初中数学鲁教版(五四制)七年级上册第五章位置与坐标本章综合与测试-章节测试习题(3)

合集下载

鲁教版(五四制) 七年级上册《第5章位置与坐标》单元练习卷

第5章位置与坐标一．选择题1．已知：点P到x轴的距离为2，到y轴的距离为3，且点P在x轴的上方，则点P的坐标为（）A．（2，3）B．（3，2）C．（2，3）或（﹣2，3）D．（3，2）或（﹣3，2）2．已知点P的坐标是（﹣2﹣，1），则点P在（）A．第一象限B．第二象限C．第三象限D．第四象限3．象棋在中国有着三千多年的历史，由于用具简单，趣味性强，成为流行极为广泛的益智游戏．如图，是一局象棋残局，已知表示棋子“馬”和“車”的点的坐标分别为（4，3），（﹣2，1），则表示棋子“炮”的点的坐标为（）A．（1，3）B．（3，2）C．（0，3）D．（﹣3，3）4．下列数据不能确定物体位置的是（）A．电影票5排8号B．北偏东30°C．希望路25号D．东经118°，北纬40°5．如图，△ABC顶点C的坐标是（﹣3，2），过点C作AB上的高线CD，则垂足D点的坐标为（）A．（2，0）B．（﹣3，0）C．（0，2）D．（0，﹣3）6．在平面直角坐标系中，点A（﹣3，2），B（3，5），C（x，y），若AC∥x轴，则线段BC 的最小值及此时点C的坐标分别为（）A．6，（﹣3，5）B．10，（3，﹣5）C．1，（3，4）D．3，（3，2）7．已知点P（a，3）、Q（﹣2，b）关于y轴对称，则＝（）A．﹣5B．5C．﹣D．8．若点A（m，n）和点B（5，﹣7）关于x轴对称，则m+n的值是（）A．2B．﹣2C．12D．﹣129．在平面直角坐标系中，点P（0，1）关于直线x＝﹣1的对称点坐标是（）A．（﹣2，1）B．（2，1）C．（0，﹣1）D．（0，1）10．在平面直角坐标系中，点A关于原点的对称点A1（3，﹣2），则点A的坐标为（）A．（﹣3，2）B．（2，﹣3）C．（3，2）D．（﹣3，﹣2）11．已知点P（﹣1，m2+1）与点Q关于原点对称，则点Q一定在（）A．第一象限B．第二象限C．第三象限D．第四象限12．在平面直角坐标系中，点P（﹣3，m2+4m+5）关于原点对称点在（）A．第一象限B．第二象限C．第三象限D．第四象限二．填空题13．如果P（m+3，2m+4）在y轴上，那么点P的坐标是．14．如图，等边△OAB的边长为，则点B的坐标为．15．在平面直角坐标系中，点A（﹣1，0）与点B（0，2）的距离是．16．若点P（3m﹣1，2+m）关于原点的对称点P′在第四象限，则m的取值范围是．17．已知点P（﹣b，2）与点Q（3，2a）关于原点对称，则a b的值是．三．解答题18．已知点P（2a﹣2，a+5），解答下列各题．（1）点P在x轴上，求出点P的坐标．（2）点Q的坐标为（4，5），直线PQ∥y轴；求出点P的坐标．（3）若点P在第二象限，且它到x轴、y轴的距离相等，求a2020+2020的值．19．在平面直角坐标系中，有A（﹣2，a+1），B（a﹣1，4），C（b﹣2，b）三点．（1）当AB∥x轴时，求A、B两点间的距离；（2）当CD⊥x轴于点D，且CD＝1时，求点C的坐标．20．在平面直角坐标系xOy中，△ABC的位置如图所示．（1）分别写出△ABC各个顶点的坐标；（2）分别写出顶点A关于x轴对称的点A′的坐标、顶点B关于y轴对称的点B′的坐标及顶点C关于原点对称的点C′的坐标；（3）求线段BC的长．21．已知点A（a+2b，1），B（7，a﹣2b）．（1）如果点A、B关于x轴对称，求a、b的值；（2）如果点A、B关于y轴对称，求a、b的值．参考答案一．选择题1．解：∵点P在x轴上方，∴点P在第一或第二象限，∵点P到x轴的距离为2，到y轴的距离为3，∴点P的横坐标为3或﹣3，纵坐标为2，∴点P的坐标为（﹣3，2）或（3，2）．故选：D．2．解：∵≥0，∴﹣2﹣＜0，∴（﹣2﹣，1）在第二象限，故选：B．3．解：如图所示：帅的位置为原点，则棋子“炮”的点的坐标为（1，3）．故选：A．4．解：不能确定物体位置的是北偏东30°，故选：B．5．解：过点C作CD垂直于x轴，垂足为D，∵点C（﹣3，2），∴点D横坐标与点C横坐标相等，∴点D（﹣3，0）．故选：B．6．解：依题意可得：∵AC∥x轴，A（﹣3，2）∴y＝2，根据垂线段最短，当BC⊥AC于点C时，点B到AC的距离最短，即BC的最小值＝5﹣2＝3，此时点C的坐标为（3，2），故选：D．7．解：∵点P（a，3）、Q（﹣2，b）关于y轴对称，∴a＝2，b＝3，则＝＝﹣．故选：C．8．解：∵点A（m，n）和点B（5，﹣7）关于x轴对称，∴m＝5，n＝7，则m+n的值是：12．故选：C．9．解：∵点P（0，1），∴点P到直线x＝﹣1的距离为1，∴点P关于直线x＝﹣1的对称点P′到直线x＝﹣1的距离为1，∴点P′的横坐标为﹣2，∴对称点P′的坐标为（﹣2，1）．故选：A．10．解：∵点A关于原点的对称点A1（3，﹣2），∴点A的坐标为（﹣3，2），故选：A．11．解：∵点P（﹣1，m2+1）与点Q关于原点对称，∴Q（1，﹣m2﹣1），∴点Q一定在第四象限，故选：D．12．解：∵m2+4m+5＝（m+2）2+1＞0，∴点P（﹣3，m2+4m+5）关于原点对称点为：[3，﹣（m2+4m+5）]，则﹣（m2+4m+5）＜0，故点P（﹣3，m2+4m+5）关于原点对称点在第四象限．故选：D．二．填空题13．解：∵P（m+3，2m+4）在y轴上，∴m+3＝0，得m＝﹣3，即2m+4＝﹣2．即点P的坐标为（0，﹣2）．故答案为：（0，﹣2）．14．解：如图，作BH⊥OA于H．∵△OAB是等边三角形，BH⊥OA，∴OH＝AH＝，∠BOH＝60°，∴BH＝OH•tan60°＝3，∴B（，3），故答案为（，3）15．解：点A（﹣1，0）与点B（0，2）的距离是：＝．故答案填：．16．解：∵点P（3m﹣1，2+m）关于原点的对称点P′（﹣3m+1，﹣2﹣m）在第四象限，∴，解得：﹣2＜m＜．故答案为：﹣2＜m＜．17．解：∵点P（﹣b，2）与点Q（3，2a）关于原点对称，∴﹣b＝﹣3，2a＝﹣2，解得：b＝3，a＝﹣1，∴a b＝（﹣1）3＝﹣1．故答案是：﹣1．三．解答题18．解：（1）∵点P在x轴上，∴a+5＝0，∴a＝﹣5，∴2a﹣2＝2×（﹣5）﹣2＝﹣12，∴点P的坐标为（﹣12，0）．（2）点Q的坐标为（4，5），直线PQ∥y轴，∴2a﹣2＝4，∴a＝3，∴a+5＝8，∴点P的坐标为（4，8）．（3）∵点P在第二象限，且它到x轴、y轴的距离相等，∴2a﹣2＝﹣（a+5），∴2a﹣2+a+5＝0，∴a＝﹣1，∴a2020+2020＝（﹣1）2020+2020＝2021．∴a2020+2020的值为2021．19．解：（1）∵AB∥x轴，∴A、B两点的纵坐标相同．∴a+1＝4，解得a＝3．∴A、B两点间的距离是|（a﹣1）+2|＝|3﹣1+2|＝4．（2）∵CD⊥x轴，∴C、D两点的横坐标相同．∴D（b﹣2，0）．∵CD＝1，∴|b|＝1，解得b＝±1．当b＝1时，点C的坐标是（﹣1，1）．当b＝﹣1时，点C的坐标是（﹣3，﹣1）．20．解：（1）A（﹣4，3），C（﹣2，5），B（3，0）；（2）如图所示：点A′的坐标为：（﹣4，﹣3），B′的坐标为：（﹣3，0），点C′的坐标为：（2，﹣5）；（3）线段BC的长为：＝5．21．解：（1）∵点A、B关于x轴对称，∴，解得：；（2））∵点A、B关于y轴对称，∴，解得：．。

鲁教版(五四制)七年级上册第五章位置与坐标测试试题(一)练习

位置与坐标测试题（一）A卷（时间：90分钟满分：100分）一、精心选一选（每小题3分，共30分）1．多层楼的电影院要确定一个座位，需要的数据个数是（）A．1个B．2个C．3个D．4个2．如图1是方格纸上画出的小旗图案，如果用（0，0）表示A点，（0，4）表示B点，那么C点的位置可表示为（）A．（0，3）B．（2，3）C．（3，2）D．（5，3）BCA图13．点P在第二象限，且到x轴、y轴的距离分别为3，4，则P点的坐标为（）A．（—4，3）B．（4，—3）C．（3，—4）D．（—3，4）4．点M（x，y）的坐标满足xy=0，那么点M在（）A．原点B．x轴上C．y轴上D．坐标轴上5．坐标平面内，点A（m，n）在第四象限，则点B（n，m）在（）A．第一象限B．第二象限C．第三象限D．第四象限6．正方形ABCD的三个顶点分别为（—1，2），（2，2），（2，—1），则第四个顶点为（）A．（0，0）B．（—1，—1）C．（5，—1）D．（—1，5）7．点P关于x轴对称的点P1的坐标为（2，3），则点P关于原点对称的点P2的坐标为（）A．（—3，—2）B．（2，—3）C．（—2，—3）D．（—2，3）8．在平面直角坐标系中，顺次连接点（—4，2），（2，2），（—4，—1），（2，—1）得到的图形是（）A．梯形B．菱形C．矩形D．正方形二、细心填一填（每小题3分，共30分）9．在A处观测到点B位于北偏东60°且距A点500m处，那么从B处观测点A时，点A位于．10．如图2，沿小正方形的边有许多方法可以把2×3的方格纸分成两个全等的图形，如，按（0，1）→（1，1）→（2，1）→（3，1）分开．请你再写出一种分法．210 1 2 3图211．点P（—5，12）到x轴的距离为，到y轴的距离为，到原点的距离为．0 1 2 3 4 5 6 77 6 5 4 3 2 1AE 2E 1F 2F 10 1 2 3 4 5 6 7 8 9 10 1111 10 9 8 7 6 5 4 3 2 1AF F 4 F 3F 2F 11 yO 1 x FE D C B A12．已知点P （x ，y ）在x 轴上，且到y 轴的距离为6，则P 点的坐标为． 13．已知点A （a ，3）与点B （4，b ）关于原点对称，则a= ，b= ． 14．当32＜m ＜1时，点P （3m —2，m —1）在第象限． 15．在同一直角坐标系中，图形a 是图形b 向上平移3个单位得到的，如果在图形a 中，点A 的坐标为（5，—3），则图形b 中与点A 对应的点A |的坐标为．16．以点（1，1），（3，1），（3，2）为顶点的三角形，变为以点（0，0），（2，0），（2，1）为顶点的三角形，前后发生的变化是．三、耐心做一做（每小题10分，共40分）17．一名邮递员每天从邮局A 出发，将报刊送到每一个订户的手中． ⑴现有如图3所示两条送报路线，分别表示出订户所在的位置，并比较两条路线的长短．A （1，0）→F 1（，）→F 2（，）；A （1，0）→E 1（，）→E 2（，）；图3 图4⑵如果⑴中的第一条送报路线又增加了几个新订户(如图4),请表示出新订户的位置： A →F 1→F 2→F 3（，）→F 4（，）→F （，）．⑶如果⑴中的第二条送报路线也增加了几个新订户，它们所在的位置可表示如下： A →E 1→E 2→E 3（7，5）→E 4（10，3）→E （11，5）．请你在图4中的方格纸上画出这条路线，并比较从A 点到F 点和从A 点到E 点这两条路线哪条长．18．已知菱形的两条对角线长分别为6和8，以两条对角线所在的直线为坐标轴建立直角坐标系，画出图形并写出各顶点的坐标（不要求写计算过程）．19．将图5中的小船沿x 轴的负方向移动5个单位长度，画出平移后的图形，并求图中所标各点变化后的坐标．图5O A （2，0） xB （0，4） yC20．在直角坐标系中描出下列各点，并用线段依次连接起来：（1，4），（1，2），（0，1），（1，0），（2，0），（3，1），（2，2），（2，4），（1，4）．观察所得的图形，你觉得它象什么？你能算出它的面积吗？B 卷（时间：50分钟满分：50分）一、精心选一选（每小题4分，共16分）1．在方格纸上，每个小方格的顶点叫做格点，以格点的连线为边的三角形叫做格点三角形．若方格纸的每个小正方形边长都为1，所作的格点三角形不可能是（）A ．直角三角形B ．钝角三角形C ．等边三角形D ．等腰三角形 2．已知点P （x ，|x|），则点P 一定（） A ．在第一象限 B ．在第一或第四象限 C ．在x 轴上方 D ．不在x 轴下方3．在直角坐标系中，坐标轴上到点P （—4，—3）的距离等于5的点的个数为（） A ．1个 B ．2个 C ．3个 D ．4个 4．已知线段AB 的两个端点分别为（1，1），（3，1），若将两个端点的横坐标都乘以—2，纵坐标不变，则得到的线段（）A ．与AB 的长相等 B ．是AB 长的一半C ．是AB 长的2倍D ．与AB 关于y 轴对称二、细心填一填（每小题4分，共16分） 5．根据指令〔s ，A 〕（s ≥0，︒≤︒3600＜A ）机器人在平面上能完成如下动作：先在原地逆时针旋转角度A ，再朝其面对的方向沿直线行走距离s ．现在机器人在平面直角坐标系的原点，且面对y 轴的负方向，为使其移动到点（—3，3），应下的指令是．6．等腰Rt △ABC 的斜边两个端点的坐标分别为A （—4，0），B （2，0），则直角顶点C 的坐标为．7．如图1，已知两点A （2，0），B （0，4），且AC=BC ，则点C 的坐标为．图1 图2 图38．如图，在直角坐标系中，第一次将△OAB 变换成△OA 1B 1，第二次将△OA 1B 1变换成△OA 2B 2，第三次将△OA 2B 2变换成△OA 3B 3．已知A （1，3），A 1（2，3），A 2（4，3），A 3（8，3）；B （2，0），B 1（4，0），B 2（8，0），B 3（16，0）．⑴观察每次变换前后的三角形有何变化，找出规律，按此变换规律再将△OA 3B 3变换成△OA 4B 4，则A 4的坐标是，B 4的坐标是；53443 B O A4 xyO 1 2 4 8 16 xB B 1 B 2 B 3 3 A A 1 A 2 A 3y ⑵若按第⑴题找出的规律将△OAB 进行了n 次变换，得到△OA n B n ，比较每次变换中三角形顶点坐标有何变化，找出规律，推测A n 的坐标是，B n 的坐标是．图三、耐心做一做（每小题9分，共18分） 9．小明没有记下作业中的图形（如图2），如果他打电话问你，请你通过建立直角坐标系，用点的坐标来描述这个图形．你还能用其他方法描述这个图形吗？10．如图3，已知直角坐标系中的两个点A （4，0）和B （0，3），连接AB ．若有一个直角三角形与Rt △ABO 全等且有一条公共的直角边，请你写出这个直角三角形第三个顶点的坐标．位置的确定测试题（一）参考答案A 卷一、1．C 2．C 3．A 4．D 5．B 6．B 7．D 8．C 二、9．南偏西60°且距B 点500m 处10．答案不惟一，如，按（1，0）→（1，1）→（2，1）→（2，2）分开 11．12，5，13 12．（6，0）或（—6，0） 13．—4，—3 14．四 15．（5，—6） 16．向左平移了1个单位长度且向下平移了1个单位长度O xy5 34 4 三、17．⑴F 1（2，2），F 2（1，5），E 1（4，1），E 2（5，3）；两条路线一样长，即AF 1+ F 1F 2= AE 1+ E 1E 2．⑵F 3（3，7），F 4（2，9），F （5，11）． ⑶画图略；两条路线一样长．18．画图略．四个顶点的坐标为（4，0），（0，3），（—4，0），（0，—3）；或（3，0），（0，4），（—3，0），（0，—4）．19．A 1（—4，2），B 1（—3，1），C 1（—2，1），D 1（0，2），E 1（—2，4），F 1（—3，3）． 20．象一个花瓶，其面积为6．B 卷一、1．C 2．D 3．C 4．C二、5．〔32，225°〕 6．（—1，3）或（—1，—3） 7．（0，1.5）8．⑴A 4（16，3），B 4（32，0）；⑵A n （2n ，3），B n （2n+1，0）．三、9．答案不惟一，建立如图的直角坐标系，则顺次连接（0，0），（9，0），（9，4），（4，4），（4，7），（0，7）各点可得到这个图形．其他方法如：将长为9、宽为7的矩形的右上角剪去一个长为5、宽为3的小矩形，即可得到这个图形．10．本题有多种情况，注意不要漏解．各种情况下第三个顶点的坐标分别为（—4，0），（—4，3），（0，—3），（4，—3），（4，3）．。

鲁教版七年级数学上册第五章位置与坐标单元测试

第五章位置与坐标单元测试一.单选题（共10题；共30分）1.若a+b<0，ab<0，则下列判断正确的是 ( )A. a、b都是正数B. a、b都是负数C. a、b异号且负数的绝对值大D. a、b异号且正数的绝对值大2.点(一2．1)所在的象限是( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限3.在平面直角坐标系中，点（-1，m2+1）一定在（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限4.小明和小刚买了两张票去观看电影，小明坐位号是11排7座记为（11，7），小刚的记为（11，9）其含义是( )A. 9座B. 11排C. 11排9座D. 9排11座5.点(-2．1)所在的象限是( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限6.点（﹣1，0）在（）A. x轴的正半轴B. x轴的负半轴C. y轴的正半轴D. y轴的负半轴7.点P（x+2，x﹣2）不可能在（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限8.在平面直角坐标系中，点P（﹣3，4）位于（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限9.在平面直角坐标系中，点（﹣2，3）所在的象限是（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限10.已知直角坐标系中，点P（x，y）满足（5x+2y﹣12）2+|3x+2y﹣6|=0，则点P坐标为（）A. （3，﹣1.5）B. （﹣3，﹣1.5）C. （﹣2，﹣3）D. （2，﹣3）二.填空题（共8题；共36分）11.在平面直角坐标系中，已知线段AB∥x轴，端点A的坐标是（﹣1，4）且AB=4，则端点B的坐标是________．12.如下图，五间亭的位置是________，飞虹桥的位置是________，下棋亭的位置是________，碑亭的位置是________．13.如果将一张“8排3号”的电影票记为（8，3），那么电影票（3，8）表示的实际意义是________ ．14.如图，在平面直角坐标系中，直线AB与y轴在正半轴、x轴正半轴分别交A、B两点，M在BA的延长线上，PA平分∠MAO，PB平分∠ABO，则∠P=________．15.点P（x﹣3，2x+4）在x轴上，则点P的坐标是________．16.若点M（a+5，a﹣3）在y轴上，则点M的坐标为________，到x轴的距离为________．17.在平面直角坐标系中，对于任意两点A（x1，y1）B (x2，y2)，规定运算：⑴A⊕B＝（x1＋x2，y1＋y2）；（2）A⊙B＝x1x2＋y1y2；（3）当x1＝x2且y1＝y2时，A＝B．有下列四个命题：①若有A（1，2），B（2，－1），则A⊕B＝（3，1），A⊙B＝0；②若有A⊕B＝B⊕C，则A＝C；③若有A⊙B＝B⊙C, 则A＝C；④(A⊕B)⊕C＝A⊕(B⊕C)对任意点A、B、C均成立。

鲁教版七年级上册第五章位置与坐标》过关测试试题

《位置与坐标》单元过关测试题（一）山东沂源县徐家庄中心学校 256116 左效平时间 120分钟分值 120分班级姓名一、选择题（共12小题，每小题4分，满分48分）1．电影院中，对电影票上的3排6座和6排3座的含义的描述，错误的是（） A ．两个3的含义不同 B ．两个6的含义不同C ．它们表示的同一个位置D ．3排6座表示的位置更靠前一些2．创建平面直角坐标系的数学家是（） A ．中国秦九韶 B ．法国笛卡尔 C ．德国康托 D ．英国莱布尼兹 3.在平面直角坐标系中，与点是一一对应的是（） A. 有理数 B.实数 C.有序实数 D.有序实数对4．已知点A(a-4,b-4)是坐标轴上的一点，则应满足的条件是（） A ．a=4 B ．b=4 C ．a=4且b=4 D ．a=4或b=45．下列各点中，位于第四象限的是（） A ．（1,3） B ．（-1,3） C ．（-1，-3） D ．（1，-3）6．已知点A(3,4),则点A 关于x 轴对称的对称点B 的坐标是（） A ．（4,3） B ．（-3,4） C ．（3，-4） D ．（4，-3）7．下列各点中，到x 轴的距离为3的是（） A ．（3，-4） B ．（3,0） C ．（0-3） D ．（-3,0）8．如图1，长方形ABCD 的长为6，宽为4，且点A 与坐标原点O 重合，则下列各结论中正确的是（）A ．点B 的坐标为（4,0） B ．点D 的坐标为（0,4）C ．点C 的坐标为（6,4）D ．点C 到x 轴的距离为6图 19．已知点A(a,b)位于第一象限，则P(-a,2()b --)位于（）A.第一象限 B ．第二象限 C ．第三象限 D ．第四象限10．若将点A（1，3）向左平移2个单位，再向下平移4个单位得到点B，则点B的坐标为（）A．（﹣2，﹣1）B．（﹣1，0）C．（﹣1，﹣1）D．（﹣2，0）11．如图2，正五边形ABCDE放入某平面直角坐标系后，若顶点A，B，C，D的坐标分别是（0，a），（﹣3，2），（b，m），（c，m），则点E的坐标是（）A．（2，﹣3）B．（2，3）C．（3，2）D．（3，﹣2）图 212．观察图3中正方形四个顶点所标的数字规律，可知，数2016应标在（）A．第504个正方形的左下角B．第504个正方形的右下角C．第505个正方形的左上角D．第505个正方形的右下角图 3二、填空题（共5小题，每小题4分，满分20分）13．点A（3，﹣2）关于y轴对称的点的坐标是．14．如图4是利用网格画出的太原市地铁1，2，3号线路部分规划示意图．若建立适当的平面直角坐标系，表示双塔西街点的坐标为（0，-1），表示桃园路的点的坐标为（-1，0），则表示太原火车站的点（正好在网格点上）的坐标是．图 415．如图5，在3×3的正方形网格中由四个格点A，B，C，D，以其中一点为原点，网格线所在直线为坐标轴，网格线所在直线为坐标轴，建立平面直角坐标系，使其余三个点中存在两个点关于一条坐标轴对称，则原点是 .图 516．已知点A(4,6)和点B（a,b）,若线段AB与坐标轴平行，则满足的条件是 .17．已知点P到x轴的距离为a，到y轴的距离为b，a+b=6,若a,b为正整数，则符合条件的点P一共有个.三、解答题（共7小题，满分52分）18．（5分）如图6，在平面直角坐标系中，描出下列各点，并将各点用线段依次连接起来：（2，1），（6，1），（6，3），（7，3），（4，6），（1，3），（2，3）观察得到的图形，你觉得它像什么？图 619．（5分）如图7，A ，B 的坐标为（2，0），（0，1），若将线段AB 平移至1A 1B ，求a+b 的值.图 720．（8分）如图8所示，等边三角形ABC 的边长为2，请你根据图2所示的坐标系，求出点A 、点B 、点C 的坐标.图 821．（8分）如图9，在平面直角坐标系xoy 中，A(-1，5) ，B(-1，0)，C(-4，3)，（1）写出点1A ，1B ，1C 的坐标．（2）在图3中作出△ABC 关于y 轴的对称图形△111C B A ．图 922．（8分）如图10，观察中国象棋的棋盘，其中红方“马”的位置可以用一个数对（3，5）来表示，红“马”走完“马3进四”后到达B点，求表示B点位置的实数对．图1023．（9分）点O（0,0），点B（1,2），点A在坐标轴上，三角形AOB的面积为2，求满足条件的点A的坐标.24．（9分）如图11，三角形AOB中，A、B两点的坐标分别是（2,4），（6,2），求三角形AOB 的面积.图11参考答案：《位置与坐标》单元过关测试题（一）一、选择题1．C2．B3.D4．D5．D6．C7．C8．C10．C11．C12．D二、填空题13．(-3,-2)14．（3,0）15B点16． a=4或b=617．20三、解答题18．解：如图，它像小房子．19．A的坐标为（3，b）,且3=2+1，所以平移的第一步是向解：因为点A的坐标为（2,0），点1B的横坐标为a，所以a=0+1=1；右平移1个单位，因为点B的横坐标为0，点1B的坐标为（a，2）,且2=1+1，所以平移的第二步是向上平因为点B的坐标为（0,1），点1A的纵坐标为b，所以b=0+1=1,移1个单位，因为点A的纵坐标为0，点1所以a+b=1+1=2.解：如图所示，过点C 作CD ⊥x 轴，垂足为D,因为等边三角形的边长为2，所以线段OA=2，因为点A 在x 轴上，且在x 轴的负半轴上，所以点A 的坐标为（-2，0）；点B 与原点重合，所以点B 的坐标为（0，0）；在直角三角形OCD 中，根据等腰三角形三线合一的性质，得：OD=1，根据勾股定理，得：CD=22OD OC -=2212-=3,即点C 到x 轴的距离为3，到y 轴的距离为1，且点C在第二象限，所以点C 的坐标为（-1，3）.21．解：因为A(-1，5) ，B(-1，0)，C(-4，3)，所以它们关于y 轴对称的对应点的坐标分别是1A （1，5），1B （1，0），1C （4，3）.如图所示，就是所求的对称图形.22．解：建立平面直角坐标系如图所示，所以点B 的坐标为（2，7）．因此应该填写：（2，7）．23．解：当点A 在x 轴正半轴时，设A 的坐标为（m ，0），此时m ＞0，因为点B （1,2），所以AOB S #=12×OA ×|B y |，所以2=12×m ×2,所以m=1，此时点A 的坐标为（1,0）；当点A 在x 轴负半轴时，设A 的坐标为（m ，0），此时m ＜0，因为点B （1,2），所以AOB S #=12×OA ×|B y |，所以2=12×|m|×2,所以 |m|=1，因为m ＜0，所以m=-1，此时点A 的坐标为（-1,0）；当点A 在y 轴正半轴时，设A 的坐标为（0，n ），此时n ＞0，因为点B （1,2），所以AOB S #=12×OA ×|B x |，所以2=12×1×n,所以n=4，此时点A 的坐标为（0,4）；当点A 在y 轴负半轴时，设A 的坐标为（0，n ），此时n ＜0，因为点B （1,2），所以AOB S #=12×OA ×|B x |，所以2=12×1×|n|,所以|n|=4，因为n ＜0，所以n=-4，此时点A 的坐标为（0，-4），综上所述，符合条件的点A 一共有四个，坐标分别为（1,0），（-1,0），（0,4），（0，-4）．24．解：过点A 作AE ⊥y 轴，垂足为E ，过点B 作BD ⊥x 轴，垂足为D ，二线交于点C ，因为点A 的坐标为（2,4），所以点E 的坐标为（0,4），所以OE=4，因为点C 在直线AE 上，所以点C 的纵坐标为4；因为点B 的坐标为（6,2），所以点C 的横坐标为6，所以点C 的坐标为（6,4），所以AE=A x -E x =2-0=2，AC=C A x x -=6-2=4，CB=C B y y -=4-2=2，BD=B D y y -=2-0=2，OD=D Ox x -=4-0=4，所以四边形OECD 的面积为：6×4=24，AOE S #=12AE OE 创=1242创=4，ABC S #=12AC CB 创=1242创=4，OBD S #=12BD OD 创=1262创=6，所以AOB S #=四边形OECD 的面积-AOE S #-ABC S #-OBD S #=24-4-4-6=10.。

鲁教版数学七上第五章《位置与坐标》单元检测含答案

第五章平面直角坐标系检测题（时间：90分钟，满分：100分）一、选择题（每小题3分，共30分）1.若点在第三象限，则应在（）A.第一象限B.第二象限C.第三象限D.第四象限2.已知点P坐标为，且P点到两坐标轴的距离相等，则点P的坐标是（）A．（3，3） B．（3，-3） C．（6，-6） D．（3，3）或（6，-6）3.设点在轴上，且位于原点的左侧，则下列结论正确的是（）A.，为一切数B.，C.为一切数，D.，4. 在直角坐标系中，一个图案上各个点的横坐标和纵坐标分别加正数，那么所得的图案与原来图案相比（）A.形状不变，大小扩大到原来的倍B.图案向右平移了个单位C.图案向上平移了个单位D.图案向右平移了个单位，并且向上平移了个单位5.已知点，在轴上有一点点与点的距离为5，则点的坐标为（）A.（6，0）B.（0，1）C.（0，－8）D.（6，0）或（0，0）6.在直角坐标系中，已知A（2，0），B（－3，－4），O（0，0），则△AOB的面积为（）A. 4B. 6C. 8D. 37. 若点P（）的坐标满足xy=0，则点P的位置是（）A.在轴上B.在轴上C.是坐标原点D.在轴上或在轴上8.点A（m＋3,m＋1）在轴上，则A点的坐标为（）A.（0，－2）B.（2，0）C.（4，0）D.（0，－4）9.已知在坐标平面内有一点，若，那么点的位置在（）A.在第一象限B.不在轴上C.不在轴上D.不在坐标轴上10. 若A （－3，2）关于原点对称的点是B ，B 关于轴对称的点是C ，则点C 的坐标是（） A.（3，2）B ．（－3，2）C ．（3，－2）D ．（－2，3）二、填空题（每小题3分，共24分）11. 已知点是第二象限的点，则的取值范围是.12. 已知点(13)A m -，与点(21)B n +，关于x 轴对称，则m =，n =．13. 一只蚂蚁由（0，0）先向上爬4个单位长度，再向右爬3个单位长度，再向下爬2个单位长度后，它所在位置的坐标是_________. 14.已知两点、，如果，则、两点关于________对称. 15. 点和点关于轴对称，而点与点关于轴对称，那么_______ ，_______ ，点和点的位置关系是__________.16.如果多边形各个顶点的横坐标保持不变，纵坐标分别加－1，那么所得到的图形与原多边形相比的变化是___________；如果多边形各个顶点的纵坐标保持不变，横坐标分别加－1，那么所得到的图形与原多边形相比的变化是___________ . 17.已知在直角坐标系中，，，△为等边三角形，则点的坐标是_______ .18.已知是整数，点在第二象限，则_____．三、解答题（共46分）19.（6分）如图所示：三角形ABC 三个顶点A 、B 、C 的坐标分别为A (1，2)、B （4，3）、C （3，1）.把三角形A 1B 1C 1向右平移4个单位，再向下平移3个单位，恰好得到三角形ABC ，试写出三角形A 1B 1C 1三个顶点的坐标.第19题图第20题图20.（8分）如图在平面网格中每个小正方形边长为1，（1）线段CD 是线段AB 经过怎样的平移后得到的？（2）线段AC 是线段BD 经过怎样的平移后得到的？ 21.（8分）在直角坐标系中，用线段顺次连接点A （，0），B （0，3），C （3，3），D （4，0）．（1）这是一个什么图形；（2）求出它的面积；（3）求出它的周长． 22.（8分）如图，点用表示，点用表示．若用→→→→表示由到的一种走法，并规定从到只能向上或向右走，用上述表示法写出另两种走法，并判断这几种走法的路程是否相等．23.（8分）如图，已知A （-1，0），B （1，1），把线段AB 平移，使点B 移动到点D （3，4）处，这时点A 移动到点C 处．（1）画出平移后的线段CD ，并写出点C 的坐标；（2）如果平移时只能左右或者上下移动，叙述线段AB 是怎样移到CD 的．24.（8分）如图所示.（1）写出三角形③的顶点坐标.（2）通过平移由③能得到④吗？为什么？第22题图第23题图第24题图（3）由对称性③可得①、②三角形，顶点坐标各是什么？第五章平面直角坐标系检测题参考答案1.B 解析：因为点在第三象限，所以，所以，所以，所以点在第二象限，故选B.2.D 解析：因为P点到两坐标轴的距离相等，所以，所以,当3.D 解析：∵点在轴上，∴纵坐标是0，即.又∵点位于原点的左侧，∴横坐标小于0，即，∴，故选D．4.D5.D 解析：过点作⊥轴于点，则点的坐标为（3，0）.因为点到轴的距离为4，所以.又因为，所以由勾股定理得，所以点的坐标为（6，0）或（0，0），故选D.6.A 解析：设点到轴的距离为，则.因为，所以，故选A.7. D 解析：若点P（）的坐标满足xy=0，则所以点P在轴上或在轴上.故选D.8. B 解析：因为点A （m ＋3,m ＋1）在轴上，所以m +1=0，所以m =-1，所以A （2，0）.9.D 解析：∵，∴且.当时，横坐标不是0，点不在轴上；当时，纵坐标不是0，点不在轴上．故点不在坐标轴上，选D ．10.A 解析：点A （－3，2）关于原点对称的点B 的坐标是（3，－2），则点B 关于轴对称的点C 的坐标是（3，2），故选A ． 11.解析：因为点是第二象限的点，所以⎩⎨⎧>-<，，030a a 解得．12.3 -4 解析：因为点(13)A m -，与点(21)B n +，关于x 轴对称，所以横坐标不变，纵坐标互为相反数，所以所以13. （3，2）解析：一只蚂蚁由（0，0）先向上爬4个单位长度，则坐标变为（0，4），再向右爬3个单位长度，坐标变为（3，4），再向下爬2个单位长度，则坐标变为（3，2），所以它所在位置的坐标为（3，2）.14.轴解析：∵ ，∴，，∴两点关于轴对称． 15. 关于原点对称解析：因为点和点关于轴对称，所以点的坐标为;因为点与点关于轴对称，所以点的坐标为，所以，点和点关于原点对称.16.向下平移了一个单位向左平移了一个单位17.解析：∵ ，以点为圆心，2为半径画弧，交轴于点，，在直角三角形和直角三角形中，由勾股定理得，∴ 点的坐标为或．18.-1 解析：因为点A 在第二象限，所以，所以.又因为是整数，所以.19. 解：设△A 1B 1C 1的三个顶点的坐标分别为A 1（,将它的三个顶点分别向右平移4个单位，再向下平移3个单位，则此时三个顶点的坐标分别为（,由题意可得=2，.20. 解：（1）将线段AB 向右（或下）平移3个小格（或4个小格），再向下（或右）平移4个小格（或3个小格），得线段CD.（2）将线段BD 向左平移（或向下平移1个小格）3个小格，再向下平移（或向左平移3个小格）1个小格，得到线段AC ． 21. 解：（1）因为（0，3）和（3，3）的纵坐标相同，因而BC ∥AD ，故四边形是梯形．作出图形如图所示. （2）因为，，高，故梯形的面积是21227．（3）在Rt△中，根据勾股定理得，同理可得，因而梯形的周长是．22. 解：路程相等. 走法一：；走法二：；答案不唯一．23.解：（1）∵ 点B （1，1）移动到点D （3，4）处，如图， ∴ C （1，3）；（2）向右平移2个单位长度再向上平移3个单位长度即可得到CD ．24. 分析：（1）根据坐标的确定方法，读出各点的纵、横坐标，即可得出各个顶点的坐标；（2）根据平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减，可得④不能由③通过平移得到；（3）根据对称性，即可得到①、②三角形顶点坐标．第21题答图第23题答图解：（1）（-1，-1），（-4，-4），（-3，-5）.（2）不能，下面两个点向右平移5个单位长度，上面一个点向右平移4个单位长度．（3）三角形②顶点坐标为（-1，1），（-4，4），（-3，5）．（三角形②与三角形③关于轴对称）；三角形①顶点坐标为（1，1），（4，4），（3，5）•（由③与①关于原点对称可得①的顶点坐标）．。

第五章位置与坐标单元测试卷（含解析）

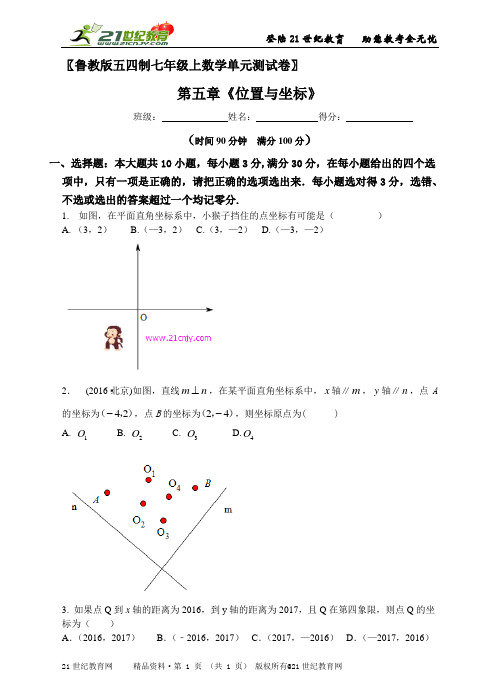
〖鲁教版五四制七年级上数学单元测试卷〗第五章《位置与坐标》班级：姓名：得分：（时间90分钟满分100分）一、选择题：本大题共10小题，每小题3分,满分30分，在每小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来．每小题选对得3分，选错、不选或选出的答案超过一个均记零分.1. 如图，在平面直角坐标系中，小猴子挡住的点坐标有可能是（） A. （3，2） B.（—3，2） C.（3，—2） D.（—3，—2）2． (2016▪北京)如图，直线m n ⊥，在某平面直角坐标系中，x 轴∥m ，y 轴∥n ，点A的坐标为42-（，），点B 的坐标为24-（，），则坐标原点为( )A. 1OB. 2OC. 3OD.4O3. 如果点Q 到x 轴的距离为2016，到y 轴的距离为2017，且Q 在第四象限，则点Q 的坐标为（）4. （2016·湖北武汉）已知点A (a ，1)与点A ′(5，b )关于坐标原点对称，则实数a 、b 的值是（）A ．a ＝5，b ＝1B ．a ＝－5，b ＝1C ．a ＝5，b ＝－1D ．a ＝－5，b ＝－15. 下列说法正确的是（）A ．若xy =0，则点P （x ，y ）表示原点B ．如果两个点的坐标相等，那么这个点在一、三象限的角平分线上；二、四象限的角平分线上的点坐标互为相反数C ．平行于x 轴的直线上的点，横坐标相同D ．点（﹣x 2，2016）在第二象限6.如图，在平面直角坐标系中，△ABC 的三个顶点都在网格图的格点上，A 点坐标（—2,1），B 点坐标（1,2），C 点坐标（2，—2），则△ABC 的面积为（）A. 7B. 6.5C. 5D.无法计算7. 在平面直角坐标系中,点()2016,122--+-b a P ，则点P 在第（）象限 A. 第一象限 B. 第二象限 C. 第三象限 D.第四象限8. 若P(a ，b )，且满足()062=++++b a b a ab ，则P 点的位置（） A. x 轴上 B. y 轴上 C. 原点 D.x 轴上或y 轴上 9. 在平面直角坐标系中,点P （2a + 1,3 -b ）在第三象限，则点⎪⎪⎭⎫ ⎝⎛-a b a b Q ,2在第（）象限10. 如图，在平面直角坐标系中，长方形ABCD ，D 点坐标（—2,4），点B 和原点重合，将长方形ABCD 沿x 轴翻滚，第1次翻滚D 点的对应点是1D ，第2次翻滚D 点的对应点是2D ，第3次翻滚D 点的对应点是3D ，……，以此类推，第2017次翻滚D 点的对应点2017D 的坐标为（）A. （6048，4）B. （6052，4）C.（6048，2）D.（6052，2）二、填空题(本大题共4小题,每小题4分,满分16分)11. （2015•绵阳第）如图是轰炸机机群的一个飞行队形，如果最后两架轰炸机的平面坐标分别为A （﹣2，1）和B （﹣2，﹣3），那么第一架轰炸机C 的平面坐标是．12. （2015江苏常州）如图是根据某公园的平面示意图建立的平面直角坐标系，公园的入口位于坐标原点O ，古塔位于点A （400，300），从古塔出发沿射线OA 方向前行300m 是盆景园B ，从盆景园B 向左转90°后直行400m 到达梅花阁C ，则点C 的坐标是_______________．y （单位：m ）（单位：m ）Ox300400CBA13. 如图，点A在y轴，坐标为（0,4）；点B在y轴，坐标为（0，—2），若△ABC的面积等于9，且点C在x轴上，则C点的坐标为。

初中数学鲁教版(五四制)七年级上册第五章位置与坐标本章综合与测试-章节测试习题

章节测试题1.【答题】若第二列第一行用数对（2，1）表示，则数对（3，6）和（7，6）表示的位置是（）A. 同一行B. 同一列C. 同行同列D. 不同行不同列【答案】A【分析】【解答】2.【答题】在直角坐标系中，点P（-2，3）关于x轴对称的点的坐标为（）A. （-2，-3）B. （2，-3）C. （-3，2）D. （3，-2）【答案】A【分析】【解答】3.【答题】在平面直角坐标系中，将点M（2，1）向下平移2个单位长度得到点N，则点N的坐标为（）A. （2，3）B. （2，-1）C. （0，1）D. （4，1）【答案】B【分析】【解答】4.【答题】如果m为任意实数，则点P（m-4，m+1）一定不在（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】D【分析】【解答】5.【答题】已知点P（a-1，3）和点M（2，b-1）关于x轴对称，则（a+b）2019的值是（）A. 0B. -1C. 1D. （-3）2019【答案】C【分析】【解答】6.【答题】已知点A（3a，5b）在x轴上方，y轴左侧，则点A到x轴、y轴的距离分别是（）A. 3a，-5bB. -3a，5bC. 5b，-3aD. -5b，3a【答案】C【分析】【解答】7.【答题】已知点0（0，0），点A（-3，2），点B在y轴的正半轴上．若△AOB的面积是12，则点B的坐标是（）A. （0，8）B. （0，4）C. （8，0）D. （0，-8）【答案】A【分析】【解答】8.【答题】已知点P（a，b）是平面直角坐标系中第二象限的点，则化简|a-b|+|b-a|的结果是（）A. -2a+2bB. 2aC. 2a-2bD. 0【答案】A【分析】【解答】9.【答题】若点N（x，y）的坐标满足xy＜0，则点N在第______象限．【答案】二、四【分析】【解答】10.【答题】在平面直角坐标系中，若点M（1，3）与点N（x，3）之间的距离是5，则x的值是______．【答案】-4或6【分析】【解答】11.【答题】已知点P的坐标为（3a+6，2-a），且点P到两坐标轴的距离相等，则点P的坐标是______．【答案】（3，3）或（-6，6）【分析】【解答】12.【答题】已知点A（a，5），B（2，2-b），C（4，2），且AB平行于x轴，AC平行于y轴，则a+b=______．【答案】1【分析】【解答】13.【题文】（10分）王霞和爸爸、妈妈到人民公园游玩，回到家后，她利用平面直角坐标系画出了公园的景区地图，如图所示，可是她忘记了在图中标出原点和x轴、y 轴，只知道游乐园D的坐标为（2，-2），湖心亭B的坐标为（-3，2），你能帮她求出其他各景点的坐标吗?【答案】【分析】【解答】由题意可知，点F为坐标原点，FA为y轴的正半轴，如图所示．A，C，E，F的坐标分别为A（0，4），C（-2，-1），E（3，3），F（0，0）．14.【题文】（12分）已知点P（4x，x-3）在平面直角坐标系中．（1）若点P在第三象限的角平分线上，求x的值；（2）若点P在第四象限，且到两坐标轴的距离之和为9，求x的值．【答案】【分析】【解答】（1）由题意得4x=x-3，解得x=-1．∴点P在第三象限的角平分线上时，x=-1．（2）由题意得4x+[-（x-3）]=9，则3x=6，解得x=2．∴当点P在第四象限，且到两坐标轴的距离之和为9时，x=2．15.【题文】（12分）已知长方形ABCD中，AB=5，BC=8，并且AB平行于y轴．若点A 的坐标为（-2，4），点B的坐标为（-2，-1），求点C的坐标．【答案】【分析】【解答】∵AB∥y轴，∴BC∥x轴．又∵点B的坐标为（-2，-1），∴点C的纵坐标是-1．而BC=8，∴点C的横坐标是-2-8=-10或-2+8=6，即C点坐标为（-10，-1）或（6，-1）．16.【题文】（14分）如图，方格纸中每个小方格都是边长为1个单位的正方形．已知学校的位置坐标为A（2，1），图书馆的位置坐标为B（-1，-2），解答以下问题：（1）在图中标出平面直角坐标系的原点，并建立直角坐标系；（2）若体育馆的位置坐标为C（1，-3），请在坐标系中标出体育馆的位置；（3）顺次连接学校、图书馆、体育馆，得到△ABC，求△ABC的面积．【答案】【分析】【解答】（1）如图，点O为原点．（2）如图，点C即为所求．（3）．17.【答题】已知点M在第二象限，距离x轴5个单位长度，距离y轴3个单位长度，则M点的坐标为（）A. （5，-3）B. （-5，3）C. （3，-5）D. （-3，5）【答案】D【分析】【解答】18.【答题】已知点P（3a，a+2）在x轴上，则P点的坐标是（）A. （3，2）B. （6，0）C. （-6，0）D. （6，2）【答案】C【分析】【解答】19.【答题】如图，将围棋棋盘放在平面直角坐标系内，已知黑棋甲的坐标为（-2，2），黑棋乙的坐标为（-1，-2），则白棋甲的坐标是（）A. （2，2）B. （0，1）C. （2，-1）D. （2，1）【答案】D【分析】【解答】20.【答题】已知点A（m+1，-2）和点B（3，m-1），若直线AB∥x轴，则m的值为（）A. -1B. -4C. 2D. 3【答案】A【分析】【解答】。

初中数学鲁教版(五四制)七年级上册第五章位置与坐标本章综合与测试-章节测试习题(1)

章节测试题1.【答题】给出下列四个说法：①坐标平面内所有的点都可以用有序数对表示；②横坐标为-3的点在经过点（-3，0）且平行于y轴的直线上；③x轴上的点的纵坐标都为0；④当x≠0时，点A（x2，-x）在第四象限．其中正确说法的个数为（）A. 1B. 2C. 3D. 4【答案】C【分析】【解答】2.【答题】如图，已知平面直角坐标系中的两点（2，0）和（0，3），则这两点之间的距离是（）A. B. C. 13 D. 5【答案】A【分析】【解答】3.【答题】已知点P1（a，2）与点P2（-3，b）关于原点对称，则a-b的值是（）A. -5B. -1C. 1D. 5【答案】D【分析】【解答】4.【答题】在平面直角坐标系上有一个轴对称图形，其中和是图形上的一对对称点．若此图形上另有一点C（-2，-9），则C点的对称点的坐标是（）A. （-2，1）B.C.D. （-2，-1）【答案】A【分析】【解答】5.【答题】如果P（m+3，2m+4）在y轴上，那么点P的坐标是______．【答案】（0，-2）【分析】【解答】6.【答题】如图是一组密码的一部分，请你运用所学的知识找到破译的“钥匙”．目前，已破译出“努力发挥”的真实意思是“今天考试”．若“努”所处的位置为（x，y），则根据你找到的密码钥匙，“祝你成功”的真实意思是______．【答案】正做数学【分析】【解答】7.【答题】如图，在平面直角坐标系中对△ABC进行循环往复的轴对称变换，若原来点A的坐标是（a，b），则经过第2016变换后A点的坐标是______．【答案】（a，b）【分析】【解答】8.【答题】如图，在平面直角坐标系中，一动点从原点O出发，沿着箭头所示方向每次移动一个单位，依次得到点P1（0，1），P2（1，1），P3（1，0），P4（1，-1），P5（2，-1），P6（2，0），…，则点P50的坐标是______．【答案】（20，0）【分析】【解答】9.【题文】（10分）在平面直角坐标系中，已知点M（m-1，2m+3）．（1）若点M在y轴上，求m的值；（2）若点M在第一、三象限的角平分线上，求m的值．【答案】【分析】【解答】（1）由题意得m-1=0，解得m=1．（2）由题意得m-1=2m+3，解得m=-4．10.【题文】（12分）如图，已知火车站的坐标为（2，2），文化馆的坐标为（-1，3）．（1）请根据题目条件画出平面直角坐标系；（2）写出体育场、市场、超市的坐标；（3）已知游乐场A、图书馆B、公园C的坐标分别为（0，5），（-2，-2），（2，-2），请在图中标出A，B，C的位置．【答案】【分析】【解答】（1）如图所示．（2）体育场（-2，5），市场（6，5），超市（4，-1）．（3）如上图所示．11.【题文】（12分）在平面直角坐标系xOy中，△ABC的位置如图所示．（1）分别写出顶点A关于x轴对称的点A'的坐标、顶点B的坐标、顶点C关于原点对称的点C'的坐标；（2）求△ABC的面积．【答案】【分析】【解答】（1）顶点A关于x轴对称的点A'的坐标为（-4，-3），顶点B的坐标为（3，0），顶点C关于原点对称的点C'的坐标为（2，-5）．（2）△ABC的面积为．12.【题文】（14分）在平面直角坐标系中，已知点A在x轴上，点C的横坐标为3，AC 的长为2，OC的长为，CB⊥OA，垂足为B．请判断△AOC的形状，并说明理由．【答案】【分析】【解答】△AOC是直角三角形．理由如下：∵点C的横坐标为3，CB⊥OA，∴OB=3，∠OBC=∠ABC=90°，∴，∴，∴OA=4．∵OC2+AC2=12+4=16，OA2=16，∴OC2+AC2=OA2，∴∠ACO=90°，∴△AOC是直角三角形．13.【答题】在直角坐标系中，点P的坐标为（-2，3），则P位于（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】B【分析】【解答】14.【答题】若点P（x，y）的坐标满足xy=0，则点P（）A. 在x轴上B. 在y轴上C. 是坐标原点D. 在x轴上或在y轴上【答案】D【分析】【解答】15.【答题】在直角坐标系中，线段AB的两个端点的坐标分别为（3，-6），（3，7），则线段AB（）A. 与x轴平行B. 与y轴平行C. 经过原点D. 与y轴相交【答案】B【解答】16.【答题】若点P在x轴上方、y轴左侧，且到x轴、y轴的距离分别为3和4，则点P的坐标为（）A. （-4，3）B. （4，-3）C. （3，-4）D. （-3，4）【答案】A【分析】【解答】17.【答题】如图，点A的坐标是（2，2）．若点P在x轴上，且△APO是等腰三角形，则点P的坐标不可能是（）A. （4，0）B. （1，0）C.D. （2，0）【答案】B【分析】【解答】18.【答题】在直角坐标系中，点P的坐标为（-3，2），将P沿y轴向上移动2个单位得到点M，则点M的坐标是______．【答案】（-3，4）【解答】19.【答题】已知线段AB=3，AB∥x轴，若点A的坐标为（-1，2），则点B的坐标是______．【答案】（-4，2）或（2，2）【分析】【解答】20.【答题】若点P（a-b，a）位于第二象限，那么点Q（a+3，ab）位于第______象限．【答案】一【分析】【解答】。

鲁教版(五四制) 七年级数学上册第五章位置与坐标单元检测题(含答案)

第五章位置与坐标单元检测题（45分钟100分）一、选择题(每小题4分,共28分)1.(2018·南通中考)在平面直角坐标系中点P(1,-2)关于x轴的对称点的坐标是（）A.(1,2)B.(-1,-2)C.(-1,2)D.(-2,1)2.如图所示,有一个方队正沿箭头所指的方向前进,A的位置为三列四行,表示为(3,4),那么B的位置是（）A.(4,5)B.(5,4)C.(4,2)D.(4,3)3.若x轴上的点P到y轴的距离为3,则点P为（）A.(3,0)B.(3,0)或(-3,0)C.(0,3)D.(0,3)或(0,-3 )4.若ab>0,则P(a,b)在( )A.第一象限B.第一或第三象限C.第二或第四象限D.以上都不对5.点M(m+1,m+3)在x轴上,则M点坐标为( )A.(0,-4)B.(4,0)C.(-2,0)D.(0,-2)6.将△ABC的三个顶点的横坐标都加上-1,纵坐标不变,则所得图形与原图形的关系是( )A.将原图形向x轴的正方向平移了1个单位B.将原图形向x轴的负方向平移了1个单位C.将原图形向y轴的正方向平移了1个单位D.将原图形向y轴的负方向平移了1个单位7.(2018·邵阳中考)如图所示,三架飞机P，Q，R保持编队飞行,某时刻在坐标系中的坐标分别为(-1,1) ，(-3,1)，(-1,-1)。

30秒后,飞机P飞到P’(4,3)位置,则飞机Q，R的位置Q’，R’分别为（）A.Q’(2,3),R’(4,1)B.Q’(2,3),R’(2,1)C.Q’(2,2),R’(4,1)D.Q’(3,3),R(3,1)二、填空题(每小题5分,共25分)8.已知点P在第二象限,点P到x轴的距离是2，到y轴的距离是3，那么点P的坐标是__________。

9.点P(2x-1，x+3)在第一、三象限的角平分线上，则x的值为_____________。

10.将平面直角坐标系平移,使原点O移至点A(3,-2),这时在新坐标系中原来点O的坐标是________。

鲁教版五四制七年级上册数学第五章位置与坐标单元测试卷

第五章测试卷一、选择题(每题3分，共30分)1．点P(4，3)所在的象限是()A．第一象限B．第二象限 C．第三象限 D．第四象限2．根据下列表述，能确定位置的是()A．红星电影院2排B．北京市四环路C．北偏东30°D．东经118°，北纬40°3．如图，在直角坐标系中，卡片盖住的点的坐标可能是() A．(2，3) B．(－2，1) C．(－2，－2.5) D．(3，－2)4．点P(－2，3)关于x轴对称的点的坐标是()A．(－3，2) B．(2，－3) C．(－2，－3) D．(2，3)5．已知点A(－1，－4)，B(－1，3)，则()A．点A，B关于x轴对称B．点A，B关于y轴对称C．直线AB平行于y轴D．直线AB垂直于y轴6．如图，若在象棋棋盘上建立平面直角坐标系，使“帅”位于点(－2，－2)，“马”位于点(1，－2)，则“兵”位于点()A．(－1，1) B．(－2，－1) C．(－4，1) D．(1，2)7．如图，将长为3的长方形ABCD放在平面直角坐标系中，AD∥x轴，若点D 的坐标为(6，3)，则点A的坐标为()A．(5，3) B．(4，3) C．(4，2) D．(3，3)8．在平面直角坐标系xOy中，若点A的坐标为(－3，3)，点B的坐标为(2，0)，则三角形ABO的面积是()A．15 B．7.5 C．6 D．39．已知点P的坐标为(2－a，3a＋6)，且点P到两坐标轴的距离相等，则点P的坐标是()A．(3，3) B．(3，－3)C．(6，－6) D．(3，3)或(6，－6)10．在平面直角坐标系中，孔明做走棋的游戏，其走法是：棋子从原点出发，第1步向右走1个单位长度，第2步向右走2个单位长度，第3步向上走1个单位长度，第4步向右走1个单位长度，……以此类推，第n步的走法是：当n能被3整除时，向上走1个单位长度；当n被3除，余数为1时，向右走1个单位长度；当n被3除，余数为2时，向右走2个单位长度，当走完第100步时，棋子所处位置的坐标是()A．(66，34) B．(67，33) C．(100，33) D．(99，34)二、填空题(每题3分，共24分)11．写出平面直角坐标系中第三象限内一个点的坐标：________．12．在直角坐标系中，第四象限内一点P到x轴的距离为2，到y轴的距离为5，那么点P的坐标是________．13．如图是益阳市行政区域图，图中益阳市区所在地用坐标表示为(1，0)，安化县城所在地用坐标表示为(－3，－1)，那么南县县城所在地用坐标表示为________．14．第二象限内的点P(x，y)满足|x|＝9，y2＝4，则点P的坐标是__________．15．已知点N的坐标为(a，a－1)，则点N一定不在第________象限．16．如图，点A，B的坐标分别为(2，4)，(6，0)，点P是x轴上一点，且△ABP 的面积为6，则点P的坐标为________．17．如图，长方形OABC的边OA，OC分别在x轴、y轴上，点B的坐标为(3，2)．点D，E分别在AB，BC边上，BD＝BE＝1.沿直线DE将三角形BDE翻折，点B落在点B′处，则点B′的坐标为________．18．如图，在平面直角坐标系中，一动点从原点O出发，按向上、向右、向下、向右的方向不断地移动，每移动一个单位长度，得到点A1(0，1)，A2(1，1)，A3(1，0)，A4(2，0)，…，那么点A4n＋1(n为自然数)的坐标为______(用n表示)．三、解答题(19题6分，20题8分，21，23题每题9分，22题10分，其余每题12分，共66分)19．如图，如果规定北偏东30°的方向记作30°，从O点出发沿这个方向走50 m 记作50，图中点A记作(30°，50)；北偏西45°的方向记作－45°，从O点出发沿着该方向的反方向走20 m记作－20，图中点B记作(－45°，－20)．(1)(－75°，－15)，(10°，－25)分别表示什么意义？(2)在图中标出点(60°，－30)和(－30°，40)．20．春天到了，七(1)班组织同学到人民公园春游，张明、李华对着景区示意图(如图)描述牡丹园的位置(图中小正方形的边长为100 m)．张明：“牡丹园的坐标是(300，300)．”李华：“牡丹园在中心广场东北方向约420 m处．”实际上，他们所说的位置都是正确的．根据所学的知识解答下列问题：(1)请指出张明同学是如何在景区示意图上建立平面直角坐标系的，并在图中画出所建立的平面直角坐标系；(2)李华同学是用什么来描述牡丹园的位置的？请用张明同学所用的方法，描述出公园内其他地方的位置．21．在平面直角坐标系中，点A(2，m＋1)和点B(m＋3，－4)都在直线l上，且直线l∥x轴．(1)求A，B两点间的距离；(2)若过点P(－1，2)的直线l′与直线l垂直于点C，求垂足C点的坐标．22．如图，在平面直角坐标系中，O，A，B，C的坐标分别为(0，0)，(－1，2)，(－3，3)和(－2，1)．(1)将图中的各个点的纵坐标不变，横坐标都乘－1，与原图形相比，所得图形有什么变化？画出图形并说明一下变化；(2)将图中的各个点的横坐标不变，纵坐标都乘－1，与原图形相比，所得图形有什么变化？画出图形并说明一下变化．23．如图，A，B，C为一个平行四边形的三个顶点，且A，B，C三点的坐标分别为(3，3)，(6，4)，(4，6)．(1)请直接写出这个平行四边形第四个顶点的坐标；(2)求这个平行四边形的面积．24．如图，四边形ABCD是边长为4的正方形，在正方形的一个角上剪去长方形CEFG，其中E，G分别是边CD，BC上的点，且CE＝3，CG＝2，剩余部分是六边形ABGFED，请你建立适当的直角坐标系求六边形ABGFED各顶点的坐标．25．先阅读一段文字，再回答问题：已知在平面直角坐标系内两点的坐标为P1(x1，y1)，P2(x2，y2)，则该两点间的距离公式为P1P2＝（x2－x1）2＋（y2－y1）2.同时，当两点在同一坐标轴上或所在直线平行于x轴或垂直于x轴时，两点间的距离公式可化简成|x2－x1|或|y2－y1|.(1)若已知两点A(3，5)，B(－2，－1)，试求A，B两点间的距离；(2)已知点A，B在平行于y轴的直线上，点A的纵坐标为5，点B的纵坐标为－1，试求A，B两点间的距离；(3)已知一个三角形各顶点的坐标分别为A(0，6)，B(－3，2)，C(3，2)，你能判断此三角形的形状吗？试说明理由．答案一、1.A 2.D 3.D 4.C 5.C 6.C7.D8.D9.D10.C二、11.(－1，－1)(答案不唯一)12.(5，－2)13.(2，4) 14．(－9，2)15.二16．(3，0)或(9，0)：设点P的坐标为(x，0)，根据题意得12×4×|6－x|＝6，解得x＝3或9，所以点P的坐标为(3，0)或(9，0)．17．(2，1)：由题意知四边形BEB′D是正方形，所以点B′的横坐标与点E的横坐标相同，点B′的纵坐标与点D的纵坐标相同．所以点B′的坐标为(2，1)．18．(2n，1)：由题图可知n＝1时，4×1＋1＝5，点A5(2，1)；n＝2时，4×2＋1＝9，点A9(4，1)；n＝3时，4×3＋1＝13，点A13(6，1)，…，所以点A4n ＋1的坐标为(2n，1)．三、19.解：(1)(－75°，－15)表示南偏东75°距O点15 m处，(10°，－25)表示南偏西10°距O点25 m处．(2)如图．20．解：(1)张明同学是以中心广场为原点、正东方向为x轴正方向、正北方向为y轴正方向建立平面直角坐标系的，图略．(2)李华同学是用方向和距离描述牡丹园的位置的．用张明同学所用的方法，描述如下：中心广场(0，0)，音乐台(0，400)，望春亭(－200，－100)，游乐园(200，－400)，南门(100，－600)．21．解：(1)因为l∥x轴，点A，B都在l上，所以m＋1＝－4.所以m＝－5.所以A(2，－4)，B(－2，－4)．所以A，B两点间的距离为4.(2)因为l∥x轴，PC⊥l，x轴⊥y轴，所以PC∥y轴．所以C点横坐标为－1.又点C在l上，所以C(－1，－4)．22．解：(1)将各个点的纵坐标不变，横坐标都乘－1，得到新的坐标分别为(0，0)，(1，2)，(3，3)，(2，1)．在坐标系中描出各点，再连接各点，如图所示．所得图形与原图形关于y轴对称．(2)将各个点的横坐标不变，纵坐标都乘－1，得到新的坐标分别为(0，0)，(－1，－2)，(－3，－3)，(－2，－1)．在坐标系中描出各点，再连接各点，如图所示．所得图形与原图形关于x轴对称．23．解：(1)(7，7)或(1，5)或(5，1)．(2)这个平行四边形的面积S＝3×5－12×1×3×2－12×2×2×2＝8或S＝4×4－12×3×1×4－2＝8或S＝3×5－12×2×2×2－12×1×3×2＝8.综上所述，这个平行四边形的面积为8.24．解：以点A为原点，分别以边AB，AD所在的直线为坐标轴，建立直角坐标系，如图所示．因为点A是原点，所以点A(0，0)．因为点B，D分别在x轴，y轴上，且AB＝AD＝4，所以点B(4，0)，点D(0，4)．因为点D，E的纵坐标相等，且DE＝CD－CE＝1，所以点E(1，4)．因为点B，G的横坐标相等，且BG＝BC－CG＝2，所以点G(4，2)．精品文档用心整理资料来源于收集整理仅供免费交流使用因为点F 与点E 的横坐标相等，与点G 的纵坐标相等，所以点F (1，2)．综上所述，六边形ABGFED 各顶点的坐标为点A (0，0)，点B (4，0)，点G (4，2)，点F (1，2)，点E (1，4)，点D (0，4)．(此题答案不唯一，建立的坐标系不同，各点坐标也不同)25．解：(1)AB ＝（－2－3）2＋（－1－5）2＝61.(2)AB ＝|－1－5|＝6.(3)能．理由：因为AB ＝（－3－0）2＋（2－6）2＝5，BC ＝[3－（－3）]2＋（2－2）2＝6，AC ＝（3－0）2＋（2－6）2＝5，所以AB ＝AC .所以△ABC 为等腰三角形．。

2021-2022学年鲁教版七年级数学上册《第5章位置与坐标》单元综合训练(附答案)

2021-2022学年鲁教版七年级数学上册《第5章位置与坐标》单元综合训练（附答案）1．在平面直角坐标系中，点（2，﹣3）绕原点逆时针旋转90°所得的点的坐标是（）A．（﹣3，2）B．（3，2）C．（2，3）D．（﹣2，3）2．已知点A（a，2019）与点B（2020，b）关于x轴对称，则a+b的值为（）A．﹣1B．1C．2D．33．若点A（a，5），在第二象限，则点A关于直线m（直线m上各点的横坐标都是1）对称的点坐标是（）A．（﹣a，5）B．（2﹣a，5）C．（﹣a﹣4，﹣5）D．（﹣a﹣2，﹣5）4．在平面直角坐标系xOy中，点P（﹣2，4）关于x轴的对称点的坐标是（）A．（2，4）B．（4，﹣2）C．（﹣4，2）D．（﹣2，﹣4）5．点P（﹣a，a+2）一定不在第（）象限．A．一B．二C．三D．四6．已知点A（0，﹣6），点B（0，3），则A，B两点间的距离是（）A．﹣9B．9C．﹣3D．37．若点P（x，y）在第二象限，且|x|＝2，|y|＝3，则x+y＝（）A．﹣1B．1C．5D．﹣58．在平面直角坐标系中，点Q（2﹣a，2a+3）在x轴上，则a的值为（）A．2B．﹣2C．﹣D．9．将点A（﹣4，﹣1）先向右平移5个单位，再向上平移3个单位得到点A1，则点A1的坐标为（）A．（1，2）B．（2，9）C．（5，3）D．（﹣9，﹣4）10．在平面直角坐标系中，把点P（﹣5，4）绕原点O顺时针旋转180°，所得到的对应点P′的坐标为（）A．（5，4）B．（﹣5，4）C．（﹣5，﹣4）D．（5，﹣4）11．在平面直角坐标系xOy中，点P（x，y）在第二象限，且点P到横轴的距离等于3，到纵轴的距离等于4，则点P坐标是（）A．（﹣3，4）B．（3，﹣4）C．（﹣4，3）D．（4，﹣3）12．已知点A（1，a）与点A′（b，﹣2）关于原点对称，则（a+b）的值是（）A．﹣1B．1C．2D．313．如图，正方形ABCD的各边分别平行于x轴或y轴，蚂蚁甲和蚂蚁乙都由点E（3，0）出发，同时沿正方形ABCD的边逆时针匀速运动，蚂蚁甲的速度为3个单位长度/秒，蚂蚁乙的速度为1个单位长度/秒，则两只蚂蚁出发后，蚂蚁甲第3次追上蚂蚁乙的坐标是．14．已知|m+5|+＝0，点P（m，n）关于x轴的对称点的坐标是．15．已知点P（2m+4，m﹣1）．（1）若点P在x轴上，则点P的坐标为；（2）若点P在第四象限，且到y轴的距离是2，则点P的坐标为．16．点A（﹣2，3）与点B（a，b）关于坐标原点对称，则a b的值为．17．在平面直角坐标系中，有点A（a，1），点B（﹣2，b），当线段AB∥y轴，且AB＝3时，则a﹣b＝．18．在平面直角坐标系中，线段AB两个端点A（1，2），B（7，5）．将线段AB平移后，点A的新坐标为（﹣6，﹣3），则点B的新坐标为．19．定义：在平面直角坐标系xOy中，把从点P出发沿纵或横方向到达点Q（至多拐一次弯）的路径长称为P，Q的“实际距离”．如图，若P（﹣1，1），Q（2，3），则P，Q 的“实际距离”为5，即PS+SQ＝5或PT+TQ＝5．若点A（3，2），B（5，﹣3），M（6，m）满足点M分别到点A和点B的“实际距离”相等，则m＝．20．已知AB∥y轴，点A的坐标为（3，2），且AB＝3，则点B的坐标为．21．如图，将含有30°角的直角三角板OAB放置在平面直角坐标系中，OB在x轴上，且A 点坐标为（，1），若将三角板绕原点O顺时针旋转75°，则点A的对应点A1的坐标为．22．在平面直角坐标系中，以点（2，0）为旋转中心，将点（1，3）顺时针旋转90°所得到的点坐标为．23．在平面直角坐标系中，若点M（1﹣m，m+2）与点N（2m+3，m+2）之间的距离是5，则m＝．24．在平面直角坐标系中，点A（6，0），点B（0，8），把△AOB绕原点O逆时针旋转，得△COD，其中，点C，D分别为点A，B旋转后的对应点．记旋转角为α（0°＜α＜360°）．（1）如图，当α＝45°时，求点C的坐标；（2）当CD∥x轴时，求点C的坐标（直接写出结果即可）．25．先阅读下列一段文字，再回答后面的问题：已知在平面直角坐标系内两点P1（x1，y1），P2（x2，y2），其两点间的距离P1P2＝，同时，当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时，两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|．（1）已知A（1，3），B（﹣3，﹣5），试求A，B两点间的距离；（2）已知线段MN∥y轴，MN＝4，若点M的坐标为（2，﹣1），试求点N的坐标；（3）已知一个三角形各顶点坐标为D（0，6），E（﹣3，2），F（3，2），你能判定此三角形的形状吗？说明理由．26．在平面直角坐标系xOy中，对于任意两点P1（x1，y1），P2（x2，y2），的“识别距离”，给出如下定义：若|x1﹣x2|≥|y1﹣y2|，则点P1（x1，y1），P2（x2，y2），的“识别距离”为|x1﹣x2|；若|x1﹣x2|＜|y1﹣y2|，则P1（x1，y1），P2（x2，y2），的“识别距离”为|y1﹣y2|；（1）已知点A（﹣2，0），B为y轴上的动点，①若点A与B的“识别距离为3”，写出满足条件的B点的坐标．②直接写出点A与点B的“识别距离”的最小值．（2）已知C点坐标为C（m，2m+2），D（0，1），写出点C与D的“识别距离”的最小值，及相应的C点坐标．27．综合与实践问题背景如图，在平面直角坐标系中，点A的坐标为（﹣3，5），点B的坐标为（0，1），点C的坐标为（4，5），将线段AB沿AC方向平移，平移距离为线段AC的长度．动手操作（1）画出AB平移后的线段CD，直接写出B的对应点D的坐标；探究证明（2）连接BD，试探究∠BAC，∠BDC的数量关系，并证明你的结论；拓展延伸（3）若点E在线段BD上，连接AD，AE，且满足∠EAD＝∠CAD，请求出∠ADB：∠AEB的值，并写出推理过程．参考答案1．解：如图，点（2，﹣3）绕原点逆时针旋转90°所得的点的坐标是（3，2）故选：B．2．解：∵点A（a，2019）与点B（2020，b）关于x轴对称，∴a＝2020，b＝﹣2019，∴a+b＝1，故选：B．3．解：∵直线m上各点的横坐标都是1，∴直线为：x＝1，∵点P（a，5）在第二象限，∴a到1的距离为：1﹣a，∴点P关于直线m对称的点的横坐标是：1﹣a+1＝2﹣a，故P点对称的点的坐标是：（2﹣a，5）．故选：B．4．解：点P（﹣2，4）关于x轴的对称点的坐标是（﹣2，﹣4），故选：D．5．解：当a＞0时，﹣a＜0，a+2为正，∴点P（﹣a，a+2）在第二象限；当a＜0时，﹣a＞0，a+2可能为正，也可能为负，∴点P（﹣a，a+2）可能在第一象限，也可能在第四象限；∴点P（﹣a，a+2）可能在第一、二、四象限；不可能在第三象限，故选：C．6．解：∵A（0，﹣6），点B（0，3），∴A，B两点间的距离＝3﹣（﹣6）＝9．故选：B．7．解：由P（x、y）在第二象限且|x|＝2，|y|＝3，得x＝﹣2，y＝3．x+y＝﹣2+3＝1，故选：B．8．解：∵点Q（2﹣a，2a+3）在x轴上，∴2a+3＝0，解得：a＝﹣．故选：C．9．解：∵把点A（﹣4，﹣1）先向右平移5个单位长度，故得到：（1，﹣1）；再向上平移3个单位长度得到点A′（1，2）．故选：A．10．解：由题意，P与P′关于原点对称，∵P（﹣5，4），∴P′（5，﹣4），故选：D．11．解：∵点P在第二象限，且第二象限内的点横坐标小于0，纵坐标大于0；∴点P的横坐标小于0，纵坐标大于0∵点P到x轴的距离等于3，到y轴的距离等于4，∴点P的坐标是（﹣4，3）．故选：C．12．解：∵点A（1，a）与点A′（b，﹣2）关于原点对称，∴b＝﹣1，a＝2，则（a+b）的值是：2﹣1＝1．故选：B．13．解：由图可知，正方形的边长为4，故正方形的周长为16∴蚂蚁甲第1次追上蚂蚁乙时间：16÷（3﹣1）＝8（秒）蚂蚁乙走的路程为：1×8＝8，∴此时相遇点的坐标为：（﹣1，0），因为蚂蚁甲和蚂蚁乙的速度比为3：1，∴再经过16秒蚂蚁甲和蚂蚁乙第三次相遇，相遇点坐标为：（﹣1，0），故答案为：（﹣1，0）．14．解：∵|m+5|+＝0，∴m+5＝0，n﹣2＝0，解得：m＝﹣5，n＝2，∴点P（m，n）关于x轴的对称点的坐标是（﹣5，﹣2）．故答案为：（﹣5，﹣2）．15．解：（1）∵点P（2m+4，m﹣1），点P在x轴上，∴m﹣1＝0，解得：m＝1，故2m+4＝6，∴点P的坐标为：（6，0）；（2）∵点P（2m+4，m﹣1），点P在第四象限，且到y轴的距离是2，∴2m+4＝2，解得：m＝﹣1，故m﹣1＝﹣2，则点P的坐标为：（2，﹣2）．故答案为：（1）（6，0）；（2）（2，﹣2）．16．解：∵点A（﹣2，3）与点B（a，b）关于坐标原点对称，∴a＝2，b＝﹣3，则a b＝2﹣3＝，故答案为：．17．解：∵当线段AB∥y轴，点A（a，1）与点B（﹣2，b）的横坐标相同，∴a＝﹣2，∵AB＝3，∴|b﹣1|＝3，∴b﹣1＝3或b﹣1＝﹣3，∴b＝4或b＝﹣2．∴a﹣b＝﹣2﹣4＝﹣6，或a﹣b＝﹣2﹣（﹣2）＝0，故答案为：﹣6或0．18．解：∵线段AB端点A（1，2），将线段AB平移后，点A的新坐标为（﹣6，﹣3），∴线段AB向左平移7个单位，向下平移5个单位，∴B点新坐标为（7﹣7，5﹣5），即（0，0），故答案为：（0，0）．19．解：如图，由题意，3+2﹣m＝1+m+3，解得m＝0.5，故答案为0.5．20．解：∵AB∥y轴，∴点B的横坐标与A点的横坐标相同，∵AB＝3，∴把A点向上（或向下）平移3个单位得到B点，而点A的坐标为（3，2），∴B点坐标为（3，﹣1）或（3，5）．故答案为：（3，﹣1）或（3，5）．21．解：如图所示：过点A1作A1C⊥OB．∵将三角板绕原点O顺时针旋转75°，∴∠AOA1＝75°，OA1＝OA．∴∠COA1＝45°．∵A（，1），∴OA＝＝2，∴OC＝2×＝，CA1＝2×＝．∴A1的坐标为（，﹣）．故答案为（，﹣）．22．解：如图，观察图象可知E（1，3）绕点A（2，0），顺时针旋转90°所得到的点F的坐标为（5，1）．故答案为：（5，1）．23．解：∵点M（1﹣m，m+2）与点N（2m+3，m+2）的纵坐标都是m+2，∴MN∥x轴，点N在点M的左边时，1﹣m﹣（2m+3）＝5，解得m＝﹣，点N在点M的右边时，2m+3﹣1+m＝5，解得m＝1，综上所述，m的值是﹣或1．故答案为：﹣或1．24．解：（1）如图，过点C作CE⊥OA于E．∵A（6，0），∵OA＝OC＝6，∵∠COE＝45°，∴EC＝OE＝3，∴C（3，3）．（2）如图，CD在x轴上方时，设CD交y轴于F，过点D作DT⊥x轴于T．∵CD∥x轴，∴CD⊥OF，∵OB＝OD＝8，OC＝OA＝6，∴CD＝＝＝10，∴DT＝OF＝＝，∴OT＝＝＝，CF＝10﹣＝，∴C（，），当CD在x轴下方时，同法可得C（﹣，﹣）．综上所述，满足条件的点C的坐标为（，）或（﹣，﹣）．25．解：（1）A，B两点间的距离＝＝4；（2）∵线段MN∥y轴，∴M、N的横坐标相同，设N（2，t），∴|t+1|＝4，解得t＝3或﹣5，∴N点坐标为（2，3）或（2，﹣5）；（3）△DEF为等腰三角形．理由如下：∵D（0，6），E（﹣3，2），F（3，2），∴DE＝＝5，DF＝＝5，EF＝＝6，∴DE＝DF，∴△DEF为等腰三角形．26．解：（1）①∵B为y轴上的一个动点，∴设点B的坐标为（0，y）．∵A、B两点的“识别距离为3”，A（﹣2，0），∵|﹣2﹣0|＝2，|y﹣0|＝3，解得：y＝3 或y＝﹣3，∴点B的坐标是（0，3）或（0，﹣3），故答案为：（0，3）或（0，﹣3）；②∵设点B的坐标为（0，y），且A（﹣2，0），∴|﹣2﹣0|＝2，|y﹣0|＝y，∴若|﹣2﹣0|≥|y﹣0|，则点A、B两点的“识别距离”为|﹣2﹣0|＝2；若|﹣2﹣0|＜|y﹣0|，则点A、B两点的“识别距离”为|y|＞2，∴A、B两点的“识别距离”的最小值为2，故答案为：2；（2）C（m，2m+2），D（0，1），①当|m﹣0|≥|2m+2﹣1|时，点C与D的“识别距离”为|m|，当m≥0 时，m≥2m+1，解得：m≤﹣1（舍弃），当﹣＜m＜0 时，﹣m≥2m+1，解得：m≤﹣，∴﹣＜m≤﹣当m≤﹣时，﹣m≥﹣2m﹣1，解得：m≥﹣1（舍弃），∴|m|的最小值为，此时，m＝﹣，C（﹣，）．②当|m﹣0|＜|2m+2﹣1|时，点C与D的“识别距离”为|2m+1|，当m≥0 时，m＜2m+1，解得：m＞﹣1，∴m≥0，则|2m+1|≥1，当﹣＜m＜0 时，﹣m＜2m+1，解得：m＞﹣，∴﹣＜m＜0，则|2m+1|＞，当m≤﹣时，﹣m＜﹣2m﹣1，解得：m＜﹣1，则|2m+1|＞1，∴|m﹣0|的最小值为，此时m＝﹣，C（﹣，）．综上所述，点C与D的“识别距离”的最小值为：，相应的C点坐标为：（﹣，），故答案为：，（﹣，）．27．解：（1）如图，CD为所作，因为AB向右平移7个单位，所以D点坐标为（7，1）；（2）∠BAC＝∠BDC．理由如下：∵AB平移后的线段CD，∴AB∥CD，AC∥BD，∴∠ABD+∠BDC＝180°，∠BAC+∠ABD＝180°，∴∠BAC＝∠BDC；（3）∠ADB：∠AEB＝1：2；理由如下：∵AC∥BD，∴∠CAD＝∠ADB，∠AEB＝∠CAE，∵∠EAD＝∠CAD，∴∠CAE＝2∠CAD，∴∠AEB＝2∠ADB，即∠ADB：∠AEB＝1：2．。

鲁教版五四制七年级数学上册第五章位置与坐标综合测评90分钟

弟五章位置与坐标综合测评时间：满分：120分班级：姓名：得分：一、精心选一选（每小题4分，共32分） 1．确定一个点的位置下列说法正确的是（）A ．东北方向B ．东经35°10′，北纬12°C ．距点A 100米D ．偏北20°，10 000米 2．若a ＞0，b ＜0，则点(-a ，-b ）在平面直角坐标系中的( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．图1是中国象棋棋盘的一部分，若在点(1，－1)上，在点(7，－1)上，则的位置标示为 ( ) A ．(－4，4) B ．(－4，-4) C ．(4，-4) D ．(4，4)4．若点P(-1，2a －6)在x 轴上，点Q （1-2b ，3）在y 轴上，则代数式(a-2b)2013的值为（）A ．－1B ．1C ．22013D ．无法确定5．某市几个著名景点：动物园、碑林公园、龙泉寺的位置如图2所示，则下列说法：①碑林公园在O 点的正北方向；②动物园在O 点的北偏东25°方向；③龙泉寺在O 点的北偏西22°方向．其中正确的有（）A ．1个B ．2个C ．3个D ．4个6．顺次连接A(2，1)，B(－1，2)，C(1，3)得到△ABC ，现将A ，B ，C 各点的横坐标不变，纵坐标分别乘以-1，得到△A 1B 1C 1，再将A ，B ，C 各点的纵坐标不变，横坐标乘以-1，得到△A 2B 2C 2，则下列说法错误的是（）A ． △ABC 与△A 1B 1C 1关于x 轴对称 B ． △ABC 与△A 2B 2C 2关于y 轴对称 C ． △A 1B 1C 1与△A 2B 2C 2关于x 轴对称D ． △A 1B 1C 1与△A 2B 2C 2既不关于x 轴对称，也不关于y 轴对称图1马兵帅马兵帅 O250300龙泉寺碑林公园动物园220东北图2·· ·· ·7．已知长方形ABCD 的顶点A 与坐标原点O 重合，边AB 在x 轴的负半轴上，边AD 在y 轴上，且AB=2，AD=3，则点C 的坐标是( )A.(2，3)或（-2，3）B. (2，-3)或（-2，-3）C ． (－2，3)或(2，－3)D ．(-2，3)或(-2，－3)8．如图3，动点P 在平面直角坐标系中按图中箭头所示的方向运动，第1次从原点运动到点（1，1），第2次运动到点（2，0），第3次运动到点（3，2），…，按这样的运动规律，经过第2011次运动后，动点P 的坐标是__________．A ．（2011，2）B ．(2011，0)C ．(2012，1)D ．(2012，0) 二、细心填一填（每小题5分，共40分）9． 2013年5月，某校组织学生收看了“心中的歌儿给党听”央视节目．到学校礼堂观看时坐位的排数和位数与坐标系类似，如果将“21排11号”简记作(21，11)，张华观看时坐在“4排15号”，可以表示为＿＿＿＿＿．10．在平面直角坐标系中，请你写出两个点的坐标，要求：①这两个点都在y 轴的负半轴上；②这两个点的距离为2个单位长度，你所选的两个点的坐标是＿＿＿＿＿＿＿，＿＿＿＿＿＿＿．11．若点A(2m+1，1）与点B （-5，n-3）关于x 轴对称，则点C （m ，n)的坐标为＿＿＿＿＿＿＿． 12．已知点P(9-2y ，y)在第二、四象限两坐标轴夹角的平分线上，则点P 在第＿＿＿＿＿＿＿象限． 13． 2012年绍兴市在加快改革创新、激发活力动力、推动城市建设中取得较大成效．图4是绍兴市行政区域图，建立直角坐标系后,若上虞市区所在地用坐标表示为(1,2)，诸暨市区所在地用坐标表示为(-5,-2)，则嵊州市区所在地用坐标可表示为________．14．观察下列各点的坐标特征:①(-1，5)，②(-2，4)，③(-3，3)，④(-4，2)，⑤(-5，1)，…，按照此规律写出第⑧个点的坐标为＿＿＿＿＿＿＿＿．15．图5所示是三轮车的“摇把”，已知“摇把”AB 的长为80厘米，BC 的长为60厘米，建立适当的坐标系，写出点A ，B ，C 的坐标依次为：＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿．16．已知点A(2，0)，B(2，3)，以A ，B ，P 为顶点的三角形与△ABO 全等，且点P 在坐标轴上，则点P 的坐ABC图5图3·上虞市·绍兴市·诸暨市·嵊州市图4标可以为＿＿＿＿＿＿＿．（P 点与O 点不重合）三、耐心做一做（共48分）17．( 10分）在如图6所示的图形中建立适当的坐标系，写出某市五大景点的坐标．18． (12分）在平面直角坐标系中描出下列六个点:(0，1)，(0，2)，(3，2)，(5，1．5)，(3，1)，（0，1），并用线段依次连接．⑴观察所得图形，你觉得它像什么?⑵若各点的横坐标不变，纵坐标变为它们的相反数，得到各对应点，在图中把这些点描出来，并用线段依次连接，得到另一个图形，这两个图形的形状、大小相同吗？这两个图形对应点的位置有什么关系？19．( 12分）已知在平面直角坐标系中，A(3，0)，B(0，3)，C(3，3)．⑴在坐标系中描出这三个点，并依次连接A ，B ，C ，得△ABC ，求△ABC 的面积．⑵分别作出△ABC 关于x 轴，y 轴的对称图形△A 1B 1C 1，△A 2B 2C 2，△A 1B 1C 1关于y 轴对称的图形△A 3B 3C 3，并求点C 1，C 2，C 3的坐标．20．（14分）如图7，有一条小河，可以近似地看成直线，河上有两点A （0,1）和B （6,1），在河的南岸有一棵树，该树的位置是（3，-2），树关于这条河成轴对称处有一口井，你能说出井的位置吗？作出图来，并确定井口的位置．第五章位置与坐标综合测评一、1．B 2． B 3．C 4．C 5．B 6．C 7．D 8．A蒙山大佛动物园晋祠博物馆漫山阁迎泽公园•图6• • • •··AB图7(0,1)(6,1)二、9．(4，15) 10．答案不唯一，如（0，-4）（0，-6） 11．（-3，2） 12．二 13．（0，-3） 14．（-8，-2） 15．答案不唯一，若以B 为原点，BC 所在的直线为x 轴，AB 所在的直线为y 轴建立坐标系，则三个点的坐标分别为A(0，80) B （0，0） C （60，0） 16．（4，0）或（0，3）三、17．解：方法不唯一，可建立如图1所示的坐标系，由图可以看出，太原动物园的坐标为（0，0），太原蒙山大佛的坐标为（-6，2），山西晋祠博物馆的坐标为（-5，-1），太原漫山阁的坐标为（2，2），太原迎泽公园的坐标为（4，-1），太原大山寺的坐标为（8，-1）．18．解：⑴所画图如图2所示，它像一支铅笔．⑵所画图形如图2所示，这两个图形的形状、大小相同，这两个图形的对应点关于x 轴对称．19．解：⑴如图3所示， S △ABC =193322⨯⨯=．⑵所画图如图3所示，点C 1(3，－3)，C 2(－3，3)，C 3(―3，―3)．20．解：建立如图4所示的平面直角坐标系，其中x 轴∥AB ，且AB 与x 轴的距离为1个单位长度，y 轴经过点A ，原点为O ，过点C 作AB 的垂线MN ，与AB 交于点D ，在DM 上截取DE=DC ，因为DE=DC=3，所以点E 的坐标为（3，4），点E 即为井口的位置．太原蒙山大佛太原动物园山西晋祠博物馆太原漫山阁太原迎泽公园 • 图1太原大山寺 • • • • • x y O x y图2 · · · · ·E A 1 C O x y 图3C 3 A B B 3A 3 C 2B 2 A 2 B 1C 1A 1B(0,1)(6,1)xy · O· (3,-2) A CD图4N M E··初中数学试卷。

鲁教五四新版七年级上学期《第5章位置与坐标》单元测试卷

鲁教五四新版七年级上学期《第5章位置与坐标》单元测试卷一．选择题（共10小题，满分30分，每小题3分）1．（3分）已知点P的坐标为（1﹣a，2a+4），且点P到两坐标轴距离相等，则a的值为（）A．﹣5B．﹣3C．﹣1或﹣5D．﹣1或﹣3 2．（3分）下列描述不能确定具体位置的是（）A．贵阳横店影城1号厅6排7座B．坐标（3，2）可以确定一个点的位置C．贵阳市筑城广场北偏东40°D．位于北纬28°，东经112°的城市3．（3分）点P（2，﹣5）关于原点对称点的坐标是（）A．（﹣5，﹣2）B．（2，5）C．（﹣2，5）D．（﹣5，2）4．（3分）平面直角坐标系中，属于第四象限的点是（）A．（5，3）B．（﹣5，3）C．（5，﹣3）D．（﹣5，﹣3）5．（3分）阳阳和亮亮喜欢下棋，阳阳持有圆形棋子，亮亮持有方形棋子．如图，若棋盘正中间的方形棋子的位置用（1，0）表示，最右上角的方形棋子的位置用（2，1）表示，阳阳应把第八枚圆形棋子放在适当位置，使所有棋子组成轴对称图形．则第八枚圆形棋子放的位置是（）A．（﹣1，0）B．（2，﹣1）C．（1，﹣1）D．（1，2）6．（3分）在平面直角坐标系中，点M（﹣3，2）关于y轴对称的点的坐标为（）A．（﹣3，﹣2）B．（﹣2，﹣3）C．（3，2）D．（3，﹣2）7．（3分）在平面直角坐标系中，点M（2021，﹣2022）的位置在（）A．第一象限B．第二象限C．第三象限D．第四象限8．（3分）如图，将一副三角板如图放置，如果DB＝2，那么点E到BC的距离为（）A．﹣1B．3﹣C．2﹣2D．+19．（3分）我们规定：在平面直角坐标系xOy中，任意不重合的两点M（x1，y1），N（x2，y2）之间的折线距离为d（M，N）＝|x1﹣x2|+|y1﹣y2|，例如图①中，点M（﹣2，3）与N （1，﹣1）之间的折线距离为d（M，N）＝|﹣2﹣1|+3﹣（﹣1）|＝3+4＝7．如图②，已知点P（3，﹣4），若点Q的坐标为（2，t），且d（P，Q）＝10，则t的值为（）A．﹣7或1B．﹣5或13C．5或﹣13D．﹣1或710．（3分）点M在第四象限，它到x轴、y轴的距离分别为8和5，则点M的坐标为（）A．（8，5）B．（5，﹣8）C．（﹣5，8）D．（﹣8，5）二．填空题（共8小题，满分24分，每小题3分）11．（3分）如图，直线l1⊥l2，在某平面直角坐标系中，x轴∥l1，y轴∥l2，点A的坐标为（﹣1，2），点B的坐标为（2，﹣1），那么点C在第象限．12．（3分）如图，平面直角坐标系中有四个点，它们的横纵坐标均为整数，若在此平面直角坐标系内移动点A至第四象限A'处，使得这四个点构成的四边形是轴对称图形，并且点A'横纵坐标仍是整数，则点A'的坐标可以为（写出一个即可）．13．（3分）如图，在平面直角坐标系xOy中，点T（4，2）．M、N分别是x轴与y轴正半轴上的动点，且线段MN＝4，P为MN的中点．在线段MN的运动过程中，PT长的最小值为．14．（3分）A（﹣3，﹣2）、B（2，﹣2）、C（﹣2，1）、D（3，1）是坐标平面内的四个点，则线段AB与CD的关系是．15．（3分）如图，点A，B分别是x轴和y轴上的动点，且OA+OB＝6，取AB的中点P，则所有满足条件的P点围成的封闭图形的面积为．16．（3分）如图，△ABC关于直线l对称的图形中，点B的对应点的坐标为．17．（3分）点P（2m+1，2）在第二象限内，则m的值可以是（写出一个即可）．18．（3分）已知点M（3，﹣2），它与点N（x，y）在同一条平行于x轴的直线上，且MN ＝4，那么点N的坐标是．三．解答题（共8小题，满分66分）19．（6分）已知点A（a﹣1，5）和点B（2，b﹣1）关于x轴对称，求（a+b）2018的值．20．（6分）如图为象棋棋盘的一部分，若象的位置用（4，2）表示．请回答下列问题：（1）表示图中“马”和“将”的位置；（2）按照“马走日”的规则，写出下一步“马”可以到达的位置．21．（8分）如图，一只蚂蚁在网格（每小格边长为1）上沿着网格线运动．它从格点A（1，2）处出发去看望格点B、C、D等处的蚂蚁，规定：向上向右走均为正，向下向左走均为负．如：从A到B记为：A→B＜+1，+3＞，从B到A记为：B→A＜﹣1，﹣3＞，其中第一个数表示左右方向，第二个数表示上下方向．填空：（1）图中A→C（，）C→（，）（2）若这只蚂蚁从A处去M处的蚂蚁的行走路线依次为＜+3，+3＞，＜+2，﹣1＞，＜﹣3，﹣3＞，＜+4，+2＞，则点M的坐标为（，）（3）若图中另有两个格点P、Q，且P→A＜m+3，n+2＞，P→Q＜m+1，n﹣2＞，则从Q到A记为（，）22．（8分）已知点P（2a+3，a﹣4）．（1）若点P在x轴上，求点P的坐标；（2）若点Q（3，2b）在第一象限，PQ∥y轴，且PQ＝10，求点Q的坐标；（3）若点P到x轴的距离比到y轴的距离多2，求点P的坐标．23．（9分）在平面直角坐标系中，已知点P（a﹣1，2a+7），请分别根据下列条件求出点P 的坐标．（1）点P在y轴上；（2）点P的纵坐标比横坐标大6；（3）点Q的坐标为（1，﹣2），直线PQ∥x轴．24．（9分）如图，在下面的直角坐标系中，已知A（0，a），B（b，0），C（b，4）三点，其中a，b满足关系式．（1）求a，b的值；（2）如果在第二象限内有一点P（m，），请用含m的式子表示四边形ABOP的面积；（3）在（2）的条件下，是否存在点P，使四边形ABOP的面积与△ABC的面积相等？若存在，求出点P的坐标；若不存在，请说明理由．25．（10分）如图，在长方形ABCD中，AB＝10cm，BC＝8cm，点E是CD边上的一点，且DE＝2cm，动点P从A点出发，以2cm/s的速度沿A﹣B﹣C﹣E运动，最终到达点E．设点P运动的时间为t秒．（1）请以A点为原点，AB为x轴，建立平面直角坐标系，并用t表示出点P处在AB、BC、CD线段时的坐标．当0＜t≤5时，P在AB上，P1（，）；当5＜t≤9时，P在BC上，P2（，）；当9＜t≤13时，P在CD上，P3（，）；（2）在（1）相同条件得到的结论下，是否存在P点使△APE的面积等于20cm2，若存在，请求出P点坐标，若不存在，请说明理由．26．（10分）如图，P1（x1、y1），P2（x1，y2）是平面直角坐标系内的两点，求证：P1P2＝．。

鲁教版七上数学-第五章位置与坐标综合测评一

· 5km 北 A 35° O 东图1 第五章位置与坐标综合测评（一）（时间: 满分：120分）（班级：姓名：得分：）一、精心选一选（每小题3分，共30分）1. 要在地球仪上准确地确定太原市的位置，需要知道的数据是（）A. 高度B. 北纬38ºC. 东经112ºD. 北纬38º和东经112º2. 在平面直角坐标系中，点（－1，－3）所在的象限是（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限3. 点A （2，－1）关于x 轴对称的点B 的坐标为（）A.（2，1）B. （－2，1）C. （2，－1）D. （－2，－1）4. 如图1，下列说法中能确定点A 的位置的是（）A. 在到点O 的距离为5 km 处B. 在北偏东35°的方向上，且到点O 的距离为5 kmC. 在点O 北偏东35°的方向上，到点O 的距离为5 kmD. 在点O 北偏东55°的方向上，到点O 的距离为5 km5. 在平面直角坐标系中，若点P （m+3，m －1）在x 轴上，则点P 的坐标为（）A.（0，－4）B.（4，0）C.（－4，0）D.（0，4）6. 在平面直角坐标系中，△ABC 的位置如图2所示，若△ABC 与△A 1B 1C 1关于y 轴对称，则点A 1的坐标为（）A.（－3，2）B.（3，－2）C.（3，2）D.（－3，－2）7. 图3所示是一局围棋比赛的棋局，为记录棋谱方便，横线用数字表示，纵线用字母表示，这样黑棋❶的位置可记为（B ，2），白棋②的位置可记为（D ，1），则白棋⑨的位置应记为（）A.（C ，5）B.（C ，4）C.（4，C ）D.（5，C ）8. 图4所示是某市几个旅游景点的大致位置示意图，如果用（0，0）表示县衙的位置，用（－2，1）表示清虚观的位置，则双林寺的位置表示为（）A.（3，－1）B.（5，3）C.（－1，－2）D.（－2，1）9. 如图5，正方形ABCD 关于x 轴、y 轴均成轴对称，若这个正方形的面积为4，则点C 的坐标为（）A.（－1，－1）B.（－2，－2）C.（1，－1）D.（2，－2）10. 已知点A （－3，2）与点B （x ，y ）在同一条平行于y 轴的直线上，且B 点到x 轴的距离等于3，则点B 的坐标为（）A.（－3，3）B.（3，－3）C.（－3，3）或（3，－3）D.（－3，3）或（－3，－3）二、细心填一填（每小题3分，共24分）11. 电影票9排21号记为（9， 21），则（21， 5）表示__________.12. 在平面直角坐标系中，点（0，－9）到x 轴的距离为__________.13. 已知点A （－1，4），B （－4，4），则线段AB 的长为__________.14. 已知点A （a ，－3）与B （－4，b ）关于x 轴对称，则a+b=_________.· · · · · 清虚观文庙城防庙双林寺县衙图4 图5 图2 1 -1 1 ❶ ⑨ ② 图315. 如图6，在象棋盘上建立平面直角坐标系，使“帅”位于点（0，－1），“炮”位于点（－1，1），则“兵”所在位置的坐标为__________.16. 已知点P （－12，2a+6）不在任何象限内，则a 的值为_________. 17. 图7所示是一台雷达探测器测的结果，图中显示在A ，B ，C ，D 处有目标出现，若目标A 的位置用（5，0°）来表示，那么其他三个目标B ，C ，D 的位置可表示为______________. 18. 在平面直角坐标系中，已知点A （6 ，0），B （6，0），点C在x 轴上，且AC+BC=10，写出满足条件的所有点C 的坐标______________________.三、耐心解一解（共66分）19.（8分）已知点P （a ，b ）在第二象限，且|a|=3，|b|=8，求点P 的坐标.20.（8分）图8所示是某市华一寄宿学校、纸坊、中南分校、藏龙岛的大致位置，直线AB ，CD ，EF ，GH 相交于点O ，OG 平分∠COE ，试分别指出华一寄宿学校、中南分校的大致位置.（说明：①OB 为正东方向，OH 为正北方向；②要有解答过程）21.（10分）写出图9中四边形ABFG 和四边形CDEF 各个顶点的坐标，并指出A ，B ，C ，D ，E ，F ，G 所在的象限或坐标轴.22.（10分）图10是一个游乐城的平面示意图，试设计一个描述这个游乐城中每个景点位置的方法，并画图说明.23.（10分）在平面直角坐标系中，顺次连接下列各点，并画出图形：（－5，2），（－1， 4），（－5，6），（－3，4），（－5，2）.（1）不改变这些点的纵坐标，将它们的横坐标都乘以－1，写出新的点的坐标；（2）在同一平面直角坐标系中，描出这些新的点，并连成图形；（3）新图形与原图形有什么关系？图6 · · · 图7 · 图10 北东图810km 11kmG H 华一寄宿学校 -1 y x 图9 (O ) 1 124.（10分）某中学八年级（3）班教室中学生座位的平面图如图11所示.（1）请你说明图中五位同学的位置（用第×排第×列说明）；（2）若用（3，2）表示第3排第2列的位置，那么（4，5）表示什么位置？王明和张强的位置怎样表示？（3，3）和（4，8）表示哪位同学的位置？（3）（3，4）和（4，3）表示的位置相同吗？25.（10分）问题情境：如图12，已知△ABC 是等腰直角三角形，∠A=90º，BC 的长为6.问题解决：（1）请你建立适当的平面直角坐标系，画出图形，并写出各个顶点的坐标；（2）画出（1）中△ABC 关于x 轴对称的图形△A 1B 1C 1，并写出各顶点的坐标；问题探究：（3）在（1）中，你还可以怎样建立平面直角坐标系？画出一种，并写出各个顶点的坐标.（拟题左丁政）第五章位置与坐标综合测评（一）参考答案一、1. D 2. C 3. A 4. D 5. B 6. C 7. B 8. A9. A 提示：因为正方形的面积为4，所以正方形的边长为2.由正方形ABCD 关于x 轴、y 轴均成轴对称，知B ，C 两点关于x 轴对称，C ，D 两点关于y 轴对称，所以C （－1，－1）.10. D 提示：由题意，得x=－3.又B 点到x 轴的距离等于3，所以y=3或y=－3.所以点B 的坐标为（－3，3）或（－3，－3）.二、11. 21排5号 12. 9 13. 3 14. －1 15.（－2， 2）16. －3 提示：由题意，得点P （－12，2a+6）在x 轴上，所以2a+6=0.所以a=－3.17. B （4，30°），C （3，120°），D （4，240°）18.（5，0）或（－5，0）提示：设点C 到原点O 的距离为a.因为AC+BC=10，所以a 1066=++-a .所以a=5.所以C （5，0）或（－5，0）.三、19. 解：因为点P （a ，b ）在第二象限，所以a<0，b>0.又|a|=3，|b|=8，所以a=-3，b=8.所以点P 的坐标为（-3，8）.20. 解：因为OG 平分∠COE ，所以∠COG=21∠COE=21×102º=51º.所以∠DOH=∠COG=51º.所以华一寄宿学校在点O 南偏西51º，距离O 点10 km 的位置上；中南分校在点O 北偏东51º，距离O 点11 km 的位置上.21. 解：A （－2，3），B （0，0），C （4，0），D （6，1），E （5，3），F （3，2），G （1，5）.点A 在第二象限，点B 在原点，点C 在x 轴上，点D ，E ，F ，G 在第一象限.22. 解：答案不唯一，给出一种供参考.如：以入口处的位置为坐标原点，建立平面直角坐标系（图略），各景点的位置表示为：入口处（0，0），辉煌花园（0，3），梦幻艺馆（－3，图11图12 C B A 图14），太空秋千（－8，2），海底世界（－4，1），激光战车（－6，－2），球幕电影（－2，－3）.23. 解：如图1所示，所画图形为第二象限中的图形.（1）不改变这些点的纵坐标，将它们的横坐标乘以－1，新的点的坐标为（5，2），（1，4），（5，6），（3，4），（5，2）.（2）如图1所示，所连图形为第一象限中的图形.（3）新图形与原图形关于y 轴对称.24. 解：（1）王明在第2排第2列，张逸在第3排第3列，张强在第5排第5列，吴俊在第4排第6列，李爽在第4排第8列.（2）因为（3，2）表示第3排第2列的位置，所以（4，5）表示第4排第5列.王明和张强的位置分别用（2，2），（5，5）表示.（3，3）表示张逸的位置，（4，8）表示李爽的位置.（3）（3，4）和（4，3）表示的位置不相同.25. 解：（1）如图2所示，以BC 所在的直线为x 轴，BC 的垂直平分线为y 轴建立平面直角坐标系.根据等腰三角形为轴对称图形可知，点A 在y 轴上.因为BC=6，所以BO=CO=3. 由勾股定理，得AB=AC=23，所以AO=223)23( =3.所以点A（0，3），B （－3，0），C （3，0）.（2）如图2所示，A 1（0，－3），B 1（－3，0），C 1（3，0）.（3）答案不唯一，如以点A 为原点，平行于BC 的直线为x 轴建立平面直角坐标系（图略）.用同样的方法可得A （0，0），B （－3，-3），C（3，－3）. A C BC 1 图2 A 1 B 1。

初中数学鲁教版(五四制)七年级上册第五章 位置与坐标本章综合与测试-章节测试习题(3)

鲁教版(五四制) 七年级上册《第5章 位置与坐标》 单元练习卷

鲁教版(五四制)七年级上册 第五章 位置与坐标测试试题(一)练习

鲁教版七年级数学上册 第五章 位置与坐标 单元测试

鲁教版七年级上册 第五章 位置与坐标》过关测试试题