高三数学课外培优练习
高三数学数学等差数列选择题专项训练的专项培优练习题(及解析

一、等差数列选择题1.已知等差数列{}n a ,且()()35710133248a a a a a ++++=,则数列{}n a 的前13项之和为( ) A .24 B .39C .104D .52解析:D 【分析】根据等差数列的性质计算求解. 【详解】由题意()()357101341041073232236()1248a a a a a a a a a a ++++=⨯+⨯=+==,74a =,∴11313713()13134522a a S a +===⨯=. 故选:D .2.等差数列{}n a 中,若26a =,43a =,则5a =( ) A .32B .92C .2D .9解析:A 【分析】由2a 和4a 求出公差d ,再根据54a a d =+可求得结果. 【详解】 设公差为d ,则423634222a a d --===--, 所以5433322a a d =+=-=. 故选:A3.在1与25之间插入五个数,使其组成等差数列,则这五个数为( ) A .3、8、13、18、23 B .4、8、12、16、20 C .5、9、13、17、21 D .6、10、14、18、22解析:C 【分析】根据首末两项求等差数列的公差,再求这5个数字. 【详解】在1与25之间插入五个数,使其组成等差数列, 则171,25a a ==,则712514716a a d --===-, 则这5个数依次是5,9,13,17,21. 故选:C4.已知等差数列{}n a 的前n 项和为n S ,且310179a a a ++=,则19S =( ) A .51 B .57C .54D .72解析:B 【分析】根据等差数列的性质求出103a =,再由求和公式得出答案. 【详解】317102a a a += 1039a ∴=,即103a =()1191019191921935722a a a S +⨯∴===⨯=故选:B5.设等差数列{}n a 的公差d ≠0,前n 项和为n S ,若425S a =,则99S a =( ) A .9 B .5C .1D .59解析:B 【分析】由已知条件,结合等差数列通项公式得1a d =,即可求99S a . 【详解】4123425S a a a a a =+++=,即有13424a a a a ++=,得1a d =,∴1999()452a a S d ⨯+==,99a d =,且0d ≠, ∴995S a =. 故选:B6.已知等差数列{}n a 的前n 项和为n S ,且2n S n =.定义数列{}n b 如下:()*1m m b m m+∈N 是使不等式()*n a m m ≥∈N 成立的所有n 中的最小值,则13519 b b b b ++++=( )A .25B .50C .75D .100解析:B 【分析】先求得21n a n =-,根据n a m ≥,求得12m n +≥,进而得到21212k k b --=,结合等差数列的求和公式,即可求解. 【详解】由题意,等差数列{}n a 的前n 项和为n S ,且2n S n =,可得21n a n =-,因为n a m ≥,即21n m -≥,解得12m n +≥, 当21m k =-,(*k N ∈)时,1m m b k m+=,即()()11212m m m mk m b m m +===++, 即21212k k b --=, 从而()13519113519502b b b b ++++=++++=.故选:B.7.设等差数列{}n a 的前n 项和为n S ,且71124a a -=,则5S =( ) A .15 B .20C .25D .30解析:B 【分析】设出数列{}n a 的公差,利用等差数列的通项公式及已知条件,得到124a d +=,然后代入求和公式即可求解 【详解】设等差数列{}n a 的公差为d ,则由已知可得()()111261024a d a d a d +-+=+=, 所以()5115455254202S a d a d ⨯=+=+=⨯= 故选:B8.《张丘建算经》卷上第22题为:“今有女善织,日益功疾(注:从第2天开始,每天比前一天多织相同量的布),第一天织5尺布,现一月(按30天计)共织390尺”,则从第2天起每天比前一天多织( ) A .12尺布 B .518尺布 C .1631尺布 D .1629尺布 解析:D 【分析】设该女子第()N n n *∈尺布,前()N n n *∈天工织布n S 尺,则数列{}n a 为等差数列,设其公差为d ,根据15a =,30390S =可求得d 的值. 【详解】设该女子第()N n n *∈尺布,前()N n n *∈天工织布n S 尺,则数列{}n a 为等差数列,设其公差为d ,由题意可得30130293015015293902S a d d ⨯=+=+⨯=,解得1629d =.故选:D.9.已知等差数列{}n a 的前n 项和为n S ,若936S S =,则612SS =( )A .177B .83C .143D .103解析:D 【分析】由等差数列前n 项和性质得3S ,63S S -,96S S -,129S S -构成等差数列,结合已知条件得633S S =和31210S S =计算得结果. 【详解】已知等差数列{}n a 的前项和为n S ,∴3S ,63S S -,96S S -,129S S -构成等差数列, 所以()()633962S S S S S ⋅-=+-,且936S S =,化简解得633S S =.又()()()96631292S S S S S S ⋅-=-+-,∴31210S S =,从而126103S S =. 故选:D 【点睛】 思路点睛:(1)利用等差数列前n 项和性质得3S ,63S S -,96S S -,129S S -构成等差数列, (2)()()633962S S S S S ⋅-=+-,且936S S =,化简解得633S S =, (3)()()()96631292S S S S S S ⋅-=-+-,化简解得31210S S =.10.已知等差数列{}n a 的前n 项和为n S ,且110a =,56S S ≥,下列四个命题:①公差d 的最大值为2-;②70S <;③记n S 的最大值为M ,则M 的最大值为30;④20192020a a >.其真命题的个数是( ) A .4个 B .3个C .2个D .1个解析:B 【分析】设公差为d ,利用等差数列的前n 项和公式,56S S ≥,得2d ≤-,由前n 项和公式,得728S ≤,同时可得n S 的最大值,2d =-,5n =或6n =时取得,结合递减数列判断D . 【详解】设公差为d ,由已知110a =,56S S ≥,得5101061015d d ⨯+≥⨯+,所以2d ≤-,A 正确;所以7710217022128S d =⨯+≤-⨯=,B 错误;1(1)10(1)0n a a n d n d =+-=+-≥,解得101n d≤-+,11100n a a nd nd +=+=+≤,解得10n d≥-, 所以10101n d d-≤≤-+,当2d =-时,56n ≤≤, 当5n =时,有最大值,此时51010(2)30M =⨯+⨯-=, 当6n =时,有最大值,此时61015(2)30M =⨯+⨯-=,C 正确. 又该数列为递减数列,所以20192020a a >,D 正确. 故选:B . 【点睛】关键点点睛:本题考查等差数列的前n 项和,掌握等差数列的前n 和公式与性质是解题关键.等差数列前n 项和n S 的最大值除可利用二次函数性质求解外还可由10n n a a +≥⎧⎨≤⎩求得.11.数列{}n a 为等差数列,11a =,34a =,则通项公式是( ) A .32n - B .322n - C .3122n - D .3122n + 解析:C 【分析】根据题中条件,求出等差数列的公差,进而可得其通项公式. 【详解】因为数列{}n a 为等差数列,11a =,34a =, 则公差为31322a a d -==, 因此通项公式为()33111222n a n n =+-=-. 故选:C.12.已知n S 为等差数列{}n a 的前n 项和,3518a S +=,633a a =+,则n a =( ) A .1n - B .nC .21n -D .2n解析:B 【分析】根据条件列出关于首项和公差的方程组,求解出首项和公差,则等差数列{}n a 的通项公式可求. 【详解】因为3518a S +=,633a a =+,所以11161218523a d a d a d +=⎧⎨+=++⎩,所以111a d =⎧⎨=⎩,所以()111n a n n =+-⨯=,故选:B.13.已知数列{}n a 是等差数列,其前n 项和为n S ,若454a a +=,则8S =( ) A .16 B .-16 C .4 D .-4解析:A 【详解】 由()()18458884816222a a a a S +⨯+⨯⨯====.故选A.14.等差数列{a n }的前n 项和为S n ,若a 1=2,S 3=12,则a 6等于( ) A .8 B .10C .12D .14解析:C 【分析】利用等差数列的通项公式即可求解. 【详解】 {a n }为等差数列,S 3=12,即1232312a a a a ++==,解得24a =. 由12a =,所以数列的公差21422d a a =-=-=, 所以()()112212n a a n d n n =+-=+-=, 所以62612a =⨯=. 故选:C15.等差数列{}n a 中,22a =,公差2d =,则10S =( ) A .200 B .100C .90D .80解析:C 【分析】先求得1a ,然后求得10S . 【详解】依题意120a a d =-=,所以101104545290S a d =+=⨯=. 故选:C二、等差数列多选题16.已知数列{}n a 满足:12a =,当2n ≥时,)212n a =-,则关于数列{}n a 的说法正确的是 ( )A .27a =B .数列{}n a 为递增数列C .221n a n n =+- D .数列{}n a 为周期数列解析:ABC 【分析】由)212n a =-1=,再利用等差数列的定义求得n a ,然后逐项判断. 【详解】当2n ≥时,由)212n a =-,得)221n a +=,1=,又12a =,所以是以2为首项,以1为公差的等差数列,2(1)11n n =+-⨯=+, 即221n a n n =+-,故C 正确; 所以27a =,故A 正确;()212n a n =+-,所以{}n a 为递增数列,故正确;数列{}n a 不具有周期性,故D 错误; 故选:ABC17.设数列{}n a 的前n 项和为*()n S n N ∈,关于数列{}n a ,下列四个命题中正确的是( )A .若1*()n n a a n N +∈=,则{}n a 既是等差数列又是等比数列B .若2n S An Bn =+(A ,B 为常数,*n N ∈),则{}n a 是等差数列 C .若()11nn S =--,则{}n a 是等比数列D .若{}n a 是等差数列,则n S ,2n n S S -,*32()n n S S n N -∈也成等差数列 解析:BCD 【分析】利用等差等比数列的定义及性质对选项判断得解. 【详解】选项A: 1*()n n a a n N +∈=,10n n a a +∴-=得{}n a 是等差数列,当0n a =时不是等比数列,故错; 选项B:2n S An Bn =+,12n n a a A -∴-=,得{}n a 是等差数列,故对;选项C: ()11nn S =--,112(1)(2)n n n n S S a n --∴-==⨯-≥,当1n =时也成立,12(1)n n a -∴=⨯-是等比数列,故对;选项D: {}n a 是等差数列,由等差数列性质得n S ,2n n S S -,*32()n n S S n N -∈是等差数列,故对; 故选:BCD【点睛】熟练运用等差数列的定义、性质、前n 项和公式是解题关键. 18.已知数列{}n a 满足112a =-,111n na a +=-,则下列各数是{}n a 的项的有( ) A .2- B .23 C .32D .3解析:BD 【分析】根据递推关系式找出规律,可得数列是周期为3的周期数列,从而可求解结论. 【详解】因为数列{}n a 满足112a =-,111n na a +=-,212131()2a ∴==--;32131a a ==-; 4131112a a a ==-=-; ∴数列{}n a 是周期为3的数列,且前3项为12-,23,3; 故选:BD . 【点睛】本题主要考查数列递推关系式的应用,考查数列的周期性,解题的关键在于求出数列的规律,属于基础题.19.首项为正数,公差不为0的等差数列{}n a ,其前n 项和为n S ,则下列4个命题中正确的有( )A .若100S =,则50a >,60a <;B .若412S S =,则使0n S >的最大的n 为15;C .若150S >,160S <,则{}n S 中7S 最大;D .若89S S <,则78S S <. 解析:ABD 【分析】利用等差数列的求和公式及等差数列的性质,逐一检验选项,即可得答案. 【详解】对于A :因为正数,公差不为0,且100S =,所以公差0d <, 所以1101010()02a a S +==,即1100a a +=,根据等差数列的性质可得561100a a a a +=+=,又0d <, 所以50a >,60a <,故A 正确; 对于B :因为412S S =,则1240S S -=,所以561112894()0a a a a a a ++⋅⋅⋅++=+=,又10a >, 所以890,0a a ><, 所以115815815()15215022a a a S a +⨯===>,116891616()16()022a a a a S ++===, 所以使0n S >的最大的n 为15,故B 正确; 对于C :因为115815815()15215022a a a S a +⨯===>,则80a >, 116891616()16()022a a a a S ++===,则890a a +=,即90a <, 所以则{}n S 中8S 最大,故C 错误;对于D :因为89S S <,则9980S a S =->,又10a >, 所以8870a S S =->,即87S S >,故D 正确, 故选:ABD 【点睛】解题的关键是先判断d 的正负,再根据等差数列的性质,对求和公式进行变形,求得项的正负,再分析和判断,考查等差数列性质的灵活应用,属中档题. 20.等差数列{}n a 的前n 项和为n S ,若10a >,公差0d ≠,则( ) A .若59S >S ,则150S > B .若59S =S ,则7S 是n S 中最大的项 C .若67S S >, 则78S S > D .若67S S >则56S S >.解析:BC 【分析】根据等差数列的前n 项和性质判断. 【详解】A 错:67895911415000S a a a a a S a S ⇒+++<>⇒+<⇒<;B 对:n S 对称轴为n =7;C 对:6770S S a >⇒<,又10a >,887700a S a d S ⇒⇒<<⇒<>;D 错:6770S S a >⇒<,但不能得出6a 是否为负,因此不一定有56S S >. 故选:BC . 【点睛】关键点点睛:本题考查等差数列的前n 项和性质,(1)n S 是关于n 的二次函数,可以利用二次函数性质得最值;(2)1n n n S S a -=+,可由n a 的正负确定n S 与1n S -的大小;(3)1()2n n n a a S +=,因此可由1n a a +的正负确定n S 的正负. 21.记n S 为等差数列{}n a 前n 项和,若81535a a = 且10a >,则下列关于数列的描述正确的是( ) A .2490a a += B .数列{}n S 中最大值的项是25S C .公差0d > D .数列{}na 也是等差数列解析:AB 【分析】根据已知条件求得1,a d 的关系式,然后结合等差数列的有关知识对选项逐一分析,从而确定正确选项. 【详解】依题意,等差数列{}n a 中81535a a =,即()()1137514a d a d +=+,1149249,2a d a d =-=-. 对于A 选项,24912490a a a d +=+=,所以A 选项正确. 对于C 选项,1492a d =-,10a >,所以0d <,所以C 选项错误. 对于B 选项,()()149511122n a a n d d n d n d ⎛⎫=+-=-+-=- ⎪⎝⎭,令0n a ≥得51510,22n n -≤≤,由于n 是正整数,所以25n ≤,所以数列{}n S 中最大值的项是25S ,所以B 选项正确.对于D 选项,由上述分析可知,125n ≤≤时,0n a ≥,当26n ≥时,0n a <,且0d <.所以数列{}na 的前25项递减,第26项后面递增,不是等差数列,所以D 选项错误.故选:AB 【点睛】等差数列有关知识的题目,主要把握住基本元的思想.要求等差数列前n 项和的最值,可以令0n a ≥或0n a ≤来求解.22.记n S 为等差数列{}n a 的前n 项和.已知450,5S a ==,则( ) A .25n a n =- B .310na nC .228n S n n =-D .24n S n n =-解析:AD 【分析】设等差数列{}n a 的公差为d ,根据已知得1145460a d a d +=⎧⎨+=⎩,进而得13,2a d =-=,故25n a n =-,24n S n n =-.【详解】解:设等差数列{}n a 的公差为d ,因为450,5S a ==所以根据等差数列前n 项和公式和通项公式得:1145460a d a d +=⎧⎨+=⎩,解方程组得:13,2a d =-=,所以()31225n a n n =-+-⨯=-,24n S n n =-.故选:AD.23.{} n a 是等差数列,公差为d ,前项和为n S ,若56S S <,678S S S =>,则下列结论正确的是( ) A .0d < B .70a =C .95S S >D .170S <解析:ABD 【分析】结合等差数列的性质、前n 项和公式,及题中的条件,可选出答案. 【详解】由67S S =,可得7670S S a -==,故B 正确; 由56S S <,可得6560S S a -=>, 由78S S >,可得8780S S a -=<,所以876a a a <<,故等差数列{}n a 是递减数列,即0d <,故A 正确; 又()9567897820S S a a a a a a -=+++=+<,所以95S S <,故C 不正确; 又因为等差数列{}n a 是单调递减数列,且80a <,所以90a <, 所以()117179171702a a S a +==<,故D 正确.故选:ABD. 【点睛】关键点点睛:本题考查等差数列性质的应用,解题的关键是熟练掌握等差数列的增减性及前n 项和的性质,本题要从题中条件入手,结合公式()12n n n a S S n --≥=,及()12n n n a a S +=,对选项逐个分析,可判断选项是否正确.考查学生的运算求解能力与逻辑推理能力,属于中档题.24.已知数列{}n a 的前n 项和为n S ,前n 项积为n T ,且3201911111a a e e +≤++,则( ) A .当数列{}n a 为等差数列时,20210S ≥ B .当数列{}n a 为等差数列时,20210S ≤ C .当数列{}n a 为等比数列时,20210T >D .当数列{}n a 为等比数列时,20210T < 解析:AC 【分析】 将3201911111a a e e +≤++变形为32019111101212a a e e -+-≤++,构造函数()1112x f x e =-+,利用函数单调性可得320190a a +≥,再结合等差数列与等比数列性质即可判断正确选项 【详解】 由3201911111a a e e +≤++,可得32019111101212a a e e -+-≤++,令()1112xf x e =-+, ()()1111101111x x x x x e f x f x e e e e --+=+-=+-=++++,所以()1112xf x e =-+是奇函数,且在R 上单调递减,所以320190a a +≥, 所以当数列{}n a 为等差数列时,()320192*********a a S +=≥;当数列{}n a 为等比数列时,且3a ,1011a ,2019a 同号,所以3a ,1011a ,2019a 均大于零, 故()2021202110110T a =>.故选:AC 【点睛】本题考查等差数列与等比数列,考查逻辑推理能力,转化与化归的数学思想,属于中档题 25.在数列{}n a 中,若22*1(2,.n n a a p n n N p --=≥∈为常数),则称{}n a 为“等方差数列”.下列对“等方差数列”的判断正确的是( ) A .若{}n a 是等差数列,则{}n a 是等方差数列 B .{(1)}n -是等方差数列C .若{}n a 是等方差数列,则{}()*,kn a k N k ∈为常数)也是等方差数列D .若{}n a 既是等方差数列,又是等差数列,则该数列为常数列 解析:BCD 【分析】根据等差数列和等方差数列定义,结合特殊反例对选项逐一判断即可. 【详解】对于A ,若{}n a 是等差数列,如n a n =,则12222(1)21n n a a n n n --=--=-不是常数,故{}n a 不是等方差数列,故A 错误;对于B ,数列(){}1n-中,222121[(1)][(1)]0n n nn a a---=---=是常数,{(1)}n ∴-是等方差数列,故B 正确;对于C ,数列{}n a 中的项列举出来是,1a ,2a ,,k a ,,2k a ,数列{}kn a 中的项列举出来是,k a ,2k a ,3k a ,,()()()()2222222212132221k k k k k k k k aa a a a a a a p +++++--=-=-==-=,将这k 个式子累加得()()()()2222222212132221k kk k k k kk aa a a a a a a kp +++++--+-+-++-=,222k k aa kp ∴-=,()221kn k n a a kp +∴-=,{}*(,kn a k N ∴∈k 为常数)是等方差数列,故C 正确; 对于D ,{}n a 是等差数列,1n n a a d -∴-=,则设n a dn m =+{}n a 是等方差数列,()()222112(2)n n n n dn m a a a a d a d d n m d d dn d m --∴-=++++=+=++是常数,故220d =,故0d =,所以(2)0m d d +=,2210n n a a --=是常数,故D 正确.故选:BCD. 【点睛】本题考查了数列的新定义问题和等差数列的定义,属于中档题.。
高三数学培优专练

高三培优专练1.单调性的判断例1:(1)函数()212log (4)f x x -=的单调递增区间是( )A .(0,)+∞B .(0),-∞C .(2,)+∞D .(),2-∞-(2)223y x x +-+=的单调递增区间为________.2.利用单调性求最值例2:函数1y x x =+-的最小值为________.3.利用单调性比较大小、解抽象函数不等式例3:(1)已知函数()f x 的图象向左平移1个单位后关于y 轴对称,当211x x >>时,()()2121()0f x f x x x -⋅-⎡⎤⎣⎦<恒成立,设12a f ⎛⎫=- ⎪⎝⎭,()2b f =,()3c f =,则a ,b ,c 的大小关系为( ) A .c a b >> B .c b a >> C .a c b >> D .b a c >>(2)定义在R 上的奇函数()y f x =在(0,)+∞上递增,且102f ⎛⎫= ⎪⎝⎭,则满足19log 0f x ⎛⎫> ⎪⎝⎭的x 的集合为________________.4.奇偶性例4:已知偶函数()f x 在区间[0,)+∞上单调递增,则满足1(21)3f x f ⎛⎫-< ⎪⎝⎭的x 的取值范围是( ) A .12,33⎛⎫ ⎪⎝⎭B .12,33⎡⎫⎪⎢⎣⎭C .12,23⎛⎫⎪⎝⎭D .12,23⎡⎫⎪⎢⎣⎭5.轴对称例5:已知定义域为R 的函数()y f x =在[]0,7上只有1和3两个零点,且()2y f x =+与()7y f x =+ 都是偶函数,则函数()y f x =在[]0,2013上的零点个数为( ) A .404 B .804C .806D .4026.中心对称例6:函数()f x 的定义域为R ,若()1f x +与()1f x -都是奇函数,则( ) A .()f x 是偶函数 B .()f x 是奇函数 C .()()2f x f x =+D .()3f x +是奇函数7.周期性的应用例7:已知()f x 是定义在R 上的偶函数,()g x 是定义在R 上的奇函数,且()()1g x f x =-, 则()()20172019f f +的值为( ) A .1-B .1C .0D .无法计算一、选择题培优点一 函数的图象与性质对点增分集训1.若函数()2f x x a =+的单调递增区间是[)3,+∞,则a 的值为( )A .2-B .2C .6-D .62.已知函数()2log 1y ax =-在()1,2上是增函数,则实数a 的取值范围是( ) A .(]0,1 B .[]1,2 C .[1,)+∞ D .[2,)+∞3.设函数()()()ln 1ln 1f x x x =-+-,则()f x 是( )A .奇函数,且在(0,1)内是增函数B .奇函数,且在(0,1)内是减函数C .偶函数,且在(0,1)内是增函数D .偶函数,且在(0,1)内是减函数4.已知函数()y f x =的图象关于1x =对称,且在(1,)+∞上单调递增,设12a f ⎛⎫=- ⎪⎝⎭,()2b f =, ()3c f =,则a ,b ,c 的大小关系为()A .c b a <<B .b a c <<C .b c a <<D .a b c <<5.已知()f x 是奇函数,()g x 是偶函数,且()2(11)f g -+=,())114(f g -=+,则()1g 等于( ) A .4 B .3 C .2 D .16.函数1()cos (0)f x x x x x x ⎛⎫=--π≤≤π≠ ⎪⎝⎭且的图象可能为( )7.奇函数()f x 的定义域为R ,若()1f x +为偶函数,且()12f =,则()()45f f +的值为( ) A .2 B .1 C .1- D .2- 8.函数()f x 的图象向右平移1个单位,所得图象与曲线e x y =关于y 轴对称,则()f x 的解析式为( ) A .()1e xf x += B .()1e xf x -= C .()1e xf x -+= D .()1e xf x --=9.使2)og (l 1x x <+-成立的x 的取值范围是( ) A .()1,0- B .[)1,0- C .()2,0- D .[)2,0-10.已知偶函数()f x 对于任意R x ∈都有()()1f x f x +=-,且()f x 在区间[]0,1上是单调递增的,则()65f -.,1()f -,()0f 的大小关系是( )A .()0 6.5()()1f f f <-<-B .()6.5()()01f f f -<<-C .()()(60)1.5f f f -<-<D .()10()( 6.5)f f f -<<-11.对任意的实数x 都有()()()221f x f x f -=+,若(1)y f x =-的图象关于1x =对称,且()02f =, 则()()20152016f f +=( ) A .0 B .2C .3D .412.已知函数()e 1x f x =-,()243g x x x =-+-,若存在()()f a g b =,则实数b 的取值范围为( ) A .[0,3] B .(1,3) C.2⎡-⎣D.(2二、填空题13.设函数()10010x x x f x >⎧⎪==⎨⎪-<⎩,()21()g x x f x -=,则函数()g x 的递减区间是_______.14.若函数()R ()f x x ∈是周期为4的奇函数,且在[0,2]上的解析式为()()101sin 12x x x x x f x ⎧-≤≤⎪=⎨π<≤⎪⎩,则294146f f ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭________.15.设函数()||f x x a =+,()1g x x =-,对于任意的R x ∈,不等式()()f x g x ≥恒成立,则实数a 的取值范围是________.16.设定义在R 上的函数()f x 同时满足以下条件:①()0()f x f x +-=;②()()2f x f x =+;③当01x ≤≤时,()21x f x =-,则()1351(2)222f f f f f ⎛⎫⎛⎫⎛⎫++++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭________.三、解答题17.已知函数()ln(2)af x x x=+-,其中a 是大于0的常数. (1)求函数()f x 的定义域;(2)当4()1,a ∈时,求函数()f x 在[2,)+∞上的最小值;(3)若对任意,[)2x ∈+∞恒有()0f x >,试确定a 的取值范围.18.设()f x 是定义域为R 的周期函数,最小正周期为2,且()1()1f x f x =+-,当10x -≤≤时,()f x x =-.(1)判定()f x 的奇偶性;(2)试求出函数()f x 在区间[]1,2-上的表达式.1.零点的判断与证明 例1:已知定义在()1,+∞上的函数()ln 2f x x x =--,求证:()f x 存在唯一的零点,且零点属于()3,4.2.零点的个数问题例2:已知函数()f x 满足()()3f x f x =,当[)1,3x ∈,()ln f x x =,若在区间[)1,9内, 函数()()g x f x ax =-有三个不同零点,则实数a 的取值范围是( )A .ln 31,3e ⎛⎫ ⎪⎝⎭B .ln 31,93e ⎛⎫ ⎪⎝⎭C .ln 31,92e ⎛⎫⎪⎝⎭D .ln3ln3,93⎛⎫⎪⎝⎭3.零点的性质例3:已知定义在R 上的函数()f x 满足:()[)[)2220,121,0x x f x xx ⎧+∈⎪=⎨-∈-⎪⎩,且()()2f x f x +=,()252x g x x +=+,则方程()()f x g x =在区间[]5,1-上的所有实根之和为( )A .5-B .6-C .7-D .8-4.复合函数的零点例4:已知函数()243f x x x =-+,若方程()()20f x bf x c ++=⎡⎤⎣⎦恰有七个不相同的实根,则实数b 的取值范围是( )A .()2,0-B .()2,1--C .()0,1D .()0,2一、选择题 1.设()ln 2f x x x +-=,则函数()f x 的零点所在的区间为( )A .()0,1B .()1,2C .()2,3D .()3,42.已知a 是函数()12log 2x x f x =-的零点,若00x a <<,则()0f x 的值满足( )A .()00f x =B .()00f x >C .()00f x <D .()0f x 的符号不确定3.函数2()2f x x a x=--的一个零点在区间()1,2内,则实数a 的取值范围是( ) A .()1,3B .()1,2C .()0,3D .()0,24.若a b c <<,则函数()()()()()()()f x x a x b x b x c x c x a -----+-=+的两个零点分别位于区间( ) A .(),a b 和(),b c 内 B .(,)a -∞和(),a b 内 C .(),b c 和(),c +∞内 D .(,)a -∞和(),c +∞内5.设函数()f x 是定义在R 上的奇函数,当0x >时,()e 3x f x x =+-,则()f x 的零点个数为( ) A .1 B .2C .3D .46.函数()2201ln 0x x x x x f x ⎧+-≤=⎨-+>⎩的零点个数为( )A .3B .2C .7D .0培优点二 函数零点对点增分集训7.已知函数()1010x x xf x ≤⎧⎪=⎨>⎪⎩,则使方程()x f x m +=有解的实数m 的取值范围是( )A .()1,2B (],2-∞-C .()(),12,-∞+∞UD .(][),12,-∞+∞U8.若函数()312f x ax a +-=在区间()1,1-内存在一个零点,则a 的取值范围是( ) A .1,5⎛⎫+∞ ⎪⎝⎭ B .()1,1,5⎛⎫-∞-+∞ ⎪⎝⎭U C .11,5⎛⎫- ⎪⎝⎭D .(),1-∞-9.已知函数()00e 0x x xf x ≤⎧=⎨>⎩,则使函数()()g x f x x m =+-有零点的实数m 的取值范围是( )A .[)0,1B .(1),-∞C .(](),12,-∞+∞UD .(](),01,-∞+∞U10.已知()f x 是奇函数且是R 上的单调函数,若函数221()()y f x f x λ++=-只有一个零点,则实数λ 的值是( ) A .14B .18C .78-D .38-11.已知当[]0,1x ∈时,函数21()y mx =-的图象与y x m =+的图象有且只有一个交点,则正实数m 的取值范围是( ) A .(0,1][23,+)∞UB .(]0,13[),+∞UC .(0,2][23,+)∞UD .(0,2][3,+)∞U12.已知函数()y f x =和()y g x =在[]2,2-的图像如下,给出下列四个命题:(1)方程()0f g x =⎡⎤⎣⎦有且只有6个根 (2)方程()0g f x =⎡⎤⎣⎦有且只有3个根 (3)方程()0f f x =⎡⎤⎣⎦有且只有5个根(4)方程()0g g x =⎡⎤⎣⎦有且只有4个根 则正确命题的个数是( ) A .1 B .2 C .3 D .4二、填空题 13.函数()052log ||x f x x -=-.的零点个数为________.14.设函数31y x =与2212x y -⎛⎫= ⎪⎝⎭的图象的交点为00(,)x y ,若0,1()x n n ∈+,n ∈N ,则0x 所在的区间是______.15.函数()22026ln 0f x x x x x x ⎧-≤=⎨-+>⎩的零点个数是________.16.已知函数()23||f x x x =+,R x ∈,若方程()1|0|f x a x --=恰有4个互异的实数根,则实数a 的取值范围是________________.三、解答题17.关于x 的二次方程21()10x m x ++-=在区间[]0,2上有解,求实数m 的取值范围.18.设函数()1()10f x x x=->.(1)作出函数()f x 的图象;(2)当0a b <<且()()f a f b =时,求11a b+的值; (3)若方程()f x m =有两个不相等的正根,求m 的取值范围.1.对于()()'0f x a a >≠,可构造()()h x f x ax =-例1:函数()f x 的定义域为R ,()12f -=,对任意R x ∈,()2f x '>,则()24f x x >+的解集为( )A .()1,1-B .()1-+∞,C .()1-∞-,D .()-∞+∞,2.对于()()'0xf x f x +>,构造()()h x xf x =;对于()()'0xf x f x ->,构造()()f x h x x=例2:已知函数()y f x =的图象关于y 轴对称,且当(),0x ∈-∞,()()0f x xf x '+<成立,()0.20.222a f =,()log 3log 3b f ππ=,()33log 9log 9c f =,则a ,b ,c 的大小关系是( )A .a b c >>B .a c b >>C .c b a >>D .b a c >>3.对于'()()0f x f x +>,构造()()e x h x f x =;对于'()()f x f x >或'()()0f x f x ->,构造()()e xf x h x = 例3:已知()f x 为R 上的可导函数,且R x ∀∈,均有()()f x f x '>,则有( )A .2016e (2016)(0)f f -<,2016(2016)e (0)f f >B .2016e (2016)(0)f f -<,2016(2016)e (0)f f <C .2016e (2016)(0)f f ->,2016(2016)e (0)f f >D .2016e (2016)(0)f f ->,2016(2016)e (0)f f <4.()f x 与sin x ,cos x 构造例4:已知函数()y f x =对任意的,22x ππ⎛⎫∈- ⎪⎝⎭满足()()cos sin 0f x x f x x '+>,则( )A .()024f f π⎛⎫> ⎪⎝⎭B .()03f f π⎛⎫<2- ⎪⎝⎭C .234f f ππ⎛⎫⎛⎫<⎪ ⎪⎝⎭⎝⎭ D .234f f ππ⎛⎫⎛⎫-<- ⎪ ⎪⎝⎭⎝⎭一、选择题 1.若函数()y f x =在R 上可导且满足不等式()()0xf x f x '+>恒成立,对任意正数a 、b ,若a b <,则必有( ) A .()()af b bf a < B .()()bf a af b <C .()()af a bf b <D .()()bf b af a <2.已知函数()()R f x x ∈满足()11f =,且()12f x '<,则()122x f x <+的解集为( ) A .}{11x x |-<<B .}{1x x |<-C .}{11x x x |<->或D .}{1x x |>3.已知函数()f x 的定义域为R ,()f x '为()f x 的导函数,且()()()10f x x f x '+->,则( ) A .()10f =B .()0f x <C .()0f x >D .()()10x f x -<培优点三 含导函数的抽象函数的构造对点增分集训4.设函数()f x '是函数()()R f x x ∈的导函数,已知()()f x f x '<,且()()4f x f x ''=-,()40f =,()21f =则使得()2e 0x f x -<成立的x 的取值范围是( )A .()2-+∞,B .()0+∞,C .()1+∞,D .()4+∞,5.已知函数()1y f x =-的图象关于点()1,0对称,函数()y f x =对于任意的()0,πx ∈满足()()sin cos f x x f x x >'(其中()f x '是函数()f x 的导函数),则下列不等式成立的是( )A .ππ36f ⎛⎫⎛⎫-> ⎪ ⎪⎝⎭⎝⎭B 3ππ42f ⎛⎫⎛⎫<--⎪ ⎪⎝⎭⎝⎭ C ππ223f ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭D 5π3π64f ⎛⎫⎛⎫<⎪ ⎪⎝⎭⎝⎭6.定义在R 上的函数()f x 的导函数为()f x ',若对任意实数x ,有()()f x f x >',且()2018f x +为奇函数,则不等式()2018e 0x f x +<的解集为( ) A .(),0-∞B .()0,+∞C .1e ,⎛⎫-∞ ⎪⎝⎭D .1e ,⎛⎫+∞ ⎪⎝⎭7.已知函数()2f x +是偶函数,且当2x >时满足()()()2xf x f x f x ''>+,则( ) A .()()214f f < B .()3232f f ⎛⎫> ⎪⎝⎭ C .()5042f f ⎛⎫< ⎪⎝⎭D .()()13f f <8.已知定义域为R 的奇函数()y f x =的导函数为()y f x =',当0x ≠时,()()0f x f x x+'>,若1133a f ⎛⎫= ⎪⎝⎭,()33b f =--,11ln ln 33c f ⎛⎫= ⎪⎝⎭,则a ,b ,c 的大小关系正确的是( ) A .a b c << B .b c a <<C .a c b <<D .c a b <<9.已知定义在R 上的函数()f x 的导函数为()f x ',()()222e x f x f x --=(e 为自然对数的底数), 且当1x ≠时,()()()10x f x f x -->⎡⎤⎣⎦',则( ) A .()()10f f <B .()()2e 0f f >C .()()33e 0f f >D .()()44e 0f f <10.定义在R 上的函数()f x 的导函数为()'f x ,()00f =若对任意R x ∈,都有()()'1f x f x >+,则使得()e 1f x x +<成立的x 的取值范围为( )A .(),1∞-B .(),0∞-C .()1,+∞-D .0,+∞()11.已知函数()f x 是定义在区间()0,+∞上的可导函数,满足()0f x >且()()'0f x f x +<(()'f x 为函数的导函数),若01a b <<<且1ab =,则下列不等式一定成立的是( ) A .()()()1f a a f b >+ B .()()()1f b a f a >- C .()()af a bf b >D .()()af b bf a >12.定义在R 上的奇函数()y f x =满足()30f =,且当0x >时,不等式()()'f x xf x >-恒成立,则函数()()lg 1g x xf x x =++的零点的个数为( )A .1B .2C .3D .4二、填空题13.设()f x 是R 上的可导函数,且'()()f x f x ≥-,(0)1f =,21(2)ef =.则(1)f 的值为________. 14.已知,22x ⎛⎫∈- ⎪⎝π⎭π,()1y f x =-为奇函数,()()'tan 0f x f x x +>,则不等式()cos f x x >的解集为_________.15.已知定义在实数集R 的函数()f x 满足()27f =,且()f x 导函数()3f x '<,则不等式()ln 3ln 1f x x >+的解集为__________.16.已知函数()f x 是定义在()(),00,-∞+∞U 上的奇函数,且()10f =.若0x <时,()()'0xf x f x ->, 则不等式()0f x >的解集为__________.1.参变分离法例1:已知函数()ln af x x x=-,若()2f x x <在()1,+∞上恒成立,则a 的取值范围是_________.2.数形结合法例2:若不等式()log sin 20,1a x x a a >>≠对于任意的π0,4x ⎛⎤∈ ⎥⎝⎦都成立,则实数a 的取值范围是___________.3.最值分析法 例3:已知函数()()ln 10f x a x a =+>,在区间()1,e 上,()f x x >恒成立,求a 的取值范围___________.一、选择题1.已知函数()()2ln 1,03,x x f x x x x ⎧-+≤⎪=⎨+>⎪⎩,若()()20f x m x -+≥,则实数m 的取值范围是( )A .(],1-∞B .[]2,1-C .[]0,3D .[)3,+∞2.已知函数()3224f x x x x =--+,当[]3,3x ∈-时,()214f x m m ≥-恒成立,则实数m 的取值范围是( ) A .()3,11- B .()3,11 C .[]3,11 D .[]2,73.若函数()2ln 2f x x ax =+-在区间1,22⎛⎫ ⎪⎝⎭内单调递增,则实数a 的取值范围是( ) A .(],2-∞- B .()2,-+∞C .12,8⎛⎫-- ⎪⎝⎭D .1,8⎡⎫-+∞⎪⎢⎣⎭4.已知对任意21,e e x ⎡⎤∈⎢⎥⎣⎦不等式2e xa x >恒成立(其中e 2.71828=L ,是自然对数的底数),则实数a 的取值范围是( )A .e 0,2⎛⎫ ⎪⎝⎭B .()0,eC .(),2e -∞-D .24,e ⎛⎫-∞ ⎪⎝⎭5.已知函数()2e x f x x =,当[]1,1x ∈-时,不等式()f x m <恒成立,则实数m 的取值范围是( )A .1,e ⎡⎫+∞⎪⎢⎣⎭B .1,e ⎛⎫+∞ ⎪⎝⎭C .[)e,+∞D .()e,+∞培优点四 恒成立问题对点增分集训6.当[]2,1x ∈-时,不等式32430ax x x -++≥恒成立,则实数a 的取值范围是( ) A .[]5,3--B .96,8⎡⎤--⎢⎥⎣⎦C .[]6,2--D .[]4,3--7.函数()2e 1xf x x=-+,若存在(]00,2x ∈使得()00m f x ->成立,则实数m 的范围是( ) A .21e 5,⎛⎫-+∞ ⎪⎝⎭ B .()1,-+∞ C .()1,+∞ D .1e,2⎛⎫-+∞ ⎪⎝⎭8.设函数()ln f x x ax =+,若存在()00,x ∈+∞,使()00f x >,则a 的取值范围是( ) A .1,1e ⎛⎫- ⎪⎝⎭B .1,e ⎛⎫-∞ ⎪⎝⎭C .()1,-+∞D .1,e ⎛⎫-+∞ ⎪⎝⎭9.若对于任意实数0x ≥,函数()e x f x ax =+恒大于零,则实数a 的取值范围是( ) A .(),e -∞B .(],e -∞-C .[)e,+∞D .()e,-+∞10.已知函数()()()3f x a x a x a =-++,()22x g x =-,若对任意x ∈R ,总有()0f x <或()0g x <成立,则实数a 的取值范围是( ) A .(),4-∞- B .()4,0-C .[)4,0-D .()4,-+∞11.已知函数()e xf x ax x=-,()0,x ∈+∞,当21x x >时,不等式()()12210f x f x x x -<恒成立,则实数a 的取值范围为( ) A .(],e -∞B .(),e -∞C .e ,2⎛⎫-∞ ⎪⎝⎭D .e ,2⎛⎤-∞ ⎥⎝⎦12.设函数()()e 31x f x x ax a =--+,其中1a <,若有且只有一个整数0x 使得()00f x ≤,则a 的取值范围是( ) A .23,e 4⎛⎫ ⎪⎝⎭B .23,e 4⎡⎫⎪⎢⎣⎭C .2,1e ⎛⎫ ⎪⎝⎭D .2,1e ⎡⎫⎪⎢⎣⎭二、填空题13.设函数()f x x a =+,()1g x x =-,对于任意的x ∈R ,不等式()()f x g x ≥恒成立,则实数a 的取值范围是__________.14.函数()ln 1f x x x ax =-+,其中a ∈R ,若对任意正数x 都有()0f x ≥,则实数a 的取值范围为____________.15.已知函数()21ln 22f x x ax x =--,若函数()f x 在1,22⎡⎤⎢⎥⎣⎦上单调递增,则实数a 的取值范围是__________.16.已知关于x 的不等式21log 02m mx x ⎛⎫+> ⎪⎝⎭-在[]1,2上恒成立,则实数m 的取值范围为___________.三、解答题17.设函数()()()2ln 1f x x a x x =++-,其中a ∈R , (1)讨论函数()f x 极值点的个数,并说明理由;(2)若0x ∀>,()0f x ≥成立,求a 的取值范围.18.设函数()2e mx f x x mx =+-,(1)证明:()f x 在(),0-∞单调递减,在()0,+∞单调递增;(2)若对于任意1x ,[]21,1x ∈-,都有()()12e 1f x f x -≤-,求m 的取值范围.1.利用导数判断单调性 例1:求函数()()32333e x f x x x x -=+--的单调区间2.函数的极值例2:求函数()e x f x x -=的极值.3.利用导数判断函数的最值例3:已知函数()()ln mf x x m x=-∈R 在区间[]1,e 上取得最小值4,则m =___________.一、单选题1.函数()ln f x x x =-的单调递减区间为( ) A .() 0,1B .() 0,+∞C .() 1,+∞D .()() ,01,-∞+∞U2.若1x =是函数()ln f x ax x =+的极值点,则( )A .()f x 有极大值1-B .()f x 有极小值1-C .()f x 有极大值0D .()f x 有极小值0培优点五 导数的应用对点增分集训3.已知函数()3f x x ax =--在(],1-∞-上单调递减,且()2ag x x x=-在区间(]1,2上既有最大值,又有最小值,则实数a 的取值范围是( ) A .2a >- B .3a ≥- C .32a -≤<- D .32a -≤≤-4.函数321y x x mx =+++是R 上的单调函数....,则m 的范围是( ) A .1,3⎛⎫+∞ ⎪⎝⎭B .1,3⎛⎫-∞ ⎪⎝⎭C .1,3⎡⎫+∞⎪⎢⎣⎭D .1,3⎛⎤-∞ ⎥⎝⎦5.遇见你的那一刻,我的心电图就如函数1ln sin 1x y x x -⎛⎫=+ ⎪+⎝⎭的图象大致为( )A .B .C .D .6.函数()321213f x x ax x =+-+在()1,2x ∈内存在极值点,则( ) A .1122a -<< B .1122a -≤≤ C .12a <-或12a >D .12a ≤-或12a ≥7.已知()22f x ax x a =++,x ∈R ,若函数()()()322g x x a x f x =---在区间()1,3-上单调递减,则实数a 的取值范围是( ) A .1a <-或3a > B .1a ≤-或3a ≥ C .9a <-或3a > D .9a ≤-或3a ≥8.函数()y f x =在定义域3,32⎡⎤-⎢⎥⎣⎦内可导,其图像如图所示.记()y f x =的导函数为()y f x =',则不等式()0f x '≤的解集为( )A .[]1,12,33⎡⎤-⎢⎥⎣⎦U B .1481,,233⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦UC .[)31,1,222⎡⎤-⎢⎥⎣⎦UD .31144,,,323233⎡⎤⎡⎤⎡⎤--⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦U U9.设函数()()1ln 03f x x x x =->,则()y f x =( ) A .在区间1,1e ⎛⎫ ⎪⎝⎭,()1,e 内均有零点 B .在区间1,1e ⎛⎫ ⎪⎝⎭,()1,e 内均无零点C .在区间1,1e ⎛⎫ ⎪⎝⎭内有零点,在区间()1,e 内无零点D .在区间1,1e ⎛⎫⎪⎝⎭内无零点,在区间()1,e 内有零点10.若函数()()323321f x x ax a x =++++既有极大值又有极小值,则实数a 的取值范围为( ) A .12a -<< B .12a -≤≤ C .1a ≤-或2a ≥ D .1a <-或2a > 11.已知函数()3223f x x ax bx c =+++的两个极值点分别在()1,0-与()0,1内,则2a b -的取值范围是( ) A .33,22⎛⎫- ⎪⎝⎭B .3,12⎛⎫- ⎪⎝⎭C .13,22⎛⎫- ⎪⎝⎭D .31,2⎛⎫ ⎪⎝⎭12.设函数()y f x =在区间(),a b 上的导函数为()f x ',()f x '在区间(),a b 上的导函数为()f x '',若在区间 (),a b 上()0f x ''>,则称函数()f x 在区间(),a b 上为“凹函数”,已知()5421122012f x x mx x =--在区间()1,3上为“凹函数”,则实数m 的取值范围为( ) A .31,9⎛⎫-∞ ⎪⎝⎭B .31,59⎡⎤⎢⎥⎣⎦C .(],5-∞D .(],3-∞-二、填空题13.函数()3222f x x x =-在区间[]1,2-上的最大值是___________.14.若函数()32334f x x ax x a =-+-在(),1-∞-,()2,+∞上都是单调增函数,则实数a 的取值集合是______.15.函数()()2ln 1f x x a x a =--∈R 在[]1,2内不存在极值点,则a 的取值范围是___________.16.已知函数()e ln x f x a x =+,①当1a =时,()f x 有最大值; ②对于任意的0a >,函数()f x 是()0,+∞上的增函数; ③对于任意的0a <,函数()f x 一定存在最小值; ④对于任意的0a >,都有()0f x >. 其中正确结论的序号是_________.(写出所有正确结论的序号)三、解答题17.已知函数()()ln f x x ax a =-∈R(1)讨论函数()f x 在()0,+∞上的单调性;(2)证明:2e e ln 0x x ->恒成立.18.已知函数()()2e ,x f x a x bx a b =+-∈R ,其导函数为()'y f x =.(1)当2b =时,若函数()'y f x =在R 上有且只有一个零点,求实数a 的取值范围;(2)设0a ≠,点()(),,P m n m n ∈R 是曲线()y f x =上的一个定点,是否存在实数()00x x m ≠使得()()000'2x m f x n f x m +⎛⎫-=- ⎪⎝⎭成立?并证明你的结论.1.求三角函数值例1:已知π3π044βα<<<<,π3cos 45α⎛⎫-= ⎪⎝⎭,3π5sin 413β⎛⎫+= ⎪⎝⎭,求()sin αβ+的值.培优点六 三角函数2.三角函数的值域与最值例2:已知函数()πππcos 22sin sin 344f x x x x ⎛⎫⎛⎫⎛⎫=-+-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,(1)求函数()f x 的最小正周期和图像的对称轴方程;(2)求函数()f x 在区间ππ,122⎡⎤-⎢⎥⎣⎦的值域.3.三角函数的性质例3:函数()3sin 2cos 2f x x x =+( )A .在ππ,36⎛⎫-- ⎪⎝⎭上单调递减B .在ππ,63⎛⎫⎪⎝⎭上单调递增C .在π,06⎛⎫- ⎪⎝⎭上单调递减D .在π0,6⎛⎫ ⎪⎝⎭上单调递增一、单选题 1.若π1sin 63α⎛⎫-=⎪⎝⎭,则2πcos 23α⎛⎫+ ⎪⎝⎭的值为( ) A .13- B .79- C .13D .792.函数()π2sin 26f x x ⎛⎫=-+ ⎪⎝⎭的一个单调递增区间是( ) A .ππ,63⎡⎤-⎢⎥⎣⎦B .π5π,36⎡⎤⎢⎥⎣⎦C .ππ,36⎡⎤-⎢⎥⎣⎦D .π2π,63⎡⎤⎢⎥⎣⎦3.已知1tan 4tan θθ+=,则2πcos 4θ⎛⎫+= ⎪⎝⎭( )A .15B .14C .13D .124.关于函数()()π3sin 213f x x x ⎛⎫=-+∈ ⎪⎝⎭R ,下列命题正确的是( ) A .由()()121f x f x ==可得12x x -是π的整数倍B .()y f x =的表达式可改写成()π3cos 216f x x ⎛⎫=++ ⎪⎝⎭C .()y f x =的图象关于点3π,14⎛⎫⎪⎝⎭对称 D .()y f x =的图象关于直线π12x =-对称5.函数()2πππcos 2sin sin 555f x x x ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭的最大值是( ) A .1B .πsin 5C .π2sin 5D .56.函数()()sin 0y x ωϕω=+>的部分图象如图所示,则ω,ϕ的值分别可以是( ) A .1,π3B .1,2π3-C .2,2π3D .2,π3-对点增分集训7.已知函数()()πsin 0,2f x x ωϕωϕ⎛⎫=+>≤ ⎪⎝⎭,π4x =-和π4x =分别是函数()f x 取得零点和最小值点横坐标,且()f x 在ππ,1224⎛⎫-⎪⎝⎭单调,则ω的最大值是( ) A .3 B .5 C .7D .98.已知函数()cos sin f x x x =⋅,给出下列四个说法:2014π3f ⎛⎫= ⎪⎝⎭①②函数()f x 的周期为π; ()f x ③在区间ππ,44⎡⎤-⎢⎥⎣⎦上单调递增;()f x ④的图象关于点π,02⎛⎫- ⎪⎝⎭中心对称其中正确说法的序号是( )A .②③B .①③C .①④D .①③④9.已知0ω>,函数()πsin 4f x x ω⎛⎫=+ ⎪⎝⎭在π,π2⎛⎫⎪⎝⎭上单调递减,则ω的取值范围是( ) A .10,2⎛⎤ ⎥⎝⎦B .(]0,2C .15,24⎡⎤⎢⎥⎣⎦D .13,24⎡⎤⎢⎥⎣⎦10.同时具有性质:①()f x 最小正周期是π;②()f x 图象关于直线π3x =对称;③()f x 在ππ,63⎡⎤-⎢⎥⎣⎦上是增函数的一个函数是( ) A .πsin 23x y ⎛⎫=+ ⎪⎝⎭ B .πsin 26y x ⎛⎫=-⎪⎝⎭ C .πcos 23y x ⎛⎫=+ ⎪⎝⎭ D .πsin 23y x ⎛⎫=+⎪⎝⎭11.关于函数()1π2sin 26f x x ⎛⎫=+ ⎪⎝⎭的图像或性质的说法中,正确的个数为( ) ①函数()f x 的图像关于直线8π3x =对称;②将函数()f x 的图像向右平移π3个单位所得图像的函数为1π2sin 23y x ⎛⎫=+ ⎪⎝⎭;③函数()f x 在区间π5π,33⎛⎫- ⎪⎝⎭上单调递增;④若()f x a =,则1πcos 233a x ⎛⎫-= ⎪⎝⎭.A .1B .2C .3D .412.函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>≤ ⎪⎝⎭的图象关于直线π3x =对称,它的最小正周期为π, 则函数()f x 图象的一个对称中心是( ) A .π,012⎛⎫-⎪⎝⎭B .π,13⎛⎫⎪⎝⎭C .5π,012⎛⎫⎪⎝⎭D .π,012⎛⎫⎪⎝⎭二、填空题13.函数πcos 24y x ⎛⎫=+ ⎪⎝⎭的单调递减区间是_________.14.已知()0,πα∈,且3cos 5α=,则πtan 4α⎛⎫-= ⎪⎝⎭_________________.15.函数()sin 23cos 2f x x x =-在π0,2x ⎛⎫∈ ⎪⎝⎭的值域为_________.16.关于()()π4sin 2,3f x x x ⎛⎫+∈ ⎪⎝⎭R =,有下列命题 ①由()()120f x f x ==可得12x x -是π的整数倍;②()y f x =的表达式可改写成π4cos 26y x ⎛⎫=- ⎪⎝⎭; ③()y f x =图象关于π,06⎛⎫- ⎪⎝⎭对称; ④()y f x =图象关于π6x =-对称. 其中正确命题的序号为________(将你认为正确的都填上).三、解答题17.已知()π2sin 2cos26f x x a x ⎛⎫=++ ⎪⎝⎭()a ∈R ,其图象在π3x =取得最大值. (1)求函数()f x 的解析式;(2)当π0,3α⎛⎫∈ ⎪⎝⎭,且()65f α=,求sin2α值.18.已知函数()()2πsin 3sin sin 02f x x x x ωωωω⎛⎫=++> ⎪⎝⎭的最小正周期为π. (1)求ω的值;(2)求函数()f x 在区间2π0,3⎡⎤⎢⎥⎣⎦上的取值范围.1.解三角形中的要素例1:ABC △的内角A ,B ,C 所对的边分别为a ,b ,c ,若2c =,6b =,60B =o ,则C =_____.2.恒等式背景例2:已知a ,b ,c 分别为ABC △三个内角A ,B ,C 的对边, 且有cos 3sin 0a C a C b c +--=.(1)求A ;(2)若2a =,且ABC △的面积为3,求b ,c .培优点七 解三角形对点增分集训一、单选题1.在ABC △中,1a =,A π∠=,4B π∠=,则c =( )A B C .D2.在ABC △中,三边长7AB =,5BC =,6AC =,则AB BC ⋅uu u v uu u v等于( ) A .19 B .19- C .18 D .18-3.在ABC △中,角A ,B ,C 所对应的边分别是a ,b ,c ,若2cos c a B =,则三角形一定是( ) A .等腰直角三角形 B .直角三角形 C .等腰三角形 D .等边三角形4.ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,若3C π=,c =3b a =,则ABC △的面积为( )A B C .D5.在ABC △中,内角A ,B ,C 的对边分别为a ,b ,c ,若22a b bc -=,sin C B =,则A =( ) A .30︒ B .60︒ C .120︒ D .150︒6.设ABC △的三个内角A ,B ,C 所对的边分别为a ,b ,c ,如果()()3a b c b c a bc +++-=,且a 那么ABC △外接圆的半径为( )A .1BC .2D .47.在ABC △中,角A ,B ,C 所对的边分别为a ,b ,c ,且222b c a bc +=+,若2sin sin sin B C A ⋅=, 则ABC △的形状是( ) A .等腰三角形 B .直角三角形 C .等边三角形 D .等腰直角三角形8.ABC △的内角A ,B ,C 的对边分别是a ,b ,c 且满足cos cos a B b A c -=,则ABC △是( ) A .锐角三角形 B .直角三角形 C .钝角三角形 D .等腰三角形9.在ABC △中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知ABC △的面积为,2b c -=,1cos 4A =-,则a 的值为( )A .8B .16C .32D .6410.在ABC △中,a ,b ,c 分别为角A ,B ,C 所对的边.若()sin cos 0b a C C +-=, 则A =( ) A .4π B .3π C .34π D .23π11.在ABC △中,内角A ,B ,C 的对边分别是a ,b ,c ,若cos cos cos a b cA B C==,则ABC △是( ) A .直角三角形 B .钝角三角形C .等腰直角三角形D .等边三角形12.在ABC △中,角A ,B ,C 所对的边分别为a ,b ,c ,已知23a =,22c =,tan 21tan A cB b+=, 则C ∠=( ) A .6π B .4π C .4π或34π D .3π二、填空题 13.在ABC △中,角A ,B ,C 的对边分别为a ,b ,c ,22c =,2216b a -=,则角C 的最大值为_____;14.已知ABC △的三边a ,b ,c 成等比数列,a ,b ,c 所对的角分别为A ,B ,C ,则sin cos B B +的取值范围是_________. 15.在ABC △中三个内角A ∠,B ∠,C ∠,所对的边分别是a ,b ,c ,若()2sin cos 2sin cos b C A A C +=-,且23a =,则ABC △面积的最大值是________16.在锐角ABC △中,角A ,B ,C 所对的边分别为a ,b ,c ,且A ,B ,C 成等差数列,3b =,则ABC △面积的取值范围是__________.三、解答题17.己知a ,b ,c 分别为ABC △三个内角A ,B ,C 的对边,且3cos 2sin a A C+=. (1)求角A 的大小;(2)若5b c +=,且ABC △的面积为3,求a 的值.18.如图,在ABC △中,点D 在BC 边上,60ADC ∠=︒,27AB =,4BD =.(1)求ABD △的面积. (2)若120BAC ∠=o ,求AC 的长.1.代数法例1:已知向量a ,b 满足=3a ,=23b ,且()⊥+a a b ,则b 在a 方向上的投影为( ) A .3B .3-C .33-D .332.几何法例2:设a ,b 是两个非零向量,且2==+=a b a b ,则=-a b _______.培优点八 平面向量3.建立直角坐标系例3:在边长为1的正三角形ABC 中,设2BC BD =uu u v uu u v ,3CA CE =uu v uu u v ,则AD BE ⋅=uuu v uu u v__________.一、单选题1.已知向量a ,b 满足1=a ,2=b ,且向量a ,b 的夹角为4π,若λ-a b 与b 垂直,则实数λ的值为( ) A .12-B .12C .24-D .242.已知向量a ,b 满足1=a ,2=b ,7+=a b ,则⋅=a b ( ) A .1 B .2 C .3 D .23.如图,平行四边形ABCD 中,2AB =,1AD =,60A ∠=o ,点M 在AB 边上,且13AM AB =,则DM DB ⋅=uuu u v uu u v( ) A .1-B .1C .33-D .334.如图,在ABC △中,BE 是边AC 的中线,O 是BE 边的中点,若AB =uu u v a ,AC =u u u vb ,则AO =uuu v( ) A .1122+a b B .1124+a b C .1142+a b D .1144+a b 5.在梯形ABCD 中,AB CD ∥,1CD =,2AB BC ==,120BCD ∠=o ,动点P 和Q 分别在线段BC 和CD上,且BP BC λ=uu v uu u v ,18DQ DC λ=uuuv uuu v ,则AP BQ ⋅uu u v uu u v 的最大值为( ) A .2-B .32-C .34D .986.已知ABC △中,2AB =,4AC =,60BAC ∠=︒,P 为线段AC 上任意一点,则PB PC ⋅uu v uu u v的范围是( ) A .[]14,B .[]04,C .944⎡⎤-⎢⎥⎣⎦, D .[]24-,7.已知非零向量a ,b ,满足22=a b 且()()320+⋅-=a b a b ,则a 与b 的夹角为( ) A .4πB .2π C .34π D .π.在Rt ABC △中斜边BC a =,以A 为中点的线段2PQ a =,则BP CQ ⋅uu v uu u v的最大值为( ) A .2- B .0C .2D .229.设向量a ,b ,c ,满足1==a b ,12⋅=-a b ,6,0--=oa b c c ,则c 的最大值等于( )A .1B .2C .3D .2对点增分集训BAE10.已知a 与b 为单位向量,且⊥a b ,向量c 满足2--=c a b ,则c 的取值范围为( )A .1,12⎡⎤+⎣⎦B .22,22⎡⎤-+⎣⎦C .2,22⎡⎤⎣⎦D .322,322⎡⎤-+⎣⎦11.平行四边形ABCD 中,AC uuu v ,BD uu u v 在AB uu u v 上投影的数量分别为3,1-,则BD uu u v 在BC uu uv 上的投影的取值范围是( )A .()1,-+∞B .()1,3-C .()0,+∞D .()0,312.如图,在等腰直角三角形ABC 中,2AB AC ==,D ,E 是线段BC 上的点,且13DE BC =,则AD AE ⋅uuu v uu u v的取值范围是( ) A .84,93⎡⎤⎢⎥⎣⎦ B .48,33⎡⎤⎢⎥⎣⎦ C .88,93⎡⎤⎢⎥⎣⎦D .4,3⎡⎫+∞⎪⎢⎣⎭二、填空题13.已知向量()1,2=a ,()2,2=-b ,()1,λ=c ,若()2+∥c a b ,则λ=________.14.若向量a ,b 满足1=a ,2=b ,且()⊥+a a b ,则a 与b 的夹角为__________.15.已知正方形的边长为2,是上的一个动点,则求的最大值为________. 16.在中,,,,为线段上一点,则的取值范围为____.1.简单的线性规划问题应注意取点是否取得到例1:已知实数,满足,则的最小值是( )A .4B .5C .6D .72.目标函数为二次式例2:若变量,满足,则的最大值为( )A .B .C .D .3.目标函数为分式例3:设变量,满足约束条件,则的取值范围是( )A .B .C .D .ABCD E CD AE BD ⋅uu u v uu u vABC △90C ∠=︒30B ∠=︒2AC =P AB PB PC +uu v uu u vx y 24240x y x y y -≥⎧⎪+≤⎨⎪≤⎩32z x y =-x y 120x x y x y ≤⎧⎪≥⎨⎪++≥⎩22z x y =+107910x y 22022010x y x y x y --≤⎧⎪-+≥⎨⎪+-≥⎩11y s x +=+31,2⎡⎤⎢⎥⎣⎦1,12⎡⎤⎢⎥⎣⎦[]1,21,22⎡⎤⎢⎥⎣⎦培优点九 线性规划4.面积问题例4:若不等式组所表示的平面区域被直线分成面积相等的两部分,则的值为( )A .B .C .D .一、单选题1.若实数,满足,则的最大值为( )A .B .1C .0D .2.已知实数,满足线性约束条件,则其表示的平面区域的面积为( )A .B .C .D .3.已知实数,满足,若只在点处取得最大值,则的取值范围是( )A .B .C .D .4.已知实数,满足约束条件,则的取值范围为( )A .B .C .D .5.若实数,满足约束条件,则的最大值是( )A .B .C .D .6.已知点,若动点的坐标满足,则的最小值为( )A .B .C .D .7.,满足约束条件,若取得最大值的最优解不唯一,则实数的值为( )A .或 B .2或C .2或1D .2或03434x x y x y ≥⎧⎪+≥⎨⎪+≤⎩4y kx =+k 7337173-317-x y 0010x y x y ≥⎧⎪≥⎨⎪+-≤⎩z x y =-21-x y 3023004x y x y x +-≤⎧⎪--≤⎨⎪≤≤⎩942749272x y 122022x y x y x y -≤⎧⎪-+≥⎨⎪+≥⎩z x ay =-()43,a ()1-∞-,()2-+∞,()1-∞,12⎛⎫+∞ ⎪⎝⎭,x y 222020x x y x y ≤⎧⎪-+≥⎨⎪++≥⎩5x z y -=2433⎡⎤-⎢⎥⎣⎦,4233⎡⎤-⎢⎥⎣⎦,3324⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭U ,,3342⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭U ,,x y 22390x y x y x +≤⎧⎪-≤⎨⎪≥⎩22z x y =+104910()12A ,()P x y ,02x y x x y ≥⎧⎪≥⎨⎪+≤⎩AP 2125x y 20220220x y x y x y +-≤⎧⎪--≤⎨⎪-+≥⎩z y ax =-a 121-121-对点增分集训8.若,满足不等式组,则成立的概率为( ) A .B .C .D . 9.若,满足不等式组,则的最小值为( ) A .7B .6C .D .410.已知平面直角坐标系上的区域由不等式组给定.若为上动点,点的坐标为.则的最大值为( ) A .B .C .4D .311.若不等式组所表示的平面区域内存在点,使成立,则实数的取值范围是( )A .B .C .D .12.已知圆,平面区域,若圆心,且圆与轴相切, 则圆心与点连线斜率的取值范围是( )A .B .C .D .二、填空题13.设,满足,则的最大值为____________.14.若变量,满足约束条件,则的最小值为_________.15.已知实数,满足,则的最小值为______.x y 40240 4x y x y x +-≥⎧⎪-+≥⎨⎪≤⎩215y x ≤+155611165838x y 20510080x y x y x y -+≥⎧⎪-+≤⎨⎪+-≤⎩32z x y =-+265xOy D 02x y x ⎧≤⎪≤⎨⎪≤⎩()M x y ,D A )z OM OA =⋅uuu v uu v 20510080x y x y x y -+≥⎧⎪-+≤⎨⎪+-≤⎩()00x y ,0020x ay ++≤a [)1,-+∞(],1-∞-(],1-∞[)1,+∞()()22:1C x a y b -+-=60:400x y x y y +-≤⎧⎪Ω-+≥⎨⎪≥⎩C ∈ΩC x (),C a b ()2,877,,35⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭U 77,,35⎛⎤⎛⎫-∞-+∞ ⎪⎥⎝⎦⎝⎭U 77,35⎛⎫- ⎪⎝⎭77,35⎡⎤-⎢⎥⎣⎦x y 10302x y x y x +-≥⎧⎪-+≥⎨⎪≤⎩21z x y =++x y 210220x x y x y ≤⎧⎪-+≤⎨⎪+-≥⎩22z x y =+x y 110x y x y x -≤⎧⎪+≤⎨⎪≥⎩22x y x ++。
高三数学 数学数列多选题专项训练的专项培优练习题(含答案

一、数列多选题1.已知数列{}n a :1,1,2,3,5,…其中从第三项起,每个数等于它前面两个数的和,记n S 为数列{}n a 的前n 项和,则下列结论正确的是( ) A .68S a = B .733S =C .135********a a a a a ++++= D .2222123202020202021a a a a a a ++++=答案:BCD 【分析】根据题意写出,,,从而判断A ,B 的正误;写出递推关系,对递推关系进行适当的变形,利用累加法即可判断C ,D 的正误. 【详解】对A ,,,故A 不正确; 对B ,,故B 正确; 对C ,由,,解析:BCD 【分析】根据题意写出8a ,6S ,7S ,从而判断A ,B 的正误;写出递推关系,对递推关系进行适当的变形,利用累加法即可判断C ,D 的正误. 【详解】对A ,821a =,620S =,故A 不正确; 对B ,761333S S =+=,故B 正确;对C ,由12a a =,342a a a =-,564a a a =-,…,202120222020a a a =-,可得135********a a a a a +++⋅⋅⋅+=,故C 正确;对D ,该数列总有21n n n a a a ++=+,2121a a a =,则()222312321a a a a a a a a =-=-,()233423423a a a a a a a a =-=-,…,()220182018201920172018201920172018a a a a a a a a =-=-, 22019a =2019202020192018a a a a -,220202020202120202019a a a a a =-,故2222123202*********a a a a a a +++⋅⋅⋅+=,故D 正确.故选:BCD 【点睛】关键点睛:解答本题的关键是对CD 的判断,即要善于利用21n n n a a a ++=+对所给式子进行变形.2.已知数列{}n a 满足0n a >,121n n n a na a n +=+-(N n *∈),数列{}n a 的前n 项和为n S ,则( ) A .11a =B .121a a =C .201920202019S a =D .201920202019S a >答案:BC 【分析】根据递推公式,得到,令,得到,可判断A 错,B 正确;根据求和公式,得到,求出,可得C 正确,D 错. 【详解】 由可知,即,当时,则,即得到,故选项B 正确;无法计算,故A 错; ,所以,则解析:BC 【分析】根据递推公式,得到11n n nn n a a a +-=-,令1n =,得到121a a =,可判断A 错,B 正确;根据求和公式,得到1n n nS a +=,求出201920202019S a =,可得C 正确,D 错. 【详解】由121n n n a n a a n +=+-可知2111n n n n n a n n n a a a a ++--==+,即11n n nn n a a a +-=-, 当1n =时,则121a a =,即得到121a a =,故选项B 正确;1a 无法计算,故A 错; 1221321111102110n n n n n n n n n n S a a a a a a a a a a a a +++⎛⎫⎛⎫⎛⎫-=+++=-+-++-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,所以1n n S a n +=,则201920202019S a =,故选项C 正确,选项D 错误. 故选:BC. 【点睛】 方法点睛:由递推公式求通项公式的常用方法:(1)累加法,形如()1n n a a f n +=+的数列,求通项时,常用累加法求解;(2)累乘法,形如()1n na f n a +=的数列,求通项时,常用累乘法求解; (3)构造法,形如1n n a pa q +=+(0p ≠且1p ≠,0q ≠,n ∈+N )的数列,求通项时,常需要构造成等比数列求解;(4)已知n a 与n S 的关系求通项时,一般可根据11,2,1n n n S S n a a n --≥⎧=⎨=⎩求解.3.已知数列{}n a 满足:12a =,当2n ≥时,)212n a =-,则关于数列{}n a 的说法正确的是 ( )A .27a =B .数列{}n a 为递增数列C .221n a n n =+-D .数列{}n a 为周期数列答案:ABC 【分析】由,变形得到,再利用等差数列的定义求得,然后逐项判断. 【详解】 当时,由, 得, 即,又,所以是以2为首项,以1为公差的等差数列, 所以,即,故C 正确; 所以,故A 正确; ,解析:ABC 【分析】由)212n a =-1=,再利用等差数列的定义求得n a ,然后逐项判断. 【详解】 当2n ≥时,由)212n a =-,得)221n a +=,1=,又12a =,所以是以2为首项,以1为公差的等差数列,2(1)11n n =+-⨯=+,即221n a n n =+-,故C 正确;所以27a =,故A 正确;()212n a n =+-,所以{}n a 为递增数列,故正确;数列{}n a 不具有周期性,故D 错误; 故选:ABC4.设等差数列{}n a 的前n 项和为n S .若30S =,46a =,则( ) A .23n S n n =- B .2392-=n n nSC .36n a n =-D .2n a n =答案:BC 【分析】由已知条件列方程组,求出公差和首项,从而可求出通项公式和前项和公式 【详解】解:设等差数列的公差为, 因为,, 所以,解得, 所以, , 故选:BC解析:BC 【分析】由已知条件列方程组,求出公差和首项,从而可求出通项公式和前n 项和公式 【详解】解:设等差数列{}n a 的公差为d , 因为30S =,46a =,所以113230236a d a d ⨯⎧+=⎪⎨⎪+=⎩,解得133a d =-⎧⎨=⎩, 所以1(1)33(1)36n a a n d n n =+-=-+-=-,21(1)3(1)393222n n n n n n nS na d n ---=+=-+=, 故选:BC5.设{}n a 是等差数列,n S 是其前n 项和,且56678,S S S S S <=>,则下列结论正确的是( ) A .0d < B .70a =C .95S S >D .67n S S S 与均为的最大值答案:ABD 【分析】由,判断,再依次判断选项. 【详解】 因为,,,所以数列是递减数列,故,AB 正确; ,所以,故C 不正确;由以上可知数列是单调递减数列,因为可知,的最大值,故D 正确. 故选:AB解析:ABD 【分析】由1n n n S S a --=()2n ≥,判断6780,0,0a a a >=<,再依次判断选项. 【详解】因为5665600S S S S a <⇒->⇒>,677670S S S S a =⇒-==,788780S S S S a >⇒-=<,所以数列{}n a 是递减数列,故0d <,AB 正确;()9567897820S S a a a a a a -=+++=+<,所以95S S <,故C 不正确;由以上可知数列{}n a 是单调递减数列,因为6780,0,0a a a >=<可知,67n S S S 与均为的最大值,故D 正确. 故选:ABD 【点睛】本题考查等差数列的前n 项和的最值,重点考查等差数列的性质,属于基础题型. 6.已知无穷等差数列{}n a 的前n 项和为n S ,67S S <,且78S S >,则( ) A .在数列{}n a 中,1a 最大 B .在数列{}n a 中,3a 或4a 最大 C .310S S =D .当8n ≥时,0n a <答案:AD 【分析】由已知得到,进而得到,从而对ABD 作出判定.对于C,利用等差数列的和与项的关系可等价转化为,可知不一定成立,从而判定C 错误. 【详解】 由已知得:,结合等差数列的性质可知,,该等差解析:AD 【分析】由已知得到780,0a a ><,进而得到0d <,从而对ABD 作出判定.对于C,利用等差数列的和与项的关系可等价转化为160a d +=,可知不一定成立,从而判定C 错误. 【详解】由已知得:780,0a a ><,结合等差数列的性质可知,0d <,该等差数列是单调递减的数列, ∴A 正确,B 错误,D 正确,310S S =,等价于1030S S -=,即45100a a a ++⋯+=,等价于4100a a +=,即160a d +=,这在已知条件中是没有的,故C 错误. 故选:AD. 【点睛】本题考查等差数列的性质和前n 项和,属基础题,关键在于掌握和与项的关系.7.首项为正数,公差不为0的等差数列{}n a ,其前n 项和为n S ,现有下列4个命题中正确的有( )A .若100S =,则280S S +=;B .若412S S =,则使0n S >的最大的n 为15C .若150S >,160S <,则{}n S 中8S 最大D .若78S S <,则89S S <答案:BC 【分析】根据等差数列的性质,以及等差数列的求和公式,逐项判断,即可得答案. 【详解】 A 选项,若,则, 那么.故A 不正确; B 选项,若,则,又因为,所以前8项为正,从第9项开始为负, 因为解析:BC 【分析】根据等差数列的性质,以及等差数列的求和公式,逐项判断,即可得答案. 【详解】A 选项,若1011091002S a d ⨯=+=,则1290a d +=, 那么()()2811128281029160S S a d a d a d d +=+++=+=-≠.故A 不正确; B 选项,若412S S =,则()5611128940a a a a a a ++++=+=,又因为10a >,所以前8项为正,从第9项开始为负,因为()()116168916802a a S a a +==+=, 所以使0n S >的最大的n 为15.故B 正确; C 选项,若()115158151502a a S a +==>,()()116168916802a a S a a +==+<, 则80a >,90a <,则{}n S 中8S 最大.故C 正确;D 选项,若78S S <,则80a >,而989S S a -=,不能判断9a 正负情况.故D 不正确. 故选:BC . 【点睛】本题考查等差数列性质的应用,涉及等差数列的求和公式,属于常考题型. 8.等差数列{}n a 的前n 项和为n S ,1385a a S +=,则下列结论一定正确的是( ) A .100a = B .当9n =或10时,n S 取最大值 C .911a a <D .613S S =答案:AD 【分析】由求出,即,由此表示出、、、,可判断C 、D 两选项;当时,,有最小值,故B 错误. 【详解】解:,,故正确A.由,当时,,有最小值,故B 错误. ,所以,故C 错误. ,,故D 正确.解析:AD 【分析】由1385a a S +=求出100a =,即19a d =-,由此表示出9a 、11a 、6S 、13S ,可判断C 、D 两选项;当0d >时,10a <,n S 有最小值,故B 错误. 【详解】解:1385a a S +=,111110875108,90,02da a d a a d a ⨯++=++==,故正确A. 由190a d +=,当0d >时,10a <,n S 有最小值,故B 错误.9101110,a a d d a a d d =-==+=,所以911a a =,故C 错误.61656+5415392dS a d d d ⨯==-+=-,131131213+11778392dS a d d d ⨯==-+=-,故D 正确. 故选:AD 【点睛】考查等差数列的有关量的计算以及性质,基础题.9.已知{}n a 为等差数列,其前n 项和为n S ,且13623a a S +=,则以下结论正确的是( ). A .10a =0B .10S 最小C .712S S =D .190S =答案:ACD 【分析】由得,故正确;当时,根据二次函数知识可知无最小值,故错误;根据等差数列的性质计算可知,故正确;根据等差数列前项和公式以及等差数列的性质可得,故正确. 【详解】因为,所以,所以,即解析:ACD 【分析】由13623a a S +=得100a =,故A 正确;当0d <时,根据二次函数知识可知n S 无最小值,故B 错误;根据等差数列的性质计算可知127S S =,故C 正确;根据等差数列前n 项和公式以及等差数列的性质可得190S =,故D 正确. 【详解】因为13623a a S +=,所以111236615a a d a d ++=+,所以190a d +=,即100a =,故A 正确;当0d <时,1(1)(1)922n n n n n S na d dn d --=+=-+2(19)2dn n =-无最小值,故B 错误;因为127891*********S S a a a a a a -=++++==,所以127S S =,故C 正确; 因为()1191910191902a a S a+⨯===,故D 正确.故选:ACD. 【点睛】本题考查了等差数列的通项公式、前n 项和公式,考查了等差数列的性质,属于中档题. 10.设公差不为0的等差数列{}n a 的前n 项和为n S ,若1718S S =,则下列各式的值为0的是( ) A .17aB .35SC .1719a a -D .1916S S -答案:BD【分析】由得,利用可知不正确;;根据可知 正确;根据可知不正确;根据可知正确. 【详解】因为,所以,所以, 因为公差,所以,故不正确; ,故正确; ,故不正确; ,故正确. 故选:BD.解析:BD 【分析】 由1718S S =得180a =,利用17180a a d d =-=-≠可知A 不正确;;根据351835S a =可知 B 正确;根据171920a a d -=-≠可知C 不正确;根据19161830S S a -==可知D 正确. 【详解】因为1718S S =,所以18170S S -=,所以180a =,因为公差0d ≠,所以17180a a d d =-=-≠,故A 不正确;13518351835()35235022a a a S a +⨯====,故B 正确; 171920a a d -=-≠,故C 不正确;19161718191830S S a a a a -=++==,故D 正确.故选:BD. 【点睛】本题考查了等差数列的求和公式,考查了等差数列的下标性质,属于基础题.。
高三数学数学数列多选题专项训练的专项培优练习题(含答案

一、数列多选题1.已知数列0,2,0,2,0,2,,则前六项适合的通项公式为( ) A .1(1)n n a =+-B .2cos 2n n a π=C .(1)2sin 2n n a π+=D .1cos(1)(1)(2)n a n n n π=--+-- 答案:AC【分析】对四个选项中的数列通项公式分别取前六项,看是否满足题意,得出答案.【详解】对于选项A ,取前六项得:,满足条件;对于选项B ,取前六项得:,不满足条件;对于选项C ,取前六项得:,解析:AC【分析】对四个选项中的数列通项公式分别取前六项,看是否满足题意,得出答案.【详解】对于选项A ,1(1)n n a =+-取前六项得:0,2,0,2,0,2,满足条件;对于选项B ,2cos2n n a π=取前六项得:0,2,0,2,0,2--,不满足条件; 对于选项C ,(1)2sin 2n n a π+=取前六项得:0,2,0,2,0,2,满足条件; 对于选项D ,1cos(1)(1)(2)n a n n n π=--+--取前六项得:0,2,2,8,12,22,不满足条件;故选:AC2.若数列{}n a 满足112,02121,12n n n n n a a a a a +⎧≤≤⎪⎪=⎨⎪-<<⎪⎩,135a =,则数列{}n a 中的项的值可能为( )A .15B .25C .45D .65答案:ABC【分析】利用数列满足的递推关系及,依次取代入计算,能得到数列是周期为4的周期数列,得项的所有可能值,判断选项即得结果.【详解】数列满足,,依次取代入计算得,,,,,因此继续下去会循环解析:ABC【分析】利用数列{}n a 满足的递推关系及135a =,依次取1,2,3,4n =代入计算2345,,,a a a a ,能得到数列{}n a 是周期为4的周期数列,得项的所有可能值,判断选项即得结果.【详解】数列{}n a 满足112,02121,12n n n n n a a a a a +⎧≤≤⎪⎪=⎨⎪-<<⎪⎩,135a =,依次取1,2,3,4,...n =代入计算得, 211215a a =-=,32225a a ==,43425a a ==,5413215a a a =-==,因此继续下去会循环,数列{}n a 是周期为4的周期数列,所有可能取值为:1234,,,5555. 故选:ABC.【点睛】本题考查了数列的递推公式的应用和周期数列,属于基础题. 3.已知数列{}n a 是等差数列,前n 项和为,n S 且13522,a a S +=下列结论中正确的是( )A .7S 最小B .130S =C .49S S =D .70a = 答案:BCD【分析】由是等差数列及,求出与的关系,结合等差数列的通项公式及求和公式即可进行判断.【详解】设等差数列数列的公差为.由有,即所以,则选项D 正确.选项A. ,无法判断其是否有最小解析:BCD【分析】由{}n a 是等差数列及13522,a a S +=,求出1a 与d 的关系,结合等差数列的通项公式及求和公式即可进行判断.【详解】设等差数列数列{}n a 的公差为d .由13522,a a S +=有()1112542252a a a d d ⨯+=++,即160a d += 所以70a =,则选项D 正确.选项A. ()71176773212S a d a d d ⨯=+=+=-,无法判断其是否有最小值,故A 错误. 选项B. 113137131302a S a a +=⨯==,故B 正确. 选项C. 9876579450a a a a S a a S -=++++==,所以49S S =,故C 正确.故选:BCD【点睛】关键点睛:本题考查等差数列的通项公式及求和公式的应用,解答本题的关键是由条件13522,a a S +=得到160a d +=,即70a =,然后由等差数列的性质和前n 项和公式判断,属于中档题.4.等差数列{}n a 的前n 项和为n S ,若10a >,公差0d ≠,则( )A .若59S >S ,则150S >B .若59S =S ,则7S 是n S 中最大的项C .若67S S >, 则78S S >D .若67S S >则56S S >.答案:BC【分析】根据等差数列的前项和性质判断.【详解】A 错:;B 对:对称轴为7;C 对:,又,;D 错:,但不能得出是否为负,因此不一定有.故选:BC .【点睛】关键点点睛:本题考查等差数列解析:BC【分析】根据等差数列的前n 项和性质判断.【详解】A 错:67895911415000S a a a a a S a S ⇒+++<>⇒+<⇒<;B 对:n S 对称轴为n =7;C 对:6770S S a >⇒<,又10a >,887700a S a d S ⇒⇒<<⇒<>;D 错:6770S S a >⇒<,但不能得出6a 是否为负,因此不一定有56S S >.故选:BC .【点睛】关键点点睛:本题考查等差数列的前n 项和性质,(1)n S 是关于n 的二次函数,可以利用二次函数性质得最值;(2)1n n n S S a -=+,可由n a 的正负确定n S 与1n S -的大小;(3)1()2n n n a a S +=,因此可由1n a a +的正负确定n S 的正负. 5.朱世杰是元代著名数学家,他所著的《算学启蒙》是一部在中国乃至世界最早的科学普及著作.《算学启蒙》中涉及一些“堆垛”问题,主要利用“堆垛”研究数列以及数列的求和问题.现有100根相同的圆形铅笔,小明模仿“堆垛”问题,将它们全部堆放成纵断面为等腰梯形的“垛”,要求层数不小于2,且从最下面一层开始,每一层比上一层多1根,则该“等腰梯形垛”应堆放的层数可以是( )A .4B .5C .7D .8答案:BD【分析】依据题意,根数从上至下构成等差数列,设首项即第一层的根数为,公差即每一层比上一层多的根数为,设一共放层,利用等差数列求和公式,分析即可得解.【详解】依据题意,根数从上至下构成等差解析:BD【分析】依据题意,根数从上至下构成等差数列,设首项即第一层的根数为1a ,公差即每一层比上一层多的根数为1d =,设一共放()2n n ≥层,利用等差数列求和公式,分析即可得解.【详解】依据题意,根数从上至下构成等差数列,设首项即第一层的根数为1a ,公差为1d =,设一共放()2n n ≥层,则总得根数为:()()111110022n n n d n n S na na --=+=+= 整理得120021a n n =+-, 因为1a *∈N ,所以n 为200的因数,()20012n n +-≥且为偶数, 验证可知5,8n =满足题意.故选:BD.【点睛】关键点睛:本题考查等差数列的求和公式,解题的关键是分析题意,把题目信息转化为等差数列,考查学生的逻辑推理能力与运算求解能力,属于基础题.6.(多选题)在数列{}n a 中,若221n n a a p --=,(2n ≥,*n N ∈,p 为常数),则称{}n a 为“等方差数列”.下列对“等方差数列”的判断正确的是( )A .若{}n a 是等差数列,则{}2n a 是等方差数列 B .(){}1n -是等方差数列 C .若{}n a 是等方差数列,则{}kn a (*k N ∈,k 为常数)也是等方差数列D .若{}n a 既是等方差数列,又是等差数列,则该数列为常数列答案:BCD【分析】根据定义以及举特殊数列来判断各选项中结论的正误.【详解】对于A 选项,取,则不是常数,则不是等方差数列,A 选项中的结论错误; 对于B 选项,为常数,则是等方差数列,B 选项中的结论正解析:BCD【分析】根据定义以及举特殊数列来判断各选项中结论的正误.【详解】对于A 选项,取n a n =,则()()()422444221111n n a a n n n n n n +⎡⎤⎡⎤-=+-=+-⋅++⎣⎦⎣⎦()()221221n n n =+++不是常数,则{}2n a 不是等方差数列,A 选项中的结论错误; 对于B 选项,()()22111110n n +⎡⎤⎡⎤---=-=⎣⎦⎣⎦为常数,则(){}1n -是等方差数列,B 选项中的结论正确;对于C 选项,若{}n a 是等方差数列,则存在常数p R ∈,使得221n n a a p +-=,则数列{}2n a 为等差数列,所以()221kn k n a a kp +-=,则数列{}kn a (*k N ∈,k 为常数)也是等方差数列,C 选项中的结论正确;对于D 选项,若数列{}n a 为等差数列,设其公差为d ,则存在m R ∈,使得n a dn m =+,则()()()()2221112222n n n n n n a a a a a a d dn m d d n m d d +++-=-+=++=++, 由于数列{}n a 也为等方差数列,所以,存在实数p ,使得221n n a a p +-=,则()222d n m d d p ++=对任意的n *∈N 恒成立,则()2202d m d d p ⎧=⎪⎨+=⎪⎩,得0p d ==,此时,数列{}n a 为常数列,D 选项正确.故选BCD.【点睛】本题考查数列中的新定义,解题时要充分利用题中的定义进行判断,也可以结合特殊数列来判断命题不成立,考查逻辑推理能力,属于中等题.7.{} n a 是等差数列,公差为d ,前项和为n S ,若56S S <,678S S S =>,则下列结论正确的是( )A .0d <B .70a =C .95S S >D .170S < 答案:ABD【分析】结合等差数列的性质、前项和公式,及题中的条件,可选出答案.【详解】由,可得,故B 正确;由,可得,由,可得,所以,故等差数列是递减数列,即,故A 正确;又,所以,故C 不正确解析:ABD【分析】结合等差数列的性质、前n 项和公式,及题中的条件,可选出答案.【详解】由67S S =,可得7670S S a -==,故B 正确;由56S S <,可得6560S S a -=>,由78S S >,可得8780S S a -=<,所以876a a a <<,故等差数列{}n a 是递减数列,即0d <,故A 正确;又()9567897820S S a a a a a a -=+++=+<,所以95S S <,故C 不正确;又因为等差数列{}n a 是单调递减数列,且80a <,所以90a <,所以()117179171702a a S a +==<,故D 正确.故选:ABD.【点睛】关键点点睛:本题考查等差数列性质的应用,解题的关键是熟练掌握等差数列的增减性及前n 项和的性质,本题要从题中条件入手,结合公式()12n n n a S S n --≥=,及()12n n n a a S +=,对选项逐个分析,可判断选项是否正确.考查学生的运算求解能力与逻辑推理能力,属于中档题.8.设d 为正项等差数列{}n a 的公差,若0d >,32a =,则( )A .244a a ⋅<B .224154a a +≥C .15111a a +>D .1524a a a a ⋅>⋅答案:ABC【分析】由已知求得公差的范围:,把各选项中的项全部用表示,并根据判断各选项.【详解】由题知,只需,,A 正确;,B 正确;,C 正确;,所以,D 错误.【点睛】本题考查等差数列的性解析:ABC【分析】由已知求得公差d 的范围:01d <<,把各选项中的项全部用d 表示,并根据01d <<判断各选项.【详解】由题知,只需1220010a d d d =->⎧⇒<<⎨>⎩, ()()2242244a a d d d ⋅=-⋅+=-<,A 正确;()()2222415223644a a d d d d +=-++=-+>≥,B 正确; 21511111122221a a d d d +=+=>-+-,C 正确; ()()()()2152422222230a a a a d d d d d ⋅-⋅=-⋅+--⋅+=-<,所以1524a a a a ⋅<⋅,D 错误.【点睛】本题考查等差数列的性质,解题方法是由已知确定d 的范围,由通项公式写出各项(用d 表示)后,可判断.9.下面是关于公差0d >的等差数列{}n a 的四个命题,其中的真命题为( ). A .数列{}n a 是递增数列B .数列{}n na 是递增数列C .数列{}n a n是递增数列 D .数列{}3n a nd +是递增数列答案:AD【分析】根据等差数列的性质,对四个选项逐一判断,即可得正确选项.【详解】, ,所以是递增数列,故①正确,,当时,数列不是递增数列,故②不正确,,当时,不是递增数列,故③不正确,,因解析:AD【分析】根据等差数列的性质,对四个选项逐一判断,即可得正确选项.【详解】0d >,10n n a a d +-=> ,所以{}n a 是递增数列,故①正确,()()2111n na n a n d dn a d n =+-=+-⎡⎤⎣⎦,当12d a n d-<时,数列{}n na 不是递增数列,故②不正确,1n a a d d n n -=+,当10a d -<时,{}n a n不是递增数列,故③不正确, 134n a nd nd a d +=+-,因为0d >,所以{}3n a nd +是递增数列,故④正确, 故选:AD【点睛】本题主要考查了等差数列的性质,属于基础题.10.等差数列{}n a 的前n 项和为n S ,若90a <,100a >,则下列结论正确的是( ) A .109S S > B .170S < C .1819S S > D .190S > 答案:ABD【分析】先根据题意可知前9项的和最小,判断出正确;根据题意可知数列为递减数列,则,又,进而可知,判断出不正确;利用等差中项的性质和求和公式可知,,故正确.【详解】根据题意可知数列为递增解析:ABD【分析】先根据题意可知前9项的和最小,判断出A 正确;根据题意可知数列为递减数列,则190a >,又181919S S a =-,进而可知1516S S >,判断出C 不正确;利用等差中项的性质和求和公式可知()01179179172171722a a a S a <+⨯⨯===,()1191019101921919022a a a S a +⨯⨯===>,故BD 正确. 【详解】根据题意可知数列为递增数列,90a <,100a >,∴前9项的和最小,故A 正确;()11791791721717022a a a S a +⨯⨯===<,故B 正确; ()1191019101921919022a a a S a +⨯⨯===>,故D 正确; 190a >,181919S S a ∴=-,1819S S ∴<,故C 不正确.故选:ABD .【点睛】本题考查等差数列的综合应用,考查逻辑思维能力和运算能力,属于常考题.。
高三数学 数学多选题的专项培优练习题(及解析

一、函数的概念与基本初等函数多选题1.已知函数222,()log ,0x x x f x x x ⎧--≤⎪=⎨>⎪⎩,若x 1<x 2<x 3<x 4,且f (x 1)=f (x 2)=f (x 3)=f (x 4),则下列结论正确的是( ) A .x 1+x 2=-1 B .x 3x 4=1 C .1<x 4<2 D .0<x 1x 2x 3x 4<1【答案】BCD 【分析】由解析式得到函数图象,结合函数各分段的性质有122x x +=-,341x x =,341122x x <<<<,即可知正确选项. 【详解】由()f x 函数解析式可得图象如下:∴由图知:122x x +=-,121x -<<-,而当1y =时,有2|log |1x =,即12x =或2, ∴341122x x <<<<,而34()()f x f x =知2324|log ||log |x x =:2324log log 0x x +=, ∴341x x =,21234121(1)1(0,1)x x x x x x x ==-++∈.故选:BCD 【点睛】关键点点睛:利用分段函数的性质确定函数图象,由二次函数、对数运算性质确定1234,,,x x x x 的范围及关系.2.已知函数()1y f x =-的图象关于1x =对称,且对(),y f x x R =∈,当12,(,0]x x ∈-∞时,()()21210f x f x x x -<-成立,若()()2221f ax f x <+对任意的x ∈R 恒成立,则a 的可能取值为( ) A. B .1- C .1 D【答案】BC 【分析】由已知得函数()f x 是偶函数,在[0,)+∞上是单调增函数,将问题转化为2|2||21|ax x <+对任意的x ∈R 恒成立,由基本不等式可求得范围得选项. 【详解】因为函数()1y f x =-的图象关于直线1x =对称,所以函数()y f x =的图象关于直线0x =(即y 轴)对称,所以函数()f x 是偶函数.又12,(,0]x x ∈-∞时,()()21210f x f x x x -<-成立,所以函数()f x 在[0,)+∞上是单调增函数.且()()2221f ax f x <+对任意的x ∈R 恒成立,所以2|2||21|ax x <+对任意的x ∈R 恒成立,当0x =时,01<恒成立,当0x ≠时,2|21|11|||||||||2|22x a x x x x x+<=+=+,又因为1||||2x x +=≥||2x =时,等号成立,所以||a <,因此a <<,故选:BC. 【点睛】方法点睛:不等式恒成立问题常见方法:① 分离参数()a f x ≥恒成立(()max a f x ≥即可)或()a f x ≤恒成立(()min a f x ≤即可);② 数形结合(()y f x = 图象在()y g x = 上方即可);③ 讨论最值()min 0f x ≥或()max 0f x ≤恒成立.3.已知函数()()124,01,21,1,x x f x af x x ⎧--≤≤⎪=⎨⎪->⎩其中a R ∈,下列关于函数()f x 的判断正确的为( ) A .当2a =时,342f ⎛⎫=⎪⎝⎭B .当1a <时,函数()f x 的值域[]22-,C .当2a =且[]()*1,x n n n ∈-∈N时,()1212242n n f x x --⎛⎫=-- ⎪⎝⎭D .当0a >时,不等式()122x f x a-≤在[)0,+∞上恒成立【答案】AC 【分析】对于A 选项,直接代入计算即可;对于B 选项,由题得当(]*,1,x m m m N ∈+∈时,()()m f x a f x m =-,进而得当(]*,1,x m m m N ∈+∈时,()()2,2f x ∈-,故()f x 的值域(]2,2-;对于C 选项,结合B 选项得当2a =且[]()*1,x n n n ∈-∈N时,()()121n f x f x n -=-+进而得解析式;对于D 选项,取特殊值即可得答案.【详解】解:对于A 选项,当2a =时,3111222442222f f ⎛⎫⎛⎫⎛⎫==--= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,故A 选项正确; 对于B 选项,由于当01x ≤≤,函数的值域为[]0,2,所以当(]*,1,x m m m N ∈+∈时,()()m f x a f x m =-,由于(]0,1x m -∈,所以()[]0,2f x m -∈,因为1a <,所以()1,1m a ∈-,所以当(]*,1,x m m m N ∈+∈时,()()2,2f x ∈-,综上,当1a <时,函数()f x 的值域(]2,2-,故B 选项错误;对于C 选项,由B 选项得当(]*,1,x m m m N ∈+∈时,()()mf x a f x m =-,故当2a =且[]()*1,x n n n ∈-∈N时,()()1112122412n n f x f x n x n --⎛⎫=-+=--+- ⎪⎝⎭1112122422422n n n x n x --⎛⎫⎛-⎫=--+=-- ⎪ ⎪⎝⎭⎝⎭,故C 选项正确; 对于D 选项,取812a =,34x =,则331241442f ⎛⎫=--= ⎪⎝⎭,122x a-=()311142482488111222222222---⎛⎫⎛⎫==⨯=⨯= ⎪ ⎪⎝⎭⎝⎭,不满足式()122x f x a -≤,故D选项错误. 故选:AC. 【点睛】本题考查函数的综合应用,考查分析能力与运算求解能力,是难题.本题解题的关键在于根据题意得当(]*,1,x m m m N ∈+∈时,()()mf x a f x m =-,且当01x ≤≤,函数的值域为[]0,2,进而利用函数平移与伸缩变换即可求解.4.设[]x 表示不超过x 的最大整数,如:[]1.21=,[]1.22-=-,[]y x =又称为取整函数,在现实生活中有着广泛的应用,诸如停车收费,出租车收费等均按“取整函数”进行计费,以下关于“取整函数”的描述,正确的是( )A .x R ∀∈,[][]22x x =B .,x y R ∀∈,若[][]x y =,则1x y ->-C .x R ∀∈,[][]122x x x ⎡⎤++=⎢⎥⎣⎦D .不等式[][]2230x x --≥的解集为{|0x x <或}2x ≥ 【答案】BCD 【分析】通过反例可得A 错误,根据取整函数的定义可证明BC 成立,求出不等式2230t t --≥的解后可得不等式[][]2230x x --≥的解集,从而可判断D 正确与否. 【详解】对于A , 1.5x =-,则[][][]()233,2224x x =-=⨯--==-,故[][]22x x ≠,故A 不成立.对于B ,[][]x y m ==,则1,1m x m m y m ≤<+≤<+, 故1m y m --<-≤-,所以1x y ->-,故B 成立. 对于C ,设x m r =+,其中[),0,1m Z r ∈∈, 则[]11222x x m r ⎡⎤⎡⎤++=++⎢⎥⎢⎥⎣⎦⎣⎦,[][]222x m r =+, 若102r ≤<,则102r ⎡⎤+=⎢⎥⎣⎦,[]20r =,故[][]122x x x ⎡⎤++=⎢⎥⎣⎦; 若112r <<,则112r ⎡⎤+=⎢⎥⎣⎦,[]21r =,故[][]122x x x ⎡⎤++=⎢⎥⎣⎦,故C 成立.对于D ,由不等式[][]2230x x --≥可得[]1x ≤-或[]32x ≥, 故0x <或2x ≥,故D 正确. 故选:BCD 【点睛】本题考查在新定义背景下恒等式的证明与不等式的解法,注意把等式的证明归结为整数部分和小数部分的关系,本题属于较难题.5.已知函数21,01()(1)1,1x x f x f x x ⎧-≤<=⎨-+≥⎩,方程()0f x x -=在区间0,2n ⎡⎤⎣⎦(*n N ∈)上的所有根的和为n b ,则( ) A .()20202019f = B .()20202020f = C .21122n n n b --=+D .(1)2n n n b +=【答案】BC 【分析】先推导出()f x 在[)()*,1n n n N+∈上的解析式,然后画出()f x 与y x =的图象,得出()f x x =时,所有交点的横坐标,然后得出n b .【详解】因为当[)0,1x ∈时,()21xf x =-,所以当[)1,2x ∈时,[)10,1x -∈,则()1121x f x --=-,故()()11112112x x f x f x --=-+=-+=,即[)10,1x -∈时,[)10,1x -∈,()12x f x -= 同理当[)2,3x ∈时,[)11,2x -∈,()()21121x f x f x -=-+=+;当[)3,4x ∈时,[)12,3x -∈,则()()31122x f x f x -=-+=+;………故当[),1x n n ∈+时,()()21x nf x n -=+-,当21,2nnx ⎡⎤∈-⎣⎦时,()()()21222n x n f x --=+-.所以()20202020f =,故B 正确;作出()f x 与y x =的图象如图所示,则当()0f x x -=且0,2n⎡⎤⎣⎦时,x 的值分别为:0,1,2,3,4,5,6,,2n则()()121122101222221222n n n n n n n n b ---+=+++++==+=+,故C 正确.故选:BC.【点睛】本题考查函数的零点综合问题,难度较大,推出原函数在每一段上的解析式并找到其规律是关键.6.已知直线2y x =-+分别与函数x y e =和ln y x =的图象交于点()()1122,,,A x y B x y ,则下列结论正确的是( ) A .122x x +=B .122x x e e e +>C .1221ln ln 0x x x x +<D .12e x x >【答案】ABC 【分析】根据互为反函数的性质可得()()1122,,,A x y B x y 的中点坐标为()1,1,从而可判断A ;利用基本不等式可判断B 、D ;利用零点存在性定理以及对数的运算性质可判断C. 【详解】函数xy e =与ln y x =互为反函数, 则xy e =与ln y x =的图象关于y x =对称,将2y x =-+与y x =联立,则1,1x y ==,由直线2y x =-+分别与函数xy e =和ln y x =的图象交于点()()1122,,,A x y B x y ,作出函数图像:则()()1122,,,A x y B x y 的中点坐标为()1,1, 对于A ,由1212x x +=,解得122x x +=,故A 正确; 对于B ,12121222222x x x x x x e e e e e e e +≥=+⋅==, 因为12x x ≠,即等号不成立,所以122x x e e e +>,故B 正确;对于C ,将2y x =-+与xy e =联立可得2x x e -+=,即20x e x +-=,设()2xf x e x =+-,且函数为单调递增函数,()010210f =+-=-<,112211320222f e e ⎛⎫=+-=-> ⎪⎝⎭,故函数的零点在10,2⎛⎫ ⎪⎝⎭上,即1102x <<,由122x x +=,则212x <<, 122112211ln ln ln lnx x x x x x x x +=- ()1222122ln ln ln 0x x x x x x x <-=-<,故C 正确;对于D,由12x x +≥,解得121x x ≤, 由于12x x ≠,则121x x <,故D 错误; 故选:ABC 【点睛】本题考查了互为反函数的性质、基本不等式的应用、零点存在性定理以及对数的运算性质,考查了数形结合的思想,属于难题.7.设函数cos2cos2()22x x f x -=-,则( ) A .()f x 在0,2π⎛⎫⎪⎝⎭单调递增B .()f x 的值域为33,22⎡⎤-⎢⎥⎣⎦ C .()f x 的一个周期为π D .4f x π⎛⎫+ ⎪⎝⎭的图像关于点,04π⎛⎫ ⎪⎝⎭对称【答案】BC 【分析】根据余弦函数及指数函数的单调性,分析复合函数的单调区间及值域,根据周期定义检验所给周期,利用函数的对称性判断对称中心即可求解. 【详解】令cos2t x =,则12222ttt t y -=-=-,显然函数12222t t tty -=-=-为增函数,当0,2x π⎛⎫∈ ⎪⎝⎭时,cos2t x =为减函数, 根据复合函数单调性可知,()f x 在0,2π⎛⎫⎪⎝⎭单调递减, 因为cos2[1,1]t x =∈-, 所以增函数12222ttt t y -=-=-在cos2[1,1]t x =∈-时,3322y -≤≤, 即()f x 的值域为33,22⎡⎤-⎢⎥⎣⎦; 因为cos2()cos2(cos2c )os222)(2()2x x x x x x f f πππ+-+-=-=+-=,所以()f x 的一个周期为π,因为sin 2sin 2224x x f x π-⎛⎫+=- ⎪⎝⎭,令sin 2sin 22(2)xx h x --=, 设(,)P x y 为sin 2sin 22(2)x x h x --=上任意一点, 则(,)2P x y π'--为(,)P x y 关于,04π⎛⎫⎪⎝⎭对称的点, 而sin 2(sin 2())22sin 2sin 2()22222x x x x h y x y πππ-----=-==≠--,知点(,)2P x y π'--不在函数图象上,故()h x 的图象不关于点,04π⎛⎫⎪⎝⎭对称,即4f x π⎛⎫+ ⎪⎝⎭的图像不关于点,04π⎛⎫ ⎪⎝⎭对称.故选:BC 【点睛】本题主要考查了余弦函数的性质,指数函数的性质,复合函数的单调性,考查了函数的周期性,值域,对称中心,属于难题.8.已知函数()2221,021,0x x x f x x x x ⎧++≥=⎨-++<⎩,则下列判断正确的是( )A .()f x 为奇函数B .对任意1x ,2x R ∈,则有()()()12120x x f x f x --≤⎡⎤⎣⎦C .对任意x ∈R ,则有()()2f x f x +-=D .若函数()y f x mx =-有两个不同的零点,则实数m 的取值范围是()()–,04,∞+∞【答案】CD 【分析】根据函数的奇偶性以及单调性判断AB 选项;对x 进行分类讨论,判断C 选项;对选项D ,构造函数,将函数的零点问题转化为函数图象的交点问题,即可得出实数m 的取值范围. 【详解】对于A 选项,当0x >时,0x -<,则()22()()2()121()f x x x x x f x -=--+-+=-+-≠-所以函数()f x 不是奇函数,故A 错误; 对于B 选项,221y x x =++的对称轴为1x =-,221y x x =-++的对称轴为1x =所以函数221y x x =++在区间[0,)+∞上单调递增,函数221y x x =-++在区间(,0)-∞上单调递增,并且2202010201+⨯+=-+⨯+ 所以()f x 在R 上单调递增即对任意()1122,,x x x x R <∈,都有()()12f x f x <则()()()()()121212120,00x x f x f x x x f x f x ⎡⎤-<-⇒--⎣⎦,故B 错误; 对于C 选项,当0x >时,0x -<,则 22()()2()121f x x x x x -=--+-+=--+ 则22()()21212f x f x x x x x +-=++--+= 当0x =时,(0)(0)1f f -==,则(0)(0)2f f -+=当0x <时,0x ->,则22()()2()121f x x x x x -=-+-+=-+ 则22()()21212f x f x x x x x +-=-+++-+= 即对任意x ∈R ,则有()()2f x f x +-=,故C 正确;对于D 选项,当0x =时,()010y f ==≠,则0x =不是该函数的零点 当0x ≠时,()()0f x f x xm x m -=⇔=令函数()()g x f x x=,函数y m =由题意可知函数y m =与函数()()g x f x x=的图象有两个不同的交点因为()0f x ≥时,)1x ⎡∈+∞⎣,()0f x <时,(,1x ∈-∞-所以12,012,12)01,1(x x x x x x x x x g x ⎧++>⎪⎪⎪-++<⎨⎪⎪--<-⎩=⎪当0x >时,设1201x x ,()()()()121212121212111x x x x g x g x x x x x x x ---=+--= 因为12120,10x x x x -<-<,所以()()120g x g x ->,即()()12g x g x > 设121x x <<,()()()()1212121210x x x x g x g x x x ---=<,即()()12g x g x <所以函数()g x 在区间(0,1)上单调递减,在区间(1,)+∞上单调递增同理可证,函数()g x 在区间)1⎡⎣上单调递减,在区间(,1-∞上单调递增11241)1(g ++==函数()g x 图象如下图所示由图可知,要使得函数y m =与函数()()g x f x x=的图象有两个不同的交点则实数m 的取值范围是()()–,04,∞+∞,故D 正确;故选:CD 【点睛】本题主要考查了利用定义证明函数的单调性以及奇偶性,由函数零点的个数求参数的范围,属于较难题.9.已知正数,,x y z ,满足3412x y z ==,则( ) A .634z x y << B .121x y z+= C .4x y z +> D .24xy z <【答案】AC 【分析】令34121x y z m ===>,根据指对互化和换底公式得:111log 3log 4log 12m m m x y z===,,,再依次讨论各选项即可. 【详解】由题意,可令34121x y z m ===>,由指对互化得:111,,log 3log 4log 12m m m x y z ===, 由换底公式得:111log 3,log 4,log 12m m m x y z ===,则有111x y z+=,故选项B 错误; 对于选项A ,124log 12log 9log 03m m m z x -=-=>,所以2x z >,又4381log 81log 64log 064m m m x y -=-=>,所以43y x >,所以436y x z >>,故选项A 正确;对于选项C 、D ,因为111x y z +=,所以xyz x y =+,所以()()()()2222222440x y xy x y xy x y z xy x y x y -+--==-<++,所以24xy z >,则()24z x y z +>,则4x y z +>,所以选项C 正确,选项D 错误;故选:AC. 【点睛】本题考查指对数的运算,换底公式,作差法比较大小等,考查运算求解能力,是中档题.本题解题的关键在于令34121xyzm ===>,进而得111,,log 3log 4log 12m m m x y z ===,再根据题意求解.10.已知函数()22,21ln 1,1x x f x x x e +-≤≤⎧=⎨-<≤⎩,若关于x 的方程()f x m =恰有两个不同解()1212,x x x x <,则()212)x x f x -(的取值可能是( ) A .3- B .1-C .0D .2【答案】BC 【分析】利用函数的单调性以及已知条件得到1122,e ,(1,0]2m m x x m +-==∈-,代入()212)x x f x -(,令121(),(1,0]2x g x xe x x x +=-+∈-,求导,利用导函数的单调性分析原函数的单调性,即可求出取值范围. 【详解】因为()f x m =的两根为()1212,x x x x <, 所以1122,e ,(1,0]2m m x x m +-==∈-, 从而()()211212222m m m m x x f x e m me m ++-⎛⎫-=-=-+ ⎪⎝⎭. 令121(),(1,0]2x g x xex x x +=-+∈-, 则1()(1)1x g x x e x +'=+-+,(1,0]x ∈-.因为(1,0]x ∈-,所以1010,1,10x x e e x ++>>=-+>, 所以()0g x '>在(1,0]-上恒成立, 从而()g x 在(1,0]-上单调递增. 又5(0)0,(1)2g g =-=-, 所以5(),02g x ⎛⎤∈-⎥⎝⎦, 即()()212x x f x -⋅的取值范围是5,02⎛⎤- ⎥⎝⎦, 故选:BC . 【点睛】关键点睛:本题考查利用导数解决函数的范围问题.构造函数121(),(1,0]2x g x xe x x x +=-+∈-,利用导数求取值范围是解决本题的关键.二、导数及其应用多选题11.已知函数()sin sin f x ax a x =-,[]0,2x π∈,其中ln 1a a ->,则下列说法中正确的是( )A .若()f x 只有一个零点,则10,2a ⎛⎫∈ ⎪⎝⎭B .若()f x 只有一个零点,则()0f x ≥恒成立C .若()f x 只有两个零点,则31,2a ⎛⎫∈ ⎪⎝⎭D .若()f x 有且只有一个极值点0x ,则()01312a a f x π+--<⋅恒成立【答案】ABD 【分析】利用()00f =以及零点存在定理推导出当1a >时,函数()f x 在[]0,2π上至少有两个零点,结合图象可知当01a <<时,函数()f x 在()0,2π上有且只有一个极值点,利用导数分析函数()f x 在()0,2π上的单调性,可判断A 选项的正误;利用A 选项中的结论可判断B 选项的正误;取12a =,解方程()0f x =可判断C 选项的正误;分析出当()f x 在()0,2π上只有一个极值点时,01a <<,分13a =、103a <<、113a <<三种情况讨论,结合sin x x <可判断D 选项的正误. 【详解】构造函数()ln 1g x x x =--,其中0x >,则()111x g x x x-'=-=. 当01x <<时,()0g x '<,函数()g x 单调递减; 当1x >时,()0g x '>,此时,函数()g x 单调递增. 所以,()()min 10g x g ==.ln 1a a ->,0a ∴>且1a ≠.()sin sin f x ax a x =-,则()00f =.当1a >时,sin sin sin 02222a a f a a ππππ⎛⎫=-=-<⎪⎝⎭,3333sin sin sin 02222a a f a a ππππ⎛⎫=-=+> ⎪⎝⎭, 由零点存在定理可知,函数()f x 在3,22ππ⎛⎫⎪⎝⎭内至少有一个零点, 所以,当1a >时,函数()f x 在区间[]0,2π上至少有两个零点, 所以,当函数()f x 在区间[]0,2π上只有一个零点时,01a <<.对于A 选项,当01a <<时,()()cos cos cos cos f x a ax a x a ax x '=-=-.01a <<,则022a ππ<<,022a ππ<<, cos 022a f a ππ⎛⎫'=> ⎪⎝⎭,()()()2cos2cos2cos210f a a a a ππππ'=-=-<,由零点存在定理可知,函数()f x 在区间,22ππ⎛⎫⎪⎝⎭上至少有一个极值点, 令()0f x '=,可得cos cos ax x =,当()0,2x π∈时,02ax x π<<<,由()cos cos cos 2ax x x π==-,可得2ax x π=-,解得21x a π=+, 所以,函数()f x 在区间()0,2π上有且只有一个极值点21x a π=+. 作出函数1cos y ax =与函数2cos y x =在区间[]0,2π上的图象如下图所示:由图象可知,函数1cos y ax =与函数2cos y x =在区间()0,2π上的图象有且只有一个交点,记该交点的横坐标为0x ,当00x x <<时,cos cos ax x >,此时()0f x '>; 当02x x π<<时,cos cos ax x <,此时()0f x '<.所以,函数()f x 在区间()00,x 上单调递增,在区间()0,2x π上单调递减. 所以,()()()0max 00f x f x f =>=,又()2sin 2f a ππ=.若函数()f x 在区间[]0,2π上有且只有一个零点,则()2sin 20f a ππ=>.01a <<,则022a ππ<<,所以,02a ππ<<,解得102a <<,A 选项正确;对于B 选项,若函数()f x 在区间[]0,2π上有且只有一个零点时,由A 选项可知,函数()f x 在区间()00,x 上单调递增,在区间()0,2x π上单调递减.()00f =,()2sin 20f a ππ=>,所以,对任意的[]0,2x π∈,()0f x ≥,B 选项正确;对于C 选项,取12a =,则()1sin sin sin sin cos sin 1cos 2222222x x x x x x f x x ⎛⎫=-=-=- ⎪⎝⎭,02x π≤≤,则02x π≤≤,令()0f x =,可得sin 02x =或cos 12x=,可得02x =或2xπ=, 解得0x =或2x π=. 所以,当12a =时,函数()f x 有两个零点,C 选项错误; 对于D 选项,当1a >时,若02x π<<,则02ax a π<<,且22a ππ>,当()0,2x π∈时,令()0f x '=,可得出()()cos cos cos 2ax x k x k Z π==±∈,至少可得出2ax x π=-或2ax x π=+,即函数()f x 在区间()0,2π上至少有两个极值点,不合乎题意,所以,01a <<.下面证明:当02x π<<时,sin x x <,构造函数()sin h x x x =-,其中02x π<<,则()1cos 0h x x '=->,所以,函数()sin h x x x =-在区间0,2π⎛⎫⎪⎝⎭上为增函数,所以,()()00h x h >=,即sin x x <.分以下三种情况来证明()01312a a f x π+--<⋅恒成立.()()000cos cos 0f x a ax x '=-=,可得00cos cos ax x =,0002ax x π<<<,由00cos cos ax x =可得出002ax x π=-,所以,021x a π=+. 则()000sin sin 2sin ax x x π=-=-. ①当13a =时,032x π=,则()1sin sin 33x f x x =-,31342sin sin 223233f ππππ⎛⎫=-=< ⎪⎝⎭, 即()01312a a f x π+--<⋅成立;②当103a <<时,023,212x a πππ⎛⎫=∈ ⎪+⎝⎭, 则()()()0000002sin sin sin sin 1sin 1sin1f x ax a x x a x a x a a π=-=--=-+=-++ ()()()()22221sin 1sin 21sin 121111a a a a a a a a a a a ππππππ⎛⎫⎛⎫=+-=+-=+<+⋅= ⎪ ⎪++++⎝⎭⎝⎭ 1312a a π+--=⋅;③当113a <<时,023,12x a πππ⎛⎫=∈ ⎪+⎝⎭, ()()()()0000000sin sin sin sin 1sin 1sin f x ax a x x a x a x a x =-=--=-+=+-()()()()()()()01121sin 1sin 1sin 1111a a a x a a a a a a πππππ--⎛⎫=+-=+-=+<+⋅⎪+++⎝⎭()13112a a a ππ+--=-=.综上所述,当函数()f x 只有一个极值点0x 时,()01312a a f x π+--<恒成立. 故选:ABD.【点睛】方法点睛:利用导数解决函数零点问题的方法:(1)直接法:先对函数求导,根据导数的方法求出函数的单调区间与极值,根据函数的基本性质作出图象,然后将问题转化为函数图象与x 轴的交点问题,突出导数的工具作用,体现了转化与化归思想、数形结合思想和分类讨论思想的应用; (2)构造新函数法:将问题转化为研究两函数图象的交点问题;(3)参变量分离法:由()0f x =分离变量得出()a g x =,将问题等价转化为直线y a =与函数()y g x =的图象的交点问题.12.关于函数()e cos xf x a x =-,()π,πx ∈-下列说法正确的是( )A .当1a =时,()f x 在0x =处的切线方程为y x =B .若函数()f x 在()π,π-上恰有一个极值,则0a =C .对任意0a >,()0f x ≥恒成立D .当1a =时,()f x 在()π,π-上恰有2个零点 【答案】ABD 【分析】直接逐一验证选项,利用导数的几何意义求切线方程,即可判断A 选项;利用分离参数法,构造新函数和利用导数研究函数的单调性和极值、最值,即可判断BC 选项;通过构造新函数,转化为两函数的交点个数来解决零点个数问题,即可判断D 选项. 【详解】解:对于A ,当1a =时,()e cos xf x x =-,()π,πx ∈-,所以()00e cos00f =-=,故切点为(0,0),则()e sin xf x x '=+,所以()00e sin01f '=+=,故切线斜率为1,所以()f x 在0x =处的切线方程为:()010y x -=⨯-,即y x =,故A 正确; 对于B ,()e cos xf x a x =-,()π,πx ∈-,则()e sin xf x a x '=+,若函数()f x 在()π,π-上恰有一个极值,即()0f x '=在()π,π-上恰有一个解, 令()0f x '=,即e sin 0x a x +=在()π,π-上恰有一个解, 则sin xxa e-=在()π,π-上恰有一个解, 即y a =与()sin xxg x e-=的图象在()π,π-上恰有一个交点, ()sin cos xx xg x e-'=,()π,πx ∈-,令()0g x '=,解得:134x π=-,24x π=, 当3,,44x ππππ⎛⎫⎛⎫∈--⎪ ⎪⎝⎭⎝⎭时,()0g x '>,当3,44x ππ⎛⎫∈-⎪⎝⎭时,()0g x '<, ()g x ∴在3,4ππ⎛⎫--⎪⎝⎭上单调递增,在443,ππ⎛⎫- ⎪⎝⎭上单调递减,在,4ππ⎛⎫ ⎪⎝⎭上单调递增, 所以极大值为3423204g e ππ-⎛⎫-=> ⎪⎝⎭,极小值为42204g e ππ-⎛⎫=< ⎪⎝⎭, 而()()()0,0,00g g g ππ-===, 作出()sinx g x e-=,()π,πx ∈-的大致图象,如下:由图可知,当0a =时,y a =与()sinx g x e-=的图象在()π,π-上恰有一个交点, 即函数()f x 在()π,π-上恰有一个极值,则0a =,故B 正确; 对于C ,要使得()0f x ≥恒成立,即在()π,πx ∈-上,()e cos 0xf x a x =-≥恒成立,即在()π,πx ∈-上,cos xxa e ≥恒成立,即maxcos x x a e ⎛⎫≥ ⎪⎝⎭,设()cos x x h x e =,()π,πx ∈-,则()sin cos xx xh x e --'=,()π,πx ∈-, 令()0h x '=,解得:14x π=-,234x π=, 当3,,44x ππππ⎛⎫⎛⎫∈--⎪ ⎪⎝⎭⎝⎭时,()0h x '>,当3,44x ππ⎛⎫∈- ⎪⎝⎭时,()0h x '<, ()h x ∴在,4ππ⎛⎫--⎪⎝⎭上单调递增,在3,44ππ⎛⎫-⎪⎝⎭上单调递减,在3,4ππ⎛⎫⎪⎝⎭上单调递增, 所以极大值为4204h e ππ-⎛⎫-=> ⎪⎝⎭,()()11,h h e e ππππ--==,所以()cos x xh x e =在()π,πx ∈-上的最大值为4204h e ππ-⎛⎫-=> ⎪⎝⎭, 所以42a e π-≥时,在()π,πx ∈-上,()e cos 0xf x a x =-≥恒成立,即当42a e π-≥时,()0f x ≥才恒成立,所以对任意0a >,()0f x ≥不恒成立,故C 不正确; 对于D ,当1a =时,()e cos xf x x =-,()π,πx ∈-,令()0f x =,则()e cos 0xf x x =-=,即e cos x x =,作出函数xy e =和cos y x =的图象,可知在()π,πx ∈-内,两个图象恰有两个交点,则()f x 在()π,π-上恰有2个零点,故D 正确.故选:ABD. 【点睛】本题考查函数和导数的综合应用,考查利用导数的几何意义求切线方程,考查分离参数法的应用和构造新函数,以及利用导数研究函数的单调性、极值最值、零点等,考查化简运算能力和数形结合思想.13.已知(0,1)x ∈,则下列正确的是( ) A .cos 2x x π+<B .22xx <C .22sin 24x x x >+D .1ln 1x x <- 【答案】ABC 【分析】构造函数()sin f x x x =-证明其在0,2π⎛⎫⎪⎝⎭单调递减,即可得sin 22x x ππ⎛⎫-<-⎪⎝⎭即可判断选项A ;作出2yx 和2x y =的函数图象可判断选项B ;作出()sin2xf x =,()224x h x x =+的图象可判断选项C ;构造函数()1ln 1x g x x =+-利用导数判断其在()0,1x ∈上的单调性即可判断选项D ,进而可得正确选项.【详解】对于选项A :因为()0,1x ∈,所以022x ππ<-<,令()sin f x x x =-,()cos 10f x x '=-≤,()sin f x x x =-在0,2π⎛⎫⎪⎝⎭单调递减,所以()()00f x f <=,即sin x x <,所以sin 22x x ππ⎛⎫-<- ⎪⎝⎭即cos 2x x π<-,可得cos 2x x π+<,故A 正确,对于选项B :由图象可得()0,1x ∈,22x x <恒成立,故选项B 正确;对于选项C :要证22sin 24xx x >+ 令()sin 2x f x =,()224xh x x =+()()f x f x -=-,()sin2xf x =是奇函数, ()()h x h x -=,()224x h x x =+是偶函数, 令2224144x t x x ==-++ ,则y t = 因为24y x =+在()0,∞+单调递增,所以2414t x =-+在()0,∞+单调递增,而y t =调递增,由符合函数的单调性可知()224x h x x =+在()0,∞+单调递增, 其函数图象如图所示:由图知当()0,1x ∈时22sin 24xx x >+C 正确; 对于选项D :令()1ln 1x g x x =+-,()01x <<,()221110x g x x x x-'=-=<, 所以()1ln 1x g x x=+-在()0,1单调递减,所以()()1ln1110g x g >=+-=, 即1ln 10x x+->,可得1ln 1x x >-,故选项D 不正确.故选:ABC 【点睛】思路点睛:证明不等式恒成立(或能成立)一般可对不等式变形,分离参数,根据分离参数后的结果,构造函数,由导数的方法求出函数的最值,进而可求出结果;有时也可根据不等式,直接构成函数,根据导数的方法,利用分类讨论求函数的最值,即可得出结果.14.函数()()320ax bx d a f x cx =+++≠有两个极值点1x 、()212x x x <,则下列结论正确的是( ) A .230b ac ->B .()f x 在区间()12,x x 上单调递减C .若()10af x <,则()f x 只有一个零点D .存在0x ,使得()()()1202f x f x f x +=【答案】ACD 【分析】利用极值点与导数的关系可判断A 选项的正误;取0a <,利用函数的单调性与导数的关系可判断B 选项的正误;分0a >、0a <两种情况讨论,分析函数()f x 的单调性,结合图象可判断C 选项的正误;计算出函数()f x 的图象关于点,33b b f a a ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭对称,可判断D 选项的正误.【详解】()()320f x ax bx cx d a =+++≠,则()232f x ax bx c '=++.对于A 选项,由题意可知,关于x 的二次方程()23200ax bx c a ++=≠有两个不等的实根,则24120b ac ∆=->,可得230b ac ->,A 选项正确;对于B 选项,当0a <时,且当()12,x x x ∈时,()0f x '>,此时函数()f x 在区间()12,x x 上单调递增,B 选项错误;对于C 选项,当0a >时,由()0f x '>,可得1x x <或2x x >;由()0f x '<,可得12x x x <<.所以,函数()f x 的单调递增区间为()1,x -∞、()2,x +∞,单调递减区间为()12,x x , 由()10af x <,可得()10<f x ,此时,函数()f x 的极大值为()10<f x ,极小值为()2f x ,且()()210f x f x <<,如下图所示:由图可知,此时函数()f x 有且只有一个零点,且零点在区间()2,x +∞内; 当0a <时,由()0f x '<,可得1x x <或2x x >;由()0f x '>,可得12x x x <<. 所以,函数()f x 的单调递减区间为()1,x -∞、()2,x +∞,单调递增区间为()12,x x , 由()10af x <,可得()10f x >,此时,函数()f x 的极小值为()10f x >,极大值为()2f x ,且()()210f x f x >>,如下图所示:由图可知,此时函数()f x 有且只有一个零点,且零点在区间()2,x +∞内,C 选项正确; 对于D 选项,由题意可知,1x 、2x 是方程2320ax bx c ++=的两根, 由韦达定理可得1223bx x a +=-,123c x x a=, ()()()()()()()()3232f t x f t x a t x b t x c t x d a t x b t x c t x d ⎡⎤⎡⎤-++=-+-+-++++++++⎣⎦⎣⎦()()()()()(322322322322332332a t t x tx x b t tx x c t x d a t t x tx x b t tx x c ⎡⎤⎡=-+-+-++-+++++++++⎣⎦⎣()()322223222a t tx b t x ct d =+++++,取3bt a=-,则322223222333333b b b b b b f x f x a x b x c d a a a a a a ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫--+-+=-+⨯-+-++⋅-+⎢⎥⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦32222223333b b b b a b c d fa a a a ⎛⎫⎛⎫⎛⎫⎛⎫=-+⋅-+⋅-+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,所以,函数()f x 的图象关于点,33b b f a a ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭对称, 1223bx x a+=-,()()1223b f x f x f a ⎛⎫∴+=- ⎪⎝⎭,D 选项正确.故选:ACD. 【点睛】方法点睛:利用导数解决函数零点问题的方法:(1)直接法:先对函数求导,根据导数的方法求出函数的单调区间与极值,根据函数的基本性质作出图象,然后将问题转化为函数图象与x 轴的交点问题,突出导数的工具作用,体现了转化与化归思想、数形结合思想和分类讨论思想的应用; (2)构造新函数法:将问题转化为研究两函数图象的交点问题;(3)参变量分离法:由()0f x =分离变量得出()a g x =,将问题等价转化为直线y a =与函数()y g x =的图象的交点问题.15.设函数cos 2()2sin cos xf x x x=+,则( )A .()()f x f x π=+B .()f x 的最大值为12C .()f x 在,04π⎛⎫- ⎪⎝⎭单调递增 D .()f x 在0,4π⎛⎫⎪⎝⎭单调递减 【答案】AD 【分析】先证明()f x 为周期函数,周期为π,从而A 正确,再利用辅助角公式可判断B 的正误,结合导数的符号可判断C D 的正误. 【详解】()f x 的定义域为R ,且cos 2()2sin cos xf x x x=+,()()()()cos 22cos 2()2sin cos 2sin cos x xf x f x x x x xππππ++===++++,故A 正确.又2cos 22cos 2()42sin cos 4sin 2x x f x x x x ==++,令2cos 24sin 2xy x=+,则()42cos 2sin 22y x y x x ϕ=-=+,其中cos ϕϕ==1≤即2415y ≤,故1515y -≤≤,当y =时,有1cos 4ϕϕ==,此时()cos 21x ϕ+=即2x k ϕπ=-,故max 15y =,故B 错误.()()()()()22222sin 24sin 22cos 2414sin 2()4sin 24sin 2x x x x f x x x ⎡⎤-+--+⎣⎦'==++,当0,4x π⎛⎫∈ ⎪⎝⎭时,()0f x '<,故()f x 在0,4π⎛⎫⎪⎝⎭为减函数,故D 正确. 当,04x π⎛⎫∈-⎪⎝⎭时,1sin20x -<<,故314sin 21x -<+<, 因为2t x =为增函数且2,02x π⎛⎫∈- ⎪⎝⎭,而14sin y t =+在,02π⎛⎫- ⎪⎝⎭为增函数,所以()14sin 2h x x =+在,04π⎛⎫- ⎪⎝⎭上为增函数, 故14sin 20x +=在,04π⎛⎫-⎪⎝⎭有唯一解0x , 故当()0,0x x ∈时,()0h x >即()0f x '<,故()f x 在()0,0x 为减函数,故C 不正确. 故选:AD 【点睛】方法点睛:与三角函数有关的复杂函数的研究,一般先研究其奇偶性和周期性,而单调性的研究需看函数解析式的形式,比如正弦型函数或余弦型函数可利用整体法来研究,而分式形式则可利用导数来研究,注意辅助角公式在求最值中的应用.16.设函数()ln f x x x =,()212g x x =,给定下列命题,其中正确的是( ) A .若方程()f x k =有两个不同的实数根,则1,0k e⎛⎫∈- ⎪⎝⎭; B .若方程()2kf x x =恰好只有一个实数根,则0k <;C .若120x x >>,总有()()()()1212m g x g x f x f x ->-⎡⎤⎣⎦恒成立,则m 1≥;D .若函数()()()2F x f x ag x =-有两个极值点,则实数10,2a ⎛⎫∈ ⎪⎝⎭. 【答案】ACD 【分析】利用导数研究函数的单调性和极值,且将题意转化为()y f x =与y k =有两个不同的交点,即可判断A 选项;易知1x =不是该方程的根,当1x ≠时,将条件等价于y k =和ln xy x=只有一个交点,利用导数研究函数的单调性和极值,从而可推出结果,即可判断B 选项;当120x x >>时,将条件等价于1122()()()()mg x f x mg x f x ->-恒成立,即函数()()y mg x f x =-在(0,)+∞上为增函数,通过构造新函数以及利用导数求出单调区间,即可求出m 的范围,即可判断C 选项;2()ln (0)F x x x ax x =->有两个不同极值点,根据导数的符号列出不等式并求解,即可判断D 选项. 【详解】解:对于A ,()f x 的定义域(0,)+∞,()ln 1f x x '=+, 令()0f x '>,有ln 1x >-,即1x e>, 可知()f x 在1(0,)e 单调递减,在1+e∞(,)单调递增,所以极小值等于最小值, min 11()()f x f e e∴==-,且当0x →时()0f x →,又(1)0f =,从而要使得方程()f x k =有两个不同的实根,即()y f x =与y k =有两个不同的交点,所以1(,0)k e∈-,故A 正确; 对于B ,易知1x =不是该方程的根,当1x ≠时,()0f x ≠,方程2()kf x x =有且只有一个实数根,等价于y k =和ln xy x=只有一个交点, 2ln 1(ln )-'=x y x ,又0x >且1x ≠, 令0y '>,即ln 1x >,有x e >, 知ln xy x=在0,1()和1e (,)单减,在+e ∞(,)上单增, 1x =是一条渐近线,极小值为e ,由ln xy x=大致图像可知0k <或=k e ,故B 错误;对于C ,当120x x >>时,[]1212()()()()m g x g x f x f x ->-恒成立, 等价于1122()()()()mg x f x mg x f x ->-恒成立, 即函数()()y mg x f x =-在(0,)+∞上为增函数, 即()()ln 10y mg x f x mx x =-''--'=≥恒成立,即ln 1+≥x m x在(0,)+∞上恒成立, 令ln 1()x r x x +=,则2ln ()xr x x -'=,令()0r x '>得ln 0x <,有01x <<,从而()r x 在(0,1)上单调递增,在(1,)+∞上单调递减, 则max ()(1)1r x r ==,于是m 1≥,故C 正确;对于D ,2()ln (0)F x x x ax x =->有两个不同极值点, 等价于()ln 120F x x ax +-'==有两个不同的正根,即方程ln 12x a x+=有两个不同的正根, 由C 可知,021a <<,即102a <<,则D 正确. 故选:ACD.【点睛】关键点点睛:本题考查导数的应用,利用导数研究函数的单调性和极值,以及利用导数解决函数的零点问题和恒成立问题从而求参数范围,解题的关键在于将零点问题转化成两个函数的交点问题,解题时注意利用数形结合,考查转化思想和运算能力.17.设函数3()(,)f x x ax b a b R =++∈,下列条件中,使得()y f x =有且仅有一个零点的是( ) A .1,2a b == B .3,3a b =-=- C .0,2a b >< D .0,0a b <>【答案】ABC 【分析】求导2()3f x x a '=+,分0a ≥和0a <进行讨论,当0a ≥时,可知函数单调递增,有且只有一个零点;当0a <时,讨论函数的单调性,要使函数有一个零点,则需比较函数的极大值与极小值与0的关系,再验证选项即可得解. 【详解】3()f x x ax b =++,求导得2()3f x x a '=+当0a ≥时,()0f x '≥,()f x ∴单调递增,当x →-∞时,()f x →-∞;当x →+∞时,()f x →+∞;由零点存在性定理知,函数()f x 有且只有一个零点,故A ,C 满足题意;当0a <时,令()0f x '=,即230x a +=,解得13ax -=-23a x -=当x 变化时,()'f x ,()f x 的变化情况如下表:x,3a ⎛⎫--∞- ⎪ ⎪⎝⎭3a-- ,33a a ⎛⎫--- ⎪ ⎪⎝⎭3a- ,3a ⎛⎫-+∞ ⎪ ⎪⎝⎭()'f x+-+()f x 极大值 极小值故当3ax -=-,函数()f x 取得极大值2333333a a a a a a f a b b ⎛⎫-----=-+=-+ ⎪ ⎪⎝⎭, 当3a x -=,函数()f x 取得极小值2333333a a a a a a f a b b ⎛⎫-----=++=+ ⎪ ⎪⎝⎭又当x →-∞时,()f x →-∞;当x →+∞时,()f x →+∞; 要使函数()f x 有且只有一个零点,作草图或则需0303a f a f ⎧⎛--<⎪ ⎪⎝⎨-⎪<⎪⎩,即20332033a a b a a b ⎧-<⎪⎪⎨-⎪<⎪⎩,即2033a ab -<<,B 选项,3,3a b =-=-,满足上式,故B 符合题意;则需0303a f a f ⎧⎛-->⎪ ⎪⎝⎨-⎪>⎪⎩,即20332033a a b a a b ⎧->⎪⎪⎨-⎪>⎪⎩,即2033a ab ->>,D 选项,0,0a b <>,不一定满足,故D 不符合题意; 故选:ABC 【点睛】思路点睛:本题考查函数的零点问题,如果函数()y f x =在区间[,]a b 上的图像是连续不断的一条曲线,并且有()()0f a f b <,那么,函数()y f x =在区间(),a b 内有零点,即存在(),c a b ∈,使得()0f c =,这个c 也就是方程()0f x =的根,考查学生的逻辑推理与运算能力,属于较难题.18.对于定义在1D 上的函数()f x 和定义在2D 上的函数()g x ,若直线y kx b =+(),k b R ∈同时满足:①1x D ∀∈,()f x kx b ≤+,②2x D ∀∈,()g x kx b ≥+,则称直线y kx b =+为()f x 与()g x 的“隔离直线”.若()ln xf x x=,()1x g x e -=,则下列为()f x 与()g x 的隔离直线的是( )A .y x =B .12y x =-C .3ex y =D .1122y x =- 【答案】AB 【分析】根据隔离直线的定义,函数()y f x =的图象总在隔离直线的下方,()y g x =的图象总在隔离直线的上方,并且可以有公共点,结合函数的图象和函数的单调性,以及直线的特征,逐项判定,即可求解. 【详解】根据隔离直线的定义,函数()y f x =的图象总在隔离直线的下方,()y g x =的图象总在隔离直线的上方,并且可以有公共点, 由函数()ln x f x x =,可得()21ln xf x x-'=, 所以函数()f x 在()0,e 上单调递增,在(),e +∞上单调递减,因为()10f =,()11f '=,此时函数()f x 的点(1,0)处的切线方程为1y x =-, 且函数()f x 的图象在直线1y x =-的下方; 又由函数()1x g x e-=,可得()1e0x g x -'=>,()g x 单调递增,因为()()111g g '==,所以函数()g x 在点(1,1)处的切线方程为11y x -=-,即y x =, 此时函数()g x 的图象在直线y x =的上方,根据上述特征可以画出()y f x =和()y g x =的大致图象,如图所示,直线1y x =-和y x =分别是两条曲线的切线,这两条切线以及它们之间与直线y x =平行的直线都满足隔离直线的条件,所以A ,B 都符合; 设过原点的直线与函数()y f x =相切于点00(,)P x y , 根据导数的几何意义,可得切线的斜率为021ln x k x -=, 又由斜002000ln 0y x k x x -==-,可得002100ln 1ln x x x x -=,解得0x =,所以12k e ==,可得切线方程为2x y e =, 又由直线3xy e=与曲()y f x =相交,故C 不符合; 由直线1122y x =-过点()1,0,斜率为12,曲线()y f x =在点()1,0处的切线斜率为1,明显不满足,排除D. 故选:AB.【点睛】对于函数的新定义试题:(1)认真审题,正确理解函数的新定义,合理转化;(2)根据隔离直线的定义,转化为函数()y f x =的图象总在隔离直线的下方,()y g x =的图象总在隔离直线的上方.19.若存在实常数k 和b ,使得函数()F x 和()G x 对其公共定义域上的任意实数x 都满足:()F x kx b ≥+和()G x kx b ≤+恒成立,则称此直线y kx b =+为()F x 和()G x 的“隔离直线”,已知函数()()2f x x R x =∈,()()10g x x x=<,()2eln h x x =(e 为自然对数的底数),则下列结论正确的是( ) A .()()()m x f x g x =-在32x ⎛⎫∈ ⎪⎝⎭内单调递增 B .()f x 和()g x 之间存在“隔离直线,且b 的最小值为4 C .()f x 和()g x 间存在“隔离直线”,且k 的取值范围是(]4,1- D .()f x 和()h x 之间存在唯一的“隔离直线”2e e y x =- 【答案】AD 【分析】求出()()()m x f x g x =-的导数,检验在32x ⎛⎫∈ ⎪⎝⎭内的导数符号,即可判断选项A ;选项B 、C 可设()f x 、()g x 的隔离直线为y kx b =+,2x kx b ≥+对一切实数x 都成立,即有10∆≤,又1kx b x≤+对一切0x <都成立,20∆≤,0k ≤,0b ≤,根据不等式的性质,求出k 、b 的范围,即可判断选项B 、C ;存在()f x 和()h x 的隔离直线,那么该直线过这个公共点,设隔离直线的斜率为k ,则隔离直线的方程为(y e k x e -=,构造函数求出函数的导数,根据导数求出函数的最值.。
高三数学培优训练(二)

高三数学培优训练(二)1、若集合A 和B 各含6个元素,A ∩B 含有3个元素,C 同时满足两个条件:①C ⊂A ∪B 且C 中含有3个元素;②C ∩A ≠φ,则如此的集合C 的个数是( ) A .82 B .83 C .84 D .219 2、下列各组命题中,满足“p 或q ”为真,“p 且q ”为假,“非p ”为确实是( ) A .p :0=φ;q :0∈φB .p :在△ABC 中,若cos2A=cos2B ,则A=B ;q :y=sinx 在第一象限是增函数 C .p :a+b ≥2ab (a ,b ∈R );q :不等式|x|>x 的解集为(-∞,0)D .p :y=|2sinx|>2;q :y=3sinx(tanxtan2x)的最小正周期为π 3、已知数列}{n a 的通项公式)(21log *2N n n n a n ∈++=,设其前n 项和为n S ,则使5-<n S 成立的自然数n ( )A .有最小值63B .有最大值63C .有最小值31D .有最大值314、等比数列{a n }中,a 1=512,公比q=21-,用n ∏表示它的前n 项之积:21a a n ⋅=∏…n a , 则21∏∏,,…,中最大的是 ( ) A .11∏ B .10∏ C .9∏ D .8∏5、已知函数f(x)=1(0)0(0)1(0)x x x -<⎧⎪=⎨⎪>⎩, 则2 b)-f(a )(•-++b a b a (a ≠b)的值应为( )A | a |B | b |C a, b 之中较少的数D a, b 之中较大的数6、已知→a ,→b ,→c 是三个非零向量,命题|||:|→→=b a p ,命题:q ||||→→→→⋅=⋅c b c a ,则p 是q 的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件7、如图甲所示,点P 在边长为1的正方形边上运动,设M 是CD 的中点,则当P 沿A —B —C —运动时,点P 通过的路程x 为自变量,△APM 的面积为y 的函数,则)(x f y =的图象形状大致是( )8、如图所示,在正方体ABCD —A 1B 1C 1D 1的侧面AB 1内有一动点P 到直线A 1B 1与直线BC 的距离相等,则动点P 所在曲线形状为( )9、抽象函数是由专门的、具体的函数抽象而得到的.如正比例函数)0()(≠=k kx x f ,)()()()(,)(,)(212121212211x f x f kx kx x x k x x f kx x f kx x f +=+=+=+==可抽象为写出下列抽象函数是由什么专门函数抽象而成(每项填入一个函数即可). 特 殊 函 数 抽 象 函 数)()()(y f x f y x f =+)()()(y f x f xy f +=)()(1)()()(y f x f y f x f y x f -+=+ 10、下列命题:①动点M 至两定点A 、B 的距离之比为常数λλλ.则动点M 的轨迹是圆.②椭圆c c b e b a by a x (,22)0(12222==>>=+则的离心率为半焦距)③双曲线)0,0(12222>>=-b a b y a x 的焦点到渐近线的距离为b ④已知抛物线),(),,(222112y x B y x A px y 上两点=且OA ⊥OB (O 为原点).则221p y y -=⋅。
高三数学数学数列多选题的专项培优练习题(含答案

高三数学数学数列多选题的专项培优练习题(含答案一、数列多选题1.已知等比数列{}n a 的公比为q ,前n 项和0n S >,设2132n n n b a a ++=-,记{}n b 的前n 项和为n T ,则下列判断正确的是( ) A .若1q =,则n n T S = B .若2q >,则n n T S > C .若14q =-,则n n T S > D .若34q =-,则n n T S > 【答案】BD 【分析】先求得q 的取值范围,根据q 的取值范围进行分类讨论,利用差比较法比较出n T 和n S 的大小关系. 【详解】由于{}n a 是等比数列,0n S >,所以110,0a S q =>≠, 当1q =时,10n S na =>,符合题意; 当1q ≠时,()1101n n a q S q-=>-,即101nq q ->-,上式等价于1010n q q ⎧->⎨->⎩①或1010n q q ⎧-<⎨-<⎩②.解②得1q >.解①,由于n 可能是奇数,也可能是偶数,所以()()1,00,1q ∈-.综上所述,q 的取值范围是()()1,00,-+∞.2213322n n n n b a a a q q ++⎛⎫=-=- ⎪⎝⎭,所以232n n T q q S ⎛⎫=- ⎪⎝⎭,所以()2311222n n n n T S S q q S q q ⎛⎫⎛⎫-=⋅--=⋅+⋅- ⎪ ⎪⎝⎭⎝⎭,而0n S >,且()()1,00,q ∈-⋃+∞.所以,当112q -<<-,或2q >时,0n n T S ->,即n n T S >,故BD 选项正确,C 选项错误. 当12(0)2q q -<<≠时,0n n T S -<,即n n T S <. 当12q =-或2q 时,0,n n n n T S T S -==,A 选项错误.综上所述,正确的选项为BD. 故选:BD 【点睛】本小题主要考查等比数列的前n 项和公式,考查差比较法比较大小,考查化归与转化的数学思想方法,考查分类讨论的数学思想方法,属于中档题.2.已知数列{}n a 的前n 项和为n S ,11a =,()1*11,221,21n n n a n ka k N a n k --+=⎧=∈⎨+=+⎩.则下列选项正确的为( ) A .614a =B .数列{}()*213k a k N-+∈是以2为公比的等比数列C .对于任意的*k N ∈,1223k k a +=-D .1000n S >的最小正整数n 的值为15 【答案】ABD 【分析】根据题设的递推关系可得2212121,21k k k k a a a a -+=-=-,从而可得22222k k a a +-=,由此可得{}2k a 的通项和{}21k a -的通项,从而可逐项判断正误.【详解】由题设可得2212121,21k k k k a a a a -+=-=-, 因为11a =,211a a -=,故2112a a =+=,所以22212121,12k k k k a a a a +++--==,所以22222k k a a +-=, 所以()222222k k a a ++=+,因为2240a +=≠,故220k a +≠,所以222222k k a a ++=+,所以{}22k a +为等比数列, 所以12242k k a -+=⨯即1222k k a +=-,故416214a =-=,故A 对,C 错. 又112122123k k k a ++-=--=-,故12132k k a +-+=,所以2121323k k a a +-+=+,即{}()*213k a k N -+∈是以2为公比的等比数列,故B 正确. ()()141214117711S a a a a a a a =+++=++++++()()2381357911132722323237981a a a a a a a =+++++++=⨯-+-++-+=,15141598150914901000S S a =+=+=>,故1000n S >的最小正整数n 的值为15,故D 正确. 故选:ABD. 【点睛】方法点睛:题设中给出的是混合递推关系,因此需要考虑奇数项的递推关系和偶数项的递推关系,另外讨论D 是否成立时注意先考虑14S 的值.3.设数列{}n a 前n 项和n S ,且21n n S a =-,21log n n b a +=,则( ) A .数列{}n a 是等差数列 B .12n n aC .22222123213n na a a a -++++= D .122334111111n n b b b b b b b b +++++< 【答案】BCD 【分析】利用n S 与n a 的关系求出数列{}n a 的通项公式,可判断AB 选项的正误;利用等比数列的求和公式可判断C 选项的正误;利用裂项求和法可判断D 选项的正误. 【详解】对任意的n *∈N ,21n n S a =-.当1n =时,11121a S a ==-,可得11a =; 当2n ≥时,由21n n S a =-可得1121n n S a --=-, 上述两式作差得122n n n a a a -=-,可得12n n a a -=,所以,数列{}n a 是首项为1,公比为2的等比数列,11122n n n a --∴=⨯=,A 选项错误,B选项正确;()221124n n na --==,所以,22221231441143nn n a a a a --==-++++,C 选项正确; 212log log 2nn n b a n +===,()1111111n n b b n n n n +==-++, 所以,12233411111111111111112233411n n b b b b b b b b n n n +++++=-+-+-++-=-<++, D 选项正确. 故选:BCD. 【点睛】方法点睛:数列求和的常用方法:(1)对于等差等比数列,利用公式法直接求和;(2)对于{}n n a b 型数列,其中{}n a 是等差数列,{}n b 是等比数列,利用错位相减法求和;(3)对于{}n n a b +型数列,利用分组求和法;(4)对于11n n a a +⎧⎫⎨⎬⎩⎭型数列,其中{}n a 是公差为()0d d ≠的等差数列,利用裂项相消法求和.4.两个等差数列{}n a 和{}n b ,其公差分别为1d 和2d ,其前n 项和分别为n S 和n T ,则下列命题中正确的是( )A .若为等差数列,则112da =B .若{}n n S T +为等差数列,则120d d +=C .若{}n n a b 为等差数列,则120d d ==D .若*n b N ∈,则{}n b a 也为等差数列,且公差为12d d +【答案】AB 【分析】对于A ,利用=对于B ,利用()2211332S T S T S T +=+++化简可得答案; 对于C ,利用2211332a b a b a b =+化简可得答案; 对于D ,根据112n n b b a a d d +-=可得答案. 【详解】对于A ,因为为等差数列,所以=即== 化简得()21120d a -=,所以112d a =,故A 正确;对于B ,因为{}n n S T +为等差数列,所以()2211332S T S T S T +=+++, 所以()11121111122223333a d b d a b a d b d +++=+++++, 所以120d d +=,故B 正确;对于C ,因为{}n n a b 为等差数列,所以2211332a b a b a b =+, 所以11121111122()()(2)(2)a d b d a b a d b d ++=+++, 化简得120d d =,所以10d =或20d =,故C 不正确;对于D ,因为11(1)n a a n d =+-,且*n b N ∈,所以11(1)n b n a a b d =+-()112111a b n d d =++--⎡⎤⎣⎦,所以()()1111211n b a a b d n d d =+-+-,所以()()()11111211112111n n b b a a a b d nd d a b d n d d +-=+-+-----12d d =, 所以{}n b a 也为等差数列,且公差为12d d ,故D 不正确. 故选:AB 【点睛】关键点点睛:利用等差数列的定义以及等差中项求解是解题关键.5.已知数列{}n a ,{}n b 满足,11a =,11n n n a a a +=+,1(1)n n b n a =+,若23100100122223100b b b T b =++++,则( ) A .n a n = B .1n n b n =+ C .100100101T =D .10099100T =【答案】BC 【分析】 先证明数列1n a 是等差数列得1n a n=,进而得1(1)1n n n b n a n ==++,进一步得()211111n b n n n n n ==-++,再结合裂项求和得100100101T =. 【详解】 解:因为11nn n a a a +=+,两边取倒数得:1111n n a a +=+,即1111n na a ,所以数列1na 是等差数列,公差为1,首项为111a ,故()1111n n n a =+-⨯=,所以1n a n=, 所以1(1)1n n nb n a n ==++,故()211111n b n n n n n ==-++, 所以31002100122211112310022334100101b b b T b =++++=++++⨯⨯⨯11111111100122334100101101101⎛⎫⎛⎫⎛⎫=+-+-++-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 故BC 正确,AD 错误; 故选:BC 【点睛】本题考查数列通项公式的求解,裂项求和,考查运算求解能力,是中档题.本题解题的关键在于证明数列1na 是等差数列,进而结合裂项求和求解100T .6.首项为正数,公差不为0的等差数列{}n a ,其前n 项和为n S ,则下列4个命题中正确的有( )A .若100S =,则50a >,60a <;B .若412S S =,则使0n S >的最大的n 为15;C .若150S >,160S <,则{}n S 中7S 最大;D .若89S S <,则78S S <. 【答案】ABD 【分析】利用等差数列的求和公式及等差数列的性质,逐一检验选项,即可得答案. 【详解】对于A :因为正数,公差不为0,且100S =,所以公差0d <, 所以1101010()02a a S +==,即1100a a +=, 根据等差数列的性质可得561100a a a a +=+=,又0d <, 所以50a >,60a <,故A 正确; 对于B :因为412S S =,则1240S S -=,所以561112894()0a a a a a a ++⋅⋅⋅++=+=,又10a >, 所以890,0a a ><, 所以115815815()15215022a a a S a +⨯===>,116891616()16()022a a a a S ++===, 所以使0n S >的最大的n 为15,故B 正确; 对于C :因为115815815()15215022a a a S a +⨯===>,则80a >, 116891616()16()022a a a a S ++===,则890a a +=,即90a <, 所以则{}n S 中8S 最大,故C 错误;对于D :因为89S S <,则9980S a S =->,又10a >, 所以8870a S S =->,即87S S >,故D 正确, 故选:ABD 【点睛】解题的关键是先判断d 的正负,再根据等差数列的性质,对求和公式进行变形,求得项的正负,再分析和判断,考查等差数列性质的灵活应用,属中档题.7.设等差数列{}n a 的前n 项和为n S ,公差为d .已知312a =,120S >,70a <则( ) A .60a > B .数列1n a ⎧⎫⎨⎬⎩⎭是递增数列 C .0nS <时,n 的最小值为13D .数列n n S a ⎧⎫⎨⎬⎩⎭中最小项为第7项 【答案】ACD由已知得()()612112712+12+220a a a a S ==>,又70a <,所以6>0a ,可判断A ;由已知得出2437d -<<-,且()12+3n a n d =-,得出[]1,6n ∈时,>0n a ,7n ≥时,0n a <,又()1112+3n a n d =-,可得出1n a 在1,6n n N上单调递增,1na 在7nnN ,上单调递增,可判断B ;由()313117713+12203213a a a S a ⨯==<=,可判断C ;判断 n a ,n S 的符号, n a 的单调性可判断D ; 【详解】由已知得311+212,122d a a a d ===-,()()612112712+12+220a a a a S ==>,又70a <,所以6>0a ,故A 正确;由7161671+612+40+512+3>0+2+1124+7>0a a d d a a d d a a a d d ==<⎧⎪==⎨⎪==⎩,解得2437d -<<-,又()()3+312+3n a n d n d a =-=-,当[]1,6n ∈时,>0n a ,7n ≥时,0n a <,又()1112+3n a n d=-,所以[]1,6n ∈时,1>0na ,7n ≥时,10n a <,所以1na 在1,6n n N上单调递增,1na 在7n n N,上单调递增,所以数列1n a ⎧⎫⎨⎬⎩⎭不是递增数列,故B 不正确; 由于()313117713+12203213a a a S a ⨯==<=,而120S >,所以0n S <时,n 的最小值为13,故C 选项正确 ;当[]1,6n ∈时,>0n a ,7n ≥时,0n a <,当[]1,12n ∈时,>0n S ,13n ≥时,0n S <,所以当[]7,12n ∈时,0n a <,>0n S ,0nnS a <,[]712n ∈,时,n a 为递增数列,n S 为正数且为递减数列,所以数列n n S a ⎧⎫⎨⎬⎩⎭中最小项为第7项,故D 正确;本题考查等差数列的公差,项的符号,数列的单调性,数列的最值项,属于较难题.8.已知等差数列{}n a 的公差0d ≠,前n 项和为n S ,且112n n n S a a +=⋅-,则( )A .12d =B .11a =C .数列{}n a 中可以取出无穷多项构成等比数列D .设(1)nn n b a =-⋅,数列{}n b 的前n 项和为n T ,则2n T n =【答案】AC 【分析】利用已知条件可得11212n n n S a a +++=-与已知条件两式相减,结合{}n a 是等差数列,可求d的值即可判断选项A ,令1n =即可求1a 的值,可判断选项B ,分别计算{}n a 的通项即可判断选项C ,分别讨论两种情况下21212n n b b -+=,即可求2n T 可判断选项D. 【详解】 因为112n n n S a a +=-,所以11212n n n S a a +++=-, 两式相减,得()11212n n n n n a a a a da ++++=-=, 因为0d ≠,所以21d =,12d =,故选项 A 正确; 当1n =时,1111122a a a ⎛⎫=+- ⎪⎝⎭,易解得11a =或112a =-,故选项B 不正确;由选项A 、B 可知,当112a =-,12d =时,()1111222n na n =-+-⨯=-,{}n a 可取遍所有正整数,所以可取出无穷多项成等比数列,同理当()()1111122n a n n =+-⨯=+时也可以取出无穷多项成等比数列,故选项C 正确; 当()112n a n =+时,()221212n n b a n ==+,()212112112n n b a n n --=-=--+=-, 因为21221212n n n n b b a a --+=-+=, 所以()()()212342122n n n n T b b b b b b -=++++++=, 当12n n a =-时,2212112n n b a n n ==⨯-=-,2121213122n n n b a n ---⎛⎫=-=--=-⎪⎝⎭,所以22131122n n b b n n -+=-+-=, 此时()()()22212223212n n n n n nT b b b b b b ---=++++++=, 所以2n T n ≠,故选项D 不正确. 故选:AC. 【点睛】方法点睛:数列求和的方法(1)倒序相加法:如果一个数列{}n a 的前n 项中首末两端等距离的两项的和相等或等于同一个常数,那么求这个数列的前n 项和即可以用倒序相加法(2)错位相减法:如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的,那么这个数列的前n 项和即可以用错位相减法来求;(3)裂项相消法:把数列的通项拆成两项之差,在求和时,中间的一些项可相互抵消,从而求得其和;(4)分组转化法:一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成,则求和时可用分组转换法分别求和再相加减;(5)并项求和法:一个数列的前n 项和可以两两结合求解,则称之为并项求和,形如()()1nn a f n =-类型,可采用两项合并求解.二、平面向量多选题9.在ABC 中,角,,A B C 所对的边分别为,,a b c ,已知()()(::5:)4:6b c c a a b +++=,下列结论正确的是( )A .::7:5:3sinA sinB sinC = B .0AB AC ⋅>C .若6c =,则ABC 的面积是D .若8+=b c ,则ABC 【答案】ACD 【分析】先利用已知条件设4,5,6b c k c a k a b k +=+=+=,进而得到3.5, 2.5, 1.5a k b c k ===,利用正弦定理可判定选项A ;利用向量的数量积公式可判断选项B ;利用余弦定理和三角形的面积公式可判定选项C ;利用余弦定理和正弦定理可判断选项D. 【详解】依题意,设4,5,6b c k c a k a b k +=+=+=, 所以 3.5, 2.5, 1.5a k b c k ===,由正弦定理得:::::7:5:3sinA sinB sinC a b c ==, 故选项A 正确;222222cos 22b c a b c a AB AC bc A bc bc +-+-⋅==⨯=222222.5 1.5 3.515028k k +-==-<,故选项B 不正确;若6c =,则4k =, 所以14,10a b ==,所以222106141cos 21062A +-==-⨯⨯,所以sin A =,故ABC 的面积是:11sin 61022bc A =⨯⨯= 故选项C 正确;若8+=b c ,则2k =, 所以7,5,3a b c ===,所以2225371cos 2532A +-==-⨯⨯,所以sin 2A =, 则利用正弦定理得:ABC 的外接圆半径是:12sin a A ⨯=, 故选项D 正确; 故选:ACD. 【点睛】关键点睛:本题主要考查正余弦定理以及三角形面积公式. 利用已知条件设4,5,6b c k c a k a b k +=+=+=,再利用正余弦定理以及三角形面积公式求解是解决本题的关键.10.如图,在平行四边形ABCD 中,,E F 分别为线段,AD CD 的中点,AF CE G =,则( )A .12AF AD AB =+ B .1()2EF AD AB =+C .2133AG AD AB =- D .3BG GD =【答案】AB【分析】 由向量的线性运算,结合其几何应用求得12AF AD AB =+、1()2EF AD AB =+、2133AG AD AB =+、2BG GD =,即可判断选项的正误 【详解】 1122AF AD DF AD DC AD AB =+=+=+,即A 正确 11()()22EF ED DF AD DC AD AB =+=+=+,即B 正确 连接AC ,知G 是△ADC 的中线交点, 如下图示由其性质有||||1||||2GF GE AG CG == ∴211121()333333AG AE AC AD AB BC AD AB =+=++=+,即C 错误 同理21212()()33333BG BF BA BC CF BA AD AB =+=++=- 211()333DG DF DA AB DA =+=+,即1()3GD AD AB =- ∴2BG GD =,即D 错误故选:AB【点睛】本题考查了向量线性运算及其几何应用,其中结合了中线的性质:三角形中线的交点分中线为1:2,以及利用三点共线时,线外一点与三点的连线所得向量的线性关系。
高三数学培优补差辅导检测试卷

高三数学辅导检测试卷一、选择题1、 已知集合 U={h 2, 3, 4, 5, 6, 7}, A={2, 4, 5, 7}, B={3, 4, 5}则心A)U(:B) =A 、{1, 6} B. {4, 5)C 、{2, 3, 4, 5, 7}D 、{1, 2, 3, 6, 7}提示:运用韦恩图解决•选D 2、 已知条件p : lx + ll>2,条件q : x>a,且「p 是F 的充分不必要条件,则"的取值范围可以是(A )A, a>\; B, t/ < 1 : C, «>-l : Dt 6/ <—3: 提示:lx + ll<2^-3<x<l ; ry : x<«.据题意:「p 中的元素都是F 中的元 素,反之不成立.运用数轴可直观得岀选AT T T T T T Iff3、 已知向量"=(2,3), b = (—l,2),若ma+nh 与a —2b 共线,则一等于(A )nA, —:B, —:C, —2:D, 2:2 2提示:两个向量共线,依据两个向量共线基本左理可得:有且只有一个非零实数几,使得 f TfJJ —几=0 1>2 因为4b 均为非零向量,所以{ => —= 一一n + 22 = 0 n 2也可以利用向量的坐标运算解决:由:=(2,3),恳=(72)可得:f f , T T T To_2b=(2,3)_2(_l,2)=(4,_l )•因为ma+nb 与 a —2b 共线,所以 4(3加 + 2”)+ (2m -;?) = 0 => 14〃? = -7z? => ~=~~24、若函数y = f(x)在[(M]上单调,则使得y = /(x+3)必为单调函数区间的是A. [«,/? +3]B. [a + 3,b + 3] C 、[°一3,/? — 3]D 、[a + 3,b]提示:本题考查函数的图彖的左右平移变换•函数y = /(x+3)的图象可由函数y = f(x)的图象向左平移3个单位得到,故y = f(x+3)的单调区间可由函数y = f(x)的单调 区间向左平移3个单位•即S — 30 —3]•故选Call P①ally其中正确的命题是(C )A, ©®; B,②③: C,①③:提示:命题1:平行于同一个平面的两个平而互相平行,正确:命题厶两个平而互相垂直,平行于其中一个平而的直线与第二个平而的位置关系有 “平行二“相交且垂直二"相交但不垂直二"在第二个平面内等多种情况:"=> mH a : D, ®@;5、设加屮是不同的直线,a 、卩、厂是不同的平而,有以下四个命题命题3:直线〃〃/0,依据直线与平而平行的性质圧理,在平而0内一泄存在一条直线nllm,则因为加丄a,所以死丄a,由两个平面垂直的判定定理可得a丄0 •正确.命题4:由直线与平而平行的判立泄理知,不正确. 故选C6、已矢口a-p )cosa-cos( a_ 卩)sina =—,那么cos 2/3的值为(A)文档从网络中收集, 已重新整理排版.word 版本可编借•欢迎下载支持.7 25提示:本题考查两角和与差三角函数公式的灵活运用,3 / 3 由 sin ( a_ 卩)cos a 一 cos ( a_ 卩)sin a =二得 sin p = -- i Q 7 所以cosip = 1 -2sin 2p = \^— = 一 •选 A 25 25 A、 725 B、 1825 C、D、18 257、已知gb 、c 成等比数列,a^b 和®”c 都成等差数列,且与H0,那么-+ -的值为 % y (B )o(A) 1 (D) 4 (B ) 2 b 2 =ac 2x = a + b 2y=b+c 2b 2+b (a + c ) ay + ex = ------- ----- 』 2 ' 4 8、 已知y = /(x )存在反函数y = g (x ),若/(3) = -l.则函数>,= g (x_l )的图象必经 过下列各点中的(B ). A. (一2,3) B. (0, 3) C ・(一2, 1) D ・(4, -1)9、 (福建•理・10题)顶点在同一球而上的正四棱柱ABCD-MCPi 中,人3 = 1,側=忑,B )C .如 D.如 4 2 10、 若直线y = kx+l 与圆x 2+y 2=l 相交于P 、Q 两点,且ZPOQ=120。
中学高三数学 课外培优练习2

广东省始兴县风度中学高三数学 课外培优练习1.从编号分别为1,2,…,9的9张卡片中任意抽取3张,将它们的编号从小到大依次记为x ,y ,z ,则y - x ≥2,z - y ≥2的概率为( )A 、13B 、512C 、14D 、5282、设l 为平面上过点()01,的直线,l 的斜率等可能地取022--,ξ表示坐标原点到l 的距离,则随机变量ξ的数学期望E ξ= 。
3、箱中装有大小相同的黄、白两种颜色的乒乓球,黄、白乒乓球的数量比为t s :.现从箱中每次任意取出一个球,若取出的是黄球则结束,若取出的是白球,则将其放回箱中,并继续从箱中任意取出一个球,但取球的次数最多不超过n 次.以ξ表示取球结束时已取到白球的次数. (Ⅰ)求ξ的分布列; (Ⅱ)求ξ的数学期望.4、据某地气象部门统计,该地区每年最低气温在C 02-以下的概率为31 (1)设ξ为该地区从2005年到2010年最低气温在C 02-以下的年数,求ξ的分布列。
(2)设η为该地区从2005年到2010年首次遇到最低气温在C 02-以下经过的年数,求η的分布列。
(3)求该地区从2005年到2010年至少遇到一次最低气温在C 02-以下的概率。
1.解:法一:(1)当x = 1,y 分别取3 , 4 ,5 , 6 , 7时,对应的取法分别有5 , 4 , 3 , 2 , 1种; (2)当x =2,y 分别取4 , 5 , 6 , 7时,对应的取法分别有4 , 3 , 2 , 1种;……共有5种情况,故适合y – x ≥2,z – y ≥ 2的取法共有 (5+4+3+2+1) + (4+3+2+1) + (3+2+1) + (2+1) + 1 = 35种.故31035512p C ==为所求. 3.解:(Ⅰ)取出黄球的概率是t s s A P +=)(,取出白球的概率是ts tA P +=)(,则 t s sP +==)0(ξ, 2)()1(t s st P +==ξ, 32)()2(t s st P +==ξ, ……, n n t s st n P )()1(1+=-=-ξ, nn t s st n P )()(1+==-ξ,∴ξ的分布列是ξ 0 1 2 …1-nnPts s + 2)(t s st + 32)(t s st +…n n t s st )(1+- nnt s t )(+(Ⅱ)++⨯++⨯++⨯=322)(2)(10t s st t s st t s s E ξ…n nn n t s t n t s st n )()()1(1+⨯++⨯-+- ①++++=+4332)(2)(t s st t s st E t s t ξ (11)11)()()1()()2(+++-+++-++-+n n n n n n t s nt t s st n t s st n ②①—②得++++++=+43322)()()(t s st t s st t s st E t s s ξ (11)11)()()1()()(+++-+-+--++++n n n n n n n n t s nt t s st n t s nt t s st∴ 11)()1()()()1(-++-++-+--=n nn n n n t s t n t s s nt t s t n s t E ξ∴ξ的数学期望是11)()1()()()1(-++-++-+--=n nn n n n t s t n t s s nt t s t n s t E ξ.4.(1)将每年的气温情况看做一次试验,则遇到最低气温在C 02-以下的概率为31,且每次实验结果是相互独立的。
高三数学 数学多选题专项训练的专项培优练习题(含答案

高三数学 数学多选题专项训练的专项培优练习题(含答案一、数列多选题1.意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一列数:1,1,2,3,5,…,其中从第三项起,每个数等于它前面两个数的和,后来人们把这样的一列数组成的数列{a n }称为“斐波那契数列”,记S n 为数列{a n }的前n 项和,则下列结论正确的是( ) A .a 8=34 B .S 8=54C .S 2020=a 2022-1D .a 1+a 3+a 5+…+a 2021=a 2022答案:BCD 【分析】由题意可得数列满足递推关系,依次判断四个选项,即可得正确答案. 【详解】对于A ,可知数列的前8项为1,1,2,3,5,8,13,21,故A 错误; 对于B ,,故B 正确; 对于C ,可解析:BCD 【分析】由题意可得数列{}n a 满足递推关系()12211,1,+3n n n a a a a a n --===≥,依次判断四个选项,即可得正确答案. 【详解】对于A ,可知数列的前8项为1,1,2,3,5,8,13,21,故A 错误; 对于B ,81+1+2+3+5+8+13+2154S ==,故B 正确; 对于C ,可得()112n n n a a a n +-=-≥, 则()()()()1234131425311++++++++++n n n a a a a a a a a a a a a a a +-=----即212++1n n n n S a a a a ++=-=-,∴202020221S a =-,故C 正确; 对于D ,由()112n n n a a a n +-=-≥可得,()()()135202124264202220202022++++++++a a a a a a a a a a a a =---=,故D 正确.故选:BCD. 【点睛】本题以“斐波那契数列”为背景,考查数列的递推关系及性质,解题的关键是得出数列的递推关系,()12211,1,+3n n n a a a a a n --===≥,能根据数列性质利用累加法求解. 2.已知数列0,2,0,2,0,2,,则前六项适合的通项公式为( )A .1(1)nn a =+- B .2cos2n n a π= C .(1)2sin2n n a π+= D .1cos(1)(1)(2)n a n n n π=--+--【分析】对四个选项中的数列通项公式分别取前六项,看是否满足题意,得出答案. 【详解】对于选项A ,取前六项得:,满足条件; 对于选项B ,取前六项得:,不满足条件; 对于选项C ,取前六项得:,解析:AC 【分析】对四个选项中的数列通项公式分别取前六项,看是否满足题意,得出答案. 【详解】对于选项A ,1(1)nn a =+-取前六项得:0,2,0,2,0,2,满足条件; 对于选项B ,2cos 2n n a π=取前六项得:0,2,0,2,0,2--,不满足条件; 对于选项C ,(1)2sin2n n a π+=取前六项得:0,2,0,2,0,2,满足条件; 对于选项D ,1cos(1)(1)(2)n a n n n π=--+--取前六项得:0,2,2,8,12,22,不满足条件; 故选:AC3.已知数列{}n a 的前n 项和为()0n n S S ≠,且满足140(2)n n n a S S n -+=≥,114a =,则下列说法错误的是( )A .数列{}n a 的前n 项和为4n S n =B .数列{}n a 的通项公式为14(1)n a n n =+C .数列{}n a 为递增数列D .数列1n S ⎧⎫⎨⎬⎩⎭为递增数列答案:ABC 【分析】数列的前项和为,且满足,,可得:,化为:,利用等差数列的通项公式可得,,时,,进而求出. 【详解】数列的前项和为,且满足,, ∴,化为:,∴数列是等差数列,公差为4, ∴,可得解析:ABC数列{}n a 的前n 项和为0n n S S ≠(),且满足1402n n n a S S n -+=≥(),114a =,可得:1140n n n n S S S S ---+=,化为:1114n n S S --=,利用等差数列的通项公式可得1nS ,n S ,2n ≥时,()()111144141n n n a S S n n n n -=-=-=---,进而求出n a . 【详解】数列{}n a 的前n 项和为0n n S S ≠(),且满足1402n n n a S S n -+=≥(),114a =, ∴1140n n n n S S S S ---+=,化为:1114n n S S --=, ∴数列1n S ⎧⎫⎨⎬⎩⎭是等差数列,公差为4, ∴()14414n n n S =+-=,可得14n S n=, ∴2n ≥时,()()111144141n n n a S S n n n n -=-=-=---, ∴()1(1)41(2)41n n a n n n ⎧=⎪⎪=⎨⎪-≥-⎪⎩,对选项逐一进行分析可得,A ,B ,C 三个选项错误,D 选项正确. 故选:ABC. 【点睛】本题考查数列递推式,解题关键是将已知递推式变形为1114n n S S --=,进而求得其它性质,考查逻辑思维能力和运算能力,属于常考题4.已知等差数列{}n a 的公差0d ≠,前n 项和为n S ,若612S S =,则下列结论中正确的有( )A .1:17:2a d =-B .180S =C .当0d >时,6140a a +>D .当0d <时,614a a >答案:ABC 【分析】因为是等差数列,由可得,利用通项转化为和即可判断选项A ;利用前项和公式以及等差数列的性质即可判断选项B ;利用等差数列的性质即可判断选项C ;由可得且,即可判断选项D ,进而得出正确选项解析:ABC 【分析】因为{}n a 是等差数列,由612S S =可得9100a a +=,利用通项转化为1a 和d 即可判断选项A ;利用前n 项和公式以及等差数列的性质即可判断选项B ;利用等差数列的性质961014a d a a d a =++=+即可判断选项C ;由0d <可得6140a a d +=<且60a >,140a <即可判断选项D ,进而得出正确选项.【详解】因为{}n a 是等差数列,前n 项和为n S ,由612S S =得:1267891011120S S a a a a a a -=+++++=,即()91030a a +=,即9100a a +=,对于选项A :由9100a a +=得12170a d +=,可得1:17:2a d =-,故选项A 正确; 对于选项B :()()118910181818022a a a a S ++===,故选项B 正确;对于选项C :911691014a a a a a a d d =+=++=+,若0d >,则6140a a d +=>,故选项C 正确;对于选项D :当0d <时,6140a a d +=<,则614a a <-,因为0d <,所以60a >,140a <,所以614a a <,故选项D 不正确, 故选:ABC 【点睛】关键点点睛:本题的关键点是由612S S =得出9100a a +=,熟记等差数列的前n 项和公式和通项公式,灵活运用等差数列的性质即可.5.已知递减的等差数列{}n a 的前n 项和为n S ,57S S =,则( ) A .60a > B .6S 最大 C .130S >D .110S >答案:ABD 【分析】转化条件为,进而可得,,再结合等差数列的性质及前n 项和公式逐项判断即可得解. 【详解】 因为,所以,即,因为数列递减,所以,则,,故A 正确; 所以最大,故B 正确; 所以,故C 错误解析:ABD 【分析】转化条件为670a a +=,进而可得60a >,70a <,再结合等差数列的性质及前n 项和公式逐项判断即可得解. 【详解】因为57S S =,所以750S S -=,即670a a +=,因为数列{}n a 递减,所以67a a >,则60a >,70a <,故A 正确; 所以6S 最大,故B 正确; 所以()113137131302a a S a+⨯==<,故C 错误; 所以()111116111102a a S a+⨯==>,故D 正确.故选:ABD.6.记n S 为等差数列{}n a 前n 项和,若81535a a = 且10a >,则下列关于数列的描述正确的是( ) A .2490a a += B .数列{}n S 中最大值的项是25S C .公差0d >D .数列{}na 也是等差数列答案:AB 【分析】根据已知条件求得的关系式,然后结合等差数列的有关知识对选项逐一分析,从而确定正确选项. 【详解】依题意,等差数列中,即, .对于A 选项,,所以A 选项正确. 对于C 选项,,,所以,解析:AB 【分析】根据已知条件求得1,a d 的关系式,然后结合等差数列的有关知识对选项逐一分析,从而确定正确选项. 【详解】依题意,等差数列{}n a 中81535a a =,即()()1137514a d a d +=+,1149249,2a d a d =-=-. 对于A 选项,24912490a a a d +=+=,所以A 选项正确.对于C 选项,1492a d =-,10a >,所以0d <,所以C 选项错误. 对于B 选项,()()149511122n a a n d d n d n d ⎛⎫=+-=-+-=- ⎪⎝⎭,令0n a ≥得51510,22n n -≤≤,由于n 是正整数,所以25n ≤,所以数列{}n S 中最大值的项是25S ,所以B 选项正确.对于D 选项,由上述分析可知,125n ≤≤时,0n a ≥,当26n ≥时,0n a <,且0d <.所以数列{}na 的前25项递减,第26项后面递增,不是等差数列,所以D 选项错误.故选:AB 【点睛】等差数列有关知识的题目,主要把握住基本元的思想.要求等差数列前n 项和的最值,可以令0n a ≥或0n a ≤来求解.7.已知数列{}n a 的前n 项和为n S ,前n 项积为n T ,且3201911111a a e e +≤++,则( ) A .当数列{}n a 为等差数列时,20210S ≥ B .当数列{}n a 为等差数列时,20210S ≤ C .当数列{}n a 为等比数列时,20210T > D .当数列{}n a 为等比数列时,20210T <答案:AC 【分析】将变形为,构造函数,利用函数单调性可得,再结合等差数列与等比数列性质即可判断正确选项 【详解】 由,可得,令, ,所以是奇函数,且在上单调递减,所以, 所以当数列为等差数列时,;解析:AC 【分析】 将3201911111a a e e +≤++变形为32019111101212a a e e -+-≤++,构造函数()1112x f x e =-+,利用函数单调性可得320190a a +≥,再结合等差数列与等比数列性质即可判断正确选项【详解】 由3201911111a a e e +≤++,可得32019111101212a a e e -+-≤++,令()1112xf x e =-+, ()()1111101111x x x x x e f x f x e e e e --+=+-=+-=++++,所以()1112xf x e =-+是奇函数,且在R 上单调递减,所以320190a a +≥, 所以当数列{}n a 为等差数列时,()320192*********a a S +=≥;当数列{}n a 为等比数列时,且3a ,1011a ,2019a 同号,所以3a ,1011a ,2019a 均大于零, 故()2021202110110T a =>.故选:AC 【点睛】本题考查等差数列与等比数列,考查逻辑推理能力,转化与化归的数学思想,属于中档题 8.已知无穷等差数列{}n a 的前n 项和为n S ,67S S <,且78S S >,则( ) A .在数列{}n a 中,1a 最大 B .在数列{}n a 中,3a 或4a 最大 C .310S S =D .当8n ≥时,0n a <答案:AD 【分析】利用等差数列的通项公式可以求,,即可求公差,然后根据等差数列的性质判断四个选项是否正确. 【详解】 因为,所以 , 因为,所以, 所以等差数列公差, 所以是递减数列, 故最大,选项A解析:AD 【分析】利用等差数列的通项公式可以求70a >,80a <,即可求公差0d <,然后根据等差数列的性质判断四个选项是否正确. 【详解】因为67S S <,所以7670S S a -=> ,因为78S S >,所以8780S S a -=<, 所以等差数列{}n a 公差870d a a =-<, 所以{}n a 是递减数列,故1a 最大,选项A 正确;选项B 不正确;10345678910770S S a a a a a a a a -=++++++=>,所以310S S ≠,故选项C 不正确;当8n ≥时,80n a a ≤<,即0n a <,故选项D 正确; 故选:AD 【点睛】本题主要考查了等差数列的性质和前n 项和n S ,属于基础题.9.等差数列{}n a 的首项10a >,设其前n 项和为{}n S ,且611S S =,则( ) A .0d > B .0d <C .80a =D .n S 的最大值是8S 或者9S答案:BD 【分析】由,即,进而可得答案. 【详解】 解:, 因为所以,,最大, 故选:. 【点睛】本题考查等差数列的性质,解题关键是等差数列性质的应用,属于中档题.解析:BD 【分析】由6111160S S S S =⇒-=,即950a =,进而可得答案. 【详解】解:1167891011950S S a a a a a a -=++++==, 因为10a >所以90a =,0d <,89S S =最大, 故选:BD . 【点睛】本题考查等差数列的性质,解题关键是等差数列性质的应用,属于中档题.10.已知等差数列{}n a 的前n 项和为n S ()*n N ∈,公差0d ≠,690S =,7a 是3a 与9a 的等比中项,则下列选项正确的是( ) A .2d =-B .120a =-C .当且仅当10n =时,n S 取最大值D .当0nS <时,n 的最小值为22答案:AD 【分析】运用等差数列的通项公式和求和公式,解方程可得首项和公差,可判断A ,B ;由二次函数的配方法,结合n 为正整数,可判断C ;由解不等式可判断D . 【详解】等差数列的前n 项和为,公差,由,可解析:AD 【分析】运用等差数列的通项公式和求和公式,解方程可得首项和公差,可判断A ,B ;由二次函数的配方法,结合n 为正整数,可判断C ;由0n S <解不等式可判断D .【详解】等差数列{}n a 的前n 项和为n S ,公差0d ≠,由690S =,可得161590a d +=,即12530a d +=,①由7a 是3a 与9a 的等比中项,得2739a a a =,即()()()2111628a d a d a d +=++,化为1100a d +=,②由①②解得120a =,2d =-,则202(1)222n a n n =--=-,21(20222)212n S n n n n =+-=-,由22144124n S n ⎛⎫=--+ ⎪⎝⎭,可得10n =或11时,n S 取得最大值110; 由2102n S n n -<=,解得21n >,则n 的最小值为22. 故选:AD 【点睛】本题考查等差数列的通项公式和求和公式,以及等比中项的性质,二次函数的最值求法,考查方程思想和运算能力,属于中档题.11.已知等差数列{}n a 的前n 项和为S n (n ∈N *),公差d ≠0,S 6=90,a 7是a 3与a 9的等比中项,则下列选项正确的是( ) A .a 1=22B .d =-2C .当n =10或n =11时,S n 取得最大值D .当S n >0时,n 的最大值为21答案:BC【分析】分别运用等差数列的通项公式和求和公式,解方程可得首项和公差,可判断A ,B ;由配方法,结合n 为正整数,可判断C ;由Sn>0解不等式可判断D . 【详解】由公差,可得,即,① 由a7是a解析:BC 【分析】分别运用等差数列的通项公式和求和公式,解方程可得首项和公差,可判断A ,B ;由配方法,结合n 为正整数,可判断C ;由S n >0解不等式可判断D . 【详解】由公差60,90d S ≠=,可得161590a d +=,即12530a d +=,①由a 7是a 3与a 9的等比中项,可得2739a a a =,即()()()2111628a d a d a d +=++,化简得110a d =-,②由①②解得120,2a d ==-,故A 错,B 对;由()()22121441201221224n S n n n n n n ⎛⎫=+-⨯-=-=--+ ⎪⎝⎭*n N ∈,可得10n =或11时,n S 取最大值110,C 对;由S n >0,解得021n <<,可得n 的最大值为20,D 错; 故选:BC 【点睛】本题考查等差数列的通项公式和求和公式的运用,考查方程思想和运算能力,属于基础题.12.设公差不为0的等差数列{}n a 的前n 项和为n S ,若1718S S =,则下列各式的值为0的是( ) A .17aB .35SC .1719a a -D .1916S S -答案:BD 【分析】由得,利用可知不正确;;根据可知 正确;根据可知不正确;根据可知正确. 【详解】因为,所以,所以, 因为公差,所以,故不正确; ,故正确; ,故不正确; ,故正确.故选:BD.解析:BD 【分析】 由1718S S =得180a =,利用17180a a d d =-=-≠可知A 不正确;;根据351835S a =可知 B 正确;根据171920a a d -=-≠可知C 不正确;根据19161830S S a -==可知D 正确. 【详解】因为1718S S =,所以18170S S -=,所以180a =,因为公差0d ≠,所以17180a a d d =-=-≠,故A 不正确;13518351835()35235022a a a S a +⨯====,故B 正确; 171920a a d -=-≠,故C 不正确;19161718191830S S a a a a -=++==,故D 正确.故选:BD. 【点睛】本题考查了等差数列的求和公式,考查了等差数列的下标性质,属于基础题.二、等差数列多选题13.已知数列{}n a 满足:12a =,当2n ≥时,)212n a =-,则关于数列{}n a 的说法正确的是 ( )A .27a =B .数列{}n a 为递增数列C .221n a n n =+- D .数列{}n a 为周期数列解析:ABC 【分析】由)212n a =-1=,再利用等差数列的定义求得n a ,然后逐项判断. 【详解】当2n ≥时,由)212n a =-,得)221n a +=,1=,又12a =,所以是以2为首项,以1为公差的等差数列,2(1)11n n =+-⨯=+, 即221n a n n =+-,故C 正确;所以27a =,故A 正确;()212n a n =+-,所以{}n a 为递增数列,故正确;数列{}n a 不具有周期性,故D 错误; 故选:ABC 14.题目文件丢失!15.已知数列{}n a 的前4项为2,0,2,0,则该数列的通项公式可能为( ) A .0,2,n n a n ⎧=⎨⎩为奇数为偶数B .1(1)1n n a -=-+C .2sin 2n n a π= D .cos(1)1n a n π=-+解析:BD 【分析】根据选项求出数列的前4项,逐一判断即可. 【详解】解:因为数列{}n a 的前4项为2,0,2,0, 选项A :不符合题设;选项B :01(1)12,a =-+=12(1)10,a =-+=23(1)12,a =-+=34(1)10a =-+=,符合题设;选项C :,12sin2,2a π==22sin 0,a π==332sin22a π==-不符合题设; 选项D :1cos012,a =+=2cos 10,a π=+=3cos212,a π=+=4cos310a π=+=,符合题设.故选:BD. 【点睛】本题考查数列的通项公式的问题,考查了基本运算求解能力,属于基础题.16.等差数列{}n a 是递增数列,公差为d ,前n 项和为n S ,满足753a a =,下列选项正确的是( ) A .0d <B .10a <C .当5n =时n S 最小D .0n S >时n 的最小值为8解析:BD 【分析】由题意可知0d >,由已知条件753a a =可得出13a d =-,可判断出AB 选项的正误,求出n S 关于d 的表达式,利用二次函数的基本性质以及二次不等式可判断出CD 选项的正误. 【详解】由于等差数列{}n a 是递增数列,则0d >,A 选项错误;753a a =,则()11634a d a d +=+,可得130a d =-<,B 选项正确;()()()22171117493222224n n n d n n d n n d S na nd n d -⎡⎤--⎛⎫=+=-+==--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦,当3n =或4时,n S 最小,C 选项错误; 令0n S >,可得270n n ->,解得0n <或7n >.n N *∈,所以,满足0n S >时n 的最小值为8,D 选项正确.故选:BD.17.等差数列{}n a 的前n 项和为n S ,若10a >,公差0d ≠,则( ) A .若59S >S ,则150S > B .若59S =S ,则7S 是n S 中最大的项 C .若67S S >, 则78S S > D .若67S S >则56S S >.解析:BC 【分析】根据等差数列的前n 项和性质判断. 【详解】A 错:67895911415000S a a a a a S a S ⇒+++<>⇒+<⇒<;B 对:n S 对称轴为n =7;C 对:6770S S a >⇒<,又10a >,887700a S a d S ⇒⇒<<⇒<>;D 错:6770S S a >⇒<,但不能得出6a 是否为负,因此不一定有56S S >. 故选:BC . 【点睛】关键点点睛:本题考查等差数列的前n 项和性质,(1)n S 是关于n 的二次函数,可以利用二次函数性质得最值;(2)1n n n S S a -=+,可由n a 的正负确定n S 与1n S -的大小;(3)1()2n n n a a S +=,因此可由1n a a +的正负确定n S 的正负. 18.记n S 为等差数列{}n a 前n 项和,若81535a a = 且10a >,则下列关于数列的描述正确的是( ) A .2490a a += B .数列{}n S 中最大值的项是25S C .公差0d > D .数列{}na 也是等差数列解析:AB 【分析】根据已知条件求得1,a d 的关系式,然后结合等差数列的有关知识对选项逐一分析,从而确【详解】依题意,等差数列{}n a 中81535a a =,即()()1137514a d a d +=+,1149249,2a d a d =-=-. 对于A 选项,24912490a a a d +=+=,所以A 选项正确. 对于C 选项,1492a d =-,10a >,所以0d <,所以C 选项错误. 对于B 选项,()()149511122n a a n d d n d n d ⎛⎫=+-=-+-=- ⎪⎝⎭,令0n a ≥得51510,22n n -≤≤,由于n 是正整数,所以25n ≤,所以数列{}n S 中最大值的项是25S ,所以B 选项正确.对于D 选项,由上述分析可知,125n ≤≤时,0n a ≥,当26n ≥时,0n a <,且0d <.所以数列{}na 的前25项递减,第26项后面递增,不是等差数列,所以D 选项错误.故选:AB 【点睛】等差数列有关知识的题目,主要把握住基本元的思想.要求等差数列前n 项和的最值,可以令0n a ≥或0n a ≤来求解.19.意大利人斐波那契于1202年从兔子繁殖问题中发现了这样的一列数:1,1,2,3,5,8,13,….即从第三项开始,每一项都是它前两项的和.后人为了纪念他,就把这列数称为斐波那契数列.下面关于斐波那契数列{}n a 说法正确的是( ) A .1055a = B .2020a 是偶数C .2020201820223a a a =+D .123a a a +++…20202022a a +=解析:AC 【分析】由该数列的性质,逐项判断即可得解. 【详解】对于A ,821a =,9211334a =+=,10213455a =+=,故A 正确; 对于B ,由该数列的性质可得只有3的倍数项是偶数,故B 错误;对于C ,20182022201820212020201820192020202020203a a a a a a a a a a +=++=+++=,故C 正确; 对于D ,202220212020a a a =+,202120202019a a a =+,202020192018a a a =+,32121,a a a a a ⋅⋅⋅=+=,各式相加得()2022202120202021202020192012182a a a a a a a a a ++⋅⋅⋅+=+++⋅⋅⋅++, 所以202220202019201811a a a a a a =++⋅⋅⋅+++,故D 错误.【点睛】关键点点睛:解决本题的关键是合理利用该数列的性质去证明选项. 20.已知数列{}n a 的前n 项和为n S ,前n 项积为n T ,且3201911111a a e e +≤++,则( ) A .当数列{}n a 为等差数列时,20210S ≥ B .当数列{}n a 为等差数列时,20210S ≤ C .当数列{}n a 为等比数列时,20210T > D .当数列{}n a 为等比数列时,20210T < 解析:AC 【分析】 将3201911111a a e e +≤++变形为32019111101212a a e e -+-≤++,构造函数()1112xf x e =-+,利用函数单调性可得320190a a +≥,再结合等差数列与等比数列性质即可判断正确选项 【详解】 由3201911111a a e e +≤++,可得32019111101212a a e e -+-≤++,令()1112x f x e =-+, ()()1111101111x x x x x e f x f x e e e e --+=+-=+-=++++,所以()1112x f x e =-+是奇函数,且在R 上单调递减,所以320190a a +≥, 所以当数列{}n a 为等差数列时,()320192*********a a S +=≥;当数列{}n a 为等比数列时,且3a ,1011a ,2019a 同号,所以3a ,1011a ,2019a 均大于零, 故()2021202110110T a =>.故选:AC 【点睛】本题考查等差数列与等比数列,考查逻辑推理能力,转化与化归的数学思想,属于中档题 21.下列命题正确的是( )A .给出数列的有限项就可以唯一确定这个数列的通项公式B .若等差数列{}n a 的公差0d >,则{}n a 是递增数列C .若a ,b ,c 成等差数列,则111,,a b c可能成等差数列 D .若数列{}n a 是等差数列,则数列{}12++n n a a 也是等差数列【分析】根据等差数列的性质即可判断选项的正误. 【详解】A 选项:给出数列的有限项不一定可以确定通项公式;B 选项:由等差数列性质知0d >,{}n a 必是递增数列;C 选项:1a b c ===时,1111a b c===是等差数列,而a = 1,b = 2,c = 3时不成立; D 选项:数列{}n a 是等差数列公差为d ,所以11112(1)223(31)n n a a a n d a nd a n d ++=+-++=+-也是等差数列;故选:BCD 【点睛】本题考查了等差数列,利用等差数列的性质判断选项的正误,属于基础题.22.首项为正数,公差不为0的等差数列{}n a ,其前n 项和为n S ,现有下列4个命题中正确的有( )A .若100S =,则280S S +=;B .若412S S =,则使0n S >的最大的n 为15C .若150S >,160S <,则{}n S 中8S 最大D .若78S S <,则89S S < 解析:BC 【分析】根据等差数列的性质,以及等差数列的求和公式,逐项判断,即可得答案. 【详解】A 选项,若1011091002S a d ⨯=+=,则1290a d +=, 那么()()2811128281029160S S a d a d a d d +=+++=+=-≠.故A 不正确; B 选项,若412S S =,则()5611128940a a a a a a ++++=+=,又因为10a >,所以前8项为正,从第9项开始为负, 因为()()116168916802a a S a a +==+=, 所以使0n S >的最大的n 为15.故B 正确; C 选项,若()115158151502a a S a +==>,()()116168916802a a S a a +==+<, 则80a >,90a <,则{}n S 中8S 最大.故C 正确;D 选项,若78S S <,则80a >,而989S S a -=,不能判断9a 正负情况.故D 不正确.【点睛】本题考查等差数列性质的应用,涉及等差数列的求和公式,属于常考题型.23.已知数列{}n a 满足:13a =,当2n ≥时,)211n a =-,则关于数列{}n a 说法正确的是( )A .28a =B .数列{}n a 为递增数列C .数列{}n a 为周期数列D .22n a n n =+解析:ABD 【分析】由已知递推式可得数列2=,公差为1的等差数列,结合选项可得结果. 【详解】)211n a =-得)211n a +=,1=,即数列2=,公差为1的等差数列,2(1)11n n =+-⨯=+,∴22n a n n =+,得28a =,由二次函数的性质得数列{}n a 为递增数列,所以易知ABD 正确, 故选:ABD. 【点睛】本题主要考查了通过递推式得出数列的通项公式,通过通项公式研究数列的函数性质,属于中档题.24.已知数列{}n a 是递增的等差数列,5105a a +=,6914a a ⋅=-.12n n n n b a a a ++=⋅⋅,数列{}n b 的前n 项和为n T ,下列结论正确的是( )A .320n a n =-B .325n a n =-+C .当4n =时,n T 取最小值D .当6n =时,n T 取最小值解析:AC 【分析】由已知求出数列{}n a 的首项与公差,得到通项公式判断A 与B ;再求出n T ,由{}n b 的项分析n T 的最小值. 【详解】解:在递增的等差数列{}n a 中,由5105a a +=,得695a a +=,又6914a a =-,联立解得62a =-,97a =, 则967(2)3963a a d ---===-,16525317a a d =-=--⨯=-. 173(1)320n a n n ∴=-+-=-.故A 正确,B 错误;12(320)(317)(314)n n n n b a a a n n n ++==---可得数列{}n b 的前4项为负,第5项为正,第六项为负,第六项以后均为正. 而5610820b b +=-=>.∴当4n =时,n T 取最小值,故C 正确,D 错误.故选:AC . 【点睛】本题考查等差数列的通项公式,考查数列的求和,考查分析问题与解决问题的能力,属于中档题.三、等比数列多选题25.一个弹性小球从100m 高处自由落下,每次着地后又跳回原来高度的23再落下.设它第n 次着地时,经过的总路程记为n S ,则当2n ≥时,下面说法正确的是( ) A .500n S < B .500n S ≤C .n S 的最小值为7003D .n S 的最大值为400解析:AC 【分析】由运动轨迹分析列出总路程n S 关于n 的表达式,再由表达式分析数值特征即可 【详解】由题可知,第一次着地时,1100S =;第二次着地时,221002003S =+⨯;第三次着地时,232210020020033S ⎛⎫=+⨯+⨯ ⎪⎝⎭;……第n 次着地后,21222100200200200333n n S -⎛⎫⎛⎫=+⨯+⨯++⨯ ⎪ ⎪⎝⎭⎝⎭则211222210020010040013333n n n S --⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=++++=+- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,显然500n S <,又n S 是关于n 的增函数,2n ≥,故当2n =时,n S 的最小值为40070010033+=; 综上所述,AC 正确 故选:AC26.设n S 为等比数列{}n a 的前n 项和,满足13a =,且1a ,22a -,34a 成等差数列,则下列结论正确的是( ) A .113()2n n a -=⋅-B .36nn S a =+C .若数列{}n a 中存在两项p a ,s a3a =,则19p s +的最小值为83D .若1n n t S m S ≤-≤恒成立,则m t -的最小值为116解析:ABD 【分析】根据等差中项列式求出12q =-,进而求出等比数列的通项和前n 项和,可知A ,B 正确;3a =求出15p s =⎧⎨=⎩或24p s =⎧⎨=⎩或42p s =⎧⎨=⎩或51p s =⎧⎨=⎩,可知19p s +的最小值为114,C 不正确;利用1n n y S S =-关于nS 单调递增,求出1n n S S -的最大、最小值可得结果. 【详解】设等比数列{}n a 的公比为q ,由13a =,21344a a a -=+得243343q q -⨯=+⨯,解得12q =-,所以113()2n n a -=⋅-,13(1())1221()121()2n n n S --⎛⎫==-- ⎪⎝⎭--;1111361()66()63()63222n n n n n S a -⎛⎫=--=--=+⋅-=+ ⎪⎝⎭;所以A ,B 正确;3a =,则23p sa a a ⋅=,1122111()p s p s a a a q a q a q --⋅==,所以114p s q q q --=,所以6p s +=,则15p s =⎧⎨=⎩或24p s =⎧⎨=⎩或42p s =⎧⎨=⎩或51p s =⎧⎨=⎩,此时19145p s +=或114或194或465;C 不正确,122,2121()2122,2nn n nn S n ⎧⎛⎫+⎪ ⎪⎪⎝⎭⎛⎫=--=⎨ ⎪⎝⎭⎛⎫⎪- ⎪⎪⎝⎭⎩为奇数为偶数, 当n 为奇数时,(2,3]n S ∈,当n 为偶数时,3[,2)2n S ∈,又1n n y S S =-关于n S 单调递增,所以当n 为奇数时,138(,]23nn S S -∈,当n 为偶数时,153[,)62n n S S -∈,所以83m ≥,56t ≤,所以8511366m t -≥-=,D 正确,故选:ABD . 【点睛】本题考查了等差中项的应用,考查了等比数列通项公式,考查了等比数列的前n 项和公式,考查了数列不等式恒成立问题,属于中档题.27.已知等比数列{}n a 的公比0q <,等差数列{}n b 的首项10b >,若99a b >,且1010a b >,则下列结论一定正确的是( )A .9100a a <B .910a a >C .100b >D .910b b >解析:AD 【分析】根据等差、等比数列的性质依次判断选项即可. 【详解】对选项A ,因为0q <,所以29109990a a a a q a q =⋅=<,故A 正确;对选项B ,因为9100a a <,所以91000a a >⎧⎨<⎩或9100a a <⎧⎨>⎩,即910a a >或910a a <,故B 错误;对选项C ,D ,因为910,a a 异号,99a b >,且1010a b >,所以910,b b 中至少有一个负数, 又因为10b >,所以0d <,910b b >,故C 错误,D 正确. 故选:AD 【点睛】本题主要考查等差、等比数列的综合应用,考查学生分析问题的能力,属于中档题. 28.已知等比数列{}n a 中,满足11a =,2q ,n S 是{}n a 的前n 项和,则下列说法正确的是( )A .数列{}2n a 是等比数列B .数列1n a ⎧⎫⎨⎬⎩⎭是递增数列 C .数列{}2log n a 是等差数列 D .数列{}n a 中,10S ,20S ,30S 仍成等比数列解析:AC 【分析】 由已知得12n na 可得以2122n n a -=,可判断A ;又1111122n n n a --⎛⎫== ⎪⎝⎭,可判断B ;由122log log 21n n a n -==-,可判断C ;求得10S ,20S ,30S ,可判断D.【详解】等比数列{}n a 中,满足11a =,2q,所以12n n a ,所以2122n n a -=,所以数列{}2n a 是等比数列,故A 正确;又1111122n n n a --⎛⎫== ⎪⎝⎭,所以数列1n a ⎧⎫⎨⎬⎩⎭是递减数列,故B 不正确;因为122log log 21n n a n -==-,所以{}2log n a 是等差数列,故C 正确;数列{}n a 中,101010111222S -==--,202021S =-,303021S =-,10S ,20S ,30S 不成等比数列,故D 不正确; 故选:AC . 【点睛】本题综合考查等差、等比数列的定义、通项公式、前n 项和公式,以及数列的单调性的判定,属于中档题.29.在公比为q 等比数列{}n a 中,n S 是数列{}n a 的前n 项和,若521127,==a a a ,则下列说法正确的是( ) A .3q = B .数列{}2n S +是等比数列 C .5121S = D .()222lg lg lg 3n n n a a a n -+=+≥解析:ACD 【分析】根据等比数列的通项公式,结合等比数列的定义和对数的运算性质进行逐一判断即可. 【详解】因为521127,==a a a ,所以有431127273q a q q q a ⋅=⋅⇒=⇒=,因此选项A 正确;因为131(31)132nn n S -==--,所以131+2+2(3+3)132nn n S -==-, 因为+1+111(3+3)+222=1+1+21+3(3+3)2n nn n n S S -=≠常数, 所以数列{}2n S +不是等比数列,故选项B 不正确; 因为551(31)=1212S =-,所以选项C 正确;11130n n n a a q --=⋅=>,因为当3n ≥时,22222lg lg =lg()=lg 2lg n n n n n n a a a a a a -+-++⋅=,所以选项D 正确. 故选:ACD 【点睛】本题考查了等比数列的通项公式的应用,考查了等比数列前n 项和公式的应用,考查了等比数列定义的应用,考查了等比数列的性质应用,考查了对数的运算性质,考查了数学运算能力.30.已知数列{}n a 是等比数列,那么下列数列一定是等比数列的是( )A .1{}na B .22log ()n aC .1{}n n a a ++D .12{}n n n a a a ++++解析:AD 【分析】主要分析数列中的项是否可能为0,如果可能为0,则不能是等比数列,在不为0时,根据等比数列的定义确定. 【详解】1n a =时,22log ()0n a =,数列22{log ()}n a 不一定是等比数列,1q =-时,10n n a a ++=,数列1{}n n a a ++不一定是等比数列,由等比数列的定义知1{}na 和12{}n n n a a a ++++都是等比数列. 故选AD . 【点睛】本题考查等比数列的定义,掌握等比数列的定义是解题基础.特别注意只要数列中有一项为0,则数列不可能是等比数列.31.在《增减算法统宗》中有这样一则故事:“三百七十八里关,初行健步不为难;次日脚痛减一半,如此六日过其关”.则下列说法正确的是( ) A .此人第六天只走了5里路B .此人第一天走的路程比后五天走的路程多6里C .此人第二天走的路程比全程的14还多1.5里 D .此人走的前三天路程之和是后三天路程之和的8倍 解析:BCD 【分析】设此人第n 天走n a 里路,则{}n a 是首项为1a ,公比为12q = 的等比数列,由6=378S 求得首项,然后逐一分析四个选项得答案. 【详解】解:根据题意此人每天行走的路程成等比数列,设此人第n 天走n a 里路,则{}n a 是首项为1a ,公比为12q =的等比数列. 所以661161[1()](1)2=3781112a a q S q --==--,解得1192a =. 选项A:5561119262a a q ⎛⎫==⨯= ⎪⎝⎭,故A 错误, 选项B:由1192a =,则61378192186S a -=-=,又1921866-=,故B 正确. 选项C:211192962a a q ==⨯=,而6194.54S =,9694.5 1.5-=,故C 正确.选项D:2123111(1)192(1)33624a a a a q q ++=++=⨯++=, 则后3天走的路程为378336=42-, 而且336428÷=,故D 正确. 故选:BCD 【点睛】本题考查等比数列的性质,考查等比数列的前n 项和,是基础题.32.设等比数列{}n a 的公比为q ,其前n 项和为n S ,前n 项积为n T ,并满足条件1201920201,1a a a >>,20192020101a a -<-,下列结论正确的是( )A .S 2019<S 2020B .2019202010a a -<C .T 2020是数列{}n T 中的最大值D .数列{}n T 无最大值解析:AB 【分析】由已知确定0q <和1q ≥均不符合题意,只有01q <<,数列{}n a 递减,从而确定20191a >,202001a <<,从可判断各选项.【详解】当0q <时,22019202020190a a a q =<,不成立;当1q ≥时,201920201,1a a >>,20192020101a a -<-不成立;故01q <<,且20191a >,202001a <<,故20202019S S >,A 正确;2201920212020110a a a -=-<,故B 正确;因为20191a >,202001a <<,所以2019T 是数列{}n T 中的最大值,C ,D 错误; 故选:AB 【点睛】本题考查等比数列的单调性,解题关键是确定20191a >,202001a <<.33.设首项为1的数列{}n a 的前n 项和为n S ,已知121n n S S n +=+-,则下列结论正确的是( )A .数列{}n S n +为等比数列B .数列{}n a 的通项公式为121n n a -=-C .数列{}1n a +为等比数列D .数列{}2n S 的前n 项和为2224n n n +--- 解析:AD 【分析】 由已知可得11222n n n n S n S nS n S n++++==++,结合等比数列的定义可判断A ;可得2n n S n =-,结合n a 和n S 的关系可求出{}n a 的通项公式,即可判断B ;由1231,1,3a a a ===可判断C ;由分组求和法结合等比数列和等差数列的前n 项和公式即可判断D. 【详解】因为121n n S S n +=+-,所以11222n n n n S n S nS n S n++++==++. 又112S +=,所以数列{}n S n +是首项为2,公比为2的等比数列,故A 正确; 所以2nn S n +=,则2nn S n =-. 当2n ≥时,1121n n n n a S S --=-=-,但11121a -≠-,故B 错误;由1231,1,3a a a ===可得12312,12,14a a a +=+=+=,即32211111a a a a ++≠++,故C 错; 因为1222n n S n +=-,所以2311222...2221222...22n n S S S n ++++=-⨯+-⨯++-()()()23122412122 (2)212 (22412)2n n n n n n n n n ++--⎡⎤=+++-+++=-+=---⎢⎥-⎣⎦ 所以数列{}2n S 的前n 项和为2224n n n +---,故D 正确. 故选:AD . 【点睛】本题考查等比数列的定义,考查了数列通项公式的求解,考查了等差数列、等比数列的前n 项和,考查了分组求和.34.记单调递增的等比数列{}n a 的前n 项和为n S ,若2410a a +=,23464a a a =,则( ) A .112n n n S S ++-=B .12n naC .21nn S =-D .121n n S -=-解析:BC 【分析】先求得3a ,然后求得q ,进而求得1a ,由此求得1,,n n n n a S S S +-,进而判断出正确选项. 【详解】由23464a a a =得3334a =,则34a =.设等比数列{}n a 的公比为()0q q ≠,由2410a a +=,得4410q q+=,即22520q q -+=,解得2q或12q =.又因为数列{}n a 单调递增,所以2q,所以112810a a +=,解得11a =.所以12n na ,()1122112n n n S ⨯-==--,所以()1121212n n nn n S S ++-=---=.故选:BC 【点睛】 本题考查等比数列的通项公式、等比数列的性质及前n 项和,属于中档题. 35.设等比数列{}n a 的公比为q ,其前n 项和为n S ,前n 项积为n T ,并且满足条件11a >,781a a >,87101a a -<-.则下列结论正确的是( ) A .01q << B .791a a <C .n T 的最大值为7TD .n S 的最大值为7S解析:ABC 【分析】由11a >,781a a >,87101a a -<-,可得71a >,81a <.由等比数列的定义即可判断A ;运用等比数列的性质可判断B ;由正数相乘,若乘以大于1的数变大,乘以小于1的数变小,可判断C; 因为71a >,801a <<,可以判断D. 【详解】11a >,781a a >,87101a a -<-, 71a ∴>,801a <<,∴A.01q <<,故正确;B.27981a a a =<,故正确; C.7T 是数列{}n T 中的最大项,故正确.D. 因为71a >,801a <<,n S 的最大值不是7S ,故不正确. 故选:ABC . 【点睛】本题考查了等比数列的通项公式及其性质、递推关系、不等式的性质,考查了推理能力与计算能力,属于中档题.36.在递增的等比数列{a n }中,S n 是数列{a n }的前n 项和,若a 1a 4=32,a 2+a 3=12,则下列。
中学高三数学 课外培优练习8

广东省始兴县风度中学高三数学 课外培优练习1. 设椭圆()2222x y C :1a b 0a b +=>>过点)M ,1,且焦点为()1F ,0。
(1)求椭圆C 的方程; (2)当过点()P 4,1的动直线与椭圆C 相交与两不同点A 、B 时,在线段AB 上取点Q ,满足AP QB AQ PB=,证明:点Q 总在某定直线上。
2. 平面直角坐标系中,O 为坐标原点,给定两点A (1,0)、B (0, -2),点C 满足αβα其中,OB OA OC +=、12,=-∈βαβ且R(1)求点C 的轨迹方程;(2)设点C 的轨迹与双曲线)0,0(12222>>=-b a b y a x 交于两点M 、N ,且以MN 为直径的圆过原点,求证:为定值2211b a -.3. 设)0,1(F ,M 、P 分别为x 轴、y 轴上的点,且PM•0=PF ,动点N 满足:NP MN 2-=.(1)求动点N 的轨迹E 的方程;(2)过定点)0)(0,(>-c c C 任意作一条直线l 与曲线E 交与不同的两点A 、B ,问在x 轴上是否存在一定点Q ,使得直线AQ 、BQ 的倾斜角互补?若存在,求出Q 点的坐标;若不存在,请说明理由.4. 如图,直角梯形ABCD 中,∠︒=90DAB ,AD ∥BC ,AB=2,AD=23,BC=21椭圆F 以A 、B 为焦点,且经过点D ,(Ⅰ)建立适当的直角坐标系,求椭圆F 的方程;(Ⅱ)是否存在直线l 与M 、F 交于椭圆N 两点,且线段C MN 的中点为点,若存在,求直线l 的方程;若不存在,说明理由.C BD5. 如图所示,B (– c ,0),C (c ,0),AH ⊥BC ,垂足为H ,且HC BH 3=. (1)若AC AB ⋅= 0,求以B 、C 为焦点并且经过点A 的椭圆的离心率; (2)D 分有向线段AB 的比为λ,A 、D 同在以B 、C 为焦点的椭圆上,当 ―5≤λ≤27-时,求椭圆的离心率e 的取值范围.6. 在直角坐标平面中,ABC ∆的两个顶点B A ,的坐标分别为)0,1(-A ,)0,1(B ,平面内两点M G ,同时满足下列条件: ①0=++GC GB GA ;②MCMB MA ==;③GM ∥AB(1)求ABC ∆的顶点C 的轨迹方程;(2)过点)0,3(P 的直线l 与(1)中轨迹交于F E ,两点,求PF PE ⋅的取值范围7. 在平面直角坐标系中,若(3,),(3,)a x y b x y =-=+,且4a b +=,(1)求动点(,)Q x y 的轨迹C 的方程;(2)已知定点(,0)(0)P t t >,若斜率为1的直线l 过点P 并与轨迹C 交于不同的两点,A B ,且对于轨迹C 上任意一点M ,都存在[0,2]θπ∈,使得cos sin OM OA OB θθ=⋅+⋅成立,试求出满足条件的实数t 的值。
中学高三数学 课外培优练习6

数学课外培优练习61. 如图,将圆分成个区域,用3种不同颜色给每一个区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为n a 。
求(Ⅰ)1234,,,a a a a ; (Ⅱ)n a 与()12n a n +≥的关系式;(Ⅲ)数列{}na 的通项公式na,并证明()*2n a n n N ≥∈。
2. 设}}{{n n b a 是两个数列,点)2,1(),2(),2,1(n n n B a A M n n n -为直角坐标平面上的点.(Ⅰ)对,*N n ∈若三点n n B A M ,,共线,求数列}{n a 的通项公式; (Ⅱ)若数列{n b }满足:nnn n a a a b a b a b a c ++++++=2122112log ,其中}{n c 是第三项为8,公比为4的等比数列.求证:点列1P (1,),(),,2(),221n n b n P b P b 在同一条直线上,并求出此直线的方程.1.解:(Ⅰ) 当1n =时,不同的染色方法种数13a = , 当2n =时,不同的染色方法种数26a = , 当3n =时,不同的染色方法种数36a = , 当4n =时,分扇形区域1,3同色与异色两种情形 ∴不同的染色方法种数43122321118a =⨯⨯⨯+⨯⨯⨯= 。
将上述2n -个等式两边分别乘以()()12,3,,1kk n -=-,再相加,得()()()()1211231221213232312312n n n n n a a ----⎡⎤--⎣⎦+-=⨯-⨯++⨯-⨯=⨯--,∴()221nn n a =+⋅-,从而()()()3,1221,2n nnn a n ⎧=⎪=⎨+⋅-≥⎪⎩ 。
(Ⅲ)证明:当1n =时,1321a =>⨯ 当2n =时,2622a =>⨯ , 当3n ≥时,()()()()()2322211121112122212n n nn n nn n n n na n C C C n n n-=+⋅-=++⋅-=++++++++⋅-≥++⋅-≥ ,故()*2n a n n N ≥∈2.解:(Ⅰ)因三点n n B A M ,,共线,1122122---=--∴n n na n得)1(22-+=n a n 故数列}{n a 的通项公式为 n a n 2=(Ⅱ)由题意323248--=⋅=n n n c)1(2)22(21+=+=+++n n n n a a a n由题意得 nnn nnn a a a b a b a b a n a a a b a b a b a n c ++++++-++++++=∴= 21221121221122,232,32212211n nn a a a b a b a b a n ++++++=-∴ )32)(1(2211-+=++∴n n n b a b a b a n n当2≥n 时,)86()52()1()32)(1(-=----+=n n n n n n n n b a n nn a n 2=43-=∴n b n .当n=1时,11-=b ,也适合上式,43-=∴n b n )(*N n ∈因为两点n P P 、1的斜率313)1(11=-⋅-=--=n n n b b K n )(*N n ∈为常数 所以点列1P (1,),(),,2(),221n n b n P b P b 在同一条直线上,且方程为:)(131-=-x b y ,即043=--y x .。
中学高三数学 课外培优练习3
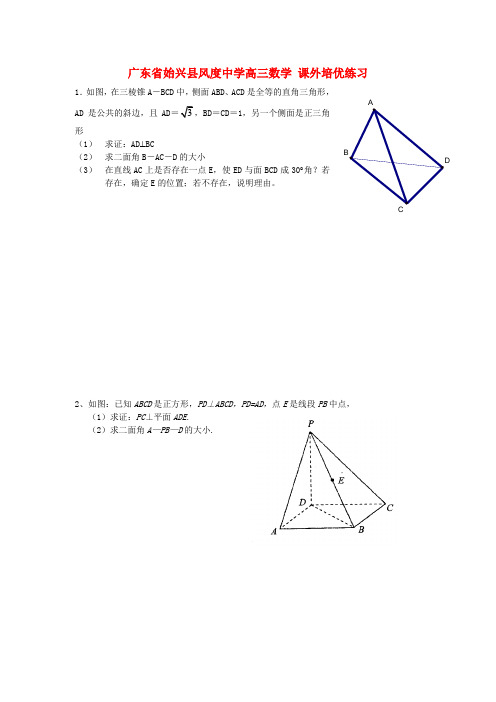
广东省始兴县风度中学高三数学课外培优练习1.如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD3BD=CD=1,另一个侧面是正三角形(1)求证:AD⊥BC(2)求二面角B-AC-D的大小(3)在直线AC上是否存在一点E,使ED与面BCD成30︒角?若存在,确定E的位置;若不存在,说明理由。
2、如图:已知ABCD是正方形,PD⊥ABCD,PD=AD,点E是线段PB中点,(1)求证:PC⊥平面ADE.(2)求二面角A—PB—D的大小.1.解法一:(1) 方法一:作AH ⊥面BCD 于H ,连DH 。
AB ⊥BD ⇒HB ⊥BD ,又AD =3,BD =1∴AB=2=BC =AC ∴BD ⊥DC又BD =CD ,则BHCD 是正方形,则DH ⊥BC ∴AD ⊥BC 方法二:取BC 的中点O ,连AO 、DO 则有AO ⊥BC ,DO ⊥BC ,∴BC ⊥面AOD ∴BC ⊥AD(2) 作BM ⊥AC 于M ,作MN ⊥AC 交AD 于N ,则∠BMN 就是二面角B -AC -D 的平面角,因为AB =AC =BC =2∴M 是AC 的中点,且MN //CD ,则BM =6,MN =12CD =12,BN =12AD =3,由余弦定理可求得cos ∠BMN =6∴∠BMN =arccos6 2.(1)解法一:由条件建立如图所示的直角坐标系,令PD=AD=2a ,则A (2a ,0,0)C (0,2a ,0),P (0,0,2a ),B (2a ,2a ,0),E (a ,a ,a )220),,()2,2,0(0020220)0,0,2()2,2,0()2,2,0(),,,(),0,0,2(=⋅-⋅+⋅=⋅-=⋅=⋅-⋅+⋅=⋅-=⋅∴-===∴a a a a a a a a a a DE PC a a a a a a a a a a a aDE PC DA PC ⊥⊥∴,∴PC ⊥平面ADE(2)联结AC ,取PA 中点G ,联结DG ,则G (a ,0,a )O EABC DHFM NPBDG PA DG DB CA DP CA a a a a a a a a a a PB DG a a a a a a a a PA DG a a a a a a a a DB CA a a a a a a DP CA a a a PB a a PA a a DG a a DB a DP a a CA ⊥⊥⊥⊥∴=-⋅+⋅+⋅=-⋅=⋅=-⋅+⋅+⋅=-⋅=⋅=⋅+⋅-⋅=⋅-=⋅=⋅+⋅-⋅=⋅-=⋅∴-=-====-=∴,,,0)2(202)2,2,2(),0,(0)2(002)2,0,2(),0,(0002222)0,2,2()0,2,2(0200202)2,0,0()0,2,2()2,2,2(),2,0,2(),,0,()0,2,2(),2,0,0(),0,2,2( ∴CA ⊥平面PBD ,DG ⊥平面PAB故向量DG CA 与分别是平面PBD 与平面PAB 的法向量。
高三数学培优九

高三数学培优(九)——等差数列与等比数列1.三个数,,1,,1,1,122成等比数列又成等差数列n m nm 的值为则n m n m ++22A .-1或3B .-3或1C .1或3D .-3或-12.在等比数列1020144117,5,6,}{a a a a a a a n 则中=+=⋅= ( )A .2332或B .2332--或 C .515--或D .2131-或 3.等比数列===302010,10,20,}{M M M M n a n n 则若项乘积记为前 ( )A .1000B .40C .425 D .81 4.已知等差数列5,8,11,…与3,7,11,…都有100项,则它们相同项的个数 A .25 B .26 C .33 D .345.已知一个等差数列的前5项的和是120,最后5项的和是180,又所有项的和为360,则此数列的项数为( ) A .12项 B .13项 C .14项 D .15项 6.两个等差数列)(27417,}{},{+∈++=N n n n B A B A n b a n n n n n n 且满足和项和分别为的前则的值是1111b a A .47 B .23 C .34 D .71787.已知公差不为零的等差数列{}n a 与等比数列{}n b 满足:,,3311b a b a ==,57b a =那么 A.=11b 13a B.=11b 31a C.=11b 63a D.1163a b =8.等差数列}{n a 的公差d 不为零,S n 是其前n 项和,则下列四个命题中的假命题是 A.若d<0,且S 3=S 8,则{S n }中,S 5和S 6都是{S n }中的最大项 B.给定n ,对于一切)(*n k N k <∈,都有n k n k n a a a 2=++- C.若d>0,则{S n }中必然有最小的项D.存在*N k ∈,使11-+--k k k k a a a a 和同号9.若n S 是等差数列{}n a 的前n 项和,其首项10a >,991000a a +>,991000a a ⋅<,则使0n S >成立的最大自然数n 是A.198 B.199 C.200 D.20110.设5021,,,a a a 是从1,0,1-这三个整数中取值的数列,若95021=+++a a a ,且107)1()1()1(2502221=++++++a a a ,则5021,,,a a a 傍边取零的个数为(A )10 (B )11 (C )15 (D )2511.在等比数列543211245,4,108,}{a a a a a a a a a a n ++++=-=-则中的值为 12.若a 、b 、c 成等比数列,a 、x 、b 成等差数列,b 、y 、c 成等差数列,则=+ycx a . 13.数列}{n a 是公差不为零的等差数列,它的第4,8,17项恰是另一等比数列}{n b 的第6,8,10项,则}{n b 的公比是 .14.在等差数列===+q p q p n a p a q a a 则中,,,}{ .在各项为正的等比数列===-+m n m n m n a q a p a a 则中,,,}{ . 15. 数列}{n a 中,1,273==a a ,且数列}11{+n a 是等差数列,则11a =___________. 16.设等差数列,324),6(144,36,}{66=>==-n n n n S n S S S n a 已知项和为的前求n a 的值.17.设等比数列的各项为正数,前n 项的和为2,这n 项后面的2n 项的和为12,求上述3n 项后面的3n 项之和.18.已知等差数列,,0},{461S S a a n =<且(Ⅰ)当n 为何值时,S n 最小?(Ⅱ)当n 为何值时,?0?0?0<>=n n n S S S (Ⅲ).2609}{,7287≤≤-=+n n a a a a 中有多少项满足问若19.有五个整数成等比数列,且第一个数为正数,若这五个整数的和为205,而它们的倒数之和为256205,求此五数.20.数列,0,,}{≠n n n a n S n a 对任意的正整数项和为的前.?}{),1|(|11说明理由是否为等比数列问数列若n n n n a k ka S S >=+++高三数学培优(九)——等差数列与等比数列参考答案一、1.B 2.A 3.D 4.A 5.A 6.C 7.C 8.D 9.A 10.B 二、11.242 12.2 13.32±14.0,pq 15. 21 16.216)(6,180361651621=+⎩⎨⎧=-=+++=+++---n n n n n n a a S S a a a a a a 得.35,1)1(,2144126,18036181181413621==∴==⇒=⨯⎩⎨⎧=+++=+++∴a a a d d a a a a a a n 得代入两式相减得 17.(1)),1(1)1(,11-=--=≠n n n q a q q a S q 时当 ,2,2,14)1(2)1(3==⎪⎩⎪⎨⎧=-=-∴a q q a q a n nn得代入得;112,126)1(3666=-∴=-=∴n n n n S S q a S(2)当q=1时,有na 1=2及2na 1=12,矛盾;综上,所求前3n 项后面的3n 项的和为112. (另解)设公比为,,,,,615621211∑∑∑+=+=====nn k nn k k nk ak Wak W a W q 且.112)(,212)(2122,,,,5431654211321621=++=++=∴=⇒⎩⎨⎧=+=⇒⎩⎨⎧=+=∴n n n n nn n q q q W W W W s q q q W W W W W q W W W 所求和的等比数列成公比为18.(Ⅰ),0029146>⇒<-=⇒=d d a S S;5],25)5[(25222最小时当n n S n n dnd n d S =∴--=-=∴(Ⅱ).0101;010;010),10(2<<≤>>==∴-=n n n n S n S n S n n n dS 时当时当时当 (Ⅲ),18,4142,727,72141487=⨯⨯=⨯=∴=+d dS S a a 得而 .15,19526099189,9918项满足条件共有∴≤≤⇒≤-≤-∴-=∴n n n a n19.设五数为,,,,,22aq aq a qa q a ①②①+② ①②①②①⎪⎪⎩⎪⎪⎨⎧=+++=+++∈>∴*256205)11(1205)11(,0,,,,2222q q q q aq q q q a N a a 由条件得且五项同号三且第一首项为正数.256,64,16,4,1,4;1,4,16,64,256,41,44104174,417)2(;,,04134,413)1(,41741302211616,1,16221)1()1(1618911,16,0,2562222222---=---=-=-=⇒=++-==+-=-==⇒=-+=+=+++⇒=+++=∴>=得所求五数为时得所求五数为时或则若不合方程无有理解则若或得令得代入得q q q q q q x q q x x x x x x q q q q q q q q qq a a a20.111112,,+++++=-=+n n n n n n n S a S S ka S S 得而,,11211,}{,12,11,01,)1()1()1()1(222,)1(12212111111矛盾则为等比数列若而=⇒-=-+-=⇒=+-+=∴≠-+=-⇒+-+-=∴+=++++++k k k k a k a a ka S S k k a a k a k a k a k a k S S a a k n n n n n n n n n n n 故.,0,,}{,).(}{213122222131232311矛盾得由则为等比若另不是等比数列故=⋅⋅=+=⇒=∴=++a a a a a a a a a a a S S a a S S a a a n n n n n n①②① ②① ① ② ①+② ① ② ①,②。
学年广东省华南师大附中高三数学培优练习(2).doc

201X-201X 学年广东省华南师大附中201X 届高三数学培优练习(2)一、选择题:1、由方程 1||||=+y y x x 确定的函数y = f (x )在(-∞,+ ∞)上是A .奇函数B .偶函数C .增函数D .减函数2、设奇函数]1,1[)(-在x f 上是增函数,且,1)1(-=-f 若函数12)(2+-≤at t x f 对所有的]1,1[-∈x 都成立,当]1,1[-∈a 时,则t 的取值范围是 A .22≤≤-tB .2121≤≤-tC .022=-≤≥t t t 或或D .02121=-≤≥t t t 或或3、从-3,-2,-1,1,2,3中任取三个不同的数作为椭圆方程022=++c by ax 中的系数,则确定不同椭圆的个数为 A .17B. 18C. 19D. 204、过双曲线12222=-by a x 的右焦点F (c ,0)的直线交双曲线于M 、N 两点,交y 轴于P点,则有NFPNMF PM +的定值为.222b a 类比双曲线这一结论,在椭圆12222=+b y a x (a >b >0)中,NFPN MFPM +是定值A. 222b a -B. 22ab 2-C. 22b a 2D. 22ab 2二、填空题 5、设等比数列)1}({1>-q qn 的前n 项和为n S ,前n+1项的和为1+n S ,1+∞→n nn S S iml =______.6、在一个棱长为cm 65的正四面体内有一点P ,它到三个面的距离分别是1cm ,2cm ,3cm ,则它到第四个面的距离为_______________cm .7、已知函数)(lo g )(221a ax x x f --=的值域为R ,且f (x )在()31,-∞-上是增函数,则a 的范围是 .8、已知函数f(x) = 2x 2-x,则使得数列{qpn n f +)(}(n ∈N +)成等差数列的非零常数p 与q 所满足的关系式为 .三、解答题9、(本题满分12分)某工厂最近用50万元购买一台德国仿型铣床,在买回来以后的第二天投入使用,使用后的第t 天应付的保养费是(t + 500)元,(买来当天的保养维修费以t = 0计算),机器从买来当天到报废共付的保养维修费与购买机器费用的和平均摊到每一天的费用叫做每天的平均损耗.当平均损耗达到最小值时,机器报废最划算.(1) 求每天平均损耗y (元)表示为天数x 的函数;(2) 求该机器买回来后多少天应报废. 10、(本题满分12分) 已知 f (θ) = a sin θ + b cos θ,θ ∈ [ 0, π ],且1与2 cos 2 θ2 的等差中项大于1与 sin 2 θ2 的等比中项的平方.求:(1) 当a = 4, b = 3时,f (θ) 的最大值及相应的 θ 值;(2) 当a > b > 0时,f (θ) 的值域.11、(本题满分12分)已知椭圆C 的方程为x 2+ y 22 = 1,点P (a , b )的坐标满足a 2+ b 22≤ 1,过点P 的直线l 与椭圆交于A 、B 两点,点Q 为线段AB 的中点,求:(1) 点Q 的轨迹方程;(2) 点Q 的轨迹与坐标轴交点个数。
高考数学精准培优专练十 等差、等比数列(文) 学生版

三、等差等比数列综合问题
例 3:已知等比数列an 中,若 4a1 , a3 , 2a2 成等差数列,则公比 q
.
四、等差等比数列的证明
例 4:已知数列
an
的首项 a1
3 5
, an1
3an , nN* 2an 1
1 .求证:数列
an
1
为等比数列.
对点增分集训
一、选择题
1.已知an 为等比数列,且 a3 4 , a7 16 ,则 a5 ( )
只有②是等比数列.
6.【答案】B
【解析】∵ a3, a4 , a8 成等比数列,∴ a42 a3a8 , a1 3d 2 a1 2d a1 7d ,
整理后可得: 3a1d
5d
2
,∴
d
3 5
a1 ,
则 a1d
3 5
a12
0 ,且 dS4
d 4a1
6d
6a12 25
0 ,∴故选 B.
n 10.已知等差数列 an 的公差 d 0 ,且 a1, a3, a13 成等比数列,若 a1 1, Sn 为数列 an 前 项和,
则 2Sn 16 的最小值为( ) an 3
A. 3
B. 4
二、填空题
C. 2 3 2
D. 9 2
11.已知等比数列 an 的公比为正数,且 a2 1, a3a9 2a52 ,则 a10
A. 64
B. 64
C. 8
D. 8
2.设 Sn 为等差数列an 的前 n 项和, S8 4a3 , a7 2 ,则 a9 ( )
A. 6
B. 4
C. 2
D. 2
3.已知等差数列an 中, a1 a2 a3 3 , a28 a29 a30 165 ,则此数列前 30 项和等于( )
高三数学-2021年华南师大附中高三数学培优试题一 精品

高三数学-2021年华南师大附中高三数学培优试题一精品培优练习(1)2021-02-24 一、选择题: 1、已知函数y?f?1,则y?f(x?1)的反函数的图象一定过点() (x)的图象过(1,0)12 A.(1,2) B.(2,1) C.(0,2) D.(2,0)2、从P点引三条射线PA,PB,PC,每两条射线夹角为60°,则平面PAB和平面PBC 所成二面角正弦值为()A.22 3B.6 3C.3 3D.3 2()?y?x223、已知x,y满足不等式组??x?2y?4则t?x?y?2x?2y?2的最小值为?y??2? A.9 5B.2 C.3D.24、在斜三棱柱ABC-A1B1C1中,A0,B0,分别为侧棱AA1,BB1上的点,且知BB0:B0B1=3:2,过A0,B0,C1 的截面将三棱柱分成上下两个部分体积之比为2:1,则 AA0:A0A1= () A.2:3 B.4:3 C.3:2 D.1:1 二、填空题:5、lim(n?n?n)? . n???26、某气象站天气预报准确率是80%,5次预报中至少有4次准确的概率是(精确到0.01). 7、设a,b都是正实数,且2a+b=1,设T?2ab?4a?b则当a=______且b=_______时,T的最大值为_______。
8、如图,矩形ABCD中,DC?3,AD=1,在DC上截取DE=1,将△ADE沿AE翻折到D′点,当D′在平面ABC上的射影落在AE上时,四棱锥D′―ABCE的体积是________;当D′在平面ABC上的射影落在AC上时,二面角D′―AE―B的平面角的余弦值是_________。
三、解答题:(过程要完整、表述要规范) 9、(本小题满分12分)是否存在常数c,使得不等式22xyxy??c??对任意正实数x、y2x?yx?2yx?2y2x?y恒成立?证明你的结论.10、(本小题满分12分)甲乙两人独立解某一道数学题,已知该题被甲独立解出的概率为0.6,被甲或乙解出的概率为0.92. (1)求该题被乙独立解出的概率;(2)求解出该题的人数?的数学期望和方差.11、(本小题满分14分)已知f(x)?x2?(a?1)x?lg|a?2|(a??2,a?R)(Ⅰ)若f(x)能表示成一个奇函数g(x)和一个偶函数h(x)的和,求g(x)和h(x) 的解析式;(Ⅱ)若f(x)和g(x)在区间(??,(a?1)2]上都是减函数,求a的取值范(Ⅲ)在(Ⅱ)的条件下,比较f(1)和1的大小. 612、(本小题满分12分)已知定义域为[0,1]的函数f (x)同时满足:(1)对于任意x∈[0,1],总有f (x)≥0;(2)f (1) =1;(3)若x1?0,x2?0,x1?x2?1,则有f(x1?x2)?f(x1)?f(x2)。
2023届高三数学培优试卷含详细答案解析(九)

2023届高三培优试卷(九)一、单选题1.设集合{}2A x x =>,{}260B x x x =-->,则RAB =( )A .[)2,-+∞B .()2,+∞C .(],2-∞-D .(],3-∞ 2.在复平面内,复数24ii+对应的点位于( ) A .第一象限 B .第二象限C .第三象限D .第四象限3.已知向量(,1)a m =-,(3,4)b =-,且||1a =,则a b ⋅=( ) A .-4B .1C .4D .74.在12nx ⎫-⎪⎭的展开式中,第4项和第5项的二项式系数相等,则展开式中5x 的系数为( ) A .358B .358-C .92D .92-5.用到球心的距离为1的平面去截球,以所得截面为底面,球心为顶点的圆锥体积为83π,则球的表面积为( ) A .16π B .32πC .36πD .48π二、多选题6.已知双曲线222:1(0)4x y C b b -=>,则( )A .C 的焦点在y 轴上B .C 的虚轴长为2C .直线x =C 相交的弦长为1D .C 的渐近线方程为2y x =±三、填空题7.已知等比数列{}n a 满足16118a a a =,则48a a =________.8.函数()2()1e 1xf x x =+-的零点个数为________.四、解答题9.已知公比大于0的等比数列{}n a 的前n 项和为n S ,24a =,15a +是2S 和3a 的等差中项.(1)求数列{}n a 的通项公式; (2)若n nnb a =,求数列{}n b 的前n 项和n T .10.已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为1F ,2F ,过点2F 作直线l 交椭圆C 于M ,N 两点(l 与x 轴不重合),1F MN △,12F F M △的周长分别为12和8. (1)求椭圆C 的方程;(2)在x 轴上是否存在一点T ,使得直线TM 与TN 的斜率之积为定值?若存在,请求出所有满足条件的点T 的坐标;若不存在,请说明理由.2023届高三培优试卷(九)答案1.【答案】A【详解】由题意得()(),23,B =-∞-+∞,所以[]R2,3B =-,所以[)R2,AB =-+∞,故选:A2.【答案】D【详解】由复数的运算法则,可得224(24)42421i i i ii i i ++-+===--,对应的点(4,2)-位于第四象限. 故选:D. 3.【答案】C【详解】因为||1a =,所以0m =,所以03(1)(4)4a b ⋅=⨯+-⨯-=.故选:C 4.【答案】B【详解】由已知可得34n n C C =,则7n =,所以二项式712x ⎫⎪⎭的展开式的通项公式为:7721771212r rr r rr r T C x C x +-+⎛⎪ ⎫-⎪⎛⎝⎫=-= ⎭⎭⎝,令752r +=解得3r =,所以33557413528T C x x ⎛⎫-=-⎪⎝= ⎭,即5x 的系数为358-,故选:B .5.【答案】C【详解】设球的半径为R ,圆锥的底面半径为r ,因为球心到截面的距离为1,所以有:221r R =-,则题中圆锥体积()2181133V R ππ=⨯⨯-=,解得3R =,故球的表面积为2436R ππ=.故选:C6.【答案】BC【详解】由222:1(0)x y C b-=>可知双曲线C 的焦点在x 轴上,A 错误;C 的离心率e ==1b =,C 的虚轴长为22b =,故B 正确; 由B 选项知1b =,把x =2214x y -=得12y =±,故弦长为1,C 正确;由B 选项知1b =且2a =,且焦点在x 轴上,双曲线C 的渐近线方程为12b y x x a =±=±,故D 错误. 故选:BC.7.【答案】4【详解】因为3161168a a a a ==,所以368a =,解得62a =. 所以24864a a a ==. 故答案为:4 8.【答案】1【详解】因为()22()2e 1e (1)0e x x xf x x x x '++=+≥=,所以()f x 单调递增,又因为(0)0f =,所以()f x 有且仅有1个零点. 故答案为:1 9.【详解】(1)设数列{}n a 的公比为(0)q q >. 由题意知()12325a S a +=+,即442544q q q⎛⎫⨯+=++ ⎪⎝⎭,化简得22320q q --=,因为0q >,所以2q . 所以222422n n nn a a q --==⨯=.(2)由(1)可知2n n n n n b a ==. 所以1231232222n n nT =+++⋅⋅⋅+,①231112122222n n n n nT +-=++⋅⋅⋅++,② 由-①②,可得12311111111111222112222222212n n n n n n n n n T +++⎛⎫- ⎪+⎝⎭=+++⋅⋅⋅+-=-=--,所以222n n n T +=-. 10.【详解】(1)设椭圆C 的焦距为2(0)c c >,由题意可得412228aa c =⎧⎨+=⎩,解得31a c =⎧⎨=⎩,所以b C 的方程为22198x y . (2)因为直线l 过点2(1,0)F 且不与x 轴重合,所以设l 的方程为1x my =+,联立方程221198x my x y =+⎧⎪⎨+=⎪⎩,消去x 并整理得()228916640m y my ++-=,设()11,M x y ,()22,N x y ,则12212216896489m y y m y y m ⎧+=-⎪⎪+⎨⎪=-⎪+⎩,所以()1212218289x x m y y m +=++=+, ()()()2212121212272911189m x x my my m y y m y y m -+=++=+++=+. 设(,0)T t ,则直线TM 与TN 的斜率分别为11TM y k x t =-,22TN y k x t =-,则()()1212TM TN y y k k x t x t ⋅=--()2122221212226489729188989y y m m x x t x x t t tm m -+==-+-++-⋅+++()222648729189t m t t -=-+-+.所以当28720t -=,即当3t =-时,m ∀∈R ,49TM TN k k ⋅=-;当3t =时,m ∀∈R ,169TM TN k k ⋅=-.因此,所有满足条件的T 的坐标为(3,0)-和(3,0).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
省始兴县风度数学 课外培优练习
2.如图,在正四棱柱ABCD —A 1B 1C 1D 1中,AA 1=2
1A B ,点E 、M 分别为A 1B 、C 1C 的中点,过点A 1,B ,M 三点的平面A 1BMN 交C 1D 1于点N.
(Ⅰ)求证:EM ∥平面A 1B 1C 1D 1; (Ⅱ)求二面角B —A 1N —B 1的正切值.
1.解法一:PO ⊥平面ABCD , PO BD ∴⊥ 又,2,2PB PD BO PO ⊥==, 由平面几何知识得:1,3,6OD PD PB ==
= (Ⅰ)过D 做//DE BC 交于AB 于E ,连结PE ,则PDE ∠或其补角为异面直线PD 与BC 所成的角,
四边形ABCD 是等腰梯形,1,2,OC OD OB OA OA OB ∴====⊥
5,22,2BC AB CD ∴===
又//AB DC ∴四边形EBCD 是平行四边形。
5,2ED BC BE CD ∴====
E ∴是AB 的中点,且2AE =
又6PA PB ==,PEA ∴∆为直角三角形,22622PE PA AE ∴=
-=-=
在PED ∆中,由余弦定理得 222215cos 215235
PD DE PE PDE PD DE +-∠===⋅⋅⋅ 故异面直线PD 与BC 所成的角的余弦值为215 (Ⅱ)连结OE ,由(Ⅰ)及三垂线定理知,PEO ∠为二面角
P AB C --的平面角
2sin 2
PO PEO PE ∴∠==,045PEO ∴∠= ∴二面角P AB C --的大小为045
(Ⅲ)连结,,MD MB MO ,
PC ⊥平面,BMD OM ⊂平面BMD ,PC OM ⊥
又在Rt POC ∆中,
3,1,2PC PD OC PO ====,
233,33PM MC ∴==,2PM MC
∴= 故2λ=时,PC ⊥平面BMD
解法二: PO ⊥平面ABCD PO BD ∴⊥
又PB PD ⊥,2,2
BO PO ==,
由平面几何知识得:1,2OD OC BO AO ====
以O 为原点,,,OA OB OP 分别为,,x y z 轴建立如图所示的空间直角坐标系,则各点坐标为(0,0,0)O ,(2,0,0)A ,(0,2,0)B ,(1,0,0)C -,(0,1,0)D -,(0,0,2)P
(Ⅲ)设00(,0,)M x y ,由于,,P M C 三点共线,0022z x = PC ⊥平面BMD ,OM PC ∴⊥00(1,0,2)(,0,)0x z ∴--⋅=0020x z ∴=
由(1)(2)知:023
x =-,023z =。
22(,0,33M ∴- 2PM MC
λ∴==,故2λ=时,PC ⊥平面BMD 。
2.解:(A )(Ⅰ)证明:取A 1B 1的中点F ,连EF ,C 1F
∵E 为A 1B 中点
∴EF ∥ 2
1BB 1…………2分 又∵M 为CC 1中点 ∴EF ∥ C 1M
∴四边形EFC 1M 为平行四边形 ∴EM ∥FC 1 ……4分
而EM ⊄平面A 1B 1C 1D 1 . FC 1⊂平面A 1B 1C 1D 1 .
∴EM ∥平面A 1B 1C 1D 1………………6分
(Ⅱ)由(Ⅰ)EM ∥平面A 1B 1C 1D 1 EM ⊂平面A 1BMN 平面A 1BMN ∩平面A 1B 1C 1D 1=A 1N ∴A 1N EM FC 1 ∴N 为C 1D 1 中点
过B 1作B 1H ⊥A 1N 于H ,连BH ,根据三垂线定理 BH ⊥A 1N ∠BHB 1即为二面角B —A 1N —B 1的平面角……8分 设AA 1=a , 则AB=2a , ∵A 1B 1C 1D 1为正方形
∴A 1H=a 5 又∵△A 1B 1H ∽△NA 1D 1 ∴B 1H=54522a
a a
a =⋅
在Rt △BB 1H 中,tan ∠BHB 1=4
55
411==a a H B BB 即二面角B —A 1N —B 1的正切值为45……12分 (B )(Ⅰ)建立如图所示空间直角坐标系,设AB=2a ,AA 1=a(a>0),则
A 1(2a ,0,a
B (2a, 2a , 0),
C (0,2a ,0C 1(0,2a ,a )……2分 ∵E 为A 1B 的中点,M 为CC 1的中点 ∴E (2a , a , 2a M (0,2a, 2a ) ∴EM A 1B 1C 1
D 1 …………6分
(Ⅱ)设平面A 1BM 的法向量为n =(x, y , z ) 又B A 1=(0,2a , -a ) )2
,0,2(a
a BM -=由BM n B A n ⊥⊥,1,得 ⎪⎪⎩
⎪⎪⎨⎧==∴⎪⎩⎪⎨⎧=+-=-24,02202z y z x az ax az ay ),2
,4(a a a n =∴…………9分
而平面A 1B 1C 1D 1的法向量为)1,0,0(1=n .设二面角为θ,则 214
||||cos |11==n n θ又:二面角为锐二面角 214
cos =∴θ,……11分
从而4
5tan =
θ………………12分。
