七年级数学竞赛培优(含解析)专题24 相交线与平行线
相交线与平行线解析含答案
相交线与平行线解析含答案一、选择题1．如图，直线AB，CD相交于点O，∠2－∠1=15°，∠3=130°．则∠2的度数是()A．37.5°B．75°C．50°D．65°【答案】D【解析】【分析】先根据条件和邻补角的性质求出∠1的度数，然后即可求出∠2的度数．【详解】）∵∠3=130°，∠1+∠3=180°，∴∠1=180°-∠3=50°，∵∠2-∠1=15°，∴∠2=15°+∠1=65°；故答案为D.【点睛】本题考查角的运算，邻补角的性质，比较简单.2．如图1，将三角板的直角顶点放在直角尺的一边上，∠1=30°，∠2=50°，则∠3的度数为A．80°B．50°C．30°D．20°【答案】D【解析】【分析】【详解】试题分析：根据平行线的性质，得∠4=∠2=50°，再根据三角形的外角的性质∠3=∠4-∠1=50°-30°=20°．故答案选D．考点：平行线的性质;三角形的外角的性质．3．如图，点D在AC上，点F、G分别在AC、BC的延长线上，CE平分∠ACB交BD于点O，且∠EOD+∠OBF＝180°，∠F＝∠G，则图中与∠ECB相等的角有( )A．6个B．5个C．4个D．3个【答案】B【解析】【分析】由对顶角关系可得∠EOD=∠COB，则由∠COB+∠OBF=180°可知EC∥BF，再结合CE是角平分线即可判断.【详解】解：由∠EOD+∠OBF=∠COB+∠OBF=180°可知EC∥BF，结合CE是角平分线可得∠ECB=∠ACE=∠CBF，再由EC∥BF可得∠ACE=∠F=∠G，则由三角形内角和定理可得∠GDC=∠CBF.综上所得，∠ECB=∠ACE=∠CBF=∠F=∠G=∠GDC，共有5个与∠ECB相等的角，故选择B.【点睛】本题综合考查了平行线的判定及性质.4．如图AD∥BC,∠B=30o,DB平分∠ADE,则∠DEC的度数为（）A．30o B．60o C．90o D．120o【答案】B【解析】∵AD∥BC，∴∠ADB=∠DBC，∵DB平分∠ADE，∴∠ADB=∠ADE，∵∠B=30°，∴∠ADB=∠BDE=30°，则∠DEC=∠B+∠BDE=60°．故选B．【点睛】此题主要考查了平行线的性质，正确得出∠ADB的度数是解题关键．5．如图，在平面内，两条直线l1，l2相交于点O，对于平面内任意一点M，若p，q分别是点M到直线l1，l2的距离，则称(p,q)为点M的“距离坐标”．根据上述规定，“距离坐标”是(2,1)的点共有（）个．A．1个B．2个C．3个D．4个【答案】D【解析】【分析】到l1距离为2的直线有2条，到l2距离为1的直线有2条，这4条直线有4个交点，这4个交点就是“距离坐标”是（2，1）的点．【详解】因为两条直线相交有四个角，因此每一个角内就有一个到直线l1，l2的距离分别是2，1的点，即距离坐标是（2，1）的点，因而共有4个．故选：D．【点睛】本题主要考查了点到直线的距离，解题时注意：到一条已知直线距离为定值的直线有两条．6．如图，一条公路修到湖边时，需拐弯绕湖而过，如果第一次拐弯处的∠A是72°，第二次拐弯处的角是∠B，第三次拐弯处的∠C是153°，这时道路恰好和第一次拐弯之前的道路平行，则∠B等于()A．81°B．99°C．108°D．120°【答案】B【解析】试题解析：过B 作BD ∥AE ，∵AE ∥CF ，∴BD ∥CF ，∴72,180A ABD DBC C ∠=∠=∠+∠=o o，∵153C ∠=o ，∴27DBC ∠=o ，则99.ABC ABD DBC ∠=∠+∠=o 故选B.7．如图，AB ∥EF ，设∠C ＝90°，那么x 、y 和z 的关系是（ ）A ．y ＝x+zB ．x+y ﹣z ＝90°C ．x+y+z ＝180°D ．y+z ﹣x ＝90°【答案】B【解析】【分析】 过C 作CM ∥AB ，延长CD 交EF 于N ，根据三角形外角性质求出∠CNE ＝y ﹣z ，根据平行线性质得出∠1＝x ，∠2＝∠CNE ，代入求出即可．【详解】解：过C 作CM ∥AB ，延长CD 交EF 于N ，则∠CDE ＝∠E+∠CNE ，即∠CNE ＝y ﹣z∵CM ∥AB ，AB ∥EF ，∴CM ∥AB ∥EF ，∴∠ABC ＝x ＝∠1，∠2＝∠CNE ，∵∠BCD ＝90°，∴∠1+∠2＝90°，∴x+y ﹣z ＝90°．故选：B ．【点睛】本题考查了平行线的性质和三角形外角性质的应用，注意：平行线的性质有：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补．8．如图，ABCD为一长方形纸带，AB∥CD，将ABCD沿EF折叠，A、D两点分别与A′、D′对应，若∠1=2∠2，则∠AEF的度数为( )A．75°B．72°C．70°D．65°【答案】B【解析】【分析】如图，由折叠的性质可知∠3=∠4，已知AB∥CD，根据两直线平行,内错角相等可得∠3=∠1，再由∠1=2∠2，∠3+∠4+∠2=180°，可得5∠2=180°，即可求得∠2=36°，所以∠AEF=∠3=∠1=72°【详解】如图，由折叠的性质可知∠3=∠4，∵AB∥CD，∴∠3=∠1，∵∠1=2∠2，∠3+∠4+∠2=180°，∴5∠2=180°，即∠2=36°，∴∠AEF=∠3=∠1=72°故选B．【点睛】本题考查的是图形翻折变换的性质及平行线的性质，熟知折叠的性质及平行线的性质是解决问题的关键．9．如图，下列条件中能判定//DE AC 的是( )A ．EDC EFC ∠=∠B ．AEF ACD ∠=∠C ．34∠=∠D ．12∠=∠【答案】C【解析】【分析】 对于A ，∠EDC=∠EFC 不是两直线被第三条直线所截得到的，据此进行判断；对于B 、D ，∠AFE=∠ACD ，∠1=∠2是EF 和BC 被AC 所截得到的同位角和内错角，据此进行判断；对于C ，∠3=∠4这两个角是AC 与DE 被EC 所截得到的内错角，据此进行判断.【详解】∠EDC=∠EFC 不是两直线被第三条直线所截得到的，因而不能判定两直线平行；∠AFE=∠ACD,∠1=∠2是EF 和BC 被AC 所截得到的同位角和内错角,因而可以判定EF ∥BC,但不能判定DE ∥AC ；∠3=∠4这两个角是AC 与DE 被EC 所截得到的内错角,可以判定DE ∥AC.故选C.【点睛】本题考查平行线的判定，掌握相关判定定理是解题的关键.10．如图，直线 a ∥b ∥c ，直角三角板的直角顶点落在直线 b 上，若∠1＝30°，则∠2 等于（ ）A ．40°B ．60°C ．50°D ．70° 【答案】B【解析】【分析】根据两直线平行内错角相等得1324==∠∠，∠∠，再根据直角三角板的性质得341290+=+=︒∠∠∠∠，即可求出∠2的度数．【详解】∵a ∥b ∥c∴1324==∠∠，∠∠∵直角三角板的直角顶点落在直线 b 上∴341290+=+=︒∠∠∠∠∵∠1＝30°∴290160=︒-=︒∠∠故答案为：B ．【点睛】本题考查了平行线和三角板的角度问题，掌握平行线的性质、三角板的性质是解题的关键．11．若a ⊥b ，c ⊥d ，则a 与c 的关系是( )A ．平行B ．垂直C ．相交D ．以上都不对【答案】D【解析】【分析】分情况讨论：①当b ∥d 时；②当b 和d 相交但不垂直时；③当b 和d 垂直时；即可得出a 与c 的关系．【详解】当b ∥d 时a ∥c ；当b 和d 相交但不垂直时，a 与c 相交；当b 和d 垂直时，a 与c 垂直；a 和c 可能平行，也可能相交，还可能垂直．故选：D ．【点睛】本题考查了直线的位置关系，掌握平行、垂直、相交的性质是解题的关键．12．如图，下列说法一定正确的是（ ）A ．∠1和∠4是内错角B ．∠1和∠3是同位角C ．∠3和∠4是同旁内角D ．∠1和∠C 是同位角【答案】D【解析】【分析】根据内错角、同位角以及同旁内角的定义进行判断即可．【详解】解：A 、∠2和∠4是内错角，故本选项错误；B 、∠1和∠C 是同位角，故本选项错误；C 、∠3和∠4是邻补角，故本选项错误；D 、∠1和∠C 是同位角，故本选项正确；故选：D ．【点睛】本题考查了同位角、内错角、同旁内角．解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．13．如图所示，某同学的家在P 处，他想尽快赶到附近公路边搭公交车，他选择P→C 路线，用几何知识解释其道理正确的是（ ）A ．两点确定一条直线B ．垂直线段最短C ．两点之间线段最短D ．三角形两边之和大于第三边【答案】B【解析】【分析】根据垂线段的定义判断即可.【详解】 解：Q 直线外一点与直线上各点连接的所有线段中，垂线段最短,∴ 选:B.【点睛】直线外任意一点到这条直线的垂线段的长度，叫做点到这条直线的距离．直线外一点与直线上各点连接的所有线段中，垂线段最短．简称“垂线段最短”．14．如图，在矩形ABCD 中，6AB =，8BC =，若P 是BD 上的一个动点，则PB PC PD ++的最小值是（ ）A ．16B ．15.2C ．15D ．14.8【答案】D【解析】【分析】 根据题意，当PC ⊥BD 时，PB PC PD ++有最小值，由勾股定理求出BD 的长度，由三角形的面积公式求出PC 的长度，即可求出最小值.【详解】解：如图，当PC ⊥BD 时，PB PC PD BD PC ++=+有最小值，在矩形ABCD 中，∠A=∠BCD=90°，AB=CD=6，AD=BC=8，由勾股定理，得226810BD +=，∴=10PB PD BD +=，在△BCD 中，由三角形的面积公式，得11=22BD PC BC CD ••， 即1110=8622PC ⨯⨯⨯⨯， 解得： 4.8PC =， ∴PB PC PD ++的最小值是：10 4.814.8PB PC PD BD PC ++=+=+=； 故选：D.【点睛】本题考查了勾股定理解直角三角形，最短路径问题，垂线段最短，以及三角形的面积公式，解题的关键是熟练掌握勾股定理，正确确定点P 的位置，得到PC 最短.15．下列命题错误的是（ ）A ．平行四边形的对角线互相平分B ．两直线平行，内错角相等C ．等腰三角形的两个底角相等D ．若两实数的平方相等，则这两个实数相等【答案】D【解析】【分析】根据平行四边形的性质、平行线的性质、等腰三角形的性质、乘方的定义，分别进行判断，即可得到答案.【详解】解：A 、平行四边形的对角线互相平分，正确；B 、两直线平行，内错角相等，正确；C 、等腰三角形的两个底角相等，正确；D 、若两实数的平方相等，则这两个实数相等或互为相反数，故D 错误；故选：D.【点睛】本题考查了判断命题的真假，以及平行四边形的性质、平行线的性质、等腰三角形的性质、乘方的定义，解题的关键是熟练掌握所学的性质进行解题.16．下列四个说法：①两点之间，线段最短；②连接两点之间的线段叫做这两点间的距离；③经过直线外一点，有且只有一条直线与这条直线平行；④直线外一点与这条直线上各点连接的所有线段中，垂线段最短.其中正确的个数有（ ）A ．1个B ．2个C ．3个D ．4个【答案】C【解析】【分析】根据线段公理，两点之间的距离的概念，平行公理，垂线段最短等知识一一判断即可．【详解】解：①两点之间，线段最短，正确．②连接两点之间的线段叫做这两点间的距离，错误，应该是连接两点之间的线段的距离叫做这两点间的距离．③经过直线外一点，有且只有一条直线与这条直线平行，正确．④直线外一点与这条直线上各点连接的所有线段中，垂线段最短．正确．故选C ．【点睛】本题考查线段公理，两点之间的距离的概念，平行公理，垂线段最短等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．17．如图，直线//a b ，将一块含45︒角的直角三角尺（90︒∠=C ）按所示摆放．若180︒∠=，则2∠的大小是（ ）A ．80︒B ．75︒C ．55︒D ．35︒【答案】C【解析】【分析】 先根据//a b 得到31∠=∠，再通过对顶角的性质得到34,25∠=∠∠=∠，最后利用三角形的内角和即可求出答案.【详解】解：给图中各角标上序号，如图所示：∵//a b∴3180︒∠=∠=（两直线平行，同位角相等），又∵34,25∠=∠∠=∠（对顶角相等），∴251804180804555A ∠=∠=︒-∠-∠=︒-︒-︒=︒.故C 为答案.【点睛】本题主要考查了直线平行的性质（两直线平行，同位角相等）、对顶角的性质（对顶角相等），熟练掌握直线平行的性质是解题的关键.18．把一块直尺与一块三角板如图放置，若∠1=45°，则∠2的度数为（ ）A ．115°B ．120°C ．145°D ．135°【答案】D【解析】【分析】由三角形的内角和等于180°，即可求得∠3的度数，又由邻补角定义，求得∠4的度数，然后由两直线平行，同位角相等，即可求得∠2的度数．【详解】在Rt△ABC中，∠A=90°，∵∠1=45°（已知），∴∠3=90°-∠1=45°（三角形的内角和定理），∴∠4=180°-∠3=135°（平角定义），∵EF∥MN（已知），∴∠2=∠4=135°（两直线平行，同位角相等）．故选D．【点睛】此题考查了三角形的内角和定理与平行线的性质．注意两直线平行，同位角相等与数形结合思想的应用．19．如图，AB∥CD，DE⊥CE，∠1=34°，则∠DCE的度数为（）A．34°B．56°C．66°D．54°【答案】B【解析】试题分析：∵AB∥CD，∴∠D=∠1=34°，∵DE⊥CE，∴∠DEC=90°，∴∠DCE=180°﹣90°﹣34°=56°．故选B．考点：平行线的性质．20．如图，在下列四组条件中，不能判断AB∥CD的是（）A．∠1＝∠2 B．∠3＝∠4C．∠ABD＝∠BDC D．∠ABC+∠BCD＝180°【答案】A【解析】【分析】根据各选项中各角的关系，利用平行线的判定定理，分别分析判断AB、CD是否平行即可．【详解】A、∵∠1＝∠2，∴AD∥BC（内错角相等，两直线平行），故A不能判断；B、∵∠3＝∠4，∴AB∥CD（内错角相等，两直线平行），故B能判断；C、∵∠ABD＝∠BDC，∴AB∥CD（内错角相等，两直线平行），故C能判断；D、∵∠ABC+∠BCD＝180°，∴AB∥CD（同旁内角互补，两直线平行），故D能判断，故选A．【点睛】本题考查了平行线的判定．掌握同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行是解题的关键．。
七年级数学竞赛培优(含解析)专题24 相交线与平行线
专题24 相交线与平行线阅读与思考在同一平面内，两条不同直线有两种位置关系：相交或平行.当两条直线相交或两条直线分别与第三条直线相交，就产生对顶角、同位角、内错角、同旁内角等位置关系角，善于从相交线中识别出以上不同名称的角是解相关问题的基础，把握对顶角有公共顶点，而同位角、内错角、同旁内角没有公共顶点且有一条边在截线上，这是识图的关键． 两直线平行的判定方法和重要性质是我们研究平行线问题的主要依据． 1．平行线的判定(1)同位角相等、内错角相等，或同旁内角互补，两直线平行； (2)平行于同一直线的两条直线平行；(3)在同一平面内，垂直于同一直线的两条直线平行． 2．平行线的性质(1)过直线外一点，有且只有一条直线和这条直线平行； (2)两直线平行，同位角相等、内错角相等、同旁内角互补；(3)如果一条直线和两条平行线中的一条垂直，那么它和另一条也垂直. 熟悉以下基本图形：例题与求解【例1】 (1) 如图①，AB ∥DE ，∠ABC ＝080，∠CDE ＝0140，则∠BCD ＝__________.（安徽省中考试题）(2) 如图②，已知直线AB ∥CD ，∠C ＝0115，∠A ＝025，则∠E ＝___________.（浙江省杭州市中考试题）DB图②FECA解题思路：作平行线，运用内错角、同旁内角的特征进行求解.【例2】如图，平行直线AB ，CD 与相交直线EF ，GH 相交，图中的同旁内角共有( )． A ．4对 B ．8对 C ．12对 D ．16对（“希望杯”邀请赛试题）解题思路：每一个“三线八角”基本图形都有两对同旁内角，从对原图进行分解入手．A BCDGHEFF DE BCA例2题图 例3题图【例3】 如图，在△ABC 中，CE ⊥AB 于E ，DF ⊥AB 于F ，AC //ED ，CE 是∠ACB 的平分线，求证：∠EDF ＝∠BDF .（天津市竞赛试题）解题思路：综合运用垂直定义、角平分线、平行线的判定与性质，由于图形复杂，因此，证明前注意分解图形．【例4】 如图，已知AB ∥CD ，∠EAF ＝41∠EAB ，∠FCF ＝41∠ECD .求证：∠AFC ＝43∠AEC . （湖北省武汉市竞赛试题）DEC AB 图1解题思路：分别过点E ，F 作平行线，利用平行线的性质找角之间的关系.ABFCD E例4题图 例5题图【例5】如图，已知∠1＝ ∠2，∠C ＝∠D ，求证：∠A ＝∠F .解题思路：从角出发，导出两直线的位置关系，再推出新的角的关系，新的两直线的位置关系，是解这类问题的基本思路.【例6】(1)已知平面内有4条直线a ，b ，c 和d ，直线a ，b 和c 相交于一点，直线b ，c 和d 也相交于一点，试确定这4条直线共有多少个交点？并说明你的理由．(2)作第5条直线e 与(1)中的直线d 平行. 说明：以这5条直线的交点为端点的线段有多少条？（“希望杯”邀请赛试题）解题思路：(1)先设直线a ，b ，c 的交点为P ，直线b ，c ，d 的交点为Q ，证得P 与Q 实为同一点，得出结论．(2)绘出图形，帮助解答，注意平行线的性质.FA BC1 DE 2能力训练A 级1．在同一平面内有1a ，2a ，3a …，10a 十条直线，如果1a //2a ，2a ⊥3a ，3a //4a ，4a ⊥5a ，5a //6a ，6a ⊥7a ，…，那么1a 与10a 的位置关系是____________.2．如图，已知AE ∥BD ，∠1＝0130，∠2＝030，则∠C ＝__________．（湖南省常德市中考试题）3．如图，直线a ，b 都与直线c 相交，下列命题中，能判断a ∥b 的条件是_____________（把你认为正确的序号填在横线上）①∠1＝∠2； ②∠3＝∠6； ③∠1＝∠8；④∠5＋∠8＝0180．（陕西省中考试题）第4题图21第3题图第2题图7865432121DA ECBab4. 将两张矩形纸片如图所示摆放，使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一边上，则∠1＋∠2__________.（山东省烟台市中考试题）5．下面四个命题中正确的是( )．A ．相等的两个角是对顶角B ．和等于0180的两个角互为邻补角 C ．连结两点的最短线是过这两点的直线D ．两条直线相交所成的四个角都相等，则这两条直线互相垂直（“希望杯”邀请赛试题）6．下列命题①两条相交直线组成的四个角相等，则这两直线垂直．②两条相交直线组成的四个角中，若有一个直角，则四角都相等． ③两条直线相交，一角的两邻补角相等，则这两直线垂直． ④两条直线相交，一角与其邻补角相等，则这两直线垂直． 其中正确的有( )．A ．4个B ．3个C ．2个D ．1个7．如图，DH ∥EG ∥BC ，且DC ∥EF ，那么图中与∠BFE 相等的角(不包括∠BFE )的个数是( )． A.2 B ．4 C ．5 D ．6（山东省菏泽地区中考试题）8．如图，AB ∥CD ∥EF ∥GH ，AE ∥DG ，点C 在AE 上，点F 在DG 上，设与∠ɑ相等的角的个数为m （不包括∠a 本身），与∠β互补的角的个数为n ．若a ≠β，则m ＋n 的值是( )．A. 8B. 9C. 10D. 11第8题图第7题图βαCFG AGDHBBEDHE9．如图，已知AB ∥ED ，∠NCB ＝030，CM 平分∠BCE ，CN ⊥CM ，求∠B 的度数．10.如图，已知E 是AB ，CD 外一点，∠D ＝∠B ＋∠E ，求证：AB ∥CD .ABED NCM11.平面上有10条直线，无任何3条交于一点，要使它们出现31个交点，怎样安排才能办到？（吉林省竞赛试题）ABEDC12.如图，已知CD ∥EF ，∠1＋∠2＝∠ABC ，求证：AB //GF .（重庆市竞赛试题）B 级1. 如图，∠A ＝060，∠1＝∠2，则∠ADC 的度数是___________. 2．如图，直线a ∥b ，那么x 的度数是____________.（五城市联赛试题）ba第1题图第2题图第3题图x48°30°30°120°21C'D'EABADBCDC F3．如图，把一个长方形纸片沿EF 折叠后，点D ，C 分别落在D '，C '的位置，若∠EFB ＝065，则∠AED '＝__________.（山东省中考试题）4．如图，已知DE ∥BC ，∠2＝070，∠1＝040，那∠EBA 的度数是_____________.AC21EBDlk4321第4题图 第5题图5. 如图，直线k ∥l ，∠4－∠3＝∠3－∠2＝∠2一∠3＝d ＞0．其中∠3＜090，∠1＝050，则∠4最大可能的整数值是( )．A. 1070B ．1080C ．1090D ．11006. 如图，AB ∥CD ∥EF ，EH ⊥CD 于H ，则∠BAC ＋∠ACE ＋∠CEH 等于( )． A ．1800B ．2700C ．3600D ．4500(北京市竞赛试题）7．如图，两直线AB ，CD 平行，则∠1＋∠2＋∠3＋∠4＋∠5＋∠6＝ ( )． A ．6300B. 7200C ．8000D. 9000（“希望杯”邀请赛试题）BDFAC654321HACBDEF GH第6题图 第7题图8．两条直线a ，b 互相平行，直线a 上顺次有10个点A 1，A 2…，A 10，直线b 上顺次有9个点B 1，B 2，…，B 3，将a 上每一个点与b 上每一个点相连可得线段．若没有三条线段相交于同一点，则这些线段的交点个数是( )A. 90B.1620C.6480D.20069．如图，已知两条平行线AB ，CD 被直线EF 所截，交点分别为G ，H ，P 为HD 上任意一点，过P 点的直线交HF 于O 点，求证：∠HOP ＝∠AGF －∠HPO .O PA BCD10．如图，在△ABC 中，AB ＝7，AC ＝11，点M 是BC 的中点，AD 是∠BAC 的平分线，MF ∥AD .求FC 的长．(2013年“《数学周报》”杯竞赛试题)D FMBC11．平面上有七条两两不平行的直线，试证：其中必有直线的交角小于260．（莫斯科八年级竞赛试题）12．⑴如图①，MA 1∥NA 2，则∠A 1＋∠A 2＝_________.如图②，MA 1∥NA 3，则∠A 1＋∠A 2＋∠A 3＝_________. 如图③，MA 1∥NA 4，则∠A 1＋∠A 2＋∠A 3＋∠A 4＝_________. 如图④，MA 1∥NA 5，则∠A 1＋∠A 2＋∠A 3＋∠A 4＋∠A 5＝_________.从上述结论中你发现了什么规律？请在图②，图③，图④中选一个证明你的结论.（2）如图5，n NA ||MA 1，则=∠++∠+∠+∠n A A A A 321 .（3）利用上述结论解决问题：如图已知CD ||AB ，AB E ∠和CDE ∠的平分线相交于F ，140E =∠，求B FD ∠的度数.A 6A nA 5A 4A 2A 1 MNA 2（第21题）A 1MNA 3A 2 A 1MNA 3A 4A 2 A 1MNA 3 A 5A 4 A 2 A 1MNA 3 图①图②图③ 图④图⑤FEBACD图⑥专题24 相交线与平行线例1 （1）40° 过点 C 作CF ∥AB ，则∠BCF ＝∠ABC ＝80°．∠DCF ＝180°—140°＝40°，∴∠BCD ＝80°－40°=40°.（2）90° 过点E 作EM ∥AB ，∴AB ∥CD ，∴EM ∥CD ，∠AEM =180°—25°=155°. ∠CEM =180°—115°=65°，∴∠E =∠AE —∠CEM =155°-65°=90°.例2 D 提示：原图可分解为8个基本图形.例3 提示：由DF ∥CE 得，∠BDF =∠BCE ，∠FDE =∠DEC ，AC ∥DE ，得∠DEC =∠ECA .例4 过E 作EM ∥AB .∴AB ∥于CD ，∴EM ∥CD . ∴∠AEC =∠AEM +∠CEM =∠EAB +∠ECD .同理：∠AFC =∠FAB +∠FCD .∴∠AEC =∠FAB +∠FCD +∠EAF +∠ECF =∠AFC +¼∠EAB +14+∠ECD =∠AFC +¼∠AEC .故∠AFC =¾∠AEC .例5 提示：先证BD ∥CE ，再证DF ∥BC .例6 （1）直线a ，b ，c ，d 共有1个交点，理由如下：设直线a ，b ，c 的交点为P ，直线b ，c ，d 的交点为Q .这意味着点P 和点Q都是直线b 和c 的交点.而两条不同直线至多有一个交点.因此P和Q 必为同一个点.即4条直线a ，b ，c 和d 相交于同一个点.因此这4条直线只有一个交点.(2)不妨设（1）中交点为O .因为作的第5条直线e 与（1）中的直线d 平行，所以直线e 和直线d 没有公共点，因此这些e 不过点O .而直线a ，b ，c 与直线e 必然都相交.如图所示.设直线e 与直线a ，b ，c 分别相交于点A ，B ，C .这时有A ，B ，C ，O 共四个不同的点.可以连出OA ，OB ，OC ，AB ，AC ，BC 共6条不同的线段.A 级1. 1a //10a2.20°3.①②③④4.90°5.D6.B7.C8.D提示：m =5，n =6，m +n =5+6=11. 9.60° 10.提示：过点E 作EF ∥AB . 11如图所示.12.作CK ∥FG ，延长GF ，CD 交于H 点，则∠1+∠2=∠ABC ，故∠ABC +∠BCK =180°，即CK ∥AB ，AB ∥GF .B级1.120°2.72°3.50°4.30°5.C 提示：∠2=50°+d，∠3=50°+2d，∠4=50°+3d，又∵∠3=50°+2d<90°，∴d<20°，∠4=50°+3d<110°.故∠4的最大整数值为109°.6.B7.D8.B 提示：由题意知每一个交点由a上两点和b上两点所确定.在a上取两点有种情况，在b上取两点有种情况，故交点个数为45*36=1620个.9.提示：过点O作CD的平行线.10.如图，设N是AC的中点，连接MN，则MN∥AB.又MF∥AD，∴∠FMN=∠BAD=∠DAC=∠MFN.∴FN=MN=½AB.因此FC=FN+NC=½AB+12AC=½(AB+AC）=½（7+11）=9.11.提示：在平面上任取一点O，将已知的七条直线平移过点O，它们把以O为圆心的圆周角分成14个彼此相邻的角a₁,a₂,……，。
(完整word版)七年级数学培优竞赛相交线与平行线
订交线与平行线一、知识重点：1.平面上两条不重合的直线，地点关系只有两种：订交和平行。
2.两条不一样的直线，若它们只有一个公共点，就说它们订交。
即，两条直线订交有且只有一个交点。
3.垂直是订交的特别状况。
相关两直线垂直，有两个重要的结论：（1）过一点有且只有一条直线与已知直线垂直；（2）直线外一点与直线上所有点的连线中，垂线段最短。
4．两条直线被第三条直线所截，组成八个角，在那些没有公共极点的角中，⑴假如两个角分别在两条直线的同一方，而且都在第三条直线的同侧，拥有这类关系的一对角叫做___________ ；⑵假如两个角都在两直线之间，而且分别在第三条直线的双侧，拥有这类关系的一对角叫做____________ ；⑶假如两个角都在两直线之间，但它们在第三条直线的同一旁，具有这类关系的一对角叫做_______________.5．平行公义：经过直线外一点，有且只有一条直线与这条直线______.推论：假如两条直线都与第三条直线平行，那么_____________________.6．平行线的判断：⑴两条直线被第三条直线所截，假如同位角相等，那么这两条直线平行. 简单说成：_______________________. ⑵两条直线被第三条直线所截，假如内错角相等，那么这两条直线平行. 简单说成：___________________________. ⑶两条直线被第三条直线所截，假如同旁内角互补，那么这两条直线平行. 简单说成：_______________________.7．在同一平面内，假如两条直线都垂直于同一条直线，那么这两条直线_______ .8．平行线的性质：⑴两条平行直线被第三条直线所截，同位角相等.简单说成：＿＿＿＿＿＿＿＿＿＿. ⑵两条平行直线被第三条直线所截，内错角相等. 简单说成： __________. ⑶两条平行直线被第三条直线所截，同旁内角互补. 简单说成： __________________ 。
七年级数学相交线与平行线 培优复习附详细答案word版本
七年级数学：相交线与平行线培优复习 )案答细详附(精品文档七年级数学：相交线与平行线培优复习例题精讲例1．如图(1)，直线a与b平行，∠1＝(3x+70)°,∠2=(5x+22)°,的度数。
求∠3la3，a∥b解：∵4b2（两直线平行，内错角相等）4∴∠3＝∠) 平角的定义4＝180°(∵∠1+∠3＝∠2+∠) 等式性质∠1＝∠2 (∴x=24 3x+70＝5x+22解得则＝142°即∠1 图(1)38°＝3180°-∠1＝∴∠评注：建立角度之间的关系，即建立方程（组），是几何计算常用的方法。
D ∠B+∠BED+，EG平分∠BEF，∠∥例2．已知：如图(2)，AB∥EFCD°，=192 的度数。
°，求∠GEF∠B-∠D=24 AB CD∥∥EF解：∵AB GE∠BEF，∠DEF=∠D（两直线平行，内错角相等）∴∠B=FCD D =192∠°（已知）∵∠B+∠BED+ °DEF+∠D=192∠即∠B+∠BEF+ °（等量代换））B+∠D=192（∠∴2°（等式性质）∠则∠B+D=96收集于网络，如有侵权请联系管理员删除．精品文档∵∠B-∠D=24°（已知）图(2)∴∠B=60°（等式性质）即∠BEF=60°（等量代换）∵EG平分∠BEF（已知）1∠BEF=30°（角平分线定义）∴∠GEF=2DEB的度数。
），已知AB∥CD，且∠B=40°，∠D=70°，求∠例3．如图（3DCAB EF∥解：过E作（已知）AB∥CD∵ABFE∴EF∥CD（平行公理）∴°（两直线平行，内错角相等）DEF=∠∠D=70∠BEF=∠B=40°BEF -∠DEB=∵∠∠DEF -∠D∠B=30°∠∴DEB =评注：证明或解有关直线平行的问题时，如果不构成“三线八角”，则应添出辅3）图（助线。
七年级下册 相交线与平行线 培优训练(含答案)
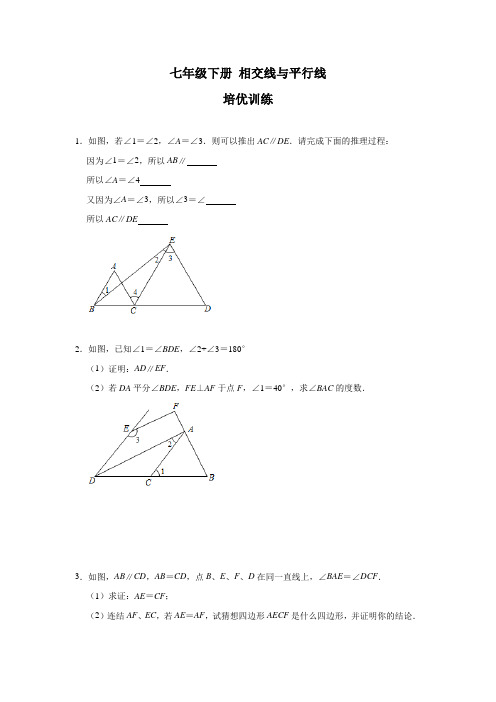
七年级下册相交线与平行线培优训练1．如图，若∠1＝∠2，∠A＝∠3．则可以推出AC∥DE．请完成下面的推理过程：因为∠1＝∠2，所以AB∥所以∠A＝∠4又因为∠A＝∠3，所以∠3＝∠所以AC∥DE2．如图，已知∠1＝∠BDE，∠2+∠3＝180°（1）证明：AD∥EF．（2）若DA平分∠BDE，FE⊥AF于点F，∠1＝40°，求∠BAC的度数．3．如图，AB∥CD，AB＝CD，点B、E、F、D在同一直线上，∠BAE＝∠DCF．（1）求证：AE＝CF；（2）连结AF、EC，若AE＝AF，试猜想四边形AECF是什么四边形，并证明你的结论．4．【问题原型】如图①，AB∥CD，点M在直线AB、CD之间，则∠M＝∠B+∠D，小明解决上述问题的过程如下：如图②，过点M作MN∥AB则∠B＝（）∵AB∥CD，（已知）MN∥AB（辅助线的做法）∴MN∥CD（）∴∠＝∠D（）∴∠B+∠D＝∠BMD请完成小明上面的过程．【问题迁移】如图③，AB∥CD，点M与直线CD分别在AB的两侧，猜想∠M、∠B、∠D之间有怎样的数量关系，并加以说明．【推广应用】（1）如图④，AB∥CD，点M在直线AB、CD之间，∠ABM的平分线与∠CDM的平分线交于点N，∠M＝96°，则∠N＝°；（2）如图⑤，AB∥CD，点M与直线CD分别在AB的两侧，∠ABM的平分线与∠CDM的平分线交于点N，∠N＝25°，则∠M＝°；（3）如图⑥，AB∥CD，∠ABG的平分线与∠CDE的平分线交于点M，∠G＝78°，∠F＝64°，∠E＝64°，则∠M＝°．5．感知：如图①，若AB∥CD，点P在AB、CD内部，则∠P、∠A、∠C满足的数量关系是．探究：如图②，若AB∥CD，点P在AB、CD外部，则∠APC、∠A、∠C满足的数量关系是．请补全以下证明过程：证明：如图③，过点P作PQ∥AB∴∠A＝∵AB∥CD，PQ∥AB∴∥CD∴∠C＝∠∵∠APC＝∠﹣∠∴∠APC＝应用：（1）如图④，为北斗七星的位置图，如图⑤，将北斗七星分别标为A、B、C、D、E、F、G，其中B、C、D三点在一条直线上，AB∥EF，则∠B、∠D、∠E满足的数量关系是．（2）如图⑥，在（1）问的条件下，延长AB到点M，延长FE到点N，过点B和点E 分别作射线BP和EP，交于点P，使得BD平分∠MBP，EN平分∠DEP，若∠MBD＝25°，则∠D﹣∠P＝°．6．如图，直线AB与CD相交于点O，OD平分∠BOE．（1）图中∠AOD的补角是（把符合条件的角都填出来）；（2）若∠AOC＝28°，求∠BOE的度数．7．如图，直线AB与CD相交于点E，射线EG在∠AEC内（如图1）．（1）若∠BEC的补角是它的余角的3倍，则∠BEC＝°；（2）在（1）的条件下，若∠CEG比∠AEG小25度，求∠AEG的大小；（3）若射线EF平分∠AED，∠FEG＝m°（m＞90°）（如图2），则∠AEG﹣∠CEG ＝°（用m的代数式表示）．8．如图，射线OA∥射线CB，∠C＝∠OAB＝120°．点D、E在线段BC上，且∠DOB＝∠BOA，OE平分∠DOC．（1）说明AB∥OC的理由；（2）求∠BOE的度数；（3）平移线段AB，若在平移过程中存在某种情况使得∠OEC＝∠OBA，试求此时∠OEC 的度数．9．如图，在△ABC中，∠A＝∠B，D、E是边AB上的点，DG∥AC，EF∥BC，DG、EF 相交于点H．（1）∠HDE与∠HED是否相等？并说明理由．解：∠HDE＝∠HED．理由如下：∵DG∥AC（已知）∴＝（）∵EF∥BC（已知）∴＝（）又∵∠A＝∠B（已知）∴＝（）．（2）如果∠C＝90°，DG、EF有何位置关系？并仿照（1）中的解答方法说明理由．解：．理由如下：10．如图，已知直线AB与CD相交于点O，OE⊥AB，OF⊥CD，OM是∠BOF的角平分线．（1）若∠AOC＝25°，求∠BOD和∠COE的度数；（2）若∠AOC＝α，求∠EOM的度数（用含α的代数式表示）．参考答案1．解：∵∠1＝∠2，∴AB∥CE，∴∠A＝∠4（两直线平行，内错角相等，∵∠A＝∠3，∴∠3＝∠4，∴AC∥DE（内错角相等，两直线平行），故答案为：CE，（内错角相等，两直线平行），4，（内错角相等，两直线平行）．2．（1）证明：∵∠1＝∠BDE，∴AC∥DE，∴∠2＝∠ADE，∵∠2+∠3＝180°，∴∠3+∠ADE＝180°，∴AD∥EF；（2）∵∠1＝∠BDE，∠1＝40°，∴∠BDE＝40°，∵DA平分∠BDE，∴∠ADE＝BDE＝20°，∴∠2＝∠ADE＝20°，∵∠2+∠3＝180°∴∠3＝160°，∵FE⊥AF，∴∠F＝90°，∴∠B＝360°﹣90°﹣160°﹣40°＝70°，在△ABC中，∠BAC＝180°﹣∠1﹣∠B＝180°﹣40°﹣70°＝70°．3．（1）证明：∵AB∥CD∴∠B＝∠D又∵AB＝CD，∠BAE＝∠DCF∴△BAE≌△DCF（ASA）∴AE＝CF（2）四边形AECF是菱形，证明如下：由（1）△BAE≌△DCF得：∠AEB＝∠CFD∴∠AEF＝∠CFE∴AE∥CF又∵AE＝CF∴四边形AECF为平行四边形∵AE＝AF∴四边形AECF为菱形．4．解：【问题原型】如图①，过点M作MN∥AB，则∠B＝∠BMN（两直线平行，内错角相等）∵AB∥CD，（已知）∴MN∥AB（辅助线的做法）∴MN∥CD（平行于同一条直线的两直线平行）∴∠NMD＝∠D（两直线平行，内错角相等）∴∠B+∠D＝∠BMD，故答案为：∠BMN，两直线平行，内错角相等，平行于同一条直线的两直线平行，∠NMD，两直线平行，内错角相等，【问题迁移】过点M作MN∥AB，∴∠1＝∠B，∵AB∥CD，∴MN∥AB，∴∠NMD＝∠D，∵∠NMD＝∠1+∠BMD，∴∠BMD＝∠D﹣∠B；【推广应用】如图④，由如图①的结论可得，∠ABM+∠CDM＝∠M＝96°，∠N＝∠ABN+∠CDN，∵BN，DN分别平分∠ABM，∠CDM，∴∠ABN+∠CDN＝＝（∠ABM+∠CDM）＝48°，∴∠N＝48°；如图⑤，由如图②的结论可得，∠M＝∠CDM﹣∠ABM，∵BN，DN分别平分∠ABM，∠CDM，∴∠CDN﹣∠ABN＝∠CDM﹣∠ABM＝（∠CDM﹣∠ABM）＝M＝∠N＝25°，∴∠M＝50°；如图⑥，过G，F，E分别作GN∥AB，FH∥AB，EP∥AB，∵AB∥CD，∴AB∥GN∥FH∥EP∥CD，∴∠2＝∠GFH，∠3＝∠EFH，∴∠2+∠3＝∠GFE＝64°，∴∠1+∠4＝∠BGF+∠DEF﹣∠GFE＝78°，∵AB∥GN，EP∥CD，∴∠ABG＝∠1，∠CDE＝∠4，∴∠ABG+∠CDE＝78°，∵BM，DM分别平分∠ABG，∠CDE，∴∠ABM＝∠ABG，∠CDM＝∠CDE，由如图①中的结论可得∠M＝∠ABM+∠CDM＝（∠ABG+∠CDE）＝78°＝39°，故答案为：48，50，39．5．解：感知：如图①，过点P作PQ∥AB∴∠A＝∠APQ，∵AB∥CD，PQ∥AB∴PQ∥CD，∴∠C＝∠QPC，∴∠APQ+∠QPC＝∠A+∠C，∠APC＝∠A+∠C．故答案为∠P＝∠A+∠C；探究：证明：如图③，过点P作PQ∥AB∴∠A＝∠APQ∵AB∥CD，PQ∥AB∴PQ∥CD∴∠C＝∠CPQ∵∠APC＝∠APQ﹣∠CPQ∴∠APC＝∠A﹣∠C．故答案为：∠APC＝∠A﹣∠C，∠APQ，PQ，∠CPQ，∠APQ，∠CPQ，∠A﹣∠C．应用：（1）如图⑤，过点D作DH∥EF，∴∠HDE＝∠E，∵AB∥EF，DH∥EF∴AB∥DH，∴∠B+∠BDH＝180°，即∠BDH＝180°﹣∠B，∴∠HDE+∠BDH＝∠E+180°﹣∠B，即∠BDE+∠B﹣∠E＝180°，故答案为∠D+∠B﹣∠E＝180°，（2）如图⑥，过点P作PH∥EF，∴∠EPH＝∠NEP，∵AB∥EF，PH∥EF，∴AB∥PH，∴∠MBP+∠BPH＝180°，∵BD平分∠MBP，∠MBD＝25°，∠MBP＝2∠MBD＝2×25°＝50°，∠BPH＝180°﹣50°＝130°，∵EN平分∠DEP，∴∠NEP＝∠DEN∴∠BPE＝∠BPH﹣∠EPH＝∠BPH﹣∠NEP＝∠BPH﹣∠DEN＝130°﹣（180°﹣∠DEF）＝∠DEF﹣50°由①∠D+∠ABD﹣∠DEF＝180°，∵∠MBD＝25°，∴∠ABD＝155°，∴∠D+∠155°﹣∠DEF＝180°，∴∠DEF＝∠D﹣25°∴∠BPE＝∠DEF﹣50°＝∠D﹣25°﹣50°＝∠D﹣75°∠D﹣∠BPE＝75°即∠D﹣∠P＝75°，故答案75．6．解：（1）由图示可得，∠AOD+∠AOC＝180°，∠AOD+∠BOD＝180°，∵OD平分∠BOE，∴∠BOD＝∠DOE，∴∠AOD+∠DOE＝180°，故∠AOD的补角是∠AOC、∠BOD、∠EOD；故答案为：∠AOC、∠EOD、∠DOB．（2）∵直线AB与CD相交于点O，∠AOC＝28°，∴∠BOD＝∠AOC＝28°．又∵OD平分∠BOE，∴∠BOE＝2∠BOD＝56°．答：∠BOE的度数是56°．7．解：（1）设∠BEC＝x°，根据题意，可列方程：180﹣x＝3（90﹣x），解得x＝45°，故∠BEC＝45°故答案为：45°（2）∵∠CEG＝∠AEG﹣25°∴∠AEG＝180°﹣∠BEC﹣∠CEG＝180°﹣45°﹣（∠AEG﹣25°）＝160°﹣∠AEG ∴∠AEG＝80°（3）∵EF平分∠AED，∴∠AEF＝∠DEF，设∠AEF＝∠DEF＝α，∠AEG＝∠FEG﹣∠AEF＝m﹣α，∠CEG＝180°﹣∠GEF﹣DEF ＝180﹣m﹣α，∴∠AEG﹣∠CEG＝m﹣α﹣（180﹣m﹣α）＝2m﹣180故答案为：2m﹣1808．解：（1）∵OA∥CB，∴∠OAB+∠ABC＝180°，∵∠C＝∠OAB＝120°，∴∠C+∠ABC＝180°，∴AB∥OC（2）∵CB∥OA，∴∠AOC＝180°﹣∠C＝180°﹣120°＝60°，∵OE平分∠COD，∴∠COE＝∠EOD，∵∠DOB＝∠AOB，∴∠EOB＝∠EOD+∠DOB＝∠AOC＝×60°＝30°；（3）在△COE和△AOB中，∵∠OEC＝∠OBA，∠C＝∠OAB，∴∠COE＝∠AOB，∴OB、OE、OD是∠AOC的四等分线，∴∠COE＝∠AOC＝×60°＝15°，∴∠OEC＝180°﹣∠C﹣∠COE＝180°﹣120°﹣15°＝45°，∴∠OEC＝∠OBA，此时∠OEC＝∠OBA＝45°9．解：（1）∠HDE＝∠HED．理由如下：∵DG∥AC（已知）∴∠A＝∠HDE（两直线平行，同位角相等）∵EF∥BC（已知）∴∠B＝∠HED（两直线平行，同位角相等）又∵∠A＝∠B（已知）∴∠HDE＝∠HED（等量代换）．（2）DG⊥EF．理由如下：∵EF∥BC∴∠AFE＝∠C＝90°∵AC∥DG∴∠DHE＝∠AFE＝90°∴DG⊥EF．故答案为：∠A，∠HDE，两直线平行，同位角相等；∠B，∠HED，两直线平行，同位角相等；∠HDE，∠HED，等量代换．DG⊥EF．10．解：（1）∵OE⊥AB，∴∠AOE＝90°，∵∠AOC＝25°，∴∠BOD＝∠AOC＝25°，∠COE＝90°﹣∠AOC＝65°；（2）∵∠AOC＝α，∴∠BOD＝α，∵OE⊥AB，OF⊥CD，∴∠BOE＝∠DOF＝90°，∴∠BOF＝90°﹣α，∵OM是∠BOF的角平分线，∴∠BOM＝∠BOF＝45°﹣α，∴∠EOM＝90°﹣∠BOM＝45°+α．。
初一数学竞赛培训相交线与平行线
A初一数学竞赛培训 相交线与平行线例题精讲例1．如图(1)，直线a 与b 平行，∠1＝(3x+70)°,∠2=(5x+22)°,求∠3的度数。
解：∵ a ∥b ，∴ ∠3＝∠4（两直线平行，内错角相等）∵ ∠1+∠3＝∠2+∠4＝180°(平角的定义) ∴ ∠1＝∠2 (等式性质) 则 3x+70＝5x+22 解得x=24 即∠1＝142°∴ ∠3＝180°-∠1＝38° 图(1) 评注：建立角度之间的关系，即建立方程（组），是几何计算常用的方法。
例2．已知：如图(2)， AB ∥EF ∥CD ，EG 平分∠BEF ，∠B+∠BED+∠D =192°，∠B-∠D=24°，求∠GEF 的度数。
解：∵AB ∥EF ∥CD∴∠B=∠BEF ，∠DEF=∠D （两直线平行，内错角相等） ∵∠B+∠BED+∠D =192°（已知） 即∠B+∠BEF+∠DEF+∠D=192°∴2（∠B+∠D ）=192°（等量代换） 图(2) 则∠B+∠D=96°（等式性质） ∵∠B-∠D=24°（已知）∴∠B=60°（等式性质） 即∠BEF=60°（等量代换） ∵EG 平分∠BEF （已知） ∴∠GEF=21∠BEF=30°（角平分线定义） 图（3）GG321FE D C B A例3．如图（3），已知AB ∥CD ，且∠B=40°，∠D=70°，求∠DEB 的度数。
解：过E 作EF ∥AB ∵ AB ∥CD （已知） ∴ EF ∥CD （平行公理）∴ ∠BEF=∠B=40° ∠DEF=∠D=70°（两直线平行，内错角相等） ∵ ∠DEB=∠DEF-∠BEF ∴ ∠DEB =∠D-∠B=30°评注：证明或解有关直线平行的问题时，如果不构成“三线八角”，则应添出辅助线。
(完整版)七年级数学培优提高讲义：相交线与平行线(一)
七年级数学：相交线与平行线一、知识要点：1•平面上两条不重合的直线，位置关系只有两种：相交和平行。
2•两条不同的直线，若它们只有一个公共点，就说它们相交。
即，两条直线相交有且只有一个交点。
3•垂直是相交的特殊情况。
有关两直线垂直，有两个重要的结论：1 ）过一点有且只有一条直线与已知直线垂直；（2 ）直线外一点与直线上所有点的连线中，垂线段最短。
4 •两条直线被第三条直线所截，构成八个角，在那些没有公共顶点的角中，⑴如果两个角分别在两条直线的同一方，并且都在第三条直线的同侧，具有这种关系的一对角叫做___________ :⑵如果两个角都在两直线之间，并且分别在第三条直线的两侧，具有这种关系的一对角叫做 _____________ :⑶如果两个角都在两直线之间，但它们在第三条直线的同一旁，具有这种关系的一对角叫做 ___________________ •5.平行公理：经过直线外一点，有且只有一条直线与这条直线______ .推论：如果两条直线都与第三条直线平行，那么___________________________ .6•平行线的判定：⑴两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行•简单说成：__________________________ •⑵两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行•简单说成：_______________________________ •⑶两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行•简单说成：7.在同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线_______ •&平行线的性质：⑴两条平行直线被第三条直线所截，同位角相等•简单说成： _______ _____________ .⑵两条平行直线被第三条直线所截，内错角相等.简单说成：_______ •⑶两条平行直线被第三条直线所截，同旁内角互补.简单说成：______ 。
七年级数学相交线与平行线培优复习附详细答案
七年级数学：相交线与平行线培优复习例题精讲例1．如图(1)，直线a与b平行，∠1＝(3x+70)°,∠2=(5x+22)°,求∠3的度数。
b，a∥解：∵la3 4（两直线平行，内错角相等）∠3＝∠∴) 平角的定义180°(3＝∠2+∠4＝1+∵∠∠4) 等式性质2 (∴∠1＝∠b2解得x=24 则3x+70＝5x+22＝142°即∠1 (1)°图-∠1＝38∴∠3＝180°评注：建立角度之间的关系，即建立方程（组），是几何计算常用的方法。
°，∠D =192，∠B+∠BED+ AB∥EF∥CD，EG平分∠BEF2例．已知：如图(2)，的度数。
°，求∠GEF∠B-∠D=24 CD EF∥解：∵AB∥（两直线平行，内错角相等）∠D∠BEF，∠DEF= ∴∠B= D =192∠°（已知）∵∠B+∠BED+D=192°BEF+∠DEF+∠即∠B+∠=192°（等量代换）B+∠D）∴2（∠D=96°（等式性质）则∠B+∠∵∠B-∠D=24°（已知）(2)图∴∠B=60°（等式性质）即∠BEF=60°（等量代换）（已知）平分∠BEF∵EG12°（角平分线定义）∴∠∠GEF=BEF=30DEB 的度数。
B=40°，∠D=70°，求∠．如图（3），已知AB∥CD，且∠例3AB EF∥解：过E作CD（已知）AB∥∵（平行公理）EF∥CD∴°（两直线平行，内错角相等）DEF=∠D=70∠B=40°∠∠∴BEF= BEF -∠∠DEB=∠DEF∵B=30°∠D-∠∠∴DEB =评注：证明或解有关直线平行的问题时，如果不构成“三线八角”，则应添出辅）图（3 助线。
条以上直线共点，有多少个不同交33n条直线两两相交且无条或．例4平面上点？1个交点，条直线产生解：2条直线共有3个交点，这时平面上条均相交，增加条直线与前面第322 个交点；1+2=3．第4条直线与前面3条均相交，增加3个交点，这时平面上4条直线共有1+2+3=6个交点；…1则n条直线共有交点个数：1+2+3+…+ (n-1)=n(n-1)2评注：此题是平面上n条直线交点个数最多的情形，需要仔细观察，由简及繁，深入思考，从中发现规律。
七年级数学相交线与平行线培优复习附详细
七年级数学：订交线与平行线培优复习例题精讲例1．如图(1)，直线a与b平行，∠1＝(3x+70)°,∠2=(5x+22)°, 求∠3的度数。
解：∵a∥b，la3 ∴∠3＝∠4（两直线平行，内错角相等）∵∠1+∠3＝∠2+∠4＝180°( 平角的定义)∴∠1＝∠2 (等式性质)则＝解得 3x+70 5x+22 x=24 即∠＝° 1 142 24b∴∠3＝180°-∠1＝38°图(1)评注：成立角度之间的关系，即成立方程（组），是几何计算常用的方法。
例2．已知：如图(2)，AB∥EF∥CD，EG均分∠BEF，∠B+∠BED+∠D =192°，∠B-∠D=24°，求∠GEF的度数。
解：∵AB∥EF∥CD∴∠B=∠BEF，∠DEF=∠D（两直线平行，内错角相等）∵∠B+∠BED+∠D =192°（已知）即∠B+∠BEF+∠DEF+∠D=192°∴2（∠B+∠D）=192°（等量代换）则∠B+∠D=96°（等式性质）∵∠B-∠D=24°（已知）图(2)∴∠B=60°（等式性质）即∠BEF=60°（等量代换）∵EG均分∠BEF（已知）1∴∠GEF=2∠BEF=30°（角均分线定义）例3．如图（3），已知AB∥CD，且∠B=40°，∠D=70°，求∠DEB的度数。
解：过E 作EF∥AB∵AB∥CD（已知）∴EF∥CD（平行公义）∴∠BEF=∠B=40°∠DEF=∠D=70°（两直线平行，内错角相等）∵∠DEB=∠DEF-∠BEF ∴∠DEB =∠D-∠B=30°评注：证明或解相关直线平行的问题时，假如不构成“三线八角”，则应添出辅助线。
图（3）例4．平面上n 条直线两两订交且无3 条或3 条以上直线共点，有多少个不一样交点？解：2条直线产生1个交点，第3 条直线与前面2 条均订交，增添2 个交点，这时平面上3 条直线共有1+2=3个交点；第4 条直线与前面3 条均订交，增添3 个交点，这时平面上4 条直线共有1+2+3=6个交点；⋯则n 条直线共有交点个数：1+2+3+⋯+ (n-1)= 12n(n-1)评注：本题是平面上n 条直线交点个数最多的情况，需要认真察看，由简及繁，深入思虑，从中发现规律。
(完整版)七年级下册数学培优资料相交线与平行线教师版[1]
![(完整版)七年级下册数学培优资料相交线与平行线教师版[1]](https://img.taocdn.com/s3/m/04ccb07cdaef5ef7bb0d3c2a.png)
第四章相交线与平行线培优4注：一般地，平面上n个点最多可确定直的条数：11+2+3+⋯+(n-1)=n(n-1)2例1．如(1)，直a与b平行，∠1＝(3x+70)°,∠2=(5x+22)°,求∠3的度数。
解：∵a∥b，∴∠3＝∠4〔两直平行，内角相等〕la3∵∠1+∠3＝∠2+∠4＝180°(平角的定)∴∠1＝∠2(等式性)4b 3x+70＝5x+22解得x=242即∠1＝142°∴∠3＝180°-∠1＝38°(1)注：建立角度之的关系，即建立方程〔〕，是几何算常用的方法。
例2．：如(2)，AB∥EF∥CD，EG平分∠BEF，∠B+∠BED+∠D=192°，B-∠D=24°，求∠GEF的度数。
解：∵AB∥EF∥CDA ∴∠B=∠BEF，∠DEF=∠D〔两直平行，内角相等〕∵∠B+∠BED+∠D=192°〔〕即∠B+∠BEF+∠DEF+∠D=192°E ∴2〔∠B+∠D〕=192°〔等量代〕C ∠B+∠D=96°〔等式性〕∵∠B-∠D=24°〔〕(2)∴∠B=60°〔等式性〕即∠BEF=60°〔等量代〕∵EG平分∠BEF〔〕∴∠GEF=1∠BEF=30°〔角平分定〕2CBGFDD例6．10条直两两相交，最多将平面分成多少不同的区域？解：2条直最多将平面分成2+2=4个不同区域；3条直中的第3条直与另两条直相交，最多有两个交点，此直被两点分成3段，每一二，区域增加3个，即最多分成2+2+3=7个不同区域；同理：4条直最多分成2+2+3+4=11个不同区域；⋯10条直最多分成2+2+3+4+5+6+7+8+9+10=56个不同区域推广：n条直两两相交，最多将平面分成2+2+3+4+⋯+n=1+1n(n+1)=1(n2+n+2)不同22思考：平面内n个两两相交，最多将平面分成多少不同的区域？例7．两条直相交于一点，所形成的的角中有2角，4角，那么，三条直相交于一点，角，多少角？四条直相交于一点，有多少角，多少角？角，多少角？直的条数345...n角的数61220...n(n-1)角的数122440...2n(n-1)二、稳固1．平面上有5个点，其中有3点在同一直上，每2点作一条直，一共可以作直〔〕条例3．如〔3〕，AB∥CD，且∠B=40°，∠D=70°，求∠DEB的度数。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
专题24 相交线与平行线阅读与思考在同一平面内，两条不同直线有两种位置关系：相交或平行.当两条直线相交或两条直线分别与第三条直线相交，就产生对顶角、同位角、内错角、同旁内角等位置关系角，善于从相交线中识别出以上不同名称的角是解相关问题的基础，把握对顶角有公共顶点，而同位角、内错角、同旁内角没有公共顶点且有一条边在截线上，这是识图的关键． 两直线平行的判定方法和重要性质是我们研究平行线问题的主要依据． 1．平行线的判定(1)同位角相等、内错角相等，或同旁内角互补，两直线平行； (2)平行于同一直线的两条直线平行；(3)在同一平面内，垂直于同一直线的两条直线平行． 2．平行线的性质(1)过直线外一点，有且只有一条直线和这条直线平行； (2)两直线平行，同位角相等、内错角相等、同旁内角互补；(3)如果一条直线和两条平行线中的一条垂直，那么它和另一条也垂直. 熟悉以下基本图形：例题与求解【例1】 (1) 如图①，AB ∥DE ，∠ABC ＝080，∠CDE ＝0140，则∠BCD ＝__________.（安徽省中考试题）(2) 如图②，已知直线AB ∥CD ，∠C ＝0115，∠A ＝025，则∠E ＝___________.（浙江省杭州市中考试题）DB图②FECA解题思路：作平行线，运用内错角、同旁内角的特征进行求解.【例2】如图，平行直线AB ，CD 与相交直线EF ，GH 相交，图中的同旁内角共有( )． A ．4对 B ．8对 C ．12对 D ．16对（“希望杯”邀请赛试题）解题思路：每一个“三线八角”基本图形都有两对同旁内角，从对原图进行分解入手．A BCDGHEFF DE BCA例2题图 例3题图【例3】 如图，在△ABC 中，CE ⊥AB 于E ，DF ⊥AB 于F ，AC //ED ，CE 是∠ACB 的平分线，求证：∠EDF ＝∠BDF .（天津市竞赛试题）解题思路：综合运用垂直定义、角平分线、平行线的判定与性质，由于图形复杂，因此，证明前注意分解图形．【例4】 如图，已知AB ∥CD ，∠EAF ＝41∠EAB ，∠FCF ＝41∠ECD .求证：∠AFC ＝43∠AEC . （湖北省武汉市竞赛试题）DEC AB 图1解题思路：分别过点E ，F 作平行线，利用平行线的性质找角之间的关系.ABFCD E例4题图 例5题图【例5】如图，已知∠1＝ ∠2，∠C ＝∠D ，求证：∠A ＝∠F .解题思路：从角出发，导出两直线的位置关系，再推出新的角的关系，新的两直线的位置关系，是解这类问题的基本思路.【例6】(1)已知平面内有4条直线a ，b ，c 和d ，直线a ，b 和c 相交于一点，直线b ，c 和d 也相交于一点，试确定这4条直线共有多少个交点？并说明你的理由．(2)作第5条直线e 与(1)中的直线d 平行. 说明：以这5条直线的交点为端点的线段有多少条？（“希望杯”邀请赛试题）解题思路：(1)先设直线a ，b ，c 的交点为P ，直线b ，c ，d 的交点为Q ，证得P 与Q 实为同一点，得出结论．(2)绘出图形，帮助解答，注意平行线的性质.FA BC1 DE 2能力训练A 级1．在同一平面内有1a ，2a ，3a …，10a 十条直线，如果1a //2a ，2a ⊥3a ，3a //4a ，4a ⊥5a ，5a //6a ，6a ⊥7a ，…，那么1a 与10a 的位置关系是____________.2．如图，已知AE ∥BD ，∠1＝0130，∠2＝030，则∠C ＝__________．（湖南省常德市中考试题）3．如图，直线a ，b 都与直线c 相交，下列命题中，能判断a ∥b 的条件是_____________（把你认为正确的序号填在横线上）①∠1＝∠2； ②∠3＝∠6； ③∠1＝∠8；④∠5＋∠8＝0180．（陕西省中考试题）第4题图21第3题图第2题图7865432121DA ECBab4. 将两张矩形纸片如图所示摆放，使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一边上，则∠1＋∠2__________.（山东省烟台市中考试题）5．下面四个命题中正确的是( )．A ．相等的两个角是对顶角B ．和等于0180的两个角互为邻补角 C ．连结两点的最短线是过这两点的直线D ．两条直线相交所成的四个角都相等，则这两条直线互相垂直（“希望杯”邀请赛试题）6．下列命题①两条相交直线组成的四个角相等，则这两直线垂直．②两条相交直线组成的四个角中，若有一个直角，则四角都相等． ③两条直线相交，一角的两邻补角相等，则这两直线垂直． ④两条直线相交，一角与其邻补角相等，则这两直线垂直． 其中正确的有( )．A ．4个B ．3个C ．2个D ．1个7．如图，DH ∥EG ∥BC ，且DC ∥EF ，那么图中与∠BFE 相等的角(不包括∠BFE )的个数是( )． A.2 B ．4 C ．5 D ．6（山东省菏泽地区中考试题）8．如图，AB ∥CD ∥EF ∥GH ，AE ∥DG ，点C 在AE 上，点F 在DG 上，设与∠ɑ相等的角的个数为m （不包括∠a 本身），与∠β互补的角的个数为n ．若a ≠β，则m ＋n 的值是( )．A. 8B. 9C. 10D. 11第8题图第7题图βαCFG AGDHBBEDHE9．如图，已知AB ∥ED ，∠NCB ＝030，CM 平分∠BCE ，CN ⊥CM ，求∠B 的度数．10.如图，已知E 是AB ，CD 外一点，∠D ＝∠B ＋∠E ，求证：AB ∥CD .ABED NCM11.平面上有10条直线，无任何3条交于一点，要使它们出现31个交点，怎样安排才能办到？（吉林省竞赛试题）ABEDC12.如图，已知CD ∥EF ，∠1＋∠2＝∠ABC ，求证：AB //GF .（重庆市竞赛试题）B 级1. 如图，∠A ＝060，∠1＝∠2，则∠ADC 的度数是___________. 2．如图，直线a ∥b ，那么x 的度数是____________.（五城市联赛试题）ba第1题图第2题图第3题图x48°30°30°120°21C'D'EABADBCDC F3．如图，把一个长方形纸片沿EF 折叠后，点D ，C 分别落在D '，C '的位置，若∠EFB ＝065，则∠AED '＝__________.（山东省中考试题）4．如图，已知DE ∥BC ，∠2＝070，∠1＝040，那∠EBA 的度数是_____________.AC21EBDlk4321第4题图 第5题图5. 如图，直线k ∥l ，∠4－∠3＝∠3－∠2＝∠2一∠3＝d ＞0．其中∠3＜090，∠1＝050，则∠4最大可能的整数值是( )．A. 1070B ．1080C ．1090D ．11006. 如图，AB ∥CD ∥EF ，EH ⊥CD 于H ，则∠BAC ＋∠ACE ＋∠CEH 等于( )． A ．1800B ．2700C ．3600D ．4500(北京市竞赛试题）7．如图，两直线AB ，CD 平行，则∠1＋∠2＋∠3＋∠4＋∠5＋∠6＝ ( )． A ．6300B. 7200C ．8000D. 9000（“希望杯”邀请赛试题）BDFAC654321HACBDEF GH第6题图 第7题图8．两条直线a ，b 互相平行，直线a 上顺次有10个点A 1，A 2…，A 10，直线b 上顺次有9个点B 1，B 2，…，B 3，将a 上每一个点与b 上每一个点相连可得线段．若没有三条线段相交于同一点，则这些线段的交点个数是( )A. 90B.1620C.6480D.20069．如图，已知两条平行线AB ，CD 被直线EF 所截，交点分别为G ，H ，P 为HD 上任意一点，过P 点的直线交HF 于O 点，求证：∠HOP ＝∠AGF －∠HPO .O PA BCD10．如图，在△ABC 中，AB ＝7，AC ＝11，点M 是BC 的中点，AD 是∠BAC 的平分线，MF ∥AD .求FC 的长．(2013年“《数学周报》”杯竞赛试题)D FMBC11．平面上有七条两两不平行的直线，试证：其中必有直线的交角小于260．（莫斯科八年级竞赛试题）12．⑴如图①，MA 1∥NA 2，则∠A 1＋∠A 2＝_________.如图②，MA 1∥NA 3，则∠A 1＋∠A 2＋∠A 3＝_________. 如图③，MA 1∥NA 4，则∠A 1＋∠A 2＋∠A 3＋∠A 4＝_________. 如图④，MA 1∥NA 5，则∠A 1＋∠A 2＋∠A 3＋∠A 4＋∠A 5＝_________.从上述结论中你发现了什么规律？请在图②，图③，图④中选一个证明你的结论.（2）如图5，n NA ||MA 1，则=∠++∠+∠+∠n A A A A 321 .（3）利用上述结论解决问题：如图已知CD ||AB ，AB E ∠和CDE ∠的平分线相交于F ，140E =∠，求B FD ∠的度数.A 6A nA 5A 4A 2A 1 MNA 2（第21题）A 1MNA 3A 2 A 1MNA 3A 4A 2 A 1MNA 3 A 5A 4 A 2 A 1MNA 3 图①图②图③ 图④图⑤FEBACD图⑥专题24 相交线与平行线例1 （1）40° 过点 C 作CF ∥AB ，则∠BCF ＝∠ABC ＝80°．∠DCF ＝180°—140°＝40°，∴∠BCD ＝80°－40°=40°.（2）90° 过点E 作EM ∥AB ，∴AB ∥CD ，∴EM ∥CD ，∠AEM =180°—25°=155°. ∠CEM =180°—115°=65°，∴∠E =∠AE —∠CEM =155°-65°=90°.例2 D 提示：原图可分解为8个基本图形.例3 提示：由DF ∥CE 得，∠BDF =∠BCE ，∠FDE =∠DEC ，AC ∥DE ，得∠DEC =∠ECA .例4 过E 作EM ∥AB .∴AB ∥于CD ，∴EM ∥CD . ∴∠AEC =∠AEM +∠CEM =∠EAB +∠ECD .同理：∠AFC =∠FAB +∠FCD .∴∠AEC =∠FAB +∠FCD +∠EAF +∠ECF =∠AFC +¼∠EAB +14+∠ECD =∠AFC +¼∠AEC .故∠AFC =¾∠AEC .例5 提示：先证BD ∥CE ，再证DF ∥BC .例6 （1）直线a ，b ，c ，d 共有1个交点，理由如下：设直线a ，b ，c 的交点为P ，直线b ，c ，d 的交点为Q .这意味着点P 和点Q都是直线b 和c 的交点.而两条不同直线至多有一个交点.因此P和Q 必为同一个点.即4条直线a ，b ，c 和d 相交于同一个点.因此这4条直线只有一个交点.(2)不妨设（1）中交点为O .因为作的第5条直线e 与（1）中的直线d 平行，所以直线e 和直线d 没有公共点，因此这些e 不过点O .而直线a ，b ，c 与直线e 必然都相交.如图所示.设直线e 与直线a ，b ，c 分别相交于点A ，B ，C .这时有A ，B ，C ，O 共四个不同的点.可以连出OA ，OB ，OC ，AB ，AC ，BC 共6条不同的线段.A 级1. 1a //10a2.20°3.①②③④4.90°5.D6.B7.C8.D提示：m =5，n =6，m +n =5+6=11. 9.60° 10.提示：过点E 作EF ∥AB . 11如图所示.12.作CK ∥FG ，延长GF ，CD 交于H 点，则∠1+∠2=∠ABC ，故∠ABC +∠BCK =180°，即CK ∥AB ，AB ∥GF .B级1.120°2.72°3.50°4.30°5.C 提示：∠2=50°+d，∠3=50°+2d，∠4=50°+3d，又∵∠3=50°+2d<90°，∴d<20°，∠4=50°+3d<110°.故∠4的最大整数值为109°.6.B7.D8.B 提示：由题意知每一个交点由a上两点和b上两点所确定.在a上取两点有种情况，在b上取两点有种情况，故交点个数为45*36=1620个.9.提示：过点O作CD的平行线.10.如图，设N是AC的中点，连接MN，则MN∥AB.又MF∥AD，∴∠FMN=∠BAD=∠DAC=∠MFN.∴FN=MN=½AB.因此FC=FN+NC=½AB+12AC=½(AB+AC）=½（7+11）=9.11.提示：在平面上任取一点O，将已知的七条直线平移过点O，它们把以O为圆心的圆周角分成14个彼此相邻的角a₁,a₂,……，。