spss作业.doc解析
spss实践题分析及答案

spss实践题分析及答案SPSS实践题习题1分析此班级不同性别的学⽣的物理和数学成绩的均值、最⾼分和最低分。
Report性别数学物理男⽣Mean 80.0769 74.5385N 13 13Std. Deviation 5.75125 5.17390Minimum 72.00 69.00Maximum 95.00 87.00⼥⽣Mean 80.7692 76.1538N 13 13Std. Deviation 8.91772 8.32512Minimum 70.00 65.00Maximum 99.00 91.00Total Mean 80.4231 75.3462N 26 26Std. Deviation 7.36029 6.84072Minimum 70.00 65.00Maximum 99.00 91.00结论:男⽣数学成绩最⾼分: 95 最低分: 72 平均分: 80.08物理成绩最⾼分: 87 最低分: 69 平均分: 74.54⼥⽣数学成绩最⾼分: 99 最低分: 70 平均分: 80.77 物理成绩最⾼分: 91 最低分: 65 平均分: 76.15 习题2分析此班级的数学成绩是否和全国平均成绩85存在显著差异。
One-Sample StatisticsNMean Std. Deviation Std. Error Mean数学2680.42317.360291.44347结论:由分析可知相伴概率为0.004,⼩于显著性⽔平0.05,因此拒绝零假设,即此班级数学成绩和全国平均⽔平85分有显著性差异习题3分析市2⽉份的平均⽓温在90年代前后有⽆明显变化。
Group Statistics分组 NMean Std. Deviation Std. Error Mean⼆⽉份⽓温0 11 -4.527273 1.2034043.3628400 118-3.2000001.3006786.3065729结论:由分析可知, ⽅差相同检验相伴概率为0.322,⼤于显著性⽔平0.05,因此接受零假设,90年代前后2⽉份温度⽅差相同。
spss练习题及简 答解读

SPSS练习题1、现有两个SPSS数据文件,分别为“学生成绩一”和“学生成绩二”,请将这两份数据文件以学号为关键变量进行横向合并,形成一个完整的数据文件。
先排序data---sort cases再合并data---merge files2、有一份关于居民储蓄调查的数据存储在EXCEL中,请将该数据转换成SPSS数据文件,并在SPSS中指定其变量名标签和变量值标签。
转换Data---transpose,输题目3、利用第2题的数据,将数据分成两份文件,其中第一份文件存储常住地是“沿海或中心繁华城市”且本次存款金额在1000-2000之间的调查数据,第二份数据文件是按照简单随机抽样所选取的70%的样本数据。
选取数据data---select cases4、利用第2题数据,将其按常住地(升序)、收入水平(升序)存款金额(降序)进行多重排序。
排序data---sort cases一个一个选,加5、根据第1题的完整数据,对每个学生计算得优课程数和得良课程数,并按得优课程数的降序排序。
计算transform---count按个输,把所有课程选取,define设区间,再排序6、根据第1题的完整数据,计算每个学生课程的平均分和标准差,同时计算男生和女生各科成绩的平均分。
描述性统计,先转换Data---transpose学号放下面,全部课程(poli到his)放上面,ok,analyze---descriptive statistics---descriptives,全选,options。
先拆分data---split file 按性别拆分,analyze---descriptive statistics---descriptives全选所有课程options---mean7、利用第2题数据,大致浏览存款金额的数据分布状况,并选择恰当的组限和组距进行组距分组。
数据分组Transform---recode---下面一个,输名字,change,old,range,new value---add 挨个输,从小加到大,等距8、在第2题的数据中,如果认为调查“今年的收入比去年增加”且“预计未来一两年收入仍会会增加”的人是对自己收入比较满意和乐观的人,请利用SPSS的计数和数据筛选功能找到这些人。
工作文档SPSS第六章作业

第六章习题习题6-4.1、问题分析:分析题目中的数据,发现影响用力肺活量的控制变量只有一个,即组别,则采取单因素方差分析进行分析数据。
2、整理数据,将数据分成两列,一列为肺活量,一为组别,进行单因素方差分析,简要步骤为:Analyze -->Compare Means -->One-Way ANOVA -->Options-->Post Hoc-->Contrast3、结果分析:根据上述步骤,整理得出如下数据:1)关于方差是否相等的检验结果及相伴概率值表格1:检验方差是否相等的相伴概率值根据数据得出,相伴概率值大于0.05,可以认为各个组总体方差是相等的,符合方差分析的前提条件,这组数据适合进行单因素方差分析。
2)关于组别之间的显著性差异的大致判断从结果看出,0.000.相伴概率小雨显著性水平0.05,表示拒绝零假设,也就是3个组当中至少有一个组和其他两个组有明显的区别,也可能3个组之间都存在显著地区别。
另外,3个组的离差平方和为12.381,其中控制变量不同水平造成的组间平方和为10.919,随机变量造成的组内平方和为1.462,在组间平方和中,能线性解释平方和10.804,不能线性解释平方和为0.115。
3)各组别之间的相互影响大小观察LSD法多重比较的结果得知,3个叙别之间的相伴概率都小雨显著性水平,说明3个组之间都存在显著性差别。
4)各组观察变量均值的折线图:4、结论:三个组矿工之间的用力肺活量存在显著性差别习题6-5.1、问题分析:分析题目中的数据,发现数据适合协方差分析,则采取协方差分析进行分析数据。
零假设:H0:个水平没有显著性差异,若相伴概率小雨0.05,则拒绝零假设2、协方差分析简要步骤为:Analyze -->General Linear Model-->Univariate-->Options-->Model -->Contrast-->Plots3、结果分析:根据上述步骤,整理得出如下数据:1)关于各组个案的个数值表格2:各组个案的个数0 61 6根据数据得出,组别06,组别二的个案数为62)控制变量对观察变量的独立部分作用观察数据得知:相伴概率大于0.05,说明不同治疗方法(不同组别)对病人血压没有造成显著的影响。
SPSS题目解答题答案解析

6、某百货公司9月份各天的服装销售数据如下(单位:万元)257 276 297 252 301 256 278 298 265 258286 234 210 322 310 278 301 290 256 249309 318 311 267 273 239 316 268 249 298(1)计算该百货公司日销售额的均值(277.4)、标准误差(5.15698)、中位数(277)、众数(249,256,278,298,301)、全距、方差(797.834)、标准差(28.24596)、四分位数、十分位数、百分位数、频数、峰度(-.518)和偏度(-.287);(2)计算日销售额的标准化Z分数及对其线性转换。
解:(1)频数298.00 2 6.7 6.7 73.3301.00 2 6.7 6.7 80.0309.00 1 3.3 3.3 83.3310.00 1 3.3 3.3 86.7311.00 1 3.3 3.3 90.0316.00 1 3.3 3.3 93.3318.00 1 3.3 3.3 96.7322.00 1 3.3 3.3 100.0合计30 100.0 100.0统计量日销售额N 有效30缺失0均值277.4000均值的标准误 5.15698中位数277a众数249.00b标准差28.24596方差797.834偏度-.287偏度的标准误.427峰度-.518峰度的标准误.833全距112.00极小值210.00极大值322.00和8322.00百分位数10 242.3333c20 253.333325 256.333330 257.500040 267.500050 276.666760 288.000070 298.000075 300.250080 306.3333.25.50,75为四分位数,10,20,30··90为十分位数百分位数 1 .c,d2 212.40003 219.60004 226.80005 234.00006 235.50007 237.00008 238.50009 240.333310 242.333311 244.333312 246.333313 248.333314 249.400015 250.000016 250.600017 251.200018 251.800019 252.533320 253.333321 254.133322 254.933323 255.733324 256.133325 256.333326 256.533327 256.733328 256.933329 257.200030 257.500031 257.800032 258.700033 260.800035 265.000036 265.600037 266.200038 266.800039 267.200040 267.500041 267.800042 268.500043 270.000044 271.500045 273.000046 273.900047 274.800048 275.700049 276.266750 276.666751 277.066752 277.466753 277.866754 279.066755 280.666756 282.266757 283.866758 285.466759 286.800060 288.000061 289.200062 290.700063 292.800064 294.900065 297.000066 297.200067 297.400068 297.600069 297.800070 298.000071 298.450073 299.350074 299.800075 300.250076 300.700077 301.533378 303.133379 304.733380 306.333381 307.933382 309.100083 309.400084 309.700085 310.000086 310.300087 310.600088 310.900089 312.000090 313.500091 315.000092 316.200093 316.800094 317.400095 318.000096 319.200097 320.400098 321.600099 .a. 利用分组数据进行计算。
SPSS操作实验作业1(附答案)

SPSS操作实验 (作业1)作为华夏儿女都曾为有着五千年的文化历史而骄傲过,作为时代青年都曾为中国所饱受的欺压而愤慨过,因为我们多是炎黄子孙。
然而,当代大学生对华夏文明究竟知道多少呢某研究机构对大学电气、管理、电信、外语、人文几个学院的同学进行了调查,各个学院发放问卷数参照各个学院的人数比例,总共发放问卷250余份,回收有效问卷228份。
调查问卷设置了调查大学生对传统文化了解程度的题目,如“佛教的来源是什么”、“儒家的思想核心是什么”、“《清明上河图》的作者是谁”等。
调查问卷给出了每位调查者对传统文化了解程度的总得分,同时也列出了被调查者的性别、专业、年级等数据信息。
请利用这些资料,分析以下问题。
问题一:分析大学生对中国传统文化的了解程度得分,并按了解程度对得分进行合理的分类。
问题二:研究获得文化来源对大学生了解传统文化的程度是否存在影响。
要求:直接导出查看器文件为.doc后打印(导出后不得修改)对分析结果进行说明,另附(手写、打印均可)。
于作业布置后,1周内上交本次作业计入期末成绩答案问题一操作过程1.打开数据文件作业。
同时单击数据浏览窗口的【变量视图】按钮,检查各个变量的数据结构定义是否合理,是否需要修改调整。
2.选择菜单栏中的【分析】→【描述统计】→【频率】命令,弹出【频率】对话框。
在此对话框左侧的候选变量列表框中选择“X9”变量,将其添加至【变量】列表框中,表示它是进行频数分析的变量。
3.单击【统计量】按钮,在弹出的对话框的【割点相等组】文本框中键入数字“5”,输出第20%、40%、60%和80%百分位数,即将数据按照题目要求分为等间隔的五类。
接着,勾选【标准差】、【均值】等选项,表示输出了解程度得分的描述性统计量。
再单击【继续】按钮,返回【频率】对话框。
4.单击【图表】按钮,勾选【直方图】和【显示正态曲线】复选框,即直方图中附带正态曲线。
再单击【继续】按钮,返回【频率】对话框。
最后,单击【确定】按钮,操作完成。
spss练习题(答案及简要分析)

Spss课程练习题1、某年纪有80名学生,男女生各40人,分成2各班级,下面表1中是某次一门课程的成绩,请分性别、班级计算平均数、标准差等结果。
表1Case Processing SummaryReport成绩2、10名学生的两门其中考试成绩见表2,请按总成绩的40%计算总分。
表23、将表1中的数据合并,即不再分组,试整理成频数分布表,绘制出频数分布图,计算出常用的统计量。
Statistics成绩N Valid 80Missing 0Mean 80.1375Std. Error of Mean .80598Median 80.5000Mode 74.00(a)Std. Deviation 7.20890Minimum 61.00Maximum 96.00Sum 6411.00Percentiles 25 74.250050 80.500075 85.0000a Multiple modes exist. The smallest value is shown成绩F r e q u e n c y4、正常人的脉搏平均 数为72次/分。
现测得15名患者的脉搏:71,55,76,68,72,69,56,70,79,67,58,77,63,66,78 试问这15名患者的脉搏与正常人的脉搏是否有差异?One-Sample Test由结果可知,因为0.088>0.05,所以在p=0.05的显著性水平上差异不显著5、收集了20名学生的自信心值,见表3,试问该指标是否与性别有关?表3Independent Samples Test由数据可知,F检验的p=0.608>0.05,所以两组样本的方差差异不显著,所以t检验应该是Equal variances assumed一项进行判断。
双侧t检验的p=0.392>0.05,表示两个样本没有显著性差异4,试问两种训练方法的效果是否相同?表4注:x1、x2表示两组学生的跳高成绩,单位厘米(cm)配对样本T检验:Analyze -Compare Means -Paried-sample T TestPaired Samples CorrelationsPaired Samples Test由配对样本相关性检验可知,两样本相关性的p=0.00<0.05,因此两者存在相关性,由配对样本T检验的数据分析可得,两组数据的p=0.006<0.05所以两者之间在0.05的差异水平上差异显著7、为了探讨不同教法对英语教学效果的影响,将一个班级随机分成3组,接受3种不同的教法,英语成绩见表5,试问不同的教法之间是否存在着差异。
spss软件应用与题解2

Spss第 2 次作业第1题(1)【实验目的】学会spss频数分析(2)【实验内容】数据居民储蓄调查数据,进行SPSS频数分析,分析被调查者的常驻地址,职业和年龄分布情况,并绘制条形图。
(3)【操作步骤】Analyze-Descriptive Statistics-Frequencies(4)【输出结果】常住地址,1沿海及中心地区;2,边远地区(5)【结果分析】说明大部分人住在沿海中心区域。
职业尽量各行各业均有所涉及。
年龄集中35岁以上。
第2题(1)【实验目的】学会分析数据的基本特征(2)【实验任务】数据居民储蓄调查数据,从数据的集中趋势,离散程度和分布形状等角度,分析被调查者本次存款金额的基本特征,并与标准正太分布曲线进行对比,进一步,对不同住地的储户存款金额的基本特征进行比对分析。
(3)【操作步骤】Analyze-Descriptive Statistics-FrequenciesStatistics:选择输出统计量:集中、离散趋势、分布特征、百分位数。
Charts:选择绘制的图形:条图、饼图、直方图(仅用于定量变量)。
(4)【输出结果】统计量A5 N有效 282缺失65均值4738.09 均值的标准误 651.799 中值 1000.00 众数 1000标准差 10945.569 方差 119805486.302 偏度5.234 偏度的标准误 .145 峰度33.656 峰度的标准误 .289 全距 100000 极小值 1极大值 100001 和 1336141A13=1时:A13=2时(5)【结果分析】说明位于沿海或中心的城市的人储蓄比较高第3题(1)【实验目的】学会用spss找出与众不同的样本。
(2)【实验内容】数据同上,假设存款金额服从正太分布,能否利用本章讲解的功能,找到存款金额与众不同的样本,并说明理由。
(提示: 可以计算”存款金额”的标准化变量,根据3*sigma 法则判断绝对值大于3 的为异常值, 也就是与众不同的值)(3)【操作步骤】(4)【输出结果】(5)【结果分析】能,1.5倍四分位距以外的数值为奇异值,3倍四分位距以外的数值为极端值,这些图和普遍集中的点相差较大,所以将其成为与众不同的样本。
SPSS作业

4-4 用药治疗6名高血压病人,对每一个人治疗前、后的舒张压进行了测量,结果如表4-4 所示(2)治疗前后病人的血压是否有显著变化?解:(1)经过统计分析的到如下结果:Statistics用药前用药后N Valid 6 6Missing 0 0Mean 124.67 118.67Variance 175.467 331.867从表中可以看出:用药前,6名病人的血压的均值是124.67,而用药后的均值则是118.67,。
可以看出均值由大变小:同理,6名病人的血压的方差则是由小变大。
以认为用药前和用药后的血压值无显著差异;T统计量的相伴概率是0.529,大于显著性水平0.05,不能拒绝T假设的零假设,即用药前和用药后病人的血压值不存在显著变化。
4-5A学校要对两位数学老师的教学质量进行评价,这两位老师分别教甲班和乙班,这两班的数学课的成绩如表4-5所示,这两个班的成绩是否存在显著差异?Group Statistics序号N Mean Std. Deviation Std. Error Mean分数甲班20 83.60 6.700 1.498乙班20 75.45 9.179 2.053和9.179.题中的F的相伴概率是0.299,大于显著性水平0.05,不能拒绝方差相等的假设,可以认为两个班的成绩无显著性差异;然后看T的相伴概率是0.003,显然小于显著性水平0.05,可以接受T的零假设,即,两个班存在显著性。
二者相互矛盾,所以不能判断出两个班成绩存在显著性差异。
5-4 谋职业病研究所对29名矿工中肺夕病患者、可疑患者和非患者进行了用力肺活量(L)测定,如表5-4所示,问三名矿工的的用力肺活量有无差别?从表中可以看出:相伴概率是0.669,大于显著性水平,可以认为总体方差是相等的,这组数据可以进行单因素分析ANOVA肺活量,表示拒绝零假设,也就是说这三组中至少有一组和其他两组有明显区别。
这是LSD法多重比较的结果,从中可以看出3个组之间的相伴概率都小于显著性水平0.05,说明这3组之间有显著差异。
第一章 SPSS概览数据分析实例详解 .doc

第一章SPSS概览--数据分析实例详解1.1 数据的输入和保存1.1.1 SPSS的界面1.1.2 定义变量1.1.3 输入数据1.1.4 保存数据1.2 数据的预分析1.2.1 数据的简单描述1.2.2 绘制直方图1.3 按题目要求进行统计分析1.4 保存和导出分析结果1.4.1 保存文件1.4.2 导出分析结果希望了解SPSS 10.0版具体情况的朋友请参见本网站的SPSS 10.0版抢鲜报道。
例1.1 某克山病区测得11例克山病患者与13名健康人的血磷值(mmol/L)如下, 问该地急性克山病患者与健康人的血磷值是否不同(卫统第三版例4.8)?患者: 0.84 1.05 1.20 1.20 1.39 1.53 1.67 1.80 1.87 2.07 2.11健康人: 0.54 0.64 0.64 0.75 0.76 0.81 1.16 1.20 1.34 1.35 1.48 1.56 1.87解题流程如下:1.将数据输入SPSS,并存盘以防断电。
2.进行必要的预分析(分布图、均数标准差的描述等),以确定应采用的检验方法。
3.按题目要求进行统计分析。
4.保存和导出分析结果。
下面就按这几步依次讲解。
§1.1 数据的输入和保存1.1.1 SPSS的界面当打开SPSS后,展现在我们面前的界面如下:请将鼠标在上图中的各处停留,很快就会弹出相应部位的名称。
请注意窗口顶部显示为“SPSS for Windows Data Editor”,表明现在所看到的是SPSS的数据管理窗口。
这是一个典型的Windows软件界面,有菜单栏、工具栏。
特别的,工具栏下方的是数据栏,数据栏下方则是数据管理窗口的主界面。
该界面和EXCEL极为相似,由若干行和列组成,每行对应了一条记录,每列则对应了一个变量。
由于现在我们没有输入任何数据,所以行、列的标号都是灰色的。
请注意第一行第一列的单元格边框为深色,表明该数据单元格为当前单元格。
Spss__作业习题答案.docx

Spss作业习题答案GRAPH/BAR(SIMPLE)二SUM(js) BY yeai\图表[数据集 1 ] C: \Users\l iuj ie\Desktop\第一次习题\习题7-1. savCOMPUTE zz=beer + wine + spirits. EXECUTE. GRAPH/BAR(SIMPLE)二SUM(zz) BY year.图表[数据集]]C: \Users\l iuj ie\Desktop\第一次习题\习题7-1 .savGRAPH/BAR(GROUPED)=MEAN(tea) MEAN(coffee) MEAN(cc) MEAN(mw) MEAN(fj) MEAN(beer) MEAN(wine)MEAN(spirits) BY country/PANEL ROWVAR二coni ROWOP=CROSS /MISSING二LISTWISE.图表[数据集 1 ] C: \Users\l iuj ic\Desktop\第一次习题\习题7・1 • savGETFILE='C:\Users\liujie\Desktop\第一次习题 \ 习题 7-2.sav'. DATASET NAME 数据集2 WINDOW 二FRONT. DATASET CLOSE 数据集 1. SORT CASES BY year (A). GRAPH/LINE(AREA)= SUM(def) SUM(eco) BY year /MISSING=LISTWISE.图表附注02-APR-2016 19:08:1612000- 1oooo- 8000- 6000- 4000- 2000-0- 12000" 10000- 8000- 6000- 4000- 2000-0- 12000- 1oooo- 8000- 6000- 4000" 2000-o- 12000- 10000- 8000- 6000- 4000-2000-westernEurope Asia "B e -gc m }Aust_・Denmark■Luxembour g —Japan 4e-ana-UK -Switzerla nd "SpainOceaniaNorth America■东 C000tons)■ 啡 cooo tons)□ C&C 饮料(million litres) ■矿泉 J :(million litres) □ 士 厂(million litres) □啤酒(million litres)□ri(millio n litres)□烈酒(million litres)创建的输出[数据集2] C:\Users\liujie\Desktop\第一次习题\习题7-2.savGETFILE=*C:\Users\ 1 iuj ie\Desktop\第一次习题\习题7-3.sav'. DATASET NAME 数据集3 WINDOW 二FRONT. DATASET CLOSE 数据集2. GRAPH/PIE=SlJNf(rus) BY sea.图表创建的输出02-APR-2016 19:11:19注释1200.00-1000.00-800.00"600.00-400.00-200.00-国防 经济gggggggggggg 9 9 9 9 9 9555556660)677777888024680246802468024[数据集3] C:\Users\l iuj ie\Desktop\第一次习题\习题7-3.sav季节■ 1 st Season■2nd Season□ 3rd Season■4th Season您对IBM SPSS Statistics的临时使用期将在11天后过期。
北语2024春《SPSS统计与分析应用》作业满分答案文档

北语2024春《SPSS统计与分析应用》作业满分答案文档问题一: 描述性统计分析数据收集首先,我们需要收集一组数据以进行描述性统计分析。
在此作业中,我们收集了100个学生的数学成绩数据。
描述性统计分析使用SPSS软件进行描述性统计分析,我们得到了以下结果:- 平均数:78.5- 标准差:9.2- 最小值:60- 最大值:95- 中位数:80- 四分位数:- 第一四分位数:72.5- 第二四分位数:80- 第三四分位数:85结论根据描述性统计分析结果,我们可以得出以下结论:- 这组学生的平均数成绩为78.5,说明整体水平中等偏上。
- 标准差为9.2,说明学生的成绩相对分散。
- 最低分为60,最高分为95,成绩分布较为广泛。
- 中位数为80,说明成绩的中等水平集中在80左右。
- 第一四分位数为72.5,第三四分位数为85,说明成绩的大部分集中在72.5到85之间。
问题二: 相关性分析数据收集我们收集了100个学生的数学成绩和英语成绩数据。
相关性分析使用SPSS软件进行相关性分析,我们得到了以下结果:- 相关系数:0.75- p值:0.001结论根据相关性分析结果,我们可以得出以下结论:- 数学成绩和英语成绩之间存在较强的正相关关系。
- 相关系数为0.75,接近于1,说明两个变量之间的关联程度较高。
- p值为0.001,小于显著性水平0.05,因此可以得出该相关关系是显著的。
问题三: T检验数据收集我们收集了两组学生的数学成绩数据:男生组和女生组。
T检验使用SPSS软件进行T检验,我们得到了以下结果:- T值:2.16- 自由度:98- p值:0.034结论根据T检验结果,我们可以得出以下结论:- 男生组和女生组的数学成绩之间存在显著差异。
- T值为2.16,自由度为98,p值为0.034,小于显著性水平0.05,因此可以得出这种差异是显著的。
问题四: 方差分析数据收集我们收集了三个不同班级的学生的数学成绩数据。
Spss作业数据分析说明
Spss作业数据分析说明本问卷构成情况:由13个分问卷组成,每个问卷在数据录入时只录入总分。
num anx焦虑exa考试焦虑mch数学成绩con学习信任cla课堂焦虑sex性别use有用性tin工作投入hom家庭背景suc成功态度ein自我投入fea压力惧怕mot探究动机
wor情绪担忧att数学态度 以下是对几个分测验总分的描述:
本表为性别差异对各分测验影响的描述:
结果:数学成绩、考试焦虑、焦虑总数、学习信任这四项在性别上差异显著,达到显著性水平(P<.05);其余各项有差异 ,但都不显著.
家庭背景对各分测验的影响:
有差异,但不显著。
各分测验成绩相关表:
结果:有用性、成功态度、自我投入与情绪担忧,有用性、成功态度、与考虑焦虑,自我投入与课堂焦虑,成功态度与焦虑总分,自我投入与学习信任,自我投入与有用性,探究动机、数学态度与自我投入,自我投入与工作投入,等相关不显著。
其余相关都非常显著。
结果:两者主效应都不显著,交互作用也不显著。
结果:数学成绩总体近似线性分布。
因素分析:
上图为因素分析的碎石图,如图所示,我们提出前三个因素即可以解释原有的这些变量。
如上表所示,新析取的三个因子变量之间只有很弱的相关性,这说明我们成功提取出三个变量,综合上述表格,我们对三个新变量解释如下:F1主要解释压力惧怕、情绪担忧、考试焦虑、课堂
焦虑、焦虑这几个项目,显然主要是关于焦虑因子;F2主要解释了学习信任、有用性、成功态度、探究动机、数学态度、工作投入这些变量,可是认为它主要是主体在学习数学时的动机和态度问题;F3主要解释了自我投入水平即自我调动水平和花费的时间多少等因素。
spss实践题分析及答案(二)
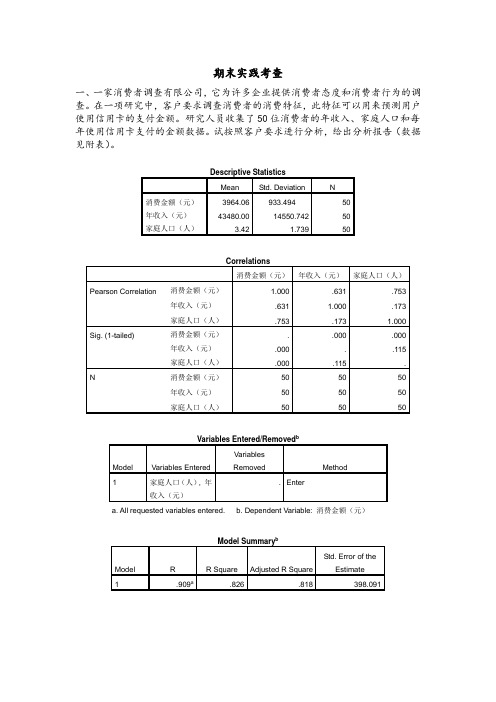
期末实践考查一、一家消费者调查有限公司,它为许多企业提供消费者态度和消费者行为的调查。
在一项研究中,客户要求调查消费者的消费特征,此特征可以用来预测用户使用信用卡的支付金额。
研究人员收集了50位消费者的年收入、家庭人口和每年使用信用卡支付的金额数据。
试按照客户要求进行分析,给出分析报告(数据见附表)。
Descriptive StatisticsMean Std. Deviation N消费金额(元)3964.06 933.494 50年收入(元)43480.00 14550.742 50家庭人口(人) 3.42 1.739 50Model Summary bModel R R Square Adjusted R Square Std. Error of the Estimate结果分析:由题目可知客户要求,是根据消费者年收入、家庭人口来预测其每年使用信用卡支付的金额数据,属于多元线性回归问题,其中年收入和家庭人口 看作两个自变量,每年信用卡支付金额看作因变量。
由分析得:121304.9050.033356.296y x x =++y :信用卡支付金额 1x :年收入 2x :家庭人口拟合优度检验2R为0.818,回归方程能很好的代表样本数据。
回归方程F检验和回归系数T检验的相伴概率都小于显著性水平,拒绝零假设即回归方程和回归系数都具显著型。
二、下表为运动员与大学生的身高(cm)与肺活量(cm3)的数据,考虑到身高与肺活量有关,而一般运动员的身高高于大学生,为进一步分析肺活量的差异是否由于体育锻炼所致,试作控制身高变量的协方差分析,并给出分析报告。
Between-Subjects FactorsValue Label N类别0 0 201 1 20Tests of Between-Subjects Effects Dependent Variable:肺活量Source Type III Sumof Squares dfMeanSquare F Sig.Corrected Model 6981685.135a2 3490842.56822.860 .000Intercept 208064.290 1 208064.290 1.363 .251身高1630762.635 1 1630762.63510.679 .002类别1407847.095 1 1407847.0959.220 .004Error 5649992.36537 152702.496 Total 6.633E8 40Corrected Total 12631677.50039a. R Squared = .553 (Adjusted R Squared = .529结果分析:控制变量的相伴概率值是0.004,小于显著性水平0.05,因此拒绝零假设,故在剔除身高对肺活量的影响前提下,是否经常进行体育锻炼对肺活量有显著影响;另外协变量相伴概率为0.002,说明身高的不同水平对肺活量也有显著影响。
教育统计学与SPSS课后作业答案祥解题目

教育统计学课后作业P118 1题目:10位大一学生平均每周所花的学习时间与他们的期末考试成绩见表6-17.试问:(1)学习时间与考试成绩之间是否相关?(2)比较两组数据谁的差异程度大一些?(3)比较学生2与学生9的期末考试测验成绩。
表6-17学习时间与期末考试成绩解题步骤:(1)第一步:定义变量:“xuexishijian”、“xuexichengji”后,输入数据.如下图:第二步:单击选择“分析(Analyze) ”中的“相关(Correlate)”中的“双变量(Bivariate Correlations)”,将上图中的“ xuexishijian”和“xuexichengji”添加到右边变量框中,如下图:第三步:点击“确定“后,输出结果如下图:相黄性水在03水平(敢侧)上显著相关。
第四步:分析结果由上图可知:学习时间与学习成绩之间的pearson 相关系数为0.714, p (双侧)为0.20。
自由度df=10-2=8时,查“皮尔逊积差相关系数显著临界值表”知:r 0.05= 0.623 ; r 0.01=0.765。
因为 0.765 > 0.714 >0.623 ,所以在 0.05水平上学习时间和学习成绩是相关显著的。
(2) SPSS 软件分析结果如下图:由上图可知:学习时间标准差和平均值为: S 1=12.037 X 1= 29.00 ;学习时间标准差和平均值为:S 2=12.437 X 2=56.00 根据差异系数公式可知: S100% =12.037/29.00X 100%=41.51%XS100% =12.437/56.00X 100%= 22.27%X有上述结果可知学习时间差异程度大于学习成绩差异程度。
(4) 把学生2和学生9的期末考试成绩转化成标准分数:Z 2=(X - X) /S= (73—56)/ 12.437=1.367 Z 9=(X- X)/S=(68— 56)/ 12.437=0.965由上计算可知:学生2期末考试测验成绩优于学生9的期末考试测验成绩。
spss实际分析word精品文档6页

06年部分省份环境污染与破坏情况调查引言:21世纪是环保的社会,建设节约型环保社会是未来几年的重大课题,环境保护的重要性不是哪个人的事情而是全社会、全球性的问题。
作为环保人我们更应该充分了解目前我国面临的环境污染与破坏事故,从而更好地投身于环保事业中去。
本文分析统计了部分省份环境污染与破坏的情况,并通过SPSS分析如下,对我国的环境保护工程有一定借鉴意义。
同时提高了分析数据统计结果的能力。
一、研究目的:1. 熟悉SPSS软件在实际中的应用;2. 根据2019年部分地区环境污染与破坏情况,了解我国目前面临的环境问题现状,为以后处理环境问题提高更好的依据。
注:由于所查数据有所缺损,故将部分数据舍弃,只取其中数据较完整的省份进行分析3. 通过对环境污染与破坏情况以及治理各类污染项目的投资额情况的调查,了解污染治理的状况,并提出相应的建议及措施;4. 培养分析数据统计结果的能力。
二、研究方法:1.资料收集:本论文从国家统计局官方网站上收集了近年来全国各地区污染事故治理及其投资情况,并选择其中的最新数据运用SPSS 11.0中文版进行统计分析。
在分析前,要进行数据格式的转换,将其汇总为可用于SPSS 分析的格式。
2.研究方法本论文主要运用了《环境统计学》中的相关知识,并运用spss软件对数据进行进行统计描述,同时将部分省份的相关数据用条形图、饼图等进行形象的表现,最后对各种数据进行相关性分析和回归分析以研究各种数据之间的相关性,借此了解我国的污染及其治理的状况。
原始数据:三、数据处理:1.部分省份总污染事故次数的比较:图1:利用简单饼图比较图2:利用简单条形图比较从图1和图2中看都出,湖南省总污染事故次数远远超出其他省份,甘肃省次之。
总污染事故次数所呈现的趋势多少与省份的人口数、工业发展情况、人民生活消费水平、生活习惯等方面有关。
2.部分省份污染事故所属类型的研究:图3:利用交互饼图比较各省份污染事故所属类型图4:利用交互条图比较各省份污染事故所属类型从系列图3和图4可以看出,湖南省的污染事故次数最多,其中水污染占将近一半;甘肃省处于第二位,其中水污染也占将近一半;黑龙江省、吉林省和我省的污染事故次数较少,其余的省份污染事故次数则较接近,都在20次左右。
spss分析.doc
其他
60
20.3
20.3
100.0
合计
295
100.0
100.0
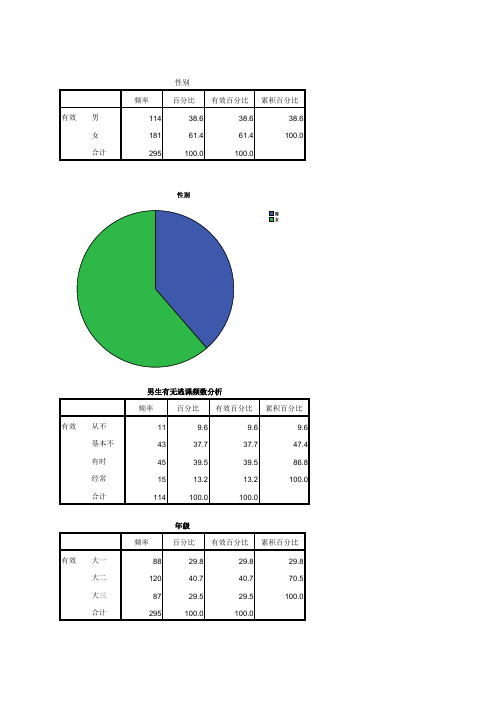
要想使学生不逃课,老师该怎样改进自己的教学
频率
百分比
有效百分比
累积百分比
有效
风趣幽默一点
136
46.1
46.1
46.1
多讲点课本以外的知识
56
19.0
19.0
65.1
学识渊博一点
42
14.2
14.2
79.3
与学生有的交流
61
20.7
频率
百分比
有效百分比
累积百分比
有效
是
61
20.7
20.7
20.7
否
234
79.3
79.3
100.0
合计
295
100.0
100.0
使大家减少逃课的措施——出勤率作为综合测评的一项指标与奖学金挂钩
频率
百分比
有效百分比
累积百分比
有效
是
82
27.8
27.8
27.8
否
213
72.2
72.2
100.0
合计
295
有效百分比
累积百分比
有效
很内疚
94
31.9
31.9
31.9
比较自责,但下次还会逃
90
30.5
30.5
62.4
无所谓
111
37.6
37.6
100.0
合计
295
100.0
100.0
对经常旷课的同学的看法
频率
百分比
spss作业以及案例分析
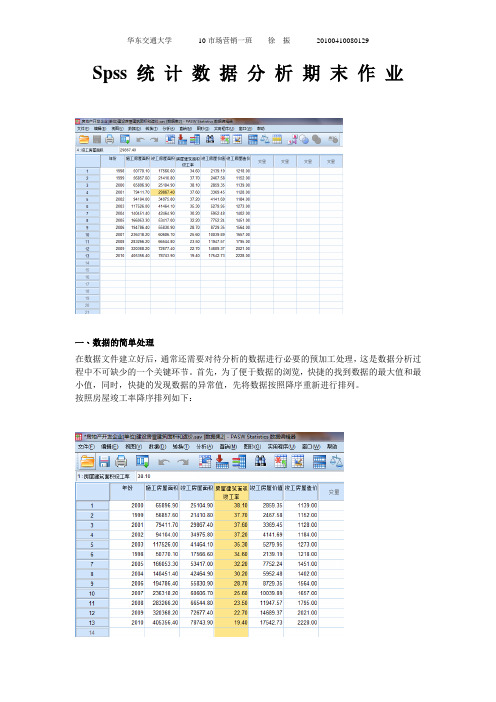
输入/移去的变量 b
模型
输入的变量 移去的变量
方法
1
施工房屋面积 a
. 输入
a. 已输入所有请求的变量。 b. 因变量: 竣工房屋价值
模型汇总 b
模型
标准 估计的误
R
R 方 调整 R 方
差
1
.998a
.996
.996
320.62046
a. 预测变量: (常量), 施工房屋面积。 b. 因变量: 竣工房屋价值
竣工房屋造价
.000
.000
.000
.000
由此表可看,大多数相关系数都较高,各变量具有较强的线性关系,能够从中提取公共因子, 适合进行因子分析。
公因子方差
初始
施工房屋面积 竣工房屋面积 房屋建筑面积竣工率 竣工房屋价值 竣工房屋造价
1.000 1.000 1.000 1.000 1.000
提取方法:主成份分析。
b. 因变量: 竣工房屋价值
Anovab df
1 11 12
均方 2.905E8
102797.480
F 2825.508
Sig. .000a
模型
1
(常量)
施工房屋面积
a. 因变量: 竣工房屋价值
系数 a
非标准化系数
标准系数
B
标准 误差 试用版
2.441
166.020
.044
.001
.998
t .015
4919.81654 306.97072
1.000 .957
N 13 13 13 13
四、单样本的T检验
房屋建筑面积竣工率
单个样本统计量
N
均值
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章
SPSS参数检验
——均值比较
1、某公司经理宣称他的雇员英语水平很高,如果按照英语六级考试的话,一般平均得
分为75分。
现从雇员中随机选出11人参加考试,得分如下:80, 81, 72, 60, 78, 65, 56, 79, 77,87, 76 请问该经理的宣称是否可信。
操作:分析→比较均值→单样本T
均值为73.7273,Q值为0.668大于0.05,均值预75没有显著性差异,接受原假设。
即该经理的宣称是可信的。
2、经济学家认为决策者是对事实做出反应,不是对提出事实的方式做出反应。
然而心理学家则倾向于认为提出事实的方式是有关系的。
为验证哪种观点更站得住脚,调查者分别以下面两种不同的方式随机访问了足球球迷。
l 方式一:假设你已经买了100元一张的足球票,当你来到足球场门口时,发现票丢了且再也找不到了。
球场还有票出售。
你会再掏出100元买一张球票吗?(1.买0.不买)。
随机访问了200人,其中:92人回答买;
l 方式二:你想看足球赛,100元一张票。
当你来到足球场买票时,发现丢了100元钱。
你口袋中还有钱,此时你还会付100元买一张球票吗?(1.买0.不买)。
随机访问了183人,其中:161人回答买;
请恰当建立SPSS数据文件,并利用本章所学习的参数检验方法,说明你更倾向于那种观点,为什么?
操作:输入数据→分析→比较均值→独立样本T检验
3、一种植物只开兰花和白花。
按照某权威建立的遗传模型,该植物杂交的后代有75%的几率开兰花,25%的几率开白花。
现从杂交种子中随机挑选200颗,种植后发现142株开了兰花,请利用SPSS进行分析,说明这与遗传模型是否一致?
操作:输入数据→分析→比较均值→独立T检验(输入值为0.75)
即:0.215大于0.05,预遗传模型没有差异性
4、给幼鼠喂以不同的饲料,用以下两种方法设计实验:
方式1:同一鼠喂不同的饲料所测得的体内钙留存量数据如下:
鼠号饲料1 饲料2 1
33.1
36.7
2
33.1
3 4 5 6 7 8 9
26.8 36.3 39.5 30.9
25.7
33.4 34.5 28.6
28.8 35.1 35.2 43.8 36.5 37.9 28.7
配对样本T检验
l 方式2:甲组有12只喂饲料1,乙组有9只喂饲料2所测得的钙留存量数据如下
甲组
饲料1
29.7 26.7 28.9 31.1 31.1 26.8 26.3 39.5 30.9 33.4 33.1 28.6
乙组
饲料2
28.7 28.3 29.3 32.2 31.1 30.0 36.2 36.8 30.0
请选用恰当方法对上述两种方式所获得的数据进行分析,研究不同饲料是否使幼鼠体内钙的留存量有显著不同。
操作:合理输入数据→分析→比较均值→独立样本T检验
即:0.811>0.5,所以认为喂不同的饲料与体内钙留存量存在非线性相关关系5、如果将习题二第4题的数据看作是来自总体的样本,试分析男生和女生的课程平均分是否存在显著差异?
操作:合理输入数据→分析→比较均值→独立样本T检验
即:语文男女存在显著性差异
6、如果将习题二第4题的数据看作是来自总体的样本,试分析哪些课程的平均分差异不显著。
操作:输入数据→分析→比较均值→配对样本T检验(只能两组)
即:英语和物理差异非常大,有线性关系
平均分美誉任何两组相关
7、以下是对促销人员进行培训前后的促销数据:
培训前440 500 580 460 490 480 600 590 430 510 320 470 培训后620 520 550 500 440 540 500 640 580 620 590 620 试分析该培训是否产生了显著效果。
操作:输入数据→分析→比较均值→配对样本T检验
8、入户推销有五种方法。
某大公司想比较这五种方法有无显著的效果差异,设计了一项实验。
从应聘人员中尚无推销经验的人员中随机挑选一部分人,并随机地将他们分为五个组,每组用一种推销方法培训。
一段时期后得到他们在一个月内的推销额,如下表所示:
第一组 20.0 16.8 17.9 21.2 23.9 26.8 22.4
第二组 24.9 21.3 22.6 30.2 29.9 22.5 20.7
第三组 16.0 20.1 17.3 20.9 22.0 26.8 20.8
第四组 17.5 18.2 20.2 17.7 19.1 18.4 16.5
第五组 25.2 26.2 26.9 29.3 30.4 29.7 28.2
1)请利用单因素方差分析方法分析这五种推销方式是否存在显著差异。
操作:输入数据→分析→比较均值→单因素
2) 绘制各组的均值对比图,并利用LSD 方法进行多重比较检验。
操作:分析→比较均值→单因素→两两比较(LSD )
9、为研究某种降血压药的适用特点,在五类具有不同临床特征的高血压患者中随机挑选了若干志愿者进行对比试验,并获得了服用该降压药后的血压变化数据。
现对该数据进行单
因素方差分析,所得部分分析结果如下表所示。
1)请根据表格数据说明以上分析是否满足方差分析的前提要求,为什么?
不满足,因为该方差不齐性。
(AMUVA参数=0.00)
2)请填写表中空缺部分的数据结果,并说明该降压药对不同组患者的降压效果是否存在显著差异。
存在
3)如果该降压药对不同组患者的降压效果存在显著差异,那么该降压药更适合哪组患者?
第一组
10、为研究某商品在不同地区和不同日期的销售差异性,调查收集了以下日平均销售量数
据。
销售量 日期
周
一~周三 周四~周五
周末
地区一
5000 6000 4000 6000 8000 7000 4000
3000 5000
地区二
7000 8000 8000 5000 5000 6000 5000
6000 4000
地区三
3000 2000 4000 6000 6000 5000 8000
9000 6000
1) 选择恰当的数据组织方式建立关于上述数据的SPSS 数据文件
2) 利用多因素方差分析方法,分析不同地区和不同日期对该商品的销售是否产生了显著影响
因为地区的sig=0.448>0.05,日期的sig=0.175>0.05,所以不同地区和不同日期对该商品的销售产生了明显的影响。
3)地区和日期是否对该商品的销售产生了交互影响。
若没有显著的交互影响,则试建立非饱和模型进行分析,并与饱和模型进行对比。
因为地区和日期相乘的sig=0.00<0.05,所以地区和日期没有显著的交
互影响;。
