“死结”与“活结”及动态平衡问题易错分析可自主编辑
攻破高中物理受力分析(3)-注意“死结”、“活结”问题

攻破⾼中物理受⼒分析(3)-注意“死结”、“活结”问题书接上⽂这篇⽂章主要是要谈谈在我们受⼒分析的时候要避过的坑这就是我们要说的“死结” 和“ 活结”准确区分“死结”和“活结”不要掉⼊陷进“死结”“活结”区别什么是“死结”?什么是“活结”?我们可以这么简单理解不是⼀根绳⼦可以理解为死结是⼀根绳⼦可以理解为活结那么“活结”和“死结”的区别是什么呢?“死结”不是⼀根绳⼦,所以绳⼦的拉⼒是不⼀样的“活结”是⼀根绳⼦,所以绳⼦上的张⼒处处相同这么理解起来还是有⼀丢丢抽象下⾯我们来举例分析⼀下举例分析题⽬:⼀根绳⼦OA⼀端系于墙上,⼀段系在⼀根横杆的右端,横杆左端固定在墙上,在横杆右端下⽅⽤绳⼦OB掉⼀重物,已知绳⼦与横杆的⾓度为θ,重物的质量为m 问题:求横杆提供的⽀持是多少?分析:这是⼀根绳⼦还是两根绳⼦呢?显然这是两根绳⼦,所以,OA和OB这两段绳⼦的受⼒是不同的“死结”问题我们对O点受⼒分析O点受⼒分析对其正交分解,列式表达Tcosθ=FTsinθ=mg解得结果为F=mg/tanθ接着来对⽐下⾯的题⽬题⽬:⼀根横杆左端固定在墙壁上,横杆右端固定着⼀个忽略摩擦的定滑轮,⼀根细绳系在墙上并且穿过定滑轮下端掉着⼀重物,绳⼦与⽔平⾯的夹⾓为θ,重物的质量为G 问题:定滑轮提供的⽀持⼒是多少?分析:这题中的绳⼦是⼏段呢?明显是⼀段绳⼦,所以,对OA、OB其实就是⼀根绳⼦,在对O点受⼒分析的时候,OA、OB⾥⾯的拉⼒是⼀样⼤的“活结”问题我们画出O点的受⼒分析⼀定要注意,OA、OB段绳⼦拉⼒是⼀样的定滑轮对O点的受⼒还是和上题⼀样的⽔平向右吗?显然不是的我们接着分析OA段与OB段绳⼦拉⼒进⾏合成,合成出红⾊的F合这个⼒这个⼒的⽅向是OA与OB这两条线的⾓平分线这个⼒的⼤⼩呢?我们来求解⼀下我们要求解的是定滑轮提供的⽀持⼒定滑轮的⽀持⼒⼀定是与这个F合这个⼒等⼤反向所以最终O点的受⼒分析O的受⼒分析其中F⽀就是定滑轮提供的⽀持⼒F⽀=F合即可得解仔细对⽐以上两题,虽然两题的图形是差不多类似,但是解决⽅法完全不同!这是我希望同学们注意的“死结”“活结”问题不要在这⾥犯错~下⾯我再给⼀题题⽬:⽤⾐架晾晒⾐服,挂在⼀根绳⼦上,绳⼦左右两端系在两根竖直的杆⼦上问题:将右端绳⼦的结点往上移动⼀定举例,⾐架左右两边的绳⼦的拉⼒是变⼤?变⼩?不变?希望各位盆友可以下去⾃主完成,可以把答案留在评论区,欢迎你的留⾔总结“死结”是不同的绳⼦,绳⼦⾥⾯的张⼒不同“活结”是⼀根绳⼦,绳⼦⾥⾯的张⼒处处相等把握好这两点,你⼀定可以避免踩坑。
高考物理专题“死结”与“活结”及动态平衡问题易错分析

二、“死结”与“活结”及动态平衡问题易错分析“死结”与“活结”的比较(1)“死结”可理解为把绳子分成两段,且不可以沿绳子移动的结点。
“死结”两侧的绳因结而变成了两根独立的绳,因此由“死结”分开的两段绳子上的弹力不一定相等。
(2)“活结”可理解为把绳子分成两段,且可以沿绳子移动的结点。
“活结”一般是由绳跨过滑轮或者绳上挂一光滑挂钩而形成的。
绳子虽然因“活结”而弯曲,但实际上是同一根绳,所以由“活结”分开的两段绳子上弹力的大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的平分线。
典例1 如图所示,AO 、BO 、CO 是完全相同的绳子,并将钢梁水平吊起,若钢梁足够重时,绳子AO 先断,则( )A.θ=120°B.θ>120°C.θ<120°D.不论θ为何值,AO 总是先断答案 C 以结点O 为研究对象,受力情况如图所示,根据对称性可知,BO 绳与CO 绳拉力大小相等,由平衡条件得,F AO =2F BO cos θ2,当钢梁足够重时,AO 绳先断,说明F AO >F BO ,则有2F BO cos θ2>F BO ,解得θ<120°,故选项C 正确。
典例2 (多选)(2016课标Ⅰ,19,6分)如图,一光滑的轻滑轮用细绳OO'悬挂于O 点;另一细绳跨过滑轮,其一端悬挂物块a,另一端系一位于水平粗糙桌面上的物块b 。
外力F 向右上方拉b,整个系统处于静止状态。
若F 方向不变,大小在一定范围内变化,物块b 仍始终保持静止,则( )A.绳OO'的张力也在一定范围内变化B.物块b所受到的支持力也在一定范围内变化C.连接a和b的绳的张力也在一定范围内变化D.物块b与桌面间的摩擦力也在一定范围内变化答案BD 系统处于静止状态,连接a和b的绳的张力大小T1等于物块a的重力Ga,C项错误;以O'点为研究对象,受力分析如图甲所示,T1恒定,夹角θ不变,由平衡条件知,绳OO'的张力T2恒定不变,A项错误;以b为研究对象,受力分析如图乙所示,则F N +T1cos θ+F sin α-Gb=0f+T1sin θ-F cos α=0FN、f均随F的变化而变化,故B、D项正确。
死结活结及动态平衡(含答案)
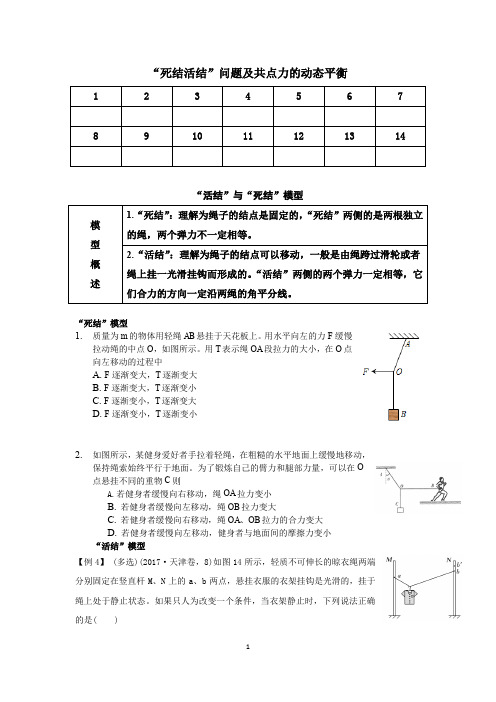
“死结活结”问题及共点力的动态平衡“活结”与“死结”模型“死结”模型1. 质量为m 的物体用轻绳AB 悬挂于天花板上。
用水平向左的力F 缓慢拉动绳的中点O ,如图所示。
用T 表示绳OA 段拉力的大小,在O 点向左移动的过程中A. F 逐渐变大,T 逐渐变大B. F 逐渐变大,T 逐渐变小C. F 逐渐变小,T 逐渐变大D. F 逐渐变小,T 逐渐变小2. 如图所示,某健身爱好者手拉着轻绳,在粗糙的水平地面上缓慢地移动,保持绳索始终平行于地面。
为了锻炼自己的臂力和腿部力量,可以在O 点悬挂不同的重物C 则A.若健身者缓慢向右移动,绳OA 拉力变小B. 若健身者缓慢向左移动,绳OB 拉力变大C. 若健身者缓慢向右移动,绳OA 、OB 拉力的合力变大D. 若健身者缓慢向左移动,健身者与地面间的摩擦力变小“活结”模型【例4】 (多选)(2017·天津卷,8)如图14所示,轻质不可伸长的晾衣绳两端分别固定在竖直杆M 、N 上的a 、b 两点,悬挂衣服的衣架挂钩是光滑的,挂于绳上处于静止状态。
如果只人为改变一个条件,当衣架静止时,下列说法正确的是( )A.绳的右端上移到b′,绳子拉力不变 B.将杆N向右移一些,绳子拉力变大C.绳的两端高度差越小,绳子拉力越小 D.若换挂质量更大的衣服,则衣架悬挂点右移3.如图,两个轻环a和b套在位于竖直面内的一段固定圆弧上:一细线穿过两轻环,其两端各系一质量为m的小球。
在a和b之间的细线上悬挂一小物块。
平衡时,a、b间的距离恰好等于圆弧的半径。
不计所有摩擦。
小物块的质量为()A. B. C. m D. 2m4.如图所示,A、B两物体的质量分别为和,且,整个系统处于静止状态,滑轮的质量和一切摩擦均不计如果绳一端由Q点缓慢地向左移到P点,整个系统重新平衡后,物体A的高度和两滑轮间绳与水平方向的夹角如何变化A. 物体A的高度升高,角变小B. 物体A的高度降低,角不变C. 物体A的高度升高,角不变D. 物体A的高度不变,角变小动态平衡5(角度变).如图所示,质量分别为M,m的两个物体系在一根通过轻滑轮的轻绳两端,M放在水平地面上,m被悬在空中,若将M沿水平地面向右缓慢移动少许后M仍静止,则( )A. 绳中张力变大B. 滑轮轴所受的压力变大C. M对地面的压力变大D. M所受的静摩擦力变大6.(大小变)一光滑的轻滑轮用细绳悬挂于O点,站在地面上的人用轻绳跨过滑轮拉住沙漏斗,在沙子缓慢漏出的过程中,人握住轻绳保持不动,则在这一过程中()A. 细线OO’与竖直方向夹角逐渐减小B. 细线OO’的张力逐渐增大C. 人对地面的压力将逐渐增大D. 人对地面的摩擦力将逐渐增大7.如图所示,光滑小球置于竖直墙壁和挡板间,挡板绕O点于图示位置缓慢转至水平的过程中,球对墙壁和挡板的压力如何变化( )A. 对墙壁的压力减小,对挡板的压力也减小B. 对墙壁的压力减小,对挡板的压力增大C. 对墙壁的压力减小,对挡板的压力先增大后减小D. 对墙壁的压力先增大后减小,对挡板的压力增大8.如图所示,一个球放在光滑斜面EF和挡板EQ中,挡板通过轴E固定在斜面上,斜面与水平面夹角为,当挡板由竖直位置转到水平位置的过程中,斜面对球的作用力,挡板对球的作用力的变化情况是( )A. 变小,先变小后变大B. 变大,先变小后变大C. 变大,变大D. 不变,变小9.如图所示,一根粗糙的水平横杆上套有A、B两个轻环,系在两环上的等长细绳拴住的书本处于静止状态,现将两环距离变小后书本仍处于静止状态,则A. 杆对A环的支持力变大B. B环对杆的摩擦力变小C. 杆对A环的力不变D. 与B环相连的细绳对书本的拉力变大10.如图所示,用OA、OB两根轻绳将花盆悬于两竖直墙之间,开始时OB绳水平。
高中物理:专题11 “活结”和“死结”、“动杆”和“定杆”模型-高一上学期同步重难讲练之相互作用

重难讲练1.“活结”和“死结”问题(1)活结:当绳绕过光滑的滑轮或挂钩时,由于滑轮或挂钩对绳无约束,因此绳上的力是相等的,即滑轮只改变力的方向不改变力的大小,例如图乙中,两段绳中的拉力大小都等于重物的重力.(2)死结:若结点不是滑轮,是固定点时,称为“死结”结点,则两侧绳上的弹力不一定相等.“死结”一般是由绳子打结而形成的,“死结”两侧的绳子因打结而变成两根独立的绳子。
死结的特点:a.绳子的结点不可随绳移动b.“死结”两侧的绳子因打结而变成两根独立的绳子,因此由“死结”分开的两端绳子上的弹力不一定相等2.“动杆”和“定杆”问题(1)动杆:若轻杆用光滑的转轴或铰链连接,当杆处于平衡时杆所受到的弹力方向一定沿着杆,否则会引起杆的转动.如图甲所示,若C为转轴,则轻杆在缓慢转动中,弹力方向始终沿杆的方向.(2)定杆:若轻杆被固定不发生转动,则杆所受到的弹力方向不一定沿杆的方向.如图乙所示.【典例1】(2016·全国卷Ⅲ·17)如图所示,两个轻环a和b套在位于竖直面内的一段固定圆弧上;一细线穿过两轻环,其两端各系一质量为m 的小球.在a 和b 之间的细线上悬挂一小物块.平衡时,a 、b 间的距离恰好等于圆弧的半径.不计所有摩擦.小物块的质量为( )A.m 2B.32m C.mD.2m【☆答案☆】 C 【解析】 如图所示,【典例2】 如图所示,一轻绳的两端分别固定在不等高的A 、B 两点,现用另一轻绳将一物体系于O 点,设轻绳AO 、BO 相互垂直,α>β,且两绳中的拉力分别为F A 、F B ,物体受到的重力为G ,下列表述正确的是( )A.F A一定大于G B.F A一定大于F BC.F A一定小于F B D.F A与F B大小之和一定等于G【☆答案☆】 B【解析】分析O点受力如图所示,由平衡条件可知,F A与F B的合力与G等大反向,因F A⊥F B,故F A、F B均小于G;因α>β,故F A>F B,B正确,A、C错误;由三角形两边之和大于第三边可知,|F A|+|F B|>G,D错误.【典例3】如图甲所示,轻绳AD跨过固定的水平横梁BC右端的定滑轮挂住一个质量M1的物体,∠ACB=30°;图乙中轻杆HG一端用铰链固定在竖直墙上,另一端G通过细绳EG拉住,EG与水平方向也成30°,轻杆的G点用细绳GF拉住一个质量M2的物体,求:(1)轻绳AC段的张力F T AC与细绳EG的张力F T EG之比;(2)轻杆BC对C端的支持力;(3)轻杆HG对G端的支持力.【☆答案☆】(1)M12M2(2)M1g方向和水平方向成30°指向右上方(3)3M2g方向水平向右【解析】题图甲和乙中的两个物体M1、M2都处于平衡状态,根据平衡的条件,首先判断与物体相连的细绳,其拉力大小等于物体的重力;分别取C点和G点为研究对象,进行受力分析如图甲和乙所示,根据平衡规律一一求解.【跟踪训练】1. 如图所示,将一细绳的两端固定于两竖直墙的A、B两点,通过一个光滑的挂钩将某重物挂在绳上,下面给出的四幅图中有可能使物体处于平衡状态的是( )【☆答案☆】C2.如图所示,当重物静止时,节点O 受三段绳的拉力,其中AO 沿水平方向,关于三段绳中承受拉力的情况,下列说法中正确的是A . AO 承受的拉力最大B . BO 承受的拉力最大C . CO 承受的拉力最大D . 三段绳承受的拉力一样大 【☆答案☆】B【解析】以结点O 为研究对象,分析受力情况,受力分析如图:由平衡条件得: 1tan T G θ=,2cos GT θ=,故T1小于T2,G 小于T2;所以BO 承受的拉力最大;故B 正确。
物体的平衡专题(二):活结、活杆问题分析

物体的平衡专题(二)——“活结,死结”、“活杆,死杆”问题一、“活结,死结”问题分析1、如图所示,长为5m 的细绳的两端分别系于竖立在地面上相距为4m 的两杆的顶端A 、B 。
绳上挂一个光滑的轻质挂钩,其下连着一个重为12N 的物体。
平衡时,绳中的张力T =_____2、如图所示,将一根不能伸长的柔软轻绳两端分别系于A 、B 两点上,一 物体用动滑轮悬挂在绳子上,达到平衡时,两段绳子间的夹角为θ1,绳 子张力为F 1;将绳子B 端移到C 点,保持整个系统达到平衡时,两段绳子间的夹角为θ2,绳子张力为F 2;将绳子B 端移到D 点,待整个系统达 到平衡时,两段绳子间的夹角为θ3,绳子张力为F 3,不计摩擦,则( ) A .123θθθ== B .123θθθ=<C .123F F F >>D .123F F F =<3、如图所示,AO 、BO 和CO 三根绳子能承受的最大拉力相等,O 为结点,OB 与竖直方向夹角为θ,悬挂物质量为m 。
求:①OA 、OB 、OC 三根绳子拉力的大小 。
②A 点向上移动少许,重新平衡后,绳中张力如何变化? 4、如图所示,用绳AC 和BC 吊起一个物体,绳AC 与竖直方向的夹角为60°,能承受的最大拉力为100N 绳BC 与竖直方向的夹角为30°,能承受的最大拉力为150N.欲使两绳都不断,物体的重力不应超过多少?5. 如图所示,轻绳绕过一光滑的小圆柱B ,上端固定于A 点,下端系一重为200 N 的物体C ,AB 段绳子与竖直方向的夹角为60°,则绳中张力大小为____________ N ,小圆柱B 受到的压力大小为____________ N. 结论:对于结受力问题,首先应明确是结否固定,若不固定,则绳两端受力相等,沿绳子方向,若结固定,则绳两端受力不一定相等,也沿绳子方向,应根据实际情况(如受力平衡等)加以分析。
平衡中的“死结”与“活结”ppt课件

20
21
22
2、A、B一起匀速向右运动,A受力个数 为 ( ) B受力个数为 ( ) 整体受力个数为( )
A
B
3、P静止,则受力个数可能为: A、2个 B、3个 C 、4个 D、5个 P
4、A、B静止,则A受力个数为(
)A
B
F
23
5、力作用物块沿粗糙水平面运动,则物块受力个数
可能是
F
A 、2个 B、3个 C、4个 D、5个
5
正交分解法
TC = mg = 50N
TB cosq = ห้องสมุดไป่ตู้g
TA A
TB
=
mg cosq
= 50 0.8
= 62.5N
TA =TB sinq = 62.5? 0.6 37.5N
B TB θ θ O
mg
6
死结的特点: 1.绳子的结点不可随绳移动 2.“死结”两侧的绳子因打结而变成两根 独立的绳子,因此由“死结”分开的两端 绳子上的弹力不一定相等
27
的穹形门窗。在竖直放置的穹形光滑支架上,一根不可伸长 的轻绳通过轻质滑轮悬挂一重物G。现将轻绳的一端固定于 支架上的A点,另一端从B点沿支架缓慢地向C点靠近(C点
与A点等高).则绳中拉力大小变化的情况是(B )
(A)先变小后变大 (B)先变大后不变 (C)先变小后不变 (D)先变大后变小。
L1
L2
θ
L1 cosq +L2 cosq = d
dd
cosq =
=
( L1 +L2) L
16
二,“活杆”与“死杆”
轻杆是物体间连接的另一种方式,根据轻杆与 墙壁连接方式的不同,可以分为“活杆”与 “死杆”。
高一物理上册专题—“活结”和“死结”及“动杆”和“定杆”模型

“活结”和“死结”、“动杆”和“定杆”模型重难讲练1.“活结”和“死结”问题(1)活结:当绳绕过光滑的滑轮或挂钩时,由于滑轮或挂钩对绳无约束,因此绳上的力是相等的,即滑轮只改变力的方向不改变力的大小,例如图乙中,两段绳中的拉力大小都等于重物的重力.(2)死结:若结点不是滑轮,是固定点时,称为“死结”结点,则两侧绳上的弹力不一定相等.“死结”一般是由绳子打结而形成的,“死结”两侧的绳子因打结而变成两根独立的绳子。
死结的特点:a.绳子的结点不可随绳移动b.“死结”两侧的绳子因打结而变成两根独立的绳子,因此由“死结”分开的两端绳子上的弹力不一定相等2.“动杆”和“定杆”问题(1)动杆:若轻杆用光滑的转轴或铰链连接,当杆处于平衡时杆所受到的弹力方向一定沿着杆,否则会引起杆的转动.如图甲所示,若C为转轴,则轻杆在缓慢转动中,弹力方向始终沿杆的方向.(2)定杆:若轻杆被固定不发生转动,则杆所受到的弹力方向不一定沿杆的方向.如图乙所示.【例1】(2016·全国卷Ⅲ·17)如图所示,两个轻环a和b套在位于竖直面内的一段固定圆弧上;一细线穿过两轻环,其两端各系一质量为m的小球.在a和b之间的细线上悬挂一小物块.平衡时,a、b间的距离恰好等于圆弧的半径.不计所有摩擦.小物块的质量为( )A.m2B.√32mC.mD.2m【答案】C【解析】如图所示,圆弧的圆心为0,悬挂小物块的点为c,由于ab=R,则△aOb为等边三角形,同一条细线上的拉力相等, F T=mg,,合力沿Oc方向,则Oc为角平分线,由几何关系知,∠acb=120°,故线的拉力的合力与物块的重力大小相等,即每条线上的拉力F T= G=mg,,所以小物块质量为m,故C对.【例2】如图甲所示,轻绳AD跨过固定的水平横梁BC右端的定滑轮挂住一个质量M₁的物体,∠ACB=30°;图乙中轻杆HG一端用铰链固定在竖直墙上,另一端G通过细绳EG 拉住,EG与水平方向也成30°,轻杆的G点用细绳GF拉住一个质量M₂的物体,求:(1)轻绳AC段的张力F TAC与细绳EG的张力F TEG;之比;(2)轻杆BC对C端的支持力;(3)轻杆HG对G端的支持力.【答案】(1)M12M2(2)M1g方向和水平方向成30°指向右上方(3)√3M2g方向水平向右【解析】题图甲和乙中的两个物体M₁、M₂都处于平衡状态,根据平衡的条件,首先判断与物体相连的细绳,其拉力大小等于物体的重力;分别取C点和G点为研究对象,进行受力分析如图甲和乙所示,根据平衡规律一一求解.(1)图甲中轻绳AD跨过定滑轮拉住质量为M₁的物体,物体处于平衡状态,轻绳AC段的拉力F24c=F TCD=M1g图乙中由.F TEG sin30∘=M2g,得F TEG=2M2g.所以F14CF126=M12M2(2)图甲中,三个力之间的夹角都为120°,根据平衡规律有F AC=F DAC=Mg,方向和水平方向成30°,指向右上方.(3)图乙中,根据平衡方程有F TEG sin30∘=Mg,F TBG cos30∘=F XG,所以F NG=M2gcot30∘=√3M2g,方向水平向右.专项训练1.如图所示,当重物静止时,节点O受三段绳的拉力,其中AO沿水平方向,关于三段绳中承受拉力的情况,下列说法中正确的是A.AO承受的拉力最大B.BO承受的拉力最大C.CO承受的拉力最大D.三段绳承受的拉力一样大【答案】B【解析】以结点O为研究对象,分析受力情况,受力分析如图:由平衡条件得:T₁=Gtanθ,T2=Gcosθ,故T1小于T2,G小于T2;所以BO承受的拉力最大;故B正确。
高一物理:平衡中的重难点问题(1)

高一物理:平衡重难点问题(1)班级__________ 座号_____ 姓名__________ 分数__________一、知识清单1.“死结”与“活结”模型(1)活结模型:跨过滑轮、光滑杆、光滑钉子的细绳为同一根细绳,其两端张力大小相等.(2)死结模型:如几个绳端有“结点”,即几段绳子系在一起,谓之“死结”,那么这几段绳子的张力不一定相等.2.“死杆”与“活杆”模型(1)“死杆”:即轻质固定杆,它的弹力方向不一定沿杆的方向,作用力的方向需要结合平衡方程或牛顿第二定律求得.(2)“活杆”:即一端有铰链相连的杆属于活动杆,轻质活动杆中的弹力方向一定沿杆的方向.3.绳杆组合问题4.活结移动问题5.定滑轮和动滑轮组合问题6. 轻环穿杆问题7. 自锁问题二、例题精讲8. (2011·海南)如图所示,墙上有两个钉子a 和b ,它们的连线与水平方向的夹角为45°,两者的高度差为l .一条不可伸长的轻质细绳一端固定于a 点,另一端跨过光滑钉子b 悬挂一质量为m 1的重物.在绳子距a 端l /2的c 点有一固定绳圈.若绳圈上悬挂质量为m 2的钩码,平衡后绳的ac 段正好水平,则重物和钩码的质量比m 1/m 2为( ) A. 5 B .2 C.52 D. 29. 如图4为三种形式的吊车的示意图,OA 为可绕O 点转动的杆,重量不计,AB 为缆绳,当它们吊起相同重物时,杆OA 在三图中的受力F a 、F b 、F c 的关系是( ) A .F a >F c =F b B .F a =F b >F cC .F a >F b >F cD .F a =F b =F c 10.(2013•天心区校级模拟)如图,长为5m 的细绳的两端系于竖立在地面上相距为4m 的两杆的顶端A 、B .绳上挂一个光滑的轻质挂钩,其下连着一个重为12N 的物体,平衡时,绳中的拉力为( ) A .10N B .12N C .16N D .20N11.(多选)[2017·天津卷] 如图所示,轻质不可伸长的晾衣绳两端分别固定在竖直杆M 、N 上的a 、b 两点, 悬挂衣服的衣架挂钩是光滑的,挂于绳上处于静止状态.如果只人为改变一个条件, 当衣架静止时,下列说法正确的是( )A .绳的右端上移到b ′,绳子拉力不变B .将杆N 向右移一些,绳子拉力变大C .绳的两端高度差越小,绳子拉力越小D .若换挂质量更大的衣服,则衣架悬挂点右移12.如图7所示,A 、B 两物体的质量分别为m A 、m B ,且m A >m B ,整个系统处于静止状态.滑轮的质量和一切摩擦均不计,如果绳一端由Q 点缓慢地向左移到P 点,整个系统重新平衡后,物体A 的高度和两滑轮间绳与水平方向的夹角θ变化情况是( ) A .物体A 的高度升高,θ角变大B .物体A 的高度降低,θ角变小C .物体A 的高度升高,θ角不变D .物体A 的高度不变,θ角变小13.如图4,AOB 为水平放置的光滑杆,∠AOB 等于60°,杆上分别套着两个质量都是m 的小环,两环由可伸缩的弹性绳连接,若在绳的中点C 施以沿∠AOB 的角平分线水平向右的拉力F ,缓慢地拉绳,待两环受力达到平衡时,绳对环的拉力T 跟F 的关系是( )A.T=F B.T >F C.T <F D.T=Fsin30°14.在机械设计中常用到下面的力学原理,如图所示,只要使连杆AB 与滑块m 所在平面间的夹角θ大于某个值,那么,无论连杆AB 对滑块施加多大的作用力,都不可能使之滑动,且连杆AB 对滑块施加的作用力越大,滑块就越稳定,工程力学上称为"自锁"现象.设滑块与所在平面间的动摩擦因数为μ,最大静摩擦力等于滑动摩擦力,为使滑块能"自锁"应满足的条件是( ) A.μ≥tanθ B.μ≥cotθ C.μ≥sinθ D.μ≥cosθ三、自我检测15.(2014·海南)如图,一不可伸长的光滑轻绳,其左端固定于O 点,右端跨过位于O ′点的固定光滑轴悬挂一质量为M 的物体;OO ′段水平,长度为L ;绳子上套一可沿绳滑动的轻环.现在轻环上悬挂一钩码,平衡后,物体上升L .则钩码的质量为( ) A.22M B.32M C.2M D.3M16.如图2所示,杆BC 的B 端用铰链固定在竖直墙上,另一端C 为一滑轮.重物G 上系一绳经过滑轮固定于墙上A 点处,杆恰好平衡.若将绳的A 端沿墙缓慢向下移(BC 杆、滑轮、绳的质量及摩擦均不计),则( )A .绳的拉力增大,BC 杆受绳的压力增大B .绳的拉力不变,BC 杆受绳的压力增大 C .绳的拉力不变,BC 杆受绳的压力减小D .绳的拉力不变,BC 杆受绳的压力不变17.如图,将一根不能伸长、柔软的轻绳两端分别系于A 、B 两点上,一物体用动滑轮悬挂在绳子上,达到平衡时,两段绳子间的夹角为θ1,绳子张力为F 1;将绳子B 端移至C 点,待整个系统达到平衡时,两段绳子间的夹角为θ2,绳子张力为F 2;将绳子B 端移至D 点,待整个系统达到平衡时,两段绳子间的夹角为θ3,绳子张力为F 3;不计摩擦,则( )A .θ1=θ2=θ3B .θ1<θ2<θ3C .F 1>F 2>F 3D .F 1=F 2<F 318.(多选)如图所示,A 物体被绕过小滑轮P 的细线所悬挂,B 物体放在粗糙的水平桌面上;小滑轮P 被一根细线系于天花板上的O 点;O ′是三根线的结点,bO ′水平拉着B 物体,cO ′沿竖直方向拉着弹簧;弹簧、细线、小滑轮的重力和细线与滑轮间的摩擦力均可忽略,整个装置处于静止状态.若悬挂小滑轮的细线OP 上的张力是20 3 N ,取g =10 m/s 2,则下列说法中正确的是( ) A .弹簧的弹力为10 N B .A 物体的质量为2 kgC .桌面对B 物体的摩擦力为10 3 ND .OP 与竖直方向的夹角为60°19.(2016·全国卷Ⅲ) 如图1-所示,两个轻环a 和b 套在位于竖直面内的一段固定圆弧上:一细线穿过两轻环,其两端各系一质量为m 的小球.在a 和b 之间的细线上悬挂一小物块.平衡时,a 、b 间的距离恰好等于圆弧的半径.不计所有摩擦.小物块的质量为( )A.m 2B.32m C .m D .2m20.如图12所示,粗糙斜面P 固定在水平面上,斜面倾角为θ,在斜面上有一个小滑块Q 。
平衡中的死结与活结

平衡中的死结与活结一、“活结”与“死结”绳是物体间连接的一种方式,当多个物体用绳连接的时候,其间必然有“结”的出现,根据“结”的形式不同,可以分为“活结”和“死结”两种。
“活结”是绳子间的一种光滑连接,其特点是结的两端同一绳上的张力相等;而“死结”是绳子间的一种固定连接,结的两端绳子上的张力不一定相等。
例1.建筑工人要将建筑材料运送到高处,常在楼顶装置一个定滑轮(图-1中未画出),用绳AB通过滑轮将建筑材料提到某一高处,为了防止材料与墙壁相碰,站在地面上的工人还另外用绳CD拉住材料,使它与竖直墙面保持一定的距离L不变。
若不计两根绳的重力,在提起材料的过程中,绳AC和CD的拉力T1和T2的大小变化情况是()A.T1增大、T2增大B.T1增大、T2不变C.T1增大、T2减小D.T1减小、T2减小解析:三根绳子连接于C点不动,所以属于“死结”的问题,三根绳上的张力不相等,画出C点的受力如图-2所示,因材料在上升过程中与墙保持L的距离不变,所以上升过程中α和β均增大,由力的平行四边形定则可知,T1、T2均增大,所以正确答案为A。
例2.如图-3所示,相距4m的两根固定柱子拴上一根长5m的细绳,小滑轮及绳子的质量、摩擦均不计。
当滑轮上吊一重180N的重物时,求绳子中的张力?解析:因滑轮可以在绳上自由滑动,所以滑轮与绳接触的点为“活结”,跨过滑轮的两段绳子上的张力相等,画出其受力如图-4所示。
由几何关系知:,所以α=530,绳中的张力:F=N=150N。
二、“活杆”与“死杆”轻杆是物体间连接的另一种方式,根据轻杆与墙壁连接方式的不同,可以分为“活杆”与“死杆”。
所谓“活杆”,就是用铰链将轻杆与墙壁连接,其特点是杆上的弹力方向一定沿着杆的方向;而“死杆”就是将轻杆固定在墙壁上(不能转动),此时轻杆上的弹力方向不一定沿着杆的方向。
例3.如图-5所示,绳与杆均轻质,承受弹力的最大值一定,A端用铰链固定,滑轮在A点正上方(滑轮大小及摩擦均可不计),B端吊一重物。
受力平衡问题中“死结”和“活结”模型

受力平衡问题中 死结 和 活结 模型ʏ孟德飞受力平衡问题中的绳模型是近年高考题中常考的模型㊂靠跨过滑轮或者绕过光滑杆㊁光滑钩等把绳子分成两段,且可以沿着绳子移动的结点称为 活结 ;而把绳子系在某位置且该结点不会沿绳子移动,这样把绳子分成两段的结点称为 死结 ㊂这类模型中的 死结 和 活结 问题考查的知识点丰富,题型变式多样,对同学们的思维能力要求高,是同学们学习的难点,同学们碰到这类问题时普遍有畏难情绪㊂但同学们如果掌握了该类问题的共性,也就是掌握其规律,再解答这类问题时就会容易得多㊂ 图1题型示例:如图1甲所示,右端固定有定滑轮的水平轻杆B C ,细绳左端固定在A 点,一质量为M 1的物体通过细绳挂在定滑轮上,其中øA C B =30ʎ;在图乙中,轻杆H G 一端用铰链(可让杆旋转)固定在竖直墙上,用固定在E 点的细绳拉住杆右端的G 点,也让E G 与水平方向成30ʎ,在G 点挂一质量为M 2的物体㊂求:(1)A C 绳与E G 段绳上的拉力之比;(2)绳在C 端对轻杆B C 的压力;(3)轻杆H G 所受到的压力㊂ 图2过程分析:(1)图甲中,物体M 1处于平衡状态,细绳A D 跨过定滑轮分成A C 段和C D 段,C 点是同一根上可移动的活结㊂由活结特点可知,绳子两端拉力相等且等于物体M 1的重力,即A C 段的拉力F T A C =F T C D =M 1g ㊂图乙中由F T EG s i n 30ʎ=M 2g ,得F T E G =2M 2g ㊂所以F T A C F T E G =M 12M 2㊂(2)要求绳在C 端对轻杆B C 的压力,需对结点C 进行受力分析㊂根据图2甲中的几何关系可知,三个力之间互成120ʎ的夹角㊂再根据平衡关系,可得F T A C =F N C =M 1g ,力的作用是相互的,压力方向与水平方向成30ʎ角指向左下方㊂(3)图乙中,对结点G 进行受力分析,根据共点力的受力平衡关系和几何关系,有F T E G s i n 30ʎ=M 2g ,F T E G c o s 30ʎ=F N G ,所以F N G =M 2g c o t 30ʎ=3M 2g ,压力方向水平向左㊂规律总结:在图2甲中,结点可以沿着绳子移动,这样的 活结 一般是由绳跨过滑轮或者绕过光滑杆㊁光滑钩等把绳子分成两段而形成的㊂因为两段绳实际上是同一根绳,在 活结 处由于弯曲而分开的两段绳上张力的大小相等㊂两分力和合力根据平行四边形定则构成菱形,菱形的对角线是两边夹角的角平分线㊂因此,两段绳子合力的方向就沿着两段绳子夹角的平分线㊂如图2乙所示,把绳子系在某位置且该结点不会沿绳子移动,这样把绳子分成两段的结点称为 死结㊂ 死结 两边的轻绳因结点不可移动而变成了两根受力相互独立的绳,要求解两段绳子上的弹力,要先根据力平行四边形定则进行力的合成与分解,再找几何关系来处理㊂因此,与 活结 不同的是,两段绳上张力不一定相等㊂综上所述,在受力平衡问题中, 死结活结 模型分析过程一般为:先明确研究对象,识别是符合 死结 还是 活结 模型;再根据 死结 活结 模型的解答规律来求解㊂在 活结 中,由结点分开的两段绳上张力的大小一定相等,且两段绳合力方向沿着其夹角的平分线㊂ 死结 分开的两段绳子要根据力平行四边形定则进行力的合成与分解,找出几何关系后分别求出两个力的大小和方向㊂作者单位:云南民族大学附属中学57基础物理 障碍分析 自主招生 2020年7 8月。
高一物理 多力平衡“活结与死结”“活杆与死杆”(学习课资)

力处处相等,而两边绳子的合力大小等于物体的重力,方
向竖直向上,由对称性可知两边绳子与竖直方向的夹角相
等,所轻而柔软的细绳,一端拴在天花板上 的A点,另一端拴在墙上的B点,A和B到O点的距离 相等,绳的长度是OA的两倍,在一个质量可忽略的 动滑轮K的下方悬挂一个质量为M的重物,现将动滑
B.不断增大
C.不断减小
D.先增大,后减小
公开课资
18
例4.如图,晒衣服的绳子轻且光滑,悬挂衣
服的衣架的挂钩也是光滑的,轻绳两端分别固 定在两根竖直杆上的A、B两点,衣服处于静 止状态,如果保持绳子A端位置不变,将B端
分别移动到不同的位置。下列判断正确的是 A.B端移到B1位置时,
绳子张力不变
公开课资
17
例3.如图所示,有两根立于水平地面上的竖 直杆,将一根不能伸长的、柔软的轻绳的两端, 分别系于竖直杆上不等高的两点a、b上,用一 个光滑的动滑轮O悬挂一个重物后再挂在绳子 上,达到平衡状态。现保持轻绳的a端不动, 将b端缓慢下移。在此过程中,轻绳的张力的
变化情况是( )A
A.保持不变
公开课资
5
例1.AO,BO,和CO三根绳子,O为节点,OB与 数值方向夹角为θ,悬挂物质量为m。已知θ角 为37°,物体质量为5kg. 求AO,BO,CO三根绳子拉力的大小。
B
θ O A
C
公开课资
6
合成法
TB
TC = mg = 50N
θ
TA
mg 50 TB = cosq = 0.8 = 62.5N
A.T1增大、T2增大 B.T1增大、T2不变 C.T1增大、T2减小 D.T1减小、T2减小
公开课资
11
练习3.轻绳AB一段固定于A点,另一端自由。在绳 中某处O点打结系另一轻绳OC,下挂一质量为m的 物体。现保持O点的位置不变,在OB段由水平方向 缓慢转到竖直方向的过程中,拉力F和绳OA的张力 变化? A
“死结”和“活结”问题
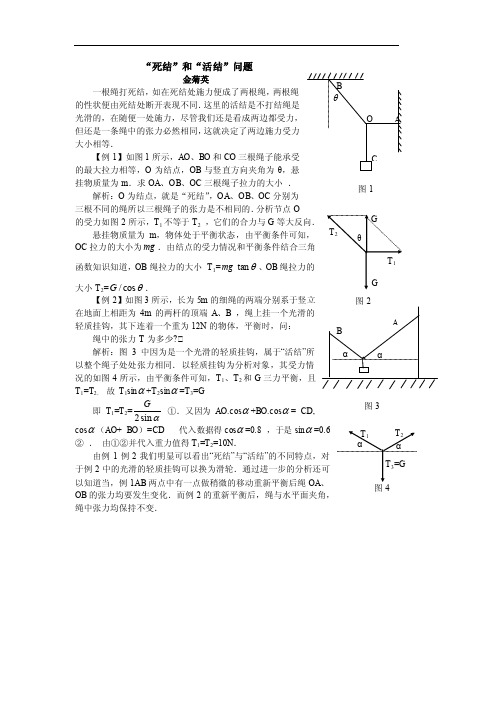
“死结”和“活结”问题金菊英一根绳打死结,如在死结处施力便成了两根绳,两根绳的性状便由死结处断开表现不同.这里的活结是不打结绳是光滑的,在随便一处施力,尽管我们还是看成两边都受力,但还是一条绳中的张力必然相同,这就决定了两边施力受力大小相等.【例1】如图1所示,AO 、BO 和CO 三根绳子能承受的最大拉力相等,O 为结点,OB 与竖直方向夹角为θ,悬挂物质量为m .求OA 、OB 、OC 三根绳子拉力的大小 .解析:O 为结点,就是“死结”,OA 、OB 、OC 分别为三根不同的绳所以三根绳子的张力是不相同的.分析节点O 的受力如图2所示,T 1不等于T 2 ,它们的合力与G 等大反向. 悬挂物质量为m ,物体处于平衡状态,由平衡条件可知,OC 拉力的大小为mg .由结点的受力情况和平衡条件结合三角函数知识知道,OB 绳拉力的大小 T 1=mg θtan 、OB 绳拉力的大小T 2=θcos /G .【例2】如图3所示,长为5m 的细绳的两端分别系于竖立在地面上相距为4m 的两杆的顶端A 、B ,绳上挂一个光滑的轻质挂钩,其下连着一个重为12N 的物体,平衡时,问:绳中的张力T 为多少?解析:图3中因为是一个光滑的轻质挂钩,属于“活结”所以整个绳子处处张力相同.以轻质挂钩为分析对象,其受力情况的如图4所示,由平衡条件可知,T 1、T 2和G 三力平衡,且T 1=T 2, 故 T 1sin α+T 2sin α=T 3=G即T 1=T 2=αsin 2G ①.又因为AO.cos α+BO.cos α= CD, cos α(AO+ BO )=CD 代入数据得cos α=0.8 ,于是sin α=0.6 ② . 由①②并代入重力值得T 1=T 2=10N .由例1例2我们明显可以看出“死结”与“活结”的不同特点,对于例2中的光滑的轻质挂钩可以换为滑轮.通过进一步的分析还可以知道当,例1AB 两点中有一点做稍微的移动重新平衡后绳OA 、OB 的张力均要发生变化.而例2的重新平衡后,绳与水平面夹角,绳中张力均保持不变.图1 图4。
高考物理难点解读:绳上死结和活结问题的分析

难点7绳上死结和活结问题的分析
“死结”可理解为把绳子分成两段,且不可以沿绳子移动的结点.“死结”一般是由结住而形成的,“死结”两侧的绳因结住而变成了两根独立的绳,因此由“死结”分开的两段绳子上的弹力不一定捆等,
“活结”可理解为把绳子分成两段,且可以沿绳子移动的结点.“活结”-般是由绳跨过滑轮或者绳上挂一光滑挂钩而形成的,绳子虽然因“活结”而弯曲,但实际上是同一根绳,所以由“活结”分开的两段绳孚上弹力的大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的平分线.
典列8
图甲图乙
如图甲所示,质量为m的物体用细绳OC悬挂在支架上的0点,沿水平方向的轻杆OB的B端由铰链固定,可绕B点自由转动,细绳OA与轻杆OB所成的角为θ,求细绳OA中张力T的大小和轻杆OB对细绳的弹力
F的大小.
N
点拨
涉及绳子的死结和活结问题时要能区别两类模型:
(1)绳与杆的一端连接为结点,如典例8,此时绳子OA 的拉力不等于物体的重力;
(2)绳跨过光滑滑轮,如图所示,此时绳子BC 的拉力等于物体的重力.滑轮受到绳的作用力是两部分绳子拉力的合力,两部分绳子拉力大小均为mg ,合力方向沿两绳的角平分线.
深化
摩擦力和弹力都属于接触力.两物体间存在摩擦力必存在弹力,存在弹力不一定存在摩擦力.
解析
由题意知,绳的结点O 相当于死结,分析结点O 的受力情况如图乙所示,它受到细绳OA 的拉力T,轻杆OB 的弹力N F 和细绳OC 的拉力
(大小等于重力mg ),其中T ,N F 的合力一定与mg 平衡,即等大反向,解力的三角形可得:θθcot ,mg F mg T N ==。
高中物理“动杆”和“定杆”与“活结”和“死结”问题 —人教版高一暑假综合易错点、易混淆点突破专题讲义

七、“动杆”和“定杆”与“活结”和“死结”问题--易错点、易混淆点突破1.“动杆”和“定杆”问题(1)动杆:若轻杆用光滑的转轴或铰链连接,当杆处于平衡时杆所受到的弹力方向一定沿着杆,否则会引起杆的转动.如图甲所示,若C为转轴,则轻杆在缓慢转动中,两绳对BC杆弹力方向:始终沿BC杆的方向.(2)定杆:若轻杆被固定不发生转动,图乙中,轻杆是插入墙中的,则杆所受到的弹力方向不一定沿杆的方向,即C Bm对轻杆A B的作用力就不一定沿BA方向。
2.“活结”和“死结”问题(1)“死结”可理解为把绳子分成两段,且不可以沿绳子移动的结点。
“死结”两侧的绳因“结”而变成了两根独立的绳,因此由“死结”分开的两段绳子上的弹力不一定相等。
(2)“活结”可理解为把绳子分成两段,且可以沿绳子移动的结点。
“活结”一般由绳跨过滑轮或者绳上挂一光滑挂钩而形成。
绳子虽然因“活结”而弯曲,但实际上“活结”两侧的绳子是同一根绳,所以由“活结”分开的两段绳子上弹力的大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的角平分线。
1.(2020·天津市南开中学月考)如图为两种形式的吊车的示意图,OA为可绕O点转动的轻杆,重量不计,AB为缆绳,当它们吊起相同重物时,杆OA在图(a)、(b)中的受力分别为F a、F b,则下列关系正确的是()A.F a=F b B.F a>F bC.F a<F b D.大小不确定答案:A解析:对题图中的A点受力分析,则由图(a)可得F a=F a′=2mg cos 30°=3mg,由图(b)可得tan30°=mgF b′,则F b=F b′=3mg,故F a=F b,A正确.2.(多选)如图所示,质量均可忽略的轻绳与轻杆,A端用铰链固定,滑轮在A点正上方(滑轮大小及摩擦均可不计),B端吊一重物.现将绳的一端拴在杆的B端,用拉力F将B端缓慢上拉,在AB杆达到竖直前()图11A.绳子拉力不变B.绳子拉力减小C.AB杆受力增大D.AB杆受力不变答案:BD解析:以B点为研究对象,受力分析如图所示,B点受重物的拉力F T1(等于重物的重力G)、轻杆的支持力F N和绳子的拉力F T2由平衡条件得,F N和F T2的合力与F T1大小相等、方向相反,根据三角形相似可得:F N AB =F T2BO =F T1AO 又F =F T2,F T1=G 解得:F N =AB AO ·G ,F =BO AO·G∠BAO 缓慢变小时,AB 、AO 保持不变,BO 变小,则F N 保持不变,F 变小,故选项B 、D 正确.3.如图所示,两个轻环a 和b 套在位于竖直面内的一段固定圆弧上;一细线穿过两轻环,其两端各系一质量为m 的小球.在a 和b 之间的细线上悬挂一小物块.平衡时,a 、b 间的距离恰好等于圆弧的半径.不计所有摩擦.小物块的质量为( )A .m 2B .32m C .m D .2m答案:C解析:如图所示,圆弧的圆心为O ,悬挂小物块的点为c ,由于ab =R ,则△aOb 为等边三角形,同一条细线上的拉力相等,F T =mg ,合力沿Oc 方向,则Oc 为角平分线,由几何关系知,∠acb =120°,故细线的拉力的合力与物块的重力大小相等,则每条细线上的拉力F T =G =m ′g ,所以小物块质量为m ′=m ,故C 对.4.如图甲所示 , 细绳AD 跨过固定的水平轻杆BC 右端的光滑定滑轮挂住一个质量为M 1的物体, ∠ACB =30°; 图乙中轻杆HG 一端用铰链固定在竖直墙上,另一端G 通过细绳EG 拉住,EG 与水平方向也成30°角,轻杆的G 点用细绳GF 拉住一个质量为M 2的物体,重力加速度为g ,求:(1)细绳AC 段的张力F T AC 与细绳EG 的张力F T EG 之比; (2)轻杆BC 对C 端的支持力; (3)轻杆HG 对G 端的支持力.解析:(1)图甲中细绳AD 跨过定滑轮拉住质量为M 1的物体,物体处于平衡状态, 细绳AC 段的拉力F T AC =F T CD =M 1g ,图乙中由F T EG sin 30°=M 2g ,得F T EG =2M 2g , 所以F T AC F TEG =M 12M 2.(2)图甲中,三个力之间的夹角都为120°,根据平衡条件有F N C =F T AC =M 1g ,方向与水平方向成30°角指向右上方.(3)图乙中,根据平衡条件有 F T E G sin 30°=M 2g , F T E G cos 30°=F N G ,所以F N G =M 2g tan 30°=3M 2g ,方向水平向右.答案:(1)M 12M 2(2)M 1g ,与水平方向成30°角指向右上方 (3) 3M 2g ,方向水平向右【题后反思】 (1)轻绳中的“活结”两侧实际是同一根轻绳,“死结”两侧是两根不同的轻绳. (2)轻杆模型中,杆顶端所受的各力中,除杆的弹力外,如果其他力的合力沿着杆的方向,则杆的弹力也必然沿着杆,如果其他力的合力不沿着杆,则杆的弹力也不会沿着杆.。
1一、“死结”与“活结”的比较

第二篇中档题防错乌申斯基说“比较是一切理解和思维的基础。
”有比较才有鉴别,通过比较,可产生强烈的刺激,促进积极思维。
采用比较的方法应对易错问题有较好的回报率,其原因是当下高考多以中档题为主,命题中出现较多的“熟面孔”问题,越熟越易错,主要是一些同学的“惯性思维”所致。
所以在平常的复习中经常采用比较的方法识“同中之异”,辨“异中之同”,不仅提高理解能力,还加强了思辨能力。
考前回归教材,以基础知识和中档题为主,其中防错是得分的强力抓手,行之有效,所以希望迎战2019年高考的广大江苏考生,在本文基础上,好好地将平时做的易错问题归类比较,在比较中“明辨是非”,仅此一点落实到位,冲A保B便水到渠成。
一、“死结”与“活结”的比较结点问题是高考考查的热点,主要以平衡状态为主,当然,还可以出现在非平衡状态中,其中受力分析和利用不同结点的特征及规律解答是纠错必备。
例1如图(a),轻绳AD跨过固定在水平横梁BC右端的定滑轮挂住一个质量为M1的物体。
∠ACB=30°;图(b)中轻杆HG一端用铰链固定在竖直墙上,另一端G通过细绳EG拉住,EG与水平方向也成30°,轻杆的G端用细绳GF拉住一个质量为M2的物体,则下列说法中正确的是( )A.图(a)中BC杆对滑轮的作用力为B.图(b)中HG杆受到的作用力为M2gC.细绳AC段的张力FAC 与细绳EG的张力FEG之比为1∶1D.细绳AC段的张力FAC 与细绳EG的张力FEG之比为M1∶2M2答案 D解析图(a)中物体处于平衡状态,根据平衡条件可判断,与物体相连的细绳的拉力大小等于物体的重力大小,取滑轮为研究对象,进行受力分析,如图所示。
绳AC段的拉力大小为F AC =FCD=M1g由几何关系得BC杆对滑轮的作用力FC =FAC=M1g方向与水平方向成30 °角斜向右上方图(b)中物体处于平衡状态,与物体相连的轻绳的拉力大小等于物体的重力,取G点为研究对象,进行受力分析,如图所示。
2024-2025年教科版物理必修第一册专项8“活结”与“死结”问题的分析(带答案)

专项 8 “活结”与“死结”问题的分析1.如图所示为三种形式的吊车示意图,OA为重力不计的杆,其O端固定,A端带有一小滑轮,AB为重力不计的缆绳,当它们吊起相同重物时,缆绳对滑轮作用力的大小关系是( )A.N甲>N乙>N丙B.N甲>N乙=N丙C.N甲=N乙>N丙D.N甲=N乙=N丙2.如图甲、乙、丙所示,弹簧测力计、绳和滑轮的重力均不计,摩擦力不计,物体的重力都是G.在甲、乙、丙三种情况下,弹簧测力计的示数分别是F1、F2、F3,则( )A.F3=F1>F2B.F3>F1=F2C.F1=F2=F3D.F1>F2=F33.(多选)如图所示,水平横梁一端插在墙壁内,另一端装有光滑的小滑轮B.一轻绳的一端C固定于墙壁上,另一端跨过滑轮后悬挂一质量m=8 kg的重物,∠CBA=30°,g取10 N/kg,则下列说法正确的是( )A.滑轮对绳子的作用力方向水平向右B.滑轮受到绳子的作用力大小为80 NC.BC段绳子的拉力为80 ND.BC段绳子的拉力大于BD段绳子的拉力4.如图所示,滑轮本身的质量可忽略不计,滑轮轴O安在一根轻木杆B上,一根轻绳AC 绕过滑轮,A端固定在墙上,且绳保持水平,C端挂一重物,BO与竖直方向的夹角θ=30°,系统保持平衡.若保持滑轮的位置不变,改变θ的大小,则滑轮受到木杆作用力大小的变化情况是( )A.只有θ变小,作用力才变大B.只有θ变大,作用力才变大C.不论θ变大或变小,作用力都是变大D.不论θ变大或变小,作用力都不变5.(多选)将砂桶P用细绳系在C点,如图所示,在两砂桶中装上一定质量的砂子,砂桶(含砂子)P、Q的总质量分别为m1、m2,系统平衡时,∠ACB=90°,∠CAB=60°,忽略滑轮的大小以及摩擦.则下列说法正确的是( )A.m1∶m2=1∶1B.m1∶m2=2∶1C.若在两桶内增加相同质量的砂子,C点的位置上升D.若在两桶内增加相同质量的砂子,C点的位置保持不变6.如图所示,物体A放在某一水平面上,已知物体A重60 N,A与水平面之间的动摩擦因数为μ=0.3,A、B均处于静止状态,绳AC水平,绳CD与水平方向成37°角,CD绳上的拉力大小为15 N.sin 37°=0.6,cos 37°=0.8.求:(1)物体A受到的摩擦力为多大?(2)物体B重力为多大?专项8 “活结”与“死结”问题的分析[提能力]1.答案:B解析:缆绳的拉力方向总是沿绳并指向绳收缩的方向,由力的合成可知,在图甲中,N甲=2mg cos 30°=3 mg;在图乙中,N乙=2mg cos 60°=mg;在图丙中,N丙=2mg cos 60°=mg.可知N甲>N乙=N丙,故B正确,A、C、D错误.2.答案:A解析:定滑轮不改变力的大小,题图甲中物体静止,有F1=G;以题图乙中物体为研究对象,作出受力图如图甲所示,根据平衡条件有F2=G sin 60°=32G;以题图丙中动滑轮为研究对象,受力图如图乙所示,由平行四边形定则得F3=G.故F3=F1>F2.3.答案:BC解析:对B点受力分析,如图所示.滑轮受到绳子的作用力应为图中两段绳中拉力F1和F2的合力F,因同一根绳子张力处处相等,则F1=F2=G=mg=80 N,即BC段绳子的拉力等于BD 段绳子的拉力,都是80 N.由平行四边形定则根据几何知识可知滑轮受到绳子的作用力大小为80 N,方向与水平方向成60°角斜向左下,根据力的作用是相互的可知,滑轮对绳子的作用力方向与水平方向成30°角斜向右上,故B、C正确.4.答案:D解析:对滑轮受力分析,如图所示,受两边绳子的拉力和杆的弹力;滑轮一直保持静止,合力为零,故杆的弹力与两边绳子的拉力的合力等大、反向、共线;由于两边绳子的拉力大小等于重物的重力,大小不变,方向也不变,故两边绳子拉力的合力大小为2 mg,与水平方向成45°角斜向右下方,选项D正确.5.答案:BC解析:以结点C为研究对象,受力分析如图所示,其中F=m1g、F B=m2g,由力的平衡条件可知F A=F cos 30°=m1g cos 30°,由几何关系可知F A=F Btan 30°,联立解得m1∶m2=2∶1,选项A错误,B正确;由以上分析可知当砂桶(含砂子)P、Q的总质量的比值为2时,AC与BC保持垂直状态,C点的位置保持不变,而若在两桶内增加相同质量的砂子,则两砂桶(含砂子)质量的比值会小于2,则Q桶向下移动,C点的位置上升,选项C正确,D错误.6.答案:(1)12 N (2)9 N解析:以结点C为研究对象,受力情况如图所示,因为A、B均处于静止状态,结点C受力平衡,F1=15 N,在x轴上,AC绳的拉力F2=F1cos 37°=12 N,在y轴上,BC绳的拉力F3=F1sin 37°=9 N,A物体处于静止,在水平方向受到的摩擦力f大小与绳AC拉力大小相等,即f=F2=12 N,B物体处于静止,则G B=F3=9 N.专项9 整体法和隔离法在平衡问题中的应用[提能力]1.答案:C解析:物块A静止时,对A进行受力分析可知,A受到重力、斜面的支持力和摩擦力;对物块和斜面体整体进行受力分析,受到重力、支持力,假设地面对整体有摩擦力,则斜面不能保持静止.对B进行受力分析可知,B受到重力、地面的支持力、A对B的压力和摩擦力,共4个力的作用.故C正确,A、B、D错误.2.答案:BC解析:对B物体受力分析,如图甲所示,根据合力等于0,运用合成法,得墙壁对B的弹力N1=m B g tan α,A对B的弹力N2=m B gcos α>m B g,即B物体对A物体的支持力大于m B g,C正确;对整体受力分析,如图乙所示,地面的支持力N A=(m A+m B)g,摩擦力f=N1=m B g tan α≠0,A、D错误,B正确.3.答案:AB解析:以整体为研究对象,地面对斜面体的支持力大小为(M +m )g ,根据摩擦力的计算公式可得地面对斜面体的摩擦力大小为f 1=μ(M +m )g ,故D 错误,B 正确;斜面体和小方块无相对运动,斜面体对小方块的摩擦力为静摩擦力,摩擦力大小为f 2=mg sin θ,故C 错误;斜面体对小方块的支持力等于小方块的重力垂直斜面的分力,大小为mg cos θ,故A 正确.4.答案:BC解析:如图对虾笼A 受力分析,由平衡条件可得T 1sin 60°=G +T 2sin 30°,T 1cos 60°=T 2c os 30°,解得T 1=3 G ,T 2=G ,A 错误,B 正确;对虾笼B 分析,水对虾笼B 的作用力与虾笼的重力及绳索2拉力的合力等大反向,有F 水=2G ·cos 120°2 =G ,C 正确,D 错误.5.答案:A解析:以圆球B 为研究对象,对圆球B 进行受力分析如图甲所示.由平衡条件可得N =F cos 30°,F sin 30°=2mg ,所以有N =23 mg ;以两球组成的整体为研究对象,其受力如图乙所示,由平衡条件有f =3mg ,N 1=N ,由题意整体恰好不滑动,有f =μN 1,联立解得μ=32,选项A 正确.6.答案:(M +m )g mg tan θ 解析:选取A 和B 整体为研究对象,它受到重力(M +m )g ,地面支持力N ,墙壁的弹力F 和地面的摩擦力f的作用(如图甲所示)而处于平衡状态.根据平衡条件得N-(M+m)g=0,F-f=0,可得N=(M+m)g,再以B为研究对象,它受到重力mg,三棱柱对它的支持力N B,墙壁对它的弹力F的作用(如图乙所示)而处于平衡状态,根据平衡条件得竖直方向上有N B cos θ-mg=0,水平方向上有N B sin θ-F=0,解得F=mg tan θ,所以f=F=mg tan θ.。
2-“死结”与“活结”及 动态平衡问题易错分析 高考物理(山东)复习专题

二、“死结”与“活结”及 动态平衡问题易错分析“死结”与“活结”的比较(1)“死结”可理解为把绳子分成两段,且不可以沿绳子移动的结点。
“死结”两侧的绳因结而变成了两根独立的绳,因此由“死结”分开的两段绳子上的弹力不一定相等。
(2)“活结”可理解为把绳子分成两段,且可以沿绳子移动的结点。
“活结”一般是由绳跨过滑轮或者绳上挂一光滑挂钩而形成的。
绳子虽然因“活结”而弯曲,但实际上是同一根绳,所以由“活结”分开的两段绳子上弹力的大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的平分线。
典例1 如图所示,AO 、BO 、CO 是完全相同的绳子,并将钢梁水平吊起,若钢梁足够重时,绳子AO 先断,则( )A.θ=120°B.θ>120°C.θ<120°D.不论θ为何值,AO 总是先断答案 C 以结点O 为研究对象,受力情况如图所示,根据对称性可知,BO 绳与CO 绳拉力大小相等,由平衡条件得,F AO =2F BO cos θ2,当钢梁足够重时,AO 绳先断,说明F AO >F BO ,则有2F BO cosθ2>F BO ,解得θ<120°,故选项C 正确。
典例2 (多选)(2016课标Ⅰ,19,6分)如图,一光滑的轻滑轮用细绳OO'悬挂于O点;另一细绳跨过滑轮,其一端悬挂物块a,另一端系一位于水平粗糙桌面上的物块b。
外力F向右上方拉b,整个系统处于静止状态。
若F方向不变,大小在一定范围内变化,物块b仍始终保持静止,则( )A.绳OO'的张力也在一定范围内变化B.物块b所受到的支持力也在一定范围内变化C.连接a和b的绳的张力也在一定范围内变化D.物块b与桌面间的摩擦力也在一定范围内变化答案BD 系统处于静止状态,连接a和b的绳的张力大小T1等于物块a的重力Ga,C项错误;以O'点为研究对象,受力分析如图甲所示,T1恒定,夹角θ不变,由平衡条件知,绳OO'的张力T2恒定不变,A项错误;以b为研究对象,受力分析如图乙所示,则F N +T1cos θ+F sin α-Gb=0f+T1sin θ-F cos α=0FN、f均随F的变化而变化,故B、D项正确。
12“死结与活结”的两个问题—【新教材】人教版(2019)高一上学期期末复习易错点精讲精练

12“死结与活结”的两个问题--高一期末复习易错点精讲精练我们知道杆既可以发生拉伸或压缩形变也可以发生弯曲或扭转形变,因此杆的弹力不一定沿杆的方向.对于杆与铰链连接的结构,杆产生的弹力必定沿杆方向时,杆才能平衡;对于杆的一端固定(即杆不能绕杆上一点转动)时,杆平衡时,杆产生的弹力不一定沿杆,现在通过下面两个“形同质异”的问题来了解一下. 例1、如图甲所示,轻绳AD 跨过固定在水平横梁BC 右端的定滑轮挂住一个质量为10 kg 的物体,∠ACB =30°;图乙中轻杆HP 一端用铰链固定在竖直墙上,另一端P 通过细绳EP 拉住,EP 与水平方向也成30°,轻杆的P 点用细绳PQ 拉住一个质量也为10 kg 的物体.g 取10 N/kg ,求:(1)轻绳AC 段的张力F AC 与细绳EP 的张力F EP 之比; (2)横梁BC 对C 端的支持力; (3)轻杆HP 对P 端的支持力.答案 (1)1:2(2)100 N ,方向与水平方向成30°角斜向右上方(3)173 N ,方向水平向右解析 题图甲和乙中的两个物体M1、M2都处于平衡状态,根据平衡条件可判断,与物体相连的细绳拉力大小等于物体的重力.分别取C 点和P 点为研究对象,进行受力分析如图甲和乙所示.(1)图甲中轻绳AD 跨过定滑轮拉住质量为M1的物体,物体处于平衡状态,绳AC 段的拉力FAC =FCD =M1g图乙中由FEPsin30°=FPQ =M2g得FEP =2M2g ,所以得FAC FEP =M12M2=12. (2)图甲中,根据几何关系得:FC =FAC =M1g =100 N ,方向和水平方向成30°角斜向右上方.(3)图乙中,根据平衡方程有FEPsin30°=M2gFEPcos30°=FP所以FP =M2gcot30°=3M2g≈173 N ,方向水平向右.[错因分析]误认为“死结”分开的两段绳子上的弹力一定相等,而由“活结”分开的两段绳子上弹力的大小不一定相等,所以两段绳子合力的方向一定沿杆的方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、“死结”与“活结”及动态平衡问题易错分析
“死结”与“活结”的比较
(1)“死结”可理解为把绳子分成两段,且不可以沿绳子移动的结点。
“死结”两侧的
绳因结而变成了两根独立的绳,因此由“死结”分开的两段绳子上的弹力不一定相等。
(2)“活结”可理解为把绳子分成两段,且可以沿绳子移动的结点。
“活结”一般是由
绳跨过滑轮或者绳上挂一光滑挂钩而形成的。
绳子虽然因“活结”而弯曲,但实际上是同一根绳,所以由“活结”分开的两段绳子上弹力的大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的平分线。
典例1如图所示,AO、BO、CO是完全相同的绳子,并将钢梁水平吊起,若钢梁足够重时,绳子AO先断,则( )
A.θ=120°
B.θ>120°
C.θ<120°
D.不论θ为何值,AO总是先断
答案 C 以结点O为研究对象,受力情况如图所示,根据对称性可知,BO绳与CO绳拉力
,当钢梁足够重时,AO绳先断,说明F AO>F BO,则有2F BO 大小相等,由平衡条件得,F AO=2F BO cos ??
2
>F BO,解得θ<120°,故选项C正确。
cos ??
2
典例2(多选)(2016课标Ⅰ,19,6分)如图,一光滑的轻滑轮用细绳OO'悬挂于O点;另一细绳跨过滑轮,其一端悬挂物块a,另一端系一位于水平粗糙桌面上的物块b。
外力F向右上方拉b,整个系统处于静止状态。
若F方向不变,大小在一定范围内变化,物块b仍始终保持静止,则( )
A.绳OO'的张力也在一定范围内变化
B.物块b所受到的支持力也在一定范围内变化
C.连接a和b的绳的张力也在一定范围内变化
D.物块b与桌面间的摩擦力也在一定范围内变化
答案BD 系统处于静止状态,连接a和b的绳的张力大小T1等于物块a的重力G a,C 项错误;以O'点为研究对象,受力分析如图甲所示,T1恒定,夹角θ不变,由平衡条件知,绳OO'的张力T2恒定不变,A项错误;以b为研究对象,受力分析如图乙所示,则
F N+T1cos θ+F sin α-
G b=0
f+T1sin θ-F cos α=0
F N、f均随F的变化而变化,故B、D项正确。
典例3(多选)如图所示,在固定好的水平和竖直的框架上,A、B两点连接着一根绕过光滑的轻小滑轮的不可伸长的细绳,重物悬挂于滑轮下,处于静止状态。
若按照以下的方式缓慢移动细绳的端点,则下列判断正确的是( )
A.只将绳的左端移向A'点,拉力变小
B.只将绳的左端移向A'点,拉力不变
C.只将绳的右端移向B'点,拉力变小
D.只将绳的右端移向B'点,拉力变大
答案BD 设滑轮两侧绳子与竖直方向的夹角为α,绳子的长度为L,B点到墙壁的距
①
离为s,根据几何知识和对称性,得sin α=??
??
以滑轮为研究对象,设绳子拉力大小为F T,根据平衡条件得
2F T cos α=mg
②
得F T=????
2cos??
当只将绳的左端移向A'点,s和L均不变,则由②式知,F T不变,故A错误,B正确。
当只将绳的右端移向B'点,s增加,而L不变,则由①式知,α增大, cos α减小,则由②式知,F T 增大,故C错误,D正确。
反思总结
(1)对于“死结”“活结”问题是经常出错的地方,我们要明确:“死结”两段绳子分
为两段,力的大小往往不同。
“活结”两段绳子拉力相等,合力沿两绳角平分线方向,这是解题的突破点,分析问题时也常常会因忽略而出错。
(2)对于“活结”问题,我们分析时要注意几何关系的分析,如典例3中我们可以看出,当绳子由A移动到A'点时通过几何的分析,得出绳子间夹角不变,因此A移动到A'点时绳子张力不变。
