复旦固体物理讲义-11倒格子

合集下载

固体物理学-倒格子

《固体物理学》固体物理学》
§3 倒格子
证明：证明：
v v a i gb j = 2πδ ij
如果所考虑的体系足够大，忽略表面效应，如果所考虑的体系足够大，忽略表面效应，布拉菲格子满足平移对称性要求，对应点的物理化学性质，菲格子满足平移对称性要求，对应点的物理化学性质，如质量、密度、电子云密度、原子实产生的势场等，如质量、密度、电子云密度、原子实产生的势场等，亦为周期函数，一般地写成：亦为周期函数，一般地写成：
v u v v Γ r + R n = Γ r L L L L (1)
(
) ()
u v v v v 其中，其中，R n = n1 a1 + n2 a 2 + n3 a 3
v 将 Γ r 展成傅里叶级数
()
v u iG h gr v uv v Γ r = ∑ A Gh e L L L L L L L ( 2)
g u v v u v v −iG h gr 1 A Gh = ∫ Γ r e L L L L L L ( 3) Ω Ω Ω为原胞体积， ) 式意味着，对所有布拉菲格子的所有格矢，应有 (1 u v v u v v u − iG h gr v 1 A Gh = ∫ Γ r + R n e dr L L L L L L ( 4 ) Ω Ω uv v u v / 引入r = r + R n , ( 4 ) 式化为 u v uv uu/v u u v v u u v v u v u v iG h gRn 1 / − iG h gr / iG h gR n A Gh = ∫ Γ r e dr ge = A Gh e L L L L L ( 5) Ω Ω 即： u u v v u v iG h gR n A G h 1 − e = 0L L L L L L L L ( 6 )

固体物理学：关于几个结构的倒格子

晶面指数和面间距从晶面指数的图可以看出密勒指数简单的晶面如100110等它们的面密度较大面间距d也较大因为单位体积中原子数目是一定的
例：简单立方晶格的倒格子
例：体心立方(bcc)晶格的倒格子体心立方晶格的初基平移矢量
其原胞的体积
例：面心立方(fcc)晶格的倒格子面心立方晶格的初基平移矢量
总结倒格子基矢的性质
1、正倒格子基矢的关系 bi a j 2 ij
2、倒格子原胞体积是正格子原胞体积倒数的 (2π)3
倍。
* (2 )3
( * b1 (b2 b3 ) 为倒（h1，h2，h3）所对应的
晶面族的法线。
4、倒格矢 K h 于晶面间距 d h1h2h3
结束
晶面间的距离称为面间距。
通常把米勒指数为（hkl）的一组晶面的面间距记为dhkl，对于不同晶系，可以求得米勒指数与面间距的关系式。
注意：晶向指数和晶面指数都依赖于晶轴的选取。
(010)
从晶面指数的图可以看出，密勒指数简单的晶面，如（100）（110）等，它们的面密度较大，面间距d也较大，因为单位体积中原子数目是一定的。
关系为 Kh
2
d h1h2h3
5、正格矢 Rl 与倒格矢 K h 的关系 Rl Kh 2 m
（m为整数）
理解： 1、如果有一矢量与正格矢点乘后等于2π的整数
倍，这个矢量一定是倒格矢。
2、如果有一矢量与正格矢点乘后为一个没有量纲的数，这个矢量一定能在倒空间中表示出来。
5.晶面指数和面间距在一组（或一族）平行的晶面中，两相邻

固体物理学：倒格子

相同。
这种周期函数可以V展(开r)为傅立叶V级 e数iGr G
G
V (r R)
V
eiG(r
R
)
V (r )
G
G
则要求 G R 2m （m为整数）
G R G.(n1a1 n2a2 n3a3) 2m
即
G a1 h1 2
h1 h2 h3 都是整数
G
a2
h2 2
G 称为倒格子平移矢量，简称倒格矢。
由a1 ，a2 ，a3 形成的格子称正格子。称R 为正格子平移矢量，简称正格矢。
每个格子有两套格子即，正格子和倒格子。
b1
b2
b3
2
V
2
V
2
V
(a2
(a3 (a1
a3 )
a1 )
a2 )
V a1 (a2 a3 )
是原胞的体积
的法线方向
(4)倒格子矢量与面间距的关系
[1]倒格子基矢与正格子基矢的关系------两个基矢正交
设
Gh1h2h3
h1b1 h2b2
所以，Gh1h2h3 • Rl1l2l3 (h1b1
h3b3 h2b2
h3b3 )
•
(n1a1
n2a2
n3a3
)
由此推论：
பைடு நூலகம்i
•
aj
2m 2 ij
[2]倒格子与正格子的原胞体积的关系
一系列规则排列的点，这些点排列的规律性只决定于函数
F(r)的周期性而与函数的具体形式无关。我们把在傅里叶
空间中规则排列着的点的列阵称为倒格子点阵（或倒易点
阵）。
倒格子点阵是晶体结构周期性在傅里叶空间中的数学

固体物理03-倒格子空间

4
dr
nj
(r )r 2
sin Gr Gr
实验发现固体中的原子形状因子与自由原子的差别不大
其它实验手段
1. 电子衍射（动量空间）
与X射线相比，电子波长更短，所以更加精确；更容易被物体吸收适合于研究微薄膜、小晶体。
2. 中子散射（动量空间）
可以测量晶体磁结构
3. 扫描隧道显微镜（实空间，表面）
S v1v2v3 f {1 exp i v2 v3 exp i v1 v3 exp i v1 v2 }
S 4 f 所有指数均为奇数，或均为偶数 S 0 其它情况
面心立方的x-ray 散射图像
原子形状因子 f j dV n j (ρ)eiGρ
对自由原子：
f j 2 dr r 2 d cos n j exp(iGr cos )
j
ρ r rj
定义原子的形状因子 f j dV n j (ρ)eiGρ
结构因子
化简后可以得到晶体的结构因子
SG
f eiGr j j
j
对于第 j 个原子
G rj v1b1 v2b2 v2b2 x ja1 y ja2 z ja3 2 v1x j v2 y j v3z j
散射幅度
SG
dV n(r)eiGr
cell
结构因子
结构因子
假设晶胞中有 s 个原子，可以把原胞中的电荷密度分配到每一个原子上（分配方法不唯一），即:
s
n(r) n j (r rj )
j 1
SG
cell dV n j (r r j )eiGr
j
eiGrj cell dV n j (ρ)eiGρ
晶体点阵的Fourier变换，晶体点阵则是倒易点阵的Fourier逆变换。正格子的量纲是长度 L, 称作坐标空间，倒格子的量钢是长度的倒数 L-1，称作波矢空间（或称动量空间）。

简述倒格子点阵的物理意义

简述倒格子点阵的物理意义
倒格子点阵是固体物理学中的一个重要概念，用于描述晶体中离子、原子或分子的排列方式。

它表示了晶体中离子在晶格中的周期性排列。

倒格子点阵在物理意义上具有以下重要特征：
1.倒格子与晶体结构的相互关系：倒格子是晶体格矢的补格。

晶体格矢是描述晶体结构的向量，而倒格子则是晶格矢的傅里叶变换。

倒格子点阵的形状和大小与晶体结构紧密相关。

2.表征晶体的动量空间：倒格子点阵的形成使得晶体在动量空间中的结构得以描述。

晶体具有动量离散化的性质，电子、声子等载流子在动量空间中的行为可以通过倒格子点阵的形态和性质来理解和
分析。

3.描述布里渊区和能带结构：倒格子点阵的布里渊区（Brillouin Zone）是动量空间中与晶格有关的基本单元。

布里渊区的形状和大小直接决定了电子能带结构、光学性质和输运特性等重要物理现象。

4.反映物质衍射性质：倒格子点阵的概念是描述晶体衍射的基础。

实验中利用晶体的衍射现象可以确定物质的结构和性质，倒格子点阵提供了理论上的基础框架。

倒格子点阵在固体物理学中具有重要的物理意义，它是描述晶体结构和性质的关键概念，并与动量空间、能带结构、衍射性质等密切相关。

通过倒格子点阵的分析，可以深入理解晶体的属性和行为，为研究材料科学和固体物理学提供了有力的工具和理论基础。

固体物理倒格矢

—— 第一布里渊区原点和12个近邻格点连线的垂直平分面围成的正十二面体
b b b 倒格矢 Kn n1 1 n2 2 n3 3
2
a
[(n2
n3 )i
(n1
n3 )
j
(n1
n2
)k ]
体心立方的倒格子是面心立方;离原点最近的有十
二个倒格点，在直角坐标系中它们的坐标为：
2
a
(n2
n3, n1
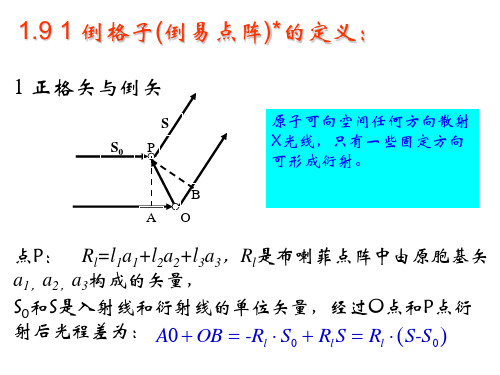
射后光程差为： A0 OB -Rl S0 RlS Rl (S-S0)
当X光为单色光;衍射加强的条件为： Rl•SS0=u •λ
令 k 2 S
k0
2
S0
，代入上式，
衍射加强条件变为： Rl• k -k0 = 2π u 根据正点阵与倒易点阵的关系，(k-k0)必是倒易空间中的位置矢量，令：
1 9 倒格子倒易点阵reciprocal
1 9 1 倒格子倒易点阵的定义：
1 正格矢与倒矢
S S0 P
原子可向空间任何方向散射 X光线;只有一些固定方向可形成衍射
B AO
点P： Rl=l1a1+l2a2+l3a3;Rl是布喇菲点阵中由原胞基矢 a1，a2，a3构成的矢量，
S0和S是入射线和衍射线的单位矢量，经过O点和P点衍
布里渊区示意图32
Γ：2 0,0,0
a
X：2 1,0,0
a
K：2 3 , 3 ,0
a 4 4
L： 2
a
1 2
,
1 2
,
1 2
简约布里渊区：十四面体
V
4
2
a
3
V倒易原胞
返回
面心立方晶格的第一布里渊区

固体物理§1.5倒格子

r r r Kh ⊥ CA Kh ⊥ CB ⇒ Kh ⊥ 晶面 ABC。，
9
r 3.倒格矢 Kh和面间距的关系倒格矢晶面ABC为晶面族中最靠近原点的晶面。为晶面族中最靠近原点的晶面。晶面为晶面族中最靠近原点的晶面
dh1h2h3 r a1 = ⋅ h1
r r r r r Kh a1 ⋅ h1b1 + h2b2 + h2b3 r = r Kh h1 Kh
( Ω Ω＝2π )
∗
3
3 r r r (2π ) (a a ) [(a a ) (a a )] r r r r r r ∗ Ω = b1 ⋅ (b2 × b3 ) = 2× 3 ⋅ 3× 1 × 1× 2 3 Ω r r r r r r r r r 利用： A 利用： × (B × C) = ( A⋅ C)B − ( A⋅ B)C r r r r r r r r r r r r r (a3 × a1 ) × (a1 × a2 ) = [(a3 × a1 ) ⋅ a2 ]a1 − [(a3 × a1 ) ⋅ a1 ]a2 = Ωa1
1
2.倒格子基矢和正格子基矢之间的关系倒格子基矢和正格子基矢之间的关系
r r r r r r 正格子基矢： a 正格子基矢： 1、a2、a3；倒格子基矢： 1、b2、b3; 倒格子基矢： b
晶面族： a d 晶面族： 1a2、a2a3、a3a1的面间距分别为 3、d1、d2;
r b3
r a3
r b2
3.倒格矢和正格矢的关系倒格矢和正格矢的关系
r r r r r r r r Kh ⋅ Rl = (l1a1 + l2a2 + l3a3 ) ⋅ (h b1 + h2b2 + h3b3 ) 1 = 2πµ (µ为整数)

固体物理(第4课)倒易空间

a 2 a3 b1 2 V a3 a1 b2 2 V b3 2 a1 a 2 V V a1 ( a 2 a3 ) 原胞体积
1 ：b1的方向沿a2、a3构成的晶面的法线方向 2：b 2 d1是a2、a3构成的晶面族的面间距 1 d1
点阵：原胞基矢 a1、a 2、a3
a 2 a3 b1 2 V a3 a1 ， V a1 (a 2 a3 ) 原胞体积 b2 2 V b 2 a1 a 2 3 V
b1、 b2、 b3：原胞基矢倒易点阵 a1、 a 2、 a 3：原胞基矢正点阵
（2）. 倒格子点阵与正格子点阵的关系
(1) 两个点阵基矢之间的关系： i j 2， ai b j 2ij 0，i j
a 2 a3 b1 2 V a3 a1 b2 2 V b 2 a1 a 2 3 V
(4) 倒格矢和正点阵晶面族之间的关系：正点阵中一族晶面，晶面指数为：（h1h2 h3）倒易点阵中倒格矢： Gh h1b1 h2 b2 h3b3 Gh // ( h1h2 h3 ) 法线方向 2 则有：证明如下： Gh ＝ d h1h2h3
1.9 1 倒格子(倒易点阵)*的定义：
1 正格矢与倒矢
S S0 P B A O
原子可向空间任何方向散射 X光线，只有一些固定方向可形成衍射。
点P： Rl=l1a1+l2a2+l3a3，Rl是布喇菲点阵中由原胞基矢 a1，a2，a3构成的矢量， S0和S是入射线和衍射线的单位矢量，经过O点和P点衍射后光程差为： A0 OB -R S R S R ( S-S )

1.10-倒格空间

4
倒格子和倒易空间
5
6
7
8
9
倒格子与正格子布喇菲格子) 与正格子(布喇菲格子 ● 倒格子与正格子布喇菲格子有什么关系？有什么关系？
10பைடு நூலகம்
一、正格子与倒格子互为对方的倒格子
证明？证明？
11
二、正格原胞体积与倒格原胞体积之积等于
12
三、倒格矢 (h1h2h3)正交正交
与正格子晶面族
13
四、倒格矢
的模与晶面族(h 的模与晶面族 1h2h3)的面间距成反比的面间距成反比
14
五、常见布喇菲格子的倒格子
证明？
15
正格子与倒格子关系示意图
16
2
第一章倒格子倒格子与X-ray衍射衍射联系一起衍射第三章倒格子与晶体格波、声子联系一起格波、声子倒格子格波第五章倒格子德布罗意波(电子倒格子与德布罗意波电子德布罗意波电子)联系一起
3
倒格子和倒易空间如何定义? ● 倒格子和倒易空间如何定义与正格子(布喇菲格子有什么关系？布喇菲格子)有什么关系 ● 与正格子布喇菲格子有什么关系？
第一章晶体的结构
1.10 倒格空间
徐智谋
华中科技大学光电子科学与工程学院
1
倒格子和倒易空间，最初是由Ewald 倒格子和倒易空间，最初是由Ewald 引入用来描述和解释晶体中x射线衍射现象的一种方法。述和解释晶体中x射线衍射现象的一种方法。然而，固体物理学的进一步发展表明，然而，固体物理学的进一步发展表明，其意义远非仅此。由于晶体微观结构的平移对称性(即周期性) 非仅此。由于晶体微观结构的平移对称性(即周期性)，平移对称性使得晶体内原子、电子等微观粒子运动的量子态量子态可用使得晶体内原子、电子等微观粒子运动的量子态可用一个几何点来标记倒易空间中的一个几何点来标记，倒易空间中的一个几何点来标记，这大大简化了对晶体内原子、电子等微观粒子运动的研究。因此，体内原子、电子等微观粒子运动的研究。因此，倒格子和倒易空间这一概念在固体物理学中是非常重要的，子和倒易空间这一概念在固体物理学中是非常重要的，它几乎贯穿于整个固体物理学领域。它几乎贯穿于整个固体物理学领域。

固体物理学倒格子

(2π ) v v v v = 2 ( a2 × a3 ) ⋅ a1 v0
3 * 0
(2π ) v = v0
* 0
3
01 04 倒格子 —— 晶体结构
2) 正格子中一簇晶面 ( h1 h2 h3 ) 和
v Gh1h2h3 正交
v v v v Gh1h2h3 = h1b1 + h2b2 + h3b3
—— 积分在一个原胞中进行
01 04 倒格子 —— 晶体结构
—— 倒格子与正格子间的关系 1) 正格子原胞体积反比于倒格子原胞体积
v v v * v0 = b1 ⋅ (b2 × b3 )
3
v v v v v v v v v A × B × C = ( A ⋅ C ) B − ( A ⋅ B )C
(2π ) v v v v v v = ( a2 × a3 ) ⋅ ( a3 × a1 ) × ( a1 × a2 ) 3 v0
v v v a2 × a3 b1 = 2π v v v a1 ⋅ a2 × a3
v v v v v v a3 × a1 a1 × a2 b2 = 2π v v v b3 = 2π v v v a1 ⋅ a2 × a3 a1 ⋅ a2 × a3
v v v 以 b1 , b2 , b3 为基矢构成一个倒格子
01 04 倒格子 —— 晶体结构
v 3) 倒格子矢量 Gh1h2h3 为晶面( h1h2 h3 ) 的法线方向
v v v v 晶面方程 ( h1b1 + h2b2 + h3b3 ) ⋅ x = 2πn
各晶面到原点O点的距离
v v v (2π n ) / h1b1 + h2b2 + h3b3
v v ai ⋅ b j = 2πδ ij

倒格子

倒格子（倒易点阵）倒格子（倒易点阵）
倒格子的定义：倒格子的定义：
• 在固体物理学中：实际观测无法直接测量在固体物理学中：正点阵，正点阵，倒格子的引入能够更好的描述很多晶体问题，多晶体问题，更适于处理声子与电子的晶格动量。格动量。 • 在X射线或电子衍射技术中：一种新的点阵，射线或电子衍射技术中：射线或电子衍射技术中一种新的点阵，该点阵的每一个结点都对应着正点阵中的一个晶面，不仅反映该晶面的取向，一个晶面，不仅反映该晶面的取向，还反映着晶面间距。映着晶面间距。
b1 =
2
(a ×a ) a ⋅ (a ×a ) 1 (a ×a ) b = a ⋅ (a ×a )
1
2 2 3 1 3 3 1
b3 =
(a ×a ) a ⋅ (a ×a )
1
1 1 2 3 2
2
3
1
确定倒格矢的方法：对于一切整数 h,k,l,作出作出 ( hb1 + k b 2 + l b3),这些向这些向量的终点就是倒格子的节点。子的节点。
倒格子（倒易点阵）的基本性质：倒格子（倒易点阵）的基本性质：
• 正点阵与倒易点阵的同名基矢的点积为，不同正点阵与倒易点阵的同名基矢的点积为1，名基矢的点积为零；名基矢的点积为零； • 正点阵晶胞的体积与倒易点阵晶胞的体积成倒数关系；关系； • 正点阵的基矢与倒易点阵的基矢互为倒易；正点阵的基矢与倒易点阵的基矢互为倒易； h • 任意倒易矢量（ b1 + kb2 + lb3 ）垂直于正点阵中的任意倒易矢量（（hkl）面；） • 倒易矢量的模等于正点阵中晶面间距的倒数。倒易矢量的模等于正点阵中晶面间距的倒数。
• 任何一个晶体结构都有两个格子：一个是任何一个晶体结构都有两个格子：正格子空间(位置空间位置空间)，正格子空间位置空间，另一个为倒格子空状态空间)。间(状态空间。二者互为倒格子，通过傅里状态空间二者互为倒格子，叶变换。叶变换。晶格振动及晶体中电子的运动都是在倒格子空间中的描述。是在倒格子空间中的描述。

复旦固体物理讲义-11倒格子(优选.)

h t t p ://10.107.0.68/~j g c h e /倒格子1上讲回顾•用轨道物理学理解晶体中原子近程结构*原子轨道之间相互作用由原子轨道角分布决定*为适应周围化学环境，与邻近原子成键，原子轨道可以杂化(重组) 以适应环境杂化最大方向由价电子数、配位、键上电子转移等共同决定*键合分类：离子、共价、金属、分子和氢键h t t p ://10.107.0.68/~j g c h e /倒格子2本讲内容•在k 空间看晶体结构*倒格子(r e c i p r o c a l l a t t i c e )倒格子基矢*正格子(d i r e c t l a t t i c e )和倒格子之间的关系h t t p ://10.107.0.68/~j g c h e /倒格子3第11讲、倒格子1.为什么倒空间？2.晶格的F o u r i e r 变换3.倒格子4.二维倒格子5.正、倒格子对应关系6.重要的例子7.B r i l l i o u n 区8.X 射线晶体衍射实验h t t p ://10.107.0.68/~j g c h e /倒格子41、为什么倒空间(r e c i p r o c a l s p a c e )？•一个物理问题，既可以在正(实，坐标)空间描写，也可以在倒(动量)空间描写*坐标表象r ，动量表象k•为什么选择不同的表象？*适当地选取一个表象，可使问题简化容易处理*比如电子在均匀空间运动，虽然坐标一直变化，但k 守衡，这时在坐标表象当然不如在动量表象简单•正空间的格矢(R l )描写周期性；在动量空间？•这两个空间完全是等价的*只是一个变换h t t p ://10.107.0.68/~j g c h e /倒格子8看格点的F o u r i e r 变换？•数学上如何用一个函数来描写格点？•δ函数！()∑-=ll R R r r δρ)(•对这个函数进行F o u r i e r 变换()()∑∑⎰⎰∙-∙-∙-=-==llli i l i ed ed eR R k R r k rk r R r r r k δρρ)(•格点满足平移周期性，则有K h 满足ml h π2=∙R K •那么乘上不变因子()∑∑∙--∙-==llh lli i eeR R K k R R k k ρh t t p ://10.107.0.68/~j g c h e /倒格子9•这告诉了我们什么信息，K h 对应什么？•坐标空间里，δ(r -R l )函数表示在R l 的格点，当满足上述条件时，其F o u r i e r 变换也是δ(k -K h )函数，表示的是倒空间里的一个点！•后面会知道，这些点就是倒格点，K h 即倒格矢*或者说前面K h 与R l 的关系定义了倒格矢，满足上述条件矢量就是倒格矢←→格矢*K h 的量纲为R l 的倒数•利用P o i s s o n 求和公式，即可得()()∑∑-==∙--hl lh h i e K R R K k k K k δρ•即当矢量K h 与R l 乘积是2π的整数倍时，在坐标空间R l 处的δ函数的F o u r i e r 变换为在动量空间以K h 为中心的δ函数！h t t p ://10.107.0.68/~j g c h e /倒格子103、倒格子(r e c i p r o c a l l a t t i c e )1=∙lh i e R K 为整数m m l h ,2π=∙R K •因此，B r a v a i s 格子也称为正格子(d i r e c t l a t t i c e )•等价关系：知道K h ，就知道R l ；反过来也一样•它们满足F o u r i e r 变换关系，因此，倒空间也称F o u r i e r 空间•定义：对B r a v a i s 格子中所有的格矢R l ，有一系列动量空间矢量K h ，满足的全部端点K h 的集合，构成该B r a v a i s 格子的倒格子，这些点称为倒格点，K h 称为倒格矢h t t p ://10.107.0.68/~j g c h e /倒格子11倒格子基矢•对正格子332211a a a R l l l l ++=•如果选择一组b ，使332211b b b K h h h h ++=•那么矢量K 就可由b 组成i jj i πδ2=⋅a b ml l l h h h l h π2332211=⋅+⋅+⋅=⋅a K a K a K R K •有•它满足上述关系，因此K h 具有平移对称性→可用基矢和整数表示的平移周期性→K h 定义倒空间的B r a v a i s 格子，b i 就是倒格子基矢•K h 为倒格矢——K h 所有的端点即为倒格点h t t p ://10.107.0.68/~j g c h e /倒格子21等价的周期性•如果K h 是倒格矢，那么物理量的F o u r i e r 级数在晶体任何平移变换下具有所期待的不变性∑+∙=+hi l l h h eF F )()(R r K K R r )(r rK K F e F hi h h ==∑∙是哪个晶面？互质？它属于哪族晶面？*是红色的这个晶面。

固体物理讲习题参考答案

B ' A' = AB(1− 2 cosθ ) 1− 2 cosθ = n cosθ : −1 ∼ +1 n = −1, 0,1, 2,3
θ = 0o , 60o , 90o ,120o ,180o
因此晶体的宏观对称操作只能是旋转以上五种角度，其转轴分别称为 1，6，4，3，2 重旋转对称轴。
ε1 0 0
1 0 0
取对称操作为绕
x
轴转
180
度， T
=
0
−1
0
代入上式，有
0 0 −1
(ε )
=
ε xx 0
0 ε yy
0
ε
yz
0 ε zy ε zz
−1 0 0
再取对称操作为绕
y
轴转
180
度， T
=
0 0
1 0
−01 代入上式，有
(ε )
=
ε xx 0
0 ε yy
0
0
0 0 ε zz
1 8
)
∆
(0
1 4
0)
Σ
(
1 8
1 8
0)
Λ
(
1 8
1 8
1 8
)
第四讲
4.1．倒格子矢量为 Kh = h1b1 + h2 b2 + h3 b3，证明布里渊区边界方程为：
2k
⋅ Kh
−
1 2
Kh
2
=0
证明此方程就是波在晶体中(h1h2h3) 晶面族上发生全反射的布喇格方程。
证：布里渊区边界垂直且平分倒格矢 K h ，故该边界面上任一矢量满足
此处a0是玻尔半径。
证明形状因子是

固体物理之之倒格子

倒格子题目：试论倒格子、倒格子空间的基本概念、与正格子的关系以及在固体物理研究中的意义和作用。

1.倒格子的基本概念：假定晶格点阵基矢1a 、2a 、3a（1、2、3表示 a 的下标）定义一个空间点阵，我们称之为正点阵或正格子，若定义： v a a b )(2321 ⨯=π v a a b )(2232 ⨯=π v a a b )(2213 ⨯=π其中)(321a a a v ⨯⋅= 为正点阵原胞的体积，新的点阵的基矢1b 、2b 、3b 是不共面的，因而由 1b 、2b 、3b 也可以构成一个新的点阵，我们称之为倒格子，而1b 、2b 、3b 称为倒格子基矢。

2.倒格子与正格子之间的关系：①基矢间关系：3,2,1,)(0)(2=⎩⎨⎧≠==*j i j i j i b a j i π ②位矢之间关系：正格子位矢：332211a l a l a l R l ++=倒格子位矢：332211b n b n b n G n ++=二者关系：m R G l n π2=⋅ （m 为整数）表明：若两矢量点积为π2的整数倍，则其中一个矢量为正格子位矢，另一个必为倒格子位矢。

③原胞体积的关系：倒格子原胞的体积v *与正格子原胞体积v 的关系为:)()2()2()(32133321*a a a vb b b v ⨯⋅==⨯⋅=ππ ④倒格矢332211b h b h b h G ++=与正格子中密勒指数为)(321h h h 的晶面族正交。

即332211b h b h b h G ++=沿晶面族)(321h h h 的法线方向。

3.固体物理研究中的意义和作用：①：倒格子中的一个基矢对应于正格子中的一族晶面，也就是说，晶格中的一族晶面可以转化为倒格子中的一个点，这在处理晶格的问题上有很大的意义。

例如，晶体的衍射是由于某种波和晶格互相作用，与一族晶面发生干涉的结果，并在照片上得出一点，所以，利用倒格子来描述晶格衍射的问题是极为直观和简便的。

固体物理学-倒空间

倒格与正格基矢的关系
՜ ՜
ℎ ⋅ = 2π
ℎ‘ =ℎ1 1 + ℎ2 2 + ℎ3 3
(1 റ1 + 2 റ 2 + 3 റ 3 ) ⋅ (ℎ1 ′1 + ℎ2 ′2 + ℎ3 ′3 ) = 2
两种点阵的基矢之间的关系：
Solid State Physics
2
Solid State Physics
倒格矢与傅里叶变换
在任意两个原胞的相对应点上，晶体的物理性质相同。
՜
՜
՜
Γ + = Γ
上式两边分别按傅里叶级数展开：
՜ ՜
ℎ ⋅ = 2π
倒格矢是傅里叶空间的矢量，它取决于正格子点阵的周期性
倒格空间=傅里叶空间
Solid State Physics
衍射加强条件的另外一种形式：
相位差
∆∅ =

λ
2 =
2
波矢 0 = 0
λ
∙− ∙0
λ
2= 2
2
=
റ
λ
՜ ՜
՜
⋅ − 0 = 2πμ
量纲互逆
∙ ℎ’ = 2
՜ ՜
՜
− 0 = ℎ′
倒格矢
ℎ ℎ
倒格空间=波矢k空间（动量 = = ）
՜
՜
՜
则， 1 ， 2 ， 3 分别与(100), (010), (001)晶面族正交
(1) 倒易点阵的一个基矢是与正点阵的一组晶面相对应的；
(2) 倒易点阵基矢的方向是该晶面的法线方向；
՜
՜
՜
՜
ℎ = ℎ1 1 + ℎ2 2 + ℎ3 3 的长度为

固体物理_倒格子与布里渊区_2013

a3 (a1 a2 )
所以：
a3 b3 2
a3 b1/ 2 0
采用同样的方法，我们可以得出：
a2 b2 2 a2 b1/3 0
2 ( a 3 a1 ) b2 2 ( a 2 a3 ) b1
二、特性：
1、第一布里渊区：在倒格子点阵中，做某一倒格点到其最近邻倒格点连线的垂直平分面，由这些垂直平分面所围成的多面体就是第一布里渊区。除第一布里渊区之外,还有第二布里渊区、第三布里渊区以及更高阶的布里渊区。
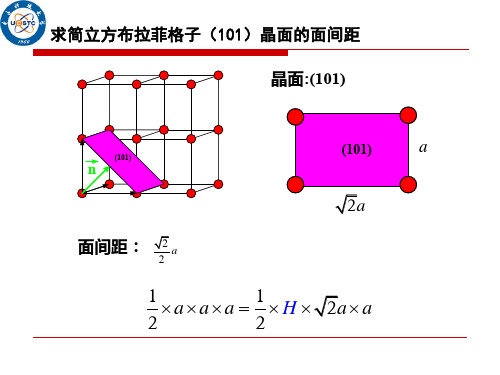
晶面:(111) 面间距：
n
(111)
(111)
法线方向： n
3 a 3
2 2 2 kh i j k 倒格矢： a a a
b3
b2 b1
2 3 k a 面间距： h k 3 h h 法线方向： k i jk kh
三、正格子和倒格子的相互关系
右手定律
2、验证：倒格矢能代表一族晶面吗？
晶面族(h1h2h3) 中最靠近坐标原点的晶面 ABC在基矢 a1 , a2 , a3
a1 a2 a3 上的截距为 , , h1 h2 h3
kh (1)倒格矢Kh垂直与晶面族 n kh
2 (2)倒格矢的模量等于面间距的倒数成正比。 k h d
3
正格子元胞与倒格子元胞体积成反比
课堂练习：
试证体心立方格子和面心立方格子互为正、倒格子。
面心立方晶格的初基原胞基矢为：P10 体心立方晶格的初基原胞基矢为：P10 a a a1 ( j k ) a1 (i j k ) 2 2 a a a2 (i j k ) a2 (k i ) 2 2 a a a3 (i j k ) a3 (i j ) 2 2 面心立方晶格的倒格子基矢如下：

固体物理(第4课)倒易空间

b2，-b2．
-b1＋b2
－b1-b2
b1＋b2 b1-b2
离原点再远的倒格点有４个：
２b1，-２b1，２b2，-２b2．
２b２
－２b1
２b1 －２b２
二维正方晶格的布里渊区
二维长方晶格的布里渊区
二维六方晶格的十个布里渊区
(3) 三维晶格a. 简来自方晶格倒易空间示意图aaa321
ai aj ak
图5 闪锌矿结构的本征GaN材料的能带结构图，导带最小和价带最大。
作
业
1 试证简单立方晶格的倒易点阵仍为简单立方晶格，体心立方和面心立方互为倒易点阵。分别计算其第一布里渊区的体积（假设其晶胞晶格常数为a）。
2 有一二维晶格，其原胞基矢分别为
a1
2
i
，a2
4j
（a1、a2的长度均以
A为单位），
布里渊区示意图2-2
：坐标原点0,0,0 ： 100 H： 2 1,0,0
a
： 110 N： 2 1 , 1 ,0
a 2 2
： 111 P： 2 1 , 1 , 1
a 2 2 2
简约布里渊区：正十二面体
V
2
2
a
3
V倒易原胞
返回
布里渊区示意图3-1
倒易
面心立方的倒易点阵是体心立方
结论：若两矢量点积为2的整数倍，且其中一个矢量
为正点阵位矢，则另一个矢量必为倒易点阵的位矢。
为什么在倒易关系中存在2π 因子，这是因为如此定义的互为倒易的两个矢量G与T之间满足下面简洁的
恒等式：
eiGT 1
(3) 两个点阵原胞体积之间的关系：
V* b1 (b2 b3 )

复旦固体物理讲义-11倒格子

固体物理学-倒格子

固体物理学：关于几个结构的倒格子

固体物理学：倒格子

固体物理03-倒格子空间

简述倒格子点阵的物理意义

固体物理倒格矢

固体物理§1.5倒格子

固体物理(第4课)倒易空间

1.10-倒格空间

固体物理学 倒格子

倒格子

复旦固体物理讲义-11倒格子(优选.)

固体物理 讲习题参考答案

固体物理之之倒格子

固体物理学-倒空间

固体物理_倒格子与布里渊区_2013

固体物理(第4课)倒易空间

固体物理学倒格子

固体物理讲习题参考答案