风荷载内力计算

合集下载

门式刚架荷载计算及内力组合

（一）荷载分析及受力简图：1、永久荷载永久荷载包括结构构件的自重和悬挂在结构上的非结构构件的重力荷载，如屋面、檩条、支撑、吊顶、墙面构件和刚架自重等。

恒载标准值（对水平投影面）：板及保温层 0.30kN/㎡檩条 0.10kN/㎡悬挂设备 0.10kN/㎡0.50kN/㎡换算为线荷载：7.50.5 3.75 3.8/=⨯=≈q KN m2、可变荷载标准值门式刚架结构设计的主要依据为《钢结构设计规范》（GB50017-2003）和《冷弯薄壁型钢结构技术规范》（GB50018-2002）。

对于屋面结构，《钢结构设计规范》m，但构件的荷载面积大于602m的可乘折减系数0.6，门规定活荷载为0.5KN/2m。

由荷载规范查得，大连地区式刚架符合此条件，故活荷载标准值取0.3KN/2雪荷载标准值为0.40kN/㎡。

屋面活荷载取为 0.30kN/㎡雪荷载为 0.40kN/㎡取二者较大值 0.40kN/㎡换算为线荷载：7.50.43/q KN m =⨯=3、风荷载标准值：0k z s z ωβμμω=（1）基本风压值 20kN/m 6825.065.005.1=⨯=ω（2）高度Z 处的风振系数z β 取1.0（门式刚架高度没有超过30m ，高宽比不大于1.5，不考虑风振系数）（3）风压高度变化系数z μ由地面粗糙度类别为B 类，查表得：h=10m ，z μ＝1.00；h=15m ，z μ＝1.14 内插：低跨刚架，h=10.5m ，z μ＝ 1.14 1.111.00(10.510)1510-+⨯--＝1.014；高跨刚架，h=15.7m ，z μ＝ 1.25 1.141.14(15.715)2015-+⨯--＝1.155。

（4）风荷载体型系数s μ-0.5-0.6-0.4-0.4-0.5-0.5-0.2+0.8μsμs1其中，s μ＝0.2010.24.760.032301230arctg -⨯=⨯=+ 1s μ＝12 1.00.6(1)0.6(12)0.36915.710.5h h ⨯-=⨯-=+-各部分风荷载标准值计算：w 1k =0z s z βμμω＝7.5×1.0×0.8×1.014×0.6825=4.15 kN/m w 2k =0z s z βμμω＝7.5×1.0×0.032×1.014×0.6825=0.17kN/m w 3k =0z s z βμμω＝7.5×1.0×（-0.6）×1.014×0.6825=-3.11kN/m w 4k = 0z s z βμμω＝7.5×1.0×0.369×1.014×0.6825=1.91 kN/m w 5k = 0z s z βμμω＝7.5×1.0×（-0.2）×1.014×0.6825=-1.04 kN/mw 6k = w 7k ＝w 8k ＝0z s z βμμω＝7.5×1.0×（-0.5）×1.014×0.6825=-2.60 kN/m w 9k = w 10k ＝0z s z βμμω＝7.5×1.0×（-0.4）×1.014×0. 6825=-2.08 kN/m 用PKPM 计算门式刚架风荷载结果如下：其中，'1k ω＝4.2KN/m ≈1k ω=4.15 kN/m ；'2kω＝0.2KN/m ≈2k ω=0.17 kN/m ； '3k ω＝-3.1N/m ≈1k ω=-3.11 kN/m ；'4kω＝2.2KN/m ≈2k ω=1.91 kN/m ； '5k ω＝-1.2KN/m ≈1k ω=-1.04kN/m ；'6kω＝-3.0KN/m ≈6k ω=-2.60kN/m ； '7kω＝-3.0KN/m ≈7k ω=-2.60kN/m ；'8k ω＝-2.6KN/m ＝8k ω； '9k ω＝-2.1KN/m ≈9k ω=-2.08kN/m ；'10kω＝-2.1KN/m ≈10k ω=-2.08kN/m 。

(整理)风荷载作用下框架内力计算

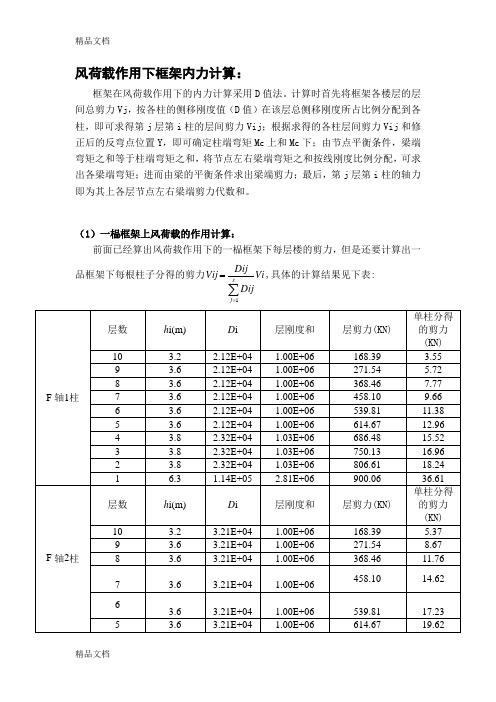
风荷载作用下框架内力计算：框架在风荷载作用下的内力计算采用D 值法。

计算时首先将框架各楼层的层间总剪力Vj ，按各柱的侧移刚度值（D 值）在该层总侧移刚度所占比例分配到各柱，即可求得第j 层第i 柱的层间剪力Vij ；根据求得的各柱层间剪力Vij 和修正后的反弯点位置Y ，即可确定柱端弯矩Mc 上和Mc 下；由节点平衡条件，梁端弯矩之和等于柱端弯矩之和，将节点左右梁端弯矩之和按线刚度比例分配，可求出各梁端弯矩；进而由梁的平衡条件求出梁端剪力；最后，第j 层第i 柱的轴力即为其上各层节点左右梁端剪力代数和。

（1）一榀框架上风荷载的作用计算：前面已经算出风荷载作用下的一榀框架下每层楼的剪力，但是还要计算出一品框架下每根柱子分得的剪力Vi DijDijVij sj ∑==1,具体的计算结果见下表:（2）风荷载作用下反弯点高度的计算:反弯点高度比即: V=V0+V1+V2+V3式中:V0 ——标准层反弯点高度比；注：本框架风荷载采用分段式均布荷载，故可查《高层建筑结构设计》表5.8a。

V1 ——因上、下层梁刚度比变化的修正值，查《高层建筑结构设计》表5.9；V2 ——因上层层高变化的修正值，查《高层建筑结构设计》表5.10；V3 ——因下层层高变化的修正值，查《高层建筑结构设计》表5.10。

具体计算结果见下表：（3）计算各柱端、梁端弯矩:①柱端弯矩计算：柱上下端弯矩按式：M u = V (1 - y)h，M d = Vyh计算；②梁端弯矩计算：梁端弯矩按式M = i b / ∑ i b ⨯ (M u + M d )具体结果如下：（4）计算各梁端剪力:计算方法：以梁为隔离体根据力矩平衡可得到梁端剪力。

具体计算结果如下表：注：单位为KN（5）计算各柱轴力:计算方法：已知梁的剪力，由上到下利用节点的竖向力平衡条件，即可得到柱的轴力，计算方法同恒。

（6）风荷载作用下的内力图绘制:风载作用下的梁端、柱端弯矩，梁端柱端剪力，柱的轴力计算完毕，恒载作用下的标准值如下几图所示：手算风荷载作用下柱端弯矩图手算风荷载作用下两端弯矩图与电算内力图的比较：电算风荷载作用下柱端弯矩图电算风荷载作用下两端弯矩图误差分析：风荷载作用下梁柱剪力图的绘制与误差分析：手算风荷载作用下的梁柱剪力图电算风荷载作用下的梁柱剪力图误差分析：风荷载作用下柱轴力图的绘制与误差分析：手算风荷载作用下的柱轴力图电算风荷载作用下的柱轴力图误差分析：水平地震作用下框架内力计算：框架在水平地震荷载作用下的内力计算采用D值法。

风荷载

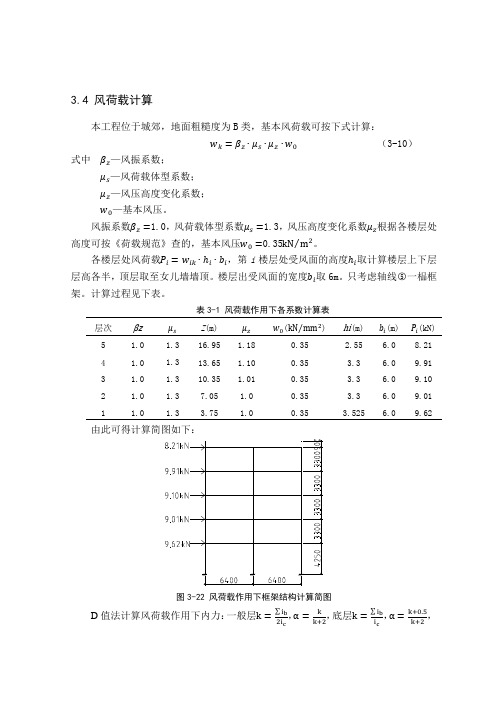
3.4 风荷载计算本工程位于城郊，地面粗糙度为B类，基本风荷载可按下式计算：w k=βz∙μs∙μz∙w0（3-10）式中βz—风振系数；μs—风荷载体型系数；μz—风压高度变化系数；w0—基本风压。

风振系数βz=1.0，风荷载体型系数μs=1.3，风压高度变化系数μz根据各楼层处高度可按《荷载规范》查的，基本风压w0=0.35kN m2⁄。

各楼层处风荷载P i=w ik∙ℎi∙b i，第i楼层处受风面的高度ℎi取计算楼层上下层层高各半，顶层取至女儿墙墙顶。

楼层出受风面的宽度b i取6m。

只考虑轴线○5一榀框架。

计算过程见下表。

表3-1 风荷载作用下各系数计算表层次βzμs Z(m) μz w0(kN mm2⁄) hi(m) b i(m) P i(kN)5 1.0 1.316.95 1.18 0.35 2.55 6.0 8.21图3-22 风荷载作用下框架结构计算简图D值法计算风荷载作用下内力：一般层k=∑i b2i c ，α=kk+2，底层k=∑i bi c，α=k+0.5k+2，柱子的抗侧移刚度D =α12i c h j2，计算结果如下表：表3-2 框架柱抗侧移刚度计算表层次柱的类型 kα D （kN m ⁄）2~5层中柱 (1根) 2.44 0.550 1.884×104 边柱（2根） 1.22 0.379 1.298×104 底层中柱（1根） 3.15 0.709 1.138×104 边柱（2根）1.570.5800.931×104注：∑i b 指框架梁线刚度之和，i c 指柱子的线刚度，k 指框架梁柱线刚度比，α指柱侧向线刚度降低系数。

3.4.1 各楼层风荷载剪力计算风荷载作用下各层剪力可按公式3-11计算： V jk =D jk∑D jk mk=1V j (3-11) 式中 V jk —第j 层第k 柱所分配到的剪力； D jk —第j 层第k 柱的侧向刚度D 值； m —第j 层框架柱数；V j —第j 层框架柱所承受的层间总剪力。

等效风荷载计算方法

等效静力风荷载的物理意义从风洞试验获取屋面风荷载气动力信息，到得到结构的风振响应整个过程来看，计算过程中涉及到风洞试验和随机振动分析等复杂过程，不易为工程设计人员所掌握，因此迫切需要研究简便的建筑结构抗风设计方法。

等效静力风荷载理论就是在这一背景下提出的。

其基本思想是将脉动风的动力效应以其等效的静力形式表达出来，从而将复杂的动力分析问题转化为易于被设计人员所接受的静力分析问题。

等效静力风荷载是联系风工程研究和结构设计的纽带[3]，是结构抗风设计理论的核心内容，近年来一直是结构风工程师研究的热点之一。

等效静力风荷载的物理意义可以用单自由度体系的简谐振动来说明[45, 108]。

图1.3 气动力作用下的单自由度体系对如图1.3的单自由度体系，在气动力()P t 作用下的振动方程为：()mx cx kx P t ++= (1.4.1)考虑粘滞阻尼系统，则振动方程可简化为：()()()200222P t x f x f x mξππ++=(1.4.2)式中0f =为该系统的自振频率，ξ=为振动系统的临界阻尼比。

假设气动力为频率为f 的简谐荷载，即()20i ft P t F e π=，那么其稳态响应为：()()()2020012i ft F kx t e f f i f f πξ=-+⋅ (1.4.3)进一步化简有：()()2i ft x t Ae πψ-= (1.4.4)其中A =，()0202arctan1f f f f ξψ=-，A 为振幅，ψ为气动力和位移响应之间的相位角。

现在假设该系统在某静力F 作用下产生幅值为A 的静力响应，那么该静力应该为：F kA ==(1.4.5)如果不考虑相位关系，静力F 与简谐气动力()P t 将产生一致的幅值响应，则这两种荷载之间存在一种“等效”的关系，那么F 可以称为()P t 的“等效静力风荷载”。

从上面这个简单的实例可以很清楚的体会到，所谓等效静力风荷载是指这样一种静力荷载，当把它作用于结构上时，其在结构上产生的静力响应（不仅指代位移响应，也包括内力响应等）与外加气动力荷载产生的动力响应最大幅值是完全相等的。

输电线路风荷载的全方位计算

输电线路风荷载的全方位计算摘要：在高压架空送电线路设计中，最不利风向时的风荷载常决定着杆塔内力大小或基础作用力的大小。

本文将通过几个工程实例详细说明在高压架空送电线路设计中，如何确定几种特殊情况下最不利风向时的风荷载计算，以确保高压架空送电线路的安全运行。

关键词：全方位;基础作用力;运行情况;不平衡张力;风荷载Abstract: In the project design of overhead transmission lines, the most unfavorable wind direction, wind load often determines the internal force of tower or base force size. This article will through several engineering examples in detail in the overhead transmission line design, how to determine some special situations the most unfavorable wind direction wind load calculation, to ensure the high voltage overhead power transmission line safe operation.Key words: all-around; base forces; operation; unbalanced tension; wind load1 引言在高压架空送电线路设计中，杆塔荷载的计算应执行《110～750kV架空输电线路设计规范》（以下简称《规程》）中第10条“杆塔荷载及材料”。

其中正常运行情况下，应计算的荷载组合是：1 基本风速、无冰、未断线；2 设计覆冰、相应风速及气温、未断线3 最低气温、无冰、无风、未断线（适用于终端和转角杆塔）本文主要针对上述第一种情况，在正常运行大风情况下计算铁塔内力或基础作用力时可能出现的漏洞。

风荷载作用下幕墙铝板内力和变形的计算

ｐａｎｔｆｎｎｉｓ（ｏｔｐａ）ａｅｃｌｌｔ．Ｔｅｓｆｎｎｂａｄｔｅａｕｉｕｌｅｌｅａｄ５ｓｆｉｇｒｔｉｅｂｐｒｌｙｅｆｍｅｒａｃａｄｈｔｆｉｇｒｎｈｌｍｎｍｐａａｔｌｕｅｉｅｉｔｃｒｅａ．Ｔｅｃｍｕａｉｄｌｓｏｎｒｒａｒｔｏｓｎｉｄｊｎｔｒｓｔｉｇｏｔｉｄｈｏｐｔｔｎｍｏｅｉｐｉｖｂｈｇｏｈｎｉｕｏ
板块内部空间狭窄，在施工现场板块内部的加劲肋连接螺丝已难以重新补装，这样原正常状态下的计
压、转角处立面受负风压作用的情况，其受力和变形较为复杂，引起业内的日益关注ＩＪ同时，由９。于单元板块在车间组装后运至现场吊装时，少数加
形计算，并与正常状态下的计算结果进行了比较。
１槽型铝板与加劲肋正常状态受力与变形计算
ＰｌｔｎｔｒａｒｅａｓｏｔｏｌｕａｉｎａｅＩｅｎｌＦｏｃｎｄＤｉｔｒｉｎＣａｃｌｔｏ
Ｄ日凡ｎ００
（ｈｎｈｎＳｅｇＸｎｏｔ，ｈｎｓａ２４２ｈｎ）ＺｏｇＳａｈｎｉｇＣ，ＬｄＺｏｇｈｎ５８１，Ｃｉａ
ｂｉｔａｄｉｓｂｇｅｔｉｔｒａｏｃｎｓｌｃｍｅｔａｅｏｔｉｅｕｌｎｔｉｇｓｎｅｎｌｆｒｅａｄｄｉｐａｅｎｒｂａｎｄ．Ｆｎｌｉａｌｈｅｐａｔｃｌａｐｉａｉｎｉｎｙ，ｔｒｃｉａｐｌｃｔｏｓｉ — ｔｏｃｄ．ｒｄｕｅ

抗风柱计算(2012年版规范)

us= uz=
Wo
B= q=
地面粗糙度可分为A、B、C、D四类：A类指近海海面和海岛、海岸、湖岸及沙漠地区； B类指田野、乡村、丛林、丘陵以及房屋比较稀疏的乡镇；C类指有密集建筑群的城市市区； D类指有密集建筑群且房屋较高的城市市区。（GB50009-2012，8.2.1）
二：柱几何参数（按“构造手册”第四版208页注6取） Hc= Hl= H= b= h1= h2= 三：求柱顶反力系数 2100 9000 11100 277.50 360 350 mm mm mm 400 600 mm 上柱高（下柱高，至基础顶面）（柱全高，至基础顶面） mm mm （柱截面宽）（下柱截面高) (上柱截面高）
mm4 mm
4
下柱惯性矩上柱惯性矩
无单位根据09SG117-1,122页,附录二表,第6栏,R= q*H*C6,C6=3/8*[1+λ ^4*(1/n-1)]/S,n=I上/I下，无单位 λ =H上/H，S=1+λ ^3*(1/n-1)，公式的来历见该图集93页；梁兴文、史庆轩主编的《混凝无单位土结构设计（2009年4月第一版）》138～139 无单位页有推导过程无单位无单位
I1=b.(h1)^3/12= I2=b.(h2)^3/12= n=I2/I1= λ =HC/H= S1=1/n-1= S2=1+λ ^4*S1= S3=1+λ^3*S1= C6=0.375*S2/S3=
四:求内力（标准值） 1.柱顶反力： R=C6*q*H=
7200000000 1429166667 0.19849537 0.189189189 4.037900875 1.005172981 1.027342902 0.366907551

风荷载标准值

风荷载标准值关于风荷载计算风荷载是高层建筑主要侧向荷载之一，结构抗风分析（包括荷载，内力，位移，加速度等）是高层建筑设计计算的重要因素。

脉动风和稳定风风荷载在建筑物表面是不均匀的，它具有静力作用（长周期哦部分）和动力作用（短周期部分）的双重特点，静力作用成为稳定风，动力部分就是我们经常接触的脉动风。

脉动风的作用就是引起高层建筑的振动（简称风振）。

以顺风向这一单一角度来分析风载，我们又常常称静力稳定风为平均风，称动力脉动风为阵风。

平均风对结构的作用相当于静力，只要知道平均风的数值，就可以按结构力学的方法来计算构件内力。

阵风对结构的作用是动力的，结构在脉动风的作用下将产生风振。

注意：不管在何种风向下，只要是在结构计算风荷载的理论当中，脉动风一定是一种随机荷载，所以分析脉动风对结构的动力作用，不能采用一般确定性的结构动力分析方法，而应以随机振动理论和概率统计法为依据。

从风振的性质看顺风向和横风向风力顺风向风力分为平均风和阵风。

平均风相当于静力，不引起振动。

阵风相当于动力，引起振动但是引起的是一种随机振动。

也就是说顺风向风力除了静风就是脉动风，根本就没有周期性风力会引起周期性风振，绝对没有，起码从结构计算风载的理论上顺风向的风力不存在周期性风力。

横风向，既有周期性振动又有随机振动。

换句话说就是既有周期性风力又有脉动风。

反映在荷载上，它可能是周期性荷载，也可能是随机性荷载，随着雷诺数的大小而定。

有的计算方法根据现有的研究成果，风对结构作用的计算，分为以下三个不同的方面：（1）对于顺风向的平均风，采用静力计算方法（2）对于顺风向的脉动风，或横风向脉动风，则应按随机振动理论计算（3）对于横风向的周期性风力，或引起扭转振动的外扭矩，通常作为稳定性荷载，对结构进行动力计算风荷载标准值的表达可有两种形式，其一为平均风压加上由脉动风引起导致结构风振的等效风压；另一种为平均风压乘以风振系数。

由于在结构的风振计算中，一般往往是第1振型起主要作用，因而我国与大多数国家相同，采用后一种表达形式，即采用风振系数βz，它综合考虑了结构在风荷载作用下的动力响应，其中包括风速随时间、空间的变异性和结构的阻尼特性等因素。

浅谈如何计算风载荷

浅谈如何计算风载荷高层建筑结构除了抵抗竖向荷载之外，风载荷和地震作用往往是结构设计的主要形成因素。

它们主要是水平荷载。

风作用出现的概率较大，而地震作用时偶然不经常的水平和竖向荷载，大风作用的时间较长，空气流动形成的风速到建筑物时，就在建筑物表面产生压力和吸力，这种风力作用称为风荷载。

随着建筑物高度的增高，风荷载的影响越来越大。

一、风载荷标准值和基本风压：《建筑结构荷载规范》GB50009-2010 8.1.1条：垂直于建筑物表层上的风载荷标准值，应按下列规定确定：1.计算主要受理结构时，应按下式计算：WK=βzusuzw0 W0-风载荷标准值，βZ-高度Z处的风振系数，US-风载荷体型系数，UZ-风压高度变化系数。

2.计算维护结构时，应按下式计算：WK=βgzUSUZW0，βgz=高度Z处的阵风系数，US-风载荷局部体型系数，基本风压是指风载荷的基准压力，一般按当地空旷平坦地层上10m高度处10min平均的风速观测数据，经概率统计得出50年一遇最大值确，承载力设计时应按基本风压的 1.1倍采用。

但围护值不乘系数。

二、风载荷体型系数Us：确定风载荷的体型系数Us是一个比较复杂的问题，它不但与建筑的平面外形，高宽比，风向与变风墙面所成的角度有关，而且还与建筑物的变层处理，周围建筑物密集程度及其高低有关。

当风流经建筑物时，对建筑物不同部位会产生不同的效果，即产生压力和吸力。

空气流动产生的涡流，对建筑物局部则会产生较大的压力和吸力。

通过对某建筑物的实测结果从中可以大致得出如下规律：○1整个迎风层上均受压力，其值中部最大，向两侧逐渐减小。

沿高度方向风压的变化很小，在整个建筑物高度的1/2-2/3处稍大，风压分布近似于矩形。

○2整个背风层上还受吸力，两侧大，中部略小，其平均值約为迎风面风压平均值的75%左右。

沿高度方向，风压的变化也很小，更近似于矩形分布。

○3整个侧面，在正面风力作用下，全部受吸力，约为迎风面风压的80%左右。

风荷载作用下框架内力计算

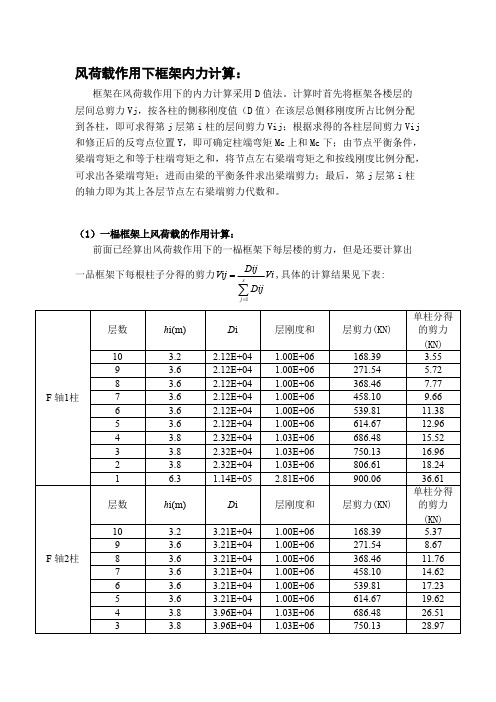
风荷载作用下框架内力计算：框架在风荷载作用下的内力计算采用D 值法。

计算时首先将框架各楼层的层间总剪力Vj ，按各柱的侧移刚度值（D 值）在该层总侧移刚度所占比例分配到各柱，即可求得第j 层第i 柱的层间剪力Vij ；根据求得的各柱层间剪力Vij和修正后的反弯点位置Y ，即可确定柱端弯矩Mc 上和Mc 下；由节点平衡条件，梁端弯矩之和等于柱端弯矩之和，将节点左右梁端弯矩之和按线刚度比例分配，可求出各梁端弯矩；进而由梁的平衡条件求出梁端剪力；最后，第j 层第i 柱的轴力即为其上各层节点左右梁端剪力代数和。

（1）一榀框架上风荷载的作用计算：前面已经算出风荷载作用下的一榀框架下每层楼的剪力，但是还要计算出一品框架下每根柱子分得的剪力,具体的计算结果见下表:Vi DijDijVij sj ∑==1层数h i(m)D i层刚度和层剪力(KN)单柱分得的剪力(KN)10 3.2 2.12E+04 1.00E+06168.39 3.55 9 3.6 2.12E+04 1.00E+06271.54 5.72 8 3.6 2.12E+04 1.00E+06368.46 7.77 7 3.6 2.12E+04 1.00E+06458.10 9.66 6 3.6 2.12E+04 1.00E+06539.81 11.38 5 3.6 2.12E+04 1.00E+06614.67 12.96 4 3.8 2.32E+04 1.03E+06686.48 15.52 3 3.8 2.32E+04 1.03E+06750.13 16.96 2 3.8 2.32E+04 1.03E+06806.61 18.24 F 轴1柱1 6.31.14E+052.81E+06900.06 36.61 层数h i(m)D i层刚度和层剪力(KN)单柱分得的剪力(KN)10 3.2 3.21E+04 1.00E+06168.39 5.37 9 3.6 3.21E+04 1.00E+06271.54 8.67 8 3.6 3.21E+04 1.00E+06368.46 11.76 7 3.6 3.21E+04 1.00E+06458.10 14.62 6 3.6 3.21E+04 1.00E+06539.81 17.23 5 3.6 3.21E+04 1.00E+06614.67 19.62 4 3.8 3.96E+04 1.03E+06686.48 26.51 F 轴2柱33.83.96E+041.03E+06750.1328.972 3.8 3.96E+04 1.03E+06806.61 31.15 1 6.3 1.31E+05 2.81E+06900.06 41.86层数h i(m)D i层刚度和层剪力(KN)单柱分得的剪力(KN)10 3.2 3.21E+04 1.00E+06168.39 5.379 3.6 3.21E+04 1.00E+06271.54 8.678 3.6 3.21E+04 1.00E+06368.46 11.767 3.6 3.21E+04 1.00E+06458.10 14.626 3.6 3.21E+04 1.00E+06539.81 17.235 3.6 3.21E+04 1.00E+06614.67 19.624 3.8 3.96E+04 1.03E+06686.48 26.513 3.8 3.96E+04 1.03E+06750.13 28.972 3.8 3.96E+04 1.03E+06806.61 31.15 F轴3柱1 6.3 1.31E+05 2.81E+06900.06 41.86层数h i(m)D i层刚度和层剪力(KN)单柱分得的剪力(KN)10 3.2 2.12E+04 1.00E+06168.39 3.559 3.6 2.12E+04 1.00E+06271.54 5.728 3.6 2.12E+04 1.00E+06368.46 7.777 3.6 2.12E+04 1.00E+06458.10 9.666 3.6 2.12E+04 1.00E+06539.81 11.385 3.6 2.12E+04 1.00E+06614.67 12.964 3.8 2.32E+04 1.03E+06686.48 15.523 3.8 2.32E+04 1.03E+06750.13 16.962 3.8 2.32E+04 1.03E+06806.61 18.24 F轴4柱1 6.3 1.14E+05 2.81E+06900.06 36.61（2）风荷载作用下反弯点高度的计算:反弯点高度比即: V=V0+V1+V2+V3式中:V0 ——标准层反弯点高度比；注：本框架风荷载采用分段式均布荷载，故可查《高层建筑结构设计》表5.8a。

建筑风荷载计算

风荷载标准值计算风荷载标准值计算公式为：0k z s z w w βμμ=，作用在屋面梁和楼面梁节点处的集中风荷载标准值计算公式为：0W z s z P w A βμμ= 式中：W P －作用于框架节点的集中风荷载标准值(KN) z β－风振系数s μ－风荷载体型系数 z μ－风压高度变化系数0w －基本风压（KN/㎡）A －一榀框架各层节点受风面积（㎡）本建筑基本风压为：200.3/w KN m =，由《荷载规范》得，地面粗糙为C 类。

s μ风荷载体系系数，根据建筑物体型查得 1.3s μ=。

z β风振系数，因结构总高度H=21.128m<30m ，故 1.0z β=。

风压高度变化系数z μ查《荷载规范》表7.2.1。

一榀框架各层节点受风面积A 计算，B 为3.3 3.9() 3.622m +=， h 取上层的一半和下层的一半之和，屋面层取到女儿墙顶，底层取底层的一半。

底层的计算高度从室外地面取()mm 45003004200=+。

一层： 24.5 3.9() 3.615.1222A m =+⨯= 二层： 23.9 3.9() 3.614.0422A m =+⨯=三层： 23.9 3.9() 3.614.0422A m =+⨯=四层： 23.9 3.9() 3.614.0422A m =+⨯=五层：23.9(1.50) 3.612.422A m =+⨯=计算过程见表所示：欠左风、右风荷载受荷简图框架梁柱线刚度计算框架梁柱线刚度计算见表表7-1 纵梁线刚度计算表表7-2 柱线刚度Ic 计算表7.2.2 侧移刚度D 值计算考虑梁柱的线刚度比，用D 值法计算柱的侧位移刚度，表7-4 柱侧移刚度计算表2～5层柱D 值计算2～5层柱D 值合计：D ∑=1.572+1.572=3.144KN/m底层柱D 值计算低层柱D 值合计：D ∑=1.612+1.612=3.224KN/m 7.2.3 风荷载作用下框架位移的计算风荷载作用下框架的层间侧移可按下式计算，即jj ijV u D∆=∑式中：j V －第j 层的总剪力；ij D ∑－第j 层所有柱的抗侧刚度之和；j u ∆－第j 层的层间位移。

地震作用内力及风荷载作用内力计算表

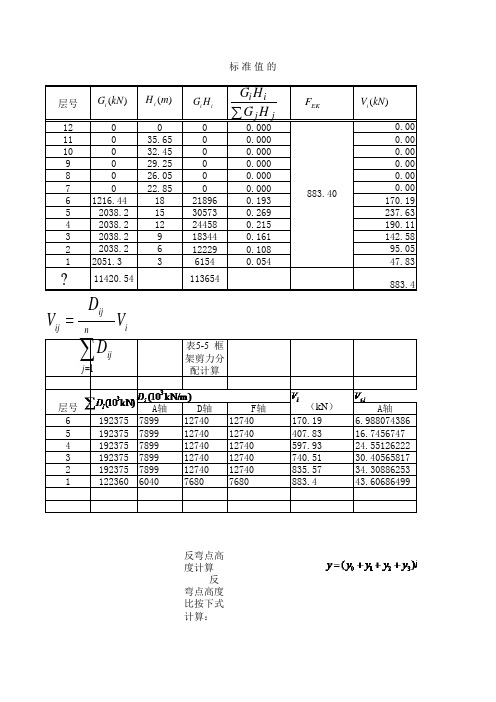
D柱梁端弯矩和
0.9 0.9 0.9 0.9 0.9 0.9
1.97 1.97 1.97 1.97 1.97 1.97
18.36380711 44.00795939
64.521 79.90781726 90.16515228 90.34764975
表5-30结构变形验
算
层间剪力层间刚度
层次 6 5
n
Gj
ji
2029.4 3138.7 3154.8
3 3 3 3 3 3
Fi H i
0.00 0.00 0.00 0.00 0.00 0.00 3063.43 3564.52 2281.29 1283.23 570.32 143.50
5447261.55
（kN）
D轴
F轴
11.27080234 11.27080234
2
381000 0.0038
1 1499.82 285000 0.0053
备注：层间相对弹性转角均满足
3
0.001266667
3
0.001766667
表5-4各楼层的刚重比和
剪重比
层号 6 5 4 3 2 1
层号 6 5 4 3 2 1
）
3
192375 3
3
192375 3
3
192375 3
h (m)
轴号 A轴
D轴 F轴
楼层 6 5
4 3 2 1 6 5
（kN）
6.988 16.745
24.551 30.405 34.308 43.606 11.27 27.008
(m)
1.125 1.35
1.425 1.5 1.5 1.8 1.35 1.5

第七章风荷载作用下的内力和位移计算

第七章风荷载作⽤下的内⼒和位移计算第7章风荷载作⽤下的内⼒和位移计算由设计任务资料知，该建筑为五层钢筋混凝⼟框架结构体系，室内外⾼差为0.45m 基本风压20m /4.0KN =ω，地⾯粗糙度为C 类，结构总⾼度19.8+0.45=20.25m （基础顶⾯⾄室内地⾯1m ）。

计算主要承重结构时，垂直于建筑物表⾯上的风荷载标准值，应按下式计算，即oz s z k w w µµβ=1、因结构⾼度H=20.25m<30m,⾼宽⽐20.25÷18.2=1.11＜1.5,故可取0.1z =β；2、s µ为风荷载体型系数，本设计按《建筑结构荷载规范》（GB50009--2012）中规定，迎风⾯取0.8，背风⾯取0.5，合计sµ=1.3。

3、z µ为风压⾼度变化系数，本设计的地⾯粗糙度类别为C 类，按下表选取风压⾼度变化系数。

7.1 横向框架在风荷载作⽤下的计算简图6轴线框架的负荷宽度B=（6.6+6.6）/2=6.6m。

各层楼⾯处集中风荷载标准值计算如表7.1：表7.1根据表7.1，画出6轴框架在风荷载作⽤下的计算简图，如图7.2所⽰：图7.2框架在风荷载作⽤下的计算简图7.2 位移计算7.2.1框架梁柱线刚度计算考虑现浇楼板对梁刚度的加强作⽤，故对6轴线框架（中框架梁）的惯性矩乘以2.0，框架梁的线刚度计算：跨度为7.3m 的梁（b ×h=250mm ×600mm ）：)(109126.0250.0212bh 24333m I -?=??=?=m KN L I E c b /105.33.7109108.2i 437b ?===-跨度为3.3m 的梁 (b ×h=200mm ×400mm ）：）（43-33m 101.2124.02.0212bh 2?=??=?=Im KN L I E c b /109.13.31013.2108.2i 437b ?===-7.2.1.1 框架柱的线刚度 1、底层柱： A 、D 轴柱：)(1021.512500500433c m I -?=?=m KN h I E c c c /100.32.51021.5100.3i 437?===-B 、C 轴柱：)(1021.512500500433c m I -?=?=m KN h I E c c c /100.32.51021.5100.3i 437?===-2、上层柱： A 、D 轴柱：)(1021.512500500433c m I -?=?=m KN h I E c c c /100.49.31021.5100.3i 437?===-B 、C 轴柱：)(1021.512500500433c m I -?=?=m KN h I E c c c /100.49.31021.5100.3i 437?===-7.2.1.2 侧移刚度D 计算框架柱刚度修正系数a 计算公式见表7.3: 表7.3表7.4 各层柱侧向刚度计算风荷载作⽤下框架的层间侧移可按下式计算，即有：∑= ijjj DV u式中jV ------第j 层的总剪⼒标准；D--------第j 层所有柱的抗侧刚度之和；ju ?--------第j 层的层间侧移。

5-风荷载计算

5 风荷载计算5.1 风荷载标准值主体结构计算时，为了简化计算，作用在外墙面上的风荷载可近似作用在屋面梁和楼面梁处的等效集中荷载替代，垂直于建筑物表面的风荷载标注值按公式5-1计算。

0k z s z ωβμμω⋅⋅⋅= （5-1）式中：k ω——风荷载标准值；s μ——风荷载体型系数；z μ——风压高度变化系数；0ω——基本风压值，本设计中的基本风压取30.00=ω； z β——高度z 处的风振系数；根据《建筑结构荷载规范》（GB50009—2012）第8.2.1条规定：地面粗糙度可分为四类：A 类指近海海面和海岛、海岸、湖岸及沙漠地区；B 类指田野、乡村、丛林、丘陵以及房屋比较稀疏的乡镇；C 类指有密集建筑群的城市市区；D 类指有密集建筑群且房屋较高的城市市区。

本设计中地面粗糙度取C 类。

高度z 处的风振系数z β的计算式见公式5-2。

1zz z ξνϕβμ=+（5-2）ξ——脉动增大系数；ν——脉动影响系数；z ϕ——振型系数；z μ——风压高度变化系数。

根据《建筑结构荷载规范》（GB50009—2012）第8.3节可知：对于框架结构的基本自振周期可以近似按照()10.08~0.10T n n =（n 为建筑层数）估算，应考虑风压脉动对结构发生顺风向风振的影响,本设计中自振周期取10.090.0960.54T n s ==⨯=，经过计算，21200.300.54=0.087T ω=⨯。

风载体型系数由《建筑结构荷载规范》（GB50009—2012）第8.3节续表8.3.1可以查得：8.0=s μ（迎风面）和5.0-=s μ（背风面）。

根据《建筑结构荷载规范》（GB50009—2012）第8.4.1条规定：当结构基本自振周期s T 25.0≥时，以及对于高度超过30m 且高宽比大于1. 5 的高柔房屋，由风引起的结构振动比较明显，而且随着结构自振周期的增长，风振也随之增强。

因此在设计中应考虑风振的影响，而且原则上还应考虑多个振型的影响。

风荷载作用下的内力和位移计算

风荷载作用下的内力和位移计算
风荷载作用下的内力和位移计算通常涉及以下步骤：
1.确定建筑物的风荷载标准以及建筑物的几何形状和尺寸参数；
2.计算建筑物的风荷载大小和方向，可采用建筑物结构设计规
范或专业软件进行计算；
3.将风荷载作用下的内力和位移分解为平面内力和垂直于平面
的剪力与弯矩，根据不同的加载条件，可以采用不同的计算方法进行计算；
4.通过应力-strain关系计算元件的应力和应变，然后对于剪切
应力和弯曲应力进行的评估。

对于抗弯性能较弱的构件，需要考虑稳定性及挠度分析；
5.通过数值算法，考虑各种边界条件下的结构位移情况，可以
计算出风荷载作用下的建筑物结构的整体变形情况，以评估结构的稳定性和安全性。

需要注意的是，针对不同的建筑物结构类型和工作条件，风荷载作用下的内力和位移计算方法可能会有所不同，需要设计师按照相关规范和标准进行具体的计算。

第七章--风荷载作用下的内力和位移计算

第7章风荷载作用下的力和位移计算由设计任务资料知，该建筑为五层钢筋混凝土框架结构体系，室外高差为0.45m 基本风压20m /4.0KN =ω，地面粗糙度为C 类，结构总高度19.8+0.45=20.25m （基础顶面至室地面1m ）。

计算主要承重结构时，垂直于建筑物表面上的风荷载标准值，应按下式计算，即o z s z k w w μμβ=1、因结构高度H=20.25m<30m,高宽比20.25÷18.2=1.11＜1.5,故可取0.1z =β；2、s μ为风荷载体型系数，本设计按《建筑结构荷载规》（GB50009--2012）中规定，迎风面取0.8，背风面取0.5，合计s μ=1.3。

3、z μ为风压高度变化系数，本设计的地面粗糙度类别为C 类，按下表选取风压高度变化系数。

7.1 横向框架在风荷载作用下的计算简图6轴线框架的负荷宽度B=（6.6+6.6）/2=6.6m。

各层楼面处集中风荷载标准值计算如表7.1：表7.1根据表7.1，画出6轴框架在风荷载作用下的计算简图，如图7.2所示：图7.2 框架在风荷载作用下的计算简图7.2 位移计算7.2.1框架梁柱线刚度计算考虑现浇楼板对梁刚度的加强作用，故对6轴线框架（中框架梁）的惯性矩乘以2.0，框架梁的线刚度计算：跨度为7.3m 的梁（b ×h=250mm ×600mm ）：)(109126.0250.0212bh 24333m I -⨯=⨯⨯=⨯= m KN L I E c b /105.33.7109108.2i 437b ⨯=⨯⨯⨯==- 跨度为3.3m 的梁 (b ×h=200mm ×400mm ）：）（43-33m 101.2124.02.0212bh 2⨯=⨯⨯=⨯=I m KN L I E c b /109.13.31013.2108.2i 437b ⨯=⨯⨯⨯==- 7.2.1.1 框架柱的线刚度 1、底层柱： A 、D 轴柱：)(1021.512500500433c m I -⨯=⨯=m KN h I E c c c /100.32.51021.5100.3i 437⨯=⨯⨯⨯==- B 、C 轴柱：)(1021.512500500433c m I -⨯=⨯=m KN h I E c c c /100.32.51021.5100.3i 437⨯=⨯⨯⨯==- 2、上层柱：A 、D 轴柱：)(1021.512500500433c m I -⨯=⨯=m KN h I E c c c /100.49.31021.5100.3i 437⨯=⨯⨯⨯==- B 、C 轴柱：)(1021.512500500433c m I -⨯=⨯=m KN h I E c c c /100.49.31021.5100.3i 437⨯=⨯⨯⨯==- 7.2.1.2 侧移刚度D 计算框架柱刚度修正系数计算公式见表7.3: 表7.3表7.4 各层柱侧向刚度计算风荷载作用下框架的层间侧移可按下式计算，即有：∑=∆ijjj DV u式中 jV ------第j 层的总剪力标准；∑ijD --------第j 层所有柱的抗侧刚度之和；ju ∆--------第j 层的层间侧移。

风荷载作用下的内力和位移计算

第7章风荷载作用下的内力和位移计算由设计任务资料知，该建筑为五层钢筋混凝土框架结构体系，室内外高差为基本风压20m /4.0KN =ω，地面粗糙度为C 类，结构总高度+=（基础顶面至室内地面1m ）。

计算主要承重结构时，垂直于建筑物表面上的风荷载标准值，应按下式计算，即o z s z k w w μμβ=1、因结构高度H=<30m,高宽比÷=＜,故可取0.1z =β；2、s μ为风荷载体型系数，本设计按《建筑结构荷载规范》（GB50009--2012）中规定，迎风面取，背风面取，合计s μ=。

3、z μ为风压高度变化系数，本设计的地面粗糙度类别为C 类，按下表选取风压高度变化系数。

横向框架在风荷载作用下的计算简图6轴线框架的负荷宽度B=（+）/2=。

各层楼面处集中风荷载标准值计算如表：表根据表，画出6轴框架在风荷载作用下的计算简图，如图所示：图框架在风荷载作用下的计算简图位移计算框架梁柱线刚度计算考虑现浇楼板对梁刚度的加强作用，故对6轴线框架（中框架梁）的惯性矩乘以，框架梁的线刚度计算：跨度为的梁（b ×h=250mm ×600mm ）：)(109126.0250.0212bh 24333m I -⨯=⨯⨯=⨯= m KN L I E c b /105.33.7109108.2i 437b ⨯=⨯⨯⨯==- 跨度为的梁 (b ×h=200mm ×400mm ）：）（43-33m 101.2124.02.0212bh 2⨯=⨯⨯=⨯=I m KN L I E c b /109.13.31013.2108.2i 437b ⨯=⨯⨯⨯==- 框架柱的线刚度 1、底层柱： A 、D 轴柱：)(1021.512500500433c m I -⨯=⨯=m KN h I E c c c /100.32.51021.5100.3i 437⨯=⨯⨯⨯==- B 、C 轴柱：)(1021.512500500433c m I -⨯=⨯=m KN h I E c c c /100.32.51021.5100.3i 437⨯=⨯⨯⨯==- 2、上层柱： A 、D 轴柱：)(1021.512500500433c m I -⨯=⨯=m KN h I E c c c /100.49.31021.5100.3i 437⨯=⨯⨯⨯==- B 、C 轴柱：)(1021.512500500433c m I -⨯=⨯=m KN h I E c c c /100.49.31021.5100.3i 437⨯=⨯⨯⨯==- 侧移刚度D 计算框架柱刚度修正系数计算公式见表: 表表各层柱侧向刚度计算风荷载作用下框架的层间侧移可按下式计算，即有：∑=∆ijjj DV u式中 jV ------第j 层的总剪力标准；∑ijD --------第j 层所有柱的抗侧刚度之和；ju ∆--------第j 层的层间侧移。

3.3.3 风荷载内力计算风荷载内力计算

三、在风荷载作用下内力计算对于作用在屋面的风荷载可以分解为水平方向的分力xq 和竖向分力yq 。

（1）在迎风面横梁上风荷载竖向分力2yqω作用下（见图）0206 3.333160.167610.04990.5973(3)30.5970.167(30.167) 4.125911=85=850.167=0.13381616 4.12591.8920kN 4.73kN 88( 1.8910 4.73)kN 14.17kN (4E A A E l H f h k h s k ql qlV V H H λμμλ===ψ=======++ψ+ψ=++⨯+=Φ+ψ⨯+⨯⨯-⨯===-=-⨯+=-==Φ=（）（）221.8920 3.3330.13384)kN 4.21kN 1.89200.1338kN=25.29kN 44BD ql MM-⨯⨯⨯=-⨯==Φ=⨯ 22[(1)]4C ql M α=-+ψΦ221.8920[0.5(10.167)0.1338]17.74kN =-⨯⨯-+=-17.74k N ·m在迎风面横梁上风荷载竖向分力作用的M 图(2) 在背风面横梁上风荷载竖向分力4yqω作用下（见图）4 1.23/q k N m ω=-0206 3.333160.167610.04990.5973(3)30.5970.167(30.167) 4.125911=85=850.167=0.13381616 4.12591.2320kN 3.08kN 88( 1.2310 3.08)kN 9.22kN 4A E A E l H f h k h s k ql qlV V H H λμμλ===ψ=======++ψ+ψ=++⨯+=Φ+ψ⨯+⨯⨯-⨯===-=-⨯+=-=-=-Φ=（）（）222222( 1.2320 3.3330.13384)kN 2.74kN 1.23200.1338kN=16.46kN 44[(1)] 1.2320[0.5(10.167)0.1338]411.54kN 4BDC ql ql MMM α--⨯⨯⨯=⨯==Φ=⨯=-+ψΦ=-⨯⨯-+=--11.54kN ·m在背风面横梁上风荷载竖向分力作用下M 图(3) 在迎风面柱上风荷载1q ω作用下（见图）A E020 3.333160.167610.04990.5973(3)30.5970.167(30.167) 4.12591l H f h k h s k λμα===ψ=======++ψ+ψ=++⨯+==222222211=[65]=[620.16750.597]=0.968744 4.12590.476kN 0.42kN22200.476(2)(20.9687)kN=4.36kN m4411(0.47 4.36)kN 2.1kN 62(0.476 2.1)kN 0.7kN[1(14A E B D A E C k qh l qh qh V V M M H H M μααΦ+ψ+++⨯⨯⨯=-==-=-⨯⨯==-Φ=-=⨯-==⨯-==-+ （2）（）220.4761)][1(10.167)0.9687]0.55kN m 4⨯⨯ψΦ=-+⨯=-(4) 在背风面柱上风荷载竖向分力3q ω作用下（见图）A E0206 3.333160.167610.04990.5973(3)30.5970.167(30.167) 4.12591l H f h k h s k λμα===ψ=======++ψ+ψ=++⨯+==22211=[65]=[620.16750.597]=0.968744 4.12591.046kN 0.94kN22201.04611(2)(20.9687)kN 4.73kN 2222(1.046 4.73) 1.51kN(4.736 1.0462)kN=9.66kN 1.516kN=9A E EA D Bk qh l qh V V H H M MμααΦ+ψ+++⨯⨯⨯=-==-=-⨯⨯⨯=--Φ=-⨯==⨯-==⨯-⨯=⨯（2）（）2222.06kN1.0461[1(1)][1(10.167)0.9687] 1.22kN 44C qh M α⨯⨯=-+ψΦ=-+⨯=-(5) 在迎风面横梁上风荷载水平分力2xq ω作用下（见图）160.167610.04990.5973(3)30.5970.167(30.167) 4.12591f h k h s k μαψ=======++ψ+ψ=++⨯+== 0.167=3=430.167=0.045588 4.12591.89161kN 0.61kN 22201.89110.0455kN 0.98kN 22(1.8910.98)0.91kN[0.5(1)]21.8916[0.50.167(10.167)2A E A E C qf h f l qf qfhV V H H M μψΦ+ψ+⨯⨯⨯=-=-+=-⨯+=⨯⨯=+Φ=+==⨯-==ψ-+ψΦ⨯⨯=⨯-+（4）（）（2）（2）（）（1）0.0455]0.17kN m0.986 5.88kN m0.916 5.46kN mB DM M⨯==⨯==⨯=C·m（6）在背风面横梁上风荷载水平分力4xq ω作用下（见图）1.89k N/mA E160.167610.04990.5973(3)30.5970.167(30.167) 4.12591f h k h s k μαψ=======++ψ+ψ=++⨯+== 0.167=3=430.167=0.045588 4.12591.23161kN 0.40kN 22201.23110.0455kN 0.64kN 22(1.2310.64)0.59kN[0.5(1)]21.2316[0.50.167(10.167)2A E E A C qf h f l qf qfhV V H H M μψΦ+ψ+⨯⨯⨯=-=-+=-⨯+=⨯⨯=+Φ=+==⨯-==ψ-+ψΦ⨯⨯=⨯-+（4）（）（2）（2）（）（1）0.0455]0.11kN m0.596 3.54kN m0.646 3.84kN mB DM M⨯==⨯==⨯=A(7) 用叠加法绘制在风荷载作用下刚加的组合内力。