重点高中物理人造卫星变轨问题专题
高中物理人造卫星变轨问题专题

人造卫星变轨问题专题(一) 人造卫星基本原理绕地球做匀速圆周运动的人造卫星所需向心力由万有引力提供..轨道半径r 确定后;与之对应的卫星线速度r GM v =、周期GM r T 32π=、向心加速度2r GMa =也都是唯一确定的..如果卫星的质量是确定的;那么与轨道半径r 对应的卫星的动能E k 、重力势能E p 和总机械能E 机也是唯一确定的..一旦卫星发生了变轨;即轨道半径r 发生变化;上述所有物理量都将随之变化E k 由线速度变化决定、E p 由卫星高度变化决定、E 机不守恒;其增减由该过程的能量转换情况决定..同理;只要上述七个物理量之一发生变化;另外六个也必将随之变化..(二) 常涉及的人造卫星的两种变轨问题1. 渐变由于某个因素的影响使原来做匀速圆周运动的卫星的轨道半径发生缓慢的变化逐渐增大或逐渐减小;由于半径变化缓慢;卫星每一周的运动仍可以看做是匀速圆周运动..解决此类问题;首先要判断这种变轨是离心还是向心;即轨道半径r 是增大还是减小;然后再判断卫星的其他相关物理量如何变化..1) 人造卫星绕地球做匀速圆周运动;无论轨道多高;都会受到稀薄大气的阻力作用..如果不及时进行轨道维持即通过启动星上小型发动机;将化学能转化为机械能;保持卫星应具有的状态;卫星就会自动变轨;偏离原来的圆周轨道;从而引起各个物理量的变化..这种变轨的起因是阻力..阻力对卫星做负功;使卫星速度减小;卫星所需要的向心力r mv 2减小了;而万有引力2r GMm的大小没有变;因此卫星将做向心运动;即轨道半径r 将减小..由基本原理中的结论可知:卫星线速度v 将增大;周期T 将减小;向心加速度a 将增大;动能E k 将增大;势能E p 将减小;有部分机械能转化为内能摩擦生热;卫星机械能E 机将减小..为什么卫星克服阻力做功;动能反而增加了呢 这是因为一旦轨道半径减小;在卫星克服阻力做功的同时;万有引力即重力将对卫星做正功..而且万有引力做的正功远大于克服空气阻力做的功;外力对卫星做的总功是正的;因此卫星动能增加..根据E机=E k+E p;该过程重力势能的减少总是大于动能的增加..2)有一种宇宙学的理论认为在漫长的宇宙演化过程中;引力常量G是逐渐减小的..如果这个结论正确;那么环绕星球将发生离心现象;即环绕星球到中心星球间的距离r将逐渐增大;环绕星球的线速度v将减小;周期T将增大;向心加速度a将减小;动能E k将减小;势能E p将增大..2.突变短时间启动飞行器上的发动机;使飞行器轨道发生突变;使其进入预定的轨道..1)发射同步卫星时;可以先将卫星发送到近地轨道Ⅰ;使其绕地球做匀速圆周运动;速率为v1;变轨时在P点点火加速;短时间内将速率由v1增加到v2;使卫星进入椭圆形的转移轨道Ⅱ;卫星运行到远地点Q时的速率为v3;此时进行第二次点火加速;在短时间内将速率由v3增加到v4;使卫星进入同步轨道Ⅲ;绕地球做匀速圆周运动..例题1. 某人造卫星运动的轨道可近似看作是以地心为中心的圆.由于阻力作用;人造卫星到地心的距离从r 1慢慢变到r 2;用E Kl .E K2分别表示卫星在这两个轨道上的动能;则A.r 1<r 2;E K1<E K2B.r 1>r 2;E K1<E K2C.r 1<r 2;E K1>E K2D.r 1>r 2;E K1>E K22. 1飞船在椭圆轨道1上运行;Q 为近地点;P 为远地点;当飞船运动到P 点时点火;使飞船沿圆轨道2运行;A .飞船在QB .飞船在PC .飞船在轨道1上P的速度小于在轨道2上P 的速度D .飞船在轨道1上P 的加速度大于在轨道2上P 的加速度 2假设由于飞船的特殊需要;美国的一艘原来在圆轨道运行的飞船前往与之对接;则飞船一定是A .从较低轨道上加速B .从较高轨道上加速C .从同一轨道上加速D .从任意轨道上加速3. 航天飞机在完成对哈勃太间望远镜的维修任务后;在A 点短时A间开动小型发动机进行变轨;从圆形轨道Ⅰ进入椭圆道Ⅱ;B 为轨道Ⅱ上的一点;如图所示..下列说法中正确的有A.在轨道Ⅱ上经过A的机械能大于经过B的机械能B.在A点短时间开动发动机后航天飞机的动能增大了C.在轨道Ⅱ上运动的周期小于在轨道Ⅰ上运动的周期D.在轨道Ⅱ上经过A的加速度小于在轨道Ⅰ上经过A的加速度4.我国成功实施了“神舟”七号的载入航天飞行;并实现了航天员首次出舱..飞船先沿椭圆轨道飞行;后在远地点343千米处点火加速;把飞船运行轨道由椭圆轨道变成离地面高度为343千米的圆轨道;在此圆轨道上飞船运行周期约为90分钟..下列正确的是A.飞船变轨前后的机械能相等B.飞船在圆轨道上时航天员出舱前后都处于超重状态C.飞船在此圆轨道上运动的角速度大于同步卫星运动的角速度D.飞船变轨前通过椭圆轨道远地点时的加速度大于变轨后沿圆轨道运动的加速度1.B2.BC A3.C4.C。
高中物理卫星变轨问题

作业:
C 卫星在轨道1上经过Q点时的加速度
大于它在轨道2上经过Q点时的加速度 D 卫星在轨道2上经过P点时的加速度 等于它在轨道3上经过P点时的加速度
p
1 23 Q
❖ 卫星变轨
练习如图所示;a b c是在地球大气层外圆形轨道上运行的3颗
人造卫星;下列说法正确的是:
A b c的线速度大小相等;且大于a的线速度 B b c的向心加速度大小相等;且大于a的向心加速度 C c加速可追上同一轨道上的b;b减速可等到同一轨道上的c D a卫星由于某种原因;轨道半径缓慢减小;其线速度将变小
卫星在圆轨 道运行速度
V1
R
1
2
V2
mv12 r
G
Mm r2
F引
θ>900
v 减小
卫星变轨原理
r
v3
F引
椭圆mv32 r
GMr2m
使
卫
星
进
v4
入
更
v3
高
轨
道
做
圆
周
运 动
使卫星 v4, 加m 使 速 r42v到 GM r2 m
卫 星 的 回 收
❖ 卫星变轨
卫星如何变轨 以发射同步卫星为例;先进入一
专题 万有引力定律的应用
1 卫星比较问题 2 卫星变轨 问题
两颗人造地球卫星;都在圆形轨道上运行;它 们的质量相等;轨道半径不同;比较它们的向心加 速度an 线速度v 角速度ω 周期T
地球
计算中心天体的质量M 密度ρ
1某星体m围绕中心天体M做圆 周运动的周期为T;圆周运动
的轨道半径为r
M
4 2r3
练习发射地球同步卫星时;先将卫星发射至近地圆轨道1;然后
高中物理 卫星变轨问题(上课课件)

此处的 万有引
力
轨道面与赤
m
(
2π) 2 T
R
G
Mm R2
道面重合, 在赤道上空, 与地面保持
的5.6倍
相对静止
课件教育
12
卫星变轨问题
课件教育
13
卫星变轨问题
课件教育
14
课件教育
15
卫星变轨原理
V
mA
F引
F引
G
Mm r2
F引<F向 F引>F向
F引 F向
F向
m
v2 r
M
在A点万有引力相同
专题 万有引力定律的应用
1、卫星“比较”问题 2、卫星“变轨” 问题
课件教育
1
课件教育
2
课件教育
3
两颗人造地球卫星,都在圆形轨道上运行, 它们的质量相等,轨道半径不同,比较它们的向心 加速度an、线速度v、角速度ω 、周期T。
地球
课件教育
4
计算中心天体的质量M、密度ρ
(1)某星体m围绕中心天体M 做圆周运动的周期为T,圆周
定态运行:看公式 动态变轨:分析供需
圆轨道与椭圆轨道的互变:
A点: 圆→ 加速 →椭圆 近地点 椭圆→减速 →圆
A
B B点: 圆→ 减速 →椭圆
远地点 椭圆→加速 →圆
课件教育
26
1、如图所示,发射同步卫星时,先将卫星发射至近地
圆轨道1,然后经点火使其沿椭圆轨道2运行;最后再次
点火将其送入同步圆轨道3。轨道1、2相切于P点,2、3
D、无论飞船采取何种措施,均不能与空间站对接
课件教育
29
【练习】发射地球同步卫星时,先将卫星发射至近地圆轨道1,
高一物理必修二第六章 专题强化4 卫星变轨问题和双星问题---学生版

专题强化4 卫星变轨问题和双星问题--学生版[学习目标] 1.会分析卫星的变轨问题,知道卫星变轨的原因和变轨前后卫星速度的变化.2.掌握双星运动的特点,会分析求解双星运动的周期和角速度.一、人造卫星的变轨问题1.变轨问题概述(1)稳定运行卫星绕天体稳定运行时,万有引力提供了卫星做圆周运动的向心力,即G Mm r 2=m v 2r. (2)变轨运行卫星变轨时,先是线速度v 发生变化导致需要的向心力发生变化,进而使轨道半径r 发生变化.①当卫星减速时,卫星所需的向心力F 向=m v 2r减小,万有引力大于所需的向心力,卫星将做近心运动,向低轨道变迁.②当卫星加速时,卫星所需的向心力F 向=m v 2r增大,万有引力不足以提供卫星所需的向心力,卫星将做离心运动,向高轨道变迁.2.实例分析(1)飞船对接问题飞船与在轨空间站对接先使飞船位于较低轨道上,然后让飞船合理地加速,使飞船沿椭圆轨道做离心运动,追上高轨道飞船完成对接(如图1甲所示).注意:若飞船和空间站在同一轨道上,飞船加速时无法追上空间站,因为飞船加速时,将做离心运动,从而离开这个轨道.通常先使后面的飞船减速降低高度,再加速提升高度,通过适当控制,使飞船追上空间站时恰好具有相同的速度,如图乙.图1(2)同步卫星的发射、变轨问题如图2所示,发射地球同步卫星时,先将卫星发射至近地圆轨道1,在Q 点点火加速做离心运动进入椭圆轨道2,在P 点点火加速,使其满足GMm r 2=m v 2r,进入同步圆轨道3做圆周运动.图2例1 (2019·通许县实验中学期末)如图3所示为卫星发射过程的示意图,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再一次点火,将卫星送入同步圆轨道3.轨道1、2相切于Q 点,轨道2、3相切于P 点,则当卫星分别在1、2、3轨道上正常运行时,以下说法中正确的是( )图3A.卫星在轨道3上的速率大于在轨道1上的速率B.卫星在轨道3上的周期大于在轨道2上的周期C.卫星在轨道1上经过Q 点时的速率大于它在轨道2上经过Q 点时的速率D.卫星在轨道2上经过P 点时的加速度小于它在轨道3上经过P 点时的加速度针对训练 (多选)(2019·定远育才实验学校期末)航天飞机在完成对哈勃空间望远镜的维修任务后,在A 点从圆形轨道Ⅰ进入椭圆轨道Ⅱ,B 为轨道Ⅱ上的一点,如图4所示.关于航天飞机的运动,下列说法中正确的有( )图4A.在轨道Ⅱ上经过A 的速度小于经过B 点的速度B.在轨道Ⅱ上经过A 的速度小于在轨道Ⅰ上经过A 的速度C.在轨道Ⅱ上运动的周期小于在轨道Ⅰ上运动的周期D.在轨道Ⅱ上经过A 的加速度小于在轨道Ⅰ上经过A 的加速度二、双星或多星问题1.双星模型(1)如图5所示,宇宙中有相距较近、质量相差不大的两个星球,它们离其他星球都较远,其他星球对它们的万有引力可以忽略不计.在这种情况下,它们将围绕其连线上的某一固定点做周期相同的匀速圆周运动,通常,我们把这样的两个星球称为“双星”.图5(2)双星问题的特点①两星围绕它们之间连线上的某一点做匀速圆周运动,两星的运行周期、角速度相同. ②两星的向心力大小相等,由它们间的万有引力提供.③两星的轨道半径之和等于两星之间的距离,即r 1+r 2=L .(3)双星问题的处理方法:双星间的万有引力提供了它们做圆周运动的向心力,即Gm 1m 2L 2=m 1ω2r 1,G m 1m 2L2=m 2ω2r 2. 2.多星系统在宇宙中存在类似于“双星”的系统,如“三星”、“四星”等多星系统,在多星系统中:(1)各个星体做圆周运动的周期、角速度相同.(2)某一星体做圆周运动的向心力是由其他星体对它引力的合力提供的.例2 两个靠得很近的天体,离其他天体非常遥远,它们以其连线上某一点O 为圆心各自做匀速圆周运动,两者的距离保持不变,科学家把这样的两个天体称为“双星”,如图6所示.已知双星的质量分别为m 1和m 2,它们之间的距离为L ,引力常量为G ,求双星的运行轨道半径r 1和r 2及运行周期T .图6例3 宇宙间存在一些离其他恒星较远的三星系统,如图7所示,三颗质量均为m 的星位于等边三角形的三个顶点,三角形边长为L ,忽略其他星体对它们的引力作用,三星在同一平面内绕三角形中心O做匀速圆周运动,引力常量为G,下列说法正确的是()图7A.每颗星做圆周运动的角速度为Gm L3B.每颗星做圆周运动的加速度与三星的质量无关C.若距离L和每颗星的质量m都变为原来的2倍,则周期变为原来的2倍D.若距离L和每颗星的质量m都变为原来的2倍,则线速度变为原来的4倍1.(卫星变轨问题)(2019·启东中学高一下学期期中)2019年春节期间,中国科幻电影里程碑的作品《流浪地球》热播,影片中为了让地球逃离太阳系,人们在地球上建造特大功率发动机,使地球完成一系列变轨操作,其逃离过程如图8所示,地球在椭圆轨道Ⅰ上运行到远日点B变轨,进入圆形轨道Ⅱ.在圆形轨道Ⅱ上运行到B点时再次加速变轨,从而最终摆脱太阳束缚.对于该过程,下列说法正确的是()图8A.沿轨道Ⅰ运动至B点时,需向前喷气减速才能进入轨道ⅡB.沿轨道Ⅰ运行的周期小于沿轨道Ⅱ运行的周期C.沿轨道Ⅰ运行时,在A点的加速度小于在B点的加速度D.在轨道Ⅰ上由A点运行到B点的过程,速度逐渐增大2.(卫星、飞船的对接问题)如图9所示,我国发射的“神舟十一号”飞船和“天宫二号”空间实验室于2016年10月19日自动交会对接成功.假设对接前“天宫二号”与“神舟十一号”都围绕地球做匀速圆周运动,为了实现飞船与空间实验室的对接,下列措施可行的是( )图9A.使飞船与空间实验室在同一轨道上运行,然后飞船加速追上空间实验室实现对接B.使飞船与空间实验室在同一轨道上运行,然后空间实验室减速等待飞船实现对接C.飞船先在比空间实验室轨道半径小的轨道上加速,加速后飞船逐渐靠近空间实验室,两者速度接近时实现对接D.飞船先在比空间实验室轨道半径小的轨道上减速,减速后飞船逐渐靠近空间实验室,两者速度接近时实现对接3.(双星问题)冥王星与其附近的另一星体卡戎可视为双星系统,冥王星与星体卡戎的质量比约为7∶1,同时绕它们连线上某点O 做匀速圆周运动,由此可知,冥王星绕O 点运动的( )A.轨道半径约为卡戎的17B.角速度大小约为卡戎的17C.线速度大小约为卡戎的7倍D.向心力大小约为卡戎的7倍4.(双星问题)(多选)宇宙中两颗相距很近的恒星常常组成一个双星系统.它们以相互间的万有引力彼此提供向心力,从而使它们绕着某一共同的圆心做匀速圆周运动,若已知某双星系统的运转周期为T ,两星到共同圆心的距离分别为R 1和R 2,引力常量为G ,那么下列说法正确的是( )A.这两颗恒星的质量必定相等B.这两颗恒星的质量之和为4π2(R 1+R 2)3GT 2C.这两颗恒星的质量之比m 1∶m 2=R 2∶R 1D.其中必有一颗恒星的质量为4π2R 1(R 1+R 2)2GT 2一、选择题1.(2019·江苏卷)1970年成功发射的“东方红一号”是我国第一颗人造地球卫星,该卫星至今仍沿椭圆轨道绕地球运动.如图1所示,设卫星在近地点、远地点的速度分别为v1、v2,近地点到地心的距离为r,地球质量为M,引力常量为G.则()图1A.v1>v2,v1=GM rB.v1>v2,v1>GM rC.v1<v2,v1=GM rD.v1<v2,v1>GM r2.(2019·北京市石景山区一模)两个质量不同的天体构成双星系统,它们以二者连线上的某一点为圆心做匀速圆周运动,下列说法正确的是()A.质量大的天体线速度较大B.质量小的天体角速度较大C.两个天体的向心力大小一定相等D.两个天体的向心加速度大小一定相等3.(2019·定州中学期末)如图2所示,“嫦娥三号”探测器经轨道Ⅰ到达P点后经过调整速度进入圆轨道Ⅱ,再经过调整速度变轨进入椭圆轨道Ⅲ,最后降落到月球表面上.下列说法正确的是()图2A.“嫦娥三号”在地球上的发射速度大于11.2 km/sB.“嫦娥三号”由轨道Ⅰ经过P 点进入轨道Ⅱ时要加速C.“嫦娥三号”在轨道Ⅲ上经过P 点的速度大于在轨道Ⅱ上经过P 点的速度D.“嫦娥三号”稳定运行时,在轨道Ⅱ上经过P 点的加速度与在轨道Ⅲ上经过P 点的加速度相等4.(多选)如图3所示,a 、b 、c 是在地球大气层外圆形轨道上运行的3颗人造卫星,下列说法正确的是( )图3A.b 、c 的线速度大小相等,且大于a 的线速度B.a 加速可能会追上bC.c 加速可追上同一轨道上的b ,b 减速可等到同一轨道上的cD.a 卫星由于某种原因,轨道半径缓慢减小,仍做匀速圆周运动,则其线速度将变大5.(2019·杨村一中期末)如图4所示,两颗星球组成的双星,在相互之间的万有引力作用下,绕其连线上的O 点做周期相同的匀速圆周运动.现测得两颗星之间的距离为L ,质量之比为m 1∶m 2=3∶2,下列说法中正确的是( )图4A.m 1、m 2做圆周运动的线速度之比为3∶2B.m 1、m 2做圆周运动的角速度之比为3∶2C.m 1做圆周运动的半径为25L D.m 2做圆周运动的半径为25L6.(2019·榆树一中期末)如图5所示,我国发射“神舟十号”飞船时,先将飞船发送到一个椭圆轨道上,其近地点M 距地面200 km ,远地点N 距地面340 km.进入该轨道正常运行时,通过M 、N 点时的速率分别是v 1和v 2,加速度大小分别为a 1和a 2.当某次飞船通过N 点时,地面指挥部发出指令,点燃飞船上的发动机,使飞船在短时间内加速后进入离地面340 km 的圆形轨道,开始绕地球做匀速圆周运动,这时飞船的速率为v 3,加速度大小为a 3,比较飞船在M 、N 、P 三点正常运行时(不包括点火加速阶段)的速率和加速度大小,下列结论正确的是( )图5A.v 1>v 3>v 2,a 1>a 3>a 2B.v 1>v 2>v 3,a 1>a 2=a 3C.v 1>v 2=v 3,a 1>a 2>a 3D.v 1>v 3>v 2,a 1>a 2=a 37.我国未来将建立月球基地,并在绕月轨道上建造空间站.如图6所示,关闭发动机的航天飞机仅在月球引力作用下沿椭圆轨道向月球靠近,并将在椭圆的近月点B 处与空间站对接.已知空间站C 绕月轨道半径为r ,周期为T ,引力常量为G ,月球的半径为R .那么以下选项正确的是( )图6A.月球的质量为4π2r 3GT 2 B.航天飞机到达B 处由椭圆轨道进入空间站圆轨道时必须加速C.航天飞机从A 处到B 处做减速运动D.月球表面的重力加速度为4π2R T 28.(2019·武邑中学调研)某双星由质量不等的星体S 1和S 2构成,两星在相互之间的万有引力作用下绕两者连线上某一定点C 做匀速圆周运动.由天文观察测得其运动周期为T ,S 1到C 点的距离为r 1,S 1和S 2之间的距离为r ,已知引力常量为G ,由此可求出S 2的质量为( )A.4π2r 2(r -r 1)GT 2B.4π2r 13GT 2C.4π2r 3GT2 D.4π2r 2r 1GT 29.(多选)如图7所示,在嫦娥探月工程中,设月球半径为R ,月球表面的重力加速度为g 0.飞船在半径为4R 的圆形轨道Ⅰ上运动,到达轨道的A 点时点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B 时,再次点火进入近月轨道Ⅲ绕月球做圆周运动,忽略月球的自转,则( )图7A.飞船在轨道Ⅲ上的运行速率大于g 0RB.飞船在轨道Ⅰ上的运行速率小于在轨道Ⅱ上B 处的运行速率C.飞船在轨道Ⅰ上的向心加速度小于在轨道Ⅱ上B 处的向心加速度D.飞船在轨道Ⅰ、轨道Ⅲ上运行的周期之比T Ⅰ∶T Ⅲ=4∶110.双星系统由两颗恒星组成,两恒星在相互引力的作用下,分别围绕其连线上的某一点做周期相同的匀速圆周运动.研究发现,双星系统演化过程中,两星的总质量、距离和周期均可能发生变化.若某双星系统中两星做匀速圆周运动的周期为T ,经过一段时间演化后,两星总质量变为原来的k 倍,两星之间的距离变为原来的n 倍,则此时匀速圆周运动的周期为( )A.n 3k 2T B.n 3k T C.n 2k T D.n kT11.(多选)(2019·雅安中学高一下学期期中)国际研究小组借助于智利的甚大望远镜,观测到了一组双星系统,它们绕两者连线上的某点O 做匀速圆周运动,如图8所示,此双星系统中体积较小成员能“吸食”另一颗体积较大星体表面物质,达到质量转移的目的,被吸食星体的质量远大于吸食星体的质量.假设在演变的过程中两者球心之间的距离保持不变,则在最初演变的过程中( )图8A.它们做圆周运动的万有引力保持不变B.它们做圆周运动的角速度不断变大C.体积较大星体圆周运动轨迹半径变大D.体积较大星体圆周运动的线速度变大12.(2019·扬州中学模拟)进行科学研究有时需要大胆的想象,假设宇宙中存在一些离其他恒星较远的、由质量相等的四颗星组成的四星系统(忽略其他星体对它们的引力作用),这四颗星恰好位于正方形的四个顶点上,并沿外接于正方形的圆形轨道运行,若此正方形边长变为原来的一半,要使此系统依然稳定存在,星体的角速度应变为原来的( )A.1倍B.2倍C.12倍 D.22倍二、非选择题13.中国自行研制、具有完全自主知识产权的“神舟号”飞船,目前已经达到或优于国际第三代载人飞船技术,其发射过程简化如下:飞船在酒泉卫星发射中心发射,由长征运载火箭送入近地点为A 、远地点为B 的椭圆轨道上,A 点距地面的高度为h 1,飞船飞行5圈后进行变轨,进入预定圆轨道,如图9所示.设飞船在预定圆轨道上飞行n 圈所用时间为t ,若已知地球表面重力加速度为g ,地球半径为R ,忽略地球的自转,求:图9(1)飞船在B 点经椭圆轨道进入预定圆轨道时是加速还是减速?(2)飞船经过椭圆轨道近地点A 时的加速度大小.(3)椭圆轨道远地点B 距地面的高度h 2.14.(2019·厦门一中模拟)如图10所示,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动,星球A和B两者中心之间距离为L.已知星球A、B的中心和O三.点始终共线,星球A和B分别在O的两侧.引力常量为G(1)求两星球做圆周运动的周期;(2)在地月系统中,若忽略其他星球的影响,可以将月球和地球看成上述星球A和B,月球绕其轨道中心运行的周期记为T1.但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期记为T2.已知地球和月球的质量分别为5.98×1024kg 和7.35×1022 kg.求T2与T1两者平方之比.(计算结果保留四位有效数字)11。
最新高中物理天体运动热点难点重点卫星变轨问题深度解析

最新高中物理天体运动热点难点重点卫星变轨问题深度解析高中物理天体运动热点难点重点卫星变轨问题深度解析(包教会)卫星变轨问题引例:飞船发射及运行过程:先由运载火箭将飞船送入椭圆轨道,然后在椭圆轨道的远地点A实施变轨,进入预定圆轨道,如图所示,飞船变轨前后速度分别为v1、v2,变轨前后的运行周期分别为T1、T2,飞船变轨前后通过A点时的加速度分别为a1、a2,则下列说法正确的是A.T1<T2,v1<v2,a1<a2B.T1<T2,v1<v2,a1=a2C.T1>T2,v1>v2,a1<a2D.T1>T2,v1=v2,a1=a2解答:首先,同样是A点,到地心的距离相等,万有引力相等,由万有引力提供的向心力也相等,向心加速度相等。
如果对开普勒定律比较熟悉,从T的角度分析:由开普勒定律知道,同样的中心体,k=a /T 为一常数。
从图中很容易知道,圆轨道的半径R大于椭圆轨道的半长轴a,这样可得圆轨道上运行的周期T2大于椭圆轨道的周期T1。
如果对离心运动规律比较熟悉,从v的角度分析:1、当合力[引力]不足以提供向心力(速度比维持圆轨道运动所需的速度大)时,物体偏离圆轨道向外运动,这一点可以说明椭圆轨道近地点天体的运动趋向。
2、当合力[引力]超过运动向心力(速度比维持圆轨道运动所需的速度小)时,物体偏离圆轨道向内运动,这一点可以说明椭圆轨道远地点天体的运动趋向。
对椭圆轨道,A点为远地点,由上述第2条不难判断,在椭圆轨道上A点的运行速度v1比圆轨道上时A点的速度v2小。
综上,正确选项为B。
注意:变轨的物理实质就是变速。
由低轨变向高轨是加速,由高轨变向低轨是减速。
其基本操作都是打开火箭发动机做功,但加速时做正功,减速时做负功。
一、人造卫星基本原理1、绕地球做匀速圆周运动的人造卫星所需向心力由万有引力提供。
2、轨道半径r确定后,与之对应的卫星线速度vGMGMr3、周期T2、向心加速度a也都是唯一确定2rrGM的。
3、如果卫星的质量是确定的,那么与轨道半径r对应的卫星的动能Ek、重力势能Ep和总机械能E机也是唯一确定的。
高中物理必修二科学思维系列(一)——卫星变轨及飞船对接问题

核心素养提升微课堂科学思维系列(一)——卫星变轨及飞船对接问题1.变轨原理及过程人造卫星的发射过程要经过多次变轨方可到达预定轨道,如图所示.(1)为了节省能量,在赤道上顺着地球自转方向发射卫星到圆轨道Ⅰ上.(2)在A点点火加速,速度变大,进入椭圆轨道Ⅱ.(3)在B点(远地点)再次点火加速进入圆轨道Ⅲ.2.卫星变轨问题分析方法(1)速度大小的分析方法.①卫星做匀速圆周运动经过某一点时,其速度满足GMm r2=m v2r即v=GMr.以此为依据可分析卫星在两个不同圆轨道上的速度大小.②卫星做椭圆运动经过近地点时,卫星做离心运动,万有引力小于所需向心力:GMmr2<m v2r.以此为依据可分析卫星沿椭圆轨道和沿圆轨道通过近地点时的速度大小(即加速离心).③卫星做椭圆运动经过远地点时,卫星做近心运动,万有引力大于所需向心力:GMmr2>m v2r.以此为依据可分析卫星沿椭圆轨道和沿圆轨道通过远地点时的速度大小(即减速近心).④卫星做椭圆运动从近地点到远地点时,根据开普勒第二定律,其速率越来越小.以此为依据可分析卫星在椭圆轨道的近地点和远地点的速度大小.(2)加速度大小的分析方法:无论卫星做圆周运动还是椭圆运动,只受万有引力时,卫星的加速度a n=Fm=G M r2.3.飞船对接问题(1)低轨道飞船与高轨道空间站对接如图甲所示,低轨道飞船通过合理地加速,沿椭圆轨道追上高轨道空间站与其完成对接.(2)同一轨道飞船与空间站对接如图乙所示,后面的飞船先减速降低高度,再加速提升高度,通过适当控制,使飞船追上空间站时恰好具有相同的速度.【典例】“嫦娥三号”探测器由“长征三号乙”运载火箭从西昌卫星发射中心发射,首次实现月球软着陆和月面巡视勘察,“嫦娥三号”的飞行轨道示意图如图所示.假设“嫦娥三号”在环月段圆轨道和椭圆轨道上运动时,只受到月球的万有引力,则以下说法正确的是()A.若已知“嫦娥三号”环月段圆轨道的半径、运动周期和引力常量,则可以计算出月球的密度B.“嫦娥三号”由环月段圆轨道变轨进入环月段椭圆轨道时,应让发动机点火使其加速C.“嫦娥三号”在从远月点P向近月点Q运动的过程中,加速度变大D.“嫦娥三号”在环月段椭圆轨道上P点的速度大于Q点的速度【解析】根据“嫦娥三号”环月段圆轨道的半径、运动周期和引力常量可以求出月球的质量,但是由于不知道月球的半径,故无法求出月球的密度,A错误;“嫦娥三号”由环月段圆轨道变轨进入环月段椭圆轨道时,轨道半径减小,故应让发动机点火使其减速,B 错误;“嫦娥三号”在从远月点P 向近月点Q 运动的过程中所受万有引力逐渐增大,故加速度变大,C 正确;“嫦娥三号”在环月段椭圆轨道上运动时离月球越近速度越大,故P 点的速度小于Q 点的速度,D 错误.【答案】 C变式训练1 如图所示是“嫦娥三号”奔月过程中某阶段的运动示意图,“嫦娥三号”沿椭圆轨道Ⅰ运动到近月点P 处变轨进入圆轨道Ⅱ,“嫦娥三号”在圆轨道Ⅱ上做圆周运动的轨道半径为r ,周期为T ,已知引力常量为G ,下列说法正确的是( )A .由题中(含图中)信息可求得月球的质量B .由题中(含图中)信息可求得月球的第一宇宙速度C .“嫦娥三号”在P 处变轨时必须点火加速D .“嫦娥三号”沿椭圆轨道Ⅰ运动到P 处时的加速度大于沿圆轨道Ⅱ运动到P 处时的加速度解析:万有引力提供向心力,G Mm r 2=m 4π2T 2r ,得M =4π2r 3GT 2,故A 正确;万有引力提供向心力,G Mm ′R 2=m ′v 2R ,得v =GM R ,由于不知道月球半径,所以不能求得月球的第一宇宙速度,故B 错误;椭圆轨道和圆轨道是不同的轨道,“嫦娥三号”在P 点不可能自主改变轨道,只有在减速后,才能进入圆轨道,故C 错误;“嫦娥三号”沿椭圆轨道Ⅰ运动到P 处时和沿圆轨道Ⅱ运动到P 处时,所受万有引力大小相等,所以加速度大小也相等,故D 错误.答案:A变式训练2(多选)如图所示,发射同步卫星的一般程序是:先让卫星进入一个近地的圆轨道,然后在P点变轨,进入椭圆形转移轨道(该椭圆轨道的近地点为近地圆轨道上的P点,远地点为同步卫星圆轨道上的Q点),到达远地点Q时再次变轨,进入同步卫星轨道.设卫星在近地圆轨道上运行的速率为v1,在椭圆形转移轨道的近地点P点的速率为v2,沿转移轨道刚到达远地点Q时的速率为v3,在同步卫星轨道上的速率为v4,三个轨道上运动的周期分别为T1、T2、T3,则下列说法正确的是()A.在P点变轨时需要加速,Q点变轨时要减速B.在P点变轨时需要减速,Q点变轨时要加速C.T1<T2< T3D.v2>v1>v4>v3答案:CD变式训练3发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3.轨道1、2相切于Q点,轨道2 3相切于P点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,以下说法不正确的是()A.要将卫星由圆轨道1送入圆轨道3,需要在圆轨道1的Q点和椭圆轨道2的远地点P分别点火加速一次B.由于卫星由圆轨道1送入圆轨道3点火加速两次,则卫星在圆轨道3上正常运行速度大于卫星在圆轨道1上正常运行速度C.卫星在椭圆轨道2上的近地点Q的速度一定大于7.9 k m/s,而在远地点P的速度一定小于7.9 km/sD .卫星在椭圆轨道2上经过P 点时的加速度一定等于它在圆轨道3上经过P 点时的加速度解析:从轨道1变轨到轨道2需在Q 处点火加速,从轨道2变轨到轨道3需要在P 处点火加速,故A 说法正确;根据公式GMm r 2=m v 2r 解得v =GMr ,即轨道半径越大,速度越小,故卫星在轨道3上正常运行的速度小于在轨道1上正常运行的速度,B 说法错误;第一宇宙速度是近地圆轨道环绕速度,即7.9 km/s ,轨道2上卫星在Q 点做离心运动,则速度大于7.9 km/s ,在P 点需要点火加速,则速度小于在轨道3上的运行速度,而轨道3上的运行速度小于第一宇宙速度,C 说法正确;卫星在椭圆轨道2上经过P 点时和在圆轨道3上经过P 点时所受万有引力相同,故加速度相同,D 说法正确.故选B.答案:B变式训练4 (多选)如图所示a 、b 、c 是在地球大气层外圆形轨道上运行的3颗人造卫星,下列说法正确的是( )A .b 、c 的线速度大小相等,且大于a 的线速度B .a 加速可能会追上bC .c 加速可追上同一轨道上的b ,b 减速可等到同一轨道上的cD .a 卫星由于某种原因,轨道半径缓慢减小,仍做匀速圆周运动,则其线速度将变大解析:因为b 、c 在同一轨道上运行,故其线速度大小、加速度大小均相等.又由b 、c 轨道半径大于a 轨道半径,v =GMr ,可知v b =v c <v a ,故A 错误;当a 加速后,会做离心运动,轨道会变成椭圆,若椭圆与b 所在轨道相切(或相交),且a 、b 同时来。
高一物理力学专题提升专题17卫星变轨问题

专题 17 卫星变轨问题【专题概括】当我们要从地球向天空发射不一样的卫星时,就牵涉到卫星的变轨问题,要想让卫星向高轨道运动,那 么我们就要让卫星加快做离心运动,使得卫星的运动轨道达到我们的要求,对于卫星的运动,我们第一需 要认识卫星在不一样轨道上运动的规律:卫星的向心加快度、线速度、角速度、周期与轨道半径的关系,依据万有引力供给卫星绕地球运动的 向心力,即有:GMm v 2 24π 2r2= ma n = m r = m ω r =m T 2 rGM(1) a n = r 2 , r 越大, a n 越小. (2) v =GMr ,r 越大, v 越小.GM(3) ω =r 3 ,r 越大, ω 越小.r 3 (4) T = 2π, r 越大, T 越大.GM卫星变轨:这是卫星变轨图:卫星先在较低的圆轨道1 上做圆周运动,当运动到近地址 A 时,经过点火加快,会使得卫星做离心运动,运动轨道变为了椭圆轨道2,在远地址在再次点火加快,上到预约轨道3,而后卫星绕地球再次做匀速圆周运动,这样就达到了发射卫星的目的,对于此类问题, A 和 B 的速度和加快度之间的关系:卫星在轨道 1 上经过 A 点到达轨道 2 上的 B 点时,引力做负功,所以动能减小,所以卫星在轨道1 上运转的速率大于在轨道2 上经过 B 点时的速率;因为 G心加快度大于在轨道2 上经过 B 点时的向心加快度,卫星在= ma 即 a = 卫星在轨道 2 上经过 A 点时的向 B点时,距离地球的距离同样,万有引力同样,依据牛顿第二定律,加快度同样对于地球的同步1.定义:相对于地面静止且与地球自转拥有同样周期的卫星叫地球同步卫星.2.“七个必定”的特色(1) 轨道平面必定:轨道平面与赤道平面共面. (2) 周期必定:与地球自转周期同样,即T = 24 h.(3) 角速度必定:与地球自转的角速度同样.(4) 高度必定:由G Mm2=4π 2( + ) 得地球同步卫星离地面的高度 h =3.6 ×10 7 m.R + h2m T R h速率必定: v =GM3 (5) R +h =3.1 ×10m/s.(6) 向心加快度必定:由 GMm2= ma 得 a =GM2,即同步卫星的向心加快度等+h +2=g h = 0.23 m/sRR h于轨道处的重力加快度.(7) 绕行方向必定:运转方向与地球自转方向同样.【典例精析】对于同步卫星典例 1利用三颗地点适合的地球同步卫星,可使地球赤道上随意两点之间保持无线电通信.当前,地球同步卫星的轨道半径约为地球半径的倍.假定地球的自转周期变小,若仍仅用三颗同步卫星来实现上述目的,则地球自转周期的最小值约为( )A . 1 hB . 4 hC. 8 hD. 16 h【答案】 BR卫星的轨道半径为r =sin 30 ° = 2Rr 1 3 r 23由T 1 2=T 2 2得R 3 R 324 2 =2.T2解得2≈4 h.T典例 2.( 多项选择 ) 据报导,北斗卫星导航系统利用其定位、导航等功能加入到马航MH370失联客机搜救工作,为指挥中心调动部署人力、物力供给决议依照,保证了搜救船只正确到达有关海疆,帮助搜救船只规划搜救航线,防止搜救出现遗漏海疆,当前北斗卫星导航定位系统由高度均约为36 000 km 的 5颗静止轨道卫星和 5 颗倾斜地球同步轨道卫星以及高度约为21 500 km 的 4 颗中轨道卫星组网运转,以下说法正确的是( )A.中轨道卫星的周期比同步卫星的周期大B.全部卫星均位于以地心为中心的圆形轨道上C.同步卫星和中轨道卫星的线速度均小于第一宇宙速度D.赤道上随处球自转的物体的向心加快度比同步卫星的向心加快度大【答案】 BC对于卫星的变轨典例 3:2013 年 5 月 2 日清晨 0 时 06 分,我国“中星11 号”通信卫星发射成功.“中星11 号”是一颗地球同步卫星,它主要用于为亚太地域等地区用户供给商业通服气务.图为发射过程的表示图,先将卫星发射至近地圆轨道1,而后经点火,使其沿椭圆轨道 2 运转,最后再一次点火,将卫星送入同步圆轨道3. 轨道 1、 2 相切于 Q点,轨道2、 3 相切于 P 点,则当卫星分别在1、 2、 3 轨道上正常运转时,以下说法正确的选项是( )A.卫星在轨道 3 上的速率大于在轨道 1 上的速率B.卫星在轨道 3 上的角速度大于在轨道 1 上的角速度C.卫星在轨道 1 上经过 Q点时的速度大于它在轨道2 上经过 Q点时的速度D.卫星在轨道 2 上经过 P 点时的速度小于它在轨道 3 上经过 P 点时的速度【答案】 D典例 4:发射地球同步卫星时,先将卫星发射至近地圆轨道1,而后点火,使其沿椭圆轨道 2 运转,最后再次点火,将卫星送入同步圆轨道 3. 轨道 1、 2 相切于 Q点,轨道2、 3 相切于 P 点,如下图.当卫星分别在 1、2、 3 轨道上正常运转时,设卫星在 1 轨道和 3 轨道正常运转的速度和加快度分别为v1、v3和 a1、a3,在 2 轨道经过 P 点时的速度和加快度为v2和 a2,且当卫星分别在1、2、3 轨道上正常运转时周期分别为T1、 T2、 T3,以下说法正确的选项是( )A.v1> v2> v3 B .v1> v3> v2C.a1> a2> a3 D .T1> T2> T3【答案】 B选项选项【分析】卫星在1 轨道运转速度大于卫星在 3 轨道运转速度,在 2 A 错误B 正确;卫星在 1 轨道和 3 轨道正常运转加快度 a1> a3,在C 错误.依据开普勒定律,卫星在 1、 2、 3 轨道上正常运转时周期轨道经过 P 点时的速度 v2小于 v3, 2轨道经过 P 点时的加快度 a2= a3,T1<T2<T3,选项 D错误【总结提高】( 1)变轨原由:当卫星因为某种原由速度忽然改变时(开启或封闭发动机或空气阻力作用),万有引力不再等于向心力,卫星将变轨运转。
专题强化训练二 卫星(近地、同步、极地)的宇宙航行运动规律与变轨问题

专题强化训练二:卫星(近地、同步、极地)的宇宙航行运动规律与变轨问题技巧归纳:人造卫星的变轨问题1.变轨问题概述 (1)稳定运行卫星绕天体稳定运行时,万有引力提供了卫星做圆周运动的向心力,即G Mmr 2=m v 2r .(2)变轨运行卫星变轨时,先是线速度大小v 发生变化导致需要的向心力发生变化,进而使轨道半径r 发生变化.①当卫星减速时,卫星所需的向心力F 向=m v 2r 减小,万有引力大于所需的向心力,卫星将做近心运动,向低轨道变轨.②当卫星加速时,卫星所需的向心力F 向=m v 2r 增大,万有引力不足以提供卫星所需的向心力,卫星将做离心运动,向高轨道变轨. 2.实例分析 (1)飞船对接问题①低轨道飞船与高轨道空间站对接时,让飞船合理地加速,使飞船沿椭圆轨道做离心运动,追上高轨道空间站完成对接(如图甲所示).②若飞船和空间站在同一轨道上,飞船加速时无法追上空间站,因为飞船加速时,将做离心运动,从而离开这个轨道.通常先使后面的飞船减速降低高度,再加速提升高度,通过适当控制,使飞船追上空间站时恰好具有相同的速度,如图乙所示.(2)卫星的发射、变轨问题如图发射卫星时,先将卫星发射至近地圆轨道1,在Q 点点火加速做离心运动进入椭圆轨道2,在P 点点火加速,使其满足GMmr 2=m v 2r,进入圆轨道3做圆周运动.一、单选题1.(2022·江苏省江都中学高三开学考试)据报道,一颗来自太阳系外的彗星擦火星而过。
如图所示,设火星绕太阳在圆轨道上运动,运动半径为r ,周期为T 。
该彗星在穿过太阳系时由于受到太阳的引力,轨道发生弯曲,彗星与火星在圆轨道的A 点“擦肩而过”。
已知万有引力常量G ,则( )A.可计算出火星的质量B.可计算出彗星经过A点时受到的引力C.可确定太阳分别对彗星和火星的引力在A点产生的加速度相等D.可确定彗星在A点的速度大小为2r vTπ=2.(2022·云南·昆明一中模拟预测)随着“嫦娥奔月”梦想的实现,我国不断刷新深空探测的“中国高度”。
2024年高考物理一轮复习(全国版) 第5章 专题强化7 卫星变轨问题 双星模型
例7 (多选)如图所示,质量相等的三颗星体组成三星系统,其他星体对
它们的引力作用可忽略.设每颗星体的质量均为m,三颗星体分别位于边
长为r的等边三角形的三个顶点上,它们绕某一共同的圆心O在三角形所
在的平面内以相同的角速度做匀速圆周运动.已知引力常量为G,下列说
法正确的是
A.每颗星体所需向心力大小为
m2 2G r2
1.双星模型
(1)定义:绕公共圆心转动的两个星体组成的系统,我们
称之为双星系统.如图所示.
(2)特点
①
各
自
所需的
向
心
力
由
彼此间
的
万
有
引力提
供
,
即
Gm1m2 L2
=
m1ω12r1
,
GmL12m2=m2ω22r2.
②两星的周期、角速度相同,即T1=T2,ω1=ω2.
③两星的轨道半径与它们之间的距离关系为r1+r2=L.
例4 北京时间2021年10月16日神舟十三号载人飞船与在轨飞行的天和核心舱 顺利实现径向自主交会对接,整个交会对接过程历时约6.5小时.为实现神舟十 三号载人飞船与空间站顺利对接,飞船安装有几十台微动力发动机,负责精 确地控制它的各种转动和平动.对接前飞船要先到达和空间站很近的相对静止 的某个停泊位置(距空间站200 m).为到达这个位置,飞船由惯性飞行状态转入 发动机调控状态,下列说法正确的是 A.飞船先到空间站同一圆周轨道上同方向运动,合适位置减速靠近即可 B.飞船先到与空间站圆周轨道垂直的同半径轨道上运动,合适位置减速靠近即可 C.飞船到空间站轨道下方圆周轨道上同方向运动,合适的位置减速即可
①G2Rm22+GRM2m=ma 向 ②GLm2 2×cos 30°×2=ma 向
高中物理人教版《必修第二册》教案讲义:卫星的变轨问题及宇宙航行的几个问题辨析

人造卫星的发射过程要经过多次变轨方可到达预定轨道,在赤道上顺着地球自转方向发射卫星到圆点点火加速,速度变大,进入椭圆轨道Ⅱ再次点火加速进入圆轨道Ⅲ卫星变轨问题分析方法速度大小的分析方法.①卫星做匀速圆周运动经过某一点时,其速度满足以此为依据可分析卫星在两个不同圆轨道上的②卫星做椭圆运动经过近地点时,卫星做离心运动,m v2.以此为依据可分析卫星沿椭圆轨r道和沿圆轨道通过近地点时的速度大小(即加速离心.发射“嫦娥三号”的速度必须达到第三宇宙速度.在绕月圆轨道上,卫星周期与卫星质量有关.卫星受月球的引力与它到月球中心距离的平方成反比.在绕月轨道上,卫星受地球的引力大于受月球的引力明白第三宇宙速度是指被发射物体能够脱离太阳系的最小发射速度,而“嫦娥三号”没有脱离太阳的引力范要熟记万有引力的表达式并清楚是万有引力提供卫星做圆如图所示,发射同步卫星的一般程序是:先让卫星进入一个近地的圆轨道,然后在P点变轨,进入椭圆形转移轨道椭圆轨道的近地点为近地圆轨道上的P点,远地点为同步卫星圆,到达远地点Q时再次变轨,进入同步卫星轨设卫星在近地圆轨道上运行的速率为v1,在椭圆形转移轨道点的速率为v2,沿转移轨道刚到达远地点,在同步卫星轨道上的速率为v4,则下列说法正确的是点变轨时需要加速,Q点变轨时要减速点变轨时需要减速,Q点变轨时要加速D.v2>v1>v4>v3练2发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火使其沿椭圆轨道2运行,最后再次点火将卫星送入同步圆轨道3,轨道1、2相切于Q点,轨道2、3相切于P点,如图所示,卫星分别在1、2、3轨道上正常运行时,以下说法正确的是()A.卫星在轨道3上的运行速率大于在轨道1上的运行速率B.卫星在轨道3上的角速度大于在轨道1上的角速度C.卫星在轨道1上运动一周的时间大于它在轨道2上运动一周的时间D.卫星在轨道2上经过P点时的加速度等于它在轨道3上经过P点时的加速度反思总结卫星变轨问题关键词转化二、有关宇宙航行的几个问题辨析辨析1.发射速度与运行速度的比较(1)发射速度在地面以某一速度发射一个物体,发射后不再对物体提供动力,在地面离开发射装置时的速度称为发射速度,三个宇宙速度都是指发射速度.(2)运行速度运行速度是指做圆周运动的人造卫星稳定飞行时的线速度,对于人造地球卫星,轨道半径越大,则运行速度越小.(3)有的同学这样认为:沿轨道半径较大的圆轨道运行的卫星的发射速度大,发射较为困难;而轨道半径较小的卫星发射速度小,发射较为容易.这种观点是片面的.因为高轨卫星的发射难易程度与发射速度没有多大关系,如果我们在地面上以7.9km/s 的速度水平发射一个物体,则这个物体可以贴着地面做圆周运动而不落到地面;如果速度增大,则会沿一个椭圆轨道运动.速度越大,椭圆轨道的半长轴就越大;如果这个速度达到11.2km/s,则这个物体可以摆脱地球的引力.可见,无论以多大速度发射一个物体或卫星,都不会使之成为沿较大的圆轨道做圆周运动的人造卫星,高轨卫星的发射过程是一个不断加速变轨的过程,并不是在地面上给一个发射速度就可以的.【典例2】(多选)如图所示,在发射地球同步卫星的过程中,卫星首先进入椭圆轨道Ⅰ,然后在Q点通过改变卫星速度,让卫星进入地球同步轨道Ⅱ,则()A.该卫星的发射速度必定大于11.2km/sB.卫星在同步轨道Ⅱ上的运行速度大于7.9km/sC.在椭圆轨道上,卫星在P点的速度大于在Q点的速度D.卫星在Q点通过加速实现由轨道Ⅰ进入轨道Ⅱ辨析2.分清三个不同(1)重力和万有引力的向心加速度等于重力加速度g 的运动周期有可能是20小时如图所示,地球赤道上的山丘e,近地资源卫星均在赤道平面上绕地心做匀速圆周运动.设、v3,向心加速度分别为v2<v33<a2已知地球赤道上的物体随地球自转的线速度大小为近地卫星线速度大小为,地球同步卫星线速度大小为设近地卫星距地面高度不计,同步卫星距地面高度约为地倍.则下列结论正确的是(。
专题 卫星的变轨问题(课件)高中物理(人教版2019必修第二册)

由于在地球表面附近大气稠密,对火箭的阻力很大,为了尽快离开大气层,
通常采用垂直向上发射;垂直发射的另一个优点有时要在适当的位
置短时间启动卫星上的
发动机,使卫星的速度
发生突变,让其运行轨
道发生改变,最终到达
于动力飞行状态,要消耗大量燃料。如果发射同步卫星,还必须在赤道上
建立发射场,有一定局限性。
变轨发射(即近地发射):运载火箭消耗的燃料少,发射场的位置也不
受限制。目前,各国发射同步卫星都采用第二种方法,但这种方法在操
作和控制上都比较复杂。
发射人造地球卫星的运载火箭一般分为三级,其发射后的飞行过程大致包括
2
向前点火减速
Mm
v
G 2 m
r
r
近心运动
三、变轨过程1——低轨到高轨
低圆轨道(Ⅰ)——P点加速(向后喷气)
Ⅲ
Ⅱ
P
v1
v2
·
Ⅰ
离心运动
v4
v3
Q
椭圆转移轨道(Ⅱ)——Q点加速(向后喷气)
离心运动
高圆轨道(Ⅲ)
3
使卫星加速到v 2
切点Q
切点P
2
mv 2
Mm
使
G 2
R
R
v4
2
v3
1
加速
v1
v2>v1
度的大小关系是(
)
P
1
2
3
Q
)所以VQ2与VQ3速
问题4、卫星在1轨道和3轨道做的都是圆周运动,所以根据“高轨低速长周期”,得
Vp1与VQ3的速度大小关系是(
)
问题5、综合以上分析得出卫星在轨道上各点速度的大小关系(
第五章 第3课时 专题强化:卫星变轨问题 双星模型-2025年高中物理大一轮复习

第3课时专题强化:卫星变轨问题双星模型目标要求 1.会处理人造卫星的变轨和对接问题。
2.掌握双星、多星系统,会解决相关问题。
3.会应用万有引力定律解决星球“瓦解”和黑洞问题。
考点一卫星的变轨和对接问题1.卫星发射模型(1)为了节省能量,在赤道上顺着地球自转方向先发射卫星到圆轨道Ⅰ上,卫星在轨道Ⅰ上做匀速圆周运动,有G Mmr12=mv2r1,如图所示。
(2)在A点(近地点)点火加速,由于速度变大,所需向心力变大,G Mmr12<mv A2r1,卫星做离心运动进入椭圆轨道Ⅱ。
(3)在椭圆轨道B点(远地点),G Mmr22>mv B2r2,将做近心运动,再次点火加速,使GMmr22=mv B′2r2,进入圆轨道Ⅲ。
思考若使在轨道Ⅲ运行的宇宙飞船返回地面,应如何操作?________________________________________________________________________2.变轨过程分析(1)速度:设卫星在圆轨道Ⅰ和Ⅲ上运行时的速率分别为v1、v3,在椭圆轨道Ⅱ上过A点和B 点时速率分别为v A、v B,四个速度关系为v A>v1>v3>v B。
(2)向心加速度在A 点,轨道Ⅰ上和轨道Ⅱ上的向心加速度关系a ⅠA ________a ⅡA ,在B 点,轨道Ⅱ上和轨道Ⅲ上的向心加速度关系a ⅡB ________a ⅢB ,A 、B 两点向心加速度关系a A ________a B 。
(均选填“>”“=”或“<”)(3)周期卫星在Ⅰ、Ⅱ、Ⅲ轨道上的运行周期T 1、T 2、T 3的关系为T 1<T 2<T 3。
(4)机械能在一个确定的圆(椭圆)轨道上机械能______。
若卫星在Ⅰ、Ⅱ、Ⅲ轨道的机械能分别为E 1、E 2、E 3,从轨道Ⅰ到轨道Ⅱ和从轨道Ⅱ到轨道Ⅲ都需要点火加速,则机械能关系为____________。
专题强化一:卫星变轨问题和双星问题—人教版高中物理必修二课件

后飞船逐渐靠近空间实验室,两者速度接近时实现对接 D.飞船先在比空间实验室轨道半径小的轨道上减速,减速
后飞船逐渐靠近空间实验室,两者速度接近时实现对接
第六章专题强化一:卫星变轨问题和 双星问 题—人 教版高 中物理 必修二 课件 (共17张PPT)
√B.沿轨道Ⅰ运行的周期小于沿轨道Ⅱ运行的周期
C.沿轨道 Ⅰ 运行时,在A点的加速度小于在B点的加速度 D.在轨道 Ⅰ 上由A点运行到B点的过程,速度逐渐增大
第六章专题强化一:卫星变轨问题和 双星问 题—人 教版高 中物理 必修二 课件 (共17张PPT)
第六章专题强化一:卫星变轨问题和 双星问 题—人 教版高 中物理 必修二 课件 (共17张PPT)
一、人造卫星的变轨问题
2.实例分析 (1)飞船对接问题 飞船与在轨空间站对接 先使飞船位于较低轨道上,然后让飞船合理地加速,使飞船沿 椭圆轨道做离心运动,追上高轨道飞船完成对接(如图甲所示). 注意:若飞船和空间站在同一轨道上,飞船加速时无法追上空 间站,因为飞船加速时,将做离心运动,从而离开这个轨道. 通常先使后面的飞船减速降低高度,再加速提升高度,通过适 当控制,使飞船追上空间站时恰好具有相同的速度,如图乙.
D.在轨道Ⅱ上经过A的加速度小于在轨道Ⅰ上经过A的加速度
第六章专题强化一:卫星变轨问题和 双星问 题—人 教版高 中物理 必修二 课件 (共17张PPT)
第六章专题强化一:卫星变轨问题和 双星问 题—人 教版高 中物理 必修二 课件 (共17张PPT)
达标检测
1.(卫星变轨问题)2019年春节期间,中国科幻电影里程碑的作品《流浪地球》热播, 影片中为了让地球逃离太阳系,人们在地球上建造特大功率发动机,使地球完成一 系列变轨操作,其逃离过程如图所示,地球在椭圆轨道 Ⅰ 上运行到远日点B变轨, 进入圆形轨道 Ⅱ.在圆形轨道 Ⅱ 上运行到B点时再次加速变轨,从而最终摆脱太阳 束缚.对于该过程,下列说法正确的是 A.沿轨道 Ⅰ 运动至B点时,需向前喷气减速才能进入轨道 Ⅱ
高中物理必修二 新教材 讲义 第7章 专题强化 卫星的变轨和双星问题

专题强化卫星的变轨和双星问题[学习目标] 1.知道卫星变轨的原因,会分析卫星变轨前后的物理量变化(重难点)。
2.知道航天器的对接问题的处理方法(重难点)。
3.掌握双星运动的特点,会分析双星的相关问题(重点)。
一、卫星的变轨问题如图是飞船从地球上发射到绕月球运动的飞行示意图。
(1)从绕地球运动的轨道上进入奔月轨道,飞船应采取什么措施?为什么?(2)从奔月轨道进入月球轨道,又应采取什么措施?为什么?________________________________________________________________________________________________________________________________________________1.变轨过程(1)为了节省能量,在赤道上顺着地球自转方向发射卫星到圆轨道Ⅰ上,如图所示。
(2)在A点(近地点)点火________(选填“加”或“减”)速,由于速度变________,万有引力不足以提供卫星在轨道Ⅰ上做圆周运动所需的向心力,卫星做离心运动进入椭圆轨道Ⅱ。
(3)在B点(远地点)再次点火________(选填“加”或“减”)速进入圆轨道Ⅲ。
2.变轨过程各物理量分析(1)两个不同轨道的“切点”处线速度v不相等,图中vⅢ____vⅡB,vⅡA____vⅠ(均选填“>”“<”或“=”)。
(2)同一个椭圆轨道上近地点和远地点线速度大小不相等,从远地点到近地点线速度逐渐________。
(3)两个不同轨道上的线速度v不相等,轨道半径越大,v越________,图中vⅠ____vⅢ(选填“>”“<”或“=”)。
(4)不同轨道上运行周期T不相等。
根据开普勒第三定律a3T2=k知,内侧轨道的周期__________外侧轨道的周期,图中TⅠ<TⅡ<TⅢ。
(5)两个不同轨道的“切点”处加速度a相同,图中aⅢ=aⅡB,aⅡA=aⅠ。
人造卫星的发射过程要一般要经过多次变轨方可到达预定轨道
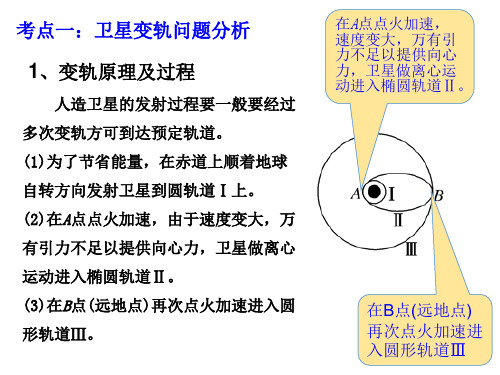
在A点点火加速,
速度变大,万有引 力不足以提供向心 力,卫星做离心运
动进入椭圆轨道Ⅱ。
在B点(远地点) 再次点火加速进 入圆形轨道Ⅲ
2、三个运行物理量的大小比较
(1)速度大小比较:设卫星在
圆轨道Ⅰ和Ⅲ上运行时的速率
分别为v1、v3,在轨道Ⅱ上过A 点和B点速率分别为vA、vB 。在 A点加速,则vA>v1 ,在B点加 速,则v3>vB,又因v1>v3,故 有 vA>v1>v3>vB 。
勒第三定律
可知:
T1<T2<T3
T1<T2<T3
T2 T3
例题:(多选)发射地球同步卫星时,先将卫星发射至近地圆轨道1, 然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入
同步圆轨道3,P点和Q点为切点,设卫星在1轨道和3轨道正常运 行的速度和加速度分别为v1、v3和a1、a3,在2轨道经过P点时的 速度和加速度为v2和a2,且当卫星分别在1、2、3轨道上正常运 行时周期分别为T1、T2 、T3,以下说法正确的是( BD )
关,由飞船到火星中心的距离决定,故 C 错误;由
GMr2m=m4Tπ22·r 可得:T=
4GπM2r3,可见飞船在轨道Ⅰ上运
动的周期与中心天体的质量也有关,B 错误。
答案:D
练习3.(多选)(2014年佛山一模)2013年12月,“嫦娥三号”经 过地月转移轨道在P点调整后进入环月圆轨道1,进一步调整后 进入环月椭圆轨道2.如图 4-4-3,有关“嫦娥三号”下列说 法正确的是( BD ) A.在地球的发射速度一定大于第二宇宙速度 B.由轨道1进入轨道2需要在P点处减速 C.在轨道2经过P点时速度大于Q点速率 D.分别由轨道1与轨道2经P点时,向心加速度相同
专题 卫星的变轨问题和追及相遇问题 高一物理(人教版2019)(解析版)

专题11 卫星的变轨问题和追及相遇问题一、卫星的变轨问题1.2018年5月21日5点28分,在我国西昌卫星发射中心,由中国航天科技集团有限公司抓总研制的嫦娥四号中继星“鹊桥”搭乘长征四号丙运载火箭升空。
卫星由火箭送入近地点约200公里、远地点约40万公里的地月转移轨道1。
在远地点40万公里处点火加速,由椭圆轨道变成高度为40万公里的圆轨道2,在此圆轨道上飞船运行周期等于月球公转周期。
下列判断正确的是( )A .卫星在轨道1的运行周期大于在轨道2的运行周期B .卫星在圆轨道2的P 点向心加速度小于轨道1上的P 点向心加速度C .卫星在此圆轨道2上运动的角速度等于月球公转运动的角速度D .卫星变轨前通过椭圆轨道远地点时的加速度大于变轨后沿圆轨道运动的加速度 【答案】C【解析】A .由开普勒第三定律得33122212R R T T 轨道1的半长轴小于轨道2的半径,故卫星在轨道1的运行周期小于在轨道2的运行周期,A 错误;BD .根据牛顿第二定律,万有引力提供向心力,提供卫星的向心加速度,同一位置,万有引力一定,向心加速度相等,卫星变轨前通过椭圆轨道远地点时的加速度等于变轨后沿圆轨道运动的加速度BD 错误;C .圆轨道2上飞船运行周期等于月球公转周期,故卫星在此圆轨道2上运动的角速度等于月球公转运动的角速度,C 正确。
故选C 。
2.如图所示,“嫦娥一号”探月卫星进入月球轨道后,首先在椭圆轨道Ⅰ上运动,P 、Q 两点是轨道Ⅰ的近月点和远月点,Ⅰ是卫星绕月做圆周运动的轨道,轨道Ⅰ和Ⅰ在P 点相切,关于该探月卫星的运动,下列说法正确的是( )A .卫星在轨道Ⅰ上运动周期大于在轨道Ⅰ上运动的周期B .卫星由轨道Ⅰ进入轨道Ⅰ必须要在P 点加速C .卫星在轨道Ⅰ上运动时,P 点的速度小于Q 点的速度D .卫星在轨道Ⅰ上运动时,P 点的加速度小于Q 点的加速度 【答案】A【解析】A .根据开普勒第三定律可知,卫星在轨道Ⅰ上运动周期大于在轨道Ⅰ上运动的周期,故A 正确;B .卫星由轨道Ⅰ进入轨道Ⅰ必须要在P 点减速,做近心运动,故B 错误;C .根据开普勒第二定律,卫星在轨道Ⅰ上运动时,近地点P 点的速度大于远地点Q 点的速度,故C 错误;D .卫星在轨道Ⅰ上运动时,根据2MmG ma R ,P 点的加速度大于Q 点的加速度,故D 错误。
高一物理【人造卫星的发射、变轨问题】专题

高一物理【人造卫星的发射、变轨问题】专题1.卫星发射及变轨过程概述人造卫星的发射过程要经过多次变轨方可到达预定轨道,如图所示。
(1)为了节省能量,在赤道上顺着地球自转方向发射卫星到圆轨道Ⅰ上。
(2)在A点(近地点)点火加速,由于速度变大,万有引力不足以提供卫星在轨道Ⅰ上做匀速圆周运动的向心力,卫星做离心运动进入椭圆轨道Ⅱ。
(3)在B点(远地点)再次点火加速进入圆形轨道Ⅲ。
2.三个运行物理量的大小比较(1)速度:设卫星在圆轨道Ⅰ和Ⅲ上运行时的速率分别为v1、v3,在轨道Ⅱ上过A点和B 点速率分别为v A、v B。
在A点加速,则v A>v1,在B点加速,则v3>v B,又因v1>v3,故有v A>v1>v3>v B。
(2)加速度:因为在A点,卫星只受到万有引力作用,故不论从轨道Ⅰ还是轨道Ⅱ上经过A点,卫星的加速度都相同,同理,经过B点加速度也相同。
(3)周期:设卫星在Ⅰ、Ⅱ、Ⅲ轨道上运行周期分别为T1、T2、T3,轨道半径分别为r1、r2(半长轴)、r3,由开普勒第三定律r3T2=k可知T1<T2<T3。
我国正在进行的探月工程是高新技术领域的一次重大科技活动,在探月工程中飞行器成功变轨至关重要。
如图所示,假设月球半径为R,月球表面的重力加速度为g0,飞行器在距月球表面高度为3R的圆形轨道Ⅰ上运动,到达轨道的A点点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动,则()A.飞行器在B点处点火后,速度增加B.由已知条件不能求出飞行器在轨道Ⅱ上的运行周期C.在只有万有引力作用的情况下,飞行器在轨道Ⅱ上通过B点的加速度大于在轨道Ⅲ上通过B点的加速度D.飞行器在轨道Ⅲ上绕月球运行一周所需的时间为2πR g0[解析]在椭圆轨道近月点变轨成为圆轨道,要实现变轨应给飞行器点火减速,减小所需的向心力,故点火后速度减小,故A错误;设飞行器在近月轨道Ⅲ绕月球运行一周所需的时间为T 3,则mg 0=mR 4π2T 32,解得T 3=2π R g 0,根据几何关系可知,轨道Ⅱ的半长轴a =2.5R ,根据开普勒第三定律a 3T2=k 以及飞行器在轨道Ⅲ上的运行周期,可求出飞行器在轨道Ⅱ上的运行周期,故B 错误,D 正确;在只有万有引力作用的情况下,飞行器在轨道Ⅱ上通过B 点的加速度与在轨道Ⅲ上通过B 点的加速度相等,故C 错误。
(完整版)人造卫星变轨问题

人造卫星变轨问题一、人造卫星基本原理绕地球做匀速圆周运动的人造卫星所需向心力由万有引力提供。
轨道半径r 确定后,与之对应的卫星线速度r GM v =、周期GMr T 32π=、向心加速度2r GM a =也都是确定的。
如果卫星的质量也确定,一旦卫星发生变轨,即轨道半径r 发生变化,上述物理量都将随之变化。
同理,只要上述物理量之一发生变化,另外几个也必将随之变化。
在高中物理中,会涉及到人造卫星的两种变轨问题。
二、渐变由于某个因素的影响使卫星的轨道半径发生缓慢的变化(逐渐增大或逐渐减小),由于半径变化缓慢,卫星每一周的运动仍可以看做是匀速圆周运动。
解决此类问题,首先要判断这种变轨是离心还是向心,即轨道半径是增大还是减小,然后再判断卫星的其他相关物理量如何变化。
如:人造卫星绕地球做匀速圆周运动,无论轨道多高,都会受到稀薄大气的阻力作用。
如果不及时进行轨道维持(即通过启动星上小型火箭,将化学能转化为机械能,保持卫星应具有的速度),卫星就会自动变轨,偏离原来的圆周轨道,从而引起各个物理量的变化。
由于这种变轨的起因是阻力,阻力对卫星做负功,使卫星速度减小,所需要的向心力r mv 2减小了,而万有引力大小2r GMm 没有变,因此卫星将做向心运动,即半径r 将减小。
由㈠中结论可知:卫星线速度v 将增大,周期T 将减小,向心加速度a 将增大。
三、突变由于技术上的需要,有时要在适当的位置短时间启动飞行器上的发动机,使飞行器轨道发生突变,使其到达预定的目标。
如:发射同步卫星时,通常先将卫星发送到近地轨道Ⅰ,使其绕地球做匀速圆周运动,速率为v 1,第一次在P 点点火加速,在短时间内将速率由v 1增加到v 2,使卫星进入椭圆形的转移轨道Ⅱ;卫星运行到远地点Q 时的速率为v 3,此时进行第二次点火加速,在短时间内将速率由v 3增加到v 4,使卫星进入同步轨道Ⅲ,绕地球做匀速圆周运动。
第一次加速:卫星需要的向心力r mv 2增大了,但万有引力2rGMm 没变,因此卫星将开始做离心运动,进入椭圆形的转移轨道Ⅱ。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人造卫星变轨问题专题
(一)人造卫星基本原理
绕地球做匀速圆周运动的人造卫星所需向心力由万有引力
半径发生缓慢的变化(逐渐增大或逐渐减小),由于半径变化缓慢,卫星每一周的运动仍可以看做是匀速圆周运动。
解决此类问题,首先要判断这种变轨是离心还是向心,即轨
道半径r是增大还是减小,然后再判断卫星的其他相关物理量如
何变化。
1)人造卫星绕地球做匀速圆周运动,无论轨道多高,都会受到
为什么卫星克服阻力做功,动能反而增加了呢?这是因为一旦轨道半径减小,在卫星克服阻力做功的同时,万有引力(即重力)将对卫星做正功。
而且万有引力做的正功远大
于克服空气阻力做的功,外力对卫星做的总功是正的,因此卫星动能增加。
根据E机=E k+E p,该过程重力势能的减少总是
大于动能的增加。
道Ⅱ;卫星运行到远地点Q时的速率为v3;此时进行第二次点火加速,在短时间内将速率由v3增加到v4,使卫星进入同步轨道Ⅲ,绕地球做匀速圆周运动。
例题
1.某人造卫星运动的轨道可近似看作是以地心为中心的圆.由
于阻力作用,人造卫星到地心的距离从r1慢慢变到r2,用
C.从同一轨道上加速D.从任意轨道上加速
3.航天飞机在完成对哈勃太间望远镜的维修任务后,在A点短
B为轨道Ⅱ上的一点,如图所示。
下列说法中正确的有
A.在轨道Ⅱ上经过A的机械能大于经过B的机械能
B.在A点短时间开动发动机后航天飞机的动能增大了
D.飞船变轨前通过椭圆轨道远地点时的加速度大于变轨后沿
圆轨道运动的加速度
1.B
2.BCA
3.C
4.C。
