机械振动课后习题和答案第三章习题和答案
第3章 多自由度机械振动系统 作业答案
⎤ ⎡ x1 ⎤ ⎡ p1 ( t ) ⎤ ⎢x ⎥ = ⎢ p t ⎥ − k3 ⎥ ⎥ ⎢ 2 ⎥ ⎢ 2 ( )⎥ k3 + k 4 ⎥ ⎦⎢ ⎣ x3 ⎥ ⎦ ⎢ ⎣ p3 ( t ) ⎥ ⎦ 0
d ∂T ∂T ∂U ∂D ( )− + + = Qi i ∂qi ∂qi ∂q i dt ∂q
2、拉格朗日法：
1 1 2 12 + m2 x 2 T = m1 x 2 2
U=
1 2 1 1 2 ⎤ k1 x1 + k2 (2 x2 − x1 ) 2 = ⎡ (k1 + k2 ) x12 + 4k2 x1 x2 + 4k2 x2 ⎣ ⎦ 2 2 2
Dr. Rong Guo
School of automotive studies, tongji university
⎡ k1r 2 K =⎢ 2 ⎣ − k1r
⎡3 2 ⎢ 2 Mr ⎢ ⎢ 0 ⎢ ⎣ 0
⎤ ⎥ ( k1 + k2 ) r 2 ⎦ − k1r 2
− k1r 2 ⎤ ⎡θ1 ⎤ ⎡0 ⎤ ⎥⎢ ⎥ = ⎢ ⎥ θ 2 ⎦ ⎣0 ⎦ ( k1 + k2 ) r 2 ⎦ ⎣
⎤ ⎤ ⎡ k1r 2 ⎥ ⎡θ ⎥ ⎢ 1 ⎥ + ⎢ 3 −k r 2 θ Mr 2 ⎥ ⎣ 2 ⎦ ⎣ 1 ⎥ ⎦ 2
x1 2l + k1 x1 2l + m2 x2l = 0 ⎧m1 ⎨ ⎩m2 x2l + k2 ( 2 x2 − x1 ) 2l = 0 x1 + m2 x2l + 2k1 x1 = 0 ⎧2m1 ⎨ x2 − 2k2 x1 + 4k2 x2 = 0 ⎩ m2 ⎡ 2m1 ⎢ 0 ⎣ m2 ⎤ ⎡ x1 ⎤ ⎡ 2k1 ⎢ ⎥ + ⎢ −2 k m2 ⎥ x 2 ⎦⎣ 2⎦ ⎣ 0 ⎤ ⎡ x1 ⎤ ⎡0 ⎤ ⎢ x ⎥ = ⎢0 ⎥ 4k 2 ⎥ ⎦⎣ 2⎦ ⎣ ⎦
机械振动基础课后习题解答_第3章习题
m
0
0 m
u1 u2
3k k
k 3k
u1 u2
2ku0
sin 0
t
K
2M
3k
2m
k
k
3k 2m
H11 ( )
3k 2m ()
H 21 ( )
k ()
u1(t) u2 (t)
H11 ( ) H21()
2ku0
sin
t
3k 为反共振频率 m
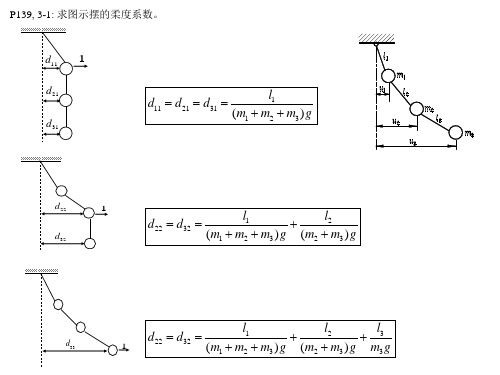
P140,3-9: 图示系统初始静止，求左端基础产生阶跃位移u0后系统的响应。
ml2 1 0 M 3 0 7 /16
K
l2k 16
9 9
9
13
| K 2M | 0
1 0.65
k m
2 2.62
k m
P139,3-3: 建立图示系统的运动微分方程，并求当ki k,i 1, 6, m1 m, m2 2m, m3 m时的固有 频率和固有振型。
m1
M
m2
u2
c
3c
2c
u2
k
3k
2k
u2
0
m u3 0 2c 2c u3 0 2k 2k u3 f0
1 0,2
k m
, 3
2k m
1 1 1
φ1
1 , φ2
0
, φ3
1
1
1/ 2
1
u1 1
u2
1
u3 1
1 0 1/ 2
1 q1
1
q2
1 q3
)d
u0 2
(1 cos1t)
q2
(t)
u0 2
(1
cos 2t )
机械振动-课后习题和答案--第三章-习题和答案
整理3.1 如图所示扭转系统。
设12122;t t I I k k ==1．写出系统的刚度矩阵和质量矩阵；2．写出系统的频率方程并求出固有频率和振型，画出振型图。
解：1)以静平衡位置为原点，设12,I I 的转角12,θθ为广义坐标，画出12,I I 隔离体，根据牛顿第二定律得到运动微分方程：111121222221()0()0t t t I k k I k θθθθθθθ⎧++-=⎪⎨+-=⎪⎩，即：1112122222122()0t t t t t I k k k I k k θθθθθθ⎧++-=⎪⎨-+=⎪⎩所以：[][]12212220,0t t t t t k k k I M K k k I +-⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦系统运动微分方程可写为：[][]11220M K θθθθ⎧⎫⎧⎫⎪⎪+=⎨⎬⎨⎬⎪⎪⎩⎭⎩⎭………… (a)或者采用能量法：系统的动能和势能分别为θθ=+2211221122T E I I整理θθθθθθθ=+-=++-222211212121221121111()()2222t t t t t t U k k k k k k 求偏导也可以得到[][],M K由于12122;t t I I k k ==，所以[][]212021,0111t M I K k -⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦2)设系统固有振动的解为： 1122cos u t u θωθ⎧⎫⎧⎫=⎨⎬⎨⎬⎩⎭⎩⎭，代入（a ）可得：[][]122()0u K M u ω⎧⎫-=⎨⎬⎩⎭………… (b)得到频率方程：22121211222()0t t t t k I k k k I ωωω--==-- 即：224222121()240t tI k I k ωωω=-+=解得：211,222(22t kI ω==所以：1ω=<2ω= ………… (c)将（c ）代入（b ）可得：整理112121211122(22)2220(22t t t t tt k k I k I u u k k k I I ⎡⎤±--⎢⎥⎧⎫⎢⎥=⎨⎬⎢⎥⎩⎭⎢⎥--⎢⎥⎣⎦解得：11212u u =-；12222u u = 令21u =，得到系统的振型为：-0.70710.7071整理3.2 求图所示系统的固有频率和振型。
大学物理(第四版)课后习题及答案 机械振动
大学物理(第四版)课后习题及答案机械振动13 机械振动解答13-1 有一弹簧振子，振幅A=2.0×10-2m，周期T=1.0s，初相ϕ=3π/4。
试写出它的运动方程，并做出x--t图、v--t 图和a--t图。
13-1分析弹簧振子的振动是简谐运动。
振幅A、初相ϕ、角频率ω是简谐运动方程x=Acos(ωt+ϕ)的三个特征量。
求运动方程就要设法确定这三个物理量。
题中除A、ϕ已知外，ω可通过关系式ω=2π确定。
振子运动的速度T和加速度的计算仍与质点运动学中的计算方法相同。
解因ω=2π，则运动方程 T⎛2πt⎛x=Acos(ωt+ϕ)=Acos t+ϕ⎛⎛T⎛根据题中给出的数据得x=(2.0⨯10-2m)cos[(2πs-1)t+0.75π]振子的速度和加速度分别为v=dx/dt=-(4π⨯10-2m⋅s-1)sin[(2πs-1)t+0.75π] a=d2x/dt2=-(8π2⨯10-2m⋅s-1)cos[(2πs-1)t+0.75πx-t、v-t及a-t图如图13-l所示π⎛⎛13-2 若简谐运动方程为x=(0.01m)cos⎛(20πs-1)t+⎛，求：（1）振幅、频率、角频率、周期和4⎛⎛初相；（2）t=2s 时的位移、速度和加速度。
13-2分析可采用比较法求解。
将已知的简谐运动方程与简谐运动方程的一般形式x=Acos(ωt+ϕ)作比较，即可求得各特征量。
运用与上题相同的处理方法，写出位移、速度、加速度的表达式，代入t值后，即可求得结果。
解（l）将x=(0.10m)cos[(20πs-1)t+0.25π]与x=Acos(ωt+ϕ)比较后可得：振幅A= 0.10 m，角频率ω=20πs-1，初相ϕ=0.25π，则周期T=2π/ω=0.1s，频率ν=1/T=10Hz。
（2）t= 2s时的位移、速度、加速度分别为x=(0.10m)cos(40π+0.25π)=7.07⨯10-2m v=dx/dt=-(2πm⋅s-1)sin(40π+0.25π)a=d2x/dt2=-(40π2m⋅s-2)cos(40π+0.25π)13-3 设地球是一个半径为R的均匀球体，密度ρ5.5×103kg•m。
机械振动课后习题集和规范标准答案第三章习题集和标准答案
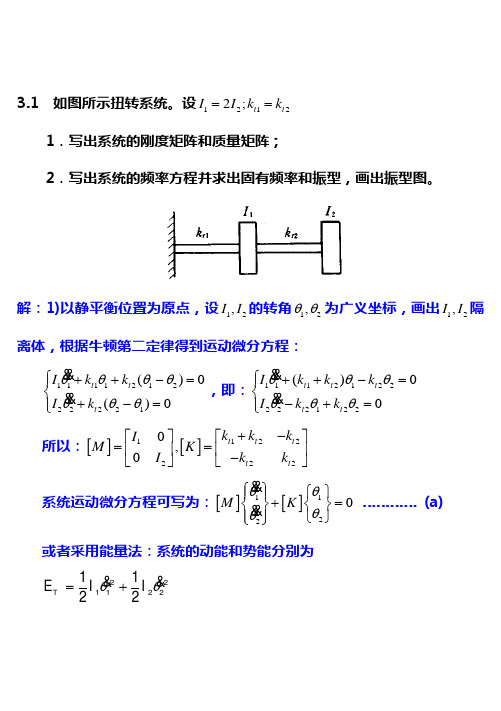
3.1 如图所示扭转系统。
设12122;t t I I k k ==1．写出系统的刚度矩阵和质量矩阵；2．写出系统的频率方程并求出固有频率和振型，画出振型图。
解：1)以静平衡位置为原点，设12,I I 的转角12,θθ为广义坐标，画出12,I I 隔离体，根据牛顿第二定律得到运动微分方程：111121222221()0()0t t t I k k I k θθθθθθθ⎧++-=⎪⎨+-=⎪⎩&&&&，即：1112122222122()00t t t t t I k k k I k k θθθθθθ⎧++-=⎪⎨-+=⎪⎩&&&&所以：[][]12212220,0t t t t t k k k IM K k k I +-⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦系统运动微分方程可写为：[][]11220M K θθθθ⎧⎫⎧⎫⎪⎪+=⎨⎬⎨⎬⎪⎪⎩⎭⎩⎭&&&& ………… (a)或者采用能量法：系统的动能和势能分别为θθ=+&&2211221122T E I Iθθθθθθθ=+-=++-222211212121221121111()()2222t t t t t t U k k k k k k 求偏导也可以得到[][],M K由于12122;t t I I k k ==，所以[][]212021,0111t M I K k -⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦2)设系统固有振动的解为： 1122cos u t u θωθ⎧⎫⎧⎫=⎨⎬⎨⎬⎩⎭⎩⎭，代入（a ）可得：[][]122()0u K M u ω⎧⎫-=⎨⎬⎩⎭………… (b)得到频率方程：22121211222()0t t t t k I k k k I ωωω--==--V即：224222121()240t t I k I k ωωω=-+=V解得：211,222(22t k I ω±==所以：1ω=<2ω= ………… (c)将（c ）代入（b ）可得：112121211122(22220(22t t t t t t k k I k I u u k k k I I ⎡⎤±--⎢⎥⎧⎫⎢⎥=⎨⎬⎢⎥⎩⎭⎢⎥--⎢⎥⎣⎦g g g解得：11212u u =-；12222u u = 令21u =，得到系统的振型为：-0.70710.70713.2 求图所示系统的固有频率和振型。
机械振动习题和答案解析
《机械振动噪声学》习题集1－1 阐明下列概念，必要时可用插图。
(a) 振动；(b) 周期振动和周期；(c) 简谐振动。
振幅、频率和相位角。
1－2 一简谐运动，振幅为0.20 cm，周期为0.15 s，求最大的速度和加速度。
1－3 一加速度计指示结构谐振在82 Hz 时具有最大加速度50 g，求其振动的振幅。
1－4 一简谐振动频率为10 Hz，最大速度为4.57 m/s，求其振幅、周期和最大加速度。
1－5 证明两个同频率但不同相位角的简谐运动的合成仍是同频率的简谐运动。
即：A cos ωn t +B cos (ωn t + φ) =C cos (ωn t + φ' )，并讨论φ＝0、π/2 和π三种特例。
1－6 一台面以一定频率作垂直正弦运动，如要求台面上的物体保持与台面接触，则台面的最大振幅可有多大？1－7 计算两简谐运动x1 = X1 cos ω t和x2 = X2 cos (ω + ε ) t之和。
其中ε << ω。
如发生拍的现象，求其振幅和拍频。
1－8 将下列复数写成指数A e i θ形式：(a) 1 + i3(b) -2 (c) 3 / (3- i ) (d) 5 i (e) 3 / (3- i )2(f) (3+ i ) (3 + 4 i ) (g) (3- i ) (3 - 4 i ) (h) [ ( 2 i ) 2 + 3 i + 8]2－1 钢结构桌子的周期τ＝0.4 s，今在桌子上放W = 30 N 的重物，如图2－1所示。
已知周期的变化∆τ＝0.1 s。
求：( a ) 放重物后桌子的周期；( b )桌子的质量和刚度。
2－2 如图2－2所示，长度为L、质量为m 的均质刚性杆由两根刚度为k 的弹簧系住，求杆绕O点微幅振动的微分方程。
2－3 如图2－3所示，质量为m、半径为r的圆柱体，可沿水平面作纯滚动，它的圆心O用刚度为k的弹簧相连，求系统的振动微分方程。
图2－1 图2－2 图2－32－4 如图2－4所示，质量为m、半径为R的圆柱体，可沿水平面作纯滚动，与圆心O 距离为a 处用两根刚度为k的弹簧相连，求系统作微振动的微分方程。
机械振动 课后习题和答案 第三章 习题和答案
3.1 如图所示扭转系统。
设12122;t t I I k k ==1．写出系统的刚度矩阵和质量矩阵；2．写出系统的频率方程并求出固有频率和振型，画出振型图。
解：1)以静平衡位置为原点，设12,I I 的转角12,θθ为广义坐标，画出12,I I 隔离体，根据牛顿第二定律得到运动微分方程：111121222221()0()0t t t I k k I k θθθθθθθ⎧++-=⎪⎨+-=⎪⎩ ，即：1112122222122()00t t t t t I k k k I k k θθθθθθ⎧++-=⎪⎨-+=⎪⎩所以：[][]12212220,0t t t t t k k k I M K k k I +-⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦系统运动微分方程可写为：[][]11220M K θθθθ⎧⎫⎧⎫⎪⎪+=⎨⎬⎨⎬⎪⎪⎩⎭⎩⎭………… (a)或者采用能量法：系统的动能和势能分别为θθ=+2211221122T E I I θθθθθθθ=+-=++-222211212121221121111()()2222t t t t t t U k k k k k k求偏导也可以得到[][],M K由于12122;t t I I k k ==，所以[][]212021,0111t M I K k -⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦2)设系统固有振动的解为： 1122cos u t u θωθ⎧⎫⎧⎫=⎨⎬⎨⎬⎩⎭⎩⎭，代入（a ）可得：[][]122()0u K M u ω⎧⎫-=⎨⎬⎩⎭………… (b)得到频率方程：22121211222()0t t t t k I k k k I ωωω--==--即：224222121()240t t I k I k ωωω=-+=解得：21,222ω==所以：1ω=2ω= ………… (c)将（c ）代入（b ）可得：112121211122(22220(22t t t t t t k k I k I u u k k k I I ⎡⎤±--⎢⎥⎧⎫⎢⎥=⎨⎬⎢⎥⎩⎭⎢⎥--⎢⎥⎣⎦解得：11212u u =-；12222u u =令21u ，得到系统的振型为：-0.70710.70713.2 求图所示系统的固有频率和振型。
机械振动基础课后答案 机械振动课件
机械振动基础课后答案机械振动课件【--文秘基础】引导语：振动物体受回复力等于零的位置;也是振动停止后,振动物体所在位置;平衡位置通常在振动轨迹的中点。
下面是为你带来的机械振动课件，希望对你有所帮助。
1、什么是简谐运动？什么是回复力？2、掌握简谐运动的特点和各量的变化规律1、机械振动：物体在平衡位置所做的往复运动叫机械振动2、回复力：总是指向平衡位置，并使物体回到平衡位置的力叫回复力注意：回复力是效果力，是物体所受力的合力或合力的分力 3、简谐运动（1）定义：物体在与偏离平衡位置的位移大小成正比，总是指向平衡位置的力作用下的振动叫简谐运动（2）简谐运动的特征：回复力F：总是指向平衡位置，其大小与偏离平衡位置的位移大小成正比。
公式:F??kx加速度a：总是指向平衡位置，其大小与偏离平衡位置的位移大小成正比。
公式:a??kxm（3）各量的方向特点：位移x：方向偏离平衡位置回复力F：总是指向平衡位置加速度a：总是指向平衡位置，速度v：除两个端点外的任何位置，速度有两个可能的方向（4）各量的大小变化规律请同学们思考：动量和动能的大小变化规律所以：简谐运动是加速度变化的变速运动。
（5）简谐运动的对称性：在简谐运动中对称的两个点有如下的几个关系：位移大小相等方向相反；回复力大小相等方向相反；加速度的大小相等方向相反；速度的大小相等，方向可能相同可能相反；动量的大小相等，方向可能相同可能相反；动能的大小相等；弹簧振子：理想化的物理模型音叉叉股的上各点的振动，弹簧片上各点的振动，钟摆摆锤的振动等简谐运动是最简单的振动形式，要研究振动只有从简谐运动开始例1：下列哪些物体的运动属于机械振动（） A、在水面上随波运动的小舟 B、在地面上拍打的篮球 C、摩托车行驶时的颠簸 D、秋千的运动例2、关于振动的平衡位置，下列说法正确的是（） A、位移为零 B、回复力为零 C、加速度为零 D、合力为零 E、速度最大例3、弹簧振子在光滑的水平地面上做简谐振动，在振子向平衡位置运动的过程中（） A、振子受回复力逐渐增大 B、振子的位移逐渐增大 C、振子的速度逐渐减小 D、振子的加速度逐渐减小例4、一个弹簧振子沿水平方向的x轴做简谐运动，原点O为平衡位置，在震动中某个时刻可能出现的情况是（）A、位移与速度均为正，加速的度为负B、位移为负值，加速度为正值C、位移与加速度均为正值，速度为负值D、位移、速度、加速度均为负值例5：证明竖直弹簧振子的振动是简谐运动。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
如图所示扭转系统。
设12122;t t I I k k ==
1．写出系统的刚度矩阵和质量矩阵；
2．写出系统的频率方程并求出固有频率和振型，画出振型图。
解：1)以静平衡位置为原点，设12,I I 的转角12,θθ为广义坐标，画出12,I I 隔离体，根据牛顿第二定律得到运动微分方程：
111121222221()0()0t t t I k k I k θθθθθθθ⎧++-=⎪⎨
+-=⎪⎩，即：1112122222122()0
t t t t t I k k k I k k θθθθθθ⎧++-=⎪⎨-+=⎪⎩
所以：[][]12
21
2220,0t t t t t k k k I M K k k I +-⎡⎤
⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦
系统运动微分方程可写为：[][]11220M K θθθθ⎧⎫⎧⎫⎪⎪
+=⎨⎬⎨⎬⎪⎪⎩⎭⎩
⎭ ………… (a)
或者采用能量法：系统的动能和势能分别为
θθ=
+22112211
22T E I I
θθθθθθθ=+-=++-222211212121221121111
()()2222t t t t t t U k k k k k k
求偏导也可以得到[][],M K
由于12122;t t I I k k ==，所以[][]212021,0111t M I K k -⎡⎤⎡⎤
==⎢⎥⎢⎥-⎣⎦⎣⎦
2)设系统固有振动的解为： 1122cos u t u θωθ⎧⎫⎧⎫
=⎨⎬⎨⎬⎩⎭⎩⎭，代入（a ）可得：
[][]12
2()0u K M u ω⎧⎫
-=⎨⎬⎩⎭
………… (b)
得到频率方程：22
12
1
2
1
12
22()0t t t t k I k k k I ωωω--=
=-- 即：224
222
121()
240t t I
k I k ωωω=-+=
解得：2
1
1,22
2
(22t k
I ω±=
=
所以：1ω=
2ω
=………… (c)
将（c ）代入（b ）可得：
1
121
2
121112
2(22)22
20(22t t t t t t k k I k I u u k k k I I ⎡⎤
±--⎢⎥
⎧⎫⎢⎥=⎨⎬⎢⎥⎩⎭⎢⎥--⎢⎥
⎣⎦
解得：11
212
u u =-
；12
22
2
u
u
=
令
21
u=，得到系统的振型为：
11
求图所示系统的固有频率和振型。
设123213;33m m k k k ===。
并画出振型图。
解：1)以静平衡位置为原点，设12,m m 的位移12,x x 为广义坐标，画出12,m m 隔离体，根据牛顿第二定律得到运动微分方程：
11112122222132()0
()0m x k x k x x m x k x x k x ++-=⎧⎨
+-+=⎩
所以：[][]122122320,0k k k m M K k k k m +-⎡⎤
⎡⎤
==⎢⎥⎢⎥-+⎣⎦⎣⎦
系统运动微分方程可写为：[][]11220x x M K x x ⎧⎫⎧⎫
+=⎨⎬⎨⎬⎩⎭⎩⎭ ………… (a)
或者采用能量法：系统的动能和势能分别为
=
+22112211
22T E m x m x =+-+2221121232111
()222U k x k x x k x
求偏导也可以得到[][],M K
由于123213;33m m k k k ===，所以[][]223021,0114M m K k -⎡⎤⎡⎤
==⎢⎥⎢⎥
-⎣⎦⎣⎦
2)设系统固有振动的解为： 1122cos x u t x u ω⎧⎫⎧⎫
=⎨⎬⎨⎬⎩⎭⎩⎭，代入（a ）可得：
[][]122()0u K M u ω⎧⎫
-=⎨⎬⎩⎭
………… (b)
得到频率方程：22
22
2
22
22
23()04k m k k k m ωωω--=
=--
即：224
222
222()314
70m k m k ωω
ω=-+=
解得：2
1,2
22
ω
== 所以：1
ω=
2ω=
………… (c)
将（c ）代入（b ）可得：
2
2
2221222222(727)2330(743k k m k m u u k k k m m ⎡⎤
±--⎢⎥
⎧⎫⎢
⎥=⎨⎬⎢⎥±⎩
⎭⎢⎥
--⎢⎥⎣⎦
解得：11
21
5 3
u u =-
；12
22
5
3
u
u
-
=
令
21
u=，得到系统的振型为
：
1
1
如图所示弹簧质量系统，写出系统的频率方程并求出固有频率和振型，画出振型图。
解：以静平衡位置为原点，设12,m m 的位移12,x x 为广义坐标，系统的动能和势能分别为 =
+221211
22T E mx mx =+-++221121211
()()22U kx k x x mg x x
求得：[][]1021,0111M m K k -⎡⎤⎡⎤==⎢⎥⎢⎥
-⎣⎦⎣⎦
系统运动微分方程可写为：[][]11220x x M K x x ⎧⎫⎧⎫
+=⎨⎬⎨⎬⎩⎭⎩⎭
………… (a)
设系统固有振动的解为： 1122cos x u t x u ω⎧⎫⎧⎫
=⎨⎬⎨⎬⎩⎭⎩⎭，代入（a ）可得：
[][]12
2()0u K M u ω⎧⎫
-=⎨⎬⎩⎭
………… (b)
得到频率方程：22
2
2()0k m k
k k m ωωω--==--
即：22422()30m km k ωωω=-+=
解得：21,2(32k
m
ω±=
所以：1ω=
2ω=………… (c)
将（c ）代入（b ）可得：
12(3220(32k k m k u m u k k k m m ⎡⎤--⎢⎥⎧⎫
⎢⎥=⎨⎬⎢⎥±⎩⎭
--⎢
⎥⎣⎦
解得：
1121u u =
；1222u u = 令21u =，得到系统的振型为：
1
1
如图T—所示，由一弹簧是连接两个质量m1，m2构成的系统以速度v撞击制动器k1，求传到基础上的力的最大值。
设v为常数且弹簧无初始变形，并设m1=m2与k1=2k。
求图所示系统的固有频率和振型，并画出振型图。
设杆质量分布均匀。
求图所示系统当左边质量有初始位移A而其余初始条件均为零时的响应
如图T—所示由弹簧耦合的双摆，杆长为L。
1．写出系统的刚度矩阵、质量矩阵和频率方程；
2．求出固有频率和振型；
3．讨论是值改变对固有频率的影响。
解：。