机械振动总结复习习题及解答

合集下载

机械振动习题及答案

机械振动一、选择题1. 下列4种运动（忽略阻力）中哪一种是简谐运动（ C ）()A 小球在地面上作完全弹性的上下运动()B 细线悬挂一小球在竖直平面上做大角度的来回摆动()C 浮在水里的一均匀矩形木块，把它部分按入水中，然后松开，使木块上下浮动()D 浮在水里的一均匀球形木块，把它部分按入水中，然后松开，使木块上下浮动解析：A 小球不是做往复运动，故A 不是简谐振动。

B 做大角度的来回摆动显然错误。

D 由于球形是非线性形体，故D 错误。

2．如图1所示，以向右为正方向，用向左的力压缩一弹簧，然后松手任其振动。

若从松手时开始计时，则该弹簧振子的初相位应为图一（ D ）()0A ()2πB()2π-C ()πD解析：3.一质量为m 的物体挂在劲度系数为k 的轻质弹簧下面，其振动周期为T 。

若将此轻质弹簧分割成3等份，将一质量为2m 的物体挂在分割后的一根弹簧上，则此弹簧振子的周期为（ B ）()63TA ()36TB ()TC 2 ()TD 6解析：有题可知：分割后的弹簧的劲度系数变为k 3，且分割后的物体质量变为m 2。

故由公式k m T π2=，可得此弹簧振子的周期为36T 4．两相同的轻质弹簧各系一物体（质量分别为21,m m ）做简谐运动（振幅分别为21,A A ）,问下列哪一种情况两振动周期不同（ B ）()21m m A =，21A A =,一个在光滑水平面上振动，另一个在竖直方向上振动()B 212m m =，212A A =,两个都在光滑的水平面上作水平振动 ()C 21m m =，212A A =，两个都在光滑的水平面上作水平振动()D 21m m =，21A A =，一个在地球上作竖直振动，另一个在月球上作竖直振动解析：由公式kmT π2=可知，周期不同于质量有关，故选B 5. 一个质点做简谐振动，已知质点由平衡位置运动到二分之一最大位移处所需要的最短时间为0t ，则该质点的振动周期T 应为（ B ）()04t A ()012t B ()06t C ()08t D解析：6. 已知月球上的重力加速度是地球的1/6，若一个单摆（只考虑小角度摆动）在地球上的振动周期为T ，将该单摆拿到月球上去，其振动周期应为（ C ）()T A 6 ()6T B ()T C 6 ()6T D解析：由公式glT π2=可知，该振动周期为T 6 7.一简谐振动的旋转矢量图如图2所示，设图中圆的半径为R ，则该简谐振动的振动方程为（ A ）()⎪⎭⎫ ⎝⎛+=4cos ππt R x A ()⎪⎭⎫ ⎝⎛+=4sin ππt R x B()⎪⎭⎫ ⎝⎛-=4cos ππt R x C ()⎪⎭⎫ ⎝⎛+42cos ππt R D解析：8.已知某简谐振动的振动曲线如图3所示，位移的单位为米，时间的单位为秒，则此简谐振动的振动方程为（ C ）()()SI t x A ⎪⎭⎫ ⎝⎛+=322411cos 10ππ ()()SI t x B ⎪⎭⎫ ⎝⎛-=67247cos 10ππ()()SI t x C ⎪⎭⎫ ⎝⎛-=32247cos 10ππ ()()SI t x D ⎪⎭⎫ ⎝⎛-=322411cos 10ππ解析：9.某弹簧振子的振动曲线如图4所示，则由图可确定s t 2=时，振子的速度为（ A ）()s m A π3 ()s m B π3- ()s m C 3 ()s m D 3-解析：10.一质量为m 的物体与一个劲度系数为k 的轻质弹簧组成弹簧振子，当其振幅为A 时，该弹簧振子的总能量为E .若将其弹簧分割成3等份，将两根弹簧并联组成新的弹簧振子，则新的弹簧振子的振幅为多少时，其总能量与原先弹簧振子的总能量E 相等（ A ）()2A A ()4A B ()2A C ()A D解析：由题可得2242121A k kA E '==,所以2A A =' 11.两同方向同频率的简谐振动的振动方程为()SI t x ⎪⎭⎫⎝⎛+=25cos 61π,()SI t x ⎪⎭⎫ ⎝⎛-=25cos 22π,则它们的合振动的振动方程应为（ D ）()()SI t x A 5cos 4= ()()()SI t x B π-=5cos 8()()SI t x C ⎪⎭⎫ ⎝⎛-=210cos 4π ()()SI t x D ⎪⎭⎫ ⎝⎛+=25cos 4π解析：12.已知两同方向同频率的简谐振动的振动方程分别为()SI t A x ⎪⎭⎫ ⎝⎛+=3cos 11πω,()SI t A x ⎪⎭⎫ ⎝⎛-=6cos 22πω,则它们的合振幅应为（ C ）()21A A A - ()21A A B +()2221+A C ()2221A A D -解析：二.填空题1.若简谐振动()0cos ϕω+=t A x 的周期为T ,则简谐振动()πϕω++='0cos t n B x 的周期为nT。

(完整版)机械振动试题(参考答案)

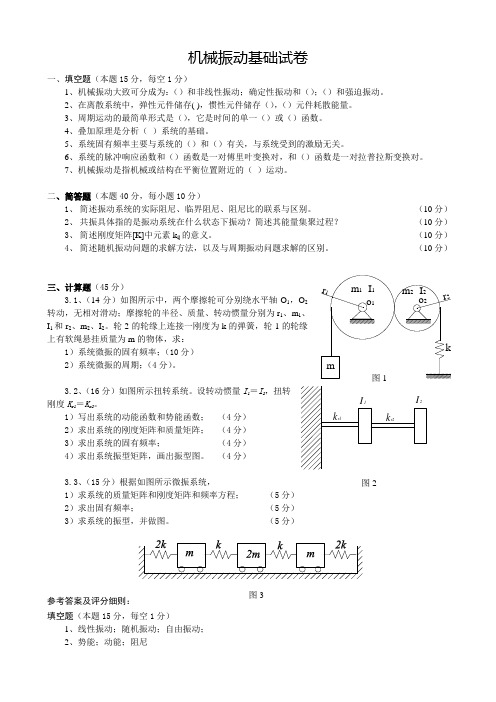
机械振动基础试卷一、填空题（本题15分，每空1分）1、机械振动大致可分成为：（）和非线性振动；确定性振动和（）；（）和强迫振动。

2、在离散系统中，弹性元件储存( )，惯性元件储存（），（）元件耗散能量。

3、周期运动的最简单形式是（），它是时间的单一（）或（）函数。

4、叠加原理是分析（）系统的基础。

5、系统固有频率主要与系统的（）和（）有关，与系统受到的激励无关。

6、系统的脉冲响应函数和（）函数是一对傅里叶变换对，和（）函数是一对拉普拉斯变换对。

7、机械振动是指机械或结构在平衡位置附近的（）运动。

二、简答题（本题40分，每小题10分）1、简述振动系统的实际阻尼、临界阻尼、阻尼比的联系与区别。

（10分）2、共振具体指的是振动系统在什么状态下振动？简述其能量集聚过程？（10分）3、简述刚度矩阵[K]中元素k ij 的意义。

（10分）4、简述随机振动问题的求解方法，以及与周期振动问题求解的区别。

（10分）三、计算题（45分） 3.1、（14分）如图所示中，两个摩擦轮可分别绕水平轴O 1，转动，无相对滑动；摩擦轮的半径、质量、转动惯量分别为r 1、m I 1和r 2、m 2、I 2。

轮2的轮缘上连接一刚度为k 的弹簧，轮1上有软绳悬挂质量为m 的物体，求： 1）系统微振的固有频率；（10分）2）系统微振的周期；（4分）。

3.2、（16分）如图所示扭转系统。

设转动惯量I 1＝I 2，扭转刚度K r1＝K r2。

1）写出系统的动能函数和势能函数；（4分） 2）求出系统的刚度矩阵和质量矩阵；（4分）3）求出系统的固有频率；（4分）4）求出系统振型矩阵，画出振型图。

（4分）3.3、（15分）根据如图所示微振系统， 1）求系统的质量矩阵和刚度矩阵和频率方程；（5分）2）求出固有频率；（5分）3）求系统的振型，并做图。

（5分）参考答案及评分细则：填空题（本题15分，每空1分）1、线性振动；随机振动；自由振动；2、势能；动能；阻尼图2图33、简谐运动；正弦；余弦4、线性5、刚度；质量6、频响函数；传递函数7、往复弹性简答题（本题40分，每小题10分）5、简述振动系统的实际阻尼、临界阻尼、阻尼比的联系与区别。

《机械振动基础》期末复习试题5套含答案.doc

中南大学考试试卷2005 - 2006学年上学期时间门o分钟《机械振动基础》课程32学时1.5学分考试形式：闭卷专业年级：机械03级总分100分，占总评成绩70 %注：此页不作答题纸，请将答案写在答题纸上一、填空题（本题15分，每空1分）1＞不同情况进行分类，振动（系统）大致可分成，（）和非线性振动；确定振动和（）；（）和强迫振动；周期振动和（）；（）和离散系统。

2、在离散系统屮，弹性元件储存（）,惯性元件储存（），（）元件耗散能量。

3、周期运动的最简单形式是（），它是时间的单一（）或（）函数。

4、叠加原理是分析（）的振动性质的基础。

5、系统的固有频率是系统（）的频率，它只与系统的（）和（）有关，与系统受到的激励无关。

二、简答题（本题40分，每小题10分）1、简述机械振动的定义和系统发生振动的原因。

（10分）2、简述振动系统的实际阻尼、临界阻尼、阻尼比的联系与区别。

（10分）3、共振具体指的是振动系统在什么状态下振动？简述其能量集聚过程？（20分）4、多自由系统振动的振型指的是什么？（10分）三、计算题（本题30分）图1 2、图2所示为3自由度无阻尼振动系统。

（1）列写系统自由振动微分方程式（含质量矩阵、刚度矩阵）（10分）；（2）设k t[=k t2=k t3=k t4=k9 /, =/2/5 = /3 = 7,求系统固有频率（10 分）。

13 Kt3四、证明题（本题15分）对振动系统的任一位移{兀},证明Rayleigh商R（x）=⑷严⑷满足材 < 尺⑴ < 忒。

{x}\M\{x}这里，［K］和［M］分别是系统的刚度矩阵和质量矩阵，®和①，分别是系统的最低和最高固有频率。

（提示：用展开定理{x} = y{M} + y2{u2}+……+ y n{u n}）3 •简述无阻尼单自由度系统共振的能量集聚过程。

（10 分） 4.简述线性多自由度系统动力响应分析方法。

（10 分）中南大学考试试卷2006 - 2007学年上学期时间120分钟机械振动课程 32 学时 2 学分考试形式：闭卷专业年级：机械04级总分100分，占总评成绩 70%注：此页不作答题纸，请将答案写在答题纸上一、填空（15分，每空1分）1. 叠加原理在（A ）中成立；在一定的条件下，可以用线性关系近似（B ） o2. 在振动系统中，弹性元件储存（C ）,惯性元件储存（D ） , （E ）元件耗散能量。

最经典机械振动总结、试题及答案(全)

最经典机械振动总结、试题及答案（全）一、简谐运动（一）知识要点1.定义：物体在跟偏离平衡位置的位移大小成正比，并且总指向平衡位置的回复力的作用下的振动，叫简谐运动。

表达式为：F = -kx⑴简谐运动的位移必须是指偏离平衡位置的位移。

也就是说，在研究简谐运动时所说的位移的起点都必须在平衡位置处。

⑵回复力是一种效果力。

是振动物体在沿振动方向上所受的合力。

⑶“平衡位置”不等于“平衡状态”。

平衡位置是指回复力为零的位置，物体在该位置所受的合外力不一定为零。

（如单摆摆到最低点时，沿振动方向的合力为零，但在指向悬点方向上的合力却不等于零，所以并不处于平衡状态）⑷F=-kx 是判断一个振动是不是简谐运动的充分必要条件。

凡是简谐运动沿振动方向的合力必须满足该条件；反之，只要沿振动方向的合力满足该条件，那么该振动一定是简谐运动。

2.几个重要的物理量间的关系要熟练掌握做简谐运动的物体在某一时刻（或某一位置）的位移x 、回复力F 、加速度a 、速度v 这四个矢量的相互关系。

⑴由定义知：F ∝x ，方向相反。

⑵由牛顿第二定律知：F ∝a ，方向相同。

⑶由以上两条可知：a ∝x ，方向相反。

⑷v 和x 、F 、a 之间的关系最复杂：当v 、a 同向（即 v 、 F 同向，也就是v 、x 反向）时v 一定增大；当v 、a 反向（即 v 、 F 反向，也就是v 、x 同向）时，v 一定减小。

3.从总体上描述简谐运动的物理量振动的最大特点是往复性或者说是周期性。

因此振动物体在空间的运动有一定的范围，用振幅A 来描述；在时间上则用周期T 来描述完成一次全振动所须的时间。

⑴振幅A 是描述振动强弱的物理量。

（一定要将振幅跟位移相区别，在简谐运动的振动过程中，振幅是不变的而位移是时刻在改变的） ⑵周期T 是描述振动快慢的物理量。

（频率f =1/T 也是描述振动快慢的物理量）周期由振动系统本身的因素决定，叫固有周期。

任何简谐振动都有共同的周期公式：km T π2=（其中m 是振动物体的质量，k 是回复力系数，即简谐运动的判定式F = -kx 中的比例系数，对于弹簧振子k 就是弹簧的劲度，对其它简谐运动它就不再是弹簧的劲度了）。

机械振动期末考试题及答案

机械振动期末考试题及答案一、选择题（每题2分，共20分）1. 简谐振动的周期与振幅无关，这是由哪个定律决定的？A. 牛顿第二定律B. 牛顿第三定律C. 胡克定律D. 能量守恒定律答案：C2. 下列哪个不是阻尼振动的特点？A. 振幅逐渐减小B. 频率逐渐增大C. 能量逐渐减少D. 振幅随时间呈指数衰减答案：B3. 一个物体做自由振动，若其振幅逐渐减小，这表明振动受到了：A. 阻尼B. 共振C. 强迫振动D. 非线性振动答案：A4. 质点的振动方程为 \( y = A \sin(\omega t + \phi) \)，其中\( \omega \) 表示：A. 振幅B. 频率C. 角频率D. 相位答案：C5. 弹簧振子的振动周期与下列哪个参数无关？A. 弹簧的劲度系数B. 振子的质量C. 振子的振幅D. 振子的初始相位答案：C6. 阻尼振动的振幅随时间呈指数衰减，其衰减速率与什么有关？A. 振幅大小B. 阻尼系数C. 振动频率D. 振动周期答案：B7. 以下哪个不是振动系统的自由度？A. 1B. 2C. 3D. 无穷大答案：D8. 共振现象发生在以下哪种情况下？A. 系统固有频率等于外部激励频率B. 系统阻尼系数最大C. 系统振幅最小D. 系统能量最大答案：A9. 以下哪个是简谐振动的特有现象？A. 振幅不变B. 频率不变C. 能量不变D. 周期不变答案：A10. 一个物体在水平面上做简谐振动，其振动能量主要由以下哪两个因素决定？A. 振幅和频率B. 振幅和阻尼系数C. 阻尼系数和频率D. 振幅和劲度系数答案：A二、填空题（每空2分，共20分）11. 简谐振动的周期公式为 \( T = \frac{2\pi}{\omega} \)，其中\( \omega \) 为________。

答案：角频率12. 当外部激励频率接近系统的________时，系统将产生共振现象。

答案：固有频率13. 阻尼振动的振幅随时间的变化规律可表示为 \( A(t) = A_0 e^{-\beta t} \)，其中 \( \beta \) 为________。

大学机械振动考试题目及答案

大学机械振动考试题目及答案一、选择题（每题2分，共10分）1. 在简谐振动中，振幅与振动的能量关系是（）。

A. 无关B. 成正比C. 成反比D. 振幅越大，能量越小答案：B2. 下列哪个不是机械振动系统的自由度？（）。

A. 转动B. 平动C. 振动D. 形变答案：C3. 一个单自由度系统在受到初始条件激励后，其振动形式是（）。

A. 简谐振动B. 阻尼振动C. 受迫振动D. 自由振动答案：D4. 在阻尼振动中，如果阻尼系数增加，振动的振幅将（）。

A. 增加B. 不变C. 减小D. 先增加后减小答案：C5. 对于一个二自由度振动系统，其振动模态数量是（）。

A. 1B. 2C. 3D. 4答案：B二、填空题（每题2分，共10分）6. 一个物体做自由振动时，其频率称为______。

答案：固有频率7. 当外力的频率与系统的固有频率相等时，系统发生的振动称为______。

答案：共振8. 阻尼力与速度成正比的阻尼称为______阻尼。

答案：线性9. 振动系统的动态响应可以通过______分析法求解。

答案：傅里叶10. 在转子动力学中，临界转速是指转子发生______振动的转速。

答案：自激三、简答题（每题5分，共20分）11. 简述什么是简谐振动，并说明其运动方程的形式。

答案：简谐振动是一种周期性的振动，其加速度与位移成正比，且方向相反。

在数学上，简谐振动的运动方程可以表示为：x(t) = A * cos(ωt + φ)其中，A 是振幅，ω 是角频率，t 是时间，φ 是初相位。

12. 解释什么是阻尼振动，并说明其特点。

答案：阻尼振动是指在振动系统中存在能量耗散，导致振幅随时间逐渐减小的振动。

其特点包括振幅逐渐衰减，振动频率可能会随着振幅的减小而发生变化，且阻尼力通常与振动速度成正比。

13. 描述什么是受迫振动，并给出其稳态响应的条件。

答案：受迫振动是指系统在周期性外力作用下的振动。

当外力的频率接近系统的固有频率时，系统将发生共振，此时振幅会显著增大。

机械振动现象练习题(含答案)

机械振动现象练习题(含答案)1. 一个弹簧常数为3000 N/m, 质量为0.2 kg的物体，在弹簧下端受到一个向下的力2 sin(10t) N，其中t为时间（秒）。

求物体的振动方程。

根据牛顿第二定律，可以得到物体的振动方程为：m * x'' + k * x = F(t)其中，m是物体的质量，x是物体的位移，x''是位移对时间的二阶导数，k是弹簧的常数，F(t)是作用在物体上的外力。

根据题目中给出的数据，代入上述公式，我们可以得到：0.2 * x'' + 3000 * x = 2 sin(10t)这就是物体的振动方程。

2. 一个质点在受到一个力F(t) = 0.1 cos(3t) N的作用下进行振动，已知质点的质量为0.5 kg。

求质点的角频率和振动周期。

根据振动方程的形式，我们可以知道物体的振动频率和周期与力的形式有关。

在这个题目中，我们可以看出力的形式为cos(3t)，它是一个正弦函数。

如果将cos(3t)函数展开，我们可以得到下面的表达式：F(t) = a cos(wt)其中，a是振幅，w是角频率。

根据题目中给出的数据，我们可以得到：a = 0.1 N，w = 3 rad/s由于振动的频率与角频率之间是有关联的，振动的周期T可以表示为：T = 2π/w代入上述数据，我们可以得到：T = 2π/3 s这就是质点的振动周期。

3. 一个质点质量为0.3 kg，在一竖直方向上的弹簧中振动，弹簧的劲度系数为2000 N/m。

当质点受到一个外力F(t) = 0.5 cos(5t) N时，求质点的振动方程。

根据题目中给出的数据，我们可以得到：m = 0.3 kg，k = 2000 N/m，F(t) = 0.5 cos(5t)代入振动方程的一般形式，我们可以得到：0.3 * x'' + 2000 * x = 0.5 cos(5t)这就是质点的振动方程。

(完整版)大学机械振动课后习题和答案(1~4章总汇)

1.1 试举出振动设计、系统识别和环境预测的实例。

1.2 如果把双轴汽车的质量分别离散到前、后轴上去，在考虑悬架质量和非悬架质量两个离散质量的情况下，画出前轴或后轴垂直振动的振动模型简图，并指出在这种化简情况下，汽车振动有几个自由度?1.3 设有两个刚度分别为1k ，2k 的线性弹簧如图T —1.3所示，试证明：1)它们并联时的总刚度eq k 为：21k k k eq +=2)它们串联时的总刚度eq k 满足：21111k k k eq +=解：1)对系统施加力P ，则两个弹簧的变形相同为x ，但受力不同，分别为：1122P k xP k x=⎧⎨=⎩由力的平衡有：1212()P P P k k x =+=+故等效刚度为：12eq Pk k k x ==+2)对系统施加力P ，则两个弹簧的变形为： 1122Px k Px k ⎧=⎪⎪⎨⎪=⎪⎩，弹簧的总变形为：121211()x x x P k k =+=+故等效刚度为：122112111eq k k P k x k k k k ===++1.4 求图所示扭转系统的总刚度。

两个串联的轴的扭转刚度分别为1t k ，2t k 。

解：对系统施加扭矩T ，则两轴的转角为： 1122t t Tk T k θθ⎧=⎪⎪⎨⎪=⎪⎩系统的总转角为：121211()t t T k k θθθ=+=+，12111()eq t t k T k k θ==+故等效刚度为：12111eq t t k k k =+1.5 两只减振器的粘性阻尼系数分别为1c ，2c ，试计算总粘性阻尼系数eq c1)在两只减振器并联时，2)在两只减振器串联时。

解：1)对系统施加力P ，则两个减振器的速度同为x &，受力分别为：1122P c x P c x =⎧⎨=⎩&& 由力的平衡有：1212()P P P c c x =+=+&故等效刚度为：12eq P c c c x ==+& 2)对系统施加力P ，则两个减振器的速度为： 1122P x c P x c ⎧=⎪⎪⎨⎪=⎪⎩&&，系统的总速度为：121211()x x x P c c =+=+&&& 故等效刚度为：1211eq P c x c c ==+&1.6 一简谐运动，振幅为0.5cm，周期为0.15s，求最大速度和加速度。

(完整版)机械振动知识点及习题练习+单元练习(含答案)

1、简谐运动的概念①简谐运动的定义：____________________________________________________________。

②简谐运动的物体的位移x、回复力F、加速度a、速度v、动能E K、势能E P的变化规律：A．在研究简谐运动时位移的起点都必须在处。

B．在平衡位置：位移最、回复力最、加速度最；速度最、动能最。

C．在离开平衡位置最远时：_________________________________________。

D．振动中：注意以上各量的矢量性和对称性。

③简谐运动机械能守恒，但机械能守恒的振动不一定时简谐运动。

④注意：A．回复力是效果力。

B．物体运动到平衡位置不一定处于平衡状态(如单摆，最低点有向心力)。

C．简谐运动定义式F=-K x中的K不一定是弹簧的劲度系数，是振动系数（如双弹簧）。

1.A关于回复力,下列说法正确的是( )A.回复力一定是物体受到的合外力B.回复力只能是弹簧的弹力提供C.回复力是根据力的作用效果命名的D.回复力总是指向平衡位置答案:CD2.A下列的运动属于简谐运动的是( )A.活塞在气缸中的往复运动B.拍皮球时,皮球的上下往复运动C.音叉叉股的振动D.小球在左右对称的两个斜面上来回滚动答案:C3.A一质点做简谐运动,当位移为正的最大值时,质点的( )A.速度为正的最大值,加速度为零B.速度为负的最大值,加速度为零C.速度为零,加速度为正的最大值D.速度为零,加速度为负的最大值答案:D4.A关于简谐运动的位移、加速度和速度的关系,正确的说法是( )A.位移减小时,加速度增大,速度增大B.位移方向总和加速度方向相反,和速度方向相同C.物体的速度增大时,加速度一定减小D.物体向平衡位置运动时,速度方向和位移方向相同答案:C6.B关于简谐运动中的平衡位置,下列说法正确的是( )A.平衡位置就是物体所受合外力为零的位置B.平衡位置就是加速度为零的位置C.平衡位置就是回复力为零的位置D.平衡位置就是受力平衡的位置答案:C7.B一平台沿竖直方向做简谐运动,一物体置于平台上随台一起运动,当振动平台处于什么位置时,物体对台面的压力最大( )A.振动平台在最高位置时B.振动平台向下振动经过平衡位置时C.振动平台在最低位置时D.振动平台向上运动经过平衡位置时答案:C8.B简谐运动是下列哪一种运动( )A.匀速直线运动B.匀加速运动C.匀变速运动D.变加速运动答案:D9.B做简谐运动的物体每次经过同一位置时,一定相同的物理量是( )A.速度B.位移C.回复力D.加速度答案:BCD10.B 对于弹簧振子,其回复力和位移的关系,在下图中正确的是()答案:C11.C 对简谐运动的回复力F=-kx 的理解,正确的是()A.k 只表示弹簧的劲度系数B.式中负号表示回复力总是负值C.位移x 是相对平衡位置的位移D.回复力只随位移变化,不随时间变化答案:C12.C 弹簧振子的质量是0.2kg,在水平方向做简谐运动,当它运动到平衡位置左侧x 1=2cm 的位置时,受到的回复力大小F 1=4N,则当它运动到平衡位置右侧x 2=4cm 的位置时,它的加速度是()A.20m/s 2,方向向左 B20m/s 2,方向向右C.40m/s 2,方向向左 D.40m/s 2,方向向右答案:C二、计算题(共16分)13.C 试证明:用轻弹簧悬挂一个振子,让它在竖直方向振动起来,在弹性限度内,振子是做简谐运动.(如图)答案:设振子的平衡位置为O,令向下为正方向,此时弹簧的形变为x 0,根据胡克定律及平衡条件有mg-kx 0=0.当振子向下偏离平衡位置x 时,有F=mg-k(x+x 0) 整理可得F=-kx(紧扣简谐运动特征及对称性)故重物的振动满足简谐运动的条件 2、总体上描述简谐运动的物理量①振幅A ：_ _称为振幅。

高二物理第九章机械振动-单摆知识点总结练习题(含答案解析)

三、单摆1、单摆：在细线的一端拴一小球，另一端固定在悬点上，如果悬挂小球的细线的伸缩和质量可以忽略，线长又比球的直径大得多，这样的装置就叫做单摆2、单摆是实际摆的理想化模型3摆长:摆球重心到摆动圆弧圆心的距离 L=L0+R4偏角:摆球摆到最高点时，细线与竖直方向的夹角（偏角一般小于5°） 2、单摆的回复力：平衡位置是最低点，kx F -=回回复力是重力沿切线方向的分力，大小为mg sin θ，方向沿切线指向平衡位置单摆的周期只与重力加速度g 以及摆长L 有关。

所以，同一个单摆具有等时性重力加速度g:由单摆所在的空间位置决定。

纬度越低，高度越高，g 值就越小。

不同星球上g 值也不同。

单摆作简谐运动时的动能和重力势能在发生相互转化，但机械能的总量保持不变，即机械能守恒。

小球摆动到最高点时的重力势能最大，动能最小；平衡位置时的动能最大，重力势能最小。

若取最低点为零势能点，小球摆动的机械能等于最高点时的重力势能，也等于平衡位置时的动能。

例一：用下列哪些材料能做成单摆( AF )悬线：细、长、伸缩可以忽略摆球：小而重（即密度大） A.长为1米的细线 B 长为1米的细铁丝 C.长为0.2米的细丝线D.长为1米的麻绳E.直径为5厘米的泡沫塑料球F.直径为1厘米的钢球G.直径为1厘米的塑料球H.直径为5厘米的钢球例2.一摆长为L 的单摆,在悬点正下方5L/9处有一钉子,则这个单摆的周期是多少？例3、有人利用安装在气球载人舱内的单摆来确定气球的高度。

已知该单摆在海平面处的周期是T 0，当气球停在某一高度时，测得该单摆周期为T 。

求该气球此时离海平面的高度h 。

把地球看作质量均匀分布的半径为R 的球体。

gL T π35=例7．如图所示为一单摆的共振曲线，求：1。

该单摆的摆长约为多少？（近似认为g=2m/s 2）2共振时摆球的最大速度大小是多少？③若摆球的质量为50克，则摆线的最大拉力是多少？例11．如图所示，在一根张紧的水平绳上，悬挂有 a 、b 、c 、d 、e 五个单摆，让a 摆略偏离平衡位置后无初速释放，在垂直纸面的平面内振动；接着其余各摆也开始振动。

机械振动复习题及解答

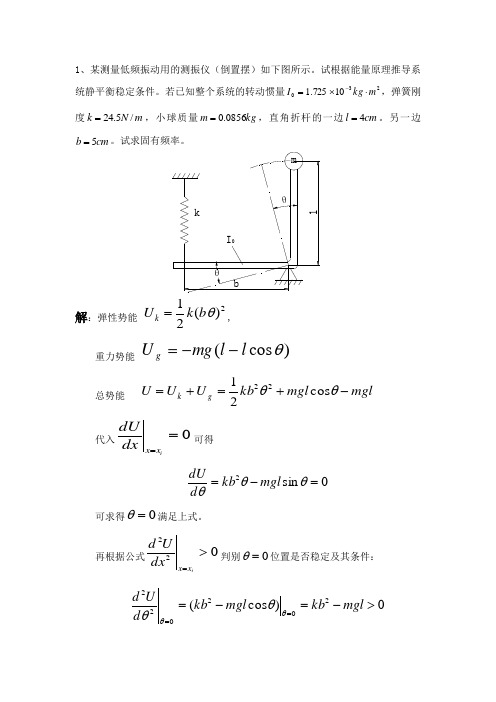
1、某测量低频振动用的测振仪（倒置摆）如下图所示。

试根据能量原理推导系统静平衡稳定条件。

若已知整个系统的转动惯量23010725.1m kg I ⋅⨯=-，弹簧刚度m N k /5.24=，小球质量kg m 0856.0=，直角折杆的一边cm l 4=。

另一边cm b 5=。

试求固有频率。

kblθθI 0m解：弹性势能 2)(21θb k U k =,重力势能)cos (θl l mg U g --=总势能 m g l m g l kb U U U g k -+=+=θθcos 2122 代入0==ix x dxdU 可得0sin 2=-=θθθmgl kb d dU可求得0=θ满足上式。

再根据公式022>=ix x dx Ud 判别0=θ位置是否稳定及其条件：0)cos (202022>-=-===mgl kb mgl kb d U d θθθθ即满足mgl kb>2条件时，振动系统方可在0=θ位置附近作微幅振动。

系统的动能为 2210θ∙=I T代入0)(=+dtU T d 可得 0sin 20=-+∙∙θθθmgl kb I由0=θ为稳定位置，则在微振动时0sin ≈θ，可得线性振动方程为：0)(20=-+∙∙θθmgl kb I固有频率2I mglkb p -=代入已知数据，可得)/(410725.104.081.90856.005.05.2432s rad p =⨯⨯⨯-⨯=-2、用能量法解此题：一个质量为均匀半圆柱体在水平面上做无滑动的往复滚动，如上图所示，设圆柱体半径为R ，重心在c 点,oc=r,，物体对重心的回转体半径为L，试导出运动微分方程。

解：如图所示，在任意角度θ（t ）时，重心c 的升高量为∆=r （1－cos θ）=2rsin 22θ取重心c 的最低位置为势能零点，并进行线性化处理，则柱体势能为 V=mg ∆=2mg r sin22θ ≈21mgr 2θ （a ）I b =I c +m bc 2=m(L 2+bc 2) （b ）bc 2=r 2+R 2-2rRcos θ(t) （c ）而柱体的动能为 T=21I b ∙θ2把（b ）式，（c ）式两式代入，并线性化有T=21m[L 2＋（R －r ）2]∙θ2（d ）根据能量守恒定理，有21m[L 2＋（R －r ）2]∙θ2＋21mgr 2θ=E=const 对上式求导并化简，得运动微分方程为[L 2＋（R －r ）2]∙∙θ＋gr θ=0 （e ）3、一质量为m 、转动惯量为I 的圆柱体作自由纯滚动，圆心受到一弹簧k 约束，如图所示，求系统的固有频率。

第10章机械振动答案

第10章机械振动答案第十章机械振动一. 选择题:【 C 】1、（基础训练3）一长为l 的均匀细棒悬于通过其一端的光滑水平固定轴上，（如图13-16所示），作成一复摆．已知细棒绕通过其一端的轴的转动惯量231ml J =，此摆作微小振动的周期为 (A)gl π2. (B)gl 22π. (C)gl 322π. (D)gl 3π.提示：均匀的细棒一段悬挂，构成一个复摆，可根据复摆的振动方程求解办法，求出复摆的振动周期。

【 C 】2（基础训练4）一质点作简谐振动，周期为T ．当它由平衡位置向x 轴正方向运动时，从二分之一最大位移处到最大位移处这段路程所需要的时间为 (A) T /12． (B) T /8． (C) T /6． (D) T /4．提示：从从二分之一最大位移处到最大位移处这段路程在旋转矢量图上，矢量转过的角位移为π31，对应的时间为T/6.[ B ] 3（基础训练8）图中所画的是两个简谐振动的振动曲线．若这两个简谐振动可叠加，则合成的余弦振动的初相为(A) π23． (B) π． (C) π21． (D) 0．提示：使用谐振动的矢量图示法，合振动的初始状态为2A-,初相位为π【 B 】 4、（自测提高5）一简谐振动曲线如图所示．则振动周期是(A) 2.62 s ． (B) 2.40 s ． (C)2.20 s ． (D) 2.00 s ．提示：使用谐振动的矢量图示法，初始状态旋转矢量位于第四象限，初始相位为3π-，到第一次回x tOA/2 -Ax 1x图13-23x (cm) t (s)O4 2 1T ，以余弦函数表达振动时，初相为零．在0≤t≤T 41范围内，系统在t =_T/8_时刻动能和势能相等．提示：动能和势能相等，为总能量的一半，此时物体偏离平衡位置的位移应为最大位移的22，相位为4π，因为初始相位为零，t=T/83、(基础训练16) 两个同方向同频率的简谐振动，其振动表达式分别为：)215cos(10621π+⨯=-t x (SI) ， )5cos(10222t x -π⨯=- (SI)它们的合振动的振辐为210102-⨯(SI),初相为3121-+tg π＝108.40提示：用旋转矢量图示法求解4、 (自测提高 8) 在静止的升降机中，长度为l的单摆的振动周期为T 0．当升降机以加速度g a 21=竖直下降时，摆的振动周期2T ．提示：当升降机以加速度加速下降时，对于单摆，等效加速度为g-a=0.5g;单摆的周期变为:022T ag lT =-=π5、(自测提高 11) 一单摆的悬线长l = 1.5 m ，在顶端固定点的竖直下方0.45 m 处有一小钉，如图13-26所示．设摆动很小，则单摆的左右两方振幅之比A 1/A 2的近似值为_0.837_．提示：当单摆在最低位置时，对左右两边有：222211)(21)(21A m A m ωω=，对于单摆lg =ω，2211A l g A l g =837.0:2121==l l A A6 (自测提高 14)、两个互相垂直的不同频率谐振动合成后的图形如图13-27所示．由图可知x 方向和y 方向两振动的频率之比νx :νy =___4:3___．提示：在同样的时间间隔内，X 方向的振动为2T x ，而y 方向的振动为1.5T y ,周期之比为3：4，频率之比相反为4：3图13-26l0.45 m小钉图13-27x y三计算题1. （基础训练23）有两个同方向的简谐振动，它们的方程(SI 单位)如下：⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+=ππ4110cos 06.04310cos 05.021t x t x ，(1) 求它们合成振动的振幅和初位相。

2023高中物理机械振动复习题集附答案

2023高中物理机械振动复习题集附答案2023高中物理机械振动复习题集附答案1. 单选题1. 在弹簧振子的简谐振动中，下列哪个量不变？A. 动能B. 势能C. 总机械能D. 振动频率答案：D2. 下列哪个不属于弹簧振子的简谐运动特征？A. 周期相等B. 频率相等C. 能量守恒D. 加速度为常数答案：D3. 振动的周期与频率的关系是：A. 周期和频率成反比B. 周期和频率成正比C. 周期和频率无关D. 周期是频率的平方答案：A4. 下列哪个条件不是机械振动的必要条件？A. 有弹性形变B. 有恢复力C. 有质量D. 有外力作用答案：D5. 一个物体做简谐振动，其振动方程为x = 5sin(2πt + π/3)，振幅为：A. 5B. 3C. 2D. 1答案：A2. 多选题1. 下列哪些是质点的简谐运动特点？A. 周期相等B. 频率相等C. 振幅相等D. 加速度恒定答案：A、B、C2. 下列哪些物体可以进行机械振动？A. 弹簧B. 摆子C. 电子D. 钢琴弦答案：A、B、D3. 一个弹簧振子的周期为2s，频率为5Hz，则它的角频率为：A. π/10 rad/sB. π/5 rad/sC. π/2 rad/sD. 2π rad/s答案：D4. 对于一个质点做直线简谐运动，振幅为3m，频率为2Hz，则振动的角频率是：A. π rad/sB. 2π rad/sC. 3π rad/sD. 6π rad/s答案：B3. 解答题1. 描述简谐振动的物理量有哪些？答：简谐振动的物理量包括振幅、周期、频率、角频率、相位等。

2. 简述谐振条件及其对应的公式。

答：谐振条件是指在机械振动中，外力频率等于振动体的固有频率时，会出现共振现象。

其对应的公式为f = 1/(2π√(l/g))。

3. 什么是阻尼振动？它与简谐振动有什么区别？答：阻尼振动是指在振动过程中，受到阻力的影响，振动幅度逐渐减小的振动。

与简谐振动不同的是，阻尼振动会消耗能量，振动的幅度逐渐衰减。

机械振动章末总复习(有答案,图形已校对)

记下所用的时间t，则单摆振动的周期。
摆长为l=l线+d/2
***应以摆球经平衡位置计时开始与停止时刻
家庭作业讲解
B BCD
D BD
BD AC
D B D
B
例题3:某简谐运动的位移与时间关系为：
x=0.1sin（100πt＋π）cm, 由此可知该振动
的振幅是_0_._1___cm，频率是 50 Ｈz，零时刻振动物体的速度与规定正方向 _相___反_ （填
单摆做简谐运动时，其周期为，故有因此测出单摆的摆长和振动周期
T，就可以求出当地的重力加速度g的数值。 • 【实验器材】
带孔小钢球两个，长约1m的细线，带铁夹的铁架台、停表、游标卡尺、米尺；
【实验步骤】
3、测周期：
把单摆从平衡位置拉开一个很小角度（＜5o）后释放
从摆球通过平衡位置开始计时，数出之后摆球通过最低点的次数n，用停表
M:m:振子质量 K:弹簧劲度系数
*பைடு நூலகம்*竖直弹簧振子
1.两种判断物体是否做简谐运动的条件：
F-x满足F=-kx的形式
竖直弹簧振子的振动是否是简谐振动？
证明步骤：设向下为正方向 1、找平衡位置:竖直弹簧振子平衡不是原长： mg=kx0 2、找弹力:F弹=k(x+x0) 3、找回复力 F回=mg-k(x+x0)=-kx 证明F=-kx,则此振动为简谐振动。
简谐运动是变加速运动，a与F方向时刻相同，与位移方向一定相反。
（1）关于平衡位置的对称点：
①a、F、S大小相同，方向相反；
动能势能相同 ②v大小相同，方向不一定相同
（2）先后通过同一位置：
①a、F、S，动能势能相同

07机械振动习题解答

解
振动方程：x=Acos(t+)=0.15cos(10t+/3) m (也可：7.5 15cos 又 v A sin 0 ）
3
0
3
v0= Asin(t+ )=Asin/3 = 1.30 m/s
第 10 页
三、计算题 2.一物体放在水平木板上，这木板以=2Hz 的频率沿水平直线作简谐运动，物体和水平木板之间的静摩擦系数S=0.5，求物体在木板上不滑动的最大振幅Amax。
2 d y 2 (m J / R ) 2 ky dt第 Nhomakorabea15 页
J T1R T2 R
T2 k (a y)
d2 y R 2 dt
1 若将滑轮当做匀质圆盘，则： J MR 2 2
1 d2 y 故： (m M ) 2 ky 2 dt
令
k / (m M / 2)
解
以物体平衡位置为坐标原点O，竖直向下为正方向建立坐标系Oy，滑轮转动轴垂直图平面向外为正。在物体平衡时，弹簧有一个伸长量，设为a，则： ka=mg 各个物理量标示如右图所示。
第 14 页
d2 y 物体m应用牛顿第二定律： m 2 mg T1 dt
滑轮应用转动定律：
绳子无质量且不可伸长：绳子在滑轮上不打滑：由上述四式化简，可得：
第9页
1. 一质量为m = 0.25kg的物体在弹性力作用下沿x轴运动，弹簧的劲度系数k = 25Nm-1。 (1) 求振动周期T和角频率。 (2) 如果振幅A = 15cm, t = 0时位移x0 = 7.5cm, 且物体沿x轴负方向运动，求初速度及初相。 (3) 写出其振动方程。
(1)振动角频率 =(k/m)1/2=10 s1，T=2/=0.628 s 。 (2)由旋转矢量求出初相， =/3，