三角形的高中线角平分线练习题
初一数学三角形的高中线与角平分线试题

初一数学三角形的高中线与角平分线试题1.如图所示,AD、AE分别是△ABC的角平分线和高,若∠B=50°,∠C=70°,求∠DAC的度数.【答案】10°【解析】本题主要考查了三角形的内角和定理和角平分线的性质.解:∵∠B=50°,∠C=70°,∴∠BAC=60°,又∵AD是△ABC的角平分线∴∠BAD=.又∵AE是△ABC的高∴∠BAE=180°-∠B-∠AEB=40°,∴∠DAC=∠BAE-∠BAD=10°2.如图,四边形ABCD中,AE平分∠BAD,DE平分∠ADC,且∠ABC=80º,∠BCD=70º,则∠AED= .【答案】75º【解析】本题考查的是角平分线的性质由∠ABC、∠BCD根据四边形的内角和即可求得∠BAD∠ADC的度数,再由AE平分∠BAD,DE平分∠ADC,即可求得∠BAE∠ADE的度数,最后根据三角形的内角和即可求得结果。
∠ABC=80º,∠BCD=70º,∠BAD∠ADC∠ABC∠BCD,AE平分∠BAD,DE平分∠ADC,∠BAE∠ADE,∠AED∠BAE∠ADE3.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是()A.等腰三角形B.锐角三角形C.直角三角形D.钝角三角形【答案】C【解析】本题考查的是三角形的高的概念作出一个直角三角形的高线进行判断,就可以得到.一个三角形的三条高的交点恰是三角形的一个顶点,这个三角形是直角三角形.故选C.4.如图,在∆ABC中,AM是中线,AD是角平分线,AH是高,则有下列结论:(1)BM== ;(2)∠CAD=∠=______________;(3)∠=∠=90°.【答案】(1)CM,BC;(2)∠BAD,∠BAC;(3)∠AHB,∠AHC【解析】本题考查的是三角形的角平分线、中线、高(1)根据三角形的中线的定义知:中线平分该中线所在的线段;(2)根据三角形角平分线的定义知:角平分线平分该角;(3)根据三角形的高的定义知,高与垂足所在的直线垂直.(1)∵AM是△ABC的中线,;(2)∵AD是△ABC的角平分线,∴∠CAD∠BAD∠BAC;(3)∵AH是△ABC的高,∴AH⊥BC,∴∠AHB=∠AHC=90°;故答案是:(1)CM,BC;(2)∠BAD,∠BAC;(3)∠AHB,∠AHC。
2021年中考数学复习:三角形的角平分线、中线和高 专项练习题(含答案)
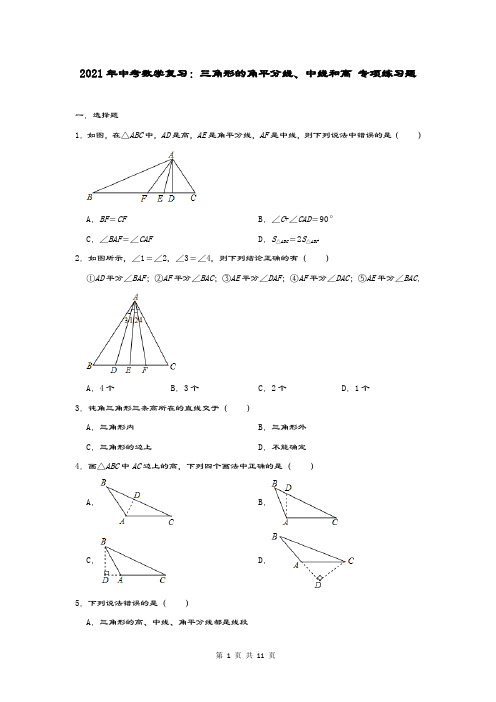
2021年中考数学复习:三角形的角平分线、中线和高专项练习题一.选择题1.如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法中错误的是()A.BF=CF B.∠C+∠CAD=90°C.∠BAF=∠CAF D.S△ABC =2S△ABF2.如图所示,∠1=∠2,∠3=∠4,则下列结论正确的有()①AD平分∠BAF;②AF平分∠BAC;③AE平分∠DAF;④AF平分∠DAC;⑤AE平分∠BAC.A.4个B.3个C.2个D.1个3.钝角三角形三条高所在的直线交于()A.三角形内B.三角形外C.三角形的边上D.不能确定4.画△ABC中AC边上的高,下列四个画法中正确的是()A.B.C.D.5.下列说法错误的是()A.三角形的高、中线、角平分线都是线段B.三角形的三条中线都在三角形内部C.锐角三角形的三条高一定交于同一点D.三角形的三条高、三条中线、三条角平分线都交于同一点6.在下列各图形中,分别画出了△ABC中BC边上的高AD,其中正确的是()A.B.C.D.7.下列四个图形中,线段BE是△ABC的高的图形是()A.B.C.D.8.如图所示,AC⊥BC于C,CD⊥AB于D,图中可以作为三角形“高”的线段有()A.1条B.2条C.3条D.5条9.如图,已知BD=CD,则AD一定是△ABC的()A.角平分线B.高线C.中线D.无法确定10.如图,在△ABC中,AB边上的高是()A.AD B.BE C.BF D.CF二.填空题11.如图,AD⊥BC于D,那么图中以AD为高的三角形有个.12.已知:AD、AE分别是△ABC的高,中线,BE=6,CD=4,则DE的长为.13.若线段AD是△ABC的中线,且BD=3,则BC长为.14.如图,在△ABC中,BC边上的中垂线DE交BC于点D,交AC于点E,AB=5cm,AC=8cm,则△ABE的周长为.15.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B=.16.如图,已知AD是△ABC的中线,且△ABD的周长比△ACD的周长多4cm.若AB=16cm,那么AC=cm.。
人教版八年级上册数学三角形的高、中线与角平分线同步训练

人教版八年级上册数学11.1.2 三角形的高、中线与角平分线同步训练一、单选题1.下列四个图形中,线段BE 是ABC 的高的是( )A .B .C .D . 2.如图,在△ABC 中,点D 是BC 的中点,点E 是AD 的中点,点F 是BE 的中点,已知△ABC 的面积为8,则△AEF 的面积为( )A .4B .2C .1D .12 3.如图,在ABC 中,BD CD =,2AE BE =,连接AD 、CE 相交于点O ,若ABC 的面积为24,则AOE △与COD △的面积之差为( )A .3B .4C .6D .8 4.如图,点D 、E 在ABC 的边上,连接AD 、BE 交于点F .若BD CD =,13CE AC =,224cm ABC S =,则图中两个阴影面积之差即AEF BDF S S -△△等于( )2cm .A .8B .4C .2D .15.如图,在ABC 中,D 、E 、F 分别为BC 、AD 、CE 的中点,且224cm ABC S =,则阴影部分AEF 的面积为( )2cm .A .2B .2.5C .3D .3.5 6.如图,ABC 中,AD BC ⊥于点D ,CE AB ⊥于点E ,则AB 边上的高是( )A .ADB .CEC .DCD .AE 7.如图,ABC 中,90C ∠=︒,8cm AC ,6cm BC ,10cm AB =.若动点P 从点C 开始,按C A B C →→→的路径运动,且速度为每秒2cm .设运动的时间为t 秒,当t =( )秒时,CP 把ABC 的面积分成相等的两部分.A .4B .6C .6.5D .7 8.如图,D 、E 分别是ABC 边BC 、AB 边上的中点,F 是AD 上一点且3AF FD =,若阴影部分的面积为9,则ABC 的面积是( )A .18B .16C .15D .14二、填空题9.如图,BD 是△ABC 的中线,AB =5cm ,BC =3cm ,那么△ABD 的周长比△CBD 的周长多_____.10.如图,△ABC 中,AB =AC =2,P 是BC 上任意一点,PE △AB 于点E ,PF △AC 于点F ,若S △ABC =3,则PE +PF =__________.11.如图,AB CD ∥,BC AB ⊥,若4cm AB =,212cm ABC S =△,求ABD △中AB 边上的高等于______.12.如图,△ABC 的面积是12,点D ,E ,F ,G 分别为BC ,AD ,BE ,CE 的中点,则△AFG 的面积是_____.13.如图,在三角形ABC 中,CD △AB 于点D ,DE △BC 于点E ,DE =8,AC =10,且CD 的长为整数,则CD 的长为________.14.如图,线段AD ,CE 分别是△ABC 中边BC ,AB 上的高.若AD =10,CE =9,AB =12,则BC 的长是________15.在Rt ABC 中,90ACB ∠=︒,CD 是AB 边上的中线,如果2AD BC =,那么:BC AB 的值是________.16.如图,在四边形ABCD 中,AD BC ∥,若210cm ABD S =△,则ACD S =______2cm .三、解答题17.如图,ABC 中,AD 是角平分线,AF 是高线,36,74B C ∠=︒∠=︒,求DAF ∠的度数.18.如图,BD和CE是△ABC的中线,AE=3cm,CD=2cm,若△ABC周长为15cm,求BC边的长.,AC边上的中线BD把三角形的周长分为10和18两部19.在ABC中,AB AC分,求腰长AB.20.如图,△ABC的顶点都在边长为1的正方形方格纸的格点上,将△ABC向上平移4格.(1)请在图中画出平移后的三角形A′B′C′;(2)在图中画出三角形△ABC的高CD、中线BE;(3)△ABC的面积是.参考答案:1.D2.C3.B4.B5.C6.B7.C8.B9.2cm10.311.6cm12.9 213.9 14.10.815.1 416.10 17.19°18.5cm 19.12 20.(3)8。
人教版八年级数学上册《三角形的高、中线与角平分线》拔高练习(1)

《三角形的高、中线与角平分线》拔高练习一、选择题(本大题共5小题,共25.0分)1.(5分)如图所示,有一条线段是△ABC(AC>AB)的中线,该线段是()A.线段AD B.线段AE C.线段AF D.线段MN2.(5分)在△ABC中,∠A是钝角,下列图中画BC边上的高线正确的是()A.B.C.D.3.(5分)如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是()A.锐角三角形B.钝角三角形C.直角三角形D.等边三角形4.(5分)三角形三条高的交点一定在()A.三角形内部B.三角形外部C.三角形内部或外部D.三角形内部、外部或顶点5.(5分)下列四个图形中,线段BE是△ABC的高的是()A.B.C.D.二、填空题(本大题共5小题,共25.0分)6.(5分)如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,AD与BE交于H,则∠CHD=.7.(5分)三角形的三条高线的交点在三角形的一个顶点上,则此三角形是.8.(5分)如图,△ABC中,AB>AC,AD是中线,AB=10,AD=7,∠CAD=45°,则BC=.9.(5分)如果一个三角形有一条边上的高等于这条边的一半,那么我们把这个三角形叫做半高三角形.已知直角三角形ABC是半高三角形,且斜边AB=5,则它的周长等于.10.(5分)如图,BD是△ABC的中线,AB=8,BC=6,△ABD和△BCD的周长的差是.三、解答题(本大题共5小题,共50.0分)11.(10分)如图,D是△ABC中BC上的一点,DE∥AC交AB于点E,DF∥AB交AC于点F,且∠ADE=∠ADF,AD是△ABC的角平分线吗?说明理由.12.(10分)我们知道,三角形三条高所在直线交于一点.规定:三角形三条高所在直线的交点叫做这个三角形的垂心.如图,AD⊥BC于点D,BE⊥AC于点E,CF⊥AB于点F;AD,BE,CF交于点G.(1)图中哪两个不共顶点的锐角一定相等?请写出一组:.(2)点G是△的垂心.(3)点A是△的垂心.13.(10分)已知AD是△ABC的高,∠BAD=70°,∠CAD=20°,求∠BAC的度数.14.(10分)如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为11cm,求AC的长.15.(10分)如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB =50°,∠C=60°,求∠DAE和∠BOA的度数.《三角形的高、中线与角平分线》拔高练习参考答案与试题解析一、选择题(本大题共5小题,共25.0分)1.(5分)如图所示,有一条线段是△ABC(AC>AB)的中线,该线段是()A.线段AD B.线段AE C.线段AF D.线段MN【分析】三角形一边的中点与此边所对顶点的连线叫做三角形的中线,逐一判断各选项即可.【解答】解:由图可得,F是BC的中点,根据三角形中线的定义,可知线段AF是△ABC的中线,故选:C.【点评】本题主要考查了三角形中线,三角形一边的中点与此边所对顶点的连线叫做三角形的中线.2.(5分)在△ABC中,∠A是钝角,下列图中画BC边上的高线正确的是()A.B.C.D.【分析】三角形的高即从三角形的顶点向对边引垂线,顶点和垂足间的线段.根据概念可知.【解答】解:过点A作直线BC的垂线段,即画BC边上的高,所以画法正确的是D.故选:D.【点评】考查了三角形的高的概念,能够正确作三角形一边上的高.3.(5分)如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是()A.锐角三角形B.钝角三角形C.直角三角形D.等边三角形【分析】直角三角形有两条高与直角边重合,另一条高在三角形内部,它们的交点是直角顶点;作出一个直角三角形的高线进行判断,就可以得到.【解答】解:一个三角形的三条高的交点恰是三角形的一个顶点,这个三角形是直角三角形.故选:C.【点评】本题主要考查了三角形的高的概念,钝角三角形的三条高所在的直线的交点在三角形的外部;锐角三角形的三条高所在的直线的交点在三角形的内部;直角三角形的三条高所在的直线的交点是三角形的直角顶点.4.(5分)三角形三条高的交点一定在()A.三角形内部B.三角形外部C.三角形内部或外部D.三角形内部、外部或顶点【分析】根据三角形的高线的定义分情况讨论高线的交点,即可得解.【解答】解:锐角三角形,三角形三条高的交点在三角形内部,直角三角形,三角形三条高的交点在三角形直角顶点,钝角三角形,三角形三条高的交点在三角形外部,故选:D.【点评】本题考查了三角形的高线,熟记三种三角形的高线的交点的位置是解题的关键.5.(5分)下列四个图形中,线段BE是△ABC的高的是()A.B.C.D.【分析】根据三角形高的画法知,过点B作AC边上的高,垂足为E,其中线段BE是△ABC的高,再结合图形进行判断.【解答】解:线段BE是△ABC的高的图是选项C.故选:C.【点评】本题主要考查了三角形的高,三角形的高是指从三角形的一个顶点向对边作垂线,连接顶点与垂足之间的线段.熟记定义是解题的关键.二、填空题(本大题共5小题,共25.0分)6.(5分)如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,AD与BE交于H,则∠CHD=45°.【分析】在三角形中,三内角之和等于180°,锐角三角形三个高交于一点.【解答】解:在△ABC中,三边的高交于一点,所以CF⊥AB,∵∠BAC=75°,且CF⊥AB,∴∠ACF=15°,∵∠ACB=60°,∴∠BCF=45°在△CDH中,三内角之和为180°,∴∠CHD=45°,故答案为∠CHD=45°.【点评】考查三角形中,三条边的高交于一点,且内角和为180°.7.(5分)三角形的三条高线的交点在三角形的一个顶点上,则此三角形是直角三角形.【分析】根据直角三角形的高的交点是直角顶点解答.【解答】解:∵三角形的三条高线的交点在三角形的一个顶点上,∴此三角形是直角三角形.故答案为:直角三角形.【点评】本题考查了三角形的高,锐角三角形的三条高在三角形内部,相交于三角形内一点;直角三角形有两条高与直角边重合,另一条高在三角形内部,它们的交点是直角顶点;钝角三角形有两条高在三角形外部,一条高在三角形内部,三条高所在直线相交于三角形外一点.8.(5分)如图,△ABC中,AB>AC,AD是中线,AB=10,AD=7,∠CAD=45°,则BC=2.【分析】作DH⊥AC于H,延长AD到E使DE=AD=7,连接CE,作EF⊥AC于F,作CH⊥AD于H,如图,先证明△ADB≌△EDC得到EC=AB=10,再利用△AEF为等腰直角三角形计算出AF=EF=7,则根据勾股定理可计算出CF=,从而得到AC =6,接着利用△ACH为等腰直角三角形得到AH=CH=6,然后利用勾股定理计算出CD,从而得到BC的长.【解答】解:作DH⊥AC于H,延长AD到E使DE=AD=7,连接CE,作EF⊥AC于F,作CH⊥AD于H,如图,∵AD是中线,∴BD=CD,在△ADB和△EDC中,∴△ADB≌△EDC(SAS),∴EC=AB=10,在RtAEF中,∵∠DAC=45°,AE=14,∴AF=EF=AE=7,在Rt△CEF中,CF==,∴AC=AF﹣CF=6,在Rt△ACH中,∵∠HAC=45°,∴AH=CH=AC=6,∴DH=AD﹣AH=1,在Rt△CDH中,CD==,∴BC=2CD=2.故答案为2.【点评】本题考查了三角形的角平分线、中线和高:熟练掌握三角形高、中线的定义;构造等腰直角三角形是解决此题的关键.9.(5分)如果一个三角形有一条边上的高等于这条边的一半,那么我们把这个三角形叫做半高三角形.已知直角三角形ABC是半高三角形,且斜边AB=5,则它的周长等于5+3或5+5.【分析】分两种情况讨论:①Rt△ABC中,CD⊥AB,CD=AB=;②Rt△ABC中,AC=BC,分别依据勾股定理和三角形的面积公式,即可得到该三角形的周长为5+3或5+5.【解答】解:如图所示,Rt△ABC中,CD⊥AB,CD=AB=,设BC=a,AC=b,则,解得a+b=5,或a+b=﹣5(舍去),∴△AB长度周长为5+5;如图所示,Rt△ABC中,AC=BC,设BC=a,AC=b,则,解得,∴△AB长度周长为3+5;综上所述,该三角形的周长为5+3或5+5.故答案为:5+3或5+5.【点评】本题主要考查了三角形的高线以及勾股定理的运用,解决问题给的关键是利用勾股定理进行推算.10.(5分)如图,BD是△ABC的中线,AB=8,BC=6,△ABD和△BCD的周长的差是2.【分析】根据三角形中线的定义可得AD=CD,然后求出△ABD和△BCD的周长差=AB ﹣BC,代入数据进行计算即可得解.【解答】解:∵BD是△ABC的中线,∴AD=CD,∴△ABD和△BCD的周长差=(AB+AD+BD)﹣(BC+CD+BD),=AB+AD+BD﹣BC﹣CD﹣BD,=AB﹣BC,∵AB=8,BC=6,∴△ABD和△BCD的周长差=8﹣6=2.答:△ABD和△BCD的周长差为2.故答案为:2【点评】本题考查了三角形的中线的定义,是基础题,数据概念并求出△ABD和△BCD 的周长差=AB﹣BC是解题的关键.三、解答题(本大题共5小题,共50.0分)11.(10分)如图,D是△ABC中BC上的一点,DE∥AC交AB于点E,DF∥AB交AC于点F,且∠ADE=∠ADF,AD是△ABC的角平分线吗?说明理由.【分析】依据DE∥AC,DF∥AB,即可得到∠ADE=∠DAF,∠ADF=∠EAD,再根据∠ADE=∠ADF,即可得出∠DAF=∠EAD,进而得到AD是∠BAC的角平分线.【解答】解:AD是△ABC的角平分线.理由:∵DE∥AC,DF∥AB,∴∠ADE=∠DAF,∠ADF=∠EAD,又∵∠ADE=∠ADF,∴∠DAF=∠EAD,又∵∠DAF+∠EAD=∠BAC,∴AD是∠BAC的角平分线.【点评】本题主要考查了角平分线的定义以及平行线的性质,三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线.12.(10分)我们知道,三角形三条高所在直线交于一点.规定:三角形三条高所在直线的交点叫做这个三角形的垂心.如图,AD⊥BC于点D,BE⊥AC于点E,CF⊥AB于点F;AD,BE,CF交于点G.(1)图中哪两个不共顶点的锐角一定相等?请写出一组:∠ABE=∠ACF或∠BAD=∠BCF或∠CAD=∠CBE.(2)点G是△ABC的垂心.(3)点A是△BCG的垂心.【分析】(1)依据BE⊥AC,CF⊥AB,可得∠ABE+∠BAE=∠ACF+∠CAF=90°,即可得到∠ABE=∠ACF;(2)三角形三条高所在直线的交点叫做这个三角形的垂心,据此进行判断;(3)三角形三条高所在直线的交点叫做这个三角形的垂心,据此进行判断.【解答】解:(1)∵BE⊥AC,CF⊥AB,∴∠ABE+∠BAE=∠ACF+∠CAF=90°,∴∠ABE=∠ACF,同理可得,∠BAD=∠BCF,∠CAD=∠CBE,故答案为:∠ABE=∠ACF或∠BAD=∠BCF或∠CAD=∠CBE;(2)∵AD⊥BC于点D,BE⊥AC于点E,CF⊥AB于点F;AD,BE,CF交于点G,∴点G是△ABC的垂心,故答案为:△ABC;(3)∵AD⊥BC于点D,BE⊥AC于点E,CF⊥AB于点F;AD,BF,CE交于点A,∴点A是△BCG的垂心,故答案为:△BCG.【点评】本题主要考查了三角形的角平分线高线以及中线,锐角三角形的三条高在三角形内部,相交于三角形内一点,直角三角形有两条高与直角边重合,另一条高在三角形内部,它们的交点是直角顶点;钝角三角形有两条高在三角形外部,一条高在三角形内部,三条高所在直线相交于三角形外一点.13.(10分)已知AD是△ABC的高,∠BAD=70°,∠CAD=20°,求∠BAC的度数.【分析】分高AD在△ABC内部和外部两种情况讨论求解即可.【解答】解:①如图1,当高AD在△ABC的内部时,∠BAC=∠BAD+∠CAD=70°+20°=90°;②如图2,当高AD在△ABC的外部时,∠BAC=∠BAD﹣∠CAD=70°﹣20°=50°,综上所述,∠BAC的度数为90°或50°.【点评】本题考查了三角形的高线,难点在于要分情况讨论.14.(10分)如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为11cm,求AC的长.【分析】根据中线的定义知CD=BD.结合三角形周长公式知AC﹣AB=5cm;又AC+AB =11cm.易求AC的长度.【解答】解:∵AD是BC边上的中线,∴D为BC的中点,CD=BD.∵△ADC的周长﹣△ABD的周长=5cm.∴AC﹣AB=5cm.又∵AB+AC=11cm,∴AC=8cm.即AC的长度是8cm.【点评】本题考查了三角形的角平分线、中线和高.三角形一边的中点与此边所对顶点的连线叫做三角形的中线.15.(10分)如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB =50°,∠C=60°,求∠DAE和∠BOA的度数.【分析】先利用三角形内角和定理可求∠ABC,在直角三角形ACD中,易求∠DAC;再根据角平分线定义可求∠CBF、∠EAF,可得∠DAE的度数;然后利用三角形外角性质,可先求∠AFB,再次利用三角形外角性质,容易求出∠BOA.【解答】解:∵∠CAB=50°,∠C=60°∴∠ABC=180°﹣50°﹣60°=70°,又∵AD是高,∴∠ADC=90°,∴∠DAC=180°﹣90°﹣∠C=30°,∵AE、BF是角平分线,∴∠CBF=∠ABF=35°,∠EAF=25°,∴∠DAE=∠DAC﹣∠EAF=5°,∠AFB=∠C+∠CBF=60°+35°=95°,∴∠BOA=∠EAF+∠AFB=25°+95°=120°,∴∠DAC=30°,∠BOA=120°.故∠DAE=5°,∠BOA=120°.【点评】本题考查了三角形内角和定理、角平分线定义、三角形外角性质.关键是利用角平分线的性质解出∠EAF、∠CBF,再运用三角形外角性质求出∠AFB.。
人教版八年级上数学第十一章 11.1.2三角形的高、中线与角平分线同步练习

11.1.2三角形的高、中线与角平分线同步练习(时间120分钟,满分150分)一、选择题:本大题共12个小题,每小题4分,共48分. 1.三角形的角平分线、中线、高线都是( )A.线段B.射线C.直线D.以上都有可能 2. 下列说法正确的是( )A .三角形三条高都在三角形内B .三角形三条中线相交于一点C .三角形的三条角平分线可能在三角形内,也可能在三角形外D .三角形的角平分线是射线 3.至少有两条高在三角形内部的三角形是( )A. 锐角三角形B. 钝角三角形C. 直角三角形D.都有可能 4.不一定在三角形内部的线段是( )(A )三角形的角平分线 (B )三角形的中线 (C )三角形的高 (D )三角形的中位线 5.可以把一个三角形分成面积相等的两部分的线段是( )A .三角形的高B .三角形的角平分线C .三角形的中线D .无法确定 7.在三角形中,交点一定在三角形内部的有( )①三角形的三条高线 ②三角形的三条中线 ③三角形的三条角平分线 ④三角形的外角平分线.A .①②③④B .①②③C .①④D .②③8.如果一个三角形三条高的交点恰是三角形的一个顶点,那么这个三角形是 ( ) A. 锐角三角形 B. 直角三角形 C.钝角三角形 D.不能确定 9.画△ABC 中AB 边上的高,下列画法中正确的是( )A B C D10. 如图,D,E 分别是△ABC 的边AC,BC 的中点,则下列说法不正确的是( )A.DE 是△BCD 的中线B.BD 是△ABC 的中线C.AD=DC,BD=ECD.∠C 的对边是DE11.如图3所示,在△ABC 中,已知点D, E,F 分别为边BC,AD,CE 的中点, 且S △ABC =4cm 2,则S 阴影等于( )A.2cm 2B.1cm 2C.12cm 2 D.14cm 212.在△ABC 中,D 是BC 上的点,且BD:CD=2:1,S △ACD =12,那么S △ABC 等于( )A. 30B. 36C. 72D.24二、填空题:本大题共6小题,每小题4分,共24分.13. 照相机的支架是三条腿,这是利用了三角形的_________. 14.如图,在△ABC 中,BC 边上的高是 ,在△AEC 中,AE 边上的高是 ,EC 边上的高是 . 15.如图所示,CD 是△ABC 的中线,AC =9cm ,BC =3cm ,那么△ACD 和△BCD 的周长差是___________cm . 16.在ABC ∆中,2,3AC cm BC cm ==,则ABC ∆的高AD 与BE 的比是FE(第11题) D CBA(第10题)17.如图所示:(1)在△ABC 中,BC 边上的高是_____(2)在△AEC 中,AE 边上的高是_____. 18.如图所示,在△ABC 中,AD ⊥BC ,BE ⊥AC ,BC=12,AC=8,AD=6,则BE的长 .三、解答题:本大题共2个小题,每小题7分,共14分. 19.如图,在⊿ABC 中画出高线AD 、中线BE 、角平分线CF .20.在△ABC 中,AB=AC,AD 是中线,△ABC 的周长为34cm,△ABD 的周长为30cm, 求AD 的长.四、解答题:本大题共4个小题,每小题10分,共40分21.如图,已知:在三角形ABC 中,∠C=90º,CD 是斜边AB 上的高,AB=5,BC=4,AC=3,求高CD 的长度.22.在等腰三角形ABC 中,AB=AC ,一腰上的中线BD 将这个等腰三角形的周长分为15和6两部分,求该等腰三角形的腰长及底边长.ABC(第17题) (第15题) E FDCBA(第14题) (第18题)23.(1)如图,在△ABC中,D、E分别是BC、AD的中点,S△ABC=4cm2,求S△ABE.(2)如图,S△ABC=1,且D是BC的中点,AE:EB=1:2,求△ADE的面积.EDCBA24.如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,求:(1)△ABC的面积;(2)CD的长;(3)作出△ABC的边AC上的中线BE,并求出△ABE的面积;(4)作出△BCD的边BC边上的高DF,当BD=11cm 时,试求出DF的长。
人教版八年级数学 《三角形的高、中线、角平分线》同步练习题(含答案)

人教版八年级数学《三角形的高、中线、角平分线》同步练习题选择题1.下面四个图形中,线段BE是△ABC的高的图是( )2.下列说法正确的是()A.三角形三条高都在三角形内B.三角形三条中线相交于一点C.三角形的三条角平分线可能在三角形内,也可能在三角形外D.三角形的角平分线是射线3.如图,D、E分别是△ABC的边AC、BC的中点,那么下列说法中不正确的是( )A.DE是△BCD的中线B.BD是△ABC的中线C.AD=DC,BE=ECD.AD=EC,DC=BE4.三角形一边上的中线把原三角形一定分成两个( )A.形状相同的三角形B.面积相等的三角形C.直角三角形D.周长相等的三角形5.如图所示,AD是△ABC的角平分线,AE是△ABD的角平分线.若∠BAC=80°,则∠E AD的度数是( )A.20°B.30°C.45°D.60°6.在△ABC中,AD为中线,BE为角平分线,则在以下等式中:①∠BAD=∠CAD;②∠ABE=∠CBE;③BD=DC;④AE=EC.正确的是()A.①②B.③④C.①④D.②③7.如图,工人师傅砌门时,常用木条EF固定矩形门框ABCD,使其不变形,这种做法的根据是()A.两点之间线段最短 B.矩形的对称性C.矩形的四个角都是直角D.三角形的稳定性8.三角形的高线是()A.直线B.线段C.射线D.三种情况都可能二、填空题9.如图,在△ABC中,∠ACB=90°,CD⊥AD,垂足为点D,有下列说法:①点A与点B的距离是线段AB的长;②点A到直线CD的距离是线段AD的长;③线段CD是△AB C边AB上的高;上述说法中,正确的个数为_________个10.如图,△ABC 的角平分线AD 、中线BE 相交于点O ,则①AO 是△ABE 的角平分线;②BO 是△ABD 的中线;③DE 是△ADC 的中线;④ED 是△EBC 的角平分线的结论中正确的有_________.11.如图,小明的父亲在院子的门板上钉了一个加固板,从数学角度看,这样做的原因是______________________.12.如图所示,CD 是△ABC 的中线,AC=9cm ,BC=3cm ,那么△ACD 和△BCD 的周长差是___________cm .13.AD 是△ABC 的一条高,如果∠BAD=65°,∠CAD=30°,则∠BAC=______.14.如图,在△ABC 中,AC ⊥BC ,CD ⊥AB 于点D .则图中共有_____个直角三角形.15.如图,在△ABC 中,BD 是角平分线,BE 是中线,若AC=24cm ,则AE= cm ,若∠ABC=72°,则∠ABD=_____度.三、解答题16.如图,D 是△ABC 中BC 边上的一点,DE ∥AC 交AB 于点E ,若∠EDA=∠EAD ,试说明AD 是△ABC 的角平分线.17.如图,在△ABC 中,AD ⊥BC,BE ⊥AC,BC=12,AC=8,AD=6,BE 的长为多少?18.如图,在3×2的正方形网格中,小正方形的边长为1,以图中A ,B ,C ,D ,E 中的三点为顶点的三角形中,面积为1的三角形有哪些?(第9题) (第10题) (第11题)(第12题) (第14题)(第15题)19.已知AD为△ABC的中线,AB=5 cm,且△ACD的周长比△ABD的周长少2 cm,求AC的长度20.张大爷的四个儿子都长大成人了,也该分家了,于是张大爷准备把如图所示的一块三角形的田地平均分给四个儿子,四个儿子要求田地的形状仍然是三角形,请你帮助张大爷提出一种平分的方案.21.如图,AD是∠CAB的角平分线,DE∥AB,DF∥AC,EF交AD于点O.请问:DO是∠EDF的角平分线吗?如果是,请给予证明;如果不是,请说明理由.22.如图1,在四边形木条框架中,任意添加1根对角线木条,就能使框架的形状稳定.判断下列说法是否正确.(正确的打“√”,错误的打“×”)(1)在图2中任意添加2根对角线木条,都能使框架的形状稳定.( )(2)在图3中任意添加3根对角线木条,都能使框架的形状稳定.( )(3)图4是一个用螺钉将木条链接成的框架,颇具美感,它的形状是稳定的.( )23.如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=4 cm2,求阴影部分的面积S阴影.参考答案1.A2.B.3.D4.B5.A 7.A 8.B9.4 10.2 11.利用三角形的稳定性使门板不变形. 12..6 13.95°或35°14.3 15.12,3616.∵DE ∥AC,∴∠EDA=∠CAD.∵∠EDA=∠EAD,∴∠CAD=∠EAD.∴AD 是△ABC 的角平分线. 17.∵S △ABC=36,又∵S△ABC=AC ·BE ,∴×8×BE=36.解得BE=9.18.以A 、B 、C 、D 、E 中的三点为顶点的三角形共有9个,其中面积为1的三角形有:△A BC,△ADE,△BCE,△ACD19.∵AD 为△ABC 的中线,∴BD=CD.∵△ACD 的周长比△ABD 的周长少2 cm ,∴(AB+BD+AD)-(AC+AD+CD)=AB-AC=2 cm ,∴AC=AB-2=5-2=3(cm).20.答案不唯一,第一种方案:四等分一条边构成的四个三角形,图略;第二种方案:由一条中线以及中线上的中线分割成的四个三角形,图略.21.DO 是∠EDF 的角平分线.证明:∵AD 是∠CAB 的角平分线,∴∠EAD=∠FAD.∵DE ∥AB ,DF ∥AC ,∴∠EDA=∠FAD ,∠FDA=∠EAD.∴∠EDA=∠FDA ,即DO 是∠EDF 的角平分线.22.(1)√(2)√(3)√23.∵D 是边BC 的中点,∴S △ABD=S △ACD=S △ABC=×4=2(cm2).∵E 是AD 的中点,∴S △B DE=S △ABD=1 cm2,S△CDE=S △A CD=1 cm2.∴S △BEC=S △BDE+S △CDE=2 cm2.又∵F 是CE 的中点,∴S 阴影=S △BEC=1 cm2.21212121212121。
人教版数学八年级上册 三角形的高、中线、角平分线 专题训练

∵AD⊥BC,∴∠ADE=90°. ∴∠B+∠BAD=90°. ∴∠BAD=90°-∠B. ∴∠DAE=∠BAE-∠BAD=90°-12(∠B+∠C)-(90°-∠B) =12(∠B-∠C). ∵∠B-∠C=40°,∴∠DAE=12×40°=20°.
16.如图,AE,AD 分别是△ABC 的高和角平分线,且∠B=36°, ∠C=75°.求∠DAE 的度数.
9.如图,在△ABC 中,AB=AC,DE⊥AB,DF⊥AC,BG⊥ AC,垂足分别为点 E,F,G.求证 DE+DF=BG. 证明:连接 AD. ∵S△ABC=S△ABD+S△ADC, ∴12AC·BG=12AB·DE+12AC·DF. 又∵AB=AC,∴DE+DF=BG.
10.如图,△ABC 的三边的中线 AD,BE,CF 的公共点为 G,
(1)求△ABC 的面积及 AC 边上的高 BE 的长;
解:S△ABC=12BC·AD=12×4×4=8. ∵S△ABC=12AC·BE=12×5×BE=8,∴BE=156.
(2)求 AD∶BE 的值. 解:AD∶BE=4∶156=54
8. 如图,已知△ABC. (1)画出 BC 边上的高 AD 和中线 AE;
解:在△ABC 中,∠BAC=180°-∠B-∠C=180°-36°-75° =69°. ∵AE,AD 分别是△ABC 的高和角平分线, ∴∠AED=90°,∠BAD=∠CAD=12∠BAC=34.5°.
∵∠ADE 是△ABD 的外角, ∴∠ADE=∠B+∠BAD=36°+34.5°=70.5°. 在 Rt△ADE 中,∠DAE=90°-∠ADE=19.5°.
(3)若 BN⊥AD 交 AD 的延长线于 N,求证 BN=CM.
证明:由题意知 S△ABD=S△ACD=12S△ABC. ∵S△ABD=12AD·BN,S△ACD=12AD·CM, ∴12AD·BN=12AD·CM. ∴BN=CM.
初中-数学-人教版-三角形的角平分线、中线和高专题练习

∴AB-AC=2(cm).
即△ABD与△ACD的周长之差为2cm.
19、【答案】115
【分析】直接根据角平分线平分对应角,三角形内角和为180度进行计算.
【解答】 BP平分∠ABC,CP平分∠ACB,
故答案为115.
20、【答案】③④
【分析】本题考查了三角形的角平分线、三角形的中线、三角形的高的概念,注意:三角形的角平分线、中线、高都是线段,且都是顶点和三角形的某条边相交的交点之间的线段.透彻理解定义是解题的关键.
③写出α与β的数量关系,并说明理由;
(2)如图(2),当E点在CA的延长线上时,其它条件不变,请直接写出α与β的数量关系.
参考答案
1、【答案】C
【分析】根据三角形的高的特点对选项进行一一分析,即可得出答案.
【解答】A、锐角三角形,三条高线交点在三角形内,故错误;
B、钝角三角形,三条高线不会交于一个顶点,故错误;
【解答】①根据三角形的角平分线的概念,知AD是△ABC的角平分线,故此说法不正确;
②根据三角形的中线的概念,知BG是△ABD的边AD上的中线,故此说法不正确;
③根据三角形的高的概念,知CH为△ACD的边AD上的高,故此说法正确;
④根据三角形的角平分线和高的概念,知AH是△ACF的角平分线和高线,故此说法正确.
∴△ABC的面积=2×△BDC的面积=16,
选C.
11、【答案】C
【分析】根据三角形的高线、中线、角平分线的性质逐一判断即可.
【解答】解:A、正确,锐角三角形的三条高线、三条中线、三条角平分线分别交于一点;
B、正确,钝角三角形有两条高线在三角形的外部;
C、错误,直角三角形也有三条高线;
三角形的高中线与角平分线练习题

4321EDCBA1CDBA三角形的高、中线与角平分线11 如图,已知△ABC 中,AQ=PQ 、PR=PS 、PR ⊥AB 于R ,PS ⊥AC 于S ,有以下三个结论:①AS=AR ;②QP ∥AR ; ③△BRP ≌△CSP ,其中( ).(A)全部正确 (B)仅①正确 (C)仅①、②正确 (D)仅①、③正确 2、 如图,点E 在BC 的延长线上,则下列条件中,不能判定AB ∥CD 的是( )A. ∠3=∠4B.∠B=∠DCEC.∠1=∠2.D.∠D+∠DAB=180° 3.如图,ΔACB 中,∠ACB=900,∠1=∠B.(1)试说明 CD 是ΔABC 的高;(2)如果AC=8,BC=6,AB=10,求CD 的长。
4如图,直线DE 交△ABC 的边AB 、AC 于D 、E , 交BC 延长线于F ,若∠B =67°,∠ACB =74°, ∠AED =48°,求∠BDF 的度数5、如图:∠1=∠2=∠3,完成说理过程并注明理由: 因为 ∠1=∠2所以 ____∥____ ( ) 因为 ∠1=∠3所以 ____∥____ ( )6.以下列各组线段为边,能组成三角形的是( ) A .2cm ,3cm ,5cm B .5cm ,6cm ,10cm C .1cm ,1cm ,3cm D .3cm ,4cm ,9cm7.等腰三角形的一边长等于4,一边长等于9,则它的周长是( ) A .17 B .22 C .17或22 D .138.适合条件∠A=12∠B=13∠C的△ABC是()A.锐角三角形B.直角三角形C.钝角三角形D.等边三角形9.已知等腰三角形的一个角为75°,则其顶角为()A.30°B.75°C.105°D.30°或75°10.一个多边形的角和比它的外角的和的2倍还大180°,这个多边形的边数是()A.5 B.6 C.7 D.811.三角形的一个外角是锐角,则此三角形的形状是()A.锐角三角形B.钝角三角形C.直角三角形D.无法确定12.三角形的三边长分别为5,1+2x,8,则x的取值围是________.13.如图,BD平分∠ABC,DA⊥AB,∠1=60°,∠BDC=80°,求∠C的度数.初一三角形的高、中线与角平分线21 如图,BC⊥CD,∠1=∠2=∠3,∠4=60°,∠5=∠6.(1)CO是△BCD的高吗?为什么?(2)∠5的度数是多少?(3)求四边形ABCD各角的度数.2.△ABC中,∠A=50°,∠B=60°,则∠A+∠C=________.3 .已知三角形的三个角的度数之比为1:2:3,则这个三角形是()A.锐角三角形B.直角三角形C.钝角三角形D.不能确定4.△ABC中,∠A=∠B+∠C,则∠A=______度.5.如图∠1+∠2+∠3+∠4=______度.6.如图,△ABC中,AD是BC上的高,AE平分∠BAC,∠B=75°,•∠C=45°,求∠DAE与∠AEC的度数.7.以下说法错误的是()6题A.三角形的三条高一定在三角形部交于一点B.三角形的三条中线一定在三角形部交于一点C.三角形的三条角平分线一定在三角形部交于一点D.三角形的三条高可能相交于外部一点8.如果一个三角形的三条高的交点恰好是这个三角形的一个顶点,•那么这个三角形是()A.锐角三角形B.直角三角形C.钝角三角形D.不能确定9.如图,BD=1BC,则BC边上的中线为______,△ABD的面积=_____的面积.2(9)10.如图,△ABC中,高CD、BE、AF相交于点O,则△BOC•的三条高分别为线段________.(10)初一三角形的高、中线与角平分线31.下列图形中具有稳定性的是()A.梯形B.菱形C.三角形D.正方形2.如图3,AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm,求△ABD•与△ACD的周长之差.3.如图,∠BAD=∠CAD,AD⊥BC,垂足为点D,且BD=CD.•可知哪些线段是哪个三角形的角平分线、中线或高?4.如图5,在等腰三角形ABC中,AB=AC,一腰上的中线BD将这个等腰三角形的周长分为15和6两部分,求该等腰三角形的腰长及底边长.5.有一块三角形优良品种试验基地,如图所示,•由于引进四个优良品种进行对比试验,需将这块土地分成面积相等的四块,请你制定出两种以上的划分方案供选择(画图说明).6.如图,在△ABC中,D、E分别是BC、AD的中点,S△ABC=4cm2,求S△ABE.7.如图,在锐角△ABC中,CD、BE分别是AB、AC上的高,•且CD、BE交于一点P,若∠A=50°,则∠BPC的度数是()8如图7-1-2-9,AD是△ABC的角平分线,DE∥AB,DF∥AC,EF交AD于点O.请问:DO是△DEF的角平分线吗?如果是,请给予证明;如果不是,请说明理由.初一三角形的高、中线与角平分线41.若三角形的外角中有一个是锐角,则这个三角形是________三角形.2.△ABC中,若∠C-∠B=∠A,则△ABC的外角中最小的角是______(填“锐角”、“直角”或“钝角”).3.如图1,x=______.(1) (2) (3) 4.如图2,△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA到E,连EF,则∠1,∠2,∠3的大小关系是_________.5.如图3,在△ABC中,AE是角平分线,且∠B=52°,∠C=78°,求∠AEB的度数.7.如图所示,在△ABC中,AB=AC,AD=AE,∠BAD=60°,则∠EDC=______.8.一个零件的形状如图7-2-2-6所示,按规定∠A应等于90°,∠B、∠D应分别是30°和20°,叔叔量得∠BCD=142°,就断定这个零件不合格,你能说出道理吗?9.(1)如图(1),求出∠A+∠B+∠C+∠D+∠E+∠F的度数;(2)如图(2),求出∠A+∠B+∠C+∠D+∠E+∠F的度数.11.如图,BD、CD分别是△ABC的两个外角∠CBE、∠BCF•的平分线,试探索∠D与∠A之间的数量关系.12 如图,BD为△ABC的角平分线,CD为△ABC的外角∠ACE的平分线,它们相交于点D,试探索∠BDC与∠A之间的数量关系.7.3 多边形及其角和基础过关作业1.四边形ABCD中,如果∠A+∠C+∠D=280°,则∠B的度数是()A.80°B.90°C.170°D.20°2.一个多边形的角和等于1080°,这个多边形的边数是()A.9 B.8 C.7 D.63.角和等于外角和2倍的多边形是()A.五边形B.六边形C.七边形D.八边形4.六边形的角和等于_______度.5.正十边形的每一个角的度数等于______,每一个外角的度数等于_______.6.如图,你能数出多少个不同的四边形?7.四边形的四个角可以都是锐角吗?可以都是钝角吗?可以都是直角吗?•为什么?8.求下列图形中x的值:综合创新作业9.(综合题)已知:如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,•DF平分∠ADC.BE与DF有怎样的位置关系?为什么?10.(应用题)有10个城市进行篮球比赛,每个城市均派3个代表队参加比赛,规定同一城市间代表队不进行比赛,其他代表队都要比赛一场,问按此规定,•所有代表队要打多少场比赛?11.(创新题)如图,以五边形的每个顶点为圆心,以1为半径画圆,求圆与五边形重合的面积.12.(1)(2005年,)已知一个多边形的角和为540°,则这个多边形为()A.三角形B.四边形C.五边形D.六边形(2)(2005年,)五边形的角和等于_______度.13.(易错题)一个多边形的每一个顶点处取一个外角,这些外角中最多有钝角(• )A.1个B.2个C.3个D.4个培优作业14.(探究题)(1)四边形有几条对角线?五边形有几条对角线?六边形有几条对角线?……猜想并探索:n边形有几条对角线?(2)一个n边形的边数增加1,对角线增加多少条?15.(开放题)如果一个多边形的边数增加1,•那么这个多边形的角和增加多少度?若将n边形的边数增加1倍,则它的角和增加多少度?数学世界攻其不备壁虎在一座油罐的下底边沿A处.它发现在自己的正上方──油罐上边缘的B•处有一只害虫.壁虎决定捕捉这只害虫.为了不引起害虫的注意,它故意不走直线,而是绕着油罐,沿着一条螺旋路线,从背后对害虫进行突然袭击如图7-3-5.结果,•壁虎的偷袭得到成功,获得了一顿美餐.请问:壁虎沿着螺旋线爬行是最短的路程吗(线段AB除外)?答案:1.A 点拨:∠B=360°-(∠A+∠C+∠D)=360°-280°=80°.故选A.2.B 点拨:设这个多边形的边数为n,则(n-2)·180=1080.解得n=8.故选B.3.B 点拨:设这个多边形的边数为n,根据题意,得(n-2)·180=2×360.解得n=6.故选B.4.7205.144°;36°点拨:正十边形每一个角的度数为:(102)18010-⨯︒=144°,每一个外角的度数为:180°-144°=36°.6.有27个不同的四边形.7.解:四边形的四个角不可以都是锐角,不可以都是钝角,可以都是直角.因为四边形的角和为360°,如果四个角都是锐角或都是钝角,•则角和小于360°或大于360°,与四边形的角和为360°矛盾.•所以四个角不可以都是锐角或都是钝角.若四个角都是直角,则四个角的和等于360°,与角和定理相符,所以四个角可以都是直角.8.解:(1)90+70+150+x=360.解得x=50.(2)90+73+82+(180-x)=360.解得x=65.(3)x+(x+30)+60+x+(x-10)=(5-2)×180.解得x=115.9.解:BE∥DF.理由:∵∠A=∠C=90°,∴∠A+∠C=180°.∴∠ABC+∠ADC=360°-180°=180°.∵∠ABE=12∠ABC,∠ADF=12∠ADC,∴∠ABE+∠ADF=12(∠ABC+∠ADC)=12×180°=90°.又∵∠ABE+∠AEB=90°,∴∠AEB=∠ADF,∴BE∥DF(同位角相等,两直线平行).10.解:12n (n-3)=12×10×(10-3)=12×10×7=35(场).答:按此规定,所有代表队要打35场比赛.点拨:问题类似于求多边形对角线的个数.11.解:(5-2)×180°÷360°×12=1.5.点拨:不能直接求出扇形的度数,用整体法圆与五边形重合部分的角度和正好是五边形的角和.12.(1)C 点拨:设这个多边形的边数为n ,依题意,得(n-2)×180°=540°,解得n=5,故选C .(2)540 点拨:(n-2)×180°=(5-3)×180°=540°.13.C14.解:(1)四边形有2条对角线;五边形有5条对角线;六边形有9条对角线;……n 边形有(3)2n n -条对角线. (2)当n 边形的边数增加1时,对角线增加(n-1)条.点拨:从n 边形的一个顶点出发,向其他顶点共可引(n-3)条对角线,n 个顶点共可引n (n-3)条,但这些对角线每一条都重复了一次,故n 边形的对角线条数为(3)2n n -. 15.180°,n ·180°.数学世界答案:是最短的路程.可用纸板做一个模型,沿AB 剪开便可看出结论.。
三角形的高、中线、角平分线练习题

三角形的高、中线、角平分线练习题
1、分别在下列锐角三角形、直角三角形、钝角三角形中画出所有的高。
2、三角形的三条中线、三条角平分线、三条高都是( )
A(直线 B(射线 C(线段 D(射线或线段
3、如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )A(锐角三角形 B(直角三角形 C(钝角三角形 D(不能确定
4、能把三角形的面积分成两个相等的三角形的线段是( )
AA(中线 B(高 C(角平分线 D(以上三种情况都正确
5、如图若?BAF=?CAF,则____是?ABD的角平分线,____是?ABC的DF角平分线BCEA
6、如图AB?AC,则AB是?ABC的边____上的高,也是?BDC的边______D上的高,也是?ABD的边____上的高.
07、如图BD、AE分别是?ABC的中线、角平分线,AC=10cm ,?BAC=70,CBA则AD=_____,?BAE=____.
D8、在?ABC中,AE是中线,AD是角平分线,AF
是高,填空: BCE1?BE,___,_____; 2
1??BAD=_____=_____;??AFB=_____=90 2
9、在?ABC中,AB=AC,AD是中线,?ABC的周长为34cm,?ABD的周长为30cm, 求AD的长.
10、在?ABC中AB=AC,AC上的中线BD把三角形的周长分为24cm和30cm的两个部分,求三角形的三边长。
11、要使四边形木架(用四根木条钉成)不变形,至少要再钉上几根木条,五边形木架和六边形木架呢,n边形木架呢,。
三角形的中线、角平分线、高线

B 三角形的中线、角平分线、高线例1、已知在△ABC 中,CE 、BD 分别是AB 、AC 边上的中线,若AE=2,AD=3,且△ABC 的周长为15,求BC 的长.练习:△ABC 的周长为18,BE 、CF 分别为AC 、AB 边上的中线,BE 、CF 相交于点O ,AO 的延长线交BC 于点D ,且AF=3cm ,AE=2cm ,求AB 、AC 、BD 的长。
例2、如图,AD 是△ABC 的中线,AB=6cm ,AC=5cm ,求△ABD 和△ADC 的周长的差。
练习:1、如图,BD 是△ABC 的中线,△ABD 和△BDC 的周长的差为3cm ,AB 的长为13cm ,求BC 的长。
2、如图,△ABC 中,AB=AC ,周长为16cm ,AC 边上的中线BD 把△ABC 分成周长差为2cm 的两个三角形,求△ABC 各边的长。
3、 已知等腰三角形的周长为25,AB AC ,一腰上的中线把三角形分成两个,两个三角形的周长的差是4,求等腰三角形各边的长。
EDO C BAB CB 第15题图B4、等腰三角形ABC 中,AB=AC ,AC 边上的中线把该三角形的周长分为15cm 和6cm 两部分,求这个等腰三角形各边的长。
5、等腰三角形ABC 中,AB=AC ,中线BD 将这个三角形的周长分为15和12两个部分,求这个三角形的底边长。
例3、如图,AD 是△ABC 的中线,AE 是△ACD 的中线,已知DE=2, (1) 求BD 、BE 、BC 的长;(2) 若△ACE 面积为4,求△ACD 、△ABC 的面积。
练习:1、如图,AD 是△ABC 的边BC 上的中线,DE 是△ACD 的边AC 上的中线,若4ABCS∆=,则ADES∆=__________________;2、如图,AD 是△ABC 的边BC 上的中线,DE=2AE ,且224ABCcm S ∆=,则ABE S ∆=__________;3、如图,在ABC ∆中,已知点D 、E 、F 分别在三边上,E 为AC 的中点,AD 、BE 、CF 交于点G ,2BD DC =,3GECS∆=,4GDC S ∆=,则ABC ∆的面积是_____________;4、如图 ,AD 为ABC ∆的中线,BE 为ABD ∆中线,(1)15,35ABE BAD ∠=︒∠=︒,求BED ∠的度数;(2)在BED ∆中作BD 边上的高;(3)图1OC B AE图3OFCB AE 图2O D CB AB若ABC ∆的面积为60,5BD =,求点E 到BC例4、(1)如图,在△ABC 中,BD 平分∠AB C ,∠A=38°,∠C=72°,则∠ADB= . (2)如图,△ABC 中,AD 平分∠CAE ,∠B=40°,∠DAE=80°,则∠ACD=______(3)如图,△ABC 中,BD 、CE 分别平分∠ABC 、∠ACB ,∠BOC=130°,则∠A=______ 例5、如图,△AB C 中,∠A=40°,(1)如图1,当∠ACB 、∠ABC 的平分线交于点O 时,则∠BOC= ; (2)如图2,当∠ABC 的平分线BD 与∠ACB 的外角平分线交于点O 时,则∠BOC= ;(3)如图3,当∠ABC 的外角平分线与∠ACB 的外角平分线交于点O 时,则∠BOC=例6、如图,D 是ABC ∆的边BC 上一点,过点D 作DE //AC 交AB 于点E ,作DF //AB 交AC 于点F ,若12∠=∠,则①AD 是ABC ∆的角平分线吗?(写出证明过程)②若33AF AE ==,,你能求出四边形AEDF 的周长吗?DCBAE DC B AEDOCB A第23题图B练习:如图,在ABC ∆中,CD 是高,点E 、F 、G 分别在BC 、AB 、AC 上,且EF AB ⊥,12∠=∠,①试判断DG 与BC 的位置关系?并说明理由。
三角形的高、中线、角平分线

8.如图,已知AD,AE分别是△ABC的高和中线,AB=6 cm, AC=8 cm,BC=10 cm,∠CAB=90°.试求:
(1)AD的长;
∴∠D+∠DEG+∠B+∠BCH=∠F+∠ACH+∠F+∠AEG. ∴∠D+∠B=2∠F. ∵∠B∶∠D∶∠F=4∶6∶x,∴x=5.
10.如图,在△ABC中,AD⊥BC于D,AE平分 ∠BAC,∠B=70°,∠C=30°.
(1)求∠BAE的度数.
解:∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°-∠B-∠C=180°-70°-30°=80°.
解:能.
∵∠B+∠C+∠BAC=180°,∴∠BAC=180°-∠B-∠C.
∵AE 平分∠BAC, ∴∠BAE=12∠BAC=12(180°-∠B-∠C)=90°-12(∠B+∠C). ∵AD⊥BC,∴∠ADE=90°.
∴∠B+∠BAD=90°. ∴∠BAD=90°-∠B.
∴∠DAE=∠BAE-∠BAD=90°-12(∠B+∠C)-(90°-∠B) =12(∠B-∠C). ∵∠B-∠C=40°,∴∠DAE=12×40°=20°.
9.如图,BE,CD相交于点A,CF为∠BCD的平分线,EF为 ∠BED的平分线.
(1)图中共有____6____个“8字形”;
(2)若∠B∶∠D∶∠F=4∶6∶x,求x的值. 解:∵EF平分∠BED,CF平分∠BCD, ∴∠DEG=∠AEG,∠ACH=∠BCH. ∵在△DGE和△FGC中,∠DGE=∠FGC, ∴∠D+∠DEG=∠F+∠ACH. ∵在△BHC和△FHE中,∠BHC=∠FHE, ∴∠B+∠BCH=∠F+∠AEG.
人教版八年级上册数学11.1.2三角形的高、中线与角平分线 同步练习

人教版八年级上册数学11.1.2三角形的高、中线与角平分线同步练习一、单选题1.三角形的重心是()A.三角形三条边上中线的交点B.三角形三条边上高线的交点C.三角形三条边垂直平分线的交点D.三角形三条内角平行线的交点2.如果一个三角形的一个顶点是它的三条高的交点,那么这个三角形是()A.锐角三角形B.直角三角形C.钝角三角形D.等边三角形3.在下列图形中,正确画出△ABC的AC边上的高的图形是()A.B.C.D.4.如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE 的中点,且△ABC的面积为4cm2,则△BEF的面积等于()A.2cm2B.1cm2C.0.5 cm2D.0.25 cm25.如图,∠ACB>90°>AD>BC>BE>AC>CF>AB,垂足分别为点D、点E、点F>>ABC中AC边上的高是()A.CF B.BE C.AD D.CD6.如图,把ABC的三边BA、CB和AC分别向外延长一倍,将得到的点A,,B,,C,顺次连接成△A,B,C,,若△ABC的面积是3,则△A,B,C,的面积是()1/ 8A .15B .18C .21D .247.如图,在△ABC 中,已知点E>F 分别是AD>CE 边上的中点,且S △BEF =4cm 2,则S △ABC 的值为( )A .1cm 2B .2cm 2C .8cm 2D .16cm 28.如图,已知ABC ∆中,AD 是BC 边上的中线,则下列结论不一定正确的是( )A .12BD BC =B .BD CD =C .12AD BC = D .12CD BC = 9.如图,CD ,CE ,CF 分别是△ABC 的高、角平分线、中线,则下列各式中错误的是( )A .AB =2BFB .∠ACE =12∠ACBC .AE =BED .CD ⊥BE 10.如图,已知正方形网格中每个小方格的边长均为1>A>B 两点在小方格的顶点上,点C 也在小方格的顶点上,且以A>B>C 为顶点的三角形的面积为1个平方单位,则点C 的个数为( )A .3B .4C .5D .611.如图所示,在ABC 中,ABC ∠与ACB ∠的平分线交于点P ,过点P 作MN BC 交AB 于点M ,交AC 于点N ,那么下列结论:①BP CP =;②MN BM CN =+;③BMP 和CNP 都是等腰三角形;④AMN的周长等于AB与AC的和,其中正确的有()A.4个B.3个C.2个D.1个二、填空题12.如图,已知AE是△ABC的边BC上的中线,若AB=8cm,△ACE的周长比△AEB的周长多2cm,则AC=_____.13.如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且△ABC的面积等于4cm2,则阴影部分图形面积等于_____cm214.如图,AD是△ABC的中线,CE是△ACD的中线,S△ACE=3cm2,则S△ABC=_____cm2.15.已知:如图,△ABC的周长为21cm,AB=6cm,BC边上中线AD=5cm,△ACD周长为16cm,则AC的长为__________cm.16.如图,△ABC中BC边上的高为___________3/ 8三、解答题17.如图:(1)在>ABC 中,BC 边上的高是______>(2)在>AEC 中,AE 边上的高是______>(3)若AB>CD>2cm>AE>3cm ,求>AEC 的面积及CE 的长.18.如图,D 是ABC △的边BC 上的一点,DE AC 交AB 于点E ,DF AB 交AC 于点F ,且ADE ADF ∠=∠,AD 是ABC △的角平分线吗?说明理由.19.如图,在△ABC 中,90ACB ︒∠=,BC a =,AC b =,CD 是△ABC 的角平分线,DE AC ⊥于点E ,DE x =.(1)用两种方法计算△ABC 的面积;(2)探究a ,b ,x 的关系,并用含有a ,b 的式子表示x . 20.阅读下列材料,并完成相应的任务.基本性质:三角形中线等分三角形的面积.如图,AD 是ABC ∆的边BC 上的中线,5 / 8则12ABD ACD ABC S S S ∆∆∆== 理由:过点A 作AH BC ⊥于点H ∵AD 是ABC ∆的边BC 上的中线. ∴BD CD =又∵12ABD S BD AH ∆=⋅,12ACD S CD AH ∆=⋅ ∴12ABD ACD ABC S S S ∆∆∆== ∴三角形中线等分三角形的面积. 任务:(1)如图,延长ABC ∆的边BC 到点D ,使CD BC =,连接DA ,则ABC S ∆和ADC S ∆的数量关系为_________.(2)如图,点D 是ABC ∆的边BC 上任意一点,点,E F 分别是线段AD ,CE 的中点,且ABC ∆的面积为236cm ,请同学们借助上述结论求BEF ∆的面积.1 / 8 答案1.A 2.B 3.C 4.B5.B6.C 7.D 8.C 9.C 10.D11.B 12.10cm 13.1 14.12cm 2. 15.7 16.AE17.解:(1)AB (2)CD(3)∵AE =3cm ,CD =2cm , ∴S △AEC =12AE ·CD =12×3×2=3(cm 2). ∵S △AEC =12CE ·AB =3cm 2,AB =2cm , ∴CE =3cm.18.解:AD 是ABC △的角平分线. 理由:∵DE AC ,DF AB , ∴ADE DAF ∠=∠,ADF EAD ∠=∠, 又∵ADE ADF ∠=∠,∴DAF EAD ∠=∠,∴AD 是BAC ∠的平分线.19.解:(1)作DF BC ⊥于点F . CD 平分ACB DE AC ∠⊥,于点E, ∴DE=DF,∴S △ABC =12ab ,()111222ABC ACD CDB S S S bx ax a b x ∆∆∆=+=+=+;(2)由(1),()11,22ab ab x a b x a b=+∴=+20.【详解】(1)CD BC =AC ∴是ABD ∆的边BD 上的中线 ABC ADC S S ∆∆∴=故答案为:ABC ADC S S ∆∆=;(2)点E 是线段AD 的中点 BE ∴是ABD ∆的边AD 上的中线,CE 是ACD ∆的边AD 上的中线 ,BDE ABE CDE ACE S S S S ∆∆∆∆∴== 11,22BDE ABD CDE ACD S S S S ∆∆∆∆∴== 1122BCE BDE CDE ABD ACD S S S S S ∆∆∆∆∆∴=+=+ 1()2ABD ACD S S ∆∆=+ 2113618()22ABC S cm ∆==⨯= 点F 是线段CE 的中点 BF ∴是BCE ∆的边CE 上的中线 BEF BCF S S ∆∆∴=211189()22BEF BCE S S cm ∆∆∴==⨯= 故BEF ∆的面积为29cm .。
八年级上经典三角形的高中线角平分线内外角练习

F E D C B A E DCB AB 'C B A 八年级上角形高、中线、角平分线,内外角练习一、选择题:1.如图1所示,在△ABC 中,∠ACB=90°,把△ABC 沿直线AC 翻折180°,使点B 落在点B ′的位置,则线段AC 具有性质( )A.是边BB ′上的中线B.是边BB ′上的高C.是∠BAB ′的角平分线D.以上三种性质合一(1) (2) (3)2.如图2所示,D,E 分别是△ABC 的边AC,BC 的中点,则下列说法正确的是( ) A.DE 是△BCD 的中线 B.BD 是△ABC 的中线 C.AD=DC,BD=EC D.∠C 的对边是DE3.如图3所示,在△ABC 中,已知点D,E,F 分别为边BC,AD,CE 的中点, 且S △ABC =4cm 2,则S 阴影等于( ) A.2cm 2 B.1cm 2 C.12cm 2 D.14cm 2 4.在△ABC,∠A=90°,角平分线AE 、中线AD 、高AH 的大小关系为( )A.AH<AE<ADB.AH<AD<AEC.AH ≤AD ≤AED.AH ≤AE ≤AD5.在△ABC 中,D 是BC 上的点,且BD:DC=2:1,S △ACD =12,那么S △ABC 等于( ) A.30 B.36 C.72 D.246.如果三角形的三个内角的度数比是2:3:4,则它是( )A.锐角三角形B.钝角三角形;C.直角三角形D.钝角或直角三角形 7.下列说法正确的是( )A.三角形的内角中最多有一个锐角;B.三角形的内角中最多有两个锐角C.三角形的内角中最多有一个直角;D.三角形的内角都大于60° 8.已知三角形的一个内角是另一个内角的23,是第三个内角的45,则这个三角形各内角的度数分别为( )A.60°,90°,75°B.48°,72°,60°C.48°,32°,38°D.40°,50°,90° 9.已知△ABC 中,∠A=2(∠B+∠C),则∠A 的度数为( ) A.100° B.120° C.140° D.160° 10.已知三角形两个内角的差等于第三个内角,则它是( )A.锐角三角形B.钝角三角形C.直角三角形D.等边三角形 11.设α,β,γ是某三角形的三个内角,则α+β,β+γ,α+γ 中 ( )A.有两个锐角、一个钝角B.有两个钝角、一个锐角C.至少有两个钝角D.三个都可能是锐角 12.在△ABC 中,∠A=12∠B=13∠C,则此三角形是( )F E D CBA 654321F E CB A 140︒80︒1 A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形 13.若一个三角形的一个外角小于与它相邻的内角,则这个三角形是( ) A.直角三角形 B.锐角三角形 C.钝角三角形 D.无法确定14.如果三角形的一个外角和与它不相邻的两个内角的和为180°,那么与这个外角相邻的内角的度数为( )A.30°B.60°C.90°D.120°15.已知三角形的三个外角的度数比为2:3:4,则它的最大内角的度数为( ) A.90° B.110° C.100° D.120° 16.已知等腰三角形的一个外角是120°,则它是( )A.等腰直角三角形;B.一般的等腰三角形;C.等边三角形;D.等腰钝角三角形 17.如图1所示,若∠A=32°,∠B=45°,∠C=38°,则∠DFE 等于( )A.120°B.115°C.110°D.105°(1) (2) (3)18.如图2所示,在△ABC 中,E,F 分别在AB,AC 上,则下列各式不能成立的是( )A.∠BOC=∠2+∠6+∠A;B.∠2=∠5-∠A;C.∠5=∠1+∠4;D.∠1=∠ABC+∠4 二、填空题:1.直角三角形两锐角的平分线所夹的钝角为_______度.2.等腰三角形的高线、角平分线、中线的总条数为________.3.在△ABC 中,∠B=80°,∠C=40°,AD,AE 分别是△ABC 的高线和角平分线, 则∠DAE 的度数为_________.4.⑴三角形的三条中线交于一点,这一点是三角形的_______心,在____________ ⑵三角形的三条角平分线交于一点,这一点是三角形的_______心,在__________ ⑶三角形的三条高线所在直线交于一点,这一点是三角形的_______心,①三角形为锐角三角形,这点在三角形___________ ②三角形为直角三角形,这点在三角形___________ ③三角形为钝角三角形,这点在三角形___________5.三角形中,若最大内角等于最小内角的2倍,最大内角又比另一个内角大20°,则此三角形的最小内角的度数是________.6.在△ABC 中, 若∠A+∠B >∠C,则此三角形为_______三角形,若∠A+∠B=∠C,则此三角形为_______三角形;若∠A+∠B <∠C,则此三角形是_____三角形.7.已知等腰三角形的两个内角的度数之比为1: 2, 则这个等腰三角形的顶角为_______.8.在△ABC 中,∠B,∠C 的平分线交于点O,若∠BOC=132°,则∠A=_______度. 5.如图所示,已知∠1=20°,∠2=25,∠A=35°,则∠BDC 的度数为________ 9.三角形的三个外角中,最多有_______个锐角. 21D CB AD C B AE D C BA10.如图3所示,∠1=_______.11.如果一个三角形的各内角与一个外角的和是225°,则与这个外角相邻的内角是____度. 12.已知等腰三角形的一个外角为150°,则它的底角为_____.13.如图所示,∠ABC,∠ACB 的内角平分线交于点O,∠ABC 的内角平分线与∠ACB 的外角平分线交于点D,∠ABC 与∠ACB 的相邻外角平分线交于点E,且∠A=60°, 则∠BOC=_______,∠D=_____,∠E=________.14.如图所示,∠A=50°,∠B=40°,∠C=30°,则∠BDC=________.三、基础训练:1.如图所示,在△ABC 中,∠C-∠B=90°,AE 是∠BAC 的平分线,求∠AEC 的度数.2.在△ABC 中,AB=AC,AD 是中线,△ABC 的周长为34cm,△ABD 的周长为30cm, 求AD 的长.3.如图所示,在△ABC 中,D 是BC 边上一点,∠1=∠2,∠3=∠4,∠BAC=63°, 求∠DAC 的度数.4321DCBA4.如图所示,在△ABC 中,AD ⊥BC 于D,AE 平分∠BAC(∠C>∠B),试说明∠EAD=12(∠C-∠B).5.如图所示,已知∠1=∠2,∠3=∠4,∠C=32°,∠D=28°,求∠P 的度数.四、提高训练:1.在△ABC 中,∠A=50°,高BE,CF 所在的直线交于点O,求∠BOC 的度数.E CB A 43P21DCB A21C 'FEC B A2.如图所示,将△ABC 沿EF 折叠,使点C 落到点C ′处,试探求∠1,∠2与∠C 的关系.3.如图所示,在△ABC 中,∠B=∠C,FD ⊥BC,DE ⊥AB,∠AFD=158°, 求∠EDF 的度数.4.如图,已知,在直角△ABC 中,∠C=90°,BD 平分∠ABC 且交AC 于D .(1)若∠BAC=30°,求证:AD=BD ;(2)若AP 平分∠BAC 且交BD 于P ,求∠BPA 的度数.五、探索发现:1. 如图5所示的是由若干盆花组成的形如三角形的图案,每条边(包括两个顶点)有n(n>1)盆花,每个图案花盆的总数为s.按此规律推断s 与n 有什么关系,并求出当n=13时,s 的值.2. 如图所示,在△ABC 中,∠A=α,△ABC 的内角平分线或外角平分线交于点P, 且∠P=β,试探求下列各图中α与β的关系,并选择一个加以说明.FE D CBAn=2,s=3n=3,s=6n=4,s=9(1)PC BA (2)PCBA(3)PCBA。
2022—2023学年人教版数学八年级上册三角形的高、中线与角平分线同步练习题含答案

2022—2023学年人教版数学八年级上册三角形的高、中线与角平分线同步练习题学校:___________姓名:___________班级:___________一、单选题1.如图,△ABC中BC边上的高和△AEC中AE边上的高分别是()A.EF和CD B.BC和CD C.AB和CD D.AB和EF2.如图,ABC的面积是2,AD是ABC的中线,13AF AD=,12CE EF=,则CDE△的面积为()A.29B.16C.23D.493.数学活动课上,小敏、小颖分别画了△ABC和△DEF,数据如图,如果把小敏画的三角形面积记作S△ABC,小颖画的三角形面积记作S△DEF,那么你认为()A.S△ABC >S△DEF B.S△ABC <S△DEFC.S△ABC =S△DEF D.不能确定4.如图,在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点,且△ABC的面积是8cm2,则阴影部分面积等于()A .2cm 2B .1.5cm 2C .1cm 2D .0.5cm 25.如图,BD 是ABC 的边AC 上的中线,AE 是ABD △的边BD 上的中线,BF 是ABE △的边AE 上的中线,若ABC 的面积是32,则阴影部分的面积是( )A .9B .12C .18D .206.请你量一量如图ABC 中BC 边上的高的长度,下列最接近的是( )A .0.5cmB .0.7cmC .1.5cmD .2cm7.如图,已知D 、E 分别为△ABC 的边BC 、AC 的中点,连接AD 、DE ,AF 为△ADE 的中线.若四边形ABDF 的面积为10,则△ABC 的面积为( )A .12B .16C .18D .208.已知A ,B 两点在数轴上的位置如图所示,原点为O ,现A 点以2m/s 的速度向左运动,B 点以1m/s 的速度向左运动,若A ,B 两点同时出发,当OA :OB =1:2时,用时为( )A .2sB .14sC .73s 或1sD .12s 或2s二、填空题 9.填空:(1)如图(1),,AD BE CF 是ABC 的三条中线,则2AB =______,BD =______,12AE =______.(2)如图(2),,AD BE CF 是ABC 的三条角平分线,则1∠=______,132∠=______,2ACB ∠=______.10.已知BD 、CE 是△ABC 的高,直线BD 、CE 相交所成的角有一个角为45︒,则BAC ∠等于______.11.如图,AC//BD ,OA ,OB 分别平分BAC ∠和ABD ∠,OE AB ⊥,垂足为E ,如果OE 5=,那么AC 与BD 的距离是________12.如图,在ABC 中,90,BAC AD ∠=︒是高,BE 是中线,CF 是角平分线,CF 交AD 于点G ,交BE 于点H ,下面说法正确的是____________.△ABE △的面积等于BCE 的面积;△AFG AGF ∠=∠;△2FAG ACF ∠=∠;△CG 是ACD △的角平分线13.如图,AD 是△ABC 的中线,BE 是△ABD 的中线,EF ⊥BC 于点F.若24ABCS=,BD = 4 ,则EF 长为___________.14.若AD是△ABC的高,△BAD=70°,△CAD=20°,则△BAC的度数为_____.15.连结三角形的一个顶点和它________________的________叫做三角形这边上的中线.如图,若BE是ABC中AC边上的中线,则AE________12EC=________.16.如图,点C、D分别是半圆AOB上的三等分点,若阴影部分的面积为32π,则半圆的半径OA的长为__________.三、解答题17.如图,△ABE中,△E=90°,AC是△BAE的角平分线.(1)若△B =40°,求△BAC 的度数;(2)若D 是BC 的中点,△ADC 的面积为16,AE =8,求BC 的长.18.如图,在ABC 中(AB BC >),2AC BC =,BC 边上的中线AD 把ABC 的周长分成60和40两部分,求AC 和AB 的长.19.在平面内,分别用3根、5根、6根……火柴棒首尾依次相接,能搭成什么形状的三角形呢?通过尝试,列表如下.问:(1)4根火柴棒能搭成三角形吗?(2)8根、12根火柴棒分别能搭成几种不同形状的三角形?并画出它们的示意图. 20.如图,在正方形网格中有一个ABC ,按要求进行作图(只用直尺)(1)画出将ABC向右平移6格,再向上平移3格后的DEF;(2)画出ABC中AC边上的高BH;(3)请在图中直接标记出3个使BCP的面积等于3的格点1P、2P、3P.参考答案:1.C【分析】根据三角形高的定义,△ABC中BC边上的高为从BC边相对的顶点A向BC边作的垂线段,△AEC中AE边上的高为从AE边相对的顶点C向AE边作的垂线段,观察图形,找出符合要求的线段即可.【详解】解:根据三角形高的定义可知,AB是△ABC中BC边上的高,CD是△AEC中AE 边上的高,故选C.【点睛】本题考查三角形高的定义:从三角形一个端点向它的对边作一条垂线,三角形顶点和它对边垂足之间的线段称三角形这条边上的高.2.A【分析】根据中线的性质即可求出S△ACD,然后根据等高时,面积之比等于底之比,即可依此求出S△CDF,S△CDE.【详解】解:△△ABC的面积是2,AD是△ABC的中线,△S△ACD=12S△ABC=1,△AF=13 AD,△DF=23AD,△S△CDF=23S△ACD=23×1=23,△CE=12EF,△CE=13 CF△S△CDE=13S△CDF=13×23=29,故选:A.【点睛】此题考查的是三角形的面积关系,掌握中线的性质和等高时,面积之比等于底之比是解决此题的关键.3.C【分析】在两个图形中分别作BC、EF边上的高,欲比较面积,由于底边相等,所以只需比较两条高即可.【详解】解:如图,过点A、D分别作AG△BC,DH△EF,垂足分别为G、H,在△ABG 和△DHE 中,AB =DE =5, △B =50°,△DEH =180°-130°=50°, △△B =△DEH ,△AGB =△DHE =90°, △△AGB △△DHE (AAS), △AG =DH . △BC =4,EF =4, △S △ABC =S △DEF . 故选:C .【点睛】要题考查全等三角形的判定和性质,等底等高两三角形面积相等.证明△AGB △△DHE 是解题的关键. 4.A【分析】先由D 为BC 中点,求出△ABD 和△ACD 面积,再由点E 为AD 中点求出△BCE 面积,再根据F 是CE 中点,知阴影部分面积等于△BCE 面积的一半,即可求解. 【详解】解:△D 是BC 中点,△ABC 的面积是8cm 2, △1=42ABD ACD ABC S S S ==△△△cm 2, △E 是AD 中点,△1=22ABE BDE ABD S S S ==△△△cm 2,1=22ACECDEACDS SS ==cm 2,△4CBE S =△cm 2, △F 为CE 中点, △1=22CBE S S =△阴影cm 2, 故选:A .【点睛】本题考查了三角形面积的等积变换,掌握三角形的中线将三角形分成面积相等的两部分是解题关键.5.B【分析】利用中线等分三角形的面积进行求解即可. 【详解】△BD 是ABC 的边AC 上的中线,△11321622ABD BCD ABC S S S ===⨯=△△,△AE 是ABD △的边BD 上的中线, △1116822ABEADEABDSSS ===⨯=, 又△BF 是ABE △的边AE 上的中线,则CF 是ACE 的边AE 上的中线, △118422BEFABFABESSS ===⨯=,182CEFACFADECEDACES SSSS =====,则4812BEFCEFS SS =+=+=阴影,故选:B .【点睛】本题考查了中线的性质,清晰明确三角形之间的等量关系,进行等量代换是解题的关键. 6.D【分析】作出三角形的高,然后利用刻度尺量取即可. 【详解】解:如图所示,过点A 作AO △BC ,用刻度尺直接量得AO 更接近2cm , 故选:D .【点睛】题目主要考查利用刻度尺量取三角形高的长度,作出三角形的高是解题关键. 7.B【分析】根据三角形的中线平分三角形的面积即可得到结论. 【详解】设AEF S x =△, △AF 为△ADE 的中线. △,2AEFADFADESSx Sx ===△E 分别为△ABC 的边AC 的中点,△2,4ADECDECDASSx Sx ===△D 分别为△ABC 的边BC 的中点, △4,8CDABDAABCSSx Sx ===△四边形ABDF 的面积=510FDABDAS Sx +==解得2x = △816ABCSx ==故选:B【点睛】本题考查了三角形的面积,熟练三角形的中线平分三角形的面积是解题的关键. 8.C【分析】设A ,B 两点同时出发运动的时间为t s ,分类讨论△当A 点在O 点右侧时和△当A 点在O 点左侧时,分别用t 表示出OA 和OB ,再列出等式,解出t 即可. 【详解】设A ,B 两点同时出发运动的时间为t s , 分类讨论△当A 点在O 点右侧时,即32t <时, 此时1OB t =+,32OA t =-, △OA :OB =1:2 △(32)t -:(1)t +=1:2 解得:312t =<,符合题意; △当A 点在O 点左侧时,即32t >, 此时1OB t =+,23OA t =-, △OA :OB =1:2 △(23)t -:(1)t +=1:2 解得:7332t =>,符合题意. 综上可知1t =或73t =时,OA :OB =1:2 故选C .【点睛】本题主要考查数轴上的动点问题,利用分类讨论的思想是解答本题的关键. 9. AF 或BF CD AC 2∠ ABC ∠ 4∠【分析】(1)根据三角形的中线定义:三角形一边的中点与此边所对顶点的连线叫做三角形的中线可得E 、F 、D 分别是AC 、AB 、BC 上的中点,进而得到答案.(2)根据角平分线定义,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线即可解答.【详解】解:(1)△CF 是AB 边上的中线,△AB =2AF =2BF ;△AD 是BC 边上的中线,△BD =CD ,△BE 是AC 边上的中线,△AE =12AC ,(2)△AD 是BAC ∠的角平分线,△12∠=∠ ,△BE 是ABC ∠的角平分线, △132∠=ABC ∠, △CF 是ACB ∠的角平分线,△2ACB ∠=4∠.故答案为:AF 或BF ;CD ;AC ;2∠;ABC ∠;4∠【点睛】此题主要考查了三角形的中线、角平分线,解题的关键是掌握三角形的中线及角平分线的定义.10.45°或135°【分析】分两种情况:(1)当△A 为锐角时,如图1,(2)当△A 为钝角时,如图2,根据三角形的内角和计算得出结果.【详解】解:分两种情况:(1)当△A 为锐角时,如图1,△△DOC =45°,△△EOD =135°,△BD 、CE 是△ABC 的高,△△AEC =△ADB =90°,△△EAO +△AEO +△AOE =180°=△DAO +△DOA +△ADO ,△△AEO +△EAD +△ADO +△EOD =360°△△A =360°−90°−90°−135°=45°;(2)当△A 为钝角时,如图2,△△F =45°,△ADF =△AEF =90°,同理△DAE =360°−90°−90°−45°=135°,△△BAC =△DAE =135°,则△BAC 的度数为45°或135°,故答案为:45°或135°.【点睛】本题考查了三角形的高和三角形的内角和,明确三角形内角和,三角形的高所构成了两个直角;本题是易错题,容易漏解,要分锐角三角形和钝角三角形两种情况进行计算. 11.10【分析】过点O 作OM AC ⊥于M ,作ON BD ⊥于N ,利用平行线的性质可证得OM△BD ,进而可证得MN 为AC 和BD 的距离,根据角平分线的性质可知OE=OM=OE ,即可求得MN 的长度.【详解】解:如图,过点O 作OM AC ⊥于M ,作ON BD ⊥于N .△OA 、OB 分别平分BAC ∠和ABD ∠,OE AB ⊥,△OM OE ON 5===,又 AC △BD ,OM AC ⊥,△OM BD ⊥,又ON BD ⊥,△M ,O ,N 三点共线,△ AC 与BD 之间的距离为MN=OM ON 10+=.故答案为:10.【点睛】本题考查求平行线间的距离、角平分线的性质、八个基本事实,熟练掌握角平分线的性质,作出AC 和BD 之间的距离是解答的关键.12.△△△△【分析】根据等底同高的三角形的面积相等即可判断△;根据直角三角形两锐角互余求出△ABC =△CAD ,根据三角形的外角性质即可推出△;根据直角三角形两锐角互余求出△BAD =△ACD ,根据角平分线定义即可判断△;根据三角形的角平分线的定义判断△即可.【详解】解:△BE 是中线,△AE =CE ,△△ABE 的面积=△BCE 的面积(等底同高的三角形的面积相等),△正确;△CF 是角平分线,△△ACF =△BCF ,△AD 为高,△△ADC =90°,△△BAC =90°,△△ABC +△ACB =90°,△ACB +△CAD =90°,△△ABC =△CAD ,△△AFG =△ABC +△BCF ,△AGF =△CAD +△ACF ,△△AFG =△AGF ,△正确;△AD 为高,△△ADB =90°,△△BAC =90°,△△ABC +△ACB =90°,△ABC +△BAD =90°,△△ACB =△BAD ,△CF 是△ACB 的平分线,△△ACB =2△ACF ,△△BAD =2△ACF ,即△F AG =2△ACF ,△正确;△CF 是△ACB 的平分线,CF 交AD 于点G ,△CG 是△ACD 的角平分线,△正确;故答案为:△△△△.【点睛】本题考查了直角三角形两锐角互余,三角形的外角性质,三角形的角平分线、中线、高线等知识点,能综合运用定理进行推理是解此题的关键.13.3【分析】因为S △ABD =12S △ABC ,S △BDE =12S △ABD ;所以S △BDE =14S △ABC ,再根据三角形的面积公式求得即可.【详解】解:△AD 是△ABC 的中线,S △ABC =24,△S △ABD =12S △ABC =12,同理,BE 是△ABD 的中线,612BDE ABD SS ==,△S △BDE =12BD •EF ,△12BD •EF =6, 即1462EF ⨯⨯= △EF =3.故答案为:3.【点睛】此题考查了三角形的面积,三角形的中线特点,理解三角形高的定义,根据三角形的面积公式求解,是解题的关键.14.90°或50°【分析】分高AD 在△ABC 内部和外部两种情况讨论求解即可.【详解】解:△如图1,当高AD 在△ABC 的内部时,△BAC =△BAD +△CAD =70°+20°=90°;△如图2,当高AD 在△ABC 的外部时,△BAC =△BAD -△CAD =70°-20°=50°,综上所述,△BAC 的度数为90°或50°.故答案为:90°或50°.【点睛】本题考查了三角形的高线,难点在于要分情况讨论.15. 所对边的中点 线段 = AC【分析】根据三角形中线的定义,即可求解.【详解】解:连结三角形的一个顶点和它所对边的中点的线段叫做三角形这边上的中线. △BE 是ABC 中AC 边上的中线, △12AE EC AC == 故答案为:所对边的中点;线段;=;AC ;【点睛】本题主要考查了三角形的中线,熟练掌握连结三角形的一个顶点和它所对边的中点的线段叫做三角形这边上的中线是解题的关键.16.3.【分析】如图,连接,,,OC OD CD 证明//,CD AB 再证明32OCD S S π=阴影扇形=,从而可以列方程求解半径.【详解】解:如图,连接,,,OC OD CD点C 、D 分别是半圆AOB 上的三等分点,60,AOC COD DOB ∴∠=∠=∠=︒,OC OD =COD ∴为等边三角形,60,OCD ∴∠=︒,AOC DCO ∴∠=∠,COD BCD S S ∴=32OCD S S π∴=阴影扇形=, 2603,3602OA ππ•∴= 解得:3,OA = (负根舍去),故答案为:3.【点睛】本题考查的圆的基本性质,弧,弦,圆心角之间的关系,平行线的判定与性质,扇形面积的计算,掌握以上知识是解题的关键.17.(1)25BAC ∠=︒;(2)8BC =【分析】(1)先利用互余计算出△BAE =50°,再利用角平分线的定义得到△BAC =12△BAE =25°;(2)先根据三角形面积公式得出DC ,利用D 是BC 的中点得到BC 即可.(1)解:△△B =40°,△E =90°,△△BAE =90°﹣40°=50°,△AC 是△BAE 的角平分线,△△BAC =12△BAE =25°;(2)△S △ADC =12DC •AE , △12×DC ×8=16,△D 是BC 的中点,△BC =2CD =8.【点睛】本题考查了角平分线的定义,线段的中点,角平分线的定义的正确运用是解题的关键.18.48AC =,28AB =【分析】由题意可得60AC CD +=,40AB BD +=,由中线的性质得244AC BC CD BD ===,故可求得48AC =,即可求得28AB =.【详解】由题意知100AC CD BD AB +++=,60AC CD +=,40AB BD +=△2AC BC =,D 为BC 中点△244AC BC CD BD === △156044AC CD AC AC AC +=+== 即460485AC =⨯= 则BC =24,CD =BD =12则40401228AB BD =-=-=且28>24符合题意.【点睛】本题考查了中线的性质,中线是三角形中从某边的中点连向对角的顶点的线段.19.(1)4根火柴棒不能搭成三角形(2)8根火柴棒能搭成一种三角形,12根火柴棒能搭成三种不同的三角形,画图见解析【分析】(1)把4分成3个数只能分成1,1,2三个数,故4根火柴棒不能搭成三角形;(2)利用三角形三边关系定理求解即可.(1)解:△把4分成3个数只能分成1,1,2三个数,而1+1=2,△4根火柴棒不能搭成三角形;(2)△ 8根火柴棒能搭成一种三角形,示意图如下:△12根火柴棒能搭成三种不同的三角形,其边长分别为:(4,4,4),(5,5,2),(3,4,5),示意图如下:【点睛】本题主要考查了三角形三边关系定理:任意两边之和大于第三边,任意两边之差小于第三边.20.(1)见解析(2)见解析(3)见解析【分析】(1)按要求分别画出平移A、B、C三点后的点D、E、F,并依次连接,即得到△ABC 平移后的△DEF;(2)按要求画即可;(3)作三格点1P、2P、3P,使CP1=CP3=BP2=3即可.(1)平移后的△DEF如下图所示:(2)所画的高BH如下图所示:(3)由于CP1=CP3=BP2=3,则此三点1P、2P、3P满足题意.【点睛】本题考查了作图:作图形的平移,画三角形边上的高、三角形的面积,学会利用数形结合是解题的关键.。
七下数学每日一练:三角形的角平分线、中线和高练习题及答案_2020年综合题版

(1) 求△ABD与△BEC的面积;
(2) △AOE与△BOD的面积相等吗?为什么?
考点: 三角形的角平分线、中线和高;三角形的面积;
答案
~~第3题~~ (2019泰兴.七下期中)
中,三个内角的平分线交于点O,过点O作
,交边AB于点D.
(1) 如图1,
①若∠ABC=40°,则∠AOC=,∠ADO=;
,垂足为 ,求
的度数;
=
AD是
的平分线,
,
.
(1) 如图2,若点 是 延长线上的一点,
、
的平分线交于点 ,求 的度数.
考点: 三角形的角平分线、中线和高;三角形内角和定理;
答案
~~第2题~~ (2019苏州.七下期末) 如图,点D与点E分别是△ABC的边长BC、AC的中点,△ABC的面积是20cm .
③ 过点B画BF⊥AC,垂足为F
(2) 填空: ① 点B、C两点的距离是线段的长度,AD的长度表示点A到直线的距离.
② 点B到直线AC的距离是线段的长度.
③点E到直线AB的距离是.
考点: 两点间的距离;点到直线的距离;三角形的角平分线、中线和高;
答案
2020年 七 下 数 学 : 图 形 的 性 质 _三 角 形 _三 角 形 的 角 平 分 线 、 中 线 和 高 练 习 题 答 案
1.答案: 2.答案: 3.答案:
4.答案: 5|+|2x﹣y|=0,试分别求出1秒钟后,线段OA、OB的长.
(2) 如图2,设∠BAO的邻补角和∠ABO的邻补角的平分线相交于点P.问:点A、B在运动的过程中,∠P的大小是
否会发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
(3) 如图3,延长BA至E,在∠ABO的内部作射线BF交x轴于点C,若∠EAC、∠FCA、∠ABC的平分线相交于点G
三角形的高、中线、角平分线练习题

三角形的高、中线、角平分线练习题
1、三角形的三条中线、三条角平分线、三条高都是()
A.直线B.射线C.线段D.射线或线段
2、如果一个三角形的三条高的交点恰是三角形的一个顶点,那么
这个三角形是()A.锐角三角形B.直角
A
D 三角形C.钝角三角形D.不能确定
F
3、能把三角形的面积分成两个相等的三角形的线段B C
E
是()
A.中线B.高C.角平分线D.以上三种情况都正确
4、如图若∠BAF=∠CAF,则____是△ABD的角平分线,
A
____是△ABC的角平分线
D
5、如图AB⊥AC,则AB是△ABC的边____上的高,也
B C
是△BDC的边______上的高,也是△ABD的边____上的高.
6、如图BD、AE分别是△ABC的中线、角平分线,
A
AC=10cm,∠BAC=70,则AD=_____,∠BAE=____.
D
BC
E
7、在△ABC中,AE是中线,AD是角平分线,AF是高,填空:
⑴BE=___=1_____;2
⑵∠BAD=_____=
1_____;⑶∠AFB=_____=90 2
8、在△ABC中AB=AC,AC上的中线BD把三角形的周长分为24cm 和30cm的两个部分,求三角形的三边长。
9、要使四边形木架(用四根木条钉成)不变形,至少要再钉上几根木条?五边形木架和六边形木架呢?n边形木架呢?。
【精品】初中数学八年级上册《三角形的高、中线与角平分线》基础练习
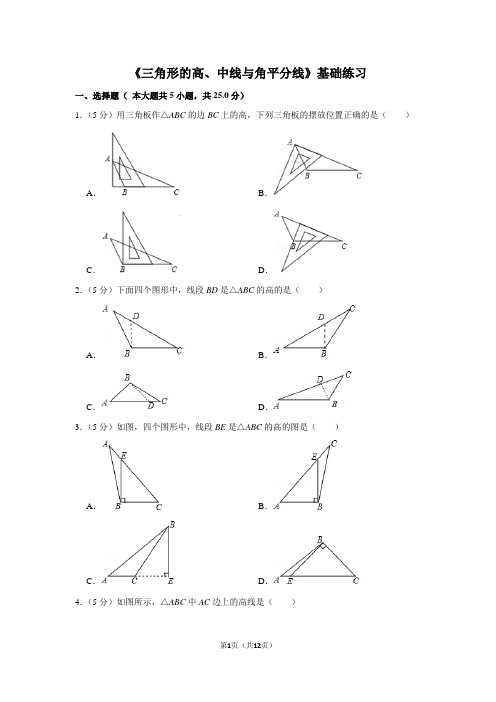
《三角形的高、中线与角平分线》基础练习一、选择题(本大题共5小题,共25.0分)1.(5分)用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是()A.B.C.D.2.(5分)下面四个图形中,线段BD是△ABC的高的是()A.B.C.D.3.(5分)如图,四个图形中,线段BE是△ABC的高的图是()A.B.C.D.4.(5分)如图所示,△ABC中AC边上的高线是()A.线段DA B.线段BA C.线段BC D.线段BD5.(5分)如图AD⊥BC于点D,那么图中以AD为高的三角形有()个A.3B.4C.5D.6二、填空题(本大题共5小题,共25.0分)6.(5分)如图所示:在△AEC中,AE边上的高是.7.(5分)如图,H若是△ABC三条高AD,BE,CF的交点,则△BHA中边BH上的高是.8.(5分)如图,AD是△ABC的中线,已知△ABD的周长为25cm,AB比AC长6cm,则△ACD的周长为cm.9.(5分)BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是.10.(5分)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B=.三、解答题(本大题共5小题,共50.0分)11.(10分)已知△ABC,如图,过点A画△ABC的角平分线AD、中线AE和高线AF.12.(10分)如图,在△ABC中,AC=8,BC=4,高BD=3,试作出BC边上的高AE,并求AE的长.13.(10分)如图,△ABC的三条高AD、BE、CF相交于点O.(1)在△BOC中,OB边上的高是,OC边上的高是,BC边上的高是.(2)在△AOC中,OA边上的高是,OC边上的高是,AC边上的高是.(3)在△AOB中,OA边上的高是,OB边上的高是,AB边上的高是.14.(10分)如图,已知CD是△ABC的中线,AC=9cm,BC=3cm,那么△ACD和△BCD 的周长之差是多少?15.(10分)如图,AD、AE分别是△ABC中∠A的内角平分线和外角平分线,它们有什么关系?《三角形的高、中线与角平分线》基础练习参考答案与试题解析一、选择题(本大题共5小题,共25.0分)1.(5分)用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是()A.B.C.D.【分析】根据高线的定义即可得出结论.【解答】解:B,C,D都不是△ABC的边BC上的高,故选:A.【点评】本题考查的是作图﹣基本作图,熟知三角形高线的定义是解答此题的关键.2.(5分)下面四个图形中,线段BD是△ABC的高的是()A.B.C.D.【分析】根据高的画法知,过点B作AC边上的高,垂足为E,其中线段BD是△ABC 的高.【解答】解:由图可得,线段BD是△ABC的高的图是D选项.故选:D.【点评】本题主要考查了三角形的高,三角形的高是指从三角形的一个顶点向对边作垂线,连接顶点与垂足之间的线段.3.(5分)如图,四个图形中,线段BE是△ABC的高的图是()A.B.C.D.【分析】根据三角形高的画法知,过点B作AC边上的高,垂足为E,其中线段BE是△ABC的高,再结合图形进行判断.【解答】解:过点B作AC边上的高,垂足为E,则线段BE是△ABC的高的图是选项C.故选:C.【点评】本题主要考查了三角形的高,三角形的高是指从三角形的一个顶点向对边作垂线,连接顶点与垂足之间的线段.熟记定义是解题的关键.4.(5分)如图所示,△ABC中AC边上的高线是()A.线段DA B.线段BA C.线段BC D.线段BD【分析】从三角形的一个顶点向底边作垂线,垂足与顶点之间的线段叫做三角形的高.【解答】解:由图可得,△ABC中AC边上的高线是BD,故选:D.【点评】本题主要考查了三角形的高线,钝角三角形有两条高在三角形外部,一条高在三角形内部,三条高所在直线相交于三角形外一点.5.(5分)如图AD⊥BC于点D,那么图中以AD为高的三角形有()个A.3B.4C.5D.6【分析】由于AD⊥BC于D,图中共有6个三角形,它们都有一边在直线CB上,由此即可确定以AD为高的三角形的个数.【解答】解:∵AD⊥BC于D,而图中有一边在直线CB上,且以A为顶点的三角形有6个,∴以AD为高的三角形有6个.故选:D.【点评】此题主要考查了三角形的高,三角形的高可以在三角形外,也可以在三角形内,所以确定三角形的高比较灵活.二、填空题(本大题共5小题,共25.0分)6.(5分)如图所示:在△AEC中,AE边上的高是CD.【分析】从三角形的一个顶点向底边作垂线,垂足与顶点之间的线段叫做三角形的高.根据三角形中高线的概念即可作答.【解答】解:由题意可得:△AEC中,AE边上的高是CD,故答案为:CD.【点评】本题考查了三角形高线的概念,三角形的高即从三角形的顶点向对边引垂线,顶点和垂足间的线段.7.(5分)如图,H若是△ABC三条高AD,BE,CF的交点,则△BHA中边BH上的高是AE.【分析】直接利用三角形高线的定义得出答案.【解答】解:如图所示:∵H是△ABC三条高AD,BE,CF的交点,∴△BHA中边BH上的高是:AE.故答案为:AE.【点评】此题主要考查了三角形的高,正确钝角三角形高线的作法是解题关键.8.(5分)如图,AD是△ABC的中线,已知△ABD的周长为25cm,AB比AC长6cm,则△ACD的周长为19cm.【分析】根据三角形中线的定义可得BD=CD,再表示出△ABD和△ACD的周长的差就是AB、AC的差,然后计算即可.【解答】解:∵AD是BC边上的中线,∴BD=CD,∴△ABD和△ACD周长的差=(AB+BD+AD)﹣(AC+AD+CD)=AB﹣AC,∵△ABD的周长为25cm,AB比AC长6cm,∴△ACD周长为:25﹣6=19cm.故答案为19.【点评】本题主要考查了三角形的中线的定义,把三角形的周长的差转化为已知两边AB、AC的长度的差是解题的关键.9.(5分)BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是2.【分析】根据三角形的中线的定义可得AD=CD,再求出△ABD和△BCD的周长的差=AB﹣BC.【解答】解:∵BD是△ABC的中线,∴AD=CD,∴△ABD和△BCD的周长的差=(AB+BD+AD)﹣(BC+BD+CD)=AB﹣BC,∵AB=5,BC=3,∴△ABD和△BCD的周长的差=5﹣3=2.故答案为:2.【点评】本题考查了三角形的角平分线、中线和高线,熟记概念并求出两个三角形的周长的差等于AB﹣BC是解题的关键.10.(5分)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B=50°.【分析】由AE平分∠BAC,可得角相等,由∠1=30°,∠2=20°,可求得∠EAD的度数,在直角三角形ABD在利用两锐角互余可求得答案.【解答】解:∵AE平分∠BAC,∴∠1=∠EAD+∠2,∴∠EAD=∠1﹣∠2=30°﹣20°=10°,Rt△ABD中,∠B=90°﹣∠BAD=90°﹣30°﹣10°=50°.故答案为50°.【点评】本题考查了三角形的角平分线、中线和高的相关知识;求得∠EAD=10°是正确解答本题的关键.三、解答题(本大题共5小题,共50.0分)11.(10分)已知△ABC,如图,过点A画△ABC的角平分线AD、中线AE和高线AF.【分析】分别根据角平分线、三角形高线作法以及垂直平分线的作法得出答案即可.【解答】解:由题意画图可得:【点评】此题主要考查了复杂作图中线段垂直平分线的作法以及角平分线作法等知识,熟练掌握作图方法是关键.12.(10分)如图,在△ABC中,AC=8,BC=4,高BD=3,试作出BC边上的高AE,并求AE的长.【分析】利用等积法求得AE的长度即可.【解答】解:如图,过点A作BC边上的高线AE,交CB延长线于点E.∵BC•AE=AC •BD,AC=8,BC=4,高BD=3,∴×4AE=×8×3,则AE=6.【点评】本题考查了三角形的角平分线、中线和高,熟记三角形的面积公式即可解题,属于基础题.13.(10分)如图,△ABC的三条高AD、BE、CF相交于点O.(1)在△BOC中,OB边上的高是CE,OC边上的高是BF,BC边上的高是OD.(2)在△AOC中,OA边上的高是CD,OC边上的高是AF,AC边上的高是OE.(3)在△AOB中,OA边上的高是BD,OB边上的高是AE,AB边上的高是OF.【分析】从三角形的一个顶点向底边作垂线,垂足与顶点之间的线段叫做三角形的高,根据三角形高的定义判断.【解答】解:(1)由图可得,在△BOC中,OB边上的高是CE,OC边上的高是BF,BC 边上的高是OD.(2)由图可得,在△AOC中,OA边上的高是CD,OC边上的高是AF,AC边上的高是OE.(3)由图可得,在△AOB中,OA边上的高是BD,OB边上的高是AE,AB边上的高是OF.故答案为:CE,BF,OD;CD,AF,OE;BD,AE,OF.【点评】本题主要考查了三角形高线的定义,解决问题的关键是掌握:钝角三角形有两条高在三角形外部,一条高在三角形内部,三条高所在直线相交于三角形外一点.14.(10分)如图,已知CD是△ABC的中线,AC=9cm,BC=3cm,那么△ACD和△BCD 的周长之差是多少?【分析】利用中线的定义可知BD=AD,可知△ACD和△BCD的周长之差即为AC和BC 的差,可求得答案.【解答】解:∵CD是△ABC的中线,∴AD=BD,∵△ACD周长=AC+CD+AD,△BCD周长=BC+CD+BD,∴△ACD周长﹣△BCD周长=(AC+CD+AD)﹣(BC+CD+BD)=AC﹣BC=9﹣3=6(cm),即△ACD和△BCD的周长之差是6cm.【点评】本题主要考查三角形中线的定义,由条件得出两三角形的周长之差即为AC和BC的差是解题的关键.15.(10分)如图,AD、AE分别是△ABC中∠A的内角平分线和外角平分线,它们有什么关系?【分析】根据角平分线的定义和邻补角的定义可得∠DAE=90°,从而得到AD⊥AE.【解答】解:AD⊥AE,理由如下:∵AD、AE分别是△ABC中∠A的内角平分线和外角平分线,∴∠DAE=∠DAC+∠EAC=∠BAC+∠CAF=(∠BAC+∠CAF)=×180°=90°,∴AD⊥AE.【点评】本题考查了三角形的角平分线:三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线,也考查了邻补角的定义以及垂直的定义.。
三角形的高中线角平分线练习题

三角形的高中线角平分线练习题文件管理序列号:[K8UY-K9IO69-O6M243-OL889-三角形的高、中线、角平分线练习题1、分别在下列锐角三角形、直角三角形、钝角三角形中画出所有的高。
2、三角形的三条中线、三条角平分线、三条高都是()A.直线 B.射线 C.线段 D.射线或线段3、如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是()A.锐角三角形 B.直角三角形C.钝角三角形 D.不能确定4、能把三角形的面积分成两个相等的三角形的线段是()A.中线B.高C.角平分线 D.以上三种情况都正确5、如图若∠BAF=∠CAF,则____是△ABD的角平分线,____是△ABC的角平分线6、如图AB⊥AC,则AB是△ABC的边____上的高,也是△BDC的边______上的高,也是△ABD的边____上的高.FB CDAB CD7、如图BD 、AE 分别是△ABC 的中线、角平分线,AC=10cm ,∠BAC=700,则AD=_____,∠BAE=____.8、在△ABC 中,AE 是中线,AD 是角平分线,AF 是高,填空: ⑴BE =___=21_____;⑵∠BAD=_____=21_____;⑶∠AFB=_____=909、在△ABC 中,AB=AC,AD 是中线,△ABC 的周长为34cm,△ABD 的周长为30cm, 求AD 的长.10、在△ABC 中AB=AC ,AC 上的中线BD 把三角形的周长分为24cm 和30cm 的两个部分,求三角形的三边长。
11、要使四边形木架(用四根木条钉成)不变形,至少要再钉上几根木条?五边形木架和六边形木架呢?n 边形木架呢?BD。
八年级数学上册《三角形的高、中线与角平分线》练习题及答案
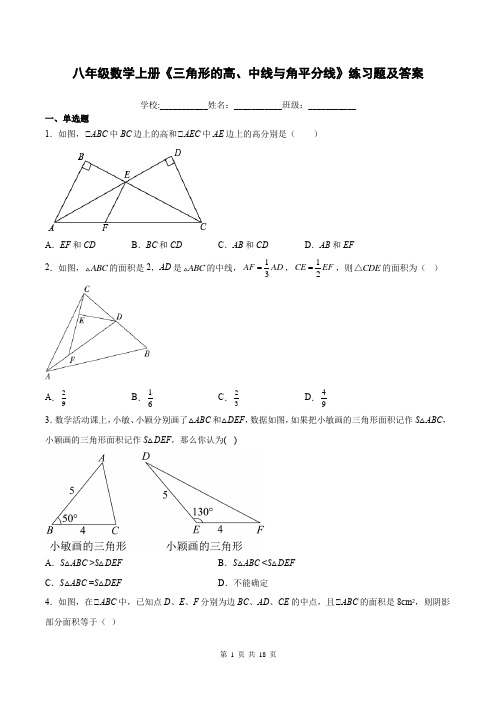
八年级数学上册《三角形的高、中线与角平分线》练习题及答案学校:___________姓名:___________班级:___________一、单选题1.如图,△ABC中BC边上的高和△AEC中AE边上的高分别是()A.EF和CD B.BC和CD C.AB和CD D.AB和EF2.如图,ABC的面积是2,AD是ABC的中线,13AF AD=,12CE EF=,则CDE△的面积为()A.29B.16C.23D.493.数学活动课上,小敏、小颖分别画了△ABC和△DEF,数据如图,如果把小敏画的三角形面积记作S△ABC,小颖画的三角形面积记作S△DEF,那么你认为()A.S△ABC >S△DEF B.S△ABC <S△DEFC.S△ABC =S△DEF D.不能确定4.如图,在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点,且△ABC的面积是8cm2,则阴影部分面积等于()A .2cm 2B .1.5cm 2C .1cm 2D .0.5cm 25.如图,BD 是ABC 的边AC 上的中线,AE 是ABD △的边BD 上的中线,BF 是ABE △的边AE 上的中线,若ABC 的面积是32,则阴影部分的面积是( )A .9B .12C .18D .206.请你量一量如图ABC 中BC 边上的高的长度,下列最接近的是( )A .0.5cmB .0.7cmC .1.5cmD .2cm7.如图,已知D 、E 分别为△ABC 的边BC 、AC 的中点,连接AD 、DE ,AF 为△ADE 的中线.若四边形ABDF 的面积为10,则△ABC 的面积为( )A .12B .16C .18D .208.已知A ,B 两点在数轴上的位置如图所示,原点为O ,现A 点以2m/s 的速度向左运动,B 点以1m/s 的速度向左运动,若A ,B 两点同时出发,当OA :OB =1:2时,用时为( )A .2sB .14sC .73s 或1sD .12s 或2s二、填空题 9.填空:(1)如图(1),,AD BE CF 是ABC 的三条中线,则2AB =______,BD =______,12AE =______. (2)如图(2),,AD BE CF 是ABC 的三条角平分线,则1∠=______,132∠=______,2ACB ∠=______.10.已知BD 、CE 是△ABC 的高,直线BD 、CE 相交所成的角有一个角为45︒,则BAC ∠等于______. 11.如图,AC//BD ,OA ,OB 分别平分BAC ∠和ABD ∠,OE AB ⊥,垂足为E ,如果OE 5=,那么AC 与BD 的距离是________12.如图,在ABC 中,90,BAC AD ∠=︒是高,BE 是中线,CF 是角平分线,CF 交AD 于点G ,交BE 于点H ,下面说法正确的是____________.△ABE △的面积等于BCE 的面积;△AFG AGF ∠=∠;△2FAG ACF ∠=∠;△CG 是ACD △的角平分线13.如图,AD 是△ABC 的中线,BE 是△ABD 的中线,EF ⊥BC 于点F.若24ABCS=,BD = 4 ,则EF 长为___________.14.若AD是△ABC的高,△BAD=70°,△CAD=20°,则△BAC的度数为_____.15.连结三角形的一个顶点和它________________的________叫做三角形这边上的中线.如图,若BE是ABC中AC边上的中线,则AE________12EC=________.16.如图,点C、D分别是半圆AOB上的三等分点,若阴影部分的面积为32π,则半圆的半径OA的长为__________.三、解答题17.如图,△ABE 中,△E =90°,AC 是△BAE 的角平分线.(1)若△B =40°,求△BAC 的度数;(2)若D 是BC 的中点,△ADC 的面积为16,AE =8,求BC 的长.18.如图,在ABC 中(AB BC >),2AC BC =,BC 边上的中线AD 把ABC 的周长分成60和40两部分,求AC 和AB 的长.19.在平面内,分别用3根、5根、6根……火柴棒首尾依次相接,能搭成什么形状的三角形呢?通过尝试,列表如下.问:(1)4根火柴棒能搭成三角形吗?(2)8根、12根火柴棒分别能搭成几种不同形状的三角形?并画出它们的示意图. 20.如图,在正方形网格中有一个ABC ,按要求进行作图(只用直尺)(1)画出将ABC向右平移6格,再向上平移3格后的DEF;(2)画出ABC中AC边上的高BH;(3)请在图中直接标记出3个使BCP的面积等于3的格点1P、2P、3P.参考答案:1.C【分析】根据三角形高的定义,△ABC中BC边上的高为从BC边相对的顶点A向BC边作的垂线段,△AEC 中AE边上的高为从AE边相对的顶点C向AE边作的垂线段,观察图形,找出符合要求的线段即可.【详解】解:根据三角形高的定义可知,AB是△ABC中BC边上的高,CD是△AEC中AE边上的高,故选C.【点睛】本题考查三角形高的定义:从三角形一个端点向它的对边作一条垂线,三角形顶点和它对边垂足之间的线段称三角形这条边上的高.2.A【分析】根据中线的性质即可求出S△ACD,然后根据等高时,面积之比等于底之比,即可依此求出S△CDF,S△CDE.【详解】解:△△ABC的面积是2,AD是△ABC的中线,△S△ACD=12S△ABC=1,△AF=13 AD,△DF=23AD,△S△CDF=23S△ACD=23×1=23,△CE=12EF,△CE=13 CF△S△CDE=13S△CDF=13×23=29,故选:A.【点睛】此题考查的是三角形的面积关系,掌握中线的性质和等高时,面积之比等于底之比是解决此题的关键.3.C【分析】在两个图形中分别作BC、EF边上的高,欲比较面积,由于底边相等,所以只需比较两条高即可.【详解】解:如图,过点A、D分别作AG△BC,DH△EF,垂足分别为G、H,在△ABG和△DHE中,AB=DE=5,△B=50°,△DEH=180°-130°=50°,△△B=△DEH,△AGB=△DHE=90°,△△AGB△△DHE(AAS),△AG=DH.△BC=4,EF=4,△S△ABC=S△DEF.故选:C.【点睛】要题考查全等三角形的判定和性质,等底等高两三角形面积相等.证明△AGB△△DHE是解题的关键.4.A【分析】先由D为BC中点,求出△ABD和△ACD面积,再由点E为AD中点求出△BCE面积,再根据F是CE中点,知阴影部分面积等于△BCE面积的一半,即可求解.【详解】解:△D是BC中点,△ABC的面积是8cm2,△1=42ABD ACD ABC S S S ==△△△cm 2, △E 是AD 中点,△1=22ABE BDE ABD S S S ==△△△cm 2,1=22ACECDEACDS SS ==cm 2,△4CBE S =△cm 2, △F 为CE 中点, △1=22CBE S S =△阴影cm 2, 故选:A .【点睛】本题考查了三角形面积的等积变换,掌握三角形的中线将三角形分成面积相等的两部分是解题关键. 5.B【分析】利用中线等分三角形的面积进行求解即可. 【详解】△BD 是ABC 的边AC 上的中线,△11321622ABD BCD ABC S S S ===⨯=△△,△AE 是ABD △的边BD 上的中线, △1116822ABEADEABDSSS ===⨯=, 又△BF 是ABE △的边AE 上的中线,则CF 是ACE 的边AE 上的中线, △118422BEFABFABESSS ===⨯=,182CEFACFADECEDACES SSSS =====,则4812BEFCEFS SS =+=+=阴影,故选:B .【点睛】本题考查了中线的性质,清晰明确三角形之间的等量关系,进行等量代换是解题的关键. 6.D【分析】作出三角形的高,然后利用刻度尺量取即可. 【详解】解:如图所示,过点A 作AO △BC ,用刻度尺直接量得AO 更接近2cm ,故选:D .【点睛】题目主要考查利用刻度尺量取三角形高的长度,作出三角形的高是解题关键. 7.B【分析】根据三角形的中线平分三角形的面积即可得到结论. 【详解】设AEF S x =△, △AF 为△ADE 的中线. △,2AEFADFADESSx Sx ===△E 分别为△ABC 的边AC 的中点, △2,4ADECDECDASSx Sx ===△D 分别为△ABC 的边BC 的中点, △4,8CDABDAABCSSx Sx ===△四边形ABDF 的面积=510FDABDAS Sx +==解得2x = △816ABCSx ==故选:B【点睛】本题考查了三角形的面积,熟练三角形的中线平分三角形的面积是解题的关键. 8.C【分析】设A ,B 两点同时出发运动的时间为t s ,分类讨论△当A 点在O 点右侧时和△当A 点在O 点左侧时,分别用t 表示出OA 和OB ,再列出等式,解出t 即可. 【详解】设A ,B 两点同时出发运动的时间为t s , 分类讨论△当A 点在O 点右侧时,即32t <时, 此时1OB t =+,32OA t =-, △OA :OB =1:2 △(32)t -:(1)t +=1:2 解得:312t =<,符合题意; △当A 点在O 点左侧时,即32t >, 此时1OB t =+,23OA t =-,△OA :OB =1:2 △(23)t -:(1)t +=1:2 解得:7332t =>,符合题意. 综上可知1t =或73t =时,OA :OB =1:2 故选C .【点睛】本题主要考查数轴上的动点问题,利用分类讨论的思想是解答本题的关键. 9. AF 或BF CD AC 2∠ ABC ∠ 4∠【分析】(1)根据三角形的中线定义:三角形一边的中点与此边所对顶点的连线叫做三角形的中线可得E 、F 、D 分别是AC 、AB 、BC 上的中点,进而得到答案.(2)根据角平分线定义,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线即可解答.【详解】解:(1)△CF 是AB 边上的中线, △AB =2AF =2BF ; △AD 是BC 边上的中线, △BD =CD ,△BE 是AC 边上的中线, △AE =12AC ,(2)△AD 是BAC ∠的角平分线, △12∠=∠ ,△BE 是ABC ∠的角平分线, △132∠=ABC ∠, △CF 是ACB ∠的角平分线, △2ACB ∠=4∠.故答案为:AF 或BF ;CD ;AC ;2∠;ABC ∠;4∠【点睛】此题主要考查了三角形的中线、角平分线,解题的关键是掌握三角形的中线及角平分线的定义. 10.45°或135°【分析】分两种情况:(1)当△A 为锐角时,如图1,(2)当△A 为钝角时,如图2,根据三角形的内角和计算得出结果.【详解】解:分两种情况:(1)当△A为锐角时,如图1,△△DOC=45°,△△EOD=135°,△BD、CE是△ABC的高,△△AEC=△ADB=90°,△△EAO+△AEO+△AOE=180°=△DAO+△DOA+△ADO,△△AEO+△EAD+△ADO+△EOD=360°△△A=360°−90°−90°−135°=45°;(2)当△A为钝角时,如图2,△△F=45°,△ADF=△AEF=90°,同理△DAE=360°−90°−90°−45°=135°,△△BAC=△DAE=135°,则△BAC的度数为45°或135°,故答案为:45°或135°.【点睛】本题考查了三角形的高和三角形的内角和,明确三角形内角和,三角形的高所构成了两个直角;本题是易错题,容易漏解,要分锐角三角形和钝角三角形两种情况进行计算.11.10【分析】过点O 作OM AC ⊥于M ,作ON BD ⊥于N ,利用平行线的性质可证得OM△BD ,进而可证得MN 为AC 和BD 的距离,根据角平分线的性质可知OE=OM=OE ,即可求得MN 的长度.【详解】解:如图,过点O 作OM AC ⊥于M ,作ON BD ⊥于N .△OA 、OB 分别平分BAC ∠和ABD ∠,OE AB ⊥,△OM OE ON 5===,又 AC △BD ,OM AC ⊥,△OM BD ⊥,又ON BD ⊥,△M ,O ,N 三点共线,△ AC 与BD 之间的距离为MN=OM ON 10+=.故答案为:10.【点睛】本题考查求平行线间的距离、角平分线的性质、八个基本事实,熟练掌握角平分线的性质,作出AC 和BD 之间的距离是解答的关键.12.△△△△【分析】根据等底同高的三角形的面积相等即可判断△;根据直角三角形两锐角互余求出△ABC =△CAD ,根据三角形的外角性质即可推出△;根据直角三角形两锐角互余求出△BAD =△ACD ,根据角平分线定义即可判断△;根据三角形的角平分线的定义判断△即可.【详解】解:△BE 是中线,△AE =CE ,△△ABE 的面积=△BCE 的面积(等底同高的三角形的面积相等),△正确;△CF 是角平分线,△△ACF =△BCF ,△AD 为高,△△ADC =90°,△△BAC =90°,△△ABC +△ACB =90°,△ACB +△CAD =90°,△△ABC =△CAD ,△△AFG =△ABC +△BCF ,△AGF =△CAD +△ACF ,△△AFG =△AGF ,△正确;△AD 为高,△△ADB =90°,△△BAC =90°,△△ABC +△ACB =90°,△ABC +△BAD =90°,△△ACB =△BAD ,△CF 是△ACB 的平分线,△△ACB =2△ACF ,△△BAD =2△ACF ,即△F AG =2△ACF ,△正确;△CF 是△ACB 的平分线,CF 交AD 于点G ,△CG 是△ACD 的角平分线,△正确;故答案为:△△△△.【点睛】本题考查了直角三角形两锐角互余,三角形的外角性质,三角形的角平分线、中线、高线等知识点,能综合运用定理进行推理是解此题的关键.13.3【分析】因为S △ABD =12S △ABC ,S △BDE =12S △ABD ;所以S △BDE =14S △ABC ,再根据三角形的面积公式求得即可.【详解】解:△AD 是△ABC 的中线,S △ABC =24,△S △ABD =12S △ABC =12,同理,BE 是△ABD 的中线,612BDE ABD SS ==,△S △BDE =12BD •EF ,△12BD •EF =6,即1462EF ⨯⨯= △EF =3.故答案为:3.【点睛】此题考查了三角形的面积,三角形的中线特点,理解三角形高的定义,根据三角形的面积公式求解,是解题的关键.14.90°或50°【分析】分高AD 在△ABC 内部和外部两种情况讨论求解即可.【详解】解:△如图1,当高AD 在△ABC 的内部时,△BAC =△BAD +△CAD =70°+20°=90°;△如图2,当高AD 在△ABC 的外部时,△BAC =△BAD -△CAD =70°-20°=50°,综上所述,△BAC 的度数为90°或50°.故答案为:90°或50°.【点睛】本题考查了三角形的高线,难点在于要分情况讨论.15. 所对边的中点 线段 = AC【分析】根据三角形中线的定义,即可求解.【详解】解:连结三角形的一个顶点和它所对边的中点的线段叫做三角形这边上的中线.△BE 是ABC 中AC 边上的中线, △12AE EC AC == 故答案为:所对边的中点;线段;=;AC ;【点睛】本题主要考查了三角形的中线,熟练掌握连结三角形的一个顶点和它所对边的中点的线段叫做三角形这边上的中线是解题的关键.16.3.【分析】如图,连接,,,OC OD CD 证明//,CD AB 再证明32OCD S S π=阴影扇形=,从而可以列方程求解半径. 【详解】解:如图,连接,,,OC OD CD点C 、D 分别是半圆AOB 上的三等分点,60,AOC COD DOB ∴∠=∠=∠=︒,OC OD =COD ∴为等边三角形,60,OCD ∴∠=︒,AOC DCO ∴∠=∠//,CD AB ∴,COD BCD S S ∴=32OCD S S π∴=阴影扇形=, 2603,3602OA ππ•∴= 解得:3,OA = (负根舍去),故答案为:3.【点睛】本题考查的圆的基本性质,弧,弦,圆心角之间的关系,平行线的判定与性质,扇形面积的计算,掌握以上知识是解题的关键.17.(1)25BAC ∠=︒;(2)8BC =【分析】(1)先利用互余计算出△BAE =50°,再利用角平分线的定义得到△BAC =12△BAE =25°;(2)先根据三角形面积公式得出DC ,利用D 是BC 的中点得到BC 即可.(1)解:△△B =40°,△E =90°,△△BAE =90°﹣40°=50°,△AC 是△BAE 的角平分线,△△BAC =12△BAE =25°;(2)△S △ADC =12DC •AE , △12×DC ×8=16,△DC =4,△D 是BC 的中点,△BC =2CD =8.【点睛】本题考查了角平分线的定义,线段的中点,角平分线的定义的正确运用是解题的关键. 18.48AC =,28AB =【分析】由题意可得60AC CD +=,40AB BD +=,由中线的性质得244AC BC CD BD ===,故可求得48AC =,即可求得28AB =. 【详解】由题意知100AC CD BD AB +++=,60AC CD +=,40AB BD +=△2AC BC =,D 为BC 中点△244AC BC CD BD === △156044AC CD AC AC AC +=+== 即460485AC =⨯= 则BC =24,CD =BD =12则40401228AB BD =-=-=且28>24符合题意.【点睛】本题考查了中线的性质,中线是三角形中从某边的中点连向对角的顶点的线段.19.(1)4根火柴棒不能搭成三角形(2)8根火柴棒能搭成一种三角形,12根火柴棒能搭成三种不同的三角形,画图见解析【分析】(1)把4分成3个数只能分成1,1,2三个数,故4根火柴棒不能搭成三角形;(2)利用三角形三边关系定理求解即可.(1)解:△把4分成3个数只能分成1,1,2三个数,而1+1=2,△4根火柴棒不能搭成三角形;(2)△ 8根火柴棒能搭成一种三角形,示意图如下:△12根火柴棒能搭成三种不同的三角形,其边长分别为:(4,4,4),(5,5,2),(3,4,5),示意图如下:【点睛】本题主要考查了三角形三边关系定理:任意两边之和大于第三边,任意两边之差小于第三边.20.(1)见解析(2)见解析(3)见解析【分析】(1)按要求分别画出平移A、B、C三点后的点D、E、F,并依次连接,即得到△ABC平移后的△DEF;(2)按要求画即可;(3)作三格点1P、2P、3P,使CP1=CP3=BP2=3即可.(1)平移后的△DEF如下图所示:(2)所画的高BH如下图所示:(3)由于CP1=CP3=BP2=3,则此三点1P、2P、3P满足题意.【点睛】本题考查了作图:作图形的平移,画三角形边上的高、三角形的面积,学会利用数形结合是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形的高、中线、角平分线练习题
1、分别在下列锐角三角形、直角三角形、钝角三角形中画出所有的高。
2、三角形的三条中线、三条角平分线、三条高都是( ) A .直线 B .射线 C .线段 D .射线或线段
3、如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )A .锐角三角形 B .直角三角形 C
.钝角三角形 D .不能确定
4、能把三角形的面积分成两个相等的三角形的线段是( )
A .中线
B .高
C .角平分线
D .以上三种情况都正确 5、如图若∠BAF=∠CAF ,则____是△ABD 的角平分线,____是△ABC 的角平分线
6、如图AB ⊥AC ,则AB 是△ABC 的边____上的高,也是△BDC 的边______上的高,也是△ABD 的边____上的高.
7、如图BD 、AE 分别是△ABC 的中线、角平分线,AC=10cm ,∠BAC=700
,则AD=_____,∠BAE=____.
F A
B
C
D A B
C
D
A
B
C
D
8、在△ABC 中,AE 是中线,AD 是角平分线,AF 是
高,填空:
⑴BE =___=2
1_____;
⑵∠BAD=_____=21_____;⑶∠AFB=_____=90
9、在△ABC 中,AB=AC,AD 是中线,△ABC 的周长为34cm,△ABD 的周长为30cm, 求AD 的长.
10、在△ABC 中AB=AC ,AC 上的中线BD 把三角形的周长分为24cm 和30cm 的两个部分,求三角形的三边长。
11、要使四边形木架(用四根木条钉成)不变形,至少要再钉上几根木条?五边形木架和六边形木架呢?n 边形木架呢?。
