物理化学:13.3 溶胶的动力性质
溶胶的物理化学性质

28
三、 溶胶的电学性质
(一) 电动现象 (1) 电泳
在外加电场作用下,带电 在外加电场作用下, 的分散相粒子在分散介质 中向相反符号电极移动的 现象叫电泳。 现象叫电泳。
29
外加电势梯度越大,胶粒带电越多,胶粒越小, 介质的粘度越小,则电泳速度越大。 通过电泳试验可以确定胶粒的电荷符号。 溶胶的电泳现象证明了胶粒是带电的,实验证明, 若在溶胶中加入电解质,则对电泳会有显著影响。 随溶胶中外加电解质的增加,电泳速度常会降低 以致变为零(等电点),甚至改变胶粒的电泳方向, 外加电解质可以改变胶粒带电的符号。 研究胶粒电泳的仪器称为电泳仪。
11
12
13
沉降速率公式的应用: 沉降速率公式的应用:
2 2 g υ = r ( ρ ρ0 ) 9 η
粘度测定
在被测液体中让一定半径一定密度的小球降落, 在被测液体中让一定半径一定密度的小球降落, 测定通过一定距离的时间求得沉降速度, 测定通过一定距离的时间求得沉降速度,由沉降 速率公式计算粘度η 速率公式计算粘度
沉降分析装置图
15
一、 溶胶的运动性质
(2) 在离心力场中的沉降
胶粒很小,在重力场中的沉降速度极为缓慢,有时无法测 定其沉降速度。 1924年,瑞典人Svedberg发明了超离心机,转速10~16 万 r/min,离心力约为地心引力的106倍。 (普通离心机转速一般为3000~5000 r/min) 利用超离心机加快沉降速率,大大扩大了测定沉降速率的 范围。可把它应用于胶团的摩尔质量或高聚物的摩尔质量 的测定上。
5
一、 溶胶的运动性质
1905年,Einstein研究了布朗运动中,粒子的平均位移与 粒子半径、介质粘度、温度和位移时间之间的关系,得到 著名的“Einstein布朗运动”公式。
溶胶的动力学性质和光学性质

溶胶的动力学性质和光学性质
第二节溶胶的动力学性质和光学性质
胶体系统是介于真溶液和粗分散系统之间的一种特殊分散系统。
由于胶体系统中粒子分散程度很高,具有很大的比表面积,表现出显著的表面特性,如胶体具有特殊的力学性质、光学性质和电学性质。
1.溶胶的力学性质
1827年,英国植物学家布朗(Brow)在显微镜下,观察悬浮在液体中的花粉颗粒时,发现这些粒子永不停息地做无规则运动。
后来还发现所有足够小的颗粒,如煤、化石、矿石、金属等无机物粉粒,也有同样的现象。
这种现象是布朗发现的,故称布朗运动,但在很长一段时间中,这种现象的本质没有得到阐明。
1903年,齐格蒙德(Zsigmondy)发明了超显微镜,用超显微镜观察溶胶,可以发现溶胶粒子在介质中不停地做无规则的运动。
对于一个粒子,每隔一定时间纪录其位置,可得到类似图9-13所示的完全不规则的运动轨迹,这种运动称为溶胶粒子的布朗运动。
图9-13 布朗运动示意图
粒子做布朗运动无需消耗能量,而是系统中分子固有的热运动的体现。
固体颗粒处于液体分子包围之中,而液体分子一直处于不停的、无序的热运动状态,撞击着固体粒子。
如果浮于液体介质中的固体远较溶胶粒子大(直径约大于5μm),一方面由于不同方向的撞击力大体已互相抵消,另一方面由于粒子质量大,其运动极不显著或根本不动。
但对于胶体分散程度的粒子(直径小于5μm)来说,每一时刻受到周围分子的撞击次数要少得多,那么在某一瞬间粒子各方向所受力不能相互抵消,就会向某一方向运动,在另一瞬间又向另一方向运动,因此形成了不停的无规则运动。
布朗运动的速率取决于粒子的大小、
温度及介质黏度等,粒子越小、温度越高、黏度越小则运动速率越快。
物理化学胶体问答题总结

(iii) 超声分散法: 用来制备乳状液 (iv) 电弧法: 电极间放电, 产生金属蒸汽,制备金、银、铂等金属溶胶 (V)气相沉积法:先将材料汽化,再反应生成纳米粒子 (2) 凝聚法: 使分子或离子聚结成胶粒。(由小变大):由此直接制出的原级粒子可以聚集成较大的次级粒子
溶胶的稳定性:聚沉稳定性(热力学)和动力学稳定性。
聚沉稳定性:胶粒比表面很大, 体系表面能高, 粒子有自发聚集从而降低体系表面能的趋向(憎液溶胶为热力学 不稳定体系,不多大分子/亲液溶胶热力学稳定)。稳定剂—>聚沉稳定性。
由于布朗运动,胶粒在重力场中不易沉降,使溶胶具有动力学稳定性。不过,布朗运动所导致的碰撞既能阻止沉 降,也能加速粒子间的粘合和聚集。
溶胶的动力性质:溶胶粒子的不规则运动, 以及由此产生的扩散, 渗透, 沉降平衡等。
布朗运动: 溶胶粒子的扩散, 渗透, 沉降平衡等现象的理解均建立在此基础上。 粒子越小,布朗运动越激烈。其运动激烈的程度不随时间而改变,但随温度的升高而增加 布朗运动的本质: 基本假定:Brown 运动与分子运动类似, 溶胶中每个粒子的平均动能和液体分子一样, 为(3/2)kT; Brown 运动是分散介质分子以大小和方向不同的力对胶体粒子不断撞击的结果; 粒子受力不平衡,导致胶粒在不同方向上以不同速度作不规则运动; 随着粒子增大,撞击的次数增多,作用力抵消的可能性增大,因而尺寸大的粒子 Brown 运动不明显。
敏化
保护
DLVO 理论(关于胶体稳定性)
胶粒之间既存在使其相互聚结的吸引力(范德华引力),又存在阻碍其聚结的相互排斥力(双电层重叠时的静电排 斥力),胶体的稳定性取决于胶粒之间这两种力的相对大小。这两种作用力与胶粒之间的距离有关(离子扩散层有无重 叠),距离较远,离子扩散层未重叠, 两胶粒以吸引为主;随距离变小,扩散层重叠, 产生斥力。 静电排斥力大小取决于粒子电荷数目和胶粒间的距离(H)。 范德华相互作用与距离的 1 次方成反比,是一种远程作用力。
溶胶

性质
特征 光学性质
动力学性质 电学性质
溶胶一般有三个特征:
图1溶胶具有丁达尔效应的光学性质,即用一束光从侧面照射溶胶,在与光路垂直的方向可以清楚地看见一条 发亮的光柱,这种现象称为丁达尔效应,又称丁铎尔(Tyndall)效应,如右图1所示。
丁达尔效应就是光的散射现象,它的产生与分散质离子的大小和入射光的波长有关。当溶质粒子大于入射光 波长,如粗分散系主要发生光的反射,观察不到散射光,所以无丁达尔现象;当溶质粒子小于入射光的波长,如 胶体溶液中溶胶粒子直径为1~100nm,小于可见光波长(400~760nm),当可见光通过溶胶时,散射现象十分明显。 真溶液中由于分散粒子太小,散射现象很弱。所以丁达尔效应是溶胶独有的光学性质。
由表可见,一价、二价三价无机离子的聚沉能力的差别。电解质的聚沉能力主要由异号离子的价态决定,价 态越高聚沉能力越大。这一规律称为叔尔采—哈迪(Schulze—Hardy)规则。
两种电解质的混合物对溶胶的聚沉的研究指出,两种与溶胶粒子相反电荷的离子对溶胶的聚沉作用有时有加 和性,有时又是相互对抗的。例如,向As2S3负溶胶中加入少量的LiCl后再加入MgCl2使As2S3聚沉,发现这时 MgCl2用量远远大于单独使用MgCl2。说明锂离子和镁离子对于As2S3聚沉作用是彼此对抗的
用各种方法制得的溶胶都会含有一定的电解质分子或离子的杂质。这些杂质会影响溶胶的稳定性,因而需要 净化。一般有两种方法:
透析法:利用溶胶粒子不能透过半透膜的性质,分离出电解质。透析时将溶胶装在透析袋中,并将其放入流 水。长时间后,大部分电解质穿过膜随水流去。可以通过检查膜外流水中的离子来监视透析情况。
图2在超显微镜下观察胶体,可以看到代表溶胶离子的发光点在不断地做不规则运动,这种运动称为布朗运动。 如图2所示
简述溶胶的动力学稳定性的定义

简述溶胶的动力学稳定性的定义溶胶的动力学稳定性( dynamic stability of colloid):是指在外加因素(如搅拌速度、离心力等)的作用下,不稳定溶胶经过一段时间后会自发地转化为稳定溶胶的特性。
溶胶分散于溶液中形成的一种胶体系统。
它具有溶液的性质,但又不完全具备溶液的性质。
可用蒸发的方法从溶液中得到的称为浓溶液;可用结晶的方法从溶液中得到的称为稀溶液。
实际上应用最广泛的还是均一稳定的稀溶液,如食盐水、蔗糖水等,在这些溶液中分散相颗粒较小,分散质浓度较高,故常称为“胶体”。
胶体的特点是具有独立的稳定系统。
其中分散相只占少数,而且多为小颗粒或小滴。
大多数分散相是大的、分散的、聚集体形式的颗粒或小滴。
例如,聚乙烯醇(分子量1000以上),分散相颗粒只有100~1000nm,相当于淀粉溶液中分散相粒子的大小。
溶胶对溶液的动力学稳定性有重要影响,并且影响程度取决于溶液的性质和胶体本身的性质,主要包括以下几个方面: 1、分散介质的性质与分散质的性质(1)当分散介质是有机溶剂时,溶胶对溶液的稳定性与其极性及溶解度有关,在水中有较好的稳定性;在非极性溶剂中分散相具有较好的稳定性。
(2)分散介质对分散质的吸附能力对分散相的稳定性也有影响,吸附能力越强,越易形成分散相,但形成的稳定系统越不稳定。
(3)当分散介质是无机胶体(如水、土壤等)时,它们对溶液的稳定性与它们的电性、粒子大小及形状有关,如土壤胶体、大分子胶体比水溶胶更稳定;溶胶对土壤胶体的稳定性比水溶胶高得多。
(4)由于溶液粘度与浓度成正比,所以分散介质对浓度也有影响,表现出良好的溶液稳定性。
(5)分散介质的温度和压力对溶液稳定性的影响,对于分散相是微小的分子和离子的溶液来说,随着温度的升高或压力的增加,分散相形成溶胶的能力增强,而且溶液粘度急剧增大,当压力增加到某一临界值时,则析出大量的分散相,形成非均相的溶液。
对于分散相是高聚物,分散相的大小与结构有关,即粒子的尺寸越小,形成的稳定系统越不稳定,聚合物越细,形成的稳定系统越不稳定,溶胶就越难形成。
简述溶胶的动力学稳定性的定义

简述溶胶的动力学稳定性的定义溶胶的动力学稳定性是指溶胶体系对溶剂和温度等因素的变化作出迅速反应而形成稳定溶液的能力,即“溶胶-凝胶转变时的转变速率”。
溶胶的这种性质,在其研究历史上曾引起过许多争论。
尽管尚未完全弄清楚这个问题,但有几点基本概念还是明确的: 1。
稳定性只表现在体系或溶液中的某一区域内,与分散体系整体的各部分无关。
是在很宽的温度范围内保持均匀状态的性质。
例如,气溶胶在水中,在-20 ℃时可以为液相;但当到达-80 ℃时,却又由固相变成液相。
它们之间存在着差别,就是由于不同的温度下溶胶体系所具有的不同性质决定的。
所以,通常都把溶胶称为非牛顿型的,并认为溶胶的这种性质主要是由溶胶的非牛顿特性决定的。
对于溶胶体系来说,溶剂不但是个重要条件,而且溶剂的分子量、分子构造等也都会影响到溶胶的稳定性。
在溶胶体系中,即使少量溶剂分子对它们的分散状态有较大的影响,但由于绝大部分是以分子尺寸很小的溶解粒子状态存在,所以,在很大程度上是受温度的影响。
即使是在浓溶液中,溶胶也具有非牛顿特性。
但当溶液冷却后,溶胶却又表现出牛顿特性。
2。
溶胶的动力学稳定性只是温度的函数,溶液和凝胶间的转变并不存在一个确定的关系式。
3。
影响溶胶动力学稳定性的主要因素有三个方面。
第一是溶液的浓度,这在溶胶聚沉中的作用是很大的。
当浓度超过某一临界值时,可以导致凝胶的产生。
第二是溶液的温度,它对体系的稳定性有直接的影响。
从经验上讲,随着温度的升高,体系的粘度会降低,在室温时,体系的粘度要比温度稍微提高一些时大得多。
这说明在温度改变的条件下,体系的稳定性也随之改变。
第三是分散体系的介质,它对体系的稳定性也有影响。
实际上,在一般情况下,溶胶的稳定性比分散体系的稳定性小。
4。
影响溶胶动力学稳定性的另一个因素是溶液的组成。
一般情况下,高分子溶液的稳定性要比非高分子溶液的稳定性差,而电解质溶液则往往比普通溶液的稳定性差。
5。
溶胶体系对外界因素的影响是有限度的。
溶胶的动力学性质
§12.3 溶胶的动力学性质
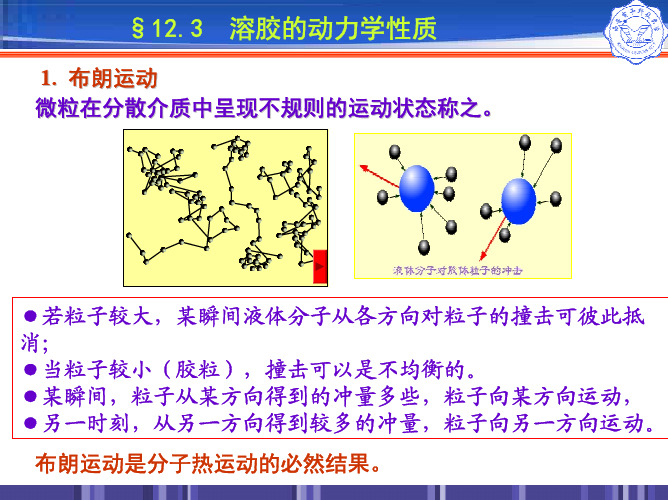
1. 布朗运动 微粒在分散介质中呈现不规则的运动状态称之。 1905年左右,爱因斯坦用几率的概念和分子运动论的观点,创 立了布朗运动的理论,推导出爱因斯坦一布朗平均位移公式。
⎛ RTt x = ⎜ ⎜ 3 L π rη ⎝ ⎞ ⎟ ⎟ ⎠
1/2
x x::tt时间间隔内粒子的平均位移 时间间隔内粒子的平均位移 T :热力学温度 T :热力学温度 L :阿伏加德罗常数 L :阿伏加德罗常数 rr:: 粒子半径 粒子半径 η η:分散介质粘度 :分散介质粘度
分散相分布 均相 沉于底部 形成浓梯
3.沉降与沉降平衡 (2)沉降平衡 扩散速率= 沉降速率,系统达到沉降平衡。
高度分布定律 可计算大小不等的粒子分布
C1,C2 :高度h1 ,h2 处粒子的数密度; M:粒子的摩尔质量; g:重力加速度; ρ0 :分散介质密度; ρ :粒子密度;
平衡时,各水平面内粒子 浓度保持不变,但从容器 底部向上形成浓度梯度。
§12.3 溶胶的动力学性质
3.沉降与沉降平衡 (1)沉降 多相分散系统中的粒子,受重力作用下沉的过程 分散相的粒子所 受到的作用力 ★重力场的作用,它力图把粒子拉向 容器的底部; ★因布朗运动所产生的扩散作用,它 力图使粒子趋于均匀分布。
沉降 ⇐⇒ 扩散 真溶液 √ 粗分散系统 √ 胶体系统 √ ←平衡→ √
1、布朗运动
斯威德伯格用超显微镜,对金溶胶作不同时间间隔 t 与平均 位移 x 测定的实验,验证爱因斯坦-布朗平均位移公式
说明:●爱因斯坦-布朗平均位移公式是准确的; ●分子运动论完全适用于溶胶分散系统。
§12.3 溶胶的动力学性质 2. 扩散
(1)扩散 有浓度梯度存在时,物质粒子因热运动,发生宏观上的定 向迁移现象。 溶胶系统中,溶胶粒子因布朗运动由高“浓度” 向低“浓度” 的定向迁移过程——溶胶粒子的扩散 。 (2)菲克第一定律 说明 : ※负号表示扩散方向与浓度梯度方 向相反。 ※扩散系数D:单位浓度梯度下,单 位时间通过单位面积的物质的量。 D的大小可衡量扩散速率。
溶胶的动力学性质和光学性质

第二节溶胶的动力学性质和光学性质
胶体系统是介于真溶液和粗分散系统之间的一种特殊分散系统。
由于胶体系统中粒子分散程度很高,具有很大的比表面积,表现出显著的表面特性,如胶体具有特殊的力学性质、光学性质和电学性质。
1.溶胶的力学性质
1827年,英国植物学家布朗(Brow)在显微镜下,观察悬浮在液体中的花粉颗粒时,发现这些粒子永不停息地做无规则运动。
后来还发现所有足够小的颗粒,如煤、化石、矿石、金属等无机物粉粒,也有同样的现象。
这种现象是布朗发现的,故称布朗运动,但在很长一段时间中,这种现象的本质没有得到阐明。
1903年,齐格蒙德(Zsigmondy)发明了超显微镜,用超显微镜观察溶胶,可以发现溶胶粒子在介质中不停地做无规则的运动。
对于一个粒子,每隔一定时间纪录其位置,可得到类似图9-13所示的完全不规则的运动轨迹,这种运动称为溶胶粒子的布朗运动。
图9-13 布朗运动示意图
粒子做布朗运动无需消耗能量,而是系统中分子固有的热运动的体现。
固体颗粒处于液体分子包围之中,而液体分子一直处于不停的、无序的热运动状态,撞击着固体粒子。
如果浮于液体介质中的固体远较溶胶粒子大(直径约大于5μm),一方面由于不同方向的撞击力大体已互相抵消,另一方面由于粒子质量大,其运动极不显著或根本不动。
但对于胶体分散程度的粒子(直径小于5μm)来说,每一时刻受到周围分子的撞击次数要少得多,那么在某一瞬间粒子各方向所受力不能相互抵消,就会向某一方向运动,在另一瞬间又向另一方向运动,因此形成了不停的无规则运动。
布朗运动的速率取决于粒子的大小、温度及介质黏度等,粒子越小、温度越高、黏度越小则运动速率越快。
溶胶动力学性质

粗分散系统
胶体系统
平衡
沉于底部
形成浓梯 19
粒子的质量越大,则其平衡浓度随高度的降低也越大。下 表列出一些不同分散体系中粒子浓度降低1/2时所需高度的 数据。
体 系 藤黄悬浮体 粗分散金溶胶 金溶胶 高分散金溶胶 氧气 不同大小的粒子的高度分布 粒子直径(m) 粒子浓度降低一半时的高度(m) 2.30×10-7 3×10-5 1.86×10-7 8.35×10-9 1.86×10-9 2.70×10-10 2×10-7 2×10-2 2.15 5×103
8.2
溶胶的动力性质
• Brown 运动 • 扩散
•沉降与沉降平衡
1. Brown运动(Brownian motion)
1827 年植物学家布朗用显微镜观察到悬浮在液
面上的花粉粉末不断地作不规则的运动。
后来又发现许多其它物质如煤、 化石、金属等
的粉末也都有类似的现象。人们称微粒的这种运动
为布朗运动。 定义:悬浮在液体的粒子的不停运动
x RT t L 3r
1
2
2. 扩散
扩散
定义:在有浓度梯度存在时,物质粒子 因热运动而发生宏观上的定向迁移,称 为扩散。 浓度梯度的存在,是扩散的推动力
溶胶粒子的布朗运动会引起溶胶中分散相粒子的扩 散作用。
8
1905年,爱因斯坦假定粒子为球形,导出了粒子在t时间
的平均位移<x>和扩散系数D之间的关系式] <x>2 = 2Dt
对于粗分散系统,或颗粒较大的胶体分散系统,当偏离沉降平衡很远时,可测定出颗粒以 一定的速率沉降。在重力场中,沉降速率 2 2 g
r ( 0 )
9
§13.3溶胶的动力性质

§13.3 溶胶的动力性质一、Brown 运动(Brownian motion)1827 年植物学家 Brown 用显微镜观察到悬浮在液面上的花粉粉末不断地做不规则的运动。
后来又发现许多其他物质如煤、 化石、金属等的粉末也都有类似的现象。
人们称微粒的这种运动为Brown 运动。
注:1、粒子越小,Brown 运动越激烈。
其运动激烈的程度不随时间而改变,但随温度的升高而增加。
2、当半径大于5 μm ,Brown 运动消失。
二、扩散和渗透压1、扩散:胶粒也有热运动,因此也具有扩散和渗透压。
只是溶胶的浓度较稀,这种现象很不显著。
斐克第一定律(Fick’s first law ):式中D 为扩散系数,其物理意义为:单位浓度梯度、单位时间内通过单位截面积的质量。
负号表示扩散发生在浓度降低的方向。
Einstein-Brown 位移方程:这就是Einstein-Brown 位移方程。
从Brown 运动实验测出x ,就可求出扩散系数 D 。
2、渗透压:由于胶粒不能透过半透膜,而介质分子或外加的电解质离子可以透过半透膜,所以有从化学势高的一方向化学势低的一方自发渗透的趋势。
溶胶的渗透压可以借用稀溶液渗透压公式计算: 注:由于憎液溶胶不稳定,浓度不能太大,所以测出的渗透压及其它依数性质都很小。
三、沉降和沉降平衡沉降平衡:溶胶是高度分散系统,胶粒一方面受到重力吸引而下降,另一方面由于Brown 运动促使浓度趋于均一。
当这两种效应相反的力相等时,粒子的分布达到平衡,粒子的浓度随高度不同有一定的梯度。
高度分布定律:达沉降平衡时,粒子随高度分布的情况与气体类似,可用高度分布定律。
或这就是高度分布公式。
粒子质量愈大,其平衡浓度随高度的降低亦愈大。
用来测蛋白质的摩尔质量 d d d d m c DA t x =-22x D t =n RT V=Π322114ln ()()3N RT r gL x x N πρρ=---粒子介质3221141exp ()()3N r gL x x N RT πρρ⎡⎤=---⎢⎥⎣⎦粒子介质21222212ln (1)()c RT c M x x ρωρ=--介质粒子。
溶胶与凝胶的基本物理化学特性
双电层结构模型和电动电位
(3) Stern模型(1924)
Stern认为Gouy—Chapman的扩散双电层可分为两 层,一层为紧靠粒子表面的紧密层(亦称Stern层或吸附 层),其厚度δ由被吸附离子的大小决定。另一层相似于 G ouy-Chapman双电层中的扩散层(电势随距离的增加呈曲 线下降),其浓度由体相溶液的浓度决定。
1941,德查金(Darjaguin)和朗道(Landau); 1948,维韦(Verwey)和奥弗比克(Overbeek): 带电胶粒稳定理论,简称DLVO理论
移率)为常数,是该带电粒 子的物化特征性常数。不同 带电粒子因所带电荷不同, 或虽所带电荷相同但荷质比 不同,在同一电场中电泳, 经一定时间后,由于移动距 离不同而相互分离。分开的
体微粒吸附阴离子,带负电荷。 距离与外加电场的电压与电
泳时间成正比。
电泳与沉降电位
按分离原理的不同,电 泳分为4类: 移动界面电泳、 区带电泳、 等电聚焦电泳 等速电泳。
工厂除尘也用到电泳。利用电泳 还可以检出被分离物,在生化和 临床诊断方面发挥重要作用。本 世纪40年代末到50年代初相继发 展利用支持物进行的电泳,如滤 纸电泳,醋酸纤维素膜电泳、琼 脂电泳;50年代末又出现淀粉凝 胶电泳和聚丙烯酰胺凝胶电泳等。 目前,电泳技术已广泛应用于分 析化学、生物化学、临床化学、 药理学、免疫学、微生物学、遗 传学等科学中。
溶胶的性质 (1)

胶粒带电原因?
氢氧化铁溶胶的电泳实验
溶胶粒子的 + 3H2O == Fe(OH)3 + 3HCl Fe(OH)3 + H+ == FeO+ + 2H2O
反离子
胶粒
电势离子 氢氧化铁胶团的结构示意图
胶核
溶胶粒子的结构
负溶胶
扩散层 反离子
胶粒
胶团
AgNO3 + KCl == AgCl + KNO3
电势离子 胶核
氯化银胶团的结构示意图
二、溶胶及其性质
3.溶胶的性质
4)溶胶的稳定性和聚沉
溶胶的稳定性 ① 动力学稳定性
② 胶粒带电(主要因素)
③ 胶粒表面水化膜的保护作用
溶胶的聚沉 ①电解质的聚沉作用
②溶胶的相互聚沉
3、使溶胶聚沉常用的方法有哪些?
溶胶中分散质的颗粒在不断地做无规则的运动,这种运动叫做布朗
。 (Brown)运动
布朗运动是大量分子做无规则运动对悬浮的固体微粒各个方向撞击作用 的不均衡性造成的,所以布朗运动是大量液体分子集体行为的结果。 是溶胶稳定的重要因素
二、溶胶及其性质
3.溶胶的性质 3)电学性质
电泳现象 电泳现象说明溶胶粒子是带电的, 根据电泳实验测定溶胶粒子的带电性。
溶胶及其性质
药学院教师 朱勇
二、溶胶及其性质
1.溶胶的概述:溶胶的胶粒是由大量分子(或原子、离子) 形成的聚集体。直径为l-100 nm的胶粒分散在分散介质中形 成的多相系统,具有很大的界面和界面能,能否长时间存在 取决于胶体的性质。
硅溶胶
二、溶胶及其性质
2.溶胶的分类:习惯上,把分散介质(分散剂)为液体的胶体 分散体系称为液溶胶或溶胶(sol);分散介质为气体的分散体 系成为气溶胶,介质为固体时,称为固溶胶。
溶胶的动力学性质

C C D 2 t x
2
C—扩散物质的体积浓度, t—扩散时间, D—扩散系 数,x—距离
沉降与沉降平衡
沉降:悬浮在液态介质中的、密度比介质大的粒 子受重力作用下沉的现象
沉降平衡:分散相中的粒子受到扩散与沉降两个 相反的作用,当两种作用相当时,粒子处于平衡 状态(动态平衡)
沉降的结果是体系下层粒子 的浓度变大,当胶粒下降产
溶胶的动力学性质
布朗运动
扩散
沉降与沉降平衡
布朗运动
罗伯特〃布朗
英国植物学家
布朗运动
发现:1827年布朗用显微镜观察到悬浮在液面上的 花粉粉粒不断地作不规则的运动
定义:微粒的连续、不规则运动
布朗运动
特点: 无规则
永不停歇
颗粒越小,布朗运动越明显 温度越高,布朗运动越明显 肉眼无法看见
布朗运动
本质:大量(水)分子做无规则运动对悬浮的固 体(花粉)微粒各个方向撞击作用的不均衡性
意义:间接反映并证明了分子热运动,同时也是 研究溶胶动力学性质的基础
布朗运动
1905年左右, 爱因斯坦用几率的概念和分子运动论 的观点, 创立了布朗运动理论,得出爱因斯坦—布 朗运动平均位移公式:
RTt x 3N πrη A
1/ 2
— x 在时间 t 内粒子沿 x 轴方向的平均位移; r — 粒子 半径;η—介质粘度;NA—阿佛加德罗常数;R— 摩尔气体常量;T—温度
扩散
如下图所示:在CDFE桶内盛溶胶,在某一截面AB 的两侧溶胶的浓度不同,C1>C2。由于分子热运动 和胶粒的布朗运动,可以观察到胶粒从 C1 区向 C2 区迁移的现象,这就是胶粒的补偿时体系处于平衡状态,
体系中胶粒沿容器高度分布
【推选】溶胶PPT资料

扩散层
胶粒
胶团
式中,m表示胶核中所含Fe(OH)3的
(胶三粒) 胶带粒负的电双荷电。层分结构子数(约为103左右),n表示胶核所
胶的粘度愈小,愈容易扩散。
吸附的FeO 离子数,n的数值比m小 + 式中,m表示胶核中所含Fe(OH)3的
相互聚沉现象:两种带相反电荷的溶胶按适当比例混合,也能引起溶胶聚沉 。 或蛋白质溶液迅速达到沉降平衡。
第三节溶胶
一、溶胶的光学性质 1869年物理学家Tyndall发现
产生的原因:溶胶粒子的直径 (1~100nm)略小于可见光波长(400~ 760nm),光波会环绕着溶胶粒子向 各个方向散射,散射出来的光称为 散射光或乳光。利用丁铎尔现象, 常可以区别溶胶与真溶液、悬浊液 和高分子溶液。
二、溶胶的动力学性质 (一) 布朗运动 1827年,植物学家布朗(Brown) 发现胶粒在介质中作无规则运动。 产生的原因:是由于周围分散介 质的分子从各个方向以不等的力撞击 这些溶胶粒子。因而在每一瞬间粒子 所受到的合力方向不断改变,所以胶 粒处于不断地无秩序运动状态。布朗 运动是溶胶的特征之一。胶粒越小, 运动越快,布朗运动越激烈。
三、溶胶的电学性质 (一) 电泳
电泳:在泳方向可以确定胶粒带有什么 电荷,Fe(OH)3胶粒带正电荷。
正溶胶:大多数金属氢氧化物溶胶 向负极迁移, 胶粒带正电荷。
负溶胶:大多数金属硫化物、硅胶、 金、银等溶胶向正极迁移, 胶粒带负电荷。
应用:
蛋白质、氨基酸和核酸等物质 各个方向散射,散射出来的光称为
离解为SiO32-和H+:
H 2Si3OSi3 2 O 2H
H+扩散到介质中去,而SiO32-留在 胶核表面,结果使胶粒带负电荷。
溶胶剂-溶胶的性质

溶胶剂-溶胶的性质溶胶剂(sols)系指固体药物以胶粒状态分散于分散介质中形成的非均匀分散的液体药剂。
又称为疏水胶体溶液。
溶胶剂中的胶粒为多分子聚集体,胶粒大小一般在1~100nm之间。
其分散度极大,但水化作用弱。
属于热力学不稳定系统。
外观与溶液剂相似,透明无沉淀。
将药物制成溶胶分散体系,可改善药物的吸收,使药效增大或异常,对药物的剌激性也会产生影响。
如粉末状的硫不被肠道吸收,但制成胶体则极易吸收,可产生毒性反应甚至中毒死亡。
具有特殊刺激性的银盐制成具有杀菌的胶体蛋白银、氧化银、碘化银则刺激性降低。
目前溶胶剂应用很少,但其性质对药剂学却有着重要童义。
溶胶的性质⒈可滤过性溶胶剂的胶粒(分散相)大小在1~100nm之间,能透过滤纸、棉花,而不能透过半透膜。
这一特性与溶液不同,与粗分散相也不同。
因此,可用透析法或电渗析法除去胶体溶液中的盐类杂质。
⒉粒子具有布朗运动溶胶的质点小,分散度大,在分散介质中存在不规则的运动,这种运动称为布朗运动。
布朗运动是由于胶粒受分散介质水分子的不规则撞击产生。
胶粒愈小,布朗运动愈强烈,其动力学稳定性就愈大。
⒊光学效应由于胶粒对光线的散射作用,当一束强光通过溶胶剂时,从侧面可见到圆锥形光束,称为丁铎尔效应。
这种光学性质在高分子溶液中表现不明显,因而可用于与溶胶剂的鉴别。
溶胶剂的颜色与胶粒对光线的吸收和散射有关,不同溶胶剂对不同波长的光线有特定的吸收作用,使溶胶剂产生不同的颜色。
如碘化银溶胶呈黄色,蛋白银溶胶呈棕色,氧化金溶胶则呈深红色。
⒋胶粒带电溶胶剂中的固体微粒可由于自身解离或吸附溶液中的某种离子而有电荷。
带电的固体微粒由于电性的作用,必然吸引带相反电荷的离子,称为反离子,部分反离子密布于固体粒子的表面,并随之运动,形成所谓胶粒。
胶粒上的吸附离子与反离子构成吸附层。
另一部分反离子散布于胶粒的周围,离胶粒愈近。
反离子愈密集,形成了与吸附层电荷相反的扩散层。
带相反电荷的吸附层与扩散层构成了胶粒的双电层结构。
12章_溶胶

3. 溶胶的光学性质-Tyndall效应
溶液
溶胶 云锁高山,哪个尖峰得出 日照漏壁,这条光棍难拿
2020/7/26
4. 溶胶的动力学性质-Brown运动
布朗用显微镜观察到悬浮在液面上的花粉不断地 作不规则的运动。 Brown运动的宏观效果使胶粒从高浓度区扩散到低 浓度区。
2020/7/26
4. 溶胶的动力学性质-沉降平衡
2020/7/26
3. 溶胶的光学性质-光散射
可见光的波长在400~700 nm。胶粒尺寸1~100nm (1)当光束通过粗分散体系,由于粒子尺寸大于入 射光的波长,主要发生反射,体系呈现混浊。
(2)当光束通过胶体溶液,由于胶粒直径小于可见 光波长,主要发生散射,即Tyndall效应。
(3)当光束通过溶液,由于溶液十分均匀,散射光因 相互干涉而完全抵消。 令一束光通过溶胶,从侧面可以看到一条光柱,这就是 Tyndall效应,是判别溶胶与溶液的最简便的方法。
结构表达式
[(AgI)m nI- (n-x)K+ ]x- xK+
胶核
紧密层
扩散层
胶粒
胶团
胶团的图示式 由内到外分别是胶 核,胶粒,胶团。
2020/7/26
5. 溶胶的电性质-胶粒的结构
若AgNO3过量,则AgI胶核吸附Ag+而带正电。反离子 NO3-一部分进入紧密层(stern层),一部分进入扩散层。 若KI过量,则AgI胶核吸附I-而带负电。反离子K+一部 分进入紧密层(stern层),一部分进入扩散层。 胶核、吸附的离子和紧密层共同组成胶粒,胶粒与扩 散层一起组成胶团,整个胶团显电中性。
2. 电离,分散相电离,一部分离子进入介质中。
2020/7/26
物理化学:13.3 溶胶的动力性质

n 1)
在大数 N ( 1023量级 ) >> n 条件下,
Nn N , nn
N
(
N
1)( Nn
N
n
1)
1
代入上式:
Wn
nn n!
(1
n N
N (n)
)n
1
nn n!
en
2021/3/19
35
Wn
nn n!
en
粒 子 数n对 平 均 粒 子 数n 的 平 均 偏 离
(最可几偏离):
均方差: (n n )2 (n n )2Wn
n0
n2Wn 2 nnWn n 2 Wn
0
0
0
(推导略) n
2021/3/19
36
平均偏离值: (n n)2 n1/2
相对偏离值:
n
n 1/ 2 n
1 n 1/ 2
即 具 有 平 均 粒 子 数 为n 的 小 体 积 元v内 粒 子数的涨落为: 1
n 1/ 2
这表明,n 越大,偏离越小。例如:
2021/3/19
37
n
100,涨落
1 n 1/ 2
10%
n
10000,涨落
1 n 1/ 2
1%
浓度为 1mol / L的 1L稀溶液中,溶质
粒子数涨落为:
1 n1/2
1
0.00013%,非常小。
6.02 1011
2021/3/19
38
四、渗透压
• 设溶胶的摩尔分 数为 x,则溶剂的 摩尔分数为 1x。
这说明用分子运动理论来阐明布朗运动十分 成功,Browm 运动的本质是质点的热运动。
相应地,Perrin 的实验结果也为分子运动理 论提供了实验依据,从而使分子运动论成为 被普遍接受的理论,推动了科学的发展。
胶体12-3

3. 瑞利(Rayleigh)散射定律 ——散光强度与哪些因素有关?
散光强度
I
24
2 A2vV 2
4
n12 n22 n12 2n22
2
A——入射光振幅
——入射光波长
v——单位体积中粒子数
V——每个粒子体积
n1、n2——分别为分散相、分散介质的折射率
公式表明:
①
I
1
4
, I
∴ 太阳光散光呈淡蓝色,透过光呈橙红色
溶胶的渗透压可用稀溶液渗透压公式:
Π n RT V
n——体积V的溶液中含溶质的物质的量
3. 沉降和沉降平衡
粒子
介质
胶粒沉降
沉降力等于扩散力(布朗运动)时,达到沉降平衡 胶粒沿高度有一定分布,类似于大气分布
Ph
P0
exp
mgh RT
N2 N1
exp
4 3
r
3
(
粒子
介质 )gL(x2
x1)
1 RT
高度分布公式
半径为r的球形粒子在重力场中沉降,当粒子所
受重力与分散介质的阻力(摩擦力)相等,粒子恒速沉
降时:
r 9 dx / dt 2 (粒子 介质)g
——落球式粘度计原理 粒子在超离心力场中沉降平衡
——测大分子或胶团的摩尔质量
x处溶胶的浓度
M
2RT ln c2 / c1
(1 介质 / 粒子 ) 2 (x22
x12 )
离心机旋转角速度
旋转轴至溶胶中 某平面的距离
说明:Brown运动、扩散和沉降都是分散体系的主要 动力性质,由于胶粒的Brown运动,使其不易沉降, 具有动力学稳定性。
二、光学性质
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021/3/19
13
1905年和1906年,爱因斯坦(Einstein)和 斯 莫 鲁 霍 夫 斯 基 ( Smoluchowski ) 独 立 地 提出了Brown 运动理论及其实验研究方法:
a)悬浮于液体中的质点的平均动能和小分 子一样,皆为 (3/2) kBT。Brown 运动是不断 热运动的液体分子对微粒冲击的结果。这一 理论可以解释以上两个实验观测结果。
一些典型的扩散系数值(20C水中)
物质
蔗糖 胶态金 纤维蛋白质 胶态硒
分子量
342 = 1.3 nm
330,000 = 56 nm
D (×10-10 m2/s)
4.586 1.63 0.197 0.038
2021/3/19
10
二、布朗运动
1. Brown运动的发现
1827年,英国植物学家Brown发现,在显微镜 下能观察到悬浮在液面(水)上的花粉末不断 地作不规则的运动。
的情况,亦即流体中各处浓度、浓度梯度恒定
的情况下稳流过程。
而实际情况往往是扩散方向上各处的浓度或浓
度梯度是变化的,所以仅用 Fick 第一定律难
以推定扩散系数 D。
2021/3/19
4
2. Fick 第二定律
考虑(t→t + d t)时间内小体积元(x→x+dx) 中溶质增加量(dm – dm )
D kBT (f:质点的阻力系数) f
对于球形质点,根据Stokes定律:
f 6 r(:介质的粘度)
D kBT RT 1
6 r L 6 r
2021/3/19
23
D kBT RT 1
6 r L 6 r
由上式可知:T ↗,扩散 D ↗;
↗,扩散 D ↘;
r ↗,扩散 D ↘。
§13.3 溶胶的动力性质
胶粒的不规则运动导致:扩散、渗透压、 外力场中的定向运动等动力性质。
一、扩散现象
当存在浓差时,胶粒由高浓区域自发地 移向低浓区域,此即扩散现象。
2021/3/19
1
在扩散传质过程中,遵守 Fick 定律。
2021/3/19
2
1. Fick第一定律
dm D A dc
dt
dx
dm 为x方向上通过截面A的扩散速度(mol / s) dt
D为扩散系数:单位浓度梯度下通过单位截面
积的物质量扩散速率(m2 / s)
dc 为浓度梯度(c:mol / m3) dx
2021/3/19
3
dm D A dc
dt
dx
显然,浓度梯度的存在是发生扩散作用的前提。
Fick 第一定律 较多适用于各处浓度梯度恒定
2021/3/19
5
c' c c dx x
对x微商
dc' dc 2c dx dx x2 dx
2021/3/19
6
dc' dx
dc dx
2c x 2
dx
由Fick 第一定律 :
2021/3/19
dm'
dc'
dc 2c
dt
D
A
dx
DA( dx
x 2
dx)
dm D A dc
dt
dx
dmBiblioteka dm' 2c DA ( x2
dx )
dt
(1)
7
dm
dm'
DA
2c ( x2
dx)
dt
(1)
显然,x → x+ dx 的浓差为
dc dm dm' (2) A dx
由 (1)、(2) 式:
dc dt
D
2c x 2
(Fick第二定律)
2021/3/19
8
dc
2c
dt D x2
2021/3/19
17
对于每个质点,由于Brown运动,其沿x轴向 左或向右移动的几率相等,故在时间 t 内经过
平面A右移的质点量为:
1 2
c1
x
A
向左移的质点量为:
1 2 c2 x A
2021/3/19
18
净的向右扩散量为:
dm
1 2
(c1
c2 )x
A
通常x值很小,故浓度梯度dc 可表为: dx
2021/3/19
14
b)在实验中不必苛求质点运动的实际路 径或实际速度 (也没有法测得),只需测 定一定时间间隔 ( t ) 内质点 ( 在 x 轴上 )
的平均位移 x。
2.Einstein 公式
2021/3/19
15
如图所示为每隔一定时间间隔 t 记下的某质
点的位置,我们考察沿某一方向(如 x 轴方
dc c1 c2 (负值表明浓度沿x方向下降)
dx
x
2021/3/19
19
dc c1 c2
dx
x
上式代入:dm
1 2
(c1
c2
) xA,得
dm 1 x2 dc A 2 dx
由Fick第一定律:
dm D A dc t(这里的t即时间间隔dt) dx
2021/3/19
20
dm 1 x2 dc A 2 dx
(Fick第二定律)
其中: dc 为x处浓度c随时间的变化率,实验可测; dt
2c x 2
为x处浓度梯度
dc dx
随x的变化率,实验可测;
• 由Fick 第二定律可求得扩散系数 D; • D 不随时间和浓度而变化 (只是温度的函数); • Fick 第二定律是扩散的普遍公式。
2021/3/19
9
胶体的扩散系数系数: 10-10 ~ 10-12 m2 / s 小分子物质的扩散系数:~10-9 m2 / s
向)上的投影,并设其在 x 轴上的位移(t
时间间隔)分别为 x1、x2、x3 …,平均位移
x。而这个平均位移值 x 是可以计算的。
2021/3/19
16
如图一截面面积为A的流体,只考虑粒子在x方向上 的位移。设粒子沿 x 方向浓度逐渐降低。考虑两个厚
度为x的相邻液层,其平均浓度分别为c1、c(2 c1 c2), x即为粒子在时间t内沿x方向的平均位移。
dm D A dc t dx
比较以上两式:
x 2Dt
— Brown运动的Einstein公式
2021/3/19
21
x 2Dt
Einstein公式揭示了Brown运动与扩散的 内在联系: 扩散是 Brown 运动的宏观表现; Brown 运动是扩散的微观基础。
2021/3/19
22
对于扩散系数 D,Einstein 曾导出关系式:
后来又发现其它细粉末(如煤、化石、金属等 粉末)也如此,这种无规则运动即Brown运动。
在很长一段时间里,Brown运动现象的本质没 有得到阐明。
2021/3/19
11
2021/3/19
12
1903年,超显微镜的发明,为研究布郎运 动提供了物质条件,观测结果表明:
1)粒子越小,布朗运动越剧烈; 2)温度升高,布郎运动变剧烈。
