1421正比例函数的图象
合集下载
正比例函数课件

正比例函数课件
contents
目录
• 正比例函数概述 • 正比例函数的图像性质 • 正比例函数的实际应用 • 正比例函数的解析式 • 正比例函数的图像变换 • 正比例函数与反比例函数的关系
01
正比例函数概述
正比例函数的定义
正比例函数是指形如 y=kx(k为常数, k≠0)的函数。
当k<0时,函数图像 过第二、四象限,y 随x的增大而减小。
04
正比例函数的解析式
解析式的推导过程
01
02
03
04
定义正比例函数:$y=kx$, 其中k为比例系数。
从已知的图像中,通过取不同 的x值,计算对应的y值。
利用已知数据,通过最小二乘 法进行线性回归分析,得出k
的值。
得出解析式:$y=kx$,其中 k为比例系数,x为自变量,y
为因变量。
解析式的应用实例
反比例函数的应用场景
反比例函数在工程、技术、经济等领域有广泛的应用。例如,在电子工程中描 述电阻、电容、电感之间的关系,在经济学中描述成本与产量之间的关系。
THANKS
感谢观看
日常生活中的应用
身高与年龄
在一定年龄范围内,身高与年龄 之间存在正比例关系。随着年龄
的增长,身高也会相应增加。
收入与工作时间
在一定时间内,收入与工作时间之 间存在正比例关系。随着工作时间 的增加,收入也会相应增加。
路程与速度
当速度保持不变时,路程与时间之 间存在正比例关系。当时间增加时 ,路程也会相应增加。
图像的平移变换
上下平移
正比例函数的图像在垂直方向上平移。
左右平移
正比例函数的图像在水平方向上平移。
平移性质
平移不改变函数的值域和定义域,也不改变函数 的单调性和奇偶性。
contents
目录
• 正比例函数概述 • 正比例函数的图像性质 • 正比例函数的实际应用 • 正比例函数的解析式 • 正比例函数的图像变换 • 正比例函数与反比例函数的关系
01
正比例函数概述
正比例函数的定义
正比例函数是指形如 y=kx(k为常数, k≠0)的函数。
当k<0时,函数图像 过第二、四象限,y 随x的增大而减小。
04
正比例函数的解析式
解析式的推导过程
01
02
03
04
定义正比例函数:$y=kx$, 其中k为比例系数。
从已知的图像中,通过取不同 的x值,计算对应的y值。
利用已知数据,通过最小二乘 法进行线性回归分析,得出k
的值。
得出解析式:$y=kx$,其中 k为比例系数,x为自变量,y
为因变量。
解析式的应用实例
反比例函数的应用场景
反比例函数在工程、技术、经济等领域有广泛的应用。例如,在电子工程中描 述电阻、电容、电感之间的关系,在经济学中描述成本与产量之间的关系。
THANKS
感谢观看
日常生活中的应用
身高与年龄
在一定年龄范围内,身高与年龄 之间存在正比例关系。随着年龄
的增长,身高也会相应增加。
收入与工作时间
在一定时间内,收入与工作时间之 间存在正比例关系。随着工作时间 的增加,收入也会相应增加。
路程与速度
当速度保持不变时,路程与时间之 间存在正比例关系。当时间增加时 ,路程也会相应增加。
图像的平移变换
上下平移
正比例函数的图像在垂直方向上平移。
左右平移
正比例函数的图像在水平方向上平移。
平移性质
平移不改变函数的值域和定义域,也不改变函数 的单调性和奇偶性。
正比例函数的图象和性质课件

们只相交于原点。
06
CHAPTER
03
正比例函数的性质
增减性
01
02
03
增减性
正比例函数在定义域内是 单调的,即随着x的增大 (或减小),y也相应增 大(或减小)。
增减性的判断
根据斜率k的正负来判断 。当k>0时,函数为增函 数;当k<0时,函数为减 函数。
增减性的应用
在解决实际问题时,可以 利用增减性判断函数的值 域或最值。
y=-3/x
提升练习题
01
总结词
深化理解与运用
02
03
04
题目1
已知某物体的速度v与时间t的 关系为v=kt,其中k为常数。 求该物体在t=3时的速度v。
题目2
画出函数y=0.5x和y=-0.2x的 图象,并比较它们的性质。
题目3
已知某物体的位移s与时间t的 关系为s=2t^2,求该物体在
t=5时的位移s。
斜率
1 2 3
斜率定义
正比例函数y=kx(k≠0)的斜率是k。
斜率与函数图像的关系
斜率决定了函数图像的形状和倾斜程度。当k>0 时,图像从左下到右上上升;当k<0时,图像从 左上到右下下降。
斜率的应用
在解决实际问题时,可以利用斜率判断函数的单 调性和变化趋势。
截距
截距定义
正比例函数y=kx(k≠0)的截距是0。
正比例函数的图象和性 质ppt课件
CONTENTS
目录
• 正比例函数的概念 • 正比例函数的图象 • 正比例函数的性质 • 正比例函数的应用 • 练习与思考
CHAPTER
01
正比例函数的概念
正比例函数的定义
《正比例函数》课件

探秘正比例函数
欢迎来到正比例函数的世界!这个PPT将会带你深入探索正比例函数,了解它 的定义、性质和应用。
定义与特点
定义
正比例函数是一种函数,其定义域和值域都是正实数,且函数的值与自变量成正比例关系。
特点
自变量为0时函数值为0。自变量每增加1,函数值增加k。函数图像为一条经过原点的直线。
公式
y=kx (k 为比例常数)
2
方法二
已知函数图像斜率为 k,取图像上两点 (x1,y1) 和 (x2,y2),代入公式 (y2-y1)/(x2x1)=k,求解比例常数 k。
3
方法三
已知函数经过点 (x,y),代入公式 y=kx,求解比例常数 k。
应用:直接比例与反比例
直接比例
两个量的比例关系为直接比例, 如果一个量增大,另一个量也相 应地增大。
3 问题三
如何通过函数图像求解正比例函数的比例常数?请列出步骤。
结论与思考
结论
正比例函数是数学中重要的函数类型之一,概念简 单易懂,应用广泛。
思考
正比例函数可以用来描述哪些现象和问题?你能设 计一道有趣的应用题吗?
结束语
感谢观看这个PPT,我们希望通过本次分享,让大家更加深入地了解正比例函数,并能够在实际问题中灵活运 用。谢谢!
反比例
两个量的比例关系为反比例,如 果一个量增大,另一个量相应地 减小。
反比例的应用
例如在物理学中,波长和频率呈 反比例关系。
小试牛刀
1 问题一
已知正比例函数 y=kx (k>0),当 x=2 时,y=6,求比例常数 k。
2 问题二
已知正比例函数 y=kx (k>0),当 x=2 时,y=6,当 x=4 时,y=12,验证斜率为常数 k。
欢迎来到正比例函数的世界!这个PPT将会带你深入探索正比例函数,了解它 的定义、性质和应用。
定义与特点
定义
正比例函数是一种函数,其定义域和值域都是正实数,且函数的值与自变量成正比例关系。
特点
自变量为0时函数值为0。自变量每增加1,函数值增加k。函数图像为一条经过原点的直线。
公式
y=kx (k 为比例常数)
2
方法二
已知函数图像斜率为 k,取图像上两点 (x1,y1) 和 (x2,y2),代入公式 (y2-y1)/(x2x1)=k,求解比例常数 k。
3
方法三
已知函数经过点 (x,y),代入公式 y=kx,求解比例常数 k。
应用:直接比例与反比例
直接比例
两个量的比例关系为直接比例, 如果一个量增大,另一个量也相 应地增大。
3 问题三
如何通过函数图像求解正比例函数的比例常数?请列出步骤。
结论与思考
结论
正比例函数是数学中重要的函数类型之一,概念简 单易懂,应用广泛。
思考
正比例函数可以用来描述哪些现象和问题?你能设 计一道有趣的应用题吗?
结束语
感谢观看这个PPT,我们希望通过本次分享,让大家更加深入地了解正比例函数,并能够在实际问题中灵活运 用。谢谢!
反比例
两个量的比例关系为反比例,如 果一个量增大,另一个量相应地 减小。
反比例的应用
例如在物理学中,波长和频率呈 反比例关系。
小试牛刀
1 问题一
已知正比例函数 y=kx (k>0),当 x=2 时,y=6,求比例常数 k。
2 问题二
已知正比例函数 y=kx (k>0),当 x=2 时,y=6,当 x=4 时,y=12,验证斜率为常数 k。
正比例函数图象和性质课件

讨 论:
画正比例函数的图像时,怎样画最简单? 为什么?
动手画一画:
用最简单的方法画(1)y= 3 x (2)y=-3x的函数的图像 2
猜 想:
y=-2x
y=3x
1、哪些正比例函数过 一、三象限?
y 1 x 3
2、哪些正比例函数过 二、四象限?
3、过一、三象限的函数有什么共同点?
4、过二、四象限的函数有什么共同点? 5、它们由什么量决定?
例1、在同个平面直角坐标系中画出下列正
比例函数的图像
y 2x
y 2x
这两个函数图像 分别有哪些什么
画图步骤:
特点?
1、列表 2、描点 3、连线
观察并找出这两个 函数的共同点和不
同点
共同点:两个图像都是 直线 线,都经过 原点 点
不同点:函数 y 2x 的比例系数 K=2 ,图像从左向右上升 趋势,经过第 一、三 象限,
图像过 第几象 限
y 10x
y 3x
y1x 4
y 11x y 3 3x y 3x
拓展演练:
1、正比例函数 y
1 3
x
的图像经过(
)A、第一,三象限B、第 Nhomakorabea,三象限
C、第二、四象限
D、第一、四象限
2、已知正比例函数y=kx的函数图像经过第二、四象限,
则k的取值范围( )
A、k>0
B、k=0
C、k<0 D、k 0
复习 1、什么是变量?什么是常量? 2、什么是自变量?什么是函数? 3、什么是正比例函数?
归 纳:
一般地,形如y=kx(k是常数,k≠0)的 函数,叫做 正比例函数,其中k叫做比例系数. 注意:正比例函数解析式y=kx (k是常数,k≠0)
1421正比例函数的图象和性质2

提高:
想一想:
一辆汽车从A站以每时80千米的速度出发,行驶时间超过 5时,但小于5时45分,你能利用正比例函数的图象估出这 辆汽车离开A站已有多远吗?
y 分析:
1)s 与 t 的函数关系式 s=80t
t 5时s 805 400 (千米)
t 5 3 时s 80 23 460 (千米)
4
4
2:根据下列图象,写出函数关系式:
(2)
y
3
0
x
2
y 6 x 3
y
y 3x
y x
y 1 x 3
1
01
y 2x yx
y1x 3
x
当 |k| 越大时,图象越靠近y轴
小结 正比例函数
解析式: y=kx(k是常数,k≠0) 图象:一条经过原点和(1,k)的直线
性质:①当k>0时,直线y=kx经过第一、三象限; 当k<0时,直线y=kx经过第二、四象限,
选做题:习题精选P18—19
下课了!
2)画图,一般地, s=80t的图象是经过(0,0) (1,80)的直线, 由于t≥0,所以它的图象 以O为端点的射线。
3)由图可见,这辆汽车离开A站约有400千米至460千米。
480 420 360 300 240 160
80
A12
x
3 45 6
布置作业:
必做题:课本P35习题11.2 第1、2题 作业本
②当k>0时,从左向右上升,即随x的增大 y而增大;
当k<0时,从左向右下降,即随着x的增大 y而减少。
③当 |k| 越大时,图象越靠近y轴
小结
1.正比例函数的定义:y=kx(k是常数, k≠0) 2.正比例函数的图象和性质:
正比例函数图像课件ppt

正比例函数的应用场景
总结词
正比例函数在现实生活中有许多应用场景,如速度-时间关系 、加速度-时间关系等。
详细描写
在物理学中,速度和时间是成正比的,可以用正比例函数表 示。同样地,加速度和时间的关系也可以用正比例函数表示 。此外,在经济学、统计学等领域中也有许多应用场景,如 收入与工作时间的关系等。
k值变化时
当k的值产生变化时,图像的斜率也 会相应变化,但始终保持垂直于x轴 。
03 正比例函数图像的性质
函数的单调性
单调递增
当比例系数大于0时,随着x的增大 ,y的值也增大。
单调递减
当比例系数小于0时,随着x的增大,y 的值减小。
函数的对称性
关于原点对称
正比例函数的图像总是经过原点,并且关于原点对称。
正比例函数的基本性质
总结词
正比例函数具有一些基本性质,包括斜率固定、过原点、y 随 x 增大而增大或 减小等。
详细描写
正比例函数的斜率为 k,即当 x 增加时,y 会以 k 的比例增加或减少。如果 k>0,则函数图像为增函数;如果 k<0,则函数图像为减函数。由于图像过原 点,因此当 x=0 时,y=0。
解决代数问题
正比例函数是线性函数的一种特殊情势,通过正比例函数图像可以直观地表示函数的增减性、交点等性质,有助 于解决代数方程、不等式等问题。
在物理中的应用
描写光强与距离的关系
在光学中,光强与光源的距离成正比。通过正比例函数图像,可以表示光强与距离之间的关系,进而 分析光学现象。
描写声音强度与距离的关系
续的学习打下坚实的基础。
提高练习题
总结词:深化理解
详细描写:提高练习题是在学生掌握正比例函数的基本概念后,进一步深化对正 比例函数的理解。这些练习题将涉及更复杂的函数情势、参数变化对函数图像的 影响等内容,有助于培养学生的思维能力和解决问题的能力。
正比例函数(共8张PPT)

在同一直角坐标平面内,分别画出下列函数的图像:
从上面的操作,画函数图像的步骤可以归纳为几个方面呢?
这条直线是函数y=2x的图像,也把它表示为“直线y=2x”.
2
根据正比例函数的图像特点,完成填空.
我们把正比例函数y=kx的图像叫做直线y=kx.
这条直线是函数y=2x的图像,也把它表示为“直线y=2x”.
函数y=-2x的图像与y=-2x的图像有哪些相同的特点?
我们把正比例函数y=kx的图像叫做直线y-4=kx.
-2
O
2
4x
我们把正比例函数y=kx的图像叫做直线y=kx.
-2
-4
第5页,共8页。
函数y=-2x的图像与y=-2x的图像有哪些相同的特点?
y
y=2x
4
y=-2x
y 4
对于一个函数y=f(x),如果一个图形(包括直线、曲线或其他图形)上任意一点的坐标都满足函数关系式y=f(x),同时以这个函数解析式所确
这条直线是函数y=2x的图像,也把它表示为“直线y=2x”.
这条直线是函数y=2x的图像,也把它表示为“直线y=2x”.
按照画函数y=2x的图像操作的步骤,画函数y=-2x的图像.
第7页,共8页。
你有什么收获?
第8页,共8页。
-4
-2
O
2
4x
按照画函数y=2x的图像操作的步骤,画函数y=-2x的图像.
函数y=-2x的图像与y=-2x的图像有哪些相同的特点?
从上面的操作,画函数图像的步骤-2可以归纳为几个方面呢?
-2
在同一直角坐标平面内,分别画出下列函数的图像:
我们把正比例函数y=kx的图像叫做直线y=kx.
我们把正比例函数y=kx的图像叫做直线y=kx.
正比例函数图像(共16张PPT)

〕
A.m=1
B.m>1
C.m<1
D.m≥1
3. 假设正比例函数图像又y=(3k-6)x的图像经过 点A〔x1,x2〕和B〔y1,y2〕,当x1<x2时 , y1>y2,那么k的取值范围B是 〔 〕 A.k>2 B.k<2 C.k=2 D.无法确定
4.正比例函数y=(3m-1)x的图像经过点A〔 x1,x2〕和B〔y1,y2〕,且该图像经过第二 、四象限.
思考
如图,三个正比例函数的图像分别对 应的解析式是 ①y=ax② y=bx ③ y=cx,那么a、b、c的大小关系是(
)
y= kx (k>0)
不同点:函数y=2x的图象经过第
象限,从左向右
,函数y=-2x的图象经过第
象
A.a>b>c ( 2 ) 正比例函数y=-2x的图象上的点(x,y)都满足
函数y=-7x的图象在第
5x,y=x,y=5x的图象,然后比较哪一个与x轴正方向所成的锐角最大,由此你得到什么猜测?再选几个图象验证你的猜测.
第十一章 一次函数
①
自学画图步骤,并在同一个直角坐标系上画出y=2x和y=-2x的图像并比较两个函数图像的相同点与不同点
自学画图步骤,并在同一个直角坐标系上画出y=2x和y=-2x的图像并比较两个函数图像的相同点与不同点
x增大时,y的值反而减小。 y随x的增大而减小
y y = 2x
y = 2x
3
y
4
4
2
2
0 12 x
-6 -3 0
x
画板演示
自学检测:
1.函数y=-7x的图象在第 二、四 象限内,经
过点(0,
0 )与点(1, -7 ),y随x的增大而
《正比例函数的性质》课件

提高练习题
总结词:深化理解
详细描述:设计一些涉及正比例函数图像变换、实际应用和复杂计算的题目,以 帮助学生更深入地理解正比例函数的性质和应用。
综合练习题
总结词:综合运用
详细描述:设计一些涉及多个知识点和解题技巧的题目,要求学生综合运用正比例函数的性质解决复杂问题,提高解题能力 和思维灵活性。
05
函数图像
当$k > 0$时,图像 为经过原点的一条直 线,且随着$x$的增 大而增大;
图像是一条经过原点 的直线,其斜率为 $k$。
当$k < 0$时,图像 为经过原点的一条直 线,且随着$x$的增 大而减小;
02
正比例函数的性质
函数值随着x的增大而增大或减小
总结词
正比例函数的单调性
详细描述
正比例函数是一种线性函数,其函数值y随着自变量x的增大而增大或减小,取 决于函数的斜率。如果斜率为正,则函数值随着x的增大而增大;如果斜率为负 ,则函数值随着x的增大而减小。
难点解析
如何判断正比例函数的单调性
通过观察正比例函数的图像,我们可以判断函数的单调性。当k>0时,函数在定义域内 单调递增;当k<0时,函数在定义域内单调递减。
如何应用正比例函数的性质解决实际问题
正比例函数的性质可以应用于解决一些实际问题,如速度、加速度、斜率等问题。通过 建立数学模型,我们可以利用正比例函数的性质解决这些问题。
03
正比例函数的应用
在物理中的应用
Hale Waihona Puke 010203
自由落体运动
正比例函数可以用来描述 物体在重力作用下的位移 与时间的关系,其中加速 度为常数。
弹簧振荡
在简谐运动中,位移与时 间的关系也可以用正比例 函数表示。
正比例函数的图像及性质共29页文档

33、如果惧怕前面跌宕的山岩,生命 就永远 只能是 死水一 潭。 34、当你眼泪忍不住要流出来的时候 ,睁大 眼睛, 千万别 眨眼!你会看到 世界由 清晰变 模糊的 全过程 ,心会 在你泪 水落下 的那一 刻变得 清澈明 晰。盐 。注定 要融化 的,也 许是用 眼泪的 方式。
35、不要以为自己成功一次就可以了 ,也不 要以为事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
25、学习是劳动,是充满思想的劳动。——乌申斯基
谢谢!
正比例函数的图像及性质
31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
35、不要以为自己成功一次就可以了 ,也不 要以为事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
25、学习是劳动,是充满思想的劳动。——乌申斯基
谢谢!
正比例函数的图像及性质
31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
正比例函数的图象和性质
1、若点A( 7,y1 ),点B ( 5,y2 ) 、若点 , , , 在双曲线 y=2x -1上,则y1 与 y2的 则 大小关系是( 大小关系是( y1 < y2 )
(1)若A( -7,y1 ),点B ( -5,y2 ) 呢?y1 > y2 ) , , , (2)若A( 7,y1 ),点B ( -5,y2 )呢? y1> y2 ) , , , 呢 (3)若A( -7,y1 ),点B ( 5,y2 )呢? y1< y2 ) , , , 呢
K、象限、增减性 、象限、
由一知二
反比例函数的复习
正比例函数与反比例函数的对比
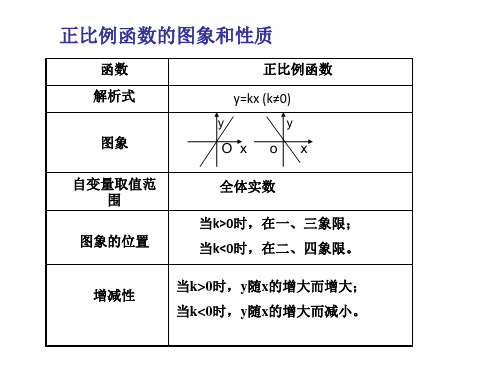
函数 解析式 正比例函数 y=kx(k≠0)
y y
反比例函数
y = k x
y
(k≠0)
y
图象
O x 自变量取值 范围
o
x
0
x
0
x
全体实数
x≠0的一切实数
图象的位置 性质
当k>0时,在一、三象限; 当k>0时,在一、三象限; 当k<0时,在二、四象限。 当k<0时,在二、四象限 当k>0时,y随x的增大 而增大; 当k<0时,y随x的增大 而减小。 当k>0时,y随x的增大而 减小; 当k<0时,y随x的增大而 增大。
(1) y=3x (3) y =5 2x (2) y =
3 x (4) y =3x-1
(5) y =4x −1 (6) y = 3 (8)-3xy=1
练习2:
是反比例函数, 已知 y = kx k +1 是反比例函数,则k=(
-2 )
例题: 例题:
已知y是 的反比例函数 且当x=2时,y=9, 的反比例函数, 例1.已知 是x的反比例函数,且当 已知 时 , 之间的比例系数, (1)求y与x之间的比例系数,并写出 与x之间的函 ) 与 之间的比例系数 并写出y与 之间的函 数解析式。 数解析式。 1 x = 3 时,y的值是多少? 的值是多少? (2 )当 2 (3)当 y = 5 时,x的值是多少? 的值是多少?
人教版数学八年级下册《正比例函数的图象和性质》PPT课件

中的值为坐标的点.将这些点连接起来,得到一条经
过原点和第三、第一象限的直线.它就是函数y=2x
的图象.
(来自《教材》)
用同样的方法,可以得到
函数y=
1 3
x 的图象(如图).
它也是一条经过原点和第
三、第一象限的直线.
(2)函数y=-1.5x中自变量x
可为任意实数.下表是y与x的几组 对应值.
知1-讲
(来自《典中点》)
知2-练
3 将2×2的正方形网格如图放置在平面直角坐标系
中,每个小正方形的顶点称为格点,每个小正方
形的边长都是1,正方形ABCD的顶点都在格点上.
若直线y=kx(k≠0)与正方形ABCD有公共点,则k
的取值范围是( C )
A.k≤2 1
C. ≤k≤2 2
B.k≥ 1 12
D. <k<2 2
x
第二、四象限
知2-讲
正比例函数y kx(k 0)的性质:
(1) 当k>0时,正比例函数的图像经过第一、三象限, 自变量x逐渐增大时,y的值也随着逐渐增大.
(2) 当k<0时,正比例函数的图像经过第二、四象限, 自变量x逐渐增大时,y的值则随着逐渐减小.
y 3x yx
y 1x 3
当 |k| 越大时, 图像越靠近y轴
y
知2-讲
y 3x
yx
1
01
y 1x 3
x
当 |k| 相等时, 图像关于坐标
轴对称
知2-讲
例3 〈珠海〉已知函数y=3x的图象经过点A(-1,y1),点 B(-2,y2),则y1__>____y2(填“>”“<”或“=”).
导引:方法一:把点A、点B的坐标分别代入函数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A. m< 1 2
B. m> 1 2
C. m<2
D. m 0
巩固训练4 探究
• (和1y)=在 同1一x直的角图坐像标,系请中你,用画量出角正器比度例量函一数下y这=两2条x直 线的交角,2你会发现什么现象?
• (2)在另一个坐标系中,画出正比例函数y=3x和 y= 1 x的图像,你发现同样存在(1)中的现象 吗? 3
y=2x
3
2
1
-4 -3 -2 -10 -1 -2
1234
-3
第三步:把这些点依次连接起-4来,得到y=2x的图象.
函数的图象的概念:
把一个函数的自变量x与对应的因变量y的值 分别作为点的横坐标和纵坐标,在直角坐标系 内描出它的对应点,所有这些点组成的图形叫 做该函数的图象.
分组活动:
作函数y=-2x,y=
14.2正比例函数的图像及 性质
上网的费用为2元/小时, 则上网x小时,费用y是多少元?
y=2x
它是什么函数?
例:画出正比例函数y=2x 的图像
解:第一步:列表
x … -2 -1 0 1 y … -4 -2 0 2
2… 4…
第二步:描点(以表中各组对应值作为点的坐标,在直角坐标中
描出相应的点)
4
限,从左向右上升,即y随x的增大而___减;小
巩固训练1
• 1正比例函数y=-4x必定经过第_二 和
•
第_四 象限,且y随x的增大而_减_小_.
• 2当m_<_2 _ 时,正比例函数 • y=(2m-4)x中y随x的增大而增大.
• 3图像经过点(1,2)的正比例函数的 • 表达式为_y_=_2x
Hale Waihona Puke 巩固训练2(2)y= 3x
观察你所画的正比例函数的图像, 并归纳正比例函数图像的性质:
• 1、正比例函数的图像是一条经过_原__点__和 (1_,__k__)点的直线;称为直线y=kx
• 2、当k>0时,直线y=kx经过第_一_、_三__象 限,从左向右上升,即y随x的增大而__增_;大
•
当k<0时,直线y=kx经过第_二_、_四__象
• (3)对于直线y=k1xy=k2x,请你大胆猜想k 1k2满足什么关系时,这两条直线存在(1)种的现象?
回顾: 正比例函数图像的性质
如图:三个正比例函数的图像分别对应
的解析式是①y=ax②y=bx③y
=cx,则a、b、c的大小关系是
(C) Aa>b>c
Bc>b>a
Cb>a>c
Db>c>a
Y
③
②
①
O
X
巩固训练3 已知正比例函数y=(2m-1)x的图像 上的两点A(x1,y1),B(x2,y2),当x1<x2 时y1 >y2,那么m的取值范围是( )A
1
x和y=-
1
x
的图象.
2
2
1、问:所有的正比例函数y=kx,(k≠0)的图象是什
么形状的?
正比例函数y=kx 的图象是一条经过原点直线.
2、问:画正比例函数的图像时,怎样画最简单?为 什么?
正比例函数y=kx 的图象经过原点和(1,k).
练习:用你认为的最简单的方法 画出下列函数的图像。
(1)y= 3 x 2
B. m> 1 2
C. m<2
D. m 0
巩固训练4 探究
• (和1y)=在 同1一x直的角图坐像标,系请中你,用画量出角正器比度例量函一数下y这=两2条x直 线的交角,2你会发现什么现象?
• (2)在另一个坐标系中,画出正比例函数y=3x和 y= 1 x的图像,你发现同样存在(1)中的现象 吗? 3
y=2x
3
2
1
-4 -3 -2 -10 -1 -2
1234
-3
第三步:把这些点依次连接起-4来,得到y=2x的图象.
函数的图象的概念:
把一个函数的自变量x与对应的因变量y的值 分别作为点的横坐标和纵坐标,在直角坐标系 内描出它的对应点,所有这些点组成的图形叫 做该函数的图象.
分组活动:
作函数y=-2x,y=
14.2正比例函数的图像及 性质
上网的费用为2元/小时, 则上网x小时,费用y是多少元?
y=2x
它是什么函数?
例:画出正比例函数y=2x 的图像
解:第一步:列表
x … -2 -1 0 1 y … -4 -2 0 2
2… 4…
第二步:描点(以表中各组对应值作为点的坐标,在直角坐标中
描出相应的点)
4
限,从左向右上升,即y随x的增大而___减;小
巩固训练1
• 1正比例函数y=-4x必定经过第_二 和
•
第_四 象限,且y随x的增大而_减_小_.
• 2当m_<_2 _ 时,正比例函数 • y=(2m-4)x中y随x的增大而增大.
• 3图像经过点(1,2)的正比例函数的 • 表达式为_y_=_2x
Hale Waihona Puke 巩固训练2(2)y= 3x
观察你所画的正比例函数的图像, 并归纳正比例函数图像的性质:
• 1、正比例函数的图像是一条经过_原__点__和 (1_,__k__)点的直线;称为直线y=kx
• 2、当k>0时,直线y=kx经过第_一_、_三__象 限,从左向右上升,即y随x的增大而__增_;大
•
当k<0时,直线y=kx经过第_二_、_四__象
• (3)对于直线y=k1xy=k2x,请你大胆猜想k 1k2满足什么关系时,这两条直线存在(1)种的现象?
回顾: 正比例函数图像的性质
如图:三个正比例函数的图像分别对应
的解析式是①y=ax②y=bx③y
=cx,则a、b、c的大小关系是
(C) Aa>b>c
Bc>b>a
Cb>a>c
Db>c>a
Y
③
②
①
O
X
巩固训练3 已知正比例函数y=(2m-1)x的图像 上的两点A(x1,y1),B(x2,y2),当x1<x2 时y1 >y2,那么m的取值范围是( )A
1
x和y=-
1
x
的图象.
2
2
1、问:所有的正比例函数y=kx,(k≠0)的图象是什
么形状的?
正比例函数y=kx 的图象是一条经过原点直线.
2、问:画正比例函数的图像时,怎样画最简单?为 什么?
正比例函数y=kx 的图象经过原点和(1,k).
练习:用你认为的最简单的方法 画出下列函数的图像。
(1)y= 3 x 2
