结构力学(拱结构)
结构力学名词解释整理

1. 框剪结构中剪力墙布置的三个原则:(1)沿结构单元的两个方向设置剪力墙,尽量做到分散、均匀、对称,使结构的质量中心和刚度中心尽量重合,防止在水平荷载的作用下,结构发生扭转。
(2)在楼盖水平刚度急剧变化处,以及楼盖较大洞口的两侧,应设置剪力墙。
(3)在同一方向各片剪力墙的抗侧刚度不应大小悬殊,以免水平地震作用过分集中到某一片剪力墙上。
2. 解决拱结构拱脚推力的三种方法:(1)推力由拉杆承受(2)推力由侧面框架结构承受(3)推力由基础直接承受3. 变形体与刚体:(1)变形体固体在外力作用下会发生变形,包括物体尺寸的改变和形状的改变,这些固体称之为变形体。
(2)刚体刚体是一种理想化的力学模型,理论力学认为刚体是这样的物体,在力的作用下,其内部任意二点之间的距离始终保持不变。
4. 索膜结构的四种主要形式:1).双曲面单元结构2).类锥形单元结构.3).索弯顶结构4).桅杆斜拉结构5. 先张法与后张法:(1)先张法张拉预应力钢筋在浇筑混凝土之前进行的方法叫先张法。
(2)后张法张拉预应力钢筋在浇筑混凝土之后,待混凝土达到一定的强度后再进行的方法叫后张法。
6. 端承桩与摩擦桩:(1)端承桩:是指桩顶竖向荷载由桩侧阻力和桩端阻力共同承受,但桩端阻力分担荷载较多的桩。
(2)摩擦桩:是指桩顶竖向荷载由桩侧阻力和桩端阻力共同承受,但桩侧阻力分担荷载较多的桩。
7. 钢骨混凝土结构的优点:(1)钢筋混凝土与型钢共同受力(2)与全钢结构相比,可节约钢材1/3左右:(3)型钢外包的钢筋混凝土不仅可以取代防腐,防火材料,而且更耐久,可节省经常性维护费用。
(4)可用于钢结构和钢筋混凝土结构各种结构体系中。
8.筒体结构类型5种:实腹筒、框筒、桁架筒、筒中筒、筒束9. 钢筋与混凝土之间的粘结力由哪四部分组成?1、化学胶结力:钢筋和混凝土接触面上的化学吸附作用力。
2、磨擦力:混凝土收缩后将钢筋紧紧地握裹住而产生的力。
3、机械咬合力:钢筋表面凹凸不平与混凝土产生的机械咬全作用而产生的力。
结构力学第4章 三铰拱

重复上述步骤,可求出各等分截面的内力,作出内力图。
§4-3 三铰拱的合理轴线
一、合理拱轴线的概念 在给定荷载作用下使拱内各截面处弯矩与剪力 都等于零,只有轴力时的拱轴线。 只适合于三铰平拱受 二、合理拱轴线的确定 竖向荷载作用
由上述的内力计算公式发现:
① 三铰拱的内力不但与荷载及三个铰的位置有关, 而且与拱轴线的形状有关。 ② 由于推力的存在,拱的弯矩比简支代梁的弯矩要小 ③ 三铰拱在竖向荷载作用下存在轴向受压。
注意: 1)该组公式仅适合平拱, 且承受竖向荷载;
2) 拱轴切线倾角k在拱的左半跨取正,右半跨取负;
三、内力图 (1)画三铰拱内力图的方法:水平基线描点法。
拱的合理轴线。设填土的容重为γ ,拱所受的竖向分布荷载为q = qC+γy。
解:将式 y M /H 对x微分两次,得
0
qC
x
d 2 y 1 d 2M0 dx 2 H dx 2
qC+γy A
C
f
q(x)为沿水平线单位长度的荷载值,则 l/2 l/2 d 2 y q(x) d 2M0 2 q(x) 2 dx dx H y 将q=qC+γy代入上式,得: 常数A和B可由边界条件确定: q qC d2y γ x 0, y 0 : A C y γ 2 dx H H dy 该微分方程的解可用双曲函数表示: q γ γ y Ach x Bsh x C H H γ
VAl P b1 P2b2 0 1
P b1 P2b2 VA 1 l Pi bi 0 VA l
结构力学第三章静定结构组合结构及拱

3.35 8.94 12.29kN (压)
二、三较拱的压力线
如果三铰拱某截面D以左(或以右)所有外力的 合力FRD已经确定,则该截面的弯矩、剪力、轴 力可按下式计算:
15kN K右
Fº =-2.5kN QK右
0 0 (FH 10kN , FQK左 12.5kN , FQK右 2.5kN )
(sin 0.447, cos 0.894)
0 FQK 左 FQK 左 cos FH sin 12.5 0.894 10 0.447
67.5kN
50
A F C G E
B
30
D
M图
kN.m
求AC杆和BC杆剪力
F
FQAC
y
0, FQAC 7.5kN
22.5kN 7.5 32.5 10kN/m FNAD
FAy
+ _
15
+
7.15 67.5kN 35 FQ图 kN
作业
3-20
§3-6 三铰拱受力分析
拱 (arch)
FN DE 135kN ,
FNDF FN EG =-67.5kN
FAy
D
FCx 135kN , FCy 15kN
FNDA
FNDF
D
FN DA FN EB= kN 151
FNDE
2m
F
50kN.m
求AC杆和BC杆弯矩
22.5kN 5kN.m
20kN.m 10kN/m
30kN.m
MD FRD
李廉锟《结构力学》笔记和课后习题(含考研真题)详解-第4章 静定拱【圣才出品】

第4章 静定拱4.1 复习笔记【知识框架】【重点难点归纳】一、拱的基本概念及特点 ★★表4-1-1 拱的基本概念及特点表4-1-2 有拉杆和无拉杆三铰拱的区别与联系二、三铰拱的计算 ★★★★★1.支座反力的计算(见表4-1-3)表4-1-3 支座反力的计算2.内力的计算(见表4-1-4)表4-1-4 三铰拱的内力计算三、三铰拱的合理拱轴线(见表4-1-5) ★★★表4-1-5 三铰拱的合理拱轴线4.2 课后习题详解复习思考题1.拱的受力情况和内力计算与梁和刚架有何异同?答:(1)拱与梁的受力情况和内力计算的区别①约束反力方面,拱在竖向荷载作用下会产生水平反力(推力),而梁在竖向荷载作用下不会产生水平反力(推力);②内力分布方面,由于水平推力的存在,拱的弯矩常比跨度、荷载相同的梁的弯矩小得多,使得拱截面上的应力分布较为均匀;③内力分析方法方面,若只有竖向荷载时,梁只需进行简单的整体分析即可求解,而拱由于水平力的存在,需要整体分析与局部分析相结合。
(2)拱与刚架的受力情况和内力计算的异同①内力分析方法方面,拱与刚架的受力情况和内力计算的特点和所应用方法基本一致,例如三铰刚架也属于拱式结构;②拱的轴线是曲线,刚架杆的轴线是直线,在应用平衡条件计算内力时,拱仍然取投2.在非竖向荷载作用下怎样计算三铰拱的反力和内力?能否使用式(4-1)和(4-2)?答:(1)对于三铰拱承受非竖向荷载的情况,可将非竖向荷载分解为水平荷载和竖向荷载。
(2)仍然可以应用式(4-1)和(4-2),将水平反力加上非竖向荷载水平方向上的分量一起代入公式中进行求解。
(4-1)o AV AV o BV BV o c H F F F F M F f ⎫⎪=⎪⎪=⎬⎪⎪=⎪⎭cos sin (4-2)sin cos o H o S S H o N S H M M F y F F F F F F ϕϕϕϕ⎫=-⎪⎪=-⎬⎪=+⎪⎭3.什么是合理拱轴线?试绘出图4-2-1各荷载作用下三铰拱的合理拱轴线形状。
结构力学—拱结构(建筑力学)

拱结构应用——大跨度体育馆
拱结构应用——农业大棚
拱结构应用——农业大棚
筒拱
砌体结构的赵州桥如果改用水平砌体的梁,是否可行?
水平的梁为纯弯曲变形,在弯矩产生的拉应力作用下砌 体会断裂,因此赵州桥无法用砌体建造水平梁
古代拱结构的应用——砌体屋顶
欧洲教堂的石砌拱形屋顶同样利用了拱结构时石材受压 而不是受拉
拱结构应用——大跨度桥梁
拱结构应用——砌体桥梁
拱结构应用——大跨度体育馆
拱截面有弯矩、剪力、轴力三个内力,
实际是弯曲变形与轴压变形的组合变形
轴向压缩产生的压应力可以抵消或者减小弯矩产生的 拉应力,使得整个横截面处于压缩状态或者仅有很 小的拉应力
拱抵抗水平力的方式
拱的矢高对水平推力的影响
拱矢高越大,拱结构的水平推力越小
拱结构特点:
1) 由于推力的存在,三铰拱截面弯矩比简支梁弯矩小。
1、拱结构
悬索 拱
拱的受力机制
竖向支座反力在 截面上产生的弯矩
外力P
外力P在截面上 产生的弯矩MP
水平支座反力H在截面上 产生的弯矩MH
水平支座反力H
竖向支座反力
拱与梁最大的差别是拱的支座反力有水平力,任意截面的弯 矩由竖向支座反力产生的弯矩、外荷载产生的弯矩、水平 支座反力产生的弯矩,水平支座反力产生的弯矩可以抵消 前两者产生的弯矩使得拱结构没有弯矩或者使得前两者产 生的弯矩减小
5) 三铰拱受向内的推力,因此需给基础施加向外的推力。 所以三铰拱的基础要比基础大,或加拉杆,以减小对 墙的推力。
古代拱结构的应用——砌体桥梁
赵州桥
砌体结构由砖石等块材用砂是抗拉能力差,拱结构为弯曲变形和轴 压变形的组合变形,轴向压应力会抵消弯曲产生的拉应力 或者减小拉应力,使得砌体处于完全受压状态或者有拉应 力也很小,因此拱结构可以建造大跨度桥梁
(结构力学)拱

y M0
称为与该荷载对应的合 理拱轴
FH
在竖向荷载作用下,三
铰拱的合理拱轴线的纵
只限于三铰平拱受 坐标与相应简支梁弯矩 竖向荷载作用 图的竖标成正比。
试求图示对称三铰拱在均布荷载作用下 的合理拱轴线
MC0=ql2/8 FH=ql2/8f M0=qlx/2-qx2 /2 =qx(l-x)/2 y=4fx(l-x)/l2
FP2 B
三请铰大拱家的反想力:只 与由荷上载述及公三式个可铰 的得位哪置些有结关论,?与
拱轴线形状无关
荷载与跨度一定
a1
FAy0
b1 a2
时,水平推力与 b2 FBy0 矢高成反比
y FP1 K C
A
x
y
f
FAH FAy
l1 l
FP2
B FBH x l2
FBy
等代梁 FP1 A
K
C
FP2 B
a1
抛物线
试求三铰拱在垂直于拱轴线的均 布荷载作用下的合理拱轴线。
FN +dFN
园
FN
R
dM ds
=FQ-m
0=0
dFN ds
=dd-FsqNt+=0FRQ
dFQ ds
=qn-
FN R
R=常数
返 章
FAy0
b1 a2
b2 FBy0
MM0FHy
F QFQ 0cosF Hsin
FNF0QsinFHcos
请大家对上述 公式进行分析
三铰拱的内力不但与荷载 及三个铰的位置有关,而且与 拱轴线的形状有关。
由于推力的存在,拱的弯矩 比相应简支梁的弯矩要小。
三铰拱在竖向荷载作用下 轴向受压。
结构力学 三铰拱

4 4 yk 2 4(16 4) 3m 求MK 16 MK 0 MK 12.5 4 10 3 20kN.m(下拉)
求MJ
yJ 3m
M
J
0
M J 7.5 4 10 3 30 30 0
3. 求FQ、FN的计算公式
拱轴任意截面D切线与水平线夹角为φ。 相应代梁中, F 设为正方向。
FP1=15kN K FHA A yk 4m
l/2
C f=4m
MC 0
FVA
4m
l l FVA FHA f FP1 0 2 4 0 MC 1 l l FHA ( FVA FP1 ) () f 2 4 f
0 上式中,M C 为代梁C截面弯矩。
M FHB () f
0 ND右 QD右 sin D H cosD 12 0.555 10.5 0.832 15.4kN
重复上述步骤,可求出各等分截面的内力,作出内力图。
三、三较拱的合理轴线
在给定荷载作用下,三铰拱任一截面弯 矩为零的轴线就线为合理拱轴。 三铰拱任一截面弯矩为 M M FH y
超静定拱
拉杆拱 静定拱
拱顶
C
拱轴线 拱高 f
B
拱趾
A
起拱线 跨度 l
f l
f
高跨比
l 通常 f l 在1-1/10之间变化,f 的值对内力有 很大影响。
工程实例
拱桥 (无铰拱)
超静定拱
世界上最古老的铸铁拱桥(英国科尔布鲁克代尔桥)
万县长江大桥:世界上跨度最大的混凝土拱桥
二、三铰拱的计算
A 12.5kN K左 Fº =12.5kN QK左 A 12.5kN
结构力学 第三章 三铰拱

B
②剪力、轴力计算公式
FQFQ 0co-sFHsin
F0yA φ FP1
M0
F0yB
FNFQ 0sin-FHcos
KM
FN
F
0 Q
—相应简支梁对应截面上的剪力
φ φ—截面处拱轴切线倾角,在左半拱
FH A
y φ FQ
为正(右半拱为负)
φ
x
FVA φ
◆ 拱截面轴力较大,且一般为压力
例3-5 作图示三铰拱的内力图,拱轴为抛物线,其方程为
1kN/m C
f=4m x
FQ0L 1kN
FV A l1=8m
4m
l=16m
4kN
D
B FH B
4m
FV B
FQ0R 5kN
1kN/m
A
C
4kN B
F0yA
F0yB
F QLF Q 0L co-sFHsin 1 0 .89 6 ( 4 0 .44 ) 4 1 .7 7k 8 2 N
F Q RF Q 0c R o -sF Hsin 5 0 .8 9 6 ( 0 4 .44 ) 4 1 7 .7k 2 8N 9
四 三铰拱的合理拱轴线(reasonable axis of arch) 1 合理拱轴线的概念 在给定荷载作用下,使拱处于无弯矩状态的拱轴线,称 为拱的合理拱轴线
2 合理拱轴线的确定 根据荷载作用下,任一截面弯矩为零条件确定。如竖向 荷载作用下的三铰拱:
MM0FHy0 y M0
FH
通过由调此整可拱见的,轴当线拱,上使荷拱载在为确已定知荷时载,作只用要下求各出截相面应上简的支弯梁 矩值的为弯零矩,方这程时,拱除截以面支上座只水有平通推过力截FH面,形即心可的求轴得向合压理力拱作轴 用,的其轴压线应方力程沿截面均匀分布,此时的材料使用最为经济
结构力学第5章静定拱的内力计算

A
FA
图5-3-2(a)
同理,截取隔离体如图5-3-2(b)
FP G FN2 e2 2` D2 FQ2 A
F2
FA
图5-3-2(b)
容易看出:
图5-3-2两隔离体上截面1、2上 合力F1、F2与各自的三个内力分量 的等效关系。
AG和GB(注意GB过C铰)直线分别 是拱AD和DB段上合内力的作用线,又 叫压力线。
例5-3-1试设计一个三铰拱的轴线。
其拱上作用荷载与拱的三个铰相对位 置已定,如图(a)示
(a)
2 m 2 m 4 m
2m
2m
解
1)求支座反力
因拱的两个底铰不在一条直线上,须 先建立关于同一个铰的两个约束力的 平衡方程,联立求解,即:
先考虑支座B的约束力。以A点为 矩心,建立拱整体的力矩平衡方 程:
(a)
解 1)求支座反力
竖向反力
0 1 R FBy [q R FP ( R R cos )] 11.33kN () 2R 2
A
M
M
FAy
B
0
1 R [q R FP ( R R cos )] 1.33kN () 2R 2
结构力学
结构力学教研室
青岛理工大学工管系
第五章 静定拱的内力分析
§5.1
概 述
什么叫拱?
一般指杆的轴线为曲线形状,并且 在竖向荷载作用下会产生水平支座 反力的结构。
静定拱分类:
三铰拱 带拉杆三铰拱
静定拱的各部名称见图5-1-1。
拱 轴
( 底 铰 )
f(拱 高)
(a)三铰拱
(b)带拉杆三铰拱
结构力学之拱结构

B
=0
A
H 6m FVA 6m
B
H FVB
FVA × 12 2 × 6 × 9 8 × 3 = 0 FVA = 11kN
∑M
A
=0
A
C
B
FVB × 12 2 × 6 × 3 8 × 9 = 0 FVA = 9kN
M C = 11× 6 2 × 6 × 3 = 30
FHA = FHB
MC = = 7.5kN f
FQ 2 = FQ02 cos 2 H sin 2 = (11 2 × 3)× 0.832 7.5 × 0.555 ≈ 0.003kN
FN 2 = FQ02 sin 2 H cos 2 = (11 2 × 3)× 0.555 7.5 × 0.832 = 9.015kN
11
(3)绘制内力图
0 Q 0 = YA P K 1
Qk = Qk0 cos H sin
0 8 N K = QK sin H cos
三铰拱的受力特点 三铰拱的受力特点 由于推力的存在,拱的弯矩比相应简支梁的弯矩要小. 由于推力的存在,拱的弯矩比相应简支梁的弯矩要小. 三铰拱在竖向荷载作用下轴向受压. 三铰拱在竖向荷载作用下轴向受压. 三铰拱的内力不但与荷载及三个铰的位置有关, 三铰拱的内力不但与荷载及三个铰的位置有关,而且与 拱轴线的形状有关. 拱轴线的形状有关.
M ( x) =
q x(l x ) 2
拱的推力为:
拱的合理轴线方程为:
MC ql 2 H= = f 8f q 8f 4f y( x ) = x( l x ) × 2 = 2 x( l x ) 2 ql l
15
�
0
y
13.300 10.958 9.015 7.749 7.500 7.433 6.796 11.235 11.665 11.700 1.421 3.325 3.331 1.060 0.600 0.472 1.000 0.003 0.354
3静定结构的受力分析-三铰拱结构力学

1 结构力学多媒体课件一、拱式结构的特征 1、拱与曲梁的区别拱式结构:指的是杆轴线是曲线,且在竖向荷载作用下会产生水平反力(推力)的结构。
FABH A =0 FABH A =0 三铰拱F PF P曲梁H≠0H≠0是否产生水平推力,是拱与梁的基本区别。
拱结构的应用:主要用于屋架结构、桥梁结构。
拱结构的应用:主要用于屋架结构、桥梁结构。
拱桥 (无铰拱)超静定拱 世界上最古老的铸铁拱桥(英国科尔布鲁克代尔桥) 万县长江大桥:世界上跨度最大的混凝土拱桥 灞陵桥是一座古典纯木结构伸臂曲拱型廊桥, 号称“渭水长虹”、“渭水第一桥” 主跨:40 米 建成时间:三峡工程对外交通专用公路下牢溪大桥(上承式钢管混凝土拱桥,主跨:160米 ,建成时间:1997)2、拱的类型三铰拱两铰拱无铰拱拉杆拱静 定 拱超 静 定 拱3、拱的优缺点a、在拱结构中,由于水平推力的存在,其各截面的弯矩要比相应简支梁或曲梁小得多,因此它的截面就可做得小一些,能节省材料、减小自重、加大跨度b、在拱结构中,主要内力是轴压力,因此可以用抗拉性能比较差而抗压性能比较好的材料来做。
c、由于拱结构会对下部支撑结构产生水平的推力,因此它需要更坚固的基础或下部结构。
同时它的外形比较复杂,导致施工比较困难,模板费用也比较大4、拱的各部分名称lf 高跨比 BACf拱顶拱轴线拱高 f拱趾 起拱线跨度 l 平拱斜拱二、三铰拱的计算 1、支座反力的计算L 2L 1Lb 2a 2b 3a 3b 1a 1k y kx kCBAfF P1F P2F P3kCBAF P1F P2F P3B M =∑0Pi iYA YAFbF FL ==∑0A M =∑0Pi iYB YBF a F FL==∑取左半跨为隔离体:CM=∑()()01111212YA P P CH F L F L a F L a M F ff⨯----==F HF H1、支座反力的计算L 2L 1Lb 2a 2b 3a 3b 1a 1k y kx kCBA fF P1F P2F P3kCBAF P1F P2F P3在竖向荷载作用下,三铰拱的支座反力有如下特点: 1)支座反力与拱轴线形状无关,而与三个铰的位置有关。
拱式结构体系

拱式结构体系-标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII拱式结构体系在本小节中我们要给大家介绍拱式结构体系的组成、优缺点及适用范围;拱式结构体系的合理布置原则及及受力特点。
在房屋建筑和桥梁工程中,拱是一种十分古老而现代仍在大量应用的结构型式。
它是以受轴向压力为主的结构,这对于混凝土、砖、石等材料是十分适宜的,特别是在没有钢材的年代,它可充分利用这些材料抗压强度高的特点,避免它们抗拉强度低的缺点。
而且能获得较好的经济和建筑效果。
因而很早以前,拱就得到了十分广泛的应用。
在我国,很早就成功地采用了拱式结构。
公元605~616年隋代人在河北赵县建造的单孔石拱桥一安济桥(又称赵州桥),横越交河,跨度37.37m。
它距今近1400年,虽经多次地震,而巍峨挺立,是驰名中外的工程技术与建筑艺术完美结合的杰作。
在古代的西方,建造了许多体型庞大、气魄雄伟的拱式建筑。
在建筑规模、空间组合、建筑技术与建筑艺术等方面都取得了辉煌的成就,并对欧洲与世界建筑产生巨大的影响。
古罗马最著名的穹顶(半圆拱)结构,当推公元前27~14年建造,后因焚毁并于公元120~123年重建的罗马万神庙(图1-29),其中央内殿为直径43.5m的半圆球形穹顶,穹顶净高距地面也是43.5m。
它是古罗马穹顶技术的最高代表作,也是世界建筑史上最早、最大的大跨结构。
图1-29罗马,万神庙a一剖面图; b一平面图; c一穹顶(半圆拱)结构近、现代的拱式结构应用范围很广,而且型式多种多样。
例如著名的澳大利亚悉尼歌剧院(图1-30,始建于1957年)是大家熟知的建筑,处于深入海中的半岛上。
建筑形象的基本元素一一拱壳,不但是主要的结构构件,而且是一个符号,一种象征,一个母题,它既象“白帆”、“浪花”,又象盛开的巨莲,使人产生丰富的联想。
图1-30 澳大利亚悉尼歌剧院一、拱结构的类型及其受力特点拱的类型很多,按结构组成和支承方式,拱可分为三铰拱、两铰拱、和无铰拱三种,如图1-31。
结构力学试题汇总
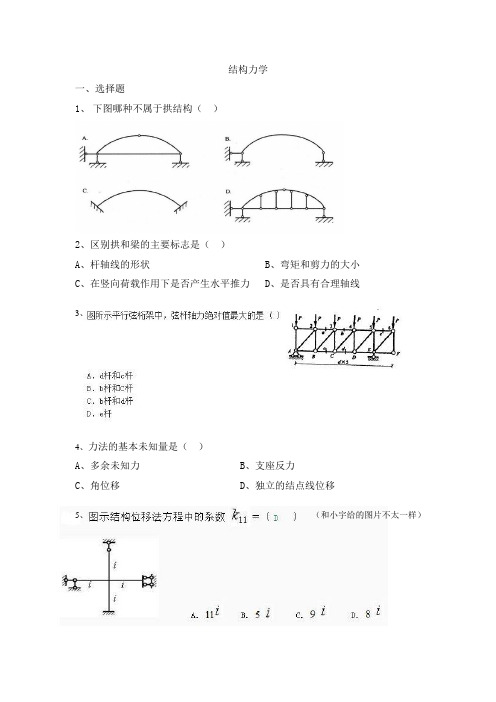
结构力学一、选择题1、下图哪种不属于拱结构()2、区别拱和梁的主要标志是()A、杆轴线的形状B、弯矩和剪力的大小C、在竖向荷载作用下是否产生水平推力D、是否具有合理轴线3、4、力法的基本未知量是()A、多余未知力B、支座反力C、角位移D、独立的结点线位移5、(和小宇给的图片不太一样)6、图示结构位移法方程中的系数r11=( )A、8iB、10iC、9iD、11i7、结构某一截面某一内力影响线将(B )改变A、随实际荷载B、不随实际荷载C、因坐标系的不同选择D、随实际荷载数值8、( C )A、L/2B、LC、0D、-L/29、等截面直杆AB的A端的转动刚度S AB:( D )。
A.仅与杆件的线刚度有关; B.仅与杆两端的支承情况有关;C.与杆件的线刚度及荷载情况有关; D.与杆件的线刚度及两端支承情况有关10、11、如下图所示,位移法典型方程中的系数K33等于()A 、12EI/L的立方B、24EI/L的立方C、48 EI/L的立方D、36 EI/L的立方12、下列说法正确的是()A、几何可变体系一定无多余联系B、静定结构一定无多余联系C、结构的制造误差不会产生内力D、有多余联系的体系是超静定结构13、影响线的基线应当与()A、梁轴线平行B、梁轴线垂直C、单位力的作用线垂直D、单位力的作用线平行14、等截面直杆的弯矩传递系数C与下列什么因素有关?()A 荷载B 线刚度C 材料的性质D 远端支承15、图示结构,i为线刚度。
AB杆的B端转动刚度(劲度)值为:()A.1B.3C.4D.716、下列那一条不是图乘法求位移的适用条件?(D )A. EI为常数B. 两个弯矩图至少有一个为直线C. 直杆D. 两个弯矩图都必须为直线(Mp 和M )17、静定结构有温度变化时(B )A:无变形,无位移,无内力B:有变形,有位移.无内力C:有变形.有位移,有内力D:无变形.有位移,无内力18、图(a)为结构在荷载作用下的弯矩图,当求C点水平位移Δch时,为使计算最简便,所选用的单位虚力状态应是( D )19、力法方程中的系数δki表示的是基本结构由( B )。
结构力学(拱与桁架)

4. 结点法计算举例
(1)首先由 桁架的整体平衡 条件求出支反力 . (2)截取各 结点解算杆件内力 .取结点G隔离体
SGE
HB=120kN
B
+60 45
75
D
0
-45
+60 40 30
50
E 20 G
15kN 4m
3m
+15
HA=120kN
A
60 C
15kN 4m
25
-120 VA=45kN
4m
YDG=SDGsinα=-(RA-P1-P2-P3)
YDG XDG RA
Ⅱ
返回
3 . 几点结论
(1) 用截面法求内力时,一般截断的 杆件一次不能多于三个(特殊情况例外). (2) 对于简单桁架,求全部杆件内力 时, 应用结点法;若只求个别杆件内力, 用截面法. 合杆件的内力求出,然后再对各简单桁架 进行分析(见图).
返回
(1)力矩法 以例说明
Ⅰ
设支反力已求出. 求CD杆的内力. 作截面Ⅰ-Ⅰ, 取左部分 为隔离体.
RA
Ⅰ
RB
由∑ME=0 得
有
RAd-P1d-P2×0-SCDh=0
SCD R Ad P1d P2 × 0 = h
(2)投影法
Ⅱ
求DG杆内力 作Ⅱ—Ⅱ截面, 取左部分为隔离体. 由∑Y=0 有 RA-P1-P2-P3+YDG=0
如图,FN—斜杆的内力 Fx—FN水平分力 Fy—FN竖向分力 l—斜杆的长度 lx—l水平投影 ly—l竖向投影
由比例关系可得
FN Fx Fy = = l lx ly
对于简单桁架,分析时与组成顺序相反 依次截取结点.
拱式结构

背景
赵州桥建于公元605年,距今1407多年,经历了10 次水灾,8次战乱和多次地震,特别是1966年3月8 日邢台发生7.6级地震,赵州桥距离震中只有40多公 里,都没有被破坏,著名桥梁专家茅以升说,先不 管桥的内部结构,仅就它能够存在1400多年就说明 了一切。1963年的水灾大水淹到桥拱的龙嘴处,据 当地的老人说,站在桥上都能感觉桥身很大的晃动。 据记载,赵州桥自建成至今共修缮9次。
伏拱的存在,一方面使赵州 桥的圆弧形的拱轴线充分接 近既经济又合理的恒载压力; 另一方面.也正是由于伏拱 的存在,既减轻了桥身自重, 又消除了拱轴线截面上的拉 应力,使赵州桥更加稳固耐 用。既美观又实用的赵州桥 深刻表现了拱桥结构的卓越 力学性能。
赵州桥是由28道各自独立的拱券沿宽度方向并列组合而成,拱厚皆为 1.03米。为加强各道拱券间的横向联系,使28道拱组成一个有机整体, 连接紧密牢固,赵州桥的建设中采取了一系列技术措施。 l)在每一拱券和少量的桥的宽度上采用了下宽上窄、略有“收分”的方 法。“收分”法使得每个拱券向里倾斜,相互挤靠,增强其横向联系, 以防止拱石向外倾倒;而且桥的宽度从桥的两端到桥顶逐渐收缩,从最 宽9.6米收缩到9米,以加强大桥的稳定性。 2)在主券上均匀沿桥宽方向设置了5个铁拉杆,穿过28道拱券,每个拉 杆的两端有半圆形杆头露在石外,以夹住28道拱券,增强其横向联系。 在4个小拱上也各有一根铁拉杆起同样作用。 3)在靠外侧的几道拱石上和两端小拱上盖有护拱石一层,以保护拱石; 在护拱石的两侧设有勾石6块,勾住主拱石使其连接牢固。 4)为了使相邻拱石紧紧贴合在一起,在两侧外券相邻拱石之间都穿有 起连接作用的“腰铁”,各道券之间的相邻石块也都在拱背穿有“腰 铁”,把拱石连锁起来。而且每块拱石的侧面都凿有细密斜纹,以增大 摩擦力,加强各券横向联系。 这些措施的采取使整个大桥连成一个紧密整体,增强了整个大桥的稳定 性和可靠性。
结构力学(拱结构)

三铰拱的内力计算
表4-1:三铰拱各截面内力计算表
内力计算时,常通过 公式、列表完成
15
合理拱轴
五、 合理拱轴的概念
1、合理拱轴的概念
定义:在给定荷载作用下,拱各截面只承受轴力, 而弯矩、剪力均为零,这样的拱轴称为合理拱轴。
?
2、合理拱轴的确定
写出任一截面的弯矩表达式,令其等于零即可确 定合理拱轴。
VA0
0 2x、 荷 载 与 跨 度 一 定 M C VAl1 P1 (l 1 a 1 ) V 0 时,水平推力与矢高 MC (4-2) 等代梁计算简图 H 成反比。 f
0 B
作为结构。
7
三铰拱的内力计算
a1
a2 b1 P1 b2 P2 f
2、弯矩计算
M K [VA x K P1 (x K a1 )] H y K
q= 1kN/m
y
4f (l x)x 2 l
P=4kN 3 4 5 C 4m
x
2
6
1
H =6kN A 0
7
B H =6kN
8
VA =7kN
8×2=16m VB =5kN
解: 1、计算支座反力
0 VA VA
1 8 12 4 4 7kN 16 1 8 4 4 12 0 VB VB 5kN 16
拱结构的组成
2、拱结构的组成
3
拱结构的种类
3、拱结构的种类 静定拱
超静定拱
三铰拱
两铰拱 超静定拱
静定拱
无铰拱
高差h
静定拱
带拉杆的三铰拱
斜拱
4
拱结构的特点
4、拱结构的特点
1、弯矩比相应等代梁小;
桁架与拱-结构力学

-8 kN
YDE CD 0.75 X DE CE 0.5
0
-33
34.8 19
-33
-33
-33
-8
-8
-5.4 -5.4
37.5
34.8 19
小结:
以结点作为平衡对象,结点承受汇交力系作用。 按与“组成顺序相反”的原则,逐次建立各结点的
平衡方程,则桁架各结点未知内力数目一定不超过 独立平衡方程数。 由结点平衡方程可求得桁架各杆内力。
Xe
3 4
10P
联合法
凡需同时应用结点法和截面法才能确 定杆件内力时,统称为联合法 (combined method)。
试求图示K式桁架指定杆1、2、3的轴力
ED杆内力如何求?
小结:
熟练掌握 计算桁架内力的基 本方法: 结点法和截面法
采取最简捷的途径计算桁架 内力
拱(arch)
一、简介
曲梁
可能的截面单杆通常有相交型 和平行型两种形式。
相
交
情 况
FP
FP
FP
FP
FP
FP
a 为 截 面 单 杆
FP FP
平行情况
b为截面单杆
用截面法灵活截取隔离体
P
P
k。
A
B
RA
RB
RB
。k
P
P
简单桁架——一般采用结点法计算;
联合桁架——一般采用截面法计算。
例1、求图示平面桁架结构中指定杆件的内力。
36
8 -75.000 -74.977
48
10 -80.000 -79.977
51
3
0.000 0.032
结构力学——三铰拱

第三部分
学习内容
三铰拱
三铰拱的组成特点及其优缺点; 三铰拱的反力和内力计算及内力图的绘制; 三铰拱的合理拱轴线。
无铰拱
拉杆拱2
斜拱
第一节 三铰拱的组成和类型
4. 三铰拱的受力特点
FP 拱的基本特点是在 竖向荷载作用下会 产生水平推力,从 而大大减小拱内弯 矩。水平推力的存 在与否是区别拱与 梁的主要标志。
曲梁
FP
拱
第二节 竖向荷载作用下三铰拱的受力分析
当两支座在同一水平线上时,称为等高拱或平拱,否 则称为斜拱。分析竖向荷载作用下三铰拱的内力和反 力时,与同跨度、同荷载的简支梁相对比,以便于计 算和对比分析拱的受力性质。 C FP1 FP2 f A B l
A
B
0 sin k FH cosk FAy P 1
Fx' 0
FS k sin k FH cos k
0
第二节 竖向荷载作用下三铰拱的受力分析
• 三铰拱的内力不但与荷载及三个铰的位置有关,而 且与拱轴线的形状有关; • 由于推力的存在,拱的弯矩比相应简支梁的弯矩要 小; • 三铰拱在竖向荷载作用下内力受压为主;
FA y
0
FS k FAy cos k P 1 cos k FH sin k F cos k FH sin k
0 Sk
0 xk a1 M k0 FAy xk P 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(VA P1)sinK HcosK
QK0 VA0 P1 VA P1
(4-5 NK QK0 sinK HcosK
三铰拱的内力计算
例4-1
杭
试作图示三铰拱的内力图。拱轴方程为
y
4f l2
(l
x)x
州
顶
q= 1kN/m
P=4kN
正
45
包
y
2 3C
6
材
1
4m
7
H =6kN A 0 VA =7kN
包
q
材
解法1:相应简支梁的弯矩方程为
y x
A
C f
M 0 1 qlx 1 qx2 1 qx(l x)
22
2
B
推力H为:
HLeabharlann M0 Cql 2
f 8f
l/2
l/2
令: M K
M
0 K
H
yK
0
q
可得三铰拱合理拱轴的轴线方程为 :
A
x
ql/2
l
17
B
y
M0 H
1 qx(l 2
ql 2
x)
4f l2
算简图 HA0 = 0 等代梁计 (4-2 7
A VA0
P1
2x、K
K
荷
C
载
与P跨2 此作度为时B一结,定H构H。MC01f
[V,Al1故 P瞬1(l1变a体1)] 系不能
VAl1 P1 (l1 a1)
时,水平推力与矢 VB0 高
成反比。
H
M
0 C
f
三铰拱的内力计算
a1
b1
杭
a2
州y 顶 正 H包A A
P1 K φK
yK f
材
xK
x
VA
P1
MK
K
NK
b2 P2
B
VB
2、弯矩计算
M K [VA xK P1(xK a1 )] H yK
M
0 K
V
0 A
x
K
P1(x K
a1
)
HB
MK
M
0 K
H
yK
3弯、剪矩力Q比K计相V算Ac应osk等 P代1cos梁k(小H4si-n3k)
QK
(VA P1)cosk Hsink
HA A
QK0
V
0 A
P1
VA
P1
VA
(4-4 HA0 = 0 A
P1 KC
P2
) xK 可用抗压性能强的工程 VA0
QK QK0 cosK HsinK
B 4、轴力计算
VB0
NK VAsinK P1sinK HcosK
材式V料 、A0 8, 列P1 Q计表K0M算完0K时成常计通 算过 。公
2
0.8
0.75
由式((44--34))3截、面注的意QM方1左1向Q半M10角1c0拱o为sH截1 负y1面H。s7的in2方112向(71角12为22)6正0.18,.756右10半..56k拱N0.m4kN
(4-5)
10
N1
N10
sin 1
H
cos1
(7
1
2)
0.6
6
0.8
7.8kN
三铰拱的内力计算 3、内力图绘制
州
顶
正
包 材
一、拱的内力计算原理仍然是截面法;
二、拱通常受压力,所以计算拱时 规定轴力以受压为正; .
三、实际计算时常将拱与相应等代梁对比 通过公式列表完成计算。 .
6
三铰拱的内力计算
四、竖向荷载作用下三铰拱计算公式的建立
杭 州
1、支座反力计算
顶 正 包 材
a1
b1
a2
b2
y
P1
φK
K
P2
1 、 三 铰C拱 的 竖 向 反
(l x)x
ql/2
8f
合理拱轴
杭 解法2:
州 顶
设三铰拱承受沿水平方向均匀分布的竖向荷载,试求其合理拱轴线。
正
q
包
材
y
C
x
f
解:研究整体
MB 0
VA
ql 2 2
A
B
研究AC
l/2
杭 州
顶 弯矩图绘制
正 包 材
11
三铰拱的内力计算
杭 弯矩图绘制
州
顶 正
等代梁弯矩图
包
材
竖向荷载作用下拱结构的受力特水平点推力引起的弯矩图
1、三铰拱与对应的等代梁相比,弯矩要小
得多,其原因是水平推力的存在所致;
12
三铰拱的内力计算
杭 州
剪力图绘制
顶
正
包
材
13
三铰拱的内力计算
轴力图绘制
杭 州 顶 正 包 材
杭
州
? 顶 1、合理拱轴的概念
正
包 材
定义:在给定荷载作用下,拱各截面只承受轴力,
而弯矩、剪力均为零,这样的拱轴称为合理拱轴。
2、合理拱轴的确定 写出任一截面的弯矩表达式,令其等于零即可确 定合理拱轴。
16
合理拱轴
杭 例 4-2 设三铰拱承受沿水平方向均匀分布的竖向荷载,试
州 顶
求其合理拱轴线。
正
y1 l 2 (l x1 )x1
N 正
包
6kN 07kN 1 Q M 材6 cos1
6 sin1
qlsin1
1
44 162
(16
2)
2
1.75m
712其 方7si、 、cnos。向法11计拱;线算轴方2原线m向理方,仍程从1然主而1是要确截用ta定1n面于13截6法确45ldd面22fyx;定,x,l上1截s22的inxm面11剪的10力46.6位,14和6置c1轴o6及s力12
竖向荷载作用下拱结构的受力特点 2、拱截面上的轴力较大,且一般为压力; 3、总体来看,拱比梁更能发挥材料的作用 ,适合较大的跨度和较重的荷载,便于利 1用4 抗压性能好而抗拉性能差的材料。
三铰拱的内力计算
杭
表4-1:三铰拱各截面内力计算表
州
顶
正
包
材
内力计算时,常通过
15
公式、列表完成
合理拱轴
五、 合理拱轴的概念
M B 0 M A 0
VA
1 l (P1b1
P2 b2
)
VB
1 l
(P1a1
P2 a 2
)
HA
A
力xK与
其yK
f
等
代
梁
的B反
力HB
(4-1 相等,水x平反力与拱
V轴A 线l1 形状无l2 关V;B
V
A
VB
VA0 VB0
) l
X 0: HA HB H
三 铰 拱 计当 f M时C ,VAl结1 构P1(为l1 瞬a1)变 H体f 系0 ,
x
8×2=16m
B H =6kN 8
VB =5kN
解: 1、计算支座反力 2、计算各截面内力
9
VA
VA0
1812 16
44
7kN
VB
VB0
18 4 16
4 12
5kN
H MC0 58 4 4 6kN
f
4
三铰拱的内力计算
2、计算各截面内力
杭 截面1 州 顶
ql qlcos1
x1 2m 4f
三铰拱
静定拱
静定拱
无铰拱
带拉杆的三铰拱
4
超静定拱
两铰拱 超静定拱 静定拱
高差h
斜拱
拱结构的特点
杭
州 顶
4、拱结构的特点
正
包
材 1、弯矩比相应等代梁小;
2、用料省、自重轻、跨度大;
?
3、可用抗压性能强的工程材料;
4、造型美观,艺术表现力强;
5、构造复杂,施工费用高。
5
三铰拱的内力计算
杭4.2 三铰拱的内力计算
江苏大学本科生课程课件
杭 州 顶 正 包 材
1
江苏大学土木工程与力学学院
第四章 静定拱
杭4.1
州 顶 正 包 材
概述
拱结构1、:拱通结常构杆的轴定线义为曲线,在竖向荷载 作用下,支座产生水平推力的结构。
2
拱结构的组成
2、拱结构的组成
杭 州 顶 正 包 材
3
拱结构的种类
3、拱结构的种类
杭 州 顶 正 包 材
