电机学电子教材
电机学教材

第六章同步电机 (272)6.1 概述 (272)6.1.1 同步电机的结构型式 (272)6.1.2 同步电机的励磁方式 (278)6.1.3 同步电机的冷却方式 (278)6.1.4 同步电机的额定值 (278)6.2 同步电机的运行原理 (279)6.2.1 同步发电机的空载运行 (279)6.2.2 同步电机的电枢反应 (282)6.2.3 隐极同步发电机的负载运行 (286)6.2.4 凸极同步发电机的负载运行 (291)6.3 同步发电机的运行特性 (295)6.3.1 同步发电机的运行特性 (296)6.3.2 特性曲线在参数计算中的应用 (299)6.3.3 同步发电机稳态参数的测定 (306)6.4 同步发电机的并联运行 (307)6.4.1 投入并联的条件和方法 (308)6.4.2 功率和转矩平衡方程 (311)6.4.3 功角特性 (312)6.4.4 有功功率调节与静态稳定 (314)6.4.5 无功功率调节和V形曲线 (318)6.5 同步电动机和调相机 (319)6.5.1 基本电磁关系 (319)6.5.2 无功功率调节 (322)6.5.3 起动与调速 (323)6.5.4 调相机 (326)6.6 同步发电机的不对称运行 (327)6.6.1 相序阻抗和等效电路 (327)6.6.2 不对称稳态短路 (330)6.6.3 负序和零序参数测定 (334)6.6.4 不对称运行的影响 (336)6.7 同步电机的突然短路 (337)6.7.1 超导回路磁链守恒原理 (337)6.7.2 三相突然短路过程中的基本电磁关系 (338)6.7.3 同步电机的瞬态参数 (343)6.7.4 突然短路电流及其衰减时间常数 (347)6.7.5 突然短路对电机的影响 (351)6.8 特殊用途的同步电机 (352)6.8.1 磁阻同步电动机 (352)6.8.2 磁滞同步电动机 (354)6.8.3 反应式步进电动机 (356)习题 (358)电机学第六章同步电机272第六章同步电机同步电机是交流电机的一种。
电机学电机绕组教学教材
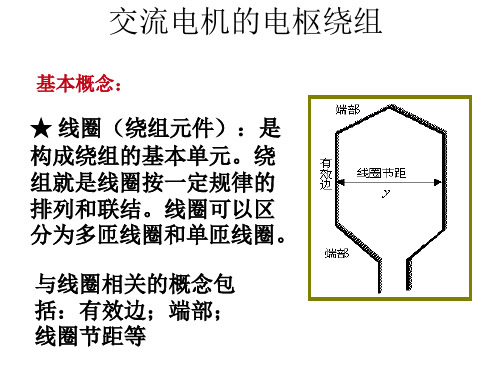
• 电机磁极对数 为p时,气隙圆 周的角度数为 p ×360电角度。
单层绕组和双层绕组
• 单层绕组一个槽中只放一个元件边; • 双层绕组一个槽中放两个元件边。
★槽距角,相数,每极每相槽 数
线圈节距
y1
Z 246 2p 4
连相绕组
• 将属于同一相的2p个线圈组连成一相绕组,并标记首尾端。 • 串联与并联,依照电势相加原则。最大并联支路数a=2p • 按照同样的方法构造其他两相。 • 连三相绕组。 • 将三个构造好的单相绕组连成完整的三相绕组。
连三相绕组
A相连接
三相连接
三相Y连接
每极每相槽数
q Z 2 pm
连线圈和线圈组
• 根据给定的线圈节距连线圈(上层边与下层边合一个线圈); • 以上层边所在槽号标记线圈编号; • 将同一极域内属于同一相的某两个线圈边连成一个线圈 (共有q个线圈,为什么?);
• 将同一极域内属于同一相的q个线圈连成一个线圈组(共有多 少个线圈组?); • 以上连接应符合电势相加原则 。
1、导体中的感应电势
• 感应电势的波形
• 感应电势随时间变化 的波形和磁感应强度在 空间的分布波形相一致。
ex(t)Bxlv
• 只考虑磁场基波时, 感应电势为正弦波。
感应电势的频率
• 磁场转过一对极,导体中的感应电势变化一个周期; • 磁场旋转一周,转过p(电机的极对数)对磁极; • 转速为n(r/min)的电机,每秒钟转过(pn/60)对极; • 导体中感应电势的频率f=(pn/60)Hz. • 问题:四极电机,要使得导体中的感应电势为50Hz, 转速应为多少?
三相电机教材(全)

技能训练5 3 技能训练5—3 三相异步电动机定子绕 组的重绕
• • • • • • 一、训练目的 1. 学会记录电动机的原始数据。 2. 掌握旧绕组的拆除工艺。 3. 掌握定子绕组的重绕工艺。 4. 学会绕组浸漆和烘烤工艺。 学会绕组嵌入工艺和通电检验方法。
三相异步电动机定子绕组的重绕
• 二、工具器材 • 绕线机、钢丝钳、线滚架、绕线模、剪刀、压 线板、裁纸刀、穿针、木榔头,铬铁、漆包线、 聚脂薄膜复合绝缘纸、黄腊管、绝缘漆。
5.2 三相异步电动机的拆装
• 5.2.1 三相异步电动机的基本结构
图5.4三相异步电动机典型结构图
笼型转子绕组
图5.5 笼型转子绕组
5.2.2 拆装电动机的常用工具
拆装电动机时,常用工具有: 拉钩、油盘、活板手、榔头、 螺丝刀、紫铜棒、钢套筒 和毛刷等(见图5.6)
图5.6拆装电动机的常用工具
三相异步电动机定子绕组的重绕
• 三、训练步骤与内容
• • • • 1.记录原始数据 记录下列原始数据: (1) 电动机铭牌数据 (2) 定子绕组数据:电动机绕组每槽的匝数; 导线规格;绕组线圈跨距;绕组的连线方式。 (3)铁心数据:槽数;铁心外径和内径尺寸;长度; 槽形。
三相异步电动机定子绕组的重绕
第二篇 电机与控制
第5章 三相异步电动机 章
•
•
内容提要
本章主要阐述三相异步电动机的安装与试 运行;三相异步电动机的拆装、注油、洗油及 小修;三相异步电动机定子绕组首末端判别; 三相异步电动机常见故障分析与排除和三相异 步电动机的绕组制作等内容。
5.1 .
三相异步动机的安装及试运行
• 5.1.1三相异步电动机的安装 三相异步电动机的安装 1. 安装前的检查 2. 基础灌制 3. 电动机的安装 4. 电动机的校正
《电机学完整》课件

直流电机控制精度高,响应速度快,因此适用于需要精确控制速度的场合,如数控机床、机器人等。同时,直流电机也具有较好的过载能力和启动性能。
总结词
通过改变交流电机的输入电源频率、电压或相位,实现对交流电机启动、制动、调速的目的。
总结词
交流电机结构简单、价格便宜、维护方便,适用于大规模生产和应用。
交流电机是指输入交流电能,输出机械能的电机。
根据工作原理的不同,交流电机可以分为异步电机和同步电机两大类。
交流电机具有结构简单、维护方便、可靠性高等优点,因此在电力、冶金、化工等领域得到广泛应用。
电机的运行原理
直流电机的基本结构
01
直流电机由定子和转子组成,定子包括主磁极和励磁绕组,转子包括电枢绕组和换向器。
专业保养
可能是电源问题、电机内部故障或负载过大。需要检查电源、电机和负载情况,找出具体原因并解决。
启动困难
可能是电机过载、通风不良或润滑不足。需要检查电机的运行状态、通风情况以及润滑情况,找出具体原因并解决。
过热
可能是电机内部有故障、轴承损坏或机械不平衡作原理
02
当直流电流通过励磁绕组时,主磁极产生磁场;当电枢绕组中有电流通过时,受到磁场的作用而产生电磁转矩,从而使转子转动。
直流电机的调速与控制
03
通过改变输入到电枢绕组的电流大小或方向,可以调节直流电机的转速或转向。
交流电机分为异步电机和同步电机,异步电机主要由定子和转子组成,同步电机还包括励磁绕组和集电环。
详细描述
交流电机结构简单、价格便宜、维护方便,因此在大规模生产和应用中得到广泛应用。同时,交流电机也具有较高的效率和可靠性。
电机学电子教材

第四节交流磁路中的激磁电流和磁通、电磁感应定律?i的波形会产在交流铁心磁路中,由于铁心磁化曲线的非线性,激磁电流和主磁通m生畸变。
下面以图1-4-1所示单一铁心材料的交流铁心磁路为例,分析激磁电流和磁通的性??f(i)的形式。
质与波形。
为分析方便,铁心材料的磁化特性使用图1-4-1 交流铁心磁路一、铁磁材料的磁化特性为基本磁化曲线当磁路内的磁通较小时,磁路不饱和,磁通与激磁电流之间的关系基本上是线性关系。
在这种情况下,如果磁通随时间按正弦规律变化,则激磁电流随时间也按正弦规律变化。
磁通到达最大值时,激磁电流也到达最大值,因此,激磁电流与磁通在时间上同相位,随时间变化的波形也相同。
当磁通较大时,磁路出现饱和,磁通与激磁电流之间呈非线性关系。
这时激磁电流和磁通的特性与波形可以用图解法进行分析,下面分两种情况讨论。
1.磁通为正弦波时激磁电流的波形??t?f(i)曲线,此时由当磁通随时间作正弦变化时,设时间为时的磁通瞬时值为11i,由此可以得到激磁电流曲线上的一点,可以查出产生该磁通所需的激磁电流如图1-4-21m i随时间变化所示。
同理,可以求出其他瞬间的激磁电流值,并进而可画出整条激磁电流m i?f(t)。
的曲线m 11-4-2 磁通为正弦波时磁路饱和对电流波形的影响图)电流波形分解)电流波形;(b(a可以看出,当磁通随时间正弦变化且磁路饱和时,由于磁路的非线性,激1-4-2 分析图磁电流波形发生畸变,成为尖顶波。
如果将激磁电流波形进行分解,除了基波外,还包含有i的波形尖顶越严重,谐其他奇次谐波,其中以三次谐波为最大。
磁路越饱和,激磁电流m?i的相位相波也越显著。
但无论激磁电流波形尖顶有多严重,它的基波相位始终与磁通m同。
.激磁电流为正弦波时磁通的波形2?i随时间随时间作正弦变化时,利用上述的作图法,同样可以求出磁通当激磁电流m?)t?f(所示。
,如图变化的曲线1-4-3 2激磁电流为正弦波时磁路饱和对磁通波形的影响图1-4-3)磁通波形分解(b(a)磁通波形;i随时间正弦变化且磁路饱和时,磁通的波形也1-4-3可以看出,当激磁电流分析图m发生畸变,成为平顶波。
电机学课件

根据使用需求和性能要求,制定电机的设计原则 和标准。
结构优化
通过对电机结构的优化设计,提高电机的性能和 稳定性。
控制优化
通过对电机控制策略的优化,提高电机的响应速 度和能源利用效率。
05
电机的控制与调速
电机的控制原理
电机控制的基本原理
说明电机的运行与哪些因素有关,以及如何通过输入电压、电流 等参数对电机进行控制。
得到广泛应用。
03
现代电机的进步
随着科技的不断进步,现代电机在设计和制造上更加精密和高效。新型
的永磁材料和电力电子控制技术的发展也推动了电机的进步。
电机的应用领域
01
02
03
04
工业领域
电机在工业领域中得到广泛应 用,如传动、生产线、包装、
泵类等。
交通运输领域
电机在交通运输领域中也有着 广泛的应用,如电动汽车、电
THANKS
感谢观看
直流电机
直流电机是指依靠直流电能驱动的电动机。
直流电机的特点是启动速度快,调速性能好,控制简单,但是维护困难,可靠性较 低。
直流电机主要应用于需要快速响应、调速性能好的场合,如电力机车、地铁、轻轨 等。
交流电机
交流电机是指依靠交流电能驱 动的电动机。
交流电机的特点是结构简单, 维护方便,可靠性高,但是启 动电流大,调速性能差。
伺服电机的特点是精度高,响应 速度快,可实现精确控制,但是
价格较高。
伺服电机主要应用于需要高精度 、高速度、高稳定性的场合,如
航空航天、精密加工等。
04
电机的性能分析
电机的性能参数
电机转速
01
电机的转速与电机的性能参数密切相关,是电机性能的重要指
电机学第6章特殊变压器讲义教材

此时两个分裂绕组之间的短路阻抗(折算到高压侧)称为分裂阻抗 Z f 。
4.分裂系数
kf
Zf Zs
3~4
是分裂变压器的基本参数,既用来定性分析分裂变压器的特性,又作为设计指标。
第6章 特殊变压器
三、等效电路
第6章 特殊变压器
6.2 自耦变压器
一、结构特点与用途
结构特点: 低压绕组是高压绕组的一部 分,一、二次绕组之间既有 磁耦合,又有电联系。
U1U2为一次绕组,匝数为 N1 ; u1u2为二次绕组,匝数为 N2,又称为公共绕组; U1u1称为串联绕组,匝数为 N1-N2 。 用途:用来连接两个电压等级相近的电力网,作为两电网的联络变压器;
第6章 特殊变压器
6.3 分裂变压器
一、结构特点与用途
1.结构特点(以单相双分裂绕组变压器为例)
高压绕组由两条支路并联组成(并非分裂绕组)。
电路上彼此分离
低压绕组是
两个分裂绕组。
磁路上松散耦合
低压两个分裂绕组的特点: 结构相同、容量相等,两个绕组容量之和等于
高压绕组的额定容量,即分裂变压器的额定容量。
如绕组3发生短路 U3 0 I2 I3 忽略 I2
残余电压
U2 U0 Z1Z3Z3U1
1.75Zs (0.1251.75)Zs
U1
0.93U1
即使分裂系数取较小值 k f 3 U2 0.8U 61
通常发电厂要求残余电压不低于65%额定电压, 因此,分裂变压器可以大大提高厂用电的可靠性。
双分裂绕组变压器实质上是三绕组变压器,二者等效电路及参数公式相同。
Z1
电机学第1章精品PPT课件

起始磁化曲线
oa段 ab段 bc段 cd段 膝点 饱和
铁磁材料 图1-7.
磁化曲线见示意
应用: 设计电机和变压器时,为使主磁路内得
到较大的磁通量而又不过分增大励磁磁动势, 通常把铁心内的工作磁通密度选择在膝点附近。
2.磁滞回线 示意图: 图1-8。 剩磁:去掉外磁场之后,铁磁材料内仍然保留的
B
=
Φ A
Wb/m2
3. 磁场强度 H
单位:A/m
电子电气工程学院
1.1 磁场的基本物理量
H 与 B 的区别
① H ∝I,与介质的性质无关。 ② B 与电流的大小和介质的性质均有关。
4. 磁导率
=
B H
单位:H / m 真空中的磁导率:
μ0 = 4π×10-7 H / m
电子电气工程学院
第1章 磁 路
1.2 物质的磁性能
按磁导率分类:非磁性物质、磁性物质。 一、非磁性物质
≈ 0 1. 顺磁物质(如空气): 略大于 0 。 2. 反磁物质(如铜): 略小于 0 。
二、 磁性物质
1. 高导磁性 0
※ 铸钢: ≈1 000 0 硅钢片: ≈ ( 6 000 ~ 7 000) 0 坡莫合金: 比 0 大几万倍。
电子电气工程学院
1.2 物质的磁性能
磁性物质内部存在着很多很小的“磁畴”。
磁畴(磁化前)
磁畴(磁化后)
磁性物质的高导磁性被广泛应用于变压器 和电机中。
电子电气工程学院
1.2 物质的磁性能
2. 磁饱和性
≠常数
磁化曲线(B-H曲线)
Bcd
B = f (H)
b a
O H
《电机学课件》PPT课件

• 使用教材:胡虔生、胡敏强、杜炎生合编《电 机学》,中国电力出版社
• 参考书:汪国梁主编《电机学》
05.12.2020
.
12
《电机学》(二)课程简介
• 课程名称: 中文名称:电机学(二) • 英文名称:Electrical Machinery (Part 2) • 教学对象:电气工程类专业、本科 • 课程定位:《电机学》是本专业的一门主要技
• 使用教材:胡虔生、胡敏强、杜炎生合编《电 机学》,中国电力出版社
•
Stephen J.Chapman, Electric Machinery
Fundamentals, McGRAW-HILL International
Editions
• 参考书:汪国梁主编《电机学》 返回
05.12.2020
.
15
变压器图片、图形、动画
变压器的空载运行 变压器运行特性 三绕组变压器 三绕组变压器向量图 变压器外特性 TR三次谐波磁通路径 YYN变压器组中性点浮动 三相变压器组铁芯磁通波形 相量图
变压器参数测定 变压器暂态运行 自耦变压器 互感器 对称分量合成 变压器并联运行 T形电路 三相变压器
05.12.2020
术基础课,定位为:
* 电气工程的基础 * 电力系统的核心
• 课程特点:课程特点是概念多、理论性强,与 工程联系密切。
05.12.2020
.
13
《电机学》(二)课程简介
主要内容:本课程主要讲述:同步电机的结构, 工作原理、运行等到方面的内容。具体为:
❖同步电机的基本理论与运行特性 ❖同步发电机在大电网上运行 ❖同步发电机不对称运行 ❖同步发电机的突然短路。
电机学第1章

if 1T Bm 1.8T then
pFe CFe f 1.3Bm2G
2020年1月23日星期四
20
1.3 磁路的计算
1.直流磁路的计算 2.直流电机的空载磁路和磁化曲线 3.永磁磁路的计算特点 4.交流磁路的特点
2020年1月23日星期四
15
3.铁磁材料
材料名称 磁性能
表1-1 永磁材料的磁性能
铝镍钴(AL 铁氧体(Y35) 稀土钴(YX 钕铁硼(N42
NICO 56/6)
G-26)
H)
剩磁T
1.35
0.39
1.03
1.33
矫顽力(kA/m)
60
200
765
907
最大磁能积
56
31.8
198
326
BH(kJ/)
2020年1月23日星期四
2
1.磁路的概念
图1-1 两种常见的磁路 a)变压器的磁路 b)四极直流电机的磁路
2020年1月23日星期四
3
2.磁路的基本定律
分析和计算磁场时,常常要用到两条基本定律: ➢ 安培环路定律, ➢ 磁通连续性定律
把这两条定律应用到磁路,可得磁路的 ➢ 欧姆定律 ➢ 磁路的基尔霍夫第一和第二定律
2020年1月23日星期四
图1-5 磁路的基尔霍夫第二定律
9
1.2 常用的铁磁材料及其特性
1.铁磁材料的磁化 2.磁化曲线和磁滞回线 3.铁磁材料 4.铁心损耗
2020年1月23日星期四
10
1.铁磁材料的磁化
磁化:铁磁材料在外磁场中呈现很强的磁性
图1-6 磁畴示意图 a)未磁化时 b)磁化后
电机学(完整版)

11.05.2020
《电机学》 第一章 导论
1.3 电机中磁路基本定律
1. 全电流定律—安培环路定律
LH dl I
i1 dl
式中,若电流的正方
向与闭合回线L的环行方 向符合右手螺旋关系时,
H
i取正号,否则取负号。
22
i2 i3
L
11.05.2020
LH•d li1i2i3
《电机学》 第一章 导论
11.05.2020
21
2.电机的近代发展及趋势
单机容量不断增加 如汽轮发电机:
1900 1920 1937空气冷却
氢气冷却
5MVA 1956水内冷 25MVA 1960 100MVA 目前 150MVA
208MVA 320MVA >1000MVA
中小型电机技术与经济指标不断改进 新的设计方法(CAD)、工艺、材料、测试手段
辜承林 华中科技大学出版社
《电机学》第三版 许实章 机械工业出版社
《电机学》
汤蕴璆 机械工业出版社
《电机学》
胡虔生 中国电力出版社
11.05.2020
《电机学》 第一章 导论
6
※ 课程要求 1. 认真听课 2. 独立完成作业
11.05.2020
《电机学》 第一章 导论
7
第一章 导论
1.1 概述 1.2 电机发展简史 1.3 电机中的基本电磁定律 1.4 铁磁材料特性 1.5 磁路基本定律及计算方法
2. 磁通本身不随时间变化,但由于线圈与磁场间有相 对运动而引起线圈中磁链的变化,这样产生的电势 称为运动电势或速度电势
11.05.2020
《电机学》 第一章 导论
13
电机学PPT课件-直流电动机、直流发电机
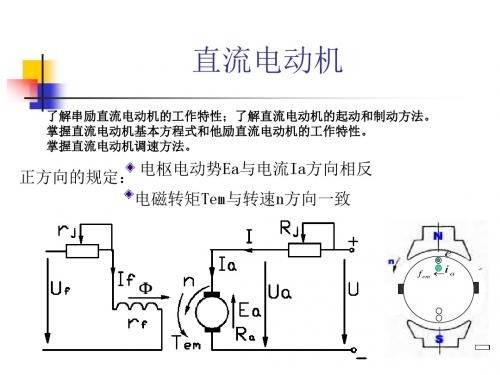
n f (I a )
n
当电动机端电压 U U N =常值,励磁电流
的函数关系 n f ( I a ) 称速率特性。
n
n0 与负载(通常用负载时电枢电流I a来表征)
I f 为常值时,
n' 0
nN
U I a Ra n C e
Ia
Tem Ia 0 CT
Tem Tc 0时
态的过程。 起动瞬间,起动转矩和起动电流分别为
Tst CT I st
I st
Ea 0 ,而且电枢电阻 起动时由于转速 n 0 , 将达很大值。
UN Ra
Ra
很小,所以起动电流
过大的起动电流将引起电网电压下降、影响电网上其它用户的正常用电; 同时过大的冲击转矩会损坏电枢绕组和传动机构。 一般直流电动机不允许直接起动。 为了限制起动电流,他励直流电动机通常采用电枢回路串电阻或降低电 枢电压起动。
并励电动机运行时,励磁绕组不能断路。
若在重负载下发生励磁绕组断开,将导致 Tem CT I a 减小,电动机停转,反电势为零,电枢电流非常大, 电机过热以致烧毁; 若在轻负载下发生励磁绕组断开, 0 将导致电动机“飞速”,可能损坏电机。
n
U I a Ra C e
2、转矩特性他励并励
n C1
U Tem
C2 ( Ra R j )
、
3、串励电动机的机械特性
当电机磁路线性时, C I a
n C1
U Tem
C2 ( Ra R j )
这是一条双曲线。可见,当负载转矩增大时,转速下降很快。 故串励电动机的机械特性很软 当电机磁路饱和时,
C I a Ra R j Tem U n Ce Ce CT
电机学(自学完整版)课件

18十月2023
《电机学》 第一章 导论
20
2. 电机的近代发展及趋势
单机容量不断增加
·如汽轮发电机:
1900 1920 1937空气冷却
氢气冷却
5MVA 25MVA 100MVA 150MVA
1956水 肉冷 1960 目前
208VA 320MVA >1000MVA
中小型电机技术与经济指标不断改进 ·新的设计方法 (CAD)、 工艺、材料、测试手段 应用范围扩大
18十月2023
14
《电机学》 第一章 导 论
发电
·我国老牌电机厂:
哈尔滨电机厂 上海电机厂
·四川:
德阳东方电机厂
上海电机厂的生产车间
18十月2023
《电机学》 第一章 导
15
论
发电
18十月2023
《电机学》 第一章 导论
16
动力
应用于洗衣机
用于有轨电车牵引的电动机 18十月2023
《电机学》 第一章 导论
39
※ 铁修材料具有的特点
它的磁化曲线具有饱和性,磁导率μpe不是常数,且随H 的变化而变化。
L. μ 变化 2. 总体非线性 3. 存在饱和特性
个= μ
18十月2023
《电机学》 第一章 导论
40
B=f(H)
B
C
b
μre =f(H)
a
B=₀H H
图1-6 铁磁材料的磁化曲线 (p16)
18十月2023
若线圈不动,穿过线圈的磁通随时间变化,则线圈中感应 的电动势——变压器电势
中=中m sin wt
感应电动势有效值:
18十月2023
28
《电机学》 第一章 导 论
《电机学》电子教案

22
4、三相交流电的应用: 在单相交流电源供电的情况下,单相交流电
动机无法自行起动。
不久,两相电流能产生旋转磁场的原理被发 现,1885年制成了两相交流异步电机的模型。
1889年,多里沃─多勃罗沃尔斯基提出了三 相制的建议并设计和制造了第一台三相变压器 和三相异步电动机。至1897年,建成了第一个 三相交流输电系统。
2 .顾绳谷主编,《电机及拖动基础》(上、下册),机 械工业出版社,1998,第2版
3.许实章主编,《电机学》(上、下册),机械工业出版 社,1994,修订版
4. 张松林主编,《电机及拖动基础习题集与实验指导 书》,机械工业出版社, 1997
5.<ELECTRIC MACHINERY FUNDAMENTALS>
8
《电机学》 (Electrical Machinery)
课程的学习方法
掌握电机的分析方法
理解、掌握各种电机的 基本概念、基本原理、 重点和难点 总结出各种电机间的 共性和个性
(听课、自学、 作业和实验)
9
基本工作原理(Fundamental Principles)
结构(Construction) ----(电路、磁路的特点) (The Feature of Electric and Magnetic circuit)
概念多,理论性强。要求:
改变以往以套公式算题就算完成学习任务 的学习方法,而把学习重点放在课后
及时复习、钻研教材
在掌握电机中主要物理量的概念、特性及 相互关系后,结合具体的条件,对电机的 运行进行分析,即认真思考老师所布置的 习题和思考题,培养分析问题和解决问题
的能力,并且勤于总结。
电机学电子教案、习题解答17第17章 直流电机的运行-PPT文档资料

指 U 为常值时,转速与电磁转矩之间的关系,即 、 I 、 ( R R ) f a s
n f ( T ) em
一、机械特性表达式
由 U E I ( + R ) a aR a s 转速特性
E n T C I em T a 可得 a C e
E U I ( R R ) a a a s n C C e e
3.励磁回路电阻 R f 小于临界电阻 R cr 空载特性 U If ) 0 f( 励磁电阻线 U 0 R f If 二者交点为空载稳定运行点
Rf Rcr ,励磁电阻线斜率& R cr ,电压不稳定; Rf R cr 不能建立电压。
第17章 直流电机的运行
p ad 取输出功率的(0.5~1)%。
3.输入、输出、电磁功率
输入功率
P1
P2
发电机:指转轴上输入的机械功率; 电动机:指电源输入的电功率 P 1 UI 发电机:指电枢两端输出的电功率 P 2 UI 电动机:指转轴输出的机械功率。
输出功率 电磁功率
Pem 指电机内部的电功率和机械功率相互转换的功率。
n f ( T ) em
R U n N a 2T n T em 0 em C C C e N e T N
并保持转速为额定转速。调节励磁电流, 可以测取整个磁滞回线,取平均曲线,作为电机的空载特性。 由于磁路有剩磁,在If = 0 时,有一个不大的剩磁电压,约为额定电压2%~4%。
第17章 直流电机的运行
二、外特性
指
I f I fN 时,U f (I) n nN,
外特性是一条略带下垂的曲线。
掌握直流电动机的起动、调速及反转的原理及方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四节 交流磁路中的激磁电流和磁通、电磁感应定律
在交流铁心磁路中,由于铁心磁化曲线的非线性,激磁电流m i 和主磁通φ的波形会产生畸变。
下面以图1-4-1所示单一铁心材料的交流铁心磁路为例,分析激磁电流和磁通的性质与波形。
为分析方便,铁心材料的磁化特性使用)(i f =φ的形式。
图1-4-1 交流铁心磁路
一、铁磁材料的磁化特性为基本磁化曲线
当磁路内的磁通较小时,磁路不饱和,磁通与激磁电流之间的关系基本上是线性关系。
在这种情况下,如果磁通随时间按正弦规律变化,则激磁电流随时间也按正弦规律变化。
磁通到达最大值时,激磁电流也到达最大值,因此,激磁电流与磁通在时间上同相位,随时间变化的波形也相同。
当磁通较大时,磁路出现饱和,磁通与激磁电流之间呈非线性关系。
这时激磁电流和磁通的特性与波形可以用图解法进行分析,下面分两种情况讨论。
1.磁通为正弦波时激磁电流的波形
当磁通随时间作正弦变化时,设时间为1t 时的磁通瞬时值为1φ,此时由)(i f =φ曲线可以查出产生该磁通所需的激磁电流1m i ,由此可以得到激磁电流曲线上的一点,如图1-4-2所示。
同理,可以求出其他瞬间的激磁电流值,并进而可画出整条激磁电流m i 随时间变化的曲线)(m t f i =。
图1-4-2 磁通为正弦波时磁路饱和对电流波形的影响
(a )电流波形;(b )电流波形分解
分析图1-4-2可以看出,当磁通随时间正弦变化且磁路饱和时,由于磁路的非线性,激磁电流波形发生畸变,成为尖顶波。
如果将激磁电流波形进行分解,除了基波外,还包含有其他奇次谐波,其中以三次谐波为最大。
磁路越饱和,激磁电流m i 的波形尖顶越严重,谐波也越显著。
但无论激磁电流m i 波形尖顶有多严重,它的基波相位始终与磁通φ的相位相同。
2.激磁电流为正弦波时磁通的波形
当激磁电流m i 随时间作正弦变化时,利用上述的作图法,同样可以求出磁通φ随时间变化的曲线)(t f =φ,如图1-4-3所示。
图1-4-3 激磁电流为正弦波时磁路饱和对磁通波形的影响
(a )磁通波形;(b )磁通波形分解
分析图1-4-3可以看出,当激磁电流m i 随时间正弦变化且磁路饱和时,磁通的波形也发生畸变,成为平顶波。
如果将磁通波形进行分解,除了基波外,亦包含有其他奇次谐波,其中也以三次谐波为最大。
磁路越饱和,磁通φ的波形平顶越严重,谐波也越显著。
但无论波形平顶有多严重,它的基波相位始终与激磁电流m i 的相位相同。
综上分析可知:激磁电流和磁通的波形是否畸变,决定于磁路是否饱和。
磁路不饱和时,磁化曲线基本上是线性的,两者的波形非常接近。
磁路饱和后,磁化曲线呈非线性,磁通与激磁电流的波形不同。
磁通为正弦波时激磁电流畸变成尖顶波;激磁电流为正弦波时磁通畸变成平顶波。
但无论是尖顶波还是平顶波,如果将其进行分解,主要成分都是基波和三次谐波。
磁通基波和激磁电流基波的相位始终相同,与磁路是否饱和以及饱和程度无关。
二、铁磁材料的磁化特性为磁滞回线
考虑磁滞现象时,铁磁材料的磁化特性为磁滞回线。
当磁通为正弦波时,通过磁滞回线,利用图解法求取激磁电流i m =f (t )的曲线,如图1-4-4所示。
可以看出,当磁通φ为正弦波时,激磁电流m i 为非正弦波。
把m i 分解成两个分量,即Fe μm i i i +=。
其中μi 分量为和φ同相位的尖顶波,与忽略磁滞现象、只考虑饱和时图1-4-2中的尖顶波完全一致;或者说,μi 是不考虑磁路有磁滞现象时的激磁电流,与基本磁化曲线相对应,称为磁化电流。
另一分量Fe i 波形近似为正弦波,相位超前于磁通φ90°、幅值为I c (与H c 相对应)。
Fe i 是反映磁滞损耗和涡流损耗的有功电流,e h Fe i i i +=,h i 是由于考虑了磁滞现象才存在的,称为磁滞损耗电流,不计磁滞现象,h i 为零。
交流磁路中除了磁滞损耗外,同时还有涡流损耗。
e i 称为涡流损耗电流。
由于h i 和e i 都反映了磁路中的铁耗,因此把它们合在一起,称为铁耗电流,
用Fe i 表示。
在各种变压器和电机中,由于铁心选用的都是较好的软磁性材料,同时又采用叠片方式,因此铁耗很小。
激磁电流中铁耗电流要比磁化电流μi 小得多。
图1-4-4 磁滞现象对激磁电流波形的影响
(a )电流波形;(b )电流波形分解
综合上述分析可知:
(1)激励产生磁通φ的电流是磁化电流μi ,它的基波与磁通φ波形同相位。
由于磁路的非线性,μi 与磁通φ的波形不一样。
当φ为正弦波时,μi 为尖顶波;当μi 为正弦波时,φ为平顶波。
(2)铁心中具有磁滞和涡流损耗。
激磁电流中除了磁化电流外,同时还存在铁心损耗电流,铁心损耗电流接近于正弦波,其相位超前于磁通90°。
(3)激磁电流是磁化电流和铁心损耗电流的合成,即m Fe i i i μ=+。
由于变压器和电机的铁心损耗很小,所以Fe i 很小,通常仅为m i 的10%左右,因此激磁电流m i 主要由μi 决定。
三、电磁感应定律
电磁感应定律描述的是磁变生电的电磁感应现象,于1831年由法拉第提出,又称法拉第电磁感应定律。
它指出,交变的磁场会产生电场,并在导体中感应电动势。
如图1-4-5所示,当规定感应电动势正方向与磁通的正方向符合右手螺旋关系时,则感应电动势与磁通对时间的变化率的负值成正比,即
t
Ψt N e d d d d -=-=φ (1-4-1) 式中:e 为回路中的感应电动势;N 为绕组匝数;φ为通过该回路面积的磁通;ψ为交链
回路的磁链,它表示N 匝线圈所匝链的总磁链,φψN =。
图1-4-5 电磁感应 根据法拉第定律可以导出,当磁场恒定,而导体在磁场中运动时,如图1-4-6(a )所示,导体中的感应电动势可表示为
⎰
⋅⨯=l B v d )(e (1-4-2) 式中:B 为磁感应强度;l 为导体的长度;v 为导体的运动速度。
感应电动势的方向可用图1-4-6(b )所示的右手定则确定。
图1-4-6 感应电动势与右手定则
(a )感应电动势;(b )右手定则
若磁场方向、导体长度方向和导体运动方向三者相互垂直时,式(1-4-2)简化为
Blv e = (1-4-3)
式(1-4--3)适用于计算恒定、均匀磁场中运动导体的切割电动势,是法拉第电磁感应定律的另一种有约束条件的表示形式, 在电机学中经常使用。
四、毕奥-萨伐尔电磁力定律
磁场最基本的特性是对场域中的载流导体有力的作用,电磁力定律是描述电与磁之间相互作用产生力的基本定律。
如图1-4-7(a )所示,取有效长度为l 的导体,导体中流过的电流为i ,导体所处的磁场为B ,则导体所受的作用力f 可表示为
⎰
⨯=B l f d i (1-4-4) 式中:l d 为导体ab 上的长度微元。
若磁场均匀且与导体相互垂直,则式(1-4-4)可简化为
Bil f = (1-4-5) 电磁力的方向可用左手定则判定,如图1-4-7(b )所示。
图1-4-7 电磁力和左手定则
(a)电磁力;(b)左手定则
五、能量守恒原理
能量守恒原理是物理学中的基本原理。
该原理可表述为:在质量不变的物理系统内,能量是守恒的,即能量不会凭空产生,亦不会凭空消灭,仅能变换其存在形式。
在电机中,能量转换包括四种能量形式,即电能、机械能、磁场储能和热能。
根据能量守恒原理,对于电动机,其能量关系为
电源输入的电能=磁场储能的增量+转换为热能的能量损耗+机械能输出
对于发电机,其能量关系为
机械能输入=磁场储能的增量+转换为热能的能量损耗+电能输出
转换为热能的能量主要包括三部分:导体中的电流在电阻中引起的电气损耗(亦称铜耗);消耗于轴承摩擦及通风中的机械损耗;电机内的磁场在铁心中产生的磁滞损耗和涡流损耗。
这些能量均转换为热能,并且是一种不可逆的过程,也就是说这部分能量很难或根本不可能再转换为电能或机械能。
