机械原理MATLAB
机械原理牛头刨床matlab源程序

七.Matlab编程及绘图clear all;clc;%初始条件theta1=linspace(-25.72,334.28,100);%单位度theta1=theta1*pi/180;%转换为弧度制W1=80*pi/30;%角速度单位rad/sH=0.6;%行程单位mL1=0.1605;%O2A的长度单位mL3=0.6914;%O3B的长度单位mL4=0.2074;%BF的长度单位mL6=0.370;%O2O3的长度单位mL6u=0.6572;%O3D的长度单位mZ=pi/180;%角度与弧度之间的转换dT=(theta1(3)-theta1(2))/W1;%时间间隔for j=1:100t(j)=dT*(j-1);%时间因素end%求解S3、Theta3、Theta4和SE四个变量S3=((L6)^2+(L1)^2-2*L6*L1*cos(theta1+pi/2)).^0.5;%求出O3A的值for i=1:100%求解角度theta3、Theta4和SE的长度theta3(i)=acos(L1*cos(theta1(i))/S3(i));theta4(i)=asin((L6u-L3*sin(theta3(i)))/L4);SE(i)=L3*cos(theta3(i))+L4*cos(theta4(i));end%求解完成%求解完成%求解VS3、W3、W4和VE四个变量for i=1:100J= inv([cos(theta3(i)),-S3(i)*sin(theta3(i)),0,0;sin(theta3(i)),S3(i)*cos(theta3(i)),0,0;0,-L3*sin(theta3(i)),-L4*sin(theta4(i)),-1;0,L3*cos(theta3(i)),L4*cos(theta4(i)),0]);K=J*W1*[-L1*sin(theta1(i));L1*cos(theta1(i));0;0];VS3(i)=K(1);W3(i)=K(2);W4(i)=K(3);VE(i)=K(4);end%求解完成%求解aS3、a3、a4、aE四个变量for i=1:100J= inv([cos(theta3(i)),-S3(i)*sin(theta3(i)),0,0;sin(theta3(i)),S3(i)*cos(theta3(i)),0,0;0,-L3*sin(theta3(i)),-L4*sin(theta4(i)),-1;0,L3*cos(theta3(i)),L4*cos(theta4(i)),0]);P=W1*W1*[-L1*cos(theta1(i));-L1*sin(theta1(i));0;0];M=[-W3(i)*sin(theta3(i)),-VS3(i)*sin(theta3(i))-S3(i)*W3(i)*cos(theta3(i)),0,0;W3(i)*cos(theta3(i)),VS3(i)*cos(theta3(i))-S3(i)*W3(i)*sin(theta3(i)),0,0;0,-L3*W3(i)*cos(theta3(i)),-L4*W4(i)*cos(theta4(i)),0;0,-L3*W3(i)*sin(theta3(i)),-L4*W4(i)*sin(theta4(i)),0];N=[VS3(i);W3(i);W4(i);VE(i)];K=J*(-M*N+P);aS3(i)=K(1);a3(i)=K(2);a4(i)=K(3);aE(i)=K(4);end%求解完成%动态静力分析%初始条件M4=22;M5=3;M6=52;Js4=0.9;Js5=0.015;Fc=1400;Ls4=0.5*L3;Ls5=0.5*L4;%给切削阻力赋值for i=1:100if((abs(SE(1)-SE(i))>0.05*H&&abs(SE(1)-SE(i))<0.95*H)&&(theta1(i)<pi))Fc(i)=1400;elseFc(i)=0;endend%赋值完成%求解平衡力矩J4=Js4+M4*(0.5*L3)*(0.5*L3);%导杆对点O3的转动惯量for i=1:100Ekk(i)=(M6*VE(i)*VE(i)+Js5*W4(i)*W4(i)+M5*VE(i)*VE(i)+J4*W3(i)*W3(i))/2;%计算总动能enddEkk(1)=Ekk(1)-Ekk(100);%动能的改变量for i=2:100dEkk(i)=Ekk(i)-Ekk(i-1);%动能的改变量endfor i=1:100MM(i)=(dEkk(i)+Fc(i)*abs(VE(i)))/W1;%求平衡力矩end%画图%画运动图figure(1);plot(t,theta3,'r');hold on;plotyy(t,theta4,t,SE);grid on;xlabel('时间t/s');ylabel('theta3、theta4(rad)');title('角度Theta3、theta4和位移SE');axis([ 0 , 0.75,-0.2,2]);figure(2);plot(t,W3,'r');hold on;grid on;plotyy(t,W4,t,VE);xlabel('时间t/s');ylabel('W3、W4(rad/s)');title('角度速度W3、W4和速度VE');axis([0 , 0.75,-5,3]);figure(3);plot(t,a3,'r');hold on;plotyy(t,a4,t,aE);grid on;xlabel('时间t/s');ylabel('a3、a4(rad/s/s)');title('角度加速度a3、a4和加速度aE');axis([0 , 0.75,-80,80]);%运动图画完%画反力图figure(4);plotyy(theta1,Fc,theta1,SE);xlabel('Theta1(时间t)');ylabel('Fc');axis([theta1(1) ,theta1(100),-50,1400]); title('切削阻力Fc与位移SE');grid on;figure(5);plotyy(theta1,MM,theta1,Fc);xlabel('Theta1(时间t)');ylabel('力矩');axis([theta1(1) ,theta1(100),-50,300]); title('平衡力矩');grid on;figure(6);plotyy(theta1,Ekk,theta1,SE);xlabel('Theta1(时间t)');ylabel('Fc');title('导杆、连杆和刨头的总动能');grid on; theta1(1)theta1(100)。
基于matlab的GUI设计——机械原理教学演示系统
机械原理教学演示系统——基于matlab的GUI设计xxx指导老师:20年月日目录一、功能简介 (3)二、总界面 (3)三、凸轮模块 (4)四、齿轮模块 (6)五.参考书目 (6)六.附录(部分程序源代码) (7)一、功能简介本系统能实现机械原理教学过程中凸轮模块与齿轮模块的设计与运动仿真,加深对机械原理课程学习的理解。
二、总界面总界面标题设置:set(gcf,'name','机械原理教学演示系统 made by 翟鲁鑫');背景图片设置:ximg=imread('机械原理课本.jpg');imshow(ximg);背景声音播放:Fs=44100;[ywav,Fs]=wavread('夜的钢琴曲 - 六3.wav');sound(ywav,Fs);到各个模块:到凸轮模块clcclose(gcf);clear allGUItulun到齿轮模块clcclose(gcf);clear allGUIchilun关闭系统:clcquestion='真的要退出吗?';title='确认退出?';button=questdlg(question,title,'是','否','是'); switch buttoncase'是'clear allclosecase'否'returnend三、凸轮模块设计要点:1.背景声音设置方法同主界面2.推程角、远休角、回程角之和不能大于360度的判别条件;基圆半径、滚子半径、行程不能为0的判别条件sr0=get(handles.edit2,'string');r0=str2num(sr0);if isequal(r0,0)errordlg('基圆半径不能为0,请重新输入','出错');returnendsrr=get(handles.edit3,'string');rr=str2num(srr);if isequal(rr,0)errordlg('滚子半径不能为0,请重新输入','出错');returnendsh=get(handles.edit4,'string');h=str2num(sh);if isequal(h,0)errordlg('行程不能为0,请重新输入','出错');returnendn3=phi01+phi02+phi03; %推程角、远休止角与回程角的总和if n3>360errordlg('角度之和大于360,请重新输入','出错');end3.仿真程序。
matlab平面连杆结构分析(机械原理课程设计)

优化参数:连杆 长度、角度、质 量等
优化结果:得到 最优的连杆结构 设计
感谢观看
汇报人:
平面连杆结构的应用范围
机械工程:用于设计、分析和优化机械设 备
生物医学:用于设计、分析和优化假肢、 康复设备等
航空航天:用于设计、分析和优化飞机、 火箭等航天器
机器人技术:用于设计、分析和优化机器 人关节、机械臂等
汽车工业:用于设计、分析和优化汽车底 盘、悬挂系统等
建筑工程:用于设计、分析和优化建筑结 构、桥梁等
03
平面连杆结构的运动学分析
平面连杆结构的运动学方程
平面连杆结构的运动学方程是描述连杆系统运动状态的数学模型 运动学方程包括位移方程、速度方程和加速度方程 运动学方程的建立需要知道连杆系统的几何参数和运动参数 运动学方程的求解可以通过数值积分方法或解析方法进行
平面连杆结构的运动学特性
运动学方程:描述连杆结构的运动状态 运动学参数:包括位移、速度、加速度等 运动学约束:限制连杆结构的运动范围 运动学仿真:通过计算机模拟连杆结构的运动过程
平面连杆结构的形状优化
优化目标:提 高连杆结构的 稳定性和刚度
优化方法:有 限元分析、拓
扑优化等
优化参数:连 杆的长度、宽
度、厚度等
优化效果:提 高连杆结构的 承载能力和使
用寿命
平面连杆结构的拓扑优化
拓扑优化:通过改变材料的分布和形状, 约束条件:结构的刚度、强度、稳定
以实现最优的结构性能
性等性能要求
目标函数:最小化重量或体积,同时 满足给定的性能要求
优化方法:遗传算法、粒子群算法、 模拟退火算法等
设计变量:材料的分布和形状
应用领域:汽车、航空航天、机械制 造等
机械原理课程设计matlab程序及成果图

Wjr_main.m%1.输入已知数据clear;l2=0.1605;%AB的长度单位ml4=0.6914;%CD的长度单位ml5=0.2074;%DE的长度单位ml1=0.370;%AC的长度单位ml1p=0.6572;%CF的长度单位momg2=8.378;af2=0;hd=pi/180;du=180/pi;%2.调用子函数abc.m计算牛头刨机构位移,角速度,角加速度for n1=1:689;tt2(n1)=-0.4488+(n1-1)*hd;ll=[l2,l4,l5,l1,l1p];[tt,omg,af]=abc(tt2(n1),omg2,af2,ll);s4(n1)=tt(1);tt4(n1)=tt(2);tt5(n1)=tt(3);sE(n1)=tt(4);v34(n1)=omg(1);omg4(n1)=omg(2);omg5(n1)=omg(3);vE(n1)=omg(4);a3(n1)=af(1);af4(n1)=af(2);af5(n1)=af(3);aE(n1)=af(4);end%3.位移,角速度,角加速度figure(1);n1=1:689;t=(n1-1)*pi/180;subplot(2,2,1); %绘角位移及位移线图plot(t,tt4*du,'r-.');grid on;hold on;axis auto;[haxes,hline1,hine2]=plotyy(t,tt5*du,t,sE);grid on;hold on;xlabel('时间/份');axes(haxes(1));ylabel('角位移/\circ');axes(haxes(2));ylabel('位移/m');hold on;grid on;text(1.15,-0.65,'tt_4');text(3.4,0.27,'tt_5');text(2.25,-0.15,'s_E');subplot(2,2,2); %绘角速度及速度线图plot(t,omg4,'r-.');grid on;hold on;axis auto;[haxes,hline1,hline2]=plotyy(t,omg5,t,vE); grid on;hold on;xlabel('时间/份')axes(haxes(1));ylabel('角速度/rad\cdots^{-1}')axes(haxes(2));ylabel('速度/m\cdots^{-1}')hold on;grid on;text(3.1,0.35,'\omg_4')text(2.1,0.1,'\omg_5')text(5.5,0.45,'v_E')subplot(2,2,3); %绘角加速度和加速度图plot(t,af4,'r-.');grid on;hold on;axis auto;[haxes,hline1,hline2]=plotyy(t,af5,t,aE); grid on;hold on;xlabel('时间/份')axes(haxes(1));ylabel('角加速度/rad\cdots^{-2}')axes(haxes(2));ylabel('加速度/m\cdots^{-2}')hold on;text(1.5,0.3,'\af_4')text(3.5,0.51,'\af_5')text(1.5,-0.11,'a_E')wjr_abc.mfunction[tt,omg,af]=abc(tt2,omg2,af2,ll)l2=ll(1);l4=ll(2);l5=ll(3);l1=ll(4);l1p=ll(5);%1.计算角位移和线位移s4=sqrt((l2*cos(tt2))*(l2*cos(tt2))+(l1+l2*sin(tt2))*(l1+l2*sin(tt2))); tt4=acos((l2*cos(tt2))/s4);tt5=asin((l1p-l4*sin(tt4))/l5);sE=l4*cos(tt4)+l5*cos(tt5);tt(1)=s4;tt(2)=tt4;tt(3)=tt5;%2.计算角速度和线速度A=[cos(tt4),-s4*sin(tt4),0,0; %速度分析矩阵之从动件位置参数矩阵sin(tt4),s4*cos(tt4),0,0;0,-l4*sin(tt4),-l5*sin(tt5),-1;0,l4*cos(tt4),l5*cos(tt5),0];B=[-l2*sin(tt2); %原动件位置参数矩阵l2*cos(tt2);0;0];omg=A\(omg2*B);v34=omg(1);omg4=omg(2);omg5=omg(3);vE=omg(4);%计算角加速度和加速度A=[cos(tt4),-s4*sin(tt4),0,0; %速度分析矩阵之从动件位置参数sin(tt4),s4*cos(tt4),0,0;0,-l4*sin(tt4),-l5*sin(tt5),-1;0,l4*cos(tt4),l5*cos(tt5),0];At=[-omg4*sin(tt4),-v34*sin(tt4)-s4*omg4*cos(tt4),0,0;omg4*cos(tt4),v34*cos(tt4)-s4*omg4*sin(tt4),0,0;0,-l4*omg4*cos(tt4),-l5*omg5*cos(tt5),0;0,-l4*omg4*sin(tt4),-l5*omg5*sin(tt5),0];Bt=[-l2*omg2*cos(tt2);-l2*omg2*sin(tt2);0;0];af=A\(-At*omg+omg2*Bt);a34=af(1);af4=af(2);af5=af(3);aE=af(4);wjr_force.m%1.输入已知数据clear;l2=0.1605;%AB的长度单位ml4=0.6914;%CD的长度单位ml5=0.2074;%DE的长度单位ml1=0.370;%AC的长度单位ml1p=0.6572;%CF的长度单位momg2=8.378;%单位rad/shd=pi/180;du=180/pi;H=0.6;%行程单位msEmax=0.5046; sEmin=0.0954;%单位mJs4=0.9; Js5=0.015;%单位kgm^2g=9.8;%单位m/s^2m4=22; m5=3; m6=52;%kgG4=196; G5=29.4; G6=509.6;%单位NFc=1400;%2.机构运动分析% 位移及角位移for n1=1:689;tt2(n1)=-0.4488+(n1-1)*hd;s4(n1)=sqrt((l2*cos(tt2(n1)))*(l2*cos(tt2(n1)))+(l1+l2*sin(tt2(n1)))*(l1+l2 *sin(tt2(n1))));tt4(n1)=acos((l2*cos(tt2(n1)))/s4(n1));tt5(n1)=asin((l1p-l4*sin(tt4(n1)))/l5);sE(n1)=l4*cos(tt4(n1))+l5*cos(tt5(n1));end%2.计算角速度和线速度for n1=1:689;A=[cos(tt4(n1)),-s4(n1)*sin(tt4(n1)),0,0; %速度分析矩阵之从动件位置参数sin(tt4(n1)),s4(n1)*cos(tt4(n1)),0,0;0,-l4*sin(tt4(n1)),-l5*sin(tt5(n1)),-1;0,l4*cos(tt4(n1)),l5*cos(tt5(n1)),0];B=[-l2*sin(tt2(n1)); %原动件位置参数矩阵l2*cos(tt2(n1));0;0];omg=A\(omg2*B);v34(n1)=omg(1);omg4(n1)=omg(2);omg5(n1)=omg(3);vE(n1)=omg(4);%计算角加速度和加速度A=[cos(tt4(n1)),-s4(n1)*sin(tt4(n1)),0,0; %速度分析矩阵之从动件位置参数sin(tt4(n1)),s4(n1)*cos(tt4(n1)),0,0;0,-l4*sin(tt4(n1)),-l5*sin(tt5(n1)),-1;0,l4*cos(tt4(n1)),l5*cos(tt5(n1)),0];At=[-omg4(n1)*sin(tt4(n1)),-v34(n1)*sin(tt4(n1))-s4(n1)*omg4(n1)*cos(tt4(n1)),0,0;omg4(n1)*cos(tt4(n1)),v34(n1)*cos(tt4(n1))-s4(n1)*omg4(n1)*sin(tt4(n1 )),0,0;0,-l4*omg4(n1)*cos(tt4(n1)),-l5*omg5(n1)*cos(tt5(n1)),0;0,-l4*omg4(n1)*sin(tt4(n1)),-l5*omg5(n1)*sin(tt5(n1)),0];Bt=[-l2*omg2*cos(tt2(n1));-l2*omg2*sin(tt2(n1));0;0];af=A\(-At*omg+omg2*Bt);a34(n1)=af(1);af4(n1)=af(2);af5(n1)=af(3);aE(n1)=af(4);end%3.机构的力平衡计算for n1=1:689;%计算各铰链点坐标xa=0;ya=l1;xb(n1)=l2*cos(tt2(n1));yb(n1)=l1+l2*sin(tt2(n1));xc=0;yc=0;xd(n1)=l4*cos(tt4(n1));yd(n1)=l4*sin(tt4(n1));xe(n1)=sE(n1);ye=l1p;%计算各质心坐标xs4(n1)=(xc+xd(n1))/2;ys4(n1)=(yc+yd(n1))/2;xs5(n1)=(xd(n1)+xe(n1))/2;ys5(n1)=(yd(n1)+ye)/2;xs6=0.15;%各质心点加速度as4x(n1)=-l4*(af4(n1)*sin(tt4(n1))+omg4(n1)^2*cos(tt4(n1)))/2;as4y(n1)=l4*(af4(n1)*cos(tt4(n1))-omg4(n1)^2*sin(tt4(n1)))/2;adx=-l4*(af4(n1)*sin(tt4(n1))+omg4(n1)^2*cos(tt4(n1)));ady=l4*(af4(n1)*cos(tt4(n1))-omg4(n1)^2*sin(tt4(n1)));as5x(n1)=adx+l5*(af5(n1)*sin(tt5(n1))+omg5(n1)^2*cos(tt5(n1)))/2; as5y(n1)=ady+l5*(af5(n1)*cos(tt5(n1))-omg5(n1)^2*sin(tt5(n1)))/2; as6(n1)=aE(n1);%惯性力及惯性力矩F4x(n1)=-m4*as4x(n1);F4y(n1)=-m4*as4y(n1);F5x(n1)=-m5*as5x(n1);F5y(n1)=-m5*as5y(n1);F6(n1)=-m6*as6(n1);M4(n1)=-Js4*af4(n1);M5(n1)=-Js5*af5(n1);%未知力系数矩阵xya=zeros(15);xya(1,2)=-1;xya(1,4)=-1;xya(2,3)=-1;xya(2,5)=-1;xya(3,1)=1;xya(3,4)=yb(n1)-ya;xya(3,5)=xa-xb(n1);xya(4,4)=1;xya(4,6)=-1;xya(5,5)=1;xya(5,7)=-1;xya(6,6)=cos(tt4(n1));xya(6,7)=sin(tt4(n1));xya(7,6)=1; xya(7,8)=-1;xya(7,10)=-1;xya(8,7)=1;xya(8,9)=-1;xya(8,11)=-1;xya(9,6)=ys4(n1)-yb(n1);xya(9,7)=xb(n1)-xs4(n1);xya(9,8)=yc-ys4(n1); xya(9,9)=xs4(n1)-xc;xya(9,10)=yd(n1)-ys4(n1);xya(9,11)=xs4(n1)-xd(n1);xya(10,10)=1;xya(10,12)=-1;xya(11,11)=1;xya(11,13)=-1;xya(12,10)=ys5(n1)-yd(n1); xya(12,11)=xd(n1)-xs5(n1);xya(12,12)=ye-ys4(n1);xya(12,13)=xs5(n1)-xe(n1);xya(13,12)=1;xya(14,13)=1;xya(14,14)=-1;xya(15,13)=xs6;xya(15,15)=1;%已知力矩阵if vE(n1)<0&sE(n1)>=(sEmin+0.05*H)&sE(n1)<=(sEmax-0.05*H)D=[0;0;0;0;0;0;-F4x(n1);-F4y(n1)+G4;-M4(n1);-F5x(n1);-F4y(n1)+G5;-M5( n1);-Fc-F6(n1);G6;0;];elseD=[0;0;0;0;0;0;-F4x(n1);-F4y(n1)+G4;-M4(n1);-F5x(n1);-F4y(n1)+G5;-M5( n1);-F6(n1);G6;0;];end%未知力矩阵FR=inv(xya)*D;M2(n1)=FR(1);FR12x(n1)=FR(2);FR12y(n1)=FR(3);FR45x(n1)=FR(10);FR45y(n1)=FR(11);FR16(n1)=FR(14);M6(n1)=FR(15);end%4.输出力的分析图figure(2);n1=1:689;t=(n1-1)*2*pi/360;subplot(2,2,1); %绘平衡力矩图plot(t,M2);grid on;hold on;axis auto;title('平衡力矩M_2')xlabel('时间/份');ylabel('力矩/N\cdotm');hold on;grid on;text(3.8,880,'M_2');subplot(2,2,2); %绘A处x方向约束反力即FR12x plot(t,FR12x,'-');grid on;hold on;axis auto;title('转动副A处约束反力')xlabel('时间/份');ylabel('力/N');hold on;grid on;text(1.1,5000,'F_R_1_2_x')plot(t,FR12y,'r-.'); %绘A处y方向约束反力即FR12y grid on;hold on;text(1.1,-3000,'F_R_1_2_y')subplot(2,2,3); %绘移动副FR16plot(t,-FR16);grid on;hold on;axis auto;title('移动副6约束反力F_R_1_6')xlabel('时间/份')ylabel('力/N')grid on;hold on;text(1.5,3100,'F_R_1_6')subplot(2,2,4); %绘转动副D处约束反力plot(t,FR45x,'-');grid on;hold on;axis auto;title('转动副D处约束反力')xlabel('时间/份')ylabel('力/N')grid on;hold on;text(1.1,-900,'F_R_4_5_x')plot(t,FR45y,'r-.');grid on;hold on;text(1.1,-3700,'F_R_4_5_y')。
matlab机械原理运动解析

matlab机械原理运动解析MATLAB机械原理运动解析是指使用MATLAB软件进行机械系统的运动学和动力学分析的过程。
通过建立数学模型,运用MATLAB进行编程计算,可以实现对机械系统的运动规律、动态特性和性能进行评估和预测。
具体来说,MATLAB机械原理运动解析包括以下步骤:1.建立数学模型:根据机械系统的物理模型,建立相应的数学模型,包括运动学和动力学方程。
这些方程可以描述系统的位移、速度、加速度、力矩等物理量之间的关系。
2.编写MATLAB程序:根据建立的数学模型,使用MATLAB编程语言编写程序,进行数值计算和分析。
MATLAB提供了丰富的数值计算函数库和图形界面工具,方便用户进行数据处理和可视化。
3.数值求解:通过MATLAB的数值计算功能,求解数学模型中的方程,得到机械系统的运动学和动力学特性。
这包括求解位置、速度、加速度等物理量的时间历程,以及分析系统的稳定性和振动等动态行为。
4.结果分析和优化:根据计算结果,对机械系统的性能进行分析和评估。
如果需要改进系统的性能,可以对数学模型进行优化设计,并重新进行数值计算和验证。
至于具体的MATLAB机械原理运动解析示例,比如平面连杆机构的分析,可以通过封闭矢量多边形法求解位置方程,得到构件的位置、速度和加速度;或者采用解析法进行机构运动分析,通过建立数学模型并对其进行封闭矢量多边形法求解,得到构件的运动规律。
此外,还可以使用MATLAB对其他类型的机械系统进行运动学和动力学分析,例如齿轮传动系统、凸轮机构等。
总之,MATLAB机械原理运动解析是一种基于数学模型的计算机辅助分析方法,通过MATLAB编程实现机械系统的运动学和动力学分析,有助于优化机械系统的设计和性能。
机械原理matlab编程

机械原理(Matlab绘图)专业班级学号姓名:图一:导杆的角位移曲线和刨刀的位移曲线x1=linspace(0,2*pi,100);l1=100;l3=360;l4=200;l6=200;y=336;w1=2*pi;x3=atan((l6+l1*sin(x1))./(l1*cos(x1)));for i = 1 : 100;if x3(i)<0x3(i)=x3(i)+pi;endendS3=l1*cos(x1)./cos(x3);V23=(-1)*w1*l1*sin(x1-x3);w3=w1*l1*cos(x1-x3)./S3;a23=w3.^2.*S3-w1.^2*l1*cos(x1-x3);A3=(w1.^2.*l1.*sin(x3-x1)-2.*w3.*V23)./S3;x4= atan((y-l3*sin(x3))./l4);Se=l3*cos(x3)+l4*cos(x4);w4=(-1)*w3.*l3.*cos(x3)./(l4.*cos(x4));Ve=(-1)*w3.*l3.*sin(x3-x4)./cos(x4);A4=(x3.^2.*l3.*sin(w3)+x4.^2.*l4.*sin(x4)-A3.*l3.*cos(x3))./(l4.*cos(x4)); ae=(-1)*(A3.*l3.*sin(x3-x4)+w3.^2.*l3.*cos(x3-x4)-w4.^2.*l4)./cos(x4); plotyy(180*x1./pi,180*x3./pi,180*x1./pi,Se/1000);xlabel('x1/(°)'),ylabel('x3(°)');title('导杆的角位移曲线和刨刀的位移曲线');text(150,108,'x3');text(200,60,'Se');grid on;plotedit on;图二:导杆的角速度曲线和刨刀的速度曲线x1=linspace(0,2*pi,100);l1=100;l3=360;l4=200;l6=200;y=336;w1=2*pi;x3=atan((l6+l1*sin(x1))./(l1*cos(x1)));for i = 1 : 100;if x3(i)<0x3(i)=x3(i)+pi;endendS3=l1*cos(x1)./cos(x3);V23=(-1)*w1*l1*sin(x1-x3);w3=w1*l1*cos(x1-x3)./S3;a23=w3.^2.*S3-w1.^2*l1*cos(x1-x3);A3=(w1.^2.*l1.*sin(x3-x1)-2.*w3.*V23)./S3;x4= atan((y-l3*sin(x3))./l4);Se=l3*cos(x3)+l4*cos(x4);w4=(-1)*w3.*l3.*cos(x3)./(l4.*cos(x4));Ve=(-1)*w3.*l3.*sin(x3-x4)./cos(x4);A4=(x3.^2.*l3.*sin(w3)+x4.^2.*l4.*sin(x4)-A3.*l3.*cos(x3))./(l4.*cos(x4)); ae=(-1)*(A3.*l3.*sin(x3-x4)+w3.^2.*l3.*cos(x3-x4)-w4.^2.*l4)./cos(x4); plotyy(180*x1./pi,w3,180*x1./pi,Ve/1000);xlabel('x1/(°)'),ylabel('w3(rad/s)');title('导杆的角速度曲线和刨刀的速度曲线');grid on;text(100,-5,'Ve');text(100,1.8,'w3');axis([0 400 -7 4]);plotedit on;图三:导杆的角加速度曲线和刨刀的加速度曲线x1=linspace(0,2*pi,100);l1=100;l3=360;l4=200;l6=200;y=336;w1=2*pi;x3=atan((l6+l1*sin(x1))./(l1*cos(x1)));for i = 1 : 100;if x3(i)<0x3(i)=x3(i)+pi;endendS3=l1*cos(x1)./cos(x3);V23=(-1)*w1*l1*sin(x1-x3);w3=w1*l1*cos(x1-x3)./S3;a23=w3.^2.*S3-w1.^2*l1*cos(x1-x3);A3=(w1.^2.*l1.*sin(x3-x1)-2.*w3.*V23)./S3;x4= atan((y-l3*sin(x3))./l4);Se=l3*cos(x3)+l4*cos(x4);w4=(-1)*w3.*l3.*cos(x3)./(l4.*cos(x4));Ve=(-1)*w3.*l3.*sin(x3-x4)./cos(x4);A4=(x3.^2.*l3.*sin(w3)+x4.^2.*l4.*sin(x4)-A3.*l3.*cos(x3))./(l4.*cos(x4)); ae=(-1)*(A3.*l3.*sin(x3-x4)+w3.^2.*l3.*cos(x3-x4)-w4.^2.*l4)./cos(x4); plotyy(180*x1./pi,A3,180*x1./pi,ae/1000);xlabel('x1/(°)'),ylabel('A3(rad/s^2)'),grid;title('导杆的角加速度曲线和刨刀的加速度曲线');text(250,25,'ae');text(300,50,'A3');plotedit on;图四:凸轮从动件位移曲线h=20;F1=2*pi/3;F2=pi/2;i=1;for x=0:0.01:2*pi;if x>=0&x<=2*pi/3;S(i)=h*(1-cos(pi*x./F1))./2;elseif x>=2*pi/3&x<=pi;S(i)=h;elseif x>=pi&x<=5*pi/4;S(i)=h-2*h*(x-pi).^2./(F2.^2);elseif x>=5*pi/4 &x<=3*pi/2;S(i)= 2*h*(F2-x+pi).^2./(F2.^2); elseif x>=3*pi/2 &x<=2*pi;S(i)=0;endi=i+1;x=0:0.01:2*pi;plot(x,S);title('从动件位移曲线');axis([0 7 0 25]);xlabel('x/(rad)');ylabel('S/(mm)');grid on;图五:凸轮的理论轮廓曲线和实际轮廓曲线e=10;Rt=10;Rb=25;w=2*pi;F1=2*pi/3;F2=pi/2;i=1;for f=0:0.01:2*pi;if f>=0&f<=2*pi/3;S(i)=h*(1-cos(pi*f./F1))./2;elseif f>=2*pi/3&f<=pi;S(i)=h;elseif f>=pi&f<=5*pi/4;S(i)=h-2*h*(f-pi).^2./(F2.^2);elseif f>=5*pi/4 &f<=3*pi/2;S(i)= 2*h*(F2-f+pi).^2./(F2.^2);elseif f>=3*pi/2 &f<=2*pi;S(i)=0;endi=i+1;endf=0:0.01:2*pi;s0=sqrt((Rb.^2)-(e.^2));x =e*cos(f)+(s0+S).*sin(f);y =(s0+S).*cos(f)-e*sin(f);d1=e*(-1).*sin(f).*w+(s0+S).*cos(f).*w;d2=(s0+S).*sin(f).*(-1).*w-e*cos(f).*w;x1=x+Rt*d2./sqrt((d1.^2)+(d2.^2));y1=y-Rt*d1./sqrt((d1.^2)+(d2.^2));plot(x,y,'k-',x1,y1,'k-.');title('凸轮的理论轮廓曲线和实际轮廓曲线'); text(-10,-30,'实际轮廓曲线');text(-10,-40,'理论轮廓曲线');axis([-40 50 -55 40 ]);hold on;plot(0,0);text(0,-3,'O');。
机械原理matlab分析大作业3-28
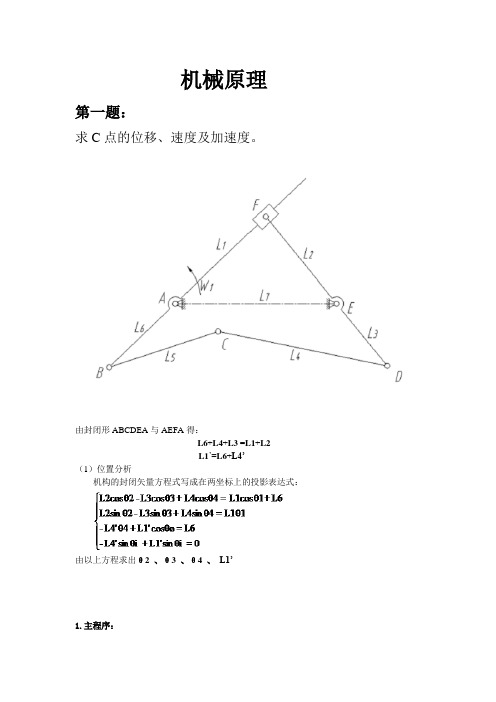
机械原理第一题:求C点的位移、速度及加速度。
由封闭形ABCDEA与AEFA得:L6+L4+L3 =L1+L2L1’=L6+L4’(1)位置分析机构的封闭矢量方程式写成在两坐标上的投影表达式:由以上方程求出θ2 、θ3 、θ4 、L1’1.主程序:%输入已知数据l2=60;l3=35;l4=75;l5=50;l6=40;l7=70;hd=pi/180;du=180/pi;omega1=10;alpha1=0;%调用子函数计算角位移,角速度及角加速度for n1=1:66 %曲柄转角范围theta1(n1)=(n1-1)*hd;ll=[l2,l3,l4,l5,l6,l7];[theta,omega,alpha]=six_bar(theta1(n1),omega1,ll);l1(n1)=theta(1);theta2(n1)=theta(2);theta4(n1)=theta(3);theta3(n1)=theta(4);v1(n1)=omega(1);omega2(n1)=omega(2);omega3(n1)=omega(3);omega4(n1)=omega(4);a1(n1)=alpha(1);alpha2(n1)=alpha(2);alpha3(n1)=alpha(3);alpha4(n1)=alpha(4);e nd%图像输出figure(1);n1=1:66;t=(n1-1)*2*pi/360;subplot(2,2,1);%滑块F线位移L1图像输出plot(theta1*du,l1,'k');title('L1线位移图');xlabel('角位移\theta_1/\circ')ylabel('线位移/mm')grid on;hold on;gtext('L1')pause(1);subplot(2,2,2);%theta2、theta3、theta4角位移图像输出plot(theta1*du,theta2*du,'g',theta1*du,theta3*du,'r',theta1*du,th eta4*du);title('\theta_2、\theta_3、\theta_4角位移图');xlabel('角位移\theta_1/\circ')ylabel('角位移/\circ')grid on;hold on;legend('\theta_2','\theta_3','\theta_4');pause(1);subplot(2,2,3);%滑块F的速度图像输出plot(theta1*du,v1,'k');title('滑块F的速度图');xlabel('角位移\theta_1/\circ')ylabel('速度/mm\cdots^{-1}')grid on;hold on;gtext('v1')pause(1);subplot(2,2,4);%滑块F的加速度图像输出plot(theta1*du,a1,'k');title('滑块F的加速度图');axis auto;xlabel('角位移\theta_1/\circ')ylabel('加速度/mm\cdots^{-2}')grid on;hold on;gtext('a1');pause(5);figure(2);subplot(1,2,1);%omega2、omega3和omega4角位移图像输出plot(theta1*du,omega2,'g',theta1*du,omega3,'r',theta1*du,omega4,' b');title('\omega_2、\omega_3、\omega_4角速度图');axis auto;grid on;hold on;xlabel('角位移\theta_1/\circ')ylabel('角速度/rad\cdots^{-1}')box on;legend('\omega_2','\omega_3','\omega_4');pause(1);subplot(1,2,2);%alpha2、alpha3和alpha4角加速度图像输出plot(theta1*du,alpha2,'g',theta1*du,alpha3,'r',theta1*du,alpha4,' b');title('\alpha_2、\alpha_3、\alpha_4角加速度图');axis auto;grid on;hold on;xlabel('角位移\theta_1/\circ')ylabel('角加速度/rad\cdots^{-2}')box on;legend('\alpha_2','\alpha_3','\alpha_4');pause(5);figure(3);xC=-l6*cos(theta1+pi)+l5*cos(theta3);yC=l6*sin(theta1+pi)+l5*sin(theta3);% rC=sqrt(xC.*xC+yC.yC)vCX=-omega1*l6*sin(theta1+pi)-omega3*l5.*sin(theta3);vCY=omega1*l6*cos(theta1+pi)+omega3*l5.*cos(theta3);% v3=sqrt(vCX.*vCX+vCY.*vCY);subplot(2,2,1);hold on;grid on;%C点x、y方向位移图像输出plot(theta1*du,xC,'r',theta1*du,yC);axis auto;hold on;grid on;title('C点位移图');xlabel('角位移\theta_1/\circ')ylabel('位移/mm')grid on;hold on;legend('xC','yC');pause(1);subplot(2,2,2);grid on;hold on;%C点x、y方向速度图像输出plot(theta1*du,vCX,'k',theta1*du,vCY);title('C点速度图');xlabel('角位移\theta_1/\circ')ylabel('速度/mm\cdots^{-1}')legend('vCX','vCY');pause(1);aCX=omega1*omega1*l6*cos(theta1)-omega3.*omega3.*l5.*cos(theta3)-alpha3.*l5.*sin(theta3);aCY=omega1*omega1*l6*sin(theta1)-omega3.*omega3.*l5.*sin(theta3)+ alpha3.*l5.*cos(theta3);%a3=sqrt(aCX.*aCX+aCY.*aCY);subplot(2,2,3);%C点x、y方向加速度图像输出plot(theta1*du,aCX,'r',theta1*du,aCY,'b');title('C点加速度图');grid on;hold on;xlabel('角位移\theta_1/\circ')ylabel('加速度/mm\cdots^{-2}')box on;legend('aCX','aCY');%主程序结束2.子程序:%子函数function[theta,omega,alpha]=six_bar(theta1,omega1,ll)l2=ll(1);l3=ll(2);l4=ll(3);l5=ll(4);l6=ll(5);l7=ll(6);%1.计算角位移和线位移l1=l7*cos(theta1)+sqrt((l7*cos(theta1))*(l7*cos(theta1))-l7*l7+l2 *l2);theta2=asin((l1*sin(theta1))/l2);A=2*l4*(l6*sin(theta1)-l3*sin(theta2).*sin(theta2));B=2*l4*(l6*cos(theta1)+l7-l3*cos(theta2));C=l4*l4-l5*l5+l6*l6+l7*l7+l3*l3-2*l3*l6*(cos(theta1)*cos(theta2)+ sin(theta1)*sin(theta1))-2*l7*l3*cos(theta2)+2*l6*l7*cos(theta1); theta4=2*atan((A+sqrt(A.*A+B.*B-C.*C))/(B-C));theta3=asin((l6*sin(theta1)+l4*sin(theta4)-l3*sin(theta2))/l5); theta(1)=l1;theta(2)=theta2;theta(3)=theta4;theta(4)=theta3;%2利用矩阵计算角速度和线速度D=[-l5*sin(theta3),l4*sin(theta4),-l3*sin(theta2+pi),0l5*cos(theta3),-l4*cos(theta4),-l3*cos(theta2+pi),00,0,l2*sin(theta2),cos(theta1)0,0,-l2*cos(theta2),sin(theta1)];E=[l6*sin(theta1+pi);-l6*cos(theta1+pi);l1*sin(theta1);-l1*cos(theta1)];omega=D\(omega1*E);v1=omega(4);omega2=omega(3);omega3=omega(1);omega4=omega(2);%3利用矩阵计算角加速度和加速度Dt=[-l5*omega3*cos(theta3),l4*omega4*cos(theta4),-l3*omega2*cos(t heta2),0-l5*omega3*sin(theta3),l4*omega4*sin(theta4),-l3*omega2*sin(theta 2),00,0,l2*omega2*cos(theta2),-omega1*sin(theta1)0,0,l2*omega2*sin(theta2),omega1*cos(theta1)];Et=[l6*omega1*cos(theta1);l6*omega1*sin(theta1);l1*omega1*cos(theta1)+v1*sin(theta1);l1*omega1*sin(theta1)-v1*cos(theta1)];alpha=D\(-Dt*omega+omega1*Et);a1=alpha(4);alpha2=alpha(3);alpha3=alpha(1);alpha4=alpha(2);%3子程序结束3.图像输出:%1.滑块F线位移L1图像输出%2.theta2、theta3、theta4角位移图像输出%3.滑块F的速度图像输出%4.滑块F的加速度图像输出%5.omega2、omega3和omega4角位移图像输出%6.alpha2、alpha3和alpha4角加速度图像输出%7.C点x、y方向位移图像输出%8.C点x、y方向速度图像输出%9.C点x、y方向加速度图像输出。
机械原理matlab课程设计

机械原理matlab课程设计一、教学目标本课程的学习目标主要包括知识目标、技能目标和情感态度价值观目标。
知识目标要求学生掌握机械原理的基本概念、理论和方法;技能目标要求学生能够运用MATLAB软件进行机械系统仿真和分析;情感态度价值观目标要求学生培养创新意识、团队合作精神和自主学习能力。
通过本课程的学习,学生将能够:1.描述和解释机械原理的基本概念和理论。
2.使用MATLAB软件进行机械系统仿真和分析。
3.提出问题、解决问题并开展创新设计。
4.能够进行团队合作,共同完成项目任务。
二、教学内容教学内容将根据课程目标进行选择和,确保内容的科学性和系统性。
教学大纲将明确教学内容的安排和进度,指出教材的章节和列举内容。
主要内容包括:1.机械原理的基本概念和理论,包括力学、动力学、运动学等方面。
2.MATLAB软件的基本操作和功能,包括矩阵运算、绘图、编程等。
3.机械系统仿真的方法和技巧,包括模型建立、参数调整、结果分析等。
4.机械系统设计案例分析,包括机器人的运动控制、机构的优化设计等。
三、教学方法为了激发学生的学习兴趣和主动性,将采用多种教学方法。
包括讲授法、讨论法、案例分析法和实验法等。
1.讲授法:通过教师的讲解和演示,向学生传授基本概念和理论知识。
2.讨论法:学生进行小组讨论,促进学生之间的交流和思维碰撞。
3.案例分析法:通过分析实际案例,引导学生运用所学知识解决实际问题。
4.实验法:安排实验课程,让学生亲自动手进行实验操作和数据分析。
四、教学资源为了支持教学内容和教学方法的实施,将选择和准备适当的教学资源。
包括教材、参考书、多媒体资料和实验设备等。
1.教材:选择权威、实用的教材,作为学生学习的主要参考资料。
2.参考书:推荐一些相关的参考书籍,供学生深入学习和拓展知识。
3.多媒体资料:制作精美的PPT、教学视频等多媒体资料,增强课堂教学的趣味性和效果。
4.实验设备:准备必要的实验设备,让学生能够进行实际操作和验证。
机械原理matlab作业

1.在图示的铰链四杆机构中,AB 为主动杆,以s rad /47.10=ω匀角速度逆时针旋转,各杆长度分别为mm l mm l mm l mm l 80,100,120,404321====,连杆点F 的位置是FE ⊥BC ,BE 长mm S 60=,EF 长mm T 10=,选取直角坐标系如图所示。
求当曲柄1与x 轴正向夹角为 360~01=ϕ时,连杆2和摇杆3所转过的角度2ϕ、3ϕ以及它们的角速度和角加速度2ω、3ω、2α、3α,并求出连杆点F 的各位置坐标、速度和加速度。
规定ϕ角从轴x 正向测量时,逆时针为正,反之为负。
y机械原理作业撰写要求机械原理电算分析是机械原理课程学习的重要环节,是检验学生综合素质与实践能力培养的手段。
1、作业内容顺序作业内容顺序一般为:题目、数学模型、程序设计、计算结果和附件M 文件。
2、作业格式要求作业格式要求见摸板,纸张大小一律使用A4复印纸。
3. 书写规定 3.1公式公式号按顺序编号,如(2)表示第2个公式。
公式应采用公式编辑器输入,选择默认格式,公式号右对齐,公式调整至基本居中。
3.2 插表每个表格均应有标题(由表序和表名组成),如第一个插表的序号为“表1”。
表格统一用三线表,表序与表名之间空一格,表名中不允许使用标点符号,表名后不加标点。
标题置于表上,要求用5号字(包括表中的内容)。
3.3 插图插图应与文字紧密配合,文图相符,内容正确。
图题置于图的下方,要求用5号字。
插图应采用AutoCAD 绘制,然后拷贝粘贴到Word 文档,以利于以后编辑。
3.4物理量的名称、符号和计量单位物理量的名称、符号和计量单位应统一按照机械原理教科书的规定书写,某一量的名称、符号和计量单位应与教科书的规定相一致。
4. 排版要求4.1正文字体要求、每部分标题左顶边、小三宋体加粗。
正文文字用宋体小四号汉字和四号“Times New Roman”英文字体,每自然段首行缩进2个字符。
matlab在机械原理中的应用实例

matlab在机械原理中的应用实例在机械原理中,MATLAB是一种常用的计算工具,可以应用于诸多领域,包括机械设计、力学分析、动力学仿真等。
下面将介绍几个MATLAB在机械原理中的应用实例。
1.机构设计与分析MATLAB可以用于机构的设计和分析,例如平面机构、空间机构、曲柄机构等。
它提供了多种机构建模方法,如刚体模型、柔性模型等。
利用MATLAB的强大计算能力和绘图功能,可以进行机构分析和优化。
例如,可以计算机构的运动学性能、动力学性能和静力学性能,并进行动态仿真。
2.动力学仿真MATLAB可以进行各种机械系统的动力学仿真,包括振动系统、运动系统和控制系统。
通过对机械系统建立微分方程或差分方程,利用MATLAB进行数值解求解,并绘制相应的图形,可以得到机械系统的响应。
例如,可以模拟机械系统的自由振动、强迫振动和阻尼振动等。
3.控制系统设计与分析MATLAB在机械原理中的应用还包括控制系统的设计与分析。
通过MATLAB中的控制系统工具箱,可以进行控制系统的模型建立、系统分析和控制器设计。
例如,可以利用MATLAB对机械系统进行稳定性分析、频域分析和时域分析,并设计相应的控制器,实现机械系统的控制。
4.声学分析MATLAB也可以用于机械系统的声学分析。
通过建立机械系统的声学模型,利用MATLAB进行声场分布和声压级分析。
可以计算机械系统的声辐射特性,例如机械振动引起的噪声。
同时,还可以进行声学优化设计,减少机械系统的噪声。
5.优化设计MATLAB在机械原理中广泛应用于优化设计。
通过建立数学模型和定义目标函数,利用MATLAB进行优化计算。
例如,可以利用MATLAB进行机械系统的拓扑优化、形状优化和尺寸优化,实现机械系统的性能优化。
同时,还可以利用MATLAB的优化算法进行参数优化和控制器设计。
综上所述,MATLAB在机械原理中具有广泛的应用,可以应用于机构设计与分析、动力学仿真、控制系统设计与分析、声学分析和优化设计等方面。
机械原理matlab

机械原理matlab
机械原理是研究机械结构运动规律和力学特性以及机械设备的设计、制造、检测和控制等方面的学科。
Matlab是一种功能强大的计算工具,对机械原理的理解和研究也有很大的帮助,以下是一些在机械原理中可以使用Matlab的应用:
1. 动力学模拟:Matlab可以用来建立机械结构的动力学模型,通过求解非线性方程组、微分方程等数学模型,模拟机械结构的运动和力学特性以及其对于外界的响应和输出。
2. 模态分析:Matlab还可以进行机械结构的动态模态分析,计算结构的固有频率、振型和振动特性,以及响应特性等。
这对于机械结构的设计、优化和降噪等方面非常有帮助。
3. 强度计算:Matlab可以计算机械结构的应力、应变等力学参数,分析结构的强度、刚度和稳定性等性能,对于结构设计、提高机械性能和耐久性等方面有很大帮助。
4. 优化设计:Matlab可以结合优化算法进行机械结构的优化设计,如遗传算法、模拟退火算法等,以达到最优性能。
同时,还可以进行优化建模、参数优化和多目标优化等方面的应用。
总之,机械原理中Matlab的应用十分广泛,对于机械结构的建模、分析和优化
等方面都有很大的帮助,可以提高机械设备的性能和效率,降低成本和风险。
机械原理4-23MATLAB平面连杆机构动力学分析

基于MATLAB/Solidworks COSMOSMotion的平面连杆机构动力学分析07208517王锡霖4-23在图示的正弦机构中,已知l AB =100 mm,h1=120 mm,h2 =80 mm,W1 =10 rad/s(常数),滑块2和构件3的重量分别为G2 =40 N和G3 =100 N,质心S2 和S3 的位置如图所示,加于构件3上的生产阻力Fr=400 N,构件1的重力和惯性力略去不计。
试用解析法求机构在Φ1=60°、150°、220°位置时各运动副反力和需加于。
构件1上的平衡力偶Mb分别对三个构件进行受力分析如图:构件3受力图构件2受力图构件1受力图(1)滑块2:V S2 =L AB W1 ①a s2 = L AB W12②构件3:S=L AB sinΦ1 ③V3=L AB W1 COSΦ1 ④a3=-L AB W12 sinΦ1 ⑤(2)确定惯性力:F12=m2as2=(G2/g)LABW12 ⑥F13=m3a3=(G3/g)LABW12sinΦ1 ⑦(3)各构件的平衡方程:构件3:∑Fy=0,FR23 =Fr-F13∑Fx=0,FR4’=FR4∑MS3 =0,FR4=FR23LAcosΦ1/h2构件2:∑Fx=0,FR12x=F12cosΦ1∑Fy=0,FR12y=FR32-F12sinΦ1构件1:∑Fx=0,FR41x=FR12x∑Fy=0,FR41y=FR12y∑MA =0,Mb=FR32LABcosΦ1总共有八个方程,八个未知数。
归纳出一元八次方程矩阵:1 0 0 0 0 0 0 0 FR23 Fr-F130 1 -1 0 0 0 0 0 FR4’ 0-LAB COSΦ1/h20 1 0 0 0 0 0 FR40 0 0 1 0 0 0 0 FR12x = F12cosΦ1-1 0 0 0 1 0 0 0 FR12y -F12sinΦ10 0 0 -1 0 1 0 0 FR41x 00 0 0 0 -1 0 1 0 FR41y 0-LABCOSΦ1 0 0 0 0 0 0 1 Mb 0 AX=B进而可得:X=A\B。
MATLAB在力学、机械中的应用举例

阵除法X=A\B直接来解。在本题中,X和B都是6×1列向量,而A
是6×6阶方阵。
在编写程序时,尽量用文字变量,先输入已知条件,在程序
开始处给它们赋值,这样得出的程序具有一定的普遍性,若要修
改参数,只需修改头几行的数据即可。
MATLAB在力学、机械中的应用举例
◆ MATLAB程序
G1=200; G2=100; L1= 2; L2=sqrt (2); %给原始参数赋值
MATLAB在力学、机械中的应用举例
MATLAB在力学、机械中的应用举例
7.1 理论力学 7.2 材料力学 7.3 机械振动
MATLAB在力学、机械中的应用举例
7.1 理论力学
【例 7-1-1】 给定由N个力 Fi (i=1,2,…,N)组成的平面
任意力系,求其合力。
解:
◆ 建模
本程序可用来对平面任意力系作简化,得出一个合力。求合
值积分的步长是MATLAB按精度自动选取的,其间隔可变,因此dt
要用数组表示。
主程序exn713:
vt=input(′vt=′); vm=input(′vm=′);
%输入主程序及函数程序共用的参数
z0=input(′[x0;y0]=′); %输入数值积分函数需要的参数
tspan=input(′tspan=[t0,tfinal]=′);
%输入数值积分函数需要的参数
[t,z]=ode23(′exn713f′,tspan,z0);
%进行数值积分
plot(z(∶,1),z(∶,2));
%绘图
MATLAB在力学、机械中的应用举例
%在惯性坐标中,M点位置的导数是相对速度,而其二次导数 则为绝对加速度
dt=diff(t); Ldt=length(dt); %为了求导数,先求各时刻处t的增量
机械原理3-28MATLAB平面连杆机构运动分析,解三角函数超越方程

根据第一步得到的数据进行数据输入,运行程序计算各速度值。程序如下:
x2=[x1' p(:,2) p(:,3) p(:,4) 10*ones(15,1) 40*ones(15,1) 50*ones(15,1)... 75*ones(15,1) 35*ones(15,1) 70*ones(15,1) p(:,1) 60*ones(15,1)]; q=zeros(4,15); for m=1:15 y2=rrrvel(x2(m,:)); q(:,m)=y2; end q
norm(f); end; y(1)=lA; y(2)=theta2; y(3)=theta3; y(4)=theta4;
再进行数据输入,运行程序进行运算。这里我们根据上面分析的θ1 的极限 位置取θ1 的范围为 40°~55°并均分成 15 个元素: clc
clear x1=linspace(40*pi/180,55*pi/180,15); x=zeros(length(x1),11); for n=1:15 x(n,:)=[x1(:,n) pi/6 8*pi/9 2*pi/3 40 50 75 35 70 75 60]; end p=zeros(length(x1),4); for k=1:15 y= rrrposi(x(k,:)); p(k,:)=y; end >> p
% while norm(f)>epsilon
J=[0 -x(6)*sin(theta2) x(7)*sin(theta3) -x(8)*sin(theta4);
0 x(6)*cos(theta2) -x(7)*cos(theta3) x(8)*cos(theta4);
cos(x(1)) 0 0 x(11)*sin(theta4); sin(x(1)) 0 0 -x(11)*cos(theta4)]; dth=inv(J)*(-1.0*f); lA=lA+dth(1); theta2=theta2+dth(2); theta3=theta3+dth(3); theta4=theta4+dth(4);
《机械原理MATLAB辅助分析》

《机械原理MATLAB辅助分析》机械原理是机械工程专业的重要课程之一,涉及到力学、材料力学、动力学等方面的内容。
MATLAB作为一种功能强大的数学软件,可以帮助学生更好地理解和分析机械原理的相关问题。
本文将介绍如何使用MATLAB进行机械原理的辅助分析。
首先,MATLAB可以帮助学生进行机械结构的力学分析。
对于一个给定的机械结构,可以通过数学计算和编程来确定其内部的应力、位移等力学参数。
例如,可以利用MATLAB求解一个给定的静力学问题,如弹簧的伸长量、杆件的应力分布等。
通过这种方式,学生可以直观地了解机械结构的力学性能,并更好地理解力学原理。
其次,MATLAB还可以帮助学生进行机械系统的动力学分析。
机械系统的动力学分析主要涉及到运动学和动力学两方面的内容。
运动学分析主要是研究机械系统的位置、速度、加速度等参数的变化规律,而动力学分析则研究机械系统在外力作用下的运动规律。
借助MATLAB的数学计算和编程功能,可以方便地对机械系统的运动学和动力学进行模拟和分析。
例如,可以通过编写MATLAB程序,模拟一个机械系统的运动轨迹,计算其速度和加速度等参数,并根据这些参数来评估机械系统的运动性能。
此外,MATLAB还可以帮助学生进行机械系统的优化设计。
在机械原理中,优化设计是一个重要的研究方向,主要涉及到对机械系统的性能进行改进和优化。
通过利用MATLAB的优化算法和模拟功能,可以对机械系统的结构参数进行优化,并自动最优解。
例如,可以通过编写MATLAB程序,对机械系统的结构参数进行优化,以使其满足一定的性能指标,如最小质量、最大刚度等。
总之,MATLAB作为一种功能强大的数学软件,可以帮助学生更好地理解和分析机械原理的相关问题。
通过利用MATLAB进行力学分析、动力学分析以及优化设计,可以使学生对机械原理的知识和理论得以更加直观和深入的理解,从而提高他们的学习效果和专业素养。
机械原理课程设计Matlab编程

/*Matlab程序*/l1 = 59.1000;l2 = 263.9000;l3=120;l4=266.83;l5=180;l6=45;x2=170;y2=132.7289;w1=9.4248;N=42:10:402;ay=119:10:479a=2*l1*l3*sin(N/180*pi);b=2*l3*(l1*cos(N/180*pi)-l4);c=l2^2-l1^2-l3^2-l4^2+2*l1*l4*cos(N/180*pi);jiao3=2*atan((a- sqrt(a.^2+b.^2-c.^2))./ (b-c))/pi*180+77g=2*l1*l2*sin(N/180*pi);h=2*l2*(l1*cos(N/180*pi)-l4);m=l1^2+l2^2+l4^2-l3^2-2*l1*l4*cos(N/180*pi);jiao2=2*atan((g- sqrt(g.^2+h.^2-m.^2))./ (h-m))/pi*180+77lof=-sqrt(l6^2-x2^2-l5^2+2*l5*x2*cos((180+jiao3)/180*pi)+l5^2*sin(j iao3/180*pi).^2)+y2-l5* sin((180+jiao3)/180*pi)j12=N-(jiao2-77);j32=jiao3-jiao2;j13=(N-(jiao3-77));j23=(jiao2-jiao3);w3=(w1*l1*sin(j12/180*pi))./ (l3*sin(j32/180*pi))w2=(-1*w1*l1*sin(j13/180*pi))./(l2*sin(j23/180*pi))a3=(w1^2*l1*cos(j12/180*pi)+w2.^2*l2-(w3.^2).*(l3*cos(j32/180*pi)) )./ (l3*sin(j32/180*pi))a2=(-w1^2*l1*cos(j13/180*pi)-(w2.^2).*(l2*cos(j23/180*pi))+l3*w3.^ 2)./ (l3*sin(j23/180*pi))jiao4=acos((x2-l5*cos((180+jiao3)/180*pi))/l6)/pi*180w4=((-l5*sin((pi+jiao3)/180*pi)).*w3)./ (l6*sin(jiao4/180*pi))vof=((l5*sin((180+jiao3-jiao4)/180*pi)).*w3).* sin(jiao4/180*pi)aof=(l6*w4.^2+(l5*w3.^2).*(cos((180+jiao3-jiao4)/180*pi))+l5*a3.*si n((180+jiao3-jiao4)/180*pi))./sin(jiao4/180*pi)作图程序:/*F点的位移*/plot(N+77,lof,'-xk')xlabel('AB杆的角度'),ylabel('F点的位移/(mm)')title('F点的位移曲线图')text(100, 171.3339,'初始值= 171.3339')text(425, 171.3339,'最高值= 180')/*F点的速度*/plot(N+77,vof,'-xk')text(100,-285,'初始值= -347.0624')text(390,-430,'终点值= -347.0624')xlabel('AB杆的角度'),ylabel('F点的速度/(mm/s)')title('F点的速度曲线图')/*F点的加速度*/plot(N+77,aof,'-xk')xlabel('AB杆的角度'),ylabel('F点的加速度/(mm/s^2)')title('F点的加速度曲线图')text(100, 1.0e+004 *-0.9848,'初始值= 1.0e+004 *(-0.9048)') text(350, 1.0e+004 *-0.9048,'终点值= 1.0e+004 *(-0.9048)')/*结果*/ay =Columns 1 through 20119 129 139 149 159 169 179 189 199 209 219 229 239 249 259 269 279 289 299 309Columns 21 through 37319 329 339 349 359 369 379 389 399 409 419 429 439 449 459 469 479jiao3 =Columns 1 through 12152.7283 155.6055 159.2201 163.3851 167.9364 172.7308 177.6411 182.5508 187.3495 191.9295 196.1844 200.0109Columns 13 through 24203.3123 206.0053 208.0272 209.3409 209.9360 209.8245 209.0330 207.5944 205.5410 202.9003 199.6946 195.9435Columns 25 through 36191.6697 186.9095 181.7262 176.2288 170.5899 165.0593 159.9573 155.6378 152.4212 150.5209 150.0024 150.7929Column 37152.7283jiao2 =Columns 1 through 1297.9329 96.9493 96.1177 95.4427 94.9235 94.5564 94.3364 94.2587 94.3188 94.5127 94.8367 95.2869Columns 13 through 2495.8585 96.5454 97.3393 98.2294 99.2013 100.2373 101.3154 102.4095 103.4889 104.5187 105.4597 106.2696Columns 25 through 36106.9048 107.3227 107.4861 107.3682 106.9579 106.2651 105.3223 104.1834 102.9167 101.5959 100.2898 99.0551Column 3797.9329lof =Columns 1 through 12171.3339 162.4831 151.6215 139.2662 125.7535 111.3249 96.2283 80.8029 65.5172 50.9387 37.6489 26.1414Columns 13 through 2416.7408 9.5650 4.5415 1.4741 0.1412 0.3882 2.1781 5.5874 10.7654 17.8808 27.0707 38.3902Columns 25 through 3651.7607 66.9223 83.4132 100.6062 117.8015 134.3068 149.4275 162.3850 172.2940 178.3195 179.9923 177.4473Column 37171.3339w3 =Columns 1 through 122.0420 2.88413.54184.0289 4.3651 4.5686 4.6533 4.6279 4.4965 4.2598 3.9173 3.4690Columns 13 through 242.9187 2.2766 1.5612 0.7980 0.0174 -0.7506 -1.4803 -2.1528 -2.7570 -3.2875 -3.7434 -4.1259Columns 25 through 36-4.4354 -4.6697 -4.8213 -4.8744 -4.8021 -4.5650 -4.1167 -3.4196 -2.4746 -1.3428 -0.1370 1.0209Column 372.0420w2 =Columns 1 through 12-1.4343 -1.1068 -0.8180 -0.5658 -0.3428 -0.1403 0.0504 0.2372 0.4268 0.6248 0.8348 1.0577Columns 13 through 241.2907 1.5265 1.7527 1.95262.1078 2.20042.2158 2.1438 1.9799 1.7238 1.3800 0.9564Columns 25 through 360.4649 -0.0783 -0.6512 -1.2249 -1.7619 -2.2168 -2.5411 -2.6940 -2.6601 -2.4610 -2.1504 -1.7915Column 37-1.4343a3 =Columns 1 through 1252.5560 41.5031 31.2310 22.2213 14.4470 7.6608 1.5603 -4.1325 -9.6312 -15.0579 -20.4136 -25.5519Columns 13 through 24-30.1734 -33.8717 -36.2458 -37.0535 -36.3289 -34.3895 -31.7205 -28.8042 -25.9756 -23.3519 -20.8311 -18.1297Columns 25 through 36-14.8311 -10.4321 -4.3902 3.8075 14.5130 27.6704 42.4330 56.8069 67.8232 72.7326 70.6513 63.0454Column 3752.5560a2 =Columns 1 through 1242.6168 37.6998 32.7111 28.4933 25.3433 23.2851 22.2337 22.0665 22.6383 23.7616 25.1694 26.4765Columns 13 through 2427.1651 26.6283 24.2896 19.7685 13.0154 4.3334 -5.7233 -16.5098 -27.4206 -37.9407 -47.6216 -56.0112Columns 25 through 36-62.5725 -66.6194 -67.2958 -63.6367 -54.7645 -40.2872 -20.8999 1.0456 21.6515 36.8894 44.6857 45.7784Column 3742.6168jiao4 =Columns 1 through 1277.1498 82.2481 87.8236 93.1653 97.6943 100.9570 102.6405 102.6068 100.9154 97.8068 93.6522 88.8959Columns 13 through 2484.0113 79.4692 75.7071 73.0882 71.8537 72.0875 73.7150 76.5391 80.2895 84.6612 89.3256 93.9195Columns 25 through 3698.0213 101.1380 102.7329 102.3311 99.6946 94.9908 88.8525 82.3019 76.5687 72.8043 71.7241 73.3615Column 3777.1498w4 =Columns 1 through 12-3.4249 -4.2204 -4.2959 -3.7606 -2.7325 -1.3398 0.2606 1.8815 3.3352 4.4720 5.1962 5.4568Columns 13 through 245.2293 4.5113 3.3352 1.7918 0.0401 -1.7169 -3.2847 -4.5255 -5.3698 -5.7983 -5.8117 -5.4089Columns 25 through 36-4.5802 -3.3225 -1.6778 0.2193 2.1277 3.7480 4.7881 4.9961 4.2100 2.4944 0.2607 -1.8728Column 37-3.4249vof =Columns 1 through 12-347.0624 -492.8494 -603.7818 -681.3764 -732.8054 -766.8573 -789.4516 -800.4475 -793.1801 -757.7000 -686.9200 -582.3864Columns 13 through 24-455.6459 -323.7142 -201.3442 -95.0327 -1.9924 86.4566 179.8406 284.1862 399.4460 519.0511 631.6416 724.6701Columns 25 through 36788.9608 822.4766 830.9271 823.5243 805.0980 769.5568 700.9268 584.3674 420.0967 225.6063 22.9226 -171.8563Column 37-347.0624aof =1.0e+004 *Columns 1 through 12-0.9048 -0.6847 -0.5221 -0.4123 -0.3300 -0.2449 -0.1309 0.0224 0.2041 0.3874 0.5412 0.6412Columns 13 through 240.6754 0.6479 0.5799 0.5058 0.4597 0.4593 0.4981 0.5531 0.5991 0.6163 0.5913 0.5159Columns 25 through 360.3871 0.2120 0.0106 -0.1886 -0.3676 -0.5349 -0.7184 -0.9361 -1.1628 -1.3170 -1.3111 -1.1438Column 37-0.9048。
《机械原理MATLAB辅助分析》

目录
第一章 平面连杆机构的运动分析 第一节 平面连杆机构运动分析概述 第二节 铰链四杆机构的运动分析 第三节 曲柄滑块机构的运动分析 第四节 导杆机构的运动分析 第五节 六杆机构的运动分析 习题
内容提要
李滨城等编著的《机械原理 MATLAB 辅助分析》介绍了数学软件 MATLAB 辅助机械 原理分析的方法。运用解析法,通过建立数学模型,对机构与机器进行精确的分析与综合, 是机械原理学科发展的重要方向。全书分为七章,分别应用 MATLAB 进行了平面连杆机构 的运动分析、平面连杆机构的力分析、连杆机构设计、凸轮机构设计、齿轮机构设计、机械 的运转及其速度波动的调节和机构优化设计,每一专题内容通过数学模型的建立、计算实例 的介绍、MATLAB 程序的编制,深入浅出地介绍了 MATLAB 在机械原理中的应用。书中大 量的程序实例不但实用,更包含作者多年在机械原理教学中使用 MATLAB 的经验。
第四章 凸轮机构设计 第一节 推杆常用的运动规律 第二节 凸轮轮廓曲线的设计 第三节 程序设计实例 习题
第五章 齿轮机构设计 第一节 渐开线函数的计算 第二节 渐开线标准直齿圆柱齿轮的设计计算 第三节 直齿圆柱齿轮机构传动设计计算 第四节 渐开线齿轮的范成
习题 第六章 机械的பைடு நூலகம்转及其速度波动的调节
第一节 机械的运转及其速度波动的调节概述 第二节 机械系统的等效动力学模型 第三节 机械运动方程式 第四节 机械运转的速度波动及其调节方法 习题 第七章 机构优化设计 第一节 平面连杆机构再现已知运动规律的优化设计 第二节 凸轮机构最大压力角及其位置的确定 习题 参考文献
机械原理课程设计用MATLAB做

机械原理课程设计用MATLAB做一、教学目标本课程旨在通过MATLAB软件的应用,让学生掌握机械原理的基本知识和技能,培养学生的创新意识和实践能力。
知识目标:使学生了解机械原理的基本概念、原理和应用,掌握MATLAB在机械原理分析中的基本使用方法。
技能目标:通过案例分析和实践操作,培养学生运用机械原理知识和MATLAB 软件解决实际问题的能力。
情感态度价值观目标:激发学生对机械原理和MATLAB软件应用的兴趣,培养学生的团队协作精神和自主学习能力。
二、教学内容本课程的教学内容主要包括机械原理的基本概念、机构和机器的设计与分析方法,以及MATLAB在机械原理分析中的应用。
教学大纲安排如下:1.机械原理概述:介绍机械原理的基本概念、研究对象和内容。
2.机构分析:讲解各种机构的工作原理和特性,包括齿轮机构、连杆机构等。
3.机器的设计与分析:介绍机器的设计方法和步骤,以及在不同工作条件下机器的性能分析。
4.MATLAB在机械原理分析中的应用:讲解MATLAB软件的基本使用方法,以及如何利用MATLAB进行机械原理分析和设计。
三、教学方法为了提高教学效果,本课程将采用多种教学方法相结合的方式,包括讲授法、案例分析法、实验法和讨论法。
1.讲授法:通过讲解机械原理的基本概念和理论知识,使学生掌握基本原理和方法。
2.案例分析法:通过分析实际案例,让学生了解机械原理在工程中的应用,培养学生的实践能力。
3.实验法:让学生动手操作,利用MATLAB软件进行机械原理分析和设计,提高学生的实际操作能力。
4.讨论法:学生进行分组讨论,培养学生的团队协作精神和批判性思维。
四、教学资源为了支持本课程的教学内容和教学方法,我们将准备以下教学资源:1.教材:《机械原理》,提供机械原理的基本知识和理论。
2.参考书:《MATLAB教程》,介绍MATLAB软件的基本使用方法。
3.多媒体资料:包括教学PPT、视频教程等,辅助学生理解和掌握知识。
