第三章 材料的断裂
第三章-断裂的微观机制

式中, 为取向因子, 接近于1; a 为施加于滑移面的外加切应力。
则垂直与OP面的正应力为:
=_x001A__x001B__x001B__x001A__x001A__x001A__x001
B__x001B__x001B__x001B__x001A__x001B__x001B__x001
或在高应变条件下, 第二相与基体变形不
第3章 断裂的微观机制
3.1 微裂纹形核方式
3.1.2 微孔聚合形成微裂纹
微孔成核与长大的位错模型: 第二相的强度高不可变形
第3章 断裂的微观机制
3.1 微裂纹形核方式
3.1.2 微孔聚合形成微裂纹
微孔形成并逐渐长大后, 微孔与微孔之间的横截面面
积减小, 使得材料所受的应力增大。
形核都是局部应力集中等于原子键合力的结果。
位错塞积应力等于原子键合力从而形成微裂纹是可
能的, 但实验上很难观察到。
裂尖无位错区中应力集中形成微裂纹适合于各种断
裂方式, 而且很容易有透射电镜原位拉伸来证实。
第3章 断裂的微观机制
3.2 位错发射和无位错区
3.2.1 裂纹和位错的交互作用
位错像力
当晶体中存在位错时, 不但在位错
金属材料中的夹杂物大多属于脆性相, 在比较
低应力下便与基体脱开或本身开裂而形成
微孔。
金属中的第二相是起强化作用的, 通常称为强
化相, 如钢中的碳化物、铝合金中时效强
化相。
在外应力作用下, 外应力足够大时启动位错,
位错沿滑移面运动, 与第二相离子相遇, 一
方面对位错运动产生阻力, 即强化作用, 另
一方面位错在强化相处塞集引起应力集中,
目增大到等于某一临界值时, 所产生的应力集中达到
第三章 断裂力学与断裂韧度

定义
也就是G表示弹性应变能的释放率或者为裂纹扩展力。 也就是 表示弹性应变能的释放率或者为裂纹扩展力。 表示弹性应变能的释放率或者为裂纹扩展力 因为G是裂纹扩展的动力,当G达到怎样的数值时, 达到怎样的数值时, 因为 是裂纹扩展的动力, 是裂纹扩展的动力 达到怎样的数值时 裂纹就开始失稳扩展呢? 裂纹就开始失稳扩展呢 按照Griffith断裂条件 断裂条件G≥R R=γs 按照 断裂条件 γ 按照Orowan修正公式 修正公式G≥R R=2(γ s+γ p) 按照 修正公式 γ γ
如对无限大平板内中心含有穿透K 如对无限大平板内中心含有穿透 1为
因此, 线弹性断裂力学并不象传统力学那样 , 单 因此 , 线弹性断裂力学并不象传统力学那样, 纯用应力大小来描述裂纹尖端的应力场, 纯用应力大小来描述裂纹尖端的应力场 , 而是同 时考虑应力与裂纹形状及尺寸的综合影响。 时考虑应力与裂纹形状及尺寸的综合影响。 教材p67 教材
其研究结果在当时并未引起重视
对于大多数金属材料, 对于大多数金属材料 , 虽然裂纹尖端由于应力集中 作用, 局部应力很高, 作用 , 局部应力很高 , 但是一旦超过材料的屈服强 就会发生塑性变形。 在裂纹尖端有一塑性区, 度 , 就会发生塑性变形 。 在裂纹尖端有一塑性区 , 材料的塑性越好强度越低, 材料的塑性越好强度越低 , 产生的塑性区尺寸就越 裂纹扩展必须首先通过塑性区, 大 。 裂纹扩展必须首先通过塑性区 , 裂纹扩展功主 要耗费在塑性变形上, 要耗费在塑性变形上 , 金属材料和陶瓷的断裂过程 不同,主要区别也在这里。 不同,主要区别也在这里。
工作应力σ<许用应力 工作应力 许用应力[σ] 许用应力
即认为是安全的
塑性材料 脆性材料
材料性能断裂力学与断裂韧性

讨论:KIC的意义,测试原理,影响因素及应 用。
3.2 Griffith断裂理论
3.2.1 理论断裂强度
理论断裂强度σC, 即相当于克服最 大引力σC
原子间结合力随距离变化示意图
力与位移的关系:
• 外因:板材或构件截面的尺 寸,服役条件下的T,应变速 率等。
• 内因:强度,合金成分和内 部组织。
3.8 金属材料的断裂韧性的测定
3.8.1 试样制备
测两种:三点弯曲试样和紧凑拉伸试样 裂纹缺口——钼丝线切割加工 0.12mm 疲劳裂纹——高频拉伸疲劳试验机上预制 为了测得稳定的值,所规定的尺寸必须满足: (1)小范围屈服(线弹性断裂力学,对裂纹长度c 应有规定 ,< 8 a )
E
3.2.2 Griffith理论
实际断裂强度<<理论计算的断裂强度
f
1 E (金属材料) 100
σf<1010 E (陶瓷,玻璃)
原因:内部存在有裂纹
材料内部含有裂纹对材料强度有多大影响?
20年代,Griffith首先研究了含有裂纹的玻 璃强度。
无限宽板中Griffith裂纹的能量平衡
断裂应力和裂纹尺寸的关系:
• 试样种类两种: 三点弯曲 紧凑拉伸试样
• 特点: 预制裂纹
B
2.5
K1C
0.2
2
• 记录P V 曲线 V -裂纹尖端张开位
移
2.确定Pa
P-V曲线
Pa是裂纹失稳扩展时临界载荷
3.计算: KQ
S 4W KQ
PQ S BW 3/ 2
f
a W
材料力学中的断裂行为模拟

材料力学中的断裂行为模拟引言材料的断裂行为在工程实践中具有重要意义。
断裂行为模拟是材料力学领域中一项重要的研究任务,它可以通过数值模拟方法来预测材料在外力作用下的断裂行为。
本文将介绍几种常用的断裂行为模拟方法,并对其原理及应用进行探讨。
第一章:线性弹性断裂力学线性弹性断裂力学是最早也是最简单的断裂行为模拟方法之一。
该方法基于线弹性理论,假设材料的力学性能在整个断裂过程中都保持不变。
通过计算应力、应变和应力强度因子的分布,可以预测材料断裂的位置和破坏形态。
线性弹性断裂力学方法适用于一些低强度、脆性材料的断裂行为模拟,但在考虑材料的非线性本质和高应变速率时效果有限。
第二章:粘弹性断裂力学粘弹性断裂力学是一种结合了线性弹性力学和粘弹性力学的方法。
它考虑了材料在断裂前后的粘性行为,能够更准确地模拟材料断裂行为。
粘弹性断裂力学方法通过定义材料的破坏准则,结合应力、应变和变形率的分析,可以模拟材料破坏的位置和形态。
该方法适用于一些温度较低、高粘性材料的断裂行为模拟。
第三章:强度折减断裂力学强度折减断裂力学是一种基于强度折减准则的方法。
它考虑了材料在局部破坏后的强度减小,能够较好地模拟材料断裂行为。
强度折减断裂力学方法通过计算应力和应力强度因子的变化,来分析材料的断裂位置和形态。
该方法适用于一些中等强度、中高应变率的材料断裂行为模拟。
第四章:塑性断裂力学塑性断裂力学是一种结合了塑性力学和断裂力学的方法。
它考虑了材料在塑性变形后的断裂行为,能够更全面地模拟材料断裂行为。
塑性断裂力学方法通过计算应力和应力强度因子的变化,结合材料的塑性变形分析,来预测材料的断裂位置和形态。
该方法适用于一些高强度、高应变率的材料断裂行为模拟。
结论断裂行为模拟是材料力学领域中的一项重要研究任务。
不同的材料和不同的工况要求使用不同的断裂行为模拟方法。
线性弹性断裂力学、粘弹性断裂力学、强度折减断裂力学和塑性断裂力学都是常用的断裂行为模拟方法。
付华-材料性能学-部分习题答案1

第一章材料的弹性变形一、填空题:1.金属材料的力学性能是指在载荷作用下其抵抗变形或断裂的能力。
2. 低碳钢拉伸试验的过程可以分为弹性变形、塑性变形和断裂三个阶段。
3. 线性无定形高聚物的三种力学状态是玻璃态、高弹态、粘流态,它们的基本运动单元相应是链节或侧基、链段、大分子链,它们相应是塑料、橡胶、流动树脂(胶粘剂的使用状态。
二、名词解释1.弹性变形:去除外力,物体恢复原形状。
弹性变形是可逆的2.弹性模量:拉伸时σ=EεE:弹性模量(杨氏模数)切变时τ=GγG:切变模量3.虎克定律:在弹性变形阶段,应力和应变间的关系为线性关系。
4.弹性比功定义:材料在弹性变形过程中吸收变形功的能力,又称为弹性比能或应变比能,表示材料的弹性好坏。
三、简答:1.金属材料、陶瓷、高分子弹性变形的本质。
答:金属和陶瓷材料的弹性变形主要是指其中的原子偏离平衡位置所作的微小的位移,这部分位移在撤除外力后可以恢复为0。
对高分子材料弹性变形在玻璃态时主要是指键角键长的微小变化,而在高弹态则是由于分子链的构型发生变化,由链段移动引起,这时弹性变形可以很大。
2.非理想弹性的概念及种类。
答:非理想弹性是应力、应变不同时响应的弹性变形,是与时间有关的弹性变形。
表现为应力应变不同步,应力和应变的关系不是单值关系。
种类主要包括滞弹性,粘弹性,伪弹性和包申格效应。
3.什么是高分子材料强度和模数的时-温等效原理?答:高分子材料的强度和模数强烈的依赖于温度和加载速率。
加载速率一定时,随温度的升高,高分子材料的会从玻璃态到高弹态再到粘流态变化,其强度和模数降低;而在温度一定时,玻璃态的高聚物又会随着加载速率的降低,加载时间的加长,同样出现从玻璃态到高弹态再到粘流态的变化,其强度和模数降低。
时间和温度对材料的强度和模数起着相同作用称为时=温等效原理。
四、计算题:气孔率对陶瓷弹性模量的影响用下式表示:E=E0 (1—1.9P+0.9P2)E0为无气孔时的弹性模量;P为气孔率,适用于P≤50 %。
材料物理第3章材料的脆性断裂和强度计算

th
s
in
2
x
近似为:
th
2x
由虎克定律知:
E E x
a
将式(2)带入式(1)得:
(式1) (式2)
x:原子位移;λ:正弦曲线波长; th : 理论断裂强度 a:晶格常数
th
2
E a
(式3)
分开单位面积原子平面所作的功为:
U
2 0
实际应用中,材料的屈服、断裂是最值得引起注意的两个问题.
3.1 理论断裂强度
理论断裂强度:完整晶体在正应力作用下沿某一晶面 拉断的强度。
两相邻原子面在拉力σ作用下,克 服原子间键合力作用 ,使原子面分开 的应力。
要推导材料的理论强度,应从原子间的结合力入手,只有克 服了原子间的结合力,材料才能断裂。
薄板
由弹性理论,人为割开长 2c 的裂纹时,平面应力 状态下应变能的降低为:
ws 4c
2 2
c
we
E
ws we
产生长度为 2c,厚度为 1 的 c 两个新断面所需的表面能为:
cc
ws 4c
2 2
c
we
E
式中为单位面积上的断裂表面能
裂纹在应力 的作用下,超过一定值以后,便发生扩展。 一方面增大表面能,另一方面又使弹性能减少(释放出弹性 能)。
E
a
2
可见,理论结合强度只与弹性模量,表面能和晶格距离等材
料常数有关。要得到高强度的固体,就要求E和 大,a小。
一般地,理论断裂强度
th
E 10
实际断裂强度
E~ E 100 1000
第三章 断裂力学与断裂韧度11

b. 另一方面,K1c和G1c虽然都是材料固有的性能,但从实验测 定来说,K1c更容易些,因此多数材料在各种热处理状态下所 给出的是K1c的实验数据。 但是,G判据的物理意义更加明确,便于接受,所以两者既是 统一的,由各有利弊。
引言
二、从选材方面考虑,对材料与裂纹的关系提出的问题
➢什么材料比较不容易萌生裂纹? ➢什么材料可以允许比较长的裂纹存在而不发生断裂? ➢什么材料抵抗裂纹扩展的性能比较好? ➢怎样冶炼、加工和热处理可以达到最佳的效果?
第一节 材料的断裂理论
一、理论断裂强度
假设:理想的、完整的晶体 理论断裂强度σc :在外加正应力作用下,将晶体的两
➢平面应力:指所有的应力都在一个平面内,平面应力问题 主要讨论的弹性体是薄板,薄壁厚度远远小于结构另外两个 方向的尺度。薄板的中面为平面,所受外力均平行于中面面 内,并沿厚度方向不变,而且薄板的两个表面不受外力作用。 ➢平面应变:指所有的应变都在一个平面内。平面应变问题 比如压力管道、水坝等,这些弹性体是具有很长的纵向轴的 柱状物体,横截面大小和形状沿轴线长度不变,作用外力与 纵向轴垂直,且沿长度不变,柱体的两段受固定约束。
几种常见裂纹的应力强度因子
(1)对无限大平板中心有穿透裂纹
几种常见裂纹的应力强度因子
(2)对无限大平板,板的一侧有单边裂纹
(3)对有限宽平板,中心有穿透裂纹 Y是2a/w的函数,可由图中实线所示查出
几种常见裂纹的应力强度因子
(4)对有限宽平板,板的两侧有双边裂纹
Y也是2a/w的函数,但由图中虚线所查出
第三章 第二部分 断裂力学与断裂韧性

纤维化能大大提升承载能力与安全性能!
(2)评价裂纹对材料力学行为的影响
2 E s 12 C ( ) c
采用无损探伤手段,监测裂纹尺寸c →构件的断裂抗力σc
c
3.4.2、Griffith理论的局限性及其修正
Griffith理论在金属材料中的应用并未引起重视,直 到 20 世纪 40 年代之后,金属的脆性断裂事故不断 发生,人们又重新开始审视Griffith断裂理论。
80℃ Griffith方程的修正 ——1950年,Orowan引入塑性变形功 p
2E S P 2E P c c c
问题6: 如何评价裂纹对材料力学行为的影响?如何对 含裂纹构件的安全性评估,判断其能否安全服役? 传统强度设计理论无法解答,因此,不能再以 传统强度设计理论为基础来设计和估算构件的承载 能力了,而必须立足于裂纹存在的前提下进行强度 设计,这就大大推动了人们对带裂纹体构件断裂问 题的研究,从而导致了新的强度设计理论诞生。
——高强度及超高强度材料的低应力断裂 二战后,高强度、超高强度材料的应用日益广泛,低应力断 裂事故层出不穷:
•20世纪50年代初,美国北极星导弹固体燃料发动机壳体在实验时发生爆炸。
•20世纪50年代,法国核电站的压力容器、英国核电站的大型锅炉爆炸,造成 严重破坏与人员伤亡。 •1954-1956,美国发生5起电站转子与叶轮的飞裂事故,加拿大发生了2起发 电机护环的飞裂事故。 •1965年12月17日,北海气田“海宝号”海洋钻机脆断事故,造成19人丧生。 •20世纪70年代初,辽阳化工厂压力容器爆破事故造成数十人伤亡。
Chapt3高分子材料的断裂力学基础

主要内容
• 线弹性断裂及表征 • 非线性断裂及表征 • 断裂表面的形貌表征
断裂力学认为材料的破坏行为是由微观-细 观-宏观多层次下,多种破坏机制相耦合而发生 和发展的。 灾难性断裂行为是由微细观损伤发展为裂纹 并扩展至完全破坏的过程。 其基本研究内容是裂纹的引发和裂纹扩展的 条件和规律性。
1、J积分及应用
J积分是塑性断裂理论的核心,可解析裂纹端 部处于较大范围屈服状态时材料的断裂特征。 利用J积分表征增韧高分子材料的破坏行为比 较普遍。
J积分的概念及物理意义
如果把弹塑性变看作为理想化的非线弹性,其应变能 密度w可表述为:
w = ∫ 0 σ ij dε ij
w仅为应变ε的函数,与在应变空间中如何达到ε的路 径无关,且不发生卸载。
假定试样尺寸如下: 宽度为D 厚度为B 裂纹长度为a 产生的塑性区长度为l
屈服类型可分为: L<<a,l<<D, L<<B:塑性区可忽略,线弹性断裂
L<D-a:裂纹端部产生小范围屈服。对于硬质塑料来说, 多数属于该情况,线弹性断裂理论仍适用,但有时需要对 塑性区进行修整
L<D-a:裂纹端部产生较大范围屈服,属于非线性断裂理 论范畴。
⎢σ xx ⎥ ⎢ ⎥ KI τ xy ⎥ = ⎢ (2πr )1/ 2 ⎢σ ⎥ ⎣ yy ⎦
θ 3θ ⎤ ⎡ ⎢1 − sin 2 sin 2 ⎥ ⎢ ⎥ θ θ 3θ ⎥ cos ⎢sin sin ⎥ 2⎢ 2 2 ⎢ θ 3θ ⎥ ⎢1 + sin sin ⎥ ⎢ 2 2⎥ ⎣ ⎦
对于裂纹端部任一点P,其坐标r、θ是已知道 的,则该点应力的大小完全有KI决定,其值大裂纹端 部各点应力就大,因此称之为应力强度因子,下标 表示张开型裂纹,量纲为MPa*m1/2。 r 0 ,全部应力趋于无穷大,即裂纹尖端应力 场具有奇异性。
第三章 材料的断裂

宏观断口 : 用肉眼或放大镜观察到的断口形貌
3、断口分析
二、断口分析
断口上分三个典型的 区域:纤维区、放射 区、剪切唇——断口 三要素。
三区域的大小、形态随试样 和实验条件而变化。
放射区较大,则材料的塑性 低(该区是裂纹快速扩展部 分,伴随的塑性变形也小)。 塑性好的材料,必然表现为 纤维区和剪切唇占很大比例, 甚至中间的辐射区可以消失。 脆性材料纤维区很小,剪切 唇几乎没有。
⑶ 剪切断裂、微孔聚合断裂与解理断裂
剪切断裂、微孔聚合断裂与解理断裂按不 同的微观断裂方式,是材料断裂的重要微观 机理. Ⅰ 剪切断裂: 剪切断裂是材料在切应力作 用下沿滑移面滑移分离而造成的断裂. 某些纯金属尤其是单晶体金属可产生纯剪切 断裂,其断口呈锋利的楔形,是充分发挥塑 性的韧性断裂,如低碳钢拉伸断口上的剪切 唇。但实际工程材料中很少见。
微观断口: 借助于扫描电镜或其它分析手段来研究 的断口形貌
断口分析是重要的分析手段。
韧断前有明显的颈缩, 断裂前有大量的塑性 变形。上下断口分别 呈杯状和锥状,合称 为杯锥状断口。 断口上分三个典型的 区域:纤维区、放射 区、剪切唇——断口 三要素。
纤维区F:位于断口中 央,呈粗糙的纤维状。 与拉力轴垂直,裂纹首 先在该区域形成; 颜色灰暗,表面有较大 的起伏,如山脊状,表 明裂纹在该区扩展时伴 有较大的塑性变形,裂 纹扩展也较慢;
•放射区R:紧挨着纤维区。 •表面较光亮平坦,有较细的 放射状条纹,放射线发散方向 为裂纹扩展方向,裂纹在该区 扩展较快,塑性变形量小,表 现为脆性断裂部分; •剪切唇S:接近试样边缘。 •应力状态为平面应力状态, 最后沿着与拉力轴向成4050°,裂纹失稳扩展,塑性变 形量较大,韧断区。表面粗糙 发深灰色。
第三章 无机材料的断裂及裂纹扩展

2
通过测得的C-c/W曲线的斜率,可求出dc/d(c/W) 进而可求Gc
求解Y
(1 ) K1c Gc E 2 Gc K1c 2 E (1 )
2 2
K1 Y c K Y c
2 1 2 2
将Gc值代入,即可求得几何形状因子Y 随c/W变化的表达式。
事实表明:结构件中不可避免地存在宏 观裂纹,在低应力下脆性破坏正是这些 裂纹扩展的结果。
所以,发展出新 学科:断裂力
学
断裂力学简介
断裂力学是研究含裂纹物体的强度与裂纹 扩展规律的科学。 意义-阐明了宏观裂纹降低断裂强度的作用, 突出了缺陷对材料性能的重要影响。
3.1断裂力学基本知识
P50,图3.1 试样伸长量u,外加载荷P,则:u P , 为试样 的柔度 系统的弹性变形能为:
)2
J.F.Knott对不同r/c的σ y分量的精确解:
1 / 2 0 1/ 2
ij (r, ) c1 f1 ( )r c2 f 2 ( )r c3 f 3 ( )r 3/ 2 c4 f 4 ( )r c5 f 5 ( )r
与Irwin近似解对比,得到:当r/c<1/15π 时,二者的相对误差小于6%。
E P
G
d (WE WP ) 2dc
或将G定义为系统释放的机械能对开裂面积A (A=2c × 厚度,厚度设为1)的导数,
d (WE WP ) G dA
采用恒位移加载,简化为:
G ( dWE ) dA
G
1 2 d P ( )p 2 dA 1 u 2 d ( ) ( )u 2 dA
3.2断裂韧性的测试方法
材料断口分析第3章-解理断裂

小刻面
放射条纹
人字纹
二、微观形貌特征及形成机理
特征: 扇形花样 解理台阶(cleavage step) 河流花样(river pattern) 舌状花样(tongue pattern) 青鱼骨花样(spine pattern) 瓦纳线(wallner line)
扇形花样
河流花样
舌状花样
青鱼骨花样
瓦纳线
(二)形成机理(模型)
1、解理台阶 解理裂纹与螺位错交截形成台阶
台阶形成过程的简化图
通过二次解理或撕裂相互连接形成台阶(撕裂棱)
台阶的性质
台阶在扩展过程中会发生合并或消失(台阶高度减小) 相同方向的台阶合并后高度增加 相反方向的台阶合并后高度减小或消失 台阶高度与柏氏矢量大小、位错密度之间存在一定关系
第三章 解理断裂
§1 概述 §2 解理断口形貌特征及形成机理 §3 影响解理断裂的因素 §4 准解理断裂
§1、概述
1、定义 正应力、解理面、穿晶脆断
2、发生条件 一般均在bcc、hcp金属中发生,而fcc只在特殊情 况下才发生,如腐蚀环境、材质较差时。
§2、解理断口形貌特征
一、宏观形貌特征 1、放射状条纹 2、人字纹 3、小刻面(facet):发亮的小晶面 解理断口上的结晶面 宏观上呈无规则取向 强光下可见到闪闪发光的特征 解理断口是由许多小刻面组成的,每个小刻 面代表一个晶粒
存在确定的位向关系
准解理裂纹形成机理示意图
准解理断口形貌
准解理断口形貌
扭转晶界——在亚晶界出产生新的裂纹,河流激增
大角度晶界:河流不能通过,在晶界处产生新的裂纹,向外扩展 ,
形成扇形花样
ቤተ መጻሕፍቲ ባይዱ
大角度晶界,扇形花样
材料性能学复习资料

第一篇材料的力学性能第一章材料的弹性变形一、名词解释1、弹性变形:外力去除后,变形消失而恢复原状的变形。
P42弹性模量:表示材料对弹性变形的抗力,即材料在弹性变形范兩内,产生单位弹性应变的需应力。
P103、比例极限:是保证材料的弹性变形按正比例关系变化的最大应力。
P154、弹性极限:是材料只发生弹性变形所能承受的最大应力。
P155、弹性比功:是材料在弹性变形过程中吸收变形功的能力。
P156、包格申效应:是指金属材料经预先加载产生少量塑性变形(残余应变小于4%), 而后再同向加载,规定残余伸长应力增加,反向加载,规定残余伸长应力降低的现象。
P207、内耗:在加载变形过程中,被材料吸收的功称为内耗。
P21二、填空题1、金属材料的力学性能是指在载荷作用下其抵抗(变形)和(断裂)的能力。
P22、低碳钢拉伸试验的过程可以分为(弹性变形)、(塑性变形)和(断裂)三个阶段。
P2三、选择题1、表示金属材料刚度的性能指标是(B )。
P10A比例极限B弹性模量C弹性比功2、弹簧作为广泛应用的减振或储能元件,应具有较高的(C )<> P16A塑性B弹性模量C弹性比功D硬度3、下列材料中(C )最适宜制作弹簧。
A 08 钢B 45 钢C 60Si:Mn C T12 钢4、下列因素中,对金属材料弹性模量影响最小的因素是(D )。
A化学成分B键合方式C晶体结构D晶粒大小四、问答题影响金属材料弹性模量的因素有哪些?为什么说它是组织不敬感参数?答:影响金属材料弹性模量的因素有:键合方式和原子结构、晶体结构、化学成分、温度及加载方式和速度。
弹性模量是组织不敬感参数,材料的晶粒大小和热处理对弹性模量的影响很小。
因为它是原子间结合力的反映和度量。
P11第二章材料的塑性变形一、名词解释1、塑性变形:材料在外力的作用于下,产生的不能恢复的永久变形。
P242、塑性:材料在外力作用下,能产生永久变形而不断裂的能力。
P523、屈服强度:表征材料抵抗起始塑性变形或产生微量塑性变形的能力。
第三章-弹塑性断裂力学

3)弹塑性断裂力学的提出 (1)解决如何通过小试样在全面屈服条件下断裂韧度 的测试去确定中、低强度重型构件的平面应变断裂韧 度KIC。
因为用线弹性断裂力学方法测定中、低强度钢的 断而裂且韧还度 由于KIC大,锻不件仅不需同用部大位型的试K件IC差和别大很吨大位,的用试大验试机, 样位所的测KIC得值的。KIC只是一个平均值,得不出各个具体部
但是由于裂纹尖端的钝化,很难确切地指出原 裂纹尖端的位置,因而亦难确定裂纹尖端的张开位移。
目前,有人用2AB作为理解纹张开位移(从变形 后的裂纹顶端测量);有人用2CD作为裂纹张开位移 (在D点测量,D为线弹性的直线与非线性的曲线的 交点);有人用2EF作为裂纹张开位移(从裂纹尖端 作450线与裂纹面相交处F的分离的大小)。
Wells
公式
e
es
2
e es
e
es
1
e
es
1
(12)
Burdekin
公式
e es
2
e es
0.25
e es
0.5
e
es
0.5
JWES2805标准:
3.5ea 或
0.5
e es
(13) (14)
1984年,我国压力容器缺陷评定规范编制组制定 了压力容器缺陷评定规范(CVDA):
裂纹张开位移的定义
2)COD判据
Wells认为;当裂纹张开位移δ达到材料的临界值δC 时,裂纹即发生失稳扩展,这就是弹塑性断裂的COD 准则,表示为:
δ =δC
(1)
件尺δC寸是改材变料的弹材塑料性常断数裂。的韧性指标,是一个不随试
对于COD准则,要解决三个方面的问题:(a) 找出裂纹尖端张开位移δ与裂纹几何尺寸、外加载荷 之间的关系式,即δ的计算公式。(2)实验测定材料 的应裂用纹。张开位移的临界值δC 。(3)COD准则的工程
第三章 零件的断裂失效

形成原因:解理沿相互平行的许多平面以不连续的方式进行. 形成原因 防止零件产生解理断裂的措施:降低韧-脆转变温度,加载速率, 防止零件产生解理断裂的措施 减少表面缺口效应和细化材料晶粒等. 切变断裂:在切应力作用下,伴随有大量塑性变形,沿着滑移面 切变断裂 且顺着滑移方向发生滑移而使晶粒分离的一种断裂形式. 切变断口的微观特征:具有“微坑”状或陷窝状,在微坑中心 切变断口的微观特征 常可见夹杂物等第二相粒子或孔穴.(图3-4).
第二节:断裂的基本原理 第二节 断裂的基本原理
一:一次加载断裂的基本原理 一次加载断裂的基本原理 正断(脱离型断裂 解理断裂):是由于外界作用的最大正应 脱离型断裂,解理断裂 正断 脱离型断裂 解理断裂 力超过材料在垂直该应力方向的平面上对脱离的抗力 所引起的. 材料的这种抗力称为正断抗力. 切断(剪切型断裂 切变断裂):是由于外界作用的最大剪应 剪切型断裂,切变断裂 切断 剪切型断裂 切变断裂 力超过了材料在剪切面上对切断的抗力所引起的.材料 的这种抗力称为切断抗力. 金属的切断抗力衡大于塑 变抗力,因此,金属都是在发生塑性变形后才产生切断的. 正断抗力,切断抗力和塑变抗力都是材料本身的特性. 零件如果在剪应力引起滑移之前,正应力超过正断抗力而 破坏,则系脆性断裂;反之,如果剪应力引起的滑移发生 在正应力引起的断裂之前,则系韧性断裂. 实际的机械零件的破断通常都是混合型的断裂. 实际的机械零件的破断通常都是混合型的断裂
二:解理断裂与切变断裂 解理断裂与切变断裂
解理断裂:在拉应力作用下,严格地沿着某些结晶学平面(解理面) 解理断裂 发生的断裂. 解理断裂常发生于低温环境,高应变速率,应力集 中,晶粒粗大和脆性材料中. 解理断裂的特征 解理断裂的特征:宏观上,断口平 坦,呈现从裂纹源开始的放射状和人字蚊的线条.如图3-1 微观上,呈河流状花样.如图3-2
第三章 断裂准则
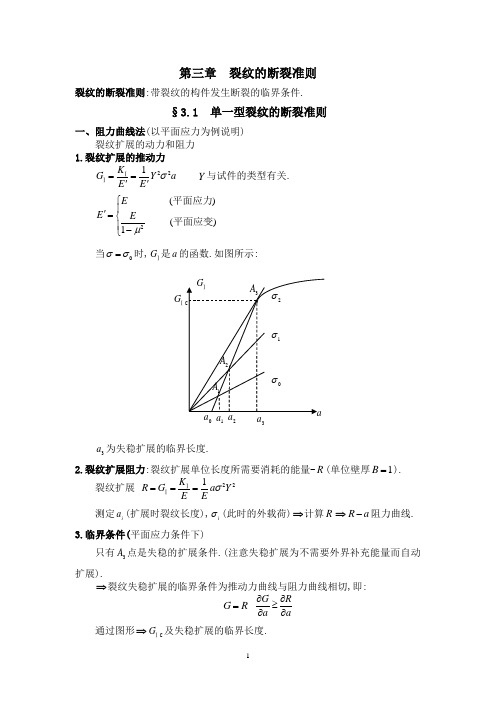
第三章 裂纹的断裂准则裂纹的断裂准则:带裂纹的构件发生断裂的临界条件.§3.1 单一型裂纹的断裂准则一、阻力曲线法(以平面应力为例说明)裂纹扩展的动力和阻力 1.裂纹扩展的推动力221K G Y a E E σ==''ⅠⅠ Y与试件的类型有关.2()()1E E Eμ⎧⎪'=⎨⎪-⎩平面应力平面应变当0σσ=时,G Ⅰ是a 的函数.如图所示:3a 为失稳扩展的临界长度.2.裂纹扩展阻力:裂纹扩展单位长度所需要消耗的能量-R (单位壁厚1B =).裂纹扩展 221K R G a YE E σ===ⅠⅠ测定i a (扩展时裂纹长度),i σ(此时的外载荷)⇒计算R ⇒R a -阻力曲线. 3.临界条件(平面应力条件下)只有3A 点是失稳的扩展条件.(注意失稳扩展为不需要外界补充能量而自动扩展).⇒裂纹失稳扩展的临界条件为推动力曲线与阻力曲线相切,即:G R=G R aa∂∂≥∂∂通过图形⇒G ⅠC 及失稳扩展的临界长度.0123aG Ⅰ二、能量判据=G GⅠⅠC 三、应力强度因子判据=K KⅠⅠC:材料的力学性能,由实验测定。
其中KⅠC§3.2 最大周向正应力理论m ax ()θσ判据.一.复合型裂纹断裂判据需要解决的问题1.裂纹沿什么方向扩展⇒确定开裂角;2.裂纹在什么条件下开始扩展⇒确定临界条件 二、 m ax ()θσ判据1.假定:裂纹初始扩展沿着周向正应力θσ为最大的方向.当这个方向上的周向正应力的最大值m ax ()θσ达到临界时,裂纹开始扩展. 2.举例:Ⅰ、Ⅱ型复合裂纹.[(1cos )3sin ]2K K θθσθθ=+-ⅠⅡ(3cos )cos(3cos 1)sin]22r K K θθσθθ=++-ⅠⅡ[sin (3cos 1)]2r K K θθτθθ=+-ⅠⅡ因0r =,各项均趋于无穷大. 取0r r =(微小值)圆周上个点的θσ0r r θθσθ=∂⎛⎫= ⎪∂⎝⎭ 220θσθ∂<∂ 000cos[sin (3cos 1)]02K K θθθ⇒+-=ⅠⅡθπ=±无实际意义00sin (3cos 1)0K K θθ⇒+-=ⅠⅡ0arccos9KK θ⇒=+ⅠⅡ开裂条件: 0m ax 001()[(1cos )3sin ]2cK K θθθσθθσ=+-=ⅠⅡc θσ:由Ⅰ型裂纹的断裂韧性来确定.即00,,0K K K θ===ⅠⅠc Ⅱ.(Ⅰ型裂纹由原裂纹面扩展)⇒临界失稳条件: 0001cos[(1cos )3sin ]22K K K θθθ+-=ⅠⅡⅠc3.几种特殊情况a.Ⅰ型, 00,0,K K K θ===ⅡⅠⅠcb.Ⅱ型, 000,(3cos 1)070.5K K K τθθ==-=⇒=± ⅠⅡⅡ 实验证明:如图所示剪应力方向,070.5θ=- 如图所示剪应力方向相反, 070.5θ= 0.87K K =ⅡⅠcc.中心斜裂纹的单向拉伸.分解σ:沿裂纹面:1cos sin τσββ=⋅τ垂直裂纹面:21sin σσβ=2,cos K K σβσββ⇒==ⅠⅡ13cos tan sin θβθ-⇒=给定0βθ⇒ 由0001cos[(1cos )3sin ]22K K K θθθ+-=ⅠⅡⅠc ,确定临界应力cσ.§3.3 能量释放率理论G判据,由帕立.尼斯威米(K.Palaniswamy)提出. 假设:(1).裂纹沿产生最大能量释放率的方向扩展.(2).当在上述确定的方向上,能量释放率达到临界值时,裂纹开始扩展.纽斯曼(Nuismer)利用连续性假设研究了能量释放率与最大周向正应力之间的关系.假设:沿0θθ=方向产生支裂纹,长度为a .平面应变下,裂纹沿本身平面扩展时的能量释放率为:22201()G K K Eμ-=+ⅠⅡ (沿裂纹方向扩展)支裂纹的能量释放率为:22201()G K K Eμ-=+ⅠⅡ谈论的问题:令0a →.假设支裂纹尖端的应力场趋近于扩展开始的原有裂纹尖端应力场.00lim |y a θθθσσ=→=00lim |xy a θθθττ=→=limr K →=Ⅰlim r K →=Ⅱ[(1cos )3sin ]2K K θθσθθ=+-ⅠⅡ--(1)[sin (3cos 1)]2r K K θθτθθ=+-ⅠⅡ --(2)⇒00001lim cos [(1cos )3sin ]22a K K K K θθσθθ→===+-Ⅰ0ⅠⅠⅡ--(3) 00001lim cos[sin (3cos 1)]22r r K K K K θθτθθ→===+-Ⅱ0ⅡⅠⅡ--(4)⇒支裂纹沿0θθ=方向开始从原有裂纹扩展时的能量释放率:22201()G K K Eθμ-=+Ⅰ0Ⅱ0 --(5)⇒决定因素⎧⎨⎩裂纹开始前的应力状态支裂纹所走的路径⇒2000021()0K G K K K E θμθθθ∂∂∂-=+=∂∂∂Ⅰ0Ⅱ0Ⅰ0Ⅱ0()结合(1),(2),(3),(4)⇒ 0()|0r r θθθθθθστστθθ=∂∂+=∂∂又由(1)式,32r θθστθ∂=-∂⇒03[()]02r r θθθθθττσθ=∂-=∂0r θτ⇒=和302r θθτσθ∂-=∂分析:03(|0cossin0arctan)2222r K K K K θθθθτθθθσθ=∂-=⇒-=⇒=∂ⅠⅠⅡⅡ⇒代入(3),(4),(5)042221()K G EKK θμ-=+ⅡⅠⅡ又22201()G K K Eμ-=+ⅠⅡ (0G 表示沿原始方向扩展)⇒00G G θ>⇒根不是解.⇒起始裂纹方向取于:002||03θθθθθθστθ==∂-==∂⇒周向应力取平稳值的方向与能量释放率取平稳值的方向又当0001|0cos[sin (3cos 1)]022r K K K θθθθτθθ==⇒=+-=Ⅱ0ⅠⅡ00122222011lim[(2)]r G K r EEθθμμπσ→--⇒==Ⅰ0⇒周向应力绝对值最大的方向是能量释放率最大的方向。
材料物理第3章材料脆性断裂与强度计算

材料物理第3章材料的脆性断裂和 强度计算
Inglis研究了具有孔洞的板的应力集中问题,得到结论:
孔洞两个端部的应力几乎取决于孔洞的长度和端部的曲率半 径,而与孔洞的形状无关。
Griffith根据弹性理论求得孔洞端部的应力
材料物理第3章材料的脆性断裂和 强度计算
a.将一单位厚度的薄板拉长到 l l ,此时板
中储存的弹性应变能为:
we1
1Fl
2
b.人为地在板上割出一条长度为2c的裂纹,产
生两个新表面,此时,板内储存的应变能为:
we212FFl
c. 应变能降低
w ew e1w e21 2Fl
d.欲使裂纹扩展,应变能降低的数量应等于 形成新表面所需的表面能。
c E(2cp)12 Ecp12
p 为塑性变形功, p >> s
材料物理第3章材料的脆性断裂和 强度计算
举例说明:
1
c
E p a
2
①典型陶瓷材料: E 3G 0,0 P 1 J a /m 2 , c 1m
临界断裂强度 c 0.4GPa
②高强度钢 E 3G 0,0 P p a 10 J/m 0 2 ,0c 0 .4 GP
断裂
韧性断裂 脆性断裂
判定依据:“断裂前是否 发生明显的塑性变形”。
效
腐蚀
变形失效
实际应用中,材料的屈服、断裂是最值得引起注意的两个问题.
材料物理第3章材料的脆性断裂和 强度计算
3.1 理论断裂强度
理论断裂强度:完整晶体在正应力作用下沿某一晶面 拉断的强度。
两相邻原子面在拉力σ作用下,克 服原子间键合力作用 ,使原子面分开 的应力。
第三章 无机材料的脆性断裂与强度

裂纹的亚临界生长(静态疲劳)
1. 亚临界生长:在应力作用下,随着时间的 推移,裂纹缓慢扩展。也叫静态疲劳。 动态疲劳:材料在循环应力或渐增应力 作用下的延时破坏。 2 裂纹缓慢生长的结果是裂纹尺寸加大,一 旦达到临界尺寸,就会失稳扩展而破坏。 研究意义:构件的使用寿命问题。
应力腐蚀理论
几种常用材料的断裂韧性
材料
M时效钢 铝合金
KIC(MP a/m)
100 44
材料
Si3N4
KIC(MPa/m)
5-6
高强度合金钢 92
Al2O3 SiC
环氧树脂 聚苯乙烯
4-4.5
Al2O3-ZrO2 4-4.5
SiAlON
Ti6Al4V ZrO2-Y2O3
5-7
40 6-15
3.5-6
0.8 0.7-1.1
阻力:
断裂韧性的测试方法
1、单边直通切口梁(SENB)法 测试方法及数据处理试样要求:光滑,要用 W7#研磨膏研磨,棱角相互垂直,B/W尺寸要 求严格,在整个试件长度范围内的变化不超过 0.02mm。用不超过0.25mm厚的锯片切口。 试件尺寸比例:a/W = 0.4~0.6, W/L = 1/4; B≈W/2。加载速度按形变速度来控制,规 定为0.05mm/min. 该方法只适合于晶粒大小在20-40μm的粗晶粒 陶瓷。对细晶粒的陶瓷,测得的数值偏大。
在一定的环境温度和应力场强度因子作用下,材料 中关键裂纹尖端处, 扩展动力与裂纹扩展阻力的 比较,构成裂纹开裂和止裂的条件。 1. 裂纹尖端处的高度的应力集中导致较大的裂纹 扩展动力。裂纹尖端处的离子键受到破坏,吸附了 表面活性物质,使材料的自由表面能降低。裂纹的 扩展阻力降低。导致低应力水平下的开裂。 2. 新开裂的断裂表面,还没来得及被介质腐蚀, 其表面能仍然大于裂纹扩展动力,裂纹立即止裂。 接着是下一个腐蚀-开裂-止裂循环。导致宏观上的 裂纹缓慢生长。
第3章 材料的断裂 习题解答

解:
因为 σ/σ0.2=150/720=0.208<0.7,所以裂纹断裂韧度 KIC 不需要修正
对于无限板的中心穿透裂纹,修正后的 KI 为: KIC=Yσcac1/2 对于表面半椭圆裂纹,Y=1.1 所以,KIC=Yσcac1/2=1.1
π /φ=1.1 π
π × 150 × 25 × 10 −3 =46.229(MPa*m1/2)
10、断裂韧度KIC与强度、塑性之间的关系:总的来说,断裂韧度随强度的升高而降低。 详见新 P80/P93 11、影响KIC的冶金因素:内因:1、学成分的影响;2、集体相结构和晶粒大小的影响; 3、杂质及第二相的影响;4、显微组织的影响。外因:1、温度;2、应变速率。P81/P95 12.有一大型板件,材料的 σ0.2=1200MPa,KIc=115MPa*m1/2,探伤发现有 20mm 长的横向 穿透裂纹,若在平均轴向拉应力 900MPa 下工作,试计算 KI 及塑性区宽度 R0,并判断该件 是否安全? 解:由题意知穿透裂纹受到的应力为σ=900MPa 根据 σ/σ0.2 的值,确定裂纹断裂韧度 KIC 是否休要修正 因为 σ/σ0.2=900/1200=0.75>0.7,所以裂纹断裂韧度 KIC 需要修正 对于无限板的中心穿透裂纹,修正后的 KI 为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
❖ 金属塑性的好坏表明了它抑制断裂能力 的高低。
❖ 在塑性加工生产中,尤其对塑性较差的 材料,断裂常常是引起人们极为关注的 问题。加工材料的表面和内部的裂纹, 以至整体性的破坏皆会使成品率和生产 率大大降低。为此,有必要了解断裂的 物理本质及其规律,有效地防止断裂, 尽可能地发挥金属材料的潜在塑性。
➢只有毫无缺陷的晶须才能近似达到理论断裂强度。
原因:
➢大多数材料都是在较低的应力水平下首先发生塑性变形, 最后因这种不可逆的损伤的积累而破坏,塑性较好的金属 就属于这种。
➢实际的材料不是完整的晶体,存在晶界、位错、空穴等 材料缺陷和擦伤、碰伤等加工缺陷。这些缺陷将在较低的 应力水平上发展成裂纹并长大,最终导致断裂。而且缺陷 会引起应力集中,对断裂的影响也是不容忽视的。
脆性断裂的特点:
Ⅰ 因为没有明显的预兆,所以脆性断裂具有很大的危险 性.
Ⅱ 脆性断裂的断口一般与正应力垂直,宏观上比较齐平光 亮,常呈放射状或结晶状.
Ⅲ 裂纹扩展速度大,往往受到的应力低于设计要求的许用 应力
❖
一般淬火钢、灰铸铁、陶瓷、玻璃等脆性材料的断裂
过程的断口常具有上述特征.
⑵ 穿晶断裂与沿晶断裂
❖ 穿晶断裂可以是韧性断裂,也可以是脆性断 裂。如常用金属材料在常温下发生韧性穿晶断裂, 低温下发生脆性穿晶断裂。
❖ 沿晶断裂则破坏了材料的连续性造成的,也可能是杂质 元素向晶界偏聚引起,是晶界结合力较弱的一种 表现。应力腐蚀、氢脆、回火脆性、淬火裂纹等 都是沿晶断裂。
❖ 因材料断裂与其他失效方式(如磨损、腐蚀等) 相比危害性最大,可能出现灾难性的后果.因此, 研究材料断裂的宏观与微观特征、断裂机理、断 裂的力学条件,以及影响材料断裂的各种因素不 仅具有重要的科学意义,而且也有很大的实用价 值.
现象:扁担从弹性变形到塑性变形,再到断裂 飞机发动机涡轮叶片从损伤到断裂
第三章 材料的断裂
❖一、断裂概述 ❖二、断裂机理 ❖三、断裂韧度
一、断裂概述
❖ 断裂 :固体材料在力的作用下变形超过其塑性极 限而呈现完全分开的状态称为断裂.
❖ 材料受力时,原子相对位置发生了改变,当局部 变形量超过一定限度时,原于间结合力遭受破坏, 使其出现了裂纹,裂纹经过扩展而使金属断开。
❖ 材料的断裂是力对材料作用的最终结果,它意味 着材料的彻底失效.
断裂; ⑶ 按照微观断裂机理分:解理断裂、微孔聚合断裂和
剪切断裂; ⑷ 按作用力的性质分:正断和切断
(二)关于各种断裂
⑴ 韧性断裂与脆性断裂 最常用,直接表明材料的韧、脆性。
❖ 韧性断裂:是材料断裂前及断裂过程中产生明显 宏观塑性变形的断裂过程.
韧性断裂的特点:
Ⅰ 韧性断裂时一般裂纹扩展过程较慢,而且要消 耗大量塑性变形能.
• 断裂是机械和工程构件失效的主要形式之一。
• 其它失效形式:如弹塑性失稳、磨损、腐蚀等。
• 断裂是材料的一种十分复杂的行为,在不同的力 学、物理和化学环境下,会有不同的断裂形式。
• 研究断裂的主要目的:防止断裂,以保证构件在服役 过程中的安全。
1、断裂的类型
(一)、断裂分类
⑴ 按照断裂性态分:断裂分为脆性断裂与韧性断裂; ⑵ 按照裂纹扩展途径分:穿晶断裂和沿晶(晶界)
Ⅱ 韧性断裂的断口用肉眼或放大镜观察时,往往 呈暗灰色、纤维状.纤维状是变形过程中微裂纹 不断扩展和相互连接造成的,而灰暗色则是纤维 断口表面对光反射能力很弱所致。
Ⅲ 不易造成重大事故,易被人察觉
❖ 一些塑性较好的金属材料及高分子材料在室 温下的静拉伸断裂具有典型的韧性断裂特征.
❖ 脆性断裂:是材料断裂前基本上不产生明显的宏观塑性 变形,没有明显预兆,往往表现为突然发生的快速断裂 过程
断裂。
平衡位置
原子间作用力最大
原子间作用力 随原间距的变 化曲线
达到破坏
❖ 由外力抵抗原子间结合力所做的功等于产生断 裂新表面的表面能,可以求得理论断裂强度为:
式中 a——断裂面间的原子间距; g——表面能; E——弹性模量。
理论断裂强度只与弹性模量、表面能和晶格间距等材料 常数有关
➢对于铁,可以估算理论断裂强度σm≈E/10。目前 强度最高的钢材为4500MPa左右,即实际材料的 断裂强度比其理论值低1~3个数量级。
➢ 共价键陶瓷晶界较弱,断裂方式主要是晶界断 裂.
➢ 离子键晶体的断裂往往具有以穿晶解理为主的特 征.
⑶ 剪切断裂、微孔聚合断裂与解理断裂
❖ 剪切断裂、微孔聚合断裂与解理断裂按不 同的微观断裂方式,是材料断裂的重要微观 机理.
❖ Ⅰ 剪切断裂: 剪切断裂是材料在切应力作 用下沿滑移面滑移分离而造成的断裂.
⑷ 正断和切断
正断:正应力引起 切断:切应力引起
正断与剪断的宏观与微观形式
2、断裂强度
(一)理论断裂强度
理论断裂强度是指完整晶体在正应力作用下沿其一晶面拉
断的强度,如图所示。
此强度就是两相邻原子面在拉应力作用下克服原子间键合
力作用,使原子面分开的应力。材料的理论结合强度,应从原
子间的结合力入 手,只有克服了原子间的结合力,材料才能
Ⅲ 解理断裂: 在正应力作用下,由于原子间结 合键的破坏而引起的沿特定晶体学平面发生分 离而导致断裂。类似大理石断裂,故叫解理断 裂。这种晶面称为解理面
❖ 属于典型的脆断,多发生在陶瓷、玻璃以及低 温下的金属中。
❖ 脆性穿晶断裂一般为解理断裂.解理裂纹的扩 展往往是沿着晶面指数相同的一族相互平行, 但位于“不同高度”的晶面进行的.不同高度 的解理面之间存在台阶,众多台阶的汇合便形 成河流花样.
❖ 某些纯金属尤其是单晶体金属可产生纯剪切 断裂,其断口呈锋利的楔形,是充分发挥塑 性的韧性断裂,如低碳钢拉伸断口上的剪切 唇。但实际工程材料中很少见。
Ⅱ 微孔聚合型断裂:剪切断裂的另一种形式为微孔聚集型 断裂,其断口在宏观上常呈现暗灰色、纤维状,微观断口 特征花样则是断口上分布大量“韧窝”。 是通过微孔形核、长大、聚合而导致的断裂,属于比较典 型的韧性断裂,常用金属材料大多属于此类。
