机车起动问题的分析及处理策略
机车启动问题的分析

机车启动问题的分析
1.两种启动方式的比较
v ↑⇒F =P 不变
v ↓
⇒a =F -F 阻
m ↓
2.三个重要关系式
(1)无论哪种运行过程,机车的最大速度都等于其匀速运动时的速度,即v m =P F min =P
F 阻
(式
中F min 为最小牵引力,其值等于阻力F 阻).
(2)机车以恒定加速度启动的运动过程中,匀加速过程结束时,功率最大,速度不是最大,即v =P F <v m =P
F 阻
.
(3)机车以恒定功率运行时,牵引力做的功W =Pt .由动能定理:Pt -F 阻
x =ΔE k .此式经
常用于求解机车以恒定功率启动过程的位移大小.
3.分析机车启动问题时的注意事项
(1)在用公式P =Fv 计算机车的功率时,F 是指机车的牵引力而不是机车所受到的合力. (2)恒定功率下的加速一定不是匀加速,这种加速过程发动机做的功可用W =Pt 计算,不能用W =Fl 计算(因为F 是变力).
(3)以恒定牵引力加速时的功率一定不恒定,这种加速过程发动机做的功常用W =Fl 计算,不能用W =Pt 计算(因为功率P 是变化的).。
机车的启动问题知识点总结

机车的启动问题知识点总结在日常使用中,机车的启动问题是常见的,有时候机车无法启动可能是因为简单的电池没电了,而有时候却可能是更加严重的问题。
在这篇文章中,我们将总结一些机车启动问题的知识点,帮助大家更好地了解并解决这些问题。
1. 电瓶机车的电瓶是启动的关键组件之一。
当机车无法启动时,首先需要检查电瓶是否充足。
如果电瓶没电了,就无法给启动电机提供足够的电力来启动发动机。
因此,我们需要定期检查电瓶的电量,并在需要时及时进行充电或更换。
此外,还需要检查电瓶的接线是否松动或者腐蚀,这可能会导致电路连接不良,影响电瓶的正常工作。
2. 燃油机车的燃油也是一个很重要的因素。
如果燃油用尽,机车自然也无法启动。
所以在使用机车时,需要注意燃油的余量,并及时加油。
此外,燃油系统也需要保持清洁,以确保燃油能够顺利供给到发动机。
3. 点火系统机车的点火系统包括点火线圈、点火塞、点火线等。
当这些部件出现故障时,也会导致机车无法启动。
所以需要定期检查这些部件的工作状态,并及时更换损坏的部件。
4. 喷油系统现代机车大多采用了电喷技术。
如果喷油系统出现故障,也会导致机车无法启动。
因此,需要检查喷油系统的工作状态,并保持其清洁和正常工作。
5. 空气滤清器空气滤清器是防止空气中灰尘和杂质进入发动机的重要组件。
如果空气滤清器堵塞,就会影响到发动机的正常工作,甚至导致无法启动。
因此,需要定期清洗或更换空气滤清器。
6. 起动机起动机是机车启动的关键组件之一。
如果起动机出现故障,就会导致机车无法启动。
因此需要定期检查起动机的工作状态,并及时更换损坏的部件。
7. 机油机油是发动机正常工作的关键润滑剂。
如果机油不足或者过于污浊,就会影响发动机的正常工作,甚至导致无法启动。
因此需要保持机油的充足和清洁。
8. 线路接口机车的线路接口是所有电气设备的重要连接部件。
当线路接口出现故障时,就会影响到机车的正常工作。
因此需要定期检查线路接口的连接状态,并及时修复损坏的部件。
高中物理:机车的启动问题

高中物理:机车的启动问题汽车之类的交通工具靠发动机对外做功,发动机的额定功率认为是其最大输出功率,实际工作的功率范围在0-P额之间.1、机车以恒定功率启动设机车在运动过程中所受的阻力F f保持不变,由F-F f =ma及F=P/v知,随着速度v的增大,F将减小,加速度a减小,所以机车做变加速运动,当a=0时,机车速度达到最大值v m=P/F f,以后机车将做匀速直线运动,v-t图如图所示.2、以恒定加速度a启动要维持机车的加速度恒定,则牵引力应为恒力. 由P=F v知,汽车的输出功率必将越来越大,而输出功率的增大是有限的,当输出功率达到额定功率以后,机车只能再以恒定的功率(额定功率)行驶,此后,随着速度v的继续增大,牵引力F将减小,加速度a将减小,当a=0时,速度达到最大值v m=P/F f,以后机车做匀速运动. 其v-t图如图所示. 图中的v0是匀加速过程能达到的最大速度,而v m是全过程所能达到的最大速度,两者不能混淆.例、图示为修建高层建筑常用的塔式起重机。
在起重机将质量m=5×103 kg的重物竖直吊起的过程中,重物由静止开始向上做匀加速直线运动,加速度a=0.2 m/s2,当起重机输出功率达到其允许的最大值时,保持该功率直到重物做v m=1.02 m/s的匀速运动。
取g=10 m/s2,不计额外功。
求:(1)起重机允许输出的最大功率。
(2)重物做匀加速运动所经历的时间和起重机在第2秒末的输出功率。
解析:(1)设起重机允许输出的最大功率为P0,重物达到最大速度时,拉力F0等于重力。
P0=F0v m ①F0=mg ②代入数据,有:P0=5.1×104W ③(2)匀加速运动结束时,起重机达到允许输出的最大功率,设此时重物受到的拉力为F,速度为v1,匀加速运动经历时间为t1,有:P0=F0v1 ④F-mg=ma ⑤V1=at1 ⑥由③④⑤⑥,代入数据,得:t1=5 s ⑦T=2 s时,重物处于匀加速运动阶段,设此时速度为v2,输出功率为P,则v2=at ⑧P=Fv2 ⑨由⑤⑧⑨,代入数据,得:P=2.04×104W。
机车启动问题doc

机车启动问题一、机车的两种启动问题当机车从静止开始沿水平面加速运动时,有两种不同的加速过程,但分析时采用的基本公式都是P=Fv和F-f=ma.为使问题简化,假定机车所受阻力大小恒定.1.恒定功率的加速问题由公式P=Fv和F-f=ma知,由于P恒定,随着v的增大,F必将减小,a也必将减小,机车做加速度不断减小的加速运动,直到F=f,a=0,这时v达到最大值可见恒定功率的加速运动一定不是匀加速运动.这种加速过程发动机做的功只能用W=Pt计算,不能用W=Fs计算(因为F为变力).2.恒定牵引力的加速问题由公式P=Fv和F-f=ma知,由于F恒定,所以a恒定,机车做匀加速运动,而随着v 的增大,功率也将不断增大,直到功率达到额定功率P,功率不能再增大了.这时匀加速运动结束,其最大速度为,此后机车要想继续加速就只能做恒定功率的变加速运动了.可见当机车做恒定牵引力的加速运动时功率一定不恒定.这种加速过程发动机做的功只能用W=F·s计算,不能用W=P·t计算(因为P为变功率).以上机车的两种启动过程可用如图所示的v-t图像来概括说明.0~t1时间内,机车从静止开始匀加速运动,牵引力F恒定,机车的输出功率P=Fv不断变大,t1时刻达到额定功率(匀加速阶段结束);t1~t2时间内,机车以恒定功率继续加速,牵引力和加速度不断减小(加速度减小的加速运动),对应图像中曲线部分;t2时刻加速度减为零,F=f,机车匀速前进(对应图像中水平直线部分),此时达到最大速度二、机车启动问题中的位移分析方法在机车启动过程中,计算机车的位移是一个难点.由于机车一般会经历多个运动过程,在匀变速运动过程中可以利用运动学公式直接求解,但在变加速运动阶段,只能借助动能定理来计算.在机车启动问题中,要注意区别“两个速度”,即匀加速阶段的最大速度(图像中的v1)和最终匀速运动的速度(图像中的v m).求匀加速阶段的位移可运用匀变速直线运动的位移公式计算变加速运动阶段的位移则不能用上述公式,但由于该阶段功率P不变,故可以用动能定理P(t2-t1)-fx2= 计算。
机车起动的两种方式分析

机车起动的两种方式分析机车起动问题是指汽车、火车、轮船、摩托等动力机械的起动问题,而起动过程分为以恒定功率起动和恒力起动(先匀加速起动至额定功率后再变加速运动)两种情况,因起动过程中各物理量相互关联而又发生变化,过程比较复杂,有一定的难度.1.以恒定功率起动在此过程中,机车不断加速,因为开始时机车已经达到额定功率,根据P=Fv 可知在速度v 不断增大的时候,牵引力F 会不断减小,加速度F-f=ma (f 表示机车运动过程中受到的阻力)也不断减小,但因为加速度的方向和速度的方向相同,所以无论加速度a 怎样小,速度v 也是增加的.即机车一直做加速度减小的加速运动,直到F f =时,达到最大速度m P P v F f==,此后以v m 做匀速直线运动.起动过程结束的标志就是“速度不变”. 例1.汽车发动机的额定功率为60kw,汽车质量为5t,汽车在水平路面上行驶时,阻力是车中的0.1倍,g=10m/s 2问(1)汽车保持以额定功率从静止启动能达到的最大速度是多少?解析:由P =F·v 可知,汽车在额定功率下行驶,牵引力与速度成反比.速度增大,牵引力减小,当汽车的牵引力与所受阻力相等时,速度达到最大.所以v m =P /F f=60000/0.1×5000×10m/s = 12m/s . 说明:此类问题主要把握住机车作加速度减小的加速运动,最终匀速的运动特点,利用F f =时,达到最大速度m P P v F f==来解题. 2.先以恒力起动至额定功率后再恒功率起动该起动过程分为两个阶段:阶段1是匀加速过程,在此过程中,速度v 由零开始不断增加,功率P 也由零开始逐渐增加;由F-f=ma ,因为加速度a 是不变的,所以在此过程中牵引力F 也是不变的.此过程的结束就是第二个过程的开始,以“功率P 达到最大即额定功率,但速度没有达到最大”为标志.阶段2中因为还有加速度的存在,所以速度v 会继续增加,在功率P 不变的情况下,根据P =Fv ,可知牵引力F 不断减小,加速度a 也相应减小.第二过程结束的标志就是“机车的功率P 最大,速度v 也是最大”,到此为止,整个起动过程结束.再以后,机车将以v m 做匀速直线运动,功率不变.例2.汽车发动机的额定功率为60 kW ,汽车的质量为4 t ,当它行驶在坡度为0.02的长直公路上时,如图1,所受阻力为车重的0.1倍(g =10 m/s 2),求:⑴汽车所能达到的最大速度v m =?⑵若汽车从静止开始以0.6 m/s 2的加速度做匀加速直线运动,则此过程能维持多长时间?解析: ⑴汽车在坡路上行驶,所受阻力由两部分构成,即f =kmg +mg sin α=4000+800N=4800 N . 又因为F =f 时达到最大速度,且P =f·v m ,所以36010/12.5/sin 4800m P v m s m s kmg mg α⨯===+. ⑵汽车从静止开始,以a =0.6 m/s 2匀加速行驶,由F =ma ,有F ′-f -mg sin α=ma .故 3sin 7.210F kmg mg ma N α'=++=⨯ 保持这一牵引力,汽车匀加速行驶到速度mv ',此时达到额定功率,据P Fv =有图18.33/m m P v m s F '=='. 由运动学规律可以求出匀加速行驶的时间8.3313.90.6m v t s s a '===. 说明:此后汽车将做加速度减小的加速运动,直到达到12.5m/s,而后匀速直线运动. 3.两种启动方式的共同点对同一机车,在相同条件下,两种启动方式最终都是F =f ,匀速时的速度v m 相同.v -t 图像如图2所示.例3.电动机通过一绳子吊起质量为8 kg 的物体,绳的拉力不能超过120 N ,电动机的功率不能超过1200 W ,要将此物体由静止起用最快的方式吊高90 m (已知此物体在被吊高接近90 m 时,已开始以最大速度匀速上升)试分析应如何吊起物体?达到最大功率的最短时间是多少?匀速时的速度是多少?解析: 此题可以采用机车起动类问题的思路,即将物体吊高分为两个过程处理:第一过程是以绳所能承受的最大拉力拉物体,使物体匀加速上升,第一个过程结束时,电动机刚达到最大功率.第二个过程是电动机一直以最大功率拉物体,拉力逐渐减小,当拉力等于重力时,物体开始匀速上升.在匀加速运动过程中加速度为a =8108120m ⨯-=-m mg F m/s 2=5 m/s 2 末速度v t =1201200=m m F P =10 m/s 上升的时间t 1=510=a v t s=2 s 此即达到最大功率的最短时间.在功率恒定的过程中,最后匀速运动的速率为v m =1081200⨯==mg F F P m m =15 m/s 说明:本题考查对机车启动两类问题的理解及迁移应用的创新能力.同学们往往对整个过程分析不透,若开始即以最大功率拉,绳会被拉断.v v 2。
机车启动问题(解析版)
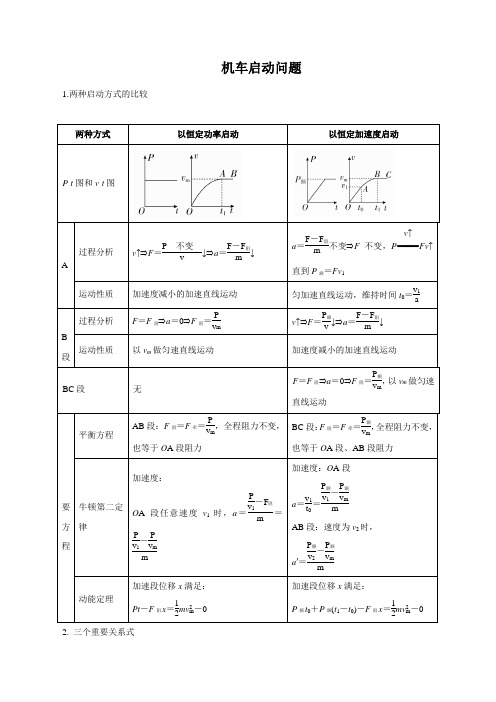
机车启动问题1.两种启动方式的比较两种方式以恒定功率启动以恒定加速度启动P -t 图和v -t 图OA段过程分析 v ↑⇒F =P不变v ↓⇒a =F -F 阻m↓ a =F -F 阻m 不变⇒F 不变,P =====v ↑Fv ↑直到P 额=Fv 1运动性质 加速度减小的加速直线运动 匀加速直线运动,维持时间t 0=v 1aA B 段过程分析 F =F 阻⇒a =0⇒F 阻=Pv mv ↑⇒F =P 额v ↓⇒a =F -F 阻m↓运动性质以v m 做匀速直线运动加速度减小的加速直线运动BC 段 无F =F 阻⇒a =0⇒F 阻=P 额v m ,以v m 做匀速直线运动重要方程平衡方程AB 段:F 阻=F 牵=P v m ,全程阻力不变,也等于O A 段阻力 BC 段:F 阻=F 牵=P 额v m,全程阻力不变,也等于O A 段、AB 段阻力 牛顿第二定律 加速度:O A 段任意速度v 1时,a =Pv 1-F 阻m =P v 1-P v mm加速度:O A 段 a =v 1t 0=P 额v 1-P 额v m mAB 段:速度为v 2时, a ′=P 额v 2-P 额v m m动能定理加速段位移x 满足:Pt -F 阻x =12mv 2m-0加速段位移x 满足:P 额t 0+P 额(t 1-t 0)-F 阻x =12mv 2m-02. 三个重要关系式(1) 无论哪种启动过程,机车的最大速度都等于其匀速运动时的速度,即v m =PF 阻。
(2) 机车以恒定加速度启动时,匀加速过程结束后功率最大,速度不是最大,即v =P F <v m =PF 阻。
(3) 机车以恒定功率运行时,牵引力做的功W =Pt ,由动能定理得Pt -F 阻x =ΔE k ,此式经常用于求解机车以恒定功率启动过程的位移或速度。
【典例】一列火车总质量m =500 t ,发动机的额定功率P =6×105 W ,在水平轨道上行驶时,轨道对火车的阻力f 是车重的0.01倍,g 取10 m/s 2。
机车起动问题

机车起动问题一、机车的两种启动问题当机车从静止开始沿水平面加速运动时,有两种不同的加速过程,但分析时采用的基本公式都是P=Fv和F-f=ma。
为使问题简化,假定机车所受阻力大小恒定。
1. 恒定功率的加速问题由公式P=Fv和F-f=ma知,由于P恒定,随着v的增大,F必将减小,a也必将减小,机车做加速度不断减小的加速运动,直到F=f,a=0,这时v达到最大值:vm =PF=Pf,可见恒定功率的加速运动一定不是匀加速运动.这种加速过程发动机做的功只能用W=Pt计算,不能用W=Fs计算(因为 F为变力)。
以上机车的启动过程可用如图所示的 v-t图像来表示。
2.恒定牵引力的加速问题由公式P=Fv和F-f=ma知,由于F恒定,所以a恒定,机车做匀加速运动,而随着v的增大,功率也将不断增大,直到功率达到额定功率P,功率不能再增大了。
这时匀加速运动结束,其最大速度为v1=PF<Pf=v m.此后机车要想继续加速就只能做恒定功率的变加速运动了。
可见当机车做恒定牵引力的加速运动时功率一定不恒定,这种加速过程发动机做的功只能用W=F⋯计算,不能用W=P-t计算(因为P为变功率)。
以上机车的启动过程可用如图所示的 v-t图像来概括说明。
0-t₁时间内,机车从静止开始匀加速运动,牵引力F恒定,机车的输出功率P=Fv不断变大,t₁时刻达到额定功率(匀加速阶段结束):t₁-t₂时间内,机车以恒定功率继续加速,牵引力和加速度不断减小(加速度减小的加速运动),对应图像中曲线部分:t₂时刻加速度减为零,F-f,机车匀速前进(对应图像中水平直线部分),此时达到最大速度vm =Pf,例题1. 一新型赛车在水平专用测试道上进行测试,该车总质量为(m=1×10³kg,由静止开始沿水平测试道运动,用传感设备记录其运动的 w r图像如图所示。
该车运动中受到的摩擦阻力(含空气阻力)恒定,且摩擦阻力跟车的重力的比值为μ=0.2,赛车在0~5s的wr图像为直线,5s末该车发动机达到额定功率并保持该功率行驶,在5~20s之间,赛车的 vt图像先是一段曲线,后为直线取g=10m/s²,试求:该车的额定功率:。
如何才能正确快速分析机车启动问题

世界 领 先 水 平 ,使人们的出行更方便快捷•复兴号动车组 是 由 动 车 和 拖 车 编 组 而 成 ,提供
由 i/ = af 得 f i = 5. 59 s. a
动 力 的 车 厢 叫 动 车 ,不 提 供 动 力
此过程动车运动的路程h = j V t = 76. 86 m
的车厢叫拖车.假设动车组每节 车 箱 质 量 m = 2 5 t,每 节 动 车 发 动 机 的 额 定 功 率 P = 9 x 106W ,某列 动 车 组 由 8 节 车 厢组成,如 图 6 所
例 1 我国高铁技术通过引进和不断创新,现在处于
收稿日期:2019 - 07 - 05 作 者 简 介 :沈 加 法 (1965. 1 2 - ) , 男 ,云 南 人 ,本 科 ,中 学 髙 级 教 师 ,从 事 高 中 物 理 教 与 学 研 究 .
— 73 —
数理化 解题研究
2019年 第 28期 总 第 449期
所以,在分析解决机车启动问题时,一 定要耐心细致 地 阅 读 题 目 ,找 到 题 中 的 关 键 词 ,准 确 定 位 好 机 车 运 动 过 程是哪种启动方式,做 到 过 程 心 中 有 底 ,并画好受力 分 析 图和运动过程图,由 功 能 关 系 列好数学方程,细心求解就 可以正确无误.
二 、应用评析和 归 纳 总 结
变 ,以 恒 定 加 速 度 启 动 ,由 公 式 P = A = 得功率均匀
图5
增大到恒定功率后,保 持 功 率 不 变 继 续 运 动 ,画出这种启 动过程的P ^ 图 象 如 图 4 所示.设机车的功率均匀增大 到 恒 定 功 率 时 的 速 度 为 此 时 牵 引 力 大 于 阻 力 ,根据图 2 对机车的受力分析,机车继续做加速度减小的加速运动 到最大速度后匀速运动,其 运 动 的 图 象 如 图 5 所示.
机车起动问题的分析

机车起动中的功率问题雷店高中石继承(一)、教学目标1.知识与技能(1)能正确计算常见情况下各力的平均功率和瞬时功率。
(2)能正确分析机车的起动过程。
2.过程与方法(1)通过实践与拓展,达到运用所学知识研究实际问题的目的。
(2)通过讨论和交流,理解P=FV中各个量的关系。
3.情感、态度与价值观(1)通过讨论与交流,培养学生敢于思考、善于思考的良好习惯。
(2)通过实践与拓展,培养学生灵活迁移知识解决实际问题的能力。
二、重点难点:1、恒定牵引力起动过程的分析。
2、额定功率和实际功率的区别和联系。
三、教学方法:练习、讨论、讲授教学过程:(一) 温故知新1.功率的定义:__________________________________________________.2.功率的物理意义:________________________________________________.3.①功率的定义式:P=______________(适用求解恒力或变力功率)(1)②若为恒力做功则:W=FScosα联立(1)式有功率的推导式:P=_______________(适用于求解恒力的功率)(2)若_________,则P表示__________;若_________,则P表示__________;※一般(1)式用于求解平均功率(2)式用于求解瞬时功率4.额定功率:机车正常工作时发动机输出的最大功率5.实际功率:机车正常工作时发动机实际输出的功率P实=F牵v(牵引力与速度同方向)(二)探究理综测试注重以现实问题立意,突出能力考查.因而以机车起动为情景的高考命题屡次出现于近几年高考试卷中,该类问题中对于a、F、p、v四个物理量间相互联系、相互制约关系的分析是考生的难点所在,但是如果我们仔细观察,却也不难发现它们的规律。
我们今天这节课就围绕机动车起动的两类问题展开学习。
当机车的功率一定时,要增大牵引力,必须(填降低或增大)机车的运动速度;加速度是如何变化的呢?本节就研究这一问题。
高中物理难点_机车启动问题

高中物理难点——机车启动问题难点分析: a 、F 、p 、v 四个物理量间相互联系、相互制约.机车起动分两类:(1)以恒定功率起动;(2)以恒定牵引力起动.(1) 以恒定功率起动——P=Fv ,所以加速度一定是变化的。
速度不断增加,F 减小,所以加速度逐渐减小阻力存在,牵引力F 减小到与阻力相等时,不能再减小,合力为零,匀速运动汽车达到最大速度时a =0,F =f ,P =Fv m =fv m . (2)以恒定牵引力起动(或以恒定加速度启动),P=Fv <额定功率P m匀加速当功率增大到额定功率P m 后,变加速(a ↓)速度增大到一定程度后,⇒ (a =0)匀速. 例1.汽车以恒定功率P 由静止出发,沿平直路面行驶,最大速度为v ,则下列判断正确的是A.汽车先做匀加速运动,最后做匀速运动B.汽车先做加速度越来越大的加速运动,最后做匀速运动C.汽车先做加速度越来越小的加速运动,最后做匀速运动D.汽车先做加速运动,再做减速运动,最后做匀速运动解析:汽车以恒定功率P 由静止出发,根据功率与速度关系式P=Fv ,F 为牵引力当功率P 一定时,速度v 越大,牵引力F 越小,刚开始速度很小,牵引力F 很大,牵引力F 大于阻力,合力向前,加速度向前,物体做加速运动随着速度的增加,牵引力F 不断变小,合力也变小,加速度也变小 当牵引力F 减小到等于阻力时,加速度减为零,速度达到最大,之后物体做匀速直线运动 故选C .例2.汽车在水平公路上行驶,车受的阻力为车重的0.01倍,当速度为4 m/s 时,加速度为0.4 m/s 2.若保持此时的功率不变继续行驶,汽车能达到的最大速度是________m/s. (g 取10 m/s 2) 解析:设汽车质量为m ,阻力f=0.01mg速度为v=4 m/s 时,加速度为a=0.4 m/s 2,F-f=ma ,因此F=f+ma=0.01mg+ma此时功率P=Fv=(0.01mg+ma)v 汽车速度最大时,此时牵引力F 最小,a=0,合力为零,m g 01.0f F min ==例3. 汽车发动机额定功率为60 kW ,汽车质量为5.0×103 kg ,汽车在水平路面行驶时,受到的阻力大小是车重的0.1倍,g 取10 m/s 2,试求:(1)汽车保持额定功率从静止出发后能达到的最大速度是多少?(2)若汽车从静止开始,以0.5 m/s 2的加速度匀加速运动,则这一加速度能维持多长时间?(3)若汽车以额定功率起动,则汽车车速为v=2m/s 时其加速度多大?解析:(1)额定功率,P=Fv ,(注意F 是牵引力,不是合力!)车质量为m ,车重为mg ,阻力f=0.1mg速度最大时,加速度a=0,牵引力m g 1.0f F min == 此时功率依然为额定功率,故max min v F P =(2)加速度m f F a -=f 、m 均不变,因此如汽车加速度不变,牵引力F 不变汽车加速运动,v 变大,P=Fv ,汽车功率必须变化,即随v 增大而增大。
难点6-机车起动问题分析

难点6 机车起动问题分析机车起动分两类:(1)以恒定功率起动;(2)以恒定牵引力起动。
其解题关键在于逐步分析v 、a 、F 、P 间关系,并把握由起动到匀速的临界条件F =f ,即汽车达到最大速度的条件.该类问题的思维流程为:(1) 以恒定功率起动的运动过程是:变加速(a ↓)(a =0)匀速。
在此过程中,F 牵、v 、a 的变化情况:所以汽车达到最大速度时a =0,F =f ,P =Fv m =fv m 。
(2)以恒定牵引力匀加速起动的运动过程是:匀加速⇒当功率增大到额定功率P m 后,变加速(a ↓) ⇒ (a =0)匀速。
各个量(牵引功率、牵引力、加速度、速度)的变化情况如下:1、汽车发动机额定功率为60 kW ,汽车质量为5.0×103 kg ,汽车在水平路面行驶时,受到的阻力大小是车重的0.1倍,试求:(1)汽车保持额定功率从静止出发后能达到的最大速度是多少? (2)若汽车从静止开始,以0.5 m/s 2的加速度匀加速运动,则这一加速度能维持多长时间?解析:(1)汽车以恒定功率起动时,它的牵引力F 将随速度v 的变化而变化,其加速度a 也随之变化,具体变化过程可采用如下示意图表示:由此可得汽车速度达到最大时,a =0,kmgP v v F P kmg f F m m =⇒⎭⎬⎫⋅====12 m/s (2)要维持汽车加速度不变,就要维持其牵引力不变,汽车功率将随v 增大而增大,当P 匀速运动保持达到最大时即时当m m v v v f F a m f F a v P F v ⇒==↓⇒-=↓⇒=↑⇒0匀速运动保持达到最大时即机车做变加速直线运动时当m m v v v f F a m f F a v P F v ⇒=→←=↓⇒-=↓⇒=↑⇒0一定即定F m f F a -=增大而增大随即定v P v F p ↑↑=↓-↓=↓↑=m fF a v P F 额此后保持匀速运动达到最大时,当m v v a 0=额定定额已经不能变大,保持还要增大,但是所以时,当P P v m f F a P P 0≠-==达到额定功率P 额后,不能再增加,即汽车就不可能再保持匀加速运动了。
机车的两种启动方式分析

机车的两种启动方式分析机车两种启动方式分析正确分析汽车启动问题,关键抓住三点: N 1、正确分析物理过程。
f F 2、抓住两个基本公式:1)功率公式:,其中是汽车的功率,是汽车的牵引力,(PFP,Fvmg v是汽车的速度。
图1 (2)牛顿第二定律:,如图1所示。
F,f,ma3、正确分析启动过程中的变化抓住不变量、变化量及变化关系。
P、F、f、v、a以恒定功率启动汽车从静止开始,保持牵引力的功率不变,假设在运动过程中汽车所受的阻力F′也不变;随速度v的增大,牵引力会减小,加速度减小;当F,F′时,加速度a,0,此时速度最大,且 ;以后以速度做匀速直线运动,其过程可由下面的框图表示:以恒定加速度启动由知,保持a不变,则牵引力F也不变,而由P,Fv知,随着速度v的增大,机车的功率增大,但任何机械的功率都是有限的,故机车的功率达到额定功率后将保持不变,以后速度虽继续增大,但并非做匀加速直线运动,因为F会变小,当F,F′时,机车就以做匀速直线运动。
由以上分析可知,车能保持加速度恒定运动一段时间,以后加速度将减小直至为零,其过程可由下面的框图表示:注意:当机车以恒定的加速度启动时,机车做匀加速直线运动的最大速度,要小于机车的最大速度。
5例:一列火车总质量m,500 t,机车发动机的额定功率P,6×10 W,在轨道上行驶时,轨道对列车2的阻力F是车重的0.01倍,g取10 m/s,求: 阻(1)火车在水平轨道上行驶的最大速度;【解析】 (1)列车以额定功率工作时~当牵引力等于阻力~F,F,kmg时列车的加速度为零~速度阻达最大v mPPP则:v,,,,12 m/s. mFkmgF阻(2)在水平轨道上,发动机以额定功率P工作,当行驶速度为v,1 m/s和v,10 m/s时,列车的瞬时12加速度a、a各是多少; 12【解析】当v<v时列车加速运动~当v,v,1 m/s时 m1P5F,,6×10 N 1v1,FF阻12据牛顿第二定律得:a, ,1.1 m/s1mP4当v,v,10 m/s时~F,,6×10 N 22v2,FF阻22据牛顿第二定律得:a,,0.02 m/s. 2m(3)在水平轨道上以36 km/h速度匀速行驶时,发动机的实际功率P′;5【解析】 (3)当v,36 km/h,10 m/s时~列车匀速运动~则发动机的实际功率P′,Fv,5×10 W. 阻2(4)若火车从静止开始,保持0.5 m/s的加速度做匀加速运动,这一过程维持的最长时间(5【解析】 (4)据牛顿第二定律得牵引力F′,F,ma,3×10 N 阻P在此过程中~速度增大~发动机功率增大(当功率为额定功率时速度大小为v′~即v′,,2 m/s mmF′v′m据v′,at~得t,,4 s. ma。
机车起动问题的分析及处理策略

机车起动问题的分析及处理策略Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】机车起动问题的分析及处理策略1.两个起动方式机车起动问题中有两种运动模式,即机车以恒定功率(通常为额定功率)和以恒定加速度a起动。
如何分析这两种方式的起动过程及相关问题的处理,这是教与学中经常碰到的问题。
2.两个基本关系“”和“”是分析与处理机车起动过程的两个重要的、基本的关系式。
它反映了机车瞬时状态的各量间的关系。
下图是机车在工作状态下的受力情况,应当明确P为机车的瞬时功率;F为机车的牵引力,而不是机车受的合力;v为机车的瞬时速度;a为瞬时加速度;f为机车所受的阻力(通常机车所受阻力设为恒力);m是机车的质量。
在实践中,我们只要抓住两个基本关系式,相关问题则会迎刃而解。
3.两个最值速度额定功率起动的情形由和可知,因功率P保持不变,速度增大,则机车的牵引力F必然减小,也就不难看出机车的加速度a因此而减小,所以该过程是一个加速度逐渐减小的运动。
显然当牵引力F减小到等于机车所受阻力f时,即F=f,其加速度a=0,则机车的速度达到最大值。
如下图所示,额定功率下起动过程的两个阶段,即从为加速度逐渐减小的加速运动;此后以速度作匀速直线运动。
恒定加速度起动的情形初速度为0的匀加速起动的过程,同样根据知,由于加速度a恒定,则牵引力F不变(通常设定机车所受阻力f恒定)。
因此随着速度v增大,其机车的瞬时功率P随之增大,当P增大到额定功率时,此刻速度便是匀加速运动过程的最大速度,其大小为。
应当注意到是匀加速运动的末状态,此刻机车的功率刚好等于额定功率,而此时此刻牵引力仍为F,且F,再由两个基本关系式,容易分析出,在功率不变的情况下,速度还会继续增大,牵引力随之减小,所以此后过程是加速度逐渐减小的加速运动,直到加速度时,机车的速度达到最终的最大速度。
如下图所示,恒定加速度起动的过程的三个阶段,即从为匀加速运动阶段;为加速度逐渐减小的加速运动;此后以速度作匀速直线运动。
发动机启动困难

发动机启动困难一、问题描述在汽车使用过程中,有时候会遇到发动机启动困难的情况。
这种情况下,汽车可能需要多次尝试才能成功启动,或者在启动后还出现了其他异常现象。
本文将就发动机启动困难的原因进行分析,并提出相应的解决方法。
二、起因分析1. 电池问题:电池电量不足是发动机启动困难的常见原因之一。
电池电量不足可能是由于长时间未使用车辆、电池老化、电路短路等问题引起的。
此时,启动电机所需的电能无法满足要求,导致启动困难。
2. 燃油问题:燃油质量不过关,或者燃油供应系统出现故障,都可能导致发动机启动困难。
例如,燃油泵损坏、燃油滤清器堵塞等情况都会影响到燃油的供应,从而导致启动困难。
3. 点火系统问题:点火系统异常也是发动机启动困难的常见原因之一。
例如,火花塞老化、火花塞间隙过大、点火线圈故障等都会影响到点火能力,使得发动机无法正常启动。
4. 空气供给问题:发动机启动需要充足的空气供给。
如果空气滤清器堵塞,或者进气管道受到异物阻塞,都会造成空气供给不足,导致启动困难。
三、解决方法1. 检查电池:首先需要检查电池电量是否充足,并注意观察电池是否老化或损坏。
如果电池电量不足,可以尝试使用电池充电器进行充电。
如果电池老化或损坏,应及时更换新电池。
2. 检查燃油系统:检查燃油是否充足,以及燃油供应系统是否正常工作。
可以检查燃油泵、燃油滤清器等部件是否损坏或堵塞,必要时进行更换或清洗。
3. 检查点火系统:检查火花塞的工作状态,观察是否有老化、间隙过大等情况。
同时,还可以检查点火线圈及其他相关部件是否正常。
必要时进行更换或维修。
4. 检查空气供给:检查空气滤清器是否干净,如有堵塞或脏污,及时清洗或更换。
同时,还要检查进气管道是否畅通,如有异物阻塞,予以清理。
四、预防措施1. 定期维护:定期进行发动机保养和维护工作,包括更换机油、空气滤清器等。
及时发现并解决潜在问题,可以减少发动机启动困难的概率。
2. 规范使用:避免频繁短途行驶和急速起步,这样可以减少对发动机的磨损,延长使用寿命。
机车启动问题

机车启动问题一、机车的两种启动问题当机车从静止开始沿水平面加速运动时,有两种不同的加速过程,但分析时采用的基本公式都是P Fv=和F f ma-=;为使问题简化,假定机车所受阻力大小恒定;1.恒定功率的加速问题由公式P Fv=和F f ma-=知,由于P恒定,随着v的增大,F必将减小,a也必将减小,机车做加速度不断减小的加速运动,直到F f=,a=0,这时v达到最大值:m P PvF f==,可见恒定功率的加速运动一定不是匀加速运动.这种加速过程发动机做的功只能用W=Pt计算,不能用W Fs=计算因为F为变力;以上机车的启动过程可用如图所示的v-t图像来表示;2.恒定牵引力的加速问题由公式P Fv=和F f ma-=知,由于F恒定,所以a恒定,机车做匀加速运动,而随着v的增大,功率也将不断增大,直到功率达到额定功率P,功率不能再增大了;这时匀加速运动结束,其最大速度为1=m P Pv vF f=<,此后机车要想继续加速就只能做恒定功率的变加速运动了;可见当机车做恒定牵引力的加速运动时功率一定不恒定;这种加速过程发动机做的功只能用W=F·s计算,不能用W=P·t计算因为P为变功率;以上机车的启动过程可用如图所示的v-t图像来概括说明;0~t1时间内,机车从静止开始匀加速运动,牵引力F恒定,机车的输出功率P=Fv不断变大,t1时刻达到额定功率匀加速阶段结束;t 1~t2时间内,机车以恒定功率继续加速,牵引力和加速度不断减小加速度减小的加速运动,对应图像中曲线部分;t2时刻加速度减为零,F=f,机车匀速前进对应图像中水平直线部分,此时达到最大速度m Pvf=;例题1.一新型赛车在水平专用测试道上进行测试,该车总质量为m=1×103kg,由静止开始沿水平测试道运动,用传感设备记录其运动的v-t图像如图所示;该车运动中受到的摩擦阻力含空气阻力恒定,且摩擦阻力跟车的重力的比值为μ=;赛车在0~5s 的v-t 图像为直线,5s 末该车发动机达到额定功率并保持该功率行驶,在5~20s 之间,赛车的v-t 图像先是一段曲线,后为直线.取g=10m/s 2,试求:1该车的额定功率;2该车的最大速度v m ;解析:10~5s 赛车做匀加速运动,其加速度:由题意得f mg μ=,则摩擦阻力为3210f N =⨯ 所以发动机牵引力的额定功率1P Fv ==×105W; 2由m P Fv =,解得:m v =60m/s;答案:1×105W260m/s点拨:弄清楚v-t 图像中各段图线所表示的运动过程,然后画出运动草图,合理运用牛顿运动定律和运动学公式是解决此类问题的基本思路和方法;二、机车启动问题中的位移分析方法在机车启动过程中,计算机车的位移是一个难点;由于机车一般会经历多个运动过程,在匀变速运动过程中可以利用运动学公式直接求解,但在变加速运动阶段,只能借助动能定理来计算;在机车启动问题中,要注意区别“两个速度”,即匀加速阶段的最大速度图像中的1v 和最终匀速运动的速度图像中的m v ;求匀加速阶段的位移可运用匀变速直线运动的位移公式21111122v x at t ==,计算变加速运动阶段的位移则不能用上述公式,但由于该阶段功率P 不变,故可以用动能定理22212111()22m P t t fx mv mv --=-计算; 如在例题1中,计算赛车出发后前20s 内的位移,分析如下:前5s 内赛车匀加速运动,位移111=50m 2v x t = 在5~20s 内即215t s =,发动机已经达到额定牵引功率,且在20s 时车的速度为最大速度m v ,由动能定理得222211122m Pt fx mv mv -=- 代入数据解得x 2=100m,总位移x =x 1+x 2=150m;例题2.节能混合动力车是一种可以利用汽油及所储存电能作为动力来源的汽车;有一质量m=1000kg 的混合动力轿车,在平直公路上以速度1v =90km/h 匀速行驶,发动机的输出功率为P=50kW,当驾驶员看到前方有80km/h 的限速标志时,保持发动机功率不变,立即启动利用电磁阻尼带动的发电机工作给电池充电,使轿车做减速运动,运动L=72m 后,速度变为2v =72km/h;此过程中发动机功率的15用于轿车的牵引,45用于供给发电机工作,发动机输送给发电机的能量最后有50%转化为电池的电能;假设轿车在上述运动过程中所受阻力保持不变;求:1轿车以90km/h 在平直公路上匀速行驶时,所受阻力f 的大小;2轿车从90km/h 减速到72km/h 过程中,获得的电能E 电;3轿车仅用其在上述减速过程中获得的电能E 电维持72km/h 匀速运动的距离L′;解析:1轿车牵引力与输出功率的关系1P Fv =将P=50kW,1v =90km/h=25m/s 代入得当轿车匀速行驶时,牵引力与阻力大小相等,有f =2×103N;2在减速过程中,发动机只有5P 用于轿车的牵引,根据动能定理有代入数据得51.57510Pt J =⨯电池获得的电能为44=0.5 6.3105E Pt J ⨯=⨯电; 3根据题设,轿车在平直公路上匀速行驶时受到的阻力仍为f =2×103N;此过程中,由能量转化及守恒定律可知,仅有电能用于克服阻力做功E 电=f L′,代入数据得L′=;答案:12×103N246.310J ⨯3点拨:本题是对机车启动问题的创新性考查,解决问题的依据和方法是学生所熟悉的,但题目情境比较新颖.首先是材料新,以节能混合动力车为题材;其次是考查角度新,没有直接考查机车启动问题的三个运动过程,而是从能量转化与守恒的角度考查学生获取信息的能力;审题过程中弄清楚发动机输出功率的分配是解题的关键;。
机车启动问题 (精编版)

机车启动的两种情况:以恒定的功率启动;以恒定的加速度a 启动(也就是以恒定牵引力启动)其解题关键在于逐步分析v 、a 、F 、p 间关系,并把握由起动到匀速的临界条件F =f ,即汽车达到最大速度的条件。
一、以恒定的功率启动(也适用于以额定功率启动)由公式P=Fv 和F-f=ma (阻力f 为定值)知,由于P 恒定,随着v 的增大,F 必将减小,a 也必将减小,机车做加速度不断减小的加速运动,直到F=f ,a=0,这时v 达到最大值max P P v F f== 可见恒定功率的加速运动一定不是匀加速运动。
这种加速过程发动机做的功只能用W=Pt 计算,不能用W=Fs 计算(因为F 为变力)。
在此过程中,F 牵、v 、a 的变化情况:max max 0||P F f v F a a F f v v v vm-↑⇒=↓⇒=↓⇒==⇒←→当时即时达到最大保持匀速运动机车做变加速直线运动所以综上所述汽车以恒定的功率启动,达到最大速度时a =0,F =f ,P =Fv max =fv max .以恒定的功率启动(也适用于以额定功率启动)的v —t 图像二、以恒定的加速度a 启动(也就是以恒定牵引力F 恒启动)由公式P=Fv 和F-f=ma (阻力f 为定值)知,由于F 恒恒定,所以a 恒定,机车做匀加速运动,而随着v 的增大,功率也将不断增大,直到功率达到额定功率P 额,功率不能再增大了.这时匀加速运动结束,其匀加速运动能达到的最大速度为,max <F P P v f=额额恒此后机车要想继续加速就只能做恒定功率的变加速运动了。
可见当机车做恒定牵引力的加速运动时功率一定不恒定.这种加速过程发动机做的功只能用W=F ·s 计算,不能用W=P ·t 计算(因为P 为变功率).各个量(牵引功率、牵引力、加速度、速度)的变化情况如下:v max 0v以恒定的加速度a 启动(也就是以恒定牵引力F 恒启动)的v —t 图像三、典型题目●案例探究[例1]汽车发动机额定功率为60kW ,汽车质量为5.0×103 kg ,汽车在水平路面行驶时,受到的阻力大小是车重的0.1倍,试求:(1)汽车保持额定功率从静止出发后能达到的最大速度是多少?(2)若汽车从静止开始,以0.5 m/s 2的加速度匀加速运动,则这一加速度能维持多长时间? 错解分析:(1)对v 、F 、a 、p 间相互制约关系分析不透,挖掘不到临界条件和临界状态,(2)在第(2)问中认为功率刚达到最大(即额定功率)时,速度亦达到了最大.可得汽车速度达到最大时,a =0,kmgPv v F P kmg f F mm =⇒⎭⎬⎫⋅====12m/s (2)要维持汽车加速度不变,就要维持其牵引力不变,汽车功率将随v 增大而增大,当P 达到额定功率P 额后,不能再增加,即汽车就不可能再保持匀加速运动了.所以,汽车达到最大速度之前已经历了两个过程:匀加速和变加速,匀加速过程能维持到汽车功率增加到P 额的时刻,设匀加速能达到最大速度为v ,则此时s 16:1=⎪⎩⎪⎨⎧=-==t ma kmg F FvP atv [例2]电动机通过一绳子吊起质量为8kg 的物体,绳的拉力不能超过120N ,电动机的功率不能超过1200 W ,要将此物体由静止起用最快的方式吊高90 m (已知此物体在被吊高接近90m 时,已开始以最大速度匀速上升)所需时间为多少?解题方法与技巧:此题可以用机车起动类问题的思路,即将物体吊高分为两个过程处理:第一过程是以绳所能承受的最大拉力拉物体,使物体匀加速上升,第一个过程结束时,电动机刚达到最大功率.第二个过程是电动机一直以最大功率拉物体,拉力逐渐减小,当拉力等于重力时,物体开始匀速上升.在匀加速运动过程中加速度为a =8108120m ⨯-=-m mg F m/s 2=5m/s 2 末速度v t =1201200=m m F P =10m/s 上升的时间t 1=510=a v t s=2s 上升高度为h =5210222⨯=a v t =5m 在功率恒定的过程中,最后匀速运动的速率为v m =1081200⨯==mg F F P m m =15 m/s 外力对物体做的总功W =P m t 2-mgh 2,动能变化量为 ΔE k =21mv 2m -21mv t 2 由动能定理得P m t 2-mgh 2=21mv m 2-21mv t 2 代入数据后解得t 2=5.75 s ,所以t =t 1+t 2=7.75 s 所需时间至少为7.75 s.1.汽车以恒定功率P 由静止出发,沿平直路面行驶,最大速度为v ,则下列判断正确的是C A.汽车先做匀加速运动,最后做匀速运动B.汽车先做加速度越来越大的加速运动,最后做匀速运动C.汽车先做加速度越来越小的加速运动,最后做匀速运动D.汽车先做加速运动,再做减速运动,最后做匀速运动2.汽车在水平公路上行驶,车受的阻力为车重的0.01倍,当速度为4 m/s 时,加速度为0.4 m/s 2.若保持此时的功率不变继续行驶,汽车能达到的最大速度是____20____m/s 。
浅谈两类机车启动模型的解题策略

高一使用-0-1年5月■荆丽明很多同学在遇到机车启动问题时,会因为不清楚机车的运动过程,而不知道该采用什么规律进行分析求解。
下面以机车在水平面上以恒定功率启动和以恒定牵引力启动两类模型为例,分析机车的启动过程,总结解题策略,供同学们参考。
一、模型构建类型一:机车以恒定功率启动当机车在水平面上以恒定功率启动时,假设机车在运动过程中受到的阻力f不变,功率P恒定,速度v增大,根据P=Fv知机车的牵引力F减小,根据牛顿第二定律F—f=ma知机车的加速度a减小,即机车做加速度逐渐减小的加速运动,直至F=f时,机车的加速度a减小至零,速度达最大,等于Pp,此后机车以这个最大速度做匀速运动。
机车以恒定功率启动问题的分析流程如图1所示。
尸两一[両天]宀丽肩加‘顾jg加速度逐渐减小的加速直线运动当F才时P=fv nRT|<max r^Ql卜匀速直线运动T图1类型二:机车以恒定牵引力启动当机车在水平面上以恒定牵引力启动时,假设机车在运动过程中受到的阻力f不变,牵引力F恒定,根据牛顿第二定律F—f=ma知机车的加速度a不变,即机车做匀加速运动;根据P=Fv知机车的速度v增大,功率P增大,当功率P达到额定值P max 时,机车的加速度不等于零,速度v继续增大,牵引力F减小,根据牛顿第二定律F—f=ma知机车的加速度a减小,即机车做加速度逐渐减小的加速运动,直至F=f时,机车的加速度a减小至零,速度达最大,等于Pf此后机车以这个最大速度做匀速运动。
机车以恒定牵引力启动问题的分析流程如图-所示。
吓尿FS,苟莎]旦讣和P二氏,丽天]匀加速直线运动当戶达Pmax时両不]<F-f=ma丽;弘P二氏両可__•加速度逐渐减小的加速直线运动当F才时P=fv nr^ol~一匀速直线运弗二「图2二、解题策略机车启动可能涉及三个运动过程:匀变速直线运动过程、变加速直线运动过程和匀速直线运动过程。
解决机车启动问题,需要正确分析机车的运动过程,针对不同的运动过程采用不同的物理规律列式求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机车起动问题的分析及处理策略
1.?两个起动方式
机车起动问题中有两种运动模式,即机车以恒定功率(通常为额定功率)和以恒定加速度a起动。
如何分析这两种方式的起动过程及相关问题的处理,这是教与学中经常碰到的问题。
2.?两个基本关系
“”和“”是分析与处理机车起动过程的两个重要的、基本的关系式。
它反映了机车瞬时状态的各量间的关系。
下图是机车在工作状态下的受力情况,应当明确P为机车的瞬时功率;F为机车的牵引力,而不是机车受的合力;v为机车的瞬时速度;a为瞬时加速度;f为机车所受的阻力(通常机车所受阻力设为恒力);m是机车的质量。
在实践中,我们只要抓住两个基本关系式,相关问题则会迎刃而解。
3.?两个最值速度
额定功率起动的情形
由和可知,因功率P保持不变,速度增大,则机车的牵引力F必然减小,也就不难看出机车的加速度a因此而减小,所以该过程是一个加速度逐渐减小的运动。
显然
当牵引力F减小到等于机车所受阻力f时,即F=f,其加速度a=0,则机车的速度达到最大值。
如下图所示,额定功率下起动过程的两个阶段,即从为加速度逐渐减小的加速运动;此后以速度作匀速直线运动。
恒定加速度起动的情形
初速度为0的匀加速起动的过程,同样根据知,由于加速度a恒定,则牵引力F不变(通常设定机车所受阻力f恒定)。
因此随着速度v增大,其机车的瞬时功率P随之增大,当P增大到额定功率时,此刻速度便是匀加速运动过程的最大速度,其
大小为。
应当注意到是匀加速运动的末状态,此刻机车的功率刚好等于额定功率,而此时此刻
牵引力仍为F,且F,再由两个基本关系式,容易分析出,在功率不变的情况下,速度还会继续增大,牵引力随之减小,所以此后过程是加速度逐渐减小的加
速运动,直到加速度时,机车的速度达到最终的最大速度。
如下图所示,恒定加速度起动的过程的三个阶段,即从为匀加速运动阶段;
为加速度逐渐减小的加速运动;此后以速度作匀速直线运动。
综合上面的分析可得:
▲两种起动过程最终所能达到的最大速度;
▲恒定加速度起动过程中,匀加速运动过程的最大速度
4.?两个图象
图象能够很好地反映机车两种起动过程的速度随时间的变化情况。
下图是保持额定功率不变的起动过程的图线。
由下图可以看出在t从O到的图线的切线斜率逐渐减小,反映了机车的加速度逐渐减小,直到时刻,斜率减小为零,即此刻机车的加速度为零,之后图线表示机车一直作匀速直线运动。
下图是保持加速度不变的起动过程的
图线。
t从O到时段为斜直线,表示机车
做匀加速运动,且时刻达到匀加速运动
过程的最大速度时段曲线的斜
率逐渐减小,表明此阶段是加速度逐渐减
小的加速运动,直到时刻速度达到最大
值。
此后即为匀速直线运动。
5.?两个典型问题
瞬时值的计算
例题1.?汽车发动机的额定牵引功率为60kW,汽车的质量为5t,汽车在水平路面上行驶时,阻力是车重的倍,试求:
(1)若汽车保持额定功率从静止起动后能达到的最大速度是多少
(2)若汽车从静止开始,保持以的加速度作匀加速运动,这段过程能维持多长时间
(3)如果阻力不变,汽车在水平路面上用速度行驶,实际功率多大此时汽车的加速度又是多大
分析与解答:
(1)汽车在水平路面上行驶时,由于牵引功率保持不变,则汽车的加速度逐渐减小,当时,汽车的速度达到最大值。
则。
(2)汽车从静止开始,以的加速度做匀加速行驶,要求得这个过程所能维持的时间,必须求出匀加速过程的最大速度。
而达到速度时汽车的实际功率恰好达到额定功率,所以根据两个基本关系式,就可以求出保持匀加速运动过程的牵引力F,自然也就求出了。
由得:
所以匀加速运动能维持的时间为:。
(3)由于表明此时汽车处于额定功率下,加速度逐渐减小的加速运动阶段,所以此刻的实际功率等于额定功率。
应该注意到,P保持不变,由知此过程中牵引力不断减小,所以当速度时,其牵引力:
则此刻汽车的加速度:
点拨:涉及功率问题中经常会计算瞬时加速度、瞬时速度、实际功率等。
我们应注意分清机车属哪个类型的起动,处在哪个阶段哪个状态的瞬时值,然后利用两个基本关系式或两个图象进行处理。
“阻力”的理解
机车起动过程的问题中,阻力是相对牵引力而言的,它可能是空气阻力、摩擦阻力、重力或重力的下滑分量等,是起阻碍机车前行的各种力的合力。
拓展:若上题中当汽车行驶在倾角为的长直斜坡上时(其他条件不变),汽车所能行驶的最大速度又是多少(已知)
错解:有不少同学在遇到汽车上坡这类问题时,往往不能正确理解阻力的内涵,会不假思索地按如下方法去计算。
即汽车上坡时所能达到的最大速度为:。
正确解答:如下图所示,汽车在坡路上行驶时,事实上汽车受到的阻力是由两部分构成,即:
又因为当时,
所以
点拨:本题的阻力时汽车速度达到最大应如何理解呢
这里还是应从两个基本关系式:
“”和“”出发来理解。
因为汽车的加速度,汽车在额定功率下工作,这个过程是加速度越来越小的加速运动,当加速度减小至零时,即时,汽车的速度达到最大值。
