用电热法测量热功当量
102 电热法测量热功当量
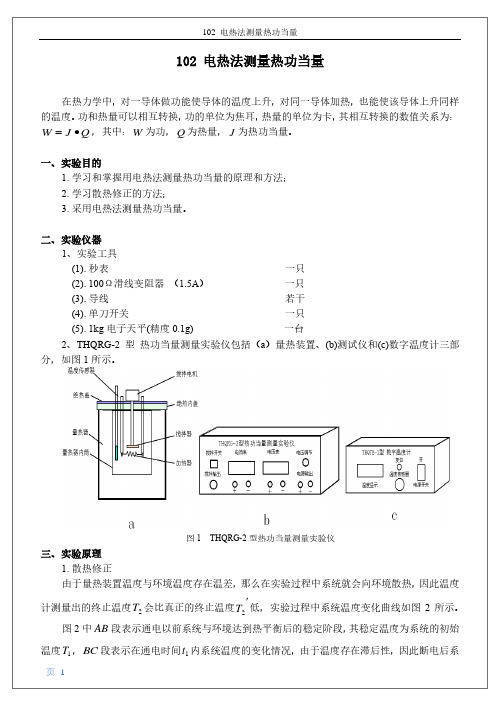
图1 THQRG-2型热功当量测量实验仪
三、实验原理
1.散热修正
由于量热装置温度与环境温度存在温差,那么在实验过程中系统就会向环境散热,因此温度计测量出的终止温度2T 会比真正的终止温度'
2T 低,实验过程中系统温度变化曲线如图2所示。
图2中AB 段表示通电以前系统与环境达到热平衡后的稳定阶段,其稳定温度为系统的初始T BC t
图2 温度随时间的变化曲线
图3 实验接线图
中的数据,通过公式(4)计算求出系统的真正终温
' 2 T。
)计算求出热功当量的数值,并与公认值进行比较,计算相对误差。
在实验前使用干燥毛巾擦净量热器,从而避免量热器表面由于水滴附着,。
中科大大学物理实验答案

中科大大学物理实验答案力学和热学电磁学光学近代物理1.是否可以测摆动一次的时间作周期值?为什么?答:不可以。
因为一次测量随机误差较大,多次测量可减少随机误差。
2.将一半径小于下圆盘半径的圆盘,放在下圆盘上,并使中心一致,讨论此时三线摆的周期和空载时的周期相比是增大、减小还是不一定?说明理由。
答:当两个圆盘的质量为均匀分布时,与空载时比较,摆动周期将会减小。
因为此时若把两盘看成为一个半径等于原下盘的圆盘时,其转动惯量I小于质量与此相等的同直径的圆盘,根据公式(3-1-5),摆动周期T将会减小。
3.三线摆在摆动中受空气阻尼,振幅越来越小,它的周期是否会变化?对测量结果影响大吗?为什么?答:周期减小,对测量结果影响不大,因为本实验测量的时间比较短。
实验2金属丝弹性模量的测量1.光杠杆有什么优点,怎样提高光杠杆测量的灵敏度?答:优点是:可以测量微小长度变化量。
提高放大倍数即适当地增大标尺距离D或适当地减小光杠杆前后脚的垂直距离b,可以提高灵敏度,因为光杠杆的放大倍数为2D/b。
2.何谓视差,怎样判断与消除视差?答:眼睛对着目镜上、下移动,若望远镜十字叉丝的水平线与标尺的刻度有相对位移,这种现象叫视差,细调调焦手轮可消除视差。
3.为什么要用逐差法处理实验数据?答:逐差法是实验数据处理的一种基本方法,实质就是充分利用实验所得的数据,减少随机误差,具有对数据取平均的效果。
因为对有些实验数据,若简单的取各次测量的平均值,中间各测量值将全部消掉,只剩始末两个读数,实际等于单次测量。
为了保持多次测量的优越性,一般对这种自变量等间隔变化的情况,常把数据分成两组,两组逐次求差再算这个差的平均值。
实验三,随即误差的统计规律1._什么是统计直方图?什么是正态分布曲线?两者有何关系与区别?答:对某一物理量在相同条件下做n次重复测量,得到一系列测量值,找出它的最大值和最小值,然后确定一个区间,使其包含全部测量数据,将区间分成若干小区间,统计测量结果出现在各小区间的频数M,以测量数据为横坐标,以频数M为纵坐标,划出各小区间及其对应的频数高度,则可得到一个矩形图,即统计直方图。
电热法测热功当量实验数据处理方法

电热法测热功当量实验数据处理方法
何建勋;唐芳
【期刊名称】《物理实验》
【年(卷),期】2018(038)010
【摘要】基于温度补偿原理和牛顿冷却定律,对电热法测量热功当量实验提出了2种散热修正方法,即温度补偿法和线性回归法.温度补偿法采用作图法,数据处理操作简单;而线性回归方法计算相对复杂,实验过程散热系数保持不变的假设也会给结果带来误差,但可以对实验结果的不确定度给出定量评估.基于此,针对不同的实验数据量和不同的数据采样间隔对实验结果进行了比较,给出了最佳方案.
【总页数】5页(P54-58)
【作者】何建勋;唐芳
【作者单位】北京航空航天大学能源与动力工程学院 ,北京100191;北京航空航天大学物理科学与核能工程学院 ,北京100191
【正文语种】中文
【中图分类】O551.1
【相关文献】
1.电热法测量热功当量实验的新探究 [J], 蔡晨;李朝荣;李英姿;王选
2.电热法测热功当量实验的改进 [J], 代伟;李骏;陈太红;兰小刚
3.用冷热补偿法做电热法测热功当量实验 [J], 岂云开
4.用电热法测定热功当量的实验探讨 [J], 李建英
5.用电热法测定热功当量的实验探讨 [J], 李建英
因版权原因,仅展示原文概要,查看原文内容请购买。
试验用电热法测量热功当量

用电热法测量热功当量教学目标:1. 用电热法测热功当量。
2. 学习用牛顿冷却定律,进行散热修正。
教学方法:采用研究式、答辩式教学方法。
实验内容1. 测量质量,填表12. 连接电路、选量程、电压。
3. 测外围温度θ14. 连接电源,记T 0 ,没隔1分钟,填表25. 断电,接着测降温温度,每隔1分钟,填表3,以求k6. 测环境温度θ2 取θ=21(θ1+θ2) 7. 求δν重点及难点:重点:自然冷却定律修正温度(终)及操作严谨 难点:牛顿自然冷却定律教学过程设计1. 电场力作功W = V I t (1)单位:焦耳、伏特、安培、秒系统吸收全部热量Q=(C 0M 0+C 1M 1+ C 2M 2+0.46δV )(T f –T 0) (2) 由(1)、(2)式可得:QJ=W ,则J=QW 焦耳/卡 称为热功当量 2. 终温修正散热后实际终温为T f ” (测的温度),不散热达到终温为T f (理想温度) 由散热导致温度下降δT测T f = T f ” +δT (4)3. 求δT 的方法:根据牛顿自然冷却定律 dtdT =K (T —θ) 自然冷却:''0fT T - t=0→t k=θθ--'0'ln 1T T t f (1/min)δT=k(θ-T )t 其中)(21"0f T T T += T f = T f ” +δT数据处理:计算法作图法,采用作图法较为直观。
例:1. C 0=1.000卡/克•度 C 1=0.092卡/克•度 C 2=0.094卡/克•度2. 电压U=8.2伏 电流I=0.975安3. 环境温度 θ环=20.0C 0 m 0=167.0克 m 1=203.0克 m 2=49.9克由图 =0.9℃ θf =θb +=28.0+0.9=28.9℃ 由计算机数据处理结果 J=4.30焦耳/卡 误差 E=%10018.430.418.4⨯-=2.9% J=4.18焦耳/卡为公认值。
电热法测热功当量

电热法测热功当量摘要:热量以卡为单位时与功的单位之间的数量关系,相当于单位热量的功的数量,叫做热功当量。
本篇文章主要围绕电热法测量热功当量的方法及其误差分析和修正展开研究。
关键词:电热法、热功当量、散热修正、误差分析1前言热量以卡为单位时与功的单位之间的数量关系,相当于单位热量的功的数量,叫做热功当量。
由焦耳通过大量实验确定。
在人们尚未认清热的本质以前,热量和功分别用不同的单位表示。
焦耳是功的单位,卡路里是热能的单位。
值得注意的是,功和热之间的转换只有通过系统内能的变化才能完成,脱离系统而去谈论功与热量的直接转换是不恰当的。
热功当量的发现,使当时的人们更好地理解了热的本质,也说明了卡路里与焦耳为相当量而非相等。
自国际单位统一热量单位为焦耳后,热功当量也就不复存在。
但其实验测定及数据对于物理学的发展的意义永远存在。
测量热功当量的方法有很多,最传统的方法是热功当量提出者焦耳采用的利用液体摩擦生热,后世人们也逐渐发明出了各种测量方法,如利用固体摩擦等,而目前操作最简便、测量误差小的方法也是我们将要采用的电热法。
2实验方法本实验所要用到的实验器材有:直流电源,导线,电压表,电流表,金属内筒,温度计,开关,玻璃搅拌器等。
图1实验装置图如图即为电热法测量热功当量的实验装置图,该实验方法是通过量热桶中的电阻丝加热液体,使其升高一定温度后通过Q=cm(t-t0)得到液体获得的热能,再通过W=UIt得到以焦耳为单位的电阻丝加热的能量,二者相比得:(1)由(1)式可得测量的热功当量数值。
具体实验步骤如下:1.用托盘天平测量量热桶内壁质量。
2.装入一定量水。
③放入量热桶内盖上盖子,注意温度计不要碰到底部。
1.用环形玻璃搅拌器搅拌,使水温度均匀。
2.读出水的初温T0。
3.组装电路。
4.调节电源电压,读出此时电压表及电流表读数。
5.等待升温。
6.升温后,断开开关并再次搅拌使温度不再变化。
7.读出此时水的温度。
⑪用W=UIt得出总共获得的热量(单位J)。
用电热法测定热功当量实验报告doc

用电热法测定热功当量实验报告篇一:T.热功当量的测量.05实验名称热功当量的测量一、前言热量和功这两个物理量,实质上是以不同形式传递的能量,它们具有相同的单位,即能量的单位焦耳(J)。
但是,在没有熟悉热的本质以前,历史上曾经对热量的计量还有规定。
热量的单位用卡路里,简称卡,1克纯水在1大气压下温度升高10C所吸收的热量为1卡。
焦耳以为热量和功之间应当有必然的当量关系,即热量的单位卡和功的单位焦耳间有必然的数量关系。
从1840年到1879年近40年的时间内,焦耳利用电热量热法和机械量热法进行了大量的实验,最终精准地求得了功和热量彼此转换的数值关系—热功当量。
若是用W表示电功或机械功,用Q表示这一切所对应的热量,则功和热量之间的关系可写成W=JQ,J即为热功当量。
目前国际上对卡和焦耳的关系有两种规定:1热工程卡=4.1868焦耳;1热化学卡=4.1840焦耳。
国际上把“卡”仅作为能量的一种辅助单位,并建议一般不利用“卡”。
国际单位制规定,功、能和热量一概利用焦耳为单位。
虽然热功当量的数值现已逐渐为人们所少用,可是,热功当量的实验及其在物理学发展史上所起的作用是不可磨灭的。
焦耳的热功当量实验为能量转化与守恒定律奠定了坚实的实验基础。
本实验采用焦耳曾经做过的电热法来测定热功当量。
二、教学目标一、了解电流作功与热量的关系,用电热法测定热功当量。
二、了解热量损失的修正方式。
三、教学重点一、了解电流作功与热量的关系。
四、教学难点一、正确读取温度的方式和机会。
五、实验原理一、用电热法来测定热功当量若是加在加热器两头的电压为U, 通过加热器的电流为I, 电流通过时间为t, 则电流作功为:W?IUt (1)若是这些功全数转化为热量,此热量用量热器测出,则可求出热功当量。
设m1表示量热器内圆筒质量,C1表示其比热。
m2表示铜电极和铜搅拌器的质量,C2表示其比热。
m3表示量热器内圆筒中水的质量,C3表示水的比热,T1和T2表示量热器内圆筒及圆筒中水的初始温度和终末温度,那么量热器内圆筒及圆筒中的水等所吸收的热量Q为Q??mC11?m2C2?m3C3??T2?T1? (2)若是进程中没有热量散失,电功W用焦耳(J)作单位,热量Q 的单位用卡(cal)时,则有W?JQ (3)式中,J为热功当量,由上式可得测量J的理论公式:J?WIUt?(J/cal) Q(m1c1?m2c2?m3c3)(T2?T1)(4)二、散热修正上述讨论是假定量热器与外界无热量互换时的结论,实际上只要有温度的不同就必然要有热互换存在。
《普通物理实验》课程标准

《普通物理实验》课程标准说明普通物理实验是三年制高等师范专科学校物理专业必修的基础课程。
通过教学,应使学生:1. 接受基本实验理论和操作技能的训练,熟练掌握基本物理量的测量原理和常用的测量方法,能合理选择与正确使用基本仪器,能正确运用有效数字并掌握基本的实验数据处理方法,能对实验结果做出正确的分析和判断,能写出符合要求的实验报告。
2. 用实验的方法去观察、研究物理现象、规律,应用所学得的理论知识指导实验,从理论和实验的结合上加深、扩展对物理基本概念和规律的认识,加强理论联系实际和提高指导中学实验的能力。
本课程总学时为114学时,每个实验为3学时。
教学内容绪论(9学时)1. 普通物理实验的地位和作用2. 普通物理实验的过程和各个教学环节的要求3. 实验室规则误差和数据处理的基本知识(一)1. 测量和误差的基本概念2. 测量结果的正确表示3. 误差的估算及其意义4. 有效数字的概念和运算法则5. 数据处理的基本方法误差和数据处理的基本知识(二)1. 随机误差的概念2. 标准误差的计算3. 系统误差的一般知识力学实验(33学时)力学实验是师专物理专业首先开设的基础物理实验,除了起到加深对物理规律认识、培养实验基本技能的作用外,还特别重视对学生进行实验课学习方法的指导,和良好科学实验习惯的培养,为以后的实验教学打下基础。
通过实验,要求学生掌握长度、时间、质量三个基本物理量的测量方法,懂得正确使用游标卡尺、螺旋测微仪、测量显微镜、秒表、数字式毫秒计及光电门、天平、气垫导轨、光杠杆等基本测量仪器和实验设备。
能应用误差理论正确处理实验数据,并对实验结果作出正确的分析。
本部分共列出15个实验。
实验一长度的测量1. 分别用游标卡尺及螺旋测微计测量长方形、球形、圆环等试样的尺寸,并求体积。
2. 利用测量显微镜测一半导体集成电路图形(或类似图形)的尺寸。
练习在弯游标及不同的测微螺旋上读数。
3. 多次测量误差的运算,求绝对误差和相对误差。
热功当量的测定
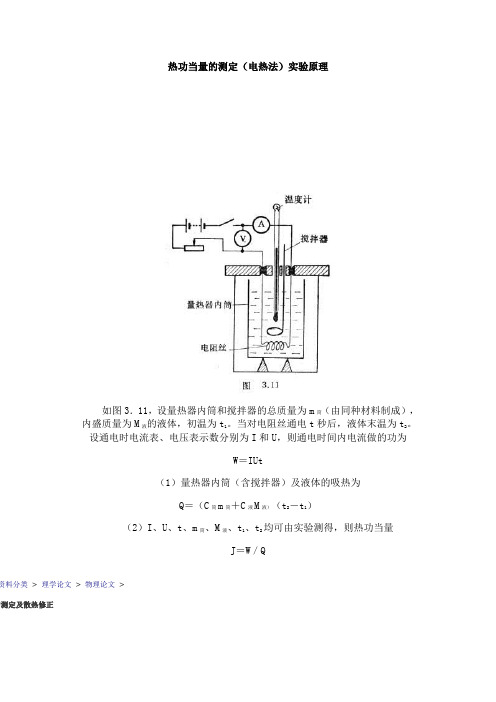
热功当量的测定(电热法)实验原理如图3.11,设量热器内筒和搅拌器的总质量为m筒(由同种材料制成),内盛质量为M液的液体,初温为t1。
当对电阻丝通电t秒后,液体末温为t2。
设通电时电流表、电压表示数分别为I和U,则通电时间内电流做的功为W=IUt(1)量热器内筒(含搅拌器)及液体的吸热为Q=(C筒m筒+C液M液)(t2-t1)(2)I、U、t、m筒、M液、t1、t2均可由实验测得,则热功当量J=W/Q资料分类> 理学论文> 物理论文> 的测定及散热修正资料星级:资料格式:Word 文档上传者:ai349744877出售次数:0上传时间:2009-01-06关键词:热功当量功热量温度牛顿冷却定律10元未知发信告诉好友收藏举报论文( 3页1894字) 图纸量守恒定律,能量既不会凭空产生,也不会自然消灭,只能从一个物体传给另一个物体,从一种形式转化为另一种形式。
功和热量之间可发生相互转化,t秒内通过电热丝,电热丝两端的电势差为U,则电场力做功为W=UIt,若这些功全部转化为热量,通过量热器测量出该热量,从而得出功与热量之间量值。
得出产生1cal热量所需做的功。
当量功热量温度牛顿冷却定律实验是证明能量守恒和转化定律的基础性实验。
焦耳从1840年起,花费了几十年的时间做了大量的实验,论证了传热和做功一样,是能量传递的一种形常数,与做功方式无关,从而为能量守恒和转换定律的确立奠定了坚实的实验基础。
当电阻R两断加上电压U,通过的电流为I时,在通电t秒时间内电些功全部转化为热量,使一个盛水的量热器系统由初温T 升高至T ,系统吸收的热量为Q,则热功当量J=W/Q。
按照能量守恒定律,若采用国际单位制,比值J=1;若Q用卡(cal)作单位,J=4.1868J/cal,该数值表示产生1cal热量所需做的功。
据能量守恒定律,通过测量热功当量,研究功与热量的转化关系,进一步了解功与热量之间转化的特点。
目录:论理实验】陈玉林李传起主编科学出版社理实验】梁家惠李朝荣唐芳编著北京航空航天大学出版社筒中的水时,应用搅拌器均匀轻轻地搅拌,避免搅拌器碰及电热丝和电极。
实验2—16a 热功当量的测定(用电热法).

实验2—16a 热功当量的测定(用电热法)【实验目的】 1.用电热法测量热功当量。
2.学会一种热量散失的修正方法—修正终止温度。
【实验仪器】量热器(附电热丝),温度计(0℃~50℃、0.1℃),电流表,电压表,直流稳压电源,秒表,物理天平,开关等。
【实验原理】仪器装置如图2-16a -1所示,M 与B 分别为量热器的内外两个圆筒,C 为绝缘垫圈,D 为绝缘盖,J 为两个铜金属棒,用以引入加热电流,F 是绕在绝缘材料上的加热电阻丝,G 是搅拌器,H 为温度计,E 为稳压电源。
1.电热法测热功当量强度为I 安培的电流在t 秒内通过电热丝,电热丝两端的电位差为U 伏特。
则电场力做功为W =IUt (2-16a -1) 这些功全部转化为热量,此热量可以用量热器来测量。
设m 1表示量热器内圆筒和搅拌器以及装有缠绕线的胶木支架(一般质料相同,否则应分别考虑)的质量,C 1表示其比热。
m 2表示缠绕线的胶木(或玻璃)的质量,C 2表示其比热。
m 3表示量热器内圆筒中水的质量,C 3表示水的比热,V 表示温度计沉入水中的体积,T 0和T f 表示量热器内圆筒及圆筒中水的初始温度和终止温度,那么量热器内圆筒及圆筒中的水等由导体发热所得的热量Q 为Q =(m 1C 1+m 2C 2+m 3C 3+0.46V )(T f -T 0) (2-16a -2) 所以,热功当量))(46.0(0332211T T V C m C m C m IUt Q W J f -+++==焦耳/卡 (2-16a -3) J 的标准值J 0=4.1868焦耳/卡。
2.散热修正如果实验是在系统(量热器内筒及筒中的水等)的温度与环境的温度平衡时,对电阻通电,那么系统加热后的温度就高于室温θ。
实验过程中将同时伴随散热作用,这样,由温度计读出的终止温度的数值T 2必须比真正的终止温度的数值T f 低。
(即假设没有散热所应达到的终温为T f )。
为了修正这个温度的误差,实验时在相等的时间间隔内,记下相对应的温度,然后以时间为横坐标,温度为纵坐标作图,如图2-16a -2所示。
电热法测热功当量[新版]
![电热法测热功当量[新版]](https://img.taocdn.com/s3/m/b649adc685254b35eefdc8d376eeaeaad1f3160e.png)
答:实验条件是系统与外界没有较大的热交换,并且系统(即水)应尽可能处于准静态变化过程。
实验方法是电热法。
系统误差的最主要来源是系统的热量散失,而终温修正往往不能完全弥补热量散失对测量的影响。
其他来源可能有①水的温度不均匀,用局部温度代替整体温度。
②水的温度与环境温度差异较大,从而给终温的修正带来误差。
③温度,质量及电功率等物理量的测量误差。
2. 试定性说明实验中发生以下情况时,实验结果是偏大还是偏小?(1) 搅拌时水被溅出;答:实验结果将会偏小。
水被溅出,即水的质量减少,在计算热功当量时,还以称横水的质量计算,即认为水的质量不变,但是由于水的质量减少,对水加热时,以同样的电功加热,系统上升的温度要比水没有上升时的温度要高,即水没溅出在同样电功加热时,应上升T度,而水溅出后上升的温度应是T+ΔT度。
用J = A / Q,有Q =(c i m i T),J = A / [(T+△T)/ mc],分母变大J变小。
(2) 搅拌不均匀;答:J 偏大、偏小由温度计插入的位置与电阻丝之间的距离而定。
离电阻丝较远时,系统温度示数比,匀均系统温度低,设T为均匀系统温度,温度计示值应为T-ΔT,用J=A/θ计算,分母变小,则J变大;离电阻丝较近时,温度计示值应为T+ΔT,分母变大,因而J变小。
为室温,若测得值偏高Δθ时,测量得到的温度值为(3) 室温测得偏高或偏低。
答:设θθ0+Δθ;偏低Δθ时,测量温度值为θ0-Δθ,在计算温度亏损时,dT i=k(T i-θ),k是与是室温无关的量(k与室温有关),只与降温初温和降温终温以及降温时间有关,测得室温偏高时,dT i =k [T i - (θ0+Δθ)],每秒内的温度亏损dT i 小于实际值,t 秒末的温度亏损δT i =∑k [T i - (θ0+Δθ)]。
此值小于实际值,由于散热造成的温度亏损δT i =T f + T f ″,修正后的温度T f ″为:T f ″= T f -δT i ,δT i 为负值,当测量值低于实际室温时,δT i 的绝对值变小:T f ″=T f +|δT i |,即T f ″变小,ΔT 变小(其中ΔT =T f ″- T f 初,T f 初:升温初始值),∑∆==Tm c AQ A J i i , J 变大,反之J 变小。
电热法测量焦耳热功当量实验

目的目的:以電熱法測出熱功當量。
實驗方法實驗方法::由於在實際環境下用電功加熱系統使溫度升高的過程中,系統會向外散熱(原因在於系統溫度高於環境溫度)。
因此系統實際上所達到的末溫必低於沒有散熱情況時的末溫,故以牛頓冷卻定律將散熱導致的溫差求出,以求得較精確的結果。
原理原理::早在1798年,德國侖福特以研究摩擦作功所產生的熱量,得知此熱量與供給的功成正比。
由能量守恆定理,當外界對一系統作功 W (單位"焦耳"),若這些功完全由系統轉換成內能(即熱量△H ,單位"卡"),我們能夠找出它們的換算關係W=J ×△H (1)其中的J 即為熱功當量,單位為"焦耳/卡"。
本實驗是要測量J 值。
若一系統是由不同比熱c i 和質量m i 的成分所構成,欲使此系統溫度升高△T ,需要的熱量△H ,可寫為△H =Σm i c i △T =C ×△T (2)其中C 代表整個系統的熱容,可寫成各成分的比熱與質量乘積之和。
若外界對系統作功W ,使系統溫度由T o 升到某一特定溫度T H ,由(2)式代回(1)式中可得其關係如下: W=J ×C ×(T H -T o ) (3)實驗儀器實驗儀器::方法說明:本實驗的設計主要分成兩部分:一是測量系統熱容C ;二是對散熱所造成的誤差做修正,再與供給的電功比較,求出得較準確之熱功當量值J 。
一、測量系統熱容C設水的比熱為S(1卡/o C),卡計系統(包括溫度計、鎳鉻線圈及銅杯等)熱容為C ,此時在卡計內的銅杯中,注入溫度T o 、質量M 克的水(約至半滿),並加熱到接近50℃ 時的溫度T H ,再量取約m 克(約與M 克差不多重),而溫度為T o 的水注入,攪勻後測得混合後的溫度T ave ,求出系統熱容C 。
(C+S ×M)(T H -T ave )=S ×m(T ave -T o )所以M S -)T -T ()T -T (m S =C ••ave H o ave (4)二、電熱法與散熱修正對於卡計系統,我們在鎳鉻線圈(電阻為R 歐姆)的兩端加電壓V (伏特),則輸入此系統的電功率為)(RV =P 2瓦特 (5)實際上,在用電功加熱系統使溫度升高的過程中,系統會向外散熱(原因在於系統溫度高於環境溫度)。
热力当量的测定实验报告模板

《热力当量的测定》实验报告实验名称:_ 热力当量的测定
姓名:_ _ _学号:_ _
实验日期:____________ 同组者:_________ __
一、实验预习部分
(一)实验目的:
1.用电热法测定热功当量。
2.学会一种热量散失的修正方法
(二)实验仪器:
量热器(附电阻丝)、数字温度计、电流表、电压表、直流稳压电源、秒表、电子天平、开关。
(三)实验步骤:
1.用天平称出量热器内同的质量m内.
2.在量热器内筒中加入约140克左右的水后用天平称出其总质量M,则水
的质量m
水
=.M - m内
3.安装好搅拌电机。
4.打开电源开关;打开搅拌开关,搅拌一分钟后,记下初温T1
5.打开加热开关,系统开始加热并开始计时。
记录电流、电压值。
6.通电加热五分钟后,即刻关闭“加热开关”,停止加热,同时,记下加
热时间,待温度不在上升时,记下矽统的末态温度T2
7.关掉“搅拌开关”,倒掉量热器中的水。
8.根据
)
/
(
)
)(
c
m
(c
1
2
cal
J
T
T
m
c
UIt
Q
UIt
J
-
+
+
=
=
ω
水
内
内
水
水
求出热功当量。
其中
C水=1 cal/g℃,C内=0.216 cal/g℃。
9.重复上述步骤多做几次。
二、实验数据:。
用杜瓦瓶改进电热法测定热功当量的实验

用杜瓦瓶改进电热法测定热功当量的实验摘要:测量热功当量的方法有很多,最传统的方法是热功当量提出者焦耳采用的利用液体摩擦生热,电热法是现在实验教学中采用较多的测量热功当量的方法。
后世人们逐渐发明出的各种测量方法,也都会出现一些误差,结合各种文献,本篇文章主要围绕用杜瓦瓶改进电热法测量热功当量的实验展开研究和讨论。
关键词:杜瓦瓶;热功当量;测量装置1前言热功当量实验是测定能量守恒和转换规律、培养学生实验设计的能力、训练操作技能和研究数据处理方法的基本实验。
所以测量热功当量的实验对于实验教育和物理学的发展都非常重要。
电热法也是现在实验教学中采用较多的测量热功当量的方法,但实验操作过程中,由于系统会受一边自然冷却的影响,产生有一定的测量误差。
为此本文用杜瓦瓶改进电热法测定热功当量的实验装置,实验设计可操作性强、方法正确、科学,实验误差小,经实验验证完全可行,实验效果非常满意.2焦耳进行过的各种测定热功当量的实验19世纪初,“热质说"特别流行,以至于焦耳认为热质是不存在的,热是一种能形式,所以他进行了很多实验。
先后介绍了四种测定热功当量的方法,其中之一是使用带电金属。
通电金属丝在水中加热。
当量是根据电流做的功和水获得的热量来计算的。
他发现:通电导体产生的热量与电流强度的平方、导体电阻和导通时间的平方成正比。
这就是后来的焦耳定律,以他的名字命名的。
测定热功当量最著名的的实验是1845年发表的关于通过摩擦加热液体的实验,即焦耳热功当量实验。
从1840年起,焦耳用电量热法和机械量热法进行了数十年的许多实验,得出结论:热功当量是一个与工作方式无关的普遍常数。
从而证明了机械能(功)和电能(功)同热量之间的转换关系;论证了传热是能量传递的一种形式。
为证实能量守恒和转换定律的正确性奠定了坚实的实验基础。
1840年焦耳指出,通过直流导体后放出的热量Q与电流l的平方、导线的电阻R、供电时间t成正比,即电流W=JQ。
测定冰的熔解热研究性报告

基础物理实验研究性报告冰的溶解热、电热法测热功当量第一作者:学号:院系:第二作者学号:院系:日期2012年12月8日冰的溶解热 一、摘要冰的溶解热实验以牛顿冷却定律为原理,采用了巧妙的散热修正的方法,减小实验误差。
虽然电阻法测温度利用函数计算之后,得到精确度较高的数字,但在用面积法对初末温度进行修正的过程中,由于数格子这一过程较为繁琐,且缺乏较高的精确性,而影响了实验的最终结果。
我们的报告利用EXCEL 拟合已经精确积分计算的方法,完成电阻和温度较为精确计算,以及面积取等的过程,力求减小实验误差,得到更加的实验结果。
二、实验目的1. 学习用混合量热法测定冰的熔解热。
2. 应用有物态变化时的热交换定律来计算冰的溶解热。
3. 学习进行散热修正的方法。
4. 熟悉热学实验中基本仪器的使用。
三、实验原理1. 基本原理本实验用混合量热法测定冰的熔解热。
其基本做法如下:把待测系统A 和一个已知热容的系统B 混合起来,并设法使它们形成一个与外界没有热量交换的孤立系统C (C=A+B )。
这样A 或(B )所放出的热量,全部为B(或A)所吸收。
因为已知热容的系统在实验过程中所传递的热量Q ,是可以由其温度的改变△T 和热容C 计算出来,即Q = C △T ,因此待测系统在实验过程中所传递的热量也就知道了。
实验时,量热器装有热水(约高于室温10℃,占内筒容积1/2),然后放入适量冰块,冰溶解后混合系统将达到热平衡。
此过程中,原实验系统放热,设为Q 放,冰吸热溶成水,继续吸热使系统达到热平衡温度,设吸收的总热量为Q 吸。
因为是孤立系统,则有:吸放Q Q =若有质量为M 、温度为T1的冰(在实验室环境下其比热容为c1,熔点为T0)。
与质量为m 、温度为T2的水(比热容为c0)混合,冰全部熔解后系统的平衡温度为T3,设量热器内筒和搅拌器的质量分别为m1、m2(比热容分别为c1 c2),数字温度计浸入水中的部分放出的热量忽略不计。
电热法测量热功当量实验的新探究

电热法测量热功当量实验的新探究蔡晨;李朝荣;李英姿;王选【摘要】提出一种新的实验方案来处理电热法测量热功当量实验中装置的散热问题.采用积分法计算热功当量,求得的热功当量数值更加接近理论值,并且一元线性拟合实验数据时得到的线性关系非常强烈.【期刊名称】《大学物理》【年(卷),期】2016(035)005【总页数】4页(P53-56)【关键词】热功当量;散热系数;线性回归;相关系数【作者】蔡晨;李朝荣;李英姿;王选【作者单位】北京航空航天大学物理科学与核能工程学院,北京 100191;北京航空航天大学物理科学与核能工程学院,北京 100191;北京航空航天大学物理科学与核能工程学院,北京 100191;北京航空航天大学物理科学与核能工程学院,北京100191【正文语种】中文【中图分类】O43电热法测量热功当量实验的散热速率与系统和环境的温差有关,是一个变化量.目前不同版本的《大学物理实验》中对此的处理方法基本都用到了短时间内“差分代替微分近似求得散热量”的方法[1-5],这一方法引起的误差没有量化估计,无法得知其对实验结果的准确性影响程度.另一方面,按照我校的做法得到的线性相关系数比较低,与大家惯常的认识不相符合,我们的研究正是从改善线性相关系数起步的.新方案从实验原理出发,采用积分法代替微分法,并且运用数学分析中泰勒展开的方法对公式进行近似,由此带来的误差可以计算并控制其在允许范围内,最终获得的实验结果不仅准确度高,而且具有理想的线性相关度.1.1 基本原理实验装置如图1所示.给电阻R两端加上电压V,在通电t秒时间内电场力作功W=V2t/R.系统吸收的热量为式(1)中:c0、c1、c2分别是水、量热装置及加热器的比热容;m0、m1、m2分别是其相应的质量;Cm=c0m0+c1m1+c2m2是系统的总热容;θ0为系统初温.于是可得热功当量:若把系统看成是理想绝热的,即只考虑系统由于通电而升温,则由式(2)对时间求导可以得到温度变化率所满足的关系式为考虑到通电时系统吸热的同时也向环境中放热,根据牛顿冷却定律,由于放热引起的温度变化率为式(4)中K为系统的散热系数.综合式(3)和式(4),系统温度的实际变化率为[5]求解此一阶线性常微分方程,得其中:;C0为常数,由初始条件可得C0=ln(A-Kθ0),再代入式(6)得ln [(A-Kθ)/(A-Kθ0)]=-Kt,经进一步转化得到温度θ随时间t变化规律为另一方面,根据牛顿冷却定律dθ/dt= -K(θ-θ环)测定散热系数K.对牛顿冷却定律积分得到令y=ln(θ-θ环),x=t,并设y=a1+b1x,即可通过一元线性拟合计算出斜率b1,进一步得到散热系数K=b1.经实验测定,散热系数K的数值约为10-5数量级(参见2.1计算结果).由于K的数值很小,在一定时间范围内可以对式(7)中指数函数项e-Kt进行泰勒展开并保留前两项,得将式(9)代入式(7),并化简可得向实验装置中加入一定量的水,并通电加热,测量一段时间内温度θ与时间t的关系(注意实验系统与环境的温差始终保持在牛顿冷却定律适用范围内).对θ与t 进行一元线性回归,得到斜率b2=,截距a2=θ0.则有1.2 误差分析下面讨论实验中两个主要的误差,并控制其在合理范围内.1)泰勒展开带来的误差.显然,总时间越长,展开带来的误差越大,如图2,令l1为实际的θ-t关系,则近似之后得到的直线为l2,其中,Δθ是时间为t时近似带来的误差,θ为t时间内温度的变化.则假设l1为一条直线(实际是弧度极小的曲线),斜率为k,则b2的相对误差为对式(11)两边取对数并求导得上式中,可由实验数据证明K(θ0-θ环)约为b2的1%,这里仅为近似计算误差,所以可以忽略.于是得到令,计算得到总时间:t<530 s.当总时间t小于530 s时,可以控制泰勒展开近似对J的误差小于0.1%.2)温度计示值误差.本实验使用金属铂电阻温度计,示值误差约为0.2℃.t时刻读取温度的相对误差为显然,σ是一个关于t的减函数,只需令t=0时,σ<1%,即可保证任何时刻温度读数的相对误差小于1%.计算得θ0>20℃,所以实验的起始温度需要在20℃以上.1.3 误差分析的验证用上述实验中得到的数据分别选取不同总时长进行一元线性拟合,并由式(11)求得不同总时长下的热功当量值J,由此做出热功当量相对误差与总测量时间的关系如图3所示.由图3可见,当总时长小于300 s时,热功当量的测量值与标准值1的相对误差较大,这是因为实验装置本身的误差(温度计的示值误差等)在总时间过小时对实验的影响不可忽略.当总时长大于500 s时,热功当量的测量值与标准值的误差随总时长的增加而增加.这与“泰勒展开带来的实验误差随总时间的增加而变大”的结论相一致.当总时间在500 s时,热功当量的实验测量值与准确值的相对误差最小,是最适合在实验中应用的总时长.由此,实验验证的结果与理论分析完全一致,从而验证了实验原理与误差分析的正确性.2.1 K值的测量向实验装置中加入高于环境温度(不超过牛顿冷却定律适用范围)的一定量的水,在不加热情况下测定50 min内温度随时间变化的规律,每5 min记录一次温度,并且记录实验前后环境温度,取平均值作为真正的环境温度θ环,测量数据及部分计算结果如表1所示.令yi≡ln(θ1i-θ环)、,xi≡t,进行一元线性拟合,得到斜率b1=-8.32×10-5s-1,u(b1)=-0.19×10-5s-1.即有K=-b1=8.32×10-5s-1,u(K)=0.19×10-5s-1.2.2 热功当量J的测定给定值电阻两端加一定电压使实验装置加热,每隔30 s记录一次系统温度,测量数据如表2所示.始末环境温度求得平均值θ环=26.898℃、负载电压V=39.875 V、电阻阻值R=201.9 Ω、内桶质量m1=131.33 g、水质量m0=218.13 g,内桶比热容c1= 0.389 J/(℃·g)、水比热容c0=4.18 J/(℃·g)、加热器热容c2m2=64.38 J/℃,前已测得散热系数K=8.32×10-5s-1.对实验数据进行一元线性回归,拟合得到斜率b2=0.00742,u(b2)=0.00005;截距a2=29.777,u(a2)=0.015;相关系数r=0.9996.将b2、a2值代入式(11),可得热功当量值J=1.0011,相对误差η=0.11%.对实验结果进行不确定度的分析和计算.由式(11)可得其中V、R、Cm、θ环的误差均可略,则所以,热功当量的最终表述为J±u(J)=1.001±0.007.本文采用“积分法泰勒展开取近似”取代“差分代替微分近似”来修正系统散热,解决了“差分代替微分是否合理”的争议.上述方案中,近似带来的实验误差是可以计算的,并且通过控制总时间可以把误差限制在合理范围内.通过泰勒展开可以得到温度θ与时间t的线性关系.利用一元线性回归拟合线性关系时用到多组数据,这样计算热功当量的实验方案实验准确度更高,实验结果更加可靠.【相关文献】[1]《大学物理实验》编写组.大学物理实验[M].北京:清华大学出版社,2008:126-128. [2]张捷民,刘汉臣.大学物理实验[M].北京:科学出版社,2007:140-141.[3]代伟,李骏,陈太红,等.电热法测热功当量实验的改进[J].西华师范大学学报,2011,32(1):95-97.[4]洪履燊,等.热功当量测量实验的改进方法[J].福州大学学报(自然科学版),2007,35(z1):106-108.[5]李朝荣,徐平,等.基础物理实验(修订版)[M].北京:北京航空航天大学出版社,2010:117-118.。
电热法测热功当量实验数据处理方法

阻,狋为加热时 间.在 不 考 虑 散 热 的 情 况 下,即 假
设电流做功全部 转 化 为 热 量,使 盛 水 的 量 热 器 系
Hale Waihona Puke 统由初温 犜0 升到 犜,系统吸收的热量为 犙ab=(犮0犿0+犮1犿1+犮2犿2)(犜-犜0)=犆犿(犜-犜0),
(2) 式中犮0,犮1,犮2 分 别 是 水、量 热 器 和 电 阻 加 热 器 的 比热容;犿0,犿1,犿2 分 别 为 其 相 应 的 质 量;犆犿 为 系统的总热容.所以热功当量犑 满足:
(3)和 (4),系 统 温 度 需 满 足
仅发生在0~狋1′、狋1′~狋3 两过程中.在 假 想 加 热 过
犆犿dd犜狋=犚犝犑2 -犽(犜-犜∞ ),
(5) 程中,系 统 和 环 境 的 传 热 可 用 图 1 所 示 面 积 表 示为
∫ 式(5)为按照牛 顿 冷 却 定 律 修 正 的 热 功 当 量 测 量
电热法测热功当量实验数据处理方法
何 建 勋a,唐 芳b
(北京航空航天大学 a.能源与动力工程学院;b.物理科学与核能工程学院,北京 100191)
摘 要:基于温度补偿原理和牛顿冷却定律,对电热法测 量 热 功 当 量 实 验 提 出 了 2 种 散 热 修 正 方 法,即 温 度 补 偿 法 和线性回归法.温度补偿法采用作图法,数据处理操作简 单;而 线 性 回 归 方 法 计 算 相 对 复 杂,实 验 过 程 散 热 系 数 保 持 不 变的假设也会给结果带来误差,但可以对实验结果的不确定度给出定量评估.基于此,针 对 不 同 的 实 验 数 据 量 和 不 同 的 数 据 采 样 间 隔 对 实 验 结 果 进 行 了 比 较 ,给 出 了 最 佳 方 案 .
电热法测热功当量实验数据处理方法

电热法测热功当量实验数据处理方法何建勋;唐芳【摘要】基于温度补偿原理和牛顿冷却定律,对电热法测量热功当量实验提出了2种散热修正方法,即温度补偿法和线性回归法.温度补偿法采用作图法,数据处理操作简单;而线性回归方法计算相对复杂,实验过程散热系数保持不变的假设也会给结果带来误差,但可以对实验结果的不确定度给出定量评估.基于此,针对不同的实验数据量和不同的数据采样间隔对实验结果进行了比较,给出了最佳方案.【期刊名称】《物理实验》【年(卷),期】2018(038)010【总页数】5页(P54-58)【关键词】热功当量;电热法;散热修正;补偿法;线性回归【作者】何建勋;唐芳【作者单位】北京航空航天大学能源与动力工程学院 ,北京100191;北京航空航天大学物理科学与核能工程学院 ,北京100191【正文语种】中文【中图分类】O551.1热功当量实验是验证能量守恒和转化定律的基础实验[1],其在装置的设计、操作技能的训练和数据处理方法的研究等方面都有助于对学生能力的培养[2],因此无论在物理学的发展还是在实验教学中,热功当量的测量实验均具有较大的意义[2].目前实验教学中普遍采用电热法测量热功当量,我校教材中该实验的数据处理采用“差分代替微分”法求解热功当量[3],这种方法只需记录加热升温数据,但从我校实验经验上看,实验所得的线性相关系数较低、且热功当量测量误差通常较大[4].本文基于温度补偿原理和牛顿冷却定律,对电热法测量热功当量实验提出了2种散热修正方法,即温度补偿法和线性回归法. 首先简单介绍电热法测量热功当量和2种新的散热修正方法;然后对同一批数据用不同的方法处理并比较;最后针对线性回归法,讨论测点数目和测点时间间隔对实验准确度的影响,给出实验方案选择建议.1 电热法测量热功当量的基本原理热功当量可定义为传热量和做功量单位之间的数量关系[1]. 电热法测量热功当量实验在量热器中进行,用电阻加热器向量热器系统加热,加热过程中电流做功为(1)式中,U为加热器两端的电压,R为加热器的电阻,t为加热时间. 在不考虑散热的情况下,即假设电流做功全部转化为热量,使盛水的量热器系统由初温T0升到T,系统吸收的热量为Qab=(c0m0+c1m1+c2m2)(T-T0)=Cm(T-T0),(2)式中c0,c1,c2分别是水、量热器和电阻加热器的比热容;m0,m1,m2分别为其相应的质量;Cm为系统的总热容. 所以热功当量J满足:(3)即如果各量均取国际单位,则热功当量理论值J=1. 然而,即使实验在量热器中进行,系统和外界不可避免地会发生热量交换,一般会根据牛顿冷却定律进行散热修正[3,5]. 当系统和环境温差较小时,牛顿冷却定律可表述为[6]:=-k(T-T∞),(4)其中δQra为系统的散热量,T和T∞分别为系统和环境的温度,k为系统的散热常量. 依据能量守恒关系,系统热力学能增量等于其从加热器的吸热量与其和外界散热量的代数和,综合式(1),(3)和(4),系统温度需满足(5)式(5)为按照牛顿冷却定律修正的热功当量测量公式.2 2种散热修正方法的基本原理2.1 温度补偿方法的原理温度补偿法借鉴了测量冰的熔解热实验中广泛使用的补偿原理[2]. 在热源供热速率恒定且不大、系统导热性能良好、搅拌充分均匀的条件下,系统的温度变化过程可以认为是准静态过程,即在任意时刻系统都处于平衡状态[7],可以通过测量系统内一点的温度来代替系统温度.设实验中系统温度随时间变化的大致趋势如图1中黑线所示,其中0-1段为加热前的过程,由于此时各时刻系统温度低于环境温度,即T<T∞,所以系统从环境吸热,温度稍有增加;1-2段为系统加热过程,在此过程中系统温度由低于环境温度转变为高于环境温度;2-3段为停止加热后的阶段,系统温度高于环境温度,系统向环境放热,温度有所下降. 0-1段和2-3段温度随时间的变化可近似为线性.对式(5)在0~t3时间段内积分:(6)式(6)中等式左边为全过程中系统的热力学能增量,等式右边第一项为系统对环境的散热量δQra,第二项为系统从加热器吸热量δQab. 根据积分定义,等式右边第一项可用系统的T-t图像和T∞所围面积的代数和表示. 若用图1所示的面积定义,则:-k[T(t)-T∞]dt=-k(-S1+S3+S4).(7)在T-t图像上取一时刻t1′,过t1′作垂直于t轴的直线,并延长线段0-1和2-3,使得其与T-t图像所围面积S2,S3和S5满足S2+S3=S5,则存在一假想加热过程,系统温度随时间的变化如图1中红线所示. 其中0~t1′为加热前的自然升温,电加热过程在t1′时刻瞬间完成,t1′~t3为加热后自然降温. 由于加热过程在瞬间完成,所以系统与环境间的传热不发生在电加热过程中,而仅发生在0~t1′、t1′~t3两过程中. 在假想加热过程中,系统和环境的传热可用图1所示面积表示为-k[T′(t)-T∞]dt=-k(-S1-S2+S4+S5).(8)图1 实验温度随时间变化的趋势和补偿原理由于作图保证S2+S3=S5,由式(7)和(8),在图1所示的0-1-2-3过程和0-1′-2′-3过程中,系统向环境间的散热量相等,又因为系统的初末状态相同(均为0状态和3状态),依据能量守恒关系,系统向外界的吸热量等于初末状态热力学能的增量与系统向外界做功量之和[8],所以两过程中系统从加热器的吸热量Qab相等,可以用0-1′-2′-3过程代替实际过程进行研究.而且,因为在0-1-2-3和0-1′-2′-3过程中,仅有1-2段和1′-2′段存在从加热器吸热的过程,所以1-2段和1′-2′段的加热量相等. 又因为1′-2′段的加热过程无时间积累,不存在对环境的散热,所以无论是0-1-2-3还是0-1′-2′-3过程,加热量Qab均等于1′状态和2′状态热力学能的差,即=Cm(T2′-T1′).(9)在实验数据处理时,延长2个散热过程的温度曲线,并在t轴上取t1′时刻,使得T-t图像上的面积满足S2+S3=S5,得到修正后的初末温度T1′和T2′,代入式(9)即可计算热功当量.2.2 二重线性回归方法的原理上述温度补偿方法可以修正实验中的散热,其原理清晰且计算量小,可行性强;但必须测量自然升温和自然降温过程,所以尝试基于牛顿冷却定律的二重线性回归法. 由实验条件可得,本实验中系统和环境的换热可近似看作大空间内的自然对流换热. 由传热学实验关系式[6],大空间自然对流换热的散热常数k与系统和环境间的温度差ΔT有关,为k=Cn(ΔT)n其中n为由实验确定的指数,操作中根据特征格拉晓夫数Gr的范围而取不同的值,可取区间为(0.25,0.33),Cn为指前系数. 对本实验对应的对流换热条件,n取值应为0.33[6].实验涉及对系统的加热升温,升温过程中ΔT的改变会导致散热常量k的变化,然而由试算可得,在升温范围不大(小于初始ΔT的50%)时,此变化在本实验中可作忽略处理. 设则有(10)求解式(10)微分方程,可得加热过程中温度的变化为(11)同理可解得自然对流过程中温度的变化T=C2e-Kt+T∞,(12)式(11)和(12)中的C1和C2均为积分常量,由初始条件确定. 对式(11)和(12)进行线性化变换,将式(12)移项并取对数得ln (T-T∞)=-Kt+ln C2.(13)令Y=ln (T-T∞),X=t,则式(13)满足Y=-KX+c的形式. 所以在自然对流过程中对ln (T-T∞)和t做线性拟合,由拟合系数可求得K.在加热过程中令Y=T,X=e-Kt,则式(11)同样满足Y=aX+b的形式. 所以,在加热过程中对T和e-Kt做线性拟合,由拟合结果可以计算热功当量:(14)而且,由于假设全过程中系统与环境的散热常量保持不变,所以第二次拟合中的K 值可用第一次拟合的结果代替,即第二次线性拟合和计算时的K值已知.3 结果与讨论以下分别用温度补偿法和二重线性回归法,对同一组实验数据进行处理,并对处理结果进行比较.3.1 温度补偿法的处理结果取某次实验测量结果,作出加热前自然升温过程、加热过程和加热后自然降温过程中的T-t图像,并对自然升温和自然降温过程做线性拟合,对加热过程做多项式拟合. 可以得到,拟合相关系数均在0.99以上.根据2.1节的温度补偿原理,做出类似图1的假想过程,用红线表示,即延长自然升温和自然降温过程,并使加热升温瞬间完成,如图2所示.图2 某次实验数据及其温度补偿结果由温度补偿法可得出已修正的加热初温T1′和末温T2′,代入式(9)即可求热功当量. 修正后的加热初末温度分别是:T1′=8.81 ℃,T2′=22.34 ℃,求得热功当量结果为J=1.03.3.2 二重线性回归法的处理结果为方便比较,现选用与3.1节相同的测量数据,用二重线性回归法进行处理. 全过程升温范围约13 ℃,散热常数k在全过程中可看作常数. 根据自然降温过程的T-t 测量结果,对ln (T-T∞)和t做线性拟合,拟合结果如图3所示.图3 自然降温过程中ln (T-T∞)和t的线性拟合结果拟合相关系数为r=-0.997 1,线性关系良好,由拟合斜率可以求得K=6.4137×10-5.假设全过程中K保持不变,在加热过程中对T和e-Kt做线性拟合如图4所示.图4 加热升温过程中T和e-Kt线性拟合结果拟合相关系数r=-0.999 2,线性关系良好,理论推导与实际测量结果无明显偏差,由拟合截距结合式(14)可计算热功当量,计算结果为J=1.049 7.现考虑由此方法求得热功当量的不确定度估计,测量结果的不确定度主要有仪器误差造成的B类不确定度和由拟合误差造成的A类不确定度. 相较于拟合误差,温度、时间、质量等测量的仪器误差很小可忽略不计. 所以这里在进行不确定度合成,仅对拟合误差造成的A类不确定度进行合成.由第一次拟合关系式(12),结合回归系数不确定度的计算方法可求得(15)同理由第二次拟合关系式(11)可求得(16)由式(15)和(16)结合式(14)以及不确定度的合成原则可求得按照上述方法,本节算例中的不确定度u(J)计算结果为u(J)=0.036 2≈0.04,所以本算例热功当量的最终表达为J=1.05±0.04.3.3 2种方法的比较2种方法均可对散热进行修正,得出较准确的热功当量结果,在原理和具体实践中都是可行的. 相较而言,温度补偿方法借助图形工具,将系统与环境的散热量转化为T-t图像中的面积,省却了复杂的散热微分方程的求解,使数据处理更加直观简便.二重线性回归法可通过求解散热常量恒定假设下的散热微分方程,得出完整而严格的数据处理原理. 然而该方法处理过程相对较复杂计算量大. 并且实际过程中的散热常量并非恒定,而是和系统与环境的温度差有关[6],由此引入的近似也会带来实验误差.4 关于二重线性回归方法的进一步讨论二重线性回归方法可以得到完整严格的数据处理原理,但计算量过大的问题仍需解决.理论上,在不影响结果准确度的前提下适当减少测量点的数目可以减少数据处理的工作量. 一般而言,在总时间不变的前提下增大相邻测点的时间间隔Δt,或在时间间隔不变的情况下减少测点的数目n均可减少测量点的数目. 为讨论这2种方法对准确度的影响,在相同条件下改变测点数目进行了多次实验,图5为加热升温阶段测点间隔及测点数目同计算结果的关系对比.图5 加热升温测点间隔和测点数目对计算结果影响总体而言,测点数目和相邻测点的时间间隔对实验结果存在影响. 加长实验时间并密集测点有助于降低实验结果的误差,提高实验结果的准确度. 然而过长的实验时间将会增加实验过程中环境因素的不确定性,不利于结果的准确.由图5可得,当Δt取为30 s时,在n≥20的情况下实验结果的分布较密集,数据的重复性好;在n=10或5时,实验结果分布则较分散,数据的稳定性欠佳,且出现了较大不确定度的情况,说明拟合相关性不好.当Δt由30 s增加到60 s而n不变时,计算结果的重复性和准确度即可得到改善,说明在测点数量不变时,适当增加实验的总时间,即增加相邻测点的时间间隔可降低实验结果的不确定性,使结果更稳定. 当Δt=60 s时,若n减小至5则同样会出现结果分散,此时实验结果的可信度低.所以为了保证实验结果的准确性,测点间的时间间隔不宜过小,一般不能小于60 s;测点数量不宜过少,一般不能小于10;当时间间隔加长至90 s时,测点数量也需为10. Δt和n的最佳取值分别为Δt=60,n=10.5 结束语基于牛顿冷却定律,提出了2种对热功当量实验的数据处理方法,即温度补偿法和二重线性回归法,二者均可降低散热带来的系统误差,得到较准确的实验结果. 温度补偿法不涉及复杂的数学推导,数据处理更加直观和简便;线性回归方法来源于对散热微分方程的求解,在数学上更加严格,且能给出实验结果的不确定度估计. 为解决线性回归方法数据处理工作量大的问题,可在保证实验准确度的前提下适当减少实验测点的数目,合适的Δt和n取值为:Δt=60,n=10. 使用此方法进行数据处理,可以明显解决“差分代替微分求解散热量”方法中线性相关系数低、误差较大的问题,得到准确的结果.【相关文献】[1] 范岱年. 从能量守恒定律的发现看科学发现的一种模式[J]. 北京航空航天大学学报,1986(2):6-20.[2] 王合英,孙文博,陈宜保,等.实验物理教学中的流白艺术[J]. 物理实验,2017,37(5):22-26.[3] 李朝荣,徐平,唐芳. 基础物理实验[M]. 北京:北京航空航天大学出版社,2010:113-120.[4] 蔡晨,李朝荣,李英姿,等. 电热法测量热功当量实验的新探究[J]. 大学物理,2016,35(5):53-56.[5] 朱鹤年. 基础物理实验教程[M]. 北京:高等教育出版社,2003:124.[6] 杨世铭,陶文铨. 传热学[M]. 4版. 北京:高等教育出版社,2006:197,268-270.[7] 刘雪林. 用电热法测定热功当量实验中的升温曲线方法[J]. 物理实验,1985,5(3):13-15.[8] 沈维道,蒋智敏,童钧耕合. 工程热力学[M]. 3版. 北京:高等教育出版社,2001:41.。
电热法测热功当量

一次电阻值,共记16次,然后断开电源。
(5) 切断电源后,待温度不再升高后,开始记录降温的初始阻值 R´ ,之后每 0
隔一分钟记录一次电阻值,共记 16
次。 数据处理
δ V=1.30 水
吕内筒 搅拌器 铜
电阻丝 降温初
1.1 261KΩ 电压
4.90V
比热容 1.000 0.210 2.10
阻值 0.093 0.105 降温终
1.1 228KΩ 电流
1.00A
质量/g 142.45 23.85 3.00
阻值 23.00 0.300 降温时
15min
1.0905
温阻值
KΩ
升
温
R 0
R 1
R 2
R 3
R 4
系统误差的最主要来源是系统的热量散失,而终温修正往往不能完全弥补热量散失对测
量的影响。其他来源可能有①水
的温度不均匀,用局部温度代替整体温度。②水的温度与环境温度差异较大,从而给终
温的修正带来误差。③温度,质
量及电功率等物理量的测量误差。 2. 试定性说明实验中发生以下情况时,实验结果是偏大还是偏小? (1) 搅拌时水被溅出; 答:实验结果将会偏小。 水被溅出,即水 的质量减少,在计算热功当量时,还以称横水的质量
实验方法原理
将一电阻放入一定量的水中 ,电阻通电 t 秒,则电功为 ,由电流的热效应 ,这些功将转化为参与热
A = VIt
作工 的 换 交
Qc
++
TT
(0m0+ c1m1+ c22
0.46δV ) (
⋅f−
如没有热量散失到环境中去,必有热功当量 J 为 J =
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用电热法测量热功当量
教学目标:
1. 用电热法测热功当量。
2. 学习用牛顿冷却定律,进行散热修正。
教学方法:
采用研究式、答辩式教学方法。
实验内容
1. 测量质量,填表1
2. 连接电路、选量程、电压。
3. 测外围温度θ1
4. 连接电源,记T 0 ,没隔1分钟,填表2
5. 断电,接着测降温温度,每隔1分钟,填表3,以求k
6. 测环境温度θ2 取θ=
21(θ1+θ2) 7. 求δν
重点及难点:
重点:自然冷却定律修正温度(终)及操作严谨
难点:牛顿自然冷却定律
教学过程设计
1. 电场力作功
W = V I t (1)
单位:焦耳、伏特、安培、秒
系统吸收全部热量
Q=(C 0M 0+C 1M 1+ C 2M 2+0.46δV )(T f –T 0) (2)
由(1)、(2)式可得:
QJ=W ,则J=Q
W 焦耳/卡 称为热功当量 2. 终温修正
散热后实际终温为T f ” (测的温度),不散热达到终温为T f (理想温度)
由散热导致温度下降δT
测T f = T f ” +δT (4)
3. 求δT 的方法:
根据牛顿自然冷却定律 dt
dT =K (T —θ) 自然冷却:''
0f
T T - t=0→t k=θθ--'0'ln 1T T t f (1/min)
δT=k(θ-T )t 其中)(2
1"0f T T T += T f = T f ” +δT
数据处理:
计算法
作图法,采用作图法较为直观。
例:
1. C 0=1.000卡/克•度 C 1=0.092卡/克•度 C 2=0.094卡/克•度
2. 电压U=8.2伏 电流I=0.975安
3. 环境温度 θ环=20.0C 0
m 0=167.0克 m 1=203.0克 m 2=49.9克
由图 =0.9℃ θf =θb +=28.0+0.9=28.9℃
由计算机数据处理结果 J=4.30焦耳/卡
误差 E=%10018.430
.418.4⨯-=2.9% J=4.18焦耳/卡为公认值。
θ℃--t(分)图
t (分)。
