高斯投影正反算 c#代码
高斯投影正反算c代码

高斯投影正反算程序设计一.程序设计流程本程序(de)设计思路如下:(1),程序采用VS08版本作为开发平台,并采用C语言作为开发语言,设计为WindowsForm窗体程序形式.(2),程序主要(de)算法来自于教材.但是本程序为了更加实用,添加了更多(de)解算基准,包括:WGS-84,国际椭球1975,克氏椭球,和2000国家大地坐标系.(3),程序为了更方便(de)读取数据和输出数据,故需要自己定义了固定(de)数据输入格式和数据输出格式或形式,请老师注意查看.二.代码using System;using Systusing SystemponentModel;using System.Data;using System.Drawing;using System.Text;namespace Gauss{public partial class Form1 : Form{//大地坐标//Geodetic Coordinatepublic struct CRDGEODETIC{public double dLongitude;public double dLatitude;public double dHeight;}//笛卡尔坐标//Cartesian Coordinatepublic struct CRDCARTESIAN{public double x;public double y;public double z;}public Form1(){InitializeComponent();}private void button1_Click(object sender, EventArgs e) {double ee = 0;double a = 0;string tt;try{}catch{MessageBox.Show("Gauss Inverse: Choose datum error");return;}if (ttpareTo("克氏椭球")==0){a = 6378245.00;}if (ttpareTo("WGS-84") == 0){a = 6378.00;}if (ttpareTo("1975国际椭球") == 0){a = 6378140.00;ee =}if (ttpareTo("2000国家大地坐标系") == 0){a = 6378.0;}const double pai = 3.1415926;double b = Math.Sqrt(a a (1 - ee ee));double c = a a / b;double epp = Math.Sqrt((a a - b b) / b / b);CRDGEODETIC pcrdGeo;CRDCARTESIAN pcrdCar;double midlong;//求纬度string[] temp;double[] tempradius = new double[3];for (int i = 0; i < 3; i++){tempradius[i] = Convert.ToDouble(temp[i]);}pcrdGeo.dLatitude = tempradius[0] / 180.0 pai + tempradius[1] / 180.0 / 60.0 pai + tempradius[2] / 180 / 60.0 / 60 pai;//求经度for (int i = 0; i < 3; i++){tempradius[i] = Convert.ToDouble(temp[i]);}pcrdGeo.dLongitude = tempradius[0] / 180.0 pai + tempradius[1] / 180.0 / 60.0 pai + tempradius[2] / 180 / 60.0 / 60 pai;int deglon = Convert.ToInt32(pcrdGeo.dLongitude180 / pai);//求中央经度int num; //带号midlong = 0; //默认值,需要制定分带try{}catch{MessageBox.Show("Choose 3/6 error");return;}if (ttpareTo("3度带") == 0){num = Convert.ToInt32(deglon / 6 + 1);midlong = (6 num - 3) / 180.0 pai;}if (ttpareTo("6度带") == 0){num = Convert.ToInt32((deglon + 1.5) / 3);midlong = num 3 pai / 180;}double lp=pcrdGeo.dLongitude - midlong;double N = c / Math.Sqrt(1 + epp eppMath.Cos(pcrdGeo.dLatitude) Math.Cos(pcrdGeo.dLatitude));double M = c / Math.Pow(1 + epp eppMath.Cos(pcrdGeo.dLatitude) Math.Cos(pcrdGeo.dLatitude), 1.5);double ita = epp Math.Cos(pcrdGeo.dLatitude);double t = Math.Tan(pcrdGeo.dLatitude);double Nscnb = N Math.Sin(pcrdGeo.dLatitude) Math.Cos(pcrdGeo.dLatitude);double Ncosb = N Math.Cos(pcrdGeo.dLatitude);double cosb = Math.Cos(pcrdGeo.dLatitude);double X;double m0, m2, m4, m6, m8;double a0, a2, a4, a6, a8;m0 = a (1 - ee ee);m2 = 3.0 / 2.0 m0 ee ee;m4 = 5.0 / 4.0 ee ee m2;m6 = 7.0 / 6.0 ee ee m4;m8 = 9.0 / 8.0 ee ee m6;a0 = m0 + m2 / 2.0 + 3.0 / 8.0 m4 + 5.0 / 16.0 m6 + 35.0 / 128.0 m8;a2 = m2 / 2 + m4 / 2 + 15.0 / 32.0 m6 + 7.0 / 16.0 m8;a4 = m4 / 8.0 + 3.0 / 16.0 m6 + 7.0 / 32.0 m8;a6 = m6 / 32.0 + m8 / 16.0;a8 = m8 / 128.0;double B = pcrdGeo.dLatitude;double sb = Math.Sin(B);double cb = Math.Cos(B);double s2b = sb cb 2;double s4b = s2b (1 - 2 sb sb) 2;double s6b = s2b Math.Sqrt(1 - s4b s4b) + s4b Math.Sqrt(1 - s2b s2b);X = a0 B - a2 / 2.0 s2b + a4 s4b / 4.0 - a6 / 6.0 s6b;pcrdCar.x = Nscnb lp lp / 2.0 + Nscnb cosb cosb Math.Pow(lp, 4) (5 - t t + 9 ita ita + 4 Math.Pow(ita, 4)) / 24.0 + Nscnb Math.Pow(cosb, 4) Math.Pow(lp, 6) (61 - 58 t t + Math.Pow(t, 4)) / 720.0 + X;pcrdCar.y = Ncosb Math.Pow(lp, 1) + Ncosb cosb cosb (1 - t t + ita ita) / 6.0 Math.Pow(lp, 3) + NcosbMath.Pow(lp, 5) Math.Pow(cosb, 4) (5 - 18 t t+ Math.Pow(t, 4) + 14 ita ita - 58 ita ita t t) / 120.0 ;if (pcrdCar.y < 0)pcrdCar.y += 500000;richTextBox1.Text = "Results:\nX:\t" +Convert.ToString(pcrdCar.x) +"\nY:\t"+ Convert.ToString(pcrdCar.y);}private void button2_Click(object sender, EventArgs e) {double ee = 0;double a = 0;string tt;int num; //带号string ytext; //利用y值求带号和中央经线try{}catch{MessageBox.Show("Gauss Inverse: Choose datumerror");return;}if (ttpareTo("克氏椭球") == 0){a = 6378245.00;}if (ttpareTo("WGS-84") == 0){a = 6378.00;}if (ttpareTo("1975国际椭球") == 0){a = 6378140.00;}if (ttpareTo("2000国家大地坐标系") == 0){a = 6378.0;}double b = Math.Sqrt(a a (1 - ee ee));double c = a a / b;double epp = Math.Sqrt((a a - b b) / b / b); CRDGEODETIC pcrdGeo;CRDCARTESIAN pcrdCar;double midlong = 0;//求X,Y和带号pcrdCar.x = Convert.ToDouble(textBox4.Text); ytext = textBox5.Text;string temp = ytext.Substring(0, 2);num = Convert.ToInt32(temp);ytext = ytext.Remove(0, 2);pcrdCar.y = Convert.ToDouble(ytext) - 500000; try{}catch{MessageBox.Show("Choose 3/6 error");return;}if (ttpareTo("3度带") == 0){midlong = num 3 pai / 180;}if (ttpareTo("6度带") == 0){midlong = (6 num - 3) pai / 180;}b = Math.Sqrt(a a (1 - ee ee));c = a a / b;epp = Math.Sqrt(a a - b b) / b;double m0, m2, m4, m6, m8;double a0, a2, a4, a6, a8;m0 = a (1 - ee ee);m2 = 3.0 / 2.0 m0 ee ee;m4 = 5.0 / 4.0 ee ee m2;m6 = 7.0 / 6.0 ee ee m4;m8 = 9.0 / 8.0 ee ee m6;a0 = m0 + m2 / 2.0 + 3.0 / 8.0 m4 + 5.0 / 16.0 m6 + 35.0 / 128.0 m8;a2 = m2 / 2 + m4 / 2 + 15.0 / 32.0 m6 + 7.0 / 16.0 m8;a4 = m4 / 8.0 + 3.0 / 16.0 m6 + 7.0 / 32.0 m8;a6 = m6 / 32.0 + m8 / 16.0;a8 = m8 / 128.0;double Bf, B;Bf = pcrdCar.x / a0;B = 0.0;while (Math.Abs(Bf - B) > 1E-10){B = Bf;double sb = Math.Sin(B);double cb = Math.Cos(B);double s2b = sb cb 2;double s4b = s2b (1 - 2 sb sb) 2;double s6b = s2b Math.Sqrt(1 - s4b s4b) + s4b Math.Sqrt(1 - s2b s2b);Bf = (pcrdCar.x - (-a2 / 2.0 s2b + a4 / 4.0 s4b - a6 / 6.0 s6b)) / a0;}double itaf, tf, Vf, Nf;itaf = epp Math.Cos(Bf);tf = Math.Tan(Bf);Vf = Math.Sqrt(1 + epp epp Math.Cos(Bf)Math.Cos(Bf));Nf = c / Vf;double ynf = pcrdCar.y / Nf;pcrdGeo.dLatitude = Bf - 1.0 / 2.0 Vf Vf tf (ynf ynf - 1.0 / 12.0 Math.Pow(ynf, 4) (5 + 3 tf tf + itaf itaf - 9 Math.Pow(itaf tf, 2)) +1.0 / 360.0 (61 + 90 tf tf + 45 Math.Pow(tf, 4)) Math.Pow(ynf, 6));pcrdGeo.dLongitude = (ynf / Math.Cos(Bf) - (1 + 2 tf tf + itaf itaf) Math.Pow(ynf, 3) / 6.0 / Math.Cos(Bf) +(5 + 28 tf tf + 24 Math.Pow(tf, 4) + 6 itaf itaf + 8 Math.Pow(itaf tf, 2)) Math.Pow(ynf, 5) / 120.0 /Math.Cos(Bf));pcrdGeo.dLongitude = pcrdGeo.dLongitude + midlong;//pcrdGeo.dLatitude = pcrdGeo.dLatitude;richTextBox2.Text = "Results:\nLatitude: " + Convert.ToString(pcrdGeo.dLatitude) + "\nLongtitude: " +Convert.ToString(pcrdGeo.dLongitude);}private void label13_Click(object sender, EventArgs e) {}}}三.程序运行结果分析通过选取书上(de)具体实例进行测试,本程序(de)精度大体满足要求,一般正算(de)精度在0.01米和0.001米之间,反算(de)精度在0.0001秒左右.以下是程序运行(de)截图.。
高斯投影坐标正反算编程报告

高斯投影坐标正反算编程报告1.编程思想高斯投影坐标正反算的编程需要涉及大量公式。
为了使程序更清晰,各模块的数据重用性更强,本文采用结构化编程思想。
程序由四大块组成。
大地测量家庭作业。
Cpp文件用于存储main()函数,是整个程序的入口。
尝试通过结构化编程简化main()函数。
myfunction.h和myfunction.cpp用于存放计算过程中进行角度弧度换算时所要用到的一些自定的转换函数。
正蒜。
H和zhengsuan CPP用于存储zhengsuan类。
在正算类中,声明了用于高斯投影坐标正演计算的所有变量。
成员变量的初始化和正向计算在类的构造函数中执行。
通过get函数获得相应的阳性结果。
fansuan.h和fansuan.cpp用于存放fansuan类,类似于zhengsuan类,fansuan类中声明了高斯投影坐标反算所要用到的所有变量,在类的构造函数中进行成员变量的初始化及反算计算。
通过get函数获得相应的反算结果。
2.计算模型高斯投影正算公式十、十、nn232244????sinbcosb?Lsimbcosb(5?t?9?4?)l2???224??? 4n5246??sinbcosb(61?58t?t)l720???6y??nn3223??cosb?Lcosb(1?t??)L6.3n5242225??cosb(5?18吨?14?58吨)l120???五tf2mfnf5f高斯投影反算公式B男朋友??tfy?2tf24mfn3f?5.3t2f224??2f?9? ftfy?720mfn46y61?90t2?45泰夫??yy32l??1.2t2f??f3nfcosbf6nfcosbf???y524222?5?28t?24t?6??8?fffftf5120nfcosbf?3.程序框图一开始输入b,l求定带号n,中央纬度l0,纬度差l正算按照实用公式计算x,y换算为国家统一坐标x,y输出x,y输入国家统一坐标x,y由y取定带号n,并换算出x,y求出中央经线l0反算按照实用公式计算b,ll=l0+l求出大地经度l输出b,l结束4.计算结果25.附录:程序代码/////主函数入口大地测量家庭作业。
(整理)高斯投影坐标正反算公式及适合电算的高斯投影公式

§8.3高斯投影坐标正反算公式任何一种投影①坐标对应关系是最主要的;②如果是正形投影,除了满足正形投影的条件外(C-R 偏微分方程),还有它本身的特殊条件。
8.3.1高斯投影坐标正算公式: B,l ⇒ x,y高斯投影必须满足以下三个条件:①中央子午线投影后为直线;②中央子午线投影后长度不变;③投影具有正形性质,即正形投影条件。
由第一条件知中央子午线东西两侧的投影必然对称于中央子午线,即(8-10)式中,x 为l 的偶函数,y 为l 的奇函数;0330'≤l ,即20/1/≈''''ρl ,如展开为l 的级数,收敛。
+++=++++=553316644220l m l m l m y l m l m l m m x (8-33)式中 ,,10m m 是待定系数,它们都是纬度B 的函数。
由第三个条件知:qy l x l y q x ∂∂-=∂∂∂∂=∂∂, (8-33)式分别对l 和q 求偏导数并代入上式----=++++++=+++5533156342442204523164253l dqdm l dq dm l dq dm l m l m l m l dqdm l dq dm dq dm l m l m m (8-34) 上两式两边相等,其必要充分条件是同次幂l 前的系数应相等,即dq dm m dqdm m dqdm m 2312013121⋅=⋅-==(8-35)(8-35)是一种递推公式,只要确定了0m 就可依次确定其余各系数。
由第二条件知:位于中央子午线上的点,投影后的纵坐标x 应等于投影前从赤道量至该点的子午线弧长X ,即(8-33)式第一式中,当0=l时有:0m X x == (8-36) 顾及(对于中央子午线)B V Mr M B N dq dB M dBdXcos cos 2==== 得:B V cB N r dq dB dB dX dq dX dq dm m cos cos 01===⋅===(8-37,38)B B Ndq dB dB dm dq dm m cos sin 22121112=⋅-=⋅-= (8-39)依次求得6543,,,m m m m 并代入(8-33)式,得到高斯投影正算公式6425644223422)5861(cos sin 720)495(cos 24cos sin 2lt t B B N lt B simB N l B B N X x ''+-''+''++-''+''⋅''+=ρηηρρ5222425532233)5814185(cos 120)1(cos 6cos l t t t B N lt B N l B N y ''-++-''+''+-''+''⋅''=ηηρηρρ (8-42) 8.3.2高斯投影坐标反算公式x,y⇒B,l投影方程:),(),(21y x l y x B ϕϕ== (8-43)满足以下三个条件:①x 坐标轴投影后为中央子午线是投影的对称轴;② x 坐标轴投影后长度不变;③投影具有正形性质,即正形投影条件。
高斯平面直角坐标与大地坐标的相互转换——高斯投影的正算与反算.

昆明冶金高等专科学校测绘学院 (4)计算公式
3 2 2 2 4 ( 5 3 t 9 t ) y f f f f 2M f N f 2 4M f N 3 f tf 2 4 6 (6 1 9 0t f 4 5t f ) y 7 2 0M f N 5 f 1 1 2 2 3 l y (1 2t f f ) y 3 N f co s B f 6 N f co s B f 1 2 5 (5 2 8t 2 t4 2 2 f 24 f 6 f 8 f t f )y 5 1 2 0N f co s B f B Bf tf y2 tf
式中:
2 e 2 cos2 B
t 2 tan2 B l (L L0) X为B对应子午线弧长 N为卯酉圈曲率半径 20626 5
昆明冶金高等专科学校测绘学院
2
高斯投影坐标反算公式
(1)高斯投影反算:
已知某点 x, y ,求该点 L, B ,即 x, y ( L, B) 的坐标变换。 (2)投影变换必须满足的条件
昆明冶金高等专科学校测绘学院
二、高斯投影坐标正反算得实用公式及算例
1 高斯投影坐标正算公式 (1)高斯投影正算: 已知某点的 L, B ,求该点的 x, y ,即 (2)投影变换必须满足的条件: 中央子午线投影后为直线; 中央子午线投影后长度不变; 投影具有正形性质,即正形投影条件。 (3)投影过程 在椭球面上有对称于中央子午线的两点 P1 和 P2 ,它们的大地坐标 分别为 ( L1 , B1 )或(l1 , B1)及 (L2 , B2)或(l2 , B2 ) 式中 l 为椭球面上点的经 度与中央子午线 ( L0 ) 的经度差:l L L0 ,点在中央子午线之东, l 为正,在西则为负,则投影后的平面坐标一定为P1 ( x1 , y1 ) 和 P2 ( x 2 , y 2 ) 。
高斯投影正反算原理

高斯投影正反算原理高斯投影是一种常用于地图制图的投影方式,也被广泛应用于其他领域的空间数据处理。
高斯投影正反算是对于已知的地球坐标系上的位置(经纬度),通过计算得到该点的平面坐标(东、北坐标),或者对于已知的平面坐标(东、北坐标),通过计算得到该点的地球坐标系上的位置(经纬度)的过程。
本文将详细介绍高斯投影正反算的原理。
一、高斯投影简介高斯投影是一种圆锥投影,其投影面在地球表面的某个经线上,也就是说,投影面是以该经线为轴的圆锥面。
经过对圆锥体的调整后,使其切于地球椭球面,在该经线上进行投影,同时保持沿该经线方向的比例尺一致,从而达到地图上各点在包括该经线的垂直面上映射的目的。
这种投影方式在某一特定区域内得到高精度的结果,因此广泛应用于地图制图。
二、高斯投影数学模型对于高斯投影正反算,需要先建立高斯投影坐标系与地球坐标系的转换模型。
1.高斯投影坐标系的建立高斯投影坐标系的建立需要确定圆锥面的基本参数,首先需要确定其所处的中央子午线,再确定该子午线上的经度为零点,并利用该经线上某一点的经度和该点的高度来确定该点所在的圆锥体。
圆锥体的底面包括所有与地球椭球面相切的圆面,通过对这些圆面进行调整,使得圆锥体转动后能够在中央子午线上进行投影。
在此基础上,可建立高斯投影坐标系,其中投影面为圆锥面,且中央子午线与投影面的交点称为该投影坐标系的中心,投影面的上端点和下端点分别对应正北方向和正南方向。
2.地球坐标系的建立地球坐标系是以地球椭球体为基础建立的,其坐标系原点确定为地球椭球体上的一个特定点。
在已知该点经纬度和高度的前提下,可确定以该点为中心的地球椭球体,并可根据它与地球坐标系之间的转换关系得到平面坐标系。
3.高斯投影坐标系与地球坐标系之间的转换关系由于高斯投影坐标系与地球坐标系存在不同的坐标体系和基准面,因此需要通过数学关系式来建立它们之间的转换关系。
(1)高斯投影坐标系转地球坐标系:已知高斯投影坐标系中任意一点的东北坐标(N,E),以及所属的中央子午线经度λ0、椭球参数a和e,则可通过以下公式求出该点的地球坐标系经纬度(φ,λ)和高度H:A0为以地球椭球体中心为原点,高斯投影坐标系中心投影坐标为(0,0)的点到椭球面的距离。
高斯投影正反算公式_新

高斯投影坐大地坐标系由大地基准面和地图投影确定,由地图投影到特定椭圆柱面后在南北两极剪开展开而成,是对地球表面的逼近,各国或地区有各自的大地基准面,我国目前主要采用的基准面为:1.WGS84基准面,为GPS基准面,17届国际大地测量协会上推荐,椭圆柱长半轴a=6378137m,短半轴b=6356752.3142451m;2.西安80坐标系,1975年国际大地测量协会上推荐,椭圆柱长半轴a=6378140m,短半轴b=6356755.2881575m;3.北京54坐标系,参照前苏联克拉索夫斯基椭球体建立,椭圆柱长半轴6度0-6度,角。
值为正,Y增加500公里;反算则是由高斯平面坐标(X,Y)求解大地坐标(L,B)。
二、计算模/***************************************本文直接依据空间立体三角函数关系得出结果。
*****/(一)正算由图表1,由方程式(1),令,可得在图表2中,,则由椭圆方程,令可知:(三、程序代doubleL=(m_L-6.0*L0//换算成弧度doublexita=atan(b*b*tan(B)/a/a/cos(L));doubledxita=0.000001;doublexi=dxita;x=0.0;doublec=a*a/b/b;while(xi<xita){x+=dxita/sqrt(c*sin(xi)*sin(xi)+cos(xi)*cos(xi));xi+=dxita;坐标*&B,do ubledoubledxi=0.000001;doublexi=dxi;doubleX=0.0;doublec=a*a/b/b;while(X<x/a){X+=dxi/sqrt(c*sin(xi)*sin(xi)+cos(xi)*cos(xi));xi+=dxi;}doubler=a/sqrt(c*sin(xi)*sin(xi)+cos(xi)*cos(xi));。
高斯投影坐标计算

B
d B dq
2
dX dq dq
c
(
cos B dV V dB
2
dB dq
sin B dB V dq
2
)
2
d B dq
2
cos B c ( tan B V
2 2
3
V
sin B cos B
)
N sin B cos B
同理得
d X dq
3
N cos B ( 1
3
3
2
0
l
L
L
0
高斯投影坐标正算的函数式:
x y
l 是以弧度为单位的经度差。
F B , l F B , l
1 2
一 高斯投影坐标正算公式计算
如图,椭球面上一点投影 到平面后为d点,椭球面上 该点的平行圈(B或q为一 常数)与中央子午线的交 点为e点,若将上式中的展 开点z0设为e处,则很据高 斯投影条件,中央子午线 的长度比m=1,且纵坐标x 等于从赤道起到该平行圈 间的子午线弧长X。此时 可以写出下列方程:
4 2
二、高斯投影坐标反算公式
最后得到坐标反算的公式为:
B B
f
2M
f
t
f
y N
f
2
t 24 M
2 f
f
f
f
N
4 f
3 f
5 3 t
6
2 f
2 f
9 f t
2
2 f
y
4
t
高斯投影坐标反算c语言代码

高斯投影坐标反算c语言代码#include<stdio.h>#include<math.h>#include<conio.h>main(){printf("#####################################################\n");printf("# 角度输入说明:如26°12′45.2″输入为26,12,45.2 #\n");printf("#####################################################\n");double x,y;int j,L0;printf("请输入高斯投影坐标(自然坐标),中间用逗号隔开:\n");scanf("%lf,%lf",&x,&y);//自然坐标输入printf("请输入中央子午线L0:\n");scanf("%d,%d,%lf",&L0); //中央子午线输入printf("请选择参考椭球:1.北京1954参考椭球。
\n 2.西安1980参考椭球。
\n");printf("选择的参考椭球为:");scanf("%d",&j);//选择椭球参数if(j==1){long double Bf0=0.157046064172*pow(10,-6)*x;long double Bf=Bf0+cos(Bf0)*(0.005051773759*sin(Bf0)-0.000029837302*pow(sin(Bf0),3)+0.00000023818 9*pow(sin(Bf0),5));long double t=tan(Bf);long double m=0.00673852541468*pow(cos(Bf),2);long double V=1+m;long double N=6378245.000/sqrt(1-0.00669342162297*pow(sin(Bf),2));long double B1=Bf-1.0/2*V*t*pow(y/N,2)+1.0/24*(5+3*pow(t,2)+m-9*m*pow(t,2))*V*t*pow(y/N,4)-1.0/72 0*(61+90*pow(t,2)+45*pow(t,4))*V*t*pow(y/N,6);long double l1=(1/cos(Bf))*(y/N)-1.0/6*(1+2*pow(t,2)+m)*(1/cos(Bf))*pow(y/N,3)+1.0/120*(5+28*pow(t,2)+24*pow(t,4)+6*m+8*m*pow(t,2))*(1/cos(Bf))*pow(y/N,5);long double B=B1*57.29577951;long double l=l1*57.29577951;long double L=L0+l;int d2=int(B);int f2=int((B-d2)*60);long double m2=((B-d2)*60-f2)*60;printf("B=%d %d %.12lf\n",d2,f2,m2);int d3=int(L);int f3=int((L-d3)*60);long double m3=((L-d3)*60-f3)*60;printf("L=%d %d %.12lf\n",d3,f3,m3); //北京1954参考椭球}if(j==2){long double Bf0=0.157048687473*pow(10,-6)*x;long double Bf=Bf0+cos(Bf0)*(0.005052505593*sin(Bf0)-0.000029847335*pow(sin(Bf0),3)+0.0000002416* pow(sin(Bf0),5)+0.0000000022*pow(sin(Bf0),7));long double t=tan(Bf);long double m=0.006739501819473*pow(cos(Bf),2);long double V=1+m;long double N=6378140.000/sqrt(1-0.006694384999588*pow(sin(Bf),2));long double B1=Bf-1.0/2*V*t*pow(y/N,2)+1.0/24*(5+3*pow(t,2)+m-9*m*pow(t,2))*V*t*pow(y/N,4)-1.0/72 0*(61+90*pow(t,2)+45*pow(t,4))*V*t*pow(y/N,6);long double l1=(1/cos(Bf))*(y/N)-1.0/6*(1+2*pow(t,2)+m)*(1/cos(Bf))*pow(y/N,3)+1.0/120*(5+28*pow(t,2)+24*pow(t,4)+6*m+8*m*pow(t,2))*(1/cos(Bf))*pow(y/N,5);long double B=B1*57.29577951;long double l=l1*57.29577951;long double L=L0+l;int d2=int(B);int f2=int((B-d2)*60);long double m2=((B-d2)*60-f2)*60;printf("B=%d %d %.12lf\n",d2,f2,m2);int d3=int(L);int f3=int((L-d2)*60);long double m3=((L-d2)*60-f2)*60;printf("L=%d %d %.12lf\n",d3,f3,m3); //西安1980参考椭球}getch();}。
测绘程序设计(VS2008)实验报告--高斯投影正反算

《测绘程序设计()》上机实验报告(Visual C++.Net)班级:学号:姓名:序号:二零一一年五月实验7 常用测量程序设计1.实验目的:1.1 巩固类的创建与使用;1.2 掌握数组参数的传递;1.3 掌握常用测绘程序设计的技巧。
1.42.实验内容:编写高斯投影正反算程序。
3.设计思路:这次的实验目的是实现高斯正反算。
需要考虑投影方式即分带的方式,又要考虑椭球参数的类型,所以我添加了两个函数来完成此功能。
分别是int SetProjectType(int m)和void SetParameter(int m,double &a,double &b)。
4.界面设计:界面设计很简单,具体见运行结果。
5.主要代码:文件名:GaussProjectDlg.cpp代码:const double PI=4*atan(1.0);//获得分带方式返回中央子午线经度int CGaussProjectDlg::SetProjectType(int m){UpdateData(TRUE);int n; //记录分带带号double L; //经度L=iDegreeL+iMinL/60+dSecondL/3600;if(m==1) //6度带{n=int(L/6)+1;L0=6*n-3;}else if(m==2) //3度带{n=int((L+1.5)/3);L0=3*n;}else if(m==3) //自主分带L0=L0;return L0;}//获取椭球参数void CGaussProjectDlg::SetParameter(int m,double &a,double &b) {if(m==1) //克拉索夫斯基椭球{a=6378245.0;b=6356863.0187730473;//e=sqrt(0.006693421622966);}else if(m==2) //1975国际协议椭球{a=6378140.0;b=6356755.2881575287;//e=sqrt(0.006694384999588);}else if(m==3) //WGS-84椭球{a=6378137.0;b=6356752.3142;//e=sqrt(0.0066943799013);}}void CGaussProjectDlg::OnBnClickedButtonpositivecal(){// TODO: 在此添加控件通知处理程序代码UpdateData(TRUE);double N;double t;double Eta;double X;double A0,A2,A4,A6,A8;double RadB;double Rou;Rou=180*3600/PI;double a,b,e1,e2; //椭球参数SetParameter(iParameterType,a,b);e1=sqrt(a*a-b*b)/a;e2=sqrt(a*a-b*b)/b;double l;L0=SetProjectType(iProjectType);double L;L=iDegreeL+double(iMinL)/60+dSecondL/3600;l=(L-L0)*3600;RadB=(iDegreeB+double(iMinB)/60+dSecondB/3600)*PI/180;N=a/sqrt(1-e1*e1*sin(RadB)*sin(RadB));t=tan(RadB);Eta=e2*cos(RadB);A0=1+3.0/4*e1*e1+45.0/64*pow(e1,4)+350.0/512*pow(e1,6)+11025.0/16384*pow(e1,8);A2=-1.0/2*(3.0/4*e1*e1+60.0/64*pow(e1,4)+525.0/512*pow(e1,6)+17640.0/16384*pow(e1,8));A4=1.0/4*(15.0/64*pow(e1,4)+210.0/512*pow(e1,6)+8820.0/16384*pow(e1,8));A6=-1.0/6*(35.0/512*pow(e1,6)+2520.0/16384*pow(e1,8));A8=1.0/8*(315.0/16384*pow(e1,8));X=a*(1-e1*e1)*(A0*RadB+A2*sin(2*RadB)+A4*sin(4*RadB)+A6*sin(6*RadB)+A8*sin(8*RadB));x=X+N/(2*Rou*Rou)*sin(RadB)*cos(RadB)*l*l+N/(24*pow(Rou,4))*sin(RadB)*pow(cos(RadB),3)*(5-t*t+9*Eta*Eta+4*pow(Eta,4))*pow(l,4)+ N/(720*pow(Rou,6))*sin(RadB)*pow(cos(RadB),5)*(61-58*t*t+pow(t,4))*pow(l,6);y=N/Rou*cos(RadB)*l+N/(6*pow(Rou,3))*pow(cos(RadB),3)*(1-t*t+Eta*Eta)*pow(l,3)+N/(120*pow(Rou,5))*pow(cos(RadB),5)*(5-18*t*t+pow(t,4)+14*Eta*Eta-58*Eta*Eta*t*t)*pow( l,5);UpdateData(FALSE);}void CGaussProjectDlg::OnBnClickedButtonantical(){// TODO: 在此添加控件通知处理程序代码UpdateData(TRUE);double t_f;double Eta_f;double B_f;double N_f;double M_f;double X=x;double B0;double K0,K2,K4,K6;double a,b,e1,e2; //椭球参数SetParameter(iParameterType,a,b);e1=sqrt(a*a-b*b)/a;e2=sqrt(a*a-b*b)/b;double A0;A0=1+3.0/4*e1*e1+45.0/64*pow(e1,4)+350.0/512*pow(e1,6)+11025.0/16384*pow(e1,8);B0=X/(a*(1-e1*e1)*A0);K0=1.0/2*(3.0/4*e1*e1+45.0/64*pow(e1,4)+350.0/512*pow(e1,6)+11025.0/16384*pow(e1,8));K2=-1.0/3*(63.0/64*pow(e1,4)+1108.0/512*pow(e1,6)+58239.0/16384*pow(e1,8));K4=1.0/3*(604.0/512*pow(e1,6)+68484.0/16384*pow(e1,8));K6=-1.0/3*(26328.0/16384*pow(e1,8));B_f=B0+sin(2*B0)*(K0+sin(B0)*sin(B0)*(K4+K6*sin(B0)*sin(B0)));t_f=tan(B_f);Eta_f=e2*cos(B_f);N_f=a/sqrt(1-e1*e1*sin(B_f)*sin(B_f));M_f=N_f/(1+e2*e2*cos(B_f)*cos(B_f));double B;B=B_f-t_f/(2*M_f*N_f)*y*y+t_f/(24*M_f*pow(N_f,3))*(5+3*t_f*t_f+Eta_f*Eta_f-9*Eta_f*Eta_f*t_f*t_f)*pow(y,4)- t_f/(720*M_f*pow(N_f,5))*(61+90*t_f*t_f+45*pow(t_f,4))*pow(y,6);double l;l=1.0/(N_f*cos(B_f))*y-1.0/(6*pow(N_f,3)*cos(B_f))*(1+2*t_f*t_f+Eta_f*Eta_f)*pow(y,3)+1.0/(120*pow(N_f,5)*cos(B_f))*(5+28*t_f*t_f+24*pow(t_f,4)+6*Eta_f*Eta_f+8*Eta_f*Eta_f* t_f*t_f)*pow(y,5);//将B转化为度分秒的形式double dDegB;dDegB=B*180/PI;iDegreeB=int(dDegB);iMinB=int((dDegB-iDegreeB)*60);dSecondB=((dDegB-iDegreeB)*60-iMinB)*60;double dDegL;dDegL=l*180/PI+L0;iDegreeL=int(dDegL);iMinL=int((dDegL-iDegreeL)*60);dSecondL=((dDegL-iDegreeL)*60-iMinL)*60;UpdateData(FALSE);}6.运行结果:实验的运行结果如下图所示:正算:反算:7.实验总结这次实验是实现高斯投影的正反算,方法很多,实现并不复杂,但是计算公式复杂,变量繁多,稍有不慎,就会造成计算错误。
高斯投影正反算-c#代码

高斯投影正反算程序设计一.程序设计流程本程序的设计思路如下:(1),程序采用VS08版本作为开发平台,并采用C#语言作为开发语言,设计为WindowsForm 窗体程序形式。
(2),程序主要的算法来自于教材。
但是本程序为了更加实用,添加了更多的解算基准,包括:WGS-84,国际椭球1975,克氏椭球,和2000国家大地坐标系。
(3),程序为了更方便的读取数据和输出数据,故需要自己定义了固定的数据输入格式和数据输出格式或形式,请老师注意查看。
二.代码using System;using System.Collections.Generic;using ponentModel;using System.Data;using System.Drawing;using System.Text;using System.Windows.Forms;namespace Gauss{public partial class Form1 : Form{//大地坐标//Geodetic Coordinatepublic struct CRDGEODETIC{public double dLongitude;public double dLatitude;public double dHeight;}//笛卡尔坐标//Cartesian Coordinatepublic struct CRDCARTESIAN{public double x;public double y;public double z;}public Form1(){InitializeComponent();}private void button1_Click(object sender, EventArgs e){double ee = 0;double a = 0;string tt;try{tt = boBox1.Items[boBox1.SelectedIndex].ToString(); }catch{MessageBox.Show("Gauss Inverse: Choose datum error!");return;}if (pareTo("克氏椭球")==0){a = 6378245.00;ee = Math.Sqrt(0.006693421622);}if (pareTo("WGS-84") == 0){a = 6378137.00;ee = Math.Sqrt(0.00669437999013);}if (pareTo("1975国际椭球") == 0){a = 6378140.00;ee = Math.Sqrt(0.006694384999588);}if (pareTo("2000国家大地坐标系") == 0){a = 6378137.0;ee =Math.Sqrt(0.0066943802290);}const double pai = 3.1415926;double b = Math.Sqrt(a * a * (1 - ee * ee));double c = a * a / b;double epp = Math.Sqrt((a * a - b * b) / b / b);CRDGEODETIC pcrdGeo;CRDCARTESIAN pcrdCar;double midlong;//求纬度string[] temp;temp = textBox1.Text.Split(' ');double[] tempradius = new double[3];for (int i = 0; i < 3; i++){tempradius[i] = Convert.ToDouble(temp[i]);}pcrdGeo.dLatitude = tempradius[0] / 180.0 * pai + tempradius[1] / 180.0 / 60.0 * pai + tempradius[2] / 180 / 60.0 / 60 * pai;//求经度temp = textBox2.Text.Split(' ');for (int i = 0; i < 3; i++){tempradius[i] = Convert.ToDouble(temp[i]);}pcrdGeo.dLongitude = tempradius[0] / 180.0 * pai + tempradius[1] / 180.0 / 60.0 * pai + tempradius[2] / 180 / 60.0 / 60 * pai;int deglon = Convert.ToInt32(pcrdGeo.dLongitude * 180 / pai);//求中央经度int num; //带号 midlong = 0; //默认值,需要制定分带try{tt = boBox3.Items[boBox3.SelectedIndex].ToString();}catch{MessageBox.Show("Choose 3/6 error!");return;}if (pareTo("3度带") == 0){num = Convert.ToInt32(deglon / 6 + 1);midlong = (6 * num - 3) / 180.0 * pai;}if (pareTo("6度带") == 0){num = Convert.ToInt32((deglon + 1.5) / 3);midlong = num * 3 * pai / 180;}double lp=pcrdGeo.dLongitude - midlong;double N = c / Math.Sqrt(1 + epp * epp * Math.Cos(pcrdGeo.dLatitude) * Math.Cos(pcrdGeo.dLatitude));double M = c / Math.Pow(1 + epp * epp * Math.Cos(pcrdGeo.dLatitude) * Math.Cos(pcrdGeo.dLatitude), 1.5);double ita = epp * Math.Cos(pcrdGeo.dLatitude);double t = Math.Tan(pcrdGeo.dLatitude);double Nscnb = N * Math.Sin(pcrdGeo.dLatitude) *Math.Cos(pcrdGeo.dLatitude);double Ncosb = N * Math.Cos(pcrdGeo.dLatitude);double cosb = Math.Cos(pcrdGeo.dLatitude);double X;double m0, m2, m4, m6, m8;double a0, a2, a4, a6, a8;m0 = a * (1 - ee * ee);m2 = 3.0 / 2.0 * m0 * ee * ee;m4 = 5.0 / 4.0 * ee * ee * m2;m6 = 7.0 / 6.0 * ee * ee * m4;m8 = 9.0 / 8.0 * ee * ee * m6;a0 = m0 + m2 / 2.0 + 3.0 / 8.0 * m4 + 5.0 / 16.0 * m6 + 35.0 / 128.0 * m8;a2 = m2 / 2 + m4 / 2 + 15.0 / 32.0 * m6 + 7.0 / 16.0 * m8;a4 = m4 / 8.0 + 3.0 / 16.0 * m6 + 7.0 / 32.0 * m8;a6 = m6 / 32.0 + m8 / 16.0;a8 = m8 / 128.0;double B = pcrdGeo.dLatitude;double sb = Math.Sin(B);double cb = Math.Cos(B);double s2b = sb * cb * 2;double s4b = s2b * (1 - 2 * sb * sb) * 2;double s6b = s2b * Math.Sqrt(1 - s4b * s4b) + s4b * Math.Sqrt(1 - s2b * s2b);X = a0 * B - a2 / 2.0 * s2b + a4 * s4b / 4.0 - a6 / 6.0 * s6b;pcrdCar.x = Nscnb * lp * lp / 2.0 + Nscnb * cosb * cosb * Math.Pow(lp, 4) * (5 - t * t + 9 * ita * ita + 4 * Math.Pow(ita, 4)) / 24.0+ Nscnb * Math.Pow(cosb, 4) * Math.Pow(lp, 6) * (61 - 58 * t * t + Math.Pow(t, 4)) / 720.0 + X;pcrdCar.y = Ncosb * Math.Pow(lp, 1) + Ncosb * cosb * cosb * (1 - t * t + ita * ita) / 6.0 * Math.Pow(lp, 3) + Ncosb * Math.Pow(lp, 5)* Math.Pow(cosb, 4) * (5 - 18 * t * t+ Math.Pow(t, 4) + 14 * ita * ita - 58 * ita * ita * t * t) / 120.0 ;if (pcrdCar.y < 0)pcrdCar.y += 500000;richTextBox1.Text = "Results:\nX:\t" + Convert.ToString(pcrdCar.x) +"\nY:\t"+ Convert.ToString(pcrdCar.y);}private void button2_Click(object sender, EventArgs e){double ee = 0;double a = 0;string tt;int num; //带号string ytext; //利用y值求带号和中央经线try{tt = boBox2.Items[boBox2.SelectedIndex].ToString(); }catch{MessageBox.Show("Gauss Inverse: Choose datum error!");return;}if (pareTo("克氏椭球") == 0){a = 6378245.00;ee = Math.Sqrt(0.006693421622);}if (pareTo("WGS-84") == 0){a = 6378137.00;ee = Math.Sqrt(0.00669437999013);}if (pareTo("1975国际椭球") == 0){a = 6378140.00;ee = Math.Sqrt(0.006694384999588);}if (pareTo("2000国家大地坐标系") == 0){a = 6378137.0;ee =Math.Sqrt(0.0066943802290);}const double pai = 3.1415926535898;double b = Math.Sqrt(a * a * (1 - ee * ee));double c = a * a / b;double epp = Math.Sqrt((a * a - b * b) / b / b);CRDGEODETIC pcrdGeo;CRDCARTESIAN pcrdCar;double midlong = 0;//求X,Y和带号pcrdCar.x = Convert.ToDouble(textBox4.Text);ytext = textBox5.Text;string temp = ytext.Substring(0, 2);num = Convert.ToInt32(temp);ytext = ytext.Remove(0, 2);pcrdCar.y = Convert.ToDouble(ytext) - 500000;try{tt = boBox4.Items[boBox4.SelectedIndex].ToString(); }catch{MessageBox.Show("Choose 3/6 error!");return;}if (pareTo("3度带") == 0){midlong = num * 3 * pai / 180;}if (pareTo("6度带") == 0){midlong = (6 * num - 3) * pai / 180;}b = Math.Sqrt(a * a * (1 - ee * ee));c = a * a / b;epp = Math.Sqrt(a * a - b * b) / b;double m0, m2, m4, m6, m8;double a0, a2, a4, a6, a8;m0 = a * (1 - ee * ee);m2 = 3.0 / 2.0 * m0 * ee * ee;m4 = 5.0 / 4.0 * ee * ee * m2;m6 = 7.0 / 6.0 * ee * ee * m4;m8 = 9.0 / 8.0 * ee * ee * m6;a0 = m0 + m2 / 2.0 + 3.0 / 8.0 * m4 + 5.0 / 16.0 * m6 + 35.0 / 128.0 * m8;a2 = m2 / 2 + m4 / 2 + 15.0 / 32.0 * m6 + 7.0 / 16.0 * m8;a4 = m4 / 8.0 + 3.0 / 16.0 * m6 + 7.0 / 32.0 * m8;a6 = m6 / 32.0 + m8 / 16.0;a8 = m8 / 128.0;double Bf, B;Bf = pcrdCar.x / a0;B = 0.0;while (Math.Abs(Bf - B) > 1E-10){B = Bf;double sb = Math.Sin(B);double cb = Math.Cos(B);double s2b = sb * cb * 2;double s4b = s2b * (1 - 2 * sb * sb) * 2;double s6b = s2b * Math.Sqrt(1 - s4b * s4b) + s4b * Math.Sqrt(1 - s2b * s2b);Bf = (pcrdCar.x - (-a2 / 2.0 * s2b + a4 / 4.0 * s4b - a6 / 6.0 * s6b)) / a0;}double itaf, tf, Vf, Nf;itaf = epp * Math.Cos(Bf);tf = Math.Tan(Bf);Vf = Math.Sqrt(1 + epp * epp * Math.Cos(Bf) * Math.Cos(Bf));Nf = c / Vf;double ynf = pcrdCar.y / Nf;pcrdGeo.dLatitude = Bf - 1.0 / 2.0 * Vf * Vf * tf * (ynf * ynf - 1.0 / 12.0 * Math.Pow(ynf, 4) * (5 + 3 * tf * tf + itaf * itaf - 9 * Math.Pow(itaf * tf, 2)) +1.0 / 360.0 * (61 + 90 * tf * tf + 45 * Math.Pow(tf, 4)) * Math.Pow(ynf, 6));pcrdGeo.dLongitude = (ynf / Math.Cos(Bf) - (1 + 2 * tf * tf + itaf * itaf) * Math.Pow(ynf, 3) / 6.0 / Math.Cos(Bf) +(5 + 28 * tf * tf + 24 * Math.Pow(tf, 4) + 6 * itaf * itaf + 8 * Math.Pow(itaf * tf, 2)) * Math.Pow(ynf, 5) / 120.0 / Math.Cos(Bf));pcrdGeo.dLongitude = pcrdGeo.dLongitude + midlong;//pcrdGeo.dLatitude = pcrdGeo.dLatitude;richTextBox2.Text = "Results:\nLatitude: " +Convert.ToString(pcrdGeo.dLatitude) + "\nLongtitude: " +Convert.ToString(pcrdGeo.dLongitude);}private void label13_Click(object sender, EventArgs e){}}}三.程序运行结果分析通过选取书上的具体实例进行测试,本程序的精度大体满足要求,一般正算的精度在0.01米和0.001米之间,反算的精度在0.0001秒左右。
高斯投影正反算 c#代码

高斯投影正反算程序设计一.程序设计流程本程序的设计思路如下:(1),程序采用VS08版本作为开发平台,并采用C#语言作为开发语言,设计为WindowsForm窗体程序形式。
(2),程序主要的算法来自于教材。
但是本程序为了更加实用,添加了更多的解算基准,包括:WGS-84,国际椭球(3{{//{p ublicdoubledLongitude;publicdoubledLatitude;publicdoubledHeight;}//笛卡尔坐标//CartesianCoordinatepublicstructCRDCARTESIAN{publicdoublex;publicdoubley;publicdoublez;}publicForm1(){InitializeComponent();}privatevoidbutton1_Click(objectsender,EventArgse) {try{tt=}{}{ee=}{ee=}if(pareTo("1975国际椭球")==0){a=6378140.00;ee=}if(pareTo("2000国家大地坐标系")==0){a=6378137.0;}constdoublepai=3.1415926;doubleb=Math.Sqrt(a*a*(1-ee*ee));doublec=a*a/b;doubleepp=Math.Sqrt((a*a-b*b)/b/b);CRDGEODETICpcrdGeo;CRDCARTESIANpcrdCar;doublemidlong;//{}ai;//{}pai;//intnum;//带号midlong=0;//默认值,需要制定分带try{tt=}catch{MessageBox.Show("Choose3/6error!");return;if(pareTo("3度带")==0){num=Convert.ToInt32(deglon/6+1);midlong=(6*num-3)/180.0*pai;}if(pareTo("6度带")==0){num=Convert.ToInt32((deglon+1.5)/3);}a4=m4/8.0+3.0/16.0*m6+7.0/32.0*m8;a6=m6/32.0+m8/16.0;a8=m8/128.0;doubleB=pcrdGeo.dLatitude;doublesb=Math.Sin(B);doublecb=Math.Cos(B);doubles2b=sb*cb*2;doubles4b=s2b*(1-2*sb*sb)*2;doubles6b=s2b*Math.Sqrt(1-s4b*s4b)+s4b*Math.Sqrt(1-s2b*s2b); X=a0*B-a2/2.0*s2b+a4*s4b/4.0-a6/6.0*s6b;pcrdCar.x=Nscnb*lp*lp/2.0+Nscnb*cosb*cosb*Math.Pow(lp,4)*(5-t*t+9*ita*ita+4*Math.Pow(ita,4))/24.0 +Nscnb*Math.Pow(cosb,4)*Math.Pow(lp,6)*(61-58*t*t+Math.Pow(t,4))/720.0+X;pcrdCar.y=Ncosb*Math.Pow(lp,1)+Ncosb*cosb*cosb*(1-t*t+ita*ita)/6.0*Math.Pow(lp,3)+Ncosb*Math.Pow(l p,5)*Math.Pow(cosb,4)*(5-18*t*t+Math.Pow(t,4)+14*ita*ita-58*ita*ita*t*t)/120.0;if(pcrdCar.y<0)pcrdCar.y+=500000;richTextBox1.Text="Results:\nX:\t"+Convert.ToString(pcrdCar.x)+"\nY:\t"+Convert.ToString(pcrdCar.y );}{try{tt=}{}{ee=}if(pareTo("WGS-84")==0){a=6378137.00;ee=}if(pareTo("1975国际椭球")==0){a=6378140.00;ee=}if(pareTo("2000国家大地坐标系")==0) {a=6378137.0;ee}constdoublepai=doubleb=Math.Sqrt(a*a*(1-ee*ee));//求Xtry{tt=}{}if(pareTo("3度带")==0){midlong=num*3*pai/180;}if(pareTo("6度带")==0){midlong=(6*num-3)*pai/180;}b=Math.Sqrt(a*a*(1-ee*ee));c=a*a/b;epp=Math.Sqrt(a*a-b*b)/b;doublem0,m2,m4,m6,m8;doublea0,a2,a4,a6,a8;m0=a*(1-ee*ee);m2=3.0/2.0*m0*ee*ee;m4=5.0/4.0*ee*ee*m2;m6=7.0/6.0*ee*ee*m4;m8=9.0/8.0*ee*ee*m6;{}tf=Math.Tan(Bf);Vf=Math.Sqrt(1+epp*epp*Math.Cos(Bf)*Math.Cos(Bf));Nf=c/Vf;doubleynf=pcrdCar.y/Nf;pcrdGeo.dLatitude=Bf-1.0/2.0*Vf*Vf*tf*(ynf*ynf-1.0/12.0*Math.Pow(ynf,4)*(5+3*tf*tf+itaf*itaf-9*Math.Pow(itaf*tf,2))+1.0/360.0*(61+90*tf*tf+45*Math.Pow(tf,4))*Math.Pow(ynf,6));pcrdGeo.dLongitude=(ynf/Math.Cos(Bf)-(1+2*tf*tf+itaf*itaf)*Math.Pow(ynf,3)/6.0/Math.Cos(Bf)+ (5+28*tf*tf+24*Math.Pow(tf,4)+6*itaf*itaf+8*Math.Pow(itaf*tf,2))*Math.Pow(ynf,5)/120.0/Math.Cos(Bf ));pcrdGeo.dLongitude=pcrdGeo.dLongitude+midlong;//pcrdGeo.dLatitude=pcrdGeo.dLatitude;richTextBox2.Text="Results:\nLatitude:"+Convert.ToString(pcrdGeo.dLatitude)+"\nLongtitude:"+Conver t.ToString(pcrdGeo.dLongitude);}privatevoidlabel13_Click(objectsender,EventArgse){}}}米之间,。
高斯投影正反算编程一.高斯投影正反算基本公式

高斯投影正反算编程一.高斯投影正反算基本公式(1)高斯正算基本公式(2)高斯反算基本公式以上主要通过大地测量学基础课程得到,这不进行详细的推导,只是列出基本公式指导编程的进行。
二.编程的基本方法和流程图(1)编程的基本方法高斯投影正反算基本上运用了所有的编程基本语句,本文中是利用C++语言进行基本的设计。
高斯正算中对椭球参数和带宽的选择主要运用了选择语句。
而高斯反算中除了选择语句的应用,在利用迭代算法求底点纬度还应用了循环语句。
编程中还应特别注意相关的度分秒和弧度之间的相互转换,这是极其重要的。
(2)相关流程图1)正算2)反算三.编程的相关代码(1)正算# include "stdio.h"# include "stdlib.h"# include "math.h"# include "assert.h"#define pi (4*atan(1.0))int i;struct jin{double B;double L;double L0;};struct jin g[100];main(int argc, double *argv[]){FILE *r=fopen("a.txt","r");assert(r!=NULL);FILE *w=fopen("b.txt","w");assert(r!=NULL);int i=0;while(fscanf(r,"%lf %lf %lf",&g[i].B,&g[i].L,&g[i].L0)!=EOF){double a,b;int zuobiao;printf("\n请输入坐标系:北京54=1,西安80=2,WGS84=3:");scanf("%d",&zuobiao);getchar();if(zuobiao==1){a=6378245;b=6356863.0187730473;}if(zuobiao==2){a=6378140;b=6356755.2881575287;}if(zuobiao==3){a=6378137;b=6356752.3142;} //选择坐标系//double f=(a-b)/a;double e,e2;e=sqrt(2*f-f*f);e2=sqrt((a/b)*(a/b)-1);//求椭球的第一,第二曲率//double m0,m2,m4,m6,m8;double a0,a2,a4,a6,a8;m0=a*(1-e*e);m2=3*e*e*m0/2;m4=5*e*e*m2/4;m6=7*e*e*m4/6;m8=9*e*e*m6/8;a0=m0+m2/2+3*m4/8+5*m6/16+35*m8/128;a2=m2/2+m4/2+15*m6/32+7*m8/16;a4=m4/8+3*m6/16+7*m8/32;a6=m6/32+m8/16;a8=m8/128;double Bmiao,Lmiao, L0miao;Bmiao=(int)(g[i].B)*3600.0+(int)((g[i].B-(int)(g[i].B))*100.0)*60.0+( g[i].B*100-(int)(g[i].B*100))*100.0;Lmiao=(int)(g[i].L)*3600.0+(int)((g[i].L-(int)(g[i].L))*100.0)*60.0+(g [i].L*100-(int)(g[i].L*100))*100.0;L0miao=(int)(g[i].L0)*3600.0+(int)((g[i].L0-(int)(g[i].L0))*100.0)*60. 0+(g[i].L0*100-(int)(g[i].L0*100))*100.0;double db;db=pi/180.0/3600.0;double B1,L1,l;B1=Bmiao*db;L1= Lmiao*db;l=L1-L0miao*db;//角度转化为弧度//double T=tan(B1)*tan(B1);double n=e2*e2*cos(B1)*cos(B1);double A=l*cos(B1);double X,x,y;X=a0*(B1)-a2*sin(2*B1)/2+a4*sin(4*B1)/4-a6*sin(6*B1)/6+a8*sin(8*B1)/8;//求弧长//double N=a/sqrt(1-e*e*sin(B1)*sin(B1));int Zonewide;int Zonenumber;printf("\n请输入带宽:3度带或6度带Zonewide=");scanf("%d",&Zonewide);getchar();if(Zonewide==3){Zonenumber=(int)((g[i].L-Zonewide/2)/Zonewide+1);}else if(Zonewide==6){Zonenumber=(int)g[i].L/Zonewide+1;}else{printf("错误");exit(0);}//选择带宽//doubleFE=Zonenumber*1000000+500000;//改写为国家通用坐标//y=FE+N*A+A*A*A*N*(1-T*T+n*n)/6+A*A*A*A*A*N*(5-18*T*T+T *T*T*T+14*n*n-58*n*n*T*T)/120;x=X+tan(B1)*N*A*A/2+tan(B1)*N*A*A*A*A*(5-T*T+9*n*n+4*n*n *n*n)/24+tan(B1)*N*A*A*A*A*A*A*(61-58*T*T+T*T*T*T)/720;printf("\n所选坐标系的转换结果:x=%lf y=%lf\n",x,y);fprintf(w,"%lf %lf\n",x,y);//输出结果到文本文件//}fclose(r);fclose(w);system("pause");return 0;}(2)反算# include "stdio.h"# include "stdlib.h"# include "math.h"# include "assert.h"#define pi (4*atan(1.0))double X,Y,B1,B2,B3,F,t;double m0,m2,m4,m6,m8;double a0,a2,a4,a6,a8,a1,b1;double BB,LL,Bf;double e,e1;int d,m,s,i,zuobiao;double sort(double,double);struct jin{double x;double y;double L0;};struct jin g[100];//x,y,L0为输入量:x,y坐标和中央子午线经度// main(int argc, double *argv[]){FILE *r=fopen("c.txt","r");assert(r!=NULL);FILE *w=fopen("d.txt","w");assert(r!=NULL);int i=0;while(fscanf(r,"%lf %lf %lf",&g[i].x,&g[i].y,&g[i].L0)!=EOF)//文件为空,无法打开//{double a1=6378245.0000000000;//克拉索夫斯基椭球参数//double b1=6356863.0187730473;double a75=6378140.0000000000;//1975国际椭球参数//double b75=6356755.2881575287;double a84=6378137.0000000000;//WGS-84系椭球参数//double b84=6356752.3142000000;double M,N;//mouyou圈曲率半径,子午圈曲率半径//double t,n;double A,B,C;double BB,LL,Bf,LL0,BB0;double a,b;printf("\n选择参考椭球:1=克拉索夫斯基椭球,2=1975国际椭球,3=WGS-84系椭球:");scanf("%d",&zuobiao);getchar();if(zuobiao==1){a=a1;b=b1;}if(zuobiao==2){a=a75;b=b75;}if(zuobiao==3){a=a84;b=b84;}//选择参考椭球,求解第一偏心率e,第二偏心率e1// Bf=sort(a,b);//调用求解底点纬度的函数//double q=sqrt(1-e*e*sin(Bf)*sin(Bf));double G=cos(Bf);M=a*(1-e*e)/(q*q*q);N=a/q;double H,I;A=g[i].y/N;H=A*A*A;I=A*A*A*A*A;t=tan(Bf);n=e1*cos(Bf);B=t*t;C=n*n;BB0=Bf-g[i].y*t*A/(2*M)+g[i].y*t*H/(24*M)*(5+3*B+C-9*B*C)-g[i] .y*t*I/(720*M)*(61+90*B+45*B*B);LL0=g[i].L0*pi/180.0+A/G-H/(6*G)*(1.0+2*B+C)+I/(120*G)*(5.0+28 *B+24*B*B+6*C+8*B*C);//利用公式求解经纬度//int Bdu,Bfen,Ldu,Lfen;double Bmiao,Lmiao;Ldu=int(LL0/pi*180);Lfen=int((LL0/pi*180)*60-Ldu*60);Lmiao=LL0/pi*180*3600-Ldu*3600-Lfen*60;Bdu=int(BB0/pi*180);Bfen=int((BB0/pi*180)*60-Bdu*60);Bmiao=BB0/pi*180*3600-Bdu*3600-Bfen*60;//将弧度转化为角度//printf("\n所选坐标系的转换结果:%d度%d分%lf秒%d 度%d分%lf秒\n",Bdu,Bfen,Bmiao,Ldu,Lfen,Lmiao);fprintf(w,"%d°%d’%lf”%d°%d’%lf”\n",Bdu,Bfen,Bmiao,Ldu,Lfen,Lmiao);//将结果输出到文本文件//}fclose(r);fclose(w);system("pause");return 0;}double sort(double a,double b){double e,e1;e=sqrt(1-(b/a)*(b/a));e1=sqrt((a/b)*(a/b)-1);double m0,m2,m4,m6,m8;double a0,a2,a4,a6,a8;m0=a*(1-e*e);m2=3*e*e*m0/2;m4=5*e*e*m2/4;m6=7*e*e*m4/6;m8=9*e*e*m6/8;a0=m0+m2/2+3*m4/8+5*m6/16+35*m8/128;a2=m2/2+m4/2+15*m6/32+7*m8/16;a4=m4/8+3*m6/16+7*m8/32;a6=m6/32+m8/16;a8=m8/128;B1=g[i].x/a0;do{F=-a2*sin(2*B1)/2+a4*sin(4*B1)/4-a6*sin(6*B1)/6+a8*sin(8*B1 )/8;B2=(g[i].x-F)/a0;B3=B1;B1=B2;} while(fabs(B3-B2)>10e-10);//利用迭代算法求解底点纬度//return B2; }。
高斯投影正反算编程

高斯投影正反算编程一.高斯投影正反算基本公式(1)高斯正算基本公式(2)高斯反算基本公式以上主要通过大地测量学基础课程得到.这不进行详细的推导.只是列出基本公式指导编程的进行。
二.编程的基本方法和流程图(1)编程的基本方法高斯投影正反算基本上运用了所有的编程基本语句.本文中是利用C++语言进行基本的设计。
高斯正算中对椭球参数和带宽的选择主要运用了选择语句。
而高斯反算中除了选择语句的应用.在利用迭代算法求底点纬度还应用了循环语句。
编程中还应特别注意相关的度分秒和弧度之间的相互转换.这是极其重要的。
(2)相关流程图1)正算2)反算三.编程的相关代码(1)正算# include "stdio.h"# include "stdlib.h"# include "math.h"# include "assert.h"#define pi (4*atan(1.0))int i;struct jin{double B;double L;double L0;};struct jin g[100];main(int argc, double *argv[]) {FILE *r=fopen("a.txt","r"); assert(r!=NULL);FILE *w=fopen("b.txt","w"); assert(r!=NULL);int i=0;while(fscanf(r,"%lf %lf %lf",&g[i].B,&g[i].L,&g[i].L 0)!=EOF){double a,b;int zuobiao;printf("\n请输入坐标系:北京54=1.西安80=2.WGS84=3:");scanf("%d",&zuobiao);getchar();if(zuobiao==1){a=6378245;b=6356863.0187730473;}if(zuobiao==2){a=6378140;b=6356755.2881575287;}if(zuobiao==3){a=6378137;b=6356752.3142;} //选择坐标系//double f=(a-b)/a;double e,e2;e=sqrt(2*f-f*f);e2=sqrt((a/b)*(a/b)-1);//求椭球的第一.第二曲率//double m0,m2,m4,m6,m8;double a0,a2,a4,a6,a8;m0=a*(1-e*e);m2=3*e*e*m0/2;m4=5*e*e*m2/4;m6=7*e*e*m4/6;m8=9*e*e*m6/8;a0=m0+m2/2+3*m4/8+5*m6/16+35*m8/128;a2=m2/2+m4/2+15*m6/32+7*m8/16;a4=m4/8+3*m6/16+7*m8/32;a6=m6/32+m8/16;a8=m8/128;double Bmiao,Lmiao, L0miao;Bmiao=(int)(g[i].B)*3600.0+(int)((g[i].B-(int)(g[i].B) )*100.0)*60.0+(g[i].B*100-(int)(g[i].B*100))*100.0;Lmiao=(int)(g[i].L)*3600.0+(int)((g[i].L-(int)(g[i].L) )*100.0)*60.0+(g[i].L*100-(int)(g[i].L*100))*100.0;L0miao=(int)(g[i].L0)*3600.0+(int)((g[i].L0-(int)(g[i] .L0))*100.0)*60.0+(g[i].L0*100-(int)(g[i].L0*100))*100 .0;double db;db=pi/180.0/3600.0;double B1,L1,l;B1=Bmiao*db;L1= Lmiao*db;l=L1-L0miao*db;//角度转化为弧度//double T=tan(B1)*tan(B1);double n=e2*e2*cos(B1)*cos(B1);double A=l*cos(B1);double X,x,y;X=a0*(B1)-a2*sin(2*B1)/2+a4*sin(4*B1)/4-a6*sin(6*B1)/6 +a8*sin(8*B1)/8;//求弧长//double N=a/sqrt(1-e*e*sin(B1)*sin(B1));int Zonewide;int Zonenumber;printf("\n请输入带宽:3度带或6度带Zonewide=");scanf("%d",&Zonewide);getchar();if(Zonewide==3){Zonenumber=(int)((g[i].L-Zonewide/2)/Zonewide+1);}else if(Zonewide==6){Zonenumber=(int)g[i].L/Zonewide+1;}else{printf("错误");exit(0);}//选择带宽//doubleFE=Zonenumber*1000000+500000;//改写为国家通用坐标//y=FE+N*A+A*A*A*N*(1-T*T+n*n)/6+A*A*A*A*A*N*(5-18*T*T+T *T*T*T+14*n*n-58*n*n*T*T)/120;x=X+tan(B1)*N*A*A/2+tan(B1)*N*A*A*A*A*(5-T*T+9*n*n+4*n *n*n*n)/24+tan(B1)*N*A*A*A*A*A*A*(61-58*T*T+T*T*T*T)/7 20;printf("\n所选坐标系的转换结果:x=%lf y=%lf\n",x,y);fprintf(w,"%lf %lf\n",x,y);//输出结果到文本文件//}fclose(r);fclose(w);system("pause");return 0;}(2)反算# include "stdio.h"# include "stdlib.h"# include "math.h"# include "assert.h"#define pi (4*atan(1.0))double X,Y,B1,B2,B3,F,t;double m0,m2,m4,m6,m8;double a0,a2,a4,a6,a8,a1,b1;double BB,LL,Bf;double e,e1;int d,m,s,i,zuobiao;double sort(double,double);struct jin{double x;double y;double L0;};struct jin g[100];//x,y,L0为输入量:x,y坐标和中央子午线经度//main(int argc, double *argv[]){FILE *r=fopen("c.txt","r");assert(r!=NULL);FILE *w=fopen("d.txt","w");assert(r!=NULL);int i=0;while(fscanf(r,"%lf %lf %lf",&g[i].x,&g[i].y,&g[i].L 0)!=EOF)//文件为空.无法打开//{double a1=6378245.0000000000;//克拉索夫斯基椭球参数//double b1=6356863.0187730473;double a75=6378140.0000000000;//1975国际椭球参数//double b75=6356755.2881575287;double a84=6378137.0000000000;//WGS-84系椭球参数//double b84=6356752.3142000000;double M,N;//mouyou圈曲率半径.子午圈曲率半径// double t,n;double A,B,C;double BB,LL,Bf,LL0,BB0;double a,b;printf("\n选择参考椭球:1=克拉索夫斯基椭球.2=1975国际椭球.3=WGS-84系椭球:");scanf("%d",&zuobiao);getchar();if(zuobiao==1){a=a1;b=b1;}if(zuobiao==2){a=a75;b=b75;}if(zuobiao==3){a=a84;b=b84;}//选择参考椭球.求解第一偏心率e,第二偏心率e1// Bf=sort(a,b);//调用求解底点纬度的函数//double q=sqrt(1-e*e*sin(Bf)*sin(Bf));double G=cos(Bf);M=a*(1-e*e)/(q*q*q);N=a/q;double H,I;A=g[i].y/N;H=A*A*A;I=A*A*A*A*A;t=tan(Bf);n=e1*cos(Bf);B=t*t;C=n*n;BB0=Bf-g[i].y*t*A/(2*M)+g[i].y*t*H/(24*M)*(5+3*B+C-9*B *C)-g[i].y*t*I/(720*M)*(61+90*B+45*B*B);LL0=g[i].L0*pi/180.0+A/G-H/(6*G)*(1.0+2*B+C)+I/(120*G)*(5.0+28*B+24*B*B+6*C+8*B*C);//利用公式求解经纬度// int Bdu,Bfen,Ldu,Lfen;double Bmiao,Lmiao;Ldu=int(LL0/pi*180);Lfen=int((LL0/pi*180)*60-Ldu*60);Lmiao=LL0/pi*180*3600-Ldu*3600-Lfen*60;Bdu=int(BB0/pi*180);Bfen=int((BB0/pi*180)*60-Bdu*60);Bmiao=BB0/pi*180*3600-Bdu*3600-Bfen*60;//将弧度转化为角度//printf("\n所选坐标系的转换结果:%d度%d分%lf秒 %d 度%d分%lf秒 \n",Bdu,Bfen,Bmiao,Ldu,Lfen,Lmiao);fprintf(w,"%d°%d’%lf”%d°%d’%lf”\n",Bdu,Bfen,Bmiao,Ldu,Lfen,Lmiao);//将结果输出到文本文件//}fclose(r);fclose(w);system("pause");return 0;}double sort(double a,double b){double e,e1;e=sqrt(1-(b/a)*(b/a));e1=sqrt((a/b)*(a/b)-1);double m0,m2,m4,m6,m8;double a0,a2,a4,a6,a8;m0=a*(1-e*e);m2=3*e*e*m0/2;m4=5*e*e*m2/4;m6=7*e*e*m4/6;m8=9*e*e*m6/8;a0=m0+m2/2+3*m4/8+5*m6/16+35*m8/128;a2=m2/2+m4/2+15*m6/32+7*m8/16;a4=m4/8+3*m6/16+7*m8/32;a6=m6/32+m8/16;a8=m8/128;B1=g[i].x/a0;do{F=-a2*sin(2*B1)/2+a4*sin(4*B1)/4-a6*sin(6*B1)/6+a8*s in(8*B1)/8;B2=(g[i].x-F)/a0;B3=B1;B1=B2;} while(fabs(B3-B2)>10e-10);//利用迭代算法求解底点纬度//return B2;}。
高斯投影的正算反算C++源代码-课程设计

高斯投影的正算反算C++源代码-课程设计高斯投影的正算反算C++源代码一、设计目的:加深理解高斯—克吕格投影的实质,掌握高斯—克吕格投影直角坐标的运用,理解通用坐标和自然坐标值的关系。
二、设计内容:1、编程实现由经纬度到直角坐标的转换;2、正确计算点所在的分度带;3、准确计算出点的通用坐标值。
三、方法与步骤:1、理解公式中每个字母的含义;2、编程。
3、编程的程序如下:// 高斯投影正反算公式.cpp : Defines the entry point for the console application.//#include "iostream.h"#include "math.h"int main(int argc, char* argv[]){int n,a,d,c;int L[4],B[4],C[3],D[3],L0;double l,N,a0,a4,a6,a3,a5,x,y,BB,P,b,Z,Bf,b2,b3,b4,b5,Nf,LL,xx,yy;cout<<"1----正算(L,B-->x,y) 2----反算(x,y-->L,B)"<<endl;cout<<"请选择正算(1)或反算(2):"<<endl;cin>>n;/////////////////正算if(n==1){cout<<"请按顺序输入L,B:"<<endl;cout<<"输入L(度,分,秒):"<<endl;cin>>L[1]>>L[2]>>L[3];cout<<"请输入B(度,分,秒):"<<endl;cin>>B[1]>>B[2]>>B[3];BB=3.141592654*(B[1]+B[2]/60.0+B[3]/3600.0)/180;P=3.141592654*(B[1]*3600+B[2]*60+B[3])/(180*3600);////////////////计算点所在投影带的中央子午线L[0]=6*(int((L[1]+L[2]/60.0+L[3]/3600.0)/6)+1)-3;cout<<"点所在投影带的中央子午线为:"<<endl;cout<<L[0]<<"度"<<endl;l=3.141592654*(L[1]+L[2]/60.0+L[3]/3600-L[0])/180;N=6399698.902-(21562.267-(108.973-0.612*cos(BB)*cos(BB))*cos(BB)*co s(BB))*cos(BB)*cos(BB);a0=32140.404-(135.3302-(0.7092-0.0040*cos(BB)*cos(BB))*cos(BB)*cos( BB))*cos(BB)*cos(BB);a4=(0.25+0.00252*cos(BB)*cos(BB))*cos(BB)*cos(BB)-0.04166;a6=(0.166*cos(BB)*cos(BB)-0.084)*cos(BB)*cos(BB);a3=(0.3333333+0.001123*cos(BB)*cos(BB))*cos(BB)*cos(BB)-0.1666667; a5=0.0083-(0.1667-(0.1968+0.0040*cos(BB)*cos(BB))*cos(BB)*cos(BB))* cos(BB)*cos(BB);///////////代号计算a=L[0]/6+1;d=L[0]-1.5;c=d/3+1;///////////////计算坐标x=6367558.4969*P-(a0-(0.5+(a4+a6*l*l)*l*l)*l*l*N)*sin(BB)*cos(BB); y=(1+(a3+a5*l*l)*l*l)*l*N*cos(BB);/////////////格式控制cout.setf(ios::fixed);cout.setf(ios::showpoint);cout.precision(3);cout<<"正算结果为:"<<endl;cout<<"平面坐标:"<<endl;cout<<"x="<<x<<endl;cout<<"y="<<y<<endl;cout<<"分度带号为:"<<endl;cout<<"六度带号为:"<<a<<endl;cout<<"三度带号为:"<<c<<endl;cout<<"通用坐标为(米):"<<endl;cout<<"x="<<x<<endl;cout<<"y="<<y+500000<<endl; //通用坐标计算}else if(n==2) /////////////////////反算{cout<<"请依次输入坐标x,y(m):"<<endl;cin>>xx>>yy;cout<<"请输入点所在投影带的中央子午线(度):"<<endl;cin>>L0;b=xx/6367558.4969;Bf=b+(50221746+(293622+(2350+22*cos(b)*cos(b))*cos(b)*cos(b))*cos(b)*cos(b))*(1.0E-10)*sin(b)*cos(b);Nf=6399698.902-(21562.267-(108.973-0.612*cos(Bf)*cos(Bf))*cos(Bf)*c os(Bf))*cos(Bf)*cos(Bf);Z=yy/(Nf*cos(Bf));b2=(0.5+0.00336975*cos(Bf)*cos(Bf))*sin(Bf)*cos(Bf);b3=0.333333-(0.1666667-0.001123*cos(Bf)*cos(Bf))*cos(Bf)*cos(Bf); b4=0.25+(0.161612+0.005617*cos(Bf)*cos(Bf))*cos(Bf)*cos(Bf);b5=0.2-(0.1667-0.00878*cos(Bf)*cos(Bf))*cos(Bf)*cos(Bf);BB=Bf*3600*180/3.141592654-(1-(b4-0.147*Z*Z)*Z*Z)*Z*Z*b2*180*3600/3.141592654;LLC[1]=int((BB-C[0]*3600)/60);C[2]=int(BB-C[0]*3600-C[1]*60);cout<<"B="<<C[0]<<"度"<<C[1]<<"分"<<C[2]<<"秒"<<endl;D[0]=int(LL/3600);D[1]=int((LL-D[0]*3600)/60);D[2]=int(LL-D[0]*3600-D[1]*60);cout<<"L="<<D[0]<<"度"<<D[1]<<"分"<<D[2]<<"秒"<<endl;}return 0;}四、成果:1、程序运行结果如下图:1260。
第四章 7高斯投影坐标正反算
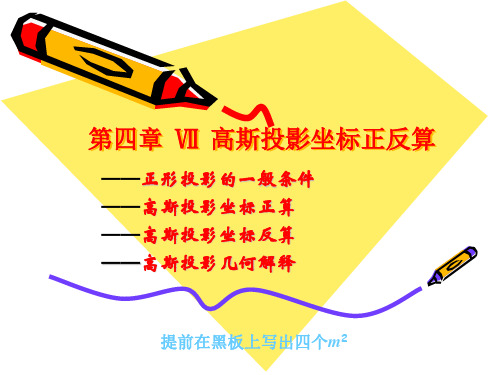
2
x y , q l
x y l q
柯西-黎曼条件(公式)是
椭球面与平面之间的正形投影的一般条件
考虑到F=0,E=G,长度比公式简化为
x y q q E m2 2 = r r2
2
2 2
x y l l G m2 2 = r r2
x m0 m 2 l 2 m 4 l 4 y m1l m3 l 3 m5 l 5
分别对l 和q 求偏导数
2) 由第三个条件正形投影条件
y x x y 和 l q l q
dm0 dm2 2 dm4 4 2 4 m1 3m3 l 5m5 l dq dq l dq l 2m l 4m l 3 dm1 l dm3 l 3 dm5 l 5 2 4 dq dq dq
§4.9.2 正形投影的一般条件
一、长度比的通用公式推导
dS 2 ( MdB)2 ( N cos Bdl )2
M dB
ds 2 dx 2 dy 2
N cos B d l
长度比平方为:
dx 2 dy 2 ds 2 m 2 2 dS ( MdB) ( N cos Bdl )
?
上式为与方向有关的长度比的通用公式。 上式在什么条件下与方向无关?
F 0
E G
柯西.黎曼条件(续)
正形条件:m与A无关,即满足: F 0
E G
2 2 2
x x y y 0 q l q l
y y x q l x l q
x y x y q q l l
「高斯投影坐标正反算公式及适合电算的高斯投影公式」

「高斯投影坐标正反算公式及适合电算的高斯投影公式」高斯投影坐标正反算公式是用于计算高斯投影坐标的数学公式。
高斯投影坐标是一种地理坐标系统,常用于测量和测绘工作中。
高斯投影坐标正算是指已知一个点的经纬度坐标,通过公式计算出该点的高斯投影坐标。
而高斯投影坐标反算是指已知一个点的高斯投影坐标,通过公式计算出该点的经纬度坐标。
一、高斯投影坐标正算公式:已知一个点的经纬度坐标(φ,λ),其中φ为纬度,λ为经度,以及椭球体参数a、f和中央经线经度L0,可以通过以下步骤计算出该点的高斯投影坐标(X,Y):1.计算扁率f':f'=(a-b)/a其中,b=a*(1-f)是椭球体的短半轴。
2.计算黄赤交角ε:ε = atan(b / a)3.计算辅助量t:t = tan(π/4 - φ/2) / [(1 - f' * sin²φ)⁰.⁵ * (1 + e' *sinφ)⁰.⁵]其中,e'=f'*(2-f')是椭球体的第一偏心率。
4.计算辅助量η:η = e'^2 * cos²φ5.计算系数A、B、C和D:A = (L - L0) * cosφC = (L - L0) * cos⁵φ * (5 - tan²φ + 9e'^² + 4e'^⁴ - 24e'^² * tan²φ - 45e'^⁴ * tan²φ)D = (L - L0) * cos⁷φ * (61 - 58tan²φ + tan⁴φ + 270e'^² - 330e'^² * tan²φ)6.计算高斯坐标X和Y:X=k0*a*(A+B/2+C/4+D/6)Y=k0*a*(C/2+D/8)其中,k0是比例系数,一般情况下取1二、高斯投影坐标反算公式:已知一个点的高斯投影坐标(X,Y),以及椭球体参数a、f、中央经线经度L0、比例系数k0和起始经度L1,可以通过以下步骤计算出该点的经纬度坐标(φ,λ):1.计算扁率f':f'=(a-b)/a其中,b=a*(1-f)是椭球体的短半轴。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高斯投影正反算程序设计一.程序设计流程本程序的设计思路如下:(1),程序采用VS08版本作为开发平台,并采用C#语言作为开发语言,设计为WindowsForm 窗体程序形式。
(2),程序主要的算法来自于教材。
但是本程序为了更加实用,添加了更多的解算基准,包括:WGS-84,国际椭球1975,克氏椭球,和2000国家大地坐标系。
(3),程序为了更方便的读取数据和输出数据,故需要自己定义了固定的数据输入格式和数据输出格式或形式,请老师注意查看。
二.代码using System;using Systusing ponentModel;using System.Data;using System.Drawing;using System.Text;namespace Gauss{public partial class Form1 : Form{//大地坐标//Geodetic Coordinatepublic struct CRDGEODETIC{public double dLongitude;public double dLatitude;public double dHeight;}//笛卡尔坐标//Cartesian Coordinatepublic struct CRDCARTESIAN{public double x;public double y;public double z;}public Form1(){InitializeComponent();}private void button1_Click(object sender, EventArgs e){double ee = 0;double a = 0;string tt;try{}catch{MessageBox.Show("Gauss Inverse: Choose datum error!"); return;}if (pareTo("克氏椭球")==0){a = 6378245.00;}if (pareTo("WGS-84") == 0){a = 6378137.00;}if (pareTo("1975国际椭球") == 0){a = 6378140.00;ee =}if (pareTo("2000国家大地坐标系") == 0){a = 6378137.0;}const double pai = 3.1415926;double b = Math.Sqrt(a * a * (1 - ee * ee));double c = a * a / b;double epp = Math.Sqrt((a * a - b * b) / b / b);CRDGEODETIC pcrdGeo;CRDCARTESIAN pcrdCar;double midlong;//求纬度string[] temp;double[] tempradius = new double[3];for (int i = 0; i < 3; i++){tempradius[i] = Convert.ToDouble(temp[i]);}pcrdGeo.dLatitude = tempradius[0] / 180.0 * pai + tempradius[1] / 180.0 / 60.0 * pai + tempradius[2] / 180 / 60.0 / 60 * pai;//求经度for (int i = 0; i < 3; i++){tempradius[i] = Convert.ToDouble(temp[i]);}pcrdGeo.dLongitude = tempradius[0] / 180.0 * pai + tempradius[1] / 180.0 / 60.0 * pai + tempradius[2] / 180 / 60.0 / 60 * pai;int deglon = Convert.ToInt32(pcrdGeo.dLongitude * 180 / pai);//求中央经度int num; //带号 midlong = 0; //默认值,需要制定分带 try{}catch{MessageBox.Show("Choose 3/6 error!");return;}if (pareTo("3度带") == 0){num = Convert.ToInt32(deglon / 6 + 1);midlong = (6 * num - 3) / 180.0 * pai;}if (pareTo("6度带") == 0){num = Convert.ToInt32((deglon + 1.5) / 3);midlong = num * 3 * pai / 180;}double lp=pcrdGeo.dLongitude - midlong;double N = c / Math.Sqrt(1 + epp * epp * Math.Cos(pcrdGeo.dLatitude) * Math.Cos(pcrdGeo.dLatitude));double M = c / Math.Pow(1 + epp * epp * Math.Cos(pcrdGeo.dLatitude) * Math.Cos(pcrdGeo.dLatitude), 1.5);double ita = epp * Math.Cos(pcrdGeo.dLatitude);double t = Math.Tan(pcrdGeo.dLatitude);double Nscnb = N * Math.Sin(pcrdGeo.dLatitude) *Math.Cos(pcrdGeo.dLatitude);double Ncosb = N * Math.Cos(pcrdGeo.dLatitude);double cosb = Math.Cos(pcrdGeo.dLatitude);double X;double m0, m2, m4, m6, m8;double a0, a2, a4, a6, a8;m0 = a * (1 - ee * ee);m2 = 3.0 / 2.0 * m0 * ee * ee;m4 = 5.0 / 4.0 * ee * ee * m2;m6 = 7.0 / 6.0 * ee * ee * m4;m8 = 9.0 / 8.0 * ee * ee * m6;a0 = m0 + m2 / 2.0 + 3.0 / 8.0 * m4 + 5.0 / 16.0 * m6 + 35.0 / 128.0 * m8;a2 = m2 / 2 + m4 / 2 + 15.0 / 32.0 * m6 + 7.0 / 16.0 * m8;a4 = m4 / 8.0 + 3.0 / 16.0 * m6 + 7.0 / 32.0 * m8;a6 = m6 / 32.0 + m8 / 16.0;a8 = m8 / 128.0;double B = pcrdGeo.dLatitude;double sb = Math.Sin(B);double cb = Math.Cos(B);double s2b = sb * cb * 2;double s4b = s2b * (1 - 2 * sb * sb) * 2;double s6b = s2b * Math.Sqrt(1 - s4b * s4b) + s4b * Math.Sqrt(1 - s2b * s2b);X = a0 * B - a2 / 2.0 * s2b + a4 * s4b / 4.0 - a6 / 6.0 * s6b;pcrdCar.x = Nscnb * lp * lp / 2.0 + Nscnb * cosb * cosb * Math.Pow(lp, 4) * (5 - t * t + 9 * ita * ita + 4 * Math.Pow(ita, 4)) / 24.0+ Nscnb * Math.Pow(cosb, 4) * Math.Pow(lp, 6) * (61 - 58 * t * t + Math.Pow(t, 4)) / 720.0 + X;pcrdCar.y = Ncosb * Math.Pow(lp, 1) + Ncosb * cosb * cosb * (1 - t * t + ita * ita) / 6.0 * Math.Pow(lp, 3) + Ncosb * Math.Pow(lp, 5)* Math.Pow(cosb, 4) * (5 - 18 * t * t+ Math.Pow(t, 4) + 14 * ita * ita - 58 * ita * ita * t * t) / 120.0 ;if (pcrdCar.y < 0)pcrdCar.y += 500000;richTextBox1.Text = "Results:\nX:\t" + Convert.ToString(pcrdCar.x) +"\nY:\t"+ Convert.ToString(pcrdCar.y);}private void button2_Click(object sender, EventArgs e){double ee = 0;double a = 0;string tt;int num; //带号 string ytext; //利用y值求带号和中央经线 try{}catch{MessageBox.Show("Gauss Inverse: Choose datum error!");return;}if (pareTo("克氏椭球") == 0){a = 6378245.00;}if (pareTo("WGS-84") == 0){a = 6378137.00;}if (pareTo("1975国际椭球") == 0){a = 6378140.00;}if (pareTo("2000国家大地坐标系") == 0){a = 6378137.0;}double b = Math.Sqrt(a * a * (1 - ee * ee));double c = a * a / b;double epp = Math.Sqrt((a * a - b * b) / b / b);CRDGEODETIC pcrdGeo;CRDCARTESIAN pcrdCar;double midlong = 0;//求X,Y和带号pcrdCar.x = Convert.ToDouble(textBox4.Text); ytext = textBox5.Text;string temp = ytext.Substring(0, 2);num = Convert.ToInt32(temp);ytext = ytext.Remove(0, 2);pcrdCar.y = Convert.ToDouble(ytext) - 500000; try{}catch{MessageBox.Show("Choose 3/6 error!");return;}if (pareTo("3度带") == 0){midlong = num * 3 * pai / 180;}if (pareTo("6度带") == 0){midlong = (6 * num - 3) * pai / 180;}b = Math.Sqrt(a * a * (1 - ee * ee));c = a * a / b;epp = Math.Sqrt(a * a - b * b) / b;double m0, m2, m4, m6, m8;double a0, a2, a4, a6, a8;m0 = a * (1 - ee * ee);m2 = 3.0 / 2.0 * m0 * ee * ee;m4 = 5.0 / 4.0 * ee * ee * m2;m6 = 7.0 / 6.0 * ee * ee * m4;m8 = 9.0 / 8.0 * ee * ee * m6;a0 = m0 + m2 / 2.0 + 3.0 / 8.0 * m4 + 5.0 / 16.0 * m6 + 35.0 / 128.0 * m8;a2 = m2 / 2 + m4 / 2 + 15.0 / 32.0 * m6 + 7.0 / 16.0 * m8;a4 = m4 / 8.0 + 3.0 / 16.0 * m6 + 7.0 / 32.0 * m8;a6 = m6 / 32.0 + m8 / 16.0;a8 = m8 / 128.0;double Bf, B;Bf = pcrdCar.x / a0;B = 0.0;while (Math.Abs(Bf - B) > 1E-10){B = Bf;double sb = Math.Sin(B);double cb = Math.Cos(B);double s2b = sb * cb * 2;double s4b = s2b * (1 - 2 * sb * sb) * 2;double s6b = s2b * Math.Sqrt(1 - s4b * s4b) + s4b * Math.Sqrt(1 - s2b * s2b);Bf = (pcrdCar.x - (-a2 / 2.0 * s2b + a4 / 4.0 * s4b - a6 / 6.0 * s6b)) / a0;}double itaf, tf, Vf, Nf;itaf = epp * Math.Cos(Bf);tf = Math.Tan(Bf);Vf = Math.Sqrt(1 + epp * epp * Math.Cos(Bf) * Math.Cos(Bf));Nf = c / Vf;double ynf = pcrdCar.y / Nf;pcrdGeo.dLatitude = Bf - 1.0 / 2.0 * Vf * Vf * tf * (ynf * ynf - 1.0 / 12.0 * Math.Pow(ynf, 4) * (5 + 3 * tf * tf + itaf * itaf - 9 * Math.Pow(itaf * tf, 2)) +1.0 / 360.0 * (61 + 90 * tf * tf + 45 * Math.Pow(tf, 4)) * Math.Pow(ynf, 6));pcrdGeo.dLongitude = (ynf / Math.Cos(Bf) - (1 + 2 * tf * tf + itaf * itaf) * Math.Pow(ynf, 3) / 6.0 / Math.Cos(Bf) +(5 + 28 * tf * tf + 24 * Math.Pow(tf, 4) + 6 * itaf * itaf + 8 * Math.Pow(itaf * tf, 2)) * Math.Pow(ynf, 5) / 120.0 / Math.Cos(Bf));pcrdGeo.dLongitude = pcrdGeo.dLongitude + midlong;//pcrdGeo.dLatitude = pcrdGeo.dLatitude;richTextBox2.Text = "Results:\nLatitude: " +Convert.ToString(pcrdGeo.dLatitude) + "\nLongtitude: " +Convert.ToString(pcrdGeo.dLongitude);}private void label13_Click(object sender, EventArgs e){}}}三.程序运行结果分析通过选取书上的具体实例进行测试,本程序的精度大体满足要求,一般正算的精度在0.01米和0.001米之间,反算的精度在0.0001秒左右。
