2008年春季中国精算师资格考试04寿险精算数学答案详解
寿险精算习题及答案讲解学习
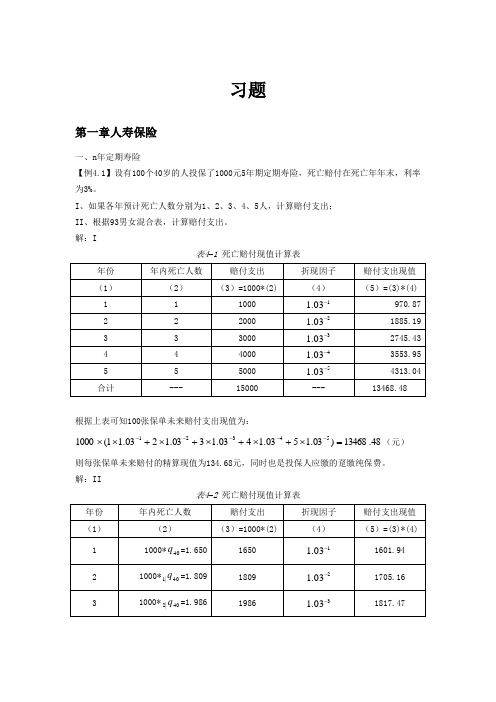
习题第一章人寿保险一、n 年定期寿险【例4.1】设有100个40岁的人投保了1000元5年期定期寿险,死亡赔付在死亡年年末,利率为3%。
I 、如果各年预计死亡人数分别为1、2、3、4、5人,计算赔付支出; II 、根据93男女混合表,计算赔付支出。
解:I表4–1 死亡赔付现值计算表根据上表可知100张保单未来赔付支出现值为:48.13468)03.1503.1403.1303.1203.11(100054321=⨯+⨯+⨯+⨯+⨯⨯-----(元)则每张保单未来赔付的精算现值为134.68元,同时也是投保人应缴的趸缴纯保费。
解:II表4–2 死亡赔付现值计算表根据上表可知100张保单未来赔付支出现值为:86.9124)03.103.103.103.103.1(1000540|4440|3340|2240|11402=⨯+⨯+⨯+⨯+⨯⨯-----q q q q q (元)则每张保单未来赔付的精算现值为91.25元,同时也是投保人应缴的趸缴纯保费。
【例4.2】某人在40岁时投保了10000元3年期定期寿险,死亡赔付在死亡年年末,利率为5%。
根据93男女混合表计算:I 、单位趸缴纯保费;II 、单位赔付现值期望的方差;III 、(总)趸缴纯保费; 解:I 、单位趸缴纯保费为,)()(424023414024040|2340|1240240|11|3:40q p v q p v vq q v q v vq q v Ak k k ++=++=⨯=∑=+]05.1001993.0)001812.01()00165.01(05.1001812.0)00165.01(05.100165.0[32⨯-⨯-+⨯-+=00492793.0=(元)。
II 、单位赔付现值期望的方差为,00444265.0)()()()(21|3:4040|2640|1440221|3:40240|)1(221|3:401|3:402=-++=-⨯=-∑=+A q v q v q v A q v AAk k k III 、趸缴纯保费为,28.49100001|3:40=⨯A (元) 【例4.3】某人在50岁时投保了100000元30年期定期寿险,利率为8%。
保险精算习题答案

第六章虫"^仏日&劳哲血」7---------------------------------d 曲__ ---------- ----- ---------------------------鼻0习* 匕叢轨g 4珂& _______________As二越丐十汹齟=陆①+ 4弘办血 ____ _____________ 7 v缶t~vfii¥尿弔n 2TI& “軀”哄心曲 -----------------------------------------------------“却L h兔购¥催停端約*松停鼠侖F询刖¥圭鳥杂f乩越曲咎任朋核保應/Alt丹袖E韦勺锁—迦缈貝必I£1L<己feo咄枷胡(皿皿虚鬲机⑹二豁 "£尊勺附)冷朴♦兹旳二也呦的乂枇区妊顶阮他彩药姐他蛆免泌纽型一無爷射柚探性X拥施柚蚪』中昭6”科朮剋霑例申變找缎冒姫務鱼和懾龙宜"120)二"«抵》4髯卩卜P【k? _h"龄虹血刍i——小二鴿人学"&也匕血吆ba "f呼虹沁严矶伽严P谕勿心显"£伽岸爲召少仲> 1(^(^ _胁阿' 拥纳—_|眼a注皿砒史他話血海对札恋乍曙戟冷确毎孫矗|弟豹貳dW Az攸初二D1题K1妙fitglaLM慢冲E4 闵速-- - ------ —-阿吐軾友沁良妇盘盘储业HSJftf橹找如__一_一姣旦曹豁J J £? ..4 h僞怜験沖钠缶花ill用E盘憾姒if Si li.fi 4熾盈赵扯St_(S 网-------------- ----- - ------------ --- 一一丄二屁广~肚砰二血沪■陶广哄叶#幻严1-召53=曲必用严)_ ¥----------------- ----------爲”显•磊二仙L一一—— .. -w VaM二血心3諾________ : ___________⑴也吋赠工十腐?土R卅* ■⑹ 血二£ k j £ A _____ ____ __ ____________包柱"“紘)L如任创二• “p“ ____________________________ 如山上£晒出栖皿L迦山丄也22Z”&乂知氐谆三也色.Ah他沖。
2008年春季中国精算师资格考试真题及参考

2008年春季中国精算师资格考试-07寿险精算实务(以下1-30题为单项选择题,每题1分,选错或不选的不给分。
)1-2题基于以下信息:已知利率为6%,2005年12月31日的评估结果如下:精算负债12万元,精算资产8万元,2006年1月1日的正常成本为1万元;2006年12 月31日的评估结果如下:精算负债13.5万元,精算资产9万元。
2006年1月1日实际缴费金额为1.4万元,2007年1月1日实际缴费金额为1.6万元,则1.2006年底的预期未纳基金负债为()。
(A)3.810万元(B)3.812万元(C)3.814万元(D)3.816万元(E)3.818万元2.2006年的运营情况为()。
(A)获利0.684万元(B)损失0.684万元(C)获利0.686万元(D)损失0.686万元(E)损失0.688万元07试题第1页(共37页)3.关于寿险公司的资产份额定价法,下列说法不正确的是()。
(A)利润检验是资产份额定价法的必要步骤(B)在建立定价模型时,模型的规划时间不一定等于最高可能保单年度(C)资产份额定价法通常通过现金流分析检验利润目标(D)资产份额定价法中的现金流分析是针对有效保单和新业务的规划结果进行的(E)资产份额定价法不能反映投资信息情况。
4.以下关于寿险产品开发的描述不正确的是()。
(A)险种开发通常是以项目的形式进行的(B)险种开发过程包括设计和实现两个部分(C)险种开发过程的终点是形成产品(D)开发的险种要体现公司的长期战略规划(E)开发的险种要满足营销人员的需要5.对于10年缴费的终身死亡保险,计算第二个保单年末最低现金价值的时候,r等于()。
(A)0.82(B)0.84(C)0.92(D)0.94(E)107试题第2页(共37页)6.以下关于加拿大资产负债法的说法中不正确的是()。
(A)含有保守的因素(B)既适用于传统寿险,又适用于新型寿险(C)基于分组的方法(D)需要对投保人的合理预期做出假设(E)为每一张保单单独计算准备金7.关于保单失效率的说法,不正确的是()。
保险精算习题及答案

第一章:利息的基本概念练 习 题1.已知()2a t at b =+,如果在0时投资100元,能在时刻5积累到180元,试确定在时刻5投资300元,在时刻8的积累值。
(0)1(5)25 1.80.8,125300*100(5)300180300*100300*100(8)(64)508180180a b a a b a b a a a b ===+=⇒===⇒=+= 2.(1)假设A(t)=100+10t, 试确定135,,i i i 。
135(1)(0)(3)(2)(5)(4)0.1,0.0833,0.0714(0)(2)(4)A A A A A A i i i A A A ---======(2)假设()()100 1.1nA n =⨯,试确定 135,,i i i 。
135(1)(0)(3)(2)(5)(4)0.1,0.1,0.1(0)(2)(4)A A A A A A i i i A A A ---======3.已知投资500元,3年后得到120元的利息,试分别确定以相同的单利利率、复利利率投资800元在5年后的积累值。
11132153500(3)500(13)6200.08800(5)800(15)1120500(3)500(1)6200.0743363800(5)800(1)1144.97a i i a i a i i a i =+=⇒=∴=+==+=⇒=∴=+=4.已知某笔投资在3年后的积累值为1000元,第1年的利率为 110%i =,第2年的利率为28%i =,第3年的利率为 36%i =,求该笔投资的原始金额。
123(3)1000(0)(1)(1)(1)(0)794.1A A i i i A ==+++⇒=5.确定10000元在第3年年末的积累值:(1)名义利率为每季度计息一次的年名义利率6%。
(2)名义贴现率为每4年计息一次的年名义贴现率6%。
(4)12341()410000(3)10000(1)11956.18410000(3)10000111750.0814i a i a =+=⎛⎫ ⎪=+= ⎪ ⎪⎝⎭6.设m >1,按从大到小的次序排列()()m m d di i δ<<<<。
中国精算师《寿险精算》章节题库-生存年金的精算现值(圣才出品)

第3章生存年金的精算现值1.设(50)岁的人以50000元的趸缴纯保费购买了每月给付k元的生存年金。
假设年金的给付从购买年金后的第一个月末开始,预定年利率i=0.005,死亡满足UDD假设,而且50=13.5 ,≈1,β12=-0.4665,则k的值为()。
[2008年真题] A.322B.333C.341D.356E.364【答案】A【解析】每月的年金精算现值为:由×12=50000 ,解得:k=322。
2.设死亡力为μ=0.06,利率力为δ=0.04,在此假设条件下,则超过的概率为()。
[2008年真题]A.0.4396B.0.4572C.0.4648D.0.4735E.0.4837【答案】C【解析】由已知,得3.根据以下条件计算=()。
[2008年真题]A.1.6B.1.8C.2.0D.2.2E.2.4【答案】D【解析】由已知,有4.支付额为1的期初生存年金从95岁开始支付,其生存模型为:已知i=0.06,以Y表示该年金的现值变量,则E(Y)和Var (Y)分别为()。
[2008年真题]A.2.03;0.55B.2.03;0.79C.2.05;0.79D.2.05;0.55E.2.07;0.79【答案】A【解析】由i=0.06,得:v=(1+i)-1=1.06-1。
5.考虑从退休基金资产中支付的期初年金组合:已知i=6%,只要年金领取人活着,每个年金的年支付额是1,若正态分布95%的分位数是1.645,则退休基金负担现值为()。
A.480B.481C.483D.485E.487【答案】C【解析】设支付的随机变量为Z,退休基金为P,则故。
6.考虑(90)的期初年金,每次年金支付额为1,生存模型为:已知利率i=0.06,则=()。
A.1.8B.1.9C.2.0D.2.1E.2.2【答案】C【解析】由于7.。
A.0.085B.0.125C.0.600D.0.650E.0.825【答案】D【解析】8.已知α(12)=1.000281,β(12)=0.46811951,=9.89693,假设死亡均匀分布。
保险精算习题及答案

第一章:利息的基本概念练 习 题1.已知()2a t at b =+,如果在0时投资100元,能在时刻5积累到180元,试确定在时刻5投资300元,在时刻8的积累值。
(0)1(5)25 1.80.8,125300*100(5)300180300*100300*100(8)(64)508180180a b a a b a b a a a b ===+=⇒===⇒=+= 2.(1)假设A(t)=100+10t, 试确定135,,i i i 。
135(1)(0)(3)(2)(5)(4)0.1,0.0833,0.0714(0)(2)(4)A A A A A A i i i A A A ---======(2)假设()()100 1.1nA n =⨯,试确定 135,,i i i 。
135(1)(0)(3)(2)(5)(4)0.1,0.1,0.1(0)(2)(4)A A A A A A i i i A A A ---======3.已知投资500元,3年后得到120元的利息,试分别确定以相同的单利利率、复利利率投资800元在5年后的积累值。
11132153500(3)500(13)6200.08800(5)800(15)1120500(3)500(1)6200.0743363800(5)800(1)1144.97a i i a i a i i a i =+=⇒=∴=+==+=⇒=∴=+=4.已知某笔投资在3年后的积累值为1000元,第1年的利率为 110%i =,第2年的利率为28%i =,第3年的利率为 36%i =,求该笔投资的原始金额。
123(3)1000(0)(1)(1)(1)(0)794.1A A i i i A ==+++⇒=5.确定10000元在第3年年末的积累值:(1)名义利率为每季度计息一次的年名义利率6%。
(2)名义贴现率为每4年计息一次的年名义贴现率6%。
(4)12341()410000(3)10000(1)11956.18410000(3)10000111750.0814i a i a =+=⎛⎫ ⎪=+= ⎪ ⎪⎝⎭6.设m >1,按从大到小的次序排列()()m m d di i δ<<<<。
保险精算习题及答案

第一章:利息的基本概念练习题1.已知()2a t at b =+,如果在0时投资100元,能在时刻5积累到180元,试确定在时刻5投资300元,在时刻8的积累值。
(0)1(5)25 1.80.8,125300*100(5)300180300*100300*100(8)(64)508180180a b a a b a b a a a b ===+=⇒===⇒=+=∵2.(1)假设A(t)=100+10t,试确定135,,i i i 。
135(1)(0)(3)(2)(5)(4)0.1,0.0833,0.0714(0)(2)(4)A A A A A A i i i A A A −−−======(2)假设()()100 1.1nA n =×,试确定135,,i i i 。
135(1)(0)(3)(2)(5)(4)0.1,0.1,0.1(0)(2)(4)A A A A A A i i i A A A −−−======3.已知投资500元,3年后得到120元的利息,试分别确定以相同的单利利率、复利利率投资800元在5年后的积累值。
11132153500(3)500(13)6200.08800(5)800(15)1120500(3)500(1)6200.0743363800(5)800(1)1144.97a i i a i a i i a i =+=⇒=∴=+==+=⇒=∴=+=4.已知某笔投资在3年后的积累值为1000元,第1年的利率为110%i =,第2年的利率为28%i =,第3年的利率为36%i =,求该笔投资的原始金额。
123(3)1000(0)(1)(1)(1)(0)794.1A A i i i A ==+++⇒=5.确定10000元在第3年年末的积累值:(1)名义利率为每季度计息一次的年名义利率6%。
(2)名义贴现率为每4年计息一次的年名义贴现率6%。
(4)12341()410000(3)10000(1)11956.18410000(3)10000111750.0814i a i a =+=⎛⎞⎜⎟=+=⎜⎟⎜⎟⎝⎠6.设m >1,按从大到小的次序排列()()m m d d i i δ<<<<。
2008年精算师考试真题

2008年精算师考试真题2008 年春季中国精算师资格考试-04 寿险精算数学(本试题共40 道单项选择题。
每题只有一个正确答案。
每题分值相同,总分100 分。
)1. 已知:(1)3 p70 = 0.95(2)2 71 p = 0.96(3)75710.107 x∫μdx =计算5 70 p 的值为()。
(A) 0.85(B) 0.86(C) 0.87(D) 0.88(E) 0.892. 已知:(1)μ(80.5) = 0.0202(2)μ(81.5)= 0.0408(3)μ(82.5) = 0.0619(4)死亡服从UDD 假设计算80.5 岁的人在两年之内死亡的概率为()。
(A) 0.0782(B) 0.0785(C) 0.0790(D) 0.0796(E) 0.08003. 已知:(1)e0 = 25 o(2), 0 x l =ω?x ≤x ≤ω(3)T(x)为未来剩余寿命随机变量计算Var[T(10)]的值为()。
(A) 65(B) 93(C) 133(D) 178(E) 3334. 设(x)的未来寿命T = T(x)的密度函数是( ) 950,TTf t< < =其它利率力为δ= 0.06,保额为一个单位的终身寿险的现值随机变量为Z ,那么满足( ) 0.9 Pr Z ≤ζ= 0.9的分位数0.9 ζ的值为()。
(A) 0.5346(B) 0.5432(C) 0.5747(D) 0.5543(E) 0.56552008 年春季-0404 试题第3 页(共21 页)5. 30 岁的人购买保额为1000 元的特殊的35 年期两全保险,已知条件如下:(1)在其购买保险时,其两个孩子的年龄分别是3 岁和6 岁(2)特殊约定为:如果被保险人死亡时两个孩子的年龄都小于11 岁,那么给付额为3000 元;如果被保险人死亡时只有一个孩子的年龄小于11 岁,那么给付额为2000 元(3)在被保险人死亡时立即给付保险金(4)μ30+t = 0.04,t ≥0(5)δ= 0.06(6)35 30 E = 0.0302则此保单的趸缴纯保费为()元。
保险精算教学大纲丶习题及答案

保险精算教学大纲本课程总课时:课程教学周,每周课时第一章:利息理论基础本章课时:学习的目的和要求要求了解利息的各种度量掌握常见利息问题的求解原理二、主要内容第一节:实际利率与实际贴现率利息的定义实际利率单利和复利实际贴现率第二节:名义利率和名义贴现率第三节:利息强度第二章年金本章课时:一、学习的目的和要求要求了解年金的定义、类别掌握年金问题求解的基本原理和常用技巧二、主要内容第一节:期末付年金第二节:期初付年金第三节:任意时刻的年金值一、在首期付款前某时刻的年金值二、在最后一期付款后某时刻的年金积累值三、付款期间某时刻的年金当前值第四节:永续年金第五节:连续年金第三章生命表基础本章课时:一、学习的目的与要求理解常用生命表函数的概率意义及彼此之间的函数关系了解生存函数与生命表的关系并掌握寿险生命表的特点与构造原理掌握各种分数年龄假定下,分数年龄的生命表函数的估计方法主要内容第一节生命函数一、分布函数二、生存函数三、剩余寿命四、取整余命五、死亡效力六、生存函数的解析表达式第二节生命表一、生命表的含义二、生命表的内容第四章人寿保险的精算现值本章课时:一、教学目的与要求掌握寿险趸缴纯保费的厘定原理理解寿险精算现值的意义,掌握寿险精算现值的表达方式及计算技巧认识常见的寿险产品并掌握各种产品趸缴纯保费的厘定及寿险精算现值方差的计算理解趸缴纯保费的现实意义主要内容第一节死亡即付的人寿保险一、精算现值的概念二、n年定期保险的精算现值(趸缴纯保费)三、终身寿险的趸缴纯保费四、延期寿险的趸缴纯保费五、生存保险与两全保险的趸缴纯保费死亡年末给付的人寿保险一、定期寿险的趸缴纯保费二、终身寿险的趸缴纯保费三、两全保险的趸缴纯保费四、延期寿险的趸缴纯保费死亡即刻赔付保险与死亡年末赔付保险的精算现值的关系递增型人寿保险与递减型人寿保险一、递增型寿险二、递减型寿险三、两类精算现值的换算第五章年金的精算现值本章课时:一、学习目的与要求理解生存年金的概念掌握各种场合计算生存年金现时值的原理和技巧。
非寿险精算数学与实务-08

第 7-8 题基于下面信息:
对于一保险组合产品,其前 2 年的总赔付额及总风险量如下表所
示:
第1年
第2年
总赔付额
60000
75000
总风险量
125
150
假设各张保单的结构参数相同。已知每张保单的保费为 600。
7. 在 Bühlmann-Straub 模型假设下,根据上述数据,信度因子中 a 的 无偏估计属于区间( )。 (A) [0, 11300) (B) [11300, 11500) (C) [11500,11700) (D) [11700, 11900) (E) [11900, +∞)
3570 5820
1620 1280
2003 年 25 岁及以上 25 岁以下
4230 6320
1910 1320
25 岁及以上 2004 年
25 岁以下
5100 6930
2200 1500
以 2007 年 7 月 1 日费率为当前费率。又已知在 2007 年 7 月 1 日, 对 2002-2004 年总损失的预测值为 54867(千元),目标损失率为 70%。
在当前费率水平下,利用平行四边形法则(这里,仅用其中的 SOA 方法)计算,2005 日历年的均衡已赚保费为( )。
(A) 2380
(B) 2381
(C) 2382
(D) 2383
(E) 2384
08 试题 第 7 页 (共 38 页)
第 13-14 题基于如下信息: 已知下表中的数据:
级别
终极赔付额 当前相对数
保障层
共保比例
自留额
¥2M
无
第一超赔层
¥5M xs ¥2M
2021中国精算师资格考试精算师《寿险精算》考试题集

2021中国精算师资格考试精算师《寿险精算》考试题集寿险精算数学第1章生存分布与生命表单项选择题(以下各小题所给出的5个选项中,只有一项最符合题目要求,请将正确选项的代码填入括号内)1.(2008年真题)已知:(1)3p70=0.95;(2)2p7l=0.96;(3)=0.107。
计算5p70的值为()。
A.0.85B.0.86C.0.87D.0.88E.0.89【答案】E !@~【解析】由于,,故。
2.(2008年真题)已知:(1)(80.5)=0.0202;(2)(81.5)=0.0408;(3)(82.5)=0.0619;(4)死亡服从UDD假设。
计算80.5岁的人在两年之内死亡的概率为()。
A.0.0782B.0.0785C.0.0790D.0.0796E.0.0800【答案】A !@~【解析】死亡服从UDD假设,故所以。
从而,,故80.5岁的人在两年之内死亡的概率为:3.(2008年真题)已知(1);(2);(3)T()为未来剩余寿命随机变量。
计算的值为()。
A.65B.93C.133D.178E.333【答案】C !@~【解析】由可知x服从均匀分布,故由=ω/2,得,所以4.(2008年真题)设()的未来寿命的密度函数是利率力为δ=0.06,保额为一个单位的终身寿险的现值随机变量为Z,那么满足Pr(Z≤ζ0.9)=0.9的分位数ζ0.9的值为()。
A.0.5346B.0.5432C.0.5747D.0.5543E.0.5655【答案】E !@~【解析】令,则解得:。
故。
5.(样题)设,0≤x≤100,则=()。
A.40.5B.41.6C.42.7D.43.8E.44.9【答案】C !@~【解析】由,得:。
故。
6.(样题)给定生命表,如表1-1所示。
求整值剩余寿命K(96)的方差=()。
表1-1 生命表A.0.39B.0.53C.0.91D.1.11E.1.50【答案】D !@~【解析】由于,。
精算师试题 寿险精算数学

中华保险学习网打造最专业的保险学习网站
/
中华保险学习网
2008 年春季-04
官方总站:圣才学习网
15. 30 岁的人购买完全离散的 10 年定期保险,若死亡在 10 年内发生,则在死
亡年末给付额为 1 个单位;若被保险人在 10 年末仍生存,则所有的保费都
∫ (3)
75 71
μxdx
=
0.107
计算 5 p70 的值为( )。
m (A) 0.85 .co (B) 0.86 bx (C) 0.87 000 (D) 0.88 .1 (E) 0.89 p://www 2. 已知: tt 10 (1) μ(80.5) = 0.0202 h w. (2) μ(81.5)= 0.0408 /ww (3) μ(82.5) = 0.0619 :/ (4) 死亡服从 UDD 假设 http 计算 80.5 岁的人在两年之内死亡的概率为( )。
18. 已知死亡在各个年龄中均匀分布,且 i = 0.04 , δ = 0.0392 , n Ex = 0.6 ,
com ( ) Ax:n = 0.804 ,则1000P Ax:n 的值为( )。 bx. (A) 153 000 (B) 155 .1 (C) 157 ww com (D) 159 http://w http://www.1000bx. (E) 161
k
a&& k
q k −1 x
1
1.00
0.33
2
1.93
0.24
3
2.80
0.16
4ห้องสมุดไป่ตู้
3.62
0.11
(A) 1.6
(B) 1.8
m (C) 2.0 .co (D) 2.2 bx (E) 2.4
中国精算师《寿险精算》章节题库-责任准备金(圣才出品)

第5章责任准备金1.年龄为x岁的人购买一份完全离散的终身寿险,已知:(1)第一年的死亡给付是0,以后各年为5000元;(2)均衡纯保费终身支付;(3)q x=0.05,v=0.90,=5.00,10V x=0.20;(4)10V表示该保险在第十个保单年度末的责任准备金。
计算10V=()元。
[2008年真题]A.795B.1000C.1090D.1180E.1225【答案】D【解析】设该保险的均衡纯保费为5000P,有2.已知:(1)死亡服从De Moivre律,其中ω=100;(2)i=0.05;计算的值为()。
[2008年真题] A.0.075B.0.077C.0.079D.0.081E.0.083【答案】A【解析】3.65岁的人购买完全连续的终身寿险,已知:(1)在时刻t的死亡给付额为b t=1000e0.04t,t≥0;(2)均衡纯保费终身支付;(3)μ65(t)=0.02,t≥0;(4)δ=0.04。
则第二年末的责任准备金=()。
[2008年真题] A.0B.29C.37D.61E.83【答案】E【解析】该险种的现值:因此,第二年末的责任准备金为:4.年龄为x岁的人购买一份保险金额为b的完全离散的终身寿险,已知:(1)q x+9=0.02904;(2)i=0.03;(3)第10个保单年度的期初责任准备金为343;(4)第10个保单年度的净风险额为872;(5)=14.65976。
则第9个保单年度的期末责任准备金为()。
[2008年真题]A.280B.288C.296D.304E.312【答案】C【解析】由已知条件得:第10个保单年度的期初责任准备金10(IV)=9V+π=343,第10个保单年度的净风险保额为b-10V=872,由准备金递推公式:10V=(9V+π)(1+i)-(b-10V)q x+9,可得10V=328,b=872+10V=1200,故5.年龄为60岁的人购买一份10年定期寿险,保险金额逐年递减,交费期为5年。
保险精算习题答案

滤讽⑹®"鑰i 保吝9徐射滋羅從躺验盘里上知陰- 為饵玄创昨看魂脩㈱加良毎妙育¥专1h 岛*》去;・/ $耐 滋陵丄譚一妙童強/凶制多为弘我 _____________________________________ -•血妇匚血僚撐钠 翻 播去 ____________________________・2际M - P 湎二伽严―护 N 伽祐)屮"孑 丄业血二90弧出仇A 虫)即2K 心fg 押 核辑祁AH 51二机0可4 弘 」込碑” • 4 ------ -------必咅, -------------- ---------------------------医占嘗*彳鸟0勺年 h m S 僦 ___________________ ___汕三甌仆山幻主月乙汨十仏力加一 ----------_______ —二总产屁歸一扌讥& ------------ _ 二匸U&i%轴M = S 呦&主创吕5«伽第六章沧二------- --- ■上 LSE^ ------------------------ TT^$、己知纬加止眠融保蜒壮L母僅加山此瞇如过遇;'■'■ 肖4主偲学醫牴fit辅保建人盒授砌材戶遍 2 g _____________________ 孕二顶比畸血⑴____________ _______________ ____________ 打曾二忽r= %解停严心5轴.A R闕十於运(1前和_______ 9二Q、6羽爭_______________二 &____________ I d^jp亍____________ : ____________________ 一,<己fao咄轴耶goT也庖牍:弘匸罄口""3)孙1韦为益芒⑼购乂柚(1肚砲元期«1如朗k即於會*沖我/和也條里菱号耐衲偲轉炷提函柚娅』w r 5円3朮谢戏例建竣均慚掬*札仗逸俺血亂F伦g)_"(炫拓力册——” 嚅人理5如叫型』^冶亦“少"伽严畀淪刃“朋"「加学此河3仲仃㈤汀咧H _忸如阿’ 眄 -一一/卯晶心三伽0 i 翌弩=7 .._/, d ~g 田7 _________bi 阻二 few二东2。
保险精算习题及答案

第一章:利息的基本概念练 习 题1.已知()2a t at b =+,如果在0时投资100元,能在时刻5积累到180元,试确定在时刻5投资300元,在时刻8的积累值。
(0)1(5)25 1.80.8,125300*100(5)300180300*100300*100(8)(64)508180180a b a a b a b a a a b ===+=⇒===⇒=+= 2.(1)假设A(t)=100+10t, 试确定135,,i i i 。
135(1)(0)(3)(2)(5)(4)0.1,0.0833,0.0714(0)(2)(4)A A A A A A i i i A A A ---======(2)假设()()100 1.1nA n =⨯,试确定 135,,i i i 。
135(1)(0)(3)(2)(5)(4)0.1,0.1,0.1(0)(2)(4)A A A A A A i i i A A A ---======3.已知投资500元,3年后得到120元的利息,试分别确定以相同的单利利率、复利利率投资800元在5年后的积累值。
11132153500(3)500(13)6200.08800(5)800(15)1120500(3)500(1)6200.0743363800(5)800(1)1144.97a i i a i a i i a i =+=⇒=∴=+==+=⇒=∴=+=4.已知某笔投资在3年后的积累值为1000元,第1年的利率为 110%i =,第2年的利率为28%i =,第3年的利率为 36%i =,求该笔投资的原始金额。
123(3)1000(0)(1)(1)(1)(0)794.1A A i i i A ==+++⇒=5.确定10000元在第3年年末的积累值:(1)名义利率为每季度计息一次的年名义利率6%。
(2)名义贴现率为每4年计息一次的年名义贴现率6%。
(4)12341()410000(3)10000(1)11956.18410000(3)10000111750.0814i a i a =+=⎛⎫ ⎪=+= ⎪ ⎪⎝⎭6.设m >1,按从大到小的次序排列()()m m d di i δ<<<<。
《寿险精算》试题及答案

《寿险精算》试题及答案(解答仅供参考)第一套一、名词解释1. 寿险精算:寿险精算是运用数学、统计学、经济学等理论和方法,对人寿保险业务中的风险进行量化分析和评估,以确定保险费率、准备金、利润分配等关键参数的学科。
2. 生命表:生命表是一种记录某一地区或群体在不同年龄阶段死亡率的统计表格,是寿险精算中计算保费和评估风险的重要工具。
3. 保险费率:保险费率是指保险公司为提供保险保障而向被保险人收取的费用比例,它是根据预期损失和运营成本等因素计算得出的。
4. 预定利率:预定利率是指保险公司为未来支付保险金而预先设定的利息率,它是计算保险产品现金价值和准备金的重要参数。
5. 保险准备金:保险准备金是指保险公司为了应对未来的保险责任和赔付风险,按照规定提取并储备的资金。
二、填空题1. 寿险精算的主要任务包括确定______、评估风险、管理资产和负债等。
答案:保险费率2. 在寿险精算中,______是预测未来死亡率的重要工具。
答案:生命表3. 保险产品的现金价值是根据______和已缴保费计算得出的。
答案:预定利率4. 保险公司提取的保险准备金主要包括未到期责任准备金和______。
答案:未决赔款准备金5. 在人寿保险中,______是一种可以在保险期间内改变保险金额和保险费的保险产品。
答案:可变寿险三、单项选择题1. 下列哪一项不属于寿险精算的主要任务?A. 确定保险费率B. 评估风险C. 管理资产和负债D. 制定营销策略答案:D. 制定营销策略2. 生命表中的死亡率通常表示为:A. 每千人的死亡人数B. 每百人的死亡人数C. 每年的死亡人数D. 每年的死亡概率答案:D. 每年的死亡概率3. 下列哪种保险产品的现金价值通常会随着投资收益的变化而变化?A. 定期寿险B. 终身寿险D. 年金保险答案:C. 变额寿险4. 在计算保险准备金时,未决赔款准备金通常是按照以下哪种方法提取的?A. 逐笔认定法B. 平均估算法C. 总和估算法D. 预期损失法答案:A. 逐笔认定法5. 下列哪种保险产品的保险金额和保险费可以在保险期间内进行调整?A. 定期寿险B. 终身寿险C. 变额寿险D. 全残保险答案:C. 变额寿险四、多项选择题1. 下列哪些因素会影响保险费率的确定?A. 预期损失B. 运营成本C. 投资收益D. 市场竞争答案:A、B、C、D2. 下列哪些保险产品具有现金价值?A. 定期寿险C. 变额寿险D. 年金保险答案:B、C、D3. 下列哪些因素可能影响生命表的编制?A. 地理位置B. 种族背景C. 性别D. 社会经济状况答案:A、B、C、D4. 下列哪些保险准备金属于长期准备金?A. 未到期责任准备金B. 未决赔款准备金C. 长期健康保险准备金D. 养老保险准备金答案:C、D5. 下列哪些保险产品具有投资功能?A. 定期寿险B. 终身寿险C. 变额寿险D. 年金保险答案:B、C、D五、判断题1. 寿险精算师只需要具备数学和统计学知识即可。
CAA2008spring-03

2008年春季中国精算师资格考试-03复利数学(以下1-30 题为单项选择题。
1-20 题每题 3 分,21-30 题每题 4 分。
每题选对的给分,选错或不选的不给分。
)1. 已知A t( ) t22t 3 ,要使i n≤ 10% ,则n至少等于()。
(A) 18(B) 19(C) 20(D) 21(E) 2222. 已知δt=t+ 1 ,则第10 年的d( )等于()。
(A) 0.1671(B) 0.1688(C) 0.1715(D) 0.1818(E) 0.187403 试题第1 页(共13 页)3. 某永久年金在第一年末支付1,第二年末支付3,第三年末支付5,LL ,则该年金的现值为()。
2v v2(A)(B)1− v v v2 1 + v v v2(C)(1− v2(D) 2v v22(E) 1 − v 2v v2 1+ v4. 如果现在投资3,第二年末投资1,则在第四年末将积累5,则实际利率为()。
(A) 6.426%(B) 6.538%(C) 6.741%(D) 6.883%(E) 6.920%5. 假定名义利率为每季度计息一次的年名义利率6%,则1000 元在3 年末的积累值为()元。
(A) 1065.2(B) 1089.4(C) 1137.3(D) 1195.6(E) 1220.103 试题第2 页(共13 页)6. 某人初始投资额为100,假定年复利为4%,则这个人从第6 年到第10 年的5 年间所赚利息为()。
(A) 26(B) 27(C) 28(D) 29(E) 307. 某人用2000 元一次性购买了15 年确定年金,假定年利率为6% ,第一次年金领取从购买时开始,计算每次可以领取的金额为()元。
(A) 167.45(B) 177.45(C) 180.13(D) 194.27(E) 204.188. 某年金分20 年于每月月初支付30 元。
利息每月转换一次,年名义利率为12%,则该年金现值为()元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
50
E(Z2)=
∫ (1 + 0.1t )
p
−2
Var(Z)= E(Z2)-( E(Z))2=0.04
1 1 8. A35:1 = A35:1 + A35:1 =v⋅
35
+ v ⋅ q35 = v =0.9439
(IA)35-A35=1E35 × (IA)36= v ⋅
p
35
× (IA)36
2
(IA)36=[(IA)35-A35]/ v ⋅
x+y= P =0.042 35:20
x+0.6099y=0.0299 解得:x=0.011 y=0.031
15. 令该保险的均衡纯保费为 P,由题意得:
1 1 P ⋅ a 30:10 = A30:10 + A30:10 ⋅10 P 1 A30:10 1 A30:10 − A30:10
..
P=
..
=
2
k=50000 ÷ 12.95 ÷ 12=322 10. a x =
1 =10 µ +δ ⎛ 1 − vt ⎞ ln 0.6 ⎞ ⎛ > 10 ⎟ = Pr ( v t < 0.6 ) = Pr ⎜ T > Pr (a T ≥ a x ) = Pr ⎜ ⎟ −δ ⎠ ⎝ ⎝ δ ⎠
= Pr (T > 12.7706 ) = =0.4648
1
故
ζ 0.9
= exp(−9.5δ ) =0.5655
5. 由题意可知,该保险相当于保额 1000 元的 35 年期两全保险+1000 元保额的 8 年期定期 保险(5-8 年内被保险人只有一个孩子小于 11 岁)+1000 元保额的 5 年期定期保险(5 年内 两个孩子都小于 11 岁) 此保单的趸交保险费=1000( A30:35 + A30:8 + A30:5 )= 1000[ +
10 x
20.
10
A40 _ V ( A40 ) = A50 − P ( A40 ) ⋅ a 50 = A50 − _ a 50 a 40
_ _
_
_ _
_
_
_
1 − A50 _ × = A50 − A40 × δ 1 − A40
_
_
_
δ
_ _ 1 − A50 _ = A50 − A40 _
1 − A40
4. 令 h =
ln ξ 0.9 , v = exp( −δ ) < 1 ,则 ln v
+∞
Pr ( Z ≤ ζ 0.9 ) = Pr (vT ≤ ζ 0.9 ) = Pr (T ≥ h) = ∫ =∫
解之得:
h = 9.5 ,即 ln ζ 0.9
+∞
h
fT (t )dt
h
1 dt 95
1 = 95 (95 − h) = 0.9 = 9.5ln v
3
2
Var (Y ) = E (Y 2 ) − ⎡ ⎣ E (Y ) ⎤ ⎦ =0.55
13.
2
Pr ⎡ ⎣ L (π ) > 0 ⎤ ⎦ < 0.5ak +1 Pr(20000v k +1 − π a k +1 > 0) < 0.5 由于 39 q40 = 0.4939及 40 q40 = 0.5109 并且L (π ) = 20000v k +1 − π 1 − v k +1 π π = (20000 + )v k +1 − d d d 是k的减函数,意味着L(π )取满足条件的最高值时,k必须取39,故
+∞
12. E (Y ) =
+∞
∑a
k =0
2
..
k +1
⋅ k | q95 =0.28×1+0.33×( 1 + v )+0.39×( 1 + v + v 2 )=2.0263
2
E (Y
2
) = ∑Y
k =0
⋅ k | q95 =0.28×1+0.33× (1 + v ) +0.39× (1 + v + v 2 ) =4.6573
17.
_
4
2 ⎛ P⎞ 由Var ( L ) = 0.1 ⇒ ⎜1 + ⎟ ⎡ 2 A49 − ( A49 ) ⎤ = 0.1 ⎣ ⎦ ⎝ d⎠ P ⇒ = 0.772598818 d ⎛ ⎛ P⎞ P⎞ ⎛ P⎞ P E ( L ) = E ⎜ V K +1 ⎜1 + ⎟ − ⎟ = A49 ⎜ 1 + ⎟ − = −0.25 ⎝ d⎠ d⎠ ⎝ d⎠ d ⎝
..
L (π ) = 20000v 39+1 − π π ≥ 121.92
1 − v 39+1 = 1944.443754 − 15.94907468π ≤ 0 d
1 1 14. 令 P35:20 =x , P35:20 =y
1 1 A35:20 + A35:20 ⋅ A55 A35 1 1 = = P35:20 + P35:20 ⋅ A55 .. 20 P 35 = .. a35:20 a35:20
2
2
Var(Z)= E(Z2)-( E(Z))2 =0.4464
当 b1 =6.048/(2 × 0.4464)=6.8 时,Var(Z)最小 7. 给付现值函数 Z = bt ⋅ vt = (1 + 0.1t ) E(Z)=
−1
∫ (1 + 0.1t )
0 50 0
50
−1
⋅ t P50 ⋅ µ 50+t dt =0.02 × 10 × ln(1 + 0.1t ) =0.35835189 ⏐ 0 ⋅ t P50 ⋅ µ 50+t dt =0.02 × 10 × (-1) (1 + 0.1t )−1 =0.16666667 ⏐ 0
0 0
+∞
+∞
a 65 = ∫ v t ⋅ t p65 dt = ∫ e −0.04t ⋅ e −0.02t dt =
0 0
_
+∞
+∞
1 50 = 0.04 + 0.02 3
APV 均衡保费π = _ = 60 a 65
2
V = ∫ b2+t ⋅ v t ⋅ t p67 µ67 ( t ) dt − π a 67
1
a 30:10 − 10 A30:10
16.
1 − A30:10
= 0.039
1
d
− 10 A30:10
保险人面临正损失的概率即Pr( L > 0) = Pr(1000vT − 10 a T > 0) 1 − vT 1 > 0) = Pr(1200vT − 200 > 0) = Pr(vT > ) δ 6 2 35.8352 35.8352 ln 6 t = Pr(T < ) = Pr(T < 35.8352) = ∫ fT ( t )dt = = 0.51 ⏐ 0 0 δ 2500 = Pr(1000vT − 10
∫0
35
exp(−δ t ) ⋅ exp(− µ30+t t ) ⋅ µ 30+t d + 35E 30
5 0
∫0
8
exp(−δ t ) ⋅ exp(− µ30+t t ) ⋅ µ 30+t dt + ∫ exp(−δ t ) ⋅ exp(− µ30+t t ) ⋅ µ 30+t dt ]
µ 30 + t µ 30 + t + δ
2
18.
_ _
Ax:n
1 Ax :n =
_
1
_
1 Ax:n = Ax:n + n Ex ⇒ Ax :n = 0.804 − 0.6 = 0.204
i 1 1 A x:n ⇒ A x = 0.204 × 0.0392 ÷ 0.04 = 0.19992 :n δ 1 = Ax + n Ex = 0.19992 + 0.6 = 0.79992 :n
l82.5 l80.5
= 1−
l80 ⋅
p80 ⋅ p81 (1 − 0.5q82 ) l80 (1 − 0.5q80 )
=0.0782
=1 − 3.
0.98 × 0.96 × (1 − 0.5 × 0.06 )
1 − 0.5 × 0.02
由 x = ω − x ,可知 x 服从均匀分布,由 e0 =25,可知 ω =50
.. a x:n = 1 − Ax:n = 5.20208 d
Ax:n 0.804 1000 P( Ax:n ) = 1000 .. = 1000 × = 155 5.20208 a x:n
19.
_
_
设该保险的均衡纯保费为P .. Ax 1 − d a x 1 − (1 − 0.9) × 5 Px = .. = .. = = 0.1 5 ax ax
=1000 (
{1 − exp[−35( µ
30 + t
+ δ
)]} + 35E 30 +
µ 30 + t µ 30 + t + δ
{1 − exp[−8( µ
30 + t
+ δ
)]} +
µ 30 + t µ 30 + t + δ
{1 − exp[−5( µ
30 + t
