激光原理第二章习题解答
激光原理第二章习题答案

2.1 证明:如图2.1所示,当光线从折射率1η的介质,向折射率为2η的介质折射时,在曲率半径R 的球面分界面上,折射光线所经受的变换矩阵为⎥⎥⎦⎤⎢⎢⎣⎡-2121201ηηηηηR 其中,当球面相对于入射光线凹(凸)面时,R 取正(负)值。
证明:由图可知 11201θ⋅+⋅=x x 又)()(222111θηθη-=-RxR x 21121122x R ηηηθθηη-∴=+ ⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡∴11212122201θηηηηηθx Rx ∴变换矩阵为⎥⎥⎦⎤⎢⎢⎣⎡-2121201ηηηηηR 2.2 试求半径R=4cm,折射率η=1.5的玻璃球的焦距和主面的位置1h 和2h 。
解:变换矩阵⎥⎥⎦⎤⎢⎢⎣⎡-⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-=2112121221210110101n n R n n n l n n R n n n M 把11=n ,5.12=n ,cm R R 421=-=,cm l 8=代入,可得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡⨯-⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡--=3531316355.1145.115.10110815.145.1101M )(12f h A -=, f C 1-=, )(11f h D -= 求得 mm f 30-= mm h 201= mm h 202=2.3 焦距1f =5cm 和2f =-10c=m 的两个透镜相距5cm 。
第一个透镜前表面和第二个透镜后表面为参考平面的系统,其等效焦距为多少?焦点和主平面位置在何处?距1f 前表面20cm 处放置高为10cm 的物体,能在2f 后多远地方成像?像高为多少? 解:(1)2110101010********1131101011110552A B L M CD f f ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥====⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-----⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦)(12f h A -=, f C 1-=, )(11f h D -=,求得cm f 5-= cm h 5.21= cm h 52-=第一个透镜前表面与前主面的距离为2.5cm ,第二个透镜后表面与后主面的距离为-5cm,前主面离焦点的距离为-5cm ,) (2)21201011===l x θ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡45252110235150235150111122θθθx x D C B A xcm l cm x 2,5.222-==(距2f 后表面-2cm )2.4 一块折射率为η,厚度为d 的介质放在空气中,其两界面分别为曲率半径等于R 的凹球面和平面,光线入射到凹球面上。
激光原理第二章答案

第二章 开放式光腔与高斯光束1. 证明121 00 ηη⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。
证明:设入射光线坐标参数为11, r θ,出射光线坐标参数为22, r θ,根据几何关系可知211122, sin sin r r ηθηθ== 傍轴光线sin θθ则1122ηθηθ=,写成矩阵形式2121121 00 r r θθηη⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦得证 2. 1210 1d ηη⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。
证明:设入射光线坐标参数为11, r θ,出射光线坐标参数为22, r θ,入射光线首先经界面1折射,然后在介质2中自由传播横向距离d ,最后经界面2折射后出射。
根据1题的结论和自由传播的光线变换矩阵可得212121121 0 1 01 0 0 0 1r r d θθηηηη⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦ 化简后2121121 0 1d r r θθηη⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦得证。
3.试利用往返矩阵证明共焦腔为稳定腔,即任意傍轴光线在其中可以往返无限多次,而且两次往返即自行闭合。
证:设光线在球面镜腔内的往返情况如下列图所示:其往返矩阵为:由于是共焦腔,则有12R R L ==将上式代入计算得往返矩阵()()()121010110101n nnn n n r L r L ⎡⎤⎡⎤⎡⎤===-=-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦A B C D T T T T T 可以看出,光线在腔内往返两次的变换矩阵为单位阵,所以光线两次往返即自行闭合。
于是光线在腔内往返任意多次均不会溢出腔外,所以共焦腔为稳定腔。
4.试求平凹、双凹、凹凸共轴球面镜腔的稳定性条件。
解:共轴球面腔稳定性条件1201g g <<其中121211,1L Lg g R R =--=- 对平凹共轴球面镜腔有12,0R R =∞>。
则1221,1Lg g R ==-,再根据稳定性条件 1201g g <<可得22011LR R L <-<>⇒。
激光原理第二章答案

第二章 开放式光腔与高斯光束1. 证明121 00 ηη⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。
证明:设入射光线坐标参数为11, r θ,出射光线坐标参数为22, r θ,根据几何关系可知211122, sin sin r r ηθηθ== 傍轴光线sin θθ则1122ηθηθ=,写成矩阵形式2121121 00 r r θθηη⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦得证 2. 1210 1d ηη⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。
证明:设入射光线坐标参数为11, r θ,出射光线坐标参数为22, r θ,入射光线首先经界面1折射,然后在介质2中自由传播横向距离d ,最后经界面2折射后出射。
根据1题的结论和自由传播的光线变换矩阵可得212121121 0 1 01 0 0 0 1r r d θθηηηη⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦ 化简后2121121 0 1d r r θθηη⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦得证。
3.试利用往返矩阵证明共焦腔为稳定腔,即任意傍轴光线在其中可以往返无限多次,而且两次往返即自行闭合。
证:设光线在球面镜腔内的往返情况如下列图所示:其往返矩阵为:由于是共焦腔,则有12R R L ==将上式代入计算得往返矩阵()()()121010110101n nnn n n r L r L ⎡⎤⎡⎤⎡⎤===-=-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦A B C D T T T T T 可以看出,光线在腔内往返两次的变换矩阵为单位阵,所以光线两次往返即自行闭合。
于是光线在腔内往返任意多次均不会溢出腔外,所以共焦腔为稳定腔。
4.试求平凹、双凹、凹凸共轴球面镜腔的稳定性条件。
解:共轴球面腔稳定性条件1201g g <<其中121211,1L Lg g R R =--=- 对平凹共轴球面镜腔有12,0R R =∞>。
则1221,1Lg g R ==-,再根据稳定性条件 1201g g <<可得22011LR R L <-<>⇒。
激光原理周炳坤-第2章习题答案

第二章 开放式光腔与高斯光束习题(缺2.18 2.19 2.20)1. 题略证明:设入射光()11,r θ,出射光()22,r θ,由折射定理1122sin sin ηθηθ=,根据近轴传输条件,则1122sin ,sin θθθθ≈≈1122ηθηθ∴=,联立21r r =,则所以变换矩阵为 2. 题略证明:由题目1知,光线进入平面介质时的变换矩阵为:经过距离d的传播矩阵为: 光线出射平面介质时: 故3. 试利用往返矩阵证明共焦腔为稳定腔,即任意傍轴光线在其中可以往返无限多次,而且两次往返即自行闭合。
证:设光线在球面镜腔内的往返情况如下图所示:其往返矩阵为:122212111210101122110101212(1) 222222[(1)][(1)(1)]A B L L T C D R R L L L R R L L L L R R R R R R ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭ ⎪ ⎪⎝⎭⎝⎭⎛⎫-- ⎪⎪= ⎪-+----- ⎪⎝⎭212211100r r θηηθ⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭21100T ηη⎛⎫= ⎪⎝⎭121100T ηη⎛⎫= ⎪⎝⎭2100d T ⎛⎫=⎪⎝⎭312100T ηη⎛⎫= ⎪⎝⎭3113213112211101010000r r r d T T T θθηηηηθ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭123211221101011000000d d T T T T ηηηηηη⎛⎫⎛⎫⎛⎫⎛⎫∴=== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭由于是共焦腔,有 12R R L == 往返矩阵变为若光线在腔内往返两次,有可以看出,光线在腔内往返两次的变换矩阵为单位阵,所以光线两次往返即自行闭合。
于是光线在腔内往返任意多次均不会溢出腔外,所以共焦腔为稳定腔。
4. 试求平凹、双凹、凹凸共轴球面镜腔的稳定性条件。
激光原理第二章答案解析

第二章 开放式光腔与高斯光束1. 证明如图2.1所示傍轴光线进入平面介质界面的光线变换矩阵为121 00 ηη⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。
证明:设入射光线坐标参数为11, r θ,出射光线坐标参数为22, r θ,根据几何关系可知211122, sin sin r r ηθηθ== 傍轴光线sin θθ则1122ηθηθ=,写成矩阵形式2121121 00 r r θθηη⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦得证 2. 证明光线通过图2.2所示厚度为d 的平行平面介质的光线变换矩阵为1210 1d ηη⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。
证明:设入射光线坐标参数为11, r θ,出射光线坐标参数为22, r θ,入射光线首先经界面1折射,然后在介质2中自由传播横向距离d ,最后经界面2折射后出射。
根据1题的结论和自由传播的光线变换矩阵可得212121121 0 1 01 0 0 0 1r r d θθηη⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦ 化简后2121121 0 1d r r θθηη⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦得证。
3.试利用往返矩阵证明共焦腔为稳定腔,即任意傍轴光线在其中可以往返无限多次,而且两次往返即自行闭合。
证:设光线在球面镜腔内的往返情况如下图所示:其往返矩阵为:由于是共焦腔,则有12R R L ==将上式代入计算得往返矩阵()()()121010110101n nnn n n r L r L ⎡⎤⎡⎤⎡⎤===-=-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦A B C D T T T T T 可以看出,光线在腔内往返两次的变换矩阵为单位阵,所以光线两次往返即自行闭合。
于是光线在腔内往返任意多次均不会溢出腔外,所以共焦腔为稳定腔。
4.试求平凹、双凹、凹凸共轴球面镜腔的稳定性条件。
解:共轴球面腔稳定性条件1201g g <<其中121211,1L Lg g R R =--=- 对平凹共轴球面镜腔有12,0R R =∞>。
激光原理第二章答案
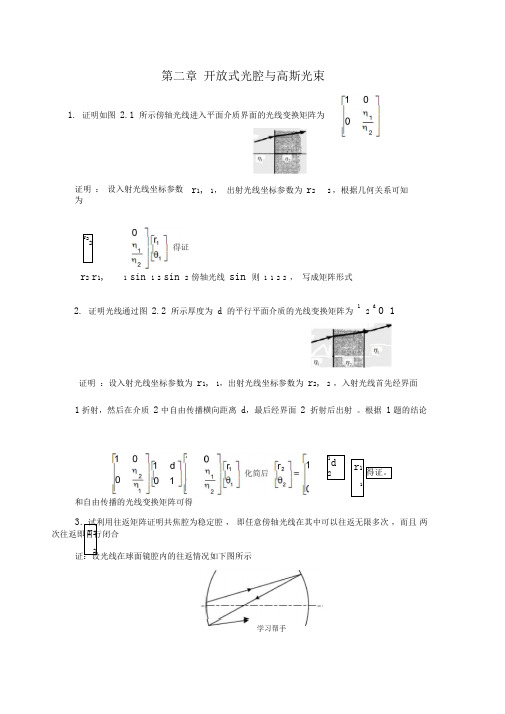
第二章 开放式光腔与高斯光束1. 证明如图2.1 所示傍轴光线进入平面介质界面的光线变换矩阵为r 2 r 1,1sin 1 2 sin 2 傍轴光线 sin 则 1 1 2 2 , 写成矩阵形式2. 证明光线通过图 2.2 所示厚度为 d 的平行平面介质的光线变换矩阵为 12 d0 1证明 :设入射光线坐标参数为 r 1, 1,出射光线坐标参数为 r 2, 2 ,入射光线首先经界面1折射,然后在介质 2中自由传播横向距离 d ,最后经界面 2 折射后出射 。
根据 1题的结论和自由传播的光线变换矩阵可得3.试利用往返矩阵证明共焦腔为稳定腔 , 即任意傍轴光线在其中可以往返无限多次 ,而且 两次往返即自行闭合证:设光线在球面镜腔内的往返情况如下图所示证明 : 设入射光线坐标参数为r 1, 1, 出射光线坐标参数为 r 22 ,根据几何关系可知学习帮手r 221d2r 11得证。
r 2 2其往返矩阵为于是光线在腔内往返任意多次均不会溢出腔外 , 所以共焦腔为稳定腔4.试求平凹 、双凹 、凹凸共轴球面镜腔的稳定性条件解: 共轴球面腔稳定性条件 0 g 1g 2 1其中 g 1 1 1 L ,g 2 1 L1 21R 1 2R 2对平凹共轴球面镜腔有 R 1,R 2 0。
则 g 1 1,g 2 1 L, 再根据稳定性条件R2L0 g 1g 2 1可得 0 1 1 R 2 L 。
1 2R22对凹凸共轴球面镜腔有 , R 1 0,R 2 0则 g 1 1L对 双 凹 共 轴 球 面 腔 有 , R 1 0,R 2 0 则 g 11 R L ,g 2R 11R2 , 根 据 稳 定 性 条 件 TA CR 1101由于是共焦腔 , 则有将上式代入计算得往返矩R1 R 2LT01 01T nT r 1T L T r 2T Ln1n 10n011n 100101可以看出 ,光线在腔内往返两次的变换矩阵为单位阵 ,所以光线两次往返即自行闭合 1L 1L 1R 1 L 或R 1R 2R 2 LR20, 根据稳定性条件R2,g 20 g 1g 2 1 可得 00 R 1 L0 R 2 L 。
激光原理周炳坤-第2章习题答案

第二章 开放式光腔与高斯光束习题(缺2.18 2.19 2.20)1. 题略证明:设入射光()11,r θ,出射光()22,r θ,由折射定理1122sin sin ηθηθ=,根据近轴传输条件,则1122sin ,sin θθθθ≈≈1122ηθηθ∴=,联立21r r =,则所以变换矩阵为 2. 题略证明:由题目1知,光线进入平面介质时的变换矩阵为:经过距离d的传播矩阵为: 光线出射平面介质时: 故3. 试利用往返矩阵证明共焦腔为稳定腔,即任意傍轴光线在其中可以往返无限多次,而且两次往返即自行闭合。
证:设光线在球面镜腔内的往返情况如下图所示:其往返矩阵为:122212111210101122110101212(1) 222222[(1)][(1)(1)]A B L L T C D R R L L L R R L L L L R R R R R R ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭⎪ ⎪⎝⎭⎝⎭⎛⎫-- ⎪⎪= ⎪-+----- ⎪⎝⎭212211100r r θηηθ⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭21100T ηη⎛⎫= ⎪⎝⎭121100T ηη⎛⎫= ⎪⎝⎭2100d T ⎛⎫=⎪⎝⎭312100T ηη⎛⎫= ⎪⎝⎭3113213112211101010000r r r d T T T θθηηηηθ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭123211221101011000000d d T T T T ηηηηηη⎛⎫⎛⎫⎛⎫⎛⎫∴=== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭由于是共焦腔,有 12R R L == 往返矩阵变为若光线在腔内往返两次,有可以看出,光线在腔内往返两次的变换矩阵为单位阵,所以光线两次往返即自行闭合。
于是光线在腔内往返任意多次均不会溢出腔外,所以共焦腔为稳定腔。
4. 试求平凹、双凹、凹凸共轴球面镜腔的稳定性条件。
激光与原理习题解答第二章

激光原理第二章习题答案1.估算2C O 气体在室温(300K)下的多普勒线宽D ν∆和碰撞线宽系数α。
并讨论在什么气压范围内从非均匀加宽过渡到均匀加宽。
解:2C O 气体在室温(300K)下的多普勒线宽D ν∆为11822770693103007.16107.161010.61044 0.05310H zD T M νν---⨯⎛⎫⎛⎫∆=⨯=⨯⨯⨯ ⎪ ⎪⨯⎝⎭⎝⎭=⨯ 2C O 气体的碰撞线宽系数α为实验测得,其值为49K H z/Pa α≈2C O 气体的碰撞线宽与气压p 的关系近似为L p να∆=当L D νν∆=∆时,其气压为930.053101081.6Pa 4910Dp να∆⨯===⨯所以,当气压小于1081.6P a 的时候以多普勒加宽为主,当气压高于1081.6P a 的时候,变为以均匀加宽为主。
2.考虑某二能级工作物质,2E 能级自发辐射寿命为s τ,无辐射跃迁寿命为τ。
假定在t=0时刻能级2E 上的原子数密度为2(0)n ,工作物质的体积为V ,自发辐射光的频率为ν,求:(1)自发辐射光功率随时间t 的变化规律;(2)能级2E 上的原子在其衰减过程中发出的自发辐射光子数;(3)自发辐射光子数与初始时刻能级2E 上的粒子数之比2η,2η称为量子产额。
解:(1) 在现在的情况下有可以解得:11()22()(0)stn t n eττ-+=可以看出,t 时刻单位时间内由于自发辐射而减小的能级之上的粒子数密度为2/s n τ,这就是t 时刻自发辐射的光子数密度,所以t 时刻自发辐射的光功率为:222()()sdn t n n dtττ=-+(2) 在t dt →时间内自发辐射的光子数为:所以(3) 量子产额为:3.根据红宝石的跃迁几率数据:7151332312121310.510,310,0.310,S s A sA s S S ---=⨯=⨯=⨯=估算13W 等于多少时红宝石对694.3n m λ=的光是透明的。
激光原理(陈钰清)第二章习题答案2

2.6 对 于 图 2.2 所 示 的 腔 , 忽 略 像 散 对 稳 定 性 影 响 。 证 明 : 当 R1 2 L1, R2 2 L2时,该腔是非稳定;仅当 R1 R2 时,该腔是临 界腔
知识点一:一些光学元件的传播矩阵 P48 图2.2
2.6 对 于 图 2.2 所 示 的 腔 , 忽 略 像 散 对 稳 定 性 影 响 。 证 明 : 当 R1 2 L1, R2 2 L2时,该腔是非稳定;仅当 R1 R2 时,该腔是临 界腔
1 (A+D) 1时,序列是稳定的 2
P49 (2-4-17)
2.14 腔内有其它元件的两镜腔中,除两个反射镜外的其余部分的变 换矩阵为 ,腔镜曲率半径为 R1 , R2 ,证明:稳定性条件为
0 g1 g 2 1
其中 = D B R1 ; g 2 A B R2
2A 2B 2 A B C( ) AB B D ( ) x R2 R2 x2 1 2 A C - 2 A )(D - 2 B ) C - 2 A )B C - 2 A )(D - 2 B ) D - 2 B )1 ( ( ( ( R1 R1 R2 R1 R1 R2
R R (1) 1 2 L1 ,2 2 L2 时,
1 1 1 L L L2 L1 L2 ( A D) 1 L( ) (1 ) 1 2 2 L1 2 L2 L1 2 L2 2 L1 L 1 L ( 2 1 ) 1 2 L1 L2
所以该腔是非稳定腔
g1 g 2 1 R2 >0 g1 g 2 <1 (1)当L< (2)当L= (3)当L>
2 R2 n0 时,0<g1 g 2 <1,该腔稳定 n0 1 2 R2 n0 时,g1 g 2 =0,该腔为临界腔 n0 1 2 R2 n0 时,g1 g 2 0,该腔不稳定 n0 1
激光原理第二章答案

第二章 开放式光腔与高斯光束1. 证明121 00 ηη⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。
证明:设入射光线坐标参数为11, r θ,出射光线坐标参数为22, r θ,根据几何关系可知211122, sin sin r r ηθηθ== 傍轴光线sin θθ则1122ηθηθ=,写成矩阵形式2121121 00 r r θθηη⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦得证 2. 1210 1d ηη⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。
证明:设入射光线坐标参数为11, r θ,出射光线坐标参数为22, r θ,入射光线首先经界面1折射,然后在介质2中自由传播横向距离d ,最后经界面2折射后出射。
根据1题的结论和自由传播的光线变换矩阵可得212121121 0 1 01 0 0 0 1r r d θθηηηη⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦ 化简后2121121 0 1d r r θθηη⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦得证。
3.试利用往返矩阵证明共焦腔为稳定腔,即任意傍轴光线在其中可以往返无限多次,而且两次往返即自行闭合。
证:设光线在球面镜腔内的往返情况如下列图所示:其往返矩阵为:由于是共焦腔,则有12R R L ==将上式代入计算得往返矩阵()()()121010110101n nnn n n r L r L ⎡⎤⎡⎤⎡⎤===-=-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦A B C D T T T T T 可以看出,光线在腔内往返两次的变换矩阵为单位阵,所以光线两次往返即自行闭合。
于是光线在腔内往返任意多次均不会溢出腔外,所以共焦腔为稳定腔。
4.试求平凹、双凹、凹凸共轴球面镜腔的稳定性条件。
解:共轴球面腔稳定性条件1201g g <<其中121211,1L Lg g R R =--=- 对平凹共轴球面镜腔有12,0R R =∞>。
则1221,1Lg g R ==-,再根据稳定性条件 1201g g <<可得22011LR R L <-<>⇒。
激光原理第二章作业的答案

0.5
M 2 R1 R2
R1 2R2
L= R1 -R2 0.3 22
R2 0.6 1.4485m 1 2
R1 2.0485m
• 当M1为输出时 ,由N的 定义知N=a2/Lλ 所以a1=0.39875mm a2= a1=0.39875mm • 当M2为输出时 ,由N的 定义知N=a2/Lλ 所以a2=0.39875mm
作业
1. 某共焦腔氦氖激光器,波长λ=0.6328um,若镜 面上基模光斑尺寸为0.5mm,试求共焦腔的腔长, 若腔长保持不变,而波长λ=3.39um,问:此时 镜面上光斑尺寸多大?
L 0s2 / 124.11mm
0s L /
1.1573mm
2. 腔长L=75cm的氦氖平凹腔激光器,波长λ= 0.6328um,腔镜曲率半径R=1m,试求凹面镜上 光斑尺寸,并计算该腔基模远场发散角θ。
z1 = -17.4545cm z2 =-1.4545cm f = 6.6656cm
g1=1-L/R1=0.2 g2 = 1-L/R2=1.5 L λ带入公式
w0 = 0.0146 cm
w1 = 0.0408 cm
w2 = 0.0149 cm
L= 160cm w0 = 0.01596cm w1 = w2 =sqrt(2)w0=0.02257cm
0
2 பைடு நூலகம்
2 (2L R1 R2 )2 2L(R1 L)(R2 L)(R1
R2
1/ 4
L)
2
L
(
g1 g2 2g1g2 )2 g1g2 (1 g1g2 )
1/ 4
Ws1=0.295mm
Ws2=0.591mm Q=0.0014rad=0.0782度
激光与原理习题解答第二章

激光原理第二章习题答案1.估算2CO 气体在室温(300K)下的多普勒线宽D ν∆和碰撞线宽系数α。
并讨论在什么气压范围内从非均匀加宽过渡到均匀加宽。
解:2CO 气体在室温(300K)下的多普勒线宽D ν∆为11822770693103007.16107.161010.61044 0.05310HzD T M νν---⨯⎛⎫⎛⎫∆=⨯=⨯⨯⨯ ⎪ ⎪⨯⎝⎭⎝⎭=⨯ 2CO 气体的碰撞线宽系数α为实验测得,其值为49KHz/Pa α≈2CO 气体的碰撞线宽与气压p 的关系近似为L p να∆=当L D νν∆=∆时,其气压为930.053101081.6Pa 4910Dp να∆⨯===⨯所以,当气压小于1081.6Pa 的时候以多普勒加宽为主,当气压高于1081.6Pa 的时候,变为以均匀加宽为主。
2.考虑某二能级工作物质,2E 能级自发辐射寿命为s τ,无辐射跃迁寿命为τ。
假定在t=0时刻能级2E 上的原子数密度为2(0)n ,工作物质的体积为V ,自发辐射光的频率为ν,求:(1)自发辐射光功率随时间t 的变化规律;(2)能级2E 上的原子在其衰减过程中发出的自发辐射光子数;(3)自发辐射光子数与初始时刻能级2E 上的粒子数之比2η,2η称为量子产额。
解:(1) 在现在的情况下有可以解得:11()22()(0)s tn t n eττ-+=可以看出,t 时刻单位时间内由于自发辐射而减小的能级之上的粒子数密度为2/s n τ,这就是t 时刻自发辐射的光子数密度,所以t 时刻自发辐射的光功率为:222()()s dn t n ndt ττ=-+(2) 在t dt →时间内自发辐射的光子数为:所以(3) 量子产额为:3.根据红宝石的跃迁几率数据:7151332312121310.510,310,0.310,S sA sA s S S ---=⨯=⨯=⨯=估算13W 等于多少时红宝石对694.3nm λ=的光是透明的。
激光原理第二章习题答案

激光原理第二章习题答案2.19某共焦腔氦氖激光器,波长λ=0.6328μm ,若镜面上基模光斑尺寸为0.5mm ,试求共焦腔的腔长,若腔长保持不变,而波长λ=3.39μm ,问:此时镜面上光斑尺寸多大?解:20/ 1.24s L m ωπλ=≈01.16mms ω==2.20考虑一台氩离子激光器,其对称稳定球面腔的腔长L=1m ,波长λ= 0.5145μm ,腔镜曲率半径R=4m ,试计算基模光斑尺寸和镜面上的光斑尺寸。
解:1/42021/42242()(2)(22)(2) 4.65104L R L R L R L RL L mωλπ-??--=??-??-==1/42121/4222422()()(2)4.9810(2)R R L L R L R L R L mRL L ωωλπ-??-==--??==-??2.21腔长L =75cm 的氦氖平凹腔激光器,波长λ=0.6328μm ,腔镜曲率半径R =1m ,试求凹面镜上光斑尺寸,并计算该腔基模远场发散角θ。
解:1/41/4212211121121/41/422112212212()0.295mm()()(1)()0.591()()(1)s s R R L g w L R L R R L g g g R R L g w mm L R L R R L g g g ??-===??-+--?-===-+--?1/42221212120212121212(2)(2)20.0014rad=0.0782()()()(1)L R R g g g g L R L R L R R L g g g g λθπ--+-===?--+--o2.22设稳定球面腔的腔长L =16cm ,两镜面曲率半径为1R =20cm ,2R =-32cm ,波长λ=410-cm ,试求:(1)最小光斑尺寸0ω和最小光斑位置;(2)镜面上光斑尺寸1s ω、2s ω;(3)0ω和1s ω、2s ω分别与共焦腔(1R =2R =L )相应值之比。
激光原理(陈钰清)第二章习题答案

2
2 1 x1 1 1 2 R 2
2.1 证明:如图2.1所示,当光线从折射率 的介质,向折射率为 时,在曲率半径R的球面分界面上,折射光线所经受的变换矩阵为
1 2 1 2 R 0 1 2
的介质折射
其中,当球面相对于入射光线凹(凸)面时,R取正(负)值。
5 35 物距s l h1 = 20- cm= cm 2 2
1 1 1 高斯公式 s s f 得像距s 7cm 7 s 像高x x x 10 cm 4cm 35 s 2
2.4 一块折射率为 ,厚度为d的介质放在空气中,其两界面分别为曲率半径等于R的 凹球面和平面,光线入射到凹球面上。求:(1)凹球面上反射光线的变换矩阵;(2) 平面界面处反射,球面界面处折射介质的光线变换矩阵;(3)透射出介质的光线的变 换矩阵。
2.1 证明:如图2.1所示,当光线从折射率 的介质,向折射率为 的介 质折射时,在曲率半径R的球面分界面上,折射光线所经受的变换矩阵 为
其中,当球面相对于入射光线凹(凸)面时,R取正(负)值。
知识点一:简单光学元件的光线矩阵
P43-44
解题思路:图上标出
x1、x2、1和 2 ,找出其中的关
图2.1
第一个透镜前表面与前主面的距离为-2.5cm,第二 个透镜后表面与后主面的距离为5cm,前主面离焦点 的距离为5cm
2.3 焦距 f1 =5cm和 f 2 =-10cm的两个透镜相距5cm。第一个透镜前表面和第二个透镜 后表面为参考平面的系统,其等效焦距为多少?焦点和主平面位置在何处?距 f1 前 表面20cm处放置高为10cm的物体,能在 f 2 后多远地方成像?像高为多少? (2)
激光原理第二章习题解答

《激光原理》习题解答 第二章习题解答1 试利用往返矩阵证明共焦腔为稳定腔,即任意傍轴光线在其中可以往返无限次,而且两次往返即自行闭合.证明如下:(共焦腔的定义——两个反射镜的焦点重合的共轴球面腔为共焦腔。
共焦腔分为实共焦腔和虚共焦腔。
公共焦点在腔内的共焦腔是实共焦腔,反之是虚共焦腔。
两个反射镜曲率相等的共焦腔称为对称共焦腔,可以证明,对称共焦腔是实双凹腔。
) 根据以上一系列定义,我们取具对称共焦腔为例来证明。
设两个凹镜的曲率半径分别是1R 和2R ,腔长为L ,根据对称共焦腔特点可知:L R R R ===21因此,一次往返转换矩阵为⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛---⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-+-⎪⎪⎭⎫⎝⎛--=⎥⎦⎤⎢⎣⎡=211121222121221221221R L R L R L R L R R R L L R L D C B A T 把条件L R R R ===21带入到转换矩阵T ,得到:⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡=1001D C B A T 共轴球面腔的稳定判别式子()1211<+<-D A 如果()121-=+D A 或者()121=+D A ,则谐振腔是临界腔,是否是稳定腔要根据情况来定。
本题中 ,因此可以断定是介稳腔(临界腔),下面证明对称共焦腔在近轴光线条件下属于稳定腔。
经过两个往返的转换矩阵式2T ,⎥⎦⎤⎢⎣⎡=10012T坐标转换公式为:⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡1111112221001θθθθr r r T r其中等式左边的坐标和角度为经过两次往返后的坐标,通过上边的式子可以看出,光线经过两次往返后回到光线的出发点,即形成了封闭,因此得到近轴光线经过两次往返形成闭合,对称共焦腔是稳定腔。
2 试求平凹、双凹、凹凸共轴球面腔的稳定条件。
解答如下:共轴球面腔的()21221222121R R L R L R L D A +--≡+,如果满足()1211<+<-D A ,则腔是稳定腔,反之为非稳腔,两者之间存在临界腔,临界腔是否是稳定腔,要具体分析。
激光原理第二章答案

第二章开放式光腔与高斯光束1.证明如图所示傍轴光线进入平面介质界面的光线变换矩阵为1 21 0ηη⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。
证明:设入射光线坐标参数为11,rθ,出射光线坐标参数为22,rθ,根据几何关系可知211122,sin sinr rηθηθ==傍轴光线sinθθ则1122ηθηθ=,写成矩阵形式2121121 0r rθθηη⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦得证2.证明光线通过图所示厚度为d的平行平面介质的光线变换矩阵为1210 1dηη⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。
证明:设入射光线坐标参数为11,rθ,出射光线坐标参数为22,rθ,入射光线首先经界面1折射,然后在介质2中自由传播横向距离d,最后经界面2折射后出射。
根据1题的结论和自由传播的光线变换矩阵可得212121121 0 1 010 00 1r rdθθηηηη⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦化简后21211210 1dr rθθηη⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦得证。
、3.试利用往返矩阵证明共焦腔为稳定腔,即任意傍轴光线在其中可以往返无限多次,而且两次往返即自行闭合。
证:设光线在球面镜腔内的往返情况如下图所示:其往返矩阵为:由于是共焦腔,则有~12R R L ==将上式代入计算得往返矩阵()()()121010110101n nnn n n r L r L ⎡⎤⎡⎤⎡⎤===-=-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦A B C D T T T T T 可以看出,光线在腔内往返两次的变换矩阵为单位阵,所以光线两次往返即自行闭合。
于是光线在腔内往返任意多次均不会溢出腔外,所以共焦腔为稳定腔。
4.试求平凹、双凹、凹凸共轴球面镜腔的稳定性条件。
解:共轴球面腔稳定性条件1201g g <<其中121211,1L Lg g R R =--=- [对平凹共轴球面镜腔有12,0R R =∞>。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
坐标转换公式为:
其中等式左边的坐标和角度为经过两次往返后的坐标,通过上边的式子可以看出,光线经过两次往返后回到光线的出发点,即形成了封闭,因此得到近轴光线经过两次往返形成闭合,对称共焦腔是稳定腔。
2试求平凹、双凹、凹凸共轴球面腔的稳定条件。
解答如下:共轴球面腔的 ,如果满足 ,则腔是稳定腔,反之为非稳腔,两者之间存在临界腔,临界腔是否是稳定腔,要具体分析。
由于反射不完全引起的损耗可以用公式2.1.24或者2.1.25来衡量
根据2.1.24得到:
δr≈-0.5lnr1r2=0.0204
根据题意,总的损耗为反射损+其他损耗,因此单程总损耗系数为
δ=0.0204+0.0003<g0L
如果考虑到衍射损耗,则还要根据菲涅尔数来确定衍射损系数:
此方形共焦腔氦氖激光器的菲涅尔数为:N=a2/(Lλ)=7.6,菲涅尔数大于一很多倍,因此可以不考虑衍射损耗的影响。
题中 ,
,在稳定腔的判别范围内,所以是稳定腔。
任意一个共焦腔与无穷多个稳定球面腔等价,一个一般稳定球面腔唯一对应一个共焦腔,他们的行波场是相同的。
等价共焦腔的参数包括:以等价共焦腔的腔中心为坐标原点,从坐标原点到一般稳定球面两个腔镜面的坐标 和 ,再加上它的共焦腔的镜面焦距 ,这三个参数就能完全确定等价共焦腔。
因此,可以在镜面上放置边长为2ω0s的光阑。
解答完毕。
6试求出方形镜共焦腔面上 模的节线位置,这些节线是等距分布吗?
解答如下:
方形镜共焦腔自再现模满足的积分方程式为
经过博伊德—戈登变换,在通过厄密-高斯近似,可以用厄密-高斯函数表示镜面上场的函数
使 就可以求出节线的位置。由上式得到:
,这些节线是等距的。
, 且 (第二种情况)
(对称双凹腔)
求解完毕。
3激光腔的谐振腔由一曲率半径为1M的凸和曲率半径为2M的凹面镜构成,工作物质长度为0.5M,其折射率为1.52,求腔长 在什么范围内谐振腔是稳定的。
解答如下:设腔长为 ,腔的光学长度为 ,已知 , , , , ,
根据 ,代入已知的凸凹镜的曲率半径,得到:
因为含有工作物质,已经不是无源腔,因此,这里L应该是光程的大小(或者说是利用光线在均匀介质里传播矩阵)。
即 ,代入上式,得到:
要达到稳定腔的条件,必须是 ,按照这个条件,得到腔的几何长度为:
,单位是米。
解答完毕。
5有一方形孔径共焦腔氦氖激光器,腔长L=30CM,方形孔径边长为d=2a=0.12CM,λ=632.8nm,镜的反射率为r1=1,r2=0.96,其他损耗以每程0.003估计。此激光器能否做单模运转?如果想在共焦镜面附近加一个方形小孔光阑来选择TEM00模,小孔的边长应为多大?试根据图2.5.5作一大略的估计。氦氖激光器增益由公式 估算,其中的l是放电管长度。
对于 ,可以做类似的分析。
,代入上式并使光波场为零,得到
显然,只要 即满足上式
最后镜面上节线圆的半径分别为:
解答完毕。
8今有一球面腔,两个曲率半径分别是R1=1.5M,R2=-1M,L=80CM,试证明该腔是稳定腔,求出它的等价共焦腔的参数,在图中画出等价共焦腔的具体位置。
解:共轴球面腔稳定判别的公式是 ,这个公式具有普适性(教材36页中间文字部分),对于简单共轴球面腔,可以利用上边式子的变换形式 判断稳定性,其中 。
通过以上分析可以断定,此谐振腔可以产生激光振荡。又根据氦氖激光器的多普勒展宽达到1.6GHZ,而纵模及横模间隔根据计算可知很小,在一个大的展宽范围内可以后很多具有不同模式的光波振荡,因此不采取技术措施不可能得到基模振荡。
为了得到基模振荡,可以在腔内加入光阑,达到基模振荡的作用。在腔镜上,基模光斑半径为:
分析:如果其他损耗包括了衍射损耗,则只考虑反射损耗及其他损耗的和是否小于激光器的增益系数,增益大于损耗,则可产生激光振荡。
如果其他损耗不包括衍射损耗,并且菲涅尔数小于一,则还要考虑衍射损耗,衍射损耗的大小可以根据书中的公式δ00=10.9*10-4.94N来确定,其中的N是菲涅尔数。
解答:根据 ,可以知道单程增益g0L=ln(1+0.0003L/d)=0.0723
解答完毕。
7求圆形镜共焦腔 和 模在镜面上光斑的节线位置。
解答如下:圆形镜共焦腔场函数在拉盖尔—高斯近似下,可以写成如下的形式
(这个场对应于 ,两个三角函数因子可以任意选择,但是当m为零时,只能选余弦,否则整个式子将为零)
对于 :
并且 ,代入上式,得到
,我们取余弦项,根据题中所要求的结果,我们取 ,就能求出镜面上节线的位置。既
《激光原理》习题解答
第二章习题解答
1试利用往返矩阵证明共焦腔为稳定腔,即任意傍轴光线在其中可以往返无限次,而且两次往返即自行闭合.
证明如下:(共焦腔的定义——两个反射镜的焦点重合的共轴球面腔为共焦腔。共焦腔分为实共焦腔和虚共焦腔。公共焦点在腔内的共焦腔是实共焦腔,反之是虚共焦腔。两个反射镜曲率相等的共焦腔称为对称共焦腔,可以证明,对称共焦腔是实双凹腔。)
根据以上一系列定义,我们取具对称共焦腔为例来证明。
设两个凹镜的曲率半径分别是 和 ,腔长为 ,根据对称共焦腔特点可知:
因此,一次往返转换矩阵为
把条件 带入到转换矩阵T,得到:
共轴球面腔的稳定判别式子
如果 或者 ,则谐振腔是临界腔,是否是稳定腔要根据情况来定。本题中,因此可以断定是介稳腔(临界腔),下面证明对称共焦腔在近轴光线条件下属于稳定腔。
根据公式(激光原理p66-2.8.4)得到:
因此
等价共焦腔示意图略。
9某二氧化碳激光器采用平-凹腔,L=50CM,R=2M,2a=1CM,波长λ面上的损耗。
解:此二氧化碳激光器是稳定腔,其中平面镜的曲率半径可以看作是无穷大。
根据公式(激光原理p67-2.8.6或2.8.7)得到:
下面我们就根据以上的内容来分别求稳定条件。
对于平凹共轴球面腔, ( )
所以,如果 ,则是稳定腔。因为 和 均大于零,所以不等式的后半部分一定成立,因此,只要满足 ,就能满足稳定腔的条件,因此, 就是平凹腔的稳定条件。
类似的分析可以知道,
凸凹腔的稳定条件是: ,且 。
双凹腔的稳定条件是: , (第一种情况)
