激光原理第二章
合集下载
激光原理与技术：第二章
件，大多数情况下，孔径是激活物质的两个端 面，但一些激光器中会另外放置元件以限制光 束为理想的形状。
➢光学谐振腔的种类：
谐振腔的开放程度: 闭腔、开腔、波导腔 开腔通常可以分为: 稳定腔、非稳定腔、临界腔 反射镜形状: 球面腔与非球面腔，端面反射腔与分
布反馈腔 反射镜的多少: 两镜腔与多镜腔（折叠腔、环形
r00
T
r00
共轴球面镜腔 往返传输矩阵：
L A 1
f2
C
1 f1
1 f2
1
L f1
B L 2
L f2
D
L f1
1
L f1
1
L f2
•往返矩阵T与光线的初始坐标参数r0和
轴光线在腔内往返传播的行为
0
无关，因而它可以描述任意近
例：
L 3 R2 4
g1
1
L R1
1;
g2
1
L R2
1 4
§2.1.3. 光学谐振腔的损耗，Q值及线宽
损耗的大小是评价谐振腔的一个重要指标，在激光振荡中， 光腔的损耗决定了振荡的阈值和激光的输出能量，也是腔 模理论的重要研究课题
➢光腔的损耗：
1. 几何损耗
选择性损耗、对不同模式，损耗不同
2. 衍射损耗 3. 腔镜反射不完全引起的损耗
非选择性损耗
4. 腔内介质不均匀引起的损耗
Q 2v R
Q
2v
R
2v
L'
C
❖腔的品质因数Q值是衡量腔质量的一个重要的物理量，它
表征腔的储能及损耗特征。
总之，腔平均单程损耗因子、光子寿命、与腔的品质因数三个 物理量之间是关联的，腔平均单程损耗因子越小，光子寿命越 长，腔的品质因数越高。
➢光学谐振腔的种类：
谐振腔的开放程度: 闭腔、开腔、波导腔 开腔通常可以分为: 稳定腔、非稳定腔、临界腔 反射镜形状: 球面腔与非球面腔，端面反射腔与分
布反馈腔 反射镜的多少: 两镜腔与多镜腔（折叠腔、环形
r00
T
r00
共轴球面镜腔 往返传输矩阵：
L A 1
f2
C
1 f1
1 f2
1
L f1
B L 2
L f2
D
L f1
1
L f1
1
L f2
•往返矩阵T与光线的初始坐标参数r0和
轴光线在腔内往返传播的行为
0
无关，因而它可以描述任意近
例：
L 3 R2 4
g1
1
L R1
1;
g2
1
L R2
1 4
§2.1.3. 光学谐振腔的损耗，Q值及线宽
损耗的大小是评价谐振腔的一个重要指标，在激光振荡中， 光腔的损耗决定了振荡的阈值和激光的输出能量，也是腔 模理论的重要研究课题
➢光腔的损耗：
1. 几何损耗
选择性损耗、对不同模式，损耗不同
2. 衍射损耗 3. 腔镜反射不完全引起的损耗
非选择性损耗
4. 腔内介质不均匀引起的损耗
Q 2v R
Q
2v
R
2v
L'
C
❖腔的品质因数Q值是衡量腔质量的一个重要的物理量，它
表征腔的储能及损耗特征。
总之，腔平均单程损耗因子、光子寿命、与腔的品质因数三个 物理量之间是关联的，腔平均单程损耗因子越小，光子寿命越 长，腔的品质因数越高。
激光原理第二章习题答案
2.1 证明：如图2.1所示，当光线从折射率1η的介质，向折射率为2η的介质折射时，在曲率半径R 的球面分界面上，折射光线所经受的变换矩阵为⎥⎥⎦⎤⎢⎢⎣⎡-2121201ηηηηηR 其中，当球面相对于入射光线凹（凸）面时，R 取正（负）值。
证明：由图可知 11201θ⋅+⋅=x x 又)()(222111θηθη-=-RxR x 21121122x R ηηηθθηη-∴=+ ⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡∴11212122201θηηηηηθx Rx ∴变换矩阵为⎥⎥⎦⎤⎢⎢⎣⎡-2121201ηηηηηR 2.2 试求半径R=4cm,折射率η=1.5的玻璃球的焦距和主面的位置1h 和2h 。
解：变换矩阵⎥⎥⎦⎤⎢⎢⎣⎡-⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-=2112121221210110101n n R n n n l n n R n n n M 把11=n ，5.12=n ，cm R R 421=-=，cm l 8=代入，可得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡⨯-⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡--=3531316355.1145.115.10110815.145.1101M )(12f h A -=, f C 1-=, )(11f h D -= 求得 mm f 30-= mm h 201= mm h 202=2.3 焦距1f =5cm 和2f =-10c=m 的两个透镜相距5cm 。
第一个透镜前表面和第二个透镜后表面为参考平面的系统，其等效焦距为多少？焦点和主平面位置在何处？距1f 前表面20cm 处放置高为10cm 的物体，能在2f 后多远地方成像？像高为多少？ 解：（1）2110101010********1131101011110552A B L M CD f f ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥====⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-----⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦)(12f h A -=, f C 1-=, )(11f h D -=，求得cm f 5-= cm h 5.21= cm h 52-=第一个透镜前表面与前主面的距离为2.5cm ，第二个透镜后表面与后主面的距离为-5cm,前主面离焦点的距离为-5cm ，） （2）21201011===l x θ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡45252110235150235150111122θθθx x D C B A xcm l cm x 2,5.222-==（距2f 后表面-2cm ）2.4 一块折射率为η，厚度为d 的介质放在空气中，其两界面分别为曲率半径等于R 的凹球面和平面，光线入射到凹球面上。
激光原理第二章答案解析
第二章 开放式光腔与高斯光束1. 证明如图2.1所示傍轴光线进入平面介质界面的光线变换矩阵为121 00 ηη⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。
证明：设入射光线坐标参数为11, r θ，出射光线坐标参数为22, r θ，根据几何关系可知211122, sin sin r r ηθηθ== 傍轴光线sin θθ则1122ηθηθ=，写成矩阵形式2121121 00 r r θθηη⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦得证 2. 证明光线通过图2.2所示厚度为d 的平行平面介质的光线变换矩阵为1210 1d ηη⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。
证明：设入射光线坐标参数为11, r θ，出射光线坐标参数为22, r θ，入射光线首先经界面1折射，然后在介质2中自由传播横向距离d ，最后经界面2折射后出射。
根据1题的结论和自由传播的光线变换矩阵可得212121121 0 1 01 0 0 0 1r r d θθηη⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦ 化简后2121121 0 1d r r θθηη⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦得证。
3．试利用往返矩阵证明共焦腔为稳定腔，即任意傍轴光线在其中可以往返无限多次，而且两次往返即自行闭合。
证：设光线在球面镜腔内的往返情况如下图所示：其往返矩阵为：由于是共焦腔，则有12R R L ==将上式代入计算得往返矩阵()()()121010110101n nnn n n r L r L ⎡⎤⎡⎤⎡⎤===-=-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦A B C D T T T T T 可以看出，光线在腔内往返两次的变换矩阵为单位阵，所以光线两次往返即自行闭合。
于是光线在腔内往返任意多次均不会溢出腔外，所以共焦腔为稳定腔。
4.试求平凹、双凹、凹凸共轴球面镜腔的稳定性条件。
解：共轴球面腔稳定性条件1201g g <<其中121211,1L Lg g R R =--=- 对平凹共轴球面镜腔有12,0R R =∞>。
激光原理第二章 激光器的工作原理
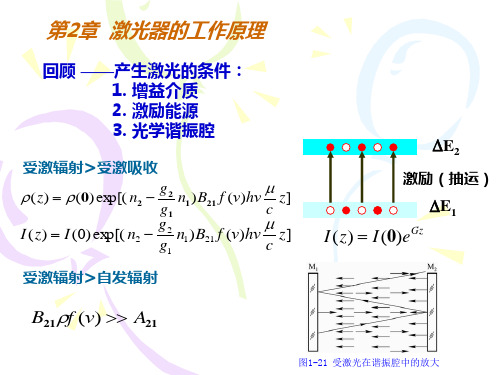
可以证明，在对称共焦腔内，任意傍轴光线可往返多次
而不横向逸出，而且经两次往返后即可自行闭合。
整个稳定球面腔的模式理论都可以建立在共焦腔振荡理 论的基础上，因此，对称共焦腔是最重要和最具有代表性的 一种稳定腔。
3.平行平面腔——由两个平面反射镜组成的共轴谐振腔
R1=R2=∞，g1=g2=1， g1 g2=1
图(2-2) 共轴球面腔的稳定图
➢凹凸稳定腔，由一个凹面镜和一个凸面镜组成，对应图中5区和6区。
➢ (g1>1,g2<1; g2>1,g1<1)
➢共焦腔，R1＝R2＝L，因而，g1=0，g2=0，对应图中的坐标原点。(特殊的稳定腔) ➢半共焦腔，由一个平面镜和一个R=2L的凹面镜组成的腔,对应图中E和F点g1=1，g2=1/2
1. 工作物质 2. 激励能源
受激辐射>受激吸收
3. 光学谐振腔
受激辐射>自发辐射
是否只要具备激励能源和工作物质就一定可以实 现粒子数反转？ 粒子数反转和什么因素有关？
速率方程方法: 量子理论的一种简化形式
——速率方程理论：把光频电磁场看成量子化的光子，把 物质体系描述成具有量子化能级的粒子体系。
(三)临界腔: g1 g2 = 0 , g1 g2= 1
临界腔属于一种极限情况,其稳定性视不同的腔而不同. 在谐振理论研究和实际应用中,临界腔具有非常重要的意义.
1.对称共焦腔——腔中心是两镜公共焦 点且：
R1=L
R2=L
R1= R2= R = L=2F F——二镜焦距
F
L
∵ g1 = g2 = 0 ∴ g1 g2 = 0
简化前提: 忽略量子化辐射场的位相特性及光子数的起伏特 性
优点: 形式特别简单, 且可给出激光的强度特性，并粗略描 述烧孔、兰姆凹陷、多模竞争等效应
激光原理与技术(第二章1)PPT课件
3. 腔镜反射不完全引起的损耗：包括镜中的吸收、散射以及镜 的透射损耗。通常镜至少有一个反射镜是部分透射的，另一 个通常称“全反射”镜，其反射率不可能做到100%。
4. 固有损耗：激光材料的吸收、散射等引起的损耗。
1和2为选择损耗：不同模式的几何损耗和衍射损耗各不相同。3和 4为非选择损耗：对各个模式大体一样。
上海大学电子信息科学与技术
损耗的参数 (loss per pass, photon lifetimes, and quality factor Q)
1. 平均单程损耗因子
初始光强I0，在腔内往返一次后，光强衰减为I1，则
I I0e2
1 2
ln
I0 I
－指数损耗因子
如果I代表每一个引起损耗缘由的损耗因子，则总损耗
1 0
Tf
1
f
1
f R 2
焦距为f=2/R的薄透镜与球面反射镜等效
5.ABCD矩阵的应用－球面镜腔的往返矩阵 上海大学电子信息科学与技术
球面镜腔中往返一周的光线矩阵（简称往返矩阵）
r44 TR1TLTR2TL r00
T
r00
A C
B D
r0
0
T
A C
B D
1 2
R1
10
1 0
0 L
1 2
2. 与腔损耗有关的参数 －光子寿命R
光子(平均)寿命R－腔内光强衰减到初始值的1/e 所需时间
根据定义，如何计算光子平均寿命
I m I0 e2 m I0e2m
m
t
2L
R称为腔的时间常数
c
1
Im
m
I 0e 2m
t 2L
c
R
4. 固有损耗：激光材料的吸收、散射等引起的损耗。
1和2为选择损耗：不同模式的几何损耗和衍射损耗各不相同。3和 4为非选择损耗：对各个模式大体一样。
上海大学电子信息科学与技术
损耗的参数 (loss per pass, photon lifetimes, and quality factor Q)
1. 平均单程损耗因子
初始光强I0，在腔内往返一次后，光强衰减为I1，则
I I0e2
1 2
ln
I0 I
－指数损耗因子
如果I代表每一个引起损耗缘由的损耗因子，则总损耗
1 0
Tf
1
f
1
f R 2
焦距为f=2/R的薄透镜与球面反射镜等效
5.ABCD矩阵的应用－球面镜腔的往返矩阵 上海大学电子信息科学与技术
球面镜腔中往返一周的光线矩阵（简称往返矩阵）
r44 TR1TLTR2TL r00
T
r00
A C
B D
r0
0
T
A C
B D
1 2
R1
10
1 0
0 L
1 2
2. 与腔损耗有关的参数 －光子寿命R
光子(平均)寿命R－腔内光强衰减到初始值的1/e 所需时间
根据定义，如何计算光子平均寿命
I m I0 e2 m I0e2m
m
t
2L
R称为腔的时间常数
c
1
Im
m
I 0e 2m
t 2L
c
R
激光原理第2章
初态： 初态：激发态原子
终态： 终态：基态原子
E2
外来光子 hν = E2 – E1
发射光子 hν = E2 – E1
E1 特点： 才能引起受激辐射； 特点：只有外来光子能量为 hv =E2-E1才能引起受激辐射； 受激辐射的光子与外来光子的特性完全相同， 受激辐射的光子与外来光子的特性完全相同，即具有相同的 频率、偏振方向、传播方向以及相同的位相；是相干光。 频率、偏振方向、传播方向以及相同的位相；是相干光。 受激辐射是激光器的物理基础
爱因斯坦A 5、 爱因斯坦A、B系数关系
在光和原子相互作用达到动平衡的条件下， (1) 在光和原子相互作用达到动平衡的条件下，
自发辐射、 自发辐射、受激辐射和受激吸收间关系
A21n2dt + B21ρ ν n2dt = B12 ρ ν n1dt
自发辐射光子数 受激辐射光子数 受激吸收光子数
n2 B12 ρ v = n1 A21 + B21ρ v
的光波， 的连续功率， 2、某激光器，输出波长500nm的光波，输出 某激光器，输出波长 的光波 输出1W的连续功率， 的连续功率 问每秒从激光上能级向下能级跃迁的粒子数是多少？ 问每秒从激光上能级向下能级跃迁的粒子数是多少？
2.3
光的受激辐射
1900年 1900年，普朗克利用辐射量子化假 设成功解释黑体辐射分布规律 1913年 1913年，波尔提出原子中电子运动状 态量子化假设
（2）自发辐射跃迁几率 设t 时刻 ，体系处于E2 的总粒子数密度为 n2(t)，从t ～t + dt 体系处于 正比于n ： 时间间隔内自发辐射粒子数密度 dn21 正比于 2(t)：
− dn2 = A21n2 (t )dt
周版激光原理课件第二章
数为：
P
nVd
8 2
c3
Vd
由此关系知，只能压缩V，但是不现实。从而提出开式腔
（无侧壁的封闭腔）。从发散角来看，封闭时为2 ，而
开式时为
a
2
L
压缩倍数为
2
/
a L
2
• 但是，我们知道开式腔是无侧壁的封闭 腔，那么内部会不会有稳定的电磁波存 在？如何求出该电磁波？
§ 2.1光腔理论的一般问题
(t
z
)
A2
A0
cos 2
(t
z
)
总波为二者叠加：
A
A1
A2
2 A0
cos
2
z
cost
稳定波存在必须满足驻波条件：
一维： L q
2
与谐振条件等价
从波动理论知：驻波是稳定存在的波。满足驻波条件的 那些光波称之为光腔的纵模，q为波节数，一般很大。一般 把由整数q所表征的腔内的纵向场分布称为腔的纵模。其特 点是：在腔的横截面内场分布是均匀的，而沿腔的轴线方向 形成驻波，驻波的波节数由q来决定。
共轴
球面 R1
共轴 R2
2. 开放式: 除二镜外其余部分开放 共轴: 二镜共轴 球面腔: 二镜都是球面反射镜(球面镜)
三.光腔按几何损耗(几何反射逸出)的分类:
稳定腔 (光腔中存在着伴轴模,它可在腔内多次传播而不逸出腔外) 光腔 临界腔 (几何光学损耗介乎上二者之间)
非稳腔 (伴轴模在腔内经有限数往返必定由侧面逸出腔外,有很高的
a
在这种条件下，可认为均匀平面波是F-P谐振腔内的最低损 耗模，从而为F-P谐振腔的模式提供一种粗略的，也是有用 的形象。
所以考虑均匀平面波在F-P谐振腔内沿轴线方向往返传播的 情形
激光原理第二章ppt课件
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的，因 此，篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
四、光腔的损耗－－光子在腔内的平均寿命
四、光腔的损耗
损耗的大小是评价谐振腔的一个重要指标，（与激 光阈值相关）本小节对无源、开腔的损耗进行分析。
• 开腔的损耗及其描述 • 光子在腔内的平均寿命 • 无源谐振腔的Q值 • 无源腔的本征振荡模式带宽 • 损耗计算举例
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的，因 此，篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的，因 此，篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
四、光腔的损耗－－开腔的损耗及其描述
2、平均单程损耗因子：
•定义：
I1 I0e2
若有多种损耗：
1 ln I0 2 I1
(与1-91比较)
n
i 12n
i
I1I0e 21e 22I0e 2
三、光腔的纵模－－多纵模振荡
1、腔内存在模式要形成稳定的振荡，还必须满足自激振荡
条件：单程小信号G0l增益大于单程损耗δ，即：G0l
2、如果以△νT表示增益曲线高于阈值部分的频带宽度，则 可能同时振荡的纵模数为：
讨论：
q [T ] 1 q
•
当 T q
1，激光器中至少有两个以上的纵模振荡。即多纵
§2.1 光腔理论的一般问题
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的，因 此，篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
一、光腔的构成与分类
激光原理(第2章)
三、光腔的损耗 损耗的大小是评价谐振腔的一个重要指标，也是腔模理论的重要研究 课题。光学的损耗大致包括如下几个方面： (1)几何偏折损耗。光线在腔内往返传播时，可能从腔的侧面偏折出 去，这种损耗为几何偏折损耗。其大小首先取决于腔的类型和几何尺寸。 例如，稳定腔内傍抽光线的几何损托应为各零，非稳腔则有较高的几何 损耗。以非稳腔而论，不同几何尺寸的非稳腔，其损耗大小亦各不相同。 其次，几何损耗的高低依模式的不同而异。比如同一平行平面腔内的高 阶横模由于其传播方向与轴的夹角较大，因而其几何损耗也比低阶横模 为大。 (2)衍射损耗。由于腔的反射镜片通常具有有限大小的孔径，因而当 光在镜面上发生衍射时，必将造成一部分能量损失。本节以及本书后面 几章的分析表明，衍射损耗的大小与腔的菲涅耳数 N＝a2/Ll有关，与 腔的几何参数g有关，而且不同横模的衍射损耗也将各不相同。
(3)腔镜反射不完全引起的损耗。它包括镜中的吸收、散射以及镜的 透射损耗，通常的光腔至少有一个反射镜是部分透射的，有时透射率还 可以很高(例如，某些固体激光器的轴输出透射率可以＞ 50％)，另一个 反射镜即使通常称为“全反射”镜，其反射率也不可能做到100％。 (4) 材料中的非激活吸收、散射，腔内插入物 ( 如布儒斯特窗、调 Q 元件、调制器等)所引起的损耗，等等。 上述 (1)(2) 两种损耗常常又称为选择损耗，因为不同模式的几何损 耗与衍射损耗各不相同。 (3)(4)两种损耗称为非选择损耗，在一般情况 下它们对各个模式都一样。 不论损耗的起源如何，我们都可以引进一个“平均单程损耗因子” d 来定量地加以描述。该因子的定义如下：如果初始出发时的光强为 I0， 在无源腔内往返一次后，光强衰减为I1，则
2.1 光腔理论的一般问题
一、光腔的构成和分类
在激活物质的两端恰当地放置两个反射镜片，就构成一个最简单的 光学谐振腔。
周炳琨激光原理第二章习题解答(完整版)
周炳琨激光原理第二章习题解答（完整版）1.试利用往返矩阵证明对称共焦腔为稳定腔，即任意傍轴光线在其中可以往返无限多次，而且两次往返即自行闭合。
证明：设从镜M 1→M 2→M 1,初始坐标为⎪⎪⎭⎫ ⎝⎛θ00r ，往返一次后坐标变为⎪⎪⎭⎫ ⎝⎛θ11r =T ⎪⎪⎭⎫⎝⎛θ00r ,往返两次后坐标变为⎪⎪⎭⎫⎝⎛θ22r =T •T ⎪⎪⎭⎫ ⎝⎛θ00r 而对称共焦腔，R 1=R 2=L 则A=1-2R L 2=-1 B=2L ⎪⎪⎭⎫⎝⎛-2R L 1=0 C=-⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-+121R L 21R 2R 2=0 D=-⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛--211R L 21R L 21R L 2=-1 所以，T=⎪⎪⎭⎫ ⎝⎛--1001故，⎪⎪⎭⎫⎝⎛θ22r =⎪⎪⎭⎫ ⎝⎛--1001⎪⎪⎭⎫ ⎝⎛--1001⎪⎪⎭⎫ ⎝⎛θ00r =⎪⎪⎭⎫⎝⎛θ00r 即，两次往返后自行闭合。
2．试求平凹、双凹、凹凸共轴球面镜腔的稳定性条件。
解：共轴球面腔的稳定性条件为0<g 1•g 2<1,其中g 1=1-1R L ,g 2=1-2R L（a 对平凹腔：R 2=∞,则g 2=1,0<1-1R L<1，即0<L<R 1 (b)对双凹腔：0<g 1•g 2<1, 0<⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-21R L 1R L 1<1 LR >1，L R >2或L R <1L R <2且LR R >+21(c)对凹凸腔：R 1=1R ,R 2=-2R ,0<⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛-21R L 1R L 1<1，L R >1且LR R <-||213．激光器的谐振腔由一面曲率半径为1m 的凸面镜和曲率半径为2m 的凹面镜组成，工作物质长0.5m ，其折射率为1.52，求腔长L 在什么范围内是稳定腔。
激光原理教案第二章
I m = I0 e
( )
−2δ
'
m
= I 0e
t
−2mδ '
t ,m = 2L '/ c
I (t ) = I 0 e
−
τR
,τ R
L' = δc
激光原理与技术
时间后， 的物理意义: 时间常数τR的物理意义 经过τR时间后， 腔内光强衰减为初始值的1／ 腔内光子数将 腔内光强衰减为初始值的 ／e,腔内光子数将 随时间依指数规律衰减， 随时间依指数规律衰减，到τR 时刻衰减为初 始值1／ 。 愈大， 愈小， 始值 ／e。δ愈大， τR愈小，说明腔的损耗 愈大，腔内光强衰减得愈快。 愈大，腔内光强衰减得愈快。 2．无源谐振腔的Q值 ．无源谐振腔的 值
c ∆ν q = ν q+1 −ν q = , (频率梳） 2L 例：L = 10cm,η = 1气体激光器, ∆ν q = 1.5 ×109 Hz L = 100cm,η = 1气体激光器, ∆ν q = 1.5 ×10 Hz
8
L = 10cm,η = 1.76的红宝石激光器∆ν q = 8.5 ×10 Hz
激光原理与技术
激光原理与技术
光 学 谐 振 腔
闭 腔 稳 定 腔 开 腔 非 稳 腔 临 界 腔 气 体 波 导 腔
激光原理与技术
谐振腔可以按不同的方法可分为： 谐振腔可以按不同的方法可分为： 端面反馈腔与分布反馈腔，球面腔与非球 端面反馈腔与分布反馈腔， 面腔，高损耗腔与低损耗腔， 面腔，高损耗腔与低损耗腔，驻波腔与行波 两镜腔与多镜腔， 腔，两镜腔与多镜腔，简单腔与复合腔 等．本章讨论两镜腔。 二、模的概念、腔与模的一般联系 模的概念、 腔的模式:光学谐振腔内可能存在的电磁场的 腔的模式 光学谐振腔内可能存在的电磁场的 本征态称。 本征态称。场的每一个本征态将具有一定的振 荡频率和一定的空间分布。 荡频率和一定的空间分布。
激光原理(陈钰清)第二章习题答案2
2.6 对 于 图 2.2 所 示 的 腔 ， 忽 略 像 散 对 稳 定 性 影 响 。 证 明 ： 当 R1 2 L1, R2 2 L2时，该腔是非稳定；仅当 R1 R2 时，该腔是临 界腔
知识点一：一些光学元件的传播矩阵 P48 图2.2
2.6 对 于 图 2.2 所 示 的 腔 ， 忽 略 像 散 对 稳 定 性 影 响 。 证 明 ： 当 R1 2 L1, R2 2 L2时，该腔是非稳定；仅当 R1 R2 时，该腔是临 界腔
1 （A+D） 1时，序列是稳定的 2
P49 （2-4-17）
2.14 腔内有其它元件的两镜腔中，除两个反射镜外的其余部分的变 换矩阵为 ,腔镜曲率半径为 R1 , R2 ,证明：稳定性条件为
0 g1 g 2 1
其中 = D B R1 ; g 2 A B R2
2A 2B 2 A B C（ ） AB B D （ ） x R2 R2 x2 1 2 A C - 2 A ）（D - 2 B ） C - 2 A ）B C - 2 A ）（D - 2 B ） D - 2 B ）1 （ （ （ （ R1 R1 R2 R1 R1 R2
R R （1） 1 2 L1 ，2 2 L2 时，
1 1 1 L L L2 L1 L2 ( A D) 1 L( ) (1 ) 1 2 2 L1 2 L2 L1 2 L2 2 L1 L 1 L ( 2 1 ) 1 2 L1 L2
所以该腔是非稳定腔
g1 g 2 1 R2 >0 g1 g 2 <1 （1）当L< （2）当L= （3）当L>
2 R2 n0 时，0<g1 g 2 <1,该腔稳定 n0 1 2 R2 n0 时，g1 g 2 =0,该腔为临界腔 n0 1 2 R2 n0 时，g1 g 2 0，该腔不稳定 n0 1
激光原理 第二章光学谐振腔理论
光学谐振腔一方面具有光学正反馈作用,另一方面 也存在各种损耗。损耗的大小是评价谐振腔质量 的一个重要指标,决定了激光振荡的阈值和激光的 输出能量。本节将分析无源开腔的损耗,并讨论表 征无源腔质量的品质因数Q值及线宽。
一、损耗及其描述 (1)几何偏折损耗: 光线在腔内往返传播时，可能从腔的侧面 偏折出去，我们称这种损耗为几何偏折损 耗。其大小首先取决于腔的类型和几何尺 寸。
概述
3.波动光学分析方法 从波动光学的菲涅耳-基尔霍夫衍射积分理论出发,可以建立 一个描述光学谐振腔模式特性的本征积分方程。 利用该方程原则上可以求得任意光腔的模式,从而得到场的 振幅、相位分布,谐振频率以及衍射损耗等腔模特性。 虽然数学上已严格证明了本征积分方程解的存在性,但只有在 腔镜几何尺寸趋于无穷大的情况下,该积分方程的解析求解 才是可能的。 对于腔镜几何尺寸有限的情况,迄今只对对称共焦腔求出了 解析解。 多数情况下,需要使用近似方法求数值解。虽然衍射积分方 程理论使用了标量场近似,也不涉及电磁波的偏振特性,但与 其他理论相比,仍可认为是一种比较普遍和严格的理论。
第一节 光学谐振腔的基本知识
本节主要讨论光学谐振腔的构成、分类、作用,以及 腔模的概念
光学谐振腔的构成和分类
根据结构、性能和机理等方面的不同,谐振腔有不同 的分类方式。
按能否忽略侧面边界,可将其分为
开腔、 闭腔 气体波导腔
第一节 光学谐振腔的基本知识
开腔而言： 1. 根据腔内傍轴光线几何逸出损耗的高低,又可分为 稳定腔、非稳腔及临界腔; 2. 按照腔镜的形状和结构,可分为球面腔和非球面腔; 3. 就腔内是否插入透镜之类的光学元件,或者是否考 虑腔镜以外的反射表面,可分为简单腔和复合腔; 4. 根据腔中辐射场的特点,可分为驻波腔和行波腔; 5. 从反馈机理的不同,可分为端面反馈腔和分布反馈 腔; 6. 根据构成谐振腔反射镜的个数,可分为两镜腔和多 镜腔等。
第2章激光产生的基本原理
f +Ze
e
f
?
Ze2
4?? 0r 2
F
f?F
F
?
V2 m
r
f
?
Ze2
4?? 0r 2
?
V2 m
r
由玻尔第三假设：电子的角动量mVr只能等于h/2π的整数倍，即
mVr ? n h
2?
(6.626176±0.000036)×10－34 J·ｓ
mVr ? n h
2?
f
?
Ze 2
4?? 0r 2
?
V2 m
? B12 ? v
?v ?
f 2 A 21
hv
? ? B21? v ? A21
f2 f1
? hv
e kbT
?
B12 ? v
f1B12e kbT ? f2B21
由黑体辐射的普朗克公式：
?v
?
8?hv3
c3
1
hv
e kbT ? 1
f1B12 ? f2 B21?
??
A21
?
8?hv3
? ?
B21
c3 ??
dn2 dt
A21为自发辐射跃迁 爱因斯坦系数
?? n2 t
?
n e ? A21t 20
?s
?
1 A21
原子数密度由n20降到1/e所 用的时间。
自发辐射产生的光都是非相干的
2.2.2 受激辐射
E2
E2
hv=E2-E1
E1
E1
特点：
（1）有外来光子； （2）发射的光子与外来光子特性完全相同。
W21
1、二能级系统
? B12 ? B21 ? W12 ? W21 ? W
激光原理第二章2.1-2.5
谐 振 腔 结 构 与 稳 定 性
§ .
(2) 临界腔 平行平面腔，对应图中的A点。只有与腔轴平行的光线才能在腔内往返。 共心腔， 满足条件R2＋R2＝L，对应图中第一象限的g1g2＝1的双曲线。 半共焦腔，由一个平面镜和一个凹面镜组成，对应图中C点和D点。 (3) 非稳腔 对应图中阴影部分的光学谐振腔都是非稳腔。
谐 振 腔 结 构 与 稳 定 性
§ .
图(2-3) 稳定图的应用
上一页 回首页 下一页 回末页 回目录
一、速率方程组
n1 B12 f ( )
n2 B21f ( )
E2
n2 A20 E1 E0
第 1. 图（2.4.1）为简化的四能级图，n0、n1、 二 n2分别为基态、上能级、下能级的粒子数密 R2 n2 A21 章 度；n为单位体积内增益介质的总粒子数， 激 R1、R2分别是激励能源将基态E0上的粒子抽 光 n1 A10 R1 运到E1、E2能级上的速率；则E2能级在单位 器 的 2 时间内增加的粒子数密度为： 图（2.4.1）简化的四能级图 dn2 工 R n A ( n B n B ) f ( ) 2 2 2 2 21 1 12 作 1 dt 原 光 理 学 同理，单位时间内E1能级上增加的粒子数密度为 ： dn1 谐 R1 n2 A21 (n2 B21 n1B12 ) f ( ) n1 A1 振 dt 腔 n0 n1 n2 n
谐 振 腔 结 构 与 稳 定 性
§ .
双凹腔：
双凸腔：
上一页 回首页 下一页 回末页 回目录
五、稳定图的使用说明
第 二 章 激 光 器 的 2 工 作 1 原 光 理 学
谐 振 腔 结 构 与 稳 定 性
1. 例一：一个腔长为L的对称稳定腔，其反射镜曲率半径如何确定？ 2. 例二：稳定腔的一块反射镜已有如R1=2L，另一块反射镜的曲率半径的取值 范围如何确定？ 3. 例三：如果两块反射镜的曲率半径分别为R1、R2，欲用它们组成稳定腔，腔 长的取值范围如何确定？
§ .
(2) 临界腔 平行平面腔，对应图中的A点。只有与腔轴平行的光线才能在腔内往返。 共心腔， 满足条件R2＋R2＝L，对应图中第一象限的g1g2＝1的双曲线。 半共焦腔，由一个平面镜和一个凹面镜组成，对应图中C点和D点。 (3) 非稳腔 对应图中阴影部分的光学谐振腔都是非稳腔。
谐 振 腔 结 构 与 稳 定 性
§ .
图(2-3) 稳定图的应用
上一页 回首页 下一页 回末页 回目录
一、速率方程组
n1 B12 f ( )
n2 B21f ( )
E2
n2 A20 E1 E0
第 1. 图（2.4.1）为简化的四能级图，n0、n1、 二 n2分别为基态、上能级、下能级的粒子数密 R2 n2 A21 章 度；n为单位体积内增益介质的总粒子数， 激 R1、R2分别是激励能源将基态E0上的粒子抽 光 n1 A10 R1 运到E1、E2能级上的速率；则E2能级在单位 器 的 2 时间内增加的粒子数密度为： 图（2.4.1）简化的四能级图 dn2 工 R n A ( n B n B ) f ( ) 2 2 2 2 21 1 12 作 1 dt 原 光 理 学 同理，单位时间内E1能级上增加的粒子数密度为 ： dn1 谐 R1 n2 A21 (n2 B21 n1B12 ) f ( ) n1 A1 振 dt 腔 n0 n1 n2 n
谐 振 腔 结 构 与 稳 定 性
§ .
双凹腔：
双凸腔：
上一页 回首页 下一页 回末页 回目录
五、稳定图的使用说明
第 二 章 激 光 器 的 2 工 作 1 原 光 理 学
谐 振 腔 结 构 与 稳 定 性
1. 例一：一个腔长为L的对称稳定腔，其反射镜曲率半径如何确定？ 2. 例二：稳定腔的一块反射镜已有如R1=2L，另一块反射镜的曲率半径的取值 范围如何确定？ 3. 例三：如果两块反射镜的曲率半径分别为R1、R2，欲用它们组成稳定腔，腔 长的取值范围如何确定？
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
r 若光线在腔内往返n次,最后的光线为：
n
n
那么有:
r rn r1 n 1 TT 内光线的往返传输矩阵
因谐振腔内的传输矩阵满足det(T)=AD-BC=1, 所以, 由Sylvester΄s theorem(希勒韦斯特定理):
1 A B n2 n1 C D n2 R 0 n1 n2
②平面媒质界面
上式中令R→∞ ，则
1 A B C D 0 0 n1 n2
一、腔内光线往返传播的矩阵表示
2、几种常用光学元件的变换矩阵：
arccos
1 A D 2
f2
r An r1 Bn1 n n Cn r1 Dn1
f1
r0 , 0
1
f2
2
f1
3 r1 ,1
f2
f1
f2
f1
L 往返周 期单位
R1 f1 2
R2 f2 2
三、共轴球面腔的稳定性条件
稳定性概念：光腔内的傍轴光线，往返任意多次而不 从横向逸出腔外。 1. 腔的稳定性条件： 从上式,当n→∞时,Tn中的各元素An、Bn、Cn、Dn都要 保持有限,即要求 应为实数 ,且 k (k=0,1,2…)
第二章 激光器工作原理
2.1 光腔理论的一般问题 2.2 共轴球面腔的稳定性条件 2.3 速率方程组与粒子数反转 2.4 均匀增宽介质的增益系数和增益饱和 2.5 非均匀增宽介质的增益饱和
2.6 激光器的阈值条件
§2. 2 共轴球面腔的稳定性条件
目标：理解掌握腔内光线往返传播的矩阵表示 、共轴 球面腔的稳定性条件 、共轴球面腔的分类 、稳区图多样 性 、稳定性的其他判别法 ，稳区图的应用 本节任务：会判定列光线传输矩阵，会写简单光学元 件传输矩阵，会运用稳定性条件判定腔的稳定性，腔 的类型，会运用稳区图及其他稳定腔判定方法。
1 A B 1 C D f
0 1
注：可证：所有的光线矩阵满足(AD-BC=1或n1/n2)
一、腔内光线往返传播的矩阵表示
2、几种常用光学元件的变换矩阵：
二、光腔内光线的往返传输矩阵
过程
①传输L
1 L T1 0 1
可得, 共轴球面腔稳定性条件: 0<g1g2<1
三、共轴球面腔的稳定性条件
1 2、腔的非稳定性条件： 当 2 A D 1 时，
不再是实数,这时sin(n)为双曲正弦函数,它随n的增大而无限增
大,所以, An、Bn、Cn、Dn也无限增大, 即rn、θn也将随之无限 增大,使光线在腔内往返数次后必将从横向逸出腔外。 A D >1是腔内非稳定性条件。 所以 1 2 3、腔的临界条件 ： 当 1 A D 1
一、腔内光线往返传播的矩阵表示
2、几种常用光学元件的变换矩阵：
⑷薄透镜： 薄透镜成象公式：
1 1 1 S S f 2 1 r 1 1 S1 r2 2 S2 r2 r1
r2 r1 1 2 r1 1 f 1 0 r r2 1 1 1 2 f 1
2 时，
此时 k ，An、Bn、Cn、Dn必为不定式，只在特定条件 下，才是稳定的，偏离这一条件又是非稳定的，因此， 是介于稳定与非稳定之间，称为临界条件。
三、共轴球面腔的稳定性条件
4. 腔的稳定性判据： r 1 A D 与光线的初始坐标 、出发位置及往返顺序无 2 关，仅与光腔本身的结构参数有关。当光腔元件选定后， 就确定了，所以，可以用，
2L L 1 2 L 1 R R2 A B 2 T C D 2 L 2 L 2 L 2 L 2 2 1 R R 1 R 1 R R R 1 2 1 1 2 1
六、稳定性的其他判别法
采用腔结构、稳区图和稳定性判据方法 。
⑴点线法：以一个反射面的曲率中心(O1或O2)与其顶点连一 直线,如果该线与另一反射面的曲率中心 (O2或O1)或者该 反射面本身二者之一相交,则腔是稳定的(一线单交); 如果 该线与二者都相交,或都不相交,则腔是非稳的(一线双交, 一线无交) ⑵σ图法: 分别以两个反射面的曲率半径 R 为直径作该反射 镜的内切圆(σ圆),圆心取在轴线上,若两个σ圆(平面镜为 反射面构成的垂直线)在两点相交,则为稳定腔; 若两圆不 相交则为非稳腔; 若两圆重合或在一点相交,则为临界腔
A B 1 C D 0 n1 L n2 1
②均匀介质中的线段(长为L)
A B 1 L C D 0 1
一、腔内光线往返传播的矩阵表示
2、几种常用光学元件的变换矩阵：
⑵不同媒质界面折射 ①球面(半径为R) 由折射定律有: n1(θ1-α)=n2(θ2-α)，(α≈r1/R; r2=r1)，
§2. 2 共轴球面腔的稳定性条件
目标：理解掌握腔内光线往返传播的矩阵表示 、共轴 球面腔的稳定性条件 、共轴球面腔的分类 、稳区图多样 性 、稳定性的其他判别法 ，稳区图的应用 本节任务：会判定列光线传输矩阵，会写简单光学元 件传输矩阵，会运用稳定性条件判定腔的稳定性，腔 的类型，会运用稳区图及其他稳定腔判定方法。
§2. 2 共轴球面腔的稳定性条件
• • • • • 腔内光线往返传播的矩阵表示 共轴球面腔的稳定性条件 共轴球面腔的分类 稳区图多样性 稳定性的其他判别法
一、腔内光线往返传播的矩阵表示
1、参数及规定：
一、腔内光线往返传播的矩阵表示
1、参数及规定 2、几种常用光学元件的变换矩阵：
⑴线段: ① 光 线 穿 过 厚 度 L, 折 射 率 为 n2 的 介 质 , r2=r1+Lθ΄1，因n1θ1=n2θ΄1，(折射定律)
arccos 1 A D 2
即
cos 1 1 A D 1
L L 0 1 1 R R 1 1 2
g2 1 L R2
1 2
对共轴球面腔: 令：
g1 1 L R1
(2－1)
(二)分类
(二)分类
五、稳区图的应用
1.制作一个腔长为L的对称稳定腔，反射镜曲率半径的取值 范围如何确定？ 2.给定稳定腔的一块反射镜，要选配另一块反射镜的曲率半 径，其取值范围如何确定? 3.如果已有两块反射镜，曲率半径分别为R1、R2，欲用它们 组成稳定腔，腔长范围如何确定？
图(2-3) 稳定图的应用
1 A sinn sinn 1 n A B T C sinn sin C D
n
An D sinn sinn 1 Cn
B sinn
Bn Dn
其中:
1 1
1 A D 2
1 来判断光腔的稳定性，故称之为腔的稳定性判据。
1 A D 1 2
1
四、共轴球面腔的分类
采用腔结构、稳区图和稳定性判据方法 。
(一)稳区图 由稳定性判据 0<g1g2<1 可以以 g1,g2 为轴作图 , 任何球面腔 (L,R1,R2)唯一地对应于g1-g2坐标上的一点。图中由坐标轴 g1=0、g2=0 和双曲线 g1g2=1 的两支围成的区域为稳区 (阴影区)。 在 g1=0、g2=0 和双曲线 g1g2=1 为临界 ( 介稳区 ), 其余为非稳 区域。 可将稳区图划分为14个区域，每个区域对应谐振腔 的一定结构。
⑶界面反射 ①球面反射：由反射定律：α-θ1=-θ2-α 且α≈r1/R；r2=r1，
1 A B C D 2 R 0 1 1 1 f 0 1
②平面反射:
上式中，令R→∞，则
A B 1 0 C D 0 1
§2. 2 共轴球面腔的稳定性条件
• • • • • 腔内光线往返传播的矩阵表示 共轴球面腔的稳定性条件 共轴球面腔的分类 稳区图多样性 稳定性的其他判别法
1 2 T2 R 2 0 1
②球面反射(R2)
③ 传输L
1 L T3 0 1
1 2 T4 R 1 0 1
④球面反射(R1)
r5 r1 r1 T T T T T 4 3 2 1 1 1 5