材料力学第五章粱弯曲时的位移
材料力学梁的位移思维导图

材料力学梁的位移思维导图
材料力学梁的位移分析是一种复杂的思维,可以很好地帮助我们研究物理系统中的物理行为.以下是材料力学梁的位移思维导图:
I、定义梁:
1. 梁定义:梁是一种结构,由支撑它的支柱或壁连接到一组顶点,其中顶点可以是拱形形状或悬挂形状,能够承受弯矩外力。
2. 梁位移:梁的位移是指支撑它的支架或壁的相对位移。
它可以是相对位移、平行位移或扭矩位移
II、物理性质:
1. 梁的弯曲性:由于梁作为物体的一部分,它受到来自外界的外力,将会产生弯曲变形。
2. 梁的挠度:梁的挠度是梁的弯曲变形的程度。
它可以在梁的不同部位分布,高挠度会使梁变形更加明显。
III、位移测定:
1. 静力学:静力学方法可以通过对梁外力和顶点位移的测量,来确定梁位移的大小和分布情况,以及如何受到外力的影响。
2. 动态位移:动态位移测量将会提供深入的信息,这些信息会反映梁的动态行为,也就是振动响应。
IV、位移分析:
1. 力/位移关系:通过分析梁的力/位移关系,可以对梁的变形情况有一定的了解,以及梁承受外力时应激变形的状况。
2. 梁模型:通过建立梁模型,可以研究梁受到不同外力大小时的位移反应,并预测梁在某一状况下应受外力的大小。
V、总结:
材料力学梁的位移分析是一种复杂的思考,它主要包括梁的定义、物理性质、位移测定以及位移分析,可以很好地帮助研究者深入了解物理系统中物体的力学行为。
通过研究梁的弯曲性、挠度、力/位移关系以及建立梁模型,可以研究出梁的变形情况、预测梁应遭受的外力范围等,从而提高工件的力学性能和强度。
孙训方第五版材料力学(I)第五章

五邑大学土木建筑系:材料力学
第五章 梁弯曲时的位移
(a)
(b)
直梁弯曲时的挠度和转角这两个位移不但与梁的弯曲 变形程度(挠曲线曲率的大小)有关,也与支座约束的条件 有关。图a和图b所示两根梁,如果它们的材料和尺寸相同,
所受的外力偶之矩Me也相等,显然它们的变形程度(也就
是挠曲线的曲率大小)相同,但两根梁相应截面的挠度和 转角则明显不同。
q w
q l 3 6lx2 4 x 3 24 EI
qx 3 l 2lx2 x 3 挠曲线方程 w 24 EI
23
五邑大学土木建筑系:材料力学
第五章 梁弯曲时的位移
根据对称性可知,两支座处的转角qA及qB的绝对值相
等,且均为最大值,故
q max
ql 3 q A qB 24 EI
以x为自变量进行积分得 x2 EIw F lx C1 2
lx 2 x 3 EIw F 2 6 C1 x C2
该梁的边界条件为:在 x=0 处 w 0,w =0
于是得
15
C1 0,C2 0
五邑大学土木建筑系:材料力学
§5-1 梁的位移——挠度和转角
直梁在对称平面xy内弯曲时其原来的轴线AB将弯曲成 平面曲线AC1B。梁的横截面形心(即轴线AB上的点)在垂直 于x轴方向的线位移w称为挠度(deflection),横截面对其原 来位置的角位移q 称为横截面的转角(angle of rotation)。
2
五邑大学土木建筑系:材料力学
挠曲线近似微分方程
b EIw1 M 1 x F x l 积分得
材料力学 梁 弯曲位移

D点的连续条件: x = a, 1' 2 ' 1 2
1 ( 0 x a)
2 (axl )
挠曲线方程
EI
1"
M1
F
b l
x
EI
2"
M
2
F
b l
x
F
(
x
a)
转角方程
EI
'
1
F b l
x2 2
C1
EI
2'
F
b l
x2 2
F
(
xa)2 2
D1
挠度方程
EI
1
F
b l
x3 6
C1 x
C2
EI
2
F
b l
式中:积分常数 C1 、C2 可通过梁挠曲线的 边界条件 和 变形 连续性条件 来确定。
1、边界条件
A
l A= 0
B
B= 0
A
A= 0
B
B= 0
在简支梁或外伸梁中, 铰支座处的挠度 都应等于零。
A 0 B 0
A
B
l A= 0 A= 0
在悬臂梁 中,固定端处的挠度 和转角 都应等于零。
A 0, A 0
F
(
xa)2 2
D1
挠度方程
EI
1
F
b l
x3 6
C1 x
C2
EI
2
F
b l
x3 6
F
(x 6
a)3
D1
x
D2
x = 0 , 1 = 0
x = l , 2= 0
再将边界条件代入方程可解得:
孙训方《材料力学》(第6版)笔记和课后习题(含考研真题)详解-梁弯曲时的位移(圣才出品)

圣才电子书
ql3/6,D=-ql4/24。
十万种考研考证电子书、题库视频学习平台
故挠曲线方程和转角方程分别为:
w(x)=qx2(x2+6l2-4lx)/(24EI),θ(x)=q(x3-3lx2+3l2x)/(6EI)
则最大挠度 wmax=w(x)|x=l=ql4/(8EI);梁端转角 θB=θ(x)| x=l=ql3/(6EI)。
表 5-1-4 叠加原理计算梁的挠度和转角
四、梁的刚度校核·提高梁的刚度的措施(见表 5-1-5)
表 5-1-5 梁的刚度校核及提高措施
3 / 41
圣才电子书 十万种考研考证电子书、题库视频学习平台
五、梁内的弯曲应变能 定义:由于梁弯曲变形而存储的能量称为梁内的弯曲应变能。梁在弹性变形过程中,其 弯曲应变能与作用在梁上的外力所作的功相等,常见梁内的弯曲应变能见表 5-1-6。
则最大挠度 wmax=w(x)|x=l=Fl3/3EI;梁端转角 θB=θ(x)| x=l=Fl2/2EI。
图 5-2-1(a)(b) (2)建立如图 5-2-1(b)所示坐标系。 首先列弯矩方程:M(x)=-q(l-x)2/2,由此可得挠曲线近似方程: EIw″=-M(x)=q(l-x)2/2 积分得: EIw′=-q(l-x)3/6+C① EIw=q(l-x)4/24+Cx+D② 该梁的边界条件:x=0,w=0,x=0,w'=0。代入式①、②可确定积分常数:C=
圣才电子书
十万种考研考证电子书、题库视频学习平台
第 5 章 梁弯曲时的位移
5.1 复习笔记
梁在承受荷载时发生相应的变形,变形后轴线相对原位置将会发生位移、梁的截面将出 现转角,梁内会因变形存储能量。本章首先介绍梁的位移概念,并基于坐标系统建立挠曲线 方程;接着介绍求解梁的位移的方法,根据挠曲线近似微分方程积分和按叠加原理计算;再 介绍梁刚度校核以及提高梁刚度的方法;最后介绍梁弯曲应变能的概念及计算方法。
材料力学-- 梁的位移计算

• 根据附录Ⅳ有: • 在 1 0 时,x1 2
•当
a 2ab 2b 3
2
2
a 2 2ab 2b 2 ab2 3 x2 2
时
挠度有最大值
(7a 2 6ab 9b2 ) (37a 2 2ab 11b2 )M (a 2 2ab 2b2 ) max 16 72(a b) 3
EIw2
qa 3 x 24
q ( x a ) 4 C2 x D2 24
1 EIw3 qa( x 3a)3 6 C3 x D3
qa 2 EI w1 x C1 8
qa 3 EIw1 x C1 x D1 24
EIw2
qa 2 x 8
EIw2
qa 3 x 24 q 9 ( x a) 4 qa3 x 24 48
(2)求
B、 D
7 qa 4 48 EI
wB w1 | x a
39 wD w3 | x 3 a qa 4 48 EI
FA
q
qa
A
Ⅰ
B
Ⅱ
C
ⅢDxFc源自方法二:奇异函数法解:(1) 初参数方程 将作用在梁BC段上的均布载荷q延续至右端B,同时,在CB 段施加等值反向的均布载荷,如图所示,写出梁(转角和挠 度)的初参数方程
选定坐标系后,梁变形后的轴线可表达为: w=f(x) —称为挠曲线方程 其中, w—该点挠度;x—横坐标 由于挠曲线是一平坦曲线,转角θ可表达为: θ ≈ tanθ = w' = f '(x)
M和w''正负号的判断
M>0,W''<0
材料力学第五章梁弯曲时的位移

实例3 :均布载荷
分析受均布载荷作用下梁的位移。
材料力学第五章梁弯曲时 的位移
在材料力学的第五章中,我们将学习有关梁在弯曲时的位移。掌握梁的基本 知识、位移方程和位移计算方法,以及梁的挠度与转角关系。
梁的基本知识
1 定义
梁是一种长条形结构,承受着沿其长度方向的外部力。
2 类型
常见的梁包括简支梁、悬臂梁和受力梁。
3 材料
梁可以由不同类型的材料制成,例如钢、木材或混凝土。
梁的位移方程
1 弯曲位移
2 挠度
3 转角
梁在弯曲时,沿梁的长度方 向发生位移。
挠度是梁的中点相对于其自 由状态的偏移量。
转角是指梁在弯曲时端部角 度的变化。
简支梁的位移计算方法
1
载荷和反力
计算简支梁上的载荷和反力分布。
2
弯矩方程
使用弯矩方程推导出简支梁的位移方程。
3
边界条件
应用适当的边界条件来解决位移方程中的未知量。
悬臂梁的位移计算方法
加载和支座反力
确定悬臂梁上的加载和支座反力。
弯曲力矩方程
通过推导弯曲力矩方程来解决悬臂 梁的位移问题。
解决边界条件
应用边界条件来计算悬臂梁的位移。
受力梁的位移计算方法
1
截面转动方程
2
推导出受力梁的截面转动方程。
3
确定力的分布
分析受力梁上的力分布,包括集中力和均布 力。
边界条件和位移方程
应用边界条件,求解受力梁的位移方程。ຫໍສະໝຸດ 梁的挠度与转角关系挠度
挠度是梁在弯曲时沿其长度方向上的位移。
转角
转角是梁在弯曲时端部偏离初始位置的角度。
关系公式
挠度和转角之间存在一定的关系,可以通过公式计算。
材料力学 积分法求梁的变形

M ( x ) = r EI Z 1
1 = ± r d 2 w dx 2 d w é 2 ù 1 + ( ) ê ú dx ë û
3
±
d 2 w dx 2 d w 2 ù é 1 + ( ) ú ê dx û ë
3
M ( x ) = EI Z
边界条件、连续条件应用举例
弯矩图分三段,共6 个积分常数需6个边界条 件和连续条件 A B
P C D
w
铰连接
ω A点: A = 0, q A = 0
B 点 : w B 左 = w B 右
C点 : w C左 = w C右
D点:w D = 0
q C 左 = q C 右
边界条件、连续条件应用举例
y
边界条件
3 qL C1 = 6 EI z
EI zw =
1 (L - x )4 + C q 1 x + C 2 24
x = 0 x = 0 x = L
q = 0 w = 0
qL3 q B = 6 EI z
q =-
3 qL C2 =24 EI z
挠曲线方程应分两段AB,BC.
F A
a
q
B
EI z
L
共有四个积分常数
C
x
边界条件
x = a x = a + L
连续条件
w B = 0 wC = 0
y
x = a
w B1 = w B 2 q B1 = q B 2
例题 5.4 &
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
材料力学(土木类)第五章 梁弯曲时的位移(2)

3 3 3
利用叠加原理求图示弯曲刚度为EI的悬臂梁 例5-6 利用叠加原理求图示弯曲刚度为 的悬臂梁 自由端B截面的挠度和转角 截面的挠度和转角。 自由端 截面的挠度和转角。
F A l C EI l F D l B
原荷载可看成为图a和 两种荷载的叠加 两种荷载的叠加, 解:原荷载可看成为图 和 b两种荷载的叠加,对应 的变形和相关量如图所示。 的变形和相关量如图所示。
Fl θ C1 = 2 EI
2
3
由位移关系可得此时B截面的挠度和转角为: 由位移关系可得此时 截面的挠度和转角为: 截面的挠度和转角为
Fl 3 Fl 2 4 Fl 3 wB1 = wC1 + θ C1 ⋅ BC = + × 2l = 向下) (向下) 3EI 2 EI 3EI Fl θ B1 = θ C1 = 2 EI
q ( x) x 2 dθ B = dθ ( x) = dx 2 EI
范围对q(x)dx的作用进行叠加,相当于 的作用进行叠加, 在x=0, l范围对 范围对 的作用进行叠加 对上两式在前述范围内积分, 对上两式在前述范围内积分,即:
wB = ∫ d wB = ∫
0
l
l
0
11q 0 l q ( x ) x (3l − x ) dx = 6 EI 120 EI
上次课回顾: 上次课回顾:
1、度量梁变形的两个基本位移量:挠度和转角 度量梁变形的两个基本位移量: 2、挠曲线近似微分方程
EIw′′ = − M ( x )
3、挠曲线近似微分方程的积分 、
EIw ' ( x ) = ∫ ( − M ( x )) dx + C1
EIw ( x ) =
材料力学第五章 梁的变形

连续条件
xa
wB1 wB2
例题 画出挠曲线大致形状。图中C为中间铰。
解: 边界条件
A
C
F
B
wA 0 qA 0
wB 0
两根梁由中间铰连接,挠
曲线在中间铰处,挠度连
续,但转角不连续。
wC左 wC右
qC左 qC右
A
挠曲线的凸向由弯矩的正
负号决定,正弯矩向下凸,
负弯矩向上凸。
例 图示等截面梁,弯曲刚度EI。设梁下有一曲面 y Ax3 ,欲
)
6l
bF l
F
b
C
Bx
x l
aF FRB l
AC段 (0 x a)
EIw1
bF l
x
EIw1
bF 2l
x2
C1
EIw1
bF 6l
x3
C1 x
D1
CB段 (a x l)
EIw2
bF l
x
F(x a)
EIw2
bF 2l
x2
F ( x a)2 2
C2
EIw2
bF 6l
x3
F ( x a)3 6
转角方程,挠度方程
EIw M ( x)
q w m 6lx 3x2 2l 2 6EIl A
m
l
C
w mx 3lx x2 2l 2 6EIl
2 m
y FRA l
l
x B
m FRB l
求 wmax w q 0
3 x0 1 3 l 0.423l
wmax
w
x0
F2 60kN
C
A
F1 200kN
F2
D
材料力学第五章 梁弯曲时的位移 PPT

M(x) E Iz
高等数学:
1
r (x)
=±(1+ww2)3/2
± w w (1+ 2)3/2
=
M(x) E Iz
M < 0,w > 0
M > 0,w < 0
取负号!
- w w (1+ 2)3/2
=
M(x) E Iz
w w (1+ 2)3/2
=-
M(x) E Iz
挠曲线微分方程
小 变 形
w
=-
DB段(a≤x≤l): M2(x)F l b xF(xa) Ew I2 Fl b xF(xa)
q E w 2 IE2I F l b x 2 2 F (x 2 a )2 C 2
E2 I w F l b x 6 3F(x 6 a )3 C 2xD 2
确定积分常数 连续条件
x = a 时:
w1 w2 w1 w2
边界条件
x = 0 时: w1 0 x = l 时: w2 0
D1D20 C1C2F 6lb(l2b2)
AD段( 0≤ x ≤ a ):
w 1 q1F(6 b lE 2b I2)l2F Eb Ix2l
w1F(6 b lE 2b I2l)x6F EbIx3 l
DB段( a ≤ x ≤ l ):
q w 2 2 F ( 6 lE 2 b b 2 I ) l2 F Ex b 2 I l 2 F E (x I a )2
对于受任意荷载的简支梁,若挠曲线上无拐点, 则可用梁中点的挠度代替最大挠度。
例3:悬臂梁如图,已知F、a,M=0.5 Fa,
梁的弯曲刚度 EI 为常数,试画出挠曲线的大致形 状。
FM
A
B
C
D
a
a
材料力学第五章梁弯曲时的位移分析

a)2
C2 x2 D2
C2
B B x
FBy
目录
5.2 积分法求梁的挠度和转角
4)由边界条件确定积分常数
位移边界条件
x1 0, w1(0) 0 x2 l, w2 (l) 0
光滑连续条件
x1 x2 a, 1(a) 2 (a)
x1 x2 a, w1(a) y2 (a) 代入求解,得
x1 ,0
x1
a
y
CB 段:
M x2
FAy
x2
F ( x2
a)
Fb l
x2
F ( x2
a),
a x2 l
目录
5.2 积分法求梁的挠度和转角
3)列挠曲线近似微分方程并积分
F
AC 段: 0 x1 a
EI
d 2w1 dx12
M (x1)
Fb l
x1
EI
dw1 dx1
EI (x1)
Fb 2l
x2 1
EI dw EI 1 F (l x)2 C
dx
2
EIw 1 F (l x)3 Cx D 6
代入求解
C 1 Fl2, D 1 Fl3
2
6
5)确定转角方程和挠度方程
EI 1 F (l x)2 1 Fl2
2
2
Ax
y
yB
l
F Bx
B
EIw 1 F (l x)3 1 Fl2x 1 Fl3
目录
5.2 积分法求梁的挠度和转角
例2 求梁的转角方程和挠度方程,并求最大转角和最大挠度,
梁的EI已知,l=a+b,a>b。
F
解 1)由梁整体平衡分析得:
材料力学笔记(第五章)

材料力学(土)笔记第五章 梁弯曲时的位移1.梁的位移——挠度及转角为研究等直梁在对称弯曲时的位移取梁在变形前的轴线为x 轴,梁横截面的铅垂对称轴为y 轴而xy 平面即为梁上荷载作用的纵向对称平面梁发生对称弯曲变形后,其轴线将变成在xy 平面内的曲线1AC B度量梁变形后横截面位移的两个基本量是挠度:横截面形心(即轴线上的点)在垂直于x 轴方向的线位移ω转角:横截面对其原来位置的角位移θ 梁变形后的轴线是一条光滑的连续曲线,且横截面仍与该曲线保持垂直因此横截面的转角θ也就是曲线在该点处的切线与x 轴之间的夹角度量等直梁弯曲变形程度的是曲线的曲率梁的变形还受到支座约束的影响通常就用这两个位移量来反映梁的变形情况梁轴线弯曲成曲线后,在x 轴方向也将发生线位移 但在小变形情况下,梁的挠度远小于跨长,梁变形后的轴线是一条平坦的曲线横截面形心沿x 轴方向的线位移与挠度相比属于高阶微量,可略去不记因此在选定坐标后,梁变形后的轴线可表达为()f x ω=式中,x 为梁在变形前轴线上任一点的横坐标;ω为该点的挠度梁变形后的轴线称为挠曲线,在线弹性范围内,也称为弹性曲线上述表达式则称为挠曲线(或弹性曲线)方程由于挠曲线为一平坦曲线,故转角θ可表达为''tan ()f x θθω≈== 称为转角方程即挠曲线上任一点处的切线斜率'ω可足够精确地代表该点处横截面的转角θ 由此可见,求得挠曲线方程后,就能确定梁任一横截面挠度的大小,指向及转角的数值 正值的挠度向下,负值的挠度向上正值的转角为逆时针转向,负值的转角为顺时针方向2.梁的挠曲线近似微分方程及其积分为求得梁的挠曲线方程,利用曲率κ与弯矩M 间的物理关系,即 1M EIκρ== 式中曲率κ为度量挠曲线弯曲程度的量,是非负的这是梁在线弹性范围内纯弯曲情况下的曲率表达式在横力弯曲时,梁横截面上除弯矩M 外尚有剪力S F 但工程用梁,其跨长l 一般均大于横截面高度的10倍剪力S F 对于梁位移的影响很小,可略去不计,故该式子依然适用式中的M 和ρ均为x 的函数,即1()()()M x x x EIκρ== 在数学中,平面曲线的曲率与曲线方程导数间的关系有'''23/21()(1)x ωρω=±+ 取x 轴向右为正,y 轴向下为正时曲线凸向上时''ω为正,凸向下时为负而按弯矩的正、负号规定,梁弯曲后凸向下时为正,凸向上为负,符号相反于是得到 '''23/2()(1)M x EIωω=-+ 由于梁的挠曲线为一平坦曲线,因此,'2ω与1相比十分微小可以略去不计故上式可近似的写为 ''()M x EIω=-上式略去了剪力S F 的影响,并略去了'2ω项 故称为梁的挠曲线近似微分方程若为等截面直梁,其弯曲刚度EI 为一常量,上式可改写为''()EI M x ω=-对于等直梁,上式进行积分,并通过由梁的变形相容条件给出的边界条件确定积分常数 即可求得梁的挠曲线方程当全梁各横截面上的弯矩可用单一的弯矩方程表示时,梁的挠曲线近似微分方程仅有一个 将上式的两端各乘以dx ,经积分一次,得'1()EI M x dx C ω=-+⎰再积分一次,即得12[()]EI M x dx dx C x C ω=-++⎰两式子中积分常数1C 、2C 可通过挠曲线的边界条件确定例如在简支梁中,左右铰支座处的挠度均等于零在悬臂梁中,固定端处的挠度和转角均等于零确定积分常数1C 、2C 后,就分别得到梁的转角方程和挠曲线方程从而可以确定任一横截面的转角和挠度1C 和2C 的几何意义 由于以x 为自变量,在坐标原点即0x =处的定积分恒等于零因此,积分常数'100x C EI EI ωθ===,20C EI ω=式中,0θ和0ω分别表示坐标原点处截面的转角和挠度若梁上的荷载不连续即分布荷载在跨度中间的某点处开始或结束,以及集中荷载或集中力偶作用处梁的弯矩需分段写出,各段梁的挠曲线近似微分方程也随之不同在对各段梁的近似微分方程积分时,均将出现两个积分常数为确定这些积分常数,除需利用支座处的约束条件外还需利用相邻两段梁在交界处位移的连续条件例如左、右两段梁在交界处的截面应具有相等的挠度和转角不论是约束条件和连续条件,均发生在各段挠曲线的边界处故均成为边界条件,即弯曲位移中的变形相容条件遵循两个原则①对各段梁,都是从同一坐标原点到截面之间的梁段上的外力列出弯矩方程所以后一段梁的弯矩方程包括前一段的弯矩方程的新增的()x a -项②对()x a -项的积分,以()x a -作为自变量于是由x a =处的连续条件,就能得到两段梁上相应的积分常数分别相等的结果 对于弯矩方程需分为任意几段的情况,只要遵循上述规则同样可以得到各梁段上相应的积分常数分别相等的结果从而简化确定积分常数的运算3.按叠加原理计算梁的挠度和转角梁在微小变形条件下,其弯矩与荷载成线性关系 在线弹性范围内,挠曲线的曲率与弯矩成正比当挠度很小时,曲率与挠度间呈线性关系梁的挠度和转角均与作用在梁上的荷载成线性关系在这种情况下梁在几项荷载(如集中力、集中力偶或分布力)同时作用下某一横截面的挠度或转角 就分别等于每项荷载单独作用下该截面的挠度或转角的叠加,即为叠加原理 已知梁在每项荷载单独作用下的挠度和转角表则按叠加原理来计算梁的最大挠度和最大转角将较为方便4.奇异函数·梁挠曲线的初参数方程5.梁的刚度校核·提高梁的刚度的措施5.1 梁的刚度校核对于梁的挠度,其许可值通常用许可挠度与跨长之比值[]l ω作为标准 梁的刚度条件可表达为 max[]ll ωω≤ max []θθ≤ 一般土建工程中的构件,强度要求是主要的刚度要求一般处于从属地位但当对构件的位移限制很严,或按强度条件所选用的构件截面过于单薄时刚度条件也可能起控制作用5.2 提高梁的刚度的措施由梁的位移表可见梁的位移(挠度和转角)除了与梁的支承和荷载情况有关还与其弯曲刚度EI 成反比,与跨长l 的n 次幂成正比减小梁的位移,可采取下列措施①增大梁的弯曲刚度EI②调整跨长和改变结构5.梁内的弯曲应变能当梁弯曲时,梁内将积蓄应变能梁在线弹性变形过程中弯曲应变能V ε在数值上等于作用在梁上的外力所作的功W梁在纯弯曲时各横截面上的弯矩M 为常数,并等于外力偶矩e M当梁处于线弹性范围内e EI EI θρ=== θ与e M 呈线性关系直线下的三角形面积就代表外力偶所作的功W ,即12e W M θ=从而得纯弯曲时梁的弯曲应变能 12e V M εθ=即得2222e M l M l V EI EIε== 横力弯曲时,梁内应变能包含两个部分:与弯曲变形相应的弯曲应变能和与切应变形相应的剪切应变能对于弯曲应变能,取长为dx 的梁段,其相邻两横截面的弯矩应分别为()M x 和()()M x dM x +在计算微段的应变能时,弯矩的增量为一阶无穷小,可略去不计 计算器弯曲应变能为2()2M x dV dx EIε= 全梁的弯曲应变能则可通过积分求得为2()2l M x V dx EIε=⎰ 式中,()M x 为梁任一横截面上的弯矩表达式 当各段梁的弯矩表达式不同时,积分需分段进行梁的剪切应变能远小于弯曲应变能,可略去不计。
材料力学第五版课后习题答案修订版

材料力学第五版课后习题答案Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】二、轴向拉伸和压缩2-1试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
(a)解:;;(b)解:;;(c)解:;。
(d)解:。
2-2 试求图示等直杆横截面1-1,2-2和3-3上的轴力,并作轴力图。
若横截面面积,试求各横截面上的应力。
解:2-3试求图示阶梯状直杆横截面1-1,2-2和3-3上的轴力,并作轴力图。
若横截面面积,,,并求各横截面上的应力。
解:2-4 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成,其截面均为两个75mm×8mm的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE和EG横截面上的应力。
解:=1)求内力取I-I分离体得(拉)取节点E为分离体,故(拉)2)求应力75×8等边角钢的面积A=11.5 cm2(拉)(拉)2-5(2-6)图示拉杆承受轴向拉力,杆的横截面面积。
如以表示斜截面与横截面的夹角,试求当,30,45,60,90时各斜截面上的正应力和切应力,并用图表示其方向。
解:2-6(2-8) 一木桩柱受力如图所示。
柱的横截面为边长200mm的正方形,材料可认为符合胡克定律,其弹性模量E=10 GPa。
如不计柱的自重,试求:(1)作轴力图;(2)各段柱横截面上的应力;(3)各段柱的纵向线应变;(4)柱的总变形。
解:(压)(压)2-7(2-9)一根直径、长的圆截面杆,承受轴向拉力,其伸长为。
试求杆横截面上的应力与材料的弹性模量E。
解:2-8(2-11)受轴向拉力F作用的箱形薄壁杆如图所示。
已知该杆材料的弹性常数为E,,试求C与D两点间的距离改变量。
解:横截面上的线应变相同因此2-9(2-12) 图示结构中,AB为水平放置的刚性杆,杆1,2,3材料相同,其弹性模量E=210GPa,已知,,,。
材料力学梁的弯曲问题
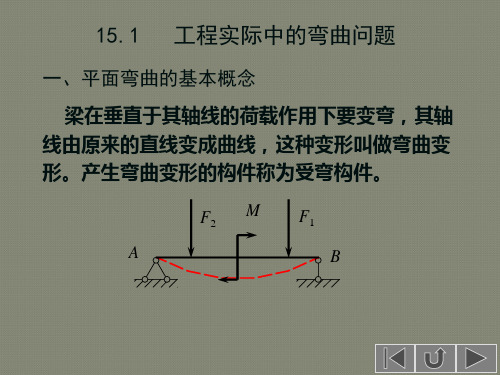
F2 M
F1
A
B
●工程实例
建筑工程中的各类梁、火车轴、水压作用下的水 槽壁等。
火车轴
厂房吊车梁
●对称(平面)弯曲 (Planar bending)
对称平面 F2
F1
(b)
F2
F1
(a)
A
B
(c)
平面弯曲:梁的轴线在变形后仍保持在同一平面( 荷载作用面)内,即梁的轴线成为一条平面曲线。
梁的荷载和支座反力
1.5m
FRB
3m
15.3 内力图──剪力图和弯矩图
为了形象地看到内力的变化规律,通常将剪力、弯 矩沿梁长的变化情况用图形表示出来,这种表示剪力 和弯矩变化规律的图形分别称为剪力图和弯矩图。
具体作法是:
剪力方程: FQFQx 函数图形 弯矩方程: MMx
例4 求作图示受均布荷载作用的简支梁的剪力图和
FQ2FRAF1F2
FQ2 FRB
M O
0
M 2 F R A 2 F 1 1 . 5 F 2 0 . 5 0 M 2 7 k N m
M 2 F R A 2 F 1 1 .5 F 2 0 .5
FQ2FRAF1F2
FQ
F1
M 2 F R A 2 F 1 1 .5 F 2 0 .5
当变形为微小时,可采用变
形前尺寸进行计算。
MB
1、叠加原理:当梁在各项
A
荷载作用下某一横截面上
的弯矩等于各荷载单独作
用下同一横截面上的弯矩
的代数和。
2、区段叠加法作弯矩图:
设简支梁同时承受跨间荷
MB
载q与端部力矩MA、MB的作用 。其弯矩图可由简支梁受端部
力矩作用下的直线弯矩图与跨
材料力学第五章 梁弯曲时的位移

分
F
F
B
M
+
B a wC (F )
C qB×a wC (F )
qB = qB ( q ) + qB ( M )
§5-5 梁的刚度校核 提高梁的刚度的措施
一、梁的刚度校核
wmax w [ ] l l
qmax [q ]
刚度条件
吊车梁:
w 1 1 [ ] ~ l 500 600
屋梁和楼板梁: 钢闸门主梁: 普通机床主轴:
wA = 0 wB = 0
wA = 0
qA = 0
边界条件 —— 支座处的约束条件
挠曲线的任意点上,有唯一确定的挠 度和转角 —— 连续条件
错!
错!
当弯矩方程需要分段建立时,在相邻梁 段的交接处,应具有相同的挠度和转角。
约束条件 本教材中 连续条件 边界条件
例1:悬臂梁在自由端受集中力F作用, 试求梁的转角方程和挠度方程,并求最大转 角和最大挠度。设梁的弯曲刚度为 EI。
F
A a B a
M
C a D
F
A H B a
M
C a D x
y
0.5Fa
-
a
+
M图
0.5Fa
M<0,挠曲线上凸; M>0,挠曲线下凸; H 为挠曲线的拐点; M=0,挠曲线为直线。
例4:已知一直梁的挠曲线方程为
试求:
q0 x 3 2 3 w (l 3lx 2 x ) 48EI
① 端点( x =0 及 x =l )的约束情况; ② 画弯矩图、剪力图; ③ 荷载情况,并画出梁的简图。
1
高等数学:
w = ± 3/2 r (x) (1+ w2)
1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料力学
第五章 梁弯曲时的位移
从而得两段梁的转角方程和挠曲线方程如下:
左段梁 (0 x a)
右段梁 (a x l)
q1
w1
Fb 2lEI
1 3
l2 b2
x
2
q2
w2
Fb 2lEI
l b
x
a
2
x2
1 3
l2
b2
根据对称性可知,两支座处的转角qA及qB的绝对值相
等,且均为最大值,故
qmax q A qB
ql3
24 EI
最大挠度在跨中,其值为
wmax
w
|xl
2
ql 2
24 EI
l 3
2l
l 2
2
l 2
3
5ql 4 384 EI
当集中荷载F作用于简支梁的跨中时(b=l/2),最大转角
qmax和最大挠度wmax为
qmax q A qB
第22页 / 共63页
材料力学
第五章 梁弯曲时的位移
例题5-3 试求图示等直梁的挠曲线方程和转角方程,
并确定其最大挠度wmax和最大转角qmax。
第23页 / 共63页
材料力学
第五章 梁弯曲时的位移
解:约束力为
FA
F
b, l
FB
Fa l
两段梁的弯矩方程分别为
M1x
FA
x
F
b l
x
0 x a
x1
l2 b2 3
aa 2b
3
显然,由于现在a>b,故上式
表明x1<a,从而证实wmax确实 在左段梁内。将上列x1的表达 式代入左段梁的挠曲线方程得
wmax w1 |xx1 9
Fb 3lEI
l2 b2 3
第31页 / 共63页
材料力学
第五章 梁弯曲时的位移
EI 2EI
挠曲线方程 w Fx2l Fx3 2EI 6EI
根据该梁边界条件和全梁横截面上弯矩均为负值, 以及挠曲线应光滑连续描出了挠曲线的示意图。
第16页 / 共63页
材料力学
第五章 梁弯曲时的位移
可见该梁的qmax和wmax均在x=l的自由端处。于是有
qmax
q
|xl
Fl 2 EI
6lEI
qB
q2
|xl
Fabl
6lEI
a
当a>b时有
qmax qB
Fabl a
6lEI
第30页 / 共63页
材料力学
第五章 梁弯曲时的位移
根据图中所示挠曲线的大致形状可知,最大挠度wmax 所在w 0 处在现在的情况下应在左段梁内。令左段梁的
转角方程 w1 等于零,得
3
2
中点C)的挠度wC为
wC
w1
|xl
2
Fb 48 EI
3l 2 4b2
Fbl 2 16 EI
0.0625
Fbl 2 EI
第32页 / 共63页
材料力学
第五章 梁弯曲时的位移
可见在集中荷载作用于右支座附近这种极端情况下,跨中
挠度与最大挠度也只相差不到3%。因此在工程计算中,只要 简支梁的挠曲线上没有拐点都可以跨中挠度代替最大挠度。
转角则明显不同。
第4页 / 共63页
材料力学
第五章 梁弯曲时的位移
在图示坐标系中,挠度w向下为正,向上为负;
顺时针转向的转角q为正,逆时针转向的转角q为负。
第5页 / 共63页
材料力学
第五章 梁弯曲时的位移
§5-2 梁的挠曲线近似微分方程及其积分
Ⅰ. 挠曲线近似微分方程的导出 在§4-4中曾得到等直梁在线弹性范围内纯弯曲情况
EIw M xd x C1
EIw M xd x d x C1x C2
以上两式中的积分常数C1, C2由边界条件确定后即可得出梁 的转角方程和挠曲线方程。
第11页 / 共63页
材料力学
第五章 梁弯曲时的位移
边界条件(这里也就是支座处的约束条件)的示例如 下图所示。
x
1
x
M x
EI
第7页 / 共63页
材料力学
第五章 梁弯曲时的位移
从几何方面来看,平面曲线的曲率可写作(参见《高等 数学上册》,同济大学,P212)
1
x
w 1 w2
3/ 2
式中,等号右边有正负号是因为曲率1/为度量平面曲线 (挠曲线)弯曲变形程度的非负值的量,而w"是q = w' 沿x方
第3页 / 共63页
材料力学
第五章 梁弯曲时的位移
(a)
(b)
直梁弯曲时的挠度和转角这两个位移不但与梁的弯曲
变形程度(挠曲线曲率的大小)有关,也与支座约束的条件
有关。图a和图b所示两根梁,如果它们的材料和尺寸相同, 所受的外力偶之矩Me也相等,显然它们的变形程度(也就 是挠曲线的曲率大小)相同,但两根梁相应截面的挠度和
第12页 / 共63页
材料力学
第五章 梁弯曲时的位移
若由于梁上的荷载不连续等原因使得梁的弯矩方程 需分段写出时,各段梁的挠曲线近似微分方程也就不同。 而对各段梁的近似微分方程积分时,都将出现两个积分 常数。要确定这些积分常数,除利用支座处的约束条件 外,还需利用相邻两段梁在交界处的连续条件。这两类 条件统称为边界条件。
下中性层的曲率为
1M EI
这也是位于中性层内的挠曲线的曲率的表达式。
第6页 / 共63页
材料力学
第五章 梁弯曲时的位移
在横力弯曲下,梁的横截面上除弯矩M=M(x)外,还 有剪力FS=FS(x),剪力产生的剪切变形对梁的变形也会产 生影响。但工程上常用的梁其跨长l 往往大于横截面高度h 的10倍,此时剪力FS对梁的变形的影响可略去不计,而有
Fb
wmax w1 |xx1 9 3lEI
l2 b2 3
由上式还可知,当集中荷载F
作用在右支座附近因而b值甚小,
以致 b2 和 l2 相比可略去不计时有
Fbl 2
Fbl 2
wmax 9
0.0642 3EI
EI
它发生在 x1
l 0.577 l 处。而此时 x l 0.500l处(跨
向的变化率,是有正负的。
第8页 / 共63页
材料力学
第五章 梁弯曲时的位移
再注意到在图示坐标系中,负弯矩对应于正值w" ,正弯矩对
应于负值的w" ,故从上列两式应有
w
1 w2
3/ 2
M x
EI
由于梁的挠曲线为一平坦的曲线,上式中的w2与1相比可略
去,于是得挠曲线近似微分方程 w M x
位移q 称为横截面的转角。
第2页 / 共63页
材料力学
第五章 梁弯曲时的位移
弯曲后梁的轴线——挠曲线为一平坦而光滑的曲线, 它可以表达为w=f(x),此式称为挠曲线方程。由于梁变形
后的横截面仍与挠曲线保持垂直,故横截面的转角q 也就
是挠曲线在该相应点的切线与x轴之间的夹角,从而有转 角方程:
q tanq w f x
第13页 / 共63页
材料力学
第五章 梁弯曲时的位移
例题5-1 试求图示等直梁的挠曲线方程和转角方程,
并确定其最大挠度wmax和最大转角qmax。
第14页 / 共63页
材料力学
第五章 梁弯曲时的位移
解:该梁的弯矩方程为
M x Fl x
挠曲线近似微分方程为
EIw M x Fl x
以x为自变量进行积分得
EIw
F lx
x2 2
C1
EIw
F
lx2 2
x3 6
C1x
C2
该梁的边界条件为:在 x=0 处 w 0,w =0
于是得
C1 0,C2 0
第15页 / 共63页
材料力学
从而有
转角方程
第五章 梁弯曲时的位移
q w Fxl Fx2
及
EIw|xl
q 2
l4 6
l4 12
C1l
0
即
C1
ql3 24
,C2
0
转角方程 q w q l3 6lx2 4x3 24EI
挠曲线方程 w qx l3 2lx2 x3 24EI
第21页 / 共63页
材料力学
第五章 梁弯曲时的位移
左段梁0 x a
右段梁 a x l
挠曲线近似微分方程
EIw1
M1x
F
b l
x
积分得
EIw2
M
2
x
F
b l
x
F
x
a
EIw1
F
b l
x2 2
C1
EIw1
F
b l
x3 6
C1x
D1
EIw2
F
b l
x2 2
F x a2
