位错反应与层错理论
Hands-on 4 面心立方金属中晶格位错的分解与层错能

Output:
dislocation: -rw-r--r-- 1 user090 -rw-r--r-- 1 user090 -rw-r--r-- 1 user090 -rw-r--r-- 1 user090 -rw-r--r-- 1 user090 -rw-r--r-- 1 user090 -rw-r--r-- 1 user090 -rw-r--r-- 1 user090 -rw-r--r-- 1 user090 -rw-r--r-- 1 user090 -rwxr-xr-x 1 user090 stacking_fault: -rw-r--r-- 1 user090 -rw-r--r-- 1 user090 -rw-r--r-- 1 user090 -rw-r--r-- 1 user090 -rwxr-xr-x 1 user090 users users users users users users users users users users users 2019541 2022271 2019554 2019942 862 870 861 869 762360 762359 904 Nov Nov Nov Nov Nov Nov Nov Nov Nov Nov Nov 25 25 25 25 25 25 25 25 25 25 25 12:50 12:50 12:50 12:50 12:50 12:50 12:50 12:50 12:50 12:50 12:50 12:50 12:50 12:50 12:50 12:50 data.screw.highSFE data.screw.highSFE.ref data.screw.lowSFE data.screw.lowSFE.ref in.screw.highSFE in.screw.highSFE.ref in.screw.lowSFE in.screw.lowSFE.ref MCu1_MendelevM_2014.eam.fs MCu7_MendelevM_2014.eam.fs
位错反应与层错理论

罗-罗向量就是fcc中全位错的12个可能的柏氏矢量
2、不对应的罗-希向量
由四面体顶点(罗马字母)和通过该顶点的外表面中心(不 对应的希腊字母)连成的向量: D 这些向量可以由三角形重心性质求得
1 B [21 1] 6 1 B [112] 6 1 1 1 A [2 11] B 6 [12 1] C [12 1] 6 6 1 1 A [121] C [1 12] 6 6 1 1 A [1 12] C [2 1 1] 6 6
实际晶体中,组态不稳定的位错可以转化为组态稳定 4. 位错反应(dislocation 的位错; : reaction) 具有不同b的位错线可以合并为一条位错线;反之,
一条位错线也可以分解为两条或多条具有不同b的位
错线。 位错反应-位错之间相互转换(即柏氏矢量的合成与 分解)。
位错反应判据
汤普森四面体位点坐标
1 1 A( , , 0) 2 2 1 1 B ( , 0, ) 2 2 1 1 C (0, , ) 2 2 D (0, 0, 0)
( , , )
1 1 1 6 6 3 1 1 1 ( , , ) 6 3 6 1 1 1 ( , , ) 3 6 6 1 1 1 ( , , ) 3 3 3
b1
B
a [10 1 ] 2
b3
C
a [21 1 ] 6
b2
b1 b3 b2 a
C
6 [112]
A
(1)扩展位错的宽度
为了降低两个不全位错间的层错能, 力求把两个不全位错的间距缩小,
则相当于给予两个不全位错一个吸
力,数值等于层错的表面张力γ(即 单位面积层错能)。 两个不全位错间的斥力则力图增加 宽度,当斥力与吸力相平衡时,不
材料微观结构第四章晶体中的位错与层错2PPT课件

+ 您的内容打在这里,或者通过复制您的文本后。
概况3
+ 您的内容打在这里,或者通过复制您的文本后。
2
4.3.3 全位错分解、层错、扩展位错
面缺陷,与材料的力学性能很相关
层错与全位错的分解密切相关
不全位错(层错和完整晶体的边界) 扩展位错
3
位错反应
位错具有很高的能量,因此它是不稳定的.在
实际晶体中,组态不稳定的位错可以转化为组 态稳定的位错,这种位错之间的相互转化称为 位错反应.位错反应的结果是降低体系自由能.
16
从面心立方金属中的位 错―汤普森作图法可知
对应着: AC->δC+A δ
17
扩展位错----
通常把一个全位错分解为两个不全位错,中间夹着一个堆垛层错的整个位 错组态称为扩展位错
由图可知,a/6[-211]和a/6[1-12]两个不全位错之间的 夹角为60度,它们之间有一 斥力,因相斥而分开,中间 夹着一片层错,两不全位错
为节点,称为束集,如图C点。此处原来分解了的两个不全
位错重新合并成为全位错。
23
形成束集所需之能量
1.不全位错间距缩小 2.束集附近位错形成弧线增加了应变能 3.因为位错线增长而增加的能量
上节课内容回顾
根据原子的滑移方向和位错线取向的几何 特征不同,位错可以分为哪几种类型?都 是什么样的?
什么是柏氏矢量b?能量最稳定的b是怎样 的?
位错按照b是否为点阵周期的整数倍可以分 为哪几种位错,哪一个能量上最稳定?
什么是柏氏矢量的守恒性?
1
整体概况
+ 概况1
您的内容打在这里,或者通过复制您的文本后。
该位错反应能够进行
6
第五章 位错和层错的电子衍射衬度分析-大学ppt

纯螺型位错g•be=g•b×u=0,所以 g•b=0就作为位错像衬度消失的判据。
表5-1 弹性各向同性材料中位错消像判据
刃Байду номын сангаас错
g•b=0 g•b×u=0
螺位错 g•b=0
混合位错
g•b=0 g•be=0 g•b×u=0
刃位错的运动
螺位错的运动
混合位错 的运动
各向同性弹性体
物理意义——物体各个方向上的弹性性质完全 相同,即物理性质的完全对称。
5.1.2 b测定的实际操作
前提:
❖ 选择好感兴趣的视场 ❖ 正确选择衍射条件 ❖ 拍摄含有待测位错的显微图像及相应的选区
域衍射谱
1. 位错衬度形成基本过程
在合适的ghkl反射下(g•b≠0),位错芯区附近的(hkl)晶 面较好地满足布拉格条件。明场下,入射电子束大部分 被衍射到物镜光阑以外,所以位错呈现暗色条纹衬度。 附近区域有时因晶体弯曲,在一个带状区内取向均匀渐 变,也会显示类似位错线的暗带,但这是“消光轮廓”, 应当加以区别.办法是微调样品取向,消光轮廓将缓慢 移动,位错线则因g改变,在原处时隐时现,却无明显 移动。明场下位错畸变场以外的完整晶体基体不满足衍 射条件,呈亮的衬度.取g反射成中心暗场像,视场衬 度反转,位错和消光轮廓显示亮衬度,基体呈暗衬度。
对于弹性各向异性材料,表5-1给出的判据,仍然 是近似有效的,特别对下述情况:
➢ 立方结构材料,垂直于弹性对称平面{110}和{100} 的纯刃型和纯螺型位错;
➢ 密排六方结构材料,垂直于或位于弹性对称的基 面的位错.
国内外大部分工作,在测定位错柏氏矢量的时候 仍是以表5-1的判据做为依据进行测量的.
缺陷存在时,缺陷附近晶体柱的畸变
位错、层错、变形孪晶以及应变诱导马氏体相变的协同

位错、层错、变形孪晶以及应变诱导马氏体相变的协同1. 引言位错、层错、变形孪晶以及应变诱导马氏体相变是固体材料中晶体微观结构发生变化的重要现象,这些现象对材料的性能和行为都具有重要的影响。
本文将围绕这些现象展开讨论,探讨它们之间的协同作用。
我们将介绍位错和层错在晶体结构中的作用,然后将深入探讨变形孪晶和应变诱导马氏体相变,最后分析它们之间的协同效应。
2. 位错和层错位错和层错是固体材料晶体中最常见的缺陷,它们可以通过使原子排列发生偏差来帮助晶体材料适应外部应力。
位错是晶体中原子排列出现偏差的线状缺陷,而层错则是晶体中原子排列偏差的面状缺陷。
这些缺陷对晶体的力学性能和行为都有显著的影响,它们能够增加材料的塑性变形能力,提高其强度和韧性。
3. 变形孪晶变形孪晶是金属材料中一种重要的微观结构,它在金属材料的加工过程中会被引入。
变形孪晶是由原始晶粒经过变形加工后产生的新晶粒,它们的晶向与原始晶粒有明显偏差。
变形孪晶的存在能够提高金属材料的强度和韧性,改善其塑性变形行为,对金属材料的机械性能有着重要的影响。
4. 应变诱导马氏体相变应变诱导马氏体相变是指在固体材料中由外部应变所导致的马氏体相变现象。
马氏体是一种具有形状记忆效应和超弹性行为的微观组织结构,它的形成可以显著改变材料的力学性能和变形行为。
应变诱导马氏体相变经常被用于制备具有记忆功能的智能材料,应用领域涵盖了医疗、航空航天等多个领域。
5. 协同效应位错、层错、变形孪晶以及应变诱导马氏体相变之间存在着协同作用,它们相互之间可以相互影响,共同作用着固体材料的力学性能和行为。
位错和层错的存在能够促进变形孪晶的形成,而变形孪晶则可以为应变诱导马氏体相变提供条件。
应变诱导马氏体相变则可能会改变材料的位错和层错结构,形成新的微观组织结构。
这种协同效应能够为材料的性能提升和新型材料的设计提供理论依据。
6. 结论位错、层错、变形孪晶以及应变诱导马氏体相变之间存在着紧密的协同作用,它们共同影响着固体材料的力学性能和行为。
位错反应与层错理论课件

位错类型
01
02
03
刃型位错
位错线与滑移面重合,滑 移面上方的一个原子平面 突然中断,形成一个额外 的半原子面。
螺型位错
位错线与滑移面不重合, 位错线周围的原子发生旋 转,形成一个螺旋状的原 子面。
混合型位错
同时具有刃型和螺型特征 的位错。
位错在晶体中的表现
01
02
03
04
位错对晶体的力学性质产生影 响,如硬度、韧性、强度等。
形成层错。
热激活
在高温条件下,原子获得足够的能 量,可以克服周围的势垒,实现晶 体的滑移和层错的产生。
应力集中
当晶体受到外力作用时,应力集中 区域容易出现层错,因为应力集中 区域容易产生滑移不协调的现象。
层错对材料性能的影响
机械性能
层错的存在会降低材料的强度和韧性,因为层错本身是一种晶体 缺陷,容易引发应力集中和裂纹扩展。
在工程领域的应用
结构材料
在建筑、航空航天、船舶等工程领域,位错反应与层错理论 的应用有助于优化结构材料的性能,提高结构的安全性和可 靠性。
机械部件
在机械部件的设计和制造过程中,位错反应与层错理论的应 用有助于预测和防止机械部件的疲劳、断裂等问题,延长机 械部件的使用寿命。
THANKS
感谢观看
陶瓷材料
在陶瓷材料的制备和优化过程中,位 错反应与层错理论有助于揭示陶瓷材 料的脆性和断裂行为,为陶瓷材料的 增韧和强韧化提供理论支持。
在物理学中的应用
晶体结构
位错反应与层错理论在晶体结构 的研究中发挥了重要作用,有助 于理解晶体结构的形成、稳定性 和相变等物理现象。
相变与热力学
位错反应与层错理论在相变和热 力学的研究中提供了微观机制的 解释,有助于理解物质在不同温 度和压力下的性质变化。
8第八节课-实际晶体位错和层错

但是,实际上此位错反应是无法进行的,因为合并后能量是增加的,需
要外力提供能量,何况同性相斥,两同号位错间的排斥力将不允许它们无 限靠拢。
23
西安石油大学材料科学与工程学院
材料科学基础
例:有两个被钉扎住的刃型位错A-B和C-D,它们的长度x相等,且具有相同的b, 而b的大小和方向相同(图3-21)。每个位错都可看做F-R位错源。试分析在其增 殖过程中二者间的交互作用。若能形成一个大的位错源,使其开动的多大?
9 西安石油大学材料科学与工程学院
材料科学基础
F-R源位错增值定义:位错两端被钉扎,在切应力作用下弯曲,位错运动导致位错线卷 曲,异号位错相遇,形成一个位错环和一根位错线,该过程重复,位错增值。
外加切应力与位错弯曲时曲率半径的关系为: Gb
曲率半径越小,切应力越大。
2r
当AB弯曲成半圆时,曲率半径最小,所需的切应力最大,此时,r=L/2,L为A和B 之间的距离。故使弗兰克-里德源发生作用的临界切应力为:
22 西安石油大学材料科学与工程学院
材料科学基础
例题:有两根左螺旋位错线,各自的能量都为E1,当它们无限靠拢时,总能 量为多少? 解:单位长度位错的能量为 T Gb 2 由于位错的应变能与b2成正比,两根同向螺型位错的能量相同,其柏氏矢 量b必然相同。若它们无限靠拢时,合并为柏氏矢量为2b的新位错,其总 能量应为4E1。
形成位错。
3)晶体内部的某些界面(如第二相质点、孪晶、晶界等)和微裂纹的附近,由 于热应力或者组织应力的作用,往往出现应力集中现象,当此应力高至足 以使该局部区域发生滑移时,该区域产生位错。
材料科学基础
3. 位错的增殖:晶体在变形过程中位错不断增殖的现象。
堆垛层错与位错的关系_概述及解释说明

堆垛层错与位错的关系概述及解释说明1. 引言1.1 概述本文将探讨堆垛层错与位错之间的关系,并对它们的定义、特性和相互影响进行解释和说明。
堆垛层错和位错是材料科学领域中重要的概念,它们在材料的晶体结构、性能以及研究中都起着关键作用。
1.2 文章结构本文主要分为五个部分。
首先,我们将介绍堆垛层错和位错的定义和特性;其次,我们将深入探讨堆垛层错与位错之间的联系和相互影响;然后,我们将分析堆垛层错和位错对材料性能的影响;紧接着,我们将介绍常用于检测和分析堆垛层错与位错的方法;最后,我们总结探讨了堆垛层错与位错的关系,并提出对材料研究和工程应用等方面的启示以及后续研究方向建议。
1.3 目的本文旨在加深读者对堆垛层错与位错之间关系的理解,并展示它们在材料科学领域的重要性。
通过对堆垛层错与位错的分析与说明,读者将能够更好地理解材料性能的变化原因,并为相关研究和工程应用提供指导和启示。
此外,本文还旨在为后续研究方向提供一些建议,以促进对堆垛层错与位错关系的深入研究。
2. 堆垛层错与位错的关系2.1 堆垛层错的定义和特性堆垛层错是固体材料中的晶格缺陷,它是由于原子或离子在结晶过程中发生了位置错误所导致的。
堆垛层错通常在晶体的平面之间形成,并且会引起局部应力场的改变。
这种错位可以是简单堆叠顺序错误(例如ABAB →ABCA),也可以是较复杂的序列重排。
2.2 位错的定义和分类位错是晶体中一维缺陷线,表示晶体内原子排序发生了偏差。
根据产生位移的类型,位错可分为边界位错和螺旋位错。
边界位错包括缩短型和伸展型,它们代表了两个相邻晶体之间原子平行于其切面方向滑战所产生的不匹配。
螺旋位错则是由于晶格上某一平面上的滑动而形成一个螺旋线。
2.3 堆垛层错与位错之间的联系和相互影响堆垛层错和位错之间存在着密切的联系和相互影响。
一方面,位错可以导致堆垛层错的形成。
例如,当晶体中发生位移时,堆垛层错可能会在这些位移区域周围形成。
另一方面,堆垛层错也可以引起位错的产生。
半导体材料层错、位错的显示

实验半导体材料层错、位错的显示通常制造电子器件要求所采用的半导体材料是单晶体,就是说要求材料的原子排列严格按照一定的规律。
但是由于种种原因,实际的单晶中往往存在某些缺陷,位错就是其中的一种。
在硅单晶中,由于种种原因,特别在高温下材料的内应力使原子面间产生滑移,晶面局部产生范性形变,这种形变即形成位错,使得完整的晶体结构受到破坏。
在外延生长过程中,原子的排列仍然要按一定的顺序,但是由于如样品表面机械损伤、表面沾污气体不纯等种种原因,使得外延层原子的排列次序发生了错误,这种原子层排列发生错乱的地方叫层错,它是一种面缺线。
半导体材料中位错的存在对晶体管集成电路器件的电学和力学性质都有影响。
层错对器件制造工艺的影响和位错相似,可以造成三极管发射区-收集区穿通,也可以不同程度的影响p-n结的反相特性,一般要求外延层中的层错密度小于102/cm2,大规模集成电路则要求更小。
位错的显示方法有X射线法、电子显微镜法和铜缀饰红外透射法等,最简单常用的是腐蚀金相法,本实验就采用腐蚀金相法。
这种方法的优点是设备简单,其缺点是只观测到与被测点相交的位错线。
本实验的目的是掌握金相显微镜的使用方法;熟悉半导体材料硅单晶片的位错、外延层层错的显示方法;掌握计算层错、位错密度以及外延层厚度的方法。
一、实验原理在硅单晶中,有位错的地方其原子的排列失去规则性,结构比较松散,在这里的原子具有较高的能量,并受到较大的张力,因此在位错线和表面相交处很容易被腐蚀形成凹下的坑,即所谓腐蚀坑,我们正是利用这个特性来显示位错和层错的。
1.层错的腐蚀硅的晶体结构是金刚石结构,在(111)方向上它的排列次序是:AA´BB´CC´即三个双层密排面一个重复周期。
假设外延衬底表面层的原子是按A原子层排列,那么按正常次序外延生长的第一层原子应为A´原子层。
但由于表面沾污、伤痕或晶格缺陷、原子在该处沉积等原因,使得表面某一区域出现反常,不是按A‘原子面排列,而是按B原子面排列,以此类推,形成了ABB´CC´AA´...... 的排列。
材料微观结构晶体中的位错与层错课件

位错是材料变形的微观机制之一,它 们在应力作用下运动和相互作用,导 致材料的塑性变形。
位错和层错在材料变形过程中相互作 用,共同决定材料的力学性能和变形 行为。
05
材料中的位错与层错实例
Chapter
金属材料中的位错与层错
金属材料中的位错
陶瓷材料中的位错是指晶体中原子排列发生扭曲的线状畸变区域。位错的存在对 陶瓷材料的力学性能、热学性能和电学性能等有显著影响。
陶瓷材料中的层错
陶瓷材料中的层错是指由于原子面的堆垛顺序发生改变而形成的缺陷。层错的形 成和扩展会影响陶瓷材料的塑性变形和断裂行为。
高分子材料中的位错与层错
高分子材料中的位错
层错的分类
根据层错的形成机制和特点,可以将层错分为偶 然层错和孪生层错两类。偶然层错是由于原子热 振动或应力作用形成的,而孪生层错则是通过晶 体结构中的对称操作形成的。
层错形成机制
热力学机制
在晶体生长或退火过程中,由于温度变化引起的原 子热振动可能导致原子偏离其平衡位置,形成层错 。此外,晶体中的应力场也可能导致原子排列的错 排或缺失,进而形成层错。
由于层错的存在,晶体的物理和化学 性质可能会发生变化。例如,在金属 材料中,层错的存在可能会导致材料 的强度和韧性发生变化。
层错与材料性能
机械性能
在金属材料中,层错的存在可以影响材料的强度、韧性、硬度等机械性能。由 于层错的界面特性,金属材料在受到外力作用时容易发生滑移和孪生变形,从 而提高材料的塑性和韧性。
02
理解位错与层错对 材料性能的影响。
03
学会位错与层错的 检测方法及其在材 料科学中的应用。
材料微观结构第五章位错和层错的电子衍射衬度分析2

下,存在一根零衬度线。应当注意沉淀相的零衬度线,
和位错环衬度中断的机理是不同的。沉淀相g总垂直于 零衬度线。对位错环,只要环上的某些部位的b与g正交,
g •b=0,即出现衬度中断。利用这个现象可以区别衍衬
照片上的弥散共格细小沉淀相和小尺寸位错环。在位错 环尺寸非常小时,看起来像一个小黑点。和时效初期的 小尺寸沉淀质点是难以区别的。
结论:
取相同的g和相同的sg,当视场中同时有间隙环和 位错环,若对间隙环满足(g•b)sg<0,对空位环则 满足(g•b)sg>0;前者表现为像在真实位置的环内, 后者与此相反,像比真实位错环直径大.
相同g条件,如果改变sg符号,则衬像反过来,即: 前者像在真实位错环外,后者像比真实位错环直 径小.
注意:
当g•b=0时,不全位错和它们中间夹着的层 错有可能均不可见.
而g•b=±1/3,层错条纹可见,其端部的不全 位错却常常是不可见的.
有经验的工作者,依靠熟练的运用倾斜台的技 巧和恰当的选择g,运用这个规律,可以区别 g•b=±1/3和g•b=0这两种不全位错.
5.2.4 位错环分析
分析位错环性质的常用方法:判定位错像在其 真实位错的哪一侧?
空位环
R矢
H量
方的
法确
定
及
间隙环
像
位
置
位错环柏氏矢量的确定
先在含不全位错的P区周围选定一个始点S (Start),顺时针方向按右手准则旋转,围绕不 全位错运行若干步,使成封闭环路,其重点为 F(Finished),F,S相重.
然后在不含位错的完整晶体部分,严格按照完 成上述环路的走向,运行同样步数,F,S不 重合,F指向S的矢量为此位错环的b.
材料微观结构晶体中的位错与层错课件

层错阻碍位错滑移,导致位错在层错附近塞积,形成应力集中。
位错和层错交互作用导致材料强化和韧性下降
材料强化
位错和层错的交互作用增加了材料的强度,提高了材料的抗变形能力。
韧性下降
位错和层错的交互作用导致材料韧性下降,容易出现脆性断裂。
04
实验方法观察和分析位错与层错
透射电子显微镜技术
原理
利用电子束穿透样品,通过电磁 透镜成像,获得晶体结构的高分
形成条件
晶体结构复杂、原子间结合力弱、外界环境干扰等。
层错对材料性能影响
01Βιβλιοθήκη 0203力学性能
层错导致晶体结构畸变, 影响材料的强度、韧性、 延展性等力学性能。
物理性能
层错影响材料的导电、导 热、光学等物理性能,可 能导致材料性能的不均匀 性。
化学性能
层错处原子排列紊乱,可 能导致材料的化学活性增 加,易受环境因素影响而 发生变化。
05
典型材料中位错和层错实例分析
金属中位错和层错现象举例
铝中的位错
在铝晶体中,位错通常呈现为线缺陷, 其滑移面为{111}。位错的存在对铝的强 度和塑性变形行为具有重要影响。
VS
铜中的层错
铜晶体中,层错通常出现在{111}面上, 表现为原子层的堆垛顺序发生改变。层错 能较低,使得铜具有较好的塑性和韧性。
陶瓷中位错和层错现象举例
氧化铝陶瓷中的位错
氧化铝陶瓷晶体中,位错主要呈现为线缺陷 和面缺陷。位错的存在对陶瓷的力学性能和 热学性能具有重要影响,如提高氧化铝陶瓷 的强度和断裂韧性。
氮化硅陶瓷中的层错
氮化硅陶瓷晶体中,层错通常出现在{100} 和{110}面上。层错的引入可以改善氮化硅 陶瓷的韧性,降低脆性。
材料微观结构第四章晶体中的位错与层错1详解

2 螺位错
形成及定义:
晶体在外加切应力作用下,沿ABCD面滑移, 图中EF线为已滑移区与未滑移区的分界处。由于位 错线周围的一组原子面形成了一个连续的螺旋形坡面, 故称为螺位错。 几何特征:位错线与原子滑移方向相平行;位错线周 围原子的配置是螺旋状的。 分类:有左、右旋之分,分别以符号“”和“” 表示。其中小圆点代表与该点垂直的位错,旋转箭头 表示螺旋的旋转方向。它们之间符合左手、右手螺旋 定则。
第四章 晶体中的 位错与层错
4.1引言
完整晶体的理论切变强度=G/2π(切变模量 G=104~105N/mm2)»实际临界切应力 1934年,Taylor提出“位错”(line defects ,
dislocation )概念-原子可能偏离其正常平衡位
置。
在此后20多年的时间里,人们一直持怀疑态度 1956年,博尔曼、赫尔什、门特实验观察到缺陷, 证实Taylor的说法。
晶体中的混合型位错
补充
无论任何位错都具有连续性。 存在状态:形成闭合位错环、终止于晶界 或其他界面、在晶体表面露头,而不会终
止于晶体内部。
4.2.2 柏氏矢量的基本性质
为了便于描述晶体中的位错,以及更为确切地表征不同类 型位错的特征,1939年柏格斯(J. M. Burgers)提出了
采用柏氏回路来定义位错,借助一个规定的矢量即柏氏矢
刃型位错结构的特点:
1).刃型位错有一个额外的半原子面。一般把多出的半原子面在滑 移面上边的称为正刃型位错,记为“┻”;而把多出在下边的称为负 刃型位错,记为“┳”。其实这种正、负之分只具相对意义而无本质 的区别。 2).刃型位错线可理解为晶体中已滑移区与未滑移区的边界线。它 不一定是直线,也可以是折线或曲线,但它必与滑移方向相垂直, 也垂直于滑移矢量. 如纯刃型位错环。 3).滑移面必定是同时包含有位错线和滑移矢量的平面,在其他面 上不能滑移。由于在刃型位错中,位错线与滑移矢量互相垂直,因 此,由它们所构成的平面只有一个。 4).晶体中存在刃型位错之后,位错周围的点阵发生弹性畸变,既 有切应变,又有正应变。就正刃型位置而言,滑移面上方点阵受到 压应力,下方点阵受到拉应力:负刃型位错与此相反。 5).在位错线周围的过渡区(畸变区)每个原子具有较大的平均能 量。但该处只有几个原子间距宽,畸变区是狭长的管道,所以刃型 位错是线缺陷。
材料微观结构第四章晶体中的位错与层错1

4.3 典型金属中的位错
4.3.1 面心立方金属中 的位错―汤普森作图法 滑移面:
BCD面(a面)=(11-1) ADC面(b面)=(1-11) ADB面(c面)=(-111) ABC面(d面)=(111)
面心立方金属中的位错―汤普森 作图法
全位错(四面体的六根棱):
DB=1/2[101],BD= 1/2[-10-1] DC= 1/2[011],DC= 1/2[0-1-1] DA= 1/2[110],AD= 1/2[-1-10]
从汤普森图形,很容易找到可能的 全位错分解反应式
例如在ΔADC和ΔCAB中,可找到下述反应: CA→Cβ+βA, 即a/2[10-1]→a/6[1-1-2]+a/6[21-1] CA→Cδ+δA, 即a/2[10-1]→a/6[2-1-1]+a/6[11-2]
4.3.2 密排六方金属 中的位错―玻赞作图法
AB= 1/2[0-11],BA= 1/2[01-1]
BC= 1/2[-110],CB= 1/2[1-10] AC= 1/2[-101],CA= 1/2[10-1]
面心立方金属中的位错―汤普森 作图法
不全位错(加上反方向,共24根)
Dα=1/6[112], Cβ=1/6[1-1-2] Bα=1/6[-21-1], Aβ=1/6[-2-11] Cα=1/6[1-2-1],Dβ=1/6[121] Bγ=1/6[-11-2],Aδ=1/6[-1-12] Dγ=1/6[211], Bδ=1/6[-12-1] Aγ=1/6[-1-21], Cδ=1/6[2-1-1]
柏氏矢量b—定量描述线状应变场给正常晶体带来畸变大小的量
1。刃位错
形成及定义 :
材料微观结构晶体中的位错与层错
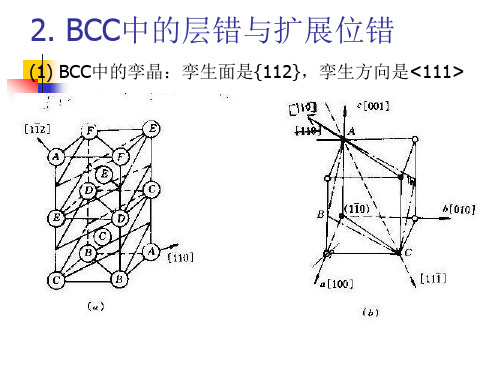
3. 密排六方晶体中的层错与扩展位错
HCP晶体中密排面是(0001), 整个晶体以它为基面一层一 层按ABABAB…顺序堆垛,如 果出现ABABABCABAB…,如 图4-15,那么其中的ABC, CAB,ABCAB都是错排,即 层错,它们其实相当于FCC的 堆垛方式。
正顺序:ABC,BCA,CAB 逆顺序:CBA,BAC,ACB
ABABCBABAB
另一种情况是从正常的HCP排列顺序中加入两个 FCC排列,如ABCBA,就形成了中间的五层孪晶。
在WC硬质合金研究工作中,在粘结相Co中曾经观 察到HCP的βCo中,出现了ABC排列的FCC胚胎, 最终形成FCC的αCo,即发生了βCo→αCo的相变。
在电镜观察HCP时,若要知道引起层错衬度的 (0001)层数的多少,可以用出现的ABC(含逆顺序) 的层数减2得到,上面两种情况下应该是5-2=3层, 这在计算层错衬度和计算由于层错引起的系统能 量升高有用。
第二种情况
参看图4-14(b),若正常排列中某C1的原子层作a/3[11-1]或 a/6[-1-11]滑移,此时C1层变成了A1层,以后各层顺序位错 a/3[11-1]或a/6[-1-11],就得到图4-14(b)的新排列: C1C2A1A2B1B2A1A2B1B2C1C2…,这相当于正常顺序中抽出了 C1C2,其结果是形成了四层层错A1A2B1B2,这和FCC的抽出型 层错相当。
a [111] a [111] a [111] a [111]
2
6
6
6
三个a/6[111]位错分别扩展到三个相交的{112}面上,如图 (a)(b),此时分解后的位错组态极不稳定,以致常转成非对称 分布,如图(c)。
全位错a/2[111]在[110]上运动,可以
材料微观结构第四章晶体中的位错与层错4分析

第四章 晶体中的位错与层错
控制晶粒大小有两种常见方法
再结晶处理,细化晶粒,同时可消除冷加工硬化.效果取决 于预加工形变的程度和再结晶的温度与时间.
控制热处理过程,使金属进行相变. 1.液相→固相,加入杂质,阻碍晶粒长大; 2.液相→固相,凝固速率愈快,成核愈多,晶粒尺寸愈小. 3.固态BCC铁(1534度) →FCC铁(1390度)
将填充的小球类比做晶粒,表面积增加意味着什么呢?
第四章 晶体中的位错与层错
3. 细晶强化
细化晶粒可以提高金属的强度,其原因在于晶界对位 错滑移的阻滞效应.当位错在多晶体中运动时,由于晶界 两侧晶粒的取向不同,加之这里杂质原子较多,增大了晶 界附近的滑移阻力,因而一侧晶粒中的滑移带不能直接进 入第二个晶粒.此外要满足晶界上形变的协调性,需要多 个滑移系统同时动作,这同样导致位错不易穿过晶界,而 是塞积在晶界处,引起强度的增高.
Strength-强度
Prevents material from Fracture Prevents material from Distortion
Rigidity-刚性 Toughness-韧性
allowable elongation deformation within a limit
Brittle materials: strength condition is critical Ductile materials: rigidity condition may become more important
晶粒愈粗,转变温度越高,这是由于晶粒越粗, 位错在滑移面上的运动,积累在晶界上的位错 越多,应力集中也越大,容易导致裂纹萌生在 晶界的薄弱部位,并迅速扩展到裂纹临界尺寸 直至脆性破坏.
材料微观结构第四章晶体中的位错与层错4

第四章 晶体中的位错与层错
3. 细晶强化 细化晶粒可以提高金属的强度,其原因在于晶界对位 错滑移的阻滞效应.当位错在多晶体中运动时,由于晶界 两侧晶粒的取向不同,加之这里杂质原子较多,增大了晶 界附近的滑移阻力,因而一侧晶粒中的滑移带不能直接进 入第二个晶粒.此外要满足晶界上形变的协调性,需要多 个滑移系统同时动作,这同样导致位错不易穿过晶界,而 是塞积在晶界处,引起强度的增高. 晶粒越细小,晶界越多,位错被阻滞的地方就越多,
解理断裂的两种机制
Stroh的位错塞积导致应力集中的理论
3 n b
3E 1v c
ቤተ መጻሕፍቲ ባይዱ
1 2
如图所示,L为滑移面上位错 塞积群所占的长度;c为障碍处 与滑移面成θ角的裂纹长度.
可以估计有效滑移面上L长度 内塞积位错的数目n.对金属 ,以抗张强度32kg/mm2, 切应力约为16kg/mm2,柏 氏矢量长度b=2*10-8cm, γ=10-7J/cm2代入,则在有 效滑移面上的位错数目为 n≈100.
晶)相结合来探讨金属断裂的位错理论.
第四章 晶体中的位错与层错
材料的强化和韧化
• 对于结构材料,最重要的性能指标是强度和韧性。 • 强度是指材料抵抗变形和断裂的能力, • 韧性是材料变形和断裂过程中吸收能量的能力。 • 提高材料的强度和韧性可以节约材料,降低成本,增加材料 在使用过程中的可靠性和延长服役寿命。人们在利用材料的 力学性质时,总是希望所使用的材料既有足够的强度,又有 较好的韧性,但通常的材料往往二者不可兼得。 • 理解材料强韧化机理,掌握材料强韧化现象的物理本质,是
第四章 晶体中的位错与层错
控制晶粒大小有两种常见方法
位错反应与层错理论

力求把两个不全位错的间距缩小,
则相当于给予两个不全位错一个吸
力,数值等于层错的表面张力γ(即
单位面积层错能)。
❖ 两个不全位错间的斥力则力图增加
宽度,当斥力与吸力相平衡时,不
全位错之间的距离一定,这个平衡
距离便是扩展位错的宽度 d。
面心立方晶体中的扩展位错
(1)扩展位错的宽度
两个平行不全位错之间的斥力
故 b 和 b 为肖克莱不全位错。也就是说,
1
2
b分解为两个肖克莱不全位错
一个全位错
b2 和 b1,全位错的运动由两个不全位错的运
动来完成,即
b b1 b2
这个位错反应从几何条件和能量条件判断均是可行的,因为
a
a
a
110 12 1 211
bs
❖ 纯螺位错在 ( 1 11) 面上分解
_
a
a
a
[110] [211] [121]
2
6
6
❖ 运动过程中,若前方受阻,
两个偏位错束集成全位错。
当杂质原子或其它因素使层
错面上某些地区的能量提高
时,该地区的扩展位错就会
变窄,甚至收缩成一个结点,
又变成原来的全位错,这个
现象称为位错的束集。 束集
可以看作位错扩展的反过程。
a
[211]
6
a
[110]
2
_
a
[12 1]
6
( 1 11)
a
[211]
6
_
a
[12 1]
6
( 1 11)
a
[211]
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(b)
A
D
对应的罗-希向量就是fcc中8个Frank不全错的柏氏矢量。
精选
4、希-希向量
所有希-希向量也都可以根据向量合成规则求得:
u u u r u u C u r C u u u r 1 [ 1 2 1 ] 1 [ 1 1 2 ] 1 [ 0 1 1 ] 1 u B u A u r 66 6 3
位错反应和层错机理
精选
面心立方晶体中的典型位错
位错名称
全位错
柏氏矢量 位错类型
a2110
刃、螺、混
位错线形状 空间曲线
可能运动方式 滑移、攀移
肖克莱位错
a6112
刃、螺、混
{111}面 上任意曲线 只滑不攀
弗兰克位错
a3111
纯刃
{111}面 上任意曲线 只攀不滑
精选
一、位错反应
4❖. 实位际错晶反体应中(,di组slo态ca不ti稳on定的位错可以转化为组态稳定 re的ac位ti错on;) :
(b)
A
D
罗-罗向量就是fcc中全位错的12个可能的柏氏矢量
精选
2、不对应的罗-希向量
由四面体顶点(罗马字母)和通过该顶点的外表面中心(不
对应的希腊字母)连成的向量:
D
这些向量可以由三角形重心性质求得
u u ur B
1
[21
1]
6
u u ur D
1
[1 1 2 ]
6
u u ur B
1
[11 2 ]
6
u u ur D
1
[1 2 1 ]
6
B
α (a)
C
u u ur A
1
[2
1 1]
6
u u ur B
1
[1 2
1]
6
u u ur C
1
[1 2
1]
6
u u ur D
1
[2 1 1]
6
(d) δ
u u ur A
1
[1 21]
6
u u ur A
1
[1
12]
6
u u ur C
1
[1
12]
6
u u ur C
以位错反应中,一般规定反应前位错
线指向节点,反应后离开节点。
b1
b3
➢ ②能量条件:反应后诸位错的总能量小于反应前诸位错的总 能量,这是热力学定律所要求的。
Q Ee b2
b前 2 b后 2
精选
位错反应类型
①一个位错分解成两个或多个具有不同柏氏矢量的位错,面心立方晶体
中一个全位错分解成两个肖克莱不全位错。
A(12 ,12 ,0) B(12 ,0,12)
C(0,12 ,12) D(0,0,0)
精选
汤普森四面体
(b)四面体外表面中心位置
定义: δ为ABC面中点 α为BCD面中点 γ为ABD面中点 β为ACD面中点
α
γ
β
精选
实例计算
精选
α
γ
β
α
γ
β
汤普森四面体的展开
1 [211] 6
1 6 [121]
对的面。这样A、B、C、D、 α、β、γ、δ等8个点中的每2个点连成的向量就表
示了fcc晶体中所精选有重要位错的柏氏矢量。
汤普森四面体位点坐标
A (1 ,1 ,0) 22
B (1 ,0,1 ) 22
C (0 , 1 , 1 ) 22
D (0 ,0 ,0 )
(1 ,1 ,1 ) 663
(1 ,1 ,1 ) 636
1
[1 1 0 ]
uuur AB
uuur DB
uuur DA
1
[0
1 1]
2
2
(a)
B
C
(d)
u u
2
u u ur DC
1
[0 1 1]
2
uuur BC
uuur DC
uuur DB
1
[110]
2
uuur AC
uuur DC
uuur DA
1
[ 1 0 1]
2
D
δ
γ
β
(c)
精选
a 10 a 0 01 a 2 0 11 a 2 1 1 1
位错反应判据详解
FCC 中,以全位错分解成两个肖克莱位错为例。 结构条件:
a2[11] 0a6[211]a6[11 2 ] 满足
能量条件:
满足
精选
汤普森四面体
Thompson四面体:可以帮 助确定fcc结构中的位错反应。 沿(111)面,定义每个面的中 点坐标为:
1]
1
[1
11]
D
2
6
3
uuur
B
uuur BC
uuur
C
1 [110]
1 [1
12]
1 [11
1]
2
6
3
uuur
C
uuur CA
uuur
A
1
[10
1]
1 [121]
1
[1
1
1]
B
2
6
3
α (a)
C
(d)
δ
uuur
D
uuur DA
uuur
A
1
[110]
1 [1 12]
1 [111]
2
6
3
D
γ
β
(c)
❖ 具有不同b的位错线可以合并为一条位错线;反之, 一条位错线也可以分解为两条或多条具有不同b的位 错线。
❖ 位错反应-位错之间相互转换(即柏氏矢量的合成与分 解)。
精选
位错反应判据
位错反应能否进行取决于两个条件:
➢ ①几何条件:反应前的柏氏矢量和等于反应后的柏氏矢量和。
b前b后
b2
注意:b的方向与规定的ξ的正向有关。所
(1 ,1 ,1 ) 366
(1 ,1 ,1 ) 333
(a) BDC (11 1)
(b) ADC (1 1 1)
(c) ABD (1 11) (d ) AB精选C (111)
C
B
αδ
β Dγ
A
1、罗-罗向量
D
由四面体顶点A、B、C、D
(罗马字母)连成的向量:
α
u u ur DA
a 211 0 a 621 a 6 1 1 1 2
②两个或多个具有不同柏氏矢量的不全位错合并成一个全位错,一个肖
克莱不全位错和一个弗兰克不全位错合并成一个全位错。
a 6112a 31 1 1 a 211 0
③两个全位错合并成另一全位错。
a 2011 a 21 1 0 a 211 0
④两个位错合并重新组合成另两个位错,如体心立方中:
同理可得:u
ur
1
[1 0
1]
1
u u ur CA
6
3
u u ur
1
[1 1 0 ]
1
u u ur DA
6
3
uur
1 [1
10]
1
u u ur CB
6
3
u u ur
1
[1 0 1 ]
1
u u ur DB
1
[2
1
1]
6
γ
β
(c)
(b)
D
A
D
不对应的罗精-选希向量是fcc中24个Shockley不全位错的柏氏矢量
3、对应的罗-希向量
4个顶点到它所对的三角形中点的连线代表8个1/3<111> 型的滑移矢量。根据矢量合成规则可以求出对应的罗-希向量:
uuur
A
uuur AB
uuur
B
1
[0
11]
1
[21
精选
汤普森四面体位点解释
用于表示fcc晶体中的位错反应
Thompson四面体在fcc晶胞中的位置:D点在坐标原点,其余顶点的坐标 分别为,A(1/2, 0, 1/2),B(0, 1/2, 1/2),C(1/2, 1/2, 0)。四面体4个外表面(等边 三角形)的中心分别用α、β、γ、δ表示,并分别对应A、B、C、D四个顶点所
