流体静力学习题-第章 水静力学ppt课件
合集下载
《流体静力学》PPT课件
21
被测管段水平放置时：
p1 p2 (ρA ρB )gR (116a)
若所测设备或管道内流体为气体时，则有：
p1 p2 ρAgR
用途：既可测量流体的压强差，也可测量流体在
任一处的压强。
若U管一端与设备或管道的测压处连接，另一端
与大气相通，则 R 所反映的是测压处流体的绝对压
强与大气压强之差（表压强）。
2020/3/2
22
缺点：若两测压点之间的压强差很小时，必须降 低被测液体与指示液两者的密度差（即选择指示液使 之密度与被测液体密度接近）来扩大读数（提高精确 度），但这种方法有时会受到限制。
问题思考：如果在U型管内存在气泡将对测量结果 产生什么影响？
⑶倾斜液柱压差计（斜管压差计）
2020/3/2
36
图1-11 压差法测量液位
2020/3/2
37
例1-7附图 远距离液位测量装置
2020/3/2
38
例1-8附图 安全液封装置
2020/3/2
39
附图 气体液封装置
2020/3/2
40
气体液封装置照片
2020/3/2
41
例1-9附图 压力平衡液封装置
2020/3/2
42
9.807 104 Pa
2020/3/2
6
三、压强的表示方法
流体的压强除用不同的单位来计量外，还可以用
不同的计量基准来表示。
计量基准：绝对零压和大气压强两种基准。
表示方法：绝对压强、表压强和真空度。
绝对压强：以绝对零压作起点计算的压强--流体
的真实压强。
表压强：当被测流体的绝对压强大于外界大气压
【例1-7】参见教材P24页。
习题 水静力学PPT课件
第27页/共54页
解:当下游无水时: 水平分力
Px rhC1 Ax1 9.813 261 3312.4KN (水平向右） 垂直分力 Pz rV1 9.8 梯形abcd1 9.8 0.5 (2618) 41 862.4KN (竖直向下）
第28页/共54页
当下游有水时 水平分力 Px rhC1 Ax1 rhc2 Ax2 3312.4 9.8 3 6 1 3316KN (水平向右z \ z） 垂直分离 Pz rV1 rV2 862.4 9.8 三角形efg 1 862.4 9.8 0.5 3 6 1 950.6KN (竖直向下）
1 ctg 60 1.73 2
1.73 P(sin 60
e)
第34页/共54页
拉T力 9.8 1 (2 0.845) .662 131.56KN 2
(h2)3当 h2 1.73m 时, AB闸门上的压强分布如AacB,
P1
9.8 1
1.73 sin 60
58.8KN
对A点取矩
T • ctg60 1.73 9.8 1 ctg 60 1.73
• 1. A、B两点之压差为多 少？
• 2. A、B两点中有无真空
第5页/共54页
• 1-2解：
• （1） 由图知道A点喝B点得压差是由h1高度得
两种密度不同PB 引 P起A 的(，0 即密A )度gh1差引起的
• 所以
0.52kPa
• （2）存在真空PA Ags m gh
• 由A点在的等压面 知5.89KN / m2 PAK 5.89KN / m2
第33页/共54页
解:
(h1)3当 0
AB 闸门上的压强分布图如AabB,
9.8
1.73
解:当下游无水时: 水平分力
Px rhC1 Ax1 9.813 261 3312.4KN (水平向右） 垂直分力 Pz rV1 9.8 梯形abcd1 9.8 0.5 (2618) 41 862.4KN (竖直向下）
第28页/共54页
当下游有水时 水平分力 Px rhC1 Ax1 rhc2 Ax2 3312.4 9.8 3 6 1 3316KN (水平向右z \ z） 垂直分离 Pz rV1 rV2 862.4 9.8 三角形efg 1 862.4 9.8 0.5 3 6 1 950.6KN (竖直向下）
1 ctg 60 1.73 2
1.73 P(sin 60
e)
第34页/共54页
拉T力 9.8 1 (2 0.845) .662 131.56KN 2
(h2)3当 h2 1.73m 时, AB闸门上的压强分布如AacB,
P1
9.8 1
1.73 sin 60
58.8KN
对A点取矩
T • ctg60 1.73 9.8 1 ctg 60 1.73
• 1. A、B两点之压差为多 少？
• 2. A、B两点中有无真空
第5页/共54页
• 1-2解：
• （1） 由图知道A点喝B点得压差是由h1高度得
两种密度不同PB 引 P起A 的(，0 即密A )度gh1差引起的
• 所以
0.52kPa
• （2）存在真空PA Ags m gh
• 由A点在的等压面 知5.89KN / m2 PAK 5.89KN / m2
第33页/共54页
解:
(h1)3当 0
AB 闸门上的压强分布图如AabB,
9.8
1.73
《水力学》第一章 水静力学
6
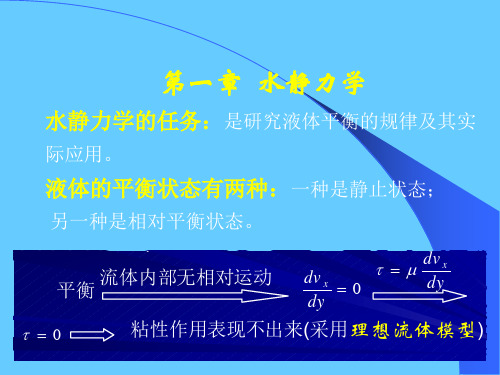
理论证明静水压力具有各项同性
四面体体积：V 1 xyz
6
总质量力在三个坐标
方向的投影为：
Fpx
1 6
xyzf x
Fpy
1 6
xyzf y
按照平衡条件，所有
Fpz
1 6
xyzf z
作用于微小四面体上
的外力在各坐标轴上
投影的代数和应分别 为零。
即在绕中心轴作等角速旋转的液体中有：只有r值相同的 那些点，即位于同心圆柱面上的各点 z p 才保持不变。
g
29
例1-1 有一圆柱形容器，内径为R，原
盛水深度为H，将容器以等角速度
绕中心轴oz旋转，试求运动稳定后容器 中心及边壁处的水深。
30
解 ： 在 容 器 边 壁 处 r ＝ R ， Zs=Zw ，
1－3 等压面
等压面：静水压强值相等的点连接成的面（可
能是平面也可能是曲面）。
等压面性质：
1．在平衡液体中等压面即是等势面。 2．等压面与质量力正交。
15
1－3 等压面
等压面性质： dp ( U dx U dy U dz) dU
x
y
dz
1．在平衡液体中等压面即是等势面。
17
等压面性质2：等压面与质量力正交。
力 F 沿 ds 移动所做的功可写作矢量F与ds的数性积：
W F ds ( fxdx f ydy fzdz)dm W dUdm
因等压面上 dU=0 ，所以W=F*ds=0。也即质量力必 须与等压面正交。
注意: (1) 静止液体质量力仅为重力时，等压面必定 是水平面;
以 p' 表示绝对压强，p表示相对压强，pa 则表示当地
理论证明静水压力具有各项同性
四面体体积：V 1 xyz
6
总质量力在三个坐标
方向的投影为：
Fpx
1 6
xyzf x
Fpy
1 6
xyzf y
按照平衡条件，所有
Fpz
1 6
xyzf z
作用于微小四面体上
的外力在各坐标轴上
投影的代数和应分别 为零。
即在绕中心轴作等角速旋转的液体中有：只有r值相同的 那些点，即位于同心圆柱面上的各点 z p 才保持不变。
g
29
例1-1 有一圆柱形容器，内径为R，原
盛水深度为H，将容器以等角速度
绕中心轴oz旋转，试求运动稳定后容器 中心及边壁处的水深。
30
解 ： 在 容 器 边 壁 处 r ＝ R ， Zs=Zw ，
1－3 等压面
等压面：静水压强值相等的点连接成的面（可
能是平面也可能是曲面）。
等压面性质：
1．在平衡液体中等压面即是等势面。 2．等压面与质量力正交。
15
1－3 等压面
等压面性质： dp ( U dx U dy U dz) dU
x
y
dz
1．在平衡液体中等压面即是等势面。
17
等压面性质2：等压面与质量力正交。
力 F 沿 ds 移动所做的功可写作矢量F与ds的数性积：
W F ds ( fxdx f ydy fzdz)dm W dUdm
因等压面上 dU=0 ，所以W=F*ds=0。也即质量力必 须与等压面正交。
注意: (1) 静止液体质量力仅为重力时，等压面必定 是水平面;
以 p' 表示绝对压强，p表示相对压强，pa 则表示当地
流体静力学习题第章水静力学
p3 p2 g(3 2 )
p4 p3 H g(3 4 ) p A p5 p4 g(5 4 )
解题步骤
联立求得
pA H g(1 2 ) g(3 2 ) H g(3 4 ) g(5 4 )
将已知值代入上式, 得 ,
pA 13.6103 kg/m3 9.8m/s2 (1.8m 0.6m)1103 kg/m3 9.8m/s2 (2.0m 0.6m)13.6103 kg/m3 9.8m/s2 (2.0m 0.8m) 1103 kg/m3 9.8m/s2 (1.5m 0.8m)
3
2.45m 0.72m 21.73m 2.45m
1P 3
3 2.11m
1.73m 2.45m 1 P
3
同理, y3 2.72m
y1 y2 y3
题目
如图所示, 水池壁面设一圆形放水闸门, 当闸门关
闭时, 求作用在圆形闸门上静水总压力和作用点的位
置。已知闸门直径d = 0.5m, 距离a= 1.0m, 闸门与
h1 h
h2 h3
P1 P2 P3
y 1 y2 y3
解题步骤
解:
首先画出平板闸门所受的
静水压强分布图。
单位宽闸门上所受的静水总压 P 力可以由图解法计算静水压强
h
D
分布图的面积求出, 即
P 1 gh h 1m
ρg h
2
1 1000 kg/m3 9.8m/s 2 3m 3m 1m 2
44100N
重力作用线距转动轴B点的距离
l1
d 2
cos 60
0.25m
启门力T到B点的距离 l2 2l1 0.5m
由力矩平衡方程 T l2 P BD G l1 解得 T 32.124KN
水力学课件 第一章 水静力学
§1.1 静水压强及其特征
联立上面各式代入后得：
1 2
pxyz
1 2
pnyz
1 6
xyzf x
0
1 2
p y xz
1 2
pnxz
1 6
xyzf y
0
1 2
pz xy
1 2
pnxy
1 6
xyzf z
0
联立上面各式代入后得：
1 2
pxyz
1 2
pnyz
1 6
xyzf x
0
1 2
p y xz
1 2
pnxz
§1.4 等压面
一、等压面(Isobaric Surface)：在平衡的液体中， 由压强相等的各点所组成的面叫做等压面。 等压面的重要特性是： 1.在静止的或相对平衡的液体中，等压面同时也是
等势面(Isopotential Surface)。 dp dU
2.在相对平衡的液体中，等压面与质量力正交。
条件：只适用于静止、同种、连续液体
三、气体压强计算
p p0
§ 1.5几种质量力同时作用下的液体平衡
z
gm h z
zs
o
x
以z轴为对称轴的旋转抛物面方程：
R
o
r
x
m
F
y 1 2rBiblioteka gz C 2§ 1.5几种质量力同时作用下的液体平衡 平衡微分方程： dp ( fxdx f ydy fzdz) 质量力：离心惯性力和重力 F m 2r, mg 单位质量力： fx 2 x, f y 2 y, fz g 自由面上压强不变为大气压： dp 0
§ 1.5几种质量力同时作用下的液体平衡
2、圆筒中液体内任一点静水压强分布规律：
流体静力学-PPT精品
n方向是任意选定的，因此静止流体中同一点各个方向 的静压强均相等。在连续介质中，仅是位置坐标的连 续函数
p=p( x , y , z )。
说明： 以上特性不仅适用于流体内部，而且也适用于 流体与固体接触的表面。
§2－2 流体平衡微分方程式
一、方程式的建立 根据流体平衡的充要条件，可建立方程。 方法：微元分析法。 在流场中取微小六面体，其边长为dx、dy、dz， 进行受力分析，列平衡方程。
二、静压强特性
1、静压强作用方向永远沿着作用面内法线方向. ——方向特性。
2、静止流体中任何一点上各个方向的静压强大小相等， 而与作用面的方位无关，即p只是位置的函数p= p(x , y , z ). ——大小特性。
特性1.静压强作用方向永远沿着作用面内法线方向
证明：反证法证明之。 有一静止流体微团，用任意平面将 其切割为两部分，取阴影部分为隔 离体。设切割面上任一点m处静压强 方向不是内法线方向，则它可分解 为pn和切应力τ 。而静止流体既不 能承受切应力，也不能承受拉应力, 如果有拉应力或切应力存在，将破坏平衡，这与静止的前 提不符。所以静压强的方向只能是沿着作用面内法线方向。
在面积A上积分：
P A d P A y s id n A s in A yd（1A ）
面积A对ox轴的面积矩，即 AydAycA
所以
P s iy n cA h cA p cA
即
PhcApcA
（2）
——总压力计算公式
总压力＝形心处压强×平面面积
二、总压力的作用点（压力中心）
设总压力P的作用点为D点，对应坐标为 yD。 根据平行力系的力矩原理：每一微小面积上所受的力
对x轴的静力矩之和应该等于作用在面积A上的合力对x轴 的静力矩。即：
p=p( x , y , z )。
说明： 以上特性不仅适用于流体内部，而且也适用于 流体与固体接触的表面。
§2－2 流体平衡微分方程式
一、方程式的建立 根据流体平衡的充要条件，可建立方程。 方法：微元分析法。 在流场中取微小六面体，其边长为dx、dy、dz， 进行受力分析，列平衡方程。
二、静压强特性
1、静压强作用方向永远沿着作用面内法线方向. ——方向特性。
2、静止流体中任何一点上各个方向的静压强大小相等， 而与作用面的方位无关，即p只是位置的函数p= p(x , y , z ). ——大小特性。
特性1.静压强作用方向永远沿着作用面内法线方向
证明：反证法证明之。 有一静止流体微团，用任意平面将 其切割为两部分，取阴影部分为隔 离体。设切割面上任一点m处静压强 方向不是内法线方向，则它可分解 为pn和切应力τ 。而静止流体既不 能承受切应力，也不能承受拉应力, 如果有拉应力或切应力存在，将破坏平衡，这与静止的前 提不符。所以静压强的方向只能是沿着作用面内法线方向。
在面积A上积分：
P A d P A y s id n A s in A yd（1A ）
面积A对ox轴的面积矩，即 AydAycA
所以
P s iy n cA h cA p cA
即
PhcApcA
（2）
——总压力计算公式
总压力＝形心处压强×平面面积
二、总压力的作用点（压力中心）
设总压力P的作用点为D点，对应坐标为 yD。 根据平行力系的力矩原理：每一微小面积上所受的力
对x轴的静力矩之和应该等于作用在面积A上的合力对x轴 的静力矩。即：
流体力学-流体静力学PPT课件-
三.流体静压强分布图
1.绘制液体静压强分布图的知识点
流体静力学基本方程； 平衡流体中的应力特征（大小性、方向性）。
2.液体静压强分布图的绘制方法
（1）根据水静力学基本方程，计算出受压面上各点压强的大小，用一定 长度比例的箭头线表示各点的压强，箭头线必须垂直并指向作用面；
（2）对于不可压缩液体，重度γ为常量，p与h呈线性关系，当受压面为平 面时，只需用直线连接箭头线的尾部，即可得到压强分布图；而当受压面 为曲面时，由于曲面上各点的法向不同，因此需用曲线连接箭头线的尾部。
z1
p1
z2
p2
(2-11) （2-12）
或
p2 p1 (z1 z2 )
对于液体，如图所示，若液面压强为p0，则由式（2-12） 可知液体内任一点的静压强为
p p0 (z0 z) p0 h
(2-13)
式（2-13）为不可压缩静止液体的压强计算公式，通常亦称 为水静力学基本方程。该式表明：
故得欧拉平衡微分方程综合式（即全微分形式）
dp ( f xdx f ydy f z dz)
上式称为流体平衡微分方程的综合式。
而 dW f xdx f y dy f z dz
又 故有
dW W dx W dy W dz
x
y
z
W
fx
x
fy
W y
W f z z
（2-5） （2-6）
•方向性: 流体静压强p垂直指向受压面
证明：采用反证法, 其要点如下: 1 因平衡流体不能承受切应力，即 τ=0，故p垂直受压面；
2 因流体几乎不能承受拉应力，故 p指向受压面。
•大小性：平衡流体中任一点的静压强大小与其作用面的方位无关
1.绘制液体静压强分布图的知识点
流体静力学基本方程； 平衡流体中的应力特征（大小性、方向性）。
2.液体静压强分布图的绘制方法
（1）根据水静力学基本方程，计算出受压面上各点压强的大小，用一定 长度比例的箭头线表示各点的压强，箭头线必须垂直并指向作用面；
（2）对于不可压缩液体，重度γ为常量，p与h呈线性关系，当受压面为平 面时，只需用直线连接箭头线的尾部，即可得到压强分布图；而当受压面 为曲面时，由于曲面上各点的法向不同，因此需用曲线连接箭头线的尾部。
z1
p1
z2
p2
(2-11) （2-12）
或
p2 p1 (z1 z2 )
对于液体，如图所示，若液面压强为p0，则由式（2-12） 可知液体内任一点的静压强为
p p0 (z0 z) p0 h
(2-13)
式（2-13）为不可压缩静止液体的压强计算公式，通常亦称 为水静力学基本方程。该式表明：
故得欧拉平衡微分方程综合式（即全微分形式）
dp ( f xdx f ydy f z dz)
上式称为流体平衡微分方程的综合式。
而 dW f xdx f y dy f z dz
又 故有
dW W dx W dy W dz
x
y
z
W
fx
x
fy
W y
W f z z
（2-5） （2-6）
•方向性: 流体静压强p垂直指向受压面
证明：采用反证法, 其要点如下: 1 因平衡流体不能承受切应力，即 τ=0，故p垂直受压面；
2 因流体几乎不能承受拉应力，故 p指向受压面。
•大小性：平衡流体中任一点的静压强大小与其作用面的方位无关
第二章--流体静力学PPT课件
.
第二章 流体静力学
流体静力学着重研究流体在外力作用下处于平衡状态的 规律及其在工程实际中的应用。
这里所指的静止包括绝对静止和相对静止两种。以地球 作为惯性参考坐标系，当流体相对于惯性坐标系静止时， 称流体处于绝对静止状态；当流体相对于非惯性参考坐标 系静止时，称流体处于相对静止状态。
流体处于静止或相对静止状态，两者都表现不出黏性作 用，即切向应力都等于零，流体只存在压应力——压强。
Pd=22.6Kpa
将以上条件代入式（2-15）积分，便可得到同温层标准大气压分布
dppgdz pgdz
RT
RT d
p dp z g
dz
pa p
zd RTd
p22 .6ex1p1( 00z0) 6334
式中z得单位为m，11000m≤z≤25000m。
35
.
2.3.2气体压强分布
2.大气层压强的分布
2.3.3压强的度量
相对压强
绝对压强
真空度 绝对压强
绝对压强、相对压强和真空之间的关系
41
.
2.3.3压强的度量
相对压强
绝对压强
真空 绝对压强
绝对压强、相对压强和真空之间的关系
42
.
2.3.3压强的度量
立置在水池中的密封罩如图所示，试求罩内A、B、C三
点的压强。
【解】：
B点： pB p0
C
A点： pAghAB pB
从11-15km，温度几乎不变，恒为216.5K（-56.5℃）， 这一层为同温层。
32
.
2.3.2气体压强分布
2.大气层压强的分布
（1）对流层
dpgdz dp pg dz
p
第二章 流体静力学
流体静力学着重研究流体在外力作用下处于平衡状态的 规律及其在工程实际中的应用。
这里所指的静止包括绝对静止和相对静止两种。以地球 作为惯性参考坐标系，当流体相对于惯性坐标系静止时， 称流体处于绝对静止状态；当流体相对于非惯性参考坐标 系静止时，称流体处于相对静止状态。
流体处于静止或相对静止状态，两者都表现不出黏性作 用，即切向应力都等于零，流体只存在压应力——压强。
Pd=22.6Kpa
将以上条件代入式（2-15）积分，便可得到同温层标准大气压分布
dppgdz pgdz
RT
RT d
p dp z g
dz
pa p
zd RTd
p22 .6ex1p1( 00z0) 6334
式中z得单位为m，11000m≤z≤25000m。
35
.
2.3.2气体压强分布
2.大气层压强的分布
2.3.3压强的度量
相对压强
绝对压强
真空度 绝对压强
绝对压强、相对压强和真空之间的关系
41
.
2.3.3压强的度量
相对压强
绝对压强
真空 绝对压强
绝对压强、相对压强和真空之间的关系
42
.
2.3.3压强的度量
立置在水池中的密封罩如图所示，试求罩内A、B、C三
点的压强。
【解】：
B点： pB p0
C
A点： pAghAB pB
从11-15km，温度几乎不变，恒为216.5K（-56.5℃）， 这一层为同温层。
32
.
2.3.2气体压强分布
2.大气层压强的分布
（1）对流层
dpgdz dp pg dz
p
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
题目
某压差计如图所示，已知hA=hB= 1m ， Δh=0.5m。求：pA - pB 。
解题步骤
解：
由图可知，１－１面为等压 面， 根据压强公式可得
p A gA h p 1 p 2 H g h
p 2p A gA hH g h
同时， p3pBghB
hA
Δh hB
空气 33 A
水 22
图a
则当最末一组测压计右
支水银面在0-0平面以
上的读数为h时，三组
水
0
U型水银测压计中水银
M
柱的高差均为2h(图b)
图b
水 0
水银 水
h
h
h
0
h
h
h
水银
解题步骤
自最末一组测压计右支起，依次推求，得
p M H g 2 h g 2 h H g 2 h g 2 h H g 2 h gh 6H g 5 hgh
p 3p 2g ( 3 2)
p 0 p 5 p 4g ( 5 4 )
解题步骤
将各式联立，得 p 0 p a H g ( 1 2 ) g ( 3 2 ) H g ( 3 4 ) g ( 5 4 )
将已知值代入上式，当地大气压取 pa 98kN/m2 , 则水箱液面上的绝对压强为
由公式 pppa，C点的相对压强为
pp p a 9.8 4 kN 2 9 /m 8k 2 N 3./2 m 2kN/m
相对压强为负值，说明C点存在真空。
解题步骤
相对压强的绝对值等于真空压强，即
pk 3.2kN/m2
或据公式 pk pap 得
pk pa p 98kN/m2 94.8kN/m2 3.2kN/m2
299.3kPa
题目
如图所示为一复式水银测压计，已知
1 2.3m 2 1.2m 3 2.5m 4 1.4m 5 1.5m
试求水箱液面上的绝对压强p0 = ?
解题步骤
解：
由图可知，1断面水银柱上
pa
方敞口，作用着大气压。
同时2-2、3-3、4-4为等压 面，根据静压强公式可得 各断面的绝对压强为
p 2p aH g ( 1 2) p 4p 3H g ( 3 4)
解题步骤
解：
已知断面1上作用着大气压， 因此可以从点1开始，通过 ， 等压面，并应用流体静力学 基本方程式，逐点推算，最 后便可求得A点压强。 ， 因2-2、3-3、4-4为等压面，根据静压强公式可得
p 2H g( 1 2) p 3p 2g ( 3 2)
p 4p 3H g ( 3 4)p A p 5 p 4g ( 5 4 )
解题步骤
联立求得
p A H g ( 1 2 ) g ( 3 2 ) H g ( 3 4 ) g ( 5 4 )
将已知值代入上式，得 ，
pA1.3613 0kg/3 m 9.8m2/s(1.80m.6 m 11 ) 3 0kg/3 m 9.8m 2 / (2.00m.6 m 13 ).163 0kg/3 m 9.8m 2(/2s.00m.8m) 113 0kg/3 m 9.8m 2(/1s.50m.8m)
题目
如图所示，盛同一种液体的两容器，用两根U形差 压计连接。上部差压计内盛密度为ρA 的液体，液面
高差为hA ；下部差压计内盛密度为ρB 的液体，液面 高差为hB 。求容器内液体的密度ρ。 （用ρA 、ρB 、 hA 、 hB 表示）。
A
hA
ρ
ρ
hB
B
解题步骤
解：
由图可知１－１、２－２ 为等压面，
流体力学
强p0 = 85
kN/m2，求水面下h = 1m点C的绝对压强、相对压强 和真空压强。已知当地大气压 pa = 98 kN/m2 , ρ= 1000kg/m3。
解题步骤
解：
由压强公式 pp0gh,
得C点绝对压强为 pp0gh
85kN/2m 1000k3g9/m .8m 2/1sm 94.8k2N/m
A
1
hA 1
则在这两个等压面之间 两端的液柱产生的压力 之和相等，即
ρ
ρ
hB
2
2
B A gA hB gB hgA hgBh
则容器内液体的密度为 AhABhB
hA hB
静止液体作用在物面上的总压力
MF2TD0251006
题目
一矩形闸门铅直放置，如图所示，闸门顶水深h1=1m ，闸门高h=2m，宽b=1.5m，试用解析法和图解法求 静水总压力P的大小及作用点。
解题步骤
解：
1. 解析法
b
hC
①求静水总压力
C
由图a知，矩形闸门几何形心
hCh1h/22m
面积 A b h 1. 5 2m m 32 m
图a
代入公式 PρgC hA ，得
P ρC g A h 1k3 g 9/.m 8 2 2 m m 3/2 m s58.8k
解题步骤
p098kN 21/m 3.163 0kg3 / m 9.8m 2(/2s.31m.2 m 11)3 0kg3/ m 9.8m 2(/2s.51m.2 m 13).163 0kg3 / m 9.8m 2(/2s.51m.4 m) 113 0kg3 / m 9.8m 2(/1s.51m.4m)
377.52kN/m
题目
如图所示，利用三组串联的U型水银测压计测量 高压水管中的压强，测压计顶端盛水。当M点压强等 于大气压强时，各支水银面均位于0-0水平面上。当 最末一组测压计右支水银面在0-0平面以上的读数为h 时，求M点的压强？
解题步骤
解：
当点压强等于大气压强 水
时，各支水银面均位于 0 M
0-0水平面上(图a)
题目
某供水管路上装一复式U形水银测压计，如图所 示。已知测压计显示的各液面的标高和A点的标高 为： 1 1 . 8 m , 2 0 .3 6 2m . 4 0 0 ,m . A 8 5 , m 1.,5 试确定管中A点压强。
(H 1.6 3 13 k 0g 3 , / 1 m 13 k 0g 3 )/m
1
1
水银
B 水
由于水银柱和水柱之间为空气，密度可忽略不
计，则p2= p3，得
p A gA hH g h p B gBh
解题步骤
将已知数代入公式，得
pApB Hghg(hAhB)
13.6103kg/m 39.8m2/s0.5m 1103kg/m 39.8m2/s(1m1m)
47.04kN/m 2