龙东地区中考数学试卷含答案

合集下载

【中考真题】2022年黑龙江省省龙东地区中考数学试卷(附答案)

2022年黑龙江省省龙东地区中考数学真题学校:___________姓名：___________班级：___________考号：___________一、单选题1．下列运算中，计算正确的是（）A ．()222b a b a -=-B ．326a a a ⋅=C ．()224x x -=D ．623a a a ÷=2．下列图形是汽车的标识，其中是中心对称图形但不是轴对称图形的是（） A ． B ． C ． D ． 3．学校举办跳绳比赛，九年（2）班参加比赛的6名同学每分钟跳绳次数分别是172，169，180，182，175，176，这6个数据的中位数是（）A ．181B ．175C ．176D ．175.5 4．如图是由若干个相同的小正方体搭成的一个几何体的左视图和俯视图，则所需的小正方体的个数最多是（）A ．7B ．8C ．9D ．10 5．2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛，单循环比赛共进行了45场，共有多少支队伍参加比赛？（）A ．8B ．10C ．7D ．9 6．已知关于x 的分式方程23111x m x x --=--的解是正数，则m 的取值范围是（） A ．4m > B ．4m <C ．4m >且5m ≠D ．4m <且1m ≠ 7．国家“双减”政策实施后，某校开展了丰富多彩的社团活动．某班同学报名参加书法和围棋两个社团，班长为参加社团的同学去商场购买毛笔和围棋（两种都购买）共花费360元．其中毛笔每支15元，围棋每副20元，共有多少种购买方案？（） A ．5 B ．6 C ．7 D ．8 8．如图，在平面直角坐标系中，点O 为坐标原点，平行四边形OBAD 的顶点B 在反比例函数3y x =的图象上，顶点A 在反比例函数k y x=的图象上，顶点D 在x 轴的负半轴上．若平行四边形OBAD 的面积是5，则k 的值是（）A ．2B ．1C ．1-D ．2-9．如图，ABC 中，AB AC =，AD 平分BAC ∠与BC 相交于点D ，点E 是AB 的中点，点F 是DC 的中点，连接EF 交AD 于点P ．若ABC 的面积是24， 1.5PD =，则PE 的长是（）A ．2.5B ．2C ．3.5D ．310．如图，正方形ABCD 的对角线AC ，BD 相交于点O ，点F 是CD 上一点，OE OF ⊥交BC 于点E ，连接AE ，BF 交于点P ，连接OP ．则下列结论：①AE BF ⊥；①45OPA ∠=︒；①AP BP -=；①若:2:3BE CE =，则4tan 7CAE ∠=；①四边形OECF 的面积是正方形ABCD 面积的14．其中正确的结论是（）A ．①①①①B ．①①①①C ．①①①①D ．①①①①二、填空题11．我国南水北调东线北延工程2021-2022年度供水任务顺利完成，共向黄河以北调水1.89亿立方米，将数据1.89亿用科学记数法表示为________．12．函数y =x 的取值范围是______．13．如图，在四边形ABCD 中，对角线AC ，BD 相交于点O ，OA OC =，请你添加一个条件________，使AOB COD ≌．14．在一个不透明的口袋中，有2个红球和4个白球，这些球除颜色外其余完全相同，摇匀后随机摸出一个球，摸到红球的概率是________．15．若关于x 的一元一次不等式组2130x x a -⎧⎨-<⎩＜的解集为2x <，则a 的取值范围是________．16．如图，在O 中，AB 是O 的弦，O 的半径为3cm ，C 为O 上一点，60ACB ∠=︒，则AB 的长为________cm ．17．若一个圆锥的母线长为5cm ，它的侧面展开图的圆心角为120°，则这个圆锥的底面半径为________cm ．18．如图，菱形ABCD 中，对角线AC ，BD 相交于点O ，60BAD ∠=︒，3AD =，AH 是BAC ∠的平分线，CE AH ⊥于点E ，点P 是直线AB 上的一个动点，则OP PE +的最小值是________．19．在矩形ABCD 中，9AB =，12AD =，点E 在边CD 上，且4CE =，点P 是直线BC 上的一个动点．若APE 是直角三角形，则BP 的长为________．20．如图，在平面直角坐标系中，点1A ，2A ，3A ，4A ……在x 轴上且11OA =，212OA OA =，322OA OA =，432OA OA =……按此规律，过点1A ，2A ，3A ，4A ……作x轴的垂线分别与直线y =交于点1B ，2B ，3B ，4B ……记11OA B ，22OA B △，33OA B ，44OA B ……的面积分别为1S ，2S ，3S ，4S ……，则2022S =______．三、解答题21．先化简，再求值：22221111a a a a a ⎛⎫---÷ ⎪-+⎝⎭，其中2cos301a =︒+． 22．如图，在正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，ABC 的三个顶点坐标分别为()1,1A -，()2,5B -，()5,4C -．(1)将ABC 先向左平移6个单位，再向上平移4个单位，得到111A B C △，画出两次平移后的111A B C △，并写出点1A 的坐标；(2)画出111A B C △绕点1C 顺时针旋转90°后得到221A B C △，并写出点2A 的坐标；(3)在（2）的条件下，求点1A 旋转到点2A 的过程中所经过的路径长（结果保留π）． 23．如图，抛物线2y x bx c =++经过点()1,0A -，点()2,3B -，与y 轴交于点C ，抛物线的顶点为D ．(1)求抛物线的解析式；(2)抛物线上是否存在点P ，使PBC 的面积是BCD △面积的4倍，若存在，请直接写出点P 的坐标：若不存在，请说明理由．24．为进一步开展“睡眠管理”工作，某校对部分学生的睡眠情况进行了问卷调查．设每名学生平均每天的睡眠时间为x 小时，其中的分组情况是：A 组：8.5x <B 组：8.59x ≤<C 组：99.5x ≤<D 组：9.510x ≤<E 组：10x ≥根据调查结果绘制成两幅不完整的统计图，请根据图中提供的信息，解答下列问题：(1)本次共调查了_______名学生；(2)补全条形统计图；(3)在扇形统计图中，求D 组所对应的扇形圆心角的度数；(4)若该校有1500名学生，请估计该校睡眠时间不足9小时的学生有多少人？25．为抗击疫情，支援B市，A市某蔬菜公司紧急调运两车蔬菜运往B市．甲、乙两辆货车从A市出发前往B市，乙车行驶途中发生故障原地维修，此时甲车刚好到达B 市．甲车卸载蔬菜后立即原路原速返回接应乙车，把乙车的蔬菜装上甲车后立即原路原速又运往B市．乙车维修完毕后立即返回A市．两车离A市的距离y（km）与乙车所用时间x（h）之间的函数图象如图所示．(1)甲车速度是_______km/h，乙车出发时速度是_______km/h；(2)求乙车返回过程中，乙车离A市的距离y（km）与乙车所用时间x（h）的函数解析式（不要求写出自变量的取值范围）；(3)乙车出发多少小时，两车之间的距离是120km？请直接写出答案．26．ABC和ADE都是等边三角形．(1)将ADE绕点A旋转到图①的位置时，连接BD，CE并延长相交于点P（点P与点+=）成立；请证明．A重合），有PA PB PC+=（或PA PC PB(2)将ADE绕点A旋转到图①的位置时，连接BD，CE相交于点P，连接P A，猜想线段P A、PB、PC之间有怎样的数量关系？并加以证明；(3)将ADE绕点A旋转到图①的位置时，连接BD，CE相交于点P，连接P A，猜想线段P A、PB、PC之间有怎样的数量关系？直接写出结论，不需要证明．27．学校开展大课间活动，某班需要购买A 、B 两种跳绳．已知购进10根A 种跳绳和5根B 种跳绳共需175元：购进15根A 种跳绳和10根B 种跳绳共需300元．(1)求购进一根A 种跳绳和一根B 种跳绳各需多少元？(2)设购买A 种跳绳m 根，若班级计划购买A 、B 两种跳绳共45根，所花费用不少于548元且不多于560元，则有哪几种购买方案？(3)在（2）的条件下，哪种购买方案需要的总费用最少？最少费用是多少元？28．如图，在平面直角坐标系中，平行四边形ABCD 的边AB 在x 轴上，顶点D 在y 轴的正半轴上，M 为BC 的中点，OA 、OB 的长分别是一元二次方程27120x x -+=的两个根()OA OB <，4tan 3DAB ∠=，动点P 从点D 出发以每秒1个单位长度的速度沿折线DC CB -向点B 运动，到达B 点停止．设运动时间为t 秒，APC △的面积为S ．(1)求点C 的坐标；(2)求S 关于t 的函数关系式，并写出自变量t 的取值范围；(3)在点P 的运动过程中，是否存在点P ，使CMP 是等腰三角形？若存在，请直接写出点P 的坐标；若不存在，请说明理由．参考答案：1．C【解析】【分析】根据完全平方公式、同底数幂相乘除，积的乘方进行计算，即可判断．【详解】()2222b=--+，故A选项错误，不符合题意；a ab b a2⋅=，故B选项错误，不符合题意；a a a326()224-=，故C选项正确，符合题意；x x624a a a÷=，，故D选项错误，不符合题意；故选：C．【点睛】本题考查了完全平方公式、同底数幂相乘除，积的乘方，熟练掌握运算法则是解题的关键．2．C【解析】【分析】根据中心对称图形的定义判断即可．【详解】解：① 是轴对称图形，也是中心对称图形，①不符合题意；①是轴对称图形，不是中心对称图形①不符合题意；①不是轴对称图形，是中心对称图形①符合题意；①是轴对称图形，不是中心对称图形①不符合题意；故选C．【点睛】本题考查了了轴对称图形即沿着某条直线折叠，直线两旁的部分完全重合、中心对称图形即将图形绕某点旋转180°后与原图形完全重合，准确理解定义是解题的关键．3．D【解析】【分析】先将这6个数从小到大进行排序，找出排在中间的两个数，求出这两个数的平均数，即为这组数据的中位数．【详解】解：将172，169，180，182，175，176从小到大进行排序为：169，172，175，176，180，182，排在中间的两个数为175，176，①这6个数据的中位数为175176175.52+=，故D正确．故选：D．【点睛】本题主要考查了求一组数据的中位数，解题的关键是将这组数据从小到大进行排序，找出排在中间的一个数或两个数，注意偶数个数是求中间两个数的平均数．4．B【解析】【分析】这个几何体共有2层，由俯视图可得第一层小正方体的个数，由左视图可得第二层小正方体的最多个数，再相加即可．【详解】由俯视图可知最底层有5个小正方体，由左视图可知这个几何体有两层，其中第二层最多有3个，那么搭成这个几何体所需小正方体最多有538+=个．故选：B．【点睛】本题主要考查了学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．5．B【解析】【分析】设有x 支队伍，根据题意，得1(1)452x x -=，解方程即可．【详解】设有x 支队伍，根据题意，得1(1)452x x -=，解方程，得x 1=10，x 2=-9（舍去），故选B ．【点睛】本题考查了一元二次方程的应用，熟练掌握一元二次方程的解法是解题的关键． 6．C【解析】【分析】先将分式方程去分母转化为整式方程，求出整式方程的解，根据分式方程的解为正数得到40m ->且410m --≠，即可求解．【详解】方程两边同时乘以(1)x -，得231x m x -+=-，解得4x m =-，关于x 的分式方程23111x m x x--=--的解是正数， 0x ∴>，且10x -≠，即40m ->且410m --≠，4m ∴>且5m ≠，故选：C ．【点睛】本题考查了分式方程的解，涉及解分式方程和分式方程分母不为0，熟练掌握知识点是解题的关键．7．A【解析】【分析】设设购买毛笔x 支，围棋y 副，根据总价=单价×数量，即可得出关于x ，y 的二元一次方程，结合x ，y 均为正整数即可得出购买方案的数量．【详解】解：设购买毛笔x 支，围棋y 副，根据题意得，15x +20y =360，即3x +4y =72，①y =18-34x ．又①x ，y 均为正整数，①415x y =⎧⎨=⎩或812x y =⎧⎨=⎩或129x y =⎧⎨=⎩或166x y =⎧⎨=⎩或203x y =⎧⎨=⎩， ①班长有5种购买方案．故选：A ．【点睛】本题考查了二元一次方程的应用，找准等量关系“共花费360元”，列出二元一次方程是解题的关键．8．D【解析】【分析】连接OA ，设AB 交y 轴于点C ，根据平行四边形的性质可得1522AOB OBAD S S ==，AB ①OD ，再根据反比例函数比例系数的几何意义，即可求解．【详解】解：如图，连接OA ，设AB 交y 轴于点C ， ①四边形OBAD 是平行四边形，平行四边形OBAD 的面积是5，①1522AOB OBAD S S ==，AB ①OD ， ①AB ①y 轴，①点B 在反比例函数3y x =的图象上，顶点A 在反比例函数k y x =的图象上， ①3,22COB COA k S S ==-， ①35222AOB COB COA k S S S =+=-=，解得：2k =-．故选：D．【点睛】本题主要考查了平行四边形的性质，反比例函数比例系数的几何意义，熟练掌握平行四边形的性质，反比例函数比例系数的几何意义是解题的关键．9．A【解析】【分析】连接DE，取AD的中点G，连接EG，先由等腰三角形“三线合一“性质，证得AD①BC，BD=CD，再由E是AB的中点，G是AD的中点，求出S△EGD=3，然后证△EGP①△FDP （AAS），得GP=CP=1.5，从而得DG=3，即可由三角形面积公式求出EG长，由勾股定理即可求出PE长．【详解】解：如图，连接DE，取AD的中点G，连接EG，①AB=AC，AD平分BAC∠与BC相交于点D，①AD①BC，BD=CD，①S△ABD=112422ABCS=⨯=12，①E是AB的中点，①S△AED=111222ABDS=⨯=6，①G是AD的中点，①S△EGD=11622AEDS=⨯=3，①E是AB的中点，G是AD的中点，①EG∥BC，EG=12BD=12CD，①①EGP=①FDP=90°，①F 是CD 的中点，①DF =12CD ， ①EG =DF ，①①EPG =①FPD ，①①EGP ①①FDP （AAS ），①GP =PD =1.5，①GD =3，①S △EGD =12GD EG ⋅=3，即1332EG ⨯=， ①EG =2，在Rt ①EGP 中，由勾股定理，得PE =，故选：A ．【点睛】本题考查等腰三角形的性质，三角形面积，全等三角形判定与性质，勾股定理，熟练掌握三角形中线分三角形两部分的面积相等是解题的关键．10．B【解析】【分析】分别对每个选项进行证明后进行判断：①通过证明()DOF COE ASA ≌得到EC =FD ，再证明()EAC FBD SAS ≌得到①EAC =①FBD ，从而证明①BPQ =①AOQ =90°，即AE BF ⊥；①通过等弦对等角可证明45OPA OBA ∠=∠=︒；①通过正切定义得tan BE BP BAE AB AP ∠==，利用合比性质变形得到CE BP AP BP BE⋅-=，再通过证明AOP AEC ∽得到OP AE CE AO ⋅=，代入前式得OP AE BP AP BP AO BE⋅⋅-=⋅，最后根据三角形面积公式得到AE BP AB BE ⋅=⋅，整体代入即可证得结论正确；①作EG ①AC 于点G 可得EG ∥BO ，根据tan EG EG CAE AG AC CG ∠==-，设正方形边长为5a ，分别求出EG 、AC 、CG 的长，可求出3tan 7CAE ∠=，结论错误；①将四边形OECF 的面积分割成两个三角形面积，利用()DOF COE ASA ≌，可证明S 四边形OECF =S △COE +S △COF = S △DOF +S △COF =S △COD 即可证明结论正确．【详解】①①四边形ABCD 是正方形，O 是对角线AC 、BD 的交点，①OC =OD ，OC ①OD ，①ODF =①OCE =45°①OE OF ⊥①①DOF +①FOC =①FOC +①EOC =90°①①DOF =①EOC在①DOF 与①COE 中ODF OCE OC ODDOF EOC ∠=∠⎧⎪=⎨⎪∠=∠⎩①()DOF COE ASA ≌①EC =FD①在①EAC 与①FBD 中45EC FD ECA FDB AC BD =⎧⎪∠=∠=︒⎨⎪=⎩①()EAC FBD SAS ≌①①EAC =①FBD又①①BQP =①AQO①①BPQ =①AOQ =90°①AE ①BF所以①正确；①①①AOB =①APB =90°①点P 、O 在以AB 为直径的圆上①AO 是该圆的弦①45OPA OBA ∠=∠=︒所以①正确； ①①tan BE BP BAE AB AP ∠== ①AB AP BE BP = ①AB BE AP BP BE BP --= ①AP BP CE BP BE-= ①CE BP AP BP BE ⋅-=①,45EAC OAP OPA ACE ∠=∠∠=∠=︒①AOP AEC ∽ ①OP AO CE AE= ①OP AE CE AO⋅= ①OP AE BP AP BP AO BE⋅⋅-=⋅ ①1122ABE AE BP AB BE S⋅=⋅= ①AE BP AB BE ⋅=⋅①OP AB BE AB AP BP OP AO BE AO⋅⋅-==⋅ 所以①正确；①作EG ①AC 于点G ，则EG ∥BO ， ①EG CE CG OB BC OC==设正方形边长为5a ，则BC =5a ，OB =OC ，若:2:3BE CE =，则23BE CE =， ①233BE CE CE ++= ①35CE BC =①35CE EG OB BC =⋅=①EG ①AC ，①ACB =45°，①①GEC =45°①CG =EG①3tan 7EG EG CAE AG AC CG ∠====- 所以①错误；①①()DOF COE ASA ≌，S 四边形OECF =S △COE +S △COF①S 四边形OECF = S △DOF +S △COF = S △COD①S △COD =14ABCD S 正方形①S 四边形OECF =14ABCD S 正方形所以①正确；综上，①①①①正确，①错误，故选 B【点睛】本题综合考查了三角形、正方形、圆和三角函数，熟练运用全等三角形、相似三角形、等弦对等角和三角函数的定义是解题的关键．11．81.8910⨯【解析】【分析】把亿写成810，最后统一写成10n a ⨯的形式即可．【详解】解：由题意得：1.89亿=81.8910⨯，故答案为：81.8910⨯．【点睛】本题考查了科学记数法表示较大的数，移动小数点，熟记科学记数法的表示形式是解题的关键．12． 1.5x ≥【解析】【分析】根据二次根式的性质，被开方数大于等于0，即可求出答案．【详解】解：根据题意，230x -≥，① 1.5x ≥；故答案为： 1.5x ≥．【点睛】本题考查了二次根式的性质，解题的关键是熟练掌握二次根式被开方数大于等于0进行解题．13．OB =OD （答案不唯一）【解析】【分析】根据SAS 添加OB =OD 即可【详解】解：添加OB =OD ，在①AOB 和①COD 中，AO CO AOB COD OB OD =⎧⎪∠=∠⎨⎪=⎩，①AOB COD ≌（SAS ）故答案为OB =OD （答案不唯一）【点睛】本题考查三角形全等判定添加条件，掌握三角形全等判定方法是解题关键．14．13【解析】【分析】利用概率公式计算即可．【详解】① 不透明的口袋中，有2个红球和4个白球，①摸到红球的概率是21243=+，故答案为：13．【点睛】本题考查了概率计算，熟练掌握概率计算公式是解题的关键．15．2a ≥##2a ≤【解析】【分析】先求出每个不等式的解集，根据已知不等式组的解集即可得出答案．【详解】解：2130x x a -⎧⎨-<⎩＜①②，解不等式①得：2x ＜，解不等式①得：x a ＜，关于x 的不等式组2130x x a -⎧⎨-<⎩＜的解集为2x ＜， 2a ∴≥．故答案为：2a ≥．【点睛】本题主要考查了一元一次不等式组解集的求法，其简便求法就是用口诀求解，求不等式组解集的口诀：同大取大，同小取小，大小小大中间找，大大小小找不到（无解）．16．【解析】【分析】连接OA 、OB ，过点O 作OD ①AB 于点D ，由垂径定理和圆周角定理可得12AD BD AB ==，120AOB ∠=︒，再根据等腰三角形的性质可得30OAB OBA ==︒∠∠，利用含30°角的直角三角形的性质和勾股定理即可求解．【详解】解：连接OA 、OB ，过点O 作OD ①AB 于点D ，12AD BD AB ∴==，90ODA =∠°， 60ACB ∠=︒，120AOB ∴∠=︒，OA OB =，30OAB OBA ∴∠=∠=︒，3cm OA =，3cm 2OD ∴=，AD ∴=，AB ∴=，故答案为：【点睛】本题考查了垂径定理，圆周角定理，等腰三角形的性质，含30°角的直角三角形的性质和勾股定理，熟练掌握知识点是解题的关键．17．5 3【解析】【分析】由于圆锥的母线长为5cm，侧面展开图是圆心角为120°扇形，设圆锥底面半径为r cm，那么圆锥底面圆周长为2πr cm，所以侧面展开图的弧长为2πr cm，然后利用弧长公式即可得到关于r的方程，解方程即可求解．【详解】解：设圆锥底面半径为r cm，则圆锥底面周长为：2rπcm，①侧面展开图的弧长为：2rπcm，①12052=180ππ⨯r，解得：r=53，故答案为：53．【点睛】本题主要考查圆锥侧面展开图的知识；正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．18【解析】【分析】作点O关于AB的对称点F，连接OF交AB于G，连接PE交直线AB于P，连接PO，则PO=PF，此时，PO+PE最小，最小值=EF，利用菱形的性质与直角三角形的性质，勾股定理，求出OF，OE长，再证明△EOF是直角三角形，然后由勾股定理求出EF长即可．【详解】解：如图，作点O关于AB的对称点F，连接OF交AB于G，连接PE交直线AB于P，连接PO，则PO=PF，此时，PO+PE最小，最小值=EF，①菱形ABCD，①AC①BD，OA=OC，O=OD，AD=AB=3，①①BAD=60°，①△ABD是等边三角形，①BD=AB=3，①BAO=30°，①OB=32，①OA①点O关于AB的对称点F，①OF①AB，OF=2OG=OA①①AOG=60°，①CE①AH于E，OA=OC，①OE=OC=OA①AH平分①BAC，①①CAE=15°，①①AEC=①CAE=15°，①①DOE=①AEC+①CAE=30°，①①DOE+①AOG=30°+60°=90°，①①FOE=90°，①由勾股定理，得EF==,①PO +PE 最小值【点睛】本题考查菱形的性质，利用轴对称求最短距离问题，直角三角形的性质，勾股定理，作点O 关于AB 的对称点F ，连接OF 交AB 于G ，连接PE 交直线AB 于P ，连接PO ，则PO =PF ，则PO +PE 最小，最小值=EF 是解题的关键．19．313或154或6 【解析】【分析】分三种情况讨论：当①APE =90°时，当①AEP =90°时，当①P AE =90°时，过点P 作PF ①DA 交DA 延长线于点F ，即可求解．【详解】解：在矩形ABCD 中，9AB CD ==，12AD BC ==，①BAD =①B =①BCD =①ADC =90°，如图，当①APE =90°时，①①APB +①CPE =90°，①①BAP +①APB =90°，①①BAP =①CPE ，①①B =①C =90°，①①ABP ①①PCE ， ①AB BP PC CE=，即9124BP BP =-，解得：BP =6；如图，当①AEP =90°时，①①AED +①PEC =90°，①①DAE +①AED =90°，①①DAE =①PEC ，①①C =①D =90°，①①ADE ①①ECP ， ①AD DE CE PC=，即12944PC -=，解得：53PC =， ①313BP BC PC =-=；如图，当①P AE =90°时，过点P 作PF ①DA 交DA 延长线于点F ，根据题意得①BAF =①ABP =①F =90°，①四边形ABPF 为矩形，①PF =AB =9，AF =PB ，①①P AF +①DAE =90°，①P AF +①APF =90°，①①DAE =①APF ，①①F =①D =90°，①①APF ①①EAD ， ①AF PF DE AD =，即99412AF =-，解得：154=AF ，即154PB =；综上所述，BP 的长为313或154或6．故答案为：313或154或6 【点睛】本题主要考查了相似三角形的判定和性质，矩形的性质，熟练掌握相似三角形的判定和性质，矩形的性质，并利用分类讨论思想解答是解题的关键．20．2【解析】【分析】先求出11A B 11OA B S =，再根据题意可得112233n n A B A B A B A B ⋯⋯∥∥∥，从而得到11OA B ①22OA B △①33OA B ①44OA B ……①n n OA B △，再利用相似三角形的性质，可得11OA B S ①22OA B S ①33OA B S ①44OA B S ……①n n OA B S =()()()2222231:2:2:2:2n ，即可求解．【详解】解：当x =1时，y =①点(1B ，①11A B①11112OA B S =⨯， ①根据题意得：112233n n A B A B A B A B ⋯⋯∥∥∥，①11OA B ①22OA B △①33OA B ①44OA B ……①n n OA B △，①11OA B S ①22OA B S ①33OA B S ①44OA B S ……①n n OA B S = OA 12①OA 22①OA 32……①OAn 2，①11OA =，212OA OA =，322OA OA =，432OA OA =……，①22OA =，2342OA ==，3482OA ==……12n n OA -=，①11OA B S ①22OA B S①33OA B S ①44OA B S ……①n n OA B S =()()()2222231246221:2:2:2:21:2:2:2:2n n --= ， ①11222n n n OA B OA B S S -=，①220222202222S ⨯-==故答案为：2【点睛】本题主要考查了图形与坐标的规律题，相似三角形的判定和性质，明确题意，准确得到规律，是解题的关键．21．11a -，【解析】【分析】先根据分式的混合运算法则化简分式，再把特殊角的三角函数值代入，求出a 值，然后把a 值代入化简式计算即可．【详解】解：原式22222112111a a a a a a a ⎛⎫--+=-⋅ ⎪---⎝⎭ 2121211a a a a -+=⋅-- 11a=-，当2cos3011a =︒+=时，原式==【点睛】本题考查分式化简求值，熟练掌握分式运算法则和熟记特殊角的三角函数值是解题的关键．22．(1)见解析；()15,3A -(2)见解析；()22,4A(3)点1A 旋转到点2A 所经过的路径长为5π2【解析】【分析】（1）根据题目中的平移方式进行平移，然后读出点的坐标即可；（2）先找出旋转后的对应点，然后顺次连接即可；（3）根据旋转可得点1A 旋转到点2A 为弧长，利用勾股定理确定圆弧半径，然后根据弧长公式求解即可．(1)解：如图所示①A 1B 1C 1即为所求，()15,3A -；(2)如图所示①A 2B 2C 2即为所求，()22,4A ；(3)①115AC ①点1A 旋转到点2A 所经过的路径长为90π55π1802⨯=．【点睛】题目主要考查坐标与图形，图形的平移，旋转，勾股定理及弧长公式等，数量掌握运用这些知识点是解题关键．23．(1)223y x x =--(2)存在，()11P ，()21P【解析】【分析】（1）将点()1,0A -，点()2,3B -，代入抛物线得10423b c b c -+=⎧⎨++=-⎩，求出b c ，的值，进而可得抛物线的解析式．（2）将解析式化成顶点式得()222314y x x x =--=--，可得D 点坐标，将0x =代入得，3y =-，可得C 点坐标，求出1BCD S =△的值，根据4PBC BCD S S =可得4PBC S =，设()2,23P m m m --，则()21223342PBC S m m =⨯⨯--+=，求出m 的值，进而可得P 点坐标．(1)解：①抛物线2y x bx c =++过点()1,0A -，点()2,3B -，①10423b c b c -+=⎧⎨++=-⎩，解得23b c =-⎧⎨=-⎩， ①抛物线的解析式为：223y x x =--．(2)解：存在．①()222314y x x x =--=--，①()1,4D -，将0x =代入得，3y =-，①()0,3C -，①D 到线段BC 的距离为1，2BC =， ①12112BCD S=⨯⨯=， ①44PBC BCD S S ==，设()2,23P m m m --，则()21223342PBC S m m =⨯⨯--+=，整理得，224m m -=，解得11m =21m =①()11P ，()21P，①存在点P ，使PBC 的面积是BCD △面积的4倍，点P 的坐标为()11P ，()21P ．【点睛】本题考查了待定系数法求二次函数解析式，二次函数顶点式，二次函数与三角形面积综合等知识．解题的关键在于对知识的熟练掌握与灵活运用．24．(1)100(2)补全统计图见解析(3)D 组所对应的扇形圆心角度数为72︒(4)估计该校睡眠时间不足9小时的学生有375人【解析】【分析】（1）根据统计图中B 组的人数与占比，计算求解即可；（2）根据E 组人数占比为15％，求出E 组人数为10015⨯％人，然后作差求出A 组人数，最后补全统计图即可；（3）根据D 组人数的占比乘以360︒计算求解即可；（4）根据A B ，两组人数的占比，乘以总人数，计算求解即可．(1)解：由统计图可知，本次共调查了2020100÷=％（人），故答案为：100．(2)解：由统计图可知，E 组人数占比为15％，①E 组人数为1001515⨯=％（人），①A 组人数为100204020155----=（人），①补全统计图如图所示(3)解：由题意知，D 组所对应的扇形圆心角度数为2036072100⨯︒=︒， ①D 组所对应的扇形圆心角度数为72︒．(4) 解：由题意知，5201500375100+⨯=（人） ①估计该校睡眠时间不足9小时的学生有375人．【点睛】本题考查了条形统计图与扇形统计图，画条形统计图，用样本估计总体等知识．解题的关键在于从统计图中获取正确的信息．25．(1)100 60(2)1001200y x =-+(3)3，6.3，9.125【解析】【分析】（1）根据图象分别得出甲车5h 的路程为500km ，乙车5h 的路程为300km ，即可确定各自的速度；（2）设()0y kx b k =+≠，由图象可得经过点（9，300），（12，0）点，利用待定系数法即可确定函数解析式；（3）乙出发的时间为t 时，相距120km ，根据图象分多个时间段进行分析，利用速度与路程、时间的关系求解即可．(1)解：根据图象可得，甲车5h 的路程为500km ，①甲的速度为：500÷5=100km/h ；乙车5h 的路程为300km ，①乙的速度为：300÷5=60km/h ；故答案为：100；60；(2)设()0y kx b k =+≠，由图象可得经过点（9，300），（12，0）点，代入得9300120k b k b +=⎧⎨+=⎩，解得1001200k b =-⎧⎨=⎩①y 与x 的函数解析式为1001200y x =-+；(3)解：设乙出发的时间为t 时，相距120km ，根据图象可得，当0<t <5时，100t -60t =120，解得：t =3；当5<t <5.5时，根据图象可得不满足条件；当5.5<t <8时，500-100（t -5.5）-300=120，解得：t =6.3；当8<t <9时，100（t -8）-300=120，解得：t =12.2，不符合题意，舍去；当9<t <12时，100×（9-8）+100（t -9）+60（t -9）=120，解得：t =9.125；综上可得：乙车出发3h 、6.3h 与9.125h 时，两车之间的距离为120km ．【点睛】题目主要考查根据函数图象获取相关信息，一次函数的应用，一元一次方程的应用等，理解题意，根据函数图象得出相关信息是解题关键．26．(1)证明见解析(2)图①结论：PB PA PC =+，证明见解析(3)图①结论：PA PB PC +=【解析】【分析】（1）由△ABC 是等边三角形，得AB =AC ，再因为点P 与点A 重合，所以PB =AB ，PC =AC ，P A =0，即可得出结论；（2）在BP 上截取BF CP =，连接AF ，证明BAD CAE ≌（SAS ），得ABD ACE ∠=∠，再证明CAP BAF ≌△△（SAS ），得CAP BAF ∠=∠，AF AP =，然后证明AFP 是等边三角形，得PF AP =，即可得出结论；（3）在CP 上截取CF BP =，连接AF ，证明BAD CAE ≌（SAS ），得ABD ACE ∠=∠，再证明BAP CAF ≌△△（SAS ），得出CAF BAP ∠=∠，AP AF =，然后证明AFP 是等边三角形，得PF AP =，即可得出结论：PA PB PF CF PC +=+=．(1)证明：①①ABC 是等边三角形，①AB =AC ，①点P 与点A 重合，①PB =AB ，PC =AC ，P A =0，①PA PB PC +=或PA PC PB +=；(2)解：图①结论：PB PA PC =+证明：在BP 上截取BF CP =，连接AF ，①ABC 和ADE 都是等边三角形，①AB AC =，AD AE =，60BAC DAE ∠=∠=︒①BAC CAD DAE CAD ∠+∠=∠+∠，①BAD CAE ∠=∠，①BAD CAE ≌（SAS ），①ABD ACE ∠=∠，①AC =AB ，CP =BF ，①CAP BAF ≌△△（SAS ），①CAP BAF ∠=∠，AF AP =，①CAP CAF BAF CAF ∠+∠=∠+∠，①60FAP BAC ∠=∠=︒，①AFP 是等边三角形，①PF AP =，①PA PC PF BF PB +=+=；(3)解：图①结论：PA PB PC +=，理由：在CP 上截取CF BP =，连接AF ，①ABC 和ADE 都是等边三角形，①AB AC =，AD AE =，60BAC DAE ∠=∠=︒①BAC BAE DAE BAE ∠+∠=∠+∠，①BAD CAE ∠=∠，①BAD CAE ≌（SAS ），①ABD ACE ∠=∠，①AB =AC ，BP =CF ，①BAP CAF ≌△△（SAS ），①CAF BAP ∠=∠，AP AF =，①BAF BAP BAF CAF ∠+∠=∠+∠，①60FAP BAC ∠=∠=︒，①AFP 是等边三角形，①PF AP =，①PA PB PF CF PC +=+=，即PA PB PC +=．【点睛】本题考查等边三角形的判定与性质，全等三角形的判定与性质，熟练掌握等边三角形的判定与性质、全等三角形的判定与性质是解题的关键．27．(1)购进一根A 种跳绳需10元，购进一根B 种跳绳需15元(2)有三种方案：方案一：购买A 种跳绳23根，B 种跳绳22根；方案二：购买A 种跳绳24根，B 种跳绳21根；方案三：购买A 种跳绳25根，B 种跳绳20根(3)方案三需要费用最少，最少费用是550元【解析】【分析】（1）设购进一根A 种跳绳需x 元，购进一根B 种跳绳需y 元，可列方程组1051751510300x y x y +=⎧⎨+=⎩，解方程组即可求得结果；（2）根据题意可列出不等式组()()101545560101545548m m m m ⎧+-≤⎪⎨+-≥⎪⎩，解得：2325.4m ≤≤，由此即可确定方案；（3）设购买跳绳所需费用为w 元，根据题意，得()1015455675w m m m =+-=-+，结合函数图像的性质，可知w 随m 的增大而减小，即当25m =时525675550=-⨯+=．(1)解：设购进一根A 种跳绳需x 元，购进一根B 种跳绳需y 元，根据题意，得1051751510300x y x y +=⎧⎨+=⎩，解得1015x y =⎧⎨=⎩，答：购进一根A 种跳绳需10元，购进一根B 种跳绳需15元；(2)根据题意，得()()101545560101545548m m m m ⎧+-≤⎪⎨+-≥⎪⎩，解得2325.4m ≤≤，①m 为整数，①m 可取23，24，25．①有三种方案：方案一：购买A 种跳绳23根，B 种跳绳22根；方案二：购买A 种跳绳24根，B 种跳绳21根；方案三：购买A 种跳绳25根，B 种跳绳20根；(3)设购买跳绳所需费用为w 元，根据题意，得()1015455675w m m m =+-=-+①50-<，①w 随m 的增大而减小，①当25m =时，w 有最小值，即w 525675550=-⨯+=（元）答：方案三需要费用最少，最少费用是550元．【点睛】本题主要考查的是不等式应用题、二元一次方程组应用题、一次函数相关应用题，根据题意列出对应的方程是解题的关键．28．(1)点C 坐标为()7,4(2)()()14207149871255t t S t t ⎧-≤<⎪=⎨-<≤⎪⎩(3)存在点P ()4,4或9,42⎛⎫ ⎪⎝⎭或59,412⎛⎫ ⎪⎝⎭，使CMP 是等腰三角形【解析】【分析】（1）先求出方程的解，可得3OA =，4OB =，再由4tan 3DAB ∠=，可得4OD =，然后根据四边形ABCD 是平行四边形，可得CD =7，90ODC AOD ∠=∠=︒，即可求解；（2）分两种情况讨论：当07t <时，当712t <时，过点A 作AF BC ⊥交CB 的延长线于点F ，即可求解；（3）分三种情况讨论：当CP =PM 时，过点M 作MF ①PC 于点F ；当52PC CM ==时；当PM =CM 时，过点M 作MG ①PC 于点G ，即可求解．(1)解：27120x x -+=，解得13x =，24x =，①OA OB <，①3OA =，4OB =， ①4tan 3DAB ∠=， ①43OD OA =， ①4OD =，①四边形ABCD 是平行四边形，①347DC AB ==+=，DC AB ∥，①点C 坐标为()7,4；(2)解：当07t <时，()117414222S CP OD t t =⋅=-⋅=-，当712t <时，过点A 作AF BC ⊥交CB 的延长线于点F ，如图，5AD ，①四边形ABCD 是平行四边形，①5BC AD ==，①BC AF AB OD ⋅=⋅，①574AF ⋅=⨯， ①285AF =， ①()11281498722555S CP AF t t =⋅=-⋅=-， ①()()14207149871255t t S t t ⎧-≤<⎪=⎨-<≤⎪⎩；(3)解：存在点P ，使CMP 是等腰三角形，理由如下：根据题意得：当点P 在CD 上运动时，CMP 可能是等腰三角形，①四边形ABCD 是平行四边形，①①C =①BAD ，BC =AD =5， ①4tan tan 3C DAB =∠=， ①点M 为BC 的中点，。

2022年黑龙江省省龙东地区中考数学真题试题及答案

2022年黑龙江省省龙东地区中考数学真题试题及答案黑龙江省龙东地区2022年初中毕业学业统一考试数学试题考生注意：1．考试时间120分钟2．全卷共三道大题，总分120分一、选择题（每题3分，满分30分）1．下列运算中，计算正确的是（）A ．()222b a b a -=-B ．326a a a ⋅=C ．()224x x -=D ．623a a a ÷=2．下列图形是汽车的标识，其中是中心对称图形但不是轴对称图形的是（）A ．B ．C ．D ．3．学校举办跳绳比赛，九年（2）班参加比赛的6名同学每分钟跳绳次数分别是172，169，180，182，175，176，这6个数据的中位数是（）A ．181B ．175C ．176D ．175.54．如图是由若干个相同的小正方体搭成的一个几何体的左视图和俯视图，则所需的小正方体的个数最多是（）A ．7B ．8C ．9D ．105．2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛，单循环比赛共进行了45场，共有多少支队伍参加比赛？（）A ．8B ．10C ．7D ．96．已知关于x 的分式方程23111x m x x --=--的解是正数，则m 的取值范围是（） A ．4m > B ．4m < C ．4m >且5m ≠ D ．4m <且1m ≠7．国家“双减”政策实施后，某校开展了丰富多彩的社团活动．某班同学报名参加书法和围棋两个社团，班长为参加社团的同学去商场购买毛笔和围棋（两种都购买）共花费360元．其中毛笔每支15元，围棋每副20元，共有多少种购买方案？（）A ．5B ．6C ．7D ．88．如图，在平面直角坐标系中，点O 为坐标原点，平行四边形OBAD 的顶点B 在反比例函数3y x =的图象上，顶点A 在反比例函数k y x=的图象上，顶点D 在x 轴的负半轴上．若平行四边形OBAD 的面积是5，则k 的值是（）A ．2B ．1C ．1-D ．2-9．如图，ABC △中，AB AC =，AD 平分BAC ∠与BC 相交于点D ，点E 是AB 的中点，点F 是DC 的中点，连接EF 交AD 于点P ．若ABC △的面积是24， 1.5PD =，则PE 的长是（）A ．2.5B ．2C ．3.5D ．310．如图，正方形ABCD 的对角线AC ，BD 相交于点O ，点F 是CD 上一点，OE OF ⊥交BC 于点E ，连接AE ，BF 交于点P ，连接OP ．则下列结论：①AE BF ⊥；②45OPA ∠=︒；③AP BP -=；④若:2:3BE CE =，则4tan 7CAE ∠=；⑤四边形OECF 的面积是正方形ABCD 面积的14．其中正确的结论是（）A ．①②④⑤B ．①②③⑤C ．①②③④D ．①③④⑤二、填空题（每题3分，满分30分）11．我国南水北调东线北延工程2021-2022年度供水任务顺利完成，共向黄河以北调水1.89亿立方米，将数据1.89亿用科学记数法表示为________．12．在函数y =x 的取值范围是________．13．如图，在四边形ABCD 中，对角线AC ，BD 相交于点O ，OA OC =，请你添加一个条件________，使AOB COD ≌△△．14．在一个不透明的口袋中，有2个红球和4个白球，这些球除颜色外其余完全相同，摇匀后随机摸出一个球，摸到红球的概率是________．15．若关于x 的一元一次不等式组2130x x a -<⎧⎨-<⎩的解集为2x <，则a 的取值范围是________． 16．如图，在O 中，AB 是O 的弦，O 的半径为3cm ，C 为O 上一点，60ACB ∠=︒，则AB 的长为________cm ．17．若一个圆锥的母线长为5cm ，它的侧面展开图的圆心角为120°，则这个圆锥的底面半径为________cm ．18．如图，菱形ABCD 中，对角线AC ，BD 相交于点O ，60BAD ∠=︒，3AD =，AH 是BAC ∠的平分线，CE AH ⊥于点E ，点P 是直线AB 上的一个动点，则OP PE +的最小值是________．19．在矩形ABCD 中，9AB =，12AD =，点E 在边CD 上，且4CE =，点P 是直线BC 上的一个动点．若APE △是直角三角形，则BP 的长为________．20．如图，在平面直角坐标系中，点1A ，2A ，3A ，4A ……在x 轴上且11OA =，212OA OA =，322OA OA =，422OA OA =……按此规律，过点1A ，2A ，3A ，4A ……作x 轴的垂线分别与直线y =交于点1B ，2B ，3B ，4B ……记11OA B △，22OA B △，13OA B △，14OA B △的面积分别为1S ，2S ，3S ，4S ……则2022S =________．三、解答题（满分60分）21．（本题满分5分）先化简，再求值：22221111a a a a a ⎛⎫---÷ ⎪-+⎝⎭，其中2cos301a =︒+．22．（本题满分6分）如图，在正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，ABC △的三个顶点坐标分别为()1,1A -，()2,5B -，()5,4C -．（1）将ABC △先向左平移6个单位，再向上平移4个单位，得到111A B C △，画出两次平移后的111A B C △，并写出点1A 的坐标；（2）画出111A B C △绕点1C 顺时针旋转90°后得到221A B C △，并写出点2A 的坐标；（3）在（2）的条件下，求点1A 旋转到点2A 的过程中所经过的路径长（结果保留π）．23．（本题满分6分）如图，抛物线2y x bx c =++经过点()1,0A -，点()2,3B -，与y 轴交于点C ，抛物线的顶点为D ．（1）求抛物线的解析式；（2）抛物线上是否存在点P ，使PBC △的面积是BCD △面积的4倍，若存在，请直接写出点P 的坐标：若不存在，请说明理由．24．（本题满分7分）为进一步开展“睡眠管理”工作，某校对部分学生的睡眠情况进行了问卷调查．设每名学生平均每天的睡眠时间为x 小时，其中的分组情况是：A 组：8.5x <B 组：8.59x ≤<C 组：99.5x ≤<D 组：9.510x ≤< E组：10x ≥根据调查结果绘制成两幅不完整的统计图，请根据图中提供的信息，解答下列问题：（1）本次共调查了________名学生；（2）补全条形统计图；（3）在扇形统计图中，求D 组所对应的扇形圆心角的度数；（4）若该校有1500名学生，请估计该校睡眠时间不足9小时的学生有多少人？25．（本题满分8分）为抗击疫情，支援B 市，A 市某蔬菜公司紧急调运两车蔬菜运往B 市．甲、乙两辆货车从A 市出发前往B 市，乙车行驶途中发生故障原地维修，此时甲车刚好到达B 市．甲车卸载蔬菜后立即原路原速返回接应乙车，把乙车的蔬菜装上甲车后立即原路原速又运往B 市．乙车维修完毕后立即返回A 市．两车离A 市的距离y （km ）与乙车所用时间x （h ）之间的函数图象如图所示．（1）甲车速度是________km/h ，乙车出发时速度是________km/h ；（2）求乙车返回过程中，乙车离A 市的距离y （km ）与乙车所用时间x （h ）的函数解析式（不要求写出自变量的取值范围）；（3）乙车出发多少小时，两车之间的距离是120km ？请直接写出答案．26．（本题满分8分）ABC △和ADE △都是等边三角形．（I ）将ADE △绕点A 旋转到图①的位置时，连接BD ，CE 并延长相交于点P （点P 与点A 重合），有PA PB PC +=（或PA PC PB +=）成立（不需证明）；（2）将ADE △绕点A 旋转到图②的位置时，连接BD ，CE 相交于点P ，连接P A ，猜想线段P A 、PB 、PC 之间有怎样的数量关系？并加以证明；（3）将ADE △绕点A 旋转到图③的位置时，连接BD ，CE 相交于点P ，连接P A ，猜想线段P A 、PB 、PC 之间有怎样的数量关系？直接写出结论，不需要证明．27．（本题满分10分）学校开展大课间活动，某班需要购买A 、B 两种跳绳．已知购进10根A 种跳绳和5根B 种跳绳共需175元：购进15根A 种跳绳和10根B 种跳绳共需300元．（1）求购进一根A 种跳绳和一根B 种跳绳各需多少元？（2）设购买A 种跳绳m 根，若班级计划购买A 、B 两种跳绳共45根，所花费用不少于548元且不多于560元，则有哪几种购买方案？（3）在（2）的条件下，哪种购买方案需要的总费用最少？最少费用是多少元？28．（本题满分10分）如图，在平面直角坐标系中，平行四边形ABCD 的边AB 在x 轴上，顶点D 在y 轴的正半轴上，M 为BC 的中点，OA 、OB 的长分别是一元二次方程27120x x -+=的两个根()OA OB <，4tan 3DAB ∠=，动点P 从点D 出发以每秒1个单位长度的速度沿折线DC CB -向点B 运动，到达B 点停止．设运动时间为t 秒，APC △的面积为S ．（1）求点C 的坐标；（2）求S 关于t 的函数关系式，并写出自变量t 的取值范围；（3）在点P 的运动过程中，是否存在点P ，使CMP △是等腰三角形？若存在，请直接写出点P 的坐标；若不存在，请说明理由．参考答案一、选择题（每小题3分，满分30分）1．C 2．C 3．D 4．B 5．B 6．C 7．A 8．D 9．A 10．B二、填空题（每小题3分，满分30分）11．81.8910⨯ 12．32x ≥ 13．OB OD =（符合题意即可）14．1315．2a ≥ 16． 17．53 1819．313或154或6 20．2三、解答题21．（本题满分5分）解：原式22222211121111211211a a a a a a a a a a a a ⎛⎫--+-+=-⋅=⋅= ⎪------⎝⎭当2cos3011a =︒+=时原式==22．（本题满分6分）（1）画出正确的图形()15,3A -（2）画出正确的图形()22,4A（3）解：∵115AC ==∴点1A 旋转到点2A 所经过的路径长为90π55π1802⨯=23．（本题满分6分）解：（1）∵抛物线2y x bx c =++过点()1,0A -，点()2,3B - ∴10423b c b c -+=⎧⎨++=-⎩解得23b c =-⎧⎨=-⎩∴抛物线的解析式为：223y x x =--（2）存在()11P ，()21P24．（本题满分7分）解：（1）100（2）补全统计图如图所示（3）D 组所对应的扇形圆心角度数为2036072100⨯︒=︒ （4）5201500375100+⨯=（人）答：估计该校睡眠时间不足9小时的学生有375人25．（本题满分8分）解：（1）100 60（2）设()0y kx b k =+≠根据题意，得9300120k b k b +=⎧⎨+=⎩解得1001200k b =-⎧⎨=⎩ ∴y 与x 的函数解析式为1001200y x =-+（3）3，6.3，9.126．（本题满分8分）（2）图②结论：PB PA PC =+证明：在BP 上截取BF CP =，连接AF∵ABC △和ADE △都是等边三角形∴AB AC =，AD AE = 60BAC DAE ∠=∠=︒ ∴BAC CAD DAE CAD ∠+∠=∠+∠∴BAD CAE ∠=∠∴BAD CAE ≌△△ ∴ABD ACE ∠=∠∴CAP BAF ≌△△∴CAP BAF ∠=∠ AF AP =∴CAP CAF BAF CAF ∠+∠=∠+∠∴60FAP BAC ∠=∠=︒∴AFP △是等边三角形∴PF AP =∴PA PC PF BF PB +=+=（3）图③结论：PA PB PC +=27．（本题满分10分）解：（1）设购进一根A 种跳绳需x 元，购进一根B 种跳绳需y 元根据题意，得1051751510300x y x y +=⎧⎨+=⎩解得1015x y =⎧⎨=⎩ 答：购进一根A 种跳绳需10元，购进一根B 种跳绳需15元．（2）根据题意，得()()101545560101545548m m m m ⎧+-≤⎪⎨+-≥⎪⎩解得2325.4m ≤≤ ∵m 为整数∴m 可取23，24，25．∴有三种方案：方案一：购买A 种跳绳23根，B 种跳绳22根；方案二：购买A 种跳绳24根，B 种跳绳21根；方案三：购买A 种跳绳25根，B 种跳绳20根（3）设购买跳绳所需费用为w 元，根据题意，得()1015455675w m m m =+-=-+ ∵50-<∴w 随m 的增大而减小∴当25m =时525675550=-⨯+=（元）答：方案三需要费用最少，最少费用是550元．28．（本题满分10分）解：（1）27120x x -+=解得13x =，24x =∵OA OB <∴3OA =，4OB =∵4tan 3DAB ∠=∴43OD OA =∴4OD = ∵四边形ABCD 是平行四边形∴347DC AB ==+= DC AB ∥∴90ODC AOD ∠=∠=︒∴点C 坐标为()7,4（2）①当07t <时()117414222S CP OD t t =⋅=-⋅=- （2）当712t <时过点A 作AF BC ⊥交CB 的延长线于点F5AD ===第11页（共11页） ∵四边形ABCD 是平行四边形∴5BC AD ==∵BC AF AB OD ⋅=⋅∴574AF ⋅=⨯∴285AF = ()11281498722555S CP AF t t =⋅=-⋅=- ∴()()14207149871255t t S t t ⎧-≤<⎪=⎨-<≤⎪⎩（3）存在()14,4p ，29,42p ⎛⎫ ⎪⎝⎭，359,412p ⎛⎫ ⎪⎝⎭。

2022年黑龙江省龙东地区中考数学试题及答案解析

2022年黑龙江省龙东地区中考数学试卷一、选择题（本大题共10小题，共30.0分）1.下列运算中，计算正确的是( )A. (b−a)2=b2−a2B. 3a⋅2a=6aC. (−x2)2=x4D. a6÷a2=a32.下列图形是汽车的标识，其中是中心对称图形但不是轴对称图形的是( )A. B.C. D.3.学校举办跳绳比赛，九年(2)班参加比赛的6名同学每分钟跳绳次数分别是172，169，180，182，175，176，这6个数据的中位数是( )A. 181B. 175C. 176D. 175.54.如图是由若干个相同的小正方体搭成的一个几何体的左视图和俯视图，则所需的小正方体的个数最多是( )A. 7B. 8C. 9D. 105.2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛，单循环比赛共进行了45场，共有多少支队伍参加比赛？( )A. 8B. 10C. 7D. 96.已知关于x的分式方程2x−mx−1−31−x=1的解是正数，则m的取值范围是( )A. m>4B. m<4C. m>4且m≠5D. m<4且m≠17.国家“双减”政策实施后，某校开展了丰富多彩的社团活动．某班同学报名参加书法和围棋两个社团，班长为参加社团的同学去商场购买毛笔和围棋(两种都购买)共花费360元．其中毛笔每支15元，围棋每副20元，共有多少种购买方案？( )A. 5B. 6C. 7D. 88.如图，在平面直角坐标系中，点O为坐标原点，平行四边形OBAD的顶点B在反比例函数y=3x 的图象上，顶点A在反比例函数y=kx的图象上，顶点D在x轴的负半轴上．若平行四边形OBAD的面积是5，则k的值是( )A. 2B. 1C. −1D. −29.如图，△ABC中，AB=AC，AD平分∠BAC与BC相交于点D，点E是AB的中点，点F是DC的中点，连接EF交AD于点P.若△ABC的面积是24，PD=1.5，则PE的长是( )A. 2.5B. 2C. 3.5D. 310.如图，正方形ABCD的对角线AC，BD相交于点O，点F是CD上一点，OE⊥OF交BC于点E，连接AE，BF交于点P，连接OP.则下列结论：①AE⊥BF；②∠OPA=45°；③AP−BP=√2OP；④若BE：CE=2：3，则tan∠CAE=47；⑤四边形OECF的面积是正方形ABCD面积的14.其中正确的结论是( )A. ①②④⑤B. ①②③⑤C. ①②③④D. ①③④⑤二、填空题（本大题共10小题，共30.0分）11.我国南水北调东线北延工程2021−2022年度供水任务顺利完成，共向黄河以北调水1.89亿立方米，将数据1.89亿用科学记数法表示为______．12.在函数y=√2x−3中，自变量x的取值范围是______．13.如图，在四边形ABCD中，对角线AC，BD相交于点O，OA=OC，请你添加一个条件______，使△AOB≌△COD．14.在一个不透明的口袋中，有2个红球和4个白球，这些球除颜色外其余完全相同，摇匀后随机摸出一个球，摸到红球的概率是______．15.若关于x的一元一次不等式组{2x−1<3x−a<0的解集为x<2，则a的取值范围是______．16.如图，在⊙O中，AB是⊙O的弦，⊙O的半径为3cm.C为⊙O上一点，∠ACB=60°，则AB的长为______cm．17.若一个圆锥的母线长为5cm，它的侧面展开图的圆心角为120°，则这个圆锥的底面半径为______cm．18.如图，菱形ABCD中，对角线AC，BD相交于点O，∠BAD=60°，AD=3，AH是∠BAC的平分线，CE⊥AH于点E，点P是直线AB上的一个动点，则OP+PE的最小值是______．19.在矩形ABCD中，AB=9，AD=12，点E在边CD上，且CE=4，点P是直线BC上的一个动点．若△APE是直角三角形，则BP的长为______．20.如图，在平面直角坐标系中，点A1，A2，A3，A4…在x轴上且OA1=1，OA2=2OA1，OA3=2OA2，OA4=2OA3…按此规律，过点A1，A2，A3，A4…作x轴的垂线分别与直线y=√3x交于点B1，B2，B3，B4…记△OA1B1，△OA2B2，△OA3B3，△OA4B4…的面积分别为S1，S2，S3，S4…则S2022=______．三、解答题（本大题共8小题，共60.0分）21.先化简，再求值：(a2−2aa2−1−1)÷2a−1a+1，其中a=2cos30°+1．22.如图，在正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，△ABC的三个顶点坐标分别为A(1,−1)，B(2,−5)，C(5,−4)．(1)将△ABC先向左平移6个单位，再向上平移4个单位，得到△A1B1C1，画出两次平移后的△A1B1C1，并写出点A1的坐标；(2)画出△A1B1C1绕点C1顺时针旋转90°后得到△A2B2C1，并写出点A2的坐标；(3)在(2)的条件下，求点A1旋转到点A2的过程中所经过的路径长(结果保留π)．23.如图，抛物线y=x2+bx+c经过点A(−1,0)，点B(2,−3)，与y轴交于点C，抛物线的顶点为D．(1)求抛物线的解析式；(2)抛物线上是否存在点P，使△PBC的面积是△BCD面积的4倍，若存在，请直接写出点P的坐标；若不存在，请说明理由．24.为进一步开展“睡眠管理”工作，某校对部分学生的睡眠情况进行了问卷调查．设每名学生平均每天的睡眠时间为x小时，其中的分组情况是：A组：x<8.5B组：8.5≤x<9C组：9≤x<9.5D组：9.5≤x<10E组：x≥10根据调查结果绘制成两幅不完整的统计图，请根据图中提供的信息，解答下列问题：(1)本次共调查了______名学生；(2)补全条形统计图；(3)在扇形统计图中，求D组所对应的扇形圆心角的度数；(4)若该校有1500名学生，请估计该校睡眠时间不足9小时的学生有多少人？25.为抗击疫情，支援B市，A市某蔬菜公司紧急调运两车蔬菜运往B市．甲、乙两辆货车从A市出发前往B市，乙车行驶途中发生故障原地维修，此时甲车刚好到达B市．甲车卸载蔬菜后立即原路原速返回接应乙车，把乙车的蔬菜装上甲车后立即原路原速又运往B市．乙车维修完毕后立即返回A市．两车离A市的距离y(km)与乙车所用时间x(ℎ)之间的函数图象如图所示．(1)甲车速度是______km/ℎ，乙车出发时速度是______km/ℎ；(2)求乙车返回过程中，乙车离A市的距离y(km)与乙车所用时间x(ℎ)的函数解析式(不要求写出自变量的取值范围)；(3)乙车出发多少小时，两车之间的距离是120km？请直接写出答案．26.△ABC和△ADE都是等边三角形．(1)将△ADE绕点A旋转到图①的位置时，连接BD，CE并延长相交于点P(点P与点A重合)，有PA+PB=PC(或PA+PC=PB)成立(不需证明)；(2)将△ADE绕点A旋转到图②的位置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？并加以证明；(3)将△ADE绕点A旋转到图③的位置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？直接写出结论，不需要证明．27.学校开展大课间活动，某班需要购买A、B两种跳绳．已知购进10根A种跳绳和5根B种跳绳共需175元：购进15根A种跳绳和10根B种跳绳共需300元．(1)求购进一根A种跳绳和一根B种跳绳各需多少元？(2)设购买A种跳绳m根，若班级计划购买A、B两种跳绳共45根，所花费用不少于548元且不多于560元，则有哪几种购买方案？(3)在(2)的条件下，哪种购买方案需要的总费用最少？最少费用是多少元？28.如图，在平面直角坐标系中，平行四边形ABCD的边AB在x轴上，顶点D在y轴的正半轴上，M为BC的中点，OA、OB的长分别是一元二次方程x2−7x+12=0的两，动点P从点D出发以每秒1个单位长度的速度沿折个根(OA<OB)，tan∠DAB=43线DC−CB向点B运动，到达B点停止．设运动时间为t秒，△APC的面积为S．(1)求点C的坐标；(2)求S关于t的函数关系式，并写出自变量t的取值范围；(3)在点P的运动过程中，是否存在点P，使△CMP是等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．答案解析1.【答案】C【解析】解：A.(b−a)2=b2−2ab+a2，故A不正确；B.3a⋅2a=6a2，故B不正确；C.(−x2)2=x4，故C正确；D.a6÷a2=a4，故D不符合题意；故选：C．利用完全平方公式，单项式乘多项式，幂的乘方的法则，同底数幂的除法的法则对各项进行运算即可．本题考查了完全平方公式，单项式乘多项式，幂的乘方的法则，同底数幂的除法，解答的关键是对相应的运算法则的掌握．2.【答案】C【解析】解：A.既是中心对称图形，也是轴对称图形，故此选项不合题意；B.不是中心对称图形，是轴对称图形，故此选项不合题意；C.是中心对称图形但不是轴对称图形，故此选项符合题意；D.不是中心对称图形，是轴对称图形，故此选项不合题意；故选：C．根据中心对称图形与轴对称图形的概念进行判断即可．本题考查的是中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后与自身重合．3.【答案】D【解析】解：将这组数据从小到大排列为：169，172，175，176，180，182，=175.5，中位数=175+1762故选：D．将这组数据从小到大排列，根据中位数的计算方法即可得出答案．本题考查了中位数，掌握将一组数据按照从小到大(或从大到小)的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数是解题的关键．4.【答案】B【解析】解：从俯视图课看出前后有三层，从左视图可看出最后面有2层高，中间最高是2层，要是最多就都是2层，最前面的最高是1层，所以最多的为：2+2×2+1×2=8．故选：B．由左视图和俯视图可以猜想到主视图的可能情况，从而得到答案．本题考查了三视图的知识，由两个识图想象几何体是解题的关键，5.【答案】B【解析】解：设共有x支队伍参加比赛，=45，根据题意，可得x(x−1)2解得x=10或x=−9(舍)，∴共有10支队伍参加比赛．故选：B．设共有x支队伍参加比赛，根据“循环比赛共进行了45场”列一元二次方程，求解即可．本题考查了一元二次方程的应用，理解题意并根据题意建立等量关系是解题的关键．6.【答案】C【解析】解：方程两边同时乘以x−1得，2x−m+3=x−1，解得x=m−4．∵x为正数，∴m−4>0，解得m>4，∵x≠1，∴m−4≠1，即m≠5，∴m的取值范围是m>4且m≠5．故选：C．先利用m表示出x的值，再由x为正数求出m的取值范围即可．本题考查了分式方程的解，掌握求出使分式方程中令等号左右两边相等且分母不等于0的未知数的值，这个值叫方程的解是解题的关键．7.【答案】A【解析】解：设购买毛笔x支，围棋y副，根据题意，得15x+20y=360，∴y=18−34x，∵两种都买，∴18−34x>0，x、y都是正整数，解得x<24，故x是4的倍数且x<24，∴x=4，y=15或x=8，y=12或x=12，y=9或x=16，y=6或x=20，y=3；∴共有5种购买方案，故选：A．设购买毛笔x支，围棋y副，根据“购买毛笔和围棋(两种都购买)共花费360元”列二元一次方程，再由x和y分别取正整数，即可确定购买方案．本题考查了二元一次方程的应用，理解题意并根据题意建立二元一次方程是解题的关键．8.【答案】D【解析】解：设B(a,3a)，∵四边形OBAD是平行四边形，∴AB//DO，∴A(ak3,3a )，∴AB=a−ak3，∵平行四边形OBAD的面积是5，∴3a (a−ak3)=5，解得k=−2，故选：D．设B(a,3a)，根据四边形OBAD是平行四边形，推出AB//DO，表示出A点的坐标，求出AB=a−ak3，再根据平行四边形面积公式列方程，解出即可．本题考查反比例函数比例系数k的几何意义、反比例函数图象上点的坐标特征、平行四边形性质，掌握反比例函数比例系数k的几何意义及函数图象上点的坐标特征，设出点的坐标、根据平行四边形面积公式列方程是解题的关键．9.【答案】A【解析】解：如图，过点E作EG⊥AD于G，∵AB=AC，AD平分∠BAC，∴AD⊥BC，BD=CD，∴∠PDF=∠EGP=90°，EG//BC，∵点E是AB的中点，∴G是AD的中点，BD，∴EG=12∵F是CD的中点，CD，∴DF=12∴EG=DF，∵∠EPG=∠DPF，∴△EGP≌△FDP(AAS)，∴PG=PD=1.5，∴AD=2DG=6，∵△ABC的面积是24，⋅BC⋅AD=24，∴12∴BC=48÷6=8，BC=2，∴DF=14∴EG=DF=2，由勾股定理得：PE=√22+1．52=2.5．故选：A．如图，过点E作EG⊥AD于G，证明△EGP≌△FDP，得PG=PD=1.5，由三角形中位线定理可得AD的长，由三角形ABC的面积是24，得BC的长，最后由勾股定理可得结论．本题考查了等腰三角形的性质，三角形的中位线定理，全等三角形的性质和判定，三角形的面积等知识，作辅助线构建全等三角形是解本题的关键．10.【答案】B【解析】解：①∵四边形ABCD是正方形，∴AB=BC=CD，AC⊥BD，∠ABD=∠DBC=∠ACD=45°．∴∠BOE+∠EOC=90°，∵OE⊥OF，∴∠FOC+∠EOC=90°．∴∠BOE=∠COF．在△BOE和△COF中，{∠OBE=∠OCF=45°OB=OC∠BOE=∠COF，∴△BOE≌△COF(ASA)，∴BE=CF．在△BAE和△CBF中，{AB=BC∠ABC=∠BCF=90°BE=CF，∴△BAE≌△CBF(SAS)，∴∠BAE=∠CBF．∵∠ABP+∠CBF=90°，∴∠ABP+∠BAE=90°，∴∠APB=90°．∴AE⊥BF．∴①的结论正确；②∵∠APB=90°，∠AOB=90°，∴点A，B，P，O四点共圆，∴∠APO=∠ABO=45°，∴②的结论正确；③过点O作OH⊥OP，交AP于点H，如图，∵∠APO=45°，OH⊥OP，∴OH=OP=√22HP，∴HP=√2OP．∵OH⊥OP，∴∠POB+∠HOB=90°，∵OA⊥OB，∴∠AOH+∠HOB=90°．∴∠AOH=∠BOP．∵∠OAH+BAE=45°，∠OBP+∠CBF=45°，，∠BAE=∠CBF，∴∠OAH=∠OBP．在△AOH和△BOP中，{∠OAH=∠OBP OA=OB∠AOH=∠BOP，∴△AOH≌△BOP(ASA)，∴AH=BP．∴AP−BP=AP−AH=HP=√2OP．∴③的结论正确；④∵BE：CE=2：3，∴设BE=2x，则CE=3x，∴AB=BC=5x，∴AE=√AB2+BE2=√29x.过点E作EG⊥AC于点G，如图，∵∠ACB=45°，∴EG=GC=√22EC=3√22x，∴AG=√AE2−GE2=7√22x，在Rt△AEG中，∵tan∠CAE=EGAG，∴tan∠CAE==3√22x7√22=37．∴④的结论不正确；⑤∵四边形ABCD是正方形，∴OA=OB=OC=OD，∠AOB=∠BOC=∠COD=∠DOA=90°，∴△OAB≌△OBC≌△OCD≌△DOA(SAS)．∴S△OBC=14S正方形ABCD．∴S△BOE+S△OEC=14S正方形ABCD．由①知：△BOE≌△COF，∴S△OBE=S△OFC，∴S△OEC+S△OFC=14S正方形ABCD．即四边形OECF的面积是正方形ABCD面积的14．∴⑤的结论正确．综上，①②③⑤的结论正确．故选：B．利用全等三角形的判定与性质，正方形的性质，圆周角定理，直角三角形的边角关系定理对每个选项的结论进行判断即可得出结论．本题主要考查了全等三角形的判定与性质，正方形的性质，圆周角定理，直角三角形的边角关系定理，等腰直角三角形的判定与性质，充分利用正方形的性质构造等腰直角三角形和全等三角形是解题的关键．11.【答案】1.89×108【解析】解：1.89亿=189000000=1.89×108．故答案为：1.89×108．用科学记数法表示较大的数时，一般形式为a×10n，其中1≤|a|<10，n为整数，且n 比原来的整数位数少1，据此判断即可．此题主要考查了用科学记数法表示较大的数，一般形式为a×10n，其中1≤|a|<10，确定a与n的值是解题的关键．12.【答案】x≥32【解析】解：根据题意得，2x−3≥0，解得x≥32．故答案为：x≥32．根据被开方数大于等于0列式计算即可得解．本题考查的知识点为：二次根式的被开方数是非负数．13.【答案】OB=OD(答案不唯一)【解析】解：添加的条件是OB=OD，理由是：在△AOB和△COD中，{AO=CO∠AOB=∠COD BO=DO，∴△AOB≌△COD(SAS)，故答案为：OB=OD(答案不唯一)．此题是一道开放型的题目，答案不唯一，只要符合全等三角形的判定定理即可．本题考查了全等三角形的判定定理，能熟记全等三角形的判定定理是解此题的关键，注意：全等三角形的判定定理是SAS，SAS，AAS，SSS，两直角三角形全等还有HL等．14.【答案】13【解析】解：∵在一个不透明的口袋中，有2个红球和4个白球，这些球除颜色外其余完全相同，摇匀后随机摸出一个球，∴摸到红球的概率是：22+4=13．故答案为：13．直接利用概率公式，进而计算得出答案．此题主要考查了概率公式，正确掌握概率求法是解题关键．15.【答案】a ≥2【解析】解：不等式组整理得：{x <2x <a， ∵不等式组的解集为x <2，∴a ≥2．故答案为：a ≥2．不等式组整理后，根据已知解集，利用同小取小法则判断即可确定出a 的范围．此题考查了解一元一次不等式组，熟练掌握不等式组取解集的方法是解本题的关键．16.【答案】3√3【解析】解：连接AO 并延长交⊙O 于点D ，∵AD 是⊙O 的直径，∴∠ADB =90°，∵∠ACB =60°，∴∠ADB =∠ACB =60°，在Rt △ABD 中，AD =6cm ，∴AB =AD ⋅sin60°=6×√32=3√3(cm)，故答案为：3√3．连接AO 并延长交⊙O 于点D ，根据直径所对的圆周角是直角可得∠ADB =90°，再利用同弧所对的圆周角相等可求出∠ADB =60°，然后在Rt △ABD 中，利用锐角三角函数的定义进行计算即可解答．本题考查了三角形的外接圆与外心，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．17.【答案】53【解析】解：c长为：120°×π×5180∘=103π，设圆锥的底面半径为r，则2πr=103π，∴r=53cm．故答案为：53．先求出圆锥侧面展开图扇形的弧长，再利用侧面展开图与底面圆的关系的关系列方程即可求出圆锥的底面半径．本题主要考查圆锥的计算，掌握侧面展开图与底面圆的关系是解题关键．18.【答案】32√6【解析】解：连接OE，过点O作OF⊥AB，垂足为F，并延长到点O′，使O′F=OF，连接O′E交直线AB于点P，连接OP，∴AP是OO′的垂直平分线，∴OP=O′P，∴OP+PE=O′P+PE=O′E，此时，OP+PE的值最小，∵四边形ABCD是菱形，∴AD=AB=3，∠BAC=12∠BAD，OA=OC=12AC，OD=OB=12BD，∠AOD=90°，∵∠BAD=60°，∴△ADB 是等边三角形，∴BD =AD =3，∴OD =12BD =32，∴AO =√AD 2−DO 2=√32−(32)2=32√3， ∴AC =2OA =3√3，∵CE ⊥AH ，∴∠AEC =90°，∴OE =OA =12AC =32√3，∴∠OAE =∠OEA ，∵AE 平分∠CAB ，∴∠OAE =∠EAB ，∴∠OEA =∠EAB ，∴OE//AB ，∴∠EOF =∠AFO =90°，在Rt △AOF 中，∠OAB =12DAB =30°，∴OF =12OA =34√3， ∴OO′=2OF =32√3，在Rt △EOO′中，O′E =√EO 2+OO ′2=√(32√3)2+(32√3)2=32√6， ∴OE +PE =32√6，∴OP +PE 的最小值为32√6，故答案为：32√6．连接OE ，过点O 作OF ⊥AB ，垂足为F ，并延长到点O′，使O′F =OF ，连接O′E 交直线AB 于点P ，连接OP ，从而可得OP =O′P ，此时OP +PE 的值最小，先利用菱形的性质可得AD =AB =3，∠BAC =12∠BAD ，OA =OC =12AC ，OD =OB =12BD ，∠AOD =90°，从而可得△ADB 是等边三角形，进而求出AD =3，然后在Rt △ADO 中，利用勾股定理求出AO 的长，从而求出AC 的长，进而利用直角三角形斜边上的中线可得OE =OA =12AC =32√3，再利用角平分线和等腰三角形的性质可得OE//AB ，从而求出∠EOF =90°，进而在Rt △AOF 中，利用锐角三角函数的定义求出OF 的长，即可求出OO′的长，最后在Rt △EOO′中，利用勾股定理进行计算即可解答．本题考查了菱形的性质，勾股定理，角平分线的定义，等边三角形的判定与性质，轴对称−最短路线问题，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．19.【答案】313或154或6【解析】解：若△APE 是直角三角形，有以下三种情况：①如图1，∠AEP =90°，∴∠AED +∠CEP =90°，∵四边形ABCD 是矩形，∴∠C =∠D =90°，∴∠CEP +∠CPE =90°，∴∠AED =∠CPE ，∴△ADE∽△ECP ，∴ADCE =DE CP，即124=9−4CP ， ∴CP =53， ∵BC =AD =12，∴BP =12−53=313；②如图2，∠PAE =90°，∵∠DAE +∠BAE =∠BAE +∠BAP =90°，∴∠DAE =∠BAP ，∵∠D =∠ABP =90°，∴△ADE∽△ABP ， ∴AD AB =DE PB ，即129=5BP ， ∴BP =154；③如图3，∠APE =90°，设BP =x ，则PC =12−x ，同理得：△ABP∽△PCE ，∴ABPC =BP CE ，即912−x =x4， ∴x 1=x 2=6，∴BP =6，综上，BP 的长是313或154或6．故答案为：313或154或6．若△APE 是直角三角形，有三种情况：①如图1，∠AEP =90°，②如图2，∠PAE =90°，③如图3，∠APE =90°，分别证明三角形相似可解答．本题考查的是相似三角形的判定与性质，矩形的性质，掌握相似三角形的判定定理和性质定理是解题的关键，并注意运用分类讨论的思想．20.【答案】【解析】解：∵OA 1=1，OA 2=2OA 1，∴OA 2=2，∵OA 3=2OA 2，∴OA 3=4，∵OA 4=2OA 3，∴OA 4=8，把x =1代入直线y =√3x 中可得：y =√3，∴A 1B 1=√3，把x =2代入直线y =√3x 中可得：y =2√3，∴A2B2=2√3，把x=4代入直线y=√3x中可得：y=4√3，∴A3B3=4√3，把x=8代入直线y=√3x中可得：y=8√3，∴A4B4=8√3，∴S1=12OA1⋅A1B1=12×1×√3=12×20×(20×√3)，S2=12OA2⋅A2B2=12×2×2√3=12×21×(21×√3)，S3=12OA3⋅A3B3=12×4×4√3=12×22×(22×√3)，S4=12OA4⋅A4B4=12×8×8√3=12×23×(23×√3)，...∴S2022=12×22021×(22021×√3)=24041×√3，故答案为：24041×√3．根据已知先求出OA2，OA3，OA4的长，再代入直线y=√3x中，分别求出A1B1，A2B2，A3B3，A4B4，然后分别计算出S1，S2，S3，S4，再从数字上找规律进行计算即可解答．本题考查了规律型：点的坐标，含30度角的直角三角形，根据已知分别求出S1，S2，S3，S4的值，然后从数字上找规律是解题的关键．21.【答案】解：(a2−2aa2−1−1)÷2a−1a+1=(a2−2aa2−1−a2−1a2−1)÷2a−1a+1=1−2a(a+1)(a−1)×a+12a−1=11−a，当a=2cos30°+1=2×√32+1=√3+1时，原式=1−√3−1=−√33．【解析】利用分式的减法法则和除法法则对分式进行计算化简，把特殊角的三角函数值代入计算求出a的值，代入化简后的分式进行计算，即可得出答案．本题考查了分式的化简求值，特殊角的三角函数值，掌握分式的混合计算及特殊角的三角函数值是解决问题的关键．22.【答案】解：(1)如图，△A1B1C1即为所求，点A1的坐标(−5,,3)；(2)如图，△A2B2C1即为所求，点A2的坐标(2,4)；(3)∵A1C1=√32+42=5，∴点A1旋转到点A2的过程中所经过的路径长=90π×5180=5π2．【解析】(1)利用平移变换的性质分别作出A，B，C的对应点A1，B1，C1即可；(2)利用旋转变换的性质分别作出A1，B1的对应点A2，B2即可；(3)利用勾股定理求出A1C1，再利用弧长公式求解．本题考查作图−平移变换，旋转变换，弧长公式等知识，解题的关键是掌握平移变换，旋转变换的性质，属于中考常考题型．23.【答案】解：(1)∵抛物线y=x2+bx+c经过点A(−1,0)，点B(2,−3)，∴{1−b+c=04+2b+c=−3，解得b=−2，c=−3，∴抛物线的解析式：y=x2−2x−3；(2)存在，理由如下：∵y=x2−2x−3=(x−1)2−4，∴D点坐标为(1,4)，令x=0，则y=x2−2x−3=−3，∴C点坐标为(0,−3)，又∵B点坐标为(2,−3)，∴BC//x轴，∴S△BCD=12×2×1=1，设抛物线上的点P坐标为(m,m2−2m−3)，∴S△PBC=1×2×|m2−2m−3−(−3)|=|m2−2m|，2当|m2−2m|=4×1时，解得m=1±√5，当m=1+√5时，m2−2m−3=1，当m=1−√5时，m2−2m−3=1，综上，P点坐标为(1+√5,1)或(1−√5,1)．【解析】(1)待定系数法求解析式即可；(2)设抛物线上的点P坐标为(m,m2−2m−3)，结合方程思想和三角形面积公式列方程求解．本题考查二次函数的性质，掌握待定系数法求函数解析式的方法，理解二次函数图象上点的坐标特征，利用方程思想解题是关键．24.【答案】100【解析】解：(1)20÷20%=100(名)，即本次共调查了100名学生，故答案为：100；(2)选择E的学生有：100×15%=15(人)，选择A的学生有：100−20−40−20−15=5(人)，补全的条形统计图如右图所示；=72°，(3)360°×20100即D组所对应的扇形圆心角的度数是72°；=375(人)，(4)1500×5+20100答：估计该校睡眠时间不足9小时的学生有375人．(1)根据B组人数和所占的百分比，可以计算出本次调查的学生总人数；(2)根据(1)中的结果、条形统计图中的时间和扇形统计图中的数据，可以计算出A组和E 组的人数，从而可以将条形统计图补充完整；(3)根据D组的人数和调查的总人数，可以计算出D组所对应的扇形圆心角的度数；(4)根据条形统计图中的数据，可以计算出该校睡眠时间不足9小时的学生有多少人．本题考查条形统计图、扇形统计图、用样本估计总体，解答本题的关键是明确题意，利25.【答案】100 60【解析】解：(1)由图象可得，甲车的速度为：500÷5=100(km/ℎ)，乙车出发时速度是：300÷5=60(km/ℎ)，故答案为：100，60；(2)乙车返回过程中，设乙车离A 市的距离y(km)与乙车所用时间x(ℎ)的函数解析式是y =kx +b ，∵点(9,300)，(12,0)在该函数图象上，∴{9k +b =30012k +b =0，解得{k =−100b =1200，即乙车返回过程中，乙车离A 市的距离y(km)与乙车所用时间x(ℎ)的函数解析式是y =−100x +1200；(3)设乙车出发m 小时，两车之间的距离是120km ，当0<m <5时，100m −60m =120，解得m =3；当5.5<m <8时，100(m −5.5)+120+300=500，解得m =6.3；当9<m <12时，乙车返回的速度为：300÷(12−9)=100(km/ℎ)，(100+100)×(m −9)=120，解得m =9.6；答：乙车出发3小时或6.3小时或9.6小时，两车之间的距离是120km ．(1)根据函数图象中的数据，可以计算出甲车速度和乙车出发时速度；(2)根据函数图象中的数据，可以计算出乙车返回过程中，乙车离A 市的距离y(km)与乙车所用时间x(ℎ)的函数解析式；(3)根据题意可知存在三种情况，然后分别计算即可．本题考查一次函数的应用，解答本题的关键是明确题意，求出相应的函数解析式，利用26.【答案】解：(2)PB=PA+PC，理由如下：如图②，在BP上截取BF=PC，连接AF，∵△ABC、△ADE都是等边三角形，∴AB=AC，AD=AE，∠BAC=∠DAE=60°，∴∠BAC+∠CAD=∠CAD+∠DAE，即∠DAB=∠EAC，∴△ABD≌△ACE(SAS)，∴∠ABD=∠ACE，∵AB=AC，BF=CP，∴△BAF≌△CAP(SAS)，∴AF=AP，∠BAF=∠CAP，∴∠BAC=∠PAF=90°，∴△AFP是等边三角形，∴PF=PA，∴PB=BF+PF=PC+PA；(3)PC=PA+PB，理由如下：如图③，在PC上截取CM=PB，连接AM，同理得：△ABD≌△ACE(SAS)，∴∠ABD =∠ACE ，∵AB =AC ，PB =CM ，∴△AMC≌△APB(SAS)，∴AM =AP ，∠BAP =∠CAM ，∴∠BAC =∠PAM =60°，∴△AMP 是等边三角形，∴PM =PA ，∴PC =PM +CM =PA +PB ．【解析】(2)证明△ABD≌△ACE(SAS)和△BAF≌△CAP(SAS)，得AF =AP ，∠BAF =∠CAP ，再证明△AFP 是等边三角形，最后由线段的和可得结论；(3)如图③，在PC 上截取CM =PB ，连接AM ，同理可得结论．本题考查了等边三角形的性质、全等三角形的判定与性质等知识，熟练掌握等边三角形的性质，证明△ABD≌△ACE 是解题的关键，属于中考常考题型．27.【答案】解：(1)设购进一根A 种跳绳需x 元，购进一根B 种跳绳需y 元，依题意得：{10x +5y =17515x +10y =300，解得：{x =10y =15．答：购进一根A 种跳绳需10元，购进一根B 种跳绳需15元．(2)∵该班级计划购买A 、B 两种跳绳共45根，且购买A 种跳绳m 根，∴购买B 种跳绳(45−m)根．依题意得：{10m +15(45−m)≤56010m +15(45−m)≥548，解得：23≤m ≤25.4，又∵m 为整数，∴m 可以取23，24，25，∴共有3种购买方案，方案1：购买23根A 种跳绳，22根B 种跳绳；方案2：购买24根A 种跳绳，21根B 种跳绳；方案3：购买25根A 种跳绳，20根B 种跳绳．(3)设购买跳绳所需总费用为w 元，则w =10m +15(45−m)=−5m +675． ∵−5<0，∴w 随m 的增大而减小，∴当m=25时，w取得最小值，最小值=−5×25+675=500．答：在(2)的条件下，购买方案3需要的总费用最少，最少费用是500元．【解析】(1)设购进一根A种跳绳需x元，购进一根B种跳绳需y元，根据“购进10根A种跳绳和5根B种跳绳共需175元：购进15根A种跳绳和10根B种跳绳共需300元”，即可得出关于x，y的二元一次方程组，解之即可得出结论；(2)设购买A种跳绳m根，则购买B种跳绳(45−m)根，利用总价=单价×数量，结合总价不少于548元且不多于560元，即可得出关于m的一元一次不等式组，解之即可得出m的取值范围，再结合m为整数，即可得出各购买方案；(3)设购买跳绳所需总费用为w元，利用总价=单价×数量，即可得出w关于m的函数关系式，再利用一次函数的性质，即可解决最值问题．本题考查了二元一次方程组的应用、一元一次不等式组的应用以及一次函数的应用，解题的关键是：(1)找准等量关系，正确列出二元一次方程组；(2)根据各数量之间的关系，正确列出一元一次不等式组；(3)根据各数量之间的关系，找出w关于m的函数关系式．28.【答案】解：(1)方程x2−7x+12=0，解得：x1=3，x2=4，∵OA<OB，∴OA=3，OB=4，∵tan∠DAB=ODOA =43，∴OD=4，∵四边形ABCD是平行四边形，∴DC=AB=3+4=7，DC//AB，∴∠ODC=∠AOD=90°，∴点C的坐标为(7,4)；(2)：①当0≤t≤7时，由题意得：PC=7−t，∴△APC的面积为S=12PC⋅OD=12(7−t)×4=14−2t；②当7<t≤12时，过点A作AF⊥BC交CB的延长线于点F，∵AD =√OA 2+OD 2=√32+42=5，四边形ABCD 是平行四边形， ∴BC =AD =5，∵S △ABC =12AB ⋅OD =12CB ⋅AF ， ∴AB ⋅OD =CB ⋅AF ，∴7×4=5AF ，∴AF =285，∴△APC 的面积为S =12PC ⋅AF =12(t −7)×285=145t −985；综上，S ={14−2t(0≤t ≤7)145t −985(7<t ≤12)；(3)∵BC =AD =5，M 为BC 的中点，C(7,4)，B(4,0)， ∴CM =52，M(112,2)， ①当CM =CP 时，∵CM =52，∴CM =CP =52，∵CD =7，∴DP=7−52=92，∴点P的坐标为(92,4)；②当CM=MP时，过点M作ME⊥CD于E，∴PE=CE，∵M(112,2)，C(7,4)，∴E(112,4)，CE=7−112=32，∴PE=CE=32，∴DP=DE−PE=112−32=4，∴点P的坐标为(4,4)；③当CP=MP时，过点P作PF⊥BC于F，∴MF=CF=12CM=54，∵四边形ABCD是平行四边形，∴∠BCD=∠DAB，∴cos∠BCD=cos∠DAB=OAAD =35，∴CFPC =35，即54PC=35，∴PC=2512，∴DP=DC−PC=7−2512=5912，∴点P的坐标为(5912,4)；综上，点P的坐标为(4,4)或(92,4)或(5912,4)．【解析】(1)解一元二次方程求出OA、OB的长度，可得出A、B的坐标，即可求解；(2)分0≤t≤7和7<t≤12两种情况考虑：①当0≤t≤7时，利用三角形的面积公式可得出S关于t的函数关系式；②当7<t≤12时，过点A作AF⊥BC交CB的延长线于点F，利用三角形的面积求出AF，即可得△APC的面积为S=12PC⋅AF=12(t−7)×285=14 5t−985；(3)要使△CMP是等腰三角形，点P一定在CD上，需分情况讨论：①当CM=CP时；②当CM=MP时；③当CP=MP时，根据等腰三角形的性质即可求解．本题是四边形综合题目，考查了一元二次方程的解法，平行四边形的性质，三角形面积的计算，解直角三角形，等腰三角形的性质等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考压轴题．第31页，共31页。

2023年黑龙江省龙东地区中考数学真题(解析版)

黑龙江省龙东地区2023年初中毕业学业统一考试数学试题考生注意：1．考试时间120分钟2．全卷共三道大题，总分120分一、选择题（每小题3分，共30分）1.下列运算正确的是（）A.22(2)4a a B.222()a b a b C. 2224m m m D. 257a a 【答案】C【解析】【分析】分别根据积的乘方，完全平方公式，平方差公式和幂的乘方法则进行判断即可．【详解】解：A. 2224a a ，原式计算错误；B.2222a b a ab b ，原式计算错误；C.2224m m m ，计算正确；D. 2510a a ，原式计算错误．故选：C ．【点睛】本题考查了积的乘方，完全平方公式，平方差公式和幂的乘方，熟练掌握运算法则，牢记乘法公式是解题的关键．2.下列新能源汽车标志图案中，既是轴对称图形，又是中心对称图形的是（）A. B. C. D.【答案】A【解析】【分析】根据轴对称图形和中心对称图形的定义进行逐一判断即可：如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形；把一个图形绕着某一个点旋转180 ，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心．【详解】解：A 、既是轴对称图形，也是中心对称图形，符合题意；B 、是轴对称图形，不是中心对称图形，不符合题意；C 、既不是轴对称图形，也不是中心对称图形，不符合题意；D 、是轴对称图形，不是中心对称图形，不符合题意；故选A ．【点睛】本题主要考查了轴对称图形和中心对称图形的识别，熟知二者的定义是解题的关键．3.一个几何体由若干大小相同的小正方体组成，它的俯视图和左视图如图所示，那么组成该几何体所需小正方体的个数最少为（）A.4B.5C.6D.7【答案】B【解析】【分析】在“俯视打地基”的前提下，结合左视图知俯视图上一行三个小正方体的上方（第2层）至少还有1个正方体，据此可得答案.【详解】解：由俯视图与左视图知，该几何体所需小正方体个数最少分布情况如下图所示：所以组成该几何体所需小正方体的个数最少为5，故选：B ．【点睛】本题主要考查由三视图判断几何体，解题的关键是掌握口诀“俯视打地基，主视疯狂盖，左视拆违章”．4.已知一组数据1,0,3,5,,2,3x 的平均数是1，则这组数据的众数是（）A.3B.5C.3 和5D.1和3【答案】C【解析】【分析】先根据平均数的定义列出关于x 的方程，求出x 的值，从而还原这组数据，再利用众数的概念求解即可．【详解】解：∵数据1,0,3,5,,2,3x 的平均数是1，∴10352371x ，解得5x ，则1,0,3,5,5,2,3 ，∴这组数据的众数是3 和5，故选：C ．【点睛】此题主要考查了众数和平均数，解题关键是掌握众数和平均数的概念．5.如图，在长为100m ，宽为50m 的矩形空地上修筑四条宽度相等的小路，若余下的部分全部种上花卉，且花圃的面积是23600m ，则小路的宽是（）A.5mB.70mC.5m 或70mD.10m【答案】A【解析】【分析】设小路宽为m x ，则种植花草部分的面积等于长为 1002m x ，宽为 502m x 的矩形的面积，根据花草的种植面积为23600m ，即可得出关于x 的一元二次方程，解之取其符合题意的值即可得出结论．【详解】解：设小路宽为m x ，则种植花草部分的面积等于长为 1002m x ，宽为 502m x 的矩形的面积，依题意得： 1002502=3600x x 解得：15 x ，270x （不合题意，舍去），∴小路宽为5m ．故选A ．【点睛】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．6.已知关于x 的分式方程122m x x x 的解是非负数，则m 的取值范围是（）A.2m B.2m C.2m 且2m D.2m 且2m 【答案】C【解析】【分析】解分式方程求出22m x，然后根据解是非负数以及解不是增根得出关于m 的不等式组，求解即可．【详解】解：分式方程去分母得：2m x x ，解得：22m x ，∵分式方程122m x x x的解是非负数，∴202m ，且222m x ，∴2m 且2m ，故选：C ．【点睛】本题考查了解分式方程，解一元一次不等式组，正确得出关于m 的不等式组是解题的关键．7.某社区为了打造“书香社区”，丰富小区居民的业余文化生活，计划出资500元全部用于采购A ，B ，C 三种图书，A 种每本30元，B 种每本25元，C 种每本20元，其中A 种图书至少买5本，最多买6本（三种图书都要买），此次采购的方案有（）A.5种B.6种C.7种D.8种【答案】B【解析】【分析】设采购A 种图书x 本，B 种图书y 本，C 种图书z 本，根据采购三种图书需500元列出方程，再依据x 的数量分两种情况讨论求解即可．【详解】解：设采购A 种图书x 本，B 种图书y 本，C 种图书z 本，其中56,0,0,x y z 且,,x y z 均为整数，根据题意得，302520500x y z ，整理得，654100x y z ，①当5x 时，6554100y z ，∴704,5z y ∵0,0,y z 且,y z 均为整数，∴当70410z 时，2y ，∴15z ；当70430z 时，6y ，∴10z ；当70450z 时，10y ，∴5z ；②当6x 时，6654100y z ，∴644,5z y ∵0,0,y z 且,y z 均为整数，∴当64420z 时，4y ，∴11z ；当64440z 时，8y ，∴6z ；当64460z 时，12y ，∴1z ；综上，此次共有6种采购方案，故选：B ．【点睛】本题主要考查了二元一次方程的应用，正确理解题意、进行分类讨论是解答本题的关键．8.如图，ABC 是等腰三角形，AB 过原点O ，底边BC x ∥轴，双曲线k y x过,A B 两点，过点C 作CD y ∥轴交双曲线于点D ，若12BCD S ，则k 的值是（）A.6B.12C.92D.9【答案】C【解析】【分析】设,k B b b ，根据反比例函数的中心对称性可得,k A b b，然后过点A 作AE BC 于E ，求出4BC b ，点D 的横坐标为3b ，再根据12BCD S 列式求出CD ，进而可得点D 的纵坐标，将点D 坐标代入反比例函数解析式即可求出k 的值．【详解】解：由题意，设,k B b b，∵AB 过原点O ，∴,k A b b，过点A 作AE BC 于E ，∵ABC 是等腰三角形，∴ 2CE BE b b b ，∴4BC b ，点D 的横坐标为3b ，∵底边BC x ∥轴，CD y ∥轴，∴1141222BCD S BC CD b CD，∴6CD b ，∴点D 的纵坐标为66k k b b b，∴63,k D b b，∴ 6336k k b k b，解得：92k ，故选：C ．【点睛】本题考查了反比例函数的图象和性质，中心对称的性质，等腰三角形的性质等知识，设出点B 坐标，正确表示出点D 的坐标是解题的关键．9.如图，在平面直角坐标中，矩形ABCD 的边5,:1:4AD OA OD ，将矩形ABCD 沿直线OE 折叠到如图所示的位置，线段1OD 恰好经过点B ，点C 落在y 轴的点1C 位置，点E 的坐标是（）A.1,2 B.()1,2- C. 51,2 D.15,2【答案】D【解析】【分析】首先证明11AOB D C O ，求出2AB CD ，连结OC ，设BC 与1OC 交于点F ，然后求出15OC OC 1252C F ，再用含EF 的式子表示出1EC ，最后在1Rt EFC 中，利用勾股定理构建方程求出EF 即可解决问题．【详解】解：∵矩形ABCD 的边5AD ，:1:4OA OD ，∴1OA ，4OD ，5BC ，由题意知1AB OC ∥，∴11ABO D OC ，又∵1190BAO OD C ，∴11AOB D C O ，∴111D C OA AB OD ，由折叠知14OD OD ，11D C DC AB ，∴14AB AB ，∴2AB ，即2CD ，连接OC ，设BC 与1OC 交于点F ，∴2222425OC OD CD ∵90FOA OAB ABF ，∴四边形OABF 是矩形，∴2AB OF ，190BFO EFC ，1OA BF ，∴514CF ，由折叠知1OC OC 14EC EC CF EF EF ，∴112C F OC OF ，∵在1Rt EFC 中，22211EF C F EC ，∴ 22224EF EF ，解得：1 EF ，∴点E 的坐标是12 ，故选：D ．【点睛】本题考查了矩形的判定和性质，相似三角形的判定和性质，折叠的性质以及勾股定理的应用等知识，通过证明三角形相似，利用相似三角形的性质求出AB 的长是解题的关键．10.如图，在正方形ABCD 中，点,E F 分别是,AB BC 上的动点，且AF D E ，垂足为G ，将ABF △沿AF 翻折，得到,AMF AM △交DE 于点P ，对角线BD 交AF 于点H ，连接,,,HM CM DM BM ，下列结论正确的是：①AF DE ；②BM DE ∥；③若CM FM ，则四边形BHMF 是菱形；④当点E 运动到AB 的中点，tan BHF ；⑤2EP DH AG BH ．（）A.①②③④⑤B.①②③⑤C.①②③D.①②⑤【答案】B【解析】【分析】利用正方形的性质和翻折的性质，逐一判断，即可解答．【详解】解：∵四边形ABCD 是正方形，90DAE ABF ，DA AB ，AF DE ∵，90BAF AED ，90BAF AFB ∵，AED BFA ，AAS ABF AED △≌△，AF DE ，故①正确，∵将ABF △沿AF 翻折，得到AMF ，BM AF ，∵AF D E ，BM DE ∥，故②正确，当CM FM 时，90CMF ，90AMF ABF ∵，180AMF CMF ，即,,A M C 在同一直线上，45MCF ，9045MFC MCF ，通过翻折的性质可得45HBF HMF ，BF MF ，∴HMF MFC ，HBC MFC ，,BC MH HB MF ∥∥，四边形BHMF 是平行四边形，BF MF ∵，平行四边形BHMF 是菱形，故③正确，当点E 运动到AB 的中点，如图，设正方形ABCD 的边长为2a ，则AE BF a ，在Rt AED △中，225DE AD AE a AF ，,45AHD FHB ADH FBH ∵，AHD FHB △∽△，122FHBFaAH AD a ，22533AH AF a ，90AGE ABF ∵，AGF ABF △∽△，555AE EG AG AF BF AB a ，5555EG BF a ，52555AG AB a ，55DG ED EG a ，4515GH AH AG a ，BHF DHA ∵，在Rt DGH △中，tan tan 3DGBHF DHA GH ，故④错误，AHD FHB ∵△∽△，12BHDH ，11222333BH BD a a ，2222333DH BD a a ，AF EP ∵，根据翻折的性质可得2525EP EG a ，25315EP DH a a a，2225315AG BH a a a，2215EP DH AG BH a，故⑤正确；综上分析可知，正确的是①②③⑤．故选：B ．【点睛】本题考查了正方形的性质，翻折的性质，相似三角形的判定和性质，正切的概念，熟练按照要求做出图形，利用寻找相似三角形是解题的关键．二、填空题（每小题3分，共30分）11.据交通运输部信息显示：2023年“五一”假期第一天，全国营运性客运量约5699万人次，将5699万用科学记数法表示为__________．【答案】75.69910 【解析】【分析】科学记数法的表示形式为10n a 的形式，其中110a ，n 为整数，确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同.当原数绝对值10 时，n 是正数；当原数的绝对值1 时，n 是负数．【详解】5699万756990000 5.69910 ，故答案为：75.69910 ．【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为10n a 的形式，其中110a ，n 为整数，表示时关键要正确确定a 的值以及n 的值．12.函数中，自变量x 的取值范围是____________．【答案】3x 【解析】【详解】解：由题意得，30x ，解得3x ．13.如图，在矩形ABCD 中对角线AC ，BD 交于点O ，请添加一个条件______________，使矩形ABCD 是正方形（填一个即可）【答案】AB BC 或AC BD 【解析】【分析】根据正方形的判定定理可知：邻边相等的矩形是正方形，对角线互相垂直的矩形是正方形.【详解】∵邻边相等的矩形是正方形，∴可添加条件AB BC或者∵对角线互相垂直的矩形是正方形∴还可以添加条件AC BD【点睛】本题考查正方形的判定，找出正方形与矩形的性质差异，即为可添加的条件.14.一个不透明的袋子中装有3个红球和2个白球，这些小球除标号外完全相同，随机摸出两个小球，恰好是一红一白的概率是__________．【答案】35##0.6【解析】【分析】首先根据题意列出表格，然后由表格求得所有等可能的结果与随机摸出一红一白的情况，再利用概率公式即可求得答案．【详解】解：列表得：红1红2红3白1白2红1（红1，红2）（红1，红3）（红1，白1）（红1，白2）红2（红2，红1）（红2，红3）（红2，白1）（红2，白2）红3（红3，红1）（红3，红2）（红3，白1）（红3，白2）白1（白1，红1）（白1，红2）（白1，红3）（白1，白2）白2（白2，红1）（白2，红2）（白2，红3）（白2，白1）由列表可知：共有20种等可能的结果，其中随机摸出两个小球，恰好是一红一白的情况有12种，∴恰好是一红一白的概率是123205，故答案为：35．【点睛】本题考查的是用列表法或画树状图法求概率．注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．用到的知识点为：概率＝所求情况数与总情况数之比．15.关于x 的不等式组501x x m有3个整数解，则实数m 的取值范围是__________．【答案】32m ##23m 【解析】【分析】解不等式组，根据不等式组有3个整数解得出关于m 的不等式组，进而可求得m 的取值范围．【详解】解：解不等式组501x x m得：1x m ，∵关于x 的不等式组501x x m有3个整数解，∴这3个整数解为4 ，3 ，2 ，∴211m ，解得：32m ，故答案为：32m ．【点睛】本题考查了解一元一次不等式组，一元一次不等式组的整数解，正确得出关于m 的不等式组是解题的关键．16.如图，AB 是O 的直径，PA 切O 于点A ，PO 交O 于点C ，连接BC ，若28B ，则P __________ ．【答案】34【解析】【分析】首先根据等边对等角得到28B OCB ，然后利用外角的性质得到56AOC B OCB ，利用切线的性质得到90OAP ，最后利用三角形内角和定理求解即可．【详解】解：∵28B ，OB OC ，∴28B OCB ，∴56AOC B OCB ，∵PA 切O 于点A ，∴90OAP ，∴18034P OAP AOP ．故答案为：34．【点睛】此题考查了切线的性质和三角形的外角的性质，三角形内角和定理等知识，解题的关键是熟练掌握以上知识点．17.已知圆锥的母线长13cm ，侧面积265cm ，则这个圆锥的高是__________cm ．【答案】12【解析】【分析】利用圆锥的侧面积公式可得到底面半径，再利用勾股定理即可得到高．【详解】解：根据圆锥侧面积公式S rl 侧变形可得m 655c 13S r l侧，根据圆锥母线公式l ，可得12cm h ，故答案为：12．【点睛】本题考查了圆锥的侧面积公式和母线公式，熟知上述公式是解题的关键．18.在Rt ACB △中，30,2BAC CB ，点E 是斜边AB 的中点，把Rt ABC △绕点A 顺时针旋转，得Rt AFD △，点C ，点B 旋转后的对应点分别是点D ，点F ，连接CF ，,EF CE ，在旋转的过程中，CEF △面积的最大值是__________．【答案】4 4【解析】【分析】过点A 作AG CE 交CE 的延长线于点G ，求出12AG AC，然后由旋转的性质可知点F 在以A 为圆心AB 的长为半径的圆上运动，则可得如图中G 、A 、F 三点共线时点F 到直线CE 的距离最大，求出距离的最大值，然后计算即可．【详解】解：如图，在Rt ACB △中，30BAC ，2CB ，点E 是斜边AB 的中点，∴24AB CB ，122CE AB AE，AC ，∴30ECA BAC ，过点A 作AG CE 交CE 的延长线于点G ，∴12AG AC，又∵在旋转的过程中，点F 在以A 为圆心AB 的长为半径的圆上运动，4AF AB ，∴点F 到直线CE 的距离的最大值为4 ，（如图，G 、A 、F 三点共线时）∴CEF △面积的最大值 11424422CE故答案为：4 ．【点睛】本题考查了含30 直角三角形的性质，直角三角形斜边中线的性质，旋转的性质，圆的基本性质等知识，根据旋转的性质求出点F 到直线CE 距离的最大值是解答本题的关键．19.矩形ABCD 中，3,9AB AD ，将矩形ABCD 沿过点A 的直线折叠，使点B 落在点E 处，若ADE V 是直角三角形，则点E 到直线BC 的距离是__________．【答案】6或3 或3 【解析】【分析】由折叠的性质可得点E 在以点A 为圆心，AB 长为半径的圆上运动，延长BA 交A 的另一侧于点E ，则此时ADE V 是直角三角形，易得点E 到直线BC 的距离；当过点D 的直线与圆相切于点E 时，ADE V 是直角三角形，分两种情况讨论即可求解．【详解】解：由题意矩形ABCD 沿过点A 的直线折叠，使点B 落在点E 处，可知点E 在以点A 为圆心，AB 长为半径的圆上运动，如图，延长BA 交A 的另一侧于点E ，则此时ADE V 是直角三角形，点E 到直线BC 的距离为BE 的长度，即26BE AB ，当过点D 的直线与圆相切与点E 时，ADE V 是直角三角形，分两种情况，①如图，过点E 作EHBC 交BC 于点H ，交AD 于点G ，∵四边形ABCD 是矩形，∴EG AD ，∴四边形ABHG 是矩形，3GH AB ∵3AE AB ，AE DE ，9AD ，由勾股定理可得229362DE ∵1122AED S AE DE AD EG，∴22EG ，∴E 到直线BC 的距离322EH EG GH ，②如图，过点E 作EN BC 交BC 于点N ，交AD 于点M ，∵四边形ABCD 是矩形，∴NM AD ，∴四边形ABNM 是矩形，3MN AB ∵3AE AB ，AE DE ，9AD ，由勾股定理可得DE ∵1122AED S AE DE AD EM△，∴EM ，∴E 到直线BC 的距离3EN MN GN ，综上，6或3 或3 ，故答案为：6或3 或3 ．【点睛】本题考查了矩形的折叠问题切线的应用，以及勾股定理，找到点E 的运动轨迹是解题的关键．20.如图，在平面直角坐标系中，ABC 的顶点A 在直线1:3l y x上，顶点B 在x 轴上，AB 垂直x 轴，且OB ，顶点C 在直线2:l y 上，2BC l ；过点A 作直线2l 的垂线，垂足为1C ，交x 轴于1B ，过点1B 作11A B 垂直x 轴，交1l 于点1A ，连接11A C ，得到第一个111A B C △；过点1A 作直线2l 的垂线，垂足为2C ，交x 轴于2B ，过点2B 作22A B 垂直x 轴，交1l 于点2A ，连接22A C ，得到第二个222A B C △；如此下去，……，则202320232023A B C 的面积是__________．【答案】2【解析】【分析】解直角三角形得出30AOB ，60BOC ，求出ABC S，证明111ABC A B C ∽△△，222ABC A B C ∽，得出1114A B C ABC S S ， 22222242A B C ABC ABC S S S ，总结得出2222n n n n n A B C ABC ABC S S S ，从而得出20232023202322023404622A B C S ．【详解】解：∵OB ，∴B ，∵AB x 轴，∴点A的横坐标为∵13:3l y x，∴点A的纵坐标为33，∴3tan 3AB AOB OB，∴30AOB ，∵2:l y ，∴设,C C C x y，则C C y ，∴tan CCy BOC x∴60BOC ，∴1cos602OC OB，3sin 602BC OB ∵130AOC BOC AOB ，∴1AOB AOC ，∴OA 平分BOC ，∵12AC l ，AB OB ，∴13AC AB，∵1AB AC ，OA OA ，∴1Rt Rt OAB OAC ≌，∴1OC OB ，∴11CC OC OC ∴12ABC OAB ACC BOCS S S S1261261223232∵2BC l ，∴90BCO ，∴906030CBO ，∵112B C l ，2BC l ，222B C l ，∴2112B B C C B C ∥∥，∴112230C B O C B O CBO ，∴1122C B O C B O CBO AOB ，∴1AO AB ，112A O A B ，∵AB x 轴，11A B x 轴，∴112OB OB，1212OB OB ，∵AB x 轴，11A B x 轴，22A B x 轴，∴1122AB A B A B ∥∥，∴11112AB OB A B OB ，22214AB OB A B OB ，∵2112B B C C B C ∥∥，∴11112BC OB B C OB ，22214BC OB B C OB ，∴1111AB BCA B B C ，∵111903060ABC A B C ，∴111ABC A B C ∽△△，同理222ABC A B C ∽，∴1114A B C ABC S S ，22222242A B C ABC ABC S S S ，∴2222n n nnn A B C ABC ABC S S S ，∴2023202320232202322A B C S故答案为：2．【点睛】本题主要考查了三角形相似的判定和性质，解直角三角形，三角形面积的计算，平行线的判定和性质，一次函数规律探究，角平分线的性质，三角形全等的判定和性质，解题的关键是得出一般规律2222n n n n n A B C ABC ABC S S S ．三、解答题（满分60分）21.先化简，再求值：2222111m m m m m，其中tan 601m ．【答案】1m m ，原式33【解析】【分析】先根据分式的混合运算法则化简，然后求出1m，最后代值计算即可．【详解】解：2222111m m m m m211121m m m m m21111m m m m m1mm，∵tan 6011m ，∴原式333．【点睛】本题主要考查了分式的化简求值，求特殊角三角函数值，正确计算是解题的关键．22.如图，在平面直角坐标系中，已知ABC 的三个顶点坐标分别是 2,1,1,2A B ， 3,3C ．（1）将ABC 向上平移4个单位，再向右平移1个单位，得到111A B C △，请画出111A B C △．（2）请画出ABC 关于y 轴对称的222A B C △．（3）将222A B C △着原点O 顺时针旋转90 ，得到333A B C △，求线段22A C 在旋转过程中扫过的面积（结果保留）．【答案】（1）见解析（2）见解析（3）134【解析】【分析】（1）根据平移的性质得出对应点的位置进而画出图形；（2）利用轴对称的性质得出对应点的位置进而画出图形；（3）画出旋转后的图形，根据33223223C A A C C DEC C OC DOE S S S S 扇扇即可得出答案．【小问1详解】解：如图所示，111A B C △即为所求；【小问2详解】如图所示，222A B C △即为所求；【小问3详解】将222A B C △着原点O 顺时针旋转90 ，得到333A B C △，设 23A A 所在圆交3OC 于点D ，交2OC 于点E ，∵23OA OA ，23OC OC ，23C E C D ，3290A OA ∵，2390C OC ，32A OD A OE ， 32A D A E ，3322A C D A C E S S 曲边曲边，332OC ，25OD OA ，332232232222390909090133603603603604C A A C C DEC C OC DOE OC OD S S S S扇扇，故线段22A C 在旋转过程中扫过的面积为134．【点睛】本题考查平移、轴对称变换作图和旋转的性质以及扇形的面积，熟练掌握网格结构准确找出对应点的位置是解题的关键．23.如图，抛物线23y ax bx 与x 轴交于 3,0,1,0A B 两点，交y 轴于点C．（1）求抛物线的解析式．（2）拋物线上是否存在一点P ，使得12PBC ABC S S ，若存在，请直接写出点P 的坐标；若不存在，请说明理由．【答案】（1）223y x x （2）存在，点P 的坐标为 2,3 或 3,12 【解析】【分析】（1）采用待定系数法，将点A 和点B 坐标直接代入抛物线23y ax bx ，即可求得抛物线的解析式．（2）过线段AB 的中点D ，且与BC 平行的直线上的点与点B ，点C 连线组成的三角形的面积都等于12ABC S ，则此直线与抛物线的交点即为所求；求出此直线的解析式，与抛物线解析式联立，即可求得答案．【小问1详解】解：因为抛物线23y ax bx 经过点 30A ,和点 10B ,两点，所以933030a b a b，解得12a b，所以抛物线解析式为：223y x x ．【小问2详解】解：如图，设线段AB 的中点为D ，可知点D 的坐标为 1,0 ，过点D 作与BC 平行的直线l ，假设与抛物线交于点1P ，2P （1P 在2P 的左边），（2P 在图中未能显示）．设直线BC 的函数解析式为 10y kx b k ．因为直线BC 经过点 10B ,和 0,3C ，所以1103k b b，解得133k b ，所以，直线BC 的函数解析式为：33y x ．又12//PP BC ，可设直线12PP 的函数解析式为23y x b ，因为直线12PP 经过点D1,0 ，所以230b ．解得23b ．所以，直线12PP 的函数解析式为33y x ．根据题意可知，12DBC ABC S S．又12//PP BC ，所以，直线12PP 上任意一点P 与点B ，点C 连线组成的P BC 的面积都满足12P BC ABC S S ．所以，直线12PP 与抛物线223y x x 的交点1P，2P 即为所求，可得23323x x x ，化简，得260x x ，解得1232x x ，，所以，点1P 的坐标为 2,3 ，点2P 的坐标为 3,12 ．故答案为：存在，点P 的坐标为 2,3 或 3,12 ．【点睛】本题主要考查二次函数的图象和性质、一次函数的图象和性质、一元二次方程、一元一次方程等，灵活结合二次函数和一次函数图象特点是解题的关键．24.某中学开展主题为“垃圾分类，绿色生活”的宣传活动、为了解学生对垃圾分类知识的掌握情况，该校团委在校园内随机抽取了部分学生进行问卷调在，将他们的得分按A ：优秀，B ：良好，C ：合格，D ：不合格四个等级进行统计，并绘制了如下不完整的条形统计图和扇形统计图．（1）这次学校抽查的学生人数是__________人；（2）将条形图补充完整；（3）扇形统计图中C组对应的扇形圆心角度数是__________ ；（4）如果该校共有2200人，请估计该校不合格的人数．【答案】（1）40（2）见解析（3）90（4）220人【解析】【分析】（1）用A：优秀的人数除以其人数占比即可求出参与调查的学生人数；（2）先求出C：合格的人数，再补全统计图即可；（3）用360度乘以C组对应人数占比即可得到答案；（4）用2200乘以样本中D组对应的人数占比即可得到答案．【小问1详解】人，解：1230%40∴这次学校抽查的学生人数是40人，故答案为：40；【小问2详解】人，解：由（1）得C：合格的人数为401214410补全统计图如下所示：【小问3详解】解：103609040，∴扇形统计图中C 组对应的扇形圆心角度数是90 ，故答案为：90；【小问4详解】解：4220022040人，∴估计该校不合格的人数为220人．【点睛】本题主要考查了条形统计图与扇形统计图信息相关联，用样本估计总体，正确读懂统计图是解题的关键．25.已知甲，乙两地相距480km ，一辆出租车从甲地出发往返于甲乙两地，一辆货车沿同一条公路从乙地前往甲地，两车同时出发，货车途经服务区时，停下来装完货物后，发现此时与出租车相距120km ，货车继续出发2h 3后与出租车相遇．出租车到达乙地后立即按原路返回，结果比货车早15分钟到达甲地．如图是两车距各自出发地的距离 km y 与货车行驶时间 h x 之间的函数图象，结合图象回答下列问题：（1）图中a 的值是__________；（2）求货车装完货物后驶往甲地的过程中，距其出发地的距离 km y 与行驶时间 h x 之间的函数关系式；（3）直接写出在出租车返回的行驶过程中，货车出发多长时间与出租车相距12km ．【答案】（1）120（2）60y x（3）12517h 或13117h 【解析】【分析】（1）利用待定系数法求得OC 的解析式，将 1,a 代入解析式，解方程即可解答；（2）根据题意可得a 的值，即为货车装货时距离乙地的长度，结合货车停下来装完货物后，发现此时与出租车相距120km ，可求出装货时间，即点B 的坐标，再根据货车继续出发2h 3后与出租车相遇，求出装完货后货车的速度，即直线BG 的解析式中k 的值，最后将点B 坐标代入直线BG 的解析式，利用待定系数法即可解答；（3）根据（2）中直线BG 的解析式求得点F 的坐标，结合题意，可得点E 的坐标，从而可得到出租车返回时的速度，然后进行分类讨论：①出租车和货车第二次相遇前，相距12km 时；②出租车和货车第二次相遇后，距离12km 时，分别进行解答即可．【小问1详解】解：结合图象，可得 4,480C ，设直线OC 的解析式为y kx ，将 4,480C 代入解析式，可得4804k ，解得120k ，直线OC 的解析式为120y x ，把 1,a 代入120y x ，得120a ，故答案为：120；【小问2详解】解：根据货车停下来装完货物后，发现此时与出租车相距120km ，可得此时出租车距离乙地为120120240km ，出租车距离甲地为480240240km ，把240y 代入120y x ，可得240120x ，解得2x ，货车装完货时，2x ，可得 2,120B ，根据货车继续出发2h 3后与出租车相遇，可得23（出租车的速度货车的速度）120 ，根据直线OC 的解析式为120y x ，可得出租车的速度为120km h ，相遇时，货车的速度为212012060km h 3，故可设直线BG 的解析式为60y x b ，将 2,120B 代入60y x b ，可得120120b ，解得0b ，直线BG 的解析式为60y x ，故货车装完货物后驶往甲地的过程中，距其出发地的距离 km y 与行驶时间 h x 之间的函数关系式为60y x ；【小问3详解】解：把480y 代入60y x ，可得48060x ，解得8x ，8,480G ， 8,0F ，根据出租车到达乙地后立即按原路返回，结果比货车早15分钟到达甲地，可得151604EF,31,04E，出租车返回时的速度为314804128km h 4，设在出租车返回的行驶过程中，货车出发t 小时，与出租车相距12km ，此时货车距离乙地为60km t ，出租车距离乙地为 1284128512km t t ，①出租车和货车第二次相遇前，相距12km 时；可得 116012851212t t ，解得112517t，②出租车和货车第二次相遇后，相距12km 时；可得 221285126012t t ，解得213117t，故在出租车返回的行驶过程中，货车出发12517h 或13117h 与出租车相距12km ．【点睛】本题考查了从函数图象获取信息，用待定系数法求一次函数，一次函数的实际应用，能准确地理解题意，根据题中信息求得所需数据是解题的关键．26.如图①，ABC 和ADE V 是等边三角形，连接DC ，点F ，G ，H 分别是,DE DC 和BC 的中点，连接,FG FH ．易证：FH．若ABC 和ADE V 都是等腰直角三角形，且90BAC DAE ，如图②：若ABC 和ADE V 都是等腰三角形，且120BAC DAE ，如图③：其他条件不变，判断FH 和FG 之间的数量关系，写出你的猜想，并利用图②或图③进行证明．【答案】图②中2FH ，图③中FH FG ，证明见解析【解析】【分析】图②：如图②所示，连接BD HG CE ，，，先由三角形中位线定理得到12FG CE FG∥，，12GH BD GH BD∥，，再证明ABD ACE ≌△△得到CE BD ACE ABD ，∠∠，则FG HG ，进一步证明90FGH ，即可证明HGF △是等腰直角三角形，则2FH FG ；图③：仿照图②证明HGF △是等边三角形，则FH FG ．【详解】解：图②中2FH FG ，图③中FH FG ，图②证明如下：如图②所示，连接BD HG CE ，，，∵点F ，G 分别是DE DC ，的中点，∴FG 是CDE 的中位线，∴12FG CE FG CE∥，，同理可得12GH BD GH BD ∥，，∵ABC 和ADE V 都是等腰直角三角形，且90BAC DAE ，∴AB AC BAD CAE AD AE ，，，∴ SAS ABD ACE △≌△，∴CE BD ACE ABD ，∠∠，∴FG HG ，∵BD GH FG CE ∥，∥，∴FGH FGD HGDDCE GHC GCH ∠∠∠DBC DCB ACD ACE ∠∠∠∠DBC ABD ACB∠∠∠ACB ABC90 ，∴HGF △是等腰直角三角形，∴FH ；图③证明如下：如图③所示，连接BD HG CE ，，，∵点F ，G 分别是DE DC ，的中点，∴FG 是CDE 的中位线，∴12FG CE FG CE ∥，，同理可得12GH BD GH BD ∥，，∵ABC 和ADE V 都是等腰三角形，且120BAC DAE ，∴AB AC BAD CAE AD AE ，，，∴ SAS ABD ACE △≌△，∴CE BD ACE ABD ，∠∠，∴FG HG ，∵BD GH FG CE ∥，∥，∴FGH FGD HGDDCE GHC GCH∠∠∠DBC DCB ACD ACE∠∠∠∠DBC ABD ACB∠∠∠ACB ABC180BAC60 ，∴HGF △是等边三角形，∴FH FG ．【点睛】本题主要考查了全等三角形的性质与判定，三角形中位线定理，等边三角形的性质与判定，勾股定理等等，正确作出辅助线构造全等三角形是解题的关键．27.2023年5月30日上午9点31分，神舟十六号载人飞船在酒泉发射中心发射升空，某中学组织毕业班的同学到当地电视台演播大厅观看现场直播，学校准备为同学们购进A ，B 两款文化衫，每件A 款文化衫比每件B 款文化衫多10元，用500元购进A 款和用400元购进B 款的文化衫的数量相同．（1）求A 款文化衫和B 款文化衫每件各多少元？（2）已知毕业班的同学一共有300人，学校计划用不多于14800元，不少于14750元购买文化衫，求有几种购买方案？（3）在实际购买时，由于数量较多，商家让利销售，A 款七折优惠，B 款每件让利m 元，采购人员发现（2）中的所有购买方案所需资金恰好相同，试求m 值．【答案】（1）A 款文化衫每件50元，则B 款文化衫每件40元，（2）一共有六种购买方案（3）5m 【解析】【分析】（1）设A 款文化衫每件x 元，则B 款文化衫每件 10x 元，然后根据用500元购进A 款和用400元购进B 款的文化衫的数量相同列出方程求解即可；（2）设购买A 款文化衫a 件，则购买B 款文化衫 300a 件，然后根据，学校计划用不多于14800元，不少于14750元购买文化衫列出不等式组求解即可；（3）设购买资金为W 元，购买A 款文化衫a 件，则购买B 款文化衫300a 件，求出 512000300W m a m ，根据（2）中的所有购买方案所需资金恰好相同，可得W 的取值与a 的值无关，由此即可求出5m ．【小问1详解】解：设A 款文化衫每件x 元，则B 款文化衫每件 10x 元，由题意得，50040010x x ，解得50x ，。

2024年黑龙江省龙东地区中考数学真题卷及答案解析

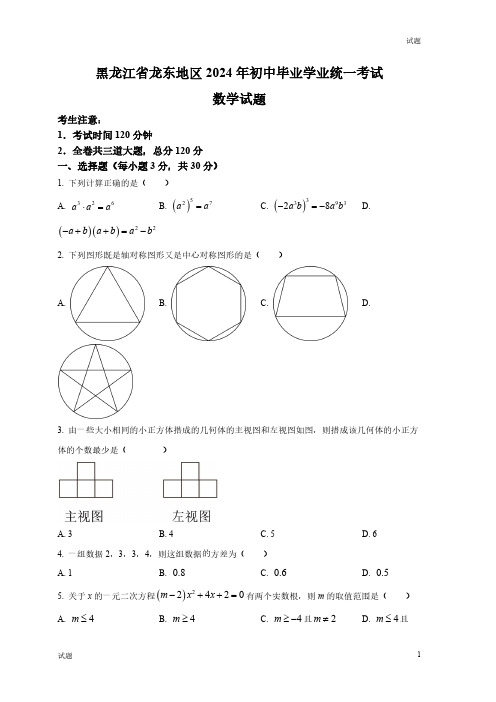
黑龙江省龙东地区2024年初中毕业学业统一考试数学试题考生注意：1．考试时间120分钟2．全卷共三道大题，总分120分一、选择题（每小题3分，共30分）1.下列计算正确的是（）A.326a a a ⋅= B.()527a a = C.()339328a b a b -=- D.()()22a b a b a b -++=-2.下列图形既是轴对称图形又是中心对称图形的是（）A. B. C. D.3.由一些大小相同的小正方体搭成的几何体的主视图和左视图如图，则搭成该几何体的小正方体的个数最少是（）A.3B.4C.5D.64.一组数据2，3，3，4，则这组数据的方差为（）A.1B.0.8C.0.6D.0.55.关于x 的一元二次方程()22420m x x -++=有两个实数根，则m 的取值范围是（）A.4m ≤ B.4m ≥ C.4m ≥-且2m ≠ D.4m ≤且2m ≠6.已知关于x 的分式方程2333x xkx -=--无解，则k 的值为（）A.2k =或1k =- B.2k =- C.2k =或1k = D.1k =-7.国家“双减”政策实施后，某班开展了主题为“书香满校园”的读书活动．班级决定为在活动中表现突出的同学购买笔记本和碳素笔进行奖励（两种奖品都买），其中笔记本每本3元，碳素笔每支2元，共花费28元，则共有几种购买方案（）A .5B.4C.3D.28.如图，双曲线()120y x x=>经过A 、B 两点，连接OA 、AB ，过点B 作BD y ⊥轴，垂足为D ，BD 交OA 于点E ，且E 为AO 的中点，则AEB △的面积是（）A.4.5B.3.5C.3D.2.59.如图，菱形ABCD 中，点O 是BD 的中点，AM BC ⊥，垂足为M ，AM 交BD 于点N ，2OM =，8BD =，则MN 的长为（）A.B.455C.355D.10.如图，在正方形ABCD 中，点H 在AD 边上（不与点A 、D 重合），90BHF ∠=︒，HF 交正方形外角的平分线DF 于点F ，连接AC 交BH 于点M ，连接BF 交AC 于点G ，交CD 于点N ，连接BD ．则下列结论：①45HBF ∠=︒；②点G 是BF 的中点；③若点H 是AD 的中点，则sin 10NBC ∠=；④BN =；⑤若12AH D H =，则112BND AHM S S =△△，其中正确的结论是（）A.①②③④B.①③⑤C.①②④⑤D.①②③④⑤二、填空题（每小题3分，共30分）11.国家统计局公布数据显示，2023年我国粮食总产量是13908亿斤，将13908亿用科学记数法表示为________．12.在函数32y x =+中，自变量x 的取值范围是________．13.已知菱形ABCD 中对角线AC BD 、相交于点O ，添加条件_________________可使菱形ABCD 成为正方形．14.七年一班要从2名男生和3名女生中选择两名学生参加朗诵比赛，恰好选择1名男生和1名女生的概率是________．15.关于x 的不等式组420102x x a -≥⎧⎪⎨->⎪⎩恰有3个整数解，则a 的取值范围是________．16.如图，ABC 内接于O ，AD 是直径，若25B ∠=︒，则CAD ∠________︒．17.若圆锥的底面半径为3，侧面积为36π，则这个圆锥侧面展开图的圆心角是________︒．18.如图，在Rt ABC △中，90ACB ∠=︒，1tan 2BAC ∠=，2BC =，1AD =，线段AD 绕点A 旋转，点P 为CD 的中点，则BP 的最大值是________．19.矩形ABCD 中，3AB =，4BC =，将AB 沿过点A 的一条直线折叠，折痕交直线BC 于点P （点P 不与点B 重合），点B 的对称点落在矩形对角线所在的直线上，则PC 长为________．20.如图，在平面直角坐标系中，正方形OMNP 顶点M 的坐标为()3,0，OAB 是等边三角形，点B 坐标是()1,0，OAB 在正方形OMNP 内部紧靠正方形OMNP 的边（方向为O M N P O M →→→→→→ ）做无滑动滚动，第一次滚动后，点A 的对应点记为1A ，1A 的坐标是()2,0；第二次滚动后，1A 的对应点记为2A ，2A 的坐标是()2,0；第三次滚动后，2A 的对应点记为3A ，3A 的坐标是313,22⎛⎫- ⎪ ⎪⎝⎭；如此下去，……，则2024A 的坐标是________．三、解答题（满分60分）21.先化简，再求值：22222111m m m m m m ⎛⎫-+÷- ⎪-+⎝⎭，其中cos60m =︒．22.如图，在正方形网格中，每个小正方形的边长都是1个单位长度，在平面直角坐标系中，ABC 的三个顶点坐标分别为()1,1A -，()2,3B -，()5,2C -．（1）画出ABC 关于y 轴对称的111A B C △，并写出点1B 的坐标；（2）画出ABC 绕点A 逆时针旋转90︒后得到的22AB C ，并写出点2B 的坐标；（3）在（2）的条件下，求点B 旋转到点2B 的过程中所经过的路径长（结果保留π）23.如图，抛物线2y x bx c =-++与x 轴交于A 、B 两点，与y 轴交于点C ，其中()1,0B ，()0,3C ．（1）求抛物线的解析式．（2）在第二象限的抛物线上是否存在一点P ，使得APC △的面积最大．若存在，请直接写出点P 坐标和APC △的面积最大值；若不存在，请说明理由．24.为贯彻落实教育部办公厅关于“保障学生每天校内、校外各一小时体育活动时间”的要求，某学校要求学生每天坚持体育锻炼．学校从全体男生中随机抽取了部分学生，调查他们的立定跳远成绩，整理如下不完整的频数分布表和统计图，结合下图解答下列问题：组别分组（cm ）频数A 50100x <≤3B 100150x <≤m C 150200x <≤20D 200250x <≤14E250300x <≤5（1）频数分布表中m =，扇形统计图中n =．（2）本次调查立定跳远成绩的中位数落在组别．（3）该校有600名男生，若立定跳远成绩大于200cm 为合格，请估计该校立定跳远成绩合格的男生有多少人？25.甲、乙两货车分别从相距225km 的A 、B 两地同时出发，甲货车从A 地出发途经配货站时，停下来卸货，半小时后继续驶往B 地，乙货车沿同一条公路从B 地驶往A 地，但乙货车到达配货站时接到紧急任务立即原路原速返回B 地，结果比甲货车晚半小时到达B 地．如图是甲、乙两货车距A 地的距离()km y 与行驶时间()h x 之间的函数图象，结合图象回答下列问题：（1）甲货车到达配货站之前的速度是km/h ，乙货车的速度是km/h ；（2）求甲货车在配货站卸货后驶往B 地的过程中，甲货车距A 地的距离()km y 与行驶时间()h x 之间的函数解析式；（3）直接写出甲、乙两货车在行驶的过程中，出发多长时间甲、乙两货车与配货站的距离相等．26.已知ABC 是等腰三角形，AB AC =，12MAN BAC ∠=∠，MAN ∠在BAC ∠的内部，点M 、N 在BC 上，点M 在点N 的左侧，探究线段BM NC MN 、、之间的数量关系．（1）如图①，当90BAC ∠=︒时，探究如下：由90BAC ∠=︒，AB AC =可知，将ACN △绕点A 顺时针旋转90︒，得到ABP ，则CN BP =且90PBM ∠=︒，连接PM ，易证AMP AMN △≌△，可得MP MN =，在Rt PBM △中，222BM BP MP +=，则有222BM NC MN +=．（2）当60BAC ∠=︒时，如图②：当120BAC ∠=︒时，如图③，分别写出线段BM NC MN、、之间的数量关系，并选择图②或图③进行证明．27.为了增强学生的体质，某学校倡导学生在大课间开展踢毽子活动，需购买甲、乙两种品牌毽子．已知购买甲种品牌毽子10个和乙种品牌毽子5个共需200元；购买甲种品牌毽子15个和乙种品牌毽子10个共需325元．（1）购买一个甲种品牌毽子和一个乙种品牌毽子各需要多少元？（2）若购买甲乙两种品牌毽子共花费1000元，甲种品牌毽子数量不低于乙种品牌毽子数量的5倍且不超过乙种品牌毽子数量的16倍，则有几种购买方案？（3）若商家每售出一个甲种品牌毽子利润是5元，每售出一个乙种品牌毽子利润是4元，在（2）的条件下，学校如何购买毽子商家获得利润最大？最大利润是多少元？28.如图，在平面直角坐标系中，等边三角形OAB 的边OB 在x 轴上，点A 在第一象限，OA 的长度是一元二次方程2560x x --=的根，动点P 从点O 出发以每秒2个单位长度的速度沿折线OA AB -运动，动点Q 从点O 出发以每秒3个单位长度的速度沿折线OB BA -运动，P 、Q 两点同时出发，相遇时停止运动．设运动时间为t 秒（0 3.6t <<），OPQ △的面积为S ．（1）求点A 的坐标；（2）求S 与t 的函数关系式；（3）在（2）的条件下，当S =M 在y 轴上，坐标平面内是否存在点N ，使得以点O 、P 、M 、N 为顶点的四边形是菱形．若存在，直接写出点N 的坐标；若不存在，说明理由．黑龙江省龙东地区2024年初中毕业学业统一考试数学试题考生注意：1．考试时间120分钟2．全卷共三道大题，总分120分一、选择题（每小题3分，共30分）1.下列计算正确的是（）A.326a a a ⋅= B.()527a a = C.()339328a b a b -=- D.()()22a b a b a b -++=-【答案】C 【解析】【分析】本题主要考查同底数幂的乘法，幂的乘方与积的乘方，平方差公式，运用相关运算法则求出各选项的结果后再进行判断即可．【详解】解：A 、3256a a a a ⋅=≠，故选项A 计算错误，此选项不符合题意；B 、()52107a a a =≠，故选项B 计算错误，此选项不符合题意；C 、()339328a b a b -=-，此选项计算正确，符合题意；D 、()()()()22a b a b b a b a b a -++=-+=-，故选项D 计算错误，此选项不符合题意；故选：C ．2.下列图形既是轴对称图形又是中心对称图形的是（）A. B. C. D.【答案】B【解析】【分析】本题主要考查了轴对称图形和中心对称图形，根据轴对称图形和中心对称图形的定义：如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形；中心对称图形的定义：把一个图形绕着某一个点旋转180 ，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心，进行逐一判断即可．【详解】解：A、是轴对称图形，不是中心对称图形，故A选项不合题意；B、既是轴对称图形又是中心对称图形，故B选项符合题意；C、是轴对称图形，不是中心对称图形，故C选项不合题意；D、是轴对称图形，不是中心对称图形，故D选项不合题意．故选：B．3.由一些大小相同的小正方体搭成的几何体的主视图和左视图如图，则搭成该几何体的小正方体的个数最少是（）A.3B.4C.5D.6【答案】B【解析】【分析】根据三视图的知识，主视图是由4个小正方形组成，而左视图是由4个小正方形组成，故这个几何体的底层最少有3个小正方体，第2层最少有1个小正方体．【详解】解：根据左视图和主视图，这个几何体的底层最少有1+1+1=3个小正方体，第二层最少有1个小正方体，因此组成这个几何体的小正方体最少有3+1=4个．故选B．【点睛】本题考查了由三视图判断几何体，意在考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，正视图疯狂盖，左视图拆违章”就容易得到答案．4.一组数据2，3，3，4，则这组数据的方差为（）A.1 B.0.8C.0.6D.0.5【答案】D 【解析】【分析】本题主要考查了方差的计算，解题的关键是方差的计算公式的识记．根据方差的计算公式，先算出数据的平均数，然后代入公式计算即可得到结果．【详解】平均数为：()233443+++÷=方差为：()()()()222221233333434S ⎡⎤=⨯-+-+-+-⎣⎦()110014=⨯+++0.5=故选：D ．5.关于x 的一元二次方程()22420m x x -++=有两个实数根，则m 的取值范围是（）A.4m ≤B.4m ≥C.4m ≥-且2m ≠D.4m ≤且2m ≠【答案】D 【解析】【分析】本题考查了一元二次方程根的判别式．根据一元二次方程20(0)ax bx c a ++=≠的根的判别式24b ac ∆=-的意义得到20m -≠且0∆≥，即244(2)20m -⨯-⨯≥，然后解不等式组即可得到m 的取值范围．【详解】解：关于x 的一元二次方程()22420m x x -++=有实数根，20m ∴-≠且0∆≥，即244(2)20m -⨯-⨯≥，解得：4m ≤，m ∴的取值范围是4m ≤且2m ≠．故选：D ．6.已知关于x 的分式方程2333x xkx -=--无解，则k 的值为（）A.2k =或1k =-B.2k =- C.2k =或1k = D.1k =-【答案】A 【解析】【分析】本题考查了解分式方程无解的情况，理解分式方程无解的意义是解题的关键．先将分式方程去分母，化为整式方程，再分两种情况分别求解即可．【详解】解：去分母得，2(3)3kx x --=-，整理得，(2)9k x -=-，当2k =时，方程无解，当2k ≠时，令3x =，解得1k =-，所以关于x 的分式方程2333x xkx -=--无解时，2k =或1k =-．故选：A ．7.国家“双减”政策实施后，某班开展了主题为“书香满校园”的读书活动．班级决定为在活动中表现突出的同学购买笔记本和碳素笔进行奖励（两种奖品都买），其中笔记本每本3元，碳素笔每支2元，共花费28元，则共有几种购买方案（）A.5B.4C.3D.2【答案】B 【解析】【分析】本题考查了二元一次方程的应用，找准等量关系，正确列出二元一次方程是解题的关键．设购买x 支笔记本，y 个碳素笔，利用总价=单价⨯数量，即可得出关于x ，y 的二元一次方程，再结合x ，y 均为正整数，即可得出购买方案的个数．【详解】解：设购买x 支笔记本，y 个碳素笔，依题意得：3228x y +=，3142y x ∴=-．又x ，y 均为正整数，∴211x y =⎧⎨=⎩或48x y =⎧⎨=⎩或65x y =⎧⎨=⎩或82x y =⎧⎨=⎩，∴共有4种不同的购买方案．故选：B ．8.如图，双曲线()120y x x=>经过A 、B 两点，连接OA 、AB ，过点B 作BD y ⊥轴，垂足为D ，BD 交OA 于点E ，且E 为AO 的中点，则AEB △的面积是（）A.4.5B.3.5C.3D.2.5【答案】A 【解析】【分析】本题考查了反比例函数，相似三角形的判定与性质等知识，过点A 作AF BD ⊥，垂足为F ，设12,A a a ⎛⎫ ⎪⎝⎭，证明AFE ODE ∽，有AF AE EFOD OE DE==，根据E 为AO 的中点，可得AF OD =，EF DE =，进而有1122EF DE DF a ===，162A AF OD y a===，可得6B y OD a ==，2B x a =，则有32BE BD DE a =-=，问题随之得解．【详解】如图，过点A 作AF BD ⊥，垂足为F ，设12,A a a ⎛⎫⎪⎝⎭，0a >，∵BD y ⊥轴，AF BD ⊥，∴AF y ∥轴，DF a =，∴AFE ODE ∽，∴AF AE EFOD OE DE==，∵E 为AO 的中点，∴AE OE =，∴1AF AE EFOD OE DE===，∴AF OD =，EF DE =∴1122EF DE DF a ===，162A AF OD y a ===，∵B OD y =，∴6B y OD a==，∴2B x a =，∴2B BD x a ==，∴32BE BD DE a =-=，∴116394.52222ABES AF BE a a =⨯⨯=⨯⨯== ，故选：A ．9.如图，菱形ABCD 中，点O 是BD 的中点，AM BC ⊥，垂足为M ，AM 交BD 于点N ，2OM =，8BD =，则MN 的长为（）A.B.455C.355D.【答案】C 【解析】【分析】本题主要考查了解三角形，菱形的性质、直角三角形斜边中线等于斜边一半．先由菱形性质可得对角线AC 与BD 交于点O ，由直角三角形斜边中线等于斜边一半可得2OA OC OM ===，进而由菱形对角线求出边长，由sin sin 5MAC OBC ∠=∠=解三角形即可求出45sin 5MC AC MAC =∠=，35tan 5MN BM OBC =∠=．【详解】解：连接AC ，如图，∵菱形ABCD 中，AC 与BD 互相垂直平分，又∵点O 是BD 的中点，∴A 、O 、C 三点在同一直线上，∴OA OC =，∵2OM =，AM BC ⊥，∴2OA OC OM ===，∵8BD =，∴142OB OD BD ===，∴BC ===，21tan 42OC OBC OB ===∠，∵90ACM MAC ∠+∠=︒，90ACM OBC ∠+∠=︒，∴MAC OBC ∠=∠∴5sin sin5OC MAC OBC BC ∠=∠==，∴sin 5MC AC MAC =∠=，∴456555BM BC MC =-==，∴65135tan 525MN BM OBC =∠=⨯=，故选：C ．10.如图，在正方形ABCD 中，点H 在AD 边上（不与点A 、D 重合），90BHF ∠=︒，HF 交正方形外角的平分线DF 于点F ，连接AC 交BH 于点M ，连接BF 交AC 于点G ，交CD 于点N ，连接BD ．则下列结论：①45HBF ∠=︒；②点G 是BF 的中点；③若点H 是AD 的中点，则10sin 10NBC ∠=；④BN =；⑤若12AH D H =，则112BND AHM S S =△△，其中正确的结论是（）A.①②③④B.①③⑤C.①②④⑤D.①②③④⑤【答案】A 【解析】【分析】连接DG，可得BDAB=AC 垂直平分BD ，先证明点B 、H 、D 、F 四点共圆，即可判断①；根据AC 垂直平分BD ，结合互余可证明DG FG =，即有DG FG BG ==，则可判断②正确；证明ABM DBN ∽，即有BN BDBM AB==，可判断④；根据相似有212ABM DBN S AB S BD ⎛⎫== ⎪⎝⎭ ，根据12AH D H =可得3AH AD =，再证明AHM CBM ∽，可得13AHM ABM S HM S BM == ，即可判断⑤；根据点H 是AD 的中点，设2AD =，即求出BH ==，同理可证明AHM CBM ∽，可得23BM BH ==，即可得BN ==，进而可判断③．【详解】连接DG ，如图，∵四边形ABCD 是正方形，∴45BDC BAC ADB ∠=∠=∠=︒，2BDAB=90BAD ADC ∠=∠=︒，AC 垂直平分BD ，∴90CDP ∠=︒，∵DF 平分CDP ∠，∴1452CDF CDP CDB ∠=∠=︒=∠，∴90BDF CDF CDB ∠=∠+∠=︒，∵90BHF BDF ∠=︒=∠，∴点B 、H 、D 、F 四点共圆，∴45HFB HDB ∠=∠=︒，DHF DBF ∠=∠，∴18045HBF HFB FHB ∠=︒-∠-∠=︒，故①正确，∵AC 垂直平分BD ，∴BG DG =，∴BDG DBG ∠=∠，∵90BDF ∠=︒，∴90BDG GDF DBG DFG ∠+∠=︒=∠+∠，∴GDF DFG ∠=∠，∴DG FG =，∴DG FG BG ==，∴点G 是BF 的中点，故②正确，∵90BHF BAH ∠=︒=∠，∴90AHB DHF AHB ABH ∠+∠=︒=∠+∠，∴DHF ABH ∠=∠，∵DHF DBF ∠=∠，∴ABH DBF ∠=∠，又∵45BAC DBC ∠=∠=︒，∴ABM DBN ∽，∴BN BDBM AB==∴BN =，故④正确，∴212ABM DBN S AB S BD ⎛⎫== ⎪⎝⎭ ，若12AH D H =，则()1122AH HD AD AH ==-，∴3AH AD =，∴13=AH AD ，即13H H A A BC AD ==，∵AD BC ∥，∴AHM CBM ∽，∴13HM AH BM BC ==，∴13AHM ABM S HM S BM == ，∴3ABM AHM S S = ，∵12ABM DBN S S = ，∴26BND ABM AHM S S S == △，故⑤错误，如图，③若点H 是AD 的中点，设2AD =，即2AB BC AD ===，∴112AH AD ==，∴BH ==，同理可证明AHM CBM ∽，∴12HM AH BM BC ==，∴32HM BM BHBM BM +==，∴23BM BH ==，∵BN =，∴BN ==，∵2BC =，∴在Rt BNC △中，23NC ==，10sin 10NC NBC BN ∠==，故③正确，则正确的有：①②③④，故选：A ．【点睛】本题是一道几何综合题，主要考查了正方形的性质，相似三角形的判定与性质，正弦，圆周角定理以及勾股定理等知识，证明点B 、H 、D 、F 四点共圆，ABM DBN ∽，是解答本题的关键．二、填空题（每小题3分，共30分）11.国家统计局公布数据显示，2023年我国粮食总产量是13908亿斤，将13908亿用科学记数法表示为________．【答案】121.390810⨯【解析】【分析】本题考查了科学记数法，科学记数法的表示形式为10n a ⨯的形式，其中1||10a ≤<，n 为整数．确定n 的值时，要看把原来的数，变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值10≥时，n 是正数；当原数的绝对值1＜时，n 是负数，确定a 与n 的值是解题的关键．【详解】1 亿81.010=⨯，13908亿48121.39081010 1.390810=⨯⨯=⨯故答案为：121.390810⨯12.在函数32y x =+中，自变量x 的取值范围是________．【答案】3x ≥##3x ≤【解析】【分析】本题主要考查函数自变量取值范围，分别根据二次根式有意义的条件和分式有意义的条件列出不等式求解即可．【详解】解：根据题意得，30x -≥，且20x +≠，解得，3x ≥，故答案为：3x ≥．13.已知菱形ABCD 中对角线AC BD 、相交于点O ，添加条件_________________可使菱形ABCD 成为正方形．【答案】AC BD =或AB BC ⊥【解析】【分析】本题主要考查的是菱形和正方形的判定，熟练掌握菱形的判定定理是解题的关键，依据正方形的判定定理进行判断即可.【详解】解：根据对角线相等的菱形是正方形，可添加：AC BD =；根据有一个角是直角的菱形是正方形，可添加的：AB BC ⊥；故添加的条件为：AC BD =或AB BC ⊥．14.七年一班要从2名男生和3名女生中选择两名学生参加朗诵比赛，恰好选择1名男生和1名女生的概率是________．【答案】35【解析】【分析】本题考查的是用树状图法求概率．树状图法可以不重复不遗漏的列出所有可能的结果，适合于两步或两步以上完成的事件．用到的知识点为：概率=所求情况数与总情况数之比．画树状图，共有12种等可能的结果，其中选取的2名学生恰好是1名男生、1名女生的结果有6种，再由概率公式求解即可．【详解】解：画树状图如下：由图可知，共有20种等可能的结果，其中选取的2名学生恰好是1名男生、1名女生的结果有12种，∴选取的2名学生恰好是1名男生、1名女生的概率为：123205=，故答案为：35．15.关于x 的不等式组420102x x a -≥⎧⎪⎨->⎪⎩恰有3个整数解，则a 的取值范围是________．【答案】102a -≤<【解析】【分析】本题考查解一元一次不等式（组)，一元一次不等式组的整数解，解答本题的关键是明确解一元一次不等式的方法．先解出不等式组中每个不等式的解集，然后根据不等式组420102x x a -≥⎧⎪⎨->⎪⎩恰有3个整数解，即可得到关于a 的不等式组，然后求解即可．【详解】解：由420-≥x ，得：2x ≤，由102x a ->，得：2x a >，不等式组420102x x a -≥⎧⎪⎨->⎪⎩恰有3个整数解，∴这3个整数解是0，1，2，120a ∴-≤<，解得102a -≤<，故答案为：102a -≤<．16.如图，ABC 内接于O ，AD 是直径，若25B ∠=︒，则CAD ∠________︒．【答案】65【解析】【分析】本题考查了圆周角定理，直角三角形的两个锐角互余，连接CD ，根据直径所对的圆周角是直角得出=90ACD ∠︒，根据同弧所对的圆周角相等得出25D B ∠=∠=︒，进而根据直角三角形的两个锐角互余，即可求解．【详解】解：如图所示，连接CD ，∵ABC 内接于O ，AD 是直径，∴=90ACD ∠︒，∵ AC AC=,25B ∠=︒，∴25D B ∠=∠=︒∴902565CAD ∠=︒-︒=︒，故答案为：65．17.若圆锥的底面半径为3，侧面积为36π，则这个圆锥侧面展开图的圆心角是________︒．【答案】90【解析】【分析】此题主要考查了圆锥的侧面积公式以及与展开图扇形面积关系，求出圆锥的母线长是解决问题的关键．根据圆锥的侧面积公式πS rl =求出圆锥的母线长，再结合扇形面积公式即可求出圆心角的度数．【详解】根据圆锥侧面积公式：πS rl =，可得π336πl ⨯⨯=解得：12l =，2π1236π360n ⨯∴=，解得90n =，∴侧面展开图的圆心角是90︒．故答案为：90．18.如图，在Rt ABC △中，90ACB ∠=︒，1tan 2BAC ∠=，2BC =，1AD =，线段AD 绕点A 旋转，点P 为CD 的中点，则BP 的最大值是________．【答案】12+【解析】【分析】本题考查了解直角三角形，三角形中位线定理，旋转的性质，解题的关键是找出BP 取最大值时B 、P 、M 三点的位置关系．取AC 的中点M ，连接PM 、BM ，利用解三角形求出BM ==形中位线定理推出1122PM AD ==，当AD 在AC 下方时，如果B 、P 、M 三点共线，则BP 有最大值．【详解】解：取AC 的中点M ，连接PM 、BM ．∵90ACB ∠=︒，1tan 2BAC ∠=，2BC =，∴124tan 2BC AC BAC ==÷=∠，∴122AM CM AC ===，∴BM ===∵P 、M 分别是CD AC 、的中点，∴1122PM AD ==．如图，当AD 在AC 下方时，如果B 、P 、M 三点共线，则BP 有最大值，最大值为12BM MP +=+，故答案为：12．19.矩形ABCD 中，3AB =，4BC =，将AB 沿过点A 的一条直线折叠，折痕交直线BC 于点P （点P 不与点B 重合），点B 的对称点落在矩形对角线所在的直线上，则PC 长为________．【答案】52或72或10【解析】【分析】本题考查了矩形与折叠问题，解直角三角形，先根据点B 的对称点落在矩形对角线所在的直线上的不同位置分三种情况，画出对应的图形，再根据矩形性质，利用解直角三角形求出PC 即可．【详解】解：①点B 的对称点落在矩形对角线BD 上，如图1，∵在矩形ABCD 中，3AB CD ==，4BC AD ==，由折叠性质可知：BB AP '⊥，∴BAP BPA BPA CBD∠+∠=∠+∠∴=BAP CBD∠∠∴3tan =tan =4CD BAP CBD BC ∠∠=，∴39tan 642BP AB BAP =∠=⨯=∴97822PC BC BP =-=-=；②点B 的对称点B '落在矩形对角线AC 上，如图2，∵在矩形ABCD 中，3AB CD ==，4BC AD ==，90B Ð=°，∴5AC ===，∴4cos 5BCACB AC ∠==，由折叠性质可知：=90ABP AB P '∠=∠︒，3AB AB '==，∴532B C AC AB ''=-=-=∴452cos 52B CPC ACB '==÷=∠；③点B 的对称点B '落在矩形对角线CA 延长线上，如图3，∵在矩形ABCD 中，3AB CD ==，4BC AD ==，90B Ð=°，∴5AC ===，∴4cos 5BCACB AC ∠==，由折叠性质可知：=90ABP AB P '∠=∠︒，3AB AB '==，∴538B C AC AB ''=+=+=∴4810cos 5B C PC ACB '==÷=∠；综上所述：则PC 长为52或72或10．故答案为：52或72或10．20.如图，在平面直角坐标系中，正方形OMNP 顶点M 的坐标为()3,0，OAB 是等边三角形，点B 坐标是()1,0，OAB 在正方形OMNP 内部紧靠正方形OMNP 的边（方向为O M N P O M →→→→→→ ）做无滑动滚动，第一次滚动后，点A 的对应点记为1A ，1A 的坐标是()2,0；第二次滚动后，1A 的对应点记为2A ，2A 的坐标是()2,0；第三次滚动后，2A 的对应点记为3A ，3A 的坐标是313,22⎛⎫- ⎪ ⎪⎝⎭；如此下去，……，则2024A 的坐标是________．【答案】()1,3【解析】【分析】本题考查了点的坐标变化规律，正方形性质，等边三角形性质，根据三角形的运动方式，依次求出点A 的对应点1A ，2A ，，12A 的坐标，发现规律即可解决问题．【详解】解：正方形OMNP 顶点M 的坐标为()3,0，3OM MN NP OP ∴====,OAB 是等边三角形，点B 坐标是()1,0，∴等边三角形高为2，由题知，1A 的坐标是()2,0；2A 的坐标是()2,0；3A 的坐标是13,22⎛⎫- ⎪ ⎪⎝⎭；继续滚动有，4A 的坐标是()3,2；5A 的坐标是()3,2；6A 的坐标是53,322⎛- ⎝⎭；7A 的坐标是()1,3；8A 的坐标是()1,3；9A 的坐标是35,22⎛⎫ ⎪ ⎪⎝⎭；10A 的坐标是()0,1；11A 的坐标是()0,1；12A 的坐标是13,22⎛⎫ ⎪ ⎪⎝⎭；13A 的坐标是()2,0；不断循环，循环规律为以1A ，2A ，，12A ，12个为一组， 2024121688÷= ，∴2024A 的坐标与8A 的坐标一样为()1,3，故答案为：()1,3．三、解答题（满分60分）21.先化简，再求值：22222111m m m m m m ⎛⎫-+÷- ⎪-+⎝⎭，其中cos60m =︒．【答案】1m -+，12【解析】【分析】本题主要考查分式的化简求值及特殊三角函数值，先对分式进行化简，然后利用特殊三角函数值进行代值求解即可．【详解】解：原式()()()()21111m m m m m m-+=⋅+--1m =-+，当1cos 602m =︒=时原式12=．22.如图，在正方形网格中，每个小正方形的边长都是1个单位长度，在平面直角坐标系中，ABC 的三个顶点坐标分别为()1,1A -，()2,3B -，()5,2C -．（1）画出ABC 关于y 轴对称的111A B C △，并写出点1B 的坐标；（2）画出ABC 绕点A 逆时针旋转90︒后得到的22AB C ，并写出点2B 的坐标；（3）在（2）的条件下，求点B 旋转到点2B 的过程中所经过的路径长（结果保留π）【答案】（1）作图见解析，()12,3B （2）作图见解析，()23,0B -（3）π2【解析】【分析】本题考查了利用旋转变换作图，轴对称和扇形面积公式等知识，熟练掌握网格结构准确找出对应点的位置是解题的关键．（1）根据题意画出即可；关于y 轴对称点的坐标横坐标互为相反数，纵坐标不变；（2）根据网格结构找出点B 、C 以点A 为旋转中心逆时针旋转90︒后的对应点，然后顺次连接即可；（3）先求出AB =90︒，利用弧长公式即可求出．【小问1详解】解：如图，111A B C △为所求；点1B 的坐标为()2,3，【小问2详解】如图，22AB C 为所求；()23,0B -，【小问3详解】AB ==点B 旋转到点2B 的过程中所经过的路径长90551802=．23.如图，抛物线2y x bx c =-++与x 轴交于A 、B 两点，与y 轴交于点C ，其中()1,0B ，()0,3C ．（1）求抛物线的解析式．（2）在第二象限的抛物线上是否存在一点P ，使得APC △的面积最大．若存在，请直接写出点P 坐标和APC △的面积最大值；若不存在，请说明理由．【答案】（1）223y x x =--+（2）存在，点P 的坐标是315,24P ⎛⎫- ⎪⎝⎭，APC △的面积最大值是278【解析】【分析】本题主要考查二次函数的图象与性质以及与几何综合：（1）将B ，C 两点坐标代入函数解析式，求出b ，c 的值即可；（2）过点P 作PE x ⊥轴于点E ，设()2,23P x x x --+，且点P 在第二象限，根据APC APE AOC PCOE S S S S =+- 梯形可得二次函数关系式，再利用二次函数的性质即可求解.【小问1详解】解：将()1,0B ，()0,3C 代入2y x bx c =-++得，103b c c -++=⎧⎨=⎩解得：23b c =-⎧⎨=⎩223y x x ∴=--+【小问2详解】解：对于223y x x =--+，令0,y =则2230,x x --+=解得，123,1x x =-=，∴()3,0A -，∴3,OA =∵()0,3C ，∴3OC =，过点P 作PE x ⊥轴于点E ，如图，设()2,23P x x x --+，且点P 在第二象限，∴,3,OE x AE x =-=+∴APC APE AOC PCOE S S S S =+- 梯形()111222AE PE OC PE OE OA OC =⨯++⨯-⨯()()()()2211132332333222x x x x x x =+--++--+--⨯⨯23327228x ⎛⎫=-++ ⎪⎝⎭∵302-<，∴S 有最大值，∴当32x =-时，S 有最大值，最大值为278，此时点P 的坐标为315,24⎛⎫- ⎪⎝⎭24.为贯彻落实教育部办公厅关于“保障学生每天校内、校外各一小时体育活动时间”的要求，某学校要求学生每天坚持体育锻炼．学校从全体男生中随机抽取了部分学生，调查他们的立定跳远成绩，整理如下不完整的频数分布表和统计图，结合下图解答下列问题：组别分组（cm ）频数A50100x <≤3B100150x <≤m C150200x <≤20D 200250x <≤14x<≤5E250300（1）频数分布表中m=，扇形统计图中n=．（2）本次调查立定跳远成绩的中位数落在组别．（3）该校有600名男生，若立定跳远成绩大于200cm为合格，请估计该校立定跳远成绩合格的男生有多少人？【答案】（1）8，40（2）C（3）估计该校立定跳远成绩合格的男生有228人【解析】【分析】本题主要考查了扇形统计图和频数表、中位数，用样本估计总体，（1）用A组的频数除以所占的百分比，即可求出调查的总人数；用总人数减去其它组的人数，即可求得B组的人数，用C组的人数除以总人数即可求解；（2）根据中位数的求法，即可求解；（3）用总人数乘以样本中立定跳远成绩合格的男生人数所占，即可求解．【小问1详解】÷=(人)解：被抽取的学生数为：36%50m=----=（人），故503201458n=，n=÷=，即40%205040%故答案为：8，40；【小问2详解】解：把这组数据从小到大排列，第25和第26个数据的平均数为这组数据的中位数，382526，5142526+<<，+<<∴把这组数据从小到大排列，第25和第26个数据都在C组，故本次调查立定跳远成绩的中位数落在C组，答案为：C；【小问3详解】解：14560022850+⨯=（人）答：该校立定跳远成绩合格的男生有228人．25.甲、乙两货车分别从相距225km 的A 、B 两地同时出发，甲货车从A 地出发途经配货站时，停下来卸货，半小时后继续驶往B 地，乙货车沿同一条公路从B 地驶往A 地，但乙货车到达配货站时接到紧急任务立即原路原速返回B 地，结果比甲货车晚半小时到达B 地．如图是甲、乙两货车距A 地的距离()km y 与行驶时间()h x 之间的函数图象，结合图象回答下列问题：（1）甲货车到达配货站之前的速度是km/h ，乙货车的速度是km/h ；（2）求甲货车在配货站卸货后驶往B 地的过程中，甲货车距A 地的距离()km y 与行驶时间()h x 之间的函数解析式；（3）直接写出甲、乙两货车在行驶的过程中，出发多长时间甲、乙两货车与配货站的距离相等．【答案】（1）30，40（2）EF 的函数解析式是()802154 5.5y x x =-≤≤（3）经过1.5h 或45h 14或5h 甲、乙两货车与配货站的距离相等【解析】【分析】本题考查一次函数的应用，待定系数法求一次函数解析式的运用，认真分析函数图象，读懂函数图象表示的意义是解题关键．（1）由图象可知甲货车到达配货站路程为105km ，所用时间为3.5h ，乙货车到达配货站路程为120km ，到达后返回，所用时间为6h ，根据速度=距离÷时间即可得；（2）甲货车从A 地出发途经配货站时，停下来卸货，半小时后继续驶往B 地，由图象结合已知条件可知(4,105)E 和点(5.5,225)F ，再利用待定系数法求出y 与x 的关系式即可得答案；（3）分两车到达配货站之前和乙货车到达配货站时接到紧急任务立即原路原速返回B 地后、甲。

2022年黑龙江省龙东地区中考数学试卷(解析版)

2022年黑龙江省龙东地区中考数学试卷一、选择题（每题3分，满分30分）1．（3分）（2022•黑龙江）下列运算中，计算正确的是（）A．（b﹣a）2＝b2﹣a2B．3a•2a＝6aC．（﹣x2）2＝x4D．a6÷a2＝a32．（3分）（2022•黑龙江）下列图形是汽车的标识，其中是中心对称图形但不是轴对称图形的是（）A．B．C．D．3．（3分）（2022•黑龙江）学校举办跳绳比赛，九年（2）班参加比赛的6名同学每分钟跳绳次数分别是172，169，180，182，175，176，这6个数据的中位数是（）A．181B．175C．176D．175.54．（3分）（2022•黑龙江）如图是由若干个相同的小正方体搭成的一个几何体的左视图和俯视图，则所需的小正方体的个数最多是（）A．7B．8C．9D．105．（3分）（2022•黑龙江）2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛，单循环比赛共进行了45场，共有多少支队伍参加比赛？（）A．8B．10C．7D．96．（3分）（2022•黑龙江）已知关于x的分式方程﹣＝1的解是正数，则m的取值范围是（）A．m＞4B．m＜4C．m＞4且m≠5D．m＜4且m≠1 7．（3分）（2022•黑龙江）国家“双减”政策实施后，某校开展了丰富多彩的社团活动．某班同学报名参加书法和围棋两个社团，班长为参加社团的同学去商场购买毛笔和围棋（两种都购买）共花费360元．其中毛笔每支15元，围棋每副20元，共有多少种购买方案？（）A．5B．6C．7D．88．（3分）（2022•黑龙江）如图，在平面直角坐标系中，点O为坐标原点，平行四边形OBAD 的顶点B在反比例函数y＝的图象上，顶点A在反比例函数y＝的图象上，顶点D在x轴的负半轴上．若平行四边形OBAD的面积是5，则k的值是（）A．2B．1C．﹣1D．﹣29．（3分）（2022•黑龙江）如图，△ABC中，AB＝AC，AD平分∠BAC与BC相交于点D，点E是AB的中点，点F是DC的中点，连接EF交AD于点P．若△ABC的面积是24，PD＝1.5，则PE的长是（）A．2.5B．2C．3.5D．310．（3分）（2022•黑龙江）如图，正方形ABCD的对角线AC，BD相交于点O，点F是CD 上一点，OE⊥OF交BC于点E，连接AE，BF交于点P，连接OP．则下列结论：①AE ⊥BF；②∠OP A＝45°；③AP﹣BP＝OP；④若BE：CE＝2：3，则tan∠CAE＝；⑤四边形OECF的面积是正方形ABCD面积的．其中正确的结论是（）A．①②④⑤B．①②③⑤C．①②③④D．①③④⑤二、填空题（每题3分，满分30分）11．（3分）（2022•黑龙江）我国南水北调东线北延工程2021﹣2022年度供水任务顺利完成，共向黄河以北调水1.89亿立方米，将数据1.89亿用科学记数法表示为．12．（3分）（2022•黑龙江）在函数中，自变量x的取值范围是．13．（3分）（2022•黑龙江）如图，在四边形ABCD中，对角线AC，BD相交于点O，OA＝OC，请你添加一个条件，使△AOB≌△COD．14．（3分）（2022•黑龙江）在一个不透明的口袋中，有2个红球和4个白球，这些球除颜色外其余完全相同，摇匀后随机摸出一个球，摸到红球的概率是．15．（3分）（2022•黑龙江）若关于x的一元一次不等式组的解集为x＜2，则a 的取值范围是．16．（3分）（2022•黑龙江）如图，在⊙O中，AB是⊙O的弦，⊙O的半径为3cm．C为⊙O 上一点，∠ACB＝60°，则AB的长为cm．17．（3分）（2022•黑龙江）若一个圆锥的母线长为5cm，它的侧面展开图的圆心角为120°，则这个圆锥的底面半径为cm．18．（3分）（2022•黑龙江）如图，菱形ABCD中，对角线AC，BD相交于点O，∠BAD＝60°，AD＝3，AH是∠BAC的平分线，CE⊥AH于点E，点P是直线AB上的一个动点，则OP+PE的最小值是．19．（3分）（2022•黑龙江）在矩形ABCD中，AB＝9，AD＝12，点E在边CD上，且CE ＝4，点P是直线BC上的一个动点．若△APE是直角三角形，则BP的长为．20．（3分）（2022•黑龙江）如图，在平面直角坐标系中，点A1，A2，A3，A4…在x轴上且OA1＝1，OA2＝2OA1，OA3＝2OA2，OA4＝2OA3…按此规律，过点A1，A2，A3，A4…作x轴的垂线分别与直线y＝x交于点B1，B2，B3，B4…记△OA1B1，△OA2B2，△OA3B3，△OA4B4…的面积分别为S1，S2，S3，S4…则S2022＝．三、解答题（满分60分）21．（5分）（2022•黑龙江）先化简，再求值：（﹣1）÷，其中a＝2cos30°+1．22．（6分）（2022•黑龙江）如图，在正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，﹣1），B（2，﹣5），C （5，﹣4）．（1）将△ABC先向左平移6个单位，再向上平移4个单位，得到△A1B1C1，画出两次平移后的△A1B1C1，并写出点A1的坐标；（2）画出△A1B1C1绕点C1顺时针旋转90°后得到△A2B2C1，并写出点A2的坐标；（3）在（2）的条件下，求点A1旋转到点A2的过程中所经过的路径长（结果保留π）．23．（6分）（2022•黑龙江）如图，抛物线y＝x2+bx+c经过点A（﹣1，0），点B（2，﹣3），与y轴交于点C，抛物线的顶点为D．（1）求抛物线的解析式；（2）抛物线上是否存在点P，使△PBC的面积是△BCD面积的4倍，若存在，请直接写出点P的坐标；若不存在，请说明理由．24．（7分）（2022•黑龙江）为进一步开展“睡眠管理”工作，某校对部分学生的睡眠情况进行了问卷调查．设每名学生平均每天的睡眠时间为x小时，其中的分组情况是：A组：x＜8.5B组：8.5≤x＜9C组：9≤x＜9.5D组：9.5≤x＜10E组：x≥10根据调查结果绘制成两幅不完整的统计图，请根据图中提供的信息，解答下列问题：（1）本次共调查了名学生；（2）补全条形统计图；（3）在扇形统计图中，求D组所对应的扇形圆心角的度数；（4）若该校有1500名学生，请估计该校睡眠时间不足9小时的学生有多少人？25．（8分）（2022•黑龙江）为抗击疫情，支援B市，A市某蔬菜公司紧急调运两车蔬菜运往B市．甲、乙两辆货车从A市出发前往B市，乙车行驶途中发生故障原地维修，此时甲车刚好到达B市．甲车卸载蔬菜后立即原路原速返回接应乙车，把乙车的蔬菜装上甲车后立即原路原速又运往B市．乙车维修完毕后立即返回A市．两车离A市的距离y（km）与乙车所用时间x（h）之间的函数图象如图所示．（1）甲车速度是km/h，乙车出发时速度是km/h；（2）求乙车返回过程中，乙车离A市的距离y（km）与乙车所用时间x（h）的函数解析式（不要求写出自变量的取值范围）；（3）乙车出发多少小时，两车之间的距离是120km？请直接写出答案．26．（8分）（2022•黑龙江）△ABC和△ADE都是等边三角形．（1）将△ADE绕点A旋转到图①的位置时，连接BD，CE并延长相交于点P（点P与点A重合），有P A+PB＝PC（或P A+PC＝PB）成立（不需证明）；（2）将△ADE绕点A旋转到图②的位置时，连接BD，CE相交于点P，连接P A，猜想线段P A、PB、PC之间有怎样的数量关系？并加以证明；（3）将△ADE绕点A旋转到图③的位置时，连接BD，CE相交于点P，连接P A，猜想线段P A、PB、PC之间有怎样的数量关系？直接写出结论，不需要证明．27．（10分）（2022•黑龙江）学校开展大课间活动，某班需要购买A、B两种跳绳．已知购进10根A种跳绳和5根B种跳绳共需175元：购进15根A种跳绳和10根B种跳绳共需300元．（1）求购进一根A种跳绳和一根B种跳绳各需多少元？（2）设购买A种跳绳m根，若班级计划购买A、B两种跳绳共45根，所花费用不少于548元且不多于560元，则有哪几种购买方案？（3）在（2）的条件下，哪种购买方案需要的总费用最少？最少费用是多少元？28．（10分）（2022•黑龙江）如图，在平面直角坐标系中，平行四边形ABCD的边AB在x 轴上，顶点D在y轴的正半轴上，M为BC的中点，OA、OB的长分别是一元二次方程x2﹣7x+12＝0的两个根（OA＜OB），tan∠DAB＝，动点P从点D出发以每秒1个单位长度的速度沿折线DC﹣CB向点B运动，到达B点停止．设运动时间为t秒，△APC的面积为S．（1）求点C的坐标；（2）求S关于t的函数关系式，并写出自变量t的取值范围；（3）在点P的运动过程中，是否存在点P，使△CMP是等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．2022年黑龙江省龙东地区中考数学试卷参考答案与试题解析一、选择题（每题3分，满分30分）1．（3分）（2022•黑龙江）下列运算中，计算正确的是（）A．（b﹣a）2＝b2﹣a2B．3a•2a＝6aC．（﹣x2）2＝x4D．a6÷a2＝a3【分析】利用完全平方公式，单项式乘多项式，幂的乘方的法则，同底数幂的除法的法则对各项进行运算即可．【解答】解：A．（b﹣a）2＝b2﹣2ab+a2，故A不正确；B.3a•2a＝6a2，故B不正确；C．（﹣x2）2＝x4，故C正确；D．a6÷a2＝a4，故D不符合题意；故选：C．【点评】本题考查了完全平方公式，单项式乘多项式，幂的乘方的法则，同底数幂的除法，解答的关键是对相应的运算法则的掌握．2．（3分）（2022•黑龙江）下列图形是汽车的标识，其中是中心对称图形但不是轴对称图形的是（）A．B．C．D．【分析】根据中心对称图形与轴对称图形的概念进行判断即可．【解答】解：A．既是中心对称图形，也是轴对称图形，故此选项不合题意；B．不是中心对称图形，是轴对称图形，故此选项不合题意；C．是中心对称图形但不是轴对称图形，故此选项符合题意；D．不是中心对称图形，是轴对称图形，故此选项不合题意；故选：C．【点评】本题考查的是中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后与自身重合．3．（3分）（2022•黑龙江）学校举办跳绳比赛，九年（2）班参加比赛的6名同学每分钟跳绳次数分别是172，169，180，182，175，176，这6个数据的中位数是（）A．181B．175C．176D．175.5【分析】将这组数据从小到大排列，根据中位数的计算方法即可得出答案．【解答】解：将这组数据从小到大排列为：169，172，175，176，180，182，中位数＝＝175.5，故选：D．【点评】本题考查了中位数，掌握将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数是解题的关键．4．（3分）（2022•黑龙江）如图是由若干个相同的小正方体搭成的一个几何体的左视图和俯视图，则所需的小正方体的个数最多是（）A．7B．8C．9D．10【分析】由左视图和俯视图可以猜想到主视图的可能情况，从而得到答案．【解答】解：从俯视图课看出前后有三层，从左视图可看出最后面有2层高，中间最高是2层，要是最多就都是2层，最前面的最高是1层，所以最多的为：2+2×2+1×2＝8．故选：B．【点评】本题考查了三视图的知识，由两个识图想象几何体是解题的关键，5．（3分）（2022•黑龙江）2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛，单循环比赛共进行了45场，共有多少支队伍参加比赛？（）A．8B．10C．7D．9【分析】设共有x支队伍参加比赛，根据“循环比赛共进行了45场”列一元二次方程，求解即可．【解答】解：设共有x支队伍参加比赛，根据题意，可得，解得x＝10或x＝﹣9（舍），∴共有10支队伍参加比赛．故选：B．【点评】本题考查了一元二次方程的应用，理解题意并根据题意建立等量关系是解题的关键．6．（3分）（2022•黑龙江）已知关于x的分式方程﹣＝1的解是正数，则m的取值范围是（）A．m＞4B．m＜4C．m＞4且m≠5D．m＜4且m≠1【分析】先利用m表示出x的值，再由x为正数求出m的取值范围即可．【解答】解：方程两边同时乘以x﹣1得，2x﹣m+3＝x﹣1，解得x＝m﹣4．∵x为正数，∴m﹣4＞0，解得m＞4，∵x≠1，∴m﹣4≠1，即m≠5，∴m的取值范围是m＞4且m≠5．故选：C．【点评】本题考查了分式方程的解，掌握求出使分式方程中令等号左右两边相等且分母不等于0的未知数的值，这个值叫方程的解是解题的关键．7．（3分）（2022•黑龙江）国家“双减”政策实施后，某校开展了丰富多彩的社团活动．某班同学报名参加书法和围棋两个社团，班长为参加社团的同学去商场购买毛笔和围棋（两种都购买）共花费360元．其中毛笔每支15元，围棋每副20元，共有多少种购买方案？（）A．5B．6C．7D．8【分析】设购买毛笔x支，围棋y副，根据“购买毛笔和围棋（两种都购买）共花费360元”列二元一次方程，再由x和y分别取正整数，即可确定购买方案．【解答】解：设购买毛笔x支，围棋y副，根据题意，得15x+20y＝360，∴y＝18﹣x，∵两种都买，∴18﹣x＞0，x、y都是正整数，解得x＜24，故x是4的倍数且x＜24，∴x＝4，y＝15或x＝8，y＝12或x＝12，y＝9或x＝16，y＝6或x＝20，y＝3；∴共有5种购买方案，故选：A．【点评】本题考查了二元一次方程的应用，理解题意并根据题意建立二元一次方程是解题的关键．8．（3分）（2022•黑龙江）如图，在平面直角坐标系中，点O为坐标原点，平行四边形OBAD 的顶点B在反比例函数y＝的图象上，顶点A在反比例函数y＝的图象上，顶点D在x轴的负半轴上．若平行四边形OBAD的面积是5，则k的值是（）A．2B．1C．﹣1D．﹣2【分析】设B（a，），根据四边形OBAD是平行四边形，推出AB∥DO，表示出A点的坐标，求出AB＝a﹣，再根据平行四边形面积公式列方程，解出即可．【解答】解：设B（a，），∵四边形OBAD是平行四边形，∴AB∥DO，∴A（，），∴AB＝a﹣，∵平行四边形OBAD的面积是5，∴（a﹣）＝5，解得k＝﹣2，故选：D．【点评】本题考查反比例函数比例系数k的几何意义、反比例函数图象上点的坐标特征、平行四边形性质，掌握反比例函数比例系数k的几何意义及函数图象上点的坐标特征，设出点的坐标、根据平行四边形面积公式列方程是解题的关键．9．（3分）（2022•黑龙江）如图，△ABC中，AB＝AC，AD平分∠BAC与BC相交于点D，点E是AB的中点，点F是DC的中点，连接EF交AD于点P．若△ABC的面积是24，PD＝1.5，则PE的长是（）A．2.5B．2C．3.5D．3【分析】如图，过点E作EG⊥AD于G，证明△EGP≌△FDP，得PG＝PD＝1.5，由三角形中位线定理可得AD的长，由三角形ABC的面积是24，得BC的长，最后由勾股定理可得结论．【解答】解：如图，过点E作EG⊥AD于G，∵AB＝AC，AD平分∠BAC，∴AD⊥BC，BD＝CD，∴∠PDF＝∠EGP＝90°，EG∥BC，∵点E是AB的中点，∴G是AD的中点，∴EG＝BD，∵F是CD的中点，∴DF＝CD，∴EG＝DF，∵∠EPG＝∠DPF，∴△EGP≌△FDP（AAS），∴PG＝PD＝1.5，∴AD＝2DG＝6，∵△ABC的面积是24，∴•BC•AD＝24，∴BC＝48÷6＝8，∴DF＝BC＝2，∴EG＝DF＝2，由勾股定理得：PE＝＝2.5．故选：A．【点评】本题考查了等腰三角形的性质，三角形的中位线定理，全等三角形的性质和判定，三角形的面积等知识，作辅助线构建全等三角形是解本题的关键．10．（3分）（2022•黑龙江）如图，正方形ABCD的对角线AC，BD相交于点O，点F是CD 上一点，OE⊥OF交BC于点E，连接AE，BF交于点P，连接OP．则下列结论：①AE ⊥BF；②∠OP A＝45°；③AP﹣BP＝OP；④若BE：CE＝2：3，则tan∠CAE＝；⑤四边形OECF的面积是正方形ABCD面积的．其中正确的结论是（）A．①②④⑤B．①②③⑤C．①②③④D．①③④⑤【分析】利用全等三角形的判定与性质，正方形的性质，圆周角定理，直角三角形的边角关系定理对每个选项的结论进行判断即可得出结论．【解答】解：①∵四边形ABCD是正方形，∴AB＝BC＝CD，AC⊥BD，∠ABD＝∠DBC＝∠ACD＝45°．∴∠BOE+∠EOC＝90°，∵OE⊥OF，∴∠FOC+∠EOC＝90°．∴∠BOE＝∠COF．在△BOE和△COF中，，∴△BOE≌△COF（ASA），∴BE＝CF．在△BAE和△CBF中，，∴△BAE≌△CBF（SAS），∴∠BAE＝∠CBF．∵∠ABP+∠CBF＝90°，∴∠ABP+∠BAE＝90°，∴∠APB＝90°．∴AE⊥BF．∴①的结论正确；②∵∠APB＝90°，∠AOB＝90°，∴点A，B，P，O四点共圆，∴∠APO＝∠ABO＝45°，∴②的结论正确；③过点O作OH⊥OP，交AP于点H，如图，∵∠APO＝45°，OH⊥OP，∴OH＝OP＝HP，∴HP＝OP．∵OH⊥OP，∴∠POB+∠HOB＝90°，∵OA⊥OB，∴∠AOH+∠HOB＝90°．∴∠AOH＝∠BOP．∵∠OAH+BAE＝45°，∠OBP+∠CBF＝45°，，∠BAE＝∠CBF，∴∠OAH＝∠OBP．在△AOH和△BOP中，，∴△AOH≌△BOP（ASA），∴AH＝BP．∴AP﹣BP＝AP﹣AH＝HP＝OP．∴③的结论正确；④∵BE：CE＝2：3，∴设BE＝2x，则CE＝3x，∴AB＝BC＝5x，∴AE＝＝x．过点E作EG⊥AC于点G，如图，∵∠ACB＝45°，∴EG＝GC＝EC＝x，∴AG＝＝x，在Rt△AEG中，∵tan∠CAE＝，∴tan∠CAE＝＝＝．∴④的结论不正确；⑤∵四边形ABCD是正方形，∴OA＝OB＝OC＝OD，∠AOB＝∠BOC＝∠COD＝∠DOA＝90°，∴△OAB≌△OBC≌△OCD≌△DOA（SAS）．∴．∴．由①知：△BOE≌△COF，∴S△OBE＝S△OFC，∴．即四边形OECF的面积是正方形ABCD面积的．∴⑤的结论正确．综上，①②③⑤的结论正确．故选：B．【点评】本题主要考查了全等三角形的判定与性质，正方形的性质，圆周角定理，直角三角形的边角关系定理，等腰直角三角形的判定与性质，充分利用正方形的性质构造等腰直角三角形和全等三角形是解题的关键．二、填空题（每题3分，满分30分）11．（3分）（2022•黑龙江）我国南水北调东线北延工程2021﹣2022年度供水任务顺利完成，共向黄河以北调水1.89亿立方米，将数据1.89亿用科学记数法表示为 1.89×108．【分析】用科学记数法表示较大的数时，一般形式为a×10n，其中1≤|a|＜10，n为整数，且n比原来的整数位数少1，据此判断即可．【解答】解：1.89亿＝189000000＝1.89×108．故答案为：1.89×108．【点评】此题主要考查了用科学记数法表示较大的数，一般形式为a×10n，其中1≤|a|＜10，确定a与n的值是解题的关键．12．（3分）（2022•黑龙江）在函数中，自变量x的取值范围是x≥．【分析】根据被开方数大于等于0列式计算即可得解．【解答】解：根据题意得，2x﹣3≥0，解得x≥．故答案为：x≥．【点评】本题考查的知识点为：二次根式的被开方数是非负数．13．（3分）（2022•黑龙江）如图，在四边形ABCD中，对角线AC，BD相交于点O，OA＝OC，请你添加一个条件OB＝OD（答案不唯一），使△AOB≌△COD．【分析】此题是一道开放型的题目，答案不唯一，只要符合全等三角形的判定定理即可．【解答】解：添加的条件是OB＝OD，理由是：在△AOB和△COD中，，∴△AOB≌△COD（SAS），故答案为：OB＝OD（答案不唯一）．【点评】本题考查了全等三角形的判定定理，能熟记全等三角形的判定定理是解此题的关键，注意：全等三角形的判定定理是SAS，SAS，AAS，SSS，两直角三角形全等还有HL等．14．（3分）（2022•黑龙江）在一个不透明的口袋中，有2个红球和4个白球，这些球除颜色外其余完全相同，摇匀后随机摸出一个球，摸到红球的概率是．【分析】直接利用概率公式，进而计算得出答案．【解答】解：∵在一个不透明的口袋中，有2个红球和4个白球，这些球除颜色外其余完全相同，摇匀后随机摸出一个球，∴摸到红球的概率是：＝．故答案为：．【点评】此题主要考查了概率公式，正确掌握概率求法是解题关键．15．（3分）（2022•黑龙江）若关于x的一元一次不等式组的解集为x＜2，则a 的取值范围是a≥2．【分析】不等式组整理后，根据已知解集，利用同小取小法则判断即可确定出a的范围．【解答】解：不等式组整理得：，∵不等式组的解集为x＜2，∴a≥2．故答案为：a≥2．【点评】此题考查了解一元一次不等式组，熟练掌握不等式组取解集的方法是解本题的关键．16．（3分）（2022•黑龙江）如图，在⊙O中，AB是⊙O的弦，⊙O的半径为3cm．C为⊙O 上一点，∠ACB＝60°，则AB的长为3cm．【分析】连接AO并延长交⊙O于点D，根据直径所对的圆周角是直角可得∠ADB＝90°，再利用同弧所对的圆周角相等可求出∠ADB＝60°，然后在Rt△ABD中，利用锐角三角函数的定义进行计算即可解答．【解答】解：连接AO并延长交⊙O于点D，∵AD是⊙O的直径，∴∠ADB＝90°，∵∠ACB＝60°，∴∠ADB＝∠ACB＝60°，在Rt△ABD中，AD＝6cm，∴AB＝AD•sin60°＝6×＝3（cm），故答案为：3．【点评】本题考查了三角形的外接圆与外心，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．17．（3分）（2022•黑龙江）若一个圆锥的母线长为5cm，它的侧面展开图的圆心角为120°，则这个圆锥的底面半径为cm．【分析】先求出圆锥侧面展开图扇形的弧长，再利用侧面展开图与底面圆的关系的关系列方程即可求出圆锥的底面半径．【解答】解：c长为：＝，设圆锥的底面半径为r，则2πr＝，∴r＝cm．故答案为：．【点评】本题主要考查圆锥的计算，掌握侧面展开图与底面圆的关系是解题关键．18．（3分）（2022•黑龙江）如图，菱形ABCD中，对角线AC，BD相交于点O，∠BAD＝60°，AD＝3，AH是∠BAC的平分线，CE⊥AH于点E，点P是直线AB上的一个动点，则OP+PE的最小值是．【分析】连接OE，过点O作OF⊥AB，垂足为F，并延长到点O′，使O′F＝OF，连接O′E交直线AB于点P，连接OP，从而可得OP＝O′P，此时OP+PE的值最小，先利用菱形的性质可得AD＝AB＝3，∠BAC＝∠BAD，OA＝OC＝AC，OD＝OB＝BD，∠AOD＝90°，从而可得△ADB是等边三角形，进而求出AD＝3，然后在Rt△ADO中，利用勾股定理求出AO的长，从而求出AC的长，进而利用直角三角形斜边上的中线可得OE＝OA＝AC＝，再利用角平分线和等腰三角形的性质可得OE∥AB，从而求出∠EOF＝90°，进而在Rt△AOF中，利用锐角三角函数的定义求出OF的长，即可求出OO′的长，最后在Rt△EOO′中，利用勾股定理进行计算即可解答．【解答】解：连接OE，过点O作OF⊥AB，垂足为F，并延长到点O′，使O′F＝OF，连接O′E交直线AB于点P，连接OP，∴AP是OO′的垂直平分线，∴OP＝O′P，∴OP+PE＝O′P+PE＝O′E，此时，OP+PE的值最小，∵四边形ABCD是菱形，∴AD＝AB＝3，∠BAC＝∠BAD，OA＝OC＝AC，OD＝OB＝BD，∠AOD＝90°，∵∠BAD＝60°，∴△ADB是等边三角形，∴BD＝AD＝3，∴OD＝BD＝，∴AO＝＝＝，∴AC＝2OA＝3，∵CE⊥AH，∴∠AEC＝90°，∴OE＝OA＝AC＝，∴∠OAE＝∠OEA，∵AE平分∠CAB，∴∠OAE＝∠EAB，∴∠OEA＝∠EAB，∴OE∥AB，∴∠EOF＝∠AFO＝90°，在Rt△AOF中，∠OAB＝DAB＝30°，∴OF＝OA＝，∴OO′＝2OF＝，在Rt△EOO′中，O′E＝＝＝，∴OE+PE＝，∴OP+PE的最小值为，故答案为：．【点评】本题考查了菱形的性质，勾股定理，角平分线的定义，等边三角形的判定与性质，轴对称﹣最短路线问题，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．19．（3分）（2022•黑龙江）在矩形ABCD中，AB＝9，AD＝12，点E在边CD上，且CE ＝4，点P是直线BC上的一个动点．若△APE是直角三角形，则BP的长为或或6．【分析】若△APE是直角三角形，有三种情况：①如图1，∠AEP＝90°，②如图2，∠P AE＝90°，③如图3，∠APE＝90°，分别证明三角形相似可解答．【解答】解：若△APE是直角三角形，有以下三种情况：①如图1，∠AEP＝90°，∴∠AED+∠CEP＝90°，∵四边形ABCD是矩形，∴∠C＝∠D＝90°，∴∠CEP+∠CPE＝90°，∴∠AED＝∠CPE，∴△ADE∽△ECP，∴＝，即＝，∴CP＝，∵BC＝AD＝12，∴BP＝12﹣＝；②如图2，∠P AE＝90°，∵∠DAE+∠BAE＝∠BAE+∠BAP＝90°，∴∠DAE＝∠BAP，∵∠D＝∠ABP＝90°，∴△ADE∽△ABP，∴＝，即＝，∴BP＝；③如图3，∠APE＝90°，设BP＝x，则PC＝12﹣x，同理得：△ABP∽△PCE，∴＝，即＝，∴x1＝x2＝6，∴BP＝6，综上，BP的长是或或6．故答案为：或或6．【点评】本题考查的是相似三角形的判定与性质，矩形的性质，掌握相似三角形的判定定理和性质定理是解题的关键，并注意运用分类讨论的思想．20．（3分）（2022•黑龙江）如图，在平面直角坐标系中，点A1，A2，A3，A4…在x轴上且OA1＝1，OA2＝2OA1，OA3＝2OA2，OA4＝2OA3…按此规律，过点A1，A2，A3，A4…作x轴的垂线分别与直线y＝x交于点B1，B2，B3，B4…记△OA1B1，△OA2B2，△OA3B3，△OA4B4…的面积分别为S1，S2，S3，S4…则S2022＝．【分析】根据已知先求出OA2，OA3，OA4的长，再代入直线y＝x中，分别求出A1B1，A2B2，A3B3，A4B4，然后分别计算出S1，S2，S3，S4，再从数字上找规律进行计算即可解答．【解答】解：∵OA1＝1，OA2＝2OA1，∴OA2＝2，∵OA3＝2OA2，∴OA3＝4，∵OA4＝2OA3，∴OA4＝8，把x＝1代入直线y＝x中可得：y＝，∴A1B1＝，把x＝2代入直线y＝x中可得：y＝2，∴A2B2＝2，把x＝4代入直线y＝x中可得：y＝4，∴A3B3＝4，把x＝8代入直线y＝x中可得：y＝8，∴A4B4＝8，∴S1＝OA1•A1B1＝×1×＝×20×（20×），S2＝OA2•A2B2＝×2×2＝×21×（21×），S3＝OA3•A3B3＝×4×4＝×22×（22×），S4＝OA4•A4B4＝×8×8＝×23×（23×），..．∴S2022＝×22021×（22021×）＝24041×，故答案为：24041×．【点评】本题考查了规律型：点的坐标，含30度角的直角三角形，根据已知分别求出S1，S2，S3，S4的值，然后从数字上找规律是解题的关键．三、解答题（满分60分）21．（5分）（2022•黑龙江）先化简，再求值：（﹣1）÷，其中a＝2cos30°+1．【分析】利用分式的减法法则和除法法则对分式进行计算化简，把特殊角的三角函数值代入计算求出a的值，代入化简后的分式进行计算，即可得出答案．【解答】解：（﹣1）÷＝÷＝×＝，当a＝2cos30°+1＝2×+1＝时，原式＝＝﹣．【点评】本题考查了分式的化简求值，特殊角的三角函数值，掌握分式的混合计算及特殊角的三角函数值是解决问题的关键．22．（6分）（2022•黑龙江）如图，在正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，﹣1），B（2，﹣5），C （5，﹣4）．（1）将△ABC先向左平移6个单位，再向上平移4个单位，得到△A1B1C1，画出两次平移后的△A1B1C1，并写出点A1的坐标；（2）画出△A1B1C1绕点C1顺时针旋转90°后得到△A2B2C1，并写出点A2的坐标；（3）在（2）的条件下，求点A1旋转到点A2的过程中所经过的路径长（结果保留π）．【分析】（1）利用平移变换的性质分别作出A，B，C的对应点A1，B1，C1即可；（2）利用旋转变换的性质分别作出A1，B1的对应点A2，B2即可；（3）利用勾股定理求出A1C1，再利用弧长公式求解．【解答】解：（1）如图，△A1B1C1即为所求，点A1的坐标（﹣5，，3）；（2）如图，△A2B2C1即为所求，点A2的坐标（2，4）；（3）∵A1C1＝＝5，∴点A1旋转到点A2的过程中所经过的路径长＝＝．【点评】本题考查作图﹣平移变换，旋转变换，弧长公式等知识，解题的关键是掌握平移变换，旋转变换的性质，属于中考常考题型．23．（6分）（2022•黑龙江）如图，抛物线y＝x2+bx+c经过点A（﹣1，0），点B（2，﹣3），与y轴交于点C，抛物线的顶点为D．（1）求抛物线的解析式；（2）抛物线上是否存在点P，使△PBC的面积是△BCD面积的4倍，若存在，请直接写出点P的坐标；若不存在，请说明理由．【分析】（1）待定系数法求解析式即可；（2）设抛物线上的点P坐标为（m，m2﹣2m﹣3），结合方程思想和三角形面积公式列方程求解．【解答】解：（1）∵抛物线y＝x2+bx+c经过点A（﹣1，0），点B（2，﹣3），∴，解得b＝﹣2，c＝﹣3，∴抛物线的解析式：y＝x2﹣2x﹣3；（2）存在，理由如下：∵y＝x2﹣2x﹣3＝（x﹣1）2﹣4，∴D点坐标为（1，4），令x＝0，则y＝x2﹣2x﹣3＝﹣3，∴C点坐标为（0，﹣3），又∵B点坐标为（2，﹣3），∴BC∥x轴，∴S△BCD＝×2×1＝1，设抛物线上的点P坐标为（m，m2﹣2m﹣3），∴S△PBC＝×2×|m2﹣2m﹣3﹣（﹣3）|＝|m2﹣2m|，当|m2﹣2m|＝4×1时，解得m＝1±，当m＝1+时，m2﹣2m﹣3＝1，当m＝1﹣时，m2﹣2m﹣3＝1，综上，P点坐标为（1+，1）或（1﹣，1）．【点评】本题考查二次函数的性质，掌握待定系数法求函数解析式的方法，理解二次函数图象上点的坐标特征，利用方程思想解题是关键．24．（7分）（2022•黑龙江）为进一步开展“睡眠管理”工作，某校对部分学生的睡眠情况进行了问卷调查．设每名学生平均每天的睡眠时间为x小时，其中的分组情况是：A组：x＜8.5B组：8.5≤x＜9C组：9≤x＜9.5D组：9.5≤x＜10E组：x≥10根据调查结果绘制成两幅不完整的统计图，请根据图中提供的信息，解答下列问题：（1）本次共调查了100名学生；（2）补全条形统计图；（3）在扇形统计图中，求D组所对应的扇形圆心角的度数；（4）若该校有1500名学生，请估计该校睡眠时间不足9小时的学生有多少人？【分析】（1）根据B组人数和所占的百分比，可以计算出本次调查的学生总人数；（2）根据（1）中的结果、条形统计图中的时间和扇形统计图中的数据，可以计算出A 组和E组的人数，从而可以将条形统计图补充完整；（3）根据D组的人数和调查的总人数，可以计算出D组所对应的扇形圆心角的度数；（4）根据条形统计图中的数据，可以计算出该校睡眠时间不足9小时的学生有多少人．【解答】解：（1）20÷20%＝100（名），即本次共调查了100名学生，故答案为：100；（2）选择E的学生有：100×15%＝15（人），选择A的学生有：100﹣20﹣40﹣20﹣15＝5（人），补全的条形统计图如右图所示；（3）360°×＝72°，即D组所对应的扇形圆心角的度数是72°；（4）1500×＝375（人），答：估计该校睡眠时间不足9小时的学生有375人．【点评】本题考查条形统计图、扇形统计图、用样本估计总体，解答本题的关键是明确题意，利用数形结合的思想解答．25．（8分）（2022•黑龙江）为抗击疫情，支援B市，A市某蔬菜公司紧急调运两车蔬菜运往B市．甲、乙两辆货车从A市出发前往B市，乙车行驶途中发生故障原地维修，此时甲车刚好到达B市．甲车卸载蔬菜后立即原路原速返回接应乙车，把乙车的蔬菜装上甲车后立即原路原速又运往B市．乙车维修完毕后立即返回A市．两车离A市的距离y（km）与乙车所用时间x（h）之间的函数图象如图所示．（1）甲车速度是100km/h，乙车出发时速度是60km/h；（2）求乙车返回过程中，乙车离A市的距离y（km）与乙车所用时间x（h）的函数解析式（不要求写出自变量的取值范围）；（3）乙车出发多少小时，两车之间的距离是120km？请直接写出答案．【分析】（1）根据函数图象中的数据，可以计算出甲车速度和乙车出发时速度；（2）根据函数图象中的数据，可以计算出乙车返回过程中，乙车离A市的距离y（km）与乙车所用时间x（h）的函数解析式；（3）根据题意可知存在三种情况，然后分别计算即可．【解答】解：（1）由图象可得，。

【真题】龙东地区中考数学试卷含答案解析(2)

黑龙江省龙东地区中考数学试卷一、填空题（每题3分，满分30分）1．在的“双11”网上促销活动中，淘宝网的交易额突破了3200000000元，将数字3200000000用科学记数法表示．【答案】3.2×109．【解析】试题解析：3200000000=3.2×109．考点：科学记数法—表示较大的数．2．在函数y =1x -1中，自变量x 的取值范围是．【答案】x ＞1．【解析】3．如图，BC ∥EF ，AC ∥DF ，添加一个条件，使得△ABC ≌△DEF ．第3题图【答案】AB=DE 或BC=EF 或AC=DF【解析】试题解析：∵BC ∥EF ，∴∠ABC=∠E ，∵AC ∥DF ，∴∠A=∠EDF ，∵在△ABC 和△DEF 中，A EDF AB DEABC E ⎧∠=∠⎪=⎨⎪∠=∠⎩，∴△ABC ≌△DEF ，同理，BC=EF 或AC=DF 也可求证△ABC ≌△DEF ．考点：全等三角形的判定．4．在一个不透明的袋子中装有除颜色外完全相同的3个红球、3个黄球、2个绿球，任意摸出一球，摸到红球的概率是．【答案】38【解析】5．不等式组⎩⎪⎨⎪⎧x +1＞0a - 13x ＜0的解集是x ＞-1，则a 的取值范围是．【答案】a ≤﹣13 【解析】试题解析：解不等式x+1＞0，得：x ＞﹣1，解不等式a ﹣13x ＜0，得：x ＞3a ， ∵不等式组的解集为x ＞﹣1，则3a ≤﹣1，∴a ≤﹣13考点：解一元一次不等式组．6．原价100元的某商品，连续两次降价后售价为81元，若每次降低的百分率相同，则降低的百分率为．【答案】10%．【解析】试题解析：设这两次的百分率是x，根据题意列方程得100×（1﹣x）2=81，解得x1=0.1=10%，x2=1.9（不符合题意，舍去）．答：这两次的百分率是10%．考点：一元二次方程的应用．7．如图，边长为4的正方形ABCD，点P是对角线BD上一动点，点E在边CD上，EC=1，则PC+PE的最小值是．第7题图【答案】5.【解析】试题解析：连接AC、AE，∴PC+PE的最小值为5．考点：轴对称﹣最短路线问题；正方形的性质．8．圆锥底面半径为3cm，母线长32cm则圆锥的侧面积为cm2．【答案】92π 【解析】考点：圆锥的计算．9．△ABC 中，AB =12，AC =39，∠B =30°则△ABC 的面积是．【答案】213或153．【解析】试题解析：①如图1，作AD ⊥BC ，垂足为点D ，在Rt △ABD 中，∵AB=12、∠B=30°，∴AD=12AB=6，BD=ABcosB=12323 在Rt △ACD 中，2222(39)6AC AD -=-3，∴333则S △ABC =12×BC ×AD=12×3×3 ②如图2，作AD ⊥BC ，交BC 延长线于点D ，考点：解直角三角形．10．观察下列图形，第一个图形中有一个三角形；第二个图形中有5个三角形；第三个图形中有9个三角形；…….则第个图形中有个三角形．第1个第2个第3个第2017个第10题图【答案】8065【解析】试题解析：第1个图形中一共有1个三角形，第2个图形中一共有1+4=5个三角形，第3个图形中一共有1+4+4=9个三角形，…第n个图形中三角形的个数是1+4（n﹣1）=4n﹣3，当n=时，4n﹣3=8065.考点：图形的变化类二、选择题（每题3分，满分30分）11．下列各运算中，计算正确的是（）A．(x-2)2=x2-4 B．(3a2)3=9a6C．x6÷x2=x3D．x3·x2=x5【答案】D.【解析】试题解析：A.原式=x2﹣4x+4，故A错误；B.原式=27a6，故B错误；C.原式=x4，故C错误；故选D.考点：整式的混合运算．12．下列图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．【答案】C．【解析】考点：中心对称图形；轴对称图形13．几个相同的小正方体所搭成的几何体的俯视图如图所示，小正方形中的数字表示在该位置小正方体的个数最多是（）俯视图左视图A．5个B．7个C．8个D．9个【答案】B．【解析】试题解析：由俯视图及左视图知，构成该几何体的小正方形体个数最多的情况如下：故选B ．考点：由三视图判断几何体．14．一组从小到大排列的数据：a ，3，4，4，6(a 为正整数)，唯一的众数是4，则该组数据的平均数是（）A ．3.6B ．3.8C ．3.6或3.8D ．4.2【答案】C ．【解析】考点：众数；算术平均数．15．如图，某工厂有两个大小相同的蓄水池，且中间有管道连通。

真题龙东地区中考数学试卷含答案

黑龙江省龙东地区20XX年初中毕业学业统一考试数学试题考生注意：Array1、考试时间120分钟二、选择题（每题3分，满分30分）11.下列各运算中，计算正确的是（）A ．()3532b a ba = B ．()632273a a = C ．326x x x =÷ D ．()222b a b a +=+12.下列图形中，既是轴对称图形又是中心对称图形的是（）A B C D13.如图,是由若干个相同的小立方体搭成的几何体的俯视图和左视图,则小立方体的个数可能是（）AB C D 第15题图A ．＞1 B. ≥1 C. ≥1且≠9 D. ≤1 18.如图,在矩形ABCD 中,AD=4,∠DAC=30°,点P 、E 分别在AC 、AD 上，则PE+PD 的最小值是（） A.2 B.32 C. 4 D.33819.“双11”促销活动中，小芳的妈妈计划用1000元在唯品会购买价格分别为80元和120元的两种商品，则可供小芳妈妈选择的购买方案有（）A.4种B.5种C.6种D.7种20.如图，在边长为4的正方形ABCD 中，E 、F 是AD 边上的两个动点,且AE=FD,连接BE 、CF 、BD ，CF 与BD 交于点G ，连接AG 交BE 于点H ，连接DH.下列结论正确的个数是（） ①△ABG ∽△FDG ②HD 平分∠EHG ③AG ⊥BE ④S △HDG : S △HBG =tan ∠DAG ⑤线段DH 的最小值是252-三、解答题（满分60分） 21.（本题满分5分）先化简，再求值：12123322--+-÷-a aa a a a a ,其中=a 1+2cos60°22.（本题满分6分）如图，在平面直角坐标系中，△ABC 的三个顶点都在格点上，点A 的坐标为（2，2）请解答下列问题: （1）画出△ABC 关于y 轴对称的△A1B 1C 1，并写出A 1的坐标. （2）画出△ABC 绕点B 逆时针旋转90°后得到的△A 2BC 2，并写出A 2的坐标.（3）画出和△A 2BC 2关于原点O 成中心对称的△A 3B 3C 3，并写出A 3的坐标. F E H D A G BC 第20题图第22题图23.（本题满分6分）如图，Rt △A O B 的直角边O A 在x 轴上，O A=2，AB=1，将Rt △A O B 绕点O 逆时针旋转90°得到Rt △C O D ，抛物线y=c bx x ++-265经过B 、D 两点.（1）求二次函数的解析式.（2）连接BD ，点P 是抛线上一点，直线O P 把△B O D 的周长分成相等的两部分，求点P 的坐标.24.（本题满分7分）我市某中学为了了解孩子们对《中国诗词大会》,《挑战不可能》,《最强大脑》,《超级演说家》,《地理中国》五种电视节目的喜爱程度,随机在七、八、九年级抽取了部分学生进行调查(每人只能选择一种喜爱的电视节目),并将获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据两幅统计图中的信息回答下列问题：（1）本次调查中共抽取了______名学生. （2）补全条形统计图.（3）在扇形统计图中，喜爱《地理中国》节目的人数所在扇形的圆心角是___ _度. （4）若该学校有2000人，请你估计该学校喜欢《最强大脑》节目的学生人数是多少人？第23题图中国大脑演说家诗词大会不可能25.（本题满分8分）在甲、乙两城市之间有一服务区,一辆客车从甲地驶往乙地,一辆货车从乙地驶往甲地,两车同时出发,匀速行驶.客车、货车离服务区的距离y1(千米),y2(千米)与行驶的时间x(小时)的函数关系图象如图1所示.(1)甲、乙两地相距千米.(2)求出发3小时后,货车离服务区的路程y2(千米)与行驶时间x(小时)之间的函数关系式.(3)在客车和货车出发的同时,有一辆邮政车从服务区匀速去甲地取货后返回乙地（取货的时间忽略不计）,邮政车离服务区的距离y3(千米)与行驶时间x(小时)之间的函数关系图象如图2中的虚线所示,直接写出在行驶的过程中,经过多长时间邮政车与客车和货车的距离相等?第25题图26.（本题满分8分）己知:△A O B 和△C O D 均为等腰直角三角形, ∠A O B=∠C O D=90°.连接AD 、BC,点H 为BC 中点,连接O H. (1)如图1所示,易证: O H=21AD 且O H ⊥AD(不需证明). (2)将△C O D 绕点O 旋转到图2、图3所示位置时，线段O H 与AD 又有怎样的关系.并选择一个图形证明你的结论.第26题图图2 B A DO C H ADB O 图3C H 图1 B A O CH27.（本题满分10分）为了推动“龙江经济带”建设,我省某蔬菜企业决定通过加大种植面积、增加种植种类，促进经济发展.20XX 年春,预计种植西红柿、马铃薯、青椒共100公顷(三种蔬菜的种植面积均为整数)，青椒的种植面积是西红柿种植面积的2倍.经预算，种植西红柿的利润可达1万元/公顷、青椒1.5万元/公顷、马铃薯2万元/公顷.设种植西红柿x 公顷,总利润为y 万元.(1)求总利润y (万元)与种植西红柿的面积x (公顷)之间的关系式. (2)若预计总利润不低于180万元,西红柿的种植面积不低于8公顷,有多少种种植方案? (3)在（2）的前提下，该企业决定投资不超过获得最大利润的81在冬季同时建造A 、B 两种类型的温室大棚,开辟新的经济增长点.经测算，投资A 种类型的大棚5万元/个、B 种类型的大棚8万元/个,请直接写出有哪几种建造方案?28.(本题满分10分)如图,矩形A O CB 的顶点A 、C 分别位于x 轴和y 轴的正半轴上,线段O A 、O C 的长度满足方程01315=-+-y x (O A ＞O C),直线b kx y +=分别与x 轴、y 轴交于M 、N 两点.将△BCN 沿直线BN 折叠,点C 恰好落在直线MN 上的点D 处,且tan ∠CBD =43. (1)求点B 的坐标.(2)求直线BN 的解析式.(3)将直线BN 以每秒1个单位长度的速度沿y 轴向下平移,求直线BN 扫过矩形A O CB 的面积S 关于运动的时间t(0＜t ≤13)的函数关系式.第28题图黑龙江省龙东地区20XX 年初中毕业学业统一考试数学试题参考答案及评分标准一、填空（每题3分，共30分）1.8×10102.x ≠13.AB=DE(BC=EF, DF=AC)等4. 55.a ≥16.39.57.34316-π8.1324+π 9.4或34 或74 10.（2016332⎪⎪⎭⎫ ⎝⎛,0)或写成⎪⎪⎭⎫ ⎝⎛0,3210082016或⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫⎝⎛0,322016二、选择题（每题3分，共30分）11.B 12.A 13.D 14.C 15.D 16. B 17. C 18 B 19. A 20.C 三、解答题（满分60分） 21.（本题满分5分）解：原式=aa )1(3-·22)1(-a a -12-a a ……………………………………… 2分 =1-a a . …………………………………………………… 1分当a=2cos60°+1=2时， ………………………………………… 1分原式=2. ……………………………………………………1分22. （本题满分6分）解; ⑴正确画出对称后的图形 ………………………………………1分 A 1（-2，2）………………………………………1分⑵正确画出旋转后的图形 ………………………………………1分 A 2（4，0）………………………………………1分⑶正确画出成中心对称的图形 ………………………………………1分 A 3（-4，0）………………………………………1分 23. （本题满分6分）解：（1）由题意得，△AOB ≌△COD ∴OC=OA=2，CD=AB=1.∴ B （2，1） D （-1，2）………………………………………………………1分 ∵抛物线y=c bx x ++-265经过B 、D 两点.⎪⎪⎩⎪⎪⎨⎧=+--⨯-=++⨯-2)1(651226522c b c b∴⎪⎪⎩⎪⎪⎨⎧==21310b c ……………………… … …… … 1分 ∴二次函数解析式是10152++-=x x y ……………1分(2) ∵直线OP 把△B O D 分成周长相等的两部分∴直线OP 必过线段BD 的中点（23,21） …………1分∴直线OP 的解析式y op =3x …………1分∵点P 是抛物线31021652++-=x x y 和直线y op =3x 的交点∴⎪⎩⎪⎨⎧++-==310216532x x y xy∴P （1，3）或P （-4，-12）………………………………2分24. （本题满分7分）解：(1)本次共调查学生200%1530=（人）. ………………………………1分（2）补全条形图的高度是50.………………………………2分（3）喜爱《地理中国》节目的人数所在扇形的圆心角是36度.…………………2分（4）估计该学校喜欢《最强大脑》节目的学生人数是600人.……2分 25. （本题满分8分）解：（1）甲、乙两地相距480 千米………………………………2分（2）设出发3小时，货车离服务区的路程y 2与时间x 的关系式为y 2=kx+b （k ≠0），则 ⎩⎨⎧=+=+3601203b k b k ………………………………………………………1分解得:⎩⎨⎧-==12040b k ………………………………………………………1分∴y 2=40x-120 ………………………………………………………1分（3）经过1.2小时、 4.8小时、 7.5小时邮政车与客车和货车的距离相等 ……3分 26. （本题满分8分）解：（1）图2的结论为：OH=21AD …………………………………1分 OH ⊥AD ………………………………1分图3的结论为: OH=21AD ………………………………1分 OH ⊥AD ………………………………1 (2) 选图2的结论证明如下：证明: 延长OH 到点Q 使OH=HQ,连接QC 易证△BHO ≌△CHQ ∴∠BOH=∠Q OH=21OQ ∵等腰Rt △AOB 和等腰Rt △COD ∴∠AOD=180°-∠COBA∠QCO=180°-(∠QOC+∠Q)=180°-∠COB∴∠AOD= ∠QCO易证△QCO ≌△AOD∴∠Q=∠OAD而∠AOC+∠COB=90°∴∠AOC+∠COQ+∠OAD=90°即OH ⊥AD ………………………2分而OM=21OQ OQ=AD ∴OH=21AD ………………………2分 ∴OH=21AD OH ⊥AD 选图3的结论证明如下：证明:延长OH 到点Q 使OH=HQ,连接QC易证△BHO ≌△CHQ∴∠BOH=∠Q OH=21OQ ∵等腰Rt △AOB 和等腰Rt △COD∴∠BOC+∠AOD=180° ∴∠BOC=∠OAD+∠ADO ∴∠Q+∠COQ=∠OAD+∠ADO ∴∠AOD=∠OCQ 易证△QCO ≌△AOD∴∠Q=∠OAD而∠BOQ+∠AON=90°∴∠DAO+∠AON=90°即OH ⊥AD ………………………2分而OM=21OQ OQ=AD ∴OH=21AD ………………………2分 ∴OH=21AD OH ⊥AD27. （本题满分10分）解（1）由已知可得：y=x+1.5×2x+2(100-x-2x)y=-2x+200 …………………………………………3分 Q 图2 BA DO C H 图3(2) 由已知可得：则⎩⎨⎧≥≥+-81802002x x ， …………………………1分解得8≤x ≤10. …………………………………………………………………1分 ∵x 为整数，∴x 可取8、9、10.∴有三种购买方案……………………………………………………………1分（3）方案一：建造A 种类型大棚1个；B 种类型大棚1个……………1分方案二：建造A 种类型大棚1个；B 种类型大棚2个……………1分方案三：建造A 种类型大棚2个；B 种类型大棚1个……………1分方案四：建造A 种类型大棚3个；B 种类型大棚1个……………1分28 .（本题满分10分）解：（1）∵01315=-+-y x ∴ x=15 ， y=13 . ………………………………………………1分 ∵O A 、O C 的长度满足方程01315=-+-y x (O A ＞O C)∴OA=15 ， OC=13. ……………………………………………………1分∴B(15,13). ………………………………………………………… 1分(2)过点D 作直线EF ∥x 轴,分别交OC 、BA 边于E 、F∴∠CBD=∠BDF∵tan ∠CBD =43 ∴tan ∠BDF = tan ∠CBD =DF BF =43 ………………………………1分 ∴在Rt △BDF 中，BD=15，由勾股定理得：BF=9，DF=12∴DE=3在Rt △DEN 中，DE=3，NE+DN=9 由勾股定理得DN=5 NE=4∴点N （0，8）, ………………………………1分设直线BN 解析式是y BN =kx+b∵N （0，8） B(15,13)∴y BN =831+x . ………………………………1分（3）S=15t ………………………………1分(0<t ≤8) …………………………1分S=9639232-+-t t ………………………………1分 (8<t ≤13) …………………………1分注：本卷中各题若有其它正确的解法，可酌情给分.。

2022年黑龙江省龙东地区中考数学试卷(解析版)

2022年黑龙江省龙东地区中考数学试卷（真题）一、选择题（每题3分，满分30分）1．（3分）（2022•黑龙江）下列运算中，计算正确的是（）A．（b﹣a）2＝b2﹣a2B．3a•2a＝6aC．（﹣x2）2＝x4D．a6÷a2＝a32．（3分）（2022•黑龙江）下列图形是汽车的标识，其中是中心对称图形但不是轴对称图形的是（）A．B．C．D．3．（3分）（2022•黑龙江）学校举办跳绳比赛，九年（2）班参加比赛的6名同学每分钟跳绳次数分别是172，169，180，182，175，176，这6个数据的中位数是（）A．181 B．175 C．176 D．175.54．（3分）（2022•黑龙江）如图是由若干个相同的小正方体搭成的一个几何体的左视图和俯视图，则所需的小正方体的个数最多是（）A．7 B．8 C．9 D．105．（3分）（2022•黑龙江）2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛，单循环比赛共进行了45场，共有多少支队伍参加比赛？（）A．8 B．10 C．7 D．96．（3分）（2022•黑龙江）已知关于x的分式方程﹣＝1的解是正数，则m的取值范围是（）A．m＞4 B．m＜4 C．m＞4且m≠5 D．m＜4且m≠17．（3分）（2022•黑龙江）国家“双减”政策实施后，某校开展了丰富多彩的社团活动．某班同学报名参加书法和围棋两个社团，班长为参加社团的同学去商场购买毛笔和围棋（两种都购买）共花费360元．其中毛笔每支15元，围棋每副20元，共有多少种购买方案？（）A．5 B．6 C．7 D．88．（3分）（2022•黑龙江）如图，在平面直角坐标系中，点O为坐标原点，平行四边形OBAD的顶点B在反比例函数y＝的图象上，顶点A在反比例函数y ＝的图象上，顶点D在x轴的负半轴上．若平行四边形OBAD的面积是5，则k的值是（）A．2 B．1 C．﹣1 D．﹣29．（3分）（2022•黑龙江）如图，△ABC中，AB＝AC，AD平分∠BAC与BC相交于点D，点E是AB的中点，点F是DC的中点，连接EF交AD于点P．若△ABC 的面积是24，PD＝1.5，则PE的长是（）A．2.5 B．2 C．3.5 D．310．（3分）（2022•黑龙江）如图，正方形ABCD的对角线AC，BD相交于点O，点F是CD上一点，OE⊥OF交BC于点E，连接AE，BF交于点P，连接OP．则下列结论：①AE⊥BF；②∠OPA＝45°；③AP﹣BP＝OP；④若BE：CE＝2：3，则tan∠CAE＝；⑤四边形OECF的面积是正方形ABCD面积的．其中正确的结论是（）A．①②④⑤B．①②③⑤C．①②③④D．①③④⑤二、填空题（每题3分，满分30分）11．（3分）（2022•黑龙江）我国南水北调东线北延工程2021﹣2022年度供水任务顺利完成，共向黄河以北调水1.89亿立方米，将数据1.89亿用科学记数法表示为．12．（3分）（2022•黑龙江）在函数中，自变量x的取值范围是．13．（3分）（2022•黑龙江）如图，在四边形ABCD中，对角线AC，BD相交于点O，OA＝OC，请你添加一个条件，使△AOB≌△COD．14．（3分）（2022•黑龙江）在一个不透明的口袋中，有2个红球和4个白球，这些球除颜色外其余完全相同，摇匀后随机摸出一个球，摸到红球的概率是．15．（3分）（2022•黑龙江）若关于x的一元一次不等式组的解集为x＜2，则a的取值范围是．16．（3分）（2022•黑龙江）如图，在⊙O中，AB是⊙O的弦，⊙O的半径为3cm．C 为⊙O上一点，∠ACB＝60°，则AB的长为cm．17．（3分）（2022•黑龙江）若一个圆锥的母线长为5cm，它的侧面展开图的圆心角为120°，则这个圆锥的底面半径为cm．18．（3分）（2022•黑龙江）如图，菱形ABCD中，对角线AC，BD相交于点O，∠BAD＝60°，AD＝3，AH是∠BAC的平分线，CE⊥AH于点E，点P是直线AB上的一个动点，则OP+PE的最小值是．19．（3分）（2022•黑龙江）在矩形ABCD中，AB＝9，AD＝12，点E在边CD上，且CE＝4，点P是直线BC上的一个动点．若△APE是直角三角形，则BP的长为．20．（3分）（2022•黑龙江）如图，在平面直角坐标系中，点A1，A2，A3，A4…在x轴上且OA＝1，OA2＝2OA1，OA3＝2OA2，OA4＝2OA3…按此规律，过点A1，A2，1A，A4…作x轴的垂线分别与直线y＝x交于点B1，B2，B3，B4…记△OA1B1，3△OA2B2，△OA3B3，△OA4B4…的面积分别为S1，S2，S3，S4…则S2022＝．三、解答题（满分60分）21．（5分）（2022•黑龙江）先化简，再求值：（﹣1）÷，其中a＝2cos30°+1．22．（6分）（2022•黑龙江）如图，在正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，﹣1），B（2，﹣5），C（5，﹣4）．（1）将△ABC先向左平移6个单位，再向上平移4个单位，得到△A1B1C1，画出两次平移后的△A1B1C1，并写出点A1的坐标；（2）画出△A1B1C1绕点C1顺时针旋转90°后得到△A2B2C1，并写出点A2的坐标；（3）在（2）的条件下，求点A1旋转到点A2的过程中所经过的路径长（结果保留π）．23．（6分）（2022•黑龙江）如图，抛物线y＝x2+bx+c经过点A（﹣1，0），点B （2，﹣3），与y轴交于点C，抛物线的顶点为D．（1）求抛物线的解析式；（2）抛物线上是否存在点P，使△PBC的面积是△BCD面积的4倍，若存在，请直接写出点P的坐标；若不存在，请说明理由．24．（7分）（2022•黑龙江）为进一步开展“睡眠管理”工作，某校对部分学生的睡眠情况进行了问卷调查．设每名学生平均每天的睡眠时间为x小时，其中的分组情况是：A组：x＜8.5B组：8.5≤x＜9C组：9≤x＜9.5D组：9.5≤x＜10E组：x≥10根据调查结果绘制成两幅不完整的统计图，请根据图中提供的信息，解答下列问题：（1）本次共调查了名学生；（2）补全条形统计图；（3）在扇形统计图中，求D组所对应的扇形圆心角的度数；（4）若该校有1500名学生，请估计该校睡眠时间不足9小时的学生有多少人？25．（8分）（2022•黑龙江）为抗击疫情，支援B市，A市某蔬菜公司紧急调运两车蔬菜运往B市．甲、乙两辆货车从A市出发前往B市，乙车行驶途中发生故障原地维修，此时甲车刚好到达B市．甲车卸载蔬菜后立即原路原速返回接应乙车，把乙车的蔬菜装上甲车后立即原路原速又运往B市．乙车维修完毕后立即返回A市．两车离A市的距离y（km）与乙车所用时间x（h）之间的函数图象如图所示．（1）甲车速度是km/h，乙车出发时速度是km/h；（2）求乙车返回过程中，乙车离A市的距离y（km）与乙车所用时间x（h）的函数解析式（不要求写出自变量的取值范围）；（3）乙车出发多少小时，两车之间的距离是120km？请直接写出答案．26．（8分）（2022•黑龙江）△ABC和△ADE都是等边三角形．（1）将△ADE绕点A旋转到图①的位置时，连接BD，CE并延长相交于点P（点P与点A重合），有PA+PB＝PC（或PA+PC＝PB）成立（不需证明）；（2）将△ADE绕点A旋转到图②的位置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？并加以证明；（3）将△ADE绕点A旋转到图③的位置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？直接写出结论，不需要证明．27．（10分）（2022•黑龙江）学校开展大课间活动，某班需要购买A、B两种跳绳．已知购进10根A种跳绳和5根B种跳绳共需175元：购进15根A种跳绳和10根B种跳绳共需300元．（1）求购进一根A种跳绳和一根B种跳绳各需多少元？（2）设购买A种跳绳m根，若班级计划购买A、B两种跳绳共45根，所花费用不少于548元且不多于560元，则有哪几种购买方案？（3）在（2）的条件下，哪种购买方案需要的总费用最少？最少费用是多少元？28．（10分）（2022•黑龙江）如图，在平面直角坐标系中，平行四边形ABCD的边AB在x轴上，顶点D在y轴的正半轴上，M为BC的中点，OA、OB的长分别是一元二次方程x2﹣7x+12＝0的两个根（OA＜OB），tan∠DAB＝，动点P 从点D出发以每秒1个单位长度的速度沿折线DC﹣CB向点B运动，到达B点停止．设运动时间为t秒，△APC的面积为S．（1）求点C的坐标；（2）求S关于t的函数关系式，并写出自变量t的取值范围；（3）在点P的运动过程中，是否存在点P，使△CMP是等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．2022年黑龙江省龙东地区中考数学试卷参考答案与试题解析一、选择题（每题3分，满分30分）1．（3分）（2022•黑龙江）下列运算中，计算正确的是（）A．（b﹣a）2＝b2﹣a2B．3a•2a＝6aC．（﹣x2）2＝x4D．a6÷a2＝a3【分析】利用完全平方公式，单项式乘多项式，幂的乘方的法则，同底数幂的除法的法则对各项进行运算即可．【解答】解：A．（b﹣a）2＝b2﹣2ab+a2，故A不正确；B.3a•2a＝6a2，故B不正确；C．（﹣x2）2＝x4，故C正确；D．a6÷a2＝a4，故D不符合题意；故选：C．【点评】本题考查了完全平方公式，单项式乘多项式，幂的乘方的法则，同底数幂的除法，解答的关键是对相应的运算法则的掌握．2．（3分）（2022•黑龙江）下列图形是汽车的标识，其中是中心对称图形但不是轴对称图形的是（）A．B．C．D．【分析】根据中心对称图形与轴对称图形的概念进行判断即可．【解答】解：A．既是中心对称图形，也是轴对称图形，故此选项不合题意；B．不是中心对称图形，是轴对称图形，故此选项不合题意；C．是中心对称图形但不是轴对称图形，故此选项符合题意；D．不是中心对称图形，是轴对称图形，故此选项不合题意；故选：C．【点评】本题考查的是中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后与自身重合．3．（3分）（2022•黑龙江）学校举办跳绳比赛，九年（2）班参加比赛的6名同学每分钟跳绳次数分别是172，169，180，182，175，176，这6个数据的中位数是（）A．181 B．175 C．176 D．175.5【分析】将这组数据从小到大排列，根据中位数的计算方法即可得出答案．【解答】解：将这组数据从小到大排列为：169，172，175，176，180，182，中位数＝＝175.5，故选：D．【点评】本题考查了中位数，掌握将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数是解题的关键．4．（3分）（2022•黑龙江）如图是由若干个相同的小正方体搭成的一个几何体的左视图和俯视图，则所需的小正方体的个数最多是（）A．7 B．8 C．9 D．10【分析】由左视图和俯视图可以猜想到主视图的可能情况，从而得到答案．【解答】解：从俯视图课看出前后有三层，从左视图可看出最后面有2层高，中间最高是2层，要是最多就都是2层，最前面的最高是1层，所以最多的为：2+2×2+1×2＝8．故选：B．【点评】本题考查了三视图的知识，由两个识图想象几何体是解题的关键，5．（3分）（2022•黑龙江）2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛，单循环比赛共进行了45场，共有多少支队伍参加比赛？（）A．8 B．10 C．7 D．9【分析】设共有x支队伍参加比赛，根据“循环比赛共进行了45场”列一元二次方程，求解即可．【解答】解：设共有x支队伍参加比赛，根据题意，可得，解得x＝10或x＝﹣9（舍），∴共有10支队伍参加比赛．故选：B．【点评】本题考查了一元二次方程的应用，理解题意并根据题意建立等量关系是解题的关键．6．（3分）（2022•黑龙江）已知关于x的分式方程﹣＝1的解是正数，则m的取值范围是（）A．m＞4 B．m＜4 C．m＞4且m≠5 D．m＜4且m≠1 【分析】先利用m表示出x的值，再由x为正数求出m的取值范围即可．【解答】解：方程两边同时乘以x﹣1得，2x﹣m+3＝x﹣1，解得x＝m﹣4．∵x为正数，∴m﹣4＞0，解得m＞4，∵x≠1，∴m﹣4≠1，即m≠5，∴m的取值范围是m＞4且m≠5．故选：C．【点评】本题考查了分式方程的解，掌握求出使分式方程中令等号左右两边相等且分母不等于0的未知数的值，这个值叫方程的解是解题的关键．7．（3分）（2022•黑龙江）国家“双减”政策实施后，某校开展了丰富多彩的社团活动．某班同学报名参加书法和围棋两个社团，班长为参加社团的同学去商场购买毛笔和围棋（两种都购买）共花费360元．其中毛笔每支15元，围棋每副20元，共有多少种购买方案？（）A．5 B．6 C．7 D．8【分析】设购买毛笔x支，围棋y副，根据“购买毛笔和围棋（两种都购买）共花费360元”列二元一次方程，再由x和y分别取正整数，即可确定购买方案．【解答】解：设购买毛笔x支，围棋y副，根据题意，得15x+20y＝360，∴y＝18﹣x，∵两种都买，∴18﹣x＞0，x、y都是正整数，解得x＜24，故x是4的倍数且x＜24，∴x＝4，y＝15或x＝8，y＝12或x＝12，y＝9或x＝16，y＝6或x＝20，y ＝3；∴共有5种购买方案，故选：A．【点评】本题考查了二元一次方程的应用，理解题意并根据题意建立二元一次方程是解题的关键．8．（3分）（2022•黑龙江）如图，在平面直角坐标系中，点O为坐标原点，平行四边形OBAD的顶点B在反比例函数y＝的图象上，顶点A在反比例函数y ＝的图象上，顶点D在x轴的负半轴上．若平行四边形OBAD的面积是5，则k的值是（）A．2 B．1 C．﹣1 D．﹣2【分析】设B（a，），根据四边形OBAD是平行四边形，推出AB∥DO，表示出A点的坐标，求出AB＝a﹣，再根据平行四边形面积公式列方程，解出即可．【解答】解：设B（a，），∵四边形OBAD是平行四边形，∴AB∥DO，∴A（，），∴AB＝a﹣，∵平行四边形OBAD的面积是5，∴（a﹣）＝5，解得k＝﹣2，故选：D．【点评】本题考查反比例函数比例系数k的几何意义、反比例函数图象上点的坐标特征、平行四边形性质，掌握反比例函数比例系数k的几何意义及函数图象上点的坐标特征，设出点的坐标、根据平行四边形面积公式列方程是解题的关键．9．（3分）（2022•黑龙江）如图，△ABC中，AB＝AC，AD平分∠BAC与BC相交于点D，点E是AB的中点，点F是DC的中点，连接EF交AD于点P．若△ABC 的面积是24，PD＝1.5，则PE的长是（）A．2.5 B．2 C．3.5 D．3【分析】如图，过点E作EG⊥AD于G，证明△EGP≌△FDP，得PG＝PD＝1.5，由三角形中位线定理可得AD的长，由三角形ABC的面积是24，得BC的长，最后由勾股定理可得结论．【解答】解：如图，过点E作EG⊥AD于G，∵AB＝AC，AD平分∠BAC，∴AD⊥BC，BD＝CD，∴∠PDF＝∠EGP＝90°，EG∥BC，∵点E是AB的中点，∴G是AD的中点，∴EG＝BD，∵F是CD的中点，∴DF＝CD，∴EG＝DF，∵∠EPG＝∠DPF，∴△EGP≌△FDP（AAS），∴PG＝PD＝1.5，∴AD＝2DG＝6，∵△ABC的面积是24，∴•BC•AD＝24，∴BC＝48÷6＝8，∴DF＝BC＝2，∴EG＝DF＝2，由勾股定理得：PE＝＝2.5．故选：A．【点评】本题考查了等腰三角形的性质，三角形的中位线定理，全等三角形的性质和判定，三角形的面积等知识，作辅助线构建全等三角形是解本题的关键．10．（3分）（2022•黑龙江）如图，正方形ABCD的对角线AC，BD相交于点O，点F是CD上一点，OE⊥OF交BC于点E，连接AE，BF交于点P，连接OP．则下列结论：①AE⊥BF；②∠OPA＝45°；③AP﹣BP＝OP；④若BE：CE＝2：3，则tan∠CAE＝；⑤四边形OECF的面积是正方形ABCD面积的．其中正确的结论是（）A．①②④⑤B．①②③⑤C．①②③④D．①③④⑤【分析】利用全等三角形的判定与性质，正方形的性质，圆周角定理，直角三角形的边角关系定理对每个选项的结论进行判断即可得出结论．【解答】解：①∵四边形ABCD是正方形，∴AB＝BC＝CD，AC⊥BD，∠ABD＝∠DBC＝∠ACD＝45°．∴∠BOE+∠EOC＝90°，∵OE⊥OF，∴∠FOC+∠EOC＝90°．∴∠BOE＝∠COF．在△BOE和△COF中，，∴△BOE≌△COF（ASA），∴BE＝CF．在△BAE和△CBF中，，∴△BAE≌△CBF（SAS），∴∠BAE＝∠CBF．∵∠ABP+∠CBF＝90°，∴∠ABP+∠BAE＝90°，∴∠APB＝90°．∴AE⊥BF．∴①的结论正确；②∵∠APB＝90°，∠AOB＝90°，∴点A，B，P，O四点共圆，∴∠APO＝∠ABO＝45°，∴②的结论正确；③过点O作OH⊥OP，交AP于点H，如图，∵∠APO＝45°，OH⊥OP，∴OH＝OP＝HP，∴HP＝OP．∵OH⊥OP，∴∠POB+∠HOB＝90°，∵OA⊥OB，∴∠AOH+∠HOB＝90°．∴∠AOH＝∠BOP．∵∠OAH+BAE＝45°，∠OBP+∠CBF＝45°，，∠BAE＝∠CBF，∴∠OAH＝∠OBP．在△AOH和△BOP中，，∴△AOH≌△BOP（ASA），∴AH＝BP．∴AP﹣BP＝AP﹣AH＝HP＝OP．∴③的结论正确；④∵BE：CE＝2：3，∴设BE＝2x，则CE＝3x，∴AB＝BC＝5x，∴AE＝＝x．过点E作EG⊥AC于点G，如图，∵∠ACB＝45°，∴EG＝GC＝EC＝x，∴AG＝＝x，在Rt△AEG中，∵tan∠CAE＝，∴tan∠CAE＝＝＝．∴④的结论不正确；⑤∵四边形ABCD是正方形，∴OA＝OB＝OC＝OD，∠AOB＝∠BOC＝∠COD＝∠DOA＝90°，∴△OAB≌△OBC≌△OCD≌△DOA（SAS）．∴．∴．由①知：△BOE≌△COF，∴S△OBE＝S△OFC，∴．即四边形OECF的面积是正方形ABCD面积的．∴⑤的结论正确．综上，①②③⑤的结论正确．故选：B．【点评】本题主要考查了全等三角形的判定与性质，正方形的性质，圆周角定理，直角三角形的边角关系定理，等腰直角三角形的判定与性质，充分利用正方形的性质构造等腰直角三角形和全等三角形是解题的关键．二、填空题（每题3分，满分30分）11．（3分）（2022•黑龙江）我国南水北调东线北延工程2021﹣2022年度供水任务顺利完成，共向黄河以北调水1.89亿立方米，将数据1.89亿用科学记数法表示为 1.89×108．【分析】用科学记数法表示较大的数时，一般形式为a×10n，其中1≤|a|＜10，n为整数，且n比原来的整数位数少1，据此判断即可．【解答】解：1.89亿＝189000000＝1.89×108．故答案为：1.89×108．【点评】此题主要考查了用科学记数法表示较大的数，一般形式为a×10n，其中1≤|a|＜10，确定a与n的值是解题的关键．12．（3分）（2022•黑龙江）在函数中，自变量x的取值范围是x≥．【分析】根据被开方数大于等于0列式计算即可得解．【解答】解：根据题意得，2x﹣3≥0，解得x≥．故答案为：x≥．【点评】本题考查的知识点为：二次根式的被开方数是非负数．13．（3分）（2022•黑龙江）如图，在四边形ABCD中，对角线AC，BD相交于点O，OA＝OC，请你添加一个条件OB＝OD（答案不唯一），使△AOB≌△COD．【分析】此题是一道开放型的题目，答案不唯一，只要符合全等三角形的判定定理即可．【解答】解：添加的条件是OB＝OD，理由是：在△AOB和△COD中，，∴△AOB≌△COD（SAS），故答案为：OB＝OD（答案不唯一）．【点评】本题考查了全等三角形的判定定理，能熟记全等三角形的判定定理是解此题的关键，注意：全等三角形的判定定理是SAS，SAS，AAS，SSS，两直角三角形全等还有HL等．14．（3分）（2022•黑龙江）在一个不透明的口袋中，有2个红球和4个白球，这些球除颜色外其余完全相同，摇匀后随机摸出一个球，摸到红球的概率是．【分析】直接利用概率公式，进而计算得出答案．【解答】解：∵在一个不透明的口袋中，有2个红球和4个白球，这些球除颜色外其余完全相同，摇匀后随机摸出一个球，∴摸到红球的概率是：＝．故答案为：．【点评】此题主要考查了概率公式，正确掌握概率求法是解题关键．15．（3分）（2022•黑龙江）若关于x的一元一次不等式组的解集为x＜2，则a的取值范围是a≥2 ．【分析】不等式组整理后，根据已知解集，利用同小取小法则判断即可确定出a的范围．【解答】解：不等式组整理得：，∵不等式组的解集为x＜2，∴a≥2．故答案为：a≥2．【点评】此题考查了解一元一次不等式组，熟练掌握不等式组取解集的方法是解本题的关键．16．（3分）（2022•黑龙江）如图，在⊙O中，AB是⊙O的弦，⊙O的半径为3cm．C 为⊙O上一点，∠ACB＝60°，则AB的长为3cm．【分析】连接AO并延长交⊙O于点D，根据直径所对的圆周角是直角可得∠ADB＝90°，再利用同弧所对的圆周角相等可求出∠ADB＝60°，然后在Rt△ABD中，利用锐角三角函数的定义进行计算即可解答．【解答】解：连接AO并延长交⊙O于点D，∵AD是⊙O的直径，∴∠ADB＝90°，∵∠ACB＝60°，∴∠ADB＝∠ACB＝60°，在Rt△ABD中，AD＝6cm，∴AB＝AD•sin60°＝6×＝3（cm），故答案为：3．【点评】本题考查了三角形的外接圆与外心，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．17．（3分）（2022•黑龙江）若一个圆锥的母线长为5cm，它的侧面展开图的圆心角为120°，则这个圆锥的底面半径为cm．【分析】先求出圆锥侧面展开图扇形的弧长，再利用侧面展开图与底面圆的关系的关系列方程即可求出圆锥的底面半径．【解答】解：c长为：＝，设圆锥的底面半径为r，则2πr＝，∴r＝cm．故答案为：．【点评】本题主要考查圆锥的计算，掌握侧面展开图与底面圆的关系是解题关键．18．（3分）（2022•黑龙江）如图，菱形ABCD中，对角线AC，BD相交于点O，∠BAD＝60°，AD＝3，AH是∠BAC的平分线，CE⊥AH于点E，点P是直线AB上的一个动点，则OP+PE的最小值是．【分析】连接OE，过点O作OF⊥AB，垂足为F，并延长到点O′，使O′F＝OF，连接O′E交直线AB于点P，连接OP，从而可得OP＝O′P，此时OP+PE 的值最小，先利用菱形的性质可得AD＝AB＝3，∠BAC＝∠BAD，OA＝OC＝AC，OD＝OB＝BD，∠AOD＝90°，从而可得△ADB是等边三角形，进而求出AD＝3，然后在Rt△ADO中，利用勾股定理求出AO的长，从而求出AC的长，进而利用直角三角形斜边上的中线可得OE＝OA＝AC＝，再利用角平分线和等腰三角形的性质可得OE∥AB，从而求出∠EOF＝90°，进而在Rt△AOF中，利用锐角三角函数的定义求出OF的长，即可求出OO′的长，最后在Rt△EOO′中，利用勾股定理进行计算即可解答．【解答】解：连接OE，过点O作OF⊥AB，垂足为F，并延长到点O′，使O′F＝OF，连接O′E交直线AB于点P，连接OP，∴AP是OO′的垂直平分线，∴OP＝O′P，∴OP+PE＝O′P+PE＝O′E，此时，OP+PE的值最小，∵四边形ABCD是菱形，∴AD＝AB＝3，∠BAC＝∠BAD，OA＝OC＝AC，OD＝OB＝BD，∠AOD＝90°，∵∠BAD＝60°，∴△ADB是等边三角形，∴BD＝AD＝3，∴OD＝BD＝，∴AO＝＝＝，∴AC＝2OA＝3，∵CE⊥AH，∴∠AEC＝90°，∴OE＝OA＝AC＝，∴∠OAE＝∠OEA，∵AE平分∠CAB，∴∠OAE＝∠EAB，∴∠OEA＝∠EAB，∴OE∥AB，∴∠EOF＝∠AFO＝90°，在Rt△AOF中，∠OAB＝DAB＝30°，∴OF＝OA＝，∴OO′＝2OF＝，在Rt△EOO′中，O′E＝＝＝，∴OE+PE＝，∴OP+PE的最小值为，故答案为：．【点评】本题考查了菱形的性质，勾股定理，角平分线的定义，等边三角形的判定与性质，轴对称﹣最短路线问题，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．19．（3分）（2022•黑龙江）在矩形ABCD中，AB＝9，AD＝12，点E在边CD上，且CE＝4，点P是直线BC上的一个动点．若△APE是直角三角形，则BP的长为或或6 ．【分析】若△APE是直角三角形，有三种情况：①如图1，∠AEP＝90°，②如图2，∠PAE＝90°，③如图3，∠APE＝90°，分别证明三角形相似可解答．【解答】解：若△APE是直角三角形，有以下三种情况：①如图1，∠AEP＝90°，∴∠AED+∠CEP＝90°，∵四边形ABCD是矩形，∴∠C＝∠D＝90°，∴∠CEP+∠CPE＝90°，∴∠AED＝∠CPE，∴△ADE∽△ECP，∴＝，即＝，∴CP＝，∵BC＝AD＝12，∴BP＝12﹣＝；②如图2，∠PAE＝90°，∵∠DAE+∠BAE＝∠BAE+∠BAP＝90°，∴∠DAE＝∠BAP，∵∠D＝∠ABP＝90°，∴△ADE∽△ABP，∴＝，即＝，∴BP＝；③如图3，∠APE＝90°，设BP＝x，则PC＝12﹣x，同理得：△ABP∽△PCE，∴＝，即＝，∴x1＝x2＝6，∴BP＝6，综上，BP的长是或或6．故答案为：或或6．【点评】本题考查的是相似三角形的判定与性质，矩形的性质，掌握相似三角形的判定定理和性质定理是解题的关键，并注意运用分类讨论的思想．20．（3分）（2022•黑龙江）如图，在平面直角坐标系中，点A1，A2，A3，A4…在x轴上且OA＝1，OA2＝2OA1，OA3＝2OA2，OA4＝2OA3…按此规律，过点A1，A2，1A，A4…作x轴的垂线分别与直线y＝x交于点B1，B2，B3，B4…记△OA1B1，3△OA2B2，△OA3B3，△OA4B4…的面积分别为S1，S2，S3，S4…则S2022＝．【分析】根据已知先求出OA2，OA3，OA4的长，再代入直线y＝x中，分别求出A1B1，A2B2，A3B3，A4B4，然后分别计算出S1，S2，S3，S4，再从数字上找规律进行计算即可解答．【解答】解：∵OA1＝1，OA2＝2OA1，∴OA2＝2，∵OA3＝2OA2，∴OA3＝4，∵OA4＝2OA3，∴OA4＝8，把x＝1代入直线y＝x中可得：y＝，∴A1B1＝，把x＝2代入直线y＝x中可得：y＝2，∴A2B2＝2，把x＝4代入直线y＝x中可得：y＝4，∴A3B3＝4，把x＝8代入直线y＝x中可得：y＝8，∴A4B4＝8，∴S1＝OA1•A1B1＝×1×＝×20×（20×），S＝OA2•A2B2＝×2×2＝×21×（21×），2S＝OA3•A3B3＝×4×4＝×22×（22×），3S＝OA4•A4B4＝×8×8＝×23×（23×），4..．∴S2022＝×22021×（22021×）＝24041×，故答案为：24041×．【点评】本题考查了规律型：点的坐标，含30度角的直角三角形，根据已知分别求出S1，S2，S3，S4的值，然后从数字上找规律是解题的关键．三、解答题（满分60分）21．（5分）（2022•黑龙江）先化简，再求值：（﹣1）÷，其中a＝2cos30°+1．【分析】利用分式的减法法则和除法法则对分式进行计算化简，把特殊角的三角函数值代入计算求出a的值，代入化简后的分式进行计算，即可得出答案．【解答】解：（﹣1）÷＝÷＝×＝，当a＝2cos30°+1＝2×+1＝时，原式＝＝﹣．【点评】本题考查了分式的化简求值，特殊角的三角函数值，掌握分式的混合计算及特殊角的三角函数值是解决问题的关键．22．（6分）（2022•黑龙江）如图，在正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，﹣1），B（2，﹣5），C（5，﹣4）．（1）将△ABC先向左平移6个单位，再向上平移4个单位，得到△A1B1C1，画出两次平移后的△A1B1C1，并写出点A1的坐标；（2）画出△A1B1C1绕点C1顺时针旋转90°后得到△A2B2C1，并写出点A2的坐标；（3）在（2）的条件下，求点A1旋转到点A2的过程中所经过的路径长（结果保留π）．【分析】（1）利用平移变换的性质分别作出A，B，C的对应点A1，B1，C1即可；（2）利用旋转变换的性质分别作出A1，B1的对应点A2，B2即可；（3）利用勾股定理求出A1C1，再利用弧长公式求解．【解答】解：（1）如图，△A1B1C1即为所求，点A1的坐标（﹣5，，3）；（2）如图，△A2B2C1即为所求，点A2的坐标（2，4）；（3）∵A1C1＝＝5，∴点A1旋转到点A2的过程中所经过的路径长＝＝．【点评】本题考查作图﹣平移变换，旋转变换，弧长公式等知识，解题的关键是掌握平移变换，旋转变换的性质，属于中考常考题型．23．（6分）（2022•黑龙江）如图，抛物线y＝x2+bx+c经过点A（﹣1，0），点B （2，﹣3），与y轴交于点C，抛物线的顶点为D．（1）求抛物线的解析式；（2）抛物线上是否存在点P，使△PBC的面积是△BCD面积的4倍，若存在，请直接写出点P的坐标；若不存在，请说明理由．【分析】（1）待定系数法求解析式即可；（2）设抛物线上的点P坐标为（m，m2﹣2m﹣3），结合方程思想和三角形面积公式列方程求解．【解答】解：（1）∵抛物线y＝x2+bx+c经过点A（﹣1，0），点B（2，﹣3），∴，解得b＝﹣2，c＝﹣3，∴抛物线的解析式：y＝x2﹣2x﹣3；（2）存在，理由如下：∵y＝x2﹣2x﹣3＝（x﹣1）2﹣4，∴D点坐标为（1，4），令x＝0，则y＝x2﹣2x﹣3＝﹣3，∴C点坐标为（0，﹣3），又∵B点坐标为（2，﹣3），∴BC∥x轴，∴S△BCD＝×2×1＝1，设抛物线上的点P坐标为（m，m2﹣2m﹣3），∴S△PBC＝×2×|m2﹣2m﹣3﹣（﹣3）|＝|m2﹣2m|，当|m2﹣2m|＝4×1时，解得m＝1±，当m＝1+时，m2﹣2m﹣3＝1，当m＝1﹣时，m2﹣2m﹣3＝1，综上，P点坐标为（1+，1）或（1﹣，1）．【点评】本题考查二次函数的性质，掌握待定系数法求函数解析式的方法，理解二次函数图象上点的坐标特征，利用方程思想解题是关键．24．（7分）（2022•黑龙江）为进一步开展“睡眠管理”工作，某校对部分学生的睡眠情况进行了问卷调查．设每名学生平均每天的睡眠时间为x小时，其中的分组情况是：A组：x＜8.5B组：8.5≤x＜9C组：9≤x＜9.5D组：9.5≤x＜10E组：x≥10根据调查结果绘制成两幅不完整的统计图，请根据图中提供的信息，解答下列问题：（1）本次共调查了100 名学生；（2）补全条形统计图；（3）在扇形统计图中，求D组所对应的扇形圆心角的度数；（4）若该校有1500名学生，请估计该校睡眠时间不足9小时的学生有多少人？【分析】（1）根据B组人数和所占的百分比，可以计算出本次调查的学生总人数；（2）根据（1）中的结果、条形统计图中的时间和扇形统计图中的数据，可以计算出A组和E组的人数，从而可以将条形统计图补充完整；（3）根据D组的人数和调查的总人数，可以计算出D组所对应的扇形圆心角的度数；（4）根据条形统计图中的数据，可以计算出该校睡眠时间不足9小时的学生有多少人．【解答】解：（1）20÷20%＝100（名），即本次共调查了100名学生，故答案为：100；（2）选择E的学生有：100×15%＝15（人），选择A的学生有：100﹣20﹣40﹣20﹣15＝5（人），补全的条形统计图如右图所示；（3）360°×＝72°，即D组所对应的扇形圆心角的度数是72°；（4）1500×＝375（人），答：估计该校睡眠时间不足9小时的学生有375人．【点评】本题考查条形统计图、扇形统计图、用样本估计总体，解答本题的关键是明确题意，利用数形结合的思想解答．25．（8分）（2022•黑龙江）为抗击疫情，支援B市，A市某蔬菜公司紧急调运两车蔬菜运往B市．甲、乙两辆货车从A市出发前往B市，乙车行驶途中发生故障原地维修，此时甲车刚好到达B市．甲车卸载蔬菜后立即原路原速返回接应乙车，把乙车的蔬菜装上甲车后立即原路原速又运往B市．乙车维修完毕后立即返回A市．两车离A市的距离y（km）与乙车所用时间x（h）之间的函数图象如图所示．（1）甲车速度是100 km/h，乙车出发时速度是60 km/h；（2）求乙车返回过程中，乙车离A市的距离y（km）与乙车所用时间x（h）的函数解析式（不要求写出自变量的取值范围）；（3）乙车出发多少小时，两车之间的距离是120km？请直接写出答案．【分析】（1）根据函数图象中的数据，可以计算出甲车速度和乙车出发时速度；（2）根据函数图象中的数据，可以计算出乙车返回过程中，乙车离A市的距。

龙东中考数学试题及答案

龙东中考数学试题及答案一、选择题（每题3分，共30分）1. 下列哪个数是无理数？A. 0.33333...（循环）B. √2C. 3.14D. 1/3答案：B2. 一个二次函数的图像开口向上，且经过点(1,0)和(-1,0)，下列哪个选项是该二次函数的对称轴？A. x = 0B. x = 1C. x = -1D. x = 2答案：A3. 一个等腰三角形的两边长分别为3和5，那么这个三角形的周长是多少？A. 11B. 13C. 16D. 14答案：B4. 如果一个数的平方等于9，那么这个数是多少？A. ±3B. 3C. -3D. 9答案：A5. 下列哪个选项是不等式2x - 3 > 5的解集？A. x > 4B. x < 4C. x > 1D. x < 1答案：A6. 一个圆的半径为5，那么它的面积是多少？A. 25πB. 50πC. 75πD. 100π答案：B7. 一个长方体的长、宽、高分别为3cm、4cm和5cm，那么它的体积是多少？A. 60cm³B. 48cm³C. 36cm³D. 12cm³答案：A8. 一个等差数列的前三项分别为2、5、8，那么它的第10项是多少？A. 27B. 29C. 31D. 23答案：C9. 一个正五边形的内角和是多少？A. 540°B. 360°C. 720°D. 1080°答案：A10. 一个函数y = 2x + 3的图像与x轴的交点坐标是什么？A. (-3/2, 0)B. (3/2, 0)C. (0, 3)D. (0, -3)答案：A二、填空题（每题3分，共15分）11. 一个直角三角形的两条直角边长分别为3和4，那么它的斜边长是_________。

答案：512. 如果一个数的立方等于-8，那么这个数是_________。

答案：-213. 一个圆的周长为12π，那么它的半径是_________。

中考龙东地区数学试卷

一、选择题（每小题3分，共30分）1. 下列数中，有理数是（）A. √9B. √-16C. πD. √02. 已知a、b是实数，且a + b = 0，则下列等式中正确的是（）A. a^2 = b^2B. a = bC. a^2 = -b^2D. a^2 = b^2 且 a = b3. 在直角坐标系中，点A（-1，2）关于x轴的对称点是（）A.（-1，-2）B.（1，-2）C.（-1，2）D.（1，2）4. 下列函数中，自变量x的取值范围是全体实数的是（）A. y = √xB. y = 1/xC. y = |x|D. y = x^2 - 15. 已知三角形的三边长分别为3，4，5，则这个三角形是（）A. 等腰三角形B. 等边三角形C. 直角三角形D. 梯形6. 在下列各组数中，成等差数列的是（）A. 1，3，5，7，9B. 2，4，6，8，10C. 1，4，7，10，13D. 3，6，9，12，157. 下列命题中，正确的是（）A. 平行四边形的对角线互相垂直B. 直角三角形的斜边中点到顶点的距离等于斜边的一半C. 对顶角相等D. 直线与平面垂直，则直线上的任意一点都在平面上8. 已知等差数列{an}的首项a1=3，公差d=2，则第10项an=（）A. 19B. 21C. 23D. 259. 下列函数中，在定义域内单调递增的是（）A. y = -2x + 1B. y = 2x - 1C. y = x^2D. y = -x^210. 已知函数y = kx + b（k≠0）的图象经过点（2，3），则下列选项中正确的是（）A. k > 0，b > 0B. k < 0，b < 0C. k > 0，b < 0D. k < 0，b > 0二、填空题（每小题3分，共30分）11. 若x^2 - 5x + 6 = 0，则x的值为______。

12. 在直角坐标系中，点B（3，-4）到原点的距离是______。

黑龙江省龙东地区中考数学试卷及答案(Word解析版)

黑龙江省龙东地区中考数学试卷一、填空题（每题3分，共30分）1．（3分）（•黑龙江）“大美大爱”的龙江人勤劳智慧，全省粮食总产量达到1152亿斤，夺得全国粮食总产第一，广袤的黑土地正成为保障国家粮食安全的大粮仓，1152亿斤用科学记数法表示为 1.152×1011斤．考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答：解：将1152亿用科学记数法表示为1.152×1011．故答案为：1.152×1011．点评：此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．2．（3分）（•黑龙江）在函数中，自变量x的取值范围是x≥﹣1且x≠0．考点：函数自变量的取值范围；分式有意义的条件；二次根式有意义的条件．分析：本题主要考查自变量的取值范围，函数关系中主要有二次根式和分式两部分．根据二次根式的意义，被开方数x+1≥0，根据分式有意义的条件，x≠0．就可以求出自变量x的取值范围．解答：解：根据题意得：x+1≥0且x≠0 解得：x≥﹣1且x≠0．故答案为：x≥﹣1且x≠0点评：函数自变量的范围一般从三个方面考虑：（1）当函数表达式是整式时，自变量可取全体实数；（2）当函数表达式是分式时，考虑分式的分母不能为0；（3）当函数表达式是二次根式时，被开方数为非负数．3．（3分）（•黑龙江）如图所示，平行四边形ABCD的对角线AC、BD相交于点O，试添加一个条件：AD=DC，使得平行四边形ABCD为菱形．考点：平行四边形的判定；平行四边形的性质．专题：开放型．分析：根据菱形的定义得出答案即可．解答：解：∵邻边相等的平行四边形是菱形，∴平行四边形ABCD的对角线AC、BD相交于点O，试添加一个条件：可以为：AD=DC；故答案为：AD=DC．点评：此题主要考查了菱形的判定以及平行四边形的性质，根据菱形的定义得出是解题关键．4．（3分）（•黑龙江）风华中学七年级（2）班的“精英小组”有男生4人，女生3人，若选出一人担任班长，则组长是男生的概率为．考点：概率公式．分析：由风华中学七年级（2）班的“精英小组”有男生4人，女生3人，直接利用概率公式求解即可求得答案．解答：解：∵风华中学七年级（2）班的“精英小组”有男生4人，女生3人，∴选出一人担任班长，则组长是男生的为：=．故答案为：．点评：此题考查了概率公式的应用．注意概率=所求情况数与总情况数之比．5．（3分）（•黑龙江）若x=1是关于x的一元二次方程x2+3mx+n=0的解，则6m+2n=﹣2．考点：一元二次方程的解．分析：先把x=1代入x2+3mx+n=0，得到3m+n=﹣1，再把要求的式子进行整理，然后代入即可．解答：解：把x=1代入x2+3mx+n=0得：1+3m+n=0，3m+n=﹣1，则6m+2n=2（3m+n）=2×（﹣1）=﹣2；故答案为：﹣2．点评：此题考查了一元二次方程的解，解题的关键是把x的值代入，得到一个关于m，n的方程，不要求m．n的值，要以整体的形式出现．6．（3分）（•黑龙江）二次函数y=﹣2（x﹣5）2+3的顶点坐标是（5，3）．考点：二次函数的性质分析：因为顶点式y=a（x﹣h）2+k，其顶点坐标是（h，k），对照求二次函数y=﹣2（x﹣5）2+3的顶点坐标．解答：解：∵二次函数y=﹣2（x﹣5）2+3是顶点式，∴顶点坐标为（5，3）．故答案为：（5，3）．点评：此题主要考查了利用二次函数顶点式求顶点坐标，此题型是中考中考查重点，同学们应熟练掌握．7．（3分）（•黑龙江）将半径为4cm的半圆围成一个圆锥，这个圆锥的高为2 cm．考点：圆锥的计算．分析：根据扇形的弧长等于圆锥的底面周长，即可求得圆锥的底面半径，底面半径、母线长以及圆锥高满足勾股定理，据此即可求得圆锥的高．解答：解：设圆锥底面的半径是r，则2πr=4π，则r=2．则圆锥的高是：=2cm．故答案是：2．点评：本题考查了圆锥的计算，正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．8．（3分）（•黑龙江）李明组织大学同学一起去看电影《致青春》，票价每张60元，20张以上（不含20张）打八折，他们一共花了1200元，他们共买了20或25张电影票．考点：一元一次方程的应用．专题：分类讨论．分析：本题分票价每张60元和票价每张60元的八折两种情况讨论，根据数量=总价÷单价，列式计算即可求解．解答：解：①1200÷60=20（张）；②1200÷（60×0.8）1200÷48=25（张）．答：他们共买了20或25张电影票．故答案为：20或25．点评：考查了销售问题，注意分类思想的实际运用，同时熟练掌握数量，总价和单价之间的关系．．9．（3分）（•黑龙江）梯形ABCD中，AB∥CD，AB=3，CD=8，点E是对角线AC上一点，连接DE并延长交直线AB于点F，若=2，则=或．考点：相似三角形的判定与性质；梯形．专题：分类讨论．分析：根据已知分别根据F在线段AB上后在AB的延长线上，进而利用平行线的分线段成比例定理得出的值．解答：解：如图1：∵AB=3，=2，∴AF=2，BF=1，∵AB∥CD，∴△AEF∽△CED，∴=，∴==；如图2：∵AB=3，=2，∴AF=6，BF=3，∵AB∥CD，∴△AEF∽△CED，∴=，∴==．故答案为：或．点评：此题主要考查了相似三角形的判定与性质，根据已知进行分类讨论得出两种不同图形是解题关键．10．（3分）（•黑龙江）已知等边三角形ABC的边长是2，以BC边上的高AB1为边作等边三角形，得到第一个等边三角形AB1C1，再以等边三角形AB1C1的B1C1边上的高AB2为边作等边三角形，得到第二个等边三角形AB2C2，再以等边三角形AB2C2的边B2C2边上的高AB3为边作等边三角形，得到第三个等边AB3C3；…，如此下去，这样得到的第n个等边三角形AB n C n的面积为（）n．考点：等边三角形的性质专题：规律型．分析：由AB1为边长为2等边三角形ABC的高，利用三线合一得到B1为BC的中点，求出BB1的长，利用勾股定理求出AB1的长，进而求出第一个等边三角形AB1C1的面积，同理求出第二个等边三角形AB2C2的面积，依此类推，得到第n个等边三角形AB n C n的面积．解答：解：∵等边三角形ABC的边长为2，AB1⊥BC，∴BB1=1，AB=2，根据勾股定理得：AB1=，∴第一个等边三角形AB1C1的面积为×（）2=（）1；∵等边三角形AB1C1的边长为，AB2⊥B1C1，∴B1B2=，AB1=，根据勾股定理得：AB2=，∴第二个等边三角形AB2C2的面积为×（）2=（）2；依此类推，第n个等边三角形AB n C n 的面积为（）n．故答案为：（）n点评：此题考查了等边三角形的性质，属于规律型试题，熟练掌握等边三角形的性质是解本题的关键．二、选择题（每题3分，满分30分）11．（3分）（•黑龙江）下列运算中，计算正确的是（）A．（x3）2=x5B．x2+x2=2x4C．（﹣2）﹣1=﹣D．（a﹣b）2=a2﹣b2考点：完全平方公式；合并同类项；幂的乘方与积的乘方；负整数指数幂．分析：A、利用幂的乘方运算法则计算得到结果，即可做出判断；B、合并同类项得到结果，即可做出判断；C、利用负指数幂法则计算得到结果，即可做出判断；D、利用完全平方公式展开得到结果，即可做出判断．解答：解：A、（x3）2=x6，本选项错误；B、x2+x2=2x2，本选项错误；C、（﹣2）﹣1=﹣，本选项正确；D、（a﹣b）2=a2﹣2ab+b2，本选项错误，故选C点评：此题考查了完全平方公式，合并同类项，以及负指数幂，幂的乘方，熟练掌握公式及法则是解本题的关键．12．（3分）（•黑龙江）下列汽车标志中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．考点：中心对称图形；轴对称图形．分根据轴对称图形与中心对称图形的概念求解．析：解答：解：A、是轴对称图形，不是中心对称图形，故本选项错误；B、既不是中心对称图形，也不是轴对称图形，故本选项错误；C、不是轴对称图形，是中心对称图形，故本选项错误；D、是中心对称图形，也是轴对称图形，故本选项正确．故选D．点评：本题考查中心对称图形和轴对称图形的知识，关键是掌握好中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，图形旋转180°后与原图重合．13．（3分）（•黑龙江）由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示，则组成这个几何体的小正方体的个数最多有（）A．4B．5C．6D．7考点：由三视图判断几何体．分析：易得这个几何体共有2层，由俯视图可得第一层小正方体的个数，由主视图可得第二层小正方体的最多个数，相加即可．解答：解：由俯视图易得最底层有4个小正方体，第二层最多有2个小正方体，那么搭成这个几何体的小正方体最多为4+2=6个．故选C．点评：考查学生对三视图的掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，主视图疯狂盖，左视图拆违章”就更容易得到答案．14．（3分）（•黑龙江）下表是我市某中学九年级（1）班右眼视力的检查结果：视力 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0 人数 1 2 5 4 3 6 1 1 5 9 6 根据表中提供的信息，这43名同学右眼视力的众数和中位数分别是（）A．4.9，4.6 B．4.9，4.7 C．4.9，4.65 D．5.0，4.65考点：众数；中位数．分析：根据众数及中位数的定义，结合所给数据即可得出答案．解答：解：视力为4.9的学生人数最多，故众数为4.9；共43为学生，中位数落在第22为学生处，故中位数为4.6．故选A．点评：本题考查了众数及中位数的知识，属于基础题，解答本题的关键是掌握众数及中位数的定义．15．（3分）（•黑龙江）如图，爸爸从家（点O）出发，沿着扇形AOB上OA →→BO的路径去匀速散步，设爸爸距家（点O）的距离为S，散步的时间为t，则下列图形中能大致刻画S与t之间函数关系的图象是（）A．B．C．D．考点：函数的图象．分析：根据当爸爸在半径AO上运动时，离出发点距离越来越远；在弧BA上运动时，距离不变；在BO上运动时，越来越近，即可得出答案．解答：解：利用图象可得出：当爸爸在半径AO上运动时，离出发点距离越来越远；在弧AB上运动时，距离不变；在OB上运动时，越来越近．故选：C．点评：此题考查了函数随自变量的变化而变化的问题，能够结合图形正确分析距离y与时间x之间的大小变化关系，从而正确选择对应的图象．16．（3分）（•黑龙江）已知关于x 的分式方程=1的解是非正数，则a的取值范围是（）A．a≤﹣1 B．a≤﹣1且a≠﹣2 C．a≤1且a≠﹣2 D．a≤1考点：分式方程的解．分析：先解关于x的分式方程，求得x的值，然后再依据“解是非正数”建立不等式求a的取值范围．解答：解：去分母，得a+2=x+1，解得，x=a+1，∵x≤0且x+1≠0，∴a+1≤0且a+1≠﹣1，∴a≤﹣1且a≠﹣2，∴a≤﹣1且a≠﹣2．故选B．点评：本题考查了分式方程的解，解一元一次不等式，需注意在任何时候都要考虑分母不为0，这也是本题最容易出错的地方．17．（3分）（•黑龙江）如图，△ABC内接于⊙O，AB=BC，∠ABC=120°，AD为⊙O的直径，AD=6，那么AB的值为（）A．3B．2C．3D．2考点：圆周角定理；含30度角的直角三角形；圆心角、弧、弦的关系．分析：首先根据AB=BC，∠ABC=120°，求出∠C的度数，然后根据圆周角定理可知：∠D=∠C，又直径AD=6，易求得AB的长度．解答：解：∵AB=BC，∴∠BAC=∠C，∵∠ABC=120°，∴∠BAC=∠C=30°，∵AD为直径，AD=6，∴∠ABD=90°，∵∠D=30°，∴AB=AD=3．故选A．点评：本题考查了圆周角定理，难度一般，关键是掌握圆周角定理：同弧所对的圆周角相等．18．（3分）（•黑龙江）如图，Rt△ABC的顶点A在双曲线y=的图象上，直角边BC在x轴上，∠ABC=90°，∠ACB=30°，OC=4，连接OA，∠ACO=60°，则k的值是（）A．4B．﹣4C．2D．﹣2考点：反比例函数综合题．分析：根据三角形外角性质得∠OAC=∠AOB﹣∠ACB=30°，易得OA=OC=4，然后再Rt△AOB中利用含30度的直角三角形三边的关系得到OB=OC=2，AB=OB=2，则可确定C点坐标为（﹣2，2），最后把C点坐标代入反比例函数解析式y=中即可得到k的值．解答：解：∵∠ACB=30°，∠ACO=60°，∴∠OAC=∠AOB﹣∠ACB=30°，∴∠OAC=∠ACO，∴OA=OC=4，在△AOB中，∠ABC=90°，∠AOB=60°，OA=4，∴∠OAB=30°，∴OB=OC=2，∴AB=OB=2，∴C点坐标为（﹣2，2），把C（﹣2，2）代入y=得k=﹣2×2=﹣4．故选B．点评：本题考查了反比例函数的综合题：掌握反比例函数图象上点的坐标特征；熟练运用含30度的直角三角形三边的关系进行几何计算．19．（3分）（•黑龙江）今年校团委举办了“中国梦，我的梦”歌咏比赛，张老师为鼓励同学们，带了50元钱取购买甲、乙两种笔记本作为奖品．已知甲种笔记本每本7元，乙种笔记本每本5元，每种笔记本至少买3本，则张老师购买笔记本的方案共有（）A．3种B．4种C．5种D．6种考点：二元一次方程的应用．分析：设甲种笔记本购买了x本，乙种笔记本y本，就可以得出7x+5y≤50，x≥3，y≥3，根据解不定方程的方法求出其解即可．解答：解：设甲种笔记本购买了x本，乙种笔记本y本，由题意，得7x+5y≤50，∵x≥3，y≥3，∴当x=3，y=3时，7×3+5×3=36＜50，当x=3，y=4时，7×3+5×4=41＜50，当x=3，y=5时，7×3+5×5=46＜50，当x=3，y=6时，7×3+5×6=51＞50舍去，当x=4，y=3时，7×4+5×3=43＜50，当x=4，y=4时，7×4+5×4=4＜50，当x=4，y=5时，7×4+5×5=53＞50舍去，当x=5，y=3时，7×5+5×3=50=50，综上所述，共有6种购买方案．故选D．点评：本题考查了列二元一次不等式解实际问题的运用，分类讨论思想在解实际问题中的运用，解答时根据条件建立不等式是关键，合理运用分类是难点．20．（3分）（•黑龙江）如图，在直角梯形ABCD中，AD∥BC，∠BCD=90°，∠ABC=45°，AD=CD，CE平分∠ACB交AB于点E，在BC上截取BF=AE，连接AF交CE于点G，连接DG交AC于点H，过点A作AN⊥BC，垂足为N，AN交CE于点M．则下列结论；①CM=AF；②CE⊥AF；③△ABF∽△DAH；④GD平分∠AGC，其中正确的个数是（）A．1B．2C．3D．4考点：相似三角形的判定与性质；全等三角形的判定与性质；直角梯形．分析：如解答图所示：结论①正确：证明△ACM≌△ABF即可；结论②正确：由△ACM≌△ABF得∠2=∠4，进而得∠4+∠6=90°，即CE⊥AF；结论③正确：证法一：利用四点共圆；证法二：利用三角形全等；结论④正确：证法一：利用四点共圆；证法二：利用三角形全等．解答：解：（1）结论①正确．理由如下：∵∠1=∠2，∠1+∠CMN=90°，∠2+∠6=90°，∴∠6=∠CMN，又∵∠5=∠CMN，∴∠5=∠6，∴AM=AE=BF．易知ADCN为正方形，△ABC为等腰直角三角形，∴AB=AC．在△ACM与△ABF中，，∴△ACM≌△ABF（SAS），∴CM=AF；（2）结论②正确．理由如下：∵△ACM≌△ABF，∴∠2=∠4，∵∠2+∠6=90°，∴∠4+∠6=90°，∴CE⊥AF；（3）结论③正确．理由如下：证法一：∵CE⊥AF，∴∠ADC+∠AGC=180°，∴A、D、C、G四点共圆，∴∠7=∠2，∵∠2=∠4，∴∠7=∠4，又∵∠DAH=∠B=45°，∴△ABF∽△DAH；证法二：∵CE⊥AF，∠1=∠2，∴△ACF为等腰三角形，AC=CF，点G为AF中点．在Rt△ANF中，点G为斜边AF中点，∴NG=AG，∴∠MNG=∠3，∴∠DAG=∠CNG．在△ADG与△NCG中，，∴△ADG≌△NCG（SAS），∴∠7=∠1，又∵∠1=∠2=∠4，∴∠7=∠4，又∵∠DAH=∠B=45°，∴△ABF∽△DAH；（4）结论④正确．理由如下：证法一：∵A、D、C、G四点共圆，∴∠DGC=∠DAC=45°，∠DGA=∠DCA=45°，∴∠DGC=∠DGA，即GD平分∠AGC．证法二：∵AM=AE，CE⊥AF，∴∠3=∠4，又∠2=∠4，∴∠3=∠2则∠CGN=180°﹣∠1﹣90°﹣∠MNG=180°﹣∠1﹣90°﹣∠3=90°﹣∠1﹣∠2=45°．∵△ADG≌△NCG，∴∠DGA=∠CGN=45°=∠AGC，∴GD平分∠AGC．综上所述，正确的结论是：①②③④，共4个．故选D．点评：本题是几何综合题，考查了相似三角形的判定、全等三角形的判定与性质、正方形、等腰直角三角形、直角梯形、等腰三角形等知识点，有一定的难度．解答中四点共圆的证法，仅供同学们参考．三、简答题（满分60分）21．（5分）（•黑龙江）先化简，再求值（1﹣）÷，其中x=2sin45°+1．考点：分式的化简求值；特殊角的三角函数值．分析：先通分，再把除法转化成乘法，然后约分，最后求出x的值，再把它代入原式，进行计算即可．解答：解：（1﹣）÷=•=，当x=2sin45°+1=2×+1=+1时，原式==．点评：此题考查了分式的化简求值，用到的知识点是分式的化简步骤和特殊角的三角函数值，关键是把分式化到最简，然后代值计算．22．（6分）（•黑龙江）如图，方格纸中每个小正方形的边长都是1个单位长度，△ABC 在平面直角坐标系中的位置如图所示．（1）将△ABC向上平移3个单位后，得到△A1B1C1，请画出△A1B1C1，并直接写出点A1的坐标．（2）将△ABC绕点O顺时针旋转90°，请画出旋转后的△A2B2C2，并求点B所经过的路径长（结果保留x）考点：作图-旋转变换；作图-平移变换．分析：（1）根据△ABC向上平移3个单位，得出对应点位置，即可得出A1的坐标；（2）得出旋转后的△A2B2C2，再利用弧长公式求出点B所经过的路径长．解答：解：（1）如图所示：A1的坐标为：（﹣3，6）；（2）如图所示：∵BO==，∴==π．点评：此题主要考查了弧长公式的应用以及图形的旋转与平移变换，根据已知得出对应点位置是解题关键．23．（6分）（•黑龙江）如图，抛物线y=x2+bx+c与x轴交于A（﹣1，0）和B（3，0）两点，交y轴于点E．（1）求此抛物线的解析式．（2）若直线y=x+1与抛物线交于A、D两点，与y轴交于点F，连接DE，求△DEF的面积．考点：待定系数法求二次函数解析式；二次函数的性质分析：（1）利用待定系数法求二次函数解析式即可；（2）首先求出直线与二次函数的交点坐标进而得出E，F点坐标，即可得出△DEF 的面积．解答：解：（1）∵抛物线y=x2+bx+c与x轴交于A（﹣1，0）和B（3，0）两点，∴，解得：，故抛物线解析式为：y=x2﹣2x﹣3；（2）根据题意得：，解得：，，∴D（4，5），对于直线y=x+1，当x=0时，y=1，∴F（0，1），对于y=x2﹣2x﹣3，当x=0时，y=﹣3，∴E（0，﹣3），∴EF=4，过点D作DM⊥y轴于点M．∴S△DEF=EF•DM=8．点评：此题主要考查了待定系数法求二次函数解析式以及三角形面积求法等知识，利用数形结合得出D，E，F点坐标是解题关键．24．（7分）（•黑龙江）在我市开展的“阳光体育”跳绳活动中，为了了解中学生跳绳活动的开展情况，随机抽查了全市八年级部分同学1分钟跳绳的次数，将抽查结果进行统计，并绘制两个不完整的统计图．请根据图中提供的信息，解答下列问题：（1）本次共抽查了多少名学生？（2）请补全频数分布直方图空缺部分，直接写出扇形统计图中跳绳次数范围135≤x≤155所在扇形的圆心角度数．（3）若本次抽查中，跳绳次数在125次以上（含125次）为优秀，请你估计全市8000名八年级学生中有多少名学生的成绩为优秀？（4）请你根据以上信息，对我市开展的学生跳绳活动谈谈自己的看法或建议．考点：频数（率）分布直方图；用样本估计总体；扇形统计图．分析：（1）利用95≤x＜115的人数是8+16=24人，所占的比例是12%即可求解；（2）求得范围是115≤x＜145的人数，扇形的圆心角度数是360度乘以对应的比例即可求解；（3）首先求得所占的比例，然后乘以总人数8000即可求解；（4）根据实际情况，提出自己的见解即可，答案不唯一．解答：解：（1）抽查的总人数：（8+16）÷12%=200（人）；（2）范围是115≤x＜145的人数是：200﹣8﹣16﹣71﹣60﹣16=29（人），则跳绳次数范围135≤x≤155所在扇形的圆心角度数是：360×=81°．；（3）优秀的比例是：×100%=52.5%，则估计全市8000名八年级学生中有多少名学生的成绩为优秀人数是：8000×52.5%=4200（人）；（4）全市达到优秀的人数有一半以上，反映了我市学生锻炼情况很好．点评：本题考查扇形统计图及相关计算．在扇形统计图中，每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°比．25．（8分）（•黑龙江）秋季，某省部分地区遭受严重的雨雪自然灾害，兴化农场34800亩的农作物面临着收割困难的局面．兴华农场积极想办法，决定采取机械收割和人工收割两种方式同时进行抢收，工作了4天，由于雨雪过大，机械收割被迫停止，此时，人工收割的工作效率也减少到原来的，第8天时，雨雪停止附近的胜利农场前来支援，合作6天，完成了兴化农场所有的收割任务．图1是机械收割的亩数y1（亩）和人工收割的亩数y2（亩）与时间x（天）之间的函数图象．图2是剩余的农作物的亩数w（亩）与时间x天之间的函数图象，请结合图象回答下列问题．（1）请直接写出：A点的纵坐标600．（2）求直线BC的解析式．（3）第几天时，机械收割的总量是人工收割总量的10倍？考点：一次函数的应用．分析：（1）根据题意可知a=8，再根据图2求出4到8天时的人工收割量，然后求出前4天的人工收割的量即可得到点A的纵坐标；（2）先求出点B、C的坐标，再设直线BC的解析式为y=kx+b，然后利用待定系数法求一次函数解析式解答；（3）利用待定系数法求出直线AB的解析式，然后列出方程求解，再求出直线EF 的解析式，根据10倍关系列出方程求解，从而最后得解．解答：解：（1）由题意可知，a=8，所以，第4到8的人工收割作物：26200﹣25800=400（亩），所以，前4天人工收割作物：400÷=600（亩），故点A的纵坐标为600；（2）∵600+400=1000，∴点B的坐标为（8，1000），∵34800﹣32000=2800，∴点C的坐标为（14，2800），设直线BC的解析式为y=kx+b，则，解得，所以，直线BC的解析式为y=300x﹣1400；（3）设直线AB的解析式为y=k1x+b1，∵A（4，600），B（8，1000），∴，解得，所以，y=100x+200，由题意得，10（100x+200）=8000，解得x=6；设直线EF的解析式为y=k2x+b2，∵E（8，8000），F（14，32000），∴，解得，所以，直线EF的解析式为y=4000x﹣24000，由题意得，4000x﹣24000=10（300x﹣1400），解得x=10．答：第6天和第10天时，机械收割的总量是人工收割总量的10倍．点评：本题考查了一次函数的应用，主要利用了待定系数法求一次函数解析式，题目信息量较大，理解两个图象并准确获取信息，确定出题目中的数量关系是解题的关键．26．（8分）（•黑龙江）正方形ABCD的顶点A在直线MN上，点O是对角线AC、BD 的交点，过点O作OE⊥MN于点E，过点B作BF⊥MN于点F．（1）如图1，当O、B两点均在直线MN上方时，易证：AF+BF=2OE（不需证明）（2）当正方形ABCD绕点A顺时针旋转至图2、图3的位置时，线段AF、BF、OE之间又有怎样的关系？请直接写出你的猜想，并选择一种情况给予证明．考点：正方形的性质；矩形的性质；旋转的性质专题：证明题．分析：（1）过点B作BG⊥OE于G，可得四边形BGEF是矩形，根据矩形的对边相等可得EF=BG，BF=GE，根据正方形的对角线相等且互相垂直平分可得OA=OB，∠AOB=90°，再根据同角的余角相等求出∠AOE=∠OBG，然后利用“角角边”证明△AOE和△OBG全等，根据全等三角形对应边相等可得OG=AE，OE=BG，再根据AF﹣EF=AE，整理即可得证；（2）选择图2，过点B作BG⊥OE交OE的延长线于G，可得四边形BGEF是矩形，根据矩形的对边相等可得EF=BG，BF=GE，根据正方形的对角线相等且互相垂直平分可得OA=OB，∠AOB=90°，再根据同角的余角相等求出∠AOE=∠OBG，然后利用“角角边”证明△AOE和△OBG全等，根据全等三角形对应边相等可得OG=AE，OE=BG，再根据AF﹣EF=AE，整理即可得证；选择图3同理可证．解答：（1）证明：如图，过点B作BG⊥OE于G，则四边形BGEF是矩形，∴EF=BG，BF=GE，在正方形ABCD中，OA=OB，∠AOB=90°，∵BG⊥OE，∴∠OBG+∠BOE=90°，又∵∠AOE+∠BOE=90°，∴∠AOE=∠OBG，∵在△AOE和△OBG中，，∴△AOE≌△OBG（AAS），∴OG=AE，OE=BG，∵AF﹣EF=AE，EF=BG=OE，AE=OG=OE﹣GE=OE﹣BF，∴AF﹣OE=OE﹣BF，∴AF+BF=2OE；（2）图2结论：AF﹣BF=2OE，图3结论：AF﹣BF=2OE．对图2证明：过点B作BG⊥OE交OE的延长线于G，则四边形BGEF是矩形，∴EF=BG，BF=GE，在正方形ABCD中，OA=OB，∠AOB=90°，∵BG⊥OE，∴∠OBG+∠BOE=90°，又∵∠AOE+∠BOE=90°，∴∠AOE=∠OBG，∵在△AOE和△OBG中，，∴△AOE≌△OBG（AAS），∴OG=AE，OE=BG，∵AF﹣EF=AE，EF=BG=OE，AE=OG=OE+GE=OE+BF，∴AF﹣OE=OE+BF，∴AF﹣BF=2OE；若选图3，其证明方法同上．点评：本题考查了正方形的性质，矩形的判定与性质，全等三角形的判定与性质，同角的余角相等的性质，作辅助线构造出全等三角形与矩形是解题的关键，也是本题的难点．27．（10分）（•黑龙江）为了落实提出的“惠民政策”，我市今年计划开发建设A、B两种户型的“廉租房”共40套．投入资金不超过200万元，又不低于198万元．开发建设办公室预算：一套A型“廉租房”的造价为5.2万元，一套B型“廉租房”的造价为4.8万元．（1）请问有几种开发建设方案？（2）哪种建设方案投入资金最少？最少资金是多少万元？（3）在（2）的方案下，为了让更多的人享受到“惠民”政策，开发建设办公室决定通过缩小“廉租房”的面积来降低造价、节省资金．每套A户型“廉租房”的造价降低0.7万元，每套B户型“廉租房”的造价降低0.3万元，将节省下来的资金全部用于再次开发建设缩小面积后的“廉租房”，如果同时建设A、B两种户型，请你直接写出再次开发建设的方案．考点：一次函数的应用；一元一次不等式组的应用．分析：（1）设建设A型x套，B型（40﹣x）套，然后根据投入资金不超过200万元，又不低于198万元列出不等式组，求出不等式组的解集，再根据x是正整数解答；（2）设总W元，建设A型x套，B型（40﹣x）套，然后根据总等于A、B两个型号的之和列式函数关系式，再根据一次函数的增减性解答；（3）设再次建设A、B两种户型分别为a套、b套，根据再建设的两种户型的资金等于（2）中方案节省的资金列出二元一次方程，再根据a、b都是正整数求解即可．解答：解：（1）设建设A型x套，则B型（40﹣x）套，根据题意得，，解不等式①得，x≥15，解不等式②得，x≤20，所以，不等式组的解集是15≤x≤20，∵x为正整数，∴x=15、16、17、18、19、20，答：共有6种方案；（2）设总W万元，建设A型x套，则B型（40﹣x）套，W=5.2x+4.8×（40﹣x）=0.4x+192，∵0.4＞0，∴W随x的增大而增大，∴当x=15时，W最小，此时W最小=0.4×15+192=198万元；（3）设再次建设A、B两种户型分别为a套、b套，则（5.2﹣0.7）a+（4.8﹣0.3）b=15×0.7+（40﹣15）×0.3，整理得，a+b=4，a=1时，b=3，a=2时，b=2，a=3时，b=1，所以，再建设方案：①A型住房1套，B型住房3套；②A型住房2套，B型住房2套；③A型住房3套，B型住房1套．点评：本题考查了一次函数的应用，一元一次不等式组的应用，读懂题目信息，理清题中不等量关系，列出不等式组是解题的关键，（2）利用一次函数的增减性求最值要注意自变量的取值范围．28．（10分）（•黑龙江）如图，在平面直角坐标系中，Rt△ABC的斜边AB在x轴上，点C在y轴上，∠ACB=90°，OA、OB的长分别是一元二次方程x2﹣25x+144=0的两个根（OA＜OB），点D是线段BC上的一个动点（不与点B、C重合），过点D作直线DE⊥OB，垂足为E．。

龙东五地市2023中考数学试卷及解析

龙东五地市2023中考数学试卷及解析全文共四篇示例，供读者参考第一篇示例：龙东五地市2023年中考数学试卷第一部分选择题（共80分）1. 已知直角三角形的直角边长分别为3cm和4cm，则斜边长是（）A. 5cmB. 6cmC. 7cmD. 8cm2. 若一个数自减去1的3倍，再乘以2，得到的结果是30，这个数是（）A. 15B. 16C. 17D. 184. 小明的爷爷今年68岁，小明今年8岁，几年以后小明的爷爷的年龄是小明的3倍？A. 12年B. 16年C. 20年D. 24年7. 甲、乙两人一起进行搬砖工作，甲每小时搬3块，乙每小时搬4块，若两人一起工作4小时，共搬砖48块，求甲、乙两人各自搬了多少块砖？A. 16，32B. 12，36C. 14，34D. 18，308. 小华每天早上骑自行车上学，平均速度为20km/h；放学后坐公交车回家，平均速度为30km/h。

如果上学和放学的路程相等，求他来回一次的总时间为多少小时？A. 2B. 3C. 4D. 510. 不等式2x + 3 > 7的解集为（）A. {x|x > 2}B. {x|x > 1}C. {x|x > 3}D. {x|x > 4}11. 若a + 3 = 7，则a的值是__________13. 小李有一堆苹果，其中一半是红色的，一半是绿色的，若共有12个红苹果，则小李手中一共有__________ 个苹果。

14. 三角形的三边长分别是5cm、8cm、9cm，其中最长的边所对的角的度数是__________ 度。

15. 不等式4x - 7 < 17的解集为{x|x < ________}18. 已知正方形的一边长为5cm，求其周长和面积分别为多少？周长为__________，面积为__________21. 解方程：5x + 3 = 1822. 某商店原价销售一种商品100元，后来打8折出售，求打折后的价格。

2022年黑龙江省省龙东地区中考数学真题及答案

（1）求抛物线的解析式；
（2）抛物线上是否存在点P，使面积是面积的4倍，若存在，请直接写出点P的坐标：若不存在，请说明理由．
24.为进一步开展“睡眠管理”工作，某校对部分学生的睡眠情况进行了问卷调查．设每名学生平均每天的睡眠时间为x小时，其中的分组情况是：
A组： B组： C组： D组： E组：
根据调查结果绘制成两幅不完整的统计图，请根据图中提供的信息，解答下列问题：
（2）将绕点A旋转到图②的位置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？并加以证明；
（3）将绕点A旋转到图③的位置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？直接写出结论，不需要证明．
（1）将先向左平移6个单位，再向上平移4个单位，得到，画出两次平移后的，并写出点的坐标；
（2）画出绕点顺时针旋转90°后得到，并写出点的坐标；
（3）在（2）的条件下，求点旋转到点的过程中所经过的路径长（结果保留）．
23.如图，抛物线经过点，点，与y轴交于点C，抛物线的顶点为D．
14.在一个不透明的口袋中，有2个红球和4个白球，这些球除颜色外其余完全相同，摇匀后随机摸出一个球，摸到红球的概率是________．
15.若关于x的一元一次不等式组的解集为，则a的取值范围是________．
16.如图，在中，AB是的弦，的半径为3cm，C为上一点，，则AB的长为________cm．
A.181B.175C.176D.175.5
4.如图是由若干个相同的小正方体搭成的一个几何体的左视图和俯视图，则所需的小正方体的个数最多是（）
A. 7B. 8C. 9D. 0

精品解析：2022年黑龙江省省龙东地区中考数学真题(解析版)

【详解】设有x支队伍，根据题意，得，
解方程，得x1=10，x2=-9（舍去），
故选B．
【点睛】本题考查了一元二次方程的应用，熟练掌握一元二次方程的解法是解题的关键．
6.已知关于x的分式方程的解是正数，则m的取值范围是（）
A. B. C. 且 D. 且
【答案】C
【解析】
【分析】先将分式方程去分母转化为整式方程，求出整式方程的解，根据分式方程的解为正数得到且，即可求解．
4.如图是由若干个相同的小正方体搭成的一个几何体的左视图和俯视图，则所需的小正方体的个数最多是（）
A.7B.8C.9D.10
【答案】B
【解析】
【分析】这个几何体共有2层，由俯视图可得第一层小正方体的个数，由左视图可得第二层小正方体的最多个数，再相加即可．
【详解】由俯视图可知最底层有5个小正方体，由左视图可知这个几何体有两层，其中第二层最多有3个，那么搭成这个几何体所需小正方体最多有个．
A.5B.6C.7D.8
【答案】A
【解析】
【分析】设设购买毛笔x支，围棋y副，根据总价=单价×数量，即可得出关于x，y的二元一次方程，结合x，y均为正整数即可得出购买方案的数量．
【详解】解：设购买毛笔x支，围棋y副，根据题意得，
15x+20y=360，即3x+4y=72，
∴y=18- x．
又∵x，y均为正整数，
A 2.5B.2C.3.5D.3
【答案】A
【解析】
【分析】连接DE，取AD的中点G，连接EG，先由等腰三角形“三线合一“性质，证得AD⊥BC，BD=CD，再由E是AB的中点，G是AD的中点，求出S△EGD=3，然后证△EGP≌△FDP（AAS），得GP=CP=1.5，从而得DG=3，即可由三角形面积公式求出EG长，由勾股定理即可求出PE长．

(中考精品卷)黑龙江省省龙东地区中考数学真题(解析版)

黑龙江省龙东地区2022年初中毕业学业统一考试数学试题一、选择题（每题3分，满分30分）1. 下列运算中，计算正确的是（）A. ()222b a b a -=-B. 326a a a ⋅=C. ()224x x -=D. 623a a a ÷= 【答案】C【解析】【分析】根据完全平方公式、同底数幂相乘除，积的乘方进行计算，即可判断．【详解】()2222b b b a a a =--+，故A 选项错误，不符合题意； 2326a a a ⋅=，故B 选项错误，不符合题意；()224x x -=，故C 选项正确，符合题意；624a a a ÷=，，故D 选项错误，不符合题意；故选：C ．【点睛】本题考查了完全平方公式、同底数幂相乘除，积的乘方，熟练掌握运算法则是解题的关键．2. 下列图形是汽车的标识，其中是中心对称图形但不是轴对称图形的是（）A. B. C. D.【答案】C【解析】【分析】根据中心对称图形的定义判断即可．【详解】解：∵是轴对称图形，也是中心对称图形，∴不符合题意；∵是轴对称图形，不是中心对称图形 ∴不符合题意；∵不是轴对称图形，是中心对称图形∴符合题意；∵是轴对称图形，不是中心对称图形∴不符合题意；故选C．【点睛】本题考查了了轴对称图形即沿着某条直线折叠，直线两旁的部分完全重合、中心对称图形即将图形绕某点旋转180°后与原图形完全重合，准确理解定义是解题的关键．3. 学校举办跳绳比赛，九年（2）班参加比赛的6名同学每分钟跳绳次数分别是172，169，180，182，175，176，这6个数据的中位数是（）A. 181B. 175C. 176D. 175.5 【答案】D【解析】【分析】先将这6个数从小到大进行排序，找出排在中间的两个数，求出这两个数的平均数，即为这组数据的中位数．【详解】解：将172，169，180，182，175，176从小到大进行排序为：169，172，175，176，180，182，排在中间的两个数为175，176，∴这6个数据的中位数为175176175.52+=，故D正确．故选：D．【点睛】本题主要考查了求一组数据的中位数，解题的关键是将这组数据从小到大进行排序，找出排在中间的一个数或两个数，注意偶数个数是求中间两个数的平均数．4. 如图是由若干个相同的小正方体搭成的一个几何体的左视图和俯视图，则所需的小正方体的个数最多是（）A. 7B. 8C. 9D. 10 【答案】B【解析】【分析】这个几何体共有2层，由俯视图可得第一层小正方体的个数，由左视图可得第二层小正方体的最多个数，再相加即可．【详解】由俯视图可知最底层有5个小正方体，由左视图可知这个几何体有两层，其中第二层最多有3个，那么搭成这个几何体所需小正方体最多有538+=个．故选：B．【点睛】本题主要考查了学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．5. 2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛，单循环比赛共进行了45场，共有多少支队伍参加比赛？（）A. 8B. 10C. 7D. 9【答案】B【解析】【分析】设有x 支队伍，根据题意，得1(1)452x x -=，解方程即可．【详解】设有x 支队伍，根据题意，得1(1)452x x -=，解方程，得x 1=10，x 2=-9（舍去），故选B ．【点睛】本题考查了一元二次方程的应用，熟练掌握一元二次方程的解法是解题的关键． 6. 已知关于x 的分式方程23111x m x x --=--的解是正数，则m 的取值范围是（） A. 4m >B. 4m <C. 4m >且5m ≠D. 4m <且1m ≠【答案】C【解析】【分析】先将分式方程去分母转化为整式方程，求出整式方程的解，根据分式方程的解为正数得到40m ->且410m --≠，即可求解．【详解】方程两边同时乘以(1)x -，得231x m x -+=-，解得4x m =-，关于x 的分式方程23111x m x x--=--的解是正数， 0x ∴>，且10x -≠，即40m ->且410m --≠，4m ∴>且5m ≠，故选：C ．【点睛】本题考查了分式方程的解，涉及解分式方程和分式方程分母不为0，熟练掌握知识点是解题的关键．7. 国家“双减”政策实施后，某校开展了丰富多彩的社团活动．某班同学报名参加书法和围棋两个社团，班长为参加社团的同学去商场购买毛笔和围棋（两种都购买）共花费360元．其中毛笔每支15元，围棋每副20元，共有多少种购买方案？（）A. 5B. 6C. 7D. 8【答案】A【解析】【分析】设设购买毛笔x 支，围棋y 副，根据总价=单价×数量，即可得出关于x ，y 的二元一次方程，结合x ，y 均为正整数即可得出购买方案的数量．【详解】解：设购买毛笔x 支，围棋y 副，根据题意得，15x +20y =360，即3x +4y =72，∴y =18-34x ．又∵x ，y 均为正整数，∴415x y =⎧⎨=⎩或812x y =⎧⎨=⎩或129x y =⎧⎨=⎩或166x y =⎧⎨=⎩或203x y =⎧⎨=⎩， ∴班长有5种购买方案．故选：A ．【点睛】本题考查了二元一次方程的应用，找准等量关系“共花费360元”，列出二元一次方程是解题的关键．8. 如图，在平面直角坐标系中，点O 为坐标原点，平行四边形OBAD 的顶点B 在反比例函数3y x =的图象上，顶点A 在反比例函数k y x=的图象上，顶点D 在x 轴的负半轴上．若平行四边形OBAD 的面积是5，则k 的值是（）A. 2B. 1C. 1-D. 2-【答案】D【解析】【分析】连接OA ，设AB 交y 轴于点C ，根据平行四边形的性质可得1522AOB OBAD S S == ，AB ∥OD ，再根据反比例函数比例系数的几何意义，即可求解．【详解】解：如图，连接OA ，设AB 交y 轴于点C ，∵四边形OBAD 是平行四边形，平行四边形OBAD 的面积是5，∴1522AOB OBAD S S == ，AB ∥OD ， ∴AB ⊥y 轴，∵点B 在反比例函数3y x =的图象上，顶点A 在反比例函数k y x =的图象上， ∴3,22COB COA k S S ==- ， ∴35222AOB COB COA k S S S =+=-= ，解得：2k =-．故选：D ．【点睛】本题主要考查了平行四边形的性质，反比例函数比例系数的几何意义，熟练掌握平行四边形的性质，反比例函数比例系数的几何意义是解题的关键．9. 如图，ABC 中，AB AC =，AD 平分BAC ∠与BC 相交于点D ，点E 是AB 的中点，点F 是DC 的中点，连接EF 交AD 于点P ．若ABC 的面积是24， 1.5PD =，则PE 的长是（）A 2.5 B. 2 C. 3.5 D. 3【答案】A【解析】【分析】连接DE ，取AD 的中点G ，连接EG ，先由等腰三角形“三线合一“性质，证得AD ⊥BC ，BD =CD ，再由E 是AB 的中点，G 是AD 的中点，求出S △EGD =3，然后证△EGP ≌△FDP （AAS ），得GP =CP =1.5，从而得DG =3，即可由三角形面积公式求出EG 长，由勾股定理即可求出PE 长．.【详解】解：如图，连接DE，取AD的中点G，连接EG，∵AB=AC，AD平分BAC∠与BC相交于点D，∴AD⊥BC，BD=CD，∴S△ABD=112422ABCS=⨯=12，∵E是AB的中点，∴S△AED=111222ABDS=⨯=6，∵G是AD的中点，∴S△EGD=11622AEDS=⨯=3，∵E是AB的中点，G是AD的中点，∴EG∥BC，EG=12BD=12CD，∴∠EGP=∠FDP=90°，∵F是CD的中点，∴DF=12CD，∴EG=DF，∵∠EPG=∠FPD，∴△EGP≌△FDP（AAS），∴GP=PD=1.5，∴GD=3，∵S△EGD=12GD EG⋅=3，即1332EG⨯=，∴EG=2，在Rt△EGP中，由勾股定理，得PE==2.5，故选：A．【点睛】本题考查等腰三角形的性质，三角形面积，全等三角形判定与性质，勾股定理，熟练掌握三角形中线分三角形两部分的面积相等是解题的关键．10. 如图，正方形ABCD 的对角线AC ，BD 相交于点O ，点F 是CD 上一点，OE OF ⊥交BC 于点E ，连接AE ，BF 交于点P ，连接OP ．则下列结论：①AE BF ⊥；②45OPA ∠=︒；③AP BP -=；④若:2:3BE CE =，则4tan 7CAE ∠=；⑤四边形OECF 的面积是正方形ABCD 面积的14．其中正确的结论是（）A. ①②④⑤B. ①②③⑤C. ①②③④D. ①③④⑤【答案】B【解析】【分析】分别对每个选项进行证明后进行判断：①通过证明()DOF COE ASA ≌ 得到EC =FD ，再证明()EAC FBD SAS ≌ 得到∠EAC =∠FBD ，从而证明∠BPQ =∠AOQ =90°，即AE BF ⊥；②通过等弦对等角可证明45OPA OBA ∠=∠=︒； ③通过正切定义得tan BE BP BAE AB AP ∠==，利用合比性质变形得到CE BP AP BP BE⋅-=，再通过证明AOP AEC ∽ 得到OP AE CE AO ⋅=，代入前式得OP AE BP AP BP AO BE ⋅⋅-=⋅，最后根据三角形面积公式得到AE BP AB BE ⋅=⋅，整体代入即可证得结论正确；④作EG ⊥AC 于点G 可得EG ∥BO ，根据tan EG EG CAE AG AC CG ∠==-，设正方形边长为5a ，分别求出EG 、AC 、CG 的长，可求出3tan 7CAE ∠=，结论错误； ⑤将四边形OECF 的面积分割成两个三角形面积，利用()DOF COE ASA ≌ ，可证明S 四边形OECF =S △COE +S △COF = S △DOF +S △COF =S △COD 即可证明结论正确．【详解】①∵四边形ABCD 是正方形，O 是对角线AC 、BD 的交点，∴OC =OD ，OC ⊥OD ，∠ODF =∠OCE =45°∵OE OF ⊥∴∠DOF +∠FOC =∠FOC +∠EOC =90°∴∠DOF =∠EOC在△DOF 与△COE 中ODF OCE OC ODDOF EOC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()DOF COE ASA ≌∴EC =FD∵在△EAC 与△FBD 中45EC FD ECA FDB AC BD =⎧⎪∠=∠=︒⎨⎪=⎩∴()EAC FBD SAS ≌∴∠EAC =∠FBD又∵∠BQP =∠AQO∴∠BPQ =∠AOQ =90°∴AE ⊥BF所以①正确；②∵∠AOB =∠APB =90°∴点P 、O 在以AB 为直径的圆上∴AO 是该圆的弦∴45OPA OBA ∠=∠=︒所以②正确； ③∵tan BE BP BAE AB AP ∠== ∴AB AP BE BP = ∴AB BE AP BP BE BP --= ∴AP BP CE BP BE-= ∴CE BP AP BP BE ⋅-=∵,45EAC OAP OPA ACE ∠=∠∠=∠=︒∴AOP AEC ∽∴OP AO CE AE= ∴OP AE CE AO⋅= ∴OP AE BP AP BP AO BE ⋅⋅-=⋅ ∵1122ABE AE BP AB BE S ⋅=⋅= ∴AE BP AB BE ⋅=⋅∴OP AB BE AB AP BP OP AO BE AO ⋅⋅-===⋅ 所以③正确；④作EG ⊥AC 于点G ，则EG ∥BO ， ∴EG CE CG OB BC OC== 设正方形边长为5a ，则BC =5a ，OB =OC，若:2:3BE CE =，则23BE CE =， ∴233BE CE CE ++= ∴35CE BC =∴35CE EG OB BC =⋅== ∵EG ⊥AC ，∠ACB =45°，∴∠GEC =45°∴CG =EG∴3tan 7EG EG CAE AG AC CG ∠====- 所以④错误；⑤∵()DOF COE ASA ≌ ，S 四边形OECF =S △COE +S △COF∴S 四边形OECF = S △DOF +S △COF = S △COD∵S △COD =14ABCD S 正方形∴S 四边形OECF =14ABCD S 正方形所以⑤正确；综上，①②③⑤正确，④错误，故选 B【点睛】本题综合考查了三角形、正方形、圆和三角函数，熟练运用全等三角形、相似三角形、等弦对等角和三角函数的定义是解题的关键．二、填空题（每题3分，满分30分）11. 我国南水北调东线北延工程2021-2022年度供水任务顺利完成，共向黄河以北调水1.89亿立方米，将数据1.89亿用科学记数法表示为________．【答案】81.8910⨯【解析】【分析】把亿写成810，最后统一写成10n a ⨯的形式即可．【详解】解：由题意得：1.89亿=81.8910⨯，故答案为：81.8910⨯．【点睛】本题考查了科学记数法表示较大的数，移动小数点，熟记科学记数法的表示形式是解题的关键．12. 函数y =中自变量x 的取值范围是______．【答案】 1.5x ≥【解析】【分析】根据二次根式的性质，被开方数大于等于0，即可求出答案．【详解】解：根据题意，230x -≥，∴ 1.5x ≥；故答案为： 1.5x ≥．【点睛】本题考查了二次根式的性质，解题的关键是熟练掌握二次根式被开方数大于等于0进行解题．13. 如图，在四边形ABCD 中，对角线AC ，BD 相交于点O ，OA OC =，请你添加一个条件________，使AOB COD ≌．【答案】OB =OD （答案不唯一）【解析】【分析】根据SAS 添加OB =OD 即可【详解】解：添加OB =OD ，在△AOB 和△COD 中，AO CO AOB COD OB OD =⎧⎪∠=∠⎨⎪=⎩，∴AOB COD ≌（SAS ）故答案为OB =OD （答案不唯一）【点睛】本题考查三角形全等判定添加条件，掌握三角形全等判定方法是解题关键． 14. 在一个不透明的口袋中，有2个红球和4个白球，这些球除颜色外其余完全相同，摇匀后随机摸出一个球，摸到红球的概率是________．【答案】13【解析】【分析】利用概率公式计算即可．【详解】∵ 不透明的口袋中，有2个红球和4个白球， ∴摸到红球的概率是21243=+，故答案为：13．【点睛】本题考查了概率计算，熟练掌握概率计算公式是解题的关键．15. 若关于x 的一元一次不等式组2130x x a -⎧⎨-<⎩＜的解集为2x <，则a 的取值范围是________．【答案】2a ≥##2a ≤【解析】【分析】先求出每个不等式的解集，根据已知不等式组的解集即可得出答案．【详解】解：2130x x a -⎧⎨-<⎩＜①②，解不等式①得：2x ＜，解不等式②得：x a ＜，关于x 的不等式组2130x x a -⎧⎨-<⎩＜的解集为2x ＜， 2a ∴≥．故答案为：2a ≥．【点睛】本题主要考查了一元一次不等式组解集的求法，其简便求法就是用口诀求解，求不等式组解集的口诀：同大取大，同小取小，大小小大中间找，大大小小找不到（无解）． 16. 如图，在O 中，AB 是O 的弦，O 的半径为3cm ，C 为O 上一点，60ACB ∠=︒，则AB 的长为________cm ．【答案】【解析】【分析】连接OA 、OB ，过点O 作OD ⊥AB 于点D ，由垂径定理和圆周角定理可得12AD BD AB ==，120AOB ∠=︒，再根据等腰三角形的性质可得30OAB OBA ==︒∠∠，利用含30°角的直角三角形的性质和勾股定理即可求解．【详解】解：连接OA 、OB ，过点O 作OD ⊥AB 于点D ，12AD BD AB ∴==，90ODA =∠°， 60ACB ∠=︒，120AOB ∴∠=︒，OA OB = ，30OAB OBA ∴∠=∠=︒，3cm OA = ，3cm 2OD ∴=，AD ∴==，AB ∴=，故答案为：【点睛】本题考查了垂径定理，圆周角定理，等腰三角形的性质，含30°角的直角三角形的性质和勾股定理，熟练掌握知识点是解题的关键．17. 若一个圆锥的母线长为5cm ，它的侧面展开图的圆心角为120°，则这个圆锥的底面半径为________cm ．【答案】53【解析】【分析】由于圆锥的母线长为5cm ，侧面展开图是圆心角为 120°扇形，设圆锥底面半径为r cm ，那么圆锥底面圆周长为2πr cm ，所以侧面展开图的弧长为2πr cm ，然后利用弧长公式即可得到关于r 的方程，解方程即可求解．【详解】解：设圆锥底面半径为r cm ，则圆锥底面周长为：2r πcm ，∴侧面展开图的弧长为：2r πcm ，∴12052=180ππ⨯r ，解得：r =53，故答案：53．【点睛】本题主要考查圆锥侧面展开图的知识；正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．18. 如图，菱形ABCD 中，对角线AC ，BD 相交于点O ，60BAD ∠=︒，3AD =，AH 是BAC ∠的平分线，CE AH ⊥于点E ，点P 是直线AB 上的一个动点，则OP PE +的最小值是________．【解析】【分析】作点O 关于AB 的对称点F ，连接OF 交AB 于G ，连接PE 交直线AB 于P ，连接PO ，则PO =PF ，此时，PO +PE 最小，最小值=EF ，利用菱形的性质与直角三角形的性质，勾股定理，求出OF ，OE 长，再证明△EOF 是直角三角形，然后由勾股定理求出EF 长即可．【详解】解：如图，作点O 关于AB 的对称点F ，连接OF 交AB 于G ，连接PE 交直线AB 于P ，连接PO ，则PO =PF ，此时，PO +PE 最小，最小值=EF ，为∵菱形ABCD ，∴AC ⊥BD ，OA =OC ，O =OD ，AD =AB =3，∵∠BAD =60°，∴△ABD 等边三角形，∴BD =AB =3，∠BAO =30°，∴OB =32， ∴OA∴点O 关于AB 的对称点F ，∴OF ⊥AB ，OF =2OG =OA∴∠AOG =60°，∵CE ⊥AH 于E ，OA =OC ，∴OE =OC =OA∵AH 平分∠BAC ，∴∠CAE =15°，∴∠AEC =∠CAE =15°，∴∠DOE =∠AEC +∠CAE =30°，∴∠DOE +∠AOG =30°+60°=90°，∴∠FOE =90°，∴由勾股定理，得EF==,∴PO +PE 最小值．．【点睛】本题考查菱形的性质，利用轴对称求最短距离问题，直角三角形的性质，勾股定理，作点O 关于AB 的对称点F ，连接OF 交AB 于G ，连接PE 交直线AB 于P ，连接PO ，则PO =PF ，则PO +PE 最小，最小值=EF 是解题的关键．19. 在矩形ABCD 中，9AB =，12AD =，点E 在边CD 上，且4CE =，点P 是直线BC 上的一个动点．若APE V 是直角三角形，则BP 的长为________．是【答案】313或154或6 【解析】【分析】分三种情况讨论：当∠APE =90°时，当∠AEP =90°时，当∠PAE =90°时，过点P 作PF ⊥DA 交DA 延长线于点F ，即可求解．【详解】解：在矩形ABCD 中，9AB CD ==，12AD BC ==，∠BAD =∠B =∠BCD =∠ADC =90°，如图，当∠APE =90°时，∴∠APB +∠CPE =90°，∵∠BAP +∠APB =90°，∴∠BAP =∠CPE ，∵∠B =∠C =90°，∴△ABP ∽△PCE ， ∴AB BP PC CE=，即9124BP BP =-，解得：BP =6；如图，当∠AEP =90°时，∴∠AED +∠PEC =90°，∵∠DAE +∠AED =90°，∴∠DAE =∠PEC ，∵∠C =∠D =90°，∴△ADE ∽△ECP ， ∴AD DE CE PC =，即12944PC-=，解得：53PC =， ∴313BP BC PC =-=；如图，当∠PAE =90°时，过点P 作PF ⊥DA 交DA 延长线于点F ，根据题意得∠BAF =∠ABP =∠F =90°，∴四边形ABPF 为矩形，∴PF =AB =9，AF =PB ，∵∠PAF +∠DAE =90°，∠PAF +∠APF =90°，∴∠DAE =∠APF ，∵∠F =∠D =90°，∴△APF ∽△EAD ， ∴AF PF DE AD =，即99412AF =-，解得：154=AF ，即154PB =；综上所述，BP 的长为313或154或6．故答案为：313或154或6 【点睛】本题主要考查了相似三角形的判定和性质，矩形的性质，熟练掌握相似三角形的判定和性质，矩形的性质，并利用分类讨论思想解答是解题的关键．20. 如图，在平面直角坐标系中，点1A ，2A ，3A ，4A ……在x 轴上且11OA =，212OA OA =，322O A O A =，432OA OA =……按此规律，过点1A ，2A ，3A ，4A ……作x 轴的垂线分别与直线y =交于点1B ，2B ，3B ，4B ……记11OA B ，22OA B △，33 OA B ，44 OA B ……的面积分别为1S ，2S ，3S ，4S ……，则2022S =______．【答案】2【解析】【分析】先求出11A B =，可得11OA B S = ，再根据题意可得112233n n A B A B A B A B ⋯⋯∥∥∥，从而得到11OA B ∽22OA B △∽33OA B ∽44 OA B ……∽n n OA B △，再利用相似三角形的性质，可得11OA B S ∶22OA B S ∶33OA B S ∶44OA B S ……∶n n OA B S =()()()2222231:2:2:2:2n ，即可求解．【详解】解：当x =1时，y =∴点(1B ，∴11A B =，∴11112OA B S =⨯= ， ∵根据题意得：112233n n A B A B A B A B ⋯⋯∥∥∥，∴11OA B ∽22OA B △∽33 OA B ∽44 OA B ……∽n n OA B △，∴11OA B S ∶22OA B S ∶33OA B S ∶44OA B S ……∶n n OA B S = OA 12∶OA 22∶OA 32……∶OA n 2，∵11OA =，212OA OA =，322O A O A =，432OA OA =……，∴22OA =，2342OA ==，3482OA ==……12n n OA -=，∴11OA B S ∶22OA B S ∶33OA B S ∶44OA B S ……∶n n OA B S =()()()2222231246221:2:2:2:21:2:2:2:2n n --= ， ∴11222n n n OA B OA B S S -= ，∴220222202222S ⨯-==．故答案为：2．【点睛】本题主要考查了图形与坐标的规律题，相似三角形的判定和性质，明确题意，准确得到规律，是解题的关键．三、解答题（满分60分）21. 先化简，再求值：22221111a a a a a ⎛⎫---÷ ⎪-+⎝⎭，其中2cos301a =︒+．【答案】11a -，【解析】【分析】先根据分式的混合运算法则化简分式，再把特殊角的三角函数值代入，求出a 值，然后把a 值代入化简式计算即可．【详解】解：原式22222112111a a a a a a a ⎛⎫--+=-⋅ ⎪---⎝⎭ 2121211a a a a -+=⋅-- 11a=-，当2cos3011a =︒+=+时，原式==【点睛】本题考查分式化简求值，熟练掌握分式运算法则和熟记特殊角的三角函数值是解题的关键．22. 如图，在正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，ABC 的三个顶点坐标分别为()1,1A -，()2,5B -，()5,4C -．（1）将ABC 先向左平移6个单位，再向上平移4个单位，得到111A B C △，画出两次平移后的111A B C △，并写出点1A 的坐标；（2）画出111A B C △绕点1C 顺时针旋转90°后得到221A B C △，并写出点2A 的坐标；（3）在（2）的条件下，求点1A 旋转到点2A 的过程中所经过的路径长（结果保留π）．【答案】（1）见解析；()15,3A -（2）见解析；()22,4A （3）点1A 旋转到点2A 所经过的路径长为5π2【解析】【分析】（1）根据题目中的平移方式进行平移，然后读出点的坐标即可；（2）先找出旋转后的对应点，然后顺次连接即可；（3）根据旋转可得点1A 旋转到点2A 为弧长，利用勾股定理确定圆弧半径，然后根据弧长公式求解即可．【小问1详解】解：如图所示△A 1B 1C 1即为所求，()15,3A -；【小问2详解】如图所示△A 2B 2C 2即为所求，()22,4A ；【小问3详解】∵115A C ==∴点1A 旋转到点2A 所经过的路径长为90π55π1802⨯=．【点睛】题目主要考查坐标与图形，图形的平移，旋转，勾股定理及弧长公式等，数量掌握运用这些知识点是解题关键．23. 如图，抛物线2y x bx c =++经过点()1,0A -，点()2,3B -，与y 轴交于点C ，抛物线的顶点为D ．（1）求抛物线的解析式；（2）抛物线上是否存在点P ，使PBC 的面积是BCD △面积的4倍，若存在，请直接写出点P 的坐标：若不存在，请说明理由．【答案】（1）223y x x =--（2）存在，()11P +，()21P - 【解析】【分析】（1）将点()1,0A -，点()2,3B -，代入抛物线得10423b c b c -+=⎧⎨++=-⎩，求出b c ，的值，进而可得抛物线的解析式．（2）将解析式化成顶点式得()222314y x x x =--=--，可得D 点坐标，将0x =代入得，3y =-，可得C 点坐标，求出1BCD S =△的值，根据4PBC BCD S S = 可得4PBC S = ，设()2,23P m m m --，则()21223342PBC S m m =⨯⨯--+= ，求出m 的值，进而可得P 点坐标．【小问1详解】解：∵抛物线2y x bx c =++过点()1,0A -，点()2,3B -， ∴10423b c b c -+=⎧⎨++=-⎩，解得23b c =-⎧⎨=-⎩，∴抛物线的解析式为：223y x x =--．【小问2详解】解：存在．∵()222314y x x x =--=--， ∴()1,4D -，将0x =代入得，3y =-， ∴()0,3C-，∴D 到线段BC 的距离为1，2BC =， ∴12112BCD S =⨯⨯=V ， ∴44PBC BCD S S == ，设()2,23P m m m --，则()21223342PBC S m m =⨯⨯--+= ，整理得，224m m -=，解得11m =+，或21m =，∴()11P +，()21P -，∴存在点P ，使PBC 的面积是BCD △面积的4倍，点P 的坐标为()11P ，()21P ．【点睛】本题考查了待定系数法求二次函数解析式，二次函数顶点式，二次函数与三角形面积综合等知识．解题的关键在于对知识的熟练掌握与灵活运用．24. 为进一步开展“睡眠管理”工作，某校对部分学生的睡眠情况进行了问卷调查．设每名学生平均每天的睡眠时间为x 小时，其中的分组情况是： A 组：8.5x < B 组：8.59x ≤<C 组：99.5x ≤<D 组：9.510x ≤<E 组：10x ≥根据调查结果绘制成两幅不完整的统计图，请根据图中提供的信息，解答下列问题：（1）本次共调查了_______名学生；（2）补全条形统计图；（3）在扇形统计图中，求D 组所对应的扇形圆心角的度数；（4）若该校有1500名学生，请估计该校睡眠时间不足9小时的学生有多少人？【答案】（1）100（2）补全统计图见解析（3）D 组所对应的扇形圆心角度数为72︒（4）估计该校睡眠时间不足9小时的学生有375人【解析】【分析】（1）根据统计图中B 组的人数与占比，计算求解即可；（2）根据E 组人数占比为15％，求出E 组人数为10015⨯％人，然后作差求出A 组人数，最后补全统计图即可；（3）根据D 组人数的占比乘以360︒计算求解即可；（4）根据A B ，两组人数的占比，乘以总人数，计算求解即可．【小问1详解】解：由统计图可知，本次共调查了2020100÷=％（人），故答案为：100．【小问2详解】解：由统计图可知，E 组人数占比为15％， ∴E 组人数为1001515⨯=％（人），∴A 组人数为100204020155----=（人）， ∴补全统计图如图所示【小问3详解】解：由题意知，D 组所对应的扇形圆心角度数为2036072100⨯︒=︒， ∴D 组所对应的扇形圆心角度数为72︒．【小问4详解】解：由题意知，5201500375100+⨯=（人） ∴估计该校睡眠时间不足9小时的学生有375人．【点睛】本题考查了条形统计图与扇形统计图，画条形统计图，用样本估计总体等知识．解题的关键在于从统计图中获取正确的信息．25. 为抗击疫情，支援B 市，A 市某蔬菜公司紧急调运两车蔬菜运往B 市．甲、乙两辆货车从A 市出发前往B 市，乙车行驶途中发生故障原地维修，此时甲车刚好到达B 市．甲车卸载蔬菜后立即原路原速返回接应乙车，把乙车的蔬菜装上甲车后立即原路原速又运往B 市．乙车维修完毕后立即返回A 市．两车离A 市的距离y （km ）与乙车所用时间x （h ）之间的函数图象如图所示．（1）甲车速度是_______km/h ，乙车出发时速度是_______km/h ；（2）求乙车返回过程中，乙车离A 市的距离y （km ）与乙车所用时间x （h ）的函数解析式（不要求写出自变量的取值范围）；（3）乙车出发多少小时，两车之间的距离是120km ？请直接写出答案．【答案】（1）100 60（2）1001200y x =-+（3）3，6.3，9.1 【解析】【分析】（1）根据图象分别得出甲车5h 的路程为500km ，乙车5h 的路程为300km ，即可确定各自的速度；（2）设()0y kx b k =+≠，由图象可得经过点（9，300），（12，0）点，利用待定系数法即可确定函数解析式；（3）乙出发的时间为t 时，相距120km ，根据图象分多个时间段进行分析，利用速度与路程、时间的关系求解即可．【小问1详解】解：根据图象可得，甲车5h 的路程为500km ， ∴甲速度为：500÷5=100km/h ；乙车5h 的路程为300km ， ∴乙的速度为：300÷5=60km/h ；故答案为：100；60；【小问2详解】设()0y kx b k =+≠，由图象可得经过点（9，300），（12，0）点，的代入得9300120k b k b +=⎧⎨+=⎩，解得1001200k b =-⎧⎨=⎩∴y 与x 的函数解析式为1001200y x =-+；【小问3详解】解：设乙出发的时间为t 时，相距120km ，根据图象可得，当0<t <5时， 100t -60t =120，解得：t =3；当5<t <5.5时，根据图象可得不满足条件；当5.5<t <8时，500-100（t -5.5）-300=120，解得：t =6.3；当8<t <9时， 100（t -8）=120，解得：t =9.2，不符合题意，舍去；当9<t <12时，100×（9-8）+100（t -9）+100（t -9）=120，解得：t =9.1；综上可得：乙车出发3h 、6.3h 与9.1h 时，两车之间的距离为120km ．【点睛】题目主要考查根据函数图象获取相关信息，一次函数的应用，一元一次方程的应用等，理解题意，根据函数图象得出相关信息是解题关键． 26. ABC 和ADE 都是等边三角形．（1）将ADE 绕点A 旋转到图①的位置时，连接BD ，CE 并延长相交于点P （点P 与点A 重合），有PA PB PC +=（或PA PC PB +=）成立；请证明．（2）将ADE 绕点A 旋转到图②的位置时，连接BD ，CE 相交于点P ，连接PA ，猜想线段PA 、PB 、PC 之间有怎样的数量关系？并加以证明；（3）将ADE 绕点A 旋转到图③的位置时，连接BD ，CE 相交于点P ，连接PA ，猜想线段PA 、PB 、PC 之间有怎样的数量关系？直接写出结论，不需要证明．【答案】（1）证明见解析（2）图②结论：PB PA PC =+，证明见解析（3）图③结论：PA PB PC += 【解析】【分析】（1）由△ABC 是等边三角形，得AB =AC ，再因为点P 与点A 重合，所以PB =AB ，PC =AC ，PA =0，即可得出结论；（2）在BP 上截取BF CP =，连接AF ，证明BAD CAE ≌（SAS ），得ABD ACE ∠=∠，再证明CAP BAF ≌△△（SAS ），得CAP BAF ∠=∠，AF AP =，然后证明AFP 是等边三角形，得PF AP =，即可得出结论；（3）在CP 上截取CF BP =，连接AF ，证明BAD CAE ≌（SAS ），得ABD ACE ∠=∠，再证明BAP CAF ≌△△（SAS ），得出CAF BAP ∠=∠，AP AF =，然后证明AFP 是等边三角形，得PF AP =，即可得出结论：PA PB PF CF PC +=+=．【小问1详解】证明：∵△ABC 是等边三角形， ∴AB =AC ，∵点P 与点A 重合， ∴PB =AB ，PC =AC ，PA =0， ∴PA PB PC +=或PA PC PB +=；【小问2详解】解：图②结论：PB PA PC =+证明：在BP 上截取BF CP =，连接AF ，∵ABC 和ADE 都是等边三角形，∴AB AC =，AD AE =，60BAC DAE ∠=∠=︒ ∴BAC CAD DAE CAD ∠+∠=∠+∠， ∴BAD CAE ∠=∠， ∴BAD CAE ≌（SAS ）， ∴ABD ACE ∠=∠， ∵AC =AB ，CP =BF ， ∴CAP BAF ≌△△（SAS ）， ∴CAP BAF ∠=∠，AF AP =， ∴CAP CAF BAF CAF ∠+∠=∠+∠， ∴60FAP BAC ∠=∠=︒， ∴AFP 是等边三角形， ∴PF AP =，∴PA PC PF BF PB +=+=；【小问3详解】解：图③结论：PA PB PC +=，理由：在CP 上截取CF BP =，连接AF ，∵ABC 和ADE 都是等边三角形，∴AB AC =，AD AE =，60BAC DAE ∠=∠=︒ ∴BAC BAE DAE BAE ∠+∠=∠+∠， ∴BAD CAE ∠=∠， ∴BAD CAE ≌（SAS ）， ∴ABD ACE ∠=∠， ∵AB =AC ，BP =CF ，∴BAP CAF ≌△△（SAS ），∴CAF BAP ∠=∠，AP AF =， ∴BAF BAP BAF CAF ∠+∠=∠+∠， ∴60FAP BAC ∠=∠=︒， ∴AFP 是等边三角形， ∴PF AP =，∴PA PB PF CF PC +=+=，即PA PB PC +=．【点睛】本题考查等边三角形的判定与性质，全等三角形的判定与性质，熟练掌握等边三角形的判定与性质、全等三角形的判定与性质是解题的关键．27. 学校开展大课间活动，某班需要购买A 、B 两种跳绳．已知购进10根A 种跳绳和5根B 种跳绳共需175元：购进15根A 种跳绳和10根B 种跳绳共需300元．（1）求购进一根A 种跳绳和一根B 种跳绳各需多少元？（2）设购买A 种跳绳m 根，若班级计划购买A 、B 两种跳绳共45根，所花费用不少于548元且不多于560元，则有哪几种购买方案？（3）在（2）的条件下，哪种购买方案需要的总费用最少？最少费用是多少元？【答案】（1）购进一根A 种跳绳需10元，购进一根B 种跳绳需15元（2）有三种方案：方案一：购买A 种跳绳23根，B 种跳绳22根；方案二：购买A 种跳绳24根，B 种跳绳21根；方案三：购买A 种跳绳25根，B 种跳绳20根（3）方案三需要费用最少，最少费用是550元【解析】【分析】（1）设购进一根A 种跳绳需x 元，购进一根B 种跳绳需y 元，可列方程组1051751510300x y x y +=⎧⎨+=⎩，解方程组即可求得结果；（2）根据题意可列出不等式组()()101545560101545548m m m m ⎧+-≤⎪⎨+-≥⎪⎩，解得：2325.4m ≤≤，由此即可确定方案；（3）设购买跳绳所需费用为w 元，根据题意，得()1015455675w m m m =+-=-+，结合函数图像的性质，可知w 随m 的增大而减小，即当25m =时525675550=-⨯+=．【小问1详解】解：设购进一根A 种跳绳需x 元，购进一根B 种跳绳需y 元，根据题意，得1051751510300x y x y +=⎧⎨+=⎩，解得1015x y =⎧⎨=⎩，答：购进一根A 种跳绳需10元，购进一根B 种跳绳需15元；【小问2详解】根据题意，得()()101545560101545548m m m m ⎧+-≤⎪⎨+-≥⎪⎩，解得2325.4m ≤≤，∵m 整数，∴m 可取23，24，25．∴有三种方案：方案一：购买A 种跳绳23根，B 种跳绳22根；方案二：购买A 种跳绳24根，B 种跳绳21根；方案三：购买A 种跳绳25根，B 种跳绳20根；【小问3详解】设购买跳绳所需费用为w 元，根据题意，得()1015455675w m m m =+-=-+ ∵50-<，∴w 随m 的增大而减小，∴当25m =时，w 有最小值，即w 525675550=-⨯+=（元）答：方案三需要费用最少，最少费用是550元．【点睛】本题主要考查的是不等式应用题、二元一次方程组应用题、一次函数相关应用题，根据题意列出对应的方程是解题的关键．28. 如图，在平面直角坐标系中，平行四边形ABCD 的边AB 在x 轴上，顶点D 在y 轴的正半轴上，M 为BC 的中点，OA 、OB 的长分别是一元二次方程27120x x -+=的两个根()OA OB <，4tan 3DAB ∠=，动点P 从点D 出发以每秒1个单位长度的速度沿折线DC CB -向点B 运动，到达B 点停止．设运动时间为t 秒，APC △的面积为S ．为（1）求点C 的坐标；（2）求S 关于t 的函数关系式，并写出自变量t 的取值范围；（3）在点P 的运动过程中，是否存在点P ，使CMP !是等腰三角形？若存在，请直接写出点P 的坐标；若不存在，请说明理由．【答案】（1）点C 坐标为()7,4（2）()()14207149871255t t S t t ⎧-≤<⎪=⎨-<≤⎪⎩（3）存在点P ()4,4或9,42⎛⎫⎪⎝⎭或59,412⎛⎫ ⎪⎝⎭，使CMP !是等腰三角形【解析】【分析】（1）先求出方程的解，可得3OA =，4OB =，再由4tan 3DAB ∠=，可得4OD =，然后根据四边形ABCD 是平行四边形，可得CD =7，90ODC AOD ∠=∠=︒，即可求解；（2）分两种情况讨论：当07t <…时，当712t <…时，过点A 作AF BC ⊥交CB 的延长线于点F ，即可求解；（3）分三种情况讨论：当CP =PM 时，过点M 作MF ⊥PC 于点F ；当52PC CM ==时；当PM =CM 时，过点M 作MG ⊥PC 于点G ，即可求解．【小问1详解】解：27120x x -+=，解得13x =，24x =，∵OA OB <，∴3OA =，4OB =， ∵4tan 3DAB ∠=，。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

黑龙江省龙东地区2017年初中毕业学业统一考试数学试题考生注意：1、考试时间120分钟2、全卷共三道大题，总分120分一、填空题（每题3分，满分30分）二、选择题（每题3分，满分30分）11.下列各运算中，计算正确的是（）A ．()3532b a b a = B ．()632273a a = C ．326x x x =÷ D ．()222b a b a +=+12.下列图形中，既是轴对称图形又是中心对称图形的是（）A B C D13.如图,是由若干个相同的小立方体搭成的几何体的俯视图和左视图,则小立方体的个数可能是（）或6 或7 或5或6 或6或7A ．＞1 B. ≥1 C. ≥1且≠9 D. ≤1 18.如图,在矩形ABCD 中,AD=4,∠DAC=30°,点P 、E 分别在AC 、AD 上，则PE+PD 的最小值是（） B.32 C. 4 D.33819.“双11”促销活动中，小芳的妈妈计划用1000元在唯品会购买价格分别为80元和120元的两种商品，则可供小芳妈妈选择的购买方案有（）种种种种20.如图，在边长为4的正方形ABCD 中，E 、F 是AD 边上的两个动点,且AE=FD,连接BE 、CF 、BD ，CF 与BD 交于点G ，连接AG 交BE 于点H ，连接DH.下列结论正确的个数是（） ①△ABG ∽△FDG ②HD 平分∠EHG ③AG ⊥BE④S △HDG : S △HBG =tan ∠DAG ⑤线段DH 的最小值是252-三、解答题（满分60分）21.（本题满分5分）先化简，再求值：12123322--+-÷-a aa a a a a ,其中=a 1+2cos60°22.（本题满分6分）如图，在平面直角坐标系中，△ABC 的三个顶点都在格点上，点A 的坐标为（2，2）请解答下列问题: （1）画出△ABC 关于y 轴对称的△A 1B 1C 1，并写出A 1的坐标. （2）画出△ABC 绕点B 逆时针旋转90°后得到的△A 2BC 2，并写出A 2的坐标.（3）画出和△A 2BC 2关于原点O 成中心对称的△A 3B 3C 3，并写出A 3的坐标.23.（本题满分6分）F E H D AG BC第20题图第22题图如图，Rt △AOB 的直角边OA 在x 轴上，OA=2，AB=1，将Rt △AOB 绕点O 逆时针旋转90°得到Rt △COD ，抛物线y=c bx x ++-265经过B 、D 两点. （1）求二次函数的解析式.（2）连接BD ，点P 是抛线上一点，直线OP 把△BOD 的周长分成相等的两部分，求点P 的坐标.24.（本题满分7分）我市某中学为了了解孩子们对《中国诗词大会》,《挑战不可能》,《最强大脑》,《超级演说家》,《地理中国》五种电视节目的喜爱程度,随机在七、八、九年级抽取了部分学生进行调查(每人只能选择一种喜爱的电视节目),并将获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据两幅统计图中的信息回答下列问题：（1）本次调查中共抽取了______名学生. （2）补全条形统计图.（3）在扇形统计图中，喜爱《地理中国》节目的人数所在扇形的圆心角是___ _度. （4）若该学校有2000人，请你估计该学校喜欢《最强大脑》节目的学生人数是多少人第23题图中国大脑演说家诗词大会不可能第24题图在甲、乙两城市之间有一服务区,一辆客车从甲地驶往乙地,一辆货车从乙地驶往甲地,两车同时出发,匀速行驶.客车、货车离服务区的距离y1(千米),y2(千米)与行驶的时间x(小时)的函数关系图象如图1所示.(1)甲、乙两地相距千米.(2)求出发3小时后,货车离服务区的路程y2(千米)与行驶时间x(小时)之间的函数关系式.(3)在客车和货车出发的同时,有一辆邮政车从服务区匀速去甲地取货后返回乙地（取货的时间忽略不计）,邮政车离服务区的距离y3(千米)与行驶时间x(小时)之间的函数关系图象如图2中的虚线所示,直接写出在行驶的过程中,经过多长时间邮政车与客车和货车的距离相等第25题图己知:△AOB 和△COD 均为等腰直角三角形, ∠AOB=∠COD=90°.连接AD 、BC,点H 为BC 中点,连接OH.(1)如图1所示,易证: OH=21AD 且OH ⊥AD(不需证明). (2)将△COD 绕点O 旋转到图2、图3所示位置时，线段OH 与AD 又有怎样的关系.并选择一个图形证明你的结论.第26题图图2 B A DO C H ADB O 图3C H 图1 AD O CH为了推动“龙江经济带”建设,我省某蔬菜企业决定通过加大种植面积、增加种植种类，促进经济发展.2017年春,预计种植西红柿、马铃薯、青椒共100公顷(三种蔬菜的种植面积均为整数)，青椒的种植面积是西红柿种植面积的2倍.经预算，种植西红柿的利润可达1万元/公顷、青椒万元/公顷、马铃薯2万元/公顷.设种植西红柿x 公顷,总利润为y 万元.(1)求总利润y (万元)与种植西红柿的面积x (公顷)之间的关系式.(2)若预计总利润不低于180万元,西红柿的种植面积不低于8公顷,有多少种种植方案 (3)在（2）的前提下，该企业决定投资不超过获得最大利润的81在冬季同时建造A 、B 两种类型的温室大棚,开辟新的经济增长点.经测算，投资A 种类型的大棚5万元/个、B 种类型的大棚8万元/个,请直接写出有哪几种建造方案28.(本题满分10分)如图,矩形AOCB 的顶点A 、C 分别位于x 轴和y 轴的正半轴上,线段OA 、OC 的长度满足方程01315=-+-y x (OA ＞OC),直线b kx y +=分别与x 轴、y 轴交于M 、N 两点.将△BCN 沿直线BN 折叠,点C 恰好落在直线MN 上的点D 处,且tan ∠CBD =43. (1)求点B 的坐标.(2)求直线BN 的解析式.(3)将直线BN 以每秒1个单位长度的速度沿y 轴向下平移,求直线BN 扫过矩形AOCB 的面积S 关于运动的时间t(0＜t ≤13)的函数关系式.第28题图黑龙江省龙东地区2017年初中毕业学业统一考试数学试题参考答案及评分标准一、填空（每题3分，共30分）×1010≠1 =DE(BC=EF, DF=AC)等 4. 5 ≥1 7.34316-π 8.1324+π 或34 或74 10.（2016332⎪⎪⎭⎫⎝⎛,0)或写成⎪⎪⎭⎫ ⎝⎛0,3210082016或⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫⎝⎛0,322016二、选择题（每题3分，共30分）16. B 17. C 18 B 19. A 三、解答题（满分60分） 21.（本题满分5分）解：原式=aa )1(3-·22)1(-a a -12-a a ……………………………………… 2分 =1-a a . …………………………………………………… 1分当a=2cos60°+1=2时， ………………………………………… 1分原式=2. ……………………………………………………1分22. （本题满分6分）解; ⑴正确画出对称后的图形 ………………………………………1分 A 1（-2，2）………………………………………1分⑵正确画出旋转后的图形 ………………………………………1分 A 2（4，0）………………………………………1分⑶正确画出成中心对称的图形 ………………………………………1分 A 3（-4，0）………………………………………1分 23. （本题满分6分）解：（1）由题意得，△AOB ≌△COD ∴OC=OA=2，CD=AB=1.∴ B （2，1） D （-1，2）………………………………………………………1分 ∵抛物线y=c bx x ++-265经过B 、D 两点.⎪⎪⎩⎪⎪⎨⎧=+--⨯-=++⨯-2)1(651226522c b c b∴⎪⎪⎩⎪⎪⎨⎧==21310b c ……………………… … …… … 1分 ∴二次函数解析式是31021652++-=x x y ……………1分(2) ∵直线OP 把△BOD 分成周长相等的两部分∴直线OP 必过线段BD 的中点（23,21） …………1分∴直线OP 的解析式y op =3x …………1分∵点P 是抛物线31021652++-=x x y 和直线y op =3x 的交点∴⎪⎩⎪⎨⎧++-==310216532x x y xy∴P （1，3）或P （-4，-12）………………………………2分24. （本题满分7分）解：(1)本次共调查学生200%1530=（人）. ………………………………1分（2）补全条形图的高度是50.………………………………2分（3）喜爱《地理中国》节目的人数所在扇形的圆心角是36度.…………………2分（4）估计该学校喜欢《最强大脑》节目的学生人数是600人.……2分 25. （本题满分8分）解：（1）甲、乙两地相距480 千米………………………………2分（2）设出发3小时，货车离服务区的路程y 2与时间x 的关系式为y 2=kx+b （k ≠0），则 ⎩⎨⎧=+=+3601203b k b k ………………………………………………………1分解得:⎩⎨⎧-==12040b k ………………………………………………………1分∴y 2=40x-120 ………………………………………………………1分（3）经过小时、小时、小时邮政车与客车和货车的距离相等 ……3分 26. （本题满分8分）解：（1）图2的结论为：OH=21AD …………………………………1分 OH ⊥AD ………………………………1分图3的结论为: OH=21AD ………………………………1分 OH ⊥AD ………………………………1 (2) 选图2的结论证明如下：证明: 延长OH 到点Q 使OH=HQ,连接QC 易证△BHO ≌△CHQ ∴∠BOH=∠Q OH=21OQ ∵等腰Rt △AOB 和等腰Rt △COD ∴∠AOD=180°-∠COB而∠COB=∠QOC+∠BOQ=∠QOC+∠Q ∠QCO=180°-(∠QOC+∠Q) =180°-∠COB∴∠AOD= ∠QCO 易证△QCO ≌△AOD∴∠Q=∠OADQ BADO CH而∠AOC+∠COB=90°∴∠AOC+∠COQ+∠OAD=90°即OH ⊥AD ………………………2分而OM=21OQ OQ=AD ∴OH=21AD ………………………2分 ∴OH=21AD OH ⊥AD 选图3的结论证明如下：证明:延长OH 到点Q 使OH=HQ,连接QC易证△BHO ≌△CHQ∴∠BOH=∠Q OH=21OQ ∵等腰Rt △AOB 和等腰Rt △COD∴∠BOC+∠AOD=180° ∴∠BOC=∠OAD+∠ADO ∴∠Q+∠COQ=∠OAD+∠ADO ∴∠AOD=∠OCQ 易证△QCO ≌△AOD∴∠Q=∠OAD而∠BOQ+∠AON=90°∴∠DAO+∠AON=90°即OH ⊥AD ………………………2分而OM=21OQ OQ=AD ∴OH=21AD ………………………2分 ∴OH=21AD OH ⊥AD27. （本题满分10分）解（1）由已知可得：y=x+×2x+2(100-x-2x)y=-2x+200 …………………………………………3分(2) 由已知可得：则⎩⎨⎧≥≥+-81802002x x ， …………………………1分解得8≤x ≤10. …………………………………………………………………1分 ∵x 为整数，∴x 可取8、9、10.∴有三种购买方案……………………………………………………………1分（3）方案一：建造A 种类型大棚1个；B 种类型大棚1个……………1分图2 BA DO C H 图3 Q方案二：建造A 种类型大棚1个；B 种类型大棚2个……………1分方案三：建造A 种类型大棚2个；B 种类型大棚1个……………1分方案四：建造A 种类型大棚3个；B 种类型大棚1个……………1分28 .（本题满分10分）解：（1）∵01315=-+-y x ∴ x=15 ， y=13 . ………………………………………………1分 ∵OA 、OC 的长度满足方程01315=-+-y x (OA ＞OC)∴OA=15 ， OC=13. ……………………………………………………1分∴B(15,13). ………………………………………………………… 1分(2)过点D 作直线EF ∥x 轴,分别交OC 、BA 边于E 、F∴∠CBD=∠BDF∵tan ∠CBD =43 ∴tan ∠BDF = tan ∠CBD =DF BF =43 ………………………………1分 ∴在Rt △BDF 中，BD=15，由勾股定理得：BF=9，DF=12∴DE=3在Rt △DEN 中，DE=3，NE+DN=9 由勾股定理得DN=5 NE=4∴点N （0，8）, ………………………………1分设直线BN 解析式是y BN =kx+b∵N （0，8） B(15,13)∴y BN =831+x . ………………………………1分（3）S=15t ………………………………1分(0<t ≤8) …………………………1分 S=9639232-+-t t ………………………………1分 (8<t ≤13) …………………………1分注：本卷中各题若有其它正确的解法，可酌情给分.。