主成分SAS程序
主成分分析、判别分析、聚类分析sas程序

一、主成分分析1、数据引入PROC IMPORT OUT= WORK.shuruDA TAFILE= "E:\****\****\数据分析\试验\shouru.xls"DBMS=EXCEL2000 REPLACE;GETNAMES=YES;RUN;2、程序proc princomp data=shouru out=defen;var x1-x9;run;proc sort data=defen;by prin1 prin2;run;proc print data=defen;run;二、判别分析程序2.2方法1:先改变shuru 数据的结构,把待判的数据去掉,再引入数据data shouru1;input diqu $ x1-x9;cards;广东211.3 114 41.44 33.2 11.2 48.72 30.77 14.9 11.1西藏175.93 163.8 57.89 4.22 3.37 17.81 82.32 15.7 0;run;proc discrim data=shourutestdata=shouru1 method=normallist all crosslist testlist;class leixing;var x1-x9;run;方法2:原shuru数据不变,直接判别,但此法虽可判断待判的两省属于那类,但无法给出误判率;proc discrim data=shouruout=a1outstat=a2 outcross=a3method=normallist all crosslist testlist;class leixing;var x1-x9;run;程序2.3proc discrim data=shourutestdata=shouru1 method=normallist all crosslist crossvalidate testlist;class leixing;var x1-x9;priors prop;run;三、聚类分析程序proc cluster data=yjshr method=sin outtree=y1 ;/*最短距离法*/ var x1-x9;run;proc tree data=y1 nclusters=3 out=z1;run;proc print data=z1;run;proc cluster data=yjshr method=com outtree=y2 ;/*最长距离法*/ var x1-x9;run;proc tree data=y2 nclusters=3 out=z2;run;proc print data=z2;run;proc cluster data=yjshr method=ave outtree=y3 ;/*类平均距离法*/ var x1-x9;run;proc tree data=y3 nclusters=3 out=z3;run;proc print data=z3;run;proc fastclus data=yjshr out=a1maxc=3 cluster=c distance list; /*快速聚类分三类情况*/ proc plot;plot x2*x1=c;run;。
SAS学习系列33.-主成分分析

SAS学习系列33.-主成分分析33. 主成分分析(一)原理一、基本思想主成份分析,是数学上对数据降维的一种方法,是将多个变量转化为少数综合变量(集中了原始变量的大部分信息)的一种多元统计方法。
其主要目的是将变量减少,并使其改变为少数几个相互独立的线性组合形成的新变量(主成份,其方差最大),使得原始资料在这些成份上显示最大的个别差异来。
在所有的线性组合中所选取的F1应该是方差最大的,称为第一主成分。
如果第一主成分不足以代表原来所有指标的信息,再考虑选取第二个线性组合F2, 称为第二主成分。
为了有效地反映原有信息,F1已有的信息就不需要再出现在F2中,用数学语言表达就是要求Cov(F1,F2)=0. 依此类推可以构造出第三、第四、…、第p个主成分。
主成份分析,可以用来综合变量之间的关系,也可用来减少回归分析或聚类分析中的变量数目。
二、基本原理设有n个样品(多元观测值),每个样品观测p项指标(变量):X1,…,X p,得到原始数据资料阵:其中,X i = (x1i,x2i,…,x ni)T,i = 1, …, p.用数据矩阵X的p个列向量(即p个指标向量)X1,…,X p作线性组合,得到综合指标向量:简写成:F i = a1i X1 + a2i X2+…+a pi X p i = 1, …, p限制系数a i = (a1i,a2i,…,a pi)T为单位向量,即且由下列原则决定:(1)F i与F j互不相关,即COV(F i, F j)=a i T∑a i=0,其中∑为X 的协方差矩阵;(2)F1是X1,X2,…,X p的所有满足上述要求的线性组合中方差最大的,即F2是与F1不相关的X1,…,X p所有线性组合中方差最大的,…,F p是与F1,…,F p-1都不相关的X1,…,X p所有线性组合中方差最方向对应。
F1,F2,…,F p可以理解为p维空间中互相垂直的p 个坐标轴。
三、基本步骤1. 计算样品数据协方差矩阵Σ = (s ij)p p,其中2. 求出Σ的特征值及相应的特征向量λ1>λ2>…>λp>0, 及相应的正交化单位特征向量:则X的第i个主成分为F i= a i T X,i=1, …, p.3. 选择主成分在已确定的全部p个主成分中合理选择m个来实现最终的评价分析。
SASprincomp

SAS/STAT主成分分析(princomp)过程一、Princomp过程语句SAS/STAT(Princomp)主要的语句如下:二、实例分析例一应收账款是指企业因对外销售产品、材料、提供劳务及其它原因,应向购货单位或接受劳务的单位收取的款项,包括应收销货款、其它应收款和应收票据等。
出于扩大销售的竞争需要,企业不得不以赊销或其它优惠的方式招揽顾客,由于销售和收款的时间差,于是产生了应收款项。
应收款赊销的效果的好坏,不仅依赖于企业的信用政策,还依赖于顾客的信用程度。
由此,评价顾客的信用等级,了解顾客的综合信用程度,做到“知己知彼,百战不殆”,对加强企业的应收账款管理大有帮助。
某企业为了了解其客户的信用程度,采用西方银行信用评估常用的5C方法,5C的目的是说明顾客违约的可能性。
它们是:1、品格(用X1表示),指顾客的信誉,履行偿还义务的可能性。
企业可以通过过去的付款记录得到此项。
2、能力(用X2表示),指顾客的偿还能力。
即其流动资产的数量和质量以及流动负载的比率。
顾客的流动资产越多,其转化为现金支付款项的能力越强。
同时,还应注意顾客流动资产的质量,看其是否会出现存货过多过时质量下降,影响其变现能力和支付能力。
3、资本(用X3表示),指顾客的财务势力和财务状况,表明顾客可能偿还债务的背景。
4、附带的担保品(用X4表示),指借款人以容易出售的资产做抵押。
5、环境条件(用X5表示),指企业的外部因素,即指非企业本身能控制或操纵的因素。
首先并抽取了10家具有可比性的同类企业作为样本,又请8位专家分别给10个企业的5个指标打分,然后分别计算企业5个指标的平均值,如表。
这5个指标是按照百分制给出的分数,它们有同样的量纲,所以我们可以利用协方差阵做主成份分析。
程序:data c;input x1-x5@@;cards;76.5 81.5 76 75.8 71.7 85 79.2 80.3 84.4 76.570.6 73 67.6 68.1 78.5 94 94 87.5 89.5 9290.7 87.3 91 81.5 80 84.6 66.9 68.8 64.8 66.477.5 73.6 70.9 69.8 74.8 57.7 60.4 57.4 60.8 6585.6 68.5 70 62.2 76.5 70 69.2 71.7 64.9 68.9;PROC PRINCOMP data=c COV OUTstat=P out=b;Var x1 x2 x3 x4 x5;proc print data=p;proc print data=b;run;程序解释:PROC Princomp语句启动Princomp过程。
SAS软件应用之主成分分析

本章小节
在大部分实际问题中,变量之间是有一定的相关性的,人们 自然希望找到较少的几个彼此不相关的综合指标尽可能多地 反映原来众多变量的信息。本章介绍了主成分分析的数学模 型、方法步骤以及主成分分析的应用。我们需要一种综合性 的分析方法,既可减少指标变量的个数,又尽量不损失原指 标变量所包含的信息,对资料进行全面的综合分析。主成分 分析正是适应这一要求产生的,是解决这类题的理想工具。 主成份分析的基本思想就是将彼此相关的一组指标变量转化 为彼此独立的一组新的指标变量,并用其中较少的几个新指 标变量就能综合反应原多个指标变量中所包含的主要信息, 符合专业含义。
主成分分析的方法步骤
计算主成分得分 如果标准化指标变量 X 1 , X 2 ,, X k 的第i个主成分是:
Z i liX li1 X 1 li 2 X 2 lik X k xij x j 其中, X ij , j, 1,2,, k sj 是xj的标准化指标变量。那么,第i个主成分可以 转换为原始指标变量的线性组合:
主成分分析的方法步骤
对原始指标数据进行标准化变换:
X ij xij x j sj , j 1,2,, k
将原始数据标准化,然后利用标准化的数据 计算主成分。X为标准化后的数据矩阵,则:
X 11 X X 21 X n1 X 12 X 22 X n2 X 1k X 2k X nk
li1 li 2 lik li1 x1 li 2 x2 lik xk zi x1 x2 xk ( ),i 1,2,, k s1 s2 sk s1 s2 sk
主成分分析的应用
主成分分析与因子分析(三):使用SAS实现主成分分析-FACTOR过程

主成分分析与因子分析(三):使用SAS实现主成分分析-FACTOR过程上一系列文章介绍了使用PRINCOMP过程进行主成分分析。
今天,我们将介绍使用FACTOR过程进行主成分分析。
FACTOR 过程除了PROC PRINCOMP外,还可以使用PROC FACTOR来进行主成分分析。
事实上,在进行标准化后,二者的结果是一样的。
为了比较二者的结果,首先介绍如何对数据进行标准化。
SAS对数据的标准化是通过PROC STDIZE实现的,PROC STDIZE的一般形式如下:其中:•选项METHOD=指定用于标准化的方法,常见的标准化方法有MEAN、SUM、EUCLEN和STD。
•VAR语句指定数据集中用来进行主成分分析的变量,变量类型必须为数值型。
若该语句缺失,那么PROC FACTOR将分析数据集中的所有数值型变量。
标准化的计算方法如下:这里LOCATION和SCALE的值与标准化方法有关。
表12.3列举了一些常见的标准化方法的LOCATION和SCALE值。
有关其他方法具体参数值建议读者参考SAS官方帮助文档。
表12.3 常见标准化方法中的LOCATION值与SCALE值这里仅简单介绍PROC FACTOR中与主成分分析相关部分的选项,在后面使用PROC FACTOR进行因子分析时,会对其他选项进行介绍。
PROC FACTOR的语法如下:其中:•常见的选项有:“DATA=”用于指定输入数据集,“SIMPLE”输出常见的统计量,“CORR”输出原始变量的相关矩阵。
•VAR语句指定数据集中用于分析的变量。
例12.2:使用PROC FACTOR对数据集sashelp.cars进行主成分分析。
示例代码如下:输出结果中基本统计量与相关矩阵的部分如图12.8所示。
图12.8 使用PROC FACTOR进行主成分分析过程中输出基本统计量与相关矩阵同时,PROC FACTOR还输出了相关矩阵的特征值与解释的变异比例,这部分内容也和PROC PRINCOMP一致(如图12.9所示)。
主成分分析和主成分回归(附实际案例和sas代码)

目录主成分分析和主成分回归(附实际案例和sas代码) (2)1 主成分分析的主要思想 (2)2 主成分分析的定义 (2)3 案例基本情况介绍餐饮业零售额相关因素 (3)4 案例相关因素的介绍相关因素的具体数据 (3)5 影响餐饮业零售额因素的主成分分析 (4)6 主成分回归 (9)主成分分析和主成分回归(附实际案例和sas 代码)1 主成分分析的主要思想在进行高维数据系统分析时,通过主成分分析,可以在纷繁的指标变量描述下,了解影响这个系统存在与发展的主要因素。
主成分分析是1933年由霍特林首先提出来的。
在信息损失最小的前提下,将描述某一系统的多个变量综合成少数几个潜变量,从而迅速揭示系统形成的主要因素,并把原来高维空间降到低维子空间。
主成分分析是研究如何通过少数几个主成分来解释多变量的方差的分析方法,也就是求出少数几个主成分,使他们尽可能多地保留原始变量的信息,且彼此不相关它是一种数学变换方法,即把给定的一组变量通过线性变换,转换为一组不相关的变量,在这种变换中保持变量的总方差不变,同时具有最大总方差,称为第一主成分;具有次大方差,成为第二主成分。
依次类推。
若共有p 个变量,实际应用中一般不是找p 个主成分,而是找出个)(p m m <主成分就够了,只要这m 个主成分能够反映原来所有变量的绝大部分的方差。
2 主成分分析的定义设研究对象涉及P 个指标,分别用p X X X ,,21表示,这个指标构成P 维随机向量为)',,,(21p X X X X =。
设随机向量的均值为u ,协方差矩阵为Σ。
主成分分析就是对随机向量进行线性变换以形成新的综合变量,用i Z 表示,满足下式:1212,1,2,,i i i ip P Z u X u X u X i p =++⋅⋅⋅+= (1)为了使新的综合变量能够充分反映原来变量的信息,则i Z 的方差尽可能大且各个i Z 之间不相关。
由于没有限制条件方差可以任意大,设有线面的约束条件:222121,(1,2,)i i ip u u u i p ++⋅⋅⋅== (2)主成分则为满足条件的i Z 。
聚类分析与主成分分析SAS的程序

实验三我国各地区城镇居民消费性支出的主成分分析和聚类分析(王学民编写)一、实验目的1.掌握如何使用SAS软件来进行主成分分析和聚类分析;2.看懂和理解SAS输出的结果,并学会以此来作出分析;3.掌握对实际数据如何来进行主成分分析;4.对同一组数据使用五种系统聚类方法及k均值法,学会对各种聚类效果的比较,获取重要经验;5.掌握使用主成分进行聚类二、实验内容数据集sasuser.examp633中含有1999年全国31个省、直辖市和自治区的城镇居民家庭平均每人全年消费性支出的八个主要变量数据。
对这些数据进行主成分分析,可将这31个地区的前两个主成分得分标示于平面坐标系内,对各地区作直观的比较分析。
对同样的数据使用五种系统聚类方法及k均值法聚类,并对聚类效果作比较。
最后,对主成分的图形聚类和正规聚类的效果进行比较。
实验1进行主成分分析,根据前两个主成分得分所作的散点图对31个地区进行比较分析。
实验2分别使用最长距离法、中间距离法、两种类平均法、离差平方和法和k均值法进行聚类分析,并比较其聚类效果。
实验3主成分聚类,并与上述正规的聚类方法进行比较三、实验要求1.用SAS软件的交互式数据分析菜单系统完成主成分分析;2.完成五种系统聚类方法及k均值法,比较其聚类效果;3.根据前两个主成分得分的散点图作直观的聚类,并与上述正规的聚类方法进行比较。
四、实验指导1.进行主成分分析在inshigt中打开数据集sasuser.examp633,见图1。
选菜单过程如下:在图1中选分析⇒多元(Y X)⇒在变量框中选x1,x2,x3,x4,x5,x6,x7,x8(见图2)⇒Y⇒选输出⇒选主分量分析,主分量选项(见图3)⇒在图4中作图中的选择(主成分个数缺省时为“自动”选项,此时只输出特征值大于1的主成分)⇒确定⇒确定⇒确定图1图2图3图4 得到如图5、图6所示的结果:图5图6从图5可以看出,前两个和前三个主成分的累计贡献率分别达到80.6%和87.8%,第一主成分1ˆy 在所有变量(除在*2x 上的载荷稍偏小外)上都有近似相等的正载荷,反映了综合消费性支出的水平,因此第一主成分可称为综合消费性支出成分。
主成份分析报告(包含sas程序)
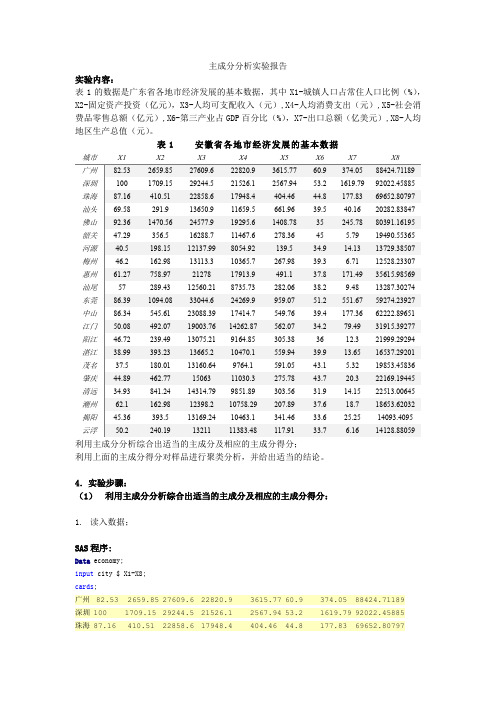
主成分分析实验报告实验内容:表1的数据是广东省各地市经济发展的基本数据,其中X1-城镇人口占常住人口比例(%),X2-固定资产投资(亿元),X3-人均可支配收入(元),X4-人均消费支出(元),X5-社会消费品零售总额(亿元),X6-第三产业占GDP百分比(%),X7-出口总额(亿美元),X8-人均地区生产总值(元)。
表1 安徽省各地市经济发展的基本数据城市X1X2X3X4X5X6X7X8广州82.532659.8527609.622820.93615.7760.9374.0588424.71189深圳1001709.1529244.521526.12567.9453.21619.7992022.45885珠海87.16410.5122858.617948.4404.4644.8177.8369652.80797汕头69.58291.913650.911659.5661.9639.540.1620282.83847佛山92.361470.5624577.919295.61408.7835245.7880391.16195韶关47.29356.516288.711467.6278.3645 5.7919490.55365河源40.5198.1512137.998054.92139.534.914.1313729.38507梅州46.2162.9813113.310365.7267.9839.3 6.7112528.23307惠州61.27758.972127817913.9491.137.8171.4935615.98569汕尾57289.4312560.218735.73282.0638.29.4813287.30274东莞86.391094.0833044.624269.9959.0751.2551.6759274.23927中山86.34545.6123088.3917414.7549.7639.4177.3662222.89651江门50.08492.0719003.7614262.87562.0734.279.4931915.39277阳江46.72239.4913075.219164.85305.383612.321999.29294湛江38.99393.2313665.210470.1559.9439.913.6516537.29201茂名37.5180.0113160.649764.1591.0543.1 5.3219853.45836肇庆44.89462.771506311030.3275.7843.720.322169.19445清远34.93841.2414314.799851.89303.5631.914.1522513.00645潮州62.1162.9812398.210758.29207.8937.618.718653.62032揭阳45.36393.513169.2410463.1341.4633.625.2514093.4095云浮50.2240.191321111383.48117.9133.7 6.1614128.88059利用主成分分析综合出适当的主成分及相应的主成分得分;利用上面的主成分得分对样品进行聚类分析,并给出适当的结论。
SAS编程:主成分分析和因子分析

SAS 统计分析与应用 从入门到精通 二、因子分析
语句说明:
4、FACTOR过程
(1)PROC语句用于规定运行FACTOR过程,并指定要分析的数据 集名。选项有: OUT=数据集名——规定一个输出数据集,其中包含原始数据以及 公共因子得分。在使用选项时,要指定公共因子的个数。 METHOD=选项——规定提取公共因子的方法。 N=n——规定被提取因子的最大数目,缺省值为变量的个数。 SCORE——规定打印因子得分系数。
SAS 统计分析与应用 从入门到精通 一、主成分分析
4、PRINCOMP过程
语句说明: (1)PROC语句用于规定运行PRINCOMP过程,并指定要分析的 数据集名。选项有: OUT=数据集名——规定一个输出数据集,其中包含原始数据以及 主成分得分。 N=n——规定要计算的主成分个数。 STANDARD——规定将OUT=的数据集中的主成分得分标准化为 单位方差。如果没有规定此选项,主成分得分的方差等于相应的特征值。 (2)VAR语句用来列出要分析的数值型变量的名字。如果不使用该 语句,则没有在其它语句规定的所有数值型变量都是要分析的变量。 (3)PARTIAl语句规定了偏出变量,使得PRINCOMP过程基于偏 相关阵或偏协方差阵进行主成分分析。
SAS 统计分析与应用 从入门到精通 二、因子分析
2、基本模型
SAS 统计分析与应用 从入门到精通 二、因子分析
2、基本模型
SAS 统计分析与应用 从入门到精通 二、因子分析
3、基本步骤
(1) 参数估计:为建立因子模型,首先要估计因子载荷和特殊因 子的方差,常用的方法有主成分法,主因子法和极大似然估计法等。
SAS 统计分析与应用 从入门到精通 二、因子分析
语句说明:
SAS主成分分析 示例
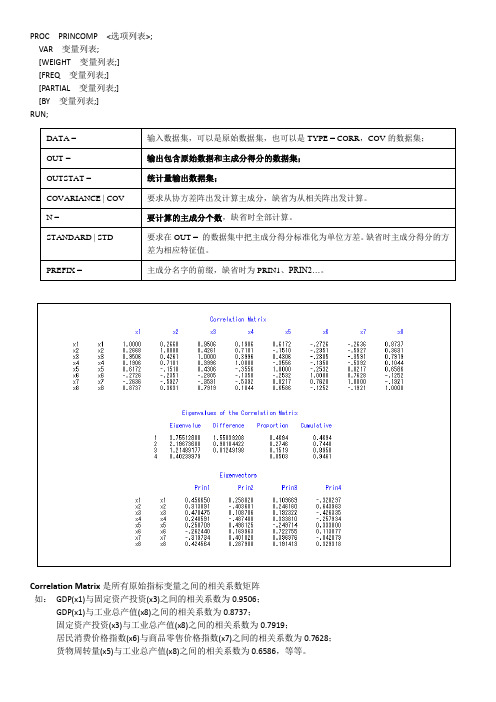
PROC PRINCOMP <选项列表>;VAR 变量列表;[WEIGHT 变量列表;][FREQ 变量列表;][PARTIAL 变量列表;][BY 变量列表;]RUN;DATA = 输入数据集,可以是原始数据集,也可以是TYPE = CORR,COV的数据集;OUT = 输出包含原始数据和主成分得分的数据集;OUTSTAT = 统计量输出数据集;COVARIANCE | COV要求从协方差阵出发计算主成分,缺省为从相关阵出发计算。
N = 要计算的主成分个数,缺省时全部计算。
STANDARD | STD要求在OUT = 的数据集中把主成分得分标准化为单位方差。
缺省时主成分得分的方差为相应特征值。
PREFIX = 主成分名字的前缀,缺省时为PRIN1、PRIN2…。
Correlation Matrix是所有原始指标变量之间的相关系数矩阵如:GDP(x1)与固定资产投资(x3)之间的相关系数为0.9506;GDP(x1)与工业总产值(x8)之间的相关系数为0.8737;固定资产投资(x3)与工业总产值(x8)之间的相关系数为0.7919;居民消费价格指数(x6)与商品零售价格指数(x7)之间的相关系数为0.7628;货物周转量(x5)与工业总产值(x8)之间的相关系数为0.6586,等等。
Eigenvalues of Correlation Matrix给出了由相关系数矩阵计算出来的全部特征值(Eigenvalue)、相邻两个特征值的差异(difference)、每个主成分的贡献率(proportion)和累积贡献率(cumulative)。
如:第一主成分对方差的贡献率为46.94%,第二主成分对方差的贡献率为27.46%,第三主成分对方差的贡献率为15.19%,之后的主成分的贡献率为0.05。
前三个主成分的累积贡献率为89.58%,因此,对第四主成分以后的主成分完全可以忽略不计,用前三个主成分就可以很好地概括这组数据。
SAS主成分分析实例

王笑(孝)权安徽省五河县临北乡石家村卫生室233316 *****************.cn主成分分析又称主分量、主轴分析,实质就是对较多的变量在尽量保存原信息的情况下加以线性概括。
在此过程前,为消除变量量纲不同造成的影响,首先要对各原始指标进行标准化处理。
迄今为止,所见教材的“主成分分析”实质都是用求得主成分再对原始变量的回归分析。
教材的通病都是未详细说明最后的回归过程,往往令初学者感觉到莫名其妙。
目前,由网上的一些所谓的“主成分分析”可知,或者其资料不适用主成分分析,还有根本就不是主成分分析。
有鉴于此,现利用网上获得的数据,进行主成分分析的探讨。
1 资料与方法1.1 资料来源资料来源于中华人民共和国卫生部网站[1],我国“2006年工业部门职业病发病及死亡情况”,剔除其中的第1、2、14号无意义指标,以及末尾的观测“其它”,剩余11个指标,观测值有缺失则用0补齐。
程序分别赋这些指标为x1-x11,其名称标签见附件1;余详见数据1。
数据1 2006年工业部门职业病发病及死亡情况相关数据name x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11煤炭4567 212 41 0 34 0 13 0 1 57 0石油 2 4 1 0 14 0 0 1 0 14 0电力110 1 1 0 28 1 0 1 1 16 1核工业0 0 0 0 0 0 0 0 0 3 0冶金494 65 40 2 159 0 0 3 5 24 11有色金属1193 120 38 4 190 11 0 7 2 38 1333 13 34 1 84 5 0 29 33 50 1电子7 0 14 3 120 0 0 51 13 3 0兵器7 0 4 0 22 0 0 0 113 6 0船舶18 0 1 0 1 1 0 0 0 2 0化工103 2 105 3 62 2 0 89 170 24 4医药 5 0 8 0 15 0 1 19 8 1 0铁道64 6 2 0 2 1 0 1 0 4 1交通61 1 6 0 14 3 0 6 6 8 0建材698 17 6 0 5 1 0 10 3 20 0建设126 1 23 8 1 3 0 5 2 3 1地质矿产253 3 1 0 4 0 0 1 0 0 0水利 2 17 0 0 0 0 0 0 0 0 0农业23 0 2 0 0 22 5 0 1 0 0森林工业 2 0 1 0 0 0 1 1 1 0 0轻工189 16 101 3 294 10 12 32 4 21 3纺织20 2 12 0 12 1 1 4 2 36 1航空航天 1 0 0 0 1 0 0 5 0 4 0商业11 0 2 0 0 3 1 2 0 2 0邮电 2 0 1 1 0 0 0 0 0 0 0石化工业9 1 5 0 6 0 0 1 1 2 0回收加工业0 0 2 2 0 0 0 0 0 0 01.2 方法将数据1倒入SAS9.1逻辑库sasuser后调用,程序默认对原始数据标准化后进行主成分分析。
主成分分析与因子分析(二):使用SAS实现主成分分析--PRINCOMP过程

主成分分析与因子分析(二):使用SAS实现主成分分析--PRINCOMP过程上一系列文章介绍了主成分分析概述。
今天,我们将介绍使用PRINCOMP过程进行主成分分析。
在SAS中,某种统计方法可能可以通过多个过程步实现。
这时候有必要了解过程步之间的区别。
比如,主成分分析就可以通过PROC FACTOR或PROCPRINCOMP实现。
PRINCOMP过程使用PROC PRINCOMP进行主成分分析时,其输入可以是原始数据集、协方差矩阵或相关矩阵等,其输出数据集包含特征根、特征向量以及标准化或未标准化的主成分得分。
此外,使用者还可以通过ODS图像选项输出陡坡图(Scree Plot)、成分特征图(Component Pattern Plot)等图形,这些图形都是进行主成分分析的有用工具。
过程步PROC PRINCOMP的一般形式为:其中:•PROC PRINCOMP语句中常见的选项如表12.1所示。
•BY语句指定分组变量。
PROC PRINCOMP根据BY语句中的变量对原数据进行分组分析。
若BY语句中的变量多于一个,那么仅最后一个变量起作用。
该语句要求原始数据已按照BY语句中的变量排序。
•VAR 语句指定数据集中用来进行主成分分析的变量,这些指定变量类型必须为数值型。
表12.1 PROC PRINCOMP常见的选项及含义例12.1:数据集sashelp.cars包含不同型号的汽车的一些参数,共有15个变量以及428条观测,具体变量的含义如表12.2所示。
现在要根据数据集sashelp.cars中的变量MPG_City、MPG_Highway、Weight、Wheelbase以及 Length,对其进行主成分分析。
表12.2 数据集sashelp.cars中的变量具体信息示例代码如下:程序的输出结果中包含了数据集的一些简单统计量,具体如图12.3所示。
图12.3 数据集sashelp.cars的简单统计量紧接着是相关矩阵以及该矩阵对应的特征值,如图12.4所示。
10_SAS中主成分分析

x4 0.96 0.74 0.38 1
x5 0.89 0.58 0.31 0.9 1
x6 0.79 0.58 0.3 0.78 0.79 1
x7 0.76 0.55 0.35 0.75 0.74 0.73 1
x8 0.26 0.19 0.58 0.25 0.25 0.18 0.24 1
x9 0.21 0.07 0.28 0.2 0.18 0.18 0.29 -0.04
78 80 75
10
11 12 13
139
140 161 158
31
29 47 49
68
64 78 78
74
74 84 83
25
26 27 28
157
151 144 141
48
36 36 30
80
74 68 67
88
80 76 76
14
15
140
137
33
31
67
66
77
73
29
30
139
148
32
-.543213 0.210246 0.724621 -.368294
主成分分析princomp过程的结果(第一、二主成 分为坐标的散布图):
书p282,表7.5,16项身体指标的相关阵
_name_ x1 x2 x3 x4 x5 x6 x7 x8
x1 1
x2 0.79 1
x3 0.36 0.31 1
1
-0.34
1
-0.16
0.23 1
-0.05
0.5 0.24 1
0.23
0.31 0.1 0.62 1
0.21
0.15 0.31 0.17 0.26 1
主成分分析SAS实验

主成分分析和因子分析也可以用下列各种统计 分析的中间结果矩阵进行分析:
CORR 相关系数矩阵 SSCP 平方和、积和矩阵 CSSCP 离均差平方和、积和矩阵 COV 方差、协方差矩阵 UCOV 为平方和、积和矩阵/n UCORR 为 XY / X 2Y 2 矩阵 FACTOR 因子矩阵
eigenvalue )>70% 碎石图(Scree plot) 能有恰当的专业解释
练习1:主成分分析(变量单位不同)
20例肝病患者4项肝功能指标: X1:转氨酶(SGPT); X2:肝大指数(F); X3:硫酸锌浊度(ZnT); X4:甲胎球蛋白(AFP)
试作主成分分析
程序: \unit4\princomp1.sas 数据: \unit4\princomp1.xls
练习2:主成分分析(变量单位相同)
我国27个少数民族体型资料
X1:头长; X2: 头宽;
X3: 额最小宽;
X4: 面宽;
X5: 下额角间宽; X6: 容貌面高;
X7: 形态面高; X8: 鼻高;
X9: 鼻宽;
X10: 口裂宽; X11:身长;
X12: 肩宽;
X13: 胸围; X14:骨盆宽; X15:全头高;
主成分分析
公共卫生学院信息数据处理教学实验室
一、主成分分析
实际工作中原始数据的变量之间常有一定 的相关性。人们希望找到较少的几个互不相关 的综合指标,尽可能多的反映原来的信息。
主成分分析就是由原变量X1~Xp中线性组 合出m个(m≤p)互不相关、且尽量少丢失信息的 新变量(主成分),并能给各主成分所包含的信 息以恰当的专业解释。
需要在数据步中指定: _TYPE_= ‘CORR';
SAS主成分分析

S A S主成分分析(总19页) -CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除SAS主成分分析分类:数据之美 2013-07-28 20:18 2343人阅读评论(0) 收藏举报目录()[-]1.主成分分析流程2.SAS主成分分析示例3.SAS主成分分析输出结果详解4.特征值和特征向量隐藏的秘密5.总结6.参考文献同事讲主成分分析,举了这么个例子:就像你选女人,有身材、相貌两个指标,如果身材、相貌都很突出,那当然很好选择;但如果两个女人,一个身材突出,一个相貌出众,看着都很喜欢,那可如何是好!这个时候通过主成分分析,汇总出一个指标,这个指标可以一定程度上代替原来的身材、相貌,这时就可以排序做出选择了。
这例子当然有很多缺陷,但至少指出了主成分分析的目的之一:减少决策变量数,也就是降维。
主成分分析的另一个目的是防范多重共线性。
实际问题往往涉及很多变量,但某些变量之间会有一定的相关性,我们希望构造较少的几个互不相关的新指标来代替原始变量,去除多重共线性,减少所需分析的变量,同时尽可能减少这一过程的信息损失。
主成分分析正是基于这样的目的而产生的有效方法。
主成分分析流程主成分分析包含以下流程:1、原始数据标准化。
2、计算标准化变量间的相关系数矩阵。
3、计算相关系数矩阵的特征值和特征向量。
4、计算主成分变量值。
5、统计结果分析,提取所需的主成分。
SAS主成分分析示例我们从实战入手,先来个简单的例子,完整体验使用SAS进行主成分分析的过程。
准备好图1所示的数据集,该数据集包含5个变量和22个观测。
其中变量num用于标识每条观测。
图1可以直接复制下面的程序完成输入:data;input num var1 var2 var3 var4;cards;1 2123 904 1256789101112131415 9016171819202122;run;我们的目的是,化简var1-var4四个变量,找出可以替代这四个变量的若干个彼此独立的新变量,也就是找出主成分。
主成分SAS程序

主成分的求解方法1求相关矩阵2、求特征值与特征向量3、确定主成分个数4、计算主成分得分。
例:求相关data p163;input x$ x1-x8;datalines;北京 1394.89 2505.00 519.01 8144 373.90 117.30 112.60 843.43 天津 920.11 2720.00 345.46 6501 342.80 115.20 110.60 582.51 河北 2849.52 1258.00 704.87 4839 2033.30 115.20 115.80 1234.85 山西 1092.48 1250.00 290.90 4721 717.30 116.90 115.60 697.25 内蒙 832.88 1387.00 250.23 4134 781.70 117.50 116.80 419.39 辽宁 2793.37 2397.00 387.99 4911 1371.10 116.10 114.00 1840.55 吉林 1129.20 1872.00 320.45 4430 497.40 115.20 114.20 762.47 黑龙江 2014.53 2334.00 435.73 4145 824.80 116.10 114.30 1240.37 上海 2462.57 5343.00 996.48 9279 207.40 118.70 113.00 1642.95 江苏 5155.25 1926.00 1434.95 5943 1025.50 115.80 114.30 2026.64 浙江 3524.79 2249.00 1006.39 6619 754.40 116.60 113.50 916.59 安徽 2003.58 1254.00 474.00 4609 908.30 114.80 112.70 824.14 福建 2160.52 2320.00 553.97 5857 609.30 115.20 114.40 433.67 江西 1205.11 1182.00 282.84 4211 411.70 116.90 115.90 571.84 山东 5002.34 1527.00 1229.55 5145 1196.60 117.60 114.20 2207.69 河南 3002.74 1034.00 670.35 4344 1574.40 116.50 114.90 1367.92 湖北 2391.42 1527.00 571.68 4685 849.00 120.00 116.60 1220.72 湖南 2195.70 1408.00 422.61 4797 1011.80 119.00 115.50 843.83 广东 5381.72 2699.00 1639.83 8250 656.50 114.00 111.60 1396.35 广西 1606.15 1314.00 382.59 5105 556.00 118.40 116.40 554.97 海南 364.17 1814.00 198.35 5340 232.10 113.50 111.30 64.33 四川 3534.00 1261.00 822.54 4645 902.30 118.50 117.00 1431.81 贵州 630.07 942.00 150.84 4475 301.10 121.40 117.20 324.72 云南 1206.68 1261.00 334.00 5149 310.40 121.30 118.10 716.65 西藏 55.98 1110.00 17.87 7382 4.20 117.30 114.90 5.57陕西 1000.03 1208.00 300.27 4396 500.90 119.00 117.00 600.98 甘肃 553.35 1007.00 114.81 5493 507.00 119.80 116.50 468.79 青海 165.31 1445.00 47.76 5753 61.60 118.00 116.30 105.80 宁夏 169.75 1355.00 61.98 5079 121.80 117.10 115.30 114.40 新疆 834.57 1469.00 376.95 5348 339.00 119.70 116.70 428.76 ;proc corr data=p163;var x1-x8;run;*将数据标准化,并存入 p1631表中proc standard data=p163 mean=0std=1out=p1631;var x1-x8;run;proc print;run;*计算主成分;proc princomp data=p163;var x1-x8;run;*计算三个主成分并保留结果存入score,显示scoreproc princomp data=p163 out=score n=3;var x1-x8;run;proc print data=score;run;*计算各省份第一主成分;data pp163;set p1631;p1=0.456650*x1+x2*0.313091+x3*0.470475+x4*0.240591+x5*0.250709+x6*(-.262440)+x7*(-.319734)+ x8*0.424564; run;proc print data=pp163;var x p1;run;*以prin2为纵轴,print1为横轴作散点图Proc plot data=score;Plot prin2*prin1=x;Run;例11、用程序求样本相关矩阵的特征值和特征向量。
SAS主成分分析

SAS 大作业主成分分析法理学院07统计学01班孙禹40708030104SAS 主成分分析利用SAS 程序我们可以进行主成分分析以及因子分析,因此首先要明白主成分分析与因子分析的概念与步骤,以方便进行后续工作1. 主成分分析的基本思想主成分分析是数学上对数据降维德一种方法。
其基本思想是设法将原来众多的具有一定相关性的指标,重新组合成一组新的互不相关的综合指标来代替原来指标。
这种线性组合有很多种,选取时,在所有的线性组合中所选取的F1应该是方差最大的,故称F1为第一主成分。
如果第一主成分不足以代表原来P 个指标的信息,再选取F2即第二个线性组合,依次类推。
一般地说,利用主成分分析得到的主成分与原始变量之间有如下的关系:(1)、每个主成分都是各原始量的线性组合。
(2)、主成分的数目大大少于原始变量的数目。
(3)、主成分保留了原始变量绝大多数信息。
(4)、各主成分之间互不相关2主成分分析的基本理论假设我们所讨论的实际问题中,有p 个指标,我们把这p 个指标看作p 维随机变量,记为X=(X 1,X 2,…,X p )T ,主成分分析就是要把这p 个指标的问题,转变为讨论p 个指标的线性组合的问题,而这些新的指标F 1,F 2,…,F k (k ≤p ),按照保留主要信息量的原则充分反映原指标的信息,并且相互独立。
3主成分分析步骤根据研究问题选取初始分析变量;根据初始变量特性判断由协方差阵求主成分还是由相关阵求主成分; 求协方差阵或相关阵的特征根与特征向量;11112121212122221122p p p p p p p pp pY u X u X u X Y u X u X u X Y u X u X u X =+++=+++=+++判断是否存在明显的多重共线性,若存在,则回到第一步;得到主成分表达式并确定主成分个数,选取主成分;结合主成分对研究问题进行分析并深入研究。
4主成分的上机实验例:北京1961~1986年冬季的气温资料如表,变量个数p=3,对这些资料进行主成分分析。
11-使用SAS进行主成分分析

例如:评价儿童的生长发育情况,某研究者收集了12 个指标,如身高、体重、胸围、肩宽、肺活量等资料。应 如何利用这12个指标进行评价?
这些指标个数很多,且指标间往往是彼此相关的。 如仅选用其中一个指标来评价,则:损失信息 如分别应用每个指标,则:评价是孤立的,非综合性
主成分分析的一般步骤
1、 收集数据并建立数据库
2、 对变量进行标准化处理
yi
xi xi si
,i1,2,p
3、 求主成分:
(1) 求相关矩阵R
r11
R
r1 p
(2) 求R的特征根:
rp1 rpp
λ1≥λ2≥….≥λP
(3) 求R的关于特征根λi的满足正规条件的特征 向量 ai, (ai1,ai2 ,…,aip ) i=1,2,…P
由表达式z2=-0.707lyl十0.707ly 2,可见y1、y2的系数绝对值相 等,符号相反,前者为负后者为正,说明前音(体重)愈大,第二主 成分的取值愈小,后者(身高)愈大,第二主成分的取值也愈大,即 矮胖者第二主成分取值大,瘦高者第二主成分取值小,说朗第二主 成分描述的是幼儿的体型。
(四)、计算主成分得分
主成分分析的好坏关键在于给综合指标所蕴藏的信 息以恰当的解释。
三、 主成分分析的基本原理:
主成分分析是对多个指标的观察数据 降维压缩,对指标间的内部从属性作客观 评价的多元分析方法。
例:对n个儿童测量其身高(x1)、体重(x2)两个指标, 显然这两个指标是高度相关的,若以x1为横,以x2 为纵轴,用n个对象的数据作散点图。
i p
i
SAS系统和数据分析主成分分析

第三十五课 主成分分析一、 主成分的导出主成分分析(principal component analysis )是1901年提出,再由Hotelling (1933)加以发展的一种统计方法。
其主要目的是在于将许多变量减少,并使其改变为少数几个相互独立的线性组合形成的变量(主成分),而在经由线性组合而得的成分之方差会变为最大,使得原始p 维资料在这些成分上显示最大的个别差异来。
用一句话来说,主成分分析是将多个变量化为少数综合变量的一种多元统计方法。
设有n 组样品,每组样品有p 个变量,记n 组样品数据见表35.1。
表35.1 p 个变量的n 组样品数据样品号 变量1 2 … n 1X 2Xp X11x21x …1n x 12x22x …2n x 错误!未定义书签。
错误!未定义书签。
错误!未定义书签。
p x 1 错误!未定义书签。
…错误!未定义书签。
如果p 个变量是相互独立的,则可以将问题化为单变量逐个处理,这是比较简单的。
但是对大量的实际问题中提出来的数据,各变量之间往往存在着不同程度的相关关系,这时要搞清这些数据之间的关系,就必须在高维空间中加以研究,这显然是比较麻烦的,为了克服这一困难,一个很自然的想法就是采取降维的方法,也就是利用全部p 个变量来重新构造q 个新的综合变量(p q ≤),并使得这些较少的变量既能尽可能多地反映原来p 个变量的统计特性,并且它们之间又是相互独立的。
假定=x 1(x ,2x ,…,)'p x 是一组随机变量,并且μ=Ex ,协方差阵V x D =)(错误!未定义书签。
考虑1x ,2x ,…,p x 的一个线性组合(或称线性变换):x a x a x a x a Z p p '=+++= 2211(35.1)这里),,,(21p a a a a ='。
对于综合变量Z ,我们要选择一组系数),,,(21p a a a a ='使得Z 的方差最大;由于Va a x a Var '=')(,对任意给定的常数c ,Va a c x a c Var '='2)(,如果对a 不加以限制,上述问题就变得毫无意义。
SAS软件与统计应用教程ch6――主成分分析与因子分析PPT课件

求出协方差矩阵Σ的特征值12…p>0及相应的正
交化单位特征向量:
a11
a12
a1p
a1
a21,
a2
a22, ...,ap
a2p
ap1
ap2
app
则X的第i个主成分为Fi = ai'X i = 1,2,…,p。
SAS软件与统计应用教程
STAT
(3) 选择主成分
图中看出,上海在第二主成分PCR2的得分远远高于 其他省市,而在第一主成分PCR1的得分则处于中间。 广东、江苏、山东和浙江则在第1主成分的得分上位于 前列。
SAS软件与统计应用教程
பைடு நூலகம்
STAT
6) 回到INSIGHT的数据窗口,可以看到前两个主成 分的得分情况(如图6-8左)。
单击数据窗口左上角的箭头,在弹出的菜单中选择 “Sort(排序)”选项,在打开的对话框中选定排序变 量PCR1,并单击“Asc/Des”按钮将其设为降序(Des), 如图6-8所示。
(5) 标准化 实际应用时,指标的量纲往往不同,所以在主成分计
算之前应先消除量纲的影响。消除数据的量纲有很多方 法,常用方法是将原始数据标准化,即做如下数据变换:
其中
xi*j,xijs jxj
i1,2,..n;.j,1,2,..p.,
,j = 1,2,…,p。
标准化x j后 的n1 i数n1 x据ij 阵s2j记为n1X1*,in1其(xi中j 每xj)个2 列向量(标准化变
对于第一主成分而言,除了x2(人均GDP)外,各变 量所占比重均在0.3左右以上,因此第一主成分(Prin1)主
要由x1、x3~x9八个变量解释;而第二主成分则主要由 x2这一个变量解释。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
主成分的求解方法
1求相关矩阵
2、求特征值与特征向量
3、确定主成分个数
4、计算主成分得分。
data p108;
input x$ x1-x8;
datalines;
北京1394.89 2505.00 519.01 8144 373.90 117.30 112.60 843.43 天津920.11 2720.00 345.46 6501 342.80 115.20 110.60 582.51 河北2849.52 1258.00 704.87 4839 2033.30 115.20 115.80 1234.85 山西1092.48 1250.00 290.90 4721 717.30 116.90 115.60 697.25 内蒙832.88 1387.00 250.23 4134 781.70 117.50 116.80 419.39 辽宁2793.37 2397.00 387.99 4911 1371.10 116.10 114.00 1840.55 吉林1129.20 1872.00 320.45 4430 497.40 115.20 114.20 762.47 黑龙江2014.53 2334.00 435.73 4145 824.80 116.10 114.30 1240.37 上海2462.57 5343.00 996.48 9279 207.40 118.70 113.00 1642.95 江苏5155.25 1926.00 1434.95 5943 1025.50 115.80 114.30 2026.64 浙江3524.79 2249.00 1006.39 6619 754.40 116.60 113.50 916.59 安徽2003.58 1254.00 474.00 4609 908.30 114.80 112.70 824.14 福建2160.52 2320.00 553.97 5857 609.30 115.20 114.40 433.67 江西1205.11 1182.00 282.84 4211 411.70 116.90 115.90 571.84 山东5002.34 1527.00 1229.55 5145 1196.60 117.60 114.20 2207.69 河南3002.74 1034.00 670.35 4344 1574.40 116.50 114.90 1367.92 湖北2391.42 1527.00 571.68 4685 849.00 120.00 116.60 1220.72 湖南2195.70 1408.00 422.61 4797 1011.80 119.00 115.50 843.83 广东5381.72 2699.00 1639.83 8250 656.50 114.00 111.60 1396.35 广西1606.15 1314.00 382.59 5105 556.00 118.40 116.40 554.97 海南364.17 1814.00 198.35 5340 232.10 113.50 111.30 64.33 四川3534.00 1261.00 822.54 4645 902.30 118.50 117.00 1431.81 贵州630.07 942.00 150.84 4475 301.10 121.40 117.20 324.72 云南1206.68 1261.00 334.00 5149 310.40 121.30 118.10 716.65 西藏55.98 1110.00 17.87 7382 4.20 117.30 114.90 5.57 陕西1000.03 1208.00 300.27 4396 500.90 119.00 117.00 600.98 甘肃553.35 1007.00 114.81 5493 507.00 119.80 116.50 468.79 青海165.31 1445.00 47.76 5753 61.60 118.00 116.30 105.80
宁夏169.75 1355.00 61.98 5079 121.80 117.10 115.30 114.40 新疆834.57 1469.00 376.95 5348 339.00 119.70 116.70 428.76 ;
proc princomp;
var x1-x8;
run;
proc princomp out=score n=3;
var x1-x8;
run;
proc print data=score;
run;
Proc plot data=score;
Plot prin2*prin1=x;
Run;
例:进行主成分分析
1、用程序求样本相关矩阵的特征值和特征向量。
2、求两个主成分的累计贡献率,写出贡献率计算表达式。
3、写出两个主成分的模型表达式。
4、计算主成分得分,并按主成分得分名次
例:对下表的指标进行主成分分析,
5、用程序求样本相关矩阵的特征值和特征向量。
6、求两个主成分的累计贡献率,写出贡献率计算表达式。
7、写出两个主成分的模型表达式。
8、计算主成分得分,并按主成分得分名次
9、按两个主成分得分作散点图
10、对主成分得分聚类
例:
学生身体各指标的主成分分析.
随机抽取30名某年级中学生,测量其身高(X1)、体重(X2)、胸围(X3)和坐高(X4),数据见
试对中学生身体指标数据做主成分分析.。
