职高一年级数学题库
中职数学高一数学试卷

中职数学高一数学试卷一、选择题(每题3分,共30分)1. 设集合A = {1, 2, 3},B={2, 3, 4},则A∩ B = ( )A. {1, 2, 3, 4}B. {2, 3}C. {1}D. {4}2. 不等式x + 3>0的解集是( )A. {xx > - 3}B. {xx < - 3}C. {xx≥ - 3}D. {xx≤ - 3}3. 函数y = 2x + 1在x = 1处的函数值为( )A. 3B. 2C. 1D. 04. 下列函数中,是奇函数的是( )A. y = x^2B. y = 2x+1C. y=(1)/(x)D. y = √(x)5. 若log_a2 = m,log_a3=n,则log_a6 = ( )A. m + nB. m - nC. mnD. (m)/(n)6. 已知向量→a=(1,2),→b=(3, - 1),则→a+→b=( )A. (4,1)B. ( - 2,3)C. (2, - 3)D. ( - 4, - 1)7. 在等差数列{a_n}中,a_1=1,d = 2,则a_3=( )A. 1B. 3C. 5D. 78. 直线y = 2x - 1的斜率是( )A. 2B. -1C. 1D. -29. 二次函数y=x^2-2x - 3的顶点坐标是( )A. (1,-4)B. ( - 1, - 4)C. (1,4)D. ( - 1,4)10. 若sinα=(1)/(2),且α∈(0,(π)/(2)),则cosα = ( )A. (√(3))/(2)B. -(√(3))/(2)C. (1)/(2)D. -(1)/(2)二、填空题(每题3分,共15分)1. 集合{x - 2用区间表示为______。
2. 函数y=√(x - 1)的定义域是______。
3. 等比数列{a_n}中,a_1 = 2,q = 3,则a_3=______。
4. 直线3x - 2y+1 = 0的截距式方程为______。
职高数学一年级上期期末测试题《一》

职高一年级上期期末测试题 (分数:150分 时间:120分钟)班级__________姓名__________分数__________一、选择题(每题4分)1、已知集合()2,2-=A ,集合()4,0=B ,则=B A I ( )。
A .()4,2- B. ()0,2- C. ()4,2 D. ()2,02.集合A ={x|0≤x<3且x ∈Z}的真子集的个数是( )A . 5B . 6C .7D .83.满足{1,2}{}1,2,3,4,5A ⊆⊆条件的集合A 的个数为( )B.6C.8D.104.下列六个关系式中正确的有( )①{}{}a b b a ,,=; ②{}{}a b b a ,,⊆; ③{}{}a b b a ,,⊇; ④{}0φ=; ⑤{}0φ≠⊂;⑥0{}0∈.A.6个B.5个C.4个D.3个及3个以下5、不等式732>-x 的解集为( )。
A .5>x B.5<x C.2>x D.2<x6、不等式02142≤-+x x 的解集为( )。
A .(][)+∞-∞-,37,Y B. []3,7- C. (][)+∞-∞-,73,Y D. []7,3-7、不等式123>-x 的解集为( )。
A .()+∞⎪⎭⎫⎝⎛-∞-,131,Y B. ⎪⎭⎫ ⎝⎛-1,31 C. ()+∞⎪⎭⎫ ⎝⎛∞-,131,Y D. ⎪⎭⎫⎝⎛1,318、不等式组⎩⎨⎧<->+0302x x 的解集为( ).A .()3,2- B. ()2,3- C. φ D. R9、要使函数42-=x y 有意义,则x 的取值范围是( )。
A .[)+∞,2 B.(][)+∞-∞-,22,Y C.[]2,2- D. R10、下列各点中,在函数13-=x y 的图像上的点是( )。
A .(1,2) B.(3,4) C.(0,1) D.(5,6)11、函数321-=x y 的定义域为( )。
中职高一年级数学期末试卷

13、若函数 且 ,则实数k=
14、若 是奇函数, ,则
15、若 ,则 =
3、解答题(10+10+10+10=10)
16、解下列不等式,解集用区间表示( )
① ②
17、求定义域,解集用区间表示( )
求① ②
18、已知函数
①求函数的定义域:
②求 的证明函数 在 是增函数
A、0 B、1 C、2 D、3
2、已知集合 ,那么集合 的真子集的个数为()
A、1B、2C、3D、4
3、方程组 的解集是( ).
A、 B、 C、 D、
4、已知U= ,A= ,B= ,C= 则(A B) =( )
A、 B、 C、 D、
5、不等式 的解集为()
A、 B、 C、 D、
6、若函数 在 上为减函数,则有 ( )
A、 B、 C、 D、
7、下列函数中,在 内是增函数的是( )
A、 B、 C、 D、
8、下列函数为偶函数的是()
A、 B、 C、 D、
9、已知函数 则 ()
A、1B、3C、-1D、1或3
10、点(2,3)关于 轴的对称点是()
A、 B、 C、 D、
2、填空题( )
11、已知集合 ,用区间表示为
12、设 则 __________
湖北前程交通职业技术学校考试试卷
A 卷
科目:一年级数学 考试时间:19-20上学期期末
题号
一
二
三
四
五
六
成绩
得分
阅卷老师
1、单项选择题(将下列各题唯一正确答案的编号填入括弧内,4’×10=40分)
1、下列三个说法中正确的个数是()
职高一年级数学题库

职高一年级《数学》(基础模块)上册试题题库第一章:集合一、填空题(每空2分)1、元素3-与集合N 之间的关系可以表示为 。
2、自然数集N 与整数集Z 之间的关系可以表示为 。
3、用列举法表示小于5 的自然数组成的集合: 。
4、用列举法表示方程243=-x 的解集 。
5、用描述法表示不等式062<-x 的解集 。
6、集合{}b a N ,=子集有 个,真子集有 个。
7、已知集合{}4,3,21,=A ,集合{},7,5,3,1=B ,则=B A ,=B A 。
8、已知集合{}5,3,1=A ,集合{}6,4,2=B ,则=B A ,=B A 。
9、已知集合{}22<<-=x x A ,集合{}40<<=x x B ,则=B A .10、已知全集{}6,5,4,3,2,1=U ,集合{}5,2,1=A ,则=A C U 。
二、选择题(每题3分)1、设{}a M =,则下列写法正确的是( )。
A .M a = B.M a ∈ C. M a ⊆ D.M a ∉2、设全集为R ,集合(]5,1-=A ,则 =A C U ( )A .(]1,-∞- B.()+∞,5 C.()()+∞-∞-,51, D. (]()+∞-∞-,51,3、已知[)4,1-=A ,集合(]5,0=B ,则=B A ( )。
A .[]5,1- B.()4,0 C.[]4,0 D. ()5,1-4、已知{}2<=x x A ,则下列写法正确的是( )。
A .A ⊆0 B.{}A ∈0 C.A ∈φ D.{}A ⊆05、设全集{}6,5,4,3,2,1,0=U ,集合{}6,5,4,3=A ,则=A U [( )。
A .{}6,2,1,0 B.φ C. {},5,4,3 D. {}2,1,06、已知集合{}3,2,1=A ,集合{}7,5,3,1=B ,则=B A ( )。
A .{}5,3,1 B.{},3,2,1 C.{}3,1 D. φ7、已知集合{}20<<=x x A ,集合{}31≤<=x x B ,则=B A ( )。
职高一年级数学测试题

职高一年级数学期中测试题总分:150分,考试时间:120分钟班级 _____ 姓名 _______ 得分 _______一、 单项选择题(共54分,共18小题,每小题3分,在每小题给出的四个选项中,只有一项是最⒈下列各式中,数值相等的是( )A 、 —32和—23 B 、 —32和(—32) C 、 —23 和(—2)3 D 、(—3×2)2和—3×22 ⒉ 任何有理数的绝对值都是()A 、负数B 、 正数C 、非负数D 、非正数 ⒊ 已知a= —5,a =b ,那么b 的值等于( )A 、 +5B 、 —5C 、±5D 、 0⒋ 若ax —b=0(a ≠0),且 ab 互为相反数,那么 x 的值为( ) A 、 ±1 B 、 —1 C 、 1 D 、 任意实数 ⒌ 下列算式运算正确的是( )A 、 (—2)+(—2)=0B 、434222)(⨯-=-2C 、( —2)1—22= + 3 D 、 —(—43)+(—437)= —7 ⒍ 如果a >b >0, c ≤0,那么下列运算一定成立的是( )A 、 ac <bcB 、 ac >bcC 、 bc >abD 、 b+c >a+b⒎ 如果x= (—2)×3,那么x 的倒数是( )A 、32 B 、 61 C 、6 D 、—61⒏下列选项能组成集合的是( )A 、明星B 、英文26个字母C 、非常接近0的数D 、勇敢的人⒐ 下列各结论中,正确的是( )。
A .{}0是空集 B .{}1,2,3¹{}3,2,1 C .{}R p Î D .R p Î⒑已知P :|x |=x ,q :0x ≥,则p 是q 的( )条件.A .充分不必要B .必要不充分C .充要D .既不充分又不必要⒒ 已知 3是关于 x 的方程 2x —a=1的解,则a 的值是( )A 、 —5B 、 5C 、 7D 、 2 ⒓ 方程 3x —4y=0的解()A 、 只有一个B 、 只有两个C 、有无数个D 、无解⒔ 不等式x 32<1 的非负整数解有() A 、 无数个 B 、 只有一个 C 、 只有两个 D 、 一个都没有 ⒕已知{}21,2,x x Î,则x 的取值为( )。
中职一年级数学期末考试卷

中职一年级数学期末考试卷考试时间:120分钟一、选择题(每题2分,共40分)1. 下列哪个是一个质数?A. 12B. 15C. 17D. 202. 以下哪个等式是恒等式?A. 3x + 5 = 7x - 9B. 2(x + 3) = 2x + 6C. 4x + 3 = 4(x + 3)D. 5x - 3 = 2x + 73. 如果一个角的补角是60度,那么这个角是多少度?A. 30度B. 60度C. 90度D. 120度4. 下面哪个数比20%的60大?A. 3B. 9C. 12D. 155. 如果一辆汽车以每小时60公里的速度行驶,那么行驶300公里需要多长时间?A. 3小时B. 4小时C. 5小时D. 6小时二、填空题(每空2分,共20分)6. 12的约数有__________。
7. 一个角的补角是90度,这个角是__________度。
8. 一个数增加50%后的数是原数的__________倍。
9. 如把一个圆的半径缩小到原来的一半,则其面积为原来的__________。
三、计算题(共40分)10. 计算:\( 5 \times (8 - 3) + 2^2 \)11. 计算:\( \frac{3}{5} + \frac{7}{10} - \frac{1}{4} \)12. 已知一个三角形的底为6厘米,高为8厘米,求其面积。
四、解答题(每题10分,共40分)13. 一个数的平方减去20的两倍等于10,求这个数。
14. 请简要说明什么是平行四边形,同理解释什么是直角三角形。
15. 解方程:\( 2x - 1 = 3x + 7 \)五、应用题(每题10分,共20分)16. 一共有120个学生参加了学校篮球比赛,其中女生占三分之一,请问有多少男生参加了比赛?17. 树上有6只猴子,它们中的4只猴子从树上摘了一部分香蕉,然后每只猴子取了相等的部分,剩下2根香蕉。
这些猴子中的每只猴子取了多少香蕉?祝同学们取得优异成绩!。
中职中专职一年级数学期末考卷

中职中专职一年级数学期末考卷一、选择题(每题5分,共25分)1. 下列哪个数是实数?A. √1B. 3.14C. log2(3)D. 4/02. 已知集合A={1, 2, 3, 4, 5},集合B={2, 4, 6, 8},则A∩B 的结果是?A. {1, 3, 5}B. {2, 4}C. {1, 2, 3, 4, 5, 6, 8}D. 空集3. 若a=3,b=2,则a+b的值是?A. 5B. 5C. 6D. 64. 已知函数f(x)=2x+1,则f(3)的值是?A. 6B. 7C. 8D. 95. 下列哪个图形是平行四边形?A. 矩形B. 正方形C. 梯形D. 圆二、填空题(每题5分,共25分)1. 已知等差数列{an}的公差为2,首项为1,则第10项的值为______。
2. 若两个角的和为90°,其中一个角为30°,则另一个角的度数为______。
3. 已知三角形ABC,AB=5,BC=8,AC=10,则三角形ABC的周长为______。
4. 一辆汽车以60km/h的速度行驶,行驶了3小时,则汽车行驶的路程为______。
5. 在平面直角坐标系中,点A(2, 3)关于原点的对称点坐标为______。
三、解答题(每题10分,共50分)1. 解方程:2x 5 = 32. 已知函数f(x) = x² 2x + 1,求f(x)在x=2时的函数值。
3. 计算下列各式的值:(1)(3²)³(2)4² × 2³(3)9 ÷ 3 + 2²4. 在直角三角形ABC中,∠C=90°,AB=10,BC=6,求AC的长度。
5. 已知数列{an}的通项公式为an = 2n + 1,求前5项的和。
四、应用题(每题20分,共40分)1. 某商店举行打折活动,原价为200元的商品,打8折后售价为多少元?2. 一辆汽车行驶了200公里,前一半路程的平均速度为60km/h,后一半路程的平均速度为80km/h,求全程的平均速度。
(完整)职高一年级数学题库

职高一年级《数学》(基础模块)上册试题题库(2010—2011学年上学期适用)第一章:集合一、填空题(每空2分)1、元素-3与集合N之间的关系可以表示为。
2、自然数集N与整数集Z之间的关系可以表示为。
3、用列举法表示小于5的自然数组成的集合:。
4、用列举法表示方程3x-4=2的解集。
5、用描述法表示不等式2x-6<0的解集。
6、集合N=%力}子集有个,真子集有个。
7、已知集合A=%,2,3,4},集合B=&,3,5,7,},则A A B=,A U B=8、已知集合A=&,3,5},集合B=b,4,6h则A A B=,A U B=9、已知集合A=(|-2<x<21集合B=,0<x<4]则A A B=10、已知全集U=&23,4,5,6],集合A=&,2,5],则CA=。
U二、选择题(每题3分)1、设M=匕},则下列写法正确的是()。
A.a=MB.a e MC.a三MD.a e M2、设全集为R,集合A=(-1,5],则CA=()UA.J8,-11B.(5,+^)C.(-^,-1)U(5,+8)D.(-8,-1]U(5,+8)3、已知A=L1,4),集合B=(0,5],则A A B=()。
A.L1,5]B.(0,4)C.b,4]D.(-1,5)4、已知A=€|x<2],则下列写法正确的是()。
A.0c AB.b}e AC.@e AD.卜兄A5、设全集U=卜,1,2,3,4,5,6},集合A=6,4,5,6],则[A=()。
UA .b,1,2,6}B.0C.6,4,5,}D.hH6、已知集合A =5,2,3},集合B =&,3,5,7},则A A B =()。
A .{1,3,5}B.{1,2,3,}C.&,3}D.07、已知集合A =(0<x <2},集合B =(1<x <3},则A U B =(8、已知集合A =&,2,3},集合B =1456,7},则A U B =()。
中职一年级数学试题

3、 ( )
A第一象限角 B第二象限角
C第三象限角 D第四象限角
4、已知角 的终边经过点( ),则tan 的值是()
A. B. C. D
5、设 <0,tan >0,则角 是( )
A第一象限角 B第二象限角
C第三象限角 D第四象限角
6、 为第三象限角, ()
A B C D
7、化简: 的结果为()
4、已知角 的终边经过点P(- ,值域是______
三解答题
1、计算(10分)
(1)
(2)
2、已知角 的终边在直线 上,求 的三个三角函数值(10分)
3、已知一段公路的弯道长度是 转过的圆心角是60°,求该弯道的半径(10分
4、已知 , ∈[0, ),求角 (10分)
(B卷)5、已知 ,且 是第三象限角,求其他三角函数(10分)
(A卷)5、已知 求下列各式的值:(10分)
(1)
(2)
A.sin B C D
8、已知 ,则 _0()
A < B > C = D无法判断
9、已知 ()
A B﹣ C± D
10、函数 的最大值是()
A.-2 B.-1 C.0 D.1
二填空题(每空2分)
1、 ________
2、与 终边相同的角的集合是________
3、75°=________弧度, ________度;
平 凉 机 电 工 程 学 校
二○一三——二○一四学年第二学期期中考试
一年级各专业《数学》试题(卷)
题号
一
二
三
四
五
总分
命题人
审题人
得分
米立春
职高数学一年级上期期末测试题《一》

职高数学一年级上期期末测试题《一》(分数:150分 时间:120分钟)班级__________姓名__________分数__________一、选择题(每题4分)1、已知集合()2,2-=A ,集合()4,0=B ,则=B A ( )。
A .()4,2- B. ()0,2- C. ()4,2 D. ()2,02.集合A ={x|0≤x<3且x ∈Z}的真子集的个数是( )A . 5B . 6C .7D .83.满足{1,2}{}1,2,3,4,5A ⊆⊆条件的集合A 的个数为( )A.4B.6C.8D.104.下列六个关系式中正确的有( )①{}{}a b b a ,,=; ②{}{}a b b a ,,⊆; ③{}{}a b b a ,,⊇; ④{}0φ=; ⑤{}0φ≠⊂;⑥0{}0∈.A.6个B.5个C.4个D.3个及3个以下5、不等式732>-x 的解集为( )。
A .5>x B.5<x C.2>x D.2<x6、不等式02142≤-+x x 的解集为( )。
A .(][)+∞-∞-,37, B. []3,7- C. (][)+∞-∞-,73, D. []7,3-7、不等式123>-x 的解集为( )。
A .()+∞⎪⎭⎫ ⎝⎛-∞-,131, B. ⎪⎭⎫ ⎝⎛-1,31C. ()+∞⎪⎭⎫⎝⎛∞-,131, D. ⎪⎭⎫ ⎝⎛1,318、不等式组⎩⎨⎧<->+0302x x 的解集为( ).A .()3,2- B. ()2,3- C. φ D. R9、要使函数42-=x y 有意义,则x 的取值范围是( )。
A .[)+∞,2 B.(][)+∞-∞-,22, C.[]2,2- D. R10、下列各点中,在函数13-=x y 的图像上的点是( )。
A .(1,2) B.(3,4) C.(0,1) D.(5,6)11、函数321-=x y 的定义域为( )。
职业高中高一数学题

高一年级 数学试题一、选择题(每空4分,共40分)1、等差数列-5,0,5,10,15的公差是( ) A.-5 B.5 C.0 D.102、数列{}a n满足an=4a n 1-+3,且a 1=0,则此数列的第5项是( )。
A.15B.255C.16D.633、56是数列1×2,2×3,3×4,4×5,…的第( )项。
A.5 B.6 C.7 D.84、数列{}a n为等差数列的充要条件是( )A.a n +常数=+a n 1B.常数=-+a a n n 1C.正数=-+a a n n 1D.负数=-+a a n n 1 5、已知等差数列{}a n的前n 项和为s n,且s 5=25,d=2,则=a 1( )。
A.5 B.3 C.-1 D.16、设a 1,a 2,a 3,a 4成等比数列,其公比为2,则a a a a 432122++的值为( )。
A. 41B.21C.81D.17、等比数列{}a n中,92=a,2435=a ,则=a a 61( )。
A.81 B.2120 C.2168 D.2187 8、化简++DM +=( ) A. B.CM C. D.9、下列四式不能化简为的是( )。
A.(+)+B.(+)+(+CM )C.+-BMD.-+10、-7与方向( )。
A.相同B.相反C.垂直D.以上都不对 二、填空题(每空3分,共30分)1、已知数列{}a n的通项公式=a n ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-)(12(1为正偶数为正奇数n n n n ,则=a 3________,=a5________。
2、两个数1与5的等差中项为_________。
3、在等差数列{}a n中,3773=+aa ,则=+++a a a a 8642_________。
4、数列m,m,m,m …既是等差数列,又是等比数列,说法对吗?____(填“√”或“×”)。
5、=“向北走20km ”,=“向南走50km ”,则=+b a_________.6、已知a=4,a b 与的方向相反,且2=b ,b m a=,则实数m=________.7、已知向量b 与a 不平行,实数x,y 满足向量等式b a y b x a626+=+,则x+y=_______.8、A (2,4),B (1,5),则的坐标是_______.9、已知向量)31(y 4a ,),,(-==b ,并且a ∥b,则y=________. 三、简答题(每题10分,共30分)1、设等差数列{}a n的前三项和为-3,前三项积为8(1)求{}a n的通项公式。
职高一年级数学练习题

职高一年级数学练习题1. 三角函数计算题(1)已知角A的终边经过点P(-3, 4),求sinA和cosA的值。
(2)已知sinB = 3/5,夹角B位于第二象限,求cosB的值。
(3)已知sinC = 4/7,夹角C位于第三象限,求tanC的值。
2. 直角三角形计算题(1)已知直角三角形的一条直角边长为8 cm,另一条直角边长为15 cm,求斜边的长度。
(2)已知直角三角形的斜边长为25 cm,一条直角边长为7 cm,求另一条直角边的长度。
(3)已知直角三角形的斜边长为10 cm,一条直角边长为6 cm,求另一条直角边的长度。
3. 平面几何计算题(1)已知矩形ABCD的边长AB为4 cm,BC为5 cm,求对角线AC的长度。
(2)已知平行四边形的一条对角线长为10 cm,另一条对角线长为6 cm,求平行四边形的面积。
(3)已知菱形的对角线长为8 cm和10 cm,求菱形的面积。
4. 平方根计算题(1)求√64的值。
(2)求√(5+12)的值。
(3)求√(9-4)的值。
5. 代数计算题(1)求解方程:2x + 5 = 17。
(2)求解方程:3y - 7 = 8。
(3)求解方程组:2x + 3y = 104x + 5y = 226. 概率计算题(1)一个袋子里有5个红球和3个蓝球,从中随机取出一个球,求取出蓝球的概率。
(2)一副扑克牌中有52张牌,从中随机抽取一张牌,求取到黑桃的概率。
(3)班级有20个男生和25个女生,从班级中随机选择一人,求选择到男生的概率。
注意:以上题目仅为示例,请结合实际教材或课堂练习题册提供的题目进行编写。
每道题目应附带详细的解题步骤,方便学生理解和学习。
不同题型可根据实际情况进行拓展和调整。
高职数学题库一年级第一学期
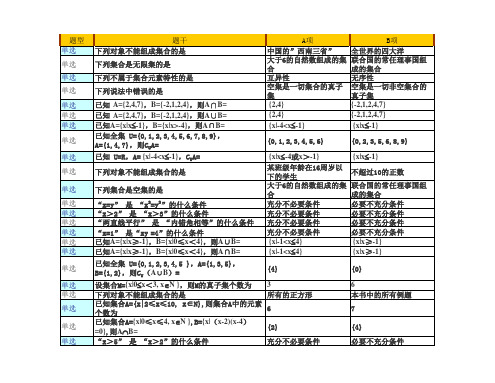
题干 -1∈N 0N+ -2.45∈Z 集合{x|1<x≤5,xZ}可用列举法表示为 {1,2,3,4,5} 小于7的所有实数组成的集合可用描述法表示为 {x|x<7}. {-2,-1,0,1,2,3}{-1,0,1} {-1,2}={x|x - x -2 =0}。 {等腰三角形}{直角三角形}={等腰直角三角形} 已知A={0,1,2},则它的子集个数是8。 18的所有正因数组成的集合是{1,2,3,6,9}。 某烹饪班有学生25人,在某次烹饪大赛中,共设冷拼 和热菜两个比赛项目,已知该班有8人未参加,有 12人参加了冷拼比赛,有11人参加了热菜比赛,问 同时参加了冷拼比赛和热菜比赛的学生有多少人? 已知A={1,2,4,8},B={-2,4,6,7,8},C={3,4,5,6,7,8}, 则(A B)(A C) {1,3,5,15}≠{x|x是15的正约数}。 由小于20的质数组成的集合用列举法表示为 {1,3,5,7,11,13,15,17,19}。 第二象限内的点组成的集合用描述法表示为 {(x,y)|x<0,y>0}。 “c<d”“c-d<0” “四边形是正方形” “四边形四边相等”。 已知A={(x,y)| y=2x+2},B={(x,y)| y=-2x4},则A B=。 已知 A={3,|m-1|,-7},B={-1,1,2},若A B={1}求m 的值。
b>0 【-2,4) |x|>3 { x| x<1} { x| -1<x<1} {x|x<-2或x>4} (-∞,-1) a =2或-2
a+b<0
一元二次方程x -ax+1=0有两个不相等的实 数根,则
若a>|b|,且b<0,则下列各式中成立的是
中职一年级期末数学试题

中职一年级第一学期期末数学试卷一、 选择题:(20分 每小题2分)1、集合A={2,3,4,5,6} , B={2,4,5,8,9} 则 A B=( ) A 、{}9,8,6,5,4,3,2 B 、{}5,4,2 C 、φ D 、{}6,5,4,3,22、集合A=(]3,1-, B=(1,5),则A B=( ) A 、(-1,5) B 、(3,5) C 、(-1,1) D 、(]3,13、函数1-=x y 的定义域为( )A 、(1,+∞)B 、[)+∞,1C 、(-∞,1)D 、(]1,∞- 4、不等式1<x 的解集是( )A 、)1,1(-B 、)1,(-∞C 、),1(+∞D 、),1()1,(+∞--∞ 5、下列对象不能组成集合的是( )A 、全体大于10的自然数B 、接近5 的实数C 、不等式23-x <0的所有解D 、平面内与点O 的距离等于5cm 的所有点 6、元素a 是集合A 中的元素,记作( )A 、A a ∈B 、A a ∉C 、A a ⊆D 、A a ⊇ 7、小于5的自然数集用列举法表示为( ) A 、{}5,4,3,2,1 B 、{1,2,3,4 } C 、{0,1,2,3,4 } D 、{0,1,2,3,4,5 }8、集合{a,b,c,d}含有元素a 的子集的个数为( ) A 、5个 B 、6个 C 、7个 D 、8个 9、不等式2x+1≤0的解集用描述法表示为( ) A 、⎭⎬⎫⎩⎨⎧≤21-/x x B 、⎭⎬⎫⎩⎨⎧-≥21/x x C 、⎭⎬⎫⎩⎨⎧≤21/x x D 、⎭⎬⎫⎩⎨⎧≥21/x x 10、函数[]3,0,3∈=x x y 的图像是( ) A 、一条直线 B 、一条射线 C 、一条线段 D 、两个点班级__________ 姓名__________ 分数___________ 二、填空题:(20分)1、设45)(2-=x x f ,=)2(f __________ ,=)2(f __________ ,=)(a f __________2、集合}{32/≤<-x x 用区间表示为__________,集合}{1/-≥x x 用区间表示为__________,集合}{31/<<x x 用区间表示为__________,集合}{1/-≤x x 用区间表示为__________3、点(-2,1)关于x 轴对称的点的坐标为__________ , 点(-1,-3)关于y 轴对称的点的坐标为__________ , 点(5,1)关于坐标原点对称的点的坐标为__________ 。
职高一年级数学 试卷及答案
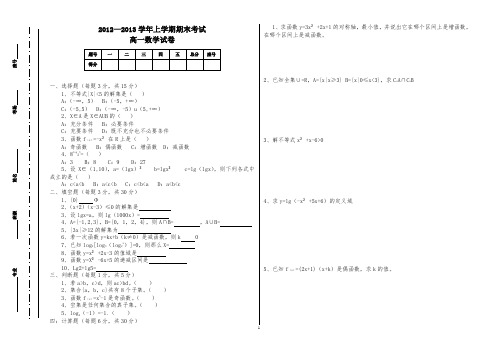
2012—2013学年上学期期末考试高一数学试卷题号 一二三四五总分 座号 得分一、选择题(每题3分,共15分)1、不等式|X|<5的解集是( ) A :(-∞,5) B :(-5,+∞) C :(-5,5) D :(-∞,-5)u (5,+∞)2、X ∈A 是X ∈AUB 的( ) A :充分条件 B :必要条件C :充要条件D :既不充分也不必要条件 3、函数f (x )=-x ²在R 上是( )A :奇函数B :偶函数C :增函数D :减函数 4、8log 23=( )A :3B :8C :9D :275、设X ∈(1,10),a=(lgx )² b=lgx ² c=lg (lgx ),则下列各式中成立的是( )A :c<a<bB :a<c<bC :c<b<aD :a<b<c 二、填空题(每题3分,共30分)1、{0} Φ2、(x+2)(x-3)≤0的解集是3、设lgx=a ,则lg (1000x )=4、A={-1,2,3},B={0,1,2,4},则A ∩B= ,A ∪B=5、|3x|≥12的解集为6、若一次函数y=kx+b (k ≠0)是减函数,则k 07、已知log 4[log 3(log 2x )]=0,则那么X=8、函数y=x ²+2x-3的值域是9、函数y=X ²-6x+5的递减区间是 10、Lg2+lg5= 三、判断题(每题1分,共5分)1、若a>b ,c>d ,则ac>bd 。
( )2、集合{a ,b ,c}共有8个子集。
( )3、函数f (x )=x 3-1是奇函数。
( )4、空集是任何集合的真子集。
( )5、log 4(-1)=-1.( ) 四:计算题(每题6分,共30分)1、求函数y=3x ²+2x+1的对称轴,最小值,并说出它在哪个区间上是增函数,在哪个区间上是减函数。
职中高一数学试题及答案

职中高一数学试题及答案一、选择题(每题4分,共40分)1. 下列哪个选项是方程x^2 - 4x + 3 = 0的解?A. x = 1B. x = 2C. x = 3D. x = 4答案:B2. 函数y = 2x + 1的斜率是多少?A. 1B. 2C. 3D. 4答案:B3. 如果一个角的余角是20°,那么这个角的度数是多少?A. 70°B. 90°C. 110°D. 160°答案:A4. 以下哪个选项是不等式2x - 5 > 3x - 1的解集?A. x < 4B. x > 4C. x < -4D. x > -4答案:C5. 圆的半径为5,那么它的面积是多少?A. 25πB. 50πC. 75πD. 100π答案:B6. 以下哪个选项是函数f(x) = x^3 - 3x^2 + 2x的零点?A. x = 0B. x = 1C. x = 2D. x = 3答案:C7. 一组数据的平均数是10,中位数是12,众数是8,那么这组数据的极差是多少?A. 4B. 6C. 8D. 10答案:A8. 以下哪个选项是函数y = 1/x的渐近线?A. y = 1B. x = 1C. y = -1D. x = -1答案:B9. 一个等差数列的前三项分别是2, 5, 8,那么它的公差是多少?A. 2B. 3C. 4D. 5答案:B10. 一个正方体的体积是27立方厘米,那么它的边长是多少?A. 3厘米B. 6厘米C. 9厘米D. 12厘米答案:A二、填空题(每题5分,共30分)1. 如果一个三角形的两边长分别为3和4,第三边长是整数,那么第三边长可能是______。
答案:1, 2, 3, 4, 52. 一个数的平方根是2,那么这个数是______。
答案:43. 一个圆的直径是10厘米,那么它的周长是______厘米。
答案:31.44. 函数f(x) = x^2 - 4x + 3的顶点坐标是______。
职高一年级数学上册第四章《指数函数》测试题及答案

职高一年级数学上册第四章《指数函数》测试题及答案4、(1)计算0.125=1/8,(2)计算5/8=0.625,(3)计算(-1)2=1,(4)计算2010+2010=4020.5、a1×a2×a3×a4的化简结果为a1+a2+a3+a4.6、(1)幂函数y=x-1的定义域为x>0,(2)幂函数y=x-2的定义域为x>0,(3)幂函数y=x的定义域为x>0.7、将指数32=9化成对数式可得log2 9=3.将对数log28=3化成指数式可得28=23.二、选择题(每题5分)1、将a写成根式的形式可以表示为A.4a。
2、将1/7a4写成分数指数幂的形式为D.a-4/7.3、9化简的结果为B.3.4、3×81的计算结果为B.9.5、下列函数中,在(-∞,+∞)内是减函数的是C.y=1/(2x)。
6、下列函数中,在(-∞,+∞)内是增函数的是 B.y=3x。
7、下列函数中,是指数函数的是A.y=2x+5.三、解答题:(每题10分)1、计算下列各题:1)(-5/8)×(-42)-0.25×(-5)×(-4)3=1052)(-10)2-5×(-3)2×22+23×10/2=3093)2-2-2+1/(10-2)-0.25×4×10=-1.754)3×3×9×7×61=5)2010++2010+=解:原式=2010(1++2010+)2010(1++++201)2010(1++)2010()xxxxxxxx02、将幂函数y=x^3-2x在x=1处的导数求出来。
解:y'=3x^2-2,所以当x=1时,y'=3(1)^2-2=1. 所以在x=1处的导数为1.3、已知函数y=2^x,求解方程2^x=8.解:2^x=8可以写成2^x=2^3,即x=3. 所以方程的解为x=3.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
职高一年级《数学》(基础模块)上册试题题库(2010—2011学年上学期适用)第一章:集合一、填空题(每空2分)1、元素3-与集合N 之间的关系可以表示为 。
2、自然数集N 与整数集Z 之间的关系可以表示为 。
3、用列举法表示小于5 的自然数组成的集合: 。
4、用列举法表示方程243=-x 的解集 。
5、用描述法表示不等式062<-x 的解集 。
6、集合{}b a N ,=子集有 个,真子集有 个。
7、已知集合{}4,3,21,=A ,集合{},7,5,3,1=B ,则=B A ,=B A 。
8、已知集合{}5,3,1=A ,集合{}6,4,2=B ,则=B A ,=B A 。
9、已知集合{}22<<-=x x A ,集合{}40<<=x x B ,则=B A .10、已知全集{}6,5,4,3,2,1=U ,集合{}5,2,1=A ,则=A C U 。
二、选择题(每题3分)1、设{}a M =,则下列写法正确的是( )。
A .M a = B.M a ∈ C. M a ⊆ D.M a ∉2、设全集为R ,集合(]5,1-=A ,则 =A C U ( )A .(]1,-∞- B.()+∞,5 C.()()+∞-∞-,51, D. (]()+∞-∞-,51,3、已知[)4,1-=A ,集合(]5,0=B ,则=B A ( )。
A .[]5,1- B.()4,0 C.[]4,0 D. ()5,1-4、已知{}2<=x x A ,则下列写法正确的是( )。
A .A ⊆0 B.{}A ∈0 C.A ∈φ D.{}A ⊆05、设全集{}6,5,4,3,2,1,0=U ,集合{}6,5,4,3=A ,则=A U [( )。
A .{}6,2,1,0 B.φ C. {},5,4,3 D. {}2,1,06、已知集合{}3,2,1=A ,集合{}7,5,3,1=B ,则=B A ( )。
A .{}5,3,1 B.{},3,2,1 C.{}3,1 D. φ 7、已知集合{}20<<=x x A ,集合{}31≤<=x x B ,则=B A ( )。
A .{}30<<=x x A B. {}30≤<=x xB C. {}21<<=x x B D. {}30<<=x x B8、已知集合{}3,2,1=A ,集合{}765,4,,=B ,则=B A ( )。
A .{}3,2 B.{},3,2,1 C.{}765,4,3,2,1,, D. φ 三、解答题。
(每题5分)1、已知集合{}5,4,3,21,=A ,集合{},987,6,5,4,=B ,求B A 和B A 。
2、设集合{}c b a M ,,=,试写出M 的所有子集,并指出其中的真子集。
3、设集合{}21≤<-=x x A ,{}30<<=x x B ,求B A 。
4、设全集{}8,7,6,5,4,3,2,1=U ,集合{}8,7,6,5=A ,{}8,6,4,2=B ,求B A ,A C U 和B C u 。
第二章:不等式一、填空题:(每空2分)1、设72<-x ,则<x 。
2、设732<-x ,则<x 。
3、设b a <,则2+a 2+b ,a 2 b 2。
4、不等式042<+x 的解集为: 。
5、不等式231>-x 的解集为: 。
6、已知集合)6,2(=A ,集合(]7,1-=B ,则=B A ,=B A7、已知集合)4,0(=A ,集合(]2,2-=B ,则=B A ,=B A8、不等式组⎩⎨⎧<->+4453x x 的解集为: 。
9、不等式062<--x x 的解集为: 。
10、不等式43>+x 的解集为: 。
二、选择题(每题3分)1、不等式732>-x 的解集为( )。
A .5>x B.5<x C.2>x D.2<x2、不等式02142≤-+x x 的解集为( )。
A .(][)+∞-∞-,37, B. []3,7-C. (][)+∞-∞-,73,D. []7,3-3、不等式123>-x 的解集为( )。
A .()+∞⎪⎭⎫ ⎝⎛-∞-,131, B. ⎪⎭⎫⎝⎛-1,31 C. ()+∞⎪⎭⎫ ⎝⎛∞-,131, D. ⎪⎭⎫⎝⎛1,314、不等式组⎩⎨⎧<->+0302xx 的解集为( ).A .()3,2- B. ()2,3- C. φ D. R5、已知集合()2,2-=A ,集合()4,0=B ,则=B A ()。
A .()4,2- B. ()0,2- C. ()4,2 D. ()2,06、要使函数42-=x y 有意义,则x 的取值范围是()。
A .[)+∞,2 B.(][)+∞-∞-,22, C.[]2,2- D. R7、不等式0122≥++x x 的解集是( )。
A .{}1- B.R C.φ D. ()()+∞--∞-,11,8、不等式()()043<-+x x 的解集为( )。
A .()3,4- B. ()()+∞-∞-,34,C. ()4,3-D. ()()+∞-∞-,43,三、解答题:(每题5分)1、当x 为何值时,代数式35-x 的值与代数式 272-x 的值之差不小于2。
2、已知集合[)2,1-=A ,集合(]3,0=B ,求B A ,B A 。
3、设全集为R ,集合(]3,0=A ,求A C U 。
4、x 是什么实数时,122--x x 有意义。
5、解下列各一元二次不等式:(1)022>--x x (2)0122<-+x x7、解下列绝对值不等式。
(1)312<-x (2)513>+x第三章:函数一、填空题:(每空2分)1、函数11)(+=x x f 的定义域是 。
2、函数23)(-=x x f 的定义域是 。
3、已知函数23)(-=x x f ,则=)0(f ,=)2(f 。
4、已知函数1)(2-=x x f ,则=)0(f ,=-)2(f 。
5、函数的表示方法有三种,即: 。
6、点()3,1-P 关于x 轴的对称点坐标是 ;点M (2,-3)关于y 轴的对称点坐标是 ;点)3,3(-N 关于原点对称点坐标是 。
7、函数12)(2+=x x f 是 函数;函数x x x f -=3)(是 函数;8、每瓶饮料的单价为2.5元,用解析法表示应付款和购买饮料瓶数之间的函数关系式可以表示为 。
9、常用对数表中,表示对数与对数值之间的关系采用的是 的方法。
二、选择题(每题3分)1、下列各点中,在函数13-=x y 的图像上的点是( )。
A .(1,2) B.(3,4) C.(0,1) D.(5,6)2、函数321-=x y 的定义域为( )。
A .()+∞∞-, B.⎪⎭⎫ ⎝⎛+∞⎪⎭⎫ ⎝⎛∞-,2323, C.⎪⎭⎫⎢⎣⎡+∞,23 D. ⎪⎭⎫ ⎝⎛+∞,23 3、下列函数中是奇函数的是( )。
A .3+=x y B.12+=x y C.3x y = D.13+=x y4、函数34+=x y 的单调递增区间是( )。
A .()+∞∞-, B. ()+∞,0 C. ()0,∞- D.[)∞+.05、点P (-2,1)关于x 轴的对称点坐标是( )。
A .(-2,1) B.(2,1) C.(2,-1) D.(-2,-1)6、点P (-2,1)关于原点O 的对称点坐标是( )。
A .(-2,1) B.(2,1) C.(2,-1) D.(-2,-1)7、函数x y 32-=的定义域是( )。
A .⎪⎭⎫ ⎝⎛∞-32, B.⎥⎦⎤ ⎝⎛∞-32, C. ⎪⎭⎫ ⎝⎛+∞,32 D.⎪⎭⎫⎢⎣⎡+∞,32 8、已知函数7)(2-=x x f ,则)3(-f =( )。
A .-16 B.-13 C. 2 D.9三、解答题:(每题5分)1、求函数63-=x y 的定义域。
2、求函数521-=x y 的定义域。
3、已知函数32)(2-=x x f ,求)1(-f ,)0(f ,)2(f ,)(a f 。
4、作函数24-=x y 的图像,并判断其单调性。
5、采购某种原料要支付固定的手续费50元,设这种原料的价格为20元/kg 。
请写出采购费y (元)与采购量()kg x 之间的函数解析式。
6、市场上土豆的价格是.83元/kg ,应付款y 是购买土豆数量x 的函数。
请用解析法表示这个函数。
7、已知函数⎩⎨⎧-+=,3,122x x x f )( .30,0≤<≤x x (1)求)(x f 的定义域;(2)求)2(-f ,)0(f ,)3(f 的值。
第四章:指数函数一、填空题(每空2分)1、将52a 写成根式的形式,可以表示为 。
2、将56a 写成分数指数幂的形式,可以表示为 。
3、将431a 写成分数指数幂的形式,可以表示为 。
4、(1)计算=31125.0 ,(2)计算121-⎪⎭⎫ ⎝⎛= (3)计算=-2)211( (4)计算=+020******* 5、4321a a a a ⋅⋅⋅的化简结果为 .6、(1)幂函数1-=x y 的定义域为 .(2)幂函数2-=x y 的定义域为 .(3)幂函数21x y =的定义域为 .7、将指数932=化成对数式可得 .将对数38log 2=化成指数式可得 .二、选择题(每题3分)1、将54a 写成根式的形式可以表示为( )。
A .4a B.5a C. 54a D.45a2、将741a 写成分数指数幂的形式为( )。
A .74a B.47a C.74-a D.47-a 3、219化简的结果为( )。
A .3± B.3 C.-3 D.29 4、432813⨯-的计算结果为( )。
A .3 B.9 C.31 D.1 5、下列函数中,在()+∞∞-,内是减函数的是( )。
A .x y 2= B. x y 3= C.xy ⎪⎭⎫ ⎝⎛=21 D. x y 10= 6、下列函数中,在()+∞∞-,内是增函数的是( )。
A .x y 2= B. x y ⎪⎭⎫ ⎝⎛=101 C.xy ⎪⎭⎫ ⎝⎛=21 D. 2x y = 7、下列函数中,是指数函数的是( )。
A .52+=x y B. x y 2= C.3x y = D.321-=x y 三、解答题:(每题5分)1、计算下列各题:(1)()()()324525.0485-⨯-⨯--⨯⎪⎭⎫ ⎝⎛- (2)()()102235103222⨯+⨯-⨯-- (3)2202122⎪⎭⎫ ⎝⎛-+--+()1010425.0⨯- (4)432793⨯⨯(5)10201020102010201010+++峨山县职业高级中学、电视中专学校2010至2011学年上学期期末考试《数学》试题题型结构、题量、布分情况适用班级:职高一年级秋季班试题题型结构、题量、布分情况:1、填空题:每空2分,共15个空,占30分。
