(完整版)定积分知识点汇总.doc
(整理)定积分 笔记.

第三节定积分一、定积分的定义设函数在上有界,在中任意插入若干个分点把区间分成个小区间,各小区间的长度依次为,,在各小区间上任取一点(),作乘积并作为,记,如果不论对怎样的分法,也不论在小区间上点怎样的取法,只要当时,和总趋于确定的极限我们称这个极限为函数在区间上的定积记为:二、定积分的性质性质1:性质2:(为常数)性质3:假设,性质4:性质5:在区间上,则性质6:设及分别是函数在区间上的最大值及最小值,则性质7(定积分中值定理)如果函数在闭区间上连续,则在积分区间上至少存在一个点,使积分中值公式的几何解释:在区间上至少存在一个点,使得以区间为底边,以曲线为曲边的曲边梯形的面积等于同一底边而高为的一个矩形的面积。
三、微积分的基本公式1.原函数存在定理:如果在上连续,则变上限积分的函数在可导,还是在上的一个原函数。
2.微积分基本公式(牛顿—莱布尼茨公式)如果是连续函数在区间上的一个原函数,则场。
微积分基本公式表明:一个连续函数在区间上的定积分等于它的任意一个原函数在区间上的增量。
求定积分问题转化为求原函数的问题。
第四节 定积分的积分方法与无穷区间上的广义积分 一、 定积分的积分方法1、定积分的换元积分法例1求4⎰.解一2d 1t tt +⎰12(1)d 1t t =-+⎰2(ln 1)t t C =-++=ln 1C++于是440ln(1=-+⎰= 42ln3- .解二 设t =,即2(0)x t t =>. 当0x =时,0t =;当 4x = 时,2t =.于是4222002d 12(1)d 2(ln 1)2(2ln 3)11t t t t t t t ==-=-+=-++⎰⎰⎰.一般地,定积分换元法可叙述如下,设()f x 在[,]a b 上连续,而()x x ϕ=满足下列条件:(1)()x x ϕ=在[,]αβ上有连续导数;(2)(),()a b ϕαϕβ==,且当 t 在[,]αβ上变化时,()x t ϕ=的值在[,]a b 上变化,则有换元公式:()d [()]()d b af x x f t t tβαϕϕ'=⎰⎰.例2求ln 0x⎰.解t =,即222ln(1),d d 1tx t x t t =+=+.换积分限:当 0x = 时,0t =, 当 ln2x =时,1t =,于是ln 11220021d 2(1)d 11t x t t t t t =⋅=-++⎰⎰⎰10π2(arctan )22t t =-=-.例3 求24d a ax x ⎰.解 设sec x a t =,则 d sec tan d x a t t t =. 换积分限:当x a =时,0t =; 2x a = 时,π3t =,于是π234440tan d sec tan d sec a aa t x a t t t x a t =⎰⎰ =π23201sin cos d t t t a ⎰π2321sin d(sin )t t a =⎰21a =.3π30sin 3t =.例4 求π20d 1sin x I x =+⎰.解一 (换元法)令2222d tan ,sin ,d 211x t t t x x t t ===++, 所以,当0x =时,0t =;当π2x =时,1t =,于是111220002d 2d 2112(1)1t I t t t t t ===-=++++⎰⎰. 解二 (凑微分法)ππ220222d d (sin cos )(tan 1)cos 2222x xI x x x x ==++⎰⎰ππ2202d tan12221(tan 1)tan 122x x x ==-=++⎰.注意:求定积分一定要注意定积分的存在性.2、定积分的分部积分法设()u x ,()v x 在[a,b]上有连续导数,则有d d b bb aaau v uv v u=-⎰⎰.[,]a b该公式称为定积分分部积分公式,使用该公式时要注意,把先积出来得那一部分代上下限求值,余下的部分继续积分.这样做比完全把原函数求出来再代上下限简便一些.例5 求π220cos d x x x⎰.解ππ22220cos d d(sin )x x x x x =⎰⎰ππ22200sin 2sin d x x x x x=-⎰ππ22222000ππ2d(cos )2cos 2cos d 44x x x x x x π=+=+-⎰⎰π2220ππ2sin 244x=-=-.例6 求e 1eln d x x⎰.解e 1e111eeln d ln d ln d x x x x x x=+⎰⎰⎰.因为11e x <<时, ln 0x <,这时ln ln x x =-;x ≥1时,ln x ≥0,这时ln ln x x=.于是e 1e111eeln d ln d ln d x x x x x x=-+⎰⎰⎰分别用分部积分求右端两个积分得11111111e e e e1112ln d ln d ln 1e e e x x x x x x x x -=-+=+=-⎰⎰,e e e111ln d ln 1x x x x x =-=⎰,最后得e 1e2ln d 2e x x =-⎰.二、 无穷区间上的广义积分设函数f (x) 在区间[a , )+∞上连续,取b >a ,如果极限lim()bab f x dx→+∞⎰存在,则称此极限为函数f (x) 在无穷区间[ a, )+∞上的广义积分,记作()a f x dx+∞⎰即()af x dx+∞⎰=lim ()ba b f x dx→+∞⎰这时也称广义积分()af x dx+∞⎰收敛。
定积分知识点总结

定积分知识点总结什么是定积分?定积分是微积分中的重要概念之一,用于求解曲线下面的面积或曲线与坐标轴所围成的图形的面积。
定积分的基本思想是将区间划分成无限小的小区间,然后对每个小区间内的函数值进行求和,最终得到曲线下的面积或图形的面积。
定积分的符号表示定积分的符号表示为∫f(x)dx,其中∫ 表示积分符号,f(x)表示被积函数,dx表示积分变量。
∫ f(x)dx的结果是一个数值,表示积分区间上的面积。
定积分的计算步骤计算定积分的一般步骤如下:1.确定积分区间:确定被积函数的积分区间,一般用[a, b] 表示。
其中,a 表示下限,b 表示上限。
2.对被积函数进行积分:根据被积函数的形式,进行积分运算。
如果被积函数是简单函数,可以直接对其进行积分。
如果被积函数比较复杂,可以利用积分的基本公式或积分的性质来进行换元、分部积分等操作。
3.计算积分结果:对积分结果进行计算,得到最终的数值结果。
定积分的性质定积分具有以下几个重要的性质:1.线性性质:定积分具有线性性质,即对于任意的常数 a 和 b,有∫(af(x) + bf(y))dx = a∫f(x)dx+ b∫f(y)dy。
2.区间可加性:如果有一个函数在区间 [a, b] 上可积分,而在 [b, c] 上也可积分,则在整个区间 [a, c] 上也可积分,并且有∫[a,c]f(x)dx = ∫[a,b]f(x)dx + ∫[b,c]f(x)dx。
3.积分与求导的关系:定积分与原函数之间存在着积分与求导的关系。
如果函数 F(x) 在区间 [a, b] 上可导,并且导函数 f(x) 连续,则有∫[a,b]f(x)dx = F(b) - F(a)。
定积分的应用定积分在科学和工程领域有着广泛的应用,下面介绍一些常见的应用场景:1.几何应用:定积分可以用于计算平面图形的面积和曲线的弧长。
例如,可以通过计算曲线所围成的面积来求解不规则图形的面积。
2.物理学应用:定积分在物理学中的应用非常广泛。
定积分的知识点总结

定积分的知识点总结一、定积分的基本概念定积分是微积分学中的重要概念,可以用来计算曲线下的面积,曲线的弧长,质心等物理量。
定积分的基本思想是将曲线下的面积划分为无穷多个微小的矩形,然后求和得到整体的面积。
定积分的符号表示为∫。
对于一个函数f(x),在区间[a, b]上的定积分表示为:∫[a, b]f(x)dx其中,a和b为区间的端点,f(x)为函数在该区间上的取值。
定积分表示在区间[a, b]上的函数f(x)所确定的曲线下的面积。
二、定积分的计算方法1. 黎曼和定积分的计算基本思想是将曲线下的面积划分为很多个小矩形,然后对这些小矩形的面积求和。
这就是定积分的计算方法。
在实际计算中,根据黎曼和的定义,我们可以将区间[a, b]等分为n个小区间,每个小区间长度为Δx=(b-a)/n,然后在每个小区间上取一个样本点xi,计算f(xi)Δx的和:∑[i=1,n]f(xi)Δx当n趋近于无穷大时,这个和就可以逼近定积分的值。
这就是黎曼和的基本思想。
2. 定积分的几何意义定积分可以用来计算曲线下的面积,也可以用来计算曲线的弧长。
对于一个函数f(x),其在区间[a, b]上的定积分表示的是曲线y=f(x)和x轴之间的面积。
这个面积就是曲线下的面积。
如果函数f(x)在区间[a, b]上非负且连续,那么函数y=f(x)、直线x=a、x=b以及x轴所围成的区域的面积就是∫[a, b]f(x)dx。
3. 定积分的物理意义定积分还可以用来计算物理量,比如质量、质心等。
在物理学中,可以用定积分来计算物体的质量、质心等物理量。
对于一个连续的物体,将其质量密度函数表示为ρ(x),则物体的质量可以表示为定积分:M=∫[a, b]ρ(x)dx三、定积分的性质1. 线性性定积分具有线性性质,即∫[a, b](c1f1(x)+c2f2(x))dx=c1∫[a, b]f1(x)dx+c2∫[a, b]f2(x)dx。
其中c1、c2为常数,f1(x)、f2(x)为函数。
定积分的计算知识点总结

定积分的计算知识点总结一、定积分的定义。
1. 概念。
- 设函数y = f(x)在区间[a,b]上连续,用分点a=x_0将区间[a,b]等分成n个小区间,每个小区间长度为Δ x=(b - a)/(n)。
在每个小区间[x_i - 1,x_i]上取一点ξ_i(i =1,2,·s,n),作和式S_n=∑_i = 1^nf(ξ_i)Δ x。
当nto∞时,如果S_n的极限存在,则称这个极限为函数y = f(x)在区间[a,b]上的定积分,记作∫_a^bf(x)dx,即∫_a^bf(x)dx=limlimits_n→∞∑_i = 1^nf(ξ_i)Δ x。
- 这里a与b分别叫做积分下限与积分上限,区间[a,b]叫做积分区间,函数f(x)叫做被积函数,x叫做积分变量,f(x)dx叫做被积表达式。
2. 几何意义。
- 当f(x)≥slant0时,∫_a^bf(x)dx表示由曲线y = f(x),直线x = a,x = b以及x 轴所围成的曲边梯形的面积。
- 当f(x)≤slant0时,∫_a^bf(x)dx表示由曲线y = f(x),直线x = a,x = b以及x 轴所围成的曲边梯形面积的相反数。
- 当f(x)在[a,b]上有正有负时,∫_a^bf(x)dx表示位于x轴上方的曲边梯形面积减去位于x轴下方的曲边梯形面积。
二、定积分的基本性质。
1. 线性性质。
- ∫_a^b[k_1f(x)+k_2g(x)]dx = k_1∫_a^bf(x)dx + k_2∫_a^bg(x)dx,其中k_1,k_2为常数。
2. 区间可加性。
- ∫_a^bf(x)dx=∫_a^cf(x)dx+∫_c^bf(x)dx,其中a < c < b。
3. 比较性质。
- 如果在区间[a,b]上f(x)≥slant g(x),那么∫_a^bf(x)dx≥slant∫_a^bg(x)dx。
- 特别地,<=ft∫_a^bf(x)dxright≤slant∫_a^b<=ftf(x)rightdx。
定积分知识点总结专科

定积分知识点总结专科一、定积分的基本概念1. 定积分的引入定积分是对曲线下面积的求解方法。
在平面直角坐标系中,给定曲线的函数关系y=f(x),我们希望计算在区间[a, b]上曲线与x轴之间的面积。
为了简化计算,我们将区间[a, b]分成无穷小的小区间,然后计算每个小区间中与x轴之间的面积,再把所有小区间的面积相加起来,就得到了曲线在区间[a, b]上的面积。
这种方法就是定积分的基本思想。
2. 定积分的定义设函数y=f(x)在区间[a, b]上有定义,且区间[a, b]上的分割为[a=x0, x1, x2, ..., xn-1, xn=b],则对应的小区间为[x0, x1], [x1, x2], ..., [xn-1, xn],每个小区间的长度为Δxi=xi-xi-1。
在每个小区间上取任意点ξi,用函数值f(ξi)乘以小区间长度Δxi,再把所有小区间的面积相加,得到Σf(ξi)Δxi。
当Δxi→0时,如果极限存在,就称曲线在区间[a, b]上的面积为定积分,用符号∫abf(x)dx表示,即∫abf(x)dx=lim(Δxi→0)Σf(ξi)Δxi。
其中f(x)是被积函数,x是积分变量,a、b是积分上下限,ξi是小区间[i-1, i]上的任意点。
3. 定积分的几何意义定积分的几何意义是曲线与x轴之间的面积,例如,对于非负函数y=f(x)在区间[a, b]上的定积分∫abf(x)dx表示曲线y=f(x)与x轴以及直线x=a、x=b所包围的平面图形的面积。
4. 定积分的物理意义定积分的物理意义通常是表示物体的质量、体积或者其它物理量,例如,对于密度为ρ(x)的连续介质在区间[a, b]上的定积分∫abρ(x)dx表示介质在区间[a, b]上的质量。
5. 定积分的符号定积分的符号是∫,这个符号来源于拉丁字母"summa"的缩写,表示对函数在一定区间内的求和。
6. 定积分的性质- 定积分的存在性只有当函数y=f(x)在区间[a, b]上是有界的(即不是无穷大)时,定积分才有意义。
(完整版)定积分知识点汇总

(完整版)定积分知识点汇总定积分是高中数学教学的重点难点之一,也是高数的基础知识。
我们通过汇总定积分的相关知识点,帮助同学们更好地掌握定积分的相关知识,以便在考试中取得好的成绩。
一、定积分的定义定积分是对函数在一定区间上的积分,也就是函数在此区间上的面积。
1. 定积分与区间的选取无关,即如果函数在 $[a,b]$ 上是可积的,则定积分$\int_a^b f(x) \mathrm{d}x$ 的值是唯一的。
2. 定积分具有可加性,即对于任意的 $c \in [a,b]$,有 $\int_a^b f(x)\mathrm{d}x = \int_a^c f(x) \mathrm{d}x + \int_c^b f(x) \mathrm{d}x$。
三、定积分的求解方法1. 函数曲线与坐标轴相交的情况:对于函数曲线与 $x$ 轴相交的区间,可以根据定义式直接求出该区间内的面积。
对于函数曲线与 $y$ 轴相交的区间,则要将积分区间平移后,再根据定义式计算面积。
2. 利用基本积分法和牛顿-莱布尼茨公式:可以利用基本积分法求出一个函数的原函数,然后利用牛顿-莱布尼茨公式,即$\int_a^b f(x) \mathrm{d}x = F(b) - F(a)$,其中 $F(x)$ 是 $f(x)$ 的一个原函数。
3. 利用换元积分法:换元积分法是利用一些特殊的代换,将积分式转化为某些基本形式的积分。
常见的代换包括:$u=g(x), x=h(u)$ 和 $\mathrm{d}u = f(x) \mathrm{d}x$。
分部积分法是将原积分式做一个变形,转化成两个积分乘积的形式,从而更容易求解。
5. 利用定积分的对称性:如积分区间对于 $0$ 对称,或者函数具有四象限对称性等,可以根据对称性减少计算量。
1. 几何应用:用定积分可以求解函数曲线与坐标轴围成的图形的面积、体积和质心等几何特征。
利用定积分可以求解质点运动的速度、加速度、位移和质量等物理量。
定积分知识点汇总

定积分知识点汇总关键信息项:1、定积分的定义2、定积分的几何意义3、定积分的基本性质4、定积分的计算方法5、定积分的应用1、定积分的定义11 定积分的概念定积分是微积分的重要概念之一。
如果函数 f(x) 在区间 a, b 上连续,用分点 a = x₀< x₁< x₂<< xₙ = b 将区间 a, b 分成 n 个小区间,在每个小区间 xᵢ₋₁, xᵢ上任取一点ξᵢ(i = 1, 2,, n),作和式∑f(ξᵢ)Δxᵢ,当 n 无限增大且Δxᵢ的最大值趋于零时,如果和式的极限存在,这个极限就叫做函数 f(x) 在区间 a, b 上的定积分,记作∫ₐᵇf(x)dx 。
12 定积分的几何定义如果在区间 a, b 上函数 f(x) 连续且非负,那么定积分∫ₐᵇf(x)dx 表示由曲线 y = f(x) 、直线 x = a 、 x = b 和 x 轴所围成的曲边梯形的面积。
如果函数 f(x) 在区间 a, b 上连续且有正有负,那么定积分∫ₐᵇf(x)dx 表示介于 x 轴上方和下方的面积的代数和。
2、定积分的几何意义21 以 x 轴上方的面积为正,x 轴下方的面积为负当函数图像在 x 轴上方时,对应的定积分值为正,表示该部分区域的面积;当函数图像在 x 轴下方时,对应的定积分值为负,表示该部分区域面积的相反数。
22 定积分表示曲线围成的面积对于一般的连续函数,定积分的值等于曲线与 x 轴之间所围成的有向面积。
3、定积分的基本性质31 线性性质若函数 f(x) 和 g(x) 在区间 a, b 上可积,k 为常数,则∫ₐᵇkf(x)dx =k∫ₐᵇf(x)dx ,∫ₐᵇf(x) ± g(x)dx =∫ₐᵇf(x)dx ±∫ₐᵇg(x)dx 。
32 区间可加性若函数 f(x) 在区间 a, c 和 c, b 上都可积,其中 a < c < b ,则∫ₐᵇf(x)dx =∫ₐᶜf(x)dx +∫ᶜᵇf(x)dx 。
定积分知识总结(总9页)

定积分知识总结(总9页)1. 定积分的定义定积分是数学中的一个概念,它表示将一个函数沿着一条给定的路径积累起来的总和。
在数学上,定积分是描述函数在一定区间上的面积、体积、虚功等概念的一种工具。
(1)可加性:若f(x)在[a,b]、[b,c]上可积,则:∫(a,c)f(x)dx=∫(a,b)f(x)dx+∫(b,c)f(x)dx∫(a,b)f(x)dx≥03. 函数可积的充分条件Riemann可积的充分条件有:(1)区间[a,b]上f(x)存在上下积分,且上下积分相等;(2)对任意ϵ>0,可找到划分P及加细之后的划分P1,使得S(P1,f)-s(P1,f)<ϵ,其中S(P1,f)表示P1的上和式,s(P1,f)表示P1的下和式。
4. 定积分的计算方法定积分可以通过换元法、分部积分法、牛顿-莱布尼茨公式等数学方法进行计算。
(1)求曲线下面的面积;(2)求曲线绕x轴或y轴旋转的体积;(3)求物理问题中的虚功;(4)求平均值、方差等统计量。
6. 常用定积分公式$\int x^ndx={x^{n+1}}/{n+1}+C$$\int\sin xdx=-\cos x+C$7. 例题(1)计算定积分: $\int_{0}^{\frac{\pi}{2}}\sin xdx$解:$ \int_{0}^{\frac{\pi}{2}}\sin xdx=\left . -\cos x \right |\begin{matrix} 0\\\frac{\pi}{2} \end{matrix} =1$8. 求导与积分的对应关系如果函数f(x)在区间[a,b]上可导,则:$\int_{a}^{b}f'(x)dx = f(b)-f(a)$微积分是数学的一个分支,其中包括微分和积分两个部分。
微积分对象是函数的导数和原函数。
定积分是微积分中的积分部分,用于计算函数在一定区间内的积累量。
因此,微积分中的求导和积分是密不可分的,两者相辅相成,是微积分学中的核心概念。
定积分知识点,DOC

定积分知识点1.定积分的概念:一般地,设函数()f x 在区间[,]a b 上连续,用分点 将区间[,]a b 等分成n 个小区间,每个小区间长度为x D (b ax n-D =),在每个小区间[]1,i i x x -上任取一点()1,2,,i i n ξ=,作和式:11()()n nn i i i i b aS f x f nξξ==-=∆=∑∑如果x D 无限接近于0(亦即n →+∞)时,上述和式n S 无限趋近于常数S ,那么称该常数S 为函数()f x 在区间[,]a b 上的定积分。
记为:()ba S f x dx =⎰,其中-⎰积分号,b -积分上限,a -积分下限,()f x -被积函数,x -积分变量,[,]a b -积分区间,()f x dx -被积式。
说明:(1)定积分()ba f x dx ⎰是一个常数,即n S 无限趋近的常数S (n →+∞时)记为()baf x dx ⎰,而不是n S .(2)用定义求定积分的一般方法是:①分割:n 等分区间[],a b ;②近似代替:取点[]1,i i i x x ξ-∈;③求和:1()ni i b a f n ξ=-∑;④取极限:()1()lim n b i a n i b a f x dx f n ξ→∞=-=∑⎰;(3)曲边图形面积:()baS f x dx =⎰;变速运动路程21()t t S v t dt =⎰;变力做功()baW F r dr =⎰2.定积分的几何意义恒有()0f x ≥,那从几何上看,如果在区间[],a b 上函数()f x 连续且么定积分()ba f x dx ⎰表示由直线,(),0x a x b a b y ==≠=和曲线()y f x =所围成的曲边梯形(如图中的阴影部分)的面积,这就是定积分()baf x dx ⎰的几何意义。
说明:一般情况下,定积分()baf x dx ⎰的几何意义是介于x 轴、函数()f x 的图形以及直线,x a x b==之间各部分面积的代数和,在x 轴上方的面积取正号,在x 轴下方的面积去负号。
高数定积分知识点总结

高数定积分知识点总结一、定积分的定义定积分是微积分中的一个重要概念,它是对一个函数在一个区间上的积分结果进行计算的过程。
在数学上,定积分是用来计算曲线下面的面积或者函数在某一区间上的平均值的方法。
定积分可以写成以下形式:\[ \int_{a}^{b} f(x)dx \]其中,\( f(x) \)是被积函数,\( a \)和\( b \)是积分区间的端点。
定积分的计算过程就是求解被积函数在给定区间上的曲线下面的面积。
定积分在物理学、工程学和经济学等领域都有着广泛的应用,是微积分中不可或缺的重要工具。
二、定积分的性质1. 定积分的可加性如果函数\( f(x) \)在区间\([a, b]\)上是可积的,那么对于任意的\( c \)满足\( a \leq c \leq b \),都有:\[ \int_{a}^{b} f(x)dx = \int_{a}^{c} f(x)dx + \int_{c}^{b} f(x)dx \]这个性质表明了定积分的可加性,即在一个区间上进行积分的结果可以根据任意划分点\( c \)进行分割。
2. 定积分的线性性对于任意的实数\( \alpha, \beta \)和函数\( f(x), g(x) \),如果\( f(x), g(x) \)在区间\([a, b]\)上是可积的,那么有:\[ \int_{a}^{b} (\alpha f(x) + \beta g(x))dx = \alpha \int_{a}^{b} f(x)dx + \beta \int_{a}^{b} g(x)dx \]这个性质表明了定积分的线性性,即在一个区间上进行线性组合的函数的积分等于线性组合的函数的积分的线性组合。
3. 定积分的保号性如果在区间\([a, b]\)上有\( f(x) \geq 0 \),那么有:\[ \int_{a}^{b} f(x)dx \geq 0 \]这个性质表明了定积分的保号性,即当被积函数在一个区间上非负时,其积分结果也是非负的。
定积分计算知识点总结

定积分计算知识点总结一、定积分的概念1.1 定积分的定义定积分是在微积分学中给定一个连续函数$f(x)$,对它在区间$[a, b]$上的积分值的确定。
具体地,定积分可以定义为:$$\int_{a}^{b} f(x) dx = \lim _{n \rightarrow \infty} \sum _{i=1}^{n} f(x_{i}^{*})\Delta x $$其中,$\Delta x = (b-a)/n$,$x_i^* \in [x_{i-1}, x_i]$。
1.2 定积分的几何意义定积分的几何意义是函数$y=f(x)$在区间$[a, b]$上的曲边梯形的面积,可以用积分来表示。
当积分区间的$[a, b]$上的函数是非负值函数时,它的定积分可以表示该函数与$x$轴所夹的曲边梯形的面积。
1.3 定积分的基本性质① 定积分与积分区间的顺序无关,即$\int_{a}^{b}f(x)dx = -\int_{b}^{a}f(x)dx$。
② 定积分的线性性:$\int_{a}^{b}(\alpha f(x)+\beta g(x))dx = \alpha \int_{a}^{b} f(x)dx + \beta \int_{a}^{b} g(x)dx$。
③ 定积分的加法性:$\int_{a}^{b} f(x)dx + \int_{b}^{c} f(x)dx = \int_{a}^{c} f(x)dx$。
1.4 定积分的计算方法定积分的计算方法主要包括:几何意义法、切割法、定积分的性质、换元积分法、分部积分法等。
这些方法在不同的情况下都有其适用范围,学习者需要根据具体问题进行选择和灵活运用。
二、定积分的计算2.1 几何意义法几何意义法是通过将定积分代表的曲边梯形进行适当的分割和逼近,最终得到定积分的值。
这种方法适用于简单的函数和几何形状,容易理解和操作。
2.2 切割法切割法是将定积分的积分区间进行适当的分割,然后对每个小区间内的函数求积分,最后将所得的和加起来。
定积分知识点汇总
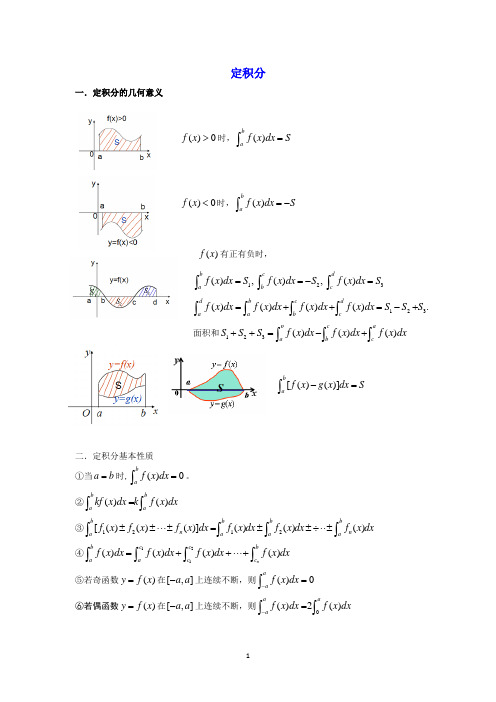
定积分一.定积分的几何意义①()0f x >时,()baf x dx S =⎰()0f x <时,()baf x dx S =-⎰()f x 有正有负时,1(),baf x dx S =⎰2(),cbf x dx S =-⎰3()dcf x dx S =⎰面积和123()()()bcdabcS S S f x dx f x dx f x dx ++=-+⎰⎰⎰[()()]baf xg x dx S -=⎰二.定积分基本性质 ①当a b =时,()0baf x dx =⎰。
②()()bb aakf x dx k f x dx =⎰⎰③1212[()()()]()()()bbb bnn aaaaf x f x f x dx f x dx f x dx f x dx±±⋅⋅⋅±=±±÷⋅⋅±⎰⎰⎰⎰④121()()()()nbc c baac c f x dx f x dx f x dx f x dx =++⋅⋅⋅+⎰⎰⎰⎰⑤若奇函数()y f x =在[,]a a -上连续不断,则()0aa f x dx -=⎰⑥若偶函数()y f x =在[,]a a -上连续不断,则0()2()aaaf x dx f x dx -=⎰⎰123()()()().d bc d a abcf x dx f x dx f x dx f x dx S S S =++=-+⎰⎰⎰⎰微分基本定理:如果()f x 是区间[,]a b 上的连续函数,且'()()F x f x =,则 ()()()()bb aaf x dx F x F b F a ==-⎰(牛顿-莱布尼兹公式)1.直线0,,0x x y π===与曲线sin y x =所围成图形的面积用定积分表示为2.用定积分表示抛物线223y x x =-+与直线3y x =+所围成图形的面积为3.曲线21,2,0,0y x x x y =-===围成的阴影部分的面积用定积分表示为4.由曲线24,4,0,0y x x x y =-===和x 轴围成的封闭图形的面积是( )42.(4)A x dx -⎰ 420.|(4)|B x dx -⎰420.|4|C x dx -⎰ 242202.(4)(4)D x dx x dx -+-⎰⎰5.计算下列定积分 (1)3239x dx --⎰(2)12144x dx --⎰(3)211(1)dx x x +⎰(4)10(2)x x e dx +⎰(5)2cos 2xdx π⎰(6)91(1)x x dx +⎰6.正方形的四个顶点(1,1),(1,1),(1,1),(1,1)A B C D ----分别在抛物线2y x =-和2y x=上,如图,若将一质点随机投入正方形ABCD 中,则质点落在图中阴影区域的概率是7。
定积分知识点总结高中

定积分知识点总结高中一、定积分的概念定积分是微积分中的重要概念之一,它是对一个区间上函数的积分进行求解的一种方法。
在数学上,定积分可以用来求解曲线与坐标轴所围成的图形的面积、求解物体的质量、求解物体的质心和求解函数的平均值等。
二、定积分的符号表示定积分的符号表示为∫abf(x)dx,其中∫表示积分的意思,a和b分别表示积分的区间,f(x)表示被积函数,而dx表示自变量。
三、定积分的基本性质1. 定积分的区间可以是一个闭区间也可以是一个开区间。
2. 定积分的积分域是一段区间上的一个函数。
3. 定积分的值只与积分的上限和下限以及积分函数的具体形式有关,与被积函数在区间上函数值的具体大小无关。
四、定积分的计算方法1. 定积分的计算方法有多种,其中最常用的方法有两种:换元积分法和分部积分法。
2. 换元积分法是将定积分中的自变量进行替换,从而使积分的形式更容易计算。
3. 分部积分法是将被积函数进行分解,从而使积分的形式更容易计算。
五、定积分的应用1. 定积分可以用来求解曲线与坐标轴所围成的图形的面积。
这是定积分最基本的应用之一。
2. 定积分可以用来求解物体的质量。
例如,如果我们知道一个物体的密度分布函数,在定积分的帮助下可以求解出物体的总质量。
3. 定积分可以用来求解物体的质心。
通过定积分可以计算出物体在某一方向上的平均位置。
4. 定积分可以用来求解函数的平均值。
通过定积分可以求解被积函数在一段区间上的平均值。
六、定积分的图形表示1. 在定积分的图形表示中,定积分表示的是曲线与坐标轴所围成的图形的面积。
2. 定积分的图形表示与被积函数在指定区间上的图像有关,可以通过被积函数的图像来判断定积分的正负值,从而得到面积的正负值。
七、定积分的应用实例1. 一块形状不规则的地块的面积可以通过定积分来求解。
2. 一根线密度不均匀的杆子的质量可以通过定积分来求解。
3. 一个质点在一段区间内的平均位置可以通过定积分来求解。
定积分应用知识点总结

定积分应用知识点总结1. 定积分的概念定积分是微积分学中的一个重要概念,用于求解曲线下面积或者曲线围成图形的面积。
在实际问题中,定积分可以用来计算曲线与坐标轴之间的面积、质心、弧长、体积、工作、功等物理量。
2. 定积分的计算定积分的计算可以通过积分的定义或者牛顿-莱布尼茨公式来进行。
积分的定义是将一个曲线f(x)在区间[a,b]上分成无穷多段,每一段的面积为f(x)与x轴之间的面积的无限和,然后通过极限的方法求得。
而牛顿-莱布尼茨公式则是通过原函数的求导与积分的关系,直接求出定积分的值。
3. 定积分的性质定积分有很多重要的性质,包括线性性质、区间可加性、保号性等。
这些性质在定积分的计算和应用中起到了非常重要的作用,可以简化定积分的计算过程。
4. 定积分的应用定积分在实际问题中有着广泛的应用,例如可以用来求解曲线围成的图形的面积、计算质心、弧长、体积、工作、功等物理量。
在工程、物理、经济学等领域都有着重要的应用价值。
5. 定积分的计算技巧对于一些特定的函数,可以通过一些积分的技巧来简化定积分的计算,例如换元积分法、分部积分法等。
这些技巧可以帮助我们更快速、准确地求解定积分。
在实际问题中,我们经常会遇到需要利用定积分来计算一些物理量或者解决一些实际问题,下面我们通过一些实际例子来解释定积分的应用知识点。
1. 计算物体的质心在物理学中,质心是一个非常重要的概念,它可以帮助我们确定物体的平衡位置。
对于一个均匀密度的物体,我们可以通过定积分来计算它的质心位置。
假设物体在x轴上的密度分布函数为ρ(x),则物体的质心位置可以通过如下公式计算得出:\[X=\frac{\int_{a}^{b}xρ(x)dx}{\int_{a}^{b}ρ(x)dx}\]其中,\(\int_{a}^{b}xρ(x)dx\)表示物体的动量矩,而\(\int_{a}^{b}ρ(x)dx\)表示物体的总质量。
通过这个公式,我们就可以求得物体的质心位置。
定积分知识复习总结

定积分知识总结一、基本概念和性质(1)定义[]()[]())()(lim )()()(,,,,0max ...,)()(lim lim )(11111111011-=∞→-=----∞→∞→=∞→-⋅-⋅=-⋅≈=→-∞→==-⋅=⋅∑∑∑∑⎰i i ni i n i i ni i i i i i i i i i i i i i i i i n i nn i n ni iban x x f x x f S x x f S I S I S I x x I x x n b x x x a n b a x x f S dx x f ξξξξξ④求极限:即③求和:,上任取一点在上用矩形代替在上的代数面积为在②记时,要求当<<<个小区间,区间分成①把的定义:[]dxx g dx x f dx x g x f ab babababa⋅⋅+⋅⋅=⋅⋅+⋅-=⎰⎰⎰⎰)()()()(12βαβα②线性运算性质:①)定积分的性质()()()(=⋅⋅-=⋅⎰⎰⎰aaabba dx x f dxx f dx x f()))(定要求的区间可积即可,不一其中,包含③区间的可加性:b a c c b a dxx f dx x f dx x f bccaba,,,()()()(∈⋅+⋅=⋅⎰⎰⎰[][][][]⎰⎰⎰⎰⎰⎰⋅⋅≥≡=⋅≥⋅≥⋅≥≥⋅≥babababab abadxx g dx x f x g x f x g x f b a x g x f x f x f dx x f x f x f b a x f dxx g dx x f x g x f b a x g x f dx x f x f b a x f )()(),()(),()(,)(),(0:0)(00:0)(0)(0)(0)(,)()()(),()(,)()(0)(0)(,)(>则:不恒等于且上连续,在区间推论:若区间上都等于则是指在整个;,也可能整个区间均为可能个别点上等于>,则不恒等于,上连续,在⑥若则上可积且在,⑤若,则上可积且在④ [][][][][])()()(,,)()()()(,)(,)()()(,)(a b f dx x f b a b a x f a b M dx x f a b m M m b a x M x f m b a x f dxx f dx x f b a x f bababa ba-⋅=⋅∈-≤⋅≤-∈≤≤⋅≤⋅⎰⎰⎰⎰ξξ,使得:点上连续,则至少存在一在闭区间若⑨(积分中值定理)均为常数,则:,,,上可积,在⑧若上可积,则在⑦若二、微积分基本公式1、积分上限函数及其导数定义:设函数)(x f 在区间],[b a 上连续,对于任意],[b a x ∈,)(x f 在区间],[x a 上也连续,所以函数)(x f 在],[x a 上也可积.显然对于],[b a 上的每一个x 的取值,都有唯一对应的定积分⎰xadt t f )(和x 对应,因此⎰xadt t f )(是定义在],[b a 上的函数.记为⎰=Φxadt t f x )()(,],[b a x ∈.称)(x Φ叫做变上限定积分,有时又称为变上限积分函数.定理1:如果函数)(x f 在区间],[b a 上连续,则⎰=Φxadt t f x )()(在],[b a 上可导,且)()()()(b x a x f dt t f dxd x xa ≤≤==Φ'⎰定理2、3:如果)(x f 在区间],[b a 上连续,则它的原函数一定存在,且其中的一个原函数为⎰=Φxadt t f x )()(.2、牛顿——莱布尼茨公式定理4(微积分基本公式)如果函数)(x f 在区间],[b a 上连续,且)(x F 是)(x f 的任意一个原函数,那么⎰-=b aa Fb F dx x f )()()(.证 由定理5.2知,⎰=Φx adt t f x )()(是)(x f 在区间],[b a 的一个原函数,则)(x Φ与)(x F 相差一个常数C ,即C x F dt t f x a+=⎰)()(.又因为C a F dt t f a a+==⎰)()(0,所以)(a F C -=.于是有)()()(a F x F dt t f x a -=⎰.所以 ⎰-=baa Fb F dx x f )()()(成立.为方便起见,通常把)()(a F b F -简记为ba x F )(或b a x F )]([,所以公式可改写为)()()()(a F b F x F dx x f b a b a-==⎰三、定积分的积分法1、定积分的换元积分法定理1设函数)(x f 在区间],[b a 上连续,并且满足下列条件:(1))(t x ϕ=,且)(αϕ=a ,)(βϕ=b ;(2))(t ϕ在区间],[βα上单调且有连续的导数)(t ϕ';(3)当t 从α变到β时,)(t ϕ从a 单调地变到b . 则有⎰⎰'=b adt t t f dx x f βαϕϕ)()]([)(上述公式称为定积分的换元积分公式.在应用该公式计算定积分时需要注意以下两点:①从左到右应用公式,相当于不定积分的第二换元法.计算时,用 把原积分变量 换成新变量 ,积分限也必须由原来的积分限 和 相应地换为新变量 的积分限 和 ,而不必代回原来的变量 ,这与不定积分的第二换元法是完全不同的.②从右到左应用公式,相当于不定积分的第一换元法(即凑微分法).一般不用设出新的积分变量,这时,原积分的上、下限不需改变,只要求出被积函数的一个原函数,就可以直接应用牛顿—莱布尼兹公式求出定积分的值. 2、定积分的分部积分法设函数)(x u u =和)(x v v =在区间],[b a 上有连续的导数,则有)()()]()([)()(x du x v x v x u x dv x u bab ab a⎰⎰-=.上述公式称为定积分的分部积分公式.选取)(x u 的方式、方法与不定积分的分部积分法完全一样.四、定积分的应用1、定积分应用的微元法为了说明定积分的微元法,我们先回顾求曲边梯形面积A 的方法和步骤: (1)将区间],[b a 分成n 个小区间,相应得到n 个小曲边梯形,小曲边梯形的面积记为i A ∆),2,1(n i =;(2)计算i A ∆的近似值,即i i i x f A ∆≈∆)(ξ(其中],[,11i i i i i i x x x x x --∈-=∆ξ); (3)求和得A 的近似值,即i ni i x f A ∆≈∑=1)(ξ;(4)对和取极限得⎰∑=∆==→bai ni i dx x f x f A )()(lim 1ξλ.下面对上述四个步骤进行具体分析:第(1)步指明了所求量(面积A )具有的特性:即A 在区间],[b a 上具有可分割性和可加性.第(2)步是关键,这一步确定的i i i x f A ∆≈∆)(ξ是被积表达式dx x f )(的雏形.这可以从以下过程来理解:由于分割的任意性,在实际应用中,为了简便起见,对i i i x f A ∆≈∆)(ξ省略下标,得x f A ∆≈∆)(ξ,用],[dx x x +表示],[b a 内的任一小区间,并取小区间的左端点x 为ξ,则A ∆的近似值就是以dx 为底,)(x f 为高的小矩形的面积(如图5.7 阴影部分),即dx x f A )(≈∆.通常称dx x f )(为面积元素,记为dx x f dA )(=.将(3),(4)两步合并,即将这些面积元素在],[b a 上“无限累加”,就得到面积A .即⎰=ba dx x f A )(.一般说来,用定积分解决实际问题时,通常按以下步骤来进行: (1)确定积分变量x ,并求出相应的积分区间],[b a ;(2)在区间],[b a 上任取一个小区间],[dx x x +,并在小区间上找出所求量F 的微元dx x f dF )(=;(3)写出所求量F 的积分表达式⎰=ba dx x f F )(,然后计算它的值.利用定积分按上述步骤解决实际问题的方法叫做定积分的微元法. 注 能够用微元法求出结果的量F 一般应满足以下两个条件: ①F 是与变量x 的变化范围],[b a 有关的量;②F 对于],[b a 具有可加性,即如果把区间],[b a 分成若干个部分区间,则F 相应地分成若干个分量.2、定积分求平面图形的面积(1)直角坐标系下面积的计算(1)由曲线)(x f y =和直线0,,===y b x a x 所围成曲边梯形的面积的求法前面已经介绍,此处不再叙述.(2)求由两条曲线)(),(x g y x f y ==,))()((x g x f ≥及直线b x a x ==,所围成平面的面积A (如图5.8所示).下面用微元法求面积A . ①取x 为积分变量,],[b a x ∈.②在区间],[b a 上任取一小区间],[dx x x +,该区间上小曲边梯形的面积dA 可以用高)()(x g x f -,底边为dx 的小矩形的面积近似代替,从而得面积元素dx x g x f dA )]()([-=. ③写出积分表达式,即⎰-=badx x g x f A )]()([.⑶求由两条曲线)(),(y x y x ϕψ==,))()((y y ϕψ≤及直线d y c y ==,所围成平面图形(如图5.9)的面积. 这里取y 为积分变量,],[d c y ∈, 用类似 (2)的方法可以推出:⎰-=dcdy y y A )]()([ψϕ.(2)极坐标系下面积的计算设曲边扇形由极坐标方程)(θρρ=与射线)(,βαβθαθ<==所围成(如图5.13所示).下面用微元法求它的面积A.以极角θ为积分变量,它的变化区间是],[βα,相应的小曲边扇形的面积近似等于半径为)(θρ,中心角为θd 的圆扇形的面积,从而得面积微元为θθρd dA 2)]([21=于是,所求曲边扇形的面积为 ⎰=βαθθρd A 2)]([21.3.定积分求体积 (1)旋转体的体积旋转体是一个平面图形绕这平面内的一条直线旋转而成的立体.这条直线叫做旋转轴.设旋转体是由连续曲线)0)()((≥=x f x f y 和直线b x a x ==,及x 轴所围成的曲边梯形绕x 轴旋转一周而成(如图5.15).取x 为积分变量,它的变化区间为],[b a ,在],[b a 上任取一小区间],[dx x x +,相应薄片的体积近似于以)(x f 为底面圆半径,dx 为高的小圆柱体的体积,从而得到体积元素为dx x f dV 2)]([π=,于是,所求旋转体体积为dx x f V bax ⎰=2)]([π.(2)平行截面面积为已知的立体体积设一物体被垂直于某直线的平面所截的面积可求,则该物体可用定积分求其体积.不妨设直线为x 轴,则在x 处的截面面积)(x A 是x 的已知连续函数,求该物体介于a x =和)(b a b x <=之间的体积(如图5.19).取x 为积分变量,它的变化区间为],[b a ,在微小区间],[dx x x +上)(x A 近似不变,即把],[dx x x +上的立体薄片近似看作)(x A 为底,dx 为高的柱片,从而得 到体积元素dx x A dV )(=.于是该物体的体积为⎰=badx x A V )(.类似地,由曲线)(y x ϕ=和直线d y c y ==,及y 轴所围成的曲边梯形绕y 轴旋转一周而成(如图5.16),所得旋转体的体积为dy y V dcy ⎰=2)]([ϕπ.。
(完整版)高等数学中有理分式定积分解法总结.doc

由十个例题掌握有理分式定积解法【摘要】 当被积函数为两多项式的商P(x)的有理函数时,解法各种各样、不易掌握,Q( x)在此由易到难将其解法进行整理、总结【关键词】有理分式 真分式 假分式 多项式除法 拆项法 凑微分法 定积分两个多项式的商P xP x称为有理函数,又称为有理分式,我们总假定分子多项式Q x与分母多项式 Q x 之间无公因式,当分子多项式P x 的次数小与分母多项式Q x ,称有理式为真分式,否则称为假分式.1. 对于假分式的积分: 利用多项式除法, 总可将其化为一个多项式与一个真分式之和的形式 .例3x 4 2x 21.1x 2 1dx解 原式3x 2 x21 x 2x21dx3x2dx x 2 dxx 2 13 x2dx 1 x 2 1 dx1 3 x2dx dx1 dxx 3 x21x arctanx C2x 4x 2 3 例 1.221 dxx2x 2 x 2 13 x2 dx解 原式x212 x 2dx 31 1 dx x2 dxx 2x 2 12 x 34arctan x x C31总结:解被积函数为假分式的有理函数时, 用多项式出发将其化简为多项式和真分式之和的形式,然后进行积分 . 对于一些常见函数积分进行记忆,有助于提高解题速度,例如:x 2 dx1 1dxx 2 1 x 2 1P x 对于真分式,若分母可分解为两个多项式乘积Q x = Q 1 x Q 2 x ,且 Q 1x ,Q xP x P xP xQ 2 x 无公因式,则可拆分成两个真分式之和:12,上述过程称为Q xQ 1 x Q 2x把真分式化为两个部分分式之和. 若 Qx 或 Q x 再分解为两个没有公因式的多项式乘12积,则最后有理函数分解式中出现多项式、P 1 xk、P 2 x 等三类函数,则多项xx 2px la q式的积分容易求的2. 先举例,有类型一、类型二、类型三,以此为基础求解较复杂的真分式积分2.1类型一(ax b) mdxcxkx31dx例 2.1.1x2解 原式 =x 33x23x1dxx 2= xdx3 dx 31dx 1dxx x 2= 1x 2 3x 3In x 1 C 2x总结:当被积函数多项式与单项式相乘的形式,将其进行化简,使被积函数为简单幂函数,然后利用常见积分公式进行运算2.2类型二cx kax m dxbx 2例 2.2.13 dxx2解 令 x+2=t , 则 xt 2 , 有 dx dt2t 2原式 = 2dxt 3= t24t4dtt 3= 14 11 dt t2 dt43 dttt=Int+ 4 - 2+Ct t 2=I n x 242Cx 2x 2 2总结:当被积函数形如时cxkm dx ,将其用换元法转换为ax b解法求解2.3 类型三P x l dxax 2bx c例 2.3.1x 32dxx 22x2原式 =x 32 dtx 1 21设=tant,x=tant+1,dx=set2x-1tdt3上式 =1+tantset 2tdtset 2t= tan 3 t 3tan 2 t 3tan t 1dtset 2t = sin 3 t cos 1 t 3sin t cost 3sin 2 t cos 2 t dtm(axb)dx ,再按照后者cx k=- 1 cos 2t costd cost +3sin 2tdt dt cos2tdt4=-Incost + 1cos 2t+2t+2sintcost2 1x 1Q tant=x-1, cost=2,sint= 2x 1 1x1 1上式122x 22 x 214 2arctan x 1 x 2 2x 2C= 2 In x4x 2x 23例2.3.2x 1 dxx 2 2x132x22=2dx22x 3x=1x 21 3 d x 22x 3 -212 dx 2 2 xx 1 2= 1In x22x 3 - 2arttanx 1+C22总结:当被积函数分母含有 ax 2 +bx+c 时,可以用凑微分法进行积分 ;对于形如 ax 2 lbx+c 时,可将其变形为 T 2 x +1或者是1-T 2 x ,然后利用三角函数恒等变形 sin 2x+cos 2x=1和1+tan 2x=set 2x 将T 2 x 降次,便于计算 .3. 以前面的几种简单类型为基础,现在来讨论较为复杂的有理真分式的积分例 3.1 2x+3dx2 3x 10x解法 12x+3 dx2 3x 10x =x 21d x 2 3x 103x 10=In x 23x 10 +C解法 22x+3dxx 23x102x+3 10 = 2x+3 = A + B 2 x 2 3x x+5 x 2 x 5 x =A B x 5B 2A1 1x 5 x 2x 5 x 2原式 =11dxx5 x 2=In x 23x 10 +C总结: 假分式分母可以因式分解, 将被积函数化为部分分式之和的形式, 然后用基本积分公4式进行运算 .x2 dx例 3.22x 1x 2 x 1原式 =2xdx2x 1 x 2 x111 2x 1 1=d 2x 1 - 2x 2 x 2dx 2x 11=1 d 2x 11x21 d x 2x 1112dx 2x 12 x121 3x24=In2x 1 - 1In x2x 1+ 1arctan x1+C232总结:遇到被积函数是复杂的有理函数,用拆分法将其分解为自己熟悉的函数,灵活变换.x 3dx 例 3.3x 2x 1 1=x 3dxx 2x11x 2 1 dxx 2 2x 1 x11 2x 2112 dxx 22xdx1 x11 x2 1 d x22x 11 2 dx1dx 2 2x 1x 1x1Inx1 x 1 Cx 11总结: 此题能够得出一个重要结论, 分母因式分解要求为各个因式之间无公约数,以此为标 准进行因式分解,拆项除此之外, 常见的还有, 可化为有理函数的积分 . 例如利用三角函数的万能公式,将被积函数中含有三角函数的分式函数,例:1+sin xdx . 例如被积函数中含有cos xsin x 1nax b 或 nax b时用换元法将根号去掉,例:x 1 xdx , 1dx . 虽然形式cxd1 x3x15各种各样 , 但只要熟练掌握以上各种类型的积分,那么在被积函数为有理分式函数时应对起来应当是信手拈来,甚是轻松6。
定积分知识点

定积分知识点定积分是微积分中非常重要的概念之一。
它在实际问题的建模和求解中起着至关重要的作用。
本文将介绍定积分的基本定义、性质以及一些常见的应用。
1. 定积分的基本定义定积分是函数积分学的重要概念,它可以将函数的定义域上的函数值从一个点到另一个点的累加。
设函数f(x)在闭区间[a, b]上有定义,将[a, b]分成n个小区间,其中第i个小区间的长度为Δx_i,选择每个小区间中任意一点ξ_i,称为取样点。
则定义Δx_i乘以f(ξ_i)的和对应的极限值,当区间的个数趋向于无穷大时,即Δx_i趋于0,就得到了函数f(x)在闭区间[a, b]上的定积分。
定积分的数值即为积分的结果。
2. 定积分的性质定积分具有一些重要的性质,下面我们简要介绍其中的几个。
2.1 可加性设函数f(x)在区间[a, b]上可积,如果将该区间分成两个子区间[a, c]和[c, b],则有定积分的可加性质,即∫[a, c]f(x)dx + ∫[c, b]f(x)dx = ∫[a, b]f(x)dx。
这个性质可以推广到多个子区间的情况。
2.2 线性性质定积分还具有线性性质。
即对于任意的实数k、l,函数f(x)和g(x)在区间[a, b]上可积,则有∫[a, b](k*f(x) + l*g(x))dx = k * ∫[a,b]f(x)dx + l * ∫[a, b]g(x)dx。
2.3 积分中值定理如果函数f(x)在闭区间[a, b]上连续,则存在一个点ξ∈[a, b],使得∫[a, b]f(x)dx = f(ξ) * (b - a)。
这个定理说明了定积分与函数在区间上的平均值的关系。
3. 定积分的应用定积分在各个领域都有广泛的应用。
下面我们介绍一些常见的应用。
3.1 几何应用通过定积分可以计算曲线与坐标轴所围的区域面积。
例如,如果给定函数f(x),在区间[a, b]上,可以通过定积分∫[a, b]f(x)dx来计算曲线y=f(x)与x轴之间的面积。
(完整版)定积分知识点总结,推荐文档

多加了 k 个新分店,则
S( , f ) S( ', f ) S( , f ) k || ||, S( , f ) S( ', f ) S( , f ) k || ||,
这里 M m, M , m 分别为 f 在[a,b]上的上、下确界.
推论 2 设 f(x)在[a,b]上有界. 对于任意两个分割 , ' ,有
定理 对于 f(x)在[a,b]上的有界函数,则有
lim S( , f ) I , lim S( , f ) I.
|| ||0
|| ||0
3.函数可积分条件 设 f(x)在[a,b]上有界,下列命题等价:
(1)f(x)在[a,b]可积;
(2) I I;
n
(3)对于[a,b]上的任何一个分割
n
n
S ( , f ) M i (xi xi1), S ( , f ) mi (xi xi1)
i 1
i 1
S( , f ) 称为 f(x)相应于分割 π 的达布上和, S( , f ) 称为 f(x)相应于分割 π 的达布下
和
特别地,当 f(x)连续时,这些和就直接是相应于任意分割法的积分和的最小者和最
原函数,则上述公式化为
b f (x)dx f ( )(b a), (a,b) a
这一类公式称之为积分中值公式,它显示出一个函数的定积分可以通过其自身进行
表达和估算.
上述公式的几何意义可以从面积的意义来考察:设 f(x)是[a,b]上的正值连续函数,则 公式左边的面积与右边表达式所代表的举矩形面积相等,而矩形的高 f ( ) 正是 f(x) 在
b
1 定积分中变量替换公式 设要计算积分 f (x)dx ,这里 f(x)是在区间[a,b]内连续的.
定积分知识点总结396

定积分知识点总结3961. 定积分的概念定积分是函数 f(x) 在区间 [a, b] 上的积分,表示为∫[a,b] f(x) dx。
其含义为将区间 [a, b] 划分成 n 个小区间,然后在每个小区间上取一个代表点 xi,利用这些代表点折线逼近函数曲线下方的面积,然后求和,将 n 趋于无穷大时所得到的极限就是定积分。
2. 定积分的性质(1)定积分的可加性:∫[a,b] (f(x) + g(x)) dx = ∫[a,b] f(x) dx + ∫[a,b] g(x) dx(2)定积分的线性性:∫[a,b] (k·f(x)) dx = k·∫[a,b] f(x) dx(3)定积分的保号性:若在区间 [a, b] 上有f(x) ≥ 0,则∫[a,b] f(x) dx ≥ 0(4)定积分的估值性:若在区间 [a, b] 上有f(x) ≤ g(x),则∫[a,b] f(x) dx ≤ ∫[a,b] g(x) dx3. 定积分的计算方法(1)定积分的计算基本原则是将区间 [a, b] 分成若干个子区间,然后在每个子区间上取代表点,利用这些代表点折线逼近函数曲线下方的面积,最后求和得到近似解,然后通过极限来求得定积分的真实值。
(2)对于一些简单的函数,可以直接利用积分表求得定积分的解析解。
例如,对于多项式、三角函数、指数函数等常见函数,都可以直接在积分表中查找对应的积分公式进行计算。
4. 定积分的应用定积分在实际生活中有着广泛的应用,常见的应用包括:(1)计算曲线与坐标轴所围成的图形的面积。
这是定积分最基本的应用之一,可以用来计算椭圆、抛物线、双曲线等图形的面积。
(2)计算质心。
利用定积分可以求得图形的质心坐标,对于物体的平衡问题具有重要的意义。
(3)计算弧长。
利用定积分可以求得曲线的弧长,对于工程领域的曲线设计有重要的应用。
(4)计算体积。
利用定积分可以求得旋转曲线所围成的立体的体积,对于工程、物理等领域有着重要的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定积分
一.定积分的几何意义
①
b
f ( x) 0 时, f (x)dx S
a
b
f ( x) 0 时, f (x)dx S
a
f(x) 有正有负时,
b c d
a f ( x)dx S1, f ( x)dx S2 , f ( x)dx S3
b c
d b c d
f ( x)dx
a
面积和 S1
二.定积分基本性质
①当 a b 时,b
f ( x)dx 0. a
b b
② kf ( x) dx k f (x)dx
a a
b b
f (x)dx f ( x)dx f (x)dx S1 S2 S3.
a b c
b c d
S2 S3
a
f (x)dx f (x)dx f (x)dx
b c
b
[ f ( x) g(x)] dx S
a
b b
③[ f1 ( x) f 2 ( x) f n (x)]dx f1 ( x)dx f 2 (x)dx f n (x)dx
a a a a
b c1 c2 b f ( x)dx
④ f (x)dx f ( x)dx f (x)dx
a a c1 c n
a
⑤若奇函数
⑥若偶函数y f ( x) 在 [a, a]
y f ( x) 在 [a, a]
上连续不断,则 f (x)dx 0
a
a
f (x)dx a
上连续不断,则 2 f ( x)dx
a 0
微分基本定理: 如果 f ( x) 是区间 [ a, b] 上的连续函数,且 F '( x)
f ( x) ,则
b a
b
F (b) F (a) (牛顿—莱布尼兹公式)
f ( x)dx F ( x)
a
1. 直线 x 0, x , y 0 与曲线 y sin x 所围成图形的面积用定积分表示为
2. 用定积分表示抛物线
y x 2 2x 3 与直线 y
x 3 所围成图形的面积为
3. 曲线 y
x 2 1, x 2, x 0, y
0 围成的阴影部分的面积用定积分表示为
4. 由曲线 y x 2
4, x
4, x 0, y 0 和 x 轴围成的封闭图形的面积是( )
4
4) dx
4
(x
2
4)dx |
A. ( x 2
B.| 0
4
4 | dx
2
4
4) dx
C. | x 2
D . (x 2
4) dx( x 2 0
2
5. 计算下列定积分
3
1
2
dx
(1)9 x 2
dx
( 2)4 4x
3
1
2
1 dx 1
(3)( 4)(2 x e x)dx
1 x( x 1) 0
(5)cos2x
dx 9 ( 6)x(1 x) dx
0 2 1
6. 正方形的四个顶点A( 1, 1), B(1, 1),C (1,1),D ( 1,1)分别在抛物线 y
2 2 x 和 y x
上,如图,若将一质点随机投入正方形ABCD 中,则质点落在图中阴影区域的概率是7. 已知函数y x2与 y kx 的图象所围成的阴影部分的面积是 4 , 则k
3
8. 求曲线y24x 与直线 y 2x 4 围成的图形面积
9. 已知函数f ( x) x3 ax 2 bx 的图象如图所示,它与直线y 0 在原点处相切,此切线
与函数图象所围区域的面积是27
, 求 a . 4。
