应用光学【第二章】习题第一部分
《应用光学》第2章课后答案全文

12. 由两个透镜组成的一个倒像系统,设第一组透镜的焦距 为f1′,第二组透镜的焦距为f2′,物平面位于第一组透镜 的物方焦面上,求该倒像系统的垂轴放大率。
解:
1
1
1
1
F2
1
1
第一组透镜
第二组透镜
1
第二组透镜
13. 由两个同心的反射球面(二球面球心重合)构成的光学系 统,按照光线反射的顺序第一个反射球面是凹的,第二个 反射球面是凸的,要求系统的像方焦点恰好位于第一个反 射球面的顶点,求两个球面的半径r1,r2和二者之间的间隔 d之间的关系。
B′
面,如图示.
l ′ = 2f′
4 试用作图法对位于空气中的正透镜组( f 0 )分别求 下列不同物距的像平面位置.
l = −f′
B
……
F
F′
A
H H′
像平面在像 空间无限远 处.
l′=∞
4 试用作图法对位于空气中的正透镜组( f 0 )分别求 下列不同物距的像平面位置.
l f' 2
B′
r1 无穷远物点
r2
r1/2
最终像点
11 2
l2 l2 r2
l2
l2
2 r2
(l2l2 )
14. 假定显微镜物镜由相隔20mm的两个薄透镜组构成,物平 面和像平面之间的距离为180mm,放大率β=-10×,要求近 轴光线通过二透镜组时的偏角Δu1和Δu2相等,求二透镜 组的焦距。
y n1u1 u1 10
l = −f′
B
……
F′
F
H H′
A
像平面在像 空间无限远 处.
5 试用作图法对位于空气中的负透镜组( f 0 )分别求 下列不同物距的像平面位置.
应用光学习题(第二章)

个面对不晕像点。
n2 n2 n 1 l2 r2 r2 n2 n n2 n2 l2 r2 n 1r2 n2
1 n n 1 n 1 r1 - r2 r1 r2 n n n 由于 d始终都是大于零的,所 以r1 r2 (由于 r1 0,r2 0,且 r1 r2,该透镜为负弯月型透 镜)
1 n2
S1
S1与S2重合,所以 r2 l2 l2
d l1 l2
n
r1
C1 l2 l2 l1 r2 l1
C2
n1 n1 1 n 而 l1 r1 r1 n1 n 1 n d r1 r2 n
b. 同心球面透镜 物像点重合且位于两个 球面的共同曲率中心 C1,C 2点上Leabharlann 所以编号出处
2_004
P193_7
什么是不晕透镜?当透 镜成无球差点实像点时 ,应采用 什么样的结构形式 ?
答: ( 1)所谓不晕透镜,是轴 上物点单色光成像时, 不产生球差的透镜
(2) 由于不晕条件,物象点 在透镜的同一侧,所以 不晕透镜 分为两种情况:一种是 实物成虚像,而另一种 是虚物成实像。 该题中得到实像点时, 采用的就是虚物成实像 的形式(会聚光入射) r1 0,r2 0 a. 正弯月单透镜 r1 r2 r1 r2,所以第一个面对球心 C 1点在 C2点的左边
,S2,S 同心球面透镜构成不晕 透镜C ( ,S1,S1 2 C1 2)
n1 1
1 n2
C1 C2
n
r1 l1 l1 r2 l2 l2
,S2与S2重合 S1,S1 d r1 r2
编号
出处
2_005
应用光学作业题答案

第二题: (1)光线由水中射向空气,求在界面处发生全反射的临界角。
解: 全反射的临界角Im arcsin(n '/ n)
光线由水中射向空气,n’=1,n=1.333
则 Im arc sin(n '/ n)=arc sin(1/1.333)=48.61
(2)光线由玻璃内部射向空气,求发生全反射的临界角。
1 l2
'
-
1 130
=
1 120
l2'=-62.4mm
A”成象于透镜2左侧62.4mm处。
(2)等效光组成象的方法:
解: H’
A
F1
F2’
F1’
F2
f1’=120mm f2’=-120mm d=70mm △= d-f1’- f2’=70mm
f ' f1 ' f2 ' 120 (120) 205.714mm
n0sini1=nsini1’ sini1=0.6552 i1=40.93° 由三角形内角和可求出太阳和幻
日之间的夹角
α=180 °-2×(i1-i1’) =158.14 °
第七题:
为了从坦克内部观察外界目标,需要在坦克上开一个孔,假 定坦克壁厚250mm,孔宽150mm,在孔内装一块折射率 n=1.52的玻璃,厚度与装甲厚度相同,问能看到外界多大的 角度范围?
O’
A’
解:(1)对于在球心的气泡,以O作为 球面顶点,根据符号规则,
O L’A=-200mm,n’=1,n=1.52
由 n ' n n ' n l' l r
1 -1.52 = 1-1.52 l=-200mm -200 l -200
应用光学习题集答案

应⽤光学习题集答案习题第⼀章1、游泳者在⽔中向上仰望,能否感觉整个⽔⾯都是明亮的?(不能,只能感觉到⼀个明亮的圆,圆的⼤⼩与游泳都所在的⽔深有关,设⽔深H ,则明亮圆半径HtgIc R =)2、有时看到窗户玻璃上映射的太阳光特别耀眼,这是否是由于窗玻璃表⾯发⽣了全反射现象?答:是。
3、⼀束在空⽓中波长为nm 3.589=λ的钠黄光从空⽓射⼊⽔中时,它的波长将变为多少?在⽔中观察这束光时其颜⾊会改变吗?答:'λλ=n ,nm 442'=λ不变 4、⼀⾼度为m 7.1的⼈⽴于路灯边(设灯为点光源)m 5.1远处,路灯⾼度为m 5,求⼈的影⼦长度。
答:设影⼦长x ,有:57.15.1=+x x ∴x=0.773m 5、为什么⾦钢⽯⽐磨成相同形状的玻璃仿制品显得更加光彩夺⽬?答:由于⾦钢⽯折射率⼤,所以其临界⾓⼩,⼊射到其中的光线⼤部分都能产⽣全反射。
6、为什么⽇出或⽇落时太阳看起来稍微有些发扁?(300例P1)答:⽇出或⽇落时,太阳位于地平线附近,来⾃太阳顶部、中部和底部的光线射向地球⼤⽓层的⼊射⾓依次增⼤(如图)。
同时,⼤⽓层密度不均匀,折射率⽔接近地⾯⽽逐渐增⼤。
当光线穿过⼤⽓层射向地⾯时,由于n 逐渐增⼤,使其折射⾓逐渐减⼩,光线的传播路径就发⽣了弯曲。
我们沿着光线去看,看到的发光点位置会⽐其实际位置⾼。
另⼀⽅⾯,折射光线的弯曲程度还与⼊射⾓有关。
⼊射⾓越⼤的光线,弯曲越厉害,视觉位置就被抬得越⾼,因为从太阳上部到下部发出的光线,⼊射⾓依次增⼤,下部的视觉位置就依次⽐上部抬⾼的更多。
第⼆章1、如图2-65所⽰,请采⽤作图法求解物体AB的像,设物像位于同⼀种介质空间。
图2-652、如图2-66所⽰,'MM 为⼀薄透镜的光轴,B 为物点,'B 为像点,试采⽤作图法求解薄透镜的主点及焦点的位置。
BM B 'M ′ B M M ′B ' ●●●●(a) (b)图2-663、如图2-67所⽰,已知物、像的⼤⼩及位置,试利⽤图解法求解出焦点的位置,设物、像位于同⼀种介质空间。
物理光学与应用光学习题解第二章

第二章习题2-1. 如图所示,两相干平行光夹角为α,在垂直于角平分线的方位上放置一观察屏,试证明屏上的干涉亮条纹间的宽度为: 2sin2αλ=l 。
2-2. 如图所示,两相干平面光波的传播方向与干涉场法线的 夹角分别为0θ和R θ,试求干涉场上的干涉条纹间距。
2-3. 在杨氏实验装置中,两小孔的间距为0.5mm ,光屏离小孔的距离为50cm 。
当以折射率为1.60的透明薄片贴住小孔S2时,发现屏上的条纹移动了1cm ,试确定该薄片的厚度。
2-4. 在双缝实验中,缝间距为0.45mm ,观察屏离缝115cm ,现用读数显微镜测得10个条纹(准确地说是11个亮纹或暗纹)之间的距离为15mm ,试求所用波长。
用白光实验时,干涉条纹有什么变化?2-5. 一波长为0.55m μ的绿光入射到间距为0.2mm 的双缝上,求离双缝2m 远处的观察屏上干涉条纹的间距。
若双缝距离增加到2mm ,条纹间距又是多少?2-6. 波长为0.40m μ~0.76m μ的可见光正入射在一块厚度为1.2×10-6 m 、折射率为1.5的薄玻璃片上,试问从玻璃片反射的光中哪些波长的光最强?2-7. 题图绘出了测量铝箔厚度D 的干涉装置结构。
两块薄玻璃板尺寸为75mm ×25mm 。
在钠黄光(λ=0.5893m μ)照明下,从劈尖开始数出60个条纹(准确地说是从劈尖开始数出61个明条纹或暗条纹),相应的距离是30mm ,试求铝箔的厚度D = ?若改用绿光照明,从劈尖开始数出100个条纹,其间距离为46.6 mm ,试求这绿光的波长。
2-8. 如图所示的尖劈形薄膜,右端厚度h 为0.005cm ,折射率n = 1.5,波长为0.707m μ的光以30°角入射到上表2-1题用图2-2题用图2-7题用图2-8题用图面,求在这个面上产生的条纹数。
若以两块玻璃片形成的空气尖劈代替,产生多少条条纹?2-9. 利用牛顿环干涉条纹可以测定凹曲面的曲率半径,结构如图所示。
《应用光学》第2章课后答案解析

l = 2f′
B F′ B′ A A′ H H′
F
像平面为 A’B’所在平 面,如图示.
5 试用作图法对位于空气中的负透镜组( f 0 )分别求 下列不同物距的像平A′ H
H′
F
像平面为 A’B’所在平 面,如图示.
5 试用作图法对位于空气中的负透镜组( f 0 )分别求 下列不同物距的像平面位置.
第二章 部分习题答案
牛顿公式 一、物像位置关系 二、物像大小关系 1、垂轴放大率 2、轴向放大率 3、角放大率 三、物方像方焦距关系 四、物像空间不变式
f' n' f n
y nl y nl
高斯公式
f' f 1 l' l
nuy n' u' y'
2. 有一放映机,使用一个凹面反光镜进行聚光照明,光源经过反
f' l 2
B
B′ A F′ A′ H H′
F
像平面为 A’B’所在平 面,如图示.
5 试用作图法对位于空气中的负透镜组( f 0 )分别求 下列不同物距的像平面位置.
l=0
B
B′
F′ H A
A′ H′
F
像平面为: 像方主平面
5 试用作图法对位于空气中的负透镜组( f 0 )分别求 下列不同物距的像平面位置.
考虑物镜组二主面之间的距离)。 解:
9. 已知航空照相机物镜的焦距f′=500mm,飞机飞行高度为
6000m,相机的幅面为300×300mm2,问每幅照片拍摄的地
面面积。 解:
10. 由一个正透镜组和一个负透镜组构成的摄远系统,前组
正透镜的焦距f1′=100,后组负透镜的焦距f2 ′=-50,要 求由第一组透镜到组合系统像方焦点的距离D与系统的组合 焦距之比为1∶1.5,求二透镜组之间的间隔d应为多少?组 合焦距等于多少?
物理光学与应用光学习题解第二章
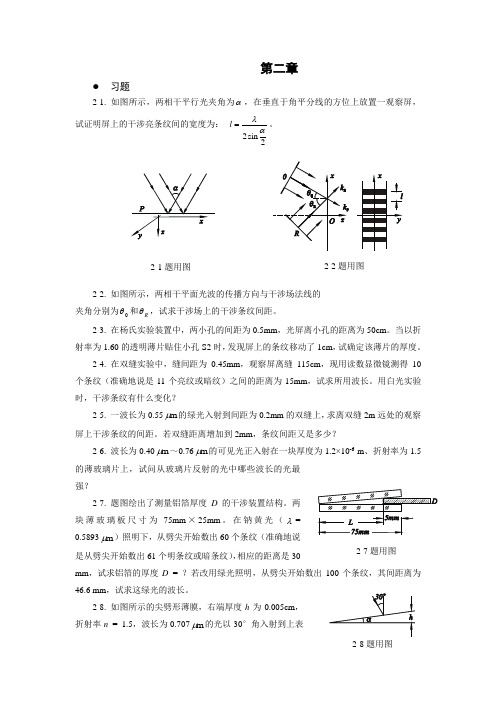
第二章习题2-1. 如图所示,两相干平行光夹角为α,在垂直于角平分线的方位上放置一观察屏,试证明屏上的干涉亮条纹间的宽度为: 2sin2αλ=l 。
2-2. 如图所示,两相干平面光波的传播方向与干涉场法线的 夹角分别为0θ和R θ,试求干涉场上的干涉条纹间距。
2-3. 在杨氏实验装置中,两小孔的间距为0.5mm ,光屏离小孔的距离为50cm 。
当以折射率为1.60的透明薄片贴住小孔S2时,发现屏上的条纹移动了1cm ,试确定该薄片的厚度。
2-4. 在双缝实验中,缝间距为0.45mm ,观察屏离缝115cm ,现用读数显微镜测得10个条纹(准确地说是11个亮纹或暗纹)之间的距离为15mm ,试求所用波长。
用白光实验时,干涉条纹有什么变化?2-5. 一波长为0.55m μ的绿光入射到间距为0.2mm 的双缝上,求离双缝2m 远处的观察屏上干涉条纹的间距。
若双缝距离增加到2mm ,条纹间距又是多少?2-6. 波长为0.40m μ~0.76m μ的可见光正入射在一块厚度为1.2×10-6 m 、折射率为1.5的薄玻璃片上,试问从玻璃片反射的光中哪些波长的光最强?2-7. 题图绘出了测量铝箔厚度D 的干涉装置结构。
两块薄玻璃板尺寸为75mm ×25mm 。
在钠黄光(λ=0.5893m μ)照明下,从劈尖开始数出60个条纹(准确地说是从劈尖开始数出61个明条纹或暗条纹),相应的距离是30mm ,试求铝箔的厚度D = ?若改用绿光照明,从劈尖开始数出100个条纹,其间距离为46.6 mm ,试求这绿光的波长。
2-8. 如图所示的尖劈形薄膜,右端厚度h 为0.005cm ,折射率n = 1.5,波长为0.707m μ的光以30°角入射到上表2-1题用图2-2题用图2-7题用图2-8题用图面,求在这个面上产生的条纹数。
若以两块玻璃片形成的空气尖劈代替,产生多少条条纹?2-9. 利用牛顿环干涉条纹可以测定凹曲面的曲率半径,结构如图所示。
应用光学第二章-1

述定义称为共线成像理论。
第二节 理想光学系统的基点与基面
共轴球面系统: 球面的曲率中心在同一轴线上的光学系统
前面讨论的单个折射球面的光路计算及成像特 性,对构成光学系统的每个球面都适用。
只要找到相邻球 面之间的关系,就可 以解决整个光学系统 的光路计算问题。
的物方焦点。
Q E’ E
F
-U
H
-f
B
h
E’B的反向延长线与FE交于Q,
过Q点做与光轴垂直的平面,与光轴交于 H点。
※ 则QH平面称为物方主平面,H点称为物方主点。 ※从物方主点H 到物方焦点F 之间的距离称为物方焦距,
用 f 表示
f 也遵从符号规则,它的起始原点是物方主点H。这里为- f
(五)物方主平面与像方主平面之间的关系
※ F ’ 就是无限远轴上物点的像点,称像方焦点
A
E
Q ’ E’
h
H’
U’
F’
※ 过F ’ 点作垂直于光轴的平面,称为像方焦平面
它是无限远处垂直于光轴的物平面的共轭像平面
将AE延长与出射光线E’F ’的反向延长线交于Q’
通过Q’点作垂直于光轴的平面交光轴于H’点,
※ 则Q’H’平面称为像方主平面,H’称为像方主点
不与主点重合。 原因:n ≠ n’
同理,对于反射球面,同样有:
l’ = l = r
单个反射球面的一对节点(J 、J’)均位于球心C。
由于单个折(反)射球面在近轴区可以看成是理想光组, 因此它的成像特性可以应用理想光组中的所有公式
注意:两边折射率不同!切勿采用光组位于同一介质
中的公式!
折射:n , n’ 反射:n , - n
物理光学与应用光学习题解第二章

第二章习题2-1. 如图所示,两相干平行光夹角为α,在垂直于角平分线的方位上放置一观察屏,试证明屏上的干涉亮条纹间的宽度为: 2sin2αλ=l 。
2-2. 如图所示,两相干平面光波的传播方向与干涉场法线的 夹角分别为0θ和R θ,试求干涉场上的干涉条纹间距。
2-3. 在杨氏实验装置中,两小孔的间距为0.5mm ,光屏离小孔的距离为50cm 。
当以折射率为1.60的透明薄片贴住小孔S2时,发现屏上的条纹移动了1cm ,试确定该薄片的厚度。
2-4. 在双缝实验中,缝间距为0.45mm ,观察屏离缝115cm ,现用读数显微镜测得10个条纹(准确地说是11个亮纹或暗纹)之间的距离为15mm ,试求所用波长。
用白光实验时,干涉条纹有什么变化?2-5. 一波长为0.55m μ的绿光入射到间距为0.2mm 的双缝上,求离双缝2m 远处的观察屏上干涉条纹的间距。
若双缝距离增加到2mm ,条纹间距又是多少?2-6. 波长为0.40m μ~0.76m μ的可见光正入射在一块厚度为1.2×10-6 m 、折射率为1.5的薄玻璃片上,试问从玻璃片反射的光中哪些波长的光最强?2-7. 题图绘出了测量铝箔厚度D 的干涉装置结构。
两块薄玻璃板尺寸为75mm ×25mm 。
在钠黄光(λ=0.5893m μ)照明下,从劈尖开始数出60个条纹(准确地说是从劈尖开始数出61个明条纹或暗条纹),相应的距离是30mm ,试求铝箔的厚度D = ?若改用绿光照明,从劈尖开始数出100个条纹,其间距离为46.6 mm ,试求这绿光的波长。
2-8. 如图所示的尖劈形薄膜,右端厚度h 为0.005cm ,折射率n = 1.5,波长为0.707m μ的光以30°角入射到上表2-1题用图2-2题用图2-7题用图2-8题用图面,求在这个面上产生的条纹数。
若以两块玻璃片形成的空气尖劈代替,产生多少条条纹?2-9. 利用牛顿环干涉条纹可以测定凹曲面的曲率半径,结构如图所示。
物理光用与应用光学习题解答(整理后全)

1-1.计算由 E = ( -2i + 2 3 j ) exp éi ( 3 x + y + 6 ´ 108 t ) ù 表示的平面波电矢量的振动方向、
ê ë
ú û
传播方向、相位速度、振幅、频率、波长。 解:由题意: E x = -2e
i ( 3 x + y + 6 ´ 108 t )
解: (1)∵ k = w / v ∵ k = 2p / l ∴ vg = v - l ∴ vg =
d (kv) dv =v+k dk dk
∴ dk = -( 2p / l2 ) dl
dv b 2l =v-l dl c 2 + b 2 l2
2 2
= c +b l 2
b 2 l2 c 2 + b 2 l2
1-4 题用图 - 2( Ex '2 sin a cos a - E y '2 sin a cos a + E x ' E y ' cos 2 a - E x ' E y ' sin 2 a ) E x 0 E y 0 cos j = E 2 E2 sin 2 j x0 y0 ( E x '2 cos 2 a + E y '2 sin 2 a - E x ' E y ' sin 2a ) E 2 + ( E x '2 sin 2 a + E y '2 cos 2 a + E x ' E y ' sin 2a ) E 2 y0 x0
i ( 3 x + y + 6 ´ 108 t )
v v ky = 1
应用光学第二章例题

第二章 例 题例题2.1 凸平透镜r 1=100mm ,r 2=∞,d=300mm ,n=1.5,当物体在-∞时候,1)求高斯像面的位置;2)在平面上刻十字,问其共轭像在什么位置;3)当入射高度为h=10mm ,问光线的像方截距是多少?和高斯像面相比相差多少?说明什么问题?解:1)根据近轴光线光路计算公式可以求出高斯像面的位置。
将1111,' 1.5,1,100l n n r mm =-∞===代入单个折射球面成像公式'''n n n n l l r--=,可以求得1'300l mm =。
又由题意d=300mm ,发现此时所成的像在凸平透镜的第二面上。
2)由光路可逆原理知道,若在平面上刻十字,其共轭像应在物方 -∞处。
3)当入射高度为h=10mm 时,光路如下图所示:此时利用物在无限远时,L =−∞时, 公式sin sin 'sin '''sin ''(1)sin 'h I r n I I n U U I I I L r U ⎧=⎪⎪⎪=⎪⎨⎪=+-⎪⎪=+⎪⎩中的第一和第四式求解得: ※ 光线经过第一面折射时,11110sin 0.1100h I r ===,所以1 5.739o I =。
又11111sin 'sin 0.10.06667' 1.5n I I n ==⨯=,所以1'arcsin 0.06667 3.822o I ==,1111''(0 5.739 3.822) 1.9172o o U U I I =+-=+-=,1111sin '0.0667'11001299.374sin '0.0334547I L r mm U ⎛⎫⎛⎫=⨯+=⨯+= ⎪ ⎪⎝⎭⎝⎭。
※ 光线再经过第二个面折射,21'0.626L L d mm =-=-,21' 1.9172o I U -==,则2222sin 'sin 1.5sin1.91720.05018'o n I I n ==-=-,2' 2.87647o I =-。
应用光学-第二章(1)

※ 物所在的空间为物空间,像所在的空间为像空间, 两者的范围都是(-∞,+∞)
物空间
像空间
物空间
两者可以重叠 像空间
※ 通常对于某一光学系统来说,某一位 置上的物会在一个相应的位置成一个清晰的 像,物与像是一一对应的,这种关系称为物 与像的共轭。
§2-3 共轴球面系统中的光路计算公式
(§2-1)
在光学仪器中 最常用的光学 零件是透镜, 目前绝大多数 是球面透镜 (系统)。 双凸 正月牙 平凸
由这些球面系 统(透镜)组 成的光学系统 有对称轴,也 称为共轴球面
系统
平凹
负月牙
双凹
• 由两个球面构成的透镜中,通过两球面球心 的直线为光轴。
光轴与透镜面的交点称为:顶点
光轴
顶点
• 若有一个面为平面,则光轴通过球面的球心 与平面垂直。
则大L公式可写成:
Lr sin I sin U r n sin I ' sin I n'
U' U I I'
lr i u r
n i' i n' u' u i i'
sin I ' L' r( 1 ) sinU '
i' l' r( 1 ) u'
称为小 l 公式
正向光路 反向光路
(二)线段
1. 沿轴线段,从起点(原点)到终点的方向与光线 传播方向相同,为正;反之为负。
即线段的原点为起点,向右为正,向左为负。
原点
+
-
原点
※ 原点规定:
(1)曲率半径 r ,以球面顶点O为原点,球 心C在右为正,在左为负。
物理光学与应用光学习题解第二章

第二章习题2-1. 如图所示,两相干平行光夹角为α,在垂直于角平分线的方位上放置一观察屏,试证明屏上的干涉亮条纹间的宽度为: 2sin2αλ=l 。
2-2. 如图所示,两相干平面光波的传播方向与干涉场法线的 夹角分别为0θ和R θ,试求干涉场上的干涉条纹间距。
2-3. 在杨氏实验装置中,两小孔的间距为0.5mm ,光屏离小孔的距离为50cm 。
当以折射率为1.60的透明薄片贴住小孔S2时,发现屏上的条纹移动了1cm ,试确定该薄片的厚度。
2-4. 在双缝实验中,缝间距为0.45mm ,观察屏离缝115cm ,现用读数显微镜测得10个条纹(准确地说是11个亮纹或暗纹)之间的距离为15mm ,试求所用波长。
用白光实验时,干涉条纹有什么变化?2-5. 一波长为0.55m μ的绿光入射到间距为0.2mm 的双缝上,求离双缝2m 远处的观察屏上干涉条纹的间距。
若双缝距离增加到2mm ,条纹间距又是多少?2-6. 波长为0.40m μ~0.76m μ的可见光正入射在一块厚度为1.2×10-6 m 、折射率为1.5的薄玻璃片上,试问从玻璃片反射的光中哪些波长的光最强?2-7. 题图绘出了测量铝箔厚度D 的干涉装置结构。
两块薄玻璃板尺寸为75mm ×25mm 。
在钠黄光(λ=0.5893m μ)照明下,从劈尖开始数出60个条纹(准确地说是从劈尖开始数出61个明条纹或暗条纹),相应的距离是30mm ,试求铝箔的厚度D = ?若改用绿光照明,从劈尖开始数出100个条纹,其间距离为46.6 mm ,试求这绿光的波长。
2-8. 如图所示的尖劈形薄膜,右端厚度h 为0.005cm ,折射率n = 1.5,波长为0.707m μ的光以30°角入射到上表2-1题用图2-2题用图2-7题用图2-8题用图面,求在这个面上产生的条纹数。
若以两块玻璃片形成的空气尖劈代替,产生多少条条纹?2-9. 利用牛顿环干涉条纹可以测定凹曲面的曲率半径,结构如图所示。
应用光学习题

应用光学习题、第一章 : 几何光学基本原理 ( 理论学时: 4 学时 )•讨论题:几何光学与物理光学有什么区别?它们研究什么内容?•思考题:汽车驾驶室两侧与马路转弯处安装的反光镜为什么要做成凸面,而不做成平面?•一束光由玻璃( n=1、5 )进入水( n=1、33 ),若以45 ° 角入射,试求折射角。
•证明光线通过二表面平行的玻璃板时,出射光线与入射光线永远平行。
•为了从坦克内部观察外界目标,需要在坦克壁上开一个孔。
假定坦克壁厚为 200mm ,孔宽为 120mm ,在孔内部安装一块折射率为 n=1、5163 的玻璃,厚度与装甲厚度相同,问在允许观察者眼睛左右移动的条件下,能瞧到外界多大的角度范围?•一个等边三角棱镜,若入射光线与出射光线对棱镜对称,出射光线对入射光线的偏转角为40 °,求该棱镜材料的折射率。
•构成透镜的两表面的球心相互重合的透镜称为同心透镜,同心透镜对光束起发散作用还就是会聚作用?•共轴理想光学系统具有哪些成像性质?第二章 : 共轴球面系统的物像关系 ( 理论学时: 10 学时,实验学时: 2 学时 )•讨论题:对于一个共轴理想光学系统,如果物平面倾斜于光轴,问其像的几何形状就是否与物相似?为什么?•思考题:符合规则有什么用处?为什么应用光学要定义符合规则?•有一放映机,使用一个凹面反光镜进行聚光照明,光源经过反光镜以后成像在投影物平面上。
光源高为10mm ,投影物高为 40mm ,要求光源像高等于物高,反光镜离投影物平面距离为 600mm ,求该反光镜的曲率半径等于多少?•试用作图法求位于凹的反光镜前的物体所成的像。
物体分别位于球心之外,球心与焦点之间,焦点与球面顶点之间三个不同的位置。
•试用作图法对位于空气中的正透镜( )分别对下列物距:求像平面位置。
•试用作图法对位于空气中的负透镜( )分别对下列物距:求像平面位置。
•已知照相物镜的焦距毫米,被摄景物位于距离米处,试求照相底片应放在离物镜的像方焦面多远的地方?•设一物体对正透镜成像,其垂轴放大率等于- 1 ,试求物平面与像平面的位置,并用作图法验证。
应用光学【第二章】习题第一部分

1.一物体在曲率半径12厘米的凹面镜的顶点左方4厘米处,求像的位置及横向放大率,并作出光路图。
2.一直径为4厘米的长玻璃棒,折射率为1.5,其一端磨成曲率半径为2厘米的半球形。
长为0.1 厘米的物垂直置于棒轴上离棒的凹面顶点8厘米处。
求像的位置及大小。
并作出光路图。
3.一玻璃半球的曲率半径为R,折射率为1.5,其平面的一边镀银。
一物高为h,放在曲面顶点2R处,求(1)由曲面所组成的第一个像的位置。
(2)这一光具所组成的最后的像在那里?4.证明:光线相继经过几个平行分界面的多层介质时,出射光线的方向只与入射方向及两边的折射率有关,与中间各层介质无关。
应用光学 课后题,作业答案

第二章作业:1、一个玻璃球直径为400mm,玻璃折射率为1.5。
球中有两个小气泡,一个在球心,一个在1/2半径处。
沿两气泡连线方向,在球的两侧观察这两个气泡,它们应在什么位置?如在水中观察(水的折射率为1.33)时,它们又应在什么位置?答案:空气中:80mm、200mm;400mm、200mm水中:93.99mm、200mm;320.48mm、200mm3、一个玻璃球直径为60mm,玻璃折射率为1.5,一束平行光射到玻璃球上,其汇聚点在何处?答案:l'=15mm4、一玻璃棒(n=1.5),长500mm,两端面为凸的半球面,半径分别为r1=50mm, r2= -100mm,两球心位于玻璃棒的中心轴线上。
一箭头高y=1mm,垂直位于左端球面顶点之前200mm处,垂直于玻璃棒轴线。
试画出结构简图,并求a)箭头经玻璃棒成像在什么位置(l2')?b)整个玻璃棒的垂轴放大率为多少?答案:l2'= -400mm、-3第三章作业:1、已知一个透镜把物体放大-3⨯,当透镜向物体移近18mm时,物体将被放大-4⨯,试求透镜的焦距。
答案:216mm2、一个薄透镜对某一物体成实像,放大率为-1⨯。
以另一薄透镜紧贴此薄透镜,则见像向透镜方向移动了20mm,放大率为原来的3/4,求两薄透镜的焦距。
答案:40mm、240mm3、一束平行光入射到平凸透镜上,汇聚于透镜后480mm处。
如在此透镜凸面上镀反射膜,则平行光汇聚于透镜前80mm处,求透镜折射率和凸面曲率半径。
答案:1.5、-240mm5、一块厚透镜,n=1.6,r1=120mm,r2=-320mm,d=30mm,试求该透镜的焦距及基点位置。
如果物距l1= -5m,像在何处?如果平行光入射时,使透镜绕一和光轴垂直的轴转动,而要求像点位置不变,问该轴安装在何处?答案:f'=149.27mm、l F'=135.28mm、l F= -144.02mm、l H'= -13.99mm、l H=5.25mm l2'=139.87mm像方节点,即像方主点6、由两薄透镜组成的对无穷远物成像的短焦距物镜,已知其焦距为35mm,筒长T=65mm,后工作距为50mm,求系统结构。
应用光学试题(第二章)

应用光学试题第二章一、填空题(建议每空1分)(请同学们不要写错别字,数字不要用大写,术语要标准,否则按错处理,不要用科学记数法如4101⨯)I 级I 级1空1、 焦点又称为后焦点或第二焦点。
像方2、过像方焦点'F 作一垂直于光轴的平面即为 焦平面。
像方3、像方焦点'F 是像方焦平面上的一个特殊点,该点对应的是物方孔径角=u 度的一束平行于光轴的平行光。
4、从物方焦点F 发出的光经过系统后均为平行于 的光。
光轴5、过 作垂直于光轴的平面称为物方焦平面。
物方焦点6、垂轴放大率为=β 倍的这对共轭平面为主平面(简称主面)。
17、主平面与光轴的交点称为 。
主点8、像方主平面与 的交点称为像方主点'H 。
光轴9、焦距属于沿轴线段,以各自的 为原点判断其符号。
主点10、 焦距可表示式为tguh 。
物方11、光学系统的 可以看作是焦距的另外一种表示形式, 光焦度12、 是指角放大率1+=γ的一对共轭点。
节点13、经过物方节点的光线其共轭光线经过 节点。
像方14、 法主要是应用光学系统基点和基面的性质,通过选用适当的光线或辅助线画出其共轭光线的方法。
图解15、牛顿公式是以各自的为原点确定物、像的具体位置。
焦点16、高斯公式是以为原点来描述物、像的具体位置。
主点17、将一个正单透镜与一个负单透镜进行胶合,称之为透镜。
双胶合18、望远系统是最典型的光学系统,其系统焦点位于无穷远处,焦距为无限大。
无焦19、望远系统的光学间隔=∆。
20、是由两个折射面包围的一种透明介质构成的光学元件,折射面可以是球面、平面或非球面。
透镜21、是指当透镜的厚度与焦距或曲率半径相比是一个很小的数值时,厚度d可忽略不计的透镜。
薄透镜22、透镜主平面与之间的距离为焦距。
焦点23、透镜物与像之间的距离称为。
共轭距24、筒长L是指第一个光组到之间的距离。
像面(或像平面)25、是指系统最后一面到像平面之间的距离。
后工作距离26、按照透镜形状的不同,正透镜又可分为透镜、平凸透镜及月凸透镜,双凸27、负透镜又分为透镜、平凹透镜及月凹透镜,其特征是中心厚度比边缘厚度薄。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.一物体在曲率半径12厘米的凹面镜的顶点左方4厘米处,求像的位置及横向放大率,并作出光路图。
2.一直径为4厘米的长玻璃棒,折射率为1.5,其一端磨成曲率半径为2厘米的半球形。
长为0.1 厘米的物垂直置于棒轴上离棒的凹面顶点8厘米处。
求像的位置及大小。
并作出光路图。
3.一玻璃半球的曲率半径为R,折射率为1.5,其平面的一边镀银。
一物高为h,放在曲面顶点2R处,求(1)由曲面所组成的第一个像的位置。
(2)这一光具所组成的最后的像在那里?4.证明:光线相继经过几个平行分界面的多层介质时,出射光线的方向只与入射方向及两边的折射率有关,与中间各层介质无关。
