应用光学习题
应用光学习题

应用光学习题应用光学习题.第一章 : 几何光学基本原理 ( 理论学时: 4 学时 )讨论题:几何光学和物理光学有什么区别它们研究什么内容思考题:汽车驾驶室两侧和马路转弯处安装的反光镜为什么要做成凸面,而不做成平面一束光由玻璃( n= )进入水( n= ),若以45 ° 角入射,试求折射角。
证明光线通过二表面平行的玻璃板时,出射光线与入射光线永远平行。
为了从坦克内部观察外界目标,需要在坦克壁上开一个孔。
假定坦克壁厚为 200mm ,孔宽为 120mm ,在孔内部安装一块折射率为n= 的玻璃,厚度与装甲厚度相同,问在允许观察者眼睛左右移动的条件下,能看到外界多大的角度范围一个等边三角棱镜,若入射光线和出射光线对棱镜对称,出射光线对入射光线的偏转角为40 °,求该棱镜材料的折射率。
构成透镜的两表面的球心相互重合的透镜称为同心透镜,同心透镜对光束起发散作用还是会聚作用?共轴理想光学系统具有哪些成像性质第二章 : 共轴球面系统的物像关系 ( 理论学时: 10 学时,实验学时: 2 学时 )讨论题:对于一个共轴理想光学系统,如果物平面倾斜于光轴,问其像的几何形状是否与物相似为什么思考题:符合规则有什么用处为什么应用光学要定义符合规则有一放映机,使用一个凹面反光镜进行聚光照明,光源经过反光镜以后成像在投影物平面上。
光源高为 10mm ,投影物高为 40mm ,要求光源像高等于物高,反光镜离投影物平面距离为600mm ,求该反光镜的曲率半径等于多少试用作图法求位于凹的反光镜前的物体所成的像。
物体分别位于球心之外,球心和焦点之间,焦点和球面顶点之间三个不同的位置。
试用作图法对位于空气中的正透镜()分别对下列物距:求像平面位置。
试用作图法对位于空气中的负透镜()分别对下列物距:求像平面位置。
已知照相物镜的焦距毫米,被摄景物位于距离米处,试求照相底片应放在离物镜的像方焦面多远的地方?设一物体对正透镜成像,其垂轴放大率等于-1 ,试求物平面与像平面的位置,并用作图法验证。
应用光学习题

' 2
)x
(l1'
xF'
dxF'
f
' 2
xF'
f
' 2
2
)
0
当d 21.13时
x
' F
f2
f
' 2
2500 78.87
86.595
x2 58.725x 86.597 0
x1 1.51 x2 57.2115
12. 由两个透镜组成的一个倒像系统,设第一组透 镜的焦距为f1′,第二组透镜的焦距 为f2′, 物平面位于第一组透镜的物方焦面上,求该倒像 系统的垂轴放大率。
5010 1.5163(40 50) _(1.5163 1) 10
50
l'H
n(r1
r2d r2 ) (n 1)d
40
11 1
l
' 2
l2
f
' 2
l2'
L
(d
)
xF'
f
' 2
1
l
' 2
1 l2
1
f
' 2
f
' 2
(l
2
l
' 2
)
l
2
l
' 2
f
' 2
(l1'
d
x
x
应用光学习题答案

7、 设一物体对正透镜成像,其垂直放大率等于-1, 试求物平面与像平面的位置,并用作图法验证。
在轴上的孔径角L1大于L2,所以L2为系统的孔径光阑
入瞳即为L2对L1成像,在L1前方2.18cm处,口径为2y=2.9cm
出瞳为L2,视场光阑为L1
3.照相物镜,f ' 50mm, D / f ' 1/ 5 2m远处目标照相, 假定底片上像点弥散斑直径小于0.05mm仍可认为成像清 晰,问物空间能清晰成像的最远、最近距离各位多少?
解:
y
f
' 1
tg
y' f2'tg
y'
f
' 2
y
f
' 1
15. 电影放映机镜头的焦距f′=120mm,影片画面的 尺寸为22×16mm2,银幕大小为6.6 ×4.8m2,问电 影机应放在离银幕多远的地方?如果把放映机移到 离银幕50m远处,要改用多大焦距的镜头?
解:
6600
300
22
l' 36.12m
• 解:
8、已知显微镜物平面和像平面之间距离180mm, 垂直放大率-5,求该物镜组的焦距和离开物平面的 距离。
• 解:
9. 已知航空照相机物镜的焦距f′=500mm,飞机 飞行高度为6000m,相机的幅面为300×300mm2, 问每幅照片拍摄的地面面积。
解:
f f f ' 8.3 105
应用光学作业题答案

第二题: (1)光线由水中射向空气,求在界面处发生全反射的临界角。
解: 全反射的临界角Im arcsin(n '/ n)
光线由水中射向空气,n’=1,n=1.333
则 Im arc sin(n '/ n)=arc sin(1/1.333)=48.61
(2)光线由玻璃内部射向空气,求发生全反射的临界角。
1 l2
'
-
1 130
=
1 120
l2'=-62.4mm
A”成象于透镜2左侧62.4mm处。
(2)等效光组成象的方法:
解: H’
A
F1
F2’
F1’
F2
f1’=120mm f2’=-120mm d=70mm △= d-f1’- f2’=70mm
f ' f1 ' f2 ' 120 (120) 205.714mm
n0sini1=nsini1’ sini1=0.6552 i1=40.93° 由三角形内角和可求出太阳和幻
日之间的夹角
α=180 °-2×(i1-i1’) =158.14 °
第七题:
为了从坦克内部观察外界目标,需要在坦克上开一个孔,假 定坦克壁厚250mm,孔宽150mm,在孔内装一块折射率 n=1.52的玻璃,厚度与装甲厚度相同,问能看到外界多大的 角度范围?
O’
A’
解:(1)对于在球心的气泡,以O作为 球面顶点,根据符号规则,
O L’A=-200mm,n’=1,n=1.52
由 n ' n n ' n l' l r
1 -1.52 = 1-1.52 l=-200mm -200 l -200
应用光学习题集答案

应⽤光学习题集答案习题第⼀章1、游泳者在⽔中向上仰望,能否感觉整个⽔⾯都是明亮的?(不能,只能感觉到⼀个明亮的圆,圆的⼤⼩与游泳都所在的⽔深有关,设⽔深H ,则明亮圆半径HtgIc R =)2、有时看到窗户玻璃上映射的太阳光特别耀眼,这是否是由于窗玻璃表⾯发⽣了全反射现象?答:是。
3、⼀束在空⽓中波长为nm 3.589=λ的钠黄光从空⽓射⼊⽔中时,它的波长将变为多少?在⽔中观察这束光时其颜⾊会改变吗?答:'λλ=n ,nm 442'=λ不变 4、⼀⾼度为m 7.1的⼈⽴于路灯边(设灯为点光源)m 5.1远处,路灯⾼度为m 5,求⼈的影⼦长度。
答:设影⼦长x ,有:57.15.1=+x x ∴x=0.773m 5、为什么⾦钢⽯⽐磨成相同形状的玻璃仿制品显得更加光彩夺⽬?答:由于⾦钢⽯折射率⼤,所以其临界⾓⼩,⼊射到其中的光线⼤部分都能产⽣全反射。
6、为什么⽇出或⽇落时太阳看起来稍微有些发扁?(300例P1)答:⽇出或⽇落时,太阳位于地平线附近,来⾃太阳顶部、中部和底部的光线射向地球⼤⽓层的⼊射⾓依次增⼤(如图)。
同时,⼤⽓层密度不均匀,折射率⽔接近地⾯⽽逐渐增⼤。
当光线穿过⼤⽓层射向地⾯时,由于n 逐渐增⼤,使其折射⾓逐渐减⼩,光线的传播路径就发⽣了弯曲。
我们沿着光线去看,看到的发光点位置会⽐其实际位置⾼。
另⼀⽅⾯,折射光线的弯曲程度还与⼊射⾓有关。
⼊射⾓越⼤的光线,弯曲越厉害,视觉位置就被抬得越⾼,因为从太阳上部到下部发出的光线,⼊射⾓依次增⼤,下部的视觉位置就依次⽐上部抬⾼的更多。
第⼆章1、如图2-65所⽰,请采⽤作图法求解物体AB的像,设物像位于同⼀种介质空间。
图2-652、如图2-66所⽰,'MM 为⼀薄透镜的光轴,B 为物点,'B 为像点,试采⽤作图法求解薄透镜的主点及焦点的位置。
BM B 'M ′ B M M ′B ' ●●●●(a) (b)图2-663、如图2-67所⽰,已知物、像的⼤⼩及位置,试利⽤图解法求解出焦点的位置,设物、像位于同⼀种介质空间。
(完整)应用光学习题

一、填空题1、光学系统中物和像具有共轭关系的原因是 光路可逆 。
2、发生全反射的条件是 光从光密媒质射向光疏媒质,且入射角大于临界角I 0,其中,sinI 0=n 2/n 1 。
3、 光学系统的三种放大率是 垂轴放大率 、 角放大率 、轴向放大率 ,当物像空间的介质的折射率给定后,对于一对给定的共轭面,可提出 一 种放大率的要求.4、 理想光学系统中,与像方焦点共轭的物点是 轴上无穷远的物点 。
5、物镜和目镜焦距分别为mm f 2'=物和mm f 25'=目的显微镜,光学筒长△= 4mm ,则该显微镜的视放大率为 -20 ,物镜的垂轴放大率为 -2 ,目镜的视放大率为 10 。
6、某物点发出的光经理想光学系统后对应的最后出射光束是会聚同心光束,则该物点所成的是实 (填“实”或“虚”)像。
7、人眼的调节包含 视度 调节和 瞳孔 调节。
8、复杂光学系统中设置场镜的目的是 在不影响系统光学特性的的情况下改变成像光束的位置,使后面系统的通光口径不致过大。
9、要使公共垂面内的光线方向改变60度,则双平面镜夹角应为30 度。
10、近轴条件下,折射率为1.4的厚为14mm 的平行玻璃板,其等效空气层厚度为 10 mm. 11、设计反射棱镜时,应使其展开后玻璃板的两个表面平行,目的是 保持系统的共轴性 。
12、有效地提高显微镜分辨率的途径是 提高数值孔径和减小波长 。
13、近轴情况下,在空气中看到水中鱼的表观深度要比实际深度 小 。
14.用垂轴放大率判断物、像虚实关系方法:当β>0时 物像虚实相反β<0时 物像虚实相同。
15.平面反射镜成像的垂轴放大率为 1 ,物像位置关系为 镜像 ,如果反射镜转过α角,则反射光线方向改变 2α 。
二、简答题1、几何光学的基本定律及其内容是什么?答:几何光学的基本定律是直线传播定律、独立传播定律、反射定律和折射定律。
直线传播定律:光线在均匀透明介质中按直线传播.独立传播定律:不同光源的光在通过介质某点时互不影响。
应用光学习题(第一章部分课后习题)
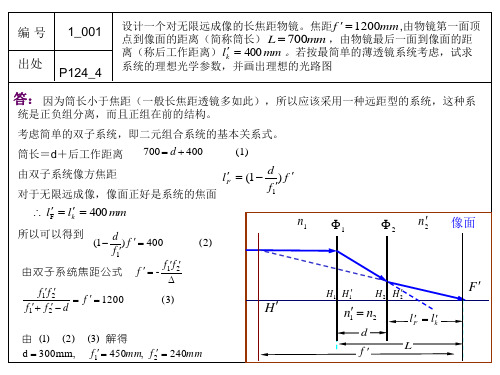
编号
出处
1_004
P124_8
答:(接上一页)
若透镜为无焦系统,则 Φ 即
n(r2 r1 ) (n 1)d 0
1 0 f
d
n (r2 r1 ) n 1
此时构成望远结构分别 有 f f ' lH lF lF lH 主面和焦面都在无穷远 处
h2 h1 d1tgu1 h1 d1tgu1 d 2 tgu 2 h3 h2 d 2 tgu 2
n1 h h tgu1 1 1 1 1 n1 n1 n1
n2 h2 2 n1 h11 h2 2 1 h11 h2 2 tgu 2 tgu2 n2 n2 n2 n1 n2 n2
d )f f1
lk 400mm lF
所以可以得到
(1 d ) f 400 f1 (2)
n1
ff1 f 2
1
2
n2
像面
由双子系统焦距公式 f1 f 2 f 1200 f1 f 2 d
(3)
H
H1 H1
H2 H2
x2 f 2 2 x1 f 2 4 x1 f 2 0 l2
x1
1 f 2 50 mm 4 物体所处的位置 -50mm x1 100mm
即,物体放在 L1左面150mm以内
(3) 假如双子系统由正负透镜组合
A
1时,如果1 0, 2 0时,
答:由组合系统光焦度公式 1 h h h 1 1 2 2 3 3 h1 如果考虑平行光入射到 这个薄透镜系统, 即 tgu1 0,薄透镜系统处于空气中
应用光学考研试题及答案

应用光学考研试题及答案一、单项选择题(每题2分,共10分)1. 下列哪种情况不属于干涉现象?A. 薄膜干涉B. 单缝衍射C. 双缝干涉D. 多普勒效应2. 激光的三个主要特性不包括以下哪一项?A. 单色性B. 相干性C. 方向性D. 发散性3. 在光纤通信中,信号传输的介质通常是:A. 空气B. 真空C. 石英玻璃D. 水4. 下列关于光的偏振现象,错误的是:A. 只有横波才能发生偏振B. 偏振片可以让自然光变成偏振光C. 偏振光通过偏振片后,光的强度会发生变化D. 偏振光的振动方向与偏振片的透振方向垂直时,透射光强度为零5. 在迈克尔逊干涉仪中,哪部分的移动会产生干涉条纹?A. 分光镜B. 反射镜C. 光源D. 观察屏二、简答题(每题10分,共20分)1. 简述全息照相的原理及其特点。
2. 解释光纤通信中的模式色散现象,并说明其对信号传输的影响。
三、计算题(每题15分,共30分)1. 一个凸透镜的焦距为20cm,物体距离透镜30cm。
求像的位置和大小。
2. 在光纤通信中,已知光纤的数值孔径为0.2,光纤的折射率为 1.5,求光纤接受光的锥角。
四、论述题(共40分)1. 论述光学薄膜在现代光学系统中的重要作用及其应用实例。
(20分)2. 分析激光冷却技术的原理及其在科学研究中的应用。
(20分)答案:一、单项选择题1. D2. D3. C4. D5. B二、简答题1. 全息照相是一种利用激光记录物体的三维图像的技术。
其原理基于光的干涉现象,通过记录物体发射或反射的光波的干涉图样,再利用参考光波与物体光波的干涉图样重合,形成全息图。
全息照相的特点包括能够记录物体的三维信息,具有真实感和立体感,以及可以进行无损检测等。
2. 模式色散是指在多模光纤中,由于不同模式的光在光纤中传播的速度不同,导致信号到达接收端的时间不同,从而引起的信号失真。
模式色散对信号传输的影响主要表现在限制了光纤的传输带宽和传输距离,降低了信号的传输质量。
应用光学习题及答案

四、分析作图题(共25分)1. 已知正光组的F 和F’,求轴上点A 的像,要求用五种方法。
(8分)2. 已知透镜的焦距公式为1122111nr f 'r d (n )n()(n )r r =⎡⎤--+-⎢⎥⎣⎦,11H n l'f 'd nr -=-,21H n l f 'd nr -=-,分析双凹透镜的基点位置,并画出FFL 、BFL 和EFL 的位置。
(9分)3. 判断下列系统的成像方向,并画出光路走向(8分)(a ) (b )五、计算题(共35分) 1.由已知150f mm '=,2150f mm '=-的两个薄透镜组成的光学系统,对一实物成一放大4倍的实像,并且第一透镜的放大率12β⨯=-,试求:1.两透镜的间隔;2.物像之间的距离;3.保持物面位置不变,移动第一透镜至何处时,仍能在原像面位置得到物体的清晰像?与此相应的垂铀放大率为多大?(15分)2. 已知一光学系统由三个零件组成,透镜1:11100f f '=-=,口径140D =;透镜2:22120f f '=-=,口径230D =,它和透镜1之间的距离为120d =;光阑3口径为20mm ,它和透镜2之间的距离230d =。
物点A 的位置1200L =-,试确定该光组中,哪一个光孔是孔径光阑,哪一个是视场光阑?(20分)试题标准答案及评分标准用纸课程名称:应用光学 (A 卷)一、选择题(每题2分,共10分)1.B ;2.A ;3.C ;4.C ;5.D二、填空题(每题2分,共10分)1.物镜的像方焦点F '物到目镜物镜焦点F 目之间的距离 2.又叫后截距,用Fl '表示,是系统最后一个面的顶点到像方焦点之间的距离 3.一般认为最大波像差小于四分之一波长,则系统质量和理想光学系统没有显著差别4.入瞳直径D 和物镜焦距f '物之比D f '物5.假设物空间不动,棱镜绕P 转θ,则像空间先绕P ’转1(1)n θ--,后绕P 转θ三、简答题(每题4分,共20分)1.限制进入光学系统的成像光束口径的光阑叫空径光阑。
物理光学与应用光学习题和答案
A、放大的字C、手影D、倒影
3.下列四个物理现象中,有一个形成的原因与另外三个不同,这个现象是()
对镜梳妆时能看到镜中的“自己”
7,模型中的凸透镜相当于晶
则
2cm,则在光
)
).
)。
5km,月球在池中的像到水面的距离是
图3 图7
图1
图6
图8
b ),则透过透镜可以看到一
),这种外墙既能透射光线⑴、外面看玻璃幕墙相当于平面镜,光线照射到光滑的玻璃幕墙上时会发生 反射,物体图13
图14 图10 图16
第四章答案参考答案
一、选择题:
1、D
2、A
3、A
4、D
5、D
6、A
7、D
8、B
9、B 10、C 11、C 12、C
二、13、日食;14、光速远大于声速;15、零;16、反射;折射;
17、3.8×105km;虚;18、800;19、红外线;紫外线;
20、焦点;21、2;1.6;22、光的直线传播;光的反射;光的折射;
三、23—26、(略);27、光屏;倒;右;28、(1)略;(2)浅一些;
29、3;正立放大的虚;
一、30、①会刺伤眼睛;②不易看清周围的物体;③在眼前的物体也有可能看不到;
31、⑴镜面;虚;⑵各块玻璃可能不在同一平面上;⑶会反射强光造成光污染;。
应用光学习题(含答案).docx

应用光学习题本习题供学习、复习使用。
精练这些习题及作业和课件上的例题有助于掌握、理解应用光学课程的基本知识、理论和规律。
应用光学的基本问题包括在本习题内,但不仅限于本习题。
本习题仅供课程学习时参考。
习题中一些问题提供了解答,限于时间,其它则略去。
一、筒答题1、几何光学的基本定律及其内容是什么?答:几何光学的基本定律是自钱传播定律、独立传播定W:、反射定律和折射定律。
直线传播定律:光线在均匀透明介质中按直线传播。
独立传播定律:不同光源的光在通过介质某点时互不影响。
反射定律:反射光线位于入射面内;反射角等于入射角:折射定律:折射光线位于入射面内:入射角和折射角正弦之比,对两种定的介j员来说,是=个和入射角无关的常数n isin/,-msin/。
22、理想光学系统的基点和基面有哪些?理想光学系统的基点包指物方焦点、{象方焦点;物方主点、像方主点:物方节点、像方节点。
基面包括:物方焦平丽、像方然平面:物方主平丽、像方主平面;物方节平面、像方节平面。
3、什么是光学系统的孔役光阑和视场光阙?答:孔径光阑是限制轴上物点成像光束立体角的光阔。
晴荡艾丽王辅前有字亩7茧事宝肯车夜夜古国的光册J。
4、常见非正常跟有哪两种?如何校正常见非正常1'常见正常目艮包括近视酬远视盹近视眼将工二(远附近点)矫正到无限远,远视眼,将一丘丛(远点就近点)矫正到明视距离。
3、光'于系统极限分辨角为多大?采取什么途径可以提岗极限分辨角?答:衍射决定的极限分辨角为0=3®。
可见其与波长和孔役有关。
订蔬小波长D和增大孔径可以提高光学系统的分辨率。
I什么是共和1)也学系统、元学系统物空间、像空间?答:光学系统以一条公共制线通过系统各表面的幽率中心,该轴线称为光轴,这样的系统称为共轴光学系统。
物体所在的空间称为物空间,像所在的空间称为像空间。
、如何确定光学系统的视场Jt阙?答:将系统中除孔径光阑以外的所有光阑对其前面所有的光学零件成像到物空间;这些像中,孔径对入暗中心张角最小的一个像所对应的光阑即为光学系统的视场光阙。
《应用光学》第六章习题

第六章 像差理论习 题1、 设计一个齐明透镜,第一面曲率半径mm r 951-=,物点位于第一面曲率半径中心处。
第二个球面满足齐明条件,透镜厚度mm d 5=,折射率5.1=n ,该透镜位于空气中。
求:1) 该透镜第二面的曲率半径;2)该齐明透镜的垂轴放大率。
解:1)由题意知:物点到第二面距离:mm d L L 10059512-=--=-=,又5.1=n ,10=n 由齐明透镜的特征:mm n nL L 150)100(5.1022-=-⨯== 第二面的曲率半径:mm n n nL r 605.2150022-=-=+=2)5.121===n βββ,该齐明透镜的垂轴放大倍率为1.5。
2、已知614.1,2,201==-=n mm d mm L ,设计负透镜(齐明),物在第一面的球心,求1r ,2r ,'2L 。
解:由题意,mm L 201-=,又物在第一面的球心处。
mm L r 2011-==∴。
又mm d L L 2212-=-=,mm n nL r 584.13614.11)22(614.1122-=+-⨯=+=∴ 同时得:mm nL L 584.35)22(614.11'22-=-⨯==3、已知某一光学系统,只包含初级球差和二阶高级球差,且边缘光球差0'=m L δ,0.707带球差015.0'-=z L δ,回答:1)写出此系统的剩余球差表达式(关于相对高度mh h ),并计算0.5带,0.85带球差;2)求出边缘光线的初级球差和高级球差;3)最大剩余球差出现在哪一带上?数值为多少?解:1)对于一般系统,我们只考虑初级和二阶高级球差的影响。
即:4221)()('mm h h A h h A L +=δ。
又此系统对边缘光校正了球差,即1=m h h 时,0'=m L δ,021=+∴A A ——① 又在0.707带,即707.0=mh h 时,有015.0)707.0()707.0(4221-=+A A ——② 由①②式得到:⎩⎨⎧=-=06.006.021A A , 所以剩余球差的表达式为42)(06.0))(06.0('mm h h h h L +-=δ。
王文生——应用光学习题集

习 题 第一章1、游泳者在水中向上仰望,能否感觉整个水面都是明亮的?(不能,只能感觉到一个明亮的圆,圆的大小与游泳都所在的水深有关,设水深H ,则明亮圆半径HtgIc R =)2、有时看到窗户玻璃上映射的太阳光特别耀眼,这是否是由于窗玻璃表面发生了全反射现象?答:是。
3、一束在空气中波长为nm 3.589=λ的钠黄光从空气射入水中时,它的波长将变为多少?在水中观察这束光时其颜色会改变吗?答:'λλ=n ,nm 442'=λ不变 4、一高度为m 7.1的人立于路灯边(设灯为点光源)m 5.1远处,路灯高度为m 5,求人的影子长度。
答:设影子长x ,有:57.15.1=+x x ∴x=0.773m 5、为什么金钢石比磨成相同形状的玻璃仿制品显得更加光彩夺目?答:由于金钢石折射率大,所以其临界角小,入射到其中的光线大部分都能产生全反射。
6、为什么日出或日落时太阳看起来稍微有些发扁?(300例P1)答:日出或日落时,太阳位于地平线附近,来自太阳顶部、中部和底部的光线射向地球大气层的入射角依次增大(如图)。
同时,大气层密度不均匀,折射率水接近地面而逐渐增大。
当光线穿过大气层射向地面时,由于n 逐渐增大,使其折射角逐渐减小,光线的传播路径就发生了弯曲。
我们沿着光线去看,看到的发光点位置会比其实际位置高。
另一方面,折射光线的弯曲程度还与入射角有关。
入射角越大的光线,弯曲越厉害,视觉位置就被抬得越高,因为从太阳上部到下部发出的光线,入射角依次增大,下部的视觉位置就依次比上部抬高的更多。
第二章1、如图2-65所示,请采用作图法求解物体AB 的像,设物像位于同一种介质空间。
A B HH 'FF 'F 'FH 'HB AFH 'HABF 'F图2-652、如图2-66所示,'MM 为一薄透镜的光轴,B 为物点,'B 为像点,试采用作图法求解薄透镜的主点及焦点的位置。
BMB 'M ′ BM M ′B' ●● ● ●(a) (b)图2-663、如图2-67所示,已知物、像的大小及位置,试利用图解法求解出焦点的位置,设物、像位于同一种介质空间。
应用光学习题及答案_百度文库

考试试题纸(A卷)课程名称题号题分备注:学生不得在试题纸上答题(含填空题、选择题等客观题应用光学四五六七专业班级八九十总分一二三一、选择题(每题1分,共5分)1.发生全反射现象的必要前提是:A)光线由光疏介质到光密介质传播B)光线由光密介质到光疏介质传播C)光线在均匀介质中传播D)以上情况都可能产生2.周视照相机可以拍摄大视场景物,其利用的:A)节点的性质B)主点的性质C)焦点的性质D)以上答案都正确3.在望远镜的视度调节中,为适应近视人群,应采取的是:A)使物镜远离目镜B)使目镜远离物镜C)使目镜靠近物镜D)应同时调节物镜和目镜4.棱镜系统中加入屋脊面,其作用是:A改变光轴的方向B)改变主截面内像的方向C)改变垂轴于主截面方向上像的方向D)以上都正确5.光学系统中场镜的作用是:A)改变成像光束的位置B)减小目镜的尺寸C)不改变像的成像性质D)以上都正确二、填空题(每题2分,共10分)1.显微镜中的光学筒长指的是(2.光学系统中像方顶截距是(3.用波像差评价系统成像质量的瑞利准则是(4.望远系统中物镜的相对孔径是(5.棱镜的转动定理是(三、简答题(共20分)1.什么叫孔径光阑?它和入瞳和出瞳的关系是什么?(4分)2.什么叫视场光阑?它和入窗和出窗的关系是什么?(4分)3.几何像差主要包括哪几种?(4分)4.什么叫远心光路?其光路特点是什么?(4分)5.照相机中F数是什么意思?光圈指的是什么?(4分))))))四、分析作图题(共25分)1.已知正光组的F和F’,求轴上点A的像,要求用五种方法。
(8分)2.已知透镜的焦距公式为f'=nr1n−1n−1,l'H=−f'd,lH=−f'd,nrnr⎡⎤rd12(n−1)⎢n(1−1)+(n−1)⎥r2r2⎦⎣分析双凹透镜的基点位置,并画出FFL、BFL和EFL的位置。
(9分)3.判断下列系统的成像方向,并画出光路走向(8分)(a)五、计算题(共35分)(b)1.由已知f1′=50mm,f2′=−150mm的两个薄透镜组成的光学系统,对一实物成一放大4倍的实像,并且第一透镜的放大率β1=−2,试求:1.两透镜的间隔;2.物像之间的距离;3.保持物面位置不变,移动第一透镜至何处时,仍能在原像面位置得到物体的清晰像?与此相应的垂铀放大率为多大?(15分)2.已知一光学系统由三个零件组成,透镜1:f1′=−f1=100,口径D1=40;透镜2:f2′=−f2=120,口径D2=30,它和透镜1之间的距离为d1=20;光阑3口径为20mm,它和透镜2之间的距离d2=30。
应用光学试题

一、填空1. 球面透镜的像差共有_____种,其中色差有两种,分别是____ _、 。
2. 球面透镜共有 种镜片形式,其中正球面透镜有 、 、 ,三种镜片形式, 型有利于消除像差。
3. 一显微镜物镜筒上标有“16×”字样,在目镜筒上标有“20×”字样,其分别 表示 和 ; 该显微镜的视放大倍数是 。
4. 、 、 是表征颜色属性的三个变量。
5. 柱镜+10.0DC ×30和柱镜-5.0DC ×120密接组合,其交替球柱式为 、 ;联合后的球柱镜的正轴和负轴分别是 、 。
6. 视场光阑是光学系统中对光束的 起限制作用的光阑,其在系统像空间的共轭像称作 。
二、判断题( )1. 晴朗的天空呈现蓝色,是由于阳光发生了瑞利散射。
( )2. 散光镜片球面面靠近眼的为内散片。
( )3. 景深是指能在影像平面上获得清晰像的物空间深度。
( )4. 目视光学系统的出射光线一般是平行光束。
( )5. 完全偏振光是振动方向单一光。
( )6. 正视眼的屈光力比近视眼的屈光力大。
三、计算题1.有一简约眼如图所示,已知角膜的曲率半径 5.6r mm ,眼内屈光介质的折射 率约为1.33,试求: (1)此简约眼的屈光力。
(2)一物体位于眼前5m 处,当眼不调节时所成理想像的位置。
2.一透镜前表面两主子午线方向分别沿水平和竖直方向,用镜度表测得水平方向的屈光力为-2.0D ;竖直方向的屈光力为-3.0D ;该透镜的另一面各方向上的屈光力均相等为+3.0D ,写出该透镜的屈光力表达式。
3. 由折射率为1.5的材料制成负柱镜,柱面轴向沿竖直方向,其最小曲率半径为0.2 m ,写出该柱面透镜的表示;并求出60°方向上的屈光力。
o4. 某一球柱镜一面为凸球面,一面为凹柱面,材料折射率为1.5,球面曲率半径为 20cm ,柱面轴向为60度,其曲率半径为10cm ,求该透镜的屈光力,并写出该透镜屈光力的所有表示形式。
《应用光学》第一章例题.

第一章例题1.P20习题1(部分):已知真空中的光速c=3Í108m/s,求光在火石玻璃(n=1.65)和加拿大树胶(n=1.526)中的光速。
解:根据折射率与光速的关系 vcn =可求得 火石玻璃 )/(10818.165.11038811s m n c v ⨯=⨯==加拿大树胶 )/(10966.1526.11038822s m n c v ⨯=⨯==3.P20习题5,解:设水中一点A 发出的光线射到水面。
若入射角为I 0(sinI 0=n 空/ n 水 ),则光线沿水面掠射;据光路可逆性,即与水面趋于平行的光线在水面折射进入水中一点A ,其折射角为I 0(临界角)。
故以水中一点A 为锥顶,半顶角为I 0 的 圆锥范围内,水面上的光线可以射到A 点(入射角不同)。
因此,游泳者向上仰 望,不能感觉整个水面都是明亮的,而只 能看到一个明亮的圆,圆的大小与游泳者 所在处水深有关,如图示。
满足水与空 气分界面的临界角为 75.033.11sin 0==I 即 '36480︒=I , 若水深为H ,则明亮圆的半径 R = H tgI 0 4. ( P20习题7 )解:依题意作图如图按等光程条件有:''''1OA n O G n MA n GM n ⋅+⋅=⋅+⋅即.1)100(5.11221+=+-⋅++O G y x x O G所以x y x -=+-⋅150)100(5.122两边平方得222)150(])100[(25.2x y x -=+-2223002250025.245022500x x y x x +-=++- 025.225.115022=++-y x x0120101822=-+x x y ——此即所求分界面的表达式。
第二章例题1.(P53习题1)一玻璃棒(n =1.5),长500mm ,两端面为半球面,半径分别为50mm 和100mm ,一箭头高1mm ,垂直位于左端球面顶点之前200mm 处的轴线上,如图所示。
应用光学习题

应用光学习题、第一章 : 几何光学基本原理 ( 理论学时: 4 学时 )•讨论题:几何光学与物理光学有什么区别?它们研究什么内容?•思考题:汽车驾驶室两侧与马路转弯处安装的反光镜为什么要做成凸面,而不做成平面?•一束光由玻璃( n=1、5 )进入水( n=1、33 ),若以45 ° 角入射,试求折射角。
•证明光线通过二表面平行的玻璃板时,出射光线与入射光线永远平行。
•为了从坦克内部观察外界目标,需要在坦克壁上开一个孔。
假定坦克壁厚为 200mm ,孔宽为 120mm ,在孔内部安装一块折射率为 n=1、5163 的玻璃,厚度与装甲厚度相同,问在允许观察者眼睛左右移动的条件下,能瞧到外界多大的角度范围?•一个等边三角棱镜,若入射光线与出射光线对棱镜对称,出射光线对入射光线的偏转角为40 °,求该棱镜材料的折射率。
•构成透镜的两表面的球心相互重合的透镜称为同心透镜,同心透镜对光束起发散作用还就是会聚作用?•共轴理想光学系统具有哪些成像性质?第二章 : 共轴球面系统的物像关系 ( 理论学时: 10 学时,实验学时: 2 学时 )•讨论题:对于一个共轴理想光学系统,如果物平面倾斜于光轴,问其像的几何形状就是否与物相似?为什么?•思考题:符合规则有什么用处?为什么应用光学要定义符合规则?•有一放映机,使用一个凹面反光镜进行聚光照明,光源经过反光镜以后成像在投影物平面上。
光源高为10mm ,投影物高为 40mm ,要求光源像高等于物高,反光镜离投影物平面距离为 600mm ,求该反光镜的曲率半径等于多少?•试用作图法求位于凹的反光镜前的物体所成的像。
物体分别位于球心之外,球心与焦点之间,焦点与球面顶点之间三个不同的位置。
•试用作图法对位于空气中的正透镜( )分别对下列物距:求像平面位置。
•试用作图法对位于空气中的负透镜( )分别对下列物距:求像平面位置。
•已知照相物镜的焦距毫米,被摄景物位于距离米处,试求照相底片应放在离物镜的像方焦面多远的地方?•设一物体对正透镜成像,其垂轴放大率等于- 1 ,试求物平面与像平面的位置,并用作图法验证。
应用光学【第二章】习题第一部分

1.一物体在曲率半径12厘米的凹面镜的顶点左方4厘米处,求像的位置及横向放大率,并作出光路图。
2.一直径为4厘米的长玻璃棒,折射率为1.5,其一端磨成曲率半径为2厘米的半球形。
长为0.1 厘米的物垂直置于棒轴上离棒的凹面顶点8厘米处。
求像的位置及大小。
并作出光路图。
3.一玻璃半球的曲率半径为R,折射率为1.5,其平面的一边镀银。
一物高为h,放在曲面顶点2R处,求(1)由曲面所组成的第一个像的位置。
(2)这一光具所组成的最后的像在那里?4.证明:光线相继经过几个平行分界面的多层介质时,出射光线的方向只与入射方向及两边的折射率有关,与中间各层介质无关。
应用光学例题

应用光学例题近轴光学系统例 1. 一厚度为 200mm 的平行平板玻璃(n=1.5)下面放着一直径为 1mm 的金属片。
若在玻璃板上盖一圆形纸片, 要求在玻璃板上方任何方向上都看不到该金属片, 问纸片的最小直径为多少?例 2. 用费马定理证明光的折射定律和反射定律。
例 3. 如图有两个平面反射镜, M1、 M2夹角为α, 今在两反射镜之间有一光线以50°角入射, 入射到 M1的反射镜上,经 M1、 M2四次反射后,起反射光线与 M1平行,求其夹角α。
例 4. 设计一个在空气中和某种玻璃之间的单个折射表面构成的光学系统,希望物在空气中离表面 15.0cm 。
实像在玻璃中,离表面 45.0cm ,放大率为 2.0。
那么玻璃的折射率应为多少?表面的曲率半径为多少?例 5. 直径为 100mm 的球形玻璃缸,将半面镀银,内有一条鱼在镀银面前 25mm 处。
问缸外的观察者看到几条鱼?位置在何处?相对大小事多少?(水的折射率为 4/3)例 6. 在一张报纸上放一个平凹透镜,通过镜面看报纸。
当平面朝着眼睛时,报纸的虚像在平面下 13.3mm 处。
当凸面朝着眼睛时, 报纸的虚像在凸面下 14.6mm 处。
若透镜中央厚度为 20mm 。
求透镜的折射率和凸球面的曲率半径。
例 7. 一凹球面镜将一实物成一实像,物与像的距离为 1m ,物高为像高的 4倍,求凹面镜的曲率半径。
例8. ①一束平行光入射到一半径 r=30mm,折射率 n=1.5的玻璃球上,求其汇聚点的位置。
②如果在凸面上镀反射膜, 其汇聚点应在何处?③如果凹面镀反射膜, 则反射光束在玻璃中的汇聚点在何处?④反射光束经前表面折射后,汇聚点在何处?说明各汇聚点的虚实。
(2)(3)(4)例 9. 一直径为 400mm ,折射率为 1.5的玻璃球中有两个小气泡,一个位于球心,另一个在 1/2半径处。
沿两气泡连线方向在球两边观察,问看到的气泡在何处?如果在水中观察者看到的气泡又在何处?例 10. 位于空气中的等腰直角棱镜折射率 n=1.54, 问当光线在斜边上发生全反射时直角边 1上入射光线的入射角 I 1 应为多大?若棱镜折射率增大, I1增大还是减小?又问若棱镜放入水中,按图中光轴方向入射的光线是否会发生全反射。
应用光学复习题

1、 一束光由玻璃(n=1.5)进入水(n=1.33),若以45°角入射,试求折射角。
(52.6°)2、 一薄透镜焦距为200mm ,一物体位于透镜前300nm ,求像的位置和垂轴放大率。
(`600,2l mm β==-)3、 一组合系统由薄正透镜(前)和薄负透镜(后)组成,1`20f mm =,2`20f mm =-,两透镜之间的距离10d mm =,当一物体位于正透镜前方100mm 处,求组合系统的垂轴放大率和像的位置。
(可用两种方法解)。
(2`60,1l mm β==-)4、 一双凸薄透镜的两表面半径分别为1250,50r mm r mm ==-,求该透镜位于空气中和浸入水(0 1.33n =)中的焦距分别为多少?(透镜材料折射率n=1.5)(`50f mm =空,`195.6f mm =水)5、 符号规则标注6、 作图求物像:掌握第二章作业里作图题7、 棱镜成像方向的判断。
8、 一凹球面反射镜浸没在水中,物在镜前300mm ,像在像前90mm ,求球面反射镜的曲率半径和焦距。
(138.46,`69.23r mm f f mm =-==-)9、 有一正薄透镜对某一物体成实像时,像高为物高的一半;若将物体向透镜移近100mm 时,则所得的实像与物大小相同,求透镜的焦距。
(`100f mm =)10、 已知显微镜的视放大率为-300,目镜的焦距为20mm ,求显微镜物镜的倍率。
假定人眼的视角分辨率为60``,问使用该显微镜观察时,能分辨的两物点的最小距离等于多少?(24,0.00024mm βσ=-=)11、 用两个焦距都是50mm 的正透镜组成一个10倍的显微镜,问目镜的倍率,物镜的倍率以及物镜和目镜之间的间隔为多少?12、 有一焦距为150mm 的望远物镜,其口径为10mm ,像的直径为20mm 。
在物镜后方80mm处放置一直角棱镜(n1.5),假如系统没有渐晕,求棱镜入射表面的通光口径及像平面离开棱镜出射表面的距离。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
应用光学习题.
第一章 : 几何光学基本原理 ( 理论学时: 4 学时 )
•讨论题:几何光学和物理光学有什么区别它们研究什么内容
•思考题:汽车驾驶室两侧和马路转弯处安装的反光镜为什么要做成凸面,而不做成平面
•一束光由玻璃( n= )进入水( n= ),若以45 ° 角入射,试求折射角。
•证明光线通过二表面平行的玻璃板时,出射光线与入射光线永远平行。
•为了从坦克内部观察外界目标,需要在坦克壁上开一个孔。
假定坦克壁厚为 200mm ,孔宽为 120mm ,在孔内部安装一块折射率为 n= 的玻璃,厚度与装甲厚度相同,问在允许观察者眼睛左右移动的条件下,能看到外界多大的角度范围
•一个等边三角棱镜,若入射光线和出射光线对棱镜对称,出射光线对入射光线的偏转角为40 °,求该棱镜材料的折射率。
•构成透镜的两表面的球心相互重合的透镜称为同心透镜,同心透镜对光束起发散作用还是会聚作用•共轴理想光学系统具有哪些成像性质
第二章 : 共轴球面系统的物像关系 ( 理论学时: 10 学时,实验学时: 2 学时 )
•讨论题:对于一个共轴理想光学系统,如果物平面倾斜于光轴,问其像的几何形状是否与物相似为什么
•思考题:符合规则有什么用处为什么应用光学要定义符合规则
•有一放映机,使用一个凹面反光镜进行聚光照明,光源经过反光镜以后成像在投影物平面上。
光源高为 10mm ,投影物高为 40mm ,要求光源像高等于物高,反光镜离投影物平面距离为 600mm ,求该反光镜的曲率半径等于多少
•试用作图法求位于凹的反光镜前的物体所成的像。
物体分别位于球心之外,球心和焦点之间,焦点和球面顶点之间三个不同的位置。
•试用作图法对位于空气中的正透镜()分别对下列物距:
求像平面位置。
•试用作图法对位于空气中的负透镜()分别对下列物距:
求像平面位置。
•已知照相物镜的焦距毫米,被摄景物位于距离
米处,试求照相底片应放在离物镜的像方焦面多远的地方•设一物体对正透镜成像,其垂轴放大率等于- 1 ,试求物平面与像平面的位置,并用作图法验证。
•已知显微物镜物平面和像平面之间的距离为 180 毫米,垂轴放大率为- 5 ,求该物镜组的焦距和离开物平面的距离(不考虑物镜组二主平面之间的距离)。
•已知航空照相机物镜的焦距= 500 毫米,飞机飞行高度为 6000 米,相机的幅面为300 × 300 毫米 2 ,问每幅照片拍摄的地面面积。
•由一个正透镜组和一个负透镜组构成的摄远系统,前组正透镜的焦距= 100 毫米,后组负透镜
的焦距=- 50 毫米。
要求由第一组透镜道组合系统像方焦点的距离为系统的组合焦距的,求二透镜组之间的间隔 d 应为多少组合焦距等于多少
•如果将第 10 题中的系统用来对 10 米远的物平面成像,用移动第二组透镜的方法,使像平面位于移动前组合系统的像方焦平面上,问透镜组移动的方向和移动距离
•由两个系统构成的一个倒像系统,设第一组透镜的焦距为,第二组透镜的焦距为,物平面位于第一组透镜的物方焦平面上,求该倒像系统的垂轴放大率。
•由两个同心的反射面(二球面的球心重合)构成的光学系统,按照光线反射的顺序第一个反射球面是凹的,第二个反射球面是凸的,要求系统的像方焦点恰好位于第一个反射球面的顶点,求两个球面的半径
、和二者之间的间隔 d 之间的关系。
•假定一显微物镜由相隔 20 毫米的两个薄透镜组构成,物平面和像平面之间的距离为 180 毫米,放大率=-10 × ,要求近轴光线通过二透镜组时的偏角和相等,求二透镜组的焦距。
•电影放映机镜头的焦距= 120 毫米,影片画面的尺寸为22 × 16 毫米 2 ,银幕大小为× 4.8 米 2 ,问电影机应放在离银幕多远的地方如果把放映机移到离银幕 50 米远处,要改用多大焦距的镜头
•一个投影仪用5 × 的投影物镜,当像平面与投影屏不重合而外伸 10 毫米时,则须移动物镜使其重合,试问物镜此时应向物平面移动还是向像平面移动移动距离为多少
•一照明聚光灯使用直径为 200 毫米的一个聚光镜,焦距为= 400 毫米,要求照明距离为 5 米远的一个直径为 3 米的圆,问灯泡应安置在什么位置
•已知一个同心透镜= 50 毫米,厚度 d = 10 毫米, n= ,求它的主平面和焦点位置。
第三章 : 眼睛的目视光学系统 ( 理论学时: 6 学时,实验学时: 2 学时 )
•讨论题:当进入已开演的电影院时,看不清周围的人和坐位,为什么过一会就能看清了当白天走出电影院时,感到光线特别强,这是为什么
•思考题:人眼的视角分辨率是什么含义为什么人眼的视角分辨率是有限的
•正常人眼的远点在什么地方若某正常人眼的最大调节范围为- 10 视度,其近点距离为多少
•用两个负透镜能否构成一个望远镜为什么
•假定用眼睛直接观察敌人的坦克时,可以在 400 米的距离上看清坦克的编号,如果要求距离 2 公里也能看清,问应该使用几倍的望远镜
•有一焦距为 150 毫米的物镜,拟装成一个 6 倍的望远镜,问组成开普勒和伽利略望远镜时,目镜的焦距各为多少镜筒长(物镜和目镜之间的距离)各为多少
•焦距仪上测微目镜的焦距为 17 毫米,使用叉线对准,问瞄准误差等于多少
•燃烧室离观察窗 1.5 米,为了看清燃烧室内的情况,需要采用一个实际视放大率为 5 倍的仪器,假定物镜和目镜之间的距离为 200 毫米(物镜和目镜的厚度均忽略不计),试问物镜焦距和目镜焦距各为多大若要求视度调节范围为± 5 视度,目镜的总移动量为多大
第四章 : 平面镜棱镜系统 ( 理论学时: 8 学时 )
•讨论题:平面镜棱镜系统有什么用途
•思考题:单平面镜和双平面镜旋转有什么实际应用
•如果要求周视瞄准镜光轴俯仰± 15 °,问端部直角棱镜应俯仰多大角度
•平面镜成像有哪些性质单平面镜和双平面镜旋转各有什么特点
•假定望远镜物镜的焦距为 80 毫米,通光口径为 20 毫米,半视场角ω=5 °,在它后面 50 毫米处放一直角屋脊棱镜90 ° 2 ,求棱镜的尺寸和像面的位置。
第五章 : 光学系统中成像光束的选择 ( 理论学时: 5 学时 )
•讨论题:光学系统成像光束选择应该根据遵循原则
•思考题:为什么望远镜系统中成像光束的选择非常重要
•在设计一个光学系统时,应如何考虑选择孔径光阑和视场光阑
•怎样表示显微镜物镜的成像光束大小和成像范围大小望远镜中是怎样表示的
•一般用显微镜的孔径光阑选在什么地方测量用显微镜的孔径光阑选在什么地方为什么
第六章 : 辐射度学和光度学基础 ( 理论学时: 8 学时 )
•讨论题:光通量和辐射通量有什么区别
•讨论题:发光强度、光照度以及光亮度分别代表什么含义
•思考题:什么叫发光点什么叫发光面如何表示人眼对发光点和发光面的主观光亮度
•一般钨丝白炽灯各方向的平均发光强度( cd )大约和灯泡的辐射功率( W )相等,问灯泡的发光效能为多大
•有一直径 20 厘米的球形磨砂灯泡,各方向均匀发光,其光视效能为 15 lm/W ,若在灯泡正下方 2 米处的光照度为 30 lx ,问该灯泡的功率为多大灯泡的光亮度多大
•用一个 250W 的溴钨灯作为 16 毫米电影放映机的光源,光源的光视效能为 30 lm/W ,灯丝的外形面积为 5 × 7mm 2 ,可以近似看作一个两面发光的发光面,采用第一种照明方式。
灯泡的后面加有球面反光镜,使灯丝的平均光亮度提高 50 % ,银幕宽度为 4 米,放映物镜的相对孔径为 1 :,系统的透过率τ =,求银幕光照度( 16 毫米放映机的片门尺寸为10 × 7mm 2 )。
•设有一个投影物镜,采用 100W 的灯泡照明,灯泡的光视效能为 20 lm/W, 发光体直径为 4 毫米、各方向均匀发光的球形灯丝,要求银幕的光照度为 60 lx ,银幕离开投影仪的距离为 10 米,投影仪片门宽为 20 毫米,整个系统的透过率τ =,求投影物镜的焦距和相对孔径。
•有一对称照相物镜,相对孔径为 1:5 ,每亿半焦距为 200 毫米,两透镜组相距 20 毫米,在透镜组中央有一个孔径光阑。
在物镜前方 400 毫米处有一个垂直光轴的物体,其光亮度为 500 cd/m 2 。
如果不考虑系统的光能损失,求像平面光照度。
当物体位于无限远时,像平面光照度又为多少
•照相时光圈数取 8 ,曝光时间用s ,为了拍摄移动目标,将曝光时间改为s ,问应取多大的光圈数
•用于跟踪天空飞行目标的电视摄影机,摄像管要求最低的像面光照度为 20 lx ,假定天空的光亮度为 2500 cd/m 2 ,光学系统的透过率τ 等于,问要求使用多大相对孔径的摄影物镜
•第五章光学系统成像光束选择中,双目望远镜的光学系统中,所有的凹透镜都是用火石玻璃制做的,凸透镜都是用冕玻璃制做的,透镜和棱镜中的总的光路长为 110 毫米,计算光学零件表面不镀增透膜和镀增透膜两种情况下系统的透过率。
第七章 : 光学系统成像质量评价 ( 理论学时: 7 学时,实验学时: 4 学时 )
•讨论题:检验实际光学系统成像质量的常用方法有哪几种
•思考题:在光学系统设计阶段常用的评价成像质量的方法有哪几种
•光学系统色差有哪几种画图说明。
•共轴光学系统轴上点有哪几种像差
•轴外点有哪几种单色像差和色差画图说明。
•什么叫理想光学系统的分辨率它具有什么实际意义理想光学系统的分辨率是怎样确定的
•试说明望远镜、照相物镜、显微物镜的分辨率表示方法。
•光学传递函数的物理意义是什么和其它评价光学系统成像质量的方法相比,光学传递函数有什么优点。
