直齿圆柱齿轮强度计算
直齿圆柱齿轮的齿根弯曲强度计算

低可靠性 0.80
SF 1.50 1.00 0.70
对于高速重载或重要的齿轮传动,应按
高可靠性选取,一般传动齿轮可适当降
低可靠性要求。
返
回
接触寿命系数ZN
返回
齿轮的弯曲疲劳极限Flim
当齿根弯曲应力为对称循环时,将查出的Flim乘以 0.7
返回
弯曲寿命系数YN
返回
尺寸系数Yx
返 回
表14-6安全系数
非对称布置 0.6 ~ 1.2 0.3 ~ 0.6
悬臂布置
0.3 ~ 0.4 0.2 ~ 0.25
直齿轮取表中的小值,斜齿轮取大值。
2、许用弯曲应力
FPFlS im F YNYx (MPa)
Flim-试验齿轮的弯曲疲劳极限, 由图14-24查得
YN-弯曲寿命系数
由图14-25查得
横坐标为实际应力循环系数 N
四、直齿圆柱齿轮的齿根弯曲强度计算 设计公式:
m3 2 dZ 01 20 K F 0 1 T P Y FY aSY a
齿形系数Yfa可由图14-19查取
齿形系数Yfa
应力修正系数YSa
重合度系数Y
齿宽系数d
表14-4
齿轮相对于轴承
齿面硬度
的位置
软齿面 硬齿面
对称布置
0.8 ~ 1.4 0.4 ~ 0.9
SF-弯曲疲劳安全系数
由表14-6查得
Yx-尺寸系数
由图14-26查得
考虑齿轮的实际尺寸大于试件尺寸 时,对弯曲疲劳的影响系数。
接触疲劳极限Hlim
在当一
区材般
域料取
的、区
上工域
半艺图
部及的
分热中
取处间
直齿圆柱齿轮传动的弯曲强度计算

齿轮传动设计时,按主要失效形式进行强度计算,确 定主要尺寸,然后按其它失效形式进行必要的校核。
软齿面闭式齿轮传动: 按接触强度进行设计,按弯曲强度校核:
2
d1
3
2KT1
H
mm
F
2KT1YFaYSa bmd1
2KT1YFaYSa bm2 z1
[ F ]
MPa
硬齿面闭式齿轮传动: 按弯曲强度进行设计,按接触强度校核:
[ F1] [ F 2 ]
3.对于传递动力的齿轮模数一般应大于1.5~2mm。
4.对于开式传动,为考虑齿面磨损,可将算得模 数值加大10%~ 15%。
三.许用弯曲应力:
[
F
]
FE
SF
MPa
弯曲疲劳极限σFE由实验确定。 SF为安全系数,查表11-5确定。
因弯曲疲劳造成的轮齿折断可能造成重大事故,而疲劳 点蚀只影响寿命,故:SF>SH
m
3
2KT1
d Z12
. YFaYsa
[ ]F
mm
H ZE ZH
2KT1 bd12
u
1 u
[
H
]
开式齿轮传动:按弯曲强度设计:
m
3
2KT1
d Z12
. YFaYsa
[ ]F
mm
载荷作用点:啮合过 程中,载荷作用点是 不断变化的。为简化 计算,一般可将齿顶 作为载荷作用点。
受力分析图
危险截面
危险截面:用30°切线法确定。 作与轮齿对称中线成30°角并 与齿根过渡圆角相切的切线, 通过两切点作平行于轴线的截 面即为危险截面(左图所示)。
弯曲应力: F
M W
6KFt hF cos F bsF2 cos
标准直齿圆柱齿轮齿面接触疲劳强度计算
三、标准直齿圆柱齿轮齿面接触疲劳强度
1.齿轮齿面接触疲劳强度条件
H ZH ZE Z
2KT1 bd12
u u
1
[ H
]
2.按齿面接触疲劳强度的设计式
a
u 1
3
KT1
2 a u
ZH ZE Z
H
2
mm
d1
3
2KT1
d
u 1
u
ZH ZE Z
H
2
mm
a
b a
;
d
ห้องสมุดไป่ตู้
b d1
5-5 标准直齿圆柱齿轮齿面接触疲劳强度计算 三、标准直齿圆柱齿轮齿面接触疲劳强度
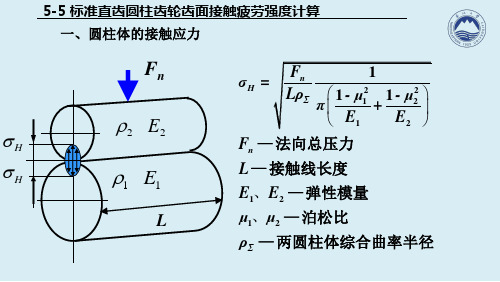
5-5 标准直齿圆柱齿轮齿面接触疲劳强度计算 一、圆柱体的接触应力
H
Fn 2 E2
σH =
Fn
1
LρΣ
π
1
- μ12 E1
+ 1 - μ22 E2
Fn — 法向总压力
H
1 E1
L — 接触线长度 E1、E2 — 弹性模量
L
μ1、μ2 — 泊松比
ρΣ — 两圆柱体综合曲率半径
5-5 标准直齿圆柱齿轮齿面接触疲劳强度计算
5-5 标准直齿圆柱齿轮齿面接触疲劳强度计算 二、标准直齿圆柱齿轮齿面接触应力 4.齿轮齿面接触应力
弹性系数:ZE
1
[(1 12 ) (1 22 )]
E1
E2
表5 5
节点区域系数:ZH
2
sin cos
齿轮齿面接触应力
H ZH ZE Z
2KT1 u 1 bd12 u
N/mm2
5-5 标准直齿圆柱齿轮齿面接触疲劳强度计算
标准直齿圆柱齿轮传动的强度计算

标准直齿圆柱齿轮传动的强度计算一、轮齿的受力分析图6-6所示为齿轮啮合传动时主动齿轮的受力情况,不考虑摩擦力时,轮齿所受总作用力f n将沿着啮合线方向,f n称为法向力。
f n在分度圆上可分解为切于分度圆的切向力f t和沿半径方向并指向轮心的径向力f r 。
圆周力f t=n径向力 f r= f t tg n (6-1)法向力 f n=n式中:d1为主动轮分度圆直径,mm;为分度圆压力角,标准齿轮=20°。
设计时可根据主动轮传递的功率p1(kw)及转速n1(r/min),由下式求主动轮力矩t1=9.55×106×(n mm)(6-2)根据作用力与反作用力原理,f t1=-f t2,f t1是主动轮上的工作阻力,故其方向与主动轮的转向相反,f t2是从动轮上的驱动力,其方向与从动轮的转向相同。
同理,f r1=-f r2,其方向指向各自的轮心。
二、载荷与载荷系数由上述求得的法向力f n 为理想状况下的名义载荷。
由于各种因素的影响,齿轮工作时实际所承受的载荷通常大于名义载荷,因此,在强度计算中,用载荷系数k 考虑各种影响载荷的因素,以计算载荷f nc 代替名义载荷f n 。
其计算公式为(6-3)式中:k 为载荷系数,见表6-3。
表6-3 载荷系数k二、齿根弯曲疲劳强度计算齿根处的弯曲强度最弱。
计算时设全部载荷由一对齿承担,且载荷作用于齿顶,将轮齿看作悬臂梁,其危险截面可用30o 切线法确定,即作与轮齿对称中心线成30o 夹角并与齿根过渡曲线相切的两条直线,连接两切点的截面即为齿根的危险截面,如图6-7所示。
运用材料力学的方法,可得轮齿弯曲强度校核的公式为= ≤或σf =≤(6-4)或由上式得计算模数m的设计公式m≥ (6-5)式中:=b/d1称齿宽系数(b为大齿轮宽度),由表6-4查取;称为齿形系数,由图6-8查取;[]为弯曲许用应力,由式6-8计算。
表6-4齿宽系数=b/d1三、齿面接触疲劳强度计算齿面接触疲劳强度计算是为了防止齿间发生疲劳点蚀的一种计算方法,它的实质是使齿面节线处所产生的最大接触应力小于齿轮的许用接触应力,齿面接触应力的计算公式是以弹性力学中的赫兹公式为依据的,对于渐开线标准直齿圆柱齿轮传动,其齿面接触疲劳强度的校核公式为≤或≤ (6-6)将上式变换得齿面接触疲劳强度的设计公式d1≥ (6-7)式中:“±”分别用于外啮合、内啮合齿轮;z e为齿轮材料弹性系数,见表6-5;z h为节点区域系数,标准直齿轮正确安装时z h =2.5;[σh]为两齿轮中较小的许用接触应力,由式6-9计算;u为齿数比,即大齿轮齿数与小齿轮齿数之比。
15直齿圆柱齿轮传动的强度计算
二、齿轮传动的强度计算
齿轮传动的强度计算是根据轮齿可能出现的失效形式和 设计准则来进行的,由于轮齿的主要失效形式是齿面疲劳点 蚀和轮齿疲劳折断,因此只讨论齿面接触疲劳强度和齿根弯 曲疲劳强度的计算
1.齿面接触疲劳强度计算 1.齿面接触疲劳强度计算
针对齿面点蚀失效进行的 齿面点蚀是因为接触应力过大引起的。 接触应力过大引起的 齿面点蚀是因为接触应力过大引起的。齿轮啮合可看 作是分别以接触处的曲率半径ρ 作是分别以接触处的曲率半径ρl、ρ2为半径的两个圆柱 赫兹应力公式计算 体的接触,其最大接触应力可由赫兹应力公式计算, 体的接触,其最大接触应力可由赫兹应力公式计算,即
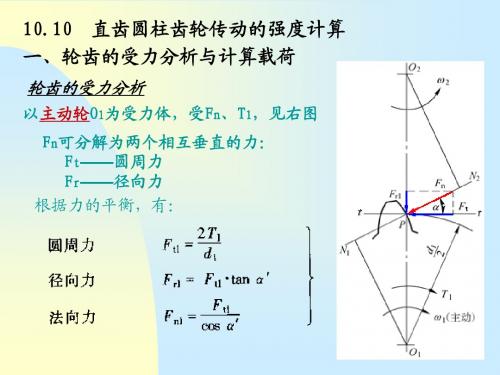
10.10 直齿圆柱齿轮传动的强度计算 一、轮齿的受力分析与计算载荷
轮齿的受力分析
以主动轮O1为受力体,受Fn、T1,见右图 主动轮O 为受力体, 可分解为两个相互垂直的力: Fn可分解为两个相互垂直的力: Ft——圆周力 圆周力 Fr——径向力 径向力 根据力的平衡,有:
其中: 其中: 主动轮传递的转矩N mm T1 -主动轮传递的转矩N·mm 主动轮分度圆直径mm; mm;非标准时用节圆直径代替 d1 -主动轮分度圆直径mm;非标准时用节圆直径代替
对于斜齿圆柱齿轮传动从前端面进入啮合到后端面脱离啮合其在啮合线上的长度比直齿圆柱齿轮增加了btg斜齿圆柱齿轮的啮合面斜齿圆柱齿轮传动的重合度端面重合度附加重合度附加重合度是由于齿的倾斜而产生它随齿宽b和的增大而增大这是斜齿轮传动平稳承载能力较高的原因之一当量齿轮及当量齿数在研究斜齿轮法面齿形时可以虚拟一个与斜齿轮的法面齿形相当的直齿轮称这个虚拟的直齿轮为该斜齿的当量齿轮其齿数则称四斜齿圆柱齿轮的当量齿数和最小齿数在进行强度计算和用成形法加工齿轮选择铣刀时必须知道斜齿轮的法面齿形通常用近似的方法来分析做法如图所示过斜齿轮分度圆柱上齿廓的任一点c作齿的法面nn该法面与分度圆柱面的交线为一椭圆椭圆的长半轴为
标准直齿圆柱齿轮传动强度

标准直齿圆柱齿轮传动的强度可以根据以下步骤进行计算:
1.确定齿轮上所受的力。
这包括圆周力(Ft)、径向力(Fr)和法向力
(Fn)。
2.根据圆周力和齿轮的节圆直径(d1),计算出转矩(T1)。
转矩可以用公
式T1 = 2 × Ft × tanα来表示,其中α是啮合角,通常取值为20°。
3.根据转矩和齿宽,计算出弯曲应力。
弯曲应力可以用公式σ= Ft/Wb来表
示,其中Wb是齿宽。
4.根据齿根处的弯曲应力,计算出弯曲疲劳强度系数。
这个系数通常由实验
确定,也可以通过查阅相关设计手册获得。
5.根据弯曲疲劳强度系数和弯曲应力,计算出弯曲疲劳极限。
弯曲疲劳极限
可以用公式σHlim = k × Wb × Ft来表示,其中k是弯曲疲劳强度系数。
6.根据弯曲疲劳极限,计算出安全系数。
安全系数可以用公式H=σHlim/σH
来表示,其中σH是工作应力。
7.根据安全系数和弯曲应力,计算出许用弯曲应力。
许用弯曲应力可以用公
式σH=σHlim/S来表示,其中S是安全系数。
以上是标准直齿圆柱齿轮传动强度的计算步骤,希望能对您有所帮助。
圆柱齿轮传动强度的计算

圆柱齿轮传动的强度计算1 直齿圆柱齿轮传动的强度计算1.齿面接触疲劳强度计算为了保证在预定寿命内齿轮不发生点蚀失效,应进行齿面接触疲劳强度计算。
因此,齿轮接触疲劳强度计算准则为:齿面接触应力σH小于或等于许用接触应力σHP,即σH≤σHP赫兹公式由于直齿轮在节点附近往往是单对齿啮合区,轮齿受力较大,故点蚀首先出现在节点附近。
因此,通常计算节点的接触疲劳强度。
图a表示一对渐开线直齿圆柱齿轮在节点接触的情况。
为了简化计算,用一对轴线平行的圆柱体代替它。
两圆柱的半径ρ1、ρ2分别等于两齿廓在节点处的曲率半径,如图b所示。
由弹性力学可知,当一对轴线平行的圆柱体相接触并受压力作用时,将由线接触变为面接触,其接触面为一狭长矩形,在接触面上产生接触应力,并且最大接触应力位于接触区中线上,其数值为式中σH-接触应力(Mpa)Fn-法向力(N)L-接触线长度(mm)rS-综合曲率半径(mm);±-正号用于外接触,负号用于内接触ZE-材料弹性系数(),,其中E1、E2分别为两圆柱体材料的弹性模量(MPa);m1、m2分别为两圆柱体材料的泊松比。
上式表明接触应力应随齿廓上各接触点的综合曲率半径的变化而不同,且靠近节点的齿根处最大(图c、d)。
但为了简化计算,通常控制节点处的接触应力。
节点处的参数(1)综合曲率半径由图可知,,代入rE公式得式中:,称为齿数比。
对减速传动,u=i;对增速传动,u=1/i。
因,则有(2)计算法向力(3)接触线长度L引入重合度系数Ze,令接触线长度将上述参数代入最大接触应力公式得接触疲劳强度计算公式令,称为节点区域系数。
则得(1) 齿面接触疲劳强度的校核公式齿面接触疲劳强度的校核公式为(2) 齿面接触疲劳强度设计公式设齿宽系数,并将代入上式,则得齿面接触疲劳强度的设计公式式中:d1-小齿轮分度圆直径(mm);ZE-材料弹性系数(),按下表查取;注:泊松比m1=m2=0.3Z H-节点区域系数,考虑节点处轮廓曲率对接触应力的影响,可由下左图查取。
10-05 标准直齿圆柱齿轮传动的强度计算

受载分析及应力计算公式
当齿顶受载时,轮齿根部
的应力如图。载荷 pca 对危险 截面产生的应力有弯曲应力和 压应力。 注意:在齿根危险截面处
的压应力仅为弯曲应力的百分
之几,故可忽略。计算时仅考 虑水平分力产生的弯曲应力。
受载分析及应力计算公式
取h = Khm,S = KSm,并将
代入,得:
齿形系数YFa及应力校正系数YFs
YFa是一个无量纲系数,它只与轮齿的齿廓形状有关,而与 齿的大小(模数m)无关。 在实际计算时,还应计入齿根危险截面处的过渡圆角所引 起的应力集中作用以及弯曲应力以外对齿根应力的影响,因此, 引入应力校正系数YSa。 齿根弯曲疲劳强度校核计算公式 :
齿形系数YFa及应力校正系数YSa 表
齿根弯曲疲劳强度公式
10-5 标准直齿圆柱齿轮传动的强度计算
(1)轮齿的受力分析
(2)齿根弯曲疲劳强度计算
(3)齿面接触疲劳强度计算
(4)齿轮传动的强度计算说明
轮齿的受力分析
• 法向载荷Fn • 圆周力Ft • 径向力Fr
T1——小齿轮传递的转矩,N.mm; d1——小齿轮的节圆直径,对标准齿轮即为分 度圆直径,mm; α——啮合角,对标准齿轮,α=20°。
齿根弯曲疲劳强度校核计算公式 :
按齿根弯曲疲劳强度设计齿轮的计算公式:
按齿根弯曲疲劳强度设计时,[σ]F1/(YFa1YSa1)或 [σ]F2/(YFa2YSa2)中较小的数值代入设计公式进行计算。
齿宽系数
装置 状况 φd 两支承相对小 齿轮对称布置 0.9-1.4 (1.2-1.9) 两支承相对小齿 轮不对称布置 0.7-1.15 (1.1-1.65) 小齿轮作 悬臂布置 0.4-0.6
直齿圆柱齿轮传动的轮齿弯曲强度计算

直齿圆柱齿轮传动的轮齿弯曲强度计算准则 为了保证在预定寿命内齿轮不发生轮齿断裂失效,应进行轮齿弯曲强度计算。
直齿圆柱齿轮传动的轮齿弯曲强度计算准则为:齿根弯曲应力σF 小于或等于许用弯曲应力[σF ],即σF ≤[σF ]轮齿弯曲强度计算公式轮齿弯曲强度的验算公式计算弯曲强度时,仍假定全部载荷仅由一对轮齿承担。
显然,当载荷作用于齿顶时,齿根所受的弯曲力矩最大。
图 11-8 齿根危险截面计算时将轮齿看作悬臂梁(如图11-8所示)。
其危险截面可用切线法确定,即作与轮齿对称中心线成夹角并与齿根圆角相切的斜线,而认为两切点连线是危险截面位置(轮齿折断的实际情况与此基本相符)。
危险截面处齿厚为。
法向力Fn 与轮齿对称中心线的垂线的夹角为,Fn 可分解为 使齿根产生弯曲应力,则产生压缩应力。
因后者较小故通常略去不计。
齿根危险截面的弯曲力矩为式中:K 为载荷系数;为弯曲力臂。
危险截面的弯曲截面系数W 为故危险截面的弯曲应力为 3030F s F α1F 2F F h F σ令式中称为齿形系数....。
因和均与模数成正比,故值只与齿形中的尺寸比例有关而与模数无关,对标准齿轮仅决定于齿数。
由此可得轮齿弯曲强度的验算公式Mpa (a)通常两齿轮的齿形系数和并不相同,两齿轮材料的许用弯曲应力[]和[]也不相同,因此应分别验算两个齿轮的弯曲强度。
轮齿弯曲强度设计公式引入齿宽系数,可得轮齿弯曲强度设计公式为mm (b)上式中的负号用于内啮合传动。
内齿轮的齿形系数可参阅有关书籍。
式(a )和(b)中为小齿轮齿数;的单位为N ·mm ;b 和m 的单位为mm ;和[]的单位为MPa 。
式(b)中的应代入和中的较大者。
算得的模数应圆整为标准模数。
传递动力的齿轮,其模数不宜小于1.5mm 。
26()cos ()cos F F F F h m Y s m αα=F Y F h F s F Y 1112122[]F F F F KTY KTY bd m bm z σσ==≤1F Y 2F Y 1F σ2F σa ba ψ=m ≥1z 1T F σF σ[]F F Y σ11[]F F Y σ22[]F F Y σ在满足弯曲强度的条件下可适当地选取较多的齿数,因齿数增多可使传动平稳;在中心距a 一定时,齿数增多则模数减小,顶圆尺寸也随之减小,有利于节省材料和加工工时。
齿轮的强度计算

直齿圆柱齿轮的强度计算受力分析:圆周力F t =112d T 径向力αtan ∙=t r F F 法向载荷αcos t n F F = 1T :小齿轮传递的转矩,mm N ∙ 1d :小齿轮的节圆直径,mm α:啮合角,对标准齿轮, 20=α齿根弯曲疲劳强度的计算: 校核公式:[]F d Sa Fa Sa Fa F z m Y Y KT bmd Y Y KT σφσ≤==21311122 计算公式:[]32112F d Sa Fa z Y Y KT m σφ≥d φ:齿宽系数,1d b d =φ Fa Y :齿形系数 Sa Y :应力校正系数齿面接触疲劳强度的计算: 校核公式:[]H E H uu bd KT Z σσ≤±∙=125.2211 设计公式:[]3211132.2⎪⎪⎭⎫ ⎝⎛∙±∙=H E d Z u u KT d σφ标准斜齿圆柱齿轮的强度计算 受力分析: 圆周力:112d T F T = 径向力:βαcos tan n t r F F ∙= 轴向力:βtan ∙=t a F F齿根弯曲疲劳强度计算: 校核公式:[]F n Sa Fa t F bm Y Y Y KF σεσαβ≤=设计计算:[]32121cos 2F Sa Fa d n Y Y z Y KT m σεφβαβ∙=齿面接触疲劳强度计算: 校核计算:H E H Z Z uu bd KT ∙±∙=111αεσ 设计计算:[]321112⎪⎪⎭⎫ ⎝⎛∙±∙≥H Sa Fa d Y Y u u KT d σεφαu :齿数比标准锥齿轮的强度计算 受力分析:11212m t t d T F F == 121cos tan δαt a r F F F == 121cos tan δαt r a F F F == αcos 1t n F F =齿根弯曲疲劳强度计算: 校核公式:()[]F R Sa Fa t F bm Y Y KF σφσ≤-=5.01 设计公式:()[]32212115.014F Sa Fa R R Y Y u z KT m σφφ∙+-≥齿面接触疲劳强度计算: 校核公式:()[]H R R E H u d KT Z σφφσ≤-=31215.015设计公式:[]()321215.0192.2u KT Z d R R H E φφσ-∙⎪⎪⎭⎫ ⎝⎛≥。
直齿圆柱齿轮传动强度计算

直齿圆柱齿轮传动的强度计算齿面接触强度计算闭式齿轮传动的主要失效形式之一是齿面点蚀,故需进行齿面接触疲劳强度计算。
齿面的 疲劳点蚀与齿面接触应力有关,齿面的最大接触应力可用赫兹公式计算如下:222121211111E E bF n H μμρρπσ-+-±⋅=式中 Fn 为法向力;b 为两轮齿的接触宽度;E1,E2为两齿轮材料的弹性模量;12,μμ为两齿轮材料的泊松比;12,ρρ为两齿面接触点处的曲率半径;“+”号用于外啮合,“一”号用于内啮合。
前已述及,齿根部分靠近节线处最易发生点蚀,故常取节点处的接触应力为计算依据。
由图11.4,a 可知,节点处的齿廓曲率半径为111sin 2N C d αρ==111sin 2N C d αρ==取传动比i=z 2/z 1≥l ,式中z 2为大齿轮齿数,z 1为小齿轮齿数,则12(1)ad i =±方向相同。
径向力F ,6勺方向由作用点指向轮心。
2.计算载荷上述的法向力Fn 为名义载荷。
理论上Fn 应沿齿宽均匀分布,但由于轴和轴承的变形,传动装置的制造,安装误差等原因,载荷沿齿宽的分布并不是均匀的,因此会出现载荷集中现象。
如图9.29所示,齿轮位置对轴承不对称时,由于轴的弯曲变形齿轮将互相倾斜,这时,轮齿左端载荷增大。
轴和轴承的刚度越小,齿宽B 越宽,载荷集中越严重。
此外,由于各种原动机和工作机特性不同,齿轮制造误差以及轮齿变形等原因,还会引起附加动载荷。
精度越低,圆周速度越高,附加动载荷就越大。
因此,计算齿轮强度时,通常用计算载荷KFn 代替名义载荷Fn ,以考虑载荷集中和附加动载荷的影响。
其中K 为载荷系数,其值可由表9.6查取。
图9.29 载荷集中现象表9.6 载荷系数K9.11.2 载荷计算1.受力分析在图9.30中,当不计齿面间的摩擦力时,作用于主动轮齿上的总压力将垂直于齿面,即为图中法向力芦n 。
芦n 可分解为圆周力F ,和径向力芦r 。
渐开线标准直齿圆柱齿轮传动的强度计算

渐开线标准直齿圆柱齿轮传动的强度计算
(4)齿数比u。齿数比u不宜过大, 以免因大齿轮的直径大而使整个齿轮传 动尺寸过大。通常直齿圆柱齿轮取u≤5, 斜齿圆柱齿轮取u≤7。
渐开线标准直齿圆柱齿轮传动的强度计算
3. 齿轮传动的设计计算步骤
(1)选择齿轮材料、热处理及许用应力。通过分析齿 轮的工作条件,选择材料牌号与热处理的方法。
应注意,通常两个相啮合的齿轮齿数是不相等的,因此YF和 YS都不相等,而且两轮材料的弯曲疲劳许用应力也不一定相等。因 此,在进行强度校核时,必须分别校核两齿轮的齿根弯曲强度,应
将两齿轮的
值进行比较,只需将其中较大者代入设计公式。
渐开线标准直齿圆柱齿轮传动的强度计算
2. 齿轮传动主要参数的选择
渐开线标准直齿圆柱齿轮传动的强度计算
(2)模数m。m应圆整,对传递动力的闭式齿轮传动,应使 圆整后的m≥2 mm;对开式齿轮传动,应使圆整后的m值大于初 算值的10%~20%,并使m≈0.02a,a为齿轮传动的中心距。
(3)齿宽系数∮d和齿宽b。增大齿宽可使齿轮的径向尺寸缩 小,但齿宽越大,载荷沿齿宽分布越不均匀。动力传动齿轮取∮ d=0.4~1.4,常用范围取∮ d=0.8~1.2。 ∮ d的选择可见表1-10。
渐开线标准直齿圆柱齿轮传动的强度计算
(4)齿根弯曲疲劳强度计算。齿轮受载时,轮齿齿根受弯曲应力 最大,为了防止轮齿根部的疲劳折断,在进行齿轮设计时,必须计算 齿根弯曲疲劳强度。为简化计算并考虑安全性,假定载荷作用于齿顶, 且全部载荷由一对轮齿承受,此时齿根部分产生的弯曲应力最大。
经推导可得轮齿齿根弯曲疲劳强度的计算公式:
渐开线标准直齿圆柱齿轮传动的强度计算
应用式(1-15)、式(1-16)时应注意以下几点:
直齿圆柱齿轮传动的强度计算

2.14
YS 1.44 1.47 1.51 1.53 1.54 1.55 1.56 1.58 1.59 1.61 1.63 1.65 1.67 1.69 1.71 1.73 1.77 1.80
1.88
返回
机械设计基础
Machine Design Foundation
直齿圆柱齿轮传动的强度计算
对于一对齿轮啮合传动而言,因为两齿轮的齿数一般不相同,所
越小,轮齿的弯曲强度越低。因此,应当在满足轮齿弯曲强度的前提
下,尽可能选取较多的齿数。对于闭式硬齿面齿轮传动或开式齿轮传
动,通常取z1=17~20;对于闭式软齿面齿轮传动,通常取z1=20~30。 当z1确定后,即可按传动比i=z2/z1,求出z2。为使两个齿轮的轮齿磨 损均匀,应尽可能使z1和z2互为质数。
按式(10-21)计算所得各力均为作用在轮齿上的名义载荷。进 行齿轮的强度计算时,要考虑由于原动机和工作机的工作特性所引起 的动力过载、齿轮副的啮合误差所引起的附加动载荷、轴的变形和齿 轮制造误差所引起的载荷沿齿宽分布不均匀、同时啮合的各对轮齿间 载荷分配不均匀等因素对轮齿受载的影响,应将名义载荷Fn修正为计 算载荷FnC,即
面,由工程力学可推得齿根弯曲疲劳强度的校核公式为
F
2FT1 bm2 z1
YFYS
[ F ]
(10-25)
σF——齿根处产生的最大弯曲应力,MPa ;
YF——反映轮齿形状对齿根弯曲应力影响的齿形系数,见表10-5;
YS——反映齿根圆角引起的应力集中和危险截面压应力等其他应力
影响的应力修正系数,见表10-5;
向转动,故[σH] 1= [σH] 2=0.9σHlim=0.9×1450=1305MPa。
齿轮传动_标准直齿圆柱齿轮传动强度计算

FYSaF0KtF b YFm Y aSa 其中:
Ft=2T1/d1 m=d1/z1
齿宽系数 :Φd=b/d1 ( 重要) 表10—7
弯曲强度校核公式:
F 2K dm 1TY3Fz1aY2SaF
弯曲强度设计公式:
m3
2KT1
d z12
YFaYSa
F
★ 由公式计算出 模数去套标准
微型电子机械系统的研究的计划,从2019年 开始, 资助MIT,加 州大学 等8所大 学和贝 尔实验 室从事 这一领 域的研 究与开 发,年 资助额
从100万、200万加到1993年的500万美 元。1994年发 布的《 美国国 防部技 术计划 》报告 ,把M EMS列 为关键 技术项 目。美 国国防 部高级 研
标准直齿圆柱齿轮传动强度计算
(一) 轮齿的受力分析
假设:单齿对啮合,力作用在节点P,不计Ff 轮齿间的法向力Fn, 沿啮合线指向齿面
1. Fn 的分解:
Fn -圆周力Ft :沿节圆切线方向指向齿面 \径向力Fr :沿半径方向指向齿面(轮心)
2. 作用力的大小: Ft=2T1/d1 Fr=Ft·tgα
后再将其装配在一起。火车的车轮外 圈也是 用加热 的方法 将其套 在基体 上,冷 却时即 可保证 其结合 的牢固 性(此 种方法 现在依 旧应用
于某些零部件的转配过程中)。
机械加工包括:灯丝电源绕组、激 光切割 、重型 加工、 金属粘 结、金 属拉拔 、等离 子切割 、精密
焊接、辊轧成型、金属板材弯曲成型 、模锻 、水喷 射切割 、精密 焊接等 。
前面",建议中央财政预支费用为五年 5000万 美元, 得到美 国领导 机构重 视,连 续大力 投资, 并把航 空航天 、信息 和MEMS作为 科技发 展
标准直齿圆柱齿轮的强度计算

齿面接触强度计算
K? :齿向载荷分布系数
两轮或其中之一是软齿面(≤350 HBS ) 两轮均为硬齿面(>350HBS) 1——齿轮对称布置于两轴承之间; 2——齿轮非对称布置于两轴承之间,且轴的刚性较大 ; 3——齿轮非对称布置于两轴承之间,且轴的刚性较小 ; 4——齿轮悬臂布置。
齿面接触强度计算
d
2 1
b
u
令: z H ?
2
cos ? sin ?
称为节点区系数
zE ?
1
?
? ? ?
1
??
E1
2 1
?
1?
?2 2
E2
? ? ?
称为弹性系数
得: ? H ? z E z H
2 KT 1 ? ( u ? 1 )
d
2 1
b
u
齿面接触强度计算
3、接触强度验算公式
? H ? ZE ZH
2 KT1 d12b
d1d 2 sin ?
u d1 sin ?
? (u ? 1)2
ua sin ?
齿面接触强度计算
在节点处,载荷由一对轮齿来承担: 一对钢制齿轮:
Fn
?
Ft
cos ?
? 2T1
d1 cos ?
弹性模量:E1=E2=2.06×105 MPa
泊松比:μ1=μ2= 0.3, α=20?
代入赫兹公式得: ? H??H32?385503535(u(u?u?1bu)1ab3)a2K32KT1T1 ? [ ? H ]
齿面接触强度计算
O1
赫兹公式
?H ?
Fn
? ? ?
1
?1
?
1?
标准直齿圆柱齿轮传动的强度计算 工程

标准直齿圆柱齿轮传动的强度计算工程(一)轮齿的受力分析进行齿轮的强度计算时,首先要知道齿轮上所受的力,这就需要对齿轮传动作受力分析,齿轮传动一般均加以润滑,啮合轮齿间的摩擦力通常很小,计算轮齿受力时,可不予考虑。
沿啮合线作用在齿面上的法向载荷Fn垂直于齿面,为了计算方便,将法向载荷Fn在节点P处分解为两个相互垂直的分力,即圆周力Ft与径向力Fr, 。
由此得Ft=2T1/d1 ;Fr=Fttanα ;Fn=Ft/cosα (a)式中:T1—小齿轮传递的转矩,N·mm;d1—小齿轮的节圆直径,对标准齿轮即为分度圆直径,mm;α—啮合角,对标准齿轮,α=20°。
(二)齿根弯曲疲劳强度计算轮齿在受载时,齿根所受的弯矩最大,因此齿根处的弯曲疲劳强度最弱。
当轮齿在齿顶处啮合时,处于双对齿啮合区,此时弯矩的力臂虽然最大,但力并不是最大,因此弯矩并不是最大。
根据分析,齿根所受的最大弯矩发生在轮齿啮合点位于单对齿啮合区最高点。
因此,齿根弯曲强度也应按载荷作用于单对齿啮合区最高点来计算。
由于这种算法比拟复杂,通常只用于高精度的齿轮传动(如6级精度以上的齿轮传动)。
对于制造精度较低的齿轮传动(如7,8,9级精度),由于制造误差大,实际上多由在齿顶处啮合的轮齿分担较多的载荷,为便于计算,通常按全部载荷作用于齿顶来计算齿根的弯曲强度。
当然,采用这样的算法,齿轮的弯曲强度比拟充裕。
右边动画所示为齿轮轮齿啮合时的受载情况。
动画演示为齿顶受载时,轮齿根部的应力图。
在齿根危险截面AB处的压应力σc仅为弯曲应力σF的百分之几,故可忽略,仅按水平分力pcacosγ所产生的弯矩进行弯曲强度计算。
假设轮齿为一悬臂梁,那么单位齿宽(b=1)时齿根危险截面的弯曲应力为取,并将(a)式代入。
对直齿圆柱齿轮,齿面上的接触线长L即为齿宽b(mm),得令YFa是一个无量纲系数,只与齿轮的齿廓形状有关,而与齿的大小(模数m)无关。
直齿圆柱齿轮强度计算

直齿圆柱齿轮强度计算一、轮齿的失效齿轮传动就装置形式来讲,有开式、半开式及闭式之分;就利用情形来讲有低速、高速及轻载、重载之别;就齿轮材料的性能及热处置工艺的不同,轮齿有较脆(如经整体淬火、齿面硬度较高的钢齿轮或铸铁齿轮)或较韧(如经调质、常化的优质钢材及合金钢齿轮),齿面有较硬(轮齿工作面的硬度大于350HBS或38HRC,并称为硬齿面齿轮)或较软(轮齿工作面的硬度小于或等于350HBS或38HRC,并称为软齿面齿轮)的不一样。
由于上述条件的不同,齿轮传动也就显现了不同的失效形式。
一样地说,齿轮传动的失效主若是轮齿的失效,而轮齿的失效形式又是多种多样的,那个地址只就较为常见的轮齿折断和工作面磨损、点蚀,胶合及塑性变形等略作介绍,其余的轮齿失效形式请参看有关标准。
至于齿轮的其它部份(如齿圈、轮辐、轮毂等),除对齿轮的质量大小需加严格限制外,通常只需按体会设计,所定的尺寸对强度及刚度均较富裕,实践中也极少失效。
轮齿折断轮齿折断有多种形式,在正常情况下,主要是齿根弯曲疲劳折断,因为在轮齿受载时,齿根处产生的弯曲应力最大,再加上齿根过渡部分的截面突变及加工刀痕等引起的应力集中作用,当轮齿重复受载后,齿根处就会产生疲劳裂纹,并逐步扩展,致使轮齿疲劳折断(见)。
此外,在轮齿受到突然过载时,也可能出现过载折断或剪断;在轮齿受到严重磨损后齿厚过分减薄时,也会在正常载荷作用下发生折断。
在斜齿圆柱齿轮(简称斜齿轮)传动中,轮齿工作面上的接触线为一斜线(参看),轮齿受载后,如有载荷集中时,就会发生局部折断。
若制造或安装不良或轴的弯曲变形过大,轮齿局部受载过大时,即使是直齿圆柱齿轮(简称直齿轮),也会发生局部折断。
为了提高齿轮的抗折断能力,可采取下列措施:1)用增加齿根过渡圆角半径及消除加工刀痕的方法来减小齿根应力集中;2)增大轴及支承的刚性,使轮齿接触线上受载较为均匀;3)采用合适的热处理方法使齿芯材料具有足够的韧性;4)采用喷丸、滚压等工艺措施对齿根表层进行强化处理。
标准直齿圆柱齿轮的强度计算

图1-21 直齿圆柱齿轮轮齿的受力分析
标准直齿圆柱齿轮的强度计算
• 1.2 载荷系数
上述作用在轮齿上的法向力Fn是在理想的工作条件下求出的理论载 荷,并未考虑到影响齿轮实际载荷的各方面因素。实际工作时,受弹性 变形、制造误差及安装误差、齿轮在轴上的布置情况以及原动机和工作 机的特性等因素的影响,会引起附加载荷。因此,为了尽量符合实际情 况,在齿轮传动强度计算中应引人载荷系数K。
齿宽系数ψd=b/d1,即齿宽与分度圆直径之比。当d1一定时,增大齿 宽系数必然增大齿宽,可提高齿轮的承载能力。但齿宽越大,载荷沿 齿宽的分布越不均匀,造成偏载而降低传动能力。 3.齿数比
大齿轮齿数与小齿轮齿数之比称为齿数比。
标准直齿圆柱齿轮的强度计算
• 七、齿轮精度等级的选择
在渐开线圆柱齿轮的精度标准中,规定了12个精度等级,其中1级精 度最高,精度依次降低,12级为最低级。常用的为6、7、8、9四个精 度等级。齿轮精度等级的选择应根据齿轮的用途,使用条件、传递的 圆周速度和功率的大小,以及其他技术、经济指标等要求来确定。 例题 已知用于带式输送机的减速器中的一对闭式直齿圆柱齿轮传动, 采用电机驱动,其转速n1=960 r/min,传动比i=4.2,P=7.4 kW,单向转 动,两班制,每年工作300天。使用期限为5年。试设计此传动中的齿 轮。
H
1
b 2u
d1
H
(1-18)
K (U 1)
d T 1 76.433
1
2
U
d
H
(1-19)
应用上式进行强度计算时,应注意以下几点:
1.式中的“+”号用于外啮合,“-”号用于内啮合;
2.两齿轮在啮合传动时,产生的齿面接触应力σH相等,但它们的许用 接触应力[σH]不一定相等,计算时,应将两者中的较小者代入公式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.5 直齿圆柱齿轮强度计算一、轮齿的失效齿轮传动就装置形式来说,有开式、半开式及闭式之分;就使用情况来说有低速、高速及轻载、重载之别;就齿轮材料的性能及热处理工艺的不同,轮齿有较脆(如经整体淬火、齿面硬度较高的钢齿轮或铸铁齿轮)或较韧(如经调质、常化的优质钢材及合金钢齿轮),齿面有较硬(轮齿工作面的硬度大于350HBS或38HRC,并称为硬齿面齿轮)或较软(轮齿工作面的硬度小于或等于350HBS或38HRC,并称为软齿面齿轮)的差别等。
由于上述条件的不同,齿轮传动也就出现了不同的失效形式。
一般地说,齿轮传动的失效主要是轮齿的失效,而轮齿的失效形式又是多种多样的,这里只就较为常见的轮齿折断和工作面磨损、点蚀,胶合及塑性变形等略作介绍,其余的轮齿失效形式请参看有关标准。
至于齿轮的其它部分(如齿圈、轮辐、轮毂等),除了对齿轮的质量大小需加严格限制外,通常只需按经验设计,所定的尺寸对强度及刚度均较富裕,实践中也极少失效。
轮齿折断轮齿折断有多种形式,在正常情况下,主要是齿根弯曲疲劳折断,因为在轮齿受载时,齿根处产生的弯曲应力最大,再加上齿根过渡部分的截面突变及加工刀痕等引起的应力集中作用,当轮齿重复受载后,齿根处就会产生疲劳裂纹,并逐步扩展,致使轮齿疲劳折断(见图1 图2 图3)。
此外,在轮齿受到突然过载时,也可能出现过载折断或剪断;在轮齿受到严重磨损后齿厚过分减薄时,也会在正常载荷作用下发生折断。
在斜齿圆柱齿轮(简称斜齿轮)传动中,轮齿工作面上的接触线为一斜线(参看),轮齿受载后,如有载荷集中时,就会发生局部折断。
若制造或安装不良或轴的弯曲变形过大,轮齿局部受载过大时,即使是直齿圆柱齿轮(简称直齿轮),也会发生局部折断。
为了提高齿轮的抗折断能力,可采取下列措施:1)用增加齿根过渡圆角半径及消除加工刀痕的方法来减小齿根应力集中;2)增大轴及支承的刚性,使轮齿接触线上受载较为均匀;3)采用合适的热处理方法使齿芯材料具有足够的韧性;4)采用喷丸、滚压等工艺措施对齿根表层进行强化处理。
齿面磨损在齿轮传动中,齿面随着工作条件的不同会出现不同的磨损形式。
例如当啮合齿面间落入磨料性物质(如砂粒、铁屑等)时,齿面即被逐渐磨损而至报废。
这种磨损称为磨粒磨损(见图4、图5、图6)。
它是开式齿轮传动的主要形式之一。
改用闭式齿轮传动是避免齿面磨粒磨损最有效的方法。
齿面点蚀点蚀是齿面疲劳损伤的现象之一。
在润滑良好的闭式齿轮传动中,常见的齿面失效形式多为点蚀。
所谓点蚀就是齿面材料变化着的接触应力作用下,由于疲劳而产生的麻点状损伤现象(见图7 图8 图9)。
齿面上最初出现的点蚀仅为针尖大小的麻点,如工作条件未加改善,麻点就会逐渐扩大,甚至数点连成一片,最后形成了明显的齿面损伤。
齿轮在啮合过程中,齿面间的相对滑动起着形成润滑油膜的作用,而且相对滑动速度愈高,愈易在齿面间形成油膜,润滑也就愈好。
当轮齿在靠近节线处啮合时,由于相对滑动速度低,形成油膜的条件差,润滑不良,摩擦力较大,特别是直齿轮传动,通常这时只有一对齿啮合,轮齿受力也最大,因此,点蚀也就首先出现在靠近节线的齿根面上,然后再向其它部位扩展。
动画演示从相对意义上说,也就是靠近节线处的齿根面抵抗点蚀的能力最差(即接触疲劳强度最低)。
提高齿轮材料的硬度,可以增强齿轮抗点蚀的能力。
在啮合的轮齿间加注润滑油可以减小摩擦,减缓点蚀,延长齿轮的工作寿命。
并且在合理的限度内,润滑油的粘度越高,上述效果也愈好。
因为当齿面上出现疲劳裂纹后,润滑油就会侵入裂纹,而且粘度愈低的油,愈易侵入裂纹。
润滑油侵入裂纹后,在轮齿啮合时,就有可能在裂纹内受到挤胀,从而加快裂纹的扩展,这是不利之处。
所以对速度不高的齿轮传动,以用粘度高一点的油来润滑为宜;对速度较高的齿轮传动(如圆周速度v>12m/s),要用喷油润滑(同时还起散热的作用),此时只宜用粘度低的油。
开式齿轮传动,由于齿面磨损较快,很少出现点蚀。
齿面胶合对于高速重载的齿轮传动(如航空发动机减速器的主传动齿轮),齿面间的压力大,瞬间温度高,润滑效果差,当瞬时温度过高时,相啮合的两齿面就会发生粘在一起的现象,由于此时两齿面又在作相对滑动,相粘结的部位即被撕破,于是在齿面上沿相对滑动的方向形成伤痕,称为胶合,如图10、图11、图12中的轮齿部分所示。
传动时齿面瞬时温度愈高、相对滑动速度愈大的地方,愈易发生胶合。
有些低速重载的重型齿轮传动,由于齿面间的油膜遭到破坏,也会产生胶合失效。
此时,齿面的瞬时温度并无明显增高,故称为冷胶合。
加强润滑措施,采用抗胶合能力强的润滑油(如硫化油),在润滑油中加入极压添加剂等,均可防止或减轻齿面的胶合。
齿面塑性变形塑性变形属于轮齿永久变形一大类的失效形式,它是由于在过大的应力作用下,轮齿材料处于屈服状态而产生的齿面或齿体塑性流动所形成的。
塑性变形一般发生在硬度低的齿轮上;但在重载作用下,硬度高的齿轮上也会出现。
塑性变形又分为滚压塑变和锤击塑变。
滚压塑变是由于啮合轮齿的相互滚压与滑动而引起的材料塑性流动所形成的。
由于材料的塑性流动方向和齿面上所受的摩擦力方向一致,所以在主动轮的轮齿上沿相对滑动速度为零的节线处被碾出沟槽,而在从动轮的轮齿上则在节线处被挤出脊棱。
这种现象称为滚压塑变(见右图)。
锤击塑变则是伴有过大的冲击而产生的塑性变形,它的特征是在齿面上出现浅的沟槽,且沟槽的取向与啮合轮齿的接触线相一致。
提高轮齿齿面硬度,采用高粘度的或加有极压添加剂的润滑油均有助于减缓或防止轮齿产生塑性变形。
图13 图14 图15动画演示提高轮齿对上述几种失效形式的抵抗能力,除上面所说的办法外,还有减小齿面粗糙度值,适当选配主、从动齿轮的材料及硬度,进行适当的磨合(跑合),以及选用合适的润滑剂及润滑方法等。
前已说明,轮齿的失效形式很多。
除上述五种主要形式外,还可能出现齿面融化、齿面烧伤、电蚀、异物啮入和由于不同原因产生的多种腐蚀和裂纹等等,可参看有关资料。
二、齿轮的受力分析和计算载荷1、受力分析进行齿轮的强度计算时,首先要知道齿轮上所受的力,这就需要对齿轮传动作受力分析。
当然,对齿轮传动进行力分析也是计算安装齿轮的轴及轴承时所必需的。
齿轮传动一般均加以润滑,啮合轮齿间的摩擦力通常很小,计算轮齿受力时,可不予考虑。
沿啮合线作用在齿面上的法向载荷F n垂直于齿面,为了计算方便,将法向载荷F n在节点P处分解为两个相互垂直的分力,即圆周力F t与径向力F r, 。
由此得F t=2T1/d1; F r=F t tanα; F n=F t/cosα(a)式中:T1—小齿轮传递的转矩,N·mm;d1—小齿轮的节圆直径,对标准齿轮即为分度圆直径,mm;α—啮合角,对标准齿轮,α=20°。
2、计算载荷为了便于分析计算,通常取沿齿面接触线单位长度上所受的载荷进行计算。
沿齿面接触线单位长度上的平均载荷p(单位为N/mm)为式中:F n--作用于齿面接触线上的法向载荷,N;L--沿齿面的接触线长,mm。
法向载荷Fn为公称载荷,在实际传动中,由于原动机及工作机性能的影响,以及齿轮的制造误差,特别是基节误差和齿形误差的影响,会使法向载荷增大。
此外,在同时啮合的齿对间,载荷的分配并不是均匀的,即使在一对齿上,载荷也不可能沿接触线均匀分布。
因此在计算齿轮传动强度时,应按接触线单位长度上的最大载荷,即计算载荷p ca(单位为N/mm)进行计算。
即式中K为载荷系数。
计算齿轮强度用的载荷系数K,包括使用系数K A,动载系数K v,齿间载荷分配系数Kα及齿向载荷分布系数Kβ,即K A--使用系数使用系数K A是考虑齿轮啮合时外部因素引起的附加动载荷影响的系数。
这种动载荷取决于原动机和工作机的特性,质量比,联轴器类型以及运行状态等。
K A的使用值应针对设计对象,通过实践确定。
下表<使用系数>所列的K A值可供参考。
使用系数K A严重冲击挖掘机,重型球磨机,橡胶揉合机,破碎机,重型给水泵,旋转式钻探装置,压砖机,带材冷轧机,压坯机等1.75 1.852.002.25或更大注:表中所列K A值仅适用于减速传动;若为增速传动,K A值约为表值的1.1倍。
当外部机械与齿轮装置间有挠性连接时,通常K A值可适当减少。
三、齿轮强度计算1、齿面接触疲劳强度计算齿面接触疲劳强度计算的基本公式为:F ca为计算载荷,L为接触线长度,为计算方便,取接触单位长度上的计算载荷式中:ρ∑—啮合齿面上啮合点的综合曲率半径;Z E—弹性影响系数,数值列于下表,则上式为(d)弹性影响系数Z E /()齿轮材料配对齿轮材料灰铸铁球墨铸铁铸钢锻钢夹布塑胶11.8×17.3×20.2×20.6×0.785×锻钢162.0181.4188.9189.856.4铸铁161.4180.5188.0——球墨铸铁156.6173.9—灰铸铁143.7—注:表中所列夹布塑胶的泊松比μ为0.5,其余材料的μ均为0.3。
渐开线齿廓上各点的曲率(1/ρ)并不相同,沿工作齿廓各点所受的载荷也不一样。
因此按式(d)计算齿面的接触强度时,就应同时考虑啮合点所受的载荷及综合曲率(1/ρ∑)的大小。
对端面重合度≤2的直齿轮传动,如图<齿面上的接触应力>所示,以小齿轮单对齿啮合的最低点(图中C点)产生的接触应力为最大,与小齿轮啮合的大齿轮,对应的啮合点是大齿轮单对齿啮合的最高点,位于大齿轮的齿顶面上。
如前所述,同一齿面往往齿根面先发生点蚀,然后才扩展到齿顶面,亦即齿顶面比齿根面具有较高的接触疲劳强度。
因此,虽然此时接触应力大,但对大齿轮不一定会构成威胁。
由图<齿面上的接触应力>可看出,大齿轮在节处的接触应力较大,同时,大齿轮单对齿啮合的最低点(图中D 点)处接触应力也较大。
但按单对齿啮合的最低点计算接触应力比较麻烦,并且当小齿轮齿数z1≥20时,按单对齿啮合的最低点所计算得的接触应力与按节点啮合计算得的接触应力极为相近。
为计算方便,通常即以节点啮合为代表进行齿面的接触强度计算。
下面即介绍按节点啮合进行接触强度计算的方法:节点啮合的综合曲率为轮齿在节点啮合时,两轮齿廓曲率半径之比与两轮的直径或齿数成正比,即ρ2/ρ1=d2/d1=z2/z1=u,故得如图所示,小齿轮轮齿节点P处的曲率半径。
对于标准齿轮,节圆就是分度圆,故得ρ1=d1sin α/2则:取L=b(b为齿轮设计工作宽度),于是(d)式为:令——区域系数(标准直齿轮α=20°时,Z H=2.5),则可写为MPa将F t=2T1/d1、φd=b/d1代入上式得σH=于是mm若将Z H=2.5代入上面两式,得MPa 及2、齿根弯曲疲劳强度计算轮齿在受载时,齿根所受的弯矩最大,因此齿根处的弯曲疲劳强度最弱。
