转动定律、转动能量
合集下载
05--2、转动定律、转动能量
T=T’ …(5)
v v v aτ = β ×r
β+ r T m2 T’
T
m1
N r
T’
m1g - T= m1a….(1) T’r=Jβ…(2) β
1 2 J = mr …(3) 2
a+
m1g
m2g
a = rβ…(4) β
Jβ β T=T’= r 代入(1)式 代入 式: Jβ β m1g = m1a r Jβ β m1g = m1rβ β r m1gr β = 所以: 所以 m1r2+J 由(2)式: 式
v F // v r
v F v ⊥ F
转动定律说明了J 3）转动定律说明了J是物体转动惯性大小的量 因为： 度。因为： M一 时 ↑Lβ ↓ J ↓Lβ ↑ 定 J 越大的物体， 即J越大的物体，保持原来转动状态的性质就 越大的物体 越强，转动惯性就越大；反之， 越小 越小， 越强，转动惯性就越大；反之，J越小，越容 易改变状态，保持原有状态的能力越弱。 易改变状态，保持原有状态的能力越弱。或 者说转动惯性越小。 者说转动惯性越小。
基本步骤 （1）隔离法选择研究对象； ）隔离法选择研究对象； （2）受力分析和运动情况分析； ）受力分析和运动情况分析； （3）对质点用牛顿定理，对刚体用转动定理； ）对质点用牛顿定理，对刚体用转动定理； （4）建立角量与线量的关系，求解方程； ）建立角量与线量的关系，求解方程； （5）结果分析及讨论。 ）结果分析及讨论。
r
r
T ' m3g T ' 1 v 2 a1 m
1
v mg 1
m2
m L 2g.T ' m 2 2 m L 3g.N THale Waihona Puke .T2 m 1 3v a2
能量的转移和转化
源的利用。
水能
利用水流驱动水轮机或潮汐能 发电，实现水能的利用。
生物质能
利用生物质资源进行燃烧或发 酵，产生热能或生物燃料，实
现生物质能的利用。
核聚变能源的研究与应用
核聚变
通过高温高压条件下，将 两个较轻的原子核聚合成 一个或多个较重的原子核， 释放出巨大能量。
核聚变能源的优势
资源丰富、清洁、高效、 可持续。
电能还可以通过电磁感应原理转换为 热能。例如，当交变磁场中的线圈通 入电流时，会产生涡流效应，使线圈 发热，从而将电能转化为热能。
核能转化为热能
• 核能可以通过核裂变或核聚变反应转换为热能。在核裂变反应 中，重原子核分裂成两个较轻的原子核，同时释放出能量，这 些能量以热能的形式释放出来。在核聚变反应中，轻原子核聚 合成重原子核，同样释放出能量，这些能量也以热能的形式释 放出来。
能量的转移和转化
目录
• 能量转移和转化的基本概念 • 能量转移的方式 • 能量转化的方式 • 能量转移和转化的应用 • 未来能源的发展趋势
01
能量转移和转化的基本概念
能量定义
能量定义
能量是物体做功的能力，表示物体运动状态变化的能力。单位制中的能量单位是焦耳（J），常用的能量单位还有卡路里（cal）、千瓦 时（kWh）等。
热量不可能自发地从低温物体传 到高温物体而不引起其他变化， 也就是说，热量的传递具有方向
性。
02
能量转移的方式
热能转移
热传导
通过物体间的直接接触，热量从高温部分传到低温部 分。
热对流
由于流体（气体或液体）的运动，热量从高温部分传 到低温部分。
热辐射
通过电磁波的辐射和吸收，热量在不同温度的物体间 传递。
水能
利用水流驱动水轮机或潮汐能 发电，实现水能的利用。
生物质能
利用生物质资源进行燃烧或发 酵，产生热能或生物燃料，实
现生物质能的利用。
核聚变能源的研究与应用
核聚变
通过高温高压条件下，将 两个较轻的原子核聚合成 一个或多个较重的原子核， 释放出巨大能量。
核聚变能源的优势
资源丰富、清洁、高效、 可持续。
电能还可以通过电磁感应原理转换为 热能。例如，当交变磁场中的线圈通 入电流时，会产生涡流效应，使线圈 发热，从而将电能转化为热能。
核能转化为热能
• 核能可以通过核裂变或核聚变反应转换为热能。在核裂变反应 中，重原子核分裂成两个较轻的原子核，同时释放出能量，这 些能量以热能的形式释放出来。在核聚变反应中，轻原子核聚 合成重原子核，同样释放出能量，这些能量也以热能的形式释 放出来。
能量的转移和转化
目录
• 能量转移和转化的基本概念 • 能量转移的方式 • 能量转化的方式 • 能量转移和转化的应用 • 未来能源的发展趋势
01
能量转移和转化的基本概念
能量定义
能量定义
能量是物体做功的能力，表示物体运动状态变化的能力。单位制中的能量单位是焦耳（J），常用的能量单位还有卡路里（cal）、千瓦 时（kWh）等。
热量不可能自发地从低温物体传 到高温物体而不引起其他变化， 也就是说，热量的传递具有方向
性。
02
能量转移的方式
热能转移
热传导
通过物体间的直接接触，热量从高温部分传到低温部 分。
热对流
由于流体（气体或液体）的运动，热量从高温部分传 到低温部分。
热辐射
通过电磁波的辐射和吸收，热量在不同温度的物体间 传递。
3、刚体定轴转动的动能定理dθd...
解: J r2dm R2dm R2 dm mR2
J是可加的，所以若为薄圆筒 （不计厚度）结果相同。
OR dm
例2.12 求质量为m、半径为R、厚为l 的均匀圆盘的转 动惯量。轴与盘平面垂直并通过盘心。
解：取半径为r宽为dr的薄圆环,
dm dV 2rdr l
dJ r 2dm 2lr3dr
M
ri
Fi
i
2、质点系对轴的角动量定理
设质点系内各质点均在各自的转动平面内绕同一轴转动
n
i 1
Miz
d dt
n i1
(ri mi vi
sini
)
因有：vi ri
i
2
n
i 1
Miz
d dt
n
[
i 1
(miri2 )]
vi O ri mi
转动惯量J
n
i 1
Miz
d dt
(Jω)
dLz dt
2L
3
因为 d d d d dt d dt d
所以 d 3g cos
d
2l
积分 d 3g cos d
0
0 2l
得 3g sin
l
四、定轴转动的动能定理
1、转动动能
Ek
n i1
1 2
mi ri 2 2
1n (
2 i1
miri2 )2
1 2
J 2
刚体绕定轴转动时转动动能等于刚体的转动惯量
2.6 刚体的定轴转动
一 刚体定轴转动的描述
1. 刚体--特殊的质点系
(1) 无限多的质点组成的有限大小的质点系（实际 上是物质连续分布的物体，其微分体积称为质元)； (2) 无论施加多大的力都不会改变形状和大小，即任 意两点间的距离不会因施力和运动而改变；
J是可加的，所以若为薄圆筒 （不计厚度）结果相同。
OR dm
例2.12 求质量为m、半径为R、厚为l 的均匀圆盘的转 动惯量。轴与盘平面垂直并通过盘心。
解：取半径为r宽为dr的薄圆环,
dm dV 2rdr l
dJ r 2dm 2lr3dr
M
ri
Fi
i
2、质点系对轴的角动量定理
设质点系内各质点均在各自的转动平面内绕同一轴转动
n
i 1
Miz
d dt
n i1
(ri mi vi
sini
)
因有：vi ri
i
2
n
i 1
Miz
d dt
n
[
i 1
(miri2 )]
vi O ri mi
转动惯量J
n
i 1
Miz
d dt
(Jω)
dLz dt
2L
3
因为 d d d d dt d dt d
所以 d 3g cos
d
2l
积分 d 3g cos d
0
0 2l
得 3g sin
l
四、定轴转动的动能定理
1、转动动能
Ek
n i1
1 2
mi ri 2 2
1n (
2 i1
miri2 )2
1 2
J 2
刚体绕定轴转动时转动动能等于刚体的转动惯量
2.6 刚体的定轴转动
一 刚体定轴转动的描述
1. 刚体--特殊的质点系
(1) 无限多的质点组成的有限大小的质点系（实际 上是物质连续分布的物体，其微分体积称为质元)； (2) 无论施加多大的力都不会改变形状和大小，即任 意两点间的距离不会因施力和运动而改变；
大学物理第5章刚体的定轴转动
d ctdt
对上式两边积分得
d c td t
0 0
t
1 2 ct 2
2 2 600π π 3 rad s 由给定条件， c 2 t 300 2 75
d π 2 由角速度的定义，则任意 t 时刻的角速度可写为： d t 150
得到： 转子转数：
A M d E K
a b
动能定理
动量定理
A F ds E K
动能定理 角动量定理 角动量 守恒
t 0Fdt P
t
动量守恒
F 0, P 0
t 0 M z dt Lz
t
M 0, L 0
§5.1 刚体、刚体运动
一、一般运动 二、刚体的定轴转动 三、解决刚体动力学问题的一般方法
基本方法： 加
质点系运动定理 刚体特性 平动：动量定理
刚体定轴转动的 动能定理 角动量定理
F mac
可以解决刚体的一般运动（平动加转动）
一、一般运动
1. 刚体 特殊的质点系， 形状和体积不变化 —— 理想化模型 在力作用下，组成物体的所有质点间的距离始终保持不变 2. 自由度 确定物体的位置所需要的独立坐标数 —— 物体的自由度数 z
刚体平面运动可看做刚体的平动与定轴转动的合成。 例如：车轮的滚动可以看成车轮随轮 轴的平动与绕轮轴的转动的组合。 描述刚体平面运动的自由度：3个
定点转动 刚体运动时，刚体上的一点固定不动，刚体绕过定点的一 瞬时转轴的转动，称作定点转动。
描述定点转动的自由度：3个
刚体的一般运动 质心的平动
+
绕质心的转动
z
描述刚体绕定轴转动的角量： 角坐标
力学10-转动定律,转动惯量,刚体绕定轴转动中的功、能量、功能关系
12
第五章 刚体力学基础 动量矩
§5-3 绕定轴转动刚体的动能 动能定理
一. 转动动能
设系统包括有 N 个质量元 取 ∆mi,其动能为 其动能为
ω
O
z
1 1 2 2 2 Eki = ∆mivi = ∆miri ω 2 2
刚体的总动能
r ri
r vi
P
• ∆mi
1 1 2 2 2 1 Ek = ∑Eki = ∑ ∆mi ri ω = ∑∆mi ri ω2 = Jω2 2 2 2
第五章 刚体力学基础 动量矩
m1g
m2g
五式联立，可解 五式联立，可解T1，T2，a1，a2，β
2012-4-16 11
总结
力的瞬时作用规律 力矩的瞬时作用规律
v F =0
v v F = ma
静止 匀速直线
M = Jβ
M = 0 静止 匀角速转动
J—转动时惯性大小的量度 转动时惯性大小的量度 力矩的持续作用规律： 力矩的持续作用规律： 空间： 空间： 时间： 时间：
(2) M、J、β必须对同一转轴定义。 必须对同一转轴定义。 、 、 必须对同一转轴定义 (3) M 正比于 β ，力矩越大，刚体的 β 越大 。 力矩相同，若转动惯量不同，产生的角加速度不同。 (4) 力矩相同，若转动惯量不同，产生的角加速度不同。
M (5) 与牛顿定律比较： → F, J → m, β → a 与牛顿定律比较：
14
讨论
(1) 力矩对刚体的功就是力对刚体的功。 力矩对刚体的功就是力对刚体的功。
θ2 θ2
1
(2) 合力矩的功
A= ∫
θ1
∑Midθ = ∑∫θ i i
Midθ = ∑Ai
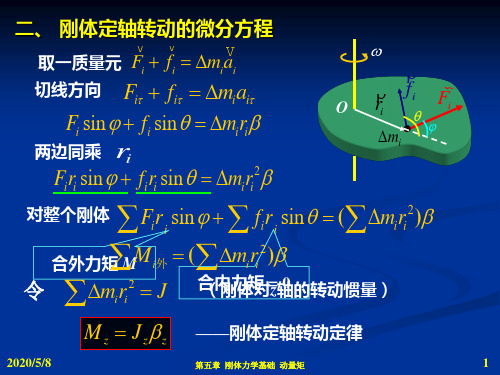
第五章 刚体力学基础 动量矩
§5-3 绕定轴转动刚体的动能 动能定理
一. 转动动能
设系统包括有 N 个质量元 取 ∆mi,其动能为 其动能为
ω
O
z
1 1 2 2 2 Eki = ∆mivi = ∆miri ω 2 2
刚体的总动能
r ri
r vi
P
• ∆mi
1 1 2 2 2 1 Ek = ∑Eki = ∑ ∆mi ri ω = ∑∆mi ri ω2 = Jω2 2 2 2
第五章 刚体力学基础 动量矩
m1g
m2g
五式联立，可解 五式联立，可解T1，T2，a1，a2，β
2012-4-16 11
总结
力的瞬时作用规律 力矩的瞬时作用规律
v F =0
v v F = ma
静止 匀速直线
M = Jβ
M = 0 静止 匀角速转动
J—转动时惯性大小的量度 转动时惯性大小的量度 力矩的持续作用规律： 力矩的持续作用规律： 空间： 空间： 时间： 时间：
(2) M、J、β必须对同一转轴定义。 必须对同一转轴定义。 、 、 必须对同一转轴定义 (3) M 正比于 β ，力矩越大，刚体的 β 越大 。 力矩相同，若转动惯量不同，产生的角加速度不同。 (4) 力矩相同，若转动惯量不同，产生的角加速度不同。
M (5) 与牛顿定律比较： → F, J → m, β → a 与牛顿定律比较：
14
讨论
(1) 力矩对刚体的功就是力对刚体的功。 力矩对刚体的功就是力对刚体的功。
θ2 θ2
1
(2) 合力矩的功
A= ∫
θ1
∑Midθ = ∑∫θ i i
Midθ = ∑Ai
力矩、转动定律、角动量守恒
mgl 1 mgl 1 mv2 v gl 4g
2
2
l
P24 1-6: As shown in below figure, the body A is connected to the body B by the light rope which is through uniform solid cylinder（圆柱体） with a mass Mand a radius R. The body A has a mass of m1 and the mass of B is m2.There is not relative motion between the rope and cylinder. Find the tension force between the solid cylinders with
a R
（4）以上三式联立，可得物体 下落的加速度和张力：
a
m2
m2
m1 2
g
T m1m2 g 2m2 m1
m2 R(m2
m1 ) 2
g
o m1
m2 x
P34.习题19 质量为m、长为L的均质细杆可绕水平光滑轴O在竖直 平面内转动。若使杆从水平位置开始由静止释放，试求杆转至铅垂
T=?
J 1 MR2 2
M,R
m1 A
B m2
解：⑴ 研究对象：A、B和圆柱体； ⑵ 受力分析如图：
A向上运动，有加速度aA，B向下运动，加速 度aB，圆柱体顺时针转动。
T
T
T
A
B
T
m1g m2g
T
T1
T2
T2
（3）列方程：
刚体的转动
J miri
i
例 如图
I m1r12 m2r22 m3r32
m2
可视为 质点
r1
m1
r2 r3
m3
转轴
•质量连续分布的物体
J rdm dm d 或 ds 或 dV
线积分
面积分
体积分
（记住：棒、圆盘和圆柱体的I）
例题 5-2
例题 5-3
例题 5-4
（4）以上三式联立，可得物体下落的加速度和速度：
a m g mM 2
V 2ah 4mgh 2m M
这时滑轮转动的角速度为 V 1 4mgh
R R 2m M
例题:质量M=1.1kg，半径=0.6m的匀质圆盘，可绕通过其
中心且垂直于盘面的水平光滑固定轴转动。圆盘边缘绕有
看成质点 水平飞行
刚体作平动，其上所有点的速度、加速度相等，运动 轨迹都相同，整个刚体可当作质点来处理，满足牛顿 定律。
转动 刚体运动时，如果刚体中所有质点都绕着一直线 作圆周运动，则这刚体的运动称为转动，这条直 线称为转轴。转轴固定的转动叫定轴转动。
转轴
地球仪转动
一般情况下，刚体十分复杂，同时存在平动和 转动；可以证明，刚体的一般运动可以当作由一平 动和一绕瞬时轴的转动组合而成。
F
ds
F
cos
ds
Ft rd
Md
The total work done during a finite angular displacement
is then
W 0 M d
(5-18)
In the special case of M is a constant
i
例 如图
I m1r12 m2r22 m3r32
m2
可视为 质点
r1
m1
r2 r3
m3
转轴
•质量连续分布的物体
J rdm dm d 或 ds 或 dV
线积分
面积分
体积分
（记住：棒、圆盘和圆柱体的I）
例题 5-2
例题 5-3
例题 5-4
（4）以上三式联立，可得物体下落的加速度和速度：
a m g mM 2
V 2ah 4mgh 2m M
这时滑轮转动的角速度为 V 1 4mgh
R R 2m M
例题:质量M=1.1kg，半径=0.6m的匀质圆盘，可绕通过其
中心且垂直于盘面的水平光滑固定轴转动。圆盘边缘绕有
看成质点 水平飞行
刚体作平动，其上所有点的速度、加速度相等，运动 轨迹都相同，整个刚体可当作质点来处理，满足牛顿 定律。
转动 刚体运动时，如果刚体中所有质点都绕着一直线 作圆周运动，则这刚体的运动称为转动，这条直 线称为转轴。转轴固定的转动叫定轴转动。
转轴
地球仪转动
一般情况下，刚体十分复杂，同时存在平动和 转动；可以证明，刚体的一般运动可以当作由一平 动和一绕瞬时轴的转动组合而成。
F
ds
F
cos
ds
Ft rd
Md
The total work done during a finite angular displacement
is then
W 0 M d
(5-18)
In the special case of M is a constant
刚体定轴转动知识点总结
刚体定轴转动知识点总结1. 刚体的转动定轴刚体的转动定轴是指固定不动的直线，沿其进行转动的刚体的每一个质点所受的力矩的代数和等于零。
在实际中，通常通过支点来实现转动定轴，比如钟摆、摇摆、旋转的转轴等。
2. 刚体的角位移、角速度和角加速度在刚体定轴转动中，刚体围绕定轴线进行旋转，其角位移、角速度和角加速度是非常重要的物理量。
角位移表示刚体在围绕定轴线旋转的过程中所经过的角度变化量，通常用θ表示；角速度表示刚体围绕定轴线旋转的速度，通常用ω表示；角加速度表示刚体围绕定轴线旋转的加速度，通常用α表示。
3. 牛顿第二定律在刚体定轴转动中的应用牛顿第二定律也适用于刚体定轴转动的情况。
在刚体定轴转动中，外力会给刚体带来转动运动，根据牛顿第二定律，刚体的角加速度与作用在其上的外力矩成正比。
因此，可以根据力矩的大小和方向来分析刚体的转动运动。
4. 转动惯量和转动动能在刚体定轴转动中，转动惯量是一个非常重要的物理量。
转动惯量描述了刚体围绕定轴线旋转的难易程度，其大小与刚体的质量分布和轴线的位置有关。
转动动能是刚体围绕定轴线旋转的能量，其大小取决于刚体的转动惯量和角速度。
5. 转动定律和角动量守恒定律在刚体定轴转动中，转动定律和角动量守恒定律是非常重要的定律。
转动定律描述了刚体受力矩产生的角加速度与所受力矩的关系，角动量守恒定律描述了刚体转动过程中角动量的守恒规律。
6. 平衡条件和稳定性分析在刚体定轴转动中，平衡条件和稳定性分析是非常重要的内容。
通过平衡条件，可以分析刚体围绕定轴线旋转的平衡状态。
稳定性分析则是分析刚体在平衡状态下的稳定性，通常通过刚体的势能函数和平衡位置的稳定性来进行分析。
7. 应用领域刚体定轴转动的理论和方法在工程技术、航空航天、机械制造、物理学等领域都有重要的应用价值。
比如在机械制造中，可以通过分析刚体的定轴转动来设计机械装置；在航空航天中，可以通过分析刚体的定轴转动来设计飞行器的运动控制系统。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2 3
gmR
1二5、–转8动多定律普勒效应
第十五章 机械波
要揭示转动惯量的物理意义，实际上是要找到
一个类似于牛顿定律的规律——转动定律。
O
v
z v F内i
F i
ri
i
i
刚体可看成是由许多小质元组成，
在p点取一质元，r
mi (dmuir), ri r
受力：外力F i ur
，与rri
成
i角
rr
Q ri ain 0
r ur ur
rr
ri (Fi F内i ) (mi )(ri ait )
r
r
r r ur
Q ait ri t0, ri ait ri2
r ur r ur
ur
ri
Fi
ri
F内i
(mi
)r
2 i
----②
1对5整–个8刚多体，普对勒②效式求应和
MZ
r
v F
力矩就可以了。
3）转动定律说明了I是物体转动惯性大小的量度。因
为：M一定时I L I L
即I越大的物体，保持原来转动状态的性质就越强， 转动惯性就越大；反之，I越小，越容易改变状态， 保持原有状态的能力越弱,或者说转动惯性越小。
15 – 8 多普勒效应
第十五章 机械波
§3--3 力矩 转动定律
一 力矩
刚体绕 O z 轴旋转 , 力F
作平用面在内刚, 体r上为点由点P ,O且到在力转的动
M
作用点 P 的径矢 .
F
对转轴Z M
的力r矩F
M Frsin Fd
O
z
M
r
d
P*
F
d : 力臂
F
F
Fi 0 , Mi 0
N
求： a1.a2.T1.T2
N
已知: m1 、m2、r
+ r
T
r
求：a、T、h
m2 T’
T’ 解：建立转动轴的
正方向，加速度的
T
m1
隔离物体 分析力：
a+ m1g
m2g
m1g - T= m1a….(1)
T’r=I…(2)
正方向.
由(2)式:T=T’=
I r
代入(1)式:
列方程：
a
r
I
1 2
m2
r
2
…(3)
第十五章 机械波
r ur r ur
ur
ri Fi
ri F内i (
(mi
)r
2 i
)
i
r uri
i
Q
ri F内i 0
I (
(mi
)r
2 i
)
uur i
r ur ur i
M 合外力 ri F i I
i
M I －转动定律
注意：M、I、β都是相对于同一转轴而言。
M z rF sin
15 – 8 多普勒效应
第十五章 机械波
2）合力矩等于各分力 矩的矢量和 M M1 M2 M3 vv v
若刚体受N个外力作用， F1 , F2 L , FN
v
M合
v M
i＝rv1
v F1
rv2
v F2
L
i
rvN
v FN
r uur r i F i －力不连续
uur i r uur
M 合 r i F i
i
i
uur r uur
力是连续的 M 合 r d F
15 – 8 多普勒效应
第十五章 机械波
3） 刚体内作用力和反作用力的力矩互相抵消
M ij
O
d
rj
ri
i
j
Fji Fij
如一个外径和质量相同的实心圆柱与空心圆筒，
若 受力和力矩一样，谁转动得快些呢？
M
I
M
M
没事！ 纸风车
不敢！ 电风扇
15 –例81 一多质普量勒为m效1的应物体绕在一半径为第r质十量五章为m机2的械波圆
盘上,开始时静止,求重物的加速度、绳中的张力和t时刻
重物下降多高?(绳的质量与轴上的磨擦力不计).
M ji
Mij M ji
15
例– 18
多普勒效应
第十五章 机械波
均匀细杆，在平面内以角速度ω转动，求M摩擦
力。
ω
解： 力是连续的
uur r ur
M合 rdF
dm
r F dr
r
其中：
dF gdm g m dr
l
所以
M合
rdF l mg 1rdr 1 mgl
定轴转动定律：绕某定轴转动的刚体，所受合外力
矩在该轴上的分量等于刚体对该轴的转动惯量与角
加速度的乘积。 M I 或 M
I
15说如–明何8求多力12））对普定M轴勒律,的I是效,矩瞬应呢应时？是对对应同关一系轴；而Z言第的十FvM五 章F机vI 械波
如图可将力分解为两个力， 只求那个垂直于轴的力的
合内力 F内i，与 ri 成i 角
ur ur
r
rr
F i F内i＝mi ai mi (ain ait )
----①
15用–rrr8i左叉多ur乘普①勒式ur 效应
第十五章 机械波
rr r
ri
(F
i
F内i r
)
r(mri )ri
r
(ain
ait
)
(mi )(ri ain ri ait )
a = r…(4)
m1g
-
I r
= m1a
T=T’ …(5)
15
–8
m1g
-多Ir普=勒m效1r应
所以:
=
m1gr m1r2+I
m1gr
=
m1r2+
1 2
m2r2
=
2m1g (2m1+m2)r
a = r =
2m1g 2m1+m2
I第十五章 机械波 T=T’= r
T=
m1m2g 2m1+m2
பைடு நூலகம்
=m1g
h 1 at 2 2
=
m1gt2 2m1+m2
注意: a等于常数且初速为零!
15例–28质多量分普别勒为效m1。应m2的物体通过轻绳第挂十在五质章量机为械m波3
r 半径为 的圆盘形滑轮上。求物体m1。m2运动的加速
度以及绳子张力T1.T2 ,（绳子质量不计）
抵消 已知： m1.m2.m3.r
0
l
2
15 –例82 现多有普一勒圆盘效在应平面内以角速度ω第转十动五，章求机摩械擦波
力产生的力矩（μ、m、R）。
dr 解： 取细圆环为质元
ωr
dm
ds
m
R2
2 rdr
dM rdf r gdm
rg
m
R2
2 rdr
M
dM
R 0
g
m
R2
2 r2dr
F
F
Fi 0 , Mi 0
15 – 8 多普勒效应
第十五章 机械波
讨论
1）若力 F 不在转动平面内，把力分解为平行和垂
直于转轴方向的两个分量
F Fz F
其中 Fz 对转轴的力
矩为零，故 F 对转轴的
力矩
v Mz
rv
v F
z
k
Fz
F
O r F