spss参数与非参数检验实验报告
SPSS应用之非参数检验

SPSS应⽤之⾮参数检验统计学的假设检验可以分为参数检验和⾮参数检验,参数检验是根据⼀些假设条件推算⽽来,当这些假设条件⽆法满⾜的时候,参数检验的效能会⼤打折扣,甚⾄出现错误的结果,⽽⾮参数检验通常是没有假设条件的,因此应⽤范围⽐参数检验要⼴。
⾮参数检验在不做任何假设的情况下,最⼤限度的使⽤样本信息,利⽤统计学、数学的⽅法和技巧构造统计量并加以检验,在某些情况下,⾮参数检验⽐参数检验拥有更⾼的效能,尽管如此,我们也不能⼀味的使⽤⾮参数检验,毕竟参数检验更加严谨,通常都是在数据不符合参数检验的条件是,才使⽤⾮参数检验,因此,对于数据的前期观察是⾮常重要的。
⾮参数检验⽅法⾮常多,但是绝⼤部分⾮参数检验⽅法都是基于秩和结来构造统计量的,中⾮参数检验是⼀个独⽴的过程,也保留了旧对话框,新对话框按照样本情况分类,根据样本情况来选择⽅法,并且更倾向于⾃动化分析,旧对话框的分类则不是很明确,分我们按照新对话框来进⾏介绍分析—⾮参数检验—单样本⼀、单样本1.⼆项式检验⼆项式检验也称为⼆项分布检验,⽤来检验样本是否来⾃⼆项分布,也就是检查样本的观测值的频数与某⼀特定⼆项分布下的期望频数是否⼀致。
不仅可以针对于⼆分类变量,对于连续变量也可以当做⼆分类变量来处理,例如成绩的及格与否,产品的合格与否等。
本例中是想检验三门学科的及格率是否都在95%以上2.卡⽅检验卡⽅检验是最常⽤的多分类⾮参数检验,卡⽅统计量也⼴泛被其他检验所引⽤,卡⽅检验依据卡⽅分布,主要包括适应性检验和独⽴性检验,适应性检验⽤于检验实际观察频数与期望频数是否⼀致,独⽴性检验⽤于检验两组或多组计数资料是否相互独⽴。
3.K-S检验全称为Kolmogorov-Smirnow检验,在探索性中,也曾出现过⽤它来检验是否服从正态分布。
该检验属于⾮参数检验,⽤来检验某⼀单样本是否服从某⼀理论分布。
4.Wilcoxon符号秩检验该检验将符号和秩相结合,效能⽐单纯的符号检验和秩和检验都⾼,因此⽐较常⽤5.游程检验我们知道样本的随机性很重要,⽽游程检验就是⽤来检验样本数据是否是随机抽取的。
SPSS的非参数检验

02
SPSS非参数检验概述
定义与特点
定义
非参数检验是在统计分析中,相对于参数检验的一种统计方法。 它不需要对总体分布做严格假定,只关注数据本身的特点,因此 具有更广泛的适用范围。
特点
非参数检验对总体分布的假设较少,强调从数据本身获取信息, 具有灵活性、稳健性和适用范围广等优点。
局限性
计算量大
对于大规模数据集,非参数检验的计算量可 能较大,需要较长的计算时间。
对数据要求高
非参数检验要求数据具有可比性,对于不可 比的数据集可能无法得出正确的结论。
解释性较差
非参数检验的结果通常较为简单,对于深入 的统计分析可能不够满足。
对异常值敏感
非参数检验对异常值较为敏感,可能导致结 果的偏差。
THANK YOU
感谢聆听
常用非参数检验方法
独立样本非参数检验
用于比较两个独立样本的差异 ,如Mann-Whitney U 检验 、Kruskal-Wallis H 检验等。
相关样本非参数检验
用于比较相关样本或配对样本 的关联性,如Wilcoxon signed-rank 检验、Kendall's tau-b 检验等。
等级排序非参数检验
案例二:两个相关样本的非参数检验
总结词
适用于两个相关样本的比较,如同一班级内不同时间点的成绩比较。
描述
使用SPSS中的两个相关样本的非参数检验,如Wilcoxon匹配对检验,可以比较两个相关样本的总体分布是否相 同。
案例二:两个相关样本的非参数检验
01
步骤
02
1. 打开SPSS软件,输入数据。
SPSS的参数检验和非参数检验
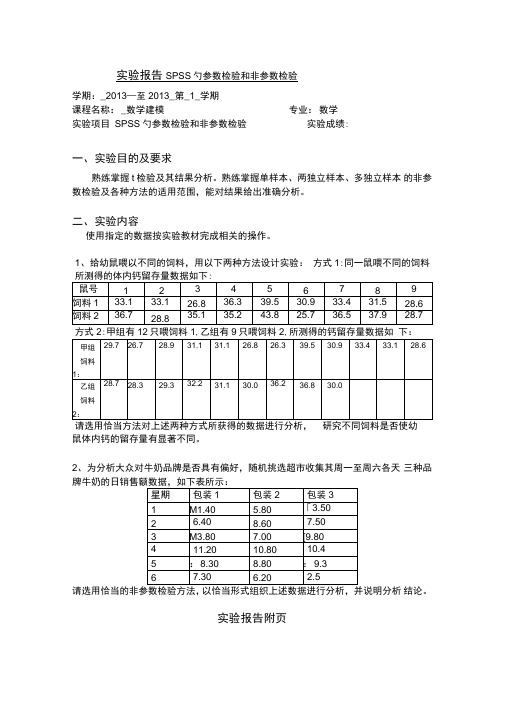
实验报告SPSS 勺参数检验和非参数检验学期:_2013—至2013_第_1_学期 课程名称:_数学建模专业:数学实验项目 SPSS 勺参数检验和非参数检验实验成绩:一、 实验目的及要求熟练掌握t 检验及其结果分析。
熟练掌握单样本、两独立样本、多独立样本 的非参数检验及各种方法的适用范围,能对结果给出准确分析。
二、 实验内容使用指定的数据按实验教材完成相关的操作。
1、给幼鼠喂以不同的饲料,用以下两种方法设计实验: 方式1:同一鼠喂不同的饲料所测得的体内钙留存量数据如下:方式2:甲组有12只喂饲料1,乙组有9只喂饲料2,所测得的钙留存量数据如 下:请选用恰当方法对上述两种方式所获得的数据进行分析,研究不同饲料是否使幼鼠体内钙的留存量有显著不同。
2、为分析大众对牛奶品牌是否具有偏好,随机挑选超市收集其周一至周六各天 三种品牌牛奶的日销售额数据,如下表所示:请选用恰当的非参数检验方法,以恰当形式组织上述数据进行分析, 并说明分析 结论。
实验报告附页三、实验步骤(一)方式1:1、打开SPSS软件,根据所给表格录入数据,建立数据文件;2、选择菜单Analyze —Compare means- Paired-Samples T Test ,出现窗口;3、把检验变量饲料1,饲料2选择到Paired Variables 框,单击OK 方式2:1、打开SPSS软件,根据所给表格录入数据,建立数据文件;2、选择菜单Analyze —Compare mean—Independent-Samples T Test,出现窗口3、选择检验变量饲料到Test Variable(s)框中。
4、选择总体标志变量组号到Group ing Variables 框中5、单击Define Groups按钮定义两总体的标志值1、2,单击OK(二)1、打开SPSS软件,根据所给表格录入数据,建立数据文件;2、选择菜单Analyze->Nonparametric->k Independent sample3、选择待检验的若干变量入包装1,包装2,包装3到Test Variable(s)框中;4、选择推广的平均秩检验(Friedman检验),单击OK四、实验结果分析与评价(一):方式1:Paired Samples Correlations由上表知:两配对变量饲料1和饲料2对应的概率p值为0.108>0.05通过了检验,可以认为两配对变量饲料1和饲料2无相关关系。
spss实验报告——非参数检验

实验报告——(非参数检验)实验目的:1、学会使用SPSS软件进行非参数检验。
2、熟悉非参数检验的概念及适用范围,掌握常见的秩和检验计算方法。
实验内容:1、某公司准备推出一个新产品,但产品名称还没有正式确定,决定进行抽样调查,在受访200人中,52人喜欢A名称,61人喜欢B名称,87人喜欢C 名称,请问ABC三种名称受欢迎的程度有无差别?(数据表自建)SPSS计算结果如下:此题为总体分布的卡方检验。
零假设:样本来自总体分布形态和期望分布没有显著差异。
即ABC三种名称受欢迎的程度无差别,分布形态为1:1:1,呈均匀分布。
观察结果,上表为200个观察数据对A、B、C三个名称(分别对应1,2,3)的喜爱的期望频数以及实际观察频数和期望频数的差。
从下表中可以看出相伴概率值为0.007小于显著性水平0.05,因此拒绝零假设,认为样本来自的总体分布与制定的期望分布有显著差异,即A、B、C三种名称受欢迎的程度有差异。
2、某村庄发生了一起集体食物中毒事件,经过调查,发现当地居民是直接饮用河水,研究者怀疑是河水污染所致,县按照可疑污染源的大致范围调查了沿河居民的中毒情况,河边33户有成员中毒(+)和均未中毒(-)的家庭分布如下:(案例数据run.sav)-+++*++++-+++-+++++----++----+----毒源问:中毒与饮水是否有关?SPSS计算结果如下:此题为单样本变量值随机检验零假设:总体某变量的变量值是随机出现的。
即中毒的家庭沿河分布的情况随机分布,与饮水无关。
相伴概率为0.036,小于显著性水平0.05,拒绝零假设,因此中毒与饮水有关。
3、某试验室用小白鼠观察某种抗癌新药的疗效,两组各10只小白鼠,以生存日数作为观察指标,试验结果如下,案例数据集为:npara1.sav,问两组小白鼠生存日数有无差别。
试验组:24 26 27 30 32 34 36 40 60 天以上对照组:4 6 7 9 10 10 12 13 16 16SPSS计算结果如下:此题为两独立样本非参数检验。
spss参数与非参数检验实验报告

(1).将一样本作为控制样本,另一样本作为实验样本。两样本混合后按升序排列;
(2).找出控制样本的跨度(最低秩和最高秩间的样品数)和截头跨度(去掉控制样本的最小值和最大值后的跨度)。若跨度(截头跨度)很小,认为样本存在极端反应。
以上四种检验的基本操作步骤:
(1)【Analyze】--->【Nonparametric Tests】--->【2 Independent Sample】
该检验可用来检验两个独立样本是否取自同一总体,它是最强的非参数检验之一。
基本思路:
1.将样本X和样本Y混合后作升序排列,计算每个数据的秩;
2.分别对两样本的秩求平均,得到两个平均秩,分别用W1=WX/m和W2=WY/n表示。
若W1和W2比较接近,则说明两个样本来自相同分布的总体,若W1和W2差异较大,则说明两个样本来自不同的总体。
(2)选择待检验变量到【Test Variable】框中
(3)指定存放样本标志值的变量到【Grouping Variable】框
(4)选择非参数检验方法
三、多个独立样本的非参数检验包括:中位数检验、Kruskal-Wallis H检验、Jonkheere-Terpstra检验
3.1中位数检验
(一)含义:通过对多组独立样本的分析,检验它们来自的总体的中位数是否存在显著差异。其原假设是:多个独立样本来自的多个总体的中位数无显著差异。
(2)选定待检验的变量到【Test Variable list】框中
(3)在【Cut Point】框中确定计算游程数的分界点
二、两个独立样本的非参数检验包括:Mann-Whitney U检验、K-S双样本检验、Wald-Wolfowitz游程检验、Moses极端反应检验
SPSS的参数检验和非参数检验

SPSS的参数检验和非参数检验SPSS是一种非常常用的统计分析软件,可以用于参数检验和非参数检验。
参数检验是假设检验的一种方法,用于判断统计样本是否代表总体。
而非参数检验则是用于检验数据是否满足一些分布假设,或判断两个或多个群体是否具有差异。
参数检验主要有t检验、方差分析和回归分析等。
其中,t检验用于比较两个样本均值是否有显著差异,包括独立样本t检验和相关样本t检验。
方差分析用于比较三个或更多样本均值是否有显著差异,可以进行单因素方差分析或多因素方差分析。
回归分析用于建立预测模型,可以通过线性回归或多项式回归进行。
非参数检验通常适用于数据不满足正态分布或方差齐性的情况,如Wilcoxon符号秩检验、Kruskal-Wallis H检验、Mann-Whitney U检验等。
Wilcoxon符号秩检验用于比较两个配对样本的差异是否有显著差异,Kruskal-Wallis H检验用于比较三个或更多独立样本的差异是否有显著差异,Mann-Whitney U检验用于比较两个独立样本的差异是否有显著差异。
在SPSS中进行参数检验和非参数检验一般需要进行以下步骤:1.导入数据:将数据导入SPSS软件,可以通过选择文件-导入功能进行操作。
2.设定分析变量:定义需要进行分析的变量,并将其添加到分析列表中。
3.选择统计方法:根据实验设计和数据分布情况,选择合适的参数检验或非参数检验方法。
4.执行分析:点击运行按钮进行分析,在分析结果中可以查看得到显著性水平、均数、方差等指标。
5.结果解释:根据分析结果进行假设检验,判断是否存在显著差异,并解释其结果。
无论是参数检验还是非参数检验,在进行分析前需要注意数据的合理性、样本的选择和实验设计的合理性等,以保证分析结果的可靠性。
同时,还应根据不同的研究目的和数据特点选择适当的方法,并合理解释分析结果。
在SPSS软件中,可以通过图表、表格和描述性统计等形式展示和解释结果,并通过结果进行科学判断和相关推断。
spss卡方检验和非参数检验

练习一、 为试验某止疼药物的效果,将178例患者随机分为两组,用药组90 人,对照组88人,试验结果见数据chi_ex,请根据此数据回答,此 药物止疼效果如何?
练习二、 用两种方法检查乳腺癌患者120名,甲法检出率60%,乙法检出率 50%,两法检出都阳性的是35%,请问两种方法检出率是否有差别?
H1:B≠C
Test Statisticsb
N Chi-Squarea
VAR00001 & VAR00002 410
86.449
Asymp. Sig.
.000
a. Continuity Corrected
b. McNemar Test
χ2 =86.45, P=0.000 P<0.05,拒绝H0,接受H1,差别有显著性,两种方法 检验结果不同。
二、 行×列表的χ2检验
a. 什么是行×列表 整理表的行数多于2,或者列数多于2。 四格表是为了比较两个率(构成比)是 否相等;行×列表是为了比较三组或者 三组以上的率(构成比)是否相等。
b. 行×列表χ2检验的假设: H0:各组构成相同 H1:各组构成不同或不全相同
c. 行×列表的自由度: (行数-1) ×(列数-1)
L i ne a r-b y-L i ne a r Asso ci a ti on
2.333
1
.127
N of Valid Cases
25
a. Computed only for a 2x2 table
b. 2 cells (50.0%) have expected count less than 5. The minimum expected count is 1. 60.
两型慢性布氏病患者得植物血凝素皮试反应
spss统计软件实验报告

岭南师范学院2014年-2015学年第一学期期末考试(考察)实验报告调查题目:岭南师院学生生活费支出情况的调查科目:统计软件成绩:姓名:陈文超学号: 2011224529 巫军福 2011224539李裕慧 2011224522李立聪 2011224515 专业:数学与应用数学班级: 11金融数学班内容: SPSS软件数据预处理、基本统计分析、参数检验非参数检验、方差分析有关说明:现在大学生的生活费大部分是家里给的,当然也有一部分的学生是通过做各种的兼职,例如:家教、派传单、送餐等,获得一小部分的零花钱。
那么,对于大学生来说,如何能让自己的一定额度的生活费用在合理的方面,这是非常重要的。
这也是一个关于生活费的理财计划,处理得好的话,可以每月都能有一点的剩余或者可以买些自己喜欢的商品。
基于这个原因,我们小组经过讨论后,确定了这个题目,也为了了解当今大学生的生活支出情况,从而可以做出相应的改善。
调查目的:大学生是一个新兴的消费群体,为了调查清楚我校大学生生活费支出状况,我们决定采用简单随机抽样发放问卷以及网上填写问卷的方法对学校的同学进行一次大学生生活费支出的调查,并进行统计分析。
主要弄清楚大学生要花多少钱,花在了什么地方,花的是否合理,如果不合理怎样改进。
我们用数据来倡导大家在校期间生活费的合理使用。
调查范围:岭南师范学院。
调查对象:我校不同学院不同专业的学生群体。
调查研究的方法:采用简单随机不重复抽样的方法发放问卷,网上不重复填写问卷的方法,并进行统计分析。
具体统计分析有:1.根据样本的生活费来源,分布状况的均值,比例等分布的数字特征,推断大学生总体分布的相应参数。
2.根据性别进行男女两个总体生活费均值之差的比较以及比例的比较。
3.根据大一、大二、大三、大四进行四个总体生活费均值之差及比例的比较4.绘制统计图使样本数据直观化并对统计量进行分析。
小组分工安排:巫军福、陈文超、李裕慧、李立聪四个人一起讨论确定选题以及调查的主体、范围、方法,也初步定出调查问卷的初稿。
非参数检验实验报告

实验报告非参数检验学院:参赛队员:参赛队员:参赛队员:指导老师:目录一、实验目的 (3)1.了解假设检验的基本容; (3)2.了解卡方检验; (3)3.了解二项分布检验; (3)4.了解两个独立样本检验; (3)5.学会运用spss软件求解问题; (3)6.加深理论与实践相结合的能力。
(3)二、实验环境 (3)三、实验方法 (3)1.卡方检验; (3)2.二项分布检验; (3)3.两个独立样本检验。
(3)四、实验过程 (3)问题一: (3)1.1实验步骤 (4)1.1.1输入数据 (4)1.1.2选择:数据加权个案 (4)1.1.3选择:分析→非参数检验→旧对话框→卡方 (4)1.1.4将变量面值放入检验变量列表 (5)1.1.5观察结果 (5)1.2输出结果 (5)1.3结果分析 (5)问题二: (5)2.1问题叙述 (5)2.2提出假设 (6)2.3实验步骤 (6)2.3.1导入excel文件数据 (6)2.3.2二项分布检验 (7)2.3.3输出结果 (8)2.4结果分析 (8)问题三: (8)3.1实验步骤 (8)3.1.1数据的输入 (8)3.1.2选择 (9)3.1.3检验变量 (9)3.2输出结果 (9)3.3结果分析 (11)五、实验总结 (11)参数检验一、实验目的1.了解假设检验的基本容;2.了解卡方检验;3.了解二项分布检验;4.了解两个独立样本检验;5.学会运用spss软件求解问题;6.加深理论与实践相结合的能力。
二、实验环境Spss、office三、实验方法1.卡方检验;2.二项分布检验;3.两个独立样本检验。
四、实验过程问题一:1.1实验步骤1.1.1输入数据1.1.2选择:数据加权个案1.1.3选择:分析→非参数检验→旧对话框→卡方1.1.4将变量面值放入检验变量列表,期望全距从数据中获取,期望值所有类别相等1.1.5观察结果1.2输出结果1.3结果分析此处,sig值为0.111>0.05,所以接受原假设,认为样本来自的总体分布形态与期望分布不存在显著差异,则认为该骰子均匀问题二:2.1问题叙述2.2提出假设H0:硬币不是均匀的 vs H1:硬币是均匀的2.3实验步骤2.3.1导入excel文件数据先将数据输入进excel表格中,用SPSS打开;在SPSS页面点击文件→打开→数据2.3.2二项分布检验选择:分析→非参数检验→旧对话框→二项式2.3.3输出结果2.4结果分析由输出结果知,精确显著性(双侧)=1.000>0.05,所以接受原假设H0,所以硬币不是均匀的。
SPSS的参数检验和非参数检验

实验二 SPSS的参数检验和非参数检验(验证性实验 4学时)1、目的要求:熟练掌握t检验及其结果分析。
熟练掌握单样本、两独立样本、多独立样本的非参数检验及各种方法的适用范围,能对结果给出准确分析。
2、实验内容:使用指定的数据按实验教材完成相关的操作。
3、主要仪器设备:计算机。
练习:1、给幼鼠喂以不同的饲料,用以下两种方法设计实验:鼠体内钙的留存量有显著不同。
2、为分析大众对牛奶品牌是否具有偏好,随机挑选超市收集其周一至周六各天并说明分析结论。
1 参数检验概述假设检验的基本思想.事先对总体参数或分布形式作出某种假设,然后利用样本信息来判断原假设是否成立;.采用逻辑上的反证法,依据统计上的小概率原理。
2 单样本的T检验2.1检验目的:•检验单个变量的均值是否与给定的常数(总体均值)之间是否存在显著差异。
如:分析学生的IQ平均分是否为100分;大学生考研率是否为5%。
•要求样本来自的总体服从或近似服从正态分布。
2.2 单样本T检验的实现思路•提出原假设:•计算检验统计量和概率P值●给定显著性水平与p值做比较:如果p值小于显著性水平,小概率事件在一次实验中发生,则我们应该拒绝原假设,反之就不能拒绝原假设。
2.3 单样本t检验的基本操作步骤1、选择选项Analyze-Compare means-One-Samples T test,出现窗口:2、在Test Value框中输入检验值。
3、单击Option按钮定义其他选项。
Option选项用来指定缺失值的处理方法。
其中,Exclude cases analysis by analysis表示计算时涉及的变量上有缺失值,则剔除在该变量上为缺失值的个案;Exclude cases listwise表示剔除所有在任意变量上含有缺失值的个案后再进行分析。
可见,较第二种方式,第一种处理方式较充分地利用了样本数据。
在后面的分析方法中,SPSS对缺失值的处理方法与此相同,不再赘述。
SPSS进行两配对样本的非参数检验(Wilcoxon符号秩检验)-实验方法-丁香通

SPSS进⾏两配对样本的⾮参数检验(Wilcoxon符号秩检验)-实验⽅法-丁⾹通⼀、概述
⾮参数检验对于总体分布没有要求,因⽽使⽤范围更⼴泛。
对于两配对样本的⾮参数检验,⾸
选Wilcoxon符号秩检验。
它与配对样本t检验相对应。
⼆、问题
为了研究某放松⽅法(如听⾳乐)对于⼊睡时间的影响,选择了10名志愿者,分别记录未进⾏
放松时的⼊睡时间及放松后的⼊睡时间(单位为分钟),数据如下笔。
请问该放松⽅法对⼊睡
时间有⽆影响。
本例可以采⽤配对样本t检验,但由于样本量少,数据可能不符合正太分布,所以考虑⽤⾮参数
检验。
三、统计操作
数据视图
菜单选择
打开如下的对话框。
SPSS管理统计 课程设计 非参数假设检验

一、实验名称:实验三二、实验要求:1、所有的文件上传到网络硬盘中。
2、数据文件保存,用文件名“学号+姓名+人员登记”。
3、撰写实验报告。
每个操作要写出实验步骤,及操作结果。
4、要求电子版实验报告,用文件名“学号+姓名+实验一”保存,学期结束上交。
5、练习上课讲过(第6-9章)的例子。
(无需写实验报告)。
三、实验步骤及结果:“CH6CH9CH10证券投资额与依据”的数据是对杭州市股民的调查数据,试进行以下分析。
(需写实验报告)(1)北京市股民的“证券外年收入”为4.8万元,杭州股民的“证券外年收入”和北京股民的相同吗?分析:此题为“单样本T检验”,检查相应总体均值是否为某个值。
1.1实验步骤:1)启动SPSS,调入样本值,2)点击Analyze->Compare Means->One-Sample T Test,弹出小窗口,将“券外收入”添加到Test Variable(s)中,3)在Test Value中输入4.8,如图1.114)点击OK.图1.11 单样本T检验窗口1.2实验结果:如图:1.12,T检验的最后结果p=0.164>0.05,可知杭州股民的“证券外年收入”和北京股民的没有显著差异。
图1.12 有关单样本T检验(2)杭州股民投入股市的资金超过他们的年收入吗?分析:此题为“配对样本的T检验”,即两组样本不可以颠倒顺序,不然将出现错误。
2.1实验步骤:1)点击Analyze->Compare Means->Paired-Samples T Test,2)从左框变量中选出“券外收入”和“投资总额”,用箭头放入右边的Test variables 框中,此时右框中的2个变量已差的形式出现,如图2.11。
3)点击OK。
图2.11 配对T检验窗口2.2实验结果:图2.12中的paired samples test表格中可知T检验的最后结果p=0.00<0.05,两者有显著性差异,从第一张表格中可以得知“投入总资金”>“卷外收入”。
SPSS的参数检验和非参数检验

实验报告 SPSS的参数检验和非参数检验学期:_2013__至2013_ 第_1_学期课程名称:_数学建模专业:数学实验项目__SPSS的参数检验和非参数检验实验成绩:_____一、实验目的及要求熟练掌握t检验及其结果分析。
熟练掌握单样本、两独立样本、多独立样本的非参数检验及各种方法的适用范围,能对结果给出准确分析。
二、实验内容使用指定的数据按实验教材完成相关的操作。
1、给幼鼠喂以不同的饲料,用以下两种方法设计实验:方式1:同一鼠喂不同的饲料所测得的体内钙留存量数据如下:方式2:甲组有12只喂饲料1,乙组有9只喂饲料2,所测得的钙留存量数据如下:请选用恰当方法对上述两种方式所获得的数据进行分析,研究不同饲料是否使幼鼠体内钙的留存量有显着不同。
2、为分析大众对牛奶品牌是否具有偏好,随机挑选超市收集其周一至周六各天三种品牌牛奶的日销售额数据,如下表所示:请选用恰当的非参数检验方法,以恰当形式组织上述数据进行分析,并说明分析结论。
实验报告附页三、实验步骤(一)方式1:1、打开SPSS软件,根据所给表格录入数据,建立数据文件;2、选择菜单Analyze-Compare means-Paired-Samples T Test,出现窗口;3、把检验变量饲料1,饲料2 选择到Paired Variables框,单击OK。
方式2:1、打开SPSS软件,根据所给表格录入数据,建立数据文件;2、选择菜单Analyze-Compare means-Independent-Samples T Test,出现窗口3、选择检验变量饲料到Test Variable(s)框中。
4、选择总体标志变量组号到Grouping Variables框中。
5、单击Define Groups按钮定义两总体的标志值1、2,单击OK。
(二)1、打开SPSS软件,根据所给表格录入数据,建立数据文件;2、选择菜单Analyze->Nonparametric->k Independent sample3、选择待检验的若干变量入包装1,包装2,包装3到Test Variable(s)框中;4、选择推广的平均秩检验(Friedman检验),单击OK。
SPSS非参数检验实验报告

实验项目非参数检验实验时间2017.10.27实验地点S308 成绩三、实验内容1、将一颗骰子连掷120次,各次所出现的点数顺次如“shai.sav” 所示,试检验掷骰子点数是否服从均匀分布?2、从随机数表中抽得20个数据如下:0.55 0.8 0.15 0.12 0.21 0.4 0.46 0.17 0.62 0.770.63 0.71 0.99 0.88 0.30 0.64 0.51 0.68 0.50 0.60要求:(1)利用单个样本的K–S检验法检验这些数据是否服从正态分布;(2)对结果进行分析,并填写新的实验报告。
1、SPSS单样本K-S检验的基本操作步骤如下:(1)选择菜单:【分析(A)】→【非参数检验(N)】→【旧对话框(L)】→【1样本K-S(1)】出现如图1-1所示的窗口。
图1-1 单样本K-S检验窗口(2)选择待检验的变量到【检验变量列表(T)】框中。
(3)在【检验分布】框中指定理论分布,这里选择【相等】,即代表均匀分布。
至此,SPSS将自动计算K-S检验统计量和对应的概率P-值,并将结果输出到查看器窗口中。
分析结果如图1-2所示。
图1-2掷骰子总体分布的K-S检验结果图1-2表明,数据极小值为1.00,极大值为6.00。
最大绝对差值为0.158,正差极值为0.158,负差极值为-0.142。
SPSS自动计算输出了√nD值(1.734)和概率P-值(0.005)。
如果显著性水平α为0.05,由于概率P-值小于显著性水平,因此拒绝原假设,接受备择假设,即掷骰子点数的总体分布为不是均匀分布。
2、SPSS单样本K-S检验的基本操作步骤如下:(1)选择菜单:【分析(A)】→【非参数检验(N)】→【旧对话框(L)】→【1样本K-S(1)】出现如图2-1所示的窗口。
图2-1单样本K-S检验窗口(2)选择待检验的变量到【检验变量列表(T)】框中。
(3)在【检验分布】框中指定理论分布,这里选择【常规】,即代表正态分布。
SPSS统计分析2:参数检验与非参数检验

参数检验与非参数检验一、参数检验与非参数检验的区别(1)参数检验:一般是数据的总体分布已知的情况下,对数据分布的参数是否落在相应范围内进行检验。
是对参数平均值、方差进行的统计检验,是推断统计的重要组成部分。
适用条件:当总体分布已知(如总体为正态分布),根据样本数据对总体分布的统计参数进行推断。
此时,总体的分布形式是给定的或是假定的,只是其中一些参数的取值或范围未知,分析的主要目的是估计参数的取值,或对其进行某种统计检验。
这类问题往往用参数检验来进行统计推断。
它不仅仅能够对总体的特征参数进行推断,还能够实现两个或多个总体的参数进行比较。
(2)非参数检验:一般是在不知道数据总体分布的前提下,检验数据的分布情况。
适用条件:在数据分析过程中,由于种种原因,往往无法对总体分布形态作简单假定,此时参数检验不再适用。
非参数检验正是基于这种考虑,在总体方差未知或知道甚少的情况下,利用样本数据对总体分布形态等进行推断的方法。
二、参数检验方法及适用条件三、非参数检验方法及适用条件四、使用方法当分析某个因素对变量的影响差异时,即检验该因素分类的若干个样本差异:(1)如果因素为两个,使用独立样本T-检验,来分析两个总体平均数相等的显著性;结果判定:先看方差齐性F检验结果,再看均值相等性的t检验结果,即a.如果方差齐性显著性>0.05,则表明方差齐性显著,再看第一行的检验统计值t及显著性p(p<0.05表示差异明显);b.如果方差齐性显著性<=0.05,则表明方差显著不齐,再看第二行的检验统计值t及显著性p(p<0.05表示差异明显);(2)如果因素为多个,使用单因素方差检验(即F检验),来分析该因素的影响差异。
结果判定:方差齐性显著则看ANOVA的检验统计值F及其显著性p。
SPSS统计软件实训报告

SPSS统计软件实训报告一、引言SPSS(Statistical Product and Service Solutions)统计软件是一种常用的统计分析软件,被广泛应用于数据分析和统计研究领域。
本报告旨在总结并分析在SPSS实训课程中所学到的基本操作和统计分析方法。
二、实训内容在SPSS统计软件实训中,我们学习了以下主要内容: 1. SPSS软件的安装和介绍; 2. 数据输入和修改; 3. 数据清洗和处理; 4. 描述性统计分析; 5. 参数检验和非参数检验; 6. 方差分析; 7. 相关分析; 8. 回归分析等。
三、实训过程1. SPSS软件的安装和介绍我们首先安装了SPSS统计软件,并对其界面和基本功能进行了介绍。
SPSS软件提供了直观的用户界面,可以进行数据输入、数据处理和统计分析等操作。
2. 数据输入和修改为了方便后续的统计分析,我们学习了数据的输入和修改方法。
在SPSS软件中,我们可以手动输入数据,也可以从Excel等其他文件中导入数据。
此外,我们还学习了如何修改数据,包括添加变量、删除变量、重命名变量等操作。
3. 数据清洗和处理在实际应用中,数据往往存在一些错误或缺失。
为了保证统计分析的准确性,我们需要对数据进行清洗和处理。
SPSS软件提供了一系列的数据清洗工具,如删除重复数据、替换缺失值、筛选数据等。
4. 描述性统计分析描述性统计分析是对收集到的数据进行总结和描述的方法。
我们学习了如何计算数据的均值、中位数、众数、标准差等统计量。
通过绘制直方图、箱线图等图表,我们可以对数据的分布进行可视化展示。
5. 参数检验和非参数检验参数检验和非参数检验是统计分析中常用的两种方法,用于判断样本间差异是否显著。
我们学习了t检验、方差分析、卡方检验等方法,并通过SPSS软件进行了实际操作。
6. 方差分析方差分析是用于比较三个或三个以上样本均值是否存在显著差异的方法。
我们学习了单因素方差分析和多因素方差分析,并通过SPSS软件进行了实际分析。
SPSS的参数检验实验报告
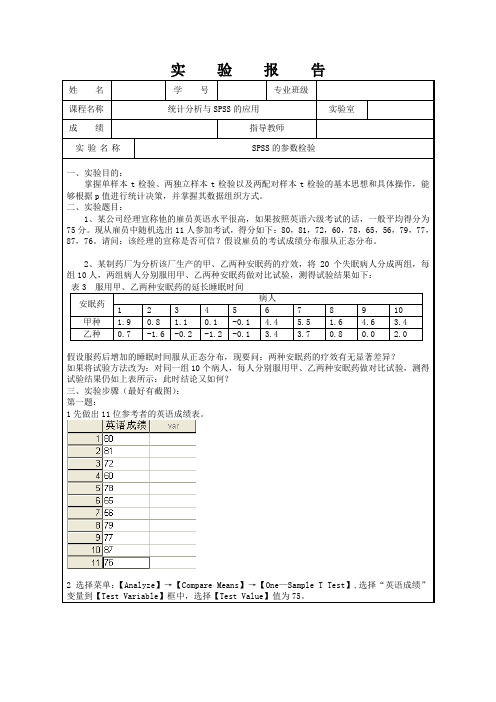
1先做出甲,乙两种安眠药效果的表格。
2选择菜单:【Analyze】→【Compare Means】→【Paired—Samples T Test】,选择“甲种”、“乙种”变量到【Paired Variables】。
四、实验结果及分析(最好有截图):
第一题结果
第二题结果
2选择菜单:【Analyze】→【Compare Means】→【One—Sample T Test】,选择“英语成绩”变量到【Test Variable】框中,选择【Test Value】值为75。
第二题(1):
1先做出10位病人服用甲,乙两种安眠药效果的表格。
2选择菜单:【Analyze】→【Compare Means】→【Independent—Samples T Test】,将“延长时间”选入【Test Variables】框中,将“病人”选入【Grouping Variables】。
2、某制药厂为分析该厂生产的甲、乙两种安眠药的疗效,将20个失眠病人分成两组,每组10人,两组病人分别服用甲、乙两种安眠药做对比试验,测得试验结果如下:
表3服用甲、乙两种安眠药的延长睡眠时间
安眠药
病人
1
2
3
4
5
6
7
8
9
10
甲种
1.9
0.8
1.1
0.1
-0.1
4.4
5.5
1.6
4.6
3.4
乙种
0.7
-1.6
实验报告
姓名
学号
专业班级
课程名称
统计分析与SPSS的应用源自实验室成绩指导教师
实验名称
SPSS的参数检验
一、实验目的:
【VIP专享】统计学实验报告——SPSS软件的参数检验与非参数检验

统计学2——SPSS软件的参数检验与非参数检验班级学号姓名日期实验目的(1)熟悉单样本t检验。
(2)熟悉两独立样本t检验。
(3)熟悉两配对样本t检验。
(4)熟悉总体分布的卡方检验。
实验内容(1)SPSS的单样本t检验操作。
(2)SPSS的两独立样本t检验。
(3)SPSS的两配对样本t检验。
(4)SPSS的总体分布的卡方检验。
实验过程(1)SPSS的单样本t检验操作。
(2)SPSS的两独立样本t检验。
(3)SPSS的两配对样本t检验。
(4)SPSS的总体分布的卡方检验。
DATASET NAME 数据集1 WINDOW=FRONT.T-TEST/TESTVAL=0.8/MISSING=ANALYSIS/VARIABLES=x5678_1/CRITERIA=CI(.95).T检验T-TEST/TESTVAL=0.8/MISSING=ANALYSIS/VARIABLES=x10_1/CRITERIA=CI(.95).T检验GETFILE='C:\Documents and Settings\admin\LocalSettings\Temp\Rar$DI02.829\商品房购买意向调查模拟数据.sav'. DATASET NAME 数据集2 WINDOW=FRONT.T-TEST GROUPS=t2(1 2)/MISSING=ANALYSIS/VARIABLES=t10_1/CRITERIA=CI(.95).T检验独立样本检验DATASET ACTIVATE 数据集1.T-TEST GROUPS=x13(1.5)/MISSING=ANALYSIS/VARIABLES=x5678_1/CRITERIA=CI(.95).T检验DATASET ACTIVATE 数据集2.GETFILE='C:\Documents and Settings\admin\Local Settings\Temp\Rar$DI67.032\减肥茶.sav'. DATASET NAME 数据集3 WINDOW=FRONT.T-TEST PAIRS=hcq WITH hch (PAIRED)/CRITERIA=CI(.9500)/MISSING=ANALYSIS.T检验DATASET ACTIVATE 数据集1.GETFILE='C:\Documents and Settings\admin\Local Settings\Temp\Rar$DI10.7860\心脏病猝死.sav'. DATASET NAME 数据集4 WINDOW=FRONT.NPAR TESTS/CHISQUARE=rq/EXPECTED=2.8 1 1 1 1 1 1/MISSING ANALYSIS.NPar 检验卡方检验频率实验心得。
spss参与非参检验实验报告参考模板
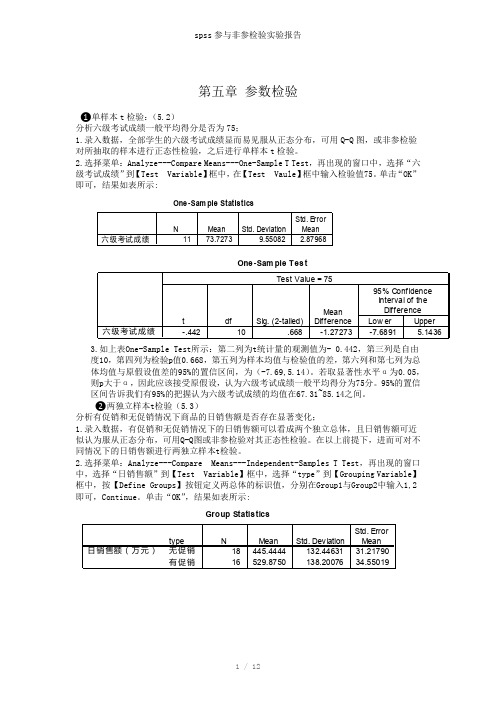
第五章 参数检验❶单样本t 检验:(5.2)分析六级考试成绩一般平均得分是否为75;1.录入数据,全部学生的六级考试成绩显而易见服从正态分布,可用Q-Q 图,或非参检验对所抽取的样本进行正态性检验,之后进行单样本t 检验。
2.选择菜单:Analyze---Compare Means---One-Sample T Test ,再出现的窗口中,选择“六级考试成绩”到【Test Variable 】框中,在【Test Vaule 】框中输入检验值75。
单击“OK ”度10,第四列为检验p 值0.668,第五列为样本均值与检验值的差,第六列和第七列为总体均值与原假设值差的95%的置信区间,为(-7.69,5.14)。
若取显著性水平α为0.05,则p 大于α,因此应该接受原假设,认为六级考试成绩一般平均得分为75分。
95%的置信区间告诉我们有95%的把握认为六级考试成绩的均值在67.31~85.14之间。
❷两独立样本t 检验(5.3)分析有促销和无促销情况下商品的日销售额是否存在显著变化;1.录入数据,有促销和无促销情况下的日销售额可以看成两个独立总体,且日销售额可近似认为服从正态分布,可用Q-Q 图或非参检验对其正态性检验。
在以上前提下,进而可对不同情况下的日销售额进行两独立样本t 检验。
2.选择菜单:Analyze---Compare Means---Independent-Samples T Test,再出现的窗口中,选择“日销售额”到【Test Variable 】框中,选择“type ”到【Grouping Variable 】框中,按【Define Groups 】按钮定义两总体的标识值,分别在Group1与Group2中输入1,23.如上表Independent Sample Test 所示,结论分析为两步:第一步,方差齐性检验。
F 统计量的观测值为0.225,对应的p 值为0.638,若取显著性水平α为0.05,则p 大于α,可以认为两总体的方差相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(一)单样本t检验的含义
1.检验某变量的总体均值与指定的检验值之间是否存在显著差异。2.前提:总体应服从正态分布。
(二)单样本t检验的基本实现思路
计算t统计量:及t值对应的p值。
(三)SPSS单样本t检验的操作步骤:
(1)打开【Analyze】---->【Compare Means】----->【One-Sample T Test】,弹出窗口。
(2)选定待检验的变量到【Test Variable】框中
(3)在【Expected Range】框中确定待检验样本的取值范围
(4)在【Test】框中给出二项分布的检验概率值
1.3单样本K-S检验
(一)单样本K-S检验含义:
该检验为拟合优度检验,可以检验样本数据是否服从指定的理论分布,适用于探索连续型随机变量的分布形态,如正态分布、均匀分布、指数分布等。
(1)若m>n,Wilcoxon W=Wx;若m<n,Wilcoxon W=Wy;若m=n,Wilcoxon W为第一个观测值所在样本的W值;
(2)Mann-WhitneyU=W-n(n+1)/2在小样本下U统计量服从曼-惠特尼分布,大样本下U近似服从正态分布。
2.2 K-S双样本检验
该检验可用来检验两个独立样本是否取自同一总体。
该检验可用来检验两个独立样本是否取自同一总体,它是最强的非参数检验之一。
基本思路:
1.将样本X和样本Y混合后作升序排列,计算每个数据的秩;
2.分别对两样本的秩求平均,得到两个平均秩,分别用W1=WX/m和W2=WY/n表示。
若W1和W2比较接近,则说明两个样本来自相同分布的总体,若W1和W2差异较大,则说明两个样本来自不同的总体。
(2)选定待检验的变量到【Test Variable list】框中
(3)在【Cut Point】框中确定计算游程数的分界点
二、两个独立样本的非参数检验包括:Mann-Whitney U检验、K-S双样本检验、Wald-Wolfowitz游程检验、Moses极端反应检验
2.1 Mann-Whitney U检验
(2)选择待检验变量到【Test Variable】框中
(3)指定存放样本标志值的变量到【Grouping Variable】框
(4)选择非参数检验方法
三、多个独立样本的非参数检验包括:中位数检验、Kruskal-Wallis H检验、Jonkheere-Terpstra检验
3.1中位数检验
(一)含义:通过对多组独立样本的分析,检验它们来自的总体的中位数是否存在显著差异。其原假设是:多个独立样本来自的多个总体的中位数无显著差异。
原假设:样本来自的总体与指定的理论分布无显著差异
(二)基本思路
假定F0(x)是一个已知的分布函数,Fn(x)是未知的总体分布函数F(x)的样本经验分布函数,取检验统计量:
D=max︳Fn(x)- F0(x)︳
在样本数据服从指定分布时,D的观测值应该较小,如果D的观测值较大,则零假设可能不成立。
(三)基本操作步骤:
(三)基本操作步骤:
(1)【Analyze】--->【Compare Means】---->【Paired Sample T Test】。
(2)指定一对或若干对配对变量作为检验变量送入【Paired Variables】框。
二、两独立样本t检验
(一)两独立样本t检验的含义
1.检验两独立的总体均值之间是否存在显著差异。
2.前提要求:(1)两样本应是相互独立的(2)样本来自的两总体应服从正态分布。
(二)基本实现思路:
(1)两个样本方差相等与不相等时使用的计算t值的公式不同,因此应先进行方差齐性检验。
(2)SPSS的输出,在给出方差齐与不齐两种计算结果的t值和t检验的显著性概率的同时,还给出对方差齐性检验的F值和F检验的显著性概率。用户需根据F检验的结果自己判断选择t检验输出中的哪个结果,得出结论。
此公式先将每一类别中的观测和期望的频数之差的平方除以相应的期望频数,然后对所有的k类求和。如果观测和期望的频数接近一致,则其差(Qi—Ei)就小,因而Χ2就小;反之,若其差大,则Χ2的值也越大。当Χ2越大时,观察的频数就越不可能是来自于以零假设为基础的整体。
(二)基本操作步骤:
(1)菜单【Analyze】--->【Nonparametric Test】--->【Chi Square】
布。
(二)基本思路:原假设:样本来自的总体与具有指定的二项分布无显著差异。
精确检验:计算二项分布概率。
近似检验:样本量大于30时,采用修正后的Z统计量:,其中X>n/2时取减号,X<n/2时取加号。
(三)基本操作步骤:
(1)菜单【Analyze】---->【Nonparametric Test】---->【Binomial】
二、两独立样本t检验
(一)两独立样本t检验的含义
1.检验两独立的总体均值之间是否存在显著差异。
2.前提要求:(1)两样本应是相互独立的(2)样本来自的两总体应服从正态分布。
(二)基本实现思路:
(1)两个样本方差相等与不相等时使用的计算t值的公式不同,因此应先进行方差齐性检验。
(2)SPSS的输出,在给出方差齐与不齐两种计算结果的t值和t检验的显著性概率的同时,还给出对方差齐性检验的F值和F检验的显著性概率。用户需根据F检验的结果自己判断选择t检验输出中的哪个结果,得出结论。
(三)操作步骤:(1)【Analyze】---->【Compare Means】---->【Independent Sample T Test】
(2)选择若干变量作为检验变量,送到【Test Variable(s)】框。
(3)选择一个变量作为标识变量到【Grouping Variable】框。
(4)选择【Define Groupes】按钮定义两总体的标识值,分别输入两个值。其中,【Use specified values】表示分别输入对应两个不同总体的标记值;【Cut point】框中应输入一个数字,大于等于该值的对应的一个总体,小于该值的对应的另一个总体。
(5)【Options】的含义与单样本t检验的相同。
三、两配对样本t检验
(一)两配对样本t检验的含义
1.检验两配对总体的均值是否有显著性差异。2.前提要求:(1)两个样本有配对关系。观测值数目相同;顺序不能随意更改(2)要求两个样本均来自正态总体
(二)、基本实现思路:转化为单样本t检验实现:首先得到差值序列,然后检验差值序列的均值是否为0。
(5)【Options】的含义与单样本t检验的相同。
三、两配对样本t检验
(一)两配对样本t检验的含义
1.检验两配对总体的均值是否有显著性差异。2.前提要求:(1)两个样本有配对关系。观测值数目相同;顺序不能随意更改(2)要求两个样本均来自正态总体
(二)、基本实现思:转化为单样本t检验实现:首先得到差值序列,然后检验差值序列的均值是否为0。
(2)在出现的窗口里,选择待检验的变量移到【Test Variable(s)】框中,在【Test Value】中输入检验值。
(3)按【Options】按钮定义其它选项,在出现的窗口里,【Exclude cases analysis by analysis】表示当计算时涉及的变量上有缺失值,则剔除在该变量上为缺失值的个案;【Exclude cases listwise】表示剔除所有在任意变量上含有缺失值的个案后再进行分析。另外,在【Confidengce Interval】框中输出默认95%的置信区间。
(1)菜单【Analyze】--->【Nonparametric Test】--->【1-Sample K-S】
(2)选定待检验的变量到【Test Variable list】框中
(3)在【test distribution】框中选择理论分布
1.4游程检验
(一)游程检验含义及思路:
假设观测结果可以表示为0和1的序列,把0和1连续出现构成的数据段称为一个游程,总的数据段称为游程总个数。例如:把下面序列:0011101100中,00、111、0、11、00当作游程,游程总个数为5。
基本思路:
(1)将样本X和样本Y混合后作升序排列;
(2)分布计算两组样本秩的累计频数和每个点上的累计频率Fn1(x)和Fn2(x);
(3)计算D=max[Fn1(x)- Fn2(x)]
如果D较小,则可以认为两个样本取自同一个总体;如果D较大,大到一定程度,则可以认为两个样本不是取自同一总体的。
2.3Wald-Wolfowitz游程检验
一、单样本非参数检验包括:卡方检验、二项检验、单样本K-S检验、游程检验。
1.1卡方检验
(一)卡方检验含义及基本思路:
Χ2检验就是根据样本数据推断总体的分布与期望分布或某一理论分布是否有显著差异。它的原假设是:样本来自的总体其分布形态与期望分布无显著差异。进行检验时,需要构造统计量:
其中,Qi=归入第i类中的观测数目;Ei=零假设成立时第i类中的期望事件数。
成绩:_________
室温:气压:课程名称:统计学软件及应用(A)教师签字:_________
实验项目
编码(L1206703)
SPSS参数与非参数检验
指导老师
实验目的
熟练掌握参数与非参数检验的具体操作步骤,并了解检验的目的和意义
实验仪器(编号)
材料、工具
SPSS 13.0软件
(原理概述)
参数检验:包括单样本t检验、两(多)独立样本t检验、两(多)配对样本t检验。
(2)选定待检验的变量到【Test Variable】框中
(3)在【Expected Range】框中确定待检验样本的取值范围
