五年级奥数进制的计算教师版
小学教育奥数数进制

数的进制相关看法同学在行整数四算,用的都是十制即“ 10 一”,于其他制感到陌生。
上,你只要留一下,在我平常生活中,不使用十制使用其他多制呢!你信不信我一些例子。
两只袜子一双,两只水桶一,里使用的是二制;十二支笔一打,十二个月算一年,里使用的是十二制;六十秒是一分,六十分是一,里使用的是六十制;二十四一天,里使用的是二十四制;100 平方分米等于一平方米,100 平方厘米等于一平方分米,里使用的是一百制;1000 米等于一千米,1000 克等于 1 千克,里使用的是一千制;⋯⋯。
怎么上可以更多的的例子。
随着科学技的展,数字子算机的使用日益宽泛,每位同学可能都使用子算器吧可是你要知道,算器内部行的算就使用的是二制数。
我常和算器打交道,懂一些二制数方面的知。
1、什么叫二制所二制,就是只用0 与 1 两个数字,在数与算必是“ 二一”。
即每两个相同的位成一个和它相的高的位(所以任意一个二制数只要用“0”与“ 1”表示就了)。
比方: 2 在二制中是10; 3 写成二制是11; 4 写成二制数即是100,那么 5 呢是101。
同学依照“逢二一”的照表:表 1(或“ 二一”)的法,很简单获取以下两种制的数字十制二制十制二制119100121010101031111101141001211005101131101611014111071111511118100016100002、二制的缺点二制的最大点是:每个数的各个数位上只有两种状—— 0 或 1。
,我便可以通的方法,比方白与黑、虚与、与正、点与划、小与大、暗与亮(在算机中主要用的高与低)等等手段加以表示。
下表中列出了在二制中 13 的几种不相同表示方法。
表 20 与 1白与黑虚与与正点与划小与大1101●●○●--⋯-++-+――·-○ ○ о ○自然,二制也有不足,正如大家看到的那,同一个数和在二制中要比在十制中位数多得多。
二进制转十进制了表达的方便,我定:用()2表示括号内写的数是二制数,如(1011)2;用() 10 表示括号中写的数是十制数,如(37)10。
五年级上册数学奥数试题第五讲——进位制问题 人教版

第五讲进位制问题例题1 (1)2013=()5=()8=()12=()16(2)(2012)5=()10;(3)(2012)2=()10练习1 (3A2)12=()10;(ADD)16=()10;(2012)5=()12;(2012)8=()12例题2 (1)把三进制数12120120110110121121改写为九进制,它从左向右数第1位数字是多少?(2)(111011001)2=()4=()8练习2 (120011221)3=()9例题3 (5453)7+(6245)7=()7练习3 (123)5 (123)5=()5例题4 在6进制中有三位数abc,化为9进制的cba,这个三位数在十进制中是多少?练习4 在7进制中有三位数abc,化为9进制为cba,这三位数在十进制中是多少?挑战极限例题五一个天平,物品必须放在左盘,砝码必须放在右盘,那么为了能称出1克到1000克,至少需要多少个砝码?例题6 一本书共有2013页,第一天看一页书,从第二天起,每天看到的页数都是以前各天的总和。
如果直到最后剩下的不足以看一次时就一次看完,共需要多少天?作业1、进制互化(1)(11202)4=()10;(2)(1CA)16=()10(2)(3120)10=()16;(4)(1248)10=()5(5)(11202)4=()9;(6)(157)9=()162 、(1)(202)4+(323)4=()4;(2)(21)5(322)5=()53 、一个十进制三位数(abc)10,其中a,b,c均代表某个数码,它的二进制表达式是一个七位数(1abcabc)2,这个十进制的三位数是多少?4 、一个自然数用三进制和四进制表示都为三位数,并且它的各位数字的排列顺序恰好相反,这个自然数用十进制表示是多少?5 、 a,b是自然数,a进制下的数47和b进制下的数74相等,a与b的和的最小值是多少?本周打卡:、1()()()()852109865=== 2、 ()=211010101 ()=87236 ()=542033、 在什么进位制里,十进位制数71记为47?4、 (110101)2+(11101)2 =_______; (1101101)2-(1011110)2 =______;222(101)(1011)(11011)⨯-=________;88888(63121)(1247)(16034)(26531)(1744)----=________;5、一个自然数的七进位制表达式是一个三位数,而这个自然数的九进位制表达式也是一个三位数,而且这两个三位数的数码顺序恰好相反。
小学五年级奥数 进制问题

2
2
2
②
Hale Waihona Puke 11010 101 2
2
2
【例3】 (★★★)
① (101)2(1011)2 (11011)2 ( )2
② ③
((131002010)4111)(6205)(17 01(0 1)2 )(1101)2
(
)2
④ (63121)8 (1247)8 (16034)8 (26531)8 (1744)8 ( )8
知识大总结 1. 进制转换:
⑴ 10转n:短除、取余、倒写 ⑵ n转10:写指、相乘、求和 2. n进制计算: ⑴ 同进制下,可以直接计算. ⑵ 不同进制,借助十进制转换计算. 3. 位值原理: ⑴ 借助数位,按数位进行计算. ⑵ 根据具体位置特征进行估算.
【今日讲题】 例1,例2,例3,例4
【讲题心得】 ______________________________________________________________
10
3
4. 关于进位制 ⑴ 本质:n进制就是逢n进一 ⑵ n进制下的数字最大为(n-1) 特别的:超过9的一般用大写英文字母表示. 例如,十六进制中,10、11、12、13、14、15、分别用A、B、C、D、E、 F表示.
5. n进制转十进制: 写指、相乘、求和. 例如:
101001 2
1
25
0
24
1
23
0
22
0
21
1
20
41 10
【例1】 (★★) ⑴将(2009)10写成二进制数 ⑵把十进制数 2008转化为十六进制数;
进制问题小学数学教案

进制问题小学数学教案
一、教学目标:
1. 知道什么是进制,了解二进制、八进制和十六进制的表示方法;
2. 能够进行不同进制间的转换;
3. 能够灵活运用不同进制进行计算。
二、教学重点:
1. 熟练掌握二进制、八进制和十六进制的表示方法;
2. 能够快速、准确地进行不同进制间的转换;
3. 能够熟练使用不同进制进行简单的计算。
三、教学内容:
1. 进制的概念及表示方法;
2. 二进制、八进制和十六进制的表示方法;
3. 不同进制间的转换方法;
4. 利用不同进制进行简单计算。
四、教学过程:
1. 导入新知识:通过口头解释和举例引导学生了解什么是进制,并介绍二进制、八进制和
十六进制的表示方法。
2. 讲解进制的表示方法:通过实际例子,详细介绍二进制、八进制和十六进制的表示方法,让学生理解其中的规律。
3. 练习不同进制转换:让学生进行一定量的练习,掌握不同进制间的转换方法,培养学生
的计算能力和转换能力。
4. 进行计算运用:设计一些实际生活中的问题,让学生利用不同进制进行简单计算,锻炼
学生的实际运用能力。
5. 总结归纳:对本节课的教学内容进行总结,强调关键知识点,帮助学生进一步巩固所学
内容。
五、教学反思:
通过本节课的教学,学生应该了解进制的概念,能够掌握二进制、八进制和十六进制的表示方法,并能够进行不同进制的转换和计算。
在教学过程中要注重培养学生的实际运用能力和解决问题的能力,使其能够灵活应用所学知识解决实际问题。
小学奥数教程之-进制的应用

1. 了解进制;2. 会对进制进行相应的转换;3. 能够运用进制进行解题一、数的进制1.十进制:我们常用的进制为十进制,特点是“逢十进一”。
在实际生活中,除了十进制计数法外,还有其他的大于1的自然数进位制。
比如二进制,八进制,十六进制等。
2.二进制:在计算机中,所采用的计数法是二进制,即“逢二进一”。
因此,二进制中只用两个数字0和1。
二进制的计数单位分别是1、21、22、23、……,二进制数也可以写做展开式的形式,例如100110在二进制中表示为:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。
二进制的运算法则:“满二进一”、“借一当二”,乘法口诀是:零零得零,一零得零,零一得零,一一得一。
注意:对于任意自然数n ,我们有n 0=1。
3.k 进制:一般地,对于k 进位制,每个数是由0,1,2,,1k -()共k 个数码组成,且“逢k 进一”.1k k >()进位制计数单位是0k ,1k ,2k ,.如二进位制的计数单位是02,12,22,,八进位制的计数单位是08,18,28,.4.k 进位制数可以写成不同计数单位的数之和的形式 1110110n n n n k n n a a a a a k a ka k a ---=⨯+⨯++⨯+()十进制表示形式:1010101010n n n n N a a a --=+++; 二进制表示形式:1010222n n n n N a a a --=+++;为了区别各进位制中的数,在给出数的右下方写上k ,表示是k 进位制的数如:8352(),21010(),123145(),分别表示八进位制,二进位制,十二进位制中的数.5.k 进制的四则混合运算和十进制一样先乘除,后加减;同级运算,先左后右;有括号时先计算括号内的。
二、进制间的转换:知识点拨教学目标5-8-2.进制的应用一般地,十进制整数化为k进制数的方法是:除以k取余数,一直除到被除数小于k为止,余数由下到上按从左到右顺序排列即为k进制数.反过来,k进制数化为十进制数的一般方法是:首先将k进制数按k的次幂形式展开,然后按十进制数相加即可得结果.如右图所示:八进制十进制二进制十六进制例题精讲模块一、进制在生活中的运用【例1】有个吝啬的老财主,总是不想付钱给长工。
(小学奥数)进制的应用

1. 瞭解進制;2. 會對進制進行相應的轉換;3. 能夠運用進制進行解題一、數的進制1.十進位:我們常用的進制為十進位,特點是“逢十進一”。
在實際生活中,除了十進位計數法外,還有其他的大於1的自然數進位制。
比如二進位,八進制,十六進制等。
2.二進位:在電腦中,所採用的計數法是二進位,即“逢二進一”。
因此,二進位中只用兩個數字0和1。
二進位的計數單位分別是1、21、22、23、……,二進位數也可以寫做展開式的形式,例如100110在二進位中表示為:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。
二進位的運算法則:“滿二進一”、“借一當二”,乘法口訣是:零零得零,一零得零,零一得零,一一得一。
注意:對於任意自然數n ,我們有n 0=1。
3.k 進制:一般地,對於k 進位制,每個數是由0,1,2,,1k -()共k 個數碼組成,且“逢k 進一”.1k k >()進位制計數單位是0k ,1k ,2k,.如二進位制的計數單位是02,12,22,,八進位制的計數單位是08,18,28,.知識點撥教學目標5-8-2.進制的應用4.k 進位制數可以寫成不同計數單位的數之和的形式1110110n n n n k n n a a a a a k a k a k a ---=⨯+⨯++⨯+()十進位表示形式:1010101010n n n n N a a a --=+++;二進位表示形式:1010222n n n n N a a a --=+++;為了區別各進位制中的數,在給出數的右下方寫上k ,表示是k 進位制的數 如:8352(),21010(),123145(),分別表示八進位制,二進位制,十二進位制中的數.5.k 進制的四則混合運算和十進位一樣先乘除,後加減;同級運算,先左後右;有括弧時先計算括弧內的。
二、進制間的轉換:一般地,十進位整數化為k 進制數的方法是:除以k 取餘數,一直除到被除數小於k 為止,餘數由下到上按從左到右順序排列即為k 進制數.反過來,k 進制數化為十進位數的一般方法是:首先將k 進制數按k 的次冪形式展開,然後按十進位數相加即可得結果.如右圖所示:模組一、進制在生活中的運用【例 1】 有個吝嗇的老財主,總是不想付錢給長工。
(完整版)五年级奥数__二进制问题_讲义

专题二二进制问题知识要点用0,1,2,3,4,5,6,7,8,9这10个数字表示所有整数的方法被叫做十进制,十进制是最常见的进制,世界上绝大数国家和地区都用这种方法来计数,它的特点是满十进一,退一当十。
除了十进制外,有其它一些进位制,如时间是60进制的,即60秒是一分,60分时1小时。
还有三进制、五进制、八进制、十六进制等。
它们和十进制计数法的道理实质是一样的。
现代计算机上大多用二进制,即满二进一,退一当二,这种进位制只用两个数字0和1,如“1”在二进制中记作1,“2”就要满二进一,记作10,“3”记作11,“4”又一次满二进一,记作100,……。
为了区别十进制和二进制,只要在这个数的右下角标上2或10即可。
任何一个十进制正整数N都可以写成各数位上的数字与10的次方数的=9×103+7×102+5×101+8×100(注:100=1)。
乘积的和的形式,如9758(10)任何一个二进制数也像十进制数一样,也可以写成各个数位上的数字与=1×25+1×24+0×23+1×22+0×21+1 2的次方数的乘积的和的形式,如110101(2)×20典例评析化成二进制例1 将139(10)【分析】要将十进制数化为二进制数,只要连续除以2.因为139=69×2+1,即有69个“2”及1个“1”,故应向第二位上进“69”,个位则有1个1;而69=34×2+1,即第二位69又要向第三位进“34”,而本位数字为“1”。
但34=17×2,即第三位上的34还应向第四位进“17”,且本位数字为“0”;接下去17=8×2+1,即第四位为1;8=4×2,即第五位为0;4=2×2,即第六位为0;2=2×1,即第七位为0,第八位为1;所以139(10)=10001011(2)。
(完整版)五年级奥数__二进制问题_讲义.doc

专题二二进制问题知要点用0,1, 2,3,4, 5, 6,7,8,9 10 个数字表示所有整数的方法被叫做十制,十制是最常的制,世界上大数国家和地区都用种方法来数,它的特点是十一,退一当十。
除了十制外,有其它一些位制,如是60 制的,即 60 秒是一分,60 分 1 小。
有三制、五制、八制、十六制等。
它和十制数法的道理是一的。
代算机上大多用二制,即二一,退一当二,种位制只用两个数字0 和 1,如“ 1”在二制中作1,“2”就要二一,作 10,“3” 作 11,“ 4”又一次二一,作 100,⋯⋯。
了区十制和二制,只要在个数的右下角上 2 或 10 即可。
任何一个十制正整数N 都可以写成各数位上的数字与10 的次方数的乘的和的形式,如9758(10)=9×103+7×102 +5×101+8× 100(注: 100=1)。
任何一个二制数也像十制数一,也可以写成各个数位上的数字与2 的次方数的乘的和的形式,如 110101(2)=1×25+1× 24+0×23+1×22+0×21+1 ×20典例析例1 将 139(10)化成二制【分析】要将十制数化二制数,只要除以2. 因 139=69×2+1,即有 69 个“ 2”及 1 个“ 1”,故向第二位上“ 69”,个位有 1 个1;而 69=34× 2+1,即第二位 69 又要向第三位“ 34”,而本位数字“ 1”。
但34=17×2,即第三位上的 34 向第四位“ 17”,且本位数字“ 0”;接下去17=8×2+1,即第四位 1;8=4×2,即第五位 0;4=2×2,即第六位 0;2=2× 1,即第七位 0,第八位 1;所以 139(10)=10001011( 2)。
个程也可以算以“短除法”求得。
五年级下册数学试题奥数专项训练:进位制人教版(2012)

N进制的本质——“逢N进1”。
N进制的换算——“换十求余”。
换算的巧解——利用进制的幂次关系。
二进制的概念请写出十进制中2、4、8、16、32在二进制中的表示,并试着总结十进制中在二进制中的表示。
1. 1.(多项选择题)判断下列哪组的两个数都不可能是二进制数:A、201,100B、243,1001C、87,520D、102,11022. 2.(多项选择题)下列十进制5、9、17、33对应的二进制的表示中正确的是_________.A、5→101B、9→1001C、17→10001D、33→1000013. 3.(多项选择题)下面十进制中1、3、7、15对应的二进制表示正确的是________。
A、1→1B、3→11C、7→111D、15→11114. 4.请写出十进制数12的二进制表示形式_________二进制与十进制的转换判断下列哪些数可能是二进制,将可能的那些数转换为十进制,将不可能的看作十进制,转换为二进制。
26、37、15、1001、11101、101001.1. 1.将下列十进制数换算成二进制:(答案中间请用一个空格隔开答案并按题目顺序填写例:1 11 111)42 = 86 = 21 =213 = 349 = 652 =2. 2.十进制中的奇数在二进制中末尾是几?偶数呢?(答案中间请用一个空格隔开答案并按题目顺序填写例:1 1)3. 3.将下列二进制数换算成十进制:(答案中间请用一个空格隔开答案并按题目顺序填写例:1 2 3)10101=_______ 11111 =_______ 1100100 =_______二进制的计算1011011+110110 1101110-1011 10111*111010 101010100-1001. 1.计算下列二进制数算式:(答案中间请用一个空格隔开答案并按题目从左到右从上到下的顺序填写例:1 1 1 1) 101+101+110 = 1011+1011+1010 =111+111+101 = 10111-1100-101 =2. 2.计算下列二进制数算式:(答案中间请用一个空格隔开答案并按题目从左到右从上到下的顺序填写例:1 1 1 1) 11*11+1011= 101*110+10101=101+1110+10*1011= 1010101*111–10101=3. 3.计算下列二进制数算式:(答案中间请用一个空格隔开答案并按题目从左到右从上到下的顺序填写例:1 1 1 1)10101 * 100 = 111110 –1011 + 11 * 1011 =111 * 101010 –1110 = 101000 * 100 * 11 =八进制的概念请写出十进制中2、4、8、16、32、64 在八进制中的表示,并试着总结十进制中在八进制中的表示;再写出二进制中1000、1000000、100000000在八进制中的表示,并试着总结二进制中在八进制中的表示。
五年级数学奥数讲义-位值原理与数的进制(讲师版)

注意:对于任意自然数 n,我们有 n0=1。 n 进制:n 进制的运算法则是“逢 n 进一,借一当 n”,n 进制的四则混合运 算和十进制一样,先乘除,后加减;同级运算,先左后右;有括号时先计算括号
内的。
【试题来源】 【题目】从 1~9 九个数字中取出三个,用这三个数可组成六个不同的三位数。若这六个三 位数之和是 3330,则这六个三位数中最小的可能是几?最大的可能是几?
【答案】951
【解析】设这三个数字分别为 a、b、c。由于每个数字都分别有两次作百位、十位、个位,
所以六个不同的三位数之和为 222×(a+b+c)=3330,推知 a+b+c=15。所以,当 a、 b、c 取 1、5、9 时,它们组成的三位数最小为 159,最大为 951。
学生姓名 教师姓名
学科培优 数学
“位值原理与数的进制”
授课日期 授课时长
知识定位
本讲是数论知识体系中的两大基本问题,也是学好数论知识所必须要掌握 的知识要点。通过本讲的学习,要求学生理解并熟练应用位值原理的表示形式, 掌握进制的表示方法、各进制间的互化以及二进制与实际问题的综合应用。并 学会在其它进制中位值原理的应用。从而使一些与数论相关的问题简单化。
99=[(100a+10b+c)-(100c
+10b+a)]÷99=(99a-99c)÷99=a-c;②( ab - ba )÷9=[(10a+b)-(10b+a)]÷9=(9a-9b)÷ 9=a-b;③( ab + ba )÷11=[(10a+b)+(10b+a)]÷11=(11a+11b)÷11=a+b。
五年级奥数第50讲 进位制与位值原理-
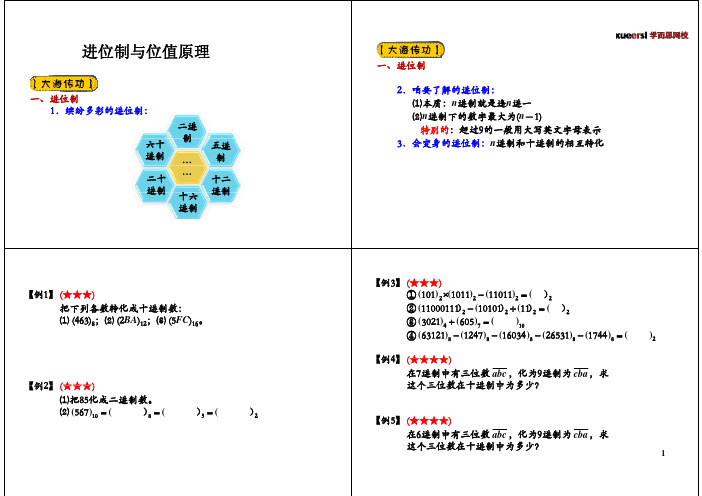
【例5】 (★★★★) 在6进制中有三位数 abc ,化为9进制为 cba,求 这个三位数在十进制中为多少?
1
二、位值原理
【例6】 (★★★) 将一个四位数的数字顺序颠倒过来,得到一个新 的四位数(这个数也叫原数的反序数),新数比原 数大8802 。求原来的四位数。
例3答案:① (11100)2 ② (11000000)2 ③ (500)10 例4答案:248
④ (13121)8
例5答案:22
)2
一、进位制 2.咱要了解的进位制: ⑴本质:n进制就是逢n进一 ⑵n进制下的数字最大为(n-1) 特别的:超过9的一般用大写英文字母表示 3.会变身的进位制:n进制和十进制的相互转化
【例3】 (★★★) ① (101)2(1011)2 (11011)2 ( )2 ② (11000111)2 (10101)2 (11)2 ( )2 ③ (3021)4 (605)7 ( )10 ④ (63121)8 (1247)8 (16034)8 (26531)8 (1744)8 ( )2
进位制与位值原理
一、进位制 1.缤纷多彩的进位制:
六十 进制 二十 进制
二进 制 … … 十六 进制
五进 制 十二 进制
【例1】 (★★★) 把下列各数转化成十进制数: ⑴ (463)8;⑵ (2BA)12;⑶ (5FC)16。
【例2】 (★★★) ⑴把85化成二进制数。 ⑵ (567)10 ( )8 ( )5 (
【例7】 (★★★) 有3个不同的数字,用它们组成6个不同的三位数, 如果这6个三位数的和是1554 ,那么这3个数字分 别是_。
(小学奥数)进制的计算

1. 瞭解進制;2. 會將十進位數轉換成多進制;3. 會將多進制轉換成十進位;4. 會多進制的混合計算;5. 能夠判斷進制.一、數的進制1.十進位:我們常用的進制為十進位,特點是“逢十進一”。
在實際生活中,除了十進位計數法外,還有其他的大於1的自然數進位制。
比如二進位,八進制,十六進制等。
2.二進位:在電腦中,所採用的計數法是二進位,即“逢二進一”。
因此,二進位中只用兩個數字0和1。
二進位的計數單位分別是1、21、22、23、……,二進位數也可以寫做展開式的形式,例如100110在二進位中表示為:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。
二進位的運算法則:“滿二進一”、“借一當二”,乘法口訣是:零零得零,一零得零,零一得零,一一得一。
注意:對於任意自然數n ,我們有n 0=1。
3.k 進制:一般地,對於k 進位制,每個數是由0,1,2,,1k -()共k 個數碼組成,且“逢k 進一”.1k k >()進位制計數單位是0k ,1k ,2k,.如二進位制的計數單位是02,12,22,,八進位制的計數單位是08,18,28,.4.k 進位制數可以寫成不同計數單位的數之和的形式知識點撥教學目標5-8-1.進制的計算1110110n n n n k n n a a a a a k a k a k a ---=⨯+⨯++⨯+()十進位表示形式:1010101010n n n n N a a a --=+++;二進位表示形式:1010222n n n n N a a a --=+++;為了區別各進位制中的數,在給出數的右下方寫上k ,表示是k 進位制的數如:8352(),21010(),123145(),分別表示八進位制,二進位制,十二進位制中的數.5.k 進制的四則混合運算和十進位一樣先乘除,後加減;同級運算,先左後右;有括弧時先計算括弧內的。
小学五年级奥数高斯课本

去组成一个数,就能很清楚地知道这个数应该是 123。
从这个例子可以看出,一个数字在不同的数位上表示不同的大小:
个位上的数字代表几个 1;
十位上的数字代表几个 10;
ቤተ መጻሕፍቲ ባይዱ
百位上的数字代表几个 100;
……
那么可以利用这种方法将一个多位数拆开,例如 123=1×100+2
,
这个结论被称为位值原理。有的时候,为了分析问题方便,我们并不能将多位数逐
-
位值原理
一、知识引领
在十进制中,每个数都是由 0~9 这十个数字中的假设干个组成的,而每个数字
在数中都占一个数位,数的大小是由数字和数字所处的数位两方面共同决定的。比
方一个数由 1、2、3 三个数字组成,我们并不能确定这个数是多少,因为 1、2、3
能组成很多数,例如 213、321、123……但如果说 1 在百位,2 在十位,3 在个位这样
2、〔1〕 =×100+×10+×1;
〔2〕
=×10000×100+×1.
3、在一个两位数的两个数字中间加一个 0,所得到的三位数是原数的 7 倍,这个两
位数是.
4、将一个两位数的个位数字和十位数字交换位置,得到一个新的两位数。它比原来
的两位数小 54,那么原来的两位数最小是.
5、将一个两位数的个位数字和十位数字交换位置,得到一个新的两位数。它与原来
三位数最大可以是多少?
例题 4:假设用一样汉字表示一样数字,不同汉字表示不同数字,那么在等式"
2=
5〞中,"学习爱〞所表示的三位数最小是多少?
练习 4:假设用一样汉字表示一样数字,不同汉字表示不同数字,那么在等式"
小学奥数之进制的计算(含详细解析)

1. 了解进制;2. 会将十进制数转换成多进制;3. 会将多进制转换成十进制;4. 会多进制的混合计算;5. 能够判断进制.一、数的进制1.十进制:我们常用的进制为十进制,特点是“逢十进一”。
在实际生活中,除了十进制计数法外,还有其他的大于1的自然数进位制。
比如二进制,八进制,十六进制等。
2.二进制:在计算机中,所采用的计数法是二进制,即“逢二进一”。
因此,二进制中只用两个数字0和1。
二进制的计数单位分别是1、21、22、23、……,二进制数也可以写做展开式的形式,例如100110在二进制中表示为:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。
二进制的运算法则:“满二进一”、“借一当二”,乘法口诀是:零零得零,一零得零,零一得零,一一得一。
注意:对于任意自然数n ,我们有n 0=1。
3.k 进制:一般地,对于k 进位制,每个数是由0,1,2,,1k -()共k 个数码组成,且“逢k 进一”.1k k >()进位制计数单位是0k ,1k ,2k ,.如二进位制的计数单位是02,12,22,,八进位制的计数单位是08,18,28,.4.k 进位制数可以写成不同计数单位的数之和的形式1110110n n n n k n n a a a a a k a ka k a ---=⨯+⨯++⨯+()十进制表示形式:1010101010n n n n N a a a --=+++; 二进制表示形式:1010222n n n n N a a a --=+++;为了区别各进位制中的数,在给出数的右下方写上k ,表示是k 进位制的数如:8352(),21010(),123145(),分别表示八进位制,二进位制,十二进位制中的数.5.k 进制的四则混合运算和十进制一样先乘除,后加减;同级运算,先左后右;有括号时先计算括号内的。
小学奥数数论讲义 15-进制与位值原理强化篇

今日关键1. n 进制运算2. n 进制3. 位值原理【例 1】(63121)8-(1247)8-(16034)8-(26531)8-(1744)8=( )8。
【巩固】在八进制中,1234-456-322= 。
【例 2】⑴(101)2⨯(1011)2-(11011)2=( )2;⑵(11000111)2-(10101)2÷(11)2=( )2;⑶(3021)4+(605)7=( )10。
【巩固】⑴(1101)2⨯(1111)2-(101)2= ;⑵(4023)5+(542)8=( )10。
【例 3】在几进制中有125⨯125=16324?【巩固】算式1534⨯25=43214是几进制数的乘法?进制与位值原理逢n 进1借1当n位值原理十进制除n 取余法【例 4】有一个两位数,如果把数码3加写在它的前面,则可得到一个三位数,如果把数码3加写在它的后面,则可得到一个三位数,如果在它前后各加写一个数码3,则可得到一个四位数。
将这两个三位数和一个四位数相加等于3600。
求原来的两位数。
【巩固】在一个两位质数的两个数字之间,添上数字6以后,所得三位数比原数大870,那么原质数是。
【例 5】(第五届希望杯培训试题)有3个不同的数字,用它们组成6个不同的三位数,如果这6个三位数的和是1554,那么这3个数字分别是。
【巩固】(迎春杯决赛)有三个数字能组成6个不同的三位数,这6个三位数的和是2886,求所有这样的6个三位数中最小的三位数。
〖答案〗【例 1】13121【巩固】234【例 2】⑴11100,⑵11000000,⑶500 【巩固】⑴10111110,⑵867【例 3】七进制【巩固】八进制【例 4】14【巩固】97【例 5】1,2,4【巩固】139。
奥数精编训练-进制的计算-精编

1. 了解进制;2. 会将十进制数转换成多进制;3. 会将多进制转换成十进制;4. 会多进制的混合计算;5. 能够判断进制.一、数的进制1.十进制:我们常用的进制为十进制,特点是“逢十进一”。
在实际生活中,除了十进制计数法外,还有其他的大于1的自然数进位制。
比如二进制,八进制,十六进制等。
2.二进制:在计算机中,所采用的计数法是二进制,即“逢二进一”。
因此,二进制中只用两个数字0和1。
二进制的计数单位分别是1、21、22、23、……,二进制数也可以写做展开式的形式,例如100110在二进制中表示为:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。
二进制的运算法则:“满二进一”、“借一当二”,乘法口诀是:零零得零,一零得零,零一得零,一一得一。
注意:对于任意自然数n ,我们有n 0=1。
3.k 进制:一般地,对于k 进位制,每个数是由0,1,2,,1k -()共k 个数码组成,且“逢k 进一”.1k k >()进位制计数单位是0k ,1k ,2k ,.如二进位制的计数单位是02,12,22,,八进位制的计数单位是08,18,28,. 4.k 进位制数可以写成不同计数单位的数之和的形式 1110110n n n n k n n a a a a a k a k a k a ---=⨯+⨯++⨯+()十进制表示形式:1010101010n n n n N a a a --=+++;二进制表示形式:1010222n n n n N a a a --=+++; 为了区别各进位制中的数,在给出数的右下方写上k ,表示是k 进位制的数如:8352(),21010(),123145(),分别表示八进位制,二进位制,十二进位制中的数.5.k 进制的四则混合运算和十进制一样先乘除,后加减;同级运算,先左后右;有括号时先计算括号内的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.五年级奥数进制的计算教师版 2.会将十进制数转换成多进制; 3.会将多进制转换成十进制; 4.会多进制的混合计算; 5.能够判断进制.一、数的进制1.十进制:我们常用的进制为十进制,特点是“逢十进一”。
在实际生活中,除了十进制计数法外,还有其他的大于1的自然数进位制。
比如二进制,八进制,十六进制等。
2.二进制:在计算机中,所采用的计数法是二进制,即“逢二进一”。
因此,二进制中只用两个数字0和1。
二进制的计数单位分别是1、21、22、23、……,二进制数也可以写做展开式的形式,例如100110在二进制中表示为:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。
二进制的运算法则:“满二进一”、“借一当二”,乘法口诀是:零零得零,一零得零,零一得零,一一得一。
注意:对于任意自然数n ,我们有n 0=1。
3.k 进制:一般地,对于k 进位制,每个数是由0,1,2,,1k -()共k 个数码组成,且“逢k 进一”.1k k >()进位制计数单位是0k ,1k ,2k ,.如二进位制的计数单位是02,12,22,,八进位制的计数单位是08,18,28,.4.k 进位制数可以写成不同计数单位的数之和的形式1110110n n n n k n n a a a a a k a k a k a ---=⨯+⨯++⨯+()十进制表示形式:1010101010n n n n N a a a --=+++; 二进制表示形式:1010222n n n n N a a a --=+++;为了区别各进位制中的数,在给出数的右下方写上k ,表示是k 进位制的数如:8352(),21010(),123145(),分别表示八进位制,二进位制,十二进位制中的数.5.k 进制的四则混合运算和十进制一样先乘除,后加减;同级运算,先左后右;有括号时先计算括号内的。
二、进制间的转换:一般地,十进制整数化为k 进制数的方法是:除以k 取余数,一直除到被除数小于k 为止,余数由下到上按从左到右顺序排列即为k 进制数.反过来,k 进制数化为十进制数的一般方法是:首先将k 进制数按k 的次幂形式展开,然后按十进制数相加即可得结果.知识点拨教学目标5-8-1.进制的计算如右图所示:模块一、十进制化成多进制【例1】把9865转化成二进制、五进制、八进制,看看谁是最细心的。
【考点】十进制化成多进制【难度】3星【题型】解答【解析】一定要强调两点(1)商到0为止,(2)自下而上的顺序写出来102(9865)(10011010001001)=105(9865)(303430)=108(9865)(23211)=【答案】102(9865)(10011010001001)=,105(9865)(303430)=,108(9865)(23211)=【巩固】852567(((=== ) ) );【考点】十进制化成多进制【难度】3星【题型】解答【解析】本题是进制的直接转化:852567(1067(4232(1000110111===)));【答案】852567(1067(4232(1000110111===)))模块二、多进制转化成十进制【例2】将二进制数(11010.11)2 化为十进制数为多少?【考点】多进制转化成十进制【难度】3星【题型】解答十进制二进制十六进制八进制例题精讲【解析】 根据二进制与十进制之间的转化方法,(11010.11)2=1×24+1×23+0×22+1×21+0×20+1×2-1+1×2-2=16+8+0+2+0+0.5+0.25=26.75。
【答案】26.75【例 3】 同学们请将258(11010101),(4203),(7236)化为十进制数,看谁算的又快又准。
【考点】多进制转化成十进制 【难度】3星 【题型】解答【解析】765432102(11010101)1212021202120212=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯ 128641641=++++213=32105(4203)45250535=⨯+⨯+⨯+⨯500503553=++=32108(7236)78283868=⨯+⨯+⨯+⨯3584128246=+++3742=【答案】213,553,3742模块三、多进制转化成多进制【例 4】 二进制数10101011110011010101101转化为8进制数是多少?【考点】多进制转化成多进制 【难度】4星 【题型】解答【解析从后往前取三合一进行求解,可以得知210101011110011010101101)825363255=【答案】()825363255【例 5】 将二进制数11101001.1011转换为十六进制数。
【考点】多进制转化成多进制 【难度】4星 【题型】解答【解析】 在转换为高于9进制的数时,遇到大于9的数用字母代替,如:A 代表10、B 代表11、C 代表12、D 代表13……。
根据取四合一法,二进制11101001.1011转换为十六进制为E 9.B 。
【答案】E 9.B【例 6】 某数在三进制中为12120120110110121121,则将其改写为九进制,其从左向右数第1位数字是几?【考点】多进制转化成多进制 【难度】4星 【题型】解答【解析】 由于32=9,所以由三进制化为9进制需要取二合一。
从后两个两个的取,取至最前边为12,用位值原理将其化为1×31+2×30=5,所以化为9进制数后第一位为5.【答案】5模块四、多进制混合计算【例 7】 ① 222(101)(1011)(11011)⨯-=________;② 2222(11000111(10101(11(-÷=))) );③88888(63121)(1247)(16034)(26531)(1744)----=________;【考点】多进制混合计算 【难度】4星 【题型】填空【解析】 ① 对于这种进位制计算,一般先将其转化成我们熟悉的十进制,再将结果转化成相应的进制: 2221010101010(101)(1011)(11011)(5)(11)(27)(28)(11100)⨯-=⨯-==; ② 可转化成十进制来计算:222101010102(11000111(10101(11(199)(21)(3)(192)(11000000-÷=-÷==))));如果对进制的知识较熟悉,可直接在二进制下对22(10101(11÷))进行除法计算,只是每次借位都是2,可得222222(11000111(10101(11(11000111(111(11000000-÷=-=))))));③十进制中,两个数的和是整十整百整千的话,我们称为“互补数”,凑出“互补数”的这种方法叫“凑整法”,在n 进制中也有“凑整法”,要凑的就是整n .原式88888(63121)[(1247)(26531)][(16034)(1744)]=-+-+8888(63121)(30000)(20000)(13121)=--=;【答案】(1)、10(11100),(2)、2(11000000),(3)、8(13121)【巩固】 ①在八进制中,1234456322--=________;②在九进制中,1443831237120117705766+--+=________.【考点】多进制混合计算 【难度】4星 【题型】填空【解析】 ①原式1234(456322)12341000234=-+=-=;②原式14438(31235766)(712011770)1443810000200004438=++-+=+-=.【答案】(1)、234,(2)、4438【例 8】 计算4710(3021)(605)()+= ;【解析】 本题涉及到3个不同的进位制,应统一到一个进制下.统一到十进制比较适宜:32471010103021)(605)(34241)(675)(500)+=⨯+⨯++⨯+=(【答案】10(500)模块五、多进制的判断【例 9】 若(1030)140n =,则n =________.【考点】多进制的判断 【难度】5星 【题型】填空【解析】 若(1030)140n =,则33140n n +=,经试验可得5n =.【答案】5【例 10】 在几进制中有413100⨯=?【考点】多进制的判断 【难度】5星 【题型】解答【解析】 利用尾数分析来解决这个问题:由于101010(4)(3)(12)⨯=,由于式中为100,尾数为0,也就是说已经将12全部进到上一位.所以说进位制n 为12的约数,也就是12,6,4,3,2中的一个.但是式子中出现了4,所以n 要比4大,不可能是4,3,2进制.另外,由于101010(4)(13)(52)⨯=,因为52100<,也就是说不到10就已经进位,才能是100,于是知道10n <,那么n 不能是12.所以,n 只能是6.【答案】6【例 11】 在几进制中有12512516324⨯=?【考点】多进制的判断 【难度】5星 【题型】解答【解析】 注意101010(125)(125)(15625)⨯=,因为1562516324<,所以一定是不到10就已经进位,才能得到16324,所以10n <.再注意尾数分析,101010(5)(5)(25)⨯=,而16324的末位为4,于是25421-=进到上一位.所以说进位制n 为21的约数,又小于10,也就是可能为7或3.因为出现了6,所以n只能是7.【答案】7【巩固】算式153********⨯=是几进制数的乘法?【考点】多进制的判断【难度】5星【题型】解答【解析】注意到尾数,在足够大的进位制中有乘积的个位数字为4520⨯=,但是现在为4,说明进走20416-=,所以进位制为16的约数,可能为16、8、4或2.因为原式中有数字5,所以不可能为4、2进位,而在十进制中有⨯=<,所以在原式中不到10就有进位,即进位制小于10,于是原1534253835043214式为8进制.【答案】8。
