关于增透膜和增反膜的几点释疑第一期
本科光纤通信试题答案(卷一)

1) 为了得到较高的信噪比,对光接收机中的前置放大器的要求是______。
A. 高增益B. 低噪声C. 低增益、低噪声D. 高增益、低噪声2) 对于半导体激光器,当外加正向电流达到某一值时,输出光功率将急剧增加,这时输出的光为______,这个电流称为______电流。
A. 自发辐射光,阈值B. 自发辐射光,阀值C. 激光,阈值D. 激光,阀值3) SDH线路码型一律采用______。
A. HDB3码B. AIM码C. NRZ码D. NRZ码加扰码4) 在SiO2单模光纤中,材料色散与波导色散互相抵消,总色散等于零时的光波长是______。
A. 0.85 μmB. 1.05 μmC. 1.27 μmD. 1.31 μm5) 在阶跃型光纤中,导波的传输条件为______。
A. V>0B. V>VcC. V>2.40483D. V<Vc6) DFA光纤放大器作为光中继器使用时,其主要作用是______。
A. 使信号放大并再生B. 使信号再生C. 使信号放大D. 降低信号的噪声7) 目前,掺铒光纤放大器的小信号增益最高可达______。
A. 40 dB左右B. 30 dB左右C. 20 dB左右D. 10 dB左右8) 对于2.048 Mb/s的数字信号,1 UI的抖动对应的时间为______。
A. 488 nsB. 2048 nsC. 488 μsD. 2048 μs9) 通常,影响光接收机灵敏度的主要因素是______。
A. 光纤色散B. 噪声C. 光纤衰减D. 光缆线路长度10) 在薄膜波导中,导波的基模是______。
A. TE0B. TM0C. TE1D. TM12. 写出下列缩写的中文全称(共10分,每题1分)1)GVD (群速度色散)2)STS (同步转移信号)3)ISDN (综合业务数字网)4)AWG (阵列波导光栅)5)OC (光载波)6)WGA (波导光栅路由器)7)GIOF (渐变折射率分布)8)OTDM (光时分复用)9)SCM副载波调制(SCM,Subcarrier modulation)。
增透膜的原理及应用(最新整理)

为 1.38)的镀膜材料很难找到,所以,现在一般都用氟化镁镀制增透膜。
另外,要使光线①和②正好反相,对薄膜的厚度有一定的要求。当光从光疏介质射向光密介质时,反射光有半 波损失。对于玻璃上的增透膜,其折射率大小介于玻璃和空气的折射率之间,所以,当光从空气透过薄膜射向玻璃 时,光线①在空气与薄膜的交界面反射时有半波损失,光线②在薄膜与介质的交界面反射时也有半波损失。所以,
长 1/4 的数量级上,增透膜的均匀度的要求也非常的苛刻
Hale Waihona Puke 。尽管如此,在人们的不懈探索中,还是掌握了不
少行之有效、先进的镀膜技术。目前,常用的镀膜方法有真空蒸镀、化学起相沉积、溶胶—凝胶镀膜等方法。三者 相比较,溶胶—凝胶镀膜设备简单、能在常温常压下操作、膜层均匀性高、微观结构可控,适于不同形状、尺寸的 基片、能通过控制配方、制备工艺得到高激光破坏阈值的光学薄膜,已成为高功率激光薄膜的最具竞争力的制备方 法之一。
事、太空探索等各行各业 ,为人类科技进步作出了重大贡献。
参考文献: [1] 姚启钧.光学教程[M].北京:高等教育出版社,2002:159-164. [2] 张彦亮.“增透膜”增透作用的理论解释[J].临沂师范学院学报,2004,26(3):1-3. [3] 王秀英.增透膜的原理及几个问题的解答[J].物理教师,2004,25(11):1-2. [4] 苗润才,周艳.光学增透膜[J].中学物理教学参考,1999,28(8):1-2. [5] 赵凯华,钟锡华.光学[M].北京:高等教育出版社,1989:152-159. [6] Ambrosc BS Shaffer PS. Steinberg R N,MeDermott L C. An investigation of student understanding of smgle slit diffraotion and double-slit interference[J] Am.J.Phvs.1999:67,146-155. [7] 俞波,陈一匡,方向明等.玻璃表面增透膜的溶胶-凝胶法制备[J].汕头大学学报,2002,17(2):1-6. [8]张厚石.薄膜干涉中的半波损失与薄膜厚度[J].中学物理教学参考,2001,30(11):1-2. [9] 孙增辉,乔学亮,程宇航.一种新型的光学增透膜—DLC 及改性 DLC 薄膜[J].材料导报,2002, 11(6):1-3. [10] 张耀平,许鸿,凌宁等.一种新型三层双波段减反膜设计研究[J].光电子技术与信息,2006,19(2):1-3. [11] 赵秀琴.增透膜与增反膜[J].太原师范学院学报,2003,2(4):1-4. [12] 李林,董连和,黄良钊.硫化锌陶瓷红外增透膜研究[J].长春理工大学学报,2004,27(1):1-3. [13] 沈自才,宋永香,王英剑等.非均匀性对增透膜增透特性的影响[J].光学技术,2005,31(1):1-3.
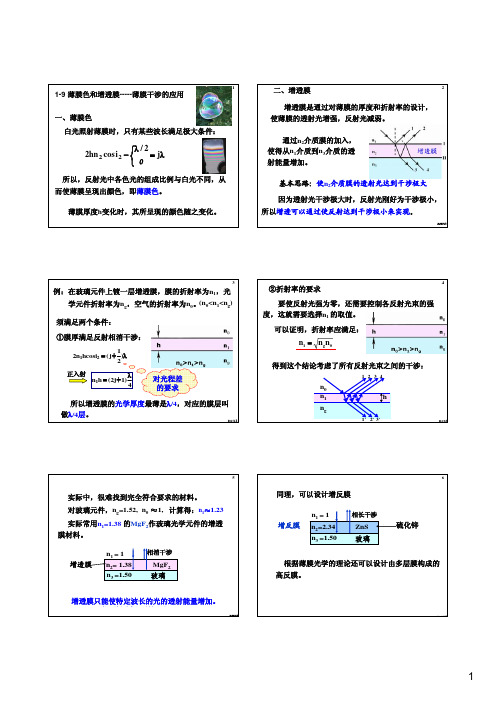
薄膜色和增透膜
1
白光照射薄膜时,只有某些波长满足极大条件:
所以,反射光中各色光的组成比例与白光不同,从2
通过n 2介质膜的加入,使得从n 1介质到n 3介质的透射能量增加。
基本思路:使n 2介质膜的透射光达到干涉极大next
因为透射光干涉极大时,反射光刚好为干涉极小,
所以增透可以通过使反射达到干涉极小来实现。
增透膜是通过对薄膜的厚度和折射率的设计,使薄膜的透射光增强,反射光减弱。
二、增透膜
光学厚度最薄是λ/4,对应的膜层叫λ2
对光程差的要求
4
②折射率的要求
要使反射光强为零,还需要控制各反射光束的强度,这就需要选择n 1 的取值。
可以证明,折射率应满足:
g 1n n n =next
得到这个结论考虑了所有反射光束之间的干涉:
1234
1'2'3'
n 0n 1n g
h。
单、双、多层增透膜的原理及应用

单、双、多层增透膜的原理及应用(转载自网络并整理)单层λ/4增透膜λ/4的光学增透膜(下面讨论时光学元件用玻璃来代替, 初始入射介质用空气来代替), 一般为在玻璃上镀一层光学厚度为λ/4的薄膜,且薄膜的折射率大于空气的折射率, 小于玻璃的折射率由菲涅耳公式知, 光线垂直人射时, 反射光在空气一薄膜界面和薄膜一玻璃界面都有半波损失设空气、镀膜、玻璃的折射率分别为n0,n1,n2 且n2>n1>n0定义R01,T01为空气-薄膜界面的反射率与透射率,R01,T01为薄膜-空气界面的反射率与透射率,R12,T12为薄膜-玻璃界面的反射率与透射率, R21,T21为玻璃-薄膜界面的反射率与透射率如图4-1所示示, 为了区分人射光线和反射光线, 这里将入射光线画成斜入射,图4-1中反射光线1和2的光程差为λ/2, 这样反射光便能完全相消由菲涅耳公式知道, 光垂直通过界面时, 反射率R 和透射率T 与折射率n 的关系为:设人射光的光强为I0, 则反射光线1的光强I1=I0R0, 反射光线2的光强I2=I0I01R12T10。
余下的反射光的光强中会出现反射率的平方, 因为反射率都比较小, 故可不再考虑。
λ/4的光学增透膜使反射光线1与反射光线2的光程差为δ=2n1d1=λ/2, 故相位差为л, 由干涉理论知, 干涉后的光强为:因为折射率n0,n1,n2比较接近,例如n0=1,n2=1.5的界面,T=96%,故可近似地取T01和T10为1,若使Ip 为0 ,则有R01=R12,即:由n2>n1>n0得201n n n =,当上式成立时,反射率最小,透射率最大。
但是涂一层膜也有不足之处,因为常用的λ/4光学增透膜MgF2,MgF2的折射率为1.38,1.38*1.38=1.9044,而玻璃的折射率一般在1.5~1.8之间,所以用MgF2增透膜不能使反射光光强最小,再者,一波长为λ+Δλ的光垂直入射到λ/4的光学增透膜同波长为λ的光一样反射光线1和反射光线2的光程差为δ=λ/2相位差为ΔΨ=2лλ/2(λ+Δλ)从而干涉后的光强为:ϕ∆++=cos 22121I I I I I p ,即可选择合适的材料,使I1=I2,从而上式变为)2.(cos 221λλλπ∆+=I I p 。
增透膜详解

用于玻璃和塑料基底上的增透膜在众多的光学系统中,一个相当重要的组成部分是镜片上能降低反射的镀膜。
在很多应用领域中,增透膜是不可缺少的,否则,无法达到应用的要求。
就拿一个由18块透镜组成的35mm的自动变焦的照相机来说,假定每个玻璃和空气的界面有4%的反射,没有增透的镜头光透过率为27%,镀有一层膜(剩余的反射为1.3%)的镜头光透过率为66%,镀多层膜(剩余的反射为0.5%)的为85%。
在这篇文章中,列举了一些简单的增透膜和使用的材料。
值得注意的是由于玻璃可以被高温加热,而塑料不能,因此,对玻璃和塑料必须选用不同的膜料和膜层设计。
用于玻璃基底的增透膜经典的单层增透膜由一薄层MgF2构成,MgF2在510nm时的折射率为n=1.38,需要的膜厚为d=92nm。
因此,在510nm波长时膜层有一个光学密度(厚度)n*d为1/4的波长。
镀在加热到250-300°C的玻璃基底上的MgF2,不但牢固,稳定,并且相当方便,经济,直接使用蒸发船便可。
想得到更低的反射率,最简单的方法是镀一层CeF3和一层MgF2(各为1/4的光学厚度),可用蒸发船。
图1是单层和2层膜的反射曲线。
2层膜的优点是在可见光范围的中段有更低的反射率,缺点在于在红,蓝端的反射率上升过快。
由于2层膜的效果不理想,为了达到理想的效果,必须使用3层或多层膜。
经典的3层膜由一层1/4光学厚度的中折射率物质(1.6-1.7),一层1/2光学厚度的高折射率物质(2.0-2.2)和一层1/4光学厚度的低折射率物质组成。
最常用的是Al2O3,ZrO2和MgF2。
图1显示在整个光学敏感段(410-680nm)的反射率低于0.5%。
3层增透膜的膜料选择膜料对膜层效果有决定性的影响。
除了理想的折射率,每次镀膜时稳定的折射率,均匀的膜层,低吸收性,牢固性,稳定性也非常重要。
MgF2是最常用的第三层低折射率物质。
但是,由于塑料不能被高温加热,用MgF2会使膜层变软和不稳定,此时,SiO2是最佳的选择。
实际情况中增透膜和高反膜的相关研究

高等教育课程教育研究学法教法研究 43够了解专业的实验仪器设备,学会工程制图、复杂系统的设计和实验,极大地提高了学生的实践动手和操作能力。
2.第二课堂的考核在第二课堂培养学生的能力,通过考核环节体现出来。
考核环节通过学生参加学科竞赛取得优异成绩,通过参与科教协同项目完成项目目标来体现。
学科竞赛:进入实验室学习的学生在1-2个学期学习后,基本上都能够具备综合运用电子、计算机、机械、测量与控制理论和技术预测、模拟和解决复杂工程问题以及设计复杂测控系统与仪器的基本能力。
学院为学生提供必要的基础条件,鼓励和支持学生组队参加全国大学生电子设计大赛、挑战杯以及大学生创新创业项目、互联网+创新创业大赛等各类学科竞赛,通过竞赛和项目检验学生第二课堂的学习成效。
科教协同项目:学校出台《桂林电子科技大学科教协同育人计划项目管理办法》,学生参与教师科研项目经认定可替代人才培养方案中的实践教学环节中的学分。
以教师科研项目为依托,通过科教协同锻炼学生的科研学习能力,培养学生的工程设计等方面的能力。
学生在参与项目的过程中,既修了学分,又学到了知识,还锻炼的能力。
四、第一课堂的实践检验第二课堂的学习最终还要回到第一课堂的实践检验当中。
根据本科培养方案,大学生要参加不少于3周时间的生产实习和专业实践。
作为联合实验室合作的延伸,学院与合作企业达成协议,在企业建设校企联合培养基地,提供条件接纳本科生到企业去修生产实习和专业实践课的学分。
学生在大三下学期末,就可以提出申请到合作企业去进行专业实践和生产实习,利用大三暑假的时间到企业体验一线生产部门的运作。
在合作企业里的培养,企业导师会悉心指导学生在企业当中的学习,企业会将在现实生产过程中所遇到的较为简单的工程问题交由实习学生去完成。
在校企联合培养的基础之上,企业将现实生产中遇到的工程问题进一步凝炼为复杂的工程技术指标,成为本科生的毕业设计题目。
学院和企业为学生提供必要的物质基础条件和制度管理政策,在导师的指导下,让学生去进行自主设计和完成毕业设计。
多层增透膜的理论解释

多层增透膜的理论解释4.1 λ/4增透膜λ/4的光学增透膜(下面讨论时光学元件用玻璃来代替, 初始入射介质用空气来代替), 一般为在玻璃上镀一层光学厚度为λ/4的薄膜,且薄膜的折射率大于空气的折射率, 小于玻璃的折射率由菲涅耳公式知, 光线垂直人射时, 反射光在空气一薄膜界面和薄膜一玻璃界面都有半波损失设空气、镀膜、玻璃的折射率分别为n0,n1,n2 且n2>n1>n0定义R01,T01为空气-薄膜界面的反射率与透射率,R01,T01为薄膜-空气界面的反射率与透射率,R12,T12为薄膜-玻璃界面的反射率与透射率, R21,T21为玻璃-薄膜界面的反射率与透射率如图4-1所示示, 为了区分人射光线和反射光线, 这里将入射光线画成斜入射,图4-1中反射光线1和2的光程差为λ/2, 这样反射光便能完全相消由菲涅耳公式知道, 光垂直通过界面时, 反射率R 和透射率T 与折射率n 的关系为:221211221122121221122101001100121011001)(41)()(41)(n n n n R T T n n n n R R n n n n R T T n n n n R R +=-==+-==+=-==+-==设人射光的光强为I0, 则反射光线1的光强I1=I0R0, 反射光线2的光强I2=I0I01R12T10。
余下的反射光的光强中会出现反射率的平方, 因为反射率都比较小, 故可不再考虑。
λ/4的光学增透膜使反射光线1与反射光线2的光程差为δ=2n1d1=λ/2, 故相位差为л, 由干涉理论知, 干涉后的光强为:212010102121)(cos R T R I I I I I I p -=++=π因为折射率n0,n1,n2比较接近,例如n0=1,n2=1.5的界面,T=96%,故可近似地取T01和T10为1,若使Ip 为0 ,则有R01=R12,即: 2121220101)()(n n nn n n n n +-=+-由n2>n1>n0得201n n n =,当上式成立时,反射率最小,透射率最大。
增透膜"增透作用的理论解释

“增透膜"增透作用的理论解释一、增透膜作用及问题的引入在比较复杂的光学器件(如望远镜、潜望镜、照相机等)中,光能的反射损失是十分严重的,虽然光学器件的每个表面在光垂直入射的情况下,反射率极低,但由于这些复杂的光学系统往往由多个透镜或棱镜组成,则最终反射而造成的光能损失不能忽略不计。
通常使用的光学材质如玻璃,在垂直入射情况下,可见光的反射率仅有4%,若考虑到透镜的两个面,总反射率也不足8%,但如果系统是由若干个透镜或棱镜所组成,反射的光能就会累积,可达百分之几十。
此外,光会在各透镜面间的发生往复反射,还会造成杂散光,继而会严重影响光学系统的成像质量。
此时,为了减少光在光学元件(透镜、棱镜)表面上的反射损失,可在其表面上镀上一层薄膜,利用薄膜的干涉相消来减少反射光的能量,是尽可能多的能量通过光透射出去。
然而对于增透膜的原理,其实很多人并不知情。
我们通过问卷对有一定物理光学基础的同学进行调查询问,发现大约有80%的人认为增透膜的作用在于当光射向它时,在膜的上下表面发生反射后,由于受干涉相消条件的限制,将重新折入光学器件;同时,约有5%的同学甚至对增透膜有所质疑,即光会在前后表面发生反射,相互抵消,那么就相当于在光的传播过程中,增加了一个反射面,进一步减弱了光的透射率,反而使增透膜无法实现增透的目的。
而在增透膜的应用问题上,比如有关使用中增透膜的厚度要求,几乎所有同学都认为只要等于反射光的四分之一波长或其奇数倍,即使得增透膜前后两列反射波的相位差为或其奇数倍,两列波就发生相消干涉,从而就实现了波的干涉相消。
但我们小组通过查阅了一些文献,发现增透膜的工作原理并非那么简单。
由于光是一种电磁波,我们就通过所学的电磁场与电磁波的理论来分析电磁波(光)通过增透膜这种介质时电场、磁场的分布,求出光在不同介质中传播的反射、投射系数等相应参数,解释增透膜增透的原理,并根据分析所得结论加深对增透膜性质的理解,并对增透膜加以推广。
单层增透、增反膜条件的一种简明推导方法

单 层 增透
,
、
增
,
奋
, ,
`
(
5 )
反 膜 的 光 学 厚 度 虽 然都 是
”
~ ”
.
通 常单 层增透 璃 的 知
。
,
增 反 膜 的 基 片都是 玻 所 以 二者
.
但这 两 种 薄 ” 一一 一 L 膜 的厚 度 的大小 却是 不 同 的 这 是 因
`
一
李 4
’
’
一
,
,
而 且 它 们都在 空 气 中工 作
: ,
,
,
的
是 正入 射
此 相 同的 同
,
,
于 是 由 菲涅 耳 公 式 知
,
,
两反射
n 光正 入 射 至 折射率 为
厚度 为 L 的 薄 膜
光振 幅 的 垂直 与 平行分 量 的 方 向变化 是 彼 所 以 它 们 的 合矢 量 方 向也 就 相
0
.
上
设上
:
、
下 界 面 上 相 邻 两 反射光 的 振 幅
_
,
。
、
1
L 丁
气“”
,
乙 + 。’
J
)
三
由( 能
,
、
`
单层 增 反膜 的 条 件
) 式知
.
式 中 d 为额外 程 差
。
1
,
要 使薄 膜具 有增 反 功 由于
A 最大 和 A 为
二
、
则 A 应 最大
、 、
零 时
,
单层 增 透 膜 的 条 件
,
所对 应 的上 由于 光 间有
单、双、多层增透膜的原理及应用

单、双、多层增透膜的原理及应用(转载自网络并整理)单层λ/4增透膜λ/4的光学增透膜(下面讨论时光学元件用玻璃来代替, 初始入射介质用空气来代替), 一般为在玻璃上镀一层光学厚度为λ/4的薄膜,且薄膜的折射率大于空气的折射率, 小于玻璃的折射率由菲涅耳公式知, 光线垂直人射时, 反射光在空气一薄膜界面和薄膜一玻璃界面都有半波损失设空气、镀膜、玻璃的折射率分别为n0,n1,n2 且n2>n1>n0定义R01,T01为空气-薄膜界面的反射率与透射率,R01,T01为薄膜-空气界面的反射率与透射率,R12,T12为薄膜-玻璃界面的反射率与透射率, R21,T21为玻璃-薄膜界面的反射率与透射率如图4-1所示示, 为了区分人射光线和反射光线, 这里将入射光线画成斜入射,图4-1中反射光线1和2的光程差为λ/2, 这样反射光便能完全相消由菲涅耳公式知道, 光垂直通过界面时, 反射率R 和透射率T 与折射率n 的关系为:设人射光的光强为I0, 则反射光线1的光强I1=I0R0, 反射光线2的光强I2=I0I01R12T10。
余下的反射光的光强中会出现反射率的平方, 因为反射率都比较小, 故可不再考虑。
λ/4的光学增透膜使反射光线1与反射光线2的光程差为δ=2n1d1=λ/2, 故相位差为л, 由干涉理论知, 干涉后的光强为:因为折射率n0,n1,n2比较接近,例如n0=1,n2=1.5的界面,T=96%,故可近似地取T01和T10为1,若使Ip 为0 ,则有R01=R12,即:由n2>n1>n0得201n n n =,当上式成立时,反射率最小,透射率最大。
但是涂一层膜也有不足之处,因为常用的λ/4光学增透膜MgF2,MgF2的折射率为1.38,1.38*1.38=1.9044,而玻璃的折射率一般在1.5~1.8之间,所以用MgF2增透膜不能使反射光光强最小,再者,一波长为λ+Δλ的光垂直入射到λ/4的光学增透膜同波长为λ的光一样反射光线1和反射光线2的光程差为δ=λ/2相位差为ΔΨ=2лλ/2(λ+Δλ)从而干涉后的光强为:ϕ∆++=cos 22121I I I I I p ,即可选择合适的材料,使I1=I2,从而上式变为)2.(cos 221λλλπ∆+=I I p 。
单、双、多层增透膜的原理及应用

单、双、多层增透膜的原理及应用〔转载自网络并整理〕➢ 单层λ/4增透膜λ/4的光学增透膜〔下面讨论时光学元件用玻璃来代替, 初始入射介质用空气来代替〕, 一般为在玻璃上镀一层光学厚度为λ/4的薄膜,且薄膜的折射率大于空气的折射率, 小于玻璃的折射率由菲涅耳公式知, 光线垂直人射时, 反射光在空气一薄膜界面和薄膜一玻璃界面都有半波损失设空气、镀膜、玻璃的折射率分别为n0,n1,n2 且n2>n1>n0定义R01,T01为空气-薄膜界面的反射率与透射率,R01,T01为薄膜-空气界面的反射率与透射率,R12,T12为薄膜-玻璃界面的反射率与透射率, R21,T21为玻璃-薄膜界面的反射率与透射率如图4-1所示示, 为了区分人射光线和反射光线, 这里将入射光线画成斜入射,图4-1中反射光线1和2的光程差为λ/2, 这样反射光便能完全相消由菲涅耳公式知道, 光垂直通过界面时, 反射率R 和透射率T 与折射率n 的关系为:221211221122121221122101001100121011001)(41)()(41)(n n n n R T T n n n n R R n n n n R T T n n n n R R +=-==+-==+=-==+-==设人射光的光强为I0, 则反射光线1的光强I1=I0R0, 反射光线2的光强I2=I0I01R12T10。
余下的反射光的光强中会出现反射率的平方, 因为反射率都比较小, 故可不再考虑。
λ/4的光学增透膜使反射光线1与反射光线2的光程差为δ=2n1d1=λ/2, 故相位差为л, 由干预理论知, 干预后的光强为:212010102121)(cos R T R I I I I I I p -=++=π因为折射率n0,n1,n2比较接近,例如n0=1,n2=1.5的界面,T=96%,故可近似地取T01和T10为1,假设使Ip 为0 ,则有R01=R12,即:2121220101)()(n n n n n n n n +-=+-由n2>n1>n0得201n n n =,当上式成立时,反射率最小,透射率最大。
增透膜和增反膜最小厚度公式

增透膜和增反膜最小厚度公式
增透膜和增反膜是光学领域中常用的薄膜材料,它们能够对光线进行干涉和反射,从而起到改变光线透过和反射的作用。
在实际应用中,我们需要计算增透膜和增反膜的最小厚度,以确保其具有预期的光学性能。
对于增透膜,最小厚度公式为:
t = λ/(4n)
其中,t表示增透膜的最小厚度,λ表示光波的波长,n表示增透膜的折射率。
对于增反膜,最小厚度公式为:
t = λ/(4n)
其中,t表示增反膜的最小厚度,λ表示光波的波长,n表示增反膜的折射率。
需要注意的是,增透膜和增反膜的厚度是一个范围,而不是一个确定的数值。
在实际应用中,我们需要根据具体情况来确定增透膜和增反膜的厚度范围,以确保其具有最佳的光学性能。
- 1 -。
增透膜和增反膜123

增透膜和增反膜1增透膜当光从空气n1= 1 到玻璃n2= 1. 5, 代入得R = 4 % , 即透镜表面约反射4%的入射光. 在各种光学仪器中, 为了矫正像差或其他原因, 往往采用多透镜的镜头. 为了避免反射损失, 在近代光学中都在透镜表面敷上一层薄膜, 其折射率小于仪器基板折射率使入射光在薄膜上下两表面的反射光干涉相消, 就可使反射光能减小, 透射光能相对增大,这样的膜, 叫做增透膜或消反膜。
显然, 仅镀一层增透膜不可能同时对所有的波长和所有入射角都是消反射的。
2对目视光学仪器人眼视觉最敏感的波长是0 = 550 nm 的绿光至黄绿光, 对照相底片最敏感的感光波长是黄绿光. 所以, 如果用白光入射到涂敷有增透膜的镜头表面上, 对波长o 来说, 若nd =0/4,30/4,50/4, ⋯, 则波长0的反射率最小, 即透射率T 最大, 这时镜头上的薄膜只是减弱黄绿光的反射, 而紫光和红光因不符合反射干涉减弱的条件所以有较高的反射. 于是涂敷有增透膜的照相机镜头在日光下呈蓝紫色。
2. 1透明膜的折射率设白光由空气垂直投射到上面涂一层折射率为n2,厚度为d的玻璃上, 使o= 550 nm 的光产生完全消失, 为达到这个目的, 先考虑两束光, 除要产生相位差为外还要求两束光的振幅相等。
设入射振幅为Ao, 由菲涅耳公式, 垂直入射, 振幅, 因光的强度与振幅的平方成正比, 所以讨论振幅的反射率和透射率分别为:r1 =|| t1= r2= t′1=r1为涂层上表面的振幅反射率, r2为下表面的振幅反射率, t1为n1到涂层上表面的振幅透射率, t′1是涂层上表面由涂层内表面向折射率为n1振幅透射率.A 1 = r1A 0 =A0A 2 = t1 r2 t′1A 0=| A 0为减小反射, 增大振幅透射, 有≈ 1 故A 2≈||A o,完全相消干涉要求, 所以≈得n2==1.225但是目前找不到一种透明介质的折射率正好是1. 225, 既稳定又能牢牢附着在玻璃上的材料, 常用M gF2附着在玻璃上, 但折射率为n2= 1. 38, 略高于完全相消反射的折射率.2. 2膜的厚度实际应用的波长有一定的波长范围, 对于不同于o 的波长的光, 光学厚度为o/4n 的薄膜, 对邻近波长的反射率与最小值差别不大, 而光学厚度为3o/4n,5o/4n 等薄膜, 反射率显著增大, 为使其他色光反射也较少, 应采用较薄的膜, 即光学厚度为0/4n 的膜, 简称o/4膜. 具体计算如下:当正入射时, 涂层的厚度d 应满足2n2d = (2j+ 1)0/2 j=0,1,2⋯首先讨论j= 0, d ==≈100 nm对黄绿光= 550 nm , 反射光束的振幅为A 1 = r1A 0=||Ao= Ao=0. 16A oA2= t1 r2 t′1 =||= 0. 04E o 因此, 反射光束1 与2 干涉相消时, 合振幅为A = A 1- A 2= 0. 12A o.相应的光强为I = A ≈0. 014A o Ao= 0. 014 Io, 故光强反射率为R = ==1. 4 %.即有涂层使反射光干涉相消时, 反射光的强度只是入射光强度的1. 4 % , 对波长为550 nm 的光降低了反射.对于紫光, v= 400 nm , 两束相干的反射光的相位差为==== 4. 23 radv反射光强Iv= A12+ A 22+ 2A 1A 2co s v= 2. 4 % I 0, 故紫光的光强反射率为2. 4 %.对于红光, r= 700 nm , 有==== 2. 47 radrI r = A12+ A 22+ 2A 1A 2co s r = 0. 017I 0所以对红光的光强反射率为1. 7 %.因此对同样厚度的涂层, 不同波长有不同的消反射效果, 三种波长相应的光强反射率分别为R = 1. 4% , R v= 2. 4 % , R r= 1. 7 % , 所谓消反层只是对特殊波长而言的, 所谓消反射也只是将该波长的光强反射率降低到最小值, 一般并非是零.当取厚度为= 2n2d = 3/2, d = 30/4n2时,计算对紫光和红光的反射率=400 nm==550=4. 125vco s (4. 125) = 0. 923 8,I v′= A 12+ A 22+ 2A 1A 2co s v = 0. 039A 02对r= 700 nm , r==550=2. 357, co s r = co s0. 357,= 0. 434 2 = A 12+ A 22+ 2A 1A 2co s r= 0. 0306A 02= 0. 033 I 0所以R ‘r == 3. 3% > R rI ′显然紫光和红光的反射率增大了.2. 3由两束光干涉扩展到多束光干涉同样把消反膜从两束光干涉扩展到多束光干涉, 从一层薄膜扩展到两层菲涅耳公式以及完全消反射的要求(反射光的位相相反, 振幅相等) 仍是讨论的基础. 反射光完全干涉相消, 薄膜起到了使入射光不透射的目的. 只要薄膜的折射率n2 小于基板的折射率n3 涂膜后的反射率总会小于不涂膜时基板的反射率.2. 4由单层膜到双层膜到多层单层膜是最简单的. 如果在折射率为n g的基板上依次涂上高折射层(n h ) 和低折射层(n1) 每层的依次光学厚度4n ,为了达到消光, 又应满足什么条件[2 ]? 如图2 所示. 光在基板上的反射率为R 0=, 先涂一层高反射层(n1 ) ,此时的反射率为R 1= ,令=,, 则R 1 =故镀一层薄膜时的反射率可等效在折射率为的基板上的反射率, 涂第二层低折射率层(n1) 时,R2==为使反射光完全干涉相消, 必须有:n0–ng=0 n1/n h=增透膜中镀一层折射率为1. 38 的氟化镁薄膜, 单面反射损失可以从4 % 减小到1. 4% , 这已可满足一般光学系统减反射的要求, 但对复杂的光学系统来说, 反射损失还太高, 因而发展多层反射膜, 但制造复杂,成本高, 应根据光学系统的总体要求, 选择合适的总体要求, 选择合适的最经济的消反射膜.对眼镜片的表面也可镀以增透膜, 这种镀膜镜片对可见光的反射很小, 而透射率可达99.5 % , 因此配带镀膜眼镜时更显得明亮. 镀膜后, 还可提高镜片的耐磨性.。
增反膜增透膜理化生光学

紫 红
k2, 2n1d 73n6m红光
21/2
色 k3, 2n1d 44 .6n1m紫光
31/2
k4,
2nd 3 增反膜增透膜1理化生光学 1 .4n 5m
13.5 薄膜等厚干涉
chsling
13.5.2 典型的等厚干涉
a. 劈 尖
n
T
L
n1
n1
d
S
劈尖角
M
D
2nd
2
nn1
k, k1,2, 明纹
13.5 薄膜等厚干涉
测量透镜的曲率半径
rk2 k R/n2
rk2m(km )R/n2
chsling
R
r
R(rk2m rk2)n2
m
2r
增反膜增透膜理化生光学
13.5 薄膜等厚干涉
chsling
例 用波长为nm的单色光做牛顿环实验,测得第
个 k mm , 第 k+5 mm,求平凸透镜的曲率半径R.
它们之间有什么关系?(已知真空中波长为 0 )
在真空中的路程为: x ct c r nr
u
介质中的相位改变: n
2 n
r
真空中的相位改变: 2 nr
0
2 uT
r
2 n cT
r
2 0
nr
t相 同 相 位 相 同
增反膜增透膜理化生光学
13.4 光程与光程差
chsling
13.4.1 光程
b
b'
b
e b' 1
b2
3 2 6 增反膜增透膜理化生光学
d L
2n b
13.5 薄膜等厚干涉
chsling
“增透膜”增透的原理解析

“增透膜”增透的原理解析摘要:当薄膜的厚度适当时,在薄膜的两个面上反射的光,路程差恰好等于半个波长,因而互相抵消。
这就大大减少了光的反射损失,增强了透射光的强度。
笔者为此查阅了有关资料,反复思考,认真探究,探究出它的原理:其一,当光从一种介质进入另一种介质时,如果两种介质的折射率相差减小,反射光的能量减小,透射光的能量增加;其二,利用了薄膜干涉的原理,增加了透射光的能量;其三,薄膜材料的选择和多数镜头呈现淡紫色的原因。
从而得出结论:在光学镜头表面涂一层厚度和材料适当的薄膜,能够增加透射光的能量,减少反射光的能量损失——“增透膜”增透。
关键词:“增透膜”增透原理现行高中物理教材讲述光的干涉在技术上的应用时,用了很短一段话介绍了增透膜的作用:“当薄膜的厚度适当时,在薄膜的两个面上反射的光,路程差恰好等于半个波长,因而互相抵消。
这就大大减少了光的反射损失,增强了透射光的强度。
”就是这段话,学生有很多疑问:两个面上反射的光相互抵消,怎么会使透射光的强度增强了?笔者带着问题查阅了有关资料并进行了反复思考,认为应从以下几个方面来理解和解释。
其一是当光从一种介质进入另一种介质时,如果两种介质的折射率相差减小,反射光的能量减小,透射光的能量增加。
原因是当光从折射率为¬n1的介质1进入折射率为n2的介质2时,根据光的反射和折射理论,反射光的振幅E与入射光的振幅E0之比:,而光的强度与光的振幅的平方成正比,所以介质1与介质2界面的反射率R(即反射光强度I与入射光强度I0之比)为:。
根据这一推论可知:(1)如果镜头表面不涂薄膜,光直接由折射率为n1=1.0空气垂直入射到折射率为n2=1.5的玻璃的介面时,反射率,即将有4%的入射光能被反射,96%的入射光能进入玻璃,这说明光学器件表面的反射光会导致光能损失。
进入玻璃的光再从玻璃垂直进入空气的分介面时,透射光与入射光相比,又要产生相同比例的能量损失。
即一个简单玻璃透镜,光通过它的两个透光表面,透射光的强度I只占原入射光强度I0 的。
_增透膜_增透作用的理论解释

×
1
+
n n2
=0
(13)
45
© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved.
临沂师范学院学报
第 26 卷
当 n 为偶数时 ,上式取正号 ,即
参考文献 :
[1 ] 姚启钧. 光学教程 (第 2 版) [M] . 北京 :高等教育出版社 ,1989. [2 ] 赵凯华 ,钟锡华. 光学 (上册) [M] . 北京 :高等教育出版社 ,1989. [3 ] G. R 福尔斯. 现代光学导论[M] . 上海 :上海科学技术出版社 ,1980. [4 ] 郭硕鸿. :电动力学 (第 2 版) [M] . 北京 :高等教育出版社 ,1997.
1
+
n1 n
×1-
n n2
+
1-
n1 n
×
1
+
n n2
=0
(14)
解得
n1
=
n2 ,此时 d
=
1 4
mλ,
m
= 2 ,4 ,6 ,8 ……,这个解说明了当两介质折射率相等时 ,由于存在着
半波损失 ,故薄膜厚度应为半波长奇数倍.
当 n 为奇数时 ,上式取负号 ,即
-
1
+
n1 n
× 1-
n n2
+
1-
2 kd = mπ, m = 0 ,1 ,2 ,3 ……
(11)
从而得出薄膜的厚度dΒιβλιοθήκη =1 4mλ,
m
= 0 ,1 ,2 ,3 ……
增透膜和增反膜最小厚度公式

增透膜和增反膜最小厚度公式
增透膜和增反膜是光学膜的一种,用于改变光线的透射与反射。
在制造增透膜和增反膜时,需要考虑其最小厚度,以保证其光学性能。
下面介绍增透膜和增反膜最小厚度公式。
增透膜最小厚度公式:
dmin = λ/(4n)
其中,dmin为增透膜的最小厚度,λ为波长,n为增透膜的折射率。
增反膜最小厚度公式:
dmin = λ/(2n)
其中,dmin为增反膜的最小厚度,λ为波长,n为增反膜的折射率。
上述公式中,波长λ和折射率n是增透膜和增反膜的两个重要参数。
波长λ决定了光线在膜层中的传播特性,而折射率n则决定了光线与膜层的相互作用程度。
根据公式可以得知,当波长λ较小或折射率n较大时,增透膜和增反膜的最小厚度会相应减小。
总之,增透膜和增反膜最小厚度公式是制造光学膜必不可少的工具,可以帮助工程师们计算出最小厚度,进而提高产品的光学性能。
- 1 -。
增透膜和增反膜最小厚度公式

增透膜和增反膜最小厚度公式
增透膜和增反膜最小厚度公式是计算光学膜材料厚度的公式。
其中,增透膜是指在光学器件表面加一层膜,使得透射率增加的膜,而增反膜是指在光学器件表面加一层膜,使得反射率减少的膜。
两种膜的最小厚度公式分别如下:
增透膜最小厚度公式: d = λ/4n
其中,d表示增透膜的最小厚度,λ表示光波的波长,n为膜的折射率。
增反膜最小厚度公式: d = λ/2n
其中,d表示增反膜的最小厚度,λ表示光波的波长,n为膜的折射率。
这两个公式是光学器件设计中非常重要的公式,可以帮助工程师选择合适的膜材料和厚度,以达到所需的光学性能。
- 1 -。
