第七章钢筋混凝土受扭构件简介
混凝土受扭构件

0.85ft
fy
V 剪力设计值,对纯扭构件取1 T 2时,取2
Vb
TTu 0.2W tcfc,当 h0/b4时 TTu 0.1W 6tcfc,当 h0/b6时
线性插值
第二节 矩形截面剪扭构件承载力
V
T
M
T
扭矩使纵筋产生拉应力,与受弯时钢筋拉应力叠加,使钢筋拉应力增大, 从而会使受弯承载力降低。
而扭矩和剪力产生的剪应力总会在构件的一个侧面上叠加,因此承载力总 是小于剪力和扭矩单独作用的承载力。
F1
F1
b/2
F2 b
理想弹塑性材料
配筋强度比 --抗扭纵筋与箍筋的配筋强度比
Astl s fy
Ast1 ucor fyv
Astl —受扭计算中对称布置在截面周边的全部抗扭纵筋的截面面积; f y ——受扭纵筋的抗拉强度设计值;
u cor —— 截面核芯部分的周长,uco r2(bco rhco)r
(3)按抗扭承载力计算需要的抗扭箍筋 Ast1 s
TT u0 .35 tftW t 1 .2 fyv A s s1 tA cor
(4)按抗扭纵筋与箍筋的配筋强度比关系,确定抗扭纵筋 A stl
Astls fy
Ast1 ucor fyv
(5)按照叠加原则计算抗弯剪扭总的纵筋和箍筋用量
受弯纵筋As和A's No 抗扭纵Imag筋e : A's
一、受扭承载力降低系数 t
t
1.5
1 0.5 VWt
Tbh0
t
1.5
10.2 1 VWt
Tbh0
t ——为剪扭构件的混凝土强度降低系数
0.5t 1.0
抗扭砼承载力
抗剪砼承载力
07 钢筋混凝土受扭构件承载力计算-精品文档

分别计算各区合力及其对截面形心的 力偶之和,可求得塑性极限开裂扭矩为
塑性开裂扭矩
2
截面抗扭塑性抵抗矩
b 3 T f h b fW c r , p t t t 6
混凝土的抗拉强度设计值
按塑性理论,对理想弹塑性材料,截面上某一点应力 达到材料强度时并不立即破坏,而是保持极限应力继续变 形,扭矩仍可继续增加,直到截面上各点应力均达到极限 强度。才达到极限承载力。此时截面上的剪应力分布为四 个区,如图7.2(b)所示。
m ax
T W te
7.2.2 矩形截面的开裂扭矩 按弹性理论, 当主拉应力σtp=τmax=ft时,构件开裂, 即
max
弹性开裂扭矩
Tcr,e ft Wte
截面抗扭弹性抵抗矩
T c r,e ft W te
混凝土的抗扭强度设计值
按塑性理论,对理想弹塑性材料,截面上某一点应力 达到材料强度时并不立即破坏,而是保持极限应力继续变 形,扭矩仍可继续增加,直到截面上各点应力均达到极限 强度。才达到极限承载力。此时截面上的剪应力分布为四 个区,如图7.2(b)所示。
T W te
截面抗扭弹性抵抗矩
由材料力学知识可知,构件侧面的主拉应力σtp和主压 应力σcp相等,主拉应力和主压应力轨迹沿构件表面呈螺旋 形。当主拉应力达到混凝土抗拉强度时,在构件长边中某 个薄弱部位首先开裂,裂缝沿主压应力轨迹迅速延伸。对 于素混凝土构件,一旦开裂就会导致构件破坏,破坏面呈 一空间扭曲面。
2 b W fw 3 h b 6 h f W tf bf b 2 hf W tf bf b 2
T .7fW c r 0 t t
对矩形截面, 截面抗扭塑性抵抗矩按下式计算:
混凝土基本原理第七章

思考题7.1按变角空间桁架模型计算扭曲截面承载力的基本思路是什么,有哪些基本假设,有几个主要计算公式?答:变角空间桁架模型计算扭曲截面承载力的基本思路:在裂缝充分发展且钢筋应力接近屈服强度时,截面核心混凝土退出工作,从而实心截面的钢筋混凝士受扭构件可以用一个空心的箱形截面构件来代替,它由螺旋形裂缝的混凝土外壳、纵筋和箍筋三者共同组成变角空间桁架以抵抗扭矩;基本假设:①混凝土只承受压力,具有螺旋形裂缝的混凝土外壳组成桁架的斜压杆,其倾角为a ;②纵筋和箍筋只承受拉力,分别为桁架的弦杆和腹杆;③忽略核心混凝土的受扭作用及钢筋的销栓作用;主要计算公式:f y At1 S— f yv A sti A corf yv A stl U cor T u 2s7.2简述钢筋混凝土纯扭和剪扭构件的扭曲截面承载力的计算步骤。
答:剪扭构件:①按公式V/(bh0) T/(0.8W t) 0.25 c f c或V/(bh0) T/(0.8W t) 0.2 c f c验算截面尺寸是否符合要求;②按公式V / ( bh 0 ) T / W t 0.7 f t 或V / (bh 0) T / W t 0.7 f t 0.07 N / (bh 0)验算是否需要按计算配置受扭、受剪箍筋和受扭纵筋;③比较剪力和扭矩是否满足V 0.35 f t bh0 , V 0.875 f t bh 0 / ( 1)或T 0.175 f t W t , T 0.175 h f t W t ,若满足,则可不考虑剪力或者扭矩的作用,按纯剪或者纯扭构件计算;否则,应考虑剪力和扭矩的作用;④按公式t 1.5/1 0.5 VW t / (Tbh 0) 或t 1.5/1 0.2( +1) VW t / (Tbh 0)计算受扭承载力降低系数,且应满足0.5 t1 ;⑤按公式V u 0.7(1.5 t)f t bh0 £丫旷,儿/$或丫” 1.75(1.5 Jf t b7U 1) f yv A sv九/s 计算剪扭构件的受剪承载力,对于T形和I形截面假设剪力全部由腹板承担,并确定受剪箍筋的用量;⑥按公式T u 0.35 t f t W t 1.2 1f yv A st1A°r/s 或T u 0.35 h t f t W t 1.2 1f yv人/儿。
钢筋混凝土受扭构件

钢筋混凝土受扭构件5.1概述1.矩形截面纯扭构件的受力性能和承载力计算方法;2.剪扭构件的相关性和矩形截面剪扭构件承载力计算方法;3.矩形截面弯、剪、扭构件的承载力计算方法;4.受扭构件的构造要求。
图5-1a所示的悬臂梁,仅在梁端A处承受一扭矩,我们把这种构件称为纯扭构件。
在钢筋混凝土结构中,纯扭构件是很少见的,一般都是扭转和弯曲同时发生。
例如钢筋混凝土雨蓬梁、钢筋混凝土现浇框架的边梁、单层工业厂房中的吊车梁以及平面曲梁或折梁(图5-1b、c)等均属既受扭转又受弯曲的构件。
由于《规范》中关于剪扭、弯扭及弯剪扭构件的承载力计算方法是以构件抗弯、抗剪承载力计算理论和纯扭构件计算理论为基础建立起来的,因此本章首先介绍纯扭构件的计5.2 纯扭构件受力和承载力计算图 5-1 受扭构件示例由材料力学知,在纯扭构件截面中将产生剪应力τ,由于τ的作用将产生主拉应力σtp和主压应力σcp,它们的绝对值都等于τ,即∣σtp∣=∣σcp∣=τ,并且作用在与构件轴线成5-2b),构件随即破坏,破坏具有突然性,属脆性破坏。
5.2.2 素混凝土纯扭构件的承载力计算1.弹性计算理论由材料力学可知,矩形截面匀质弹性材料杆件在扭矩作用下,截面中各点均产生剪应力τ,剪应力的分布规律如图5-3所示。
最大剪应力τmax发生在截面长边的中点,与该点剪应力作用对应的主拉应力σtp和主压应力σcp分别与构件轴线成45方向,其大小为σtp=σcp= τmax当该处主拉应力σtp达到混凝土抗拉极限时,构件将沿与主拉应力σtp垂直方向开裂,其开裂扭矩就是当σtp=τmax=ft时作用在构件上的扭矩。
试验表明,按弹性计算理论来确定混凝土构件的开裂扭矩,比实测值偏小较多。
这说明按弹性计算理论低估了混凝土构件的实际抗扭能力。
2.塑性计算理论对于理想塑性材料的构件,只有当截面上各点的剪应力全部都达到材料的强度极限时,构件才丧失承载力而破坏。
这时截面上剪应力分布如图5-4a所示。
七章钢筋混凝土受扭构件承载力计算
翼缘 —— 纯扭;
腹板—— 剪扭;
全截面——弯剪扭分别配筋再叠加。
(五)箱形截面剪扭构件承载力计算
1、一般剪扭构件 抗扭承载力下式计算:
T 0.35ht ftWt 1.2
f yv
Ast1 Acor s
2、集中力作用下的独立剪扭构件
(7-14)
(六)箱形截面弯剪扭构件承载力计算
(3)按照叠加原则计算剪扭的箍筋用量和纵筋用量。
(二)矩形截面弯扭构件承载力计算
图7-11 弯扭构件的钢筋叠加
(三)矩形截面弯剪扭构件承载力计算
﹡《规范》规定,其纵筋截面面积由受弯承载力和受扭 承载力所需的钢筋截面面积相叠加,箍筋截面面积则由 受剪承载力和受扭承载力所需的箍筋截面面积相叠加, 其具体计算方法如下:
(3)当箍筋或纵筋过多时,为部分超配筋破坏。
(4)当箍筋和纵筋过多时,为完全超配筋破坏。
因此,在实际工程中,尽量把构件设计成(2)、(3), 避免出现(1)、(4)。
(二)抗扭钢筋配筋率对受扭构件受力性能的影响
《规范》采用纵向钢筋与箍筋的配筋强度比值 进行控制, (0.6≤ ≤1.7)
f y Astl s
﹡像矩形、T形和I形截面一样,箱形截面弯剪扭 构件承载力计算中,弯矩按纯弯构件计算剪力和 扭矩按剪扭构件计算。
三、受扭构件计算公式的适用条件及构造要求
(一)截面尺寸限制条件
当 hw b 4
时,
V bh0
T 0.8Wt
0.25c
fc
(7-15)
当
hw
b6
时,
V bh0
T 0.8Wt
0.2c
fc
——混凝土抗拉强度设计值;
受扭构件承载力

2 1
1
2
Tmax
T(T)
裂缝
受压区
5.2 纯扭构件的破坏特征和承载力计算
5.2.2 矩形截面开裂扭矩 弹性开裂扭矩 按弹性理论,当主拉应力
时,构件开裂:
其中,弹性抗扭截面系数
, a 是与h/b有关的系数。
弹性剪应力分布
5.2 纯扭构件的破坏特征和承载力计算
5.2.2 矩形截面开裂扭矩 塑性开裂扭矩 按塑性理论,截面上各点均达到极限强度,才达到极限 承载力。塑性极限开裂扭矩为:
5.3.2 弯剪扭构件的承载力计算
5.3.2.2 在剪、扭作用下的承载力计算
(2)受扭的纵向钢筋和受扭箍筋的配筋强度比ξ 当抗扭纵筋和抗扭箍筋的配筋强度(配筋量及钢筋
强度值)的比例失调,破坏时会发生一种钢筋达到屈服强 度而另一种则没有达到,出现“部分超筋破坏”的破坏状 态。它虽也有一定延性,但比适筋破坏时的延性小。为防 止出现这种破坏,规范对抗扭纵筋和抗扭箍筋的配筋强度 比值ξ的适合范围做出了限定。
5.2.3 纯扭构件的承载力计算
5.2.3.2 纯扭构件的破坏特征
钢筋混凝土纯扭构件,开裂前钢筋中的应力很小,开裂后 不立即破坏,裂缝可以不断增加,随着钢筋用量的不同,有不 同的破坏形态。 (1) 少筋破坏:裂后钢筋应力激增,构件破坏,呈脆性破坏特征。 承载力取决与混凝土的抗拉强度。 (2) 适筋破坏:裂后钢筋应力增加,继续开裂,钢筋屈服,混凝 土压碎,构件破坏,具有一定的延性。 (3) 超筋破坏:受扭的纵向钢筋和受扭箍筋都过量配置,裂后钢 筋应力增加,继续开裂,混凝土压碎,构件破坏,钢筋未屈服。 属于无预兆的脆性破坏。承载力取决于混凝土的抗压强度。 (4) 部分超筋破坏:裂后钢筋应力增加,继续开裂,混凝土压碎, 构件破坏,纵筋或箍筋未屈服。
混凝土结构设计原理第7章抗扭

1 矩形截面弯剪扭构件承载力计算
破坏特征 V不起控制作用,且T/M
较小,配筋适量时
T
•
斜裂缝首先在弯曲受拉的底部开裂
M V
,再发展
第Ⅰ类型——弯形破坏
破坏时,底部受拉纵筋已屈服 M不起控制作用
V、T的共同工作使得一侧混凝土剪 应力增大,一侧混凝土应力减小
剪应力大的一侧先受拉开裂,最后破 第Ⅱ类型——剪扭形破坏 坏, T很小时,仅发生剪切破坏
z
f yv
Ast1 Acor s
式中: βt 按前式计算;Wt 应以 hWt代替。
➢ 弯剪扭构件
像矩形、T形和I形截面一样,弯矩按纯弯构件计算和扭矩按 剪扭构件计算。
➢ 压弯剪扭构件
V
1.51
t
1.75
1
ftbh0
0.07 N
•
f yv
Asv s
h0
T
t
0.35
ft
0.07
N A
Wt
1.2
z A A st1 cor
(2)当Vc/Vco ≤ 0.5时,即V≤ 0.35ftbh0时,可忽略剪影响,按纯扭构件 设计;
(3)当T>0.175ftWt和V> 0.35ftbh0时,要考虑剪扭的相关性。
考虑剪扭相关性的计算
V
0.7
ftbh0 (1.5 t )
f yv
nAs v1 •sv
h0
T 0.35t f Wt t 1.2
ft
d2
b/2
ft ft
h
d1
F2
F1
F1
h
max h
b/2
ft
F2
b
b
混凝土结构设计原理第7章

7.2.2 裂缝出现后的性能
图7-3 扭矩—扭转角曲线
图7-4 钢筋混凝土受扭试件的螺 旋形裂缝展开图 注:图中所注数字是该裂缝出现 时的扭矩值(kN·m),未注数字 的裂缝是破坏时出现的裂缝。
图7-5 纯扭构件纵筋和箍筋的扭矩-钢筋拉应变曲线
7.2.3 破坏形态
受扭构件的破坏形态与受扭纵筋和受扭箍筋配筋率的大小有关,可 分为适筋破坏、部分超筋破坏、超筋破坏和少筋破坏四类。
VT bh0 ? wt ? 0.7 ft
或V bh0
?
T wt
?
0.7 ft
?
N 0.07
bh0
N ? 0.3 fc A
?
0.2 N
? ??
?
Asv s
f yv h0 ?
Asv s
f yv h0
(2)受扭承载力
Tu
?
?t
??? 0.35
ft
?
0.2
N A
???Wt
?
1.2
?
f yv
Ast1 Acor s
? 1.2
?
f yv
Ast1 Acor s
7.6 协调扭转的钢筋混凝土构件扭曲截面承载力
协调扭转的钢筋混凝土构件开裂以后,受扭刚度降低, 由于内力重分布将导致作用于构件上的扭矩减小。一般情况 下,为简化计算,可取扭转刚度为零,即忽略扭矩的作用, 但应按构造要求配置受扭纵向钢筋和箍筋,以保证构件有足 够的延性和满足正常使用时裂缝宽度的要求,此即一些国外 规范采用的零刚度设计法。我国《混凝土结构设计规范》没 有采用上述简化计算法,而是规定宜考虑内力重分布的影响, 将扭矩设计值T降低,按弯剪扭构件进行承载力计算。
钢筋混凝土受扭构件

—Acor—截面核心部分的面积: ,此 Acor bcor hcor 处 、 为bcor箍筋hcor内表面范围内截面核 心部分的短边、长边尺寸;
— —受扭构件纵向钢筋与箍筋的配筋强度 比值。
2. 混凝土纯扭构件的极限扭矩
配置受扭钢筋对提高受扭构件抗裂性能的作用不 大,但当混凝土开裂后,可由钢筋继续承担拉力. (1)受扭钢筋的形式
受扭构件中主拉应力与构件轴线成45°角,因此合 理的配筋方式应采用与轴线成45°的螺旋形箍筋。 但螺旋形箍筋施工复杂,且只能适应一个方向的扭 矩,一般多采用横向箍筋与纵向钢筋组成的钢筋骨 架来抵抗扭矩作用。
建筑结构概论
钢筋混凝土受扭构件
扭转是构件除承受弯矩、剪力、轴力外另一种基 本受力形式之一。钢筋混凝土受扭构件中,常见的 有现浇框架结构中的边梁,厂房结构中受横向制动 力作用时的吊车梁,以及钢筋混凝土雨蓬梁等构件。
钢筋混凝土构件受扭可以分成两大类: 一类为平衡扭转:构件中的扭矩由外荷载直接作 用产生,扭矩可以直接由荷载静力平衡求出,与构 件的抗扭刚度无关。如图6-1中的吊车梁、挑檐梁。 另一类为协调扭转:在超静定结构,扭矩是由相 邻构件的变形受到约束而产生的,扭矩大小与受扭 构件的抗扭刚度有关。如图6-2中现浇框架中的边 梁。
b2 6
3h b
ft
称为矩形截面抗扭塑性抵抗矩。
ft
素混凝土既非完全弹性,又非理想塑性,是介于
两者之间的弹塑性材料。因而受扭时的极限应力分
布将介于上述两种情况之间。素混凝土构件的受扭
承载力即开裂扭矩为
Tcr 0.7Wt ft
当荷载产生的扭矩满足下式
Tcr 0.7Wt ft
则认为混凝土的抗扭能力足以承受由荷载产生的外 扭矩作用,抗扭钢筋仅需按构造设置。
07--水工钢筋砼--钢筋混凝土受扭构件承载力计算 2012

后为弯、剪、扭作用下的承载力计算。 2、作用荷载:
包括:弯曲和剪切作用,实质上是弯、剪、扭 (有时还有压)的复合受力问题。 3、受扭构件分类:
根据截面上存在的内力情况分为纯扭、弯扭、剪 扭、弯剪扭。工程中的受扭构件一般都是弯、剪、扭 构件,纯扭极为少见。
7.1 钢筋混凝土受扭构件的破坏形态及开裂扭矩
二、矩形截面构件在弯、剪、扭共同作用下破坏形态 2、扭型破坏 (2)发生条件: a. 扭矩T / 弯矩M 的比值较大,剪力很小 b. 上部纵筋较少时的情况 (3)原因:
扭矩T引起。
7.1 钢筋混凝土受扭构件的破坏形态及开裂扭矩
二、矩形截面构件在弯、剪、扭共同作用下破坏形态
《规范》取混凝土抗拉强度ft降低系数为0.7,因此, 开裂扭矩Tcr的计算公式为:
Tcr 0.7 ftWt (7 4)
7.1 钢筋混凝土受扭构件的破坏形态及开裂扭矩
四、带翼缘截面纯扭构件的开裂扭矩 1、考虑因素
破坏时构件截面的扭转角较 大。破坏前有预兆,属于塑性破 坏,这类破坏称为适筋破坏。
7.1 钢筋混凝土受扭构件的破坏形态及开裂扭矩
一、矩形截面纯扭构件的破坏形态
3、破坏形态 (3)抗扭钢筋配得适量时--适筋破坏: c. 意义
该类破坏模型是设计的试验依据。
7.1 钢筋混凝土受扭构件的破坏形态及开裂扭矩
7.1 钢筋混凝土受扭构件的破坏形态及开裂扭矩
三、矩形截面纯扭构件的开裂扭矩 2、基于弹性理论的开裂扭矩
在扭矩作用下,矩形截面受扭构件最大剪应力τmax
发生在截面长边中点。当主拉应力σtp达到砼抗拉强度
ft时,出现沿450方向的斜裂缝。
混凝土结构设计原理-受扭构件

' T fd
5.4 箱形截面受扭构件
箱形截面抗扭刚度大。研究表明,箱梁的抗扭承载力与实心矩形梁相近。
h
t1
t2
b
箱形截面的受扭塑性抵抗矩:
(b 2t1 ) 2 b2 Wt (3h b) [3(h 2t 2 ) (b 2t1 )] 6 6
承载力按实心矩形梁计算,引入有效壁厚折减系数 a : 两者较小值
第二项系数1.2是考虑钢筋不能充分发挥作用的影响。
0.5 t 1.0
5.3 T形、I形截面受扭构件
T形截面、I形截面——分块计算,将扭矩 Td 按受扭抵抗矩 分配到各分块。
bf bf
hf
h
h
b
b bf
hf
hf
腹板的受扭塑性抵抗矩
b2 Wtw (3h b) 6
Wt ' f
5.5 构造要点
受扭纵向钢筋:四角必须布置,周边均匀对称布置,间距 300 mm 。 受扭箍筋:封闭式,末端做成135o弯钩,长度最少10d。 !不允许采用有内折角的箍筋
例题5-1
As
Md 986106 A0 0.071 ' 2 2 f cd b f h0 18.4 920 905
Wt f
受压翼缘受扭塑性抵抗矩 受拉翼缘受扭塑性抵抗矩 截面总的受扭塑性抵抗矩 腹板的扭矩 受压翼缘的扭矩 受拉翼缘的扭矩
h 'f2 2
h2 f 2
(b 'f b)
(b f b)
Wt Wtw Wt ' f Wt f
Twd
Wtw Td Wt
Wt ' f Td
Wt Wt f T fd Td Wt
受扭构件承载力

max
T Wte
σpt σpt
理想匀质构件的受扭裂缝 从主拉应力最大处开始
对匀质材料,理想的受扭裂缝应当呈螺旋形。
1
第2页/共43页
二、素混凝土纯扭构件
◆ 由材料力学知,构件侧面主拉应力stp和主压应力scp相等。
◆ 主拉应力和主压应力迹线沿构件表面成螺旋型。 ◆ 当主拉应力达到混凝土抗拉强度时,在构件中某个薄弱部位
11
第12页/共43页
《规范》受扭承载力计算公式
Tu 0.35 ftWt 1.2
f yv Ast1 s
Acor
为避免配筋过多产生超筋脆性破坏
Wt
b2 6
(3h b)
T 0.2c fcWt
为防止少筋脆性破坏
st
2 Ast1 bs
st ,min
0.28
ft f yv
tl
Astl bh
tl,min
(2) 少筋破坏
配筋数量过少时,配筋不足以承担混凝土开裂后释放的拉 应力,一旦开裂,将导致扭转角迅速增大,与受弯少筋梁类似, 呈脆性破坏特征,受扭承载力取决于混凝土的抗拉强度。
(3) 超筋破坏
当箍筋和纵筋配置都过大时,则会在钢筋屈服前混凝土就 压坏,为受压脆性破坏。受扭构件的这种超筋破坏称为完全超 筋,受扭承载力取决于混凝土的抗压强度。
b2 6
(3h
b)
按弹性理论
Tcr,e ftWte
45° ft
ft ft
按塑性理论
Tcr, p ftWt
7
第8页/共43页
6.2.2 矩形截面纯扭构件受扭承载力计算 一、变角空间桁架模型
对比试验表明,在其他参数均相同的情况下,钢筋混凝土实心 截面与空心截面构件的极限受扭承载力基本相同。
第七章 钢筋混凝土受扭构件简介

第二节
矩形截面混凝土纯扭构件
一、素混凝土构件开裂扭矩
1 、开裂前的受力性能
构件在扭矩作用下主要产生剪应力。最大剪应力发生 在截面长边中点(见教材139页图7-2),与该点剪应 力作用相对应的主拉应力σ
tp和主压应力σ cp分别与构 tp
件轴线成45°角,其大小为 σ
= σ
cp
容
1. 受扭构件的受力特点; 2. 受扭构件的配筋构造要求。
重 点
受扭构件的配筋特点及配筋构造要求。
难 点
受扭构件的受力特点。
第一节
1 、受扭构件的定义:
概
述
在构件截面中有扭矩
(T)作用的构件。 2 、受扭构件的分类: 1 、纯扭 2 、剪扭、
3 、弯扭、
max。当主
拉应力超过混凝土的抗拉强度时,混凝土将首先在截
面长边中点处,垂直于主拉应力方向开裂,在纯扭构件 中,构件裂缝与轴线成45°角
对于理想的弹塑性材料而言,截面上某点的应力达到强 度极限时并不会立即破坏,该点能保持极限应力不变而 继续变形,整个截面仍能继续承受荷载,直到截面上各 点的应力都达到极限值ft时,构件才达到极限抗扭能力
一长边压区混凝土压碎。此类破坏主要因剪力和扭矩 引起。
二、
受扭构件的配筋构造要求
1.受扭纵筋 受扭纵筋应沿构件截面
周边均匀对称布置。矩形截
面的四角以及T形和Ι 形截面 各分块矩形的四角,均必须 设置受扭纵筋。受扭纵筋的 间距不应大于200mm,也不应
大于梁截面短边长度。
受扭纵向钢筋的接头和锚固要求均应按受拉钢筋 的相应要求考虑。 架立筋和梁侧构造纵筋也可利用作为受扭纵筋。
钢筋未达到屈服强度,构件即由于斜裂缝间混凝土被压
钢筋混凝土受扭构件承载力设计计算

式中,Tcr为矩形截面纯扭构件的开裂扭矩;
Wt为矩形截面的抗塑性抵抗矩;
ftd为混凝土抗拉强度设计值。
(2)承载力的计算:在《公路钢筋混凝土及应力混凝土桥涵设计规范》(JTG D62-2004)中,对受扭构件的承载力计算是建立在变角度空间桁架理论基础上的。基于变角度空间桁架的计算模型,通过受扭构件的室内试验数据分析,并使总的抗扭能力取试验数据的偏下值,得到矩形截面构件抗扭承载能力计算公式如:
2钢筋混凝土弯、剪、扭构件的配筋设计与计算
在《公路钢筋混凝土及应力混凝土桥涵设计规范》(JTG D62-2004)中规定,弯、剪、扭构件的配筋计算,也采取叠加计算的截面设计简化方法。
(1)受剪扭的构件承载力计算:现行设计规范中规定,钢筋混凝土剪扭构件的承载能力,一般按受扭和受剪构件分别计算承载能力,然后再它们叠加起来。但是,剪、扭共同作用的构件,剪力和扭矩对混凝土和箍筋的承载能力均有一定影响。如果采取简单地叠加,对箍筋和混凝土尤其是混凝土是偏于不安全的。构件在剪扭的共同作用下,其截面的某一受压区内承受剪切和扭转应力的双重作用,这不仅会降低构件内混凝土的抗剪和抗扭能力,而且分别小于单独受剪和受扭时相应的承载能力。由于受扭钢筋混凝土构件的受力情况比较复杂,所以对箍筋所承担的承载能力采取简单叠加,混凝土的抗扭和抗剪承载能力考虑其相互影响,在混凝土的抗扭承载能力计算式中,应引入剪扭构件混凝土承载能力的降低系数。根据试验资料分析,在《公路钢筋混凝土及应力混凝土桥涵设计规范》中,对剪扭共同作用下矩形截面钢筋混凝土构件和抗扭承载能力计算分别可采用以下公式:
(3)在弯矩、剪力和扭矩共同作用下的配筋计算:对于在弯矩、剪力和扭矩共同作用下的构件,其纵向钢筋和箍筋应按以下规定计算并分别进行配置。抗弯纵向钢筋应按受弯构件正截面承载能力计算所需的钢筋截面面积,配置在受拉区的边缘;按剪扭构件计算纵向钢筋和箍筋。由抗扭承载能力计算公式计算所需的纵向抗扭钢筋面积,并均匀、对称地布置在矩形截面的周边,其间距不应大于300 mm。在矩形截面的四角必须配置纵向钢筋;箍筋为按抗剪和抗扭承载能力计算所需的截面面积之和进行布置。《公路钢筋混凝土及应力混凝土桥涵设计规范》中规定,纵向受力钢筋的配筋率,不应小于受弯构件纵向受力钢筋的最小配筋率与受剪扭构件纵向受力钢筋最小配筋率之和,如配置在截面弯曲受拉边的纵向受力钢筋,其截面面积不应小于按受弯构件受拉钢筋最小配筋率计算出的面积与按受扭纵向钢筋最小配筋率并分配到弯曲受拉边的面积之和;同时,其箍筋最小配筋率不应小于剪扭构件的箍筋最小配筋率。
第七章受扭构件承载力计算

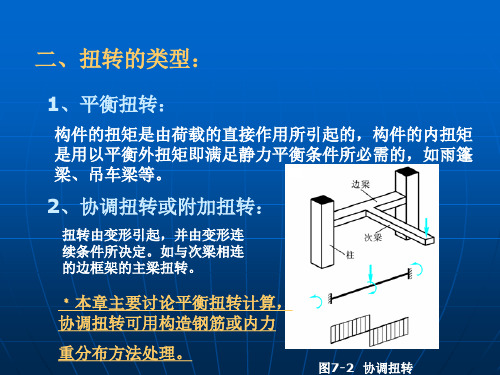
第七章 受扭构件承载力计算7.1 概述工程中的钢筋砼受扭构件有两类:● 一类是 —— 平衡扭矩:是静定结构由于荷载的直接作用所产生的扭矩,这种构件所承受的扭矩可由静力平衡条件求得,与构件的抗扭刚度无关。
如:教材图7·1a 、b 所示受檐口竖向荷载作用的挑檐梁,及受水平制动力作用的吊车梁以及平面曲梁、折线梁、螺旋楼梯等。
● 另一类是 —— 协调扭矩:是超静定结构中由于变形协调条件使截面产生的扭矩,构件所承受的扭矩与其抗扭刚度有关。
如:教材图7·2 所示现浇框架的边梁。
由于次梁在支座(边梁)处的转角产生的扭转,边梁开裂后其抗扭刚度降低,对次梁转角的约束作用减小,相应地边梁的扭矩也减小。
● 本章只讨论平衡扭转情况下的受扭构件承载力计算。
在工程结构中,直接承受扭矩、弯矩、剪力和轴向力复合作用的构件是常遇的。
但规范对弯扭、剪扭和弯剪扭构件的设计计算,是以抗弯、抗剪能力计算理论和纯扭构件的承载力计算理论为基础,采用分别计算和叠加配筋的方法进行的,故有必要先了解纯扭构件的受力性能和承载力的计算方法。
7.2 纯扭构件的受力性能7.2.1 素砼纯扭构件的受力性能素砼构件也能承受一定的扭矩。
素砼构件在扭矩T 的作用下,在构件截面中产生剪应力τ及相应的主拉应力tp σ 和主压应力cp σ(教材图7·3)。
根据微元体平衡条件可知:τστσ==cp tp ,由于砼的抗拉强度远低于它的抗压程度,因此当主拉应力达到砼的抗拉强度时,即t tp f ≥=τσ时,砼就会沿垂直于主拉应力方向裂开(教材图7·3)。
所以在纯扭矩作用下的砼构件的裂缝方向总是与构件轴线成45o的角度。
并且砼开裂时的扭矩T 也就是相当于t f =τ时的扭矩,即砼纯扭构件的受扭承载力co T 。
为了求得co T ,需要建立扭矩和剪应力之间的关系,然后根据强度条件,即砼纯扭构件的破坏条件求出受扭承载力co T 。
7.2.2 素砼纯扭构件的承载力计算(一) 、弹性分析法:用弹性分析方法计算砼纯扭构件承载力时,认为砼构件为单一匀质弹性材料。
第七章-受扭构件

第七章 受扭构件(94)判断题:1 构件因为受扭而产生的裂缝,总体上呈螺旋形,与构件轴线的夹角大致为45º,螺旋形裂缝是连续贯通的。
( )2 受扭构件扭曲截面承载力计算中。
ζ是变角空间模型混凝土斜压杆与构件纵轴线夹角α的余切,即αζcot =。
( ) 3 受扭构件扭曲截面承载力计算中,系数ξ是受扭的纵向钢筋与箍筋的配筋强度比值,cor sv yv stl y A f s A f μξ1/..=,ξ应满足大于1.7的要求。
( )4 stl A 是指受扭计算中取对称布置的全部纵向非预应力钢筋截面面积;1sv A 是指受扭计算中沿截面周边布置的箍筋单肢截面面积。
( )5 素混凝土纯扭构件的开裂扭矩与破坏扭矩基本相等。
( )6 受扭钢筋对钢筋混凝土纯扭构件开裂扭矩影响很大。
( )7 受扭钢筋的配筋量对钢筋混凝土纯扭构件的破坏形态有很大影响。
( )8 对受扭起作用的钢筋主要是箍筋,纵筋对受扭构件不起作用。
( )9 箍筋和纵筋对受扭都有作用,因此在受扭构件的扭曲截面承载力计算中,可以既设置受扭箍筋又设置受扭纵筋,也可以只设置一种形式受扭钢筋。
( )10 变角度空间桁梁模型中没有考虑截面核心混凝土的作用。
( )11 我国《混凝土结构设计规范》和变角空间桁梁模型中都考虑了混凝土的抗扭作用。
( )12 弯剪扭构件的承载力配筋计算中,纵筋是由受弯承载力及受扭承载力所需纵筋叠加而得,这与弯扭构件的承载力计算结果是相同的。
( )13 t β称为一般剪扭构件混凝土受扭承载力降低系数,(1.5-t β)可称为一般剪扭构件混凝土受剪承载力降低系数。
( )14 受扭纵向钢筋的布置要求是,沿截面周边均匀对称布置,间距不应大于200mm ,截面四角必须布置。
( ) 15 素混凝土开列扭矩一般也是其破坏扭矩。
( )16 当扭矩或剪力不超过混凝土部分所承受的扭矩或剪力的一半时,为简化计算,可不考虑其影响。
( ) 17 剪扭构件承载力计算中,混凝土的承载力考虑剪扭相关关系,而钢筋的承载力按纯扭和纯剪的承载力叠加。
第7章 钢筋混凝土受扭构件承载力计算

第7章 钢筋混凝土受扭构件承载力计算1.简述钢筋混凝土矩形截面纯扭构件的四种破坏形态及其与设计的关系。
答:矩形截面纯扭构件的破坏形态以下四种类型:(1)少筋破坏当抗扭钢筋数量过少时,裂缝首先出现在截面长边中点处,并迅速沿45°方向向邻近两个短边的面上发展,在第四个面上出现裂缝后(压区很小),构件立即破坏。
破坏形态如图7-3(a),其破坏类似于受弯构件的少筋梁,破坏时扭转角较小(图7-4曲线1),属于脆性破坏,构件受扭极限承载力取决于混凝土抗拉强度和截面尺寸,设计中应予避免。
该类破坏模型是计算混凝土开裂扭矩的试验依据,并可按此求得抗扭钢筋数量的最小值。
(2)适筋破坏 当抗扭钢筋数量适中时,破坏形态如图7-3(b)。
混凝土开裂并退出工作,由其承担的拉力转给钢筋,钢筋的应力突增,但没有达到屈服,使构件在破坏前形成多条裂缝。
当通过主裂缝处的纵筋和箍筋达到屈服强度后,第四个面上的受压区混凝土被压碎而破坏。
适筋破坏扭转角较大(图7-4曲线2),属于延性破坏,该类破坏模型是建立构件受扭承载力设计方法的试验依据。
(3)超筋破坏当抗扭钢筋数量过多,构件破坏时抗扭纵筋和箍筋均未达到屈服,破坏是由某相邻两条45°螺旋缝间混凝土被压碎引起的。
破坏形态见图7-3(c),构件破坏时螺旋裂缝条数多而细,扭转角较小(图7-4曲线3),属于超筋脆性破坏,构件承载力主要取决于截面尺寸及混凝土抗压强度。
这类破坏称为完全超筋破坏,在设计中应避免。
该类破坏模型是计算抗扭钢筋数量最大值的试验依据。
(4)部分超筋破坏当抗扭纵筋和抗扭箍筋数量比例不当,致使混凝土压碎时,箍筋或纵筋两者之一不能达到屈服点,这种破坏属于部分超筋破坏。
虽然结构在破坏时有一定延性,设计可用,但不经济。
2.什么是配筋强度比ζ的物理意义、计算公式与合理的取值范围。
答:配筋强度比ζ的物理意义:ζ为受扭构件纵向钢筋与箍筋的配筋强度比,如图7-5,其物理意义是协调抗扭纵筋和箍筋应合理配置,充分利用抗扭钢筋的作用,使受扭构件的破坏形态呈现适筋破坏。
水工钢筋混凝土 第七章 受扭构件

混凝土部分承载力相关关系可近似取1/4圆,
Tc Vc , v 取 t Tc 0 Vc 0
V Vc 并近似取 T Tc
Tc 0 Vc 2 t 1 ( ) 1 Tc Vc 0
2
Tc 2 Vc 2 ( ) ( ) 1 Tc 0 Vc 0
t
②部分超筋受扭构件:受扭箍筋和受扭纵筋两者配筋量相差过大
时,会出现一个未达到屈服、另一个达到屈服的部分超筋破坏 情况。具有一定的延性。
③超筋受扭构件当箍筋和纵筋配置都过大时,则会在钢筋屈服前
混凝土就压坏,为受压脆性破坏。受扭承载力取决于混凝土的 抗压强度。 ④少筋受扭构件:当配筋量过少时,配筋不足以承担混凝土开裂后 释放的拉应力,一旦开裂,将导致扭转角迅速增大,此时纵筋 和箍筋不仅达到屈服强度而且可能进入强化阶段,与受弯少筋 梁类似,呈受拉脆性破坏特征,受扭承载力取决于混凝土的抗 拉强度。
而扭矩和剪力产生的剪应力总会在构件的一个侧面上叠加,因 此承载力总是小于剪力和扭矩单独作用的承载力。
剪扭相关图
无腹筋构件剪扭承载力相 关曲线基本符合1/4圆曲线 规律。 Tc、Tc0分别为剪扭、纯扭 构件的受扭承载力; Vc、Vc0分别为剪扭及扭 矩为0的受剪构件的受剪 承载力。
无腹筋
把配有箍筋的有腹筋构件混凝土的剪扭承载力相关曲线也假 定符合1/4圆曲线规律,并将其简化为三折线。
-称为受扭构件纵筋与箍筋的配筋强度比。
Ast-取对称布置的全部纵向钢筋截面面积;
Ast1-沿截面周边所配置箍筋的单肢截面面积;
Acor-按箍筋内表面计算的截面核心面积, Acor =bcorhcor; s-受扭箍筋的间距;
fy,fyv-分别为受扭纵筋和受扭箍筋的屈服强度;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
受扭纵向钢筋的接头和锚固要求均应按受拉钢筋 的相应要求考虑。
架立筋和梁侧构造纵筋也可利用作为受扭纵筋。
2.受扭箍筋 在受扭构件中,箍筋在整个周长上均承受拉力,因此, 受扭箍筋必须做成封闭式,且应沿截面周边布置。箍筋末 端弯折135°,弯钩端头平直段长度不应小于10d。 受扭箍筋的间距s及直径d 均应满足受弯构件的最大箍 筋间距smax及最小箍筋直径的要求。
第二节 矩形截面混凝土纯扭构件 一、素混凝土构件开裂扭矩
1 、开裂前的受力性能 构件在扭矩作用下主要产生剪应力。最大剪应力发生 在截面长边中点(见教材139页图7-2),与该点剪应
力作用相对应的主拉应力σtp和主压应力σcp分别与构 件轴线成45°角,其大小为 σtp = σcp =τmax。当主
பைடு நூலகம்
小结
1.受扭构件的受力特点。 2. 受扭构件的配筋特点及配筋构造要求。
作业布置
预 习:第八章:受压构件 思考题 7-6,7-7
结束! 谢谢大家!
弯剪扭复合受扭构件由于其三种内力的比值及配筋 情况的不同影响,有三种典型的破坏形态:
(1)弯型破坏。构件破坏开始于底面及两侧的混 凝土开裂,底部钢筋屈服,然后顶部混凝土压碎。这类 破坏主要因弯矩引起。
(2)扭型破坏。构件破坏开始于构件顶面及两侧 面的混凝土开裂,顶部钢筋因受扭而先屈服,最 后底部混凝土压碎。此类破坏主要因扭矩引起。
第七章 钢筋混凝土受扭构件简介
本章主要内容
1. 受扭构件的受力特点; 2. 受扭构件的配筋构造要求。
重点
受扭构件的配筋特点及配筋构造要求。
难点
受扭构件的受力特点。
第一节 概 述
1 、受扭构件的定义: 在构件截面中有扭矩 (T)作用的构件。
2 、受扭构件的分类: 1 、纯扭 2 、剪扭、 3 、弯扭、 4 、弯剪扭构件。
(2)少筋受扭构件 构件的受扭承载力与素混凝土没有实质差别,破坏过程 迅速而突然,类似于受弯构件的少筋破坏。 (3)超筋受扭构件 钢筋未达到屈服强度,构件即由于斜裂缝间混凝土被压 碎而破坏,这种破坏与受弯构件的超筋梁类似。
注意:少筋受扭构件和超筋受扭构件均属脆性破坏, 设计中应予避免。
第三节 钢筋混凝土弯、剪、扭构件
继续
2,破坏形态
(1)适筋受扭构件 配置了适量受扭钢筋的构件,在裂缝出现以后不会立
即破坏。随着外扭矩的不断增大,在构件表面逐渐形成多 条大致沿45°方向呈螺旋形发展的裂缝(图5.1.3 b◆)。在 裂缝处,原来由混凝土承担的主拉应力主要改由与裂缝相 交的钢筋来承担。随着其中一条裂缝所穿越的纵筋和箍筋 达到屈服时,该裂缝不断加宽,直到最后形成三面开裂一 边受压的空间扭曲破坏面,进而受压边混凝土被压碎,构 件破坏(图5.1.4)。整个破坏过程具有一定延性和较明显 的预兆,类似受弯构件适筋破坏。
(3)剪扭破坏。构件破坏开始于截面长边的一侧开 裂和该侧的受扭纵筋和受扭、受剪箍筋屈服,最后另 一长边压区混凝土压碎。此类破坏主要因剪力和扭矩 引起。
二、 受扭构件的配筋构造要求
1.受扭纵筋 受扭纵筋应沿构件截面 周边均匀对称布置。矩形截 面的四角以及T形和Ι形截面 各分块矩形的四角,均必须 设置受扭纵筋。受扭纵筋的 间距不应大于200mm,也不应 大于梁截面短边长度。
2 、矩形截面开裂扭矩
素混凝土既非完全弹性,又非理想塑性,是介于两者
之间的弹塑性材料。因而受扭时的极限应力分布将介于
上述两种情况之间。素混凝土构件的受扭承载力即开裂
扭矩
Tcr=0.7ftWt
(7-3)
式中ft―混凝土抗拉强度设计值;
Wt―受扭构件的截面抗扭塑性抵抗矩。对矩形截面
Wt=b2(3h - b) / 6。
一、扭矩对受弯、受剪构件承载力的影响
承载力之间的相关性:扭矩与弯矩或剪力同时作用于构件时, 一种承载力会因另一种内力的存在而降低。
(1)弯扭相关性 扭矩的作用使纵筋产生拉应力,加重了受弯构件纵向受拉 钢筋的负担,使其应力提前达到屈服,因而降低了受弯承载 力
(2)剪扭相关性
两者的剪应力在构件一个侧面上是叠加的,扭矩 的存在降低了受剪承载力。图5.1.5、图5.1.6分别为 弯扭和剪扭承载力相关曲线。
拉应力超过混凝土的抗拉强度时,混凝土将首先在截 面长边中点处,垂直于主拉应力方向开裂,在纯扭构件 中,构件裂缝与轴线成45°角
对于理想的弹塑性材料而言,截面上某点的应力达到强 度极限时并不会立即破坏,该点能保持极限应力不变而 继续变形,整个截面仍能继续承受荷载,直到截面上各 点的应力都达到极限值ft时,构件才达到极限抗扭能力
二.钢筋混凝土纯扭构件 1,配筋方式: 配置受扭钢筋对提高受扭构件
抗裂性能的作用不大,当混凝土开裂后,可由钢筋继 续承担拉力,最合理的配筋方式是在构件靠近表面处 设置呈45°走向的螺旋形钢筋。但这种配筋方式不便 于施工,且当扭矩改变方向后则将完全失去效用。在 实际工程中,一般是采用由靠近构件表面设置的横向 箍筋和沿构件周边均匀对称布置的纵向钢筋共同组成 的抗扭钢筋骨架。
