实验四纠错码Hamming码编译码(新)
汉明码编码译码实验报告(信息论与编码)及源程序

一个二元(7,4)汉明码的系统码形式的矩阵和校验矩阵分别为
1 0 0 0 1 0 1 1 1 1 0 1 0 0
G=0 1 0 0 1 1 1 H= 0 1 1 1 0 1 0
0 0 1 0 1 1 0 1 1 0 1 0 0 1
0 0 0 1 0 1 1
等价的编码方程为
Ci=mi, i=0,1,2,3
到现在为止,我已经学了C语言程序设计、数据结构等课程,这次的信息论与编码实验让我感觉到以前学习的东西有了用武之地,把知识和理论付诸实践才能有所提高。在编程的过程中,我发现自己的编程能力还非常有待提高,以前C语言课程里的很多知识掌握还不牢,时常需要翻书查阅。对信息论与编码这门课的学习还要加深,只有深刻理解了要做的事情,才能把事情做好。以后我要更加努力,逐步解决这些问题。
int f[3];
int ww[10000/4*7];
printf("汉明(7,4)码的编码与译码程序:\n");
printf("请输入你想产生的二进制个数:");
scanf("%d",&N); //输入想产生的信源的个数
while(N<4)
{
printf("输入无效,请重新输入");
printf("请输入你想产生的二进制个数:");
汉明码是一种能够纠正一位错码且编码效率较高的线性分组码。
汉明码是一种多重(复式)奇偶检错系统。它将信息用逻辑形式编码,以便能够检错和纠错。用在汉明码中的全部传输码字是由原来的信息和附加的奇偶监督位组成的。每一个这种奇偶位被编在传输码字的特定比特位置上。
推导并使用长度为m位的码字的汉明码,所需步骤如下:
汉明码纠错

汉明码纠错汉明码的编码检错原理针对4位数据的汉明码编码示意图汉明码是一个在原有数据中插入若干校验码来进行错误检查和纠正的编码技术。
以典型的4位数据编码为例,汉明码将加入3个校验码,从而使实际传输的数据位达到7个(位),它们的位置如果把上图中的位置横过来就是:数据位1234567代码P1P2D8P3D4D2D1说明第1个汉明码第2个汉明码第1个数据码第3个汉明码第2个数据码第3个数据码第4个数据码注:Dx中的x是2的整数幂(下面的幂都是指整数幂)结果,多少幂取决于码位,D1是0次幂,D8是3次幂,想想二进制编码就知道了现以数据码1101为例讲讲汉明码的编码原理,此时D8=1、D4=1、D2=0、D1=1,在P1编码时,先将D8、D4、D1的二进制码相加,结果为奇数3,汉明码对奇数结果编码为1,偶数结果为0,因此P1值为1,D8+D2+D1=2,为偶数,那么P2值为0,D4+D2+D1=2,为偶数,P3值为0。
这样,参照上文的位置表,汉明码处理的结果就是1010101。
在这个4位数据码的例子中,我们可以发现每个汉明码都是以三个数据码为基准进行编码的。
下面就是它们的对应表:汉明码编码用的数据码P1D8、D4、D1P2D8、D2、D1P3D4、D2、D1从编码形式上,我们可以发现汉明码是一个校验很严谨的编码方式。
在这个例子中,通过对4个数据位的3个位的3次组合检测来达到具体码位的校验与修正目的(不过只允许一个位出错,两个出错就无法检查出来了,这从下面的纠错例子中就能体现出来)。
在校验时则把每个汉明码与各自对应的数据位值相加,如果结果为偶数(纠错代码为0)就是正确,如果为奇数(纠错代码为1)则说明当前汉明码所对应的三个数据位中有错误,此时再通过其他两个汉明码各自的运算来确定具体是哪个位出了问题。
还是刚才的1101的例子,正确的编码应该是1010101,如果第三个数据位在传输途中因干扰而变成了1,就成了1010111。
常见的纠错编码

常见的纠错编码介绍纠错编码是一种在数字通信和数据存储中常见的技术,用于检测和纠正发生在数据传输或存储过程中的错误。
常见的纠错编码方法包括海明码、汉明码、布尔码等。
这些编码方法通过添加冗余信息来实现错误检测和纠正的功能,提高数据传输和存储的可靠性。
海明码(Hamming Code)海明码是一种最早被提出的纠错编码方法。
它通过向数据中添加冗余位,使数据可以进行错误检测和纠正。
海明码的原理是利用奇偶校验位进行错误检测,并利用冗余位进行错误纠正。
海明码可以检测和纠正单个比特位的错误,并且具有较高的纠错能力。
海明码的编码过程如下: 1. 计算奇偶校验位的位置。
根据数据位的数量,确定奇偶校验位的位置。
2. 计算奇偶校验位的值。
根据奇偶校验位所对应的数据位,计算奇偶校验位的值。
3. 添加奇偶校验位。
将计算得到的奇偶校验位添加到数据中。
海明码的解码过程如下: 1. 检测错误位的位置。
利用奇偶校验位检测错误位的位置。
2. 纠正错误位的值。
根据错误位的位置,进行错误位的纠正。
海明码通过使用冗余位,可以检测和纠正单个比特位的错误,提高了数据传输的可靠性。
汉明码(Hamming Distance)汉明码是一种用于衡量两个等长字符串之间的距离的概念。
在纠错编码中,汉明码被用来计算错误比特位的数量,从而实现错误的检测和纠正。
汉明码的计算方法如下: 1. 将两个等长字符串进行比较,逐位比较。
2. 当两个字符串的对应位不同,汉明距离加一。
3. 汉明距离即为错误比特位的数量。
汉明码能够衡量两个字符串之间的差异程度,为纠错编码提供了基础。
布尔码(BCH Code)布尔码是一种纠错编码的方法,可以用来检测和纠正多个比特位的错误。
布尔码的原理是利用多项式算法进行错误检测和纠正。
它通过添加冗余位,生成校验码,并在接收端使用算法计算接收到的校验码,从而进行错误的检测和纠正。
布尔码主要包括以下几个步骤: 1. 确定多项式生成器的选择。
汉明码的编码和译码算法

汉明码(Hamming)的编码和译码算法本文所讨论的汉明码是一种性能良好的码,它是在纠错编码的实践中较早发现的一类具有纠单个错误能力的纠错码,在通信和计算机工程中都有应用。
例如:在“计算机组成原理”课程中,我们知道当计算机存储或移动数据时,可能会产生数据位错误,这时可以利用汉明码来检测并纠错。
简单的说,汉明码是一个错误校验码码集,由Bell实验室的R.W.Hamming发明,因此定名为汉明码。
如果对汉明码作进一步推广,就得出了能纠正多个错误的纠错码,其中最典型的是BCH码,而且汉明码是只纠1bit错误的BCH码,可将它们都归纳到循环码中。
各种码之间的大致关系显示如下。
一、汉明码的编码算法输入:信源消息u(消息分组u)输出:码字v处理:信源输出为一系列二进制数字0和1。
在分组码中,这些二进制信息序列分成固定长度的消息分组(message blocks)。
每个消息分组记为u,由k个信息位组成。
因此共有2k种不同的消息。
编码器按照一定的规则将输入的消息u转换为二进制n 维向量v ,这里n >k 。
此n 维向量v 就叫做消息u 的码字(codeword )或码向量(code vector )。
因此,对应于2k 种不同的消息,也有2k 种码字。
这2k 个码字的集合就叫一个分组码(block code )。
若一个分组码可用,2k 个码字必须各不相同。
因此,消息u 和码字v 存在一一对应关系。
由于n 符号输出码字只取决于对应的k 比特输入消息,即每个消息是独立编码的,从而编码器是无记忆的,且可用组合逻辑电路来实现。
定义:一个长度为n ,有2k 个码字的分组码,当且仅当其2k 个码字构成域GF(2)上所有n 维向量组成的向量空间的一个K 维子空间时被称为线性(linear )(n, k)码。
汉明码(n ,k ,d )就是线性分组(n, k)码的一种。
其编码算法即为使用生成矩阵G :v = u ·G 。
通信原理实验 汉明编码和译码实验 实验报告

姓名:学号:班级:
第周星期第大节
实验名称:汉明编码和译码实验
一、实验目的
1.掌握汉明码编译码原理。
2.掌握汉明码纠错检错原理。
3.通过纠错编解码实验,加深对纠错编解码理论的理解。
二、实验仪器
1.ZH5001A通信原理综合实验系统
2.20MHz双踪示波器
三、实验内容
2.编码规则验证
(1)输入数据为0011
(2)输入数据为1100
3.译码数据输出观测
(1)m序列方式为11
(1)不加错
♦观测加错指示TPC03与错码检测指示输出波形TPW03波形
(2)加1位错
♦观测加错指示TPC03与错码检测指示输出波形TPW03波形
(4)加3位错
(1)不加错
加2位错不能全部正确译码
(4)加3位错
四、思考题
2.汉明编码器模块的使能开关,译码器模块的使能模块(H_EN断路器)起什么作用?
从电路图中可以看出,没有插入H_EN时,汉明编码器被短路,输出数据没有经过汉明编码。
插入H_EN时,输出数据经过汉明编码。
汉明码编译码

图中绿线为BSC信道误码率,红线为设定Pe值,蓝线为Hamming码解码误码率。由图线可以看出仿真的BSC信道误码率与Pe一致。
在Pe<0.2时,Hamming码的解码误码率随着BSC信道错误传输概率Pe的减小而减小。Hamming码的解码误码率显著下降,约为Pe的1/2。Hamming码的纠1位错起到了很好的效果。
附录
clear all
[H,G,n,k] =hammgen(3,'D^3+D+1');%
2)产生随机的信息序列M
3)由 得到码字
4)进入信道传输
假设是BSC信道,错误转移概率设定为0.1
传输后接收端得到的码流为
红色表示错误比特。
5)计算 得到伴随式
错误图样
伴随式
1
001
010
100
查表可知第一行码字错误图样为0100000,第二行码字错误图样为1000000,第三行码字错误图样为0000001。
进行 即可得到纠错解码的码字C2。
6)得到解码码流
7)得到解码信息序列
可以看出解码信息序列与原信息序列一样,体现了汉明码的纠错能力。
2.性能分析
1)BSC信道仿真
设置BSC错误转移概率Pe从0到1变化,步进为0.01,在每个Pe值进行1000次蒙特卡洛仿真,得到图4所示误码率随Pe变化曲线图和图5所示误帧率随Pe变化曲线图。
0.2<Pe<0.5时,Hamming码的解码误码率大于Pe。这是因为在Pe>0.2时,传一个码字错误比特数近似为2,而Hamming码只能纠一位错,两位同时出错时会纠成另一个码字,这样就可能增加误比特数,使得“越纠越错”。
Pe>0.5时,情况恰好相反。
汉明码的编码和译码算法

汉明码(Hamming)的编码和译码算法本文所讨论的汉明码是一种性能良好的码,它是在纠错编码的实践中较早发现的一类具有纠单个错误能力的纠错码,在通信和计算机工程中都有应用。
例如:在“计算机组成原理”课程中,我们知道当计算机存储或移动数据时,可能会产生数据位错误,这时可以利用汉明码来检测并纠错。
简单的说,汉明码是一个错误校验码码集,由Bell实验室的R.W.Hamming发明,因此定名为汉明码。
如果对汉明码作进一步推广,就得出了能纠正多个错误的纠错码,其中最典型的是BCH码,而且汉明码是只纠1bit错误的BCH码,可将它们都归纳到循环码中。
各种码之间的大致关系显示如下。
一、汉明码的编码算法输入:信源消息u(消息分组u)输出:码字v处理:信源输出为一系列二进制数字0和1。
在分组码中,这些二进制信息序列分成固定长度的消息分组(message blocks)。
每个消息分组记为u,由k个信息位组成。
因此共有2k种不同的消息。
编码器按照一定的规则将输入的消息u转换为二进制n 维向量v ,这里n >k 。
此n 维向量v 就叫做消息u 的码字(codeword )或码向量(code vector )。
因此,对应于2k 种不同的消息,也有2k 种码字。
这2k 个码字的集合就叫一个分组码(block code )。
若一个分组码可用,2k 个码字必须各不相同。
因此,消息u 和码字v 存在一一对应关系。
由于n 符号输出码字只取决于对应的k 比特输入消息,即每个消息是独立编码的,从而编码器是无记忆的,且可用组合逻辑电路来实现。
定义:一个长度为n ,有2k 个码字的分组码,当且仅当其2k 个码字构成域GF(2)上所有n 维向量组成的向量空间的一个K 维子空间时被称为线性(linear )(n, k)码。
汉明码(n ,k ,d )就是线性分组(n, k)码的一种。
其编码算法即为使用生成矩阵G :v = u ·G 。
汉明码编译码实验(新编)-作业
汉明码编译码实验班级学号姓名时间1、实验目的1、掌握汉明码编译码原理2、掌握汉明码纠错检错原理3、掌握用CPLD实现汉明码编译码的方法2、实验内容1、汉明码编码实验。
2、汉明码译码实验。
3、汉明码纠错检错能力验证实验。
三|、实验步骤1、验证汉明码编码规则实验将S2拨为“1110”,设置8号板为汉明码的工作模式。
将S1拨为“0000”。
此时,将对S3的数据进行汉明编码(COMRXA的输入无效)。
以FS0(汉明编码的帧同步信号)为触发,观测FJOUT(汉明码输出)。
将S3拨为0~15之间的数,然后观测汉明编码。
并填写下表,验证汉明码编码结果。
输入编码输出输入编码输出α6α5α4α3α6α5α4α3α2α1α0α6α5α4α3α6α5α4α3α2α1α000001000000110010010101000111011010011000101110101101110011111112、译码数据输出测量:S2保持不变,将S1拨为“0001”。
此时,将对COMRXA的数据进行汉明编码(S3的输入无效)。
用示波器同时观察FS3(汉明码编码输入)和TS_SEL(汉明码译码输出)的波形,回答译码输出数据与发端信号是否保持一致,测出时延,并写出输出数据序列(从1111开始记录一个周期),验证汉明编译码的正确性。
3、发端加错信号观测(1)保持S2为“1110”,将S1拨为“0000”(此时无误码)。
用示波器同时观测FS2(发端加错指示)和TS0(收端检错指示),说明这两点的波形的状态;(2)将S1拨为“0001”(表示插入一个误码)。
用示波器同时观测FS2(发端加错指示和TS0(收端错码指示),上下对应记录这两点的波形,定性说明汉明译码能否检测出错码。
(3)将S1拨为“0010”(表示插入两个误码)。
用示波器同时观测FS2(发端加错指示)和TS0(收端检错指示),定性说明汉明译码能否检测出错码。
回答:为什么TS0(收端错码指示)的脉冲有时窄,有时宽(宽度是窄脉冲的2倍)?(4)将S1拨为“0011”(表示插入三个误码),用示波器同时观测FS2(发端加错指示)和TS0(收端检错指示),定性说明汉明译码能否检测出错码。
汉明码编译码实验报告

汉明码编译码实验报告引言:汉明码是一种检错纠错编码方法,常用于数字通信和计算机存储中。
它通过在数据中插入冗余位,以检测和纠正错误,提高数据传输的可靠性。
本实验旨在通过编写汉明码的编码和解码程序,对汉明码的编译码原理进行实际验证,并分析其性能。
一、实验目的:1. 了解汉明码的编码和解码原理;2. 掌握汉明码编码和解码的具体实现方法;3. 验证汉明码在检测和纠正错误方面的有效性;4. 分析汉明码的性能及其应用范围。
二、实验原理:1. 汉明码编码原理:汉明码的编码过程主要包括以下几个步骤:(1)确定数据位数和冗余位数:根据要传输的数据确定数据位数n,并计算冗余位数m。
(2)确定冗余位的位置:将数据位和冗余位按照特定规则排列,确定冗余位的位置。
(3)计算冗余位的值:根据冗余位的位置和数据位的值,计算每个冗余位的值。
(4)生成汉明码:将数据位和冗余位按照一定顺序排列,得到最终的汉明码。
2. 汉明码解码原理:汉明码的解码过程主要包括以下几个步骤:(1)接收数据:接收到经过传输的汉明码数据。
(2)计算冗余位的值:根据接收到的数据,计算每个冗余位的值。
(3)检测错误位置:根据冗余位的值,检测是否存在错误,并确定错误位的位置。
(4)纠正错误:根据错误位的位置,纠正错误的数据位。
(5)输出正确数据:输出经过纠正后的正确数据。
三、实验过程:1. 编码程序设计:根据汉明码编码原理,编写编码程序,实现将输入的数据进行编码的功能。
2. 解码程序设计:根据汉明码解码原理,编写解码程序,实现将输入的汉明码进行解码的功能。
3. 实验数据准备:准备一组数据,包括数据位和冗余位,用于进行编码和解码的实验。
4. 编码实验:将准备好的数据输入编码程序,得到编码后的汉明码。
5. 传输和接收实验:将编码后的汉明码进行传输,模拟数据传输过程,并接收传输后的数据。
6. 解码实验:将接收到的数据输入解码程序,进行解码,检测和纠正错误。
7. 实验结果分析:分析编码和解码的正确性,检测和纠正错误的能力,并对汉明码的性能进行评估。
汉明码编译码实验

本次实验较为简单,我们小组很快就能做出来,而且实验原理及实验结果也很容易看懂,所以我们在很短的时间就完成了本次实验,唯一就是需要记录的数据较前两次实验较多,所以本次记录的时间就较多,不过我们还是成功的完成了本次实验。
1100
1101
1110
1111
五、实验记录与处理(数据、图表、计算等)
汉明码编码规则验证:
输入
编码输出
α6α500
0000000
0001
0001011
0010
0010101
0011
0011110
0100
0100110
0101
0101101
0110
0110011
(1)将2号模块的拨码开关S12#拨为10100000,拨码开关S22#、S32#、S42#均拨为00000000;
(2)将6号模块的拨码开关S16#拨为0001,即编码方式为汉明码。开关S36#拨为0000,即无错模式。按下6号模块S2系统复位键。
3、此时系统初始状态为:2号模块提供32K编码输入数据,6号模块进行汉明编译码,无差错插入模式。
0111
0111000
输入
编码输出
α6α5α4α3
α6α5α4α3α2α1α0
1000
1000111
1001
1001100
1010
1010010
1011
1011001
1100
1100001
1101
1101010
1110
1110100
1111
1111111
六、实验结果及分析
本项目通过改变输入数字信号的码型,观测延时输出,编码输出及译码输出,验证汉明码编译码规则。
汉明码编译码实验

0111000
输入
编码输出
α6α5α4α3
α6α5α4α3α2α1α0
1000
10001
1010010
1011
1011001
1100
1100001
1101
1101010
1110
1110100
1111
1111111
六、实验结果及分析
本项目通过改变输入数字信号的码型,观测延时输出,编码输出及译码输出,验证汉明码编译码规则。
模块6:TH3(辅助观测-帧头指示)
编码帧头指示
模块6:TH5(编码输出-编码数据)
模块6:TH7(译码输入-数据)
将数据送入译码
模块6:TH6(编码输出-时钟)
模块6:TH8(译码输入-时钟)
提供译码时钟
模块6:TH4(延时输出1)
模块6:TH9(辅助观测-NRZD-IN)
延时输出
2、开电,设置主控菜单,选择【主菜单】→【通信原理】→【汉明码】。
实验报告
课程名称:《通信原理》开课学期:17-18学年第1学期
实验室地点:实训楼512学生姓名:
学号:专业班级:
电子信息学院
实验项目名称
实验日期
2017.12.08
学生姓名
学 号
专业班级
指导教师
一、实验目的和要求
1、了解信道编码在通信系统中的重要性。
2、掌握汉明码编译码的原理。
3、掌握汉明码检错纠错原理。
4、实验操作及波形观测。
(1)TH2(编码输入-时钟);
(2)TH3(辅助观测-帧头指示)。
输入
编码输出
α6α5α4α3
α6α5α4α3α2α1α0
实验四 纠错码Hamming码编译码

实验四纠错码Hamming码编译码一、实验原理差错控制编码的基本作法是:在发送端被传输的信息序列上附加一些监督码元,这些多余的码元与信息之间以某种确定的规则建立校验关系。
接收端按照既定的规则检验信息码元与监督码元之间的关系,一旦传输过程中发生差错,则信息码元与监督码元之间的校验关系将受到破坏,从而可以发现错误,乃至纠正错误。
通信原理综合实验系统中的纠错码系统采用汉明码(7,4)。
所谓汉明码是能纠正单个错误的线性分组码。
它有以下特点:码长n=2m-1 最小码距d=3信息码位k=2n-m-1 纠错能力t=1监督码位r=n-k这里m位≥2的正整数,给定m后,既可构造出具体的汉明码(n,k)。
汉明码的监督矩阵有n列m行,它的n列分别由除了全0之外的m位码组构成,每个码组只在某列中出现一次。
系统中的监督矩阵如下图所示:其相应的生成矩阵为:汉明译码的方法,可以采用计算校正子,然后确定错误图样并加以纠正的方法。
表3.4.1 (7,4)汉明编码输入数据与监督码元生成表二、实验仪器1、JH5001通信原理综合实验系统一台2、20MHz双踪示波器一台3、JH9001型误码测试仪(或GZ9001型)一台三、实验目的通过纠错编解码实验,加深对纠错编译码理论的理解;掌握纠错编译码的实现和应用。
AS CVSD四、 实验内容准备工作:(1)首先通过菜单将调制方式设置为BPSK 或DBPSK 方式;将汉明编码模块内工作方式选择开关SWC01中,编码使能开关插入(H_EN ),ADPCM 数据断开(ADPCM );将输入数据选择开关KC01设置在m 序列(DT_M )位置;设置m 序列方式为(00:M_SEL2和M_SEL1拔下),此时m 序列输出为1/0码。
(2)将汉明译码模块内输入信号和时钟选择开关KW01、KW02设置在LOOP 位置(右端),输入信号直接来自汉明编码模块;将译码器使能开关KW03设置在工作位置0N (左端)。
实验四纠错码编译码概要

实验四 纠错码编译码一、 实验原理编译码原理和方法: (一) 汉明码编译码编码汉明码的编码就是如何根据信息位数k ,求出纠正一个错误的监督矩阵H ,然后根据H 求出信息位所对应的码字。
构造汉明码监督矩阵H 的方法很多,这里仅介绍一种。
1)根据已知的信息位数k ,从汉明不等式中求出校验位数m=n-k ;2)在每个码字C :(C 1,C 2,⋯ ,C n )中,用C n ,C n-1 ,C n-2作为监督位,剩下的位作为信息位;3)用二进制数字表示2m-1 列,得到2m-1列和m 行监督矩阵H ;4)用3步的H 形成HC T=0,从而得出m 个监督方程;5)将已知的信息代入方程组,然后求出满足上述方程组的监督位c (i=0,1,⋯ ,m 一1)。
例如,用以上方法,很容易求出[7,4,3]汉明码的监督矩阵:111010011010101011001H ⎛⎫ ⎪= ⎪ ⎪⎝⎭由H 得到G1 0 0 0 1 1 1G = I k Q = 0 1 0 0 1 1 0 0 0 1 0 1 0 1 0 0 0 1 0 1 1译码 当收到一个接收码字 R 后,可用监督矩阵H 来检验R 是否满足监督方程,即HR T =0T 是否成立。
若关系式成立,则认为 R 是一个码字,否则判为码字在传输中发生了错误。
因此,HR T 的值是否为0 是检验码字出错与否的依据。
把 S =RH T 或 S T =HR T ,称为接收码字 R 的伴随式(或监督子,或校验子)。
设发送码字 C =(c n -1,c n -2,…,c 0),信道的错误图样为E =(e n -1,e n -2,…,e 0) 式中:若e i =0,表示第i 位无错,若e i =1,则表示第i 位有错,i =n -1,n -2,…,0 那么,接收码字 R 为R =(r n -1,r n -2,…,r 0) =C +E =(c n -1+e n -1,c n -2+e n -2,…,c 0+e 0) 将接收字用监督矩阵进行检验,即求接收码字的伴随式: S T = HR T = H (C +E ) T = HC T + HE T 由于 HC T = 0 T ,所以:S T = HE TH =(h 1,h 2,…,h n )(h i 表示H 的列,i =1,2,…,n )代入式(5―35)得: S T =h 1e n -1+h 2e n -2+…+h n e 0(1)伴随式仅与错误图样有关,而与发送的具体码字无关,即伴随式仅由错误图样决定。
实验四 纠错码编译码

实验四 纠错码编译码一、 实验原理编译码原理和方法: (一) 汉明码编译码编码汉明码的编码就是如何根据信息位数k ,求出纠正一个错误的监督矩阵H ,然后根据H 求出信息位所对应的码字。
构造汉明码监督矩阵H 的方法很多,这里仅介绍一种。
1)根据已知的信息位数k ,从汉明不等式中求出校验位数m=n-k ;2)在每个码字C :(C 1,C 2,⋯ ,C n )中,用C n ,C n-1 ,C n-2作为监督位,剩下的位作为信息位;3)用二进制数字表示2m-1 列,得到2m-1列和m 行监督矩阵H ;4)用3步的H 形成HC T=0,从而得出m 个监督方程;5)将已知的信息代入方程组,然后求出满足上述方程组的监督位c (i=0,1,⋯ ,m 一1)。
例如,用以上方法,很容易求出[7,4,3]汉明码的监督矩阵:111010011010101011001H ⎛⎫ ⎪= ⎪ ⎪⎝⎭由H 得到G1 0 0 0 1 1 1G = I k Q = 0 1 0 0 1 1 0 0 0 1 0 1 0 1 0 0 0 1 0 1 1译码 当收到一个接收码字 R 后,可用监督矩阵H 来检验R 是否满足监督方程,即HR T =0T 是否成立。
若关系式成立,则认为 R 是一个码字,否则判为码字在传输中发生了错误。
因此,HR T 的值是否为0 是检验码字出错与否的依据。
把 S =RH T 或 S T =HR T ,称为接收码字 R 的伴随式(或监督子,或校验子)。
设发送码字 C =(c n -1,c n -2,…,c 0),信道的错误图样为E =(e n -1,e n -2,…,e 0) 式中:若e i =0,表示第i 位无错,若e i =1,则表示第i 位有错,i =n -1,n -2,…,0。
那么,接收码字 R 为R =(r n -1,r n -2,…,r 0) =C +E =(c n -1+e n -1,c n -2+e n -2,…,c 0+e 0) 将接收字用监督矩阵进行检验,即求接收码字的伴随式: S T = HR T = H (C +E ) T = HC T + HE T 由于 HC T = 0 T ,所以:S T = HE T将 H =(h 1,h 2,…,h n )(h i 表示H 的列,i =1,2,…,n )代入式(5―35)得: S T =h 1e n -1+h 2e n -2+…+h n e 0 由上面分析得到如下结论:(1)伴随式仅与错误图样有关,而与发送的具体码字无关,即伴随式仅由错误图样决定。
汉明码实验报告

汉明码实验报告汉明码实验报告引言:汉明码是一种用于错误检测和纠正的编码技术。
在通信和存储系统中,数据传输和存储过程中常常会出现错误,而汉明码可以帮助我们检测出这些错误,并且在一定程度上还能够纠正这些错误。
本实验旨在通过实际操作,深入理解和掌握汉明码的原理和应用。
实验目的:1. 了解汉明码的基本原理和编码方式;2. 实际操作中,通过添加冗余位实现错误检测和纠正。
实验步骤:1. 汉明码的编码过程首先,我们需要选择合适的汉明码位数。
在本实验中,我们选择了4位汉明码进行编码。
接下来,将待传输的数据进行编码。
假设我们要传输的数据是1010,我们可以通过以下步骤进行编码:- 第一步,确定冗余位的位置。
在4位汉明码中,第1、2、4位是冗余位,而第3位是数据位。
- 第二步,计算冗余位的值。
冗余位的值是通过数据位和冗余位的异或运算得到的。
具体计算如下:- 第1位冗余位的值:1 xor 0 xor 1 xor 0 = 0- 第2位冗余位的值:1 xor 0 xor 1 xor 0 = 0- 第4位冗余位的值:1 xor 0 xor 1 xor 0 = 0- 第三步,将数据位和冗余位按顺序排列,得到最终的汉明码。
在本例中,最终的汉明码为0110100。
2. 汉明码的解码过程在接收端,我们需要对接收到的汉明码进行解码,以检测和纠正可能存在的错误。
解码的步骤如下:- 第一步,确定冗余位的位置。
根据汉明码的编码方式,我们可以得知冗余位的位置。
- 第二步,计算冗余位的值。
与编码过程相反,我们通过数据位和冗余位的异或运算得到冗余位的值。
- 第三步,检测错误位。
如果冗余位的值为0,则说明传输过程中没有错误;如果冗余位的值为1,则说明传输过程中存在错误。
通过对冗余位的值进行判断,我们可以确定错误位的位置。
- 第四步,纠正错误位。
根据错误位的位置,我们可以将该位的值进行翻转,从而纠正错误。
实验结果:通过实验,我们成功地进行了汉明码的编码和解码过程。
汉明码的编码和译码算法

汉明码(Hamming)的编码和译码算法本文所讨论的汉明码是一种性能良好的码,它是在纠错编码的实践中较早发现的一类具有纠单个错误能力的纠错码,在通信和计算机工程中都有应用。
例如:在“计算机组成原理”课程中,我们知道当计算机存储或移动数据时,可能会产生数据位错误,这时可以利用汉明码来检测并纠错。
简单的说,汉明码是一个错误校验码码集,由Bell实验室的R.W.Hamming发明,因此定名为汉明码。
如果对汉明码作进一步推广,就得出了能纠正多个错误的纠错码,其中最典型的是BCH码,而且汉明码是只纠1bit错误的BCH码,可将它们都归纳到循环码中。
各种码之间的大致关系显示如下。
一、汉明码的编码算法输入:信源消息u(消息分组u)输出:码字v处理:信源输出为一系列二进制数字0和1。
在分组码中,这些二进制信息序列分成固定长度的消息分组(message blocks)。
每个消息分组记为u,由k个信息位组成。
因此共有2k种不同的消息。
编码器按照一定的规则将输入的消息u转换为二进制n 维向量v ,这里n >k 。
此n 维向量v 就叫做消息u 的码字(codeword )或码向量(code vector )。
因此,对应于2k 种不同的消息,也有2k 种码字。
这2k 个码字的集合就叫一个分组码(block code )。
若一个分组码可用,2k 个码字必须各不相同。
因此,消息u 和码字v 存在一一对应关系。
由于n 符号输出码字只取决于对应的k 比特输入消息,即每个消息是独立编码的,从而编码器是无记忆的,且可用组合逻辑电路来实现。
定义:一个长度为n ,有2k 个码字的分组码,当且仅当其2k 个码字构成域GF(2)上所有n 维向量组成的向量空间的一个K 维子空间时被称为线性(linear )(n, k)码。
汉明码(n ,k ,d )就是线性分组(n, k)码的一种。
其编码算法即为使用生成矩阵G :v = u ·G 。
汉明码编译码及纠错能力验证实验

课程名称通信原理实验序号实验8实验名称汉明码编译码及纠错能力验证实验实验地点B702实验学时 2 实验类型验证性指导教师实验员专业 _电子信息工程__ 班级14电信一班学号姓名2016年12 月15 日五、测试/调试及实验结果分析图片说明:CH1(黄色)帧同步信号CH2(浅蓝色)编码后信号CH3(粉红色)编码前信号CH4(深蓝色)译码后信号保护位无加错的时候设置的原始信号是:1100,编码后的信号是:1100001,译码后的信号为:1100。
对照图片的波形图,无误输出,汉明码正确。
有延时的现象。
1位加错的时候:设置的原始信号是:1100,编码后的信号是:1101001译码后的信号是:1100 通过计算S1、S2、S3可知错误位为:a3 对照译码后的波形与编码前的波形,可知已经纠错成功。
汉明码的一位纠错功能实现。
有延时的现象。
2位加错的时候:设置的原始信号是:1100,编码后的信号是:1111001码后的信号是:0111 对照无错的编码后序列,可知错误位为:a3、a4 对照译码后的波形与编码前的波形,可知译码后的波形与编码前的波形对不上。
(7,4)汉明码的2位纠错功能无法实现。
3位加错的时候:设置的原始信号是:1100,编码后的信号是:1011001码后的信号是:0111 对照无错的编码后序列,可知错误位为:a3、a4、a5 ,对照译码后的波形与编码前的波形,可知译码后的波形与编码前的波形对不上。
(7,4)汉明码的3位纠错功能无法实现。
4位加错的时候:设置的原始信号是:1100,编码后的信号是:0011001码后的信号是:0111 对照无错的编码后序列,可知错误位为:a3、a4、a5 、a6 ,对照译码后的波形与编码前的波形,可知译码后的波形与编码前的波形对不上。
(7,4)汉明码的4位纠错功能无法实现。
六、实验结论与体会1.课堂上对汉明码的理解不够深入,经过本次实验明显加深了我对汉明码的理论的认识和理解,实际动手才是关键2.经过编码后的编码序列,在加错码的时候,对a0、a1、a2位没有影响,也就是说这三位不会在无错的时候编码是什么,加错后这三位的编码还是一样3.一位加错时,(7,4)汉明码有检错以及纠错的功能,两位加错的时候,只有检错的功能,却没有纠错的功能,三位或三位以上加错时,既没有检错的功能,也没有纠错的功能;4.(7,4)汉明码作为一种信道编码的方式,具有一定的纠错检错能力。
汉明码编译码
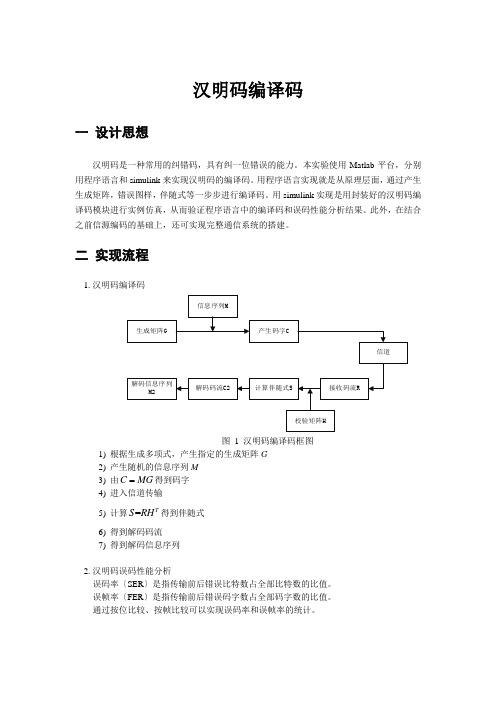
汉明码编译码一设计思想汉明码是一种常用的纠错码,具有纠一位错误的能力。
本实验使用Matlab平台,分别用程序语言和simulink来实现汉明码的编译码。
用程序语言实现就是从原理层面,通过产生生成矩阵,错误图样,伴随式等一步步进行编译码。
用simulink实现是用封装好的汉明码编译码模块进行实例仿真,从而验证程序语言中的编译码和误码性能分析结果。
此外,在结合之前信源编码的基础上,还可实现完整通信系统的搭建。
二实现流程1.汉明码编译码图 1 汉明码编译码框图1)根据生成多项式,产生指定的生成矩阵G2)产生随机的信息序列M得到码字3)由C MG4)进入信道传输S RH得到伴随式5)计算=T6)得到解码码流7)得到解码信息序列2.汉明码误码性能分析误码率〔SER〕是指传输前后错误比特数占全部比特数的比值。
误帧率〔FER〕是指传输前后错误码字数占全部码字数的比值。
通过按位比较、按帧比较可以实现误码率和误帧率的统计。
3. 构建完整通信系统图 2 完整通信系统框图三 结论分析1. 汉明码编译码编写了GUI 界面方便呈现过程和结果。
图 3 汉明码编译码演示GUI 界面以产生〔7,4〕汉明码为例说明过程的具体实现。
1) 根据生成多项式,产生指定的生成矩阵G用[H,G,n,k] = hammgen(3,'D^3+D+1')函数得到系统码形式的校验矩阵H 、G 以及码字长度n 和信息位数k100101101011100010111H ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦1101000011010011100101010001G ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦2) 产生随机的信息序列M输入信息序列Huffman 编码Hamming 编码信道Hamming 译码Huffman 译码输出信息序列噪声0010=01000111M ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦3) 由C MG =得到码字010001101101000010111C ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦4) 进入信道传输传输后接收端得到的码流为000011110100000111101R ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦红色表示错误比特。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验四纠错码Hamming码编译码
一、实验原理
差错控制编码的基本作法是:在发送端被传输的信息序列上附加一些监督码元,这些多余的码元与信息之间以某种确定的规则建立校验关系。
接收端按照既定的规则检验信息码元与监督码元之间的关系,一旦传输过程中发生差错,则信息码元与监督码元之间的校验关系将受到破坏,从而可以发现错误,乃至纠正错误。
通信原理综合实验系统中的纠错码系统采用汉明码(7,4)。
所谓汉明码是能纠正单个错误的线性分组码。
它有以下特点:
码长n=2m-1 最小码距d=3
信息码位k=2n-m-1 纠错能力t=1
监督码位r=n-k
这里m位≥2的正整数,给定m后,既可构造出具体的汉明码(n,k)。
汉明码的监督矩阵有n列m行,它的n列分别由除了全0之外的m位码组构成,每个码组只在某列中出现一次。
系统中的监督矩阵如下图所示:
1110100
H=0111010
1101001
其相应的生成矩阵为:
1000101
0100111
G=
0010110
0001011
汉明译码的方法,可以采用计算校正子,然后确定错误图样并加以纠正的方法。
表3.4.1 (7,4)汉明编码输入数据与监督码元生成表
二、实验仪器
1、1 JH5001通信原理综合实验系统一台
2、20MHz双踪示波器一台
三、实验目的
1、通过纠错编解码实验,加深对纠错编解码理论的理解;
四、实验内容
准备工作
(1)将汉明编码模块内工作方式选择开关SWC01中,编码使能开关插入(H_EN);;
设置m序列方式为(M_SEL1拔除、M_SEL0接入),此时m序列输出为全1码。
(2)将汉明译码模块内输入信号和时钟选择开关KW01、KW02设置在(右端),输入信号直接来自汉明编码模块;将译码器使能开关KW03设置在工作位置0N(左端)。
1.编码规则验证
(1)用示波器同时观测编码输入信号TPC03波形和编码输出波形TPC05,观测是否符合汉明编码规则(参见表3.4.1所示)。
(2)设置m序列方式为(10:M_SEL1插入、M_SEL0拔下),此时m序列输出为16进制码0000~1111(参见表3.4.2所示)。
通过接入M-PAUSE跳线,选择某一静态
码。
用示波器同时观测编码输入信号TPC01波形和编码输出波形TPC05,观测时
以TPC01同步,观测是否符合汉明编码规则。
(3)设置其它m序列方式,重复上述测量步骤。
注:m序列周期因非4bit的倍数,所以输入的4bit数据为其周期内的某一段截取码字。
2.译码数据输出测量
(1)用示波器同时观测汉明编码模块的编码输入信号TPC03波形和汉明译码模块译码输出m序列波形TPW06,测量译码输出数据与发端信号是否保持一致,以及
延时。
(2)设置不同的m序列方式,重复上述实验,验证汉明编译码的正确性。
3.译码同步过程观测
将汉明编码模块工作方式选择开关SWC01的编码使能开关插入(H_EN)。
将汉明译码模块的输入信号和时钟选择开关KW01、KW02设置在2_3位置(右端),输入信号直接来自汉明编码模块。
(1)用示波器检测汉明译码模块内错码检测指示输出波形TPW03。
将汉明编码模块内工作方式选择开关SWC01的编码使能开关断开(H_EN),使汉明译码模块失步,
观测TPW03变化;将编码使能开关插入(H_EN),观测汉明译码的同步过程,
记录测量结果。
(2)将输入数据换为其它测试码型,重复上述测量步骤,分析测量结果。
4.发端加错信号观测
将汉明编码模块工作方式选择开关SWC01的编码使能开关插入(H_EN)。
将汉明译码模块内输入信号和时钟选择开关KW01、KW02设置(右端),输入信号直接来自汉明编码模块;将译码器使能开关KW03设置在工作位置0N(左端)。
加的错码个数设置参见表3.4.3 (1)无加错:用示波器同时测量编码输出TPC03和汉明译码模块内错码位置指示输出波形TPW05的波形。
此时无错码。
(2)末位错1bit: 将汉明编码模块工作方式选择开关SWC01的加错开关E_MOD0接入,产生1位错码,定性观测明译码能否检测出错码,记录结果。
(3)首位错1bit; 将汉明编码模块工作方式选择开关SWC01的加错开关E_MOD1接入,产生2位错码,定性观测明译码能否检测出错码,记录结果。
(4)错2bit: 将汉明编码模块工作方式选择开关SWC01的加错开关E_MOD0、E_MOD1都插入,定性观测明译码能否检测出错码,记录结果。
5.收端错码检测能力观测和错码纠错性能测量
将汉明编码模块工作方式选择开关SWC01的编码使能开关插入(H_EN),将输入数据选择为任意一种测试码型。
将汉明译码模块内输入信号和时钟选择开关KW01、KW02设置在(右端);将译码器使能开关KW03设置在工作位置0N(左端)。
错码个数从1bit 到2bit分别开始。
用示波器同时观察TPC03和TPW06,观察7/4汉明码的纠错能力。
五、实验报告
1、画出输入为0/1码、00/11码和1110010 m序列码的汉明编码输出波形。
2、分析整理测试数据。
3、纠错译码时为什么要同步?如何同步?
4、纠错编码对误码率有何影响?
5、Hamming码有何优点和局限?。
