FLUENT数值模拟离散笔记

合集下载

FLUENT数值模拟离散笔记

一旦使用了离散相模型，下面的模型将不能使用：● 选择了离散相模型后，不能再使用周期性边界条件● 可调整时间步长方法不能与离散相模型同时使用● 预混燃烧模型中只能使用非反应颗粒模型● 同时选择了多参考坐标系与离散相颗粒模型时，在缺省情况下，颗粒轨道的显示失却了其原有意义；同样，相间耦合计算是没有意义的。

FLUENT 提供的离散相模型选择如下：● 对稳态与非稳态流动，可以应用拉氏公式考虑离散相的惯性、曳力、重力● 预报连续相中，由于湍流涡旋的作用而对颗粒造成的影响● 离散相的加热/冷却● 液滴的蒸发与沸腾● 颗粒燃烧模型，包括挥发份析出以及焦炭燃烧模型（因而可以模拟煤粉燃烧）● 连续相与离散相间的耦合● 液滴的迸裂与合并热泳力（热致迁移力或辐射力）Saffman 升力在附加力中也可以考虑由于横向速度梯度（剪切层流动）引致的Saffman 升力。

离散相边界条件当颗粒与壁面发生碰撞时，将会发生下述几种情况：l 颗粒发生弹性或非弹性碰撞反射l 穿过壁面而逃逸（颗粒的轨道计算在此处终止）l 在壁面处被捕集。

非挥发性颗粒在此处终止计算；颗粒或液滴中的挥发性物质在此处被释放到气相中l 穿过内部的诸如辐射或多孔介质间断面区域！！如果选择了Spalart-Allmaras 湍流模型，那么，轨道计算中就不能包含颗粒的湍流扩散。

颗粒类型l 惯性颗粒（``inert''）是服从力平衡（方程19.2-1）以及受到加热／冷却影响（由定律1 确定，请参阅19.3.2）的一种离散相类型（颗粒、液滴或气泡）。

在FLUENT 任何模型中，惯性颗粒总是可选的。

2液滴（``droplet''）是一种存在于连续相气流中的液体颗粒。

它服从力的平衡并受到加热／冷却的影响（由定律1 确定）。

此外，他还由定律2 和3 确定自身的蒸发与沸腾（请参阅19.3.3、19.3.4）。

只有传热选项被激活并且至少两种化学组份在计算中是被激活的，或者已经选择了非预混燃烧或部分预混燃烧模型，液滴类型才是可选的。

fluent学习笔记

fluent技术基础与应用实例fluent数值模拟步骤简介主要步骤：1、根据实际问题选择2D或3Dfluent求解器从而进行数值模拟。

2、导入网格（File→Read→Case,然后选择有gambit导出的.msh文件）3、检查网格（Grid→Check）。

如果网格最小体积为负值，就要重新进行网格划分。

4、选择计算模型。

5、确定流体物理性质（Define→Material）。

6、定义操作环境（Define→operating condition）7、制定边界条件（Define→Boundary Conditions）8、求解方法的设置及其控制。

9、流场初始化（Solve→Initialize）10、迭代求解（Solve→Iterate）11、检查结果。

12、保存结果，后处理等。

具体操作步骤：1、fluent2d或3d求解器的选择。

2、网格的相关操作（1）、读入网格文件（2）、检查网格文件文件读入后，一定要对网格进行检查。

上述的操作可以得到网格信息，从中看出几何区域的大小。

另外从minimum volume 可以知道最小网格的体积，若是它的值大于零，网格可以用于计算，否则就要重新划分网格。

（3）、设置计算区域在gambit中画出的图形是没有单位的，它是一个纯数量的模型。

故在进行实际计算的时候，要根据实际将模型放大或缩小。

方法是改变fluent总求解器的单位。

（4）、显示网格。

Display→Grid3、选择计算模型（1）、基本求解器的定义Define→Models→SolverFluent中提供了三种求解方法：·非耦合求解segregated·耦合隐式求解coupled implicit·耦合显示求解coupled explicit非耦合求解方法主要用于不可压缩流体或者压缩性不强的流体。

耦合求解方法用在高速可压缩流体fluent默认设置是非耦合求解方法，但对于高速可压缩流动，有强的体积力（浮力或离心力）的流动，求解问题时网格要比较密集，建议采用耦合隐式求解方法。

FLUENT离散相设置终极教程

FLUENT离散相设置终极教程离散相设置是一种流体动力学中的模拟方法，用于模拟流体行为。

FLUENT是一种广泛使用的计算流体力学软件，可以用于离散相设置。

下面是一个离散相设置的终极教程，详细介绍了FLUENT中的离散相设置。

第一步是导入几何模型。

在FLUENT中，可以通过导入几何模型文件（通常是.stl或.step格式）来创建模拟实验的几何模型。

导入后，可以使用FLUENT的几何建模工具对模型进行修复和优化。

第三步是定义物理模型。

在离散相设置中，需要定义流体和颗粒的物理属性。

可以使用FLUENT中的材料库来定义流体的性质，如密度、黏度、温度等。

对于离散相，需要定义颗粒的粒径、密度、形状等。

第四步是定义边界条件。

在离散相设置中，通常需要定义流体和颗粒的进出口条件。

可以通过FLUENT的边界条件工具来定义进出口条件，如速度、质量流率等。

第五步是设置离散相模型。

在FLUENT中，提供了多种离散相模型，如欧拉-拉格朗日方法（Euler-Lagrange）和欧拉-欧拉方法（Euler-Euler）。

根据模拟对象的特点，选择合适的离散相模型。

第六步是配置模拟参数。

在离散相设置中，需要配置模拟的时间步长、迭代收敛准则、迭代次数等参数。

可以通过FLUENT的求解控制面板来配置这些参数。

第七步是运行模拟。

在配置好所有设置后，可以点击FLUENT的求解按钮来开始模拟。

FLUENT将根据定义的设置和参数进行仿真，并输出结果。

第八步是分析结果。

FLUENT可以输出各种结果数据，如流场、颗粒轨迹、颗粒浓度等。

可以使用FLUENT的后处理工具对结果进行可视化和分析。

总结：离散相设置是FLUENT中的一个重要功能，可以模拟流体与颗粒的复杂相互作用。

通过导入几何模型、定义网格、定义物理模型、设置边界条件、设置离散相模型、配置模拟参数、运行模拟和分析结果等步骤，可以完成FLUENT中的离散相设置。

希望这个终极教程能够帮助你更好地理解和应用FLUENT中的离散相设置。

FLUENT学习经验总结(狠珍贵,学长传授)

1对于刚接触到FLUENT新手来说，面对铺天盖地的学习资料和令人难读的FLUENT help，如何学习才能在最短的时间内入门并掌握基本学习方法呢？答：学习任何一个软件，对于每一个人来说，都存在入门的时期。

认真勤学是必须的，什么是最好的学习方法，我也不能妄加定论，在此，我愿意将我三年前入门FLUENT心得介绍一下，希望能给学习FLUENT的新手一点帮助。

由于当时我需要学习FLUENT来做毕业设计，老师给了我一本书，韩占忠的《FLUENT流体工程仿真计算实例与应用》，当然，学这本书之前必须要有两个条件，第一，具有流体力学的基础，第二，有FLUENT 安装软件可以应用。

然后就照着书上二维的计算例子，一个例子，一个步骤地去学习，然后学习三维，再针对具体你所遇到的项目进行针对性的计算。

不能急于求成，从前处理器GAMBIT，到通过FLUENT进行仿真，再到后处理，如TECPLOT，进行循序渐进的学习，坚持，效果是非常显著的。

如果身边有懂得FLUENT的老师，那么遇到问题向老师请教是最有效的方法，碰到不懂的问题也可以上网或者查找相关书籍来得到答案。

另外我还有本《计算流体动力学分析》王福军的，两者结合起来学习效果更好。

2 CFD计算中涉及到的流体及流动的基本概念和术语：理想流体和粘性流体；牛顿流体和非牛顿流体；可压缩流体和不可压缩流体；层流和湍流；定常流动和非定常流动；亚音速与超音速流动；热传导和扩散等。

A.理想流体（Ideal Fluid）和粘性流体（Viscous Fluid）：流体在静止时虽不能承受切应力，但在运动时，对相邻的两层流体间的相对运动，即相对滑动速度却是有抵抗的，这种抵抗力称为粘性应力。

流体所具备的这种抵抗两层流体相对滑动速度，或普遍说来抵抗变形的性质称为粘性。

粘性的大小依赖于流体的性质，并显著地随温度变化。

实验表明，粘性应力的大小与粘性及相对速度成正比。

当流体的粘性较小（实际上最重要的流体如空气、水等的粘性都是很小的），运动的相对速度也不大时，所产生的粘性应力比起其他类型的力如惯性力可忽略不计。

fluent笔记讲解

fluent笔记讲解Discretization离散Node values节点值，coarsen粗糙refine 细化curvature曲率，X-WALL shear Stress 壁面切应力的X方向。

strain rate应变率1、求解器:（solver）分为分离方式(segeragated)和耦合方式(coupled)，耦合方式计算高速可压流和旋转流动等复杂高参数问题时比较好，耦合隐式(implicit)耗时短内存大，耦合显式(explicit)相反；2.收敛判据:观察残差曲线。

可以在残差监视器面板中设置Convergence Criterion（收敛判据），比如设为10 -3 ，则残差下降到小于10 -3 时，系统既认为计算已经收敛并同时终止计算。

（2）流场变量不再变化。

有时候不论怎样计算，残差都不能降到收敛判据以下。

此时可以用具有代表性的流场变量来判断计算是否已经收敛——如果流场变量在经过很多次迭代后不再发生变化，就可以认为计算已经收敛。

（3）总体质量、动量、能量达到平衡。

在Flux Reports （通量报告）面板中检查质量、动量、能量和其他变量的总体平衡情况。

通过计算域的净通量应该小于0.1%。

Flux Reports（通量报告）面板如图2-17 所示，其启动方法为：Report -> Fluxes3.一阶精度与二阶精度：First Oder Upwind and Second Oder Upwind(一阶迎风和二阶迎风)①一阶耗散性大，有比较严重的抹平现象；稳定性好②二阶耗散性小，精度高；稳定性较差，需要减小松弛因子4.流动模型的选择①inviscid无粘模型：当粘性对流场影响可以忽略时使用；例如计算升力。

②laminar层流模型：考虑粘性，且流动类型为层流。

③Spalart-Allmaras （S-A模型）：单方程模型，适用于翼型、壁面边界层流动，不适于射流等自由剪切湍流问题。

学习fluent (流体常识及软件计算参数设置)

luent中一些问题----(目录)1 如何入门2 CFD计算中涉及到的流体及流动的基本概念和术语2.1 理想流体（Ideal Fluid）和粘性流体（Viscous Fluid）2.2 牛顿流体（Newtonian Fluid）和非牛顿流体（non-Newtonian Fluid）2.3 可压缩流体（Compressible Fluid）和不可压缩流体（Incompressible Fluid）2.4 层流（Laminar Flow）和湍流（Turbulent Flow）2.5 定常流动（Steady Flow）和非定常流动（Unsteady Flow）2.6 亚音速流动(Subsonic)与超音速流动（Supersonic）2.7 热传导（Heat Transfer）及扩散（Diffusion）3 在数值模拟过程中，离散化的目的是什么？如何对计算区域进行离散化？离散化时通常使用哪些网格？如何对控制方程进行离散？离散化常用的方法有哪些？它们有什么不同？3.1 离散化的目的3.2 计算区域的离散及通常使用的网格3.3 控制方程的离散及其方法3.4 各种离散化方法的区别4 常见离散格式的性能的对比（稳定性、精度和经济性）5 流场数值计算的目的是什么？主要方法有哪些？其基本思路是什么？各自的适用范围是什么？6 可压缩流动和不可压缩流动，在数值解法上各有何特点？为何不可压缩流动在求解时反而比可压缩流动有更多的困难？6.1 可压缩Euler及Navier-Stokes方程数值解6.2 不可压缩Navier-Stokes方程求解7 什么叫边界条件？有何物理意义？它与初始条件有什么关系？8 在数值计算中，偏微分方程的双曲型方程、椭圆型方程、抛物型方程有什么区别？9 在网格生成技术中，什么叫贴体坐标系？什么叫网格独立解？10 在GAMBIT中显示的“check”主要通过哪几种来判断其网格的质量？及其在做网格时大致注意到哪些细节？11 在两个面的交界线上如果出现网格间距不同的情况时，即两块网格不连续时，怎么样克服这种情况呢？12 在设置GAMBIT边界层类型时需要注意的几个问题：a、没有定义的边界线如何处理？b、计算域内的内部边界如何处理（2D）？13 为何在划分网格后，还要指定边界类型和区域类型？常用的边界类型和区域类型有哪些？14 20 何为流体区域（fluid zone）和固体区域（solid zone）？为什么要使用区域的概念？FLUENT是怎样使用区域的？15 21 如何监视FLUENT的计算结果？如何判断计算是否收敛？在FLUENT中收敛准则是如何定义的？分析计算收敛性的各控制参数，并说明如何选择和设置这些参数？解决不收敛问题通常的几个解决方法是什么？16 22 什么叫松弛因子？松弛因子对计算结果有什么样的影响？它对计算的收敛情况又有什么样的影响？17 23 在FLUENT运行过程中，经常会出现“turbulence viscous rate”超过了极限值，此时如何解决？而这里的极限值指的是什么值？修正后它对计算结果有何影响18 24 在FLUENT运行计算时，为什么有时候总是出现“reversed flow”？其具体意义是什么？有没有办法避免？如果一直这样显示，它对最终的计算结果有什么样的影响26 什么叫问题的初始化？在FLUENT中初始化的方法对计算结果有什么样的影响？初始化中的“patch”怎么理解？27 什么叫PDF方法？FLUENT中模拟煤粉燃烧的方法有哪些？30 FLUENT运行过程中，出现残差曲线震荡是怎么回事？如何解决残差震荡的问题？残差震荡对计算收敛性和计算结果有什么影响？31数值模拟过程中，什么情况下出现伪扩散的情况？以及对于伪扩散在数值模拟过程中如何避免？32 FLUENT轮廓（contour）显示过程中，有时候标准轮廓线显示通常不能精确地显示其细节，特别是对于封闭的3D物体（如柱体），其原因是什么？如何解决？33 如果采用非稳态计算完毕后，如何才能更形象地显示出动态的效果图？34 在FLUENT的学习过程中，通常会涉及几个压力的概念，比如压力是相对值还是绝对值？参考压力有何作用？如何设置和利用它？35 在FLUENT结果的后处理过程中，如何将美观漂亮的定性分析的效果图和定量分析示意图插入到论文中来说明问题？36 在DPM模型中，粒子轨迹能表示粒子在计算域内的行程，如何显示单一粒径粒子的轨道（如20微米的粒子）？37 在FLUENT定义速度入口时，速度入口的适用范围是什么？湍流参数的定义方法有哪些？各自有什么不同？38 在计算完成后，如何显示某一断面上的温度值？如何得到速度矢量图？如何得到流线？39 分离式求解器和耦合式求解器的适用场合是什么？分析两种求解器在计算效率与精度方面的区别43 FLUENT中常用的文件格式类型：dbs，msh，cas，dat，trn，jou，profile等有什么用处？44 在计算区域内的某一个面（2D）或一个体（3D）内定义体积热源或组分质量源。

中科大FLUENT讲稿离散相模拟

中科大FLUENT讲稿离散相模拟离散相模拟FLUENT 程序除了模拟连续相以外，也可以在Lagrangian 坐标系下模拟离散相。

离散相为球形颗粒（也可以是水滴或气泡）弥散在连续相中。

FLUENT 可以计算离散相的颗粒轨道，以及其与连续相之间的质量和能量交换。

耦合求解连续相和离散相，可以考虑相间的相互作用及影响。

离散相处理过程中，可以考虑以下因素：1，在Lagrangian 坐标系下，计算离散相在定常和非定常流动中的颗粒轨道。

2，连续相涡旋产生的湍流对离散相的影响3，离散相的加热与冷却过程4，液滴的蒸发与沸腾5，颗粒燃烧，包括挥发分挥发和碳核燃烧，用以模拟粉煤燃烧过程。

Fluent 假设离散相足够稀疏，忽略颗粒与颗粒之间的相互作用，也不考虑颗粒体积分数对连续相的影响。

因此在用该方法模拟实际过程时，要保证离散相的体积分数应该小于10％～12％。

离散相模型对以下流动过程不适合。

1，流向周期性流动2，如果采用预混燃烧模型，就不能考虑颗粒的化学反应。

3，采用多坐标系的流动采用颗粒轨道模型计算离散相时，需要给出颗粒的初始位置，速度，颗粒大小，温度及颗粒的物性参数。

颗粒轨道的计算根据颗粒的力平衡计算。

颗粒的传热传质则根据颗粒与连续相间的对流和辐射换热及质量交换来计算。

颗粒轨道，颗粒传热传质计算结果可以用图的形式给出。

颗粒轨道计算根据作用在颗粒（液滴，气泡）上力平衡，可以给出颗粒在Lagrangian 坐标系下的运动方程：x p p x p D pF g u u F dt du +-+-=ρρρ/)()( （8－1）其中，24Re 182D pp D C D F ρμ=，u 是连续相速度，p u 是颗粒速度，μ是流体的分子粘性系数，p ρρ,分别是流体与颗粒的密度；p D 是颗粒直径，Re 是相对雷诺数，定义为：μρuu D p p -=Re 阻力系数2321Re Re ααα++=D C ，1α，2α，3α为常数，根据光滑球颗粒实验结果给出[L114]。

fluent中文教程笔记

fluent中文教程笔记1.FLUENT 提供三种不同的解格式：分离解；隐式耦合解；显式耦合解。

三种解法都可以在很大流动范围内提供准确的结果，但是它们也各有优缺点。

分离解和耦合解方法的区别在于，连续性方程、动量方程、能量方程以及组分方程的解的步骤不同，分离解是按顺序解，耦合解是同时解。

两种解法都是最后解附加的标量方程（比如：湍流或辐射)。

隐式解法和显式解法的区别在于线化耦合方程的方式不同。

2. 分离解以前用于FLUENT 4 和FLUENT/UNS，耦合显式解以前用于RAMPANT。

分离解以前是用于不可压流和一般可压流的。

而耦合方法最初是用来解高速可压流的。

现在，两种方法都适用于很大范围的流动(从不可压到高速可压)，但是计算高速可压流时耦合格式比分离格式更合适。

FLUENT 默认使用分离解算器，但是对于高速可压流（如上所述），强体积力导致的强烈耦合流动(比如浮力或者旋转力)，或者在非常精细的网格上的流动，你需要考虑隐式解法。

这一解法耦合了流动和能量方程，常常很快便可以收敛。

耦合隐式解所需要内存大约是分离解的1.5 到2 倍，选择时可以通过这一性能来权衡利弊。

在需要隐式耦合解的时候，如果计算机的内存不够就可以采用分离解或者耦合显式解。

耦合显式解虽然也耦合了流动和能量方程，但是它还是比耦合隐式解需要的内存少，但是它的收敛性相应的也就差一些。

注意：分离解中提供的几个物理模型，在耦合解中是没有的：多项流模型；混合组分/PDF 燃烧模型/预混合燃烧模型/Pollutant formation models/相变模型/Rosseland 辐射模型/指定质量流周期流动模型/周期性热传导模型。

3. FLUENT 不会管所解能量方程是温度还是焓形式，它都会设定默认的亚松弛因子为1.0。

在能量场影响流体流动（通过温度相关属性或者焓）的问题中，你应该是用较小的亚松弛因子，一般在0.8 到1.0之间。

当流场和温度场解耦时（没有温度相关属性或者浮力），你可以保留松弛因子的默认值1.0。

Fluent的气固两相流中离散颗粒的数值模拟

对气固流动系统，双流体模型以其大规模模拟的可行性在数值模拟领域占据重要地位，但双流体模型中的颗粒连续假设从本质上削弱了颗粒流体系统中非均匀特性的描述[1]。与传统两相流数值模拟方法相比，离散单元法 (DEM，Discrete/Distinct Element Method，又称软球模型)可跟踪每个颗粒的运动信息，并考虑颗粒-颗粒、颗粒-壁面碰撞及颗粒-流体相互作用，在气固非均匀流数值模拟方面具有强大优势。
2、数学模型
2.1 颗粒相控制方程在气(液)固系统中，颗粒主要受四种力作用—气体对颗粒的曳力、压力梯度力、颗粒重力及颗粒-颗粒间碰
撞力。根据牛顿第二定律，颗粒运动方程可表述为：
mi
dVi dt
= Fd ,i
+ mi g + Σ(Fn,ij
+ Ft,ij ) − V p∇p
(1)
Ii
dωi dt
= ΣTt,ij
连续相对颗粒作用力包括曳力、压力梯度力、浮力、附加质量力等，本文只考虑曳力及压力梯度力，其中压
力梯度力已在式(1)中给出。本算法基于双流体模型气相方程中的耦合项推广到颗粒轨道模型，再反作用于颗粒相。
流体运动方程中的动量交换源项取为：
S fp = β (u − υ )
(12)
其中相间动量交换系数β为：
启动阶段，入口附近形成一个椭圆形气泡，气泡向上运动，床层上部演变为活塞流。被抬起的颗粒回落床层，而
后形成稳定的流化态，本文结果与 Tsuji et al[4], Xud Yu[3]试验及模拟结果定性一致。
5 结论
基于通用计算流体软件 FlUENT，通过用户自定义函数(User Defined Function) 实现了伪三维 DEM-CFD 耦合算法，其中连续相控制方程由通用计算流体软件 FLUENT 求解。构建空隙率标量场，重组基于局部平均并考虑流 -固耦合作用的连续相控制方程，提高了连续相控制方程的求解稳定性。最后，将该算法用于球形颗粒的节涌及鼓

fluent离散相dpm模拟实例

fluent离散相dpm模拟实例【原创版】目录1.Fluent 软件介绍2.离散相 DPM 模拟的概念3.Fluent 离散相 DPM 模拟实例的具体操作步骤4.Fluent 离散相 DPM 模拟实例的应用效果5.总结正文一、Fluent 软件介绍Fluent 是一款由美国 CFD 公司开发的流体动力学分析软件，广泛应用于化工、能源、环境等领域。

该软件具有强大的数值模拟能力，可以模拟流体流动、传热和化学反应等多种物理现象。

Fluent 采用基于有限体积法的求解方法，可以模拟复杂几何结构和非牛顿流体。

同时，Fluent 支持多种计算模型和边界条件，为用户提供了灵活的分析手段。

二、离散相 DPM 模拟的概念离散相 DPM（Discrete Phase Model）模拟是一种处理流体中离散相颗粒的方法，主要用于研究气液、气固等两相或多相流体系统。

DPM 模拟采用离散颗粒跟踪方法，可以准确地描述颗粒在流体中的运动和分布，以及颗粒与流体之间的相互作用。

这种方法可以揭示多相流体系统中的复杂现象，为工程应用提供理论依据。

三、Fluent 离散相 DPM 模拟实例的具体操作步骤1.准备模型：首先，根据实际问题，建立或导入 Fluent 中的三维几何模型。

2.设置物理参数：设置流体和颗粒的物性参数，如密度、粘度、比热容等。

3.定义流动模型：选择合适的流动模型，如层流或湍流模型。

4.定义离散相模型：选择 DPM 模型，并设置颗粒追踪算法、颗粒间相互作用力等参数。

5.设置边界条件和初始条件：设置流体和颗粒的边界条件和初始条件，如入口速度、压力、温度等。

6.进行仿真计算：运行 Fluent 软件，进行仿真计算。

7.后处理：对计算结果进行后处理，提取感兴趣的物理量，如流速、压力、颗粒浓度等。

四、Fluent 离散相 DPM 模拟实例的应用效果Fluent 离散相 DPM 模拟实例在多相流体系统研究中具有广泛的应用。

例如，在气液输送过程中，通过 DPM 模拟可以研究气泡在液相中的生成、成长和破裂过程，以及气泡对流体流动的影响。

完整word版,FLUENT中的求解器、算法和离散方法

FLUENT中的求解器、算法和离散方法作为一个非科班出身的CFD工程师，一开始常常被CFD软件里各种概念搞的晕头转向。

最近终于静下心来看了看CFD 理论的书，理清了一些概念。

就此写一遍博文，顺便整理一下所学内容。

I 求解器：FLUENT中求解器的选择在如下图所示界面中设置：FLUENT中的求解器主要是按照是否联立求解各控制方程来区分的，详见下图：II 算法：算法是求解时的策略，即按照什么样的方式和步骤进行求解。

FLUENT中算法的选择在如下图所示的界面中设置：这里简单介绍一下SIMPLE、SIMPLEC、PISO等算法的基本思想和适用范围。

SIMPLE算法：基本思想如前面讲求解器的那张图中解释分离式求解器的例子所示的一样，这里再贴一遍：1.假设初始压力场分布。

2.利用压力场求解动量方程，得到速度场。

3.利用速度场求解连续性方程，使压力场得到修正。

4.根据需要，求解湍流方程及其他方程5.判断但前计算是否收敛。

若不收敛，返回第二步。

简单说来，SIMPLE算法就是分两步走：第一步预测，第二步修正，即预测－修正。

SIMPLC算法：是对SIMPLE算法的一种改进，其计算步骤与SIMPLE算法相同，只是压力修正项中的一些系数不同，可以加快迭代过程的收敛。

PISO算法：比SIMPLE算法增加了一个修正步，即分三步：第一步预测，第二步修正得到一个修正的场分布，第三步在第二步基础上在进行一侧修正。

即预测－修正－修正。

PISO算法在求解瞬态问题时有明显优势。

对于稳态问题可能SIMPLE或SIMPLEC更合适。

如果你实在不知道该如何选择，就保持FLUENT的默认选项好了。

因为默认选项可以很好解决70％以上的问题，而且对于大部分出了问题的计算来说，也很少是因为算法选择不恰当所致。

III 离散方法：离散方法是指按照什么样的方式将控制方程在网格节点离散，即将偏微分格式的控制方程转化为各节点上的代数方程组。

FLUENT中离散方法的选择在如下图所示的界面中设置：简单介绍常用的几种离散方法：一阶迎风格式/ Fisrst order upwind：一阶迎风格式考虑了流动方向，可以得到物理上看起来合理的解。

FLUENT基本概念与常见问题汇总（一）

FLUENT基本概念与常见问题汇总（一）1、理想流体和粘性流体流体在静止时虽不能承受切应力，但在运动时，对相邻的两层流体间的相对运动，即相对滑动速度却是有抵抗的，这种抵抗力称为粘性应力。

流体所具备的这种抵抗两层流体相对滑动速度，或普遍说来抵抗变形的性质称为粘性。

粘性的大小依赖于流体的性质，并显著地随溫度变化。

实验表明，粘性应力的大小与粘性及相对速度成正比。

当流体的粘性较小（实际上最重要的流体如空气、水等的粘性都是很小的），运动的相对速度也不大时，所产生的粘性应力比起其他类型的力如惯性力可忽咯小计。

此时我们可以近似地把流体看成无粘性的, 这样的流体称为理想流体。

十分明显，埋想流体对于切向变形没有任何抗拒能力。

这样对于粘性而言，我们可以将流体分为理想流体和粘性流体两大类。

应该强调指出，真正的理想流体在客观实际中是不存在的，它只是实际流体在某些条件下的一种近似模型。

2、牛顿流体和非牛顿流体日常生活和工程实践中最常遇到的流体其切应力与剪切变形速率符合线性关系，称为牛顿流体。

而切应力与变形速率不成线性关系者称为非牛顿流体。

非牛顿流体中又因其切应力与变形速率关系特点分为膨胀性流体，拟塑性流体，具有屈服应力的理想宾厄流体和塑性流体等。

通常油脂、油漆、牛奶、牙音、血液、泥浆等均为非牛顿流体。

非牛顿流体的研究在化纤、塑料、石油、化工、食品及很多轻工业中有着广泛的应用。

对于有些非牛顿流体，其粘滞特性具有时间效应，即剪切应力不仅与变形速率有关而且与作用时间有关。

当变形速率保持常量，切应力随时间增大，这种非牛顿流体称为震凝性流体。

当变形速率保持常量而切应力随时间减小的非牛顿流体则称为触变性流体。

3、可压缩流体和不可压缩流体在流体的运动过程中，由于压力、温度等因素的改变，流体质点的体积（或密度，因质点的质量一定），或多或少有所改变。

流体质点的体积或密度在受到一定压力差或温度差的条件下可以改变的这个性质称为压缩性。

真实流体都是可以压缩的。

FLUENT 离散相设置终极教程

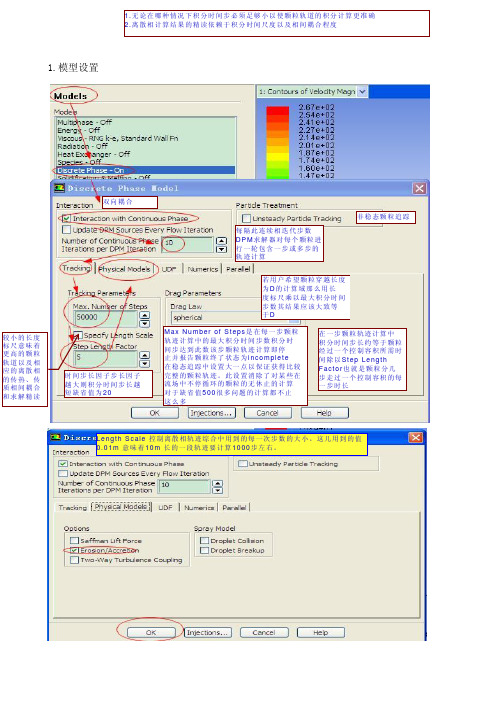
1.模型设置
双向耦合
每隔此连续相迭代步数丆
D P M求解器对每个颗粒进
行一轮包含一步或多步的
轨迹计算
M a x N u m b e r o f S t e p s是在每一步颗粒轨迹计算中的最大积分时间步数丆积分时间步达到此数丆该步颗粒轨迹计算即停
止丆并报告颗粒终了状态为i n c o m p l e t e•C 在稳态追踪中设置大一点以保证获得比较完整的颗粒轨迹。

此设置消除了对某些在流场中不停循环的颗粒的无休止的计算丆对于缺省值500•C很多问题的计算都不止这么多在一步颗粒轨迹计算中丆积分时间步长约等于颗粒经过一个控制容积所需时间除以S t e p L e n g t h
F a c t o r•C也就是颗粒分几步走过一个控制容积的每一步时长
非稳态颗粒追
踪
若用户希望颗粒穿越长度
为D的计算域丆那么用长
度标尺乘以最大积分时间
步数丆其结果应该大致等
于D
L e n g t h S c a l e控制离散相轨迹综合中用到的每一次步数的大小。

这儿用到的值0.01m意味着10m长的一段轨迹要计算1000步左右。

2.材料 material 设定介质属性
3.工作条件 opertation condition
4.加粒子injection
5.设定粒子材料属性
6.边界条件设定（流体）
6.2设定壁面边界条件
粒子速度显示
显示磨损率
计算平均磨损率。

Fluent指南｜01空间离散方法

Fluent指南｜01空间离散⽅法本⽂描述Fluent中空间离散格式的选取⽅法。

注：本⽂内容译⾃Fluent UserGuide 32.2，留待后期查阅。

”1 Gradient计算梯度不仅⽤于构造⽹格⾯上的标量值，⽽且还⽤于计算⼆次扩散项和速度导数。

Fluent中包括三种梯度计算⽅法：Green-Gauss Cell BasedGreen-Gauss Node BasedLeast Squares Cell Based梯度算法可以在Solution > Methods ⾯板中的Gradient下拉列表中进⾏选择。

此外，Fluent还允许为每个控制⽅程的对流项选择离散格式(粘性项⾃动使⽤⼆阶精度)。

默认情况下，使⽤压⼒基求解器或密度基求解器求解单相流问题时，对于流动⽅程和所有标量⽅程(湍流除外)的对流项使⽤⼆阶迎风格式（Second Order Upwind），湍流物理量相关⽅程则使⽤⼀阶迎风格式（First Order Upwind）进⾏离散求解。

对于多相流问题，流动⽅程默认使⽤⼀阶迎风离散化。

当使⽤压⼒基求解器时，可以指定压⼒插值算法。

2 ⼀阶精度 vs. ⼆阶精度当流动⽅向与⽹格⽅向⼀致时(如⽤四边形或六⾯体⽹格模拟的矩形管道中的层流流动)，⼀阶迎风离散格式的计算精度是可以接受的。

然⽽当流动与⽹格⽅向不⼀致时(即当流动斜穿过⽹格线时)，对流项的⼀阶离散会增加数值离散误差(出现数值扩散)。

对于三⾓形和四⾯体⽹格，由于流动⽆法与⽹格对齐，因此通常使⽤⼆阶离散⽅法。

对于四边形/六⾯体⽹格，使⽤⼆阶离散也可以获得更好的结果，特别是对于复杂的流动问题。

总⽽⾔之，虽然⼀阶格式通常⽐⼆阶格式有更好的收敛性，但它常常会产⽣不太精确的结果，特别是在使⽤三⾓形/四⾯体⽹格时表现更糟。

多数情况下，可以直接使⽤⼆阶格式进⾏计算。

但是在⼀些情况下，可能需要先从⼀阶格式开始计算，然后在进⾏⼏次迭代之后切换到⼆阶格式继续进⾏计算。

Fluent 第2章

●边界元法
针对于有限差分法和有限元法占用计算机内存资源过多的缺点而发展起来。源过多的缺点而发展起来。最大的优点是降维，最大的优点是降维，只在求解区域的边界进行离散就能求得整个流场的解。三维问题可降为二维。散就能求得整个流场的解。三维问题可降为二维。如大空间外部扰流。适合于无粘势流的计算，如大空间外部扰流。但对于粘性N-S方程，对应的全函数算子基本解不方程，对于粘性方程一定只能找到。一定只能找到。
Method， ●有限体积法(Finite Vo1ume Method，有限体积法(Finite FVW)
将计算区域划分为一系列控制体积，将计算区域划分为一系列控制体积，将待解微分方程对每一个控制体积积分得出离散方程。方程对每一个控制体积积分得出离散方程。用有限体积法导出的离散方程可以保证具有守恒特性，而且离散方程系数物理意义明确．特性，而且离散方程系数物理意义明确．计算量相对较小。相对较小。
第二章基于有限体积法的控制方程离散
本章授课内容
离散化概述有限体积法及其网格简介常用的离散格式
2.1 பைடு நூலகம்散化概述
2.1.1 离散化的目的
通过数值的方法把计算域内有限数量位置( 通过数值的方法把计算域内有限数量位置(即网格节点)上的因变量值当作基本未知量来处理，格节点)上的因变量值当作基本未知量来处理，从而建立一组关于这些未知量的代数方程，而建立一组关于这些未知量的代数方程，然后通过求解代数方程组来得到这些节点值，过求解代数方程组来得到这些节点值，而计算域内其他位置上的值则根据节点位置上的值来确定。内其他位置上的值则根据节点位置上的值来确定。
2.4 常用的离散格式
中心差分格式
一阶迎风格式

fluent中离散相项模型中udf的使用

《深度探讨：fluent中离散相项模型中udf的使用》在使用fluent进行离散相项模拟的过程中，用户定义函数（User Defined Function，UDF）的使用是非常重要的一环。

本文将从简单到复杂的方式，深入探讨在fluent中离散相项模型中UDF的使用，以帮助读者更全面地理解这一主题。

1. UDF在fluent中的基本原理在fluent中，用户定义函数是指用户可以编写自己的代码，并将其嵌入到fluent的求解过程中。

这样可以实现一些fluent本身不具备的功能，进而拓展了fluent的应用范围和灵活性。

在离散相项模拟中，UDF可以用于定义离散相的性质、参数和行为等，从而更精确地模拟实际工程问题。

2. UDF的基本结构和语法通常情况下，在fluent中定义UDF需要遵循一定的语法和结构。

需要包括必要的头文件引用、变量定义、函数定义等。

还需要注意在fluent中使用的特定关键词和函数，以确保UDF能够正确地嵌入到fluent的求解过程中，并得到正确的计算结果。

3. UDF在离散相项模拟中的具体应用UDF在离散相项模拟中可以发挥重要作用。

用户可以通过编写UDF来定义离散相的颗粒物性质，如密度、粘度等；或者定义离散相的边界条件，如离散相的速度场、温度场等。

通过合理地定义这些参数和条件，可以更准确地模拟离散相在流体中的运动和相互作用，从而得到更可靠的工程分析结果。

4. 我对UDF在fluent中的个人观点和理解作为一名工程师，我个人认为UDF在fluent中的使用是非常有价值的。

它可以帮助用户更灵活地定制自己的模拟模型，满足实际工程问题的需求。

尤其在离散相项模拟中，UDF的使用可以让模拟更加真实和可靠，对工程设计和优化有着重要意义。

总结回顾通过本文的深度探讨，我们对fluent中离散相项模型中UDF的使用有了更深入的了解。

我们从UDF的基本原理、结构和语法，到在离散相项模拟中的具体应用，进一步认识了UDF的重要性和价值。

fluent学习总结报告5

9. 求解。

1.设置求解控制参数∙离散格式对求解器性能的影响控制方程中的扩散项一般采用中心差分格式离散，而对流项则可采用多种不同的格式进行离散4。

FLUENT允许用户为对流项选择不同的离散格式(注意粘性项总是自动使用二阶精确度的离散格式)。

默认情况下，当使用分离式求解器时，所有方程中的对流项均用一阶迎风格式离散;当使用祸合式求解器时，流动方程使用二阶精度格式、其他方程使用一阶精度格式进行离散。

此外，当使用分离式求解器时，用户还可为压力选择插值方式。

当流动与网格对齐时，如使用四边形或六面体网格模拟层流流动，使用一阶精度离散格式是可以接受的。

但当流动斜穿网格线时，一阶精度格式将产生明显的离散误差(数值扩散)。

因此，对于2D三角形及3D四面体网格，注意要使用二阶精度格式，特别是对复杂流动更是如此。

一般来讲，.在一阶精度格式下容易收散，但精度较差。

有时，为了加快计算速度，可先在一阶精度格式下计算，然后再转到二阶精度格式下计算。

如果使用二阶精度格式遇到难于收敛的情况，则可考虑改换一阶精度格式。

对于转动及有旋流的计算，在使用四边形及六面体网格时，具有三阶精度的QUICK格式可能产生比二阶精度更好的结果。

但是，一般情况下，用二阶精度就已足够，即使使用QUICK 格式，结果也不一定好。

乘方格式(Power-law scheme)一般产生与一阶精度格式相同精度的结果。

中心差分格式一般只用于大涡模拟模型，而且要求网格很细的情况。

∙欠松弛因子对性能的影响欠松弛（Under Relaxation）：所谓欠松弛就是将本层次计算结果与上一层次结果的差值作适当缩减，以避免由于差值过大而引起非线性迭代过程的发散。

用通用变量来写出时，为松弛因子（Relaxation Factors）。

《数值传热学-214》FLUENT中的欠松弛：由于FLUENT所解方程组的非线性，我们有必要控制的变化。

一般用欠松弛方法来实现控制，该方法在每一部迭代中减少了的变化量。

FLUENT离散相设置终极教程

FLUENT离散相设置终极教程离散相设置是指将一个连续域分割为离散的小区域，然后在每个小区域内进行计算和模拟的一种方法。

它在计算机图形学、计算流体力学和分子动力学等领域有广泛的应用。

本文将为您介绍离散相设置的终极教程。

离散相设置的第一步是将连续域分割成离散的小区域。

这可以通过网格划分来实现。

常见的网格类型包括结构化网格和非结构化网格。

结构化网格是由规则的小方格组成的网格，适用于简单的几何形状。

非结构化网格由不规则的多边形或多面体组成，适用于复杂的几何形状。

选择适当的网格类型取决于具体应用和几何形状的复杂程度。

一旦网格划分完成，接下来需要为每个小区域分配相应的属性。

这些属性可以包括物理属性、材料属性和初始条件。

物理属性可以包括速度、密度和温度等。

材料属性可以包括材料的性质和特性。

初始条件是指在模拟开始时每个小区域内的初始状态。

这些属性的设置将直接影响到模拟结果的准确性和可靠性。

在离散相设置的过程中，通常需要选择适当的模拟方法。

常见的模拟方法包括有限差分法、有限元法和边界元法等。

有限差分法是通过近似导数和积分的方法来求解偏微分方程。

有限元法是通过将连续域划分成有限数量的小单元，然后在每个小单元内通过简单的数学方程来近似求解原始偏微分方程。

边界元法是通过在边界上求解边界积分方程来近似求解原始偏微分方程。

选择适当的模拟方法取决于模拟的复杂度和准确性要求。

在离散相设置的最后一步是进行模拟和计算。

模拟和计算的过程可以使用各种数值方法来实现。

其中一个常用的方法是迭代法。

迭代法通过反复迭代求解模拟方程，直到达到特定的收敛准则。

另一个常用的方法是显式求解法。

显式求解法通过将模拟方程转化为线性方程组，然后使用数值方法直接求解线性方程组。

这些数值方法的选择取决于模拟的复杂度和计算机的性能。

总结一下，离散相设置是将连续域划分为离散的小区域，并为每个小区域分配相应的属性。

然后通过选择适当的模拟方法和数值方法来进行模拟和计算。

FLUENT中离散相的设置(翻译FLUENT手册)

FLUENT除了可以计算连续相的输运方程，也可以求解拉格朗日坐标系下的离散的第二相。

计算离散相的轨迹、热量和质量的传递、相间耦合及对两相的影响。

提供以下的离散相模型：（1）利用拉格朗日方程计算离散相轨迹（利用其它模型求得轨迹与这个有什么不同）（2）连续相中的湍流对离散相分布的影响；（3）连续相对离散相的耦合计算（4）颗粒的碰撞和空隙率……..其他用不到的没记录1概述当前有三种求解多相流模型的数值方法：欧拉-拉格朗日、欧拉-欧拉及浓相离散相模型。

2局限（1）对于体积分数的限制由于离散相模型有一个假设前提：第二相要足够的稀以致于颗粒与颗粒的相互作用和颗粒对空气的影响可以忽略。

在实际的操作中，就要求颗粒相有足够低的体积分数，通常在10-12%。

如果你求解的问题的颗粒相的体积分数超过这个限制，可以考虑采用多相流模型。

比如浓离散相模型。

（2）局限于连续的颗粒悬浮模型具有稳定的拉格朗日方程的离散相并且具有颗粒相注入连续相的定义完善的入口和出口条件。

拉格朗日模型对于在连续相中不具有确定的悬浮是无效的，比如密闭的搅拌容器，混合容器和流化床等。

不稳定的颗粒离散相模型可以对于离散相的连续悬浮进行模拟。

（3）离散相模型与其它FLUENT模型的共用限制a.当并行追踪颗粒时，如果分享内存选项被选中，DPM模型不能与任何的多相流模型共用。

当进行并行处理时，记得使用信息传递选项，这样就可以使多相流模型和离散相模型并用。

b.当使用离散相模型时，不能获得沿流动方向的周期流动的参数（质量流量和压力降等）c.当使用预混合-燃烧模型时只能包含不反应颗粒。

d.如果使用滑移、移动和变形网格时，表面注入将随着网格一起变化，但是只有与边界有关的表面会重新计算。

剖面上的注入将不随网格移动，而会被删除当重画网格时。

e.cloud model对于不稳定的颗粒追踪是不可得的，或者，当对颗粒使用信息传递选项时，是不能够并行计算地。

f.当连同离散相使用多个坐标系时，颗粒的轨迹图是默认没有意义的。

fluent离散相DPM模型模拟

1、导入网格，设置边界条件，一阶计算，solve—controls—solution controls速度压力耦合选择SIMPLE,2、一阶收敛后，改为SIMPLEC，如图注意：不要初始化，迭代6000步左右3、QUICK模式迭代收敛或稳定后，改为非稳状态计算液相Define—Models—Solver注意：中间不要初始化4、单相非稳态迭代至1.1s后，加颗粒，选DPM模型，设置颗粒喷射源参数具体设置如下文5、效率计算方法：6、设定出口截面方法：Surface—plane…，设置如下图，通过三点确定一个面，（x0为圆心，x1、x2为圆上两个点）设定监视面：7、模型设定：Define—Models—Discrete Phase,勾选Interaction with Continuous Phase，即考虑连续相的影响，设定连续相的迭代数为10；设定计算步数100000，步长5图18、设置注射源Define—Injections…，选择注射类型：surface，选择注射面：inlet，图29、设定物料选择calcium-carbonate代替滑石粉，并选择物料类型“inert-particle”图310、再设置入口参数Define—Injections…，选择源面，set..，见下图，Diameter distribution(粒径分布)选择“distribution”，重点设定“Point properties”，其中包括三位速度、开始时间、停止时间、质量流量、最大粒径、最小粒径、Spread parameter（文后方法计算的n值），Number of Diameters(粒径分成的份数，也就是每个单元格计算的颗粒数目)。

图4图5图6图7图8图9图10图11附：颗粒离散数计算方法关于rosin-rammler分布举例说明，有一组颗粒服从这样一种粒径分布，见下表：定义一个变量Y d，其定义为：比指定粒径d 大的颗粒的质量分数。