2122对数函数及其性质运算1
对数与指数函数的性质与运算

对数与指数函数的性质与运算对数与指数函数是高中数学中的重要部分,它们在数学和实际应用中都有广泛的应用。
本文将介绍对数与指数函数的性质与运算。
一、对数函数的性质对数函数是指以某个正数为底的对数函数,用常用对数以10为底或自然对数以e为底为例进行说明。
对数函数的性质如下:1. 定义域与值域常用对数函数的定义域是正实数集(0, +∞),值域是实数集;自然对数函数的定义域是正实数集(0, +∞),值域是实数集。
2. 增减性常用对数函数和自然对数函数均是严格增函数,即当x1 < x2时,对数值logx1 < logx2。
3. 对数函数的图像常用对数函数和自然对数函数的图像均具有特殊的形状,且图像关于y轴对称。
二、指数函数的性质指数函数是以常数e为底的指数函数,以指数函数y = a^x为例进行说明。
指数函数的性质如下:1. 定义域与值域指数函数的定义域是实数集,值域是正实数集(0, +∞)。
2. 增减性指数函数a^x的增减性与指数a的大小有关。
当a > 1时,指数函数是增函数;当0 < a < 1时,指数函数是减函数。
3. 指数函数的图像指数函数的图像具有特殊的形状,与指数底a的大小有关。
当a > 1时,指数函数图像递增;当0 < a < 1时,指数函数图像递减。
三、对数与指数函数的运算性质对数与指数函数在运算中有一些重要的性质,包括以下几个方面:1. 对数的运算性质(1)对数的乘法性质:loga(M * N) = logaM + logaN,其中a为底数,M,N为正数。
(2)对数的除法性质:loga(M / N) = logaM - logaN。
(3)对数的幂运算性质:loga(M^p) = p * logaM,其中a为底数,M为正数,p为任意实数。
2. 指数的运算性质(1)指数的乘法性质:a^m * a^n = a^(m+n),其中a为底数,m,n 为实数。
高中数学2.2.2 对数函数及其性质(1)优秀课件

例 1 求下列函数的定义域:
(1)y=log3(1-x);(2)y=log12x;(3)y=log71-13x;
(4)y= log3x.
(3)由1-13x>0 1-3x≠0
,得 x<13;
∴所求函数定义域为x|x<13; (4)由lxo>g03x≥0 ,得xx>≥01 ; ∴x≥1,∴所求函数定义域为{x|x≥1}.
(2) y log0.7 x 在 (0, ) 上是减函数 ,
且 1.6 1.8, log0.7 1.6 log0.7 1.8 .
例 2:比较大小
(1) log2 3 , log2 3.5 (2)log0.71.6 ,log0.71.8 (3)log3 2 , log3.5 2 (4)log1.6 0.7 , log1.8 0.7
2.2.2 对数函数及其性质〔1〕
问题: 某种细胞分裂时,由1个分裂为2个,2个分为4 个,……,一个这样的细胞分裂x次后,得到的细胞的
个数 y 与 x 的函数关系是: y 2x .
现在我们来研究相反的问题.如果要求这种细胞 经过多少次分裂,大约可以得到1万个,10万个…… 细胞,那么,分裂次数 x 就是要得到的细胞个数 y
解:(3) 0 log 2 3 log2 3.5,
即 0 1 1 , log3 2 log3.5 2
log3 2 log3.5 2 . 法2: ∵ 3<3.5,2>1 , log3 2 log3.5 2 .
〔4〕 ∵ 1.6<1.8,0<0.7<1, log1.6 0.7 log1.8 0.7 .
y 2x .
x=log2y
思考:〔1〕为什么定义域为(0,+∞)? 〔2〕为什么规定底数a>0且a≠1呢? 〔3〕函数y=logax的值域是什么?
对数函数及其性质-对数的公式互化-详尽的讲解

2.1 对数与对数运算1.对数的概念一般地,如果a x=N (a >0,且a ≠1),那么数x 叫做以a 为底N 的对数,记作x =log a N ,其中a 叫做对数的底数,N 叫做真数.说明:(1)实质上,上述对数表达式,不过是指数函数y =a x的另一种表达形式,例如:34=81与4=log 381这两个式子表达是同一关系,因此,有关系式a x=N ⇔x =log a N ,从而得对数恒等式:a log a N =N .(2)“log ”同“+”“×”“ ”等符号一样,表示一种运算,即已知一个数和它的幂求指数的运算,这种运算叫对数运算,不过对数运算的符号写在数的前面.(3)根据对数的定义,对数log a N (a >0,且a ≠1)具有下列性质: ①零和负数没有对数,即N >0; ②1的对数为零,即log a 1=0; ③底的对数等于1,即log a a =1. 2.对数的运算法则利用对数的运算法则,可以把乘、除、乘方、开方的运算转化为对数的加、减、乘、除运算,反之亦然.这种运算的互化可简化计算方法,加快计算速度.(1)基本公式①log a (MN )=log a M +log a N (a >0,a ≠1,M >0,N >0),即正数的积的对数,等于同一底数的各个因数的对数的和.②log a MN=log a M -log a N (a >0,a ≠1,M >0,N >0),即两个正数的商的对数,等于被除数的对数减去除数的对数.③log a M n=n ·log a M (a >0,a ≠1,M >0,n ∈R ),即正数的幂的对数等于幂的底数的对数乘以幂指数.(2)对数的运算性质注意点①必须注意M >0,N >0,例如log a [(-3)×(-4)]是存在的,但是log a (-3)与log a (-4)均不存在,故不能写成log a [(-3)×(-4)]=log a (-3)+log a (-4).②防止出现以下错误:log a (M ±N )=log a M ±log a N ,log a (M ·N )=log a M ·log a N ,log a M N =log a Mlog a N,log a M n=(log a M )n .3.对数换底公式在实际应用中,常碰到底数不为10的对数,如何求这类对数,我们有下面的对数换底公式:log b N =log c Nlog c b(b >0,且b ≠1;c >0,且c ≠1;N >0).证明 设log b N =x ,则b x=N .两边取以c 为底的对数, 得x log c b =log c N .所以x =log c N log c b ,即log b N =log c Nlog c b.换底公式体现了对数运算中一种常用的转化,即将复杂的或未知的底数转化为已知的或需要的底数,这是数学转化思想的具体应用.由换底公式可推出下面两个常用公式: (1)log b N =1log N b或log b N ·log N b =1 (N >0,且N ≠1;b >0,且b ≠1); (2)log bn N m=m nlog b N (N >0;b >0,且b ≠1;n ≠0,m ∈R ).题型一 正确理解对数运算性质对于a >0且a ≠1,下列说法中,正确的是( )①若M =N ,则log a M =log a N ; ②若log a M =log a N ,则M =N ; ③若log a M 2=log a N 2,则M =N ; ④若M =N ,则log a M 2=log a N 2.A .①与③B .②与④C .②D .①、②、③、④解析 在①中,当M =N ≤0时,log a M 与log a N 均无意义,因此log a M =log a N 不成立. 在②中,当log a M =log a N 时,必有M >0,N >0,且M =N ,因此M =N 成立.在③中,当log a M 2=log a N 2时,有M ≠0,N ≠0,且M 2=N 2,即|M |=|N |,但未必有M =N .例如,M =2,N =-2时,也有log a M 2=log a N 2,但M ≠N .在④中,若M =N =0,则log a M 2与log a N 2均无意义,因此log a M 2=log a N 2不成立. 所以,只有②成立. 答案 C点评 正确理解对数运算性质公式,是利用对数运算性质公式解题的前提条件,使用运算性质时,应牢记公式的形式及公式成立的条件.题型二 对数运算性质的应用求下列各式的值:(1)2log 32-log 3329+log 38-5log 53;(2)lg25+23lg8+lg5·lg20+(lg2)2;(3)log 52·log 79log 513·log 734.分析 利用对数的性质求值,首先要明确解题目标是化异为同,先使各项底数相同,才能使用性质,再找真数间的联系,对于复杂的真数,可以先化简再计算.解 (1)原式=2log 32-(log 332-log 39)+3log 32-3 =2log 32-5log 32+2+3log 32-3=-1. (2)原式=2lg5+2lg2+lg 102·lg(2×10)+(lg2)2=2lg(5×2)+(1-lg2)·(lg2+1)+(lg2)2=2+1-(lg2)2+(lg2)2=3. (3)∵log 52·log 79log 513·log 734=12log 52·2log 73-log 53·13log 74=-lg2lg5·lg3lg7lg3lg5·13·lg4lg7=-32.点评 对数的求值方法一般有两种:一种是将式中真数的积、商、幂、方根利用对数的运算性质将它们化为对数的和、差、积、商,然后化简求值;另一种方法是将式中的和、差、积、商运用对数的运算法则将它们化为真数的积、商、幂、方根,然后化简求值.题型三 对数换底公式的应用计算:(log 2125+log 425+log 85)(log 52+log 254+log 1258).分析 由题目可获取以下主要信息:本题是一道对数化简求值题,在题目中各个对数的底数都各不相同.解答本题可先通过对数换底公式统一底数再进行化简求值. 解 方法一 原式=⎝ ⎛⎭⎪⎫log 253+log 225log 24+log 25log 28⎝ ⎛⎭⎪⎫log 52+log 54log 525+log 58log 5125 =⎝ ⎛⎭⎪⎫3log 25+2log 252log 22+log 253log 22⎝ ⎛⎭⎪⎫log 52+2log 522log 55+3log 523log 55 =⎝⎛⎭⎪⎫3+1+13log 25·(3log 52) =13log 25·log 22log 25=13.方法二 原式=⎝ ⎛⎭⎪⎫lg125lg2+lg25lg4+lg5lg8⎝ ⎛⎭⎪⎫lg2lg5+lg4lg25+lg8lg125=⎝ ⎛⎭⎪⎫3lg5lg2+2lg52lg2+lg53lg2⎝ ⎛⎭⎪⎫lg2lg5+2lg22lg5+3lg23lg5=⎝⎛⎭⎪⎫13lg53lg2⎝ ⎛⎭⎪⎫3lg2lg5=13.点评 方法一是先将括号内换底,然后再将底统一;方法二是在解题方向还不清楚的情况下,一次性地统一为常用对数(当然也可以换成其他非1的正数为底),然后再化简.上述方法是不同底数对数的计算、化简和恒等证明的常用方法.已知log (x +3)(x 2+3x )=1,求实数x 的值.错解 由对数的性质可得x 2+3x =x +3. 解得x =1或x =-3.错因分析 对数的底数和真数必须大于0且底数不等于1,这点在解题中忽略了.正解 由对数的性质知⎩⎪⎨⎪⎧x 2+3x =x +3,x 2+3x >0,x +3>0且x +3≠1.解得x =1,故实数x 的值为1.对数的定义及其性质是高考中的重要考点之一,主要性质有:log a 1=0,log a a =1,a log a N =N (a >0,且a ≠1,N >0).1.(上海高考)方程9x -6·3x-7=0的解是________. 解析 ∵9x-6·3x-7=0,即32x-6·3x-7=0 ∴(3x-7)(3x +1)=0 ∴3x=7或3x=-1(舍去) ∴x =log 37. 答案 log 372.(辽宁高考)设g (x )=⎩⎪⎨⎪⎧e x,x ≤0,ln x ,x >0,则g ⎝ ⎛⎭⎪⎫g ⎝ ⎛⎭⎪⎫12=____.解析 g ⎝ ⎛⎭⎪⎫12=ln 12<0,g ⎝ ⎛⎭⎪⎫ln 12=eln 12=12, ∴g ⎝ ⎛⎭⎪⎫g ⎝ ⎛⎭⎪⎫12=12. 答案 121.对数式log (a -3)(7-a )=b ,实数a 的取值范围是( )A .(-∞,7)B .(3,7)C .(3,4)∪(4,7)D .(3,+∞) 答案 C解析 由题意得⎩⎪⎨⎪⎧a -3>0,a -3≠1,7-a >0,解得3<a <7且a ≠4.2.设a =log 32,则log 38-2log 36用a 表示的形式是( ) A .a -2 B .3a -(1+a )2C .5a -2D .-a 2+3a -1 答案 A解析 ∵a =log 32,∴log 38-2log 36=3log 32-2(log 32+1) =3a -2(a +1)=a -2.3.log 56·log 67·log 78·log 89·log 910的值为( ) A .1 B .lg5 C.1lg5D .1+lg2答案 C解析 原式=lg6lg5·lg7lg6·lg8lg7·lg9lg8·lg10lg9=lg10lg5=1lg5.4.已知log a (a 2+1)<log a 2a <0,则a 的取值范围是( )A .(0,1) B.⎝ ⎛⎭⎪⎫0,12 C.⎝ ⎛⎭⎪⎫12,1 D .(1,+∞) 答案 C解析 由题意,得⎩⎪⎨⎪⎧0<a <1,2a >1,∵a >0,a ≠1,log a (a 2+1)<log a 2a ,∴0<a <1.∴12<a <1.5.已知函数f (x )=a x -1+log a x (a >0,a ≠1)在[1,3]上最大值与最小值之和为a 2,则a的值为( )A .4 B.14 C .3 D.13答案 D6.若方程(lg x )2+(lg7+lg5)lg x +lg7·lg5=0的两根为α,β,则αβ等于( ) A .lg7·lg5 B .lg35 C .35 D.135答案 D解析 ∵lg α+lg β=-(lg7+lg5)=-lg35=lg 135∴α·β=135.7.已知f (log 2x )=x ,则f ⎝ ⎛⎭⎪⎫12=________. 答案2解析 令log 2x =12,则212=x ,∴f ⎝ ⎛⎭⎪⎫12=212= 2.8.log (2-1)(2+1)=________.答案 -1 解析 log 2-1(2+1)=log 2-1(2+1)(2-1)2-1=log (2-1)12-1=-1.9.已知lg2=0.301 0,lg3=0.477 1,lg x =-2+0.778 1,则x =________. 答案 0.06解析 ∵lg2=0.301 0,lg3=0.477 1,而0.301 0+0.477 1=0.778 1,∴lg x =-2+lg2+lg3, 即lg x =lg10-2+lg6.∴lg x =lg(6×10-2),即x =6×10-2=0.06.10.(1)已知lg x +lg y =2lg(x -2y ),求log 2xy的值; (2)已知log 189=a,18b=5,试用a ,b 表示log 365. 解 (1)lg x +lg y =2lg(x -2y ), ∴xy =(x -2y )2,即x 2-5xy +4y 2=0. 即(x -y )(x -4y )=0,解得x =y 或x =4y ,又∵⎩⎪⎨⎪⎧x >0,y >0,x -2y >0,∴x >2y >0,∴x =y ,应舍去,取x =4y . 则log 2xy=log 24y y =log 24=lg4lg 2=4. (2)∵18b=5,∴log 185=b, 又∵log 189=a , ∴log 365=log 185lg 1836=blog 18(18×2)=b 1+log 182=b1+log 18189=b 1+(1-log 189)=b2-a.11.设a ,b ,c 均为不等于1的正数,且a x =b y =c z,1x +1y +1z=0,求abc 的值.解 令a x =b y =c z=t (t >0且t ≠1), 则有1x =log t a ,1y =log t b ,1z=log t c ,又1x +1y +1z=0,∴log t abc =0,∴abc =1.12.已知a ,b ,c 是△ABC 的三边,且关于x 的方程x 2-2x +lg(c 2-b 2)-2lg a +1=0有等根,试判定△ABC 的形状.解 ∵关于x 的方程x 2-2x +lg(c 2-b 2)-2lg a +1=0有等根,∴Δ=0,即4-4[lg(c2-b2)-2lg a+1]=0.即lg(c2-b2)-2lg a=0,故c2-b2=a2,∴a2+b2=c2,∴△ABC为直角三角形.2.2.1 对数与对数运算(一)学习目标1.理解对数的概念,能进行指数式与对数式的互化.2.了解常用对数与自然对数的意义.3.理解对数恒等式并能用于有关对数的计算.自学导引1.如果a(a>0且a≠1)的b次幂等于N,就是a b=N,那么数b叫做以a为底N的对数,记作b=log a N,其中a叫做对数的底数,N叫做真数.2.对数的性质有:(1)1的对数为零;(2)底的对数为1;(3)零和负数没有对数.3.通常将以10为底的对数叫做常用对数,以e为底的对数叫做自然对数,log10N可简记为lg N,log e N简记为ln N.4.若a>0,且a≠1,则a b=N等价于log a N=b.5.对数恒等式:a log a N=N(a>0且a≠1).一、对数式有意义的条件例1 求下列各式中x的取值范围:(1)log2(x-10);(2)log(x-1)(x+2);(3)log(x+1)(x-1)2.分析由真数大于零,底数大于零且不等于1可得到关于x的不等式(组),解之即可.解 (1)由题意有x -10>0,∴x >10,即为所求. (2)由题意有⎩⎪⎨⎪⎧ x +2>0,x -1>0且x -1≠1,即⎩⎪⎨⎪⎧x >-2,x >1且x ≠2,∴x >1且x ≠2.(3)由题意有⎩⎪⎨⎪⎧(x -1)2>0,x +1>0且x +1≠1,解得x >-1且x ≠0,x ≠1.点评 在解决与对数有关的问题时,一定要注意:对数真数大于零,对数的底数大于零且不等于1.变式迁移1 在b =log (a -2)(5-a )中,实数a 的取值范围是( ) A .a >5或a <2 B .2<a <5 C .2<a <3或3<a <5 D .3<a <4 答案 C解析 由题意得⎩⎪⎨⎪⎧5-a >0a -2>0a -2≠1,∴2<a <5且a ≠3.二、对数式与指数式的互化例2 将下列对数形式化成指数形式或将指数形式转化为对数形式: (1)54=625; (2)log 128=-3;(3)⎝ ⎛⎭⎪⎫14-2=16; (4)log 101 000=3. 分析 利用a x=N ⇔x =log a N 进行互化. 解 (1)∵54=625,∴log 5625=4. (2)∵log 128=-3,∴⎝ ⎛⎭⎪⎫12-3=8.(3)∵⎝ ⎛⎭⎪⎫14-2=16,∴log 1416=-2.(4)∵log 101 000=3,∴103=1 000.点评 指数和对数运算是一对互逆运算,在解题过程中,互相转化是解决相关问题的重要途径.在利用a x=N ⇔x =log a N 进行互化时,要分清各字母分别在指数式和对数式中的位置.变式迁移2 将下列对数式化为指数式求x 值: (1)log x 27=32; (2)log 2x =-23;(3)log 5(log 2x )=0; (4)x =log 2719;(5)x =log 1216.解 (1)由log x 27=32,得x 32=27,∴x =2723=32=9.(2)由log 2x =-23,得2-23=x ,∴x =1322=322.(3)由log 5(log 2x )=0,得log 2x =1,∴x =21=2. (4)由x =log 2719,得27x =19,即33x =3-2,∴x =-23.(5)由x =log 1216,得⎝ ⎛⎭⎪⎫12x =16,即2-x =24,∴x =-4.三、对数恒等式的应用例3 (1)a log a b ·log b c ·log c N 的值(a ,b ,c ∈R +,且不等于1,N >0); (2)412(log 29-log 25).解 (1)原式=(a log a b )log b c ·log c N =b log b c ·log c N =(b log b c )log c N =c log c N =N .(2)原式=2(log 29-log 25)=2log 292log 25=95. 点评 对数恒等式a log a N =N 中要注意格式:(1)它们是同底的;(2)指数中含有对数形式;(3)其值为真数.变式迁移3 计算:3log 35+(3)log 315.解 原式=5+312log 315=5+(3log 315)12=5+15=655.1.一般地,如果a (a >0,a ≠1)的b 次幂等于N ,就是a b=N ,那么b 叫做以a 为底N 的对数,记作log a N =b ,其中a 叫做对数的底数,N 叫做真数.2.利用a b=N ⇔b =log a N (其中a >0,a ≠1,N >0)可以进行指数与对数式的互化. 3.对数恒等式:a log a N =N (a >0且a ≠1).一、选择题1.下列指数式与对数式互化不正确的一组是( ) A .100=1与lg1=0 B .27-13=13与log 2713=-13C .log 312=9与912=3D .log 55=1与51=5 答案 C2.指数式b 6=a (b >0,b ≠1)所对应的对数式是( )A .log 6a =aB .log 6b =aC .log a b =6D .log b a =6 答案 D3.若log x (5-2)=-1,则x 的值为( ) A.5-2 B.5+2C.5-2或5+2 D .2- 5 答案 B4.如果f (10x)=x ,则f (3)等于( ) A .log 310 B .lg3 C .103D .310答案 B解析 方法一 令10x=t ,则x =lg t , ∴f (t )=lg t ,f (3)=lg3.方法二 令10x=3,则x =lg3,∴f (3)=lg3. 5.21+12·log 25的值等于( )A .2+ 5B .2 5C .2+52 D .1+52答案 B解析 21+12log 25=2×212log 25=2×2log 2512=2×512=2 5.二、填空题6.若5lg x=25,则x 的值为________. 答案 100解析 ∵5lg x=52,∴lg x =2,∴x =102=100. 7.设log a 2=m ,log a 3=n ,则a 2m +n的值为________.答案 12解析 ∵log a 2=m ,log a 3=n ,∴a m =2,a n=3, ∴a2m +n=a 2m ·a n =(a m )2·a n =22×3=12.8.已知lg6≈0.778 2,则102.778 2≈________.答案 600 解析 102.778 2≈102×10lg6=600.三、解答题9.求下列各式中x 的值 (1)若log 3⎝⎛⎭⎪⎫1-2x 9=1,则求x 值;(2)若log 2 003(x 2-1)=0,则求x 值. 解 (1)∵log 3⎝⎛⎭⎪⎫1-2x 9=1,∴1-2x 9=3∴1-2x =27,即x =-13(2)∵log 2 003(x 2-1)=0 ∴x 2-1=1,即x 2=2 ∴x =± 210.求x 的值:(1)x =log224;(2)x =log 93;(3)x =71-log 75; (4)log x 8=-3;(5)log 12x =4.解 (1)由已知得:⎝⎛⎭⎪⎫22x=4, ∴2-12x =22,-x 2=2,x =-4.(2)由已知得:9x =3,即32x=312.∴2x =12,x =14.(3)x =7÷7log 75=7÷5=75.(4)由已知得:x -3=8, 即⎝ ⎛⎭⎪⎫1x 3=23,1x =2,x =12.(5)由已知得:x =⎝ ⎛⎭⎪⎫124=116.2.2.1 对数与对数运算(二)学习目标1.掌握对数的运算性质及其推导.2.能运用对数运算性质进行化简、求值和证明.自学导引1.对数的运算性质:如果a >0,a ≠1,M >0,N >0,那么, (1)log a (MN )=log a M +log a N ; (2)log a M N=log a M -log a N ; (3)log a M n=n log a M (n ∈R ). 2.对数换底公式:log a b =log c blog c a.一、正确理解对数运算性质例1 若a >0,a ≠1,x >0,y >0,x >y ,下列式子中正确的个数有( ) ①log a x · log a y =log a (x +y ); ②log a x -log a y =log a (x -y ); ③log a x y=log a x ÷log a y ; ④log a (xy )=log a x ·log a y .A .0个B .1个C .2个D .3个 答案 A解析 对数的运算实质是把积、商、幂的对数运算分别转化为对数的加、减、乘的运算.在运算中要注意不能把对数的符号当作表示数的字母参与运算,如log a x ≠log a ·x ,log a x 是不可分开的一个整体.四个选项都把对数符号当作字母参与运算,因而都是错误的.点评 正确理解对数运算性质公式,是利用对数运算性质公式解题的前提条件. 变式迁移1 若a >0且a ≠1,x >0,n ∈N *,则下列各式正确的是( ) A .log a x =-log a 1xB .(log a x )n=n log a xC .(log a x )n =log a x nD .log a x =log a 1x答案 A二、对数运算性质的应用例2 计算:(1)log 535-2log 573+log 57-log 51.8;(2)2(lg 2)2+lg 2·lg5+(lg 2)2-lg2+1; (3)lg 27+lg8-lg 1 000lg1.2;(4)(lg5)2+lg2·lg50.分析 利用对数运算性质计算.解 (1)原式=log 5(5×7)-2(log 57-log 53)+log 57-log 595=log 55+log 57-2log 57+2log 53+log 57-2log 53+log 55 =2log 55=2.(2)原式=lg 2(2lg 2+lg5)+(lg 2-1)2=lg 2(lg2+lg5)+1-lg 2=lg 2+1-lg 2=1. (3)原式=32lg3+3lg2-32lg3+2lg2-1=3lg3+6lg2-32(lg3+2lg2-1)=32.(4)原式=(lg5)2+lg2·(lg2+2lg5)=(lg5)2+2lg5·lg2+(lg2)2=(lg5+lg2)2=1.点评 要灵活运用有关公式.注意公式的正用、逆用及变形使用. 变式迁移2 求下列各式的值: (1)log 535+2log 122-log 5150-log 514;(2)[(1-log 63)2+log 62·log 618]÷log 64. 解 (1)原式=log 5(5×7)-2log 2212+log 5(52×2)-log 5(2×7)=1+log 57-1+2+log 52-log 52-log 57=2. (2)原式=[log 262+log 62·log 6(3×6)]÷log 622=log 62(log 62+log 63+1)÷(2log 62)=1.三、换底公式的应用例3 (1)设3x =4y=36,求2x +1y的值;(2)已知log 189=a,18b=5,求log 3645. 解 (1)由已知分别求出x 和y . ∵3x=36,4y=36, ∴x =log 336,y =log 436,由换底公式得:x =log 3636log 363=1log 363,y =log 3636log 364=1log 364, ∴1x =log 363,1y=log 364,∴2x +1y=2log 363+log 364=log 36(32×4)=log 3636=1.(2)∵log 189=a,18b=5,∴log 185=b . ∴log 3645=log 1845log 1836=log 18(9×5)log 18(18×2)=log 189+log 1851+log 182=a +b 1+log 18189=a +b2-a.点评 指数式化为对数式后,两对数式的底不同,但式子两端取倒数后,利用对数的换底公式可将差异消除.变式迁移3 (1)设log 34·log 48·log 8m =log 416,求m ; (2)已知log 1227=a ,求log 616的值. 解 (1)利用换底公式,得lg4lg3·lg8lg4·lg mlg8=2,∴lg m =2lg3,于是m =9.(2)由log 1227=a ,得3lg32lg2+lg3=a ,∴lg3=2a lg23-a ,∴lg3lg2=2a3-a .∴log 616=4lg2lg3+lg2=42a3-a +1=4(3-a )3+a.1.对于同底的对数的化简常用方法是:(1)“收”,将同底的两对数的和(差)化成积(商)的对数; (2)“拆”,将积(商)的对数拆成对数的和(差).2.对于常用对数的化简要充分利用“lg5+lg2=1”来解题.3.对于多重对数符号对数的化简,应从内向外逐层化简求值.一、选择题1.lg8+3lg5的值为( )A .-3B .-1C .1D .3 答案 D解析 lg8+3lg5=lg8+lg53=lg1 000=3. 2.已知lg2=a ,lg3=b ,则log 36等于( ) A.a +b a B.a +bb C.a a +bD.ba +b答案 B解析 log 36=lg6lg3=lg2+lg3lg3=a +b b.3.若lg a ,lg b 是方程2x 2-4x +1=0的两个根,则⎝ ⎛⎭⎪⎫lg a b 2的值等于( )A .2 B.12 C .4 D.14答案 A解析 由根与系数的关系,得lg a +lg b =2,lg a ·lg b =12,∴⎝ ⎛⎭⎪⎫lg a b 2=(lg a -lg b )2=(lg a +lg b )2-4lg a ·lg b =22-4×12=2.4.若2.5x =1 000,0.25y=1 000,则1x -1y等于( )A.13 B .3 C .-13 D .-3 答案 A解析 由指数式转化为对数式:x =log 2.51 000,y =log 0.251 000,则1x -1y =log 1 0002.5-log 1 0000.25=log 1 00010=13. 5.设函数f (x )=log a x (a >0,且a ≠1),若f (x 1x 2…x 2 005)=8,则f (x 21)+f (x 22)+…+f (x 22 005)的值等于( )A .4B .8C .16D .2log a 8 答案 C解析 因为f (x )=log a x ,f (x 1x 2…x 2 005)=8, 所以f (x 21)+f (x 22)+…+f (x 22 005) =log a x 21+log a x 22+…+log a x 22 005=2log a |x 1|+2log a |x 2|+…+2log a |x 2 005| =2log a |x 1x 2…x 2 005| =2f (x 1x 2…x 2 005)=2×8=16. 二、填空题6.设lg2=a ,lg3=b ,那么lg 1.8=__________. 答案a +2b -12解析 lg 1.8=12lg1.8=12lg 1810=12lg 2×910=12(lg2+lg9-1)=12(a +2b -1). 7.若log a x =2,log b x =3,log c x =6,则log abc x 的值为____. 答案 1解析 log abc x =1log x abc =1log x a +log x b +log x c∵log a x =2,log b x =3,log c x =6 ∴log x a =12,log x b =13,log x c =16,∴log abc x =112+13+16=11=1.8.已知log 63=0.613 1,log 6x =0.386 9,则x =________. 答案 2解析 由log 63+log 6x =0.613 1+0.386 9=1. 得log 6(3x )=1.故3x =6,x =2. 三、解答题9.求下列各式的值:(1)12lg 3249-43lg 8+lg 245; (2)(lg5)2+2lg2-(lg2)2.解 (1)方法一 原式=12(5lg2-2lg7)-43·32lg2+12(2lg7+lg5) =52lg2-lg7-2lg2+lg7+12lg5 =12lg2+12lg5=12(lg2+lg5) =12lg10=12. 方法二 原式=lg 427-lg4+lg7 5=lg 42×757×4=lg(2·5)=lg 10=12.(2)方法一 原式=(lg5+lg2)(lg5-lg2)+2lg2 =lg10·lg 52+lg4=lg ⎝ ⎛⎭⎪⎫52×4=lg10=1. 方法二 原式=(lg10-lg2)2+2lg2-lg 22 =1-2lg2+lg 22+2lg2-lg 22=1. 10.若26a =33b =62c,求证:1a +2b =3c.证明 设26a =33b =62c=k (k >0),那么⎩⎪⎨⎪⎧6a =log 2k ,3b =log 3k ,2c =log 6k ,∴⎩⎪⎨⎪⎧1a =6log 2k=6log k 2,1b =3log 3k =3log k3,1c =2log 6k =2log k6.∴1a +2b=6·log k 2+2×3log k 3=log k (26×36)=6log k 6=3×2log k 6=3c,即1a+2b=3c.2.2.2 对数函数及其性质1.对数函数的概念形如y=log a x (a>0且a≠1)的函数叫做对数函数.对于对数函数定义的理解,要注意:(1)对数函数是由指数函数变化而来的,由指数式与对数式关系知,对数函数的自变量x恰好是指数函数的函数值y,所以对数函数的定义域是(0,+∞);(2)对数函数的解析式y=log a x中,log a x前面的系数为1,自变量在真数的位置,底数a必须满足a>0,且a≠1;(3)以10为底的对数函数为y=lg x,以e为底的对数函数为y=ln x.2.对数函数的图象及性质:3.指数函数与对数函数的关系比较m (1)当(m -1)(n -1)>0,即m 、n 范围相同(相对于“1”而言),则log m n >0;(2)当(m -1)(n -1)<0,即m 、n 范围相反(相对于“1”而言),则log m n <0.有了这个规律,我们再判断对数值的正负就很简单了,如log 213<0,log 52>0等,一眼就看出来了!题型一 求函数定义域求下列函数的定义域:(1)y =log 3x -12x +3x -1; (2)y =11-log a (x +a )(a >0,a ≠1).分析 定义域即使函数解析式有意义的x 的范围.解 (1)要使函数有意义,必须{ 2x +3>0,x -1>0,3x -1>0,3x -1≠1同时成立,解得⎩⎨⎧x >-32,x >1,x >13,x ≠23.∴x >1.∴定义域为(1,+∞).(2)要使原函数有意义,需1-log a (x +a )>0, 即log a (x +a )<1=log a a .当a >1时,0<x +a <a ,∴-a <x <0. 当0<a <1时,x +a >a ,∴x >0.∴当a >1时,原函数定义域为{x |-a <x <0}; 当0<a <1时,原函数定义域为{x |x >0}.点评 求与对数函数有关的定义域问题,首先要考虑:真数大于零,底数大于零且不等于1,若分母中含有x ,还要考虑不能使分母为零.题型二 对数单调性的应用(1)log 43,log 34,log 4334的大小顺序为( )A .log 34<log 43<log 4334B .log 34>log 43>log 4334C .log 34>log 4334>log 43D .log 4334>log 34>log 43(2)若a 2>b >a >1,试比较log a a b ,log b b a,log b a ,log a b 的大小. (1)解析 ∵log 34>1,0<log 43<1, log 4334=log 43⎝ ⎛⎭⎪⎫43-1=-1, ∴log 34>log 43>log 4334.答案 B(2)解 ∵b >a >1,∴0<a b<1.∴log a ab <0,log b b a∈(0,1),log b a ∈(0,1). 又a >b a >1,且b >1,∴log b b a<log b a , 故有log a a b <log b b a<log b a <log a b .点评 比较对数的大小,一般遵循以下几条原则:①如果两对数的底数相同,则由对数函数的单调性(底数a >1为增;0<a <1为减)比较. ②如果两对数的底数和真数均不相同,通常引入中间变量进行比较.③如果两对数的底数不同而真数相同,如y =log a 1x 与y =log a 2x 的比较(a 1>0,a 1≠1,a 2>0,a 2≠1).当a 1>a 2>1时,曲线y 1比y 2的图象(在第一象限内)上升得慢.即当x >1时,y 1<y 2;当0<x <1时,y 1>y 2.而在第一象限内,图象越靠近x 轴对数函数的底数越大.当0<a 2<a 1<1时,曲线y 1比y 2的图象(在第四象限内)下降得快.即当x >1时,y 1<y 2;当0<x <1时,y 1>y 2即在第四象限内,图象越靠近x 轴的对数函数的底数越小.已知log a 12<1,那么a 的取值范围是________.分析 利用函数单调性或利用数形结合求解.解析 由log a 12<1=log a a ,得当a >1时,显然符合上述不等式,∴a >1;当0<a <1时,a <12,∴0<a <12.故a >1或0<a <12.答案 a >1或0<a <12点评 解含有对数符号的不等式时,必须注意对数的底数是大于1还是小于1,然后再利用相应的对数函数的单调性进行解答.理解会用以下几个结论很有必要:(1)当a >1时,log a x >0⇔x >1,log a x <0⇔0<x <1; (2)当0<a <1时,log a x >0⇔0<x <1,log a x <0⇔x >1.题型三 函数图象的应用若不等式2x-log a x <0,当x ∈⎝ ⎛⎭⎪⎫0,12时恒成立,求实数a 的取值范围.解要使不等式2x<logax 在x ∈⎪⎭⎫ ⎝⎛21,0时恒成立,即函数y=logax 的图象在⎪⎭⎫ ⎝⎛21,0内恒在函数y=2x 图象的上方,而y=2x 图象过点⎪⎭⎫⎝⎛2,21.由图可知,loga 21>2,显然这里0<a<1,∴函数y=logax 递减.又loga21>2=log 2a a ,∴a2>21,即a>2221⎪⎭⎫ ⎝⎛.∴所求的a 的取值范围为2221⎪⎭⎫ ⎝⎛<a<1.点评 原问题等价于当x ∈⎪⎭⎫ ⎝⎛21,0时,y1=2x 的图象在y2=logax 的图象的下方,由于a的大小不确定,当a>1时,显然y2<y1,因此a 必为小于1的正数,当y2的图象通过点⎪⎭⎫⎝⎛2,21时,y2满足条件,此时a 0=2221⎪⎭⎫⎝⎛.那么a 是大于a 0还是小于a 0才满足呢?可以画图象观察,请试着画一画.这样可以对数形结合的方法有更好地掌握.设函数f (x )=lg(ax 2+2x +1),若f (x )的值域是R ,求实数a 的取值范围.错解 ∵f (x )的值域是R , ∴ax 2+2x +1>0对x ∈R 恒成立, 即{ a >0<0⇔{ a >04-4a <0⇔a >1.错因分析 出错的原因是分不清定义域为R 与值域为R 的区别. 正解 函数f (x )=lg(ax 2+2x +1)的值域是R ⇔真数t =ax 2+2x +1能取到所有的正数.当a =0时,只要x >-12,即可使真数t 取到所有的正数,符合要求;当a ≠0时,必须有{ a >00⇔{ a >04-4a ≥0⇔0<a ≤1.∴f (x )的值域为R 时,实数a 的取值范围为[0,1].本节内容在高考中考查的形式、地位与指数函数相似,着重考查对数的概念与对数函数的单调性,考查指数、对数函数的图象、性质及其应用.1.(广东高考)已知函数f (x )=11-x 的定义域为M ,g (x )=ln(1+x )的定义域为N ,则M ∩N 等于( )A .{x |x >-1}B .{x |x <1}C .{x |-1<x <1}D .∅解析 由题意知M ={x |x <1},N ={x |x >-1}. 故M ∩N ={x |-1<x <1}. 答案 C2.(湖南高考)下列不等式成立的是( ) A .log 32<log 23<log 25 B .log 32<log 25<log 23 C .log 23<log 32<log 25 D .log 23<log 25<log 32解析 ∵y =log 2x 在(0,+∞)上是增函数, ∴log 25>log 23>log 22=1.又y =log 3x 在(0,+∞)上为增函数, ∴log 32<log 33=1.∴log 32<log 23<log 25. 答案 A3.(全国高考)若x ∈(e -1,1),a =ln x ,b =2ln x ,c =ln 3x ,则( )A .a <b <cB .c <a <bC .b <a <cD .b <c <a解析 ∵1e <x <1,∴-1<ln x <0.令t =ln x ,则-1<t <0. ∴a -b =t -2t =-t >0.∴a >b .c -a =t 3-t =t (t 2-1)=t (t +1)(t -1),又∵-1<t <0,∴0<t +1<1,-2<t -1<-1,∴c -a >0,∴c >a . ∴c >a >b .1.已知函数f (x )=1+2x 的定义域为集合M ,g (x )=ln(1-x )的定义域为集合N ,则M ∩N 等于( )A .{x |x >-1}B .{x |x <1}C.⎩⎨⎧⎭⎬⎫x |-12<x <1 D .∅答案 C2.已知函数f (x )=lg 1-x 1+x ,若f (a )=12,则f (-a )等于( )A.12 B .-12 C .-2 D .2 答案 B解析 f (-a )=lg 1+a 1-a =-lg ⎝ ⎛⎭⎪⎫1+a 1-a -1 =-lg 1-a 1+a =-f (a )=-12.3.已知a =log 23,b =log 32,c =log 42,则a ,b ,c 的大小关系是( ) A .c <b <a B .a <b <c C .b <c <a D .c <a <b 答案 A解析 因为a =log 23>1,b =log 3 2<1,所以a >b ; 又因为2>3,则log 32>log 33=12,而log 42=log 22=12,所以b >12,c =12,即b >c .从而a >b >c .4.函数f (x )=lg|x |为( )A .奇函数,在区间(0,+∞)上是减函数B .奇函数,在区间(0,+∞)上是增函数C .偶函数,在区间(-∞,0)上是增函数D .偶函数,在区间(-∞,0)上是减函数解析 已知函数定义域为(-∞,0)∪(0,+∞),关于坐标原点对称,且f (-x )=lg|-x |=lg|x |=f (x ),所以它是偶函数.又当x >0时,|x |=x ,即函数y =lg|x |在区间(0,+∞)上是增函数. 又f (x )为偶函数,所以f (x )=lg|x |在区间(-∞,0)上是减函数.5.函数y =a x与y =-log a x (a >0,且a ≠1)在同一坐标系中的图象只可能为( )答案 A解析 方法一 若0<a <1,则曲线y =a x下降且过(0,1),而曲线y =-log a x 上升且过(1,0);若a >1,则曲线y =a x上升且过(0,1),而曲线y =-log a x 下降且过(1,0).只有选项A 满足条件.方法二 注意到y =-log a x 的图象关于x 轴对称的图象的表达式为y =log a x ,又y =log a x 与y =a x互为反函数(图象关于直线y =x 对称),则可直接选定选项A.6.设函数f (x )=log 2a (x +1),若对于区间(-1,0)内的每一个x 值都有f (x )>0,则实数a 的取值范围为( )A .(0,+∞) B.⎝ ⎛⎭⎪⎫12,+∞ C.⎝ ⎛⎭⎪⎫12,1 D.⎝ ⎛⎭⎪⎫0,12答案 D解析 已知-1<x <0,则0<x +1<1,又当-1<x <0时,都有f (x )>0,即0<x +1<1时都有f (x )>0,所以0<2a <1,即0<a <12.7.若指数函数f (x )=a x(x ∈R )的部分对应值如下表:则不等式log a (x -1)<0答案 {x |1<x <2}解析 由题可知a =1.2,∴log 1.2(x -1)<0, ∴log 1.2(x -1)<log 1.21,解得x <2, 又∵x -1>0,即x >1,∴1<x <2. 故原不等式的解集为{x |1<x <2}.8.函数y =log a x (1≤x ≤2)的值域为[-1,0],那么a 的值为________. 答案 12解析 若a >1,则函数y =log a x 在区间[1,2]上为增函数,其值域不可能为[-1,0]; 故0<a <1,此时当x =2时,y 取最小值-1, 即log a 2=-1,得a -1=2,所以a =12.9.已知函数f (x )=⎩⎪⎨⎪⎧(3a -1)x +4a ,x <1log a x ,x ≥1是实数集R 上的减函数,那么实数a 的取值范围为__________.答案 ⎣⎢⎡⎭⎪⎫17,13解析 函数f (x )为实数集R 上的减函数, 一方面,0<a <1且3a -1<0,所以0<a <13,另一方面,由于f (x )在R 上为减函数, 因此应有(3a -1)×1+4a ≥log a 1,即a ≥17.因此满足题意的实数a 的取值范围为17≤a <13.10.已知f (x )=1+log 2x (1≤x ≤4),求函数g (x )=f 2(x )+f (x 2)的最大值和最小值. 解 ∵f (x )的定义域为[1,4], ∴g (x )的定义域为[1,2].∵g (x )=f 2(x )+f (x 2)=(1+log 2x )2+(1+log 2x 2) =(log 2x +2)2-2, 又1≤x ≤2,∴0≤log 2x ≤1. ∴当x =1时,g (x )min =2;当x =2时,g (x )max =7.学习目标1.掌握对数函数的概念、图象和性质.2.能够根据指数函数的图象和性质得出对数函数的图象和性质,把握指数函数与对数函数关系的实质.自学导引1.对数函数的定义:一般地,我们把函数y=log a x(a>0,且a≠1)叫做对数函数,其中x是自变量,函数的定义域是(0,+∞).2.对数函数的图象与性质对数函数y =log a x (a >0且a ≠1)和指数函数y =a x_(a >0且a ≠1)互为反函数.一、对数函数的图象例1 下图是对数函数y =log a x 的图象,已知a 值取3,43,35,110,则图象C 1,C 2,C 3,C 4相应的a 值依次是( )A.101,53,34,3B .53,101,34,3 C .101,53,3,34 D .53,101,3,34 答案 A解析 方法一 因为对数的底数越大,函数的图象越远离y 轴的正方向,所以C1,C2,C3,C4的a 值依次由大到小,即C1,C2,C3,C4的a 值依次为101,53,34,3. 方法二过(0,1)作平行于x 轴的直线,与C1,C2,C3,C4的交点的横坐标为(a1,1),(a2,1),(a3,1),(a4,1),其中a1,a2,a3,a4分别为各对数的底,显然a1>a2>a3>a4,所以C1,C2,C3,C4的底值依次由大到小.点评 函数y=logax (a>0,且a ≠1)的底数a 的变化对图象位置的影响如下:①上下比较:在直线x=1的右侧,底数大于1时,底数越大,图象越靠近x 轴;底数大于0且小于1时,底数越小,图象越靠近x 轴.②左右比较:(比较图象与y=1的交点)交点的横坐标越大,对应的对数函数的底数越大. 变式迁移1 借助图象比较m ,n 的大小关系:(1)若logm5>logn5,则m n ;(2)若logm0.5>logn0.5,则m n.答案 (1)< (2)>二、求函数的定义域例2 求下列函数的定义域:(1)y =3log 2x ;(2)y =log 0.5(4x -3);(3)y =log (x +1)(2-x ).分析 定义域即使函数解析式有意义的x 的范围.解 (1)∵该函数是奇次根式,要使函数有意义,只要对数的真数是正数即可,∴定义域是{x |x >0}.(2)要使函数y =log 0.5(4x -3)有意义,必须log 0.5(4x -3)≥0=log 0.51,∴0<4x -3≤1.解得34<x ≤1. ∴定义域是⎩⎨⎧⎭⎬⎫x |34<x ≤1. (3)由⎩⎪⎨⎪⎧ x +1>0x +1≠12-x >0,得⎩⎪⎨⎪⎧ x >-1x ≠0,x <2即0<x <2或-1<x <0,所求定义域为(-1,0)∪(0,2).点评 求与对数函数有关的函数定义域时,除遵循前面已学习过的求函数定义域的方法外,还要对这种函数自身有如下要求:一是要特别注意真数大于零;二是要注意对数的底数;三是按底数的取值应用单调性,有针对性的解不等式.变式迁移2 求y =log a (4x -3)(a >0,a ≠1)的定义域.解 log a (4x -3)≥0.(*)当a >1时,(*)可化为log a (4x -3)≥log a 1,∴4x -3≥1,x ≥1.当0<a <1时,(*)可化为log a (4x -3)≥log a 1,∴0<4x -3≤1,34<x ≤1. 综上所述,当a >1时,函数定义域为[1,+∞),当0<a <1时,函数定义域为⎝ ⎛⎦⎥⎤34,1.三、对数函数单调性的应用例3 比较大小:(1)log 0.81.5与log 0.82;(2)log 35与log 64.分析 从比较底数、真数是否相同入手.解 (1)考查对数函数y =log 0.8x 在(0,+∞)内是减函数,∵1.5<2,∴log 0.81.5>log 0.82.(2)log 35和log 64的底数和真数都不相同,找出中间量“搭桥”,再利用对数函数的单调性,即可求解.∵log 35>log 33=1=log 66>log 64,∴log 35>log 64.点评 比较两个对数值的大小,常用方法有:①底数相同真数不同时,用函数的单调性来比较;②底数不同而真数相同时,常借助图象比较,也可用换底公式转化为同底数的对数后比较;③底数与真数都不同,需寻求中间值比较.变式迁移3 比较下列各组中两个值的大小:(1)log 0.52.7,log 0.52.8; (2)log 34,log 65;(3)log a π,log a e (a >0且a ≠1).解 (1)∵0<0.5<1,∴对数函数y =log 0.5x 在(0,+∞)上是减函数.又∵2.7<2.8,∴log 0.52.7>log 0.52.8.(2)∵y =log 3x 在(0,+∞)上是增函数,∴log 34>log 33=1.∵y =log 6x 在(0,+∞)上是增函数,∴log 65<log 66=1.∴log 34>log 65.(3)当a >1时,y =log a x 在(0,+∞)上是增函数.∵π>e ,∴log a π>log a e.当0<a <1时,y =log a x 在(0,+∞)上是减函数.∵π>e ,∴log a π<log a e.综上可知,当a >1时,log a π>log a e ;当0<a <1时,log a π<log a e.例4 若-1<log a 34<1,求a 的取值范围. 分析 此不等式为对数不等式且底数为参数.解答本题可根据对数函数的单调性转化为一般不等式求解,同时应注意分类讨论.解 -1<log a 34<1⇔log a 1a <log a 34<log a a . 当a >1时,1a <34<a ,∴a >43. 当0<a <1时,1a >34>a ,∴0<a <34. ∴a 的取值范围是⎝ ⎛⎭⎪⎫0,34∪⎝ ⎛⎭⎪⎫43,+∞. 点评 (1)解对数不等式问题通常转化为不等式组求解,其依据是对数函数的单调性.(2)解决与对数函数相关的问题时要遵循“定义域优先”原则.(3)若含有字母,应考虑分类讨论.变式迁移4 已知log a (2a +1)<log a 3a <0,求a 的取值范围.解 log a (2a +1)<log a 3a <0(*)当a >1时,(*)可化为⎩⎪⎨⎪⎧ 0<2a +1<10<3a <12a +1<3a ,解得⎩⎪⎨⎪⎧ -12<a <00<a <13a >1,∴此时a 无解.当0<a <1时,(*)可化为⎩⎪⎨⎪⎧ 2a +1>13a >12a +1>3a,解得⎩⎪⎨⎪⎧ a >0a >13a <1,∴13<a <1. 综上所述,a 的取值范围为⎝ ⎛⎭⎪⎫13,1.1.求对数函数定义域要注意底数中是否含有自变量,此时底数大于0且不等于1.2.应用对数函数的图象和性质时要注意a >1还是0<a <1。
2.2.2对数函数及其性质(1)

2.2.2 对数函数及其性质(1)一、目标:1.理解对数函数的概念,体会对数函数是一类重要的函数模型;2.能用画出具体对数函数的简图;3.掌握对数函数的性质并会应用;4.在学习过程中体会研究具体函数及其性质的过程与方法,如具体到一般的过程、数形结合的方法等。
二、重点:对数函数的定义、图象和性质。
三、难点:底数a 对对数函数性质的影响,不同底数的对数比较大小。
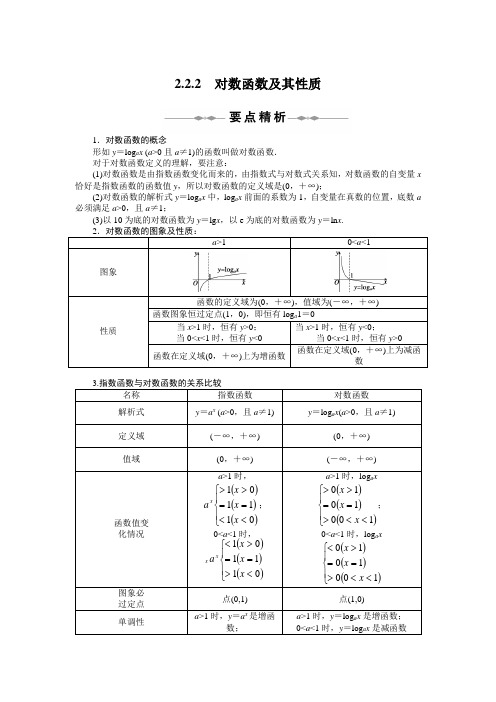
四、教学过程 1.引入用清水漂洗衣服,若每次能洗去污垢的43,写出存留污垢x 表示的漂洗次数y 的关系式,请根据关系式计算,若要使存留的污垢不超过原有的641,则至少要漂洗几次?x y 41log =2.对数函数的定义“你能否根据上面的函数解析式,给出一个一般性的概念?” “对于式子x y 41log =,如果用字母a 替代41,这就是一般性的结论.”即对数函数的定义:(板书)一般地,函数)1,0(log ≠=a a x y a 且 叫做对数函数。
思考:(1)为什么对数函数的概念中明确规定1,0≠a a ?根据对数与指数式的关系,知x y a log =可化为x a y =,有指数的概念,要使x a y =有意义,必须规定0 a ,1≠a .(2)对数函数的定义域、值域分别是什么?因为x y a log =可化为x a y =,不管y 取怎样的值,有指数函数的性质0 y a ,所以),0(+∞∈x ,对数函数的值域为R .(3)如何根据对数函数的定义判断一个函数是否为一个对数函数?1 a10 a)1(log +=x y a ,x y a log 2=,1log +=x y a 是不是对数函数?只有形如..),1,0(log o x a a x y a ≠=且对函数才叫对数函数.像)1(log +=x y a ,x y a log 2=,1log +=x y a 等函数,它们是由对数函数变化(平移、伸缩)而得到的,都不是对数函数.例1 求下列函数的定义域:(1)2log x y a =; (2))4(log x y a -=; (3))9(log 2x y a -=; (4))54(log 2--=x x y a . 变式练习:求下列函数的定义域:(1)3)4(lg )(--=x x x f a ; (2))32(log 2)1(++-=-x x y x .3.对数函数的图象与性质“回忆:前面我们学习指数函数的时候,根据什么思路研究指数函数的性质?”“根据图象研究函数的性质,从具体到一般,考虑函数的定义域、值域、是否过定点、单调性、奇偶性.”(板书)请在同一坐标系中作出函数x y 2log =与x y 3log =的图象.(板书) 思考:(1)x y 2log =与)(log log 221x x y -==的图象有什么关系?x y 3log =与)(log log 331x x y -==的图象又有什么关系?请在刚才的坐标系中作出函数x y 21log =与x y 31log =的图象.(2)根据刚才作出的4个函数图象,你认为对数函数的图象可分成几类?你的分类依据是什么?(板书)(3)根据上述两类图象的特点,你能归纳出对数函数的性质吗? (板书)(4)x y 2log =与x y 3log =的图象的区别在哪? x y 21log =与x y 31log =的图象区别在哪?x y 3log =的图象比x y 2log =的图象更靠近x 轴; x y 31log =的图象比x y 21log =的图象更靠近x 轴.即:“顺时针方向,底数越大”. 3.例题与练习:例2 比较下列各组数中两个值的大小:(1)4.3log 2,5.8log 2; (2)8.1log 3.0,7.2log 3.0;(3)1.5log a ,9.5log a (0 a ,且1≠a ). 变式练习:1.3log 4,4log 3,43log 34的大小顺序为 .2.已知121log a,那么a 的取值范围是 . 例3 求下列函数的值域:(1))4(log 22+=x y ; (2))23(log 221x x y -+=.例4 函数)1,0(2)1(log ≠-+=a a x y a 的图象恒过定点 . 例5 溶液酸碱度的测量.溶液酸碱度是通过pH 刻画的. pH 的计算公式为]lg[+-=H pH ,其中][+H 表示溶液中氢离子的浓度,单位是摩尔/升.(1)根据对数函数性质及上述pH 的计算公式,说明溶液酸碱度与溶液中氢离子的浓度之间的变化关系;(2)已知纯净水中氢离子的浓度为710][-+=H 摩尔/升,计算纯净水的pH . 4.小结:(1)对数函数的定义;(2)对数函数的图像与性质. 5.作业:1.课本P74习题2.2 第7题. 2.课本P74习题2.2 第8题.3.设1 a ,函数x x f a log )(=在区间]2,[a a 上的最大值与最小值之差为21,求a .4.求函数)32(log )(221++=x x x f 的值域.。
复2.2.2对数函数及其性质(1)

y =l 1 x og
2
x 0.5 1 2 4 6 8 12 16 y 1 0 -1 -2 -2.45 -3 -3.46 -4
y = log 2 x 和 y = log 1 x的图象: 的图象:
y
8 7 6 5 4 3 2 1 -1 -2 -3
2
y=log2x =
-3 -2 -10 1 2 3 4 5 6 7 8 x
5.9(a> ⑶loga5.1,loga5.9(a>0,a≠1)
(0,+∞)上是增函数 上是增函数, 解:当a>1时,函数y=log ax在(0,+∞)上是增函数, 函数y=log 于是 5.1< log a5.1<log a5.9 函数y=log (0,+∞)上是减函 当0<a<1时,函数y=log ax在(0,+∞)上是减函 数,于是 5.1> log a5.1>log a5.9
复习回顾: 复习回顾:函数 y = ax ( a > 0, 且 a ≠ 1 )
叫做指数函数,其中x是自变量. 指数函数 叫做指数函数,其中x是自变量.函数的定义域是 R.
图 象
y=1
a > 1
y y=1
(0,1)Biblioteka 0 < a < 1
y
(0,1)
0
x
0
x
定 义 域 : R 值 域 : (0 ,+∞) 过点(0,1) x=0 时,y = 1. (0,1),即x=0 (0,1) y
x,因为它的底数 因为它的底数2 解 ⑴考察对数函数 y = log 2x,因为它的底数2>1, 所以它在(0,+∞)上是增函数, (0,+∞)上是增函数 所以它在(0,+∞)上是增函数,于是 3.4< log 23.4<log 28.5 x,因为它的底数为 因为它的底数为0.3, ⑵考察对数函数 y = log 0.3 x,因为它的底数为0.3, 0.3<1,所以它在(0,+∞)上是减函数 所以它在(0,+∞)上是减函数, 即0<0.3<1,所以它在(0,+∞)上是减函数,于是 1.8> log 0.31.8>log 0.32.7
对数函数及其性质(1)(精)

对数函数及其性质(1)一、教材分析本小节选自《普通高中课程标准数学教科书-数学必修(一)》(人教版)第二章基本初等函数(1)2.2.2对数函数及其性质(第一课时),主要内容是学习对数函数的定义、图象、性质及初步应用。
对数函数是继指数函数之后的又一个重要初等函数,无论从知识或思想方法的角度对数函数与指数函数都有许多类似之处。
与指数函数相比,对数函数所涉及的知识更丰富、方法更灵活,能力要求也更高。
学习对数函数是对指数函数知识和方法的巩固、深化和提高,也为解决函数综合问题及其在实际上的应用奠定良好的基础。
虽然这个内容十分熟悉,但新教材做了一定的改动,如何设计能够符合新课标理念,是人们十分关注的,正因如此,本人选择这课题立求某些方面有所突破。
二、学生学习情况分析刚从初中升入高一的学生,仍保留着初中生许多学习特点,能力发展正处于形象思维向抽象思维转折阶段,但更注重形象思维。
由于函数概念十分抽象,又以对数运算为基础,同时,初中函数教学要求降低,初中生运算能力有所下降,这双重问题增加了对数函数教学的难度。
教师必须认识到这一点,教学中要控制要求的拔高,关注学习过程。
三、设计理念本节课以建构主义基本理论为指导,以新课标基本理念为依据进行设计的,针对学生的学习背景,对数函数的教学首先要挖掘其知识背景贴近学生实际,其次,激发学生的学习热情,把学习的主动权交给学生,为他们提供自主探究、合作交流的机会,确实改变学生的学习方式。
四、教学目标1.通过具体实例,直观了解对数函数模型所刻画的数量关系,初步理解对数函数的概念,体会对数函数是一类重要的函数模型;2.能借助计算器或计算机画出具体对数函数的图象,探索并了解对数函数的单调性与特殊点;3.通过比较、对照的方法,引导学生结合图象类比指数函数,探索研究对数函数的性质,培养学生运用函数的观点解决实际问题。
五、教学重点与难点重点是掌握对数函数的图象和性质,难点是底数对对数函数值变化的影响.六、教学过程设计教学流程:背景材料→引出课题→函数图象→函数性质→问题解决→归纳小结(一)熟悉背景、引入课题1.让学生看材料:材料1(幻灯):马王堆女尸千年不腐之谜:一九七二年,马王堆考古发现震惊世界,专家发掘西汉辛追遗尸时,形体完整,全身润泽,皮肤仍有弹性,关节还可以活动,骨质比现在六十岁的正常人还好,是世界上发现的首例历史悠久的湿尸。
2.2.2对数函数及其性质(1)

0, 2
二、基础知识讲解
2、对数函数y loga x a 0, 且a 1的图像和性质
用描点法在同一个直角坐标系中作出下列函数 的图像
y log 2 x; y log 1 x
2
(1)列表
x y=log2x
2
y log 1 x
0.5 1 -1 0 1 0
2 1
4 2
(2)指数函数的值域是什么? 0,
二、基础知识讲解 1、对数函数的定义
一般的,函数 y loga x a 0, 且a 1 叫做对数函数。
其中x是自变量,定义域是
0,
随练:下列函数是对数函数的是(
( A) y log 2 3 x 2 ( B ) y log( x 1) x
三、举例应用
例1、求下列函数的定义域:
(1) y log a x ;
2
2 解: 要使函数有意义,则须有 x 0
即:x 0 2 y log a x 的定义域为 x | x 0
(2) y loga 4 x ;
解:要使函数有意义,则须有 4 x 0
解之得:x 4 函数y loga 4 x 的定义域是 x | x 4
(C ) y log 1 x
3 2
D)
( D) y ln x
三、举例应用
例1、求下列函数的定义域:
(1) y log a x ;
2
(2) y loga 4 x ;
(3) y log x 1 16 4 x .
分析:应用对数函数定义中的条件解决问题。
y loga x a 0, 且a 1 , x 0,
课件10:2.2.2 对数函数及其性质 第一课时

∴x>23且 x≠1.
故原函数的定义域为xx>23且x≠1 .
1.求下列函数的定义域:
(1)y= lg2-x;
(2)y=log331x-2.
解:(1)由题意,得 lg(2-x)≥0,即 2-x≥1,所以 x≤1,
则 y= lg2-x的定义域为{x|x≤1}.
(2)由l3oxg-332x>-0,2≠0, 得33xx- >22,≠1, 解得 x>23且 x≠1. 所以 y=log331x-2的定义域为xx>23且x≠1 .
题型二 对数函数的图象 【例2】 已知a>0且a≠1,函数y=ax与y=loga(-x)的图象 可能是下图中的( )
思路点拨:利用对数函数的图象与性质求解.
解析:首先,曲线y=ax只可能在上半平面,y=loga(-x) 只可能在左半平面,从而排除A,D.
其次,从单调性着眼,y=ax与y=loga(-x)的增减性正好 相反,又可排除C.∴应选B.
2.2 对数函数
2.2.2 对数函数及其性质
第1课时 对数函数的图ห้องสมุดไป่ตู้及性质
自学导引
1.对数函数的定义:一般地,我们把函数y=logax(a>0且 a≠1)叫做__对__数__函__数___,其中x是自变量,函数的定义域是(0, +∞).
2.对数函数的图象与性质:
定义
y=logax(a>0,且 a≠1)
2.对数函数单调性等重要性质要借助图象来理解与掌握. 3.掌握对数函数不但要清楚对数函数自身的图象和性质, 还要结合指数函数的图象和性质来对比掌握.
本节内容结束 更多精彩内容请登录:
因为 0<x<3,所以 3x(3-x)=-3x-322+247∈0,247,
对数函数及其性质(1)

. . . O . . .
2 1 4 2 8 3
y log 2 x
.
x
y log 1 x
2
练习 教材P.73练习第1题 画出函数 y log 3 x 及 y log 1 x 的图象,并且说明这两个函数的相 同点和不同点.
y
3
y log 3 x
O
y log 1 x
3
x
y
y log 2 x
(2) y log0.2 (4 x 3)
练习
已知函数f(x)= log2x,x>0 1 x ,则 f(f(4))的值是( 3 ,x≤0
A.9 1 B.9 C.-9
) 1 D.-9
(2)(lg2)2+lg2lg5+lg5=________.
[答案] (1)B (2)1
1.函数 f ( x) lg( x 1) 4 x 的定义域为( A.(1,4] B.(1,4) C.[1,4]
且 3 3.5,
log2 3 log2 3.5 .
(2) y log0.7 x 在 (0, ) 上是减函数,
且 1.6 1.8, log0.7 1.6 log0.7 1.8 .
例 2:比较大小
(1) log2 3 , log2 3.5 (3) log3 2 , log3.5 2 (2) log0.7 1.6 , log0.7 1.8 (4) log1.6 0.7 , log1.8 0.7
【点拨】 一个函数为对数函数的条件是: ①系数为1;②底数为大于0且不等于1的常数; ③真数为单个自变量.
2. 对数函数的图象: 用描点法作 y log 2 x 与 y log 1 x 的图象.
对数函数的基本性质与公式

对数函数的基本性质与公式对数函数是数学中一种重要的函数形式,其基本性质和公式在解决各种问题中具有广泛应用。
本文将介绍对数函数的基本性质和常见的公式,帮助读者更好地理解和应用对数函数。
一、对数函数的定义和性质对数函数的定义如下:对于任意给定的正实数a(a>0且a≠1)和正实数x(x>0),以a为底的对数函数y=loga(x)表示满足a^y=x的实数y。
其中,a称为底数,x称为真数,y为对数。
对数函数具有以下基本性质:1. 对于任意正实数a和b,以a为底的对数函数和以b为底的对数函数是等价的,即loga(x)=ln(x)/ln(a)(其中ln(x)表示以自然数e为底的对数函数)。
2. 对于任意正实数a,a^loga(x)=x。
3. 对于任意正实数a和b,loga(b)×logb(a)=1。
4. 对于任意正实数a、b和c,loga(b×c)=loga(b)+loga(c)。
二、常见对数函数公式1. 换底公式:loga(b)=logc(b)/logc(a),其中a、b、c为任意正实数。
2. 对数乘方公式:a^loga(x)=x,其中a为正实数,x为正实数且x≠0。
3. 对数运算公式:loga(b×c)=loga(b)+loga(c),其中a为正实数,b、c为正实数且b≠0,c≠0。
4. 对数倒数公式:loga(1/b)=-loga(b),其中a为正实数,b为正实数且b≠0。
5. 对数除法公式:loga(b/c)=loga(b)-loga(c),其中a为正实数,b、c 为正实数且b≠0,c≠0。
6. 对数幂公式:loga(b^n)=n×loga(b),其中a为正实数,b为正实数且b≠0,n为任意实数。
三、对数函数在实际问题中的应用对数函数的公式和性质在各个领域中有着广泛的应用。
以下是一些实际应用的例子:1. 在金融领域,对数函数的性质被用于计算复利问题,如投资收益率和贷款利率的计算。
对数函数及其性质

2.2.2 对数函数及其性质1.对数函数的概念(1)定义:一般地,我们把函数y =log a x (a >0,且a ≠1)叫做对数函数,其中x 是自变量,函数的定义域是(0,+∞).(2)对数函数的特征:特征⎩⎪⎨⎪⎧log a x 的系数:1log a x 的底数:常数,且是不等于1的正实数log a x 的真数:仅是自变量x判断一个函数是否为对数函数,只需看此函数是否具备了对数函数的特征.比如函数y =log 7x 是对数函数,而函数y =-3log 4x 和y =log x 2均不是对数函数,其原因是不符合对数函数解析式的特点.【例1-1】函数f (x )=(a 2-a +1)log (a +1)x 是对数函数,则实数a =__________. 解析:由a 2-a +1=1,解得a =0,1. 又a +1>0,且a +1≠1,∴a =1. 答案:1【例1-2】下列函数中是对数函数的为__________.(1)y =log(a >0,且a ≠1);(2)y =log 2x +2; (3)y =8log 2(x +1);(4)y =log x 6(x >0,且x ≠1); (5)y =log 6x . 解析:答案:2.对数函数y =log a x (a >0,且a ≠1)的图象与性质 (1)底数.a >1时,函数单调递增;0<a <1时,函数单调递减.理解和掌握对数函数的图象和性质的关键是会画对数函数的图象,在掌握图象的基础上性质就容易理解了.我们要注意数形结合思想的应用.(2)指数函数与对数函数的性质比较(3)①底数a 与1的大小关系决定了对数函数图象的“升降”:当a >1时,对数函数的图象“上升”;当0<a <1时,对数函数的图象“下降”.②底数的大小决定了图象相对位置的高低:不论是a >1还是0<a <1,在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大.点技巧 对数函数图象的记忆口诀 两支喇叭花手中拿,(1,0)点处把花扎,若是底数小于1,左上穿点渐右下, 若是底数大于1,左下穿点渐右上, 绕点旋转底变化,顺时方向底变大, 可用直线y =1来切,自左到右a 变大.【例2】如图所示的曲线是对数函数y =log a x 的图象.已知a ,43,35,110中取值,则相应曲线C 1,C 2,C 3,C 4的a 值依次为( )A .,43,35,110B ,43,110,35C .43,35,110D .43,110,35解析:由底数对对数函数图象的影响这一性质可知,C 4的底数<C 3的底数<C 2的底数<C 1的底数.故相应于曲线C 1,C 2,C 3,C 443,35,110. 答案:A点技巧 根据图象判断对数函数的底数大小的方法 (1)方法一:利用底数对对数函数图象影响的规律:在x 轴上方“底大图右”,在x 轴下方“底大图左”;(2)方法二:作直线y =1,它与各曲线的交点的横坐标就是各对数的底数,由此判断各底数的大小.3.反函数(1)对数函数的反函数指数函数y =a x (a >0,且a ≠1)与对数函数y =log a x (a >0,且a ≠1)互为反函数. (2)互为反函数的两个函数之间的关系①原函数的定义域、值域是其反函数的值域、定义域; ②互为反函数的两个函数的图象关于直线y =x 对称. (3)求已知函数的反函数,一般步骤如下:①由y =f (x )解出x ,即用y 表示出x ; ②把x 替换为y ,y 替换为x ;③根据y =f (x )的值域,写出其反函数的定义域. 【例3-1】若函数y =f (x )是函数y =a x (a >0,且a ≠1)的反函数,且f (2)=1,则f (x )=( ) A .log 2x B .12x C .12log x D .2x -2解析:因为函数y =a x (a >0,且a ≠1)的反函数是f (x )=log a x , 又f (2)=1,即log a 2=1,所以a =2.故f (x )=log 2x . 答案:A【例3-2】函数f (x )=3x (0<x ≤2)的反函数的定义域为( ) A .(0,+∞) B .(1,9]C .(0,1)D .[9,+∞) 解析:∵ 0<x ≤2,∴1<3x ≤9, 即函数f (x )的值域为(1,9].故函数f (x )的反函数的定义域为(1,9]. 答案:B【例3-3】若函数y =f (x )的反函数图象过点(1,5),则函数y =f (x )的图象必过点( ) A .(5,1) B .(1,5) C .(1,1) D .(5,5)解析:由于原函数与反函数的图象关于直线y =x 对称,而点(1,5)关于直线y =x 的对称点为(5,1),所以函数y =f (x )的图象必经过点(5,1).答案:A4.利用待定系数法求对数函数的解析式及函数值对数函数的解析式y =log a x (a >0,且a ≠1)中仅含有一个常数a ,则只需要一个条件即可确定对数函数的解析式,这样的条件往往是已知f (m )=n 或图象过点(m ,n )等等.通常利用待定系数法求解,设出对数函数的解析式f (x )=log a x (a >0,且a ≠1),利用已知条件列方程求出常数a 的值.利用待定系数法求对数函数的解析式时,常常遇到解方程,比如log a m =n ,这时先把对数式log a m =n 化为指数式的形式a n =m ,把m 化为以n 为指数的指数幂形式m =k n (k >0,且k ≠1),则解得a =k >0.还可以直接写出1n am =,再利用指数幂的运算性质化简1nm .例如:解方程log a 4=-2,则a -2=4,由于2142-⎛⎫= ⎪⎝⎭,所以12a =±.又a >0,所以12a =.当然,也可以直接写出124a -=,再利用指数幂的运算性质,得11212214(2)22a ---====.【例4-1】已知f (e x )=x ,则f (5)=( )A .e 5B .5eC .ln 5D .log 5e解析:(方法一)令t =e x ,则x =ln t ,所以f (t )=ln t ,即f (x )=ln x . 所以f (5)=ln 5.(方法二)令e x =5,则x =ln 5,所以f (5)=ln 5. 答案:C【例4-2】已知对数函数f (x )的图象经过点1,29⎛⎫⎪⎝⎭,试求f (3)的值. 分析:设出函数f (x )的解析式,利用待定系数法即可求出. 解:设f (x )=log a x (a >0,且a ≠1),∵对数函数f (x )的图象经过点1,29⎛⎫⎪⎝⎭,∴11log 299a f ⎛⎫== ⎪⎝⎭.∴a 2=19.∴a =11222111933⎡⎤⎛⎫⎛⎫==⎢⎥⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦.∴f (x )=13log x . ∴f (3)=111331log 3log 3-⎛⎫= ⎪⎝⎭=-1.【例4-3】已知对数函数f (x )的反函数的图象过点(2,9),且f (b )=12,试求b 的值. 解:设f (x )=log a x (a >0,且a ≠1),则它的反函数为y =a x (a >0,且a ≠1),由条件知a 2=9=32,从而a =3.于是f (x )=log 3x ,则f (b )=log 3b =12,解得b=123=5.对数型函数的定义域的求解 (1)对数函数的定义域为(0,+∞).(2)在求对数型函数的定义域时,要考虑到真数大于0,底数大于0,且不等于1.若底数和真数中都含有变量,或式子中含有分式、根式等,在解答问题时需要保证各个方面都有意义.一般地,判断类似于y =log a f (x )的定义域时,应首先保证f (x )>0.(3)求函数的定义域应满足以下原则: ①分式中分母不等于零;②偶次根式中被开方数大于或等于零; ③指数为零的幂的底数不等于零; ④对数的底数大于零且不等于1;⑤对数的真数大于零,如果在一个函数中数条并存,求交集. 【例5】求下列函数的定义域.(1)y =log(1-x );(2)y =log (2x -1)(5x -4);(3)y=.分析:利用对数函数y =log a x (a >0,且a ≠1)的定义求解. 解:(1)要使函数有意义,则1-x >0,解得x <1, 所以函数y =log 5(1-x )的定义域是{x |x <1}.(2)要使函数有意义,则54>0,21>0,211,x x x -⎧⎪-⎨⎪-≠⎩解得x >45且x ≠1,所以函数y =log (2x -1)(5x -4)的定义域是4,15⎛⎫⎪⎝⎭(1,+∞).(3)要使函数有意义,则0.5430,log (43)0,x x ->⎧⎨-≥⎩解得34<x ≤1,所以函数y =的定义域是3<14x x ⎧⎫≤⎨⎬⎩⎭.6.对数型函数的值域的求解(1)充分利用函数的单调性和图象是求函数值域的常用方法.(2)对于形如y =log a f (x )(a >0,且a ≠1)的复合函数,其值域的求解步骤如下: ①分解成y =log a u ,u =f (x )这两个函数; ②求f (x )的定义域; ③求u 的取值范围;④利用y =log a u 的单调性求解.(3)对于函数y =f (log a x )(a >0,且a ≠1),可利用换元法,设log a x =t ,则函数f (t )(t ∈R )的值域就是函数f (log a x )(a >0,且a ≠1)的值域.注意:(1)若对数函数的底数是含字母的代数式(或单独一个字母),要考查其单调性,就必须对底数进行分类讨论.(2)求对数函数的值域时,一定要注意定义域对它的影响.当对数函数中含有参数时,有时需讨论参数的取值范围.【例6-1】求下列函数的值域:(1)y =log 2(x 2+4);(2)y =212log (32)x x +-.解:(1)∵x 2+4≥4,∴log 2(x 2+4)≥log 24=2. ∴函数y =log 2(x 2+4)的值域为[2,+∞).(2)设u =3+2x -x 2,则u =-(x -1)2+4≤4.∵u >0,∴0<u ≤4. 又y =12log u 在(0,+∞)上为减函数,∴12log u ≥-2.∴函数y =212log (32)x x +-的值域为[-2,+∞).【例6-2】已知f (x )=2+log 3x ,x ∈[1,3],求y =[f (x )]2+f (x 2)的最大值及相应的x 的值. 分析:先确定y =[f (x )]2+f (x 2)的定义域,然后转化成关于log 3x 的一个一元二次函数,利用一元二次函数求最值.解:∵f (x )=2+log 3x ,x ∈[1,3],∴y =[f (x )]2+f (x 2)=(log 3x )2+6log 3x +6且定义域为[1,3]. 令t =log 3x (x ∈[1,3]).∵t =log 3x 在区间[1,3]上是增函数,∴0≤t ≤1.从而要求y =[f (x )]2+f (x 2)在区间[1,3]上的最大值,只需求y =t 2+6t +6在区间[0,1]上的最大值即可.∵y =t 2+6t +6在[-3,+∞)上是增函数,∴当t =1,即x =3时,y max =1+6+6=13.综上可知,当x =3时,y =[f (x )]2+f (x 2)的最大值为13. 7.对数函数的图象变换及定点问题(1)与对数函数有关的函数图象过定点问题对数函数y =log a x (a >0,且a ≠1)过定点(1,0),即对任意的a >0,且a ≠1都有log a 1=0.这是解决与对数函数有关的函数图象问题的关键.对于函数y =b +k log a f (x )(k ,b 均为常数,且k ≠0),令f (x )=1,解方程得x =m ,则该函数恒过定点(m ,b ).方程f (x )=0的解的个数等于该函数图象恒过定点的个数.(2)对数函数的图象变换的问题①函数y =log a x (a >0,且a ≠1)――----------------→向左(b >0)或向右(b <0)平移|b |个单位长度函数y =log a (x +b )(a >0,且a ≠1) ②函数y =log a x (a >0,且a ≠1)――---------------→向上(b >0)或向下(b <0)平移|b |个单位长度函数y =log a x +b (a >0,且a ≠1) ③函数y =log a x (a >0,且a ≠1)―----------------―→当x >0时,两函数图象相同当x <0时,将x >0时的图象关于y 轴对称函数y =log a |x |(a >0,且a ≠1)④函数y =log a x (a >0,且a ≠1)――----------------------------------------→保留x 轴上方的图象同时将x 轴下方的图象作关于x 轴的对称变换函数y =|log a x |(a >0,且a ≠1)【例7-1】若函数y =log a (x +b )+c (a >0,且a ≠1)的图象恒过定点(3,2),则实数b ,c 的值分别为__________.解析:∵函数的图象恒过定点(3,2),∴将(3,2)代入y =log a (x +b )+c (a >0,且a ≠1),得2=log a (3+b )+c . 又∵当a >0,且a ≠1时,log a 1=0恒成立, ∴c =2.∴log a (3+b )=0. ∴b =-2. 答案:-2,2【例7-2】作出函数y =|log 2(x +1)|+2的图象. 解:(第一步)作函数y =log 2x 的图象,如图①;(第二步)将函数y =log 2x 的图象沿x 轴向左平移1个单位长度,得函数y =log 2(x +1)的图象,如图②;(第三步)将函数y=log2(x+1)在x轴下方的图象作关于x轴的对称变换,得函数y=|log2(x+1)|的图象,如图③;(第四步)将函数y=|log2(x+1)|的图象,沿y轴方向向上平移2个单位长度,便得到所求函数的图象,如图④.8.利用对数函数的单调性比较大小两个对数式的大小比较有以下几种情况:(1)底数相同,真数不同.比较同底数(是具体的数值)的对数大小,构造对数函数,利用对数函数的单调性比较大小.要注意:明确所给的两个值是哪个对数函数的两个函数值;明确对数函数的底数与1的大小关系;最后根据对数函数的单调性判断大小.(2)底数不同,真数相同.若对数式的底数不同而真数相同时,可以利用顺时针方向底数增大画出函数的图象,再进行比较,也可以先用换底公式化为同底后,再进行比较.(3)底数不同,真数也不同.对数式的底数不同且指数也不同时,常借助中间量0,1进行比较.(4)对于多个对数式的大小比较,应先根据每个数的结构特征,以及它们与“0”和“1”的大小情况,进行分组,再比较各组内的数值的大小即可.注意:对于含有参数的两个对数值的大小比较,要注意对底数是否大于1进行分类讨论.【例8-1】比较下列各组中两个值的大小.(1)log31.9,log32;(2)log23,log0.32;(3)log aπ,log a3.141.分析:(1)构造函数y=log3x,利用其单调性比较;(2)分别比较与0的大小;(3)分类讨论底数的取值范围.解:(1)因为函数y=log3x在(0,+∞)上是增函数,所以f(1.9)<f(2).所以log31.9<log32.(2)因为log23>log21=0,log0.32<log0.31=0,所以log23>log0.32.(3)当a>1时,函数y=log a x在定义域上是增函数,则有log aπ>log a3.141;当0<a<1时,函数y=log a x在定义域上是减函数,则有log aπ<log a3.141.综上所得,当a>1时,log aπ>log a3.141;当0<a<1时,log aπ<log a3.141.【例8-2】若a2>b>a>1,试比较log a ab,log bba,log b a,log a b的大小.分析:利用对数函数的单调性或图象进行判断.解:∵b >a >1,∴0<ab<1. ∴log aab<0,log a b >log a a =1,log b 1<log b a <log b b ,即0<log b a <1. 由于1<b a <b ,∴0<log b b a <1.由log b a -log b ba=2log b a b ,∵a 2>b >1,∴2a b>1.∴2log b a b >0,即log b a >log b b a.∴log a b >log b a >log b b a >log a ab.9.利用对数函数的单调性解对数不等式(1)根据对数函数的单调性,当a >0,且a ≠1时,有 ①log a f (x )=log a g (x )⇔f (x )=g (x )(f (x )>0,g (x )>0);②当a >1时,log a f (x )>log a g (x )⇔f (x )>g (x )(f (x )>0,g (x )>0); ③当0<a <1时,log a f (x )>log a g (x )⇔f (x )<g (x )(f (x )>0,g (x )>0). (2)常见的对数不等式有三种类型:①形如log a f (x )>log a g (x )的不等式,借助函数y =log a x 的单调性求解,如果a 的取值不确定,需分a >1与0<a <1两种情况讨论.②形如log a f (x )>b 的不等式,应将b 化为以a 为对数的对数式的形式,再借助函数y =log a x 的单调性求解.③形如log a f (x )>log b g (x )的不等式,基本方法是将不等式两边化为同底的两个对数值,利用对数函数的单调性来脱去对数符号,同时应保证真数大于零,取交集作为不等式的解集.④形如f (log a x )>0的不等式,可用换元法(令t =log a x ),先解f (t )>0,得到t 的取值范围.然后再解x 的范围.【例9-1】解下列不等式:(1)1177log log (4)x x >-;(2)log x (2x +1)>log x (3-x ).解:(1)由已知,得>0,4>0,<4,x x x x ⎧⎪-⎨⎪-⎩解得0<x <2.所以原不等式的解集是{x |0<x <2}.(2)当x >1时,有21>3,21>0,3>0,x x x x +-⎧⎪+⎨⎪-⎩解得1<x <3;当0<x <1时,有21<3,21>0,3>0,x x x x +-⎧⎪+⎨⎪-⎩解得0<x <23.所以原不等式的解集是20<<1<<33xx x ⎧⎫⎨⎬⎩⎭或.【例9-2】若22log 3a ⎛⎫ ⎪⎝⎭<1,求a 的取值范围.解:∵22log 3a ⎛⎫ ⎪⎝⎭<1,∴-1<2log 3a <1,即12log log log 3a a a a a <<.(1)∵当a >1时,y =log a x 为增函数,∴123a a <<.∴a >32,结合a >1,可知a >32. (2)∵当0<a <1时,y =log a x 为减函数,∴12>>3a a .∴a <23,结合0<a <1,知0<a <23.∴a 的取值范围是230<<>32a a a ⎧⎫⎨⎬⎩⎭,或.10.对数型函数单调性的讨论(1)解决与对数函数有关的函数的单调性问题的关键:一是看底数是否大于1,当底数未明确给出时,则应对底数a 是否大于1进行讨论;二是运用复合法来判断其单调性;三是注意其定义域.(2)关于形如y =log a f (x )一类函数的单调性,有以下结论:函数y =log a f (x )的单调性与函数u =f (x )(f (x )>0)的单调性,当a >1时相同,当0<a <1时相反.例如:求函数y =log 2(3-2x )的单调区间.分析:首先确定函数的定义域,函数y =log 2(3-2x )是由对数函数y =log 2u 和一次函数u =3-2x 复合而成,求其单调区间或值域时,应从函数u =3-2x 的单调性、值域入手,并结合函数y =log 2u 的单调性考虑.解:由3-2x >0,解得函数y =log 2(3-2x )的定义域是⎝⎛⎭⎫-∞,32. 设u =3-2x ,x ∈⎝⎛⎭⎫-∞,32, ∵u =3-2x 在⎝⎛⎭⎫-∞,32上是减函数,且y =log 2u 在(0,+∞)上单调递增, ∴函数y =log 2(3-2x )在⎝⎛⎭⎫-∞,32上是减函数. ∴函数y =log 2(3-2x )的单调减区间是⎝⎛⎭⎫-∞,32. 【例10-1】求函数y =log a (a -a x)的单调区间.解:(1)若a >1,则函数y =log a t 递增,且函数t =a -a x 递减. 又∵a -a x >0,即a x <a ,∴x <1.∴函数y =log a (a -a x )在(-∞,1)上递减.(2)若0<a <1,则函数y =log a t 递减,且函数t =a -a x 递增. 又∵a -a x >0,即a x <a ,∴x >1.∴函数y =log a (a -a x )在(1,+∞)上递减.综上所述,函数y =log a (a -a x )在其定义域上递减.析规律 判断函数y =log a f (x )的单调性的方法 函数y =log a f (x )可看成是y =log a u 与u =f (x )两个简单函数复合而成的,由复合函数单调性“同增异减”的规律即可判断.需特别注意的是,在求复合函数的单调性时,首先要考虑函数的定义域,即“定义域优先”.【例10-2】已知f (x )=12log (x 2-ax -a )在1,2⎛⎫-∞-⎪⎝⎭上是增函数,求a 的取值范围. 解:1,2⎛⎫-∞- ⎪⎝⎭是函数f (x )的递增区间,说明1,2⎛⎫-∞- ⎪⎝⎭是函数u =x 2-ax -a 的递减区间,由于是对数函数,还需保证真数大于0.令u (x )=x 2-ax -a ,∵f (x )=12log ()u x 在1,2⎛⎫-∞- ⎪⎝⎭上是增函数,∴u (x )在1,2⎛⎫-∞- ⎪⎝⎭上是减函数,且u (x )>0在1,2⎛⎫-∞- ⎪⎝⎭上恒成立.∴1,2210,2a u ⎧≥-⎪⎪⎨⎛⎫⎪-≥ ⎪⎪⎝⎭⎩即1,10.42a a a ≥-⎧⎪⎨+-≥⎪⎩∴-1≤a ≤12.∴满足条件的a 的取值范围是112a a ⎧⎫-≤≤⎨⎬⎩⎭.11.对数型函数的奇偶性问题判断与对数函数有关的函数奇偶性的步骤是:(1)求函数的定义域,当定义域关于原点不对称时,则此函数既不是奇函数也不是偶函数,当定义域关于原点对称时,判断f (-x )与f (x )或-f (x )是否相等;(2)当f (-x )=f (x )时,此函数是偶函数;当f (-x )=-f (x )时,此函数是奇函数; (3)当f (-x )=f (x )且f (-x )=-f (x )时,此函数既是奇函数又是偶函数;(4)当f (-x )≠f (x )且f (-x )≠-f (x )时,此函数既不是奇函数也不是偶函数.例如,判断函数f (x )=log )a x (x ∈R ,a >0,且a ≠1)的奇偶性. 解:∵f (-x )+f (x )==log )a x -+log )a x ) =log a (x 2+1-x 2)=log a 1=0,∴f (-x )=-f (x ).∴f (x )为奇函数. 【例11】已知函数f (x )=1log 1axx+-(a >0,且a ≠1). (1)求函数f (x )的定义域; (2)判断函数f (x )的奇偶性;(3)求使f (x )>0的x 的取值范围.分析:对于第(2)问,依据函数奇偶性的定义证明即可.对于第(3)问,利用函数的单调性去掉对数符号,解出不等式.解:(1)由11xx+->0,得-1<x <1, 故函数f (x )的定义域为(-1,1). (2)∵f (-x )=1log 1ax x -+=1log 1a xx+--=-f (x ), 又由(1)知函数f (x )的定义域关于原点对称,∴函数f (x )是奇函数. (3)当a >1时,由1log 1a x x +->0=log a 1,得11xx+->1,解得0<x <1; 当0<a <1时, 由1log 1ax x +->0=log a 1,得0<11xx+-<1,解得-1<x <0. 故当a >1时,x 的取值范围是{x |0<x <1};当0<a <1时,x 的取值范围是{x |-1<x <0}. 12.对数型函数模型的实际应用地震震级的变化规律、溶液pH的变化规律、航天问题等,可以用对数函数模型来研究.此类题目,通常给出函数解析式模型,但是解析式中含有其他字母参数.其解决步骤是:(1)审题:弄清题意,分清条件和结论,抓住关键的词和量,理顺数量关系;(2)建模:将文字语言转化成数学语言,利用数学知识,求出函数解析式模型中参数的值;(3)求模:求解函数模型,得到数学结论;(4)还原:将用数学方法得到的结论还原为实际问题的结论.由此看,直接给定参数待定的函数模型时,利用待定系数法的思想,代入已知的数据得到相关的方程而求得待定系数.一般求出函数模型后,还利用模型来研究一些其他问题.代入法、方程思想、对数运算性质,是解答此类问题的方法精髓.【例12】我国用长征二号F型运载火箭成功发射了“神舟”七号载人飞船,实现了中国历史上第一次的太空漫步,令中国成为世界上第三个有能力把人送上太空并进行太空漫步的国家(其中,翟志刚完全出舱,刘伯明的头部和手部部分出舱).在不考虑空气阻力的条件下,假设火箭的最大速度y(单位:km/s)关于燃料重量x(单位:吨)的函数关系式为y=k ln(m+x)-k)+4ln 2(k≠0),其中m是箭体、搭载的飞行器、航天员的重量和.当燃料重量为-1)m吨时,火箭的最大速度是4 km/s.(1)求y=f(x);(2)已知长征二号F型运载火箭的起飞重量是479.8吨(箭体、搭载的飞行器、航天员、燃料),火箭的最大速度为8 km/s,求装载的燃料重量(e=2.7,精确到0.1).解:(1)由题意得当x=-1)m时,y=4,则4=k ln[m+-1)m]-k)+4ln 2,解得k=8.所以y=8ln(m+x)-)+4ln 2,即y=8ln m x m+.(2)由于m+x=479.8,则m=479.8-x,令479.888ln479.8x=-,解得x≈302.1.故火箭装载的燃料重量约为302.1吨.。
2.2.2对数函数及其性质(一)

y
(a>1) (0<a<1)
象
O
x
O
x
定义域 R;值域(0,+∞)
性 过点(0,1),即x=0时,y=1
质 在 R 上是增函数
x>0时,ax>1;
在 R 上是减函数
x<0时,0<ax<1
第6页,共54页。
2. 指数函数的图象和性质
a>1
0<a<1
图
y
y=ax y=ax
y
(a>1) (0<a<1)
象
x<0时,0<ax<1 x<0时,ax>1
第12页,共54页。
3. 某种细胞分裂时,得到的细胞的个 数y是分裂次数x的函数,这个函数可
以用指数函数y=2x表示.
第13页,共54页。
3. 某种细胞分裂时,得到的细胞的个 数y是分裂次数x的函数,这个函数可 以用指数函数y=2x表示.
这种细胞经过多少次分裂,大约
讲授新课
1. 对数函数的定义: 函数y=logax (a>0且a≠1)叫做
对数函数,定义域为(0,+∞),
第20页,共54页。
讲授新课
1. 对数函数的定义:
函数y=logax (a>0且a≠1)叫做 对数函数,定义域为(0,+∞),
第21页,共54页。
讲授新课
1. 对数函数的定义: 函数y=logax (a>0且a≠1)叫做
第46页,共54页。
三、指数函数和对数函数的关系
• 在统一坐标系中作出下列函数的图象并思考它们之间有什么 关系?
• (1)
• (2)
y 2x 和y log2 x
y
1 x 2
和y
log 1
2
x
第47页,共54页。
对数函数的性质及运算法则

对数函数的性质及运算法则
数学中的对数函数是一个非常重要的函数,它以一组等式将指数函数和自然对数函数联系
起来。
对数函数满足多项式和幂函数的性质,在金融计算,物理学和化学中应用广泛。
对数函数的性质和运算概括如下:
1.复合性:给定任意实数x和t,有 log(x^t)=t*logx。
2.乘性:给定任意实数x,y,有log(xy)=logx+logy。
3.除法性:给定任意实数x,y,有log(x/y)=logx-logy。
4.反比性:给定任意实数x,y,有logy/logx=log(x/y)。
5.幂性:给定任意实数x,y,有logx^y=y*logx。
6.指数性:给定任意实数x,有e^logx=x。
上述性质可有效用来解决复杂的数学运算问题。
比如,解决2的3次方等于多少的问题,可以将对数函数的性质和运算应用到这一问题上,得出公式 log2^3=3*log2,故 2的3次
方等于8。
以上是对数函数的性质及运算法则的简单介绍,它包括多种基本性质和运算法则,以及扩
展到多种相关问题的应用。
正确理解和运用对数函数,可以有效解决复杂的数学运算问题。
人教A版数学必修一2.2.2对数函数及其性质运算(1)课件.pptx

练习2: 已知下列不等式,比较正数m,n的大小:
(1)log3m<log3n (2)log0.3m>log0.3n (3)logam<logan(0<a<1) (4)logam>logan(a>1)
答案:(1)m<n (3)m>n
(2)m<n (4)m>n
例2.比较下列各组中两个值的大小: (4) log67,log76; (5) log3π,log20.8.
函数 底数
a>1
y=logax(a>0且a≠1) 0<a<1
y
y
图象
o
1
x
1
o
x
定义域 值域 定点
值分布
趋势 单调性
(0,+∞)
R
(1,0)即x=1时,y=0
当x>1时,y>0 当0<x<1时,y<0
当x>1时,y<0 当0<x<1时,y>0
底数越大,图象越靠近x轴 底数越小,图象越靠近x轴
在(0,+∞)上是增函数
应为(). y=log2x
对数函数的定义:
一般地
函数y=logax(a>0,且a≠1)
叫做对数函数.其中x是自变量,函数 的定义域是(0,+∞).
对数函数图像的作法:
作对数图像的三个步骤:
一、列表(根据给定的自变量分别计算 出应变量的值)
二、描点(根据列表中的坐标分别在坐 标系中标出其对应点)
三、连线(将所描的点用平滑的曲线连 接起来)
log 3
(x),
x
0.
函数
y=logax(a>0且a≠1)
图像
定义域 值域
单调性
R+ R 增函数
2.2.2对数函数及其性质(一)

的大小,并利用函数图象给予几何解释 的大小,并利用函数图象给予几何解释.
小 结 1. 两个同底数的对数比较大小的一般 两个同底数 同底数的对数比较大小的一般 步骤: 步骤: 确定所要考查的对数函数; ①确定所要考查的对数函数; 根据对数底数判断对数函数增减性; ②根据对数底数判断对数函数增减性; 比较真数大小, ③比较真数大小,然后利用对数函数 的增减性判断两对数值的大小. 的增减性判断两对数值的大小. 2. 分类讨论的思想. 分类讨论的思想 的思想.
(1) log 2 3.4, log 2 8.5
( 2) log 0.3 1.8, log 0.3 2.7
( 3) log a 5.1, log a 5.9(a > 0, a ≠ 1)
9 例3 已知a= 4 时,
不等式log - > - + 不等式 a(x2-x-2)>loga(-x2+2x+3) 成立,求使此不等式成立的 的取值范围 的取值范围. 成立,求使此不等式成立的x的取值范围
若函数f(x)=logax (0<a<1)在 例4 若函数 = < < 在 区间[a, 区间 2a]上的最大值是最小值的 上的最大值是最小值的 3倍,求a的值 倍 的值. 的值
x 求证: 函数f(x)= log 2 例5 求证 函数 = 1− x
在[0, 1]上是增函数 上是增函数. 上是增函数
2.2.2对数函数 2.2.2对数函数 及其性质
临沂第24中学 临沂第24中学
复习引入
1. 指数与对数的互化关系 ab=N ⇔ logaN=b. =
2. 指数函数的图象和性质 a>1 > 图 象
2.2.2对数函数及其性质
2.2.2对数函数及其性质1.对数函数的概念形如y=log a x (a>0且a≠1)的函数叫做对数函数.对于对数函数定义的理解,要注意:(1)对数函数是由指数函数变化而来的,由指数式与对数式关系知,对数函数的自变量x 恰好是指数函数的函数值y,所以对数函数的定义域是(0,+∞);(2)对数函数的解析式y=log a x中,log a x前面的系数为1,自变量在真数的位置,底数a 必须满足a>0,且a≠1;(3)以10为底的对数函数为y=lg x,以e为底的对数函数为y=ln x.m (1)当(m -1)(n -1)>0,即m 、n 范围相同(相对于“1”而言),则log m n >0;(2)当(m -1)(n -1)<0,即m 、n 范围相反(相对于“1”而言),则log m n <0.有了这个规律,我们再判断对数值的正负就很简单了,如log 213<0,log 52>0等,一眼就看出来了!题型一 求函数定义域求下列函数的定义域:(1)y =log 3x -12x +3x -1;(2)y =11-log a (x +a )(a >0,a ≠1).分析 定义域即使函数解析式有意义的x 的范围.解 (1)要使函数有意义,必须{ 2x +3>0, x -1>0, 3x -1>0, 3x -1≠1同时成立,解得⎩⎨⎧x >-32, x >1, x >13, x ≠23. ∴x >1.∴定义域为(1,+∞).(2)要使原函数有意义,需1-log a (x +a )>0, 即log a (x +a )<1=log a a .当a >1时,0<x +a <a ,∴-a <x <0. 当0<a <1时,x +a >a ,∴x >0.∴当a >1时,原函数定义域为{x |-a <x <0}; 当0<a <1时,原函数定义域为{x |x >0}.点评 求与对数函数有关的定义域问题,首先要考虑:真数大于零,底数大于零且不等于1,若分母中含有x ,还要考虑不能使分母为零.题型二 对数单调性的应用(1)log 43,log 34,log 4334的大小顺序为( )A .log 34<log 43<log 4334B .log 34>log 43>log 4334C .log 34>log 4334>log 43D .log 4334>log 34>log 43(2)若a 2>b >a >1,试比较log a a b ,log b ba,log b a ,log a b 的大小.(1)解析 ∵log 34>1,0<log 43<1, log 4334=log 43⎝⎛⎭⎫43-1=-1, ∴log 34>log 43>log 4334.答案 B(2)解 ∵b >a >1,∴0<ab<1.∴log a a b <0,log b ba ∈(0,1),logb a ∈(0,1).又a >b a >1,且b >1,∴log b ba<log b a ,故有log a a b <log b ba<log b a <log a b .点评 比较对数的大小,一般遵循以下几条原则:①如果两对数的底数相同,则由对数函数的单调性(底数a >1为增;0<a <1为减)比较. ②如果两对数的底数和真数均不相同,通常引入中间变量进行比较.③如果两对数的底数不同而真数相同,如y =log a 1x 与y =log a 2x 的比较(a 1>0,a 1≠1,a 2>0,a 2≠1).当a 1>a 2>1时,曲线y 1比y 2的图象(在第一象限内)上升得慢.即当x >1时,y 1<y 2;当0<x <1时,y 1>y 2.而在第一象限内,图象越靠近x 轴对数函数的底数越大.当0<a 2<a 1<1时,曲线y 1比y 2的图象(在第四象限内)下降得快.即当x >1时,y 1<y 2;当0<x <1时,y 1>y 2即在第四象限内,图象越靠近x 轴的对数函数的底数越小.已知log a 12<1,那么a 的取值范围是________.分析 利用函数单调性或利用数形结合求解.解析 由log a 12<1=log a a ,得当a >1时,显然符合上述不等式,∴a >1;当0<a <1时,a <12,∴0<a <12. 故a >1或0<a <12.答案 a >1或0<a <12点评 解含有对数符号的不等式时,必须注意对数的底数是大于1还是小于1,然后再利用相应的对数函数的单调性进行解答.理解会用以下几个结论很有必要:(1)当a >1时,log a x >0⇔x >1,log a x <0⇔0<x <1; (2)当0<a <1时,log a x >0⇔0<x <1,log a x <0⇔x >1.题型三 函数图象的应用若不等式2x -log a x <0,当x ∈⎝⎛⎭⎫0,12时恒成立,求实数a 的取值范围. 解要使不等式2x<logax 在x ∈⎪⎭⎫ ⎝⎛21,0时恒成立,即函数y=logax 的图象在⎪⎭⎫ ⎝⎛21,0内恒在函数y=2x 图象的上方,而y=2x 图象过点⎪⎭⎫⎝⎛2,21.由图可知,loga 21>2,显然这里0<a<1,∴函数y=logax 递减. 又loga21>2=log 2a a ,∴a2>21,即a>2221⎪⎭⎫ ⎝⎛.∴所求的a 的取值范围为2221⎪⎭⎫⎝⎛<a<1.点评 原问题等价于当x ∈⎪⎭⎫⎝⎛21,0时,y1=2x 的图象在y2=logax 的图象的下方,由于a的大小不确定,当a>1时,显然y2<y1,因此a 必为小于1的正数,当y2的图象通过点⎪⎭⎫⎝⎛2,21时,y2满足条件,此时a 0=2221⎪⎭⎫⎝⎛.那么a 是大于a 0还是小于a 0才满足呢?可以画图象观察,请试着画一画.这样可以对数形结合的方法有更好地掌握.设函数f (x )=lg(ax 2+2x +1),若f (x )的值域是R ,求实数a 的取值范围.错解 ∵f (x )的值域是R ,∴ax 2+2x +1>0对x ∈R 恒成立,即{ a >0 Δ<0⇔{ a >0 4-4a <0⇔a >1. 错因分析 出错的原因是分不清定义域为R 与值域为R 的区别. 正解 函数f (x )=lg(ax 2+2x +1)的值域是R ⇔真数t =ax 2+2x +1能取到所有的正数.当a =0时,只要x >-12,即可使真数t 取到所有的正数,符合要求;当a ≠0时,必须有{ a >0 Δ≥0⇔{ a >0 4-4a ≥0⇔0<a ≤1. ∴f (x )的值域为R 时,实数a 的取值范围为[0,1].本节内容在高考中考查的形式、地位与指数函数相似,着重考查对数的概念与对数函数的单调性,考查指数、对数函数的图象、性质及其应用.1.(广东高考)已知函数f (x )=11-x的定义域为M ,g (x )=ln(1+x )的定义域为N ,则M ∩N等于( )A .{x |x >-1}B .{x |x <1}C .{x |-1<x <1}D .∅解析 由题意知M ={x |x <1},N ={x |x >-1}. 故M ∩N ={x |-1<x <1}. 答案 C2.(湖南高考)下列不等式成立的是( ) A .log 32<log 23<log 25 B .log 32<log 25<log 23 C .log 23<log 32<log 25 D .log 23<log 25<log 32解析 ∵y =log 2x 在(0,+∞)上是增函数, ∴log 25>log 23>log 22=1.又y =log 3x 在(0,+∞)上为增函数, ∴log 32<log 33=1.∴log 32<log 23<log 25. 答案 A3.(全国高考)若x ∈(e -1,1),a =ln x ,b =2ln x ,c =ln 3x ,则( ) A .a <b <c B .c <a <b C .b <a <c D .b <c <a解析 ∵1e<x <1,∴-1<ln x <0.令t =ln x ,则-1<t <0.∴a -b =t -2t =-t >0.∴a >b .c -a =t 3-t =t (t 2-1)=t (t +1)(t -1), 又∵-1<t <0,∴0<t +1<1,-2<t -1<-1,∴c -a >0,∴c >a . ∴c >a >b . 答案 C1.已知函数f (x )=1+2x 的定义域为集合M ,g (x )=ln(1-x )的定义域为集合N ,则M ∩N 等于( )A .{x |x >-1}B .{x |x <1}C.⎩⎨⎧⎭⎬⎫x |-12<x <1 D .∅ 答案 C2.已知函数f (x )=lg 1-x 1+x,若f (a )=12,则f (-a )等于( )A.12 B .-12 C .-2 D .2 答案 B解析 f (-a )=lg 1+a 1-a =-lg ⎝ ⎛⎭⎪⎫1+a 1-a -1=-lg 1-a 1+a=-f (a )=-12.3.已知a =log 23,b =log 32,c =log 42,则a ,b ,c 的大小关系是( ) A .c <b <a B .a <b <c C .b <c <a D .c <a <b 答案 A解析 因为a =log 23>1,b =log 3 2<1,所以a >b ;又因为2>3,则log 32>log 33=12,而log 42=log 22=12,所以b >12,c =12,即b >c .从而a >b >c .4.函数f (x )=lg|x |为( )A .奇函数,在区间(0,+∞)上是减函数B .奇函数,在区间(0,+∞)上是增函数C .偶函数,在区间(-∞,0)上是增函数D .偶函数,在区间(-∞,0)上是减函数 答案 D解析 已知函数定义域为(-∞,0)∪(0,+∞),关于坐标原点对称,且f (-x )=lg|-x |=lg|x |=f (x ),所以它是偶函数.又当x >0时,|x |=x ,即函数y =lg|x |在区间(0,+∞)上是增函数. 又f (x )为偶函数,所以f (x )=lg|x |在区间(-∞,0)上是减函数.5.函数y =a x 与y =-log a x (a >0,且a ≠1)在同一坐标系中的图象只可能为( )答案 A解析 方法一 若0<a <1,则曲线y =a x 下降且过(0,1),而曲线y =-log a x 上升且过(1,0);若a >1,则曲线y =a x上升且过(0,1),而曲线y =-log a x 下降且过(1,0).只有选项A 满足条件.方法二 注意到y =-log a x 的图象关于x 轴对称的图象的表达式为y =log a x ,又y =log a x 与y =a x 互为反函数(图象关于直线y =x 对称),则可直接选定选项A.6.设函数f (x )=log 2a (x +1),若对于区间(-1,0)内的每一个x 值都有f (x )>0,则实数a 的取值范围为( )A .(0,+∞) B.⎝⎛⎭⎫12,+∞C.⎝⎛⎭⎫12,1D.⎝⎛⎭⎫0,12 答案 D解析 已知-1<x <0,则0<x +1<1,又当-1<x <0时,都有f (x )>0,即0<x +1<1时都有f (x )>0,所以0<2a <1,即0<a <12.7.若指数函数f (x )=a x(x ∈R )的部分对应值如下表:则不等式log a (x -1)<0答案 {x |1<x <2}解析 由题可知a =1.2,∴log 1.2(x -1)<0, ∴log 1.2(x -1)<log 1.21,解得x <2, 又∵x -1>0,即x >1,∴1<x <2. 故原不等式的解集为{x |1<x <2}.8.函数y =log a x (1≤x ≤2)的值域为[-1,0],那么a 的值为________.答案 12解析 若a >1,则函数y =log a x 在区间[1,2]上为增函数,其值域不可能为[-1,0]; 故0<a <1,此时当x =2时,y 取最小值-1,即log a 2=-1,得a -1=2,所以a =12.9.已知函数f (x )=⎩⎪⎨⎪⎧(3a -1)x +4a ,x <1log a x ,x ≥1是实数集R 上的减函数,那么实数a 的取值范围为__________.答案 ⎣⎡⎭⎫17,13解析 函数f (x )为实数集R 上的减函数,一方面,0<a <1且3a -1<0,所以0<a <13,另一方面,由于f (x )在R 上为减函数,因此应有(3a -1)×1+4a ≥log a 1,即a ≥17.因此满足题意的实数a 的取值范围为17≤a <13.10.已知f (x )=1+log 2x (1≤x ≤4),求函数g (x )=f 2(x )+f (x 2)的最大值和最小值. 解 ∵f (x )的定义域为[1,4], ∴g (x )的定义域为[1,2].∵g (x )=f 2(x )+f (x 2)=(1+log 2x )2+(1+log 2x 2) =(log 2x +2)2-2,又1≤x ≤2,∴0≤log 2x ≤1.∴当x =1时,g (x )min =2;当x =2时,g (x )max =7.学习目标1.掌握对数函数的概念、图象和性质.2.能够根据指数函数的图象和性质得出对数函数的图象和性质,把握指数函数与对数函数关系的实质.自学导引1.对数函数的定义:一般地,我们把函数y =log a x (a >0,且a ≠1)叫做对数函数,其中x 是自变量,函数的定义域是(0,+∞).对数函数y =log a x (a >0且a ≠1)和指数函数y =a x _(a >0且a ≠1)互为反函数.一、对数函数的图象例1 下图是对数函数y =log a x 的图象,已知a 值取3,43,35,110,则图象C 1,C 2,C 3,C 4相应的a 值依次是( )A.101,53,34,3B .53,101,34,3C .101,53,3,34D .53,101,3,34答案 A解析 方法一 因为对数的底数越大,函数的图象越远离y 轴的正方向,所以C1,C2,C3,C4的a 值依次由大到小,即C1,C2,C3,C4的a 值依次为101,53,34,3.方法二过(0,1)作平行于x 轴的直线,与C1,C2,C3,C4的交点的横坐标为(a1,1),(a2,1),(a3,1),(a4,1),其中a1,a2,a3,a4分别为各对数的底,显然a1>a2>a3>a4,所以C1,C2,C3,C4的底值依次由大到小.点评 函数y=logax (a>0,且a ≠1)的底数a 的变化对图象位置的影响如下:①上下比较:在直线x=1的右侧,底数大于1时,底数越大,图象越靠近x 轴;底数大于0且小于1时,底数越小,图象越靠近x 轴.②左右比较:(比较图象与y=1的交点)交点的横坐标越大,对应的对数函数的底数越大. 变式迁移1 借助图象比较m ,n 的大小关系: (1)若logm5>logn5,则m n ; (2)若logm0.5>logn0.5,则m n. 答案 (1)< (2)>二、求函数的定义域例2 求下列函数的定义域:(1)y =3log 2x ;(2)y =log 0.5(4x -3); (3)y =log (x +1)(2-x ).分析 定义域即使函数解析式有意义的x 的范围.解 (1)∵该函数是奇次根式,要使函数有意义,只要对数的真数是正数即可, ∴定义域是{x |x >0}.(2)要使函数y =log 0.5(4x -3)有意义, 必须log 0.5(4x -3)≥0=log 0.51,∴0<4x -3≤1.解得34<x ≤1.∴定义域是⎩⎨⎧⎭⎬⎫x |34<x ≤1.(3)由⎩⎪⎨⎪⎧x +1>0x +1≠12-x >0,得⎩⎪⎨⎪⎧x >-1x ≠0,x <2即0<x <2或-1<x <0,所求定义域为(-1,0)∪(0,2).点评 求与对数函数有关的函数定义域时,除遵循前面已学习过的求函数定义域的方法外,还要对这种函数自身有如下要求:一是要特别注意真数大于零;二是要注意对数的底数;三是按底数的取值应用单调性,有针对性的解不等式.变式迁移2 求y =log a (4x -3)(a >0,a ≠1)的定义域. 解 log a (4x -3)≥0.(*)当a >1时,(*)可化为log a (4x -3)≥log a 1, ∴4x -3≥1,x ≥1.当0<a <1时,(*)可化为 log a (4x -3)≥log a 1,∴0<4x -3≤1,34<x ≤1.综上所述,当a >1时,函数定义域为[1,+∞),当0<a <1时,函数定义域为⎝⎛⎦⎤34,1.三、对数函数单调性的应用例3 比较大小: (1)log 0.81.5与log 0.82; (2)log 35与log 64.分析 从比较底数、真数是否相同入手.解 (1)考查对数函数y =log 0.8x 在(0,+∞)内是减函数, ∵1.5<2,∴log 0.81.5>log 0.82.(2)log 35和log 64的底数和真数都不相同,找出中间量“搭桥”,再利用对数函数的单调性,即可求解.∵log 35>log 33=1=log 66>log 64, ∴log 35>log 64.点评 比较两个对数值的大小,常用方法有:①底数相同真数不同时,用函数的单调性来比较;②底数不同而真数相同时,常借助图象比较,也可用换底公式转化为同底数的对数后比较;③底数与真数都不同,需寻求中间值比较.变式迁移3 比较下列各组中两个值的大小: (1)log 0.52.7,log 0.52.8; (2)log 34,log 65; (3)log a π,log a e (a >0且a ≠1). 解 (1)∵0<0.5<1,∴对数函数y =log 0.5x 在(0,+∞)上是减函数. 又∵2.7<2.8,∴log 0.52.7>log 0.52.8.(2)∵y =log 3x 在(0,+∞)上是增函数, ∴log 34>log 33=1.∵y =log 6x 在(0,+∞)上是增函数, ∴log 65<log 66=1. ∴log 34>log 65.(3)当a >1时,y =log a x 在(0,+∞)上是增函数. ∵π>e ,∴log a π>log a e.当0<a <1时,y =log a x 在(0,+∞)上是减函数. ∵π>e ,∴log a π<log a e.综上可知,当a >1时,log a π>log a e ; 当0<a <1时,log a π<log a e.例4 若-1<log a 34<1,求a 的取值范围.分析 此不等式为对数不等式且底数为参数.解答本题可根据对数函数的单调性转化为一般不等式求解,同时应注意分类讨论.解 -1<log a 34<1⇔log a 1a <log a 34<log a a .当a >1时,1a <34<a ,∴a >43.当0<a <1时,1a >34>a ,∴0<a <34.∴a 的取值范围是⎝⎛⎭⎫0,34∪⎝⎛⎭⎫43,+∞. 点评 (1)解对数不等式问题通常转化为不等式组求解,其依据是对数函数的单调性. (2)解决与对数函数相关的问题时要遵循“定义域优先”原则. (3)若含有字母,应考虑分类讨论.变式迁移4 已知log a (2a +1)<log a 3a <0,求a 的取值范围. 解 log a (2a +1)<log a 3a <0(*)当a >1时,(*)可化为⎩⎪⎨⎪⎧0<2a +1<10<3a <12a +1<3a,解得⎩⎪⎨⎪⎧ -12<a <00<a <13a >1,∴此时a 无解.当0<a <1时,(*)可化为⎩⎪⎨⎪⎧ 2a +1>13a >12a +1>3a ,解得⎩⎨⎧ a >0a >13a <1,∴13<a <1. 综上所述,a 的取值范围为⎝⎛⎭⎫13,1.1.求对数函数定义域要注意底数中是否含有自变量,此时底数大于0且不等于1.2.应用对数函数的图象和性质时要注意a >1还是0<a <1。
课件4:2.2.2 对数函数及其性质 第一课时

解析:由底数对对数函数图象的影响,知 C4 的底数<C3 的
底数<C2 的底数<C1 的底数.故相应的曲线 C1,C2,C3,C4 的底数依次是 3,43,35,110. 答案:A
[例3] 求函数y=log2(x2-4x+6)的值域. [思路点拨] 先确定真数的取值范围,再运用对数 函数的单调性求解.
3.函数y=lg(x+1)的图象大致是( ) 答案:C
4.如图所示的曲线是对数函数 y=logax
的图象,已知 a 的取值可为 3,43,35,
110,则相应曲线 C1,C2,C3,C4 的底
数 a 的值依次为
()
A. 3,43,35,110 C.43, 3,35,110
B. 3,43,110,35 D.43, 3,110,35
(3)由题意得- 22xx- - 4x+ 11>≠80>1,,0,解得xxx<>≠2121, ,. ∴y=log(2x-1)(-4x+8)的定义域为{x|12<x<2,且 x≠1}.
1.若 f(x)= log1(12x+1),则 f(x) 2 的定义域为
()
Hale Waihona Puke A.(-12,0) C.(-12,+∞)
[精解详析] ∵x2-4x+6=(x-2)2+2≥2,
又f(x)=log2u在(0,+∞)上是增函数, ∴log2(x2-4x+6)≥log22=1. ∴函数的值域是[1,+∞).
(6分) (8分)
5.函数f(x)=log2(3x+1)的值域为
A.(0,+∞)
B.[0,+∞)
()
C.(1,+∞)
[精解详析] (1)由题意得l2g-(x2>-0,x)≥0,即22- -xx≥ >01. , ∴x≤1,即 y= lg(2-x)的定义域为{x|x≤1}. (2)由l3oxg-3(2>30x,-2)≠0,得33xx>-22,≠1, 解得 x>23,且 x≠1. ∴y=log3(31x-2)的定义域为{x|x>23,且 x≠1}.
2122对数函数及其性质1

y log1 x
2
对数函数y=log a x (a>0, a≠1)
a>1
0<a<1
图
y
y
象
o (1, 0)
(1, 0) xo
x
(1) 定义域: (0,+∞)
性 (2) 值域:R
(3) 过点(1,0), 即x=1 时, y=0
(4) 0<x<1时, y<0;
质 x>1时, y>0
(4) 0<x<1时, y>0; x>1时, y<0
确定的年代 t 与它对应,所以,t 是P的函数.
对数函数:
一般地,我们把函数 ylogax(a 叫0 做且 对a 数 函1)
数,其中x是自变量,函数的定义域是(0,+∞).
注意:①对数函数的定义与指数函数类似,都是形式定义,
注都意不辨是别对.数如 函: 数,而y只能2称lo其2g为x对数,y型 函log数5 .5x
设A,B分别为函数y=f(x)的定义域和值域,如果由函数y=f(x)
所解得 x(y)也是一个函数(即对任意一个yB,都
有唯一的 xA与之对应),那么就称函数 x(y)是函
数y=f(x)的反函数,记作:x f1(y) 。习惯上,用x表示 自变量,y表示函数,因此的反函数 y f1(x)通常改写成:
x f 1(y)
2 4… 1 2…
x
x … 1/4 1/2 1 2 4 …
列 表
ylog2 x…
y log1 x…
2
-2 -1 2
0 1 2… 1 0 -1 -…2
y
描
2
点
1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作y=log2x图像
列
x
1/4 1/2 1 2 4 …
表 y=log2x -2 -1 0 1 2 …
描 点
连 线
y
1
O
1
ylog2 x ylog3 x y log6 x
x y log 1 x y log61 x y log13 x
2
对数函数的图象与性质:
解:⑴考察对数函数y=log2x,因为它的底数2>1,
所以它在(0,+∞)上是增函数. 因为3.4<8.5,
于是log23.4<log28.5;
⑵因为函数y=log0.3x在(0,+∞)上是减函数, 且1.8<2.7,所以log 0.31.8>log 0.32.7.
⑶ loga5.1 , loga5.9 ( a>0 , a≠1 )
值分布
趋势 单调性
(0,+∞)
R
( 1 , 0 ) 即 x = 1 时,y = 0
当 x>1 时,y>0 当 0<x <1 时, y<0
当 x>1 时,y<0 当 0<x<1 时,y>0
底数越大,图象越靠近 x 轴 底数越小,图象越靠近 x 轴
在 ( 0 , + ∞ ) 上是增函数
在( 0 , + ∞ )上是减函数
R+ R 减函数 (1,0)
底数越小,图象越靠近 x 轴
0<x<1时,y>0 x>1时,y<0
1.对数函数定义: y = log a x ( a>0 且 a ≠1 ). 2.对数函数的图象与性质:
函数 底数
y = log a x ( a>0 且 a≠1 )
a>1
0<a<1
y
y
图象
o
1
x
1
o
x
定义域 值域 定点
练习:判断下列函数是否是对数函数?
1yloagx1 2y2loagx 3yloagx1 4yloxgx
5ylo(g2)x 6ya25a4loagx
对数函数图像的作法:
作对数图像的三个步骤:
一、列表(根据给定的自变量分别计算 出应变量的值)
二、描点(根据列表中的坐标分别在坐 标系中标出其对应点)
对数y函l数oaxg (a0 且 a1 ) 的性质的助记口诀:4x0 x4Fra bibliotek由 x0
x0
0 x 1,或 1 x 4.
x1
x1
(5) 求函数 y lo0g.5(4x3)的定义域.
解:要使函数有意义,必有
4x-3>0, log0.5(4x-3)≥0.
4x>3,
即 4x-3≤1.
解得3x1. 4
所以所求函数的定义域为{x| 3 x 1 }.
4
例2.比较下列各组数中两个值的大小: (1) log23.4 , log28.5; ⑵ log0.31.8, log0.32.7; ⑶ loga5.1 , loga5.9 (a>0,a≠1 ).
又f(x) 为奇函数,
∴ f(x)=-f(-x) =-log3(-x).
故f(x)
l o 0,
g3 x,
x 0, x 0,
l og3(x),x0.
函数
y = log a x ( a>0 且 a≠1 )
图像
定义域 值域 单调性
R+ R 增函数
过定点
(1,0)
趋 势 底数越大,图象越靠近 x 轴
0<x<1时,y<0 取值范围 x>1时,y>0
函数 底数
图象
y = log a x ( a>0 且 a≠1 )
a>1
0<a<1
y
y
o
1
x
1
o
x
定义域 值域 定点
值分布
单调性 趋势
(0,+∞)
R (1,0) 当 x>1 时,y>0 当 0<x <1 时, y<0 在( 0 , + ∞ ) 上是增函数 底数越大,图象越靠近x轴
(0,+∞) R
(1,0) 当 x>1 时,y<0 当 0<x<1 时,y>0 在( 0 , + ∞ )上是减函数 底数越小,图象越靠近x 轴
(2) m < n (4) m > n
例2.比较下列各组中两个值的大小: (4) log 67 , log 7 6 ; (5) log 3π, log 2 0.8 .
分析 : (1) log aa=1
(2) log a1=0
(1)解:∵注 :lo比g6较7>两lo个g6对6=数1,的(2大)解小:∵时lo,g可3π>log31=0, 在log两76个<对log数77中=间1, 插入一个l已og2知0.8<log21=0,
∴ 数log(如67>1或lo0g7等6;),间接比较∴这lo两g3π个>log20.8. 对数的大小.
(6)log750 log67 log54 log40.5
例3.已知定义域为R的奇函数f(x),当x>0 时, f(x)=log3x,求f(x). 解:当x=0时,f(0) = 0;
当 x<0 时,-x >0,
注: 例2是利用对数函数的增减性比较两个对数的大 小的,对底数与1的大小关系未明确指出时,要分情况 对底数进行讨论来比较两个对数的大小.
练习1:
比较下列各题中两个值的大小: ⑴ log106 < log108 ⑵ log0.56 < log0.54 ⑶ log0.10.5 > log0.10.6 ⑷ log1.51.6 > log1.51.4
分析:对数函数的增减性决定于对数的底数是大 于1还是小于1.而已知条件中并未指出底数a与1 哪个大,因此需要对底数a进行讨论:
解:①当a>1时,函数y=log ax在(0,+∞)上是增函 数,于是log a5.1<log a5.9;
②当0<a<1时,函数y=log ax在(0,+∞)上是 减函数,于是log a5.1>log a5.9.
练习2: 已知下列不等式,比较正数m,n 的大小:
(1) log 3 m < log 3 n (2) log 0.3 m > log 0.3 n (3) log a m < loga n (0<a<1) (4) log a m > log a n (a>1)
答案: (1) m < n (3) m > n
讲解范例 例1.求下列函数的定义域: (1)y = log a x 2
解 : 由 x2 0, 得 x 0.
所以函 y数 loagx2的定义x域 |x是 0.
(2) y = log a ( 4-x ) 定义域:(-∞, 4 )
(3) y = log a ( 9-x 2 ) 定义域: (-3, 3 ) (4) y = log x ( 4-x ) 定义域:( 0 , 1 )∪( 1 , 4 )
