各种熵变的计算
2.6熵变的计算(物理化学)

Q 2244.8 S环境= 7.48 JK 1 T 300
S孤立=S系统+S环境= 19.14-7.48= 11.66 JK1 0
f Hm V Hm
S气 S液 S固
四、可逆相变化过程中熵变的计算
例 1 mol冰在零度熔化成水,熔化热为6006.97 J/mol,求熵变。 解: 此过程是在等温等压条件下发生的正常相变。
S系统
Qr H 6006.97 21.99 JK 1 T T 273.2
终态混合气中各物质的分压 pA(终) p xA
S A nA R ln pA( 始) p A( 终 ) pD (终 ) p nA R ln p xA nA R ln p p xD
pD(终) p xD
Smix S A S D nA R ln x A nD R ln x D R ( nB ln x B )
Q 6006.97 S环境= 21.99 JK 1 T环境 237.2
S孤立=S系统+S环境=0
这是一个可逆过程。
五、理想气体混合过程的熵变计算
理想气体在等温等压混合
A(T,p) (nA, VA) D(T,p) (nD, VD)
U 0,W 0, Q 0
A+D(T,p) (nA,+nD ,VA+VD)
S
T2
Qr
T
T1
T2
T1
CV dT T2 CV ln T T1
(完整版)各种熵变的计算

热力学第二定律的经典表述
克劳休斯说法 :不可能把热由低温物体转 移到高温物体,而不留下其他变化。
开尔文说法:不可能从单一热源吸热使之完全变 为功,而不留下其他变化。
能否找到一个统一的判据来判断可能 发生的过程的方向和限度呢?
熵判据
1.10 熵
1. 定义
Q1 Q2 0 T1 T2
不可逆热机 可逆热机
p2 p1
C
p
,m
ln
V2 V1
)
定容
定压
练习1.
2molH2 由 300K , 100kPa 定 压 加 热 到 1200K , 求ΔS 已知Cp,m(H2) / (J•K-1 • mol-1 )=
28.83-0.84х10-3(T/K)+2.00×10-6(T/K)2
S δQp T 2 nCp, mdT
(2) 熵判据
隔离系统,Q= 0
ΔS隔≥0
不可逆过程 可逆过程
隔离系统,W= 0 所以,隔离系统的不可逆过程是自发过程
可逆过程是无限慢的变化,实际是平衡态
ΔS隔≥0
自发过程 平衡态
平衡的熵判据
(只能用于隔离系统!!!)
隔离系统 状态A
状态B
ΔS = 0 ΔS > 0 ΔS < 0
A 、B平衡态 自发从A 变到B的趋势 不可能发生
相平衡条件下发生的相变化是可逆过程,否 则是不可逆过程。
一般条件下发生的化学反应,都是不可逆过程。
(1) 单纯 p,V,T 变化过程熵变的计算
① 实际气体,液体或固体的 p,V,T 变化
(i) 定压变温
Qp= dH =nCp,mdT
S δQp T 2 nCp, mdT
3-4、5熵变计算

理想气体、恒温
物质(气体)之间的混合, 导致系统的熵增大.
物质之间的传热, 导致各物质的总熵增大.
p1 T S nR ln p2 V T S nRln 2 n V1
以上熵增大过程伴随着微观分子无序热运动速率或空间 V↑ 的增大, 即物质状态的混乱程度、分散程度增大了. S↑
第一定律:U(总) = U(系统) + U (环境)= 0
第二定律: S(总) = S(系统) + S (环境)≥ 0
第一定律数学式:
第二定律数学式:
U = Q + W
S
δQ T
任意不可逆过程 任意可逆过程
熵变计算式
ΔS
δ Qr T
δ Qir Tex
dS (环)
δ Q(环) T (环)
T2 T1
Q 6025J S (环) 5649J / 22.1J/K 263K = 21.5J/K T (环) 273K S(总)= S(系统)+ S (环境) = 0.8 J/K
>0
∴是自发过程
不可逆相变过程
§3-6 熵变的计算
1. PVT 变化的熵变
2. 相变化的熵变 3. 环境熵变 熵判据
T1
T3
T3
T1 +dT
+dT
+dT
+dT
传热过程
(4) pVT同时改变的过程 V2 n (理想气体, pVT都变) V1 T nC
S V S T S
2
V S
Q p1 rT1 V1
p T2 V1
T S
第二章热力学第二定律-2系统熵变的计算

解:(1)等温可逆膨胀 △S系统 = nRln(V2/V1)=10.0mol×8.3145J·K-1·mol-1
× ln(2.00/1.00) =57.6J·K-1。 ΔS 环境= -Q实际/Tex= - nRln(V2/V1)
= -ΔS系统 =- 57.6 J·K-1。 ΔS 隔离 = 0 (可逆过程)
△mixS = -(0.041mol ×ln0.66 +0.021mol×ln0.34)×8.3145J.K-1.mol-1 =0.33 J.K-1.
23
理想气体等温等容进行混合求混合熵△mixS ? 理想气体等温等容进行混合,U=0,H=0,
实际上是绝热可逆过程,混合熵△mixS =0. 同种理想气体等温等容混合,mixS≠0,因
§2-6 热力学第三定律及规定熵
18
对A来说,发生的是在恒温下从体积VA可 逆膨胀到体积V的过程。
SA
nA Rln
VA VB VA
对B
SB
nB Rln
VA VB VB
19
m ix S
nA Rln
VA VB VA
nB Rln
VA VB VB
因为
VA VB VA
yA
, VB VA VB
yB
则 mixS =- ( nARlnyA+nBRlnyB) 因为 yA<1,yB<1, 所以
故 S = ( 2.81-22.1-1.41)JK-1 =-20.7JK-1
31
寻求可逆途径的依据: (i)途径中的每一步必须可逆; (ii)途径中每步S 的计算有相应的公式可利用; (iii)有相应于每步S 计算式所需的热数据。
32
因为 S系统 = -20.7JK-1,不能用来判 断过冷水结冰过程的自发与否。欲用熵判 据,还需要计算环境的熵变。
化学反应的熵变计算方法

化学反应的熵变计算方法熵变(ΔS)是描述化学反应中系统混乱程度的指标,它与反应的自发性密切相关。
在化学领域中,我们经常需要计算化学反应的熵变,以揭示反应的热力学性质和熵效应。
本文将介绍几种常用的化学反应熵变的计算方法。
一、标准熵变的计算方法标准熵变(ΔS°)是指在标准状态下,物质从纯单质状态转变成产物状态时的熵变。
标准熵变的计算方法为:ΔS° = ΣnS°(产物) - ΣmS°(反应物)其中,ΔS°表示标准熵变,n代表产物的摩尔数,S°代表物质的标准摩尔熵,m代表反应物的摩尔数。
二、非标准熵变的计算方法对于非标准状态下的化学反应,我们需要通过其他方法来计算熵变。
以下是几种常用的非标准熵变计算方法。
1. 熵差法(ΔS差法)熵差法是通过比较反应物和产物在不同温度下的熵值来计算熵变。
具体步骤如下:(1) 计算反应物和产物在不同温度下的熵值。
(2) 计算反应物和产物熵值的差值。
(3) 将差值代入以下公式计算熵变:ΔS = ΣnS(产物) - ΣmS(反应物)2. 统计热力学法统计热力学法基于分子动力学理论,可以通过统计物质中各个自由度的能量和熵来计算熵变。
该方法较为复杂,需要使用计算机软件进行模拟和计算。
3. 混合熵法混合熵法是利用熔解、溶解、混合等过程的熵变来计算反应的熵变。
具体步骤如下:(1) 计算反应物和产物在纯物质状态下的熵值。
(2) 计算混合过程中的熵变。
(3) 将两部分熵变相加得到反应的熵变。
三、例题分析为了更好地理解这些计算方法,我们来看一个简单的例子:氢气和氧气反应生成水的熵变计算。
2H2(g) + O2(g) → 2H2O(l)我们知道水是液体状态,而氢气和氧气都是气体状态,因此我们需要先计算气体到液体的ΔS,并且考虑到反应物和产物的摩尔数比为1:2,故有:ΔS = 2×S(2H2O(l)) - [2×S(H2(g)) + S(O2(g))]根据参考资料,我们可以找到相应的标准摩尔熵值,然后代入计算即可得到氢气和氧气反应生成水的熵变值。
各种熵变的计算范文

各种熵变的计算范文熵是一个重要的物理概念,用于描述系统的无序程度或混乱程度。
在物理学、信息论和热力学等领域,经常需要计算各种熵变。
1.熵的定义熵在热力学中的定义为:ΔS = S_final - S_initial其中,ΔS表示熵变,S_final表示系统的末态熵值,S_initial表示系统的初态熵值。
2.系统的微观熵变对于一个牛顿力学体系,它的微观熵变可以表示为:ΔS = k ln W其中,ΔS表示微观熵变,k是玻尔兹曼常数,W是系统的微观状态数。
3.统计熵变对于一个分子系统,如果它处于均匀平衡的状态,其统计熵变可以表示为:ΔS = k ln Ω其中,ΔS表示统计熵变,k是玻尔兹曼常数,Ω是系统的配分函数。
这个公式可以用于计算固态、液态和气态系统的熵变。
4.信息熵变在信息论中,熵被用来描述信息的不确定性。
对于一个离散随机变量X,其信息熵可以表示为:H(X) = -ΣP(x) log P(x)其中,H(X)表示信息熵,P(x)表示随机变量X取一些值x的概率。
5.热力学熵变在热力学中,熵可以用来描述系统的热量转移和无序程度。
对于一个开放系统,其热力学熵变可以表示为:ΔS=∫(dQ/T)其中,ΔS表示热力学熵变,dQ表示系统吸收或释放的热量,T表示系统的温度。
这个公式可以用来计算系统在热平衡过程中的熵变。
总结:各种熵变的计算方法有微观熵变、统计熵变、信息熵变和热力学熵变等。
这些熵变的计算方法不同,适用于不同的物理系统和情况。
熵变的计算是物理学、信息论和热力学等领域的基础概念,对于深入理解系统的行为和性质非常重要。
第3章 熵变的计算

等温,等压,可逆
1mol H 2 O g 373.15 K,p o
S SⅠ SⅡ SⅢ 373.15 40.60 103 298.15 33 ln 298.15 373.15 373.15 118 J K 1 75 ln
等压 可逆
1mol H 2 O l 373.15 K,p o
S
理想气体混合物 A(g) + B(g) + C(g) + …
* * * U UA UB UC * * * H HA HB HC
S B nB R ln
p nB R ln xB n xB R ln xB nR xB ln xB pB
思考:因为 S > 0,该过程为自发过程;此推理正确吗?
3. 环境熵变的计算
环 境 系 统
环境通常由不发生相变及化学变化的物质 组成,即使环境与系统有功与热的交换,其 温度、压力并没有发生可觉察的变化。所以 认为 环境内部过程都是可逆过程
Samb
Qamb Tamb
Qsys Tamb
Qsys 为系统实际从环境得到的热; Qamb为环境实际由系统得到的热 两者绝对值相等,符号相反
O
3. 先恒压后恒容
V p S nC p ,m ln 2 nCV ,m ln 2 V1 p1
前提:设定理想气体的 CV,m和 Cp,m 均为常数
V1
V2
V
(4) 混合或传热过程 (理想气体/凝聚态物质)
混合过程:种类很多,都不可逆;所以,需要设计可逆过程; 总的原则:分别计算各个组分的熵变,然后加和
(1) 可逆相变 (恒温恒压可逆相变)
24熵变的计算.

解题思路:
268K的液态苯变为 268K固态苯是一个非正常相变 过程,求此变化的熵变需要设计可逆过程来计算。
1 mol 苯(l) 不可逆过程
268 K
S
1 mol 苯(s) 268 K
S1 可逆
S3 可逆
1 mol 苯(l)
S2
278 K
可逆
1 mol 苯(s) 278 K
不可逆相变系统熵变的计算
S环境=
Q T
9812.3 268
36.61J
K -1
S孤立=S系统+S环境 = 35.30 36.61=1.31J K-1 0
该过程为自发过程。
不可逆相变系统熵变的计算
例 假设保温瓶内有20g25℃的水,再加入5g-5℃的冰。 (1)保温瓶最终平衡态; (2)计算系统的ΔS。
解题思路:(1)系统变化为绝热过程。Q=0,计算终态t:
pA(始) pA(终)
nAR ln
p p xA
SD
nD R ln
pD(始) pD(终)
nAR ln
p p xD
Smix SA SD
nAR ln xA nD R ln xD
R (nB ln xB ) B
xB为B物质的摩尔分数
理想气体混合过程的熵变计算
例 设在273K时,用一隔板将容器分割为两部分,一边装有 02 mol、100kPa的O2,另一边是08 mol、100kPa 的N2, 抽去隔板后,两气体混合均匀,试求混合熵,并判断过程 的可逆性。
环境熵变的计算
环境熵变的计算:
S环境=
- Q实际 T环境
与系统相比,环境很大,当系统发生变化时,吸收或放出的热 量不至于影响环境的温度和压力,环境的温度和压力均可看做 常数,实际过程的热即为可逆热.
各种熵变的计算范文

各种熵变的计算范文熵是热力学中的一个重要概念,用于描述系统的无序程度和混乱程度。
熵变则是指在化学或物理过程中系统熵的变化。
本文将介绍各种熵变的计算方法。
1.体系熵变的计算方法在化学和物理过程中,体系的熵变可以通过以下公式计算:ΔS = S_final - S_initial其中,ΔS表示体系的熵变,S_final表示过程结束后体系的熵,S_initial表示过程开始前体系的熵。
在计算体系熵变时,需要注意以下几点:- 使用适当的单位:熵通常以焦耳/摄氏度(J/(K•mol))或卡路里/摄氏度(cal/(K•mol))为单位。
-考虑转化的摩尔比例:如果反应涉及到2个或多个物质的摩尔比例的变化,那么应考虑这些变化对体系熵变的影响。
-考虑相变和化学反应:相变(如液体转为气体)和化学反应(如物质的反应生成新的物质)会导致体系熵变的变化,应相应考虑。
2.熵变的计算方法在一定条件下,温度变化(T)是熵变(ΔS)的一个重要因素。
根据热力学第二定律,对于可逆过程,熵变可以通过以下公式计算:ΔS=∫(Cp/T)dT其中,Cp表示恒压条件下的摩尔热容。
在计算熵变时,需要注意以下几点:-温度的选择:公式中的温度范围应选择与相变或反应发生的范围相匹配。
-热容的选择:应使用与反应物和产物相应的热容值。
对于多个物质的反应,需要计算每个物质的热容,并考虑其摩尔比例。
3.稳态熵变的计算方法在热力学中,稳态过程是指系统的各个宏观性质在其内部平衡时不随时间而变化的过程。
在稳态条件下,系统的熵变可以通过以下公式计算:ΔS = Σ(mi × ΔSi)其中,ΔS表示稳态熵变,mi表示稳态过程中每个物体的摩尔数,ΔSi表示每个物体的熵变。
稳态熵变的计算需要注意以下几点:-系统内物质的贡献:稳态过程中,如果有不止一个物体参与,需要考虑每个物质的熵变。
- 选择适当的单位:与体系熵变类似,稳态熵变通常以焦耳/摄氏度(J/(K•mol))或卡路里/摄氏度(cal/(K•mol))为单位。
计算熵变的三个公式

计算熵变的三个公式
熵变是概率论中一个重要的概念,它表示随机变量之间的相互依赖性。
它反映了系统中变量的复杂性。
通过熵变可以更清楚地看到系统的结果,从而帮助我们更好地理解系统的规律性。
这也是为什么熵变如此重要。
熵变可以用三个公式来计算:
1、香农熵变公式:
H(X) = - P(X)logP(X)
这个公式表明,熵变可由随机变量X的不同取值及其概率之间的关系来计算,其结果以重要的熵单位度量。
Σ表示一个求和符号,P(X)表示随机变量X的概率,log表示自然对数函数。
2、条件熵变公式:
H(X|Y) = - P(X,Y)logP(X|Y)
条件熵变公式由香农熵变公式派生而成,它表示Y给定时,X的不确定度。
由于Y通常由其他更多的变量和其他因素决定,因此P(X,Y)表示X和Y的联合概率,而P(X|Y)表示X在给定Y的情况下的概率。
3、熵变增强公式:
H(X,Y)=H(X)+H(Y|X)
熵变增强公式由香农熵变和条件熵变公式组合而成,它表示X和Y的总熵变是它们各自的熵变之和。
当X和Y之间存在相互依赖性,则X和Y的总熵变会比它们各自的熵变大。
熵变是计算机系统研究中最重要的概念之一,它不仅可以用来衡
量一个系统的复杂性,还可以用来衡量一个系统的可靠性。
使用熵变可以更准确地估计一个系统的性能。
因此,熵变具有重要的科学价值和应用价值。
总之,熵变是概率论中一个重要概念,它不仅可以用来衡量一个系统的复杂性,而且还可以用来衡量一个系统的可靠性。
以计算熵变的三个公式为核心,熵变对计算机系统研究具有重要的科学价值和应用价值。
计算熵变的三个公式

计算熵变的三个公式热力学第二定律指出,系统内有定值工作时,其总熵变趋近于零,即稳定状态下的熵变为零。
那么,在给定的条件下,我们怎样计算物理系统中的熵变呢?本文将讨论计算熵变的三个公式,它们是Carnot 公式、Clausius公式和Gibbs公式。
### Carnot公式Carnot公式是弗朗索瓦卡诺(17961832)首先提出的,是热力学第二定律的早期表达形式,旨在描述可逆热力学过程中熵变的大小。
在一个可逆过程中,由Carnot公式定义,熵变为:△S = -Qc/Tc其中,Qc是热量,Tc是温室效应热(开尔文温度)。
### Clausius公式安德鲁克劳西斯(18221888)修改了卡诺公式,以形成克劳西斯公式,定义了熵变为:△S =qrev/Td其中,qrev是微分反应,Td是系统的微分温度。
在使用Clausius公式时,系统的总熵变将与系统的绝对温度无关,只与相对温度有关。
### Gibbs公式约翰霍尔斯特吉布斯(18391903)提出的吉布斯公式是一个完善的热力学第二定律的表达式,其定义的熵变为:△S =dQrev/T +dQirr/T其中,dQrev是微分反应,dQirr是无序过程。
因此,Gibbs公式不仅充分考虑了可逆反应,而且充分考虑了无序过程,它是一个完善的定律,可以用来描述热力学系统中的熵变。
综上所述,Carnot公式、Clausius公式和Gibbs公式是计算热力学系统内熵变的三个公式,每种公式均有其独特的应用场景,如果搞清楚这三种公式,就可以更好地了解物理系统中熵变的情况。
在说热力学系统熵变以及计算熵变公式时,我们不可不提热力学第二定律,即系统可以通过热力学过程接受热量,但总熵不会增加。
Carnot公式、Clausius公式和Gibbs公式都是从该定律出发,根据不同的物理情况分别表现出来的,最终的目的都是描述系统的熵变情况。
在实际工程中,我们需要根据实际情况选择不同的公式来对系统进行分析,并通过对熵变的计算来发现系统内的动态变化,从而更有效地进行设计和控制。
各种熵变的计算范文

各种熵变的计算范文熵是热力学的一个重要概念,用来描述系统的无序程度。
在各种过程中,系统的熵会发生变化,可以通过熵变值来表示。
本文将介绍各种熵变的计算方法,包括气体的熵变、固体的熵变、溶液的熵变以及化学反应的熵变。
一、气体的熵变计算气体的熵变计算依赖于气体的状态方程,其中最常用的是理想气体状态方程:PV=nRT其中P为气体的压强,V为气体的体积,n为气体的摩尔数,R为气体常数,T为气体的温度。
在恒温、恒压条件下,气体的熵变可以通过下式计算:ΔS = nR ln(V2/V1)其中ΔS为熵变值,n为摩尔数,R为气体常数,V2和V1分别为气体的体积2和体积1二、固体的熵变计算固体的熵变计算相对较为简单,可以通过以下公式计算:ΔS=∫(Cp/T)dT其中ΔS为固体的熵变值,Cp为固体的摩尔热容,T为固体的温度。
需要注意的是,固体的熵变值与温度变化相关,需要进行积分计算。
三、溶液的熵变计算溶液的熵变计算与溶液的浓度相关,可以通过下列公式计算:ΔS = -nR[X ln(X) + (1-X) ln(1-X)]其中ΔS为溶液的熵变值,n为摩尔数,R为气体常数,X为溶液的摩尔分数。
四、化学反应的熵变计算化学反应的熵变计算涉及到物质的物态变化和摩尔数的变化。
根据熵的加性原理,化学反应的熵变可以通过以下公式计算:ΔS=ΣνS(m)-ΣνS(n)其中ΔS为化学反应的熵变值,ΣνS(m)为生成物的摩尔熵之和,ΣνS(n)为反应物的摩尔熵之和。
需要注意的是,摩尔熵的计算需要参考热力学表格,根据相应物质的熵值计算。
总结:熵变是热力学中描述系统无序程度的一个重要指标,其计算方法与物质的状态、浓度和反应过程相关。
本文简要介绍了气体、固体、溶液和化学反应的熵变计算方法,希望能对读者有所帮助。
需要注意的是,在具体应用中,熵变计算还需要综合考虑温度、压强等因素,以获得准确的计算结果。
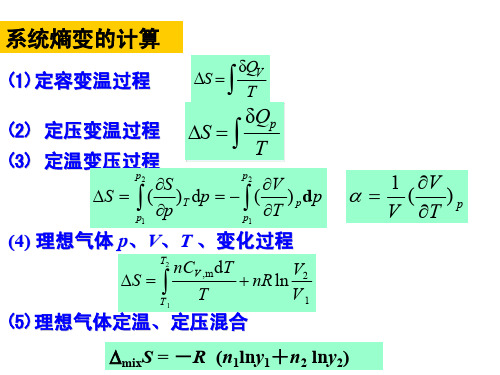
物理化学1.12-4 熵变的计算
T1
T
V1
(5)理想气体定温、定压混合
1 V
( V T
)p
mixS = -R (n1lny1+n2 lny2)
(6)在平衡温度、压力下的相变
(正常相变,可逆相变)
Qr
Qp=H相变= n ·ΔHm
S Qr nHm(相变焓)
T
T
fusHm>0, vapHm>0
同一物质在一定T 、p下 : Sm(s) < Sm(l),
H2O(l,90℃,101 325Pa)
H2O(g,90℃,101 325Pa)
不可逆相变
定压可逆升温 S1
S3
定压可逆降温
H2O(l,100℃,101 325Pa)
S2 可逆相变
H2O(g,100℃,101 325Pa)
T eq
S1 T1 nCp,m (H2O, l)dT/T
S2
系统熵变的计算
(1)定容变温过程
S δQV T
(2) 定压变温过程 S δQp
(3) 定温变压过程
T
S
p2 S p1 ( p )T dp
p2 ( V p1 T
) pdp
(4) 理想气体 p、V、T 、变化过程
S T2 nCV ,mdT nR ln V2
Sm(l) < Sm(g)
(7)非平p1) S1
B(,Teq, peq)
S=? 不可逆相变
S2 可逆相变
p1=p2=psu×
B(, T2, p2) S3
B(, Teq, peq)
则 S=S1+S2+S3
S =?
S隔离 Ssy Ssu 0自可发逆
总结各种过程熵变的计算

总结各种过程熵变的计算1.总结等温过程熵变的计算公式答:(1)(2)(3)公式(1)适用于一定量理想气体的恒温过程。
公式(2)适用于等温、等压可逆相变,若是不可逆相变,则设计可逆过程进行计算。
公式(3)适用于理想气体或理想溶液的等温混合过程,并符合分体积定律,即2.总结变温过程熵变的计算公式答:(1)公式1适用于物质的量一定的恒容变温过程;(2)公式2适用于物质的量一定的恒压变温过程;(3)公式3适用于物质的量一定的从p1,V1,T1到p2,,V2,,T2的过程。
这要分两步计算,先等温,后等容或先等温后等压,或先恒压后恒容,一步是无法计算的。
(4)公式4适用于两个恒温热源之间的热传导,并无相变发生。
(5)公式5适用于无相变、两个变温物体的热传导。
首先要求出终态温度T的值。
3.总结化学过程中熵变的计算公式答:(1)公式1适用于标准压力下,298K时化学反应的熵变计算。
n B是反应式中B物质的计量系数,对产物取正值,反应物取负值。
各物质的标准摩尔熵值有表可查。
(2)公式2适用于标准压力下,求反应温度T时的熵变值。
298。
15 K时的熵变值从查表可得。
(3)公式3适用于等温298K时,求反应在压力为p时的熵变。
在标准压力下的熵变值从查表可得。
(4)公式4是从电动势随温度的变化率求电池反应的熵变,或从可逆电池的热效应求熵变。
4.总结环境熵变的计算公式答:(1)d S(环) = d Q R(环) / T (环)(2)d S(环) = -d Q R(体系) / T (环)公式(1)适用于环境在任何可逆变化时的熵变计算。
公式(2)中,体系的热效应可能是不可逆的,但由于环境很大,对环境这热效应可看作是可逆的。
5.总结规定熵值的计算公式答:(1)公式(1)用来计算温度从0 K到T时等压过程中的规定熵值。
规定在0 K时完整晶体的熵值为零,从0 K到T无相变发生,否则积分不连续。
也可用图解积分求熵值,如0 K至400K时水的积分图。
熵变△s怎么计算

熵变△s怎么计算
在一个过程中,系统混乱度发生改变,称之为熵变,也就是△S。
对于化学反应而言,若反应物和产物都处于标准状态下,则反应过程的熵变,即为该反应的标准熵变。
计算公式:一般地,对于反应:mA+nB=xC+yD,DrSmq=[x Sq,C+y Sq,D]–[m Sq,A+n Sq,B]。
判断:往混乱度增大的方向反应,则△S大于零,反之则△S小于零。
一般来说,气体大于液体大于固体,所以生成气体越多,熵变越大。
例如,水蒸气冷凝成水,△S<0;乙烯聚合成聚乙烯,△S<0;CaCO ₃(s)=CaO(s)+CO₂(g),△S>0;N₂O₄(g)=2NO₂(g),△S>0。
扩展资料
影响因素
1、熵变与体系中反应前后物质的量的变化值有关
(1)对有气体参加的反应
主要看反应前后气体物质的量的变化值即Δn(g),Δn(g)正值越大,反应后熵增加越大;Δn(g)负值越大,反应后熵减越多。
(2)对没有气体参加的反应
主要看各物质总的物质的量的变化值即Δn(总),Δn(总)正值越大,熵变正值越大;Δn(总)负值绝对值越大,熵变也是负值的绝对值越大,但总的来说熵变在数值上都不是特别大。
2、温度的高低
熵变值随温度的改变变化不大,一般可不考虑温度对反应熵变的
影响。
3、压力的大小
熵变值随压力的改变变化也不大,所以可不考虑压力对反应熵变的影响。
化学熵变△s三个公式

化学熵变△s三个公式
高校与高等教育中,化学熵变△s极为重要。
它指的是某一物理或化学过程中,熵的变化量,是衡量系统是否从某种热力学势垒出发以顺利进行反应的一个程度指标。
它由三个公式表达:△s=Δq/T、△s都=qrev/T和△s的=Δq/T的。
首先,△s=Δq/T表示:若某系统处在未改变温度的条件下,进行一定量的热
转移,如Δq(单位:焦耳),则熵变量△s(单位:焦耳/绝对温度)等于热转移
量Δq除以温度T。
其次,△s都=qrev/T表示:反应在完成过程中,所产生的焓变量与温度的乘
积就是熵变△s的大小,其中,qrev是指热力学过程反应的发热量(单位:焦耳),而T代表反应温度(单位:绝对温度),二者的乘积就是△s的大小(焦耳/绝对
温度)。
最后,△s的=Δq/T的表达的是:某物理或化学过程中,熵变量△s等于热转
移量Δq除以温度T的负值,而T代表热力学均衡所确定的温度(绝对温度)。
综上所述,化学熵变△s必须通过上述三个方程中指定的三个参数 - △q、T
和qrev来求得,它有助于我们简单、明确、准确地表达一个化学系统处于热力学
势垒出发的变化趋势,从而提供一个在高校与高等教育中的重要指标。
热力学中的熵产生与熵减的计算方法

热力学中的熵产生与熵减的计算方法熵是热力学中的一个重要概念,常用来描述系统的无序程度或混乱程度。
熵的变化可以用于描述自然界中的各种现象和过程,包括化学反应、热力学循环、热传导等。
为了能够准确计算系统的熵变,我们需要掌握熵产生和熵减的计算方法。
熵产生的计算方法一般包括以下几种情况:1. 理想气体的熵产生:对于理想气体的过程,其熵的变化可以通过熵产生的计算方法来确定。
根据理想气体的状态方程和热力学基本关系,可以得到理想气体熵变的表达式为ΔS = R × ln(V₂/V₁),其中R 为气体常数,V₁和V₂分别为初态和末态的体积。
2. 化学反应的熵产生:在化学反应中,物质的摩尔数变化会导致熵的变化。
根据热力学基本关系和化学反应方程,可以得到化学反应熵变的表达式为ΔS = ∑(ν_i × S_i),其中ν_i为反应物或生成物的摩尔系数,S_i为相应物质的摩尔熵。
3. 热传导的熵产生:热传导是指由于温度差异而导致的热量传递过程。
在热传导中,熵的变化可以用以下形式表示:ΔS = Q/T,其中Q 为热量,T为温度。
与熵产生相反,熵减是指系统经过某个过程后熵的减少。
以下是几种常见的熵减计算方法:1. 理想气体的熵减:对于理想气体的等温过程,其熵减可以通过熵减的计算方法来确定。
根据理想气体的状态方程和热力学基本关系,可以得到理想气体熵减的表达式为ΔS = R × ln(P₂/P₁),其中P₁和P₂分别为初态和末态的压强。
2. 系统的熵减:对于一个封闭系统而言,在无外界能量输入的情况下,系统的熵减可以通过ΔS = Q/T来计算,其中Q为系统吸收的热量,T为系统的温度。
3. 化学反应的熵减:在化学反应中,有些反应会导致产物的熵减。
根据热力学基本关系和化学反应方程,可以得到化学反应熵减的表达式为ΔS = ∑(ν_i × S_i),其中ν_i为反应物或生成物的摩尔系数,S_i为相应物质的摩尔熵。
熵变计算方法总结

解:对于一些较复杂的过程可用一些 示意图简示:
0.4atm,80.1C, g 1atm,80.1C, g 1atm,80.1C,l 1atm, 60C,l
S Sg S相 Sl T2 p1 H 相 C p ,m (l) ln R ln T1 T相 p2 30878 0.4 8.314 ln 1 273.2 80.1 273.2 60 J/K 103.4J/K 142.7 ln 273.2 80.1
S相 Sl S g
能 不 能 进 行
例题:今有两个容器接触,外面用绝热外 套围着,均处于压力101.325 kPa下,一 个容器中有0.5mol的液态苯与 0.5mol的固 态苯成平衡。在另一个容器中有0.8mol的 冰与 0.2mol的水成平衡。求两容器互相 接触达到平衡后的熵变。已知常压下苯的 熔点为5℃,冰的熔点为0℃。固态苯的热 容为122.59J/mol,苯的熔化热为 9916J/mol,冰的熔化热为6004J/mol。
解:
S S2 S1 ( QR / T )
A
B
QR Q p H T T T
108.9J K
1
B
A
(δQ/ T环 ) Q1 / T 40.66 103 /373.2 J K-1
108.9J K-1
不可逆程度: S A ( QR / T环 ) 0
T2 300 S nC p , m ln 3 29.1 ln J/K T1 400 25.1J/K
S环境
Q体系,实际 T环境
nC p , m T T环境
3 29.1(300 400) J/K 29.1J/K 300
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
S nRln V2 nR ln p1
V1
p2
2 8.314 ln 1103 J • K1 114 .86J • K1 1
练习3
1mol 单 原 子 理 想 气 体 , 从 273.15K 、 1013.25kPa的始态,经绝热可逆膨胀至终态 压力为101.325kPa ,求ΔS
S 0
0
可逆循环
积分定理:若封闭曲线闭积分等于零,则被积变 量应为某状态函数的全微分
δQr 是某状态函数的全微分 T
令该状态函数以S 表示,称为熵
dS δQr T
熵的定义式
dS δQr T
S S2 S1
2 δQr 1T
熵 是状态函数 是广度性质 SI单位 J·K-1
熵的物理意义 〈待讨论〉
2. 热力学第二定律的数学表达式
Siso Ssy s Ssu
Siso 236 .71 293 .81J K1 57.1J K1 <0
不能自动进行
化学反应熵变
已会求任意反应的 rHm 298K; rHm T rUm 298K rUm T
如何求 rSm 298K rSm T
研究化学变化方向要求此值 一般条件下发生的化学反应,都是不可逆过程。
推广到任意循环过程
δQ 0 Tsu
不可逆热机 可逆热机
或
δQ
不可逆热机
0
Tsu
可逆热机
δQ 0 不可逆热机
Tsu
可逆热机
热温商
δQ Tsu
沿任意可逆循环闭积分等于零,
沿任意不可逆循环的闭积分总是小于零。
克劳休斯定理
δQr 0 Tsu
可逆循环
δ Qir 0 Tsu
不可逆循环
δQr T
练习4
设在恒温273K时,将一个22.4dm3的盒子 用 隔 板 从 中 间 隔 开 。 一 方 放 0.5molO2 , 另 一 方 放 0.5molN2 , 抽 去 隔 板 后 , 两 种 气 体 均匀混合。求过程的ΔS
m ix S
n1Rln
V1
V2 V1
n2
Rln
V1 V2 V2
0.5Rln 22.4 0.5Rln 22.4 5.76J K1
S
nC p ,m ln
T2 T1
若Cp,m不为常数?
(ii) 定容变温
QV= dU =nCv,mdT
S δ QV T 2 nCV ,mdT
T
T1
T
若Cv,m视为常数,则
S
nCV ,mln
T2 T1
(iii) 液体或固体定温下 p,V 变化 定T,而p,V变化不大时,液、固体的熵变很小, S ≈0。 实际气体,定T,而p,V变化时,熵变较大
S B δQr AT
合并表示
S B δQ 不可逆过程 A Tsu 可逆过程 δQ 不可逆过程 dS
Tsu 可逆过程
热力学第二定律数学表达式
3. 熵增原理和熵判据
(1) 熵增原理
B δQ
S A Tsu
绝热过程
不可逆过程 可逆过程
ΔS≥0
不可逆过程 可逆过程
熵增原理数学表示式
系统经绝热过程由一个状态达到另一个状态,熵值 不减少 — 熵增原理
T
T1
T
T 2(a bT cT 2 )dT
n T1
T
n(a
ln
T2 T1
b(T2
T1 )
c 2
(T2
2
T12
)
练习2
2mol H2由300K,1.0MPa分别经下述三种不 同 径 途 变 到 300K , 1.0kPa 求 经 各 种 变 化 系 统
的ΔS。(1)自由膨胀;
(2)恒温可逆膨胀; (3)作最大功的50% 。
1.12 热力学第三定律
( third law of thermodynamics)
1. 热力学第三定律的经典表述及数学表达式
能斯特热定理(1906):
Nernst 1864-1941年(德国)
1920年诺贝尔化学奖
随着绝对温度趋于零, 凝聚系统定温反应的熵 变趋于零
lim S*(T ) 0J K1
重点回顾
热力学第二定律的经典表述
克劳休斯说法 :不可能把热由低温物体转 移到高温物体,而不留下其他变化。
开尔文说法:不可能从单一热源吸热使之完全变 为功,而不留下其他变化。
能否找到一个统一的判据来判断可能 发生的过程的方向和限度呢?
熵判据
1.10 熵
1. 定义
Q1 Q2 0 T1 T2
不可逆热机 可逆热机
T 0
普朗克修正说法:
纯物质完美晶体在0 K 时的熵值为零 S *( 完美晶体,0 K )=0 J•K-1
练习4
1mol 单 原 子 理 想 气 体 , 从 273.15K 、 1013.25kPa 的 始 态 , 对 抗 恒 外 压 为 101.325kPa , 绝 热 膨 胀 至 终 态 压 力 为 101.325kPa ,求ΔS
解: Q 0
U W
U
T2 T1
nCV
,m
(T
)dT
W psu (V2 V1)
S
n(CV
,mln
T2 T1
Rln
V2 V1
)
定容
定温
(T1, p1
p1,V1,T1
T2, p2)
p2,V2,T2
定压
定温
p1,V´,T2
S
n(C p,mln
T2 T1
Rln
p1 ) p2
定压 定温
(V1, p1
p1,V1,T1
定容
p2,V1,T´
V2, p2)
p2,V2,T2
定压
S
n(CV ,mln
求该过程的S 。 已知100℃水的汽化焓为40.67 kJ•mol-1
S nHm (相变焓) T
2 40.67 KJ K1 218J K1 373.15
练习6.
2mol H2O( l,25℃,101.325kPa )在定温定压下 汽化为H2O( g,25℃,101.325kPa ) 求该过程的S 。已知100℃水的汽化焓为40.67kJ•mol-1 ,水和水 蒸气的定压摩尔热容分别为75.31J • K-1 • mol-1和 33.6 J •K-1 • mol-1
p2 p1
C
p
,m
ln
V2 V1
)
定容
定压
练习1.
2molH2 由 300K , 100kPa 定 压 加 热 到 1200K , 求ΔS 已知Cp,m(H2) / (J•K-1 • mol-1 )=
28.83-0.84х10-3(T/K)+2.00×10-6(T/K)2
S δQp T 2 nCp, mdT
ΔS隔≥0
自发过程 平衡态
ΔS(系统)+ ΔS(环境) =ΔS(新的隔离系统)
练习5.
2molH2O(l,25℃,101.325kPa)在定温定压下汽 化为H2O(g,25℃,101.325kPa) 求该过程的S 。
已知100℃水的汽化焓为40.67kJ•mol-1 ,水和 水蒸气的定压摩尔热容分别为75.31J • K-1 • mol-1 和33.6 J •K-1 • mol-1
2
273.15
101.325
(3) 理想气体定温,定压下的混合
A,n(A) T,p,V1
+ B,n(B)
T,p,V2
n(A)+n(B) A--B T,p,(V1+ V2)
m ix S
n1Rln
V1 V2 V1
n2 Rln
V1 V2 V2
应用条件:宏观性质不同的理想气体的混合。
宏观性质相同的理想气体的混合 mixS 0
〈本课程不讨论〉
② 理想气体的 p,V,T 变化
W′=0
dS δ Qr dU pdV
T
T
dU=nCV,mdT,则 dS nCV ,mdT nRdV
T
V
若 CV,m为常数,
S
n(CV ,mln
T2 T1
Rln
V2 V1
)
(T1,V1
p1,V1,T1
T2,V2)
p2,V2,T2
定容
定温
p',V1,T2
nCV ,m (T2
T1)
psu
(
nRT2 p2
nRT1 ) p1
3 2
(T2
T1)
p2
(
T2 p2
T1 p1
)
T2 174 .8K
(T1, p1
T2, p2)p ,m
T
p
1
2
1 (3 R R) ln 174.8 1 R ln 1013.25 9.86J K-1
(2) 熵判据
隔离系统,Q= 0
ΔS隔≥0
不可逆过程 可逆过程
隔离系统,W= 0 所以,隔离系统的不可逆过程是自发过程
可逆过程是无限慢的变化,实际是平衡态
ΔS隔≥0
自发过程 平衡态
平衡的熵判据
(只能用于隔离系统!!!)
隔离系统 状态A
状态B
ΔS = 0 ΔS > 0 ΔS < 0
A 、B平衡态 自发从A 变到B的趋势 不可能发生
Ssys S1 S2 S3 236.71J K1
H = ?
H2O(l,25℃,101.325kPa)
H1 H2
H2O(l,100℃,101.325kPa )
H2O(g,25℃,101.325kPa ) H3
H2O( g,100℃,101.325kPa )
