初二三角形压轴题分类解析(完整资料).doc
专题03 全等三角形的六种模型全梳理(解析版)-2024年常考压轴题攻略(8年级上册人教版)

专题03全等三角形的六种模型全梳理几何探究类问题一直属于考试压轴题范围,在三角形这一章,压轴题主要考查是证明三角形各种模型,或证明线段数量关系等,接来下我们针对其做出详细分析与梳理。
类型一、倍长中线模型目的:①构造出一组全等三角形;②构造出一组平行线。
将分散的条件集中到一个三角形中。
如图1,ABC 中,若86AB AC ==,,求BC 边上的中线小明在组内经过合作交流,得到了如下的解决方法:如图连接BE .请根据小明的方法思考:(1)如图2,由已知和作图能得到ADC EDB ≌△△A .SSS B .SAS C .AAS D .ASA(2)如图2,AD 长的取值范围是.(2)根据全等三角形的性质得到6AC BE ==,由三角形三边关系得到AB BE AE AB BE -<<+,即可求出17AD <<;(3)延长AD 到点M ,使AD DM =,连接BM ,证明ADC MDB △△≌,得到BM AC CAD M =∠=∠,,由AE EF =得到CAD AFE ∠=∠,进而推出BF BM =,即可证明AC BF =.【详解】解:(1)如图2,延长AD 到点E ,使DE AD =,连接BE .∵AD 为BC 的中线,∴BD CD =,又∵AD DE ADC BDE =∠=∠,,∴()SAS ADC EDB ≌△△,故答案为:B ;(2)解:∵ADC EDB ≌△△,∴6AC BE ==,在ABE 中,AB BE AE AB BE -<<+,∴86286AD -<<+,∴17AD <<,故答案为:C ;(3)证明:延长AD 到点M ,使AD DM =,连接BM ,∵AD 是ABC 中线,∴CD BD =,∵在ADC △和MDB △中,DC DB ADC MDB AD HD =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ADC MDB ≌△△,∴BM AC CAD M =∠=∠,,∵AE EF =,(1)如图1,求证:12BF AD =;(2)将DCE △绕C 点旋转到如图2所示的位置,连接,AE BD ,过C 点作CM ⊥①探究AE 和BD 的关系,并说明理由;②连接FC ,求证:F ,C ,M 三点共线.【答案】(1)见解析(2)①,AE BD AE BD =⊥,理由见解析②见解析【分析】(1)证明≌ACD BCE V V ,得到AD BE =,再根据点F 为BE 中点,即可得证;则:AGB CBD BHG ∠=∠+∠=∠∵CBD EAC ∠=∠,∴90BHG ACB ∠=∠=︒,∴AE BD ⊥,综上:,AE BD AE BD =⊥;②延长CF 至点P ,使PF CF =∵F 为BE 中点,∴BF FE =,∴()SAS BFP EFC ≌,∴,BP CE BPF ECF =∠=∠,∴CE BP ,∴180CBP BCE ∠+∠=︒,∵360180BCE ACD ACB DCE ∠+∠=︒-∠-∠=︒,∴CBP ACD ∠=∠,又,CE CD BP AC BC ===,∴()SAS PBC DCA ≌,∴BCP CAD ∠=∠,延长FC 交AD 于点N ,则:18090BCP ACN ACB ∠+∠=︒-∠=︒,∴90CAD ACN ∠+∠=︒,∴90ANC ∠=︒,∴CN AD ⊥,∵CM AD ⊥,∴点,M N 重合,即:F ,C ,M 三点共线.【点睛】本题考查全等三角形的判定和性质,等腰三角形判定和性质.熟练掌握手拉手全等模型,倍长中线法构造全等三角形,是解题的关键.【变式训练1】如图,ABC 中,BD DC AC ==,E 是DC 的中点,求证:2AB AE =.【答案】见解析【分析】利用中线加倍证DEF CEA △≌△(SAS ),可得DF AC BD ==,FDE C ∠=∠,由DC AC =,可得ADC CAD ∠=∠进而可证ADF ADB ∠=∠.,再证ADB ADF △≌△(SAS )即可.【详解】证明:延长AE 到F ,使EF AE =,连结DF ,∵E 是DC 中点,∴DE CE =,∴在DEF 和CEA 中,DE CE DEF CEA EF EA =⎧⎪∠=∠⎨⎪=⎩,∴DEF CEA △≌△(SAS ),∴DF AC BD ==,FDE C ∠=∠,∵DC AC =,∴ADC CAD ∠=∠,又∵ADB C CAD ∠=∠+∠,ADF FDE ADC ∠=∠+∠,∴ADF ADB ∠=∠,在ADB 和ADF △中,AD AD ADB ADF DB DF =⎧⎪∠=∠⎨⎪=⎩,∴ADB ADF △≌△(SAS ),∴2AB AF AE ==.【点睛】本题考查中线加倍构图,三角形全等判定与性质,等腰三角形性质,掌握中线加倍构图,三角形全等判定与性质,等腰三角形性质是解题关键.【变式训练2】(1)如图1,已知ABC 中,AD 是中线,求证:2AB AC AD +>;(2)如图2,在ABC 中,D ,E 是BC 的三等分点,求证:AB AC AD AE +>+;(3)如图3,在ABC 中,D ,E 在边BC 上,且BD CE =.求证:AB AC AD AE +>+.【答案】(1)见解析;(2)见解析;(3)见解析【分析】(1)利用“倍长中线”法,延长AD ,然后通过全等以及三角形的三边关系证明即可;(2)取DE 中点H ,连接AH 并延长至Q 点,使得AH =QH ,连接QE 和QC ,通过“倍长中线”思想全等证明,进而得到AB =CQ ,AD =EQ ,然后结合三角形的三边关系建立不等式证明即可得出结论;(3)同(2)处理方式一样,取DE 中点M ,连接AM 并延长至N 点,使得AM =NM ,连接NE ,CE ,结合“倍长中线”思想证明全等后,结合三角形的三边关系建立不等式证明即可得出结论.【详解】证:(1)如图所示,延长AD 至P 点,使得AD =PD ,连接CP ,∵AD 是△ABC 的中线,∴D 为BC 的中点,BD =CD ,在△ABD 与△PCD 中,BD CD ADB PDC AD PD =⎧⎪∠=∠⎨⎪=⎩∴△ABD ≌△PCD (SAS ),∴AB =CP ,在△APC 中,由三边关系可得AC +PC >AP ,∴2AB AC AD +>;(2)如图所示,取DE 中点H ,连接AH 并延长至Q 点,使得AH =QH ,连接QE 和QC ,∵H 为DE 中点,D 、E 为BC 三等分点,∴DH =EH ,BD =DE =CE ,∴DH =CH ,在△ABH 和△QCH 中,BH CH BHA CHQ AH QH =⎧⎪∠=∠⎨⎪=⎩,∴△ABH ≌△QCH (SAS ),同理可得:△ADH ≌△QEH ,∴AB =CQ ,AD =EQ ,此时,延长AE ,交CQ 于K 点,∵AC +CQ =AC +CK +QK ,AC +CK >AK ,∴AC +CQ >AK +QK ,又∵AK +QK =AE +EK +QK ,EK +QK >QE ,∴AK +QK >AE +QE ,∴AC +CQ >AK +QK >AE +QE ,∵AB =CQ ,AD =EQ ,∴AB AC AD AE +>+;(3)如图所示,取DE 中点M ,连接AM 并延长至N 点,使得AM =NM ,连接NE ,CE ,∵M 为DE 中点,∴DM =EM ,∵BD =CE ,∴BM =CM ,在△ABM 和△NCM 中,BM CM BMA CMN AM NM =⎧⎪∠=∠⎨⎪=⎩∴△ABM ≌△NCM (SAS ),同理可证△ADM ≌△NEM ,∴AB =NC ,AD =NE ,此时,延长AE ,交CN 于T 点,∵AC +CN =AC +CT +NT ,AC +CT >AT ,∴AC +CN >AT +NT ,又∵AT +NT =AE +ET +NT ,ET +NT >NE ,∴AT +NT >AE +NE ,∴AC +CN >AT +NT >AE +NE ,∵AB =NC ,AD =NE ,∴AB AC AD AE +>+.【点睛】本题考查全等三角形证明问题中辅助线的添加,掌握“倍长中线”的基本思想,以及熟练运用三角形的三边关系是解题关键.【答案】(1)1.5 6.5AE <<;(2)见解析;(3)BE DF EF +=,理由见解析【分析】(1)如图①:将ACD △绕着点D 逆时针旋转180 得到EBD △可得BDE ≅ 得出5BE AC ==,然后根据三角形的三边关系求出AE 的取值范围,进而求得AD 范围;(2)如图②:FDC △绕着点D 旋转180︒得到NDB 可得BND CFD ≅ ,得出BN∴1.5 6.5AD <<;故答案为1.5 6.5AD <<;(2)证明:如图②:FDC △绕着点D 旋转180︒得到NDB∴BND CFD ≅ (SAS ),∴BN CF =,DN DF=∵DE DF⊥∴EN EF =,在BNE 中,由三角形的三边关系得:BE BN EN +>,∴BE CF EF +>;(3)BE DF EF +=,理由如下:如图③,将DCF 绕着点C 按逆时针方向旋转100︒∴△DCF ≌△BCH ,∴100CH CF DCB FCH ∠∠=︒=,=∴HBC D DF BH∠∠==,∵180ABC D ∠+∠︒=∴180HBC ABC ∠+∠︒=,∴点A 、B 、H 三点共线∵100FCH ∠=︒,50FCE ∠=︒,∴50ECH ∠=︒∴FCE ECH ∠∠=,在HCE 和FCE △中,===CF CH ECF ECH CE CE ∠∠⎧⎪⎨⎪⎩,∴HCE FCE ≌ (SAS )∴EH EF =,∵BE BH EH DF BH+==,∴BE DF EF +=.【点睛】本题属于三角形综合题,主要考查对全等三角形的性质和判定、三角形的三边关系定理、旋转的性质等知识点,通过旋转得到构造全等三角形是解答本题的关键.类型二、截长补短模型截长补短法使用范围:线段和差的证明(往往需证2次全等)(1)求证:CD BC DE=+;(2)若75B∠=︒,求E∠的度数.【答案】(1)见解析(2)105︒【分析】(1)在CD上截取CF∵CA平分BCD∠,∴BCA FCA∠=∠.在BCAV和FCA△中,⎧⎪∠⎨⎪⎩,∠=︒BAC60【答案】(1)5.8;(2)4.3【分析】(1)由已知条件和辅助线的作法,证得△ACD≌△ECD,得到由于∠A=2∠B,推出∠DEC=2∠B,等量代换得到∠B=∠EDB形,得出AC =CE =3.6,DE =BE =2.2,相加可得BC 的长;(2)在BA 边上取点E ,使BE =BC =2,连接DE ,得到△DEB ≌△DBC (SAS ),在DA 边上取点F ,使DF =DB ,连接FE ,得到△BDE ≌△FDE ,即可推出结论.【详解】解:(1)如图2,在BC 边上取点E ,使EC =AC ,连接DE .在△ACD 与△ECD 中,AC CE ACD ECD CD CD =⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△ECD (SAS ),∴AD =DE ,∠A =∠DEC ,∵∠A =2∠B ,∴∠DEC =2∠B ,∴∠B =∠EDB ,∴△BDE 是等腰三角形;∴BE =DE =AD =2.2,AC =EC =3.6,∴BC 的长为5.8;(2)∵△ABC 中,AB =AC ,∠A =20°,∴∠ABC =∠C =80°,∵BD 平分∠B ,∴∠1=∠2=40°,∠BDC =60°,在BA 边上取点E ,使BE =BC =2,连接DE ,在△DEB 和△DBC 中,12BE BC BD BD =⎧⎪∠=∠⎨⎪=⎩,∴△DEB ≌△DBC (SAS ),∴∠BED =∠C =80°,∴∠4=60°,∴∠3=60°,在DA 边上取点F ,使DF =DB ,连接FE ,同理可得△BDE ≌△FDE ,∴∠5=∠1=40°,BE =EF =2,∵∠A =20°,∴∠6=20°,∴AF =EF =2,∵BD =DF =2.3,∴AD =BD +BC =4.3.【点睛】本题考查了全等三角形的性质与判定,等腰三角形的性质,熟悉这些定理是解决本题的关键.类型三、一线三等角模型应用:①通过证明全等实现边角关系的转化,便于解决对应的几何问题;②与函数综合应用中有利于点的坐标的求解。
全等三角形中的常见压轴题五种模型全攻略—2023-2024学年八年级数学上册(浙教版)(解析版)

全等模型专题:全等三角形中的常见压轴题五种模型全攻略【考点导航】目录【典型例题】 (1)【解题模型一 四边形中构造全等三角形解题】 ........................................................................................ 1 【解题模型二 一线三等角模型】 ............................................................................................................... 8 【解题模型三 三垂直模型】..................................................................................................................... 15 【解题模型四 倍长中线模型】 ................................................................................................................. 22 【解题模型五 旋转模型】 (28)【典型例题】【解题模型一 四边形中构造全等三角形解题】例题:(2023春·广东梅州·八年级校联考开学考试)已知如图,四边形ABCD 中,AB BC =,AD CD =,求证:A C ∠=∠.【答案】见解析【分析】连接BD ,已知两边对应相等,加之一个公共边BD ,则可利用SSS 判定ABD CBD ≌△△,根据全等三角形的对应角相等即可证得. 【详解】证明:连接BD ,AB CB =,BD BD =,AD CD =,SSS ABD CBD ∴≌(). A C ∴∠=∠.【点睛】此题主要考查学生对全等三角形的判定方法的理解及运用,常用的判定方法有SSS ,SAS ,ASA ,HL 等.【变式训练】【答案】他的发现正确,理由见解析【分析】根据全等三角形的判定和性质直接证明即可. 【详解】解:他的发现正确,理由如下: 在ABD △与ACD 中,AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩,∴ABD ACD △≌△,∴BAD CAD ∠=∠,ADB ADC ∠=∠,∴AD 不仅平分BAC ∠,且平分BDC ∠.【点睛】题目主要考查全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题关键. 2.(2023秋·湖南常德·八年级统考期末)中国现役的第五代隐形战斗机歼−20的机翼如图,为适应空气动力的要求,两个翼角,A B ∠∠必须相等.(1)实际制造中,工作人员只需用刻度尺测量PA PB =,CA CB =就能满足要求,说明理由; (2)若30,40A P ∠=︒∠=︒,求ACB ∠的度数. 【答案】(1)见解析 (2)100°【分析】(1)连接PC ,证明APC BPC ≌△△,即可解答. (2)由三角形的外角的性质即可解答. 【详解】(1)证明:如图,连接PC ,在APC △和BPC △中,PA PB CA CB PC PC =⎧⎪=⎨⎪=⎩,∴APC BPC ≌△△(SSS ), ∴A B ∠=∠.(2)∵APC BPC ≌△△,30,40A P ∠=︒∠=︒, ∴30A B ==︒∠∠,∵C C A B A E C B E =+∠∠∠,,,ACE APC A BCE BPC B ∠=∠+∠∠=∠+∠ ∴23040100ACB APC A BPC B A BPA B ∠=∠+∠+∠+∠=∠+∠+∠=⨯︒+︒=︒. 【点睛】本题考查了三角形全等和外角的性质,掌握三角形全等是解题的关键.3.如图,在四边形ABCD 中,CB AB ⊥于点B ,CD AD ⊥于点D ,点E ,F 分别在AB ,AD 上,AE AF =,CE CF =.(1)若8AE =,6CD =,求四边形AECF 的面积;(2)猜想∠DAB ,∠ECF ,∠DFC 三者之间的数量关系,并证明你的猜想. 【答案】(1)48(2)∠DAB +∠ECF =2∠DFC ,证明见解析 【解析】 【分析】(1)连接AC ,证明△ACE ≌△ACF ,则S △ACE =S △ACF ,根据三角形面积公式求得S △ACF 与S △ACE ,根据S 四边形AECF =S △ACF +S △ACE 求解即可;(2)由△ACE ≌△ACF 可得∠FCA =,∠FAC =∠EAC ,∠AFC =∠AEC ,根据垂直关系,以及三角形的外角性质可得∠DFC +∠BEC =∠FCA +∠FAC +∠ECA +∠EAC =∠DAB +∠ECF .可得∠DAB +∠ECF =2∠DFC (1)解:连接AC ,如图,在△ACE 和△ACF 中AE AFCE CF AC AC =⎧⎪=⎨⎪=⎩∴△ACE ≌△ACF (SSS ).∴S △ACE =S △ACF ,∠FAC =∠EAC .∵CB⊥AB,CD⊥AD,∴CD=CB=6.∴S△ACF=S△ACE=12AE·CB=12×8×6=24.∴S四边形AECF=S△ACF+S△ACE=24+24=48.(2)∠DAB+∠ECF=2∠DFC证明:∵△ACE ≌△ACF,∴∠FCA=∠ECA,∠FAC=∠EAC,∠AFC=∠AEC.∵∠DFC与∠AFC互补,∠BEC与∠AEC互补,∴∠DFC=∠BEC.∵∠DFC=∠FCA+∠FAC,∠BEC=∠ECA+∠EAC,∴∠DFC+∠BEC=∠FCA+∠FAC+∠ECA+∠EAC=∠DAB+∠ECF.∴∠DAB+∠ECF=2∠DFC【点睛】本题考查了三角形全等的性质与判定,三角形的外角的性质,掌握三角形全等的性质与判定是解题的关键.4.在四边形ABDC中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF.(1)试说明:DE=DF:(2)在图中,若G在AB上且∠EDG=60°,试猜想CE,EG,BG之间的数量关系并证明所归纳结论.(3)若题中条件“∠CAB=60°,∠CDB=120°改为∠CAB=α,∠CDB=180°﹣α,G在AB上,∠EDG满足什么条件时,(2)中结论仍然成立?【答案】(1)见解析;(2)CE+BG=EG,理由见解析;(3)当∠EDG=90°-12α时,(2)中结论仍然成立.【解析】 【分析】(1)首先判断出C DBF ∠=∠,然后根据全等三角形判定的方法,判断出ΔΔCDE BDF ≅,即可判断出DE DF =.(2)猜想CE 、EG 、BG 之间的数量关系为:CE BG EG +=.首先根据全等三角形判定的方法,判断出ABD ACD∆≅∆,即可判断出60BDA CDA ∠=∠=︒;然后根据60EDG ∠=︒,可得CDE ADG ∠=∠,ADE BDG ∠=∠,再根据CDE BDF ∠=∠,判断出EDG FDG ∠=∠,据此推得ΔΔDEG DFG ≅,所以EG FG =,最后根据CE BF =,判断出CE BG EG +=即可.(3)根据(2)的证明过程,要使CE BG EG +=仍然成立,则12EDG BDA CDA CDB ∠=∠=∠=∠,即11(180)9022EDG αα∠=︒−=︒−,据此解答即可.(1)证明:360CAB C CDB ABD ∠+∠+∠+∠=︒,60CAB ∠=︒,120CDB ∠=︒,36060120180C ABD ∴∠+∠=︒−︒−︒=︒,又180DBF ABD ∠+∠=︒,C DBF ∴∠=∠,在CDE ∆和BDF ∆中,CD BDC DBF CE BF =⎧⎪∠=∠⎨⎪=⎩ΔΔ()CDE BDF SAS ∴≅,DE DF ∴=.(2)解:如图,连接AD ,猜想CE 、EG 、BG 之间的数量关系为:CE BG EG +=. 证明:在ABD ∆和ACD ∆中,AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩,ΔΔ()ABD ACD SSS ∴≅,111206022BDA CDA CDB ∴∠=∠=∠=⨯︒=︒,又60EDG ∠=︒,CDE ADG ∴∠=∠,ADE BDG ∠=∠,由(1),可得ΔΔCDE BDF ≅,CDE BDF ∴∠=∠,60BDG BDF ∴∠+∠=︒,即60FDG ∠=︒,EDG FDG ∴∠=∠,在DEG ∆和DFG ∆中,DE DF EDG FDG DG DG =⎧⎪∠=∠⎨⎪=⎩ΔΔ()DEG DFG SAS ∴≅, EG FG ∴=,又CE BF =,FG BF BG =+,CE BG EG ∴+=;(3)解:要使CE BG EG +=仍然成立, 则12EDG BDA CDA CDB ∠=∠=∠=∠,即11(180)9022EDG αα∠=︒−=︒−,∴当1902EDG α∠=︒−时,CE BG EG +=仍然成立. 【点睛】本题综合考查了全等三角形的性质和判定,此题是一道综合性比较强的题目,有一定的难度,能根据题意推出规律是解此题的关键.【解题模型二 一线三等角模型】例题:(2023春·七年级课时练习)【探究】如图①,点B 、C 在MAN ∠的边AM AN 、上,点E 、F 在MAN ∠内部的射线AD 上,12∠∠、分别是ABE 、CAF V 的外角.若AB AC =,12BAC ∠=∠=∠,求证:ABE CAF V V ≌.【应用】如图②,在等腰三角形ABC 中,AB AC =,AB BC >,点D 在边BC 上,2CD BD =,点E 、F 在线段AD 上,12BAC ∠=∠=∠,若ABC 的面积为9,则ABE 与CDF 的面积之和为 .【答案】探究:见解析;应用:6【分析】探究:根据A BAE ABE ∠=∠∠,BAC CAF BAE ∠=∠+∠,得出ABE CAF ∠=∠,根据12∠=∠,得出AEB CFA ∠=∠,再根据AAS 证明即可; 应用:根据全等三角形的性质得出:ABECAFSS=,进而得出CDFCAFACDSSS+=,根据2CD BD =,ABC的面积为9,得出263ACDABCSS ==,即可得出答案.【详解】探究证明:∵A BAE ABE ∠=∠+∠,BAC CAF BAE ∠=∠+∠, 又∵1BAC ∠=∠, ∴ABE CAF ∠=∠, ∵12∠=∠, ∴AEB CFA ∠=∠, 在ABE 和CAF V 中,AEB CFA ABE CAF AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()AAS ABE CAF △≌△;应用解:∵ABE CAF V V ≌, ∴ABECAFS S=,∴CDFCAFACDSSS+=,∵2CD BD =,ABC 的面积为9, ∴263ACDABCSS ==,∴ABE 与CDF 的面积之和为6, 故答案为:6.【点睛】本题考查全等三角形的判定与性质,掌握全等三角形的判定是解题的关键.【变式训练】≌ABF CAD ;,在ABC 中,.若ABC 的面积为与CDE 的面积之比. 【答案】(1)证明见详解;(2)成立,证明见详解;(3)1:4【分析】(1)根据90BAC BFE CDE ∠=∠=∠=︒即可得到90BAF CAF ∠+∠=︒,90DCA CAF ∠+∠=︒,从而得到BAF DCA ∠=∠,即可得到证明;(2)根据BAC BFE CDE ∠=∠=∠得到BAF CAF DCA CAF ∠+∠=∠+∠,即可得到BAF DCA ∠=∠,即可得到证明;(3)根据ABC 的面积为15,2CE BE =,即可得到5ABE S =△,10AEC S =,结合2DE AD =可得103ADC S =△,203EDC S =,根据AB AC =,BAC BFE CDE ∠=∠=∠得到≌ABF CAD ,即可得到BEF S ,即可得到答案;【详解】(1)证明:∵90BAC BFE CDE ∠=∠=∠=︒,∴90BFA CDA ∠=∠=︒,90BAF CAF ∠+∠=︒,90DCA CAF ∠+∠=︒, ∴BAF DCA ∠=∠, 在ABF △与CAD 中,∵BFA CDA BAF DCA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴(AAS)ABF CAD ≌; (2)解:成立,理由如下, ∵BAC BFE CDE ∠=∠=∠,∴BAF CAF DCA CAF ∠+∠=∠+∠,BFA CDA ∠=∠, ∴BAF DCA ∠=∠, 在ABF △与CAD 中,∵BFA CDA BAF DCA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴(AAS)ABF CAD ≌;(3)解:∵ABC 的面积为15,2CE BE =, ∴5ABE S =△,10AECS=,∵2DE AD =, ∴103ADC S =△,203EDCS =,∵BAC BFE CDE ∠=∠=∠,∴BAF CAF DCA CAF ∠+∠=∠+∠,BFA CDA ∠=∠,∴BAF DCA ∠=∠,在ABF △与CAD 中,∵BFA CDA BAF DCA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴(AAS)ABF CAD ≌ ∴105533BEF S =−=, ∴520:1433BEF CDE S S ==::; 【点睛】本题考查三角形全等的判定与性质及同高不同底三角形的面积,解题的关键是根据内外角关系得到三角形全等的条件.【答案】(1)①BE CF =;②180BCA α+∠=︒(2)EF BE AF =+【分析】(1)①由90BCA ∠=︒,90BEC CFA α∠=∠==︒,可得BCE CAF ∠=∠,从而可证BCE CAF ≌△△,故BE CF =;②添加180BCA α+∠=︒,可证明BCA BEF ∠=∠,则ACF CBE ∠=∠,根据AAS 可证明BCE CAF ≌△△,即可得证①中的结论仍然成立;(2)题干已知条件可证BCE CAF ≌△△,故BE CF =,EC FA =,从而可证明EF BE AF =+.【详解】(1)解:①BE CF =,理由如下:∵90BCA ∠=︒,∴90ACF BCE ∠+∠=︒,∵90BEC AFC α∠===∠︒,∴90ACF CAF ∠+∠=︒,∴BCE CAF ∠=∠,∵AC BC =,∴()AAS BCE CAF △≌△,∴BE CF =;②添加180BCA α+∠=︒,使①中的结论仍然成立,理由如下:∵BEC CFA α∠=∠=,∴180180BEF BEC α∠=︒−∠=︒−,∵BEF EBC BCE ∠=∠+∠,∴180EBC BCE α∠+∠=︒−,∵180BCA α+∠=︒,∴180BCA α∠=︒−,∴180BCA BCE ACF α∠=∠+∠=︒−,∴EBC ACF ∠=∠,∵AC BC =,BEC CFA α∠=∠=,∴()AAS BCE CAF △≌△,∴BE CF =;故答案为:180BCA α+∠=︒;(2)EF BE AF =+,理由如下:∵BCA α∠=,∴180180BCE FCA BCA α∠+∠=︒−∠=︒−,∵BEC α∠=,∴180180EBC BCE BEC α∠+∠=︒−∠=︒−,∴EBC FCA ∠=∠,∵AC BC =,BEC CFA α∠=∠=,∴()AAS BEC CFA △≌△,∴BE CF =,EC FA =,∴EF EC CF FA BE =+=+,即EF BE AF =+.【点睛】本题是三角形的综合题,主要考查全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.3.在直线m 上依次取互不重合的三个点,,D A E ,在直线m 上方有AB AC =,且满足BDA AEC BAC α∠=∠=∠=.(1)如图1,当90α=︒时,猜想线段,,DE BD CE 之间的数量关系是____________;(2)如图2,当0180α<<︒时,问题(1)中结论是否仍然成立?如成立,请你给出证明;若不成立,请说明理由;(3)应用:如图3,在ABC 中,BAC ∠是钝角,AB AC =,,BAD CAE BDA AEC BAC ∠<∠∠=∠=∠,直线m 与CB 的延长线交于点F ,若3BC FB =,ABC 的面积是12,求FBD 与ACE 的面积之和.【答案】(1)DE =BD+CE(2)DE =BD+CE 仍然成立,理由见解析(3)△FBD 与△ACE 的面积之和为4【解析】【分析】(1)由∠BDA =∠BAC =∠AEC =90°得到∠BAD+∠EAC =∠BAD+∠DBA =90°,进而得到∠DBA =∠EAC ,然后结合AB=AC得证△DBA≌△EAC,最后得到DE=BD+CE;(2)由∠BDA=∠BAC=∠AEC=α得到∠BAD+∠EAC=∠BAD+∠DBA=180°﹣α,进而得到∠DBA=∠EAC,然后结合AB=AC得证△DBA≌△EAC,最后得到DE=BD+CE;(3)由∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,得出∠CAE=∠ABD,由AAS证得△ADB≌△CAE,得出S△ABD =S△CEA,再由不同底等高的两个三角形的面积之比等于底的比,得出S△ABF即可得出结果.(1)解:DE=BD+CE,理由如下,∵∠BDA=∠BAC=∠AEC=90°,∴∠BAD+∠EAC=∠BAD+∠DBA=90°,∴∠DBA=∠EAC,∵AB=AC,∴△DBA≌△EAC(AAS),∴AD=CE,BD=AE,∴DE=AD+AE=BD+CE,故答案为:DE=BD+CE.(2)DE=BD+CE仍然成立,理由如下,∵∠BDA=∠BAC=∠AEC=α,∴∠BAD+∠EAC=∠BAD+∠DBA=180°﹣α,∴∠DBA=∠EAC,∵AB=AC,∴△DBA≌△EAC(AAS),∴BD=AE,AD=CE,∴DE=AD+AE=BD+CE;(3)解:∵∠BAD<∠CAE,∠BDA=∠AEC=∠BAC,∴∠CAE=∠ABD,在△ABD和△CAE中,ABD CAEBDA CEAAB AC∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABD≌△CAE(AAS),∴S△ABD=S△CAE,设△ABC 的底边BC 上的高为h ,则△ABF 的底边BF 上的高为h ,∴S △ABC =12BC•h =12,S △ABF =12BF•h ,∵BC =3BF ,∴S △ABF =4,∵S △ABF =S △BDF+S △ABD =S △FBD+S △ACE =4,∴△FBD 与△ACE 的面积之和为4.【点睛】本题考查了全等三角形的判定与性质、直角三角形的性质,三角形的面积,解题的关键是熟练掌握全等三角形的判定与性质.【解题模型三 三垂直模型】例题:(2023春·广东广州·九年级专题练习)如图,90,,ACB AC BC BE CE ∠=︒=⊥于E ,AD CE ⊥于D ,2.7cm, 1.8cm AD DE ==.(1)求证:ACD CBE ≌.(2)求BE 的长.【答案】(1)见解析;(2)0.9cm BE =.【分析】(1)由垂直得90ADC CEB ∠=∠=︒,求出ACD CBE ∠=∠,然后利用AAS 即可证明ACD CBE ≌;(2)根据全等三角形的性质可得 2.7cm CE AD ==,BE CD =,根据CD CE DE =−求出CD 即可得到BE 的长.【详解】(1)证明:∵AD CE ⊥,BE CE ⊥,∴90ADC CEB ∠=∠=︒,∵90ACB ∠=︒,∴90ACD ACB BCE BCE ∠=∠−∠=︒−∠,∵90CBE BCE ∠=︒−∠,∴ACD CBE ∠=∠,在ACD 与CBE △中,ADC CEB ACD CBE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴()AAS ACD CBE ≌; (2)解: 由(1)知,ACD CBE △△≌, ∴ 2.7cm CE AD ==,BE CD =,∵ 2.7 1.80.9cm CD CE DE =−=−=,∴0.9cm BE =.【点睛】本题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定定理和全等三角形对应边相等的性质是解题的关键.【变式训练】 1.(2023春·河北邯郸·七年级校考阶段练习)已知:90ACB ∠=︒,AC BC =,AD CM ⊥,BE CM ⊥,垂足分别为D ,E .在ACD 和CBE ∴ACD CBE ≌,( CD BE =∵ACD CBE ≌,【答案】(1)①CBE ∠;同角的余角相等;ADC BEC ∠∠=,ACD CBE ∠=∠,AC BC =;AAS ;②AD CE =(2)不成立,DE BE AD −=,见解析【分析】(1)根据同角的余角相等,全等三形的判定方法角角边分析处理;(2)根据同角的余角相等,全等三形的判定方法角角边分析处理,注意观察图形,得出线段间的数量关系;【详解】(1)∵AD CM ⊥,BE CM ⊥,∴90ACB BEC ADC Ð=Ð=Ð=°,∴90ACD BCE ∠+∠=︒,90BCE CBE ∠+∠=︒,∴ACD ∠= CBE ∠ ( 同角的余角相等 )在ACD 和CBE 中, ADC BEC ∠∠=,ACD CBE ∠=∠,AC BC = ,∴ACD CBE ≌,( AAS )∴CD BE =.②结论:AD BE DE =+.理由:∵ACD CBE ≌,∴ AD CE = ,∵CE CD DE BE DE =+=+,∴AD BE DE =+.(2)不成立,结论:DE BE AD −=.理由:∵AD CM ⊥,BE CM ⊥,∴90ACB BEC ADC Ð=Ð=Ð=°,∴90ACD BCE ∠+∠=︒,90BCE CBE ∠+∠=︒,∴ACD CBE ∠=∠在ACD 和CBE △中,ADC CEB ACD CBE AC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴ACD CBE △△≌,(AAS )∴AD CE =,CD BE =,∴DE BE DE DC CE AD -=-==.【点睛】本题考查全等三角形的判定和性质,能够由图形的位置关系得出线段之间、角之间的数量关系是解题的关键.2.在△ABC 中,∠BAC =90°,AC=AB ,直线MN 经过点A ,且CD ⊥MN 于D ,BE ⊥MN 于E .(1)当直线MN绕点A旋转到图1的位置时,EAB DAC∠+∠=度;(2)求证:DE=CD+BE;(3)当直线MN绕点A旋转到图2的位置时,试问DE、CD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.【答案】(1)90°(2)见解析(3)CD= BE + DE,证明见解析【解析】【分析】(1)由∠BAC=90°可直接得到EAB DAC∠+∠=90°;(2)由CD⊥MN,BE⊥MN,得∠ADC=∠BEA=∠BAC=90°,根据等角的余角相等得到∠DCA=∠EAB,根据AAS可证△DCA≌△EAB,所以AD=CE,DC=BE,即可得到DE = EA+AD = DC+BE.(3)同(2)易证△DCA≌△EAB,得到AD=CE,DC=BE,由图可知AE = AD +DE,所以CD= BE + DE.(1)∵∠BAC=90°∴∠EAB+∠DAC=180°-∠BAC=180°-90°=90°故答案为:90°.(2)证明:∵ CD⊥MN于D,BE⊥MN于E∴∠ADC=∠BEA=∠BAC=90°∵∠DAC+∠DCA=90°且∠DAC+∠EAB=90°∴∠DCA=∠EAB∵在△DCA和△EAB中90 ADC BEA DCA EABAC AB ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∴△DCA≌△EAB (AAS)∴ AD=BE且EA=DC由图可知:DE = EA+AD = DC+BE.(3)∵ CD⊥MN于D,BE⊥MN于E∴∠ADC=∠BEA=∠BAC=90°∵∠DAC+∠DCA=90°且∠DAC+∠EAB=90°∴∠DCA=∠EAB∵在△DCA和△EAB中90 ADC BEA DCA EABAC AB ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∴△DCA≌△EAB (AAS)∴ AD=BE且AE=CD由图可知:AE = AD +DE∴ CD= BE + DE.【点睛】本题考查了旋转的性质:旋转前后两图形全等,对应点到旋转中心的距离相等,对应点与旋转中心的连线段所夹的角等于旋转角,也考查了三角形全等的判定与性质..如图,已知:在ABC中,)的位置时,求证:ADC CEB≅;【答案】(1)见解析;(2)见解析;(3)DE=BE-AD【分析】(1)由已知推出∠ADC=∠BEC=90°,因为∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,推出∠DAC=∠BCE,根据AAS即可得到答案;(2)结论:DE=AD -BE .与(1)证法类似可证出∠ACD=∠EBC ,能推出△ADC ≌△CEB ,得到AD=CE ,CD=BE ,即可得到答案.(3)结论:DE=BE -AD .证明方法类似.【详解】解:(1)证明:如图1,∵AD ⊥DE ,BE ⊥DE ,∴∠ADC=∠BEC=90°,∵∠ACB=90°,∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,∴∠DAC=∠BCE ,在△ADC 和△CEB 中,CDA BEC DAC ECBAC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△CEB (AAS );(2)如图2,∵BE ⊥EC ,AD ⊥CE ,∴∠ADC=∠BEC=90°,∴∠EBC+∠ECB=90°,∵∠ACB=90°,∴∠ECB+∠ACE=90°,∴∠ACD=∠EBC ,在△ADC 和△CEB 中,ACD CBE ADC BECAC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△CEB (AAS ),∴AD=CE ,CD=BE ,∴DE=EC -CD=AD -BE .(3)DE=BE -AD ;如图3,∵∠ACB=90°,∴∠ACD+∠BCE=90°∵AD ⊥MN ,BE ⊥MN ,∴∠ADC=∠CEB=90°,∴∠ACD+∠DAC=90°,∴∠DAC=∠ECB ,在△ACD 和△CBE 中,ADC CEB DAC ECBAC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△CBE (AAS ),∴AD=CE ,CD=BE ,∴DE=CD -CE=BE -AD .【点睛】本题主要考查了余角的性质,全等三角形的性质和判定等知识点,能根据已知证明△ACD ≌△CBE 是解此题的关键,题型较好,综合性比较强.【解题模型四 倍长中线模型】 八年级统考期中)如图,在ABC 中, (1)求BC 边的长的取值范围?(2)若AD 是ABC 的中线,求AD 【答案】(1)17BC <<(2)1722AD << 【分析】(1)根据三角形三边的关系求解即可;(2)延长AD 至E ,使AD DE =,连接BE ,证明ADC EDB V V ≌,得到AC BE =,由三角形三边关系得到17AE <<,则1722AD <<.【详解】(1)解:由三角形的三边关系可知:AC AB BC AC AB −<<+,∵34AB AC ==,,∴17BC <<;(2)解:延长AD 至E ,使AD DE =,连接BE ,在ABE 中,∵BD DC ADC BDE AD DE =∠=∠=,,,∴()SAS ADC EDB ≌△△,∴AC BE =,由三角形的三边关系:BE AB AE BE AB −<<+,∴17AE <<, ∴1722AD <<.【点睛】本题主要考查了三角形三边的关系,全等三角形的性质与判定,正确作出辅助线构造全等三角形是解题的关键.【变式训练】 .如图,在ABC 中, 【答案】(1)见解析(2)AC BE =,AC BE ∥(3)2AD BC =,证明见解析【分析】(1)根据三角形全等的判定定理SAS ,即可证得;(2)由ACD EBD △△≌,可得AC BE =,C EBC ∠=∠,据此即可解答;(3)根据三角形全等的判定定理SAS ,可证得BAC ABE ≌,据此即可解答.【详解】(1)证明:AD 是BC 边上的中线,BD CD ∴=,在ACD △与EBD △中AD ED ADC EDBBD CD =⎧⎪∠=∠⎨⎪=⎩,()SAS ACD EBD ∴≌; (2)解:ACD EBD ≌,AC BE ∴=,C EBC ∠=∠,∴∥AC BE ,故答案为:AC BE =,AC BE ∥;(3)解:2AD BC =证明:ACD EBD ≌,AC BE ∴=,C EBC ∠=∠,∴∥AC BE ,90BAC ∠=︒90BAC ABE ∴∠=∠=︒在BAC △和ABE △中,90AB BA BAC ABE AC BE =⎧⎪∠=∠=︒⎨⎪=⎩()SAS BAC ABE ∴≌, 2BC AE AD ∴==.【点睛】本题考查了全等三角形的判定与性质,平行线的判定与性质,熟练掌握和运用全等三角形的判定与性质是解决本题的关键. 2.(2023·全国·八年级假期作业)如图1,AD 为△ABC 的中线,延长AD 至E ,使DE =AD .(1)试证明:△ACD ≌△EBD ;(2)用上述方法解答下列问题:如图2,AD 为△ABC 的中线,BMI 交AD 于C ,交AC 于M ,若AM =GM ,求证:BG =AC .【答案】(1)详见解析;(2)详见解析.【分析】(1)根据中线的定义,即可得到BD =CD ,再根据SAS 即可判定△ACD ≌△EBD .(2)延长AD 到F ,使AD =DF ,连接BF ,根据SAS 证△ADC ≌△FDB ,推出BF =AC ,∠CAD =∠F ,根据AM =GM ,推出∠CAD =∠AGM =∠BGF ,求出∠BGF =∠F ,根据等腰三角形的性质求出即可.【详解】(1)证明:∵AD 是△ABC 的中线,∴BD =CD ,在△ACD 和△EBD 中,CD BD ADC EDBAD ED =⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△EBD (SAS ).(2)证明:延长AD 到F ,使AD =DF ,连接BF ,∵AD 是△ABC 中线,∴BD =DC ,∵在△ADC 和△FDB 中BD DC ADC BDFAD DF =⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△FDB (SAS ),∴BF =AC ,∠CAD =∠F ,∵AM =GM ,∴∠CAD =∠AGM ,∵∠AGM =∠BGF ,∴∠BGF =∠CAD =∠F ,∴BG =BF =AC ,即BG =AC .【点睛】此题考查的是全等三角形的判定及性质,掌握倍长中线法构造全等三角形是解决此题的关键. 【探究与发现】(1)如图1,AD 是ABC 的中线,延长AD 至点E ,使ED AD =,连接【理解与应用】是DEF 的中线,若是ABC 的中线,【答案】(1)见解析;(2)14x <<;(3)见解析【分析】(1)根据全等三角形的判定即可得到结论;(2)延长EP 至点Q ,使PQ PE =,连接FQ ,根据全等三角形的性质得到3FQ DE ==,根据三角形的三边关系即可得到结论;(3)延长FD 至G ,使得GD DF =,连接BG ,EG ,结合前面的做题思路,利用三角形三边关系判断即可.【详解】(1)证明:CD BD =,ADC EDB ∠=∠,AD ED =,ACD EBD ∴≌,(2)14x <<;如图,延长EP 至点Q ,使PQ PE =,连接FQ ,在PDE ∆与PQF ∆中,PE PQ EPD QPFPD PF =⎧⎪∠=∠⎨⎪=⎩,PEP QFP ∴∆≅∆,3FQ DE ∴==, 在EFQ ∆中,EF FQ QE EF FQ −<<+,即53253x −<<+,x ∴的取值范围是14x <<;故答案为:14x <<;(3)延长FD 至G ,使得GD =BG ,EG ,在DFC △和DGB 中,DF DG =,CDF BDG ∠=∠,DC DB =,(SAS)DFC DGB ∴≌,BG CF ∴=,在EDF 和EDG △中,DF DG =,90FDE GDE ∠=∠=︒,DE DE =,(SAS)EDF EDG ∴≌,EF EG ∴=,在BEG 中,两边之和大于第三边,BG BE EG ∴+>,又EF EG =,BG CF =,BE CF EF ∴+>【点睛】本题考查了全等三角形的判定和性质,三角形的中线的定义,三角形的三边关系,正确的作出图形是解题的关键.【解题模型五旋转模型】【答案】(1)见详解;(2)BD=CE,BD⊥CE;(3)902︒−【分析】(1)根据三角形全等的证明方法SAS证明两三角形全等即可;(2)由(1)△AEC≌△ADB可知CE=BD且CE⊥BD;利用角度的等量代换证明即可;(3)过A分别做AM⊥CE,AN⊥BD,易知AF平分∠DFC,进而可知∠CFA【详解】(1)∵∠CAB=∠EAD∴∠CAB+∠BAE=∠EAD+∠BAE,∴∠CAE=∠BAD,∵AB=AC,AE=AD在△AEC和△ADB中,AB ACCAE BAD AE AD=⎧⎪⎨⎪⎩∠=∠=∴△AEC≌△ADB(SAS)(2)CE=BD且CE⊥BD,证明如下:将直线CE与AB的交点记为点O,由(1)可知△AEC≌△ADB,∴ CE=BD,∠ACE=∠ABD,∵∠BOF=∠AOC,∠α=90°,∴∠BFO=∠CAB=∠α=90°,∴ CE⊥BD.(3)过A分别做AM⊥CE,AN⊥BD 由(1)知△AEC≌△ADB,∴两个三角形面积相等故AM·CE=AN·BD∴AM=AN∴AF平分∠DFC由(2)可知∠BFC=∠BAC=α∴∠DFC=180°-α∴∠CFA=12∠DFC=902α︒−【点睛】本题考查了全等三角形的证明,以及全等三角形性质的应用,正确掌握全等三角形的性质是解题的关键;【变式训练】 1.如图,在△ABC 中,AB =BC ,∠ABC =120°,点D 在边AC 上,且线段BD 绕着点B 按逆时针方向旋转120°能与BE 重合,点F 是ED 与AB 的交点.(1)求证:AE =CD ;(2)若∠DBC =45°,求∠BFE 的度数.【答案】(1)证明见解析;(2)∠BFE =105°.【分析】(1)根据旋转的性质证明△ABE ≌△CBD (SAS ),进而得证;(2)由(1)得出∠DBC=∠ABE=45°,BD=BE ,∠EBD=120°,最后根据三角形内角和定理进行求解即可.【详解】(1)证明:∵线段BD 绕着点B 按逆时针方向旋转120°能与BE 重合,∴BD =BE ,∠EBD =120°,∵AB =BC ,∠ABC =120°,∴∠ABD+∠DBC =∠ABD+∠ABE =120°,∴∠DBC =∠ABE ,∴△ABE ≌△CBD (SAS ),∴AE =CD ;(2)解:由(1)知∠DBC =∠ABE =45°,BD =BE ,∠EBD =120°,∴∠BED =∠BDE =12(180°﹣120°)=30°,∴∠BFE =180°﹣∠BED ﹣∠ABE=180°﹣30°﹣45°=105°.【点睛】本题考查了旋转的性质,全等三角形的判定与性质,三角形内角和定理,利用旋转的性质证明是解题的关键.2.问题发现:如图1,已知C 为线段AB 上一点,分别以线段AC ,BC 为直角边作等腰直角三角形,=90ACD ∠︒,CA CD =,CB CE =,连接AE ,BD ,线段AE ,BD 之间的数量关系为______;位置关系为_______.拓展探究:如图2,把Rt ACD △绕点C 逆时针旋转,线段AE ,BD 交于点F ,则AE 与BD 之间的关系是否仍然成立?请说明理由.【答案】问题发现:AE BD =,AE BD ⊥;拓展探究:成立,理由见解析【分析】问题发现:根据题目条件证△ACE ≌△DCB ,再根据全等三角形的性质即可得出答案;拓展探究:用SAS 证ACE DCB ∆≅∆,根据全等三角形的性质即可证得.【详解】解:问题发现:延长BD ,交AE 于点F ,如图所示:∵90ACD ︒=∠,∴90ACE DCB ︒∠=∠=,又∵,CA CD CB CE ==,∴ACE DCB ∆≅∆(SAS ),,AE ED CAE CDB ∴=∠=∠, ∵90CDB CBD ︒∠+∠=,∴90CAE CBD ︒∠+∠=,∴90AFD ︒∠=,∴AF FB ⊥,AE BD ∴⊥, 故答案为:AE BD =,AE BD ⊥;拓展探究:成立.理由如下:设CE 与BD 相交于点G ,如图1所示:∵90ACD BCE ︒∠=∠=,∴ACE BCD ∠=∠,又∵CB CE =,AC CD =,∴ACE DCB ∆≅∆(SAS ),∴AE BD =,AEC DBC ∠=∠,∵90CBD CGB ︒∠+∠=,∴90AEC EGF ︒∠+∠=, ∴90AFB ︒∠=,∴BD AE ⊥,即AE BD =,AE BD ⊥【点睛】本题考查全等三角形的判定和性质,三角形三边关系,手拉手模型,熟练掌握全等三角形的判定和手拉手模型是解决本题的关键. 3.(2023春·全国·七年级专题练习)在△ABC 中,∠BAC =90°,AC=AB ,直线MN 经过点A ,且CD ⊥MN 于D ,BE ⊥MN 于E .(1)当直线MN绕点A旋转到图1的位置时,EAB DAC∠+∠=度;(2)求证:DE=CD+BE;(3)当直线MN绕点A旋转到图2的位置时,试问DE、CD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.【答案】(1)90°(2)见解析(3)CD= BE + DE,证明见解析【分析】(1)由∠BAC=90°可直接得到EAB DAC∠+∠=90°;(2)由CD⊥MN,BE⊥MN,得∠ADC=∠BEA=∠BAC=90°,根据等角的余角相等得到∠DCA=∠EAB,根据AAS可证△DCA≌△EAB,所以AD=CE,DC=BE,即可得到DE = EA+AD = DC+BE.(3)同(2)易证△DCA≌△EAB,得到AD=CE,DC=BE,由图可知AE = AD +DE,所以CD= BE + DE.【详解】(1)∵∠BAC=90°∴∠EAB+∠DAC=180°-∠BAC=180°-90°=90°故答案为:90°.(2)证明:∵ CD⊥MN于D,BE⊥MN于E∴∠ADC=∠BEA=∠BAC=90°∵∠DAC+∠DCA=90°且∠DAC+∠EAB=90°∴∠DCA=∠EAB∵在△DCA和△EAB中90 ADC BEA DCA EABAC AB ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∴△DCA≌△EAB (AAS)∴ AD=BE且EA=DC由图可知:DE = EA+AD = DC+BE.(3)∵ CD⊥MN于D,BE⊥MN于E ∴∠ADC=∠BEA=∠BAC=90°∵∠DAC+∠DCA=90°且∠DAC+∠EAB=90°∴∠DCA=∠EAB∵在△DCA 和△EAB 中90ADC BEA DCA EABAC AB ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∴△DCA ≌△EAB (AAS)∴ AD=BE 且AE=CD 由图可知:AE = AD +DE∴ CD= BE + DE .【点睛】本题考查了旋转的性质:旋转前后两图形全等,对应点到旋转中心的距离相等,对应点与旋转中心的连线段所夹的角等于旋转角,也考查了三角形全等的判定与性质. 八年级假期作业)在ABC 中, (1)【证明推断】求证:DN DM =;小明给出的思路:若要证明DN DM =,只需证明BDN △≌△你根据小明的思路完成证明过程;(2)【延伸发现】连接AE ,BF ,如图所示,求证:AE BF =;【答案】(1)见解析(2)见解析(3)AE BF ⊥,见解析【分析】(1)在ABC 中,根据点D 是BC 的中点,得出2AD BD BC==,由AD BC ⊥,DEF 是直角三角尺,得出90EDF ∠=︒,从而得到BDN ADM ∠=∠,在BDN 和ADM △中,立即证明全等,由性质即可解答DN DM =;(2)根据BDN ADM △≌△,得出BN AM =,BND AMD ∠=∠,DN DM =,从而得到BNF AME ∠=∠,由于DEF 是含45°直角三角尺,推出FN EM =,利用SAS 即可证明BNF 和AME △全等,从而求解;(3)猜想:AE BF ⊥,理由:根据BNF AME △≌△和90FDE ∠=︒,得出90AEM APD ∠+∠=︒,又根据APD FPQ ∠=∠,等量代换得到90FQP ∠=︒从而证明.【详解】(1)证明:在ABC 中,∵AB AC =,90BAC ∠=︒,∴45B C ∠==︒∠,又∵点D 是BC 的中点, ∴2AD BD BC ==,且AD BC ⊥,1452BAD CAD BAC ∠=∠=∠=︒∴90ADN BDN ∠+∠=︒,又∵DEF 是直角三角尺,∴90EDF ∠=︒,即90ADN ADM ∠+∠=︒,∴BDN ADM ∠=∠ 在BDN 和ADM △中45B DAM BD AD BDN ADM ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩∴BDN ADM △≌△,∴DN DM =;(2)证明:∵BDN ADM △≌△∴BN AM =,BND AMD ∠=∠,DN DM =∴BNF AME ∠=∠,且由于DEF 是含45°直角三角尺,∴DF DE =,∴DF DN DE DM −=−即FN EM =在BNF 和AME △中BN AM BNF AMEFN EM =⎧⎪∠=∠⎨⎪=⎩∴BNF AME △≌△,∴AE BF =;(3)解:作图正确(如图所示)猜想:AE BF ⊥,理由如下:∵BNF AME △≌△,∴BFN AEM ∠=∠,∵90FDE ∠=︒,∴90AEM APD ∠+∠=︒又∵APD FPQ ∠=∠,∴90FPQ BFN ∠+∠=︒,∴90FQP ∠=︒,∴AE BF ⊥.【点睛】本题考查了旋转的性质、直角三角尺的特征、全等三角形的判定及性质,解题的关键是掌握三角形全等的判定及性质.。
专题02三角形压轴题真题分类(原卷版)—2022-2023学年八年级数学上册重难点题型分类高分必刷题

专题02《三角形》压轴题真题分类-高分必刷题(原卷版)专题简介:本份资料包含《三角形》这一章中求角度的的四种类型的常考压轴题,所选题目源自各名校期中、期末试题中的典型考题,具体包含的题型有:与内角外角平分线有关的压轴题、与8字模型有关的压轴题、与燕尾模型有关的压轴题、与动角有关的压轴题。
适合于培训机构的老师给学生作复习培训时使用或者学生考前刷题时使用。
题型一:与内角外角平分线有关的压轴题1.(上海)(1)在锐角ABC ∆中,AC 边上的高所在直线和AB 边上的高所在直线的交点为P ,110BPC ∠=︒,求A ∠的度数.(2)如图,AF 和CE 分别平分BAD ∠和BCD ∠,当点D 在直线AC 上时,且B 、P 、D 三点共线,100APC ∠=︒,则B ∠=_________.(3)在(2)的基础上,当点D 在直线AC 外时,如下图:130ADC ∠=︒,100APC ∠=︒,求B Ð的度数.2.∠MOQ=90°,点A,B分别在射线OM、OQ上运动(不与点O重合).(1)如图1,AI平分∠BAO,BI平分∠ABO,若∠BAO=40°,求∠AIB的度数.(2)如图2,AI平分∠BAO,BC平分∠ABM,BC的反向延长线交AI于点D.①若∠BAO=40°,则∠ADB=°;②点A、B在运动的过程中,∠ADB是否发生变化,若不变,试求∠ADB的度数;若变化,请说明变化规律.3.(江苏)直线MN 与直线PQ 垂直相交于点O ,点A 在直线PQ 上运动,点B 在直线MN 上运动.(1)如图1,已知AE BE 、分别是BAO ∠和ABO ∠角的平分线,点AB 、在运动的过程中,AEB ∠的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出AEB ∠的大小.(2)如图2,已知AB 不平行CD AD BC ,、分别是BAP ∠和ABM ∠的角平分线,又DE CE 、分别是ADC∠和BCD ∠的角平分线,点AB 、在运动的过程中,CED ∠的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出CED ∠的度数.(3)如图3,延长BA 至G ,已知BAO OAG ∠∠、的角平分线与BOQ ∠的角平分线及反向延长线相交于E F 、,在AEF 中,如果有一个角是另一个角的3倍,则ABO ∠的度数为____(直接写答案)4.已知△ABC在平面直角坐标系内,满足:点A在y轴正半轴上移动,点B在x轴负半轴上移动,点C 为y轴右侧一动点.(1)若点A(0,a)和点B(b,0)坐标恰好满足:(a﹣2)2+|a+b+1|=0,直接写出a、b的值.(2)如图①,当点C在第四象限时,若AM、AO将∠BAC三等分,BM、BO将∠ABC三等分,在A、B、C的运动过程中,试求出∠C和∠M的大小.探究:(1)如图②,当点C在第四象限时,若AM平分∠CAO,BM平分∠CBO,在A、B、C的运动过程中,∠C和∠M是否存在确定的数量关系?若存在,请证明你的结论;若不存在,请说明理由.(2)如图③,当点C在第一象限时,且在(1)中的条件不变的前提下,∠C和∠M又有何数量关系?证明你的结论.题型二:与8字模型有关的压轴题5.(江苏)图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:;(2)仔细观察,在图2中“8字形”的个数:个;(3)图2中,当∠D=50度,∠B=40度时,求∠P的度数.(4)图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结果,不必证明).6.(四川)(1)如图1的图形我们把它称为“8字形”,请说理证明∠A+∠B=∠C+∠D.(2)(可直接使用问题(1)中的结论)如图2,BP、DP分别平分∠ABC、∠ADC;①若∠A=36°,∠C=28°,求∠P的度数;②∠A和∠C为任意角时,其他条件不变,猜想∠P与∠A、∠C之间数量关系,并给出证明.(3)在图3中,点E为CD延长线上一点,BQ、DP分别是∠ABC、∠ADE的四等分线,且∠CBQ=14∠ABC,∠EDP=14∠ADE,QB的延长线与DP交于点P,请直接写出∠P与∠A、∠C的关系,无需证明.7.(江苏)已知:线段AD 、BC 相交于点O ,连接AB 、C D .(1)如图1的图形我们把它称为“8字形”,则∠A 、∠B 、∠C 、∠D 之间的数量关系为;(2)如图2,AP 、CP 分别平分∠BAD 、∠BC D .若∠B =36°,∠D =44°,则∠P 的度数=°;(3)如图3,∠BAD 和∠BCD 的三等分线AP 和CP 相交于点P ,123BAD ∠=∠,143BCD ∠=∠,试探究∠B 、∠D 、∠P 三者之间存在的数量关系,并说明理由.(4)如图4,CP 、AG 分别平分∠BCE 、∠FAD ,AG 反向延长线交CP 于点P ,请猜想∠P 、∠B 、∠D 之间的数量关系,直接写出结论,不需要说明理由.6.如图①,已知线段AB ,CD 相交于点O ,连接AC ,BD ,我们把形如图①的图形称之为“8字形”.如图②,∠CAB 和∠BDC 的平分线AP 和DP 相交于点P ,并且与CD ,AB 分别相交于M ,N .试解答下列问题:(1)在图①中,写出一个关于∠A 、∠B 、∠C 、∠D 的关系的等式.(2)在图②中,若∠B =96°,∠C =100°,求∠P 的度数;(3)在图②中,若设∠C =α,∠B =β,∠CAP =13∠CAB ,∠CDP =13∠CDB ,试问∠P 与∠C ,∠B 之间存在着怎样的数量关系(用α,β表示∠P ),并说明理由;(4)如图③,则∠A +∠B +∠C +∠D +∠E +∠F 的度数为.8.(江苏)如图1的图形我们把它称为“8字形”,显然有A B C D ∠+∠=∠+∠;阅读下面的内容,并解决后面的问题:(1)如图2,AP 、CP 分别平分BAD ∠、BCD ∠,若36ABC ∠=︒,16ADC ∠=︒,求P ∠的度数;(2)①在图3中,直线AP 平分BAD ∠的外角FAD ∠,CP 平分BCD ∠的外角BCE ∠,猜想P ∠与B ∠、D ∠的关系,并说明理由.②在图4中,直线AP 平分BAD ∠的外角FAD ∠,CP 平分BCD ∠的外角BCE ∠,猜想P ∠与B ∠、D ∠的关系,直接写出结论,无需说明理由.③在图5中,AP 平分BAD ∠,CP 平分BCD ∠的外角BCE ∠,猜想P ∠与B ∠、D ∠的关系,直接写出结论,无需说明理由.题型三:与燕尾模型有关的压轴题9.利用“模型”解决几何综合问题往往会取得事半功倍的效果.几何模型:如图(1),我们称它为“A”型图案,易证明:∠EDF=∠A+∠B+∠C.运用以上模型结论解决问题:(1)如图(2),“五角星”形,求∠A1+∠A2+∠A3+∠A4+∠A5=?分析:图中A1A3DA4是“A”型图,于是∠A2DA5=∠A1+∠A3+∠A4,所以∠A1+∠A2+∠A3+∠A4+∠A5=;(2)如图(3),“七角星”形,求∠A1+∠A2+∠A3+∠A4+∠A5+∠A6+∠A7的度数.10.(山西晋中)请阅读下列材料,并完成相应的任务:有趣的“飞镖图”如图,这种形似飞镖的四边形,可以形象地称它为“飞镖图”.当我们仔细观察后发现,它实际上就是凹四边形.那么它具有哪些性质呢?又将怎样应用呢?下面我们进行认识与探究:凹四边形通俗地说,就是一个角“凹”进去的四边形,其性质有:凹四边形中最大内角外面的角等于其余三个内角之和.(即如图1,∠ADB=∠A+∠B+∠C)理由如下:方法一:如图2,连接AB,则在△ABC中,∠C+∠CAB+∠CBA=180°,即∠1+∠2+∠3+∠4+∠C=180°,又∵在△ABD中,∠1+∠2+∠ADB=180°,∴∠ADB=∠3+∠4+∠C,即∠ADB=∠CAD+∠CBD+∠C.方法二:如图3,连接CD并延长至F,∵∠1和∠3分别是△ACD和△BCD的一个外角,......大家在探究的过程中,还发现有很多方法可以证明这一结论,你有自己的方法吗?任务:(1)填空:“方法一”主要依据的一个数学定理是;(2)探索:根据“方法二”中辅助线的添加方式,写出该证明过程的剩余部分;(3)应用:如图4,AE是∠CAD的平分线,BF是∠CBD的平分线,AE与BF交于G,若∠ADB=150°,∠AGB=110°,请你直接写出∠C的大小.11.(江苏)模型规律:如图1,延长CO 交AB 于点D ,则1BOC B A C B ∠=∠+∠=∠+∠+∠.因为凹四边形ABOC 形似箭头,其四角具有“BOC A B C ∠=∠+∠+∠”这个规律,所以我们把这个模型叫做“箭头四角形”.模型应用(1)直接应用:①如图2,60,20,30A B C ∠=︒∠=︒∠=︒,则BOC ∠=__________︒;②如图3,A B C D E F ∠+∠+∠+∠+∠+∠=__________︒;(2)拓展应用:①如图4,ABO ∠、ACO ∠的2等分线(即角平分线)1BO 、1CO 交于点1O ,已知120BOC ∠=︒,50BAC ∠=︒,则1BO C ∠=__________︒;②如图5,BO 、CO 分别为ABO ∠、ACO ∠的10等分线1,2,3,,(,)89i =⋯.它们的交点从上到下依次为1O 、2O 、3O 、…、9O .已知120BOC ∠=︒,50BAC ∠=︒,则7BOC ∠=__________︒;③如图6,ABO ∠、BAC ∠的角平分线BD 、AD 交于点D ,已知120,44BOC C ∠=︒∠=︒,则ADB =∠__________︒;④如图7,BAC ∠、BOC ∠的角平分线AD 、OD 交于点D ,则B Ð、C ∠、D ∠之同的数量关系为__________.12.(福建)如图1所示的图形,像我们常见的符号——箭号.我们不妨把这样图形叫做“箭头四角形”.探究:(1)观察“箭头四角形”,试探究BDC ∠与A ∠、B Ð、C ∠之间的关系,并说明理由;应用:(2)请你直接利用以上结论,解决以下两个问题:①如图2,把一块三角尺XYZ 放置在ABC ∆上,使三角尺的两条直角边XY 、XZ 恰好经过点B 、C ,若60A ∠=︒,则ABX ACX ∠+∠=o ;②如图3,ABE ∠、ACE ∠的2等分线(即角平分线)BF 、CF 相交于点F ,若60BAC ∠=︒,130BEC ∠=︒,求BFC ∠的度数;拓展:(3)如图4,i BO ,i CO 分别是ABO ∠、ACO ∠的2020等分线(12320182019i = ,,,,,),它们的交点从上到下依次为1O 、2O 、3O 、…、2019O .已知BOC m ∠=︒,BAC n ∠=︒,则1000BO C ∠=度.题型四:与动角有关的压轴题13.(江苏泰州)直线AB、CD相交于点O,∠AOC=α,点F在直线AB上且在点O的右侧,点E在直线CD上(点E与点O不重合),连接EF,直线EM、FN交于点G.(1)如图1,若点E在射线OC上,α=60°,EM、FN分别平分∠CEF和∠AFE,求∠EGF的度数;(2)如图2,点E在射线OC上,∠MEF=m∠CEF,∠NFE=(1﹣2m)∠AFE,若∠EGF的度数与∠AFE 的度数无关,求m的值及∠EGF的度数(用含有α的代数式表示);(3)如图3,若将(2)中的“点E在射线OC上”改为“点E在射线OD上”,其他条件不变,直接写出∠EGF 的度数(用含有a的代数式表示)14.如图1,含30°角的直角三角板()30DEF EDF ∠=︒与含45︒角的直角三角板的斜边在同一直线上,D 为BC 的中点,将直角三角板DEF 绕点D 按逆时针方向旋转()0180αα∠︒<<︒,在旋转过程中:(1)如图2,当α∠=________︒时,//DE AB ;当α∠=______︒时,DE AB ⊥;(2)如图③,当直角三角板DEF 的边DF 、DE 分别交BA 、CA 的延长线于点M 、N 时;①1∠与2∠度数的和是否变化?若不变,求出1∠与2∠度数的和;若变化,请说明理由;②若使得122∠=∠,求出1∠、2∠的度数,并直接写出此时α∠的度数;③若使得2123∠≥∠,求α∠的度数范围.15.(河南郑州)如图,在△ABC中,∠ACB=90°,O是AB边上的中点,三角板OMN的直角顶点与O重台,∠MON=90°,直角三角形板MON绕点O旋转使边OM交AC于点D,边ON交BC于点E(D、E不与A、B重合),连接DE.(1)如图①,当CA=CB=4时,①请直接写出DE的取值范围:②判断△DOE的形状并说明理由;③判断四边形ODCB的面积在旋转的过程中是否变化,若不变,求出该四边形的面积;若变化,请说明变化的范围;(2)如图②,判断并说明线段AD,DE和BE的数量关系.16.(辽宁大连)已知:△ABC,点M是平面上一点,射线BM与直线AC交于点D,射线CM与直线AB交于点E.过点A作AF∥CE,AF与BC所在的直线交于点F.(1)如图1,当BD⊥AC,CE⊥AB时,写出∠BAD的一个余角,并证明∠ABD=∠CAF;(2)若∠BAC=80°,∠BMC=120°.①如图2,当点M在△ABC内部时,用等式表示∠ABD与∠CAF之间的数量关系,并加以证明;②如图3,当点M在△ABC外部时,依题意补全图形,并直接写出用等式表示的∠ABD与∠CAF之间的数量关系.。
初二三角形所有知识点总结和常考题提高难题压轴题练习(含答案解析)

初二三角形所有知识点总结和常考题知识点:1.三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.2.三边关系:三角形任意两边的和大于第三边,任意两边的差小于第三边.3.高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足间的线段叫做三角形的高.4.中线:在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线.5.角平分线:三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.6.三角形的稳定性:三角形的形状是固定的,三角形的这个性质叫三角形的稳定性.7.多边形:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.8.多边形的内角:多边形相邻两边组成的角叫做它的内角.9.多边形的外角:多边形的一边与它的邻边的延长线组成的角叫做多边形的外角.10.多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.11.正多边形:在平面内,各个角都相等,各条边都相等的多边形叫正多边形.12.平面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做用多边形覆盖平面,13.公式与性质:⑴三角形的内角和:三角形的内角和为180°⑵三角形外角的性质:性质1:三角形的一个外角等于和它不相邻的两个内角的和.性质2:三角形的一个外角大于任何一个和它不相邻的内角.⑶多边形内角和公式:n 边形的内角和等于(2)n ·180°⑷多边形的外角和:多边形的外角和为360°. ⑸多边形对角线的条数:①从n 边形的一个顶点出发可以引(3)n 条对角线,把多边形分成(2)n 个三角形.②n 边形共有(3)2n n 条对角线.常考题:一.选择题(共13小题)1.已知三角形的两边长分别为4cm 和9cm ,则下列长度的四条线段中能作为第三边的是()A .13cmB .6cmC .5cmD .4cm2.一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=()A.90°B.100°C.130° D.180°3.已知如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于()A.315°B.270° C.180° D.135°4.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是()A.B.C.D.5.如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=()A.90°﹣αB.90°+αC.D.360°﹣α6.如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=()A.40°B.30°C.20°D.10°7.如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE相交。
2024学年八年级数学上学期真题分类汇编(人教版)-三角形与角有关的压轴题训练(解析版)(人教版)

三角形与角有关的压轴题训练多边形内角和(n−3602∵AMD EMF ∠=∠,180AMD FAD ADE ∠+∠+∠=︒,180E F EMF ∠+∠+∠=︒ E F ADE FAD ∴∠+∠=∠+∠∴BAF B C CDE E F ∠+∠+∠+∠+∠+∠BAD ADC B C =∠+∠+∠+∠360=; 故答案为:360°(2)如图,连接AE ,FE 交AH 于点M∴360F G H FMH ∠+∠+∠+∠=︒,180AME MAE MEA ∠+∠+∠=︒ ∵AME FMH ∠=∠∴()180360F G H MAE MEA ∠+∠+∠+︒−∠−∠=︒ ∴180MAE MEA F G H ∠+∠=∠+∠+∠−︒∵()52180540BAM B C D MED MEA MAE ∠+∠+∠+∠+∠+∠+∠=−⨯︒= ∴()180540BAM B C D MED F G H ∠+∠+∠+∠+∠+∠+∠+∠−︒= ∴540180720BAM B C D MED F G H ∠+∠+∠+∠+∠+∠+∠+∠=+︒=︒ ∴二环四边形的内角和为:720︒∵二环三角形的内角和为:()36036032︒=︒⨯− 二环四边形的内角和为:()720360236042︒=︒⨯=︒⨯−∴二环五边形的内角和为:()360521080︒⨯−=︒ ∴二环n 边形的内角和为:()3602n − 故答案为:720,1080,()3602n −.【点睛】本题考查了多边形内角和、对顶角、数字规律的知识;解题的关键是熟练掌握三角形内角和、多边形内角和、数字规律的性质,从而完成求解.3.如图,ACP PCD ∠=∠,ABP PBD ∠=∠,且80A ∠=︒,120D ∠=︒,则P ∠的度数为 °.【答案】100【分析】设ACP PCD x ∠=∠=,ABP PBD y ∠=∠=,根据三角形内角和公式可求得1002AEC x ∠=︒−,602DEB y ∠=︒−,推得20x y =+,根据三角形内角和公式可求得120P x y ∠=︒−+,将20x y =+代入即可求解.【详解】解:设ACP PCD x ∠=∠=,ABP PBD y ∠=∠=,如图:∵80A ∠=︒,120D ∠=︒,在ACE △中,1801808021002AEC ACE A x x ∠=︒−∠−∠=︒−︒−=︒−, 在DBE 中,1801801202602DEB DBE D y y ∠=︒−∠−∠=︒−︒−=︒−, 又∵AEC DEB ∠=∠,∴1002602x y ︒−=︒−,故20x y =+, 在DBF 中,180********DFB DBF D y y ∠=︒−∠−∠=︒−︒−=︒−, 在DBF 中,60PFC DFB y ∠=∠=︒−,()180********P PCE DFB x y x y ∠=︒−∠−∠=︒−−︒−=︒−+,将20x y =+代入可得12020100P ∠=︒−=︒;故答案为:100.【点睛】本题考查了三角形内角和定理,熟练掌握三角形内角和定理是解题的关键.4.(1)如图①,你知道∠BOC=∠B+∠C+∠A的奥秘吗?请用你学过的知识予以证明;(2)如图②,设x=∠A+∠B+∠C+∠D+∠E,运用(1)中的结论填空.x=____________°;x=____________°;x=____________°;(3)如图③,一个六角星,其中∠BOD=70°,则∠A+∠B+∠C+∠D+∠E+∠F=________°.【答案】(1)证明见解析. (2)180;180;180;(3)140【分析】(1)首先延长BO交AC于点D,可得BOC=∠BDC+∠C,然后根据∠BDC=∠A+∠B,判断出∠BOC=∠B+∠C+∠A即可.(2)a、首先根据外角的性质,可得∠1=∠A+∠B,∠2=∠C+∠D,然后根据∠1+∠2+∠E=180°,可得x=∠A+∠B+∠C+∠D+∠E=180,据此解答即可.b、首先根据外角的性质,可得∠1=∠A+∠B,∠2=∠C+∠D,然后根据∠1+∠2+∠E=180°,可得x=∠A+∠B+∠C+∠D+∠E=180,据此解答即可.c、首先延长EA交CD于点F,EA和BC交于点G,然后根据外角的性质,可得∠GFC=∠D+∠E,∠FGC=∠A+∠B,再根据∠GFC+∠FGC+∠C=180°,可得x=∠A+∠B+∠C+∠D+∠E=180°,据此解答即可.(3)根据∠BOD=70°,可得∠A+∠C+∠E=70°,∠B+∠D+∠F=70°,据此求出∠A+∠B+∠C+∠D+∠E+∠F的度数是多少即可.【详解】(1)证明:如图,延长BO交AC于点D,则∠BOC=∠BDC+∠C,又∵∠BDC=∠A+∠B,∴∠BOC=∠B+∠C+∠A.(2)180;180;180;(3)140【点睛】(1)此题主要考查了三角形的内角和定理,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°.(2)此题还考查了三角形的外角的性质和应用,要熟练掌握,解答此题的关键是要明确:①三角形的外角和为360°.②三角形的一个外角等于和它不相邻的两个内角的和.③三角形的一个外角角度之间的数量关系ABC 中, 【变式拓展】当点E 与点A 不重合时,连接ED ,设ADE α∠=,ACB β∠=. (1)如图2,BED ∠的平分线交BD 于点O . ①当50α=︒,80β=︒时,EOD ∠=____________︒; αβ在ABC内部和点在ABC外部,利用角平分线的定义,三角形内角)ABC中,∠=BAC∠=ABC∠=︒)C mAO平分∠=ADE∠=ACB②ADE α∠=,ACB β∠=,CDG α∴∠=,180ACG β∠=︒−,180G CDG ACG βα∴∠=︒−∠−∠=−, 180180ABG BEG G αβ∴∠+∠=︒−∠=︒+−,在ABC 内部时,令 ACB β∠=,CF 平分∠1122ACF ACB β∴∠=∠=,ADE ACF CHD ∠=∠+∠AED ∠+EF 平分F DEF ∠+∠ABC ∠+∠在ABC 外部时,令 ACB β∠=,CF 平分ACB ∠,1122ACF ACB β∴∠=∠=, 12CKB A ACF A β∴∠=∠+∠=∠+,1AED ∠=F FEK ∠+∠COD ∠= (1)如图2,一束光线DE 射到平面镜AB 上,被AB 反射到平面镜BC 上,又被BC 反射,若被射出的光线FM (与光线DE 平行,且120EFM ∠=︒,则AED =∠_______°,B ∠=______°;(2)如图3,有三块平面镜AB ,BC ,CH ,入射光线DE 与镜面AB 的夹角35AED ∠=︒,镜面BC 的夹角115B ∠=︒,当光线DE 经过平面镜AB ,BC ,CH 的三次反射后,入射光线DE 光线MN 平行时,请求出FMN ∠的度数;根据题意,AED BEF∠=∠,EFB∠120EFM∠=︒,∴180120302EFB CFM︒−︒∠=∠== ED FM∥,18012060DEF∠=︒−︒=︒,在BEF中,由三角形内角和定理可得ED MN∥,ED FG MN ∴∥∥,180DEF EFG ∴∠+∠=︒,180NMF MFG ∠+∠=︒,360DEF EFM FMN ∴∠+∠+∠=︒,35AED ∠=︒,35BEF AED ∴∠=∠=︒,则180352110DEF ∠=︒−︒⨯=︒,在BEF 中,35BEF ∠=︒,115B ∠=︒,则由三角形内角和定理可得1803511530BFE ∠=︒−︒−︒=︒, 30MFC BFE ∴∠=∠=︒,则180302120EFM ∠=︒−︒⨯=︒,∴360120110130FMN ∠=︒−︒−︒=︒;(3)解:如图所示:由(2)知120EFM ∠=︒,130FMN ∠=︒,35BEF ∠=︒,115B ∠=︒,由于一个四边形可以分成两个三角形,由三角形内角和定理可知,在四边形FMQI 中,360FIQ EFM FMN PQM ∠+∠+∠+∠=︒,AEG BEP ∠=∠,115B ∠=︒,18011565BPE AEG AEG ∴∠=︒−︒−∠=︒−∠,则65QPF BPE AEG ∠=∠=︒−∠,()18065115QPB AEG AEG ∴∠=︒−︒−∠=︒+∠,由于一个四边形可以分成两个三角形,由三角形内角和定理可知,在四边形PBEI 中,360BEI EIP QPB B ∠+∠+∠+∠=︒,EIP FIQ ∠=∠,∴由360FIQ EFM FMN PQM ∠+∠+∠+∠=︒与360BEI EIP QPB B ∠+∠+∠+∠=︒,代入已知角度有120130360FIQ PQM ∠+︒+︒+∠=︒与35115360EIP QPB ∠+︒+∠+︒=︒,可得100QPB PQM ∠−∠=︒,(1)=a ___________,b =___________;(2)如图2,若AC BC BQ ⊥,平分ABC ∠交AC 于点Q ,交OC 于点P ,求证:CPQ CQP ∠∠=(3)如图3,若点A 、点B 分别在x 轴负半轴和正半轴上运动,ACB ∠的角平分线交x 轴于点N 在x 轴上,且BCM DCN ∠=∠,请补全图形,探究OCM ACN∠∠的值的变化情况,并直接写出结论BQ 平分CBA ∠,∴OBP CBQ ∠=∠,AC BC ⊥Q ,90ACB ∴∠=︒,理由:AC BC ⊥Q ,90ACB ∴∠=︒,∴90ACD BCF ∠+∠=︒,CB 平分ECF ∠,∴ECB ∠=(1)如图①,若90AOB ∠=︒,求C ∠的度数;(2)若AOB n ∠=,则C ∠=________(结果用含n 的代数表示(3)如图②,若点E 是射线OM 上一点,连接BE BF EF ,、为BOE 的角平分线.①随着点A B E 、、的移动,C ∠与BFE ∠存在什么样的数量关系,②过点F 作FK MN ∥交BE 于点K ,则BGO ∠,KFE ∠为BOE的角平分线,1为BOE的角平分线,定值问题在ABC 中,αC ∠=(1)当80α=︒,30β=︒时,求E ∠的度数;(2)试问E ∠与B ∠、C ∠之间存在着怎样的数量关系,试用,αβ表示E ∠,并说明理由(3)若EFB ∠与BAE ∠平分线交于点P (如图2),当点E 在AD 线上运动时,P ∠是否发生变化,若不变,请用,αβ表示P ∠;若变化,请说明理由【答案】(1)25︒)解:80B ∠=︒3070−︒=︒,AD 平分EF BC⊥)EDF∠= EFD∠=AD平分AP平分(1)求点C 的坐标.(2)如图2,设D 为线段OB 上一动点,当AD AC ⊥时,ODA ∠的角平分线与向延长线交于点P ,求APD ∠的度数;(点E 在x 轴的正半轴)(3)在(2)的基础上,如果将“ODA ∠的角平分线与CAE ∠的角平分线的反向延长线交于点AGC S =∵()2340a b −++=,∴30a −=,40b +=,解得:3a =,4b =−,AGC S =∠,MN平分∵AN平分OAD,在ABC 中, (1)若40C ∠=︒.①求P ∠的度数;DE BC ∥AB AC 、AP平分AP平分∠−APE。
初二全等三角形所有知识点总结和常考题提高难题压轴题练习(含答案解析)

初二全等三角形所有知识点总结和常考题1.基本定义:⑴全等形:能够完全重合的两个图形叫做全等形 .⑵全等三角形:能够完全重合的两个三角形叫做全等三角形.⑶对应顶点:全等三角形中互相重合的顶点叫做对应顶点.⑷对应边:全等三角形中互相重合的边叫做对应边 .⑸对应角:全等三角形中互相重合的角叫做对应角 .2.基本性质:⑴三角形的稳定性:三角形三边的长度确定了,这个三角形的形状、大小就全确定,这个性质叫做三角形的稳定性.⑵全等三角形的性质:全等三角形的对应边相等,对应角相等.3.全等三角形的判定定理:⑴边边边(SSS):三边对应相等的两个三角形全等.⑵边角边(SAS):两边和它们的夹角对应相等的两个三角形全等.⑶角边角(ASA):两角和它们的夹边对应相等的两个三角形全等.⑷角角边(AAS):两角和其中一个角的对边对应相等的两个三角形全等⑸斜边、直角边(HL ):斜边和一条直角边对应相等的两个直角三角形全等.4.角平分线:⑴画法:⑵性质定理:角平分线上的点到角的两边的距离相等 .⑶性质定理的逆定理:角的内部到角的两边距离相等的点在角的平分线上5.证明的基本方法:⑴明确命题中的已知和求证.(包括隐含条件,如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形等所隐含的边角关系)⑵根据题意,画出图形,并用数字符号表示已知和求证.⑶经过分析,找出由已知推出求证的途径,写出证明过程 .一.选择题(共14小题)1.使两个直角三角形全等的条件是()A. 一个锐角又t应相等B.两个锐角对应相等C. 一条边对应相等D.两条边对应相等2.如图,已知AE=CF /AFD=/ CEB那么添加下列一个条件后,仍无法判定△AD陷4CBE的是()A. /A=/ CB. AD=CBC. BE=DFD. AD // BC3.如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是()A. SSSB. SASC. AASD. ASA4.到三角形三条边的距离都相等的点是这个三角形的(A.三条中线的交点B.三条高的交点C.三条边的垂直平分线的交点D.三条角平分线的交点5.如图,△ AC阴NA CB'/BCB =30°则/ ACA的度数为(A. 20°B. 300C. 350D. 40°6.如图,直线11、12、13表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则供选择的地址有()A. 1处B. 2处C. 3处D. 4处7.如图,AD是4ABC中/ BAC的角平分线,D已AB于点E, S AABC=7, DE=ZAB=4,则AC长是()8.如图,在△ ABC和4DEC中,已知AB=DE还需添加两个条件才能使△ ABCDEC不能添加的一组条件是()A. BC=EC /B=/ EB. BC=EC AC=DCC. BC=DC /A=/DD. / B=/ E,/ A=/ D9.如图,已知在△ ABC中,CD是AB边上的高线,BE平分/ ABC,交CD于点E, BC=5 DE=2,贝BCE的面积等于()A. 10B. 7C. 5D. 410.要测量河两岸相对的两点A, B的距离,先在AB的垂线BF上取两点C, D, 使CD=BC再定出BF的垂线DE,使A, C, E在一条直线上(如图所示),可以说明△ED8 AABC,彳3ED=AB因此测得ED的长就是AB的长,判定△ ED8 △ ABC最恰当的理由是()A.边角边B.角边角C.边边边D.边边角11.如图,4ABC的三边AB, BC, CA长分别是20, 30, 40,其三条角平分线将△ ABC分为三个三角形,则S A ABO):S A BCO:S A CAO等于()BC AA. 1:1:1B. 1: 2: 3C. 2: 3: 4D. 3: 4: 512.尺规作图作/ AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA, OB于C, D,再分别以点C, D为圆心,以大于tCD长为半径画弧,两弧交于点P,作射线OP由作法得^ OC国4ODP的根据是()A.有两边和其中一边的对角对应相等的两个三角形全等B.有两边对应相等,且有一角为 30°的两个等腰三角形全等C.有一角和一边对应相等的两个直角三角形全等D.有两角和一边对应相等的两个三角形全等14.如图,已知/ 1=/2, AC=AD,增加下列条件:① AB=AE ②BC=ED ③C C= /D;④/ B=/ E.其中能使△ AB ®ZXAED 的条件有( )A. 4个B. 3个C. 2个D. 1个二.填空题(共11小题)15 .如图,在△ ABC 中,/C=90°, AD 平分/CAB BC=8cm, BD=5cm,那么点 D 到线段AB 的距离是 cm.16 .如图,△ ABC 中,/ C=90°, AD 平分/BAC AB=5, CD=2,则△ ABD 的面积17 .如图为6个边长等的正方形的组合图形,则/ 1+/ 2+/3=19 .如图所示,某同学把一块三角形的玻璃打碎成了三块, 现在要到玻璃店去配 一块完全一样的玻璃,那么最省事的办法是带 去玻璃店.18.如图,△AB ®ADEF5请根据图中提供的信息,写出* F x= ______是 _______20.如图,已知AB// CF, E为DF的中点,若AB=9cm, CF=5cm 贝U BD=cm.B C21.在数学活动课上,小明提出这样一个问题:/ B=Z C=90°, E是BC的中点, DE 平分/ADC, /CED=35,如图,则/ EAB是多少度?大家一起热烈地讨论交流,小英第一个得出正确答案,是度.D C22.如图,/XABeAADEE, / B=100°, / BAC=30,那么/ AED=度.23.如图所示,将两根钢条AA', BB'的中点。
专题 全等三角形压轴题训练(30题)(解析版)

(苏科版)八年级上册数学《第1章全等三角形》专题全等三角形压轴题训练(30题)1.如图,△ABC中,AB=AC,D为AC边上一点,E为AB延长线上一点,且CD=BE,DE与BC相交于点F.(1)求证:DF=EF.(2)过点F作FG⊥DE,交线段CE于点G,若CE⊥AC,CD=4,S=5,求EG的长.△EFG【分析】(1)过点D作DH∥AB交BC于点H,根据等腰三角形的性质及平行线的性质得到∠BEF=∠HDF,∠DHC=∠DCH,则DH=CD,结合∠BFE=∠HFD,即可利用AAS判定△BEF≌△HDF,根据全等三角形的性质即可得解;(2)根据三角形的面积公式求解即可.【解答】(1)过点D作DH∥AB交BC于点H,∵AB=AC,∴∠ABC=∠ACB,∵DH∥AB,∴∠DHC=∠ABC,∴∠DHC=∠ACB=∠DCH,∴DH=CD,∵CD=BE,∴DH=BE,∵DH∥AB,∴∠BEF=∠HDF,在△BEF和△HDF中,∠BFE=∠HFD∠BEF=∠HDFBE=DH,∴△BEF≌△HDF(AAS),∴DF=EF;(2)连接DG,∵DF=EF,FG⊥DE,∴S△DFG =S△EFG=5,∴S△DEG=10,∵CE⊥AC,CD=4,∴S△DEG =12EG•CD=12EG×4,∴12EG×4=10,∴EG=5.【点评】此题考查了全等三角形的判定与性质,利用AAS判定△BEF≌△HDF是解题的关键.2.如图,四边形ABCD中,AB=BC=2CD,AB∥CD,∠C=90°,E是BC的中点,AE与BD相交于点F,连接DE.(1)求证:△ABE≌△BCD;(2)判断线段AE与BD的数量关系及位置关系,并说明理由;【分析】(1)由平行线的性质得出∠ABE+∠C=180°,得出∠ABE=90°=∠C,再证出BE=CD,由SAS证明△ABE≌△BCD即可;(2)由全等三角形的性质得出AE=BD,证出∠ABF+∠BAE=90°,得出∠AFB=90°,即可得出结论.【解答】(1)证明:∵AB∥CD,∴∠ABE+∠C=180°,∵∠C=90°,∴∠ABE=90°=∠C,∵E是BC的中点,∴BC=2BE,∵BC=2CD,∴BE=CD,在△ABE和△BCD中,AB=BC∠ABE=∠C BE=CD,∴△ABE≌△BCD(SAS);(2)解:AE=BD,AE⊥BD,理由如下:由(1)得:△ABE≌△BCD,∴AE=BD,∵∠BAE=∠CBD,∠ABF+∠CBD=90°,∴∠ABF+∠BAE=90°,∴∠AFB=90°,∴AE⊥BD.【点评】本题考查了全等三角形的判定与性质、直角三角形的性质等知识;证明三角形全等是解题的关键.3.如图1,在等腰直角三角形ABC中,AB=AC,∠BAC=90°,点P为BC边上的一个动点,连接AP,以AP为直角边,A为直角顶点,在AP右侧作等腰直角三角形PAD,连接CD.(1)当点P在线段BC上时(不与点B重合),求证:△BAP≌△CAD;(2)当点P在线段BC的延长线上时(如图2),试猜想线段BP和CD的数量关系与位置关系分别是什么?请给予证明.【分析】(1)证得∠BAP=∠CAD,根据SAS可证明△BAP≌△CAD;(2)可得∠BAP=∠CAD,由SAS可证明△BAP≌△CAD,可得BP=CD,∠B=∠ACD,则结论得证.【解答】(1)证明:∵∠BAC=∠PAD=90°,∴∠BAC﹣∠PAC=∠PAD﹣∠PAC,即:∠BAP=∠CAD,在△BAP和△CAD中AB=AC∠BAP=∠CAD,PA=DA∴△BAP≌△CAD(SAS);(2)猜想:BP=CD,BP⊥CD.证明:∵∠BAC=∠PAD=90°,∴∠BAC+∠PAC=∠PAD+∠PAC,即:∠BAP=∠CAD,在△BAP和△CAD中AB=AC∠BAP=∠CAD,PA=DA∴△BAP≌△CAD(SAS),∴BP=CD(全等三角形的对应边相等),∠B=∠ACD(全等三角形的对应角相等),∵∠B+∠ACB=90°,∴∠ACD+∠ACB=90°,即:BP⊥CD.【点评】本题考查了全等三角形的判定与性质,等腰直角三角形的性质,根据同角的余角相等求出两边的夹角相等是证明三角形全等的关键.4.(2023春•市南区期末)如图,在△ABC中,AB=AC,AD⊥BC于点D,E为AC边上一点,连接BE与AD交于点F,G为△ABC外一点,满足∠ACG=∠ABE,∠FAG=∠BAC,连接EG.(1)求证:△ABF≌△ACG;(2)求证:BE=CG+EG.【分析】(1)根据已知条件可得∠BAD=∠CAG,然后利用ASA即可证明△ABF≌△ACG;(2)结合(1)的结论,再证明△AEF≌△AEG,即可解决问题.【解答】(1)证明:∵∠BAC=∠FAG,∴∠BAC﹣∠CAD=∠FAG﹣∠CAD,∴∠BAD=∠CAG,在△ABF和△ACG中,∠BAD=∠CAGAB=AC,∠ABF=∠ACG∴△ABF≌△ACG(ASA);(2)证明:∵△ABF≌△ACG,∴AF=AG,BF=CG,∵AB=AC,AD⊥BC,∴∠BAD=∠CAD,∵∠BAD=∠CAG,∴∠CAD=∠CAG,在△AEF和△AEG中,AF=AG∠FAE=∠GAE,AE=AE∴△AEF≌△AEG(SAS).∴EF=EG,∴BE=BF+FE=CG+EG.【点评】本题考查了全等三角形的判定与性质,解决本题的关键是得到△AEF≌△AEG.5.(2022秋•新宾县期中)如图(1)所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,若AB=CD.(1)求证:EG=FG.(2)若将△DEC的边EC沿AC方向移动,变为图(2)时,其余条件不变,上述结论是否成立?请说明理由.【分析】(1)先利用HL判定Rt△ABF≌Rt△CDE,得出BF=DE;再利用AAS判定△BFG≌△DEG,从而得出GE=GF;(2)结论仍然成立,同理可以证明得到.【解答】解:(1)证明:∵DE⊥AC,BF⊥AC,∴∠DEF=∠BFE=90°.∵AE=CF,AE+EF=CF+EF.即AF=CE.在Rt△ABF和Rt△CDE中,AB=CDAF=CE,∴Rt△ABF≌Rt△CDE(HL),∴BF=DE.在△BFG和△DEG中,∵∠BFG=∠DEG ∠BGF=∠DGE BF=DE,∴△BFG≌△DGE(AAS),∴GE=GF;(2)结论依然成立.理由:∵DE⊥AC,BF⊥AC,∴∠BFA=∠DEC=90°∵AE=CF∴AE﹣EF=CF﹣EF,即AF=CE,在Rt△ABF和Rt△CDE中,AB=CDAF=CE,∴Rt△ABF≌Rt△CDE(HL),∴DE=BF在△BFG和△DEG中,∵∠BFG=∠DEG ∠BGF=∠DGE BF=DE,∴△BFG≌△DGE(AAS),∴GE=GF.【点评】本题考查三角形全等的判定与性质,判定两个三角形全等的一般方法有:SSS、SAS、ASA、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.6.(2023春•市南区期末)如图,在△ABC中,AB=AC,AD⊥BC于点D,E为AC边上一点,连接BE与AD交于点F,G为△ABC外一点,满足∠ACG=∠ABE,∠FAG=∠BAC,连接EG.(1)求证:△ABF≌△ACG;(2)求证:BE=CG+EG.【分析】(1)根据已知条件可得∠BAD=∠CAG,然后利用ASA即可证明△ABF≌△ACG;(2)结合(1)的结论,再证明△AEF≌△AEG,即可解决问题.【解答】(1)证明:∵∠BAC=∠FAG,∴∠BAC﹣∠CAD=∠FAG﹣∠CAD,∴∠BAD=∠CAG,在△ABF和△ACG中,∠BAD=∠CAGAB=AC,∠ABF=∠ACG∴△ABF≌△ACG(ASA);(2)证明:∵△ABF≌△ACG,∴AF=AG,BF=CG,∵AB=AC,AD⊥BC,∴∠BAD=∠CAD,∵∠BAD=∠CAG,∴∠CAD=∠CAG,在△AEF和△AEG中,AF=AG∠FAE=∠GAE,AE=AE∴△AEF≌△AEG(SAS).∴EF=EG,∴BE=BF+FE=CG+EG.【点评】本题考查了全等三角形的判定与性质,解决本题的关键是得到△AEF≌△AEG.7.(2022秋•忠县期末)在△ABC中,点D、E分别在AB、AC边上,设BE与CD相交于点F.(1)如图①,设∠A=60°,BE、CD分别平分∠ABC、∠ACB,证明:DF=EF.(2)如图②,设BE⊥AC,CD⊥AB,点G在CD的延长线上,连接AG、AF;若∠G=∠6,BD=CD,证明:GD=DF.【分析】(1)在BC上截取BM=BD,连接FM,证明△BFD≌△BFM,△ECF≌△MCF,进而可以解决问题;(2)根据已知条件证明△BDF≌△CDA,进而可以解决问题.【解答】证明:(1)如图,在BC上截取BM=BD,连接FM,∵∠A=60,∴∠BFC=90°+60°÷2=120°,∴∠BFD=60°,∵BE平分∠ABC,∴∠1=∠2,在△BFD和△BFM中,BD=BM∠1=∠2,BF=BF∴△BFD≌△BFM(SAS),∴∠BFM=∠BFD=60°,DF=MF,∴∠CFM=120°﹣60°=60°,∵∠CFE=∠BFD=60°,∴∠CFM=∠CFE,∵CD平分∠ACB,∴∠3=∠4,又CF=CF,在△ECF和△MCF中,∠CFE=∠CFMFC=FC,∠3=∠4∴△ECF≌△MCF(ASA),∴EF=MF,∴DF=EF;(2)∵BE⊥AC,CD⊥AB,∴∠BDF=∠CDA=90°,∴∠1+∠BFD=90°,∠3+∠CFE=90°,∠BFD=∠CFE,∴∠1=∠3,∵BD=CD,在△BDF和△CDA中,∠BDF=∠CDABD=CD,∠1=∠3∴△BDF≌△CDA(ASA),∴DF=DA,∵∠ADF=90°,∴∠6=45°,∵∠G=∠6,∴∠5=45°∴∠G=∠5,∴GD=DA,∴GD=DF.【点评】本题属于三角形的综合题,考查了全等三角形的判定与性质,角平分线的性质,解决本题的关键是掌握全等三角形的判定与性质.8.(2023春•宣汉县校级期末)已知:∠ACB=90°,AC=BC,AD⊥CM,BE⊥CM,垂足分别为D,E,(1)如图1,把下面的解答过程补充完整,并在括号内注明理由.①线段CD和BE的数量关系是:CD=BE;②请写出线段AD,BE,DE之间的数量关系并证明.解:①结论:CD=BE.理由:∵AD⊥CM,BE⊥CM,∴∠ACB=∠BEC=∠ADC=90°,∴∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,∴∠ACD= 在△ACD和△CBE中,( )∴△ACD≌△CBE,( )∴CD=BE.②结论:AD=BE+DE.理由:∵△ACD≌△CBE,∴ ∵CE=CD+DE=BE+DE,∴AD=BE+DE.(2)如图2,上述结论②还成立吗?如果不成立,请写出线段AD,BE,DE之间的数量关系.并说明理由.【分析】(1)根据同角的余角相等,全等三角形的判定和性质即可解决问题;(2)结论:DE﹣BE=AD,只要证明△ACD≌△CBE即可解决问题;【解答】解:(1)∵AD⊥CM,BE⊥CM,∴∠ACB=∠BEC=∠ADC=90°,∴∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,∴∠ACD=∠CBE在△ACD和△CBE中,(∠ADC=∠BEC ∠ACD=∠CBE AC=BC)∴△ACD≌△CBE,(AAS)∴CD=BE.②结论:AD=BE+DE.理由:∵△ACD≌△CBE,∴AD=CE∵CE=CD+DE=BE+DE,∴AD=BE+DE.故答案为:∠CBE,∠ADC=∠BEC∠ACD=∠CBEAC=BC,AAS,AD=CE.(2)不成立,结论:DE﹣BE=AD.理由:∵AD⊥CM,BE⊥CM,∴∠ACB=∠BEC=∠ADC=90°,∴∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,∴∠ACD=∠CBE在△ACD和△CBE中,∠ADC=∠BEC∠ACD=∠CBEAC=BC,∴△ACD≌△CBE,(AAS)∴AD=CE,CD=BE,∴DE﹣BE=DE﹣DC=CE=AD.【点评】本题考查全等三角形的判定和性质,解题的关键是正确寻找全等三角形的全等条件,灵活运用知识解决问题.9.如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,点E、F分别在BC、CD上,且∠EAF=1 2∠BAD,求证:DF=EF﹣BE.【分析】由边角边证明△ADF≌△ABH得AF=AH,∠DAF=∠BAH,同理可得△HAE≌△FAE,其性质得HE=EF,最后由线段和差和等式的性质得DF=EF﹣BE.【解答】证明:在CB的延长线上取BH=DF,如图所示:∵∠ABE+∠ABH=180°,∠ABE+∠D=180°,∴∠ABH=∠D,在△ADF和△ABH中,AD=AB∠D=∠ABHDF=BH,∴△ADF≌△ABH(SAS),∴AF=AH,∠DAF=∠BAH,∴∠BAD=∠HAF,∵∠EAF=12∠BAD,∴∠EAF=∠HAE=12∠HAF,在△HAE和△FAE中,AH=AF∠HAE=∠FAEAE=AE,∴△HAE≌△FAE(SAS),∴HE=EF,又∵HE=HB+BE,HB=DF,∴EF=BE+DF,∴DF=EF﹣BE.【点评】本题综合考查了全等三角形的判定与性质,角平分线的定义,同角的补角相等,线段的和差和等量代换等知识点,重点掌握全等三角形的判定与性质,难点是构建全等三角形和角平分线.10.在Rt△ABC中,∠ABC=90°,点D是CB延长线上一点,点E是线段AB上一点,连接DE.AC=DE,BC=BE.(1)求证:AB=BD;(2)BF平分∠ABC交AC于点F,点G是线段FB延长线上一点,连接DG,点H是线段DG上一点,连接AH交BD于点K,连接KG.当KB平分∠AKG时,求证:AK=DG+KG.【分析】(1)证明Rt△ACB≌Rt△DEB即可解决问题;(2)作BM平分∠ABD交AK于点M,证明△BMK≌△BGK,△ABM≌△DBG,即可解决问题.【解答】证明:(1)在Rt△ACB和Rt△DEB中,AC=DEBC=BE,∴Rt△ACB≌Rt△DEB(HL),∴AB=BD,(2)如图:作BM平分∠ABD交AK于点M,∵BM平分∠ABD,KB平分∠AKG,∴∠ABM=∠MBD=45°,∠AKB=∠BKG,∵∠ABF=∠DBG=45°∴∠MBD=∠GBD,在△BMK和△BGK中,∠MBD=∠GBDBK=BK,∠AKB=∠BKG∴△BMK≌△BGK(ASA),∴BM=BG,MK=KG,在△ABM和△DBG中,AB=BD∠ABM=∠DBG,BM=BG∴△ABM≌△DBG(SAS),∴AM=DG,∵AK=AM+MK,∴AK=DG+KG.【点评】本题考查了全等三角形的判定与性质,解决本题的关键是得到△BMK≌△BGK.11.(2023春•余江区期末)如图,大小不同的两块三角板△ABC和△DEC直角顶点重合在点C处,AC=BC,DC=EC,连接AE、BD,点A恰好在线段BD上.(1)找出图中的全等三角形,并说明理由;(2)当AD=AB=4cm,则AE的长度为 cm.(3)猜想AE与BD的位置关系,并说明理由.【分析】(1)根据SAS证明△CBD≌△CAE即可;(2)根据全等三角形的性质解答即可;(3)根据全等三角形的性质和垂直的定义解答即可.【解答】解:(1)△CBD≌△CAE,理由如下:∵∠ACB=∠DCE=90°,∴∠ACB+∠ACD=∠DCE+∠ACD,即∠BCD=∠ACE,在△CBD与△CAE中,BC=AC∠BCD=∠ACE,DC=EC∴△CBD≌△CAE(SAS);(2)∵△CBD≌△CAE,∴BD=AE=AD+AB=4+4=8(cm),故答案为:8;(3)AE⊥BD,理由如下:AE与CD相交于点O,在△AOD与△COE中,∵△CBD≌△CAE,∴∠ADO=∠CEO,∵∠AOD=∠COE,∴∠OAD=∠OCE=90°,∴AE⊥BD.【点评】此题考查全等三角形的判定和性质,关键是根据SAS得出△CBD与△CAE全等解答.12.如图①点A、B、C、D在同一直线上,AB=CD,作CE⊥AD,BF⊥AD,且AE=DF.(1)证明:EF平分线段BC;(2)若△BFD沿AD方向平移得到图②时,其他条件不变,(1)中的结论是否仍成立?请说明理由.【分析】(1)由AB=CD,利用等式的性质得到AC=BD,再由AE=DF,利用HL得到直角三角形ACE 与直角三角形DBF全等,利用全等三角形对应边相等得到EC=BF,再利用AAS得到三角形ECG与三角形FBG全等,利用全等三角形对应边相等得到BG=CG,即可得证;(2)(1)中的结论成立,理由为:由AC=DB,利用等式的性质得到AC=BD,再由AE=DF,利用HL 得到直角三角形ACE与直角三角形DBF全等,利用全等三角形对应边相等得到EC=BF,再利用AAS 得到三角形ECG与三角形FBG全等,利用全等三角形对应边相等得到BG=CG,即可得证.【解答】(1)证明:∵CE⊥AD,BF⊥AD,∴∠ACE=∠DBF=90°,∵AB=CD,∴AB+BC=BC+CD,即AC=DB,在Rt△ACE和Rt△DBF中,AE=DFAC=DB,∴Rt△ACE≌Rt△DBF(HL),∴CE=FB,在△CEG和△BFG中,∠ECG=∠FBG=90°∠EGC=∠BGF,EC=FB∴△CEG≌△BFG(AAS),∴CG=BG,即EF平分线段BC;(2)(1)中结论成立,理由为:证明:∵CE⊥AD,BF⊥AD,∴∠ACE=∠DBF=90°,∵AB=CD,∴AB﹣BC=CD﹣BC,即AC=DB,在Rt△ACE和Rt△DBF中,AE=DFAC=DB,∴Rt△ACE≌Rt△DBF(HL),∴CE=FB,在△CEG和△BFG中,∠ECG=∠FBG=90°∠EGC=∠BGF,EC=FB∴△CEG≌△BFG(AAS),∴CG=BG,即EF平分线段BC.【点评】此题考查了全等三角形的判定与性质,以及平移的性质,熟练掌握全等三角形的判定与性质是解本题的关键.13.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.(1)当直线MN绕点C旋转到图1的位置时①请说明△ADC≌△CEB的理由;②请说明DE=AD+BE的理由;(2)当直线MN绕点C旋转到图2的位置时,DE、AD、BE具有怎样的等量关系?请直接在横线上写出这个等量关系: .(3)当直线MN绕点C旋转到图3的位置时,DE、AD、BE具有怎样的等量关系?请直接在横线上写出这个等量关系: .【分析】(1)①由已知推出∠ADC=∠BEC=90°,因为∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,推出∠DAC=∠BCE,根据AAS即可得到答案;②由①得到AD=CE,CD=BE,即可求出答案;(2)结论:DE=AD﹣BE.与(1)证法类似可证出∠ACD=∠EBC,能推出△ADC≌△CEB,得到AD =CE,CD=BE,代入已知即可得到答案.(3)结论:DE=BE﹣AD.证明方法类似.【解答】解:(1)①证明:如图1中,∵AD⊥DE,BE⊥DE,∴∠ADC=∠BEC=90°,∵∠ACB=90°,∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,∴∠DAC=∠BCE,在△ADC和△CEB中,∠CDA=∠BEC∠DAC=∠ECB,AC=BC∴△ADC≌△CEB(AAS).②证明:由(1)知:△ADC≌△CEB,∴AD=CE,CD=BE,∵DC+CE=DE,∴AD+BE=DE.(2)结论:DE=AD﹣BE.理由:如图2中,∵BE⊥EC,AD⊥CE,∴∠ADC=∠BEC=90°,∴∠EBC+∠ECB=90°,∵∠ACB=90°,∴∠ECB+∠ACE=90°,∴∠ACD=∠EBC,在△ADC和△CEB中,∠ACD=∠CBE∠ADC=∠BEC,AC=BC∴△ADC≌△CEB(AAS),∴AD=CE,CD=BE,∴DE=EC﹣CD=AD﹣BE.(3)结论:DE=BE﹣AD.理由如下:如图3中,∵∠ACB=90°,∴∠ACD+∠BCE=90°∵AD⊥MN,BE⊥MN,∴∠ADC=∠CED=90°,∴∠ACD+∠DAC=90°,∴∠DAC=∠ECB,在△ACD和△CBE中,∠ADC=∠CEB∠DAC=∠ECB,AC=CB∴△ACD≌△CBE(AAS),∴AD=CE,CD=BE,∴DE=CD﹣CE=BE﹣AD.故答案为DE=AD﹣BE,DE=BE﹣AD.【点评】本题主要考查了邻补角的意义,全等三角形的性质和判定等知识点,能根据已知证出符合全等的条件是解此题的关键,题型较好,综合性比较强.14.已知:在△AOB和△COD中,OA=OB,OC=OD.(1)如图①,若∠AOB=∠COD=60°.①求证:AC=BD.②求∠APB的度数.(2)如图②,若∠AOB=∠COD=α,∠APD的大小为 (直接写出结果,不证明).【分析】(1)①根据已知先证明∠AOC=∠BOD,再由SAS证明△AOC≌△BOD,所以AC=BD.②由△AOC≌△BOD,可得∠OAC=∠OBD,再结合图形,利用角的和差,可得∠APB=60°.(2)由(1)小题的证明可知,∠APB=α,则可得出答案.【解答】(1)①证明:∵∠AOB=∠COD=60°,∴∠AOB+∠BOC=∠COD+∠BOC,∴∠AOC=∠BOD,在△AOC和△BOD中,AO=BO∠AOC=∠BOD,OC=OD∴△AOC≌△BOD(SAS),∴AC=BD;②解:∵△AOC≌△BOD,∴∠OAC=∠OBD,∴∠OAC+∠AOB=∠OBD+∠APB,∴∠OAC+60°=∠OBD+∠APB,∴∠APB=60°;(2)解:由(1)可知:△AOC≌△BOD(SAS),∴∠OAC=∠OBD,∴∠OAC+∠AOB=∠OBD+∠APB,∴∠OAC+α=∠OBD+∠APB,∴∠APB=α,∴∠APD=180°﹣α.故答案为:180°﹣α.【点评】本题主要考查了全等三角形的判定和性质,正确运用全等三角形的性质是解题的关键.15.(1)已知,如图①,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E,求证:DE=BD+CE.(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE是否成立?若成立,请你给出证明;若不成立,请说明理由.【分析】(1)根据BD⊥直线m,CE⊥直线m得∠BDA=∠CEA=90°,而∠BAC=90°,根据等角的余角相等得∠CAE=∠ABD,然后根据“AAS”可判断△ADB≌△CEA,则AE=BD,AD=CE,于是DE=AE+AD=BD+CE;(2)利用∠BDA=∠BAC=α,则∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,得出∠CAE=∠ABD,进而得出△ADB≌△CEA即可得出答案.【解答】证明:(1)∵BD⊥直线m,CE⊥直线m,∴∠BDA=∠CEA=90°,∵∠BAC=90°,∴∠BAD+∠CAE=90°,∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD,∵在△ADB和△CEA中∠ABD=∠CAE∠BDA=∠CEA,AB=AC∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE;(2)结论DE=BD+CE仍然成立,理由是:∵∠BDA=∠BAC=α,∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,∴∠CAE=∠ABD,∵在△ADB和△CEA中∠ABD=∠CAE∠BDA=∠CEAAB=AC,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE.【点评】本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;得出∠CAE=∠ABD是解题关键.16.已知:如图AC∥BD,AE和BE分别平分∠CAB和∠DBA,CD过点E.求证:(1)AE⊥BE;(2)AB=AC+BD.【分析】(1)首先证明∠CAB+∠DBA=180°,再利用角平分线的性质证明∠EAB=12∠CAB,∠EBA=12∠DBA,可得到∠EAB+∠EBA=90°,进而可证出AE⊥BE;(2)首先在AB上截取AF=AC,连接EF,证明△CAE≌△FAE,可证出∠CEA=∠FEA,可得到∠FEB =∠DEB,再证明△DEB≌△FEB,可得到BD=BF,即可证出AB=AC+BD.【解答】证明:(1)∵AC∥BD,∴∠CAB+∠DBA=180°又∵AE和BE分别平分∠CAB和∠DBA,∴∠EAB=12∠CAB,∠EBA=12∠DBA,∴∠EAB+∠EBA=12(∠CAB+∠DBA)=90°,∴AE⊥BE(2)在AB上截取AF=AC,连接EF,在△CAE和△FAE中AC=AF∠CAE=∠FAE AE=AE,∴△CAE≌△FAE,则∠CEA=∠FEA,又∠CEA+∠BED=∠FEA+∠FEB=90°,∴∠FEB=∠DEB,∵BE平分∠DBA,∴∠DBE=∠FBE,在△DEB和△FEB中∠DEB=∠FEB EB=EB∠DBE=∠FBE,∴△DEB≌△FEB(ASA),∴BD=BF,又∵AF=AC,∴AB=AF+FB=AC+BD.【点评】此题主要考查了垂直,角平分线,以及三角形全等的判定和性质,证明三角形全等是证明线段和角相等的重要手段.17.问题情境:如图①,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D.可知:∠BAD=∠C(不需要证明);(1)特例探究:如图②,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN 上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;(2)归纳证明:如图③,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF;(3)拓展应用:如图④,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为24,则△ACF与△BDE的面积之和为 .(直接写出结果)【分析】(1)证明∠ABD=∠CAF,利用AAS定理证明;(2)根据三角形的外角的性质证明∠ABE=∠CAF,∠BAE=∠FCA,利用ASA定理证明;(3)根据CD=2BD,求出△ABD的面积,根据全等三角形的性质计算即可.【解答】(1)证明:如图②,∵CF⊥AE,BD⊥AE,∠MAN=90°,∴∠BDA=∠AFC=90°,∴∠ABD+∠BAD=90°,∠ABD+∠CAF=90°,∴∠ABD=∠CAF,在△ABD和△CAF中,∠ADB=∠CFA∠ABD=∠CAF,AB=AC∴△ABD≌△CAF(AAS);(2)证明:如图③,∵∠1=∠2=∠BAC,∠1=∠BAE+∠ABE,∠BAC=∠BAE+∠CAF,∠2=∠FCA+∠CAF,∴∠ABE=∠CAF,∠BAE=∠FCA,在△ABE和△CAF中,∠ABE =∠CAF AB =AC ∠BAE =∠ACF,∴△ABE ≌△CAF (ASA );(3)解:如图④,∵△ABC 的面积为24,CD =2BD ,∴△ABD 的面积是:13×24=8,由(2)可知,△ABE ≌△CAF ,∴△ACF 与△BDE 的面积之和等于△ABE 与△BDE 的面积之和,即等于△ABD 的面积是8,故答案为:8.【点评】本题考查的是三角形的知识的综合应用,掌握全等三角形的判定定理和性质定理、三角形的面积公式是解题的关键.18.在△ABC 中,AB =AC ,D 是直线BC 上一点,以AD 为一条边在AD 的右侧作△ADE ,使AE =AD ,∠DAE =∠BAC ,连接DE ,CE .(1)如图,当点D 在BC 延长线上移动时,求证:BD =CE .(2)设∠BAC =α,∠DCE =β.①当点D 在线段BC 的延长线上移动时,α与β之间有什么数量关系?请说明理由.②当点D 分别在线段BC 上、线段BC 的反向延长线上移动时,α与β之间有什么数量关系?请说明理由.【分析】(1)根据SAS 证△BAD ≌△CAE ,可得结论;(2)①由△BAD ≌△CAE ,推出∠B =∠ACE ,根据三角形外角性质求出即可;②α+β=180°或α=β,根据三角形外角性质求出即可.【解答】(1)证明:∵∠DAE =∠BAC ,∴∠DAE +∠CAD =∠BAC +∠CAD ,∴∠BAD=∠CAE,在△BAD和△CAE中,AB=AC∠BAD=∠CAE,AD=AE∴△BAD≌△CAE(SAS),(2)解:①当点D在线段BC的延长线上移动时,α与β之间的数量关系是α=β,理由是:由(1)知△BAD≌△CAE,∴∠B=∠ACE,∵∠ACD=∠B+∠BAC=∠ACE+∠DCE,∴∠BAC=∠DCE,∵∠BAC=α,∠DCE=β,∴α=β;②分三种情况:i)当D在线段BC上时,如图2,α+β=180°,理由是:同理可证明:△ABD≌△ACE(SAS),∴∠ADB=∠AEC,∠ABC=∠ACE,∵∠ADC+∠ADB=180°,∴∠ADC+∠AEC=180°,∴∠DAE+∠DCE=180°,∵∠BAC=∠DAE=α,∠DCE=β,∴α+β=180°,ii)当点D在线段BC反向延长线上时,如图3,α=β.如图3,同理可证明:△ABD≌△ACE(SAS),∴∠ABD=∠ACE,∵∠ACE=∠ACD+∠DCE,∠ABD=∠ACD+∠BAC,∴∠ACD+∠DCE=∠ACD+∠BAC,∴∠BAC=∠DCE,∵∠BAC=α,∠DCE=β,∴α=β;ii)当点D在线段BC的延长线上时,如图1,α=β.综上,当点D在BC上移动时,α=β或α+β=180°.【点评】本题是三角形的综合题,考查了全等三角形的性质和判定,三角形的外角性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.19.(2023春•新市区期末)在△ABC中,∠ACB=90°,AC=BC,D是直线AB上一点(点D不与点A、B重合),连接DC并延长到E,使得CE=CD,过点E作EF⊥直线BC,交直线BC于点F.(1)如图1,当点D为线段AB上的任意一点时,用等式表示线段EF、CF、AC的数量关系,并证明;(2)如图2,当点D为线段BA的延长线上一点时,依题意补全图2,猜想线段EF、CF、AC的数量关系是否发生改变,并证明;(3)如图3,当点D在线段AB的延长线上时,直接写出线段EF、CF、AC之间的数量关系.【分析】(1)过D作DH⊥CB于H,由“AAS”可证△FEC≌△HDC,可得CH=FC,DH=EF,可得结论;(2)过D作DH⊥CB于H,由“AAS”可证△FEC≌△HDC,可得CH=FC,DH=EF,可得结论.(3)过D作DH⊥CB交CB的延长线于H,由“AAS”可证△FEC≌△HDC,可得CH=FC,DH=EF,可得结论.【解答】解:(1)结论:AC=EF+FC.理由如下:过D作DH⊥CB于H,∴∠DHC=∠DHB=90°,∵EF⊥CF,∴∠EFC=∠DHC=90°,在△FEC和△HDC中,∠EFC=∠DHC=90°∠FCE=∠DCH,EC=DC∴△FEC≌△HDC(AAS),∴CH=FC,DH=EF,∵∠ACB=90°,AC=BC,∴∠B=45°,∵∠DHB=90°,∴∠B=∠HDB=45°,∴DH=HB=EF,∵BC=CB+HB,∴AC=FC+EF;(2)依题意补全图形,结论:AC=EF﹣CF,理由如下:过D作DH⊥CB交BC的延长线于H,∵EF⊥CF,∴∠EFC=∠DHC=90°,在△FEC和△HDC中,∠FCE=∠DCH∠EFC=∠DHC=90°,EC=DC∴△FEC≌△HDC(AAS),∴CH=FC,DH=EF,∵∠DHB=90°,∴∠B=∠HDB=45°,∴DH=HB=EF,∵BC=HB﹣CH,∴AC=EF﹣CF;(3)AC=CF﹣EF.如图3,过D作DH⊥CB交CB的延长线于H,同理可证△FEC≌△HDC(AAS),∴CH=FC,DH=EF,∵∠DHB=90°,∴∠B=∠HDB=45°,∴DH=HB=EF,∵BC=CH﹣BH,∴AC=CF﹣EF.【点评】本题是三角形综合题,考查了全等三角形的判定和性质,添加恰当辅助线构造全等三角形是本题的关键.20.如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.(1)如果AB=AC,∠BAC=90°,①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD所在直线的位置关系为 ,线段CF、BD的数量关系为 ;②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F 不重合),并说明理由.【分析】(1)当点D在BC的延长线上时①的结论仍成立.由正方形ADEF的性质可推出△DAB≌△FAC,所以CF=BD,∠ACF=∠ABD.结合∠BAC=90°,AB=AC,得到∠BCF=∠ACB+∠ACF=90°.即CF⊥BD.(2)当∠ACB=45°时,过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,可推出∠ACB=∠AGC,所以AC=AG,由(1)①可知CF⊥BD.【解答】证明:(1)①正方形ADEF中,AD=AF,∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF,又∵AB=AC,∴△DAB≌△FAC,∴CF=BD,∠B=∠ACF,∴∠ACB+∠ACF=90°,即CF⊥BD.②当点D在BC的延长线上时①的结论仍成立.由正方形ADEF得AD=AF,∠DAF=90度.∵∠BAC=90°,∴∠DAF=∠BAC,∴∠DAB=∠FAC,又∵AB=AC,∴△DAB≌△FAC,∴CF=BD,∠ACF=∠ABD.∵∠BAC=90°,AB=AC,∴∠ABC=45°,∴∠ACF=45°,∴∠BCF=∠ACB+∠ACF=90度.即CF⊥BD.(2)当∠ACB=45°时,CF⊥BD(如图).理由:过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,∵∠ACB=45°,∠AGC=90°﹣∠ACB,∴∠AGC =90°﹣45°=45°,∴∠ACB =∠AGC =45°,∴AC =AG ,∵∠DAG =∠FAC (同角的余角相等),AD =AF ,∴△GAD ≌△CAF ,∴∠ACF =∠AGC =45°,∠BCF =∠ACB +∠ACF =45°+45°=90°,即CF ⊥BC .【点评】本题考查三角形全等的判定和直角三角形的判定,判定两个三角形全等的一般方法有:SSS 、SAS 、ASA 、AAS 、HL .判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.21.(2022春•沙坪坝区校级期中)如图,在△ABC 中,∠ABC 、∠ACB 的平分线交于点D ,延长BD 交AC 于E ,G 、F 分别在BD 、BC 上,连接DF 、GF ,其中∠A =2∠BDF ,GD =DE .(1)当∠A =80°时,求∠EDC 的度数;(2)求证:CF =FG +CE .【分析】(1)方法一:先求∠ABC 和∠ACB 的和为100°,再根据角平分线求∠DBC +∠DCB =50°,再根据外角即可解决问题;方法二:在BC 上取点M ,使CM =CE ,证明△CDE ≌△CDM (SAS ),可得DE =DM ,∠DEC =∠DMC ,∠EDC =∠MDC ,证明∠BDM =180°―12∠ABC ﹣∠DMB =180°―12∠ABC ﹣∠AEB =∠A =80°,进而可以解决问题.(2)结合(1)然后证明△DGF≌△DMF(SAS),可得GF=MF,进而可以解决问题.【解答】(1)解:方法一:∵∠A=80°,∴∠ABC+∠ACB=100°,∵BE平分∠ABC、CD平分∠ACB,∴∠DBC+∠DCB=50°,∴∠EDC=∠DBC+∠DCB=50°;方法二:如图,在BC上取点M,使CM=CE,∵CD平分∠ACB,∴∠ACD=∠BCD,在△CDE和△CDM中,CE=CM∠ECD=∠MCDCD=CD,∴△CDE≌△CDM(SAS),∴DE=DM,∠DEC=∠DMC,∠EDC=∠MDC,∵GD=DE,∴GD=MD,∵∠DEC+∠AEB=180°,∠DMC+∠DMF=180°,∴∠AEB=∠DMF,∵BE平分∠ABC,∴∠ABE=∠CBE=12∠ABC,∴∠BDM=180°―12∠ABC﹣∠DMB=180°―12∠ABC﹣∠AEB=∠A=80°,∴∠EDM=100°,∴∠EDC=50°;(2)证明:∵∠A=2∠BDF,∴∠BDM=2∠BDF,∴∠FDM=∠BDF,在△DGF和△DMF中,DG=DM∠GDF=∠MDF,DF=DF∴△DGF≌△DMF(SAS),∴GF=MF,∴CF=CM+FM=CE+GF.∴CF=FG+CE.【点评】本题考查了全等三角形的判定与性质,角平分线的定义,解决本题的关键是根据题意准确作出辅助线得到△DGF≌△DMF.22.(2022秋•大同月考)已知△ABC和△CDE中,CA=CB,CD=CE,∠ACB=∠DCE=α,AE与BD交于点F.(1)如图1.当α=90°时.求证:①△ACE≌△BCD;②AE⊥BD;(2)如图2.当α=60°时,直接写出∠AFB的度数为 ;(3)如图3,直接写出∠AFD的度数为 (用含α的式子表示).【分析】(1)先根据等角的余角相等得到∠ACE=∠BCD,再根据等腰直角三角形的性质得AC=BC,EC=DC,于是可根据“SAS”判断△ACE≌△BCD,然后根据相似三角形的性质得到∠CAE=∠CBD,根据三角形的内角和即可得到结论;(2)由已知条件得到∠ACE=∠BCD,推出△ACE≌△BCD(SAS),根据全等三角形的性质得到∠CAE =∠CBD,推出A,B,F,C四点共圆,根据圆周角定理即可得到结论.(3)由已知条件得到∠ACE=∠BCD,推出△ACE≌△BCD(SAS),根据全等三角形的性质得到∠CAE =∠CBD即可得到结论.【解答】证明:(1)∵∠ACB=∠DCE=90°,∴∠ACB+∠BCE=∠DCE+∠BCE,即∠ACE=∠BCD,又∵△ABC和△ECD都是等腰直角三角形∴AC=BC,EC=DC,在△ACE和△BCD中,AC=BC∠ACE=∠BCD,CE=CD∴△ACE≌△BCD(SAS),∴∠CAE=∠CBD,∵∠CAE+∠EAB+∠ABC=90°,∴∠CBD+∠EAB+∠ABC=90°,∴∠AFB=90°,∴AE⊥BD;(2)∵∠ACB=∠DCE=60°,∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,即∠ACE=∠BCD,在△ACE和△BCD中,AC=BC∠ACE=∠BCD,CE=CD∴△ACE≌△BCD(SAS),∴∠CAE=∠CBD,∵∠CAE+∠EAB+∠ABC=120°,∴∠CBD+∠EAB+∠ABC=120°,∴∠AFB=∠ACB=60°;故答案为:60°;(3))∵∠ACB=∠DCE=α,∴∠ACB+∠BCE=∠DCE+∠BCE即∠ACE=∠BCD,在△ACE和△BCD中,AC=BC∠ACE=∠BCD,CE=CD∴△ACE≌△BCD(SAS),∴∠CAE=∠CBD,∵∠CAE+∠EAB+∠ABC=180°﹣α,∴∠CBD+∠EAB+∠ABC=180°﹣α∴∠AFB=∠ACB=α,∴∠AFD=180°﹣α.故答案为:180°﹣α.【点评】本题考查了全等三角形的判定与性质:判断三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应角相等,对应边相等.23.将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.(1)求证:AF+EF=DE;(2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图②中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立;(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图③.你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.【分析】(1)我们已知了三角形BED和CAB全等,那么DE=AF+CF,因此只要求出EF=CF就能得出本题所求的结论,可通过全等三角形来实现,连接BF,那么证明三角形BEF和BCF全等就是解题的关键,这两三角形中已知的条件有BE=BC,一条公共边,根据斜边直角边定理,这两个直角三角形就全等了,也就得出EF=CF,也就能证得本题的结论了;(2)解题思路和辅助线的作法与(1)完全一样;(3)结论不成立.结论:AF=DE+EF.同(1)得CF=EF,由△ABC≌△DBE,可得AC=DE,AF=AC+FC=DE+EF.【解答】(1)证明:连接BF(如图①),∵△ABC≌△DBE(已知),∴BC=BE,AC=DE.∵∠ACB=∠DEB=90°,∴∠BCF=∠BEF=90°.在Rt△BFC和Rt△BFE中,BF=BFBC=BE∴Rt△BFC≌Rt△BFE(HL).∴CF=EF.又∵AF+CF=AC,∴AF+EF=DE.(2)解:画出正确图形如图②∴(1)中的结论AF+EF=DE仍然成立;(3)不成立.结论:AF=DE+EF.证明:连接BF,∵△ABC≌△DBE,∴BC=BE,∵∠ACB=∠DEB=90°,∴△BCF和△BEF是直角三角形,在Rt△BCF和Rt△BEF中,BC=BEBF=BF,∴△BCF≌△BEF(HL),∴CF=EF;∵△ABC≌△DBE,∴AC=DE,∴AF=AC+FC=DE+EF.【点评】本题考查了全等三角形的判定和性质,通过构建全等三角形来得出简单的线段相等是解题的关键.24.(2023春•沙坪坝区校级期中)如图,在△ABC和△DCE中,∠ACB=90°,CA=CB,∠DCE=90°,CD=CE.(1)如图1,当点D在BC上时,CB=10,AE=4,则S四边形ABDE= ;(2)如图2,当B、C、E三点共线时,D在AC上,连接BD、AE,F是AD的中点,过点A作AG∥BD,交BF的延长线于点G,求证:AG=AE且AG⊥AE;(3)如图3,B、C、E三点共线,且∠DBE=15°,将线段AE绕点A以每秒10°的速度逆时针旋转,同时线段BE绕点E以每秒20°的速度顺时针旋转180°后立即以相同速度回转,设转动时间为t秒,当BE回到出发时的位置时同时停止旋转,则在转动过程中.当BE和AE互相平行或者垂直时,请直接写出此时t的值.【分析】(1)根据S四边形ABDE =S△ABC﹣S△DCE,求解即可.(2)如图2中,延长BD交AE于T.证明△BCD≌△ACE(SAS),推出BD=AE,∠CBD=∠CAE,推出BD⊥AE,证明△AFG≌△DFB(AAS),推出AG=BD,可得结论.(3)从开始到结束出现平行,垂直,平行,平行四种情形,分别构建方程求解即可.【解答】(1)解:如图1中,∵CA=CB=10,AE=4,∴CE=CD=AC﹣AE=10﹣4=6,∴S四边形ABDE =S△ABC﹣S△DCE=12×10×10―12×6×6=32,故答案为:32.(2)证明:如图2中,延长BD 交AE 于T .∵∠BCD =∠ACE =90°,BC =AC ,DC =EC ,∴△BCD ≌△ACE (SAS ),∴BD =AE ,∠CBD =∠CAE ,∵∠BDC =∠ADT ,∴∠BCD =∠ATD =90°,∴BD ⊥AE ,∵AG ∥BD ,∴∠G =∠FBD ,∵AF =FD ,∠AFG =∠DFB ,∴△AFG ≌△DFB (AAS ),∴AG =BD ,∴AG =AE ,∵AG ∥BD ,BD ⊥AE ,∴AG ⊥AE .(3)由题意,第一次平行时,10t =75°﹣20t ,解得t =52,第一次垂直时,10t +20t ﹣75°=90°,解得t =112,第二次平行时,20t ﹣75°+10t =180°.解得y =516,第三次平行时,105°﹣(20t ﹣180°)+10t =180°,解得t =212,综上所述,满足条件的t 的值为52或112或516或212.【点评】本题属于四边形综合题,考查了全等三角形的判定和性质,平行线的判定和性质,三角形的面。
初二数学:三角形知识点总结及压轴题练习(附答案解析)

初二三角形所有知识点总结和常考题知识点:1.三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.2.三边关系:三角形任意两边的和大于第三边,任意两边的差小于第三边.3.高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足间的线段叫做三角形的高.4.中线:在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线.5.角平分线:三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.6.三角形的稳定性:三角形的形状是固定的,三角形的这个性质叫三角形的稳定性.7.多边形:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.8.多边形的内角:多边形相邻两边组成的角叫做它的内角.9.多边形的外角:多边形的一边与它的邻边的延长线组成的角叫做多边形的外角.10.多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.11.正多边形:在平面内,各个角都相等,各条边都相等的多边形叫正多边形.12.平面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做用多边形覆盖平面,13.公式与性质:⑴三角形的内角和:三角形的内角和为180°⑵三角形外角的性质:性质1:三角形的一个外角等于和它不相邻的两个内角的和.性质2:三角形的一个外角大于任何一个和它不相邻的内角.⑶多边形内角和公式:n边形的内角和等于(2)n-·180°⑷多边形的外角和:多边形的外角和为360°.⑸多边形对角线的条数:①从n边形的一个顶点出发可以引(3)n-条对角线,把多边形分成(2)n-个三角形.②n边形共有(3)2n n-条对角线.常考题:一.选择题(共13小题)1.已知三角形的两边长分别为4cm和9cm,则下列长度的四条线段中能作为第三边的是()A.13cm B.6cm C.5cm D.4cm2.一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=()A.90°B.100°C.130° D.180°3.已知如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于()A.315°B.270° C.180° D.135°4.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是()A.B.C.D.5.如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=()A.90°﹣αB.90°+αC.D.360°﹣α6.如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=()A.40°B.30°C.20°D.10°7.如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE相交于一点P,若∠A=50°,则∠BPC=()A.150°B.130°C.120° D.100°8.如图,为估计池塘岸边A、B的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是()A.20米B.15米C.10米D.5米9.将一个n边形变成n+1边形,内角和将()A.减少180°B.增加90°C.增加180°D.增加360°10.一个多边形除一个内角外其余内角的和为1510°,则这个多边形对角线的条数是()A.27 B.35 C.44 D.5411.一个多边形的边数每增加一条,这个多边形的()A.内角和增加360°B.外角和增加360°C.对角线增加一条 D.内角和增加180°12.一个三角形三个内角的度数之比为2:3:7,这个三角形一定是()A.等腰三角形B.直角三角形C.锐角三角形D.钝角三角形13.如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为()A.13 B.14 C.15 D.16二.填空题(共13小题)14.若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是.15.如图,小亮从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,…,照这样走下去,他第一次回到出发地A点时,一共走了米.16.将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为度.17.当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为.18.若一个多边形内角和等于1260°,则该多边形边数是.19.如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5=.20.一个多边形的内角和比外角和的3倍多180°,则它的边数是.21.若正多边形的一个内角等于140°,则这个正多边形的边数是.22.在△ABC中,三个内角∠A、∠B、∠C满足∠B﹣∠A=∠C﹣∠B,则∠B=度.23.如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2012BC和∠A2012CD的平分线交于点A2013,则∠A2013=度.24.如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=度.25.用一条宽相等的足够长的纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE,其中∠BAC=度.26.平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,如图,则∠3+∠1﹣∠2=.三.解答题(共14小题)27.如图,直线DE交△ABC的边AB、AC于D、E,交BC延长线于F,若∠B=67°,∠ACB=74°,∠AED=48°,求∠BDF的度数.28.如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=42°,求∠ACD的度数.29.已知△ABC中,∠ACB=90°,CD为AB边上的高,BE平分∠ABC,分别交CD、AC于点F、E,求证:∠CFE=∠CEF.30.如图,AD为△ABC的中线,BE为△ABD的中线,(1)若∠ABE=25°,∠BAD=50°,则∠BED的度数是度.(2)在△ADC中过点C作AD边上的高CH.(3)若△ABC的面积为60,BD=5,求点E到BC边的距离.31.如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.(1)若∠B=35°,∠ACB=85°,求∠E的度数;(2)当P点在线段AD上运动时,猜想∠E与∠B、∠ACB的数量关系,写出结论无需证明.32.如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,垂足分别为D,E,∠AFD=158°,求∠EDF的度数.33.如图,AD平分∠BAC,∠EAD=∠EDA.(1)∠EAC与∠B相等吗?为什么?(2)若∠B=50°,∠CAD:∠E=1:3,求∠E的度数.34.(1)如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.△ABC中,∠A=30°,则∠ABC+∠ACB=,∠XBC+∠XCB=.(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ 仍然分别经过B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.35.已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON 上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.(1)如图1,若AB∥ON,则①∠ABO的度数是;②当∠BAD=∠ABD时,x=;当∠BAD=∠BDA时,x=.(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.36.平面内的两条直线有相交和平行两种位置关系(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD 是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B﹣∠D.将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系?(不需证明)(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.37.如下几个图形是五角星和它的变形.(1)图(1)中是一个五角星,求∠A+∠B+∠C+∠D+∠E.(2)图(2)中的点A向下移到BE上时,五个角的和(即∠CAD+∠B+∠C+∠D+∠E)有无变化说明你的结论的正确性.(3)把图(2)中的点C向上移到BD上时(1)如图(3)所示,五个角的和(即∠CAD+∠B+∠ACE+∠D+∠E)有无变化说明你的结论的正确性.38.Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2=°;(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为:;(3)若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.(4)若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间的关系为:.39.如图所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数.40.将纸片△ABC沿DE折叠使点A落在A′处的位置.(1)如果A′落在四边形BCDE的内部(如图1),∠A′与∠1+∠2之间存在怎样的数量关系?并说明理由.(2)如果A′落在四边形BCDE的BE边上,这时图1中的∠1变为0°角,则∠A′与∠2之间的关系是.(3)如果A′落在四边形BCDE的外部(如图2),这时∠A′与∠1、∠2之间又存在怎样的数量关系?并说明理由.初二三角形所有知识点总结和常考题提高难题压轴题练习(含答案解析)参考答案与试题解析一.选择题(共13小题)1.(2008•福州)已知三角形的两边长分别为4cm和9cm,则下列长度的四条线段中能作为第三边的是()A.13cm B.6cm C.5cm D.4cm【分析】此题首先根据三角形的三边关系,求得第三边的取值范围,再进一步找到符合条件的数值.【解答】解:根据三角形的三边关系,得:第三边应大于两边之差,且小于两边之和,即9﹣4=5,9+4=13.∴第三边取值范围应该为:5<第三边长度<13,故只有B选项符合条件.故选:B.【点评】本题考查了三角形三边关系,一定要注意构成三角形的条件:两边之和>第三边,两边之差<第三边.2.(2013•河北)一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=()A.90°B.100°C.130° D.180°【分析】设围成的小三角形为△ABC,分别用∠1、∠2、∠3表示出△ABC的三个内角,再利用三角形的内角和等于180°列式整理即可得解.【解答】解:如图,∠BAC=180°﹣90°﹣∠1=90°﹣∠1,∠ABC=180°﹣60°﹣∠3=120°﹣∠3,∠ACB=180°﹣60°﹣∠2=120°﹣∠2,在△ABC中,∠BAC+∠ABC+∠ACB=180°,∴90°﹣∠1+120°﹣∠3+120°﹣∠2=180°,∴∠1+∠2=150°﹣∠3,∵∠3=50°,∴∠1+∠2=150°﹣50°=100°.故选:B.【点评】本题考查了三角形的内角和定理,用∠1、∠2、∠3表示出△ABC的三个内角是解题的关键,也是本题的难点.3.(2010•西藏)已知如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于()A.315°B.270° C.180° D.135°【分析】利用三角形内角与外角的关系:三角形的任一外角等于和它不相邻的两个内角之和解答.【解答】解:∵∠1、∠2是△CDE的外角,∴∠1=∠4+∠C,∠2=∠3+∠C,即∠1+∠2=2∠C+(∠3+∠4),∵∠3+∠4=180°﹣∠C=90°,∴∠1+∠2=2×90°+90°=270°.故选:B.【点评】此题主要考查了三角形内角与外角的关系:三角形的任一外角等于和它不相邻的两个内角之和.4.(2015•长沙)如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是()A.B.C.D.【分析】根据三角形高线的定义:过三角形的顶点向对边引垂线,顶点和垂足之间的线段叫做三角形的高线解答.【解答】解:为△ABC中BC边上的高的是A选项.故选A.【点评】本题考查了三角形的角平分线、中线、高线,熟记高线的定义是解题的关键.5.(2014•达州)如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD 的平分线交于点P,则∠P=()A.90°﹣αB.90°+αC.D.360°﹣α【分析】先求出∠ABC+∠BCD的度数,然后根据角平分线的性质以及三角形的内角和定理求解∠P的度数.【解答】解:∵四边形ABCD中,∠ABC+∠BCD=360°﹣(∠A+∠D)=360°﹣α,∵PB和PC分别为∠ABC、∠BCD的平分线,∴∠PBC+∠PCB=(∠ABC+∠BCD)=(360°﹣α)=180°﹣α,则∠P=180°﹣(∠PBC+∠PCB)=180°﹣(180°﹣α)=α.故选:C.【点评】本题考查了多边形的内角和外角以及三角形的内角和定理,属于基础题.6.(2009•荆门)如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A 落在边CB上A′处,折痕为CD,则∠A′DB=()A.40°B.30°C.20°D.10°【分析】由三角形的一个外角等于与它不相邻的两个内角的和,得∠A′DB=∠CA'D ﹣∠B,又折叠前后图形的形状和大小不变,∠CA'D=∠A=50°,易求∠B=90°﹣∠A=40°,从而求出∠A′DB的度数.【解答】解:∵Rt△ABC中,∠ACB=90°,∠A=50°,∴∠B=90°﹣50°=40°,∵将其折叠,使点A落在边CB上A′处,折痕为CD,则∠CA'D=∠A,∵∠CA'D是△A'BD的外角,∴∠A′DB=∠CA'D﹣∠B=50°﹣40°=10°.故选:D.【点评】本题考查图形的折叠变化及三角形的外角性质.关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.解答此题的关键是要明白图形折叠后与折叠前所对应的角相等.7.(2004•陕西)如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE相交于一点P,若∠A=50°,则∠BPC=()A.150°B.130°C.120° D.100°【分析】根据垂直的定义和四边形的内角和是360°求得.【解答】解:∵BE⊥AC,CD⊥AB,∴∠ADC=∠AEB=90°,∴∠BPC=∠DPE=180°﹣50°=130°.故选B.【点评】主要考查了垂直的定义以及四边形内角和是360度.注意∠BPC与∠DPE 互为对顶角.8.(2009•黑河)如图,为估计池塘岸边A、B的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是()A.20米B.15米C.10米D.5米【分析】根据三角形的三边关系,第三边的长一定大于已知的两边的差,而小于两边的和,求得相应范围,看哪个数值不在范围即可.【解答】解:∵15﹣10<AB<10+15,∴5<AB<25.∴所以不可能是5米.故选:D.【点评】已知三角形的两边,则第三边的范围是:>已知的两边的差,而<两边的和.9.(2014•临沂)将一个n边形变成n+1边形,内角和将()A.减少180°B.增加90°C.增加180°D.增加360°【分析】利用多边形的内角和公式即可求出答案.【解答】解:n边形的内角和是(n﹣2)•180°,n+1边形的内角和是(n﹣1)•180°,因而(n+1)边形的内角和比n边形的内角和大(n﹣1)•180°﹣(n﹣2)•180=180°.故选:C.【点评】本题主要考查了多边形的内角和公式,是需要识记的内容.10.(2015•莱芜)一个多边形除一个内角外其余内角的和为1510°,则这个多边形对角线的条数是()A.27 B.35 C.44 D.54【分析】设出题中所给的两个未知数,利用内角和公式列出相应等式,根据边数为整数求解即可,再进一步代入多边形的对角线计算方法,即可解答.【解答】解:设这个内角度数为x°,边数为n,∴(n﹣2)×180﹣x=1510,180n=1870+x=1800+(70+x),∵n为正整数,∴n=11,∴=44,故选:C.【点评】此题考查多边形的内角和计算公式以及多边形的对角线条数的计算方法,属于需要识记的知识.11.(2011春•滨城区期末)一个多边形的边数每增加一条,这个多边形的()A.内角和增加360°B.外角和增加360°C.对角线增加一条 D.内角和增加180°【分析】利用多边形的内角和定理和外角和特征即可解决问题.【解答】解:因为n边形的内角和是(n﹣2)•180°,当边数增加一条就变成n+1,则内角和是(n﹣1)•180°,内角和增加:(n﹣1)•180°﹣(n﹣2)•180°=180°;根据多边形的外角和特征,边数变化外角和不变.故选:D.【点评】本题主要考查了多边形的内角和定理与外角和特征.先设这是一个n 边形是解题的关键.12.(2012•滨州)一个三角形三个内角的度数之比为2:3:7,这个三角形一定是()A.等腰三角形B.直角三角形C.锐角三角形D.钝角三角形【分析】已知三角形三个内角的度数之比,根据三角形内角和定理,可求得三角的度数,由此判断三角形的类型.【解答】解:三角形的三个角依次为180°×=30°,180°×=45°,180°×=105°,所以这个三角形是钝角三角形.故选:D.【点评】本题考查三角形的分类,这个三角形最大角为180°×>90°.本题也可以利用方程思想来解答,即2x+3x+7x=180,解得x=15,所以最大角为7×15°=105°.13.(2014•毕节市)如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为()A.13 B.14 C.15 D.16【分析】根据多边形内角和公式,可得新多边形的边数,根据新多边形比原多边形多1条边,可得答案.【解答】解:设新多边形是n边形,由多边形内角和公式得(n﹣2)180°=2340°,解得n=15,原多边形是15﹣1=14,故选:B.【点评】本题考查了多边形内角与外角,多边形的内角和公式是解题关键.二.填空题(共13小题)14.(2015•资阳)若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是8.【分析】任何多边形的外角和是360°,即这个多边形的内角和是3×360°.n边形的内角和是(n﹣2)•180°,如果已知多边形的边数,就可以得到一个关于边数的方程,解方程就可以求出多边形的边数.【解答】解:设多边形的边数为n,根据题意,得(n﹣2)•180=3×360,解得n=8.则这个多边形的边数是8.【点评】已知多边形的内角和求边数,可以转化为方程的问题来解决.15.(2006•镇江)如图,小亮从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,…,照这样走下去,他第一次回到出发地A点时,一共走了120米.【分析】由题意可知小亮所走的路线为一个正多边形,根据多边形的外角和即可求出答案.【解答】解:∵360÷30=12,∴他需要走12次才会回到原来的起点,即一共走了12×10=120米.故答案为:120.【点评】本题主要考查了多边形的外角和定理.任何一个多边形的外角和都是360°.16.(2014•随州)将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为75度.【分析】根据三角形三内角之和等于180°求解.【解答】解:如图.∵∠3=60°,∠4=45°,∴∠1=∠5=180°﹣∠3﹣∠4=75°.故答案为:75.【点评】考查三角形内角之和等于180°.17.(2013•上海)当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为30°.【分析】根据已知一个内角α是另一个内角β的两倍得出β的度数,进而求出最小内角即可.【解答】解:由题意得:α=2β,α=100°,则β=50°,180°﹣100°﹣50°=30°,故答案为:30°.【点评】此题主要考查了新定义以及三角形的内角和定理,根据已知得出β的度数是解题关键.18.(2013•遂宁)若一个多边形内角和等于1260°,则该多边形边数是9.【分析】根据多边形内角和定理及其公式,即可解答;【解答】解:∵一个多边形内角和等于1260°,∴(n﹣2)×180°=1260°,解得,n=9.故答案为9.【点评】本题考查了多边形的内角定理及其公式,关键是记住多边形内角和的计算公式.19.(2015•北京)如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5=360°.【分析】首先根据图示,可得∠1=180°﹣∠BAE,∠2=180°﹣∠ABC,∠3=180°﹣∠BCD,∠4=180°﹣∠CDE,∠5=180°﹣∠DEA,然后根据三角形的内角和定理,求出五边形ABCDE的内角和是多少,再用180°×5减去五边形ABCDE的内角和,求出∠1+∠2+∠3+∠4+∠5等于多少即可.【解答】解:∠1+∠2+∠3+∠4+∠5=(180°﹣∠BAE)+(180°﹣∠ABC)+(180°﹣∠BCD)+(180°﹣∠CDE)+(180°﹣∠DEA)=180°×5﹣(∠BAE+∠ABC+∠BCD+∠CDE+∠DEA)=900°﹣(5﹣2)×180°=900°﹣540°=360°.故答案为:360°.【点评】此题主要考查了多边形内角和定理,要熟练掌握,解答此题的关键是要明确:(1)n边形的内角和=(n﹣2)•180 (n≥3)且n为整数).(2)多边形的外角和指每个顶点处取一个外角,则n边形取n个外角,无论边数是几,其外角和永远为360°.20.(2014•自贡)一个多边形的内角和比外角和的3倍多180°,则它的边数是9.【分析】多边形的内角和比外角和的3倍多180°,而多边形的外角和是360°,则内角和是3×360°+180°.n边形的内角和可以表示成(n﹣2)•180°,设这个多边形的边数是n,得到方程,从而求出边数.【解答】解:根据题意,得(n﹣2)•180°=3×360°+180°,解得:n=9.则这个多边形的边数是9.故答案为:9.【点评】考查了多边形内角与外角,此题只要结合多边形的内角和公式寻求等量关系,构建方程即可求解.21.(2015•徐州)若正多边形的一个内角等于140°,则这个正多边形的边数是 9 .【分析】首先根据求出外角度数,再利用外角和定理求出边数.【解答】解:∵正多边形的一个内角是140°,∴它的外角是:180°﹣140°=40°,360°÷40°=9.故答案为:9.【点评】此题主要考查了多边形的外角与内角,做此类题目,首先求出正多边形的外角度数,再利用外角和定理求出求边数.22.(2013•黔东南州)在△ABC 中,三个内角∠A 、∠B 、∠C 满足∠B ﹣∠A=∠C ﹣∠B ,则∠B= 60 度.【分析】先整理得到∠A +∠C=2∠B ,再利用三角形的内角和等于180°列出方程求解即可.【解答】解:∵∠B ﹣∠A=∠C ﹣∠B ,∴∠A +∠C=2∠B ,又∵∠A +∠C +∠B=180°,∴3∠B=180°,∴∠B=60°.故答案为:60.【点评】本题考查了三角形的内角和定理,是基础题,求出∠A +∠C=2∠B 是解题的关键.23.(2013•达州)如图,在△ABC 中,∠A=m°,∠ABC 和∠ACD 的平分线交于点A 1,得∠A 1;∠A 1BC 和∠A 1CD 的平分线交于点A 2,得∠A 2;…∠A 2012BC 和∠A 2012CD的平分线交于点A 2013,则∠A 2013= 度.【分析】利用角平分线的性质、三角形外角性质,易证∠A 1=∠A ,进而可求∠A 1,由于∠A 1=∠A ,∠A 2=∠A 1=∠A ,…,以此类推可知∠A 2013=∠A=°. 【解答】解:∵A 1B 平分∠ABC ,A 1C 平分∠ACD ,∴∠A1BC=∠ABC,∠A1CA=∠ACD,∵∠A1CD=∠A1+∠A1BC,即∠ACD=∠A1+∠ABC,∴∠A1=(∠ACD﹣∠ABC),∵∠A+∠ABC=∠ACD,∴∠A=∠ACD﹣∠ABC,∴∠A1=∠A,∴∠A1=m°,∵∠A1=∠A,∠A2=∠A1=∠A,…以此类推∠A2013=∠A=°.故答案为:.【点评】本题考查了角平分线性质、三角形外角性质,解题的关键是推导出∠A1=∠A,并能找出规律.24.(2012春•金台区期末)如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=74度.【分析】利用三角形的内角和外角之间的关系计算.【解答】解:∵∠A=40°,∠B=72°,∴∠ACB=68°,∵CE平分∠ACB,CD⊥AB于D,∴∠BCE=34°,∠BCD=90﹣72=18°,∵DF⊥CE,∴∠CDF=90°﹣(34°﹣18°)=74°.故答案为:74.【点评】主要考查了三角形的内角和外角之间的关系.(1)三角形的外角等于与它不相邻的两个内角和;(2)三角形的内角和是180度,求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件;(3)三角形的一个外角>任何一个和它不相邻的内角.注意:垂直和直角总是联系在一起.25.(2006•临安市)用一条宽相等的足够长的纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE,其中∠BAC= 36度.【分析】利用多边形的内角和定理和等腰三角形的性质即可解决问题.【解答】解:∵∠ABC==108°,△ABC是等腰三角形,∴∠BAC=∠BCA=36度.【点评】本题主要考查了多边形的内角和定理和等腰三角形的性质.n边形的内角和为:180°(n﹣2).26.(2015•河北)平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,如图,则∠3+∠1﹣∠2=24°.【分析】首先根据多边形内角和定理,分别求出正三角形、正方形、正五边形、正六边形的每个内角的度数是多少,然后分别求出∠3、∠1、∠2的度数是多少,进而求出∠3+∠1﹣∠2的度数即可.【解答】解:正三角形的每个内角是:180°÷3=60°,正方形的每个内角是:360°÷4=90°,正五边形的每个内角是:(5﹣2)×180°÷5=3×180°÷5=540°÷5=108°,正六边形的每个内角是:(6﹣2)×180°÷6=4×180°÷6=720°÷6=120°,则∠3+∠1﹣∠2=(90°﹣60°)+(120°﹣108°)﹣(108°﹣90°)=30°+12°﹣18°=24°.故答案为:24°.【点评】此题主要考查了多边形内角和定理,要熟练掌握,解答此题的关键是要明确:(1)n边形的内角和=(n﹣2)•180 (n≥3)且n为整数).(2)多边形的外角和指每个顶点处取一个外角,则n边形取n个外角,无论边数是几,其外角和永远为360°.三.解答题(共14小题)27.(2013春•临清市期末)如图,直线DE交△ABC的边AB、AC于D、E,交BC延长线于F,若∠B=67°,∠ACB=74°,∠AED=48°,求∠BDF的度数.【分析】先根据三角形的内角和定理求出∠A的度数,再根据三角形外角的性质求出∠BDF的度数.【解答】解:因为∠A+∠B+∠ACB=180°,所以∠A=180°﹣67°﹣74°=39°,所以∠BDF=∠A+∠AED=39°+48°=87°.【点评】本题考查三角形外角的性质及三角形的内角和定理,解答的关键是外角和内角的关系.28.(2013•湖州校级模拟)如图,已知D为△ABC边BC延长线上一点,DF⊥AB 于F交AC于E,∠A=35°,∠D=42°,求∠ACD的度数.【分析】根据三角形外角与内角的关系及三角形内角和定理解答.【解答】解:∵∠AFE=90°,∴∠AEF=90°﹣∠A=90°﹣35°=55°,∴∠CED=∠AEF=55°,∴∠ACD=180°﹣∠CED﹣∠D=180°﹣55°﹣42°=83°.答:∠ACD的度数为83°.【点评】三角形外角与内角的关系:三角形的一个外角等于和它不相邻的两个内角的和.三角形内角和定理:三角形的三个内角和为180°.29.(2015秋•全椒县期中)已知△ABC中,∠ACB=90°,CD为AB边上的高,BE 平分∠ABC,分别交CD、AC于点F、E,求证:∠CFE=∠CEF.【分析】题目中有两对直角,可得两对角互余,由角平分线及对顶角可得两对角相等,然后利用等量代换可得答案.【解答】证明:∵∠ACB=90°,∴∠1+∠3=90°,∵CD⊥AB,∴∠2+∠4=90°,又∵BE平分∠ABC,∴∠1=∠2,∴∠3=∠4,∵∠4=∠5,∴∠3=∠5,即∠CFE=∠CEF.【点评】本题考查了三角形角平分线、中线和高的有关知识;正确利用角的等量代换是解答本题的关键.30.(2010春•横峰县校级期末)如图,AD为△ABC的中线,BE为△ABD的中线,(1)若∠ABE=25°,∠BAD=50°,则∠BED的度数是度.(2)在△ADC中过点C作AD边上的高CH.(3)若△ABC的面积为60,BD=5,求点E到BC边的距离.【分析】(1)根据三角形的一个外角等于与它不相邻的两个内角和,∠BED=∠ABE+∠BAE=75°;(2)三角形高的基本作法:用圆规以一边两端点为圆心,任意长为半径作两段弧,交于角的两边,再以交点为圆心,用交轨法作两段弧,找到两段弧的交点,连接两个交点,并过另一端点作所成直线的平行线,叫该边所在直线一点,连接该点和另一端点,则为高线;(3)我们通过证明不难得出三角形中线将三角形分成面积相等的两个三角形,那么可依据D是BC中点,E是AD中点,求出三角形BED的面积.三角形BDE 中,E到BD的距离就是BD边上的高,有了三角形BDE的面积,BD的长也容易求得.那么高就求出来了.【解答】解:(1)∠BED=∠ABE+∠BAE=75°;(2)CH为所求的高.(3)解:如图,过点E作EF⊥BD于点F,∵AD是BC的中线∴BD=CD=S△ACD==×60=30∴S△ABD=S△ABE==×30=15同理S△BED又∵S=BD•EF=×5EF=15△BED∴EF=6即点E到BC边的距离为6.【点评】本题主要考查了基本作图中,三角形高的作法,三角形的内角和外角等知识点.31.(2015春•单县期末)如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.(1)若∠B=35°,∠ACB=85°,求∠E的度数;(2)当P点在线段AD上运动时,猜想∠E与∠B、∠ACB的数量关系,写出结论无需证明.【分析】(1)中,首先根据三角形的内角和定理求得∠BAC的度数,再根据角平分线的定义求得∠DAC的度数,从而根据三角形的内角和定理即可求出∠ADC的度数,进一步求得∠E的度数;(2)中,根据第(1)小题的思路即可推导这些角之间的关系.【解答】解:(1)∵∠B=35°,∠ACB=85°,∴∠BAC=60°,∵AD平分∠BAC,∴∠DAC=30°,∴∠ADC=65°,∴∠E=25°;(2).设∠B=n°,∠ACB=m°,∵AD平分∠BAC,∴∠1=∠2=∠BAC,∵∠B+∠ACB+∠BAC=180°,∵∠B=n°,∠ACB=m°,∴∠CAB=(180﹣n﹣m)°,∴∠BAD=(180﹣n﹣m)°,∴∠3=∠B+∠1=n°+(180﹣n﹣m)°=90°+n°﹣m°,∵PE⊥AD,∴∠DPE=90°,∴∠E=90°﹣(90°+n°﹣m°)=(m﹣n)°=(∠ACB﹣∠B).【点评】运用了三角形的内角和定理以及角平分线的定义.特别注意第(2)小题,由于∠B和∠ACB的大小不确定,故表达式应写为两种情况.32.(2010春•朝阳区期末)如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,垂足分别为D,E,∠AFD=158°,求∠EDF的度数.【分析】要求∠EDF的度数,只需求出∠BDE和∠FDC的度数即可,由FD⊥BC,得∠FDC=90°;而∠BDE在Rt△BDE中,故只需求出∠B的度数.因∠B=∠C,只需求出∠C的度数即可.因∠AFD是△CDF的外角,∠AFD=158°∴∠C=∠AFD﹣∠FDC=158°﹣90°=68°.【解答】解:∵FD⊥BC,所以∠FDC=90°,∵∠AFD=∠C+∠FDC,∴∠C=∠AFD﹣∠FDC=158°﹣90°=68°,∴∠B=∠C=68°.∵DE⊥AB,∵∠DEB=90°,∴∠BDE=90°﹣∠B=22°.又∵∠BDE+∠EDF+∠FDC=180°,∴∠EDF=180°﹣∠BDE﹣∠FDC=180°﹣22°﹣90°=68°.【点评】考查三角形内角和定理,外角性质,垂直定义等知识.33.(2014春•岱岳区期末)如图,AD平分∠BAC,∠EAD=∠EDA.(1)∠EAC与∠B相等吗?为什么?(2)若∠B=50°,∠CAD:∠E=1:3,求∠E的度数.【分析】(1)由于AD平分∠BAC,根据角平分线的概念可得∠BAD=∠CAD,再根据三角形的一个外角等于和它不相邻的两个内角和,结合已知条件可得∠EAC 与∠B相等;(2)若设∠CAD=x°,则∠E=3x°.根据(1)中的结论以及三角形的内角和定理及其推论列方程进行求解即可.【解答】解:(1)相等.理由如下:∵AD平分∠BAC,∴∠BAD=∠CAD.又∠EAD=∠EDA,∴∠EAC=∠EAD﹣∠CAD=∠EDA﹣∠BAD=∠B;。
三角形(五大压轴题专练)(解析版)-2023-2024学年八年级数学上册单元速记巧练(人教版)

三角形(五大压轴题专练)【题型一三角形中高线的综合问题】(1)如图1,连接AB 、AC ,求ABC 的面积;(2)如图2,延长BA 交直线m 交于点D ,在CD 上存在点P 坐标;(3)请在备用图中画图探究:若点P 是直线m 上的一个动点,连接1CMP BCM S S -=△时,直接写出点M的坐标.【答案】(1)3(2)点P 的坐标(3,2)或(9,2),(3)点M 的坐标为2(,0)3或2(,0)3-【分析】(1)根据点A 、B 、C 的坐标得2,OA OC OB ===(2)设(,2),(,2)D m P n ,根据BCD △的面积:113322m ⨯=⨯113(6)3(6)2222n n ⨯-⨯-⨯-⨯=,或11(6)3(6)22n n ⨯-⨯-⨯-(3)设(,2),(,2)D m P n ,根据+PCB BCM PCM S S S =△△△得132⨯1CMP BCM S S -=△得111231223t t ⨯⨯-⨯⨯=,计算得2t =,则BCD △的面积:11322m ⨯=⨯6m =,∵12ABP ABC S S =△△,∴11(6)3(6)22n n ⨯-⨯-⨯-⨯解得,3n =或9n =,∴点P 的坐标(3,2)或(9,2);(3)解:如图3中,设(D m +PCB BCM PCM S S S =△△△,111332222t a t ⨯⨯=⨯⨯=⨯⨯,13a t =,∵1CMP BCM S S -=△,(1)在题干的基础上,①如图2,点P 为BC 上一点,作PM AB ⊥,PN AC ⊥,设②如图3,当点P 在CB 延长线上时,猜想1d 、2d 之间又有什么样的数量关系,请证明你的猜想;(2)如图4,在ABC 中,10AB AC ==,12BC =,ABC S △点B 作BE BC ⊥,点P 是直线BE 上一动点,点Q 是直线值.【答案】(1)①见解析;②猜想:213412d d -=,证明见解析222∴124312d d +=②猜想:213412d d -=理由如下:,作PM AB ⊥,PN (2)作点D 关于直线BE 的对称点∴PD PD '=,PD PQ PD PQ'+=+∵点D 在BC 延长线上,则D ¢、B 、【点睛】本题考查了三角形高的定义,垂线段最短,熟练掌握等面积法求线段的长是解题的关键.3.在平面直角坐标系中,有点(),0A a ,(0,B 单位得到线段CD .(1)直接写出=a ______,b =______;(2)如图1,点E 为线段CD 上任意一点,点F 为线段AB 上任意一点,,求则OP CD AB ∥∥,∴180DEO EOP ∠+∠=︒,∴DEO EOP AFO ∠+∠+∠即33135360x y ++︒=︒,∴75x y +=︒,过G 作GH CD ∥,则GH ∴EGH DEG x ∠=∠=,∵6k =,∴()0,3C ,()6,6D ,设(),3K n ,∵BCK ABC ACK S S S =+△△△,∴1116663222n n ⨯⨯=⨯⨯+⨯⨯,【题型二三角形中中线的综合问题】【深入探究】(1)如图2,点D 在ABC 的边BC 上,点P 在AD 上.①若AD 是ABC 的中线,求证:APB APC S S =△△;②若3BD DC =,则:APB APC S S =△△______.【拓展延伸】∵点A、B、C、D分别为∴AG,BC,CE,∴12 GAH GADS S S==∴12 ADC ADGS S S==(1)如图2,延长ABC 的边BC 到点D ,使CD BC =,连接DA .若ACD 的面积为1S ,则1S =代数式表示);(2)如图3,延长ABC 的边BC 到点D ,延长边CA 到点E ,使CD BC =,AE CA =,连接DE .若面积为2S ,则2S =(用含a 的代数式表示);(3)在图3的基础上延长AB 到点F ,使BF AB =,连接FD ,FE ,得到DEF (如图4).若阴影部分的面积为3S ,则3S =(用含a 的代数式表示);拓展应用:(4)如图5,点D 是ABC 的边BC 上任意一点,点E ,F 分别是线段AD ,CE 的中点,且ABC 的面积为延长ABC 的边BC ∴12ACD AED ECD S S S ∆∆∆==22ECD ABC S S a ∆∆∴==,即22S a =;(3)由(2)得ECD S ∆同理:2EFA ABC S S ∆∆=3ECD EFA S S S ∆∆∴=++(4)2BEF S a =△,理由如下:理由:∵点E 是线段∴ABE BDE S S = ,S △∴12BCE ABC S S = .=,连接FD,FE,得到(3)在图3的基础上延长AB到点F,使BF AB积为3S,则3S=___________;(用含a的代数式表示)拓展与应用:(4)如图5,已知四边形ABCD的面积是a,E、F、G、H分别是AB、BC【答案】(1)a;(2)2a;(3)6a;(4)12 a.延长ABC∆的边BC∴12ACD AED ECD S S S∆∆∆==22ECD ABCS S a∆∆∴==,(4)解:如图5所示,连接则1,2AEO ABO S S S ∆∆=∴AEO AHO S S S ∆∆∆++【点睛】此题考查了阅读与理解:三角形中线的性质即等底同高的三角形面积相等,灵活运用这个结论并适当添加辅助线是解答此题的关键.【题型三三角形中角平分线的综合问题】1.已知,AB DE ∥,点C 是直线AB ,DE 下方一点,连接BC ,DC .【点睛】本题考查平方数、二次根式的非负性,利用面积法求点的坐标,角平分线的定义,三角形内角和定理等,难度一般,解第二问的关键是熟练运用数形结合思想,解第三问的关键是利用角度等量代换.【题型四三角形内角和与外角和的综合问题】1.在ABC 中,点E 是CA 延长线上一点.(1)如图1,过点B 作BD BC ⊥,交CE 于点F ,D C ∠=∠.①若36C ∠=︒,则DAF ∠=______°;②试写出DAF ∠与C ∠的数量关系,并说明理由;③当DAF D ∠=∠时,求C ∠的度数;④若D ABD ∠=∠,请说明BA CF ⊥;(2)如图2,BD 交CE 于点F ,D C ∠=∠,直接写出DAC ∠、C ∠与DBC ∠之间的数量关系.【答案】(1)①18;②290DAF C ∠+∠=︒,理由见解析;③30C ∠=︒;④见解析(2)2DAC C DBC∠=∠+∠【分析】(1)①根据180BFC C DBC ∠=︒-∠-∠,DAF BFC D ∠=∠-∠,即可求得答案.②根据180BFC C DBC ∠=︒-∠-∠,DAF BFC D ∠=∠-∠,结合等量代换,即可求得答案.③根据②的结论,采用等量代换即可求得答案.④根据2+18090DAF C DAF D ABD FAB ∠+∠=∠+∠∠=︒-∠=︒,即可求得FAB ∠的度数,问题即可得证.(2)延长BA 至K ,根据DAC DAK CAK ∠=∠+∠,结合三角形的外角的性质可求得答案.【详解】(1)①∵0910********BFC C DBC ∠︒=︒-∠-∠=︒-︒=︒-,∴543618DAF BFC D ∠︒=︒-∠-==∠︒.故答案为:18.②290DAF C ∠+∠=︒.理由如下:∵DAK D DBA∠∠=∠+∠,CAK∴DAC DAK CAK D∠=∠+∠=∠+【点睛】本题主要考查三角形内角和定理、三角形的外角的性质(三角形的一个外角等于与它不相邻的两个内角的和),牢记三角形的外角的性质是解题的关键.中,点2.(1)如图①所示,ABC,不用说明理由,直接填空.(2)如图③所示,13OBC DBC ∠=∠,13OCB ECB ∠=∠,若A α∠=,则BOC ∠填空并说明理由.【答案】(1)902α︒+,1203α︒+.;(2)1203α︒-1(1)如图1,若AD BC ∥,求证:AC BD ∥;(2)如图2,若BD BC ⊥,垂足为B ,BD 交CE 于点G ,请探究DAE ∠论,并说明理由;(3)如图3,在(2)的条件下,过点D 作DF BC ∥交射线CE 于点F ,当(1)如图1,如果点F 在线段AE 上,且50C ∠=︒,30B ∠=︒,则EFD ∠=______.(2)如果点F 在ABC 的外部,分別作出CAE ∠和EDF ∠的角平分线,交于点K ,请在图2中补全图形,探究AKD ∠、C ∠、B ∠三者之间的数量关系,并说明理由:(3)如图3,若点F 与点A 重合,PE 、PC 分别平分AEC ∠和ABC 的外角ACM ∠,连接PA PG BC ⊥交BC 延长线于点G ,PH AB ⊥交BA 的延长线于点H ,若EAD CAD ∠=∠,且44(3)解:设EAD CAD ∠=∠=∵AE 平分BAC ∠,∴BAE CAE EAD ∠=∠=+∠∠∴6BAD α∠=,∵AD BC⊥【题型五多边形的内角和与外角和综合问题】1.【感知】如图1所示,在四边形AEFC 中,EB FD 、分别是边AE CF 、的延长线,我们把BEF DFE ∠∠、称为四边形AEFC 的外角,若220A C ∠+∠=︒,则BEF DFE ∠+∠=___________;【探究】如图2所示,在四边形AECF 中,EB FD 、分别是边AE AF 、的延长线,我们把BEC DFC ∠∠、称为四边形AECF 的外角,试探究A C ∠∠、与BEC DFC ∠∠、之间的数量关系,并说明理由;【应用】如图3所示,FM EM 、分别是四边形AEFC 的外角DFE BEF ∠∠、的平分线,若200A C ∠+∠=︒,则M ∠的度数为___________.【答案】(感知)220︒;(探究)A C BEC DFC∠+∠=∠+∠,理由见解析;(应用)【分析】(感知)根据四边形的内角和和邻补角的定义即可求出答案.(探究)根据四边形的内角和和邻补角的定义即可求出答案.(应用)根据四边形的内角和和邻补角定义可求出BEF DFE∠+∠的度数,结合角平分线的定义即可求出∠的度数.MFE MEF∠+∠度数,最后利用三角形内角和即可求出M①如图1,若B C ∠=∠,则C ∠=________︒;②如图2,若ABC ∠的平分线BE 交DC 于点E 、且BE AD ∥,则C ∠=③如图3,若ABC ∠和BCD ∠的平分线相交于点E ,则BEC ∠=________(2)如图3,当A D αβ∠=∠=,时,若ABC ∠和BCD ∠的平分线交于点数量关系.∵,BE CE 平分,ABC ∠∴111,222ABC ∠=∠∠=∴112(2ABC ∠+∠=∠∴在BCE 中,BEC ∠故答案为:110︒.(2)解:在四边形ABCD ∴360ABC BCD ∠+∠=∵ABC ∠和BCD ∠的平分线交于点∴111,222ABC ∠=∠∠=、两外角平分线所成的(1)如图2,在四边形ABCD 中,BP 、CP 分别平分ABC ∠和BCD ∠,则(2)如图3,在四边形ABCD 中,BM 、CM 分别平分EBC ∠和BCF ∠,请探究并说明理由.(3)在四边形ABCD 中,F ∠为ABC ∠的平分线与边CD 和BC 延长线所成角的平分线所在的直线构成的锐角,若设A α∠=,D β∠=,则F ∠=.(用α、β表示)【答案】(1)()1P A D ∠=∠+∠BF 平分ABC ∠,CF 平分12CBF ABC ∴∠=∠,DCF ∠180DCG BCD ∠=︒-∠ ,。
专题 全等三角形压轴题(30题)(解析版)

八年级上册数学《第十二章全等三角形》专题全等三角形压轴题训练(30题)1.(2022秋•忠县期末)在△ABC中,点D、E分别在AB、AC边上,设BE与CD相交于点F.(1)如图①,设∠A=60°,BE、CD分别平分∠ABC、∠ACB,证明:DF=EF.(2)如图②,设BE⊥AC,CD⊥AB,点G在CD的延长线上,连接AG、AF;若∠G=∠6,BD=CD,证明:GD=DF.【分析】(1)在BC上截取BM=BD,连接FM,证明△BFD≌△BFM,△ECF≌△MCF,进而可以解决问题;(2)根据已知条件证明△BDF≌△CDA,进而可以解决问题.【解答】证明:(1)如图,在BC上截取BM=BD,连接FM,∵∠A=60,∴∠BFC=90°+60°÷2=120°,∴∠BFD=60°,∵BE平分∠ABC,∴∠1=∠2,在△BFD和△BFM中,BD=BM∠1=∠2,BF=BF∴△BFD≌△BFM(SAS),∴∠BFM=∠BFD=60°,DF=MF,∴∠CFM=120°﹣60°=60°,∵∠CFE=∠BFD=60°,∴∠CFM=∠CFE,∵CD平分∠ACB,∴∠3=∠4,又CF=CF,在△ECF和△MCF中,∠CFE=∠CFMFC=FC,∠3=∠4∴△ECF≌△MCF(ASA),∴EF=MF,∴DF=EF;(2)∵BE⊥AC,CD⊥AB,∴∠BDF=∠CDA=90°,∴∠1+∠BFD=90°,∠3+∠CFE=90°,∠BFD=∠CFE,∴∠1=∠3,∵BD=CD,在△BDF和△CDA中,∠BDF=∠CDABD=CD,∠1=∠3∴△BDF≌△CDA(ASA),∴DF=DA,∵∠ADF=90°,∴∠6=45°,∵∠G=∠6,∴∠5=45°∴∠G=∠5,∴GD=DA,∴GD=DF.【点评】本题属于三角形的综合题,考查了全等三角形的判定与性质,角平分线的性质,解决本题的关键是掌握全等三角形的判定与性质.2.如图,△ABC中,AB=AC,D为AC边上一点,E为AB延长线上一点,且CD=BE,DE与BC相交于点F.(1)求证:DF=EF.=5,求EG的长.(2)过点F作FG⊥DE,交线段CE于点G,若CE⊥AC,CD=4,S△EFG【分析】(1)过点D作DH∥AB交BC于点H,根据等腰三角形的性质及平行线的性质得到∠BEF=∠HDF,∠DHC=∠DCH,则DH=CD,结合∠BFE=∠HFD,即可利用AAS判定△BEF≌△HDF,根据全等三角形的性质即可得解;(2)根据三角形的面积公式求解即可.【解答】(1)过点D作DH∥AB交BC于点H,∵AB=AC,∴∠ABC=∠ACB,∵DH∥AB,∴∠DHC=∠ABC,∴∠DHC=∠ACB=∠DCH,∴DH=CD,∵CD=BE,∴DH=BE,∵DH∥AB,∴∠BEF=∠HDF,在△BEF和△HDF中,∠BFE=∠HFD∠BEF=∠HDFBE=DH,∴△BEF≌△HDF(AAS),∴DF=EF;(2)连接DG,∵DF=EF,FG⊥DE,∴S△DFG =S△EFG=5,∴S△DEG=10,∵CE⊥AC,CD=4,∴S△DEG =12EG•CD=12EG×4,∴12EG×4=10,∴EG=5.【点评】此题考查了全等三角形的判定与性质,利用AAS判定△BEF≌△HDF是解题的关键.3.如图1,在等腰直角三角形ABC中,AB=AC,∠BAC=90°,点P为BC边上的一个动点,连接AP,以AP为直角边,A为直角顶点,在AP右侧作等腰直角三角形PAD,连接CD.(1)当点P在线段BC上时(不与点B重合),求证:△BAP≌△CAD;(2)当点P在线段BC的延长线上时(如图2),试猜想线段BP和CD的数量关系与位置关系分别是什么?请给予证明.【分析】(1)证得∠BAP=∠CAD,根据SAS可证明△BAP≌△CAD;(2)可得∠BAP=∠CAD,由SAS可证明△BAP≌△CAD,可得BP=CD,∠B=∠ACD,则结论得证.【解答】(1)证明:∵∠BAC=∠PAD=90°,∴∠BAC﹣∠PAC=∠PAD﹣∠PAC,即:∠BAP=∠CAD,在△BAP和△CAD中AB=AC∠BAP=∠CAD,PA=DA∴△BAP≌△CAD(SAS);(2)猜想:BP=CD,BP⊥CD.证明:∵∠BAC=∠PAD=90°,∴∠BAC+∠PAC=∠PAD+∠PAC,即:∠BAP=∠CAD,在△BAP和△CAD中AB=AC∠BAP=∠CAD,PA=DA∴△BAP≌△CAD(SAS),∴BP=CD(全等三角形的对应边相等),∠B=∠ACD(全等三角形的对应角相等),∵∠B+∠ACB=90°,∴∠ACD+∠ACB=90°,即:BP⊥CD.【点评】本题考查了全等三角形的判定与性质,等腰直角三角形的性质,根据同角的余角相等求出两边的夹角相等是证明三角形全等的关键.4.在△ABC中,∠ABC=90°.点G在直线BC上,点E在直线AB上,且AG与CE相交于点F,过点A 作边AB的垂线AD,且CD∥AG,EB=AD,AE=BC.(1)如图①,当点E在△ABC的边AB上时,求∠DCE的度数;(2)如图②,当点E在线段BA的延长线上时,求证:AB=BG.【分析】(1)如图①,连接ED,根据已知条件得到△ADE≌△BEC(SAS),根据全等三角形的性质得到∠AED=∠BCE,ED=CE,于是得到结论;(2)如图②,连接DE,根据已知条件得到△ADE≌△BEC(SAS),根据全等三角形的性质得到∠AED =∠BCE,ED=CE,根据等腰三角形的性质得到∠EDC=∠ECD,推出AF平分∠DAE,于是得到结论.【解答】解:(1)如图①连接ED,∵AD⊥AB,∴∠DAE=90°,∵∠ABC=90°,∵AD=EB,AE=BC,∴△ADE≌△BEC(SAS),∴∠AED=∠BCE,ED=CE,∴∠AED+∠BEC=∠BCE+∠BEC;∴∠AED+∠CEB=90°,∴∠DEC=90°,∴∠DCE=45°;(2)如图②,连接DE,∵AD⊥AB,∴∠DAE=90°,∵∠ABC=90°,∴∠DAE=∠ABC,∵AD=EB,AE=BC,∴△ADE≌△BEC(SAS),∴∠ADE=∠BEC,ED=CE,∵ED=CE,∴∠EDC=∠ECD,即∠ADE+∠ADC=∠ECD,∴∠BEC+∠DAF=∠AFC,∵∠BEC+∠EAF=∠AFC,∴∠DAF=∠EAF,∴AF平分∠DAE,∵∠DAE=90°,∴∠EAF=45°,∵∠EAF=∠BAG,∴∠BAG=45°,∵∠ABC=90°,∴∠ABG=90°,∴∠BGA=∠BAG,∴AB=BG.【点评】本题考查了平行线的性质,全等三角形的判定和性质,角平分线的定义,等腰直角三角形的判定和性质,正确的识别图形是解题的关键.5.在Rt△ABC中,∠ABC=90°,点D是CB延长线上一点,点E是线段AB上一点,连接DE.AC=DE,BC=BE.(1)求证:AB=BD;(2)BF平分∠ABC交AC于点F,点G是线段FB延长线上一点,连接DG,点H是线段DG上一点,连接AH交BD于点K,连接KG.当KB平分∠AKG时,求证:AK=DG+KG.【分析】(1)证明Rt△ACB≌Rt△DEB即可解决问题;(2)作BM平分∠ABD交AK于点M,证明△BMK≌△BGK,△ABM≌△DBG,即可解决问题.【解答】证明:(1)在Rt△ACB和Rt△DEB中,AC=DEBC=BE,∴Rt△ACB≌Rt△DEB(HL),∴AB=BD,(2)如图:作BM平分∠ABD交AK于点M,∵BM平分∠ABD,KB平分∠AKG,∴∠ABM=∠MBD=45°,∠AKB=∠BKG,∵∠ABF=∠DBG=45°∴∠MBD=∠GBD,在△BMK和△BGK中,∠MBD=∠GBDBK=BK,∠AKB=∠BKG∴△BMK≌△BGK(ASA),∴BM=BG,MK=KG,在△ABM和△DBG中,AB=BD∠ABM=∠DBG,BM=BG∴△ABM≌△DBG(SAS),∴AM=DG,∵AK=AM+MK,∴AK=DG+KG.【点评】本题考查了全等三角形的判定与性质,解决本题的关键是得到△BMK≌△BGK.6.(2023春•市南区期末)如图,在△ABC中,AB=AC,AD⊥BC于点D,E为AC边上一点,连接BE与AD交于点F,G为△ABC外一点,满足∠ACG=∠ABE,∠FAG=∠BAC,连接EG.(1)求证:△ABF≌△ACG;(2)求证:BE=CG+EG.【分析】(1)根据已知条件可得∠BAD=∠CAG,然后利用ASA即可证明△ABF≌△ACG;(2)结合(1)的结论,再证明△AEF≌△AEG,即可解决问题.【解答】(1)证明:∵∠BAC=∠FAG,∴∠BAC﹣∠CAD=∠FAG﹣∠CAD,∴∠BAD=∠CAG,在△ABF和△ACG中,∠BAD=∠CAGAB=AC,∠ABF=∠ACG∴△ABF≌△ACG(ASA);(2)证明:∵△ABF≌△ACG,∴AF=AG,BF=CG,∵AB=AC,AD⊥BC,∴∠BAD=∠CAD,∵∠BAD=∠CAG,∴∠CAD=∠CAG,在△AEF和△AEG中,AF=AG∠FAE=∠GAE,AE=AE∴△AEF≌△AEG(SAS).∴EF=EG,∴BE=BF+FE=CG+EG.【点评】本题考查了全等三角形的判定与性质,解决本题的关键是得到△AEF≌△AEG.7.(2022秋•新市区校级期中)已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.求证:(1)AD=AE=EC.(2)BA+BC=2BF.【分析】(1)由△BCD和△BEA为等腰三角形,∠ABD=∠EBC,得出∠BCD=∠BEA,由△ABD≌△EBC可得∠BCE=∠BDA,由∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA得出∠BCD+∠DCE=∠DAE+∠BEA,进而得出∠DCE=∠DAE,即可证明AE=EC;(2)过点E作EG⊥BC交BC的延长线于点G,由“HL”得出Rt△BFE≌Rt△BGE和Rt△BFE≌Rt△BGE,从而得出BF=BG,FA=CG,再通过等量代换即可得出结论.【解答】(1)证明:∵BD为△ABC的角平分线,∴∠ABD=∠EBC,在△ABD与△EBC中,AB=EB∠ABD=∠EBD,BD=BC∴△ABD≌△EBC(SAS),∴∠BCE=∠BDA,∵∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,∴∠BCD+∠DCE=∠DAE+∠BEA,∵BD=BC,BE=BA,∴△BCD和△BEA为等腰三角形,∵∠ABD=∠EBC,∴∠BCD=∠BEA,∴∠DCE=∠DAE,∴AE=EC,∵△ABD≌△EBC,∴AD=EC,∴AD=EC=AE;(2)证明:如图,过点E作EG⊥BC交BC的延长线于点G,∵BE平分∠ABC,EF⊥AB,EG⊥BG,∴EF=EG,在Rt△BFE与Rt△BGE中,EF=EGBE=BE,∴Rt△BFE≌Rt△BGE(HL),∴BF=BG,在Rt△AFE与Rt△CGE中,EF=EGEA=EC,∴Rt△AFE≌Rt△CGE(HL),∴FA=CG,∴BA+BC=BF+FA+BG﹣CG=BF+BG=2BF.【点评】本题考查了全等三角形的判定与性质,掌握三角形全等的判定方法是解决问题的关键.8.(2023春•余江区期末)如图,大小不同的两块三角板△ABC和△DEC直角顶点重合在点C处,AC=BC,DC=EC,连接AE、BD,点A恰好在线段BD上.(1)找出图中的全等三角形,并说明理由;(2)当AD=AB=4cm,则AE的长度为 cm.(3)猜想AE与BD的位置关系,并说明理由.【分析】(1)根据SAS证明△CBD≌△CAE即可;(2)根据全等三角形的性质解答即可;(3)根据全等三角形的性质和垂直的定义解答即可.【解答】解:(1)△CBD≌△CAE,理由如下:∵∠ACB=∠DCE=90°,∴∠ACB+∠ACD=∠DCE+∠ACD,即∠BCD=∠ACE,在△CBD与△CAE中,BC=AC∠BCD=∠ACE,DC=EC∴△CBD≌△CAE(SAS);(2)∵△CBD≌△CAE,∴BD=AE=AD+AB=4+4=8(cm),故答案为:8;(3)AE⊥BD,理由如下:AE与CD相交于点O,在△AOD与△COE中,∵△CBD≌△CAE,∴∠ADO=∠CEO,∵∠AOD=∠COE,∴∠OAD=∠OCE=90°,∴AE⊥BD.【点评】此题考查全等三角形的判定和性质,关键是根据SAS得出△CBD与△CAE全等解答.9.已知,△ABC中,∠ACB=90°,AC=BC,点E是BC上一点,连接AE(1)如图1,当AE平分∠BAC时,EH⊥AB于H,△EHB的周长为10m,求AB的长;(2)如图2,延长BC至D,使DC=BC,将线段AE绕点A顺时针旋转90°得线段AF,连接DF,过点B作BG⊥BC,交FC的延长线于点G,求证:BG=BE.【分析】(1)根据等腰三角形的性质得到∠B=45°,根据角平分线的性质得到CE=EH=BH,根据全等三角形的性质得到AH=AC,于是得到结论;(2)先连接AD,依据AAS判定△ADF≌△ABE,得到DF=BE,再判定△BCG≌△DCF,得出DF=BG,进而得到BG=BE.【解答】解:(1)∵∠ACB=90°,AC=BC,∴∠B=45°,∵AE平分∠BAC时,EH⊥AB于H,∴CE=EH=BH,在Rt△ACE与Rt△AHE中,CE=EH AE=AE,∴Rt△ACE与Rt△AHE(HL),∴AH=AC,∴AH=BC,∵△EHB的周长为10m,∴AB=AH+BH=BC+BH=10m;(2)如图所示,连接AD,线段AE绕点A顺时针旋转90°得线段AF,则AE=AF,∠EAF=90°,∵AC⊥BD,DC=BC,∴AD=AB,∠ABE=∠ADC=45°,∴∠BAD=90°=∠EAF,∴∠BAE=∠DAF,∴△ABE≌△ADF(SAS),∴DF=BE,∠ADF=∠ABE=45°,∴∠FDC=90°,∵BG⊥BC,∴∠CBG=∠CDF=90°,又∵BC=DC,∠BCG=∠DCF,∴△BCG≌△DCF(ASA),∴DF=BG,∴BG=BE.【点评】本题主要考查了旋转的性质,等腰直角三角形的性质以及全等三角形的判定与性质的综合运用,解决问题的关键是作辅助线构造全等三角形,依据全等三角形的对应边相等得出结论.10.在△ABC中,∠ABC=45°,AM⊥MB,垂足为M,点C是BM延长线上一点,连接AC.(1)如图①,点D在线段AM上,且DM=CM.求证:△BDM≌△ACM;(2)如图②,在(1)的条件下,点E是△ABC外一点,且满足EC=AC,连接ED并延长交BC于点F,且F为线段BC的中点,求证:∠BDF=∠CEF.【分析】(1)利用SAS即可证明△BMD≌△AMC.(2)延长EF到点G,使得FG=EF,证△BMD≌△AMC得AC=BD,再证△BFG≌△CFE可得BG=CE,∠G=∠E,从而得BD=BG=CE,即可得∠BDG=∠G=∠CEF.【解答】(1)证明:∵∠ABM=45°,AM⊥BM,在△BMD和△AMC中,DM=CM∠BMD=∠AMC BM=AM,∴△BMD≌△AMC(SAS);(2)证明:延长EF到点G,使得FG=EF,连接BG.如图所示:∵△BMD≌△AMC∴BD=AC,又∵CE=AC,∴BD=CE,在△BFG和△CFE中,BF=FC∠BFG=∠EFC FG=FE,∴△BFG≌△CFE(SAS),∴BG=CE,∠G=∠CEF,∴BD=CE=BG,∴∠BDF=∠G=∠CEF.∴∠BDF=∠CEF.【点评】本题主要考查全等三角形的判定与性质,等腰直角三角形的性质等知识点,熟练掌握全等三角形的判定与性质是解题的关键.11.如图1,在△ABC中,∠A=120°,∠C=20°,BD平分∠ABC,交AC于点D.(1)求证:BD=CD.(2)如图2,若∠BAC的角平分线AE交BC于点E,求证:AB+BE=AC.(3)如图3,若∠BAC的外角平分线AE交CB的延长线于点E,则(2)中的结论是否成立?若成立,给出证明,若不成立,写出正确的结论.【分析】(1)根据∠A=120°,∠C=20°,可得∠ABC的度数,再根据BD平分∠ABC,可得∠DBC=∠C=20°,进而可得结论;(2)如图2,过点E作EF∥BD交AC于点F,证明△ABE≌△AFE,可得BE=EF=FC,进而可得AB+BE =AC;(3)如图3,过点A作AF∥BD交BE于点F,结合(1)和AE是∠BAC的外角平分线,可得FE=AF=AC,进而可得结论BE﹣AB=AC.【解答】(1)证明:∵∠A=120°,∠C=20°,∴∠ABC=180°﹣120°﹣20°=40°,∵BD平分∠ABC,∴∠ABD=∠DBC=12∠ABC=20°,∴∠DBC=∠C=20°,∴BD=CD;(2)证明:如图2,过点E作EF∥BD交AC于点F,∴∠FEC=∠DBC=20°,∴∠FEC=∠C=20°,∴∠AFE=40°,FE=FC,∴∠AFE=∠ABC,∵AE是∠BAC的平分线,∴∠BAE=∠FAE,在△ABE和△AFE中,∠BAE=∠FAE∠ABE=∠AFE,AE=AE∴△ABE≌△AFE(AAS),∴BE=EF,∴BE=EF=FC,∴AB+BE=AF+FC=AC;(3)(2)中的结论不成立,正确的结论是BE﹣AB=AC.理由如下:如图3,过点A作AF∥BD交BE于点F,∴∠AFC=∠DBC=20°,∴∠AFC=∠C=20°,∴AF=AC,∵AE是∠BAC的外角平分线,∴∠EAB=12(180°﹣∠ABC)=30°,∵∠ABC=40°,∴∠E=∠ABC﹣∠EAB=10°,∴∠E=∠FAE=10°,∴FE=AF,∴FE=AF=AC,∴BE﹣AB=BE﹣BF=EF=AC.【点评】本题考查了全等三角形的判定与性质,解决本题的关键是掌握全等三角形的判定与性质.12.(2022秋•渝北区校级期末)已在等腰Rt△ABC中,∠ABC=90°,AB=CB,D为直线AB上一点,连接CD,过点C作CE⊥CD,且CE=CD,连接DE,交AC于点F.(1)如图1,当点D在线段AB上,且∠DCB=30°时,请探究DF,EF,CF之间的数量关系,并说明理由;(2)如图2,在(1)的条件下,在FC上任取一点G,连接DG,作射线GP使∠DGP=60°,交∠DFG 的平分线于点Q,求证:FD+FG=FQ.【分析】(1)在EF上找到G点使得FG=CF,易证△CFG是等边三角形,可得CG=CF=GF,即可求得∠ECG=∠ACD,即可证明△ECG≌△CDF,可得DF=EG,即可解题;(2)在FP上找到H点,使得FH=FG,易证△FGH是等边三角形,可得∠GHF=∠FGH=60°,GH =FG=FH,即可求得∠FGD=∠QGH,即可证明△DFG≌△QHG,可得DF=QH,即可解题.【解答】(1)解:EF=DF+CF;在EF上找到G点使得FG=CF,如图2,∵∠BCD=30°,∠ACB=45°,∴∠ACD=15°,∴∠CFG=∠CDE+∠ACD=60°,∵FG=CF,∴△CFG是等边三角形,∴CG=CF=GF,∠FCG=60°,∴∠GCE=90°﹣15°﹣60°=15°,在△ECG和△CDF中,CG=CF∠ECG=∠ACD,CE=CD∴△ECG≌△CDF,(SAS)∴DF=EG,∵EF=EG+GF,∴EF=DF+CF;(2)证明:在FQ上找到H点,使得FH=FG,如图3,∵FQ平分∠DFG,∴∠QFG=60°,∵FG=FH,∴△FGH是等边三角形,∴∠GHF=∠FGH=60°,GH=FG=FH,∵∠AFD=∠CDE+∠ACD=60°,∴∠GHQ=∠DFG=120°,∵∠FGD+∠DGH=60°,∠DGH+∠QGH=60°,∠QGH=∠DGF,∴∠FGD=∠QGH,在△DFG和△QHG中,∠DFG=∠QHG=120°FG=HG,∠FGD=∠QGH∴△DFG≌△QHG,(ASA)∴DF=QH,∵FQ=FH+QH,∴FQ=FG+FD.【点评】本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ECG≌△CDF和△DFG≌△QHG是解题的关键.13.(2022春•运城期末)综合与探究如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,CE的延长线交BD于点F.(1)求证:△ACE≌△ABD.(2)若∠BAC=∠DAE=50°,请直接写出∠BFC的度数.(3)过点A作AH⊥BD于点H,求证:EF+DH=HF.【分析】(1)可利用SAS证明结论;(2)由全等三角形的性质可得∠AEC=∠ADB,结合平角的定义可得∠DAE+∠DFE=180°,根据∠BFC+∠DFE=180°,可求得∠BFC=∠DAE,即可求解;(3)连接AF,过点A作AJ⊥CF于点J.结合全等三角形的性质利用HL证明Rt△AFJ≌Rt△AFH,Rt△AJE≌Rt△AHD可得FJ=FH,EJ=DH,进而可证明结论.【解答】(1)证明:∵∠BAC=∠DAE.∴∠CAE=∠BAD.在△ACE和△ABD中,AC=AB∠CAE=∠BAD,AE=AD∴△ACE ≌△ABD (SAS );(2)解:∵△ACE ≌△ABD ,∴∠AEC =∠ADB ,∴∠AEF +∠AEC =∠AEF +∠ADB =180°.∴∠DAE +∠DFE =180°,∵∠BFC +∠DFE =180°,∴∠BFC =∠DAE =∠BAC =50°;(3)证明:如图,连接AF ,过点A 作AJ ⊥CF 于点J .∵△ACE ≌△ABD ,∴S △ACE =S △ABD ,CE =BD ,∵AJ ⊥CE ,AH ⊥BD .∴12CE ⋅AJ =12BD ⋅AH ,∴AJ =AH .在Rt △AFJ 和Rt △AFH 中,AF =AF AJ =AH ,∴Rt △AFJ ≌Rt △AFH (HL ),∴FJ =FH .在Rt △AJE 和Rt △AHD 中,AE =AD AJ =AH ,∴Rt △AJE ≌Rt △AHD (HL ),∴EJ =DH ,∴EF +DH =EF +EJ =FJ =FH .【点评】本题主要考查全等三角形的判定与性质,掌握全等三角形的判定条件是解题的关键.14.(2022春•沙坪坝区校级期中)如图,在△ABC 中,∠ABC 、∠ACB 的平分线交于点D ,延长BD 交AC 于E ,G 、F 分别在BD 、BC 上,连接DF 、GF ,其中∠A =2∠BDF ,GD =DE .(1)当∠A =80°时,求∠EDC 的度数;(2)求证:CF =FG +CE .【分析】(1)方法一:先求∠ABC 和∠ACB 的和为100°,再根据角平分线求∠DBC +∠DCB =50°,再根据外角即可解决问题;方法二:在BC 上取点M ,使CM =CE ,证明△CDE ≌△CDM (SAS ),可得DE =DM ,∠DEC =∠DMC ,∠EDC =∠MDC ,证明∠BDM =180°−12∠ABC ﹣∠DMB =180°−12∠ABC ﹣∠AEB =∠A =80°,进而可以解决问题.(2)结合(1)然后证明△DGF ≌△DMF (SAS ),可得GF =MF ,进而可以解决问题.【解答】(1)解:方法一:∵∠A =80°,∴∠ABC +∠ACB =100°,∵BE 平分∠ABC 、CD 平分∠ACB ,∴∠DBC +∠DCB =50°,∴∠EDC =∠DBC +∠DCB =50°;方法二:如图,在BC 上取点M ,使CM =CE ,∵CD 平分∠ACB ,∴∠ACD=∠BCD,在△CDE和△CDM中,CE=CM∠ECD=∠MCDCD=CD,∴△CDE≌△CDM(SAS),∴DE=DM,∠DEC=∠DMC,∠EDC=∠MDC,∵GD=DE,∴GD=MD,∵∠DEC+∠AEB=180°,∠DMC+∠DMF=180°,∴∠AEB=∠DMF,∵BE平分∠ABC,∴∠ABE=∠CBE=12∠ABC,∴∠BDM=180°−12∠ABC﹣∠DMB=180°−12∠ABC﹣∠AEB=∠A=80°,∴∠EDM=100°,∴∠EDC=50°;(2)证明:∵∠A=2∠BDF,∴∠BDM=2∠BDF,∴∠FDM=∠BDF,在△DGF和△DMF中,DG=DM∠GDF=∠MDFDF=DF,∴△DGF≌△DMF(SAS),∴GF=MF,∴CF=CM+FM=CE+GF.∴CF=FG+CE.【点评】本题考查了全等三角形的判定与性质,角平分线的定义,解决本题的关键是根据题意准确作出辅助线得到△DGF≌△DMF.15.如图,在△ABC中,∠C=90°,AD是∠BAC的角平分线交BC于点D,过D作DE⊥BA于点E,点F在AC上,且BD=DF.(1)求证:AC=AE;(2)求证:∠BAC+∠FDB=180°;(3)若AB=9.5,AF=1.5,求线段BE的长.【分析】(1)证△ACD≌△AED(AAS),即可得出结论;(2)设∠DAC=∠DAE=α,在AB上截取AM=AF,连接MD,证△FAD≌△MAD(SAS),得FD=MD,∠ADF=∠ADM,再证Rt△MDE≌Rt△BDE(HL),得∠DME=∠B,然后证∠FDB=90°+90°﹣2α=180°﹣2α,即可得出结论;(3)求出MB=AB﹣AM=8,由全等三角形的性质得ME=BE,即可求解.【解答】(1)证明:∵AD平分∠BAC,∴∠DAC=∠DAE,∵DE⊥BA,∴∠DEA=∠DEB=90°,∵∠C=90°,∴∠C=∠DEA=90°,在△ACD和△AED中,∠C=∠DEA∠DAC=∠DAE,AD=AD∴△ACD≌△AED(AAS),∴AC=AE;(2)证明:设∠DAC=∠DAE=α,∵∠C=∠DEA=90°,∴∠ADC=90°﹣α,∠ADE=90°﹣α,则∠FDB=∠FCD+∠DFC=90°+∠DFC,在AB上截取AM=AF,连接MD,如图所示:在△FAD和△MAD中,AF=AM∠DAF=∠DAM,AD=AD∴△FAD≌△MAD(SAS),∴FD=MD,∠ADF=∠ADM,∵BD=DF,∴BD=MD,在Rt△MDE和Rt△BDE中,MD=BDDE=DE∴Rt△MDE≌Rt△BDE(HL),∴∠DME=∠B,∵∠DAC=∠DAE=α,∴∠DAC+∠ADF=∠ADM+∠ADM,在△FAD中,∠DAC+∠ADF=∠DFC,在△AMD中,∠DAE+∠ADM=∠DME,∴∠DFC=∠DME,∴∠DFC=∠B,∵∠C=90°,在△ABC中,∠B=90°﹣2α,∴∠DFC=90°﹣2α,∴∠FDB=90°+90°﹣2α=180°﹣2α,∵∠BAC=∠DAC+∠DAE=2α,∴∠FDB+∠BAC=180°﹣2α+2α=180°;(3)解:∵AF=AM,且AF=1.5,∴AM=1.5,∵AB=9.5,∴MB=AB﹣AM=9.5﹣1.5=8,由(2)得:Rt△MDE≌Rt△BDE,∴ME=BE,∴BE=12BM=4,即BM的长为4.【点评】本题考查了全等三角形的判定与性质、角平分线定义、直角三角形的性质、三角形的外角性质等知识;证明△FAD≌△MAD和Rt△MDE≌Rt△BDE是解题的关键.16.在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接DE,CE.(1)如图,当点D在BC延长线上移动时,求证:BD=CE.(2)设∠BAC=α,∠DCE=β.①当点D在线段BC的延长线上移动时,α与β之间有什么数量关系?请说明理由.②当点D分别在线段BC上、线段BC的反向延长线上移动时,α与β之间有什么数量关系?请说明理由.【分析】(1)根据SAS证△BAD≌△CAE,可得结论;(2)①由△BAD≌△CAE,推出∠B=∠ACE,根据三角形外角性质求出即可;②α+β=180°或α=β,根据三角形外角性质求出即可.【解答】(1)证明:∵∠DAE=∠BAC,∴∠DAE+∠CAD=∠BAC+∠CAD,∴∠BAD=∠CAE,在△BAD和△CAE中,AB=AC∠BAD=∠CAE,AD=AE∴△BAD≌△CAE(SAS),(2)解:①当点D在线段BC的延长线上移动时,α与β之间的数量关系是α=β,理由是:由(1)知△BAD≌△CAE,∴∠B=∠ACE,∵∠ACD=∠B+∠BAC=∠ACE+∠DCE,∴∠BAC=∠DCE,∵∠BAC=α,∠DCE=β,∴α=β;②分三种情况:i)当D在线段BC上时,如图2,α+β=180°,理由是:同理可证明:△ABD≌△ACE(SAS),∴∠ADB=∠AEC,∠ABC=∠ACE,∵∠ADC+∠ADB=180°,∴∠ADC+∠AEC=180°,∴∠DAE+∠DCE=180°,∵∠BAC=∠DAE=α,∠DCE=β,∴α+β=180°,ii)当点D在线段BC反向延长线上时,如图3,α=β.如图3,同理可证明:△ABD≌△ACE(SAS),∴∠ABD=∠ACE,∵∠ACE=∠ACD+∠DCE,∠ABD=∠ACD+∠BAC,∴∠ACD+∠DCE=∠ACD+∠BAC,∴∠BAC=∠DCE,∵∠BAC=α,∠DCE=β,∴α=β;ii)当点D在线段BC的延长线上时,如图1,α=β.综上,当点D在BC上移动时,α=β或α+β=180°.【点评】本题是三角形的综合题,考查了全等三角形的性质和判定,三角形的外角性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.17.(2022春•南海区校级月考)如图,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD.以AD为直角边且在AD的上方作等腰直角三角形ADF.(1)若AB=AC,∠BAC=90°.①当点D在线段BC上时(与点B不重合),试探讨CF与BD的数量关系和位置关系;②当点D在线段BC的延长线上时,①中的结论是否仍然成立,请在图②中画出相应的图形并说明理由;(2)如图③,若AB≠AC,∠BAC≠90°,∠BCA=45°,点D在线段BC上运动,试探究CF与BD 的位置关系.【分析】(1)①根据同角的余角相等求出∠CAF=∠BAD,然后利用“边角边”证明△ACF和△ABD全等,根据全等三角形的性质及等腰直角三角形的性质求解即可;②先求出∠CAF=∠BAD,然后与①的思路相同求解即可;(2)过点A作AE⊥AC交BC于E,可得△ACE是等腰直角三角形,根据等腰直角三角形的性质可得AC=AE,∠AED=45°,再根据同角的余角相等求出∠CAF=∠EAD,然后利用“边角边”证明△ACF 和△AED全等,根据全等三角形对应角相等可得∠ACF=∠AED,然后求出∠BCF=90°,从而得到CF ⊥BD.【解答】解:(1)①CF=BD,CF⊥BD,理由如下:∵∠BAC=90°,△ADF是等腰直角三角形,AB=AC,∴∠CAF+∠CAD=90°,∠BAD+∠CAD=90°,∠B=∠ACB=45°,∴∠CAF=∠BAD,在△ACF和△ABD中,AC=AB∠CAF=∠BAD,AF=AD∴△ACF≌△ABD(SAS),∴CF=BD,∠ACF=∠B=45°,∵∠ACB=45°,∴∠FCB=45°+45°=90°,∴CF⊥BD;②①中的结论成立,理由如下:如图②:∵∠BAC=90°,△ADF是等腰直角三角形,AB=AC,∴∠BAC=∠DAF=90°,∠B=∠ACB=45°,∴∠BAC+∠CAD=∠DAF+∠CAD,即∠CAF=∠BAD,在△ACF和△ABD中,AC=AB∠CAF=∠BAD,AF=AD∴△ACF≌△ABD(SAS),∴CF=BD,∠ACF=∠B,∴∠BCF=∠ACF+∠ACB=45°+45°=90°,∴CF⊥BD;(3)如图③,过点A作AE⊥AC交BC于E,∵∠BCA=45°,∴△ACE是等腰直角三角形,∴AC=AE,∠AED=45°,∵∠CAF+∠CAD=90°,∠EAD+∠CAD=90°,∴∠CAF=∠EAD,在△ACF和△AED中,AC=AE∠CAF=∠EAD,AF=AD∴△ACF≌△AED(SAS),∴∠ACF=∠AED=45°,∴∠BCF=∠ACF+∠BCA=45°+45°=90°,∴CF⊥BC.【点评】此题是三角形综合题,主要考查了全等三角形的判定与性质,等腰直角三角形的性质,作出合理的辅助线根据同角的余角相等求出两边的夹角相等是证明三角形全等的关键.18.如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.(1)△ABC≌△ADE吗?为什么?(2)求∠FAE的度数;(3)延长BF到G,使得FG=FB,试说明CD=2BF+DE.【分析】(1)由“SAS”可证△ABC≌△ADE;(2)由等腰直角三角形的性质可得∠AEC=∠ACE=45°,由全等三角形的性质可得∠ACB=∠AED=45°,即可求解;(3)由全等三角形的性质可得∠ABC=∠ADE,BC=DE,由线段垂直平分线的性质和等腰三角形的性质可得AB=AG=AD,∠ABG=∠AGB=∠ADC,由“AAS”可证△ACD≌△ACG,可得CD=CG,可得结论.【解答】证明:(1)△ABC≌△ADE,理由如下:∵∠BAD=∠CAE=90°,∴∠EAD=∠CAB,在△ABC和△ADE中,AB=AD∠BAC=∠DAE,AC=AE∴△ABC≌△ADE(SAS);(2)∵∠CAE=90°,AC=AE,∴∠AEC=∠ACE=45°,∵△ABC≌△ADE,∴∠ACB=∠AED=45°,∵AF⊥CB,∴∠FAC=45°,∴∠FAE=135°;(3)∵△ABC≌△ADE,∴∠ABC=∠ADE,BC=DE,∴∠ADC=∠ABG,∵AF⊥BF,BF=FG,∴AB=AG,∴AG=AD,∠ABG=∠AGB=∠ADC,又∵∠ACG=∠ACD=45°,∴△ACD≌△ACG(AAS),∴CD=CG,∴CD=BG+CB=2BF+DE.【点评】本题是三角形综合题,考查了全等三角形的判定和性质,等腰三角形的判定和性质,线段垂直平分线的性质等知识,证明△ACD≌△ACG是解题的关键.19.Rt△ABC中,∠C=90°,点D在直线AC上,点E在直线AB上,∠ADE=∠ABC.(1)如图1,当点D、E分别在边AC、AB上时,求证:DE⊥AB;(2)如图2,当点D在CA延长线上,点E在BA延长线上时,DE、BC延长线交于点F,作∠EAC的角平分线AG交DF于点G,求证:∠D+2∠DGA=90°;(3)如图3,在(2)的条件下,连接BG交CD于点H,若∠DGH=∠DHG,∠AGB=3∠CBH,求∠DGA的度数.【分析】(1)根据直角三角形的两锐角互余得到∠ABC+∠A=90°,等量代换得出∠ADE+∠A=90°,进而得出∠AED=90°,根据垂直的定义即可得解;(2)过点G作GN∥FB交CD于点N,根据平行线的性质及垂直的定义推出∠AEG=∠ANG=90°,根据角平分线定义得出∠EAG=∠NAG,利用AAS证明△EAG≌△NAG,根据全等三角形的性质及直角三角形的性质即可得解;(3)根据直角三角形的性质及对顶角相等得出∠DGH=90°−13∠AGB,根据等腰三角形的性质推出∠DGH=90°−12∠D,则90°−13∠AGB=90°−12∠D,进而推出∠AGB=32∠D,则∠DGA+32∠D=90°−12∠D,结合(2)求解即可.【解答】(1)证明:∵∠C=90°,∴∠ABC+∠A=90°,∵∠ADE=∠ABC,∴∠ADE+∠A=90°,∴∠AED=90°,∴DE⊥AB;(2)证明:如图2,过点G作GN∥FB交CD于点N,则∠GNC=∠ACB=90°,∴GN⊥CD,∵∠ACB=90°,∴∠ABC+∠BAC=90°,∵∠ADE=∠ABC,∠BAC=∠DAE,∴∠ADE+∠DAE=90°,∴∠DEA=90°,∴BE⊥DF,∴∠AEG=∠ANG=90°,∵AG平分∠EAC,∴∠EAG=∠NAG,在△EAG和△NAG中,∠AEG=∠ANG∠EAG=∠NAGAG=AG,∴△EAG≌△NAG(AAS),∴∠DGA=∠NGA,∴∠DGN=2∠DGA,∵∠D+∠DGN=90°,∴∠D+2∠DGA=90°;(3)解:∵∠AGB=3∠CBH,∴∠CBH=13∠AGB,∵∠DHG=∠CHB=90°﹣∠CBH,∴∠DGH=90°−13∠AGB,∵∠DGH=∠DHG,∴∠DGH=12(180°﹣∠D)=90°−12∠D,∴90°−13∠AGB=90°−12∠D,∴∠AGB=32∠D,∵∠DGH=∠DGA+∠AGB,∴∠DGA+∠AGB=90°−12∠D,∴∠DGA+32∠D=90°−12∠D,∴2∠D+∠DGA=90°,由(2)知,∠D+2∠DGA=90°,∴∠D=∠DGA,∴3∠DGA=90°,∴∠DGA=30°.【点评】此题是三角形综合题,考查了直角三角形的判定与性质、全等三角形的判定与性质、等腰三角形的性质、平行线的性质等知识,熟练掌握直角三角形的判定与性质、全等三角形的判定与性质、等腰三角形的性质并作出合理的辅助线是解题的关键.20.(2023春•新市区期末)在△ABC中,∠ACB=90°,AC=BC,D是直线AB上一点(点D不与点A、B重合),连接DC并延长到E,使得CE=CD,过点E作EF⊥直线BC,交直线BC于点F.(1)如图1,当点D为线段AB上的任意一点时,用等式表示线段EF、CF、AC的数量关系,并证明;(2)如图2,当点D为线段BA的延长线上一点时,依题意补全图2,猜想线段EF、CF、AC的数量关系是否发生改变,并证明;(3)如图3,当点D在线段AB的延长线上时,直接写出线段EF、CF、AC之间的数量关系.【分析】(1)过D作DH⊥CB于H,由“AAS”可证△FEC≌△HDC,可得CH=FC,DH=EF,可得结论;(2)过D作DH⊥CB于H,由“AAS”可证△FEC≌△HDC,可得CH=FC,DH=EF,可得结论.(3)过D作DH⊥CB交CB的延长线于H,由“AAS”可证△FEC≌△HDC,可得CH=FC,DH=EF,可得结论.【解答】解:(1)结论:AC=EF+FC.理由如下:过D作DH⊥CB于H,∴∠DHC=∠DHB=90°,∵EF⊥CF,∴∠EFC=∠DHC=90°,在△FEC和△HDC中,∠EFC=∠DHC=90°∠FCE=∠DCH,EC=DC∴△FEC≌△HDC(AAS),∴CH=FC,DH=EF,∵∠ACB=90°,AC=BC,∴∠B=45°,∵∠DHB=90°,∴∠B=∠HDB=45°,∴DH=HB=EF,∵BC=CB+HB,∴AC=FC+EF;(2)依题意补全图形,结论:AC=EF﹣CF,理由如下:过D作DH⊥CB交BC的延长线于H,∵EF⊥CF,∴∠EFC=∠DHC=90°,在△FEC和△HDC中,∠FCE=∠DCH∠EFC=∠DHC=90°,EC=DC∴△FEC≌△HDC(AAS),∴CH=FC,DH=EF,∵∠DHB=90°,∴∠B=∠HDB=45°,∴DH=HB=EF,∵BC=HB﹣CH,∴AC=EF﹣CF;(3)AC=CF﹣EF.如图3,过D作DH⊥CB交CB的延长线于H,同理可证△FEC≌△HDC(AAS),∴CH=FC,DH=EF,∵∠DHB=90°,∴∠B=∠HDB=45°,∴DH=HB=EF,∵BC=CH﹣BH,∴AC=CF﹣EF.【点评】本题是三角形综合题,考查了全等三角形的判定和性质,添加恰当辅助线构造全等三角形是本题的关键.21.如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.(1)如果AB=AC,∠BAC=90°,①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD所在直线的位置关系为 ,线段CF、BD的数量关系为 ;②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F 不重合),并说明理由.【分析】(1)当点D在BC的延长线上时①的结论仍成立.由正方形ADEF的性质可推出△DAB≌△FAC,所以CF=BD,∠ACF=∠ABD.结合∠BAC=90°,AB=AC,得到∠BCF=∠ACB+∠ACF=90°.即CF⊥BD.(2)当∠ACB=45°时,过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,可推出∠ACB=∠AGC,所以AC=AG,由(1)①可知CF⊥BD.【解答】证明:(1)①正方形ADEF中,AD=AF,∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF,又∵AB=AC,∴△DAB≌△FAC,∴CF=BD,∠B=∠ACF,∴∠ACB+∠ACF=90°,即CF⊥BD.②当点D在BC的延长线上时①的结论仍成立.由正方形ADEF得AD=AF,∠DAF=90度.∵∠BAC=90°,∴∠DAF=∠BAC,∴∠DAB=∠FAC,又∵AB=AC,∴△DAB≌△FAC,∴CF=BD,∠ACF=∠ABD.∵∠BAC=90°,AB=AC,∴∠ABC=45°,∴∠ACF=45°,∴∠BCF=∠ACB+∠ACF=90度.即CF⊥BD.(2)当∠ACB=45°时,CF⊥BD(如图).理由:过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,∵∠ACB=45°,∠AGC=90°﹣∠ACB,∴∠AGC=90°﹣45°=45°,∴∠ACB=∠AGC=45°,∴AC=AG,∵∠DAG=∠FAC(同角的余角相等),AD=AF,∴△GAD≌△CAF,∴∠ACF=∠AGC=45°,∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.【点评】本题考查三角形全等的判定和直角三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.22.(1)如图1,∠B=∠D=90°,E是BD的中点,AE平分∠BAC,求证:CE平分∠ACD.(2)如图2,AM∥CN,∠BAC和∠ACD的平分线并于点E,过点E作BD⊥AM,分别交AM、CN于B、D,请猜想AB、CD、AC三者之间的数量关系,请直接写出结论,不要求证明.(3)如图3,AM∥CN,∠BAC和∠ACD的平分线交于点E,过点E作不垂直于AM的线段BD,分别交AM、CN于B、D点,且B、D两点都在AC的同侧,(2)中的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.【分析】(1)过点E作EF⊥AC于F,根据角平分线上的点到角的两边的距离相等可得OB=OE,从而求出OE=OD,然后根据到角的两边距离相等的点在角的平分线上证明;(2)如图2,过E作EF⊥AC于F,根据平行线的性质得到BD⊥CD,由角平分线的性质得到BE=EF,证得Rt△AEF≌Rt△ABE,根据全等三角形到现在得到AF=AB,同理CF=CD,等量代换得到结论;(3)成立,如图3,在AC上截取AF=AB,根据角平分线的定义得到∠BAE=∠FAE,推出△ABE≌△AFE,根据全等三角形的性质得到∠AFE=∠ABE,根据角平行线的性质得到∠ABE+∠CDE=180°,求得∠CFE=∠CDE,证得△CEF≌△CDE,根据全等三角形的性质即可得到结论.【解答】解:(1)如图1,过E作EF⊥AC于F,∵∠B=90°,AE平分∠BAC,∴EF=BE,∵E是BD的中点,∴BE=DE,∴EF=DE,∵∠D=90°,∴CE平分∠ACD;(2)如图2,过E作EF⊥AC于F,∵AM∥CN,BD⊥AM,∴BD⊥CD,∵AE平分∠BAC,∴BE=EF,在Rt△AEF与Rt△ABE中,BE=EF AE=AE,∴Rt△AEF≌Rt△ABE,∴AF=AB,同理CF=CD,∵AC=AF+CF,∴AC=AB+CD;(3)成立,如图3,在AC上截取AF=AB,∵AE平分∠BAC,∴∠BAE=∠FAE,在△ABE与△AFE中,AB=AF∠BAE=∠FAEAE=AE,∴△ABE≌△AFE,∴∠AFE=∠ABE,∵AM∥CN,∴∠ABE+∠CDE=180°,∵∠AFE+∠EFC=180°,∴∠CFE=∠CDE,∵CE平分∠ACD,∴∠FCE=∠DCE,在△CEF与△CDE中,∠CFE=∠CDE ∠FCE=∠DCE CE=CE,∴△CEF≌△CDE,∴CF=CD,∵AC=AF+CF,∴AC=AB+CD.【点评】本题考查了全等三角形的判定和性质,角平分线的性质,角平分线的定义,平行线的性质,正确的作出辅助线构造全等三角形是解题的关键.23.将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.(1)求证:AF+EF=DE;(2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图②中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立;(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图③.你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.【分析】(1)我们已知了三角形BED和CAB全等,那么DE=AF+CF,因此只要求出EF=CF就能得出本题所求的结论,可通过全等三角形来实现,连接BF,那么证明三角形BEF和BCF全等就是解题的关键,这两三角形中已知的条件有BE=BC,一条公共边,根据斜边直角边定理,这两个直角三角形就全等了,也就得出EF=CF,也就能证得本题的结论了;(2)解题思路和辅助线的作法与(1)完全一样;(3)结论不成立.结论:AF=DE+EF.同(1)得CF=EF,由△ABC≌△DBE,可得AC=DE,AF=AC+FC=DE+EF.【解答】(1)证明:连接BF(如图①),∵△ABC≌△DBE(已知),∴BC=BE,AC=DE.∵∠ACB=∠DEB=90°,∴∠BCF=∠BEF=90°.在Rt△BFC和Rt△BFE中,BF=BFBC=BE∴Rt△BFC≌Rt△BFE(HL).∴CF=EF.又∵AF+CF=AC,∴AF+EF=DE.(2)解:画出正确图形如图②∴(1)中的结论AF+EF=DE仍然成立;(3)不成立.结论:AF=DE+EF.。
三角形(压轴必刷30题5种题型专项训练)—2023-2024学年八年级数学上册(人教版)(解析版)

三角形(压轴必刷30题5种题型专项训练)一.三角形的角平分线、中线和高(共1小题)1.(2022秋•瑞金市校级月考)如图,△ABC的周长是21cm,AB=AC,中线BD分△ABC为两个三角形,且△ABD的周长比△BCD的周长大6cm,求AB,BC.【分析】由BD是中线,可得AD=CD,又由△ABD的周长比△BCD的周长大6cm,△ABC的周长是21cm,AB=AC,可得AB﹣BC=6cm,2AB+BC=21cm,继而求得答案.【解答】解:∵BD是中线,∴AD=CD=AC,∵△ABD的周长比△BCD的周长大6cm,∴(AB+AD+BD)﹣(BD+CD+BC)=AB﹣BC=6cm①,∵△ABC的周长是21cm,AB=AC,∴2AB+BC=21cm②,联立①②得:AB=9cm,BC=3cm.【点评】此题考查了三角形面积与三角形的中线.注意掌握数形结合思想与方程思想的应用.二.三角形三边关系(共1小题)2.(2022春•徐汇区校级期末)周长为30,各边互不相等且都是整数的三角形共有个.【分析】不妨设三角形三边为a、b、c,且a<b<c,由三角形三边关系定理及题设条件可确定c的取值范围,以此作为解题的突破口.【解答】解:设三角形三边为a、b、c,且a<b<c.∵a+b+c=30,a+b>c∴10<c<15∵c为整数∴c为11,12,13,14∵①当c为14时,有5个三角形,分别是:14,13,3;14,12,4;14,11,5;14,10,6;14,9,7;②当c为13时,有4个三角形,分别是:13,12,5;13,11,6;13,10,7;13,9,8;③当c为12时,有2个三角形,分别是:12,11,7;12,10,8;④当c为11时,有1个三角形,分别是:11,10,9;故答案为:12个.【点评】此题主要考查学生对三角形三边关系的理解及运用能力.三.三角形内角和定理(共12小题)3.(2021秋•新罗区校级月考)在△ABC中,∠A=36°,当∠C=,△ABC为等腰三角形.【分析】分三种情形分别讨论,运用三角形内角和定理即可解决问题【解答】解:①当AB=AC时,∵∠A=36°,∴∠C=∠B=72°.②当CA=CB时,∵∠A=∠B=36°,∴∠C=108°.③当BA=BC时,∴∠C=∠A=36°,综上所述,∠C的值为72°或108°或36°,故答案为:72°,36°,108°.【点评】本题考查等腰三角形的判定和性质以及三角形内角和定理的运用,解题的关键是用分类讨论的思想思考问题.4.(2022秋•潍坊期末)如图,AB和CD相交于点O,∠C=∠COA,∠BDC=∠BOD,AP,DP分别平分∠CAO和∠BDC,若∠C+∠P+∠B=165°,则∠C的度数是.【分析】设∠C=∠AOC=∠BOD=∠BDO=x,∠CAP=∠PAB=y,∠P=z,则∠B=2y,构建方程组解决问题即可.【解答】解:∵∠C=∠COA,∠BDC=∠BOD,∠AOC=∠BOD,∴∠C=∠AOC=∠BOD=∠BDO,∴∠B=∠CAO,设∠C=∠AOC=∠BOD=∠BDO=x,∠CAP=∠PAB=y,∠P=z,则∠B=2y,则有,解得,∴∠C=70°,故答案为70°.【点评】本题考查三角形内角和定理,三角形的外角的性质等知识,解题的关键是学会利用参数构建方程组解决问题.5.(2021秋•武昌区期末)如图,在△ABC中,∠ACB=2α,CD平分∠ACB,∠CAD=30°﹣α,∠BAD=30°,则∠BDC=.(用含α的式子表示)【分析】延长CB到E,使CE=CA,连接DE,EA,利用SAS证明△ADC≌△EDC,得AD=ED,∠ADC=∠EDC,再证明△EDA为等边三角形,得出AB是∠EAD的角平分线,再通过导角得出答案.【解答】解:如图,延长CB到E,使CE=CA,连接DE,EA,∵CD平分∠ACB,∴∠ACD=∠BCD=,在△ADC与△EDC中,,∴△ADC≌△EDC(SAS),∴AD=ED,∠ADC=∠EDC,∵∠CAD=30°﹣α,∠ACD=α,∴∠ADC=180°﹣(30°﹣α)﹣α=150°,∴∠EDC=∠ADC=150°,∴∠EDA=360°﹣150°﹣150°=60°,∵ED=AD,∴△EDA为等边三角形,∴∠EAD=∠AED=60°,∵∠BAD=30°,∴∠EAB=60°﹣30°=30°,∴AB是∠EAD的角平分线,∵AB是ED的垂直平分线,∴BD=BE,∴∠BED=∠BDE,∵∠ACB=2α,∠EAC=∠EAD+∠DAC=60°+30°﹣α=90°﹣α,∴∠AEC=180°﹣2α﹣(90°﹣α)=90°﹣α,∴∠EDB=∠AEC﹣∠AED=90°﹣α﹣60°=30°﹣α,∴∠EDB=∠BED=30°﹣α,∴∠DBC=∠BDE+∠BED=(30°﹣α)×2=60°﹣2α,∴∠BDC=180°﹣∠DBC﹣∠DCB=180°﹣(60°﹣2α)﹣α=120°+α,故答案为:120°+α.【点评】本题主要考查了三角形内角和定理,全等三角形的判定与性质,等边三角形的判定与性质等知识,作辅助线构造全等三角形是解题的关键.6.(2020秋•杏花岭区校级月考)如图,在第1个△ABA1中,∠B=40°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到A2,使得在第2个△A1CA2中,∠A1CA2=∠A1A2C;在A2C上取一点D,延长A1A2到A3,使得在第3个△A2DA3中,∠A2DA3=∠A2A3D;…,按此做法进行下去,第3个三角形中以A3为顶点的内角的度数为;第n个三角形中以A n为顶点的底角的度数为.【分析】先根据等腰三角形的性质求出∠BA1A的度数,再根据三角形外角的性质及等腰三角形的性质分别求出∠CA2A1,∠DA3A2及∠EA4A3的度数,找出规律即可得出第n个三角形的以An为顶点的底角的度数.【解答】解:∵在△ABA1中,∠B=40°,AB=A1B,∴∠BA1A=(180°﹣∠B)=(180°﹣40°)=70°,∵A1A2=A1C,∠BA1A是△A1A2C的外角,∴∠CA2A1=∠BA1A=×70°=35°;同理可得,∠DA3A2=×70°=17.5°,∠EA4A3=×70°,以此类推,第n个三角形的以An为顶点的底角的度数=.故答案为:17.5°,.【点评】本题考查的是等腰三角形的性质及三角形外角的性质,根据题意得出∠CA2A1,∠DA3A2及∠EA4A3的度数,进而找出规律是解答此题的关键.7.(2022春•台江区校级期末)如图,在△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,∠BAC>∠C,FH⊥BE交BD于G,交BC于H,下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=(∠BAC﹣∠C);④∠BGH=∠ABE+∠C.其中正确的是.【分析】①根据BD⊥FD,FH⊥BE和∠FJD=∠BJH,证明结论正确;②根据角平分线的定义和三角形外角的性质证明结论正确;③证明∠DBE=∠BAC﹣∠C,根据①的结论,证明结论正确;④根据角平分线的定义和三角形外角的性质证明结论正确.【解答】解:设BE交FH于点J.①∵BD⊥FD,∴∠FGD+∠F=90°∵FH⊥BE,∴∠BGJ+∠DBE=90°,∵∠FGD=∠BGJ,∴∠DBE=∠F,①正确;②∵BE平分∠ABC,∴∠ABE=∠CBE,∠BEF=∠CBE+∠C,∴2∠BEF=∠ABC+2∠C,∠BAF=∠ABC+∠C,∴2∠BEF=∠BAF+∠C,②正确;③∠ABD=90°﹣∠BAC,∠DBE=∠ABE﹣∠ABD=∠ABE﹣90°+∠BAC=∠CBD﹣∠DBE﹣90°+∠BAC,∵∠CBD=90°﹣∠C,∴∠DBE=∠BAC﹣∠C﹣∠DBE,由①得,∠DBE=∠F,∴∠F=∠BAC﹣∠C﹣∠DBE,∴∠F=(∠BAC﹣∠C);③正确;④∵∠AEB=∠EBC+∠C,∵∠ABE=∠CBE,∴∠AEB=∠ABE+∠C,∵BD⊥FC,FH⊥BE,∴∠FGD=∠BGH=∠FEB,∴∠BGH=∠ABE+∠C,④正确,故答案为:①②③④.【点评】本题考查的是三角形内角和定理,正确运用三角形的高、中线和角平分线的概念以及三角形外角的性质是解题的关键.8.(2021秋•雷州市月考)如图,D是△ABC的BC边上的一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.(1)求∠B的度数.(2)求∠C的度数.【分析】(1)先由三角形外角的性质得出∠ADC=∠B+∠BAD,再由∠ADC=80°,∠B=∠BAD即可得出∠B的度数;(2)直接根据三角形的内角和定理得出∠C的度数.【解答】解:(1)∵∠ADC是△ABD的一个外角,∴∠ADC=∠B+∠BAD,又∵∠ADC=80°,∠B=∠BAD,∴∠B=∠ADC=×80°=40°;(2)在△ABC 中,∵∠BAC+∠B+∠C=180°,∴∠C=180°﹣∠B﹣∠BAC=180°﹣40°﹣70°=70°.【点评】本题考查的是三角形内角和定理及外角的性质,熟知三角形的内角和是180°是解答此题的关键.9.(2021春•东台市月考)如图,AD平分∠BAC,∠EAD=∠EDA.(1)∠EAC与∠B相等吗?为什么?(2)若∠B=50°,∠CAD:∠E=1:3,求∠E的度数.【分析】(1)由于AD平分∠BAC,根据角平分线的概念可得∠BAD=∠CAD,再根据三角形的一个外角等于和它不相邻的两个内角和,结合已知条件可得∠EAC与∠B相等;(2)若设∠CAD=x°,则∠E=3x°.根据(1)中的结论以及三角形的内角和定理及其推论列方程进行求解即可.【解答】解:(1)相等.理由如下:∵AD平分∠BAC,∴∠BAD=∠CAD.又∠EAD=∠EDA,∴∠EAC=∠EAD﹣∠CAD=∠EDA﹣∠BAD=∠B;(2)设∠CAD=x°,则∠E=3x°,由(1)知:∠EAC=∠B=50°,∴∠EAD=∠EDA=(x+50)°在△EAD中,∵∠E+∠EAD+∠EDA=180°,∴3x+2(x+50)=180,解得:x=16.∴∠E=48°.【点评】(1)建立要证明的两个角和已知角之间的关系,根据已知的相等的角,即可证明;(2)注意应用(1)中的结论,主要是根据三角形的内角和定理及其推论用同一个未知数表示相关的角,再列方程求解.10.(2021秋•新建区校级月考)如图,∠B=50°,点P在∠ABC内部,∠P的两边分别交AB,BC于点E,F.(1)若PE⊥AB,PF⊥BC.①如图1,则∠P=°;②如图2,EQ平分∠BEP,FQ平分∠BFP,求∠Q的度数.(2)若∠BEP与∠BFP两角的平分线交于ABC内一点Q,请写出∠Q与∠P的数量关系,并说明理由.【分析】(1)①由∠BEP=∠BFP=90°,∠ABC=50°,解可得∠EPF=130°;②根据EQ平分∠BEP,FQ平分∠BFP,得∠QEP=45°,∠QFP=45°,即可得∠Q=140°;(2)分两种情况:①四边形BEPF为凸四边形时,由∠B+2∠2+2∠4+∠P=360°,∠2+∠4=360°﹣∠P﹣∠Q,消去∠2、∠4即可得∠Q+∠P=200°;②四边形BEPF为凹四边形时,可得2∠Q﹣∠P=40°.【解答】解:(1)①∵PE⊥AB,PF⊥BC,∴∠BEP=∠BFP=90°,∵∠ABC=50°,∴∠EPF=360°﹣∠BEP﹣∠BFP﹣∠ABC=130°,故答案为:130;②∵EQ平分∠BEP,FQ平分∠BFP,∴∠QEP=∠BEP=45°,∠QFP=∠BFP=45°,∴∠Q=360°﹣∠QEP﹣∠QFP﹣∠EPF=140°;(2)①四边形BEPF为凸四边形时,如图:∵EQ平分∠BEP,FQ平分∠BFP,∴∠BEP=2∠2,∠BFP=2∠4,∵∠B+∠BEP+∠BFP+∠P=360°,∴∠B+2∠2+2∠4+∠P=360°,而∠B=50°,∴2∠2+2∠4=310°﹣∠P,即∠2+∠4=155°﹣∠P①,又∠2+∠4=360°﹣∠P﹣∠Q②,由①②可得:155°﹣∠P=360°﹣∠P﹣∠Q,整理得:∠Q+∠P=205°.②四边形BEPF为凹四边形时,如图:∵EQ平分∠BEP,FQ平分∠BFP,∴∠1=∠2,∠3=∠4,∵∠B=50°,∴2(∠2+∠3)+∠PEF+∠PFE=130°(Ⅰ),又∠Q+(∠2+∠3)+∠PEF+∠PFE=180°(Ⅱ),(Ⅱ)×2﹣(Ⅰ)得:2∠Q+∠PEF+∠PFE=230°(Ⅲ),而∠P+∠PEF+∠PFE=180°(Ⅳ),(Ⅲ)﹣(Ⅳ)得:2∠Q﹣∠P=50°;同理当四边形BEPF、四边形BEQF均为凸四边形时,2∠Q﹣∠P=310°,综上所述,∠Q与∠P的数量关系为∠Q+∠P=205°或2∠Q﹣∠P=50°或2∠Q﹣∠P=310°.【点评】本题考查多边形内角和,涉及角平分线、角的和差等知识,解题的关键是掌握四边形的内角和是360°.11.(2022秋•东港区校级月考)已知:如图,在△ABC中,AD是BC边上的高,AE是∠BAC平分线,∠B=30°,∠DAE=15°,(1)求∠BAE的度数;(2)求∠C的度数.【分析】(1)由AD是BC边上的高可得出∠ADE=90°,在△ADE中利用三角形内角和可求出∠AED的度数,再利用三角形外角的性质即可求出∠BAE的度数;(2)根据角平分线的定义可得出∠BAC的度数,在△ABC中利用三角形内角和可求出∠C的度数.【解答】解:(1)∵AD是BC边上的高,∴∠ADE=90°.∵∠ADE+∠AED+∠DAE=180°,∴∠AED=180°﹣∠ADE﹣∠DAE=180°﹣90°﹣15°=75°.∵∠B+∠BAE=∠AED,∴∠BAE=∠AED﹣∠B=75°﹣30°=45°.(2)∵AE是∠BAC平分线,∴∠BAC=2∠BAE=2×45°=90°.∵∠B+∠BAC+∠C=180°,∴∠C=180°﹣∠B﹣∠BAC=180°﹣90°﹣30°=60°.【点评】本题考查了三角形内角和定理以及三角形外角的性质,解题的关键是:(1)在△ADE中利用三角形内角和求出∠AED的度数;(2)利用角平分线的定义求出∠BAC的度数.12.(2022秋•香洲区校级月考)△ABC中,∠C=80°,点D、E分别是△ABC边AC、BC上的点,点P是一动点,令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.(1)若点P在边AB上,且∠α=50°,如图1,则∠1+∠2=;(2)若点P在边AB上运动,如图2所示,则∠α、∠1、∠2之间的关系为.(3)若点P运动到边AB的延长线上,如图3,则∠α、∠1、∠2之间有何关系?猜想并说明理由【分析】(1)连接CP,根据三角形外角性质,即可得到∠1=∠DCP+∠DPC,∠2=∠ECP+∠EPC,再根据∠1+∠2=∠ACB+∠DPE进行计算即可;(2)连接CP,根据三角形外角性质,即可得到∠1=∠DCP+∠DPC,∠2=∠ECP+∠EPC,再根据∠1+∠2=∠ACB+∠DPE进行计算即可得到∠α、∠1、∠2之间的关系;(3)根据三角形外角性质,即可得到∠1=∠C+∠CMD,∠CMD=∠2+∠α,进而得到∠1=∠C+∠2+∠α,据此可得∠α、∠1、∠2之间的关系.【解答】解:(1)如图1,连接CP,∵∠1是△CDP的外角,∴∠1=∠DCP+∠DPC,同理可得,∠2=∠ECP+∠EPC,∴∠1+∠2=∠ACB+∠DPE=80°+50°=130°,故答案为:130°;(2)如图,连接CP,∵∠1是△CDP的外角,∴∠1=∠DCP+∠DPC,同理可得,∠2=∠ECP+∠EPC,∴∠1+∠2=∠ACB+∠DPE=80°+∠α,故答案为:∠1+∠2=80°+∠α;(3)∠1=80°+∠2+∠α,理由如下:如图3,∵在△CDM中,∠1=∠C+∠CMD,在△EMP中,∠CMD=∠2+∠α,∴∠1=∠C+∠2+∠α,即∠1=80°+∠2+∠α.【点评】本题主要考查了三角形外角性质以及三角形内角和定理的运用,解题时注意:三角形的一个外角等于与它不相邻的两个内角的和.13.(2021秋•仙桃校级月考)如图,在△ABC中,AD⊥BC于D,AE平分∠DAC,∠BAC=80°,∠B=60°,求∠AEC的度数.【分析】根据三角形的内角和定理求出∠C,再根据直角三角形两锐角互余求出∠DAC,然后根据角平分线的定义求出∠DAE,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.【解答】解:∵∠BAC=80°,∠B=60°,∴∠C=180°﹣∠BAC﹣∠B=180°﹣80°﹣60°=40°,∵AD⊥BC,∴∠DAC=90°﹣∠C=90°﹣40°=50°,∵AE平分∠DAC,∴∠DAE=∠DAC=×50°=25°,∴∠AEC=∠DAE+∠ADE=25°+90°=115°.【点评】本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的角平分线和高线的定义,解题的关键是学会用分类的思想思考问题,属于中考常考题型.14.(2020秋•官渡区校级月考)如图,AD是△ABC的BC边上的高,AE是△ABC的一条角平分线,若∠B=42°,∠C=70°,求∠AEC和∠DAE的度数.【分析】由三角形内角和定理可求得∠BAC的度数,在Rt△ADC中,可求得∠DAC的度数,AE是角平分线,有∠EAC=∠BAC,故∠EAD=∠EAC﹣∠DAC.【解答】解:∵∠B=42°,∠C=70°,∴∠BAC=180°﹣∠B﹣∠C=68°,∵AE是角平分线,∴∠EAC=∠BAC=34°.∵AD是高,∠C=70°,∴∠DAC=90°﹣∠C=20°,∴∠EAD=∠EAC﹣∠DAC=34°﹣20°=14°,∠AEC=90°﹣14°=76°.【点评】本题考查三角形的内角和定理及角平分线的性质,高线的性质,解答的关键是熟练掌握三角形的内角和定理.四.三角形的外角性质(共10小题)15.(2022春•云龙区校级月考)如图,在△ABC中,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC,内角∠ABC,外角∠ACF,以下结论:①AD∥BC;②∠ACB=∠ADB;③∠ADC+∠ABD=90°;④,其中正确的结论有.【分析】根据角平分线定义得出∠ABC=2∠ABD=2∠DBC,∠EAC=2∠EAD,∠ACF=2∠DCF,根据三角形的内角和定理得出∠BAC+∠ABC+∠ACB=180°,根据三角形外角性质得出∠ACF=∠ABC+∠BAC,∠EAC=∠ABC+∠ACB,根据已知结论逐步推理,即可判断各项.【解答】解:①∵AD平分∠EAC,∴∠EAC=2∠EAD,∵∠ABC=∠ACB,∴∠EAD=∠ABC,∴AD∥BC,故①正确;②∵AD∥BC,∴∠ADB=∠DBC,∵BD平分∠ABC,∠ABC=∠ACB,∴∠ABC=∠ACB=2∠DBC,∴∠ACB=2∠ADB,故②错误;③在△ADC中,∠ADC+∠CAD+∠ACD=180°,∵CD平分△ABC的外角∠ACF,∴∠ACD=∠DCF,∵AD∥BC,∴∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB∴∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,∴∠ADC+∠ABD=90°,故③正确;④∵BD平分∠ABC,∴∠ABD=∠DBC,∵AD∥BC,∴∠ADB=∠DBC,∠DCF=∠ADC,∵∠ADC+∠ABD=90°,∵∠DCF=90°﹣∠ABC=∠DBC+∠BDC,∴∠BDC=90°﹣2∠DBC,∴∠ADB=∠DBC=45°﹣∠BDC,故④正确;故答案为:①③④.【点评】此题考查了三角形外角性质,平行线的判定与性质,主要考查学生的推理能力,有一定的难度.16.(2022秋•游仙区校级月考)如图,D是△ABC内一点,连接AD、BD、CD,P是∠BDC的角平分线的反向延长线上的一点,连接BP,∠ABP=2∠PBD,△ABC和△ACD的外角平分线相交于点Q,若∠Q =45°,∠BDC=4∠ABD,则∠P的度数为°.【分析】设∠PBD=α,表示出∠BDE=6α,于是∠P=5α,由∠Q=45°可推出∠BAC+∠ACD=90°,根据∠BDC=∠ABD+∠BAC+∠ACD求得α的值,进一步得出结果.【解答】解:如图,设PD的延长线交BC于E,设∠PBD=α,则∠ABP=2α,∴∠ABD=∠ABP+∠PBD=3α,∴∠BDC=4∠ABD=12α,∵DE平分∠BDC,∴∠BDE==6α,∴∠P=∠BDE﹣∠PBD=6α﹣α=5α,在△ACQ中,∠QAC+∠ACQ=180°﹣∠Q=135°,∵AQ平分∠FAC,CQ平分∠ACG,∴∠FAC=2∠QAC,∠ACG=2∠ACQ,∴∠FAC+∠ACG=2(∠QAC+∠ACQ)=270°,∴∠BAC+∠ACD=180°﹣∠FAC+180°﹣∠ACG=90°,∵∠BDC=∠ABD+∠BAC+∠ACD,∴12α=3α+90°,∴α=10°,∴∠P=5α=50°,故答案为:50.【点评】本题考查了角平分线的性质,三角形内角和定理及其推论等知识,解决问题的关键是设未知数,寻找角之间的数量关系.17.(2021•惠济区校级开学)认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+,理由如下:∵BO和CO分别是∠ABC和∠ACB的角平分线∴∴又∵∠ABC+∠ACB=180°﹣∠A∴∴∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣∠A)=探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)结论:.【分析】(1)根据提供的信息,根据三角形的一个外角等于与它不相邻的两个内角的和,用∠A与∠1表示出∠2,再利用∠O与∠1表示出∠2,然后整理即可得到∠BOC与∠A的关系;(2)根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出∠OBC与∠OCB,然后再根据三角形的内角和定理列式整理即可得解.【解答】解:(1)探究2结论:∠BOC=∠A,理由如下:∵BO和CO分别是∠ABC和∠ACD的角平分线,∴∠1=∠ABC,∠2=∠ACD,又∵∠ACD是△ABC的一外角,∴∠ACD=∠A+∠ABC,∴∠2=(∠A+∠ABC)=∠A+∠1,∵∠2是△BOC的一外角,∴∠BOC=∠2﹣∠1=∠A+∠1﹣∠1=∠A;(2)探究3:∠OBC=(∠A+∠ACB),∠OCB=(∠A+∠ABC),∠BOC=180°﹣∠0BC﹣∠OCB,=180°﹣(∠A+∠ACB)﹣(∠A+∠ABC),=180°﹣∠A﹣(∠A+∠ABC+∠ACB),结论∠BOC=90°﹣∠A.【点评】本题考查了三角形的外角性质与内角和定理,熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键,读懂题目提供的信息,然后利用提供信息的思路也很重要.18.(2021秋•回民区校级月考)如图,在△ABC中,∠B=40°,∠C=70°,AD是△ABC的角平分线,点E在BD上,点F在CA的延长线上,EF∥AD.(1)求∠BAF的度数.(2)求∠F的度数.【分析】(1)根据外角的性质即可得到结论;(2)根据角平分线的定义得到∠DAC=BAC=35°,根据平行线的性质即可得到结论.【解答】解:(1)∵∠BAF=∠B+∠C,∵∠B=40°,∠C=70°,∴∠BAF=110°;(2)∵∠BAF=110°,∴∠BAC=70°,∵AD是△ABC的角平分线,∴∠DAC=BAC=35°,∵EF∥AD,∴∠F=∠DAC=35°.【点评】本题考查了三角形外角的性质,平行线的性质,三角形的内角和,角平分线的定义,熟练掌握三角形外角的性质是解题的关键.19.(2020秋•顺昌县月考)如图,已知:点P是△ABC内一点.(1)求证:∠BPC>∠A;(2)若PB平分∠ABC,PC平分∠ACB,∠A=40°,求∠P的度数.【分析】(1)延长BP交AC于D,根据△PDC外角的性质知∠BPC>∠1;根据△ABD外角的性质知∠1>∠A,所以易证∠BPC>∠A.(2)由三角形内角和定理求出∠ABC+∠ACB=140°,由角平分线和三角形内角和定理即可得出结果.【解答】(1)证明:延长BP交AC于D,如图所示:∵∠BPC是△CDP的一个外角,∠1是△ABD的一个外角,∴∠BPC>∠1,∠1>∠A,∴∠BPC>∠A;(2)在△ABC中,∵∠A=40°,∴∠ABC+∠ACB=180°﹣∠A=180°﹣40°=140°,∵PB平分∠ABC,PC平分∠ACB,∴∠PBC=∠ABC,∠PCB=∠ACB,在△ABC中,∠P=180°﹣(∠PBC+∠PCB)=180°﹣(∠ABC+∠ACB)=180°﹣(∠ABC+∠ACB)=180°﹣×140°=110°.【点评】此题主要考查了三角形的外角性质、三角形内角和定理、三角形的角平分线定义;熟练掌握三角形的外角性质和三角形内角和定理是解决问题的关键.20.(2022秋•威县校级月考)综合与探究:【情境引入】(1)如图1,BD,CD分别是△ABC的内角∠ABC,∠ACB的平分线,说明∠D=90°+∠A的理由.【深入探究】(2)①如图2,BD,CD分别是△ABC的两个外角∠EBC,∠FCB的平分线,∠D与∠A之间的等量关系是;②如图3,BD,CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线,BD,CD交于点D,探究∠D与∠A之间的等量关系,并说明理由.【拓展应用】(3)请用以上结论解决下列问题:如图4,在△ABC中,BD,CD分别平分∠ABC,∠ACB,M,N,Q 分别在DB,DC,BC的延长线上,BE,CE分别平分∠MBC,∠BCN,BF,CF分别平分∠EBC,∠ECQ.若∠A=80°,则∠F的度数是.【分析】(1)利用角平分线的定义得出∠1+∠2=(∠ABC+∠ACB),再利用三角形内角和定理即可求解;(2)①利用三角形内角和定理可得∠DBC+∠DCB+∠D=180°,∠A+∠ABC+∠ACB=180°,利用角平分线的定义可得∠EBD=∠DBC,∠BCD=∠DCF,从而得到∠A﹣2(180°﹣∠D)=﹣180°,化简即可求解;②利用三角形的外角性质可得∠DCE=∠DBC+∠D,∠A+2∠DBC=2∠DCE,从而得到∠A+2∠DBC=2∠DBC+2∠D,化简即可求解;(3)由(1)知:∠D=90°+∠A,即可求出∠A,利用三角形内角和定理可得∠MBC+∠NCB,再利用角平分线的性质可得∠CBE+∠BCE,利用三角形内角和定理可得∠E,再由(2)②可知∠F=∠E,求解即可.【解答】解:(1)∵BD、CD分别是∠ABC、∠ACB的平分线,∴∠1=∠ABC,∠2=∠ACB,∴∠1+∠2=(∠ABC+∠ACB),∵∠A+∠ABC+∠ACB=180°,∠1+∠2+∠D=180°,∴∠D=180°﹣∠1﹣∠2=180°﹣(∠ABC+∠ACB),∴∠D=90°+∠A;(2)①∠D与∠A之间的等量关系是:∠D=90°﹣∠A,理由如下:∵BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线,∴∠EBD=∠DBC,∠BCD=∠DCF,∵∠DBC+∠DCB+∠D=180°,∠A+∠ABC+∠ACB=180°,∠ABC=180°﹣2∠DBC,∠ACB=180°﹣2∠DCB,∴∠A+180°﹣2∠DBC+180°﹣2∠DCB=180°,∠DBC+∠DCB=180°﹣∠D,∴∠A﹣2(∠DBC+∠DCB)=﹣180°,∴∠A﹣2(180°﹣∠D)=﹣180°,∴∠A+2∠D=180°,∴∠D=90°﹣∠A,故答案为:∠D=90°﹣∠A;②∠D与∠A之间的等量关系是:∠D=∠A,理由如下:∵BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线,∵∠DCE=∠DBC+∠D,∠A+2∠DBC=2∠DCE,∴∠A+2∠DBC=2∠DBC+2∠D,∴∠A=2∠D,∴∠D=∠A;(3)由(1)知:∠D=90°+∠A,∵∠A=80°,∴∠D=130°,∴∠DBC+∠DCB=50°,∴∠MBC+∠NCB=360°﹣50°=310°,∵BE、CE分别平分∠MBC、∠BCN,∴∠CBE+∠BCE=(∠MBC+∠NCB)=155°,∴∠E=180°﹣155°=25°.由(2)②知:∠F=∠E,∴∠F=∠E=12.5°,故答案为:12.5°.【点评】本题考查三角形的外角性质,三角形的内角和定理,角平分线的定义,解题的关键是熟记三角形外角性质,内角和定理,角平分线的定义.21.(2021秋•信丰县校级月考)如图,求∠A+∠B+∠C+∠D+∠E的度数.【分析】要求∠A+∠B+∠C+∠D+∠E的度数,只要求出∠D+∠1+∠2的度数,利用三角形外角性质得,∠1=∠A+∠E,∠2=∠B+∠C;在△DOF中,∠D+∠1+∠2=180°,∴∠A+∠B+∠C+∠D+∠E=∠D+∠1+∠2=180°.【解答】解:∵∠1是△AEF的外角,∴∠1=∠A+∠E.∵∠2是△BOC的外角,∴∠2=∠B+∠C.在△DOF中,∠D+∠1+∠2=180°,∴∠A+∠B+∠C+∠D+∠E=∠D+∠1+∠2=180°.【点评】考查三角形外角性质与内角和定理.将∠A+∠B+∠C+∠D+∠E拼凑在一个三角形中是解题的关键.22.(2020秋•兴义市校级月考)(1)如图1,这是一个五角星ABCDE,你能计算出∠A+∠B+∠C+∠D+∠E的度数吗?为什么?(必须写推理过程)(2)如图2,如果点B向右移动到AC上,那么还能求出∠A+∠DBE+∠C+∠D+∠E的大小吗?若能结果是多少?(可不写推理过程)(3)如图,当点B向右移动到AC的另一侧时,上面的结论还成立吗?(4)如图4,当点B、E移动到∠CAD的内部时,结论又如何?根据图3或图4,说明你计算的理由.【分析】(1)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠A+∠C=∠1,∠B+∠D=∠2,然后利用三角形的内角和定理列式即可得解;(2)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠A+∠D=∠1,在△BCE中,利用三角形的内角和列式计算即可得解;(3)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠A+∠C=∠1,∠B+∠D=∠2,然后利用三角形的内角和定理列式即可得解;(4)延长CE与AD相交,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠A+∠C=∠1,∠B+∠E=∠2,然后利用三角形的内角和定理列式即可得解.【解答】解:(1)如图,由三角形的外角性质,∠A+∠C=∠1,∠B+∠D=∠2,∵∠1+∠2+∠E=180°,∴∠A+∠B+∠C+∠D+∠E=180°;(2)如图,由三角形的外角性质,∠A+∠D=∠1,∵∠1+∠DBE+∠C+∠E=180°,∴∠A+∠DBE+∠C+∠D+∠E=180°;(3)如图,由三角形的外角性质,∠A+∠C=∠1,∠B+∠D=∠2,∵∠1+∠2+∠E=180°,∴∠A+∠B+∠C+∠D+∠E=180°;(4)如图,延长CE与AD相交,由三角形的外角性质,∠A+∠C=∠1,∠B+∠E=∠2,∵∠1+∠2+∠D=180°,∴∠A+∠B+∠C+∠D+∠E=180°.【点评】本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形内角和定理,比较简单,关键在于准确识图,理清图中各角度之间的联系与转化.23.(2022秋•冷水滩区校级月考)认真阅读下面关于三角形内外角平分线所夹的探究片段,完成所提出的问题.探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+∠A,理由如下:∵BO和CO分别是∠ABC和∠ACB的角平分线,∴∠1=∠ABC,∠2=∠ACB,∴∠1+∠2=(∠ABC+∠ACB)=(180°﹣∠A)=90°﹣∠A,∴∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣∠A)=90°+∠A.(1)探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.(2)探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(直接写出结论)(3)拓展:如图4,在四边形ABCD中,O是∠ABC与∠DCB的平分线BO和CO的交点,则∠BOC与∠A+∠D有怎样的关系?(直接写出结论)【分析】(1)根据角平分线的定义表示出∠OBC,∠OCD,再根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠ACD和∠OCD,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式整理即可得解;(2)根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠DBC和∠BCE,再根据角平分线的定义求出∠OBC+∠OCB,然后根据三角形内角和定理列式整理即可得解;(3)根据四边形内角和等于360°求出∠ABC+∠BCD,再根据角平分线的定义求出∠OBC+∠OCB,然后利用三角形内角和定理列式整理即可得解.【解答】解:(1)探究2结论:∠BOC=∠A.理由如下:∵BO和CO分别是∠ABC和∠ACD的角平分线,∴∠OBC=∠ABC,∠OCD=∠ACD,又∵∠ACD是△ABC的一个外角,∴∠ACD=∠A+∠ABC,∴∠OCD=(∠A+∠ABC)=∠A+∠ABC=∠A+∠OBC,又∵∠OCD是△BOC的一个外角,∴∠BOC=∠OCD﹣∠OBC=∠A+∠OBC﹣∠OBC=∠A;(2)探究3:结论∠BOC=90°﹣∠A.根据三角形的外角性质,∠DBC=∠A+∠ACB,∠BCE=∠A+∠ABC,∵O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,∴∠OBC=∠DBC,∠OCB=∠BCE,∴∠OBC+∠OCB=(∠DBC+∠BCE)=(∠A+∠ACB+∠A+∠ABC),∵∠A+∠ACB+∠ABC=180°,∴∠OBC+∠OCB=90°+∠A,在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(90°+∠A)=90°﹣∠A;(3)拓展:结论∠BOC=(∠A+∠D).在四边形ABCD中,∠ABC+∠BCD=(360°﹣∠A﹣∠D),∵O是∠ABC与∠DCB的平分线BO和CO的交点,∴∠OBC=∠ABC,∠OCB=∠BCD,∴∠OBC+∠OCB=(∠ABC+∠BCD)=(360°﹣∠A﹣∠D),在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(360°﹣∠A﹣∠D)=(∠A+∠D),即∠BOC=(∠A+∠D).【点评】本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.24.(2023•东兴区校级二模)如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.(1)如果∠A=80°,求∠BPC的度数;(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.【分析】(1)运用三角形的内角和定理及角平分线的定义,首先求出∠PBC+∠PCB,进而求出∠BPC即可解决问题;(2)根据三角形的外角性质分别表示出∠MBC与∠BCN,再根据角平分线的性质可求得∠CBQ+∠BCQ,最后根据三角形内角和定理即可求解;(3)在△BQE中,由于∠Q=90°﹣∠A,求出∠E=∠A,∠EBQ=90°,所以如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况进行讨论:①∠EBQ=2∠E=90°;②∠EBQ=2∠Q=90°;③∠Q=2∠E;④∠E=2∠Q;分别列出方程,求解即可.【解答】(1)解:∵∠A=80°.∴∠ABC+∠ACB=100°,∵点P是∠ABC和∠ACB的平分线的交点,∴∠P=180°﹣(∠ABC+∠ACB)=180°﹣×100°=130°,(2)∵外角∠MBC,∠NCB的角平分线交于点Q,∴∠QBC+∠QCB=(∠MBC+∠NCB)=(360°﹣∠ABC﹣∠ACB)=(180°+∠A)=90°+∠A∴∠Q=180°﹣(90°+∠A)=90°﹣∠A;(3)延长BC至F,∵CQ为△ABC的外角∠NCB的角平分线,∴CE是△ABC的外角∠ACF的平分线,∴∠ACF=2∠ECF,∵BE平分∠ABC,∴∠ABC=2∠EBC,∵∠ECF=∠EBC+∠E,∴2∠ECF=2∠EBC+2∠E,即∠ACF=∠ABC+2∠E,又∵∠ACF=∠ABC+∠A,∴∠A=2∠E,即∠E=∠A;∵∠EBQ=∠EBC+∠CBQ=∠ABC+∠MBC=(∠ABC+∠A+∠ACB)=90°.如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;③∠Q=2∠E,则90°﹣∠A=∠A,解得∠A=60°;④∠E=2∠Q,则∠A=2(90°﹣∠A),解得∠A=120°.综上所述,∠A的度数是90°或60°或120°.【点评】本题是三角形综合题,考查了三角形内角和定理、外角的性质,角平分线定义等知识;灵活运用三角形的内角和定理、外角的性质进行分类讨论是解题的关键.五.多边形内角与外角(共6小题)25.(2021秋•盖州市校级月考)如果一个多边形的内角和等于1800°,则这个多边形是边形;如果一个n边形每一个内角都是135°,则n=;如果一个n边形每一个外角都是36°,则n =.【分析】n边形的内角和可以表示成(n﹣2)•180°,设这个正多边形的边数是n,就得到方程,从而求出边数.【解答】解:这个多边形的边数是n,则(n﹣2)•180°=1800°,解得:n=12,则这个多边形是12.如果一个n边形每一个内角都是135°,∴每一个外角=45°,则n==8,如果一个n边形每一个外角都是36°,则n==10,故答案为:十二,8,10.【点评】此题考查了多边形的内角和定理.注意多边形的内角和为:(n﹣2)×180°.26.(2021秋•河东区校级期末)如图,AD,CE是△ABC的两条高,它们相交于点P,已知∠BAC的度数为α,∠BCA的度数为β,则∠APC的度数是.【分析】利用三角形的内角和定理和三角形的外角性质解决问题即可.【解答】解:∠B=180°﹣∠BAC﹣∠ACB=180°﹣(α+β),∵AD⊥BC,CE⊥AB,∴∠AEC=∠ADB=90°,∴∠BAD=90°﹣[180°﹣(α+β)]=α+β﹣90°,∴∠APC=∠AEC+∠BAD=α+β故填α+β.【点评】主要考查了三角形的内角和是180度.求角的度数常常要用到“三角形的内角和是180°这一隐含的条件,同时考查了四边形内角和定理.垂直和直角总是联系在一起.27.(2021秋•仙桃校级月考)如图,在五边形ABCDE中,AP平分∠EAB,BP平分∠ABC.(1)五边形ABCDE的内角和为度;(2)若∠C=100°,∠D=75°,∠E=135°,求∠P的度数.【分析】(1)根据多边形内角和公式求出即可;(2)求出∠EAB+∠ABC,根据角平分线定义求出∠PAB+∠PBA,即可求出答案.【解答】解:(1)五边形ABCDE的内角和为(5﹣2)×180°=540°,故答案为:540;(2)∵在五边形ABCDE中,∠EAB+∠ABC+∠C+∠D+∠E=540°,∠C=100°,∠D=75°,∠E=135°,∴∠EAB+∠ABC=230°,∵AP平分∠EAB,BP平分∠ABC,∴∠PAB=∠EAB,∠PBA=∠ABC,∴∠PAB+∠PBA=115°,∴∠P=180°﹣(∠PAB+∠PBA)=65°.【点评】本题考查了多边形的内角和外角,能熟记多边形的内角和定理是解此题的关键.28.(2022秋•礼县月考)小明计算一个多边形的内角和时误把一个外角加进去了,得其和为2620°.(1)求这个多加的外角的度数;(2)求这个多边形的边数.【分析】根据多边形的内角和公式(n﹣2)•180°可知,多边形的内角和是180°的倍数,然后求出多边形的边数以及多加的外角的度数即可得解.【解答】解:设多边形的边数为n,多加的外角度数为α,则(n﹣2)•180°=2620°﹣α,∵2620°=14×180°+100°,内角和应是180°的倍数,∴小明多加的一个外角为100°,∴这是14+2=16边形的内角和.故这个多加的外角的度数为100°,这个多边形的边数是16.【点评】本题考查了多边形的内角和公式,根据多边形的内角和公式判断出多边形的内角和公式是180°的倍数是解题的关键.29.(2020秋•夏津县校级月考)如图,AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线.(1)判断∠AOB与∠COD有怎样的数量关系,为什么?(2)若∠AOD=∠BOC,AB、CD有怎样的位置关系,为什么?【分析】(1)根据角平分线的定义得到∠1=DAB,∠2=ABC,∠3=ADC,∠4=BCD,根据四边形的内角和即可得到结论;(2)由(1)证得∠AOB+∠COD=180°,得到∠AOD+∠BOC=180°,根据角平分线的定义得到∠BAD+∠ADC=180°,由平行线的判定定理即可得到结论.【解答】解:(1)∠AOB+∠COD=180°,理由:∵AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线,∴∠1=DAB,∠2=ABC,∠3=ADC,∠4=BCD,∴∠1+∠2+∠3+∠4=(∠DAB+∠ABC+∠ADC+∠BCD)==180°,∴∠AOB+∠COD=360°﹣∠1﹣∠2﹣∠3﹣∠4=180°;(2)AB∥CD;理由:由(1)证得∠AOB+∠COD=180°,∴∠AOD+∠BOC=180°,∵∠AOD=∠BOC,∴∠AOD=90°,∵AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线,∴∠OAD+∠ADO=(∠BAD+∠ADC)=90°,∴∠BAD+∠ADC=180°,∴AB∥CD.【点评】本题考查了多边形的内角和外角,平行线的判定,角平分线的定义,正确的识别图形是解题的关键.30.(2019秋•广丰区校级月考)请你参与下面探究过程,完成所提出的问题.(1)探究1:如图1,P是△ABC的内角∠ABC与∠ACB的平分线BP和CP的交点,若∠A=70°,则∠BPC=度;(2)探究2:如图2,P是△ABC的外角∠DBC与外角∠ECB的平分线BP和CP的交点,求∠BPC与∠A的数量关系?并说明理由.(3)拓展:如图3,P是四边形ABCD的外角∠EBC与∠BCF的平分线BP和CP的交点,设∠A+∠D =α.①直接写出∠BPC与α的数量关系;②根据α的值的情况,判断△BPC的形状(按角分类).。
专题02 直角三角形三种压轴题型全攻略(解析版)

专题02 直角三角形三种压轴题型全攻略 类型一、与直角三角形有关最值问题例、如图,在ABC 中,90C ∠=︒,30A ∠=︒,点D 为边AB 的中点,点P 在边AC 上,则PDB△周长的最小值等于( ).A .AC AB +B .ABC .AC BC +D .AC【答案】C 【详解】解:作点B 关于AC 的对称点H ,连接HP 、HD ,如图所示:∴BP HP =,BC HC =,∴90C ∠=︒,30A ∠=︒,∴2AB BC BH ==,∴点D 为边AB 的中点,∴2AB BD =,∴BC BD =,∴ABC HBD ∠=∠,∴ABC HBD ≌(SAS ),∴AC HD =,∴PBD C BP PD BD HP PD BD =++=++,要使其最小,则需满足H 、P 、D 三点共线,即BP PD +的最小值为HD 的长,∴PBD △的周长最小值为AC BC +;故选C .【变式训练1】如图,在R t∴ABC 中,∴ACB =90°,将R t∴ABC 绕顶点C 逆时针旋转得到R t∴A 'B 'C ,M 是BC 的中点,P 是A ′B '的中点,连接PM .若BC =2,∴BAC =30°,则线段PM 的最大值为( ).A .2.5B .C .3D .4【答案】C 【详解】如图,连接PC在Rt ABC 中,2BC =,30BAC ∠=︒,∴24AB BC ==∴将ABC 绕顶点C 逆时针旋转得到A B C ''△∴A B C ''△也是直角三角形,且4A B AB ''==∴P 是A B ''的中点,∴122PC A B =''= ∴M 是BC 的中点。
∴1CM BM ==则由三角形的三边关系定理得:PC CM PM PC CM -<<+即13PM <<当点P 恰好在MC 的延长线上时,213PM PC CM =+=+=当点P 恰好在CM 的延长线上时,211PM PC CM =-=-=综上,13PM ≤≤则线段PM 的最大值为3故选:C .【变式训练2】如图,在ABC 中,90ACB ∠=︒,30CAB ∠=︒,=AC D 为AB 上一动点(不与点A 重合),AED 为等边三角形,过D 点作DE 的垂线,F 为垂线上任意一点,G 为EF 的中点,则线段BG 长的最小值是( )A.B .6 C.D .9【答案】B 【详解】解:如图,连接DG ,AG ,设AG 交DE 于点H ,DE DF ⊥,G 为EF 的中点,DG GE ∴=,∴点G 在线段DE 的垂直平分线上, AED 为等边三角形,AD AE ∴=,∴点A 在线段DE 的垂直平分线上,AG ∴为线段DE 的垂直平分线,AG DE ∴⊥,1302DAG DAE ∠=∠=︒, ∴点G 在射线AH 上,当BG AH ⊥时,BG 的值最小,如图所示,设点G '为垂足, 90ACB ∠=︒,30CAB ∠=︒,ACB AG B '∴∠=∠,CAB BAG '∠=∠,则在BAC 和BAG '△中,ACB AG B CAB BAG AB AB ∠=∠⎧⎪∠=∠='⎨'⎪⎩,()BAC BAG AAS '∴≅.BG BC '∴=,∴90ACB ∠=︒,30CAB ∠=︒,=AC ∴12BC AB =,222BC AB +=,∴222(2)BC BC +=,解得:6BC =,∴6BG BC '==故选:B . 【变式训练3】如图,长方形ABCD 中,6AB =,8BC =,E 为BC 上一点,且2BE =,F 为AB 边上的一个动点,连接EF ,将EF 绕着点E 顺时针旋转30°到EG 的位置,连接FG 和CG ,则CG 的最小值为______.【答案】2【详解】解:如图,将线段BE 绕点E 顺时针旋转30°得到线段ET ,连接GT ,过E 作EJ CG ⊥,垂足为J ,∴四边形ABCD 是矩形,∴AB =CD =6,∴B =∴BCD =90°,∴∴BET =∴FEG =30°,∴∴BEF =∴TEG ,在∴EBF 和∴TEG 中,EB ET BEF TEG EF EG =⎧⎪∠=∠⎨⎪=⎩,∴∴EBF ∴∴ETG (SAS ),∴∴B =∴ETG =90°,∴点G 的在射线TG 上运动,∴当CG ∴TG 时,CG 的值最小,∴∴EJG =∴ETG =∴JGT =90°,∴四边形ETGJ 是矩形,∴∴JET =90°,GJ =TE =BE =2,∴∴BET =30°,∴∴JEC =180°-∴JET -∴BET =60°,∴8BC =,∴6,3,EC BC BE EJ CJ =-===∴CG =CJ +GJ=2.∴CG的最小值为2+.故答案为:2.类型二、直角三角形中的存在性问题例、(1)在图1中,已知△ABC 中,∴B >∴C ,AD ∴BC 于D ,AE 平分∴BAC ,∴B =70°,∴C =40°,求∴DAE 的度数.(2)在图2中,∴B =x ,∴C =y ,其他条件不变,若把AD ∴BC 于D 改为F 是AE 上一点,FD ∴BC 于D ,试用x 、y 表示∴DFE = :(3)在图3中,当点F 是AE 延长线上一点,其余条件不变,则(2)中的结论还成立吗?若成立,请说明为什么;若不成立,请写出成立的结论,并说明为什么.(4)在图3中,分别作出∴BAE 和∴EDF 的角平分线,交于点P ,如图4.试用x 、y 表示∴P = .【答案】(1)15°;(2)1122x y -;(3)结论应成立.1122x y -(4)3144x y -. 【详解】解:(1)∴∴B =70°,∴C =40°,∴∴BAC =180°-∴B -∴C =180°-70°-40°=70°,∴AE 平分∴BAC ,∴∴BAE =11703522BAC ∠=⨯︒=︒, ∴AD ∴BC ,∴∴BDA =90°,∴∴B +∴BAD =90°,∴∴BAD =90°-∴B =90°-70°=20°,∴∴DAE =∴BAE -∴BAD =35°-20°=15°;(2)∴∴B =x ,∴C =y ,∴∴BAC =180°-∴B -∴C =180°- x -y ,∴AE 平分∴BAC ,∴∴EAC =()1111180902222BAC x y x y ∠=⨯︒--=︒--, ∴FD ∴BC ,∴∴EDE =90°,∴∴DFE +∴FED =90°,∴∴FED 是△AEC 的外角,∴∴FED =∴C +∴EAC =111190902222y x y x y +︒--=︒-+, ∴∴DFE =90°-∴FED =1122x y -, 故答案为:1122x y -; (3)结论应成立.过点A 作AG ∴BC 于G ,∴∴B =x ,∴C =y ,∴∴BAC =180°-∴B -∴C =180°- x -y ,∴AE 平分∴BAC ,∴∴BAE =()1111180902222BAC x y x y ∠=⨯︒--=︒--, ∴AG ∴BC ,∴∴AGB =90°,∴∴B +∴BAG =90°,∴∴BAG =90°-∴B =90°-x ,∴∴GAE =∴BAE -∴BAG =()11909022x y x ︒---︒-=1122x y -, ∴FD ∴BC ,AG ∴BC ,∴AG ∥FD ,∴∴EFD =∴GAE =1122x y -(4)设AF 与PD 交于H ,∴FD ∴BC ,PD 平分∴EDF ,∴∴HDF =11904522EDF ∠=⨯︒=︒, ∴P A 平分∴BAE ,∴BAE =()1111180902222BAC x y x y ∠=⨯︒--=︒--, ∴∴P AE =1111119045222244BAE x y x y ⎛⎫∠=︒--=︒-- ⎪⎝⎭, ∴∴AHP =∴FHD ,∴EFD =1122x y - ∴∴P +∴P AE =∴HDF +∴EFD ,即∴P +114544x y ︒--=45°+1122x y -, ∴∴P =1111314545224444x y x y x y ⎛⎫︒+--︒--=- ⎪⎝⎭, 故答案为:3144x y -.【变式训练1】综合与探究:如图①,在∴ABC 中,∴C >∴B ,AD 是∴BAC 角平分线.(1)探究与发现:如图①,AE ∴BC 于点E ,①若∴B =30°,∴C =70°,则∴CAD = °,∴DAE = °;②若∴B =45°,∴C =65°,则∴DAE = °;③试探究∴DAE 与∴B 、∴C 的数量关系,并说明理由.(2)判断与思考:如图②,F 是AD 上一点,FE ∴BC 于点E ,这时∴DFE 与∴B 、∴C 又有怎样的数量关系?【答案】(1)①40,20;②10;③∴DAE =12(∴C -∴B ),理由见解析;(2)∴DFE =12(∴C ﹣∴B ),理由见解析【详解】解:(1)①∴∴B =30°,∴C =70°,∴18080BAC B C ∠=︒-∠-∠=︒,∴AD 是∴BAC 角平分线,∴1402CAD BAD CAB ∠=∠=∠=︒,∴AE ∴BC ,∴90AEC ∠=︒,∴907020CAE ∠=︒-︒=︒,∴402020DAE CAD CAE ∠=∠-∠=︒-︒=︒,故答案为:40,20;②∴∴B =45°,∴C =65°,∴18070BAC B C ∠=-∠-∠=︒︒,∴AD 是∴BAC 角平分线,∴1352CAD BAD CAB ∠=∠=∠=︒,∴AE ∴BC ,∴90AEC ∠=︒,∴906525CAE ∠=︒-︒=︒,∴352510DAE CAD CAE ∠=∠-∠=︒-︒=︒,故答案为:10;③∴DAE =12(∴C -∴B ),理由如下:在∴AEC 中,∴AEC +∴C +∴EAC =180°,∴∴EAC =180°-∴AEC -∴C =180°-90°-∴C =90°-∴C ,∴∴DAE =∴CAD -∴EAC =12×(180°-∴B -∴C )=(90°-12∴B -12∴C )-( 90°-∴C )=12 (∴C -∴B ); (2)判断与思考;∴DFE =12(∴C ﹣∴B ),理由如下:证明:∴AD 平分∴BAC ,∴∴BAD =01802B C -∠-∠=90°-12(∴C +∴B ), ∴∴ADC 为∴ABD 的外角,∴∴ADC =∴B +90°-12(∴C +∴B )=90°+12(∴B -∴C ),∴FE ∴BC ,∴∴FED =90°,∴∴DFE =90°- [90°+12(∴B -∴C )]=90°-90°-12(∴B -∴C ),∴∴DFE =12(∴C -∴B ).【变式训练2】已知在直角三角形ABC 中,90C ∠=︒,AD 平分CAB ∠.(1)如图1,若DA DB =,求B 的度数;(2)如图2,点E 在AB 上,连接CE 交AD 于F ,若BCE BAD ∠=∠,求证:AC AE =; (3)如图3,在(2)的条件下,点M 在AB 上,连接CM 交AD 于G ,过点G 作GN BC ⊥于N ,交CF 于H ,2ACM B ∠=∠,2CH =,3DF =,求CGD △的面积.【答案】(1)30°;(2)见解析;(3)20【详解】证明:(1)∴DA =DB ,∴∴DAB =∴B ,∴AD 平分∴CAB ,∴∴CAD =∴DAB ,∴∴C =90°,∴∴B +∴CAB =90°,∴3∴B =90°,∴∴B =30°.(2)∴AD 平分∴CAB ,∴∴CAD =∴BAD ,∴∴BAD =∴BCE ,∴∴CAD =∴BCE ,∴∴BCE +∴ACE =90°,∴∴CAD +∴ACE =90°,∴∴AFE =∴AFC =90°,∴∴F AE +∴AEC =90°,∴∴ACE =∴AEC ,∴AC =AE .(3)设∴ACM =α,∴CAB =2β,∴∴BCM =90°-α.∴2∴ACM =∴B ,∴∴B =2α,∴∴BMC =90°-α.∴AC =AE ,∴∴AEC =90°-β,∴∴MCE =180°-∴BMC -∴AEC =α+β.∴2α+2β=90°,∴∴MCE =45°.∴∴CFG =90°,∴∴FGC =∴FCG ,∴FC =FG .∴GN ∴CD ,∴∴GNC =90°.∴∴FCD +∴FDC =∴FGH +∴FDC ,∴∴FCD =∴FGH .∴∴FGH ∴∴FCD ,∴FH =FD =3.∴CH =2,∴CF =GF =5,GD =8,∴∴CGD 的面积为11852022DG CF ⋅=⨯⨯=. 【变式训练3】已知:40MON ∠=︒,OE 平分MON ∠,点A 、B 、C 分别是射线OM 、OE 、ON 上的动点(A 、B 、C 不与点O 重合),连接AC 交射线OE 于点D .设OAC x ∠=︒. (1)如图,若//AB ON ,则①ABO ∠的度数是______;②当BAD ABD ∠=∠时,x =______;当BAD BDA ∠=∠时,x =______.(2)如图,若AB OM ⊥,则是否存在这样的x 的值,使得ADB △中有两个相等的角?若存在,请画出图形,并求出x 的值;若不存在,说明理由.【答案】(1)①20°;②120,60;(2)存在,图形见解析,20x 、35、50、125【详解】解:(1)解:(1)①∴40MON ∠=︒,OE 平分MON ∠,∴20AOB BON ∠=∠=︒, ∴//AB ON ,∴20ABO ∠=︒;②当BAD ABD ∠=∠,∴20BAD ABD ︒∠=∠=,∴180OAC BAD MAB ∠+∠+∠=︒,∴//AB ON ,∴40MAB MON ∠=∠=︒,∴180120OAC MAB BAD ∠=︒-∠-∠=︒,当BAD BDA ∠=∠,20ABO ∠=︒,∴80BAD ∠=︒,∴180OAC BAD MAB ∠+∠+∠=︒,∴//AB ON ,∴40MAB MON ∠=∠=︒,∴18060OAC MAB BAD ∠=︒-∠-∠=︒;故答案为:①20°;②120,60;(2)①当点D 在线段OB 上时,∴OE 是MON ∠的角平分线,∴1202AOB MON ∠=∠=︒, ∴AB OM ⊥,∴90AOB ABO ∠+∠=︒,∴70ABO ∠=︒,若70BAD ABD ∠=∠=︒,则907020OACOAB BAD ,∴20x ; 若()118070552BAD BDA ∠=∠=-︒=︒︒,则905535OAC OAB BAD ,∴35x =;若70ADB ABD ∠=∠=︒,则18027040BAD ∠=-︒⨯=︒︒,904050OAC OAB BAD ,∴50x =;②当点D 在射线BE 上时,因为110ABE ∠=︒,且三角形的内角和为180°, 所以只有1(180110)352BAD BDA ∠=∠=︒-︒=︒, 则9035125OAC OAB BAD ,∴125x =,综上可知,存在这样的x 的值,使得ADB △中有两个相等的角,且20x 、35、50、125.类型三、等腰三角形中的动点问题例、如图,在∴ABC 中,BC =7cm ,AC =24cm ,AB =25cm ,CD 为AB 边上的高,点E 从点B 出发沿直线BC 以2cm/s 的速度移动,过点E 作BC 的垂线交直线CD 于点F . (1)求证:∴A =∴BCD ;(2)问:点E 运动多长时间,CF =AB ?说明理由.【答案】(1)见解析;(2)312或172,理由见解析 【详解】解:(1)22222272425AC BC AB +=+==,∴∴ACB =90°∴CD ∴AB ,∴∴ADC =90°∴∴A +∴ACD =90°,∴BCD +∴ACD =90°,∴∴A =∴BCD ;(2)①点E 在BC 延长线上∴∴A =∴BCD =∴ECF ,∴ACB =∴FEC =90°, CF =AB∴∴ACB ∴∴CEF (AAS ),∴EC =AC =24 ,∴EB =31,∴t =312; ②点E 在CB 延长线上,同理∴ACB ∴∴CE''F'(AAS ),24E C AC '==,∴17E B '=,∴172t =综上所述,t =312或172.【变式训练1】如图1,在∴ABC 中,∴B <∴C ,AD 平分∴BAC ,E 为AD (不与点A ,D 重合)上的一动点,EF ∴BC 于点F .(1)若∴B =40°,∴DEF =20°,求∴C 的度数.(2)求证:∴C ﹣∴B =2∴DEF .(3)如图2,在∴ABC 中,∴B <∴C ,AD 平分∴BAC ,E 为AD 上一点,EF ∴AD 交BC 延长线于点F ,∴ACB =m °,∴B =n °,直接写出∴F 的度数(用含m ,n 的代数式表示).【答案】(1)80︒;(2)证明过程见解析;(3)1122F m n ∠=︒-︒ 【详解】(1)∴EF ∴BC ,∴90EFD ∠=︒,又∴20DEF ∠=︒,∴90902070EDF DEF ∠=︒-∠=︒-︒=︒,又∴EDF B BAD ∠=∠+∠,∴704030BAD EDF B ∠=∠-∠=︒-︒=︒,又∴AD 平分∴BAC ,∴223060BAC BAD ∠=∠=⨯︒=︒,∴180180406080C B BAC ∠=︒-∠-∠=︒-︒-︒=︒;(2)由(1)可知,90EDF DEF B BAD ∠=︒-∠=∠+∠,90DEF B BAD ∠=︒-∠-∠,1902B BAC =︒-∠-∠, ()1901802B C B =︒-∠-︒-∠-∠, 1122C B =∠-∠, ∴2C B DEF ∠-∠=∠;(3)∴AD 平分∴BAC , ∴12BAD BAC ∠=∠,EDF B BAD ∠=∠+∠, ∴EF AD ⊥,∴90FED ∠=︒,∴9090F EDF B BAD ∠=︒-∠=︒-∠-∠,1902B BAC =︒-∠-∠, ()1901802B B ACB =︒-∠-︒-∠-∠, 1122ACB B =∠-∠, 1122m n =︒-︒, ∴1122F m n ∠=︒-︒. 【变式训练2】如图所示,在ABC 中,9cm,12cm,15cm AB BC CA ===,点P 从点A 开始沿AB 边向B 点以每秒1cm 的速度移动,点Q 从点B 沿BC 边向点C 以每秒2cm 的速度移动,如果同时出发,问过3秒时,BPQ 的面积为多少?【答案】218cm 【详解】解:AB =9cm ,BC =12cm ,AC =15cm , ∴AB 2+BC 2=AC 2,∴∴ABC 是直角三角形,过3秒时,9316BP =-⨯=cm ,BQ =2×3=6cm , 11661822BPQ S BP BQ ∴==⨯⨯=2cm , 故过3秒时,∴BPQ 的面积为218cm .。
专题02 全等三角形的性质与判定压轴题八种模型全攻略(解析版)

专题02全等三角形的性质与判定压轴题八种模型全攻略考点一全等三角形的概念考点二利用全等图形求正方形网格中角度之和考点三全等三角形的性质考点四用SSS证明三角形全等考点五用SAS证明三角形全等考点六用ASA证明三角形全等考点七用AAS证明三角形全等考点八用HL证明三角形全等考点一全等三角形的概念例题:(2021·福建·福州三牧中学八年级期中)有下面的说法:①全等三角形的形状相同;②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等.其中正确的说法有() A.1个B.2个C.3个D.4个【答案】D【解析】【分析】先分别验证①②③④的正确性,并数出正确的个数,即可得到答案.【详解】①全等三角形的形状相同,根据图形全等的定义,正确;②全等三角形的对应边相等,根据全等三角形的性质,正确;③全等三角形的对应角相等,根据全等三角形的性质,正确;④全等三角形的周长、面积分别相等,正确;故四个命题都正确,故D为答案.【点睛】本题主要考查了全等的定义、全等三角形图形的性质,即全等三角形对应边相等、对应角相等、面积周长均相等.【变式训练】1.(2022·上海·七年级专题练习)如图,在△ABC和△A′B′C′中,已知AB=A′B′,∠A=∠A′,AC=A′C′,那么△ABC≌△A′B′C′.说理过程如下:把△ABC放到△A′B′C′上,使点A与点A′重合,由于=,所以可以使点B与点B′重合.又因为=,所以射线能落在射线上,这时因为=,所以点与重合.这样△ABC和△A′B′C′重合,即△ABC≌△A′B′C′.【答案】AB,A'B',∠A,∠A′,AC,A'C',AC=A'C',C,C'【解析】【分析】直接利用已知结合全等的定义得出答案.【详解】解:把△ABC放到△A′B′C′上,使点A与点A′重合,由于AB=A'B',所以可以使点B与点B′重合.又因为∠A=∠A′,所以射线AC能落在射线A'C'上,这时因为AC=A'C',所以点C与C'重合.这样△ABC和△A′B′C′重合,即△ABC≌△A′B′C′.故答案为:AB,A'B',∠A,∠A′,AC,A'C',AC=A'C',C,C'.【点睛】本题考查了全等三角形的判定,解答本题的关键是仔细读题,理解填空.考点二利用全等图形求正方形网格中角度之和例题:(2021·全国·八年级专题练习)如图为6个边长相等的正方形的组合图形,则∠1+∠3-∠2=()A.30°B.45°C.60°D.135°【答案】B【解析】【分析】首先利用SAS定理判定△ABC≌△DBE,根据全等三角形的性质可得∠3=∠ACB,再由∠ACB+∠1=∠1+∠3=90°,可得∠1+∠3-∠2.【详解】∵在△ABC 和△DBE 中AB BD A D AC ED ⎧⎪∠∠⎨⎪⎩===,∴△ABC ≌△DBE (SAS ),∴∠3=∠ACB ,∵∠ACB +∠1=90°,∴∠1+∠3=90°,∵∠2=45°∴∠1+∠3-∠2=90°-45°=45°,故选B .【点睛】此题主要考查了全等图形,关键是掌握全等三角形的判定,以及全等三角形对应角相等.【变式训练】1.(2022·山东·济南市槐荫区教育教学研究中心二模)如图,在44⨯的正方形网格中,求αβ+=______度.【答案】45【解析】【分析】连接AB ,根据正方形网格的特征即可求解.【详解】解:如图所示,连接AB∵图中是44⨯的正方形网格∴AD CE =,ADB AEC ∠=∠,DB AE =∴()ADB CEA SAS △≌△∴EAC ABD α∠=∠=,AB AC =∵90ABD BAD ∠+∠=︒∴90EAC BAD ∠+∠=︒,即90CAB ∠=︒∴45ACB ABC ∠=∠=︒∵BD CE ∥∴BCE DBC β==∠∠∵ABC ABD DBC αβ=+=+∠∠∠∴45αβ+=︒故答案为:45.【点睛】本题考查了正方形网格中求角的度数,利用了平行线的性质、同角的余角相等、等腰直角三角形的性质等知识点,解题的关键是能够掌握正方形网格的特征.2.(2020·江苏省灌云高级中学城西分校八年级阶段练习)如图,由4个相同的小正方形组成的格点图中,∠1+∠2+∠3=________度.【答案】135【解析】【分析】首先利用全等三角形的判定和性质求出13∠+∠的值,即可得出答案;【详解】 如图所示,在△ACB 和△DCE 中,AB DE A D AC DC ⎧=⎪∠=∠⎨⎪=⎩,∴()△△ACB DCE SAS ≅,∴3ABE ∠=∠,∴()12313459045135∠+∠+∠=∠+∠+︒=︒+︒=︒;故答案是:135︒.【点睛】本题主要考查了全等图形的应用,准确分析计算是解题的关键.考点三 全等三角形的性质例题:(2021·重庆大足·八年级期末)如图,ABC 和DEF 全等,且A D ∠=∠,AC 对应DE .若6AC =,5BC =,4AB =,则DF 的长为( )A .4B .5C .6D .无法确定【答案】A【解析】【分析】 全等三角形对应边相等,对应角相等,根据题中信息得出对应关系即可.【详解】∵ABC 和DEF 全等,A D ∠=∠,AC 对应DE∴ABC DFE ≅∴AB =DF =4故选:A .【点睛】本题考查了全等三角形的概念及性质,应注意①对应边、对应角是对两个三角形而言的,指两条边、两个角的关系,而对边、对角是指同一个三角形的边和角的位置关系②可以进一步推广到全等三角形对应边上的高相等,对应角的平分线相等,对应边上的中线相等,周长及面积相等③全等三角形有传递性.【变式训练】1.(2022·云南昆明·三模)如图,ABC DEF △≌△,若80,30A F ∠=︒∠=︒,则B 的度数是( )A .80°B .70°C .65°D .60°【答案】B【解析】【分析】 由ABC DEF △≌△根据全等三角形的性质可得30C F ∠=∠=︒,再利用三角形内角和进行求解即可.【详解】ABC DEF ≌,C F ∠=∠∴,30F ∠=︒,30C ∴∠=︒,80,180A A B C ∠=︒∠+∠+∠=︒,18070B A C ∴∠=︒-∠-∠=︒,故选:B .【点睛】本题考查了全等三角形的性质及三角形的内角和定理,熟练掌握知识点是解题的关键.2.(2022·上海·七年级专题练习)如图所示,D ,A ,E 在同一条直线上,BD ⊥DE 于D ,CE ⊥DE 于E ,且△ABD ≌△CAE ,AD =2cm ,BD =4cm ,求(1)DE 的长;(2)∠BAC 的度数.【答案】(1)6cm DE =;(2)90BAC ︒∠=【解析】【分析】(1)根据全等三角形的性质即可得到结论;(2)根据垂直的定义得到∠D =90°,求得∠DBA +∠BAD =90°,根据全等三角形的性质得到∠DBA =∠CAE 等量代换即可得到结论.(1)解:∵△ABD ≌△CAE ,AD =2cm ,BD =4cm ,∴AE =BD =4cm ,∴DE =AD +AE =6cm .(2)∵BD ⊥DE ,∴∠D =90°,∴∠DBA +∠BAD =90°,∵△ABD ≌△CAE ,∴∠DBA =∠CAE∴∠BAD +∠CAE =90°,∴∠BAC =90°.【点睛】本题主要考查了全等三角形的性质,垂直的定义,熟练掌握全等三角形的性质是解题的关键.考点四 用SSS 证明三角形全等例题:(2022·河北·平泉市教育局教研室二模)如图,BD BC =,点E 在BC 上,且BE AC =,DE AB =.(1)求证:ABC EDB ≌;(2)判断AC 和BD 的位置关系,并说明理由.【答案】(1)见解析(2)AC BD ,理由见解析【解析】【分析】(1)运用SSS 证明即可;(2)由(1)得DBE BCA ∠=∠,根据内错角相等,两直线平行可得结论.(1)在ABC ∆和EDB ∆中,BD BC BE AC DE AB =⎧⎪=⎨⎪=⎩,∴ABC EDB ∆≅∆(SSS );(2)AC 和BD 的位置关系是AC BD ,理由如下:∵ABC EDB ∆≅∆∴DBE BCA ∠=∠,∴AC BD .【点睛】本题主要考查了全等三角形的判定与性质,熟练掌握全等三角形的判定定理是解答本题的关键.【变式训练】1.(2021·河南省实验中学七年级期中)如图,在线段BC 上有两点E ,F ,在线段CB 的异侧有两点A ,D ,且满足AB CD =,AE DF =,CE BF =,连接AF;(1)B 与C ∠相等吗?请说明理由.(2)若40B ∠=︒,20∠=DFC °,AF 平分BAE ∠时,求BAF ∠的度数.【答案】(1)B C ∠=∠,理由见解析(2)60︒【解析】【分析】(1)由“SSS ”可证△AEB ≌△DFC ,可得结论;(2)由全等三角形的性质可得∠AEB =∠DFC =20°,可求∠EAB =120°,由角平分线的性质可求解.(1)解:B C ∠=∠,理由如下:∵CE BF =∴BE CF =在AEB △和DFC △中AB CD AE DF BE CF =⎧⎪=⎨⎪=⎩∴()SSS AEB DFC ≌△△∴B C ∠=∠(2)解:∵AEB DFC ≌∴20AEB DFC ∠=∠=︒∴180120EAB B AEB ∠=︒-∠-∠=︒∵AF 平分BAE ∠ ∴1602BAF BAE ∠=∠=︒ 【点睛】本题考查了全等三角形的判定和性质,掌握全等三角形的判定是本题的关键.2.(2022·山东济宁·八年级期末)如图,在四边形ABCD 中,CB AB ⊥于点B ,CD AD ⊥于点D ,点E ,F 分别在AB ,AD 上,AE AF =,CE CF =.(1)若8AE =,6CD =,求四边形AECF 的面积;(2)猜想∠DAB ,∠ECF ,∠DFC 三者之间的数量关系,并证明你的猜想.【答案】(1)48(2)∠DAB +∠ECF =2∠DFC ,证明见解析【解析】【分析】(1)连接AC ,证明△ACE ≌△ACF ,则S △ACE =S △ACF ,根据三角形面积公式求得S △ACF 与S △ACE ,根据S 四边形AECF =S △ACF +S △ACE 求解即可;(2)由△ACE ≌△ACF 可得∠FCA =∠ECA ,∠F AC =∠EAC ,∠AFC =∠AEC ,根据垂直关系,以及三角形的外角性质可得∠DFC +∠BEC =∠FCA +∠F AC +∠ECA +∠EAC =∠DAB +∠ECF .可得∠DAB +∠ECF =2∠DFC(1)解:连接AC ,如图,在△ACE 和△ACF 中AE AF CE CF AC AC =⎧⎪=⎨⎪=⎩∴△ACE ≌△ACF (SSS ).∴S △ACE =S △ACF ,∠F AC =∠EAC .∵CB ⊥AB ,CD ⊥AD ,∴CD =CB =6.∴S △ACF =S △ACE =12AE ·CB =12×8×6=24.∴S 四边形AECF =S △ACF +S △ACE =24+24=48.(2)∠DAB +∠ECF =2∠DFC证明:∵△ACE ≌△ACF ,∴∠FCA =∠ECA ,∠F AC =∠EAC ,∠AFC =∠AEC .∵∠DFC 与∠AFC 互补,∠BEC 与∠AEC 互补,∴∠DFC =∠BEC .∵∠DFC =∠FCA +∠F AC ,∠BEC =∠ECA +∠EAC ,∴∠DFC +∠BEC =∠FCA +∠F AC +∠ECA +∠EAC=∠DAB +∠ECF .∴∠DAB +∠ECF =2∠DFC【点睛】本题考查了三角形全等的性质与判定,三角形的外角的性质,掌握三角形全等的性质与判定是解题的关键.考点五 用SAS 证明三角形全等例题:(2022·福建省福州第十九中学模拟预测)如图,点O 是线段AB 的中点,∥OD BC 且OD BC =.求证:AOD OBC ≌.【答案】见解析【解析】【分析】根据线段中点的定义得到AO BO =,根据平行线的性质得到AOD OBC ∠=∠,根据全等三角形的判定定理即可得到结论.【详解】证明:∵点O 是线段AB 的中点,∴AO BO =,∵∥OD BC ,∴AOD OBC ∠=∠,在△AOD 与△OBC 中,AO BO AOD OBC OD BC =⎧⎪∠=∠⎨⎪=⎩,∴()AOD OBC SAS ≌.【点睛】本题考查了全等三角形的判定,平行线的性质,熟练掌握全等三角形的判定是解题的关键.【变式训练】1.(2022·云南普洱·二模)如图,ABC 和EFD 分别在线段AE 的两侧,点C ,D 在线段AE 上,AC DE =,//AB EF ,.AB EF =求证:BC FD =.【答案】见解析【解析】【分析】利用//AB EF ,得到A E ∠=∠,再用AC DE =,AB EF =,得到ABC ≌EFD △(SAS ),然后用三角形全等的性质得到结论即可.【详解】证明://AB EF ,A E ∴∠=∠,在ABC 和EFD △中AC DE A E AB EF =⎧⎪∠=∠⎨⎪=⎩,ABC ∴≌EFD △(SAS ),BC FD ∴=.【点睛】本题考查三角形全等的判定,平行线的性质,找到三角形全等的条件是解答本题的关键.2.(2022·四川省南充市白塔中学八年级阶段练习)如图,点B 、C 、E 、F 共线,AB =DC ,∠B =∠C ,BF =CE . 求证:△ABE ≌△DCF.【答案】证明见解析;【解析】【分析】根据两边和它们的夹角对应相等的两个三角形全等(简写成“边角边”或“SAS”);即可证明;【详解】证明:∵点B、C、E、F共线,BF=CE,∴BF+EF=CE+EF,∴BE=CF,△ABE和△DCF中:BA=CD,∠ABE=∠DCF,BE=CF,∴△ABE≌△DCF(SAS);【点睛】本题考查了全等三角形的判定;掌握(SAS)的判定条件是解题关键.考点六用ASA证明三角形全等例题:(2022·上海·七年级专题练习)已知:如图,AB⊥BD,ED⊥BD,C是BD上的一点,AC⊥CE,AB =CD,求证:BC=DE.【答案】见解析【解析】【分析】根据直角三角形全等的判定方法,ASA即可判定三角形全等.【详解】证明:∵AB⊥BD,ED⊥BD,AC⊥CE(已知)∴∠ACE=∠B=∠D=90°(垂直的意义)∵∠BCA+∠DCE+∠ACE=180°(平角的意义)∠ACE=90°(已证)∴∠BCA +∠DCE =90°(等式性质)∵∠BCA +∠A +∠B =180°(三角形内角和等于180°)∠B =90°(已证)∴∠BCA +∠A =90°(等式性质)∴∠DCE =∠A (同角的余角相等)在△ABC 和△CDE 中,A DCE AB CD B D ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ABC ≌△CDE (ASA )∴BC =DE (全等三角形对应边相等)【点睛】本题考查了全等三角形的判定和性质;熟练掌握三角形全等的判定定理是解题的关键.【变式训练】1.(2022·广西百色·二模)如图,在△ABC 和△DCB 中,∠A =∠D ,AC 和DB 相交于点O ,OA =OD .(1)AB =DC ;(2)△ABC ≌△DCB .【答案】(1)证明见解析;(2)证明见解析【解析】【分析】(1)证明△ABO ≌△DCO (ASA ),即可得到结论;(2)由△ABO ≌△DCO ,得到OB =OC ,又OA =OD ,得到BD =AC ,又由∠A =∠D ,即可证得结论.(1)证明:在△ABO 与△DCO 中,A D OA ODAOB DOC ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△ABO ≌△DCO (ASA )∴AB =DC ;(2)证明:∵△ABO ≌△DCO ,∴OB =OC ,∵OA =OD ,∴OB +OD =OC +OA ,∴BD =AC ,在△ABC 与△DCB 中,AC BD A D AB DC =⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△DCB (SAS ).【点睛】此题考查了全等三角形的判定和性质,熟练掌握并灵活选择全等三角形的判定方法是解题的关键. 2.(2022·贵州遵义·八年级期末)如图,已知AB DE ∥,ACB D ∠=∠,AC DE =.(1)求证:ABC EAD ≅.(2)若60BCE ∠=︒,求BAD ∠的度数.【答案】(1)见解析(2)60︒【解析】【分析】(1)利用平行线的性质得CAB E ∠=∠,利用“角边角”即可证明ABC EAD ≅;(2)由邻补角的定义求出180120ACB BCE ∠=︒-∠=︒,进而得到120D ∠=︒,再利用两直线平行同旁内角互补求出BAD ∠.由两直线平行得(1)证明:AB DE ,CAB E ∴∠=∠,在ABC 和EAD中,CAB E AC DEACB D ∠=∠⎧⎪=⎨⎪∠=∠⎩, ABC EAD ∴≅.(2)解:60BCE ∠=︒,180ACB BCE ∠+∠=︒,180120ACB BCE ∴∠=︒-∠=︒,120D ACB ∴∠=∠=︒,AB DE ,180∴∠+∠=︒D BAD ,180********BAD D ∴∠=︒-∠=︒-︒=︒.【点睛】本题考查平行线的性质、邻补角的定义、全等三角形的判定等知识,熟练掌握平行线的性质是解题的关键.平行线的性质:两直线平行,内错角相等;两直线平行,同位角相等;两直线平行,同旁内角互补.考点七 用AAS 证明三角形全等例题:(2022·上海·七年级专题练习)如图,已知BE 与CD 相交于点O ,且BO =CO ,∠ADC =∠AEB ,那么△BDO 与△CEO 全等吗?为什么?【答案】△BDO ≌△CEO (AAS );原因见解析【解析】【分析】根据AAS 证明△BDO 与△CEO 全等即可.【详解】解:△BDO 与△CEO 全等;∵∠BDO =180°﹣∠ADC ,∠CEO =180°﹣∠AEB ,又∵∠ADC =∠AEB ,∴∠BDO =∠CEO,∵在△BDO 与△CEO 中,BDO CEO BOD COE BO CO ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BDO ≌△CEO (AAS ).【点睛】本题主要考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS 、SAS 、ASA 、AAS 、HL .注意:AAA 、SSA 不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.【变式训练】1.(2022·福建省福州第一中学模拟预测)如图,已知A ,F ,E ,C 在同一直线上,AB ∥CD ,∠ABE =∠CDF ,AF =CE .求证:AB =CD .【答案】见详解【解析】【分析】根据全等三角形证明△ABE ≌△CDF ,再根据全等三角形的性质解答即可.【详解】证明:∵AB ∥CD ,∴∠ACD =∠CAB ,∵AF=CE ,∴AF+EF=CE+EF ,即AE =FC ,在△ABE 和△CDF 中,ACD CAB ABE CDF AE CF ∠∠⎧⎪∠∠⎨⎪⎩=== ∴△ABE ≌△CDF (AAS ).∴AB =CD .【点睛】此题主要考查了三角形全等的判定及性质,一般证明线段相等先大致判断两个线段所在三角形是否全等,然后再看证明全等的条件有哪些.2.(2022·全国·九年级专题练习)如图,D 是△ABC 的边AB 上一点,CF //AB ,DF 交AC 于E 点,DE=EF .(1)求证:△ADE ≌△CFE ;(2)若AB =5,CF =4,求BD 的长.【答案】(1)证明见解析(2)BD =1【解析】【分析】(1)利用角角边定理判定即可;(2)利用全等三角形对应边相等可得AD 的长,用AB ﹣AD 即可得出结论.(1)证明:∵CF ∥AB ,∴∠ADF =∠F ,∠A =∠ECF .在△ADE 和△CFE 中,A ECF ADE F DE FE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADE ≌△CFE (AAS ).(2)∵△ADE ≌△CFE ,∴AD =CF =4.∴BD =AB ﹣AD =5﹣4=1.【点睛】此题考查了全等三角形的判定及性质,熟记全等三角形的判定定理是解题的关键.考点八 用HL 证明三角形全等例题:(2022·四川省南充市白塔中学八年级阶段练习)如图,AB =CD ,AE ⊥BC 于E ,DF ⊥BC 于F ,且BF =CE.(1)求证AE=DF;(2)判定AB和CD的位置关系,并说明理由.【答案】(1)见解析∥,理由见解析(2)AB CD【解析】【分析】(1)只需要利用HL证明Rt△ABE≌Rt△DCF即可证明结论;∥.(2)根据Rt△ABE≌Rt△DCF即可得到∠B=∠C,即可证明AB CD(1)解:∵BF=CE,∴BF-EF=CE-EF,即BE=CF,∵AE⊥BC,DF⊥BC,∴∠AEB=∠DFC=90°,又∵AB=DC,∴Rt△ABE≌Rt△DCF(HL),∴AE=DF;(2)∥,理由如下:解:AB CD∵Rt△ABE≌Rt△DCF,∴∠B=∠C,∥.∴AB CD【点睛】本题主要考查了全等三角形的性质与判定,平行线的判定,熟知全等三角形的性质与判定条件是解题的关键.【变式训练】1.(2022·安徽安庆·八年级期末)如图,AD,BC相交于点O,AD=BC,∠C=∠D=90°.(1)求证:△ACB ≌△BDA ;(2)若∠CAB =54°,求∠CAO 的度数.【答案】(1)见解析(2)18°【解析】【分析】(1)根据HL 证明Rt △ABC ≌Rt △BAD ;(2)先求出∠ABC 的度数,即可利用全等三角形的性质求出∠BAD 的度数,由此即可得到答案.(1)证明:∵∠D =∠C =90°,∴△ABC 和△BAD 都是直角三角形,在Rt △ABC 和Rt △BAD 中,BC AD AB BA ⎧⎨⎩==, ∴Rt △ABC ≌Rt △BAD (HL );(2)解:在Rt △ABC 中,∠CAB =54°,∠ACB =90°,∴∠ABC =36°,∵Rt △ABC ≌Rt △BAD ,∴∠ABC =∠BAD =36°,∴∠CAO =∠CAB -∠BAD =54°-36°=18°.【点睛】本题主要考查了全等三角形的性质与判定,直角三角形两锐角互余,熟练掌握全等三角形的性质与判定条件是解题的关键.2.(2022·江西·永丰县恩江中学八年级阶段练习)如图,在△ABC 中,BC =AB ,∠ABC =90°,F 为AB 延长线上一点,点E 在BC 上,且AE =CF .(1)求证:Rt △ABE ≌Rt △CBF ;(2)若∠CAB =30°,求∠ACF 的度数.【答案】(1)证明见解析(2)60︒【解析】【分析】(1)由“HL ”可证Rt △ABE ≌Rt △CBF ;(2)由AB =CB ,∠ABC =90°,即可求得∠CAB 与∠ACB 的度数,即可得∠BAE 的度数,又由Rt △ABE ≌Rt △CBF ,即可求得∠BCF 的度数,则由∠ACF =∠BCF +∠ACB 即可求得答案.(1)∵∠ABC =90°,∴∠CBF =∠ABE =90°,在Rt △ABE 和Rt △CBF 中,AE CF AB BC=⎧⎨=⎩ ∴Rt △ABE ≌Rt △CBF (HL );(2)∵AB =BC ,∠ABC =90°,∴∠CAB =∠ACB =45°,∴∠BAE =∠CAB -∠CAE =45°-30°=15°。
人教版八年级上册《全等三角形》解答题压轴题能力提升专练(含详细解析)
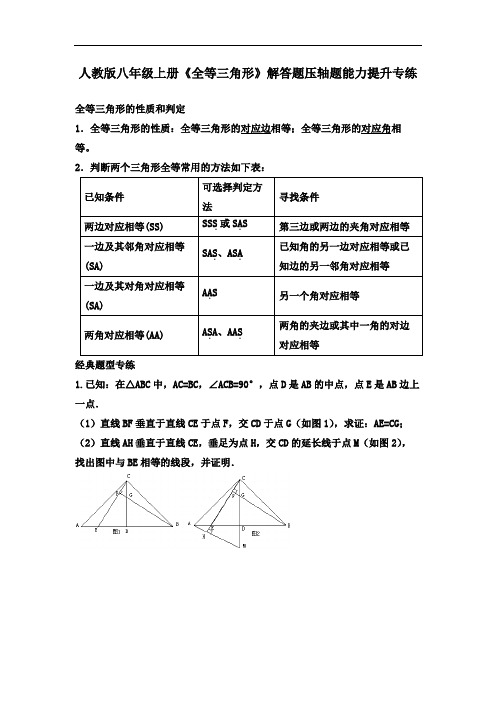
人教版八年级上册《全等三角形》解答题压轴题能力提升专练全等三角形的性质和判定1.全等三角形的性质:全等三角形的对应边相等;全等三角形的对应角相等。
2.判断两个三角形全等常用的方法如下表:经典题型专练1.已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.(1)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.2.如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.3.如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交CD 于点F,BD分别交CE、AE于点G、H.试猜测线段AE和BD的数量和位置关系,并说明理由.4.课外兴趣小组活动时,许老师出示了如下问题:如图1,己知四边形ABCD 中,AC平分∠DAB,∠DAB=60°,∠B与∠D互补,求证:AB+AD=√3AC.小敏反复探索,不得其解.她想,若将四边形ABCD特殊化,看如何解决该问题.(1)特殊情况入手添加条件:“∠B=∠D”,如图2,可证AB+AD=√3AC;(请你完成此证明)(2)解决原来问题受到(1)的启发,在原问题中,添加辅助线:如图3,过C点分别作AB、AD的垂线,垂足分别为E、F.(请你补全证明)5.如图,△ABC中,AD⊥BC于D,点E在AD上,△ADC和△BDE是等腰三角形,EC=5cm,求AB的长.6. CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:①如图1,若∠BCA=90°,∠α=90°,则BE CF;EF |BE﹣AF|(填“>”,“<”或“=”);②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件,使①中的两个结论仍然成立,并证明两个结论成立.(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF 三条线段数量关系的合理猜想(不要求证明).7.在△ABC中,∠ACB=2∠B,如图①,当∠C=90°,AD为∠ABC的角平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD.(1)如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?不需要证明,请直接写出你的猜想:(2)如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.8. 如图,在锐角△ABC中,AB=4√2,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,求BM+MN的最小值.9. 如图,在△ABC中,AB≠AC,∠BAC的外角平分线交直线BC于D,过D作DE⊥AB,DF⊥AC分别交直线AB,AC于E,F,连接EF.(1)求证:EF⊥AD;(2)若DE∥AC,且DE=1,求AD的长.10.如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:(1)FC=AD;(2)AB=BC+AD.11. 如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.(1)求证:DE平分∠BDC;(2)若点M在DE上,且DC=DM,求证:ME=BD.12. 图1、图2中,点C为线段AB上一点,△ACM与△CBN都是等边三角形.(1)如图1,线段AN与线段BM是否相等?证明你的结论;(2)如图2,AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.人教版八年级上册《全等三角形》解答题压轴题能力提升专练(答案版)全等三角形的性质和判定1.全等三角形的性质:全等三角形的对应边相等;全等三角形的对应角相等。
初二三角形所有知识点总结和常考题提高难题压轴题练习(含答案解析)(K12教育文档)

初二三角形所有知识点总结和常考题提高难题压轴题练习(含答案解析)(word 版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(初二三角形所有知识点总结和常考题提高难题压轴题练习(含答案解析)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为初二三角形所有知识点总结和常考题提高难题压轴题练习(含答案解析)(word版可编辑修改)的全部内容。
初二三角形所有知识点总结和常考题知识点:1.三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
2。
三边关系:三角形任意两边的和大于第三边,任意两边的差小于第三边。
3.高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足间的线段叫做三角形的高.4.中线:在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线.5.角平分线:三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.6.三角形的稳定性:三角形的形状是固定的,三角形的这个性质叫三角形的稳定性。
7.多边形:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.8.多边形的内角:多边形相邻两边组成的角叫做它的内角。
9.多边形的外角:多边形的一边与它的邻边的延长线组成的角叫做多边形的外角.10.多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.11.正多边形:在平面内,各个角都相等,各条边都相等的多边形叫正多边形。
12。
平面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做用多边形覆盖平面,13.公式与性质:⑴三角形的内角和:三角形的内角和为180°⑵三角形外角的性质:性质1:三角形的一个外角等于和它不相邻的两个内角的和。
初二三角形压轴题

初二三角形压轴题1. 引言三角形是初中数学中的重要概念之一,也是几何学的基础知识。
在初二阶段,我们已经学习了三角形的性质、分类和计算方法等内容。
本文将围绕初二三角形相关的知识点,给出一道压轴题,并详细解答。
2. 题目描述求解下列问题:已知三角形ABC中,AB=AC,∠BAC=40°,点D是BC边上的一个点,且AD=AC。
连接线段CD,并延长至点E使得CE=CD。
问题1:求证:∠AEC=100°。
问题2:若AD的延长线与BE相交于点F,则求证:∠FEC=30°。
3. 解题过程3.1 问题1的证明首先,根据已知条件可得:AB = AC (AB与AC相等)∠BAC = 40° (∠BAC的度数为40°)AD = AC (AD与AC相等)由于AD = AC,所以△ADC为等腰三角形。
又因为CE = CD,所以△CED也为等腰三角形。
根据等腰三角形的性质可知:∠CAD = ∠CDA (△ADC中底角相等)∠CED = ∠CDE (△CED中底角相等)由于∠BAC = 40°,所以∠CAD = ∠CDA = 20°。
又因为CE = CD,所以∠CED = ∠CDE。
根据三角形内角和定理可得:∠CED + ∠CAD + ∠CDA = 180°代入已知条件,得到:∠CED + 20° + 20° = 180°化简后可得:∠CED = 140°由于CE = CD,所以△CED为等腰三角形。
根据等腰三角形的性质可知:∠AEC = (180° - ∠CED) / 2代入已知条件,得到:∠AEC = (180° - 140°) / 2化简后可得:∠AEC = 40°因此,证明了∠AEC的度数为40°。
3.2 问题2的证明首先,根据已知条件可得:AB = AC (AB与AC相等)AD = AC (AD与AC相等)连接点D和E,并延长线段AD和BE。
初二三角形压轴题

初二三角形压轴题1. 引言初中数学中,三角形是一个非常重要的几何图形,也是很多数学知识的基础。
在初二阶段,学生们已经学习了三角形的基本性质和相关定理,掌握了计算三角形面积、周长、角度等的方法。
为了检验学生对这些知识的掌握程度以及能力的综合运用,老师通常会出一道“三角形压轴题”,要求学生综合运用所学知识解答问题。
本文将围绕初二三角形压轴题展开讨论。
2. 什么是三角形压轴题三角形压轴题是一道要求综合运用所学知识解答的难题,通常涉及到多个概念和定理。
它不仅考察了学生对基本概念和定理的理解和记忆,更重要的是考察他们是否能够将这些知识灵活应用于实际问题中,并且进行推理和证明。
3. 解决三角形压轴题的思路解决三角形压轴题需要有一定的思维方法和解题技巧。
下面将介绍一些常用的解题思路和技巧,帮助学生更好地应对三角形压轴题。
3.1 利用已知条件三角形压轴题通常会给出一些已知条件,比如边长、角度等。
我们可以首先利用这些已知条件进行计算,找出一些有用的信息。
例如,如果已知一个角的度数,可以根据三角形内角和定理计算出其他两个角的度数。
3.2 运用三角形性质三角形有很多重要的性质和定理,比如勾股定理、正弦定理、余弦定理等。
在解决问题时,可以根据具体情况选择合适的性质或定理进行运用。
例如,在计算三角形面积时,可以使用海伦公式或正弦公式。
3.3 运用图形变换图形变换是解决几何问题的重要方法之一。
通过对图形进行平移、旋转、翻转等变换,可以得到新的图形,并从中获得新的信息。
例如,在证明两个三角形全等时,可以通过平移或旋转使它们重合。
3.4 推理和证明在解决三角形压轴题时,通常需要进行推理和证明。
推理是根据已知条件和已有结论得出新的结论,而证明是用严密的逻辑推理来证明一个命题的真实性。
在进行推理和证明时,应该注意逻辑的严密性和合理性。
4. 例题分析下面通过一个例题来进一步说明解决三角形压轴题的思路和方法。
例题:已知三角形ABC中,AB=AC,∠B=50°,∠C=70°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
BAO CE图8此文档下载后即可编辑济南初中数学压轴--------姜姜老师北师大版七年级下三角形综合题归类一、 双等边三角形模型1. (1)如图7,点O 是线段AD 的中点,分别以AO 和DO 为边在线段AD 的同侧作等边三角形OAB 和等边三角形OCD ,连结AC 和BD ,相交于点E ,连结BC .求∠AEB 的大小;(2)如图8,ΔOAB 固定不动,保持ΔOCD 的形状和大小不变,将ΔOCD 绕着点O 旋转(ΔOAB 和ΔOCD 不能重叠),求∠AEB 的大小.同类变式: 如图a ,△ABC 和△CEF 是两个大小不等的等边三角形,且有一个公共顶点C ,连接AF 和BE.(1)线段AF 和BE 有怎样的大小关系?请证明你的结论;(2)将图a 中的△CEF 绕点C 旋转一定的角度,得到图b ,(1)中的结论还成立吗?作出判断并说明理由;(3)若将图a 中的△ABC 绕点C 旋转一定的角度,请你画出一个变换后的图形c(草图即可),(1)中的结论还成立吗?作出判断不必说明理由.图c3. 如图9,若△ABC 和△ADE 为等边三角形,,M N 分别为,EB CD 的中点,易证:CBO D图7AECD BE =,△AMN 是等边三角形.(1)当把△ADE 绕A 点旋转到图10的位置时,CD BE =是否仍然成立?若成立,请证明;若不成立,请说明理由;(2)当△ADE 绕A 点旋转到图11的位置时,△AMN 是否还是等边三角形?若是,请给出证明,若不是,请说明理由.同类变式:已知,如图①所示,在ABC △和ADE △中,AB AC =,AD AE =,BAC DAE ∠=∠,且点B A D ,,在一条直线上,连接BE CD M N ,,,分别为BE CD ,的中点. (1)求证:①BE CD =;②AN AM =;(2)在图①的基础上,将ADE △绕点A 按顺时针方向旋转180o ,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立.CF GEDAH图9 图10 图11CEN DABM图①C AEM BDN 图②4. 如图,四边形ABCD和四边形AEFG均为正方形,连接BG与DE相交于点H.(1)证明:△ABG ≌△ADE ;(2)试猜想∠BHD的度数,并说明理由;(3)将图中正方形ABCD绕点A逆时针旋转(0°<∠BAE<180°),设△ABE 的面积为1S,△ADG的面积为2S,判断1S与2S的大小关系,并给予证明.5.已知:如图,ABC△是等边三角形,过AB边上的点D作DG BC∥,交AC于点G,在GD的延长线上取点E,使DE DB=,连接AE CD,.(1)求证:AGE DAC△≌△;(2)过点E作EF DC∥,交BC于点F,请你连接AF,并判断AEF△是怎样的三角形,试证明你的结论.CGAEDB F二、垂直模型(该模型在基础题和综合题中均为重点考察内容)考点1:利用垂直证明角相等1.如图,△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.求证:(1)AE=CD;(2)若AC=12 cm,求BD的长.2.(西安中考)如图(1), 已知△ABC 中, ∠BAC=900, AB=AC, AE 是过A 的一条直线, 且B 、C 在A 、E 的异侧, BD ⊥AE 于D, CE ⊥AE 于E 。
图(1) 图(2) 图(3) (1)试说明: BD=DE+CE.(2) 若直线AE 绕A 点旋转到图(2)位置时(BD<CE), 其余条件不变, 问BD 与DE 、CE 的关系如何?写结论,并说明理由。
(3) 若直线AE 绕A 点旋转到图(3)位置时(BD>CE), 其余条件不变, 问BD 与DE 、CE 的关系如何? 写出结论,可不说明理由。
3. 直线CD 经过BCA ∠的顶点C ,CA=CB .E 、F 分别是直线CD 上两点,且BEC CFA α∠=∠=∠.(1)若直线CD 经过BCA ∠的内部,且E 、F 在射线CD 上,请解决下面两个问题: ①如图1,若90,90BCA α∠=∠=o o ,则EF AF -(填“>”,“<”或“=”号);②如图2,若0180BCA <∠<o o ,若使①中的结论仍然成立,则 α∠与BCA ∠ 应满足的关系是 ;(2)如图3,若直线CD 经过BCA ∠的外部,BCA α∠=∠,请探究EF 、与BE 、AF 三条线段的数量关系,并给予证明.考点2:利用角相等证明垂直1. 已知BE ,CF 是△ABC 的高,且BP=AC ,CQ=AB ,试确定AP 与AQ 的数量关系和位置关系2. 如图,在等腰R t△ABC 中,∠ACB =90°,D 为BC 的中点,DE ⊥AB ,垂足为E ,过点B 作BF ∥AC 交DE 的延长线于点F ,连接CF . (1)求证:CD=BF ; (2)求证:AD ⊥CF ;(3)连接AF ,试判断△ACF 的形状.拓展巩固:如图9所示,△ABC 是等腰直角三角形,∠ACB =90°,AD 是BC 边上的中线,过C 作AD 的垂线,交AB 于点E ,交AD 于点F ,求证:∠ADC =∠BDE .3. 如图1,已知正方形ABCD 的边CD 在正方形DEFG 的边DE 上,连接AE ,GC . (1)试猜想AE 与GC 有怎样的位置关系,并证明你的结论;(2)将正方形DEFG 绕点D 按顺时针方向旋转,使E 点落在BC 边上,如图2,连接AEABC E F DDAB CE F ADFC EB图1图2 图3B A CE FQ P D ABC DEF 图9和GC .你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.4.如图1,ABC ∆的边BC 在直线l 上,,AC BC ⊥且,AC BC =EFP ∆的边FP 也 在直线l 上,边EF 与边AC 重合,且EF FP =(1) 在图1中,请你通过观察、测量,猜想并写出AB 与AP 所满足的 数量关系和位置关系;(2) 将EFP ∆沿直线l 向左平移到图2的位置时,EP 交AC 于点Q ,连接,AP BQ .猜想并写出BQ 与AP 所满足的数量关系和位置关系,请证明你的猜想; (3)将EFP ∆沿直线l 向左平移到图3的位置时,EP 的延长线交AC 的延长 线于点Q,连结,AP BQ ,你认为(2)中所猜想的BQ 与AP 的数量关系和位置关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.三、 等腰三角形(中考重难点之一) 考点1:等腰三角形性质的应用1. 如图,ABC ∆中,AB AC =,90BAC ∠=︒,D 是BC 中点,ED FD ⊥,ED 与AB 交于E ,FD 与AC交于F .求证:BE AF =,AE CF =.l(1)A B (F) (E) C PAB EC FP Q(2)lAB EC F P l(3)QABCDE F2. 两个全等的含30o,60o角的三角板ADE 和三角板ABC ,如图所示放置,,,E A C 三点在一条直线上,连结BD ,取BD 的中点M ,连结,ME MC .试判断EMC ∆的形状,并说明理由.MED CBA压轴题拓展:(三线合一性质的应用)已知Rt ABC ∆中,AC BC =,90C ∠=︒,D 为AB 边的中点,90EDF ∠=︒,EDF ∠绕D 点旋转,它的两边分别交AC 、CB (或它们的延长线)于E 、F .当EDF ∠绕D 点旋转到DE AC ⊥于E 时(如图1),易证12DEF CEF ABC S S S ∆∆∆+=.当EDF ∠绕D 点旋转到DE 和AC 不垂直时,在图2和图3这两种情况下,上述结论是否成立? 若成立,请给予证明;若不成立,DEF S ∆,CEF S ∆,ABC S ∆又有怎样的数量关系?请写出你的猜想,不需证明.FEDCBA图1AECF BD图2AECFBD图33. 已知:如图,△ABC 中,∠ABC =45°,CD ⊥AB 于D ,BE 平分∠ABC ,且BE ⊥AC 于E ,与CD 相交于点F ,H 是BC 边的中点,连结DH 与BE 相交于点G 。
(1) BF =AC (2) CE =12BF (3)CE 与BC 的大小关系如何。
考点2:等腰直角三角形(45度的联想)1. 如图1,四边形ABCD 是正方形,M 是AB 延长线上一点。
直角三角尺的一条直角边经过点D ,且直角顶点E 在AB 边上滑动(点E 不与点A ,B 重合),另一条直角边与∠CBM的平分线BF 相交于点F.⑴ 如图14―1,当点E 在AB 边的中点位置时:① 通过测量DE ,EF 的长度,猜想DE 与EF 满足的数量关系是; ② 连接点E 与AD 边的中点N ,猜想NE 与BF 满足的数量关系是 ; ③ 请证明你的上述两猜想. ⑵ 如图14―2,当点E 在AB 边上的任意位置时,请你在AD 边上找到一点N, 使得NE=BF ,进而猜想此时DE 与EF 有怎样的数量关系并证明2. 在Rt △ABC 中,AC =BC ,∠ACB =90°,D 是AC 的中点,DG ⊥AC 交AB 于点G.(1)如图1,E 为线段DC 上任意一点,点F 在线段DG 上,且DE=DF ,连结EF 与 CF ,过点F 作FH ⊥FC ,交直线AB 于点H . ①求证:DG=DC②判断FH 与FC 的数量关系并加以证明.(2)若E 为线段DC 的延长线上任意一点,点F 在射线DG 上,(1)中的其他条件不变,借助图2画出图形。
在你所画图形中找出一对全等三角形,并判断你在(1)中得出的结论是否发生改变.AB G HF E DCBA同类变式:(期末考试原题哦) 已知:△ABC 为等边三角形,M 是BC 延长线上一点,直角三角尺的一条直角边经过点A ,且60º角的顶点E 在BC 上滑动,(点E 不与点B 、C 重合),斜边与∠ACM 的平分线CF 交于点F (1)如图(1)当点E 在BC 边得中点位置时 ○1猜想AE 与EF 满足的数量关系是 . ○2连结点E 与AB边得中点N,猜想BE和CF满足的数量关系是 . ○3请证明你的上述猜想;(2)如图(2)当点E在BC边得任意位置时,AE和EF 有怎样的数量关系,并说明你的理由?四、 角平分线问题1. 如图:E 在线段CD 上,EA 、EB 分别平分∠DAB 和∠CBA, ∠AEB=90°,设AD =x ,BC =y ,且,x y 满足2268250x y x y +--+=(1)求AD 和BC 的长;(2)你认为AD 和BC还有什么关系?并验证你的结论;(3)你能求出AB 的长度吗?若能,请写出推理过程;若不能,请说明理由.图(1)E图(2)ACBD E2. 如图①,OP 是∠MON 的平分线,请你利用该图形画一对以OP 所在直线为对称轴的全等三角形。
