全等三角形压轴题分类解析
全等三角形压轴题及其详解

全等三角形压轴题1.在△ABC中,AB=AC,∠BAC=α(0°<α<60°),将线段BC绕点B逆时针旋转60°得到线段BD.(1)如图1,直接写出∠ABD的大小(用含α的式子表示);(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;(3)在(2)的条件下,连接DE,若∠DEC=45°,求α的值.【分析】(1)求出∠ABC的度数,即可求出答案;(2)连接AD,CD,ED,根据旋转性质得出BC=BD,∠DBC=60°,求出∠ABD=∠EBC=30°﹣α,且△BCD为等边三角形,证△ABD≌△ACD,推出∠BAD=∠CAD=∠BAC=α,求出∠BEC=α=∠BAD,证△ABD≌△EBC,推出AB=BE即可;(3)求出∠DCE=90°,△DEC为等腰直角三角形,推出DC=CE=BC,求出∠EBC=15°,得出方程30°﹣α=15°,求出即可.【解答】(1)解:∵AB=AC,∠A=α,∴∠ABC=∠ACB=(180°﹣∠A)=90°﹣α,∵∠ABD=∠ABC﹣∠DBC,∠DBC=60°,即∠ABD=30°﹣α;(2)△ABE是等边三角形,证明:连接AD,CD,ED,∵线段BC绕B逆时针旋转60°得到线段BD,则BC=BD,∠DBC=60°,∵∠ABE=60°,∴∠ABD=60°﹣∠DBE=∠EBC=30°﹣α,且△BCD为等边三角形,在△ABD与△ACD中∴△ABD≌△ACD(SSS),∴∠BAD=∠CAD=∠BAC=α,∵∠BCE=150°,∴∠BEC=180°﹣(30°﹣α)﹣150°=α=∠BAD,在△ABD和△EBC中∴△ABD≌△EBC(AAS),∴AB=BE,∴△ABE是等边三角形;(3)解:∵∠BCD=60°,∠BCE=150°,∴∠DCE=150°﹣60°=90°,∵∠DEC=45°,∴△DEC为等腰直角三角形,∴DC=CE=BC,∵∠BCE=150°,∴∠EBC=(180°﹣150°)=15°,∵∠EBC=30°﹣α=15°,∴α=30°.【点评】本题考查了全等三角形的性质和判定,等边三角形的性质和判定,等腰直角三角形的判定和性质的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的性质是全等三角形的对应边相等,对应角相等.2.已知,Rt△ABC中,∠ACB=90°,∠CAB=30°.分别以AB、AC为边,向三角形外作等边△ABD和等边△ACE.(1)如图1,连接线段BE、CD.求证:BE=CD;(2)如图2,连接DE交AB于点F.求证:F为DE中点.【解答】证明:(1)∵△ABD和△ACE是等边三角形,∴AB=AD,AC=AE,∠DAB=∠EAC=60°,∴∠DAB+∠BAC=∠EAC+∠BAC,即∠DAC=∠BAE,在△DAC和△BAE中,,∴△DAC≌△BAE(SAS),∴DC=BE;(2)如图,作DG∥AE,交AB于点G,由∠EAC=60°,∠CAB=30°得:∠FAE=∠EAC+∠CAB=90°,∴∠DGF=∠FAE=90°,又∵∠ACB=90°,∠CAB=30°,∴∠ABC=60°,又∵△ABD为等边三角形,∠DBG=60°,DB=AB,∴∠DBG=∠ABC=60°,在△DGB和△ACB中,,∴△DGB≌△ACB(AAS),∴DG=AC,又∵△AEC为等边三角形,∴AE=AC,∴DG=AE,在△DGF和△EAF中,,∴△DGF≌△EAF(AAS),∴DF=EF,即F为DE中点.3.在课外小组活动时,小慧拿来一道题(原问题)和小东、小明交流.原问题:如图1,已知△ABC,∠ACB=90°,∠ABC=45°,分别以AB、BC为边向外作△ABD与△BCE,且DA=DB,EB=EC,∠ADB=∠BEC=90°,连接DE交AB于点F.探究线段DF与EF的数量关系.小慧同学的思路是:过点D作DG⊥AB于G,构造全等三角形,通过推理使问题得解.小东同学说:我做过一道类似的题目,不同的是∠ABC=30°,∠ADB=∠BEC=60度.小明同学经过合情推理,提出一个猜想,我们可以把问题推广到一般情况.请你参考小慧同学的思路,探究并解决这三位同学提出的问题:(1)写出原问题中DF与EF的数量关系;(2)如图2,若∠ABC=30°,∠ADB=∠BEC=60°,原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明;(3)如图3,若∠ADB=∠BEC=2∠ABC,原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明.【分析】本题的解题思路是通过构建全等三角形来求解.先根据直角三角形的性质,等边三角形的性质得到一些隐含的条件,然后根据所得的条件来证明所构建的三角形的全等;再根据全等三角形的对应边相等得出DF=EF的猜想.【解答】解:(1)DF=EF.(2)猜想:DF=FE.证明:过点D作DG⊥AB于G,则∠DGB=90度.∵DA=DB,∠ADB=60度.∴AG=BG,△DBA是等边三角形.∴DB=BA.∵∠ACB=90°,∠ABC=30°,∴AC=AB=BG.在Rt△DBG和Rt△BAC中∴Rt△DBG≌Rt△BAC(HL).∴DG=BC.∵BE=EC,∠BEC=60°,∴△EBC是等边三角形.∴BC=BE,∠CBE=60度.∴DG=BE,∠ABE=∠ABC+∠CBE=90°.∵∠DFG=∠EFB,∠DGF=∠EBF,在△DFG和△EFB中∴△DFG≌△EFB(AAS).∴DF=EF.(3)猜想:DF=FE.证法一:过点D作DH⊥AB于H,连接HC,HE,HE交CB于K,则∠DHB=90度.∵DA=DB,∴AH=BH,∠1=∠HDB.∵∠ACB=90°,∴HC=HB.在△HBE和△HCE中∴△HBE≌△HCE(SSS).∴∠2=∠3,∠4=∠BEH.∴HK⊥BC.∴∠BKE=90°.∴∠3+∠ABC=90°∵∠ADB=∠BEC=2∠ABC,∴∠HDB=∠BEH=∠ABC.∴∠DBC=∠DBH+∠ABC=∠DBH+∠HDB=90°,∴∠3=∠DBH∠EBH=∠EBK+∠ABC=∠EBK+∠BEK=90°=∠DHB又∵HB是公共边,所以△DBH≌△EHB∴DH=BE同理可以证明△DHF≌△EBF∴DF=EF.4.已知,点P是Rt△ABC斜边AB上一动点(不与A、B重合),分别过A、B向直线CP作垂线,垂足分别为E、F,Q为斜边AB的中点.(1)如图1,当点P与点Q重合时,AE与BF的位置关系是AE∥BF,QE与QF的数量关系是QE=QF;(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.【分析】(1)根据AAS推出△AEQ≌△BFQ,推出AE=BF即可;(2)延长EQ交BF于D,求出△AEQ≌△BDQ,根据全等三角形的性质得出EQ=QD,根据直角三角形斜边上中点性质得出即可;(3)延长EQ交FB于D,求出△AEQ≌△BDQ,根据全等三角形的性质得出EQ=QD,根据直角三角形斜边上中点性质得出即可.【解答】解:(1)如图1,当点P与点Q重合时,AE与BF的位置关系是AE∥BF,QE与QF的数量关系是AE=BF,理由是:∵Q为AB的中点,∴AQ=BQ,∵AE⊥CQ,BF⊥CQ,∴AE∥BF,∠AEQ=∠BFQ=90°,在△AEQ和△BFQ中∴△AEQ≌△BFQ,∴QE=QF,故答案为:AE∥BF,QE=QF;(2)QE=QF,证明:延长EQ交BF于D,∵由(1)知:AE∥BF,∴∠AEQ=∠BDQ,在△AEQ和△BDQ中∴△AEQ≌△BDQ,∴EQ=DQ,∵∠BFE=90°,∴QE=QF;,(3)当点P在线段BA(或AB)的延长线上时,此时(2)中的结论成立,证明:延长EQ交FB于D,如图3,∵由(1)知:AE∥BF,∴∠AEQ=∠BDQ,在△AEQ和△BDQ中∴△AEQ≌△BDQ,∴EQ=DQ,∵∠BFE=90°,∴QE=QF.5.在△ABC中,AB=AC,∠BAC=60°,点E为直线AC上一点,D为直线BC上的一点,且DA=DE.当点D在线段BC上时,如图①,易证:BD+AB=AE;当点D在线段CB的延长线上时,如图②、图③,猜想线段BD,AB和AE之间又有怎样的数量关系?写出你的猜想,并选择一种情况给予证明.【分析】图②中,论:BD+AE=AB,作EM∥AB交BC于M,先证明△EMC是等边三角形得CE=CM,AE=BM,再证明△ABD≌△DEM,得DB=EM=MC由此可以对称结论.图③中,结论:BD﹣AE=AB,证明方法类似.【解答】解;如图②中,结论:BD+AE=AB.理由:作EM∥AB交BC于M,∵△ABC是等边三角形,∴∠ABC=∠C=∠BAC=60°,AB=BC=AC,∴∠CEM=∠CAB=60°,∠CME=∠CBA=60°,∴△CME是等边三角形,∴CE=CM=EM,∠EMC=60°,∴AE=BM,∵DA=DE,∴∠DAE=∠DEA,∴∠BAC+∠DAB=∠C+∠EDM,∴∠DAB=∠EDM,∵∠ABD=180°﹣∠ABC=120°,∠EMD=180°﹣∠EMC=120°,∴∠ABD=∠DME,在△ABD和△DEM中,,∴△ABD≌△DEM,∴DB=EM=CM,∴DB+AE=CM+BM=BC=AB.如图③中,结论:BD﹣AE=AB.理由:作EM∥AB交BC于M,∵△ABC是等边三角形,∴∠ABC=∠C=∠BAC=60°,AB=BC=AC,∴∠CEM=∠CAB=60°,∠CME=∠CBA=60°,∴△CME是等边三角形,∴CE=CM=EM,∠EMC=∠MEC=60°,∴AE=BM,∵DA=DE,∴∠DAE=∠DEA,∴∠C+∠ADC=∠MEC+∠EDDEM,∴∠ADB=∠DEM,∵∠ABD=180°﹣∠ABC=120°,∠EMD=180°﹣∠EMC=120°,∴∠ABD=∠DME,在△ABD和△DEM中,,∴△ABD≌△DME,∴DB=EM=CM,∴DB﹣AE=CM﹣BM=BC=AB.【点评】本题考查全等三角形的判定和性质、等边三角形的性质、等腰三角形的性质等知识,解题的关键是添加辅助线构造全等三角形,注意形变证明方法基本不变,属于中考常考题型.6.如图1,我们定义:在四边形ABCD中,若AD=BC,且∠ADB+∠BCA=180°,则把四边形ABCD叫做互补等对边四边形.(1)如图2,在等腰△ABE中,AE=BE,四边形ABCD是互补等对边四边形,求证:∠ABD=∠BAC=∠AEB.(2)如图3,在非等腰△ABE中,若四边形ABCD仍是互补等对边四边形,试问∠ABD=∠BAC=∠AEB是否仍然成立?若成立,请加以证明;若不成立,请说明理由.【分析】(1)根据等边对等角可得∠EAB=∠EBA,根据四边形ABCD是互补等对边四边形,可得AD=BC,根据SAS可证△ABD≌△BAC,根据全等三角形的性质可得∠ABD=∠BAC,再根据等腰三角形的性质即可证明;(2)仍然成立;理由如下:如图所示:过点A、B分别作BD的延长线与AC的垂线,垂足分别为G、F,证明△AGD≌△BFC,得到AG=BF,又AB=BA,所以△ABC≌△BAF,得到∠ABD=∠BAC,根据∠ADB+∠BCA=180°,得到∠EDB+∠ECA=180°,进而得到∠AEB+∠DHC=180°,由∠DHC+∠BHC=180°,所以∠AEB=∠BHC.因为∠BHC=∠BAC+∠ABD,∠ABD=∠BAC,所以∠ABD=∠BAC=∠AEB.【解答】解:(1)∵AE=BE,∴∠EAB=∠EBA,∵四边形ABCD是互补等对边四边形,∴AD=BC,在△ABD和△BAC中,,∴△ABD≌△BAC(SAS),∴∠ADB=∠BCA,又∵∠ADB+∠BCA=180°,∴∠ADB=∠BCA=90°,在△ABE中,∵∠EAB=∠EBA==90°﹣∠AEB,∴∠ABD=90°﹣∠EAB=90°﹣(90°﹣∠AEB)=∠AEB,同理:∠BAC=∠AEB,∴∠ABD=∠BAC=∠AEB;(2)仍然成立;理由如下:如图③所示:过点A、B分别作BD的延长线与AC的垂线,垂足分别为G、F,∵四边形ABCD是互补等对边四边形,∴AD=BC,∠ADB+∠BCA=180°,又∠ADB+ADG=180°,∴∠BCA=∠ADC,又∵AG⊥BD,BF⊥AC,∴∠AGD=∠BFC=90°,在△AGD和△BFC中,∴△AGD≌△BFC,∴AG=BF,在△ABG和△BAF中,∴△ABG≌△BAF,∴∠ABD=∠BAC,∵∠ADB+∠BCA=180°,∴∠EDB+∠ECA=180°,∴∠AEB+∠DHC=180°,∵∠DHC+∠BHC=180°,∴∠AEB=∠BHC.∵∠BHC=∠BAC+∠ABD,∠ABD=∠BAC,∴∠ABD=∠BAC=∠AEB.【点评】本题考查了等腰三角形的性质、全等三角形的判定与性质,解决本题的关键是根据SAS证明△ABD≌△BAC.7.已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作等边△ADE(顶点A、D、E按逆时针方向排列),连接CE.(1)如图1,当点D在边BC上时,求证:①BD=CE,②AC=CE+CD;(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CE+CD是否成立?若不成立,请写出AC、CE、CD之间存在的数量关系,并说明理由;(3)如图3,当点D在边BC的反向延长线上且其他条件不变时,补全图形,并直接写出AC、CE、CD之间存在的数量关系.【分析】(1)根据等边三角形的性质及等式的性质就可以得出△ABD≌△ACE,从而得出结论;(2)根据等边三角形的性质及等式的性质就可以得出△ABD≌△ACE,就可以得出BD=CE,就可以得出AC=CE﹣CD;(3)先根据条件画出图形,根据等边三角形的性质及等式的性质就可以得出△ABD≌△ACE,就可以得出BD=CE,就可以得出AC=CD﹣CE.【解答】解:(1)∵△ABC和△ADE都是等边三角形,∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°.∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,即∠BAD=∠CAE.在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴BD=CE.∵BC=BD+CD,AC=BC,∴AC=CE+CD;(2)AC=CE+CD不成立,AC、CE、CD之间存在的数量关系是:AC=CE﹣CD.理由:∵△ABC和△ADE都是等边三角形,∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°.∴∠BAC+∠CAD=∠DAE+∠CAD,∴∠BAD=∠CAE在△ABD和△ACE中,∴△ABD≌△ACE(SAS)∴BD=CE∴CE﹣CD=BD﹣CD=BC=AC,∴AC=CE﹣CD;(3)补全图形(如图)AC、CE、CD之间存在的数量关系是:AC=CD﹣CE.理由:∵△ABC和△ADE都是等边三角形,∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°.∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,∴∠BAD=∠CAE在△ABD和△ACE中,∴△ABD≌△ACE(SAS)∴BD=CE.∵BC=CD﹣BD,∴BC=CD﹣CE,∴AC=CD﹣CE.【点评】本题考查了等边三角形的性质的运用,等式的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.8.如图,已知△ABC,分别以AB、AC为边作△ABD和△ACE,且AD=AB,AC=AE,∠DAB=∠CAE,连接DC与BE.G、F分别是DC与BE的中点.(1)求证:DC=BE;(2)当∠DAB=80°,求∠AFG的度数;(3)若∠DAB=α,则∠AFG与α的数量关系是.【分析】(1)根据等式的性质就可以得出∠DAC=∠BAE.就可以得出△ADC≌△ABE就可以得出DC=BE;(2)连接AG,根据条件就可以得出△ADG≌△ABF,就可以求出AG=AF,∠GAF=∠DAB,由等腰三角形的性质就可以求出∠AFG的值,(3)连接AG,根据条件就可以得出△ADG≌△ABF,就可以求出AG=AF,∠GAF=∠DAB,由等腰三角形的性质就可以表示∠AFG与a的关系.【解答】解:(1)∵∠DAB=∠CAE,∴∠DAB+∠BAC=∠CAE+∠BAC,∴∠DAC=∠BAE.在△ADC和△ABE中,∴△ADC≌△ABE(SAS),∴DC=BE;(2)连接AG.∵△ADC≌△ABE,∴∠ADC=∠ABE.AD=AB.∵G、F分别是DC与BE的中点,∴DG=DC,BF=BE,∴DG=BF.在△ADG和△ABF中,∴△ADG≌△ABF(SAS),∴AG=AF,∠DAG=∠BAF,∴∠AGF=∠AFG,∠DAG﹣∠BAG=∠BAF﹣∠BAG,∴∠DAB=∠GAF.∵∠DAB=80°,∴∠GAF=80°.∵∠GAF+∠AFG+∠AGF=180°,∴∠AFG=50°.答:∠AFG=50°;(3)∵∠DAB=α,∴∠GAF=α.∵∠GAF+∠AFG+∠AGF=180°,∴α+2∠AFG=180°,∴∠AFG=90°﹣α.故答案为:∠AFG=50°,90°﹣α.【点评】本题考查了全等三角形的判定及性质的运用,等式的性质的运用,等腰三角形的性质的运用,三角形内角和定理的运用,解答时证明三角形全等是关键.9.△ABC是等边三角形,点D、E分别在边AB、BC上,CD、AE交于点F,∠AFD=60°.(1)如图1,求证:BD=CE;(2)如图2,FG为△AFC的角平分线,点H在FG的延长线上,HG=CD,连接HA、HC,求证:∠AHC=60°;(3)在(2)的条件下,若AD=2BD,FH=9,求AF长.【分析】(1)根据等边三角形的性质得出AB=BC,∠BAC=∠C=∠ABE=60°,根据SAS推出△ABE≌△BCD,即可证得结论;(2)根据角平分线的性质定理证得CM=CN,利用∠CEM=∠ACE+∠CAE=60°+∠CAE,∠CGN=∠AFH+∠CAE=60°+∠CAE,得出∠CEM=∠CGN,然后根据AAS证得△ECM≌△GCN,得出CG=CE,EM=GN,∠ECM=∠GCN,进而证得△AMC≌△HNC,得出∠ACM=∠HCN,AC=HC,从而证得△ACH是等边三角形,证得∠AHC=60°;(3)在FH上截取FK=FC,得出△FCK是等边三角形,进一步得出FC=KC=FK,∠ACF=∠HCK,证得△AFC≌△HKC得出AF=HK,从而得到HF=AF+FC=9,由AD=2BD 可知AG=2CG,再由=,根据等高三角形面积比等于底的比得出===2,再由AF+FC=9求得.【解答】解:(1)如图1,∵△ABC是等边三角形,∴∠B=∠ACE=60°BC=AC,∵∠AFD=∠CAE+∠ACD=60°∠BCD+∠ACD=∠ACB=60°,∴∠BCD=∠CAE,在△ABE和△BCD中,∴△ABE≌△BCD(ASA),∴BD=CE;(2)如图2,作CM⊥AE交AE的延长线于M,作CN⊥HF于N,∵∠EFC=∠AFD=60°∴∠AFC=120°,∵FG为△AFC的角平分线,∴∠CFH=∠AFH=60°,∴∠CFH=∠CFE=60°,∵CM⊥AE,CN⊥HF,∴CM=CN,∵∠CEM=∠ACE+∠CAE=60°+∠CAE,∠CGN=∠AFH+∠CAE=60°+∠CAE,∴∠CEM=∠CGN,在△ECM和△GCN中∴△ECM≌△GCN(AAS),∴CE=CG,EM=GN,∠ECM=∠GCN,∴∠MCN=∠ECG=60°,∵△ABE≌△BCD,∵AE=CD,∵HG=CD,∴AE=HG,∴AE+EM=HG+GN,即AM=HN,在△AMC和△HNC中∴△AMC≌△HNC(SAS),∴∠ACM=∠HCN,AC=HC,∴∠ACM﹣∠ECM=∠HCN﹣∠GCN,即∠ACE=∠HCG=60°,∴△ACH是等边三角形,∴∠AHC=60°;(3)如图3,在FH上截取FK=FC,∵∠HFC=60°,∴△FCK是等边三角形,∴∠FKC=60°,FC=KC=FK,∵∠ACH=60°,∴∠ACF=∠HCK,在△AFC和△HKC中∴△AFC≌△HKC(SAS),∴AF=HK,∴HF=AF+FC=9,∵AD=2BD,BD=CE=CG,AB=AC,∴AG=2CG,∴==,作GW⊥AE于W,GQ⊥DC于Q,∵FG为△AFC的角平分线,∴GW=GQ,∵===,∴AF=2CF,∴AF=6.【点评】本题考查了全等三角形的判定和性质,等边三角形的判定和性质,角平分线的性质,找出辅助线根据全等三角形和等边三角形是解题的关键.10.如图1,△ABE是等腰三角形,AB=AE,∠BAE=45°,过点B作BC⊥AE于点C,在BC上截取CD=CE,连接AD、DE并延长AD交BE于点P;(1)求证:AD=BE;(2)试说明AD平分∠BAE;(3)如图2,将△CDE绕着点C旋转一定的角度,那么AD与BE的位置关系是否发生变化,说明理由.【分析】(1)利用SAS证明△BCE≌△ACD,根据全等三角形的对应边相等得到AD=BE.(2)根据△BCE≌△ACD,得到∠EBC=∠DAC,由∠BDP=∠ADC,得到∠BPD=∠DCA=90°,利用等腰三角形的三线合一,即可得到AD平分∠BAE;(3)AD⊥BE不发生变化.由△BCE≌△ACD,得到∠EBC=∠DAC,由对顶角相等得到∠BFP=∠ACF,根据三角形内角和为180°,所以∠BPF=∠ACF=90°,即AD⊥BE.【解答】解:(1)∵BC⊥AE,∠BAE=45°,∴∠CBA=∠CAB,∴BC=CA,在△BCE和△ACD中,∴△BCE≌△ACD,∴AD=BE.(2)∵△BCE≌△ACD,∴∠EBC=∠DAC,∵∠BDP=∠ADC,∴∠BPD=∠DCA=90°,∵AB=AE,∴AD平分∠BAE.(3)AD⊥BE不发生变化.如图2,∵△BCE≌△ACD,∴∠EBC=∠DAC,∵∠BFP=∠ACF,∴∠BPF=∠ACF=90°,∴AD⊥BE.【点评】本题考查了全等三角形的性质定理与判定定理,解决本题的关键是证明△BCE≌△ACD.11.情境观察:如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.①写出图1中所有的全等三角形△ABE≌△ACE,△ADF≌△CDB;②线段AF与线段CE问题探究:如图2,△ABC中,∠BAC=45°,BAC,AD⊥CD,垂足为D,AD与BC交于点E.求证:AE=2CD.拓展延伸:如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC=∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明.【分析】情境观察:①由全等三角形的判定方法容易得出结果;②由全等三角形的性质即可得出结论;问题探究:延长AB、CD交于点G,由ASA证明△ADC≌△ADG,得出对应边相等CD=GD,即CG=2CD,证出∠BAE=∠BCG,由ASA证明△ADC≌△CBG,得出AE=CG=2CD即可.拓展延伸:作DG⊥BC交CE的延长线于G,同上证明三角形全等,得出DF=CG即可.【解答】情境观察:解:①图1中所有的全等三角形为△ABE≌△ACE,△ADF≌△CDB;故答案为:△ABE≌△ACE,△ADF≌△CDB②线段AF与线段CE的数量关系是:AF=2CE;故答案为:AF=2CE.问题探究:证明:延长AB、CD交于点G,如图2所示:∵AD平分∠BAC,∴∠CAD=∠GAD,∵AD⊥CD,∴∠ADC=∠ADG=90°,在△ADC和△ADG中,,∴△ADC≌△ADG(ASA),∴CD=GD,即CG=2CD,∵∠BAC=45°,AB=BC,∴∠ABC=90°,∴∠CBG=90°,∴∠G+∠BCG=90°,∵∠G+∠BAE=90°,∴∠BAE=∠BCG,在△ABE和△CBG中,,∴△ADC≌△CBG中(ASA),∴AE=CG=2CD.拓展延伸:解:作DG⊥BC交CE的延长线于G,如图3所示.【点评】本题考查了全等三角形的判定与性质、等腰三角形的性质等知识;熟练掌握等腰三角形的性质,证明三角形全等是解决问题的关键.12.如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.(1)求证:△ABQ≌△CAP;(2)如图1,当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说理由;若不变,求出它的度数.(3)如图2,若点P、Q在分别运动到点B和点C后,继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC=120度.(直接填写度数)【分析】(1)根据等边三角形的性质,利用SAS证明△ABQ≌△CAP;(2)由△ABQ≌△CAP根据全等三角形的性质可得∠BAQ=∠ACP,从而得到∠QMC=60°;(3)由△ABQ≌△CAP根据全等三角形的性质可得∠BAQ=∠ACP,从而得到∠QMC=120°.【解答】(1)证明:∵△ABC是等边三角形∴∠ABQ=∠CAP,AB=CA,又∵点P、Q运动速度相同,∴AP=BQ,在△ABQ与△CAP中,,∴△ABQ≌△CAP(SAS);(2)解:点P、Q在运动的过程中,∠QMC不变.理由:∵△ABQ≌△CAP,∴∠BAQ=∠ACP,∵∠QMC=∠ACP+∠MAC,∴∠QMC=∠BAQ+∠MAC=∠BAC=60°;(3)解:∵△ABQ≌△CAP,∴∠BAQ=∠ACP,∵∠QMC=∠BAQ+∠APM,∴∠QMC=∠ACP+∠APM=180°﹣∠PAC=180°﹣60°=120°.故答案为:120°.【点评】本题考查了等边三角形的性质,全等三角形的判定与性质,熟练掌握全等三角形的判定是解题的关键.13.如图,在等腰Rt△ABC中,∠C=90°,D是斜边上AB上任一点,AE⊥CD于E,BF⊥CD交CD的延长线于F,CH⊥AB于H点,交AE于G.(1)试说明AH=BH(2)求证:BD=CG.(3)探索AE与EF、BF之间的数量关系.【分析】(1)根据等腰三角形的三线合一证明;(2)证明△ACG≌△CBD,根据全等三角形的性质证明;(3)证明△ACE≌△CBF即可.【解答】证明:(1)∵AC=BC,CH⊥AB,∴AH=BH;(2)∵ABC为等腰直角三角形,CH⊥AB,∴∠ACG=45°,∵∠CAG+∠ACE=90°,∠BCF+∠ACE=90°,∴∠CAG=∠BCF,在△ACG和△CBD中,,∴△ACG≌△CBD(ASA),∴BD=CG;(3)AE=EF+BF,理由如下:在△ACE和△CBF中,,∴△ACE≌△CBF,∴AE=CF,CE=BF,∴AE=CF=CE+EF=BF+EF.【点评】本题考查的是全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理是解题的关键.14.在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,△ABD和△AFD关于直线AD对称,∠FAC的平分线交BC于点G,连接FG.(1)求∠DFG的度数;(2)设∠BAD=θ,①当θ为何值时,△DFG为等腰三角形;②△DFG有可能是直角三角形吗?若有,请求出相应的θ值;若没有,请说明理由.【分析】(1)由轴对称可以得出△ADB≌△ADF,就可以得出∠B=∠AFD,AB=AF,在证明△AGF≌△AGC就可以得出∠AFG=∠C,就可以求出∠DFG的值;(2)①当GD=GF时,就可以得出∠GDF═80°,根据∠ADG=40+θ,就有40°+80°+40°+θ+θ=180°就可以求出结论;当DF=GF时,就可以得出∠GDF=50°,就有40°+50°+40°+2θ=180°,当DF=DG时,∠GDF=20°,就有40°+20°+40°+2θ=180°,从而求出结论;②有条件可以得出∠DFG=80°,当∠GDF=90°时,就有40°+90°+40°+2θ=180°就可以求出结论,当∠DGF=90°时,就有∠GDF=10°,得出40°+10°+40°+2θ=180°求出结论.【解答】解:(1)∵AB=AC,∠BAC=100°,∴∠B=∠C=40°.∵△ABD和△AFD关于直线AD对称,∴△ADB≌△ADF,∴∠B=∠AFD=40°,AB=AF∠BAD=∠FAD=θ,∴AF=AC.∵AG平分∠FAC,∴∠FAG=∠CAG.在△AGF和△AGC中,,∴△AGF≌△AGC(SAS),∴∠AFG=∠C.∵∠DFG=∠AFD+∠AFG,∴∠DFG=∠B+∠C=40°+40°=80°.答:∠DFG的度数为80°;(2)①当GD=GF时,∴∠GDF=∠GFD=80°.∵∠ADG=40°+θ,∴40°+80°+40°+θ+θ=180°,∴θ=10°.当DF=GF时,∴∠FDG=∠FGD.∵∠DFG=80°,∴∠FDG=∠FGD=50°.∴40°+50°+40°+2θ=180°,∴θ=25°.当DF=DG时,∴∠DFG=∠DGF=80°,∴∠GDF=20°,∴40°+20°+40°+2θ=180°,∴θ=40°.∴当θ=10°,25°或40°时,△DFG为等腰三角形;②当∠GDF=90°时,∵∠DFG=80°,∴40°+90°+40°+2θ=180°,∴θ=5°.当∠DGF=90°时,∵∠DFG=80°,∴∠GDF=10°,∴40°+10°+40°+2θ=180°,∴θ=45°∴当θ=5°或45°时,△DFG为直角三角形.【点评】本题考查了轴对称的性质的运用,全等三角形的判定及性质的运用,等腰三角形的判定及性质的运用,直角三角形的判定及性质的运用,解答时证明三角形的全等是关键.15.如图,在△ABC中,∠BAC=90°,AB=AC,点D是AB的中点,连接CD,过B 作BE⊥CD交CD的延长线于点E,连接AE,过A作AF⊥AE交CD于点F.(1)求证:AE=AF;(2)求证:CD=2BE+DE.【分析】(1)通过证△AEB≌△AFC(SAS),得到AE=AF;(2)如图,过点A作AG⊥EC,垂足为G,通过证△BED≌△AGD(AAS),得到ED=GD,BE=AG,易证CF=BE=AG=GF.因为CD=DG+GF+FC,所以CD=DE+BE+BE,故CD=2BE+DE.【解答】证明:(1)如图,∵∠BAC=90°,AF⊥AE,∴∠EAB+∠BAF=∠BAF+∠FAC=90°,∴∠EAB=∠FAC,∵BE⊥CD,∴∠BEC=90°,∴∠EBD+∠EDB=∠ADC+∠ACD=90°,∵∠EDB=∠ADC,∴∠EBA=∠ACF,∴在△AEB与△AFC中,,∴△AEB≌△AFC(ASA),∴AE=AF;(2)如图,过点A作AG⊥EC,垂足为G.∵AG⊥EC,BE⊥CE,∴∠BED=∠AGD=90°,∵点D是AB的中点,∴BD=AD.∴在△BED与△AGD中,,∴△BED≌△AGD(AAS),∴ED=GD,BE=AG,∵AE=AF∴∠AEF=∠AFE=45°∴∠FAG=45°∴∠GAF=∠GFA,∴GA=GF,∴CF=BE=AG=GF,∵CD=DG+GF+FC,∴CD=DE+BE+BE,∴CD=2BE+DE.【点评】本题考查了全等三角形的判定与性质.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.16.如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.(1)求证:BE=CF;(2)在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.求证:①ME⊥BC;②CM平分∠ACE.【分析】(1)根据等腰直角三角形的性质求出∠B=∠ACB=45°,再求出∠ACF=45°,从而得到∠B=∠ACF,根据同角的余角相等求出∠BAE=∠CAF,然后利用“角边角”证明△ABE和△ACF全等,根据全等三角形对应边相等证明即可;(2)①过点E作EH⊥AB于H,求出△BEH是等腰直角三角形,然后求出HE=BH,再根据角平分线上的点到角的两边距离相等可得DE=HE,然后求出HE=HM,从而得到△HEM是等腰直角三角形,再根据等腰直角三角形的性质求解即可;②求出∠CAE=∠CEA=67.5°,根据等角对等边可得AC=CE,再利用“HL”证明Rt△ACM和Rt△ECM全等即可得到结论.【解答】证明:(1)∵∠BAC=90°,AB=AC,∴∠B=∠ACB=45°,∵FC⊥BC,∴∠BCF=90°,∴∠ACF=90°﹣45°=45°,∴∠B=∠ACF,∵∠BAC=90°,FA⊥AE,∴∠BAE+∠CAE=90°,∠CAF+∠CAE=90°,∴∠BAE=∠CAF,在△ABE和△ACF中,,∴△ABE≌△ACF(ASA),∴BE=CF;(2)①如图,过点E作EH⊥AB于H,则△BEH是等腰直角三角形,∴HE=BH,∠BEH=45°,∵AE平分∠BAD,AD⊥BC,∴DE=HE,∴DE=BH=HE,∵BM=2DE,∴HE=HM,∴△HEM是等腰直角三角形,∴∠MEH=45°,∴∠BEM=45°+45°=90°,∴ME⊥BC;②由题意得,∠CAE=45°+×45°=67.5°,∴∠CEA=180°﹣45°﹣67.5°=67.5°,∴∠CAE=∠CEA=67.5°,∴AC=CE,在Rt△ACM和Rt△ECM中,,∴Rt△ACM≌Rt△ECM(HL),∴∠ACM=∠ECM,∴CM平分∠ACE.【点评】本题考查了全等三角形的判定与性质,等腰直角三角形的判定与性质,角平分线上的点到角的两边距离相等的性质,熟记性质并作辅助线构造出等腰直角三角形和全等三角形是解题的关键,难点在于最后一问根据角的度数得到相等的角.17.如图,在△ABC中,已知∠ABC=45°,过点C作CD⊥AB于点D,过点B作BM ⊥AC于点M,CD与BM相交于点E,且点E是CD的中点,连接MD,过点D作DN⊥MD,交BM于点N.(1)求证:△DBN≌△DCM;(2)请探究线段NE、ME、CM之间的数量关系,并证明你的结论.【分析】(1)根据两角夹边相等的两个三角形全等即可证明.(2)结论:NE﹣ME=CM.作DF⊥MN于点F,由(1)△DBN≌△DCM 可得DM=DN,由△DEF≌△CEM,推出ME=EF,CM=DF,由此即可证明.【解答】(1)证明:∵∠ABC=45°,CD⊥AB,∴∠ABC=∠DCB=45°,∴BD=DC,∵∠BDC=∠MDN=90°,∴∠BDN=∠CDM,∵CD⊥AB,BM⊥AC,∴∠ABM=90°﹣∠A=∠ACD,在△DBN和△DCM中,,∴△DBN≌△DCM.(2)结论:NE﹣ME=CM.证明:由(1)△DBN≌△DCM 可得DM=DN.作DF⊥MN于点F,又ND⊥MD,∴DF=FN,在△DEF和△CEM中,,∴△DEF≌△CEM,∴ME=EF,CM=DF,∴CM=DF=FN=NE﹣FE=NE﹣ME.【点评】本题考查全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,属于中考常考题型.18.问题情境:如图①,在△ABD与△CAE中,BD=AE,∠DBA=∠EAC,AB=AC,易证:△ABD≌△CAE.(不需要证明)特例探究:如图②,在等边△ABC中,点D、E分别在边BC、AB上,且BD=AE,AD与CE交于点F.求证:△ABD≌△CAE.归纳证明:如图③,在等边△ABC中,点D、E分别在边CB、BA的延长线上,且BD=AE.△ABD与△CAE是否全等?如果全等,请证明;如果不全等,请说明理由.拓展应用:如图④,在等腰三角形中,AB=AC,点O是AB边的垂直平分线与AC 的交点,点D、E分别在OB、BA的延长线上.若BD=AE,∠BAC=50°,∠AEC=32°,求∠BAD的度数.【分析】特例探究:利用等边三角形的三条边都相等、三个内角都是60°的性质推知AB=AC,∠DBA=∠EAC=60°,然后结合已知条件BD=AE,利用全等三角形的判定定理SAS证得△ABD≌△CAE.归纳证明:△ABD与△CAE全等.利用等边三角形的三条边都相等、三个内角都是60°的性质以及三角形外角定理推知AB=AC,∠DBA=∠EAC=120°,然后结合已知条件BD=AE,利用全等三角形的判定定理SAS证得△ABD≌△CAE;拓展应用:利用全等三角形(△ABD≌△CAE)的对应角∠BDA=∠AEC=32°,然后由三角形的外角定理求得∠BAD的度数.【解答】特例探究:证明:∵△ABC是等边三角形,∴AB=AC,∠DBA=∠EAC=60°,在△ABD与△CAE中,,∴△ABD≌△CAE(SAS);解:归纳证明:△ABD与△CAE全等.理由如下:∵在等边△ABC中,AB=AC,∠ABC=∠BAC=60°,∴∠DBA=∠EAC=120°.在△ABD与△CAE中,,∴△ABD≌△CAE(SAS);拓展应用:∵点O在AB的垂直平分线上,∴OA=OB,∴∠OBA=∠BAC=50°,∴∠EAC=∠DBC.在△ABD与△CAE中,,∴△ABD≌△CAE(SAS),∴∠BDA=∠AEC=32°,∴∠BAD=∠OBA﹣∠BDA=18°.【点评】本题考查了全等三角形的判定与性质,等边三角形的性质,线段垂直平分线的性质等知识点.在证明两个三角形全等时,一定要找准对应角和对应边.19.情境创设:如图1,两块全等的直角三角板,△ABC≌△DEF,且∠C=∠F=90°,现如图放置,则∠ABE=90°.问题探究:如图2,△ABC中,AH⊥BC于H,以A为直角顶点,分别以AB、AC为直角边,向△ABC形外作等腰直角△ABE和等腰直角△ACF,过点E、F作射线HA的垂线,垂足分别为M、N,试探究线段EM和FN之间的数量关系,并说明理由.拓展延伸:如图3,△ABC中,AH⊥BC于H,以A为直角顶点,分别以AB、AC为一边,向△ABC形外作正方形ABME和正方形ACNF,连接E、F交射线HA于G点,试探究线段EG和FG之间的数量关系,并说明理由.【分析】(1)求出∠A=∠EDF,∠A+∠ABC=90°,推出∠EDF+∠ADC=90°,求出∠ADE的度数即可;(2)根据全等三角形的判定得出△EAM≌△ABH,进而求出EM=AH.同理AH=FN,因而EM=FN.(3)与(2)证法类似求出EG=FG,求出△EPG≌△FQG即可.【解答】解:(1)∵△ABC≌△DEF,∴∠A=∠EDF,∵∠C=90°,∴∠A+∠ABC=90°,∴∠EDF+∠ADC=90°,∴∠ADE=180°﹣90°=90°,故答案为:90;(2)解:EM=FN,如图2,理由如下:∵Rt△ABE是等腰三角形,∴EA=BA,∠BAE=90°,∴∠BAH+∠MAE=90°,∵AH⊥BC,EM⊥AH,∴∠AME=∠AHB=90°,∴∠ABH+∠BAH=90°,∴∠ABH=∠MAE,在△EAM与△ABH中∴△EAM≌△ABH(AAS),∴EM=AH.同理AH=FN.∴EM=FN;(3)解:EG=FG,如图3,作EP⊥HG,FQ⊥HG,垂足分别为P、Q,由(2)可得EP=FQ,∵EP⊥HG,FQ⊥HG,∴∠EPG=∠FQG=90°,在△EPG和△FQG中∵,∴△EPG≌△FQG,∴EG=FG.【点评】本题考查了全等三角形的性质和判定,注意:①全等三角形的对应角相等,对应边相等,②全等三角形的判定定理有SAS,ASA,AAS,SSS.。
专题03 全等三角形的六种模型全梳理(解析版)-2024年常考压轴题攻略(8年级上册人教版)

专题03全等三角形的六种模型全梳理几何探究类问题一直属于考试压轴题范围,在三角形这一章,压轴题主要考查是证明三角形各种模型,或证明线段数量关系等,接来下我们针对其做出详细分析与梳理。
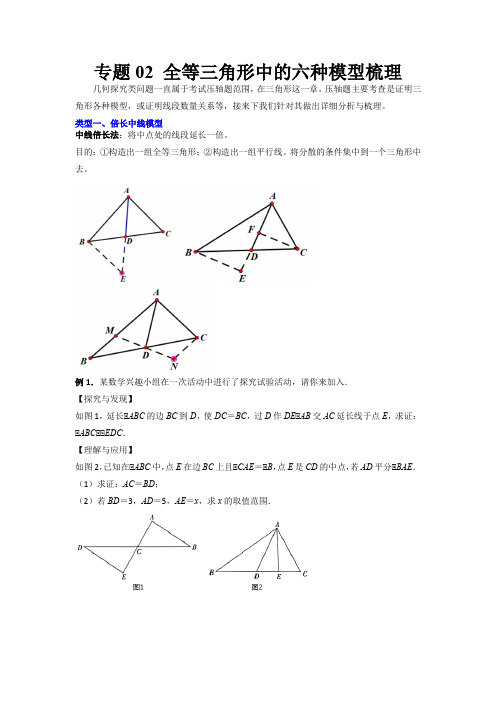
类型一、倍长中线模型目的:①构造出一组全等三角形;②构造出一组平行线。
将分散的条件集中到一个三角形中。
如图1,ABC 中,若86AB AC ==,,求BC 边上的中线小明在组内经过合作交流,得到了如下的解决方法:如图连接BE .请根据小明的方法思考:(1)如图2,由已知和作图能得到ADC EDB ≌△△A .SSS B .SAS C .AAS D .ASA(2)如图2,AD 长的取值范围是.(2)根据全等三角形的性质得到6AC BE ==,由三角形三边关系得到AB BE AE AB BE -<<+,即可求出17AD <<;(3)延长AD 到点M ,使AD DM =,连接BM ,证明ADC MDB △△≌,得到BM AC CAD M =∠=∠,,由AE EF =得到CAD AFE ∠=∠,进而推出BF BM =,即可证明AC BF =.【详解】解:(1)如图2,延长AD 到点E ,使DE AD =,连接BE .∵AD 为BC 的中线,∴BD CD =,又∵AD DE ADC BDE =∠=∠,,∴()SAS ADC EDB ≌△△,故答案为:B ;(2)解:∵ADC EDB ≌△△,∴6AC BE ==,在ABE 中,AB BE AE AB BE -<<+,∴86286AD -<<+,∴17AD <<,故答案为:C ;(3)证明:延长AD 到点M ,使AD DM =,连接BM ,∵AD 是ABC 中线,∴CD BD =,∵在ADC △和MDB △中,DC DB ADC MDB AD HD =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ADC MDB ≌△△,∴BM AC CAD M =∠=∠,,∵AE EF =,(1)如图1,求证:12BF AD =;(2)将DCE △绕C 点旋转到如图2所示的位置,连接,AE BD ,过C 点作CM ⊥①探究AE 和BD 的关系,并说明理由;②连接FC ,求证:F ,C ,M 三点共线.【答案】(1)见解析(2)①,AE BD AE BD =⊥,理由见解析②见解析【分析】(1)证明≌ACD BCE V V ,得到AD BE =,再根据点F 为BE 中点,即可得证;则:AGB CBD BHG ∠=∠+∠=∠∵CBD EAC ∠=∠,∴90BHG ACB ∠=∠=︒,∴AE BD ⊥,综上:,AE BD AE BD =⊥;②延长CF 至点P ,使PF CF =∵F 为BE 中点,∴BF FE =,∴()SAS BFP EFC ≌,∴,BP CE BPF ECF =∠=∠,∴CE BP ,∴180CBP BCE ∠+∠=︒,∵360180BCE ACD ACB DCE ∠+∠=︒-∠-∠=︒,∴CBP ACD ∠=∠,又,CE CD BP AC BC ===,∴()SAS PBC DCA ≌,∴BCP CAD ∠=∠,延长FC 交AD 于点N ,则:18090BCP ACN ACB ∠+∠=︒-∠=︒,∴90CAD ACN ∠+∠=︒,∴90ANC ∠=︒,∴CN AD ⊥,∵CM AD ⊥,∴点,M N 重合,即:F ,C ,M 三点共线.【点睛】本题考查全等三角形的判定和性质,等腰三角形判定和性质.熟练掌握手拉手全等模型,倍长中线法构造全等三角形,是解题的关键.【变式训练1】如图,ABC 中,BD DC AC ==,E 是DC 的中点,求证:2AB AE =.【答案】见解析【分析】利用中线加倍证DEF CEA △≌△(SAS ),可得DF AC BD ==,FDE C ∠=∠,由DC AC =,可得ADC CAD ∠=∠进而可证ADF ADB ∠=∠.,再证ADB ADF △≌△(SAS )即可.【详解】证明:延长AE 到F ,使EF AE =,连结DF ,∵E 是DC 中点,∴DE CE =,∴在DEF 和CEA 中,DE CE DEF CEA EF EA =⎧⎪∠=∠⎨⎪=⎩,∴DEF CEA △≌△(SAS ),∴DF AC BD ==,FDE C ∠=∠,∵DC AC =,∴ADC CAD ∠=∠,又∵ADB C CAD ∠=∠+∠,ADF FDE ADC ∠=∠+∠,∴ADF ADB ∠=∠,在ADB 和ADF △中,AD AD ADB ADF DB DF =⎧⎪∠=∠⎨⎪=⎩,∴ADB ADF △≌△(SAS ),∴2AB AF AE ==.【点睛】本题考查中线加倍构图,三角形全等判定与性质,等腰三角形性质,掌握中线加倍构图,三角形全等判定与性质,等腰三角形性质是解题关键.【变式训练2】(1)如图1,已知ABC 中,AD 是中线,求证:2AB AC AD +>;(2)如图2,在ABC 中,D ,E 是BC 的三等分点,求证:AB AC AD AE +>+;(3)如图3,在ABC 中,D ,E 在边BC 上,且BD CE =.求证:AB AC AD AE +>+.【答案】(1)见解析;(2)见解析;(3)见解析【分析】(1)利用“倍长中线”法,延长AD ,然后通过全等以及三角形的三边关系证明即可;(2)取DE 中点H ,连接AH 并延长至Q 点,使得AH =QH ,连接QE 和QC ,通过“倍长中线”思想全等证明,进而得到AB =CQ ,AD =EQ ,然后结合三角形的三边关系建立不等式证明即可得出结论;(3)同(2)处理方式一样,取DE 中点M ,连接AM 并延长至N 点,使得AM =NM ,连接NE ,CE ,结合“倍长中线”思想证明全等后,结合三角形的三边关系建立不等式证明即可得出结论.【详解】证:(1)如图所示,延长AD 至P 点,使得AD =PD ,连接CP ,∵AD 是△ABC 的中线,∴D 为BC 的中点,BD =CD ,在△ABD 与△PCD 中,BD CD ADB PDC AD PD =⎧⎪∠=∠⎨⎪=⎩∴△ABD ≌△PCD (SAS ),∴AB =CP ,在△APC 中,由三边关系可得AC +PC >AP ,∴2AB AC AD +>;(2)如图所示,取DE 中点H ,连接AH 并延长至Q 点,使得AH =QH ,连接QE 和QC ,∵H 为DE 中点,D 、E 为BC 三等分点,∴DH =EH ,BD =DE =CE ,∴DH =CH ,在△ABH 和△QCH 中,BH CH BHA CHQ AH QH =⎧⎪∠=∠⎨⎪=⎩,∴△ABH ≌△QCH (SAS ),同理可得:△ADH ≌△QEH ,∴AB =CQ ,AD =EQ ,此时,延长AE ,交CQ 于K 点,∵AC +CQ =AC +CK +QK ,AC +CK >AK ,∴AC +CQ >AK +QK ,又∵AK +QK =AE +EK +QK ,EK +QK >QE ,∴AK +QK >AE +QE ,∴AC +CQ >AK +QK >AE +QE ,∵AB =CQ ,AD =EQ ,∴AB AC AD AE +>+;(3)如图所示,取DE 中点M ,连接AM 并延长至N 点,使得AM =NM ,连接NE ,CE ,∵M 为DE 中点,∴DM =EM ,∵BD =CE ,∴BM =CM ,在△ABM 和△NCM 中,BM CM BMA CMN AM NM =⎧⎪∠=∠⎨⎪=⎩∴△ABM ≌△NCM (SAS ),同理可证△ADM ≌△NEM ,∴AB =NC ,AD =NE ,此时,延长AE ,交CN 于T 点,∵AC +CN =AC +CT +NT ,AC +CT >AT ,∴AC +CN >AT +NT ,又∵AT +NT =AE +ET +NT ,ET +NT >NE ,∴AT +NT >AE +NE ,∴AC +CN >AT +NT >AE +NE ,∵AB =NC ,AD =NE ,∴AB AC AD AE +>+.【点睛】本题考查全等三角形证明问题中辅助线的添加,掌握“倍长中线”的基本思想,以及熟练运用三角形的三边关系是解题关键.【答案】(1)1.5 6.5AE <<;(2)见解析;(3)BE DF EF +=,理由见解析【分析】(1)如图①:将ACD △绕着点D 逆时针旋转180 得到EBD △可得BDE ≅ 得出5BE AC ==,然后根据三角形的三边关系求出AE 的取值范围,进而求得AD 范围;(2)如图②:FDC △绕着点D 旋转180︒得到NDB 可得BND CFD ≅ ,得出BN∴1.5 6.5AD <<;故答案为1.5 6.5AD <<;(2)证明:如图②:FDC △绕着点D 旋转180︒得到NDB∴BND CFD ≅ (SAS ),∴BN CF =,DN DF=∵DE DF⊥∴EN EF =,在BNE 中,由三角形的三边关系得:BE BN EN +>,∴BE CF EF +>;(3)BE DF EF +=,理由如下:如图③,将DCF 绕着点C 按逆时针方向旋转100︒∴△DCF ≌△BCH ,∴100CH CF DCB FCH ∠∠=︒=,=∴HBC D DF BH∠∠==,∵180ABC D ∠+∠︒=∴180HBC ABC ∠+∠︒=,∴点A 、B 、H 三点共线∵100FCH ∠=︒,50FCE ∠=︒,∴50ECH ∠=︒∴FCE ECH ∠∠=,在HCE 和FCE △中,===CF CH ECF ECH CE CE ∠∠⎧⎪⎨⎪⎩,∴HCE FCE ≌ (SAS )∴EH EF =,∵BE BH EH DF BH+==,∴BE DF EF +=.【点睛】本题属于三角形综合题,主要考查对全等三角形的性质和判定、三角形的三边关系定理、旋转的性质等知识点,通过旋转得到构造全等三角形是解答本题的关键.类型二、截长补短模型截长补短法使用范围:线段和差的证明(往往需证2次全等)(1)求证:CD BC DE=+;(2)若75B∠=︒,求E∠的度数.【答案】(1)见解析(2)105︒【分析】(1)在CD上截取CF∵CA平分BCD∠,∴BCA FCA∠=∠.在BCAV和FCA△中,⎧⎪∠⎨⎪⎩,∠=︒BAC60【答案】(1)5.8;(2)4.3【分析】(1)由已知条件和辅助线的作法,证得△ACD≌△ECD,得到由于∠A=2∠B,推出∠DEC=2∠B,等量代换得到∠B=∠EDB形,得出AC =CE =3.6,DE =BE =2.2,相加可得BC 的长;(2)在BA 边上取点E ,使BE =BC =2,连接DE ,得到△DEB ≌△DBC (SAS ),在DA 边上取点F ,使DF =DB ,连接FE ,得到△BDE ≌△FDE ,即可推出结论.【详解】解:(1)如图2,在BC 边上取点E ,使EC =AC ,连接DE .在△ACD 与△ECD 中,AC CE ACD ECD CD CD =⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△ECD (SAS ),∴AD =DE ,∠A =∠DEC ,∵∠A =2∠B ,∴∠DEC =2∠B ,∴∠B =∠EDB ,∴△BDE 是等腰三角形;∴BE =DE =AD =2.2,AC =EC =3.6,∴BC 的长为5.8;(2)∵△ABC 中,AB =AC ,∠A =20°,∴∠ABC =∠C =80°,∵BD 平分∠B ,∴∠1=∠2=40°,∠BDC =60°,在BA 边上取点E ,使BE =BC =2,连接DE ,在△DEB 和△DBC 中,12BE BC BD BD =⎧⎪∠=∠⎨⎪=⎩,∴△DEB ≌△DBC (SAS ),∴∠BED =∠C =80°,∴∠4=60°,∴∠3=60°,在DA 边上取点F ,使DF =DB ,连接FE ,同理可得△BDE ≌△FDE ,∴∠5=∠1=40°,BE =EF =2,∵∠A =20°,∴∠6=20°,∴AF =EF =2,∵BD =DF =2.3,∴AD =BD +BC =4.3.【点睛】本题考查了全等三角形的性质与判定,等腰三角形的性质,熟悉这些定理是解决本题的关键.类型三、一线三等角模型应用:①通过证明全等实现边角关系的转化,便于解决对应的几何问题;②与函数综合应用中有利于点的坐标的求解。
2018中考数学专题复习 全等三角形压轴题分类解析(无答案)

三角形综合题归类考点:利用角相等证明垂直1. 已知BE ,CF 是△ABC 的高,且BP=AC ,CQ=AB ,试确定AP 与AQ 的数量关系和位置关系2. 如图,在等腰R t△ABC 中,∠ACB =90°,D 为BC 的中点,DE ⊥AB ,垂足为E ,过点B 作BF ∥AC 交DE 的延长线于点F ,连接CF .(1)求证:CD=BF ;(2)求证:AD ⊥CF ;(3)连接AF ,试判断△ACF 的形状.拓展巩固:如图9所示,△ABC 是等腰直角三角形,∠ACB =90°,AD 是BC 边上的中线,过C 作AD 的垂线,交AB 于点E ,交AD 于点F ,求证:∠ADC =∠BDE .3. 如图1,已知正方形ABCD 的边CD 在正方形DEFG 的边DE 上,连接AE ,GC . (1)试猜想AE 与GC 有怎样的位置关系,并证明你的结论;(2)将正方形DEFG 绕点D 按顺时针方向旋转,使E 点落在BC 边上,如图2,连接AE 和GC .你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.BAC E FQPD A BCDEF图9ABCDE F4.如图1,ABC ∆的边BC 在直线l 上,,AC BC ⊥且,AC BC =EFP ∆的边FP 也 在直线l 上,边EF 与边AC 重合,且EF FP =(1) 在图1中,请你通过观察、测量,猜想并写出AB 与AP 所满足的 数量关系和位置关系;(2) 将EFP ∆沿直线l 向左平移到图2的位置时,EP 交AC 于点Q ,连接 ,AP BQ .猜想并写出BQ 与AP 所满足的数量关系和位置关系,请证明你的猜想; (3)将EFP ∆沿直线l 向左平移到图3的位置时,EP 的延长线交AC 的延长 线于点Q,连结,AP BQ ,你认为(2)中所猜想的BQ 与AP 的数量关系和位置关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.等腰三角形(中考重难点之一) 考点1:等腰三角形性质的应用1. 两个全等的含30,60角的三角板ADE 和三角板ABC ,如图所示放置,,,E A C 三点在一条直线上,连结BD ,取BD 的中点M ,连结,ME MC .试判断EMC ∆的形状,并说明理由. MED CBA压轴题拓展:(三线合一性质的应用)已知Rt ABC ∆中,AC BC =,90C ∠=︒,D 为AB 边的中点,90EDF ∠=︒,EDF ∠绕D 点旋转,它的两边分别交AC 、CB (或它们的延长线)于E 、F .l(1)A B(F) (E)C PABECFPQ (2) lABEC FP l(3)Q当EDF ∠绕D 点旋转到DE AC ⊥于E 时(如图1),易证12DEF CEF ABC S S S ∆∆∆+=.当EDF ∠绕D 点旋转到DE 和AC 不垂直时,在图2和图3这两种情况下,上述结论是否成立? 若成立,请给予证明;若不成立,DEF S ∆,CEF S ∆,ABC S ∆又有怎样的数量关系?请写出你的猜想,不需证明.FEDCBA图1AECF BD图2AECFBD图32. 已知:如图,△ABC 中,∠ABC =45°,CD ⊥AB 于D ,BE 平分∠ABC ,且BE ⊥AC 于E ,与CD 相交于点F ,H 是BC 边的中点,连结DH 与BE 相交于点G 。
初二全等三角形所有知识点总结和常考题提高难题压轴题练习(含答案解析)

初二全等三角形所有知识点总结和常考题1.基本定义:⑴全等形:能够完全重合的两个图形叫做全等形 .⑵全等三角形:能够完全重合的两个三角形叫做全等三角形.⑶对应顶点:全等三角形中互相重合的顶点叫做对应顶点.⑷对应边:全等三角形中互相重合的边叫做对应边 .⑸对应角:全等三角形中互相重合的角叫做对应角 .2.基本性质:⑴三角形的稳定性:三角形三边的长度确定了,这个三角形的形状、大小就全确定,这个性质叫做三角形的稳定性.⑵全等三角形的性质:全等三角形的对应边相等,对应角相等.3.全等三角形的判定定理:⑴边边边(SSS):三边对应相等的两个三角形全等.⑵边角边(SAS):两边和它们的夹角对应相等的两个三角形全等.⑶角边角(ASA):两角和它们的夹边对应相等的两个三角形全等.⑷角角边(AAS):两角和其中一个角的对边对应相等的两个三角形全等⑸斜边、直角边(HL ):斜边和一条直角边对应相等的两个直角三角形全等.4.角平分线:⑴画法:⑵性质定理:角平分线上的点到角的两边的距离相等 .⑶性质定理的逆定理:角的内部到角的两边距离相等的点在角的平分线上5.证明的基本方法:⑴明确命题中的已知和求证.(包括隐含条件,如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形等所隐含的边角关系)⑵根据题意,画出图形,并用数字符号表示已知和求证.⑶经过分析,找出由已知推出求证的途径,写出证明过程 .一.选择题(共14小题)1.使两个直角三角形全等的条件是()A. 一个锐角又t应相等B.两个锐角对应相等C. 一条边对应相等D.两条边对应相等2.如图,已知AE=CF /AFD=/ CEB那么添加下列一个条件后,仍无法判定△AD陷4CBE的是()A. /A=/ CB. AD=CBC. BE=DFD. AD // BC3.如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是()A. SSSB. SASC. AASD. ASA4.到三角形三条边的距离都相等的点是这个三角形的(A.三条中线的交点B.三条高的交点C.三条边的垂直平分线的交点D.三条角平分线的交点5.如图,△ AC阴NA CB'/BCB =30°则/ ACA的度数为(A. 20°B. 300C. 350D. 40°6.如图,直线11、12、13表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则供选择的地址有()A. 1处B. 2处C. 3处D. 4处7.如图,AD是4ABC中/ BAC的角平分线,D已AB于点E, S AABC=7, DE=ZAB=4,则AC长是()8.如图,在△ ABC和4DEC中,已知AB=DE还需添加两个条件才能使△ ABCDEC不能添加的一组条件是()A. BC=EC /B=/ EB. BC=EC AC=DCC. BC=DC /A=/DD. / B=/ E,/ A=/ D9.如图,已知在△ ABC中,CD是AB边上的高线,BE平分/ ABC,交CD于点E, BC=5 DE=2,贝BCE的面积等于()A. 10B. 7C. 5D. 410.要测量河两岸相对的两点A, B的距离,先在AB的垂线BF上取两点C, D, 使CD=BC再定出BF的垂线DE,使A, C, E在一条直线上(如图所示),可以说明△ED8 AABC,彳3ED=AB因此测得ED的长就是AB的长,判定△ ED8 △ ABC最恰当的理由是()A.边角边B.角边角C.边边边D.边边角11.如图,4ABC的三边AB, BC, CA长分别是20, 30, 40,其三条角平分线将△ ABC分为三个三角形,则S A ABO):S A BCO:S A CAO等于()BC AA. 1:1:1B. 1: 2: 3C. 2: 3: 4D. 3: 4: 512.尺规作图作/ AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA, OB于C, D,再分别以点C, D为圆心,以大于tCD长为半径画弧,两弧交于点P,作射线OP由作法得^ OC国4ODP的根据是()A.有两边和其中一边的对角对应相等的两个三角形全等B.有两边对应相等,且有一角为 30°的两个等腰三角形全等C.有一角和一边对应相等的两个直角三角形全等D.有两角和一边对应相等的两个三角形全等14.如图,已知/ 1=/2, AC=AD,增加下列条件:① AB=AE ②BC=ED ③C C= /D;④/ B=/ E.其中能使△ AB ®ZXAED 的条件有( )A. 4个B. 3个C. 2个D. 1个二.填空题(共11小题)15 .如图,在△ ABC 中,/C=90°, AD 平分/CAB BC=8cm, BD=5cm,那么点 D 到线段AB 的距离是 cm.16 .如图,△ ABC 中,/ C=90°, AD 平分/BAC AB=5, CD=2,则△ ABD 的面积17 .如图为6个边长等的正方形的组合图形,则/ 1+/ 2+/3=19 .如图所示,某同学把一块三角形的玻璃打碎成了三块, 现在要到玻璃店去配 一块完全一样的玻璃,那么最省事的办法是带 去玻璃店.18.如图,△AB ®ADEF5请根据图中提供的信息,写出* F x= ______是 _______20.如图,已知AB// CF, E为DF的中点,若AB=9cm, CF=5cm 贝U BD=cm.B C21.在数学活动课上,小明提出这样一个问题:/ B=Z C=90°, E是BC的中点, DE 平分/ADC, /CED=35,如图,则/ EAB是多少度?大家一起热烈地讨论交流,小英第一个得出正确答案,是度.D C22.如图,/XABeAADEE, / B=100°, / BAC=30,那么/ AED=度.23.如图所示,将两根钢条AA', BB'的中点。
专题03 全等三角形压轴题真题(解析版)-初中数学七年级上学期重难点题型分类高分必刷题(人教版)

专题03高分必刷题-全等三角形压轴题真题(解析版)题型一:全等三角形小压轴题考向1:多项选择题1.如图,已知AB=AC,AF=AE,∠EAF=∠BAC,点C、D、E、F共线.则下列结论,其中正确的是()①△AFB≌△AEC;②BF=CE;③∠BFC=∠EAF;④AB=BC.A.①②③B.①②④C.①②D.①②③④【解答】解:∵∠EAF=∠BAC,∴∠BAF=∠CAE,∵AF=AE,AB=AC,∴△F AB≌△EAC(SAS),故①正确,∴BF=EC,故②正确,∴∠ABF=∠ACE,∵∠BDF=∠ADC,∴∠BFC=∠DAC,∵∠DAC=∠EAF,∴∠BFC=∠EAF,故③正确,无法判断AB=BC,故④错误,故选:A.2.如图,△ABC中,∠C=90°、AD是角平分线,E为AC边上的点,DE=DB,下列结论:①∠DEA+∠B=180°;②∠CDE=∠CAB;③AC=(AB+AE);④S△ADC=S四,其中正确的结论个数为()边形ABDEA.4个B.3个C.2个D.1个【解答】解:如图,过D作DF⊥AB于F,∵∠C=90°,AD是角平分线,∴DC=DF,∠C=∠DFB,又∵DE=DB,∴Rt△CDE≌Rt△FDB,∴∠B=∠CED,∠CDE=∠FDB,CE=BF,又∵∠DEA+∠DEC=180°,∴∠DEA+∠B=180°,故①正确;∵∠C=∠DFB,∠B=∠B,∴∠BDF=∠BAC,∴∠CDE=∠CAB,故②正确;∵AD是角平分线,∴∠CAD=∠F AD,又∵∠C=∠AFD,AD=AD,∴△ACD≌△AFD,∴AC=AF,∴AB+AE=(AF+FB)+(AC ﹣CE)=AF+AC=2AC,∴AC=(AB+AE),故③正确;∵Rt△CDE≌Rt△FDB,∴S△CDE=S△FDB,∴S四边形ABDE=S四边形ACDF,又∵△ACD≌△AFD,∴S△ACD=S△ADF,∴S△ADC=S四边形ACDF=S四边形ABDE,故④正确;故选:A.3.如图,直线AC上取点B,在其同一侧作两个等边三角形△ABD和△BCE,连接AE,CD 与GF,下列结论正确的有()①AE=DC;②∠AHC=120°;③△AGB≌△DFB;④BH平分∠AHC;⑤GF∥AC.A.①②④B.①③⑤C.①③④⑤D.①②③④⑤【解答】解:∵△ABD和△BCE都是等边三角形,∴BA=BD,BE=BC,∠ABD=∠CBE =60°,∵∠DBE=180°﹣60°﹣60°=60°,∴∠ABE=∠DBC=120°,∵BA=BD,∠ABD=∠DBC,BE=BC,∴△ABE≌△DBC(SAS),∴AE=DC,所以①正确;∠BAE=∠BDC,∵∠BDC+∠BCD =∠ABD=60°,∴∠BAE+∠BCD=60°,∴∠AHC=180°﹣(∠BAH+∠BCH)=180°﹣60°=120°,所以②正确;∵∠BAG=∠BDF,BA=BD,∠ABG=∠DBF=60°,∴△AGB≌△DFB(ASA);所以③正确;∵△ABE≌△DBC,∴AE和DC边上的高相等,即B点到AE和DC的距离相等,∴BH平分∠AHC,所以④正确;∵△AGB≌△DFB,∴BG=BF,∵∠GBF=60°,∴△BGF为等边三角形,∴∠BGF=60°,∴∠ABG=∠BGF,∴GF∥AC,所以⑤正确.故选:D.考向2:动点问题4.如图,已知△ABC中,∠B=∠C,BC=8cm,BD=6cm,如果点P在线段BC上以1cm/s 的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,当一个点停止运动时,另一个点也随之停止运动,设点Q的速度为xcm/s,则当△BPD与△CQP全等时,x=1或.【解答】解:设运动的时间为ts,则BP=t,PC=8﹣t,CQ=tx,∵∠B=∠C,∴当BD=CQ,BP=CP时,△BPD≌△CPQ(SAS),即tx=6,t=8﹣t,解得t=4,x=;当BD=CP,BP=CQ时,△BPD≌△CQP(SAS),即8﹣t=6,t=tx,解得t=2,x=1;综上所述,x的值为1或.故答案为1或.5.如图,AB=4cm,AC=BD=3cm.∠CAB=∠DBA=60°,点P在线段AB上以1cm/s 的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).设点Q的运动速度为xcm/s,若使得△ACP与△BPQ全等.x的值为1或1.5.【解答】解:要使△ACP与△BPQ全等,有两种情况:①AP=BQ,∵点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).设点Q的运动速度为xcm/s,∴x=1;②AC=BQ=3cm,AP=BP=AB==2cm,∴时间为=2秒,即x==1.5,所以x的值是1或1.5.题型二:全等三角形的大压轴题6.根据全等多边形的定义,我们把四个角,四条边分别相等的两个凸四边形叫做全等四边形,记作:四边形ABCD≌四边形A1B1C1D1.(1)若四边形ABCD≌四边形A1B1C1D1,已知AB=3,BC=4,AD=CD=5,∠B=90°,∠D=60°,则A1D1=5,∠B1=90°,∠A1+∠C1=210°.(直接写出答案);(2)如图1,四边形ABEF≌四边形CBED,连接AD交BE于点O,连接OF,求证:∠AOB=∠FOE;(3)如图2,若AB=A1B1,BC=B1C1,CD=C1D1,AD=A1D1,∠B=∠B1,求证:四边形ABCD≌四边形A1B1C1D1.【解答】解:(1)∵四边形ABCD≌四边形A1B1C1D1,∴A1D1=AD=5,∠B1=∠B=90°,∠D=∠D1=60°,∠A=∠A1,∠C=∠C1,∵∠A+∠C=160°﹣90°﹣60°=210°,∴∠A1+∠C1=210°,故答案为5,90°,210°.(2)如图1中,∵四边形ABEF≌四边形CBED,∴EF=ED,∠FEO=∠DEO,∵EO=EO,∴△FEO≌△DEO(SAS),∴∠EOF=∠DOE,∵∠AOB=∠DOE,∴∠AOB=∠EOF.(3)如图2中,连接AC,A1C1.∵AB=A1B1,∠B=∠B1,BC=B1C1,∴△ABC≌△A1B1C1,∴AC=A1C1,∠BAC=∠B1A1C1,∠BCA=∠B1C1A1,∵AD=A1D1,CD=C1D1,∴△ADC≌△A1D1C1(SSS),∴∠D=∠D1,∠DAC=∠D1A1C1,∠ACD=∠A1C1D1,∴∠BAD=∠B A A1D1,∠BCD =∠B1C1D1,∴四边形ABCD≌四边形A1B1C1D1.7.(1)如图1,已知∠EOF=120°,OM平分∠EOF,A是OM上一点,∠BAC=60°,且与OF、OE分别相交于点B、C,求证:AB=AC;(2)如图2,在如上的(1)中,当∠BAC绕点A逆时针旋转使得点B落在OF的反向延长线上时,(1)中的结论是否还成立?若成立,给出证明;若不成立,说明理由;(3)如图3,已知∠AOC=∠BOC=∠BAC=60°,求证:①△ABC是等边三角形;②OC=OA+OB.【解答】(1)证明:过A作AG⊥OF于G,AH⊥OE于H,则∠AHO=∠AGO=90°,∵∠EOF=120°,∴∠HAG=60°=∠BAC,∴∠HAG﹣∠BAH=∠BAC﹣∠BAH,∴∠BAG =∠CAH,∵OM平分∠EOF,AG⊥OF,AH⊥OE,∴AG=AH,在△BAG和△CAH中,∵,∴△BAG≌△CAH(ASA),∴AB=AC;(2)结论还成立,证明:过A作AG⊥OF于G,AH⊥OE于H,与(1)证法类似根据ASA 证△BAG≌△CAH(ASA),则AB=AC;(3)证明:①如图,∠FOA=180°﹣120°=60°,∠FOC=60°+60°=120°,即OM 平分∠COF,由(2)知:AC=AB,∵∠CAB=60°,∴△ABC是等边三角形;②在OC上截取BO=ON,连接BN,∵∠COB=60°,∴△BON是等边三角形,∴ON=OB,∠OBN=60°,∵△ABC是等边三角形,∴∠ABC=60°=∠NBO,∴都减去∠ABN 得:∠ABO=∠CBN,在△AOB和△CNB中∵,∴△AOB≌△CNB(SAS),∴NC=OA,∴OC=ON+CN=OB+OA,即OC=OA+OB.8.如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC.(1)求C点的坐标;(2)如图2,P为y轴负半轴上一个动点,当P点向y轴负半轴向下运动时,以P为顶点,P A为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求OP﹣DE的值;(3)如图3,已知点F坐标为(﹣2,﹣2),当G在y轴的负半轴上沿负方向运动时,作Rt△FGH,始终保持∠GFH=90°,FG与y轴负半轴交于点G(0,m),FH与x轴正半轴交于点H(n,0),当G点在y轴的负半轴上沿负方向运动时,求证m+n为定值,并求出其值.【解答】解:(1)过C作CM⊥x轴于M点,如图1,∵CM⊥OA,AC⊥AB,∴∠MAC+∠OAB=90°,∠OAB+∠OBA=90°,则∠MAC=∠OBA,在△MAC和△OBA中,,∴△MAC≌△OBA(AAS)∴CM=OA=2,MA=OB=4,∴点C的坐标为(﹣6,﹣2);(2)如图2,过D作DQ⊥OP于Q点,∵DQ⊥OP,DE⊥OE,∠POE=90°∴四边形OEDQ是矩形,∴OE=QD,DE=OQ,∴OP=PQ+OQ=DE+PQ,∵∠APO+∠QPD=90°,∠APO+∠OAP=90°,∴∠QPD=∠OAP,在△AOP和△PDQ中,,∴△AOP≌△PDQ(AAS),∴QP=AO=2,∴OP﹣DE=2;(3)结论②是正确的,m+n=﹣4,理由如下:如图3,过点F分别作FS⊥x轴于S点,FT ⊥y轴于T点,∴FS=FT=2,∠FHS=∠HFT=∠FGT,在△FSH和△FTG中,,∴△FSH≌△FTG(AAS)∴GT=HS,又∵G(0,m),H(n,0),点F坐标为(﹣2,﹣2),∴OT═OS=2,OG=|m|=﹣m,OH=n,∴GT=OG﹣OT=﹣m﹣2,HS=OH+OS=n+2,∴﹣2﹣m=n+2,∴m+n=﹣4.9.在△ABC中,AB=AC,CG⊥BA交BA的延长线于点G.一等腰直角三角尺按如图1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边在一条直线上,另一条直角边恰好经过点B.(1)在图1中请你通过观察、测量BF与CG的长度,猜想并写出BF与CG满足的数量关系,然后证明你的猜想;(2)当三角尺沿AC方向平移到图2所示的位置时,一条直角边仍与AC边在同一直线上,另一条直角边交BC边于点D,过点D作DE⊥BA于点E.此时请你通过观察、测量DE、DF与CG的长度,猜想并写出DE+DF与CG之间满足的数量关系,然后证明你的猜想;(3)当三角尺在(2)的基础上沿AC方向继续平移到图3所示的位置(点F在线段AC 上,且点F与点C不重合)时,若AG:AB=5:13,BC=4,求DE+DF的值.【解答】解:(1)猜想:BF=CG.理由:如图1.∵BF⊥AC,CG⊥AB,∴S△ABC=AC•BF=AB•CG.∵AB=AC,∴BF=CG;(2)猜想:DE+DF=CG.理由:连接AD,如图2.∵DF⊥AC,DE⊥AB,CG⊥AB,∴S△ACD=AC•DF,S△ABD=AB•DE,S△ABC=AB•CG.∵S△ACD+S△ABD=S△ABC,∴AC•DF+AB•DE=AB•CG.∵AB=AC,∴DF+DE=CG;(3)连接AD,如图3.同(2)可得:DF+DE=CG.设AG=5x,∵AG:AB=5:13,AB =AC,∴AC=AB=13x.∴∠G=90°,∴GC==12x.在Rt△BGC中,∵BG=AB+AG=13x+5x=18x,GC=12x,BC=4,∴(18x)2+(12x)2=(4)2,解得:x=,∴DE+DF=CG=12x=8.10.如图1,在平面直角坐标系中,A(﹣2,0)、B(0,5),AB=AD,∠ABC+∠ADC=180°,BC⊥CD.(1)求证:∠ABO=∠CAD;(2)求点D坐标;(3)如图2,若OC=OB=5,E为∠BCO的邻补角的平分线上的一点,且∠BEO=45°,OE交BC于点F,求BF的长.【解答】解:(1)如图1,在四边形ABCD中,∵∠ABC+∠ADC=180°,∴∠BAD+∠BCD =180°,∵BC⊥CD,∴∠BCD=90°,∴∠BAD=90°.∴∠BAC+∠CAD=90°,又∵∠BAC+∠ABO=90°.∴∠ABO=∠CAD.(2)如图1,过点D作DG⊥AC,∴∠AGD=∠BOA=90°,又∵∠ABO=∠CAD,AB=AD,∴△ABO≌△DAG(AAS),∴DG=AO=2,AG=BO=5,∴OG=AG﹣AO=3,则点D的坐标为(3,﹣2);(3)如图2,过点E作EH⊥BC于点H,作EG⊥x轴于点G,∵E点在∠BCO的邻补角的平分线上,∴EH=EG.又∵∠BCO=∠BEO=45°,∴∠EBC=∠EOC.∴△EBH≌△EOG(AAS),∴EB=EO.又∵∠BEO=45°,∴∠EBO=∠EOB=67.5°,∵∠OBC=45°,∴∠BOE=∠BFO=67.5°.∴BF=BO=5.11.在平面直角坐标系中,点A在x轴上,点B、C在y轴上,且点B与点C关于x轴对称,点D在线段AB上,点E为该坐标平面内一点.(1)已知BD=CE.①如图1,若点E在线段AC上,求证:CD=BE;②如图2,若点E在线段BC上,且∠DEA=∠ABC,求证:∠ACO=2∠OAE.(2)如图3,已知BD=AE,点E在线段CA的延长线上,F为CD中点,且∠OAB=30°,求证:BF⊥EF.【解答】证明:(1)①∵点B和点C关于x轴对称,∴AB=AC,∴∠CBD=∠BCE,在△CBD和△BCE中,,∴△CBD≌△BCE(SAS),∴CD=BE;②∵∠DEA+∠DEB=∠ACB+∠CAE,∠DEA=∠ABC=∠ACB,∴∠DEB=∠CAE,在△BED和△CAE中,,∴△BED≌△CAE(AAS),∴BE=AC=AB,∴∠BEA=∠BAE,∵点B和点C关于x轴对称,∴AB=AC,OB=OC,∴∠BAO=∠CAO,∴∠BAE=2∠CAO﹣∠EAC=2∠OAE+∠EAC,∵∠DEB=∠CAE,∴∠DEA=2∠OAE,∵∠DEA=∠ABC=∠ACO,∴∠ACO=2∠OAE;(2)延长BF到点G,使BF=FG,连接CG、EG、BE,如图3所示:∵点B和点C关于x轴对称,∴AB=AC,OB=OC,∴∠OAB=∠OAC=30°,∴∠BAC=60°,∴△ABC是等边三角形,∴CB=AB,∠BCA=60°,∵F为DC中点,∴DF=CF,在△BDF和△GCF中,,∴△BDF≌△GCF(SAS),∴CG=BD=AE,∠CGF=∠DBF,∴BD∥CG,∴∠GCA=∠BAC=60°,∴∠BCG=∠BCA+∠GCA=60°+60°=120°,∵∠BAE=180°﹣∠OAB﹣∠EAx=180°﹣∠OAB﹣∠OAC=180°﹣30°﹣30°=120°,∴∠BCG=∠BAE,在△BCG和△BAE中,,∴△BCG≌△BAE(SAS),∴∠CBG=∠ABE,BG=BE,∵∠CBG+∠GBA=60°,∴∠ABE+∠GBA=60°,即∠GBE =60°,∴△GBE是等边三角形,∵F是BG的中点,∴EF⊥BG,∴BF⊥EF.12.如图,平面直角坐标系中,已知点A(a﹣1,a+b),B(a,0),且+(a﹣2b)2=0,C为x轴上点B右侧的动点,以AC为腰作等腰△ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.(1)求证:AO=AB;(2)求证:OC=BD;(3)当点C运动时,点P在y轴上的位置是否发生改变,为什么?【解答】证明:(1)∵+(a﹣2b)2=0,≥0,(a﹣2b)2≥0,∴=0,(a﹣2b)2=0,解得:a=2,b=1,∴A(1,3),B(2,0),∴OA==,AB==,∴OA=AB;(2)∵∠CAD=∠OAB,∴∠CAD+∠BAC=∠OAB+∠BAC,即∠OAC=∠BAD,在△OAC 和△BAD中,,∴△OAC≌△BAD(SAS),∴OC=BD;(3)点P在y轴上的位置不发生改变.理由:设∠AOB=∠ABO=α,∵由(2)知△AOC≌△ABD,∴∠ABD=∠AOB=α,∵OB =2,∠OBP=180°﹣∠ABO﹣∠ABD=180°﹣2α为定值,∵∠POB=90°,∴OP长度不变,∴点P在y轴上的位置不发生改变.13.在△ABC中,∠A<60°,以AB,AC为边分别向外作等边△ABD,△ACE,连接DC,BE交于点H.(如图1)(1)求证:△DAC≌△BAE;(2)求DC与BE相交的∠DHB的度数;(3)又以BC边向内作等边三角形△BCF,连接DF(如图2),试判断AE与DF的位置与数量关系,并证明你的结论.【解答】(1)证明:如图1中,∵△ABD、△ACE都是等边三角形,∴AD=AB,AC=AE,∠DAB=∠CAE=60°,∴∠DAC=∠BAE,在△DAC和△BAE中,,∴△DAC≌△BAE.(2)如图1中,∵△DAC≌△BAE,∴∠ADC=∠ABE,∵∠AOD=∠BOH,∠AOD+∠ADC+∠DAO=180°,∠BOH+∠OHB+∠ABE=180°,∴∠OHB=∠DAO=60°,∴∠DHB=60°.(3)结论AE=DF,AE∥FD.如图2中,连接EF,∵△ABD,△BCF,△ACE都是等边三角形,∴BD=BA=AD,BF=BC,CA=CE=AE,∠ABD=∠CBF=∠BCF=∠ACE=60°,∴∠DBF=∠CBA,∠BCA=∠ECF,在△ABC和△DBF中,,∴△ABC≌△DBF,同理△ABC≌△EFC,∴DF=AC=AE,EF=AB=AD,∴四边形ADFE是平行四边形,∴DF=AE,DF∥AE.14.已知,△ABC是等腰直角三角形,BC=AB,A点在x负半轴上,直角顶点B在y轴上,点C在x轴上方.(1)如图1所示,若A的坐标是(﹣3,0),点B的坐标是(0,1),求点C的坐标;(2)如图2,过点C作CD⊥y轴于D,请直接写出线段OA,OD,CD之间等量关系;(3)如图3,若x轴恰好平分∠BAC,BC与x轴交于点E,过点C作CF⊥x轴于F,问CF与AE有怎样的数量关系?并说明理由.【解答】解:(1)作CH⊥y轴于H,如图1,∵点A的坐标是(﹣3,0),点B的坐标是(0,1),∴OA=3,OB=1,∵△ABC是等腰直角三角形,∴BA=BC,∠ABC=90°,∴∠ABO+∠CBH=90°,∵∠ABO+∠BAO=90°,∴∠CBH=∠BAO,在△ABO和△BCH中,∴△ABO≌△BCH,∴OB=CH=1,OA=BH=3,∴OH=OB+BH=1+3=4,∴C(﹣1,4);(2)OA=CD+OD.理由如下:如图2,∵△ABC是等腰直角三角形,∴BA=BC,∠ABC =90°,∴∠ABO+∠CBD=90°,∵∠ABO+∠BAO=90°,∴∠CBD=∠BAO,在△ABO和△BCD中,∴△ABO≌△BCD,∴OB=CD,OA=BD,而BD=OB+OD=CD+OD,∴OA=CD+OD;(3)CF=AE.理由如下:如图3,CF和AB的延长线相交于点D,∴∠CBD=90°,∵CF⊥x,∴∠BCD+∠D=90°,而∠DAF+∠D=90°,∴∠BCD=∠DAF,在△ABE和△CBD中,,∴△ABE≌△CBD(ASA),∴AE=CD,∵x轴平分∠BAC,CF⊥x轴,∴CF=DF,∴CF=CD=AE.15.在△ABC中,AB=AC,D是直线BC上一点(不与点B、C重合),以AD为一边在AD 的右侧作△ADE,AD=AE,∠DAE=∠BAC,连接CE.(1)如图1,当点D在线段BC上时,写出△ABD≌△ACE的理由;(2)如图2,当点D在线段BC上,∠BAC=90°,直接写出∠BCE的度数;(3)如图3,若∠BCE=α,∠BAC=β,点D在线段CB的延长线上时,则α、β之间有怎样的数量关系?写出你的理由.【解答】(1)证明:∵∠BAC=∠DAE,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS);(2)解:∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,同(1)的方法可得,△ABD≌△ACE(SAS),∴∠ACE=∠ABD=45°,∴∠BCE=∠ACB+∠ACE=45°+45°=90°;(3)解:α=β.理由如下:同(1)的方法可得,△ABD≌△ACE(SAS),∴∠ACE=∠ABD,∵∠BCE=α,∴∠ACE=∠ACB+∠BCE=∠ACB+α,∵∠ABD是△ABC的一个外角,∴∠ABD=∠ACB+∠BAC=∠ACB+β,∴α=β.。
中考数学专题《全等三角形中的六种模型梳理》解析
专题02 全等三角形中的六种模型梳理几何探究类问题一直属于考试压轴题范围,在三角形这一章,压轴题主要考查是证明三角形各种模型,或证明线段数量关系等,接来下我们针对其做出详细分析与梳理。
类型一、倍长中线模型中线倍长法:将中点处的线段延长一倍。
目的:①构造出一组全等三角形;②构造出一组平行线。
将分散的条件集中到一个三角形中去。
例1.某数学兴趣小组在一次活动中进行了探究试验活动,请你来加入.【探究与发现】如图1,延长△ABC的边BC到D,使DC=BC,过D作DE△AB交AC延长线于点E,求证:△ABC△△EDC.【理解与应用】如图2,已知在△ABC中,点E在边BC上且△CAE=△B,点E是CD的中点,若AD平分△BAE.(1)求证:AC=BD;(2)若BD=3,AD=5,AE=x,求x的取值范围.【变式训练1】如图1,在ABC 中,CM 是AB 边的中线,BCN BCM ∠=∠交AB 延长线于点N ,2CM CN =.(1)求证AC BN =;(2)如图2,NP 平分ANC ∠交CM 于点P ,交BC 于点O ,若120AMC ∠=︒,CP kAC =,求CPCM的值.【变式训练2】(1)如图1,已知ABC 中,AD 是中线,求证:2AB AC AD +>; (2)如图2,在ABC 中,D ,E 是BC 的三等分点,求证:AB AC AD AE +>+; (3)如图3,在ABC 中,D ,E 在边BC 上,且BD CE =.求证:AB AC AD AE +>+.【变式训练3】在ABC 中,点P 为BC 边中点,直线a 绕顶点A 旋转,BM ⊥直线a 于点M .CN ⊥直线a 于点N ,连接PM ,PN .(1)如图1,若点B ,P 在直线a 的异侧,延长MP 交CN 于点E .求证:PM PE =.(2)若直线a 绕点A 旋转到图2的位置时,点B ,P 在直线a 的同侧,其它条件不变,此时7BMP CNP S S +=△△,1BM =,3CN =,求MN 的长度.(3)若过P 点作PG ⊥直线a 于点G .试探究线段PG 、BM 和CN 的关系.类型二、截长补短模型截长补短法使用范围:线段和差的证明(往往需证2次全等)例.在等边三角形ABC 的两边AB 、AC 所在直线上分别有两点M 、N ,P 为△ABC 外一点,且△MPN =60°,△BPC =120°,BP =CP .探究:当点M 、N 分别在直线AB 、AC 上移动时,BM ,NC ,MN 之间的数量关系.(1)如图①,当点M 、N 在边AB 、AC 上,且PM =PN 时,试说明MN =BM +CN . (2)如图②,当点M 、N 在边AB 、AC 上,且PM ≠PN 时,MN =BM +CN 还成立吗? 答: .(请在空格内填“一定成立”“不一定成立”或“一定不成立”).(3)如图③,当点M 、N 分别在边AB 、CA 的延长线上时,请直接写出BM ,NC ,MN 之间的数量关系.【变式训练1】如图,在四边形ABCD 中,,180AB AD B ADC =∠+∠=︒,点E 、F 分别在直线BC 、CD 上,且12EAF BAD ∠=∠.(1)当点E 、F 分别在边BC 、CD 上时(如图1),请说明EF BE FD =+的理由.(2)当点E 、F 分别在边BC 、CD 延长线上时(如图2),(1)中的结论是否仍然成立?若成立,请说明理由;若不成立,请写出EF 、BE 、FD 之间的数量关系,并说明理由.【变式训练2】(1)阅读理解:问题:如图1,在四边形ABCD 中,对角线BD 平分ABC ∠,180A C ∠+∠=︒.求证:DA DC =.思考:“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题.方法1:在BC 上截取BM BA =,连接DM ,得到全等三角形,进而解决问题; 方法2:延长BA 到点N ,使得BN BC =,连接DN ,得到全等三角形,进而解决问题. 结合图1,在方法1和方法2中任选一种....,添加辅助线并完成证明. (2)问题解决:如图2,在(1)的条件下,连接AC ,当60DAC ∠=︒时,探究线段AB ,BC ,BD 之间的数量关系,并说明理由;(3)问题拓展:如图3,在四边形ABCD 中,180A C ∠+∠=︒,DA DC =,过点D 作DE BC ⊥,垂足为点E ,请直接写出线段AB 、CE 、BC 之间的数量关系.【变式训练3】在ABC 中,BE ,CD 为ABC 的角平分线,BE ,CD 交于点F . (1)求证:1902BFC A ∠=︒+∠;(2)已知60A ∠=︒.①如图1,若4BD =, 6.5BC =,求CE 的长; ②如图2,若BF AC =,求AEB ∠的大小.类型三、做平行线证明全等 例1.如图所示:ABC 是等边三角形,D 、E 分别是AB 及AC 延长线上的一点,且BD CE =,连接DE 交BC 于点M . 求让:MD ME =【变式训练1】 P 为等边△ABC 的边AB 上一点,Q 为BC 延长线上一点,且P A =CQ ,连PQ 交AC 边于D . (1)证明:PD =DQ .(2)如图2,过P 作PE △AC 于E ,若AB =6,求DE 的长.【变式训练2】已知在等腰△ABC 中,AB =AC ,在射线CA 上截取线段CE ,在射线AB 上截取线段BD ,连接DE ,DE 所在直线交直线BC 与点M .请探究:(1)如图(1),当点E 在线段AC 上,点D 在AB 延长线上时,若BD =CE ,请判断线段MD 和线段ME 的数量关系,并证明你的结论.(2)如图(2),当点E 在CA 的延长线上,点D 在AB 的延长线上时,若BD =CE ,则(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由;类型四、旋转模型 例.如图1,AC BC =,CD CE =,ACB DCE α∠=∠=,AD 、BE 相交于点M ,连接CM .(1)求证:BE AD =,并用含α的式子表示AMB ∠的度数;(2)当90α=︒时,取AD ,BE 的中点分别为点P 、Q ,连接CP ,CQ ,PQ ,如图2,判断CPQ 的形状,并加以证明.【变式训练1】四边形ABCD 是由等边ABC ∆和顶角为120︒的等腰ABD ∆排成,将一个60︒角顶点放在D 处,将60︒角绕D 点旋转,该60︒交两边分别交直线BC 、AC 于M 、N ,交直线AB 于E 、F 两点.(1)当E 、F 都在线段AB 上时(如图1),请证明:BM AN MN +=;(2)当点E 在边BA 的延长线上时(如图2),请你写出线段MB ,AN 和MN 之间的数量关系,并证明你的结论;(3)在(1)的条件下,若7AC =, 2.1AE =,请直接写出MB 的长为 .【变式训练2】(1)问题发现:如图1,△ACB 和△DCE 均为等边三角形,当△DCE 旋转至点A ,D ,E 在同一直线上,连接BE .则:①△AEB 的度数为 °;②线段AD 、BE 之间的数量关系是 . (2)拓展研究:如图2,△ACB 和△DCE 均为等腰三角形,且△ACB =△DCE =90°,点 A 、D 、E 在同一直线上,若AD =a ,AE =b ,AB =c ,求a 、b 、c 之间的数量关系. (3)探究发现:图1中的△ACB 和△DCE ,在△DCE 旋转过程中,当点A ,D ,E 不在同一直线上时,设直线AD 与BE 相交于点O ,试在备用图中探索△AOE 的度数,直接写出结果,不必说明理由.【变式训练3】如图1,在Rt ABC 中,90A ∠=︒,AB AC =,点D ,E 分别在边AB ,AC 上,AD AE =,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.(1)观察猜想:图1中,线段PM 与PN 的数量关系是______,位置关系是______. (2)探究证明:把ADE 绕点A 逆时针方向旋转到图2的位置,连接MN ,BD ,CE ,判断PMN 的形状,并说明理由;(3)拓展延伸:把ADE 绕点A 在平面内自由旋转,若4=AD ,10AB =,请直接写出PMN 面积的最大值.类型五、手拉手模型例.在等边ABC 中,点D 在AB 上,点E 在BC 上,将线段DE 绕点D 逆时针旋转60°得到线段DF ,连接CF .(1)如图(1),点D 是AB 的中点,点E 与点C 重合,连接AF .若6AB =,求AF 的长; (2)如图(2),点G 在AC 上且60AGD FCB ∠=︒+∠,求证:CF DG =;(3)如图(3),6AB =,2BD CE =,连接AF .过点F 作AF 的垂线交AC 于点P ,连接BP 、DP .将BDP △沿着BP 翻折得到BQP ,连接QC .当ADP △的周长最小时,直接写出CPQ 的面积.【变式训练1】△ACB 和△DCE 是共顶点C 的两个大小不一样的等边三角形.(1)问题发现:如图1,若点A ,D ,E 在同一直线上,连接AE ,BE . ①求证:△ACD △△BCE ;②求△AEB 的度数.(2)类比探究:如图2,点B 、D 、E 在同一直线上,连接AE ,AD ,BE ,CM 为△DCE 中DE 边上的高,请求△ADB 的度数及线段DB ,AD ,DM 之间的数量关系,并说明理由. (3)拓展延伸:如图3,若设AD (或其延长线)与BE 的所夹锐角为α,则你认为α为多少度,并证明.【变式训练2】(1)如图1,锐角△ABC 中,分别以AB 、AC 为边向外作等腰直角△ABE 和等腰直角△ACD ,使AE =AB ,AD =AC ,∠BAE =∠CAD =90°,连接BD ,CE ,试猜想BD 与CE 的大小关系,不需要证明.【深入探究】(2)如图2,四边形ABCD 中,AB =5,BC =2,∠ABC =∠ACD =∠ADC =45°,求BD 2的值;甲同学受到第一问的启发构造了如图所示的一个和△ABD 全等的三角形,将BD 进行转化再计算,请你准确的叙述辅助线的作法,再计算;【变式思考】(3)如图3,四边形ABCD 中,AB =BC ,∠ABC =60°,∠ADC =30°,AD =6,BD =10,则CD = .【变式训练3】(1)问题发现:如图1,ACB △和DCE 均为等腰直角三角形,90ACB DCE ∠=∠=︒,连接AD ,BE ,点A 、D 、E 在同一条直线上,则AEB ∠的度数为__________,线段AD 、BE 之间的数量关系__________;(2)拓展探究:如图2,ACB △和DCE 均为等腰直角三角形,90ACB DCE ∠=∠=︒,连接AD ,BE ,点A 、D 、E 不在一条直线上,请判断线段AD 、BE 之间的数量关系和位置关系,并说明理由. (3)解决问题:如图3,ACB △和DCE 均为等腰三角形,ACB DCE α∠=∠=,则直线AD 和BE 的夹角为__________.(请用含α的式子表示)类型六、一线三角模型例.在ABC 中,90ACB ∠=︒,AC BC =,直线MN 经过点C 且AD MN ⊥于D ,BE MN ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时,求证:①ADC △CEB △;②DE AD BE =+;(2)当直线MN 烧点C 旋转到图2的位置时,求证:DE AD BE =-;(3)当直线MN 绕点C 旋转到图3的位置时,试问DE 、AD 、BE 具有怎样的等量关系?请写出这个等量关系,并加以证明.【变式训练1】【问题解决】(1)已知△ABC 中,AB =AC ,D ,A ,E 三点都在直线l 上,且有△BDA =△AEC =△BAC .如图①,当△BAC =90°时,线段DE ,BD ,CE 的数量关系为:______________;【类比探究】(2)如图②,在(1)的条件下,当0°<△BAC<180°时,线段DE,BD,CE的数量关系是否变化,若不变,请证明:若变化,写出它们的关系式;【拓展应用】(3)如图③,AC=BC,△ACB=90°,点C的坐标为(-2,0),点B的坐标为(1,2),请求出点A的坐标.【变式训练2】(1)如图1,在△ABC中,△BAC=90°,AB=AC,直线m经过点A,BD△直线m,CE△直线m,垂足分别为点D、E.求证:△ABD△△CAE;(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有△BDA=△AEC=△BAC=α,其中α为任意锐角或钝角.请问结论△ABD△△CAE是否成立?如成立,请给出证明;若不成立,请说明理由.(3)拓展应用:如图3,D,E是D,A,E三点所在直线m上的两动点(D,A,E三点互不重合),点F为△BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD,CE,若△BDA=△AEC=△BAC,求证:△DEF是等边三角形.【变式训练3】探究:(1)如图(1),已知:在△ABC中,△BAC=90°,AB=AC,直线m经过点A,BD△直线m,CE△直线m,垂足分别为点D、E.请直接写出线段BD,DE,CE之间的数量关系是.拓展:(2)如图(2),将探究中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有△BDA=△AEC=△BAC=α,其中α为任意锐角或钝角.请问探究中的结论是否成立?如成立,请你给出证明;若不成立,请说明理由.应用:(3)如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为△BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若△BDA=△AEC=△BAC,请直接写出△DEF的形状是.。
专题 全等三角形压轴题(30题)(解析版)

八年级上册数学《第十二章全等三角形》专题全等三角形压轴题训练(30题)1.(2022秋•忠县期末)在△ABC中,点D、E分别在AB、AC边上,设BE与CD相交于点F.(1)如图①,设∠A=60°,BE、CD分别平分∠ABC、∠ACB,证明:DF=EF.(2)如图②,设BE⊥AC,CD⊥AB,点G在CD的延长线上,连接AG、AF;若∠G=∠6,BD=CD,证明:GD=DF.【分析】(1)在BC上截取BM=BD,连接FM,证明△BFD≌△BFM,△ECF≌△MCF,进而可以解决问题;(2)根据已知条件证明△BDF≌△CDA,进而可以解决问题.【解答】证明:(1)如图,在BC上截取BM=BD,连接FM,∵∠A=60,∴∠BFC=90°+60°÷2=120°,∴∠BFD=60°,∵BE平分∠ABC,∴∠1=∠2,在△BFD和△BFM中,BD=BM∠1=∠2,BF=BF∴△BFD≌△BFM(SAS),∴∠BFM=∠BFD=60°,DF=MF,∴∠CFM=120°﹣60°=60°,∵∠CFE=∠BFD=60°,∴∠CFM=∠CFE,∵CD平分∠ACB,∴∠3=∠4,又CF=CF,在△ECF和△MCF中,∠CFE=∠CFMFC=FC,∠3=∠4∴△ECF≌△MCF(ASA),∴EF=MF,∴DF=EF;(2)∵BE⊥AC,CD⊥AB,∴∠BDF=∠CDA=90°,∴∠1+∠BFD=90°,∠3+∠CFE=90°,∠BFD=∠CFE,∴∠1=∠3,∵BD=CD,在△BDF和△CDA中,∠BDF=∠CDABD=CD,∠1=∠3∴△BDF≌△CDA(ASA),∴DF=DA,∵∠ADF=90°,∴∠6=45°,∵∠G=∠6,∴∠5=45°∴∠G=∠5,∴GD=DA,∴GD=DF.【点评】本题属于三角形的综合题,考查了全等三角形的判定与性质,角平分线的性质,解决本题的关键是掌握全等三角形的判定与性质.2.如图,△ABC中,AB=AC,D为AC边上一点,E为AB延长线上一点,且CD=BE,DE与BC相交于点F.(1)求证:DF=EF.=5,求EG的长.(2)过点F作FG⊥DE,交线段CE于点G,若CE⊥AC,CD=4,S△EFG【分析】(1)过点D作DH∥AB交BC于点H,根据等腰三角形的性质及平行线的性质得到∠BEF=∠HDF,∠DHC=∠DCH,则DH=CD,结合∠BFE=∠HFD,即可利用AAS判定△BEF≌△HDF,根据全等三角形的性质即可得解;(2)根据三角形的面积公式求解即可.【解答】(1)过点D作DH∥AB交BC于点H,∵AB=AC,∴∠ABC=∠ACB,∵DH∥AB,∴∠DHC=∠ABC,∴∠DHC=∠ACB=∠DCH,∴DH=CD,∵CD=BE,∴DH=BE,∵DH∥AB,∴∠BEF=∠HDF,在△BEF和△HDF中,∠BFE=∠HFD∠BEF=∠HDFBE=DH,∴△BEF≌△HDF(AAS),∴DF=EF;(2)连接DG,∵DF=EF,FG⊥DE,∴S△DFG =S△EFG=5,∴S△DEG=10,∵CE⊥AC,CD=4,∴S△DEG =12EG•CD=12EG×4,∴12EG×4=10,∴EG=5.【点评】此题考查了全等三角形的判定与性质,利用AAS判定△BEF≌△HDF是解题的关键.3.如图1,在等腰直角三角形ABC中,AB=AC,∠BAC=90°,点P为BC边上的一个动点,连接AP,以AP为直角边,A为直角顶点,在AP右侧作等腰直角三角形PAD,连接CD.(1)当点P在线段BC上时(不与点B重合),求证:△BAP≌△CAD;(2)当点P在线段BC的延长线上时(如图2),试猜想线段BP和CD的数量关系与位置关系分别是什么?请给予证明.【分析】(1)证得∠BAP=∠CAD,根据SAS可证明△BAP≌△CAD;(2)可得∠BAP=∠CAD,由SAS可证明△BAP≌△CAD,可得BP=CD,∠B=∠ACD,则结论得证.【解答】(1)证明:∵∠BAC=∠PAD=90°,∴∠BAC﹣∠PAC=∠PAD﹣∠PAC,即:∠BAP=∠CAD,在△BAP和△CAD中AB=AC∠BAP=∠CAD,PA=DA∴△BAP≌△CAD(SAS);(2)猜想:BP=CD,BP⊥CD.证明:∵∠BAC=∠PAD=90°,∴∠BAC+∠PAC=∠PAD+∠PAC,即:∠BAP=∠CAD,在△BAP和△CAD中AB=AC∠BAP=∠CAD,PA=DA∴△BAP≌△CAD(SAS),∴BP=CD(全等三角形的对应边相等),∠B=∠ACD(全等三角形的对应角相等),∵∠B+∠ACB=90°,∴∠ACD+∠ACB=90°,即:BP⊥CD.【点评】本题考查了全等三角形的判定与性质,等腰直角三角形的性质,根据同角的余角相等求出两边的夹角相等是证明三角形全等的关键.4.在△ABC中,∠ABC=90°.点G在直线BC上,点E在直线AB上,且AG与CE相交于点F,过点A 作边AB的垂线AD,且CD∥AG,EB=AD,AE=BC.(1)如图①,当点E在△ABC的边AB上时,求∠DCE的度数;(2)如图②,当点E在线段BA的延长线上时,求证:AB=BG.【分析】(1)如图①,连接ED,根据已知条件得到△ADE≌△BEC(SAS),根据全等三角形的性质得到∠AED=∠BCE,ED=CE,于是得到结论;(2)如图②,连接DE,根据已知条件得到△ADE≌△BEC(SAS),根据全等三角形的性质得到∠AED =∠BCE,ED=CE,根据等腰三角形的性质得到∠EDC=∠ECD,推出AF平分∠DAE,于是得到结论.【解答】解:(1)如图①连接ED,∵AD⊥AB,∴∠DAE=90°,∵∠ABC=90°,∵AD=EB,AE=BC,∴△ADE≌△BEC(SAS),∴∠AED=∠BCE,ED=CE,∴∠AED+∠BEC=∠BCE+∠BEC;∴∠AED+∠CEB=90°,∴∠DEC=90°,∴∠DCE=45°;(2)如图②,连接DE,∵AD⊥AB,∴∠DAE=90°,∵∠ABC=90°,∴∠DAE=∠ABC,∵AD=EB,AE=BC,∴△ADE≌△BEC(SAS),∴∠ADE=∠BEC,ED=CE,∵ED=CE,∴∠EDC=∠ECD,即∠ADE+∠ADC=∠ECD,∴∠BEC+∠DAF=∠AFC,∵∠BEC+∠EAF=∠AFC,∴∠DAF=∠EAF,∴AF平分∠DAE,∵∠DAE=90°,∴∠EAF=45°,∵∠EAF=∠BAG,∴∠BAG=45°,∵∠ABC=90°,∴∠ABG=90°,∴∠BGA=∠BAG,∴AB=BG.【点评】本题考查了平行线的性质,全等三角形的判定和性质,角平分线的定义,等腰直角三角形的判定和性质,正确的识别图形是解题的关键.5.在Rt△ABC中,∠ABC=90°,点D是CB延长线上一点,点E是线段AB上一点,连接DE.AC=DE,BC=BE.(1)求证:AB=BD;(2)BF平分∠ABC交AC于点F,点G是线段FB延长线上一点,连接DG,点H是线段DG上一点,连接AH交BD于点K,连接KG.当KB平分∠AKG时,求证:AK=DG+KG.【分析】(1)证明Rt△ACB≌Rt△DEB即可解决问题;(2)作BM平分∠ABD交AK于点M,证明△BMK≌△BGK,△ABM≌△DBG,即可解决问题.【解答】证明:(1)在Rt△ACB和Rt△DEB中,AC=DEBC=BE,∴Rt△ACB≌Rt△DEB(HL),∴AB=BD,(2)如图:作BM平分∠ABD交AK于点M,∵BM平分∠ABD,KB平分∠AKG,∴∠ABM=∠MBD=45°,∠AKB=∠BKG,∵∠ABF=∠DBG=45°∴∠MBD=∠GBD,在△BMK和△BGK中,∠MBD=∠GBDBK=BK,∠AKB=∠BKG∴△BMK≌△BGK(ASA),∴BM=BG,MK=KG,在△ABM和△DBG中,AB=BD∠ABM=∠DBG,BM=BG∴△ABM≌△DBG(SAS),∴AM=DG,∵AK=AM+MK,∴AK=DG+KG.【点评】本题考查了全等三角形的判定与性质,解决本题的关键是得到△BMK≌△BGK.6.(2023春•市南区期末)如图,在△ABC中,AB=AC,AD⊥BC于点D,E为AC边上一点,连接BE与AD交于点F,G为△ABC外一点,满足∠ACG=∠ABE,∠FAG=∠BAC,连接EG.(1)求证:△ABF≌△ACG;(2)求证:BE=CG+EG.【分析】(1)根据已知条件可得∠BAD=∠CAG,然后利用ASA即可证明△ABF≌△ACG;(2)结合(1)的结论,再证明△AEF≌△AEG,即可解决问题.【解答】(1)证明:∵∠BAC=∠FAG,∴∠BAC﹣∠CAD=∠FAG﹣∠CAD,∴∠BAD=∠CAG,在△ABF和△ACG中,∠BAD=∠CAGAB=AC,∠ABF=∠ACG∴△ABF≌△ACG(ASA);(2)证明:∵△ABF≌△ACG,∴AF=AG,BF=CG,∵AB=AC,AD⊥BC,∴∠BAD=∠CAD,∵∠BAD=∠CAG,∴∠CAD=∠CAG,在△AEF和△AEG中,AF=AG∠FAE=∠GAE,AE=AE∴△AEF≌△AEG(SAS).∴EF=EG,∴BE=BF+FE=CG+EG.【点评】本题考查了全等三角形的判定与性质,解决本题的关键是得到△AEF≌△AEG.7.(2022秋•新市区校级期中)已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.求证:(1)AD=AE=EC.(2)BA+BC=2BF.【分析】(1)由△BCD和△BEA为等腰三角形,∠ABD=∠EBC,得出∠BCD=∠BEA,由△ABD≌△EBC可得∠BCE=∠BDA,由∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA得出∠BCD+∠DCE=∠DAE+∠BEA,进而得出∠DCE=∠DAE,即可证明AE=EC;(2)过点E作EG⊥BC交BC的延长线于点G,由“HL”得出Rt△BFE≌Rt△BGE和Rt△BFE≌Rt△BGE,从而得出BF=BG,FA=CG,再通过等量代换即可得出结论.【解答】(1)证明:∵BD为△ABC的角平分线,∴∠ABD=∠EBC,在△ABD与△EBC中,AB=EB∠ABD=∠EBD,BD=BC∴△ABD≌△EBC(SAS),∴∠BCE=∠BDA,∵∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,∴∠BCD+∠DCE=∠DAE+∠BEA,∵BD=BC,BE=BA,∴△BCD和△BEA为等腰三角形,∵∠ABD=∠EBC,∴∠BCD=∠BEA,∴∠DCE=∠DAE,∴AE=EC,∵△ABD≌△EBC,∴AD=EC,∴AD=EC=AE;(2)证明:如图,过点E作EG⊥BC交BC的延长线于点G,∵BE平分∠ABC,EF⊥AB,EG⊥BG,∴EF=EG,在Rt△BFE与Rt△BGE中,EF=EGBE=BE,∴Rt△BFE≌Rt△BGE(HL),∴BF=BG,在Rt△AFE与Rt△CGE中,EF=EGEA=EC,∴Rt△AFE≌Rt△CGE(HL),∴FA=CG,∴BA+BC=BF+FA+BG﹣CG=BF+BG=2BF.【点评】本题考查了全等三角形的判定与性质,掌握三角形全等的判定方法是解决问题的关键.8.(2023春•余江区期末)如图,大小不同的两块三角板△ABC和△DEC直角顶点重合在点C处,AC=BC,DC=EC,连接AE、BD,点A恰好在线段BD上.(1)找出图中的全等三角形,并说明理由;(2)当AD=AB=4cm,则AE的长度为 cm.(3)猜想AE与BD的位置关系,并说明理由.【分析】(1)根据SAS证明△CBD≌△CAE即可;(2)根据全等三角形的性质解答即可;(3)根据全等三角形的性质和垂直的定义解答即可.【解答】解:(1)△CBD≌△CAE,理由如下:∵∠ACB=∠DCE=90°,∴∠ACB+∠ACD=∠DCE+∠ACD,即∠BCD=∠ACE,在△CBD与△CAE中,BC=AC∠BCD=∠ACE,DC=EC∴△CBD≌△CAE(SAS);(2)∵△CBD≌△CAE,∴BD=AE=AD+AB=4+4=8(cm),故答案为:8;(3)AE⊥BD,理由如下:AE与CD相交于点O,在△AOD与△COE中,∵△CBD≌△CAE,∴∠ADO=∠CEO,∵∠AOD=∠COE,∴∠OAD=∠OCE=90°,∴AE⊥BD.【点评】此题考查全等三角形的判定和性质,关键是根据SAS得出△CBD与△CAE全等解答.9.已知,△ABC中,∠ACB=90°,AC=BC,点E是BC上一点,连接AE(1)如图1,当AE平分∠BAC时,EH⊥AB于H,△EHB的周长为10m,求AB的长;(2)如图2,延长BC至D,使DC=BC,将线段AE绕点A顺时针旋转90°得线段AF,连接DF,过点B作BG⊥BC,交FC的延长线于点G,求证:BG=BE.【分析】(1)根据等腰三角形的性质得到∠B=45°,根据角平分线的性质得到CE=EH=BH,根据全等三角形的性质得到AH=AC,于是得到结论;(2)先连接AD,依据AAS判定△ADF≌△ABE,得到DF=BE,再判定△BCG≌△DCF,得出DF=BG,进而得到BG=BE.【解答】解:(1)∵∠ACB=90°,AC=BC,∴∠B=45°,∵AE平分∠BAC时,EH⊥AB于H,∴CE=EH=BH,在Rt△ACE与Rt△AHE中,CE=EH AE=AE,∴Rt△ACE与Rt△AHE(HL),∴AH=AC,∴AH=BC,∵△EHB的周长为10m,∴AB=AH+BH=BC+BH=10m;(2)如图所示,连接AD,线段AE绕点A顺时针旋转90°得线段AF,则AE=AF,∠EAF=90°,∵AC⊥BD,DC=BC,∴AD=AB,∠ABE=∠ADC=45°,∴∠BAD=90°=∠EAF,∴∠BAE=∠DAF,∴△ABE≌△ADF(SAS),∴DF=BE,∠ADF=∠ABE=45°,∴∠FDC=90°,∵BG⊥BC,∴∠CBG=∠CDF=90°,又∵BC=DC,∠BCG=∠DCF,∴△BCG≌△DCF(ASA),∴DF=BG,∴BG=BE.【点评】本题主要考查了旋转的性质,等腰直角三角形的性质以及全等三角形的判定与性质的综合运用,解决问题的关键是作辅助线构造全等三角形,依据全等三角形的对应边相等得出结论.10.在△ABC中,∠ABC=45°,AM⊥MB,垂足为M,点C是BM延长线上一点,连接AC.(1)如图①,点D在线段AM上,且DM=CM.求证:△BDM≌△ACM;(2)如图②,在(1)的条件下,点E是△ABC外一点,且满足EC=AC,连接ED并延长交BC于点F,且F为线段BC的中点,求证:∠BDF=∠CEF.【分析】(1)利用SAS即可证明△BMD≌△AMC.(2)延长EF到点G,使得FG=EF,证△BMD≌△AMC得AC=BD,再证△BFG≌△CFE可得BG=CE,∠G=∠E,从而得BD=BG=CE,即可得∠BDG=∠G=∠CEF.【解答】(1)证明:∵∠ABM=45°,AM⊥BM,在△BMD和△AMC中,DM=CM∠BMD=∠AMC BM=AM,∴△BMD≌△AMC(SAS);(2)证明:延长EF到点G,使得FG=EF,连接BG.如图所示:∵△BMD≌△AMC∴BD=AC,又∵CE=AC,∴BD=CE,在△BFG和△CFE中,BF=FC∠BFG=∠EFC FG=FE,∴△BFG≌△CFE(SAS),∴BG=CE,∠G=∠CEF,∴BD=CE=BG,∴∠BDF=∠G=∠CEF.∴∠BDF=∠CEF.【点评】本题主要考查全等三角形的判定与性质,等腰直角三角形的性质等知识点,熟练掌握全等三角形的判定与性质是解题的关键.11.如图1,在△ABC中,∠A=120°,∠C=20°,BD平分∠ABC,交AC于点D.(1)求证:BD=CD.(2)如图2,若∠BAC的角平分线AE交BC于点E,求证:AB+BE=AC.(3)如图3,若∠BAC的外角平分线AE交CB的延长线于点E,则(2)中的结论是否成立?若成立,给出证明,若不成立,写出正确的结论.【分析】(1)根据∠A=120°,∠C=20°,可得∠ABC的度数,再根据BD平分∠ABC,可得∠DBC=∠C=20°,进而可得结论;(2)如图2,过点E作EF∥BD交AC于点F,证明△ABE≌△AFE,可得BE=EF=FC,进而可得AB+BE =AC;(3)如图3,过点A作AF∥BD交BE于点F,结合(1)和AE是∠BAC的外角平分线,可得FE=AF=AC,进而可得结论BE﹣AB=AC.【解答】(1)证明:∵∠A=120°,∠C=20°,∴∠ABC=180°﹣120°﹣20°=40°,∵BD平分∠ABC,∴∠ABD=∠DBC=12∠ABC=20°,∴∠DBC=∠C=20°,∴BD=CD;(2)证明:如图2,过点E作EF∥BD交AC于点F,∴∠FEC=∠DBC=20°,∴∠FEC=∠C=20°,∴∠AFE=40°,FE=FC,∴∠AFE=∠ABC,∵AE是∠BAC的平分线,∴∠BAE=∠FAE,在△ABE和△AFE中,∠BAE=∠FAE∠ABE=∠AFE,AE=AE∴△ABE≌△AFE(AAS),∴BE=EF,∴BE=EF=FC,∴AB+BE=AF+FC=AC;(3)(2)中的结论不成立,正确的结论是BE﹣AB=AC.理由如下:如图3,过点A作AF∥BD交BE于点F,∴∠AFC=∠DBC=20°,∴∠AFC=∠C=20°,∴AF=AC,∵AE是∠BAC的外角平分线,∴∠EAB=12(180°﹣∠ABC)=30°,∵∠ABC=40°,∴∠E=∠ABC﹣∠EAB=10°,∴∠E=∠FAE=10°,∴FE=AF,∴FE=AF=AC,∴BE﹣AB=BE﹣BF=EF=AC.【点评】本题考查了全等三角形的判定与性质,解决本题的关键是掌握全等三角形的判定与性质.12.(2022秋•渝北区校级期末)已在等腰Rt△ABC中,∠ABC=90°,AB=CB,D为直线AB上一点,连接CD,过点C作CE⊥CD,且CE=CD,连接DE,交AC于点F.(1)如图1,当点D在线段AB上,且∠DCB=30°时,请探究DF,EF,CF之间的数量关系,并说明理由;(2)如图2,在(1)的条件下,在FC上任取一点G,连接DG,作射线GP使∠DGP=60°,交∠DFG 的平分线于点Q,求证:FD+FG=FQ.【分析】(1)在EF上找到G点使得FG=CF,易证△CFG是等边三角形,可得CG=CF=GF,即可求得∠ECG=∠ACD,即可证明△ECG≌△CDF,可得DF=EG,即可解题;(2)在FP上找到H点,使得FH=FG,易证△FGH是等边三角形,可得∠GHF=∠FGH=60°,GH =FG=FH,即可求得∠FGD=∠QGH,即可证明△DFG≌△QHG,可得DF=QH,即可解题.【解答】(1)解:EF=DF+CF;在EF上找到G点使得FG=CF,如图2,∵∠BCD=30°,∠ACB=45°,∴∠ACD=15°,∴∠CFG=∠CDE+∠ACD=60°,∵FG=CF,∴△CFG是等边三角形,∴CG=CF=GF,∠FCG=60°,∴∠GCE=90°﹣15°﹣60°=15°,在△ECG和△CDF中,CG=CF∠ECG=∠ACD,CE=CD∴△ECG≌△CDF,(SAS)∴DF=EG,∵EF=EG+GF,∴EF=DF+CF;(2)证明:在FQ上找到H点,使得FH=FG,如图3,∵FQ平分∠DFG,∴∠QFG=60°,∵FG=FH,∴△FGH是等边三角形,∴∠GHF=∠FGH=60°,GH=FG=FH,∵∠AFD=∠CDE+∠ACD=60°,∴∠GHQ=∠DFG=120°,∵∠FGD+∠DGH=60°,∠DGH+∠QGH=60°,∠QGH=∠DGF,∴∠FGD=∠QGH,在△DFG和△QHG中,∠DFG=∠QHG=120°FG=HG,∠FGD=∠QGH∴△DFG≌△QHG,(ASA)∴DF=QH,∵FQ=FH+QH,∴FQ=FG+FD.【点评】本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ECG≌△CDF和△DFG≌△QHG是解题的关键.13.(2022春•运城期末)综合与探究如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,CE的延长线交BD于点F.(1)求证:△ACE≌△ABD.(2)若∠BAC=∠DAE=50°,请直接写出∠BFC的度数.(3)过点A作AH⊥BD于点H,求证:EF+DH=HF.【分析】(1)可利用SAS证明结论;(2)由全等三角形的性质可得∠AEC=∠ADB,结合平角的定义可得∠DAE+∠DFE=180°,根据∠BFC+∠DFE=180°,可求得∠BFC=∠DAE,即可求解;(3)连接AF,过点A作AJ⊥CF于点J.结合全等三角形的性质利用HL证明Rt△AFJ≌Rt△AFH,Rt△AJE≌Rt△AHD可得FJ=FH,EJ=DH,进而可证明结论.【解答】(1)证明:∵∠BAC=∠DAE.∴∠CAE=∠BAD.在△ACE和△ABD中,AC=AB∠CAE=∠BAD,AE=AD∴△ACE ≌△ABD (SAS );(2)解:∵△ACE ≌△ABD ,∴∠AEC =∠ADB ,∴∠AEF +∠AEC =∠AEF +∠ADB =180°.∴∠DAE +∠DFE =180°,∵∠BFC +∠DFE =180°,∴∠BFC =∠DAE =∠BAC =50°;(3)证明:如图,连接AF ,过点A 作AJ ⊥CF 于点J .∵△ACE ≌△ABD ,∴S △ACE =S △ABD ,CE =BD ,∵AJ ⊥CE ,AH ⊥BD .∴12CE ⋅AJ =12BD ⋅AH ,∴AJ =AH .在Rt △AFJ 和Rt △AFH 中,AF =AF AJ =AH ,∴Rt △AFJ ≌Rt △AFH (HL ),∴FJ =FH .在Rt △AJE 和Rt △AHD 中,AE =AD AJ =AH ,∴Rt △AJE ≌Rt △AHD (HL ),∴EJ =DH ,∴EF +DH =EF +EJ =FJ =FH .【点评】本题主要考查全等三角形的判定与性质,掌握全等三角形的判定条件是解题的关键.14.(2022春•沙坪坝区校级期中)如图,在△ABC 中,∠ABC 、∠ACB 的平分线交于点D ,延长BD 交AC 于E ,G 、F 分别在BD 、BC 上,连接DF 、GF ,其中∠A =2∠BDF ,GD =DE .(1)当∠A =80°时,求∠EDC 的度数;(2)求证:CF =FG +CE .【分析】(1)方法一:先求∠ABC 和∠ACB 的和为100°,再根据角平分线求∠DBC +∠DCB =50°,再根据外角即可解决问题;方法二:在BC 上取点M ,使CM =CE ,证明△CDE ≌△CDM (SAS ),可得DE =DM ,∠DEC =∠DMC ,∠EDC =∠MDC ,证明∠BDM =180°−12∠ABC ﹣∠DMB =180°−12∠ABC ﹣∠AEB =∠A =80°,进而可以解决问题.(2)结合(1)然后证明△DGF ≌△DMF (SAS ),可得GF =MF ,进而可以解决问题.【解答】(1)解:方法一:∵∠A =80°,∴∠ABC +∠ACB =100°,∵BE 平分∠ABC 、CD 平分∠ACB ,∴∠DBC +∠DCB =50°,∴∠EDC =∠DBC +∠DCB =50°;方法二:如图,在BC 上取点M ,使CM =CE ,∵CD 平分∠ACB ,∴∠ACD=∠BCD,在△CDE和△CDM中,CE=CM∠ECD=∠MCDCD=CD,∴△CDE≌△CDM(SAS),∴DE=DM,∠DEC=∠DMC,∠EDC=∠MDC,∵GD=DE,∴GD=MD,∵∠DEC+∠AEB=180°,∠DMC+∠DMF=180°,∴∠AEB=∠DMF,∵BE平分∠ABC,∴∠ABE=∠CBE=12∠ABC,∴∠BDM=180°−12∠ABC﹣∠DMB=180°−12∠ABC﹣∠AEB=∠A=80°,∴∠EDM=100°,∴∠EDC=50°;(2)证明:∵∠A=2∠BDF,∴∠BDM=2∠BDF,∴∠FDM=∠BDF,在△DGF和△DMF中,DG=DM∠GDF=∠MDFDF=DF,∴△DGF≌△DMF(SAS),∴GF=MF,∴CF=CM+FM=CE+GF.∴CF=FG+CE.【点评】本题考查了全等三角形的判定与性质,角平分线的定义,解决本题的关键是根据题意准确作出辅助线得到△DGF≌△DMF.15.如图,在△ABC中,∠C=90°,AD是∠BAC的角平分线交BC于点D,过D作DE⊥BA于点E,点F在AC上,且BD=DF.(1)求证:AC=AE;(2)求证:∠BAC+∠FDB=180°;(3)若AB=9.5,AF=1.5,求线段BE的长.【分析】(1)证△ACD≌△AED(AAS),即可得出结论;(2)设∠DAC=∠DAE=α,在AB上截取AM=AF,连接MD,证△FAD≌△MAD(SAS),得FD=MD,∠ADF=∠ADM,再证Rt△MDE≌Rt△BDE(HL),得∠DME=∠B,然后证∠FDB=90°+90°﹣2α=180°﹣2α,即可得出结论;(3)求出MB=AB﹣AM=8,由全等三角形的性质得ME=BE,即可求解.【解答】(1)证明:∵AD平分∠BAC,∴∠DAC=∠DAE,∵DE⊥BA,∴∠DEA=∠DEB=90°,∵∠C=90°,∴∠C=∠DEA=90°,在△ACD和△AED中,∠C=∠DEA∠DAC=∠DAE,AD=AD∴△ACD≌△AED(AAS),∴AC=AE;(2)证明:设∠DAC=∠DAE=α,∵∠C=∠DEA=90°,∴∠ADC=90°﹣α,∠ADE=90°﹣α,则∠FDB=∠FCD+∠DFC=90°+∠DFC,在AB上截取AM=AF,连接MD,如图所示:在△FAD和△MAD中,AF=AM∠DAF=∠DAM,AD=AD∴△FAD≌△MAD(SAS),∴FD=MD,∠ADF=∠ADM,∵BD=DF,∴BD=MD,在Rt△MDE和Rt△BDE中,MD=BDDE=DE∴Rt△MDE≌Rt△BDE(HL),∴∠DME=∠B,∵∠DAC=∠DAE=α,∴∠DAC+∠ADF=∠ADM+∠ADM,在△FAD中,∠DAC+∠ADF=∠DFC,在△AMD中,∠DAE+∠ADM=∠DME,∴∠DFC=∠DME,∴∠DFC=∠B,∵∠C=90°,在△ABC中,∠B=90°﹣2α,∴∠DFC=90°﹣2α,∴∠FDB=90°+90°﹣2α=180°﹣2α,∵∠BAC=∠DAC+∠DAE=2α,∴∠FDB+∠BAC=180°﹣2α+2α=180°;(3)解:∵AF=AM,且AF=1.5,∴AM=1.5,∵AB=9.5,∴MB=AB﹣AM=9.5﹣1.5=8,由(2)得:Rt△MDE≌Rt△BDE,∴ME=BE,∴BE=12BM=4,即BM的长为4.【点评】本题考查了全等三角形的判定与性质、角平分线定义、直角三角形的性质、三角形的外角性质等知识;证明△FAD≌△MAD和Rt△MDE≌Rt△BDE是解题的关键.16.在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接DE,CE.(1)如图,当点D在BC延长线上移动时,求证:BD=CE.(2)设∠BAC=α,∠DCE=β.①当点D在线段BC的延长线上移动时,α与β之间有什么数量关系?请说明理由.②当点D分别在线段BC上、线段BC的反向延长线上移动时,α与β之间有什么数量关系?请说明理由.【分析】(1)根据SAS证△BAD≌△CAE,可得结论;(2)①由△BAD≌△CAE,推出∠B=∠ACE,根据三角形外角性质求出即可;②α+β=180°或α=β,根据三角形外角性质求出即可.【解答】(1)证明:∵∠DAE=∠BAC,∴∠DAE+∠CAD=∠BAC+∠CAD,∴∠BAD=∠CAE,在△BAD和△CAE中,AB=AC∠BAD=∠CAE,AD=AE∴△BAD≌△CAE(SAS),(2)解:①当点D在线段BC的延长线上移动时,α与β之间的数量关系是α=β,理由是:由(1)知△BAD≌△CAE,∴∠B=∠ACE,∵∠ACD=∠B+∠BAC=∠ACE+∠DCE,∴∠BAC=∠DCE,∵∠BAC=α,∠DCE=β,∴α=β;②分三种情况:i)当D在线段BC上时,如图2,α+β=180°,理由是:同理可证明:△ABD≌△ACE(SAS),∴∠ADB=∠AEC,∠ABC=∠ACE,∵∠ADC+∠ADB=180°,∴∠ADC+∠AEC=180°,∴∠DAE+∠DCE=180°,∵∠BAC=∠DAE=α,∠DCE=β,∴α+β=180°,ii)当点D在线段BC反向延长线上时,如图3,α=β.如图3,同理可证明:△ABD≌△ACE(SAS),∴∠ABD=∠ACE,∵∠ACE=∠ACD+∠DCE,∠ABD=∠ACD+∠BAC,∴∠ACD+∠DCE=∠ACD+∠BAC,∴∠BAC=∠DCE,∵∠BAC=α,∠DCE=β,∴α=β;ii)当点D在线段BC的延长线上时,如图1,α=β.综上,当点D在BC上移动时,α=β或α+β=180°.【点评】本题是三角形的综合题,考查了全等三角形的性质和判定,三角形的外角性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.17.(2022春•南海区校级月考)如图,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD.以AD为直角边且在AD的上方作等腰直角三角形ADF.(1)若AB=AC,∠BAC=90°.①当点D在线段BC上时(与点B不重合),试探讨CF与BD的数量关系和位置关系;②当点D在线段BC的延长线上时,①中的结论是否仍然成立,请在图②中画出相应的图形并说明理由;(2)如图③,若AB≠AC,∠BAC≠90°,∠BCA=45°,点D在线段BC上运动,试探究CF与BD 的位置关系.【分析】(1)①根据同角的余角相等求出∠CAF=∠BAD,然后利用“边角边”证明△ACF和△ABD全等,根据全等三角形的性质及等腰直角三角形的性质求解即可;②先求出∠CAF=∠BAD,然后与①的思路相同求解即可;(2)过点A作AE⊥AC交BC于E,可得△ACE是等腰直角三角形,根据等腰直角三角形的性质可得AC=AE,∠AED=45°,再根据同角的余角相等求出∠CAF=∠EAD,然后利用“边角边”证明△ACF 和△AED全等,根据全等三角形对应角相等可得∠ACF=∠AED,然后求出∠BCF=90°,从而得到CF ⊥BD.【解答】解:(1)①CF=BD,CF⊥BD,理由如下:∵∠BAC=90°,△ADF是等腰直角三角形,AB=AC,∴∠CAF+∠CAD=90°,∠BAD+∠CAD=90°,∠B=∠ACB=45°,∴∠CAF=∠BAD,在△ACF和△ABD中,AC=AB∠CAF=∠BAD,AF=AD∴△ACF≌△ABD(SAS),∴CF=BD,∠ACF=∠B=45°,∵∠ACB=45°,∴∠FCB=45°+45°=90°,∴CF⊥BD;②①中的结论成立,理由如下:如图②:∵∠BAC=90°,△ADF是等腰直角三角形,AB=AC,∴∠BAC=∠DAF=90°,∠B=∠ACB=45°,∴∠BAC+∠CAD=∠DAF+∠CAD,即∠CAF=∠BAD,在△ACF和△ABD中,AC=AB∠CAF=∠BAD,AF=AD∴△ACF≌△ABD(SAS),∴CF=BD,∠ACF=∠B,∴∠BCF=∠ACF+∠ACB=45°+45°=90°,∴CF⊥BD;(3)如图③,过点A作AE⊥AC交BC于E,∵∠BCA=45°,∴△ACE是等腰直角三角形,∴AC=AE,∠AED=45°,∵∠CAF+∠CAD=90°,∠EAD+∠CAD=90°,∴∠CAF=∠EAD,在△ACF和△AED中,AC=AE∠CAF=∠EAD,AF=AD∴△ACF≌△AED(SAS),∴∠ACF=∠AED=45°,∴∠BCF=∠ACF+∠BCA=45°+45°=90°,∴CF⊥BC.【点评】此题是三角形综合题,主要考查了全等三角形的判定与性质,等腰直角三角形的性质,作出合理的辅助线根据同角的余角相等求出两边的夹角相等是证明三角形全等的关键.18.如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.(1)△ABC≌△ADE吗?为什么?(2)求∠FAE的度数;(3)延长BF到G,使得FG=FB,试说明CD=2BF+DE.【分析】(1)由“SAS”可证△ABC≌△ADE;(2)由等腰直角三角形的性质可得∠AEC=∠ACE=45°,由全等三角形的性质可得∠ACB=∠AED=45°,即可求解;(3)由全等三角形的性质可得∠ABC=∠ADE,BC=DE,由线段垂直平分线的性质和等腰三角形的性质可得AB=AG=AD,∠ABG=∠AGB=∠ADC,由“AAS”可证△ACD≌△ACG,可得CD=CG,可得结论.【解答】证明:(1)△ABC≌△ADE,理由如下:∵∠BAD=∠CAE=90°,∴∠EAD=∠CAB,在△ABC和△ADE中,AB=AD∠BAC=∠DAE,AC=AE∴△ABC≌△ADE(SAS);(2)∵∠CAE=90°,AC=AE,∴∠AEC=∠ACE=45°,∵△ABC≌△ADE,∴∠ACB=∠AED=45°,∵AF⊥CB,∴∠FAC=45°,∴∠FAE=135°;(3)∵△ABC≌△ADE,∴∠ABC=∠ADE,BC=DE,∴∠ADC=∠ABG,∵AF⊥BF,BF=FG,∴AB=AG,∴AG=AD,∠ABG=∠AGB=∠ADC,又∵∠ACG=∠ACD=45°,∴△ACD≌△ACG(AAS),∴CD=CG,∴CD=BG+CB=2BF+DE.【点评】本题是三角形综合题,考查了全等三角形的判定和性质,等腰三角形的判定和性质,线段垂直平分线的性质等知识,证明△ACD≌△ACG是解题的关键.19.Rt△ABC中,∠C=90°,点D在直线AC上,点E在直线AB上,∠ADE=∠ABC.(1)如图1,当点D、E分别在边AC、AB上时,求证:DE⊥AB;(2)如图2,当点D在CA延长线上,点E在BA延长线上时,DE、BC延长线交于点F,作∠EAC的角平分线AG交DF于点G,求证:∠D+2∠DGA=90°;(3)如图3,在(2)的条件下,连接BG交CD于点H,若∠DGH=∠DHG,∠AGB=3∠CBH,求∠DGA的度数.【分析】(1)根据直角三角形的两锐角互余得到∠ABC+∠A=90°,等量代换得出∠ADE+∠A=90°,进而得出∠AED=90°,根据垂直的定义即可得解;(2)过点G作GN∥FB交CD于点N,根据平行线的性质及垂直的定义推出∠AEG=∠ANG=90°,根据角平分线定义得出∠EAG=∠NAG,利用AAS证明△EAG≌△NAG,根据全等三角形的性质及直角三角形的性质即可得解;(3)根据直角三角形的性质及对顶角相等得出∠DGH=90°−13∠AGB,根据等腰三角形的性质推出∠DGH=90°−12∠D,则90°−13∠AGB=90°−12∠D,进而推出∠AGB=32∠D,则∠DGA+32∠D=90°−12∠D,结合(2)求解即可.【解答】(1)证明:∵∠C=90°,∴∠ABC+∠A=90°,∵∠ADE=∠ABC,∴∠ADE+∠A=90°,∴∠AED=90°,∴DE⊥AB;(2)证明:如图2,过点G作GN∥FB交CD于点N,则∠GNC=∠ACB=90°,∴GN⊥CD,∵∠ACB=90°,∴∠ABC+∠BAC=90°,∵∠ADE=∠ABC,∠BAC=∠DAE,∴∠ADE+∠DAE=90°,∴∠DEA=90°,∴BE⊥DF,∴∠AEG=∠ANG=90°,∵AG平分∠EAC,∴∠EAG=∠NAG,在△EAG和△NAG中,∠AEG=∠ANG∠EAG=∠NAGAG=AG,∴△EAG≌△NAG(AAS),∴∠DGA=∠NGA,∴∠DGN=2∠DGA,∵∠D+∠DGN=90°,∴∠D+2∠DGA=90°;(3)解:∵∠AGB=3∠CBH,∴∠CBH=13∠AGB,∵∠DHG=∠CHB=90°﹣∠CBH,∴∠DGH=90°−13∠AGB,∵∠DGH=∠DHG,∴∠DGH=12(180°﹣∠D)=90°−12∠D,∴90°−13∠AGB=90°−12∠D,∴∠AGB=32∠D,∵∠DGH=∠DGA+∠AGB,∴∠DGA+∠AGB=90°−12∠D,∴∠DGA+32∠D=90°−12∠D,∴2∠D+∠DGA=90°,由(2)知,∠D+2∠DGA=90°,∴∠D=∠DGA,∴3∠DGA=90°,∴∠DGA=30°.【点评】此题是三角形综合题,考查了直角三角形的判定与性质、全等三角形的判定与性质、等腰三角形的性质、平行线的性质等知识,熟练掌握直角三角形的判定与性质、全等三角形的判定与性质、等腰三角形的性质并作出合理的辅助线是解题的关键.20.(2023春•新市区期末)在△ABC中,∠ACB=90°,AC=BC,D是直线AB上一点(点D不与点A、B重合),连接DC并延长到E,使得CE=CD,过点E作EF⊥直线BC,交直线BC于点F.(1)如图1,当点D为线段AB上的任意一点时,用等式表示线段EF、CF、AC的数量关系,并证明;(2)如图2,当点D为线段BA的延长线上一点时,依题意补全图2,猜想线段EF、CF、AC的数量关系是否发生改变,并证明;(3)如图3,当点D在线段AB的延长线上时,直接写出线段EF、CF、AC之间的数量关系.【分析】(1)过D作DH⊥CB于H,由“AAS”可证△FEC≌△HDC,可得CH=FC,DH=EF,可得结论;(2)过D作DH⊥CB于H,由“AAS”可证△FEC≌△HDC,可得CH=FC,DH=EF,可得结论.(3)过D作DH⊥CB交CB的延长线于H,由“AAS”可证△FEC≌△HDC,可得CH=FC,DH=EF,可得结论.【解答】解:(1)结论:AC=EF+FC.理由如下:过D作DH⊥CB于H,∴∠DHC=∠DHB=90°,∵EF⊥CF,∴∠EFC=∠DHC=90°,在△FEC和△HDC中,∠EFC=∠DHC=90°∠FCE=∠DCH,EC=DC∴△FEC≌△HDC(AAS),∴CH=FC,DH=EF,∵∠ACB=90°,AC=BC,∴∠B=45°,∵∠DHB=90°,∴∠B=∠HDB=45°,∴DH=HB=EF,∵BC=CB+HB,∴AC=FC+EF;(2)依题意补全图形,结论:AC=EF﹣CF,理由如下:过D作DH⊥CB交BC的延长线于H,∵EF⊥CF,∴∠EFC=∠DHC=90°,在△FEC和△HDC中,∠FCE=∠DCH∠EFC=∠DHC=90°,EC=DC∴△FEC≌△HDC(AAS),∴CH=FC,DH=EF,∵∠DHB=90°,∴∠B=∠HDB=45°,∴DH=HB=EF,∵BC=HB﹣CH,∴AC=EF﹣CF;(3)AC=CF﹣EF.如图3,过D作DH⊥CB交CB的延长线于H,同理可证△FEC≌△HDC(AAS),∴CH=FC,DH=EF,∵∠DHB=90°,∴∠B=∠HDB=45°,∴DH=HB=EF,∵BC=CH﹣BH,∴AC=CF﹣EF.【点评】本题是三角形综合题,考查了全等三角形的判定和性质,添加恰当辅助线构造全等三角形是本题的关键.21.如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.(1)如果AB=AC,∠BAC=90°,①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD所在直线的位置关系为 ,线段CF、BD的数量关系为 ;②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F 不重合),并说明理由.【分析】(1)当点D在BC的延长线上时①的结论仍成立.由正方形ADEF的性质可推出△DAB≌△FAC,所以CF=BD,∠ACF=∠ABD.结合∠BAC=90°,AB=AC,得到∠BCF=∠ACB+∠ACF=90°.即CF⊥BD.(2)当∠ACB=45°时,过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,可推出∠ACB=∠AGC,所以AC=AG,由(1)①可知CF⊥BD.【解答】证明:(1)①正方形ADEF中,AD=AF,∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF,又∵AB=AC,∴△DAB≌△FAC,∴CF=BD,∠B=∠ACF,∴∠ACB+∠ACF=90°,即CF⊥BD.②当点D在BC的延长线上时①的结论仍成立.由正方形ADEF得AD=AF,∠DAF=90度.∵∠BAC=90°,∴∠DAF=∠BAC,∴∠DAB=∠FAC,又∵AB=AC,∴△DAB≌△FAC,∴CF=BD,∠ACF=∠ABD.∵∠BAC=90°,AB=AC,∴∠ABC=45°,∴∠ACF=45°,∴∠BCF=∠ACB+∠ACF=90度.即CF⊥BD.(2)当∠ACB=45°时,CF⊥BD(如图).理由:过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,∵∠ACB=45°,∠AGC=90°﹣∠ACB,∴∠AGC=90°﹣45°=45°,∴∠ACB=∠AGC=45°,∴AC=AG,∵∠DAG=∠FAC(同角的余角相等),AD=AF,∴△GAD≌△CAF,∴∠ACF=∠AGC=45°,∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.【点评】本题考查三角形全等的判定和直角三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.22.(1)如图1,∠B=∠D=90°,E是BD的中点,AE平分∠BAC,求证:CE平分∠ACD.(2)如图2,AM∥CN,∠BAC和∠ACD的平分线并于点E,过点E作BD⊥AM,分别交AM、CN于B、D,请猜想AB、CD、AC三者之间的数量关系,请直接写出结论,不要求证明.(3)如图3,AM∥CN,∠BAC和∠ACD的平分线交于点E,过点E作不垂直于AM的线段BD,分别交AM、CN于B、D点,且B、D两点都在AC的同侧,(2)中的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.【分析】(1)过点E作EF⊥AC于F,根据角平分线上的点到角的两边的距离相等可得OB=OE,从而求出OE=OD,然后根据到角的两边距离相等的点在角的平分线上证明;(2)如图2,过E作EF⊥AC于F,根据平行线的性质得到BD⊥CD,由角平分线的性质得到BE=EF,证得Rt△AEF≌Rt△ABE,根据全等三角形到现在得到AF=AB,同理CF=CD,等量代换得到结论;(3)成立,如图3,在AC上截取AF=AB,根据角平分线的定义得到∠BAE=∠FAE,推出△ABE≌△AFE,根据全等三角形的性质得到∠AFE=∠ABE,根据角平行线的性质得到∠ABE+∠CDE=180°,求得∠CFE=∠CDE,证得△CEF≌△CDE,根据全等三角形的性质即可得到结论.【解答】解:(1)如图1,过E作EF⊥AC于F,∵∠B=90°,AE平分∠BAC,∴EF=BE,∵E是BD的中点,∴BE=DE,∴EF=DE,∵∠D=90°,∴CE平分∠ACD;(2)如图2,过E作EF⊥AC于F,∵AM∥CN,BD⊥AM,∴BD⊥CD,∵AE平分∠BAC,∴BE=EF,在Rt△AEF与Rt△ABE中,BE=EF AE=AE,∴Rt△AEF≌Rt△ABE,∴AF=AB,同理CF=CD,∵AC=AF+CF,∴AC=AB+CD;(3)成立,如图3,在AC上截取AF=AB,∵AE平分∠BAC,∴∠BAE=∠FAE,在△ABE与△AFE中,AB=AF∠BAE=∠FAEAE=AE,∴△ABE≌△AFE,∴∠AFE=∠ABE,∵AM∥CN,∴∠ABE+∠CDE=180°,∵∠AFE+∠EFC=180°,∴∠CFE=∠CDE,∵CE平分∠ACD,∴∠FCE=∠DCE,在△CEF与△CDE中,∠CFE=∠CDE ∠FCE=∠DCE CE=CE,∴△CEF≌△CDE,∴CF=CD,∵AC=AF+CF,∴AC=AB+CD.【点评】本题考查了全等三角形的判定和性质,角平分线的性质,角平分线的定义,平行线的性质,正确的作出辅助线构造全等三角形是解题的关键.23.将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.(1)求证:AF+EF=DE;(2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图②中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立;(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图③.你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.【分析】(1)我们已知了三角形BED和CAB全等,那么DE=AF+CF,因此只要求出EF=CF就能得出本题所求的结论,可通过全等三角形来实现,连接BF,那么证明三角形BEF和BCF全等就是解题的关键,这两三角形中已知的条件有BE=BC,一条公共边,根据斜边直角边定理,这两个直角三角形就全等了,也就得出EF=CF,也就能证得本题的结论了;(2)解题思路和辅助线的作法与(1)完全一样;(3)结论不成立.结论:AF=DE+EF.同(1)得CF=EF,由△ABC≌△DBE,可得AC=DE,AF=AC+FC=DE+EF.【解答】(1)证明:连接BF(如图①),∵△ABC≌△DBE(已知),∴BC=BE,AC=DE.∵∠ACB=∠DEB=90°,∴∠BCF=∠BEF=90°.在Rt△BFC和Rt△BFE中,BF=BFBC=BE∴Rt△BFC≌Rt△BFE(HL).∴CF=EF.又∵AF+CF=AC,∴AF+EF=DE.(2)解:画出正确图形如图②∴(1)中的结论AF+EF=DE仍然成立;(3)不成立.结论:AF=DE+EF.。
全等模型专题:全等三角形中的常见压轴题五种模型全攻略(解析版)

全等模型专题:全等三角形中的常见压轴题五种模型全攻略【考点导航】目录【典型例题】1【解题模型一四边形中构造全等三角形解题】【解题模型二一线三等角模型】【解题模型三三垂直模型】【解题模型四倍长中线模型】【解题模型五旋转模型】【典型例题】【解题模型一四边形中构造全等三角形解题】1(2023春·广东梅州·八年级校联考开学考试)已知如图,四边形ABCD中,AB=BC,AD=CD,求证:∠A=∠C.【答案】见解析【分析】连接BD,已知两边对应相等,加之一个公共边BD,则可利用SSS判定△ABD≌△CBD,根据全等三角形的对应角相等即可证得.【详解】证明:连接BD,∵AB=CB,BD=BD,AD=CD,∴△ABD≌△CBD(SSS).∴∠A=∠C.【点睛】此题主要考查学生对全等三角形的判定方法的理解及运用,常用的判定方法有SSS,SAS,ASA,HL等.【变式训练】1(2023秋·云南昆明·八年级统考期末)放风筝是中国民间的传统游戏之一,风筝又称风琴,纸鹞,鹞子,纸鸢.如图1,小华制作了一个风筝,示意图如图2所示,AB=AC,DB=DC,他发现AD不仅平分你觉得他的发现正确吗?请说明理由.∠BAC,且平分∠BDC,【答案】他的发现正确,理由见解析【分析】根据全等三角形的判定和性质直接证明即可.【详解】解:他的发现正确,理由如下:在△ABD与△ACD中,AB=AC,BD=CDAD=AD∴△ABD≌△ACD,∴∠BAD=∠CAD,∠ADB=∠ADC,∴AD不仅平分∠BAC,且平分∠BDC.【点睛】题目主要考查全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题关键.2(2023秋·湖南常德·八年级统考期末)中国现役的第五代隐形战斗机歼-20的机翼如图,为适应空气必须相等.动力的要求,两个翼角∠A,∠B(1)实际制造中,工作人员只需用刻度尺测量PA=PB,CA=CB就能满足要求,说明理由;(2)若∠A=30°,∠P=40°,求∠ACB的度数.【答案】(1)见解析(2)100°【分析】(1)连接PC,证明△APC≌△BPC,即可解答.(2)由三角形的外角的性质即可解答.【详解】(1)证明:如图,连接PC,在△APC 和△BPC 中,PA =PBCA =CB PC =PC,∴△APC ≌△BPC (SSS ),∴∠A =∠B .(2)∵△APC ≌△BPC ,∠A =30°,∠P =40°,∴∠A =∠B =30°,∵∠ACB =∠ACE +∠BCE ,∠ACE =∠APC +∠A ,∠BCE =∠BPC +∠B ,∴∠ACB =∠APC +∠A +∠BPC +∠B =∠A +∠BPA +∠B =2×30°+40°=100°.【点睛】本题考查了三角形全等和外角的性质,掌握三角形全等是解题的关键.3如图,在四边形ABCD 中,CB ⊥AB 于点B ,CD ⊥AD 于点D ,点E ,F 分别在AB ,AD 上,AE =AF ,CE =CF.(1)若AE =8,CD =6,求四边形AECF 的面积;(2)猜想∠DAB ,∠ECF ,∠DFC 三者之间的数量关系,并证明你的猜想.【答案】(1)48(2)∠DAB +∠ECF =2∠DFC ,证明见解析【解析】【分析】(1)连接AC ,证明△ACE ≌△ACF ,则S △ACE =S △ACF ,根据三角形面积公式求得S △ACF 与S △ACE ,根据S 四边形AECF =S △ACF +S △ACE 求解即可;(2)由△ACE ≌△ACF 可得∠FCA =∠ECA ,∠FAC =∠EAC ,∠AFC =∠AEC ,根据垂直关系,以及三角形的外角性质可得∠DFC +∠BEC =∠FCA +∠FAC +∠ECA +∠EAC =∠DAB +∠ECF .可得∠DAB +∠ECF =2∠DFC(1)解:连接AC ,如图,在△ACE 和△ACF 中AE =AFCE =CFAC =AC∴△ACE ≌△ACF (SSS ).∴S △ACE =S △ACF ,∠FAC =∠EAC .∵CB ⊥AB ,CD ⊥AD ,∴CD =CB =6.∴S △ACF =S △ACE =12AE ·CB =12×8×6=24.∴S 四边形AECF =S △ACF +S △ACE =24+24=48.(2)∠DAB +∠ECF =2∠DFC证明:∵△ACE ≌△ACF ,∴∠FCA =∠ECA ,∠FAC =∠EAC ,∠AFC =∠AEC .∵∠DFC 与∠AFC 互补,∠BEC 与∠AEC 互补,∴∠DFC =∠BEC .∵∠DFC =∠FCA +∠FAC ,∠BEC =∠ECA +∠EAC ,∴∠DFC +∠BEC =∠FCA +∠FAC +∠ECA +∠EAC=∠DAB +∠ECF .∴∠DAB +∠ECF =2∠DFC【点睛】本题考查了三角形全等的性质与判定,三角形的外角的性质,掌握三角形全等的性质与判定是解题的关键.4在四边形ABDC 中,AC =AB ,DC =DB ,∠CAB =60°,∠CDB =120°,E 是AC 上一点,F 是AB 延长线上一点,且CE =BF .(1)试说明:DE =DF :(2)在图中,若G 在AB 上且∠EDG =60°,试猜想CE ,EG ,BG 之间的数量关系并证明所归纳结论.(3)若题中条件“∠CAB =60°,∠CDB =120°改为∠CAB =α,∠CDB =180°-α,G 在AB 上,∠EDG 满足什么条件时,(2)中结论仍然成立?【答案】(1)见解析;(2)CE +BG =EG ,理由见解析;(3)当∠EDG =90°-12α时,(2)中结论仍然成立.【解析】【分析】(1)首先判断出∠C =∠DBF ,然后根据全等三角形判定的方法,判断出ΔCDE ≅ΔBDF ,即可判断出DE =DF .(2)猜想CE 、EG 、BG 之间的数量关系为:CE +BG =EG .首先根据全等三角形判定的方法,判断出ΔABD ≅ΔACD ,即可判断出∠BDA =∠CDA =60°;然后根据∠EDG =60°,可得∠CDE =∠ADG ,∠ADE =∠BDG ,再根据∠CDE =∠BDF ,判断出∠EDG =∠FDG ,据此推得ΔDEG ≅ΔDFG ,所以EG =FG ,最后根据CE =BF ,判断出CE +BG =EG 即可.(3)根据(2)的证明过程,要使CE +BG =EG 仍然成立,则∠EDG =∠BDA =∠CDA =12∠CDB ,即∠EDG =12(180°-α)=90°-12α,据此解答即可.(1)证明:∵∠CAB +∠C +∠CDB +∠ABD =360°,∠CAB =60°,∠CDB =120°,∴∠C +∠ABD =360°-60°-120°=180°,又∵∠DBF +∠ABD =180°,∴∠C=∠DBF ,在ΔCDE 和ΔBDF 中,CD =BD∠C =∠DBFCE =BF∴ΔCDE ≅ΔBDF (SAS ),∴DE =DF .(2)解:如图,连接AD ,猜想CE 、EG 、BG 之间的数量关系为:CE +BG =EG .证明:在ΔABD 和ΔACD 中,AB =ACBD =CD AD =AD,∴ΔABD ≅ΔACD (SSS ),∴∠BDA =∠CDA =12∠CDB =12×120°=60°,又∵∠EDG =60°,∴∠CDE =∠ADG ,∠ADE =∠BDG ,由(1),可得ΔCDE ≅ΔBDF ,∴∠CDE =∠BDF ,∴∠BDG +∠BDF =60°,即∠FDG =60°,∴∠EDG =∠FDG ,在ΔDEG 和ΔDFG 中,DE =DF∠EDG =∠FDGDG =DG∴ΔDEG ≅ΔDFG (SAS ),∴EG =FG ,又∵CE =BF ,FG =BF +BG ,∴CE +BG =EG ;(3)解:要使CE +BG =EG 仍然成立,则∠EDG =∠BDA =∠CDA =12∠CDB ,即∠EDG =12(180°-α)=90°-12α,∴当∠EDG =90°-12α时,CE +BG =EG 仍然成立.【点睛】本题综合考查了全等三角形的性质和判定,此题是一道综合性比较强的题目,有一定的难度,能根据题意推出规律是解此题的关键.【解题模型二一线三等角模型】1(2023春·七年级课时练习)【探究】如图①,点B 、C 在∠MAN 的边AM 、AN 上,点E 、F 在∠MAN 内部的射线AD 上,∠1、∠2分别是△ABE 、△CAF 的外角.若AB =AC ,∠1=∠2=∠BAC ,求证:△ABE ≌△CAF .【应用】如图②,在等腰三角形ABC 中,AB =AC ,AB >BC ,点D 在边BC 上,CD =2BD ,点E 、F 在线段AD 上,∠1=∠2=∠BAC ,若△ABC 的面积为9,则△ABE 与△CDF 的面积之和为.【答案】探究:见解析;应用:6【分析】探究:根据∠A =∠BAE +∠ABE ,∠BAC =∠CAF +∠BAE ,得出∠ABE =∠CAF ,根据∠1=∠2,得出∠AEB =∠CFA ,再根据AAS 证明即可;应用:根据全等三角形的性质得出:S△ABE=S△CAF,进而得出S△CDF+S△CAF=S△ACD,根据CD=2BD,△ABC的面积为9,得出S△ACD=23S△ABC=6,即可得出答案.【详解】探究证明:∵∠A=∠BAE+∠ABE,∠BAC=∠CAF+∠BAE,又∵∠BAC=∠1,∴∠ABE=∠CAF,∵∠1=∠2,∴∠AEB=∠CFA,在△ABE和△CAF中,∠AEB=∠CFA ∠ABE=∠CAF AB=AC∴△ABE≌△CAF AAS;应用解:∵△ABE≌△CAF,∴S△ABE=S△CAF,∴S△CDF+S△CAF=S△ACD,∵CD=2BD ,△ABC的面积为9,∴S△ACD=23S△ABC=6,∴△ABE与△CDF的面积之和为6,故答案为:6.【点睛】本题考查全等三角形的判定与性质,掌握全等三角形的判定是解题的关键.【变式训练】1(2023春·广西南宁·七年级南宁市天桃实验学校校考期末)(1)问题发现:如图1,射线AE在∠MAN 的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,若∠BAC=∠BFE=∠CDE=90°,求证:△ABF≌△CAD;(2)类比探究:如图2,AB=AC,且∠BAC=∠BFE=∠CDE.(1)中的结论是否仍然成立,请说明理由;(3)拓展延伸:如图3,在△ABC中,AB=AC,AB>BC.点E在BC边上,CE=2BE,点D、F在线段AE上,∠BAC=∠BFE=∠CDE.若△ABC的面积为15,DE=2AD,求△BEF与△CDE的面积之比.【答案】(1)证明见详解;(2)成立,证明见详解;(3)1:4【分析】(1)根据∠BAC=∠BFE=∠CDE=90°即可得到∠BAF+∠CAF=90°,∠DCA+∠CAF=90°,从而得到∠BAF=∠DCA,即可得到证明;(2)根据∠BAC=∠BFE=∠CDE得到∠BAF+∠CAF=∠DCA+∠CAF,即可得到∠BAF=∠DCA,即可得到证明;(3)根据△ABC的面积为15,CE=2BE,即可得到S△ABE=5,S△AEC=10,结合DE=2AD可得S△ADC=103,S△EDC =203,根据AB=AC,∠BAC=∠BFE=∠CDE得到△ABF≌△CAD,即可得到S△BEF,即可得到答案;【详解】(1)证明:∵∠BAC=∠BFE=∠CDE=90°,∴∠BFA=∠CDA=90°,∠BAF+∠CAF=90°,∠DCA+∠CAF=90°,∴∠BAF=∠DCA,在△ABF与△CAD中,∵∠BFA=∠CDA ∠BAF=∠DCA AB=AC,∴△ABF≌△CAD(AAS);(2)解:成立,理由如下,∵∠BAC=∠BFE=∠CDE,∴∠BAF+∠CAF=∠DCA+∠CAF,∠BFA=∠CDA,∴∠BAF=∠DCA,在△ABF与△CAD中,∵∠BFA=∠CDA ∠BAF=∠DCA AB=AC,∴△ABF≌△CAD(AAS);(3)解:∵△ABC的面积为15,CE=2BE,∴S△ABE=5,S△AEC=10,∵DE=2AD,∴S△ADC=103,S△EDC =203,∵∠BAC=∠BFE=∠CDE,∴∠BAF+∠CAF=∠DCA+∠CAF,∠BFA=∠CDA,∴∠BAF=∠DCA,在△ABF与△CAD中,∵∠BFA=∠CDA ∠BAF=∠DCA AB=AC,∴△ABF≌△CAD(AAS)∴S△BEF=5-103=53,∴S△BEF:S△CDE=53:203=1:4;【点睛】本题考查三角形全等的判定与性质及同高不同底三角形的面积,解题的关键是根据内外角关系得到三角形全等的条件.2(2023春·广东佛山·七年级校考期中)如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E、F 分别是直线CD上两点,且∠BEC=∠CFA=α.(1)若直线CD经过∠BCA的内部,且E、F在射线CD上.①如图1,若∠BCA=90°,α=90°,试判断BE和CF的数量关系,并说明理由.②如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件,使①中的结论仍然成立;(2)如图3,若直线CD经过∠BCA的外部,α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想,并说明理由.【答案】(1)①BE=CF;②α+∠BCA=180°(2)EF=BE+AF【分析】(1)①由∠BCA=90°,∠BEC=∠CFA=α=90°,可得∠BCE=∠CAF,从而可证△BCE≌△CAF,故BE=CF;②添加α+∠BCA=180°,可证明∠BCA=∠BEF,则∠ACF=∠CBE,根据AAS可证明△BCE≌△CAF,即可得证①中的结论仍然成立;(2)题干已知条件可证△BCE≌△CAF,故BE=CF,EC=FA,从而可证明EF=BE+AF.【详解】(1)解:①BE=CF,理由如下:∵∠BCA=90°,∴∠ACF+∠BCE=90°,∵∠BEC=∠AFC=α=90°,∴∠ACF+∠CAF=90°,∴∠BCE=∠CAF,∵AC=BC,∴△BCE≌△CAF AAS,∴BE=CF;②添加α+∠BCA=180°,使①中的结论仍然成立,理由如下:∵∠BEC=∠CFA=α,∴∠BEF=180°-∠BEC=180°-α,∵∠BEF=∠EBC+∠BCE,∴∠EBC+∠BCE=180°-α,∵α+∠BCA=180°,∴∠BCA=180°-α,∴∠BCA=∠BCE+∠ACF=180°-α,∴∠EBC=∠ACF,∵AC=BC,∠BEC=∠CFA=α,∴△BCE≌△CAF AAS,∴BE=CF;故答案为:α+∠BCA=180°;(2)EF=BE+AF,理由如下:∵∠BCA=α,∴∠BCE+∠FCA=180°-∠BCA=180°-α,∵∠BEC=α,∴∠EBC+∠BCE=180°-∠BEC=180°-α,∴∠EBC=∠FCA,∵AC=BC,∠BEC=∠CFA=α,∴△BEC≌△CFA AAS,∴BE=CF,EC=FA,∴EF=EC+CF=FA+BE,即EF=BE+AF.【点睛】本题是三角形的综合题,主要考查全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.3在直线m上依次取互不重合的三个点D,A,E,在直线m上方有AB=AC,且满足∠BDA=∠AEC =∠BAC=α.(1)如图1,当α=90°时,猜想线段DE,BD,CE之间的数量关系是;(2)如图2,当0<α<180°时,问题(1)中结论是否仍然成立?如成立,请你给出证明;若不成立,请说明理由;(3)应用:如图3,在△ABC中,∠BAC是钝角,AB=AC,∠BAD<∠CAE,∠BDA=∠AEC=∠BAC,直线m与CB的延长线交于点F,若BC=3FB,△ABC的面积是12,求△FBD与△ACE的面积之和.【答案】(1)DE=BD+CE(2)DE=BD+CE仍然成立,理由见解析(3)△FBD与△ACE的面积之和为4【解析】【分析】(1)由∠BDA=∠BAC=∠AEC=90°得到∠BAD+∠EAC=∠BAD+∠DBA=90°,进而得到∠DBA=∠EAC,然后结合AB=AC得证△DBA≌△EAC,最后得到DE=BD+CE;(2)由∠BDA=∠BAC=∠AEC=α得到∠BAD+∠EAC=∠BAD+∠DBA=180°-α,进而得到∠DBA=∠EAC,然后结合AB=AC得证△DBA≌△EAC,最后得到DE=BD+CE;(3)由∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,得出∠CAE=∠ABD,由AAS证得△ADB≌△CAE,得出S△ABD=S△CEA,再由不同底等高的两个三角形的面积之比等于底的比,得出S△ABF即可得出结果.(1)解:DE=BD+CE,理由如下,∵∠BDA=∠BAC=∠AEC=90°,∴∠BAD+∠EAC=∠BAD+∠DBA=90°,∴∠DBA=∠EAC,∵AB=AC,∴△DBA ≌△EAC (AAS ),∴AD =CE ,BD =AE ,∴DE =AD +AE =BD +CE ,故答案为:DE =BD +CE .(2)DE =BD +CE 仍然成立,理由如下,∵∠BDA =∠BAC =∠AEC =α,∴∠BAD +∠EAC =∠BAD +∠DBA =180°-α,∴∠DBA =∠EAC ,∵AB =AC ,∴△DBA ≌△EAC (AAS ),∴BD =AE ,AD =CE ,∴DE =AD +AE =BD +CE ;(3)解:∵∠BAD <∠CAE ,∠BDA =∠AEC =∠BAC ,∴∠CAE =∠ABD ,在△ABD 和△CAE 中,∠ABD =∠CAE∠BDA =∠CEA AB =AC,∴△ABD ≌△CAE (AAS ),∴S △ABD =S △CAE ,设△ABC 的底边BC 上的高为h ,则△ABF 的底边BF 上的高为h ,∴S △ABC =12BC •h =12,S △ABF =12BF •h ,∵BC =3BF ,∴S △ABF =4,∵S △ABF =S △BDF +S △ABD =S △FBD +S △ACE =4,∴△FBD 与△ACE 的面积之和为4.【点睛】本题考查了全等三角形的判定与性质、直角三角形的性质,三角形的面积,解题的关键是熟练掌握全等三角形的判定与性质.【解题模型三三垂直模型】1(2023春·广东广州·九年级专题练习)如图,∠ACB =90°,AC =BC ,BE ⊥CE 于E ,AD ⊥CE 于D ,AD =2.7cm ,DE =1.8cm.(1)求证:△ACD ≌△CBE .(2)求BE 的长.【答案】(1)见解析;(2)BE =0.9cm .【分析】(1)由垂直得∠ADC =∠CEB =90°,求出∠ACD =∠CBE ,然后利用AAS 即可证明△ACD ≌△CBE ;(2)根据全等三角形的性质可得CE =AD =2.7cm ,BE =CD ,根据CD =CE -DE 求出CD 即可得到BE 的长.【详解】(1)证明:∵AD ⊥CE ,BE ⊥CE ,∴∠ADC =∠CEB =90°,∵∠ACB =90°,∴∠ACD =∠ACB -∠BCE =90°-∠BCE ,∵∠CBE =90°-∠BCE ,∴∠ACD =∠CBE ,在△ACD 与△CBE 中,∠ADC =∠CEB∠ACD =∠CBE AC =BC,∴△ACD ≌△CBE AAS ;(2)解:由(1)知,△ACD ≌△CBE ,∴CE =AD =2.7cm ,BE =CD ,∵CD =CE -DE =2.7-1.8=0.9cm ,∴BE =0.9cm .【点睛】本题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定定理和全等三角形对应边相等的性质是解题的关键.【变式训练】1(2023春·河北邯郸·七年级校考阶段练习)已知:∠ACB =90°,AC =BC ,AD ⊥CM ,BE ⊥CM ,垂足分别为D ,E .(1)如图1,把下面的解答过程补充完整,并在括号内注明理由.①线段CD和BE的数量关系是:CD=BE;②请写出线段AD,BE,DE之间的数量关系并证明.解:①结论:CD=BE.理由:∵AD⊥CM,BE⊥CM,∴∠ACB=∠BEC=∠ADC=90°,∴∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,∴∠ACD=( )在△ACD和△CBE中,,∴△ACD≌△CBE,( )∴CD=BE.②结论:AD=BE+DE.理由:∵△ACD≌△CBE,∴,∵CE=CD+DE=BE+DE,∴AD=BE+DE.(2)如图2,上述结论②还成立吗?如果不成立,请写出线段AD,BE,DE之间的数量关系,并说明理由.【答案】(1)①∠CBE;同角的余角相等;∠ADC=∠BEC,∠ACD=∠CBE,AC=BC;AAS;②AD=CE (2)不成立,DE-BE=AD,见解析【分析】(1)根据同角的余角相等,全等三形的判定方法角角边分析处理;(2)根据同角的余角相等,全等三形的判定方法角角边分析处理,注意观察图形,得出线段间的数量关系;【详解】(1)∵AD⊥CM,BE⊥CM,∴∠ACB=∠BEC=∠ADC=90°,∴∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,∴∠ACD=∠CBE(同角的余角相等 )在△ACD和△CBE中,∠ADC=∠BEC,∠ACD=∠CBE,AC=BC,∴△ACD≌△CBE,(AAS )∴CD=BE.②结论:AD=BE+DE.理由:∵△ACD≌△CBE,∴AD=CE,∵CE=CD+DE=BE+DE,∴AD=BE+DE.(2)不成立,结论:DE -BE =AD.理由:∵AD ⊥CM ,BE ⊥CM ,∴∠ACB =∠BEC =∠ADC =90°,∴∠ACD +∠BCE =90°,∠BCE +∠CBE =90°,∴∠ACD =∠CBE在△ACD 和△CBE 中,∠ADC =∠CEB∠ACD =∠CBE AC =CB,∴△ACD ≌△CBE ,(AAS )∴AD =CE ,CD =BE ,∴DE -BE =DE -DC =CE =AD .【点睛】本题考查全等三角形的判定和性质,能够由图形的位置关系得出线段之间、角之间的数量关系是解题的关键.2在△ABC 中,∠BAC =90°,AC =AB ,直线MN 经过点A ,且CD ⊥MN 于D ,BE ⊥MN 于E.(1)当直线MN 绕点A 旋转到图1的位置时,∠EAB +∠DAC =度;(2)求证:DE =CD +BE ;(3)当直线MN 绕点A 旋转到图2的位置时,试问DE 、CD 、BE 具有怎样的等量关系?请写出这个等量关系,并加以证明.【答案】(1)90°(2)见解析(3)CD =BE +DE ,证明见解析【解析】【分析】(1)由∠BAC =90°可直接得到∠EAB +∠DAC =90°;(2)由CD ⊥MN ,BE ⊥MN ,得∠ADC =∠BEA =∠BAC =90°,根据等角的余角相等得到∠DCA =∠EAB ,根据AAS 可证△DCA ≌△EAB ,所以AD =CE ,DC =BE ,即可得到DE =EA +AD =DC +BE.(3)同(2)易证△DCA≌△EAB,得到AD=CE,DC=BE,由图可知AE=AD+DE,所以CD=BE +DE.(1)∵∠BAC=90°∴∠EAB+∠DAC=180°-∠BAC=180°-90°=90°故答案为:90°.(2)证明:∵CD⊥MN于D,BE⊥MN于E∴∠ADC=∠BEA=∠BAC=90°∵ ∠DAC+∠DCA=90°且∠DAC+∠EAB=90°∴∠DCA=∠EAB∵在△DCA和△EAB中∠ADC=∠BEA=90°∠DCA=∠EABAC=AB∴△DCA≌△EAB(AAS)∴AD=BE且EA=DC由图可知:DE=EA+AD=DC+BE.(3)∵CD⊥MN于D,BE⊥MN于E∴∠ADC=∠BEA=∠BAC=90°∵∠DAC+∠DCA=90°且∠DAC+∠EAB=90°∴∠DCA=∠EAB∵在△DCA和△EAB中∠ADC=∠BEA=90°∠DCA=∠EABAC=AB∴△DCA≌△EAB(AAS)∴AD=BE且AE=CD由图可知:AE=AD+DE∴CD=BE+DE.【点睛】本题考查了旋转的性质:旋转前后两图形全等,对应点到旋转中心的距离相等,对应点与旋转中心的连线段所夹的角等于旋转角,也考查了三角形全等的判定与性质.3如图,已知:在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,AD⊥MN,BE⊥MN.(1)当直线MN绕点C旋转到图(1)的位置时,求证:△ADC≅△CEB;(2)当直线MN绕点C旋转到图(2)的位置时,求证:DE=AD-BE;(3)当直线MN绕点C旋转到图(3)的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系:.【答案】(1)见解析;(2)见解析;(3)DE=BE-AD【分析】(1)由已知推出∠ADC=∠BEC=90°,因为∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,推出∠DAC=∠BCE,根据AAS即可得到答案;(2)结论:DE=AD-BE.与(1)证法类似可证出∠ACD=∠EBC,能推出△ADC≌△CEB,得到AD= CE,CD=BE,即可得到答案.(3)结论:DE=BE-AD.证明方法类似.【详解】解:(1)证明:如图1,∵AD⊥DE,BE⊥DE,∴∠ADC=∠BEC=90°,∵∠ACB=90°,∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,∴∠DAC=∠BCE,在△ADC和△CEB中,∠CDA=∠BEC∠DAC=∠ECBAC=BC,∴△ADC≌△CEB(AAS);(2)如图2,∵BE⊥EC,AD⊥CE,∴∠ADC=∠BEC=90°,∴∠EBC+∠ECB=90°,∵∠ACB=90°,∴∠ECB+∠ACE=90°,∴∠ACD=∠EBC,在△ADC和△CEB中,∠ACD=∠CBE∠ADC=∠BECAC=BC,∴△ADC≌△CEB(AAS),∴AD=CE,CD=BE,∴DE=EC-CD=AD-BE.(3)DE=BE-AD;如图3,∵∠ACB=90°,∴∠ACD+∠BCE=90°∵AD⊥MN,BE⊥MN,∴∠ADC=∠CEB=90°,∴∠ACD+∠DAC=90°,∴∠DAC=∠ECB,在△ACD和△CBE中,∠ADC=∠CEB ∠DAC=∠ECB AC=BC,∴△ACD≌△CBE(AAS),∴AD=CE,CD=BE,∴DE=CD-CE=BE-AD.【点睛】本题主要考查了余角的性质,全等三角形的性质和判定等知识点,能根据已知证明△ACD≌△CBE 是解此题的关键,题型较好,综合性比较强.【解题模型四倍长中线模型】1(2023春·山东临沂·八年级统考期中)如图,在△ABC中,AB=3,AC=4,(1)求BC边的长的取值范围?(2)若AD是△ABC的中线,求AD取值范围?【答案】(1)1<BC<7(2)12<AD<72【分析】(1)根据三角形三边的关系求解即可;(2)延长AD至E,使AD=DE,连接BE,证明△ADC≌△EDB,得到AC=BE,由三角形三边关系得到1<AE<7,则12<AD<72.【详解】(1)解:由三角形的三边关系可知:AC-AB<BC<AC+AB,∵AB=3,AC=4,∴1<BC<7;(2)解:延长AD至E,使AD=DE,连接BE ,在△ABE中,∵BD=DC,∠ADC=∠BDE,AD=DE,∴△ADC≌△EDB SAS,∴AC=BE,由三角形的三边关系:BE-AB<AE<BE+AB,∴1<AE<7,∴1 2<AD<72.【点睛】本题主要考查了三角形三边的关系,全等三角形的性质与判定,正确作出辅助线构造全等三角形是解题的关键.【变式训练】1如图,在△ABC中,AD是BC边上的中线.延长AD到点E,使DE=AD,连接BE.(1)求证:△ACD≌△EBD;(2)AC与BE的数量关系是:,位置关系是:;(3)若∠BAC=90°,猜想AD与BC的数量关系,并加以证明.【答案】(1)见解析(2)AC=BE,AC∥BE(3)2AD=BC,证明见解析【分析】(1)根据三角形全等的判定定理SAS,即可证得;(2)由△ACD≌△EBD,可得AC=BE,∠C=∠EBC,据此即可解答;(3)根据三角形全等的判定定理SAS,可证得△BAC≌△ABE,据此即可解答.【详解】(1)证明:∵AD是BC边上的中线,∴BD=CD,在△ACD与△EBD中,AD=ED∠ADC=∠EDB BD=CD,∴△ACD≌△EBD SAS;(2)解:∵△ACD≌△EBD,∴AC=BE,∠C=∠EBC,∴AC∥BE,故答案为:AC=BE,AC∥BE;(3)解:2AD=BC证明:∵△ACD≌△EBD,∴AC=BE,∠C=∠EBC,∴AC∥BE,∵∠BAC=90°∴∠BAC=∠ABE=90°在△BAC和△ABE中,AB=BA∠BAC=∠ABE=90°AC=BE∴△BAC≌△ABE SAS,∴BC=AE=2AD.【点睛】本题考查了全等三角形的判定与性质,平行线的判定与性质,熟练掌握和运用全等三角形的判定与性质是解决本题的关键.2(2023·全国·八年级假期作业)如图1,AD为△ABC的中线,延长AD至E,使DE=AD.(1)试证明:△ACD≌△EBD;(2)用上述方法解答下列问题:如图2,AD为△ABC的中线,BMI交AD于C,交AC于M,若AM=GM,求证:BG =AC.【答案】(1)详见解析;(2)详见解析.【分析】(1)根据中线的定义,即可得到BD =CD ,再根据SAS 即可判定△ACD ≌△EBD .(2)延长AD 到F ,使AD =DF ,连接BF ,根据SAS 证△ADC ≌△FDB ,推出BF =AC ,∠CAD =∠F ,根据AM =GM ,推出∠CAD =∠AGM =∠BGF ,求出∠BGF =∠F ,根据等腰三角形的性质求出即可.【详解】(1)证明:∵AD 是△ABC 的中线,∴BD =CD ,在△ACD 和△EBD 中,CD =BD∠ADC =∠EDB AD =ED,∴△ACD ≌△EBD (SAS ).(2)证明:延长AD 到F ,使AD =DF ,连接BF ,∵AD 是△ABC 中线,∴BD =DC ,∵在△ADC 和△FDB 中,BD =DC∠ADC =∠BDF AD =DF,∴△ADC ≌△FDB (SAS ),∴BF =AC ,∠CAD =∠F ,∵AM =GM ,∴∠CAD =∠AGM ,∵∠AGM =∠BGF ,∴∠BGF =∠CAD =∠F ,∴BG =BF =AC ,即BG =AC .【点睛】此题考查的是全等三角形的判定及性质,掌握倍长中线法构造全等三角形是解决此题的关键.3(2023春·上海·七年级专题练习)某数学兴趣小组在一次活动中进行了探究试验活动,请你来加入.【探究与发现】(1)如图1,AD 是△ABC 的中线,延长AD 至点E ,使ED =AD ,连接BE ,证明:△ACD ≌△EBD .【理解与应用】(2)如图2,EP 是△DEF 的中线,若EF =5,DE =3,设EP =x ,则x 的取值范围是.(3)如图3,AD 是△ABC 的中线,E 、F 分别在AB 、AC 上,且DE ⊥DF ,求证:BE +CF >EF .【答案】(1)见解析;(2)1<x <4;(3)见解析【分析】(1)根据全等三角形的判定即可得到结论;(2)延长EP 至点Q ,使PQ =PE ,连接FQ ,根据全等三角形的性质得到FQ =DE =3,根据三角形的三边关系即可得到结论;(3)延长FD 至G ,使得GD =DF ,连接BG ,EG ,结合前面的做题思路,利用三角形三边关系判断即可.【详解】(1)证明:CD =BD ,∠ADC =∠EDB ,AD =ED ,∴△ACD ≌△EBD ,(2)1<x <4;如图,延长EP 至点Q ,使PQ =PE ,连接FQ ,在ΔPDE 与ΔPQF 中,PE =PQ∠EPD =∠QPF PD =PF,∴ΔPEP ≅ΔQFP ,∴FQ =DE =3,在ΔEFQ 中,EF -FQ <QE <EF +FQ ,即5-3<2x <5+3,∴x 的取值范围是1<x <4;故答案为:1<x <4;(3)延长FD 至G ,使得GD =DF ,连接BG ,EG ,在△DFC 和△DGB 中,DF =DG ,∠CDF =∠BDG ,DC =DB ,∴△DFC ≌△DGB (SAS ),∴BG =CF ,∵在△EDF 和△EDG 中,DF =DG ,∠FDE =∠GDE =90°,DE =DE ,∴△EDF ≌△EDG (SAS ),∴EF =EG ,在△BEG 中,两边之和大于第三边,∴BG +BE >EG ,又∵EF =EG ,BG =CF,∴BE +CF >EF【点睛】本题考查了全等三角形的判定和性质,三角形的中线的定义,三角形的三边关系,正确的作出图形是解题的关键.【解题模型五旋转模型】1如图,AB =AC ,AE =AD ,∠CAB =∠EAD =α.(1)求证:△AEC≅△ADB;(2)若α=90°,试判断BD与CE的数量及位置关系并证明;(3)若∠CAB=∠EAD=α,求∠CFA的度数.【答案】(1)见详解;(2)BD=CE,BD⊥CE;(3)90°-α2【分析】(1)根据三角形全等的证明方法SAS证明两三角形全等即可;(2)由(1)△AEC≌△ADB可知CE=BD且CE⊥BD;利用角度的等量代换证明即可;(3)过A分别做AM⊥CE,AN⊥BD,易知AF平分∠DFC,进而可知∠CFA【详解】(1)∵∠CAB=∠EAD∴∠CAB+∠BAE=∠EAD+∠BAE,∴∠CAE=∠BAD,∵AB=AC,AE=AD在△AEC和△ADB中,AB=AC∠CAE=∠BAD AE=AD∴△AEC≌△ADB(SAS)(2)CE=BD且CE⊥BD,证明如下:将直线CE与AB的交点记为点O,由(1)可知△AEC≌△ADB,∴CE=BD,∠ACE=∠ABD,∵∠BOF=∠AOC,∠α=90°,∴∠BFO=∠CAB=∠α=90°,∴CE⊥BD.(3)过A分别做AM⊥CE,AN⊥BD 由(1)知△AEC≌△ADB,∴两个三角形面积相等故AM·CE=AN·BD∴AM=AN∴AF平分∠DFC由(2)可知∠BFC=∠BAC=α∴∠DFC=180°-α∴∠CFA=12∠DFC=90°-α2【点睛】本题考查了全等三角形的证明,以及全等三角形性质的应用,正确掌握全等三角形的性质是解题的关键;【变式训练】1如图,在△ABC中,AB=BC,∠ABC=120°,点D在边AC上,且线段BD绕着点B按逆时针方向旋转120°能与BE重合,点F是ED与AB的交点.(1)求证:AE=CD;(2)若∠DBC=45°,求∠BFE的度数.【答案】(1)证明见解析;(2)∠BFE=105°.【分析】(1)根据旋转的性质证明△ABE≌△CBD(SAS),进而得证;(2)由(1)得出∠DBC=∠ABE=45°,BD=BE,∠EBD=120°,最后根据三角形内角和定理进行求解即可.【详解】(1)证明:∵线段BD绕着点B按逆时针方向旋转120°能与BE重合,∴BD=BE,∠EBD=120°,∵AB=BC,∠ABC=120°,∴∠ABD+∠DBC=∠ABD+∠ABE=120°,∴∠DBC=∠ABE,∴△ABE≌△CBD(SAS),∴AE=CD;(2)解:由(1)知∠DBC=∠ABE=45°,BD=BE,∠EBD=120°,(180°-120°)=30°,∴∠BED=∠BDE=12∴∠BFE=180°-∠BED-∠ABE=180°-30°-45°=105°.【点睛】本题考查了旋转的性质,全等三角形的判定与性质,三角形内角和定理,利用旋转的性质证明是解题的关键.2问题发现:如图1,已知C为线段AB上一点,分别以线段AC,BC为直角边作等腰直角三角形,∠ACD=90°,CA=CD,CB=CE,连接AE,BD,线段AE,BD之间的数量关系为;位置关系为.拓展探究:如图2,把Rt△ACD绕点C逆时针旋转,线段AE,BD交于点F,则AE与BD之间的关系是否仍然成立?请说明理由.【答案】问题发现:AE=BD,AE⊥BD;拓展探究:成立,理由见解析【分析】问题发现:根据题目条件证△ACE≌△DCB,再根据全等三角形的性质即可得出答案;拓展探究:用SAS证ΔACE≅ΔDCB,根据全等三角形的性质即可证得.【详解】解:问题发现:延长BD,交AE于点F,如图所示:∵∠ACD=90°,∴∠ACE=∠DCB=90°,又∵CA=CD,CB=CE,∴ΔACE≅ΔDCB(SAS),∴AE=ED,∠CAE=∠CDB,∵∠CDB+∠CBD=90°,∴∠CAE+∠CBD=90°,∴∠AFD=90°,∴AF⊥FB,∴AE⊥BD,故答案为:AE=BD,AE⊥BD;拓展探究:成立.理由如下:设CE与BD相交于点G,如图1所示:∵∠ACD=∠BCE=90°,∴∠ACE=∠BCD,又∵CB=CE,AC=CD,∴ΔACE≅ΔDCB(SAS),∴AE=BD,∠AEC=∠DBC,∵∠CBD+∠CGB=90°,∴∠AEC+∠EGF=90°,∴∠AFB=90°,∴BD⊥AE,即AE=BD,AE⊥BD依然成立.【点睛】本题考查全等三角形的判定和性质,三角形三边关系,手拉手模型,熟练掌握全等三角形的判定和手拉手模型是解决本题的关键.3(2023春·全国·七年级专题练习)在△ABC中,∠BAC=90°,AC=AB,直线MN经过点A,且CD ⊥MN于D,BE⊥MN于E.(1)当直线MN绕点A旋转到图1的位置时,∠EAB+∠DAC=度;(2)求证:DE=CD+BE;(3)当直线MN绕点A旋转到图2的位置时,试问DE、CD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.【答案】(1)90°(2)见解析(3)CD=BE+DE,证明见解析【分析】(1)由∠BAC=90°可直接得到∠EAB+∠DAC=90°;(2)由CD⊥MN,BE⊥MN,得∠ADC=∠BEA=∠BAC=90°,根据等角的余角相等得到∠DCA=∠EAB,根据AAS可证△DCA≌△EAB,所以AD=CE,DC=BE,即可得到DE=EA+AD=DC+ BE.(3)同(2)易证△DCA≌△EAB,得到AD=CE,DC=BE,由图可知AE=AD+DE,所以CD=BE +DE.【详解】(1)∵∠BAC=90°∴∠EAB+∠DAC=180°-∠BAC=180°-90°=90°故答案为:90°.(2)证明:∵CD⊥MN于D,BE⊥MN于E∴∠ADC=∠BEA=∠BAC=90°∵ ∠DAC+∠DCA=90°且∠DAC+∠EAB=90°∴∠DCA=∠EAB∵在△DCA和△EAB中,∠ADC=∠BEA=90°∠DCA=∠EABAC=AB∴△DCA≌△EAB(AAS)∴AD=BE且EA=DC由图可知:DE=EA+AD=DC+BE.(3)∵CD⊥MN于D,BE⊥MN于E∴∠ADC=∠BEA=∠BAC=90°∵∠DAC+∠DCA=90°且∠DAC+∠EAB=90°∴∠DCA=∠EAB∵在△DCA和△EAB中,∠ADC=∠BEA=90°∠DCA=∠EABAC=AB∴△DCA≌△EAB(AAS)∴AD=BE且AE=CD由图可知:AE=AD+DE∴CD=BE+DE.【点睛】本题考查了旋转的性质:旋转前后两图形全等,对应点到旋转中心的距离相等,对应点与旋转中心的连线段所夹的角等于旋转角,也考查了三角形全等的判定与性质.4(2023·江苏·八年级假期作业)在△ABC中,AB=AC,∠BAC=90°.将一个含45°角的直角三角尺DEF按图所示放置,使直角三角尺的直角顶点D恰好落在BC边的中点处.将直角三角尺DEF绕点D旋转,设AB交DF于点N,AC交DE于点M,示意图如图所示.(1)【证明推断】求证:DN=DM;小明给出的思路:若要证明DN=DM,只需证明△BDN≌△ADM即可.请你根据小明的思路完成证明过程;(2)【延伸发现】连接AE,BF,如图所示,求证:AE=BF;(3)【迁移应用】延长EA交DF于点P,交BF于点Q.在图中完成如上作图过程,猜想并证明AE和BF的位置关系.【答案】(1)见解析(2)见解析(3)AE⊥BF,见解析【分析】(1)在△ABC中,根据点D是BC的中点,得出AD=BD=BC2,由AD⊥BC,△DEF是直角三角尺,得出∠EDF=90°,从而得到∠BDN=∠ADM,在△BDN和△ADM中,立即证明全等,由性质即可解答DN=DM;(2)根据△BDN≌△ADM,得出BN=AM,∠BND=∠AMD,DN=DM,从而得到∠BNF=∠AME,由于△DEF是含45°直角三角尺,推出FN=EM,利用SAS即可证明△BNF和△AME全等,从而求解;(3)猜想:AE⊥BF,理由:根据△BNF≌△AME和∠FDE=90°,得出∠AEM+∠APD=90°,又根据∠APD=∠FPQ,等量代换得到∠FQP=90°从而证明.【详解】(1)证明:在△ABC中,∵AB=AC,∠BAC=90°,∴∠B=∠C=45°,又∵点D是BC的中点,∴AD=BD=BC2,且AD⊥BC,∠BAD=∠CAD=12∠BAC=45°∴∠ADN+∠BDN=90°,又∵△DEF是直角三角尺,∴∠EDF=90°,即∠ADN+∠ADM=90°,∴∠BDN=∠ADM在△BDN和△ADM中,∠B=∠DAM=45°BD=AD∠BDN=∠ADM∴△BDN≌△ADM,∴DN=DM;(2)证明:∵△BDN≌△ADM∴BN=AM,∠BND=∠AMD,DN=DM∴∠BNF=∠AME,且由于△DEF是含45°直角三角尺,∴DF=DE,∴DF-DN=DE-DM即FN=EM在△BNF和△AME中,BN=AM∠BNF=∠AME FN=EM∴△BNF≌△AME,∴AE=BF;(3)解:作图正确(如图所示)猜想:AE⊥BF,理由如下:∵△BNF≌△AME,∴∠BFN=∠AEM,∵∠FDE=90°,∴∠AEM+∠APD=90°又∵∠APD=∠FPQ,∴∠FPQ+∠BFN=90°,∴∠FQP=90°,∴AE⊥BF.【点睛】本题考查了旋转的性质、直角三角尺的特征、全等三角形的判定及性质,解题的关键是掌握三角形全等的判定及性质.。
中考数学复习---《三角形综合》压轴题练习(含答案解析)

中考数学复习---《三角形综合》压轴题练习(含答案解析)一.全等三角形的判定与性质1.(2022•淄博)如图,在△ABC中,AB=AC,点D在AC边上,过△ABD的内心I作IE⊥BD于点E.若BD=10,CD=4,则BE的长为()A.6B.7C.8D.9【答案】B【解答】解:如图,连接AI,BI,CI,DI,过点I作IT⊥AC于点T.∵I是△ABD的内心,∴∠BAI=∠CAI,∵AB=AC,AI=AI,∴△BAI≌△CAI(SAS),∴IB=IC,∵∠ITD=∠IED=90°,∠IDT=∠IDE,DI=DI,∴△IDT≌△IDE(AAS),∴DE=DT,IT=IE,∵∠BEI=∠CTI=90°,∴Rt△BEI≌Rt△CTI(HL),∴BE=CT,设BE=CT=x,∵DE=DT,∴10﹣x=x﹣4,∴x=7,∴BE=7.故选:B.2.(2022•湘西州)如图,在Rt△ABC中,∠A=90°,M为BC的中点,H为AB上一点,过点C作CG∥AB,交HM的延长线于点G,若AC=8,AB=6,则四边形ACGH周长的最小值是()A.24B.22C.20D.18【答案】B【解答】解:∵CG∥AB,∴∠B=∠MCG,∵M是BC的中点,∴BM=CM,在△BMH和△CMG中,,∴△BMH≌△CMG(ASA),∴HM=GM,BH=CG,∵AB=6,AC=8,∴四边形ACGH的周长=AC+CG+AH+GH=AB+AC+GH=14+GH,∴当GH最小时,即MH⊥AB时四边形ACGH的周长有最小值,∵∠A=90°,MH⊥AB,∴GH∥AC,∴四边形ACGH为矩形,∴GH=8,∴四边形ACGH的周长最小值为14+8=22,故选:B.3.(2022•南充)如图,正方形ABCD边长为1,点E在边AB上(不与A,B重合),将△ADE沿直线DE折叠,点A落在点A1处,连接A1B,将A1B绕点B 顺时针旋转90°得到A2B,连接A1A,A1C,A2C.给出下列四个结论:①△ABA1≌△CBA2;②∠ADE+∠A1CB=45°;③点P是直线DE上动点,则CP+A1P的最小值为;④当∠ADE=30°时,△A1BE的面积为.其中正确的结论是.(填写序号)【答案】①②③【解答】解:∵四边形ABCD是正方形,∴BA=BC,∠ABC=90°,∵∠A1BA2=∠ABC=90∴∠ABA1=∠CBA2,∵BA1=BA2,∴△ABA1≌△CBA2(SAS),故①正确,过点D作DT⊥CA1于点T,∵CD=DA1,∴∠CDT=∠A1DT,∵∠ADE=∠A1DE,∠ADC=90°,∴∠ADE+∠CDT=45°,∵∠CDT+∠DCT=90°,∠DCT+∠BCA1=90°,∴∠CDT=∠BCA1,∴∠ADE+∠BCA1=45°,故②正确.连接P A,AC.∵A,A1关于DE对称,∴P A=P A1,∴P A1+PC=P A+PC≥AC=,∴P A1+PC的最小值为,故③正确,过点A1作A1H⊥AB于点H,∵∠ADE=30°,∴AE=A1E=AD•tan30°=,∴EB=AB﹣AE=1﹣,∵∠A1EB=60°,∴A1H=A1E•sin60°=×=,∴=×(1﹣)×=,故④错误.故答案为:①②③.4.(2022•朝阳)等边三角形ABC中,D是边BC上的一点,BD=2CD,以AD 为边作等边三角形ADE,连接CE.若CE=2,则等边三角形ABC的边长为.【答案】3或.【解答】解:如图,E点在AD的右边,∵△ADE与△ABC都是等边三角形,∴AC=AB,AE=AD,∠DAE=∠BAC=60°,∴∠DAE﹣∠CAD=∠BAC﹣∠CAD,即∠CAE=∠BAD.在△CAE和△BAD中,,∴△CAE≌△BAD(SAS),∴CE=BD=2,∵BD=2CD,∴CD=1,∴BC=BD+CD=2+1=3,∴等边三角形ABC3,如图,E点在AD的左边,同上,△BAE≌△CAD(SAS),∴BE=CD,∠ABE=∠ACD=60°,∴∠EBD=120°,过点E作EF⊥BC交CB的延长线于点F,则∠EBF=60°,∴EF=BE=CD,BF=BE=CD,∴CF=BF+BD+CD=CD,在Rt△EFC中,CE=2,∴EF2+CF2=CE2=4,∴+=4,∴CD=或CD=﹣(舍去),∴BC=,∴等边三角形ABC的边长为,故答案为:3或.5.(2022•日照)如图,在平面直角坐标系xOy中,点A的坐标为(0,4),P 是x轴上一动点,把线段P A绕点P顺时针旋转60°得到线段PF,连接OF,则线段OF长的最小值是.【答案】2【解答】解:方法一:∵将线段P A绕点P顺时针旋转60°得到线段PF,∴∠APF=60°,PF=P A,∴△APF是等边三角形,∴AP=AF,如图,当点F1在x轴上时,△P1AF1为等边三角形,则P1A=P1F1=AF1,∠AP1F1=60°,∵AO⊥P1F1,∴P1O=F1O,∠AOP1=90°,∴∠P1AO=30°,且AO=4,由勾股定理得:P1O=F1O=,∴P1A=P1F1=AF1=,∴点F1的坐标为(,0),如图,当点F2在y轴上时,∵△P2AF2为等边三角形,AO⊥P2O,∴AO=F2O=4,∴点F2的坐标为(0,﹣4),∵tan∠OF1F2===,∴∠OF1F2=60°,∴点F运动所形成的图象是一条直线,∴当OF⊥F1F2时,线段OF最短,设直线F1F2的解析式为y=kx+b,则,解得,∴直线F1F2的解析式为y=x﹣4,∵AO=F2O=4,AO⊥P1F1,∴F1F2=AF1=,在Rt△OF1F2中,设点O到F1F2的距离为h,则×OF1×OF2=×F1F2×h,∴××4=××h,解得h=2,即线段OF的最小值为2;方法二:如图,在第二象限作等边三角形AOB,连接BP、AF,过点B作BP′⊥x轴于点P′,∵将线段P A绕点P顺时针旋转60°得到线段PF,∴∠APF=60°,PF=P A,∴△APF是等边三角形,∴AP=AF,∠P AF=60°,∵△AOB是等边三角形,∴AB=AO=OB=4,∠BAO=60°,∴∠BAP=60°+∠OAP=∠OAF,在△BAP和△OAF中,,∴△BAP≌△OAF(SAS),∴BP=OF,∵P是x轴上一动点,∴当BP⊥x轴时,BP最小,即点P与点P′重合时BP=BP′最小,∵∠BOP′=30°,∠BP′O=90°,∴BP′=OB=×4=2,∴OF的最小值为2,故答案为2.二.勾股定理6.(2022•内江)勾股定理被记载于我国古代的数学著作《周髀算经》中,汉代数学家赵爽为了证明勾股定理,创制了一幅如图①所示的“弦图”,后人称之为“赵爽弦图”.图②由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD、正方形EFGH、正方形MNXT的面积分别为S1、S2、S3.若正方形EFGH的边长为4,则S1+S2+S3=.【答案】48【解答】解:设八个全等的直角三角形的长直角边为a,短直角边是b,则:S1=(a+b)2,S2=42=16,S3=(a﹣b)2,且:a2+b2=EF2=16,∴S1+S2+S3=(a+b)2+16+(a﹣b)2=2(a2+b2)+16=2×16+16=48.故答案为:48.7.(2022•常州)如图,在Rt△ABC中,∠C=90°,AC=9,BC=12.在Rt △DEF中,∠F=90°,DF=3,EF=4.用一条始终绷直的弹性染色线连接CF,Rt△DEF从起始位置(点D与点B重合)平移至终止位置(点E与点A 重合),且斜边DE始终在线段AB上,则Rt△ABC的外部被染色的区域面积是.【答案】21【解答】解:如图,连接CF交AB于点M,连接CF′交AB于点N,过点F 作FG⊥AB于点H,过点F′作F′H⊥AB于点H,连接FF′,则四边形FGHF′是矩形,Rt△ABC的外部被染色的区域是梯形MFF′N.在Rt△DEF中,DF=3,EF=4,∴DE===5,在Rt△ABC中,AC=9,BC=12,∴AB===15,∵•DF•EF=•DE•GF,∴FG=,∴BG===,∴GE=BE﹣BG=,AH=GE=,∴F′H=FG=,∴FF′=GH=AB﹣BG﹣AH=15﹣5=10,∵BF∥AC,∴==,∴BM=AB=,同法可证AN=AB=,∴MN=15﹣﹣=,∴Rt△ABC的外部被染色的区域的面积=×(10+)×=21,故答案为:21.8.(2022•武汉)如图,在Rt△ABC中,∠ACB=90°,AC>BC,分别以△ABC的三边为边向外作三个正方形ABHL,ACDE,BCFG,连接DF.过点C作AB的垂线CJ,垂足为J,分别交DF,LH于点I,K.若CI=5,CJ=4,则四边形AJKL的面积是.【答案】80【解答】解:过点D作DM⊥CI,交CI的延长线于点M,过点F作FN⊥CI 于点N,∵△ABC为直角三角形,四边形ACDE,BCFG为正方形,过点C作AB的垂线CJ,CJ=4,∴AC=CD,∠ACD=90°,∠AJC=∠CMD=90°,∠CAJ+∠ACJ=90°,BC=CF,∠BCF=90°,∠CNF=∠BJC=90°,∠FCN+∠CFN=90°,∴∠ACJ+∠DCM=90°,∠FCN+∠BCJ=90°,∴∠CAJ=∠DCM,∠BCJ=∠CFN,∴△ACJ≌△CDM(AAS),△BCJ≌△CFN(AAS),∴AJ=CM,DM=CJ=4,BJ=CN,NF=CJ=4,∴DM=NF,∴△DMI≌△FNI(AAS),∴DI=FI,MI=NI,∵∠DCF=90°,∴DI=FI=CI=5,在Rt△DMI中,由勾股定理可得:MI===3,∴NI=MI=3,∴AJ=CM=CI+MI=5+3=8,BJ=CN=CI﹣NI=5﹣3=2,∴AB=AJ+BJ=8+2=10,∵四边形ABHL为正方形,∴AL=AB=10,∵四边形AJKL为矩形,∴四边形AJKL的面积为:AL•AJ=10×8=80,故答案为:80.三.等腰直角三角形(共2小题)9.(2022•宜宾)如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE =90°,点D是BC边上的动点(不与点B、C重合),DE与AC交于点F,连结CE.下列结论:①BD=CE;②∠DAC=∠CED;③若BD=2CD,则=;④在△ABC内存在唯一一点P,使得P A+PB+PC的值最小,若点D在AP的延长线上,且AP的长为2,则CE=2+.其中含所有正确结论的选项是()A.①②④B.①②③C.①③④D.①②③④【答案】B【解答】解:如图1中,∵∠BAC=∠DAE=90°,∴∠BAD=∠CAE,∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS),∴BD=EC,∠ADB=∠AEC,故①正确,∵∠ADB+∠ADC=180°,∴∠AEC+∠ADC=180°,∴∠DAE+∠DCE=180°,∴∠DAE=∠DCE=90°,取DE的中点O,连接OA,OA,OC,则OA=OD=OE=OC,∴A,D,C,E四点共圆,∴∠DAC=∠CED,故②正确,设CD=m,则BD=CE=2m.DE=m,OA=m,过点C作CJ⊥DF于点J,∵tan∠CDF===2,∴CJ=m,∵AO⊥DE,CJ⊥DE,∴AO∥CJ,∴===,故③正确.如图2中,将△BPC绕点B顺时针旋转60°得到△BNM,连接PN,∴BP=BN,PC=NM,∠PBN=60°,∴△BPN是等边三角形,∴BP=PN,∴P A+PB+PC=AP+PN+MN,∴当点A,点P,点N,点M共线时,P A+PB+PC值最小,此时∠APB=∠APC =∠BPC=120°,PB=PC,AD⊥BC,∴∠BPD=∠CPD=60°,设PD=t,则BD=AD=t,∴2+t=t,∴t=+1,∴CE=BD=t=3+,故④错误.故选:B.10.(2022•绵阳)如图,四边形ABCD中,∠ADC=90°,AC⊥BC,∠ABC=45°,AC与BD交于点E,若AB=2,CD=2,则△ABE的面积为.【答案】【解答】解:过点D作DF⊥AC于点F,∵AC⊥BC,∠ABC=45°,∴AC=BC=AB=2,∵∠ADC=90°,CD=2,∴AD=,∵,∴DF=,∴AF=,∴CF=,∵DF∥BC,∴△DEF∽△BEC,∴,即,∴EF=,∴AE=,∴.故答案为:.11.(2022•安徽)已知点O是边长为6的等边△ABC的中心,点P在△ABC外,△ABC,△P AB,△PBC,△PCA的面积分别记为S0,S1,S2,S3.若S1+S2+S3=2S0,则线段OP长的最小值是()A.B.C.3D.【答案】B【解答】解:如图,不妨假设点P在AB的左侧,∵S△P AB +S△ABC=S△PBC+S△P AC,∴S1+S0=S2+S3,∵S1+S2+S3=2S0,∴S1+S1+S0=2,∴S1=S0,∵△ABC是等边三角形,边长为6,∴S0=×62=9,∴S1=,过点P作AB的平行线PM,连接CO延长CO交AB于点R,交PM于点T.∵△P AB的面积是定值,∴点P的运动轨迹是直线PM,∵O是△ABC的中心,∴CT⊥AB,CT⊥PM,∴•AB•RT=,CR=3,OR=,∴RT=,∴OT=OR+TR=,∵OP≥OT,∴OP的最小值为,当点P在②区域时,同法可得OP的最小值为,如图,当点P在①③⑤区域时,OP的最小值为,当点P在②④⑥区域时,最小值为,∵<,故选:B.12.(2022•温州)如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,连结CF,作GM⊥CF于点M,BJ⊥GM于点J,AK⊥BJ于点K,交CF于点L.若正方形ABGF与正方形JKLM的面积之比为5,CE=+,则CH的长为()A.B.C.2D.【答案】C【解答】解:设CF交AB于点P,过C作CN⊥AB于点N,如图:设正方形JKLM边长为m,∴正方形JKLM面积为m2,∵正方形ABGF与正方形JKLM的面积之比为5,∴正方形ABGF的面积为5m2,∴AF=AB=m,由已知可得:∠AFL=90°﹣∠MFG=∠MGF,∠ALF=90°=∠FMG,AF =GF,∴△AFL≌△FGM(AAS),∴AL=FM,设AL=FM=x,则FL=FM+ML=x+m,在Rt△AFL中,AL2+FL2=2,∴x2+(x+m)2=(m)2,解得x=m或x=﹣2m(舍去),∴AL=FM=m,FL=2m,∵tan∠AFL====,∴=,∴AP=,∴FP===m,BP=AB﹣AP=m﹣=,∴AP=BP,即P为AB中点,∵∠ACB=90°,∴CP=AP=BP=,∵∠CPN=∠APF,∠CNP=90°=∠F AP,∴△CPN∽△FP A,∴==,即==,∴CN=m,PN=m,∴AN=AP+PN=m,∴tan∠BAC====,∵△AEC和△BCH是等腰直角三角形,∴△AEC∽△BCH,∴=,∵CE=+,∴=,∴CH=2,故选:C.13.(2022•湖州)在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,在6×6的正方形网格图形ABCD中,M,N分别是AB,BC上的格点,BM=4,BN=2.若点P是这个网格图形中的格点,连结PM,PN,则所有满足∠MPN=45°的△PMN中,边PM的长的最大值是()A.4B.6C.2D.3【答案】C【解答】解:如图所示:∵BM=NC=4,BN=CP=2,且∠B=∠C=90°,∴△BMN≌△CNP(SAS),∴MN=NP,∠BMN=∠CNP,∵∠BMN+∠BNM=90°,∴∠BNM+∠CNP=90°,∴∠MNP=90°,∴△NMP为等腰直角三角形,根据题意得到点P的轨迹为圆弧,当MP为直径时最长,在Rt△BMN和Rt△NCP中,根据勾股定理得:MN=NP==2,则PM==2.故选:C.14.(2022•苏州)如图,点A的坐标为(0,2),点B是x轴正半轴上的一点,将线段AB绕点A按逆时针方向旋转60°得到线段AC.若点C的坐标为(m,3),则m的值为()A.B.C.D.【答案】C【解答】解:过C作CD⊥x轴于点D,CE⊥y轴于点E,如图:∵CD⊥x轴,CE⊥y=90°,∴四边形EODC是矩形,∵将线段AB绕点A按逆时针方向旋转60°得到线段AC,∴AB=AC,∠BAC=60°,∴△ABC是等边三角形,∴AB=AC=BC,∵A(0,2),C(m,3),∴CE=m=OD,CD=3,OA=2,∴AE=OE﹣OA=CD﹣OA=1,∴AC===BC=AB,在Rt△BCD中,BD===,在Rt△AOB中,OB===,∵OB+BD=OD=m,∴+=m,化简变形得:3m4﹣22m2﹣25=0,解得m=或m=﹣(舍去),∴m=,故选:C.三.等腰直角三角形(共1小题)15.(2022•成都)如图,在△ABC中,按以下步骤作图:①分别以点B和C为圆心,以大于BC的长为半径作弧,两弧相交于点M和N;②作直线MN交边AB于点E.若AC=5,BE=4,∠B=45°,则AB的长为.【答案】7【解答】解:设MN交BC于D,连接EC,如图:由作图可知:MN是线段BC的垂直平分线,∴BE=CE=4,∴∠ECB=∠B=45°,∴∠AEC=∠ECB+∠B=90°,在Rt△ACE中,AE===3,∴AB=AE+BE=3+4=7,故答案为:7.四.等边三角形的性质(共2小题)16.(2022•张家界)如图,点O是等边三角形ABC内一点,OA=2,OB=1,OC=,则△AOB与△BOC的面积之和为()A.B.C.D.【答案】C【解答】解:将△AOB绕点B顺时针旋转60°得△CDB,连接OD,∴OB=BD,∠OBD=60°,CD=OA=2,∴△BOD是等边三角形,∴OD=OB=1,∵OD2+OC2=12+()2=4,CD2=22=4,∴OD2+OC2=CD2,∴∠DOC=90°,∴△AOB与△BOC的面积之和为S△BOC +S△BCD=S△BOD+S△COD=×12+=,故选:C.17.(2022•鄂州)如图,在边长为6的等边△ABC中,D、E分别为边BC、AC 上的点,AD与BE相交于点P,若BD=CE=2,则△ABP的周长为.【答案】【解答】解:∵△ABC是等边三角形,∴AB=BC,∠ABD=∠C=60°,在△ABD和△BCE中,∴△ABD≌△BCE(SAS)∴∠BAD=∠CBE,∴∠APE=∠ABP+∠BAD=∠ABP+∠CBE=∠ABD=60°,∴∠APB=120°,在CB上取一点F使CF=CE=2,则BF=BC﹣CF=4,∴∠C=60°,∴△CEF是等边三角形,∴∠BFE=120°,即∠APB=∠BFE,∴△APB∽△BFE,∴==2,设BP=x,则AP=2x,作BH⊥AD延长线于H,∵∠BPD=∠APE=60°,∴∠PBH=30°,∴PH=,BH=,∴AH=AP+PH=2x+=x,在Rt△ABH中,AH2+BH2=AB2,即(x)2+(x)2=62,解得x=或﹣(舍去),∴AP=,BP=,∴△ABP的周长为AB+AP+BP=6++=6+=,故答案为:.五.含30度角的直角三角形(共1小题)18.(2022•十堰)【阅读材料】如图①,四边形ABCD中,AB=AD,∠B+∠D =180°,点E,F分别在BC,CD上,若∠BAD=2∠EAF,则EF=BE+DF.【解决问题】如图②,在某公园的同一水平面上,四条道路围成四边形ABCD.已知CD=CB=100m,∠D=60°,∠ABC=120°,∠BCD=150°,道路AD,AB上分别有景点M,N,且DM=100m,BN=50(﹣1)m,若在M,N之间修一条直路,则路线M→N的长比路线M→A→N的长少m (结果取整数,参考数据:≈1.7).【答案】370【解答】解:解法一:如图,延长DC,AB交于点G,过点N作NH⊥AD于H,∵∠D=60°,∠ABC=120°,∠BCD=150°,∴∠A=360°﹣60°﹣120°﹣150°=30°,∴∠G=90°,∴AD=2DG,Rt△CGB中,∠BCG=180°﹣150°=30°,∴BG=BC=50,CG=50,∴DG=CD+CG=100+50,∴AD=2DG=200+100,AG=DG=150+100,∵DM=100,∴AM=AD﹣DM=200+100﹣100=100+100,∵BG=50,BN=50(﹣1),∴AN=AG﹣BG﹣BN=150+100﹣50﹣50(﹣1)=150+50,Rt△ANH中,∵∠A=30°,∴NH=AN=75+25,AH=NH=75+75,由勾股定理得:MN===50(+1),∴AM+AN﹣MN=100+100+150+50﹣50(+1)=200+100≈370(m).答:路线M→N的长比路线M→A→N的长少370m.解法二:如图,延长DC,AB交于点G,连接CN,CM,则∠G=90°,∵CD=DM,∠D=60°,∴△DCM是等边三角形,∴∠DCM=60°,由解法一可知:CG=50,GN=BG+BN=50+50(﹣1)=50,∴△CGN是等腰直角三角形,∴∠GCN=45°,∴∠BCN=45°﹣30°=15°,∴∠MCN=150°﹣60°﹣15°=75°=∠BCD,由【阅读材料】的结论得:MN=DM+BN=100+50(﹣1)=50+50,∵AM+AN﹣MN=100+100+150+50﹣50(+1)=200+100≈370(m).答:路线M→N的长比路线M→A→N的长少370m.故答案为:370.六.等腰直角三角形(共2小题)19.(2022•长沙)如图,在△ABC中,按以下步骤作图:①分别以点A、B为圆心,大于AB的长为半径画弧,两弧交于P、Q两点;②作直线PQ交AB于点D;③以点D为圆心,AD长为半径画弧交PQ于点M,连接AM、BM.若AB=2,则AM的长为()A.4B.2C.D.【答案】B【解答】解:由作图可知,PQ是AB的垂直平分线,∴AM=BM,∵以点D为圆心,AD长为半径画弧交PQ于点M,∴DA=DM=DB,∴∠DAM=∠DMA,∠DBM=∠DMB,∵∠DAM+∠DMA+∠DBM+∠DMB=180°,∴2∠DMA+2∠DMB=180°,∴∠DMA+∠DMB=90°,即∠AMB=90°,∴△AMB是等腰直角三角形,∴AM=AB=×2=2,故选:B.20.(2022•河南)如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,点D 为AB的中点,点P在AC上,且CP=1,将CP绕点C在平面内旋转,点P 的对应点为点Q,连接AQ,DQ.当∠ADQ=90°时,AQ的长为.【答案】或【解答】解:如图:∵∠ACB=90°,AC=BC=2,∴AB=AC=4,∵点D为AB的中点,∴CD=AD=AB=2,∠ADC=90°,∵∠ADQ=90°,∴点C、D、Q在同一条直线上,由旋转得:CQ=CP=CQ′=1,分两种情况:当点Q在CD上,在Rt△ADQ中,DQ=CD﹣CQ=1,∴AQ===,当点Q在DC的延长线上,在Rt△ADQ′中,DQ′=CD+CQ′=3,∴AQ′===,综上所述:当∠ADQ=90°时,AQ的长为或,故答案为:或.30。
专题02 全等三角形的性质与判定压轴题八种模型全攻略(解析版)

专题02全等三角形的性质与判定压轴题八种模型全攻略考点一全等三角形的概念考点二利用全等图形求正方形网格中角度之和考点三全等三角形的性质考点四用SSS证明三角形全等考点五用SAS证明三角形全等考点六用ASA证明三角形全等考点七用AAS证明三角形全等考点八用HL证明三角形全等考点一全等三角形的概念例题:(2021·福建·福州三牧中学八年级期中)有下面的说法:①全等三角形的形状相同;②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等.其中正确的说法有() A.1个B.2个C.3个D.4个【答案】D【解析】【分析】先分别验证①②③④的正确性,并数出正确的个数,即可得到答案.【详解】①全等三角形的形状相同,根据图形全等的定义,正确;②全等三角形的对应边相等,根据全等三角形的性质,正确;③全等三角形的对应角相等,根据全等三角形的性质,正确;④全等三角形的周长、面积分别相等,正确;故四个命题都正确,故D为答案.【点睛】本题主要考查了全等的定义、全等三角形图形的性质,即全等三角形对应边相等、对应角相等、面积周长均相等.【变式训练】1.(2022·上海·七年级专题练习)如图,在△ABC和△A′B′C′中,已知AB=A′B′,∠A=∠A′,AC=A′C′,那么△ABC≌△A′B′C′.说理过程如下:把△ABC放到△A′B′C′上,使点A与点A′重合,由于=,所以可以使点B与点B′重合.又因为=,所以射线能落在射线上,这时因为=,所以点与重合.这样△ABC和△A′B′C′重合,即△ABC≌△A′B′C′.【答案】AB,A'B',∠A,∠A′,AC,A'C',AC=A'C',C,C'【解析】【分析】直接利用已知结合全等的定义得出答案.【详解】解:把△ABC放到△A′B′C′上,使点A与点A′重合,由于AB=A'B',所以可以使点B与点B′重合.又因为∠A=∠A′,所以射线AC能落在射线A'C'上,这时因为AC=A'C',所以点C与C'重合.这样△ABC和△A′B′C′重合,即△ABC≌△A′B′C′.故答案为:AB,A'B',∠A,∠A′,AC,A'C',AC=A'C',C,C'.【点睛】本题考查了全等三角形的判定,解答本题的关键是仔细读题,理解填空.考点二利用全等图形求正方形网格中角度之和例题:(2021·全国·八年级专题练习)如图为6个边长相等的正方形的组合图形,则∠1+∠3-∠2=()A.30°B.45°C.60°D.135°【答案】B【解析】【分析】首先利用SAS定理判定△ABC≌△DBE,根据全等三角形的性质可得∠3=∠ACB,再由∠ACB+∠1=∠1+∠3=90°,可得∠1+∠3-∠2.【详解】∵在△ABC 和△DBE 中AB BD A D AC ED ⎧⎪∠∠⎨⎪⎩===,∴△ABC ≌△DBE (SAS ),∴∠3=∠ACB ,∵∠ACB +∠1=90°,∴∠1+∠3=90°,∵∠2=45°∴∠1+∠3-∠2=90°-45°=45°,故选B .【点睛】此题主要考查了全等图形,关键是掌握全等三角形的判定,以及全等三角形对应角相等.【变式训练】1.(2022·山东·济南市槐荫区教育教学研究中心二模)如图,在44⨯的正方形网格中,求αβ+=______度.【答案】45【解析】【分析】连接AB ,根据正方形网格的特征即可求解.【详解】解:如图所示,连接AB∵图中是44⨯的正方形网格∴AD CE =,ADB AEC ∠=∠,DB AE =∴()ADB CEA SAS △≌△∴EAC ABD α∠=∠=,AB AC =∵90ABD BAD ∠+∠=︒∴90EAC BAD ∠+∠=︒,即90CAB ∠=︒∴45ACB ABC ∠=∠=︒∵BD CE ∥∴BCE DBC β==∠∠∵ABC ABD DBC αβ=+=+∠∠∠∴45αβ+=︒故答案为:45.【点睛】本题考查了正方形网格中求角的度数,利用了平行线的性质、同角的余角相等、等腰直角三角形的性质等知识点,解题的关键是能够掌握正方形网格的特征.2.(2020·江苏省灌云高级中学城西分校八年级阶段练习)如图,由4个相同的小正方形组成的格点图中,∠1+∠2+∠3=________度.【答案】135【解析】【分析】首先利用全等三角形的判定和性质求出13∠+∠的值,即可得出答案;【详解】 如图所示,在△ACB 和△DCE 中,AB DE A D AC DC ⎧=⎪∠=∠⎨⎪=⎩,∴()△△ACB DCE SAS ≅,∴3ABE ∠=∠,∴()12313459045135∠+∠+∠=∠+∠+︒=︒+︒=︒;故答案是:135︒.【点睛】本题主要考查了全等图形的应用,准确分析计算是解题的关键.考点三 全等三角形的性质例题:(2021·重庆大足·八年级期末)如图,ABC 和DEF 全等,且A D ∠=∠,AC 对应DE .若6AC =,5BC =,4AB =,则DF 的长为( )A .4B .5C .6D .无法确定【答案】A【解析】【分析】 全等三角形对应边相等,对应角相等,根据题中信息得出对应关系即可.【详解】∵ABC 和DEF 全等,A D ∠=∠,AC 对应DE∴ABC DFE ≅∴AB =DF =4故选:A .【点睛】本题考查了全等三角形的概念及性质,应注意①对应边、对应角是对两个三角形而言的,指两条边、两个角的关系,而对边、对角是指同一个三角形的边和角的位置关系②可以进一步推广到全等三角形对应边上的高相等,对应角的平分线相等,对应边上的中线相等,周长及面积相等③全等三角形有传递性.【变式训练】1.(2022·云南昆明·三模)如图,ABC DEF △≌△,若80,30A F ∠=︒∠=︒,则B 的度数是( )A .80°B .70°C .65°D .60°【答案】B【解析】【分析】 由ABC DEF △≌△根据全等三角形的性质可得30C F ∠=∠=︒,再利用三角形内角和进行求解即可.【详解】ABC DEF ≌,C F ∠=∠∴,30F ∠=︒,30C ∴∠=︒,80,180A A B C ∠=︒∠+∠+∠=︒,18070B A C ∴∠=︒-∠-∠=︒,故选:B .【点睛】本题考查了全等三角形的性质及三角形的内角和定理,熟练掌握知识点是解题的关键.2.(2022·上海·七年级专题练习)如图所示,D ,A ,E 在同一条直线上,BD ⊥DE 于D ,CE ⊥DE 于E ,且△ABD ≌△CAE ,AD =2cm ,BD =4cm ,求(1)DE 的长;(2)∠BAC 的度数.【答案】(1)6cm DE =;(2)90BAC ︒∠=【解析】【分析】(1)根据全等三角形的性质即可得到结论;(2)根据垂直的定义得到∠D =90°,求得∠DBA +∠BAD =90°,根据全等三角形的性质得到∠DBA =∠CAE 等量代换即可得到结论.(1)解:∵△ABD ≌△CAE ,AD =2cm ,BD =4cm ,∴AE =BD =4cm ,∴DE =AD +AE =6cm .(2)∵BD ⊥DE ,∴∠D =90°,∴∠DBA +∠BAD =90°,∵△ABD ≌△CAE ,∴∠DBA =∠CAE∴∠BAD +∠CAE =90°,∴∠BAC =90°.【点睛】本题主要考查了全等三角形的性质,垂直的定义,熟练掌握全等三角形的性质是解题的关键.考点四 用SSS 证明三角形全等例题:(2022·河北·平泉市教育局教研室二模)如图,BD BC =,点E 在BC 上,且BE AC =,DE AB =.(1)求证:ABC EDB ≌;(2)判断AC 和BD 的位置关系,并说明理由.【答案】(1)见解析(2)AC BD ,理由见解析【解析】【分析】(1)运用SSS 证明即可;(2)由(1)得DBE BCA ∠=∠,根据内错角相等,两直线平行可得结论.(1)在ABC ∆和EDB ∆中,BD BC BE AC DE AB =⎧⎪=⎨⎪=⎩,∴ABC EDB ∆≅∆(SSS );(2)AC 和BD 的位置关系是AC BD ,理由如下:∵ABC EDB ∆≅∆∴DBE BCA ∠=∠,∴AC BD .【点睛】本题主要考查了全等三角形的判定与性质,熟练掌握全等三角形的判定定理是解答本题的关键.【变式训练】1.(2021·河南省实验中学七年级期中)如图,在线段BC 上有两点E ,F ,在线段CB 的异侧有两点A ,D ,且满足AB CD =,AE DF =,CE BF =,连接AF;(1)B 与C ∠相等吗?请说明理由.(2)若40B ∠=︒,20∠=DFC °,AF 平分BAE ∠时,求BAF ∠的度数.【答案】(1)B C ∠=∠,理由见解析(2)60︒【解析】【分析】(1)由“SSS ”可证△AEB ≌△DFC ,可得结论;(2)由全等三角形的性质可得∠AEB =∠DFC =20°,可求∠EAB =120°,由角平分线的性质可求解.(1)解:B C ∠=∠,理由如下:∵CE BF =∴BE CF =在AEB △和DFC △中AB CD AE DF BE CF =⎧⎪=⎨⎪=⎩∴()SSS AEB DFC ≌△△∴B C ∠=∠(2)解:∵AEB DFC ≌∴20AEB DFC ∠=∠=︒∴180120EAB B AEB ∠=︒-∠-∠=︒∵AF 平分BAE ∠ ∴1602BAF BAE ∠=∠=︒ 【点睛】本题考查了全等三角形的判定和性质,掌握全等三角形的判定是本题的关键.2.(2022·山东济宁·八年级期末)如图,在四边形ABCD 中,CB AB ⊥于点B ,CD AD ⊥于点D ,点E ,F 分别在AB ,AD 上,AE AF =,CE CF =.(1)若8AE =,6CD =,求四边形AECF 的面积;(2)猜想∠DAB ,∠ECF ,∠DFC 三者之间的数量关系,并证明你的猜想.【答案】(1)48(2)∠DAB +∠ECF =2∠DFC ,证明见解析【解析】【分析】(1)连接AC ,证明△ACE ≌△ACF ,则S △ACE =S △ACF ,根据三角形面积公式求得S △ACF 与S △ACE ,根据S 四边形AECF =S △ACF +S △ACE 求解即可;(2)由△ACE ≌△ACF 可得∠FCA =∠ECA ,∠F AC =∠EAC ,∠AFC =∠AEC ,根据垂直关系,以及三角形的外角性质可得∠DFC +∠BEC =∠FCA +∠F AC +∠ECA +∠EAC =∠DAB +∠ECF .可得∠DAB +∠ECF =2∠DFC(1)解:连接AC ,如图,在△ACE 和△ACF 中AE AF CE CF AC AC =⎧⎪=⎨⎪=⎩∴△ACE ≌△ACF (SSS ).∴S △ACE =S △ACF ,∠F AC =∠EAC .∵CB ⊥AB ,CD ⊥AD ,∴CD =CB =6.∴S △ACF =S △ACE =12AE ·CB =12×8×6=24.∴S 四边形AECF =S △ACF +S △ACE =24+24=48.(2)∠DAB +∠ECF =2∠DFC证明:∵△ACE ≌△ACF ,∴∠FCA =∠ECA ,∠F AC =∠EAC ,∠AFC =∠AEC .∵∠DFC 与∠AFC 互补,∠BEC 与∠AEC 互补,∴∠DFC =∠BEC .∵∠DFC =∠FCA +∠F AC ,∠BEC =∠ECA +∠EAC ,∴∠DFC +∠BEC =∠FCA +∠F AC +∠ECA +∠EAC=∠DAB +∠ECF .∴∠DAB +∠ECF =2∠DFC【点睛】本题考查了三角形全等的性质与判定,三角形的外角的性质,掌握三角形全等的性质与判定是解题的关键.考点五 用SAS 证明三角形全等例题:(2022·福建省福州第十九中学模拟预测)如图,点O 是线段AB 的中点,∥OD BC 且OD BC =.求证:AOD OBC ≌.【答案】见解析【解析】【分析】根据线段中点的定义得到AO BO =,根据平行线的性质得到AOD OBC ∠=∠,根据全等三角形的判定定理即可得到结论.【详解】证明:∵点O 是线段AB 的中点,∴AO BO =,∵∥OD BC ,∴AOD OBC ∠=∠,在△AOD 与△OBC 中,AO BO AOD OBC OD BC =⎧⎪∠=∠⎨⎪=⎩,∴()AOD OBC SAS ≌.【点睛】本题考查了全等三角形的判定,平行线的性质,熟练掌握全等三角形的判定是解题的关键.【变式训练】1.(2022·云南普洱·二模)如图,ABC 和EFD 分别在线段AE 的两侧,点C ,D 在线段AE 上,AC DE =,//AB EF ,.AB EF =求证:BC FD =.【答案】见解析【解析】【分析】利用//AB EF ,得到A E ∠=∠,再用AC DE =,AB EF =,得到ABC ≌EFD △(SAS ),然后用三角形全等的性质得到结论即可.【详解】证明://AB EF ,A E ∴∠=∠,在ABC 和EFD △中AC DE A E AB EF =⎧⎪∠=∠⎨⎪=⎩,ABC ∴≌EFD △(SAS ),BC FD ∴=.【点睛】本题考查三角形全等的判定,平行线的性质,找到三角形全等的条件是解答本题的关键.2.(2022·四川省南充市白塔中学八年级阶段练习)如图,点B 、C 、E 、F 共线,AB =DC ,∠B =∠C ,BF =CE . 求证:△ABE ≌△DCF.【答案】证明见解析;【解析】【分析】根据两边和它们的夹角对应相等的两个三角形全等(简写成“边角边”或“SAS”);即可证明;【详解】证明:∵点B、C、E、F共线,BF=CE,∴BF+EF=CE+EF,∴BE=CF,△ABE和△DCF中:BA=CD,∠ABE=∠DCF,BE=CF,∴△ABE≌△DCF(SAS);【点睛】本题考查了全等三角形的判定;掌握(SAS)的判定条件是解题关键.考点六用ASA证明三角形全等例题:(2022·上海·七年级专题练习)已知:如图,AB⊥BD,ED⊥BD,C是BD上的一点,AC⊥CE,AB =CD,求证:BC=DE.【答案】见解析【解析】【分析】根据直角三角形全等的判定方法,ASA即可判定三角形全等.【详解】证明:∵AB⊥BD,ED⊥BD,AC⊥CE(已知)∴∠ACE=∠B=∠D=90°(垂直的意义)∵∠BCA+∠DCE+∠ACE=180°(平角的意义)∠ACE=90°(已证)∴∠BCA +∠DCE =90°(等式性质)∵∠BCA +∠A +∠B =180°(三角形内角和等于180°)∠B =90°(已证)∴∠BCA +∠A =90°(等式性质)∴∠DCE =∠A (同角的余角相等)在△ABC 和△CDE 中,A DCE AB CD B D ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ABC ≌△CDE (ASA )∴BC =DE (全等三角形对应边相等)【点睛】本题考查了全等三角形的判定和性质;熟练掌握三角形全等的判定定理是解题的关键.【变式训练】1.(2022·广西百色·二模)如图,在△ABC 和△DCB 中,∠A =∠D ,AC 和DB 相交于点O ,OA =OD .(1)AB =DC ;(2)△ABC ≌△DCB .【答案】(1)证明见解析;(2)证明见解析【解析】【分析】(1)证明△ABO ≌△DCO (ASA ),即可得到结论;(2)由△ABO ≌△DCO ,得到OB =OC ,又OA =OD ,得到BD =AC ,又由∠A =∠D ,即可证得结论.(1)证明:在△ABO 与△DCO 中,A D OA ODAOB DOC ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△ABO ≌△DCO (ASA )∴AB =DC ;(2)证明:∵△ABO ≌△DCO ,∴OB =OC ,∵OA =OD ,∴OB +OD =OC +OA ,∴BD =AC ,在△ABC 与△DCB 中,AC BD A D AB DC =⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△DCB (SAS ).【点睛】此题考查了全等三角形的判定和性质,熟练掌握并灵活选择全等三角形的判定方法是解题的关键. 2.(2022·贵州遵义·八年级期末)如图,已知AB DE ∥,ACB D ∠=∠,AC DE =.(1)求证:ABC EAD ≅.(2)若60BCE ∠=︒,求BAD ∠的度数.【答案】(1)见解析(2)60︒【解析】【分析】(1)利用平行线的性质得CAB E ∠=∠,利用“角边角”即可证明ABC EAD ≅;(2)由邻补角的定义求出180120ACB BCE ∠=︒-∠=︒,进而得到120D ∠=︒,再利用两直线平行同旁内角互补求出BAD ∠.由两直线平行得(1)证明:AB DE ,CAB E ∴∠=∠,在ABC 和EAD中,CAB E AC DEACB D ∠=∠⎧⎪=⎨⎪∠=∠⎩, ABC EAD ∴≅.(2)解:60BCE ∠=︒,180ACB BCE ∠+∠=︒,180120ACB BCE ∴∠=︒-∠=︒,120D ACB ∴∠=∠=︒,AB DE ,180∴∠+∠=︒D BAD ,180********BAD D ∴∠=︒-∠=︒-︒=︒.【点睛】本题考查平行线的性质、邻补角的定义、全等三角形的判定等知识,熟练掌握平行线的性质是解题的关键.平行线的性质:两直线平行,内错角相等;两直线平行,同位角相等;两直线平行,同旁内角互补.考点七 用AAS 证明三角形全等例题:(2022·上海·七年级专题练习)如图,已知BE 与CD 相交于点O ,且BO =CO ,∠ADC =∠AEB ,那么△BDO 与△CEO 全等吗?为什么?【答案】△BDO ≌△CEO (AAS );原因见解析【解析】【分析】根据AAS 证明△BDO 与△CEO 全等即可.【详解】解:△BDO 与△CEO 全等;∵∠BDO =180°﹣∠ADC ,∠CEO =180°﹣∠AEB ,又∵∠ADC =∠AEB ,∴∠BDO =∠CEO,∵在△BDO 与△CEO 中,BDO CEO BOD COE BO CO ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BDO ≌△CEO (AAS ).【点睛】本题主要考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS 、SAS 、ASA 、AAS 、HL .注意:AAA 、SSA 不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.【变式训练】1.(2022·福建省福州第一中学模拟预测)如图,已知A ,F ,E ,C 在同一直线上,AB ∥CD ,∠ABE =∠CDF ,AF =CE .求证:AB =CD .【答案】见详解【解析】【分析】根据全等三角形证明△ABE ≌△CDF ,再根据全等三角形的性质解答即可.【详解】证明:∵AB ∥CD ,∴∠ACD =∠CAB ,∵AF=CE ,∴AF+EF=CE+EF ,即AE =FC ,在△ABE 和△CDF 中,ACD CAB ABE CDF AE CF ∠∠⎧⎪∠∠⎨⎪⎩=== ∴△ABE ≌△CDF (AAS ).∴AB =CD .【点睛】此题主要考查了三角形全等的判定及性质,一般证明线段相等先大致判断两个线段所在三角形是否全等,然后再看证明全等的条件有哪些.2.(2022·全国·九年级专题练习)如图,D 是△ABC 的边AB 上一点,CF //AB ,DF 交AC 于E 点,DE=EF .(1)求证:△ADE ≌△CFE ;(2)若AB =5,CF =4,求BD 的长.【答案】(1)证明见解析(2)BD =1【解析】【分析】(1)利用角角边定理判定即可;(2)利用全等三角形对应边相等可得AD 的长,用AB ﹣AD 即可得出结论.(1)证明:∵CF ∥AB ,∴∠ADF =∠F ,∠A =∠ECF .在△ADE 和△CFE 中,A ECF ADE F DE FE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADE ≌△CFE (AAS ).(2)∵△ADE ≌△CFE ,∴AD =CF =4.∴BD =AB ﹣AD =5﹣4=1.【点睛】此题考查了全等三角形的判定及性质,熟记全等三角形的判定定理是解题的关键.考点八 用HL 证明三角形全等例题:(2022·四川省南充市白塔中学八年级阶段练习)如图,AB =CD ,AE ⊥BC 于E ,DF ⊥BC 于F ,且BF =CE.(1)求证AE=DF;(2)判定AB和CD的位置关系,并说明理由.【答案】(1)见解析∥,理由见解析(2)AB CD【解析】【分析】(1)只需要利用HL证明Rt△ABE≌Rt△DCF即可证明结论;∥.(2)根据Rt△ABE≌Rt△DCF即可得到∠B=∠C,即可证明AB CD(1)解:∵BF=CE,∴BF-EF=CE-EF,即BE=CF,∵AE⊥BC,DF⊥BC,∴∠AEB=∠DFC=90°,又∵AB=DC,∴Rt△ABE≌Rt△DCF(HL),∴AE=DF;(2)∥,理由如下:解:AB CD∵Rt△ABE≌Rt△DCF,∴∠B=∠C,∥.∴AB CD【点睛】本题主要考查了全等三角形的性质与判定,平行线的判定,熟知全等三角形的性质与判定条件是解题的关键.【变式训练】1.(2022·安徽安庆·八年级期末)如图,AD,BC相交于点O,AD=BC,∠C=∠D=90°.(1)求证:△ACB ≌△BDA ;(2)若∠CAB =54°,求∠CAO 的度数.【答案】(1)见解析(2)18°【解析】【分析】(1)根据HL 证明Rt △ABC ≌Rt △BAD ;(2)先求出∠ABC 的度数,即可利用全等三角形的性质求出∠BAD 的度数,由此即可得到答案.(1)证明:∵∠D =∠C =90°,∴△ABC 和△BAD 都是直角三角形,在Rt △ABC 和Rt △BAD 中,BC AD AB BA ⎧⎨⎩==, ∴Rt △ABC ≌Rt △BAD (HL );(2)解:在Rt △ABC 中,∠CAB =54°,∠ACB =90°,∴∠ABC =36°,∵Rt △ABC ≌Rt △BAD ,∴∠ABC =∠BAD =36°,∴∠CAO =∠CAB -∠BAD =54°-36°=18°.【点睛】本题主要考查了全等三角形的性质与判定,直角三角形两锐角互余,熟练掌握全等三角形的性质与判定条件是解题的关键.2.(2022·江西·永丰县恩江中学八年级阶段练习)如图,在△ABC 中,BC =AB ,∠ABC =90°,F 为AB 延长线上一点,点E 在BC 上,且AE =CF .(1)求证:Rt △ABE ≌Rt △CBF ;(2)若∠CAB =30°,求∠ACF 的度数.【答案】(1)证明见解析(2)60︒【解析】【分析】(1)由“HL ”可证Rt △ABE ≌Rt △CBF ;(2)由AB =CB ,∠ABC =90°,即可求得∠CAB 与∠ACB 的度数,即可得∠BAE 的度数,又由Rt △ABE ≌Rt △CBF ,即可求得∠BCF 的度数,则由∠ACF =∠BCF +∠ACB 即可求得答案.(1)∵∠ABC =90°,∴∠CBF =∠ABE =90°,在Rt △ABE 和Rt △CBF 中,AE CF AB BC=⎧⎨=⎩ ∴Rt △ABE ≌Rt △CBF (HL );(2)∵AB =BC ,∠ABC =90°,∴∠CAB =∠ACB =45°,∴∠BAE =∠CAB -∠CAE =45°-30°=15°。
三角形全等的判定方法压轴题五种模型全攻略(解析版)

三角形全等的判定方法压轴题五种模型全攻略【考点导航】目录【典型例题】【考点一用SAS证明两三角形全等】【考点二用ASA证明两三角形全等】【考点三用AAS证明两三角形全等】【考点四用SSS证明两三角形全等】【考点五添一个条件使两三角形全等】【过关检测】【典型例题】【考点一用SAS证明两三角形全等】1(2023春·江苏苏州·七年级校联考阶段练习)如图,在△ABC中,AC>AB,射线AD平分∠BAC,交BC 于点E,点F在边AB的延长线上,AF=AC,连接EF.(1)求证:△AEC≌△AEF.(2)若∠AEB=50°,求∠BEF的度数.【答案】(1)证明见解析(2)80°【分析】(1)由射线AD平分∠BAC,可得∠CAE=∠FAE,进而可证△AEC≌△AEF SAS;(2)由△AEC≌△AEF SAS,可得∠C=∠F,由三角形外角的性质可得∠AEB=∠CAE+∠C=50°,则∠FAE+∠F=50°,根据∠FAE+∠F+∠AEB+∠BEF=180°,计算求解即可.【详解】(1)证明:射线AD平分∠BAC,∴∠CAE=∠FAE,在△AEC和△AEF中,∵AC=AF∠CAE=∠FAEAE=AE,∴△AEC≌△AEF SAS;(2)解:∵△AEC≌△AEF SAS,∴∠C =∠F ,∵∠AEB =∠CAE +∠C =50°,∴∠FAE +∠F =50°,∵∠FAE +∠F +∠AEB +∠BEF =180°,∴∠BEF =80°,∴∠BEF 为80°.【点睛】本题考查了角平分线,全等三角形的判定与性质,三角形外角的性质,三角形内角和定理.解题的关键在于对知识的熟练掌握与灵活运用.【变式训练】1(2023春·云南昭通·九年级校考阶段练习)如图,点A 、C 、F 、D 在同一直线上,AF =DC ,∠A =∠D ,AB =DE .求证:△ABC ≌△DEF.【答案】见解析【分析】由AF =CD ,可求得AC =DF ,利用SAS 可得出结论.【详解】解:∵ AF =CD ,∴AF -FC =CD -FC ,即AC =DF ,在△ABC 和△DEF 中,AB =DE∠A =∠D AC =DF,∴△ABC ≌△DEF (SAS ).【点睛】本题主要考查全等三角形的判定,掌握全等三角形的判定方法是解题的关键.2(2023春·四川成都·七年级统考期末)如图在△ABC 中,D 是BC 边上的一点,AB =DB ,BE 平分∠ABC ,交AC 边于点E ,连接DE.(1)求证:△ABE ≌△DBE ;(2)若∠A =100°,∠C =40°,求∠DEC 的度数.【答案】(1)证明见解析(2)60°【分析】(1)根据BE 平分∠ABC ,可得∠ABE =∠DBE ,进而利用SAS 证明△ABE ≌△DBE 即可;(2)根据全等三角形的性质可得∠BDE =∠A =100°,再由三角形外角的性质即可求解.【详解】(1)解:∵BE 平分∠ABC ,∴∠ABE =∠DBE .∵AB=DB,BE=BE,∴△ABE≌△DBE SAS;(2)解:∵△ABE≌△DBE,∴∠BDE=∠A=100°,∴∠DEC=∠BDE-∠C=60°.【点睛】本题主要考查了全等三角形的判定和性质,三角形外角的性质,熟练掌握全等三角形的判定和性质定理是解题的关键.3(2023春·江苏泰州·七年级统考期末)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°,连接BD、CE.(1)求证:△ABD≌△ACE.(2)图中BD和CE有怎样的关系?试证明你的结论.【答案】(1)见详解(2)见详解【分析】(1)先证明∠BAD=∠EAC,又因为AB=AC,AD=AE,即可求出三角形全等;(2)根据△ABD≌△ACE,得到∠ACE=∠ABD,进而证得∠ABD+∠DBC+∠ACB=90°,等量代换得∠ACE+∠DBC+∠ACB=90°即∠ECB+∠DBC=90°,再利用内角和,即可证明垂直.【详解】(1)解:∵∠BAC=∠DAE=90°∴∠BAC+∠CAD=∠DAE+∠CAD∴∠BAD=∠EAC∵AB=AC,AD=AE∴△ABD≌△ACE.(2)解:如图,设BD和CE交点为F∵△ABD≌△ACE∴∠ACE=∠ABD∵∠BAC=90°∴∠ABD+∠DBC+∠ACB=90°∴∠ACE+∠DBC+∠ACB=90°即∠ECB+∠DBC=90°∴∠BFC=180°-∠ECB+∠DBC=90°∴BD⊥CE.【点睛】此题考查全等三角形的判定和性质,和角与角之间关系,解题的关键是根据SAS三角形全等.4(2023·江苏南通·统考一模)如图,点A,B,C,D在同一条直线上,AB=CD=13BC,AE=DF,AE∥DF.(1)求证:△AEC ≌△DFB ;(2)若S △AEC =6,求四边形BECF 的面积.【答案】(1)见解析(2)9【分析】(1)由AE ∥DF ,得∠A =∠D ,进一步证得AC =DB ,根据边角边求证△AEC ≌△DFB SAS ;(2)以AC 为底作EH 为高,则S △AEC =12EH ∙AC ,S △BCE =12EH ·BC ,由AB =CD =13BC ,求得S △BEC =34S △AEC=4.5;求证△BEC ≌△CFB SAS ,得S △BEC =S △CFB ,所以S 四边形BECF =2S △BEC =9.【详解】(1)证明:∵AE ∥DF ,∴∠A =∠D ,∵AB =CD ,∴AC =DB ,在△AEC 和△DFB 中,AE =DF∠A =∠DAC =DB∴△AEC ≌△DFB SAS ;(2)解:在△AEC 中,以AC 为底作EH 为高,∴S △AEC =12EH ∙AC ,S △BCE =12EH ∙BC ,∵AB =CD =13BC ,∴AC =43BC ,∵S △AEC =6,∴S △BEC =34S △AEC =4.5,∵△AEC ≌△DFB ,∴∠ACE =∠DBF ,EC =FB ,在△BEC 和△CFB 中,EC =FB∠BCE =∠CBF BC =CB,∴△BEC ≌△CFB SAS ,∴S △BEC =S △CFB ,∴S 四边形BECF =2S △BEC =9.【点睛】本题考查平行的性质,全等三角形的判定和性质,三角形面积计算;能够灵活运用全等三角形性质是解题的关键.【考点二用ASA 证明两三角形全等】1(2023春·广东惠州·八年级校考期中)如图,BC ∥EF ,点C ,点F 在AD 上,AF =DC ,∠A =∠D .求证:△ABC ≌△DEF.【答案】见解析【分析】首先根据平行线的性质可得∠ACB =∠DFE ,利用等式的性质可得AC =DF ,然后再利用ASA 判定△ABC ≌△DEF 即可.【详解】证明:∵BC ∥EF ,∴∠ACB =∠DFE ,∵AF =DC ,∴AF +CF =DC +CF ,即AC =DF ,在△ABC 和△DEF 中,∠A =∠DAC =DF ∠ACB =∠DFE,∴△ABC ≌△DEF ASA .【点睛】本题考查三角形全等的判定方法,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.【变式训练】1(2023·校联考一模)如图,点A 、D 、B 、E 在同一条直线上,若AD =BE ,∠A =∠EDF ,∠E =∠ABC .求证:AC =DF.【答案】见解析【分析】由AD =BE 知AB =ED ,结合∠A =∠EDF ,∠E =∠ABC ,依据“ASA ”可判定△ABC ≌△DEF ,依据两三角形全等对应边相等可得AC =DF .【详解】证明:∵AD =BE ,∴AD +BD =BE +BD ,即AB =ED ,在△ABC 和△DEF 中,∠ABC =∠EAB =ED ∠A =∠EDF,∴△ABC≌△DEF ASA,∴AC=DF.【点睛】本题主要考查全等三角形的判定与性质,掌握全等三角形的判定与性质是解题的关键.2(2023·浙江温州·温州市第八中学校考三模)如图,在△ABC和△ECD中,∠ABC=∠EDC=90°,点B为CE中点,BC=CD.(1)求证:△ABC≌△ECD.(2)若CD=2,求AC的长.【答案】(1)见解析(2)4,见解析【分析】(1)根据ASA判定即可;(2)根据△ABC≌△ECD ASA和点B为CE中点即可求出.【详解】(1)证明:∵∠ABC=∠EDC=90°,BC=CD,∠C=∠C,∴△ABC≌△ECD ASA(2)解:∵CD=2,△ABC≌△ECD ASA,∴BC=CD=2,AC=CE,∵点B为CE中点,∴BE=BC=CD=2,∴CE=4,∴AC=4;【点睛】本题考查全等三角形的判定和性质,掌握全等三角形的判定条件是解答本题的关键.【考点三用AAS证明两三角形全等】1(2023·广东汕头·广东省汕头市聿怀初级中学校考三模)如图,点E在△ABC边AC上,AE=BC,BC∥AD,∠CED=∠BAD.求证:△ABC≌△DEA【答案】证明见解析【分析】根据平行线的性质,得到∠DAC=∠C,再根据三角形外角的性质,得出∠D=∠BAC,即可利用“AAS”证明△ΑBC≌△DEA.【详解】证明:∵BC∥AD,∴∠DAC=∠C,∵∠CED=∠BAD,∠CED=∠D+∠DAC,∠BAD=∠DAC+∠BAC,∴∠D=∠BAC,在△ABC和△DEA中,∠BAC=∠D ∠C=∠DAC BC=AE,∴△ΑBC≌△DEA AAS.【点睛】本题考查了全等三角形的判定,平行线的性质,三角形外角的性质,熟练掌握全等三角形的判定定理是解题关键.【变式训练】1(2023·浙江温州·统考二模)如图,AB=BD,DE∥AB,∠C=∠E.(1)求证:△ABC≅△BDE.(2)当∠A=80°,∠ABE=120°时,求∠EDB的度数.【答案】(1)见解析(2)40°【分析】(1)根据平行线的性质,利用三角形全等的判定定理即可证明;(2)根据三角形全等的性质和平行线的性质即可求解【详解】(1)解:∵DE∥AB,∴∠BDE=∠ABC,又∵∠E=∠C,BD=AB,∴△ABC≅△BDE.(2)解:∵∠A=80°,△ABC≅△BDE,∴∠A=∠BDE=80°,∵∠ABE=120°,∴∠ABD=40°,∵DE∥AB,∴∠EDB=40°.【点睛】本题考查了平行线的性质,三角形全等的判定和性质,熟练掌握各知识点,利用好数形结合的思想是解本题的关键.2(2023秋·八年级课时练习)如图,已知点C是线段AB上一点,∠DCE=∠A=∠B,CD=CE.(1)求证:△ACD ≌△BEC ;(2)求证:AB =AD +BE .【答案】(1)见解析(2)见解析【分析】(1)由∠DCE =∠A 得∠D +∠ACD =∠ACD +∠BCE ,即∠D =∠BCE ,从而即可证得△ACD ≌△BEC ;(2)由△ACD ≌△BEC 可得AD =BC ,AC =BE ,即可得到AC +BC =AD +BE ,从而即可得证.【详解】(1)证明:∵∠DCE =∠A ,∴∠D +∠ACD =∠ACD +∠BCE ,∴∠D =∠BCE ,在△ACD 和△BEC 中,∠A =∠B∠D =∠BCE CD =EC,∴△ACD ≌△BEC AAS ;(2)解:∵△ACD ≌△BEC ,∴AD =BC ,AC =BE ,∴AC +BC =AD +BE ,∴AB =AD +BE .【点睛】本题主要考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键.【考点四用SSS 证明两三角形全等】1(2023·云南玉溪·统考三模)如图,点B ,E ,C ,F 在一条直线上,AB =DF ,AC =DE ,BE =CF ,求证:△ABC ≌△DFC.【答案】见解析【分析】根据题意,运用“边边边”的方法证明三角形全等.【详解】证明:∵BE =CF ,∴BE +CE =CF +CE ,即BC =EF ,在△ABC 和△DFE 中,AB =DFAC =DEBC =FE∴△ABC ≌△DFE (SSS ).【点睛】本题主要考查三角形全等的判定,掌握全等三角形的判定方法解题的关键.【变式训练】1(2023·云南·统考中考真题)如图,C 是BD 的中点,AB =ED ,AC =EC .求证:△ABC ≌△EDC.【答案】见解析【分析】根据C 是BD 的中点,得到BC =CD ,再利用SSS 证明两个三角形全等.【详解】证明:∵C 是BD 的中点,∴BC =CD ,在△ABC 和△EDC 中,BC =CDAB =ED AC =EC,∴△ABC ≌△EDC SSS 【点睛】本题考查了线段中点,三角形全等的判定,其中对三角形判定条件的确定是解决本题的关键.2(2023春·全国·七年级专题练习)如图,已知∠E =∠F =90°,点B ,C 分别在AE ,AF 上,AB =AC ,BD =CD.(1)求证:△ABD ≌△ACD ;(2)求证:DE =DF .【答案】(1)见解析(2)见解析【分析】(1)直接根据SSS 证明即可.(2)根据(1)得∠EAD =∠FAD ,然后证明△AED ≌△AFD 即可.【详解】(1)解:证明:在△ABD 和△ACD 中,AB =ACAD =AD BD =CD∴△ABD ≌△ACD (SSS ).(2)解:由(1)知△ABD ≌△ACD (SSS ),∴∠EAD =∠FAD ,在△AED和△AFD中,∠E=∠F∠EAD=∠FAD AD=AD∴△AED≌△AFD(AAS),∴DE=DF.【点睛】本题考查了全等三角形的性质与判定,熟记全等三角形的性质与判定是解题关键.【考点五添一个条件使两三角形全等】1(2023春·宁夏银川·七年级校考期末)如图,在△ABC和△FED中,AD=FC,∠A=∠F,要使△ABC≌△FED,需添加的一个条件是.【答案】AB=EF(∠B=∠E或∠ACB=∠FDE答案不唯一)【分析】要使△ABC≌△FED,现有一边一角分别对应相等,还少一个条件,可结合图形选择利用求解即可.【详解】解:∵AD=FC,∴AC=FD又∵∠A=∠F,∴添加AB=EF,利用SAS可以证明△ABC≌△FED;添加∠B=∠E,利用AAS可以证明△ABC≌△FED;添加∠ACB=∠FDE,利用ASA可以证明△ABC≌△FED故答案为:AB=EF(∠B=∠E或∠ACB=∠FDE(.【点睛】本题考查三角形全等的判定方法;判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.添加时注意:AAA、SSA不能判定两个三角形全等,不能添加,根据已知结合图形及判定方法选择条件是正确解答本题的关键.【变式训练】1(2023·北京大兴·统考二模)如图,点B,E,C,F在一条直线上,AC∥DF,BE=CF,只需添加一个条件即可证明△ABC≌△DEF,这个条件可以是(写出一个即可).【答案】AC=DF或∠A=∠D或∠ABC=∠DEF或AB∥DE(答案不唯一).【分析】根据SAS,AAS或ASA添加条件即可求解.【详解】解:∵AC∥DF,∴∠ACB=∠DFE,∵BE=CF,∴BE+EC=CF+EC,即BC=EF,则有边角AS两个条件,要添加一个条件分三种情况,(1)根据“SAS”,则可添加:AC=DF,(2)根据“ASA”,则可添加:∠ABC=∠DEF或AB∥DE,(3)根据“AAS”,则可添加:∠A=∠D,故答案为:AC=DF或∠ABC=∠DEF或AB∥DE或∠A=∠D(答案不唯一).【点睛】本题考查了全等三角形的判定,解此题的关键是熟练掌握全等三角形的几种判断方法.2(2023春·山东青岛·七年级统考期末)如图,点E,F在BC上,BE=CF,∠AFB=∠DEC,请你添加一个条件(不添加字母和辅助线),使得△ABF≌△DCE,你添加的条件是.【答案】AF=DE或∠ABF=∠DCE或∠A=∠D【分析】本题要判定△ABF≌△DCE,已知∠AFB=∠DEC,由BE=CF可得BF=CE,那么只需添加一个条件即可.添边可以是AF=DE或添角可以是∠ABF=∠DCE或∠A=∠D.【详解】解:所添加条件为:AF=DE或∠ABF=∠DCE或∠A=∠D,∵BE=CF,∴BE+EF=CF+EF,即BF=CE,添加:AF=DE,在△ABF和△DCE中,AF=DE∠AFB=∠DECBF=CE,∴△ABF≌△DCE SAS;添加:∠ABF=∠DCE,在△ABF和△DCE中,∠ABF=∠DCEBF=CE∠AFB=∠DEC,∴△ABF≌△DCE ASA添加:∠A=∠D,在△ABF和△DCE中,∠A=∠D∠AFB=∠DECBF=CE,∴△ABF≌△DCE AAS.故答案为:AF=DE或∠ABF=∠DCE或∠A=∠D.【点睛】本题考查三角形全等的判定方法,解题的关键是掌握判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.3(2023秋·八年级课前预习)如图,AB=AC,D,E分别是AB,AC上的点,要使△ABE≌△ACD,则还需添加的条件是.(只需填写一个合适的条件即可,图中不能再添加其他点或线)【答案】AE=AD或∠B=∠C或∠AEB=∠ADC(答案不唯一)【分析】根据全等三角形的判定方法即可求解.【详解】解:①∵AB=AC,∠A=∠A,AE=AD,∴△ABE≌△ACD(SAS),∴添加的条件为AE=AD;②∵∠B=∠C,AB=AC,∠A=∠A,∴△ABE≌△ACD(ASA),∴添加的条件为∠B=∠C;③∵∠A=∠A,∠AEB=∠ADC,AB=AC,∴△ABE≌△ACD(ASA),∴添加的条件为∠AEB=∠ADC;综上所述,添加的条件为AE=AD或∠B=∠C或∠AEB=∠ADC,故答案为:AE=AD或∠B=∠C或∠AEB=∠ADC(答案不唯一).【点睛】本题主要考查全等三角形的判定,掌握以上知识是解题的关键.【过关检测】一、单选题1(2023春·四川达州·七年级四川省大竹中学校考期末)如图,已知BE=DF,AF∥CE,不能使△ABF≌△CDE的是()A.BF=DEB.AF=CEC.AB∥CDD.∠A=∠C【答案】A【分析】根据BE =DF ,可得BF =DE ,根据AF ∥CE ,可得∠AFE =∠CEF ,由等角的补角相等可得∠AFB =∠CED ,然后根据全等三角形的判定定理逐一判断即可.【详解】解:∵BE =DF ,∴BF =DE ,∵AF ∥CE ,∴∠AFE =∠CEF ,∴∠AFB =∠CED .A 、添加BF =DE 时,不能判定△ABF ≌△CDE ,故选项符合题意;B 、添加AF =CE ,根据SAS ,能判定△ABF ≌△CDE ,故选项不符合题意;C 、由AB ∥CD 可得∠B =∠D ,所以添加AB ∥CD ,根据ASA ,能判定△ABF ≌△CDE ,故选项不符合题意;D 、添加∠A =∠C ,根据AAS ,能判定△ABF ≌△CDE ,故选项不符合题意;故选:A .【点睛】本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS 、ASA 、SAS 、SSS ,直角三角形可用HL 定理,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.2(2023秋·河南漯河·八年级校考期末)如图,∠A =∠B ,AE =BE ,点D 在AC 边上,∠1=∠2,AE 和BD 相交于点O ,若∠1=42°,则∠BDE 的度数为()A.71°B.69°C.67°D.65°【答案】B【分析】证明△BED ≌△AEC ,得到DE =CE ,∠C =∠BDE 等边对等角,求出∠C 的度数,即可.【详解】解:∵∠A =∠B ,∠BOE =∠AOD ,∴∠2=∠3,∵∠1=∠2,∴∠1=∠3,∴∠BED =∠AEC ,又AE =BE ,∴△BED ≌△AEC ,∴DE =CE ,∠C =∠BDE ,∴∠CDE =∠C =12180°-∠1 =69°,∴∠BDE =69°.【点睛】本题考查全等三角形的判定和性质,等腰三角形的判定和性质.解题的关键是证明三角形全等.3(2023春·辽宁丹东·八年级校考期中)如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=42°,则∠P的度数为()A.42°B.74°C.84°D.96°【答案】D【分析】根据等腰三角形的性质得出两个底角相等,根据三角形全等的判定定理得出∠AMK=∠BKN,根据三角形的外角性质得出∠A的度数,即可得答案.【详解】解:∵PA=PB,∴∠A=∠B,∵AM=BK,BN=AK,∴△AMK≌△BKN,∴∠AMK=∠BKN,∵∠MKB=∠A+∠AMK=∠MKN+∠BKN,∴∠A=∠MKN=42°,∴∠P=180°-2×42°=96°.故选:D.【点睛】本题考查等腰三角形的性质、全等三角形的判定与性质、三角形内角和定理及三角形外角性质,熟练掌握相关判定定理及性质是解题关键.二、填空题4(2023春·山东青岛·七年级统考期末)如图,∠l=∠2,现要添加一个条件使△ABD≌△ACD,可以添加.(只添一个即可).【答案】CD=BD(答案不唯一)【分析】根据三角形全等的判定方法进行解答即可.【详解】解:∵∠l=∠2,∴180°-∠1=180°-∠2,即∠ADC =∠ADB ,∵AD =AD ,∴添加条件CD =BD ,根据SAS 证明△ABD ≌△ACD ;添加条件∠C =∠B ,根据AAS 证明△ABD ≌△ACD ;添加条件∠CAD =∠BAD ,根据ASA 证明△ABD ≌△ACD .故答案为:CD =BD (答案不唯一).【点睛】本题主要考查了三角形全等的判定,解题的关键是熟练掌握三角形全等的判定方法,SAS ,AAS ,ASA ,HL ,SSS .5(2023秋·湖南娄底·八年级统考期末)如图,∠ACB =90°,AC =BC ,BE ⊥CE 于E ,AD ⊥CE 于D .下面四个结论:①∠ABE =∠BAD ;②△CBE ≌△ACD ;③AB =CE ;④AD -BE =DE ,其中正确的有.【答案】①②④【分析】由BE ⊥CE 于E ,AD ⊥CE 于D ,得BE ∥AD ,则∠ABE =∠BAD ,可判断①正确;根据“同角的余角相等”推导出∠BCE =∠CAD ,即可证明△CBE ≌△ACD ,可判断②正确;由垂线段最短可证明AB >BC ,BC >CE ,则AB >CE ,可判断③错误;由CE =AD ,BE =CD ,且CE -CD =DE ,得AD -BE =DE ,可判断④正确,于是得到问题的答案.【详解】∵BE ⊥CE ,AD ⊥CE ,∴AD ∥BE ,∴∠ABE =∠BAD ,故①正确;∵∠E =∠ADC =∠ACB =90°,∴∠BCE =∠CAD =90°-∠ACD ,在△CBE 和△ACD 中,∠E =∠ADC∠BCE =∠CAD BC =CA,∴△CBE ≌△ACD AAS ,故②正确;∵BC ⊥AC ,CE ⊥BE ,∴AB >BC ,BC >CE ,∴AB >CE ,故③错误;∵△CBE ≌△ACD ,∴CE =AD ,BE =CD ,∵CE -CD =DE ,∴AD -BE =DE ,故④正确;故答案为:①②④.【点睛】此题考查了同角的余角相等、垂线段最短、平行线的判定与性质、全等三角形的判定与性质等知识,证明∠BCE =∠CAD 及△CBE ≌△ACD 是解题的关键.6(2023秋·江苏淮安·八年级淮安市浦东实验中学校考开学考试)如图,已知正方形ABCD中,边长为10cm,点E在AB边上,BE=6cm.如果点P在线段BC上以4cm/s的速度由B点向C点运动.同时,点Q在线段CD上以acm/s的速度由C点向D点运动.当a=时,△EBP和△PCQ全等.【答案】4或24 5【分析】分两种情况:当△EBP≌△PCQ时和当△EBP≌QCP时,根据边对应相等,分别求出a的值即可.【详解】解:当△EBP≌△PCQ时,此时BE=CP,BP=CQ,则有BP=4t=at,CP=BC-BP=10-4t=6,此时t=1,a=4,当△EBP≌QCP时,此时BE=CQ,BP=CP,则有CQ=at=6,CP=BC-BP=10-4t=4t,此时t=54,a=245,综上所述,a的值为4或24 5,故答案为:4或24 5.【点睛】本题主要考查了全等三角形的性质,熟练掌握全等三角形的性质,采用分类讨论的思想是解题的关键.三、解答题7(2023春·上海嘉定·七年级校考期末)如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD=BE.(1)求证:△ABD≌△ECB;(2)如果∠BDC=75°,求∠ADB的度数.【答案】(1)见解析(2)∠ADB=30°【分析】(1)由平行线性质可得∠ADB=∠CBE,再由ASA可证△ABD≌△ECB;(2)由全等三角形的性质可得BD=BC,由等腰三角形的性质可求出∠DBC=30°,再由两直线平行内错角相等即可求解.【详解】(1)证明∵AD∥BC,∴∠ADB=∠CBE,在△ABD和△ECB中,∠A=∠BECAD=BE∠ADB=∠CBE,∴△ABD≌△ECB ASA;(2)∵△ABD≌△ECB,∴BD=BC,∴∠BDC=∠BCD=75°,∴∠DBC=180°-∠BDC-∠BCD=30°,∵AD∥BC,∴∠ADB=∠DBC=30°.【点睛】本题考查了全等三角形的判定和性质,平行线的性质,三角形内角和,熟练掌握两直线平行内错角相等是解答本题的关键.8(2023秋·江苏·八年级校考周测)如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.(1)试说明AE=CD;(2)若AC=12cm,求BD的长.【答案】(1)见解析(2)BD=6cm【分析】(1)由题意可得∠D+∠DCB=90°,∠DCB+∠AEC=90°,即∠D=∠AEC,根据“AAS”可证△DBC≌△ECA,可得;(2)先求出,然后根据全等三角形的性质即可求解.【详解】(1)∵,,∴,,∴,∵,,∴,∴;(2)∵,,∴.∵是边上的中线,∴.∵,∴.【点睛】本题考查了全等三角形的判定与性质,熟练运用全等三角形的判定是本题的关键.9(2023秋·湖南长沙·八年级长沙市开福区青竹湖湘一外国语学校校考开学考试)如图所示,在中,于D,于E,与交于点F,且.(1)求证:;(2)已知,求的长.【答案】(1)见解析(2)【分析】(1)根据垂直的定义得出,再根据同角的余角相等得出,然后由证明即可;(2)由全等三角形的性质得出,再根据线段的和差即可解决问题.【详解】(1)证明:∵,,∴,∴,∴,在和中∴,(2)解:∵,∴,∵,∴,∴;【点睛】此题考查了全等三角形的判定与性质的应用,证明三角形全等是解决问题的关键,属于中考常考题型.10(2023春·四川成都·七年级成都实外校考期末)已知:如图,点是等边三角形内一点,且,外一点满足,平分.(1)求证:;(2)求的度数.(3)若,试判断与的位置关系,并说明理由.【答案】(1)见解析(2)(3),理由见解析【分析】(1)由三角形是等边三角形和可得,由角平分线的性质可得,由“”即可证明;(2)由三角形是等边三角形和可得,,由“”证明,从而得到,再由,;(3)由全等三角形的性质可得,由等腰三角形的性质可得,令交于点,通过计算得出,最后由三角形内角和定理可得出,从而得到答案.【详解】(1)证明:三角形是等边三角形,,,,平分,,在和中,,;(2)解:三角形是等边三角形,,,在和中,,,,,,由(1)得,,;(3)解:,理由如下:由(1)得,,,由(2)得,,,,,,如图,令交于点,,则,,,.【点睛】本题主要考查了等边三角形的性质、三角形全等的判定与性质、等腰三角形的性质、三角形内角和定理、角平分线的性质,熟练掌握等边三角形的性质、三角形全等的判定与性质、等腰三角形的性质、三角形内角和定理、角平分线的性质,是解题的关键.11(2023春·四川达州·七年级校考期末)如图,在中,,,点在线段上运动(不与、重合),连接,作,交线段于.(1)当时,,;点从向的运动过程中,逐渐变(填“大”或“小”);(2)当等于多少时,,请说明理由.(3)在点的运动过程中,与的长度可能相等吗?若可以,请直接写出的度数,请说明理由.【答案】(1);;小;(2),理由见解析;(3)可能相等,,理由见解析【分析】(1)现根据邻补角的定义,得到,进而得到,然后利用三角形内角和定理,得到,,又因为点从向的运动过程中,逐渐增大,所以逐渐变小;(2)利用三角形内角和定理,得到,根据平角的性质,得到,进而得到,再根据“”证明,即可得到答案;(3)根据等边对等角的性质,得到,再利用三角形内角和定理,得出,由三角形外角的性质,得到,进而得到,最后利用邻补角,即可求出的度数.【详解】(1)解:,,,,,,,,点从向的运动过程中,逐渐增大,逐渐变小,故答案为:;;小;(2)解:当时,,理由如下:,,又,,,,当时,,,在和中,,,即当时,,;(3)解:在点的运动过程中,与的长度可能相等,理由如下:,,,,,,,,.【点睛】本题考查了邻补角,三角形内角和定理,全等三角形的判定和性质,等腰三角形的判定和性质,三角形外角的性质,灵活运用相关知识解决问题是解题关键.12(2023春·广东梅州·八年级校考开学考试)在四边形中.(1)如图1,,,,分别是,上的点,且,探究图中,,之间的数量关系.小林同学探究此问题的方法是:延长到点,使.连接,先对比与结论是;(2)如图2,在四边形中,,,、分别是,上的点,且,则上述结论是否仍然成立,请说明理由.(3)如图3,在四边形中,,,若点在的延长线上,点在的延长线上,若,请写出与的数量关系,并给出证明过程.【答案】(1),理由见解析(2)成立,理由见解析(3),证明见解析【分析】(1)延长到点,使,连接,可判定,进而得出,,再判定,可得结论;(2)延长到点,使,连接,先判定,进而得出,,再判定,可得结论;(3)在延长线上取一点,使得,连接,先判定,再判定,得出,最后根据,推导得到【详解】(1)解:结论:.理由:如图1,延长到点,使,连接,在和中,,,,,,,,在和中,,,.故答案为:;(2)解:仍成立,理由:如图2,延长到点,使,连接,,,,在和中,,,,,,,,在和中,,,;(3)解:结论:.理由:如图3,在延长线上取一点,使得,连接,,,,在和中,,,,,在和中,,,,,,,即,.【点睛】本题属于三角形综合题,主要考查了全等三角形的判定以及全等三角形的性质的综合应用,解题的关键是作辅助线构造全等三角形,根据全等三角形的对应角相等进行推导变形.解题时注意:同角的补角相等.。
北师大版七年级下全等三角形压轴题分类解析

七年级下三角形综合题归类一、双等边三角形模型1.(1)如图7,点O 是线段AD 的中点,分别以AO 和DO 为边在线段AD 的同侧作等边三角形OAB和等边三角形OCD ,连结AC 和BD ,相交于点E ,连结BC .求∠AEB 的大小;(2)如图8,ΔOAB 固定不动,保持ΔOCD 的形状和大小不变,将ΔOCD 绕着点O 旋转(ΔOAB 和ΔOCD 不能重叠),求∠AEB 的大小.2.已知:AN 、BM相交于潭·中考题)ADE△中,AB 点B A D ,,分别为BE CD ,(1(24.(1(2(3 为1S ,△ADG 的面积为2S ,判断1S 与2S 的大小关系,并给予证明.5.已知:如图,ABC △是等边三角形,过AB 边上的点D 作DG BC ∥,交AC 于点G ,在GD 的延长线上取点E ,使DE DB =,连接AE CD ,. (1)求证:AGE DAC △≌△; (2)过点E 作EF DC ∥,交BC 于点F ,请你连接AF ,并判断AEF △是怎样的三角形,试证明你的结论.二、垂直模型(该模型在基础题和综合题中均为重点考察内容) 考点1:利用垂直证明角相等C FGEDBAH 图① 图②1. 如图,△ABC 中,∠ACB =90°,AC =BC ,AE 是BC 边上的中线,过C 作CF ⊥AE ,垂足为F ,过B 作BD ⊥BC 交CF 的延长线于D .求证:(1)AE =CD ; (2)若AC =12cm ,求BD 的长. 考点2:利用角相等证明垂直1. 已知BE ,CF 是△ABC 的高,且BP=AC ,CQ=AB ,试确定AP 与AQ 的数量关系和位置关系2.如图,在等腰R t△ABC 中,∠ACB =90°,D 为BC 的中点,DE ⊥AB ,垂足为E ,过点B 作BF ∥AC 交DE 的延长线于点F ,连接CF . (1)(2)(3)连接是等腰直角三角形,90°,AD 是BC ,F ,求证:∠ADC(提示:) 3.如图1(1(2和GC .4.如图1在直线l (1)(2),AP BQ .(3线于点Q,连结,AP BQ ,你认为(2)中所猜想的BQ 与AP 的数量关系和位置关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.三、等腰三角形(中考重难点之一)考点1:等腰三角形性质的应用 1. 如图,ABC ∆中,AB AC =,90BAC ∠=︒,D 是BC 中点,ED FD ⊥,ED 与AB 交于E ,FD 与AC l (1) A B (F) (E)C PAB EC F P Q (2) l AB EC F P l交于F .求证:BE AF =,AE CF =.2. 两个全等的含30,60角的三角板ADE 和三角板ABC ,如图所示放置,,,E A C 三点在一条直线上,连结BD ,取BD 的中点M ,连结,ME MC .试判断EMC ∆的形状,并说明理由. 压轴题拓展:(三线合一性质的应用)已知Rt ABC ∆中,AC BC =,90C ∠=︒,D 为AB 边的中点,90EDF ∠=︒,EDF ∠绕D 点旋转,它的两边分别交AC 、CB (或它们的延长线)于E 、F . 当EDF ∠绕D 点旋转到DE AC ⊥于E 时(如图1),易证12DEF CEF ABC S S S ∆∆∆+=.当E D F ∠绕D 点旋转到DE 和AC 不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,DEF S ∆,CEF S ∆,ABC S ∆又有怎样的数量关系?请写出你的猜想,不需证明.3. CD 相交于点BC 的大小考点21. 如图经过点D 的平分线⑴①②③⑵2.在Rt △(1F 作FH ⊥FC ①求证:DG=DC②判断FH 与FC 的数量关系并加以证明.(2)若E 为线段DC 的延长线上任意一点,点F 在射线DG 上,(1)中的其他条件不变,借助图2画出图形。
全等三角形压轴题精选

全等三角形压轴题精选全等三角形是初中数学中的重要概念之一,下面我将从多个角度给出一些精选的全等三角形压轴题的解答。
1. 题目,已知△ABC和△DEF,且∠A = ∠D,∠B = ∠E,AB= DE,证明△ABC ≌ △DEF。
解答,根据已知条件,可以得出两个对应的角相等,以及一条边相等。
根据全等三角形的判定条件之一SAS(边角边),可以得出△ABC ≌ △DEF。
2. 题目,已知△ABC和△DEF,且AB = DE,BC = EF,∠B =∠E,证明△ABC ≌ △DEF。
解答,根据已知条件,可以得出两个对应的边相等,以及一个对应的角相等。
根据全等三角形的判定条件之一SAS(边角边),可以得出△ABC ≌ △DEF。
3. 题目,已知△ABC和△DEF,且AB = DE,BC = EF,AC = DF,证明△ABC ≌ △DEF。
解答,根据已知条件,可以得出三个边全部相等。
根据全等三角形的判定条件之一SSS(边边边),可以得出△ABC ≌ △DEF。
4. 题目,已知△ABC和△DEF,且∠A = ∠D,∠B = ∠E,AC= DF,证明△ABC ≌ △DEF。
解答,根据已知条件,可以得出两个对应的角相等,以及一条边相等。
根据全等三角形的判定条件之一SAS(边角边),可以得出△ABC ≌ △DEF。
这些题目涵盖了全等三角形的常见情况,通过给出已知条件并运用全等三角形的判定条件,可以得出两个三角形全等的结论。
需要注意的是,在证明过程中要严谨正确地使用标点符号,以确保解答的准确性。
希望以上解答能够满足你的需求,如果你还有其他问题,请继续提问。
人教版八年级上册《全等三角形》解答题压轴题能力提升专练(含详细解析)
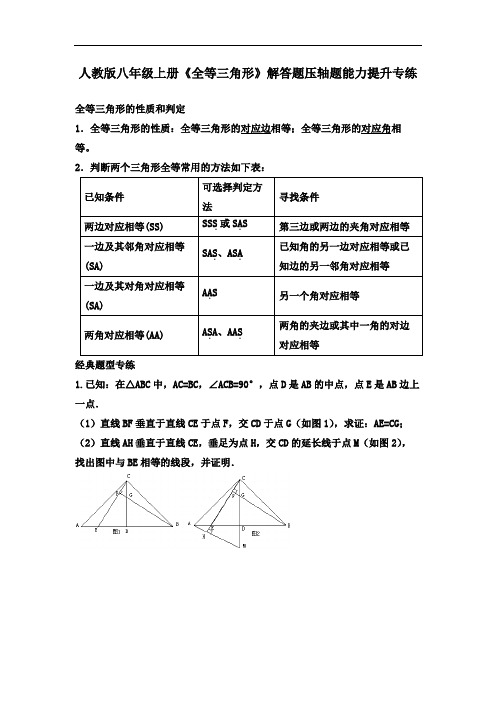
人教版八年级上册《全等三角形》解答题压轴题能力提升专练全等三角形的性质和判定1.全等三角形的性质:全等三角形的对应边相等;全等三角形的对应角相等。
2.判断两个三角形全等常用的方法如下表:经典题型专练1.已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.(1)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.2.如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.3.如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交CD 于点F,BD分别交CE、AE于点G、H.试猜测线段AE和BD的数量和位置关系,并说明理由.4.课外兴趣小组活动时,许老师出示了如下问题:如图1,己知四边形ABCD 中,AC平分∠DAB,∠DAB=60°,∠B与∠D互补,求证:AB+AD=√3AC.小敏反复探索,不得其解.她想,若将四边形ABCD特殊化,看如何解决该问题.(1)特殊情况入手添加条件:“∠B=∠D”,如图2,可证AB+AD=√3AC;(请你完成此证明)(2)解决原来问题受到(1)的启发,在原问题中,添加辅助线:如图3,过C点分别作AB、AD的垂线,垂足分别为E、F.(请你补全证明)5.如图,△ABC中,AD⊥BC于D,点E在AD上,△ADC和△BDE是等腰三角形,EC=5cm,求AB的长.6. CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:①如图1,若∠BCA=90°,∠α=90°,则BE CF;EF |BE﹣AF|(填“>”,“<”或“=”);②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件,使①中的两个结论仍然成立,并证明两个结论成立.(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF 三条线段数量关系的合理猜想(不要求证明).7.在△ABC中,∠ACB=2∠B,如图①,当∠C=90°,AD为∠ABC的角平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD.(1)如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?不需要证明,请直接写出你的猜想:(2)如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.8. 如图,在锐角△ABC中,AB=4√2,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,求BM+MN的最小值.9. 如图,在△ABC中,AB≠AC,∠BAC的外角平分线交直线BC于D,过D作DE⊥AB,DF⊥AC分别交直线AB,AC于E,F,连接EF.(1)求证:EF⊥AD;(2)若DE∥AC,且DE=1,求AD的长.10.如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:(1)FC=AD;(2)AB=BC+AD.11. 如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.(1)求证:DE平分∠BDC;(2)若点M在DE上,且DC=DM,求证:ME=BD.12. 图1、图2中,点C为线段AB上一点,△ACM与△CBN都是等边三角形.(1)如图1,线段AN与线段BM是否相等?证明你的结论;(2)如图2,AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.人教版八年级上册《全等三角形》解答题压轴题能力提升专练(答案版)全等三角形的性质和判定1.全等三角形的性质:全等三角形的对应边相等;全等三角形的对应角相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形全等综合题归类一、 双等边三角形模型 1. (1)如图1,点0是线段AD 的中点,分别以 AO 和 DO 为边在线段AD 的同侧作等边三角形 OAB 和等边三角形 OCD 连结AC和BD,相交于点 E ,连结BC 求/ AEB 的大小; (2)如图2, △ OAB 固定不动, 求/ AEB 的大小.G 连接AF 和BE. 如图a , △ ABC 和厶CEF 是两个大小不等的等边三角形,且有一个公共顶点 ⑴线段AF 和BE 有怎样的大小关系?请证明你的结论; (2) 将图a 中的△ CEF 绕点C 旋转一定的角度,得到图 b ,⑴ 中的结论还成立吗?作出判断并说明理由; (3) 若将图a 中的△ ABC 绕点C 旋转一定的角度,请你画出一个变换后的图形 c(草图即可),⑴ 中的结论还成 立吗?作出判断不必说明理由 2、 C C3.如图 ( (2)^ 理由. 1,若^ ABC 和^ ADE 为等边三角形,M ,N 分别为EB ,CD的中点ADE 绕A 点旋转到图2的位置时,ADE 绕A 点旋转到图3的位置时,△ AMN 是否还是等边三角形?若是,CD =BE 是否成立?若成立,请证明;若不成立,请说明理由;若不是,请说明 请给出证明,4、已知,如图①所示,在△ ABC 和^ ADE 中,AB=AC , AD =AE , N BAC =NDAE,且点B, A, D 在一条直线上,连接BE, CD, M , N分别为BE, CD的中点.(1)求证:① BE =CD :② AM =AN ;(2)在图①的基础上,将△ ADE绕点A按顺时针方向旋转180,其他条件不变,得到图②所示的图形.请直接(1)中的两个结论是否仍然成立写出DA5.如图,四边形ABCD和四边形AEFG匀为正方形,连接BG与DE相交于点H.(1)证明:△ ABG = △ ADE ;(2)试猜想N BHD的度数,并说明理由;(3)将图中正方形ABCD绕点A逆时针旋转(0 °v N BAE < 180 °),设△ ABE的面积为S , △ ADG的面积为S2,判断S与S2的大小关系,并给予证明. GCBF E6.已知:如图,△ ABC是等边三角形,过AB边上的点D作DG // BC ,交AC于点G,在GD的延长线上取点E ,使DE = DB,连接AE,CD .(1)求证:△ AGE =△ DAC;(2)过点E作EF // DC,交BC于点F,请你连接AF ,并判断△ AEF是怎样的三角形,试证明你的结论.考点2 :利用角相等证明垂直垂直模型(该模型在基础题和综合题中均为重点考察内容) 考点1 :利用垂直证明角相等 1、如图,△ ABC 中,/ ACB= 90°, AC = BC AE 是BC 边上的中线,过 C 作CF 丄AE,垂足为 F ,过B 作BD 丄BC 交 CF 的延长线于D. 求证:(1) AE = CD (2)若 AC= 12 cm ,求 BD 的长.2、如图(1), 已知△ ABC 中,/ BAC=900, AB=AC, AE 是过A 的一条直线 CE 丄AE 于E 。
(1) ⑵ ⑶ ,且B C 在 A E 的异侧,BD 丄AE 于D,3.试说明:BD=DE+CE. 若直线AE 绕A 点旋转到图 若直线AE 绕A 点旋转到图(2)位置时(BD<CE),其余条件不变,问 BD 与 DE CE 的关系如何?说明理由。
直线CD 经过N BCA 的顶点 (1)若直线CD 经过N BCA 的内部,且E 、F 在射线CD 上,请解决下面两个问题: 若 N BCA =90",则 E F 若 BCA <180 \若使①中的结论仍然成立,则Na 与N BCA 应满足的关系 C , CA=CB E 、F 分别是直线CD 上两点,且N BEC =N CFA =Na ①如图1,BE-AF (填“ >”,“ C ” 或“=”号); ②如图2, (2)如图 予证明. 3,若直线CD 经过N BCA 的外部,Z* = NBCA ,请探究EF 、 BE AF 三条线段的数量关系,并给 图1图2 图31、如图,在等腰Rt △ ABC中,/ ACB=90 , D为BC的中点,DE I AB,垂足为E,过点B作BF// AC交DE的延长线于点F,连接CF. (1)求证:CD=BF (2)求证:ADI CF; (3)连接AF,试判断△ ACF的形状.2、如图9所示,△ ABC是等腰直角三角形, / ACB= 90°, AD是BC边上的中线,过交AD于点F,求证:/ ADC=/ BDE3.如图1,已知正方形ABCD的边CD在正方形DEFG的边DE上,连接AE ,(1)试猜想AE与GC有怎样的位置关系,并证明你的结论;(2)将正方形DEFG绕点D按顺时针方向旋转,使E点落在BC边上,如图2,中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.4.如图1,也ABC的边BC在直线I上,AC丄BC,且A C=BC,A E FP的边FP也在直线重合,且EF=FPC作AD的垂线,交AB于点E ,GC连接AE和GC.你认为(1)上,边EF与边ACE 图9(SGIAB 与AP 所满足的数量关系和位置关系;EP 交AC 于点Q,连接AP ,B Q.猜想并写出BQ 与AP 所满EP 的延长线交AC 的延长线于点Q,连结AP ,BQ ,你认为(2)中所猜想的BQ与AP 的数量关系和位置关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由等腰三角形(中考重难点之一)AC =BC , Z C =90°, D 为AB 边的中点, ^EDF =90°,也EDF 绕D 点旋转,它的两边I考点1 :等腰三角形性质的应用 如图,MBC 中,AB =AC , NBAC证:BE =AF , AE =CF . 1. =90 °, D 是BC 中点,ED 丄FD ,ED 与AB 交于E ,FD 与AC 交于2. 两个全等的含30取BD 的中点M ,,60'角的三角板 连结ME,MC .试判断AEMC 的形状,并说明理由.ADE 和三角板ABC ,如图所示放置,E, AC 三点在一条直线上, 连结BD ,CA(1) 在图1中,请你通过观察、测量,猜想并写出 (2) 将AEFP 沿直线I 向左平移到图2的位置时, 足的数量关系和位置关系,请证明你的猜想; (3) 将iEFP 沿直线I 向左平移到图3的位置时, 已知 Rt AABC 中,分别交AC 、CB (或它们的延长线)于 E 、F .当N EDF 绕D 点旋转到DE 丄AC 于E 时(如图1),易证S g EF +S g EF=2$誉BC -当ZEDF 绕D 点旋转到DE 和AC 不垂直时,在图2和图3这两种情况下,上述结论是否成立 证明;若不成立,1DH 与BE 相交于点 G 。
(1) BF=AC (2) CE=—BF (3)CE 与BC 的大小关系如何。
?若成立,请给予S 应EF , S 虑EF , S ^BC 又有怎样的数量关系?请写出你的猜想,并证明.4、已知:如图,△ ABC 中,/ ABC=45°, CD 丄AB 于 D , BE 平分/ ABC, 且BE 丄AC 于E ,与CD 相交于点 F ,H 是BC 边的中点,连结 考点2 :等腰直角三角形(45度的联想)1、如图1,四边形ABCD 是正方形,M 是AB 延长线上一点。
直角三角尺的一条直角边经过点 在AB 边上滑动(点 E 不与点A , B 重合),另一条直角边与/ CBM 的平分线BF 相交于点 如图14—1,当点E 在AB 边的中点位置时: 通过测量DE , EF 的长度,猜想DE 与EF 满足的数量关系是 — 连接点E 与AD 边的中点N ,猜想NE 与BF 满足的数量关系是 _ 请证明你的上述两猜想.如图14—2 ,当点E 在AB 边上的任意位置时,请你在 AD 边上找 到一点N,使得NE=BF,进而猜想此时 DE 与EF 有怎样的数量关系并 D 证明D ,且直角顶点 EF. ⑴① ② ③ ⑵2.在 Rt A ABC 中,AC = BC , / ACB = 90 ° D 是 AC 的中点,DG 丄 AC 交 AB 于点 G. (1)如图1, E 为线段DC 上任意一点,点 F 在线段DG 上,且DE=DR 连结EF 与CE 过点F 作FH 丄FC,交直线图1图2F1ON胚A SB @14-123、已知:△ ABC 为等边三角形,M 是BC 延长线上一点,直角三角尺的一条直角边经过点 在BC 上滑动,(点E 不与点B 、C 重合),斜边与/ ACM 的平分线CF 交于点F (1) 如图(1)当点E 在BC 边得中点位置时①猜想AE 与EF 满足的数量关系是 . ①连结点E 与AB 边得中点N,猜想BE 和CF 满足的数量关系是O 请证明你的上述猜想;(2) 如图(2)当点E 在BC 边得任意位置时,AE 和 怎样的数量关系,并说明你的理由?四、角平分线问题1.如图:E 在线段 CD 上,EA 、EB 分别平分/ DAB 和/ CBA, / AEB=90,设AD = x,2 2BC = y ,且 x,y 满足 x +y -6x-8厂25 = 0(1)求AD 和BC 的长;(2)你认为AD 和BC 还有什么关系?并验证你的结论; (3)你能求出AB 的长度吗?若能,请写出推理过程;若不能,请说明理由 .AB 于点H . ① 求证:DG=DC ② 判断FH 与FC 的数量关系并加以证明.(2)若E 为线段DC 的延长线上任意一点,点 F 在射线DG 上,(1)中的其他条件不变,借助图 2画出图形。
在你 所画图形中找出一对全等三角形,并判断你在 (1)中得出的结论是否发生改变.(本小题直接写出结论,不必证明)A ,600角的顶点 EEF 有M图(1)BE C 图(2)2.如图①,OP是/ MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形。
请你参考这个作全等三角形的方法,解答下列问题:(1) 如图②,在△ ABC 中,/ ACB 是直角,/ B=60 点F 。
请你判断并写出 FE 与FD 之间的数量关系; (2) 如图③,在△ ABC 中,如果/ ACB 不是直角,而 立?若成立,请证明;若不成立,请说明理由。
4.如图,△ ABC 中,AD 平分/ BAC, DG 丄BC 且平分BC, DE 丄AB 于E , DF 丄AC 于F.(1)说明BE=CF 的理由;(2)如果AB=a , AC=b ,求AE 、BE 的长.五、中点问题,AD 、CE 分别是/ BAC / BCA 的平分线,AD 、CE 相交于(1)中的其它条件不变,请问,你在 (1)中所得结论是否仍然成3.如图,在四边形ABCD中,AC 平分Z BAD ,过C 作CE 丄A 盯E ,并且 等于多少? AE =-(AB +AD)2 ,则N ABC +N ADC图FB3、已知:如图,矩形ABCD 中点G 为BC 延长线上一点,连接DG, B H 丄DG 于H ,且2、已知 MBC 中,AB =AC ,BD 为AB 的延长线,且BD =AB ,CE 为AABC 的AB 边上的中线. 求证CD =2CE3、以 M BC 的两边 AB 、AC 为腰分别向外作等腰 RUABD 和等腰Rt 心ACE , Z BADCAE =90°.连接DE , M 、N 分别是BC 、DE 的中点.探究: AM 与DE 的位置关系及数量关系. ⑴如图① 当M BC 为直角三角形时,AM 与DE 的位置关系是 ________________ ;线段AM 与DE 的数量关系是 ___________ ; ⑵将图①中的等腰RUABD 绕点A 沿逆时针方向旋转0°(O v0<:9O)后,如图②所示,⑴问中得到的两个结论是 否发生改变?并说明理由.1.在^ ABC 中,D 为BC 的中点, 过D 点的直线GF 交AC于F ,交AC 的平行线 BG 于点G 。
