智慧作业---圆周角定理

圆周角定理一条弧所对圆周角等于它所对圆心角的一半

圆周角定理：一条弧所对圆周角等于它所对圆心角的一半证明：已知在⊙O中，∠BOC与圆周角∠BAC同对弧BC，求证：∠BOC=2∠BAC.证明：情况1：如图1，当圆心O在∠BAC的一边上时，即A、O、B在同一直线上时：图1向左转|向右转∵OA、OC是半径解：∴OA=OC∴∠BAC=∠ACO（等边对等角）∵∠BOC是△AOC的外角∴∠BOC=∠BAC+∠ACO=2∠BAC情况2：如图2,，当圆心O在∠BAC的内部时：连接AO，并延长AO交⊙O于D图2向左转|向右转∵OA、OB、OC是半径解：∴OA=OB=OC∴∠BAD=∠ABO，∠CAD=∠ACO（等边对等角）∵∠BOD、∠COD分别是△AOB、△AOC的外角∴∠BOD=∠BAD+∠ABO=2∠BAD(三角形的外角等于两个不相邻两个内角的和）∠COD=∠CAD+∠ACO=2∠CAD(三角形的外角等于两个不相邻两个内角的和）∴∠BOC=∠BOD+∠COD=2(∠BAD+∠CAD)=2∠BAC情况3：如图3，当圆心O在∠BAC的外部时：图3向左转|向右转连接AO，并延长AO交⊙O于D连接OA,OB。

解：∵OA、OB、OC、是半径∴OA=OB=OC∴∠BAD=∠ABO（等边对等角）,∠CAD=∠ACO(OA=OC）∵∠DOB、∠DOC分别是△AOB、△AOC的外角∴∠DOB=∠BAD+∠ABO=2∠BAD(三角形的外角等于两个不相邻两个内角的和）∠DOC=∠CAD+∠ACO=2∠CAD(三角形的外角等于两个不相邻两个内角的和）∴∠BOC=∠DOC-∠DOB=2(∠CAD-∠BAD)=2∠BAC从而得证：∠BOC=2∠BAC.。

圆周角定理及其推论

圆周⾓定理及其推论
圆周⾓定理指的是⼀条弧所对圆周⾓等于它所对圆⼼⾓的⼀半。

这⼀定理叫做圆周⾓定理。

定理推论：在同圆或等圆中，同弧或等弧所对的圆周⾓相等，相等的圆周⾓所对的弧也相等。

定理内容
圆周⾓的度数等于它所对弧上的圆⼼⾓度数的⼀半，同弧或等弧所对的圆周⾓相等。

圆周⾓：顶点在圆上，并且两边都和圆相交的⾓叫做圆周⾓，这⼀定义实质上反映的是圆周⾓所具备的两个特征：①顶点在圆上，②两边都和圆相交。

这两个条件缺⼀不可。

定理推论
1.在同圆或等圆中，同弧或等弧所对的圆周⾓相等，相等的圆周⾓所对的弧也相等。

2.半圆（直径）所对的圆周⾓是直⾓；90°的圆周⾓所对的弦是直径。

3.圆的内接四边形的对⾓互补，并且任何⼀个外⾓都等于它的内对⾓。

2.1圆周角定理

推论１：在同圆或等圆中，同弧或等弧所对的圆周角相等；相等的圆周角所对的弧也相等．推论２：半圆（或直径）所对的圆周角是直角；９０°的圆周角所对的弦是直径．
例1:如图:AB,AC是⊙O的两条弦,延长CA到D, 使AD=AB.若∠ADB=40°, 求∠BOC的度数．
B O C
D A
160°
例２．ＡＢ是⊙Ｏ的直径，ＢＤ是⊙Ｏ的弦，延长ＢＤ到点Ｃ，使ＣＤ＝ＢＤ，连接ＡＣ．判断ＡＢ与ＡＣ的大小有什么关系？为什么？
C
小结：圆周角／圆心角定理
圆周角定理：
圆上一条弧所对的圆周角等于它所对的圆心角的一半. 圆心角定理：圆心角的度数等于它所对弧的度数．推论１：在同圆或等圆中，同弧或等弧所对的圆周角相等；相等的圆周角所对的弧也相等．推论２：半圆（或直径）所对的圆周角是直角；
９０°的圆周角所对的弦是直径．
小结：圆周角／圆心角定理
B E · O H D G C
３.如图，BC是半圆的直径,P是半圆上的一点,过 BP 的中点Ａ，作ＡＤ⊥ＢＣ，垂足为Ｄ，ＢＰ交ＡＤ于Ｅ，交ＡＣ于Ｆ，求证：ＢＥ＝ＡＥ＝ＥＦ
︵
Ａ
2
Ｂ
ＥＦＤ
1
3 4
Ｐ
Ｃ
４、如图， Δ ABC内接于⊙Ｏ，ＡＨ⊥ＢＣ于点Ｈ，求证：（１）∠ＯＡＢ＝∠ＨＡＣ（２）ＯＡ·ＡＨ＝１／２ＡＢ·ＡＣ
(第1题) (第2题) (第3题)
2.如图,圆的直径AB=13cm,C为圆上一点,CD⊥AB,垂足D,且CD=6cm.求AD的长. ⌒ ⌒ 3.如图,BC是⊙O的直径, AD⊥BC,垂足D.AB=AF,BF 和 AD相交于E.求证:AE=BE.
2、如图，设AD,CF是Δ ABC的两条高, AD,CF的延长线交Δ ABC的外接圆O于G,AE 是⊙O的直径,求证: (1)AB·AC=AD·AE F A (2)DG=DH

初中数学易错题流程化-圆周角定理

初中数学易错题流程化-圆周角定理重庆中考中，有关圆的考点相对比较简单，但正因为比较简单，导致很多学生对圆不太敏感，很多时候看似都做对了，其实逻辑性并不严明，属于蒙对的，所以在考试中并不能保证百分之百做对。

今天我们就先讲其中一个考点—圆周角定理。

知识点：圆周角定理，圆中边角弦的关系流程化讲解例：如图，BC是⊙O的直径，点A在圆上，连接AO，AC，∠AOB=64°，则∠ACB= ．（出自2017重庆中考15题）解题过程：1. 标注∠AOB=64°，所求∠ACB的位置（几何计算中，第一步都是读题标注好已知信息）2. ∵∠ACB和∠AOB是均是弧AB所对应的圆周角和圆心角∴∠ACB=1/2∠AOB=32°（这道题解题过程很简单，直接用圆周角定理就能做对，所以圆的内容在重庆中考中不难，大家不要担心自己不会做）总结：这道题很简单，很多同学总觉得没什么可讲的，那么我所表达的流程化到底在哪儿呢，我们来分析一下：第一步：标注已知信息（这一步是所有几何题都都应该先做的，不只是计算题，几何证明题也同样重要）第二步：看问题，分析找所求角对应弧，比如这道题对应的就是弧AB（在几何计算中，我们重要的就是看问题所求的量，角也好，边也好，我们得分析出这个角如何求，边如何求）第三步：找对应弧上的圆周角或圆心角，如果没有，可添加辅助线构造那么这道题简单就简单在这里，弧AB所对应的就只有圆心角AOB第四步：求出对应的圆心角或者圆周角，那么这道题简单就简单在这里，弧AB所对应的就只有圆心角AOB已知其度数，所以利用圆周角定理就求出答案了。

（如果不知道角的度数，我们就要导角，那么导角对于圆的题来说相对比较简单，就是与已知角产生关系）流程化巩固（为了更好地帮助大家理解到这简单三步的好处，我们下面再来看一道题）例：如图，CD 是⊙O的直径，A、B两点在⊙O上，且 AB与CD 交于点E，若∠BAO=30°，AO∥BC，则∠AOD的度数为（）A．120° B．100° C．170° D．150°解：第一步：标注已知信息相信大家都做好了第二步：第二步所求∠AOD对应的弧是弧AD第三步：弧AD所对应的圆周角图中没有，可以连接BD构造∠ABD，此时我们知道求出∠ABD乘以2，就求出了∠AOD第四步：求∠ABD，∠ABD挨着∠ABC，∠ABC=∠BAO=30°，且∠ABC+∠ABD=∠BCD（这样就与已知角产生了关系），又因为∠BCD=90°，所以∠ABD=90°-30°=60°所以就求出来∠AOD=120°注：今天给大家讲了一个很简单的几何计算题，并不是说这道题难，而是在给大家提供一个思路，就是几何题的逻辑思路，很多同学在做几何的时候就是没有方向，自己把每个角每条边能算的都算出来，最后来看能否求出答案，很明显就算最后选对了答案，也浪费了很多时间，所以一定要注意，不管多简单的几何题，都能明白解题的方向在哪儿，能理清楚解题的逻辑性，那么才算真的掌握到了几何解题的要点。

圆周角定理的应用

圆周角定理的应用圆周角定理是圆中的一个非常重要的定理，通过它，我们可以在求角度、算线段等方面有所作为。

我们一起来看几例。

一、求出相关角度。

圆周角定理揭示了它和同弧所对的圆心角度数之间的关系。

例1如图，点A、B、C都在⊙O上，若∠C=34°，则∠AOB的度数为多少分析：观察图形，发现∠C和∠AOB都是AB所对的角，一个是圆周角，另一个是圆心角，根据圆周角定理可得出结论。

解：因为∠C和∠AOB都是AB所对，则∠AOB＝2∠C，得∠AOB＝68°。

评：理解定理，运用定理。

例2如图，点A、B、C、D、E都在⊙O上，若∠A=14°，∠E＝12°，则∠DOB的度数为多少分析：观察图形，∠A和∠E这两个圆周角共起来，才和圆心角∠DOB同对一弧，问题可解。

解：∠A和∠E这两个圆周角共起来，才和圆心角∠DOB同对一弧BD，所以∠DOB＝2（∠A＋∠E）＝52°。

评：寻求已知和求知之间的联系。

二、求相关线段之间的关系通过圆周角定理，可找出相关线段所在三角形中角度之间的关系，从而可进一步加以探索。

例3 如图，△ABC内接于⊙O，AD平分∠BAC交⊙O于D，DE∥BA交⊙O于E。

求证：AC＝DE。

分析：因为相等的圆周角所对的弦相等，则要证AC＝DE，只需证∠DAE ＝∠ADC。

证：连结AE、DC，因为AD平分∠BAC，所以∠BAD＝∠DAC，因为DE∥BA，所以∠BAD＝∠EDA，所以∠DAC＝∠EDA，因为EC公共，所以∠EAC＝∠EDC，所以∠DAC＋∠CAE＝∠ADE＋∠EDC所以∠DAE＝∠ADC，所以AC＝DE。

评：通过寻求同一圆中，同弧或等弧所对的圆周角与弦等元素之间的对应关系，寻求解题思路。

例4 已知：如图，△ABC是⊙O的内接三角形，AD⊥BC于D，AE是⊙O 的直径，若S△ABC=S，⊙O的半径为R．求证：AB·AC=AD·AE分析：本题要证明的结论是“等积式”，•通常的思路是把等积式转化成比例式，再找相似三角形．上式可改成AB AEAD AC，则寻求△ADC∽△ABE。

圆周角定理及其运用

2
求证： △ABC 为直角三角形.
C
证明：以AB为直径作⊙O，
1
∵AO=BO， CO= 2 AB,
A
·
B
O
∴AO=BO=CO.
∴点C在⊙O上.
又∵AB为直径,
∴∠ACB=
1 2
×180°=90°.源自∴ △ABC 为直角三角形.
3. 如图，在直径为AB的半圆中，O为圆心，C、D 为半圆上的两点，∠COD=50°，则
圆周角定理
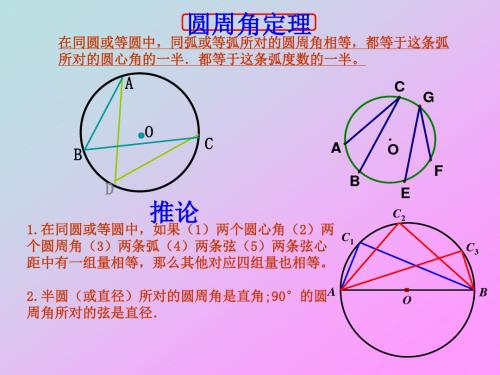
在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．都等于这条弧度数的一半。
A
C
G
B
●O
C
A
D
B
推论
1.在同圆或等圆中，如果（1）两个圆心角（2）两个圆周角（3）两条弧（4）两条弦（5）两条弦心 C1
距中有一组量相等，那么其他对应四组量也相等。
2.半圆（或直径）所对的圆周角是直角;90°的圆A 周角所对的弦是直径．
∠CAD=_2_5__°__；
4、在⊙O中，一条弧所对的圆心角和圆周角分别为
(2x+100)°和(5x-30)°，则x=_20°_；
D
A
O 40° B
C
例题
例如图，⊙O直径AB为10cm，弦AC为6cm，∠ACB的平
分线交⊙O于D，求BC、AD、BD的长．
解：∵AB是直径，
∴ ∠ACB= ∠ADB=90°．
C
在Rt△ABC中，
BC AB2 AC2 102 62 8
A
O
B
∵CD平分∠ACB，
ACD BCD.
O F
E
C2
C3
·O

圆周角定理的推论2及圆

圆周角定理的推论2及圆
圆周角定理是几何学中的重要定理，它指的是：在任意三角形中，其三个内角的和为180°；而在任意园形内，相应的三角形所有内角的和为园周角，即360°，这就是圆周角定理。

圆周角定理是根据三角形和圆形的基础知识来说明的，其中三角形在几何学中是一种重要的几何体，其有三个角度。

任意三角形中，其三个角度的和是180°，而圆则是一个完整的圆形，因而其一个圈中包含了好多条边缘，所有的角度的和就是360°，这也正好等于园周角。

圆周角定理的推论2是：如果三点不在一条直线上，则这三点可以构成一个三角形，而在三角形内，其三个内角的和为180°；另一方面，一个圆中包含了很多条边缘，而它们如果组成三角形，那么它们的和是360°，因此，三角形内角的和等于园周角的和，就是圆周角定理。

因此，圆周角定理的推论2的意义在于，它使得对于所有的园形，可以很容易构绘出来，也可以更方便地计算出其内部的角度数。

圆周角定理的推论2也可以用来帮助解决许多几何问题，比如求椭圆的长短轴长度等。

总而言之，圆周角定理是一个重要的定理，它反映了三角形和圆形之间的关系，并由此推论出了圆周角定理的推论2，使得求解复杂几何问题更加容易，不仅提高了几何的计算应用，而且也成为了几何学的一大宝贵知识。

圆周角定理

∵∠1=∠2,∴ = ,
∴BF=CG, = ,
∴∠FBD=∠GCE.
又 ∵BD=CE,∴△BFD≌△CGE,
∴∠F=∠G,∴ = ,
∴AB=AC.
题型一
题型二
题型三
题型三
易错辨析
易错点:误认为同弦或等弦所对圆周角相等而致错
【例3】如图,若∠BAD=75°,则∠BCD=
分成两条弧:优弧和劣弧,若圆周角的顶点同在优弧上或同在劣弧
上,同弦或等弦所对的圆周角相等;若一个圆周角的顶点在优弧上,
另一个圆周角的顶点在劣弧上,则同弦或等弦所对的圆周角不相等,
它们互补(如本题).
(2)在圆周角定理的证明中,运用了数学中分类讨论和化归的思想
以及归纳的证明方法.这个定理是从特殊情况入手研究的,首先研
究当角的一边过圆心时,得到圆周角与同弧所对的圆心角的关系,
然后研究当角的一边不经过圆心时,圆周角与同弧所对的圆心角之
间的关系.当角的一边不经过圆心时,又有两种情况:一是圆心在圆
周角内部;二是圆心在圆周角外部.经过这样不同情况的讨论,最后
第二讲
直线与圆的位置关系
一
圆周角定理
1.了解圆心角定理,并能应用定理解决问题.
2.理解圆周角定理及其两个推论,并能应用定理解决有关问题.
圆周角定理的理解
剖析:(1)应用圆周角定理时,要注意的问题如下:
圆周角定理推论1中,同圆或等圆中,相等的圆周角所对的弧相等.
这一定理成立的前提是同圆或等圆,否则不成立.
角形,从而得到成比例线段,再列方程求得线段长.
题型一
题型二
题型三
【变式训练 1】如图,已知△ABC 内接于☉O, = , 点是

圆周角定理及推论

1 / 624.1.4圆周角第1课时圆周角定理及推论教学内容1．圆周角的概念．2．圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，?都等于这条弦所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径及其它们的应用．教学目标1．了解圆周角的概念．2．理解圆周角的定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，?都等于这条弧所对的圆心角的一半．3．理解圆周角定理的推论：半圆（或直径）所对的圆周角是直角，90?°的圆周角所对的弦是直径．4．熟练掌握圆周角的定理及其推理的灵活运用．设置情景，给出圆周角概念，探究这些圆周角与圆心角的关系，运用数学分类思想给予逻辑证明定理，得出推导，让学生活动证明定理推论的正确性，最后运用定理及其推导解决一些实际问题．重难点、关键2 / 61．重点：圆周角的定理、圆周角的定理的推导及运用它们解题．2．难点：运用数学分类思想证明圆周角的定理．3．关键：探究圆周角的定理的存在．教学过程一、复习引入（学生活动）请同学们口答下面两个问题．1．什么叫圆心角？2．圆心角、弦、弧之间有什么内在联系呢？老师点评：（1）我们把顶点在圆心的角叫圆心角．（2）在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，?那么它们所对的其余各组量都分别相等．刚才讲的，顶点在圆心上的角，有一组等量的关系，如果顶点不在圆心上，它在其它的位置上？如在圆周上，是否还存在一些等量关系呢？这就是我们今天要探讨，要研究，要解决的问题．二、探索新知问题：如图所示的⊙O，我们在射门游戏中，设E、F是球门，?设球员们只能在所在的⊙O其它位置射门，如图所示的3 / 6A、B、C点．通过观察，我们可以发现像∠EAF、∠EBF、∠ECF这样的角，它们的顶点在圆上，?并且两边都与圆相交的角叫做圆周角．现在通过圆周角的概念和度量的方法回答下面的问题．1．一个弧上所对的圆周角的个数有多少个？2．同弧所对的圆周角的度数是否发生变化？3．同弧上的圆周角与圆心角有什么关系？（学生分组讨论）提问二、三位同学代表发言．老师点评：1．一个弧上所对的圆周角的个数有无数多个．2．通过度量，我们可以发现，同弧所对的圆周角是没有变化的．3．通过度量，我们可以得出，同弧上的圆周角是圆心角的一半．下面，我们通过逻辑证明来说明“同弧所对的圆周角的度数没有变化，?并且它的度数恰好等于这条弧所对的圆心角的度数的一半．”（1）设圆周角∠ABC的一边BC是⊙O的直径，如图所示∵∠AOC是△ABO的外角∴∠AOC=∠ABO+∠BAO∵OA=OB∴∠ABO=∠BAO∴∠AOC=∠ABO∴∠ABC=∠AOC4 / 6（2）如图，圆周角∠ABC的两边AB、AC在一条直径OD的两侧，那么∠ABC=∠AOC吗？请同学们独立完成这道题的说明过程．老师点评：连结BO交⊙O于D同理∠AOD是△ABO的外角，∠COD是△BOC 的外角，?那么就有∠AOD=2∠ABO，∠DOC=2∠CBO，因此∠AOC=2∠ABC．（3）如图，圆周角∠ABC的两边AB、AC在一条直径OD的同侧，那么∠ABC=∠AOC吗？请同学们独立完成证明．老师点评：连结OA、OC，连结BO并延长交⊙O于D，那么∠AOD=2∠ABD，∠COD=2∠CBO，而∠ABC=∠ABD-∠CBO=∠AOD-∠COD=∠AOC现在，我如果在画一个任意的圆周角∠AB′C，?同样可证得它等于同弧上圆心角一半，因此，同弧上的圆周角是相等的．从（1）、（2）、（3），我们可以总结归纳出圆周角定理：在同圆或等圆中，同弧等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．进一步，我们还可以得到下面的推导：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．下面，我们通过这个定理和推论来解一些题目．例1．如图，AB 是⊙O的直径，BD是⊙O的弦，延长BD到C，使AC=AB，BD与CD的大小有什么关系？为什么？5 / 6分析：BD=CD，因为AB=AC，所以这个△ABC是等腰，要证明D是BC 的中点，?只要连结AD证明AD是高或是∠BAC的平分线即可．解：BD=CD理由是：如图24-30，连接AD∵AB是⊙O的直径∴∠ADB=90°即AD⊥BC又∵AC=AB∴BD=CD三、巩固练习1．教材P92思考题．2．教材P93练习．四、应用拓展例2．如图，已知△ABC内接于⊙O，∠A、∠B、∠C的对边分别设为a，b，c，⊙O半径为R，求证：===2R．分析：要证明===2R，只要证明=2R，=2R，=2R，即sinA=，sinB=，sinC=，因此，十分明显要在直角三角形中进行．6 / 6证明：连接CO并延长交⊙O于D，连接DB∵CD是直径∴∠DBC=90°又∵∠A=∠D在Rt△DBCxx，sinD=，即2R= 同理可证：=2R，=2R ∴===2R五、归纳小结（学生归纳，老师点评）本节课应掌握：1．圆周角的概念；2．圆周角的定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，?都相等这条弧所对的圆心角的一半；3．半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．。

圆周角定理及其推论

圆周角定理及其推论
观察：
•在圆A上点C、G固定，观察点B运动的同时弧CB圆周角大小与它的圆心角大小的关系。

结论：同圆或等圆中，圆周角等于它所对的弧上的圆心角的一
半。

观察：
•保持圆A的大小不变固定C点F点，点G在圆上任意移动，观察圆周角CGF的大小的变化？
结论：同弧或等弧所对的圆周角相等。

观察：
•在圆A中，点T沿圆运动，观察直径RS所对圆周角的大小。

结论：半圆或直径所对的圆周角是直角。

观察：
•任意改变圆内接四边形的形状，观察对角的和。

结论:圆的内接四边形的对角互补，并且任何一个外角都它的内对
角。

总结:
定理：同圆或等圆中，圆周角等于它所对的弧上的圆心角的一半。

推理1：同弧或等弧所对的圆周角相等。

推理2：半圆或直径所对的圆周角是直角。

推理3：圆的内接四边形的对角互补，并且任何一个外角都它的内对角。

中考数学复习----《圆周角定理》知识点总结与专项练习题(含答案)

中考数学复习----《圆周角定理》知识点总结与专项练习题（含答案）知识点总结1.圆心角、弦以及弧之间的关系：①定理：在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等。

②推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等。

说明：同一条弦对应两条弧，其中一条是优弧，一条是劣弧，而在本定理和推论中的“弧”是指同为优弧或劣弧。

2.圆周角的定义：顶点在圆上，并且两边都与圆相交的角叫做圆周角。

3.圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。

4.圆周角定理的推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径。

5.圆的内接四边形：①定义：四个顶点都在圆上的四边形叫做圆的内接四边形。

②性质：I：圆内接四边形的对角互补。

II：圆内接四边形的任意一个外角等于它的内对角。

练习题1、（2022•襄阳）已知⊙O的直径AB长为2，弦AC长为2，那么弦AC所对的圆周角的度数等于．【分析】首先利用勾股定理逆定理得∠AOC＝90°，再根据一条弦对着两种圆周角可得答案．【解答】解：如图，∵OA＝OC＝1，AC＝，∴OA2+OC2＝AC2，∴∠AOC＝90°，∴∠ADC＝45°，∴∠AD'C＝135°，故答案为：45°或135°．2、（2022•日照）一圆形玻璃镜面损坏了一部分，为得到同样大小的镜面，工人师傅用直角尺作如图所示的测量，测得AB＝12cm，BC＝5cm，则圆形镜面的半径为．【分析】连接AC，根据∠ABC＝90°得出AC是圆形镜面的直径，再根据勾股定理求出AC 即可．【解答】解：连接AC，∵∠ABC＝90°，且∠ABC是圆周角，∴AC是圆形镜面的直径，由勾股定理得：AC＝＝＝13（cm），所以圆形镜面的半径为cm，故答案为：cm．3、（2022•永州）如图，AB是⊙O的直径，点C、D在⊙O上，∠ADC＝30°，则∠BOC＝度．【分析】根据在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半求出∠AOC的度数，根据平角的定义即可得到∠BOC＝180°﹣∠AOC的度数．【解答】解：∵∠ADC是所对的圆周角，∴∠AOC＝2∠ADC＝2×30°＝60°，∴∠BOC＝180°﹣∠AOC＝180°﹣60°＝120°．故答案为：120．4、（2022•苏州）如图，AB是⊙O的直径，弦CD交AB于点E，连接AC，AD．若∠BAC＝28°，则∠D＝°．【分析】如图，连接BC，证明∠ACB＝90°，求出∠ABC，可得结论．【解答】解：如图，连接BC．∵AB是直径，∴∠ACB＝90°，∴∠ABC＝90°﹣∠CAB＝62°，∴∠D＝∠ABC＝62°，故答案为：62．5、（2022•湖州）如图，已知AB 是⊙O 的弦，∠AOB ＝120°，OC ⊥AB ，垂足为C ，OC 的延长线交⊙O 于点D ．若∠APD 是AB ⌒所对的圆周角，则∠APD 的度数是．【分析】由垂径定理得出，由圆心角、弧、弦的关系定理得出∠AOD ＝∠BOD ，进而得出∠AOD ＝60°，由圆周角定理得出∠APD ＝∠AOD ＝30°，得出答案．【解答】解：∵OC ⊥AB ，∴，∴∠AOD ＝∠BOD ，∵∠AOB ＝120°，∴∠AOD ＝∠BOD ＝∠AOB ＝60°，∴∠APD ＝∠AOD ＝×60°＝30°，故答案为：30°．6、（2022•徐州）如图，A 、B 、C 点在圆O 上，若∠ACB ＝36°，则∠AOB ＝．【分析】利用一条弧所对的圆周角等于它所对的圆心角的一半即可得出结论．【解答】解：∵∠ACB ＝∠AOB ，∠ACB ＝36°，∴∠AOB ＝2×∠ACB ＝72°．故答案为：72°．7、（2022•锦州）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，∠ADC＝130°，连接AC，则∠BAC的度数为．【分析】利用圆内接四边形的性质和∠ADC的度数求得∠B的度数，利用直径所对的圆周角是直角得到∠ACB＝90°，然后利用直角三角形的两个锐角互余计算即可．【解答】解：∵四边形ABCD内接于⊙O，∠ADC＝130°，∴∠B＝180°﹣∠ADC＝180°﹣130°＝50°，∵AB为⊙O的直径，∴∠ACB＝90°，∴∠CAB＝90°﹣∠B＝90°﹣50°＝40°，故答案为：40°．8、（2022•雅安）如图，∠DCE是⊙O内接四边形ABCD的一个外角，若∠DCE＝72°，那么∠BOD的度数为．【分析】根据邻补角的概念求出∠BCD，根据圆内接四边形的性质求出∠A，根据圆周角定理解答即可．【解答】解：∵∠DCE＝72°，∴∠BCD＝180°﹣∠DCE＝108°，∵四边形ABCD内接于⊙O，∴∠A＝180°﹣∠BCD＝72°，由圆周角定理，得∠BOD＝2∠A＝144°，故答案为：144°．9、（2022•甘肃）如图，⊙O是四边形ABCD的外接圆，若∠ABC＝110°，则∠ADC＝°．【分析】根据圆内接四边形的对角互补即可得到结论．【解答】解：∵四边形ABCD内接于⊙O，∠ABC＝110°，∴∠ADC＝180°﹣∠ABC＝180°﹣110°＝70°，故答案为：70．。

圆周角定理及其推论

圆周角定理及其推论一、圆周角定理圆周角定理是几何学的重要定理，它源于古希腊数学家弥尔顿（Archimedes）的研究。

圆周角定理规定：任何两个正夹角的正弦之积等于它们之间的乘积，也就是学术上说的“正夹角全乘积等于余弦。

”以上是圆周角定理的文字表示，而在数学上，圆周角定理又有如下式子体现：Sin（α+β）= Sinα×Cosβ+Cosα×Sinβ二、圆周角定理的推论1、正弦定理：一个三角形角α，β，γ的正弦值分别为Sinα，Sinβ，Sinγ，那么有Sinα：Sinβ：Sinγ=a：b：c；2、余弦定理：每个三角形角α，β，γ的余弦值分别为Cosα，Cosβ，Cosγ，那么有a2+b2=c2-2abCosγ；3、正切定理：任一三角形角α，β，γ的正切值分别为tanα，tanβ，tanγ，那么有tanα×tanβ=tanγ/1-tanαtanβ；4、正割定理：一个三角形角α，β，γ的正割值分别为cotα，cotβ，cotγ，那么有cotα+cotβ=cotγ/1+cotα cotβ；5、互补定理：任一角α，它的余角β满足Cosα=Sinβ；Cosβ=Sinα；6、倒数定理：对一角α，其余角β均有Secα=1/Cosα；Secβ=1/Cosβ；7、士角定理：一角α，其余角β乘积等于正弦定理，那么Sinα×Sinβ=Cos角γ/2;8、三边定理：任一三角形角α，β，γ的边长分别为a，b，c，那么有a/(Sinα)=b/(Sinβ)=c/(Sinγ)；9、兰勃托定理：一个等腰三角形，其底边和对边相较于当前对角之正弦的比值之和等于1，也就是说：Sinα/(a/2)+Sinβ/(a/2)=1；10、马克斯定理：一个三角形边长abc，那么有cosA+cosB+cosC=4cosA/2cosB/2cosC/2=3/2。

专题04 圆周角定理(解析版) -2021-2022学年九年级数学之专攻圆各种类型题的解法(人教版)

专题04 圆周角定理1.圆周角的定义顶点在圆上，并且两边都与圆相交的角叫做圆周角.2.圆周角定理及其推论定理：一条弧所对的圆周角等于它所对的圆心角的一半．如图，连接BO,CO,得圆心角∠BOC.试猜想∠BAC 与∠BOC 存在怎样的数量关系.推论：1）在同圆或等圆中，同弧或等弧所对的圆周角相等．2）直径所对的圆周角是直角．圆内接四边形的对角互补．在圆中求角度时，通常需要通过一些圆的性质进行转化．比如圆心角与圆周角间的转化；同弧或等弧的圆周角间的转化；连直径，得到直角三角形，通过两锐角互余进行转化等．3.圆周角与圆心角的关系中圆心的位置存在的情形（1）圆心O 在∠BAC 的一边上（如图甲）（2）圆心O 在∠BAC 的内部（如图乙）（3）圆心O 在∠BAC 的外部（如图丙）甲乙丙4.圆周角和直径的关系概念规律重在理解12BAC BOC ∠=∠半圆或直径所对的圆周角都相等，都等于90°.5.方法总结在圆中，如果有直径，一般要找直径所对的圆周角，构造直角三角形解题．6.圆内接四边形如果一个多边形所有顶点都在同一个圆上，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆.推论1：圆的内接四边形的对角互补.推论2：圆的内接四边形的任何一个外角都等于它的内对角.注意：圆内接四边形的性质是沟通角相等关系的重要依据．典例解析掌握方法【例题1】（2021湖南邵阳）如图，点A，B，C是⊙O上的三点．若∠AOC＝90°，∠BAC＝30°，则∠AOB 的大小为（）A．25°B．30°C．35°D．40°【答案】B【解析】由圆周角定理可得∠BOC＝2∠BAC＝60°，继而∠AOB＝∠AOC﹣∠BOC＝90°﹣60°＝30°．∵∠BAC与∠BOC所对弧为，由圆周角定理可知：∠BOC＝2∠BAC＝60°，又∠AOC＝90°，∴∠AOB＝∠AOC﹣∠BOC＝90°﹣60°＝30°．【例题2】（2021黑龙江鹤岗）如图，在⊙O中，AB是直径，弦AC的长为5cm，点D在圆上且∠ADC＝30°，则⊙O的半径为cm．【答案】5．【解析】连接OC，证明△AOC是等边三角形，可得结论．解：如图，连接OC．∵∠AOC＝2∠ADC，∠ADC＝30°，∴∠AOC＝60°，∵OA＝OC，∴△AOC是等边三角形，∴OA＝AC＝5（cm），∴⊙O的半径为5cm．【例题3】如图，线段AB是☉O的直径，点C是☉O上的任意一点（除点A、B外），那么，∠ACB就是直径AB所对的圆周角，想一想，∠ACB会是怎样的角？【答案】见解析。

人教版数学高二选修4-1课时作业一圆周角定理

一圆周角定理1.下列命题中，真命题的个数是( )①顶点在圆周上的角是圆周角；②圆周角的度数等于圆心角度数的一半； ③90°的圆周角所对的弦是直径；④直径所对的角是直角；⑤圆周角相等，则它们所对的弦也相等；⑥同弧或等弧所对的圆周角相等． A.1个 B.2个C.3个 D.4个2.已知点O 是△ABC 的外心，∠A ＝α，则∠BOC 为( ) A ．2α B ．360°－2αC ．2α或360°－2αD ．180°－2α3.在半径为2 cm 的⊙O 内有长为2 3 cm 的弦AB ，则此弦所对的圆心角∠AOB 等于________．4.如图所示，⊙O 直径MN ⊥AB 于点P ，∠BMN ＝30°，则∠AON ＝________．5.如图所示，若圆内接四边形的对角线交于点E ，则图中相似三角形有( )A ．1对B ．2对C ．3对D ．4对6．如图所示，点D 是AC ︵的中点，与∠ABD 相等的角的个数是( )A ．7个B ．3个C ．2个D ．1个7.已知点C 、D 是以AB 为直径的圆弧上的两点，若BC ︵所对的圆周角为25°，AD ︵所对的圆周角为35°，则DC ︵所对的圆周角为( ) A ．30° B ．40°C ．30°或80° D ．80°8．在Rt △AB C 中，∠C ＝90°，∠A ＝30°，b ＝23，则此三角形外接圆半径为( ) A.3B ．2C ．2 3 D ．49．半径为4的圆上一段弧长等于半径为2的圆的周长，则这段弧所对的圆心角是________． 10．如图，点A ，B ，C 是圆O 上的点，且AB ＝4，∠ACB ＝45°，则圆O 的面积等于________．11．如图所示，若AD ︵＋BC ︵＝AB ︵＋CD ︵，且∠ADB ＝30°，则CD ︵的度数是________． 12．如下图，弦AB 与CD 相交于圆O 内一点E ，过E 作BC 的平行线与AD 的延长线相交于点P .已知PD ＝2DA ＝2，则PE ＝____．13．如图，已知圆O 内接△ABC 的∠C 的平分线CD 延长后交圆于点E ，连接BE ，已知BD ＝3，CE ＝7，BC ＝5，则线段BE ＝________．14．如图，AB 是圆O 的直径，D ，E 为圆O 上位于AB 异侧的两点，连接BD 并延长至点C ，使BD ＝DC ，连接AC ，AE ，DE .求证：∠E ＝∠C .参考答案1.A2.C3.120°4．解析：连BO ，则AO ＝BO ，即∠OAB ＝∠OBA ，又MN ⊥AB ，则∠AON ＝∠NOB ＝2∠BMN ＝60°. 答案：60° 5．B 6.B7．解析：若C 、D 在AB 同侧，则DC ︵所对圆周角为30°，若C 、D 在AB 异侧，则所对圆周角为80°. 答案：C8.解析：易推得斜边AB 为外接圆直径．答案：B9.180°10.8π 11.120°12．解析：PE ∥BC ，则∠PED ＝∠C .又同弧BD ︵所对的角∠C 及∠A 相等，则∠PED ＝∠A . 易推△PED ∽△P AE ，即PE P A ＝PDPE .PE ＝P A ·PD ＝ 6.答案： 613．解析：∠ACE ＝∠BCE ，∠ABE ＝∠ACE ，则∠ABE ＝∠BCE ，易得△BDE ∽△CBE ， BE CE ＝BD BC ，即BE ＝215. 答案：21514．证明：如图，连接OD ，∵BD ＝DC ，O 为AB 的中点，∴OD ∥AC ，∴∠ODB ＝∠C . ∵OB ＝OD ，∴∠ODB ＝∠B .∴∠B ＝∠C .∵点A ，E ，B ，D 都在圆O 上，且D ，E 为圆O 上位于AB 异侧的两点，∴∠E 和∠B 为同弧所对的圆周角．故∠E ＝∠B ，∴∠E ＝∠C .。

圆周角定理及其推论 (2)

圆周角和圆心角的关系
1.首先考虑一种特殊情况：
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角 ∠ABC与圆心角∠AOC的大小关系.
∵∠AOC是△ABO的外角， ∴∠AOC=∠B+∠A.
A C
∵OA=OB，
●O
∴∠A=∠B.
∴∠AOC=2∠B.
B
即 ∠ABC = 1 ∠ AOC.
2
根据以上证明你能得到什么结论？
如图,点A、B、C、D在同一个圆上，四边形ABCD的对角线把4 个内角分成8个角，这些角中哪些是相等的角？
∠1=∠4 ∠2=∠7
★
★
★
★
∠3=∠6 ∠5=∠8
★
★
★
★
思考
如图，线段AB是⊙O的直径，点C是⊙O上任意一点（除点A、B），那么，∠ACB就是直径AB所对的圆周角，想想看，∠ACB会是怎样的角？
一. 复习引入:
1.圆心角的定义?
O.
答:顶点在圆心的角叫圆心角
2.上节课我们学习了一个反映圆
心角、弧、弦、弦心距四个量之 B
C
间关系的一个结论，这个结论是
什么？
在同圆（或等圆）中，如果圆心角、弧、弦、
弦心距有一组量相等，那么它们所对应的其余
两个量都分别相等。
探探索索1:
我们知道：顶点在圆心的角叫圆心角，当圆心角的顶点发生变化时,我们得到以下三种情况A:
,若∠ABD=40°,则∠BCD=＿5＿0°＿＿＿.
D
A
O 40° B
C
4.如图：OA、OB、OC都是⊙O 的半径，且∠AOB=2∠BOC.
求证：∠ACB=2∠BAC.
A
证明：∵BAC 1 BOC，ACB 1 AOB,

圆周角定理及其运用

A
O
B
∵CD平分∠ACB，
ACD BCD.D∴AD=BD.又在Rt△ABD中，AD2+BD2=AB2，
AD BD 2 AB 2 10 5 2(cm)
2
2
课本练习
3.求证：如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形．（提示：作出以这条边为直径的圆.）
已知：△ABC 中，CO为AB边上的中线，且CO= 1 AB
是
顶点在圆上，两边和圆相交。
不是
两边不和圆相交。
不是
有一边和圆不相交。
生活实践
• 当球员在B,D,E处射门时, 他所处的位置对球门AC 分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?.
A
E B
C D
A
E ●O
B
A⌒C所对的圆周角∠ AEC ∠ ABC ∠ ADC的大小 C 有什么关系？
在同圆或等圆中，如果两个圆周角相等，它们所对弧一定相等吗？为什么？
在同圆或等圆中，如果两个圆周角相等，它们所对的弧一定相等．
巩固练习：
如图，点A,B,C,D在同一个圆上，四边形ABCD的对角线把4个内角分成 8个角，这些角中哪些是相等的角？
D
A1
87
2
3
6
45
B
C
探究与思考：
问题1：如图，AB是⊙O的直径，请问：
∠BCD=100°，求∠BOD（所对的圆心角）
和∠BAD的大小。
A
O
D
B
C
探究
3、如图，AB是⊙O的直径，BD是⊙O的弦，延长 BD到点C，使DC=BD，连接AC交⊙O于点F，点 F不与点A重合。

圆周角定理及运用

• 4、All that you do, do with your might; things done by halves are never done right. ----R.H. Stoddard, American poet做一切事都应尽力而为，半途而废永远不行6.17.20216.17.202110:5110:5110:51:1910:51:19
提示:能否也转化为1的情况? 过点B作直径BD.由1可得:
●O
B A C
∠ABD
=
1∠AOD,∠CBD
2
= 1 ∠COD,
2
B
●O
∴ ∠ABC = 1∠AOC.
2
你能写出这个命题吗? 同弧所对的圆周角等于它所对的圆心角的一半.
巩固练习：
如图，点A,B,C,D在同一个圆上，四边形ABCD的对角线把4个内角分成 8个角，这些角中哪些是相等的角？
BD是⊙O的直径，则∠AEB等于（ B）
A、70°；
B、110°；
C、90°；
D、120°
B
4、如图，△ABC的顶点A、B、C
都在⊙O上，∠C＝30 °，AB＝2，
则⊙O的半径是 2 。
解：连接OA、OB
A
∵∠C=30 ° ，∴∠AOB=60 °
又∵OA=OB ，∴△AOB是等边三角形 ∴OA=OB=AB=2，即半径为2。
因此，甲应将球回传给乙，让乙射门.
如图所示，已知⊿ABC的三个顶点都在⊙O 上，AD是⊿ABC的高，AE是⊙O的直径. 求证：∠BAE＝∠CAD
A
B E
O DC
第二课时应用
• 回顾：圆周角定理及推论？
• 思考：判断正误：
1.同弧或等弧所对的圆周角相等（）

圆周角定理

圆周角定理圆周角定理：在圆中，一条弧所对圆周角等于它所对圆心角的一半。

要素：圆、同一条弧、圆周角、圆心角、12要素的正向运用：(2015·六盘水)如图所示，A 、B 、C 三点均在⊙O 上，若∠AOB ＝80°，则∠ACB ＝要素的逆向运用：（2015•株洲）如图，圆O 是△ABC 的外接圆，∠A ＝68°，则∠OBC 的大小是( ) A ．22° B ．26° C ．32° D ．68°隐藏圆：（2015•威海）如图，已知AB =AC =AD ，∠CBD =2∠BDC ，∠BAC =44°，则∠CAD 的度数为（） A ．68°B ．88°C ．90°D ． 112°隐藏圆心角：将量角器按如图所示的方式放置在三角形纸板上，使顶点C 在半圆上，点A 、B 的读数分别为0100、0150 ，则ACB 的大小为_____度.（2015•海南）如图，将⊙O沿弦AB折叠，圆弧恰好经过圆心O，点P是优弧上一点，则∠APB的度数为（）A．45°B．30°C．75°D．60°(2015南宁)如图，AB是⊙O的直径，AB=8，点M在⊙O上，∠MAB=20°，N是弧MB的中点,P是直径AB上的一动点，若MN=1，则△PMN周长的最小值为（）.（A）4 （B）5 （C）6 （D）7隐藏圆周角：（2014•泰州）如图，A、B、C、D依次为一直线上四个点，BC=2，△BCE为等边三角形，⊙O过A、D、E三点，且∠AOD=120°．设AB=x，CD=y，则y与x 的函数关系式为．隐藏圆心角和圆周角：如图，圆O的半径为1cm，弦AB、CD，1cm，则弦AC、BD所夹的锐角a=经典题型：（2013宁波）如图，△ABC中，∠BAC=60°，∠ABC=45°，D是边BC上（不与端点重合）的一个动点，以AD为直径画⊙O分别交AB，AC于E，F，连接EF，若线段AD长度的最小值为3，则线段EF长度的最小值为．。