2 kmeans用户聚类R

统计分析方法论：K-Means算法

K-Means课前准备下载Anaconda软件。

课堂主题本次课讲解K-Means聚类算法与算法的改进与优化。

课堂目标学习本次课，我们能够达到如下目标：熟知K-Means算法的原理与步骤。

熟知K-Means++算法的原理与初始化方式。

熟知Mini Batch K-Means算法的原理与步骤。

能够选择最佳的值。

知识要点聚类之前我们接触的算法，都是监督学习，即训练数据是包含我们要预测的结果（训练数据中是含有样本的标签）。

我们对含有标签的训练集建立模型，从而能够对未知标签的样本进行预测。

与监督学习对应的，聚类属于无监督学习，即训练数据中是不含有标签的。

聚类的目的是根据样本数据内部的特征，将数据划分为若干个类别，每个类别就是一个簇。

结果为，使得同一个簇内的数据，相似度较大，而不同簇内的数据，相似度较小。

聚类也称为“无监督的分类”。

其样本的相似性是根据距离来度量的。

K-Means算法算法步骤K-Mean算法，即均值算法，是最常见的一种聚类算法。

顾名思义，该算法会将数据集分为个簇，每个簇使用簇内所有样本的均值来表示，我们将该均值称为“质心”。

具体步骤如下：1. 从样本中选择个点作为初始质心。

2. 计算每个样本到各个质心的距离，将样本划分到距离最近的质心所对应的簇中。

3. 计算每个簇内所有样本的均值，并使用该均值更新簇的质心。

4. 重复步骤2与3，直到达到以下条件之一结束：质心的位置变化小于指定的阈值。

达到最大迭代次数。

过程演示下图给出了使用K-Means算法聚类的过程。

优化目标KMeans算法的目标就是选择合适的质心，使得在每个簇内，样本距离质心的距离尽可能的小。

这样就可以保证簇内样本具有较高的相似性。

我们可以使用最小化簇内误差平方和（within-cluster sum-of-squares ）来作为优化算法的量化目标（目标函数），簇内误差平方和也称为簇惯性（inertia）。

：簇的数量。

：第个簇含有的样本数量。

kmeans 聚类算法

kmeans 聚类算法Kmeans聚类算法Kmeans聚类算法是一种基于距离的无监督机器学习算法，它可以将数据集分为多个类别。

Kmeans算法最初由J. MacQueen于1967年提出，而后由S. Lloyd和L. Forgy独立提出。

目前，Kmeans算法已经成为了机器学习领域中最常用的聚类算法之一。

Kmeans算法的基本思想是将数据集划分为k个不同的簇，每个簇具有相似的特征。

簇的数量k是由用户指定的，算法会根据数据集的特征自动将数据集分成k个簇。

Kmeans算法通过迭代的方式来更新每个簇的中心点，以此来不断优化簇的划分。

Kmeans算法的步骤Kmeans算法的步骤可以概括为以下几个步骤：1. 随机选择k个点作为中心点；2. 将每个数据点与离它最近的中心点关联，形成k个簇；3. 对于每个簇，重新计算中心点；4. 重复2-3步骤，直到簇不再变化或达到最大迭代次数。

Kmeans算法的优缺点Kmeans算法的优点包括：1. 算法简单易实现；2. 能够处理大规模数据集；3. 可以处理多维数据。

Kmeans算法的缺点包括：1. 需要用户指定簇的数量；2. 对于不规则形状的簇，效果不佳；3. 对于包含噪声的数据集，效果不佳。

Kmeans算法的应用Kmeans算法在机器学习和数据挖掘中有着广泛的应用。

以下是Kmeans算法的一些应用：1. 图像分割：将图像分为多个不同的区域；2. 文本聚类：将文本数据划分为多个主题；3. 市场分析：将消费者分为不同的群体，以便进行更好的市场分析；4. 生物学研究：将生物数据分为不同的分类。

总结Kmeans聚类算法是一种基于距离的无监督机器学习算法，它可以将数据集分为多个类别。

Kmeans算法的步骤包括随机选择中心点、形成簇、重新计算中心点等。

Kmeans算法的优缺点分别是算法简单易实现、需要用户指定簇的数量、对于不规则形状的簇效果不佳等。

Kmeans算法在图像分割、文本聚类、市场分析和生物学研究等领域有着广泛的应用。

kmeans聚类和两步分类法

kmeans聚类和两步分类法Kmeans聚类和两步分类法在机器学习领域中，聚类和分类是两个重要的任务。

聚类是将数据集中的数据分成不同的组，每个组内的数据具有相似的特征。

而分类是将数据集中的数据分成不同的类别，每个类别内的数据具有相似的特征。

在聚类和分类中，Kmeans聚类和两步分类法是两种常用的方法。

Kmeans聚类是一种基于距离的聚类方法，它将数据集中的数据分成K个不同的组，每个组内的数据具有相似的特征。

Kmeans聚类的过程包括以下几个步骤：1. 随机选择K个数据点作为聚类中心。

2. 将每个数据点分配到距离最近的聚类中心所在的组。

3. 计算每个组的平均值，并将其作为新的聚类中心。

4. 重复步骤2和步骤3，直到聚类中心不再改变或达到预定的迭代次数。

Kmeans聚类的优点是简单易用，适用于大规模数据集。

但是，Kmeans聚类的缺点是需要预先确定聚类的数量K，而且对初始聚类中心的选择非常敏感。

两步分类法是一种基于特征选择和分类器的分类方法，它将数据集中的数据分成不同的类别，每个类别内的数据具有相似的特征。

两步分类法的过程包括以下几个步骤：1. 特征选择：选择最具有区分性的特征，以提高分类器的准确性。

2. 分类器训练：使用选择的特征训练分类器，以将数据集中的数据分成不同的类别。

3. 分类器测试：使用测试数据集测试分类器的准确性。

两步分类法的优点是可以自动选择最具有区分性的特征，提高分类器的准确性。

但是，两步分类法的缺点是需要大量的计算资源和时间，适用于小规模数据集。

Kmeans聚类和两步分类法是两种常用的聚类和分类方法。

在实际应用中，应根据数据集的特点和需求选择合适的方法。

【计算机应用】_k-means聚类_期刊发文热词逐年推荐_20140725

推荐指数 5 4 3 3 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46
推荐指数 7 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

2010年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106
科研热词聚类 k-means 马尔可夫模型非凸形状遗传算法资源查找节点关联度色度直方图网格维数约简粗糙集粗k-means方法神经网络社团结构用户在线行为灰度共生矩阵滤波算法混沌优化水平集样本生成数据挖掘恢复机制层次聚类算法对等系统密度孤立点检测复杂网络协同过滤动态模型创新设计创新方向识别分类内极线约束光流场主成分分析不均衡数据集 silhouette均值 p2p网络 lab颜色空间 k均值聚类 k均值 k-means聚类算法 k-means聚类 k-means算法 delaunay三角剖分 7色印刷

四种常用聚类方法

聚类就是按照某个特定标准把一个数据集分割成不同的类或簇，使得同一个簇内的数据对象的相似性尽可能大，同时不在同一个簇中的数据对象的差异性也尽可能地大。

即聚类后同一类的数据尽可能聚集到一起，不同类数据尽量分离。

主要的聚类算法可以划分为如下几类：划分方法、层次方法、基于密度的方法、基于网格的方法以及基于模型的方法。

下面主要对k-means聚类算法、凝聚型层次聚类算法、神经网络聚类算法之SOM,以及模糊聚类的FCM算法通过通用测试数据集进行聚类效果的比较和分析。

k-means聚类算法k-means是划分方法中较经典的聚类算法之一。

由于该算法的效率高，所以在对大规模数据进行聚类时被广泛应用。

目前，许多算法均围绕着该算法进行扩展和改进。

k-means算法以k为参数，把n个对象分成k个簇，使簇内具有较高的相似度，而簇间的相似度较低。

k-means算法的处理过程如下：首先，随机地选择k个对象，每个对象初始地代表了一个簇的平均值或中心;对剩余的每个对象，根据其与各簇中心的距离，将它赋给最近的簇;然后重新计算每个簇的平均值。

这个过程不断重复，直到准则函数收敛。

通常，采用平方误差准则，其定义如下：E=\sum_{i=1}^{k}\sum_{p\in C_i}\left\|p-m_i\right\|^2这里E是数据中所有对象的平方误差的总和，p是空间中的点，$m_i$是簇$C_i$的平均值[9]。

该目标函数使生成的簇尽可能紧凑独立，使用的距离度量是欧几里得距离，当然也可以用其他距离度量。

算法流程：输入：包含n个对象的数据和簇的数目k；输出：n个对象到k个簇，使平方误差准则最小。

步骤：(1) 任意选择k个对象作为初始的簇中心；(2) 根据簇中对象的平均值，将每个对象(重新)赋予最类似的簇；(3) 更新簇的平均值，即计算每个簇中对象的平均值；(4) 重复步骤(2)、(3)直到簇中心不再变化；层次聚类算法根据层次分解的顺序是自底向上的还是自上向下的，层次聚类算法分为凝聚的层次聚类算法和分裂的层次聚类算法。

第12.1章 k-Means聚类算法【本科研究生通用机器学习课程精品PPT系列】

（1）K-means 算法在散货船代货运系统中的应用（2）K-Means 算法在客户细分中的应用
4 小结本章详细地介绍了K-means算法的基本概念、基本原理,并介绍了该算法的
特点和存在的缺陷,最后介绍了K-means算法的应用,从中可以看出K-means算法的应用非常广泛。
k-均值算法 (k-Means)
其中p表示簇中的点，X是簇内点的集合，distance(p, centroid)即点p到簇质心的距离
聚类结果的SSE即各个簇的SSE之和，其值越小表示聚类质量越好
主要内容
K-Means聚类算法 k-均值算法的改进 K-中心点聚类算法
考虑改对如进下学1生: 兴归趣数一据进化行聚类
学生编号喜欢吃零食喜欢看韩剧
A
8
B
7
C
8
D
8
E
0
F
0
G
1
H
2
喜欢打篮球喜欢玩游戏工资
8
0
0 5000
8
0
1 5100
7
0
1 5080
8
1
0 5030
0
10
8 5010
2
9
8 5090
2
9
9 5020
1
8
9 5040
结果被“工资”主导了！
改进1: 归一化
为什么结果被“工资”主导了？
解决方案: 归一化
例如x2,y2的差值很大，而x1,y1等差异很小，则计算得到的欧氏距离几乎
图: 4个簇及其质心
k-均值算法 (k-Means)
指定 k = 3 (即要将数据点分成3组)
1. 随机挑选3个点作为初始簇质心(centroid)

简述k均值聚类的实现步骤

k均值聚类的实现步骤1. 简介k均值聚类（k-means clustering）是一种常用的无监督学习算法，用于将数据集划分为k个不重叠的类别。

该算法通过寻找数据集中各个样本之间的相似性，将相似的样本归为一类，从而实现聚类分析。

2. 算法步骤k均值聚类算法主要包含以下几个步骤：步骤1：初始化首先需要确定要划分的类别数k，并随机选择k个样本作为初始聚类中心。

这些聚类中心可以是随机选择的，也可以根据领域知识或经验来确定。

步骤2：分配样本到最近的聚类中心对于每个样本，计算它与各个聚类中心之间的距离，并将其分配到距离最近的聚类中心所代表的类别。

步骤3：更新聚类中心对于每个聚类，计算该类别内所有样本的平均值，作为新的聚类中心。

步骤4：重复步骤2和步骤3重复执行步骤2和步骤3，直到满足停止条件。

停止条件可以是达到最大迭代次数、聚类中心不再发生变化等。

步骤5：输出聚类结果k均值聚类算法输出每个样本所属的类别，即完成了对数据集的聚类分析。

3. 距离度量在k均值聚类算法中，需要选择合适的距离度量方法来计算样本之间的相似性。

常用的距离度量方法包括欧氏距离、曼哈顿距离和余弦相似度等。

欧氏距离欧氏距离是最常用的距离度量方法之一，它表示两个点在n维空间中的直线距离。

假设有两个点A(x1, y1)和B(x2, y2)，则它们之间的欧氏距离为：d(A, B) = sqrt((x2 - x1)^2 + (y2 - y1)^2)曼哈顿距离曼哈顿距离是另一种常用的距离度量方法，它表示两个点在n维空间中沿坐标轴方向的绝对差值之和。

假设有两个点A(x1, y1)和B(x2, y2)，则它们之间的曼哈顿距离为：d(A, B) = |x2 - x1| + |y2 - y1|余弦相似度余弦相似度是用于衡量两个向量之间的相似性的度量方法，它通过计算两个向量的夹角余弦值来确定它们的相似程度。

假设有两个向量A和B，则它们之间的余弦相似度为：sim(A, B) = (A·B) / (||A|| * ||B||)其中，A·B表示向量A和向量B的内积，||A||和||B||分别表示向量A和向量B 的模长。

外汇领域的洗钱侦测系统及关键算法研究

3)基金资助:国家自然科学基金(60403027)。

陈云开　博士研究生,研究方向为数据挖掘;孙小林　博士研究生,研究方向为数据挖掘,语义网。

计算机科学2007Vol 134№13外汇领域的洗钱侦测系统及关键算法研究3)陈云开　孙小林　马君华(华中科技大学计算机科学与技术学院　武汉430074)摘　要　目前,反洗钱成为世界各政府机构关注的热点领域。

本文从技术角度探讨了外汇领域的洗钱侦测系统及其关键算法的实现。

首先,描述了我国第一个外汇反洗钱侦测系统的架构;然后提出了一个以语义核心树SCT (Seman 2tic Core Tree )为基础的增量概念聚类算法。

该算法能解决以下问题:1)能处理海量数据集;2)能处理分类和数值型混合的数据集;3)能够清楚地解释聚类结果,使得结果易于理解。

该算法已在反洗钱框架下实现并投入使用。

关键词　反洗钱系统,数据挖掘,增量概念聚类,语义核心树,分类属性　Study on Money 2Laundering Detection System and a K ey AlgorithmCH EN Yun 2Kai SUN Xiao 2Lin MA J un 2Hua(School of Computer Science and Technology ,Huazhong University of Science &Technology ,Wuhan 430074)Abstract At present ,anti 2money laundering has become a hot topic of the entire world.From the point of view of technique ,this paper discusses a money 2laundering detection system for administration of foreign exchange and one of its key algorithms.It first gives the framework of the system ,which is the first anti 2money laundering system of our nation.And then it proposes an SCT (Semantic Core Tree )2based incremental conceptual clustering algorithm.The al 2gorithm could solve the problems of 1)large volume of data set ;2)mixture of categorical and numerical data ;3)easy understanding of result.The algorithm has been employed in the money laundering detection system.K eyw ords Anti 2money laundering system ,Data mining ,Incremental conceptual clustering ,Semantic core tree ,Cate 2gorical 1　引言洗钱活动与走私、贩毒、恐怖活动、贪污腐败等刑事犯罪相联系,对国家的政治稳定、社会安定、经济安全及国际政治经济体系的安全构成严重威胁。

改进K-means算法在B2C电子商务客户细分中的应用

时红军，韩兵
摘要：客户细分是企业精确制定营销策略和成功管理客户群的基础，随着网络和电子商务的迅猛发展，对个性化客户服务提出更高要求。提出一种改进的Ｋ－ａｓ算法，该算法依照同心圆的方式对整个区域划分，并充分考虑小区域内个体的密ｍｅｎ度。并运用改进的Ｋｍｅｎ算法对客户进行划分，显著提高聚类质量，提高电子商务企业开展营销活动的针对性和有效性。－ａｓ关键词：数据挖掘；Ｋｍｅｓ－ａ算法；客户细分ｎ中图分类号：Ｔ３１Ｐ９．９文献标志码：Ａ
０引言
在激烈竞争的网络商业时代，电子商务企业必须留住老顾客，发展新顾客并锁定利润最高的客户，预测客户客户未来的购买趋势，制定相应的营销策略和客户管理策略。为了实现这个目标，企业就需要尽可能地了解客户的行为，尽可能收集顾客的信息，借助各种分析方法，透过无序的、表层的信息挖掘出内在的知识和规律。利用聚类算法分析出具有相似浏览或购买行为的客户群，并分析客户的共同特征，进而对客户进行细分，帮助电子商务企业了解自己的客户，为客户聚类群体提供更合适、更全面的个性化服务，选择最有开发价值的目标客户群体，发现潜在客户，集中企业优势，制定有效的营销策略…。
一
（）１从数据集中随机选择个对象，每一个对象作为一个类的 “ 心 ” ，别代表要分成的个类；中分
（）据距离中心最近的原则，找与各对象最为相近的２根寻

gis中的k聚类函数

gis中的k聚类函数在GIS（地理信息系统）中，K-means聚类是一种常用的聚类分析方法。

K-means聚类是一种迭代算法，它将数据集划分为K个聚类，使得每个数据点与其所在聚类的中心点之间的平方距离之和最小。

下面是使用Python中的Scikit-learn库进行K-means聚类的基本步骤：1. 导入必要的库：```pythonimport numpy as npimport as pltfrom import KMeans```2. 创建数据集：这里以二维数据为例。

您可以使用自己的GIS数据替换以下示例数据。

```python示例数据data = ([[1, 2], [1, 4], [1, 0], [4, 2], [4, 4], [4, 0]]) ```3. 创建KMeans对象并拟合数据：```python设置聚类数量为2kmeans = KMeans(n_clusters=2)拟合数据(data)```4. 获取聚类结果：```python获取每个点的聚类标签labels = _获取每个聚类的中心点cluster_centers = _centers_```5. 可视化结果：```python可视化聚类结果和中心点(data[:, 0], data[:, 1], c=labels) 使用标签进行颜色编码(cluster_centers[:, 0], cluster_centers[:, 1], c='red') 将中心点绘制为红色圆圈()```以上代码将绘制一个散点图，其中每个点的颜色表示其所属的聚类，红色的圆圈表示每个聚类的中心点。

您可以根据实际需要修改数据集、聚类数量以及可视化部分的代码来满足您的需求。

R语言-层次聚类、k-means聚类、PAM

R语⾔-层次聚类、k-means聚类、PAM 层次聚类1、定义每⼀个观测量为⼀类2、计算每⼀类与其他各类的距离3、把距离最短的两类合为⼀类4、重复步骤2和3，直到包含所有的观测量合并成单类时> ##########################聚类算法> ####层次聚类> par(mfrow = c(1,1))> data(nutrient,package = "flexclust")> s(nutrient)<-tolower(s(nutrient))> #数据中⼼标准化scale（）> nutrient_s<-scale(nutrient,center = T)> View(nutrient_s)> #⽤dist()函数求出距离euclidean-欧⼏⾥得距离常⽤> d<-dist(nutrient_s,method = "euclidean")> #求出距离带⼊hclust函数中⽤ward⽅法聚类> cnutrient<-hclust(d,method = "ward.D")> plot(cnutrient,hang = -1,cex=.8,main='averher linkage clustering')探究模型确定聚成⼏类合适> ####⽤NbClust函数确定聚类K值> library(NbClust)> NC<-NbClust(nutrient_s,distance = "euclidean",min.nc = 2,max.nc = 15,method = "average")> table(NC$Best.n[1,])0 1 2 3 4 5 9 10 13 14 152 1 4 4 2 4 1 1 2 1 4> barplot(table(NC$Best.n[1,]))根据列表和柱状图我们可知聚为2、3、5、15类为不错的选项下⾯我们看看聚为5类的结果#####确定聚类个数后cut树clusters<-cutree(cnutrient,k=5)table(clusters)plot(cnutrient,hang = -1,cex=.8,main='averher linkage clustering')rect.hclust(cnutrient,k=5)因为层次聚类计算距离⾮常复杂，所以能计算较⼩是数据集K-Means聚类1、选k个聚类中⼼点（随机⽣成）2、把每个样本划分到距离最近的中⼼点3、更新每类的中⼼点（可以把类的质⼼作为中⼼点）4、重复2、3步骤，直⾄数据收敛> #############k-means聚类> data(wine,package = "rattle")Type Alcohol Malic Ash Alcalinity Magnesium Phenols Flavanoids Nonflavanoids1 1 14.23 1.71 2.43 15.6 127 2.80 3.06 0.282 1 13.20 1.78 2.14 11.2 100 2.65 2.76 0.263 1 13.16 2.36 2.67 18.6 101 2.80 3.24 0.30Proanthocyanins Color Hue Dilution Proline1 2.29 5.64 1.04 3.92 10652 1.28 4.38 1.05 3.40 10503 2.81 5.68 1.03 3.17 1185> df<-scale(wine[,-1],center = T)> #确定聚类个数> library(NbClust)> nck<-NbClust(df,distance = "euclidean",min.nc = 2,max.nc = 15,method = "kmeans")> table(nck$Best.n[1,])0 1 2 3 14 152 1 2 19 1 1> barplot(table(nck$Best.n[1,]))从数据和图像可知聚为3类最好。

一种基于K—means的自适应聚类算法的研究

◇ 业育职教 ◇
科技国向导
２１年第０期０２２
一
种基于Ｋ— ａｓ自适应聚类算法的研究ｍｅｎ的
唐燕雯（西工商职业技术学院广西广南宁５００）３０３
【要】摘聚类（１ｔｉ是数据挖掘中的一种主要技术， — ｅｎ算法是一种重要的经典的划分方法，算法在Ｋ值的确定、ｃｕｅｎｓｒＫｍａｓ但该质心的选
取、维数的依赖上存在问题，对本文提出了一种改进的自适应算法，用于解决Ｋ值的确定、质心的选取等问题。聚类效果较好。【关键词】聚；— ｅ自Ｋｍａｍ；适应；算法・
好的聚类结果应该是同一类间的各数据对象间相似度大．同而不０引言．ＤＩ分母越大聚类（１ｔｉ）数据挖掘中的一种主要技术．ＣＵｅｎ；Ｓｒｇｌ￣是按照一定要求类之间的相似度小．Ｂ能够满足这个条件，即分子越小．ＤＩ则代表各聚类内数据相似度大而类间的相似度小，和规律对一组个体进行区分和分类的过程．主要目的是使的属于同一时，Ｂ的值越小．类别的个体之间的距离尽可能的小．同类别上的个体间的距离尽从这个值可以确定通过Ｄｍｘｍｎ（ｌ）（，｝而不＝ａ｛ｉ（ｅ，，ｃｊ，ｄＪｄ２）查找到的ｘ是否ｊ可能的大．聚类属于无监督分类的范畴。划分聚类（ａｉｏｉ是最佳中心，Ｐｒｔｎｎｔｉｇ既而确定最佳的聚类数目。Ｍｔｏｓｅｄ）ｈ是聚类中的重要方法．指对于一个给定包含ｎ对象或元组个找到新聚类中心ｘ．聚类．ｉ进行重新计算聚类的中心。目前形成对的数据库．通过基于划分的方法由用户给定构建数据的ｋ个划分．每的ｋ个聚类．计算其ＤＩ前一次计算的ＤＩ行比较．如果Ｂ和Ｂ进个划分表示一个簇．并且ｋ＝＜ｎＤＩｗＤＩｄ则ｘ可以作为聚类中心．Ｂｎ＜Ｂｏ．ｊｅｌ同时ｋ原来的基础上加在１Ｋ－．ｍｅａｓ算法ｎ１否则算法终止。．Ｋｍａｓ法是重要的划分方法，Ｊ．ａＱｅｎ出． — ｅｎ算由．Ｍｃｕｅ提Ｂ具有广（如果找到的数据对象是中心，４）则计算Ｄｍｘｉｄｅ，，（，＝ａ｛ｎ（ｊｄ２ｍ（１）ｅ泛的影响力。其基本原理是，首先指定聚类数ｋ从含有ｎ，个对象的数ｄ３ｊｊ ’ １２ …，。（，）ｊ＝，，ｎ存在这样的数据对象，到（。依次类推直ｅ），转３）据集合中随机地选择ｋ个对象作为一个簇的初始平均值或中心。计算到跳出循环剩余的各个对象到这些簇中心的距离．然后根据其与各个簇中心的距从确定的过程可以看出．少了人为的干预．免了由于参数设减避离．将它赋给最近的簇。然后重新计算每个簇的平均值作为该簇新的定不当对聚类结果造成的影响聚类中心．相邻的聚类中心没有任何变化，如果则样本调整结束，聚类２３－对改进ｋｍａｓ法的描述 — ｅｎ算

lloyd算法和k-mean算法

Lloyd算法和K-means算法是在数据挖掘和机器学习领域中常用的聚类算法。

它们都是基于迭代优化方法，通过将数据点分配到不同的聚类中心来实现聚类。

在本文中，我们将对这两种算法进行详细的介绍和比较。

1. Lloyd算法Lloyd算法，也称为K-means算法，是一种迭代优化算法，用于将数据点分配到K个聚类中心中。

该算法的基本思想是不断迭代地更新聚类中心，直到达到收敛条件为止。

具体步骤如下：1) 随机初始化K个聚类中心；2) 将每个数据点分配到距离最近的聚类中心所在的类别中；3) 更新每个聚类中心为其所包含数据点的平均值；4) 重复步骤2和步骤3，直到满足收敛条件。

Lloyd算法的优点在于简单、直观，并且易于实现。

然而，该算法也有一些缺点，例如对初始聚类中心的选择敏感，容易陷入局部最优解等。

2. K-means算法与Lloyd算法相似，K-means算法也是一种聚类算法，用于将数据点分配到K个聚类中心中。

与Lloyd算法不同的是，K-means算法在每次迭代中优化的是目标函数，而不是直接更新聚类中心。

具体步骤如下：1) 随机初始化K个聚类中心；2) 将每个数据点分配到距离最近的聚类中心所在的类别中；3) 更新目标函数，如聚类距离的总平方和；4) 重复步骤2和步骤3，直到满足收敛条件。

K-means算法相对于Lloyd算法的优点在于可以更灵活地定义目标函数，从而更好地适应不同的数据分布。

然而，K-means算法也有一些缺点，如对初始聚类中心的选择敏感，容易陷入局部最优解等。

3. 对比分析在实际应用中，Lloyd算法和K-means算法都有各自的优劣势。

Lloyd算法相对简单直观，易于理解和实现，适用于大规模数据集。

但是，Lloyd算法容易受到初始聚类中心的选择影响，从而得到不理想的聚类结果。

相比之下，K-means算法可以更灵活地定义目标函数，适应不同的数据分布，提高聚类效果。

但是，K-means算法要求目标函数的连续性和可微性，适用范围相对较窄。

基于SPSS和KNIME的K_means聚类结果研究

但是，K -means 方法只有在簇的平均值被定义的情况下才能使用,这可能不适用于某些应用，例如涉及有分类属性的数据。该方法的一个缺点是要求用户必须事先给出 k ( 要生成的簇的数目 ) 。 K -means 方法不适用于发现非凸面形状的簇。此外，它对于“噪声”和孤立点数据敏感,少量的该种数据能够对平均值产生极大的影响。 2 SPSS 和 KNIME 的介绍
1 K-means 算法
K - means [2] 算法是一种著名的并且常用的聚类方法。
K -means 以 k 为参数，把 n 个对象分为 k 个簇 (cluster),
以使簇内具有较高的相似度，而簇间的相似度较低。相
似度的计算是根据一个簇中对象的平均值(被看作簇的
5
表 5 SPSS 中 K-means 运算的结果 (k=3)
Cluster 组织文化组织氛围领导角色员工发展包含数目
1 89 . 50 88 . 75 82 . 25 83 . 25
8
2 68 . 33 69 . 83 90 . 17 86 . 67
6
3 79 . 00 87 . 00 50 . 00 51 . 00
《微型机与应用》 2010 年第 12 期
综述与评论 Review and Comment
表 4 SPSS 中 K-means 运算的结果 (k=2)
Cluster 组织文化组织氛围领导角色员工发展包含数目
1 75 . 20 75 . 60 87 . 60 87 . 20
10
2 90 . 60 92 . 00 74 . 60 73 . 00

基于k-means算法的数据挖掘与客户细分研究

大数据时代，善于从中挖掘对企业有用的信息，可以开拓新的市场和机会。图 1 简单说明了数据分析的过程。
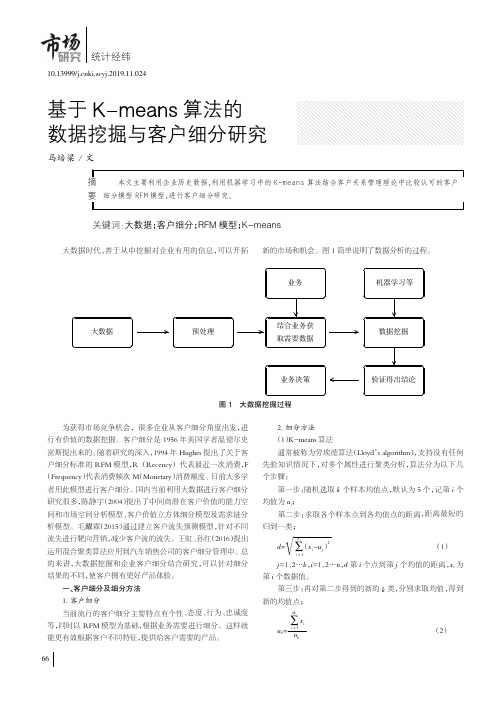
业务
机器学习等
大数据
预处理
结合业务获取需要数据
数据挖掘
业务决策
验证得出结论
图 1 大数据挖掘过程
为获得市场竞争机会，很多企业从客户细分角度出发，进行有价值的数据挖掘。客户细分是 1956 年美国学者温德尔史密斯提出来的。随着研究的深入，1994 年 Hughes 提出了关于客户细分标准的 RFM 模型，R （Recency）代表最近一次消费，F （Frequency）代表消费频次 M（Monetary）消费额度。目前大多学者用此模型进行客户细分。国内当前利用大数据进行客户细分研究很多，陈静宇（2004）提出了中间商潜在客户价值的能力空间和市场空间分析模型、客户价值立方体细分模型及需求链分析模型。毛躍霖（2015）通过建立客户流失预测模型，针对不同流失进行靶向营销，减少客户流的流失。王虹、孙红（2016）提出运用混合聚类算法应用到汽车销售公司的客户细分管理中。总的来讲，大数据挖掘和企业客户细分结合研究，可以针对细分结果的不同，使客户拥有更好产品体验。
由于 k-means 均值算法分类 k 值随机选取，为了选取更好
的分类结果，评估最优的聚类个数，有两种方法：平均轮廓系数
和手肘法.平均轮廓系数公式表示：
Si=
xi -yi max{xi ，yi
}
（4）
xi 表示第 i 个聚类点到本类其他店的平均距离。yi 表示第 i 个聚类点到其他类中点的平均距离 Si 取值范围为（-1，1）越接近 1 表明分类越好。
一尧客户细分及细分方法 1. 客户细分当前流行的客户细分主要特点有个性、态度、行为、忠诚度等，同时以 RFM 模型为基础，根据业务需要进行细分。这样就能更有效根据客户不同特征，提供给客户需要的产品。

第7章某移动公司客户价值分析

聚类后RFM每个维度上取平均值（也就是聚类中心），再根据RFM三个指标组成的元组判断每个群体分别属于哪种价值类别的客户。
7.3.1 读入数据并进行数据预处理
（2）数据准备
首先，创建一个用于本章代码运行的工作目录，将准备好的数据集拷贝到此工作目录下，数据文件名命名为 “ RFM 聚类分析 .xlsx ” ，然后在 Jupyter Notebook中将数据读入以进行后续分析预处理。
➢TEXT add here
7.2 K-Means聚类算法简介
3.K-Means算法流程
数据初始状态如下图所示。
➢TEXT add here ➢TEXT add here ➢TEXT add here
7.2 K-Means聚类算法简介
3.K-Means算法流程
（1）选择聚类的个数k，此时会生成k个类的初始中心，例如：k=3，生成k个聚类中心点，如下图所示。
#统计数据缺失值 data.isnull().sum()
7.3.1 读入数据并进行数据预处理
（6）检测和过滤异常值
首先需要检测有哪些列存在0值，以便观察出哪些列的0值会造成行数据的无效统计，统计结果如右图所示。
#统计有0值的数据列 (data == 0).any()
接着观察结果可以看到，除了user_id（用户id），last_pay_time（最后一次消费时间），online_time（网络在线时间）三列外，其他的列均存在0值。为了进一步观察数据，需要对每一列0值个数进行统计。
7.3.1 读入数据并进行数据预处理
（6）检测和过滤异常值
通过对每列的各行数据进行遍历判断，可以统计出每列0值个数，结果如右图所示。

手写KMeans算法

⼿写KMeans算法KMeans算法是⼀种⽆监督学习，它会将相似的对象归到同⼀类中。

其基本思想是：1.随机计算k个类中⼼作为起始点。

2. 将数据点分配到理其最近的类中⼼。

3.移动类中⼼。

4.重复2,3直⾄类中⼼不再改变或者达到限定迭代次数。

具体的实现如下：from numpy import *import matplotlib.pyplot as pltimport pandas as pd# Load dataseturl = "https:///ml/machine-learning-databases/iris/iris.data"names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'class']dataset = pd.read_csv(url, names=names)dataset['class'][dataset['class']=='Iris-setosa']=0dataset['class'][dataset['class']=='Iris-versicolor']=1dataset['class'][dataset['class']=='Iris-virginica']=2#对类别进⾏编码，3个类别分别赋值0，1，2#算距离def distEclud(vecA, vecB): #两个向量间欧式距离return sqrt(sum(power(vecA - vecB, 2))) #la.norm(vecA-vecB)#初始化聚类中⼼：通过在区间范围随机产⽣的值作为新的中⼼点def randCent(dataSet, k):#获取特征维度n = shape(dataSet)[1]#创建聚类中⼼0矩阵 k x ncentroids = mat(zeros((k,n)))#遍历n维特征for j in range(n):#第j维特征属性值min ,1x1矩阵minJ = min(dataSet[:,j])#区间值max-min，float数值rangeJ = float(max(dataSet[:,j]) - minJ)#第j维，每次随机⽣成k个中⼼centroids[:,j] = mat(minJ + rangeJ * random.rand(k,1))return centroidsdef randChosenCent(dataSet,k):# 样本数m=shape(dataSet)[0]# 初始化列表centroidsIndex=[]#⽣成类似于样本索引的列表dataIndex=list(range(m))for i in range(k):#⽣成随机数randIndex=random.randint(0,len(dataIndex))#将随机产⽣的样本的索引放⼊centroidsIndexcentroidsIndex.append(dataIndex[randIndex])#删除已经被抽中的样本del dataIndex[randIndex]#根据索引获取样本centroids = dataSet.iloc[centroidsIndex]return mat(centroids)def kMeans(dataSet, k):# 样本总数m = shape(dataSet)[0]# 分配样本到最近的簇：存[簇序号,距离的平⽅]# m⾏ 2 列clusterAssment = mat(zeros((m, 2)))# step1:# 通过随机产⽣的样本点初始化聚类中⼼centroids = randChosenCent(dataSet, k)print('最初的中⼼=', centroids)# 标志位，如果迭代前后样本分类发⽣变化值为Tree，否则为FalseclusterChanged = True# 查看迭代次数iterTime = 0# 所有样本分配结果不再改变，迭代终⽌while clusterChanged:clusterChanged = False# step2:分配到最近的聚类中⼼对应的簇中for i in range(m):# 初始定义距离为⽆穷⼤minDist = inf;# 初始化索引值minIndex = -1# 计算每个样本与k个中⼼点距离for j in range(k):# 计算第i个样本到第j个中⼼点的距离distJI = distEclud(centroids[j, :], dataSet.values[i, :])# 判断距离是否为最⼩if distJI < minDist:# 更新获取到最⼩距离minDist = distJI# 获取对应的簇序号minIndex = j# 样本上次分配结果跟本次不⼀样，标志位clusterChanged置Trueif clusterAssment[i, 0] != minIndex:clusterChanged = TrueclusterAssment[i, :] = minIndex, minDist ** 2 # 分配样本到最近的簇iterTime += 1sse = sum(clusterAssment[:, 1])print('the SSE of %d' % iterTime + 'th iteration is %f' % sse)# step3:更新聚类中⼼for cent in range(k): # 样本分配结束后，重新计算聚类中⼼# 获取该簇所有的样本点ptsInClust = dataSet.iloc[nonzero(clusterAssment[:, 0].A == cent)[0]]# 更新聚类中⼼：axis=0沿列⽅向求均值。

解释k-mean聚类、系统聚类、二阶聚类的概念

解释k-mean聚类、系统聚类、二阶聚类的概念K-means聚类是一种常用的无监督学习算法，用于将数据集分成k个不同的类别。

算法通过迭代计算各个数据点与聚类中心的距离，将其分配到距离最近的聚类中心所属的类别中。

系统聚类是将数据集中的数据点按照相似度进行树形结构的聚类，从而形成一个层次结构。

系统聚类有两种方法：聚合法和分裂法，两者的具体实现方式略有不同，但都是基于相似度进行聚类。

二阶聚类是一种特殊的聚类方法，也称为子空间聚类。

它将数据集看作多个子空间的交，将每个子空间看作一个单独的聚类问题，通过对子空间进行聚类，最终形成完整的数据聚类。

二阶聚类可用于处理高维数据，也可用于解决数据集中存在多个子簇的情况。