材料力学第六版答案第06章
材料力学(金忠谋)第六版课后习题及答案

解
(1) ∆l1
=
1 3
Ρxl1
Ε 1Α1
∆l1 = ∆l2 x = 0.6m
∆l 2
=
1 3
Ρ (3 − x)l2
Ε 2Α2
(2) Ρ ≤ 3Ε1Α1 = 3× 200 × 2 ×10−1 = 200ΚΝ
xl1
0.6× 2
2-11 铰接的正方形结构如图所示,各杆材料皆为铸铁,许用拉应力[σ +]=400kg/cm2, 许用压应力[σ − ]=600kg/cm2,各杆的截面积均等于25cm2。试求结构的许用载荷P。
习题
2-1 一木柱受力如图示,柱的横截面为边长20cm的正方形,材料服从虎克定律,其
弹性模量 E = 0.10 ×105 MPa.如不计柱自重,试求:
(1) (2) (3) (4)
作轴力图; 各段柱横截面上的应力; 各段柱的纵向线应变; 柱的总变形.
解:
(1) 轴力图
(2) AC 段应力
σ
=
−100 ×103 0.2 2
= −2.5×106 Ρa = −2.5ΜΡa
CB 段应力
σ
=
− 260 ×103 0.2 2
= −6.5×106 Ρa = −6.5ΜΡa
(3) AC 段线应变
ε = σ = −2.5 = −2.5×10−4 Ε 0.1×105 CB 段线应变
ε
=σ Ε
=
−6.5 0.1×10 5
解:
AC、CB、BD、DA 杆受拉力,大小为 Τ1 =
Ρ 2
DC 杆受压力,大小为 Τ2 = Ρ
[σ
+
]≥
Τ1 Α
得 Ρ1 ≤ 2 × 400 × 25 = 14142kg
材料力学06(第六章 弯曲应力)分析

F / 4 2 103 mm 134 mm
30 MPa 5493104 mm4
F 24.6 kN
因此梁的强度由截面B上的最大拉应力控制
[F] 19.2 kN
§6-3 梁横截面上的切应力•梁的切应力强度条件
Ⅰ、梁横截面上的切应力
分离体的平衡
横截面上切应力 分布规律的假设
横截面上弯曲切 应力的计算公式
二.工字形截面梁 1、腹板上的切应力
h
d
y
d
O
y b
O
' A*
y dA
FS
S
* z
Izd
S
* z
bd
2
h
d
d 2
h 2
d
2
y2
腹板与翼缘交界处
max
min
FS Izd
bd
h d
max O
中性轴处
max
FS
S
* z,m
ax
Izd
y
min
FS
bd
h
d
d
h
d
2
I z d 2
160 MPa 148 MPa
2
Ⅲ 梁的正应力强度条件
max 材料的许用弯曲正应力
中性轴为横截面对称轴的等直梁
M max
Wz
拉、压强度不相等的铸铁等脆性材料制成的梁
为充分发挥材料的强度,最合理的设计为
t,max
M max yt,max Iz
[
t]
c,max
M max yc,max Iz
Myc,max Iz
典型截面的惯性矩与抗弯截面系数 ( d D)
b
材料力学(金忠谋)第六版答案第06章.doc

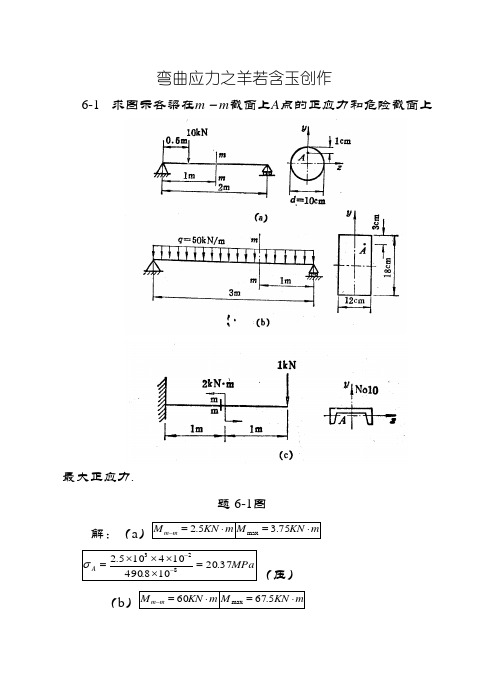
弯曲应力6-1 求图示各梁在m-m截面上A点的正应力和危险截面上最大正应力。
题6-1图解:(a)mKNMmm⋅=-5.2mKNM⋅=75.3max48844108.49064101064mdJx--⨯=⨯⨯==ππMPaA37.20108.490104105.2823=⨯⨯⨯⨯=--σ(压)MPa2.38108.4901051075.3823max=⨯⨯⨯⨯=--σ(b )m KN M m m ⋅=-60 m KN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯== MPa A 73.611058321061060823=⨯⨯⨯⨯=--σ (压) MPa 2.104105832109105.67823max =⨯⨯⨯⨯=--σ (c )m KN M m m ⋅=-1 m KN M ⋅=1max48106.25m J x -⨯=36108.7m W x -⨯=cm y A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ (压) MPa 2.128106.2510183max =⨯⨯=-σ 6-2 图示为直径D =6 cm 的圆轴,其外伸段为空心,内径d =4cm ,求轴内最大正应力。
解:)1(32431απ-=D W x⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π 361002.17m -⨯=3463321021.213210632m D W x --⨯=⨯⨯==ππMPa 88.521002.17109.0631=⨯⨯=-σ MPa 26.551021.2110172.1631=⨯⨯=-σ MPa 26.55max =σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。
试求梁内最大拉应力与最大压应力。
已知I z =10170cm 4,h 1=9.65cm ,h 2=15.35cm 。
材料力学(金忠谋)第六版完整版问题详解

第一章 绪论1-1 求图示杆在各截面(I )、(II )、(III )上的力,并说明它的性质.解:(a )I-I 截面: N = 20KN (拉)II-II 截面: N = -10KN (压)III-III 截面: N = -50KN (压)(b )I-I 截面: N = 40KN (拉)II-II 截面: N = 10KN (拉)III-III 截面: N = 20KN (拉)1-2 已知P 、M 0、l 、a ,分别求山下列图示各杆指定截面(I )、(II)上的力解:(a ):(I )截面:力为零。
(II )截面:M = Pa (弯矩)Q = -P (剪力)(b ):(I )截面:θsin 31P Q =θsin 61PL M = (II )截面:θsin 32P Q = θsin 92PL M =(c ):(I )截面:L M Q 0-= 021M M = (II )截面:L M Q 0-= 031M M =1-3 图示AB 梁之左端固定在墙,试求(1)支座反力,(2)1-1、2-2、3-3各横截面上的力(1-1,2-2是无限接近集中力偶作用点.)解:10110=⨯=A Y (KN )1055.110-=+⨯-=A M (KN-M )(1-1) 截面:10110=⨯=Q (KN )521110-=⨯⨯-=M (KN-M ) (2-2)截面:10=Q (KN )055=-=M (KN-M )(2-3)截面:10=Q (KN )551110-=+⨯⨯-=M (KN-M )1-4 求图示挂钩AB 在截面 1-1、2-2上的力.解:(1-1)截面:P N 32=a P M ⋅=43 (2-2)截面:P Q 32=a P M ⋅=321-5 水平横梁AB 在A 端为固定铰支座,B 端用拉杆约束住,求拉杆的力和在梁1-1截面上的力.解:(1)拉杆力T :1230sin 0⨯=⨯⋅=∑P T M A ο 10030sin 2100=⨯=οT (KN )(拉) (2)(1-1)截面力:Q 、N 、M :5030sin -=-=οT Q (KN )6.8630cos -=-=οT N (KN )(压)()2550.030sin =⨯=οT M (KN-M )1-6 一重物 P =10 kN 由均质杆 AB 及绳索 CD 支持如图示,杆的自重不计。
材料力学(金忠谋)第六版完整编辑版规范标准答案

解:(a):(I)截面:内力为零。
(II)截面:M = Pa(弯矩)
Q = -P(剪力)
(b):(I)截面:
(II)截面:
(c):(I)截面:
(II)截面:
1-3图示AB梁之左端固定在墙内,试求(1)支座反力,(2)1-1、2-2、3-3各横截面上的内力(1-1,2-2是无限接近集中力偶作用点.)
解:
(1)
(2)
即
解得
各杆的长度为
2-37图示三杆结构中,杆(1)是铸铁的,E1=120Gpa, =80MPa;杆(2)是铜的,EA=100GPa, =60Gpa;杆(3)是钢的,EA=200GPa, =120Mpa。载荷P=160kN,设A1:A2:A3=2:2:1,试确定各杆的截面积。
解:
各杆的应力关系为
解
(1)
(2)
2-11铰接的正方形结构如图所示,各杆材料皆为铸铁,许用拉应力[ +]=400kg/cm2,许用压应力[ ]=600kg/cm2,各杆的截面积均等于25cm2。试求结构的许用载荷P。
解:
AC、CB、BD、DA杆受拉力,大小为
DC杆受压力,大小为
得
得
故
2-12图示拉杆沿斜截面m-n由两部分胶合而成,设在胶合面上许用拉应力[ ]=100MPa,许用剪应力 =50MPa,胶合面的强度控制杆件的拉力,试求:为使杆件承受最大拉力P, 角的值应为多少?若横截面面积为4cm2,并规定 ,试确定许可载荷P。
解:
只计P时,有
只计2P时,有
且有
联立,解得
(方向水平向左) (方向水平向右)
(b)
材料力学课后标准答案

解:取轴向长为 的管分析:微元 上,作用力为
向分量 ,积分得
则: ,而
则:
题6-12图题6-13图
6-13长输水管受内压 ,管的内径为 , , ,用第四强度理论计算壁厚。(提示:可设管的轴向应变为零。)
解: ,数据代入,得:
,
所以
现已知
,
得
题6-5图
题6-6图题6-7图
6-6图示简支梁为 工字梁, , 。 点所在截面在集中力 的左侧,且无限接近 力作用的截面。试求: 点在指定斜截面上的应力; 点的主应力及主平面位置(用单元体表示)。
解: 所处截面上弯矩、剪力:
,
查型钢表后, 点以下表面对中性轴静矩:
,
同理,积分得
所以, 处转角为 ,为顺时针方向; 处挠度为 ,为竖直向下。
8-6试求图示各刚架 点的竖直位移,已知刚架各杆的 相等。
解: 段: ; 段上
由卡氏定理, 处的竖直位移
分段带入后面积分:
为正值,则与 同向,竖直向下
分析可知, 处已经作用有竖直方向的力,为了能利用卡氏定理解题, 处和竖杆中间处的 分别为
(压), (拉)
进而求得 (拉),由
求得:
8-3计算图示各杆件结构的变形能。
题8-3图
解: 首先求解 处的约束反力为
弯矩方程为:
则
分段积分:
解: 以逆时针方向为正,
,积分得
8-4试求图示各梁的 点的挠度的转角。
题8-4图
解: 以 点为 轴起点,结构的弯矩方程为:
则:
得
撤去 和 ,在 处作用逆时针向
材料力学(金忠谋)第六版答案第06章
弯曲应力之羊若含玉创作6-1 求图示各梁在m -m 截面上A 点的正应力和危险截面上最大正应力.题 6-1图解:(a )m KNM m m ⋅=-5.2m KN M ⋅=75.3maxMPa A 37.20108.490104105.2823=⨯⨯⨯⨯=--σ (压)(b )m KN M m m ⋅=-60m KN M ⋅=5.67maxMPa A 73.611058321061060823=⨯⨯⨯⨯=--σ (压)(c )m KN M m m ⋅=-1m KN M ⋅=1maxMPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ (压)6-2 图示为直径D =6 cm 的圆轴,其外伸段为空心,内径d =4cm ,求轴内最大正应力.解:)1(32431απ-=D W x6-3T 字形截面铸铁梁的尺寸与所受载荷如图示.试求梁内最大拉应力与最大压应力.已知I z =10170cm 4,h 1,h 2.解:A 截面:Mpa 95.371065.9101017010402831max =⨯⨯⨯⨯=--σ (拉)E截面(拉)(压)6-4 一根直径为d的钢丝绕于直径为D的圆轴上.(1)求钢丝由于弯曲而产生的最大弯曲正应力(设钢丝处于弹性状态)(2)若d=lmm,弹性模量E=210GPa,求不使钢丝产生残存变形的轴径D.6-5 矩形悬臂梁如图示.已知l= 4 m,,q=10kN/m,许用应力[σ]=10Mpa.试确定此梁横截面尺寸.6-6 20a工字钢梁的支承和受力情况如图所示.若[σ]=160MPa,试求许用载荷P.[][]P W M 32102371016066=⨯⨯⨯=⋅=-σ (M 图) P 32 6-7压板的尺寸和载荷情况如图所示.资料为 45钢,s σ=380 MPa ,取平安系数5.1=n .试校核压板强度.解:2331568)121230122030(101m m W =⨯-⨯⨯=6-8由两个槽钢组成的梁受力如图示.已知资料的许用应力[σ]=150 MPa ,试选择槽钢号码.解:m KN M ⋅=60max查表:(22a , 332006.217cm cm W x >=)( M 图)6-9割刀在切割工件时,受到P =1kN 的切销力的作用.割刀尺寸如图所示.试求割刀内最大弯曲应力.解:m N p M ⋅=⨯⨯=-I 81083 6-10 图示圆木,直径为D ,需要从中切取一矩形截面梁.试问(1)如要使所切矩形截面的抗弯强度最高,h 、b 分离为何值?(2)如要使所切矩形截面的抗弯刚度最高,h 、b 又分离为何值?解:6)(6222b D b bh W -==∴从强度讲:D b 57735.0=∴从刚度讲D b 50.0=6-11T 字形截面的铸铁梁受纯弯曲如图示,欲使其最大压应力为最大拉应力的3倍,巳知h = 12cm ,t =3cm ,试确定其翼板宽度b 之值.解:3max max =下上拉压y y =σσ6-12 图示简支梁,由工字钢制成,在外载荷作用下,测得横截面A 处梁底面的纵向正应变4100.3-⨯=ε,试盘算梁的最大弯曲正应力σmax .已知钢的弹性模量E =200GPa, a =1m.解:MPa E A 60100.31020049=⨯⨯⨯==-εσ (M 图)6-13 试盘算图示矩形截面简支梁的1-1面上a 点和b 点的正应力和剪应力.解:1-1截面6-14 盘算在均布载荷q =10 kN /m 作用下,圆截面简支梁的最大正应力和最大剪应力,并指出它们产生在何处.解:232max 110108181⨯⨯⨯==ql MMPa86.101= 在跨中点上、下边沿 MPa 46.25= 在梁端,中性轴上6-15试盘算6-12题工字钢简支梁在图示载荷下梁内的最大剪应力.解:(Q 图)6-16 矩形截面木梁所受载荷如图示,资料的许用应力[σ]=10Mpa.(Q 图) (M 图)6-17 试为图示外伸梁选择一工字形截面,资料的许用应力[σ]= 160MPa ,[τ]=80Mpa.故 取No16工字钢(Q 图) (M 图)6-18 图示起重机装置在两根工字形钢梁上,试求起重机在移动时的最危险位置及所采取工字型钢的号码.已知 l =10 m ,a =4 m ,d =2 m.起重机的重量W =50 kN ,起重机的吊重P =10 kN ,钢梁资料的许用应力[σ]=160 MPa ,[τ]=100Mpa.取6-19等腰梯形截面梁,其截面高度为h .用应变仪测得其上试求此截面形心的位置.6-20 简支梁承受均布载荷q 模量E ,试求梁最底层纤维的总伸长.6-21矩形截面悬臂梁受力如图(a )所示,若设想沿中性层把梁离开为上下两部分:(1)试求中性层截面上剪应力沿x 轴向的变更纪律,拜见图(b );(2)试说明梁被截下的部分是怎样平衡的?解:(1(2T由弯曲产生的轴间力为N6-22 正方形截面边长为a ,设水平对角线为中性轴.试求(1最大;(2)若截面上的弯矩不变,新截面的最大正应力是原截面的几倍?(提示:盘算I z 时可按图中虚线分三块来处理). 解:原来正方形:6-23 悬臂梁AB 受均布载荷q 及集中力P 作用如图示.横截.试盘算最大剪应力τmax 值及其所在位置.6-24试绘出图中所示各截面的剪应力流偏向,并指出弯曲中心的大致位置.解:6-25确定启齿薄壁圆环截面弯曲中心的位置.设环的平均半径R 0,壁厚t ,设壁厚t 与半径0R 相比很小.解:ϕϕsin 00⋅⋅⋅=R t d R dS6-26试导出图示不合错误称工字形截面的弯曲中心位置(当在垂直于对称轴的平面内弯曲时).假设厚度t 与其他尺寸相比很小.解:z J t h b e 4)2(221= 6-27 在均布载荷作用下的等强度悬臂梁,其横截面为矩形,并宽度b =常量,试求截面高度沿梁轴线的变更纪律解:2022023621bh ql bh ql W M l ===σ6-28 图示变截面梁,自由端受铅垂载荷P 作用,梁的尺寸l 、b 、h 均为已知.试盘算梁内的最大弯曲正应力.解:x P x M ⋅=)(6-29当载荷P 直接作用在跨长为l =6m 的简支梁AB 的中点时,梁内最大正应力超出容许值30%.为了消除此过载现象,设置装备摆设如图所示的帮助梁CD ,试求此梁的最小跨长a .解:x P Pl 270.04=⨯ 6-30 图示外伸梁由25a 号工字钢制成,跨长l =6 rn ,在全梁上受集度为q的均布载荷作用.当支座截面A、B处及跨度中央截面C的最大正应力σ均为140MPa时,试问外伸部分的长度及载荷集度q等于若干?查表:(M图)6-31 图示悬臂梁跨长L=40cm,集中力P=250N,作用在弯曲中心上,梁的截面为等肢角形,尺寸如图,试绘剪应.6-32 圆锥形变截面悬臂梁其两头直径之比d b:d a=3:1,在自由端承受集中力P作用,试求梁内的最大弯曲正应力,并将此应力与支承处的最大应力比较.6-33工字形截面的简支钢梁,跨度l=4m,跨度中央受集中载荷P作用.,平安系数n,试按极限载荷法盘算此梁的许可载荷.6-34 矩形截面简支梁,在跨度中央承受集中力P.论确定故故。
材料力学第六章

极惯性矩: d r d d4 2dA=2d/2r2· ddr = z Ip= A r· 0 0 32 C 轴惯性矩: Ip=IZ+IY d4 IZ= IY = Ip/2= 64 2 sin· cos· ddr =0 12 r· r· 惯性积:IZY= AyzdA= 0 d/2 r· 0
z h 2
h1 2
C b 2 b 2
11
例6-4 圆形对其对称轴的几何性质
面积: A=AdA=d2/4 2 sin· ddr =0 静矩: SZ=AydA=0 d/2r· r· 0
2 SY=AzdA= 0 d/2r· cos· ddr =0 r· 0
dA=rddr y dr
计算主惯性矩的一般公式
由式: 2 IZY tg20 = IZ IY 2 IZY sin20 = ( IZ IY)2+4 I2ZY cos20 = 2 ( IZ IY) ( IZ IY)2+4 I2ZY
可得:
代入上节的IZ1、 IY1计算式便可得: IZ+ IY 1 + ( IZ IY)2+4 I2ZY IZ0= 2 2 IZ+ IY 1 – ( IZ IY)2+4 I2ZY IY0= 2 2
例6-5
23
a1 zO a2 z
截面对yO轴的惯性矩为两个矩形面积对yO轴的惯性矩之 和: 0.120.63 0.40.23 IZo= II + III = + =0.242 10-2m4 YO YO 12 12
24
求图示图形的形心主轴位置和形心主惯性矩。 6 解:该图形由I、II、III三个 y 矩形组成组合图形。显然组 合图形的形心与矩形II的形 I C1 心重合。 为计算形心主轴的位置及 b1 形心主惯性矩 ,过形心选择 一对便于计算惯性矩和惯性 C z 积的z、y轴如图示。 II 矩形I、III的形心坐标为: 2 a1=0.04m a3=-0.04m C3 III b1=-0.02m b3=0.02m b3 组合截面对z、y轴的惯性矩 尺寸单位 cm 6 和惯性积分别为
材料力学第06章 复杂应力状态分析及强度理论

2
s′
p
A πD
πD 2 F p 4 pD s A πD 4
n
D
(2)假想用一直径平面将圆筒截分为二,并取下半环为研究对象
s"
p
直径平面
FN
O
FN
d
y
D Fy 0 0 pl 2 sin d plD pD 2s l plD 0 s 2
理论分析表明,在复杂应力状态下(平面应力状态和空 间应力状态),一点处的最大正应力为 s max s 1 ,最小 正应力为 s min s 3 ,最大切应力的值为t s 1 s 3。
max
2
例题1 简支梁如图所示.已知 m-m 截面上A点的弯曲正应力和 切应力分别为s =-70MPa,t =50MPa.确定A点的主应力及主平面 的方位.
t xy
s x s y 0
txy
Mn t xy t WP
求极值应力
tyx
y O
s x s y 2 2 s 1 s x s y ( )t xy 2 2 s 2
2 t xy t
x
s 1t ;s 2 0;s 3 t
s x s y 2 2 t max ( )t xy t 2 t min
铸铁
在圆杆的扭转试验中,对于剪切强度低于拉伸强度的材料(例如低碳 钢),破坏是从杆的最外层沿横截面发生剪断产生的(图c),而对于 拉伸强度低于剪切强度的材料(例如铸铁),其破坏是由杆的最外层 沿杆轴线约成450倾角的螺旋形曲面发生拉断而产生的(图d)
2
平面应力状态分析——图解法
一、应力圆( Stress Circle)
2 2
材料力学第六版答案刘鸿文

材料力学第六版答案刘鸿文pdf_刘鸿文材料力学课件铸铁比低碳钢脆性高。
低碳钢的屈服强度高于铸铁。
(铸铁很脆,几乎不存在屈服强度),但是铸铁的拉伸强度大于低碳钢,由于铸铁含碳量高于低碳钢。
冲击强度低碳钢明显要优于铸铁。
低碳钢由于含碳量低,它的延展性、韧性和可塑性都是高于铸铁的,拉伸开头时,低碳钢试棒受力大,先发生变形,随着变形的增大,受力渐渐减小,当试棒断开的瞬间,受力为“0”,其受力曲线是呈正弦波>0的外形。
铸铁由于轫性差,拉伸开头时,受力是逐步加大的,当到达并超过它的拉伸极限时,试棒断开,受力瞬间为“0”,其受力曲线是随受力时间延长,一条直线向斜上方进展,试棒断开,直线垂直向下归“0”。
同样的道理:低碳钢抗压缩的力量比铸铁要低,当对低碳钢试块进展压缩试验时,受力渐渐加大,试块随外力变形,当试块变形到达极限时,其受力也到达最大值,其受力曲线是一条向斜上方的直线。
铸铁则不然,开头时与低碳钢受力状况根本一样,只是当铸铁试块受力到达本身的破坏极限时,受力渐渐减小,直到试块在外力下被破坏(裂开),受力为“0”其受力曲线与低碳钢拉伸时的受力曲线一样。
以上就是低碳钢和铸铁在拉伸和压缩时力学性质的异同点。
赞同4| 评论低碳钢:低碳钢为塑性材料.开头时遵守胡克定律沿直线上升,比例极限以后变形加快,但无明显屈服阶段。
相反地,图形渐渐向上弯曲。
这是由于在过了比例极限后,随着塑性变形的快速增长,而试件的横截面积渐渐增大,因而承受的载荷也随之增大。
从试验我们知道,低碳钢试件可以被压成极簿的平板而一般不破坏。
因此,其强度极限一般是不能确定的。
我们只能确定的是压缩的屈服极限应力。
2.铸铁:铸铁为脆性材料,其压缩图在开头时接近于直线,与纵轴之夹角很小,以后曲率渐渐增大,最终至破坏,因此只确定其强度极限。
ζbc=Fbc/S 铸铁试件受压力作用而缩短,说明有很少的塑性变形的存在。
当载荷到达最大值时,试件即破坏,并在其外表上消失了倾斜的裂缝(裂缝一般大致在与横截面成45°的平面上发生)铸铁受压后的破坏是突然发生的,这是脆性材料的特征。
昆明理工大学材料力学第六章 材料拉伸和压缩的力学性能

⑵ 试验和计算表明,该公式不能描述载荷作用点附 近截面上的应力情况,因为这些区域的应力变化比 较复杂,截面变形较大。
公式不能描述载荷作用点附近的应力情况。
●圣维南原理 力作用于杆端的方式不同,只会使与杆端距离 不大于杆的横向尺寸的范围内受到影响。
F
F
F 2
F 2
影响区
影响区 F
F
F 2
F 2
}
二、应力集中 在实际工程中,由于约束与连接的需要或构造与工 艺的要求,通常须在杆件上钻孔或切槽,如图所示。
应力峰值须借助弹性理论的精确计算或实验应力 分析的方法得到。 应力峰值σmax与剩余面积上的平均应力值σ0之 比称为应力集中系数(或称因数),记为 应力集中因数
max 为局部最大应力, 0 为削弱处的平均应力。
max K 0
用来描述应力集中的程度。可参阅相关资料和手册。
●静载荷作用下: 塑性材料所制成的构件对应力集中的敏感程度较小;
脆性材料所制成的构件必须要考虑应力集中的影响。
b
即当σmax 达到σb 时,该处首先产生破坏。
●动载荷作用下: 无论是塑性材料制成的构件还是 F 脆性材料所制成的构件都必须要考虑 应力集中的影响。
本章完
对于没有屈服阶段的塑性 材料,是将卸载后产生0.2% 的塑性应变所对应的应力值作 为屈服极限,称为名义屈服极 限或条件屈服极限。
p0.2
0.002残余应变
名义屈服极限
三、 铸铁拉伸时的 — 曲线 ①无明显直线阶段,故认为 近似线弹性,胡克定律近似成 立。弹性模量由一条割线的斜 率来确定,切割点通常定在应 变为0.1%的点处。 ②没有屈服、强化、颈缩现 象,试件在很小的变形下突然 断裂,断口平齐。 ③只能测出强度极限 bt (拉断时的最大应力)。其值远 低于低碳钢。 典型脆性材料
材料力学习题册概念答案

第一章绪论一、是非判断题1.1资料力学的研究方法与理论力学的研究方法完整相同。
(×) 1.2内力只作用在杆件截面的形心处。
(×) 1.3杆件某截面上的内力是该截面上应力的代数和。
(×) 1.4确立截面内力的截面法,合用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或随意截面的广泛状况。
(∨) 1.5依据各向同性假定,可以为资料的弹性常数在各方向都相同。
(∨) 1.6依据均匀性假定,可以为构件的弹性常数在各点处都相同。
(∨) 1.7同一截面上正应力σ与切应力τ必互相垂直。
(∨) 1.8同一截面上各点的正应力σ必然大小相等,方向相同。
(×) 1.9同一截面上各点的切应力τ必互相平行。
(×)1.10应变分为正应变ε和切应变γ。
(∨)1.11应变为无量纲量。
(∨) 1.12若物体各部分均无变形,则物体内各点的应变均为零。
(∨) 1.13若物体内各点的应变均为零,则物体无位移。
(×) 1.14均衡状态弹性体的随意部分的内力都与外力保持均衡。
(∨) 1.15题 1.15 图所示构造中, AD 杆发生的变形为曲折与压缩的组合变形。
(∨) 1.16题 1.16 图所示构造中, AB 杆将发生曲折与压缩的组合变形。
(×)FFA A CBBCD D题 1.15 图题 1.16 图二、填空题1.1资料力学主要研究杆件受力后发生的变形,以及由此产生的应力,应变。
1.2拉伸或压缩的受力特色是外力的协力作用线经过杆轴线,变形特色是。
1沿杆轴线伸长或缩短1.3剪切的受力特色是受一平等值,反向,作用线距离很近的力的作用,变形特色是沿剪切面发生相对错动。
1.4扭转的受力特征是外力偶作用面垂直杆轴线,变形特色是随意二横截面发生绕杆轴线的相对转动。
1.5曲折的受力特色是外力作用线垂直杆轴线,外力偶作用面经过杆轴线,变形特征是梁轴线由直线变为曲线。
1.6组合受力与变形是指包含两种或两种以上基本变形的组合。
第6章梁的应力分析与强度计算教程

eBook材料力学习题详细解答教师用书(第6章)2008-8-8范 钦 珊 教 育 教 学 工 作 室FAN Qin-Shan’s Education & Teaching Studio习题6-1 习题6-2 习题6-3 习题6-4 习题6-5 习题6-6 习题6-7 习题6-8 习题6-9 习题6-10 习题6-11 习题6-12 习题6-13 习题6-14 习题6-15 习题6-16 习题6-17 习题6-18 习题6-19 习题6-20材料力学习题详细解答之六第6章 梁的应力分析与强度计算6-1 悬臂梁受力及截面尺寸如图所示。
图中的尺寸单位为mm 。
求:梁的1-1截面上A 、B 两点的正应力。
解:1。
计算梁的1-1截面上的弯矩:31m 110N 1m+600N/m 1m 1300N m 2M ⎛⎞=−××××=−⋅⎜⎟⎝⎠ 2。
确定梁的1-1截面上A 、B 两点的正应力:A 点:()336-3-315010m 1300N m 2010m 210Pa MPa ()10010m 15010m12z A z M y I σ−−⎛⎞×⋅×−×⎜⎟⎝⎠==×=××× 2.54拉应力 B 点:()3363-3-315010m 1300N m 4010m 216210Pa 162MPa ()10010m 15010m12..z A z M y I σ−−⎛⎞×⋅×−×⎜⎟⎝⎠===×=×××压应力6-2 加热炉炉前机械操作装置如图所示,图中的尺寸单位为mm。
其操作臂由两根无习题6-2图习题6-1图缝钢管所组成。
外伸端装有夹具,夹具与所夹持钢料的总重F P =2200 N ,平均分配到两根钢管上。
求:梁内最大正应力(不考虑钢管自重)。
材料力学 第06章 强度理论

可见:由第三强度理论,图b所示应力状态比 图a所示的安全;而由第四强度理论,两者的危险 程度一样。 注意:图a所示应力状态实际上为拉扭和弯扭组 合加载对应的应力状态,其相当应力如下:
s r 3 s 2 4 2
s r 4 s 2 3 2
例 工字钢梁如图a所示。已知材料(Q235钢)的许 用应力为[s]=170MPa和[]= 100MPa。试按强度条 件选择工字钢号码。 (a) 200 kN 解:确定危险截面。 200 kN
1 2s s2 6E
因此:
1 2 2 2 s 1 s 2 s 2 s 3 s 1 s 3 s s 2
由此可得强度条件为:
ss 1 2 2 2 s 1 s 2 s 2 s 3 s 1 s 3 [s ] 2 n
s r4
1 2 2 2 s 1 s 2 s 2 s 3 s 1 s 3 2
§7-7 强度理论的应用
应用范围: a) 仅适用于常温、静载条件下的均匀、连续、各 向同性的材料; b) 不论塑性或脆性材料,在三向拉应力状态都 发生脆性断裂,宜采用第一强度理论; c) 对于脆性材料,在二向拉应力状态下宜采用第 一强度理论; d) 对塑性材料,除三向拉应力状态外都会发生 屈服,宜采用第三或第四强度理论; e) 不论塑性或脆性材料,在三向压应力状态都发 生屈服失效,宜采用第四强度理论。
假设形状改变能密度vd是引起材料塑性屈服的 因素,即:
vd vd u
vd u
所以:
可通过单拉试验来确定。
因为材料单拉屈服时有: s 1 s s s 2 s 3 0
材力习题册(第六版)参考答案(1-3章)

D
)
2.轴向拉伸细长杆件如图 2 所示,其中 1-1 面靠近集中力作用的左端面,则正确的说法 A.1-1、2-2 面上应力皆均匀分布 B.1-1、2-2 面上应力皆非均匀分布 C.1-1 面上应力非均匀分布, 2-2 面上应力均匀分布 D.1-1 面上应力均匀分布, 2-2 面上应力非均匀分布
(图 B 端 D 任意点 A ) B 都是横截面 D 都是 45 斜截面
0 0
14. 轴向拉伸杆,正应力最大的截面和剪应力最大的截面 (
15. 设轴向拉伸杆横截面上的正应力为 σ ,则 45 斜截面上的正应力和剪应力 ( D )。 B 均为 σ D 均为 σ /2 C δ 和ψ D σ s、 δ 和 ψ
17. 由拉压变形公式 l A C A C
F l FN l 即 E N 可知,弹性模量 ( A )。 A l EA
B 与载荷成正比 D 与横截面面积成正比
与载荷、杆长、横截面面积无关 与杆长成正比 A )是正确的。 内力随外力增大而增大 内力随外力增大而减小 C B D
18. 在下列说法,(
B 内力与外力无关 D 内力沿杆轴不变 ) 。 σ >300MPa σ <200MPa B ) 。 B. 剪切面面积为 bh,挤压面面积为 bc; D. 剪切面面积为 bh,挤压面面积为 ch。 C ) ,计算挤压面积
19. 一拉伸钢杆,弹性模量 E=200GPa,比例极限为 200MPa,今测得其轴向应变 ε = 0.0015,则横截面上的正应力 ( A C σ =Eε =300MPa 200MPa<σ <300Mpa
= -2(arctan
)=2.5×
rad
2.试求图示结构 m m 和 n n 两截面的内
-2-
材料力学性能06_缺口试样

断裂韧度测定试验-JⅠc的测定
临界点的确定对JⅠc值的影响很大,一般认为
,采用裂纹开裂点作为临界点较为合适,这样
规定比较符合JⅠc的定义。但在多数JⅠc测定试
验中,由于裂纹扩展前其尖端会产生塑性变形
,致使P-Δ曲线上裂纹的开始扩展点不明显,
因而,需要借助于电位法或声发射法辅助标定 裂纹开裂点。
若在Fmax处突然断裂,则Fmax/F=1,表示裂纹扩展极 快,材料产生突然脆性断裂,缺口敏感度最大。
如果仅有第I和第Ⅱ部分,断裂功为零,即当F= Fmax时试样突然脆性断裂,说明材料对缺口敏感 。而且第Ⅱ部分愈小,缺口敏感度愈高。 第Ⅲ部分代表裂纹产生后材料阻碍裂纹继续扩展 的能力,其面积愈大,说明裂纹可缓慢扩展较长 距离,材料具有良好塑性和低的缺口敏感度。
2020/7/9
33/39
疲劳裂纹扩展试验
当材料中存在裂纹并且外加应力达到某一临界值后,裂纹就会发生失 稳扩展。因此含裂纹材料的断裂可根据断裂韧度加以判别。不过在很 多情况下,这种足够大的宏观临界裂纹是在载荷作用下由萌生的小裂 纹逐渐扩展而成的,这也就是所谓的亚临界裂纹扩展过程。 疲劳载荷下的亚临界裂纹扩展尤为重要,这也是导致材料疲劳破坏的 主要原因。通过疲劳裂纹扩展试验,得到疲劳裂纹从萌生到亚临界扩 展再到最后失稳扩展的全过程,可以测定材料中疲劳裂纹扩展的门槛 值,得到疲劳裂纹扩展速率的变化规律,进而估算材料的疲劳寿命。
2020/7/9
帕里思(Paris)从断裂力学的角度分析了疲 劳裂纹扩展的规律,发现决定裂纹扩展速率
da/dN的主要力学参量是应力强度因子差值 ΔK。ΔK是应力循环过程中最大应力和最小应
力所对应的应力强度因子之差。
典型的疲劳裂纹扩展速率曲线(lgda/dNlgΔK)可以分为三个区域
材料力学答案第六章
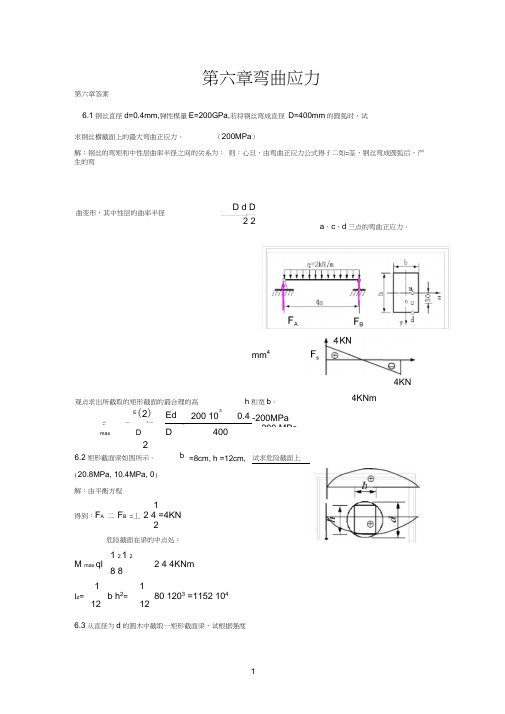
第六章答案第六章弯曲应力6.1钢丝直径d=0.4mm,弹性模量E=200GPa,若将钢丝弯成直径 D=400mm 的圆弧时,试求钢丝横截面上的最大弯曲正应力。
(200MPa )解:钢丝的弯矩和中性层曲率半径之间的关系为: 则:心旦,由弯曲正应力公式得f 二如=荃,钢丝弯成圆弧后,产生的弯E(2) rr —J —Ed 3200 100.4 -200MPakJ——200 MPa -maxDD40026.2矩形截面梁如图所示。
b ==8cm, h =12cm, 试求危险截面上(20.8MPa, 10.4MPa, 0) 解:由平衡方程1得到:F A 二 F B =丄 2 4 =4KN2危险截面在梁的中点处:1 2 1 2 M max ql2 4 4KNm 8 8 11 I z =b h 2=80 1203 =1152 10412126.3从直径为d 的圆木中截取一矩形截面梁,试根据强度曲变形,其中性层的曲率半径D d D------------ &——2 2mm 44KN观点求出所截取的矩形截面的最合理的高h 和宽b 。
4KNma 、c 、d 三点的弯曲正应力。
(h= -d , b=」d)3 3机械解:最大弯曲正应力:max-max一y max-max土木W z4KNm系数:1 2 1 2 2 1 2 3 W=1bh二b(d _b)=1(db_b)dW dt d2 -3b2h/b的最佳值应应使梁的抗弯截面系数为最大。
抗弯截面为b为自变量的函数。
6.4图示两根简支梁,其跨度、荷载及截面面积都相同。
一个是整体截面梁,另一个是由两 根方木叠置而成(二方木之间不加任何联1 3 1 3 8 4bh 3 150 2003 = 108 mm 412 12再有矩形截面梁的弯曲正应力弯曲正应力为L.T-10MP a ,许用剪应力为• ‘ = 1MPa , 试求许可荷载P 。
(P=8.1kN )解:依题给条件,对梁进行受力分析,由平衡条件,列平衡方程,做出剪力图 和弯矩图如右所示 (1)按木材弯曲正应力强度要求确定许可荷载F s S ; T = -----------------I z b ,故 9 =0, aF S240 1033 __ 2.0 A 2 150 200MPaF S S ZI z b 40 103 5.625 105108 150= 1.5 MPa6.6图示简支梁由三块木板胶合而成, l=1m,胶缝的许用剪应力为!. l-0.5MPa木材的许用系),试画出沿截面高度的弯曲正应力分布 图,并分别计算梁中的最大弯曲正应力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弯曲应力6-1 求图示各梁在m -m 截面上A 点的正应力和危险截面上最大正应力。
题 6-1图解:(a )m KN M m m ⋅=-5.2 m KN M ⋅=75.3max 48844108.49064101064m d J x --⨯=⨯⨯==ππMPa A37.20108.490104105.2823=⨯⨯⨯⨯=--σ (压)MPa 2.38108.4901051075.3823max=⨯⨯⨯⨯=--σ (b )m KN M m m ⋅=-60 m KN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯== MPa A 73.611058321061060823=⨯⨯⨯⨯=--σ (压) MPa 2.104105832109105.67823max=⨯⨯⨯⨯=--σ (c )m KN M m m ⋅=-1 m KN M ⋅=1max48106.25m J x -⨯= 36108.7m W x -⨯=cm y A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ (压) MPa 2.128106.2510183max=⨯⨯=-σ 6-2 图示为直径D =6 cm 的圆轴,其外伸段为空心,内径d =4cm ,求轴内最大正应力。
解:)1(32431απ-=D W x⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π361002.17m -⨯= 3463321021.213210632m D W x --⨯=⨯⨯==ππMPa 88.521002.17109.0631=⨯⨯=-σ MPa 26.551021.2110172.1631=⨯⨯=-σMPa 26.55max =σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。
试求梁内最大拉应力与最大压应力。
已知I z =10170cm 4,h 1=9.65cm ,h 2=15.35cm 。
解:A 截面:Mpa 95.371065.9101017010402831max =⨯⨯⨯⨯=--σ (拉)Mpa 37.501035.15101017010402831min -=⨯⨯⨯⨯-=--σ(压) E 截面Mpa 19.301035.15101017010202832max =⨯⨯⨯⨯=--σ (拉)Mpa 98.181065.9101017010202832min -=⨯⨯⨯⨯-=--σ (压) 6-4 一根直径为d 的钢丝绕于直径为D 的圆轴上。
(1) 求钢丝由于弯曲而产生的最大弯曲正应力(设钢丝处于弹性状态)(2) 若 d =lmm ,材料的屈服极限s σ=700MPa ,弹性模量E =210GPa ,求不使钢丝产生残余变形的轴径D 。
解:EJ M =ρ1Dd E EJM 324πρ== D dE d M W M ⋅===3max 32πσ cm m dE D s303.01070010110210639==⨯⨯⨯⨯=⋅≥-σ6-5 矩形悬臂梁如图示.已知l = 4 m ,32=h b ,q =10kN/m ,许用应力[σ]=10Mpa 。
试确定此梁横截面尺寸。
解:m KN ql M ⋅=⨯⨯==80410212122max 963266322h h h h W =⨯== 910101080263h M W W M =⨯⨯==⇒=σσcm m h 6.41416.0== cm b 7.27=6-6 20a 工字钢梁的支承和受力情况如图所示。
若[σ]=160MPa ,试求许用载荷P 。
解:3237cm W = P 32 m KN PM ⋅=32max[][]P W M 32102371016066=⨯⨯⨯=⋅=-σ (M 图) P 32 []KN P 880.5623716023=⨯⨯=6-7 压板的尺寸和载荷情况如图所示。
材料为 45钢,s σ=380 MPa ,取安全系数5.1=n 。
试校核压板强度。
解:2331568)121230122030(101mm W =⨯-⨯⨯= m N M ⋅=⨯⨯⨯=-3601020101833[]σσ<=⨯==-MPa W M 6.22910156836096-8 由两个槽钢组成的梁受力如图示。
已知材料的许用应力[σ]=150 MPa ,试选择槽钢号码。
解:m KN M ⋅=60max[]33363m ax400104.0101501060cm m M W x =⨯=⨯⨯==-σ 查表:(22a , 332006.217cm cm W x >=)m KN ⋅60( M 图)6-9 割刀在切割工件时,受到P =1kN 的切销力的作用。
割刀尺寸如图所示。
试求割刀内最大弯曲应力。
解:m N p M ⋅=⨯⨯=-I 81083m N p M ⋅=⨯⨯=-∏30103033242.706135.2mm W =⨯=I 321506154mm W =⨯=∏()MPa W M 114104.7089m ax =⨯==-I I I σ ()MPa W M 20010150309m ax =⨯==-∏∏∏σ6-10 图示圆木,直径为D ,需要从中切取一矩形截面梁。
试问(1)如要使所切矩形截面的抗弯强度最高,h 、b 分别为何值?(2)如要使所切矩形截面的抗弯刚度最高,h 、b 又分别为何值?解:6)(6222b D b bh W -== 0=dbdW∴06322=-b D ∴322D b =2222323D D D h =-=∴从强度讲:D b 57735.0=∴ D h 8165.0=12)(123222b D b bhJ -==0=dbdJ0)2()(23)(21222322=-⨯-⨯⨯+-b b D b b D∴从刚度讲 D b 50.0=D h 866.0=6-11 T 字形截面的铸铁梁受纯弯曲如图示,欲使其最大压应力为最大拉应力的3倍,巳知h = 12cm ,t =3cm ,试确定其翼板宽度b 之值。
解:3max max =下上拉压y y =σσ下上=y y 3 12=h y y =+下上cm y 3412==下05.4)39()233)(3(=⨯⨯--⨯=b Scm b 275.135.439=⨯⨯⨯=6-12 图示简支梁,由No.18工字钢制成,在外载荷作用下,测得横截面A 处梁底面的纵向正应变4100.3-⨯=ε,试计算梁的最大弯曲正应力σmax 。
已知钢的弹性模量E =200GPa, a =1m 。
解:MPa E A 60100.31020049=⨯⨯⨯==-εσ28/34/3max max ===A A M M σσ MPa A 1206022max =⨯==σσ243qa 283qa24qa (M 图)6-13 试计算图示矩形截面简支梁的1-1面上a 点和b 点的正应力和剪应力。
解:1-1截面KN Q 6364.3=m KN M ⋅=6364.3433375.210912155.712cm bh J =⨯==283105.310375.2109106364.3--⨯⨯⨯⨯==y J M a σ MPa 03.6=82310375.2109105.7106364.3--⨯⨯⨯⨯=b σ MPa 93.12=2863105.710375.2109105.5)5.74(106364.3---⨯⨯⨯⨯⨯⨯⨯⨯==Jb QS a τMPa 379.0=6-14 计算在均布载荷 q =10 kN /m 作用下,圆截面简支梁的最大正应力和最大剪应力,并指出它们发生在何处。
解:232max 110108181⨯⨯⨯==ql M m N ⋅⨯=31025.1 1101021213max ⨯⨯⨯==ql Q N 3105⨯=633m ax 105321025.1-⨯⨯⨯==πσWMMPa 86.101= 在跨中点上、下边缘 34105410534423max⨯⨯⨯⨯=⨯=-πτA Q MPa 46.25= 在梁端,中性轴上6-15 试计算6-12题工字钢简支梁在图示载荷下梁内的最大剪应力。
解: MPa Wqa 60832= qa 413185cm W =KN q 6.29123810185106066=⨯⨯⨯⨯⨯=- qa 43KN qa Q 2.2216.294343max =⨯⨯== (Q 图) MPa Jt QS 12.22105.6104.15102.22323max=⨯⨯⨯⨯==--τ6-16 矩形截面木梁所受载荷如图示,材料的许用应力[σ]=10Mpa 。
试选择该梁的截面尺寸,设1:2:=b hKN 19(Q 图) ( M 图)解:KN R A 19= KN R B 29=126132h bh W ==[]σσ≤⨯==12101433m axh W M cm m h 6.25256.01010121014363==⨯⨯⨯=cm b 8.12= []ττ<=⨯⨯⨯⨯==-MPa A Q 961.0106.258.1210215.15.143max6-17 试为图示外伸梁选择一工字形截面,材料的许用应力[σ]= 160MPa ,[τ]=80Mpa 。
解:[]3612510160100020cm MW =⨯⨯==σ 取16I , 3141cm W =)(8.13:cm S J =[]ττ<=⨯⨯⨯==-MPa Jt QS 181.01068.13101533故 取No16工字钢)(x Q KN 15 )(x M m KN ⋅20KN 5 m KN ⋅10KN 10(Q 图) (M 图)6-18 图示起重机安装在两根工字形钢梁上,试求起重机在移动时的最危险位置及所采用工字型钢的号码。
已知 l =10 m ,a =4 m ,d =2 m 。
起重机的重量 W =50 kN ,起重机的吊重P =10 kN ,钢梁材料的许用应力[σ]=160 MPa ,[τ]= 100Mpa 。
解:轻压:KN 10 ,KN 50[]x x x R 658)8(10)10(50101-=-+-=x x Rx x M ⋅-==)658()(0=dxdM01258=-x m x 833.4=m KN M ⋅=⨯⨯-=17.140833.4)833.4658(max []63m ax101601017.140⨯⨯==σM W33387610876.0cm m =⨯=- 取 两个 a I 28 33438215.508cm Wcm W z =>=KN 10 KN 50d m 106-19 等腰梯形截面梁,其截面高度为h 。
用应变仪测得其上边的纵向线应变611042-⨯-=ε,下边的纵向线应变621014-⨯=ε。
