工程力学课后答案摘录概要
(完整版)工程力学课后详细答案
第一章静力学的基本概念受力图第二章 平面汇交力系2-1解:由解析法,23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故:22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故: 223R RX RY F F F KN=+= 方向沿OB 。
2-3 解:所有杆件均为二力杆件,受力沿直杆轴线。
(a ) 由平衡方程有:0X =∑sin 300AC AB F F -=0Y =∑cos300AC F W -=0.577AB F W=(拉力)1.155AC F W=(压力)(b ) 由平衡方程有:0X =∑ cos 700AC AB F F -=0Y =∑sin 700AB F W -=1.064AB F W=(拉力)0.364AC F W=(压力)(c ) 由平衡方程有:0X =∑cos 60cos300AC AB F F -=0Y =∑sin 30sin 600AB AC F F W +-=0.5AB F W= (拉力)0.866AC F W=(压力)(d ) 由平衡方程有:0X =∑sin 30sin 300AB AC F F -=0Y =∑cos30cos300AB AC F F W +-=0.577AB F W= (拉力)0.577AC F W= (拉力)2-4 解:(a )受力分析如图所示:由x =∑ 22cos 45042RA F P -=+15.8RA F KN∴=由Y =∑ 22sin 45042RA RB F F P +-=+7.1RB F KN∴=(b)解:受力分析如图所示:由x =∑3cos 45cos 45010RA RB F F P ⋅--=0Y =∑1sin 45sin 45010RA RB F F P ⋅+-=联立上二式,得:22.410RA RB F KN F KN==2-5解:几何法:系统受力如图所示三力汇交于点D ,其封闭的力三角形如图示所以:5RA F KN= (压力)5RB F KN=(与X 轴正向夹150度)2-6解:受力如图所示:已知,1R F G = ,2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解:受力分析如图所示,取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后,解得:0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600AB AC F F W +-=联立上二式,解得:7.32AB F KN=-(受压)27.3AC F KN=(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D ,B 点分别列平衡方程(1)取D 点,列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==(2)取B 点列平衡方程:由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解:取B 为研究对象:由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象:由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BCBC F F '= 解得:2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象:由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有:22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解:取A 点平衡:x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得: 2cos 75AD AB PF F ==取D 点平衡,取如图坐标系:x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD P F F F KN'∴===⋅=2-12解:整体受力交于O 点,列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得:2.92RA F KN=1.33DC F KN=(压力)列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得: 1.67AC F KN=(拉力)1.0BC F KN=-(压力)2-13解:(1)取DEH 部分,对H 点列平衡x =∑05RD REF F '= 0Y =∑05RD F Q =联立方程后解得: 5RD F Q =2REF Q '=(2)取ABCE 部分,对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得: 22RA F Q =2RB F Q P=+(3)取BCE 部分。
工程力学课后习题答案(静力学和材料力学)
解:图(a):θ = arcsin 4 ,
5
∑ Fx = 0 ,
F sin(60° − θ ) − W sinθ = 0 , F = 1672 N
图(b):θ = 53.13° ,
∑ Fx = 0 , F cos(θ − 30°) − W sinθ = 0 , F = 217N
Fy
x
30D B
Wθ
y
可推出图(b)中 FAB = 10FDB = 100F = 80 kN。
FED αD
FDB FD′ B
FCB
α
B
F 习题 1-12 解 1 图
F AB 习题 1-12 解 2 图
1—13 杆 AB 及其两端滚子的整体重心在 G 点,滚子搁置在倾斜的光滑刚性平面上,如
图所示。对于给定的θ 角,试求平衡时的 β 角。
=
25 kN 6
即
FR
= ( 5 , 10 )kN 23
作用线方程: y = 4 x + 4 3
讨论:本题由于已知数值的特殊性,实际 G 点与 E 点重合。
2-3三个小拖船拖着一条大船,如图所示。每根拖缆的拉力为5kN。试求:(1)作用于大 船上的合力的大小和方向。(2)当A船与大船轴线x的夹角θ为何值时,合力沿大船轴线方向。
投影: Fx1 = F cosα , Fy1 = F sinα
讨论: ϕ = 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
图(b):
分力: Fx2 = (F cosα − F sin α tan ϕ )i2 ,
Fy2
=
F sinα sinϕ
j2
投影: Fx2 = F cosα ,
Fy2 = F cos(ϕ − α )
《工程力学》课后习题与答案全集

由 ,作出速度平行四边形,如图示:
即:
7.图示平行连杆机构中, mm, 。曲柄 以匀角速度 2rad/s绕 轴转动,通过连杆AB上的套筒C带动杆CD沿垂直于 的导轨运动。试示当 时杆CD的速度和加速度。
解:取CD杆上的点C为动点,AB杆为动系。对动点作速度分析和加速度分析,如图(a)、(b)所示。图中:
解:设该力系主矢为 ,其在两坐标轴上的投影分别为 、 。由合力投影定理有:
=-1.5kN
kN
kN
;
由合力矩定理可求出主矩:
合力大小为: kN,方向
位置: m cm,位于O点的右侧。
2.火箭沿与水平面成 角的方向作匀速直线运动,如图所示。火箭的推力 kN与运动方向成 角。如火箭重 kN,求空气动力 和它与飞行方向的交角 。
(d)由于不计杆重,杆AB在A、C两处受绳索作用的拉力 和 ,在B点受到支座反力 。 和 相交于O点,
根据三力平衡汇交定理,
可以判断 必沿通过
B、O两点的连线。
见图(d).
第二章力系的简化与平衡
思考题:1.√;2.×;3.×;4.×;5.√;6.×;7.×;8.×;9.√.
1.平面力系由三个力和两个力偶组成,它们的大小和作用位置如图示,长度单位为cm,求此力系向O点简化的结果,并确定其合力位置。
则
(mm/s)
故 =100(mm/s)
又有: ,因
故:
即:
第四章刚体的平面运动
思考题
1.×;2.√; 3.√;4.√;5.×.
习题四
1.图示自行车的车速 m/s,此瞬时后轮角速度 rad/s,车轮接触点A打滑,试求点A的速度。
(完整版)工程力学课后详细答案

第一章静力学的基本概念受力图第二章 平面汇交力系2-1解:由解析法,23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故:22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故: 223R RX RY F F F KN=+= 方向沿OB 。
2-3 解:所有杆件均为二力杆件,受力沿直杆轴线。
(a ) 由平衡方程有:0X =∑sin 300AC AB F F -=0Y =∑cos300AC F W -=0.577AB F W=(拉力)1.155AC F W=(压力)(b ) 由平衡方程有:0X =∑ cos 700AC AB F F -=0Y =∑sin 700AB F W -=1.064AB F W=(拉力)0.364AC F W=(压力)(c ) 由平衡方程有:0X =∑cos 60cos300AC AB F F -=0Y =∑sin 30sin 600AB AC F F W +-=0.5AB F W= (拉力)0.866AC F W=(压力)(d ) 由平衡方程有:0X =∑sin 30sin 300AB AC F F -=0Y =∑cos30cos300AB AC F F W +-=0.577AB F W= (拉力)0.577AC F W= (拉力)2-4 解:(a )受力分析如图所示:由x =∑ 22cos 45042RA F P -=+15.8RA F KN∴=由Y =∑ 22sin 45042RA RB F F P +-=+7.1RB F KN∴=(b)解:受力分析如图所示:由x =∑3cos 45cos 45010RA RB F F P ⋅--=0Y =∑1sin 45sin 45010RA RB F F P ⋅+-=联立上二式,得:22.410RA RB F KN F KN==2-5解:几何法:系统受力如图所示三力汇交于点D ,其封闭的力三角形如图示所以:5RA F KN= (压力)5RB F KN=(与X 轴正向夹150度)2-6解:受力如图所示:已知,1R F G = ,2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解:受力分析如图所示,取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后,解得:0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600AB AC F F W +-=联立上二式,解得:7.32AB F KN=-(受压)27.3AC F KN=(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D ,B 点分别列平衡方程(1)取D 点,列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==(2)取B 点列平衡方程:由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解:取B 为研究对象:由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象:由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BCBC F F '= 解得:2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象:由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有:22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解:取A 点平衡:x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得: 2cos 75AD AB PF F ==取D 点平衡,取如图坐标系:x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD P F F F KN'∴===⋅=2-12解:整体受力交于O 点,列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得:2.92RA F KN=1.33DC F KN=(压力)列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得: 1.67AC F KN=(拉力)1.0BC F KN=-(压力)2-13解:(1)取DEH 部分,对H 点列平衡x =∑05RD REF F '= 0Y =∑05RD F Q =联立方程后解得: 5RD F Q =2REF Q '=(2)取ABCE 部分,对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得: 22RA F Q =2RB F Q P=+(3)取BCE 部分。
(完整版)工程力学课后习题答案

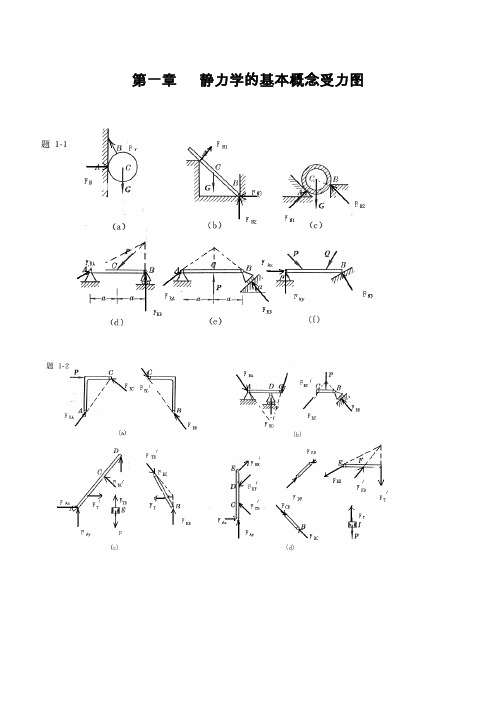
工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)2 第一章静力学基础(d)(e)(f)(g)第一章静力学基础 3 1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)4 第一章静力学基础1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)第一章静力学基础 5 (b)(c)(d)6 第一章静力学基础(e)第一章静力学基础7 (f)(g)8 第二章 平面力系第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如第二章 平面力系 9图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
工程力学课后习题答案

题2-12图
受力分析如图:
受力分析如图:
2-16在图示刚架中,已知 , , ,不计刚架自重。求固定端A处的约束力。
2-17在图示a,b两连续梁中,已知q,M,a,及 ,不计梁的自重。求各连续梁在A,B,C三处的约束反力。
2-13 在图示a,b两连续梁中,已知q,M,a,及 ,不计梁的自重。求各连续梁在A,B,C三处的约束反力。
题6-2图
6-3题6-2图所示圆截面杆,已知载荷 , , 段的直径 ,如欲使 与 段横截面上的正应力相同,试求 段的直径。
6-4设图示结构的1和2两部分皆为刚体,刚拉杆 的横截面直径为 ,试求拉杆内的应力。
题6-4图
1做受力图
2列平衡方程求解
解得F=6kN, FN=3kN, AB杆的应力为:
6-5某受扭圆管,外径 ,内径 ,横截面上的扭矩 ,试计算距轴心21mm处圆管横截面与纵截面上的扭转切应力。
题2-1图
解得:
2-2 物体重P=20kN,用绳子挂在支架的滑轮B上,绳子的另一端接在绞车D上,如图所示。转动绞车,物体便能升起。设滑轮的大小及轴承的摩擦略去不计,杆重不计,A、B、C三处均为铰链连接。当物体处于平衡状态时,求拉杆AB和支杆BC所受的力。
题2-2图
解得:
2-3 如图所示,输电线ACB架在两电线杆之间,形成一下垂线,下垂距离CD=f=1m,两电线杆间距离AB=40m。电线ACB段重P=400N,可近视认为沿AB直线均匀分布,求电线的中点和两端的拉力。
工 程 力 学
练 习 册
学 校
学 院
专 业
学 号
教 师
姓 名
第一章 静力学基础
1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
《工程力学》课后习题与答案全集

工程力学习题答案第一章静力学基础知识思考题:1. X ;2. V ;3. V ;4. V ;5. K 6. K 7. V ;8. V习题一1•根据三力汇交定理,画出下面各图中A 点的约束反力方向。
解:(a )杆AB 在 A B 、C 三处受力作用。
u由于力p和uuv R B 的作用线交于点Q 如图(a )所示,根据三力平衡汇交定理, 可以判断支座A 点的约束反力必沿 通过A 0两点的连线。
uP 3uvB 处受绳索作用的拉力uuv R B (b )同上。
由于力交于0点,根据三力平衡汇交定理, 可判断A 点的约束反力方向如 下图(b )所示。
的作用线 2.不计杆重,画出下列各图中 AB 杆的受力图。
uP 解:(a )取杆AB 和E 两处还受光滑接触面约束。
约束力UJVN E uuvuuN A 和 N E,在A的方向分别沿其接触表面的公法线, 外,在 并指向杆。
其中力uuvN A 与杆垂直,通过半圆槽的圆心 Q力 AB 杆受力图见下图(a )。
和C 对它作用的约束力 NBo------- r -------- —y —uuv N C铰销此两力的作用线必须通过(b )由于不计杆重,曲杆 BC 只在两端受 故曲杆BC 是二力构件或二力体,和 B 、C 两点的连线,且B O两点的连线。
见图(d).第二章力系的简化与平衡思考题:1. V ;2.>;3. X ;4. K 5. V ;6.$7.>;8. x ;9. V .1.平面力系由三个力和两个力偶组成, 它们的大小和作用位置如图示,长度单位为cm 求此力系向O 点简化的结果,并确定其合力位置。
uvR R 解:设该力系主矢为 R ,其在两坐标轴上的投影分别为Rx、y。
由合力投影定理有:。
4.梁AB 的支承和荷载如图, 小为多少?解:梁受力如图所示:2. 位置:d M o /R 25000.232 火箭沿与水平面成F ,100 0.6100 80 2000 0.5 580m 23.2cm,位于O 点的右侧。
工程力学课后习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触.(a)(b)(c)2 第一章静力学基础(d)(e)(f)(g)第一章静力学基础 3 1—2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)4 第一章静力学基础1—3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计.(a)第一章静力学基础 5 (b)(c)(d)6 第一章静力学基础(e)第一章静力学基础7 (f)(g)8 第二章 平面力系第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0.如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图第二章 平面力系 9所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m.电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力.题2—3图以AC 段电线为研究对象,三力汇交NF N F F F FF F F C A GA yC A x 200020110/1tan sin ,0,cos ,0=======∑∑解得:ααα2-4 图示为一拔桩装置。
工程力学课后习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)2 第一章静力学基础(d)(e)(f)(g)第一章静力学基础 31-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)4 第一章静力学基础1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)第一章静力学基础 5(b)(c)(d)6 第一章静力学基础(e)第一章静力学基础7(f)(g)8第二章 平面力系第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如第二章 平面力系9图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F FBC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
工程力学课后题答案

第二章汇交力系习题2.1在刚体的A 点作用有四个平面汇交力。
其中F 1=2kN ,F 2=3kN ,F 3=lkN , F 4=2.5kN ,方向如题2.1图所示。
用解析法求该力系的合成结果。
题2.1图解 0001423c o s 30c o s 45c o s 60c o s 45 1.29Rx F X F F F F KN ==+--=∑ 00001423sin30cos45sin60cos45 2.54Ry F Y F F F F KN ==-+-=∑2.85R F KN ==0(,)tan63.07Ry R RxF F X arc F ∠==2.2 题2.2图所示固定环受三条绳的作用,已知F 1=1kN ,F 2=2kN ,F 3=l.5kN 。
求该力系的合成结果。
23解:2.2图示可简化为如右图所示023cos60 2.75Rx F X F F KN ==+=∑ 013sin600.3Ry F Y F F KN ==-=-∑2.77R F KN ==0(,)tan6.2Ry R RxF F X arc F ∠==-2.3 力系如题2.3图所示。
已知:F 1=100N ,F 2=50N ,F 3=50N ,求力系的合力。
32F 1解:2.3图示可简化为如右图所示080arctan5360BAC θ∠=== 32cos 80Rx F X F F KN θ==-=∑12sin 140Ry F Y F F KN θ==+=∑161.25R F KN ==0(,)tan60.25Ry R RxF F X arc F ∠==2.4 球重为W =100N ,悬挂于绳上,并与光滑墙相接触,如题2.4图所示。
已知30α=,试求绳所受的拉力及墙所受的压力。
题2.4图解:2.4图示可简化为如右图所示sin 0X FF α=-=∑拉推 cos W 0Y Fα=-=∑拉115.47N 57.74N F F ∴==拉推,∴墙所受的压力F=57.74N2.5 均质杆AB 重为W 、长为 l ,两端置于相互垂直的两光滑斜面上,如题2.5图所示。
工程力学课后习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)(d)(e)(f)(g)1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)(b)(c)(d)(e)(f)(g)第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图解得: P F PF AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
题2-3图以AC 段电线为研究对象,三力汇交2-4 图示为一拔桩装置。
在木桩的点A 上系一绳,将绳的另一端固定在点C ,在绳的点B 系另一绳BE ,将它的另一端固定在点E 。
然后在绳的点D 用力向下拉,并使绳BD 段水平,AB 段铅直;DE 段与水平线、CB 段与铅直线成等角α=0.1rad (弧度)(当α很小时,tanα≈α)。
如向下的拉力F=800N ,求绳AB 作用于桩上的拉力。
题2-4图 作BD 两节点的受力图 联合解得:kN F F F A80100tan 2=≈=α 2-5 在四连杆机构ABCD 的铰链B 和C 上分别作用有力F 1和F 2,,机构在图示位置平衡。
工程力学(第二版)课后答案
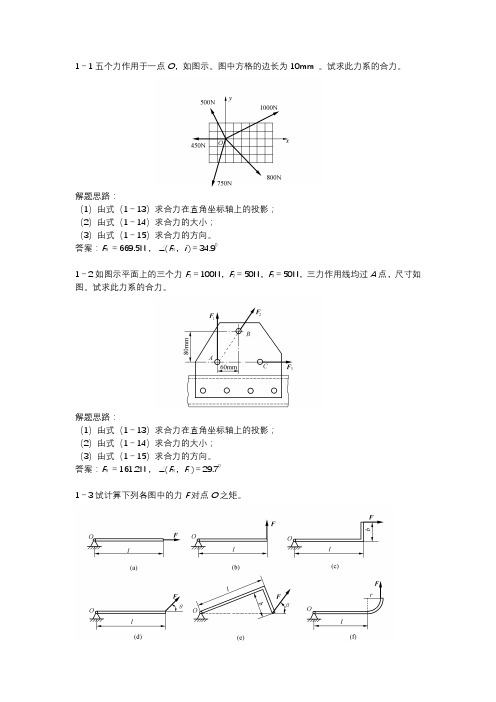
1-1五个力作用于一点O,如图示。
图中方格的边长为10mm 。
试求此力系的合力。
解题思路:(1)由式(1-13)求合力在直角坐标轴上的投影;(2)由式(1-14)求合力的大小;(3)由式(1-15)求合力的方向。
答案:F R =669.5N , ∠(F R,i )=34.901-2如图示平面上的三个力F1=100N,F2=50N,F3=50N,三力作用线均过A点,尺寸如图。
试求此力系的合力。
解题思路:(1)由式(1-13)求合力在直角坐标轴上的投影;(2)由式(1-14)求合力的大小;(3)由式(1-15)求合力的方向。
答案:F R =161.2N , ∠(F R,F i)=29.701-3试计算下列各图中的力F对点O之矩。
解题思路:各小题均由式(1-16)求力矩。
答案:略1-4如图所示的挡土墙重G 1=75 kN ,铅直土压力G 2=120 kN ,水平土压力F p =90 kN 。
试求三力对前趾A 点之矩的和,并判断挡土墙是否会倾倒。
解题思路:(1)由式(1-16)求三力对前趾A 点之矩的代数和; (2)若其值为负(顺时针转),则挡土墙不会翻倒。
答案:∑M A =-180kN.m ,不会倾倒。
1-5如图所示,边长为a 的正六面体上沿对角线AH 作用一力F 。
试求力F 在三个坐标轴上的投影,力F 对三个坐标轴之矩以及对点O 之矩矢。
解题思路:(1)由式(1-13)、(1-14)、(1-15)求合力的大小和方向; (2)由式(1-25)求力对三个坐标轴之矩; (3)由式(1-26)求力对坐标原点之矩。
答案:M x =0,Fa M y 33=,Fa M 33z =-, k Fa j Fa M O 3333-=1-7试画出下列各图中物体A ,构件AB 的受力图。
未画重力的物体重量不计,所有接触面均为光滑接触。
解题思路:(1)画出研究对象的轮廓形状; (2)画出已知的主动力;(3)在解除约束处按约束的性质画出约束力。
(完整版)工程力学课后习题答案

工程力学练习册学校 ______________学院 _______________专业 ______________学号 _______________教师 _______________姓名 ______________第一章静力学基础1-1画出下列各图中物体A,构件AB, BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
1-3画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(1 J AB杆(2)CTJff(3)整体(1 ) K段槊(2) CD段梁r 3)鹫佐t 1)滑轮日⑵ABff(3) DF 样C I 】CDW⑵曲杵⑶CA杵(e)t 1,直(并tlikkiv t n OA IT(g)第二章平面力系2-1电动机重P=5000N,放在水平梁AC的中央,如图所示。
梁的A端以皎链固定,另一端以撑杆BC支持,撑杆与水平梁的夹角为30 °。
如忽略撑杆与梁的重量,求绞支座A、B处的约束反力。
F x0, F B CO S30F A COS300F y0, F A sin30F B sin30P解得:F A F B P5000N2-2 物体重P=20kN,用绳子挂在支架的滑轮B上,绳子的另一端接在绞车D上,如图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为皎链连接。
当物体处于平衡状态时,求拉杆 AB 和支杆BC 所受的力。
2-3如图所示,输电线 ACB 架在两电线杆之间,形成一下垂线,下垂距离 CD=f=1m, 两电线杆间距离 AB=40m 。
电线ACB 段重P=400N,可近视认为沿 AB 直线均匀分布,求电 线的中点和两端的拉力。
F x0, F AB F BC F y0, F BC sin 30 解得:F BC 3.732P F AB 2.732Pcos30 Psin30 0 Pcos30 P 0F x 0,F A COS F C,F y 0, F A Sin F Gtan 1/10解得:F A 201NF C 2000 N2-4 图示为一拔桩装置。
工程力学课后详细答案
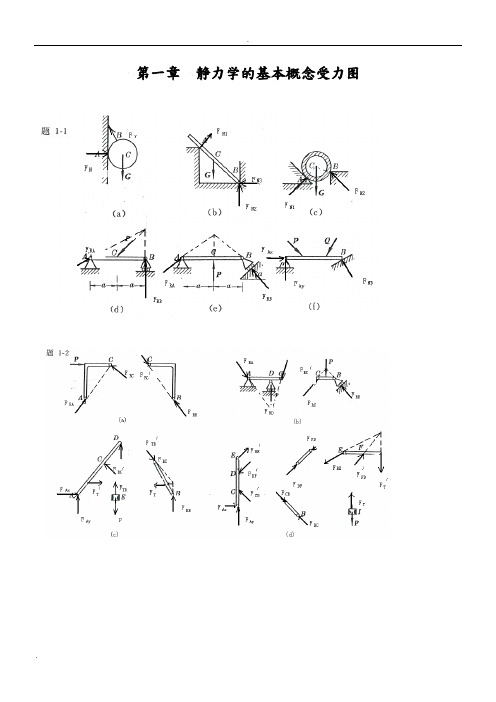
第一章静力学的基本概念受力图第二章 平面汇交力系2-1解:由解析法,23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P N θ==+=∑故:161.2R F N==1(,)arccos2944RYR RF F P F '∠==2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故:3R F KN== 方向沿OB 。
2-3 解:所有杆件均为二力杆件,受力沿直杆轴线。
(a ) 由平衡方程有:0X =∑ sin 300ACAB FF -=0Y =∑ cos300ACFW -=0.577AB F W=(拉力)1.155AC F W=(压力)(b ) 由平衡方程有:0X =∑ cos 700ACAB FF -=0Y =∑ sin 700ABFW -=1.064AB F W=(拉力)0.364AC F W=(压力)(c ) 由平衡方程有:0X =∑ cos 60cos300ACAB FF -=0Y =∑ sin 30sin 600ABAC FF W +-=0.5AB F W= (拉力)0.866AC F W=(压力)(d ) 由平衡方程有:0X =∑ sin 30sin 300ABAC FF -=0Y =∑ cos30cos300ABAC FF W +-=0.577AB F W= (拉力)0.577AC F W= (拉力)2-4 解:(a )受力分析如图所示:由x =∑cos 450RA F P -=15.8RA F KN∴=由Y =∑sin 450RA RB F F P +-=7.1RB F KN∴=(b)解:受力分析如图所示:由x =∑cos 45cos 450RA RB F F P --= 0Y =∑sin 45sin 450RA RB F F P -=联立上二式,得:22.410RA RB F KN F KN==2-5解:几何法:系统受力如图所示三力汇交于点D ,其封闭的力三角形如图示所以: 5RA F KN= (压力) 5RB F KN=(与X 轴正向夹150度)2-6解:受力如图所示:已知,1R F G = ,2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=2sin N F W G W α∴=-⋅=2-7解:受力分析如图所示,取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑ sin 45sin 450CBRA F F '-=联立后,解得:0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由x=∑cos60cos300AC ABF F W⋅--= 0Y=∑sin30sin600AB ACF F W+-=联立上二式,解得:7.32ABF KN=-(受压)27.3ACF KN=(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D,B点分别列平衡方程(1)取D点,列平衡方程由x=∑sin cos0DBT Wαα-=DBT Wctgα∴==(2)取B点列平衡方程:由Y=∑sin cos0BDT Tαα'-=230BDT T ctg Wctg KNαα'∴===2-10解:取B为研究对象:由0Y =∑ sin 0BC F P α-= sin BC PF α∴=取C 为研究对象:由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BCBC F F '= 解得:2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象:由0Y =∑ cos 0NH CE F F α'-=CECE F F '= 故有:22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解:取A 点平衡:x =∑sin 75sin 750AB AD F F -=0Y =∑ cos 75cos 750ABAD FF P +-=联立后可得:2cos 75AD AB PF F ==取D 点平衡,取如图坐标系:x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD PF F F KN'∴===⋅=2-12解:整体受力交于O 点,列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑ sin sin 300RAFP α-=联立上二式得:2.92RA F KN=1.33DC F KN=(压力)列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得: 1.67AC F KN=(拉力)1.0BC F KN=-(压力)2-13解:(1)取DEH 部分,对H 点列平衡x =∑0RD REF F '= 0Y =∑0RD F Q =联立方程后解得:RD F =2REF Q '=(2)取ABCE 部分,对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑ sin 450RBRA FF P --=且RE REF F '=联立上面各式得:RA F =2RB F Q P=+(3)取BCE 部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2-6 图示平面任意力系中F 1 = 402N ,F 2 = 80N ,F 3 = 40N ,F 4 = 110M ,M = 2000 N ·mm 。
各力作用位置如图所示,图中尺寸的单位为mm 。
求(1)力系向O 点简化的结果;(2)力系的合力的大小、方向及合力作用线方程。
FFFF(0,30)(20,20)(20,-30)(-50,0)45yxRF 'ooM yxoRF (0,-6)解:N 15045cos 421R -=--︒=∑=F F F F F x x 045sin 31R =-︒=∑=F F F F y yN 150)()(22'R =∑+∑=y x F F Fmm N 900305030)(432⋅-=--+=∑=M F F F M M O O F 向O 点简化结果如图(b );合力如图(c ),其大小与方向为N 150'R R i F F -==设合力作用线上一点坐标为(y x ,),则x y O O yF xF M M R R R )(-==F将O M 、'R y F 和'R x F 值代入此式,即得合力作用线方程为:mm 6-=y2-7 图示等边三角形板ABC ,边长a ,今沿其边缘作用大小均为F P 的力,方向如图(a )所示,求三力的合成结果。
若三力的方向改变成如图(b )所示,其合成结果如何?解(a )0'R =∑=i F Fa F a F M A P P 2323=⋅=(逆) 合成结果为一合力偶a F M P 23=(逆) (b )向A 点简化i F P 'R 2F -=(←)a F M A P 23=(逆) F F FF F F 习题2-10图 F F F A 'A d R F R F 'AM 习题2-9图EDF D DBF Fα(a) αCB F BDBF 'AB F (b) F C F CF A F BF BF D (c )(d ) O 再向'A 点简化,a F M d A 43'R ==合力i F P R 2F A -=(←)3-2 图示为一绳索拔桩装置。
绳索的E 、C 两点拴在架子上,点B 与拴在桩A 上的绳索AB 连接,在点D 加一铅垂向下的力F ,AB 可视为铅垂,DB 可视为水平。
已知α= 0.1rad.,力F = 800N 。
试求绳AB 中产生的拔桩力(当α很小时,tan α≈α)。
解:0=∑y F ,F F ED =αsin αs i nF F ED =0=∑x F ,DB ED F F =αcosF FF DB 10tan ==α由图(a )计算结果,可推出图(b )中:F AB = 10F DB = 100F = 80 kN3–6 梁AB 用三根杆支承,如图所示。
已知F 1=30kN ,F 2 = 40kN ,M =30kN ·m, q = 20N/m ,试求三杆的约束力。
解:(1)图(a )中梁的受力如图(c )所示。
0=∑x F ,060cos 60cos 1=︒+︒-F F C ;kN 301==F F C0)(=∑F BM ,035.160sin 3460sin 8821=⨯+︒++-︒+q F F M F F C A ;kN 22.63-=A F0)(=∑F AM ,035.660sin 5482=⨯+︒+++q F F M F C B ;kN 74.88-=A F(2)图(b )中梁的受力如图(d )所示。
0)(=∑F O M ,030cos 24621=︒--+F M F F C ;kN 45.3-=CF0)(=∑F BM,030sin 245sin 46821=︒+︒+-+F F M F F D C ;kN 41.57-=D F习题3-2图0)(=∑F DM,045sin 430sin 22421=︒-︒-+-B C F F F M F ;kN 42.8-=B F3-10 试求图示多跨梁的支座反力。
已知: (a )M = 8kN ·m , q = 4kN/m ; (b )M = 40kN ·m ,q = 10kN/m 。
习题3-19图解:(1)取图(a )中多跨梁的BC 段为研究对象,受力如图(c )所示。
0)(=∑F B M ,0634=⨯-q F C ;kN 18=C F 取图整体为研究对象,受力如图(d )所示。
0)(=∑F A M ,0678=⨯-+-q F M M C A ;m kN 32⋅=A M0=∑yF ,06=+-C Ay F q F ;kN 6=Ay F 0=∑xF,0=Ax F(2)取图(b )中多跨梁的CD 段为研究对象,受力如图(e )所示。
0)(=∑F C M ,024=--q M F D ;kN 15=D F 取图整体为研究对象,受力如图(f )所示。
0)(=∑F A M ,01682=--+q M F F D B ;kN 40=B F0=∑yF ,04=+-+D B Ay F q F F ;kN 15-=Ay F 0=∑xF,0=Ax F3-12 图示为汽车台秤简图,BCF 为整体台面,杠杆AB 可绕轴O 转动,B 、习题3-19图 (c ) (d ) (e ) (f )F Ax F Ax F Ay F Ay F C F CF Cx F Cy F BxF ByF DF BF D M ABy F 2WC B (a)A1W O B By F '(b)C 、D 三处均为铰链。
杆DC 处于水平位置。
试求平衡时砝码重W 1与汽车重W 2的关系。
解:图(a ):ΣF y = 0,F By = W 2 (1)图(b ):ΣM O = 0,01=⋅'-⋅a F l W By (2) 由式(1)、(2),得laW W =213-15 图示构架中,物体P 重1200N ,由细绳跨过滑轮E 而水平系于墙上,尺寸如图。
不计杆和滑轮的自重,求支承A 和B 处的约束力,以及杆BC 的内力F BC 。
习题3-28图 (a )(b )解:(1)整体为研究对象,受力图(a ),W F =T0=∑A M ,0)5.1()2(4T R =--+-⋅r F r W F B ,N 1050R =B F 0=∑x F ,N 1200T ===W F F Ax0=∑y F ,N 501=Ay F(2)研究对象CDE (BC 为二力杆),受力图(b ) 0=∑D M ,0)5.1(5.1sin T =-+⋅+⨯r F r W F BC θN 1500541200sin -=-=-=θW F BC (压力) 5-4 点作圆周运动,孤坐标的原点在O 点,顺钟向为孤坐标的正方向,运动方程为221Rt s π=,式中s 以厘米计,t 以秒计。
轨迹图形和直角坐标的关系如右图所示。
当点第一次到达y 坐标值最大的位置时,求点的加速度在x 和y 轴上的习题3-21图2ωe 2ωe -t ωO υaυ(c) ωe νωe -tωO υ (b) y R e -R t ωe R +πO υ (a) 投影。
解:Rt s v π== ,R v a π== t ,222n Rt Rv a π==y 坐标值最大的位置时:R Rt s 2212ππ== ,12=∴tR a a x π==t ,R a y 2π-=5-5 凸轮顶板机构中,偏心凸轮的半径为R ,偏心距OC = e ,绕轴O 以等角速转动,从而带动顶板A 作平移。
试列写顶板的运动方程,求其速度和加速度,并作三者的曲线图像。
解:(1)顶板A 作平移,其上与轮C 接触点坐标: t e R y s i n ω+=(ω为轮O 角速度) t e y v c o s ωω== t e y a s i n 2ωω-==(2)三者曲线如图(a )、(b )、(c )。
5-8滑座B 沿水平面以匀速v 0向右移动,由其上固连的销钉C 固定的滑块C 带动槽杆OA 绕O 轴转动。
当开始时槽杆OA 恰在铅垂位置,即ϕ0;销钉C 位于C 0,OC 0=b 。
试求槽杆的转动方程、角速度和角加速度。
解:bt v 0tan =ϕ,bt v 0arctan =ϕ rad22020tv b bv +==ϕωrad/s 2220230)(2t v b t bv +-==ωα6-1 图示曲柄滑杆机构中、滑杆上有圆弧滑道,其半径cm 10=R ,圆心O 1在导杆BC 上。
曲柄长cm 10=OA ,以匀角速rad/s 4πω=绕O 轴转动。
当机构在图示位置时,曲柄与水平线交角 30=φ。
求此时滑杆CB 的速度。
解:1、运动分析:动点:A ,动系:BC ,牵连运动:平移,相对运动:圆周运动,绝对运动:圆周运动。
2、速度分析:r e a v v v +=πω401a =⋅=A O v cm/s ;12640a e ====πv v v BC cm/sROMxy习题4-3图b ϕ BA v 0C 0习题4-10图 O o Av ωϕAv 习题5-2图v av r v eϕϕCCa Ba τe a ra nea(d)CϕϕeυOυrυBυ(c)AϕrOυeυa υrυ(e)6-3 曲柄摇杆机构如图所示。
已知:曲柄O 1A 以匀角速度ω1绕轴O 1转动,O 1A = R ,O 1O 2 =b ,O 2O = L 。
试求当O 1A 水平位置时,杆BC 的速度。
解:1、A 点:动点:A ,动系:杆O 2A ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
1a ωR v A =;221222ae R b R R b R v v A A +=+=ω 2、B 点:动点:B ,动系:杆O 2A ,牵连运动:定轴转动,相对运动:直线,绝对运动:直线。
221222e e R b b LR AO B O v v A B +==ω21222ea b LR b R b v v v B B BC ω=+==v A r 6-4 图a 、b 所示两种情形下,物块B 均以速度B υ、加速度a B 沿水平直线向左作平移,从而推动杆OA 绕点O 作定轴转动,OA = r ,ϕ= 40°。
试问若应用点的复合运动方法求解杆OA 的角速度与角加速度,其计算方案与步骤应当怎样?将两种情况下的速度与加速度分量标注在图上,并写出计算表达式。
解:(a ):1、运动分析:动点:C (B 上);动系:OA ;绝对运动:直线;相对运动:直线;牵连运动:定轴转动。
2、v 分析(图c ) r e v v v +=B (1)ϕs i n e B v v =OC v OC v B OA ϕωsin e ==(2)ϕc o s r B v v =3、a 分析(图d )C r te n e a a a a a +++=B (3)(3)向a C 向投影,得 C t e s i n a a a B +-=-ϕ其中OCv v a B OA ϕω2sin 22r C ==C t es i n a a a B +=ϕ OCa OAt e =α(b ):1、运动分析:动点:A (OA 上);动系:B ;绝对运动:圆周运动;相对运动:直线;牵连运动:平移。
