产业集聚度的测算.doc
产业集聚水平测度定量方法综述

产业集聚一般 指由一定 数量的企业共同组成 的产业在
一
市场集 中度 , x代表 X 产业 中第 i 位企业 的生产 额或销售 额、 职工人数等 ,N 代表 x 产业 的全部企业数 。行业集 中度
能够形象地反映产业市场集 中水平 , 测定产业 内主要企业在
重要标志 。 行业集 中度是指某一产业规模最大 的 n位企业 的
有关数值 ( 如生产额、 销售额 、 职工人数 、 资产总额等) 占整个 市场或行业的份额 。其计算公式为 :
,
对于 我国乃 至各地区产业竞争力的提升和地 区产业 的有序
协调发展具有重要 的现实意义。
C R ∑一 z /
经
济 ∽ 与 , 管
摘
要: 随着经济的发展 , 厚有产业模 式面临着新 的挑战, 产业集聚 的作用逐渐显现。本文通过分析产业集聚水平测度 的
定性与定量方法, 介绍 了一些主要的产业集聚涮度定量方法 , 以便各部门在进行产业集聚研 究时参考。 徐
关键 词 : 业 集 聚 ;测度 ;定 量 玮 产 中 图分 类号 :F 6 . 0 29
定地 域范围内的集 中, 一般包括同一类型或不同类型产业
的集 聚, 是一种集聚经济 。目前学术界对于界定地区产业集 聚程 度主要有 定性分析与定量分析两类方法 。 定性分析方法 主要为 专家意见法 、 企业调研法等。专家意见 法一般通过邀
请政府官 员、大学教授等专家,面谈后采用 D lh 法等方 epi 法, 调研 收集所需关键信息, 分析 某个 特定产 业在一定区域 的集 中程度 。企业调研法 是通过对研 究区内的企业进行调 研, 以此获取它们对 ( 域) 内外 贸易情况 、 合作联盟模 式、 研
产业集聚水平测度方法综述

n
=
年代 以来 ,从新 熊彼特 主义 的观点 出发 ,研究产 业集 聚的创 新体 系。K um n(9 1 9 5 rg a 19 ,19 )应用 不完 全竞争经济 学等解 释产业 的空 间集 聚。Pr r(9 0 94 ot 19 ,19 )提 出地 区竞 争力 的 e 著名的 “ 钻石 ”模型 ,他特别强 调产业集 聚对一定 地 区产 业 国际竞争力 的作用 。 对于产业集 聚现象 ,我 国学者也 给予 了高度 关注 ,分别
2 基 于 区域 的 产 业 集 聚 水 平 测 度 .1
经济学者和经济地理学者从 不 同的视 角对 产业集 聚理 论进 行 了研究 。2 0世纪 3 0年代 ,H oe 13 )首次将集 聚经济分 ovr(9 7 解为内部规模经济 、地方化经济 和城市化 经济 。2 0世纪 7 0— 8 0年代 ,对产业集 聚现 象 的研 究 主要 集 中在 灵活 的 “ 业 产
为了解决方法都以行政单元为基础只能描述单一空间尺度上的产业空间基尼系数失真的问题ellision和glaeser于1997年提出集聚程度这些行政单元通常规模差异很大比如中国的新了新的集聚指数来测定产业空间集聚程度即eg指数弥疆和内蒙古比安徽江西浙江等省区空间上大很多倍
20 0 9年第 5期
S in e a d T c n lg n g me tR s a c ce c n e h oo y Ma a e n e e r h
2 产 业 集聚 研 究方 法评 述
经 C K 数 据库检索 ,检索起 止 时问 从 19 NI 9 8—20 0 8年 8 月 ,篇名检索词 为 : “ 业集 聚 ” 产 ,产业 集聚 研究 文献 共 有
产业集聚度几种测度方法的比较

产业集聚度几种测度方法的比较一、标准差比例指数(SD Ratio)标准差比例指数是用来衡量企业在一个地域范围内聚集程度的方法之一、它的计算公式为SD Ratio = (标准差/平均值) * 100。
该方法可以直观地给出一个地区的产业分布的稳定程度,当SD Ratio越高时,表示产业集聚度越高。
二、本聚指数(Location Quotient)本聚指数是用来衡量一个地区特定产业在国家或地区整体产业中的比重程度。
它的计算公式为LQ=(地区特定产业的就业人数/地区所有产业的就业人数)/(国家或地区特定产业的就业人数/国家或地区所有产业的就业人数)。
当LQ大于1时,表示该地区的产业集聚度高于国家或地区整体水平,说明该地区在该产业上有较高的竞争力和优势。
三、格兰斯贝克指数(Gini Coefficient)格兰斯贝克指数是用来衡量地区产业集聚度不平衡程度的方法之一,它的计算公式为Gini = 1 - (2 * 集聚度区域面积)。
Gini值越大,表示该地区的产业集聚度越不平衡,即存在较大的集聚区和较多的边缘化地区。
四、差异系数(Coefficient of Variation)差异系数是用来衡量不同地区内部产业集聚度差异的方法之一,它的计算公式为CV=(标准差/平均值)*100。
通过计算不同地区的差异系数,可以判断不同地区内部产业分布的不均匀程度。
以上几种方法各有其优势和适用范围。
标准差比例指数可以直观地反映产业分布的稳定程度,适用于研究地区内部产业聚集程度的差异。
本聚指数适用于比较不同地区特定产业在国家或地区整体产业中的比重,可以判断地区的产业竞争力。
格兰斯贝克指数可以衡量地区产业集聚度的不平衡程度,适用于研究地区内部产业集聚的均衡性。
差异系数适用于比较不同地区内部产业聚集度的差异,可以揭示地区产业分布的不均匀程度。
综上所述,不同的产业集聚度测度方法在衡量地区产业集聚度时各有其独特的作用和适用范围。
结合这些方法的应用,可以全面地了解一个地区的产业集聚情况,为地区经济发展提供参考和指导。
论产业集聚度的测度

论产业集聚度的测度作者:刘志坚侯春峰来源:《现代商贸工业》2008年第03期摘要:随着产业集聚理论的不断发展成熟,一系列衡量产业集聚度的指标应运而生,其中最具代表性的即是区位基尼系数,它的出现为我们测度产业集聚提供了一个很好的工具。
详细论述了区位基尼系数的产生、发展以及运用时应当注意的问题,以期更好地运用区位基尼系数解释、预测社会经济的运行。
关键词:产业集聚;区位基尼系数;分析工具中图分类号:F062.9文献标识码:A文章编号:1672-3198(2008)03-0007-1 区位基尼系数的应用1.1 产业集聚理论的发展早在上世纪20年代,韦伯(A·Weber)和马歇尔(A · Marshall)就对产业集聚的问题给予了高度的重视,并由此开辟了一个新的研究领域——空间经济。
进入20世纪80年代,世界范围内产业集聚明显加快,各种形式的产业集聚现象大量涌现,一大批著名的经济学家敏锐地观察到了这一趋势,开始介入到产业集聚的空间或区域问题的研究,并希望将其引入到主流经济学的范畴。
在这些工作中,首推以保罗·克鲁格曼(Krugram, Paul)等为代表的“新经济地理学”的贡献。
克鲁格曼甚至认为“新经济地理学”是继新产业组织理论、新贸易理论和新增长理论之后的最新经济理论前沿。
随着产业集聚理论的不断发展成熟,现在该理论已经成为经济学、管理学等诸多学科的研究热点。
1.2 区位基尼系数的计算深入地研究集聚理论,不仅要探索产业集聚的形成机理以及动力机制等定性因素,而且要求产业集聚度量等定量分析,以便更好地检验或者完善产业集聚理论。
在这一要求下,一系列衡量产业集聚度的指标应运而生,如标准差系数、集中率、集中指数、区位基尼系数等,其中最具代表性的应该是区位基尼系数。
区位基尼系数的产生要追溯到洛伦茨,洛伦兹(M · Lorenz)在研究居民收入分配时,发现将居民家庭户数累积百分比与居民收入百分比联系在一起,可以揭示收入分配的均衡性。
产业集聚度的测度方法和区位熵

场的份额来度量。
Xi
n➢ 1)计算公式:
N
➢ 其中, 是 产业的集聚度;
CRn
是第i个地区的产值、产量、销售额、销售量、职工人数、资产总额
等;
是要计算的某一产业中规模最大的几个地区数目,一般取值为4或8;
二、方法比较——产业集聚度的几种 测度方法
➢ 2)优点:计算方法简单,采用最常用的指标, 能够形象的反应产业集聚 水平。
➢ 缺点:集聚度的测算季节容易受到n值选取 的影响; 忽略了规模最大地区之外其它地区
二、方法比较——产业集聚度的几种 测度方法
➢
➢
2赫、芬赫达芬达尔尔指-H赫数希iN1是Z曼i2 指指 i数N1某(XX特iHe2 定rfin市dah场l -H上irs所chm有an企in业dex的)市
场X份额的平方和,其的原始用途是用于衡量市
Xi
Zi
➢
场竞X争i 和垄断的关系。 1)X计算公式
N
➢ 其中, 代表产业市场总规模(就业或产值),
二、方法比较——产业集聚度的几种 测度方法
➢ 2)优点: 能够相对准确反映产业或企业市场 集中度, 因为它考虑了企业总数
和企业规模两个因素的影响;
变化;
能够反映市场垄断与竞争程度的
对产业内企业的合并与分解反映
➢ 缺点:基尼系数大于零并不表明有集聚现 象存在, 因为它没有考虑到企业 的规模差异。 空间基尼系数没有考虑到
二、方法比较——产业集聚度的几种 测度方法
➢ 4、 EG 指数( EG index)空M间集聚指数 M N
sxi内这i 1N有假)个N定计企个某算业企一公=分业(G1经式布,(i1济:于且xi2)i体(1M将xi2()H个H该) 国区经i家1域(济s(i1或之划xiiM地)1中2分xi2区()。1(为1)ijM1N1xZi2)2j的)j个1 Z某地2j 一理产区业域,
产业集聚度的测算

一 产业集聚度概念和测度方法产业集中度的概念:产业集中度也叫市场集中度,是指市场上的某种行业内少数企业的生产量、销售量、资产总额等方面对某一行业的支配程度,它一般是用这几家企业的某一指标(大多数情况下用销售额指标)占该行业总量的百分比来表示。
产业集聚测度方法1、 集中度(Concentrion ration of industry )行业集中度是用规模最大的几个地区有关数值(销售额、就业人数、生产额等) 占整个行业的份额来度量。
计算公式为:11n i i n N i i XCR X===∑∑其中n CR 代表X 产业的集聚度,1ni i X =∑代表规模最大几个地区X 产业的销售额或者生产额、就业人数等,1Ni i X =∑代表全部地区X 产业的销售额或者生产额、就业人数等。
优点:计算方法简单,采用最常用的指标,能够形象的反应产业集聚水平。
缺点:一是集聚度的测算季节容易受到n 值选取的影响,二是忽略了规模最大地区之外其它地区的规模分布情况, 三是不能反映规模最大地区内部之间产业结构与分布的差别。
2、 区位熵(Entropy index )所谓熵, 就是比率的比率,它由哈盖特(P ·Haggett )首先提出并用于区位分析中。
区位熵, 又称专门化率,用以衡量某一区域要素的空间分布情况,反映某一产业部门的专业化程度,以及某一区域在高层次区域的地位和作用等方面。
在产业结构研究中,通常用于分析区域主导专业化部门的状况。
计算公式为:11E /i i ij n n i i i i q Q q Q ===∑∑ 其中E ij 表示某区域i 部门对于高层次区域的区域熵;i q 为某区域部门的有关指标(通常可用产值、产量、生产能力、就业人数等指标);i Q 为高层次区域部门的有关指标; n 为某类产业的部门数量。
E ij 值越大,表示产业的集聚程度越高。
优点:计算操作简单方便,指标选取目标明确。
缺点:不能反映区域经济发展水平的差异性,某产业区位熵最大的地区不一定是该产业集聚水平最高的地区。
产业集聚度的测算(最新整理)

一 产业集聚度概念和测度方法产业集中度的概念:产业集中度也叫市场集中度,是指市场上的某种行业内少数企业的生产量、销售量、资产总额等方面对某一行业的支配程度,它一般是用这几家企业的某一指标(大多数情况下用销售额指标)占该行业总量的百分比来表示。
产业集聚测度方法1、集中度(Concentrion ration of industry )行业集中度是用规模最大的几个地区有关数值(销售额、就业人数、生产额等) 占整个行业的份额来度量。
计算公式为:11n i i n N ii XCR X===∑∑其中代表X 产业的集聚度,代表规模最大几个地区X 产业的销售额n CR 1ni i X =∑或者生产额、就业人数等,代表全部地区X 产业的销售额或者生产额、1Ni i X =∑就业人数等。
优点:计算方法简单,采用最常用的指标,能够形象的反应产业集聚水平。
缺点:一是集聚度的测算季节容易受到n 值选取的影响,二是忽略了规模最大地区之外其它地区的规模分布情况, 三是不能反映规模最大地区内部之间产业结构与分布的差别。
2、区位熵(Entropy index )所谓熵, 就是比率的比率,它由哈盖特(P ·Haggett )首先提出并用于区位分析中。
区位熵, 又称专门化率,用以衡量某一区域要素的空间分布情况,反映某一产业部门的专业化程度,以及某一区域在高层次区域的地位和作用等方面。
在产业结构研究中,通常用于分析区域主导专业化部门的状况。
计算公式为:11E /i i ij n n i i i i q Q q Q ===∑∑其中表示某区域i 部门对于高层次区域的区域熵;为某区域部门的有关E ij i q指标(通常可用产值、产量、生产能力、就业人数等指标);为高层次区域i Q 部门的有关指标; n 为某类产业的部门数量。
值越大,表示产业的集聚E ij 程度越高。
优点:计算操作简单方便,指标选取目标明确。
缺点:不能反映区域经济发展水平的差异性,某产业区位熵最大的地区不一定是该产业集聚水平最高的地区。
产业集聚度的测算

一产业集聚度概念和测度方法产业集中度的概念:产业集中度也叫市场集中度,是指市场上的某种行业内少数企业的生产量、销售量、资产总额等方面对某一行业的支配程度,它一般是用这几家企业的某一指标(大多数情况下用销售额指标)占该行业总量的百分比来表示。
产业集聚测度方法1、集中度(Concentrion ration of industry )行业集中度是用规模最大的几个地区有关数值(销售额、就业人数、生产额等)占整个行业的份额来度量。
计算公式为:nX iCR n 1X ii 1n其中CR n代表X产业的集聚度,X i代表规模最大几个地区X产业的销售额i 1N或者生产额、就业人数等,X i代表全部地区X产业的销售额或者生产额、i 1就业人数等。
优点:计算方法简单,采用最常用的指标,能够形象的反应产业集聚水平。
缺点:一是集聚度的测算季节容易受到n值选取的影响,二是忽略了规模最大地区之外其它地区的规模分布情况,三是不能反映规模最大地区内部之间产业结构与分布的差别。
2、区位熵(Entropy index )所谓熵,就是比率的比率,它由哈盖特( P • Haggett )首先提出并用于区位分析中。
区位熵,又称专门化率,用以衡量某一区域要素的空间分布情况,反映某一产业部门的专业化程度,以及某一区域在高层次区域的地位和作用等方面。
在产业结构研究中,通常用于分析区域主导专业化部门的状况。
计算公式为:E q i / Q i匚j ~/ ~nq i Q ii 1 i 1其中E j表示某区域i部门对于高层次区域的区域熵;qi为某区域部门的有关指标(通常可用产值、产量、生产能力、就业人数等指标);Qi为高层次区E域部门的有关指标;n为某类产业的部门数量。
E j值越大,表示产业的集聚程度越高。
优点:计算操作简单方便,指标选取目标明确。
缺点:不能反映区域经济发展水平的差异性,某产业区位熵最大的地区不一定是该产业集聚水平最高的地区。
3、赫芬达尔-赫希曼指数(Hefindahl-Hirschman index )该指数是衡量产业集聚程度的重要指标,最初由 A. Hirschma n 提出,后经哥伦比亚大学O. Hirschman加以改进,该指数产生的理论基础来源于贝恩(Bain) 的“结构一一行为一一绩效”(SCP) 理论。
产业集聚度的几种测算方法

产业集聚度的几种测算方法第一种方法是格里芬指数(Gini coefficient)。
格里芬指数最初用于测算个体之间的收入不平等程度,后来也被应用于衡量产业集聚度。
格里芬指数的计算方法如下:1.收集区域内所有企业的市场份额数据,份额可以是销售额、就业人数、净利润等。
2.将这些份额按照从小到大的顺序排列,并计算企业市场份额的累计占比。
3.根据累计占比计算格里芬系数,公式为:G=(n+1)/n-(2×累计份额占比)格里芬指数的取值范围为0到1,值越高表示产业集聚度越高。
第二种方法是默顿指数(Herfindahl index)。
默顿指数用于衡量市场份额集中度,也可以用于衡量产业集聚度。
计算方法如下:1.收集区域内所有企业的市场份额数据,份额可以是销售额、就业人数、净利润等。
2.将这些份额按照从小到大的顺序排列,并计算企业市场份额的平方。
3.将所有企业的市场份额平方相加,得到总和。
4.根据总和计算默顿指数,公式为:H=总和默顿指数的取值范围为0到1,值越高表示产业集聚度越高。
第三种方法是位置熵(Location entropy)。
位置熵用于测算不同地区之间同一产业占比的差异程度,可以反映产业集聚的情况。
计算方法如下:1.统计不同地区内同一产业的市场份额数据,份额可以是销售额、就业人数、净利润等。
2.计算每个地区内同一产业份额的占比,并计算位置熵,公式为:E = -∑(p × log(p))位置熵的取值范围为0到1,值越高表示产业集聚度越高。
此外,还有一些其他方法可以用于测算产业集聚度,如罗森鲍姆指数、可达性指数等。
这些方法都在不同的背景和需求下应用,可以根据具体情况选择适当的方法。
总之,产业集聚度的测算方法多样,可以根据数据可获得性和研究目的选择合适的方法进行测算。
不同的方法有不同的特点和适用范围,需要根据具体情况进行选择和应用。
产业集聚度的测算.pdf

一 产业集聚度概念和测度方法产业集中度的概念:产业集中度也叫市场集中度,是指市场上的某种行业内少数企业的生产量、销售量、资产总额等方面对某一行业的支配程度,它一般是用这几家企业的某一指标(大多数情况下用销售额指标)占该行业总量的百分比来表示。
产业集聚测度方法1、 集中度(Concentrion ration of industry )行业集中度是用规模最大的几个地区有关数值(销售额、就业人数、生产额等) 占整个行业的份额来度量。
计算公式为:11n i i n N i i XCR X===∑∑其中n CR 代表X 产业的集聚度,1ni i X =∑代表规模最大几个地区X 产业的销售额或者生产额、就业人数等,1Ni i X =∑代表全部地区X 产业的销售额或者生产额、就业人数等。
优点:计算方法简单,采用最常用的指标,能够形象的反应产业集聚水平。
缺点:一是集聚度的测算季节容易受到n 值选取的影响,二是忽略了规模最大地区之外其它地区的规模分布情况, 三是不能反映规模最大地区内部之间产业结构与分布的差别。
2、 区位熵(Entropy index )所谓熵, 就是比率的比率,它由哈盖特(P ·Haggett )首先提出并用于区位分析中。
区位熵, 又称专门化率,用以衡量某一区域要素的空间分布情况,反映某一产业部门的专业化程度,以及某一区域在高层次区域的地位和作用等方面。
在产业结构研究中,通常用于分析区域主导专业化部门的状况。
计算公式为:11E /i i ij n n i i i i q Q q Q ===∑∑ 其中E ij 表示某区域i 部门对于高层次区域的区域熵;i q 为某区域部门的有关指标(通常可用产值、产量、生产能力、就业人数等指标);i Q 为高层次区域部门的有关指标; n 为某类产业的部门数量。
E ij 值越大,表示产业的集聚程度越高。
优点:计算操作简单方便,指标选取目标明确。
缺点:不能反映区域经济发展水平的差异性,某产业区位熵最大的地区不一定是该产业集聚水平最高的地区。
贵州省产业集群的集聚度测算
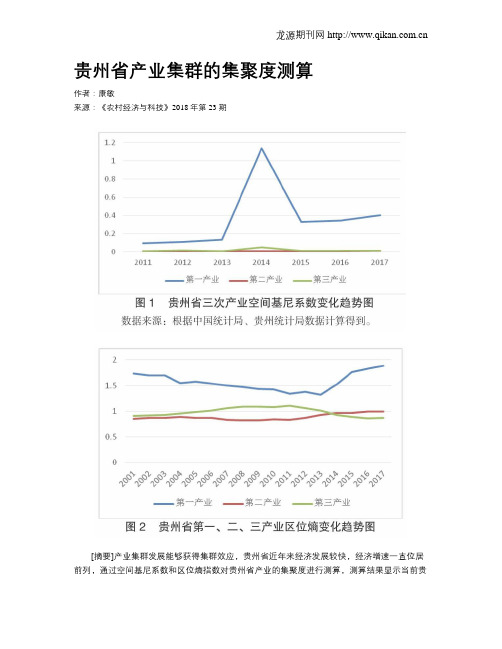
贵州省产业集群的集聚度测算作者:康敏来源:《农村经济与科技》2018年第23期[摘要]产业集群发展能够获得集群效应,贵州省近年来经济发展较快,经济增速一直位居前列,通过空间基尼系数和区位熵指数对贵州省产业的集聚度进行测算,测算结果显示当前贵州省产业集群的集聚度均比较低,提出加大政策支持力度、完善产业集聚平台建设、创建产城融合机制以及坚持走技术创新的可持续发展道路的对策建议。
[关键词]产业集群;集聚度;空间基尼系数;区位熵[中图分类号]F062.9 [文献标识码]A1; ; 引言自2001年以來,国家大力实施西部大开发战略,西部地区迎来发展的新机遇,获得了更多的政策优惠与支持,促进了西部地区经济的快速发展,产业结构更趋合理,产业竞争力不断提高。
贵州省作为西部内陆省份,不沿江、不沿海、不沿边,同时土地碎片化、石漠化严重,是我国喀斯特地貌主要集中地区,山地面积广大,是我国唯一一个没有平原支撑的山地省份,交通不便,信息闭塞,长期处于“欠开发、欠发展”状态。
但贵州是一个传统的资源大省,资源丰裕,具有发展的先天优势与条件,特别是近几年贵州省经济增速一直保持前列,在经济转型升级的重要阶段,思考贵州省产业发展应如何从集群发展的角度出发,通过专业化的分工与合作,增强集群企业间的上下游产业关联,提高地区经济发展的竞争力具有重要意义。
2; ; 产业集群的意义2.1; ; 产业集群能够获得“集群”效应产业集群能够带来规模经济、范围经济、技术外溢等集群效应,相关企业聚集能够扩大地区产业规模,加大基础设施、人力资本的利用效率,加强企业的沟通与交流,增强企业信任与信息交换能力,降低企业间交易成本;促进健康有序的竞争合作秩序建立,促进企业进行产品创新与质量提高,增加产品品种,提高产品质量与丰裕度;促进生产工艺、产业设计、管理与运营等新思想、新技术的产生,形成区域间不断创新、不断进步的良性循环态势。
2.2; ; 产业集群能够促进专业化的分工与合作聚集企业之间存在明显的上下游产业关系,主导企业与上下游企业之间、核心企业与其配套企业之间存在着密切的专业化分工与合作。
产业集聚测度方法

1.赫芬代尔系数和赫希曼-赫芬代尔系数赫芬代尔系数是各区域某产业产值或就业比重的平方和,即∑=ii s H 2如果所有经济活动都集中在一个区域,那么H=1最大,如果经济活动平均分布在各个区域,H=1/n 。
这个系数实际上仅衡量了产业的空间分布,并没有与其他经济活动相对比较,衡量的是产业绝对集中程度。
为了衡量产业的相对集中程度,赫希曼改善课赫芬代尔系数,()21∑=-=m j j ij i x s HH其中s ij 表示产业i 在区域j 中的就业或产值比重,x j 区域j 中的总就业或者产值占全国的比重。
如果某产业的就业或产值的空间分布与总体经济活动是一致的,那么HH 值为零。
2.信息熵和锡尔系数信息熵原本用来测量一个系统的复杂程度。
一个产业的空间分布越分散,表明这个系统越复杂;反之,产业在空间上越集中,则该系统越简单。
产业空间分布的信息熵如下()()i ij ji ij i x x x x E /ln /∑-=其中x ij 表示产业i 在区域j 中的就业人数或产值,x i 产业i 的总就业人数或总产值。
如果某个产业全部集中在一个区域,E 值为零。
锡尔系数经常用来测量收入的区域差异,也可以衡量产业的地理集中程度,计算如下:⎪⎪⎭⎫ ⎝⎛-=∑=J x x x x T i ij Jr i ij i 1log log 1 其中x ij 产业i 在区域j 总的就业或产值,x i 产业i 的总就业或总产值,J 为总区域数。
3.基尼系数基尼系数将某产业分布于其他产业对比,是使用最广泛的系数之一,计算公式如下:ik ij k j i s s n G -=∑∑μ221其中s ij 和s ik 事产业i 在区域j 和k 的比重,μ是产业在各个区域比重的平均值,n 为区域个数。
基尼系数等于洛伦兹曲线与45°线之间面积的两倍,洛伦兹曲线是基于s ij 递增排序,并将累计s ij 置于纵轴,而累计的区域数置于横轴绘制而成的。
产业集聚度的测度方法和区位熵

产业集聚度的测度方法和区位熵
区位熵是由经济地理学家阿尔弗雷德·韦伯于1909年提出的概念,
用于衡量产业集聚度。
区位熵是根据产业在地理上的相对分布情况计算的。
区位熵的计算方法如下:
首先,确定研究区域的范围和要研究的产业类型。
然后,将研究区域划分为若干个单位区域(例如县级单位或乡镇单位)。
接下来,根据产业在每个单位区域的就业人数或产值等指标,计算每
个单位区域内产业的相对分布情况。
最后,根据单位区域内产业的相对分布情况,计算区位熵的值。
区位
熵的计算公式为:
E = - ∑(pi * log(pi))
其中,pi表示第i个单位区域内的产业就业人数或产值占总区域内
产业总就业人数或产值的比重,log表示以2为底的对数。
区位熵的数值范围为0到1之间,数值越小表示产业的集聚度越高,
数值越大表示产业的分散度越高。
区位熵的优点是简单易计算,并且能够综合考虑地理上的相对分布情况。
然而,区位熵也存在一些局限性。
首先,区位熵只能反映产业在空间上的集聚程度,无法考虑其他因素
对产业集聚度的影响。
其次,区位熵的计算结果受到单位区域的划分方式和产业类型的选择等因素的影响,可能存在主观性和不确定性。
此外,区位熵只能测度当前时期的产业集聚度,无法对产业集聚度的变化趋势进行预测。
因此,在进行产业集聚度的测度时,需要综合考虑区位熵以外的其他因素,例如产业链条的完整度、企业间的关联度、创新能力等,以充分评估产业集聚的程度和发展潜力。
(完整版)产业集聚测量方法

(完整版)产业集聚测量⽅法摘要:本⽂介绍了⽬前常⽤的产业集聚测量⽅法,主要包括:⾏业集中度、赫芬达尔指数、熵指数、空间基尼系数、E-G指数。
通过对⽐分析,阐述了各种测量⽅法的优缺点。
分析认为,E-G指数是测量产业集聚⽐较适合的⽅法,但受制于数据的可获取性。
关键词:产业集聚测量⼀、前⾔区域经济理论认为,产业集聚对⼀个地区整体产业竞争⼒及区域经济增长具有重要影响。
因此推动产业集聚成为了许多地⽅政府发展区域经济的重要⼿段。
制定产业集聚相关政策必须以实证研究为基本前提,⽽对于产业集聚的实证研究,⼀个最根本的问题是如何测度产业的集聚度⽔平,因为⽆论是单纯进⾏产业集聚的研究还是探讨产业集聚对经济增长、经济稳定以及其他⽅⾯的影响,它都直接影响到最终研究结论的可信程度。
⼆、产业集聚常⽤的测量⽅法⽬前⽐较常⽤的产业集聚测量⽅法主要有:⾏业集中度、赫芬达尔指数、熵指数、空间基尼系数、E-G集聚指数。
1、⾏业集中度⾏业集中度是⼀种⽐较简单的指标,⽤来衡量某产业规模最⼤的前⼏个地区在全国所占的份额。
其计算公式如下:其中IC代表⾏业集中度;A i代表产业A中排名第i位区域的产值或者销售额、从业⼈员等;N代表产业A中的地区数⽬。
上式表明⾏业集中度等于产业A中规模排名前n位 (n⼀般取4或8)的区域企业规模之和占产业A全国总规模的⽐例。
由于IC主要反映⾏业在⼏个区域的集中程度,没有涉及到⾏业的企业数⽬与⾏业总规模之间的差异,⾏业集中系数就是为了弥补这个缺陷。
以P表⽰计算的企业占⾏业企业总数的⽐例:那么,⾏业集中系数 CC可表⽰为:⾏业集中度与集中系数能够形象地反映产业区域集中⽔平以及⾏业中企业数量的影响,测算⽅法便捷直观。
然⽽,⾏业集中度指标存在⼀些缺点:第⼀,仅说明了产业分布规模最⼤的⼏个地区的情况,⽽忽略了其余地区的规模分布情况;第⼆,不能反映最⼤⼏个地区的个别情况;第三,存在选取规模最⼤的区域数⽬不同集中度结果不同的问题。
产业集聚测度方法

1.赫芬代尔系数和赫希曼-赫芬代尔系数赫芬代尔系数是各区域某产业产值或就业比重的平方和,即∑=ii s H 2如果所有经济活动都集中在一个区域,那么H=1最大,如果经济活动平均分布在各个区域,H=1/n 。
这个系数实际上仅衡量了产业的空间分布,并没有与其他经济活动相对比较,衡量的是产业绝对集中程度。
为了衡量产业的相对集中程度,赫希曼改善课赫芬代尔系数,()21∑=-=m j j ij i x s HH其中s ij 表示产业i 在区域j 中的就业或产值比重,x j 区域j 中的总就业或者产值占全国的比重。
如果某产业的就业或产值的空间分布与总体经济活动是一致的,那么HH 值为零。
2.信息熵和锡尔系数信息熵原本用来测量一个系统的复杂程度。
一个产业的空间分布越分散,表明这个系统越复杂;反之,产业在空间上越集中,则该系统越简单。
产业空间分布的信息熵如下()()i ij ji ij i x x x x E /ln /∑-=其中x ij 表示产业i 在区域j 中的就业人数或产值,x i 产业i 的总就业人数或总产值。
如果某个产业全部集中在一个区域,E 值为零。
锡尔系数经常用来测量收入的区域差异,也可以衡量产业的地理集中程度,计算如下:⎪⎪⎭⎫ ⎝⎛-=∑=J x x x x T i ij Jr i ij i 1log log 1 其中x ij 产业i 在区域j 总的就业或产值,x i 产业i 的总就业或总产值,J 为总区域数。
3.基尼系数基尼系数将某产业分布于其他产业对比,是使用最广泛的系数之一,计算公式如下:ik ij k j i s s n G -=∑∑μ221其中s ij 和s ik 事产业i 在区域j 和k 的比重,μ是产业在各个区域比重的平均值,n 为区域个数。
基尼系数等于洛伦兹曲线与45°线之间面积的两倍,洛伦兹曲线是基于s ij 递增排序,并将累计s ij 置于纵轴,而累计的区域数置于横轴绘制而成的。
论产业集聚度的测度

论产业集聚度的测度[摘要]21世纪初以来,产业集群在推动着我国国民经济迅速发展方面起着越来越重要的作用,业界和学界关于产业集群的探索研究方兴未艾。
其中,有关产业集聚度测度的研究成为一个热门研究领域。
目前,产业地理集聚程度的测度方法多是从传统的集中度测度方法演变而来,其基本方法是利用经济学中衡量分布均衡状态的指标,利用因子分析、层次分析、结构方程等一些定量方法进行研究。
而无论采取何种方法,关键部分始终是产业集聚度测度指标的选择。
本文试图将串联目前各种有关产业集聚度测度指标的研究成果,总结它们的贡献与不足,以期能促进对产业集聚度测度的研究进展。
[关键词]产业集聚度;测度指标;产业集群1 产业集聚度问题的提出从目前区域经济研究来看,产业集群问题无疑是其中的热点议题,而对产业集群集聚度的研究是产业集群研究中的亮点。
对产业集群集聚度的研究主要通过一系列指标来判断某一区域是否存在产业集群,以及产业集群的聚合程度。
其实质是利用集群在区域内的影响力加以衡量,这是一种未知判断并得出结论的研究方式。
目前,国内外学者对产业集群集聚度的研究多从产业集群的表层出发进行测度,并没有考虑产业集群内部的经济关系。
因此,产业集群的研究,首先必须明确产业集聚度的界定与测度方法以及相应的理论基础。
1.1 产业集聚度的测度从目前的研究来看,产业集聚度的测度大都通过某一产业的区位集中程度来判定产业集群是否存在。
当前常用到的两个测定产业集聚度的指标区位商系数LQ与空间基尼系数G,都把产业集群一个“黑箱”同外部的经济组织进行比较,以测定产业集群的集聚程度。
然而,产业集群的三个基本特征——弹性专精、竞争合作、社会根植性是相互关联、共同发展的,集群内的经济活动是以网状的方式交织在一起的。
因此,产业集聚度其实就是对产业集群内部网络系统的衡量和外部影响力的评价。
它包含两方面的内容:一是产业集群内部网络系统的完善度和紧密度;二是产业集群在区位内的影响力和在产业内的影响力。
(完整版)产业集聚度的测算

一 产业集聚度概念和测度方法产业集中度的概念:产业集中度也叫市场集中度,是指市场上的某种行业内少数企业的生产量、销售量、资产总额等方面对某一行业的支配程度,它一般是用这几家企业的某一指标(大多数情况下用销售额指标)占该行业总量的百分比来表示。
产业集聚测度方法1、 集中度(Concentrion ration of industry )行业集中度是用规模最大的几个地区有关数值(销售额、就业人数、生产额等) 占整个行业的份额来度量。
计算公式为:11n i i n N i i XCR X===∑∑其中n CR 代表X 产业的集聚度,1ni i X =∑代表规模最大几个地区X 产业的销售额或者生产额、就业人数等,1Ni i X =∑代表全部地区X 产业的销售额或者生产额、就业人数等。
优点:计算方法简单,采用最常用的指标,能够形象的反应产业集聚水平。
缺点:一是集聚度的测算季节容易受到n 值选取的影响,二是忽略了规模最大地区之外其它地区的规模分布情况, 三是不能反映规模最大地区内部之间产业结构与分布的差别。
2、 区位熵(Entropy index )所谓熵, 就是比率的比率,它由哈盖特(P ·Haggett )首先提出并用于区位分析中。
区位熵, 又称专门化率,用以衡量某一区域要素的空间分布情况,反映某一产业部门的专业化程度,以及某一区域在高层次区域的地位和作用等方面。
在产业结构研究中,通常用于分析区域主导专业化部门的状况。
计算公式为:11E /i i ij n n i i i i q Q q Q ===∑∑ 其中E ij 表示某区域i 部门对于高层次区域的区域熵;i q 为某区域部门的有关指标(通常可用产值、产量、生产能力、就业人数等指标);i Q 为高层次区域部门的有关指标; n 为某类产业的部门数量。
E ij 值越大,表示产业的集聚程度越高。
优点:计算操作简单方便,指标选取目标明确。
缺点:不能反映区域经济发展水平的差异性,某产业区位熵最大的地区不一定是该产业集聚水平最高的地区。
(完整版)产业集聚度的测算.doc

一产业集聚度概念和测度方法产业集中度的概念:产业集中度也叫市场集中度,是指市场上的某种行业内少数企业的生产量、销售量、资产总额等方面对某一行业的支配程度,它一般是用这几家企业的某一指标(大多数情况下用销售额指标)占该行业总量的百分比来表示。
产业集聚测度方法1、集中度( Concentrion ration of industry )行业集中度是用规模最大的几个地区有关数值( 销售额、就业人数、生产额等 ) 占整个行业的份额来度量。
计算公式为:nX iCR n i 1 NX ii 1其中 CR n代表X产业的集聚度,n代表规模最大几个地区 X产业的销售额X ii 1N或者生产额、就业人数等,X i代表全部地区X产业的销售额或者生产额、i 1就业人数等。
优点:计算方法简单,采用最常用的指标,能够形象的反应产业集聚水平。
缺点:一是集聚度的测算季节容易受到n 值选取的影响,二是忽略了规模最大地区之外其它地区的规模分布情况,三是不能反映规模最大地区内部之间产业结构与分布的差别。
2、区位熵( Entropy index)所谓熵 , 就是比率的比率,它由哈盖特(P · Haggett )首先提出并用于区位分析中。
区位熵,又称专门化率,用以衡量某一区域要素的空间分布情况,反映某一产业部门的专业化程度,以及某一区域在高层次区域的地位和作用等方面。
在产业结构研究中,通常用于分析区域主导专业化部门的状况。
计算公式为:q i Q iEij n / nq i Q ii 1 i 1其中Eij表示某区域 i 部门对于高层次区域的区域熵;q i为某区域部门的有关指标 ( 通常可用产值、产量、生产能力、就业人数等指标);Qi为高层次区域部门的有关指标;n 为某类产业的部门数量。
Eij值越大,表示产业的集聚程度越高。
优点:计算操作简单方便,指标选取目标明确。
缺点:不能反映区域经济发展水平的差异性,某产业区位熵最大的地区不一定是该产业集聚水平最高的地区。
(2020年整理)产业集聚度的测算.doc

一 产业集聚度概念和测度方法产业集中度的概念:产业集中度也叫市场集中度,是指市场上的某种行业内少数企业的生产量、销售量、资产总额等方面对某一行业的支配程度,它一般是用这几家企业的某一指标(大多数情况下用销售额指标)占该行业总量的百分比来表示。
产业集聚测度方法1、 集中度(Concentrion ration of industry )行业集中度是用规模最大的几个地区有关数值(销售额、就业人数、生产额等) 占整个行业的份额来度量。
计算公式为:11nii n Nii X CR X===∑∑其中n CR 代表X 产业的集聚度,1ni i X =∑代表规模最大几个地区X 产业的销售额或者生产额、就业人数等,1Ni i X =∑代表全部地区X 产业的销售额或者生产额、就业人数等。
优点:计算方法简单,采用最常用的指标,能够形象的反应产业集聚水平。
缺点:一是集聚度的测算季节容易受到n 值选取的影响,二是忽略了规模最大地区之外其它地区的规模分布情况, 三是不能反映规模最大地区内部之间产业结构与分布的差别。
2、 区位熵(Entropy index )所谓熵, 就是比率的比率,它由哈盖特(P ·Haggett )首先提出并用于区位分析中。
区位熵, 又称专门化率,用以衡量某一区域要素的空间分布情况,反映某一产业部门的专业化程度,以及某一区域在高层次区域的地位和作用等方面。
在产业结构研究中,通常用于分析区域主导专业化部门的状况。
计算公式为:11E /iiij nni ii i q Q q Q===∑∑其中E ij表示某区域i 部门对于高层次区域的区域熵;i q为某区域部门的有关指标(通常可用产值、产量、生产能力、就业人数等指标);iQ 为高层次区域部门的有关指标; n 为某类产业的部门数量。
E ij值越大,表示产业的集聚程度越高。
优点:计算操作简单方便,指标选取目标明确。
缺点:不能反映区域经济发展水平的差异性,某产业区位熵最大的地区不一定是该产业集聚水平最高的地区。
论产业集聚度的测度

两种 方 法 :一 是 运 用 区位 商 系 数 L ( oao ut n) Q Lct nQ o et i i 判别 产业 集群 存 在 的 可 能 性 ;二 是 基 于 空 间 基 尼 系 数 G (ptl i ofc n)来 计算 产 业 集群 集 聚 度 。二 者 的 S aa Gn cei et i i fi 计算 公式 如下 :
L = ( / / E / Q E)( E)
面 的 内容 :一是 产 业 集 群 内部 网 络 系 统 的 完 善 度 和 紧密 度 ;二是 产业 集 群 在 区位 内 的影 响力 和 在 产 业 内 的影 响
力 。本文 第 三部分 的 产业 集聚度 的测 度 指标 体系 也将 围绕
产业 集群 的探 索研 究 方兴 未艾 。其 中,有 关产业 集聚度 测 度 的研 究成 为一个 热 门研 究领 域 。 目 ,产 业地理 集 聚程 度 的 前 测度 方 法 多是 从传 统 的集 中度 测度 方 法演 变而 来 ,其基 本 方 法 是利 用经 济 学 中衡 量 分 布 均衡 状 态 的指 标 ,利 用 因子 分
测 度 的研 究 进 展 。
[ 关键 词 ] 产 业集 聚度 ;测度 指标 ;产 业 集群 [ 图分类 号 ] F6 . 中 0 29 [ 文献标 识码 ]A
[ 文章 编 号 ]10 6 3 (0 1 3— 20— 3 05— 42 2 1 )2 00 0
上从 不 同的角 度对 产业 关联 进行 了细致 的划分 :按 产业 之
和 环 向关 联关 系 ;按产 业之 间相 互依 托 的方式 分 ,有产 品 或 劳务联 系 、生产 技术 联 系 、价格 联 系 、劳动就 业联 系 和 投 资联 系 ;按 产业 之 间技术 工艺 的方 向和 特点 分 ,有单 向 联 系和 多 向联 系 等 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一 产业集聚度概念和测度方法产业集中度的概念:产业集中度也叫市场集中度,是指市场上的某种行业内少数企业的生产量、销售量、资产总额等方面对某一行业的支配程度,它一般是用这几家企业的某一指标(大多数情况下用销售额指标)占该行业总量的百分比来表示。
产业集聚测度方法1、 集中度(Concentrion ration of industry )行业集中度是用规模最大的几个地区有关数值(销售额、就业人数、生产额等) 占整个行业的份额来度量。
计算公式为:11n i i n N i i XCR X===∑∑其中n CR 代表X 产业的集聚度,1ni i X =∑代表规模最大几个地区X 产业的销售额或者生产额、就业人数等,1Ni i X =∑代表全部地区X 产业的销售额或者生产额、就业人数等。
优点:计算方法简单,采用最常用的指标,能够形象的反应产业集聚水平。
缺点:一是集聚度的测算季节容易受到n 值选取的影响,二是忽略了规模最大地区之外其它地区的规模分布情况, 三是不能反映规模最大地区内部之间产业结构与分布的差别。
2、 区位熵(Entropy index )所谓熵, 就是比率的比率,它由哈盖特(P ·Haggett )首先提出并用于区位分析中。
区位熵, 又称专门化率,用以衡量某一区域要素的空间分布情况,反映某一产业部门的专业化程度,以及某一区域在高层次区域的地位和作用等方面。
在产业结构研究中,通常用于分析区域主导专业化部门的状况。
计算公式为:11E /i i ij n n i i i i q Q q Q ===∑∑ 其中E ij 表示某区域i 部门对于高层次区域的区域熵;i q 为某区域部门的有关指标(通常可用产值、产量、生产能力、就业人数等指标);i Q 为高层次区域部门的有关指标; n 为某类产业的部门数量。
E ij 值越大,表示产业的集聚程度越高。
优点:计算操作简单方便,指标选取目标明确。
缺点:不能反映区域经济发展水平的差异性,某产业区位熵最大的地区不一定是该产业集聚水平最高的地区。
3、 赫芬达尔- 赫希曼指数(Herfindahl-Hirschman index )该指数是衡量产业集聚程度的重要指标,最初由A. Hirschman 提出,后经哥伦比亚大学O. Hirschman 加以改进,该指数产生的理论基础来源于贝恩(Bain) 的“结构——行为——绩效” ( SCP) 理论。
计算公式为:2211(/)(1,2,3...,)N Njj j j H Z X X j n =====∑∑ 其中, X 代表产业市场总规模(就业或产值), j X 代表j 企业的规模,j Z = /j X X 代表第j 个企业的市场占有率,N 代表该产业内部的企业数。
在实际分析中,经常运用H 指数的倒数作为产业多样化的测度。
优点:第一是能够准确反映产业或企业市场集中度,因为它考虑了企业总数和企业规模两个因素的影响;第二是能够反映市场垄断与竞争程度的变化; 第三是对产业内企业的合并与分解反映灵敏且计算方法相对容易。
缺点:直观性比较差。
4、 空间基尼系数(Space Gini coefficient )洛伦茨(Lorenz) 在研究居民收入分配时,创造了解释社会分配平均程度的洛伦茨曲线。
基尼( Gini )依据洛伦茨曲线, 提出了计算收入分配公平程度的统计指标——基尼系数。
Krugman 等利用洛伦茨曲线和基尼系数的原理和方法,构造了测定行业在空间分布均衡程度的空间基尼系数。
Krugman ( 1991) 等在研究美国制造业集聚程度测量时定义了空间基尼系数,计算公式为:2()i i iG S x =-∑ 其中,G 为空间基尼系数,i S 是i 地区某产业占全国该产业就业人数的比重,i x 是该地区就业人数占全国总就业人数的比重。
G = 0时,产业在空间分布是均匀的,G (最大值为1) 越大,表明地区产业的集聚程度越高。
优点:相对而言比较简便直观,可以很方便地把基尼系数转化成非常直观的图形。
缺点:基尼系数大于零并不表明有集聚现象存在, 因为它没有考虑到企业的规模差异。
空间基尼系数没有考虑到具体的产业组织状况及区域差异,因此在表示产业集聚程度时往往含有虚假的成分。
5、 EG 指数( EG index )为解决基尼系数失真问题,Ellision 和Glaeser (1997)提出了新的集聚指数来测定产业空间集聚程度。
假定某一经济体(国家或地区) 的某一产业内有N 个企业,且将该经济体划分为M 个地理区域,这N 个企业分布于M 个区域之中。
Ellision 和Glaeser 建立的产业空间集聚指数计算公式为:22221112221()(1)(1)1(1)(1)M M N i i i j i i j i i N i i i j i j s x x Z G x H x H x Z γ====-----==---∑∑∑∑∑∑∑()(1-)其中, i s 表示i 区域某产业就业人数占该产业全部就业人数的比重,i x 表示i 区域全部就业人数占经济体就业总人数的比重。
赫芬达尔指数(Herf indah lIndex) 21Nj j H Z ==∑N 表示该产业中以就业人数为标准计算的企业分布。
优点:充分考虑了企业规模及区域差异带来的影响,弥补了空间基尼系数的缺陷, 使能够进行跨产业、跨时间、甚至跨国的比较。
缺点:该方法没有对其中的H 给出合理的解释。
6、 DO 指数(DO index )Duranton 和Overman (XXXX )则采用了无参数回归模型分析方法,构造了新的产业集聚测度指数,计算公式为:,,111()1(),()A B A B n n i j A i j j n n d d k d f p h h ==≠-=∑∑、B其中, h 是窗宽,,f 是核函数,A 、B 是总企业地点S 的两个子集。
,()A B n n p 是不同企业双边距离的总数,其中每个企业属于一个子集。
如果A 、B 是相同的集合,则,()A B n n p = ,(1)2A A n n -;如果A,B 属于不相交的集合,则,()A B n n p =.A B n n 。
优点:与前面几种方法相比, 这种方法能够评价偏离随即性的统计显著性,避免了与规模和边界有关的问题。
缺点:由于这种计算是基于企业层面的数据且与企业间的距离有关,因此该方法的可操作性比较差。
二 实例解析EG 指数测算实例:该指标的计算公式中融合了空间基尼系数和赫芬达尔指数优点,也是目前国内用于测算产业集聚度的常用指标,具有普遍性。
下面是一个测算高技术产业集聚度的例子,采用的评价指标是EG 指数,测算了1995~XXXX 年我国高技术企业的集聚变动趋势,同时,考虑到我国的经济发展不平衡,东部地区开放程度高,基础设施较为完善,经济发展水平较高,交通便利,并且高技术产业发展的时间较早,技术成熟,拥有良好的供应链和技术链环境,从而引发了越来越多的高技术企业向东部靠拢,所以东部地区的地理集中程度会明显高于全国的平均水平。
若仅把全国当成一个经济体来测算高技术企业的地理集中度,所得的结果会有一定的偏差,体现不出分地区的集聚状况,因此有必要按传统的方法把全国分为东部、中部和西部三大区域。
根据EG 指数计算公式:22221112221()(1)(1)1(1)(1)M M N i i i j i i j i i N i i i j i j s x x Z G x H x H x Z γ====-----==---∑∑∑∑∑∑∑()(1-)将γ的大小分成三个区间:当0.02γ<时,表示该产业没有地方化的现象;0.020.05γ≤≤ 时,表示该产业在区域上分布较为均衡;当0.05γ> 时,表明产业在地区上的分布聚集程度较高。
计算出95、97、99、01、02、03、04、05年的EG 指数如下表所示:态势。
就全国范围内来看,在1995~XXXX 年间,我国高技术产业的区域分布还是较为均衡的,但在XXXX 年以后,全国的地理集中指数γ就超过了0.05(γ=0.0542),并且还有进一步集中的趋势。
这一结论可以从前五省市的市场集中度CR5 得到进一步的验证①,全国前五省市的市场集中度CR5 显示了在1995~1999 年间,全国前五省市的市场占有率增加了3.09%,平均每年增加0.773%,而在1999~XXXX 年,全国前五省市的市场占有率增加了8.31%,平均每年增1.38%,所以,我国高技术企业的地理集中度指数的变化趋势与前五省市的市场占有率的变动方向相吻合。
再从分地区来看,当我们把东部地区视为一个整体来考察区内高技术企业的集聚指数时,可以发现在1995年东部地区的地理集中指数已经超过了0.05,说明此时该地区已经出现了明显的企业聚集现象。
从1995 年东部地区前五省市的市场占有率排名上看,高技术企业主要聚集在长江三角洲、珠江三角洲和首都北京,这五省市的高技术企业总产值达2675.4 亿,占东部地区企业生产总值的74.78%,占全国总产值的56.77%。
可以说此时的长江三角洲、珠江三角洲高技术产业带和以首都北京为中心的高技术产业区已经初见端倪。
随着时间的进一步推进,东部的地理集中指数增长越来越快,从1995~1997 年两年增长7.56%,到时XXXX~XXXX 年增长率为21.02%,XXXX~XXXX 年增长率为32.20%,这说明我国东部地区的高技术企业的集聚程度还在进一步加强,出现了所谓的“集聚导致集聚”的现象。
这一结论还可以从前五省市的市场占有率中得到时进一步的印证,因为XXXX年前五省市的市场占有率已从1995 年的56.77%上升到71.91%,占东部地区的比例已从1995 年的74.78%是升80.31%。
与东部地区相比,中部地区的高技术产业集聚现象出现的时间比较晚,地理集中指数明显的不如东部,但中部地区的地理集中指数也在逐年增大,在XXXX年前,中部地区所有年份的γ值均小于0.02,说明在XXXX 年以前中部地区的高技术企业并没有形成明显的地方化现象,但到XXXX 年中部地区的γ值已经超过0.02(γ=0.0272)。
在XXXX 年γ值已经达到0.04133,这说明经过一段时间的发展,高技术产业已经形成自东向西扩散的产业格局。
同时从产业的市场集中度表格中可以看出,中部地区的高技术企业主要集聚在湖北省的周围,这与湖北拥有诸多著名的高等学府是分不开的。
西部地区是我国高技术企业集聚程度最低的地区,XXXX 年西部地区的地理集中指数仅为0.02459,不过该地区的地理集中指数的年平均增长率最高,从1995~XXXX 年西部地区的高技术企业地理集中指数年平均增长率为79.065%。
