铆钉连接的计算
铆钉长度的确定方法

铆钉长度的确定方法(实用版4篇)《铆钉长度的确定方法》篇1铆钉长度的确定方法通常根据被连接材料的厚度、材质和连接方式来确定。
以下是一些常见的确定铆钉长度的方法:1. 根据被连接材料的厚度确定铆钉长度:对于较薄的材料,铆钉长度应该略大于材料的厚度,以确保铆钉能够穿过材料并形成足够的强度。
对于较厚的材料,铆钉长度应该更长,以确保铆钉能够穿过材料并形成足够的强度。
2. 根据被连接材料的材质确定铆钉长度:不同材质的铆钉适用于不同材质的被连接材料。
例如,不锈钢铆钉适用于连接不锈钢材料,而碳钢铆钉适用于连接碳钢材料。
因此,根据被连接材料的材质选择适当的铆钉长度是非常重要的。
3. 根据连接方式确定铆钉长度:不同的连接方式需要不同长度的铆钉。
例如,对于单面连接,铆钉长度应该略短于被连接材料的厚度,而对于双面连接,铆钉长度应该与被连接材料的厚度相等。
4. 根据实际需要确定铆钉长度:在某些情况下,铆钉长度可能需要根据实际需要进行调整。
例如,如果需要连接两个不同厚度的材料,可能需要使用较长的铆钉来确保连接强度。
总之,铆钉长度的确定需要考虑多个因素,包括被连接材料的厚度、材质和连接方式等。
《铆钉长度的确定方法》篇2铆钉长度的确定方法通常根据被连接材料的厚度、材质和连接方式来确定。
以下是一些常见的确定铆钉长度的方法:1. 根据被连接材料的厚度确定铆钉长度:适用于被连接材料厚度较薄的情况。
铆钉的长度应该略大于被连接材料的厚度,以确保铆钉能够穿透材料并形成牢固的连接。
2. 根据被连接材料的材质确定铆钉长度:适用于被连接材料硬度较高的情况。
铆钉的长度应该足够长,以确保铆钉能够穿透材料并形成牢固的连接。
3. 根据连接方式确定铆钉长度:适用于不同的连接方式。
例如,对于单面铆接,铆钉的长度应该足够长,以确保铆钉能够穿透材料并形成牢固的连接。
对于双面铆接,铆钉的长度应该略短,以确保铆钉不会穿透材料太深。
4. 根据经验确定铆钉长度:适用于经验丰富的铆工。
铆钉连接及计算

第三章连接返回§3-7铆钉连接3.7.1铆钉的排列和构造要求一、铆钉的形状铆钉按照铆头的形状分为:半圆头铆钉、高头铆钉、埋头铆钉和半埋头铆钉四种。
二.铆钉的构造要求:(1)在钢结构中一般多采用半圆头铆钉(图a);(2)当铆合钢板的总厚度超过铆钉直径的5倍时,宜采用高头铆钉;(图b)(3)当构件表面要求平整或钉头处的空间受到限制时,可采用沉头铆钉(图c、d)(4)沉头和半沉头铆钉不得用于钉杆受拉的连接。
三、铆钉连接的形式:对接、搭接和顶接(表3.7.1)。
四、铆钉按受力分为:剪力铆钉、拉力铆钉和剪拉铆钉三类(表3.7.1)。
3.7.2铆钉连接的计算一、受剪连接二、每个受拉铆钉的承载力设计值三、铆钉群连接的计算:(同普通螺栓)返回第三章连接返回§3-8轻钢结构紧固件连接的构造和计算3.8.1紧固件连接的构造要求用于薄壁型钢结构中的紧固件应满足下述构造要求:(1)抽芯铆钉(拉铆钉)和自攻螺钉的钉头部分应靠在较薄的板件一侧。
连接件的中距和端距不得小于连接件直径的3倍,边距不得小于连接件直径的1.5倍。
受力连接中的连接件不宜少于2个。
(2)抽芯铆钉的适用直径为2.6~6.4mm,在受力蒙皮结构中宜选用直径不小于4mm的抽芯铆钉;自攻螺钉的适用直径为3.0~8.0mm,在受力蒙皮结构中宜选用直径不小于5mm的自攻螺钉。
(3)自攻螺钉连接的板件上的预制孔径d0应符合下式要求:(4)射钉只用于薄板与支承构件(即基材如檩条)的连接。
射钉的间距不得小于射钉直径的4.5倍,且其中距不得小于20mm,到基材的端部和边缘的距离不得小于15mm,射钉的适用直径为3.7~6.0mm。
射钉的穿透深度(指射钉尖端到基材表面的深度,如图3.8.1所示)应不小于10mm。
(5)在抗拉连接中,自攻螺钉和射钉的钉头或垫圈直径不得小于14mm;且应通过试验保证连接件由基材中的拔出强度不小于连接件的抗拉承载力设计值。
上述规定大部分引自国外的相关规,项次(3)是根据我国自己的试验结果归纳出的经验公式。
材料力学 第6章 连接件的实用计算

故销钉安全
6.2 连接件的实用计算
D
思考题
(1)销钉的剪切面面积 A
h
(2)销钉的挤压面面积 AbS
d
F
6.2 连接件的实用计算
D
挤压面
思考题
(1)销钉的剪切面面积 A
h
(2)销钉的挤压面面积 AbS
A = πdh
d
剪切面
π(D2 - d2)
F
Abs =
4
挤压面
6.2 连接件的实用计算
冲床的最大冲压力F=400kN,冲头材料的许用压应力[]=440MPa,钢板的
对错动。
F
5. 连接处的破坏形式
6.1 引言
一、基本概念和实例
5. 连接处的破坏形式
FS n
(1)剪切破坏 连接件沿剪切面的剪断
(2)挤压破坏 连接件与被连接件在
相互接触面上因挤压 挤压面
而使连接松动,发生 破坏。
(3)拉伸破坏 被连接件在受连接件 处削弱的截面处,应 力增大,易在连接处 拉断。
F n
挤压面和挤压力为:
F AQ
b
仰视图
Abs
Fbs
F :切应力和挤压应力
τ Fs F 40 107 0.952MPa
AQ bh 12 35
F
σbs
=
Fbs Abs
=
F cb
=
40 ×107 4.5×12
=
7.4MPa
6.2 连接件的实用计算
例6-2 齿轮与轴由平键连接,已知轴的直径d=70mm, 键的尺寸为b×h×L=20
2. 工程实例
(1) 螺栓连接
可拆卸
M
特点:可传递一般力
36普通螺栓和铆钉连接的构造和计算
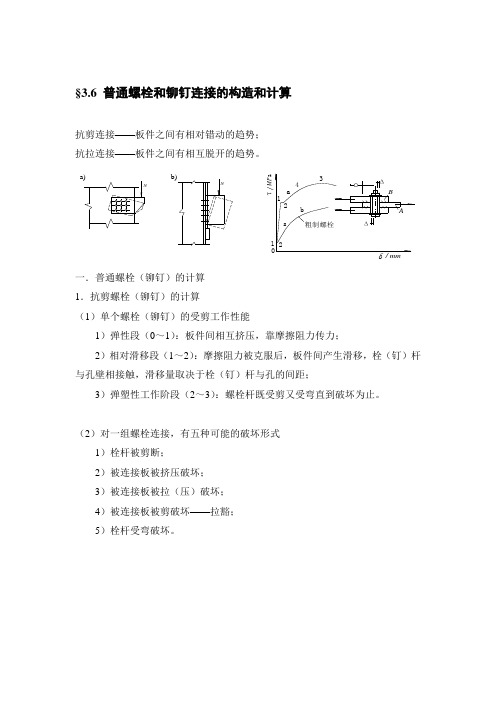
§3.6 普通螺栓和铆钉连接的构造和计算抗剪连接——板件之间有相对错动的趋势;抗拉连接——板件之间有相互脱开的趋势。
一.普通螺栓(铆钉)的计算1.抗剪螺栓(铆钉)的计算(1)单个螺栓(铆钉)的受剪工作性能1)弹性段(0~1):板件间相互挤压,靠摩擦阻力传力;2)相对滑移段(1~2):摩擦阻力被克服后,板件间产生滑移,栓(钉)杆与孔壁相接触,滑移量取决于栓(钉)杆与孔的间距;3)弹塑性工作阶段(2~3):螺栓杆既受剪又受弯直到破坏为止。
(2)对一组螺栓连接,有五种可能的破坏形式1)栓杆被剪断;2)被连接板被挤压破坏;3)被连接板被拉(压)破坏;4)被连接板被剪破坏——拉豁;5)栓杆受弯破坏。
tc)(3)针对如上情况,应避免所有破坏的可能性1)栓(钉)杆长度(t ∑)≤05d ——防止受弯破坏; 2)1a ≥02d ,栓距≥03d ——避免拉豁; 3)通过计算保证螺栓(铆钉)抗剪; 4)通过计算保证螺栓(铆钉)抗挤压;5)通过计算保证被连接构件具有足够的拉压强度。
(4)螺栓群受剪计算1)轴心受力基本假定:螺栓群均匀受力。
一个螺栓的抗剪承载能力:bv 2v b v4πn f d N =v n ——剪切面数;d ——螺栓直径;b v f ——螺栓抗剪设计强度。
一个螺栓抗挤压承载能力:b c m in b c f t d N ⋅∑⋅=d ——螺栓直径;m in t ∑——被连接板中受力一侧的总厚度的较小值;b c f ——螺栓承压设计强度。
当受力一边螺栓分布长度0115d l >时,会出现较严重的传力不均匀现象,故采用强度折减系数对螺栓的承载能力进行折减:11501.1d l -=β当0160d l >时,取0.7=β这样,设计计算时,对受力最大的螺栓进行验算:max N ≤{}bcb v ,min N N ⋅β2)螺栓群受扭 基本假定:① 被连接板是刚性的; ② 螺栓是弹性的;③ 在扭矩作用下,绕螺栓群中心旋转,每个螺栓受力大小与其到形心的距离成正比,方向垂直于矢径。
材料力学(I)第八章-铆钉连接的计算

§8-6 铆钉连接的计算
1
铆钉连接主要有三种方式: 1.搭接(图a),铆钉受单剪; 2.单盖板对接(图b),铆钉受单剪; 3.双盖板对接(图c),铆钉受双剪。
2
铆钉组承受横向荷载
实际铆钉组中位于 两端的铆钉所传递的力 要比中间的铆钉所传递 的力大。
为了简化计算,假设: (1) 如果作用于连接上的力其作用线通过铆钉组 中所有铆钉横截面的形心,而且各铆钉的材料和直径 均相同,则认为每个铆钉传递相等的力。 (2) 不考虑弯曲的影响。 铆钉连接与螺栓连接的计算方法相同。
i 1
2.754 103 N 2.754 kN
22
例题 8-10
F F
'' 2 '' 5
M e r2
2 r i i 1 6
2.928kN
F F
'' 3 '' 4
M e r3
2 r i i 1 6
4.344kN
Fi 的方向垂直于ri。
23
例题 8-10
将Fi'和Fi''按矢量合成以得出每一铆钉所受的力 Fi。图b中示出了1,2,3三个铆钉所受力的情况。 经比较按矢量合成后的力F1,F2,…,F6 知,铆钉 1和6所受力最大,F1=F6=4.41 kN。
24
例题 8-10
5. 此连接为搭接,铆钉受单剪,故受力最大的铆 钉1和6剪切面上的切应力为
F1 4.41 103 N 6 t1 t 6 14 10 Pa 14 MPa A s1 π (0.02 m)2 4
257
例题 8-10
解: 1. 将外力F向铆
铆钉连接计算

P
P1
A
a1
B
o
e
承受偏心横向荷载作用的铆钉组(图a)
Pe
P
将偏心荷载 P 向铆钉组 截面形心O点简化,得到 一个通过O的荷载 P 和一个绕O点旋转的 转矩 m = Pe
m
O
(a)
若同一铆钉组中每一铆钉 的直径相同
Pe
P
横向力 P 引起的力P1’ 转矩 m 引起的力 P1”, 每一铆钉的受力是 P1’ 和
c z1 M
M1
z
S
S
(a)
(b)
解:上,下两钢轨作为整体弯曲时,上面钢轨的横截面上全是 压应力,下面钢轨的横截面上全是拉应力。
由于相邻横截面上弯矩不同, 相应点处的正应力不等,故上
T 下钢轨有沿其接触面纵向错动 的趋势,铆钉承受剪力。 每排铆钉承受的剪力等于一 根钢轨在距离为纵向间距 S 的两个横截面上压(拉)力 之差。
P3"
3
2P1"r1 2P2"r2 2P3"r3 m
P1" r1 P2" r2
P1" r1 P3" r3
2P1" r1
2P1"
r2 2
r1
2P1"
r2 3
r1
m
由此解出
P1"
2(
r2 1
mr1
r2 2
r 32 )
P3'
2 P2"
r3 P2'
r2 r1 P1'
O
1
P1"
P3"
3
径和材料均相同,故每 个铆钉上受的力相等。
材料力学第2章 连接部分的计算
b
d
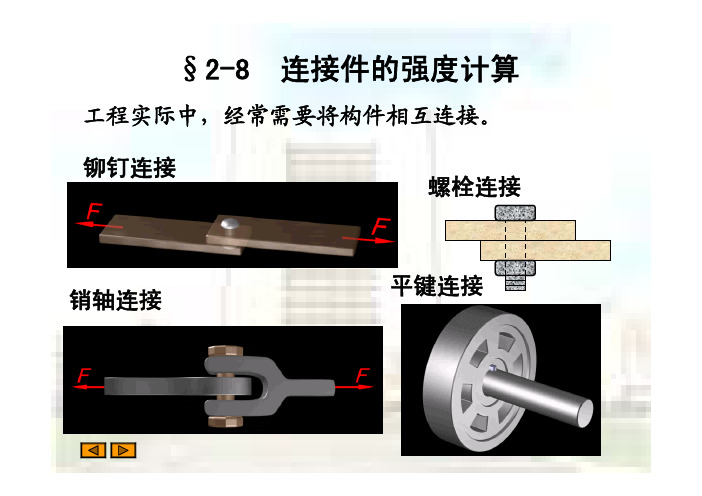
3.铆钉的剪切强度
a
Fs 4F 2F 2 2 A 2 πd πd 2 50 10 3 2 π 0.017 110 10 6 110 MPa [ ]
4.板和铆钉的挤压强度 Fbs F 50 103 bs Abs 2d 2 0.017 0.01
40 10 3 4 2 ba 50 10 m bs 8 10 6 FS P 2. 顺纹剪切强度条件为 A bl P
ba
b 11.4 10 2 m 114 mm l 35.1 10 2 m 351mm a 4.4 10 2 m 44 mm
bs 2
为充分利用材料,切 应力和挤压应力应满足
Fbs F bs Abs dh
4F 8h F 2 2 d d dh
b
d
a
图示接头,受轴向力F 作 用。已知F=50kN,b=150mm, δ=10mm,d=17mm,a=80mm, [σ]=160MPa,[τ]=120MPa, [σbs]=320MPa,铆钉和板的材 料相同,试校核其强度。
例: t=2mm,b=15mm,d=4mm, []= 100MPa, [bs]= 300MPa, []= 160MPa,计算许用载荷[F]。
F
b
F
F
t
F
F 3-3 2-2 F t 1-1
b
F
F
解:一、破坏形式分析 1.剪断(沿1-1截面) 2.拉断(沿2-2截面) 3.“剪豁” (剪出缺口 3-3截面) 4.挤压破坏
d 2
F td 2.4kN
半空心铆钉 翻边长度

半空心铆钉翻边长度半空心铆钉是一种常见的连接件,广泛应用于各种工程和工业领域。
半空心铆钉的特点是钉身中部有圆形空洞,这样可以减轻重量,提高强度。
在半空心铆钉的使用中,翻边长度是一个关键参数,它直接影响到连接的稳定性和强度。
翻边长度是指铆钉头部翻边部分的尺寸,通常用毫米表示。
翻边长度的选择需要考虑以下几个因素:1.连接材料的性质:不同材料的连接,需要的翻边长度有所不同。
例如,对于软质材料,翻边长度可以适当减小,以提高连接强度;对于硬质材料,翻边长度应适当增大,以防止铆钉头部断裂。
2.连接件的形状:连接件的形状会影响翻边长度的选择。
在保证连接强度的前提下,应尽量选择较短的翻边长度,以提高连接件的稳定性。
3.受力方向:受力方向也会影响翻边长度的选择。
在垂直于受力方向的连接中,翻边长度应适当增大,以提高连接强度。
计算半空心铆钉翻边长度的方法如下:翻边长度= (连接强度要求× 安全系数)/ 铆钉直径注意事项:1.翻边长度的选择应结合实际情况,不能盲目追求过大或过小。
2.在选择翻边长度时,应考虑连接件的形状和受力方向,以确保连接稳定。
3.翻边长度与铆钉直径的比例应适当,过大会导致铆钉头部过于沉重,容易断裂;过小则会使连接强度不足。
4.半空心铆钉的翻边长度计算公式仅供参考,实际应用中需根据具体情况调整。
实用性建议:1.根据实际需求选择合适的翻边长度,以提高连接强度和稳定性。
2.针对不同材料和连接件形状,调整翻边长度,确保连接可靠。
3.在受力较大的情况下,可以选择加大翻边长度,提高连接安全性。
4.注意翻边长度与铆钉直径的比例,避免出现过长或过短的情况。
通过掌握半空心铆钉翻边长度的选择方法,我们可以更好地应用这种连接件,提高工程和工业领域的连接效果。
铆钉长度计算公式

铆钉长度计算公式铆钉是一种在机械连接中常用的零件,它能够将两个或多个部件牢固地连接在一起。
而要确定合适的铆钉长度,就需要用到铆钉长度计算公式啦。
先来说说铆钉的作用吧。
想象一下,你有一个精致的小书架,板子和架子之间需要紧紧相连,这时候铆钉就派上用场了。
它就像一个小小的大力士,默默地在背后发力,让整个书架稳稳当当的。
那铆钉长度到底怎么算呢?其实铆钉长度的计算并不是一件特别复杂的事儿,但也需要我们认真对待。
一般来说,铆钉长度的计算公式是这样的:铆钉长度 = 被连接件总厚度 + 铆钉伸出长度。
这里的被连接件总厚度很好理解,就是需要连接的那些板子、零件啥的加在一起的厚度。
那铆钉伸出长度又是啥呢?这就有点讲究了。
通常情况下,铆钉伸出长度会根据不同的连接要求和材料有所变化。
比如说,在一些比较软的材料连接中,铆钉伸出长度可能相对短一点;而在硬度较高的材料连接时,铆钉伸出长度就要适当增加,以保证连接的牢固性。
我曾经在一个小车间里帮忙,当时师傅正在组装一批金属零件。
他拿着卡尺仔细地测量着被连接件的厚度,嘴里还念叨着铆钉长度的计算。
我在旁边好奇地看着,只见他熟练地运用公式,算出了合适的铆钉长度,然后拿起铆钉,用工具一敲,就稳稳地连接好了零件。
那一瞬间,我深刻地感受到了这个公式的实用和重要。
再来说说实际应用中的一些小技巧。
如果被连接件的表面不太平整,那在计算总厚度时,要多考虑一些余量,免得铆钉长度不够。
还有啊,如果是在振动比较大的环境中使用铆钉连接,也要适当增加铆钉长度,这样能更好地防止松动。
另外,不同类型的铆钉,其长度计算可能会有一些细微的差别。
比如抽芯铆钉和实心铆钉,在计算时就需要根据它们各自的特点进行调整。
总之,铆钉长度计算公式虽然看起来简单,但在实际应用中,需要我们结合具体情况,灵活运用,才能确保连接的质量和可靠性。
就像生活中的很多事情一样,看似简单的背后,往往需要我们用心去琢磨、去实践。
希望大家以后在遇到需要使用铆钉连接的时候,都能准确算出合适的铆钉长度,让工作和生活中的连接更加牢固、可靠!。
铆钉连接计算

u
FS As
5103 3104
16.7106 Pa
16.7MPa
剪切与连接件的实用计算
[例二] 如图螺钉,已知:[]=0.6[s],求其d:h的合理比值。
h d
d h
F
剪切面
解
s
FN A
4F
d 2
s
当 s , 分 别 达 到 [] , [s] 时 ,
FS
F
材料的利用最合理
AS dh
第四节 铆钉连接的计算
剪切与连接件的实用计算
铆钉连接方式:单剪-----搭接、单盖板对接 双剪-----双盖板对接。
F F
F F
一、铆钉组承受横向荷载
假设:1.不考虑弯曲的影响;2.外力通过铆钉组的形心, 且各铆钉直径相同,则每个铆钉的受力也相等。
每个铆钉受相同的力F 1 =F/n 其中:n为铆钉组中的铆钉个数
计算方法:与上 一节方法相同
二、铆钉组承受扭转荷载
F
剪切与连接件的实用计算
此时每个铆钉的受力不相
同,每个铆钉上所受的力与到 形心的距离成正比,方向垂直 于该点与形心O点的连线。
F
e
m Fe Fiai
其中: m为钢板所受的转矩; Fi为每个铆钉所受的力; ai为铆钉截面中心至铆钉组形心的距离
剪切与连接件的实用计算FSFn 2 NhomakorabeaF 2n
1.由剪应力强度条件:
剪切与连接件的实用计算
F
FS AS
2n
d2
2 140 1000
n 162 106
130MPa
得:
4
2、校核挤压强度
n 2.68
取: n 3
F
铆钉连接及计算

铆钉连接及计算 The manuscript was revised on the evening of 2021第三章?连接§3-7铆钉连接铆钉的排列和构造要求一、铆钉的形状铆钉按照铆头的形状分为:半圆头铆钉、高头铆钉、埋头铆钉和半埋头铆钉四种。
二.铆钉的构造要求:(1)在钢结构中一般多采用半圆头铆钉(图a);(2)当铆合钢板的总厚度超过铆钉直径的5倍时,宜采用高头铆钉;(图b)(3)当构件表面要求平整或钉头处的空间受到限制时,可采用沉头铆钉(图c、d)(4)沉头和半沉头铆钉不得用于钉杆受拉的连接。
三、铆钉连接的形式:对接、搭接和顶接(表)。
四、铆钉按受力分为:剪力铆钉、拉力铆钉和剪拉铆钉三类(表)。
铆钉连接的计算一、受剪连接二、每个受拉铆钉的承载力设计值三、铆钉群连接的计算:(同普通螺栓)第三章?连接§3-8轻钢结构紧固件连接的构造和计算紧固件连接的构造要求用于薄壁型钢结构中的紧固件应满足下述构造要求:(1)抽芯铆钉(拉铆钉)和自攻螺钉的钉头部分应靠在较薄的板件一侧。
连接件的中距和端距不得小于连接件直径的3倍,边距不得小于连接件直径的倍。
受力连接中的连接件不宜少于2个。
(2)抽芯铆钉的适用直径为~,在受力蒙皮结构中宜选用直径不小于4mm的抽芯铆钉;自攻螺钉的适用直径为~,在受力蒙皮结构中宜选用直径不小于5mm的自攻螺钉。
(3)自攻螺钉连接的板件上的预制孔径d0应符合下式要求:(4)射钉只用于薄板与支承构件(即基材如檩条)的连接。
射钉的间距不得小于射钉直径的倍,且其中距不得小于20mm,到基材的端部和边缘的距离不得小于15mm,射钉的适用直径为~。
射钉的穿透深度(指射钉尖端到基材表面的深度,如图所示)应不小于10mm。
(5)在抗拉连接中,自攻螺钉和射钉的钉头或垫圈直径不得小于14mm;且应通过试验保证连接件由基材中的拔出强度不小于连接件的抗拉承载力设计值。
上述规定大部分引自国外的相关规范,项次(3)是根据我国自己的试验结果归纳出的经验公式。
铆钉连接及计算

铆钉连接及计算铆钉连接及计算 Document serial number【LGGKGB-LGG98YT-LGGT8CB-LGUT-第三章连接§3-7 铆钉连接铆钉的排列和构造要求⼀、铆钉的形状铆钉按照铆头的形状分为:半圆头铆钉、⾼头铆钉、埋头铆钉和半埋头铆钉四种。
⼆.铆钉的构造要求:(1)在钢结构中⼀般多采⽤半圆头铆钉(图a);(2)当铆合钢板的总厚度超过铆钉直径的5倍时,宜采⽤⾼头铆钉;(图b)(3)当构件表⾯要求平整或钉头处的空间受到限制时,可采⽤沉头铆钉(图c、d)(4)沉头和半沉头铆钉不得⽤于钉杆受拉的连接。
三、铆钉连接的形式:对接、搭接和顶接(表)。
四、铆钉按受⼒分为:剪⼒铆钉、拉⼒铆钉和剪拉铆钉三类(表)。
铆钉连接的计算⼀、受剪连接⼆、每个受拉铆钉的承载⼒设计值三、铆钉群连接的计算:(同普通螺栓)第三章连接§3-8 轻钢结构紧固件连接的构造和计算紧固件连接的构造要求⽤于薄壁型钢结构中的紧固件应满⾜下述构造要求:(1)抽芯铆钉(拉铆钉)和⾃攻螺钉的钉头部分应靠在较薄的板件⼀侧。
连接件的中距和端距不得⼩于连接件直径的3倍,边距不得⼩于连接件直径的倍。
受⼒连接中的连接件不宜少于2个。
(2)抽芯铆钉的适⽤直径为~,在受⼒蒙⽪结构中宜选⽤直径不⼩于4mm的抽芯铆钉;⾃攻螺钉的适⽤直径为~,在受⼒蒙⽪结构中宜选⽤直径不⼩于5mm的⾃攻螺钉。
(3)⾃攻螺钉连接的板件上的预制孔径d0应符合下式要求:(4)射钉只⽤于薄板与⽀承构件(即基材如檩条)的连接。
射钉的间距不得⼩于射钉直径的倍,且其中距不得⼩于20mm,到基材的端部和边缘的距离不得⼩于15mm,射钉的适⽤直径为~。
射钉的穿透深度(指射钉尖端到基材表⾯的深度,如图所⽰)应不⼩于10mm。
(5)在抗拉连接中,⾃攻螺钉和射钉的钉头或垫圈直径不得⼩于14mm;且应通过试验保证连接件由基材中的拔出强度不⼩于连接件的抗拉承载⼒设计值。
铆钉连接及计算

铆钉连接及计算 Document serial number【LGGKGB-LGG98YT-LGGT8CB-LGUT-第三章连接§3-7 铆钉连接铆钉的排列和构造要求一、铆钉的形状铆钉按照铆头的形状分为:半圆头铆钉、高头铆钉、埋头铆钉和半埋头铆钉四种。
二.铆钉的构造要求:(1)在钢结构中一般多采用半圆头铆钉(图a);(2)当铆合钢板的总厚度超过铆钉直径的5倍时,宜采用高头铆钉;(图b)(3)当构件表面要求平整或钉头处的空间受到限制时,可采用沉头铆钉(图c、d)(4)沉头和半沉头铆钉不得用于钉杆受拉的连接。
三、铆钉连接的形式:对接、搭接和顶接(表)。
四、铆钉按受力分为:剪力铆钉、拉力铆钉和剪拉铆钉三类(表)。
铆钉连接的计算一、受剪连接二、每个受拉铆钉的承载力设计值三、铆钉群连接的计算:(同普通螺栓)第三章连接§3-8 轻钢结构紧固件连接的构造和计算紧固件连接的构造要求用于薄壁型钢结构中的紧固件应满足下述构造要求:(1)抽芯铆钉(拉铆钉)和自攻螺钉的钉头部分应靠在较薄的板件一侧。
连接件的中距和端距不得小于连接件直径的3倍,边距不得小于连接件直径的倍。
受力连接中的连接件不宜少于2个。
(2)抽芯铆钉的适用直径为~,在受力蒙皮结构中宜选用直径不小于4mm的抽芯铆钉;自攻螺钉的适用直径为~,在受力蒙皮结构中宜选用直径不小于5mm的自攻螺钉。
(3)自攻螺钉连接的板件上的预制孔径d0应符合下式要求:(4)射钉只用于薄板与支承构件(即基材如檩条)的连接。
射钉的间距不得小于射钉直径的倍,且其中距不得小于20mm,到基材的端部和边缘的距离不得小于15mm,射钉的适用直径为~。
射钉的穿透深度(指射钉尖端到基材表面的深度,如图所示)应不小于10mm。
(5)在抗拉连接中,自攻螺钉和射钉的钉头或垫圈直径不得小于14mm;且应通过试验保证连接件由基材中的拔出强度不小于连接件的抗拉承载力设计值。
上述规定大部分引自国外的相关规范,项次(3)是根据我国自己的试验结果归纳出的经验公式。
铆钉铆接装配应力的分析和计算

应力具有很大影响 。椭圆形刀顶参数 a = 016 的刀 具所加工出的齿轮与一般圆角形刀顶参数的刀具所 加工出的齿轮相比 ,应力值下降幅度为 1019 %。
(4) 在保持齿轮制造工艺不变的前提下 ,通过合 理地设计刀顶形状及其参数 ,就可大幅度地提高齿 轮的抗弯曲疲劳强度 ,延长齿轮的工作寿命 。
参考文献 :
εe3 =ε′3 - ε″3
由广义胡克定理 (铆钉的横向变形系数 μ 取
0128)
εe1
=ε′1 - ε″1 =
1 E
[σ1
-
μ(σ2
+σ3)
]
(5)
(下转第 48 页)
·48 ·
图 6 圆角刀顶曲线
4 结论
(1) 齿根应力有限元分析中选用二维模型是合 理的 ,且可保证计算精度 。与单齿模型相比 ,这种 模型是较理想的 。
试铆确定) ,再由塑性变形时铆钉的体积不变得关系
式Δ d
=
1 2
·Δδδ·d (δ为两块板的厚度之和)
,即可求
出钉孔处板的被压缩量Δδ= 0105mm 。
这时 ,铆钉直径为
d1 = 1013 + 01026 = 101326mm 铆钉杆长为 δ1 = 10 - 0105 = 9195mm
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P
P
e
令铆钉组横截面的形心 为O点(图 )。 假设 钢板上任一直线(如 或 ) 钢板上任一直线 如OA或OB) 在转动后仍保持为直线, 在转动后仍保持为直线 因而每一铆钉的平均剪应变 与该铆钉截面中心至O点的 与该铆钉截面中心至 点的 距离成正比。 距离成正比。
(b)
P A
a1
o
B
P
e
若每个铆钉的直径相同, 若每个铆钉的直径相同, 则每个铆钉受的力与铆钉 截面中心到铆钉组截面中 的距离成正比。 心O的距离成正比。方向 的距离成正比 垂直于该点与O点的连线。 垂直于该点与 点的连线。 点的连线
§7-2 铆钉连接的计算
铆钉连接的主要方式
搭接 P P
P P
一个受剪面
单盖板对接
P P
P P
双盖板对接
P
双
P
P P
两 个 受 剪 面
( c )
图
8 - 6
I、 铆钉组承受横向荷载
P P
P P
为了简化计算, 在铆钉组连接 ( 图 8-7 ) 中, 为了简化计算 设: 不论铆接的方式如何, 均不考虑弯曲的影响。 不论铆接的方式如何 均不考虑弯曲的影响。 若外力的作用线通过铆钉组横截面的形心, 若外力的作用线通过铆钉组横截面的形心 且同一组内各 铆钉的直径相同, 则每个铆钉的受力也相等。 铆钉的直径相同 则每个铆钉的受力也相等。 每个 铆钉受力为
P
b
P
t t P P
P
b
P
P4
P
P4
受剪面
b
P
(1) 铆钉的剪切强度 每个铆钉受力为 P/4 每个铆钉受剪面上的剪力为
Q=
P = 22.5K N 4
τ=
Q Q = 2 =112M a <[τ] P A πd 4
(2) 铆钉的挤压强度
挤压面
每个铆钉受挤压力为
P4
Pjy =
P 4
受剪面
P4
挤压面面积为
P
冲头
d
钢板
冲模
P
P
冲头
d
钢板
P 冲模
剪切面
解:冲头为轴向压缩变形
P P = 2 ≤[σ] A πd 4
δ =34mm
P
P
冲头
d
钢板
P 冲模
剪切面
由钢板的剪切破坏条件
P = ≥ τb d A πδ
Q
δ =10.4m m
例题 3-5
用两根钢轨铆接成组合梁, 其连接情况如图a,b所示 所示. 用两根钢轨铆接成组合梁 其连接情况如图 所示
根据平衡方程
∑P"ri = m i
P3 "
3 2
2P"r1 + 2P "r2 + 2P "r3 = m 1 2 3
P2 "
1
P" = r1 1 P2" r2
P" = r1 1 P " r3 3
2 2
r 3 P2 ' r2
r 2 1"r1 + 2 1" P P r1
+ 2P"r = m 1
2 3
r1
O
e
P
(a)
若同一铆钉组中每一铆钉 的直径相同 引起的力P 横向力 P 引起的力 1’ 转矩 m 引起的力 P1”, 每一铆钉的受力是 P1’ 和 P1” 的矢量和 求得每个铆钉的受力P 求得每个铆钉的受力 1 后,即可分别校核受力 最大铆钉的剪切和挤压 强度。 强度。
O
P
e
P
m
P1"
P1'
P1
(a)
Ajy = d ⋅t
σjy = Pjy =141 P <[σjy] Ma Ajy
P4 P4 P4 P4
P
p
3P 4 P 4
+
1
P4 P4 P4 P4
P
1
(3) 钢板的拉伸强度
P =107M a <[σ] P σ −1 = 1 (b−d)t
2
P4 P4 P4
1
P4
P
2
1
3P 4 =99.3M a <[σ] P σ2−2 = (b−2d)t
例题 8-6
的作用, 一铆钉连接的托架受集中力 P 的作用 如图 a 所示 ,
已知外力 P = 12kN 。铆钉直径 d =20mm ,每个铆钉都受 每个铆钉都受 单剪 , 试求受力最大的铆钉横截面上的剪应力。 试求受力最大的铆钉横截面上的剪应力。
y 3 2 80 1 o 40 40 80 6 5 4
P P= 1 n
例4-3
一铆钉接头用四个铆钉连接两快钢板。 一铆钉接头用四个铆钉连接两快钢板。钢板与铆钉 材料相同。铆钉直径d=16mm,钢板的尺寸为b=100mm, 材料相同。铆钉直径 ,钢板的尺寸为 ,
t=10mm,P=90KN,铆钉的许用应力是 τ]=120MPa, , ,铆钉的许用应力是[τ , [σjy]=120MPa,钢板的许用拉应力 σ]=160MPa。 σ ,钢板的许用拉应力[σ 。 试校核铆钉接头的强度。 试校核铆钉接头的强度。
(b)
P
P1
A
a1
B o
m= Pe = ∑Pi ai
P 为每个铆钉受的力 i
a i
为该铆钉截面中心 到铆钉组截面形心O 到铆钉组截面形心 的距离 P e
承受偏心横向荷载作用的铆钉组(图 承受偏心横向荷载作用的铆钉组 图a) P 将偏心荷载 P 向铆钉组 截面形心O点简化 得到 截面形心 点简化,得到 点简化 一个通过O的荷载 一个通过O的荷载 P 和一个绕O点旋转的 和一个绕 点旋转的 转矩 m = Pe m
整个接头是安全的
D
思考题 销钉的剪切面面积 A 销钉的挤压面面积 Ajy
h
d
P
D
h
d
剪切面 h d P
A = πdh
D
挤压面
h
d
剪切面
挤压面 P
A jy = π ( D 2 − d 2) 4
补充题:在厚度 的钢板上冲出形状如图的孔, 补充题:在厚度t=5mm的钢板上冲出形状如图的孔,若钢 的钢板上冲出形状如图的孔 板材料的剪切强度极限τ 板材料的剪切强度极限τb=300MPa,求冲床所需的冲压力 。 求冲床所需的冲压力F。
c
z1 M z
S S
M1
(a)
(b)
解:上,下两钢轨作为整体弯曲时,上面钢轨的横截面上全是 下两钢轨作为整体弯曲时, 压应力,下面钢轨的横截面上全是拉应力。 压应力,下面钢轨的横截面上全是拉应力。
由于相邻横截面上弯矩不同, 由于相邻横截面上弯矩不同, 相应点处的正应力不等, 相应点处的正应力不等,故上 下钢轨有沿其接触面纵向错动 的趋势,铆钉承受剪力。 的趋势,铆钉承受剪力。 每排铆钉承受的剪力等于一 根钢轨在距离为纵向间距 S 的两个横截面上压( 的两个横截面上压(拉)力 之差。 之差。 T
4 − . = Ac = 640 6m
s
T =τ 'b ' s
τ '= = Q *m x S a z
S T T1
bz I
IZ 为整个横截面对中性轴
的惯性矩
.C IZ = 2(IZ1 + A )
2
4 − =1 334 10 4m . ×
T ' = 2Q '
Q '
sQ * m T' 1 SZ ax Q = = τ 'bS= ' 2 2 2IZ
(a)
解:铆钉组与x轴对 铆钉组与 轴对 称,转动中心在铆钉2 转动中心在铆钉 的连线与x轴的 与 5 的连线与 轴的 交点 O 处。
x
点简 1 将力 P 向 O点简 化得 力 P = 12 KN
P
力偶矩 m=1230.12=1.44KN.m 3
例题 8-6 图
2
在过转动中心的力 P 作 用下, 用下,因每个铆钉的直 径和材料均相同, 径和材料均相同,故每 个铆钉上受的力相等。 个铆钉上受的力相等。
R=50
R=50
400
解:剪切面的面积为
3 m A = 2bt +πdt = 2×400×5+3.14×2×50×5 =5570m
τ=
F A
≥ τb
F ≥ A τb =1671K N
补充题:冲床的最大冲压力 补充题:冲床的最大冲压力P=400KN,冲头材料的许用压应力 , [σ]=440MPa,钢板的剪切强度极限τb=360MPa。试求冲头能冲剪 σ 剪切强度极限τ ,钢板的剪切强度极限 。试求冲头能冲剪 的最小孔径d和最大的钢板厚度δ 的最小孔径 和最大的钢板厚度δ。 和最大的钢板厚度
N =17.86K
s
sQ * m T' 1 SZ ax Q = = τ 'bS= ' 2 2 2IZ
S T T1
N =17.86K
铆钉的剪应力为
τ=
Q '
2
πd
4
P = 56.9M a <[τ ]
T ' = 2Q '
Q '
铆钉的剪应力满足强度条件。 铆钉的剪应力满足强度条件。 s
II、 铆钉组承受扭转荷载 II、 承受扭转荷载的铆钉组( 承受扭转荷载的铆钉组(图 )
3
P3 "
2
P2 "
1
'= P '=⋅⋅⋅ = P ' = P = 2K N P 1 2 i 6
3 的作用下, 在力偶 m 的作用下, 它们所承受的力与其到 转动中心的距离成正比。 转动中心的距离成正比。
